Чему равна равнодействующая сил F1 и F2 действующих На тележку что. Равнодействующая двух сил Чему равны силы f1 и f2
Часто на тело действует одновременно не одна, а несколько сил. Рассмотрим случай, когда на тело оказывают воздействие две силы ( и ). Например, на тело, покоящееся на горизонтальной поверхности действуют сила тяжести () и реакция опоры поверхности () (рис.1).
Эти две силы можно заменить одной, которую называют равнодействующей силой (). Находят ее как векторную сумму сил и :
Определение равнодействующей двух сил
ОПРЕДЕЛЕНИЕ
Равнодействующей двух сил называют силу, которая производит на тело действие аналогичное, действию двух отдельных сил.
Отметим, что действие каждой силы не зависит от того, есть ли другие силы или их нет.
Второй закон Ньютона для равнодействующей двух сил
Если на тело действуют две силы, то второй закон Ньютона запишем как:
Направление равнодействующей всегда совпадает по направлению с направлением ускорения движения тела.
Это означает, что, если на тело оказывают воздействие две силы () в один и тот же момент времени, то ускорение () этого тела будет прямо пропорционально векторной сумме этих сил (или пропорционально равнодействующей сил):
M — масса, рассматриваемого тела. Суть второго закона Ньютона заключается в том, что силы, действующие на тело, определяют как изменяется скорость тела, а не просто величину скорости тела. Отмети, что второй закон Ньютона выполняется исключительно в инерциальных системах отсчета.
Равнодействующая двух сил может быть равна нулю, если силы, действующие на тело направлены в разные стороны и равны по модулю.
Нахождение величины равнодействующей двух сил
Для нахождения равнодействующей, следует изобразить на чертеже все силы, которые необходимо учитывать в задаче, действующие на тело. Складывать силы следует по правилам сложения векторов.
Допустим, что на тело действуют две силы, которые направлены по одной прямой (рис.1). Из рисунка видно, что они направлены в разные стороны.
Равнодействующая сил (), приложенных к телу, будет равна:
Для нахождения модуля равнодействующей сил выберем ось, обозначим ее X, направим вдоль направления действия сил. Тогда проектируя выражение (4) на ось X мы получим, что величина (модуль) равнодействующей (F) равен:
где — модули соответствующих сил.
Представим, что на тело действуют две силы и , направленные под некоторым углом друг к другу (рис.2). Равнодействующую этих сил находим по правилу параллелограмма. Величина равнодействующей будет равен длине диагонали этого параллелограмма.
Примеры решения задач
ПРИМЕР 1
| Задание | Тело массой 2 кг перемещают вертикально за нить вверх, при этом его ускорение равно 1 Какова величина и направление равнодействующей силы? Какие силы приложены к телу? |
| Решение | К телу (рис.3) приложены сила тяжести () и сила реакции нити (). Равнодействующую указанных выше сил можно найти используя второй закон Ньютона: В проекции на ось X уравнение (1. |
| Ответ | Н, равнодействующая сила направлена так же как ускорение движения тела, то есть вертикально вверх. На тело действует две силы и . |
Для ответа на этот вопрос, необходимо из условия задачи сделать некоторые выводы:
- Направление этих сил;
- Модульное значение сил F1 и F2;
- Могут ли эти силы создать такую равнодействующую силу, чтобы сдвинуть тележку с места.
Направление сил
Для того, чтобы определить основные характеристики движения тележки, находящейся под воздействием двух сил, необходимо знать их направление. Например, если тележку вправо тянет сила, равная 5 Н и такая же сила тянет тележку влево, то логично предположить, что тележка будет стоять на месте. Если силы сонаправлены, для нахождения результирующей силы необходимо лишь найти их сумму. Если какая либо сила направлена под углом к плоскости движения тележки, то значение этой силы надо умножить на косинус угла между направлением действия силы и плоскостью. Математически это будет выглядеть так:
Математически это будет выглядеть так:
F = F1 * cosa; где
F – сила, направленная параллельно поверхности движения.
Теорема косинусов для нахождения результирующего вектора сил
Если две силы имеют свое начало в одной точке и есть определенный угол между их направлением, то тогда необходимо достроить треугольник результирующим вектором (то есть тем, который соединяет концы векторов F1 и F2). Найдем результирующую силу с помощью теоремы косинусов, которая гласит, что квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними. Запишем это в математическом виде:
F = F 1 2 + F 2 2 — 2 * F 1 * F 2 * cosa.
Подставив все известные величины можно определить величину результирующей силы.
Содержание статьи
СТАТИКА, раздел механики, предметом которого являются материальные тела, находящиеся в состоянии покоя при действии на них внешних сил.
См . ГИДРОАЭРОМЕХАНИКА .
Историческая справка.
Статика – самый старый раздел механики; некоторые из ее принципов были известны уже древним египтянам и вавилонянам, о чем свидетельствуют построенные ими пирамиды и храмы. Среди первых создателей теоретической статики был Архимед (ок. 287–212 до н.э.), который разработал теорию рычага и сформулировал основной закон гидростатики. Родоначальником современной статики стал голландец С.Стевин (1548–1620), который в 1586 сформулировал закон сложения сил, или правило параллелограмма, и применил его в решении ряда задач.
Основные законы.
Законы статики вытекают из общих законов динамики как частный случай, когда скорости твердых тел стремятся к нулю, но по историческим причинам и педагогическим соображениям статику часто излагают независимо от динамики, строя ее на следующих постулируемых законах и принципах: а) законе сложения сил, б) принципе равновесия и в) принципе действия и противодействия. В случае твердых тел (точнее, идеально твердых тел, которые не деформируются под действием сил) вводится еще один принцип, основанный на определении твердого тела. Это принцип переносимости силы: состояние твердого тела не изменяется при перемещении точки приложения силы вдоль линии ее действия.
В случае твердых тел (точнее, идеально твердых тел, которые не деформируются под действием сил) вводится еще один принцип, основанный на определении твердого тела. Это принцип переносимости силы: состояние твердого тела не изменяется при перемещении точки приложения силы вдоль линии ее действия.
Сила как вектор.
В статике силу можно рассматривать как тянущее или толкающее усилие, имеющее определенные направление, величину и точку приложения. С математической точки зрения, это вектор, а потому ее можно представить направленным отрезком прямой, длина которого пропорциональна величине силы. (Векторные величины, в отличие от других величин, не имеющих направления, обозначаются полужирными буквами.)
Параллелограмм сил.
Рассмотрим тело (рис. 1,а ), на которое действуют силы F 1 и F 2 , приложенные в точке O и представленные на рисунке направленными отрезками OA и OB . Как показывает опыт, действие сил
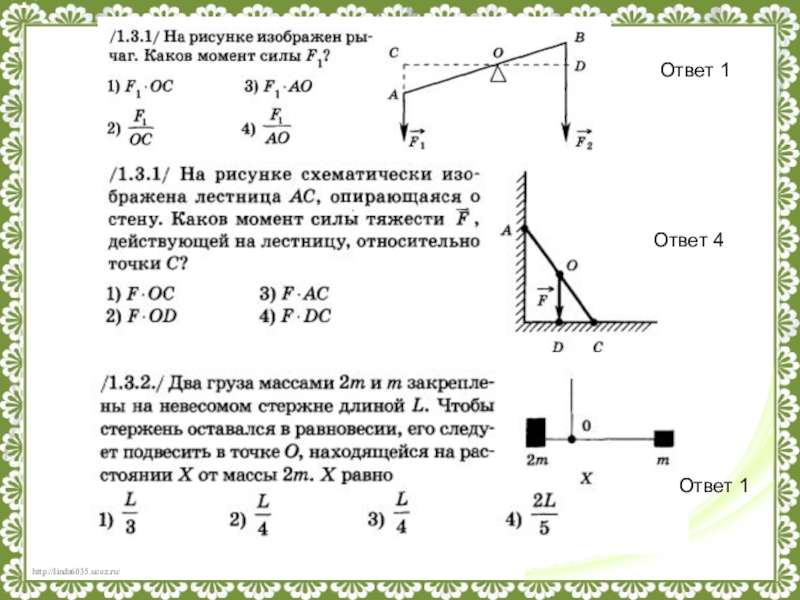 Величина силы R равна длине диагонали параллелограмма, построенного на векторах OA и OB как его сторонах; ее направление показано на рис. 1,а . Сила R называется равнодействующей сил F 1 и F 2 . Математически это записывается в виде R = F 1 + F 2 , где сложение понимается в геометрическом смысле слова, указанном выше. Таков первый закон статики, называемый правилом параллелограмма сил.
Величина силы R равна длине диагонали параллелограмма, построенного на векторах OA и OB как его сторонах; ее направление показано на рис. 1,а . Сила R называется равнодействующей сил F 1 и F 2 . Математически это записывается в виде R = F 1 + F 2 , где сложение понимается в геометрическом смысле слова, указанном выше. Таков первый закон статики, называемый правилом параллелограмма сил.Равнодействующая сила.
Вместо того чтобы строить параллелограмм OACB, для определения направления и величины равнодействующей
 .., F n , приложенных в одной и той же точке O рассматриваемого тела. Так, если система состоит из четырех сил (рис. 1,в ), то можно найти равнодействующую сил
.., F n , приложенных в одной и той же точке O рассматриваемого тела. Так, если система состоит из четырех сил (рис. 1,в ), то можно найти равнодействующую сил Данное выше определение равнодействующей можно обобщить на систему сил F 1 , F 2 ,…, F n , приложенных в точках O 1 , O 2 ,…, O n твердого тела. Выбирается точка O, называемая точкой приведения, и в ней строится система параллельно перенесенных сил, равных по величине и направлению силам F 1 , F 2 ,…, F
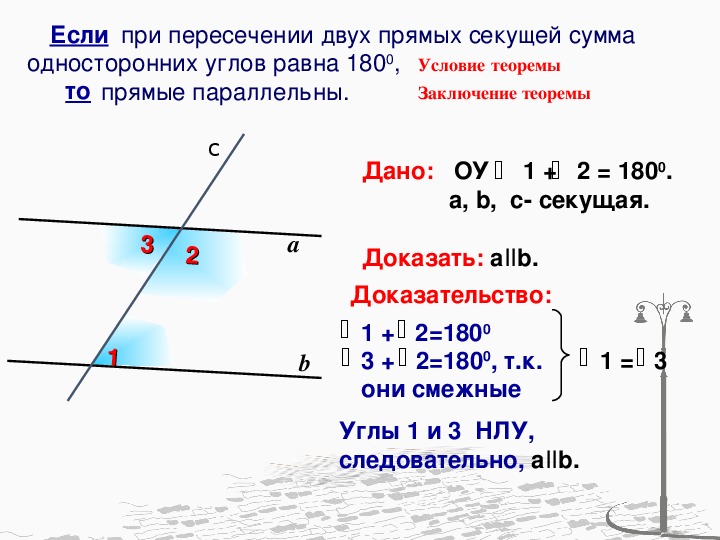 2). Ясно, что вектор R не зависит от выбранной точки приведения. Если величина вектора R (отрезок ON) не равна нулю, то тело не может находиться в покое: в соответствии с законом Ньютона всякое тело, на которое действует сила, должно двигаться с ускорением. Таким образом, тело может находиться в состоянии равновесия только при условии, что равнодействующая всех сил, приложенных к нему, равна нулю. Однако это необходимое условие нельзя считать достаточным – тело может двигаться, когда равнодействующая всех приложенных к нему сил равна нулю.
2). Ясно, что вектор R не зависит от выбранной точки приведения. Если величина вектора R (отрезок ON) не равна нулю, то тело не может находиться в покое: в соответствии с законом Ньютона всякое тело, на которое действует сила, должно двигаться с ускорением. Таким образом, тело может находиться в состоянии равновесия только при условии, что равнодействующая всех сил, приложенных к нему, равна нулю. Однако это необходимое условие нельзя считать достаточным – тело может двигаться, когда равнодействующая всех приложенных к нему сил равна нулю.В качестве простого, но важного примера, поясняющего сказанное, рассмотрим тонкий жесткий стержень длиной l , вес которого пренебрежимо мал по сравнению с величиной приложенных к нему сил. Пусть на стержень действуют две силы F и -F , приложенные к его концам, равные по величине, но противоположно направленные, как показано на рис. 3,а . В этом случае равнодействующая R равна F – F = 0, но стержень не будет находиться в состоянии равновесия; очевидно, он будет вращаться вокруг своей средней точки O.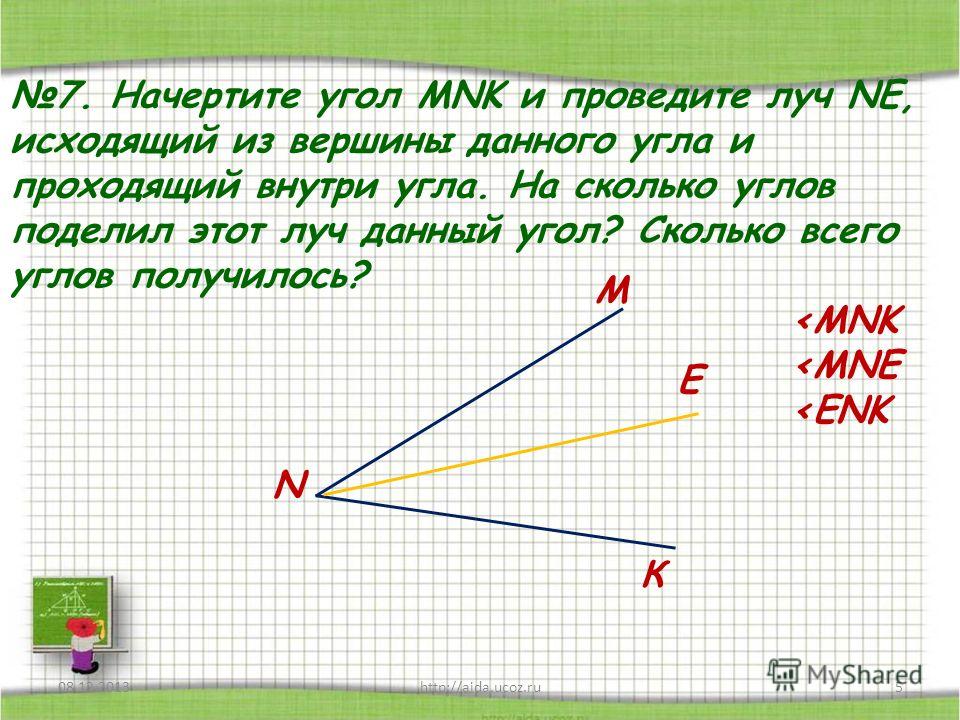
Таким образом, вращение можно предотвратить бесчисленными способами. Важно лишь выбрать силу и точку ее приложения так, чтобы произведение силы на плечо было равно F 1 l 1 . Это и есть правило рычага.
Это и есть правило рычага.
Нетрудно вывести условия равновесия системы. Действие сил F 1 и F 2 на ось вызывает противодействие в виде силы реакции
 4,а , то эту силу можно представить в виде суммы двух составляющих, одна из которых (F p), величиной F cosq , действует параллельно стержню и уравновешивается реакцией опоры —F p , а другая (F n), величиной F sinq , направлена под прямым углом к рычагу. В этом случае крутящий момент равен F l sinq ; он может быть уравновешен любой силой, которая создает равный ему момент, действующий против часовой стрелки.
4,а , то эту силу можно представить в виде суммы двух составляющих, одна из которых (F p), величиной F cosq , действует параллельно стержню и уравновешивается реакцией опоры —F p , а другая (F n), величиной F sinq , направлена под прямым углом к рычагу. В этом случае крутящий момент равен F l sinq ; он может быть уравновешен любой силой, которая создает равный ему момент, действующий против часовой стрелки.Чтобы проще было учитывать знаки моментов в тех случаях, когда на тело действует много сил, момент силы F относительно любой точки O тела (рис. 4,б ) можно рассматривать как вектор L , равный векторному произведению r ґ F вектора положения r на силу F . Таким образом, L = r ґ F . Нетрудно показать, что если на твердое тело действует система сил, приложенных в точках O 1 , O 2 ,…, O n (рис. 5), то эту систему можно заменить равнодействующей R сил F 1 , F 2 ,. .., F n , приложенной в любой точке Oў тела, и парой сил L , момент которых равен сумме [r 1 ґ F 1 ] + [r 2 ґ F 2 ] +… + [r n ґ F n ]. Чтобы убедиться в этом, достаточно мысленно приложить в точке Oў систему пар равных, но противоположно направленных сил F 1 и —F 1 ; F 2 и —F 2 ;…; F n и —F n , что, очевидно, не изменит состояния твердого тела.
.., F n , приложенной в любой точке Oў тела, и парой сил L , момент которых равен сумме [r 1 ґ F 1 ] + [r 2 ґ F 2 ] +… + [r n ґ F n ]. Чтобы убедиться в этом, достаточно мысленно приложить в точке Oў систему пар равных, но противоположно направленных сил F 1 и —F 1 ; F 2 и —F 2 ;…; F n и —F n , что, очевидно, не изменит состояния твердого тела.
Но сила F 1 , приложенная в точке O 1 , и сила –F 1 , приложенная в точке Oў, образуют пару сил, момент которых относительно точки Oў равен r 1 ґ F 1 . Точно так же силы F 2 и —F 2 , приложенные в точках O 2 и Oў соответственно, образуют пару с моментом r 2 ґ F 2 , и т.д. Суммарный момент L всех таких пар относительно точки Oў дается векторным равенством L = [r 1 ґ F 1 ] + [r 2 ґ F 2 ] +… + [r n ґ F n ].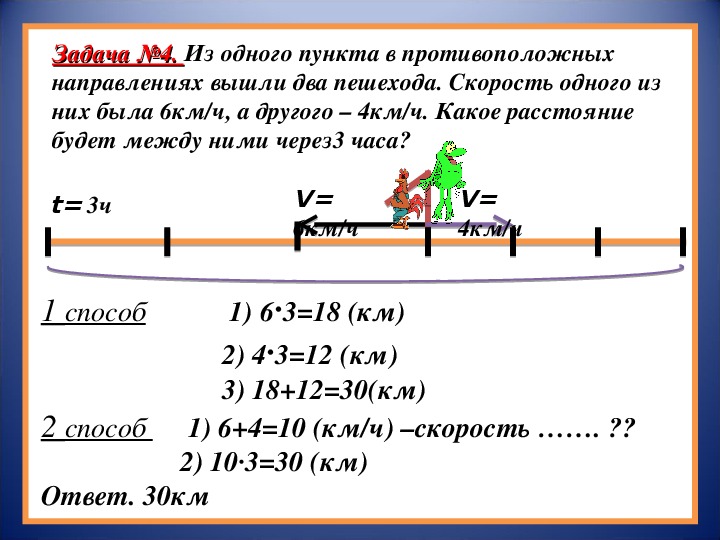 Остальные силы F 1 , F 2 ,…, F n , приложенные в точке Oў, в сумме дают равнодействующую R . Но система не может находиться в равновесии, если величины R и L отличны от нуля. Следовательно, условие равенства нулю одновременно величин R и L является необходимым условием равновесия. Можно показать, что оно же является и достаточным, если тело первоначально покоится. Итак, задача о равновесии сводится к двум аналитическим условиям: R = 0 и L = 0. Эти два уравнения представляют собой математическую запись принципа равновесия.
Остальные силы F 1 , F 2 ,…, F n , приложенные в точке Oў, в сумме дают равнодействующую R . Но система не может находиться в равновесии, если величины R и L отличны от нуля. Следовательно, условие равенства нулю одновременно величин R и L является необходимым условием равновесия. Можно показать, что оно же является и достаточным, если тело первоначально покоится. Итак, задача о равновесии сводится к двум аналитическим условиям: R = 0 и L = 0. Эти два уравнения представляют собой математическую запись принципа равновесия.
Теоретические положения статики широко применяются при анализе сил, действующих на конструкции и сооружения. В случае непрерывного распределения сил суммы, которые дают результирующий момент L и равнодействующую R , заменяются интегралами и в соответствии с обычными методами интегрального исчисления.
Равнодействующая. Вы уже знаете, что две силы уравновешивают друг друга, когда они равны по модулю и направлены противоположно. Таковы, например, сила тяжести и сила нормальной реакции, действующие на лежащую на столе книгу. В этом случае говорят, что равнодействующая двух сил равна нулю. В общем случае равнодействующей двух или нескольких сил называют силу, которая производит на тело такое же действие, как одновременное действие этих сил.
Таковы, например, сила тяжести и сила нормальной реакции, действующие на лежащую на столе книгу. В этом случае говорят, что равнодействующая двух сил равна нулю. В общем случае равнодействующей двух или нескольких сил называют силу, которая производит на тело такое же действие, как одновременное действие этих сил.
Рассмотрим на опыте, как найти равнодействующую двух сил, направленных вдоль одной прямой.
Поставим опыт
Положим легкий брусок на гладкую горизонтальную поверхность стола (чтобы трением между бруском и поверхностью стола можно было пренебречь). Будем тянуть брусок вправо с помощью одного динамометра, а влево — с помощью двух динамометров, как показано на рис. 16.3. Обратите внимание, что находящиеся слева динамометры прикреплены к бруску так, что силы натяжения пружин этих динамометров различны.
Рис. 16.3. Как можно найти равнодействующую двух сил
Мы увидим, что брусок находится в покое, если модуль силы, которая тянет его вправо, равен сумме модулей сил, тянущих брусок влево. Схема этого опыта изображена на рис. 16.4.
Схема этого опыта изображена на рис. 16.4.
Рис. 16.4. Схематическое изображение сил, действующих на брусок
Сила F 3 уравновешивает равнодействующую сил F 1 и F 2 , то есть равна ей по модулю и противоположна по направлению. Значит, равнодействующая сил F 1 и F 2 направлена влево (как и эти силы), а ее модуль равен F 1 + F 2 . Таким образом, если две силы направлены одинаково, их равнодействующая направлена так же, как эти силы, а модуль равнодействующей равен сумме модулей сил-слагаемых.
Рассмотрим силу F 1 . Она уравновешивает равнодействующую сил F 2 и F 3 , направленных противоположно. Значит, равнодействующая сил F 2 и F 3 направлена вправо (то есть в сторону большей из этих сил), а ее модуль равен F 3 — F 2 . Таким образом, если две не равные по модулю силы направлены противоположно, их равнодействующая направлена как большая из этих сил, а модуль равнодействующей равен разности модулей большей и меньшей силы.
Нахождение равнодействующей нескольких сил называют сложением этих сил.
Две силы направлены вдоль одной прямой. Модуль одной силы равен 1 Н, а модуль другой силы равен 2 Н. Может ли модуль равнодействующей этих сил быть равен: а) нулю; б) 1 Н; в) 2 Н; г) 3 Н?
Задача 3.2.1
Определить равнодействующую двух сил F 1 =50Н и F 2 =30Н, образующие между собой угол 30° (рис.3.2а).
Рисунок 3.2
Перенесем векторы сил F 1 и F 2 до точки пересечения линий действий и сложим по правилу параллелограмма (рис.2.2б). Точка приложения и направление равнодействующей показано на рисунке. Модуль полученной равнодействующей определим по формуле:
Ответ: R=77,44Н
Задача 3.2.2
Определить равнодействующую системы сходящихся сил F 1 =10Н, F 2 =15Н, F 3 =20Н, если известны углы, образованные векторами этих сил с осью Ох: α 1 =30 ° , α 2 =45 ° и α 3 =60 ° (рис.3.3а)
Рисунок 3.3
Проецируем силы на оси Оx и Оy:
Модуль равнодействующей
На основе полученных проекций определяем направление равнодействующей (рис. 3.3б)
3.3б)
Ответ: R=44,04Н
Задача 3.2.3
В точке соединения двух нитей приложена вертикальная сила P=100Н (рис.3.4а). Определить усилия в нитях, если в состояния равновесия углы образованные нитями с осью OY равны α=30°, β=75°.
Рисунок 3.4
Силы натяжения нитей будут направлены вдоль нитей от узла соединения (рис.3.4б). Система сил T 1 , T 2 , P является системой сходящихся сил, т.к. линии действия сил пересекаются в точке соединения нитей. Условие равновесия данной системы:
Составляем аналитические уравнения равновесия системы сходящихся сил, проецирую векторное уравнение на оси.
Решаем систему полученных уравнений. Из первого выражаем T 2 .
Подставим полученное выражение во второе и определим T 1 и T 2 .
Н,
Проверим решение из условия, что модуль P’суммы сил T 1 и T 2 должен быть равен Р (рис.3.4в).
Ответ: T 1 =100Н, T 2 =51,76Н.
Задача 3.2.4
Определить равнодействующую системы сходящихся сил, если заданы их модули F 1 =12Н, F 2 =10Н, F 3 =15Н и угол α=60 ° (рис. 3.5а).
3.5а).
Рисунок 3.5
Определяем проекции равнодействующей
Модуль равнодействующей:
На основе полученных проекций определяем направление равнодействующей (рис.3.5б)
Ответ: R=27,17Н
Задача 3.2.6
Три стержня АС, ВС, DC соединены шарнирно в точке C. Определить усилия в стержнях, если задана сила F=50Н, угол α=60° и угол β=75°. Сила F находится в плоскости Оyz. (рис.3.6)
Рисунок 3.6
Первоначально предполагаем, что все стержни растянуты, соответственно направляем реакции в стержнях от узла С. Полученная система N 1 , N 2 , N 3 , F является системой сходящихся сил. Условие равновесия данной системы.
Объяснение урока: Равнодействующая двух сил
В этом объяснителе мы узнаем, как найти равнодействующую двух сил, действующих в одной точке, и как найти направление равнодействующей.
Начнем с определения силы и изучения ее свойств.
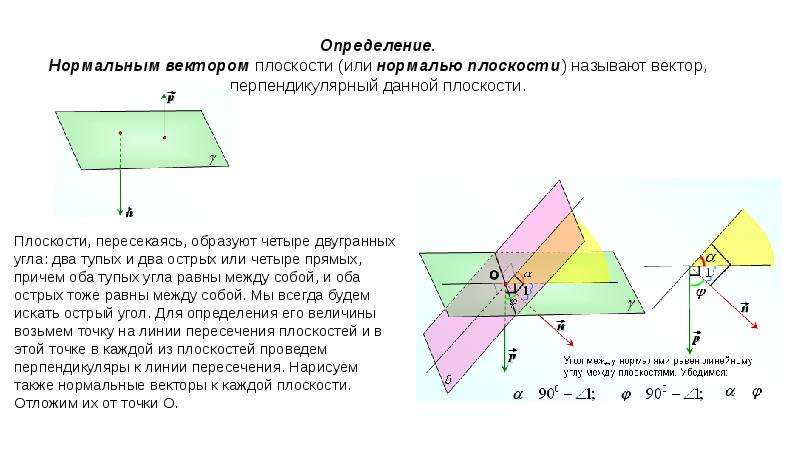
Определение: Сила
Сила определяется как воздействие одного природного тела на другое. Каждая сила описывается с точки зрения ее величины (размера), направления, точки действия и линии действия.
Каждая сила описывается с точки зрения ее величины (размера), направления, точки действия и линии действия.
Мы часто представляем силу, используя обозначение ⃑𝐹.
Свойства: Силы
- Величина силы – это ее величина, которая измеряется в ньютонах (Н). Используя направленный отрезок линии для представления силы ⃑𝐹 и рисуя линию в подходящем масштабе, мы можем использовать длину линии для обозначения величины, ‖‖⃑𝐹‖‖.
- направление силы — это направление, в котором она действует. Используя направленный отрезок для представления силы ⃑𝐹, мы можем использовать направление стрелки, чтобы показать направление силы.
- Точка действия силы — это точка, к которой она приложена.
- линия действия силы представляет собой геометрический способ представления приложения силы. Он рисуется как линия через точку действия в том же направлении, что и ⃑𝐹.
Например, на диаграмме ниже показана сила ⃑𝐹, представленная направленным отрезком 𝐴𝐵.
Величина силы определяется ‖‖𝐴𝐵‖‖. Направление стрелки соответствует направлению ⃑𝐹. Точка действия 𝐴. Линия действия обозначается расширением 𝐴𝐵 в том же направлении (как показано пунктирной линией).
Сила, действующая на тело, представлена вектором ⃑𝐹. Когда на тело действуют две силы, мы называем их равнодействующей силой, которая описывает их совместное действие.
Определение: результирующая сила
Когда две силы, ⃑𝐹 и ⃑𝐹, действуют на тело в одной и той же точке, совокупный эффект этих двух сил такой же, как эффект одной силы, называемой равнодействующей силой.
Результирующая сила ⃑𝑅 определяется выражением ⃑𝑅=⃑𝐹+⃑𝐹.
Векторное равенство ⃑𝑅=⃑𝐹+⃑𝐹 можно представить двумя способами, как показано на следующей диаграмме.
Поскольку ⃑𝐹, ⃑𝐹 и ⃑𝑅 — три стороны треугольника, мы можем использовать закон синусов или закон косинусов в треугольнике, чтобы найти равнодействующую двух сил, углы между равнодействующей и силы или любые другие неизвестные.
Пусть 𝛼 угол между силами ⃑𝐹 и ⃑𝐹, 𝜃 угол между ⃑𝑅 и ⃑𝐹, а 𝜃 угол между ⃑𝑅 и ⃑𝐹, как показано на диаграмме ниже.
Закон синусов в этом треугольнике дает нам 𝐹𝜃=𝐹𝜃=𝑅(180−𝛼),∘sinsinsin где 𝐹, 𝐹 и 𝑅 — величины ⃑𝐹, ⃑𝐹 и ⃑𝑅 соответственно.
Поскольку sinsin(180−𝑥)=𝑥∘ для всех 𝑥, мы находим соотношение, указанное в следующем поле.
Свойство: закон синусов в треугольнике, образованном двумя силами и их равнодействующей
Имеем 𝐹𝜃=𝐹𝜃=𝑅𝛼,sinsinsin где 𝐹, 𝐹, 𝑅 — величины ⃑𝐹, ⃑𝐹 и ⃑𝑅 соответственно, 𝛼 — угол между силами ⃑𝐹 и ⃑𝐹, 𝜃 — угол между ⃑𝐹 и ⃑𝜐 угол между ⃑𝑅 и ⃑𝐹.
Применяя закон косинусов к нашему треугольнику, находим, что 𝑅=𝐹+𝐹−2𝐹𝐹(180−𝛼).∘cos
Поскольку coscos(180−𝑥)=−𝑥∘ для всех 𝑥, мы находим соотношение, указанное в следующем поле.
Свойство: Закон косинусов в треугольнике, образованном двумя силами и их равнодействующей
Имеем
𝑅=𝐹+𝐹+2𝐹𝐹𝛼,кос
где 𝐹, 𝐹 и 𝑅 — величины ⃑𝐹, ⃑𝐹 и ⃑𝑅 соответственно, а 𝛼 — угол между силами ⃑𝐹 и ⃑𝐹.
Извлекая квадратный корень из обеих частей приведенного выше равенства и учитывая, что величина вектора положительна, мы можем получить явную формулу для 𝑅, величины ⃑𝑅. Также несложно вывести сопутствующую формулу для направления ⃑𝑅. Мы приводим эти результаты ниже.
Формула: Величина и направление равнодействующей двух сил
Пусть ⃑𝑅 будет равнодействующей силой двух сил, ⃑𝐹 и ⃑𝐹, действующих в одной точке под углом 𝛼 между ними. Затем, 𝑅=𝐹+𝐹+2𝐹𝐹𝛼𝜃=𝐹𝛼𝐹+𝐹𝛼,косандтансинкос где 𝐹, 𝐹 и 𝑅 — величины ⃑𝐹, ⃑𝐹 и ⃑𝑅 соответственно и 𝜃 угол между ⃑𝑅 и ⃑𝐹.
Начнем с примера, в котором определяется модуль равнодействующей двух сил, действующих в точке.
Пример 1: Нахождение модуля равнодействующей двух сил
На частицу действуют две силы с величинами 35 Н и 91 Н. Учитывая, что равнодействующая перпендикулярна первой силе, найти модуль равнодействующей.
Ответ
Удобно считать, что первая сила действует горизонтально. Назовем эту силу ⃑𝐹, а другую силу ⃑𝐹. Равнодействующая этих сил, ⃑𝐹+⃑𝐹, действует вертикально, поскольку она перпендикулярна ⃑𝐹, как показано на следующем рисунке.
Назовем эту силу ⃑𝐹, а другую силу ⃑𝐹. Равнодействующая этих сил, ⃑𝐹+⃑𝐹, действует вертикально, поскольку она перпендикулярна ⃑𝐹, как показано на следующем рисунке.
Сила ⃑𝐹 может быть представлена стрелкой с концом в начале ⃑𝐹 и концом в начале ⃑𝐹+⃑𝐹, как показано на следующем рисунке.
Результирующая сила ⃑𝑅 определяется выражением ⃑𝑅=⃑𝐹+⃑𝐹.
Поскольку ⃑𝐹 и ⃑𝑅 перпендикулярны, мы видим, что две силы и их равнодействующая образуют прямоугольный треугольник. Следовательно, применение теоремы Пифагора дает ‖‖⃑𝐹‖‖+‖‖⃑𝑅‖‖=‖‖⃑𝐹‖‖.
Стоит отметить, что теорема Пифагора – это всего лишь частный случай закона косинусов.
Подставляя значения ‖‖⃑𝐹‖‖ и ‖‖⃑𝐹‖‖, находим, что 35+‖‖⃑𝑅‖‖=91‖‖⃑𝑅‖‖=91−35=7056‖‖⃑𝑅‖‖=√7056=84.N
Обратите внимание, что величина вектора всегда положительный, -84 Н не является допустимым решением.
Модуль равнодействующей сил равен 84 Н.
Рассмотрим теперь пример, в котором определяется направление линии действия равнодействующей двух сил, действующих в точке.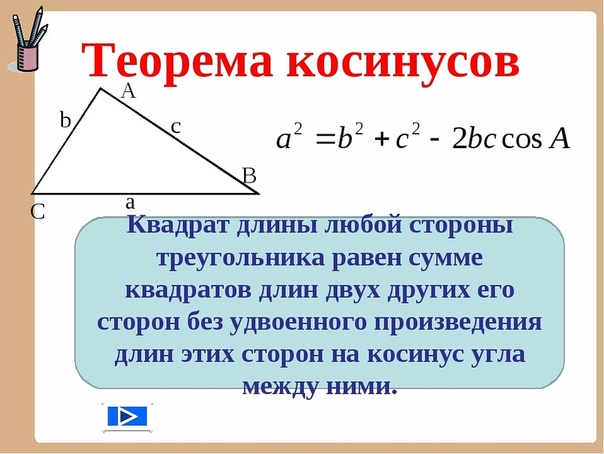
Пример 2. Нахождение направления равнодействующей двух сил, действующих в одной точке
Две перпендикулярные силы величинами 88 Н и 44 Н действуют на точку. Их равнодействующая образует угол 𝜃 с силой 88 Н. Найдите значение sin𝜃.
Ответ
Удобно предположить, что одна из сил действует горизонтально. Назовем эту силу ⃑𝐹, а другую силу ⃑𝐹, как показано на следующем рисунке.
Решив сделать так, чтобы ⃑𝐹 соответствовал линии, примыкающей к 𝜃, мы выбрали эту силу как силу в 88 ньютонов. Величина ⃑𝐹 составляет 44 ньютона; следовательно, величина ⃑𝐹 вдвое меньше, чем ⃑𝐹. Величина равнодействующей сил 𝑅 может быть выражена как 𝑅=𝐹+𝐹=𝐹+𝐹2.
Отсюда видно, что 𝑅=𝐹+𝐹2=𝐹+𝐹4=54𝐹.
Взяв квадратный корень, мы имеем, что 𝑅=√5𝐹2.
Применение закона синусов к треугольнику дает sinsin𝜃𝐹=90𝑅.∘
Поскольку sin90=1∘, имеем sinsin𝜃=𝐹𝑅𝜃==1√5=√55.√
Таким образом, мы имеем, что
грех𝜃=√55.
Рассмотрим теперь пример, в котором известна величина и направление линии действия равнодействующей двух перпендикулярных сил и необходимо определить величины этих сил.
Пример 3. Нахождение двух сил по величине и направлению их равнодействующей
Две перпендикулярные силы, ⃑𝐹 и ⃑𝐹, действуют в точке. Их равнодействующая ⃑𝑅 имеет звездную величину 188 N и составляет угол 60∘ с ⃑𝐹. Найдите величины ⃑𝐹 и ⃑𝐹.
Ответ
Перпендикулярные силы ⃑𝐹 и ⃑𝐹 и их равнодействующая показаны на следующем рисунке.
Мы видим, что ⃑𝐹 и ⃑𝐹 перпендикулярны, а равнодействующая ⃑𝐹+⃑𝐹 образует угол 60∘ с ⃑𝐹. Так как у нас есть прямоугольный треугольник, мы имеем coscosN60=‖‖⃑𝐹‖‖188‖‖⃑𝐹‖‖=18860=12×188=94∘∘ и sinsinN60=‖‖⃑𝐹‖‖188‖‖⃑𝐹‖‖=18860=√32×188=94√3.∘∘
⃑𝐹 имеет звездную величину 94 N, а ⃨4 имеет ⃑𝐹3 звездную величину N.
Давайте теперь рассмотрим пример с участием двух неперпендикулярных сил.
Пример 4: Нахождение недостающей силы по информации о равнодействующей силе
Угол между силами ⃑𝐹 и ⃑𝐹 равен 112∘, а угол между их равнодействующей и ⃑𝐹 равен 56∘. Если величина ⃑𝐹 равна 28 Н, какова величина ⃑𝐹?
Если величина ⃑𝐹 равна 28 Н, какова величина ⃑𝐹?
Ответ
На следующем рисунке показаны силы ⃑𝐹 и ⃑𝐹 и их равнодействующая ⃑𝐹+⃑𝐹. Силы действуют в точке 𝑃.
Равнодействующие сил ⃑𝐹 и ⃑𝐹 образуют параллелограмм, диагональ которого, проходящая через 𝑃, является равнодействующей.
Угол 𝜃 между ⃑𝐹 и равнодействующей ⃑𝐹 и ⃑𝐹 определяется выражением 𝜃=112−56=56.∘
Теперь мы можем добавить этот угол и его альтернативный внутренний угол на нашу диаграмму, как показано.
Применяя закон синусов к треугольнику, образованному ⃑𝐹, ⃑𝐹 и ⃑𝐹+⃑𝐹, находим, что ‖‖⃑𝐹‖‖56=‖‖⃑𝐹‖‖56,∘∘грех то есть, ‖‖⃑𝐹‖‖=‖‖⃑𝐹‖‖.
Величина ⃑𝐹 равна 28 Н, поэтому величина ⃑𝐹 также равна 28 Н.
Давайте посмотрим на наш последний пример, где направление одной из сил меняется на противоположное.
Пример 5: Нахождение модуля двух сил одинаковой величины по их равнодействующей в двух случаях
Две силы, каждая из которых имеет величину 𝐹 Н, действуют в одной и той же точке. Величина их равнодействующей равна 90 Н. Когда направление одной из сил меняется на противоположное, величина их равнодействующей равна 90 N. Определите значение 𝐹.
Величина их равнодействующей равна 90 Н. Когда направление одной из сил меняется на противоположное, величина их равнодействующей равна 90 N. Определите значение 𝐹.
Ответ
Представим первую ситуацию.
Когда мы складываем две силы, ⃑𝐹 и ⃑𝐹, равнодействующей является диагональ параллелограмма, образованного ⃑𝐹 и ⃑𝐹, а его хвост является точкой приложения ⃑𝐹 и ⃑𝐹. Если две силы имеют одинаковую величину, то параллелограмм представляет собой ромб, а две силы и их равнодействующая образуют равнобедренный треугольник, как показано на следующей диаграмме.
Применяя закон косинусов, находим, что 𝑅=𝐹+𝐹+2𝐹𝐹𝛼,кос с 𝐹=‖‖⃑𝐹‖‖, 𝐹=‖‖⃑𝐹‖‖ и 𝑅=‖‖⃑𝑅‖‖.
Поскольку 𝐹=𝐹=𝐹, имеем 𝑅=2𝐹+2𝐹𝛼.cos
Если мы теперь повернем направление одной из сил (из соображений симметрии не имеет значения, какая сила поменяет направление на противоположное; мы получим тот же результат), равнодействующая будет по-прежнему будет диагональю ромба, конгруэнтного предыдущему, но это будет другая диагональ, а угол между силами −⃑𝐹 и ⃑𝐹 будет равен 180−𝛼∘.
Величина −⃑𝐹 такая же, как величина ⃑𝐹, 𝐹.
Применение закона косинусов в треугольнике, образованном −⃑𝐹, ⃑𝐹, и их равнодействующая дает нам 𝑅′=2𝐹+2𝐹(180−𝛼),∘cos то есть, 𝑅′=2𝐹−2𝐹𝛼.cos
Нам говорят, что величина равнодействующей в обоих случаях одинакова, 90 Н. Отсюда имеем 𝑅=𝑅′=90,Н Который означает, что 2𝐹+2𝐹𝛼=2𝐹−2𝐹𝛼=90.coscos
Это верно, только если cos𝛼=0, то есть, если 𝛼=90∘. Таким образом, силы ⃑𝐹 и ⃑𝐹 перпендикулярны.
Отсюда имеем 2𝐹=90𝐹=902𝐹=9012𝐹=45√2.N
Стоит отметить, что в предыдущем примере мы могли бы заключить, что две силы перпендикулярны, с помощью простых геометрических соображений: диагонали в ромб имеет одинаковую длину, только если ромб является квадратом.
Давайте теперь обобщим то, что мы узнали из этих примеров.
Ключевые моменты
- Сила определяется как воздействие одного природного тела на другое. Каждая сила описывается с точки зрения ее величины (размера),
направление, точка действия и линия действия.
 Мы часто представляем силу, используя обозначение ⃑𝐹.
Мы часто представляем силу, используя обозначение ⃑𝐹. - Равнодействующая ⃑𝑅 двух сил, ⃑𝐹 и ⃑𝐹, действующих на тело в одной и той же точке, представляет собой единую силу, определяемую выражением ⃑𝑅=⃑𝐹+⃑𝐹.
- Комбинированный эффект ⃑𝐹 и ⃑𝐹 такой же, как эффект только ⃑𝑅.
- ⃑𝐹, ⃑𝐹 и ⃑𝑅 — три стороны треугольника или две смежные стороны и диагональ параллелограмма.
- Применение закона синусов к треугольнику, образованному двумя силами ⃑𝐹 и ⃑𝐹 и их равнодействующей ⃑𝑅, дает 𝐹𝜃=𝐹𝜃=𝑅𝛼,sinsinsin где 𝐹, 𝐹, 𝑅 — величины ⃑𝐹, ⃑𝐹 и ⃑𝑅 соответственно, 𝛼 — угол между силами ⃑𝐹 и ⃑𝐹, 𝜃 — угол между ⃑𝐹 и ⃑𝜐 угол между ⃑𝑅 и ⃑𝐹.
- Применение закона косинусов к треугольнику, образованному двумя силами ⃑𝐹 и ⃑𝐹 и их равнодействующей ⃑𝑅, дает 𝑅=𝐹+𝐹+2𝐹𝐹𝛼,кос где 𝐹, 𝐹 и 𝑅 — величины ⃑𝐹, ⃑𝐹 и ⃑𝑅 соответственно, а 𝛼 — угол между силами ⃑𝐹 и ⃑𝐹.
- Пусть ⃑𝑅 будет результирующей силой
двух сил, ⃑𝐹 и ⃑𝐹,
которые действуют в одной точке с углом 𝛼 между ними.
 Затем,
𝑅=𝐹+𝐹+2𝐹𝐹𝛼𝜃=𝐹𝛼𝐹+𝐹𝛼,косандтансинкос
где 𝐹, 𝐹 и 𝑅 — величины ⃑𝐹,
⃑𝐹 и ⃑𝑅 соответственно и 𝜃
угол между ⃑𝑅 и ⃑𝐹.
Затем,
𝑅=𝐹+𝐹+2𝐹𝐹𝛼𝜃=𝐹𝛼𝐹+𝐹𝛼,косандтансинкос
где 𝐹, 𝐹 и 𝑅 — величины ⃑𝐹,
⃑𝐹 и ⃑𝑅 соответственно и 𝜃
угол между ⃑𝑅 и ⃑𝐹.
Равновесие и статика
Когда все силы, действующие на объект, уравновешены, говорят, что объект находится в состоянии равновесия . Силы считаются уравновешенными
, если силы, направленные вправо, уравновешиваются силами, направленными влево, а силы, направленные вверх, уравновешиваются силами, направленными вниз. Это, однако, не обязательно означает, что все силы равны друг другу. Рассмотрим два объекта, изображенных на силовой диаграмме, показанной ниже. Обратите внимание, что два объекта находятся в равновесии, потому что силы, действующие на них, уравновешены; однако отдельные силы не равны друг другу. Сила 50 Н не равна силе 30 Н.
Если объект находится в равновесии, то силы уравновешены. Сбалансированный — ключевое слово, которое используется для описания равновесных ситуаций. Таким образом, результирующая сила равна нулю, а ускорение равно 0 м/с/с. Объекты в равновесии должны иметь ускорение 0 м/с/с. Это следует из первого закона движения Ньютона. Но наличие ускорения 0 м/с/с не означает, что объект находится в состоянии покоя. Объект в равновесии либо …
Сбалансированный — ключевое слово, которое используется для описания равновесных ситуаций. Таким образом, результирующая сила равна нулю, а ускорение равно 0 м/с/с. Объекты в равновесии должны иметь ускорение 0 м/с/с. Это следует из первого закона движения Ньютона. Но наличие ускорения 0 м/с/с не означает, что объект находится в состоянии покоя. Объект в равновесии либо …
- в состоянии покоя и в состоянии покоя или
- в движении и продолжают движение с той же скоростью и направлением.
Это тоже следует из первого закона движения Ньютона.
Анализ ситуации статического равновесия
Если объект покоится и находится в состоянии равновесия, то мы бы сказали, что объект находится в «статическом равновесии». «Статический» означает стационарный или в покое . Обычная физическая лаборатория состоит в том, чтобы подвешивать объект на двух или более веревках и измерять силы, действующие под углом на объект, чтобы выдержать его вес. Состояние объекта анализируется с точки зрения сил, действующих на объект. Объект представляет собой точку на струне, на которую действовали три силы. См. схему справа. Если объект находится в равновесии, то результирующая сила, действующая на объект, должна быть равна 0 ньютонов. Таким образом, если все силы сложить как векторы, то результирующая сила (сумма векторов) должна быть равна 0 ньютонов. (Напомним, что результирующая сила представляет собой «векторную сумму всех сил» или равнодействующую сложения всех отдельных сил лицом к хвосту.) Таким образом, можно построить точно нарисованную диаграмму сложения векторов для определения равнодействующей. Примеры данных для такой лаборатории показаны ниже.
Состояние объекта анализируется с точки зрения сил, действующих на объект. Объект представляет собой точку на струне, на которую действовали три силы. См. схему справа. Если объект находится в равновесии, то результирующая сила, действующая на объект, должна быть равна 0 ньютонов. Таким образом, если все силы сложить как векторы, то результирующая сила (сумма векторов) должна быть равна 0 ньютонов. (Напомним, что результирующая сила представляет собой «векторную сумму всех сил» или равнодействующую сложения всех отдельных сил лицом к хвосту.) Таким образом, можно построить точно нарисованную диаграмму сложения векторов для определения равнодействующей. Примеры данных для такой лаборатории показаны ниже.
|
Для большинства студентов результатом было 0 ньютонов (или, по крайней мере, очень близко к 0 Н). Это то, что мы ожидали — поскольку объект находился в равновесии, результирующая сила (векторная сумма всех сил) должна быть 0 Н.
Другой способ определения результирующей силы (векторной суммы всех сил) заключается в использовании тригонометрических функций для разложения каждой силы на ее горизонтальную и вертикальную составляющие. Когда компоненты известны, их можно сравнить, чтобы увидеть, уравновешены ли вертикальные силы и уравновешены ли горизонтальные силы. На приведенной ниже диаграмме показаны векторы A, B и C и их соответствующие компоненты. Для векторов A и B вертикальные компоненты можно определить с помощью синуса угла, а горизонтальные компоненты можно проанализировать с помощью косинуса угла. Величина и направление каждого компонента для выборочных данных показаны в таблице под диаграммой.
Величина и направление каждого компонента для выборочных данных показаны в таблице под диаграммой.
Данные в таблице выше показывают, что силы 90 211 почти равны 90 212. Анализ горизонтальных компонентов показывает, что левый компонент A почти уравновешивает правый компонент B. Анализ вертикальных компонентов показывает, что сумма восходящих компонентов A + B почти уравновешивает нисходящий компонент C , Векторная сумма всех сил равна ( почти ) равно 0 ньютонов. Но как быть с разницей в 0,1 Н между силами, направленными вправо и влево, и разницей в 0,2 Н между силами, направленными вверх и вниз? Почему компоненты силы только почти уравновешиваются? Данные образца, используемые в этом анализе, являются результатом измеренных данных реальной экспериментальной установки. Разница между фактическими и ожидаемыми результатами связана с ошибкой, возникающей при измерении силы A и силы B. Мы должны были бы заключить, что этот низкий предел экспериментальной погрешности отражает эксперимент с отличными результатами.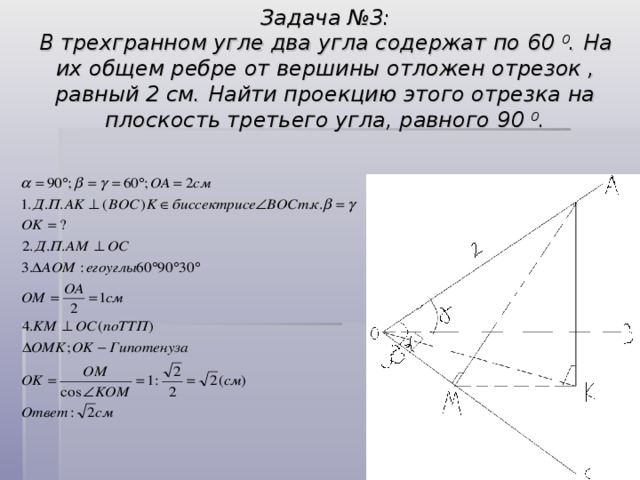 Мы могли бы сказать, что это «достаточно близко для работы правительства».
Мы могли бы сказать, что это «достаточно близко для работы правительства».
Приведенный выше анализ сил, действующих на объект, находящийся в равновесии, обычно используется для анализа ситуаций, связанных с объектами, находящимися в статическом равновесии. Наиболее распространенное приложение включает анализ сил, действующих на знак, который находится в состоянии покоя. Например, рассмотрим картину справа, которая висит на стене. Картина находится в состоянии равновесия, а значит, все силы, действующие на картину, должны быть уравновешены. То есть все горизонтальные компоненты должны составлять 0 ньютонов, а все вертикальные компоненты должны составлять 0 ньютонов. Натяжение троса A, направленное влево, должно уравновешивать натяжение троса B, направленного вправо, а сумма натяжения троса A и троса B вверх должна уравновешивать вес знака.
Предположим, что измеренное натяжение обоих тросов равно 50 Н, и известно, что угол, который каждый трос образует с горизонтом, равен 30 градусам. Каков вес знака? На этот вопрос можно ответить, проведя силовой анализ с использованием тригонометрических функций. Вес знака равен сумме восходящих составляющих натяжения двух тросов. Таким образом, для определения этой вертикальной составляющей можно использовать тригонометрическую функцию. Схема и сопутствующие работы показаны ниже.
Каков вес знака? На этот вопрос можно ответить, проведя силовой анализ с использованием тригонометрических функций. Вес знака равен сумме восходящих составляющих натяжения двух тросов. Таким образом, для определения этой вертикальной составляющей можно использовать тригонометрическую функцию. Схема и сопутствующие работы показаны ниже.
Поскольку каждый трос тянет вверх с силой 25 Н, общая сила тяги знака вверх составляет 50 Н. Следовательно, сила тяжести (также известная как вес) составляет 50 Н, направленная вниз. Знак весит 50 Н.
В приведенной выше задаче натяжение троса и угол , который трос образует с горизонталью, используются для определения веса знака. Идея состоит в том, что натяжение, угол и вес связаны. Если известны любые две из этих трех, то третью величину можно определить с помощью тригонометрических функций.
В качестве другого примера, иллюстрирующего эту идею, рассмотрим симметрично подвешенный знак, как показано справа. Если известно, что знак имеет массу 5 кг и если угол между двумя тросами составляет 100 градусов, то можно определить натяжение троса. Предполагая, что знак находится в равновесии (хорошее предположение, если он остается в покое), два троса должны создавать достаточную направленную вверх силу, чтобы уравновесить направленную вниз силу тяжести. Сила тяжести (также известная как вес) равна 49.Н (Fgrav = m*g), поэтому каждый из двух тросов должен тянуть вверх с силой 24,5 Н. Поскольку угол между кабелями равен 100 градусам, каждый кабель должен составлять угол 50 градусов с вертикалью и угол 40 градусов с горизонталью. Эскиз этой ситуации (см. диаграмму ниже) показывает, что натяжение троса можно найти с помощью функции синуса. Треугольник ниже иллюстрирует эти отношения.
Если известно, что знак имеет массу 5 кг и если угол между двумя тросами составляет 100 градусов, то можно определить натяжение троса. Предполагая, что знак находится в равновесии (хорошее предположение, если он остается в покое), два троса должны создавать достаточную направленную вверх силу, чтобы уравновесить направленную вниз силу тяжести. Сила тяжести (также известная как вес) равна 49.Н (Fgrav = m*g), поэтому каждый из двух тросов должен тянуть вверх с силой 24,5 Н. Поскольку угол между кабелями равен 100 градусам, каждый кабель должен составлять угол 50 градусов с вертикалью и угол 40 градусов с горизонталью. Эскиз этой ситуации (см. диаграмму ниже) показывает, что натяжение троса можно найти с помощью функции синуса. Треугольник ниже иллюстрирует эти отношения.
Концептуальное мышление
Существует важный принцип, вытекающий из некоторых тригонометрических вычислений, выполненных выше. Принцип заключается в том, что по мере увеличения угла с горизонталью сила натяжения, необходимая для удержания знака в равновесии, уменьшается. Чтобы проиллюстрировать это, рассмотрим изображение силой 10 ньютонов, удерживаемое проводами с тремя разными ориентациями, как показано на диаграммах ниже. В каждом случае для поддержки изображения используются два провода; каждый провод должен выдерживать половину веса знака (5 Н). Угол, который провода образуют с горизонтом, варьируется от 60 до 15 градусов. Используйте эту информацию и приведенную ниже диаграмму, чтобы определить натяжение проволоки для каждой ориентации. Когда закончите, нажмите кнопку, чтобы просмотреть ответы.
Чтобы проиллюстрировать это, рассмотрим изображение силой 10 ньютонов, удерживаемое проводами с тремя разными ориентациями, как показано на диаграммах ниже. В каждом случае для поддержки изображения используются два провода; каждый провод должен выдерживать половину веса знака (5 Н). Угол, который провода образуют с горизонтом, варьируется от 60 до 15 градусов. Используйте эту информацию и приведенную ниже диаграмму, чтобы определить натяжение проволоки для каждой ориентации. Когда закончите, нажмите кнопку, чтобы просмотреть ответы.
В заключение, равновесие – это состояние объекта, при котором все действующие на него силы уравновешены. В таких случаях результирующая сила равна 0 ньютонов. Зная силы, действующие на объект, можно использовать тригонометрические функции для определения горизонтальной и вертикальной составляющих каждой силы. Если в равновесии, то все вертикальные компоненты должны уравновешиваться, и все горизонтальные компоненты должны уравновешиваться.
Мы хотели бы предложить …
Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашей Сбалансировать! Interactive или Go For The Gold! Интерактивный. Оба интерактива можно найти в разделе Physics Interactive на нашем веб-сайте, и они обеспечивают интерактивный опыт с возможностью добавления векторов.
Посетите: Сбалансируйте это! || Иди за золотом!
Следующие вопросы предназначены для проверки вашего понимания равновесных ситуаций. Нажмите кнопку, чтобы просмотреть ответы на эти вопросы.
1. На стене висит следующая картина. Используйте тригонометрические функции, чтобы определить вес изображения.
На стене висит следующая картина. Используйте тригонометрические функции, чтобы определить вес изображения.
2. Вывеска внизу висит снаружи кабинета физики, рекламируя самую важную истину, которую можно найти внутри. Знак поддерживается диагональным тросом и жесткой горизонтальной перекладиной. Если знак имеет массу 50 кг, то определить натяжение диагонального троса, поддерживающего его вес.
3. В Гленвью можно найти следующий знак. Знак имеет массу 50 кг. Определить натяжение тросов.
4. После последней доставки печально известный аист сообщает хорошие новости. Если знак имеет массу 10 кг, то какова сила натяжения в каждом тросе? Используйте тригонометрические функции и эскиз, чтобы помочь в решении.
5. Предположим, что студент тянет двумя большими силами (F 1 и F 2 ), чтобы поднять 1-килограммовую книгу двумя тросами.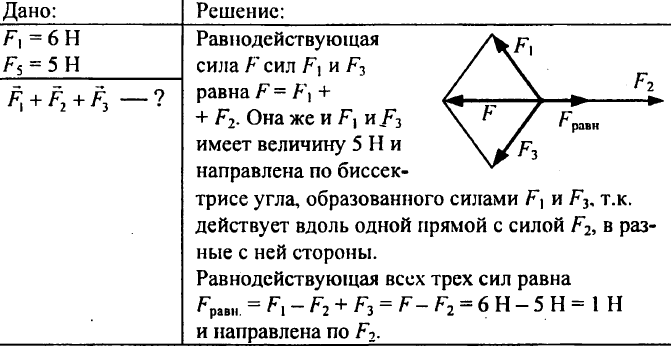

 1) принимает форму:
1) принимает форму: Мы часто представляем силу, используя обозначение ⃑𝐹.
Мы часто представляем силу, используя обозначение ⃑𝐹. Затем,
𝑅=𝐹+𝐹+2𝐹𝐹𝛼𝜃=𝐹𝛼𝐹+𝐹𝛼,косандтансинкос
где 𝐹, 𝐹 и 𝑅 — величины ⃑𝐹,
⃑𝐹 и ⃑𝑅 соответственно и 𝜃
угол между ⃑𝑅 и ⃑𝐹.
Затем,
𝑅=𝐹+𝐹+2𝐹𝐹𝛼𝜃=𝐹𝛼𝐹+𝐹𝛼,косандтансинкос
где 𝐹, 𝐹 и 𝑅 — величины ⃑𝐹,
⃑𝐹 и ⃑𝑅 соответственно и 𝜃
угол между ⃑𝑅 и ⃑𝐹.
Leave A Comment