| Утверждение | Верно? |
| Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части. | Да |
| Внешний угол треугольника больше каждого не смежного с ним внутреннего угла. | Да |
| В прямоугольном треугольнике катет больше гипотенузы. | Нет |
| В треугольнике АВС, для которого АВ = 4, ВС = 5, АС = 6, угол B — наибольший. | Да |
| Диагонали параллелограмма пересекаются под прямым углом и в точке пересечения делятся пополам. | Нет |
| Биссектриса равнобедренного треугольника, проведённая из вершины перпендикулярна основанию. | Да |
| Биссектриса треугольника делит пополам сторону, к которой проведена? | Нет |
Биссектриса угла делит угол пополам. | Да |
| Биссектриса угла любого параллелограмма является его диагональю. | Нет |
| Биссектриса угла треугольника делит противоположную сторону на отрезки, пропорциональные двум другим сторонам. | Да |
| Биссектрисы смежных углов взаимно перпендикулярны. | Да |
| Биссектрисы треугольника не могут пересекаться в одной точке | Нет |
| Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, описанной около этого треугольника. | Нет |
| Биссектрисы треугольника пересекаются в центре его вписанной окружности. | Да |
| Биссектрисы углов параллелограмма прилежащих к одной стороне, пересекаются под прямым углом. | Да |
| Вертикальные углы равны. | Да |
| В каждом треугольнике углы при основании равны. | Нет |
В квадрате диагонали пересекаются под прямым углом. | Да |
| В любой выпуклый семиугольник можно вписать окружность. | Нет |
| В любой прямоугольник можно вписать окружность. | Нет |
| В любой прямоугольный треугольник можно вписать окружность. | Да |
| В любой ромб можно вписать окружность. | Да |
| В любой трапеции диагонали перпендикулярны. | Нет |
| В любой трапеции диагонали равны. | Нет |
| В любой треугольник можно вписать окружность. | Да |
| В любой четырёхугольник можно вписать не более одной окружности. | Да |
| В любой четырёхугольник можно вписать окружность. | Нет |
| В любом выпуклом четырёхугольнике все углы острые. | Нет |
| В любом выпуклом четырёхугольнике все углы прямые. | Нет |
| В любом выпуклом четырёхугольнике все углы тупые. | |
В любом описанном около окружности четырехугольнике суммы противоположных сторон равны. | Да |
| В любом описанном четырёхугольнике сумма противоположных углов равна 180°. | Да |
| В любом параллелограмме диагонали равны. | Нет |
| В любом параллелограмме диагонали точкой пересечения делятся пополам. | Да |
| В любом прямоугольнике все стороны равны. | Нет |
| В любом прямоугольнике диагонали взаимно перпендикулярны. | Нет |
| В любом прямоугольнике диагонали равны. | Да |
| В любом равнобедренном треугольнике медиана, проведённая из вершины основания, является биссектрисой и высотой. | Да |
| В любом ромбе диагонали перпендикулярны. | Да |
| В любом треугольнике выполняется теорема Пифагора. | Нет |
| В любом треугольнике против большего угла лежит большая сторона. | Да |
В любом треугольнике против большей стороны лежит меньший угол. | Нет |
| В любом треугольнике сумма двух сторон больше третьей стороны. | Да |
| В любом треугольнике сумма двух сторон меньше третьей стороны. | Нет |
| В любом тупоугольном треугольнике есть острый угол. | Да |
| В любую окружность можно вписать два подобных, но неравных треугольника. | Нет |
| В любую окружность можно вписать прямоугольник. | Да |
| В любую равнобедренную трапецию можно вписать окружность. | Нет |
| Внешний угол треугольника больше каждого внутреннего угла. | Нет |
| Внешний угол треугольника больше не смежного с ним внутреннего угла. | Да |
| Внешний угол треугольника всегда тупой. | Нет |
| Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. | Да |
Внешний угол треугольника равен сумме его внутренних углов. | Нет |
| Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны. | Да |
| Во всякий четырёхугольник можно вписать окружность. | Нет |
| Во всяком треугольнике биссектриса угла равна его медиане. | Нет |
| Во всяком треугольнике высота проведённая к основанию, совпадает с медианой. | Нет |
| Вокруг любого выпуклого восьмиугольника можно описать окружность. | Нет |
| Вокруг любого параллелограмма можно описать окружность. | Нет |
| Вокруг любого треугольника можно описать окружность. | Да |
| Вокруг любого четырёхугольника можно описать окружность. | Нет |
| Вокруг параллелограмма всегда можно описать окружность. | Нет |
| Вокруг равнобедренной трапеции можно описать окружность. | Да |
Вокруг тупоугольного треугольника нельзя описать окружность.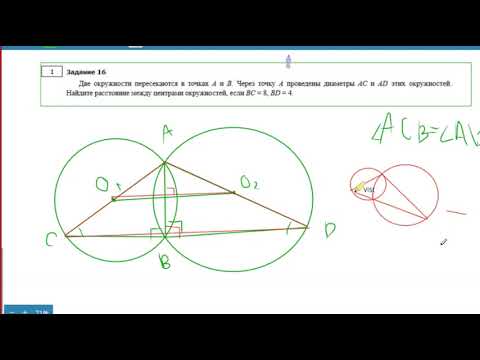 | Нет |
| В окружности на диаметр опирается прямой угол. | Да |
| В окружности радиуса 2 можно провести хорду длиной 3. | Да |
| В окружность можно вписать угол, равный 200° | Нет |
| В параллелограмме все стороны равны. | Нет |
| В параллелограмме диагонали точкой пересечения делятся пополам. | Да |
| В параллелограмме есть два равных угла. | Да |
| В параллелограмме противоположные углы равны. | Да |
| Вписанные углы окружности равны. | Нет |
| Вписанные углы, опирающиеся на одну и ту же дугу, равны. | Да |
| Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны. | Нет |
| Вписанный угол измеряется дугой, на которую он опирается. | Нет |
Вписанный угол измеряется половиной дуги, на которую он опирается. | Да |
| Вписанный угол, опирающийся на диаметр окружности, прямой. | Да |
| Вписанный угол, опирающийся на диаметр окружности, равен 90°. | Да |
| Вписанный угол, опирающийся на полуокружность — развёрнутый. | Нет |
| Вписанный угол равен половине угловой величины дуги, на которую он опирается. | Да |
| Вписанный угол равен половине центрального, опирающегося на туже дугу. | Да |
| В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности. | Да |
| В плоскости для точки, лежащей вне круга, расстояние до центра круга больше его радиуса. | Да |
| В подобных треугольниках соответствующие стороны равны. | Нет |
| В подобных треугольниках сходственные стороны пропорциональны. | Да |
| В правильном многоугольнике все стороны равны. | Да |
В правильном многоугольнике все углы равны. | Да |
| В правильном треугольнике все углы прямые. | Нет |
| В прямоугольнике диагонали являются биссектрисами. | Нет |
| В прямоугольнике диагонали являются биссектрисами его углов. | Нет |
| В прямоугольной трапеции основания параллельны. | Да |
| В прямоугольном треугольнике гипотенуза больше катета. | Да |
| В прямоугольном треугольнике гипотенуза меньше катета. | Нет |
| В прямоугольном треугольнике гипотенуза в два раза больше каждого из катетов. | Нет |
| В прямоугольном треугольнике гипотенуза всегда меньше суммы его катетов. | Да |
| В прямоугольном треугольнике гипотенуза равна сумме катетов. | Нет |
| В прямоугольном треугольнике катет больше гипотенузы. | Нет |
В прямоугольном треугольнике катет, лежащий против угла к 30° равен половине гипотенузы. | Да |
| В прямоугольном треугольнике квадрат гипотенузы равен разности квадратов катетов. | Нет |
| В прямоугольном треугольнике квадрат гипотенузы равен сумме катетов. | Нет |
| В прямоугольном треугольнике любой катет меньше гипотенузы. | Да |
| В прямоугольном треугольнике синус одного из углов равен 0. | Нет |
| В прямоугольном треугольнике тангенсом острого угла а называется отношение sin a / cos a. | Да |
| В равнобедренной трапеции диагонали равны. | Да |
| В равнобедренной трапеции углы при основании равны. | Да |
| В равнобедренном прямоугольном треугольнике все стороны равны. | Нет |
| В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°. | Да |
| В равнобедренном треугольнике все стороны равны. | Нет |
В равнобедренном треугольнике все углы равны. | Нет |
| В равнобедренном треугольнике имеется не более двух равных углов. | Нет |
| В равнобедренном треугольнике медиана, проведённая к основанию, является одновременно и биссектрисой. | Да |
| В равнобедренном треугольнике медиана, проведённая к основанию, является одновременно и высотой. | Да |
| В равнобедренном треугольнике углы при основании равны. | Да |
| В равностороннем треугольнике АВС медиана AK равна высоте CH. | Да |
| В равностороннем треугольнике все углы острые. | Да |
| В равностороннем треугольнике все углы равны. | Да |
| В равностороннем треугольнике каждый угол равен 45°. | Нет |
| В равностороннем треугольнике медианы пересекаются в одной точке. | Да |
| В ромбе все углы прямые. | Нет |
В ромбе диагонали пересекаются под прямым углом. | Да |
| В ромбе противоположные углы равны. | Да |
| В ромб нельзя вписать окружность. | Нет |
| Все вписанные углы окружности равны. | Нет |
| Все высоты равностороннего треугольника равны. | Да |
| Все диаметры окружности равны между собой. | Да |
| Все квадраты имеют равные площади. | Нет |
| Все прямоугольные треугольники подобны. | Нет |
| Все прямоугольные треугольники подобны друг другу. | Нет |
| Все равнобедренные треугольники подобны. | Нет |
| Все равнобедренные треугольники равны. | Нет |
| Все точки каждой из двух параллельных прямых равноудалены от другой прямой. | Да |
| Все углы квадрата прямые. | Да |
| Все углы правильного пятиугольника равны 112°. | Нет |
Все углы правильного шестиугольника равны 135°. | Нет |
| Все углы пятиугольника равны. | Да |
| Все углы ромба равны. | Нет |
| Все хорды одной окружности равны между собой. | Нет |
| Всякий равнобедренный треугольник является остроугольным. | Нет |
| Всякий равносторонний треугольник является остроугольным. | Да |
| Всякий равносторонний треугольник является равнобедренным. | Да |
| В трапеции боковые стороны параллельны. | Нет |
| В трапеции сумма длин боковых сторон всегда меньше суммы оснований. | Нет |
| В трапецию АВCD с основаниями ВС = 7, AD = 10, и боковыми сторонами AB = CD = 8 можно вписать окружность. | Нет |
| В трапецию с основаниями 6 и 3 и боковыми сторонами 4 и 4 можно вписать окружность. | Нет |
В треугольнике ABC, для которого AB = 3, BC = 4, АС = 5, угол С наименьший. | Да |
| В треугольнике АВС, для которого АВ = 4, BC = 5, AC = 6, угол A наибольший. | Нет |
| В треугольнике АВС, для которого АВ = 4, ВС = 5, АС = 6, угол B — наибольший | Да |
| В треугольнике АВС, для которого АВ = 6, BC = 8, АС = 11, угол при вершине С — наименьший. | Да |
| В треугольнике АВС, для которого ∠A = 40°, ∠B = 60°, ∠C = 80°, сторона AC — наибольшая. | Нет |
| В треугольнике АВС, для которого ∠A = 40°, ∠B = 55°, ∠C = 85° сторона AC — наименьшая. | Нет |
| В треугольнике АВС, для которого ∠A = 44°, ∠B = 55°, ∠C = 81° сторона BC — наибольшая. | Нет |
| В треугольнике АВС, для которого ∠A = 45°, ∠B = 55°, ∠C = 80° сторона AC — наименьшая | Нет |
| В треугольнике АВС, для которого ∠A = 47°, ∠B — 64°, сторона АВ — наибольшая. | Да |
| В треугольнике АВС, для которого ∠A = 50°, ∠B = 60°, ∠C = 70° сторона AB — наибольшая | Да |
В треугольнике АВС, для которого ∠A = 50°, ∠B = 60°, ∠C = 70° сторона BC — наименьшая. | Да |
| В треугольнике любая сторона меньше суммы двух других сторон. | Да |
| В треугольнике может быть только один тупой угол. | Да |
| В треугольнике против большего угла лежит большая сторона. | Да |
| В треугольнике против большего угла лежит меньшая сторона. | Нет |
| В треугольнике против большей стороны лежит больший угол. | Да |
| В треугольнике против большей стороны лежит меньший угол. | Нет |
| В треугольнике против меньшего угла лежит меньшая сторона. | Да |
| В треугольнике против меньшего угла лежит большая сторона. | Нет |
| В треугольнике против меньшей стороны лежит больший угол. | Нет |
| В треугольнике против меньшей стороны лежит меньший угол. | Да |
| В треугольнике сумма двух сторон больше третьей стороны. | Да |
В тупоугольном треугольнике все углы тупые. | Нет |
| В тупоугольном треугольнике сумма углов больше 180 градусов. | Нет |
| Высота прямоугольного треугольника, опущенная на гипотенузу, делит его на два подобных треугольника. | Да |
| Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой. | Да |
| Высота равнобедренного треугольника проведённая к основанию, является медианой и биссектрисой. | Да |
| Гипотенуза длиннее катета. | Да |
| Гипотенуза прямоугольного треугольника, вписанного в окружность, в два раза больше её радиуса. | Да |
| Гипотенуза равна сумме квадратов катетов. | Нет |
| Гипотенуза — самая длинная сторона в прямоугольном треугольнике. | Да |
| Два угла с общей стороной называются смежными. | Нет |
Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности. | Нет |
| Две прямые всегда пересекаются. | Нет |
| Две прямые, параллельные третьей прямой, перпендикулярны друг другу. | Нет |
| Две прямые, перпендикулярные к третьей, не пересекаются. | Да |
| Две прямые, перпендикулярные одной и той же прямой, не пересекаются. | Да |
| Две прямые, перпендикулярные третьей прямой, параллельны друг другу. | Да |
| Две прямые, перпендикулярные третьей прямой, перпендикулярны друг другу. | Нет |
| Диагонали квадрата взаимно перпендикулярны. | Да |
| Диагонали квадрата делят его углы пополам. | Да |
| Диагонали квадрата пересекаются под прямым углом. | Да |
| Диагонали квадрата равны. | Да |
| Диагонали квадрата точкой пересечения делятся пополам. | Да |
Диагонали любого прямоугольника делят его на 4 равных треугольника. | Нет |
| Диагонали любого прямоугольника равны. | Да |
| Диагонали параллелограмма делят его углы пополам. | Нет |
| Диагонали параллелограмма пересекаются под прямым углом и в точке пересечения делятся пополам. | Нет |
| Диагонали параллелограмма перпендикулярны. | Нет |
| Диагонали параллелограмма равны. | Нет |
| Диагонали прямоугольника взаимно перпендикулярны. | Нет |
| Диагонали прямоугольника пересекаются под прямым углом и точкой пересечения делятся пополам. | Нет |
| Диагонали прямоугольника равны. | Да |
| Диагонали прямоугольника точкой пересечения делятся пополам. | Да |
| Диагонали прямоугольной трапеции равны. | Нет |
| Диагонали равнобедренной трапеции равны. | Да |
Диагонали ромба взаимно перпендикулярны. | Да |
| Диагонали ромба в точке пересечения делятся пополам. | Да |
| Диагонали ромба пересекаются под прямым углом. | Да |
| Диагонали ромба пересекаются под углом 60°. | Нет |
| Диагонали ромба перпендикулярны. | Да |
| Диагонали ромба равны. | Нет |
| Диагонали ромба точкой пересечения делятся пополам. | Да |
| Диагонали трапеции пересекаются и делятся точкой пересечения пополам. | Нет |
| Диагонали трапеции пересекаются под прямым углом. | Нет |
| Диагонали трапеции равны. | Нет |
| Диагонали трапеции точкой пересечения делятся пополам. | Нет |
| Диагональ квадрата равна его стороне. | Нет |
| Диагональ параллелограмма делит его на два равных треугольника | Да |
Диагональ параллелограмма делит его углы пополам. | Нет |
| Диагональ равнобедренной трапеции делит её на два равных треугольника. | Нет |
| Диагональ трапеции делит её на два равных треугольника. | Нет |
| Диагональ трапеции равна квадратному корню из суммы квадратов её оснований. | Нет |
| Диаметр делит окружность на две равные дуги. | Да |
| Диаметр окружности в два раза больше её радиуса. | Да |
| Диаметр окружности в два раза меньше его радиуса. | Нет |
| Длина вектора равна квадратному корню из суммы его координат. | Да |
| Длина вектора, равного сумме двух векторов, не превосходит сумму длин этих векторов. | Нет |
| Длина гипотенузы прямоугольного треугольника больше суммы длин его катетов. | Нет |
| Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов. | Да |
Длина катета прямоугольного треугольника равна длине гипотенузы, умноженной на косинус угла, образованного этим катетом и гипотенузой. | Да |
| Длина окружности вычисляется по формуле С = 2πR. | Да |
| Длина окружности равна её удвоенному радиусу. | Нет |
| Длина окружности равна πR. | Нет |
| Длина окружности радиуса R равна 2πR. | Да |
| Длина суммы двух векторов равна сумме их длин. | Нет |
| Для любого четырёхугольника, вписанного в окружность, сумма углов, прилежащих к одной стороне, равна 180° | Нет |
Для любого числа к и любых векторов а, b справедливо равенство | Да |
| Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу. | Да |
| Для точки, лежащей внутри круга, расстояние до центра круга меньше его радиуса. | Да |
| Если в выпуклом четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник — ромб. | Нет |
Если в параллелограмме две высоты равны, то этот параллелограмм — ромб.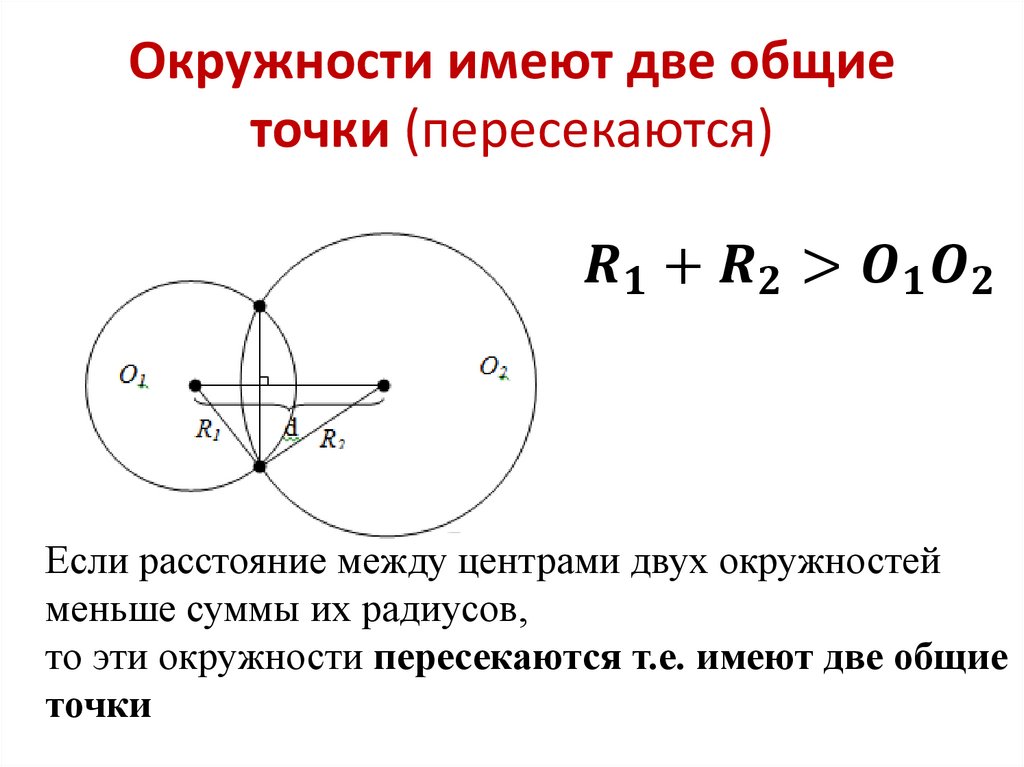 | Да |
| Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом. | Да |
| Если в параллелограмме две соседние стороны равны, то такой параллелограмм является ромбом. | Да |
Билеты по геометрии для 8 класса
Билет №1.
1.Найти смежные углы, если один из них на 70º больше второго.
2.Найти гипотенузу прямоугольного треугольника, если его катеты равны 3 см и 4 см.
3.Какое из следующих утверждений верно?
1)Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
2)Вертикальные углы равны.
3) Диагонали трапеции пересекаются и делятся точкой пересечения пополам.
Билет №2.
1.Найти смежные углы, если один из них в восемь раз меньше другого.
2.Сторона ромба равна 17 см, а одна из его диагоналей 16 см. Найти вторую диагональ ромба.
3.Какое из следующих утверждений верно?
1) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм – квадрат.
2)Смежные углы всегда равны.
3) Каждая из биссектрис равнобедренного треугольника является его высотой.
Билет №3.
1Найти смежные углы, если их градусные меры относятся как 3:2.
2.Периметр ромба 12 см, а один из углов равен 30º .Найти площадь ромба.
3.Какое из следующих утверждений верно?
1)Если диагонали параллелограмма равны, то он является ромбом.
2)Площадь параллелограмма равна половине произведения его диагоналей.
3)Вписанный угол, опирающийся на диаметр окружности, прямой.
Билет №4.
1.Один из углов, образовавшихся при пересечении двух прямых , равен 118º.Найти градусные меры остальных углов.
2.Найти площадь прямоугольного треугольника, катеты которого равны 6см и 9см.
3.Какое из следующих утверждений верно?
1)Точка пересечения двух окружностей равноудалена от центров этих окружностей.
2)В параллелограмме есть два равных угла.
3)Площадь прямоугольного треугольника равна произведению длин его катетов.
Билет №5.
1.Найти угол треугольника, если два других его угла равны 53º и 62º.
2.Найти среднюю линию трапеции, если её основания равны 6см и 11 см.
3.Какие из следующих утверждений равны?
1)Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
2)Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла.
3)Если диагонали параллелограмма равны, то он является ромбом.
Билет №6.
1.В равнобедренном треугольнике АВС с основанием АС угол АВС равен 98º. Найти внешний угол при вершине С.
2.Диагонали прямоугольника АВСД пересекаются в точке О.ВС=16 см, АС=24см. Найти периметр треугольника АОД.
3.Какие из следующих утверждений верны?
1)Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
2) Средняя линия трапеции параллельна её основаниям.
3) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
Билет №7.
1.Отрезки АС и ВД- диаметры окружности с центром О. Угол АСВ равен 53º. Найдите угол АОД.
2.Катеты прямоугольного треугольника равны 12 см и 5 см. Найти гипотенузу этого треугольника.
3.Какое из следующих утверждений верно?
1)Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
2)Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
3) Сумма острых углов прямоугольного треугольника равна 90º.
Билет №8.
1.Один из смежных углов на 20º больше другого. Найдите эти углы.
2.Найти средние линии треугольника, если его стороны равны 8см, 14 см и 18 см.
3.Какое из следующих утверждений верно?
1)Диагонали прямоугольника точкой пересечения делятся пополам.
2)Любая биссектриса равнобедренного треугольника является его медианой.
3)Диагональ трапеции делит её на два равных треугольника.
Билет №9.
1.Отрезки АВ и СД — диаметры некоторой окружности. Докажите, что прямые АС и ВД параллельны.
2.Одна из сторон параллелограмма в три раза меньше другой, а его периметр равен 72 см .Найдите стороны параллелограмма.
3.Какие из следующих утверждений верны?
1)Все квадраты имеют равные площади.
2)Существует прямоугольник, диагонали которого взаимно перпендикулярны.
3)Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
Билет №10.
1.В равнобедренном треугольнике АВС с основанием АС внешний угол при вершине С равен 144º. Найти величину угла АВС.
2.Периметр равнобокой трапеции равен 52 см, основания трапеции 13см и 21 см. Найти боковую сторону трапеции.
3.Какие из следующих утверждений верны?
1)Один из углов треугольника всегда не превышает 60º.
2)У любой трапеции боковые стороны равны.
3)Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
Билет №11.
1.Отрезки АВ и СД пересекаются в их общей середине. Докажите, что прямые АС и ВД параллельны.
2.Угол А трапеции АВСД с основаниями АД и ВС, вписанной в окружность, равен 77º. Найдите угол С этой трапеции.
3.Какое из следующих утверждений верно?
1)Площадь трапеции равна произведению основания трапеции на высоту.
2)Если диагонали параллелограмма равны, то он является ромбом.
3)Биссектрисы треугольника пересекаются в точке, которая является центром окружности, вписанной в треугольник.
Билет №12.
1.Один из углов, получившихся при пересечении двух прямых, равен 20º. Найдите остальные углы.
2.Четырёхугольник АВСД описан около окружности, АВ=8, ВС=12, СД=13. Найти АД.
3.Какое из следующих утверждений верно?
1)Средняя линия трапеции параллельна её основаниям
2)Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны.
3)Диагонали ромба равны.
Билет №13.
1.Сумма накрест лежащих углов, полученных при пересечении двух параллельных прямых секущей, равна 210º. Найдите эти углы.
2.Найдите сумму углов выпуклого пятиугольника.
3.Какие из следующих утверждений верны?
1)Сумма углов равнобедренного треугольника равна 180º.
2)Диагонали параллелограмма равны.
3)Все диаметры окружности равны между собой.
Билет №14.
1.Отрезки АВ и СД пересекаются в середине О отрезка АВ, угол ОАД равен углу ОВС. Докажите, что треугольник СВО равен треугольнику ДАО.
2.Сумма двух углов равнобедренной трапеции равна 94º. Найти больший угол трапеции.
3.Какое из следующих утверждений верно?
1)Площадь прямоугольного треугольника равна произведению длин его катетов.
2)Существует прямоугольник, диагонали которого взаимно перпендикулярны.
3)Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
Билет №15.
1.Найти периметр треугольника, если два угла его равны, а две стороны имеют длины 20 см и 10 см.
2.Сумма двух углов равнобедренной трапеции равна 218º. Найти меньший угол трапеции.
3.Какое из следующих утверждений верно?
1)Основания равнобедренной трапеции равны.
2)Все высоты равностороннего треугольника равны.
3)Смежные углы всегда равны.
Билет №16.
1.Найти углы равнобедренного треугольника, если один из его углов равен 40º.
2.Диагональ ВД параллелограмма АВСД образует с его сторонами углы, равные 65º и 50º. Найти меньший угол параллелограмма.
3.Какие из следующих утверждений верны?
1)Вертикальные углы равны.
2)Площадь квадрата равна произведению двух его смежных сторон.
3)Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
Билет №17.
1.Один из внешних углов равнобедренного треугольника равен 115º. Найти углы треугольника.
2.Два катета прямоугольного треугольника равны 7 см и 12 см. Найти его площадь.
3.Какое из следующих утверждений верно?
1)В прямоугольном треугольнике гипотенуза равна сумме катетов.
2)Всегда один из смежных углов острый, а другой тупой.
3)Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
Билет №18.
1.Найти угол С треугольника АВС, если угол А=65º, а угол В=57º.
2.Высота равнобедренной трапеции АВСД, проведённая из вершины С, делит основание АД на отрезки длиной 14 см и 19 см. Найти длину основания ВС.
3.Какое из следующих утверждений верно?
1)Все прямоугольные треугольники подобны.
2)Диагонали прямоугольника равны.
3)Сумма углов прямоугольного треугольника равна 90º.
Билет №19.
1.Найти углы прямоугольного равнобедренного треугольника.
2.В равнобедренной трапеции основания равны 3см и 9см, а один из углов между боковой стороной и основанием равен 45º. Найти площадь трапеции.
Найти площадь трапеции.
3.Какие из следующих утверждений верны?
1)Треугольника со сторонами 1,2,4 не существует.
2)Медиана треугольника делит пополам угол, из которого проведена.
3)Все радиусы окружности равны между собой.
Билет №20.
1.В треугольнике АВС АВ=ВС, угол АВС равен 122º. Найти угол ВСА.
2.Периметр параллелограмма равен 48 см. Найти стороны параллелограмма, если одна из сторон в два раза больше другой.
3.Какие из следующих утверждений верны?
1) В любой ромб можно вписать окружность.
2) Диагонали прямоугольной трапеции равны.
3)Сумма углов четырёхугольника равна 360º.
Билет №21.
1. Найти все углы, образованные при пересечении двух параллельных прямых секущей, если один из углов равен 150º.
2.Боковая сторона равнобедренного треугольника равна17см, а основание равно 16 см. Найти высоту, проведённую к основанию.
3.Какое из следующих утверждений верно?
1) В тупоугольном треугольнике все углы тупые.
2)Градусная мера вписанного угла равна градусной мере дуги, на которую он опирается.
3) Существует прямоугольник, диагонали которого взаимно перпендикулярны.
Билет №22.
1.Один из острых углов прямоугольного треугольника равен 53º. Найти его другой острый угол.
2.Периметр квадрата равен 68 см. Найти его площадь.
3.Какое из следующих утверждений верно?
1)У любой трапеции боковые стороны равны.
2)Всякий равнобедренный треугольник является остроугольным.
3)Если в выпуклом четырёхугольнике суммы противолежащих сторон равны, то в него можно вписать окружность.
Билет №23.
1.Разность двух односторонних углов, полученных при пересечении двух параллельных прямых секущей , равна 50º.Найдите эти углы.
2.Найти среднюю линию трапеции, если её основания равны 12см и 14 см.
3.Какое из следующих утверждений верно?
1)Все хорды одной окружности равны между собой.
2)Диагональ равнобедренной трапеции делит её на два равных треугольника.
3)Сумма углов равнобедренного треугольника равна 180º.
Билет №24.
1.Один из смежных углов на 38º больше другого. Найдите эти углы.
2.Найти вписанный угол, если градусная мера дуги, на которую он опирается, равна 226º.
3.Какое из следующих утверждений верно?
1)В прямоугольном треугольнике квадрат гипотенузы равен разности квадратов катетов.
2)Сумма смежных углов равна 180º.
3)Все углы ромба равны.
Билет №25.
1.Периметр равнобедренного треугольника равен 19см, а его основание равно 7 см. Найти боковую сторону треугольника.
2.Сторона квадрата равна 5см. Найти его диагональ.
3.Какие из следующих утверждений верны?
1)Диагональ параллелограмма делит его на два равных треугольника.
2)Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
3)Каждая из биссектрис равнобедренного треугольника является его высотой.
Билет №26.
1.Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из этих углов равен 72º.
2.Найдите площадь параллелограмма, сторона которого равна 12см, а высота, проведённая к ней, равна 8см.
3.Какое из следующих утверждений верно?
1)Диагонали прямоугольника точкой пересечения делятся пополам.
2)Площадь трапеции равна произведению основания трапеции на высоту.
3)В прямоугольном треугольнике гипотенуза меньше катета.
Билет №27.
1.Найти углы треугольника, если их градусные меры относятся как 3:4:5.
2.Найти площадь треугольника, если сторона треугольника равна 16 см, а высота, проведённая к ней, равна 3,5 см.
3.Какие из следующих утверждений верны?
1)Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
2)В прямоугольно треугольнике катет, лежащий против угла в 30º, равен половине гипотенузы.
3)Диагонали параллелограмма равны.
Билет №28.
1.Найти углы, образованные в результате пересечения двух прямых, если сумма трёх из них равна 305º.
2. Периметр параллелограмма равен 112 см. Найти его стороны, если две его стороны относятся как 5:9.
Периметр параллелограмма равен 112 см. Найти его стороны, если две его стороны относятся как 5:9.
3.Какие из следующих утверждений верны?
1)Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники подобны.
2.Средняя линия трапеции параллельна основаниям и равна их полусумме.
3)Если один из смежных углов острый, то другой тупой.
Билет №29.
1.Периметр равнобедренного треугольника равен 28 см, а боковая сторона равна 10 см. Найти основание треугольника.
2.Найти углы трапеции АВСД , прилежащие к боковой стороне СД, если
3.Какие из следующих утверждений верны?
1)Площадь треугольника меньше произведения двух его сторон.
2)Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
3)Основания трапеции могут быть равными.
Билет №30.
1.Угол при основании равнобедренного треугольника равен 67. ºНайти угол при вершине этого треугольника.
ºНайти угол при вершине этого треугольника.
2.Найти площадь равнобедренной трапеции , основания которой равны 10 см и 14см, а высота 5см.
3.Какое из следующих утверждений верно?
1)Диагонали ромба точкой пересечения делятся пополам.
2)Касательная к окружности параллельна радиусу, проведённому в точку касания.
3)В прямоугольном треугольнике гипотенуза равна сумме катетов.
геометрия — Как найти радиус, если две окружности пересекаются в двух разных точках?
Задавать вопрос
спросил
Изменено 7 лет, 11 месяцев назад
Просмотрено 5к раз
92-8x+2y+8=0$ .Теперь я хочу узнать диапазон r .
Я нашел центр $(4,-1)$ и радиус как 3 второй окружности.

В моей книге упоминается условие пересечения окружностей в двух местах.
$r_1-r_2
- геометрия
$\endgroup$
3
$\begingroup$
Итак, у вас есть круг с центром $(1,3)$ и радиусом $r$ и еще один круг с центром $(4,-1)$ и радиусом $3$. Чтобы они пересеклись в двух местах, должны произойти две вещи: внутренние части должны перекрываться (поэтому $r$ не может быть слишком маленьким) и первая окружность не может полностью окружать вторую окружность (поэтому $r$ не может быть слишком большой).
Мы можем упростить задачу, сдвинув и повернув координаты так, чтобы центр первой окружности находился в начале координат, а центр второй окружности находился на положительной оси $x$. 2}=\sqrt{9+16}=5$ и $y=0$.
2}=\sqrt{9+16}=5$ и $y=0$.
Сделав это, обратите внимание, что точка второго круга, ближайшая к центру первого круга, равна $(2,0)$ (крайняя левая точка). Если мы хотим, чтобы внутренности перекрывались, то эта точка должна быть внутри первого круга, поэтому вам понадобится $r>2$.
Теперь попробуйте найти условие, чтобы первый круг не окружал полностью второй круг. Подсказка: какая самая дальняя точка на втором круге от центра первого круга?
$\endgroup$
$\begingroup$
Для 2 окружностей, пересекающихся друг с другом как 2 точки, расстояние между центрами $C_1$ и $C_2$ должно быть меньше, чем расстояние, когда 2 окружности соприкасаются (соприкасаются) только в 1 точке, что имеет место в случае $C_1C_2= r_1+r_2$, так как центры образуют прямую линию с единственной точкой пересечения. Итак, мы имеем:
$$C_1C_2 Хотя минимальное расстояние между центрами существует, когда меньший круг касается большего внутри. $\endgroup$ Этот урок проиллюстрирует довольно простую концепцию — взаимное расположение двух окружностей. То есть найти, лежат ли две окружности с известными центрами и радиусами полностью вне друг друга, касаются друг друга, пересекаются в двух точках или таковы, что одна лежит внутри другой. Для всех этих случаев рассмотрим две окружности с центрами C 1 и C 2 и радиусы r 1 и r 2 соответственно. Я немного рассказывал об этом случае в предыдущем уроке. Взгляните на рисунок ниже. У нас есть два круга, внешне соприкасающиеся друг с другом. И совершенно очевидно, что расстояние между центрами двух окружностей равно сумме их радиусов. То есть С 1 С 2 = r 1 + r 2 , что будет необходимым условием для того, чтобы два круга касались друг друга снаружи. Имеет смысл? В предыдущем случае, что если мы немного отодвинем одну из окружностей от другой? Два круга больше не будут касаться друг друга и лежат вне друг друга. Поскольку, разделив их, мы увеличили расстояние между их центрами, расстояние C 1 C 2 станет больше, чем r 1 + r 2 . Поэтому требуемое условие будет C 1 C 2 > R 1 + R 2 . Посмотрите на рисунок. В этом случае расстояние между центрами равно разнице радиусов окружностей, т. Теперь давайте немного сдвинем меньший круг вправо, чтобы он полностью лежал внутри большего круга. Сдвигая круг, мы делаем C 1 C 2 меньше, чем в предыдущем случае. Значит, искомое условие для этого случая будет C 1 C 2 < r 1 – r 2 . Снова рассмотрим третий случай. Что, если мы сдвинем меньший круг влево? (Или больший справа?). Окружности теперь будут пересекаться в двух точках. И теперь мы увеличиваем расстояние между их центрами, подразумевая C 1 C 2 > r 1 – r 2 . Но мы не можем толкать его бесконечно влево, потому что возникнет ситуация, когда C 1 C 2 станет равным r 1 +r 2 , и круги снова будут касаться друг друга, но внешне. Учитывая все это, получаем требуемое условие для этого случая: 2 Уведомление что в последних трех случаях я предполагал, что r 1 > r 2 (иначе r 1 – r 2 получилось бы отрицательным). Для любых двух заданных окружностей вы всегда можете считать, что больший радиус равен r 1 , или же вы можете использовать абсолютное значение их разницы. И это все о взаимном расположении двух кругов. Я надеюсь, что это было довольно легко понять. Я резюмировал урок в следующей таблице: В следующем уроке я приведу несколько примеров, чтобы продемонстрировать эти случаи. Итак, минимальное расстояние $C_1C_2\ge{r_1}-r_2$. Однако, поскольку 2 окружности пересекаются друг с другом в 2 точках, случай касания ($C_1C_2=r_1-r_2$) следует отбросить. Так 92}<|r+3|
$$
$$
|r-3|<5 \cap |r+3|>5
$$
Вы можете решить после этого.
Итак, минимальное расстояние $C_1C_2\ge{r_1}-r_2$. Однако, поскольку 2 окружности пересекаются друг с другом в 2 точках, случай касания ($C_1C_2=r_1-r_2$) следует отбросить. Так 92}<|r+3|
$$
$$
|r-3|<5 \cap |r+3|>5
$$
Вы можете решить после этого. Взаимное расположение двух окружностей
Две окружности, соприкасающиеся друг с другом снаружи

Две окружности, лежащие вне друг друга
Два круга, касающихся друг друга внутренне
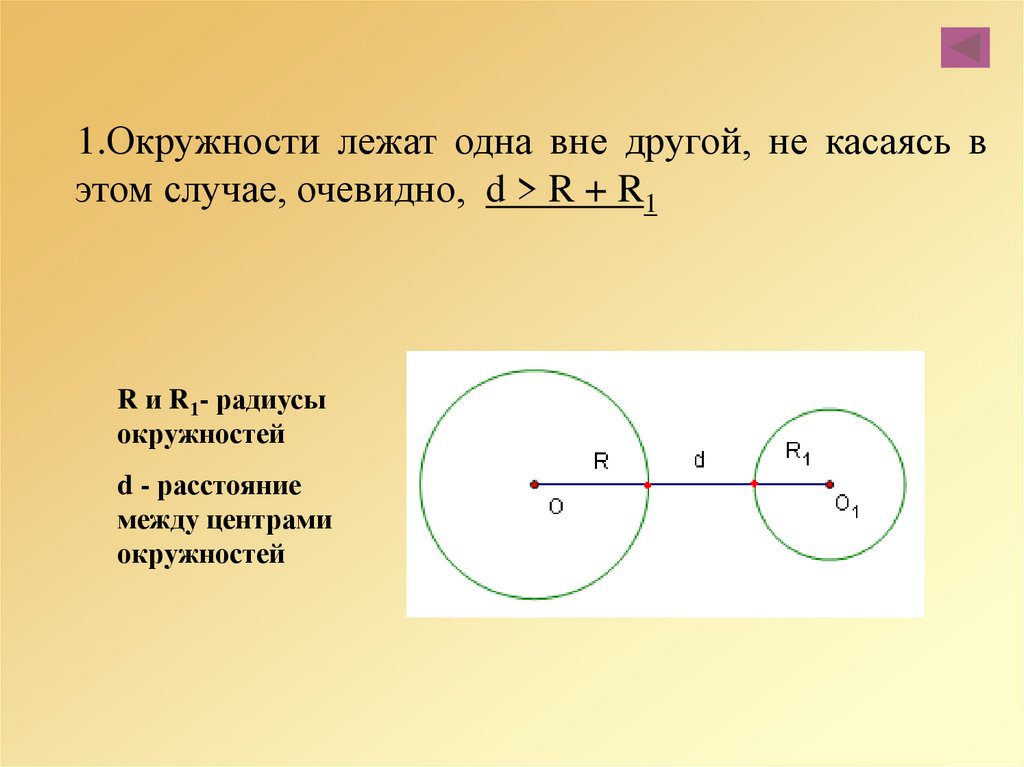 е.0077 . Вы видите это?
е.0077 . Вы видите это? Один круг лежит внутри другого
Две окружности, пересекающиеся в двух точках
 Это означает, что если мы хотим, чтобы окружности пересекались в двух точках, мы должны сохранить расстояние между их центрами меньше суммы их радиусов.
Это означает, что если мы хотим, чтобы окружности пересекались в двух точках, мы должны сохранить расстояние между их центрами меньше суммы их радиусов. Резюме урока
Позиция
Состояние
Лежащие друг за другом
С
1 С 2 > r 1 + r 2 Внешнее прикосновение
С
1 С 2 = г 1 + г 2 Пересечение в двух точках
|r
1 – r 2 | < С 1 С 2 < r 1 + r 2 Внутреннее касание
С
1 С 2 = |r 1 – r 2 | Один лежит внутри другого
C
1 C 2 < |r 1 – r 2 |

Leave A Comment