ВПР по Математике 8 класс (2023г) — Задание 17
Образцы вариантов ВПР 2023 года, демоверсии всероссийской проверочной работы для 8 класса по Математике.
1. В прямоугольном треугольнике ABC с прямым углом C известны катеты: Найдите медиану CK этого треугольника.
2. В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
3. Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АС, если сторона АВ равна 4.
4. Найдите градусную меру ∠ACB, если известно, что BC является диаметром окружности, а градусная мера центрального ∠AOC равна 96°.
5. В угол величиной 70° вписана окружность, которая касается его сторон в точках A и B. На одной из дуг этой окружности выбрали точку C так, как показано на рисунке. Найдите величину угла ACB.
На одной из дуг этой окружности выбрали точку C так, как показано на рисунке. Найдите величину угла ACB.
6. Найдите отношение двух сторон треугольника, если его медиана, выходящая из их общей вершины, образует с этими сторонами углы в 30° и 90°.
7. Высота треугольника разбивает его основание на два отрезка с длинами 8 и 9. Найдите длину этой высоты, если известно, что другая высота треугольника делит ее пополам.
8. Медианы треугольника пересекаются в точке Найдите длину медианы, проведённой к стороне если угол BAC равен 47°, угол равен 133°,
9. В треугольнике АВС углы А и С равны 40° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
10. Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АС, если сторона АВ равна 3.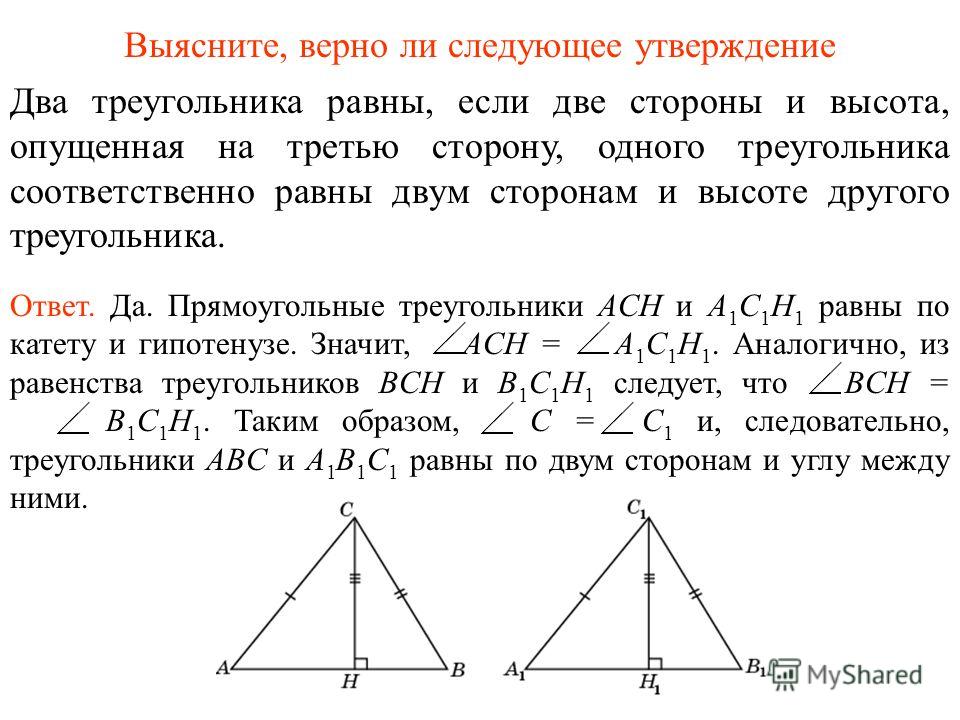
11. Катет и гипотенуза прямоугольного треугольника равны 18 и 30. Найдите высоту, проведённую к гипотенузе.
12. Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 10, DC = 25, AC = 56 .
13. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN = 13, AC = 65, NC = 28.
14. AC и BD — диаметры окружности с центром O. Угол ACB равен 79°. Найдите угол AOD. Ответ дайте в градусах.
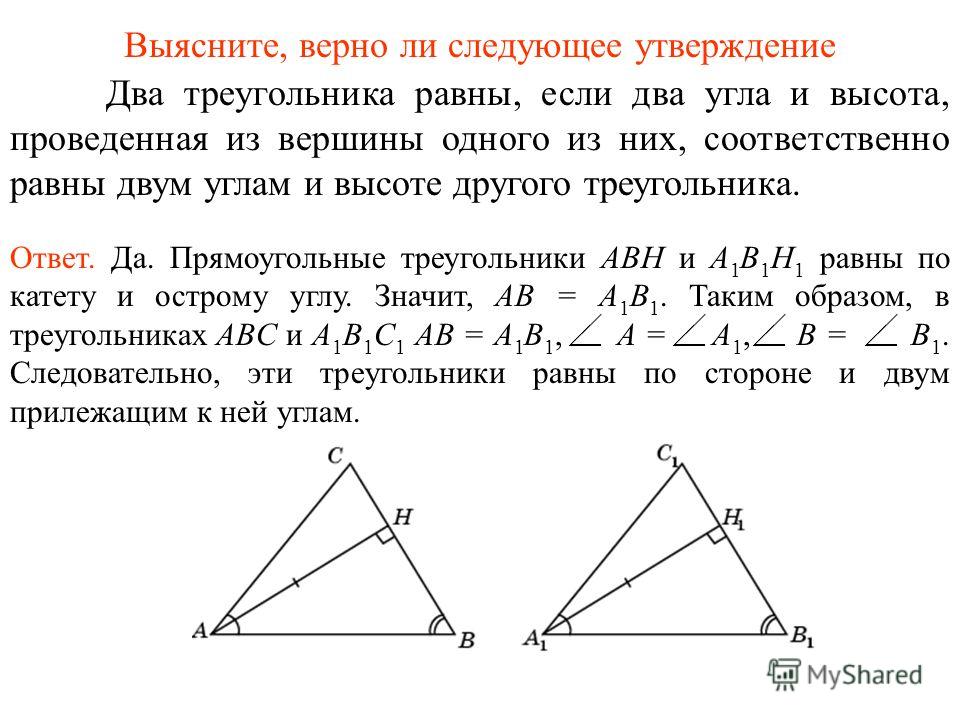
15. Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC.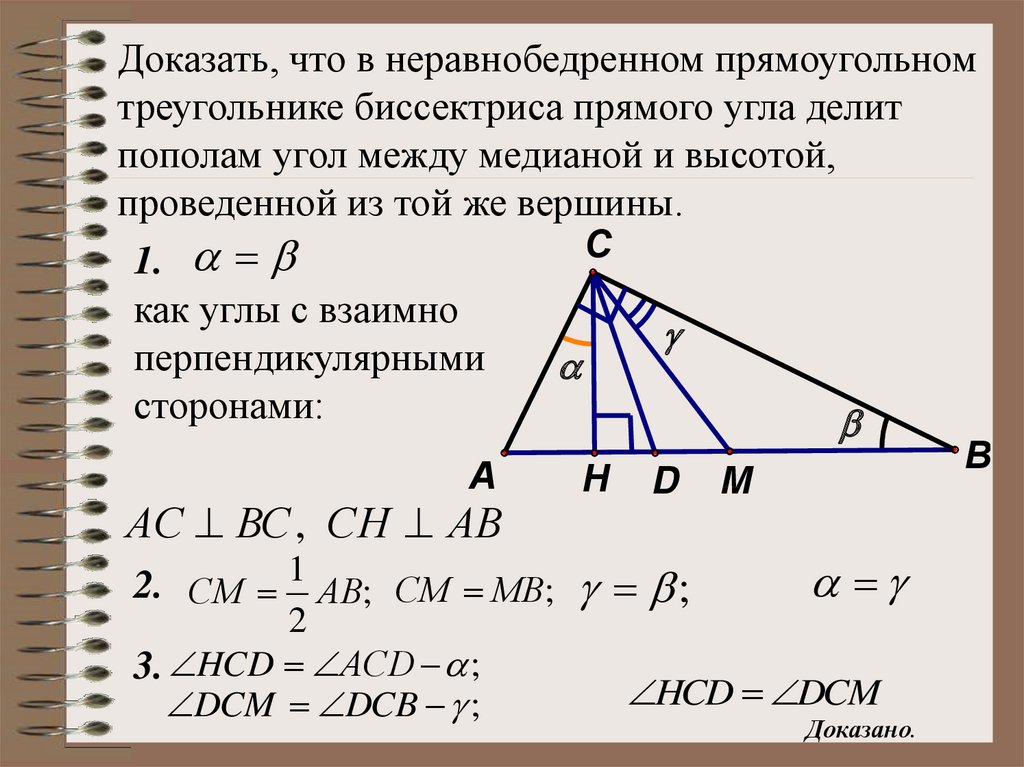 Найдите AB, если AH = 5, AC = 20.
Найдите AB, если AH = 5, AC = 20.
16. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и Найдите меньший угол между диагоналями параллелограмма. Ответ дайте в градусах.
17. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD = 63°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
18. В треугольнике ABC проведена биссектриса AL, угол ALC равен 78°, угол ABC равен 52°. Найдите угол ACB. Ответ дайте в градусах.
19. В равнобедренном треугольнике АВС с основанием ВС проведена медиана АМ. Найдите медиану АМ, если периметр треугольника АВС равен 56 см, а периметр треугольника АВМ равен 42 см.
20. Отрезки AB и CD — диаметры окружности с центром O. Найдите периметр треугольника AOD, если известно, что CB = 13 см, AB = 16 см.
Найдите периметр треугольника AOD, если известно, что CB = 13 см, AB = 16 см.
21. Большее основание равнобедренной трапеции равно 34. Боковая сторона равна 14. Синус острого угла равен Найдите меньшее основание.
22. В равнобедренной трапеции основания равны 12 и 27, острый угол равен Найдите ее периметр.
23. Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.
24. В прямоугольном треугольнике ABC с гипотенузой AB провели высоту CD и биссектрису CL. Найдите угол DCL, если угол CAB равен 25°. Запишите решение и ответ.
25. В треугольнике АВС стороны АВ и BС равны, На стороне ВС взяли точки Х и Y так, что точка Х лежит между точками В и Y, АХ = ВХ и Найдите длину отрезка AY, если
26. В треугольнике АВС стороны АВ и BС равны, На стороне ВС взяли точки Х и Y так, что точка Х лежит между точками В и Y, АХ = ВХ и Найдите длину отрезка AY, если
В треугольнике АВС стороны АВ и BС равны, На стороне ВС взяли точки Х и Y так, что точка Х лежит между точками В и Y, АХ = ВХ и Найдите длину отрезка AY, если
27. К окружности с диаметром АВ в точке А проведена касательная. Через точку В проведена прямая, пересекающая окружность в точке С и касательную в точке К. Через точку D проведена хорда СD параллельно АВ так, что получилась трапеция ACDB. Через точку D проведена касательная, пересекающая прямую АК в точке Е. Найдите радиус окружности, если прямые DE и BC параллельны, и
28. В прямоугольной трапеции ABCD с основаниями AD и BC диагональ АС является биссектрисой угла А, равного 45°. Найдите длину диагонали BD, если меньшее основание трапеции равно Запишите решение и ответ.
29. Из точки М к окружности с центром О проведены касательные MA и MB. Найдите расстояние между точками касания A и B, если и MO = 4.
30. К окружности с диаметром AB в точке A проведена касательная. Через точку B проведена прямая, пересекающая окружность в точке C и касательную в точке K. Через точку C проведена хорда CD параллельно AB так, что получилась трапеция ACDB. Через точку D проведена касательная, пересекающая прямую AK в точке E. Найдите длину отрезка AK, если прямые DE и BC параллельны, и
31. К окружности с диаметром AB в точке A проведена касательная. Через точку B проведена прямая, пересекающая окружность в точке C и касательную в точке K. Через точку C проведена хорда CD параллельно AB так, что получилась трапеция ACDB. Через точку D проведена касательная, пересекающая прямую AK в точке E. Найдите радиус окружности, если прямые DE и BC параллельны, и
Через точку D проведена касательная, пересекающая прямую AK в точке E. Найдите радиус окружности, если прямые DE и BC параллельны, и
32. В прямоугольной трапеции ABCD с основаниями AD и BC диагональ BD равна 32, а угол А равен 45°. Найдите бо́льшую боковую сторону, если меньшее основание трапеции равно
33. Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке М, лежащей на стороне ВС. Найдите периметр параллелограмма ABCD, если АB = 6.
34. Из точки М к окружности с центром О проведены касательные MA и MB. Найдите расстояние между точками касания A и B, если и MO = 22.
35. Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке М, лежащей на стороне ВС. Найдите периметр параллелограмма ABCD, если АB = 2.
Найдите периметр параллелограмма ABCD, если АB = 2.
36. Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке М, лежащей на стороне ВС. Найдите периметр параллелограмма ABCD, если АB = 9.
37. К окружности с диаметром AB в точке A проведена касательная. Через точку B проведена прямая, пересекающая окружность в точке C и касательную в точке K. Через точку C проведена хорда CD параллельно AB так, что получилась трапеция ACDB. Через точку D проведена касательная, пересекающая прямую AK в точке E. Найдите длину отрезка AK, если прямые DE и BC параллельны, и
38. К окружности с диаметром AB в точке A проведена касательная. Через точку B проведена прямая, пересекающая окружность в точке C и касательную в точке K.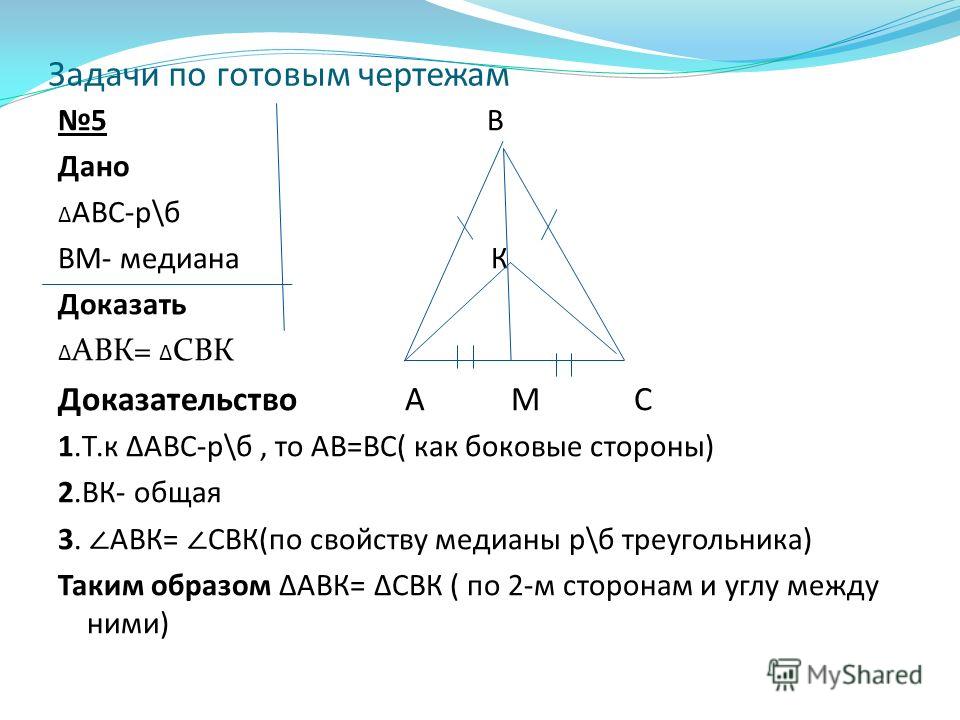 Через точку C проведена хорда CD параллельно AB так, что получилась трапеция ACDB. Через точку D проведена касательная, пересекающая прямую AK в точке E. Найдите радиус окружности, если прямые DE и BC параллельны, и
Через точку C проведена хорда CD параллельно AB так, что получилась трапеция ACDB. Через точку D проведена касательная, пересекающая прямую AK в точке E. Найдите радиус окружности, если прямые DE и BC параллельны, и
39. В треугольнике АВС стороны АВ и АС равны. На стороне АС взяли точки Х и Y так, что точка Х лежит между точками А и Y и AX = BX = BY. Найдите величину угла CBY, если .
40. В треугольнике АВС стороны АВ и BС равны, На стороне ВС взяли точки Х и Y так, что точка Х лежит между точками В и Y, АХ = ВХ и Найдите длину отрезка AY, если AX = 20.
41. В треугольнике АВС стороны АВ и BС равны, На стороне ВС взяли точки Х и Y так, что точка Х лежит между точками В и Y, АХ = ВХ и Найдите длину отрезка AY, если AX = 24.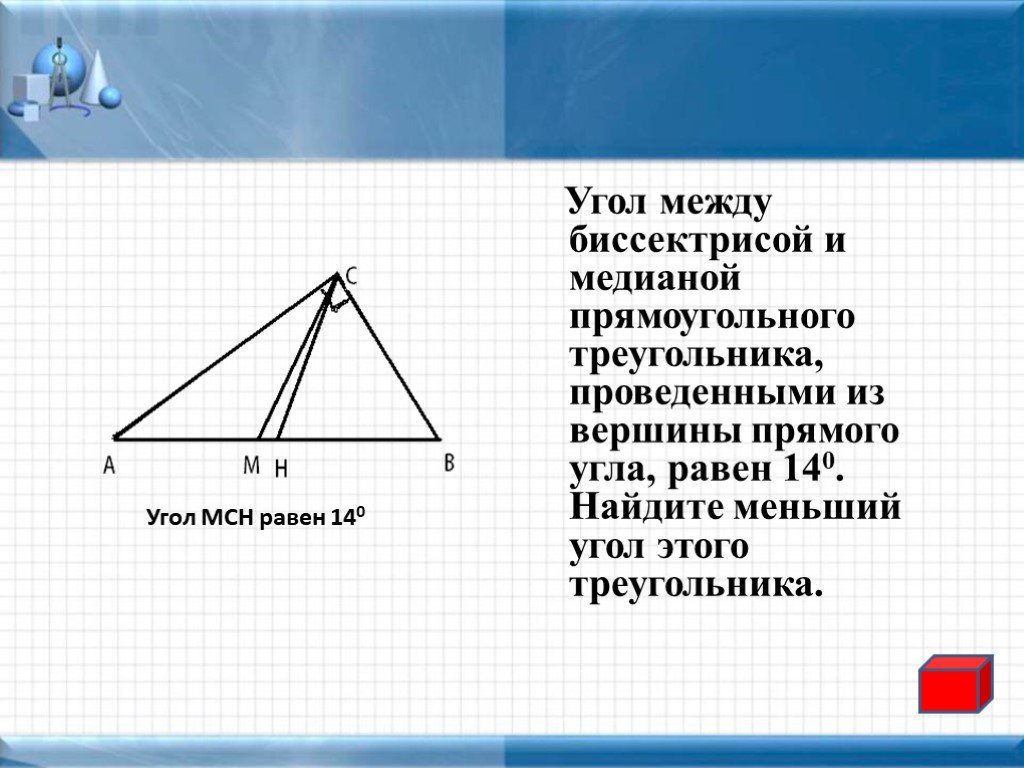
42. Из точки М к окружности с центром О проведены касательные MA и MB. Найдите расстояние между точками касания A и B, если и MA = 20.
43. В параллелограмме ABCD биссектриса угла А, равного 60°, пересекает сторону ВС в точке М. Отрезки АМ и DM перпендикулярны. Найдите периметр параллелограмма, если AB = 6. Запишите решение и ответ.
44. В параллелограмме ABCD биссектриса угла А, равного 60°, пересекает сторону ВС в точке М. Отрезки АМ и DM перпендикулярны. Найдите периметр параллелограмма, если AB = 10. Запишите решение и ответ.
45. В треугольнике АВС стороны АВ и BС равны, На стороне ВС взяли точки Х и Y так, что точка Х лежит между точками В и Y, АХ = ВХ и Найдите длину отрезка AY, если AX = 10.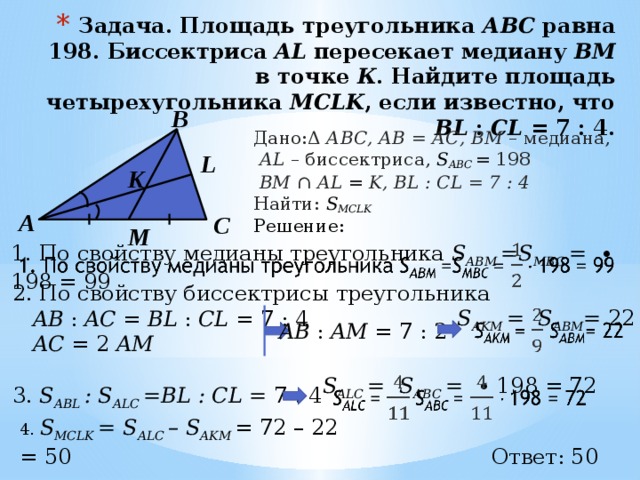
46.В треугольнике АВС стороны АВ и BС равны, На стороне ВС взяли точки Х и Y так, что точка Х лежит между точками В и Y, АХ = ВХ и Найдите длину отрезка AY, если AX = 6.
47. В треугольнике АВС стороны АВ и АС равны. На стороне АС взяли точки Х и Y так, что точка Х лежит между точками А и Y и AX = BX = BY. Найдите величину угла CBY, если .
48. В прямоугольной трапеции ABCD с основаниями AD и BC диагональ АС является биссектрисой угла А, равного 45°. Найдите длину диагонали BD, если меньшее основание трапеции равно Запишите решение и ответ.
49. Из точки М к окружности с центром О проведены касательные MA и MB. Найдите расстояние между точками касания A и B, если и MA = 7.
Найдите расстояние между точками касания A и B, если и MA = 7.
50. В треугольнике АВС стороны АВ и BС равны, На стороне ВС взяли точки Х и Y так, что точка Х лежит между точками В и Y, АХ = ВХ и Найдите длину отрезка AY, если AX = 22.
51. В прямоугольной трапеции ABCD с основаниями AD и BC диагональ АС является биссектрисой угла А, равного 45°. Найдите длину диагонали BD, если меньшее основание трапеции равно Запишите решение и ответ.
52. Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке М, лежащей на стороне ВС. Найдите периметр параллелограмма ABCD, если АB = 7.
53. Из точки М к окружности с центром О проведены касательные MA и MB. Найдите расстояние между точками касания A и B, если и MA = 6.
Найдите расстояние между точками касания A и B, если и MA = 6.
54. В прямоугольной трапеции ABCD с основаниями AD и BC диагональ BD равна 32, а угол А равен 45°. Найдите бо́льшую боковую сторону, если меньшее основание трапеции равно
55. В параллелограмме ABCD биссектриса угла А, равного 60°, пересекает сторону ВС в точке М. Отрезки АМ и DM перпендикулярны. Найдите периметр параллелограмма, если AB = 5. Запишите решение и ответ.
56. В прямоугольной трапеции ABCD с основаниями AD и BC диагональ BD равна 10, а угол А равен 45°. Найдите бо́льшую боковую сторону, если меньшее основание трапеции равно
57. В параллелограмме ABCD биссектриса угла А, равного 60°, пересекает сторону ВС в точке М.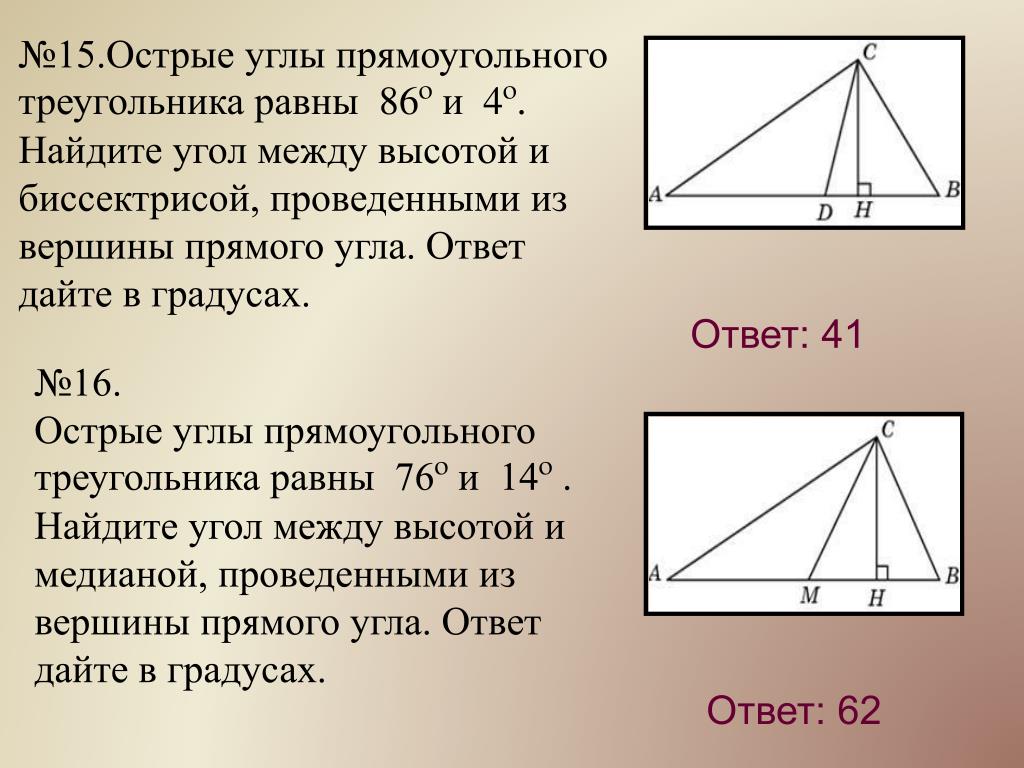 Отрезки АМ и DM перпендикулярны. Найдите периметр параллелограмма, если AB = 2. Запишите решение и ответ.
Отрезки АМ и DM перпендикулярны. Найдите периметр параллелограмма, если AB = 2. Запишите решение и ответ.
58. Из точки М к окружности с центром О проведены касательные MA и MB. Найдите расстояние между точками касания A и B, если и MA = 9.
59. В треугольнике АВС стороны АВ и АС равны. На стороне АС взяли точки Х и Y так, что точка Х лежит между точками А и Y и AX = BX = BY. Найдите величину угла CBY, если Запишите решение и ответ.
60. В треугольнике АВС стороны АВ и АС равны. На стороне АС взяли точки Х и Y так, что точка Х лежит между точками А и Y и AX = BX = BY. Найдите величину угла CBY, если Запишите решение и ответ.
61. В треугольнике АВС стороны АВ и АС равны. На стороне АС взяли точки Х и Y так, что точка Х лежит между точками А и Y и AX = BX = BY. Найдите величину угла CBY, если Запишите решение и ответ.
62. Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке М, лежащей на стороне ВС. Найдите периметр параллелограмма ABCD, если АB = 11.
63. В прямоугольной трапеции ABCD с основаниями AD и BC диагональ BD равна 18, а угол А равен 45°. Найдите большую боковую сторону, если меньшее основание трапеции равно Запишите решение и ответ.
Готовимся к зачету — презентация онлайн
ГОТОВИМСЯ К ЗАЧЕТУ.
МОБУ « Новочеркасская СОШ
Булдакова Л.П
2. Готовимся к ЗАЧЕТУ( билет1)
1. Дайте определение отрезка, луча, угла.
Дайте определение отрезка, луча, угла.Определение развернутого угла.
Обозначение лучей и углов.
2. В прямоугольном треугольнике DEF
катет DF=12 см., ∟E=300 . Найдите
гипотенузу DE.
3. 3. Докажите признак равенства треугольников по двум сторонам и углу между ними.
1.Докажите, что угол 1 равен углу 2.Угол ВАС = углу 1 – вертикальные;
Угол ВСА = углу 2 – вертикальные;
Угол ВАС = углу ВСА так как
треугольник АВС равнобедренный,
значит угол 1= углу 2
Билет №2
1.Дайте определение равных фигур.
Определение середины отрезка и
биссектрисы угла.
2.Докажите признак равенства треугольников
по стороне и двум прилежащим углам.
3.Угол при основании равнобедренного
треугольника равен 370 . Найдите угол при
вершине.
4.На прямой отмечены точки A, B, C и D ,
AB=8 см., BD=6 см., BC=3 см. Найдите AD.
1.Дайте определение равных фигур. Определение
середины отрезка и биссектрисы угла.
2.Докажите признак равенства треугольников по стороне и
двум прилежащим углам.
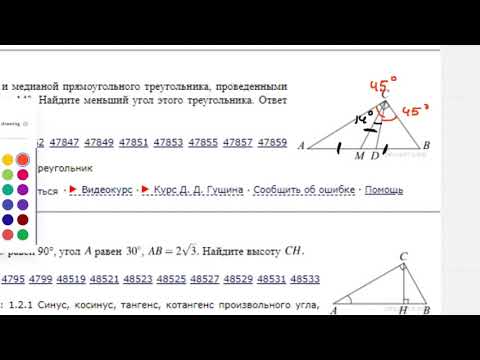
3.Угол при основании равнобедренного
треугольника равен 370 . Найдите угол
при вершине.
В
Дано
АВС – равнобедренный
АВ = ВС
Угол А = 37
Найти угол В
РЕШЕНИЕ:
1) т.к. АВС – равнобедренный,
2)<А =<В
3) < В = 180 – ( 37+37 ) = 106
А
С
4.На прямой отмечены точки A, B, C и D ,
AB=8 см., BD=6 см., BC=3 см. Найдите AD.
А
В
АД = 8+6 = 14
С
Д
10. Билет 3
1. Дайте определение смежных углов.Сформулируйте свойство смежных углов.
.Смежные углы — это углы, у которых одна сторона —
общая, а другие стороны лежат на одной прямой.
Сумма смежных углов равна 180º
.
11. Вопрос 2 Докажите признак равенства треугольников по трем сторонам.
1.Вопрос 2 Докажите признак равенстватреугольников по трем сторонам.
• Если три стороны одного треугольника равны
соответственно трем сторонам другого
треугольника, то такие треугольники равны.
3)один из углов, образованных при пересечении двух
прямых, равен 700.
 Найти остальные три угла.
Найти остальные три угла.70; 110
4)В треугольнике ABC ∟A=800 , ∟B=400. Биссектриса угла A
пересекает сторону BC в точке F. Найдите угол ACF.
(Как мы помним, биссектриса делит угол пополам,
соответственно углы BAF и FАС будут равны 40 градусам.
Рассмотрим треугольник BAF:
Угол В равен 40 градусов и угол А равен 40 градусов, найдём угол F:
180 — (40 + 40) = 100 градусов.
Теперь рассмотрим треугольник FАС:
Углы ВFА и АFС смежные, находим угол АFС:
180 — 100 = 80.
Теперь из треугольника FАС находим угол С:
180 — (80 + 40) = 60 градусов.
Этот же угол и АСF.
13. Билет 4
• 1)Дайте определение вертикальных углов.Сформулируйте свойство вертикальных углов
• Вертикальные углы — это пары углов с
общей вершиной, которые образованы при
пересечении двух прямых так, что стороны
одного угла являются продолжением сторон
другого.
• Вертикальные углы равны. При пересечении
двух прямых образуются две пары
вертикальных углов
14.
 2. Докажите теорему о сумме углов треугольника
2. Докажите теорему о сумме углов треугольника15. 3) Доказать равенство треугольников ADM и AFE
16. 4) Один из внутренних односторонних углов, образованных при пересечении двух параллельных прямых третьей, в 3 раза больше
другого. Чему равныэти углы?
Пусть меньший из углов равен х,
тогда другой равен 3х Значит
3х + х = 4х = 180°, следовательно, х =
45°. Ответ: 45° и 135°
17. Билет 5
• 1) Дайте определение острого, прямого итупого угла
• 2) Докажите свойство биссектрисы
равнобедренного треугольника
• Докажите равенство треугольников COD и AOD.
градусные меры двух внешних углов треугольника равны 1390 и 870.
Найдите третий внешний угол треугольника
• Т.к. градусные меры внешних углов Δ=
139°и 87°. то смежные с ними
внутренние углы Δ будут 180°-139°=41°
и 180°-87°=93°
сумма углов в любом Δ=180° ⇒ третий угол
в Δ=180°-41°-93°=46°
тогда смежный внешний угол будет 180°46°=134°
20.
 Билет №6• 1. Дайте определение равнобедренного
Билет №6• 1. Дайте определение равнобедренноготреугольника. Сформулируйте свойства
равнобедренного треугольника.
• 2. Докажите свойства смежных и вертикальных
углов.
• 3. Один из острых углов прямоугольного
треугольника 370. Найти второй острый угол.
• 4. AC II DB, CO=OD. Доказать, что
треугольники СОА и DOB равны.
21. 1. Дайте определение равнобедренного треугольника. Сформулируйте свойства равнобедренного треугольника.
• Равнобедренный треугольник треугольник, у которого две стороныравны. Эти равные стороны называются
боковыми, а третья — основание. В
равнобедренном треугольнике: Боковые
стороны равны; Углы при основании
равны Высота, опущенная к основанию,
является также и биссектрисой и
медианой этого
• 3. Один из острых углов прямоугольного
треугольника 370. Найти второй острый
угол.
• Два угла в прямоугольном треугольнике
90 градусов, значит второй угол 90-37
=53
• Ответ 53 градуса
24.
 4. AC II DB, CO=OD. Доказать, что треугольники СОА и DOB равны.
4. AC II DB, CO=OD. Доказать, что треугольники СОА и DOB равны.• Треугольники СОА и ДОВ
• равны:1) ОД = ОС
2) <ОДВ = < АСД вн накрест леж;
3) < АОС = < ДОВ вертикальные
• ( второй признак)
25. БИЛЕТ№ 7
• 1. Дайте определение медианы, биссектрисы ивысоты треугольника.
• 2. Сформулируйте признаки параллельных
прямых. Доказать один по выбору.
• 3. Периметр равнобедренного треугольника 19
см, а основание – 7 см. Найти боковую сторону
треугольника.
• 4. В прямоугольном треугольнике острый угол
равен 600 , а биссектриса этого угла – 8 см.
Найдите длину катета, лежащего против этого
угла.
26. ВОПРОС 1
• 1. Дайте определение медианы, биссектрисы ивысоты треугольника
• Медиана треугольника – это отрезок, соединяющий
вершину треугольника с серединой противоположной
стороны.
• Биссектриса треугольника — это отрезок биссектрисы
угла треугольника( Луч делящий угол треугольника
пополам).
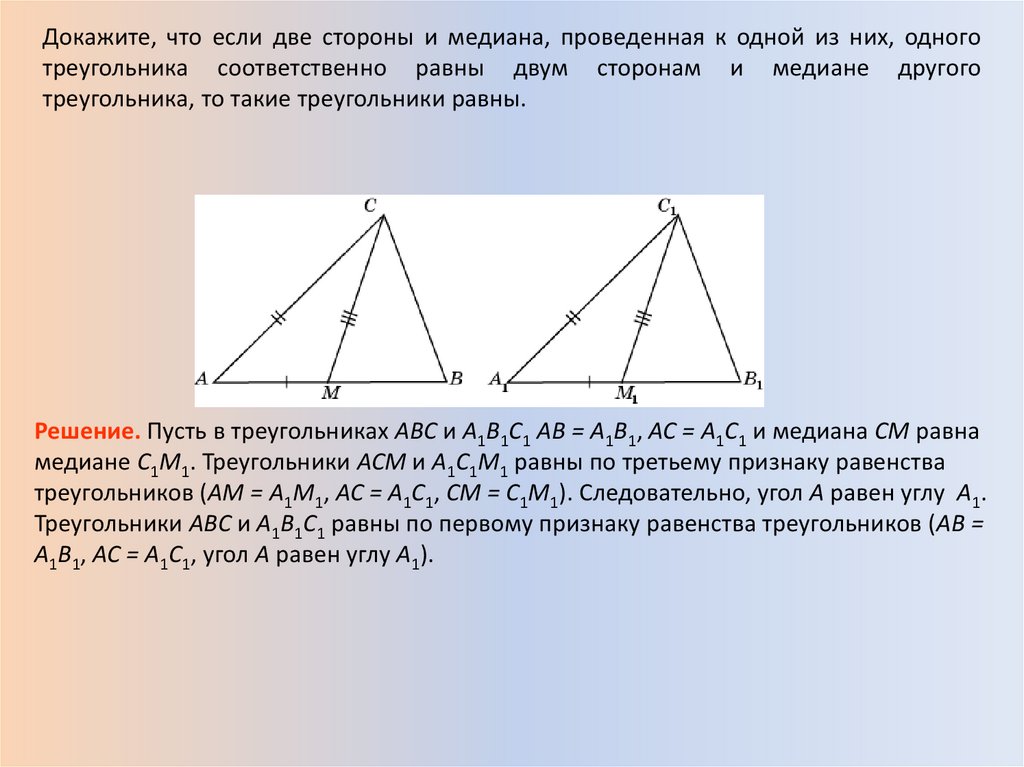
• Высота треугольника – это перпендикуляр,
опущенный из вершины угла треугольника на
противоположную сторону треугольника.
ВОПРОС 2
• 2. Сформулируйте признаки параллельных
прямых. Доказать один по выбору.
• ТЕОРЕМА1:
• ТЕОРЕМА 2
Докажем признак №2
Текст слайда
ТЕОРЕМА – третий признак параллельности прямых
Вопрос 3
• . Периметр равнобедренного треугольника 19
см, а основание – 7 см. Найти боковую сторону
треугольника.
Треугольник равнобедренный, то две его
стороны равны
Значит, Боковая сторона = (19 — 7):2=
12:2=6.
Ответ: 6 см.
Вопрос 4
• 4. В прямоугольном треугольнике острый угол
равен 600 , а биссектриса этого угла – 8 см.
Найдите длину катета, лежащего против этого
угла.
В
К
С
ДАНО:
< А = 60°, АК = 8см
Найти :
ВС
Решение:
Δ АСК прямоуг, КС против 30 градусов, равна
Половине АК; КС = 4см
Δ ВАК равнобедренный, ВК = АК = 8 см;
ВС = 12 см
А
.

Билет 8
Вопрос 1
1. Дайте определение внешнего угла треугольника.
Сформулируйте свойство внешнего угла треугольника.
Внешним углом треугольника называется угол, смежный с каким – нибудь
углом треугольника
Внешний угол треугольника равен сумме острых углов не смежных с ним
.
ВОПРОС 2. Докажите,
что при пересечении двух параллельных
прямых секущей накрест лежащие углы равны.
3. Один из углов, образованных при пересечении двух
прямых, на 500 меньше другого. Найти эти углы.
4 . Найти углы треугольника ABC.
М
ΔАМС
<МАС = < МСА = (180-140) : 2 = 20°
< ВМС = 180 – 140 = 40°
ВМ = АМ значит < МВА и
< МАВ = (180-40) :2 =70
< С = 20°, < В = 70°; < А = 90°
БИЛЕТ 9
1. Дайте определение остроугольного, прямоугольного,
тупоугольного треугольника.
Треугольник у которого все углы острые –
остроугольный;
Если есть прямой угол – треугольник
прямоугольный;
Если есть тупой угол – треугольник
тупоугольный
2.
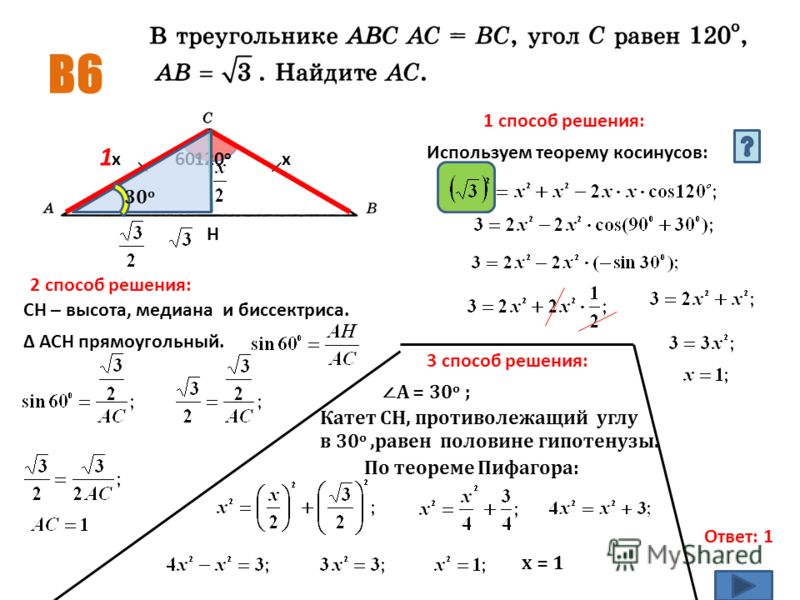 Доказать, что при пересечении двух параллельных прямых
Доказать, что при пересечении двух параллельных прямыхсекущей а) соответственные углы равны, б) сумма
односторонних равна 180 0.
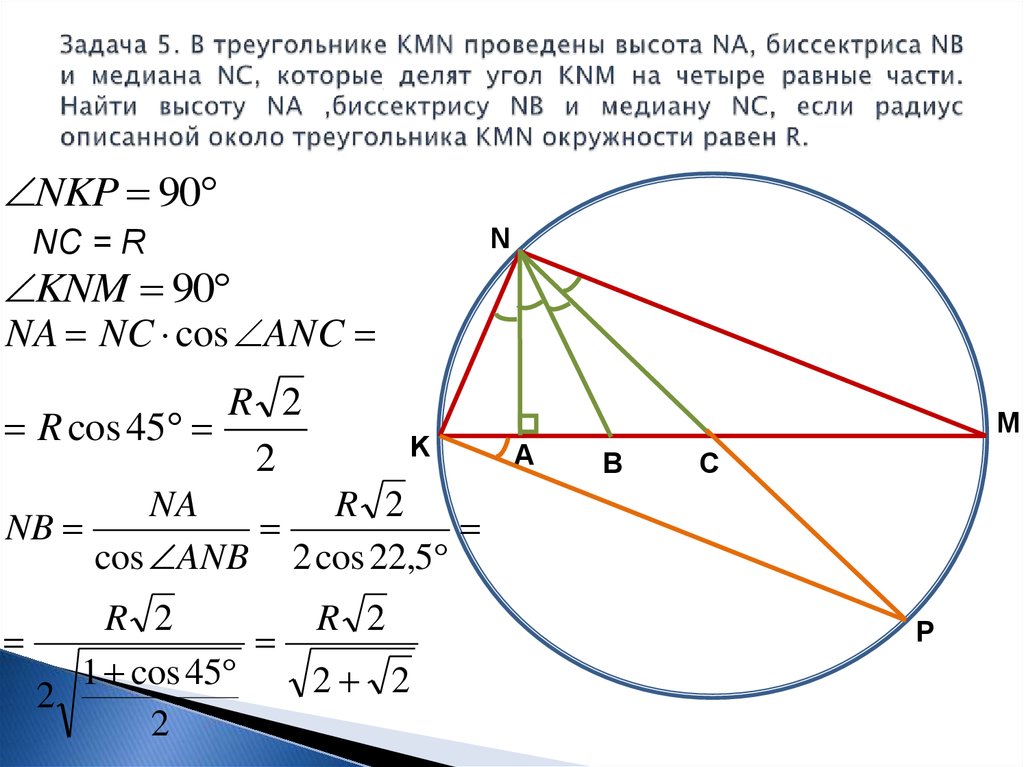
3. Один из острых углов прямоугольного треугольника равен 210. Найдите
угол между биссектрисой и высотой, проведенной из вершины прямого угла.
Угол А = 21 °,
угол В = 90 -21 = 69 °
<АСД = < ВСД = 45°
< НСВ = 90-69 = 21°
< ДСН = 45 -21 = 24 °
4. Доказать, что в равнобедренном треугольнике медианы,
проведенные к боковым сторонам, равны.
БИЛЕТ 10
1) Дайте определение параллельных прямых и параллельных отрезков
)Две прямые называются параллельными , если они не пересекаются.
Два отрезка называются параллельными, если они лежат на параллельных
прямых.
2)Докажите теорему о соотношении между сторонами и углами треугольника
( прямую или обратную).
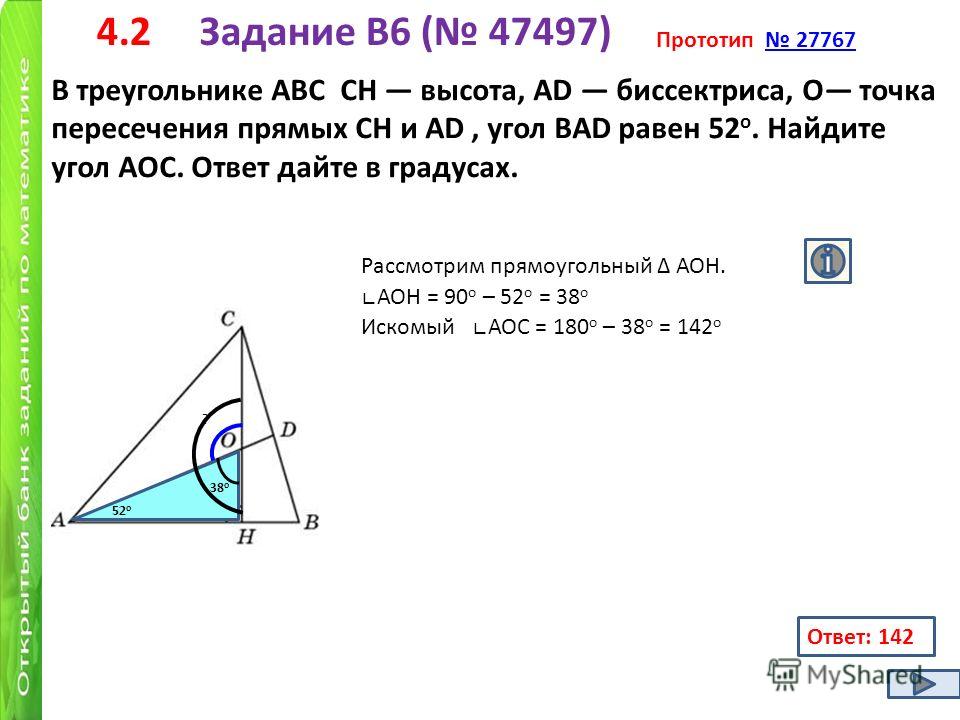
3. Найти углы треугольника АВС
Угол АВС = 136 – вертикальные;
Угол С = 180 -136 -23 = 21°
4. Доказать, что в равнобедренном треугольнике медианы,
проведенные к боковым сторонам, равны.
44. Билет 11
Билет 11
1)Дайте определение окружности, центра, радиуса, хорды, диаметра и
дуги окружности
Окружность — это замкнутая кривая линия, все точки которой
находятся на равном расстоянии от данной точки плоскости,
называемой центром окружности.
°
Круг — это часть плоскости, ограниченная окружностью. Расстояние
от любой точки круга до центра круга не превышает расстояния от
центра круга до любой точки на окружности.
Радиус — отрезок прямой линии, соединяющий центр с любой точкой
окружности.
Диаметр – отрезок прямой линии, соединяющии две точки окружности
и проходящий через центр. Можно так — это наибольшая из хорд
окружности.
Дуга — часть окружности или другой кривой линии, заключенная между
двумя точками.
Хорда — прямая, соединяющая две точки кривой линии.
45. 2) . Докажите свойство углов при основании равнобедренного треугольника
°.∟ABC=∟DCB=900, АС=BD.
Доказать, что AB=CD.

°
4)Высоты остроугольного треугольника NPT, проведенные
из вершин N и P, пересекаются в точке K, ∟T = 560.
Найдите угол NKP.
Пусть высота из N будет NM,
высота из Р – РН
Высоты треугольника
пересекаются в одной точке.
В прямоугольных ∆ РНТ и
∆ РКМ угол НРТ — общий.
Сумма острых углов треугольника
90°.
Поэтому ∠РКМ=∠РТN=56°
Искомый угол NKPсмежный углу
РКМ. В сумме они составляют
развёрнутый угол=180°.
Угол NKP=180°-56°=124°
48. Билет 12 1) Дайте определение параллельных прямых и параллельных отрезков. Сформулируйте аксиому параллельных прямых.
• Параллельные прямые — это двенепересекающиеся прямые, лежащие в одной
плоскости. Параллельные прямые записываются
через знак параллельности «||».
• Аксиома параллельных прямых. Через данную
точку, не лежащую на данной прямой, проходит
только одна прямая, параллельная данной.
• Если при пересечении двух прямых секущей:
• накрест лежащие углы равны, или соответственные
углы равны, или сумма односторонних углов равна
180°, то прямые параллельны
• Если две параллельные прямые пересечены
секущей, то:
• накрест лежащие углы равны; соответственные
углы равны; сумма односторонних углов равна 180°.

49. 2) Докажите теорему о соотношении между сторонами и углами треугольника ( прямую или обратную). Следствия из теоремы
В треугольнике: 1) против большей стороны лежит больший угол;2) обратно, против большего угла лежит большая сторона.
Отложим на стороне АВ отрезок АD, равный стороне АС.
АD АВ, т.к. по построению АD = АС, а по условию АС
АВ, значит, точка D лежит между точками А и В.
Следовательно, 1 является частью С, т.е. С 1.
Угол 2 внешний угол DBC, поэтому 2 В. АDС равнобедренный с основанием DC, т.к. по
построению АD = АС, следовательно, 1 = 2 (углы при
основании).
Итак, С 1, 1 = 2, значит, С 2, при этом 2 В,
следовательно, С В.
• Предположим, что это не так. Тогда возможны два варианта:
1. либо АВ = АС, тогда АВС — равнобедренный с
основанием ВС, значит, С = В (как углы при основании), что
противоречит условию: С В.
2. либо АВ АС, тогда С В, т.к. против большей
стороны лежит больший угол (смотри 1 часть
доказательства), что противоречит условию: С В.

• Значит, наше предположение неверно, следовательно, АВ
АС. Что и требовалось доказать.
51. Следствие
1)В прямоугольном треугольнике гипотенуза больше катета.Если два угла треугольника равны, то
треугольник равнобедренный (признак равнобедренного
треугольника).
• .3) Внешний угол равнобедренного треугольника
равен 640. Найдите углы треугольника.
• если внешний угол при вершине равен 64
градуса.
1)180-64=116(один угол)
2)180-116=64(сумма двух углов)
3)64:2=32
Ответ: Два угла равны 32 градусов и один
равен 116градуса.
53. ОА=ОС, угол 1 равен углу 2. Доказать, что АВ=ВС.
ОА=ОС, угол 1 равен углу 2. Доказать, чтоАВ=ВС.
54. Билет №13
• 1. Дайте определение расстояния от точки допрямой. Наклонная. Определение расстояния между
параллельными прямыми.
• Расстояние от точки до прямой — это длина
перпендикуляра, опущенного из данной точки
на данную прямую.
Расстоянием между параллельными прямыми
называется расстояние от какой-нибудь
точки одной прямой до другой прямой.

Поэтому, чтобы найти расстояние между
параллельными прямыми, надо:
1) выбрать на одной из параллельных прямых
точку;
2) опустить из выбранной точки к другой
прямой перпендикуляр;
3) найти длину этого перпендикуляра.
• 2. Докажите, что каждая сторона треугольника
меньше суммы двух других. Что такое неравенство
треугольника.
• сумма углов треугольника равно 180
градусов. а если бы каждая сторона
треугольника была бы больше суммы
двух других сторон, то сумма углов
была бы больше 180, что невозможно.
следовательно — каждая сторона
треугольника меньше суммы двух
других сторон
• 3. Углы FDB и CBD равны, углы FBD и CDB равны.
Доказать, что равны углы F и C.
решение:
I. Рассмотрим треугольник CBD и
треугольник FDB.
BD – общая
Угол FDB = углу CBD(по условию)
Угол FBD = углу CDB(по условию),
следовательно треугольник CBD =
треугольнику FDB(II признак равенства),
следовательно угол F = углу
C(соответственные элементы), ЧТД.

• 4. Доказать, что в равнобедренном треугольнике
медианы, проведенные к боковым сторонам, равны.
58. Билет №14
• 1) Сформулируйте признаки равенствапрямоугольных треугольников
59. 2)Докажите свойство внешнего угла треугольника.
• Доказать, что прямые a и b параллельны• 4) . В прямоугольном треугольнике KPE ∟P=900, ∟K=600. На
катете PE отметили точку M такую, что ∟KMP=600.
Найдите PM , если EM = 16 см.
• Рассмотрим треугольник КМР:
• ∟ РКМ=90- ∟ КМР=90-60=30
• 2. ∟ РКЕ= ∟ РКМ+ ∟ МКЕ ∟ МКЕ= ∟ РКЕ- ∟ МКЕ=9030=60= ∟ РКМ,значит КМ-биссектриса угла РКЕ
• 3. ∟ КЕР=90- ∟ РКЕ=90-60=30
• ∟ МКЕ= ∟ КЕМ, значит треугольник КЕМравнобедренный, отсюда КМ=МЕ=16
4.Рассмотрим треугольник КМР. т.к. в прямоугольном
треугольнике катет, лежащий против угла в 30
градусов равен половине гипотенузы, то РМ=1/2КМ
РМ=1/2*16=8
• Ответ:8см
62. Билет 15
• 1). Дайте определение секущей? Назовитепары углов, которые образуются при
пересечении двух прямых секущей.
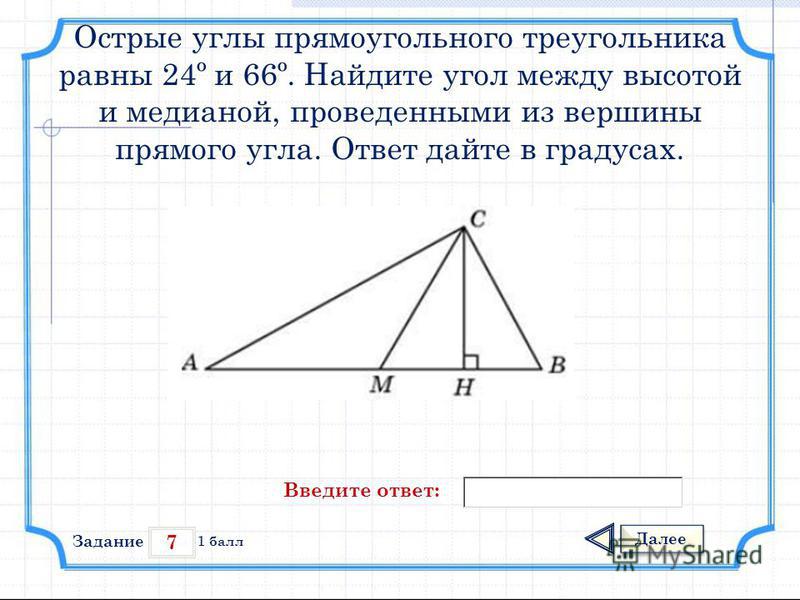
• Секущая — прямая по отношению к двум
прямым, которая пересекает их в двух точках.
При пересечении двух прямых секущей
образуются накрест лежащие, односторонние
и соответственные углы. Каждых видов
углов по 4 пары.
• 2)Докажите свойство катета прямоугольного
треугольника, лежащего против угла в 300.
Сформулировать обратное утверждение
• Луч BD проходит между сторонами угла ABC . Найдите
угол DBC, если ∟ABC = 630, ∟ABD = 510.
• дано:
угол ABC,
луч BD проходит между сторон ABC,
угол ABC = 63 градус,
угол ABD = 51 градус.
Найти градусную меру угла DBC — ?
Решение:
Рассмотрим угол АВС.
Угол АВС состоит из углов АВD и DВС, то есть угол АВС = угол
АВD + угол DВС.
Тогда угол DВС = угол АВС — угол АВD;
угол DВС = 63 градусов — 51 градус;
угол DВС = 12 градусов.
Ответ: угол DВС = 12 градусов.
• 4.В треугольнике АВС (АВ=ВС) на сторонах АВ
и ВС отложены равные отрезки АМ и СN
соответственно.
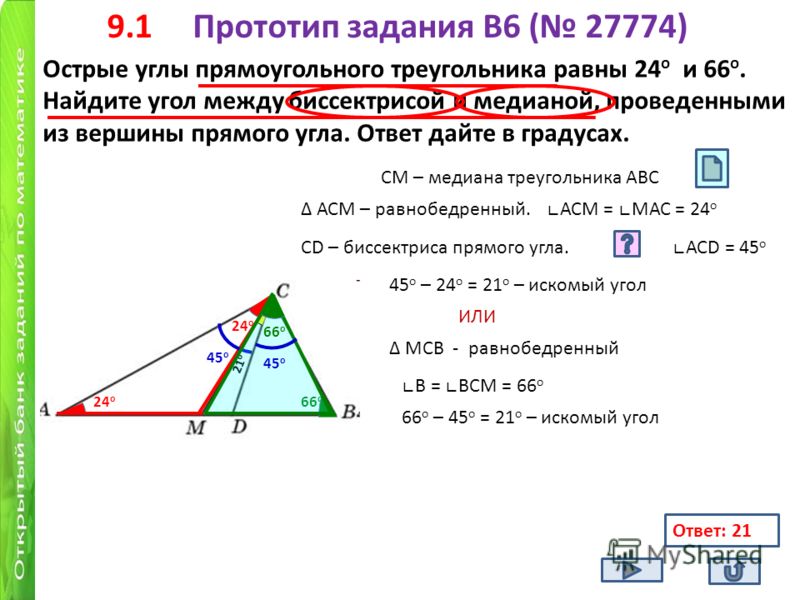 Докажите, что AN=СМ.
Докажите, что AN=СМ.• Угол М равен углу N и угол А равен углу С
точка пересечения будет О пусть
угол AOM равен углу CON
Следует что AN=CM
[ЛУЧШИЙ] План уроков математики 2023
План урока математики для школьных учителей, B.Ed, D.EL.ED, BTC, BSTC, NIOS, CBSE, NCERT, M.Ed, а также для всех курсов и советов по подготовке учителей .
Если вы ищете план урока математики, то вы находитесь в правильном месте. Здесь вы найдете множество планов уроков по математике по различным навыкам обучения, таким как микрообучение, мегаобучение, обсуждение, преподавание и практика в реальной школе, а также план урока по навыкам наблюдения. С помощью этих планов уроков вы сможете очень легко составить свой собственный план уроков математики. Все ссылки плана урока математики приведены ниже.
Примечание. Ниже вы найдете несколько планов уроков по некоторым темам. Вы должны проверить все планы уроков по математике, прежде чем составлять свой собственный план урока. И помните, что это примеры планов уроков. Вы можете использовать их в соответствии со своими потребностями и требованиями, внеся небольшие изменения в название, класс, курс, дату, продолжительность и т. д. на английском Скачать PDF бесплатно | План урока математики на английском языке
И помните, что это примеры планов уроков. Вы можете использовать их в соответствии со своими потребностями и требованиями, внеся небольшие изменения в название, класс, курс, дату, продолжительность и т. д. на английском Скачать PDF бесплатно | План урока математики на английском языке
Планы уроков математики в микрообучении
- Навык введения
- Навык изменения стимула
- Навык наводящих вопросов
- Навык подкрепления
- Навык объяснения
- Круг — Навык зондирования Вопрос
- Прибыли и убытки — Навык объяснения
- Целое число — Навык интеграции (опрос, объяснение и работа на доске)
- Трехмерные фигуры (трехмерные фигуры) — Навык интеграции (Навык изменения стимула, Навык объяснения, Навык иллюстрации и Навык работы с доской)
- Сложные проценты — Навык изменения стимула, Навык объяснения и Навык иллюстрирования примерами
Мегаплан учебного урока по математике
- Изогнутая и общая площадь поверхности конуса
- Изогнутая и общая площадь поверхности цилиндра
- Многочлены
- Алгебраические выражения
- Объем правого кругового цилиндра
Урок-дискуссия Математика
- Сумма углов треугольника
- Площадь поверхности куба и прямоугольного параллелепипеда
Преподавание и практика в реальной школе План урока математики
- Треугольники
- Тригонометрия
- Высота и расстояние с использованием тригонометрии
- Объем конуса и цилиндра
- Площадь поверхности конуса и цилиндра
- Круг
- Квадранты тригонометрии
- Площадь поверхности объема сферы
- Четырехугольники
- областей, связанных с кругом
- Координатная геометрия
- Координата Геометрия расстояния и сечения Формула
- Формула преобразования тригонометрии
- Статистика
- Доля
- Тригонометрическое отношение
- Круговая диаграмма
- Теорема
- Свойства угла в окружности
- 3D-фигуры (трехмерные фигуры)
Дополнительная ссылка:
www. learningclassesonline.com План урока математики для B.Ed
learningclassesonline.com План урока математики для B.Ed
Еще несколько планов уроков математики на английском языке
Макро/Имитация/Обсуждение/Наблюдение/Критика и реальное школьное преподавание и практика Список планов уроков математики
- План урока 1 – Прямая пропорция
- План урока 2 — Площадь поверхности прямоугольного параллелепипеда
- План урока 3 — Площадь ромба
- План урока 4 — Круговая диаграмма
- План урока 5. Уравнение алгебры и его типы
- План урока 6 — Алгебраическое выражение
- План урока 7 — Теоремы круга
- План урока 8 — Конгруэнтность треугольников
- План урока 9. Обратная пропорция
- План урока 10. Площадь прямоугольника, треугольника и квадрата
- План урока 11 — Выразители сил
- План урока 12. Рациональное число
- План урока 13. Рациональные числа между двумя числами
- План урока 14.
 Факторизация простых чисел
Факторизация простых чисел - План урока 15 — Теорема Пифагора
- План урока 16 — Свойства треугольника
- План урока 18 — Угол
- План урока 19 — Свойства круга
- План урока 20 — Площадь прямоугольника для преподавания математики
- План урока 21 — Площадь поверхности и объем
- План урока 22 — Сфера
- План урока 23 — Периметр прямоугольника квадрата
- План урока 24 — Простой интерес
- План урока 25 — Поверхность конуса
- План урока 26 — Квадратный корень Тема
- План урока 27 — Треугольник со своей площадью
- План урока 28 — Уравнение
- План урока 29 — Прибыли и убытки
- План урока 30 — Площадь и периметр квадрата и прямоугольника
- План урока 31 — Классификация треугольника
- План урока 32 — Круг
- План урока 33- Многочлены
- План урока 34. Целые числа
- План урока 35 — Типы рациональных чисел
- План урока 36.
 Дробь и десятичная дробь
Дробь и десятичная дробь - План урока 37 — Hcf
- План урока 38 — Lcm
- План урока 39 — Уравнение с одной переменной
- План урока 40 — Процент
- План урока 41 — Формула цапель
- План урока 42 — Четырехугольник
- План урока 43 — Квадратные и квадратные корни
- План урока 44 — Экспоненты
- План урока 46 — Объем цилиндра
- План Урока 47 — Объем Конуса
- План урока 48 — Объем цилиндра
- План урока 49 — Площадь сектора
- План урока 50 — Круговые сегменты
- План урока 51 — Оценка
- План урока 52 — Расширенные скобки
- План урока 53 — Преемник и предшественник
- План урока 54 — Смешанная фракция
- План урока 55. Неправильная дробь
- План урока 56. Эквивалентная дробь
- План урока 57 — Сравните дробь Тема
- План урока 58 — Сложение похожей дроби
- План урока 59 — Добавление смешанной дроби
- План урока 60 — Фракция
- План урока 61 — Десятичная система счисления
- План урока 62 — Прибыли и убытки
- План урока 63 — Соотношение
- План урока 64 — Эквивалентное сравнение соотношения
- План урока 65 — Пропорция
- План урока 66 — Унитарный метод
- План урока 67 — Симметрия
- План урока 68.
 Отражение и симметрия
Отражение и симметрия - План урока 69 — Угол
- План урока 70 — 3D-фигуры
- План урока 71 — Целые числа Тема
- План урока 72 — Числовая строка
- План урока 73 — Сложение, вычитание, деление и умножение числа
- План урока 74 — Целое число
- План урока 75. Фактор и умножение
- План урока 76 — Нечетные, четные, составные и простые числа
- План урока 77 — Правила делимости
- План урока 78 — Общий множитель и умножение
- План урока 79. Типы рациональных чисел
- План урока 80. Линейное уравнение
- План урока 81 — Десятичный вес
- План урока 82 — Деньги в десятичном формате
- План урока 83 — Квадратное уравнение
- План урока 84 — Среднее
- План урока 85 — Объем цилиндра
- План урока 86 — Объем сферы
- План урока 87 — Правый круговой цилиндр
- План урока 88 — Правый круговой конус
- План урока 89- Площадь прямоугольника
- План урока 90 — Площадь квадрата
- План урока 91 — План урока наблюдения
- План урока 92 — План урока критики о типах четырехугольников и их типах
- План урока 93 — Планы уроков критики по углу и его типам
 Ed на 2021 год (новинка)
Ed на 2021 год (новинка) Серийный номер | Название навыка | Ссылка |
1 | Написание инструкций Цели Поведенческие термины | Нажмите |
2 | Знакомство с уроком | Нажмите |
3 | Навык письма на доске | Нажмите |
4 | Свободное владение вопросами | Нажмите |
5 | Зондирование Опрос | Нажмите |
6 | Вариация стимула | Нажмите |
7 | Навык объяснения | Нажмите |
8 | Демонстрация | Нажмите |
9 | Закрепление навыка микрообучения | Нажмите |
10 | Достижение закрытия | Нажмите |
Как составить план урока математики
Как вы знаете, План урока представляет собой подробное описание курса инструкций или «Траектории обучения» Для учителей.
Опытные преподаватели Можно составить краткое описание деятельности Учителя. Полуподробный план урока составляется новыми учителями и включает все мероприятия и вопросы учителей.
Учитель-стажер должен составить подробный план урока, в котором записаны все задания, вопросы учителя и ожидаемые ответы учащихся.
Компоненты плана урока математики
Планы урока математики состоят из следующих компонентов:
1. Общие цели:
Это общие знания, полученные ребенком. Это полезно в обучении в реальной жизни.
2. Конкретные цели:
Включает:
- Цели знаний: Учащиеся смогут получить знания по конкретной теме математики.
- Цель понимания: Учащиеся смогут понять концепцию конкретной темы математики.

- Задачи приложения: Студенты смогут применять полученные знания в повседневной жизни.
3. Учебные мероприятия:
1. Подготовительные мероприятия:
Это
- Упражнение: Упражнение, позволяющее учащимся автоматизировать ответ на предварительные навыки нового урока.
- Обзор: Упражнение, которое освежит или обновит ранее пройденный материал.
- Введение: Упражнение, которое определит цель дневного урока.
- Мотивация: Все виды деятельности, вызывающие интерес учащихся (как внутренние, так и внешние)
2. Развивающие занятия
Сюда входят:
- Презентация урока математики: Учитель использует различные занятия в качестве средства преобразования знаний, ценностей и навыков в обучение, которое может быть получено Их жизнь вне школы.

- Обсуждение/Анализ: Учитель задает ряд эффективных или познавательных вопросов о представленном уроке.
- Абстракция/Обобщение: Полное обобщение информации происходит до фактического представления.
- Closer / Application: Это относится к уроку с другими ситуациями в формах
- Драматизация,
- Моделирование и игра,
- Рассказывание историй,
- Устное чтение,
- Конструкция/чертеж,
- Письменное сочинение,
- Пение или чтение стихотворения,
- Тест,
- или решение проблем.
Оценка:
Это метод или способ проверки или оценки целей, достигнутых на предыдущих уроках. Опрос, подведение итогов, сравнение, презентация предыдущего обучения, назначение работы, проведение короткой викторины и т. д. Попадают под это.
Назначение:
- Учителя готовят это задание за пределами школы или дома.
 Студенты приносят материал, необходимый в классе.
Студенты приносят материал, необходимый в классе. - Эти действия должны помочь в достижении цели урока.
- Он должен быть интересным и дифференцированным (с учетом мероприятий по исправлению, усилению и обогащению.)
План урока математики
План урока математики
План урока математики для B.Ed На английском языке Скачать бесплатно Pdf
Micro Teaching Math Lesson Plan
Mega Teaching Mathematics Lesson Plans
Simulation Teaching Mathematics Plan Lesson
Real School Teaching and Practice Plan Math Lessons для B.Ed и Deled 1st Year 2th Year
JAMIA, MDU, CRSU, DU, IGNOU, IPU Университетский урок математики Планы
Привет, друзья,
Если вы ищете лучшую коллекцию планов уроков математики для B.Ed, M.Ed, DELED, DED, BTC, NIOS, NCERT, CBSE и среднего уровня, средняя школа, средняя, старшая средняя, начальная школа, то вы находитесь в правильном месте. Здесь вы получите весь план урока математики для всех классов и классов, то есть 1-й, 2-й, 3-й, 4-й, 5-й, 6-й, 7-й, 8-й, 9-й.10-й, 11-й и 12-й на английском и хинди Medium.
Здесь вы получите весь план урока математики для всех классов и классов, то есть 1-й, 2-й, 3-й, 4-й, 5-й, 6-й, 7-й, 8-й, 9-й.10-й, 11-й и 12-й на английском и хинди Medium.
Здесь вы получите все микрообучение, мегаобучение, реальное обучение, обсуждение и план уроков по математике с наблюдением бесплатно для учителей и студентов бакалавриата первого и второго года обучения и семестра. Некоторые планы уроков по математике будут полуподробными, а некоторые подробные планы уроков вы найдете здесь. Список планов уроков математики по разным темам приведен выше. Эти примеры планов уроков окажут большую помощь учителям математики.
Здесь вы найдете множество тем для преподавания математики в школах, таких как круг, прибыль и убытки, сложные проценты, трехмерные фигуры, целые числа, поверхности конуса и цилиндра, многочлены, алгебраические выражения, треугольники, тригонометрия, объем Конус и цилиндр, квадранты, четырехугольники, статистика, среднее значение, медиана, мода, пропорция, круговые тележки, теоремы и т. д.
д.
сможете узнать, как составить план урока математики и как очень легко научить студентов математике с помощью этих планов урока.
план урока математики pdf
план урока математики с использованием технологий
формат плана урока по математике
план урока математики для детского сада
план урока математики для 4 класса
план урока математики
план урока математики для детского сада
план урока математики для дошкольного учреждения
план урока математики pdf
план урока математики для 1 класса
планиспользуя таксономию Блума
математика план урока математики для 3 класса
план урока математики для 4 класса
образец плана урока математики для детского сада
план урока математики для 4 класса
образец плана урока математики
5e план урока математики
образец плана урока математики для 6 класса
5 класс 4 математика подробный 90 0003 план урока 4 математики 90 0003 план урока математики 4 подробный 90 0003 подробный план урока математики
4а план урока математики
план урока математики
план урока математики
план урока математики
план урока математики по наборам
подробный план урока математики
план урока математики для b. ed pdf
ed pdf
план урока математики для 5 класса
20 09003 подробный план4 урока математики 900 0003 формат плана урока математики
план урока математики в б эд pdf
план урока математики для старшей школы pdf
план урока математики 4 класс
b.ed план урока математики для 8 класса
подробный план урока математики
план урока математики для JHS
план урока математики для 1 класса
план урока математики для средней школы
2 4план урока математики для 9 класса
план урока математики для 6 класса
план урока математики для 3 класса
план урока математики r
план урока математики 1 класс
план урока математики 3 класс
план урока математики 2 класс
0 общий план урока математики 2 9 005пример урока математики план
образец плана урока математики
план урока математики 5 класс
план урока математики 10 класс
план урока математики в средней школе
план урока математики 3 классплан урока математики 2 класс
математика год 1 план урока 4 03 полудетальный план урока математики
Образец плана урока математики 5e
Макроплан урока математики
План урока математики для 8 класса
план урока математики
план урока математики 4 класс
план урока математики 10 класс
план урока математики 8 класс 9003 план урока математики 8 класс 04
план урока математики 1 класс
план урока математики дошкольный
план урока математики 1 класс
план урока математики 6 класс
план урока математики 12 класс
план урока математики herbartian
образец плана урока математики
пример плана урока 90 0055е типовой план урока математики
мегаплан урока математики
конструктивистский план урока математики
5e план урока математики
подробный план урока математики
план урока микрообучения по математике
план урока b. 5  ed по математике на английском языке 0
ed по математике на английском языке 0
план урока математики для 6 класса
план урока математики на хинди
план урока математики для 8 класса
план урока математики
план урока математики 1 класс
план урока математики 3 класс
план урока математики 2 класс 003 90 план урока 90 для детского сада по математике
план урока математики 4 класс
план урока математики 7 класс
план урока математики 5 класс
план урока математики дошкольный
план урока математики 8 класс
подробный план урока математики
подробный план урока математики 2 класс
подробный план урока математики 1 класс4 3 подробный план урока по математике 3
примерный план урока по математике 6 класс
примерный план урока по математике
5e план урока по математике
подробный план урока по математике 9 класс0004
полудетальный план урока по математике
план урока по математике
план урока по математике для 6 класса pdf
план урока математики 7 класс pdf
план урока математики 8 класс pdf
план урока математики 10 класс pdf
Mathematics Lesson Planmatic0005
💁Здравствуйте, друзья! Если вы хотите внести свой вклад, чтобы помочь другим учащимся найти все материалы в одном месте, не стесняйтесь присылать нам свои заметки, задания, учебные материалы, файлы, план урока, бумагу, PDF или PPT.

 Факторизация простых чисел
Факторизация простых чисел Дробь и десятичная дробь
Дробь и десятичная дробь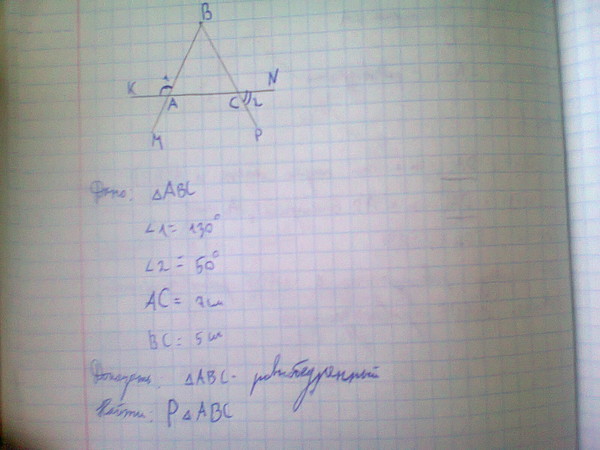 Отражение и симметрия
Отражение и симметрия
 Студенты приносят материал, необходимый в классе.
Студенты приносят материал, необходимый в классе.
Leave A Comment