Итоговая контрольная работа по геометрии для учащихся 8 класса
Итоговая контрольная работа по геометрии Вариант 1. 1. Два катета прямоугольного треугольника АВС равны 5 и 12. Найдите гипотенузу этого треугольника. 2. Найди острый угол параллелограмма АВСD, если биссектриса угла А образует со стороной ВС угол равный 150. 3. На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии. 4. В треугольнике АВС угол В равен 90 0, АС=15см., Cos С=0,2. Найти ВС. 5 . Прямая AB касается окружности в точке С, причем OA=1,7, OC=0,8. Найти АС. | Итоговая контрольная работа по геометрии Вариант 2. 1. Два катета прямоугольного треугольника АВС равны 9 и 12. Найдите гипотенузу этого треугольника. Найди острый угол параллелограмма АВСD, если биссектриса угла В образует со стороной АD угол равный 200. 3. На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии. 4 . В треугольнике АВС угол С равен 90 0, АС=12см., SinВ=0,5. Найти АВ. 5. Прямая AB касается окружности в точке C, причем OC=5, AC=12. Найти ОА. |
Итоговая контрольная работа по геометрии Вариант 1. 1. Два катета прямоугольного треугольника АВС равны 5 и 12. Найдите гипотенузу этого треугольника. 2. Найди острый угол параллелограмма АВСD, если биссектриса угла А образует со стороной ВС угол равный 150. 3. На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии. 4. В треугольнике АВС угол В равен 90 0, АС=15см., Cos С=0,2. 5 . Прямая AB касается окружности в точке С, причем OA=1,7, OC=0,8. Найти АС. | Итоговая контрольная работа по геометрии Вариант 2. 1. Два катета прямоугольного треугольника АВС равны 9 и 12. Найдите гипотенузу этого треугольника. Найди острый угол параллелограмма АВСD, если биссектриса угла В образует со стороной АD угол равный 200. 3. На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии. 4 . В треугольнике АВС угол С равен 90 0, АС=12см., SinВ=0,5. Найти АВ. 5. Прямая AB касается окружности в точке C, причем OC=5, AC=12. Найти ОА. |
Итоговая контрольная работа по геометрии Вариант 1. 1. Два катета прямоугольного треугольника АВС равны 5 и 12. Найдите гипотенузу этого треугольника. 2. Найди острый угол параллелограмма АВСD, если биссектриса угла А образует со стороной ВС угол равный 150. 3. На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии. 4. В треугольнике АВС угол В равен 90 0, АС=15см., Cos С=0,2. Найти ВС. 5 . Прямая AB касается окружности в точке С, причем OA=1,7, OC=0,8. Найти АС. | Итоговая контрольная работа по геометрии Вариант 2. 1. Два катета прямоугольного треугольника АВС равны 9 и 12. Найдите гипотенузу этого треугольника. Найди острый угол параллелограмма АВСD, если биссектриса угла В образует со стороной АD угол равный 200. 3. На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии. 4 . В треугольнике АВС угол С равен 90 0, АС=12см., SinВ=0,5. Найти АВ. 5. |
Итоговая контрольная работа по геометрии
Вариант 1.
1. Два катета прямоугольного треугольника равны 6 и 13. Найдите площадь этого треугольника.
Ответ ______________________
2. Найди острый угол параллелограмма АВС D, если биссектриса угла А образует со стороной ВС угол равный 150.
Ответ_________________________________
3.На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
Ответ_____________________
4. Пожарную лестницу длиной 10м приставили к окну третьего этажа. Нижний конец лестницы отстоит от стены на 6м. На какой высоте расположено окно?
Ответ _____________________________________
5. В треугольнике АВС угол В равен 90 0, АС=15см., Cos С=0,2. Найти ВС
Ответ____________________________
6.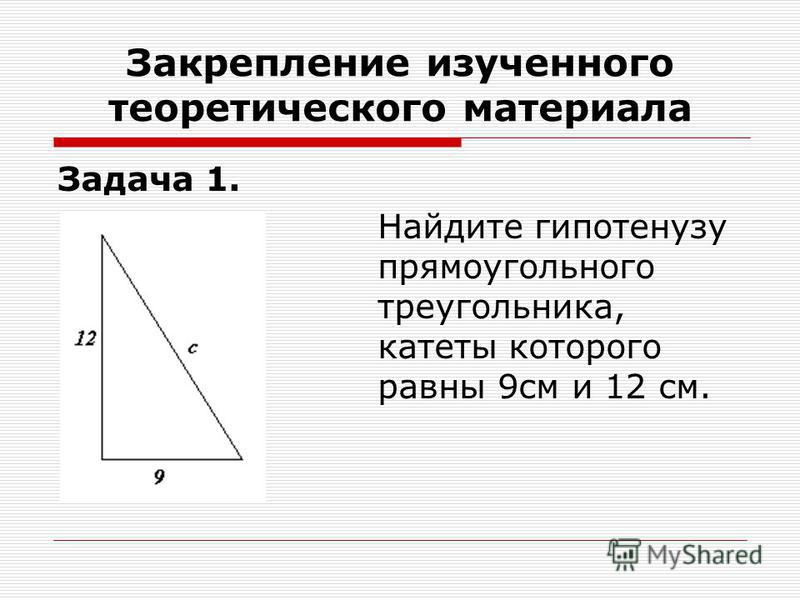 Периметр ромба равен 20, а один из углов 300. Найдите площадь ромба.
Периметр ромба равен 20, а один из углов 300. Найдите площадь ромба.
Ответ____________________________
7. В окружности с центром в точке О отрезки АС и ВD – диаметры. Угол АОD равен 880. Найдите угол АСВ.
Ответ______________________
8. Основания ВС и AD трапеции АВСD равны соответственно5 и 20, ВD =10. Докажите, что треугольники СВD и ВDА подобны.
Класс 8 «____»
ФИ______________________________
Итоговая контрольная работа по геометрии
Вариант2.
1. Два катета прямоугольного треугольника равны 4 и 11. Найдите площадь этого треугольника.
Ответ ______________________
2. Найди острый угол параллелограмма АВС D, если биссектриса угла А образует со стороной ВС угол равный 200.
Ответ_________________________________
3. На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
Ответ __________________________
4. Пожарную лестницу приставили к окну расположенному на высоте 12м. Нижний конец лестницы отстоит от стены на 5м. Какова длина лестницы?
Ответ _________________________
5. В треугольнике АВС угол С равен 90 0, АС=12см., SinВ=0,5. Найти АВ
6. Периметр ромба равен 12, а один из углов 300. Найдите площадь ромба.
Ответ____________________________
7. В окружности с центром в точке О отрезки АС и ВD – диаметры. Угол АОD равен 1140. Найдите угол АСВ.
Ответ___________________
8. Основания ВС и AD трапеции АВСD равны соответственно 3 и 12, ВD =6. Докажите, что треугольники СВD и ВDА подобны.
Класс 8 «____»
ФИ______________________________
Итоговая контрольная работа по геометрии
Вариант 3.
1. Два катета прямоугольного треугольника равны 8 и 3. Найдите площадь этого треугольника.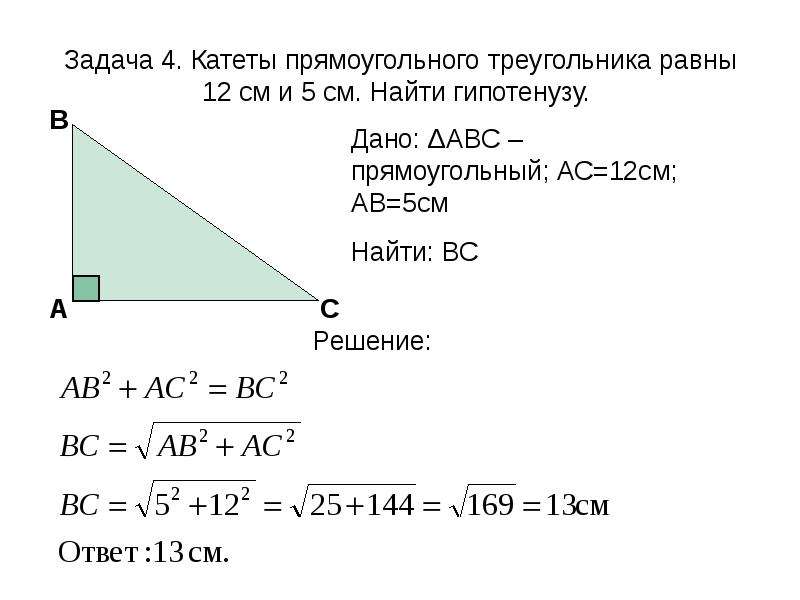
Ответ ______________________
2. Найди острый угол параллелограмма АВСD, если биссектриса угла А образует со стороной ВС угол равный 250.
Ответ_________________________________
3. На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
Ответ ____________
4. Пожарную лестницу длиной 17м приставили к окну третьего этажа. Нижний конец лестницы отстоит от стены на 8м. На какой высоте расположено окно?
Ответ___________________________________
5. В треугольнике АВС угол С равен 90 0, АВ=21см., Cos В= . Найти ВС
6. Периметр ромба равен 88, а один из углов 300. Найдите площадь ромба.
Ответ____________________________
7. В окружности с центром в точке О отрезки АС и ВD – диаметры. Угол АОD равен 1080. Найдите угол АСВ.
Ответ_________________________
8. Основания ВС и AD трапеции АВСD равны соответственно 6 и 24, ВD =12. Докажите, что треугольники СВD и ВDА подобны.
Докажите, что треугольники СВD и ВDА подобны.
Класс 8 «____»
ФИ______________________________
Итоговая контрольная работа по геометрии
Вариант 4.
1. Два катета прямоугольного треугольника равны 12 и 11. Найдите площадь этого треугольника.
Ответ ______________________
2. Найди острый угол параллелограмма АВС D, если биссектриса угла А образует со стороной ВС угол равный 190.
3. На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
Ответ _____________________________
4. Флагшток удерживается в вертикальном положении при помощи троса. Расстояние от основания флагштока до места крепления троса на земле равно 3м. Длина троса 5м. найдите расстояние от земли до точки крепления троса.
Ответ___________________________
5. В треугольнике АВС угол А равен 90 0, АВ=20см., Cos В= . Найти ВС
6. Периметр ромба равен 32, а один из углов 300. Найдите площадь ромба.
Периметр ромба равен 32, а один из углов 300. Найдите площадь ромба.
Ответ____________________________
7. В окружности с центром в точке О отрезки АС и ВD – диаметры. Угол АОD равен 500. Найдите угол АСВ.
Ответ___________________________
8. Основания ВС и AD трапеции АВСD равны соответственно 7 и 28, ВD =14. Докажите, что треугольники СВD и ВDА подобны.
Ответы
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
Вариант 1 | 39 | 30 | 6 | 8 | 3 | 12,5 | 46 | |
Вариант 2 | 22 | 40 | 4 | 13 | 24 | 4,5 | 33 | |
Вариант 3 | 12 | 50 | 7 | 15 | 12 | 242 | 36 | |
Вариант 4 | 66 | 38 | 4 | 4 | 35 | 32 | 65 |
Пропорциональные отрезки в прямоугольном треугольнике
Геометрия. 8 класс. Глава VII. Параграф 3. Тест 1.
8 класс. Глава VII. Параграф 3. Тест 1.
Вариант I.
1. Найти высоту прямоугольного треугольника, проведенную к гипотенузе, если она делит гипотенузу на отрезки 25 см и 81 см.
A) 70 см; B) 55 см; C) 53 см; D) 45 см.
2. Высота прямоугольного треугольника, проведенная к гипотенузе, делит гипотенузу на отрезки 9 и 36. Определить длину этой высоты.
A) 22,5; B) 19; C) 18; D) 12.
4. Высота прямоугольного треугольника, проведенная к гипотенузе, равна 22, проекция одного из катетов равна 16. Найти проекцию другого катета.
A) 30,25;
5. Катет прямоугольного треугольника равен 18, а его проекция на гипотенузу 12. Найти гипотенузу.
Найти гипотенузу.
A) 25; B) 24; C) 27; D) 26.
6. Гипотенуза равна 32. Найти катет, проекция которого на гипотенузу равна 2.
A) 8; B) 7; C) 6; D) 5.
7. Гипотенуза прямоугольного треугольника равна 45. Найти катет, проекция которого на гипотенузу равна 9.
8. Катет прямоугольного треугольника равен 30. Найти расстояние от вершины прямого угла до гипотенузы, если радиус описанной около этого треугольника окружности равен 17.
A) 17; B) 16; C) 15; D) 14.
10. Гипотенуза прямоугольного треугольника равна 41, а проекция одного из катетов 16. Найти длину высоты, проведенной из вершины прямого угла к гипотенузе.
A) 15; B) 18; C) 20; D) 16.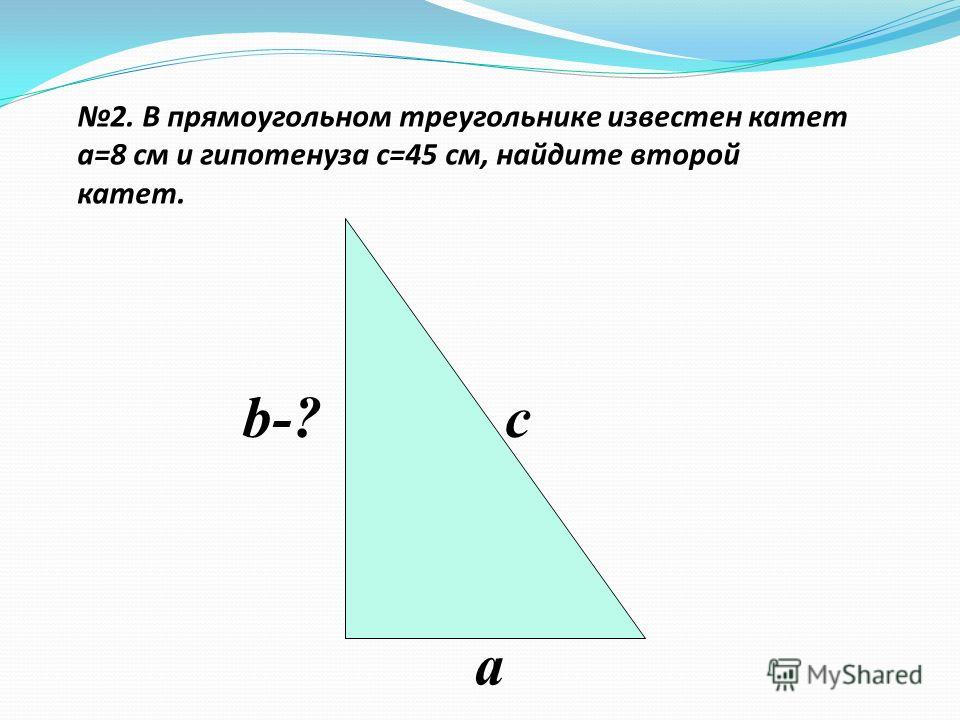
A) 80; B) 72; C)
12. Разность проекций катетов на гипотенузу равна 15, а расстояние от вершины прямого угла до гипотенузы равно 4. Найти радиус описанной окружности.
A) 7,5; B) 8; C) 6,25; D) 8,5.
Вариант II.
1. Найти высоту прямоугольного треугольника, проведенную к гипотенузе, если она делит гипотенузу на отрезки 4 см и 9 см.
A) 7 см; B) 6 см; C) 5 см; D) 8 см.
2. Высота прямоугольного треугольника, проведенная к гипотенузе, делит гипотенузу на отрезки 2 и 32. Определить длину этой высоты.
A) 8; B) 9; C) 8,5; D) 7.
Найти высоту, проведённую из вершины прямого угла.
A) 5 см;B) 6 см; C) 9 см; D) 7 см.
4. Высота прямоугольного треугольника, проведенная к гипотенузе, равна 14, проекция одного из катетов равна 8. Найти проекцию другого катета.
A) 30,25; B) 24,5; C) 18,45; D) 32.
5.
A) 23,5; B) 22,5; C) 24; D) 21,5.
6. Гипотенуза равна 27. Найти катет, проекция которого на гипотенузу равна 3.
A) 8; B) 9; C) 6; D) 7.
7. Гипотенуза прямоугольного треугольника равна 75. Найти катет, проекция которого на гипотенузу равна 12.
A) 30; B) 27; C) 28; D
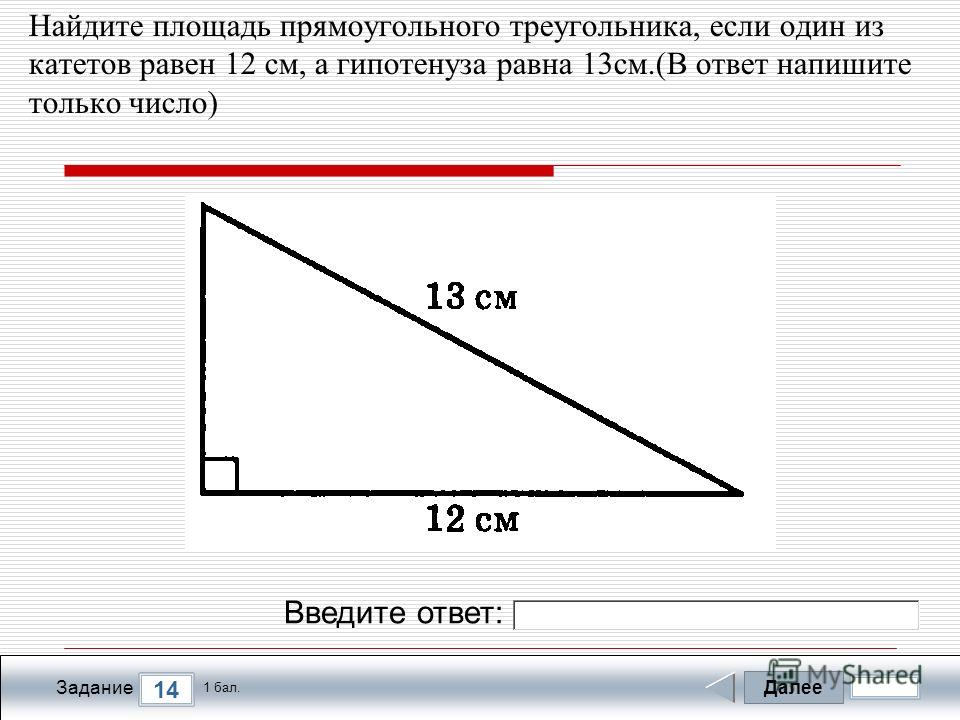
8. Катет прямоугольного треугольника равен 8. Найти расстояние от вершины прямого угла до гипотенузы, если радиус описанной около этого треугольника окружности равен 8,5.
A) 2,7; B) 3,6; C) 4,2; D) 5,4.
10. Гипотенуза прямоугольного треугольника равна 26, а проекция одного из катетов 8. Найти длину высоты, проведенной из вершины прямого угла к гипотенузе.
A) 12; B) 13; C) 14; D) 15.
A) 30; B) 32; C) 28; D) 36.
12. Разность проекций катетов на гипотенузу равна 8, а расстояние от вершины прямого угла до гипотенузы равно 3. Найти радиус описанной окружности.
A) 5,5; B) 5; C) 6; D) 6,5.
Справочные материалы.
В Δ АВС ∠АСВ = 90°. АС и ВС — катеты, АВ — гипотенуза.
CD — высота треугольника, проведенная к гипотенузе.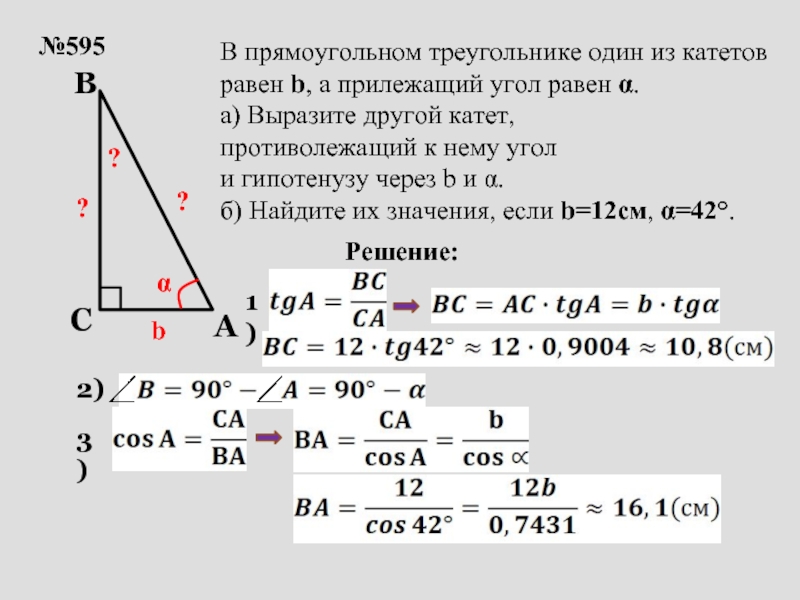
AD — проекция катета АС на гипотенузу,
BD — проекция катета ВС на гипотенузу.
Высота CD делит треугольник АВС на два подобных ему (и друг другу) треугольника: ΔADC и ΔCDB.
Из пропорциональности сторон подобных ΔADC и ΔCDB следует:
AD : CD = CD : BD. Отсюда CD2 = AD ∙ BD. Говорят: высота прямоугольного треугольника, проведенная к гипотенузе, есть средняя пропорциональная величина между проекциями катетов на гипотенузу.
Из подобия ΔADC и ΔАCB следует:
AD : AC = AC : AB. Отсюда AC2 = AB ∙ AD. Говорят: каждый катет есть средняя пропорциональная величина между всей гипотенузой и проекцией данного катета на гипотенузу.
Аналогично, из подобия ΔСDВ и ΔАCB следует:
BD : BC = BC : AB. Отсюда
Сверить ответы.
Поделиться новостью в соцсетях
Метки: высота, Геометрия 8 класс, пропорциональные отрезки, прямоугольный треугольник, треугольник
Справка по базовой геометрии
Студенты, нуждающиеся в помощи по основам геометрии, получат большую пользу от нашей интерактивной программы. Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по базовой геометрии.
Имея под рукой обязательные концепции изучения и актуальные практические вопросы, вы быстро получите массу помощи по базовой геометрии.
Получите помощь сегодня с нашей обширной коллекцией важной информации по базовой геометрии.
Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по базовой геометрии.
Имея под рукой обязательные концепции изучения и актуальные практические вопросы, вы быстро получите массу помощи по базовой геометрии.
Получите помощь сегодня с нашей обширной коллекцией важной информации по базовой геометрии. Геометрия является наиболее распространенным математическим предметом в средней школе США. По оценкам Института педагогических наук, в 2009 году 88 процентов учащихся средних школ США прошли курс геометрии. Этот раздел математики знакомит учащихся со свойствами и взаимосвязями углов, линий, поверхностей и других элементов основных форм. Этот предмет, который большинство учащихся могут освоить к 10-му классу, является обязательным для любого студента колледжа, который хочет изучать математику, а также междисциплинарные области, такие как физика и инженерия. Независимо от планов учащегося на будущее, изучение основ геометрии обеспечит необходимые строительные блоки для более сложных математических концепций как в старшей школе, так и в колледже.
Справка по базовой геометрии, доступная с помощью бесплатного инструмента обучения Varsity Tutors «Learn by Concept Learning Tool», охватывает множество тем для студентов, плохо знакомых с предметом. Студенты, которым нужна учеба, помогут получить ее, ответив на ряд примеров вопросов на веб-сайте Varsity Tutors Learning Tools. Темы организованы как учебная программа класса, с несколькими общими разделами и серией подтем. В каждом примере вопроса вам дается проблема и несколько возможных ответов. Вы решаете задачу и выбираете правильный ответ, а затем проверяете, правильно ли вы его поняли. Varsity Tutors предлагает такие ресурсы, как бесплатные практические тесты по базовой геометрии, которые помогут вам в самостоятельном обучении, или вы можете подумать о репетиторстве по геометрии.
Что еще более важно, Learn by Concept выходит за рамки простого предоставления проблем и решений, сосредоточив внимание на процессе решения проблем. Каждый образец вопроса содержит подробное объяснение того, как прийти к правильному ответу. Каждое релевантное понятие или формула отмечены, и каждый отдельный шаг описан в этих объяснениях. Если существует несколько правильных методов решения проблемы, то каждый метод включается. Если вы дали неправильный ответ, вы можете повторить свои шаги, чтобы точно определить, где вы сбились с пути и как вернуться. Если вы ответили правильно, вы можете проверить свою работу и убедиться, что процесс был правильным, а не просто повезло с ответом. В дополнение к разделу справки по основам геометрии и урокам геометрии вы также можете рассмотреть некоторые из наших карточек по основам геометрии.
Любой учащийся, планирующий изучать высшую математику в колледже или просто желающий хорошо учиться в старшей школе, может использовать инструмент «Учиться по понятиям» в качестве учебного пособия по основам геометрии. Инструмент охватывает основные темы кругов, линий, четырехугольников и треугольников. Каждая подтема структурирована как «Как сделать», например «Как найти диаметр». Количество вопросов варьируется в зависимости от предмета: некоторые подтемы содержат более 50 вопросов, а другие относятся к младшим подросткам.
Инструмент охватывает основные темы кругов, линий, четырехугольников и треугольников. Каждая подтема структурирована как «Как сделать», например «Как найти диаметр». Количество вопросов варьируется в зависимости от предмета: некоторые подтемы содержат более 50 вопросов, а другие относятся к младшим подросткам.
На веб-сайте учебных материалов Varsity Tutors также можно найти дополнительные материалы для изучения геометрии. Наряду с инструментом «Изучение концепций» вы можете пройти один из нескольких бесплатных полноразмерных практических тестов по базовой геометрии, чтобы определить, какие концепции вы понимаете, а на каких следует сосредоточить внимание при изучении. Существуют также сотни практических тестов, посвященных конкретным областям, которые позволяют вам определить, в чем вам нужна помощь. Изучив бесплатные примеры вопросов «Учитесь по концепции», вы также можете использовать карточки для обучения по инструментам обучения преподавателей Varsity Tutors, чтобы проверить себя по тем же темам. Карточки можно сортировать по категориям или настраивать в соответствии с вашими конкретными потребностями. Инструмент «Вопрос дня» рандомизирует вопросы из всех основных тем и концепций геометрии, чтобы помочь вам проверить свои общие знания по предмету. Используйте инструменты обучения Varsity Tutors, чтобы оставаться сосредоточенным, когда вы изучаете базовую геометрию и начинаете переходить к более продвинутым концепциям.
Карточки можно сортировать по категориям или настраивать в соответствии с вашими конкретными потребностями. Инструмент «Вопрос дня» рандомизирует вопросы из всех основных тем и концепций геометрии, чтобы помочь вам проверить свои общие знания по предмету. Используйте инструменты обучения Varsity Tutors, чтобы оставаться сосредоточенным, когда вы изучаете базовую геометрию и начинаете переходить к более продвинутым концепциям.
Базовая геометрия
Плоская геометрия
Круги
Математика часов
Как найти угол часовых стрелок
Как найти расстояние между стрелками часов
Диаметр
Как найти длину диаметра
Как найти соотношение диаметра и длины окружности
Радиус
Как найти длину окружности
Как найти площадь круга
Как найти длину радиуса
строки
Как найти луч
Как найти угол линии
Четырехугольники
прямоугольники
Как определить, подобны ли прямоугольники
Как найти площадь прямоугольника
Как найти длину диагонали прямоугольника
Как найти длину стороны прямоугольника
Как найти периметр прямоугольника
Квадраты
Как найти площадь квадрата
Как найти длину диагонали квадрата
Как найти длину стороны квадрата
Как найти периметр квадрата
Треугольники
45/45/90 Прямоугольные равнобедренные треугольники
Как найти площадь прямоугольного равнобедренного треугольника 45/45/90
Как найти высоту прямоугольного равнобедренного треугольника 45/45/90
Как найти длину гипотенузы прямоугольного равнобедренного треугольника 45/45/90 : теорема Пифагора
Как найти длину стороны прямоугольного равнобедренного треугольника 45/45/90
Как найти периметр 45/45/90 прямоугольный равнобедренный треугольник
Прямоугольные треугольники
Как найти угол в прямоугольном треугольнике
Как определить конгруэнтность прямоугольных треугольников
Как определить, подобны ли прямоугольные треугольники
Как найти площадь прямоугольного треугольника
Как найти высоту прямоугольного треугольника
Как найти длину гипотенузы прямоугольного треугольника : Теорема Пифагора
Как найти длину стороны прямоугольного треугольника
Как найти периметр прямоугольного треугольника
Теорема Пифагора
Теорема Пифагора
На этом уроке мы узнаем, что такое теорема Пифагора и как ее использовать. найти недостающую сторону прямоугольного треугольника.
найти недостающую сторону прямоугольного треугольника.
Тысячи лет назад греческая организация под названием пифагорейцы, возглавляемая человек по имени Пифагор, исследовал геометрию. Самое главное их достижение связано с открытием соотношения между длинами сторон правой треугольник. Это соотношение, называемое теоремой Пифагора, рассматривается самая важная формула в математике.
Сначала напомним некоторую терминологию. Напомним, что Прямоугольный треугольник – это треугольник, один из углов которого 90 градусов. Для прямоугольного треугольника сторона противоположный прямому углу называется гипотенуза. Эта сторона всегда будет самой длинной стороной справа. треугольник. Две другие (более короткие) стороны называются ноги.
Теорема Пифагора утверждает, что если сложить квадраты длин из двух катетов прямоугольного треугольника вы всегда получите квадрат длины гипотенузы.
|
Пример 1
Рассмотрим прямоугольный треугольник, показанный ниже. Найдите значение х .
Раствор
Сначала обратите внимание, что длины двух ног равны 4. и 3. Длина гипотенузы равна х . Используя буквы из Теорема Пифагора, имеем
а = 4
б = 3
c = x
Теперь воспользуемся теоремой Пифагора
а 2 + б 2 = в 2
или
4 2 + 3 2 = x 2
Теперь возведите числа в квадрат
16 + 9 = x 2
Добавьте, чтобы получить
25 = х 2
Наконец, найдите положительное число, квадрат которого равен 25.
х = 5
Теперь попробуйте сами. Если хотите увидеть ответ, наведите мышку на желтом прямоугольнике и появится ответ.
Упражнение 1
Рассмотрим прямоугольный треугольник, показанный ниже. Найдите значение х .
Ответить
Иногда в CAHSEE задача дает длины одной ноги и гипотенуза прямоугольного треугольника. Задача попросит вас найти третий нога. Вот пример.
Пример 2
Рассмотрим прямоугольный треугольник, показанный ниже. Найдите значение х .
Раствор
Сначала обратите внимание, что длина двух ног равна х и 6. Длина гипотенузы равна 10. Использование буквы из теоремы Пифагора, имеем
а = х
б = 6
с = 10
Теперь воспользуемся теоремой Пифагора
а 2 + б 2 = в 2
или
х 2 + 6 2 = 10 2
Теперь возведите числа в квадрат
х 2 + 36 = 100
Вычесть, чтобы получить
x 2 = 100 — 36
= 64
Наконец, найдите положительное число, квадрат которого равен 64.
х = 8
Теперь попробуйте сами. Если хотите увидеть ответ, наведите мышку на желтом прямоугольнике и появится ответ.
Упражнение 2
Рассмотрим прямоугольный треугольник, показанный ниже. Найдите значение х .
Ответить
Пример 3
Компания сотовой связи рекламирует такую длину своего прямоугольного экрана. (между противоположными углами) составляет 5 дюймов. высота экрана 4 дюйма. Что ширина экрана?
Раствор
Схема экрана сотового телефона показана ниже
Верхняя часть образует прямоугольный треугольник с длиной двух сторон х и 4. Длина гипотенузы равна 5. Используя буквы из теоремы Пифагора, имеем
а = x
б = 4
с = 5
Теперь воспользуемся теоремой Пифагора
а 2 + б 2 = в 2
или
х 2 + 4 2 = 5 2
Теперь возведите числа в квадрат
х 2 + 16 = 25
Вычесть, чтобы получить
x 2 = 25–16
= 9
Наконец, найдите положительное число, квадрат которого равен 9.


 Найти ВС.
Найти ВС.
 Прямая AB касается окружности в точке C, причем OC=5, AC=12. Найти ОА.
Прямая AB касается окружности в точке C, причем OC=5, AC=12. Найти ОА. Затем
Затем
Leave A Comment