Для изменения температуры металлической детали массой 100 г от 20° до 40 С потребовалось 280
Средний балл по физике — 4.25,возможна ли 5?Или может надо брать доп. задания чтобы исправить оценку?
Яке зусилля потрібно прикласти, щоб утримувати під водою бетонний блок розмірами 20 x 30х 40 см? На скільки це зусилля потрібно збільшити, щоб дістати … блок з-під води? Помогите пожалуйста ((
СРОЧНО, ФИЗИКА 8 — 25 БАЛЛОВКакова скорость заряженного тела, перемещающегося в магнитном поле с индукцией 2 Тл, если на него со стороны магнитного … поля действует сила32 Н. Скорость и магнитное поле взаимно перпендикулярны. Заряд тела равен 0,5 мКл.(с дано/найти)!!БЕЗ СИЛЫ ЛОРЕНСА!!
срочно пж очень надо
Знайти прискорення вільного падіння на планеті, якщо її маса в 3 рази більша за масу Землі, а радіус у 4 рази менший за радіус Землі. Прискорення віл … ьного падіння на Землі 9,8 м/с2.
Сопротивление лампочки накаливание используемой в фонаре автомаюиля ровно 30 Ом Найдитк силу тока которой течёт через лампочку если напряжение на ней … 9 В
Сопротивление лампочки накаливание используемой в фонаре автомаюиля ровно 30 Ом Найдитк силу тока которой течёт через лампочку если напряжение на ней … 9 В
Решите хотя один,дам 20 баллов(каждому по 10)
срочно, физика.В магнитном поле с индукцией 20 мТл находится проводник длиной 0,2. Определите силу тока в проводнике, если известно, что при расположе … нии его перпендикулярно линиям индукции магнитного поля сила тяжести равная 40 мН, уравновешивается силой, действующей на проводник со стороны поля.(если можно с дано/найти)!БЕЗ СИЛЫ ЛОРЕНСА!
Вычисли, с какой силой человек будет выталкиваться из морской воды, если в пресной воде на него действует выталкивающая сила, равная 656 Н.
(Плотность
… морской воды принять равной ρм.в.=1030 кг/м³, коэффициент тяжести g=10 Н/кг.)
Ответ (округли до сотых): Fм.в.=…Н.
MrFlyguy на ваш ответ я надеюсь.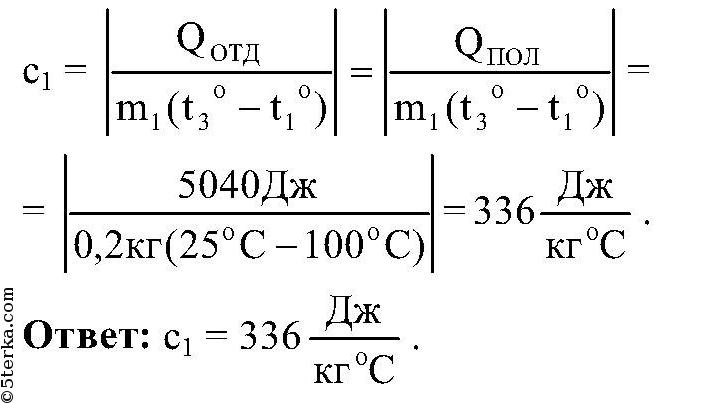
Тема №6326 Задачи по физике для самостоятельного решения Тепловые явления 44
Тема №6326
§2. Внутренняя энергия. Качественные задачи.
Задача 1. Закрытую пробирку поместили в горячую воду. Изменилась ли кинетическая и потенциальная энергия молекул воздуха в пробирке? Если изменилась, то как?
Задача 2 . В один стакан налита холодная вода, в другой – кипяток. В каком стакане вода обладает большей внутренней энергией?
Задача 3. Два медных бруска массами 100 и 500 г, взятых при комнатной температуре, погрузили в горячую воду на одинаковое время. Изменилась ли их внутренняя энергия? Одинаково ли изменилось значение внутренней энергии этих брусков относительно друг друга? Ответ обоснуйте.
Задача 5. После обработки на точильном круге зубило стало горячим. Зубило, вынутое из горна, тоже горячее. Одинакова ли причина повышения температуры зубила?
Задача 6 В закрытой трубке находится капля ртути. Трубку с одного конца нагрели. Объясните, за счет какой энергии совершается работа по перемещению ртути в трубке.
Задача 8. Спичка загорается при трении ее о коробок. Она вспыхивает и при внесении ее в пламя свечи. В чем сходство и различие причин, приведших к воспламенению спички?
Задача 9. Можно ли сказать (см. предыдущую задачу), что внутренняя энергия спичечной головки увеличилась, что ей передано некоторое количество теплоты, что она нагрелась до температуры воспламенения?
Задача 10. Почему воспламеняется горючее в капсюле патрона при ударе по ней бойком во время выстрела?
Задача 11. В пробирку наливают немного воды, затыкают пробкой и нагревают воду. Спустя некоторое время пробка вылетает. Какие превращения энергии происходят в опыте?
 За счет чего увеличивается его потенциальная энергия?
За счет чего увеличивается его потенциальная энергия?Задача 13. Объясните, почему происходит изменение внутренней энергии: а) при сжатии и расширении воздуха; б) при нагревании воды в кастрюле; в) при сжатии и растяжении резины; г) при таянии льда.
Задача 14. Приведите примеры изменения внутренней энергии тела в процессе совершения работы при: а) трении; б) ударе; в) сжатии.
Задача 15. В одном сосуде разреженный газ. В другом таком же сосуде — сжатый. Какой газ имеет большую потенциальную энергию взаимодействия молекул и почему?
Задача 17. Объясните, на каком физическом явлении основан способ добывания огня трением.
Задача 18. Почему коньки легко скользят по льду, а по стеклу, поверхность которого более гладкая, на коньках катится невозможно?
Задача 19. Почему при вбивании гвоздя его шляпка нагревается слабо, а когда гвоздь уже вбит, достаточно нескольких ударов, чтобы сильно нагреть шляпку?
Задача 20. Какие превращения энергии происходят при торможении движущегося автомобиля?
Задача 21. Как изменяется внутренняя энергия газа в пузырьке, который поднимается со дня водоема?
Задача 22. Почему шариковые подшипники у машин нагреваются меньше, чем подшипники скольжения?
Задача 24. При скоростной обработке металла температура в точках отделения стружки от изделия повышается на 800 – 900 . Объясните причину явления.
Задача 25. При опиловке металла один ученик за 5 мин снял слой толщиной 2 мм. Другой ученик при обработке такой же детали за то же время снял слой толщиной 3 мм. Почему повысилась температура деталей? У какого из учащихся деталь после обработки приобрела более высокую температуру? Почему?
Задача 26. Как объяснить, что при откачивании воздуха из баллона внутренняя энергия оставшейся части воздуха уменьшилась?
§3. Виды теплопередачи. Качественные задачи.
Виды теплопередачи. Качественные задачи.
Задача 27. В стакан налит горячий чай. Как осуществляется теплообмен между чаем и стенками стакана?
Задача 28. Как изменится внутренняя энергия нагретого тела при опускании его в холодную воду? Почему?
Задача 29. Железная и медная заклепки имеют одинаковую массу и температуру. Заклепки опустили в холодную воду. Какая из них быстрее охладится?
Задача 30. Почему нагретые детали в воде охлаждаются быстрее, чем на воздухе?
Задача 31. Приведите примеры изменения внутренней энергии тела в процессе теплообмена.
Задача 33. Зачем канализационные и водопроводные трубы зарывают в землю на значительную глубину?
Задача 34. Зачем ствол винтовки покрывают деревянной ствольной накладкой?
Задача 35. В медный и стеклянный сосуд налили жидкость. Какой из стаканов быстрее примет температуру налитой жидкости?
Задача 36. Почему вы обжигаете губы, когда пьете чай из металлической кружки и не обжигаете, когда пьете из чай из фарфоровой кружки (температура чая одинакова)?
Задача 37. В каком чайнике вода скорее нагреется: в новом или в старом, на стенках которого имеется накипь?
Задача 39. При одинаковой температуре гранита и кирпича кирпич на ощупь кажется теплее гранита. Какой из этих строительных материалов обладает лучшей теплопроводностью?
Задача 40. Зимой на улице металл на ощупь холоднее дерева. Какими будут казаться на ощупь металл и дерево в тридцатиградусную жару? Почему?
Задача 41. Почему шерстяная одежда сохраняет теплоту лучше, чем хлопчатобумажная?
Задача 42. Зачем на зиму приствольные круги земли у плодовых деревьев покрывают слоями торфа, навоза или древесных опилок?
Задача 43.

Задача 44. Зачем в южных широтах нашей Родины местные жители во время сильной жары носят шапки-папахи и ватные халаты?
Задача 45. Какой дом теплее – деревянный или каменный, если толщина стен одинакова?
Задача 46. Почему все пористые строительные материалы (пористый кирпич, пеностекло, пенистый бетон и др.) обладают лучшими теплоизоляционными свойствами, чем плотные стройматериалы?
Задача 47. Почему в безветрие пламя свечи устанавливается вертикально?
Задача 48. Объясните, почему радиаторы центрального отопления ставят обычно под окнами.
Задача 49. Как образуются бризы (местные ветры, дующие днем с моря на сушу, а ночью с суши на море)?
Задача 51. В промышленных холодильниках воздух охлаждается с помощью труб, по которым течет охлажденная жидкость. Где надо располагать эти трубы – вверху или внизу помещения?
Задача 52. Сильная струя воздуха, которая идет от вентилятора, создает прохладу. Можно ли этой струей сохранить мороженное в твердом виде?
Задача 53. Почему в печах с высокими трубами тяга выше, чем в печах с низкими трубами?
Задача 54. Почему в металлических печных трубах тяга меньше, чем в кирпичных трубах?
Задача 56. Почему грязный снег в солнечную погоду тает быстрее, чем чистый?
Задача 57. Зачем оболочку стратостата красят «серебряной» краской?
Задача 58. Какие почвы лучше нагреваются солнечными лучами: черноземные или подзолистые, имеющие более светлую окраску?
Задача 59. Зачем в железнодорожных вагонах-ледниках, служащих для перевозки фруктов, мяса, рыбы и других скоропортящихся продуктов, промежутки между двойными стенками заполняют войлоком или несколькими слоями каких-либо пористых веществ, а снаружи вагоны окрашивают в белый или светло-желтый цвет?
Задача 60.
 В каком платье летом менее жарко: в белом или в темном? Объясните почему.
В каком платье летом менее жарко: в белом или в темном? Объясните почему.Задача 61. Объясните назначение стеклянных рам в парниках.
Задача 62. Почему вода в открытых водоемах нагревается солнечными лучами медленнее, чем суша?
Задача 63. Почему горячая вода, оставленная в термосе, со временем охлаждается?
Задача 64. Можно ли термос временно использовать как холодильник?
§4. Расчет количества теплоты.
Задача 65. Кубики, изготовленные из меди, стали и алюминия, массой 1 кг охлаждают на 1. На сколько Джоулей и как изменится внутренняя энергия каждого кубика?
Задача 66. На что больше расходуется энергии: на нагревание чугунного горшка или воды, налитой в него, если их массы одинаковы?
Задача 67. Алюминиевую и серебряную ложки одинаковой массы и температуры опустили в кипяток. Равное ли количество теплоты получили они от воды?
Задача 68. По стальной и свинцовой заготовкам равных масс ударили молотком равное число раз. Какая из них больше нагрелась? Ответ обоснуйте.
Задача 69. Термос, вместимость которого 3 л, наполнили кипятком. Через сутки температура воды в нем понизилась до 77. Определите, на сколько изменилась внутренняя энергия воды.
Задача 70. В алюминиевом чайнике нагрели воду и построили графики зависимости количества теплоты, полученной чайником и водой, от времени нагревания. Постройте эти графики зависимости для чайника и для воды в одних координатных осях. Объясните результат.
Задача 71. На одинаковых горелках нагревались вода, медь и железо равной массы. Постройте графики зависимости количества теплоты от времени нагревания для воды, для меди и для железа в одних координатных осях. Объясните результат..
Задача 72. Для изменения температуры нафталина, никеля и фарфора массой 1 кг на 1 соответственно требуется 130; 460; и 750 Дж энергии. Чему равна удельная теплоемкость этих веществ?
Задача 73. Для нагревания золота, бронзы, никеля, глицерина и молока массой 2 кг на 1 соответственно расходуется 260; 760; 920; 4800 и 7800 Дж энергии. Чему равна удельная теплоемкость этих веществ?
Чему равна удельная теплоемкость этих веществ?
Задача 74. Нагретый камень массой 5 кг, охлаждаясь в воде на 1, передает ей 2,1 кДж энергии. Чему равна удельная теплоемкость камня?
Задача 75. Какое количество теплоты потребуется для нагревания на 1 воды объемом 0,5 л; олова массой 500 г; серебра объемом 2 см3; стали объемом 0,5 м3; латуни массой 0,2 т?
Задача 76. Стальная деталь массой 20 кг при обработке на токарном станке нагревается на 50. Сколько энергии израсходовано двигателем на нагревание детали?
Задача 77. Стальное сверло массой 100 г при работе нагрелось от 15 до 115. Сколько энергии израсходовано двигателем на нагревание сверла?
Задача 78. В каком отношении нужно взять объемы свинца и олова, чтобы их теплоемкости были одинаковы?
Задача 79. Перед горячей штамповкой латунную болванку массой 15 кг нагрели от 15 до 750. Какое количество теплоты для этого потребовалось?
Задача 80. Какое количество теплоты отдаст стакан кипятка (250 см3), остывая до температуры 14?
Задача 81. Какое количество теплоты отдаст кирпичная печь массой 0,35 т, остывая с изменением температуры на 50?
Задача 82. Какое количество теплоты выделилось при охлаждении чугунной болванки массой 32 кг, если ее температура изменилась от 1115 до 15?
Задача 83. Какое количество теплоты потребуется, чтобы в алюминиевом котелке массой 200 г нагреть 1,5 л воды от 20 до кипения?
Задача 84. В алюминиевой кастрюле, масса которой 800 г, нагревается вода, объем которой 5л, от 10 до кипения. Какое количество теплоты пойдет на нагревание кастрюли и воды?
Задача 85. В железный душевой бак, масса которого 65 кг, налили холодной колодезной воды объемом 200 л. В результате нагревания солнечным излучением температура воды повысилась от 4 до 29. Какое количество теплоты получили бак и вода?
Задача 86. Рассчитайте, какое количество теплоты отдаст кирпичная печь, сложенная из 300 кирпичей, при остывании от температуры 70 до 20. Масса одного кирпича 5 кг.
Задача 87. Какое количество теплоты пойдет на нагревание воды от 15 до 25 в бассейне, длина которого 100 м, ширина 6 м и глубина 2 м?
Какое количество теплоты пойдет на нагревание воды от 15 до 25 в бассейне, длина которого 100 м, ширина 6 м и глубина 2 м?
Задача 88. Для изменения температуры металлической детали массой 100 г от 20 до 40 потребовалось 280 Дж энергии. Определите, из какого металла сделана деталь.
Задача 89. При охлаждении куска олова массой 100 г до температуры 32 выделилось 5 кДж энергии. Определите температуру олова до охлаждения.
Задача 90. До какой температуры остынет 5 л кипятка в кастрюле, отдав в окружающее пространство 1680 кДж энергии?
Задача 91. При охлаждении медного паяльника до 20 выделилось 30,4 кДж энергии. До какой температуры был нагрет паяльник, если его масса 200 г?
Задача 92. Для аквариума смешали 20 кг воды при 8, 6 кг воды при 50 и 10 кг воды при 40. Определить температуру смеси.
Задача 93. Смешали 39 л воды при 20 и 21 л воды при 60. Определить температуру смеси.
Задача 94. Смешали 6 кг воды при 42, 4 кг воды при 72 и 20 кг воды при 18. Определить температуру смеси.
Задача 95. Сколько литров воды при 95 нужно добавить к 30 л воды при 25, чтобы получить воду с температурой 67?
Задача 96. Смешали 0,4 м3 воды при 20 и 0,1 м3 воды при 70. Какова температура смеси при тепловом равновесии?
Задача 97. В ванну налито 80 л воды при температуре 10. Сколько литров воды при 100 нужно добавить в ванну, чтобы температура смеси была 25?
Задача 98. Чтобы охладить 2 л воды, взятой при 80, до 60, в нее добавляют холодную воду при 10. Какое количество холодной воды требуется добавить?
Задача 99. Для приготовления ванны нужно смешать холодную воду при t1 = 11 с горячей при t2 = 66. Какое количество той и другой воды необходимо взять для получения V = 110 л воды при t3 = 36?
Задача 100. В каком отношении нужно смешать две массы воды при температурах 50 и 0, чтобы температура смеси была 20?
Задача 101. Необходимо смешать воду при 20 с водой при 100 для получения 300 л воды при 40. Сколько литров той и другой воды нужно взять?
Задача 102. Паровой котел содержит 40 м3 воды при температуре 225. Какое количество воды при 9 было добавлено, если установилась общая температура 200?
Паровой котел содержит 40 м3 воды при температуре 225. Какое количество воды при 9 было добавлено, если установилась общая температура 200?
Задача 103. В паровой котел, содержащий 50 m воды при температуре 240, с помощью насоса добавили 3 m воды при температуре 10. Какая установится температура смеси?
Задача 104. Для ванны нужно приготовить 300 кг воды при 36. В водогрейной колонке температура воды 70, а в водопроводе температура воды 10. Сколько той и другой воды нужно взять для приготовления ванны?
Задача 105. В стеклянный стакан массой 0,12 кг при температуре 15 налили 0,2 кг воды при 100. Какая температура воды установилась в стакане?
Задача 106. В стеклянный стакан массой 100 г налито 200 г воды. Температура воды и стакана 75. На сколько понизится температура воды при опускании в нее серебряной ложки массой 80 г при 15?
Задача 107. Стальную деталь машины массой 0,3 кг нагрели до высокой температуры, а затем погрузили для закалки в масло, взятое при 10. Определить начальную температуру стальной детали, если масса масла 3 кг, а конечная температура установилась 30 (удельная теплоемкость масла равна ).
Задача 108. Определить удельную теплоемкость свинца, зная, что 100 г свинца при 100 погрузили в алюминиевый калориметр массой 40 г, содержащий 240 г воды при 15, и температура смеси установилась 16. Проведите подобный опыт.
Задача 109. В латунный калориметр массой 80 г, содержащий 200 г воды при температуре 20, был опущен кусочек алюминия массой 40 г при температуре 100. Температура смеси стала равной 23. Определить удельную теплоемкость алюминия.
Задача 110. До какой средней температуры нагрелась стальная фреза массой 0,2 кг, если после погружения ее в алюминиевый калориметр массой 100 г, содержащий 178 г воды при температуре 16, установилась температура 22?
Задача 111. Для определения температуры топки котла в нее внесли стальной шарик массой 20 г. Затем перенесли шарик в алюминиевый калориметр массой 60 г, содержащий 200 г воды при температуре 18. Температура смеси установилась 26. Определить температуру топки.
Температура смеси установилась 26. Определить температуру топки.
Задача 112. Стальной резец массой 400 г нагрели до 800 и погрузили для закалки в 5 кг воды при 20. До какой температуры охладился резец?
Задача 113. До какой температуры нагрелась во время работы стальная фреза массой 1 кг, если после опускания ее в калориметр температура 1 л воды повысилась от 11,3 до 30? Теплоемкость калориметра не учитывать.
Задача 114. В сосуд, содержащий 2,35 кг воды при 20, опускают кусок олова, нагретого до 230; температура воды в сосуде повысилась на 15. Вычислить массу олова. Испарением воды пренебречь.
Задача 115. Как велика масса стальной детали, нагретой предварительно до 500, если при опускании ее в сосуд, содержащий 18,6 л воды при 13, последняя нагрелась до 35? Испарением воды пренебречь.
Задача 116. Чугунный брусок массой 0,2 кг, предварительно нагретый, опускают в сосуд, содержащий 0,8 кг керосина при 15. Окончательная температура керосина установилась 20. Определить первоначальную температуру бруска.
Задача 117. Для определения удельной теплоемкости вещества проводят следующий опыт: пластинку массой 0,3 кг, предварительно нагретую до 85, опускают в алюминиевый калориметр массой 0,03 кг, содержащий 0,25 кг воды при 22. Общая конечная температура, установившаяся в калориметре, равна 28. Определить удельную теплоемкость вещества пластинки.
Задача 118. В стеклянной колбе, масса которой 50 г, находилось 185 г воды при 20. В колбу вылили некоторое количество ртути при 100, и температура воды в колбе повысилась до 22. Определить массу ртути.
Задача 119. Для определения температуры печи нагретый в ней стальной болт массой 0,3 кг бросили в медный сосуд массой 0,2 кг, содержащий 1,27 кг воды при 15. Температура воды повысилась до 32. Вычислить температуру печи.
Задача 120. В латунный калориметр массой 200 г влили 400 г воды при 17 и опустили тело из серебра массой 600 г при 85. Вода нагрелась до 22. Определить удельную теплоемкость серебра.
Задача 121.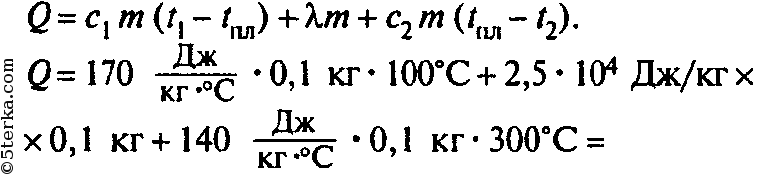 После опускания в воду, имеющую температуру 10, тела, нагретого до 100, через некоторое время установилась общая температура 40. Какой станет температура воды, если, не вынимая первого тела, в нее опустить еще одно такое же тело, нагретое до 100.
После опускания в воду, имеющую температуру 10, тела, нагретого до 100, через некоторое время установилась общая температура 40. Какой станет температура воды, если, не вынимая первого тела, в нее опустить еще одно такое же тело, нагретое до 100.
Задача 122. Для измерения температуры воды, имеющей массу 66 г, в нее погрузили термометр, который показал 32,4. Какова действительная температура воды, если теплоемкость термометра 1,9 Дж/ и перед погружением в воду он показывал температуру помещения 17,8?
Задача 123. В стакане содержится 250 см3 воды. Опущенный в стакан термометр показал 78. Какова действительная температура воды, если теплоемкость термометра 20 Дж/, а до опускания в воду он показывал 20?
Задача 124. В калориметре смешиваются три химически не взаимодействующие жидкости массами 1 кг, 10 кг, 5 кг, имеющие соответственно температуры: 6, — 40, 60. Удельные теплоемкости жидкостей равны соответственно 2 , 4, 2. Определить температуру смеси.
Задача 125. В каком отношении должны быть взяты массы m1 и m2 двух жидкостей с удельными теплоемкостями c1 и c2, начальными температурами T1 и T2 (T1>T2), чтобы общая температура после их смещения получилась равной T0? Теплоемкость сосуда, в котором находятся жидкости, не учитывать.
Задача 126. Вычислите, сколько энергии выделится при полном сгорании древесного угля массой 15 кг; керосина массой 200 г.
Задача 127. Какое количество теплоты выделится при полном сгорании бензина массой 5 кг; каменного угля массой 10 кг?
Задача 128. Какое количество теплоты выделится при полном сгорании пороха массой 25 г; торфа массой 0,5 т; каменного угля массой 1,5 т?
Задача 129. Сколько теплоты выделится при полном сгорании сухих березовых дров объемом 5 м3?
Задача 130. Сколько теплоты выделится при полном сгорании керосина объемом 0,25 м3; спирта объемом 0,00005 м3; бензина объемом 25 л; нефти объемом 250 л?
Задача 131. На сколько больше теплоты выделится при полном сгорании бензина массой 2 кг, чем сухих березовых дров той же массы?
Задача 132. Во сколько раз больше выделится теплоты при полном сгорании водорода массой 1 кг, чем при полном сгорании сухих березовых дров той же массы?
Во сколько раз больше выделится теплоты при полном сгорании водорода массой 1 кг, чем при полном сгорании сухих березовых дров той же массы?
Задача 133. Смешали бензин массой 2 кг и спирт массой 3 кг. Какое количество теплоты выделится при полном сгорании полученного топлива?
Задача 134. Смешали бензин объемом 1,5 л и спирт объемом 0,5 л. Какое количество теплоты выделится при полном сгорании этого топлива?
Задача 135. В печи сгорели сухие сосновые дрова объемом 0,01 м3 и торф массой 5 кг. Сколько теплоты выделилось в печи?
Задача 136. К зиме заготовили сухие сосновые дрова объемом 2 м3 и каменный уголь массой 1,5 т. Сколько теплоты выделится в печи при полном сгорании в ней заготовленного топлива?
Задача 137. При полном сгорании тротила массой 10 кг выделяется Дж энергии. Чему равна удельная теплота сгорания тротила?
Задача 138. При сгорании пороха массой 3 кг выделилось 11400 кДж энергии. Вычислите удельную теплоту сгорания пороха.
Задача 139. Сколько надо сжечь каменного угля, чтобы выделилось Дж энергии? Дж энергии?
Задача 140. В топке котла парового двигателя сожгли торф массой 20 т. Какой массой каменного угля можно было бы заменить сгоревший торф (удельную теплоту сгорания торфа принять равной Дж/кг)?
Задача 141. Сколько каменного угля нужно сжечь, чтобы получить столько же энергии, сколько ее выделяется при сгорания бензина объемом 6 м3?
Задача 142. Сколько спирта надо сжечь, чтобы изменить температуру воды массой 2 кг от 14 до 50, если вся теплота, выделенная спиртом, пойдет на нагревание воды?
Задача 143. Сколько воды, взятой при температуре 14, можно нагреть до 50, сжигая спирт массой 30 г и считая, что вся выделяемая при горении спирта энергия идет на нагревание воды?
Задача 144. На сколько изменится температура воды объемом 100 л, если считать, что вся теплота, выделяемая при сгорании древесного угля массой 0,5, пойдет на нагревание воды?
Задача 145. На сколько изменится температура воды, масса которой 22 кг, если ей передать всю энергию, выделившуюся при сгорании керосина массой 10 г?
Задача 146. В чем заключается процесс сгорания топлива? В чем разница между сгоранием (нефти, угля) и взрывом (пороха, гремучего газа)?
В чем заключается процесс сгорания топлива? В чем разница между сгоранием (нефти, угля) и взрывом (пороха, гремучего газа)?
Задача 147. Определить КПД примуса, зная, что при сжигании 300 г керосина можно вскипятить 15 л воды, взятой при 10.
Задача 148. На спиртовке нагрели 224 г воды от 15 до 75 и сожгли при этом 5 г спирта. Определить КПД спиртовки. Проведите подобный опыт.
Задача 149. Каков КПД кузнечного горна, если для нагревания 2 кг стали на 1000 расходуется 0,6 кг кокса?
Задача 150. На нагревание 2 л воды от 5 до 100 затрачено 0,1 м3 природного газа. Определить КПД горелки.
Задача 151. Чтобы нагреть 1,8 кг воды от 18 до кипения на горелке с КПД 25% потребовалось 92 г горючего. Какова удельная теплота сгорания горючего?
Задача 152. Определить КПД нагревателя, в котором израсходовано 80 г керосина для нагревания 3 л воды на 90.
Задача 153. Какое количество воды можно нагреть от 15 до кипения на горелке с КПД 40%, если сжечь 100 л природного газа?
Задача 154. Сколько времени потребуется, чтобы нагреть 1,55 л воды от 20 до 100, если горелка потребляет 0,3 кг спирта в час, а КПД ее 24%?
Задача 155. На спиртовке нагревали воду массой 100 г от 16 до 71. При этом был сожжен спирт массой 10 г. Найти КПД установки.
Задача 156. Для нагревания воды объемом 2 л, находящейся в алюминиевой кастрюле массой 400 г, от 15 до 75 был израсходован газ массой 30 г. Определить КПД газовой плиты, считая теплоту, израсходованную на нагревание сосуда, полезной. Как изменится результат, если полезной считать только теплоту, израсходованную на нагревание воды?
Задача 157. Каково отношение масс спирта и бензина, если удельная теплота сгорания этих горючих веществ оказалась равной Дж/кг? Удельная теплота сгорания спирта Дж/кг и бензина Дж/кг.
Задача 158. Почему лед не сразу начинает таять, если его внести с мороза в натопленную комнату?
Задача 159. Температура плавления стали 1400. При сгорании пороха в канале ствола орудия достигается температура 3600. Почему ствол орудия не плавится при выстреле?
Почему ствол орудия не плавится при выстреле?
Задача 160. Два тигля с одинаковой массой расплавленного свинца остывают в помещениях с разной температурой. Какой график (см. рис.) построен для теплого помещения и какой – для холодного? Найдите различия в графиках и объясните причины этих различий.
Задача 161. Почему зимой при длительных остановках воду из радиатора автомобиля выливают?
Задача 162. Оболочки космических кораблей и ракет делают из тугоплавких металлов и специальных сплавов. Почему?
Задача 163. При спаивании стальных деталей иногда пользуются медным припоем. Почему нельзя паять медные детали стальным припоем?
Задача 164. Почему невозможно пользоваться очень маленьким паяльником при пайке массивных кусков меди или железа?
Задача 165. Объясните на основании молекулярно-кинетической теории, почему не повышается температура в момент плавления и кристаллизации тела.
Задача 166. Два одинаковых сосуда из полиэтилена заполнили водой, температура которой 0. Один сосуд поместили в воду, другой – в измельченный лед, имеющих, как и окружающий воздух, температуру 0. Замерзнет ли вода в каком-нибудь из этих сосудов?
Задача 167. Можно ли заморозить воду расплавленным металлом?
Задача 168. На рисунке ниже показано, как со временем изменяется температура при нагревании и охлаждении свинца. Твердому или жидкому состоянию соответствуют участки графика AB, BC, CD, GH? Что может быть причиной того, что участок GH круто падает вниз? Чему равны температуры плавления и кристаллизации свинца?
Задача 169. График, приведенный на рисунке ниже, выражает зависимость температуры вещества при его нагревании и плавлении от времени. а) Какую температуру имело вещество в первоначальный момент? б) Через сколько времени от начала наблюдения температура достигла 635? в) Какова продолжительность перехода вещества из одного агрегатного состояния в другое? г) Какому веществу соответствует график?
Задача 170. Начертите график плавления меди, откладывая по вертикальной оси температуру в масштабе 20 в 1 см, а по горизонтальной – время в масштабе 10 мин в 1 см. Начальную температуру меди примите равной 1000, время нагревания до температуры плавления – 20 мин, а время перехода меди в жидкое состояние – 30 мин.
Начальную температуру меди примите равной 1000, время нагревания до температуры плавления – 20 мин, а время перехода меди в жидкое состояние – 30 мин.
Задача 171. Постройте примерный график для нагревания, плавления и кристаллизации олова.
Задача 172. В сосуде находится лед при температуре –10. Сосуд поставили на горелку, которая дает в равные промежутки времени равное количество теплоты. Укажите, какой график (см. рисунок ниже) соответствует описанному случаю и в чем ошибочны другие графики.
Задача 173. Внимательно рассмотрев график охлаждения и кристаллизации вещества (см. рисунок ниже), ответьте: а) Для какого вещества составлен график? б) Сколько времени охлаждалось вещество от 20 до температуры кристаллизации? в) Сколько времени длился процесс кристаллизации? г) О чем говорит участок графика DE? д) Как приблизительно расположились бы точки A, B, C относительно друг друга и точки 0, если бы при той же температуре окружающей среды был бы составлен график для того же вещества, но большей массы?
Задача 174. Какому из двух тел одинакового объема – слитке алюминия или отливке из винца – надо передать большее количество теплоты и во сколько раз, чтобы перевести их из твердого состояния в жидкое при их температурах плавления?
Задача 175. Возможно ли такое явление: физическое тело передает некоторое количество теплоты окружающей среде, но при этом не охлаждается (предполагается, что расход теплоты не восполняется).
Задача 176. Изменяется ли общая кинетическая энергия молекул тела, когда во время его плавления к нему подводится некоторое количество теплоты? Изменяется ли в этом случае внутренняя энергия тела?
Задача 177. Одинаковый ли физический смысл имеют выражения: «передача телу теплоты» и «нагревание тела»?
Задача 178. В чем проявляется закон сохранения и превращения энергии при плавлении и кристаллизации вещества?
Задача 179. На сколько увеличится при плавлении внутренняя энергия ртути, свинца, меди массой 1 кг, взятых при температурах плавления?
Задача 180. На сколько уменьшится внутренняя энергия при кристаллизации брусков из белого чугуна массой 2 кг; олова массой 1 кг; железа массой 5 кг; льда массой 10 кг, охлажденных до температуры их кристаллизации?
На сколько уменьшится внутренняя энергия при кристаллизации брусков из белого чугуна массой 2 кг; олова массой 1 кг; железа массой 5 кг; льда массой 10 кг, охлажденных до температуры их кристаллизации?
Задача 181. Масса какого металла – золота и серебра – должна быть больше и во сколько раз, чтобы количество теплоты, достаточное для плавления металла, было в каждом случае одинаковым?
Задача 182. Во сколько раз требуется больше энергии для плавления льда при температуре 0, чем для изменения температуры той же массы льда на 1?
Задача 183. Какое количество теплоты потребуется для плавления тел из нафталина, золота, платины массой 10 г, взятых при температуре плавления?
Задача 184. Какое количество теплоты необходимо затратить, чтобы расплавить лед массой 5 кг, если начальная температура льда 0; -1; -10?
Задача 185. Какое количество теплоты необходимо для плавления куска свинца массой 1 г, начальная температура которого равна 27? олова массой 10 г, взятого при температуре 32?
Задача 186. Сколько энергии требуется для плавления куска свинца массой 0,5 кг, взятого при температуре 27?
Задача 187. Сколько энергии необходимо для плавления бруска из цинка массой 0,5 кг, взятого при температуре 20?
Задача 188. Сколько энергии необходимо для плавления железного металлолома массой 4 т, если начальная температура железа равна 39?
Задача 189. Масса серебра 10 г. Сколько энергии выделится при его кристаллизации и охлаждении до 60, если серебро взято при температуре плавления?
Задача 190. Сколько энергии выделится при кристаллизации и охлаждении от температуры плавления до 27 свинцовой пластинки размером см?
Задача 191. Из копильника вагранки для отливки детали выпустили расплавленное железо массой 50 кг. Какое количество теплоты выделилось при его кристаллизации и охлаждении до температуры 39?
Задача 192. Для приготовления пищи полярники используют воду, полученную из расплавленного льда. Какое количество теплоты потребуется для того, чтобы расплавить лед массой 20 кг и полученную воду вскипятить, если начальная температура льда -10?
Задача 193. Объем формы для пищевого льда 750 см3. Сколько энергии отдают вода и лед форме и окружающему ее воздуху в холодильнике, если начальная температура воды 12, а температура образовавшегося льда -5?
Объем формы для пищевого льда 750 см3. Сколько энергии отдают вода и лед форме и окружающему ее воздуху в холодильнике, если начальная температура воды 12, а температура образовавшегося льда -5?
Задача 194. Какое количество теплоты пошло на приготовление в полярных условиях питьевой воды из льда массой 10 кг, взятого при температуре -20, если температура воды должна быть равной 15?
Задача 195. Сколько энергии выделилось при отвердевании и охлаждении до 25 заготовки маховика массой 80 кг, отлитой из белого чугуна? Удельную теплоемкость чугуна принять равной удельной теплоемкости железа. Температура плавления чугуна 1165.
Задача 196. Свинцовая деталь массой 100 г охлаждается от 427 до температуры плавления, отвердевает и охлаждается до 27. Какое количество теплоты отдает деталь окружающим телам? (Удельную теплоемкость расплавленного свинца принять равной 170 .)
Задача 197. В железной коробке массой 300 г мальчик расплавил 100 г олова. Какое количество теплоты пошло на нагревание коробки и плавление олова, если их начальная температура была равна 32?
Задача 198. Железная заготовка, охлаждаясь от температуры 800 до 0, растопила лед массой 3 кг, взятый при 0. Какова масса заготовки, если вся энергия, выделенная ею, пошла на плавление льда?
Задача 199. Чтобы охладить 4,5 л воды от 30 до 10, в воду бросают кусочки льда при 0. Какое количество льда потребуется для охлаждения воды?
Задача 200. Для приготовления дроби расплавленный свинец при температуре плавления влили струями в воду с начальной температурой 17. Сколько потребовалось воды, чтобы охладить 40 кг свинцовой дроби при конечной температуре воды не выше 47?
Задача 201. В сосуд, содержащий воду массой 100 кг при температуре 10, положили кусок льда, охлажденный до –50. После установления теплового равновесия температура ледяной массы оказалась равной –4. Какова масса куска льда?
Задача 202. В калориметр налита вода массой 2 кг при температуре 5 и положен кусок льда массой 5 кг, имеющий температуру –4. Определите температуру и объем содержимого калориметра после установления теплового равновесия. Теплоемкостью калориметра и теплообменом со средой пренебречь.
Определите температуру и объем содержимого калориметра после установления теплового равновесия. Теплоемкостью калориметра и теплообменом со средой пренебречь.
Задача 203. В сосуд, содержащий 10 кг воды при температуре 10, положили кусок льда, охлажденный до –50, после чего температура образовавшейся ледяной массы оказалась равной –4. Какое количество льда было положено в сосуд?
Задача 204. Кусок свинца массой 1 кг расплавился наполовину при сообщении ему количества теплоты Дж. Какова была начальная температура свинца?
Задача 205. Тигель, содержащий некоторое количество олова, нагревается электрическим током. Выделяемое в единицу времени количество теплоты постоянно. За 10 мин температура олова повышается от 20 до 70. Спустя еще 83 мин олово полностью расплавилось. Найти удельную теплоемкость олова.
Задача 206. Чтобы охладить 200 г воды, имеющей температуру 25, в нее бросают взятые из холодильника ледяные брусочки объемом 6,4 см3, температура которых –5. Сколько надо бросить брусочков для охлаждения воды до 5?
Задача 207. В стальной сосуд массой 300 г налили 1,5 л воды при 17. В воду опустили кусок мокрого снега массой 200 г. Когда снег растаял, установилась температура 7. Сколько воды было в комке снега?
Задача 208. В воду массой 1,5 кг положили лед, температура которого 0. Начальная температура воды 30. Сколько нужно взять льда, чтобы он весь растаял?
Задача 209. В калориметре находятся лед и вода при температуре 0. Масса льда о воды одинакова и равна 500 г. В калориметр вливают воду массой 1 кг при температуре 50. Какая температура установится в нем?
Задача 210. В углубление, сделанное во льду, вливают свинец. Сколько было влито свинца, если он остыл до температуры 0 и растопил лед массой 270 г? Начальная температура льда 0, свинца 400.
Задача 211. В термос с водой поместили лед при температуре –10. Масса воды 400 г, масса льда 100 г, начальная температура воды 20. Определите конечную температуру воды в термосе.
Задача 212. В медном сосуде массой 400 г находится вода массой 500 г при температуре 40. В воду бросили кусок льда при температуре –10. Когда установилось тепловое равновесие, остался нерасплавленный лед массой 75 г. Определите начальную массу льда.
В воду бросили кусок льда при температуре –10. Когда установилось тепловое равновесие, остался нерасплавленный лед массой 75 г. Определите начальную массу льда.
Задача 213. Кусок льда массой 700 г поместили в калориметр с водой. Масса воды 2,5 кг, начальная температура 5. Когда установилось тепловое равновесие, оказалось, что масса льда увеличилась на 64 г. Определите начальную температуру льда.
Задача 214. В калориметр с водой объемом 1 л опустили мокрый снег. Масса снега 250 г, начальная температура воды 20. После плавления снега температура воды в калориметре стала равной 5. Сколько воды содержалось в снегу?
Задача 215. 1 кг льда, взятому при температуре –50, сообщили 520 кДж теплоты. Построить график зависимости температуры от времени поступления теплоты. Скорость поступления теплоты постоянная.
Задача 216. В сосуд с водой с общей теплоемкостью 1,5 кДж/К при температуре 20 поместили 56 г льда при температуре –8. Какая установится температура?
Задача 217. В сосуд с водой с общей теплоемкостью 1,7 кДж/К при 20 поместили 100 г льда при –8. Какая температура установится в сосуде?
Задача 218. В медный калориметр массой 100 г, содержащий воду массой 50 г при температуре 5, опустили лед при температуре –30. Масса льда 300 г. Какая температура установится в калориметре?
Задача 219. При 0 почва покрыта слоем снега толщиной 10 см и плотностью 500 кг/м3. Какой слой дождевой воды при 4 расплавит весь слой снега?
Задача 220. Сколько потребуется каменного угля, чтобы расплавить 1000 кг серого чугуна, взятого при температуре 50? Тепловая отдача вагранки 60%.
Задача 221. В плавильной печи сожгли 0,1 m угля и расплавили 2 m меди, взятой при 23. Определить КПД печи.
Задача 222. Сколько керосина нужно сжечь в примусе с КПД 40%, чтобы расплавить 4 кг льда, взятого при –10, если q = 42000 кДж/кг?
Задача 223. В 480 г воды при 22 бросили кусок льда при температуре –8. Сколько бросили льда, если температура смеси установилась 12?
Задача 224. Определить КПД вагранки, работающей на коксе, если кокса расходуется 300 кг, а серого чугуна расплавляется 1,5 m при начальной температуре 20.
Определить КПД вагранки, работающей на коксе, если кокса расходуется 300 кг, а серого чугуна расплавляется 1,5 m при начальной температуре 20.
Задача 225. Сколько кокса потребуется для расплавления 4 m серого чугуна, взятого при температуре 30, если КПД вагранки 12%?
Задача 226. Сколько меди можно расплавить в плавильной печи с КПД 30%, сжигая 2 m кокса, если начальная температура меди 20?
Задача 227. Вода при соблюдении некоторых предосторожностей может быть переохлаждена до температуры -10. Такое состояние воды неустойчиво, и при любом возмущении вода превращается в лед с температурой 0. Какова масса льда, образовавшегося из переохлажденной воды, масса которой 1 кг? Считать, что удельная теплоемкость воды не зависит от температуры и равна ее табличному значению.
Задача 228. К воде, переохлажденной до температуры -12, бросили маленький кусочек льда. Какая часть массы воды превратится в лед?
Задача 229. Железный шарик радиусом 1 см, нагретый до 120, положили на лед. На какую глубину погрузится шарик в лед? Плотность льда и воды считать одинаковой. Температура окружающей воды 0.
Задача 230. До какой температуры надо нагреть алюминиевый куб, чтобы он, будучи положен на лед, полностью в него погрузился? Температура льда 0, плотность 920 .
Задача 231. Для определения удельной теплоты плавления олова был проделан такой опыт: 100 г расплавленного олова при температуре 250 влили в алюминиевый калориметр массой 60 г, содержащий 200 г воды при 10. Окончательная температура установилась 23. Определить удельную теплоту плавления олова, принимая удельную теплоемкость жидкого олова равной удельной теплоемкости твердого олова (СИ). Проведите подобный опыт в физическом кабинете.
Задача 232. При температуре -5 каждый квадратный метр поверхности водоема теряет каждый час 168 кДж теплоты. Найти толщину слоя льда, образовавшегося за сутки, если температура воды на поверхности водоема 0.
Задача 233. При изготовлении льда в комнатном холодильнике требуется 5 мин для охлаждения воды от 4 до 0 и еще 1 ч 40 мин, чтобы превратить ее в лед. Определить удельную теплоту плавления льда.
Определить удельную теплоту плавления льда.
§4. Испарение и кипение. Качественные задачи.
Задача 234. Почему температура воды в открытом стакане всегда бывает немного ниже температуры воздуха в комнате?
Задача 235. В один стакан налили эфир при температуре 20, в другой – воду при той же температуре. В стаканы опустили термометры. Какой из них будет показывать более низкую температуру?
Задача 236. Почему в комнате после мытья пола становится прохладнее?
Задача 237. Почему написанное тушью просыхает быстрее, чем написанное чернилами?
Задача 238. Почему после дождя становится холоднее?
Задача 239. Почему мокрое развешенное белье, скошенная трава высыхают быстрее в ветреную погоду?
Задача 240. Почему пловец, вышедший из воды, ощущает холод, и это ощущение особенно сильно в ветреную погоду?
Задача 241. Мокрое белье, вывешенное зимой во дворе, замерзает. Но через некоторое время оно становится сухим, даже при сильных морозах. Чем это можно объяснить?
Задача 242. Почему вода, пролитая на пол, высыхает значительно быстрее, чем такое же количество воды в стакане?
Задача 243. Зачем овощи и фрукты, предназначенные для сушки, разрезают на тонкие ломтики?
Задача 244. В листву дерева непрерывно поступает большое количество воды из почвы через корни и ствол дерева. Куда девается эта вода?
Задача 245. На чашки рычажных весов поставили и уравновесили стакан с холодной водой и стакан с горячим чаем. Почему равновесие быстро нарушилось?
Задача 246. Объясните на основе представления о молекулах такой факт: температура эфира значительно понижается, если его вылить из закрытой склянки в открытый сосуд.
Задача 247. Для музыкальных инструментов очень сухой воздух вреден. Объясните, почему в комнате, где находится пианино рекомендуется держать аквариум.
Задача 248. Зачем при скоростной обработке металлов на станках на резцы направляется струя распыленной жидкости?
Задача 249. Люди, плохо переносящие жару, пользуются летом на открытом воздухе зонтом, а в помещении – веером. Объясните охлаждающее действие этих предметов.
Объясните охлаждающее действие этих предметов.
Задача 250. Почему летним утром туман «рассеивается» с первыми лучами солнца?
Задача 251. Подышите на зеркало и объясните, что произошло при этом на его поверхности.
Задача 252. Почему в банях и прачечных некоторые металлические трубы, по которым подается вода, покрыты капельками воды, тогда как поверхность других труб сухая?
Задача 253. При безоблачном небе выпадает, обычно, больше утренней росы, чем при пасмурном. Какова причина такого явления?
Задача 254. Над чайником с кипящей водой почти не видно пара, пока чайник стоит на пламени газовой плиты. Однако тотчас после выключения горелки пар на некоторое время становится виден. Объясните это явление.
Задача 255. Как объяснить на основании молекулярно-кинетической теории о строении вещества охлаждение жидкости при испарении?
Задача 256. Почему самовар с раскаленными углями не распаивается, когда в него налита вода, и распаивается, когда воды в нем нет?
Задача 257. В двух сосудах конической и сферической формы с одинаковой площадью дна налита вода одинаковой массы. В каком сосуде вода закипит быстрее, если их поставить на одну и ту же электрическую плиту?
Задача 258. На рисунке показано, как со временем изменяется температура при нагревании и охлаждении воды. Какому состоянию воды соответствуют участки графика AB, BC? Объясните, почему участок BC параллелен оси времени.
Задача 259. В чем проявляется закон сохранения и превращения энергии при парообразовании и конденсации пара?
Задача 260. На рисунке даны графики нагревания и кипения жидкостей одинаковой массы: воды, спирта, эфира. Определите, какой график построен для воды, какой – для спирта, какой – для эфира.
Задача 261. Что обладает большей внутренней энергией: вода при температуре 100 или ее пар той же массы при той же температуре?
Задача 262. Как и на сколько изменится внутренняя энергия пара массой 1 г при его конденсации, если он имеет температуру 100?
Задача 263. Две жидкости (А, В) равных масс нагревают на одинаковых горелках до кипения. Определите по графикам (см. рисунок), у какой жидкости выше температура кипения; больше удельная теплоемкость; больше удельная теплота парообразования.
Две жидкости (А, В) равных масс нагревают на одинаковых горелках до кипения. Определите по графикам (см. рисунок), у какой жидкости выше температура кипения; больше удельная теплоемкость; больше удельная теплота парообразования.
Задача 264. Почему не кипит вода в открытой стеклянной пробирке, опущенной в кипящую воду?
Задача 265. В каком состоянии в жидком при 100 или в газообразном при той же температуре 1 г воды имеет меньшую внутреннюю энергию: ?
Задача 266. Как заставить воду кипеть, подвергая ее охлаждению?
Задача 267. В каком агрегатном состоянии находится при нормальном давлении каждое из следующих веществ: спирт при 100, кислород при -200, железо при 2000, эфир при 45, вода при 173, цинк при 980?
Задача 268. Закипит ли медь, если кусочек ее погрузить в жидкий свинец, нагретый до температуры его кипения? Изменится ли ответ, если все будет сделано наоборот: кусочек свинца брошен в кипящую медь?
Задачи и упражнения к главе 4 «Внутренняя энергия»
115. В один стакан налили 100 мл холодной воды, в другой — такое же количество горячей воды. В каком стакане вода обладает большей внутренней энергией?
116. Что происходит с внутренней энергией человека, когда после жара у него восстанавливается нормальная температура?
117. Почему, если быстро скользить вниз по шесту или канату, можно обжечь руки?
118. При обработке детали напильником и деталь, и напильник нагреваются. Почему?
119. Почему конькобежец легко скользит по льду, в то время как по стеклу, обладающему более гладкой поверхностью, он скользить не может?
120. Почему метеорит, пролетая через атмосферу Земли, раскаляется?
121. Ножницы и карандаш, лежащие на столе, имеют одинаковую температуру. Почему же на ощупь ножницы кажутся холоднее карандаша?
Решение:
Рука человека в обычных условиях имеет большую температуру, чем ножницы и карандаш. Поэтому при контакте руки с этими предметами начинается теплообмен: рука теряет некоторое количество теплоты, а карандаш и ножницы его получают. Но теплопроводность дерева, из которого изготовлен карандаш, значительно меньше теплопроводности металлических ножниц. Поэтому теплообмен между рукой и карандашом будет осуществляться намного медленнее, чем между рукой и ножницами. Более быстрая теплоотдача в последнем случае и вызывает то ощущение холода, которое возникает, когда мы дотрагиваемся до ножниц.
Но теплопроводность дерева, из которого изготовлен карандаш, значительно меньше теплопроводности металлических ножниц. Поэтому теплообмен между рукой и карандашом будет осуществляться намного медленнее, чем между рукой и ножницами. Более быстрая теплоотдача в последнем случае и вызывает то ощущение холода, которое возникает, когда мы дотрагиваемся до ножниц.
122. Почему на воздухе при температуре 25 °С человеку жарко, а в воде, имеющей такую же температуру, ему прохладно?
123. Почему глубокий рыхлый снег защищает озимые хлеба от вымерзания?
124. Почему меховые пальто и шапки защищают тело человека и от мороза, и от сильной жары? При какой примерно температуре имеет смысл надевать такую одежду в жару?
125. Ускорится ли таяние мороженого в теплой комнате, если укутать его шубой?
126. Что теплее: три рубашки или рубашка тройной толщины?
127. Почему в безветрие пламя свечи устанавливается вертикально?
128. Почему подвал — самое холодное место в доме?
129. В какой одежде летом менее жарко: в белой или темной? Почему?
130. Почему вспаханное поле сильнее нагревается солнечным излучением, чем зеленый луг?
131. Внутренняя энергия газа была равна 0,03 МДж. В результате теплообмена она стала равной 38 кДж. Найдите изменение внутренней энергии этого газа. Как изменилась при этом температура газа — повысилась или понизилась? Чему равно количество теплоты, полученное газом?
132. Чему была равна внутренняя энергия газа, если в результате теплообмена она уменьшилась на 10 кДж и стала равной 0,05 МДж? Как при этом изменилась температура газа — повысилась или понизилась? Какое количество теплоты было получено газом?
133. На сколько изменилась внутренняя энергия газа, если, получив количество теплоты 8 МДж, газ совершил работу 6 Мдж?
134. При передаче газу количества теплоты 15 кДж он совершил работу, равную 40 кДж. Чему равно изменение внутренней энергии газа? Охладился газ или нагрелся?
135. Получив количество теплоты 500 кДж, газ совершил некоторую работу. Какую работу совершил газ, если полное изменение его внутренней энергии составило 200 кДж?
Получив количество теплоты 500 кДж, газ совершил некоторую работу. Какую работу совершил газ, если полное изменение его внутренней энергии составило 200 кДж?
136. Какое количество теплоты было получено газом, если его внутренняя энергия увеличилась на 0,2 МДж и при этом он совершил работу 100 кДж?
137. Пользуясь таблицей 8, вычислите (устно) количество теплоты, необходимое для нагревания на 1 °С: а) воды массой 2 кг; б) льда массой 2 кг.
138. Пользуясь таблицей 8, вычислите (устно) количество теплоты, выделяющееся при охлаждении на 2 °С: а) воды массой 1 кг; б) льда массой 1 кг.
139. Какое количество теплоты необходимо для нагревания алюминиевой ложки массой 50 г на 50 °С?
140. Какое количество теплоты необходимо для нагревания стальной детали массой 500 г на 20 °С?
141. Какое количество теплоты выделяется при охлаждении куска льда массой 200 г от 0 до –10 °С?
142. Какое количество теплоты выделяется при охлаждении воды массой 100 г от 90 до 20 °С?
143. Имеется два предмета одинаковой массы и одинаковой температуры: один из свинца, другой из стали. Какой из них отдаст при охлаждении до одной и той же температуры большее количество теплоты?
144. Имеется два предмета одинаковой массы и одинаковой температуры: один из меди, другой из алюминия. Какой из них нагреется до большей температуры при передаче им одинакового количества теплоты?
145. Вынутые из кипятка цилиндры из свинца и меди массой 1 кг каждый поместили на лед. Под каким из них растает больше льда? Какая из лунок (рис. 102) образовалась под свинцовым цилиндром, какая — под медным?
146. Вынутые из кипятка цилиндры из стали и алюминия одинаковой массы поместили на парафин. Под каким из них расплавится больше парафина? Какая из лунок (рис. 103) образовалась под стальным цилиндром, какая — под алюминиевым?
147. В каком случае 1 кг свинца нагреется сильнее: когда его температуру повысят на 10 °С или когда ему сообщат количество теплоты 10 Дж?
148. В каком случае 1 г свинца нагреется сильнее: когда его температуру повысят на 5 °С или когда ему сообщат количество теплоты 5 Дж?
149. В железный котел массой 10 кг налита вода массой 20 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100 °С?
150. Какое количество теплоты необходимо для нагревания от 20 до 100 °С алюминиевой кастрюли массой 800 г с водой, масса которой 5 кг?
151. В ведро налита вода массой 5 кг, температура которой 9 °С. Сколько кипятку нужно долить в ведро, чтобы температура воды стала равной 30 °С? Тепловыми потерями пренебречь.
152. Металлический цилиндр массой 200 г нагрели в кипятке до 100 °С и затем опустили в воду массой 400 г, имеющую температуру 22 °С. Через некоторое время температура воды и цилиндра стала равной 25 °С. Чему равна удельная теплоемкость металла, из которого изготовлен цилиндр? Тепловыми потерями пренебречь.
instr_2018_1.indd
%PDF-1.6 % 525 0 obj > endobj 547 0 obj >/Font>>>/Fields[]>> endobj 522 0 obj >stream Acrobat Distiller 10.0.1 (Windows)PScript5.dll Version 5.2.22018-01-16T16:22:51+03:002018-01-16T16:18:41+03:002018-01-16T16:22:51+03:00application/pdf
Конечная температура после помещения теплого металла в более холодную воду
Конечная температура после помещения теплого металла в более холодную водуКакова конечная температура, когда теплый металл помещают в более холодную воду?
Перейти к расчету конечной температуры при смешивании металла и воды: задачи 1-15
Переход к расчету конечной температуры при смешивании двух проб воды
Назад в меню термохимии
Эти проблемы подобны смешиванию двух количеств воды, за одним небольшим исключением: значения удельной теплоемкости на двух сторонах уравнения будут разными.Удельная теплоемкость воды останется на уровне 4,184, но значение для металла будет другим. Эти значения сведены в таблицы, а списки выбранных значений есть в большинстве учебников.
Пример № 1: Определите конечную температуру, когда кусок железа весом 25,0 г при 85,0 ° C помещают в 75,0 г воды при 20,0 ° C.
Сначала обсуждение, затем решение. Простите меня, если пункты кажутся очевидными:
а) Более холодная вода нагреется (к ней «течет» тепловая энергия).Более теплый металл остынет (из него «потечет» тепловая энергия).
б) Вся смесь будет наматываться при температуре ТАК ЖЕ . Это очень и очень важно.
c) Энергия, которая «вытекла» (из более теплой воды) равна энергии, которая «втекала» (в более холодную воду).
Ключевой элемент решения номер один: Мы начинаем с того, что называем конечную конечную температуру «х». Имейте в виду, что И железо, и вода нагреваются до температуры, которую мы называем «х». Также убедитесь, что вы понимаете, что мы используем «x» НЕ Δt, а температуру FINAL .Это то, что мы решаем.
Более теплое железо понижается с 85,0 до x, это означает, что его Δt равно 85,0 минус x. Более холодная вода нагревается, поэтому ее Δt равно x минус 20,0.
Этот последний абзац может немного сбивать с толку, поэтому давайте сравним его с числовой строкой:
Для вычисления абсолютного расстояния это большее значение минус меньшее, поэтому от 85,0 до x равно 85,0 минус x, а расстояние от x до 20,0 равно x минус 20,0.
Ключевой номер решения номер два: количество энергии, выходящей из теплой воды, равно количеству энергии, уходящей в холодную воду.Это означает:
q потеря = q прирост
Итак, подстановкой мы получаем:
(25,0) (85,0 — x) (0,45) = (75,0) (x — 20,0) (4,184)
Решить относительно x
Обратите внимание на значение удельной теплоемкости железа. Это 0,45 Дж на грамм градуса Цельсия.
Учитывая, что 75/25 = 3, получаем:
38,25 — 0,45x = 12,552x — 251,04
тогда
13,002x = 289,29
Ответ
22.25 ° С
, если вы не слишком привередничать со значащими цифрами.
Обратите внимание, что температура утюга немного падает, в то время как вода перемещается всего на несколько (в данном случае 2,25) градуса. Это типичная ситуация для такого типа проблем.
Пример № 2: Определите конечную температуру, когда 10,0 г алюминия при 130,0 ° C смешиваются с 200,0 г воды при 25,0 ° C.
Нет отличий в методике расчета от примера №1.Обратите внимание: начальная температура металла выше точки кипения воды. На самом деле образец может испарить небольшое количество воды, но мы предположим, что это не так для целей расчета.
Решение:
1) Настроить номера:
q алюминий = q вода(10) (130 — x) (0,901) = (200,0) (x — 25) (4,18)
2) Заметив, что 200/10 = 20, я получаю:
117,13 — 0,901x = 83.6x — 2090x = 26,12 ° С.
Имейте в виду, что «x» отождествлялся с конечной температурой, а НЕ с Δt.
Также я делал эту проблему с 4.18. Выполнение этого с 4.184 дает немного другой ответ. Убедитесь, что вы уточняете у своего учителя значения различных констант, которые он / она хочет, чтобы вы использовали.
Пример № 3: Определите конечную температуру, когда 20,0 г ртути при 165,0 ° C смешиваются с 200,0 г воды при 60.0 ° С. (C p для Hg = 0,14 Дж на грамм градуса Цельсия.)
Не будем обращать внимания на то, что ртуть жидкая. не растворяется в воде.
Решение:
(20,0) (165,0 — x) (0,14) = (200,0) (x — 60,0) (4,18)Заметив, что 200/20 = 10, я получаю:
23,1 — 0,14x = 41,8x — 2508
41,94x = 2531,1
x = 60,35 ° C
Обратите внимание, что вода перемещается только на 0,35 градуса. Имейте в виду, что существует большое количество воды по сравнению с ртутью, И что для перемещения воды на один градус требуется гораздо больше энергии по сравнению с тем же количеством ртути, перемещающейся на один градус.
Пример № 4: 10,0 г воды имеют температуру 59,0 ° C. Если в калориметр поместить 3,00 г золота при 15,2 ° C, какова конечная температура воды в калориметре? (Удельная теплоемкость золота составляет 0,128 Дж / г ° C.)
Решение:
1) Настройте следующее:
q вода = q золота(10,0) (59,0 — x) (4,184) = (3,00) (x — 15,2) (0,128)
2) Алгебра:
2468,56 — 41.84x = 0,384x — 5,836842,224x = 2474,3968
x = 58,6 ° C
Обратите внимание, что в этом случае вода остывает, а золото нагревается. Это противоположно самой распространенной проблеме этого типа, но метод решения такой же.
Пример 5: 105,0 мл H 2 O первоначально находится при комнатной температуре (22,0 ° C). Охлажденный стальной стержень (2,00 ° C) помещается в воду. Если конечная температура системы составляет 21,5 ° C, какова масса стального стержня? (удельная теплоемкость воды = 4.184 Дж / г ° С; удельная теплоемкость стали = 0,452 Дж / г ° C)
Решение:
(105,0 г) (0,5 ° C) (4,184 Дж ° C -1 г -1 ) = (x) (19,5 ° C) (0,452 Дж ° C -1 г -1 )x = 24,9 г
Пример № 6: Кольцо из чистого золота и кольцо из чистого серебра имеют общую массу 15,0 г. Два кольца нагревают до 62,4 ° C и помещают в 13,6 мл воды при 22,1 ° C. Когда равновесие достигнуто, температура воды составляет 23.9 ° С. (Предположим, что плотность воды составляет 0,998 г / мл.)
а) Какова масса золотого кольца?
(б) Какова масса серебряного кольца?
Комментарий: значения удельной теплоемкости можно найти во многих местах в Интернете и в учебниках. Вот пример.
Решение:
1) Используемое основное уравнение:
Полученное или потерянное тепло = (масса) (изменение температуры) (удельная теплоемкость)В более компактном виде: q = (м) (Δt) (C p )
Ниже будут использованы три из них.
2) Две массы, связанные с золотым и серебряным кольцами:
Пусть y = граммы золота
Следовательно, 15,0 — y = грамм серебра
3) Масса воды:
13,6 мл x 0,998 г / мл = 13,5728 г
4) Тепло, получаемое водой:
q = (13,5728 г) x (1,8 ° C) (4,184 Дж г ¯ 1 ° C ¯ 1 )q = 102,2195 Дж
1,8 получается таким образом: 23,9 — 22,1
5) Когда золотое кольцо и серебряное кольцо остывают, они выделяют энергию, которая в сумме составляет 102.2195 J. Сумму можно выразить следующим образом:
(y) (38,5 ° C) (0,129 Дж ¯ 1 ° C ¯ 1 ) + (15 — y) (38,5 ° C) (0,235 Дж g ¯ 1 ° C ¯ 1 ) = 102,2195 ДжПомните, изменение на 1 ° C равно изменению на 1 К. Это означает, что 0,129 Дж ¯ 1 ° C ¯ 1 то же самое, что 0,129 Дж ¯ 1 K ¯ 1
38,5 был получен таким же образом, как и 1,8, чуть выше.
6) Алгебра!
4.9665y + (15 — y) (9,0475) = 102,21954.9665y + 135.7125 — 9.0475y = 102.2195
-4,081y = -33,493
y = 8,21 г Au
15,0 — 8,21 = 6,79 г Ag
Пример № 7: Кольцо имеет массу 8,352 грамма и изготовлено из золота и серебра. Когда кольцо нагревали до 94,52 ° C, а затем опускали в 13,40 г воды при 20,00 ° C, температура воды после достижения теплового равновесия составляла 22,00 ° C. Каков массовый процент золота и серебра в кольце?
Решение:
Тепло, выделяемое серебром, плюс тепло, выделяемое золотом, равняется теплу, поглощаемому водой.Установите массу серебра равной «x». Это означает, что масса золота равна 8,352 минус x.
(x) (72,52 ° C) (0,235 Дж / г ° C) + (8,352 — x) (72,52 ° C) (0,129 Дж / г ° C) = (13,40 г) (2,00 ° C) (4,184 Дж / г ° C)
72,52 получается из 94,52 минус 22,00
17,0422x + (8,352 — x) (9,35508) = 112,1312
17,0422x + 78,13362816 — 9,35508x = 112,1312
7,68712x = 33,99757184
x = 4,422667 г
массовый процент золота: (4.422667 / 8.352) * 100 = 52,95%
массовый процент серебра: 100,00 — 52,95 = 47,05%
Пример № 8: Куб льда массой 74,0 г при температуре –12,0 ° C помещается на блок меди массой 10,5 кг при температуре 23,0 ° C, и вся система изолируется от окружающей среды. Через несколько минут лед растает, и температура системы достигла равновесия. Рассчитайте конечную температуру системы.
Комментарий: ни одна из подходящих констант не указана. Если вы столкнетесь с такой проблемой, вам придется искать правильные значения.Если вы изучите свои источники информации, вы можете обнаружить, что они немного отличаются от значений, которые я использую. Это обычное дело. Многие из используемых значений были определены экспериментально, и разные источники часто содержат немного разные значения.
Решение:
1) Лед изменяется от −12 до 0:
q = (74,0 г) (12,0 ° C) (2,06 Дж / г ° C) = 1829,28 Дж
2) Лед тает:
q = (74,0 г / 18,0 г / моль) (6,02) = 24,7489 кДж
3) Жидкая вода подвергается неизвестному повышению температуры до конечного значения x
q = (74.0 г) (x — 0) (4,184 Дж / г ° C) = 309,616x
4) Медь теряет тепло и ее температура падает до конечного значения x:
q = (10500 г) (23,0 — x) (0,385 Дж / г ° C)
5) Количество тепла, потерянного медью, равно теплу, полученному водой:
(10500) (23,0 — x) (0,385) = 1829,28 + 24748,9 + 309,616xОбратите внимание, как кДж от таяния льда используется как J, а не как кДж. Масса меди выражается в граммах, а не в килограммах.
(23,0 — х) (4042.5) = 26578,18 + 309,616x
92977,5 — 4042,5x = 26578,18 + 309,616x
66399,32 = 4352,116x
x = 15,2568 ° С
x = 15,2 ° C (для трех сигнатур я следовал правилу округления с 5)
Пример № 9: Сколько граммов воды можно нагреть от 25,0 ° C до 35,0 ° C за счет тепла, выделяемого 85,0 г железа, которое охлаждается с 85,0 ° C до 35,0 ° C? Удельная теплоемкость железа составляет 0,450 Дж / г ° C.
Решение:
1) Сколько тепла теряет утюг?
изменение температуры —> 85.0 ° C — 35,0 0 ° C = 50,0 ° Cq = (масса) (изменение температуры) (удельная теплоемкость)
q = (85,0 г) (50,0 ° C) (0,450 Дж / г ° C)
q = 1912,5 Дж
2) Предположим, что все 1912,5 Дж идут на нагрев воды:
q = (масса) (изменение температуры) (удельная теплоемкость)1912,5 Дж = (x) (10,0 ° C) (4,184 Дж / г ° C)
x = 45,7 г
Обратите внимание, что удельная теплоемкость жидкой воды в тексте задачи не указывается.
3) Эта проблема могла быть решена путем приравнивания двух уравнений и решения относительно ‘x.’:
(85,0 г) (50,0 ° C) (0,450 Дж / г ° C) = (x) (10,0 ° C) (4,184 Дж / г ° C)
Пример № 10: Найти массу жидкости H 2 O при 100,0 ° C, которая может быть превращена в газообразный H 2 O при 100,0 ° C с помощью блока алюминия 130,0 г при температуре 402,0 ° C? Предположим, что алюминий способен кипятить воду до тех пор, пока его температура не упадет ниже 100,0 ° C. Теплоемкость алюминия составляет 0,900 Дж ¯ 1 ° C ¯ 1 , а теплота испарения воды при 100 ° C равна 40.65 кДж моль ¯ 1
Раствор:
1) Тепло, которое Al может терять при переходе от начальной до конечной температуры:
q = m Δt C pq = (130.) г (302,0 ° C) (0,900 Дж г ¯ 1 ° C ¯ 1 ) = 35334 Дж = 35,334 кДж
Для испарения воды доступно 35,334 кДж тепла.
2) Используйте 35,334 кДж и теплоту испарения воды для расчета молей, а затем массу испаренной воды:
q = (ΔH) (моль)35.334 кДж = (40,65 кДж / моль) (x)
x = 0,869225 моль H 2 O
масса H 2 O = (0,869225 моль) (18,015 г / моль) = 15,659 г
Для трех сиг-инжиров это 15,6 г
Бонус Пример: 250-граммовый образец металла нагревают до температуры 98,0 ° C. Его помещают в 100 граммов воды в латунную чашку калориметра с латунной мешалкой. Общая масса чашки и мешалки составляет 50,0 грамма. Начальная температура воды, мешалки и калориметра — 20.0 ° С. Конечная равновесная температура системы составляет 30,0 ° C. Какова удельная теплоемкость металлического образца? (Удельная теплоемкость латуни составляет 0,0920 кал. Г ¯ 1 ° C ¯ 1 .)
Решение:
1) Количество тепла, выделяемого металлическим образцом, поглощается (а) водой и (б) латунным калориметром и мешалкой. Сколько тепла уловила вода?
q = m Δt C pq = (100. г) (10,0 ° C) (1,00 г кал. ¯ 1 C ¯ 1 )
q = 1000 кал.
Примечание: 1.00 г кал g ¯ 1 C ¯ 1 — удельная теплоемкость жидкой воды.
2) Сколько тепла поглотили латунный калориметр и мешалка?
q = m Δt C pq = (50,0 г) (10,0 ° C) (0,092 кал г ¯ 1 C ¯ 1 )
q = 54,28 ккал
3) Общее количество тепла, отдаваемого металлическим образцом:
1000 кал + 54,28 кал = 1054,28 кал
4) Определите удельную теплоемкость металлического образца:
q = м Δt C p1054.28 кал = (250. г) (68,0 ° C) (C p )
C p = 0,062 г кал г ¯ 1 C ¯ 1
Переход к расчету конечной температуры при смешивании металла и воды. Проблемы 1-15
Переход к расчету конечной температуры при смешивании двух проб воды
Назад в меню термохимии
Конечная температура после помещения теплого металла в более холодную воду: Задачи 1
Конечная температура после того, как теплый металл помещают в более холодную воду: Задачи 1-15Какова конечная температура, когда теплый металл помещают в более холодную воду?
Задачи 1-15
Перейти к расчету конечной температуры при смешивании металла и воды
Переход к расчету конечной температуры при смешивании двух проб воды
Назад в меню термохимии
Проблема № 1: A 610.Г кусок медной трубки нагревают до 95,3 ° C и помещают в изотермический сосуд, содержащий 45,0 г воды при температуре 36,5 ° C. При условии отсутствия потерь воды и теплоемкости для емкости 10,0 Дж / К, какова конечная температура системы (C p меди = 0,387 Дж / г-К)?
Решение:
1) Эту проблему можно резюмировать следующим образом:
q потеря меди = q получено водой + q получено калориметром
2) Следовательно:
(610.г) (95,3 ° C — x) (0,387 Дж г ¯ 1 K ¯ 1 ) = (45,0 г) (x — 36,5 ° C) (4,184 Дж г ¯ 1 ° C ¯ 1 ) + [(10,0 Дж / К) (x — 36,5 ° C)]Комментарий: K и ° C отменяются, потому что ° C в этой задаче — это разница температур (а не одно конкретное значение) и «размер» одного K = один ° C.
3) Разве алгебра не развлекает?
22497,471 — 236,07x = 198,28x — 7237,22424,35x = 29734,691
x = 70,1 ° C
Проблема № 2: A 45.0 г образца вещества при 55,0 ° C (s = 1,66 кал / г ° C) помещали в калориметр кофейной чашки (c = 4,20 кал / ° C), который содержал 50,0 г этилового спирта при 25,0 ° C (s = 0,590 кал / г ° C). Какая в результате температура?
Комментарий перед решением: обратите внимание, что в этой задаче используются калории, а не джоули. Это не влияет на технику решения.
Решение:
1) Задайте следующее уравнение:
(масса вещества) (Δt вещества) (C p вещества) = (масса спирта) (Δt спирта) (C p спирта) + (калориметрическая константа) (Δt спирта)Существует неявное предположение, что спирт и калориметр запускаются при одинаковой температуре.Это очень безопасное предположение.
2) Введите соответствующие значения:
(45,0 г) (55,0 — x) (1,66 кал / г ° C) = (50,0 г) (x — 25,0) (0,590 кал / г ° C) + (4,20 кал / ° C) (x — 25,0)
3) Алгебра следует:
4108,5 — 74,7x = 29,5x — 737,5 + 4,2x — 105x = 45,7 ° C
Проблема № 3: Кольцо из чистого золота и кольцо из чистого серебра имеют общую массу 17,0 г. Два кольца нагревают до 65,4 ° C и помещают в 12,4 мл воды при температуре 22 ° C.3 ° С. Когда достигается равновесие, температура воды составляет 24,7 ° C. Какая масса у золотого кольца?
Решение:
1) Задайте следующее уравнение:
(масса золота) (Δt золота) (C p золота) + (масса серебра) (Δt серебра) (C p серебра) = (масса воды) (Δt воды) (C p вода)
2) Введите соответствующие значения:
(x) (40,7 ° C) (0,129 Дж г ¯ 1 ° C ¯ 1 ) + (17,0 г — x) (40.7 ° C) (0,237 Дж г ¯ 1 ° C ¯ 1 ) = (12,4 г) (2,4 ° C) (4,184 Дж г ¯ 1 ° C ¯ 1 )
3) Алгебра:
x = 8,98 г
4) Комментарии:
а) Я посмотрел в Интернете значения удельной плавки золота и серебра. Кстати, вы уже должны были запомнить удельную теплоемкость жидкой воды.
б) Масса золотого и серебряного колец исходит из того факта, что их сумма составляет 17,0 г. Мы присвоили «x» массу золотого кольца, поэтому масса серебряного кольца равна 17.0 минус х.
Задача № 4: Образец алюминия массой 5,00 г (удельная теплоемкость = 0,89 Дж · г ¯ 1 ° C ¯ 1 ) и образец железа 10,00 г (удельная теплоемкость = 0,45 Дж · г ¯ 1 ° C ¯ 1 ) нагревают до 100,0 ° C. Затем смесь горячего железа и алюминия по каплям добавляют в 91,9 г воды при 23,7 ° C. Рассчитайте конечную температуру смеси металла и воды, предполагая, что потери тепла в окружающую среду отсутствуют.
Решение:
1) Настройте это:
q Al + q Fe = q вода(5.00 г) (100 ° C — x) (0,89 Дж г ¯ 1 ° C ¯ 1 ) + (10,00 г) (100 ° C — x) (0,45 Дж г ¯ 1 ° C ¯ 1 ) = (91,9 г) (x — 23,7 ° C) (4,184 Дж г ¯ 1 ° C ¯ 1 )
2) Давайте займемся алгеброй (и отбросим все единицы):
(445 — 4,45x) + (450 — 4,5x) = 384,5096x — 9112,87752393,4596x = 10007,87752
x = 25,4 ° C
Задача № 5: Образец металлического железа весом 50,6 г нагревают и помещают в камеру 104.0 г воды при 19,7 ° C в калориметре. Если конечная температура образца железа и воды составляет 24,3 ° C, какой была температура образца железа, когда он был помещен в воду?
Решение:
1) тепло, потерянное железом = тепло, полученное водой:
(масса железа) (Δt железа) (C p железа) = (масса воды) (Δt воды) (C p вода)(50,6 г) (x — 24,3 ° C) (0,450 Дж / г ° C) = (104,0 г) (4,6 ° C) (4,184 Дж / г ° C)
4.6 из 24,3 минус 19,7.
x — 24,3 ° C — это Δt железа. Она перешла от высокой температуры «х» к более холодной 24,3 ° C.
2) Решите относительно x:
(50,6x — 1229,58) (0,450) = 2001,625622,77x — 553,311 = 2001,6256
22,77x = 2554,9366
x = 112,2 ° C
Проблема № 6: Кусок медной трубки весом 505,0 г нагревают до 99,9 ° C и помещают в изолированный сосуд, содержащий 59.8 г воды при 24,8 ° C. При условии отсутствия потерь воды и теплоемкости емкости 10,0 Дж / К, какова конечная температура системы? (C p меди = 0,387 Дж / г К)
Решение:
Нет решения.
Обратите внимание, что значения K и ° C отменяются в задаче. Это связано с тем, что (а) температуры в фактическом расчете являются разницей между двумя значениями температуры и (б) «размер» 1 K равен «размеру» 1 ° C.
Задача № 7: Какой объем 18.Необходимо добавить воду с температурой 5 ° C вместе с куском железа весом 1,23 кг (C p = 0,449 Дж / г градусов C) при температуре 68,5 ° C в изолированном контейнере, чтобы конечная температура смеси вода / металл остается постоянной при 25,6 ° C?
Решение:
тепло, потерянное металлом = тепло, полученное водой(1230 г) (42,9 ° C) (0,449 Дж / г ° C) = (масса) (4,184 Дж / г ° C) (7,1 ° C)
масса = 797,562 грамма
Округление до 3 фиг кажется разумным
798 мл
Проблема № 8: A 2.00 x 10 2 г латунного блока при 85,0 ° C помещают в стакан из пенопласта, содержащий 2,00 x 10 2 г воды при 50,0 ° C. Чашка и окружающая среда не теряют тепло. Найдите конечную температуру смеси.
Решение:
Решение этой проблемы требует теплоемкости латуни. Используйте этот сайт, чтобы узнать стоимость.
Решение предоставляется читателю.
Проблема № 9: Для двух идентичных блоков T f — это среднее значение начальных температур, так что T f = 1/2 (T 1 + T 2 ).Покажите, что это верно для системы из двух блоков, полностью изолированных от окружающей среды. (Подсказка: поскольку блоки сделаны из одного материала, они будут иметь одинаковый C p .)
Решение:
Я буду использовать T 1 для начальной температуры теплого блока и T 2 для начальной температуры холодного блока.тепла, потерянного теплым блоком = тепло, полученное холодным блоком
(масса) (ΔT теплый ) (C p ) = (масса) (ΔT холодный ) (C p )
для одинаковых блоков, масса = масса и C p = C p ; следовательно:
ΔT теплый = ΔT холодный
T 1 — T f = T f — T 2
2T f = T 1 + T 2
T f = 1/2 (T 1 + T 2 )
Проблема № 10: 50.0 г меди при 200,0 ° C помещают во лед при 0,0 ° C. Сколько граммов льда растает?
Решение:
1) Медь опустится до нуля по Цельсию, выделяя определенное количество тепла:
(50,0 г) (200,0 ° C) (0,385 Дж / г ° C) = 3850 Дж
2) Все тепло от меди тает лед:
(334,16 Дж / г) (x) = 3850 Джx = 11,5 г (на три сига)
Проблема № 11: Предположим, что 0.82 г воды конденсируется на железном блоке массой 75,0 г, который первоначально имеет температуру 24,0 ° C. Если тепло, выделяющееся при конденсации, идет только на нагрев железного блока, какова конечная температура (в ° C) железного блока?
Решение:
(0,82 г / 18,01532 г / моль) (40,7 кДж / моль) = 1,8525673 кДж = 1852,5673 Дж, потерянных водойЧтобы продолжить расчет, вам необходимо знать удельную теплоемкость железа. В этом источнике указано 0,444 Дж / г ° C.
1852,5673 J = (75.0 г) (x) (0,444 Дж / г ° C)
x = 55,6 ° C изменение
24,0 ° C + 55,6 ° C = 79,6 ° C
Задача № 12: 400,0 г железа нагревают в пламени и затем сбрасывают в химический стакан, содержащий 1,00 кг воды. Исходная температура воды составляла 20,0 ° C, а конечная температура воды и железа составляла 32,8 ° C после достижения теплового равновесия. Какова была исходная температура горячего железного прутка? (Предположим, что химический стакан или окружающий воздух не теряют тепло.)
Решение:
q железо = q вода(400,0 г) (x — 32,8 ° C) (0,444 Дж / г ° C) = (1000 г) (12,8 ° C) (4,184 Дж / г ° C)
177,6x — 5825,28 = 53555,2
x = 334,35 ° С
Для трех сигнатур, 334 ° C
Задача № 13: Образец металла весом 30,66 г находится при температуре 81,0 ° C, когда его помещают в стакан из пенополистирола, содержащий 40,0 г воды при 23,0 ° C. Температура воды поднялась до 25.0 ° С. Теплостойкость чашки 42 Дж / ° C.
а) Сколько джоулей потерял металл из-за воды?
(б) Какова удельная теплоемкость металла?
(c) Какова атомная масса металла?
(d) Что это за металл?
Решение:
q = [(40,0 г) (2,0 ° C) (4,184 Дж / г ° C)] + [(42 Дж / ° C) (2,0 ° C)] = 418,72 Дж (ответ на вопрос a)418,72 Дж = (30,66 г) (56,0 ° C) (x)
x = 0,244 Дж / г ° C) (ответ на b)
Используйте закон Дюлонга-Пети для атомной массы:
(удельная теплоемкость) умножить на (атомную массу) = 3R
(0.244 Дж / г ° C) (x) = (3) (8,31447 Дж / К моль)
x = 102,2 г / моль (ответ на вопрос c)
Примечание: ° C и K отменяются, потому что «размер» каждой единицы температуры одинаков: 1 ° C = 1 K.
Родий наиболее близок к 102,9 г / моль (ответ на d)
Просматривая удельную теплоемкость Rh, я нашел 0,242 Дж / г C.
Вот вопрос Yahoo Answers о законе D-P (обратите внимание, что это приблизительный закон).
Задача № 14: Неочищенный образец цинка имеет массу 7.35 г. Образец реагирует с 150,00 г разбавленной соляной кислоты внутри калориметра. Масса калориметра 520,57 г, удельная теплоемкость 0,400 Дж / г ° C. Когда происходит реакция, температура внутри калориметра повышается с 14,5 ° C до 29,7 ° C. Какова процентная чистота образца цинка?
Комментарий: мы предполагаем, что плотность раствора HCl составляет 1,00 г / мл, а удельная теплоемкость раствора HCl такая же, как у чистой воды.
Решение:
1) Общая энергия, выделяемая при реакции цинка с HCl:
q = (масса воды) (Δt) (C p вода) + (массовый калориметр) (Δt) (C p калориметр)q = (150.0 г) (15,2 ° C) (4,184 Дж / г ° C) + (370,57 г) (15,2 ° C) (0,400 Дж / (г ° C))
q = 9539,52 + 2253,0656 = 11792,5856 Дж
Примечание: 370,57 происходит от 520,57 минус 150,00
2) Теперь нам нужно посмотреть, сколько цинка выделяет указанное выше количество тепла. Для этого нам понадобится энтальпия этой реакции:
Zn (т.) + 2HCl (водн.) —> ZnCl 2 (водн.) + H 2 (г)Некоторый поиск в Интернете (см. Задачу 5.66) дает значение -152,4 кДж на моль Zn.
Этот расчет:
11792,5856 Дж разделить на 152400 Дж / моль = 0,07738 моль Zn
Тогда этот расчет:
0,07738 моль раз 65,409 г / моль = 5,06 г
3) Определите процентное содержание цинка в образце:
(5,06 г / 7,35 г) умножить на 100 = 68,8% (до трех сигнатур)
Задача № 15: Кусок железа весом 25,75 г и кусок золота 28,45 г, каждый при 100,0 ° C, были опущены в 570,0 мл воды при 17,70 ° C. Молярная теплоемкость железа и золота 25.19 Дж моль ¯ 1 ° C ¯ 1 и 25,41 Дж моль ¯ 1 ° C ¯ 1 соответственно. Какова конечная температура воды и кусков металла?
Решение:
1) Настройка проблемы:
джоулей, высвобожденных железом + общее количество джоулей, высвобожденных золотом = общее количество джоулей, поглощенных водой(25,75 г / 55,845 г / моль) (100,0 — x) (25,19 Дж / моль ° C) + (28,45 г / 196,97 г / моль) (100,0 — x) (25,41 Дж / моль ° C) = (570.00 г) (x — 17,70) (4,184 Дж / г ° C)
Найдите x, который является конечной температурой.
2) Вот что означают несколько терминов:
(25,75 г / 55,845 г / моль) —> моль Fe(28,45 г / 196,97 г / моль) —> моль Au
(100,0 — x) —> изменение температуры Fe и Au (каждый из них начинается при 100 ° C и снижается до конечной температуры, обозначенной символом ‘x’)
(x — 17,70) —> изменение температуры воды
Обратите внимание, что удельная теплоемкость воды выражается в граммах, а Fe и Au — в молях.Это нормально, так как я использую моль Fe и Au (чтобы отменить с помощью моля в Fe и в удельной теплоемкости Au), и я использую граммы воды (чтобы отменить с помощью граммов в удельной теплоемкости для воды). Каждый блок будет отменен должным образом.
Задача № 16: Подсчитайте количество граммов льда, которое растает, если 1000,0 г железа при 500,0 ° C поместить в смесь льда с водой. Теплота плавления воды 334,166 Дж / г. Удельная теплоемкость железа = 0,448 Дж / г ° C. Предположим, что льда достаточно, чтобы немного осталось после достижения теплового равновесия.
Решение:
Последнее предложение имеет решающее значение, поскольку оно гарантирует, что температура не изменится, будет таять только лед, а температура всей системы останется на уровне нуля по Цельсию.
1) Определите энергию, выделяемую утюгом:
q = (масса) (изменение температуры) удельная теплоемкость)q = (1000,0 г) (500,0 ° C) (0,448 Дж / г ° C)
q = 224000 Дж
Тот факт, что остается немного льда, позволяет нам точно знать, что железо упадет с 500.От 0 ° C до 0 ° C.
2) Определите лед, который растает:
224000 Дж разделить на 334,166 Дж / г = 670,3 г
3) Эту проблему можно было решить следующим образом:
(1000,0 г) (500,0 ° C) (0,448 Дж / г ° C) = x / 334,166 Дж / гПредполагается, что 100% энергии, теряемой железом, идет на таяние льда.
Проблема № 17: 18,0 мл воды при 28,0 ° C добавляют в горячую сковороду. Вся вода превращается в пар при 100.0 ° С. Масса сковороды 1,25 кг, а молярная теплоемкость железа 25,19 Дж / моль ° C. Какое изменение температуры сковороды?
Решение:
1) Определите количество энергии, необходимое для нагрева и кипячения воды:
тепло: q = (18,0 г) (72,0 ° C) (4,184 Дж / г ° C) = 5422,464 Дж = 5,422464 кДжкипения: q = (40,7 кДж / моль) (18,0 г / 18,0 г / моль) = 40,7 кДж
Всего: 40,7 кДж + 5,422464 кДж = 46,122464 кДж
Не буду округлять до окончательного ответа.
2) Определите изменение температуры сковороды:
46122,464 Дж = (22,38338 моль) (Δt) (25,19 Дж / моль ° C)Δt = 81,8 ° С
Обратите внимание, что используются моль железа, а не граммы. Это из-за единиц удельной теплоемкости, указанных в задаче.
Задача № 18: Медный шар имеет массу 125 граммов и имеет температуру 145 ° C. Этот шар помещается в калориметр, содержащий 25,0 граммов льда при -35.0 ° С. Какова будет конечная температура медного шара? (удельная теплоемкость меди = 0,387 Дж / г ° C)
Решение:
Медный шар будет отдавать тепло льду. Весь лед сначала нагреется до 0 ° C, а затем начнет таять. По мере таяния льда создается система жидкого льда, температура которой сохраняется при 0 ° C. Если медь растопит весь лед, только тогда жидкая вода переместится от нуля ° C до некоторой конечной температуры равновесия с медью.
1) Давайте нагреем лед с -35 ° C до 0 ° C и посмотрим, сколько энергии на это потребуется.
q = (25 г) (35 ° C) (2,06 Дж / г ° C) q = 1802,5 Дж
2) Посмотрим, что произойдет с температурой меди при снятии 1802,5 Дж.
1802,5 Дж = (125 г) (x) (0,387 Дж / г ° C)х = 37,26 ° С
145 — 37,26 = 107,74 ° С
3) Теперь давайте охладим медный шар до нуля и посмотрим, сколько энергии при этом выделяется.
q = (125) (107,74) (0,387) = 5211,9225 Дж4) Далее нам нужно выяснить, сколько льда растаяло с использованием 5211.9225 Дж энергии.
5211,9225 Дж = (x) (6020 Дж / моль) x = 0,86577 моль0,86577 моль, умноженная на 18,015 г / моль = 15,6 г
Поскольку для начала у нас было 25 г льда, при таянии 15,6 г льда в системе остается некоторое количество льда. Поскольку весь лед должен растаять, прежде чем мы сможем перейти от 0 ° C, мы заключаем, что вся система жидкий лед-медь находится при 0 ° C, когда достигается равновесие.
Задача № 19: Медный куб массой 100 грамм нагревают на кипящей водяной бане до 100.0 по Цельсию. Куб вынимают из ванны и кладут на очень большой кусок льда, имеющий температуру 0,00 по Цельсию. Какова максимальная масса льда, который предположительно может быть растоплен за счет теплообмена, если предположить, что вся тепловая энергия используется для плавления льда?
Решение:
1) Давайте определим, сколько энергии высвободила медь, когда растопила лед:
q = (масса) (Δt) (удельная теплота)q = (100,0 г) (100,0 ° C) (0,385 Дж / г ° C)
q = 3850 Дж
2) Теперь определяем, сколько льда можно растопить:
q = (масса) (теплота плавления)3850 Дж = (334.166 Дж / г) (x)
x = 17,25 г
до трех сигарей, 17,2 г (с использованием правила округления на пять)
3) Комментарии:
(a) удельную теплоемкость меди можно найти в учебнике или в Интернете.
(b) теплоту плавления можно найти (или рассчитать, исходя из молярной теплоты плавления, 6,02 кДж / моль)Задача № 20: Кусок алюминия весом 12,0 г при 22,0 ° C помещают в 175,0 мл воды при 85,0 ° C и дают ему достичь теплового равновесия.Какая будет конечная температура? (Другие факторы, такие как передача тепла воздуху, следует игнорировать.) Удельная теплоемкость алюминия составляет 0,215 кал / г ° C.
Решение:
1) Перед тем, как приступить к решению, можете ли вы обнаружить ошибку в этом предложенном решении (а дело не в том, что ни на чем нет блоков)?
(175,0) (4,184) (85,0 — Т) = (12) (0,215) (Т — 22,0)Ошибка в неправильном смешивании единиц. 4,184 — удельная теплоемкость жидкой воды в Дж ¯ г ¯ 1 ° C ¯ 1 и 0.215 — удельная теплоемкость алюминия в кал. ¯ 1 ° C ¯ 1 .
Вы не можете использовать эти две единицы удельной теплоемкости в одной задаче и быть правильным. Единицы должны совпадать, так что обе удельные температуры должны быть в Дж ¯ 1 ° C ¯ 1 или оба должны быть в кал g ¯ 1 ° C ¯ 1 . Вы не можете, чтобы один был в одном блоке, а другой — в другом, и при этом оставался правильным.
Исходный вопрос в Yahoo Answers содержал несколько ответов с несколькими вариантами ответов, и один из них был ответом, полученным в результате вышеупомянутой ошибки.
2) Правильная установка (и решение) с использованием калорий:
(175,0) (1,00) (85,0 — Т) = (12) (0,215) (Т — 22,0)14875 — 175 зуб. = 2,58 зуб. — 56,76
14818,24 = 177,58 т
Т = 83,4 ° С
Решение в J g ¯ 1 ° C ¯ 1 предоставляется читателю.
Перейти к расчету конечной температуры при смешивании металла и воды
Переход к расчету конечной температуры при смешивании двух проб воды
Назад в меню термохимии
Плотность воды | Глава 3: Плотность
Тебе это нравится? Разве это не нравится? Пожалуйста, уделите время и поделитесь с нами своим мнением.Спасибо!
Урок 3.3
Ключевые понятия
- Жидкости, как и твердые тела, обладают собственной характеристической плотностью.
- Объем жидкости можно измерить непосредственно с помощью градуированного цилиндра.
- Молекулы разных жидкостей имеют разный размер и массу.
- Масса и размер молекул в жидкости, а также то, насколько плотно они упакованы вместе, определяют плотность жидкости.
- Так же, как и твердое тело, плотность жидкости равна массе жидкости, деленной на ее объем; D = м / об.
- Плотность воды — 1 грамм на кубический сантиметр.
- Плотность вещества одинакова независимо от размера образца.
Сводка
Учащиеся измеряют объем и массу воды, чтобы определить ее плотность. Затем они измеряют массу разных объемов воды и обнаруживают, что плотность всегда одинакова.Учащиеся составляют график зависимости между объемом и массой воды.
Цель
Студенты смогут измерять объем и массу воды и рассчитывать ее плотность. Студенты смогут объяснить, что, поскольку любой объем воды всегда имеет одинаковую плотность при данной температуре, эта плотность является характерным свойством воды.
Оценка
Загрузите лист активности учащегося и раздайте по одному каждому учащемуся, если это указано в задании.Лист упражнений будет служить компонентом «Оценить» каждого плана урока 5-E.
Безопасность
Убедитесь, что вы и ваши ученики носите правильно подогнанные очки.
материалов для каждой группы
- Градуированный цилиндр, 100 мл
- Вода
- Весы с граммовой суммой (более 100 г)
- Капельница
Материалы для демонстрации
- Вода
- Два одинаковых ведра или большие емкости
Проведите демонстрацию, чтобы представить идею о плотности воды.
Материалы
- Вода
- Два одинаковых ведра или большие емкости
Подготовка учителей
Наполните одно ведро наполовину и добавьте примерно 1 стакан воды в другое.
Процедура
- Выберите ученика, который поднимет оба ведра с водой.
- Спросите студента-добровольца, какое ведро имеет большую массу.
Ожидаемые результаты
Ведро с большим количеством воды имеет большую массу.
Спросите студентов:
- В уроках 3.1 — Что такое плотность? и 3.2 — Метод вытеснения воды, плотность твердых тел определяется путем измерения их массы и объема. Как вы думаете, жидкость, такая как вода, может иметь плотность?
- Студенты должны понимать, что вода имеет объем и массу. Поскольку D = m / v, вода также должна иметь плотность.
- Как вы думаете, можно определить плотность жидкости, такой как вода?
- Ожидается, что на данный момент студенты не смогут полностью ответить на этот вопрос.Это сделано как начало расследования. Но студенты могут понять, что сначала им нужно каким-то образом определить массу и объем воды.
- Может ли и небольшое, и большое количество воды, которое поднял ваш одноклассник, иметь одинаковую плотность?
- Студенты могут указать, что ведро с большим количеством воды имеет большую массу, но больший объем. Ковш с меньшей массой имеет меньший объем. Таким образом, возможно, что разное количество воды может иметь одинаковую плотность.
Раздайте каждому учащемуся лист с упражнениями.
Студенты будут записывать свои наблюдения и отвечать на вопросы о деятельности в листе действий. «Объясни это с помощью атомов и молекул» и «Возьми это». Дальнейшие разделы рабочего листа будут заполнены либо в классе, либо в группах, либо индивидуально в зависимости от ваших инструкций. Посмотрите на версию листа с заданиями для учителя, чтобы найти вопросы и ответы.
Обсудите со студентами, как найти объем и массу воды.
Скажите студентам, что они попытаются найти плотность воды.
Спросите студентов:
- Какие две вещи вам нужно знать, чтобы определить плотность воды?
- Студенты должны понимать, что им нужен объем и масса пробы воды, чтобы определить ее плотность.
- Как можно измерить объем воды?
- Предложите учащимся использовать мерный цилиндр для измерения объема в миллилитрах.Напомните учащимся, что каждый миллилитр равен 1 см 3 .
- Как можно измерить массу воды?
- Предложите учащимся использовать весы для измерения массы в граммах. Скажите студентам, что они могут набрать массу, взвесив воду. Однако, поскольку вода — это жидкость, она должна быть в каком-то контейнере. Таким образом, чтобы взвесить воду, они должны взвесить и контейнер. Объясните учащимся, что им придется вычесть массу пустого градуированного цилиндра из массы цилиндра и воды, чтобы получить массу только воды.
Попросите учащихся найти массу различных объемов воды, чтобы показать, что плотность воды не зависит от размера образца.
Вопрос для расследования
Имеет ли разное количество воды одинаковую плотность?
Материалы для каждой группы
- Градуированный цилиндр, 100 мл
- Вода
- Весы с граммовой суммой (более 100 г)
- Капельница
Процедура
- Найдите массу пустого градуированного цилиндра.Запишите массу в граммах в таблице на листе активности.
Налейте 100 мл воды в мерный цилиндр. Постарайтесь быть максимально точными, убедившись, что мениск находится прямо на отметке 100 мл. Используйте пипетку, чтобы добавить или удалить небольшое количество воды.
- Взвесьте мерный цилиндр с водой. Запишите массу в граммах.
- Найдите массу только воды, вычтя массу пустого градуированного цилиндра.Запишите в таблицу массу 100 мл воды.
- Используйте массу и объем воды для расчета плотности. Запишите в таблицу плотность в г / см 3 .
- Слейте воду, пока в мерном цилиндре не будет 50 мл воды. Если вы случайно вылили слишком много воды, добавляйте воду, пока не дойдете до 50 мл.
Найдите массу 50 мл воды. Запишите массу в листе деятельности. Рассчитайте и запишите плотность.
- Затем слейте воду, пока в мерном цилиндре не будет 25 мл воды. Найдите массу 25 мл воды и запишите ее в таблицу. Рассчитайте и запишите плотность.
Таблица 1. Определение плотности различных объемов воды. Объем воды 100 миллилитров 50 миллилитров 25 миллилитров Масса мерного цилиндра + вода (г) Масса пустого градуированного цилиндра (г) Масса воды (г) Плотность воды (г / см 3 ) Ожидаемые результаты
Плотность воды должна быть близка к 1 г / см 3 .Это верно для 100, 50 или 25 мл.
Спросите студентов:
- Посмотрите на свои значения плотности на диаграмме. Кажется ли, что плотность разных объемов воды примерно одинакова?
- Помогите учащимся увидеть, что большинство различных значений плотности составляют около 1 г / см 3 . Они могут задаться вопросом, почему не все их значения равны 1 г / см 3 . Одной из причин могут быть неточности в измерениях. Другая причина в том, что плотность воды меняется в зависимости от температуры.Вода наиболее плотная при 4 ° C и при этой температуре имеет плотность 1 г / см 3 . При комнатной температуре около 20–25 ° C плотность составляет около 0,99 г / см 3 .
- Какова плотность воды в г / см3?
- Ответы учащихся могут быть разными, но в большинстве случаев их значения должны составлять около 1 г / см. 3 .
Попросите учащихся построить график своих результатов.
Помогите учащимся составить график данных из их листа деятельности.Ось X должна быть объемом, а ось Y — массой.
Когда ученики наносят на график свои данные, должна быть прямая линия, показывающая, что по мере увеличения объема масса увеличивается на ту же величину.
Обсудите наблюдения, данные и графики учащихся.
Спросите студентов:
- С помощью графика найдите массу 40 мл воды. Какова плотность этого объема воды?
- Масса 40 мл воды 40 грамм.Поскольку D = m / v и mL = cm 3 , плотность воды составляет 1 г / см 3 .
- Выберите объем от 1 до 100 мл. Используйте свой график, чтобы найти массу. Какова плотность этого объема воды?
- Независимо от того, весят ли учащиеся 100, 50, 25 мл или любое другое количество, плотность воды всегда будет 1 г / см 3 .
Скажите студентам, что плотность — это характерное свойство вещества. Это означает, что плотность вещества одинакова независимо от размера образца.
Спросите студентов:
- Является ли плотность характерным свойством воды? Откуда вы знаете?
- Плотность — это характерное свойство воды, потому что плотность любого образца воды (при той же температуре) всегда одинакова. Плотность 1 г / см 3 .
Объясните, почему плотность воды любого размера всегда одинакова.
Спроецировать изображение Плотность воды.
Все молекулы воды имеют одинаковую массу и размер. Молекулы воды также расположены довольно близко друг к другу. Они упакованы одинаково во всей пробе воды. Таким образом, если объем воды имеет определенную массу, удвоенный объем будет иметь удвоенную массу, трехкратный объем будет иметь трехкратную массу и т. Д. Независимо от того, какой размер образца воды вы измеряете, соотношение между массой и объемом всегда будет таким же. Поскольку D = m / v, плотность одинакова для любого количества воды.
Спроектируйте анимацию «Жидкая вода».
Молекулы воды всегда в движении. Но в среднем они все упакованы одинаково. Следовательно, соотношение между массой и объемом одинаково, а плотность одинакова. Это верно независимо от размера выборки или от того, где вы ее выбрали.
Попросите учащихся подумать, совпадает ли плотность большого куска твердого вещества с плотностью меньшего куска.
Дайте учащимся время для расчета плотности каждого из трех образцов, нарисованных на их листе с заданиями, и ответьте на соответствующие вопросы.
Спросите студентов:
- Плотность жидкости не зависит от размера образца. Может ли это быть верно и для твердых тел? Чтобы выяснить это, вычислите плотность каждого из трех образцов.
- Да. Плотность твердого вещества одинакова независимо от размера образца.
- Образец А имеет массу 200 г. Какова плотность образца А?
- D = м / об
- D = 200 г / 100 см 3
- D = 2 г / см 3
- Если разрезать образец A пополам и посмотреть только одну половину, получится образец B. Какова плотность образца B?
- Если учащиеся не знают, какова масса, скажите им, что это половина массы образца А.Поскольку образец A был 200 г, образец B составляет половину объема и, следовательно, половину массы (100 г).
- D = м / об
- D = 100 г / 50 см 3
- D = 2 г / см 3
- Если разрезать образец B пополам, вы получите образец C. Какова плотность образца C?
- D = м / об
- D = 50 г / 25 см 3
- D = 2 г / см 3
Как откалибровать малые весы с помощью четвертей
Обычной практикой при покупке какого-либо измерительного устройства, такого как шкала или линейка, является его калибровка.Калибровка важна для определения точности этого измерительного устройства.
Например, если ваш друг дает вам старую деревянную 12-дюймовую линейку, вы можете откалибровать линейку, чтобы определить, действительно ли она 12 дюймов, поскольку древесина может сжиматься и расширяться из-за температуры.
Вы можете использовать новую пластиковую 12-дюймовую линейку, которую не гнули и не меняли с момента изготовления, чтобы определить, действительно ли деревянная линейка 12 дюймов или нет. Вы должны предположить, что производители также откалибровали машины, которые делают пластиковые линейки, потому что, конечно, вы должны принять, что пластиковая линейка на самом деле 12 дюймов.
А как насчет калибровки весов для правильного измерения массы? Давайте рассмотрим процедуру быстрой калибровки цифровых весов.
TL; DR (слишком долго; не читал)
Калибровка — это процедура сравнения измерения некоторой величины, измеренной устройством, с известным стандартом.
D.I.Y. Процедура калибровки весов
Во-первых, поскольку мы находимся на Земле, вес объекта равен массе, умноженной на ускорение свободного падения.Иногда «масса» и «вес» используются как синонимы, потому что вес объекта — это просто масса, масштабируемая по ускорению свободного падения. Однако важно помнить, что масса — это количество вещества в объекте, а вес — это сила тяжести, действующая на этот объект.
Чтобы начать калибровку, вам нужно найти что-то, что можно использовать в качестве стандартной массы.
Новые кварталы Монетного двора США — вариант; новенький квартал в США имеет массу 5,670 грамма.Другие варианты — новые гроши или никели США; монета имеет массу ровно 2,500 граммов, а монета — 5,000 граммов.
Поместите выбранную монету на весы и прочитайте результат. Если вы поместили на шкалу пенни, вы должны прочитать 2,500 грамма. Если вы поместите четверть на шкале, результат должен составить 5,670 грамма.
Если весы показывают 5,671 грамма, очевидно, что разница между показанием и известной массой составляет 0,001 грамма. Таким образом, вы также определили, что любая ошибка калибровки, вероятно, будет около 10 -3 грамм, что означает, что шкала достаточно точна для десятых и сотых долей.
Если показание для пенни было 2,500, но показание для четверти было 5,700 граммов, вы можете видеть, что разрешение шкалы составляет только одну десятую грамма. Это еще одна форма калибровки.
Объекты весом 10 грамм
Может оказаться полезным иметь ряд объектов известной массы, чтобы определить, есть ли какие-либо изменения в калибровке шкалы для экстремальных значений массы. Таким образом, найдите несколько разных предметов, например предметы, которые весят 10 граммов (или имеют массу 10 граммов), такие как монеты, а также предметы домашнего обихода, которые весят 100 граммов.
Почему бы просто не сложить тонну монет? Если у вас есть 20 центов или 40 пенни, у вас есть 100 граммов, которые вы можете использовать для калибровки. Поместите монеты на весы и наблюдайте за показаниями. Масса должна быть ровно 100 000 граммов. Если показание больше или меньше 100 000 грамм, вы снова можете определить значение калибровки.
Некоторые шкалы более точны для больших масс, поэтому возможно, что для небольших масс (например, одной монеты) существует заметная разница между измерением и известной массой, которая исчезает при добавлении монет.
Калибровка — это общий метод, который можно использовать для определения того, насколько точно любое измерительное устройство способно измерить заданное количество.
Алюминий и углеродное волокно — сравнение материалов
Какой материал может заменить алюминий и обеспечить повышенную прочность, а также меньший вес?
Можно ли изготавливать компоненты, которые весят на 50% меньше алюминия, но обладают такой же или большей прочностью?
Алюминий — широко используемый материал, но углеродное волокно представляет собой новое решение для многих инженеров-строителей.В этой статье указаны различия между этими материалами и описаны их сильные и слабые стороны.
Каковы сильные и слабые стороны этих материалов?
Прочтите эту статью, чтобы узнать больше о сильных и слабых сторонах алюминия и углеродного волокна.
ВведениеУглеродное волокно используется в отраслях, где требуется высокая прочность и жесткость по отношению к весу. например в авиации, автоматизированные машины, гоночные автомобили, профессиональные велосипеды, реабилитационное оборудование.
Благодаря своему уникальному дизайну, углеродное волокно также используется в производстве предметов роскоши, включая часы, кошельки и т. Д. Этот материал делает продукт уникальным в мире роскоши и элегантности и помогает ему быть на шаг впереди конкурентов.
Сопоставить свойства углеродного волокна со сталью или алюминием непросто. В отличие от углеродного волокна, металлы обычно однородны. — изотропны, что обеспечивает одинаковые свойства во всех направлениях.
Прочность и жесткость компонента из углеродного волокна достигается путем размещения тканей определенным образом. Это открывает возможности для производителя, но также требует больших знаний и опыта.
В этом исследовании анализируются 10 наиболее важных свойств для инженеров-строителей:
- Жесткость и прочность материала по отношению к весу.
- Жесткость и прочность материала одинаковой толщины.
- Вес / плотность.
- Механическая обработка.
- Тепловое расширение.
- Теплопроводность.
- Температурная стойкость
- Долгосрочная работа.
- Осуществление производственного процесса.
- Сводка
Обратите внимание, что любое упоминание углеродного волокна и его характеристик в этом документе относится к композитному материалу, изготовленному из углеродного волокна и эпоксидной смолы.
1. Жесткость и прочность материала по отношению к весу
Чтобы объяснить жесткость по отношению к весу, представьте себе лист шириной 5 см, длиной 50 см и толщиной 2 мм.Когда вы подвешиваете груз весом 5 кг к концу листа, нагрузка приведет к изгибу, а степень изгиба будет соответствовать жесткости. Для разных материалов лист одинаковой толщины будет иметь разные свойства изгиба. Чем жестче материал, тем меньше будет изгибов. После снятия нагрузки лист примет первоначальную форму.
А теперь представьте, что полоса материала подвергается более высокой нагрузке — это вызовет текучесть полосы, и после сброса нагрузки полоса восстанавливает свою первоначальную форму.Это сила делает это возможным. Чем выше прочность материала, тем большую нагрузку ему потребуется, прежде чем последует постоянная текучесть.
Помимо прочности и жесткости, еще одним важным свойством для инженеров-проектировщиков является вес элемента, который определяется плотностью.
Жесткость материала измеряется модулем Юнга. Однако одного этого параметра недостаточно для определения жесткости материала без учета веса данного элемента.
Например, в случае велосипедной рамы (размеры, геометрия, толщина стенки) из двух разных металлов: стали и алюминия, стальная будет иметь в 3 раза большую жесткость, чем алюминиевая. Но если учитывать еще и вес элементов, то стальная рама, хотя она имеет в 3 раза большую жесткость, чем алюминиевая, она также будет в 3 раза тяжелее .
Эти числа являются приблизительными, поскольку на практике инженер-конструктор указывает геометрию для выбранного материала, например.грамм. в случае алюминиевой рамы велосипеда чаще всего увеличивают диаметр рамы, а также толщину стенок. В случае велосипедной рамы жесткость и прочность напрямую связаны с геометрией и толщиной стенки (увеличение толщины стенки в 2 раза приводит к увеличению жесткости примерно в 8 раз).
Прочность зависит не только от материала и толщины секции, но и от ее геометрии.На самом деле существует много разных факторов, но именно отношение жесткости материала к его весу является общим знаменателем и упрощает сравнение и анализ различных материалов.
Отношение жесткости к весу (а именно удельный модуль) на практике является наиболее эффективным для определения жесткости материала , поскольку для большинства инженеров-конструкторов жесткость и вес являются наиболее важными параметрами.
Углеродное волокно — это материал, обладающий жесткостью и прочностью при низкой плотности. — он легче алюминия и стали, что дает множество практических преимуществ.
Удельный вес. Углеродное волокно обеспечивает от 2 до 5 раз большую жесткость (в зависимости от используемого волокна) , чем алюминий и сталь .В случае конкретных компонентов, которые будут подвергаться нагрузке только в одной плоскости, изготовленных из однонаправленного углеродного волокна, его жесткость будет в 5-10 раз больше, чем у стали или алюминия (того же веса).
В следующих таблицах сравниваются жесткость и устойчивость к повреждениям для различных материалов с одинаковым весом . Для анализа было применено двунаправленное углеродное волокно — одно из них чаще всего используется для производства композитов, а однонаправленное углеродное волокно — иногда используется, в основном для изделий, в которых напряжение ожидается только в одной плоскости.
Анализ алюминия, стали и двунаправленного углеродного волокна на жесткость по отношению к весу и прочность по отношению к весу:
| Алюминий | Сталь | Углеродное волокно в двух направлениях — общий модуль | Углеродное волокно с двухсторонним направлением — улучшенный модуль | Углеродное волокно в двух направлениях — максимальный модуль | |
| Жесткость против веса (Удельный модуль) | 26 | 25 | 56 | 83 | 120 |
| Устойчивость к повреждениям (Удельная прочность) | 214 | 254 | 392 | 211 | 126 |
Анализ алюминия, стали и однонаправленного углеродного волокна на жесткость по отношению к весу и прочность по отношению к весу:
| Алюминий | Сталь | Углеродное волокно в одном направлении — общий модуль | Углеродное волокно с односторонним направлением — улучшенный модуль | Углеродное волокно в одном направлении — максимальный модуль | |
| Жесткость против веса (Удельный модуль) | 26 | 25 | 113 | 166 | 240 |
| Устойчивость к повреждениям (Удельная прочность) | 214 | 254 | 785 | 423 | 252 |
Приведенные выше данные для листов из углеродного волокна относятся к образцу, изготовленному с использованием технологии вливания эпоксидной смолы (соотношение углеродного волокна к смоле 70/30%).
Приведенное выше утверждение демонстрирует множество преимуществ, которые дает углеродное волокно, а также элементы, разработанные и изготовленные из углеродного волокна. Ткани с улучшенным и самым высоким модулем относятся к специальным материалам (к сожалению, очень дорогостоящим), которые обладают характеристиками жесткости в 2 или 3 раза больше, чем стандартное углеродное волокно, и используются в основном в военных приложениях и в аэрокосмической промышленности.
Чтобы интерпретировать результаты, представленные в таблице, представьте, что инженер-конструктор собирается сконструировать прочный и легкий лист из углеродного волокна толщиной 1 м 2 с максимальным весом 10 кг и он рассматривает алюминий, сталь и углеродное волокно.
Помня о предельном весе в 10 кг , инженер-конструктор может выбрать:
- Стальной лист толщиной около 1,5 мм.
- Лист алюминиевый толщиной 4 мм.
- Углеродное волокно лист около толщиной 7 мм.
Углеродное волокно обеспечивает 2 важных преимущества.
Углеродное волокно предлагает большую жесткость (как описано выше) при более низкой плотности, и, следовательно, продукт того же веса может быть толще, что приведет к повышению жесткости только за счет увеличения толщины.Проще говоря, увеличение толщины материала в 2 раза обеспечивает жесткость 2 3 — то есть примерно в 8 раз больше. Это дает много возможностей для снижения веса за счет использования углеродного волокна.
2. Жесткость и прочность материала при одинаковой толщине стенки элементаОчень часто инженеры-конструкторы ищут материал, который позволил бы им изготовить компонент, идентичный алюминиевому по всем размерам, включая толщину .В таблицах ниже показаны сравнения жесткости и прочности компонентов одинаковой толщины, изготовленных из алюминия, стали и углеродного волокна. Обратите внимание, что компонент из углеродного волокна тех же размеров будет на 42% легче алюминиевого и более чем в 5 раз легче стального. Подробнее читайте в разделе 3. Вес / плотность материала .
Жесткость и прочность при одинаковой толщине стенки: для алюминия, стали и двунаправленного углеродного волокна:
| Алюминий | Сталь | Углеродное волокно в двух направлениях — общий модуль | Углеродное волокно с двухсторонним направлением — улучшенный модуль | Углеродное волокно в двух направлениях — максимальный модуль | |
| Жесткость (модуль Юнга) Единица: ГПа | 69 | 200 | 90,5 | 132 | 190 |
| Предел прочности (Предел прочности — Предел прочности) Единица кН · м / кг | 500 | 1000 | 800 | 368 | 126 |
Жесткость и прочность при одинаковой толщине стенки: для алюминия, стали и однонаправленного углеродного волокна:
| Материал | Алюминий | Сталь | Углеродное волокно в одном направлении — общий модуль | Углеродное волокно с односторонним направлением — улучшенный модуль | Углеродное волокно в одном направлении — максимальный модуль |
| Жесткость (модуль Юнга) Единица: ГПа | 69 | 200 | 181 | 264 | 380 |
| Предел прочности (Предел прочности — Предел прочности ) Единица кН · м / кг | 500 | 1000 | 1600 | 736 | 252 |
Компонент, сделанный из стандартного углеродного волокна той же толщины, что и алюминиевый, будет иметь на 31% большую жесткость, чем алюминиевый , и в то же время вес на 42% меньше и на 60% больше прочности.
Использование углеродного волокна с более высоким модулем упругости и однонаправленной ткани может обеспечить в 4 раза большую жесткость по сравнению с алюминием при аналогичной или улучшенной предельной прочности.
Обратите внимание, что на практике сталь и алюминий имеют предел прочности ниже указанного в таблице.Это связано с тем, что до полного разрушения (расчет предела прочности был основан на этом моменте) металлический элемент подвергнется остаточной деформации (не восстановит свои первоначальные размеры).
Момент возникновения остаточного изгиба (без разрушения) относится к пределу текучести. Для устойчивости к повреждению в приведенных выше данных применялась прочность на разрыв — максимальная прочность, которая относится к сопротивлению полному разрушению (растрескиванию).
Например, при гибке листового алюминия до полного разрушения и растрескивания образец сначала сломается (без возможности восстановить свои первоначальные размеры).Данные, представленные в таблице, относятся к полностью разрушенным образцам (растрескиванию) с предположением, что изгиб приведет к полному разрушению (что не совсем правильно). Углеродное волокно имеет другие характеристики — в случае нагрузки, которая вызывает постоянный изгиб алюминия без восстановления первоначальных размеров, углеродное волокно будет демонстрировать большую эластичность и после кратковременного изгиба восстановит свою форму после снятия нагрузки (эффект возврата пружины). Полное разрушение элемента из углеродного волокна произойдет внезапно и без каких-либо предупреждений — в отличие от алюминия, который имеет некоторые предупреждения, связанные с постоянным изгибом.Всегда помните вышеизложенное при проектировании компонента из углеродного волокна, чтобы предусмотреть некоторый припуск.
В ролике ниже представлено сравнение устойчивости к повреждениям карданного вала из углеродного волокна и стального, а также описан процесс разрушения материала:
Что касается интерпретации результатов в таблице, очевидно, что углеродное волокно с наивысшим модулем упругости обеспечивает исключительную жесткость. Однако сопротивление повреждению уменьшается с увеличением жесткости (более высокий модуль).
Другой пример: лист из углеродного волокна с максимальной жесткостью, сделанный из тканей с наивысшим модулем упругости, будет иметь меньшую устойчивость к повреждениям. Чем больше компонент армирован тканями с наивысшим модулем упругости, тем больше он будет подвержен разрушению при изгибе.
Дальнейший анализ будет проводиться с углеродным волокном со стандартным модулем упругости, и композиты, сделанные из тканей с наивысшим модулем упругости, предоставят возможности благодаря углеродным композитам.
Обратите внимание, что и алюминий, и углеродное волокно могут использоваться в качестве «гибридов», которые придают детали другие рабочие характеристики. В случае алюминия это относится к сплавам наряду с другими металлами, а в случае углеродного волокна — к одновременному использованию арамидных, стеклянных, базальтовых или вектроновых волокон.
Очень распространены композиты кевлар и арамид-кевлар-углерод, которые обеспечивают жесткость и высокую устойчивость к повреждениям , но это будет предметом другого исследования.
3. Вес / плотность материалаВес важен для многих продуктов.Например, снижает вес рычага / улавливателя автоматизированной машины для тяжелых условий эксплуатации, которая работает со скоростью 10 м / сек. позволит увеличить его скорость и продлить срок его службы. В промышленных масштабах это может привести к увеличению производственных мощностей и значительной экономии.
Другим примером может быть инвалидная коляска, уменьшение веса которой облегчает подъем в машину и выход из нее, а также обеспечивает лучший контроль. Это очень очевидно в случае с гоночными автомобилями Формулы 1, где замена алюминия на углеродное волокно привело к снижению веса, что имеет решающее значение в этом виде спорта.
Автоматическая стрела KUKA из углеродного волокна позволяет увеличить рабочую скорость и в то же время уменьшить ее вес, что приводит к уменьшению нагрузки на подшипники и другие детали, подверженные износу.Автоматическая стрела KUKA из углеродного волокна позволяет увеличить рабочую скорость и в то же время уменьшить ее вес, что приводит к уменьшению нагрузки на подшипники и другие детали, подверженные износу.
Из сравнения алюминия с углеродным волокном мы знаем, что плотность материала напрямую влияет на его вес.
Композиты из углеродного волокна имеют плотность 1,55 г / см 3 (эпоксидная смола 30%, углеродное волокно 70%), что в случае алюминия составляет 2,7 г / см 3 и 4,5 г / см 3 для титана или 7,9 г / см 3 для стали.
Композит из углеродного волокна имеет плотность почти в 2 раза меньше, чем у алюминия, и более чем в 5 раз меньше, чем у стали. Следовательно, в компоненте тех же размеров замена алюминия углеродным волокном снизит его вес на ~ 42% . Замена стали углеродным волокном уменьшит вес в 5 раз.
Чтобы проиллюстрировать это, представьте себе лист толщиной 6 мм и площадью 1 м 2 .
Один квадратный метр листа углеродного волокна толщиной 6 мм имеет вес:
- 47,4 кг для стального листа
- 16,2 кг для алюминиевого листа
- 9,3 кг для листа углеродного волокна.
При проектировании изделий и выборе материала необходимо учитывать жесткость, а также прочность данного материала, как описано в разделах 1 и 2 настоящего исследования. На практике возможности снижения веса компонентов за счет замены алюминия углеродным волокном потребовали дополнительных испытаний и экспериментов. Каждый элемент относится к индивидуальному случаю с уникальной геометрией и параметрами. Обычно можно снизить вес на 20-40%, используя углеродное волокно.
Кузов автомобиля из углеродного волокна позволил BMW снизить вес модели IS на 300 кг.BMW запустила производство полных кузовов из углеродного волокна для своей модели I3.Карбоновый кузов позволил снизить вес каждой машины на 300 кг. Ежегодно компания производит десятки тысяч таких автомобилей. На самом деле эта модель интересует больше клиентов, чем первоначально прогнозировала BMW.
Снижение веса за счет использования углеродного волокна возможно и выгодно, особенно для продуктов, в которых значительна направленная сила. В отличие от металлов композиты не демонстрируют одинаковой прочности в любом направлении (не однородны). Фактически именно во время производственного процесса принимаются решения относительно направления тканей (при использовании однонаправленных тканей) и направления, обеспечивающего наибольшую прочность за счет снижения прочности в других местах.Это решение позволяет еще больше снизить вес компонентов из углеродного волокна.
4. Обработка / резкаУглеродное волокно из-за его низкой плотности представляет собой материал, который легко обрабатывается станками с ЧПУ или ручными инструментами, включая угловую шлифовальную машину или дремель.
Углеродное волокно — это материал, который можно легко обработать на станке с ЧПУ — на фото изображен тату-станок, сделанный из углеродного волокна.Несмотря на то, что высококачественные конструкции из углеродного волокна, полученные вакуумным методом (введение смолы, препрег), могут иметь резьбу, там, где требуется много резьбовых соединений, вместо них используются специальные вставки.
Алюминиевые элементы соединяют чаще всего сваркой, клепкой или вставками. С углеродным волокном чаще всего применяется склейка, при необходимости с армирующими заклепками и вставками. Современные эпоксидные клеи обеспечивают прочность склеивания, аналогичную сварке.
Интересно, что Ferrari постепенно внедряла новую технологию, которая заменила сварку алюминия склеиванием эпоксидным клеем . В настоящее время Ferrari 458 Italia имеет 70 м сварных швов и 8 м клея .Главный инженер Ferrari Moruzzi ожидает, что в будущем из-за изменения производственных процессов в кузовах автомобилей будет больше склеивания, чем сварки. Для Ferrari это возможность использовать другие алюминиевые сплавы, которые обладают улучшенными характеристиками, но не поддаются сварке.
Сравнивая склеивание со сваркой, обратите внимание, что склеивание требует простого внедрения технологии (хотя требуются ноу-хау и опыт).
Технология склеивания широко используется в авиационной промышленности для снижения веса и, в то же время, снижения расхода топлива.
Однако склеивание имеет некоторые недостатки, в том числе подготовку поверхности или время, необходимое для приклеивания клеевого покрытия. Во многих случаях компоненты, которые могут подвергнуться удару (например, в автомобильной аварии), усилены специальными вставками для противодействия внезапной разрушающей нагрузке.
Технология склеиваниябудет использоваться чаще в связи с разработкой более мощных клеев и повышением осведомленности о ее преимуществах и возможных возможностях.
5.Тепловое расширениеКаждый материал обладает разными характеристиками теплового расширения.
Тепловое расширение связано с изменением размеров материала из-за изменения температуры. Углеродное волокно на практике показывает почти нулевое тепловое расширение, поэтому оно широко используется в устройствах, включая 3D-сканеры.
Поскольку на практике углеродное волокно показывает почти нулевое тепловое расширение, оно широко используется в устройствах, включая 3D-сканеры.Поскольку на практике углеродное волокно показывает почти нулевое тепловое расширение, оно широко используется в устройствах, включая 3D-сканеры .
Инженеры-конструкторывсе чаще убеждаются во многих преимуществах углеродного волокна благодаря низкому тепловому расширению по сравнению с традиционными материалами, такими как сталь или алюминий. Углеродное волокно демонстрирует исключительные параметры в этом отношении и подходит, в частности, для высокоточных элементов, таких как оптические устройства, 3D-сканеры, телескопы и другие, где крайне важно минимальное низкое тепловое расширение.
Углеродное волокно (композит из углеродного волокна и эпоксидной смолы) — это материал с тепловым расширением в 6 раз меньше алюминия и более чем в 3 раза меньше стали.
Приведенная ниже таблица включает анализ теплового расширения различных материалов с учетом соотношения дюйм / градус Фаренгейта. Указанные единицы предназначены только для справки с учетом различий между материалами.
| Материал | Тепловое расширение |
| Алюминий | 13 |
| Сталь | 7 |
| Стекловолокно — эпоксидный композит | 7-8 |
| Кевлар / арамид — эпоксидный композит | 3 |
| Углеродно-эпоксидный композит | 2 |
Углеродное волокно — это материал с низкими характеристиками теплопроводности.
Углеродное волокно — идеальный изолятор — на фотографии выше показан входной патрубок турбины из углеродного волокна.Теплопроводность в основном зависит от передачи / проводимости энергии из областей с высокой температурой в области с низкой температурой. Материалы с высокой теплопроводностью переносят температуру легче, чем материалы с низкой теплопроводностью.
Композит из углеродного волокна и эпоксидной смолы — это материал, теплопроводность которого в 40 раз меньше, чем у алюминия, и в 10 раз меньше, чем у стали. Таким образом, можно предположить, что углеродное волокно является очень хорошим изолятором.
В этой таблице сравнивается теплопроводность различных материалов, включая углеродное волокно (единица измерения Вт / м *)
| Материал | Теплопроводность |
| Углеродно-эпоксидный композит | 5-7 |
| Сталь | 50 |
| Алюминий | 210 |
Алюминий — это материал, устойчивый к высоким температурам, и в этом отношении он имеет преимущества перед композитами из углеродного волокна.
Характеристики и устойчивость углеродного волокна к высоким температурам зависят от структуры композита и технологии выпечки. Это правда, что композит из углеродного волокна устойчив к высоким температурам , но, к сожалению, часто это не так. На самом деле это происходит из-за использования неподходящих материалов, неправильного обжига композита или недостаточного ноу-хау и опыта в этом отношении многих поставщиков композитов.
Для обеспечения устойчивости к высоким температурам во время производства могут использоваться только материалы, демонстрирующие такую стойкость, при условии, что обжиг композита осуществляется надлежащим образом в диапазоне температур, близком к желаемой стойкости композита. Использование смол, устойчивых к высоким температурам, без дополнительного отверждения внутри духовки не обеспечит требуемой стойкости.
Стандартные эпоксидные композиты из углеродного волокна, прошедшие надлежащую устойчивость к выпечке при температуре до 70–100 ° C (160–210 ° F).
Если требуется устойчивость к температурам более 100 ° C, чаще всего подходит препрег из углеродного волокна , часто вместе с отверждением композита при температурах около 150 ° C / 300 ° F, что обеспечивает повышенную стойкость до температур 200 ° C / 400 ° F. Например, Prepreg Gurit EP127 обладает стойкостью до 230 ° C / 445 ° F.
Если требуется устойчивость к более высоким температурам, используются фенольные смолы, и эти композиты обладают кратковременной стойкостью до 500 ° C / 930 ° F.
Хотя такое сопротивление может быть обеспечено для композитов, обратите внимание, что эти специальные материалы являются дорогостоящими и требуют не только закалки в печи при высокой температуре, но и ноу-хау. Поэтому все это приводит к высокой цене на композиты, устойчивые к очень высоким температурам.
8. Долгосрочная работаУглеродный композит при строительстве должен изготавливаться вакуумным методом — настаиванием смолы или препрега.Такая технология обеспечивает долгий срок службы углеродного композита. Углеродный композит, изготовленный вручную «валиком и кистью», имеет низкую прочность и небольшой срок службы.
Углеродное волокно обладает коррозионной стойкостью, что дает еще одно преимущество по сравнению с алюминием.
Углеродно-эпоксидный композит имеет недостаток, связанный с пониженной стойкостью к УФ-излучению, поэтому композит, подвергающийся воздействию УФ-излучения, следует защищать путем нанесения верхнего покрытия, что, как дополнительный процесс, приводит к более высоким производственным затратам.
9. Осуществление производстваПочему углеродное волокно не широко используется в производстве, хотя оно имеет много преимуществ по сравнению с очень популярным алюминием?
Чаще всего это связано с ценой: элементы из углеродного волокна стоят дороже алюминиевых, потому что углеродное волокно стоит дороже, а производство углеродных изделий требует больше времени.
С другой стороны, при сравнении затрат, связанных с внедрением производства алюминия и углеродного волокна, во многих случаях именно производство элемента из углеродного волокна будет дешевле и, что более важно, доступно в случае небольшого тиража, для которого внедрение производства алюминиевых элементов было бы нерентабельным.
В следующем фильме показано производство элементов из углеродного волокна с использованием технологии препрега.
Наконец, мы должны упомянуть широко распространенное отсутствие осведомленности о преимуществах и преимуществах углеродного волокна по сравнению с традиционными материалами, включая алюминий или сталь. Мы надеемся, что эта статья дает больше информации об углеродном волокне и о том, чем этот материал отличается от алюминия, а также о том, какие преимущества возможны при замене алюминия углеродным волокном.
Мы надеемся, что это исследование предоставило больше информации о свойствах углеродного волокна по сравнению с алюминием. Со временем все больше и больше инженеров-конструкторов будут использовать этот материал, поскольку углеродное волокно предлагает множество преимуществ, включая легкий вес, практически нулевое тепловое расширение, простоту обработки и высокую жесткость.
Наша компания является поставщиком компонентов из углеродного волокна . Мы поставляем нестандартные компоненты, а также партии изделий из углеродного волокна.Местонахождение: Воломин, Польша (Европа), доставка по всему миру.
Пример удельной теплоемкости Задача
Энергия, необходимая для нагрева чего-либо, пропорциональна изменению массы и температуры материала. Константа пропорциональности называется удельной теплоемкостью.Фотография Johannes W на Unsplash
Удельная теплоемкость — это количество тепла на единицу массы, необходимое для повышения температуры материала на один градус Цельсия или Кельвина. Эти три примера задач удельной теплоемкости покажут, как найти удельную теплоемкость материала или другую информацию, связанную с удельной теплоемкостью.
Уравнение удельной теплоемкости
Уравнение, наиболее часто связанное с удельной теплоемкостью:
Q = mcΔT
, где
Q = тепловая энергия
m = масса
c = удельная теплоемкость
ΔT = изменение температуры = (T final — T начальный )
Хороший способ запомнить эту формулу — Q = «em cat»
По сути, это уравнение используется для определения количества тепла, добавляемого к материалу для повышения температуры на определенную величину (или количество теряется при остывании материала).
Это уравнение применимо только к материалам, которые остаются в одном и том же состоянии вещества (твердое, жидкое или газообразное) при изменении температуры. Фазовые изменения требуют дополнительных энергетических соображений.
Удельная теплоемкость Пример задачи — найти количество тепла
Вопрос : 500-граммовый куб свинца нагревают с 25 ° C до 75 ° C. Сколько энергии требовалось для нагрева свинца? Удельная теплоемкость свинца составляет 0,129 Дж / г ° C.
Решение : Во-первых, давайте перейдем к известным нам переменным.
m = 500 грамм
c = 0,129 Дж / г ° C
ΔT = (T конечный — T начальный ) = (75 ° C — 25 ° C) = 50 ° C
Вставьте эти значения в уравнение теплоемкости сверху.
Q = mcΔT
Q = (500 грамм) · (0,129 Дж / г ° C) · (50 ° C)
Q = 3225 Дж
Ответ : Для нагрева свинца потребовалось 3225 Джоулей энергии куб от 25 ° C до 75 ° C.
Пример удельной теплоемкости Задача — найти удельную теплоемкость
Вопрос: 25-граммовый металлический шар нагревается до 200 ° C с помощью энергии 2330 Дж.Какова удельная теплоемкость металла?
Решение : Перечислите известную нам информацию.
m = 25 граммов
ΔT = 200 ° C
Q = 2330 Дж
Поместите их в уравнение теплоемкости.
Q = mcΔT
2330 Дж = (25 г) c (200 ° C)
2330 Дж = (5000 г ° C) c
Разделите обе стороны на 5000 г ° C
c = 0,466 Дж / г ° C
Ответ : Удельная теплоемкость металла составляет 0,466 Дж / г ° C.
Пример удельной теплоемкости Задача — определение начальной температуры
Вопрос: Горячему куску меди весом 1 кг дают остыть до 100 ° C.Если медь выделяет 231 кДж энергии, какова начальная температура меди? Удельная теплоемкость меди составляет 0,385 Дж / г ° C.
Решение : Перечислите данные переменные:
m = 1 кг
T final = 100 ° C
Q = -231 кДж (отрицательный знак означает, что медь охлаждается и теряет энергию.)
c = 0,385 Дж / г ° C
Нам нужно привести наши единицы в соответствие с единицами удельной теплоемкости, поэтому давайте преобразуем единицы массы и энергии.
м = 1 кг = 1000 грамм
1 кДж = 1000 Дж
Q = -231 кДж · (1000 Дж / кДж) = -231000 Дж
Подставьте эти значения в формулу теплоемкости.
Q = mcΔT
-231000 Дж = 1000 г · (0,385 Дж / г ° C) · ΔT
-231000 Дж = 385 Дж / ° C · ΔT
ΔT = -600 ° C
ΔT = (T final — T initial )
Вставьте значения ΔT и T final .
-600 ° C = (100 ° C — T начальная )
Вычтем 100 ° C из обеих частей уравнения.
-600 ° C — 100 ° C = — T начальная
-700 ° C = — T начальная
T начальная = 700 ° C
Ответ : Начальная температура меди кусок был 700 ° C.
Связанные сообщения
Leave A Comment