Диаметры окружности равны между собой: Все диаметры окружности равны между собой

Ребят, какие из следующих утверждений верны? Вариант 9. Часть 1. Задание 13. ОГЭ 36 вариантов ответов по Математике 9 класс Ященко. – Рамблер/класс

Ребят, какие из следующих утверждений верны? Вариант 9. Часть 1. Задание 13. ОГЭ 36 вариантов ответов по Математике 9 класс Ященко. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Какие из следующих утверждений верны?

 
1)     Треугольника со сторонами 1, 2, 4 не существует.
2)      Площадь трапеции равна произведению основания трапеции на высоту.
3)      Все диаметры окружности равны между собой.
 
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
 

ответы

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Олимпиады

Экзамены

Оценки

3 класс

похожие вопросы 5

Вариант 1. Часть 2. Задание 26. ОГЭ 36 вариантов ответов по Математике 9 класс Ященко. Помогите найти АН.

На стороне ВС остроугольного треугольника АВС (АВ ≠ АС) как на диаметре построена полуокружность, пересекающая высоту АD в точке М, АD (Подробнее…)

ГДЗМатематикаОГЭ9 классЯщенко И.В.

Вариант 3.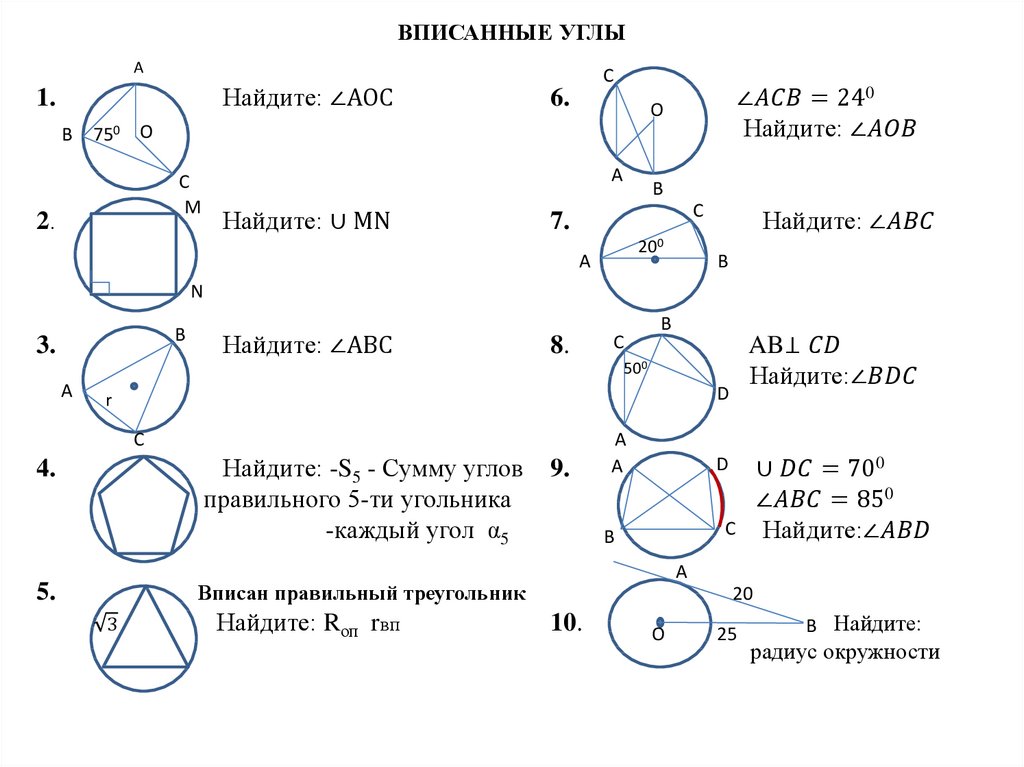 Часть 1. Задание 4. ОГЭ 36 вариантов ответов по Математике 9 класс Ященко. Помогите с корнями!

Решите уравнение х2- 5х = 14 .
Если уравнение имеет более одного корня, в ответе запишите больший из корней.

ГДЗМатематикаОГЭ9 классЯщенко И.В.

ГДЗ. Математика. Базовый уровень ЕГЭ — 2017. Вар.№26. Зад.№9.Под руководством Ященко. Помогите установить соответствие.

   Здравствуйте! Помогите установить соответствие между величинами и их возможными значениями: к каждому элементу первого столбца (Подробнее…)

ЕГЭЭкзаменыМатематикаЯщенко И.В.

Задание 38 Однородные члены предложения. Что такое однородные члены предложения? Русский язык.4 класс. Канакина В.П., Горецкий В.Г. ГДЗ

Всем привет, поделитесь ответом на задание
Прочитайте.
Рассмотрите условные обозначения однородных членов. (Подробнее…)

ГДЗРусский языкКанакина В.П.Горецкий В.Г.4 класс

А что интересного будет происходить в эти выходные? Куда сходить с учителем?

А что интересного будет происходить в эти выходные? Куда сходить с учителем?

9 класс

Задача 19 ОГЭ по математике.

Практика

По материалам открытого банка ФИПИ.

Из спецификации к 19 номеру:

Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения.

Более 100 задач с ответами: z19.docx

1.Какое из следующих утверждений верно?

1) В прямоугольном треугольнике гипотенуза равна сумме катетов.
2) Всегда один из двух смежных углов острый, а другой тупой.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.

2. Какие из следующих утверждений верны?

1) Сумма углов равнобедренного треугольника равна 180 градусам.
2) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
3) В прямоугольном треугольнике квадрат гипотенузы равен разности квадратов катетов.

3. Какие из следующих утверждений верны?

1) Через заданную точку плоскости можно провести только одну прямую.
2) Все равносторонние треугольники подобны.
3) Сумма острых углов прямоугольного треугольника равна 90 градусам.

4. Какое из следующих утверждений верно?

1) Все равнобедренные треугольники подобны.
2) Существует прямоугольник, диагонали которого взаимно перпендикулярны.
3) Сумма углов прямоугольного треугольника равна 90 градусам.

5. Какие из следующих утверждений верны?

1) Все диаметры окружности равны между собой.
2) Если в параллелограмме две соседние стороны равны, то этот параллелограмм является ромбом.
3) Сумма углов любого треугольника равна 360 градусам.

6. Какое из следующих утверждений верно?

1) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
2) Основания равнобедренной трапеции равны.
3) Все высоты равностороннего треугольника равны.

7. Какие из следующих утверждений верны?
1) Диагонали трапеции пересекаются и делятся точкой пересечения пополам.
2) Все диаметры окружности равны между собой.
3) Один из углов треугольника всегда не превышает 60 градусов

8.Какое из следующих утверждений верно?

1) Площадь любого параллелограмма равна произведению длин его сторон.
2) Треугольник со сторонами 1, 2, 4 существует.
3) Основания любой трапеции параллельны.

9.Какое из следующих утверждений верно?

1) Всегда один из двух смежных углов острый, а другой тупой.
2) Площадь квадрата равна произведению двух его смежных сторон.
3)Все хорды одной окружности равны между собой.

10.Какое из следующих утверждений верно?

1) Отношение площадей подобных треугольников равно коэффициенту подобия.
2) Диагонали прямоугольника точкой пересечения делятся пополам.
3) Биссектриса треугольника делит пополам сторону, к которой проведена.

11.Какие из следующих утверждений верны?

1) Треугольника со сторонами 1, 2, 4 не существует.
2) Медиана треугольника делит пополам угол, из вершины которого проведена.
3) Все диаметры окружности равны между собой.

12.Какое из следующих утверждений верно?

1) Диагонали параллелограмма равны.
2) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу
другого треугольника, то такие треугольники равны.

13.Какое из следующих утверждений верно?

1) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
2) Сумма углов равнобедренного треугольника равна 180 градусам.
3) Все квадраты имеют равные площади.

14.Какое из следующих утверждений верно?

1) Диагональ трапеции делит её на два равных треугольника.
2) Косинус острого угла прямоугольного треугольника равен отношению гипотенузы
к прилежащему к этому углу катету.
3) Расстояние от точки, лежащей на окружности, до центра окружности равно радиусу.

15.Какое из следующих утверждений верно?

1) Если три угла одного треугольника равны соответственно трём углам другого треугольника,
то такие треугольники равны.
2) Все диаметры окружности равны между собой.
3) Площадь параллелограмма равна половине произведения его диагоналей.

16.Какие из следующих утверждений верны?

1) Все высоты равностороннего треугольника равны.
2) Существуют три прямые, которые проходят через одну точку.
3) Если диагонали параллелограмма равны, то этот параллелограмм является ромбом.

17.Какие из следующих утверждений верны?

1) Любые два диаметра окружности пересекаются.
2) Две прямые, перпендикулярные третьей прямой, перпендикулярны.
3) Треугольника со сторонами 1, 2, 4 не существует.

18.Какое из следующих утверждений верно?

1) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
2) Сумма углов равнобедренного треугольника равна 180 градусам.
3) Диагонали ромба равны.

19.Какие из следующих утверждений верны?

1) Один из углов треугольника всегда не превышает 60 градусов.
2) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
3) Две прямые, параллельные третьей прямой, перпендикулярны.

20.Какое из следующих утверждений верно?

1) Через точку, не лежащую на данной прямой, можно провести прямую,
перпендикулярную этой прямой.
2) Все углы ромба равны.
3) Если диагонали выпуклого четырёхугольника равны и перпендикулярны,
то этот четырёхугольник является квадратом.

21.Какое из следующих утверждений верно?

1) Смежные углы всегда равны.
2) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
3) Площадь параллелограмма равна половине произведения его диагоналей.

22.Какое из следующих утверждений верно?

1) Площадь прямоугольного треугольника равна произведению длин его катетов.
2) Существует прямоугольник, диагонали которого взаимно перпендикулярны.
3) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника,
то такие четырехугольники равны

23.Какое из следующих утверждений верно?

1) Если диагонали параллелограмма равны, то этот параллелограмм является ромбом.
2) Тангенс любого острого угла меньше единицы.
3) Сумма углов равнобедренного треугольника равна 180 градусам.

24.Какое из следующих утверждений верно?

1) Тангенс любого острого угла меньше единицы.
2) Средняя линия трапеции равна сумме её оснований.
3) В параллелограмме есть два равных угла.

25.Какое из следующих утверждений верно?

1) Диагонали равнобедренной трапеции равны.
2) Если три угла одного треугольника равны соответственно трём углам другого треугольника,
то такие треугольники равны.
3) Тангенс любого острого угла меньше единицы.

26.Какие из следующих утверждений верны?

1) Один из углов треугольника всегда не превышает 60 градусов.
2) Если диагонали параллелограмма равны, то это прямоугольник.
3) Две прямые, параллельные третьей прямой, перпендикулярны.

27.Какое из следующих утверждений верно?

1) Диагонали ромба равны.
2) Отношение площадей подобных треугольников равно коэффициенту подобия.
3) В треугольнике против большего угла лежит большая сторона.

28.Какое из следующих утверждений верно?

1) Если угол острый, то смежный с ним угол также является острым.
2) Если диагонали параллелограмма перпендикулярны, то этот параллелограмм является ромбом.
3) Касательная к окружности параллельна радиусу, проведённому в точку касания.

29.Какое из следующих утверждений верно?

1) Средняя линия трапеции параллельна её основаниям.
2) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника,
то такие треугольники равны.
3) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.

30.Какие из следующих утверждений верны?

1) Один из углов треугольника всегда не превышает 60 градусов.
2) Средняя линия трапеции равна сумме её оснований.
3) Касательная к окружности перпендикулярна радиусу, проведённому
в точку касания.

31.Какое из следующих утверждений верно?

1) Все углы ромба равны.
2) Вписанный угол, опирающийся на диаметр окружности, прямой.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.

32.Какое из следующих утверждений верно?

1) Сумма углов выпуклого четырёхугольника равна 360 градусам.
2) Средняя линия трапеции равна сумме её оснований.
3) Любой параллелограмм можно вписать в окружность.

33.Какие из следующих утверждений верны?

1) Все хорды одной окружности равны между собой.
2) Треугольника со сторонами 1, 2, 4 не существует.
3) Все углы прямоугольника равны.

34.Какое из следующих утверждений верно?

1) Сумма острых углов прямоугольного треугольника равна 90 градусам.
2) Средняя линия трапеции равна сумме её оснований.
3) В любой четырёхугольник можно вписать окружность

35.Какое из следующих утверждений верно?

1) Боковые стороны любой трапеции равны.
2) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
3) Площадь квадрата равна произведению его диагоналей.

36.Какие из следующих утверждений верны?

1) Косинус острого угла прямоугольного треугольника равен отношению гипотенузы
к прилежащему к этому углу катету.
2) Диагонали ромба перпендикулярны.
3) Существуют три прямые, которые проходят через одну точку.

37.Какое из следующих утверждений верно?

1) Две различные прямые, перпендикулярные третьей прямой, параллельны.
2) Если диагонали выпуклого четырёхугольника равны и перпендикулярны,
то этот четырёхугольник является квадратом.
3) Все углы ромба равны.

38.Какое из следующих утверждений верно?

1) Вертикальные углы равны.
2) Две прямые, параллельные третьей прямой, перпендикулярны.
3) Диагонали любого прямоугольника делят его на четыре равных треугольника.

39.Какое из следующих утверждений верно?

1) Боковые стороны любой трапеции равны.
2) Площадь прямоугольника равна произведению длин его смежных сторон.
3) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.

40.Какое из следующих утверждений верно?

1) Площадь параллелограмма равна половине произведения его диагоналей.
2) Сумма углов прямоугольного треугольника равна 90 градусам.
3) Биссектрисы треугольника пересекаются в точке, которая является центром окружности,
вписанной в треугольник.

41.Какое из следующих утверждений верно?

1) В параллелограмме есть два равных угла.
2) В тупоугольном треугольнике все углы тупые.
3) Площадь прямоугольника равна произведению длин всех его сторон.

42.Какие из следующих утверждений верны?

1) Через заданную точку плоскости можно провести только одну прямую.
2) Серединные перпендикуляры к сторонам треугольника пересекаются
в точке, являющейся центром окружности, описанной около треугольника.
3) Если в параллелограмме две соседние стороны равны, то этот параллелограмм является ромбом.

43. Какое из следующих утверждений верно?

1) В треугольнике против большего угла лежит большая сторона.
2) Диагонали ромба равны.
3) Площадь параллелограмма равна половине произведения его диагоналей.

44. Какие из следующих утверждений верны?

1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
2) Сумма острых углов прямоугольного треугольника равна 90 градусам.
3) Любые два равносторонних треугольника подобны.

45.Какие из следующих утверждений верны?

1) Сумма углов прямоугольного треугольника равна 90 градусам.
2) Существуют три прямые, которые проходят через одну точку.
3) Диагонали ромба точкой пересечения делятся пополам.

46.Какое из следующих утверждений верно?

1) Если угол острый, то смежный с ним угол также является острым.
2) Диагонали прямоугольника точкой пересечения делятся пополам.
3) В прямоугольном треугольнике гипотенуза равна сумме катетов.

47.Какие из следующих утверждений верны?

1) Площадь ромба равна произведению двух его смежных сторон на синус угла между ними.
2) В тупоугольном треугольнике все углы тупые.
3) Существуют три прямые, которые проходят через одну точку.

48.Какое из следующих утверждений верно?

1) Все квадраты имеют равные площади.
2) Точка пересечения двух окружностей равноудалена от центров этих окружностей.
3) В остроугольном треугольнике все углы острые.

49.Какое из следующих утверждений верно?

1) Тангенс любого острого угла меньше единицы.
2) Средняя линия трапеции равна сумме её оснований.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.

50.Какое из следующих утверждений верно?

1) Площадь трапеции равна произведению основания трапеции на высоту.
2) Если в треугольнике есть один острый угол, то этот треугольник остроугольный.
3) Диагонали прямоугольника точкой пересечения делятся пополам.

51.Какие из следующих утверждений верны?

1) Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла.
2) Если в параллелограмме две соседние стороны равны, то этот параллелограмм является ромбом.
3) Касательная к окружности параллельна радиусу, проведённому в точку касания.

52. Какое из следующих утверждений верно?

1) Любой параллелограмм можно вписать в окружность.
2) Касательная к окружности параллельна радиусу, проведённому в точку касания.
3) Сумма острых углов прямоугольного треугольника равна 90 градусам.

53. Какое из следующих утверждений верно?

1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
2) Точка пересечения двух окружностей равноудалена от центров этих окружностей.
3) Диагонали ромба точкой пересечения делятся пополам.

54. Какие из следующих утверждений верны?

1) Все диаметры окружности равны между собой.
2) Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
3) Любые два равносторонних треугольника подобны.

55. Какие из следующих утверждений верны?

1) Один из углов треугольника всегда не превышает 60 градусов.
2) Боковые стороны любой трапеции равны.
3) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.

56. Какие из следующих утверждений верны?

1) Смежные углы всегда равны.
2) Площадь квадрата равна произведению двух его смежных сторон.
3) Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.

57.Какие из следующих утверждений верны?

1) Существует квадрат, который не является прямоугольником.
2) Если в параллелограмме две соседние стороны равны, то этот параллелограмм является ромбом.
3) Все диаметры окружности равны между собой.

58. Какие из следующих утверждений верны?

1)
В любой прямоугольной трапеции есть два равных угла.
2) Касательная к окружности параллельна радиусу, проведённому в точку касания.
3) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.

59.Какое из следующих утверждений верно?

1) Все углы ромба равны.
2) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.

60.Какое из следующих утверждений верно?

1) Расстояние от точки, лежащей на окружности, до центра окружности равно радиусу.
2) Средняя линия трапеции равна сумме её оснований.
3) Площадь параллелограмма равна половине произведения его диагоналей.

61. Какое из следующих утверждений верно?

1) Средняя линия трапеции равна полусумме её оснований.
2) Диагонали любого прямоугольника делят его на четыре равных треугольника.
3) Косинус острого угла прямоугольного треугольника равен отношению гипотенузы к прилежащему к этому углу катету.

62. Какое из следующих утверждений верно?

1) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
2) Через заданную точку плоскости можно провести только одну прямую.
3) Диагонали ромба точкой пересечения делятся пополам.

63.Какие из следующих утверждений верны?

1) Сумма углов равнобедренного треугольника равна 180 градусам.
2) Боковые стороны любой трапеции равны.
3) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.

64. Какое из следующих утверждений верно?

1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
2) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
3) Смежные углы всегда равны.

65. Какие из следующих утверждений верны?

1) Существует прямоугольник, диагонали которого взаимно перпендикулярны.
2) Все квадраты имеют равные площади.
3) Один из углов треугольника всегда не превышает 60 градусов.

66. Какое из следующих утверждений верно?

1) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
2) В параллелограмме есть два равных угла.
3) Площадь прямоугольного треугольника равна произведению длин его катетов.

67. Какие из следующих утверждений верны?

1) Любые два равносторонних треугольника подобны.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) Все диаметры окружности равны между собой.

68. Какое из следующих утверждений верно?

1) Боковые стороны любой трапеции равны.
2) Серединные перпендикуляры к сторонам треугольника пересекаются
в точке, являющейся центром окружности, описанной около треугольника.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.

69. Какое из следующих утверждений верно?

1) Диагонали прямоугольника точкой пересечения делятся пополам.
2) Точка пересечения двух окружностей равноудалена от центров этих окружностей.
3) Площадь любого параллелограмма равна произведению длин его сторон.

70. Какое из следующих утверждений верно?

1) Вписанный угол, опирающийся на диаметр окружности, прямой.
2) Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны.
3) Отношение площадей подобных треугольников равно коэффициенту подобия

Диаметр круга – определение, формула, примеры

В круге диаметр – это линия, проходящая через центр и пересекающаяся с окружностью на противоположных концах. Он в два раза больше радиуса окружности. Другими словами, диаметр круга — это линия, проходящая через центр и делящая круг на две равные части. Давайте узнаем больше об определении диаметра и свойствах в этой статье.

1.	Каков диаметр круга?
2.	Диаметр окружности Формула
3.	Как найти диаметр круга?
4.	Диаметр против радиуса
5.	Часто задаваемые вопросы о Diameter

Каков диаметр круга?

Диаметром окружности называется любой отрезок прямой линии, проходящий через центр окружности и концы которого лежат на окружности окружности. Диаметр также известен как самая длинная хорда окружности.

Определение диаметра

Диаметр определяется как удвоенная длина радиуса окружности. Радиус измеряется от центра круга до одной конечной точки на границе круга, тогда как расстояние диаметра измеряется от одного конца круга до точки на другом конце круга, проходящей через центр. Обозначается буквой D. На окружности окружности бесконечное количество точек, это означает, что окружность имеет бесконечное число диаметров, и каждый диаметр окружности имеет одинаковую длину.

Символ диаметра

Ø — это символ, который используется в технике для обозначения диаметра. Этот символ обычно используется в технических спецификациях и чертежах. Ø25 мм означает, что диаметр круга составляет 25 мм.

Диаметр окружности Формула

Все мы знаем, что диаметр является частью круга. Давайте разберемся с некоторыми терминами, прежде чем мы узнаем формулу диаметра круга.

• Радиус (r) — это длина отрезка от центра окружности до конечной точки окружности.
• Окружность (C) относится к замкнутой границе круга. Он также известен как периметр круга.
• Площадь круга — это общее пространство внутри границы круга. Он рассчитывается по формуле πr ² , где r — радиус.

Мы можем вывести формулу диаметра из длины окружности, площади и радиуса круга.

Диаметр круга с использованием длины окружности

Мы можем легко вывести формулу диаметра из длины окружности. Формула длины окружности: C = πd; здесь, C = длина окружности, d = диаметр окружности, π = 22/7 или 3,142 прибл. Формула диаметра с использованием окружности:

Диаметр = Окружность ÷ π.

Диаметр круга с использованием радиуса

Радиус — это длина отрезка от центра круга до конечной точки на круге, а диаметр в два раза превышает длину радиуса круга. Используя это определение, формула для диаметра равна D = Радиус × 2 .

Формула диаметра, использующая площадь круга

Мы можем вывести формулу диаметра круга, используя формулу площади круга, то есть площадь (A) = π(радиус) ² . Подставляя значение радиуса в качестве D/2, мы получаем A/π = (D/2) ² .

⇒ D/2 = √(A/π)

⇒ D = 2 × √(A/π)

Следовательно, формула диаметра круга с использованием площади: D = 2√Площадь/π .

Как найти диаметр круга?

Диаметр круга можно рассчитать, если известны радиус, длина окружности или площадь. Выполните шаги, указанные ниже, чтобы найти диаметр круга:

• Шаг 1: Первый шаг — определить, что дано в вопросе: радиус, площадь или окружность.
• Шаг 2: Примените соответствующую формулу из трех приведенных выше формул.
• Шаг 3: Упрости и получи ответ.

Попробуем найти диаметр с помощью приведенных выше формул на практическом примере. Обратите внимание на приведенный ниже пример.

Пример: Джек нарисовал круг радиусом 3 единицы. Каков диаметр круга?

Решение:

Дано: Радиус окружности = 3 единицы.
Диаметр круга = 2 × радиус

= 2 × 3 = 6 шт.
Следовательно, диаметр круга равен 6 единицам.

Диаметр против радиуса

Как мы уже говорили, длина диаметра в два раза больше радиуса. Есть некоторые сходства и различия между диаметром и радиусом, которые мы собираемся изучить в этом разделе.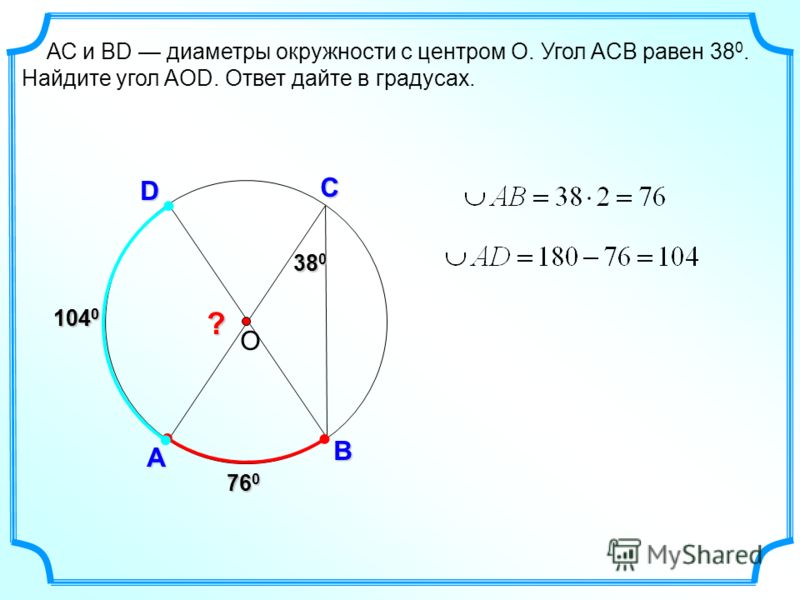 Прежде чем перейти к разнице между диаметром и радиусом, сначала поговорим об их сходстве. И диаметр, и радиус являются частями круга, которые определяют различные свойства, такие как размер круга, длина окружности и площадь круга. Они разделяют отношения в форме уравнения. и.в. Диаметр = 2 × Радиус.

Посмотрите на приведенную ниже таблицу, чтобы понять диаметр и радиус.

Диаметр	Радиус
Диаметр круга в два раза больше его радиуса.	Это половина длины от диаметра.
Для любой окружности длина диаметра больше длины радиуса.	Длина радиуса меньше диаметра.
Начинается с границы круга и заканчивается на самой границе.	Начинается из центра и в точке касается окружности круга.

☛ Похожие темы

Проверьте эти интересные статьи, связанные с диаметром круга.

• Хорды ​​и диаметры
• Формула диаметра сферы с использованием объема
• Окружность к диаметру

 

Примеры диаметров

1. Пример 1: Радиус круга составляет 15 единиц. Вычислите его диаметр.

   Решение:
   Дано, радиус = 15 единиц
   Мы это знаем,
   Диаметр = 2 × радиус 90 141 = 2 × 15
   Следовательно, диаметр = 30 единиц.

2. Пример 2: Можете ли вы определить значение радиуса, если диаметр окружности равен 36 единицам?

   Решение:
   Дано: Диаметр = 36 единиц
   Мы знаем, что диаметр в два раза больше радиуса. Это означает, что радиус равен половине значения диаметра.
   

   Диаметр = 2 × радиус 90 141 Р = Д ÷ 2
   Радиус = 36 ÷ 2 = 18 единиц
   Следовательно, радиус = 18 единиц.

3. Пример 3: Диаметр круглого бассейна составляет 7 футов. Какова окружность бассейна? Выразите ответ через число π.

   Решение:
   Дано: Диаметр = 7 футов
   Мы знаем, что длина окружности = π × d
   . Таким образом, длина окружности бассейна = π × 7 
   . Следовательно, окружность бассейна = 7π футов.

перейти к слайдуперейти к слайдуперейти к слайду

Готовы увидеть мир глазами математика?

Математика — это жизненный навык. Помогите своему ребенку усовершенствовать это с помощью реального приложения с Cuemath.

Записаться на бесплатный пробный урок

Практические вопросы по Diameter

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по диаметру

Какой диаметр?

Диаметр – это прямая линия, проходящая через центр окружности и делящая окружность на две части/полуокружности. Это самая длинная хорда окружности, которая пересекает окружность на противоположных концах.

Какой символ используется для обозначения диаметра?

В технике для обозначения диаметра используется символ ⌀. Его часто называют «фи». Этот символ фи используется для описания диаметра круглого сечения. Например, «⌀20» означает, что диаметр круга составляет 20 единиц измерения.

Что такое радиус и диаметр?

Радиус и диаметр круга являются двумя важными частями круга, которые взаимозависимы друг от друга. Радиус круга — это отрезок, который начинается от центра круга и заканчивается на окружности круга. Это половина длины диаметра круга, т. Е. Радиус = диаметр / 2. Диаметр окружности — это отрезок, проходящий через центр окружности и имеющий две точки на окружности. Это в два раза больше длины радиуса окружности, т. е. диаметр = 2 × радиус.

Как рассчитать диаметр?

Диаметр круга можно рассчитать по заданным параметрам. Если заданы такие параметры, как радиус, окружность или площадь, мы можем напрямую использовать следующие формулы.

• Диаметр = длина окружности ÷ π (если дана длина окружности)
• Диаметр = 2 × радиус (если указан радиус)
• Диаметр = 2√[Площадь/π] (если дана площадь)

Пример диаметра?

Если вы посмотрите на колесо цикла, шипы, идущие от одного конца к другому через центр, являются примером диаметра. Мы можем связать это с диаметром круга, поскольку диаметр — это отрезок, который начинается с одного конца круга и заканчивается на другом конце круга, проходящем через центр.

Как найти диаметр по окружности?

Если длина окружности известна, то мы можем легко найти значение диаметра, подставив значения в формулу: Диаметр = C ÷ π; где «C» — длина окружности, а значение π равно примерно 22/7 или 3,14.

Как найти площадь круга по диаметру?

Площадь круга рассчитывается по формуле: πr ² . Если диаметр задан, мы можем найти радиус, разделив значение диаметра на 2. Получив радиус, мы можем подставить его значение в формулу: πr ² , чтобы получить площадь круга, или напрямую применить формулу площади. с диаметром, A = π(d/2) ² = πd ² /4 кв.

Для чего нужен калькулятор отношения диаметра к окружности?

Калькулятор отношения диаметра к окружности — это онлайн-инструмент, используемый для определения значения длины окружности. В калькуляторе диаметра окружности введите размер диаметра и получите значение окружности в течение нескольких секунд. Вы также можете попробовать калькулятор диаметра для прямых расчетов.

Какова формула диаметра круга, если известен радиус круга?

Если радиус окружности указан в единицах ‘r’, то легко определить диаметр окружности по формуле. С определением радиуса мы знаем, что это половина диаметра, следовательно, формула диаметра = 2r.

Как называется половина диаметра круга?

Диаметр круга — это отрезок линии от одного конца круга до другого конца круга, проходящий через центр круга. Принимая во внимание, что радиус круга — это длина отрезка линии от центра круга до точки на окружности круга. Следовательно, радиус равен половине диаметра окружности.

Как диаметр связан с радиусом окружности?

Радиус круга равен половине диаметра. Отношение между радиусом и диаметром можно математически выразить формулой: Диаметр = 2 × радиус.

Является ли диаметр половиной радиуса?

Нет, диаметр не равен половине радиуса. Это в два раза больше радиуса окружности. Он представлен формулой: Диаметр = 2 × Радиус.

Диаметр, радиус и длина окружности (видео и практика)

Расшифровка FAQsPractice

Привет, ребята! Добро пожаловать в это видео о радиусе, диаметре и длине окружности.

Круги существуют столько же, сколько существует Земля. Люди могли видеть естественные круги, наблюдая за луной, солнцем и другими различными природными круглыми формами.

Первое технологическое изобретение с использованием круглой формы, однако, не было до 3500 г. до н.э., и это было изобретение гончарного круга. Затем, 300 лет спустя, их использовали для колес колесниц. Когда люди начали видеть ценность и использование объектов круглой формы, они начали изучать круги.

Такие термины, как радиус , диаметр и окружность , помогают нам отслеживать различные измерения окружности.

Итак, теперь давайте посмотрим, что представляет собой каждое из этих измерений.

Определения

Середина окружности

Во-первых, давайте определим середину , чтобы вы поняли, о чем я говорю, когда я на нее ссылаюсь. Вот круг:

Середина — это точный центр круга, где находится точка.

Теперь давайте посмотрим на эти другие термины.

Радиус круга

Радиус — это длина от середины круга до внешнего края круга. Радиус обозначается строчной буквой \(r\).

Диаметр круга

Диаметр — это полная длина круга, проходящая от края через середину до другой стороны. То есть вся эта длина прямо здесь. Диаметр круга обозначается буквой \(d\).

Окружность круга

Окружность — это расстояние вокруг внешнего края этого круга. Окружность обозначается заглавной буквой \(C\).

Окружность сравнима с периметром фигуры, например параллелограмма . Если бы вы разрезали линию круга, как если бы это была нить, и выложили ее по размеру. Эта длина будет эквивалентна окружности. Однако, поскольку круг имеет непрерывную кривую, мы используем слово окружность , а не периметр , чтобы отличить его.

Теперь, когда мы рассмотрели, что такое радиус, диаметр и длина окружности, давайте посмотрим, как их рассчитать.

Расчеты

Если бы кто-то просто вручил вам лист бумаги с кружком на нем…. Ну, на самом деле, это было бы довольно странно.

Но допустим, мы хотим найти радиус, диаметр и длину окружности этого круга, и все, что у нас есть, это линейка.

Для начала проще всего взять линейку и измерить от самого центра круга расстояние между внешним краем. Это будет диаметр.

Предположим, что при измерении мы получили длину 9см для диаметра.

Ну, мы знаем, что если наш радиус проходит от середины до внешнего края, то все, что нам нужно сделать, чтобы найти длину нашего радиуса, это разделить длину диаметра на 2.

Итак, когда мы берем 9 и делим на 2 получаем длину радиуса 4,5см.

Формула радиуса

Формула радиуса может быть записана как \(r=\frac{d}{2}\)

Формула диаметра

Формула диаметра может быть записана как \(d=2r\)

Формула длины окружности

Формула длины окружности: \(C=\pi \times d\) или может быть записана как \(C=2\times \pi \times r\). Любой работает!

Теперь вы можете спросить: «Откуда взялось число пи и почему мы вдруг получаем длину окружности, если умножаем это число пи на наш диаметр? Кто это решил?» Если вы не задаете этот вопрос… Вы должны, и я все равно отвечу на него.

Пи — это символ, который мы используем в математике для обозначения числа 3,14. А на самом деле это просто пи, округленное до сотых. Пи на самом деле не имеет ни конца, ни предсказуемой закономерности. Это просто продолжается.

Однако, когда вы видите символ \(\pi\), обычно (и в нашем случае) будет достаточно 3.14.

Пи — это не случайное число, которое придумали математики и заявили: «Мы каждый раз будем умножать диаметр на число и называть его окружностью». Наоборот, было обнаружено, что пи есть постоянное отношение между длиной окружности и диаметром.

Именно поэтому и как мы получили формулу длины окружности.

Теперь возьмем круг диаметром 9см, а радиус 4,5 см, и вычислить длину окружности.

Я собираюсь использовать формулу с диаметром для этого.

Итак, длина окружности равна (я просто перепишу формулу, чтобы помочь нам следить за нашей работой), \(C=\pi \times d\), равно pi, умноженному на диаметр. Итак, теперь все, что нам нужно сделать, это подставить наше число для диаметра. Это равно, а также мы сказали, что пи равно 3,14, \(C=(3,14)(9\text{см})=28,26\текст{см}\).

А вот и наш ответ! Теперь, чтобы попрактиковаться, попробуйте нарисовать круг на листе бумаги и измерьте его диаметр линейкой. Затем найдите свой радиус и длину окружности.

Надеюсь, это видео было для вас полезным.

Увидимся в следующий раз!

Часто задаваемые вопросы

Q

Каков радиус окружности?

A

Если бы нам нужно было измерить расстояние от центра круга до внешнего края этого круга, мы бы нашли радиус.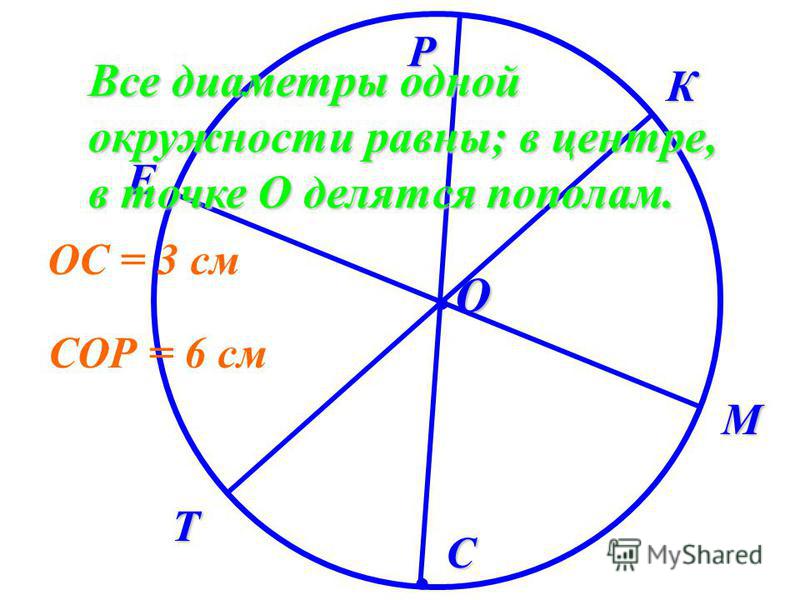 Подумайте о часах; если бы одна из стрелок была достаточно длинной, чтобы достать до края часов, эту стрелку можно было бы считать радиусом часов – независимо от того, сколько сейчас времени!

Q

Что такое радиус и диаметр?

A

В то время как радиус окружности проходит от центра к краю, диаметр проходит от края к краю и проходит через центр. Диаметр круга по существу делит фигуру пополам. Радиус и диаметр — близкие друзья — радиус круга равен половине длины его диаметра (или: диаметр круга в два раза больше длины его радиуса).

Q

Как называется радиус?

A

Радиус — это отрезок линии. Следовательно, у него есть две конечные точки: точка в центре круга и точка на краю круга, с которым мы его соединили. Имея все это в виду, мы знаем, что называть радиус так же, как и все сегменты линии: имена обеих конечных точек перечислены рядом (часто с чертой над двумя буквами).

Q

Является ли радиус половиной диаметра?

А

Да! Если вы помните только один факт о кругах, пусть это будет он. Просверлите это в своем уме! Радиус равен половине длины диаметра.

Q

Как найти радиус и диаметр?

A

Если мы знаем только радиус круга, мы просто умножим это значение на 2, чтобы получить диаметр \((d=2r)\). Точно так же, если мы знаем только диаметр круга, мы делим его на 2 и получаем радиус \((r=\frac{d}{2})\)!

Но что, если мы не получили ни одно из этих значений? Чтобы определить радиус или диаметр круга, нам нужно знать либо его длину окружности, либо его площадь. 92\)

\(±3=r\)

(Обратите внимание, что квадратный корень из 9 может быть либо 3, либо -3. Поскольку мы имеем дело с реальным кругом, мы будем просто использовать

\( d=2r=6\text{ дюймов}\)

Q

Как вычислить длину окружности

A

его радиус. Затем мы используем соответствующее значение в этом уравнении: \(C=2πr\) (где « r » представляет радиус, конечно)

Пример.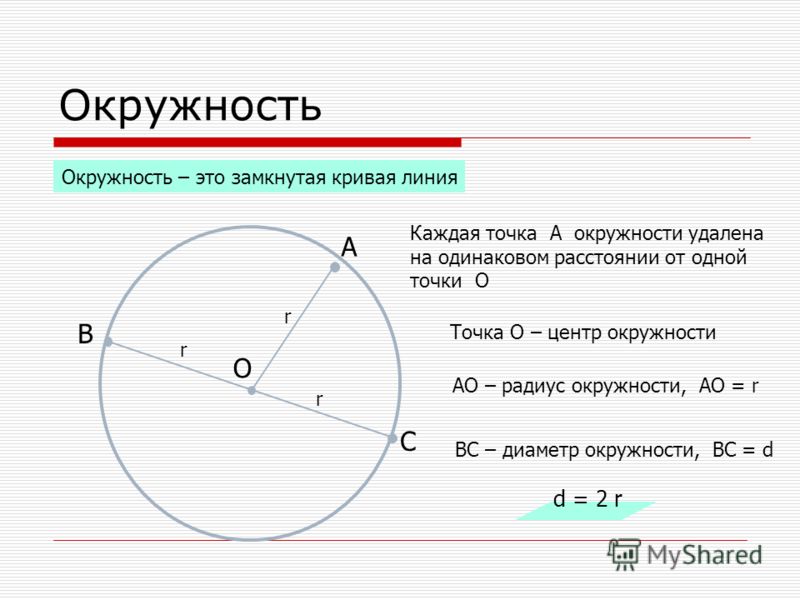 Найдите длину окружности этого круга:

\(r=\frac{10\text{ единиц}}{2}=5\text{ единиц}\)

\(C=2πr=2π\times5= 10π\text{ единиц}\)

Q

Почему длина окружности \(2πr\)?

A

Мы знаем, что длина окружности — это длина всего внешнего края круга. (Можно думать об этом так: длина окружности для кругов равна периметру для треугольников, прямоугольников, пятиугольников и т. д.!) Имея это в виду, давайте переставим переменные в уравнении \(C=2πr\), чтобы получить \ (С=2r\timesπ\). Помните, что \(2r=d\) (где d представляет собой диаметр), поэтому мы могли бы переписать это уравнение еще раз: \(C=d\timesπ\). Другими словами, мы можем обернуть нить (длина которой равна диаметру) вокруг круга 3,1415926… раз.

Q

Как мы используем длину окружности в повседневной жизни?

A

Применение окружности в повседневной жизни поистине безгранично! Однако одним из примеров является определение размера шины, необходимой для велосипеда или автомобиля. Другим примером может быть определение количества древесины в дереве: для очень-очень старого дерева было бы довольно сложно измерить диаметр основания дерева; но было бы просто обернуть веревку вокруг основания и измерить окружность. Затем вы можете использовать это измерение окружности и «реконструировать» уравнение окружности, чтобы определить диаметр дерева. С помощью этого измерения (и высоты дерева) мы могли бы найти объем древесины внутри этого дерева. Опять же, список примеров можно продолжать бесконечно, поэтому следите за другими способами использования окружности на протяжении всей своей жизни!

Q

Чем отличается длина окружности от диаметра?

A

Окружность — это длина одного полного «круга» вокруг окружности, а диаметр — это длина отрезка, который делит окружность пополам. Думайте об окружности как о внешнем измерении, а о диаметре — как о внутреннем измерении круга!

Q

Является ли диаметр половиной длины окружности?

А

Нет! Помните, что уравнение \(C=2πr\) можно переписать так: \(C=2r\timesπ\), \(C=d\timesπ\) или \(C=d\). Итак, возможно, мы могли бы сказать, что диаметр равен 3,14159.26… ^й окружности…

Q

Является ли диаметр длиной?

A

Если длина определяется как расстояние между двумя точками, тогда да, диаметр является длиной. Диаметр окружности измеряет расстояние между двумя самыми дальними точками окружности.

Практические вопросы

Вопрос №1:

 
Определите длину окружности.

23,16 см

24,14 см

25,12 см

26,11 см

Показать ответ

Ответ:

Длину окружности можно рассчитать по одной из следующих формул: \(C=𝜋d\) или \(C=2)𝜋 .

Мы знаем, что диаметр круга равен 8 см, а приближенное число пи равно 3,14, поэтому мы можем подставить эти значения в формулу \(C=𝜋d\). Формула принимает вид \(C=(3.14)(8)\), что упрощается до 25. 12. Длина окружности 25,12 см.

Скрыть ответ

Вопрос № 2:

 
Определите радиус окружности, если длина окружности составляет двадцать три дюйма. Округлите ответ до сотых.

3,66 дюйма

4,65 дюйма

3,44 дюйма

4,76 дюйма

Показать Ответ

Ответ:

5 Мы знаем, что длина окружности равна двадцати трем дюймам, поэтому мы можем подставить это значение в формулу \(C=2𝜋r\). Мы также знаем, что приблизительное число пи равно 3,14, поэтому единственное неизвестное нам значение — это 9.0343 р , радиус. Когда C и 𝜋 подставляются в формулу, получается \(23=2(3.14)r\). Его можно упростить до \(23=6,28r\), а затем обе части уравнения можно разделить на 6,28, чтобы выделить переменную r . 23 разделить на 6,28 равно 3,66 при округлении до сотых. Радиус круга равен 3,66 дюйма.

Скрыть ответ

Вопрос № 3:

 
Если C представляет длину окружности, r представляет радиус, а d представляет диаметр, какая формула неверна?

\(d=2r\)

\(C=𝜋d\)

\(C=2𝜋r\)

\(r=𝜋dC\)

Показать ответ

r=𝜋dC\) неверно, потому что умножение пи, умноженное на диаметр, умноженное на длину окружности, не равно радиусу. Если диаметр известен, то радиус равен половине значения d .

Скрыть ответ

Вопрос № 4:

 
Велосипеды 1800-х годов сильно отличаются от велосипедов, которые мы видим сегодня. На фотографии ниже заднее колесо велосипеда имеет радиус 9 дюймов, а переднее колесо имеет диаметр 60 дюймов. Используя 3,14 в качестве приближения для пи, какова разница между окружностями переднего и заднего колеса?

161,88 дюйма

151,88 дюйма

171,88 дюйма

131,88 дюйма

Показать ответ

Ответ:

Прежде чем сравнивать переднее и заднее колесо, нам нужно рассчитать длину окружности каждого колеса в отдельности.