Квадрат. Формулы и свойства квадрата
Навигация по странице: Определение квадрата Основные свойства квадрата Диагональ квадрата Периметр квадрата Площадь квадрата Окружность описанная вокруг квадрата Окружность вписанная в квадрат
Определение.
Квадрат — это четырехугольник у которого все четыре стороны и углы одинаковы. Квадраты отличаются между собой только длиной стороны, но все четыре угла у них прямые, то есть по 90°.
| Рис.1 | Рис.2 |
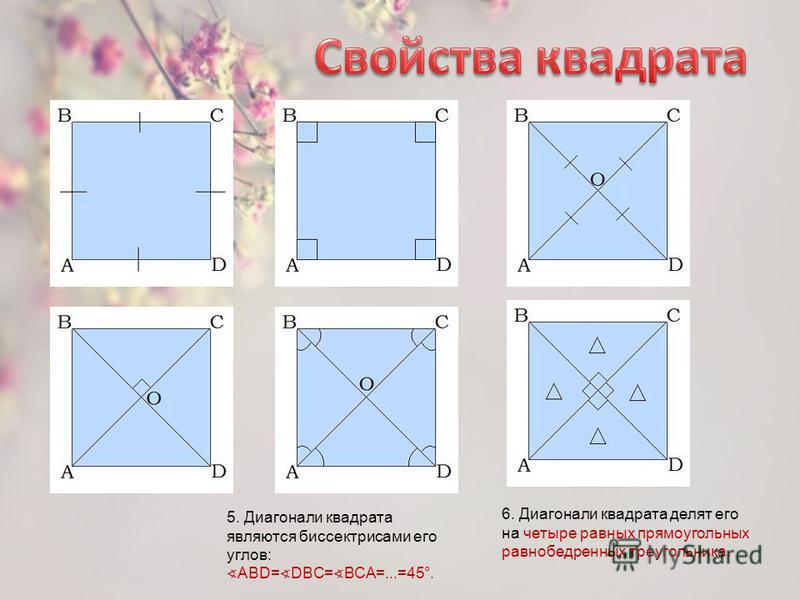
Основные свойства квадрата
Квадратом также могут быть параллелограмм, ромб или прямоугольник если они имеют одинаковые длины диагоналей, сторон и одинаковые углы.
1. Все четыре стороны квадрата имеют одинаковую длину, то есть они равны:
AB = BC = CD = AD
Противоположные стороны квадрата параллельны:AB||CD, BC||AD
3. Все четыре угла квадрата прямые:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
4. Сумма углов квадрата равна 360 градусов:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
5. Диагонали квадрата имеют одинаковой длины:
AC = BD
6. Каждая диагональ квадрата делит квадрат на две одинаковые симметричные фигуры
7. Диагонали квадрата пересекаются под прямым углом, и разделяют друг друга пополам:
| AC┴BD | d | ||
| 2 |
8. Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружности
9. Каждая диагональ делит угол квадрата пополам, то есть они являются биссектрисами углов квадрата:
ΔABC = ΔADC = ΔBAD = ΔBCD
∠ACB = ∠ACD = ∠BDC = ∠BDA = ∠CAB = ∠CAD = ∠DBC = ∠DBA = 45°
10.
Обе диагонали разделяют квадрат на четыре равные треугольника, причем эти треугольники одновременно и равнобедренные и прямоугольные:
ΔAOB = ΔBOC = ΔCOD = ΔDOA
Диагональ квадрата
Определение.
Диагональю квадрата называется любой отрезок, соединяющий две вершины противоположных углов квадрата.
Диагональ любого квадрата всегда больше его стороны в√2 раз.
Формулы определения длины диагонали квадрата
1. Формула диагонали квадрата через сторону квадрата:
d = a·√2
2. Формула диагонали квадрата через площадь квадрата:
d = √2S
3. Формула диагонали квадрата через периметр квадрата:
| d = | P |
| 2√2 |
4. Формула диагонали квадрата через радиус описанной окружности:
d = 2R
5.
d = Dо
6. Формула диагонали квадрата через радиус вписанной окружности:
d = 2r√2
7. Формула диагонали квадрата через диаметр вписанной окружности:
d = Dв√2
8. Формула диагонали квадрата через длину отрезка l:
| d = l | 2√10 |
| 5 |
Периметр квадрата
Определение.
Периметром квадрата называется сумма длин всех сторон квадрата.
Формулы определения длины периметра квадрата
1. Формула периметра квадрата через сторону квадрата:
P = 4a
P = 4√S
3. Формула периметра квадрата через диагональ квадрата:
P = 2d√2
4.
Формула периметра квадрата через радиус описанной окружности:
P = 4R√2
5. Формула периметра квадрата через диаметр описанной окружности:
P = 2Dо√2
6. Формула периметра квадрата через радиус вписанной окружности:
P = 8r
7. Формула периметра квадрата через диаметр вписанной окружности:
8. Формула периметра квадрата через длину отрезка l:
| P = l | 8 |
| √5 |
Площадь квадрата
Определение.
Площадью квадрата называется пространство, ограниченное сторонами квадрата, то есть в пределах периметра квадрата.
Площадь квадрата больше площади любого четырехугольника с таким же периметром.
Формулы определения площади квадрата
1.
Формула площади квадрата через сторону квадрата:
S = a2
2. Формула площади квадрата через периметр квадрата:
| S = | P2 |
| 16 |
3. Формула площади квадрата через диагональ квадрата:
| S = | d |
| 2 |
4. Формула площади квадрата через радиус описанной окружности:
S = 2R2
5. Формула площади квадрата через диаметр описанной окружности:
| S = | Do2 |
| 2 |
6. Формула площади квадрата через радиус вписанной окружности:
S = 4r2
7. Формула площади квадрата через диаметр вписанной окружности:
S = Dв2
8.
| S = l 2 | 16 |
| √5 |
Окружность описанная вокруг квадрата
Определение.
Кругом описанным вокруг квадрата называется круг проходящий через четыре вершины квадрата и имеющий центр на пересечении диагоналей квадрата.
Радиус окружности описанной вокруг квадрата всегда больше радиуса вписанной окружности в√2 раз.
Радиус окружности описанной вокруг квадрата равен половине диагонали.
Площадь круга описанного вокруг квадрата большая площадь того же квадрата в π/2 раз.
Формулы определения радиуса окружности описанной вокруг квадрата
1. Формула радиуса окружности описанной вокруг квадрата через сторону квадрата:
| R = a | √2 |
| 2 |
2. Формула радиуса окружности описанной вокруг квадрата через периметр квадрата:
| R = | P |
| 4√2 |
3.
| R = | √2S |
| 2 |
4. Формула радиуса круга описанного вокруг квадрата через диагональ квадрата:
| R = | d |
| 2 |
5. Формула радиуса круга описанного вокруг квадрата через диаметр описанной окружности:
| R = | Dо |
| 2 |
6. Формула радиуса круга описанного вокруг квадрата через радиус вписанной окружности:
R = r √2
7. Формула радиуса круга описанного вокруг квадрата через диаметр вписанной окружности:
| R = Dв | √2 |
| 2 |
8. формула радиуса круга описанного вокруг квадрата через длину отрезка l:
| R = l | √10 |
| 5 |
Окружность вписанная в квадрата
Определение.
Кругом вписанным в квадрат называется круг, который примыкает к серединам сторон квадрата и имеет центр на пересечении диагоналей квадрата.
Радиус вписанной окружности равен половине стороны квадрата.
Площадь круга вписанного в квадрат меньше площади квадрата в 4/π раза.
Формулы определения радиуса круга вписанного в квадрат
1. Формула радиуса круга вписанного в квадрат через сторону квадрата:
| r = | a |
| 2 |
2. Формула радиуса круга вписанного в квадрат через диагональ квадрата:
| r = | d |
| 2√2 |
3. Формула радиуса круга вписанного в квадрат через периметр квадрата:
| r = | P |
| 8 |
4. Формула радиуса круга вписанного в квадрат через площадь квадрата:
| r = | √S |
| 2 |
5.
Формула радиуса круга вписанного в квадрат через радиус описанной окружности:
| r = | R |
| √2 |
6. Формула радиуса круга вписанного в квадрат через диаметр, описанной окружности:
| r = | Dо |
| 2√2 |
7 Формула радиуса круга вписанного в квадрат через диаметр вписанной окружности:
| r = | Dв |
| 2 |
8. Формула радиуса круга вписанного в квадрат через длину отрезка l:
| r = | l |
| √5 |
Все таблицы и формулы
Квадрат. Периметр и площадь квадрата. / Геометрия / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Геометрия
- Квадрат.
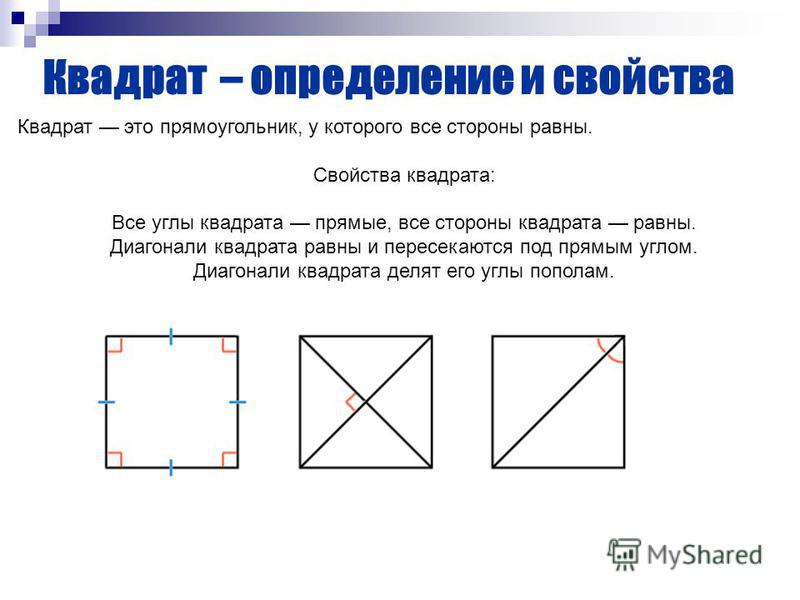
Рассмотрим фигуру она называеться квадрат.
Квадрат — это прямоугольник у которого все стороны равны AB=BC=CD=DA.
Стороны AB, BC, CD, DA другое название они имеют ребра; углы A, B, C, D; второе название вершины, зеленим цветом обозначаются диагонали AD, BC. Диагонали в квадрате равны и точкой пересечения делятся пополам.
Периметр P=4•a, Площадь S=a·а
Свойства квадрата
1. Длины сторон квадрата равны.
AB=BC=CD=DA
2. Все углы квадрата прямые.
∠ABC=∠BCD=∠CDA=∠DAB=90∘
3. Противолежащие стороны квадрата параллельны друг другу AB∥CD,BC∥AD
4. Сумма всех углов квадрата равна 360 градусов ∠ABC+∠BCD+∠CDA+∠DAB=360∘
5. Величина угла между диагональю и стороной равна 45 градусов ∠BAC=∠BCA=∠CAD=∠ACD=45∘
6.
Диагонали квадрата — тождественны, перпендикулярны и разделяются точкой пересечения пополам.
AO = BO = CO = DO
7. Каждая из диагоналей делит квадрат на два равнобедренных прямоугольных треугольника.
△ABD=△CBD=△ABC=△ACD
8. Обе диагонали делят квадрат на 4 равнобедренных прямоугольных треугольника.
△AOB=△BOC=△COD=△AOD
Советуем посмотреть:
Отрезок
Ломаная
Четырехугольники
Единицы измерения площадей. Свойства площадей
Прямоугольник, его периметр и площадь. Ось симметрии фигуры
Многоугольники. Правильные многоугольники. Равенство фигур.
Плоскость
Прямая
Луч
Шкалы и координаты
Прямоугольный параллелепипед. Пирамида.
Объем прямоугольного параллелепипеда
Куб. Площадь поверхности куба
Куб. Объем куба
Угол. Обозначение углов
Прямой и развернутый угол
Чертежный треугольник
Измерение углов. Транспортир.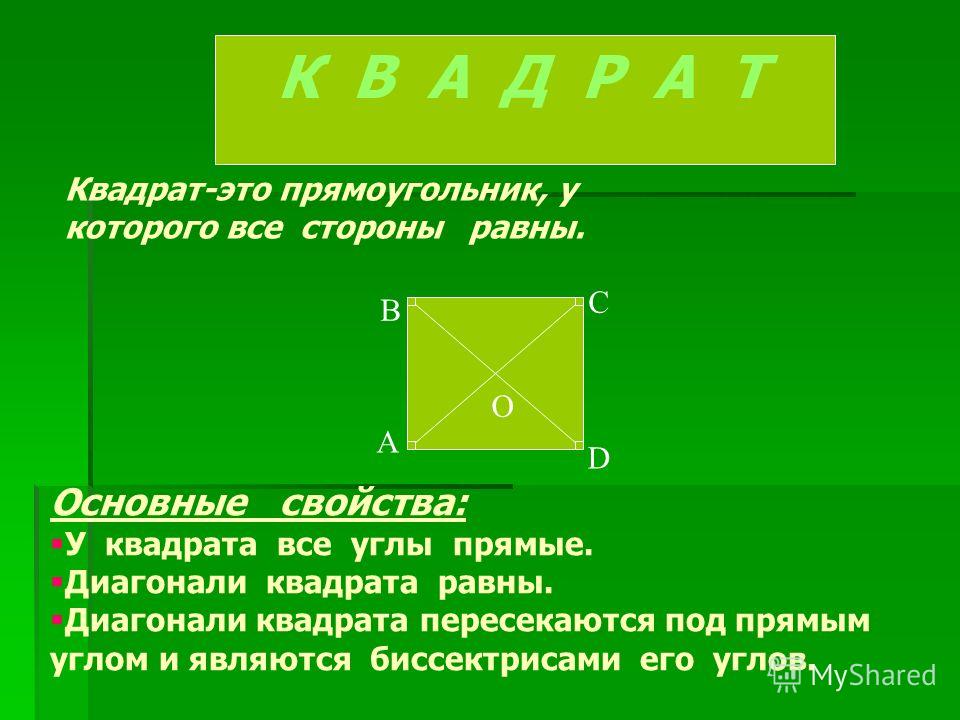
Виды углов
Треугольник и его виды
Окружность, круг, шар
Цилиндр, конус
Отрезок-xx
Геометрия
Правило встречается в следующих упражнениях:
5 класс
Задание 237 , Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 720, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 772, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 957, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 370, Мерзляк, Полонский, Якир, Учебник
Номер 374, Мерзляк, Полонский, Якир, Учебник
Номер 581, Мерзляк, Полонский, Якир, Учебник
Номер 1060, Мерзляк, Полонский, Якир, Учебник
Номер 1061, Мерзляк, Полонский, Якир, Учебник
Номер 1197, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 121, Мерзляк, Полонский, Якир, Учебник
Номер 130, Мерзляк, Полонский, Якир, Учебник
Номер 658, Мерзляк, Полонский, Якир, Учебник
Номер 729, Мерзляк, Полонский, Якир, Учебник
Номер 758, Мерзляк, Полонский, Якир, Учебник
Номер 1219, Мерзляк, Полонский, Якир, Учебник
Задание 191, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 519, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1413, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 2, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
7 класс
Номер 229, Мерзляк, Полонский, Якир, Учебник
Номер 409, Мерзляк, Полонский, Якир, Учебник
Номер 544, Мерзляк, Полонский, Якир, Учебник
Номер 601, Мерзляк, Полонский, Якир, Учебник
Номер 643, Мерзляк, Полонский, Якир, Учебник
Номер 751, Мерзляк, Полонский, Якир, Учебник
Номер 754, Мерзляк, Полонский, Якир, Учебник
Номер 848, Мерзляк, Полонский, Якир, Учебник
Номер 892, Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 372, Мерзляк, Полонский, Якир, Учебник
Показать, что диагонали квадрата равны и делят друг друга пополам под прямым углом.
..Перейти к
- Четырехугольники — упражнение 8.1
- Четырехугольники — упражнение 8.2
- Система счисления
- Полиномы
- Координатная геометрия
- Линейные уравнения с двумя переменными
- Введение в геометрию Евклида
- Линии и углы
- Треугольники
- Четырехугольники
- Площади параллелограммов и треугольников
- Круги
- Конструкции
- Формула Герона
- Площади поверхности и объемы
- Статистика
- Вероятность
Главная >
Решения НЦЭРТ
Класс 9
Математика
>
Глава 8 — Четырехугольники
>
Четырехугольники — упражнение 8.
1
>
Вопрос 3
Вопрос 3 Четырехугольники – Упражнение 8.1
Докажите, что диагонали квадрата равны и делят друг друга пополам под прямым углом.
Ответ:
Пусть ABCD — квадрат и его диагонали AC и BD пересекаются в точке O.
Доказательство,
В ΔABC и ΔBAD,
BC = BA (Общий)
∠ABC = ∠BAD = 90°0003
Таким образом,
AC = BD (CPCT)
∴, диагонали равны.
Теперь,
в ΔAOB и ΔCOD,
♂ = Ϫdco (альтернативные внутренние углы)
↑AOB = ↑COD (вертикально противоположность)
AB = CD (дан)
∴ , ΔAOB ΔCODCOD. (ААС-конгруэнтность)
Таким образом,
AO = CO (CPCT)
∴, Диагонали делят друг друга пополам.
Сейчас,
В ΔAOB и ΔCOB,
OB = OB (Дано)
AO = CO (диагонали разделены пополам)
AB = CB (стороны квадрата)
∴, ΔAOB ≅ ΔCOB (конгруэнтность SSS)
также, ∠AOB = ∠COB
∠AOB + ∠COB = 180° (линейная пара 00) ∠AOB = ∠COB = 90°
∴, Диагонали делят друг друга пополам под прямым углом
Связанные вопросы
Углы четырехугольника относятся как 3 : 5 : 9 : 13.
Найдите все углы четырехугольника…
Если диагонали параллелограмма равны, то докажите, что это прямоугольник.
ABCD — прямоугольник, в котором диагональ AC делит пополам ∠A и ∠C. Покажите, что: (i) ABCD — квадрат (ii…
ABCD — параллелограмм, а AP и CQ — перпендикуляры из вершин A и C на диагонали BD (см.
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Exercises
Quadrilaterals — Exercise 8.1
Quadrilaterals — Exercise 8.
2
Chapters
Number System
Polynomials
Coordinate Geometry
Linear Equations in Two Variables
Introduction to Euclids Geometry
Lines and Angles
Triangles
Четырехугольники
Площади параллелограммов и треугольников
Окружности
Построения
Формула Герона
Площади поверхностей и объемы
Статистика
Вероятность
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены
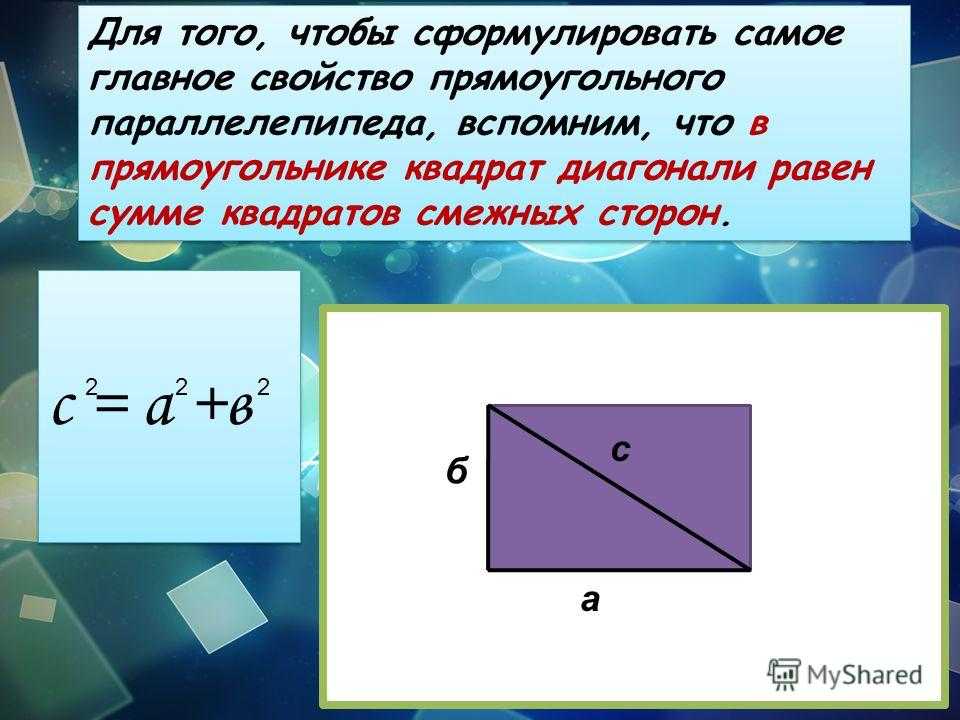
Как найти длину диагонали квадрата
9 Все ресурсы по базовой геометрии0187
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
Справка по базовой геометрии » Плоская геометрия » Четырехугольники » Площади » Как найти длину диагонали квадрата
Сторона в квадрате имеет длину 12.
Какова длина диагонали?
Возможные ответы:
На основании предоставленной информации определить невозможно.
Правильный ответ:
Объяснение:
Диагональ образует треугольник со смежными сторонами. Поскольку это квадрат, мы знаем, что это прямоугольный треугольник, и мы можем использовать теорему Пифагора, чтобы определить длину . Стороны длины формируют каждый из катетов и являются гипотенузой. Таким образом, уравнение выглядит так: 9Мы можем упростить это до достаточно места, чтобы сделать расстояние между домашней площадкой и первой базой 44 фута. Какое расстояние (ближайший фут) будет от домашней площадки до второй базы, если предположить, что он построил ее в соответствии с этой спецификацией?
(Примечание: четыре основания являются вершинами идеального квадрата, причем основания называются исходной пластиной, первое основание, второе основание, третье основание, в указанном порядке).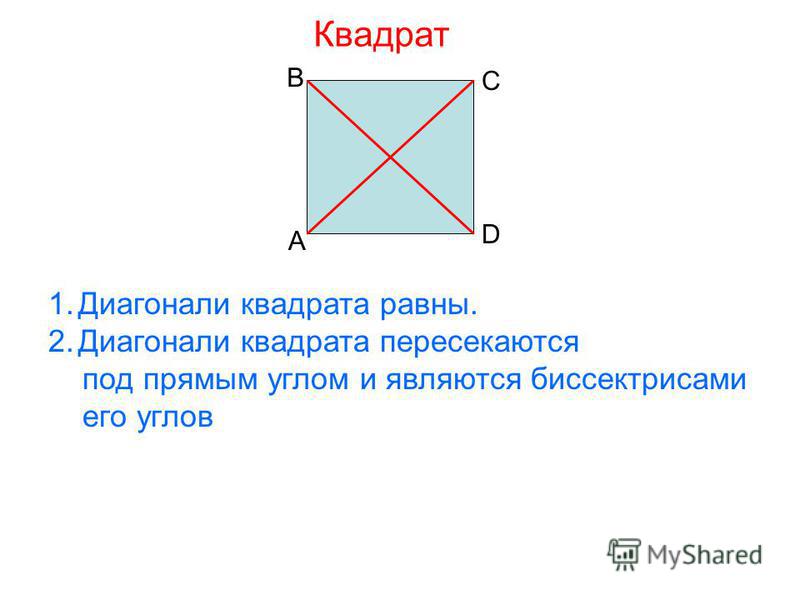
Возможные ответы:
Правильный ответ:
Объяснение:
Путь от домашней пластины до первой базы является стороной правильного квадрата; путь от домашней пластины до второй базы является диагональю. Поскольку две стороны и диагональ образуют треугольник, длина диагонали равна длине стороны.
Расстояние до второй базы от дома умножено на расстояние до первой базы:
Сообщить об ошибке
Квадратный участок площадью 1200 квадратных метров. С точностью до метра, какое расстояние от одного угла до противоположного?
Возможные ответы:
Правильный ответ:
Объяснение:
Квадрат также является ромбом, поэтому его площадь можно вычислить как половину произведения его диагоналей:
,
, где .
С , .
Расстояние между противоположными углами около 49 метров.
Сообщить об ошибке
Найдите длину диагонали квадрата.
Возможные ответы:
Ни один из других ответов не является правильным.
Правильный ответ:
Пояснение:
Диагональная линия делит квадрат на два равных треугольника. Их гипотенуза является диагональю квадрата, поэтому мы можем найти гипотенузу.
Нам нужно использовать теорему Пифагора: , где a и b — катеты, а c — гипотенуза.
Длина двух катетов равна 8. Подставьте это число и решите для c:
Сообщить об ошибке
Найдите длину диагонали квадрата со стороной см.
Возможные ответы:
Правильный ответ:
Объяснение:
Вы можете решить эту задачу двумя разными способами, которые приведут к окончательному ответу:
1.
Теорема Пифагора
2. Специальные треугольники (45-45-90)
1. Для первой идеи используйте теорему Пифагора: , где a и b — длины сторон квадрата, а c — длина диагонали.
2. Если вы знаете, что ВСЕ квадраты можно составить из двух особых прямоугольных треугольников с углами 45-45-90, то можно использовать следующую формулу:
скажем, что длина стороны квадрата равна «а». Тогда диагональ квадрата (или гипотенуза прямоугольного треугольника) будет равна .Итак, используя это с a=4:
Сообщить об ошибке
Периметр квадрата равен 48. Какова длина его диагонали?
Возможные ответы:
Правильный ответ:
Объяснение:
Периметр = сторона * 4
48 = сторона * 4
Сторона = 12
Квадрат можно разбить на два равных прямоугольных треугольника.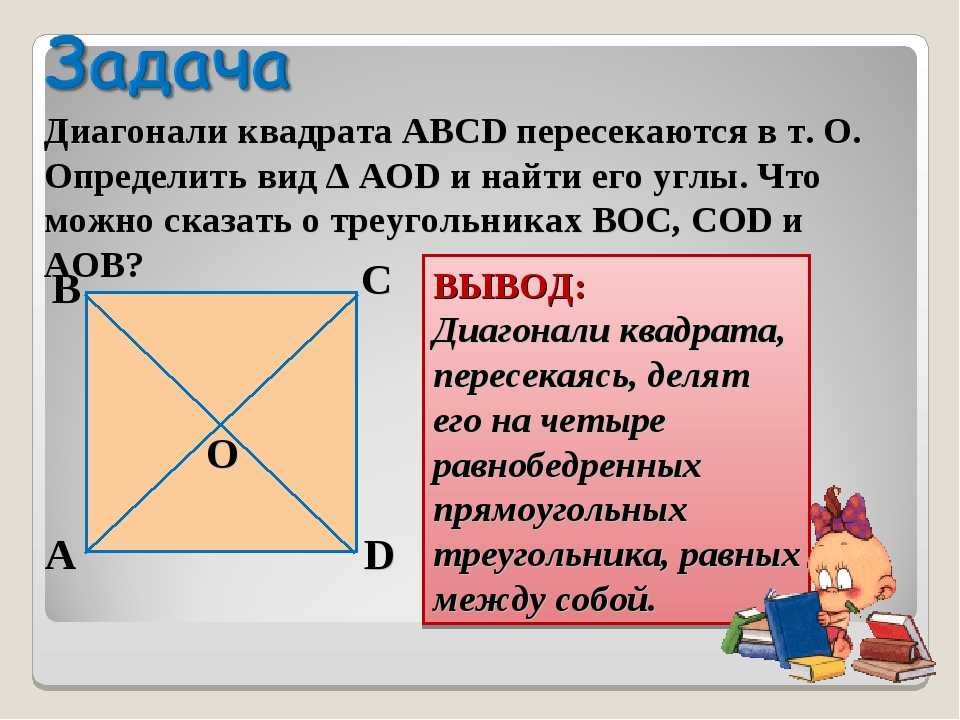
Тогда диагональ квадрата является гипотенузой этих двух треугольников.
Следовательно, мы можем использовать теорему Пифагора для вычисления диагонали:
Сообщить об ошибке площади
23
. Сколько единиц длины диагонали квадрата?
Возможные ответы:
Правильный ответ:
Пояснение:
Из периметра мы можем найти длину каждой стороны квадрата. Длины сторон квадрата равны по определению, поэтому периметр можно переписать как
Затем мы используем теорему Пифагора, чтобы найти диагональ, которая является гипотенузой прямоугольного треугольника, каждый катет которого является стороной квадрата.
Сообщить об ошибке
Найдите длину диагонали квадрата со стороной .
Возможные ответы:
Правильный ответ:
Объяснение:
Диагональ квадрата также является гипотенузой прямоугольного треугольника с длинами сторон как катетами треугольника.
Используйте теорему Пифагора, чтобы найти длину диагонали.
Для квадрата, указанного в вопросе,
Сообщить об ошибке
Найдите длину диагонали квадрата со сторонами .
Возможные ответы:
Правильный ответ:
Объяснение:
Диагональ квадрата также является гипотенузой прямоугольного треугольника с длинами сторон как катетами треугольника.
Используйте теорему Пифагора, чтобы найти длину диагонали.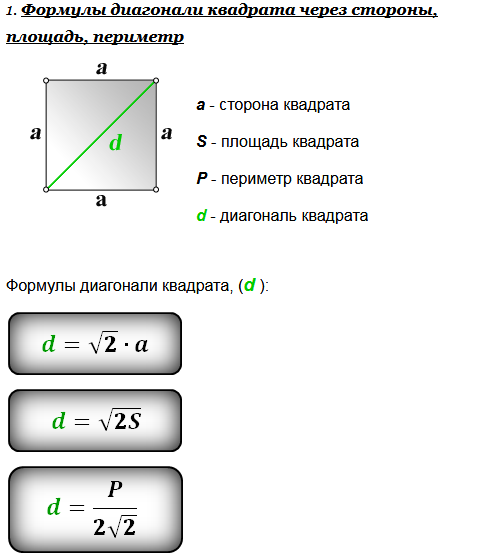
Leave A Comment