Действия со степенями примеры: Свойства степеней, действия со степенями

Действия со степенями | СПАДИЛО

Что такое степень?

Степенью числа a с натуральным показателем n называют произведение n одинаковых множителей, каждый из которых равен а. То есть аⁿ=a×a×a×a …..a (а берется n раз). Число а называют основанием, а число n показателем степени. Показатель показывает, сколько раз берется основание как множитель.

Пример №1.

• 3⁴=3×3×3×3 число 3 берем 4 раза (показатель 4)
• 21³=21×21×21 число 21 берем 3 раза (показатель 3)

Свойства степени (применимы для степеней с одинаковым основанием)

Умножение степеней

При умножении степеней с одинаковым основанием основание оставляют тем же, а показатели складывают:

aⁿ× a^m=a^n+m

Пример №2.

а²×а⁸=а²⁺⁸=а¹⁰

5⁵×5³×5⁴=5⁵⁺³⁺⁴=5¹²

Деление степеней

При делении степеней с одинаковым основанием  основание оставляют тем же, а показатели вычитают:

aⁿ : a^m=a^n–m

Пример №3.

с¹²:с⁵=с^12-5= с⁷

3²³:3²⁰=3^23-20= 3³

Возведение степени в степень

При возведении степени в степень основание оставляют тем же, а показатели умножают:

(aⁿ)^m=a^n×m

Пример №4.

(с¹⁰)²=с²⁰

(6³)⁵=6¹⁵

Степень произведения

При возведении в степень произведения разных множителей необходимо возвести в эту степень каждый множитель:

(a×b×c)^m=a^m×b^m×c^m

Пример №5.

(сmn)⁵=c⁵m⁵n⁵

(3²5⁴)⁶=3¹²5²⁴

Степень дроби  (степень частного)

При возведении в степень обыкновенной дроби необходимо возвести в данную степень числитель и знаменатель дроби:

Важные правила для работы со степенями

Запомните!

1. Любое число в нулевой степени равно 1 (а⁰=1).
2. Нуль в любой степени равен нулю (0ⁿ=0).
3. Свойства степени с натуральным показателем применимы для степени с целым отрицательным показателем.

Пример №6.

с^-21× с^-2=с^-21+(-2)=с^-23

х¹² : х^-2= х^12-(-2)=х¹⁴

(с^-3)⁵=с^-15

Правила для степени с целым отрицательным показателем

1. Степень с целым отрицательным показателем можно представить в виде обыкновенной дроби, числитель которой равен единице, а знаменатель степени с натуральным показателем.
2. Если дана дробь, в знаменателе которой есть степень с целым отрицательным показателем, то ее можно представить в виде степени с натуральным показателем.
3. Если дана дробь, в числителе и знаменателе которой есть степень с целым отрицательным показателем, то можно заменить её дробью, содержащей степень с натуральным показателем, просто поменяв числитель и знаменатель местами.

Задание OM2004 Сократите дробь 36n4n−2∙32n−1 .

---

Чтобы решить данное задание, необходимо понимать, что выполнять действия умножение и деление степеней мы можем в том случае, если они имеют одинаковые основания. Поэтому разложим на множители основание 36 нашего числителя так, чтобы вместо 36 были числа 4 и 3, которые есть в знаменателе.

(3∙3∙4)n4n−2∙32n−1 ..

Теперь представим каждый множитель в виде степени:

3n∙3n∙4n4n−2∙32n−1 ..

Разложим знаменатель дроби на множители по свойству степеней

3n∙3n∙4n4n∙4−2∙32n∙3−1 ..

Теперь можно сократить числитель и знаменатель на 3n и в 4n степени

Получим дробь, которую преобразуем по свойству степеней:

. .14−2∙3−1 ..= 42∙311..=16∙3=48

Ответ: 48

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание 8OM21R Найти значение выражения

(3∙8)737∙85..

 

---

В числителе дроби возведем в степень каждый множитель:

(3∙8)737 ∙85..=37∙8737∙85.

Теперь сократим (выполним деление степеней), сократятся 37 полностью, а при сокращении на 85 по свойству степеней останется 82, возведем 8 во вторую степень, получим 64, т.е.

 (3∙8)737 ∙85..=37∙8737∙85..=82=64

Ответ: 64

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1302o

Найдите значение выражения:

при a = 13, b = 6,8

---

В данном случае, в отличие от первого, мы будем упрощать выражение вынося за скобки, а не раскрывая их.

Сразу можно заметить, что b присутствует у первой дроби в числителе, а у второй – в знаменателе, поэтому можем их сократить.

Семь и четырнадцать тоже сокращаются на семь:

Далее выносим из числителя второй дроби a:

 Сокращаем (a-b):

 И получаем:

a/2

Подставляем значение a = 13:

13 / 2 = 6,5

Ответ: 6,5

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1301o

Найдите значение выражения: (x + 5)² — x (x- 10) при x = — 1/20

---

В данном случае необходимо сначала упростить выражение, для этого раскроем скобки:

(x + 5)² – x (x – 10) = x² + 2 • 5 • x + 25 – x² + 10x

Затем приведем подобные слагаемые:

x² + 2 • 5 • x + 25 – x² + 10x = 20 x + 25

Далее подставим x из условия:

20 x + 25 = 20 • (-1/20) + 25 = – 1 + 25 = 24

Ответ: 24

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0807o Найдите значение выражения:

---

Используем правило умножения и деления степеней с одинаковым основанием.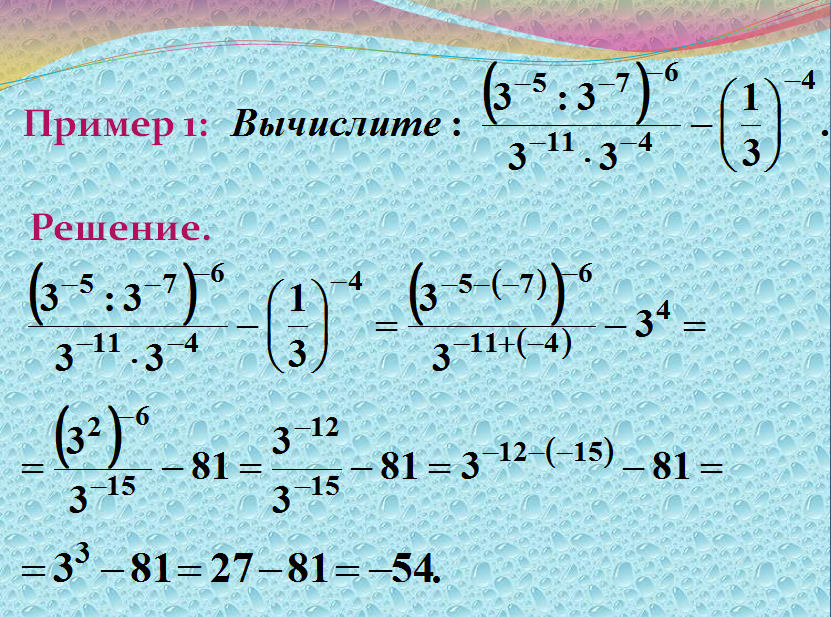

Заключается оно в том, что при их умножении показатели степеней суммируются, а при делении вычитаются (от показателя в числителе вычитается показатель, стоящий в знаменателе). Тогда получаем:

Ответ: 81

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0806o

Найдите значение выражения:

---

В 1-м корне представляем 4900 в виде произведения 49·100. Оба эти числа являются точными квадратами: 49=7² и 100=10². И, значит, число под корнем можно полностью вынести из-под него, применив правила работы с подкоренными выражениями. В целом получаем:   По аналогии извлекаем и 2-й корень: В итоге получаем:

Ответ: 70,7

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0805o

Значение какого из выражений является рациональным числом?

1. √6-3
2. √3•√5
3. (√5)²
4. (√6-3)²

---

В данном задании у нас проверяют навыки операций с иррациональными числами.

Разберем каждый вариант ответа в решении:

1) √6-3

√6 само по себе является иррациональным числом, для решения подобных задач достаточно помнить, что рационально извлечь корень можно из квадратов натуральных чисел, например, 4, 9, 16, 25…

При вычитании из иррационального числа любого другого, кроме его же самого, приведет вновь к иррациональному числу, таким образом, в этом варианте получается иррациональное число.

2) √3•√5

При умножении корней, мы можем извлечь корень из произведения подкоренных выражений, то есть:

√3•√5 = √(3•5) = √15

Но √15 является иррациональным, поэтому данный вариант ответа не подходит.

3) (√5)²

При возведении квадратного корня в квадрат, мы получаем просто подкоренное выражение (если уж быть точнее, то подкоренное выражение по модулю, но в случае числа, как в данном варианте, это не имеет значения), поэтому:

(√5)² = 5

Данный вариант ответа нам подходит.

4) (√6-3)²

Данное выражение представляет продолжение 1 пункта, но если √6-3 иррациональное число, то никакими известными нам операциями перевести в рациональное его нельзя.

Ответ: 3

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0804o

Какое из данных ниже чисел является значением выражения?

---

Заметим, что в знаменателе присутствует разность (4 – √14), от которой нам необходимо избавиться. Как же это сделать?

Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.

После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² – (√14)². После этого знаменатель легко вычисляется:

16 – 14 = 2

Суммарно наши действия выглядят так:

Ответ: 4

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0801o

Какое из данных ниже выражений при любых значениях n равно произведению 121 • 11ⁿ ?

1. 121ⁿ
2. 11ⁿ⁺²
3. 11²ⁿ
4. 11ⁿ⁺³

---

Для решения данной задачи необходимо вспомнить следующие правила обращения со степенями:

• при умножении степени складываются
• приделении степени вычитаются
• при возведении степени в степень степени перемножаются
• при извлечении корня степени делятся

Кроме того, для решения необходимо представить 121 как степень 11, а именно это 11².

121 • 11ⁿ = 11² • 11ⁿ

С учетом правила умножения, складываем степени:

  11² • 11ⁿ = 11ⁿ⁺²

Следовательно, нам подходит второй ответ.

Ответ: 2

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM0606o Найдите значение выражения:

–0,3·(–10)⁴+4·(–10)²–59

---

Для получения результата необходимо последовательно выполнить математические действия в соответствии с их приоритетом.

–0,3·(–10)⁴+4·(–10)²–59 =

Выполняем возведение в степень. Получаем числа, состоящие из единицы и следующего за ней количества нулей, равного показателю степени. При этом знаки «–» в скобках исчезают, поскольку показатели степеней четные. Получаем:

= –0,3·10000+4·100–59 =

Выполняем умножение. Для этого в числе 0,3 переносим десятичную запятую на 4 знака вправо (так как в 10000 четыре нуля), а к 4 дописываем, соответственно, 2 нуля. Получаем:

= –3000+400–59 =

Выполняем сложение –3000+400. Поскольку это числа с разными знаками, то вычитаем из большего модуля меньший и перед результатом ставим «–», поскольку число с большим модулем отрицательное. Получаем:

= –2600–59 =

Так как оба числа отрицательные, то складываем их модули и перед результатом ставим «–». Получаем:

= –(2600+59) = –2659

Ответ: -2659

pазбирался: Даниил Романович | обсудить разбор | оценить

Алла Василевская | Просмотров: 7.5k

Действия со степенями с примерами решения

Содержание:

1. Поговорим о действиях со степенями
2. Отрицательные степени

Поговорим о действиях со степенями

Пусть — натуральные числа. Тогда То есть — это указание умножить число само на себя раз. Пример. Обсуждение. А что такое ? Это Типовая ошибка. Пожалуйста, не путайте умножение и сложение. Еще раз повторим:

Для действий со степенями существуют ровно три базовые формулы, а все остальные формулы выводятся из них. Дальше мы узнаем, что бывают различные степени, в том числе отрицательные и дробные (т. е. ). Базовые формулы верны для любых степеней. По для натуральных степеней их легко проверить и вывести. Итак, давайте перейдем к формулам.

Обсуждение.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

В какой степени? Сколько раз мы умножали 2 само на себя? Обратите внимание, какую операцию мы произвели со степенями. Л теперь продолжите формулу:

Обсуждение. Продолжим формулу.

Какую операцию мы произвели со степенями?

А теперь продолжите формулу:

Замечание Мы увидели, что То есть

Возможно вам будут полезны данные страницы:

Реляционная модель данных

Поверхность второго порядка

Действия с корнями

Формулы сокращенного умножения

Пример 1:

На игре формул строится алгоритм быстрого возведения в степень. Свойства степени с натуральным показателем.

Эти свойства верны и для степени с целым и рациональным показателями. Действия со степенями.

Упростите выражения:

Отрицательные степени

Натуральные степени имели интуитивно понятный смысл. Дальше мы будем говорить о степенях, которые вводятся определениями. То есть мы сами договариваемся о том, какой смысл они имеют.

В этом случаи мы используем обозначение

Мы договоримся:

Пример 2:

Теперь осталось обсудить отрицательные и дробные степени. Можно понимать так: отрицательная степень — это «лифт», перемещающий все, кроме минуса, в другую часть дроби: сверху-вниз, снизу вверх. Минус при вынесении его из отрицательной степени никогда не меняет знак самого выражения!

Проще говоря: посмотрите на формулу. В левой части имеется минус в степени, а в правой части минуса нет. Разберем решение некоторых типовых задач из ЕГЭ. Будем разбирать по шагам. Будем использовать таблицу степеней.

Пример 3:

Пример. Как я это узнала? Знаю, что и сдвиг равен трем знакам. Можете проверить умножением. Пример. и сдвиг равен четырем знакам.

Правила экспоненты

: 7 ключевых стратегий решения сложных уравнений

Правила экспоненты объясняют, как решать различные уравнения, в которых, как и следовало ожидать, есть экспоненты. Но есть несколько различных типов экспоненциальных уравнений и экспоненциальных выражений, которые могут показаться сложными… поначалу.

Овладение этими основными правилами экспоненты вместе с основными правилами логарифмирования (также известными как «логарифмические правила») сделает ваше изучение алгебры очень продуктивным и приятным. Имейте в виду, что во время этого процесса по-прежнему будет применяться порядок операций.

Как и большинство математических приемов, существуют стратегии обучения, которые можно использовать для упрощения выполнения правил экспоненты.

Чтобы помочь вам в обучении этим понятиям, у нас есть бесплатный рабочий лист правил экспоненты , который вы можете загрузить и использовать в своем классе!

Что такое показатели?

Показатель степени, также известный как степень, представляет собой величину, показывающую, сколько раз нужно умножить базовое число само на себя. Например, 43 говорит вам умножить четыре само на себя три раза.

43= 4 × 4 × 4 = 64

Число, возведенное в степень, известно как по основанию , а надстрочное число над ним — это показатель или степень .

Кредит: To The Square Inch

Вышеприведенное уравнение звучит как «четыре в степени три». Степень двойки также может быть выражена как « в квадрате », а степень числа три — как « в кубе ». Эти термины часто используются при нахождении площади или объема различных фигур.

Запись числа в экспоненциальной форме означает его упрощение до основания со степенью. Например, преобразование 5 × 5 × 5 в экспоненциальную форму выглядит как 53 .

Экспоненты — это способ упростить уравнения, чтобы их было легче читать. Это становится особенно важным, когда вы имеете дело с такими переменными, как «𝒙» и «𝑦» — как 𝒙7× 𝑦5= ? легче читать, чем (𝒙)(𝒙)(𝒙)(𝒙)(𝒙)(𝒙)(𝒙)(𝑦)(𝑦)(𝑦)(𝑦)(𝑦) = ?

Правила экспоненты в быту

Понимание свойств экспоненты не только поможет вам решать различные алгебраические задачи, экспоненты также используются на практике в повседневной жизни при расчете квадратных футов, квадратных метров и даже кубических сантиметров.

Экспоненциальные правила также упрощают вычисление очень больших или очень малых величин. Они также используются в мире компьютеров и технологий при описании мегабайтов, гигабайтов и терабайтов.

Каковы различные правила показателей степени?

Существует семь правил экспоненты, или законов экспоненты, которые необходимо изучить вашим ученикам. Каждое правило показывает, как решать различные типы математических уравнений и как складывать, вычитать, умножать и делить степени.

Тщательно изучите каждое правило экспоненты в классе, так как каждое из них играет важную роль в решении уравнений на основе экспоненты.

1. Правило произведения степеней

При умножении двух оснований одного и того же значения оставьте основания одинаковыми, а затем сложите их показатели, чтобы получить решение.

42× 45 = ?

Поскольку оба базовых значения равны четырем, оставьте их одинаковыми, а затем сложите вместе показатели степени (2 + 5).

42 × 45= 47

Затем умножьте четыре на себя семь раз, чтобы получить ответ.

47 = 4 × 4 × 4 × 4 × 4 × 4 × 4 = 16 384

Давайте расширим приведенное выше уравнение, чтобы увидеть, как работает это правило:

ответ.

Попробуйте задать более сложный вопрос:

(4𝒙2)(2𝒙3) = ?

Перемножьте коэффициенты вместе (четыре и два), так как они не являются одним и тем же основанием. Затем оставьте «𝒙» таким же и добавьте показатели степени.

(4𝒙2)(2𝒙3) = 8𝒙5

2. Правило отношения степеней

Умножение и деление противоположны друг другу — во многом то же самое, правило частного действует как противоположность правила произведения.

При делении двух оснований одного и того же значения оставьте основание одинаковым, а затем вычтите значения степени.

55 ÷ 53 = ?

Оба основания в этом уравнении равны пяти, что означает, что они остаются прежними. Затем возьмите показатели и вычтите делитель из делимого.

55÷ 53 = 52

Наконец, упростим уравнение, если это необходимо:

52= 5 × 5 = 25

Еще раз, расширение уравнения показывает нам, что это сокращение дает правильный ответ:

Взгляните на этот более сложный пример:

5𝒙4 / 10𝒙2 = ?

Одинаковые переменные в знаменателе отменяют переменные в числителе. Вы можете показать это своим ученикам, зачеркнув равное количество 𝒙 сверху и снизу дроби.

5𝒙4 / 10𝒙2 = 5𝒙/10

Затем упростите, где это возможно, как с любой дробью. Пять можно превратить в десять, пять раз превратив дробь в ½ с оставшимися 𝒙 переменными.

5𝒙4/10𝒙2= 1𝒙2/2 = 𝒙2/2

3. Степень правила степени

Это правило показывает, как решать уравнения, где степень возводится в другой степенью.

(𝒙3)3 = ?

В уравнениях, подобных приведенному выше, умножьте показатели степени и оставьте основание одинаковым.

(𝒙3) 3 = 𝒙9

Взгляните на расширенное уравнение, чтобы увидеть, как это работает:

4. Мощность правила продукта

Когда любая база умножается на показатель, Распределение показатель степени до каждая часть основания.

(𝒙𝑦)3 = ?

В этом уравнении степень троицы должна быть распределена как по 𝒙, так и по 𝑦 переменным.

(𝒙𝑦)3 = 𝒙3𝑦3

Это правило применяется, если к основанию также присоединены экспоненты.

(𝒙2𝑦2)3 = 𝒙6𝑦6

В расширенном виде уравнение будет выглядеть так:

Обе переменные в этом уравнении равны в квадрате и представляют собой , возведенное в степень 3. Это означает, что три умножаются на показатели степени в обеих переменных, превращая их в переменные, которые возводятся в степень шесть.

5. Сила правила отношения

Частное просто означает, что вы делите две величины. В этом правиле тебе возведение частного в степень. Подобно силе правила произведения, показатель степени должен распространяться на все значения в скобках, к которым он присоединен.

(𝒙/𝑦)4 = ?

Здесь обе переменные в квадратных скобках увеличьте в четыре степени.

Взгляните на это более сложное уравнение:

(4𝒙3/5𝑦4)2 = ?

Не забудьте распределить показатель степени, на который вы умножаете, на как на коэффициент, так и на переменную. Затем упростите, где это возможно.

(4𝒙3/5𝑦4)2= 42𝒙6/52𝑦8 = 16𝒙6/25𝑦8

6. Правило нулевой степени

Любое основание, возведенное в нулевую степень, равно единице.

Самый простой способ объяснить это правило — использовать правило отношения степеней.

43/43 = ?

Следуя правилу отношения степеней, вычтите показатели степени друг из друга, что аннулирует их, оставив только основание. Любое число, деленное само на себя, равно единице.

43/43= 4/4 = 1

Независимо от длины уравнения, все, что возводится в нулевую степень, становится единицей.

(82𝒙4𝑦6)0 = ?

Как правило, внешний показатель степени должен быть умножен на каждое число и переменную в скобках. Однако, поскольку это уравнение возводится в нулевую степень, эти шаги можно пропустить, и ответ просто станет единицей.

(82𝒙4𝑦6)0 = 1

Полностью развернутое уравнение будет выглядеть так: 3 7. Правило отрицательного показателя степени

Когда есть число, возводимое в отрицательную степень, превратите его в обратную, чтобы превратить степень в положительную. Не используйте отрицательную степень для превращения основания в отрицательное.

Авторы и права: Thinglink

Мы уже говорили об обратных величинах в нашей статье « Как делить дроби за 3 простых шага ». По сути, обратные числа — это то, на что вы умножаете число, чтобы получить значение единицы. Например, чтобы превратить два в один, умножьте его на ½.

Теперь посмотрите на этот пример с показателем степени:

𝒙-2 = ?

Чтобы сделать число обратным:

1. Превратить число в дробь (поставить над единицей)
2. Переставить числитель в знаменатель и наоборот
3. Когда отрицательное число меняется местами в дроби, оно становится положительным числом

Цель уравнений с отрицательными показателями заключается в том, чтобы сделать их положительными.

Теперь взгляните на более сложное уравнение:

4𝒙-3𝑦2/20𝒙𝑧-3 = ?

В этом уравнении есть два показателя степени с отрицательными степенями. Упростите то, что можете, а затем преобразуйте отрицательные показатели в их обратную форму. В решении 𝒙-3 перемещается в знаменатель, а 𝑧-3 перемещается в числитель.

Поскольку в знаменателе уже есть значение 𝒙, к этому значению добавляется 𝒙3.

4𝒙-3𝑦2/20𝒙z-3 = 𝑦2𝑧3/5𝒙4

Имея эти семь правил в задних карманах ваших учеников, они смогут ответить на большинство экспоненциальных вопросов, с которыми они столкнутся!

Таблица правил экспоненты

Как Prodigy может помочь вам обучать правилам экспоненты

Prodigy — это математическая игра, адаптированная к учебной программе, которую вы можете использовать для постановки вопросов, отслеживания прогресса и выявления проблем в обучении ваших учеников . И вы можете бесплатно создавать учетные записи учителей и учеников!

С таким количеством различных правил экспоненты, которым нужно следовать, и нескольким ученикам, которых нужно отслеживать, может быть трудно понять, кому и в чем нужна помощь. Prodigy позволяет легко отслеживать прогресс и создавать уникальные игровые возможности для каждого учащегося в зависимости от его потребностей.

Статистика отслеживается в режиме реального времени, когда ученики играют в игру, и обратная связь доступна мгновенно. В большинстве случаев ваши ученики даже не осознают, что они участвуют в уроках математики. Все это часть их персонализированного игрового опыта!

На панели управления учителя вы можете создавать планы уроков, просматривать статистику в реальном времени, вводить пользовательские задания и готовить своих учеников к предстоящим тестам. Вот как вы можете использовать Prodigy для :

• Подготовить учащихся к стандартизированным тестам
• Закрепить понятия в классе (например, правила экспоненты)
• Различить математические упражнения в математическом классе и дома

9 0003 Рабочий лист правил произвольной экспоненты

Рабочие листы по математике — это удобные инструменты, которые могут показать, как учащиеся понимают ключевые понятия. Вы можете увидеть, как учащиеся придумывают ответы, где они борются, и нужно ли более подробно осветить какие-либо концепции.

С помощью нашей команды учителей мы составили рабочий лист правил экспоненты, чтобы помочь вам с уроками экспоненты.

Щелкните здесь , чтобы загрузить нашу таблицу правил экспоненты с ключом ответа!

Вывод: практика правил экспоненты

Экспоненты используются, чтобы показать, сколько раз базовое значение умножается само на себя. Это упрощает уравнения до более удобного для чтения формата. (𝒙𝒙𝒙𝒙𝒙𝒙𝒙𝒙𝒙)(𝑦𝑦𝑦𝑦𝑦𝑦)(𝑧𝑧𝑧𝑧𝑧) = 𝒙9𝑦6𝑧5

Напомним, есть семь основные правила, объясняющие, как решать большинство математических уравнений, в которых используются показатели степени. Правила экспоненты:

• Правило произведения степеней — Сложите степени при умножении подобных оснований
• Правило отношения степеней — — Вычтите степени при делении одинаковых оснований
• Правило степеней  — Умножайте силы вместе, когда повышаете силу другой показатель степени
• Степень правила произведения  — Распределить степень по каждому основанию при возведении нескольких переменных в степень
• Степень правила частного  — Распределить степень по всем значениям в частном
• Правило нулевой степени  — Любое основание, возведенное в нулевую степень, становится единицей
• Правило отрицательного показателя степени  — Чтобы изменить отрицательный показатель степени на положительный, превратите его в обратный

Показатель степени имеет тенденцию появляться на протяжении всей нашей жизни, поэтому важно, чтобы учащиеся понимали, как они работают, двигаясь вперед. Есть много правил, которые нужно запомнить, но как только ваши ученики поймут их, решать показатели степени, вероятно, станет легче!

Prodigy Math Game — это адаптивная игровая обучающая платформа. Успех в Prodigy требует, чтобы учащиеся правильно отвечали на вопросы учебной программы, адаптированные к их учебным потребностям, и дает учителям больше способов сделать уроки математики увлекательными! Зарегистрируйте бесплатную учетную запись учителя сегодня, чтобы начать.

Экспоненты в реальном мире

Экспоненты, порядковые номера, степени и индексы используются во многих частях нашего современного технологического мира.

Экспоненты используются в физике компьютерных игр, шкалах измерения pH и Рихтера, науке, технике, экономике, бухгалтерском учете, финансах и многих других дисциплинах.

Экспоненциальный рост является критически важным аспектом финансов, демографии, биологии, экономики, ресурсов, электроники и многих других областей.

Экспоненциальный распад связан со светом, звуком, спортивным оборудованием, опасными химическими веществами и радиоактивными отходами.

Exponents используют экономисты, банкиры, финансовые консультанты, специалисты по оценке страховых рисков, биологи, инженеры, программисты, химики, физики, географы, звукорежиссеры, статистики, математики, геологи и представители многих других профессий.

В этом уроке мы покажем несколько способов использования экспонентов в реальной жизни, а также их влияние на наше понимание современного мира вокруг нас.

 

Экспоненты имеют фундаментальное значение, особенно в вычислениях с основанием 2 и 16, а также в формулах физики и электроники, используемых в вычислениях.

 

 
 

В последние годы наблюдается экспоненциальный рост скорости и мощности компьютеров, и, по прогнозам, примерно к 2030 году вычислительная мощность сравняется с человеческим мозгом.

 
 

Экспоненты имеют решающее значение в современных интернет-продажах и маркетинге,

 
 

Экспоненты важны в инвестициях и финансах.

Сложные проценты также работают против людей с задолженностью по кредитной карте, которую они не выплачивают, потому что задолженность растет все быстрее и быстрее с каждым расчетным периодом и может быстро выйти из-под контроля.
 
 

Показатели являются основой «Демографии» (прироста населения)

 
 

Население мира увеличивается с невероятной скоростью, особенно в развивающихся регионах Африки, Индии и Китая.

 

Массовый рост населения приводит к массовому использованию ископаемого топлива для промышленности, отопления, электроснабжения и транспорта.

 
 

За последние несколько лет наблюдается значительный экспоненциальный рост использования мобильных телефонов и их проникновения на рынок.

 
 

Задолженность по потребительскому кредиту увеличилась за последние годы до рекордно высокого уровня.

 
 

Экспоненты также являются частью пищевых технологий и микробиологии.

 
 

Вирусная болезнь (а также многие вирусы электронной почты и компьютерные вирусы) могут распространяться с постоянно возрастающей скоростью, вызывая обширные зараженные области.

Это происходит так же, как вирусный маркетинг разветвляется на все более широкие ветви, когда все больше и больше людей передают что-то все большему количеству людей.

 
 

При взрыве мы получаем неконтролируемое массовое увеличение выхода энергии и силы за очень короткий период времени.

Представьте это как очень крутой экспоненциальный график, по сравнению с горящей спичкой, выделяющей энергию на довольно плоском прямолинейном графике.

 
 

Экспоненциальный рост

Ситуации, которые мы рассматривали до сих пор, включают «экспоненциальный рост».

Уравнения для графиков этих ситуаций содержат показатели степени, и это приводит к тому, что график начинается медленно, но затем очень быстро растет.

Например. Подумайте о квадратных числах и о том, как они быстро становятся все больше и больше:

1 4 9 16 25 36 49 64 81 100 121 132 и т. д.

Чтобы достичь 100, нам нужно всего девять квадратных чисел. диаграмма ниже.

Противоположностью «Экспоненциальному росту» является применение показателей степени к дробям, что приводит к «Экспоненциальному затуханию».

 
 

Экспоненциальный спад

Использование отрицательных значений мощности приводит к дробям, и когда к этим дробям применяются показатели степени, мы получаем «Распад».

В процессе «Распада» количество участвующего в нем процесса падает довольно быстро в начале, но затем падение становится все медленнее и медленнее.

Типичный график экспоненциального спада выглядит следующим образом:

 
 

Составление графика экспоненциального спада 0002 Забавный способ сделать экспоненциальное затухание График состоит в том, чтобы взять пачку M&M’s или Skittles и продолжать выливать их из чашки, но каждый раз удаляя все конфеты, которые приземляются с лицевой стороны.

Это должно создать требуемый график.

Существует отличный набор инструкций о том, как сделать это по следующей ссылке:

Нажмите здесь, чтобы получить инструкции по экспоненциальному графику с M & MS

Экспонентный распад — Реальные примеры

Некоторые примеры экспоненциального распада в реальном мире — реальные примеры

. являются следующие.

Экспоненциальный распад и период полураспада

Многим вредным материалам, особенно радиоактивным отходам, требуется очень много времени, чтобы разложиться до безопасного уровня в окружающей среде.

Это связано с тем, что эти материалы подвергаются экспоненциальному распаду, и даже небольшое количество оставшегося материала может быть вредным.

 
 

 
 

Экспоненциальные шкалы

Шкала Рихтера используется для измерения силы землетрясений.

Фактическая энергия каждого землетрясения равна степени 10, но на шкале мы просто берем значение индекса 1, 2, 3, 4 и т. д., а не полное значение показателя степени.

Это означает, что землетрясение по шкале Рихтера 6 на самом деле в 10 раз сильнее, чем землетрясение по шкале Рихтера 5. (Например, 1000000 против 100000).

Точно так же землетрясение по шкале Рихтера 7 на самом деле в 100 раз сильнее, чем землетрясение по шкале Рихтера 5. (Например, 10000000 против 100000).

 

Шкала рН для измерения кислотности материалов также создается путем получения значений мощности из измеренных мощностей 10 значений концентрации кислоты.

 
 

Экспоненты и научная запись

Очень большие числа, такие как расстояние между планетами или население стран, выражаются с использованием степеней 10 в формате, называемом «Научная запись».

Научное обозначение также используется для выражения очень малых десятичных значений, таких как размер молекул вируса гриппа или расстояние между атомами в кристаллической структуре.

 
 

Онлайн-презентация об экспонентах в реальном мире

Онлайн-презентация этого урока доступна на SlideShare по следующей ссылке:

Нажмите здесь, чтобы просмотреть нашу презентацию SlideShare
 
 

Музыкальное видео об экспонентах

Следующее музыкальное видео, посвященное экспонентам, возможно, является самым успешным математическим видео. когда-либо загруженные на YouTube.

На данный момент у него более 850 000 просмотров на YouTube, и это просто потрясающее произведение!

Достойно просмотра для всех, кто изучает индексы и экспоненты.

 
 

Связанные элементы

Основные индексы и показатели
Умножение показателей
Деление выражений алгебры
Деление показателей с использованием правила вычитания
Расширение показателя степени s Использование степени степени Правило
Расширение экспоненциальных произведений Правило
Расширение коэффициентов экспоненты Правило
Нуль и отрицательное значение Экспоненты
Научное обозначение

 

Подписаться

Если вам понравился этот урок, почему бы не получить бесплатную подписку на наш сайт.
После этого вы сможете получать уведомления о новых страницах прямо на свой адрес электронной почты.

Перейдите в область подписки на правой боковой панели, введите свой адрес электронной почты и нажмите кнопку «Подписаться».

Чтобы точно узнать, как работает бесплатная подписка, нажмите на следующую ссылку:

Как работает бесплатная подписка

Если вы хотите предложить идею для статьи или стать приглашенным автором на нашем веб-сайте, напишите нам по адресу адрес горячей почты, показанный в правой части этой страницы.

 

Отметьте нас на Facebook

 

Помогите Passy’s World расти

Каждый день Passy’s World предоставляет сотням людей бесплатные уроки математики.

Помогите нам поддерживать этот бесплатный сервис и поддерживать его рост.

Пожертвуйте любую сумму от $2 и выше через PayPal, щелкнув изображение PayPal ниже. Спасибо!

PayPal принимает кредитные карты, но вам нужно будет указать адрес электронной почты и пароль, чтобы PayPal мог создать для вас учетную запись PayPal для обработки транзакции. За это действие с вас не будет взиматься плата за обработку, так как PayPal вычитает комиссию из вашего пожертвования до того, как оно попадет в Passy’s World.

 
 

Наслаждайтесь,
Passy

Эта запись была опубликована в Алгебра, Экспоненты, Математика в реальном мире и помечена как сложные проценты, шкала землетрясений, степени экспоненты, экспоненциальное затухание, экспоненциальное уменьшение, экспоненциальные графики, экспоненциальный рост, экспоненты, экспоненты сложные проценты, экспоненты в реальном мире, экспоненты музыкальное видео, экспоненты рэп, период полураспада, как люди используют экспоненты, индексы, индексы в реальном мире, индексы, индексы в реальном мире, индексы рэп, рабочие места, которые используют экспоненты , задания, использующие индексы, задания, использующие индексы, логарифмы, экспоненциальный распад M&M, мощности, мощности в реальном мире, радиоактивный распад, радиоактивный период полураспада, показатели реальной жизни, индексы реальной жизни, индексы реальной жизни, мощности реальной жизни, экспоненциальные примеры реального мира, показатели реального мира, индексы реального мира, индексы реального мира, силы реального мира, музыкальное видео undices, кто использует показатели степени, кто использует числа индексов, кто использует индексы, кто использует степени, зачем изучать показатели, зачем изучать индекс числа, зачем изучать индексы, зачем изучать степени, зачем использовать показатели, зачем использовать числа индексов, зачем использовать индексы, зачем использовать степени, работа с показателями.