Действия со степенями и корнями
- Свойства степени с натуральным показателем
- Степень с целым и дробным показателем
- Преобразования арифметических корней
1. При умножении степеней с одинаковыми основаниями показатели складываются, а основание остаётся прежним:
.
Например, .
2. При делении степеней с одинаковыми основаниями показатели степеней вычитаются, а основание остаётся прежним:
.
Например, .
3. При возведении степени в степень показатели степеней перемножаются, а основание остаётся прежним:
.
Например, .
4. Степень произведения равна произведению степеней множителей:
.
Например, .
5. Степень частного равна частному степеней делимого и делителя:
.
Например, .
Пример 1. Найти значение выражения
.
Решение. В данном случае в явной форме ни одно из свойств степени с натуральным показателем применить нельзя, так как все степени имеют разные основания. Запишем некоторые степени в другом виде:
(степень произведения равна произведению степеней множителей),
(при умножении степеней с одинаковыми основаниями показатели складываются, а основание остаётся прежним, при возведении степени в степень показатели степеней перемножаются, а основание остаётся прежним).
Теперь получим:
В данном примере были использованы первые четыре свойства степени с натуральным показателем.
Свойства степеней и корней интенсивно используются при упрощении выражений в задачах
математического анализа, например, для нахождения производной параметрически заданной функции и производной функции, заданной неявно.
Нет времени вникать в решение? Можно заказать работу!
Имеют место следующие тождества:
1) ;
2) ;
3) .
Выполнить действия со степенями самостоятельно, а затем посмотреть решения
.
Пример 3. Найти значение выражения
.
Пример 4. Найти значение выражения
.
Правильные ответы и решения примеров 2, 3, 4.
1. Корень k-й степени из произведения неотрицательных чисел равен произведению корней той же степени из сомножителей: , где (правило извлечения корня из произведения).
2. Если , то (правило извлечения корня из дроби).
3. Если ,
то
(правило извлечения корня из корня).
4. Если , то (правило возведения корня в степень).
5. Если , то , где , т. е. показатель корня и показатель подкоренного выражения можно умножить на одно и то же число.
6. Если , то , т. е. большему положительному подкоренному выражению соответствует и большее значение корня.
7. Все указанные выше формулы часто применяются в обратном порядке (т. е. справа налево). Например:
(правило умножения корней),
(правило деления корней),
.
8. Правило вынесения множителя из-под знака корня. При .
9. Обратная задача — внесение множителя под знак корня. Например,
10. Уничтожение иррациональности в знаменателе дроби. Рассмотрим некоторые типичные случаи.
а) , так как .
Например, .
б)
Например,
в)
и т. д.
д.
11. Применение тождеств сокращённого умножения к действиям с арифметическими корнями:
1) ;
2) ;
3)
| Назад | Листать | Вперёд>>> |
К началу страницы
Другие темы в блоке «Школьная математика»
Действия с дробями
Решение квадратных уравнений
Решение дробных уравнений с преобразованием в квадратное уравнение
Примеры решения задач со степенями с ответами
Простое объяснение принципов решения задач со степенями и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Алгоритм решения задач со степенями
Теорема
Алгебраические выражения, содержащие неизвестные в основании или показателе степени, относятся к классу выражений со степенями.
При решении задач на упрощение выражений, содержащих переменные в основании или показателе степени, используются свойства степеней.
Нужна помощь в написании работы?
Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Заказать работу
Примеры решений задач со степенями
Пример 1
Задача
Упростить выражение:
Решение
ОДЗ:
Ответ
Пример 2
Упростить выражение:
Решение
ОДЗ:
Ответ
Пример 3
Задача
Упростить выражение:
Решение
ОДЗ:
Ответ
Пример 4
Задача
Упростить выражение:
Решение
ОДЗ:
Ответ
Пример 5
Задача
Упростить выражение:
Решение
ОДЗ:
Ответ
Пример 6
Задача
Упростить выражение:
Решение
ОДЗ:
Ответ
Пример 7
Задача
Упростить выражение:
Решение
ОДЗ:
Ответ
Пример 8
Задача
Упростить выражение:
Решение
Ответ
Пример 9
Задача
Упростить выражение:
Решение
Ответ
Пример 10
Задача
Упростить выражение:
Решение
ОДЗ:
Ответ
Средняя оценка 3 / 5. Количество оценок: 3
Количество оценок: 3
Поставьте вашу оценку
Сожалеем, что вы поставили низкую оценку!
Позвольте нам стать лучше!
Расскажите, как нам стать лучше?
19452
Закажите помощь с работой
Не отобразилась форма расчета стоимости? Переходи по ссылке
Не отобразилась форма расчета стоимости? Переходи по ссылке
Полезно
РЕШЕННЫЕ УПРАЖНЕНИЯ: ПОКАЗАТЕЛИ УПРОЩЕНИЯ: ВТОРИЧНЫЕ
Содержание этой страницы:
Введение
Мощность является выражением этого типа
9001 3 а б = а · а · · · а · а, который представляет собой результат умножения на основание , на , сама по себе столько раз, сколько показывает показатель степени , b . Мы читаем это как « a в степени б «.
Например, 2 3 = 2·2·2 = 8 (основание равно 2, показатель степени равен 3).
Как правило, основание и показатель степени могут быть любым числом (действительные или комплексные) или они могут быть даже переменными, неизвестными факторами или параметрами. Уравнения с неизвестным множителем в показателе степени известны как показательных уравнений .
Особым случаем являются степени, показатели степени которых являются дробями. В этом случае мощность представляет собой квадратный корень. Они появляются из-за к необходимости решить уравнение типа х н = а.
Другим особым случаем являются степени с основанием из 10 , с этим внешний вид 10 n . Если n
 Эти
тип полномочий, используемых в научное обозначение .
Эти
тип полномочий, используемых в научное обозначение .Наконец, мы скажем, что степень, возведенная в 0, всегда равна 1 , поэтому x 0 = 1 .
В этом разделе задания расположены в порядке возрастания сложности: мы используем свойства экспонент (мощность произведений, степень частного, степень степени,..) и, после того, как мы упростим выражения, образованные степенями (круглые скобки, дроби, отрицательные показатели, параметры…).
| СВОЙСТВА ПОЛНОМОЧИЙ | ||
| Продукт | Мощность | |
| Частное | Отрицательный показатель степени | |
| Обратный | Инверсия инверсии | |
Упражнение 1
Показать решение
Упражнение 2
Показать решение
Упражнение 3
Показать решение
Упражнение 4
Показать решение
Упражнение 5
Показать решение
Упражнение 6
Показать решение
Упражнение 7 900 03
Показать решение
Упражнение 8
Показать решение
Упражнение 9
Показать решение
Упражнение 10
Показать решение
Упражнение 11
Показать решение
Задание 12
Показать решение
Задание 13 90 009
Показать решение
Упражнение 14
Показать решение
Упражнение 15
Показать решение
Matesfacil. com
J. Llopis имеет лицензию
творческий
Commons Attribution-NonCommercial 4.0 Международная лицензия.
com
J. Llopis имеет лицензию
творческий
Commons Attribution-NonCommercial 4.0 Международная лицензия.
Мощность
Количественная работа связана с силой, вызывающей перемещение. Работа не имеет ничего общего с количеством времени, в течение которого эта сила действует, вызывая смещение. Иногда работа выполняется очень быстро, а иногда работа выполняется довольно медленно. Например, скалолазу требуется аномально много времени, чтобы поднять свое тело на несколько метров вверх по склону утеса. С другой стороны, турист (который выбирает более легкий путь в гору) может поднять свое тело на несколько метров за короткий промежуток времени. Два человека могут выполнить один и тот же объем работы, но турист сделает ее за значительно меньшее время, чем скалолаз. Величина, связанная со скоростью, с которой выполняется определенный объем работы, называется мощностью. У туриста больше номинальная мощность , чем скалолаз.
Мощность – это скорость выполнения работы. Это соотношение работа/время. Математически это вычисляется с использованием следующего уравнения.
Это соотношение работа/время. Математически это вычисляется с использованием следующего уравнения.
или
P = Вт/т
Стандартной метрической единицей мощности является Вт . Как следует из уравнения мощности, единица мощности эквивалентна единице работы, деленной на единицу времени. Таким образом, ватт эквивалентен джоулю в секунду. По историческим причинам л.с. иногда используется для описания мощности, выдаваемой машиной. Одна лошадиная сила эквивалентна примерно 750 Вт.
Большинство машин спроектированы и изготовлены для работы с объектами. Все машины обычно описываются номинальной мощностью. Номинальная мощность указывает скорость, с которой эта машина может работать с другими объектами. Таким образом, мощность машины — это отношение работы к времени для этой конкретной машины. Автомобильный двигатель является примером машины, которой присваивается номинальная мощность. Номинальная мощность относится к тому, насколько быстро автомобиль может разогнать автомобиль. Предположим, что двигатель мощностью 40 лошадиных сил может разогнать автомобиль с 0 до 60 миль/ч за 16 секунд. Если бы это было так, то автомобиль, мощность которого в четыре раза превышала бы мощность, мог бы выполнить тот же объем работы за четверть времени. То есть 160-сильный двигатель мог разогнать тот же автомобиль с 0 до 60 миль/ч за 4 секунды. Дело в том, что при одном и том же объеме работы мощность и время обратно пропорциональны. Уравнение мощности предполагает, что более мощный двигатель может выполнить тот же объем работы за меньшее время.
Номинальная мощность относится к тому, насколько быстро автомобиль может разогнать автомобиль. Предположим, что двигатель мощностью 40 лошадиных сил может разогнать автомобиль с 0 до 60 миль/ч за 16 секунд. Если бы это было так, то автомобиль, мощность которого в четыре раза превышала бы мощность, мог бы выполнить тот же объем работы за четверть времени. То есть 160-сильный двигатель мог разогнать тот же автомобиль с 0 до 60 миль/ч за 4 секунды. Дело в том, что при одном и том же объеме работы мощность и время обратно пропорциональны. Уравнение мощности предполагает, что более мощный двигатель может выполнить тот же объем работы за меньшее время.
Человек также является машиной с номинальной мощностью . Некоторые люди обладают большей силой, чем другие. То есть некоторые люди способны выполнять тот же объем работы за меньшее время или больший объем работы за то же время. Обычная физическая лаборатория включает в себя быстрый подъем по лестнице и использование информации о массе, росте и времени для определения личной силы студента.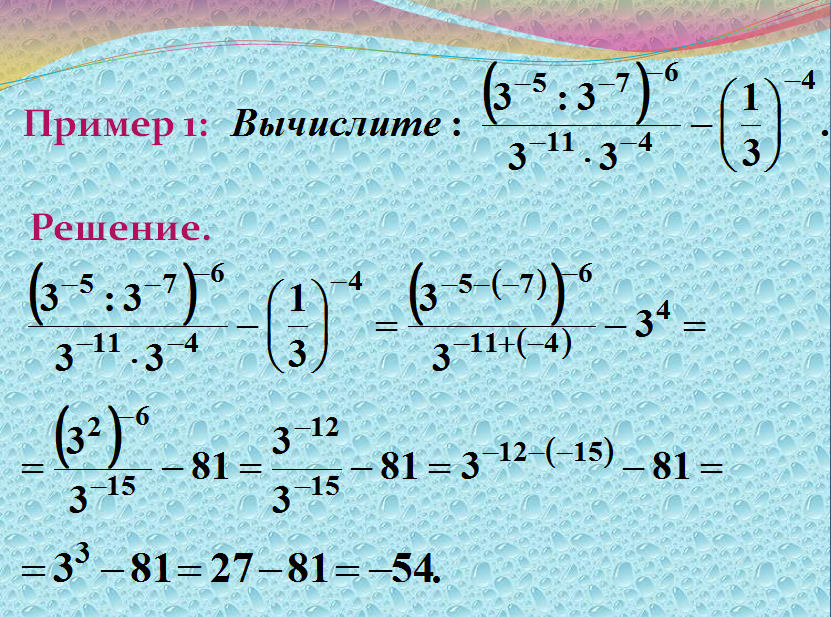 Несмотря на диагональное движение по лестнице, часто предполагается, что горизонтальное движение является постоянным и вся сила от ступенек используется для подъема ученика вверх с постоянной скоростью. Таким образом, вес ученика равен силе, совершающей работу над учеником, а высота лестницы — смещению вверх. Предположим, что Бен Пумпинирон поднимает свое 80-килограммовое тело по 2,0-метровой лестнице за 1,8 секунды. Если бы это было так, то мы могли бы вычислить 9 Бена.0283 номинальная мощность . Можно предположить, что Бен должен приложить к лестнице направленную вниз силу в 800 ньютонов, чтобы поднять свое тело. При этом лестница будет толкать тело Бена вверх с достаточной силой, чтобы поднять его тело вверх по лестнице. Также можно предположить, что угол между силой лестницы, действующей на Бена, и смещением Бена равен 0 градусов. С этими двумя приближениями номинальная мощность Бена может быть определена, как показано ниже.
Несмотря на диагональное движение по лестнице, часто предполагается, что горизонтальное движение является постоянным и вся сила от ступенек используется для подъема ученика вверх с постоянной скоростью. Таким образом, вес ученика равен силе, совершающей работу над учеником, а высота лестницы — смещению вверх. Предположим, что Бен Пумпинирон поднимает свое 80-килограммовое тело по 2,0-метровой лестнице за 1,8 секунды. Если бы это было так, то мы могли бы вычислить 9 Бена.0283 номинальная мощность . Можно предположить, что Бен должен приложить к лестнице направленную вниз силу в 800 ньютонов, чтобы поднять свое тело. При этом лестница будет толкать тело Бена вверх с достаточной силой, чтобы поднять его тело вверх по лестнице. Также можно предположить, что угол между силой лестницы, действующей на Бена, и смещением Бена равен 0 градусов. С этими двумя приближениями номинальная мощность Бена может быть определена, как показано ниже.
Мощность Бена составляет 871 Вт. Он довольно лошадь .
Он довольно лошадь .
Другая формула мощности
Выражением мощности является работа/время. А поскольку выражение для работы есть сила*смещение, выражение для мощности можно переписать как (сила*смещение)/время. Поскольку выражение для скорости есть перемещение/время, выражение для мощности можно еще раз переписать как сила*скорость. Это показано ниже.
Это новое уравнение для мощности показывает, что мощная машина одновременно мощная (большая сила) и быстрая (большая скорость). Мощный автомобильный двигатель силен и быстр. Мощная сельскохозяйственная техника надежна и быстра. Мощный тяжелоатлет силен и быстр. Сильный лайнсмен в футбольной команде силен и быстр. А 9Машина 0283 , которая достаточно мощна, чтобы приложить большую силу, чтобы вызвать перемещение за небольшой промежуток времени (т. е. с большой скоростью), является мощной машиной.
Используйте свое понимание работы и мощности, чтобы ответить на следующие вопросы.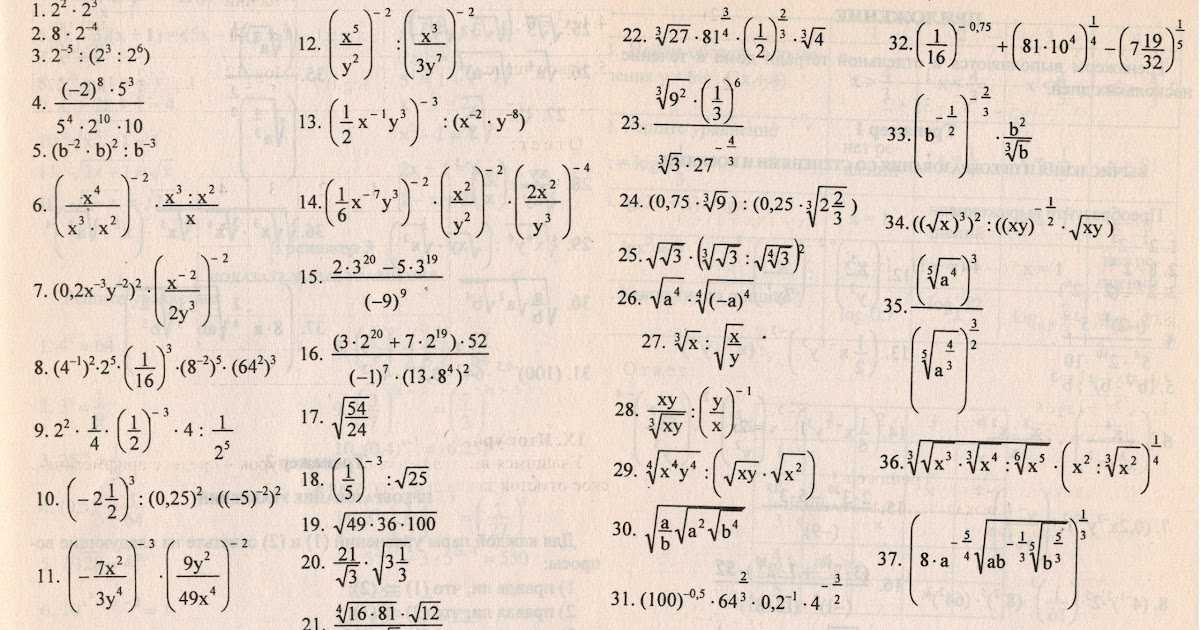 Когда закончите, нажмите кнопку, чтобы просмотреть ответы.
Когда закончите, нажмите кнопку, чтобы просмотреть ответы.
1. Два студента-физика, Уилл Н. Эндэйбл и Бен Пумпинайрон, в зале тяжелой атлетики. Уилл поднимает над головой 100-фунтовую штангу 10 раз за одну минуту; Бен поднимает 100-фунтовую штангу над головой 10 раз за 10 секунд. Кто из учеников больше всего работает? ______________ Кто из учеников проявляет наибольшую силу? ______________ Объясните свои ответы.
2. Во время физического кабинета Джек и Джилл взбежали на холм. Джек вдвое массивнее Джилл; однако Джилл преодолевает то же расстояние вдвое быстрее. Кто работал больше всех? ______________ Кто приложил больше всего усилий? ______________ Объясните свои ответы.
3. Усталая белка (массой около 1 кг) отжимается, прикладывая силу, чтобы поднять ее центр масс на 5 см, чтобы совершить работу всего лишь в 0,50 Дж. Если усталая белка проделает всю эту работу за 2 секунды, то определите ее мощность.

Leave A Comment