ПОДГОТОВКА К ГОДОВОЙ КОНТРОЛЬНОЙ РАБОТЕ ПО ГЕОМЕТРИИ 8 класс | Материал для подготовки к ЕГЭ (ГИА) по геометрии (8 класс) по теме:
ПОДГОТОВКА К ГИА, Задачи по геометрии за курс 8 класса
1. Найти сумму углов шестиугольника, семиугольника, одиннадцатиугольника.
ПАРАЛЛЕЛОГРАММ
2. Найти все углы параллелограмма, если один из них равен 132°.
3. Определить углы параллелограмма, если:
1) один из них больше другого на 70°;
2) один из них меньше другого в 11 раз;
3) сумма двух из них равна 82°.
4. Найти периметр параллелограмма, если известны две его стороны 5 м и 11 м.
5. Определить стороны параллелограмма, если:
1) его периметр равен 38 дм, а одна из сторон на 7 дм меньше другой
2) его периметр равен 60 м, а одна из сторон в 4 раза больше другой.
6. В параллелограмме BCDE диагонали пересекаются в точке М. Найти периметр треугольника ВСМ, если DE = 7 см, BD = 12 см, СЕ = 16 см.
7. Диагонали параллелограмма КМОР пересекаются в точке С.
Доказать, что ΔКМС = ΔОРС.
8. В параллелограмме АCDE на сторонах АE и CD отложены равные отрезки АК и DМ . Доказать, что ΔАКС = ΔDME.
9. В параллелограмме BDEF на сторонах BF и DE отложены равные отрезки BO и ND. Доказать, что четырёхугольник ONEF также является параллелограммом.
10. Диагонали параллелограмма продолжены за вершины на одинаковую длину. Полученные точки последовательно соединены. Доказать, что образовавшийся четырёхугольник является параллелограммом.
11. В параллелограмме АBCD биссектриса угла В пересекает сторону АD в точке М, а биссектриса угла D пересекает сторону ВС в точке К. Доказать, что ВМDК параллелограмм.
12. В параллелограмме АBCD биссектриса угла А пересекает сторону ВС в точке М. Найдите периметр параллелограмма, если АВ= 4,6см и МС= 3,8.
13. На диагонали МК параллелограмма MNKO отложены равные отрезки МА и КВ. доказать, что ΔМАN = ΔКBO.
14. В параллелограмме АВСД точки М, Р, К, Е- являются серединами сторон параллелограмма.
Определите вид четырехугольника МРКЕ,
ТЕОРЕМА ФАЛЕСА.
15. Прямые AM, BN, и СО параллельны и DM = MN = NO. Найти длину отрезка DC, если АВ = 12.
16. Начертить произвольный отрезок АВ. Разделить его на 5 равных частей.
17. Начертить отрезок а. Построить отрезок .
ТРАПЕЦИЯ,
18. Дана трапеция МРОК с основаниями МК и ОР. Найти:
1) все углы трапеции, если К = 81°, Р = 110°;
2) ОРК и РОМ, если КМО = 54°, МКР = 38°;
3) углы треугольника МКN (где N — точка пересечения диагоналей трапеции), если углы ОКР и РОМ соответственно равны 36° и 54°.
19. Дана трапеция МРОК с основаниями МК и ОР. Найти:
1) среднюю линию трапеции АВ, если МК= 12см, ОР= 8см.
2) основание МК, если средняя линия АВ=10см, основание ОР=14см.
3) основания трапеции МК и ОР, если МК в 5 раз больше ОР и средняя линия АВ=33см.
4) основания трапеции МК и ОР, если МК:ОР=4:9 и средняя линия АВ=26см.
20. Трапеция CDEF — равнобокая, CF и DE — её основания.
1) Найти все углы трапеции, если Е = α.
2) Доказать, что ΔFCE = ΔCDF.
3) Найти углы треугольника FCE, если известно, что DEC = 60°.
21. Дано: KMNO — трапеция, (см. рис.).
1) Определить вид четырёхугольника KMNA.
2) Доказать, что К = NAO = MNA.
3) Найти углы треугольника ANO и четырёхугольника KMNA, если О = 68°, OAN = 58°.
4) Доказать, что если трапеция равнобокая, то ΔONA — равнобедренный с основанием ОА.
22. Меньшее основание равнобокой трапеции равно боковой стороне и в 2 раза меньше другого основания. Найти углы трапеции.
23. Доказать, что диагонали равнобокой трапеции равны.
24. По данным рисунка определите среднюю В 12см С
линию трапеции
4см
45
А К Д
25.
По данным рисунка определите периметр В 8см С
равнобокой трапеции.
6см
А 4см К 30 Д
р
26. В равнобокой трапеции DEFC на большее основание DC опущены перпендикуляры ЕА и FB.
1) Доказать, что ΔDEA = ΔFCB.
2) Чему равны отрезки DA и CB, если EF = 8 см; CD = 30 см.
ПРЯМОУГОЛЬНИК.
27. В прямоугольнике АBCD проведена диагональ АC. Найти острые углы треугольника АBC, если один из них больше другого в 5 раз.
28. В прямоугольнике BCDЕ диагонали пересекаются в точке О. Найти отрезки ОD и ОВ, если диагональ ВD равна 17 см.
29. Диагонали прямоугольника CDЕF пересекаются в точке N. Доказать, что
1) ΔDNE –равнобедренный;
2) если точка О является серединой стороны EF, то .
30. Точка пересечения диагоналей прямоугольника соединена с серединами двух соседних сторон. Определить:
1) вид отсекаемого четырёхугольника;
2) периметр отсекаемого четырёхугольника, если периметр данного прямоугольника равен 52 см.
31. В прямоугольнике АBCD биссектриса угла D пересекает сторону АВ в точке М.
1) Доказать, что ΔADM — равнобедренный.
2) Найти периметр прямоугольника, если сторона АВ оказалась разбита на отрезки длиной 3 см и 5 см. Сколько решений имеет задача?
32. В прямоугольнике DEFK биссектриса угла D пересекает сторону EF в точке С, причём отрезок CF в 2 раза больше отрезка ЕС. Найти стороны прямоугольника, если периметр равен 32 см.
33. Дан прямоугольник MNCK (см. рис.).
1) Найти углы треугольника MNB, если А = β.
2) Доказать, что ΔAMК = ΔMBN, если точка М — середина стороны АВ.
3) Найти стороны и диагонали прямоугольника MNCK, если М — середина стороны АВ, АС = 12 м, АВ = 13 м, ВС = 5 м.
34.По данным рисунка определите В С
периметр прямоугольника.
8см
45
А Д
35. По данным рисунка определите В С
периметр треугольника СДО.
О
АД=12 см, АВ= 8см
60
А Д
КВАДРАТ.
36.В квадрате АВСД сторона равна 4,5см. Определите периметр квадрата.
37. Площадь квадрата равна: а) 49кв.см; в)78 кв.см.
38. В квадрате АВСД точка О- пересечение диагоналей. Определите углы треугольника АОВ.
39.
В квадрате АВСД точки М,Р,К,Е- середины сторон квадрата. Определите вид четырехугольника
МРКЕ.
40. В квадрате проведены диагонали.
1) Доказать, что они разбивают квадрат на четыре равных равнобедренных треугольника.
2) Найти углы этих треугольников.
41. В равнобедренный прямоугольный треугольник вписан квадрат, причём две его вершины лежат на гипотенузе и две — на катетах. Доказать, что гипотенуза в три раза больше стороны квадрата.
42. Диагонали квадрата ABCD пересекаются в точке О, из которой опущен перпендикуляр ОК на сторону ВС. Определить вид четырёхугольника АВКО и найти его углы
РОМБ.
43. Найти периметр ромба, если его сторона равна 11 см .
44. Найти стороны ромба, если его периметр равен 30 см.
45. Найти все углы ромба, если они относятся как 1:3.
46.
В ромбе CDEF проведена диагональ DF. Определить углы треугольника CDF, если СFЕ = 42°.
47. В ромбе проведены диагонали.
1)Доказать, что они разбивают ромб на четыре равных треугольника.
2) Найти боковые стороны этих треугольников, если диагонали равны12 см и 18 см.
3) Найдите сторону ромба, если диагонали равны 24см и 10 см.
4) Найти углы этих треугольников, если один из углов ромба равен α.
5) . В ромбе АВСД проведены диагонали АС и ВД, О -точка пересечения диагоналей,
48. Доказать, что одна из диагоналей ромба равна его стороне, если один из углов ромба равен 120°.
49. Диагонали ромба BCDE пересекаются в точке М, отрезок МК — перпендикуляр к стороне CD. Найти углы треугольника СМК, если СВЕ = 82°
.
Симметрия.
50. Начертить треугольник АВС. Построить симметричный ему треугольник
1) относительно вершины С; в
2) относительно стороны АС.
3)ОТНОСИТЕЛЬНО ПРЯМОЙ В.
А с
Окружность.
Вписанные углы.
51.
м
К д М
52. Градусная мера дуги МР=128°.
Определите
Р Р
54. АВ- диаметр окружности. Определите угол АРВ.
А В
А
55.Определие градусные меры дуг окружности, В
Если дуги относятся как АВ:ВС:АС = 6:4:8
С
56. В окружности с центром О проведены диаметры MK и NP.
1) Доказать, что MNKP — прямоугольник.
2) Найти углы треугольника MKP, если МOР = 140°
57. В АС и ВС касательные к окружности (А и С- точки касания),
расстояние от центра окружности до точки С.
60° С
А
58. В окружности с центром О проведены два взаимно перпендикулярных радиуса ОА и ОВ. Касательные, проходящие через точки А и В, пересекаются в точке С.
Найти периметр четырёхугольника ОАСВ, если радиус окружности равен 23 см.
59. В окружности проведены два взаимно перпендикулярных диаметра АС и BD. Определить вид четырёхугольника ABCD.
60. В окружности проведены диаметры АB и СD. Доказать, что АBCD параллелограмм.
61. А
О АВ- диаметр, О- центр окружности,
С
В
62. В прямоугольном треугольнике АВС
63. А
К
Д С А
64. Где находится центр вписанной окружности?
А и М точки касания, радиус равен 12см. О
Расстояние от вершины О до центра окружности
13см. Найдите длину ОМ.
М
65. Около треугольника АВС описана окружность, разделенная вершинами треугольника на части пропорциональные числам 5 : 7 : 6. Определите углы треугольника.
66. Две хорды окружности АВ и СД пересекаются в точке О, АО=12см, ОС=4см, СО=8см. Найдите длину отрезка ОД.
67.
Если О- центр окружности.
68.МР- диаметр, О_ центр окружности, ОМ=ОК=МК А В
Р
Найдите
М К
69.
А С
70.КД и МС хорды одной окружности, причем Е- точка их
пересечения. Найдите
а
71. Дано: КВ =12см, КС=30см, периметр треугольника АКВ равен 28см. В
Найдите периметр треугольника СКД, если К- пересечение
АС и ВД. С
А
Д
72. Дано: КМ и СД- хорды, Е- точка их пересечения, СЕ=6см, ЕД=8см, КЕ на 8см меньше ЕМ.
Найдите КМ.
73. Дано: АВ=26см, АС=4см, АЕ=16см.
А
Найдите ДЕ. С
Д В
74. Е
В
А АВ- касательная к окружности, АВ=6дм, СД=5дм
Д
Найдите АД.
С
МНОГОУГОЛЬНИКИ
75. Найти сумму углов шестиугольника, семиугольника, одиннадцатиугольника.
76.Один из внутренних углов правильного n-угольника равен 150°. Найдите число сторон многоугольника.
77. Величины углов выпуклого пятиугольника пропорциональны числам 2:3:4:5:6. Найдите величину большего из углов.
78.Периметр равностороннего треугольника равен 6 3. Найдите радиус описанной окружности.
79.Около квадрата описана окружность, и в квадрат вписана окружность. Найдите радиус вписанной окружности, если радиус описанной окружности равен 10 2.
80. Внешний угол правильного многоугольника меньше внутреннего на 140°.
Найдите сумму углов данного многоугольника.
81.Меньшая диагональ правильного шестиугольника равна 5 3 см. Найдите периметр шестиугольника.
82. В некотором многоугольнике можно провести 20 диагоналей. Найдите число сторон этого многоугольника.
ПЛОЩАДИ ФИГУР.
83.Найдите площадь треугольника: б)
А) в)
7,2
4 3
8 5 30°
7,2
14
13
г) д)Угол при основании равнобедренного треугольника
15 равен 30°, а площадь 9 3 . Найдите боковую сторону
треугольника.
е) Стороны треугольника равны 8см, 6см, 4см. Найдите
меньшую высоту треугольника.
84..jpg)
Найдите площадь параллелограмма:
В С
А) б) Р Е в)К С
Н АС= 5,6
5,2 8 КМ=4
А Д О- пересечение
ВН= 5 М 1,4 К Д М диагоналей.
85. Найдите площадь ромба:
А) В В С б) Д К М Н ДН=4,8
МЕ= 4
5 6
Е
А Н Д Р
ВН=4,2
86. Найдите площадь трапеции АВСД, где АД || ВС.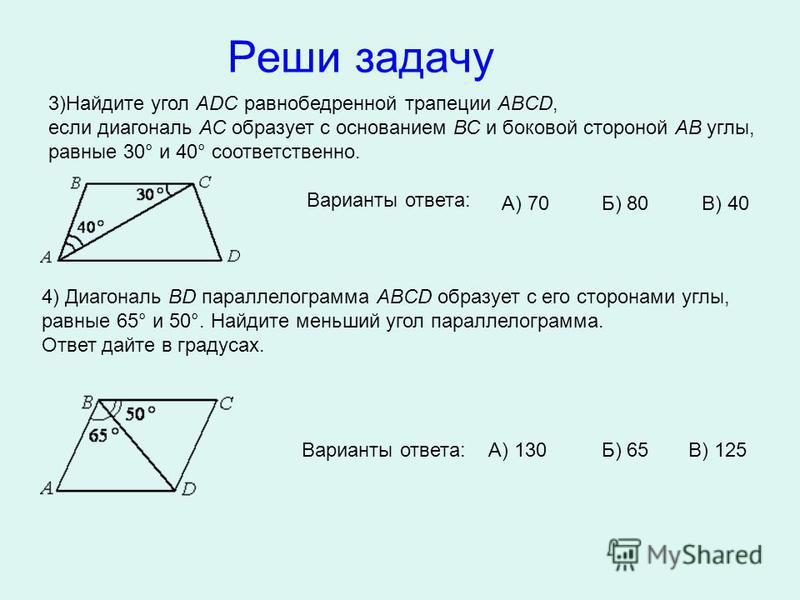
87. Найдите площадь квадрата:
1. А В 2. М Р 3.
КР=2,4 Площадь квадрата
равна 6. Найдите
сторону квадрата.
С 2,3 В
Д 4,2 С К В
88.Сторона ромба 20см, а одна из диагоналей 24см. Найдите площадь ромба.
89.В равнобедренной трапеции диагональ перпендикулярна боковой стороне.
Найдите площадь трапеции, если большее основание равно 16 3, а один из углов
трапеции равен 60°.
90.Угол при вершине равнобедренного треугольника равен 120°, а основание 14 3 см. Найдите
площадь треугольника.
91.Площадь прямоугольного равнобедренного треугольника 16. Найдите гипотенузу этого
треугольника.
92.Площадь равностороннего треугольника равна 24 3 . Найдите сторону этого треугольника.
ТЕОРЕМА ПИФАГОРА.
93. Найдите неизвестные стороны треугольника:
1. 2. 3. В
АВ=18 АВ=2 2
4 5 17
С А С В В
3
94.Стороны прямоугольника относятся как 2 : 3, диагональ прямоугольника равна 13. Найдите стороны прямоугольника.
95.Сторона равностороннего треугольника равна 18 3 . Найдите биссектрису этого треугольника.
96. Гипотенуза АВ прямоугольного треугольника АВС равна 2 22, а катет ВС=6.
Найдите длину медианы ВК.
97. В Δ СДЕ СД=15, ДЕ=13, СЕ=14. Найдите высоту ДМ.
98. Дано:ΔАВС,
АС=15, АД=9, СВ= 52
Найти АВ.
С В
СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА И ТРАПЕЦИИ.
99. Определите среднюю линию мк : 15см
М К М К
34см 23см
100.Средняя линия треугольника на 3,6 меньше основания треугольника. Найдите сумму средней линии треугольника и основания.
В С
101. В трапеции АВСД АД=23, ВС =18,
МК- средняя . М Е Р К
Найдите ЕР.
А Д
102. К Е
А В Дано: МКЕР- трапеция, АК=АС=СО=МО,
АВ||СД||ОН||МР, МР=18, КЕ=12
С Д Найдите АВ и ОН.
Leave A Comment