дана трапеция abcd с основаниями ad=15 dc=10 о-точка пересечения диагоналей.разложите вектор BO по векторам AD=a и AB=b — Спрашивалка

Дима Зайцев

дана трапеция abcd с основаниями ad=15 dc=10 о-точка пересечения диагоналей.разложите вектор BO по векторам AD=a и AB=b точка основание диагональ вектор пересечение трапеция

204

22

0

Ответы

ЛС

Левый Сектор!

дано:лезет баба к нам в окно…допустим мы её впустим…предположим мы её положим, из точки Х в точку Р опустим перпендикуляр..через 9 месяцев получим экземпляр…как то так..)))

0

. ..s.k.l.b.r…

…нарисуй всё так как написал…обозначь пересечение в необходимой точке…и проведи траекторию линий по трактовке диагоналей…

0

МГ

Марина Горлач

ну нельзя же после тяжелого трудового дня такие задачи задавать)))

0

Дима Зайцев

окау

1

КП

Ким Палыч

ни как по геометрии домашнее задание не можешь сделать!?

0

ТА

Татьяна Андрюшина

дорогой, ты не по адресу обратился,я давно это забыла.

0

СД

Сабит Досаев

Лучше скажите что появилось первым курица или яйцо.

9 лет

0

Дима Зайцев

любая курица появилась из яйца, которое, в свою очередь, было снесено другой курицей.

1

СД

Сабит Досаев

Нет яйцо это и есть начало оно произошло от метаморфозы энергетического импульса данного некой силой.

1

Эвр

Про это наверное в твоем учебнике хорошо написано…

0

КД

Коля Дикий

ты чё тут заплутал малость?тебе надо на спиши. ру

0

Дима Зайцев

ахаха

1

Морошка

Ой Дима…не делай мне беременной голову:)))

0

Marina Margo

Это ты сейчас домашнее задание делаешь???)

0

Дима Зайцев

да

1

Капитанская Дочка

ай -яй-яй…спрашка решает, а Дима сдает…

0

Игорь

Дима, кофейку? На хрена нам твоя трапеция?

0

Fcpugros Fcpugros

чо ,домашку нам скидываешь?сам решай!

0

ИГ

Ирина Грицевич

как могут быть основания ad и dc?

0

ЕК

Елена К.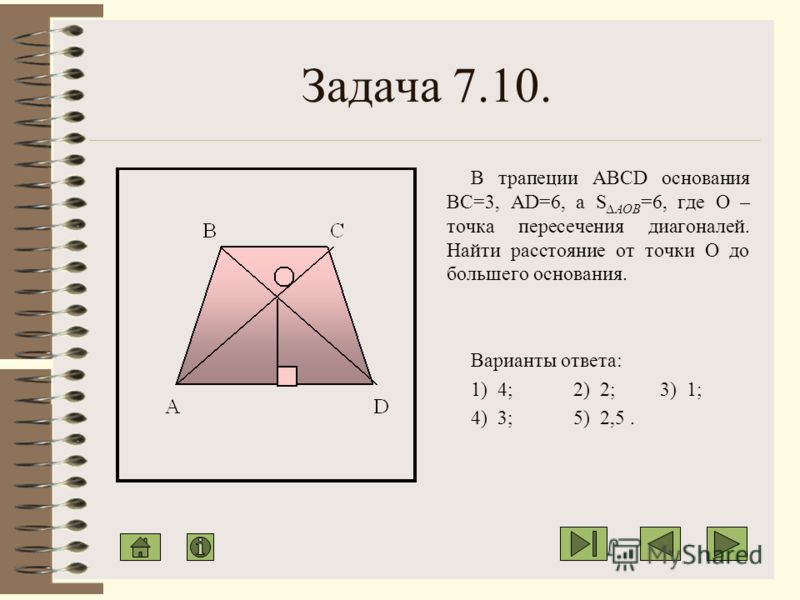

а мне это надо? думаю нафига)))

0

Дима Зайцев

._.

1

Larissa Arzhanova

Не получается с геометрией

0

Ba

Bakiev.1992

net net takov wa nexochu mozg parit)))))))

0

АЖ

Аркадий Жарков

….нет… сами подумайте

0

Bad Girl

чувак.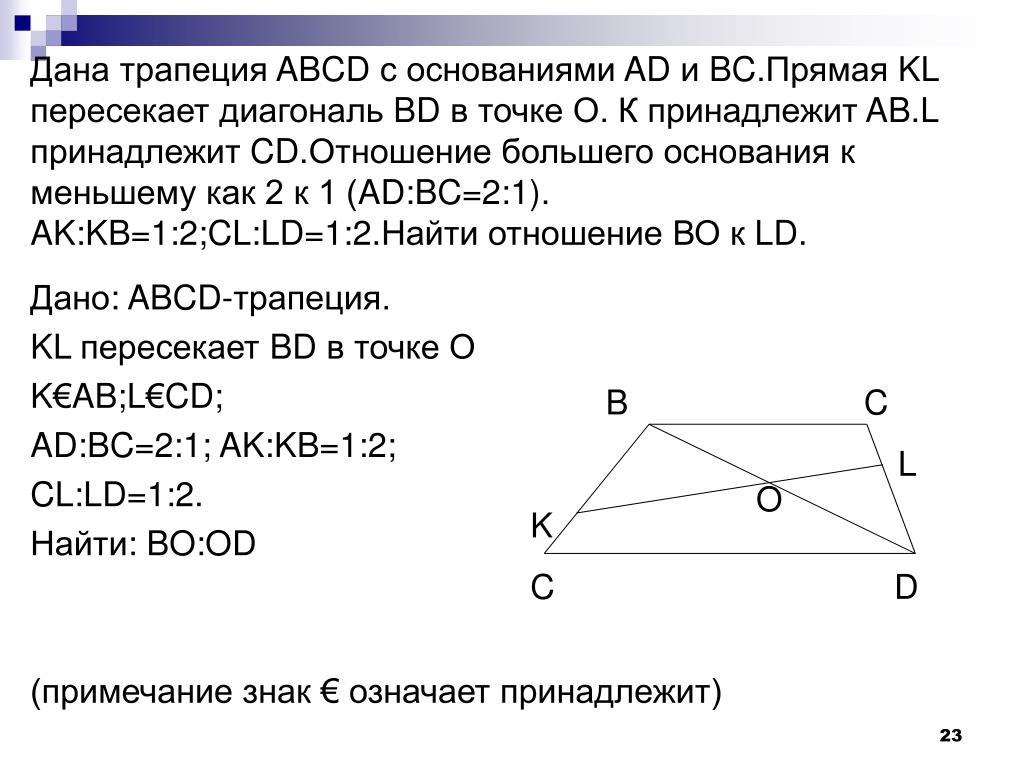 мы не на алгебре

0

ЗИ

Зелёный Ио Прынца Даццкого

а нафига оно мне ))))

9 лет

0

Дима Зайцев

уж я хз

1

ЗИ

Зелёный Ио Прынца Даццкого

вот и я о том же ))

1

Дима Зайцев

ахаха

1

Следующая страница

Другие вопросы

какая модель моновпрыска скорее всего стоит в AUDI 80. Audi 80 1989г двигатель A3 2.

0 кузов B3 АКПП

Какое влияние на работу двигателя оказывает состояние коренных и шатунных шеек? коленчатого вала?? ? не пойму ((

СРОЧНОНашла человека из прошлого. Возможны ли отношения? Прошу вас погадать!

Можно ли оформить отпуск по уходу за ребенком до 3 лет на работающую дочь?

я служил срочку в в/ч 22179 33 ОРБр (г) р. ДАГЕСТАН. н/п БОТЛИХ 2010-2011г, смогу ли я подписать контракт и попасть туда ж

когда в моей жизни начнет уже что то хорошее происходить? надоели уже все проблемы, когда ждать хороших перемен и в чем?

Могу ли я приватизировать квартиру, если до этого я принимал участие в приватизации квартиры своей мамы (тогда был не со

У кого есть ненужные запчасти на ВАЗ 2101-07? СПБ

Вот если вы приглашаете человека на очную консультацию

Нужен перечень заболеваний, при которых запрещено усыновление в Украине

со скольки лет можно носить пистолет аникс А-101 мощность 3,0 Дж

Каким аппаратом делают полную шлифовку двигателя сколько он стоит ?

чем можно удалить желтизну с прозрачного пластмасса, панель скутера.

Обтянул пленкой кузов авто (ВАЗ 2107) по докам светло бежевая, стала зеленая=) что за это могут предъявить Гаишники

Закон о продаже алкоголя в Украине, и про безалкогольные напитки(пиво). Внутри смешная история и вопрос.

Задание №16. Планиметрия с доказательством. ЕГЭ. Математика. 3

1.  Планиметрия 

2.  Стереометрия 
3.  Начала теории вероятностей 

4.  Теория вероятностей

5.  Простейшие уравнения
6.  Преобразование выражений 
7.  Производная функции 
8.  Практические задачи 
9.  Текствые задачи 
10.  Графики функций 
11.  Исследование функций
12.  Уравнения 
13.  Стереометрия с доказ-вом
14.  Неравенства 


15.  Финансовая математика 
16.  Планиметрия с доказ-вом 
17.   Задачи с параметром 
18.  Задачи на логику 

      БАЗА ЗАДАНИЙ

Задание № 16. Планиметрия с доказательством.

57. Одна окружность вписана в прямоугольную трапецию, а вторая касается большей боковой стороны и продолжений оснований.

а) Докажите, что расстояние между центрами окружностей равно большей боковой стороне трапеции.
б) Найдите расстояние от вершины одного из прямых углов трапеции до центра второй окружности, если точка касания первой окружности с большей боковой стороной трапеции делит её на отрезки, равные 2 и 50.

58. В остроугольном треугольнике ABC проведены высоты AK и CM. На них из точек M и K опущены перпендикуляры ME и KH соответственно.
а) Докажите, что прямые EH и AC параллельны.
б) Найдите отношение EH и AC, если ∠ABC=45°
Ответ: б) 1:2

59. Точка М – середина гипотенузы АВ треугольника АВС. Серединный перпендикуляр к гипотенузе пересекает катет ВС в точке N.

 а) Докажите, что ∠ CAN = ∠ CMN
б) Найдите отношение радиусов окружностей, описанных около треугольников ANB и CBM, если tg BAC = 4/3.

Ответ: б) 5:4

60. В равнобедренной трапеции ABCD основание AD в два раза больше основания BC.
а) Докажите, что высота CH трапеции разбивает основание AD на отрезки, один из которых втрое больше другого.
б) Пусть O — точка пересечения диагоналей трапеции ABCD. Найдите расстояние от вершины C до середины отрезка OD, если BC=16 и AB=10.
Ответ: б) 4

61. В трапеции ABCD основание AD в два раза больше основания BC. Внутри трапеции взяли точку M так, что углы ABM и DCM прямые.
а) Докажите, что AM=DM.
б) Найдите угол BAD, если угол ADC равен 70°, а расстояние от точки M до прямой AD равно стороне BC.
Ответ: б) 65°

62. Около остроугольного треугольника ABC описана окружность с центром O. На продолжении отрезка AO за точку O отмечена точка K так, что ∠BAC +∠AKC=90°.

а) Докажите, что четырёхугольник OBKC вписанный.

б) Найдите радиус окружности, описанной около четырёхугольника OBKC, если cos ∠BAC=3/5, а BC=48.

Ответ: б) 25

63. В равнобедренной трапеции ABCD основание AD в три раза больше основания BC.
а) Докажите, что высота CH трапеции разбивает основание AD на отрезки, один из которых вдвое больше другого.
б) Найдите расстояние от вершины C до середины диагонали BD, если AD=15 и AC=2√61.
Ответ: б) 6

64. В трапеции ABCD боковая сторона AB перпендикулярна основаниям. Из точки A на сторону CD опустили перпендикуляр AH. На стороне AB отмечена точка E так, что прямые CD и CE перпендикулярны.
а) Докажите, что прямые BH и ED параллельны.
б) Найдите отношение BH к ED, если ∠BCD=120°.
Ответ: б) 3:4

65. В треугольнике ABC угол ABC тупой, H — точка пересечения продолжений высот, угол AHC равен 60°.
а) Докажите, что угол ABC равен 120°.
б) Найдите BH, если AB=7, BC=8.

66. В трапеции ABCD с основаниями ВС и AD углы ABD и ACD прямые.
а) Докажите, что АВ = CD.
б) Найдите AD, если AB = 2, BC = 7.
Ответ: б) 8

67. Точка Е — середина стороны BС квадрата АВСD. Серединные перпендикуляры к отрезкам АЕ и ЕС пересекаются в точке O.
а) Докажите, что ∠AOE=90°.
б) Найдите BO:OD.
Ответ: б) 3:1

68. Точка O — центр окружности, описанной около остроугольного треугольника ABC, а BH — высота этого треугольника.
а) Докажите, что углы ABH и CBO равны.
б) Найдите BH, если AB=8, BC=9, BH=BO.
Ответ: б) 6

69. В выпуклом четырёхугольнике ABCD известны стороны и диагональ:  AB = 3,  BC = CD = 5,  AD = 8,  AC = 7.
а) Докажите, что вокруг этого четырёхугольника можно описать окружность.
б) Найдите BD.
Ответ: б) 55/7

70. Четырёхугольник ABCD вписан в окружность радиуса R = 8. Известно, что AB=BC=CD=12.
а) Докажите, что прямые BC и AD параллельны.
б) Найдите AD.
Ответ: б) 9

71.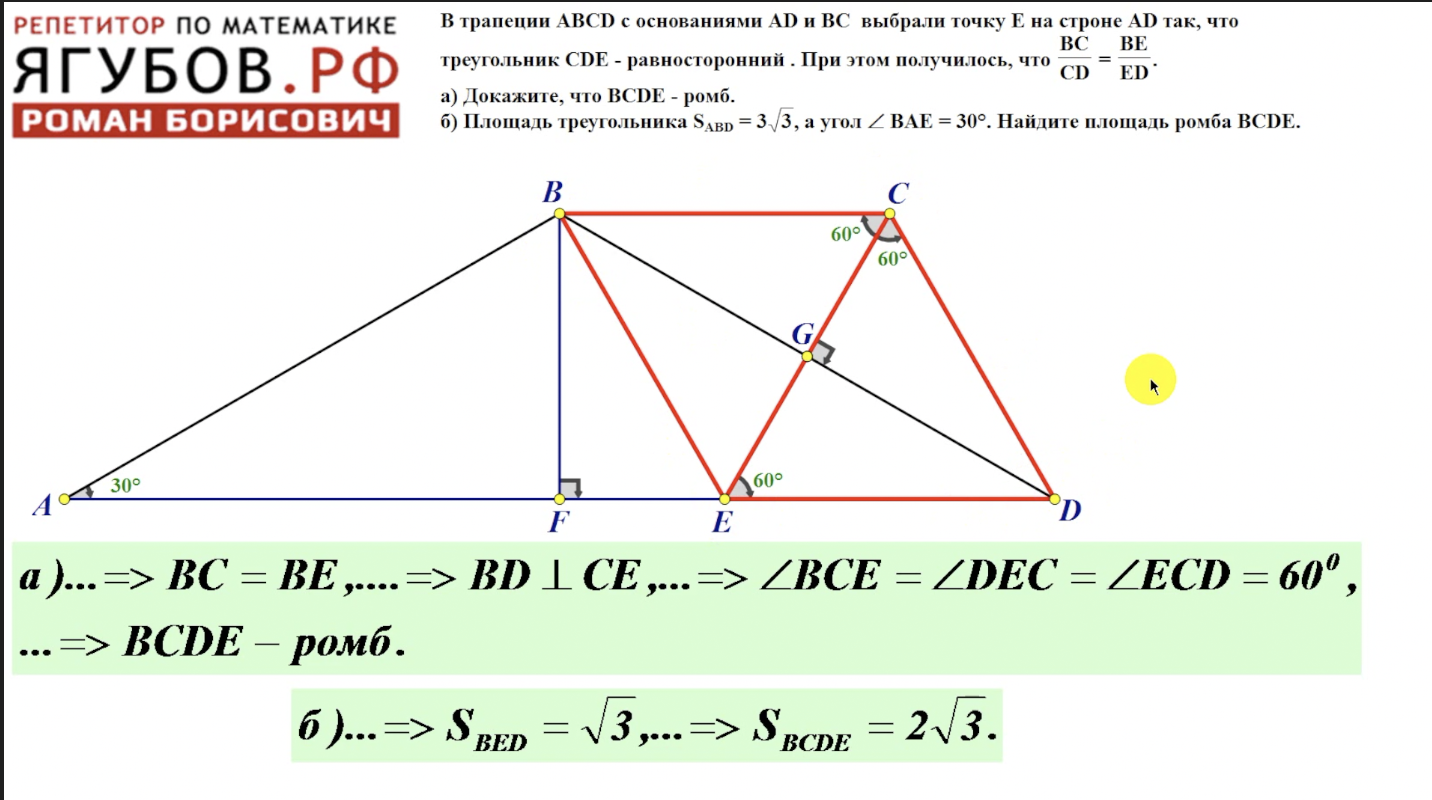 Окружность с центром О1 касается оснований ВС и AD и боковой стороны АВ трапеции ABCD. Окружность с центром O2 касается сторон ВС, CD и AD. Известно, что АВ = 10, ВС = 9, CD = 30, AD = 39.
а) Докажите, что прямая О1О2 параллельна основаниям трапеции АВСD.
б) Найдите О1О2.
Ответ: б) 4

72. Окружность с центром в точке O высекает на всех сторонах трапеции ABCD равные хорды.
а) Докажите, что биссектрисы всех углов трапеции пересекаются в одной и той же точке.

б) Найдите высоту трапеции, если окружность пересекает боковую сторону AB в точках K и L так, что AK = 11, KL = 10, LB = 4.

Ответ: б) 24

73. Окружность проходит через вершины A, B и D параллелограмма ABCD, пересекает сторону BC в точках B и E и пересекает сторону CD в точках K и D.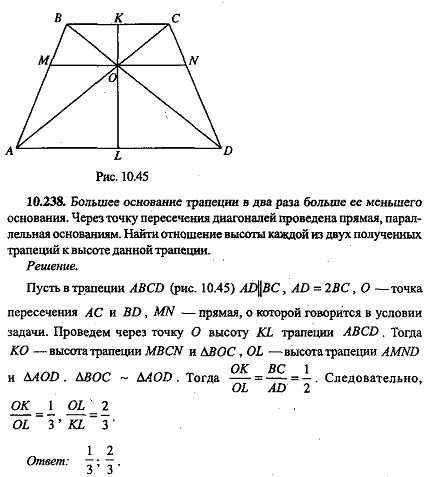
а) Докажите, что AE = AK.
б) Найдите AD, если CE =10, DK = 9 и cos ∠BAD=0,2.

Ответ: б) 40

74. Высоты тупоугольного треугольника АВС с тупым углом АВС пересекаются в точке Н. Угол АНС равен 60 градусов.
а) Докажите, что угол АВС равен 120 градусов.

б) Найдите ВН, если АВ=7, ВС=8.

75. В трапецию ABCD c основаниями ВС и AD вписана окружность с центром О, СН – высота трапеции, Е – точка пересечения диагоналей.
а) Докажите, что ∠OHC= ∠ADC / 2.  
б) Найдите площадь четырехугольника СЕОН, если известно, что ∠BAD=90°, BC=9, AD=18.

Ответ: б) 21

76. Серединный перпендикуляр к стороне АВ треугольника АВС пересекает сторону АС в точке D. Окружность с центром О, вписанная в треугольник ADB, касается отрезка AD в точке Р, а прямая ОР пересекает сторону АВ в точке К.

а) Докажите, что около четырехугольника ВDОК можно описать окружность.

б) Найдите радиус этой окружности, если АВ = 10, АС = 8, ВС = 6.

77. Окружность, вписанная в треугольник ABC, касается сторон BC и AC в точках M и N соответственно, E и F — середины сторон AB соответственно. Прямые MN и EF пересекаются в точке D.

а) Докажите, что треугольник DFN равнобедренный.

б) Найдите площадь треугольника BED, если AB = 20 и ∠ABC = 60°.

78. Медианы AA1, BB1, CC1 треугольника ABC пересекаются в точке M. Известно, что AC = 3MB.

а) Докажите, что треугольник ABC прямоугольный.

б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 12.

Ответ: б) 180

79. Четырёхугольник ABCD вписан в окружность. Диаметр CC1 перпендикулярен стороне AD и пересекает её в точке M, а диаметр DD1 перпендикулярен стороне AB и пересекает её в точке N.

а)  Пусть AA1  также диаметр окружности. Докажите, что ∠DNM =∠BA1D1.

б) Найдите углы четырёхугольника ABCD, если угол CDB вдвое меньше угла ADB.

Ответ: б) 72°, 126°, 108°, 54°

80. В прямоугольном треугольнике ABC с прямым углом C известны стороны AC=12, BC=5. Окружность радиусом 0,5 с центром O на стороне BC проходит через вершину C. Вторая окружность касается катета AC, гипотенузы треугольника, а также внешним образом касается первой окружности.

а) Докажите, что радиус второй окружности меньше, чем 1/5 длины катета AC.

б) Найдите радиус второй окружности.

Ответ: б) 2

81. Окружность с центром O проходит через вершины B и C большей боковой стороны прямоугольной трапеции ABCD и касается боковой стороны AD в точке T.

а) Докажите, что угол BOC вдвое больше угла BTC.

б) Найдите расстояние от точки T до прямой BC, если основания трапеции AB и CD равны 4 и 9 соответственно.

Ответ: б) 6

82. Окружность с центром O, вписанная в треугольник ABC, касается его сторон BC, AB и AC в точках K, L и M соответственно. Прямая KM вторично пересекает в точке P окружность радиуса AM с центром A.

а) Докажите, что прямая AP параллельна прямой BC.

б) Пусть ∠ABC =90°, AM =3, CM =2, Q— точка пересечения прямых KM и AB, а T—такая точка на отрезке PQ, что ∠OAT= 45°. Найдите QT.

83. На гипотенузе AB и на катетах BC и AC прямоугольного треугольника ABC отмечены точки M, N и K соответственно, причем прямая KN параллельна прямой AB и BM =BN =KN/2. Точка P — середина отрезка KN.

а) Докажите, что четырехугольник BCPM — равнобедренная трапеция.

б) Найдите площадь треугольника ABC, если BM=1 и ∠BCM=15°.

84. В прямоугольном треугольнике ABC точка M лежит на катете AC, а точка N лежит на продолжении катета BC за точку C, причём CM=BC и CN=AC. Отрезки CP и CQ — биссектрисы треугольников ACB и NCM соответственно.

а) Докажите, что CP и СQ перпендикулярны.

б) Найдите PQ, если BC=3, а AC=5. 

Ответ: б) 15/4

85. Дана трапеция ABCD с основаниями BC и AD. Точки M и N являются серединами сторон AB и CD соответственно. Окружность, проходящая через точки B и С, пересекает отрезки BM и CN в точках P и Q (отличных от концов отрезков).

а) Докажите, что точки M, N, P и Q лежат на одной окружности.

б) Найдите радиус окружности, описанной около треугольника MPQ, если прямая DP перпендикулярна прямой PC,  AB= 25, BC = 3, CD = 28, AD = 20.

Ответ: б) 85/12

86. В остроугольном треугольнике ABC, ∠A=60°. Высоты BN и CM треугольника ABC пересекаются в точке H. Точка O — центр окружности, описанной около ∆ABC.

а) Докажите, что AH=AO.

б) Найдите площадь ∆AHO, если BC=6√3, ∠ABC=45°.

Ответ: б) 9

87. Точка O — центр вписанной в треугольник ABC окружности. Прямая OB вторично пересекает описанную около этого треугольника окружность в точке P.

а) Докажите, что ∠POC=∠PCO.
б) Найдите площадь треугольника APC, если радиус описанной около треугольника ABC окружности равен 4, а ∠ABC=120°.

Ответ: б) 12√3

88. Около остроугольного треугольника ABC с различными сторонами описали окружность с диаметром BN. Высота BH пересекает эту окружность в точке K.

а) Докажите, что AN=CK.

б) Найдите KN, если ∠BAC=35°, ∠ACB=65°, а радиус окружности = 12.

 Ответ: б) 12

89. Около ∆ABC описана окружность. Прямая BO, где O — центр вписанной окружности, вторично пересекает описанную окружность в точке P. 

а) Докажите, что OP=AP.  

б) Найдите расстояние от точки P до прямой AC, если ∠ABC=120°. а радиус описанной окружности равен 18.  

Ответ: б) 27

1     2    3

Главная

Вопрос Видео: Нахождение площади трапеции

𝐴𝐵𝐶𝐷 — трапеция, где отрезок 𝐴𝐷 ⫽ отрезок 𝐵𝐶, 𝐴𝐷 = 22 см, а 𝐵𝐶 = 13 см. Если площадь △𝐴𝐵𝐶 равна 65 см², какова площадь трапеции?

Стенограмма видео

𝐴𝐵𝐶𝐷 — трапеция, где линия отрезок 𝐴𝐷 параллелен отрезку 𝐵𝐶, 𝐴𝐷 равен 22 сантиметрам, а 𝐵𝐶 равняется 13 сантиметрам. Если площадь треугольника 𝐴𝐵𝐶 равна 65 квадратных сантиметров, какова площадь трапеции?

Нам дали разные информацию об этой трапеции и попросили вычислить ее площадь. Площадь трапеции равна половина суммы длин его параллельных сторон, обычно обозначаемых 𝑎 и 𝑏, умножается на высоту, обозначаемую ℎ.

Нам известны длины параллельные стороны, отрезки 𝐴𝐷 и 𝐵𝐶, равные 22 и 13 сантиметрам, соответственно. Но нам не дали высота трапеции. Нам нужно использовать другой информация в вопросе, чтобы вычислить это, прежде чем мы сможем найти трапецию область.

Другая предоставленная информация заключается в том, что площадь треугольника 𝐴𝐵𝐶 равна 65 квадратных сантиметров. Вот этот треугольник. Теперь площадь треугольника находится по формуле: половина умножается на его основание, умноженное на его перпендикулярная высота. Основание треугольника 𝐴𝐵𝐶 равно общая со стороной трапеции, стороной 𝐵𝐶, которая имеет длину 13 сантиметры. Высота треугольника 𝐴𝐵𝐶 равна равно высоте трапеции. И так мы можем составить уравнение. 65 равно половине, умноженной на 13ℎ.

Мы можем решить это уравнение, чтобы найти высота треугольника и, следовательно, высота трапеции.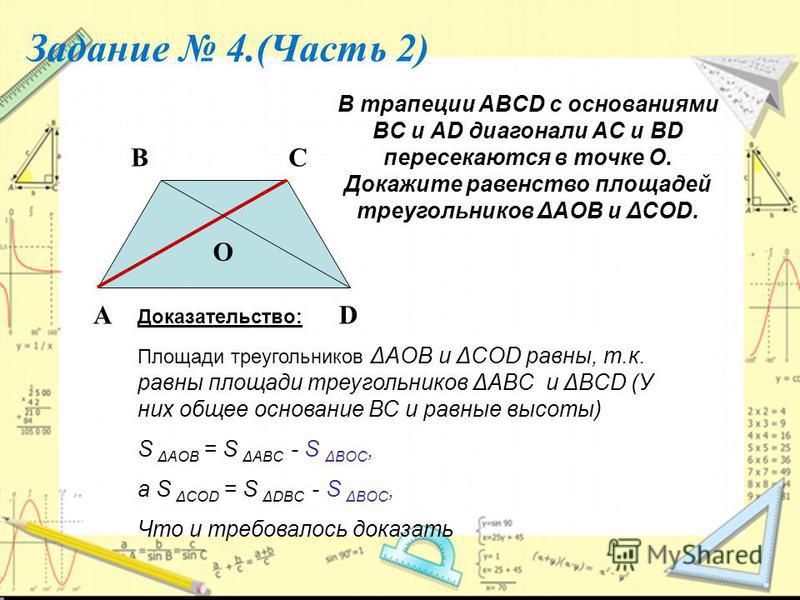 Умножение обеих сторон уравнение на два дает 130 равно 13ℎ. А затем разделив обе стороны уравнение на 13 дает ℎ равно 10.

Теперь мы обнаружили, что высота трапеция равна 10 см. Итак, мы готовы вычислить его область. Подставляем 13 и 22 вместо длины параллельных сторон и 10 высоты в формулу площади трапеции дает, что площадь трапеции 𝐴𝐵𝐶𝐷 равна половине умножить на 13 плюс 22 умножить на 10. 13 плюс 22 будет 35 с половиной умножить на 10 будет пять. Таким образом, расчет упрощается до пять умножить на 35, что равно 175.

Сначала используя площадь треугольника 𝐴𝐵𝐶 для вычисления высоты трапеции мы нашли, что площадь трапеция 175 квадратных сантиметров.

Эти треугольники не равны, но их площади равны.

Вопрос

Обновлено: 26/04/2023

NCERT BANGLISH-AREAS – ДУМАЙ, ОБСУЖДАЙ И НАПИШИ

4 видео

РЕКЛАМА

Ответ

Шаг за шагом решение от экспертов, которое поможет вам разобраться с сомнениями и получить отличные оценки оценки на экзаменах.

Ab Padhai каро бина объявления ке

Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!

Видео по теме

На рис. 6.44 ABC и DBC — два треугольника с одним и тем же основанием BC. Если AD пересекает BC в точке O, покажите, что (ar (ABC))/( ar (DBC))= (AO)/(DO)

На данном рисунке дельта ABC и дельта DBC лежат на одном основании BC. Если AD пересекает BC в точке O , докажите, что (ar(Delta ABC))/(ar(Delta DBC))=(AO)/(DO)

आकृति 6 .44 में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए है यदि AD , BC को O पर प्रतिच्छेद करे , तो दर्शाइए कि ar(ABC) ar(DBC)=AODO है

52808304

На том же рисунке ΔABC и ΔDBC лежат в одной базе BC. Если AD пересекает BC в точке O, докажите, что
ar(ΔABC)ar(ΔDBC)=AODO

53084596

На данном рисунке ΔABC и ΔDBC имеют одно и то же основание BC. Если AD и BC пересекаются в точке O, докажите, что ar(ΔABC)ar(ΔDBC)=AODO

53084862

र BC पर दो त्रिभुज ABC और DBC बने हुए है। यदि AD,BD को O पर प्रतिच्छेद पर तो दर्शाइए कि ar(ΔABC)ar(ΔDBC)=AODO है।

58114404

Утверждение (A): В трапеции ABCD имеем AB ||DC и диагонали AC и BD пересекаются в точке O.
Тогда ar(△AOD)=ar(△BOC).

Причина (R ) : Треугольники на одном основании между одинаковыми параллелями равны по площади.

61726500

चित्र में AB आधार पर दो त्रिभुजों ABC त था ABD है है यदि रेखाखण्ड CD को रेखा AB बिंदु O पर प्रतिच ्छेद करती है, तो प्रदर्शित कीजिए कि ar(ΔABC)=ar(ΔABD)

900 02 105884898

त्रिभुज ABC की AD एक माध्यिका है तथा भुजा AC पर बिंदु P इस प्रका र है कि
ar(ΔADP):ar(ΔABD)=2:3, तो ar(ΔPDC):ar(ΔABC)

105884960

ABC और DBC दो त्रिभुज एकही आधार BC पर विपरीत पार्शव में है । यदि AD,BC को P पर प्रतिच्छेद करती है
तो दिखाएँ कि ar( ΔABC)ar(DBC)=APDP

127318285

На рисунке ABC и DBC — два треугольника с одним и тем же основанием BC.