Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
Высота конуса равна 6 см, угол при вершин осевого сечения равен 120 градусов. Найдите 1) площадь сечения конуса плоскостью проходящей через две…
Найдите 1) площадь сечения конуса плоскостью проходящей через две…Решено
В корзине лежат 25 грибов: рыжики и грузди. Известно, что среди любых 11 грибов имеется хотя бы один рыжик ,а среди любых 16 грибов хотя бы один груздь. Сколько рыжиков в корзине?У Ани есть 30 одинаковых кубиков. Сколько различных прямоугольных параллелепипедов она может из них составить, если для построения одного параллелепипеда надо использовать все имеющиеся 30 кубиков?
Высота конуса равна 6 см, угол при вершин осевого сечения равен 120 градусов. Найдите 1) площадь сечения конуса плоскостью проходящей через две…
валя решает задачу на 3 минуты быстрее чем оля и на одну минуту дольше чем решая эту же задачу вместе с олей. за сколько минут валя решит задачу в одиночку
дан прямоугольный треугольник ABC,у которого угол C-прямой ,катет BC равен 6 см. и уголA=60°.
 найдите:остальные стороны треугольника ABC,площадь ABC,длину высоты,опущенной из вершины C
найдите:остальные стороны треугольника ABC,площадь ABC,длину высоты,опущенной из вершины CОтветы 1
1. sin A = BC : AB, отсюда
АВ = BC : sin 60° = 6 : √3/2 = 4√3 см
2. Зная, что сумма острых углов прямоугольного треуг-ка равна 90°, находим неизвестный угол В:
<B=90-<A=90-60=30°
3. В прямоугольном треуг-ке АВС катет АС, лежащий против угла В в 30°, равен половине гипотенузы АВ, значит:
АС=1/2АВ=1/2*4√3=2√3 см
4. Площадь прямоугольного треугольника равна половине произведения его катетов:
S=1/2AC*BC=1/2*2√3*6=6√3 см²
5. В прямоугольном треуг-ке ВНС катет СН (он же высота), лежащий против угла В в 30°, равен половине гипотенузы ВС, значит:
Автор:
amiya
Оценить ответ:
0
Знаешь ответ? Добавь его сюда!
Последние вопросы
- Математика
1 час назад
Помогите пожалуйста от этой оценки зависит годовая оценка
9 часов назад
3 вариант
- Информатика
9 часов назад
Помогите
- Физика
12 часов назад
Реохорд. x+1 y(0)=2; y'(0)=1.
x+1 y(0)=2; y'(0)=1. - Математика
13 часов назад
1. Случайная величина распределена равномерно на отрезке [−2; 5]. Найти математическое ожидание и дисперсию. Что вероятнее: в результате ис- пытания случайная величина окажется в интервале (2,5; 3) или вне его?
- Математика
13 часов назад
1. В цехе работают 8 мужчин и 12 женщин. По табельным номерам отбира- ют 6 человек. Какова вероятность того, что среди них будут только 2 женщины?
- Физика
14 часов назад
определи фокусное расстояние лупы с точностью до сантиметра если её оптическая сила равна d 5.3 дптр.
- Алгебра
15 часов назад
-6x^2+x+2>0.
 Решение квадратных неравенств
Решение квадратных неравенств - Физика
15 часов назад
2.3. Блок укреплен на вершине двух наклонных плоскостей, составляющих с горизонтом углы а = 30° и (3 = 45°. Гири равной массы
(т
х = т2 = 2 кг) соединены нитью, перекинутой через блок. Считая нить и блок невесомыми, принимая коэффициенты трения гирь о наклонные плоскости равными f1= f2= =0,1 и пренебрегая трением в блоке, определите: 1) ускорение, с которым движутся гири; 2) силу натяжения нити. [1) 0,24 м/с2; 2) 12 Н]
- История
20 часов назад
ПЖ помогите КТО ЭТО Я НЕЗНАЮ
- Алгебра
20 часов назад
Негр и мексиканец падают с небоскрёба.
 Кто упадёт первым?
Кто упадёт первым? - Математика
1 день назад
В машине сидят негр и мексиканец. Кто за рулём?
- Математика
1 день назад
В чём разница между негром и апельсином?
- Математика
1 день назад
Братья Лёша и Саша решили добраться из дома до скейт‑парка. Они вышли одновременно, но Лёша пошёл пешком со скейтом в руках, а Саша поехал на скейте. Известно, что Саша едет на скейте в 3
3 раза быстрее, чем Лёша идёт пешком со скейтом. Через некоторое время они одновременно поменяли способ передвижения: Лёша поехал на скейте, а Саша пошёл пешком. При этом скорость движения каждого из них изменилась в 2
2 раза: у Лёши увеличилась, а у Саши уменьшилась.
 Оказалось, что до скейт‑парка они добрались одновременно. Сколько метров проехал на скейте Саша, если расстояние от дома до скейт‑парка составляет 3600
Оказалось, что до скейт‑парка они добрались одновременно. Сколько метров проехал на скейте Саша, если расстояние от дома до скейт‑парка составляет 3600метров? срочноо принимаются только норм ответы
How much to ban the user?
1 hour 1 day 100 yearsКак найти длину стороны прямоугольного треугольника
Все ресурсы по математике для средней школы
8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
Справка по математике для средней школы » Геометрия » Плоская геометрия » Треугольники » Прямоугольные треугольники » Как найти длину стороны прямоугольного треугольника
Найдите (округлив до десятых). Рисунок выполнен не в масштабе.
Возможные ответы: Правильный ответ: Пояснение: Мы воспользуемся теоремой Пифагора, чтобы найти недостающую длину стороны.
Сообщить об ошибке
Периметр квадратного боксерского ринга составляет футы. Когда два боксера сидят в противоположных углах между раундами, на каком расстоянии они друг от друга?
Возможные ответы:фута
фута
фута
фута
фута
90 015 Правильный ответ:футов
Объяснение:Поскольку периметр кольца – футы, а кольцо – квадрат, найдите длину одной стороны кольца, разделив его на .
Расстояние между двумя боксерами в противоположных углах представляет собой прямую линию от одного угла до другого. Эта прямая образует гипотенузу прямоугольного треугольника, две другие стороны которого имеют длину фута (поскольку каждая из них является стороной квадрата).
Решение длины гипотенузы этого прямоугольного треугольника с помощью теоремы Пифагора дает расстояние между двумя боксерами, когда они находятся в противоположных углах.
Сообщить об ошибке
Дан прямоугольный треугольник с длиной катета 6 и длиной гипотенузы 10, найдите длину другого катета, х .
Возможные ответы:
16
4
64
8
Правильный ответ:8
Объяснение:Используя теорему Пифагора, мы можем найти длину ноги x :
x 2 + 6 2 = 10 2
Теперь находим x :
x 2 + 36 = 100
x 2 = 100 – 36
x 2 = 64
x = 8
Также обратите внимание, что это пропорционально прямоугольный треугольник 3/4/5, который очень распространен. Всегда следите за отношением стороны к гипотенезе 3/5 или 4/5 или отношением стороны к стороне 3/4 в любом прямоугольном треугольнике, чтобы вы могли быстро решать такие треугольники.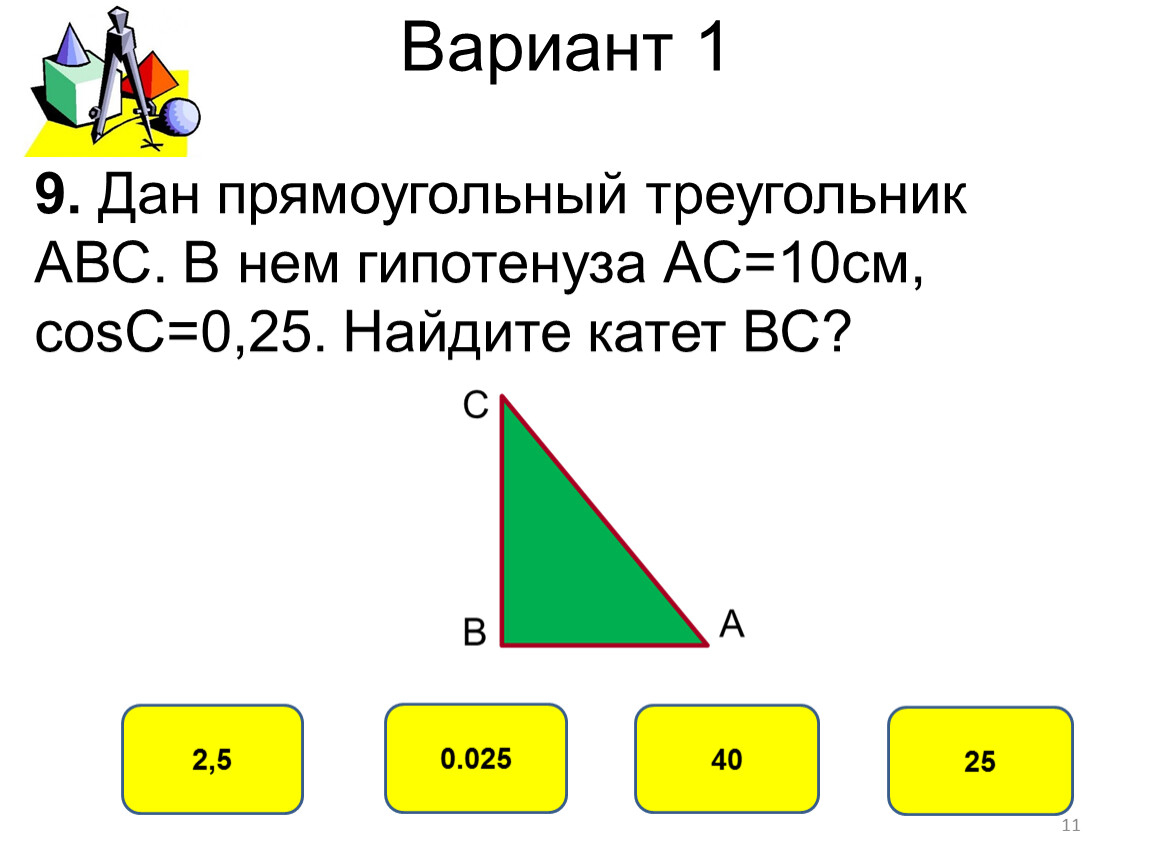
Сообщить об ошибке
В прямоугольном треугольнике длина гипотенузы равна 8, а длина катета равна 7. Какова длина третьей стороны с точностью до десятых?
Возможные ответы:3.9
2.4
3.6
1.0
Правильный ответ: 3.9
Объяснение: Используя теорему Пифагора, 8 2 = 7 2 +x 2 . Решение для x дает квадратный корень из 15, который равен 3,9
Сообщить об ошибке
Дан прямоугольный треугольник с длиной катета 2 и длиной гипотенузы √8, найдите длину другого катета, х .
Возможные ответы:4
√8
2
6
10
9 0014 Правильный ответ:2
Объяснение:Используя теорему Пифагора, мы можем найти длину ноги x :
x 2 + 2 2 = (√8) 2 901 22 = 8
Теперь находим х :
х 2 + 4 = 8
x 2 = 8 – 4
x 2 = 4
900 04 x = 2Сообщить об ошибке
Катеты прямоугольного треугольника и . Округлив до ближайшего целого числа, какова длина гипотенузы?
Округлив до ближайшего целого числа, какова длина гипотенузы?
Используйте теорему Пифагора. Сумма квадратов обоих катетов равна квадрату гипотенузы.
Сообщить об ошибке
Решить для .
(Рисунок выполнен не в масштабе).
Возможные ответы: Правильный ответ: Объяснение:Используйте теорему Пифагора: .
Мы знаем длину одной стороны и гипотенузу.
Теперь мы можем найти недостающую сторону.
Сообщить об ошибке
Прямоугольный треугольник имеет одну сторону, равную 5, и гипотенузу, равную 14. Его третья сторона равна:
Возможные ответы:12
171
9
13. 07
14,87
Правильно ответ: 13. 07
07
Теорема Пифагора дает нам a 2 + b 2 = c 2 для прямоугольного треугольника, где c — это гипотенуза, а a и b — меньшие стороны. Здесь a равно 5, а c равно 14, поэтому b 2 = 14 2 – 5 2 = 171. Следовательно, b 90 008 равно квадратному корню из 171 или ориентировочно 13.07.
Сообщить об ошибке
Что из следующего НЕ может быть длинами сторон прямоугольного треугольника?
Возможные ответы:12, 16, 20
5, 7, 10
5, 12, 13
8, 15, 17
14, 48, 50
Правильный ответ:5, 7, 10
Объяснение: Мы используем теорему Пифагора и вычисляем, что 25 + 49 не равно 100.
Все остальные варианты ответов соблюдают теорему с 2
Сообщить об ошибке
Какой набор сторон может составить прямоугольный треугольник?
Возможные ответы:4, 6, 9
10, 12, 16
6, 7, 8
9, 12, 15
90 014 Правильный ответ:9, 12, 15
Пояснение: По теореме Пифагора в прямоугольном треугольнике сумма квадратов меньших двух сторон равна квадрату наибольшей стороны. Только 9, 12 и 15 соответствуют этому правилу.
Только 9, 12 и 15 соответствуют этому правилу.
Сообщить об ошибке
← Назад 1 2 3 Далее →
Уведомление об авторских правах
Все ресурсы по математике для старших классов
8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Learn by Concept
Тригонометрия и прямоугольные треугольники | безграничная алгебра |
Тригонометрия
Прямоугольные треугольники и теорема Пифагора
Теорема Пифагора, 9{2},}a2+b2=c2, используется для нахождения длины любой стороны прямоугольного треугольника.ccc
, а длины других сторон помечены какaaa
иbbb
, теорема Пифагора утверждает, что 9\circ90∘ ). Прямоугольный треугольник – это треугольник, в котором один угол прямой. Соотношение между сторонами и углами прямоугольного треугольника является основой тригонометрии.
Прямоугольный треугольник – это треугольник, в котором один угол прямой. Соотношение между сторонами и углами прямоугольного треугольника является основой тригонометрии.Сторона, противолежащая прямому углу, называется гипотенузой (на рисунке сторона
ссс
). Стороны, примыкающие к прямому углу, называются катетами (стороныaaa
иbbb
). Сторонаaaa
может быть идентифицирована как сторона, прилегающая к углуBBB
и напротив (или напротив) углаAAA
. Сторонаbbb
— сторона, примыкающая к углуAAA
и противолежащая углуBBB
. Прямоугольный треугольник: Теорему Пифагора можно использовать для нахождения значения длины недостающей стороны в прямоугольном треугольнике. Если длины всех трех сторон прямоугольного треугольника являются целыми числами, такой треугольник называется пифагорейским треугольником, а длины его сторон в совокупности называются пифагорейской тройкой.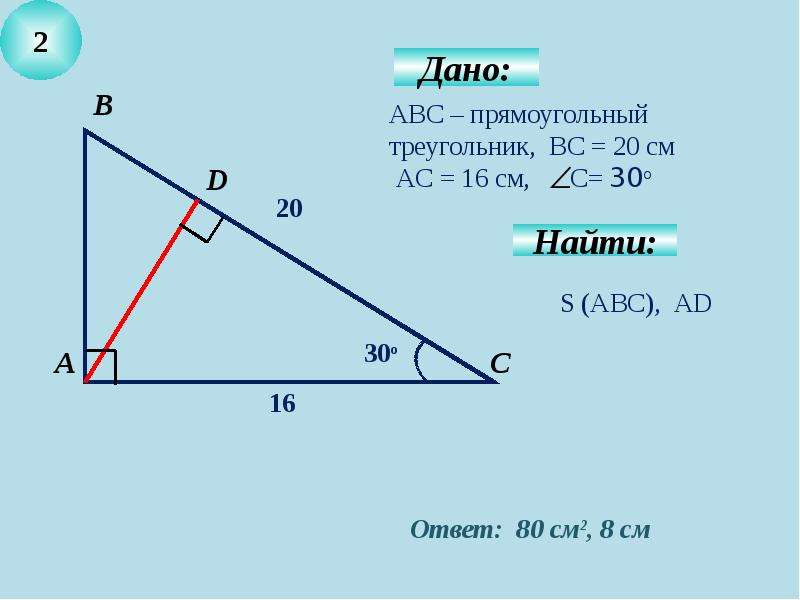
Теорема Пифагора
Теорема Пифагора, также известная как теорема Пифагора, является фундаментальным соотношением в евклидовой геометрии. Он определяет отношение между тремя сторонами прямоугольного треугольника. В нем говорится, что квадрат гипотенузы (сторона, противоположная прямому углу) равен сумме квадратов двух других сторон. Теорему можно записать в виде уравнения, связывающего длины сторонaaa
,bbb
9{2}}a2+b2=c2В этом уравнении
ccc
представляют длину гипотенузы, аaaa
иbbb
длины гипотенузы две другие стороны треугольника.Хотя часто говорят, что знание теоремы предшествовало ему, [2] теорема названа в честь древнегреческого математика Пифагора (ок. 570 – ок. 495 до н.э.). Ему приписывают первое зарегистрированное доказательство.
Теорема Пифагора: 92a2+b2=c2 .Поиск недостающей длины стороны
Пример 1. Прямоугольный треугольник имеет длину стороны101010
футов и длину гипотенузы202020
футов. Найдите длину другой стороны. (округлить до десятых долей фута)
Найдите длину другой стороны. (округлить до десятых долей фута)Подставить
a=10a=10a=10
иc=20c=20c=20
в теорему Пифагора и найтиббб
. 92} &=\sqrt{300} \\ б &=17,3 ~\mathrm{футов} \end{выравнивание} }a2+b2(10)2+b2100+b2b2b2 b=c2=(20)2=400=300=300 =17,3 футаПример 2. Длина сторон прямоугольного треугольника равна
333
см и444
см. Найдите длину гипотенузы.Подставить
a=3a=3a=3
иb=4b=4b=4
в теорему Пифагора и найтиccc
900 14 . 92} &=\sqrt{25} \\ с &=5~\mathrm{см} \end{выравнивание} }a2+b232+429+1625c2c2 c=c2=c2=c2=c2=25=25 =5 смКак работают тригонометрические функции
Тригонометрические функции можно использовать для нахождения отсутствующих длин сторон в прямоугольных треугольниках.Цели обучения
Узнайте, как тригонометрические функции используются для решения задач о прямоугольных треугольниках, и определите их входы и выходыОсновные выводы
Ключевые моменты 9{\ circ} 90 ∘
) Три тригонометрические функции, наиболее часто используемые для определения недостающей стороны прямоугольного треугольника: }sint=hypotenuseopposite ,cost=adjacenthypotenuse\displaystyle{\cos{t} = \frac {adjacent}{hypotenuse}}cost=hypotenuseadjacent
, иtant=oppositeadjacent\displaystyle{\tan{ t} = \frac {противоположный} {смежный}} tant=соседнийпротивоположный
Тригонометрические функции
Мы можем определить тригонометрические функции через уголttt
и длины сторон треугольника. Прилегающая сторона – это сторона, ближайшая к углу. (Смежный означает «рядом с».) Противоположная сторона – это сторона, расположенная напротив угла. Гипотенуза — это сторона треугольника, противоположная прямому углу, и она самая длинная. Прямоугольный треугольник: Стороны прямоугольного треугольника относительно угла
Прилегающая сторона – это сторона, ближайшая к углу. (Смежный означает «рядом с».) Противоположная сторона – это сторона, расположенная напротив угла. Гипотенуза — это сторона треугольника, противоположная прямому углу, и она самая длинная. Прямоугольный треугольник: Стороны прямоугольного треугольника относительно углаttt
.При поиске отсутствующей стороны прямоугольного треугольника, но единственной полученной информацией является измерение острого угла и длина стороны, используйте тригонометрические функции, перечисленные ниже:
- Синус {t} = \frac {напротив} {гипотенуза}}sint=гипотенузанапротив
- Косинус
cost=adjacenthypotenuse\displaystyle{\cos{t} = \frac {adjacent}{hypotenuse}}cost=hypotenuseadjacent
- Тангенс
tant=противоположныйсмежный\displaystyle{\tan{t} = \frac {напротив}{смежный}}tant=adjacentopposite
Тригонометрические функции равны отношениям, которые связывают определенные длины сторон прямоугольного треугольника. При поиске отсутствующей стороны первым шагом является определение того, какие стороны и какой угол даны, а затем выбор подходящей функции для решения проблемы.
При поиске отсутствующей стороны первым шагом является определение того, какие стороны и какой угол даны, а затем выбор подходящей функции для решения проблемы.
Оценка тригонометрической функции прямоугольного треугольника
Иногда вы знаете длину одной стороны треугольника и угла, и вам нужно найти другие измерения. Используйте одну из тригонометрических функций ( 9{\circ}34∘ и длину гипотенузы252525
футов, найдите длину стороны, противоположной острому углу (округлите до десятых): Прямоугольный треугольник: Дан прямоугольный треугольник с острого угла343434
градусов и длины гипотенузы252525
футов, найдите длину противоположной стороны.Глядя на рисунок, найдите сторону, противоположную острому углу
343434 9{\circ}83∘
и длину гипотенузы300300300
футов, найдите длину гипотенузы (округлив до десятых): Прямоугольный треугольник: Дан прямоугольный треугольник с острым углом838383
градусов и длину гипотенузы300300300
футов, найдите длину гипотенузы.
Глядя на рисунок, найдите гипотенузу острого угла
838383
градусов. Отношение сторон равно 9{\circ}\right)}} \\ x &= \frac{300}{\left(0,1218\dots\right)} \\ х &=2461,7~\mathrm{футы} \end{выравнивание} }costcos(83∘)x⋅cos(83∘)xxx=hypotenuseadjacent=x300=300=cos(83∘)300=(0,1218…)300=2461,7 футовСинус, косинус и Тангенс
МнемоникуSohCahToa можно использовать для определения длины стороны прямоугольного треугольника.
Цели обучения
Используйте аббревиатуру SohCahToa для определения синуса, косинуса и тангенса в терминах прямоугольных треугольниковKey Takeaways
Key Points
- Общая мнемоника для запоминания взаимосвязей между функциями синуса, косинуса и тангенса — SohCahToa.
- SohCahToa образован из первых букв « S ine is o pposite over h ypotenuse ( Soh ), C osine is 900 07 a djacent более h ypotenuse ( Cah ), Тангенс противоположен соседнему ( Тоа ).

Определения тригонометрических функций
Для прямоугольного треугольника с острым угломttt
первые три тригонометрические функции таковы:- сайт}{гипотенуза} } sint=hypotenuseopposite
- Косинус
cost=adjacenthypotenuse\displaystyle{ \cos{t} = \frac {adjacent}{hypotenuse} }cost=hypotenuseadjacent
- Тангенс
tant=oppositeadjacent\displaystyle{ \tan{t} = \frac {противоположный}{adjacent} }tant=adjacentopposite
Общая мнемоника для запоминания этих взаимосвязей — SohCahToa , образованная из первых букв « S ine is o pposite over h ypotenuse ( Soh ), 9 0007 C осин — это a djacent более ч ypotenuse ( Cah ), Тангенс противоположен соседнему ( 9{\ circ} 62∘
и смежная сторона454545
футов, найдите длину противоположной стороны. (округлить до десятых) Прямоугольный треугольник: Дан прямоугольный треугольник с острым углом626262
градусов и смежной стороной454545
футов, найти противоположную сторону длина.
Сначала определите, какую тригонометрическую функцию использовать, если дана смежная сторона, и вам нужно решить для противоположной стороны. Всегда определяйте, какая сторона дана, а какая неизвестна по острому углу ( 9\circ32∘
, гипотенуза равна 30 футам, а недостающая длина стороны равна противоположному катету,xxx
футов.Определите, какую тригонометрическую функцию использовать, если задана гипотенуза, и вам нужно решить для противоположной стороны. Вспоминая мнемонику « S ohCahToa», указанные стороны представляют собой гипотенузу и противолежащие стороны, или «h» и «o», которые использовали бы «S» или синусоидальную тригонометрическую функцию.
sint=противоположная гипотенуза in(32∘)=x3030⋅sin(32∘)=xx=30⋅sin(32∘)x=30⋅(0,529{\ круг} \ справа)} \\ x &= 30\cdot\left( 0.5299\dots\right) \\ х &= 15,9 ~\mathrm{футов} \end{выравнивание} }sintsin(32∘)30⋅sin(32∘)xxx=hypotenuseopposite=30x=x=30⋅sin(32∘)=30⋅(0,5299…)=15,9 футов
Нахождение углов из отношений : Обратные тригонометрические функции
Обратные тригонометрические функции можно использовать для нахождения измерения острого угла прямоугольного треугольника.
Цели обучения
Использование обратных тригонометрических функций при решении задач на прямоугольные треугольники 9{-1}tan−1 . Использование тригонометрических функций для определения отсутствующей стороны при заданном остром угле так же просто, как определение сторон относительно острого угла, выбор правильной функции, составление уравнения и решение. Найти недостающий острый угол по двум сторонам прямоугольного треугольника так же просто.Обратные тригонометрические функции
Чтобы найти недостающий острый угол, используйте те же три тригонометрические функции, но используйте обратный ключ ( 9\circA∘ с противоположной стороной12 футов12~\mathrm{feet}12 футов
, найдите острый угол с точностью до ближайшего градуса: Прямоугольный треугольник: Найдите величину угла 9000 4 ААА , если даны противолежащий катет и гипотенуза.Из угла
AAA
даны стороны напротив и гипотенуза .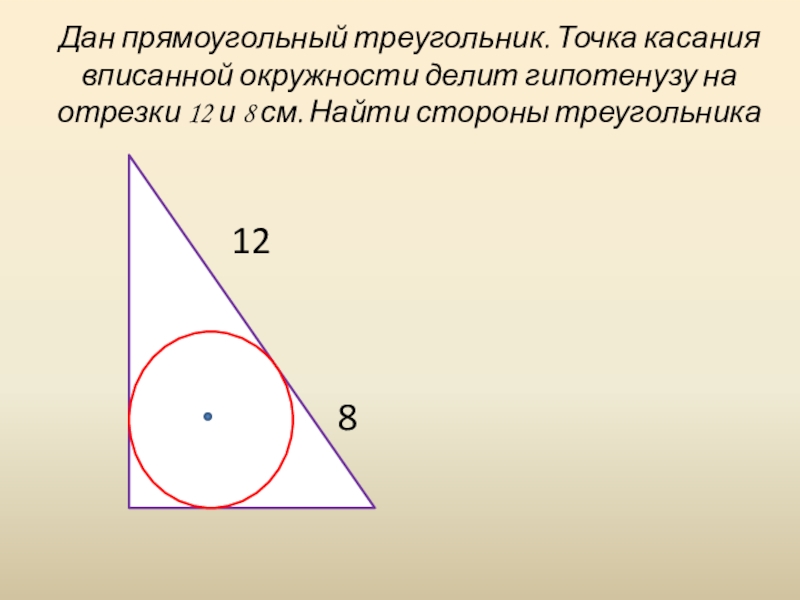 Поэтому используйте тригонометрическую функцию синуса. ( Soh от SohCahToa) Напишите уравнение и решите его, используя обратный ключ для синуса.
9{\ круг}
\end{выравнивание}
}sinA∘sinA∘A∘A∘A=hypotenuseopposite=2512=sin-1(2512)=sin-1(0.48)=29∘
Поэтому используйте тригонометрическую функцию синуса. ( Soh от SohCahToa) Напишите уравнение и решите его, используя обратный ключ для синуса.
9{\ круг}
\end{выравнивание}
}sinA∘sinA∘A∘A∘A=hypotenuseopposite=2512=sin-1(2512)=sin-1(0.48)=29∘Лицензии и атрибуты
Лицензионный контент CC, опубликованный ранее
- Курирование и доработка. Автор : Boundless.com. Лицензия : Общественное достояние: Неизвестно Авторские права
Лицензионный контент CC, конкретное указание авторства
- Прямоугольный треугольник. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Теорема Пифагора. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- 346px-Rtriangle.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- 265px-Pythagorean.
 svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike - Тригонометрия прямоугольного треугольника. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike
- Тригонометрические функции. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- 346px-Rtriangle.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- 265px-Pythagorean.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигура Джанет Хеймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах.
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - Оригинальная фигура Джанет Хеймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
- CNX_Precalc_Figure_05_04_002.jpg. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike
- Тригонометрические функции. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Trigonometric_functions. Лицензия : CC BY-SA: Attribution-ShareAlike
- Тригонометрия прямоугольного треугольника. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry.
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - 346px-Rtriangle.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- 265px-Pythagorean.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигура Джанет Хаймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигура Джанет Хеймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
- CNX_Precalc_Figure_05_04_002.jpg. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигура Джанет Хеймбах.
 Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike - CNX_Precalc_Figure_05_04_002.jpg. Предоставлено : OpenStax. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигурка Джанет Хаймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
- Тригонометрия прямоугольного треугольника. Предоставлено : openstax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike
- Тригонометрические функции. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- 346px-Rtriangle.svg.jpg.
 Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike - 265px-Pythagorean.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигура Джанет Хеймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигура Джанет Хаймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
- CNX_Precalc_Figure_05_04_002.jpg. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигурка Джанет Хаймбах.


 01.15
01.15 x+1 y(0)=2; y'(0)=1.
x+1 y(0)=2; y'(0)=1. Решение квадратных неравенств
Решение квадратных неравенств Кто упадёт первым?
Кто упадёт первым?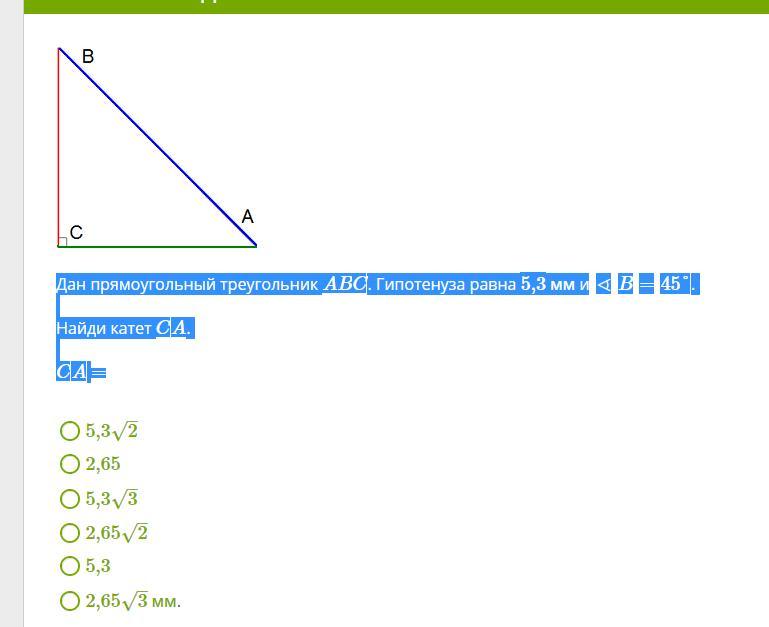 Оказалось, что до скейт‑парка они добрались одновременно. Сколько метров проехал на скейте Саша, если расстояние от дома до скейт‑парка составляет 3600
Оказалось, что до скейт‑парка они добрались одновременно. Сколько метров проехал на скейте Саша, если расстояние от дома до скейт‑парка составляет 3600
 svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike  Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike  Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike  Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike  Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike 
Leave A Comment