ГДЗ по геометрии 8 класс Атанасян. Гл.IX №759. Докажите, что… – Рамблер/класс

ГДЗ по геометрии 8 класс Атанасян. Гл.IX №759. Докажите, что… – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Что делать, как решить задание Гл. IX №759.
Дан произвольный четырёхугольник MNPQ. Докажите, что:

 

ответы

Привет, я решил задачу Гл.IX №759, помогаю:

а)

(по правилу треугольника). Следовательно:

б) Аналогично: 

Следовательно:

 

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Психология

Химия

похожие вопросы 5

ГДЗ по геометрии 8 класс Атанасян. Гл.VIII №704. Докажите, что точка О — середина гипотенузы…

 Не могу додуматься, как решить задачу Гл.VIII №704, необходима помощь.
Окружность с центром О описана около прямоугольного (Подробнее…)

ГДЗАтанасян Л.С.Геометрия

ГДЗ по геометрии 8 класс Атанасян.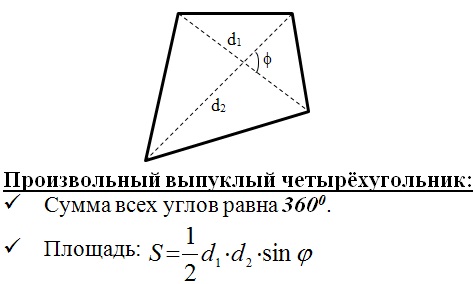 Гл.VIII №727. Докажите, что точки О1 и O2 лежат на серединном перпендикуляре..

Не могу решить задачу Гл.VIII №727.
В равнобедренный треугольник вписана окружность с центром O1 и около него описана окружность с (Подробнее…)

ГДЗ8 классГеометрияАтанасян Л.С.

влияет ли спинер на мозг?

влияет ли спинер на человеческий мозг ?

9 классГДЗВыпускнойАнглийский языкЭкзаменыЕГЭШкола11 классГИАДосуг

Стороны параллелограмма

Стороны параллелограмма находятся в отношении 4:5. Найти стороны параллелограмма если периметр равен 10.8 см   (Подробнее…)

ГДЗ

ГДЗ по геометрии Атанасян 8 класс. Гл.VIII №732. Докажите, что углы МНС и МВС равны.

Не понимаю, как решить задачу Гл.VIII №732.
 В прямоугольном треугольнике АВС из точки М стороны АС проведён перпендикуляр МН к (Подробнее…)

ГДЗ8 классГеометрияАтанасян Л.С.

Вписанная и описанная окружности — видеоурок по геометрии за 8 класс

Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.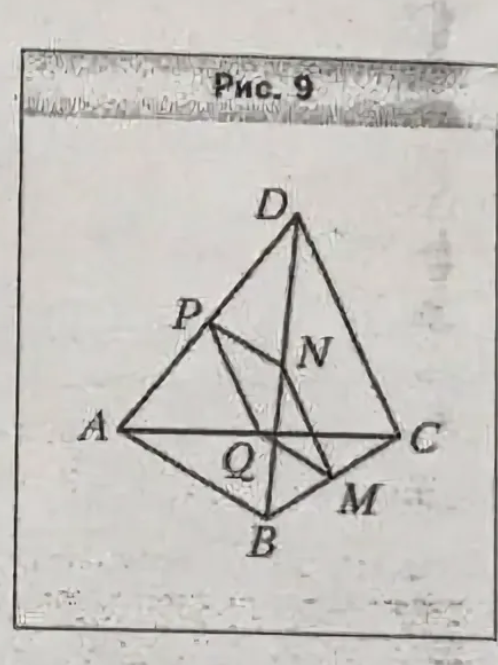

Окружность называется вписанной в угол, если она лежит внутри угла и касается его сторон.

Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.

Окружность называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника и касается всех прямых, проходящих через его стороны.

Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех углов данного многоугольника пересекаются в одной точке, которая является центром вписанной окружности. Сам многоугольник в таком случае называется описанным около данной окружности. Таким образом, в выпуклый многоугольник можно вписать не более одной окружности.

Для произвольного многоугольника невозможно вписать в него и описать около него окружность. Для треугольника это всегда возможно.

Окружность называется вписанной в треугольник, если она касается всех трех его сторон, а ее центр находится внутри окружности.

СУЩЕСТВУЮТ СПЕЦИАЛЬНЫЕ ФОРМУЛЫ, БЛАГОДАРЯ КОТОРЫМ И МОЖНО ПРОИЗВЕСТИ РАЗЛИЧНЫЕ РАСЧЕТЫ.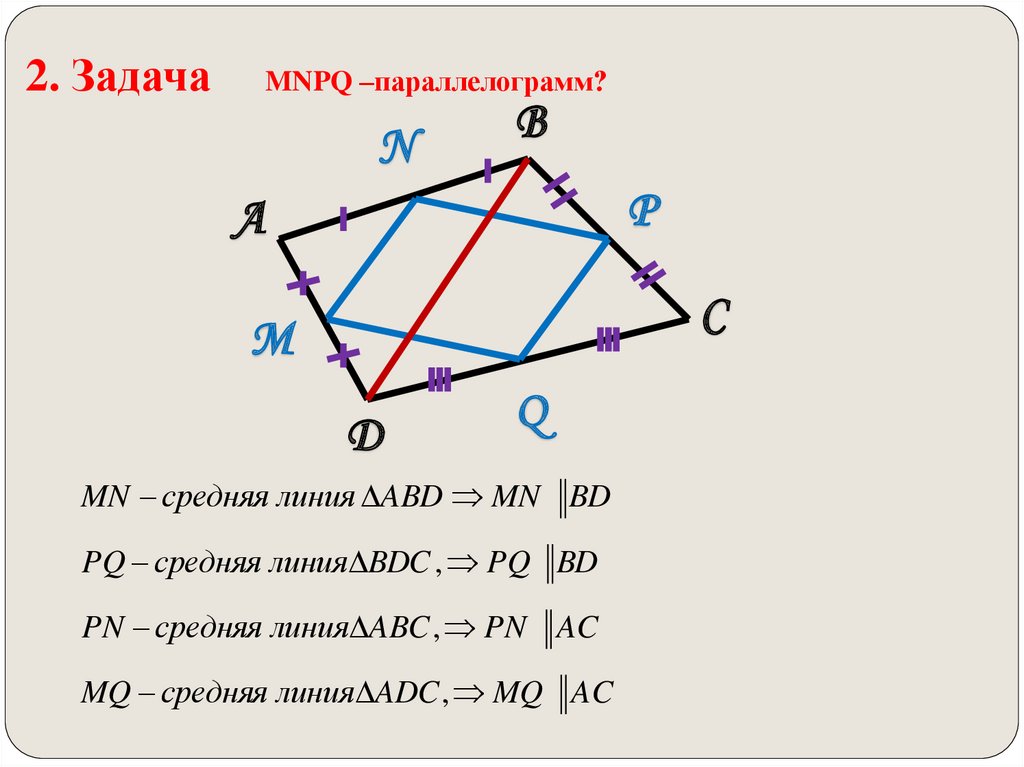

РАССМОТРИМ ИХ.

  • Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
  • В любой треугольник можно вписать окружность, и только одну.
  • Радиус вписанной в треугольник окружности равен отношению площади треугольника и его полупериметра: r=S/p, где S — площадь треугольника, а p=(a+b+c)/2 — полупериметр треугольника.

Серединным перпендикуляром называют прямую перпендикулярную отрезку и проходящую через его середину.

Окружность называется описанной около треугольника, если она проходит через три его вершины.

  • Вокруг любого треугольника можно описать окружность, и только одну.
  • В любом треугольнике сторона равна произведению диаметра описанной окружности и синуса противолежащего угла.
  • Площадь треугольника равна отношению произведения длин всех его сторон к учетверенному радиусу окружности, описанной около этого треугольника: R=(a⋅b⋅c)/4S, где S — площадь треугольника.

Окружность, касающаяся одной стороны треугольника и продолжений двух других его сторон, называется вневписанной.

  • Центр вневписанной окружности лежит на пересечении биссектрис внешних углов, при вершинах касаемой стороны, и биссектрисы угла при третей вершине.

Окружность, вписанная в прямоугольный треугольник

  • Радиус вписанной окружности находят по формулам: r=(a⋅b)/(a+b+c), и r=(a+b−c)/2, где a и b катеты прямоугольного треугольника, а c гипотенуза прямоугольного треугольника.

Окружность, описанная около прямоугольного треугольника
  • Центр описанной окружности совпадает с серединой гипотенузы.
  • Радиус равен половине гипотенузы: R=c/2.
  • Радиус равен медиане, проведенной к гипотенузе: R=mс.

Четырехугольник, описанный около окружности
  • Четырехугольник ABCD можно описать около окружности, если суммы противолежащих сторон равны AB + CD = BC + AD. Если четырехугольник описан около окружности, то суммы противолежащих сторон равны. Площадь: S=p⋅r, где
    r     — радиус вписанной окружности, а p=(a+b+c+d)/2 — полупериметр.

Перед собой вы видите четырехугольник ABCD, треугольник STF и четырехугольник MNPQ. Заметим, что четырехугольник ABCD и треугольник STF описаны около окружности с центрами в точке О. Что нельзя сказать о четырехугольнике MNPQ. Он не является описанным около окружности с центром О, так как его сторона NP не касается окружности.

Теорема об окружности, вписанной в треугольник

Для начала рассмотрим свойства вписанной окружности.

  1. Окружность можно списать в любой треугольник.
  2. Окружность можно вписать в четырехугольник, если суммы длин его противоположных сторон равны.

Так, окружность можно вписать в ромб или квадрат, но нельзя вписать в прямоугольник или параллелограмм.

Сформулируем и докажем теорему об окружности, вписанной в треугольник.

В любой треугольник можно вписать окружность.

Доказательство. Пусть дан произвольный треугольник ABC. Проведем биссектрисы его углов. Напомним, что все биссектрисы треугольника пересекаются в одной точке. Обозначим эту точку буквой О.

Обратите внимание, точка О равноудалена от сторон угла A, так как принадлежит биссектрисе этого угла. Аналогично она равноудалена и от сторон углов B и C. Т.е. точка О равноудалена от трех сторон треугольника ABC. Проведем из точки О перпендикуляры OK к AB, OL к BC, OM  к AC.

Так как точка О равноудалена от сторон этого треугольника, то перпендикуляры OK=OL=OM. Значит, окружность с центром в точке О и радиусом равным OK, проходит через точки K, L и M. Таким образом, окружность касается всех трех сторон треугольника ABC. Следовательно, она вписана в треугольник.

Теорема доказана.

Из данной теоремы вытекают следствия.

В треугольник можно вписать только одну окружность.

В отличие от треугольника не во всякий четырехугольник можно вписать окружность.

Если же в четырехугольник можно вписать окружность, то его стороны обладают следующим замечательным свойством:

В любом описанном четырехугольнике суммы противоположных сторон равны.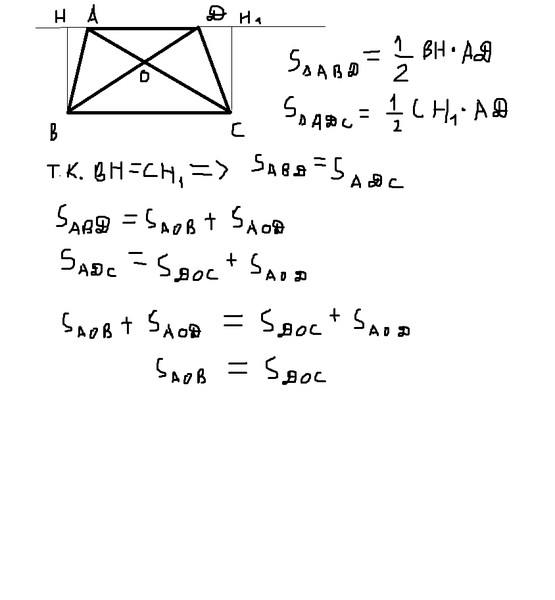

Докажем это утверждение. Рассмотрим четырехугольник ABCD, описанный около окружности с центром О. Напомним, что отрезки касательных к окружности, проведенные из одной точки, равны. Тогда касательные к окружности, выходящие из точки А равны. Аналогично, равны и касательные, выходящие из точек В, С и D.

Обозначим равные отрезки касательных маленькими буквами а, b, c и d соответственно. Тогда, смотрите, сумма противоположных сторон четырехугольника АВ+CD=a+b+c+d.

Аналогично, и сумма сторон BC+AD=a+b+c+d. Раз равны правые части равенств, то можем приравнять их левые части. Тогда видим, что AB+CD=BC+AD. Следовательно, суммы противоположных сторон в описанном четырехугольнике равны.

Что и требовалось доказать.

Верно и обратное утверждение: если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.

Теорема об окружности, описанной около треугольника

Для начала рассмотрим свойства описанной окружности.

  1. Окружность можно описать около любого треугольника.
  2. Окружность можно описать вокруг любого четырехугольника, если суммы его противолежащих углов равны.

Таким образом, окружность можно описать около квадрата или прямоугольника, но нельзя описать около ромба или параллелограмма.

Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.

Окружность называется описанной около треугольника, если она проходит через все его вершины.

На рисунке изображена окружность с радиусом R и центром описанная около треугольника АВС.

Так как ОА = ОВ = ОС = R, то центр описанной окружности равноудален от вершин треугольника.

Вместо слов «окружность, описанная около треугольника АВС», также говорят «окружность, описанная вокруг треугольника АВС», или «описанная окружность треугольника АВС».

Теорема (об окружности, описанной около треугольника).

Около любого треугольника можно описать окружность, причем только одну, ее центр находится в точке пересечения серединных перпендикуляров к сторонам треугольника.

Рассмотрим произвольный треугольник АВС (на рисунке выше). Пусть О — точка пересечения серединных перпендикуляров к его сторонам. Проведем отрезки ОА, ОВ и ОС. По свойству серединного перпендикуляра ОА = ОС, ОС = ОВ. Так как точка О равноудалена от всех вершин треугольника АВС, то окружность с центром в точке О и радиусом ОА проходит через все вершины треугольника АВС, т. е. является его описанной окружностью. Единственность описанной окружности докажите самостоятельно.

Замечание. Так как все три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке, то для нахождения центра описанной окружности достаточно построить точку пересечения любых двух из них.

Итог

Итак, на этом уроке мы доказали, что в любой треугольник можно вписать окружность, и центр этой окружности совпадает с точкой пересечения биссектрис треугольника.

Мы также доказали, что около любого треугольника можно описать окружность, и ее центр совпадет с точкой пересечения серединных перпендикуляров.

Кроме того, мы увидели, что в некоторые четырехугольники можно вписать окружность, и для этого нужно, чтобы суммы противоположных сторон четырехугольника были равны.

Мы также показали, что около некоторых четырехугольников можно описать окружность, и необходимым и достаточным условием для этого является равенство суммы противоположных углов.

геометрия — Равносторонние треугольники на сторонах параллелограмма

$\begingroup$

На сторонах параллелограмма $ABCD$ постройте одинаково ориентированные равносторонние треугольники $ABC_1, BCA_1, CDD_1$ и $DAB_1$. Пусть $N,P,Q$ и $M$ — центры треугольников соответственно. Докажите, что четырехугольник $MNPQ$ является параллелограммом.

Я думаю, что это действительно интересная задача. Я нашел это в блоке 9 геометрических преобразований 0010 в моем учебнике.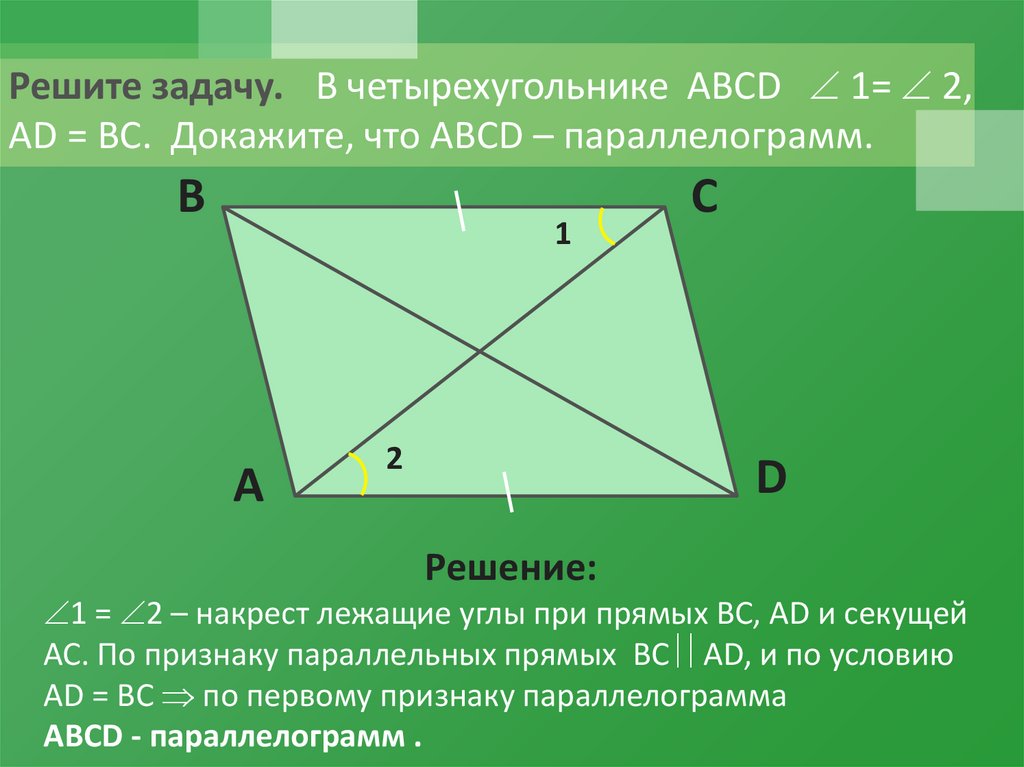 Данный совет состоит в том, чтобы использовать (центральную) симметрию с центром в пересечении диагоналей данного параллелограмма ($ABCD$). Хотя я не уверен, что вижу это. Любая помощь будет оценена по достоинству. Заранее спасибо!

  • геометрия
  • евклидова геометрия
  • преобразование
  • симметрия

$\endgroup$

8

$\begingroup$ 9\circ$ вращение точки $X$ вокруг центра параллелограмма $ABCD$.

Показать, что

  • $R(A) = C, R(B) = D. $
  • $R(C_1) = D_1, R(A_1) = B_1$. -> Обратите внимание, что это не так симметрично, как остальные, из-за именования в вопросе. Если бы мы использовали циклическую запись типа $ABC_1, CDA_1$, то мы бы имели $R(C_1) = A_1$. На самом деле $R(ABC_1) = R(CDA_1)$.
  • $R(N) = Q, R(P) = M$.
  • $NQ, PM$ делят друг друга пополам вокруг центра,
  • Эти точки образуют параллелограмм.

$\endgroup$

11

$\begingroup$

На приведенном выше рисунке мы можем использовать три пары конгруэнтных треугольников, чтобы доказать вывод.

1. Для $\triangle MDQ$ $ и $$\triangle PBN$,

$\alpha=\alpha’$, MD=BP,NB=DQ, $\triangle MDQ$ $\equiv$ $\triangle PBN$ (SAS), $\to$ MQ=NP (1)

2.Для $\треугольника MAN$ и $\треугольника PCQ$,

$\beta=\beta’$,MA=PC,AN=QC,$\triangle MAN$ $\equiv$ $\triangle PCQ$ (SAS), $\to$ MN=PQ (2)

3 .Для $\треугольника MNP$ и $\треугольника MPQ$ бб MP=MP ,MQ=NP и MN=PQ из (1)(2), $\треугольник MNP$$\equiv$ $\triangle MPQ$ (SSS) $\to$

$\angle NMP=\angle QMP$, NP//MQ, при NP=MQ из (1), MNPQ — параллелограмм.

$\endgroup$

$\begingroup$

Еще одно «другое» доказательство. Следующее изображение…

вводит немного другие обозначения, чтобы упростить бухгалтерский учет (и набор текста). Здесь $O$ — пересечение диагоналей в заданном параллелограмме $ABCD$, равносторонний треугольник, построенный на $AB$, имеет третью вершину $X_{AB}$ и центр $O_{AB}$, и аналогичные обозначения применяются к остальные.

Из сравнения (записанного как равенство) $\Delta DAO_{DA}=\Delta BCO_{BC}$ из равнобедренных треугольников (случай ASA по основаниям $AD=BC$) получаем $AO_{DA}=CO_{BC}$. Вместе с $OA=OC$ получаем $$ \тег{$*$} \Дельта OAO_{DA}=\Дельта OCO_{BC}\ , $$ так как углы между парами соответствующих сторон также совпадают. Тогда из $(*)$ следует

  • $\widehat{ AOO_{DA}}=\widehat{ COO_{BC}}$, и из колинеарности $A,O,C$ получаем коллинеарность $O_{DA},O,O_{ БК}$,
  • $OO_{DA}=OO_{BC}$.

Аналогичные свойства можно экстраполировать «от фиолетовых фигур к коричневым фигурам» на рисунке.

Таким образом, $O$ является средней точкой обоих сегментов. $O_{DA}O_{BC}$ и $O_{AB}O_{CD}$, следовательно, четырехугольник $\color{blue}{O_{AB}O_{BC}O_{CD}O_{DA}}$ — параллелограмм.

(Чтобы получить $O_{AB}O_{DA}=O_{BC}O_{CD}$, сравните два треугольника с этими сегментами в качестве соответствующих сторон и с общей вершиной в $O$.)

$\square$

Примечание. Вышеизложенное представляет собой длинную историю доказательства с использованием отражения относительно. центр $O$ кольца $ABCD$. Это отражение меняет местами противоположные стороны параллелограмма, а значит, и противоположные построенные равносторонние треугольники, а значит, и их центры, и мы приземляемся сразу же в показанном выше свойстве для $\color{blue}{O_{AB}O_{BC}O_{CD}O_{DA}}$, что завершает доказательство.

$\endgroup$

$\begingroup$ 9{i\frac\pi3})$$

Тогда несложно проверить

$$Y-X=Z-W,\>\>\>\>\>Z-Y = W-X$$ ​​

Таким образом, $XYZW$ параллелограмм.

$\endgroup$

Параллелограммы — четырехугольник | Wyzant Спросите эксперта

Геометрия Четырехсторонние параллелограммы

Габриэль Л.

спросил 05.09.15

1- Дан параллелограмм MNPQ такой, что MN = 2a-3b и NO = 20-3b. Найдите значение a и все возможные значения b , которые делают MNPQ ромбом.

 

2- Дан четырехугольник ABCd такой, что ∠A и ∠B дополнительные и ∠A = ∠C. Докажите, что ABCD — параллелограмм.

 

3- Докажите, что каждый ромб является параллелограммом.

Подписаться І 2

Подробнее

Отчет

1 ответ эксперта

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Майкл Дж. ответил 0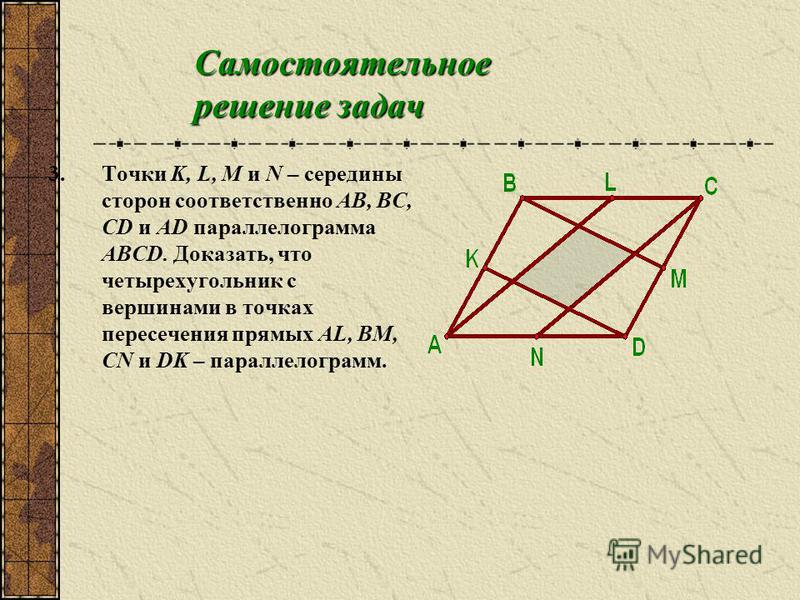5. 09.15

Репетитор

5 (5)

Эффективный репетитор STEM средней школы и лидер CUNY по математике

См. таких репетиторов

Смотрите таких репетиторов

Примечание: я думаю, вы имели в виду NP вместо NO. Ваш палец, должно быть, нажал не на ту клавишу.

1)

Ромб будет иметь 4 последовательных сторона:

мн, NP, PQ и MQ

AROMBUS имеет 4 равных санда. Таким образом, мы устанавливаем данные стороны равными друг другу.

 

2a — 3b = 20 — 3b

 

Поскольку -3b находится в обеих частях уравнения, b может принимать бесконечное число значений, пока b является постоянным. Остается только приравнять 2а и 20.

2a = 20

a = 10

2)

Стороны четырехсторонних

∠A и ∠B примыкают друг к другу.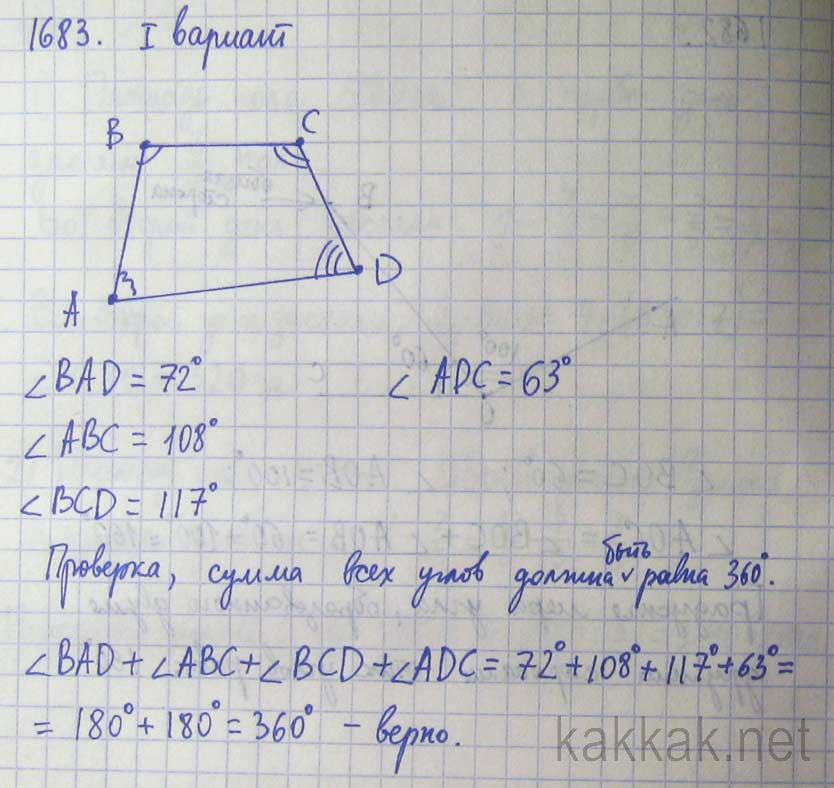 ∠C и ∠D также смежны друг с другом. ∠A и ∠C противоположны друг другу. Эти углы всегда равны по размеру.

 

Вы можете нарисовать это, чтобы лучше видеть.

 

Параллелограммы – это четырехсторонние замкнутые фигуры, имеющие две пары равных параллельных сторон, две пары равных и противоположных углов и две пары дополнительных углов. Если ∠A — угол меньше 90 градусов, а ∠B — угол больше 90 градусов, эти два угла вместе должны образовывать прямую линию. Эти углы дополняют друг друга.

 

 

3)

 

Параллелограмм – это четырехсторонняя фигура с 2 парами параллельных сторон, 2 парами сторон одинаковой длины и 2 парами противоположных и равных углов. Под это описание подходит ромб.

0 9 0 004 3 0 9 0004 3

Голосовать за 0 Понизить

Подробнее

Отчет

Все еще ищете помощь? Получите правильный ответ, быстро.