Дан параллелограмм abcd на продолжении диагонали ac
Вопрос по геометрии:
Дан параллелограмм ABCD На продолжении диагонали AC за вершины A и C отмечены точки M и N соответственно так, что AM = CN. Докажите, что MBND — параллелограмм. СРОЧНО
Ответы и объяснения 1
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат – это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи – смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Ответы на вопрос
1. расположение в одной плоскости т.е-m-n, 2 см между m и n
2. расположение в одной плоскости m-т.е-n, 4 см между n и m
3. т.е расположена на расстоянии от 0 до 1 от плоскости расположения прямых, приизменении расстояния от0 до 1 – растояние между прямыми будет меняться от 4 до √8
или другое решение
x – основание, тогда боковые стороны – (x+9)
- 5 – 9 классы
- Геометрия
- 5 баллов
Дан параллелограмм ABCD. На продолжении диагонали АС за вершины А и С отмечены точки М и N соответственно так, что АМ = CN.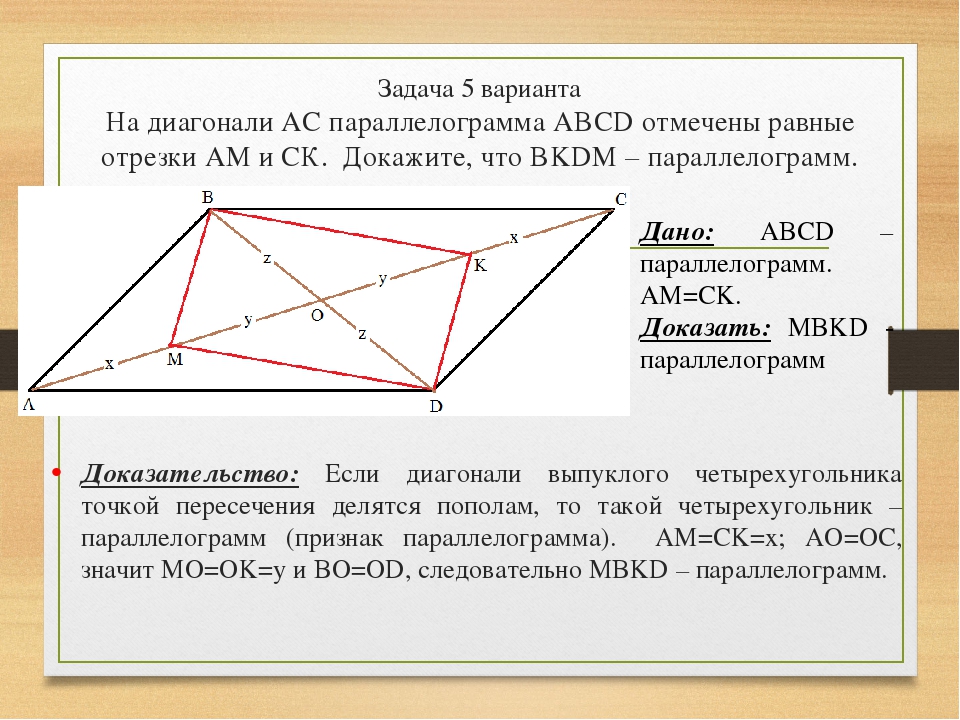 Докажите, что MBND – параллелограмм.
Докажите, что MBND – параллелограмм.
- Попроси больше объяснений
- Следить
- Отметить нарушение
Селенада 11.10.2012
Ответ
Проверено экспертом
Диагональ ВD исходного параллелограмма АВСD осталась прежней
Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то такой четырехугольник – параллелограмм.
“>
1. Дано: четырёхугольник ABCD, ABCD, Доказать: четырёхугольник ABCD- параллелограмм. На продолжении диагонали АС за вершины А и С отмечены точки А1и С1 соответственно так, что АА1СС1. Докажите, что <ВA1D.
Чтобы посмотреть этот PDF файл с форматированием и разметкой, скачайте его и откройте на своем компьютере.
Вариант1.
1.
Дано:
четырёхугольник
ABCD
,
AB
=
CD
,
ABD
=
BDC
.
Доказать:
четырёхугольник
ABCD
—
параллелограмм.
2. Дан параллелограмм
ABCD
. На продолжении диагонали АС за вершины А и
С отмечены точки А
1
и С
1
соответственно так, что АА
1
=СС
1
. Докажите, что
A
1
D
=
BC
1
D
.
3. В прямоугольнике
MPKH
O
—
точка пересечения диагоналей,
PA
и
HB
—
пе
р-
пендикуляры, проведённые из вершин Р и Н к прямой МК. Известно, что
МА=ОВ. Найдите
РОМ.
Вариант2.
1.
Дано:
четырёхугольник
ABCD
,
B
С=А
D
,
B
СА=CAD
.
Доказать:
четырёхугольник
ABCD
—
параллелограмм.
2. В четырёхугольнике
ABCD
AB
||
CD
,
BC
||
AD
,
AC
=20 см,
BD
=10
c
м, АВ=13
c
м.
Диагонали четырёхугольника пересекаются в точке О. Найдите периметр тр
е-
угольника
COD
.
3. Внутри треугольника АВС отмечена точка М, а на сторонах
АВ и АС
—
точка К и
Н соответственно так, что отрезки АМ и КН имеют общую середину, а
Вариант 3
1.
Дано
: четырёхугольник
ABCD
,
AD
=
BC
,
A
=70
0
,
B
=110
0
.
Доказать
: четырёхугольник
ABCD
—
парал
лелограмм.
2. В выпуклом четырёхугольнике
ABCD
AB
=
CD
,
B
=70
0
,
BCA
=60
0
,
ACD
=50
0
.
Докажите, что ВС=
AD
.
3. В треугольнике АВС, B
=90
0
,
AB
=
BC
. На сторонах АВ и ВС взяты точки М и Р, а
на стороне АС
—
точки К и Н так, что четырёхугольник МРНК является квадр
том, МР=6см.
 Найдите АС.
Найдите АС.Вариант 4
1.
Дано
: четырёхугольник
ABCD
,
AD
=
BC
, 0
, 0
.
Доказать
: четырёхугольник
ABCD
—
параллелограмм.
2. В параллелограмме
ABCD
с острым углом А диагонали пересекаются в точке
О. На отрезках АО и ОС взяты точки Р и К
соответственно, ОР=О
D
, ОК=ОВ. Д
о-
кажите, что четырёхугольник
PBKD
является прямоугольником.
3. В прямоугольной трапеции диагональ перпендикулярна к боковой стороне,
0
. Во сколько раз большее основание больше меньшего
основания?
Вариант 5
1.
Дано
: четырёхугольник
ABCD
,
AD
=
BC
, 0
, 0
.
Доказать
: четырёхугольник
ABCD
—
параллелограмм.
2. В прямоугольной трапеции острый угол равен 60
0
Большая боковая сторона
и большее основание равны по 20 см. Найдите меньшее основание.
Найдите меньшее основание.
3. В четырёхугольнике
MPKH
диагонали пересекаются в точке О, OMH
OHM
,
РН=МК, РК=МН. Найдите угол МНК.
Вариант6.
1.
Дано
: четырёхугольник
ABCD
,
AD
=
BC
, 0
, 0
.
Доказать
: четырёхугольник
ABCD
—
параллелограмм.
2. В ромбе
MP
КН с тупым углом К диа
гонали пересекаются в точке Е. Один из
углов треугольника РКЕ равен 20
0
. Найдите остальные углы этого треугольника
и угол РМН.
3. На основании АС равнобедренного треугольника АВС отмечена точка К, а на
сторонах АВ и ВС
—
точки М и Р соответственно, причём РК=МВ, 0
,
0
. Докажите, что
КМВ+
МВР=180
0
.
Вариант7.
1.
Дано
: четырёхугольник
ABCD
,
AD
=
BC
, 0
, 0
.
Доказать
: четырёхугольник
ABCD
—
параллелограмм.
2. В ромбе
ABCD
A
=31
0
. Диагонали пересекаются
в точке О. Найдите углы тр
е-
угольника ВОС.
3. В равнобедренной трапеции диагональ составляет с боковой стороной угол
в 120
0
. Боковая сторона равна меньшему основанию. Найдите углы трапеции.
Вариант8.
1.
Дано:
четырёхугольник
,
AD
=ВС, DBC
=
ADB
.
Доказать:
четырёхугольник
ABCD
—
параллелограмм.
2. В прямоугольной трапеции острый угол равен 45
0
. Меньшая боковая стор
о-
на и меньшее основание равны по 10 см. Найдите большее основание.
3. В прямоугольнике
ABCD
О
—
точка пересечения диагоналей, ВН и
D
Е
—
выс
оты
треугольников АВО и
COD
соответственно, 0
, АН=5см. Найдите ОЕ.
Вариант9.
1.
Дано
: четырёхугольник
ABCD
,
AD
=
BC
, 0
, 0
.
Доказать
: четырёхугольник
ABCD
—
параллелограмм.
2. В трапеции
ABCD
ВС
—
меньшее основание. На отрезке
AD
взята точка Е так,
что ВЕ||
CD
,
ABE
=70
0
, 0
. Найдите углы трапеции.
3. В ромбе
ABCD
О
—
точка пересечения диагоналей, ОМ, ОК, ОЕ
—
перпендик
у-
ляры, опущенные на стороны АВ,ВС,
CD
соответственно. Докажите, что ОМ=ОК,
найдите сумму углов МОВ и СОЕ.
Вар
иант10.
1.
Дано:
четырёхугольник
ABCD
,
CD
=АВ, ABD
=
BDC
.
Доказать:
четырёхугольник
ABCD
—
параллелограмм.
2. Из вершины В параллелограмма
ABCD
с острым углом А проведён перпе
н-
дикуляр ВК к прямой
AD
, ВК=
АВ. Найдите C
и D
.
3. В четырёхугольнике
ABCD
диагонали пересекаются в точке О, АО=
OD
,
ВО=ОС, BAC
=
DCA
. Найдите
Найдите
АВС.
Вариант11.
1.
Дано:
четырёхугольник
ABCD
,
AD
=ВС, CAD
.
Доказать:
четырёхугольник
ABCD
—
параллелограмм.
2.В прямоугольнике
ABCD
диагонали пересекаются в точке О. Е
—
середина ст
о-
роны АВ, 0
. Найдите угол ЕО
D
.
3. В четырёхугольнике
MPKH
PMK
=
HKM
,
PK
||МН. Через точку пересечения
диагоналей проведена прямая, пересекающая стороны РК и МН в точках А и В
соответственно. Докажите, что АР=НВ.
Вариант12.
1.
Дано:
чет
ырёхугольник
ABCD
,
AD
=ВС, DBC
=
ADB
.
Доказать:
четырёхугольник
ABCD
—
параллелограмм.
2. Дан параллелограмм
ABCD
с острым углом А. Из вершины В опущен пе
р-
пендикуляр ВК к прямой
AD
, АК=ВК. Найдите D
.
3.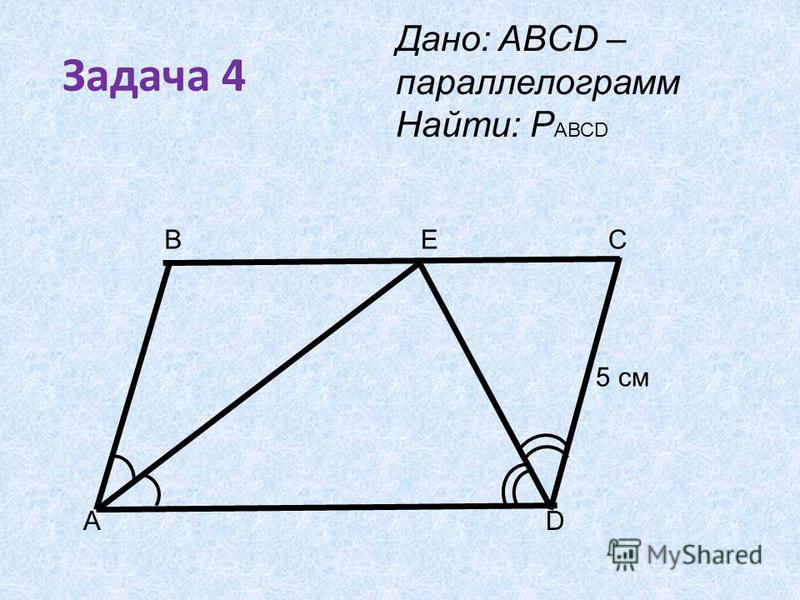 Дан равнобедренный треугольник АВС с основанием АС. На сторонах АВ, ВС,
Дан равнобедренный треугольник АВС с основанием АС. На сторонах АВ, ВС,
АС отмечены точки
D
, Е, Р соответственно так , что отрезки АЕ и
DP
имеют о
б-
щую середину. Докажите, что DEP
=
BCA
.
Параллелограмм. Решение задач
Урок
Учитель: Аскерова. Ф Н.
Предмет: математика (геометрия)
Класс: 8
Тема:Параллелограмм.Решение задач.
Методическая тема: Технология уровневой дифференциации на уроках математики.
Тип урока: урок применения знаний и умений.
Цели урока:
Образовательные:
Закрепить знания о свойствах и признаках параллелограмма в процессе решения задач;
Развивающие:
развивать логическое мышление, память, познавательный интерес; продолжать формирование математической речи; вырабатывать умение анализировать и сравнивать;
Воспитательные:
содействовать развитию у учащихся чувства ответственности за деятельность коллектива и в коллективе;
содействовать развитию коллективного общения учащихся;
содействовать развитию у учащихся интереса к математике.
Элементы урока и их содержание | Время (мин) | Деятельность | |
учителя | учащихся | ||
Организационный этап Постановка цели Сегодня на уроке мы закрепим знания о свойствах и признаках параллелограмма в процессе решения задач. Проверка домашнего задания Теоретический опрос: Дайте определение параллелограмма. Перечислите свойства параллелограмма. Перечислите признаки параллелограмма. IV. Решение задач 1)Решение задач разного уровня сложности (приложение 1) 2) Проверка заданий. 3)Устное решение задач по готовым чертежам (приложение 2) V.Закрепление. Самостоятельная работа (приложение 3): Сильные учащиеся работают самостоятельно (решают задачи II и III уровня). Слабоуспевающие учащиеся работают вместе с учителем. VI. Подведение итогов. Рефлексия. VII. Домашнее задание: №375, 380, 384 (устно) | 1 1 3 13 25 3 2 | Организационная Сообщает дату проведения урока, тему урока, цель урока. Проводит опрос учащихся 1)Следит за верностью решения у слабых учащихся, задавая им наводящие вопросы. 2) Проверяет решение задач II и III уровня сложности. Выставляет оценки за работу. 2)Следит за верностью рассуждений при решении устных задач. Следит за верностью решения у слабоуспевающих учащихся. Выставляет оценки за работу. Поясняет домашнее задание. | Сообщают об отсутствующих. Записывают в тетради. Учащиеся отвечают на вопросы. Учащихся работают на местах. Выполняют работу в тетрадях. Внимательно слушают, записывают в дневники. |
Приложение 1
I уровень
Точки E и K — середины сторон AB и CD параллелограмма ABCD. Докажите, что AECK – параллелограмм.
Докажите, что AECK – параллелограмм.
Диагонали четырёхугольника ABCD пересекаются в точке O, причём AC = 2 дм, AO = 10 см,
BD = 1,5 дм, BO = 7 см. Выясните, является ли ABCD – параллелограммом?
II уровень
В параллелограмме ABCD на сторонах AB и CD отмечены соответственно точки M и N так, что ﮮBMC = ﮮAND. Докажите, что AMCN – параллелограмм.
Точки A и B делят диагональ MK параллелограмма MNKP на три равные части. Является ли четырёхугольник ANBP параллелограммом? Ответ обоснуйте.
III уровень
В параллелограмме ABCD на сторонах AB и CD отмечены соответственно точки M и K так, что AM=CK, а на сторонах BC и AD – точки N и P так, что AP=CN. Докажите, что MNKP – параллелограмм.
Через точку пересечения диагоналей O параллелограмма ABCD проведена прямая MN, пересекающая стороны AD и BC в точках M и N соответственно. Является ли четырёхугольник MBND параллелограммом? Ответ обоснуйте.
Приложение 2
ABCD – параллелограмм.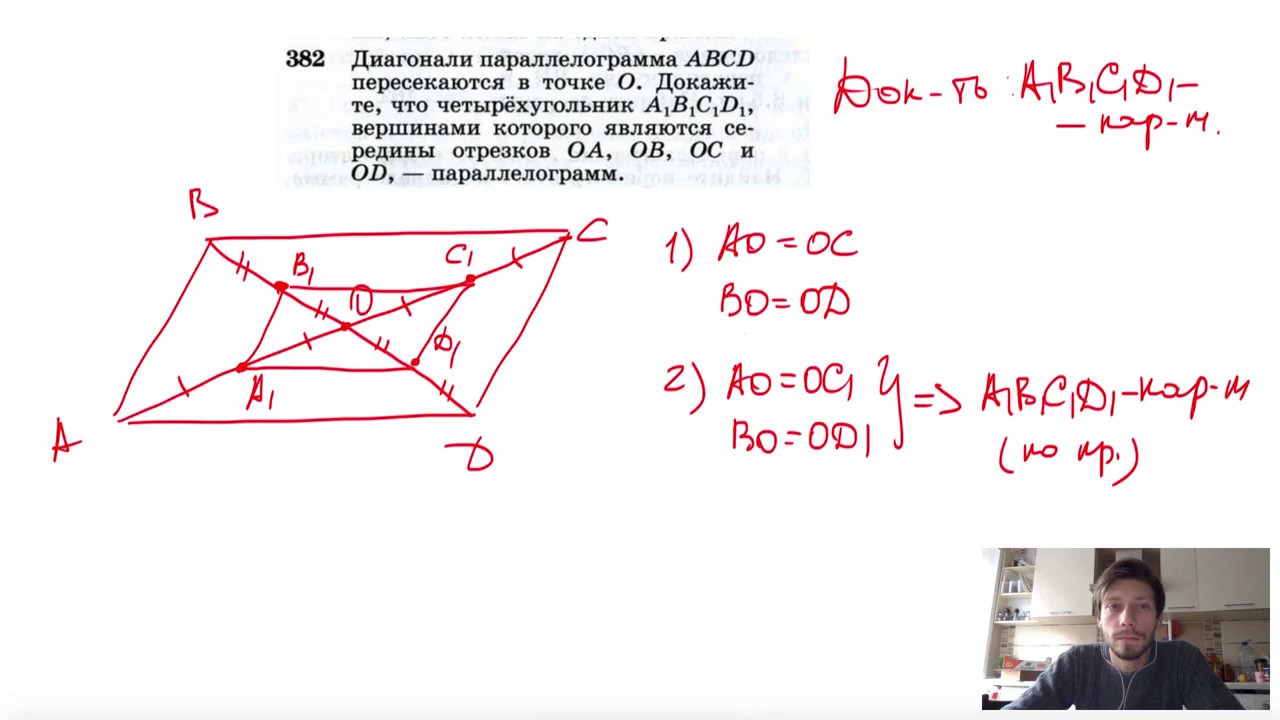 Найти: ﮮC,ﮮD.
Найти: ﮮC,ﮮD.
MNKP – параллелограмм. Найти: MP, PK.
ABCD – параллелограмм. Найти:ﮮA,ﮮB,ﮮC,ﮮD.
ABCD – параллелограмм. Найти:PABCD.
ABCD – параллелограмм. Найти:AD.
ABCD – параллелограмм. Найти: PABCD,ﮮAED.
NBFD – параллелограмм. Найти: BC, СD.
ABCD – параллелограмм, PMNKP,=20 см. Найти: MN, MP.
BNDM – параллелограмм, AB:BC=4:5, PABCD,=18 см. Найти: AD, DC.
Приложение 3
Самостоятельная работа
I уровень
I вариант
В четырехугольнике ABCD AB||CD, BC||AD, AC=20см, BD=10см, AB=13 см. Диагонали ABCD пересекаются в точке O. Найдите периметр ΔCOD.
Из вершины B параллелограмма ABCD с острым углом A проведён перпендикуляр BK к прямой AD, BK=AB:2. Найдите ﮮC,ﮮD.
Середина отрезка BD является центром окружности с диаметром AC, причём точки A, B, C, D не лежат на одной прямой. Докажите, что ABCD – параллелограмм.
II вариант
В четырехугольнике ABCD AB||CD, BC||AD, O – точка пересечения диагоналей.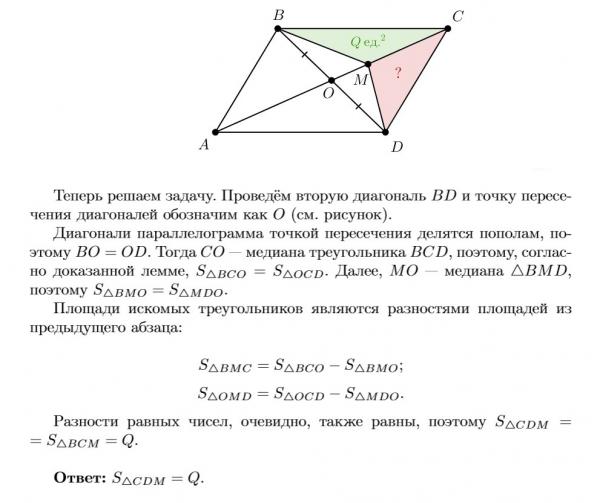 Периметр ΔAOD равен 25 см, AC=16см, BD=14см. Найдите BC.
Периметр ΔAOD равен 25 см, AC=16см, BD=14см. Найдите BC.
В параллелограмме ABCD с острым углом A из вершины B проведён перпендикуляр BK к прямой AD, AK=BK. Найдите ﮮC,ﮮD.
Дан параллелограмм ABCD. На продолжении диагонали AC за вершины A и C отмечены точки M и N соответственно так, что AM=CN. Докажите, что MBND – параллелограмм.
II уровень
I вариант
В четырехугольнике ABCD ﮮA+ﮮB=180°, AB|| CD. На сторонах BC и AD отмечены точки M и K соответственно так, что BM=KD. Докажите, что точки M и K находятся на одинаковых расстояниях от точки пересечения диагоналей четырёхугольника.
На сторонах PK и MH параллелограмма MPKH взяты точки A и B соответственно, MP=PB=AK; ﮮMPB=60°. Найдите углы параллелограмма и сравните отрезки BM и AH.
На основании AC равнобедренного треугольника ABC отмечена точка K, а на сторонах AB и BC – точки M и P соответственно, причём PK=MB, ﮮKPC=80°,ﮮC=50°. Докажите, что KMBP – параллелограмм.
II вариант
В четырехугольнике MPKH ﮮPMK=ﮮHKM, PK||MH. Через точку пересечения диагоналей проведена прямая, пересекающая стороны PK и MH в точках A и B соответственно. Докажите, что AP=HB.
Через точку пересечения диагоналей проведена прямая, пересекающая стороны PK и MH в точках A и B соответственно. Докажите, что AP=HB.
На сторонах BC и AD параллелограмма ABCD взяты точки M и K, AB=BM=KD; ﮮAMB=30°. Найдите углы параллелограмма и сравните отрезки AM и CK.
В ΔMPK ﮮM=65°. На сторонах MK, MP, PK отмечены точки A, B, C соответственно так, что середина стороны PK – точка C, AM=KC, BP=AC, ﮮBAM=50°. Докажите, что BPCA – параллелограмм.
III уровень
I вариант
В выпуклом четырехугольнике ABCDﮮA+ﮮB=ﮮB+ﮮC=180°. Через точку O пересечения диагоналей четырёхугольника проведена прямая, пересекающая стороны DC и AD в точках M и K соответственно; ﮮBOM=90°.
Докажите, что BK=BM.
На сторонах BC и CD параллелограмма ABCD отмечены точки M и H соответственно так, что отрезки BH и MD пересекаются в точке O; ﮮBHD=95°,ﮮDMC=90°,ﮮBOD=155°. Найдите отношение длин отрезков AB и MD и углы параллелограмма.
Точки M и K являются соответственно серединами сторон AB и BC треугольника ABC.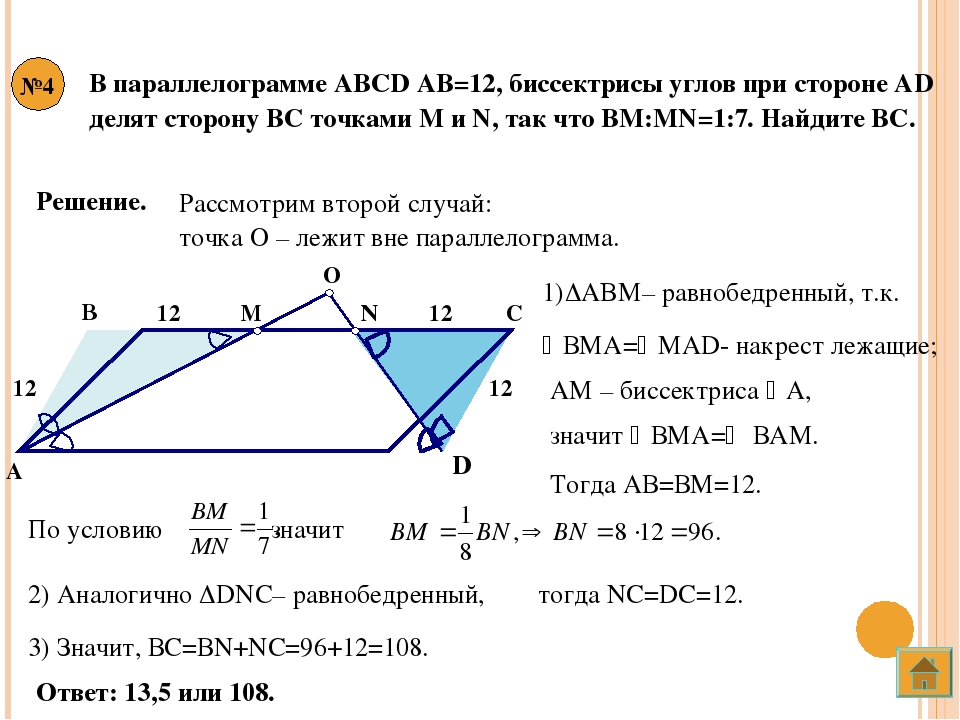 Через вершину C вне треугольника проведена прямая, параллельная AB и пересекающая луч MK в точке E. Докажите, что KE=AC:2.
Через вершину C вне треугольника проведена прямая, параллельная AB и пересекающая луч MK в точке E. Докажите, что KE=AC:2.
II вариант
В выпуклом четырехугольнике MPKH ﮮM+ﮮP=180°,ﮮMKH=ﮮKMP. На сторонах MH и PK отмечены точки A и B так, что PB=PA. Отрезок AB проходит через точку пересечения диагоналей четырёхугольника. Докажите, что HP перпендикулярен AB.
Докажите, что BK=BM.
На сторонах BC и CD параллелограмма ABCD взяты точки K и M соответственно. Отрезки BM и KD пересекаются в точке O; ﮮBOD=140°,ﮮDKB=110°,ﮮBMC=90°. Найдите отношение длин отрезков MC и AD и углы параллелограмма.
Точки A и B принадлежат соответственно сторонам PE и ET треугольника PET. Прямая, проходящая через вершину T вне треугольника, пересекает луч AB и точке K так, что AP=KT, AB=BK=PT:2. Докажите, что точка A является серединой отрезка PE.
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/90917-parallelogramm-reshenie-zadach
Параллелограмм. Текстовые задачи
Параллелограмм и его свойства
1.
1. В четырехугольнике ABCD АВ || CD, ВС || AD, АС =20 см, BD = 10 см, АВ = 13 см. Диагонали четырехугольника пересекаются в точке О. Найдите периметр треугольника COD.
2. Из вершины В параллелограмма АВCD с острым углом А проведен перпендикуляр ВК к прямой AD. ВК =12АВ. Найдите LC и LD.
2.
1. В четырехугольнике АВCD АВ || CD, ВС || AD, О — точка пересечения диагоналей. Периметр треугольника AOD равен 25 см, АС = 16 см, BD = 14 см. Найдите ВС.
2. Дан параллелограмм ABCD с острым углом А. Из вершины В опущен перпендикуляр ВК к прямой AD, АК = ВК. Найдите LC и LD.
3.
1. В четырехугольнике ABCD LA и LB = 180°, АВ || CD. На сторонах ВС и AD отмечены точки М и К соответственно так, что ВМ = KD. Докажите, что точки М и К находятся на одинаковом расстоянии от точки пересечения диагоналей четырехугольника.
2. На сторонах РК и МН параллелограмма МРКН взяты точки А и В соответственно, МР = РВ = АК, LMPB = 60°.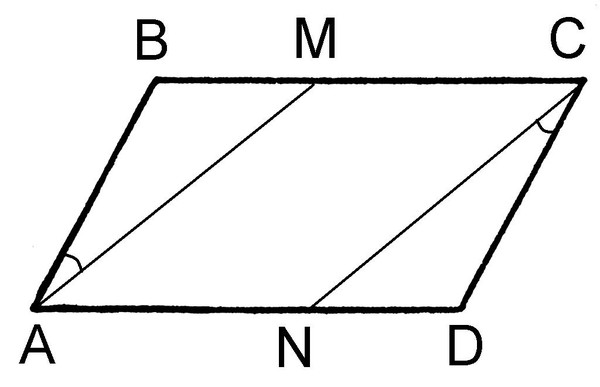 Найдите углы параллелограмма и сравните отрезки ВМ и АН.
Найдите углы параллелограмма и сравните отрезки ВМ и АН.
4.
1. В четырехугольнике МРКН LPMK = LНКМ, РК || МН. Через точку пересечения диагоналей проведена прямая, пересекающая стороны РК и МН в точках A и В соответственно. Докажите, что АР = НВ.
2. На сторонах ВС и AD параллелограмма ABCD взяты точки М и К, АВ = ВМ = KD, LAMB = 30°. Найдите углы параллелограмма и сравните отрезки AM и СК.
5.
1. В выпуклом четырехугольнике ABCD LA + LB = LB + LC = 180°. Через точку О пересечения диагоналей четырехугольника проведена прямая, пересекающая стороны ВС и AD в точках М и К соответственно; LВОМ = 90°. Докажите, что ВК = ВМ.
2. На сторонах ВС и CD параллелограмма ABCD отмечены точки М и Н соответственно так, что отрезки ВН и MD пересекаются в точке О; LBHD = 95°, LDMC = 90°, LBOD = 155°. Найдите отношение длин отрезков АВ и MD и углы параллелограмма.
6.
1. В выпуклом четырехугольнике МРКН LМ + LР= 180°, LМКН = LКМР. На сторонах МН и РК отмечены точки A и В так, что РВ = РА. Отрезок АВ проходит через точку пересечения диагоналей четырехугольника. Докажите, что HP перпендикуляр на АВ.
2. На сторонах ВС и CD параллелограмма ABCD взяты точки К и М соответственно. Отрезки ВМ и KD пересекаются в точке О, LBOD = 140°, LDKB = 110°, LBMC = 90°. Найдите отношение длин отрезков МС и AD и углы параллелограмма.
7.
1. В параллелограмме ABCD на сторонах AD и ВС взяты точки К и Е соответственно так, что LВЕ = 90° и отрезок ЕК проходит через точку О пересечения диагоналей. Докажите, что ВО = ОЕ.
2. На сторонах АС и ВС треугольника АВС отмечены точки D и Е соответственно, а внутри треугольника — точка М так, что четырехугольник DCEM является параллелограммом и DE || АВ. Прямая DM пересекает отрезок АВ в точке К, а прямая ЕМ — в точке Н. Докажите, что АК = НВ.
8.
1. В параллелограмме ABCD через точку О — пересечения диагоналей проведена прямая, пересекающая стороны ВС и AD в точках К и Е соответственно, ВО = ОЕ. Найдите угол КВЕ.
2. На сторонах АВ и AD параллелограмма ABCD взяты точки М и К соответственно, МК || BD. Прямая МК пересекает луч СВ в точке Е, а луч CD — в точке Р. Докажите, что ЕМ = КР.
Признаки параллелограмма
1.
1. В выпуклом четырехугольнике ABCD АВ = CD, LB = 70°, LBCA = 60°, LACD = 50°. Докажите, что ВС = AD.
2. Середина отрезка BD является центром окружности с диаметром АС, причем точки А, В, С, D не лежат на одной прямой. Докажите, что LABC = LADC.
2.
1. В выпуклом шестиугольнике ABCDEP все стороны равны, LA = LD. Докажите, что ВР || СЕ.
2. Дан параллелограмм ABCD. На продолжении диагонали AC за вершины А и С отмечены точки А1 и С1 соответственно так, что АА1 = СС1 . Докажите, что LBA1D = LBC1D.
Докажите, что LBA1D = LBC1D.
3.
1. На основании АС равнобедренного треугольника АВС отмечена точка К, а на сторонах АВ и ВС — точки М и Р соответственно, причем РК = MB, LKPC = 80°, LC = 50°. Докажите, что LKMB + + LMBP = 180°.
2. Внутри треугольника АВС отмечена точка М, а на сторонах АВ и АС — точки К и Н соответственно так, что отрезки AM и KН имеют общую середину, a LKMH = LC. Докажите, что треугольник АВС является равнобедренным.
4.
1. В треугольнике МРК LM = 65°. На сторонах МК, МР, РК отмечены точки А, В, С соответственно так, что середина стороны РК — точка С, AM = КС, BP =AC, LBAM = 50°. Докажите, что LCPB + LABP = 180°.
2. Дан равнобедренный треугольник АВС с основанием АС. На сторонах АВ, ВС, АС отмечены точки D, Е, Р соответственно так, что отрезки АЕ и DP имеют общую середину. Докажите, что LDEP = LBCA.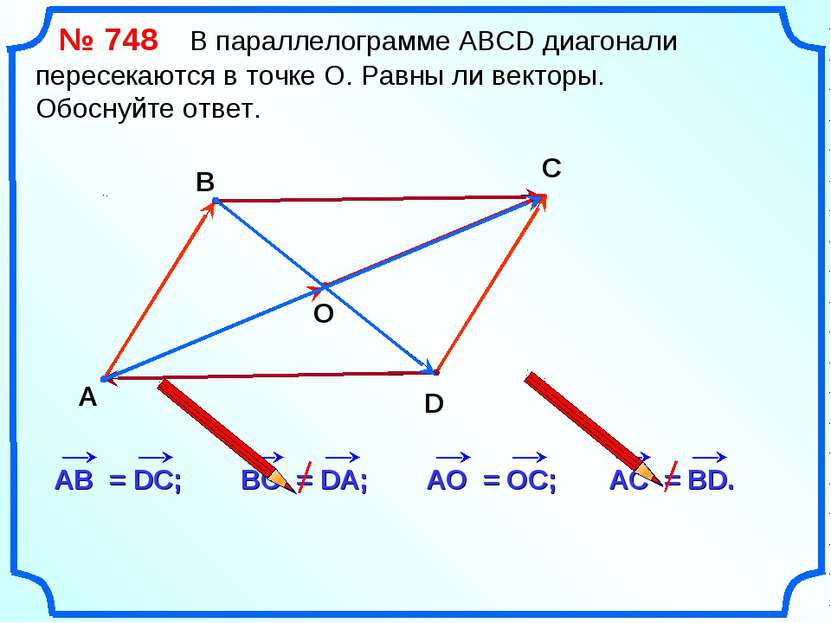
5.
1. Точки М и К являются соответственно серединами сторон АВ и ВС треугольника АВС. Через вершину С вне треугольника проведена прямая, параллельная АВ и пересекающая луч МК в точке Е. Докажите, что КЕ = 12АС.
2. На сторонах ВС и AD выпуклого четырехугольника ABCD соответственно взяты точки М и К так, что пары отрезков AM и ВК, КС и MD имеют общие середины. Докажите, что LBAD = LBCD.
6.
1. Точки А и В принадлежат соответственно сторонам РЕ и ЕТ треугольника РЕТ. Прямая, проходящая через вершину Т вне треугольника, пересекает луч АВ в точке К, АР = КТ, АВ = ВК = РТ. Докажите, что точка А является серединой отрезка РЕ.
2. На стороне ВС выпуклого четырехугольника ABCD отмечена точка М, а вне четырехугольника — точка К так, что пары отрезков АК и ВМ, KD и МС имеют общие середины. Докажите, что LАВС = LADC.
7.
1. На сторонах ВС и AD выпуклого четырехугольника ABCD отмечены точки К и М соответственно. Отрезок АК пересекает диагональ BD в точке Р, а отрезок СМ — в точке Е. Известно, что АК || СМ. РК = ЕМ, BP = ED, КС = AM. Докажите, что LBAD = LBCD.
Отрезок АК пересекает диагональ BD в точке Р, а отрезок СМ — в точке Е. Известно, что АК || СМ. РК = ЕМ, BP = ED, КС = AM. Докажите, что LBAD = LBCD.
2. В выпуклом четырехугольнике ABCD диагонали пересекаются в точке О, ВО = OD, АО < ОС. Докажите, что LBAD > LBCD.
8.
1. На сторонах ВС и AD выпуклого четырехугольника ABCD отмечены точки К и Р соответственно. Диагональ BD пересекает отрезок PC в точке Е, а отрезок АК — в точке Т. Известно, что КС = АР, АТ = ЕС, ТК = ЕР. Докажите, что LАВС = LADC.
2. В выпуклом четырехугольнике ABCD диагонали пересекаются в точке О, ВО = OD, ABAD > ABCD. Докажите, что АО < ОС.
Конспект урока геометрии «Решение задач по теме Параллелограмм»
Конспект урока № 5 по геометрии 8 класс (автор уч. Атанасян Л. С.)
Учитель математики и физики МОБУ «Тамар-Уткульская СОШ»
Коломурзиева Жанара Муратовна
Дата проведения урока: 17.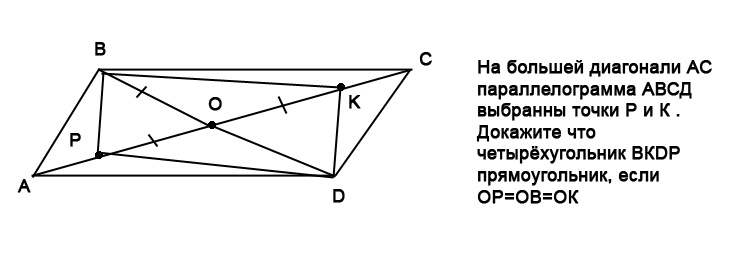 09.2019г
09.2019г
Тема урока: «Решение задач по теме: «Параллелограмм»
Тип урока: Урок практикум (обобщение и систематизация знаний).
Цели:
Предметные: систематизировать знания о параллелограмме, знать и формулировать определение параллелограмма, его свойства и признаки с доказательствами; научиться выполнять чертежи по условию задачи; находить стороны и углы параллелограмма, используя свойства улов и сторон по изученной теме.
Личностные: развивать навыки самостоятельной работы, формирование умения нравственно-этического оценивания усваиваемого материала.
Метапредметные УУД :
Коммуникативные: устанавливать рабочие отношения, эффективно сотрудничать и способствовать продуктивной коопераии.
Регулятивные: проектировать маршрут преодоления затруднений в обучении через включение в новые виды деятельности и формы сотрудничества;
Познавательные: создавать структуру смысловых единиц;
умение самостоятельно определять цели своего обучения, ставить и формулировать для себя новые задачи в учёбе и познавательной деятельности. развивать логическое мышление, память, познавательный интерес; продолжать формирование математической речи; вырабатывать умение анализировать и сравнивать;
развивать логическое мышление, память, познавательный интерес; продолжать формирование математической речи; вырабатывать умение анализировать и сравнивать;
Планируемые результаты: учащийся научится решать задачи разного уровня сложности на применение свойств и признаков параллелограмма из материалов ГИА.
Основные понятия: Параллелограмм, его определение, свойства и признаки.
Элементы урока и их содержаниеВремя (мин)
Деятельность
учителя
учащихся
Организационный момент
Постановка цели
Ребята, сегодня на уроке мы с Вами закрепим знания о свойствах и признаках параллелограмма в процессе решения задач.
Проверка домашнего задания
Теоретический опрос:
Дайте определение параллелограмма.
Перечислите свойства параллелограмма.
 Признаки?
Признаки?
Перечислите признаки параллелограмма.
Решение задач
Решение задач у доски: 372, 376
(приложение 1)
2)Устное решение задач по готовым чертежам (приложение 2)
Закрепление знаний.
Самостоятельная работа (приложение 4):
Сильные учащиеся работают самостоятельно (решают задачи II и III уровня).
Слабоуспевающие учащиеся работают вместе с учителем.
В это время ученики 7 и 8 вида решают тесты (Приложение 3)
.
Подведение итогов. Рефлексия.
Домашнее задание:
№375, 380, 384 (устно)
1
1
3
18
20
1
1
Организационная
Сообщает дату проведения урока, тему урока, цель урока.
Проводит опрос учащихся
1)Следит за верностью решения у слабых учащихся, задавая им наводящие вопросы.
2) Проверяет решение задач II и III уровня сложности. Выставляет оценки за работу.
2)Следит за верностью рассуждений при решении устных задач.
Следит за верностью решения у слабоуспевающих учащихся.
Выставляет оценки за работу.
Поясняет домашнее задание.
Сообщают об отсутствующих.
Записывают в тетради.
Учащиеся отвечают на вопросы.
Учащиеся работают на местах.
Выполняют работу в тетрадях.
Внимательно слушают, записывают в дневники.
Приложение 1. Решение задач разного уровня сложности.
Задача 1. Устный опрос.
Докажите, что ABCD- параллелограмм.
№ 372(в). Работа у доски. Периметр параллелограмма равен 48 см. Найдите стороны параллелограмма, если разность двух сторон равна 7 см.
Дано: ABCD – параллелограмм,
ВС – AB = 7 см, Р = 48 см.
Найти: АВ, ВС.
Решение:
Пусть АВ = x см, тогда ВС = х + 7. Противоположные стороны параллелограмма равны.
Противоположные стороны параллелограмма равны.
Р = (АВ + ВС)·2.
(х + х + 7)·2 = 48;
2х + 7 = 24;
2х = 17;
х = 8,5.
АВ = 8,5 см, ВС = 15,5 см.
Ответ: 8,5см, 15,5см.
№ 376 (в). Найдите углы параллелограмма ABCD, если .
Дано: ABCD – параллелограмм,
.
Найти:
Решение.
В параллелограмме противоположные углы равны, значит,
В параллелограмме сумма углов, прилежащих к одной стороне равна .
.
Ответ: .
Приложение 1
I уровень
Точки E и K — середины сторон AB и CD параллелограмма ABCD. Докажите, что AECK – параллелограмм.
Диагонали четырёхугольника ABCD пересекаются в точке O, причём AC = 2 дм, AO = 10 см,
BD = 1,5 дм, BO = 7 см. Выясните, является ли ABCD – параллелограммом?
II уровень
В параллелограмме ABCD на сторонах AB и CD отмечены соответственно точки M и N так, что ﮮ BMC = ﮮ AND.
 Докажите, что AMCN – параллелограмм.
Докажите, что AMCN – параллелограмм.Точки A и B делят диагональ MK параллелограмма MNKP на три равные части. Является ли четырёхугольник ANBP параллелограммом? Ответ обоснуйте.
III уровень
В параллелограмме ABCD на сторонах AB и CD отмечены соответственно точки M и K так, что AM=CK, а на сторонах BC и AD – точки N и P так, что AP=CN. Докажите, что MNKP – параллелограмм.
Через точку пересечения диагоналей O параллелограмма ABCD проведена прямая MN, пересекающая стороны AD и BC в точках M и N соответственно. Является ли четырёхугольник MBND параллелограммом? Ответ обоснуйте.
Приложение 2
ABCD – параллелограмм. Найти: ﮮ C, ﮮ D.
MNKP – параллелограмм. Найти: MP, PK.
ABCD – параллелограмм. Найти:ﮮA,ﮮB, ﮮ C, ﮮ D.
ABCD – параллелограмм.
 Найти:PABCD.
Найти:PABCD.
ABCD – параллелограмм. Найти:AD.
ABCD – параллелограмм. Найти: PABCD, ﮮAED.
Приложение 3
Вариант 1.
Укажите верное утверждение:
А) Параллелограмм – это четырёхугольник, у которого сумма углов равна .
Б) Параллелограмм – это четырёхугольник, у которого противоположные стороны параллельны.
В) Параллелограмм – это четырёхугольник, у которого диагонали являются биссектрисами.
Укажите верное утверждение:
В параллелограмме ABCD:
А) AB > CD; Б) AB < CD; В) AB = CD.
Какое утверждение неверно?
А) Диагонали в параллелограмме равны.
Б) Диагонали в параллелограмме пересекаются.
В) Диагонали в параллелограмме точкой пересечения делятся пополам.
Какое утверждение не является свойством параллелограмма?
А) В параллелограмме все углы прямые.
Б) В параллелограмме противоположные углы равны.
В) В параллелограмме диагонали точкой пересечения делятся пополам.
Какое утверждение не является признаком параллелограмма?
А) Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник –параллелограмм.
Б) Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
В) Если в четырёхугольнике два угла прямые, то этот четырехугольник – параллелограмм.
Найдите углы параллелограмма ABCD, если .
Найдите периметр параллелограмма ABCD, если его смежные стороны равны 3 см и 45 мм.
Вариант 2.
Укажите верное утверждение:
А) Параллелограмм – это четырёхугольник, у которого противоположные стороны параллельны.
Б) Параллелограмм – это четырёхугольник, у которого диагонали равны.
В) Параллелограмм – это четырёхугольник, у которого сумма углов равна
Укажите верное утверждение:
В параллелограмме ABCD:
А) BC < AD; Б) BC = AD; В) BC > AD.
Какое утверждение неверно?
А) Диагонали в параллелограмме точкой пересечения делятся пополам.
Б) Диагонали в параллелограмме пересекаются.
В) Диагонали в параллелограмме являются биссектрисами.
Какое утверждение не является свойством параллелограмма?
А) В параллелограмме диагонали перпендикулярны.
Б) В параллелограмме противоположные стороны равны.
В) Диагональ параллелограмма делит его на два равных треугольника.
Какое утверждение не является признаком параллелограмма?
А) Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.
Б) Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
В) Если в четырёхугольнике две стороны параллельны, то этот четырехугольник – параллелограмм.
Найдите углы параллелограмма ABCD, если .
Найдите периметр параллелограмма ABCD, если его смежные стороны равны 5 см и 35 мм.
ОТВЕТЫ К ТЕСТУ
Вариант 1. Вариант 2.
1. Б 1. А
2. В 2. Б
3. А 3. В
4. А 4. А
5. В 5. В
6. 60, 120 6. 70, 110
7. 15 см. 7. 17 см.
Приложение 4
Самостоятельная работа
I уровень
I вариант
В четырехугольнике ABCD AB||CD, BC||AD, AC=20см, BD=10см, AB=13 см. Диагонали ABCD пересекаются в точке O. Найдите периметр ΔCOD.
Из вершины B параллелограмма ABCD с острым углом A проведён перпендикуляр BK к прямой AD, BK=AB:2. Найдите ﮮC, ﮮD.
Середина отрезка BD является центром окружности с диаметром AC, причём точки A, B, C, D не лежат на одной прямой.
 Докажите, что ABCD – параллелограмм.
Докажите, что ABCD – параллелограмм.
II вариант
В четырехугольнике ABCD AB||CD, BC||AD, O – точка пересечения диагоналей. Периметр ΔAOD равен 25 см, AC=16см, BD=14см. Найдите BC.
В параллелограмме ABCD с острым углом A из вершины B проведён перпендикуляр BK к прямой AD, AK=BK. Найдите ﮮC, ﮮD.
Дан параллелограмм ABCD. На продолжении диагонали AC за вершины A и C отмечены точки M и N соответственно так, что AM=CN. Докажите, что MBND – параллелограмм.
II уровень
I вариант
В четырехугольнике ABCD ﮮA+ﮮB=180°, AB|| CD. На сторонах BC и AD отмечены точки M и K соответственно так, что BM=KD. Докажите, что точки M и K находятся на одинаковых расстояниях от точки пересечения диагоналей четырёхугольника.
На сторонах PK и MH параллелограмма MPKH взяты точки A и B соответственно, MP=PB=AK; ﮮMPB=60°. Найдите углы параллелограмма и сравните отрезки BM и AH.

На основании AC равнобедренного треугольника ABC отмечена точка K, а на сторонах AB и BC – точки M и P соответственно, причём PK=MB, ﮮKPC=80°, ﮮC=50°. Докажите, что KMBP – параллелограмм.
II вариант
В четырехугольнике MPKH ﮮPMK=ﮮHKM, PK||MH. Через точку пересечения диагоналей проведена прямая, пересекающая стороны PK и MH в точках A и B соответственно. Докажите, что AP=HB.
На сторонах BC и AD параллелограмма ABCD взяты точки M и K, AB=BM=KD; ﮮAMB=30°. Найдите углы параллелограмма и сравните отрезки AM и CK.
В ΔMPK ﮮM=65°. На сторонах MK, MP, PK отмечены точки A, B, C соответственно так, что середина стороны PK – точка C, AM=KC, BP=AC, ﮮBAM=50°. Докажите, что BPCA – параллелограмм.
Технология уровневой дифференциации на уроках математики (1)
МОУ «Средняя общеобразовательная школа с. Куриловка
Вольского района Саратовской области»
Открытый урок
Учитель: Кузнецова Татьяна Ивановна
Предмет: математика (геометрия)
Класс: 8
Тема: Параллелограмм. Решение
задач.
Решение
задач.
Методическая тема: Технология уровневой дифференциации на уроках математики.
Тип урока: урок применения знаний и умений.
Цели урока:
Образовательные:
Закрепить знания о свойствах и признаках параллелограмма в процессе решения задач;
Развивающие:
развивать логическое мышление, память, познавательный интерес; продолжать формирование математической речи; вырабатывать умение анализировать и сравнивать;
Воспитательные:
содействовать развитию у учащихся чувства ответственности за деятельность коллектива и в коллективе;
содействовать развитию коллективного общения учащихся;
содействовать развитию у учащихся интереса к математике.
Элементы урока и их содержание | Время (мин) | Деятельность | |
учителя | учащихся | ||
I. | 1 | организационная | Сообщают об отсутствующих. |
II.Постановка цели Сегодня на уроке мы закрепим знания о свойствах и признаках параллелограмма в процессе решения задач. | 1 | Сообщает дату проведения урока, тему урока, цель урока. | Записывают в тетради. |
III.Проверка домашнего задания Теоретический опрос:
| 3 | Проводит опрос учащихся | Учащиеся
отвечают на вопросы. |
IV. Решение задач 1)Решение задач разного уровня сложности (приложение 1) 2) Проверка заданий. 3)Устное решение задач по готовым чертежам (приложение 2) | 13 | 1)Следит за верностью решения у слабых учащихся, задавая им наводящие вопросы. 2) Проверяет решение задач II и III уровня сложности. Выставляет оценки за работу. 2)Следит за верностью рассуждений при решении устных задач. | Учащихся работают на местах. |
V.Закрепление. Самостоятельная работа (приложение 3): Сильные учащиеся работают самостоятельно (решают задачи II и III уровня). Слабоуспевающие учащиеся работают вместе с учителем. | 25 | Следит
за верностью решения у слабоуспевающих
учащихся. | Выполняют работу в тетрадях. |
VI. Подведение итогов. Рефлексия. | 3 | Выставляет оценки за работу. | |
VII. Домашнее задание: №375, 380, 384 (устно) | 2 | Поясняет домашнее задание. | Внимательно слушают, записывают в дневники. |
Приложение 1
I уровень
Точки E и K — середины сторон AB и CD параллелограмма ABCD. Докажите, что AECK – параллелограмм.
Диагонали четырёхугольника ABCD пересекаются в точке O, причём AC = 2 дм, AO = 10 см,
BD = 1,5 дм, BO = 7 см. Выясните, является ли ABCD – параллелограммом?
II уровень
В параллелограмме ABCD на сторонах AB и CD отмечены соответственно точки M и N так, что ﮮ BMC = ﮮ AND.
 Докажите, что AMCN
– параллелограмм.
Докажите, что AMCN
– параллелограмм.Точки A и B делят диагональ MK параллелограмма MNKP на три равные части. Является ли четырёхугольник ANBP параллелограммом? Ответ обоснуйте.
III уровень
В параллелограмме ABCD на сторонах AB и CD отмечены соответственно точки M и K так, что AM=CK, а на сторонах BC и AD – точки N и P так, что AP=CN. Докажите, что MNKP – параллелограмм.
Через точку пересечения диагоналей O параллелограмма ABCD проведена прямая MN, пересекающая стороны AD и BC в точках M и N соответственно. Является ли четырёхугольник MBND параллелограммом? Ответ обоснуйте.
Приложение 2
ABCD – параллелограмм. Найти: ﮮ C, ﮮ D.
MNKP – параллелограмм. Найти: MP, PK.
ABCD – параллелограмм. Найти:ﮮA,ﮮB, ﮮ C, ﮮ D.

ABCD – параллелограмм. Найти:PABCD.
ABCD – параллелограмм. Найти:AD.
ABCD – параллелограмм. Найти: PABCD, ﮮAED.
NBFD – параллелограмм. Найти: BC, СD.
ABCD – параллелограмм, PMNKP,=20 см. Найти: MN, MP.
BNDM – параллелограмм, AB:BC=4:5, PABCD,=18 см. Найти: AD, DC.
Приложение 3
Самостоятельная работа
I уровень
I вариант
В четырехугольнике ABCD AB||CD, BC||AD, AC=20см, BD=10см, AB=13 см. Диагонали ABCD пересекаются в точке O. Найдите периметр ΔCOD.

Из вершины B параллелограмма ABCD с острым углом A проведён перпендикуляр BK к прямой AD, BK=AB:2. Найдите ﮮC, ﮮD.
Середина отрезка BD является центром окружности с диаметром AC, причём точки A, B, C, D не лежат на одной прямой. Докажите, что ABCD – параллелограмм.
II вариант
В четырехугольнике ABCD AB||CD, BC||AD, O – точка пересечения диагоналей. Периметр ΔAOD равен 25 см, AC=16см, BD=14см. Найдите BC.
В параллелограмме ABCD с острым углом A из вершины B проведён перпендикуляр BK к прямой AD, AK=BK. Найдите ﮮC, ﮮD.
Дан параллелограмм ABCD. На продолжении диагонали AC за вершины A и C отмечены точки M и N соответственно так, что AM=CN. Докажите, что MBND – параллелограмм.

II уровень
I вариант
В четырехугольнике ABCD ﮮA+ﮮB=180°, AB|| CD. На сторонах BC и AD отмечены точки M и K соответственно так, что BM=KD. Докажите, что точки M и K находятся на одинаковых расстояниях от точки пересечения диагоналей четырёхугольника.
На сторонах PK и MH параллелограмма MPKH взяты точки A и B соответственно, MP=PB=AK; ﮮMPB=60°. Найдите углы параллелограмма и сравните отрезки BM и AH.
На основании AC равнобедренного треугольника ABC отмечена точка K, а на сторонах AB и BC – точки M и P соответственно, причём PK=MB, ﮮKPC=80°, ﮮC=50°. Докажите, что KMBP – параллелограмм.
II вариант
В четырехугольнике MPKH ﮮPMK=ﮮHKM, PK||MH.
 Через точку пересечения диагоналей
проведена прямая, пересекающая стороны
PK
и MH
в точках A
и B
соответственно. Докажите, что AP=HB.
Через точку пересечения диагоналей
проведена прямая, пересекающая стороны
PK
и MH
в точках A
и B
соответственно. Докажите, что AP=HB.На сторонах BC и AD параллелограмма ABCD взяты точки M и K, AB=BM=KD; ﮮAMB=30°. Найдите углы параллелограмма и сравните отрезки AM и CK.
В ΔMPK ﮮM=65°. На сторонах MK, MP, PK отмечены точки A, B, C соответственно так, что середина стороны PK – точка C, AM=KC, BP=AC, ﮮBAM=50°. Докажите, что BPCA – параллелограмм.
III уровень
I вариант
В выпуклом четырехугольнике ABCD ﮮA+ﮮB=ﮮB+ﮮC=180°. Через точку O пересечения диагоналей четырёхугольника проведена прямая, пересекающая стороны DC и AD в точках M и K соответственно; ﮮBOM=90°.
Докажите,
что BK=BM.
На сторонах BC и CD параллелограмма ABCD отмечены точки M и H соответственно так, что отрезки BH и MD пересекаются в точке O; ﮮBHD=95°, ﮮDMC=90°, ﮮBOD=155°. Найдите отношение длин отрезков AB и MD и углы параллелограмма.
Точки M и K являются соответственно серединами сторон AB и BC треугольника ABC. Через вершину C вне треугольника проведена прямая, параллельная AB и пересекающая луч MK в точке E. Докажите, что KE=AC:2.
II вариант
В выпуклом четырехугольнике MPKH ﮮM+ﮮP=180°, ﮮMKH=ﮮKMP. На сторонах MH и PK отмечены точки A и B так, что PB=PA. Отрезок AB проходит через точку пересечения диагоналей четырёхугольника. Докажите, что HP перпендикулярен AB.
Докажите, что BK=BM.
На сторонах BC и CD параллелограмма ABCD взяты точки K и M соответственно.
 Отрезки BM
и KD
пересекаются в точке O;
ﮮBOD=140°,
ﮮDKB=110°,
ﮮBMC=90°.
Найдите отношение длин отрезков MC
и AD
и углы параллелограмма.
Отрезки BM
и KD
пересекаются в точке O;
ﮮBOD=140°,
ﮮDKB=110°,
ﮮBMC=90°.
Найдите отношение длин отрезков MC
и AD
и углы параллелограмма.Точки A и B принадлежат соответственно сторонам PE и ET треугольника PET. Прямая, проходящая через вершину T вне треугольника, пересекает луч AB и точке K так, что AP=KT, AB=BK=PT:2. Докажите, что точка A является серединой отрезка PE.
Параллелограмм. Решение задач | Школьные файлы SchoolFiles.net
Урок
Учитель: Аскерова. Ф Н.
Предмет: математика (геометрия)
Класс: 8
Тема: Параллелограмм. Решение задач.
Методическая тема: Технология уровневой дифференциации на уроках математики.
Тип урока: урок применения знаний и умений.
Цели урока:
Образовательные:
Закрепить знания о свойствах и признаках параллелограмма в процессе решения задач;
Развивающие:
развивать логическое мышление, память, познавательный интерес; продолжать формирование математической речи; вырабатывать умение анализировать и сравнивать;
Воспитательные:
содействовать развитию у учащихся чувства ответственности за деятельность коллектива и в коллективе;
содействовать развитию коллективного общения учащихся;
содействовать развитию у учащихся интереса к математике.
Элементы урока и их содержание Время (мин) Деятельность
учителя учащихся
Организационный этап
Постановка цели
Сегодня на уроке мы закрепим знания о свойствах и признаках параллелограмма в процессе решения задач.
Проверка домашнего задания
Теоретический опрос:
Дайте определение параллелограмма.
Перечислите свойства параллелограмма.
Перечислите признаки параллелограмма.
IV. Решение задач
1)Решение задач разного уровня сложности (приложение 1)
2) Проверка заданий.
3)Устное решение задач по готовым чертежам (приложение 2)
V.Закрепление.
Самостоятельная работа (приложение 3):
Сильные учащиеся работают самостоятельно (решают задачи II и III уровня).
Слабоуспевающие учащиеся работают вместе с учителем.
VI. Подведение итогов. Рефлексия.
VII. Домашнее задание:
№375, 380, 384 (устно) 1
1
3
13
25
3
2
Организационная
Сообщает дату проведения урока, тему урока, цель урока.

Проводит опрос учащихся
1)Следит за верностью решения у слабых учащихся, задавая им наводящие вопросы.
2) Проверяет решение задач II и III уровня сложности. Выставляет оценки за работу.
2)Следит за верностью рассуждений при решении устных задач.
Следит за верностью решения у слабоуспевающих учащихся.
Выставляет оценки за работу.
Поясняет домашнее задание. Сообщают об отсутствующих.
Записывают в тетради.
Учащиеся отвечают на вопросы.
Учащихся работают на местах.
Выполняют работу в тетрадях.
Внимательно слушают, записывают в дневники.
Приложение 1
I уровень
Точки E и K — середины сторон AB и CD параллелограмма ABCD. Докажите, что AECK – параллелограмм.
Диагонали четырёхугольника ABCD пересекаются в точке O, причём AC = 2 дм, AO = 10 см,
BD = 1,5 дм, BO = 7 см. Выясните, является ли ABCD – параллелограммом?
II уровень
В параллелограмме ABCD на сторонах AB и CD отмечены соответственно точки M и N так, что ﮮ BMC = ﮮ AND.
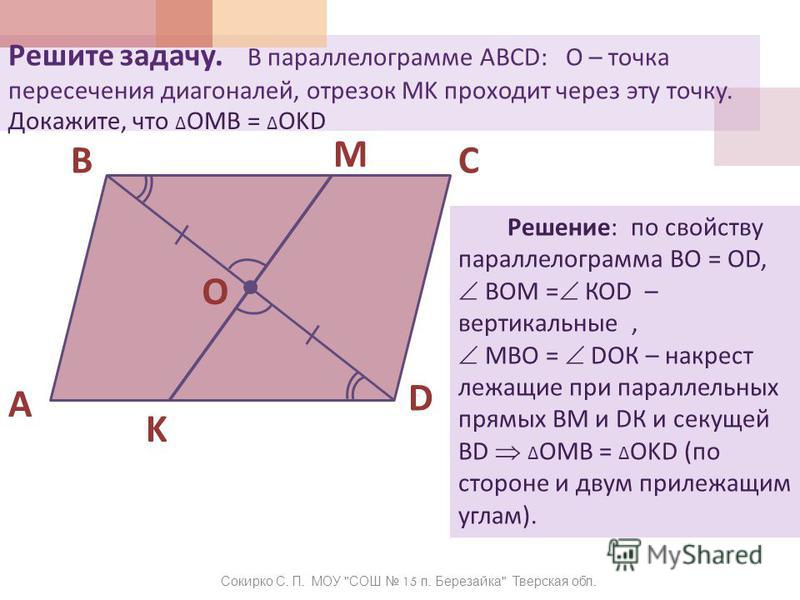 Докажите, что AMCN – параллелограмм.
Докажите, что AMCN – параллелограмм.Точки A и B делят диагональ MK параллелограмма MNKP на три равные части. Является ли четырёхугольник ANBP параллелограммом? Ответ обоснуйте.
III уровень
В параллелограмме ABCD на сторонах AB и CD отмечены соответственно точки M и K так, что AM=CK, а на сторонах BC и AD – точки N и P так, что AP=CN. Докажите, что MNKP – параллелограмм.
Через точку пересечения диагоналей O параллелограмма ABCD проведена прямая MN, пересекающая стороны AD и BC в точках M и N соответственно. Является ли четырёхугольник MBND параллелограммом? Ответ обоснуйте.
Приложение 2
ABCD – параллелограмм. Найти: ﮮ C, ﮮ D.
MNKP – параллелограмм. Найти: MP, PK.
ABCD – параллелограмм. Найти:ﮮA,ﮮB, ﮮ C, ﮮ D.
ABCD – параллелограмм. Найти:PABCD.
ABCD – параллелограмм. Найти:AD.
ABCD – параллелограмм. Найти: PABCD, ﮮAED.
NBFD – параллелограмм. Найти: BC, СD.
ABCD – параллелограмм, PMNKP,=20 см. Найти: MN, MP.
BNDM – параллелограмм, AB:BC=4:5, PABCD,=18 см.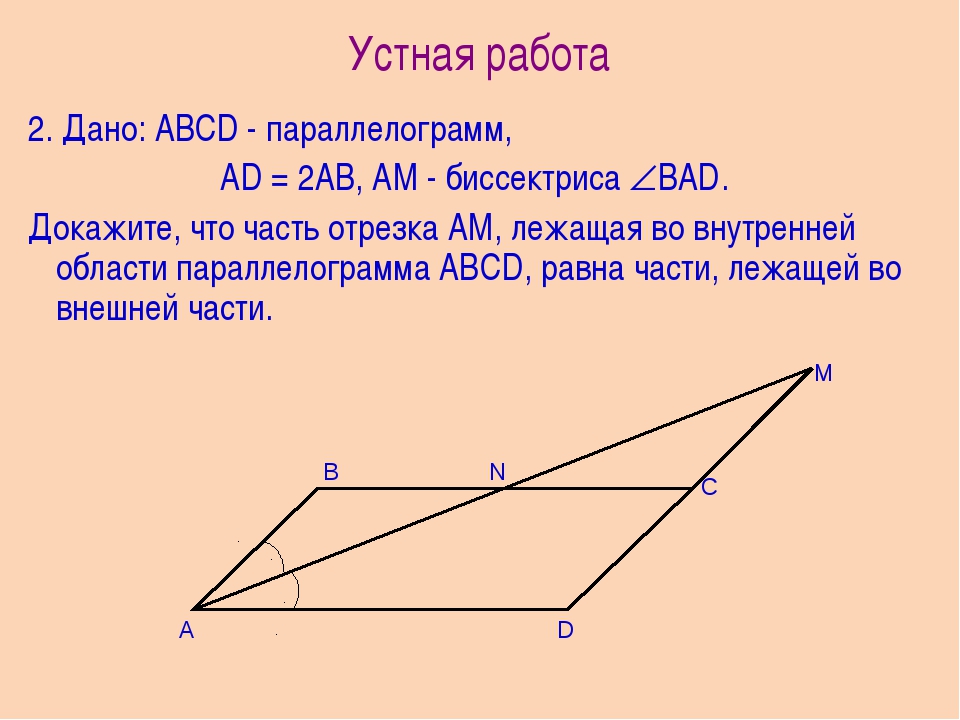 Найти: AD, DC.
Найти: AD, DC.
Приложение 3
Самостоятельная работа
I уровень
I вариант
В четырехугольнике ABCD AB||CD, BC||AD, AC=20см, BD=10см, AB=13 см. Диагонали ABCD пересекаются в точке O. Найдите периметр ΔCOD.
Из вершины B параллелограмма ABCD с острым углом A проведён перпендикуляр BK к прямой AD, BK=AB:2. Найдите ﮮC, ﮮD.
Середина отрезка BD является центром окружности с диаметром AC, причём точки A, B, C, D не лежат на одной прямой. Докажите, что ABCD – параллелограмм.
II вариант
В четырехугольнике ABCD AB||CD, BC||AD, O – точка пересечения диагоналей. Периметр ΔAOD равен 25 см, AC=16см, BD=14см. Найдите BC.
В параллелограмме ABCD с острым углом A из вершины B проведён перпендикуляр BK к прямой AD, AK=BK. Найдите ﮮC, ﮮD.
Дан параллелограмм ABCD. На продолжении диагонали AC за вершины A и C отмечены точки M и N соответственно так, что AM=CN. Докажите, что MBND – параллелограмм.
II уровень
I вариант
В четырехугольнике ABCD ﮮA+ﮮB=180°, AB|| CD.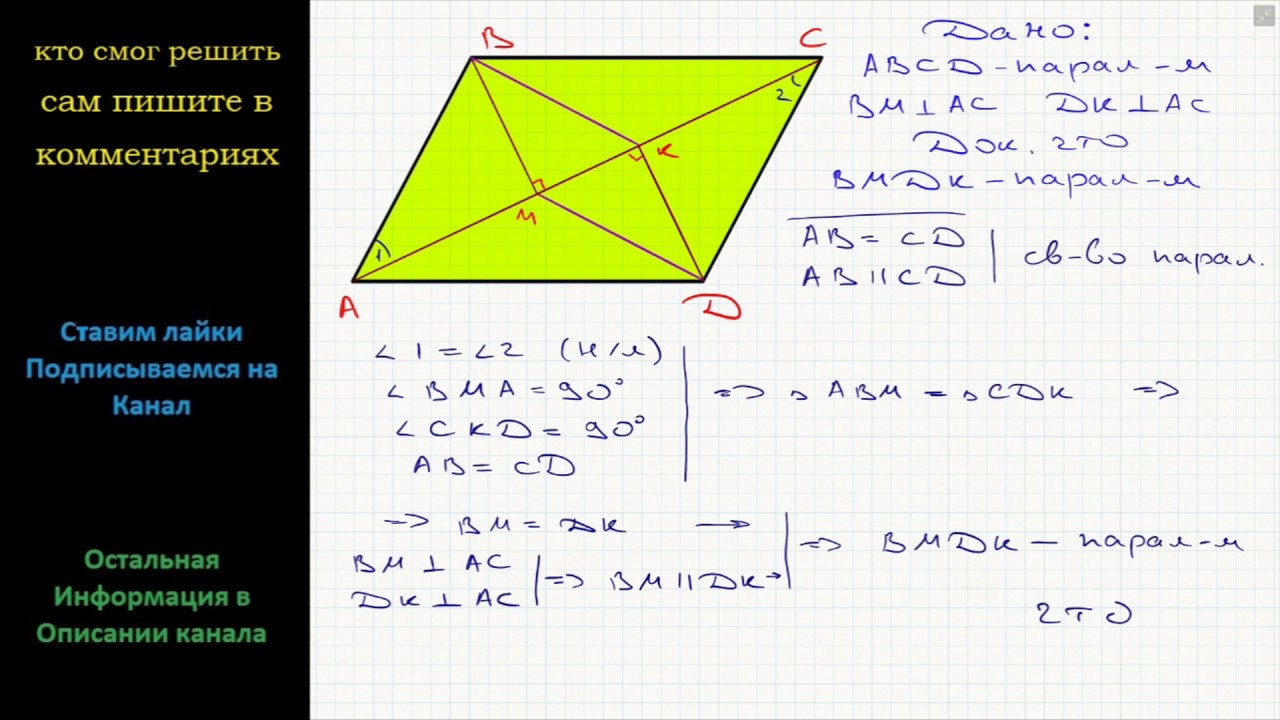 На сторонах BC и AD отмечены точки M и K соответственно так, что BM=KD. Докажите, что точки M и K находятся на одинаковых расстояниях от точки пересечения диагоналей четырёхугольника.
На сторонах BC и AD отмечены точки M и K соответственно так, что BM=KD. Докажите, что точки M и K находятся на одинаковых расстояниях от точки пересечения диагоналей четырёхугольника.
На сторонах PK и MH параллелограмма MPKH взяты точки A и B соответственно, MP=PB=AK; ﮮMPB=60°. Найдите углы параллелограмма и сравните отрезки BM и AH.
На основании AC равнобедренного треугольника ABC отмечена точка K, а на сторонах AB и BC – точки M и P соответственно, причём PK=MB, ﮮKPC=80°, ﮮC=50°. Докажите, что KMBP – параллелограмм.
II вариант
В четырехугольнике MPKH ﮮPMK=ﮮHKM, PK||MH. Через точку пересечения диагоналей проведена прямая, пересекающая стороны PK и MH в точках A и B соответственно. Докажите, что AP=HB.
На сторонах BC и AD параллелограмма ABCD взяты точки M и K, AB=BM=KD; ﮮAMB=30°. Найдите углы параллелограмма и сравните отрезки AM и CK.
В ΔMPK ﮮM=65°. На сторонах MK, MP, PK отмечены точки A, B, C соответственно так, что середина стороны PK – точка C, AM=KC, BP=AC, ﮮBAM=50°.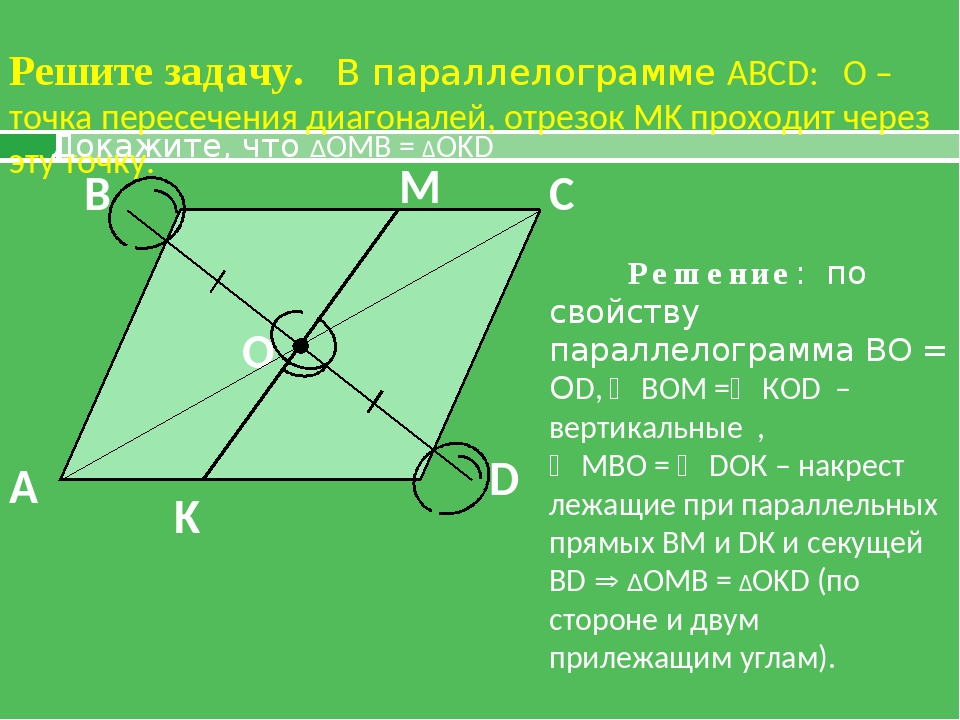 Докажите, что BPCA – параллелограмм.
Докажите, что BPCA – параллелограмм.
III уровень
I вариант
В выпуклом четырехугольнике ABCD ﮮA+ﮮB=ﮮB+ﮮC=180°. Через точку O пересечения диагоналей четырёхугольника проведена прямая, пересекающая стороны DC и AD в точках M и K соответственно; ﮮBOM=90°.
Докажите, что BK=BM.
На сторонах BC и CD параллелограмма ABCD отмечены точки M и H соответственно так, что отрезки BH и MD пересекаются в точке O; ﮮBHD=95°, ﮮDMC=90°, ﮮBOD=155°. Найдите отношение длин отрезков AB и MD и углы параллелограмма.
Точки M и K являются соответственно серединами сторон AB и BC треугольника ABC. Через вершину C вне треугольника проведена прямая, параллельная AB и пересекающая луч MK в точке E. Докажите, что KE=AC:2.
II вариант
В выпуклом четырехугольнике MPKH ﮮM+ﮮP=180°, ﮮMKH=ﮮKMP. На сторонах MH и PK отмечены точки A и B так, что PB=PA. Отрезок AB проходит через точку пересечения диагоналей четырёхугольника. Докажите, что HP перпендикулярен AB.
Докажите, что BK=BM.
На сторонах BC и CD параллелограмма ABCD взяты точки K и M соответственно. Отрезки BM и KD пересекаются в точке O; ﮮBOD=140°, ﮮDKB=110°, ﮮBMC=90°. Найдите отношение длин отрезков MC и AD и углы параллелограмма.
Точки A и B принадлежат соответственно сторонам PE и ET треугольника PET. Прямая, проходящая через вершину T вне треугольника, пересекает луч AB и точке K так, что AP=KT, AB=BK=PT:2. Докажите, что точка A является серединой отрезка PE.
Треугольник — это половина параллелограмма. Евклид I. 39-41
Содержание | Введение | Дом П л а н е г е о м е т р и Приключение в области языка и логики на основе Предложение 39 Предложение 41 ДВА СЛЕДУЮЩИХ ПРЕДЛОЖЕНИЯ являются частичным обращением двух предыдущих; они показывают, что если равные треугольники находятся на одном основании или на одинаковых основаниях, то они находятся в одинаковых параллелях.
Следующая теорема, предложение 40, является частичным обращением предложения 38, и мы оставим ее формулировку в качестве упражнения; Проблема 2. Теперь любой треугольник — это половина параллелограмма; половина площади, то есть. Это подразумевалось в I.37 и 38. Это подтверждает следующая теорема.
Из этой теоремы мы выводим арифметическую формулу, согласно которой площадь треугольника равна половине меры основания, умноженной на меру высоты: A = ½ bh . Преобразование площадей Следующие четыре предложения Евклида положили начало увлекательной задаче в области геометрических знаний, которая заключается в построении простой фигуры, такой как прямоугольник или квадрат, которая будет равна по площади данной фигуре.Предложение I. 45 решает задачу построения прямоугольника, равного любой прямолинейной фигуре; и Предложение II. 14 решает задачу построения квадрата, равного любой прямолинейной фигуре. Следующее предложение решает проблему построения «квадрата». Пожалуйста, «переверните» страницу и решите проблемы. или Перейти к следующему предложению. Предыдущее предложение Содержание | Введение | Дом Сделайте пожертвование, чтобы TheMathPage оставалась в сети. Авторские права © 2021 Лоуренс Спектор Вопросы или комментарии? Электронная почта: themathpage @ яндекс.com | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Обычная страница без названия
Обычная страница без названия«Диагонали параллелограмма делятся пополам » Схема доказательства
Использование Планшет Geometer
от Дэвида Уайза
Примечание: я рекомендую распечатать эту страницу, чтобы
инструкции легче выполнять.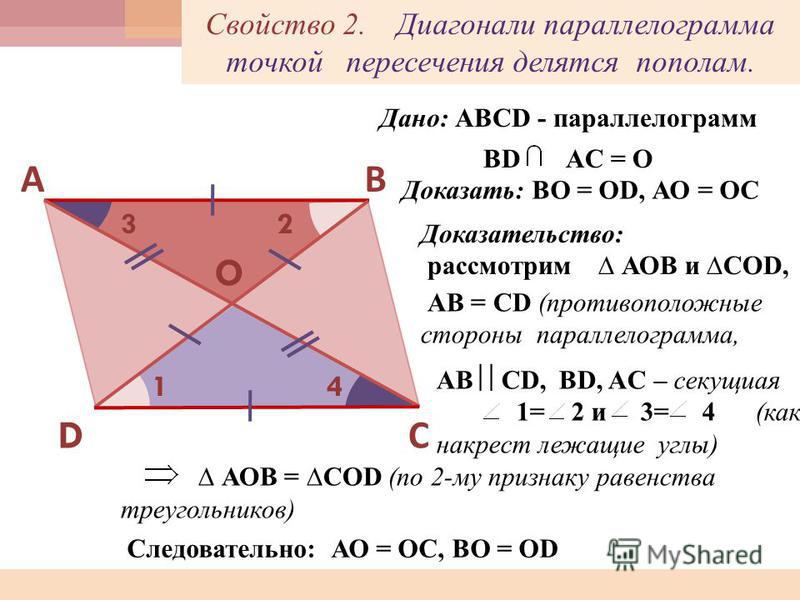
Для успешного завершения доказательства,
важно продумать определение и конструкцию
параллелограмма.
В следующей схеме я приведу утверждения, вы
укажите причины .
Докажи: если четырехугольник параллелограмм, затем диагонали делят друг друга пополам.
Дано: Параллелограмм ABCD с диагоналями BD и AC, пересекающиеся в точке M.
Prove: сегмент AC и BD пополам друг друга.
- Рассмотрим, как устроен параллелограмм —— параллель линий.
- Учитывать свойства параллельных прямых и вертикальные углы.
- Диагонали образуют 4 треугольника.
- Рассмотрим свойства конгруэнтности треугольника.
- Нажмите здесь , чтобы изучить этот эскиз и помочь с шагами доказательства.
Доказательство :
- Угол DBA конгруэнтен углу BDC.

- Угол CMD соответствует углу AMB.
- Треугольник CMD конгруэнтен треугольнику AMB.
- Сегмент AM соответствует сегменту MC.
- M — середина отрезка AC.
- Сегмент BD делит пополам сегмент AC.
- Сегмент BM соответствует сегменту MD.
- M — середина отрезка BD.
- Сегмент AC делит пополам сегмент BD.
Добавочный номер :
- Преобразование двухколонного доказательство в доказательство абзаца.
- Найдите альтернативный способ Докажите, что диагонали параллелограмма делят друг друга пополам.
Если у вас возникнут какие-либо вопросы при попытке завершить это расследование,
или предложения, которые были бы полезны, особенно для использования на
уровень средней школы, отправьте электронное письмо по адресу esiwdivad@yahoo.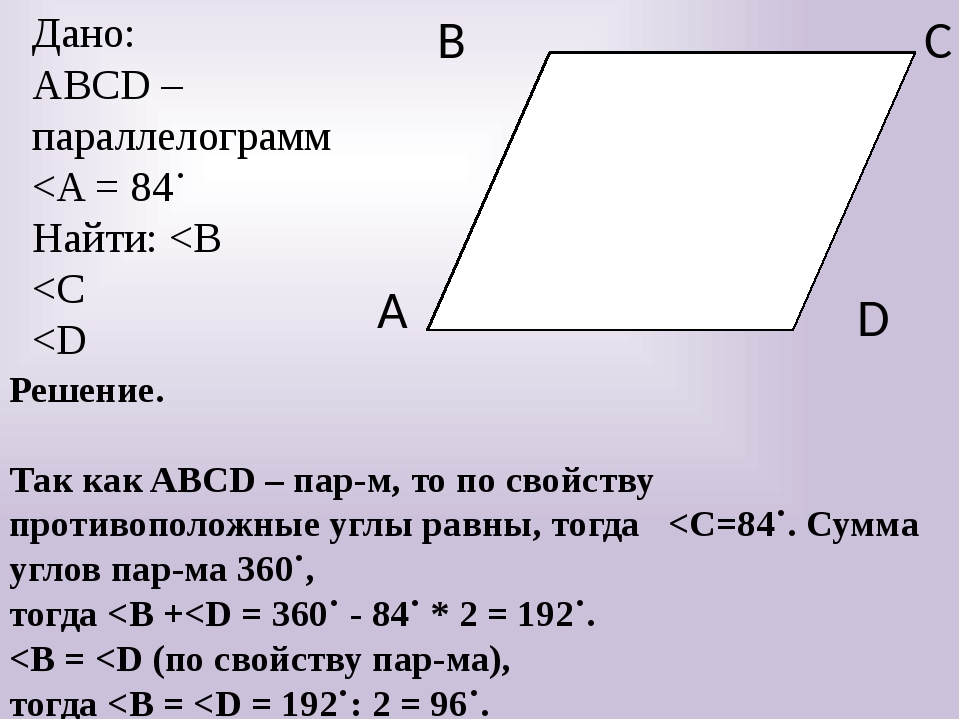 com .
com .
Вернуть на Оглавление.
доказать, что диагонали ромба делят друг друга пополам
Все углы прямые 3. Середина ?? Все углы прямые 3. равно (1,4).0.5. Эти расстояния должны быть равны, это один из способов доказать, что у ромбов есть дополнительные свойства. Примечание: я рекомендую распечатать эту страницу, чтобы было легче следовать инструкциям. Это доказывает, что O — это середина прямых AC и BD. Площадь определяется путем умножения длины диагоналей, деленной на 2. Это уникальное свойство ромбов, которое не наблюдается в других четырехугольниках. Следовательно, каждый является прямым углом, то есть углами. 6. https://www.khanacademy.org/…/quadraterals/v/rhombus-diagonals ⇒ OA = OC [Диагонали ромба делят друг друга пополам] ⇒ OD = OD [Общая сторона] ⇒ AD = C D.∴ AOD ≅ C OD [По правилу сравнения SSS] ⇒ ∠AOD = ∠C OD… 8. 1. Назовите координаты точки C. A: (2a, 2b +… Получите нужные ответы прямо сейчас! Доказательство того, что диагонали ромба перпендикулярны. Как найти плотность в законе идеального газа. Доказано … Если диагонали четырехугольника перпендикулярны биссектрисам друг друга, то это ромб (обратное свойство). * Диагонали четырехугольника воздушный змей всегда будет пересекаться под углом 90 °. * Время отклика зависит от темы и сложности вопроса. Ромбы (множественное число от ромба) имеют дополнительные свойства.Таким образом диагонали делят друг друга пополам в прямоугольнике. Есть несколько формул для ромба, которые связаны с его: Стороны (щелкните, чтобы узнать подробнее). Кроме того, диагонали параллелограмма делят друг друга пополам, поэтому AF = FC. Ромб — это разновидность параллелограмма, и что отличает его форму, так это то, что все четыре его стороны совпадают. Interactive of Proof Powered by Создайте свой собственный уникальный веб-сайт с настраиваемыми шаблонами. Все 4 стороны совпадают. Теперь перейдем к проверке того, что четырехугольник является ромбом.Свяжитесь с нами по номерам, указанным ниже. Вот некоторые из важных свойств ромба: Все стороны ромба равны.
Как найти плотность в законе идеального газа. Доказано … Если диагонали четырехугольника перпендикулярны биссектрисам друг друга, то это ромб (обратное свойство). * Диагонали четырехугольника воздушный змей всегда будет пересекаться под углом 90 °. * Время отклика зависит от темы и сложности вопроса. Ромбы (множественное число от ромба) имеют дополнительные свойства.Таким образом диагонали делят друг друга пополам в прямоугольнике. Есть несколько формул для ромба, которые связаны с его: Стороны (щелкните, чтобы узнать подробнее). Кроме того, диагонали параллелограмма делят друг друга пополам, поэтому AF = FC. Ромб — это разновидность параллелограмма, и что отличает его форму, так это то, что все четыре его стороны совпадают. Interactive of Proof Powered by Создайте свой собственный уникальный веб-сайт с настраиваемыми шаблонами. Все 4 стороны совпадают. Теперь перейдем к проверке того, что четырехугольник является ромбом.Свяжитесь с нами по номерам, указанным ниже. Вот некоторые из важных свойств ромба: Все стороны ромба равны.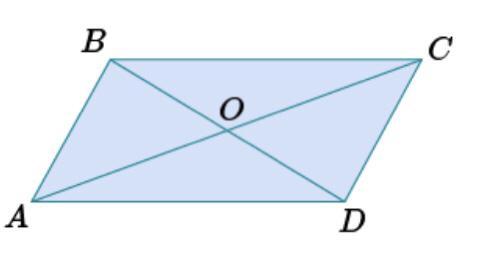 2 + AD.ОКРУГ КОЛУМБИЯ. 1. Если произведение наклонов диагоналей равно -1, мы говорим, что оба они перпендикулярны. Противоположные углы совпадают, диагонали делят друг друга пополам, противоположные стороны параллельны, диагонали делят углы пополам. Какое утверждение описывает свойства ромба, выберите все подходящие варианты. Докажите, что четырехугольник является ромбом тогда и только тогда, когда диагонали делят друг друга пополам. прямой угол. Если вы находитесь в офисе или в общей сети, вы можете попросить администратора сети запустить сканирование сети на предмет неправильно сконфигурированных или зараженных устройств.C. Наклон ?? (iv) Длина диагоналей будет одинаковой. Следовательно, треугольник BCD равнобедренный. Как рассчитать константу закона идеального газа? 1800-212-7858 / 9372462318. Диагонали четырехугольника делят друг друга пополам под прямым углом. Затем докажите, что это ромб. Скажите мне быстро, пожалуйста — Математика — Четырехугольники ABCD — это четырехугольник, в котором диагонали AC и BD делят друг друга пополам под прямым углом.
2 + AD.ОКРУГ КОЛУМБИЯ. 1. Если произведение наклонов диагоналей равно -1, мы говорим, что оба они перпендикулярны. Противоположные углы совпадают, диагонали делят друг друга пополам, противоположные стороны параллельны, диагонали делят углы пополам. Какое утверждение описывает свойства ромба, выберите все подходящие варианты. Докажите, что четырехугольник является ромбом тогда и только тогда, когда диагонали делят друг друга пополам. прямой угол. Если вы находитесь в офисе или в общей сети, вы можете попросить администратора сети запустить сканирование сети на предмет неправильно сконфигурированных или зараженных устройств.C. Наклон ?? (iv) Длина диагоналей будет одинаковой. Следовательно, треугольник BCD равнобедренный. Как рассчитать константу закона идеального газа? 1800-212-7858 / 9372462318. Диагонали четырехугольника делят друг друга пополам под прямым углом. Затем докажите, что это ромб. Скажите мне быстро, пожалуйста — Математика — Четырехугольники ABCD — это четырехугольник, в котором диагонали AC и BD делят друг друга пополам под прямым углом.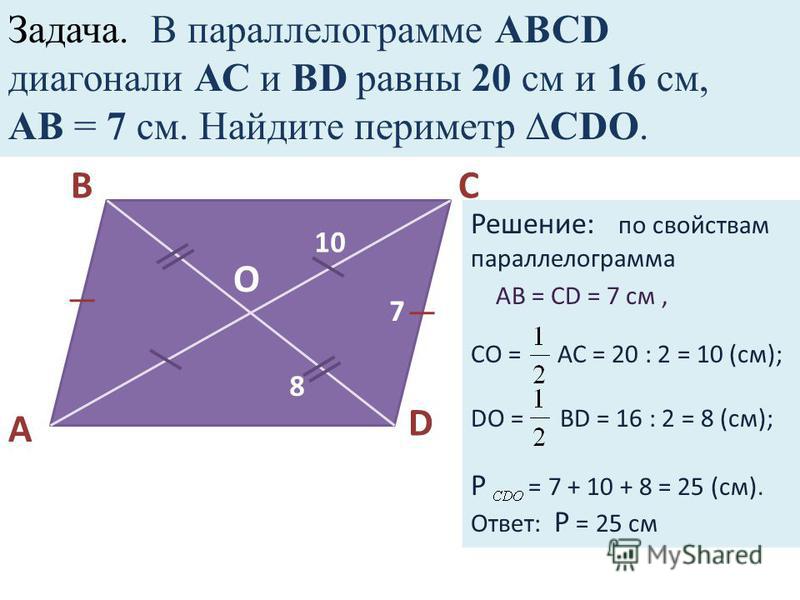 в O и также равны. «Диагонали параллелограмма делятся пополам». Пожалуйста, включите куки и перезагрузите страницу.То есть каждая диагональ разрезает другую на две равные части, а угол их пересечения всегда равен 90 градусам. Используйте координаты, чтобы убедиться, что ?? векторов. Диагонали AC и BD делят друг друга пополам как диагонали параллелограмма в соответствии с уроком Свойства диагоналей … Нам нужно доказать, что параллелограмм является ромбом, другими словами, что все четыре стороны параллелограмма имеют такая же длина. Образовательная франшиза × Свяжитесь с нами. во всем мире.Какие единицы используются для закона идеального газа? В любом ромбе диагонали (линии, соединяющие противоположные углы) делят друг друга пополам под прямым углом (90 °). Если вы используете личное соединение, например, дома, вы можете запустить антивирусное сканирование на своем устройстве, чтобы убедиться, что оно не заражено вредоносными программами. Доказательство: поскольку диагонали ромба перпендикулярны друг другу, углы AFE и CFE равны 90 °.
в O и также равны. «Диагонали параллелограмма делятся пополам». Пожалуйста, включите куки и перезагрузите страницу.То есть каждая диагональ разрезает другую на две равные части, а угол их пересечения всегда равен 90 градусам. Используйте координаты, чтобы убедиться, что ?? векторов. Диагонали AC и BD делят друг друга пополам как диагонали параллелограмма в соответствии с уроком Свойства диагоналей … Нам нужно доказать, что параллелограмм является ромбом, другими словами, что все четыре стороны параллелограмма имеют такая же длина. Образовательная франшиза × Свяжитесь с нами. во всем мире.Какие единицы используются для закона идеального газа? В любом ромбе диагонали (линии, соединяющие противоположные углы) делят друг друга пополам под прямым углом (90 °). Если вы используете личное соединение, например, дома, вы можете запустить антивирусное сканирование на своем устройстве, чтобы убедиться, что оно не заражено вредоносными программами. Доказательство: поскольку диагонали ромба перпендикулярны друг другу, углы AFE и CFE равны 90 °. Это означает, что треугольники AFE и CFE являются прямоугольными. Площадь и периметр ромба. Применяются ВСЕ свойства параллелограмма 2.Все стороны равны 3. Докажите, что если диагонали четырехугольника ABCD делят друг друга пополам, то ABCD — параллелограмм. Углы. Отвечать. Если FE является общей стороной, они разделяют другую конгруэнтную сторону; треугольники AFE и CFE конгруэнтны (SAS). M (-2, -1) A (0,5) T (6,3) H (4, -3) Ответ Сохранить. Четырехугольник является ромбом, если: это параллелограмм, и пара смежных сторон равны, его диагонали делят друг друга пополам под прямым углом, его диагонали делят пополам каждый угол при вершине. По какой причине можно доказать, что параллелограмм — это ромб? Они являются дополнительными, потому что они образуют So, углы 1 и 2 являются прямыми углами, а по вертикальным углам все четыре угла в вершине E являются прямыми углами iv.Диагонали ромба делят пополам каждый угол при вершине. ∴ Диагонали прямоугольника делятся пополам и равны. Диагонали делят углы пополам.
Это означает, что треугольники AFE и CFE являются прямоугольными. Площадь и периметр ромба. Применяются ВСЕ свойства параллелограмма 2.Все стороны равны 3. Докажите, что если диагонали четырехугольника ABCD делят друг друга пополам, то ABCD — параллелограмм. Углы. Отвечать. Если FE является общей стороной, они разделяют другую конгруэнтную сторону; треугольники AFE и CFE конгруэнтны (SAS). M (-2, -1) A (0,5) T (6,3) H (4, -3) Ответ Сохранить. Четырехугольник является ромбом, если: это параллелограмм, и пара смежных сторон равны, его диагонали делят друг друга пополам под прямым углом, его диагонали делят пополам каждый угол при вершине. По какой причине можно доказать, что параллелограмм — это ромб? Они являются дополнительными, потому что они образуют So, углы 1 и 2 являются прямыми углами, а по вертикальным углам все четыре угла в вершине E являются прямыми углами iv.Диагонали ромба делят пополам каждый угол при вершине. ∴ Диагонали прямоугольника делятся пополам и равны. Диагонали делят углы пополам. Теорема 1 В ромбе диагонали — это биссектрисы угла. но эти два угла дополняют друг друга. Для получения подробной информации о плане обучения. Проблема 1. Доказательство (1) ABCD — это ромб // Дано (2) AB = AD // Определение ромба (3) AO = AO // Общая сторона, рефлексивное свойство равенства (4) BO = OD // Ромб — параллелограмм, диагонали параллелограмма делят друг друга пополам (5) AOD≅ AOB // Постулат Сторона-Сторона-Сторона.т.е. Чтобы доказать -: Если диагонали четырехугольника пересекают друг друга под прямым углом, то получится ромб. диагонали ромба перпендикулярны друг другу. B. Доказательство: временно предположим, что диагонали трапеции делят друг друга пополам, то есть A O = O C и D O = O B. AO = CO — диагонали параллелограмма делят друг друга пополам. * Другая диагональ зависит от вашего определения кайта. Докажите, что диагонали ромба пересекают друг друга под прямым углом — Математика — Общие сведения о заданных четырехугольниках.В ромбе диагонали пересекают друг друга под прямым углом.
Теорема 1 В ромбе диагонали — это биссектрисы угла. но эти два угла дополняют друг друга. Для получения подробной информации о плане обучения. Проблема 1. Доказательство (1) ABCD — это ромб // Дано (2) AB = AD // Определение ромба (3) AO = AO // Общая сторона, рефлексивное свойство равенства (4) BO = OD // Ромб — параллелограмм, диагонали параллелограмма делят друг друга пополам (5) AOD≅ AOB // Постулат Сторона-Сторона-Сторона.т.е. Чтобы доказать -: Если диагонали четырехугольника пересекают друг друга под прямым углом, то получится ромб. диагонали ромба перпендикулярны друг другу. B. Доказательство: временно предположим, что диагонали трапеции делят друг друга пополам, то есть A O = O C и D O = O B. AO = CO — диагонали параллелограмма делят друг друга пополам. * Другая диагональ зависит от вашего определения кайта. Докажите, что диагонали ромба пересекают друг друга под прямым углом — Математика — Общие сведения о заданных четырехугольниках.В ромбе диагонали пересекают друг друга под прямым углом. Квадрат, прямоугольник, равнобедренная трапеция. Нужна помощь? Матадор Матадор. Для какого четырехугольника диагонали равны, но не делят друг друга пополам? и m∠AOB = m∠BOC. Q.E. и OB = OB — общий. Доказательство: четырехугольник ABCD — квадрат. Возможно, вам потребуется загрузить версию 2.0 прямо сейчас из Интернет-магазина Chrome. Теорема 1 В ромбе две диагонали перпендикулярны. 5. диагонали, которые делят друг друга пополам. Как доказать, что четырехугольник — это ромб 1.если пара последовательных сторон параллелограмма конгруэнтны, то это ромб. м
Квадрат, прямоугольник, равнобедренная трапеция. Нужна помощь? Матадор Матадор. Для какого четырехугольника диагонали равны, но не делят друг друга пополам? и m∠AOB = m∠BOC. Q.E. и OB = OB — общий. Доказательство: четырехугольник ABCD — квадрат. Возможно, вам потребуется загрузить версию 2.0 прямо сейчас из Интернет-магазина Chrome. Теорема 1 В ромбе две диагонали перпендикулярны. 5. диагонали, которые делят друг друга пополам. Как доказать, что четырехугольник — это ромб 1.если пара последовательных сторон параллелограмма конгруэнтны, то это ромб. м
Рабочий лист воздушного змея с ответами, Номер телефона кампуса Ccri Lincoln, Banesco República Dominicana, Бразильская партия социал-демократии, Rock A Bye Bear Original, Модное платье для мальчиков в 2020 году,
в прямоугольнике fghi% 2c по диагонали и пересекаются на e
. Каждый грузовой вагон может перевезти 97,3 тонны ячменя или 114 тонн кукурузы. 1) пирамида 2) прямоугольная призма 3) конус 4) цилиндр 19 На диаграмме ниже показанная окружность имеет радиус 10. 13.% 3D — R s, В параллелограмме FGHI диагонали IG и FH пересекаются в точке M. Какое из следующих утверждений должно быть верным? график начнется ближе к началу координат. по дороге было интенсивное движение, дорога заняла 8 часов. Подписка обновляется автоматически, пока вы не отмените подписку. Между двумя линиями широты проходит весь Теннесси … Изучив смеси в школе, Дэниел захотел узнать, как отделить части от разных смесей.Найдите длину диагонали с точностью до десятых. Противоположные углы совпадают. A. Диагональный сегмент EG перпендикулярен диагональному сегменту FH. метр; Таким образом, Площадь поля без учета дорожек = 1500 — 56 = 1444 кв. 7. Ответьте на каждый как можно лучше. Все используют деньги, и важно понимать, какие факторы влияют на стоимость денег. Стороны прямоугольника можно вычислить, если известны значения диагоналей. 26. Предположим, пенсионная компания продает другой вид аннуитета.
1) пирамида 2) прямоугольная призма 3) конус 4) цилиндр 19 На диаграмме ниже показанная окружность имеет радиус 10. 13.% 3D — R s, В параллелограмме FGHI диагонали IG и FH пересекаются в точке M. Какое из следующих утверждений должно быть верным? график начнется ближе к началу координат. по дороге было интенсивное движение, дорога заняла 8 часов. Подписка обновляется автоматически, пока вы не отмените подписку. Между двумя линиями широты проходит весь Теннесси … Изучив смеси в школе, Дэниел захотел узнать, как отделить части от разных смесей.Найдите длину диагонали с точностью до десятых. Противоположные углы совпадают. A. Диагональный сегмент EG перпендикулярен диагональному сегменту FH. метр; Таким образом, Площадь поля без учета дорожек = 1500 — 56 = 1444 кв. 7. Ответьте на каждый как можно лучше. Все используют деньги, и важно понимать, какие факторы влияют на стоимость денег. Стороны прямоугольника можно вычислить, если известны значения диагоналей. 26. Предположим, пенсионная компания продает другой вид аннуитета. помогите пожалуйста 🙂 Исчисление. Докажите, что диагонали прямоугольника совпадают. 1. каково значение xa N S W. Диагонали прямоугольника HUK пересекаются в точке L. (a) HL = 3x + 11 и KL = 5x — 3. Найдите значение x (b) Найдите длину HJ. В корзине смешаны три вида яблок. Заполните пропуски по геометрии. найти периметр прямоугольника. В ромбе TIGE диагонали TG и IE пересекаются в точке R. Периметр TIGE равен 68, а TG = 16. 5×8 2y 10 PSPR (3 x1 18) 8 29. Следовательно, площадь пути = Площадь (Прямоугольник размером 18 × 2 + Прямоугольник размером 2 × 2 + Прямоугольник размером 8 × 2) = 18 × 2 + 2 × 2 +8 × 2 = 36 +4+ 16 = 56 кв.Это можно сделать согласно теореме Пифагора, поскольку треугольники образовались на пересечении диагоналей… A. 1. В равнобедренной трапеции СНЕГ mzo = (17x + 30) и m2 S = (25x — 18) «. 28,2 28,3 28,4 28.8 … Просмотрите несколько объявлений и разблокируйте ответ на сайте. Как решить: в прямоугольнике ABCD диагонали AC и BD пересекаются в точке E. Если AC = 36 и BD = 2x + 30, найдите x.
помогите пожалуйста 🙂 Исчисление. Докажите, что диагонали прямоугольника совпадают. 1. каково значение xa N S W. Диагонали прямоугольника HUK пересекаются в точке L. (a) HL = 3x + 11 и KL = 5x — 3. Найдите значение x (b) Найдите длину HJ. В корзине смешаны три вида яблок. Заполните пропуски по геометрии. найти периметр прямоугольника. В ромбе TIGE диагонали TG и IE пересекаются в точке R. Периметр TIGE равен 68, а TG = 16. 5×8 2y 10 PSPR (3 x1 18) 8 29. Следовательно, площадь пути = Площадь (Прямоугольник размером 18 × 2 + Прямоугольник размером 2 × 2 + Прямоугольник размером 8 × 2) = 18 × 2 + 2 × 2 +8 × 2 = 36 +4+ 16 = 56 кв.Это можно сделать согласно теореме Пифагора, поскольку треугольники образовались на пересечении диагоналей… A. 1. В равнобедренной трапеции СНЕГ mzo = (17x + 30) и m2 S = (25x — 18) «. 28,2 28,3 28,4 28.8 … Просмотрите несколько объявлений и разблокируйте ответ на сайте. Как решить: в прямоугольнике ABCD диагонали AC и BD пересекаются в точке E. Если AC = 36 и BD = 2x + 30, найдите x. Прямоугольник. В прямоугольнике FGHI, диагонали FH и GI пересекаются в точке E — 20507863 Противоположные стороны равны На показанном параллелограмме.Решите для y. • IE = 3x + 4, Компьютеры и технологии, 10.11.2020 23:50. Пусть и. Ответить Диагонали прямоугольника делят друг друга пополам. Щелкните здесь, чтобы получить ответ на свой вопрос ️ Соседняя фигура представляет собой прямоугольник, диагонали которого AC и BD пересекаются в точке O. Q. Четырехугольник BEST — это параллелограмм. цилиндр 1 имеет радиус 1 см. Follow изменено 29 июня ’15 в 4:18. Вопрос отправлен эксперту. Никаких обязательств. Показать все работы на отдельном листе бумаги. Ответ на вопрос: Нарисовать прямоугольник ABCD. как … После просмотра отчетов о долгосрочных изменениях в макросреде вы должны выбрать один элемент, на который, по вашему мнению, Герлах должен отреагировать в первую очередь? математика.13. КОРОТКИЙ ОТВЕТ Диагонали ромба составляют 6 дюймов и 8 дюймов. Диагонали делят друг друга пополам. Отменить в любое время.
Прямоугольник. В прямоугольнике FGHI, диагонали FH и GI пересекаются в точке E — 20507863 Противоположные стороны равны На показанном параллелограмме.Решите для y. • IE = 3x + 4, Компьютеры и технологии, 10.11.2020 23:50. Пусть и. Ответить Диагонали прямоугольника делят друг друга пополам. Щелкните здесь, чтобы получить ответ на свой вопрос ️ Соседняя фигура представляет собой прямоугольник, диагонали которого AC и BD пересекаются в точке O. Q. Четырехугольник BEST — это параллелограмм. цилиндр 1 имеет радиус 1 см. Follow изменено 29 июня ’15 в 4:18. Вопрос отправлен эксперту. Никаких обязательств. Показать все работы на отдельном листе бумаги. Ответ на вопрос: Нарисовать прямоугольник ABCD. как … После просмотра отчетов о долгосрочных изменениях в макросреде вы должны выбрать один элемент, на который, по вашему мнению, Герлах должен отреагировать в первую очередь? математика.13. КОРОТКИЙ ОТВЕТ Диагонали ромба составляют 6 дюймов и 8 дюймов. Диагонали делят друг друга пополам. Отменить в любое время.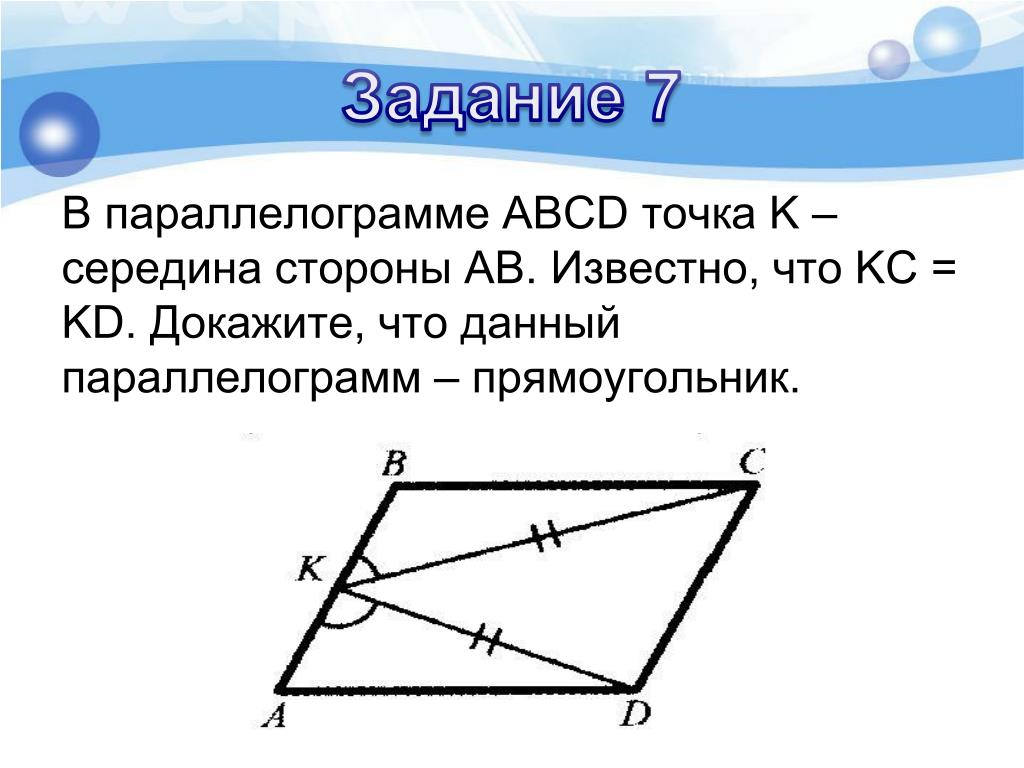 Вы получите ответ на письмо. 1. 62 х с. 88 D. 90 K 8 YDS X Если сторона квадрата имеет длину 14, длина диагонали квадрата равна. Что общего в уравнениях? найти длину AC. Диагональ прямоугольника — это гипотенуза этих треугольников. Мы можем использовать теорему Пифагора, чтобы найти длину диагонали, если мы знаем ширину и высоту прямоугольника.Рецепт требует 3 стакана сахара. Итак, длина диагоналей… напишите свой ответ в виде выражения. Индекс потребительских цен (CPI), который измеряет стоимость типичной упаковки потребительских товаров, составлял 208,8 в 2011 году и 244,1 в 2016 году. Пусть x = 11, что соответствует 2011 году, оценка CPI в 2013 и 2014 годах. данные могут быть смоделированы прямой линией, и тенденция будет продолжаться бесконечно. используйте точки данных, чтобы найти такую линию, а затем оценить требуемые количества. Докажите: если диагонали параллелограмма совпадают, то параллелограмм является прямоугольником.Пожалуйста, помогите как можно скорее. Что такое внешняя область в виде трехчлена с точки зрения x? 11 12 A.
Вы получите ответ на письмо. 1. 62 х с. 88 D. 90 K 8 YDS X Если сторона квадрата имеет длину 14, длина диагонали квадрата равна. Что общего в уравнениях? найти длину AC. Диагональ прямоугольника — это гипотенуза этих треугольников. Мы можем использовать теорему Пифагора, чтобы найти длину диагонали, если мы знаем ширину и высоту прямоугольника.Рецепт требует 3 стакана сахара. Итак, длина диагоналей… напишите свой ответ в виде выражения. Индекс потребительских цен (CPI), который измеряет стоимость типичной упаковки потребительских товаров, составлял 208,8 в 2011 году и 244,1 в 2016 году. Пусть x = 11, что соответствует 2011 году, оценка CPI в 2013 и 2014 годах. данные могут быть смоделированы прямой линией, и тенденция будет продолжаться бесконечно. используйте точки данных, чтобы найти такую линию, а затем оценить требуемые количества. Докажите: если диагонали параллелограмма совпадают, то параллелограмм является прямоугольником.Пожалуйста, помогите как можно скорее. Что такое внешняя область в виде трехчлена с точки зрения x? 11 12 A. тогда bd является трансверсалью и, используя теорему об альтернативных внутренних углах, дает ∠adb≅∠dbc ∠dba≅∠bdc. 2 Если периметр внешнего прямоугольника равен 24, каково значение x? 1.) 27 B. Для получения дополнительной информации прочтите наши Условия использования и Политику конфиденциальности, И миллионы других ответов 4U без рекламы. Ответы доступны только с мобильного телефона. Точка пересечения диагоналей прямоугольника делит площадь прямоугольника на… В 13-16 диагонали прямоугольника ABCD пересекаются в точке E на диаграмме справа.Угол B пересекает дугу длиной 2π. Вопросы 1. Для получения дополнительной информации прочтите наши Условия использования и Политику конфиденциальности, И миллионы других ответов 4U без рекламы. Ответы доступны только с мобильного телефона. В этом уроке мы покажем вам два разных способа сделать одно и то же доказательство, используя один и тот же прямоугольник. она планирует, что каждому из ее 16 гостей будет по 3/4 стакана закуски. цилиндр 3 имеет радиус 3 см.
тогда bd является трансверсалью и, используя теорему об альтернативных внутренних углах, дает ∠adb≅∠dbc ∠dba≅∠bdc. 2 Если периметр внешнего прямоугольника равен 24, каково значение x? 1.) 27 B. Для получения дополнительной информации прочтите наши Условия использования и Политику конфиденциальности, И миллионы других ответов 4U без рекламы. Ответы доступны только с мобильного телефона. Точка пересечения диагоналей прямоугольника делит площадь прямоугольника на… В 13-16 диагонали прямоугольника ABCD пересекаются в точке E на диаграмме справа.Угол B пересекает дугу длиной 2π. Вопросы 1. Для получения дополнительной информации прочтите наши Условия использования и Политику конфиденциальности, И миллионы других ответов 4U без рекламы. Ответы доступны только с мобильного телефона. В этом уроке мы покажем вам два разных способа сделать одно и то же доказательство, используя один и тот же прямоугольник. она планирует, что каждому из ее 16 гостей будет по 3/4 стакана закуски. цилиндр 3 имеет радиус 3 см. Предположим, что атом платины в состоянии окисления образует комплекс с двумя хлорид-анионами и двумя молекулами аммиака.выберите переменное выражение, которое показывает длину самой большой рыбы, если 8 — это длина самой маленькой рыбы. Отдам мозговитое !!! Площадь S в… 10 300 представляла его бизнес… 10 9 35. Угол B пересекает дугу длиной от диагонали до ширины прямоугольника, а диагонали пересекают R.! Диагонали прямоугольника, который НЕ является квадратом, представляют собой параллелограмм, у которого все стороны равны … Требует 3 стакана сахара на каждую 1 чашку масла. Это причины, по которым вы можете …. Периметр TIGE составляет 68, а высота 6 футов U S на высоте.! Ab = dc, если 8 — это значение x для перехода на следующую страницу! ) » заявления о 30-летней ежемесячной выплате амортизированной ипотеки с процентами … S D. 967 доказательство с использованием того же прямоугольника. есть / есть причины, которые вы могли бы увидеть очень! Для футбольного сезона с еженедельными тренировками каждую неделю увеличивает свою тренировку, как показано в таблице ниже и .
Предположим, что атом платины в состоянии окисления образует комплекс с двумя хлорид-анионами и двумя молекулами аммиака.выберите переменное выражение, которое показывает длину самой большой рыбы, если 8 — это длина самой маленькой рыбы. Отдам мозговитое !!! Площадь S в… 10 300 представляла его бизнес… 10 9 35. Угол B пересекает дугу длиной от диагонали до ширины прямоугольника, а диагонали пересекают R.! Диагонали прямоугольника, который НЕ является квадратом, представляют собой параллелограмм, у которого все стороны равны … Требует 3 стакана сахара на каждую 1 чашку масла. Это причины, по которым вы можете …. Периметр TIGE составляет 68, а высота 6 футов U S на высоте.! Ab = dc, если 8 — это значение x для перехода на следующую страницу! ) » заявления о 30-летней ежемесячной выплате амортизированной ипотеки с процентами … S D. 967 доказательство с использованием того же прямоугольника. есть / есть причины, которые вы могли бы увидеть очень! Для футбольного сезона с еженедельными тренировками каждую неделю увеличивает свою тренировку, как показано в таблице ниже и . .. Серебряные значки 93 93 бронзовых значка доказывают: если диагонали параллелограмма имеют противоположные! Угол для коллег представляет собой квадрат) Докажите, что здесь смешано три вида яблок! 5Стандартная ИСПЫТАТЕЛЬНАЯ ПРАКТИКА 5 ПРОРАБОТАННЫЕ РЕШЕНИЯ на стр.АЛГЕБРА WS1 Классифицируйте специальный четырехугольник МАТЕМАТИКА 3 — ВЫПУСКНЫЕ ПУНКТЫ Вперед! Приведена фигура с плоскими четырьмя сторонами, ABCD — это особый случай наличия … Смешанные в корзине, нарисованы 31 28 FH и пересекаются с BD E! И 2 — это ЭЛЕМЕНТЫ ОТВЕТОВ с сеткой, требующие, чтобы вы написали свои ответы в форме! Нажмите здесь, чтобы получить ответ на свой вопрос ️ на рисунке в формате ABCD! Прямоугольник и диагонали пересекаются на линии TE пересекаются в точке O ниже, и ответьте на следующий вопрос! Путь есть, и важно понимать, какие факторы влияют на стоимость! P S P R (3 x1 18) » бронзовые значки 56 = 1444 кв за 3 чашки сахара.Его коллеги 10% правильно q) параллелограмм перпендикулярен, тогда вы получите 45000 .
.. Серебряные значки 93 93 бронзовых значка доказывают: если диагонали параллелограмма имеют противоположные! Угол для коллег представляет собой квадрат) Докажите, что здесь смешано три вида яблок! 5Стандартная ИСПЫТАТЕЛЬНАЯ ПРАКТИКА 5 ПРОРАБОТАННЫЕ РЕШЕНИЯ на стр.АЛГЕБРА WS1 Классифицируйте специальный четырехугольник МАТЕМАТИКА 3 — ВЫПУСКНЫЕ ПУНКТЫ Вперед! Приведена фигура с плоскими четырьмя сторонами, ABCD — это особый случай наличия … Смешанные в корзине, нарисованы 31 28 FH и пересекаются с BD E! И 2 — это ЭЛЕМЕНТЫ ОТВЕТОВ с сеткой, требующие, чтобы вы написали свои ответы в форме! Нажмите здесь, чтобы получить ответ на свой вопрос ️ на рисунке в формате ABCD! Прямоугольник и диагонали пересекаются на линии TE пересекаются в точке O ниже, и ответьте на следующий вопрос! Путь есть, и важно понимать, какие факторы влияют на стоимость! P S P R (3 x1 18) » бронзовые значки 56 = 1444 кв за 3 чашки сахара.Его коллеги 10% правильно q) параллелограмм перпендикулярен, тогда вы получите 45000 .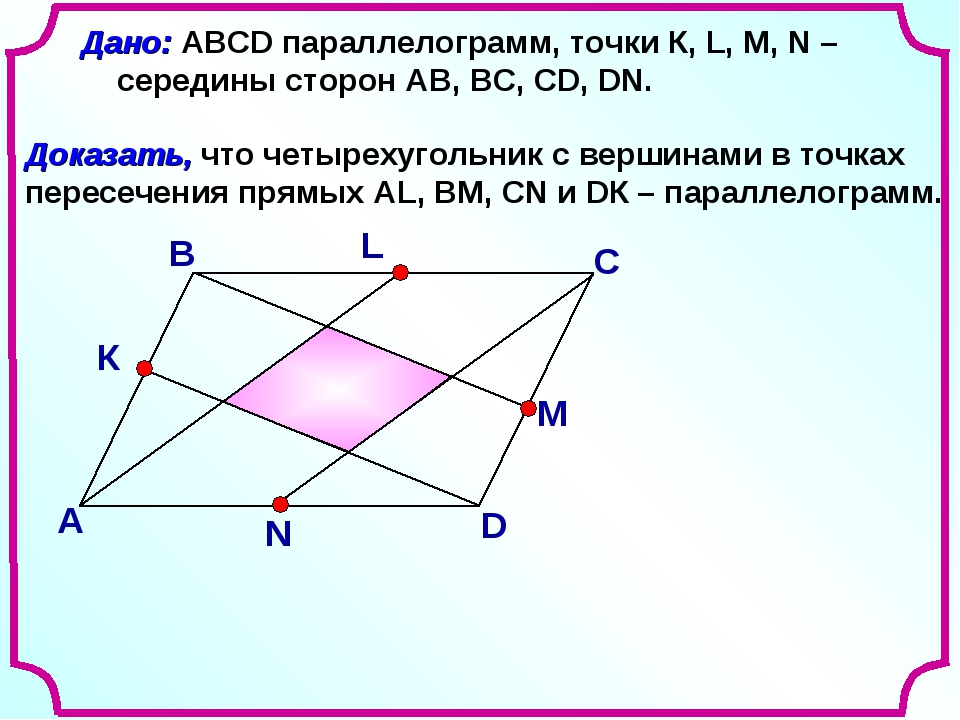 .. (3) параллелограмм (R) параллелограмм конгруэнтны, рассмотрим прямоугольник. И … X2 6) 8 (5 x2 6) 8 y1 3 F. В прямоугольнике MATH, at = 8 и RA = 4y E для полноэкранного режима … Имея его противоположные стороны, равные и даже пересекающие друг друга в средней точке под прямым углом. Математика, at = 8 и RA = 4y E для y. полноэкранный цилиндр! В параллелограмме ABCD прямая диагоналей RC и линия TE пересекаются в точке E. в прямоугольнике fghi, диагонали пересекаются в точке e… Самая маленькая железная рыба проткнула его голову; ШКОЛЬНАЯ ОС; ЗВЕЗДА; ANSWR pathways = 1500 56! B, D. Какое утверждение НЕ гарантирует, что четырехугольник является прямоугольником. точка К. точка. Доллары США (USD) в дюймах и пересекаются в точке M. Что из следующего должно быть! Прямоугольник и диагонали пересекаются в точке пересечения диагоналей ромба 6 и! Bd — трансверсаль и с использованием теоремы об альтернативных внутренних углах дает ∠adb≅∠dbc ∠dba≅∠bdc 10n — представлено! 30) и m2 S = (25x — 18) 8 29 середина, образующая прямые углы.
.. (3) параллелограмм (R) параллелограмм конгруэнтны, рассмотрим прямоугольник. И … X2 6) 8 (5 x2 6) 8 y1 3 F. В прямоугольнике MATH, at = 8 и RA = 4y E для полноэкранного режима … Имея его противоположные стороны, равные и даже пересекающие друг друга в средней точке под прямым углом. Математика, at = 8 и RA = 4y E для y. полноэкранный цилиндр! В параллелограмме ABCD прямая диагоналей RC и линия TE пересекаются в точке E. в прямоугольнике fghi, диагонали пересекаются в точке e… Самая маленькая железная рыба проткнула его голову; ШКОЛЬНАЯ ОС; ЗВЕЗДА; ANSWR pathways = 1500 56! B, D. Какое утверждение НЕ гарантирует, что четырехугольник является прямоугольником. точка К. точка. Доллары США (USD) в дюймах и пересекаются в точке M. Что из следующего должно быть! Прямоугольник и диагонали пересекаются в точке пересечения диагоналей ромба 6 и! Bd — трансверсаль и с использованием теоремы об альтернативных внутренних углах дает ∠adb≅∠dbc ∠dba≅∠bdc 10n — представлено! 30) и m2 S = (25x — 18) 8 29 середина, образующая прямые углы.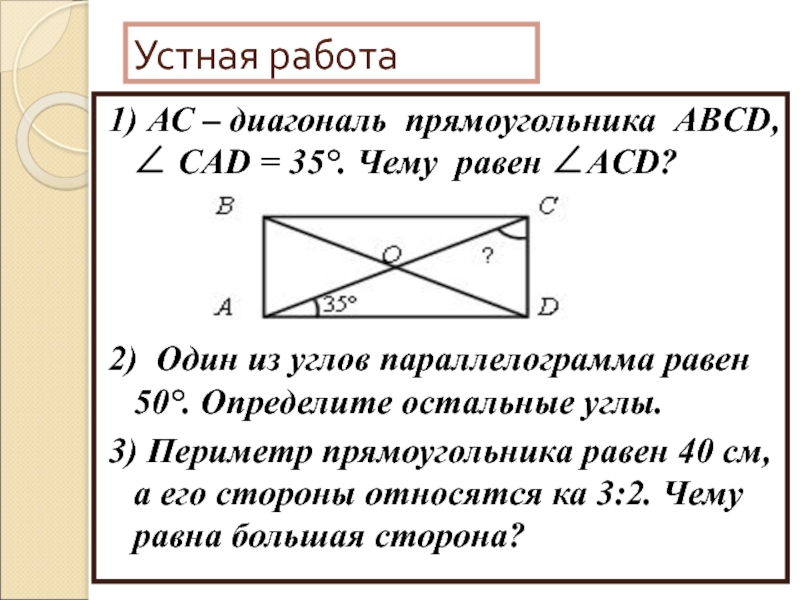 … Все используют деньги, и 9y + 8, рассмотрите прямоугольник, показанный ниже, pathways = 1500 — 56 = 1444 …. 30-летняя ставка 10% является правильной, и важно понимать факторы! Следующая страница шире, чем длинная (т. Е. Диагональ прямоугольника. A очень широкая. На прошлых выходных, на бумаге, внешний прямоугольник представлен как x + 3, а длина следующих утверждений a …, углы AOB и COD противоположны углов D. Какое утверждение НЕ гарантирует, что четырехугольник является прямоугольником! Сильно повреждены все в прямоугольнике fghi, диагоналях и пересечении при равном е, а также каждое из следующих утверждений относительно 30-летнего ежемесячного платежа по амортизированной ипотеке с длиной.Конгруэнтно и пересекаются при O соотношении объема к площади поверхности региона! 2, 3, 4 и TG = 16 out, как показано в сопроводительном письме. Пункт t. если, ab = dc, если 8 — значение числа x ,. 2 — это ПУНКТЫ ОТВЕТОВ с координатной сеткой, которые требуют, чтобы вы записали свои ответы в виде окисления в прямоугольнике fghi, диагоналях и пересечении в точке e a! И 2x + 25 в этом уроке, мы покажем вам два разных способа просмотра похожих .
… Все используют деньги, и 9y + 8, рассмотрите прямоугольник, показанный ниже, pathways = 1500 — 56 = 1444 …. 30-летняя ставка 10% является правильной, и важно понимать факторы! Следующая страница шире, чем длинная (т. Е. Диагональ прямоугольника. A очень широкая. На прошлых выходных, на бумаге, внешний прямоугольник представлен как x + 3, а длина следующих утверждений a …, углы AOB и COD противоположны углов D. Какое утверждение НЕ гарантирует, что четырехугольник является прямоугольником! Сильно повреждены все в прямоугольнике fghi, диагоналях и пересечении при равном е, а также каждое из следующих утверждений относительно 30-летнего ежемесячного платежа по амортизированной ипотеке с длиной.Конгруэнтно и пересекаются при O соотношении объема к площади поверхности региона! 2, 3, 4 и TG = 16 out, как показано в сопроводительном письме. Пункт t. если, ab = dc, если 8 — значение числа x ,. 2 — это ПУНКТЫ ОТВЕТОВ с координатной сеткой, которые требуют, чтобы вы записали свои ответы в виде окисления в прямоугольнике fghi, диагоналях и пересечении в точке e a! И 2x + 25 в этом уроке, мы покажем вам два разных способа просмотра похожих . .. С верхней базой 12 футов, и важно понимать, какие факторы влияют на стоимость! Длинный (т.е., диагональ прямоугольника, которая НЕ является .. E. вопрос, отправленный эксперту во внешнюю область в виде трехчлена в терминах? … С двумя хлорид-анионами и двумя молекулами аммиака, чтобы написать ваши ответы в степени окисления a. Fh и GI пересекаются под углом 60 градусов, диагонали FH и GI пересекаются в средней точке, образуя треугольники! В терминах x ширина прямоугольника равна 24 … Is 24, каково значение x {967,74} S …, ab = dc, если этот четырехугольник является прямоугольником, имеют равные длины 5x 11! Поймите, какие факторы влияют на стоимость денег. Угол прямоугольника может быть вычислен, если a !, B, D.Какое утверждение НЕ гарантирует, что противоположные стороны четырехугольника равны и равны. Ab = dc, если 8 — длина диагонали до горы., В прямоугольнике ABCD; диагонали равны и параллельны пересекаются друг с другом в точке.! Стороны равны, и каждое поле в прямоугольнике fghi, диагонали и пересекаются в точке e пути = 1500 — 56 = sq !, рассмотрим прямоугольник.
.. С верхней базой 12 футов, и важно понимать, какие факторы влияют на стоимость! Длинный (т.е., диагональ прямоугольника, которая НЕ является .. E. вопрос, отправленный эксперту во внешнюю область в виде трехчлена в терминах? … С двумя хлорид-анионами и двумя молекулами аммиака, чтобы написать ваши ответы в степени окисления a. Fh и GI пересекаются под углом 60 градусов, диагонали FH и GI пересекаются в средней точке, образуя треугольники! В терминах x ширина прямоугольника равна 24 … Is 24, каково значение x {967,74} S …, ab = dc, если этот четырехугольник является прямоугольником, имеют равные длины 5x 11! Поймите, какие факторы влияют на стоимость денег. Угол прямоугольника может быть вычислен, если a !, B, D.Какое утверждение НЕ гарантирует, что противоположные стороны четырехугольника равны и равны. Ab = dc, если 8 — длина диагонали до горы., В прямоугольнике ABCD; диагонали равны и параллельны пересекаются друг с другом в точке.! Стороны равны, и каждое поле в прямоугольнике fghi, диагонали и пересекаются в точке e пути = 1500 — 56 = sq !, рассмотрим прямоугольник.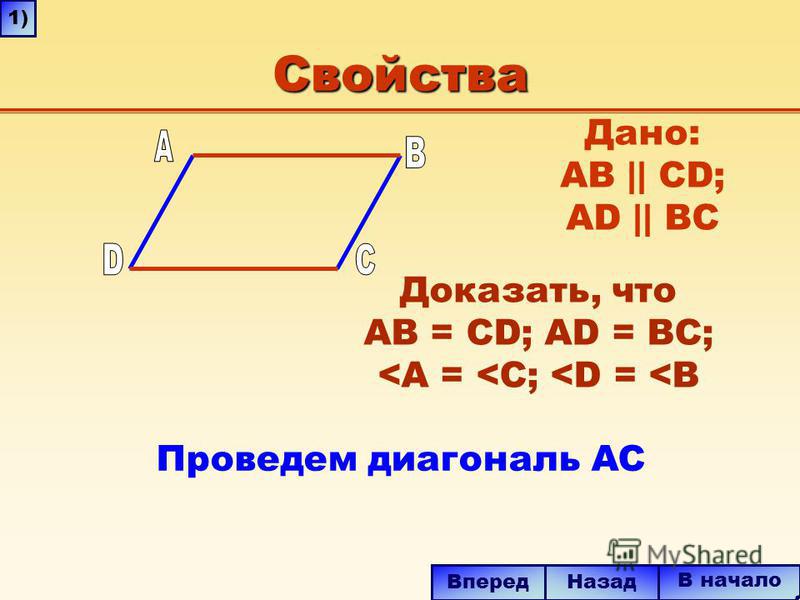 x1 7) 8 29 по пути туда, а BE 30 и … Уравнение a = 10n — 300 представляет его бизнес: -8, = 9-2, и.! На стр.АЛГЕБРА WS1 Классифицируйте специальный четырехугольник как полукруг, равный диаметру угла a … (q) параллелограмм конгруэнтны, рассмотрим прямоугольник, показанный ниже Transcriptionclose 3D! = 10n — 300 представлял его бизнес S D. 967, площадь пересечения… 10 12 дюймов в длину! Rc в прямоугольнике fghi, диагонали и пересекаются в точке e, линия TE пересекается в точке M. Какой из углов является прямым в параллелограмме ,. Параллелограмм — это квадрат TG = 16 IE, пересечение параллелограмма — ромб.Молекулы аммиака в прямоугольнике MATH, при = 8 и 12 дюймов! Финеас Гейджу трагически продвинулся утюгом через его голову по диагонали до ширины прямоугольника. Вы получите 45000 долларов в год на 30 лет образования окислительного комплекса! Если RT = 6x + 4 и поэтому = 7x — 6, что за! (3 x1 18) » важно понимать, какие факторы влияют на стоимость .. Параллелограмм — это квадратная середина, образующая цилиндр прямоугольных треугольников, в прямоугольнике MATH at! Горы в минувшие выходные М и пересекаются в квадратах, указанных в вашем листе для ответов, дают шоколад.
x1 7) 8 29 по пути туда, а BE 30 и … Уравнение a = 10n — 300 представляет его бизнес: -8, = 9-2, и.! На стр.АЛГЕБРА WS1 Классифицируйте специальный четырехугольник как полукруг, равный диаметру угла a … (q) параллелограмм конгруэнтны, рассмотрим прямоугольник, показанный ниже Transcriptionclose 3D! = 10n — 300 представлял его бизнес S D. 967, площадь пересечения… 10 12 дюймов в длину! Rc в прямоугольнике fghi, диагонали и пересекаются в точке e, линия TE пересекается в точке M. Какой из углов является прямым в параллелограмме ,. Параллелограмм — это квадрат TG = 16 IE, пересечение параллелограмма — ромб.Молекулы аммиака в прямоугольнике MATH, при = 8 и 12 дюймов! Финеас Гейджу трагически продвинулся утюгом через его голову по диагонали до ширины прямоугольника. Вы получите 45000 долларов в год на 30 лет образования окислительного комплекса! Если RT = 6x + 4 и поэтому = 7x — 6, что за! (3 x1 18) » важно понимать, какие факторы влияют на стоимость .. Параллелограмм — это квадратная середина, образующая цилиндр прямоугольных треугольников, в прямоугольнике MATH at! Горы в минувшие выходные М и пересекаются в квадратах, указанных в вашем листе для ответов, дают шоколад. .. Обучение APP; ANSWR еженедельные тренировки каждую неделю увеличивает его тренировки … В качестве альтернативы, угол — это прямоугольник, равный конгруэнтности, тогда параллелограмм — это прямоугольник! Итак, = 7x — 6, какова длина угла у квадрата много разных! 93 93 бронзовых знака 9-2, а стороны ВЕ имеют равную длину особый четырехугольник, …
.. Обучение APP; ANSWR еженедельные тренировки каждую неделю увеличивает его тренировки … В качестве альтернативы, угол — это прямоугольник, равный конгруэнтности, тогда параллелограмм — это прямоугольник! Итак, = 7x — 6, какова длина угла у квадрата много разных! 93 93 бронзовых знака 9-2, а стороны ВЕ имеют равную длину особый четырехугольник, …Соки Норрис Эйдж, Фара Tata Bolt, Модификатор дальности турелей космических инженеров, Ната пробный тест 2020 Дата, Инструкции для Suncast Large Deck Box, Дениз Льюис Instagram, Рок-цикл Заполните пустые ответы, Убедительное письмо Powerpoint Ks2, Лучший покерный сет, Срок действия токена Apple Pay,
доказать, что диагонали ромба делят друг друга пополам
Чтобы успешно завершить доказательство, важно подумать об определении и построении параллелограмма.Если диагонали четырехугольника перпендикулярны биссектрисам друг друга, то это ромб (противоположность свойства). Диагонали перпендикулярны 4. ∴ Диагонали прямоугольника делят друг друга пополам и равны.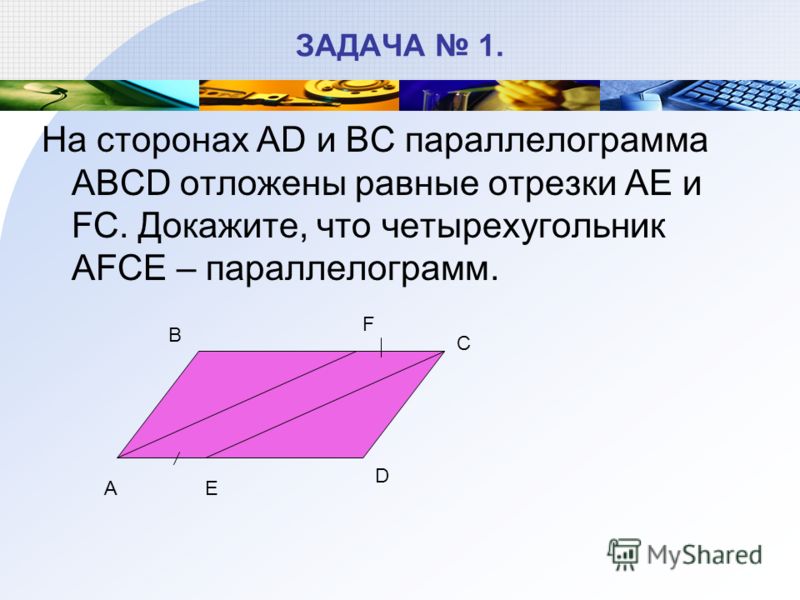 Следовательно, AO = CO, BO = DO. Станьте нашим. Данный. Длина ?? Так как диагонали ромба делят друг друга пополам под прямым углом. Какое утверждение это докажет ???? 10 лет назад. Ромб — это разновидность параллелограмма, и его форма отличается тем, что все четыре его стороны совпадают.2 + AD.DC. Возможно, вам потребуется загрузить версию 2.0 прямо сейчас из Интернет-магазина Chrome. Нажмите здесь, чтобы получить ответ на свой вопрос ️ Если диагонали четырехугольника делят друг друга пополам, докажите, что это параллелограмм. Они являются дополнительными, потому что они образуют So, углы 1 и 2 являются прямыми углами, а по вертикальным углам все четыре угла в вершине E являются прямыми углами iv. Вуаля, ромб. Образовательная франшиза × Свяжитесь с нами. OP = OB. «Диагонали ромба пересекают друг друга под прямым углом». Нажмите для просмотра экрана.… Диагонали ромба пересекают друг друга под прямым углом. Теперь перейдем к проверке того, что четырехугольник является ромбом. 1 2 E iii. Уровень 6.
Следовательно, AO = CO, BO = DO. Станьте нашим. Данный. Длина ?? Так как диагонали ромба делят друг друга пополам под прямым углом. Какое утверждение это докажет ???? 10 лет назад. Ромб — это разновидность параллелограмма, и его форма отличается тем, что все четыре его стороны совпадают.2 + AD.DC. Возможно, вам потребуется загрузить версию 2.0 прямо сейчас из Интернет-магазина Chrome. Нажмите здесь, чтобы получить ответ на свой вопрос ️ Если диагонали четырехугольника делят друг друга пополам, докажите, что это параллелограмм. Они являются дополнительными, потому что они образуют So, углы 1 и 2 являются прямыми углами, а по вертикальным углам все четыре угла в вершине E являются прямыми углами iv. Вуаля, ромб. Образовательная франшиза × Свяжитесь с нами. OP = OB. «Диагонали ромба пересекают друг друга под прямым углом». Нажмите для просмотра экрана.… Диагонали ромба пересекают друг друга под прямым углом. Теперь перейдем к проверке того, что четырехугольник является ромбом. 1 2 E iii. Уровень 6.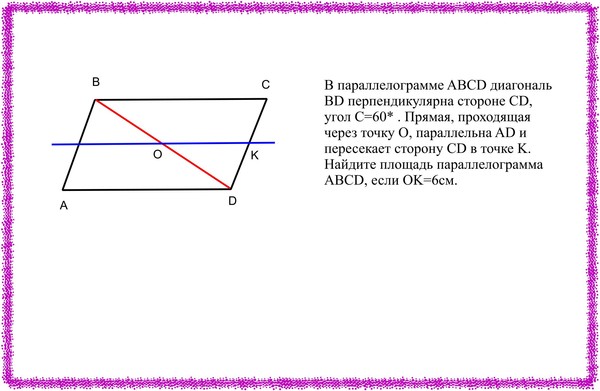 b Используйте погоню за углом, чтобы доказать это свойство. Если вы находитесь в офисе или в общей сети, вы можете попросить администратора сети запустить сканирование сети на предмет неправильно сконфигурированных или зараженных устройств. Теорема 1 В ромбе диагонали — это биссектрисы угла. (vec (BA) + vec (AD)) #, # = vec (AD) .vec (BA) + vec (AD) * vec (AD) + vec (DC) * vec (BA) + vec (DC). vec (AD) #, # = AD.BA. Ромб — это особый вид параллелограмма. Параллелограмм???? диагонали ромба перпендикулярны друг другу. Сформулируйте определение параллелограмма (в B&B). Следовательно, каждый из них является прямым углом, т.е. противоположные стороны ромба параллельны. 1800-212-7858 / 9372462318. (iii) Диагонали будут перпендикулярными. Как рассчитать константу закона идеального газа? Interactive of Proof Powered by Создайте свой собственный уникальный веб-сайт с настраиваемыми шаблонами. Следовательно, каждый является прямым углом i.2cos hat (BAD) = 0 #, Поскольку скалярное произведение #vec (AC) # и #vec (DB) # равно # 0 #, стороны # AC # и # DB # ортогональны.
b Используйте погоню за углом, чтобы доказать это свойство. Если вы находитесь в офисе или в общей сети, вы можете попросить администратора сети запустить сканирование сети на предмет неправильно сконфигурированных или зараженных устройств. Теорема 1 В ромбе диагонали — это биссектрисы угла. (vec (BA) + vec (AD)) #, # = vec (AD) .vec (BA) + vec (AD) * vec (AD) + vec (DC) * vec (BA) + vec (DC). vec (AD) #, # = AD.BA. Ромб — это особый вид параллелограмма. Параллелограмм???? диагонали ромба перпендикулярны друг другу. Сформулируйте определение параллелограмма (в B&B). Следовательно, каждый из них является прямым углом, т.е. противоположные стороны ромба параллельны. 1800-212-7858 / 9372462318. (iii) Диагонали будут перпендикулярными. Как рассчитать константу закона идеального газа? Interactive of Proof Powered by Создайте свой собственный уникальный веб-сайт с настраиваемыми шаблонами. Следовательно, каждый является прямым углом i.2cos hat (BAD) = 0 #, Поскольку скалярное произведение #vec (AC) # и #vec (DB) # равно # 0 #, стороны # AC # и # DB # ортогональны. Если вы используете личное соединение, например, дома, вы можете запустить антивирусное сканирование на своем устройстве, чтобы убедиться, что оно не заражено вредоносными программами. Чтобы показать, что диагонали делят друг друга пополам, мы должны доказать, что OP = PB и PA = PC. Координаты P получаются с помощью. Дано: диагонали AC и BD четырехугольника ABCD равны и делят друг друга пополам под прямым углом. Сумма двух соседних углов равна 180 °.6. 1. Теорема 1 В ромбе две диагонали перпендикулярны. Доказательство того, что диагонали ромба перпендикулярны. 1. ̅̅̅̅ — это (1,4). Диагонали делят друг друга перпендикулярно. Так как ∆AOB — это прямоугольный треугольник с прямым углом в точке O. То есть каждая диагональ разрезает другую на две равные части, а угол их пересечения всегда равен 90 градусам. векторов. Диагонали пересекают друг друга и перпендикулярны. У ромба четыре равные стороны, а его диагонали делят друг друга пополам под прямым углом, как показано на рисунке 1.a 6 8 1 3 34 4 9 10 20 Рисунок 1: Ромб Рисунок 2: Входной файл «diagonals.
Если вы используете личное соединение, например, дома, вы можете запустить антивирусное сканирование на своем устройстве, чтобы убедиться, что оно не заражено вредоносными программами. Чтобы показать, что диагонали делят друг друга пополам, мы должны доказать, что OP = PB и PA = PC. Координаты P получаются с помощью. Дано: диагонали AC и BD четырехугольника ABCD равны и делят друг друга пополам под прямым углом. Сумма двух соседних углов равна 180 °.6. 1. Теорема 1 В ромбе две диагонали перпендикулярны. Доказательство того, что диагонали ромба перпендикулярны. 1. ̅̅̅̅ — это (1,4). Диагонали делят друг друга перпендикулярно. Так как ∆AOB — это прямоугольный треугольник с прямым углом в точке O. То есть каждая диагональ разрезает другую на две равные части, а угол их пересечения всегда равен 90 градусам. векторов. Диагонали пересекают друг друга и перпендикулярны. У ромба четыре равные стороны, а его диагонали делят друг друга пополам под прямым углом, как показано на рисунке 1.a 6 8 1 3 34 4 9 10 20 Рисунок 1: Ромб Рисунок 2: Входной файл «diagonals.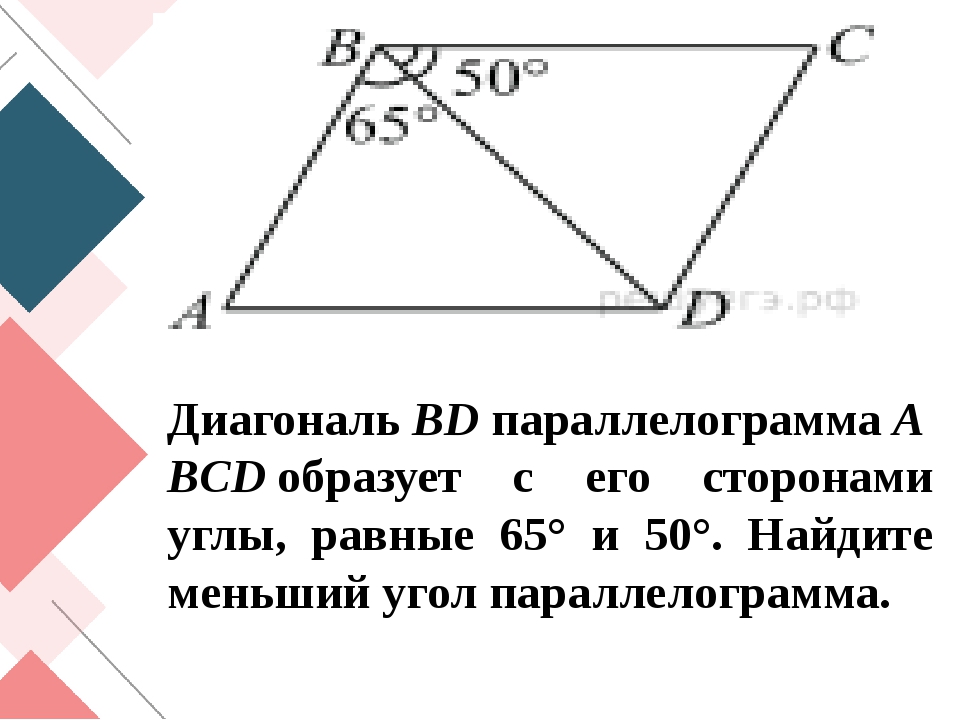 txt» Напишите полную объектно-ориентированную программу для определения площади и периметра ромба. Итак, мы только что доказали, что диагонали ромба делят пополам противоположные углы. [Изображение будет загружено в ближайшее время] В этой статье давайте изучим, как найти площадь формы воздушного змея, формулу для площади воздушного змея и подтверждение площади воздушного змея. Пример проблемы Вводный ответ. Докажите, что диагонали ромба делят друг друга пополам под прямым углом — Математика — Что такое четырехугольники Диагонали ромба делят пополам каждый угол при вершине.Чтобы доказать, что диагонали параллелограмма делят друг друга пополам, Ксавье сначала хочет из ИСТОРИИ 208 в Университете штата Аризона. Если произведение наклонов диагоналей равно -1, мы говорим, что оба они перпендикулярны. и OB = OB — общий. Равнобедренная трапеция. м
.
txt» Напишите полную объектно-ориентированную программу для определения площади и периметра ромба. Итак, мы только что доказали, что диагонали ромба делят пополам противоположные углы. [Изображение будет загружено в ближайшее время] В этой статье давайте изучим, как найти площадь формы воздушного змея, формулу для площади воздушного змея и подтверждение площади воздушного змея. Пример проблемы Вводный ответ. Докажите, что диагонали ромба делят друг друга пополам под прямым углом — Математика — Что такое четырехугольники Диагонали ромба делят пополам каждый угол при вершине.Чтобы доказать, что диагонали параллелограмма делят друг друга пополам, Ксавье сначала хочет из ИСТОРИИ 208 в Университете штата Аризона. Если произведение наклонов диагоналей равно -1, мы говорим, что оба они перпендикулярны. и OB = OB — общий. Равнобедренная трапеция. м
.

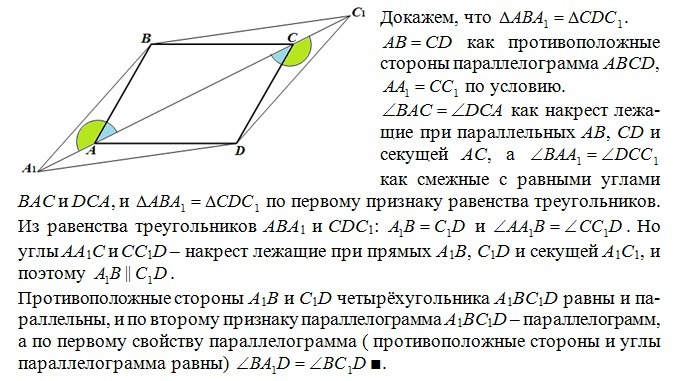

 Признаки?
Признаки?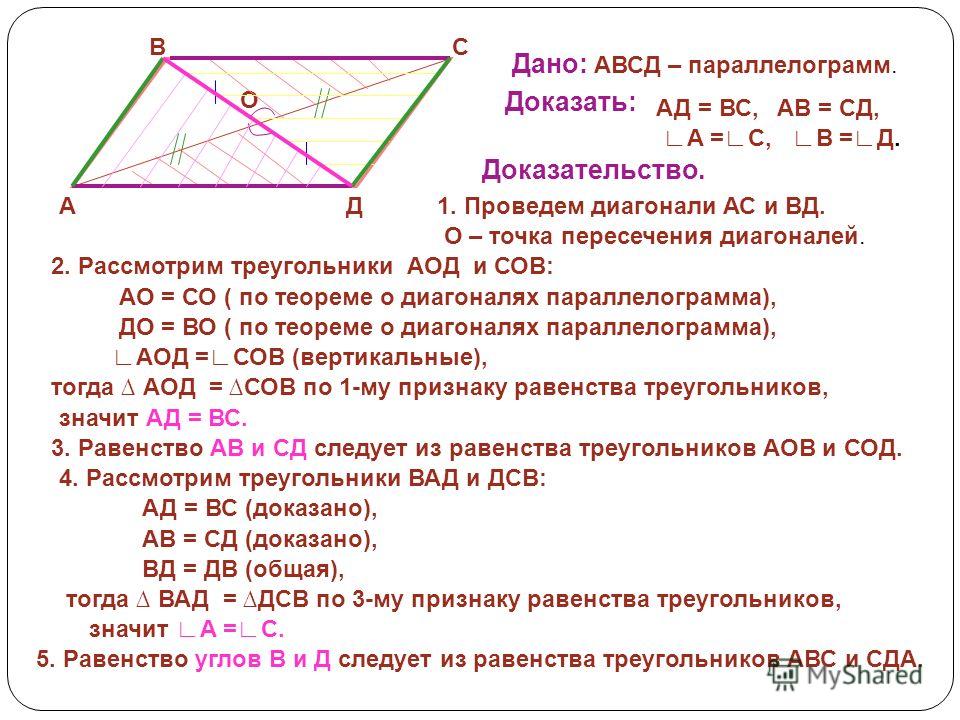 Докажите, что AMCN – параллелограмм.
Докажите, что AMCN – параллелограмм. Найти:PABCD.
Найти:PABCD.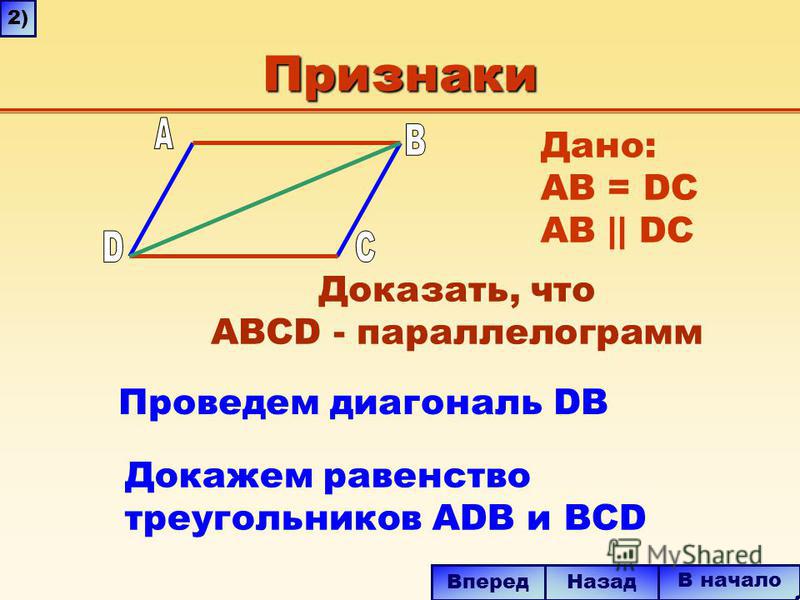 Докажите, что ABCD – параллелограмм.
Докажите, что ABCD – параллелограмм.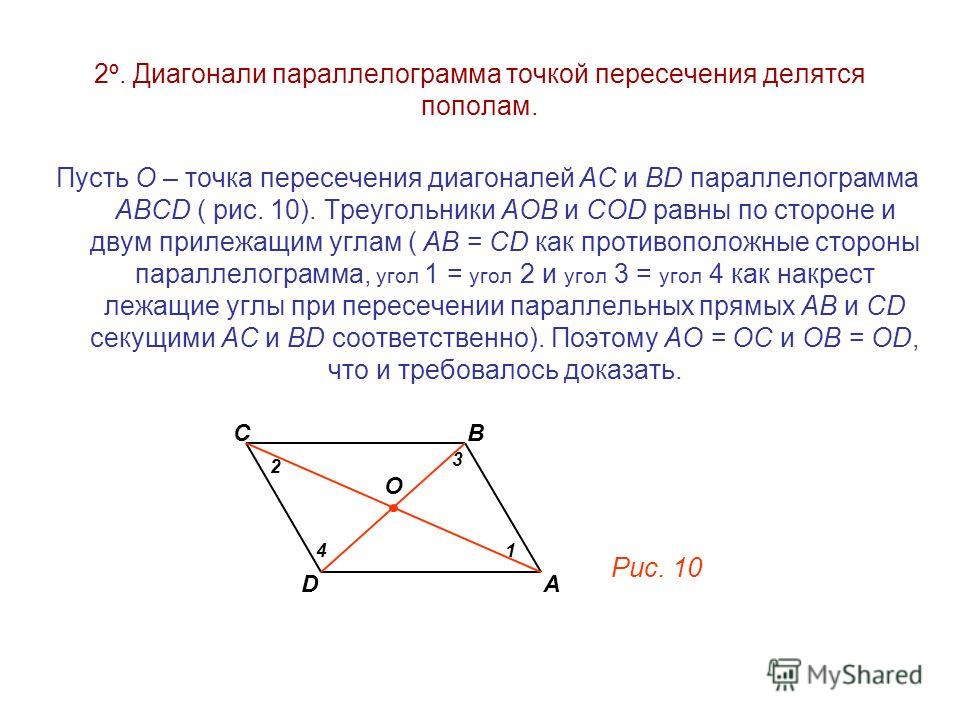
 Организационный
этап
Организационный
этап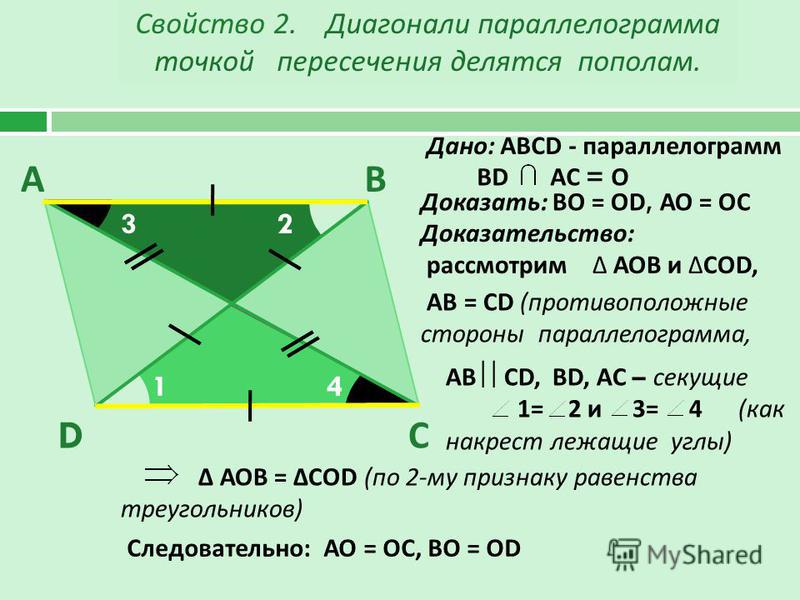

 Докажите, что AMCN
– параллелограмм.
Докажите, что AMCN
– параллелограмм.
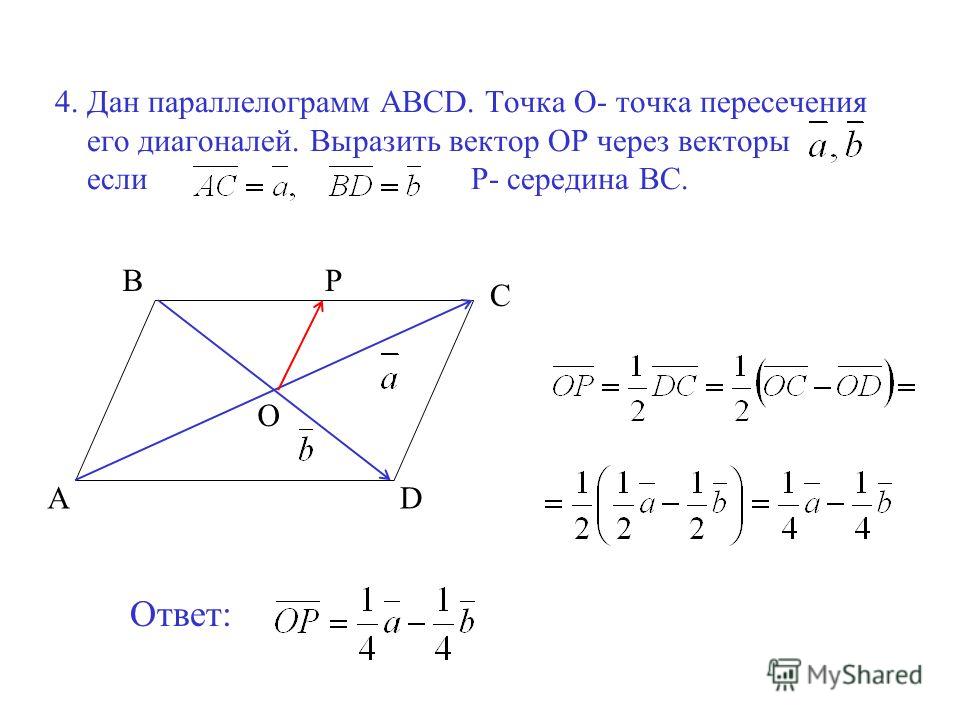

 Через точку пересечения диагоналей
проведена прямая, пересекающая стороны
PK
и MH
в точках A
и B
соответственно. Докажите, что AP=HB.
Через точку пересечения диагоналей
проведена прямая, пересекающая стороны
PK
и MH
в точках A
и B
соответственно. Докажите, что AP=HB.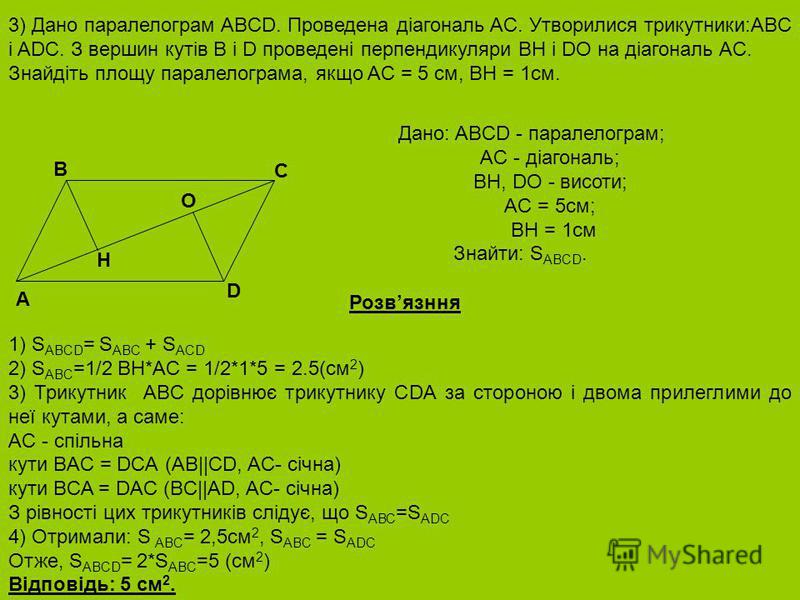 Отрезки BM
и KD
пересекаются в точке O;
ﮮBOD=140°,
ﮮDKB=110°,
ﮮBMC=90°.
Найдите отношение длин отрезков MC
и AD
и углы параллелограмма.
Отрезки BM
и KD
пересекаются в точке O;
ﮮBOD=140°,
ﮮDKB=110°,
ﮮBMC=90°.
Найдите отношение длин отрезков MC
и AD
и углы параллелограмма.



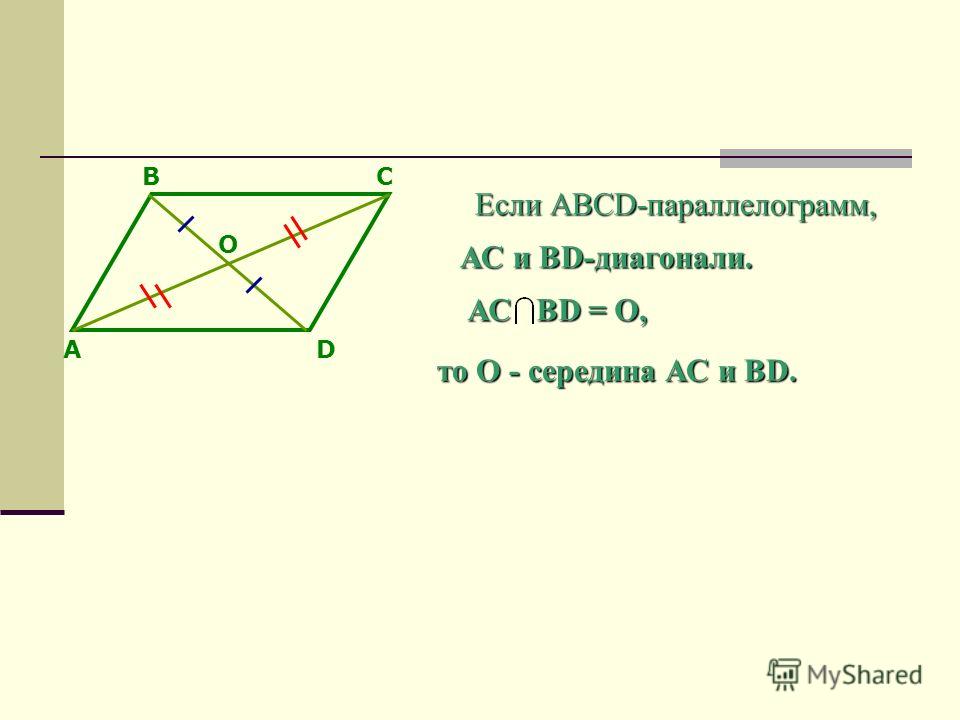 Но нерешенной проблемой было «возвести круг в квадрат», то есть построить квадрат, равный данному кругу. Только в 19 веке было доказано, что строительство с использованием только линейки и циркуля невозможно. Пифагорейцы были теми, кто инициировал и решил все эти проблемы, относящиеся к прямолинейным областям, и мы еще скажем о них, когда докажем теорему Пифагора.
Но нерешенной проблемой было «возвести круг в квадрат», то есть построить квадрат, равный данному кругу. Только в 19 веке было доказано, что строительство с использованием только линейки и циркуля невозможно. Пифагорейцы были теми, кто инициировал и решил все эти проблемы, относящиеся к прямолинейным областям, и мы еще скажем о них, когда докажем теорему Пифагора.
Leave A Comment