Докажите Контрольная работа 1. Вариант 2. № 1 Геометрия 8 класс Зив Б.Г. – Рамблер/класс

Докажите Контрольная работа 1. Вариант 2. № 1 Геометрия 8 класс Зив Б.Г. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Дан четырехугольник ABCD, в котором диагона-
ли имеют общую середину.

На продолжении стороны AD
за вершину D взята точка В, DC = ЕС. Докажите, что
четырехугольник АВСЕ является равнобедренной трапецией.

ответы

Т.к. диагонали имеют общую середину, то ABCD — параллелограмм => ВС || AD. Д DCE — равнобедренный, т.е.
 

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Психология

Химия

похожие вопросы 5

Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.

Привет. Запуталась при решении, нужна помощь знатоков!!!
 
Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее…)

ГДЗГеометрия11 класс10 классАтанасян Л.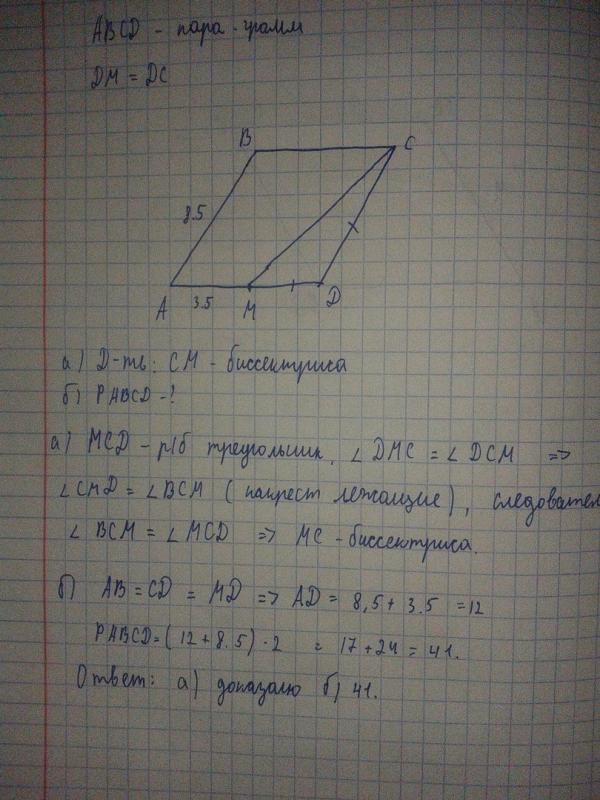 С.

Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1. Практ. работа № 5.

Попробуйте провести следующий опыт. Приготовление раствора
сахара и расчёт его массовой доли в растворе.
Отмерьте мерным (Подробнее…)

ГДЗШкола8 классХимияГабриелян О.С.

Самостоятельная работа 19. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос

Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.
 

ГДЗЭкзаменыГеометрия9 классЗив Б. Г.

11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.

11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 12. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…

18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

Дан четырёхугольник АБСД: А(-1; 7), Б(5;5), С(7;-5), Д(3;-7). Докажите, что 1)отрезки, соединяющие середины сторон АБ и СД, АД и БС, в точке их пересечения делятся пополам; 2) середины сторон данного — вопрос №2785838

Прочитайте отрывок из комедии Д.И.Фонвизина «Недоросль» (Действие 4, явление 8) 2. Исследуйте сцену экзамена Митрофанушки и определите роль художественных средств и фигур поэтического синтаксиса в

Зная что самолет в течении 4 ч20 мин летел со средней скоростью 540 км\ч, ответь на следующий вопросы. 1) Какой должна быть средняя скорость самолета,…

1)В воду объемом 1 л ,температура которой 20С°, бросают кусок железа массой 100г, нагретый до 500С°. При этом температура воды повышается до 24С° и некоторое количество её обращается в пар.

Боковое ребро правильной треугольной призмы равно 9 см,а диагональ боковой грани равна 15 см. Найти площадь боковой и полной поверхности призмы

Медиана равностороннего треугольника равна 13√3.Найдите его сторону. Решение плиз

Пользуйтесь нашим приложением

Ответов пока нет

Михаил Александров

от 0 p.
Читать ответы

Татьяна Александровна

от 500 p.
Читать ответы

Татьяна

от 100 p.
Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука

Похожие вопросы

Четырехугольник — Практический учебный материал

9.1. ВВЕДЕНИЕ
Если на плоскости есть четыре точки, никакие три из которых не лежат на одной прямой, то фигура, полученная соединением четырех точек по порядку, называется четырехугольником. Мы можем сказать, что четырехугольник — это замкнутая фигура с четырьмя сторонами:

, например. ABCD — четырехугольник с четырьмя сторонами AB, BC, CD и DA, четырьмя углами ∠A, ∠B, ∠C и ∠D и четырьмя вершинами A, B, C и D, а также двумя диагоналями AC и BD. То есть четырехугольник имеет четыре стороны, четыре угла, четыре вершины и две диагонали.
9.2. Свойство суммы углов четырехсторонней
Теорема: Сумма углов четырехстороннего — 360 O
Дано: Let ABCD будет четырехсторонней и AC — это один диагональный ∠A + ∠B + ∠C + ∠D = 360 o
Решение: В △ACD имеем
∠DAC + ∠ACD + ∠D = 180 o    … (05) сумма углов 0 свойство ]
В △ABC имеем
∠BAC + ∠ACB + ∠B = 180 o   … (ii)
[Свойство суммы углов]
Складывая (i) и (ii), получаем
∠DAC + ∠ACD + ∠D + ∠BAC + ∠ACB + ∠B
= 180 o + 180 o
⇒ (∠DAC + ∠BAC) + (∠ACD + ∠ACB) + ∠D + ∠B = 360 o
∴ A + ∠C + ∠D + ∠7 Следовательно, ∠A + ∠B + ∠C + ∠D = 360 o Доказано.
9.3. ТИПЫ ЧЕТЫРЕХСТОРОННИХ
I. Трапеция: В четырехугольнике, если одна пара противоположных сторон параллельна, то он называется трапецией, т.е. если AB || CD, то четырехугольник ABCD является трапецией.

II. Параллелограмм: В четырехугольнике, если обе пары противоположных сторон параллельны и равны, то он называется параллелограммом. т. е. АВ || CD и AB = CD; н.э. || BC и AD = BC, то ABCD — параллелограмм.

III. Прямоугольник: Если в четырехугольнике (параллелограмме) все углы прямые, то он называется прямоугольником. то есть АВ || CD, AB = CD, AD || ДО Н.Э; AD = BC и ∠A = ∠B = ∠C = ∠D = 90 o , тогда ABCD — прямоугольник.

IV A Ромб: В четырехугольнике (параллелограмме), если все стороны равны, то он называется ромбом, т. е. AB || CD, AD || BC и AB = BC = CD = DA, тогда ABCD — ромб.

V Квадрат: В четырехугольнике (параллелограмме), если все стороны равны и все углы равны 90 o , то он называется квадратом. то есть АВ || CD, AD || BC, AB = BC = CD = DA и ∠A = ∠B = ∠C = ∠D = 90 o

VI Воздушный змей: В четырехугольнике ABCD, если AD = CD и AB = CB, то он называется коршун; т. е. две пары смежных сторон равны, но это не параллелограмм.

УЗНАТЬ ЭТО
(i) Квадрат является прямоугольником, а также ромбом
(ii) Параллелограмм является трапецией
(iii) Трапеция не является параллелограммом
(iv) Трапеция не является параллелограммом
(v) Прямоугольник или ромб не является квадратом.
9.4. СВОЙСТВА ПАРАЛЛЕЛОГРАММА
Теорема : Диагональ параллелограмма делит его на два конгруэнтных треугольника.
Дано: ABCD — параллелограмм, а AC — диагональ.

Чтобы доказать: △ ABC ≅△CDA,
Решение: В △ABC и △CDA мы имеем
BC || AD и AC являются секущей
∴∠BCA = ∠DAC [Пара противоположных углов]
Аналогично, AB || DC и AC являются секущими
∴∠BAC = ∠DCA [Пара противоположных углов]
и AC = AC [Общий]
Следовательно, △ABC ≅△CDA [По правилу конгруэнтности ASA]
, т. е. диагональ AC делит параллелограмм ABCD на два равные треугольники ABC и CDA.
Теорема : Если каждая пара противоположных сторон четырехугольника равна, то это параллелограмм.
Дано: Пусть ABCD четырехугольник, в котором AB = CD и BC = AD.

Чтобы доказать: ABCD — параллелограмм.
Конструкция: Соединение AC
Решение : В △s ABC и CDA мы имеем
AB = CD [Дано]
BC = AD [Дано]
и AC = AC [Общее]
∴ △ABC≅△CDA [По правилу соответствия SSS]
∴∠CAB = ∠ACD   … (i)
и ∠ACB = ∠CAD … (ii)  [По CPCT]
Теперь линия AC пересекает AB и DC в точках A и C, так что
∠CAB = ∠ACD [Из (i)]
Но это альтернативные внутренние углы
∴ АВ || DC  … (iii)
Аналогично, прямая AC пересекает BC и AD в точках C и A так, что
∠ACB = ∠CAD [из (ii)]
Но это альтернативные внутренние углы
∴ BC || AD  … (iv)
Из (iii) и (iv) имеем
AB || DC и БК || AD
Следовательно, ABCD — параллелограмм. Доказано.
Теорема : В параллелограмме противоположные углы равны.
Если ABCD — параллелограмм,

Тогда ∠A = ∠C и ∠B = ∠D
Теорема : Если в четырехугольнике каждая пара противоположных углов равна, то это параллелограмм.
Дано: ABCD — четырехугольник, в котором ∠A = ∠C и ∠B = ∠D.

Чтобы доказать: ABCD — параллелограмм
Решение: В четырехугольнике ABCD у нас есть
∠A = ∠C   … (i) [Дано]
∠B = ∠D   …(ii) [Дано]
Теперь, складывая (i) и (ii), мы получаем
∠A + ∠B = ∠C + ∠ D … (iii)
Мы знаем, что сумма углов четырехугольника равна 360 o .
∴∠A + ∠B + ∠C + ∠D = 360 o
⇒∠A + ∠B) + (∠A + ∠B) = 360 o [Из (iii)]
⇒2(∠ A+∠B)=360°
∴∠A + ∠B = 180 o … (iv)
т.е. ∠A + ∠B = ∠C + ∠D = 180 o  … (v)
[Из (iii ) и (iv)]
линия AB пересекает AD и BC в точках A и B соответственно, так что
∠A + ∠B = 180 o
[Сумма последовательных внутренних углов равна 180 o ]
∴ AD || BC … (vi)
Опять же, ∠A + ∠B = 180 o   
⇒∠C + ∠B = 180 o [ ∵∠A = ∠C задано]
Прямая BC пересекает AB и DC в точках A и C соответственно такие, что
∠B + ∠C = 180 o
∴ AB || DC [Сумма последовательных внутренних углов равна 180 o ]   … (vii)
Из (vi) и (vii) получаем
AD || до н. э. и АВ || DC
Следовательно, ABCD — параллелограмм.
Теорема : Диагонали параллелограмма делят друг друга пополам.
Дано : ABCD — параллелограмм, в котором AB = CD, AB || CD и ВС = AD; до нашей эры || Диагонали AD AC и BD пересекаются в точке O.

Доказать:
OA = OC и OB = OD
Решение:
В △OAB и △OCD
AB || CD и BD являются секущей [Дано]
∴∠ABD = ∠CDB [Пара противоположных углов]
⇒∠BAO = ∠CDO
Опять же, ∵ до н.э. || AD и AC являются секущими [Дано]
∴ ∠BAC = ∠DCA [Пара противоположных углов]
⇒∠BAO = ∠DCO
и AB = CD [Дано]
∴△OAB ≅ △OCD [По правилу соответствия ASA]
Следовательно, OA = OC [По CPCT] и OB = OD Доказано.
Обратная теорема
Если диагонали четырехугольника делят друг друга пополам, то это параллелограмм.
Дано:
Пусть ABCD — четырехугольник, в котором диагонали AC и BD делят друг друга пополам в точке O;
, т. е. OA = OC и OB = OD.

Чтобы доказать:
Четырехугольник ABCD является параллелограммом
Решение:
В △S AOD и COB мы имеем
AO = CO [Дано]
OD = ∈OD = 9005 OB [Дано] BOC [Вертикально противоположные углы]
∴△AOD ≅ △COB [По правилу конгруэнтности SAS]
∴∠OAD = ∠OCB [По CPCT]  … (i)
Но это альтернативные внутренние углы
∴ AD || ДО Н.Э. Аналогично, АВ || CD
Значит, ABCD — параллелограмм. Доказано.
Теорема:
Четырехугольник является параллелограммом, если пара противоположных сторон равна и параллельна
Дано:
ABCD — четырехугольник, в котором AB = CD и AB || CD .

Чтобы доказать:
ABCD — параллелограмм.
Конструкция:
Присоединился к AC.
Решение:
В △s ABC и CDA мы имеем
AB = CD [Дано]
AC = AC [Общее]
и ∠BAC = ∠DCA
[∵ AB||CD и AC является секущей.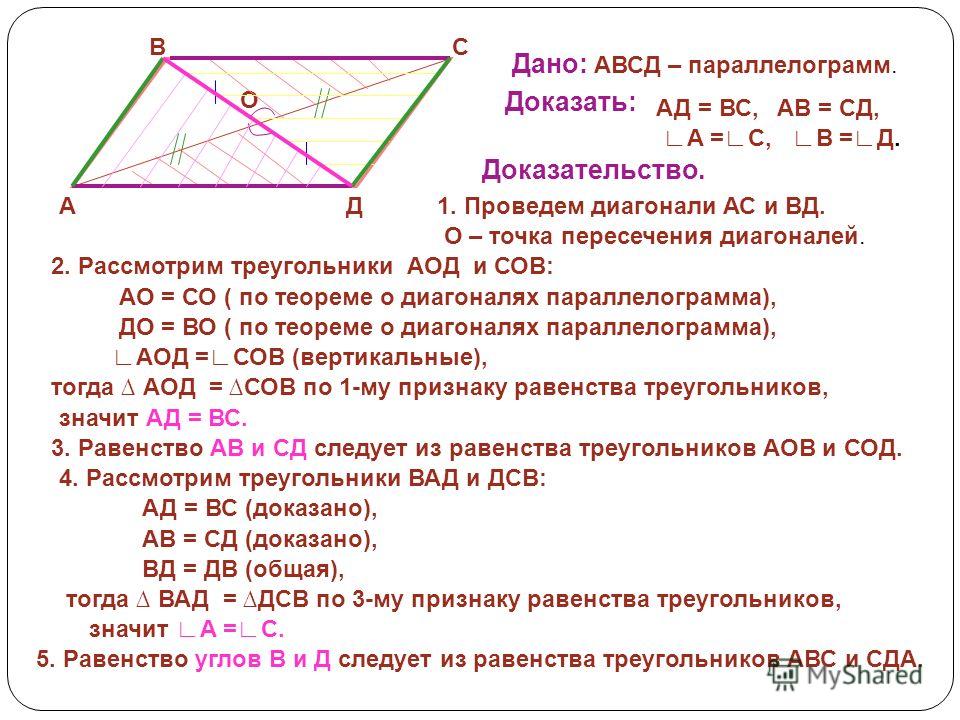 ∴ Альтернативные внутренние углы равны]
∴ △ABC ≅ △CDA [правило соответствия SAS]
∴∠BCA = ∠DAC [по CPCT]
Но это альтернативные ракурсы.
∴ н.э. ||
г. до н.э. Сейчас, AB || CD и AD || ДО Н.Э. Следовательно, четырехугольник ABCD является параллелограммом. Доказано.  
9.5. Теорема о средней точке
Отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне.
Дано :
ABC — треугольник, в котором D и E — середины сторон AB и AC соответственно DE соединены.

Доказать:
DE || до н.э. и DE = 1/2 до н.э.
Конструкция : Отрезок DE, произведенный до F, такой, что DE = EF присоединился к FC.
Доказательство : В △s AED и CEF имеем
AE = CE [ ∵ E — середина заданного AC]
∠AED = ∠CEF [вертикально противоположные углы]
и DE = EF [По построению]
∴ △AED≅△CEF [По правилу соответствия SAS]
∴ AD = CF … (i) [По CPCT]
и ∠ADE = ∠CFE … (ii) [По CPCT]
Теперь D — середина AB
 ∴ AD = BD
⇒ DB = CF … (iii) [Из (i) AD = CF]
DF пересекает AD и FC в точках D и F соответственно, так что
∠ADE = ∠CFE … [Из (ii)]
, т. е. альтернативные внутренние углы равны
∴ AD || FC
⇒ ДБ || CF … (iv)
Из (iii) и (iv) получаем, что DBCF — четырехугольник, у которого одна пара сторон равна и параллельна
∴ DBCF — параллелограмм
∴ DF || BC и DF = BC [ ∵ противоположные стороны || gm равны, параллельны]
Но D, E, F коллинеарны и DE = EF
Следовательно, DE || до н.э. и DE = ½ до н.э. Доказано.
Обратная теорема: Прямая, проведенная через середину одной стороны треугольника параллельно другой стороне, делит третью сторону пополам.
Дано : Пусть ABC — треугольник, в котором E — середина AB, прямая l проходит через E и параллельна BC, а CM || BA пересекает AC в точке F.

Доказать: AF = CF
Построение: CM || BE и линия пересечения l в точке D нарисованы
Доказательство: ∵ CM || БЫТЬ и л || BC
∴ BCDE — параллелограмм.
∴ BE = CD [противоположные стороны ||gm]
Но BE = AE [Дано]
∴ AE = CD … (i)
Теперь в △AEF и △CDF имеем
∠AFE = ∠CFD [вертикально противоположные углы]
∠A = ∠FCD [альтернативные углы]
AE = CD … [из (i)]
∴△AEF≅△CDF [правило соответствия AAS]
Следовательно, AF = CF [КПП].

Четырехугольники — Параллелограммы | Shmoop

Параллелограммы повсюду. Они прячутся у всех на виду, глядя нам прямо в лицо. Как вешалки для полотенец и туалеты, мы используем их каждый день и никогда не задумываемся о них. Прямо сейчас, когда вы читаете это, вы смотрите на параллелограмм. Да, это верно. Экран вашего компьютера представляет собой параллелограмм. Если только у вас не особенно шаткий экран.

Параллелограмм — это любой четырехугольник с двумя наборами параллельных сторон. Когда мы думаем о параллелограммах, мы обычно думаем о чем-то подобном.

Если вы не серьезно повредили экран своего компьютера, это, вероятно, не выглядит так. Ради вашего банковского счета, мы искренне надеемся, что это не так. Он должен быть прямоугольным. Так что дает?

У прямоугольника два набора параллельных сторон, не так ли? Так что это такой же параллелограмм, как и выше. На самом деле квадраты, ромбы и прямоугольники являются частными случаями параллелограммов.

Пока не забивайте себе голову этими специфическими параллелограммами. Мы рассмотрим их более подробно позже.

Поскольку параллелограммы так же распространены, как заморозки мозга в магазине мороженого, давайте разберёмся с ними. Только не в магазине мороженого. Это просто антисанитарно.

Поскольку параллелограмм представляет собой особый тип четырехугольника, он обладает всеми достоинствами четырехугольников, такими как 360° внутренних углов, противоположные углы, стороны и вершины, а также две почетные и широкие диагонали.

Да, мы только что назвали эти диагонали «благородными и щедрыми», и это не потому, что они жертвуют на благотворительность или работают волонтерами в столовых. Дело в том, что диагонали параллелограмма делят его на два равных треугольника.

Не верите нам? Мы можем доказать это. Не могли бы вы?

Пример задачи

Учитывая, что ABCD является параллелограммом, докажите, что Δ ABC и Δ CDA конгруэнтны.

1 29435
Заявления Причины
1. ABCD — параллелограмм, данный . CD и до н.э. || DA Определение параллелограммы (1)
3. тий BAC ≅ тий DCA , ▲ BCA ∠ . 9035. 9035. 9035. 9035. 9035. . 9035. 9035. 9035. . 9035. . . . . . . . .0431 4. AC ≅ AC Reflexive property
5. Δ ABC ≅ Δ CDA ASA Postulate (3, 4)


Bam! Конгруэнтные треугольники. Мы не хотим говорить, что сказали вам об этом, поэтому мы выберем «Мы сообщили вам об этом».

А знаете, что еще лучше? Благодаря CPCTC (соответствующие части конгруэнтных треугольников конгруэнтны) мы можем сразу доказать еще три теоремы:

  1. Обе пары противоположных сторон параллелограмма равны. Таким образом, для ABCD , AB ≅ CD и BC ≅ DA .
  2. Обе пары противоположных углов равны Таким образом, для ABCD , ∠ B ≅ ∠ D и ∠ A ≅ ∠ C .
  3. Два последовательных угла являются дополнительными. Таким образом, ∠ A и ∠ B являются дополнительными, как и ∠ C и ∠ D 9.0395 .

Со всеми этими теоремами о параллелограммах мы словно нашли математическое золото. Но подождите, есть еще! Закажите в течение следующих десяти минут, и мы добавим еще одну теорему абсолютно бесплатно! Просто заплатите 4,95 доллара за доставку и обработку. Или, если вы не хотите, вы можете получить теорему бесплатно! Просто справляйтесь с этим сами.

Пример задачи

Учитывая, что ABCD является параллелограммом, докажите, что его диагонали AC и BD делят друг друга пополам.

Statements Reasons
1. ABCD is a parallelogram Given
2. ∠ BAE ≅ ∠ DCE and ∠ ABE ≅ ∠ CDE Теорема о чередующихся внутренних углах (1)
3. AB ≅ CD Противоположные стороны параллелограмма1 3 904 равны0431 4. Δ ABE ≅ Δ CDE ASA Postulate (2, 3)
5. AE ≅ CE and BE ≅ DE CPCTC (4)
6. E is the midpoint of AC and BD Definition of midpoint (5)
7. AC and BD bisect each other Definition of segment bisector ( 6)


Ключом к этому доказательству (и, вероятно, к большинству доказательств четырехугольников) является теорема о треугольниках. О, вы думали, что с ними покончено, не так ли? Что ж, нам не хочется лопать твой пузырь, приятель, но мы узнали об этих треугольниках не просто так. И не только для того, чтобы порадовать учителя математики.

Мы установили пять различных теорем о параллелограммах. Так что вполне разумно, что мы задаем наши любимые вопросы о математике. «Почему мы заботимся?» «Какое это имеет значение?» «Как это вообще относится к моей жизни?» «Почему так важны эти маленькие золотые крупицы мудрости?»

Что ж, мы могли бы продолжить собирать эти самородки и, в конечном счете, дать Форту Ноксу шанс заработать деньги. С другой стороны, мы накопили бы кучу бесполезных фактов, когда могли бы использовать их в качестве учебников для параллелограмма.

Допустим, вы обвинили четырехугольник в том, что он является параллелограммом. Теперь вам нужно изложить свое дело. Вот несколько способов убедить присяжных, что четырехугольник является параллелограммом:

  1. Две пары противоположных сторон параллельны. (Это определение параллелограмма.)
  2. Обе пары противоположных сторон конгруэнтны.
  3. Одна пара противоположных сторон конгруэнтна и параллельна.
  4. Обе пары противоположных углов равны.
  5. Диагонали делят друг друга пополам.

Многие из этих утверждений являются обратными утверждениями доказательств, которые мы уже придумали. Ранее мы предполагали, что фигура является параллелограммом, и показали, что эта фигура обладает некоторыми особыми свойствами. Теперь мы говорим, что если фигура обладает этими свойствами, она должно быть параллелограммом. Помимо определения, мы должны показать, что каждое из этих утверждений истинно. К счастью для нас, нам просто нужно применить факты, которые мы уже знаем.

Пример задачи

Дано: Четырехугольник ABCD имеет две пары противоположных сторон, которые конгруэнтны.
Докажите: ABCD — параллелограмм.

Заявления Причины
1. AB ≅ CD and BC ≅ DA Given
2.

Related Posts

Leave A Comment