График функции с переменной в знаменателе
График функции с переменной в знаменателе — следующая группа заданий из номера 23 ОГЭ по математике.
Исследование любой функции начинается с нахождения её области определения.
Дробь имеет смысл, если знаменатель отличен от нуля. Следовательно, те значения переменной, при которых знаменатель обращается в нуль, не входят в область определения функции.
В этом случае возможно появление на графике выколотых точек.
Рассмотрим примеры построения графиков функций, содержащих переменную в знаменателе дроби.
1) Постройте график функции
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
В знаменателе вынесем за скобки общий множитель x:
ВАЖНО: прежде чем сократить дробь, следует найти область определения функции!
Дробь имеет смысл, если знаменатель отличен от нуля:
x(5x-8)≠0,
x≠0, x≠8/5.
(или D(y): x∈R, кроме x=0 и x=8/5).
Теперь сократим дробь на 5x-8:
y=1/x — функция обратной пропорциональности. Её график — гипербола. Не забываем про выколотую точку: x≠8/5 (0 не входит в область определения функции y=1/x).
Для построения гиперболы возьмём несколько точек (в том числе, выколотую):
Отмечаем эти точки на координатной плоскости.
Строим гиперболу с выколотой точкой (8/5; 5/8):
Прямая y=kx имеет с графиком ровно одну общую точку, если она проходит через выколотую точку:
Чтобы найти k, подставляем координаты выколотой точки
(8/5; 5/8)
в формулу y=kx и находим k:
Ответ : 25/64.
2) Постройте график функции
и определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
Решение:
В знаменателе вынесем за скобки общий множитель
(Не забываем: сначала следует найти область определения функции, и лишь после этого упрощать выражение!)
Ищем область определения функции.
x(x+5)≠0
x≠0; x≠-5;
D(y): x∈(-∞;-5)∪(-5;0)∪(0;∞).
Сокращаем дробь на x+5:
— функция обратной пропорциональности. График — гипербола, полученная из гиперболы
параллельным переносом на 3 единицы вверх вдоль оси Oy.
Сначала найдём несколько точек для построения графика y=-1/x:
Отметим эти точки на координатной плоскости. Затем каждую из них перенесем на 3 единицы вверх вдоль оси ординат.
Прямая y=0 (ось абсцисс) для гиперболы y=-1/x является асимптотой (то есть прямой, к которой график стремится, но никогда её не достигнет). Асимптоты принято изображать пунктирными линиями. Так как y=0 совпадает с осью Ox, то она изображена сплошной линией. При параллельном переносе на 3 единицы вверх прямая y=0 переходит в прямую y=3. Прямая y=3 — асимптота, поэтому изображаем её пунктиром.
Через полученные точки проведём гиперболу y=3-1/x:
Прямая y=m не имеет с графиком ни одной общей точки, если она проходит через выколотую точку либо совпадает с асимптотой y=3, то есть при m=3,2 и m=3:
Ответ: 3; 3,2.
3) Постройте график функции
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
Найдём область определения функции.
-1-x≠0
x≠-1.
Преобразуем дробь:
и сократим её на (x+1):
y=-x²-4 — квадратичная функция. График — парабола ветвями вниз (так как a=-1<0).
График может быть получен из графика функции y=-x² параллельным переносом на 4 единицы вниз вдоль оси Oy (не забываем про выколотую точку! x≠-1):
Прямая y=kx имеет с графиком ровно одну общую точку, если она проходит через выколотую точку либо если она является касательной к параболе:
Значения k в данном случае удобнее искать аналитически, а не с помощью графика.
Прямая y=kx имеет с графиком функции y=-x²-4, где x≠-1 ровно одну общую точку, если система
имеет одно решение.
Приравниваем правые части равенств:
-x²-4=kx
x²+kx+4=0.
Это квадратное уравнение имеет один корень в двух случаях: либо дискриминант равен нулю, либо дискриминант положителен, но один из корней равен -1.
D=b²-4ac=k²-4·1·4=k²-16.
k²-16=0 при k=4 или k=-4.
Если x=-1, подставив это значение в уравнение, найдём k:
(-1)²+k·(-1)+4=0
k=5.
Ответ: -4; 4; 5.
4) Постройте график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Решение:
Формула функции содержит три квадратных трёхчлена. Чтобы разложить каждый из них на множители, решим три квадратных уравнения и воспользуемся теоремой о разложении квадратного трёхчлена на множители.
1)x²-4x+3=0
x1=1; x2=3
x²-4x+3=(x-1)(x-3).
2)x²-x-2=0
x1=-1; x2=2
x²-x-2=(x+1)(x-2).
3)x²-2x-3=0
x1=-1; x2=3
x²-2x-3=(x+1)(x-3).
Ищем область определения функции.
(x+1)(x-3)≠0
x≠-1, x≠3.
D(y): x∈(-∞;-1)∪(-1;3)∪(3;∞).
Сокращаем дробь на (x+1)(x+3):
-квадратичная функция. График — парабола ветвями вверх (так как a=1>0).
Координаты вершины параболы
От вершины — точки (1,5; -0,25) — строим параболу y=x². Поскольку координаты вершины — не целые числа, для построения графика удобно найти дополнительные точки с целыми координатами.
При y=0 (x — 1)(x — 2)=0,
x=1; x=2.
При x=0 y=0²-3·0+2=2.
Находим координаты выколотых точек
При x=-1 y=(-1)²-3·(-1)+2=6,
при x=3 y=3²-3·3+2=2.
Прямая y=m имеет с графиком ровно одну общую точку, если она проходит через одну из выколотых точек либо через вершину, то есть при m=2, m=6 и m=-0,25.
Ответ: -0,25; 2; 6.
Рубрика: ОГЭ задание 22 | Комментарии§ 5. Непрерывность функций
 Учиться строить
графики лучше непосредственно на
практическом занятии. Здесь в основном
показано исследование на непрерывность.
Учиться строить
графики лучше непосредственно на
практическом занятии. Здесь в основном
показано исследование на непрерывность.Известно, что элементарная функция (см. с. 16) непрерывна во всех точках, в которых определена. Поэтому нарушение непрерывности у элементарных функций возможно только в точках двух типов:
а) в точках, где функция «переопределяется»;
б) в точках, где функция не существует.
Соответственно только такие точки и проверяются при исследовании на непрерывность, что показано в примерах.
Для неэлементарных функций исследование сложнее. Например, функция (целая часть числа) определена на всей числовой оси, но терпит разрыв при каждом целом x. Подобные вопросы выходят за рамки пособия.
Перед изучением материала следует повторить по лекции или учебнику, какими (какого рода) бывают точки разрыва.
Функция задана кусочно,
если она на разных участках области
определения задаётся разными формулами.
Основная идея при исследовании таких функций – выяснить, задана ли функция в тех точках, в которых переопределяется, и как. Затем проверяется, совпадают ли значения функции слева и справа от таких точек.
Пример 1. Покажем, что функция непрерывна.
Функция элементарна и потому непрерывна в тех точках, в которых определена. Но, очевидно, она определена во всех точках. Следовательно, во всех точках она и непрерывна, в том числе при , как требует условие.
То же справедливо для функции , и при она непрерывна.
а) ;
б) .
Пределы слева и справа совпадают. Остаётся узнать:
а) определена ли функция в самой точке ;
б) если да, то
совпадает ли со значениями пределов слева и справа.
По условию, если , то . Поэтому .
Видим, что (все равны числу 2). Это означает, что в точке
Замечания к решению
а) При вычислениях не играло роли, подставляем мы в конкретную формулу число или . Обычно это важно, когда получается деление на бесконечно малую величину, поскольку влияет на знак бесконечности. Здесь же и отвечают только за выбор функции;
б) как правило, обозначения и равноправны, то же касается обозначений и (и справедливо для любой точки, а не только для ). Дальше для краткости применяются обозначения вида ;
в) когда пределы слева и справа равны, для проверки на непрерывность фактически остаётся посмотреть, будет ли одно из неравенств нестрогим. В примере таковым оказалось 2-е неравенство.
Пример 2.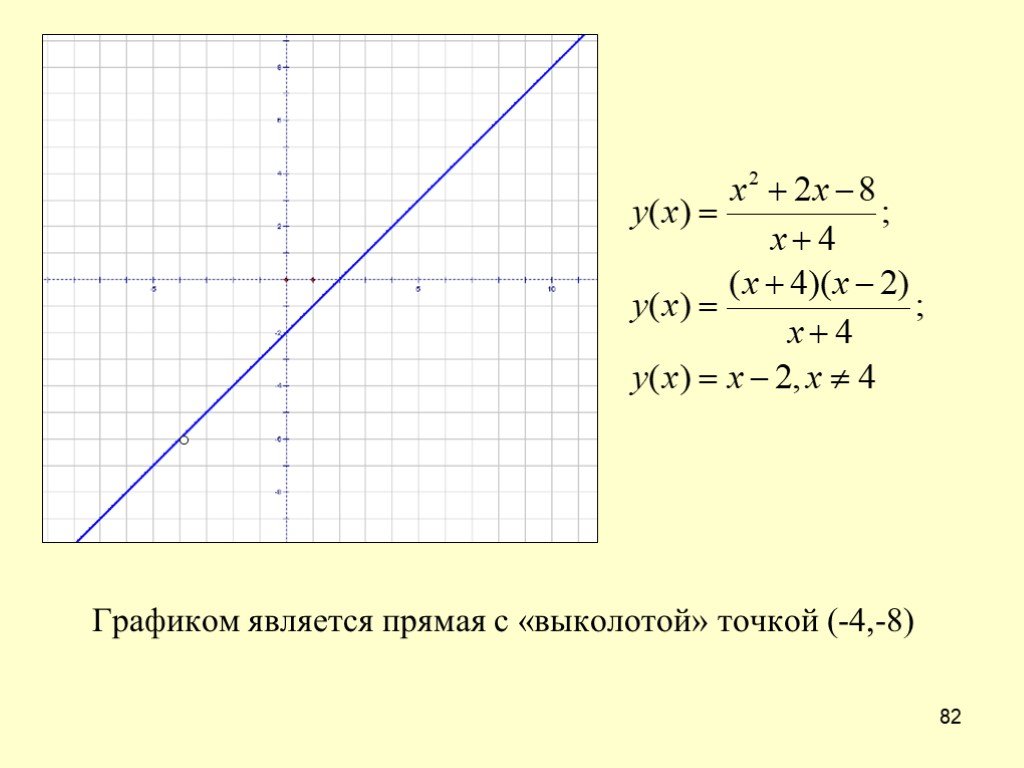 Исследуем на непрерывность функцию .
Исследуем на непрерывность функцию .
По тем же причинам, что в примере 1, непрерывность может нарушаться только в точке . Проверим:
а) ;
б) .
Пределы слева и справа равны, но в самой точке функция не определена (неравенства строгие). Это означает, что – точка устранимого разрыва.
«Устранимый разрыв» означает, что достаточно или сделать любое из неравенств нестрогим, или придумать для отдельной точки функцию, значение которой при равно –5, или просто указать, что , чтобы вся функция стала непрерывной.
Ответ: точка – точка устранимого разрыва.
Замечание 1. В литературе устранимый разрыв обычно
считается частным случаем разрыва 1-го
рода, однако студентами чаще понимается
как отдельный тип разрыва. Во избежание
разночтений будем придерживаться 1-й
точки зрения, а «неустранимый» разрыв
1-го рода оговаривать особо.
Пример 3. Проверим, непрерывна ли функция
В точке
а) ;
б) .
Пределы слева и справа различны: . Независимо от того, определена ли функция при (да) и если да, то чему равна (равна 2), точка – точка неустранимого разрыва 1-го рода.
В точке происходит конечный скачок (от 1 к 2).
Ответ: точка – точка неустранимого разрыва 1-го рода.
Замечание 2. Вместо и обычно пишут и соответственно.
Возможен вопрос: чем отличаются функции
и ,
а также их графики? Правильный ответ:
а) 2-я функция не определена в точке ;
б) на графике 1-й функции точка «закрашена», на графике 2-й – нет («выколотая точка»).
Точка ,
где обрывается график ,
не закрашена на обоих графиках.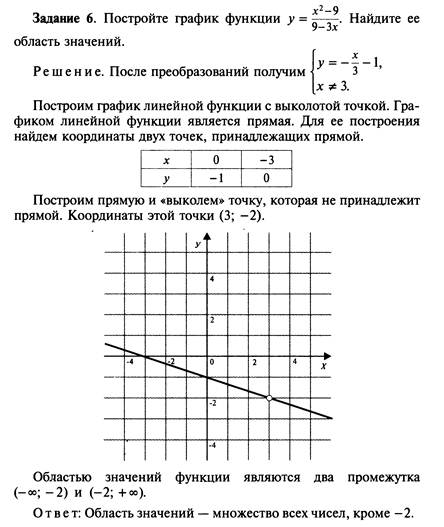
Сложнее исследовать функции, по-разному определённые на трёх участках.
Пример 4. Непрерывна ли функция ?
Так же, как в примерах 1 – 3, каждая из функций , и непрерывна на всей числовой оси, в том числе – на участке, на котором задана. Разрыв возможен только в точке или (и) в точке , где функция переопределяется.
Задача распадается на 2 подзадачи: исследовать на непрерывность функции
и ,
причём точка не представляет интереса для функции , а точка – для функции .
1-й шаг. Проверяем точку и функцию (индекс не пишем):
а) ;
б) .
Пределы совпадают. По условию, (если пределы слева и справа равны, то фактически функция непрерывна, когда одно и из неравенств нестрогое). Итак, в точке функция непрерывна.
2-й
шаг.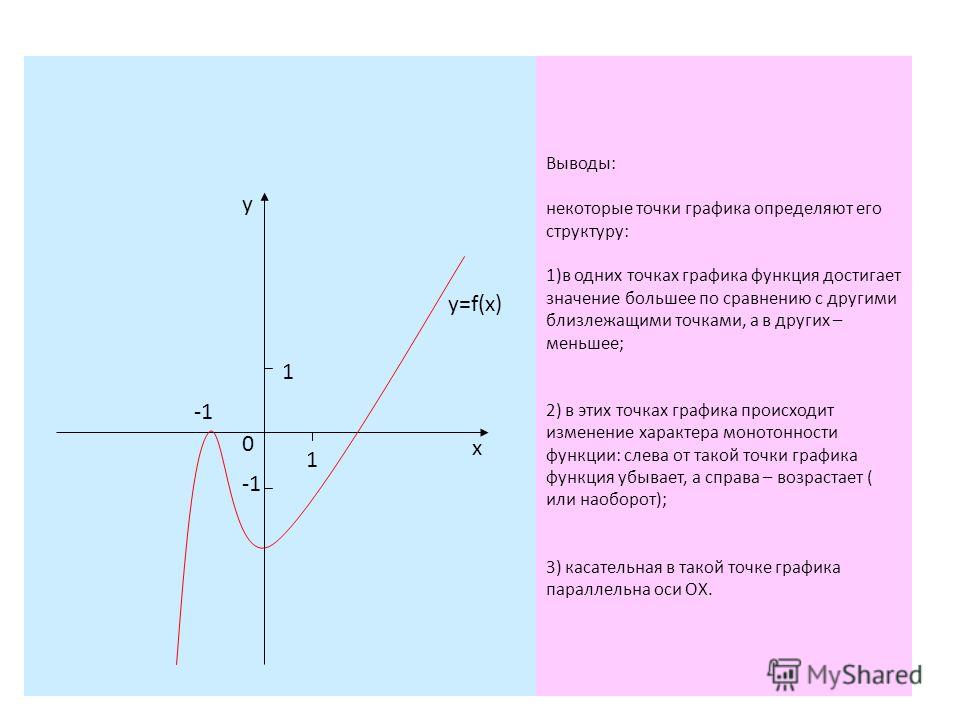 Проверяем
точку
и функцию
:
Проверяем
точку
и функцию
:
а) ;
б) .
Поскольку , точка – точка разрыва 1-го рода, и значение (и то, есть ли оно вообще) уже не играет роли.
Ответ: функция непрерывна во всех точках, кроме точки , где имеет место неустранимый разрыв 1-го рода – скачок от 6 к 4.
Пример 5. Найти точки разрыва функции .
Действуем по той же схеме, что в примере 4.
1-й шаг. Проверяем точку :
а) , поскольку слева от функция постоянна и равна 0;
б) ( – чётная функция).
Пределы совпадают, но при функция по условию не определена, и получается, что – точка устранимого разрыва.
2-й шаг. Проверяем точку :
а) ;
б) – значение функции не зависит от переменной.
Пределы различны: ,
точка
– точка неустранимого разрыва 1-го рода.
Ответ: – точка устранимого разрыва, – точка неустранимого разрыва 1-го рода, в остальных точках функция непрерывна.
Пример 6. Непрерывна ли функция ?
Функция определена при , поэтому условие превращается в условие .
С другой стороны, функция определена при , т.е. при . Значит, условие превращается в условие .
Получается, что должно выполняться условие , и область определения всей функции – отрезок .
Сами по себе функции и элементарны и потому непрерывны во всех точках, в которых определены – в частности, и при .
Остаётся проверить, что происходит в точке :
а) ;
б) .
Поскольку , смотрим, определена ли функция в точке . Да, 1-е неравенство – нестрогое относительно , и этого достаточно.
Ответ: функция определена на отрезке
и непрерывна на нём.
Более сложные случаи, когда одна из составляющих функций неэлементарна или не определена в какой-либо точке своего отрезка, выходят за рамки пособия.
НФ1. Постройте графики функций. Обратите внимание, определена ли функция в той точке, в которой переопределяется, и если да – каково значение функции (слово «если» в определении функции для краткости пропущено):
1) а) б) в) г)
2) а) б) в) г)
3) а) б) в) г)
4) а) б) в) г)
Пример 7. Пусть . Тогда на участке строим горизонтальную прямую , а на участке строим горизонтальную прямую . При этом точка с координатами «выколота», а точка «закрашена». В точке получается разрыв 1-го рода («скачок»), и .
НФ2. Исследуйте на непрерывность
функции, по-разному определённые на 3-х
интервалах.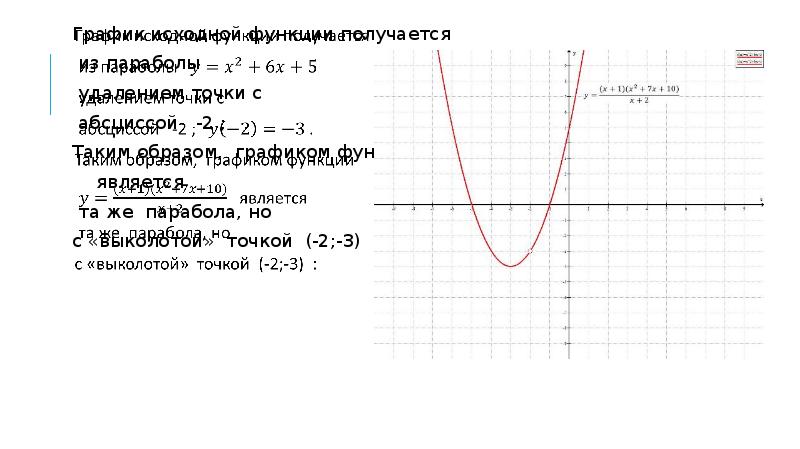 Постройте графики:
Постройте графики:
1) а) б) в)
г) д) е)
2) а) б) в)
г) д) е)
3) а) б) в)
г) д) е)
Пример 8. Пусть . На участке строим прямую , для чего находим и . Соединяем точки и отрезком. Сами точки не включаем, поскольку при и функция по условию не определена.
На участке и обводим ось OX (на ней ), однако точки и «выколоты». В точке получаем устранимый разрыв, а в точке – разрыв 1-го рода («скачок»).
НФ3. Постройте графики функций и убедитесь в их непрерывности:
1) а) б) в)
г) д) е)
2) а) б) в)
г) д) е)
НФ4. Убедитесь в непрерывности функций и постройте их графики:
1) а) б) в)
2 а) б) в)
3) а) б) в)
НФ5. Постройте графики функций. Обратите
внимание на непрерывность:
Постройте графики функций. Обратите
внимание на непрерывность:
1) а) б) в)
г) д) е)
2) а) б) в)
г) д) е)
3) а) б) в)
г) д) е)
4) а) б) в)
г) д) е)
5) а) б) в)
г) д) е)
НФ6. Постройте графики разрывных функций. Обратите внимание на значение функции в той точке, где функция переопределяется (и существует ли оно):
1) а) б) в)
г) д) е)
2) а) б) в)
г) д) е)
3) а) б) в)
г) д) е)
4) а) б) в)
г) д) е)
5) а) б) в)
г) д) е)
НФ7. То же задание, что и в НФ6:
То же задание, что и в НФ6:
1) а) б) в)
г) д) е)
2) а) б) в)
г) д) е)
3) а) б) в)
г) д) е)
4) а) б) в)
г) д) е)
2 — х — 2}{х — 2}$ имеют вертикальную асимптоту в точке $\,x = 2\,$? Нет! Некоторые благонамеренные веб-сайты заключают, что эта функция имеет вертикальную асимптоту
в $\,x = 2\,$
просто потому, что знаменатель там нулевой.
Это неверно.
 $
$, тогда вам придется приложить больше усилий, чтобы понять, что происходит.
Вы должны определить, что происходит БЛИЗКО к интересующему значению $x$. 92-x-2}{x-2}}
\cssId{s21}{= \frac{(x+1)(x-2)}{x-2}}
\cssId{s22}{= (x+1)\cdot\frac{x-2}{x-2}}
$$
Отмена дополнительного коэффициента единицы:
$$\cssId{s24}{R(x) = x + 1\,}\
\cssId{s25}{\text{предоставление} x\ne 2}$$
Функция $\,R\,$ не определена, когда $\,x = 2\,$, так как деление на ноль не допускается.
Для всех значений $\,x\ne 2\,$ ‘$\,\frac{x-2}{x-2}\,$’ — это просто число $\,1\,$!
Таким образом, график $\,R\,$ совпадает с линией $\,y = x + 1\,$
за исключением того, что он был «проколот» в $\,x = 2\,. $
$
Из этого переименования теперь ясно, что когда $\,x\,$ близко к $\,2\,$ выходы близки к $\,2 + 1 = 3\,.$
График функции $\,R\,$ показан ниже:
Функция $\,R\,$ имеет точку прокола (дырку) в точке $\,x = c\,$ если и только если выполняются следующие три условия:
- $D(c) = 0\,$ (знаменатель равен нулю при $\,c\,$)
- $N(c) = 0\,$ (числитель равен нулю в точке $\,c\,$)
- при приближении $\,x\,$ к $\,c\,$ значения $\,R(x)\,$ приближаются к конечному числу
Примечание:
В исчислении «дыра» является примером устранимого разрыва .
Если недостаточно , просто требуется, чтобы и числитель, и знаменатель были равны нулю.
Почему? Вместо точки прокола у вас может быть вертикальная асимптота. 92 — 4x + 4} = \frac{x-2}{(x-2)(x-2)}\,$ имеет вертикальная асимптота в $\,x = 2\,.$
Почему? Для всех $\,x\ne 2\,$ $\displaystyle\,R(x) = \frac{1}{x-2}\,.$
- Приравняем знаменатель к нулю.
- Проверьте полученное значение(я) в числителе.
- Если знаменатель равен нулю, а числитель отличен от нуля, то вы гарантированно имеете вертикальную асимптоту.
- Если и числитель, и знаменатель ОБА равны нулю, то вам необходимо провести дополнительный анализ:
у вас есть либо вертикальная асимптота, либо дыра.
Введение в точки прокола (отверстия)
Введение в точки прокола (отверстия) ВНИМАНИЕ:
MathJax
требует JavaScript для обработки математики на этой странице.
Убедитесь, что он включен.
Ваш браузер не поддерживает аудио элементы. ПРОЧИТАНИЕ УРОКА
доктором Кэрол Дж. В. Ф. Бернс (создатель веб-сайта)
Следуйте вместе с выделенным текстом во время прослушивания!
Спасибо за поддержку!
- ПРАКТИКА (онлайн-упражнения и рабочие листы для печати)
Рациональные функции могут иметь точек прокола (также называемых «дырами»).
Как вы узнаете из «Исчисления», точки прокола являются примером «устранимой прерывности».


Leave A Comment