Вписанный угол окружности. Теорема с доказательством
- Теорема о вписанном угле
- Следствия из теоремы
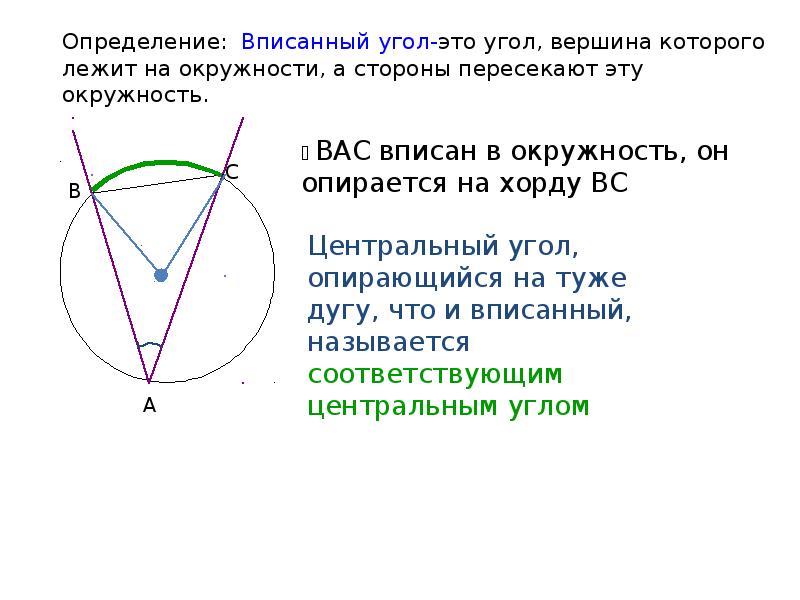
Вписанный угол окружности — это угол, образованный двумя хордами, исходящими из одной точки, то есть вписанным углом называется угол, вершина которого лежит на окружности.
Угол ABC — вписанный угол. ∠ABC опирается на дугу AC, заключённую между его сторонами.
Теорема о вписанном угле
Теорема:
Вписанный угол измеряется половиной дуги, на которую он опирается.
Это следует понимать так: вписанный угол содержит в два раза меньше градусов, чем дуга, на которую он опирается:
| ∠ABC = | 1 | AC. |
| 2 |
Доказательство:
При доказательстве этой теоремы следует рассмотреть три возможных случая расположения вписанного угла относительно центра окружности.
Первый случай. Сторона вписанного угла проходит через центр окружности.
Соединим точку A с центром круга (точкой O). Получим равнобедренный треугольник AOB, в котором AO = OB, как радиусы одной окружности. Следовательно, ∠A = ∠B, как углы при основании равнобедренного треугольника.
Так как ∠AOC — внешний угол равнобедренного треугольника, то:
∠AOC = ∠A + ∠B,
а так как углы A и B равны, то
| ∠B = | 1 | ∠AOC. |
| 2 |
Но ∠AOC — центральный угол, значит ∠AOC = AC, следовательно ∠B измеряется половиной дуги AC:
| ∠ABC = ∠B = | 1 | AC. |
| 2 |
Второй случай. Центр окружности лежит между сторонами вписанного угла.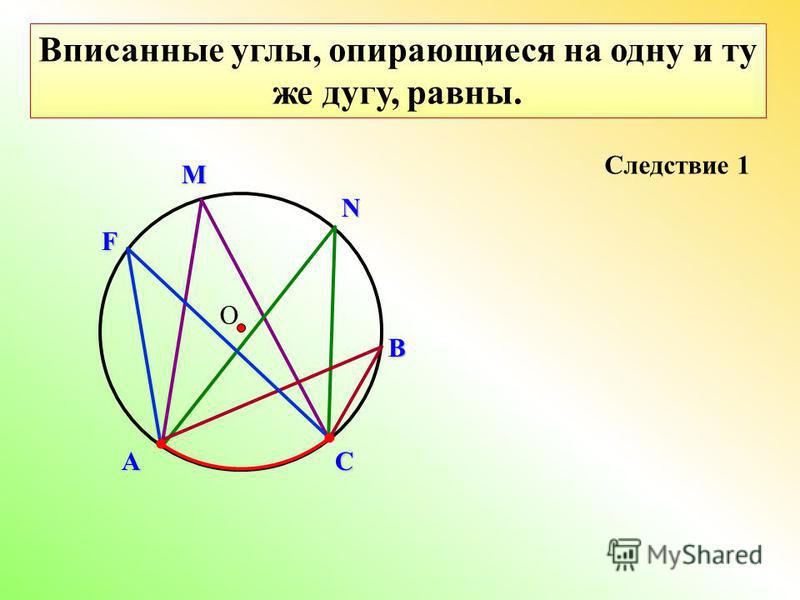
Проведём диаметр BD. Угол ABC разбился на два угла: ∠1 и ∠2.
Точка D разделяет дугу AC на две дуги: AD и DC. По доказательству, рассмотренному в первом случае:
| ∠1 = | 1 | AD и ∠2 = | 1 | DC. |
| 2 | 2 |
Следовательно, весь угол ABC будет измеряться половиной дуги AC:
| ∠1 + ∠2 = | 1 | AD + | 1 | DC |
| 2 | 2 |
или
| ∠ABC = | 1 | AC. |
| 2 |
Третий случай. Центр окружности лежит вне вписанного угла.
Проведём диаметр BD.
∠ABC = ∠ABD — ∠CBD.
Но ∠ABD измеряется половиной дуги AD , а ∠CBD измеряется половиной дуги CD. Следовательно,
| ∠ABC = | 1 | (AD — CD), |
| 2 |
то есть
| ∠ABC = | 1 | AC. |
| 2 |
Следствия из теоремы
1. Все вписанные углы, опирающиеся на одну и ту же дугу, равны между собой, так как они измеряются половиной одной и той же дуги.
2. Вписанный угол, опирающийся на диаметр, — прямой, так как он опирается на половину окружности.
Половина окружности содержит 180°, значит, угол, опирающийся на диаметр, содержит 90°.
Центральные и вписанные углы 8 класс онлайн-подготовка на Ростелеком Лицей
Тема 4: Окружность
- Видео
- Тренажер
- Теория
Заметили ошибку?
Центральные и вписанные углы
Угол с вершиной в центре окружности называется ее центральным углом.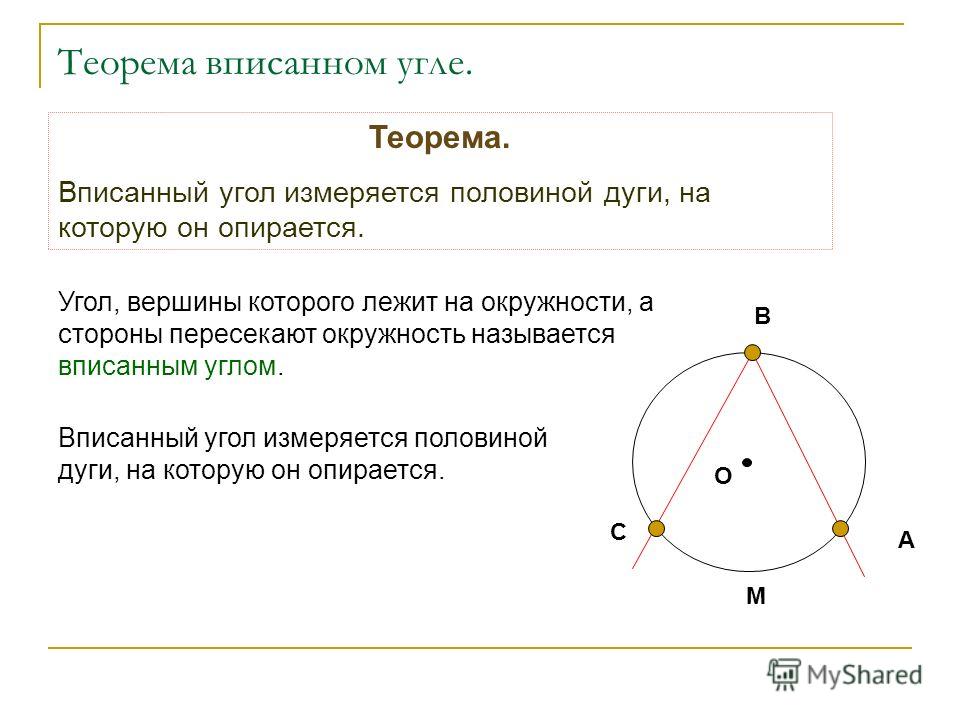
Центральный угол – угол между двумя радиусами.
Центральному углу АОВ соответствуют две дуги с концами А и В. Если дуга АВ окружности с центром в точке О меньше полуокружности или является полуокружностью, то ее градусная мера считается равной градусной мере центрального угла АОВ. Если же дуга АВ больше полуокружности, то ее градусная мера считается равной 360°-∠AOB.
Центральный угол измеряется дугой, на которую опирается.
Сумма градусных мер дуг окружности с общими концами равна 3600.
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
Вписанный угол – угол между двумя хордами, которые пересекаются в точке на окружности.
При этом говорят, что вписанный угол ABC опирается на дугу AC.
Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается.
Доказательство.
Пусть ∠АВС – вписанный угол окружности с центром О, опирающийся на дугу АС. Докажем, что ∠АВС=12AC. Рассмотрим три возможных случая расположения луча ВО относительно угла АВС.
-
Луч ОВ совпадает с одной из сторон угла АВС, например со стороной ВС. В этом случае дуга АС меньше полуокружности, поэтому центральный угол АОС равен дуге АС. Так как угол АОС – внешний угол равнобедренного треугольника АВО, а углы 1 и 2 при основании равнобедренного треугольника равны, то ∠АОС=∠1+∠2=2·∠1.
Отсюда следует, что удвоенный ∠1 равен дуге АС или ∠АВС=∠1=12AC.
-
Луч ВО делит угол АВС на два угла. В этом случае ВО пересекает дугу АС в некоторой точке D. Точка D разделяет дугу АС на две дуги: АD и DC. По доказанному в теореме о вписанном угле ∠ABD=12AD, ∠DBC=12DC. Складывая эти равенства попарно, получаем ∠ABD+∠DBC=12AD+12DC или ∠ABC=12AC.
-
Луч ВО не делит угол АВС на два угла и не совпадает со стороной этого угла.
Из теоремы о вписанном угле следует два утверждения:
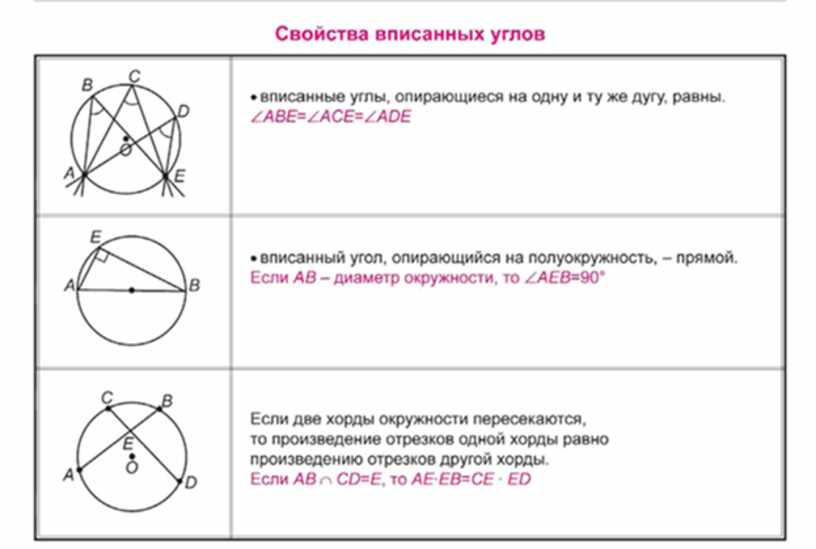
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Вписанный угол, опирающийся на полуокружность – прямой.
Докажем еще одну теорему, которая пригодится для решения задач.
Теорема. Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Пусть хорды АВ и СD пересекаются в точке Е. Докажем, что АЕ·ВЕ = СЕ·DE.
Рассмотрим треугольники ADE и CBE. В этих треугольниках углы 1 и 4 равны, так как они вписанные и опираются на одну и ту же дугу BD, а углы 2 и 3 равны как вертикальные. По первому признаку подобия треугольников △ADE ∼△CBE. Отсюда следует, что АЕСЕ=DEBE, или AE·BE = CE·DE.
Решим задачу, используя изученные свойства центральных и вписанных углов.
Центральный угол на 17° больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.
Пусть центральный угол равен х, а вписанный угол, опирающийся на ту же дугу, равен у:
Мы знаем, что х = 2у. Отсюда 2у = 17+у; у = 17.
Ответ: 17.
Заметили ошибку?
Расскажите нам об ошибке, и мы ее исправим.Объяснение урока: Вписанные углы в окружность
В этом объяснении мы узнаем, как определить теоремы нахождения меры вписанного угла относительно его образующего дуга или центральный угол, опирающийся на ту же дугу и меры вписанных углов в полуокружность.
Сначала определим вписанный угол.
Определение: вписанный угол
Вписанный угол — это внутренний угол между двумя хордами, пересекающимися по окружности.
Теперь мы собираемся доказать важную связь между мерой вписанного угла и мерой центрального угла
опирается на одну и ту же дугу.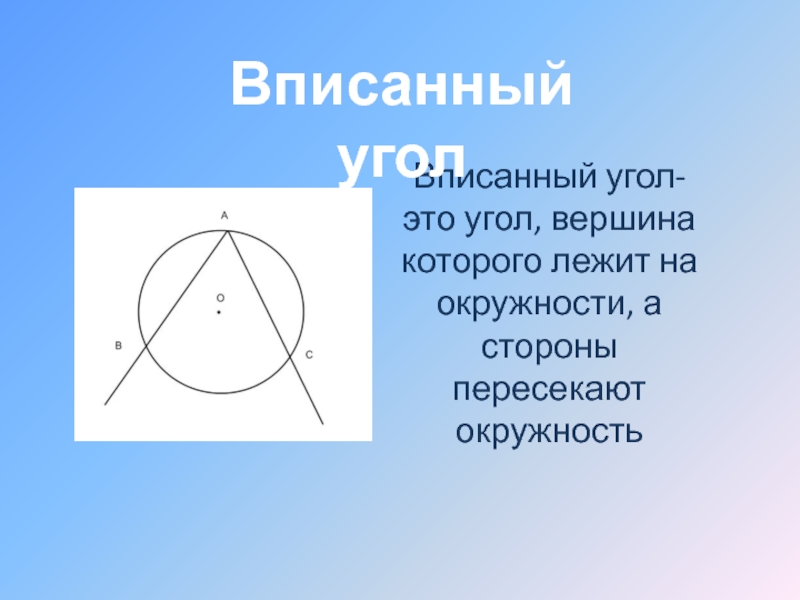
Рассмотрим сначала случай, когда центр окружности 𝑀 принадлежит одной из сторон вписанного угла.
Вписанный угол ∠𝐴𝐶𝐵 и центральный угол ∠𝐴𝑀𝐵 опираются на один и тот же дуга, 𝐴𝐵. Стоит отметить, что дуга 𝐴𝐵, о которой говорят, что она тянется угол ∠𝐴𝐶𝐵 — это дуга, которая делает , а не содержат точку 𝐶 (это дуга красного цвета на схеме).
Так как две стороны треугольника 𝐴𝐶𝑀 равны двум радиусам окружности, то это равнобедренный треугольник. Это значит, что, в треугольнике 𝐴𝐶𝑀, 𝑚∠𝐴𝐶𝐵=𝑚∠𝐴.
Следовательно, поскольку сумма углов треугольника составляет 180∘, мы имеем
| 𝑚 ВИТИТЕЛЬНОСТЬ = 180–2𝑚тка. ∘ | (1) |
У углы тий и тий находятся на прямой линии; следовательно, у нас есть
| 0026 | (2) |
Уравнения (1) и (2) приводят к
𝑚∠𝐴𝑀𝐵=2𝑚∠𝐴𝐶𝐵;
то есть,
𝑚∠𝐴𝐶𝐵=12𝑚∠𝐴𝑀𝐵.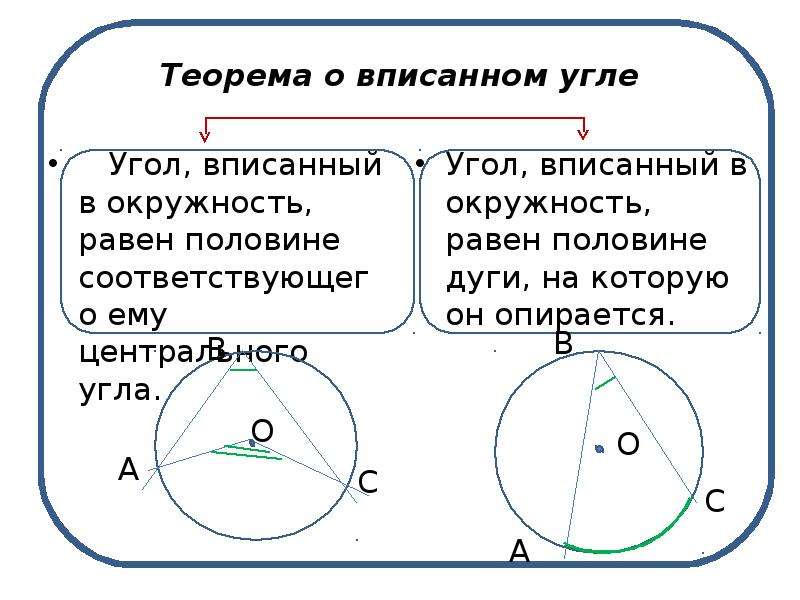
Теперь рассмотрим другую ситуацию для вписанного угла и центрального угла, опирающихся на одну и ту же дугу, а именно, когда окружность центр, 𝑀, является точкой внутри вписанного угла.
Мы можем использовать наш предыдущий результат для вписанного угла, сторона которого содержит центр окружности, разделив вписанный угол угол ∠𝐴𝐶𝐵 на два вписанных угла, ∠𝐴𝐶𝐷 и ∠𝐷𝐶𝐵, у которых есть сторона, содержащая центр круга (поскольку 𝐶𝐷 — это диаметр круга).
У нас есть 𝑚∠𝐴𝑀𝐷=2𝑚∠𝐴𝐶𝐷 и 𝑚∠𝐷𝑀𝐵=2𝑚∠𝐷𝐶𝐵.
С 𝑚∠𝐴𝑀𝐵=𝑚∠𝐴𝑀𝐷+𝑚∠𝐷𝑀𝐵 и 𝑚∠𝐴𝐶𝐵=𝑚∠𝐴𝐶𝐷+𝑚∠𝐷𝐶𝐵, находим, что 𝑚 Хорошо = 2𝑚 ВИДА+2𝑚 ВИТИТЕЛЬНОЕ
Итак, 𝑚∠𝐴𝐶𝐵=12𝑚∠𝐴𝑀𝐵.
Наконец, рассмотрим третью ситуацию, когда центр окружности 𝑀 находится вне вписанного угла.
Как и в предыдущей ситуации, мы рассматриваем два вписанных угла, у которых есть сторона, содержащая центр окружности, ∠𝐴𝐶𝐷 и ∠𝐵𝐶𝐷, где 𝐶𝐷 — диаметр круга.
Поскольку 𝑚∠𝐴𝑀𝐵=𝑚∠𝐴𝑀𝐷−𝑚∠𝐵𝑀𝐷 и
𝑚∠𝐴𝐶𝐵=𝑚∠𝐴𝐶𝐷−𝑚∠𝐵𝐶𝐷, находим, что
𝑚 Хорошо = 2𝑚 ВИТ -2𝑚 ВneT𝐵𝐶𝐷𝑚 = 2 (𝑚om -𝑚 — 𝑚 𝑚 𝐵𝐶𝐷 𝑚 𝑚 𝐴𝑀𝐵 = 2𝑚 ВИД.
Итак, 𝑚∠𝐴𝐶𝐵=12𝑚∠𝐴𝑀𝐵.
Мы нашли один и тот же результат в трех возможных положениях центра окружности 𝑀 относительно вписанного угла: (i) на одной стороне вписанного угла, (ii) внутри вписанного угла и (iii) вне вписанного угла.
Помните, что мера центрального угла, образуемого дугой, такая же, как мера этой дуги.
Теорема: Теорема о вписанном угле
Мера вписанного угла, опирающегося на дугу, равна половине меры этой дуги, то есть половине меры центральной угол, опирающийся на эту дугу.
Давайте теперь посмотрим на нашем первом примере, как использовать эту теорему, чтобы найти меру вписанного угла.
Пример 1. Нахождение меры вписанного угла по величине центрального угла, опирающегося на ту же дугу
Найдите 𝑚∠𝐴𝐶𝐷.
Ответ
Назовем 𝑀 центром круга. Это точка пересечения 𝐶𝐷 и 𝐴𝐵.
Угол ∠𝐴𝐶𝐷 является вписанным, так как точки 𝐴, 𝐶,
и 𝐷 находятся на круге. ∠𝐶𝑀𝐵 и ∠𝐴𝑀𝐷 — вертикально противоположные углы;
следовательно, они имеют одинаковую меру, 72∘.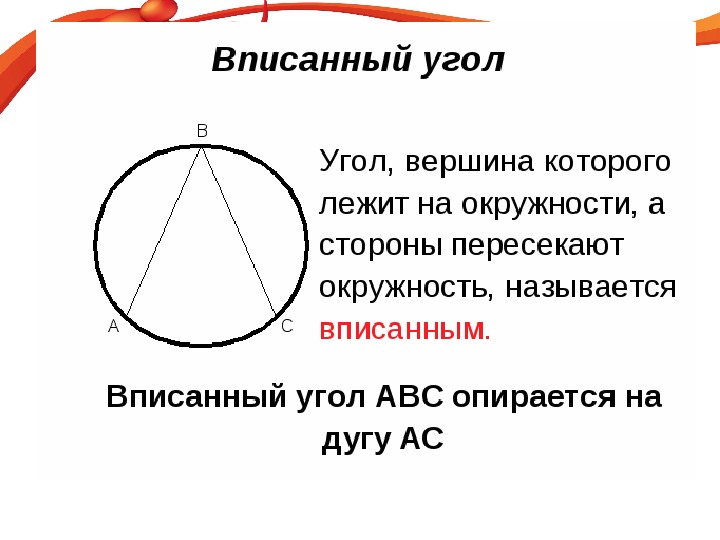
Отсюда имеем 𝑚∠𝐴𝐶𝐷=12𝑚∠𝐴𝑀𝐷𝑚∠𝐴𝐶𝐷=12×72𝑚∠𝐴𝐶𝐷=36,∘
Рассмотрим пример решения линейных уравнений.
Пример 2. Нахождение меры вписанного угла по величине его дуги путем решения двух линейных уравнений
Что такое 𝑥 на рисунке?
Ответ
В окружность с центром 𝑀 угол ∠𝐴𝐶𝐵 является вписанным, потому что точки 𝐴, 𝐶 и 𝐵 находятся на окружности. Центральный угол, опирающийся на та же дуга (большая дуга 𝐴𝐵) имеет меру (2𝑥+8)∘. Теорема о вписанном угле утверждает что мера вписанного угла, опирающегося на дугу, равна половине меры центрального угла, опирающегося на эту дугу.
Отсюда имеем 𝑚∠𝐴𝐶𝐵=12𝑚∠𝐴𝑀𝐵101=12(2𝑥+8)101=𝑥+4101−4=𝑥+4−4𝑥=97,∘∘
Теперь рассмотрим пример, включающий измерение дуги и решение линейное уравнение.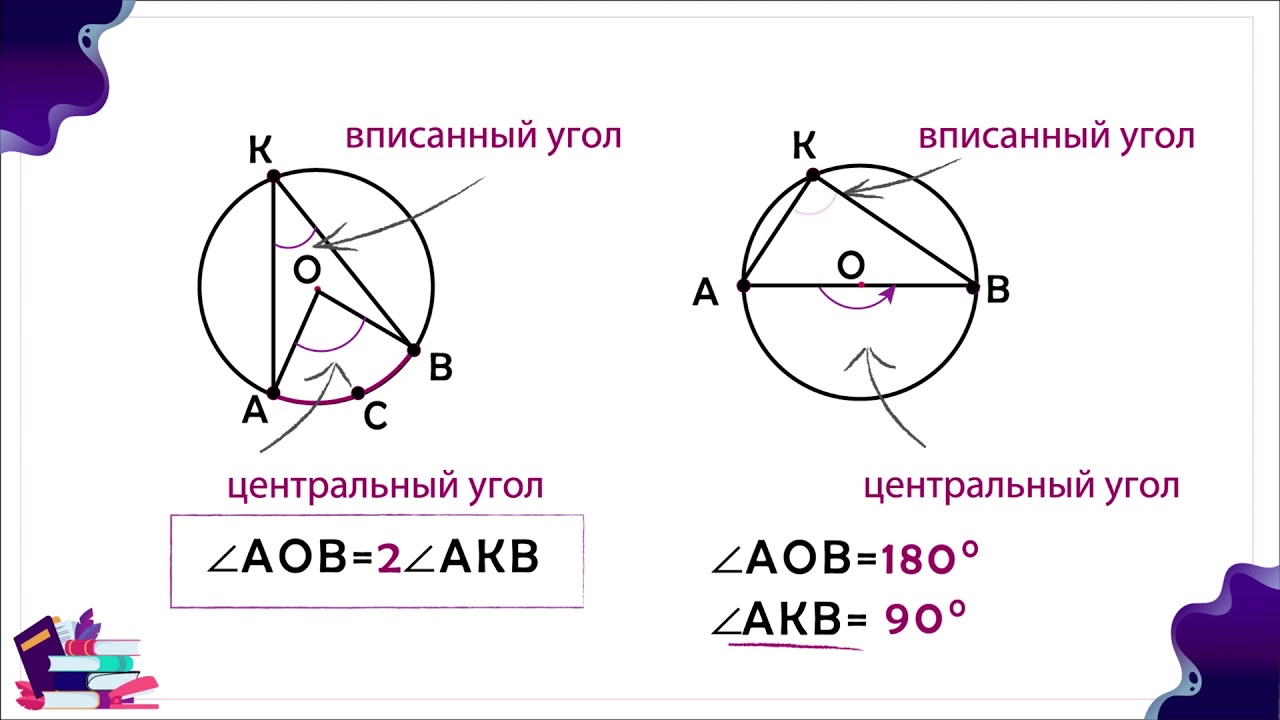
Пример 3. Решение уравнений с использованием меры вписанного угла по заданной мере его дуги
Учитывая, что 𝑚∠𝐵𝐴𝐶=(𝑥+15)∘, найти 𝑥.
Ответ
Угол ∠𝐵𝐴𝐶 — вписанный угол, опирающийся на дугу 𝐵𝐶 меры 118∘.
Теорема о вписанном угле утверждает, что мера вписанного угла, опирающегося на дугу, равна половине меры этой дуги. Таким образом, у нас есть 𝑚∠𝐵𝐴𝐶=12𝑚𝐵𝐶𝑚∠𝐵𝐴𝐶=12×118=59.∘∘
Кроме того, нам говорят, что 𝑚∠𝐵𝐴𝐶=(𝑥+15)∘; следовательно, 𝑥+15=59𝑥=59−15𝑥=44.
В следующем примере мы собираемся решить многошаговую задачу, в которой нам задана мера дуги.
Пример 4. Нахождение меры вписанного угла с помощью меры его дуги
Найдите 𝑚∠𝐷𝐶𝐵.
Ответ
Угол ∠𝐴𝐷𝐵 — вписанный угол, опирающийся на дугу 𝐴𝐵. Теорема о вписанном угле утверждает, что мера вписанного угла, опирающегося на дугу, равна половине меры этой дуги. Таким образом, у нас есть 𝑚∠𝐴𝐷𝐵=12𝑚𝐴𝐵52=12×𝑚𝐴𝐵𝑚𝐴𝐵=2×52=104.∘∘∘
Угол ∠𝐷𝐶𝐵 — вписанный угол, опирающийся на
дуга 𝐷𝐵=𝐴𝐵+𝐴𝐷.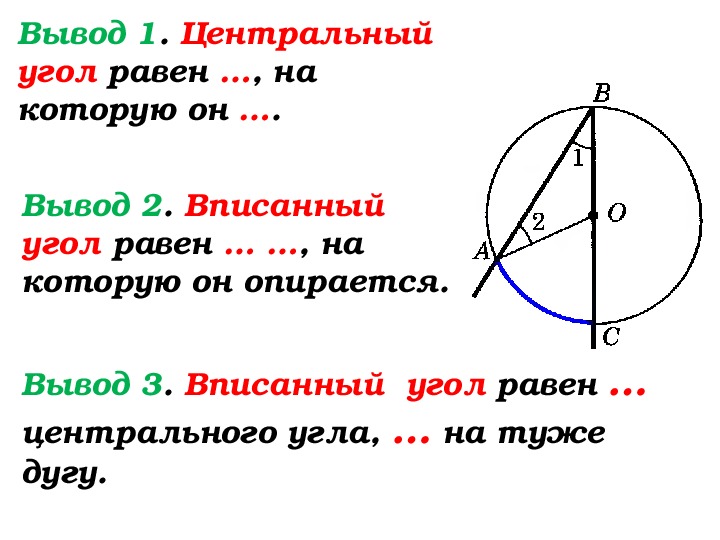
Следовательно,
𝑚𝐷𝐵=𝑚𝐴𝐵+𝑚𝐴𝐷𝑚𝐷𝐵=104+60=164.∘
Теорема о вписанном угле утверждает, что мера вписанного угла, опирающегося на дугу, равна половине меры этой дуги. Таким образом, у нас есть 𝑚∠𝐷𝐶𝐵=12𝑚𝐷𝐵𝑚∠𝐷𝐶𝐵=12×164=82.∘∘
Рассмотрим следствие теоремы о вписанном угле, а именно, когда вписанный угол описывается полуокружностью (что означает что вписанный угол опирается на дугу размером 180∘) или, другими словами, когда центральный угол прямой (центральный угол ∠𝐴𝑀𝐵 имеет меру 180∘).
Применение теоремы о вписанном угле дает нам 𝑚∠𝐴𝐶𝐵=12×180=90.∘∘
Следствие: угол, вписанный в полукруг
Вписанный угол, проведенный в полукруг, является прямым углом.
Теперь решим систему линейных уравнений, чтобы найти меру вписанного угла в полуокружность.
Пример 5. Нахождение меры вписанного угла в полуокружность
Учитывая, что 𝑚∠𝐶𝐴𝐵=31∘, найти 𝑦 и 𝑥.
Ответ
Вписанный угол ∠𝐵𝐶𝐴 очерчен полуокружностью, так как 𝐴𝐵
это диаметр окружности.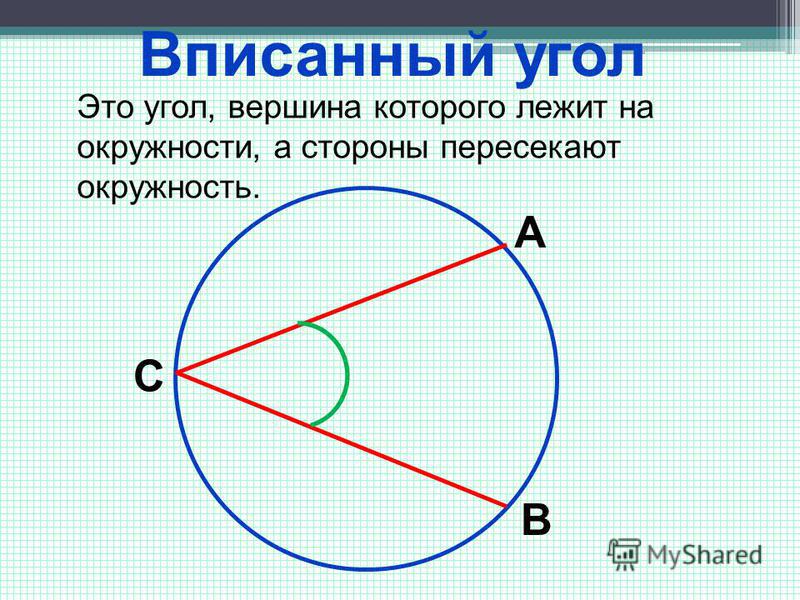
Вписанный угол, очерченный полуокружностью, является прямым углом. Таким образом, у нас есть
𝑚∠𝐵𝐶𝐴=𝑦=90,∘∘
Кроме того, сумма углов треугольника равна 180∘, что дает 𝑥+𝑦+31=180.
Подстановка значения, которое мы нашли для 𝑦, в это уравнение дает 𝑥+90+31=180𝑥+121=180𝑥=180−121=59.
Мы обнаружили, что 𝑦=90𝑥=59.and
В нашем последнем примере мы решаем задачу, включающую вписанный угол, проведенный в полуокружность, и решим уравнение.
Пример 6. Решение уравнений с использованием меры угла, вписанного в полуокружность
Учитывая, что 𝑚∠𝐴𝐵𝐶=(6𝑥+15)∘ и 𝑚∠𝐶𝐴𝐵=(11𝑥−10)∘, найдите значение 𝑥.
Ответ
Вписанный угол ∠𝐵𝐶𝐴 очерчен полуокружностью, так как 𝐴𝐵 это диаметр окружности. Вписанный угол, очерченный полуокружностью, является прямым углом. Таким образом, у нас есть 𝑚∠𝐵𝐶𝐴=90.∘
Поскольку сумма углов треугольника равна 180∘, находим, учитывая
треугольник 𝐴𝐵𝐶, что
𝑚 Хорошо+𝑚 𝑚 В+90 = 180𝑚 𝑚+𝑚 Вор.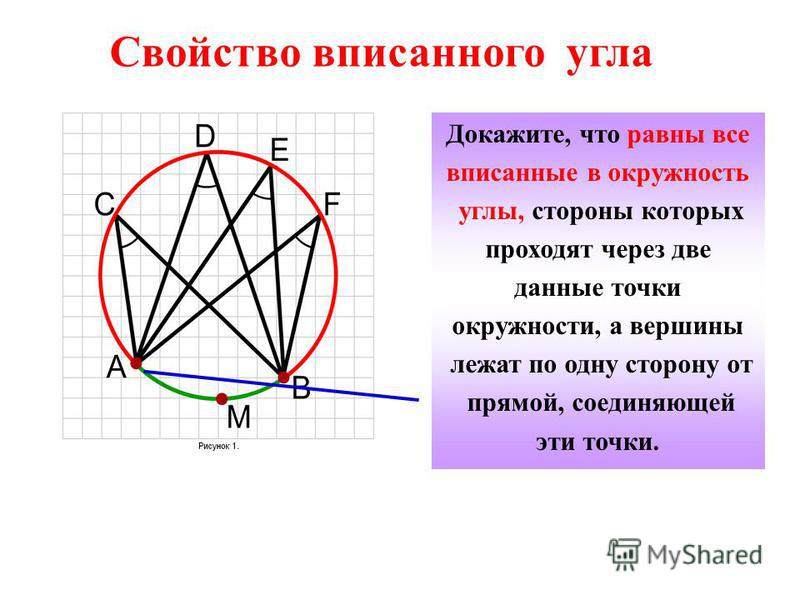
Резюмируем ключевые моменты этого объяснения.
Ключевые точки
- Вписанный угол – это угол, вершина которого лежит на окружности, а стороны содержат две хорды окружности.
- Теорема о вписанном угле утверждает, что мера вписанного угла, опирающегося на дугу, равна половине меры этой дуги, то есть половина меры центрального угла, опирающегося на эту дугу.
- Следствием теоремы о вписанном угле является то, что вписанный угол, проведенный через полуокружность, является прямым углом.
вписанных углов: определение, примеры и формула
Круг уникален тем, что у него нет ни углов, ни углов, что отличает его от других фигур, таких как треугольники, прямоугольники и треугольники. Но конкретные свойства можно детально изучить, введя углы внутри круга. Например, самый простой способ создать угол внутри круга — нарисовать две хорды так, чтобы они начинались в одной точке. Поначалу это может показаться ненужным, но при этом мы можем использовать многие правила тригонометрии и геометрии, тем самым более подробно изучая свойства окружности.
Что такое вписанный угол окружности?
Вписанные углы — это углы, образованные в окружности двумя хордами, имеющими одну конечную точку на окружности. Общая конечная точка также известна как вершина угла. Это показано на рис. 1, где две хорды AB¯ и BC¯ образуют вписанный угол m Вписанные углы, оригиналы StudySmarter Другие конечные точки двух хорд образуют дугу на окружности, которая представляет собой дугу AC, показанную ниже. Есть два вида дуг, которые образованы вписанным углом. Если размер дуги меньше полукруга или 180°, то дуга определяется как малая дуга, как показано на рисунке 2а. Если размер дуги больше полукруга или 180°, то дуга определяется как большая дуга, как показано на рисунке 2b. Но как создать такую дугу? Натянув два шнура, как мы обсуждали выше. Но что такое аккорд? Возьмите любые две точки на окружности и соедините их, чтобы получился отрезок: Хорда — это отрезок, соединяющий две точки окружности. Большая дуга и Малая дуга окружности, StudySmarter Originals Теперь, когда определена хорда, что можно построить вокруг хорды? Начнем с дуги , и, как бы очевидно это ни звучало, это простая часть окружности, определенная ниже: Дуга окружности — это кривая, образованная двумя точками окружности. Длина дуги — это расстояние между этими двумя точками. Длину дуги можно измерить, используя центральный угол в градусах или радианах и радиус, как показано в формуле ниже, где θ — центральный угол, а π — математическая константа. В то же время r — это радиус окружности. Длина дуги (градусы)=θ360·2π·rДлина дуги (радианы)=θ·r Несколько типов вписанных углов моделируются с помощью различных формул, основанных на количестве углов и их форме. Давайте рассмотрим различные теоремы о вписанном угле. Теорема о вписанном угле связывает меру вписанного угла и его дугу. Он утверждает, что мера вписанного угла в градусах равна половине меры дуги, на которую опирается точка, где мера дуги также является мерой центрального угла. m Теорема о вписанном угле, StudySmarter Originals Если два вписанных угла опираются на одну дугу, то углы равны. Конгруэнтные углы имеют одинаковую градусную меру. Пример показан на рисунке 4, где m m Конгруэнтные вписанные углы, StudySmarter Originals Когда вписанный угол пересекает дугу, являющуюся полуокружностью, вписанный угол является прямым углом, равным 90 °. Вписанный угол в полуокружность, StudySmarter Originals Если четырехугольник вписан в окружность, а это означает, что четырехугольник образован хордами в окружности, то его противоположные углы являются дополнительными. Например, на следующей диаграмме показан вписанный четырехугольник, где m m m Вписанный четырехугольник, StudySmarter Originals Найдите углы m Пример вписанных углов, StudySmarter Originals Решение: Поскольку углы m m Используя теорему о вписанном угле, мы знаем, что центральный угол в два раза больше вписанного угла, опирающегося на ту же дугу. м Следовательно, угол равен 37,5°. Какова мера угла m Конгруэнтные вписанные углы, оригиналы StudySmarter Решение: Так как углы m Чтобы решить любой пример вписанных углов, запишите все данные углы. Распознайте заданные углы, нарисовав схему, если она не дана. Давайте посмотрим на некоторые примеры. Найдите m Решение: Используя теорему о вписанном угле, получаем, что вписанный угол равен половине центрального угла. m Найдите m Вписанный четырехугольник Пример, StudySmarter Originals Решение: Поскольку показанный четырехугольник вписан в окружность, его противоположные углы дополняют друг друга. Затем мы подставляем заданные углы в уравнения и перестраиваем уравнения, чтобы сделать неизвестный угол предметом. 98°+ Найти m Вписанный четырехугольник, StudySmarter Originals Решение: Вписанные углы m Угол m Так как четырехугольник ABCD вписан в окружность, то его противоположные углы должны быть смежными. 
Формула вписанных углов
Таким образом, нельзя создать общую формулу, но такие углы можно разделить на определенные группы. Теоремы о вписанном угле
Это показано ниже на рисунке, где дуга АВ — полуокружность с мерой 180°, а вписанный в нее угол m Примеры вписанных углов
Метод решения задач с вписанными углами
Вписанные углы – основные выводы
Leave A Comment