Решение неравенств, все формулы и примеры
Определение и формулы неравенств
Знаки > называются знаками строгого неравенства, а знаки — знаками нестрогого неравенства.
Если в неравенство входят только числовые величины, то такое неравенство называется числовым неравенством.
Неравенства называют равносильными, если они имеют одно и тоже множество решений.
Основные правила, применяемые при решении неравенств
- Если какое-либо слагаемое перенести из одной части неравенства в другую, изменив при этом его знак на противоположный, то получим неравенство, равносильное данному.
- Если обе части неравенства умножить (разделить) на одно и то же положительное число, то получим неравенство, равносильное данному.
- Если обе части неравенства умножить (разделить) на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получим неравенство, равносильное данному.
В зависимости от того, какие функции входят в неравенство, различают линейные, квадратные, дробно-рациональные, иррациональные, логарифмические, показательные неравенства, неравенства с параметром.
Если требуется все общие решения двух или нескольких неравенств, то решают систему неравенств. Как и систему уравнений, систему неравенств записывают с помощью фигурной скобки. Решение системы неравенств есть пересечение решений всех входящих в нее неравенств.
Одним из основных методов решения неравенств является метод интервалов.
Примеры решения неравенств
| Понравился сайт? Расскажи друзьям! | |||
Двойные неравенства. 2 способа решения
Например:
\(5<11<17\)
\(-2\leq3x+5\leq2\)
\(2x-5\leq3x+7\leq8x\)
Двойное неравенство по своей сути – это система из двух неравенств, записанных в одну строку. Поэтому их всегда можно представить в виде системы.
Например:
\(-2\leq3x+5\leq2\Leftrightarrow\begin{cases}-2\leq3x+5\\3x+5\leq2\end{cases}\)
Но делать это нужно не всегда.
2 способа решения двойного неравенства
1) Если в крайней левой и крайней правой частях двойного неравенства нет неизвестных, то удобнее оставить его как есть. При этом в процессе решения стремится равносильными преобразованиями привести неравенство к виду \([число]\)\(<\)\(x\)\(<\)\([число]\).
Пример: Решите двойное неравенство:
|
\(-2\leq3x+5\leq2\) \(|-5\) |
Здесь нет неизвестных по краям, поэтому к системе переходить не будем. Вместо этого делаем такие преобразования, чтоб в центре остался голый икс, а по краям — числа. |
|
|
\(-7≤3x≤-3\) \(|:3\) |
Теперь нам мешает \(3\). Поделим все три части неравенства на \(3\). |
|
|
\(-\)\(\frac{7}{3}\)\(\leq x \leq-1\) |
Готово, наш икс «голый». Можно записывать ответ. |
2) Если в крайних частях двойного неравенства есть неизвестные лучше перевести неравенство в систему и решать его как обычную систему неравенств.
Пример: Решите двойное неравенство:
\(2x-5<3x+7≤8x\) |
В крайней левой и крайней правой частях есть неизвестные –значит переходим к системе. |
|
\(\begin{cases}2x-5<3x+7\\3x+7\leq8x\end{cases}\) |
Решаем обычные линейные неравенства: все, что с иксами переносим в левую сторону, все что без иксов — в правую. |
|
\(\begin{cases}2x-3x<7+5\\3x-8x\leq-7\end{cases}\) |
Приводим |
|
\(\begin{cases}-x<12 \\-5x\leq-7 \end{cases}\) |
«Оголим» иксы, поделив верхнее неравенство на \((-1)\), нижнее на \((-5)\). Не забываем при этом перевернуть знаки сравнения, так как мы делим на отрицательное число. |
|
\(\begin{cases}x>-12 \\x\geq \frac{7}{5}\end{cases}\) |
Отметим на числовой оси оба решения |
|
Так как у нас система, то мы ищем значения иксов, которые подойдут обоим неравенствам, т.е. |
Ответ: \([\)\(\frac{7}{5}\)\(;\infty)\)
Скачать статьюЕсли в выражении с переменными вы увидели знак = , то это уравнение.
Если знак < или ˃ или ≤ или ≥ — то это, конечно, неравенство.
Как правило, неравенства решаются сложнее, чем аналогичные им уравнения. И знать надо больше – чтобы не наделать ошибок
В этом разделе – все основные способы и приемы решения неравенств на ЕГЭ по математике. Повторите их. Даже такие неравенства, как квадратичные или дробно-рациональные, содержат немало ловушек для неопытного школьника. И тем более — показательные и логарифмические. А иррациональные неравенства и неравенства с модулями вообще считаются одними из самых сложных тем школьного курса алгебры.
Здесь рассказано также о методе замены множителя (еще он называется методом рационализации неравенства). В учебнике вы его не найдете. И еще – об основных ошибках и полезных лайфхаках для решения неравенств.
Квадратичные неравенства
Метод интервалов
Иррациональные неравенства
Задача 15 Репетиционного ЕГЭ онлайн, май 2020, Анна Малкова
Неравенства с модулем
Показательные неравенства
Логарифмические неравенства
Метод замены множителя (рационализации)
Решение неравенств: основные ошибки и полезные лайфхаки
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 15
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 32, задача 15
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 15
Логарифмические неравенства повышенной сложности
Еще раз повторим основные правила:
— Равносильными называются неравенства, множества решений которых совпадают.
— Если обе части неравенства умножить на отрицательное число, знак неравенства поменяется на противоположный. А если на положительное число – знак неравенства останется тем же.
— Возводить обе части неравенства в квадрат можно только если они неотрицательны.
— Извлекать корень из неравенства нельзя. Нет такого действия!
— Если в неравенстве можно сделать замену переменной – сделайте замену переменной. А потом аккуратно вернитесь к той переменной, которая была вначале.
— Если вы решаете простейшее показательное или логарифмическое неравенство – не забудьте сравнить основание степени (или логарифма) с единицей.
— Если в неравенстве есть дроби, корни четной степени или логарифмы – там обязательно будет
— Решение неравенства лучше всего записывать в виде цепочки равносильных переходов.
— Если вы воспользовались методом рационализации (замены множителя) – соответствующие формулы лучше доказать.
основные ошибки и полезные лайфхаки
Вы умеете решать неравенства? Уверены?
Вспомним для начала, что вообще можно делать с неравенствами и чего с ними делать нельзя.
При решении неравенств мы можем:
1. Умножать обе части неравенства на число или выражение, не равное нулю.
При умножении обеих частей неравенства на положительное число знак неравенства сохраняется.
При умножении обеих частей неравенства на отрицательное число знак неравенства меняется на противоположный.
2. Можем возводить обе части неравенства в квадрат при условии, что они неотрицательны
3. Имея дело с показательным или логарифмическим неравенством, мы можем «отбрасывать» основания или логарифмы. Если основание степени или логарифма больше единицы – знак неравенства будет тот же. Если основание степени или логарифма положительно и меньше единицы – знак неравенства меняется на противоположный.
Конечно, мы не просто «отбрасываем» основания степеней или логарифмы. Мы пользуемся свойствами монотонности соответствующих функций. Если основание степени больше единицы, показательная функция монотонно возрастает. Если основание положительно и меньше единицы – показательная функция монотонно убывает. Аналогично ведет себя и логарифмическая функция.

4. При решении показательных или логарифмических неравенств применяется метод рационализации (замены множителя).
5. Общее правило. Если неравенство можно хоть как-то упростить – это необходимо сделать! Иначе его решение может занять восемь страниц и два часа времени.
Чего нельзя делать при решении неравенств? Вот 7 ловушек, в которые часто попадают абитуриенты.
1. Нельзя умножать (или делить) неравенство на выражение, знака которого мы не знаем.
Например, в неравенстве > нельзя поделить левую и правую часть на . Правильный способ: перенести всё в левую часть неравенства, разложить на множители и решить неравенство методом интервалов.
> 0
> 0
Получаем, что < 0 или > . «Сократив» на , который может быть отрицательным, мы не получили бы правильного ответа.
2. Извлекать из неравенства корень тоже нельзя. Такого действия просто нет.
Как, например, решить неравенство
>
Перенесем все в левую часть неравенства, чтобы в правой остался ноль.
> 0
Разложим левую часть на множители.
> 0
Решим неравенство, пользуясь свойствами квадратичной функции , и запишем ответ: < или > .
Запомним: ответы типа « > » абсурдны.
Как решать неравенство > 0? Это типичная «ловушка для абитуриентов». Так и хочется сказать, что > 0 (то есть извлечь корень из неравенства). Но этого делать нельзя. Выражение положительно при всех , кроме нуля. Правильное решение неравенства: .
4. Возводить обе части неравенства в квадрат можно только если они неотрицательны.
5. Помним о том, в каких случаях знак показательного или логарифмического неравенства меняется, а в каких – остается тем же. «Отбрасывая» логарифмы, делаем это грамотно.
6. Если в неравенстве есть дроби, корни четной степени или логарифмы – там обязательно будет область допустимых значений.
7. Сложная тем для старшеклассников – задачи с модулем. Проверьте, умеете ли вы их решать.
При решении неравенств большое значение имеет правильное оформление. Рекомендуется оформлять решение как цепочку равносильных переходов: от исходного неравенства к равносильному ему неравенству или системе.
Обратите внимание на приемы, позволяющие решать неравенства легко, быстро и без лишних вычислений.
А теперь – полезный лайфхак для решения дробно-рациональных неравенств.
Решите неравенство
Запишем ОДЗ:
Что будет, если действовать «по шаблону» — то есть собрать всё в левой части неравенства и привести к одному знаменателю? — Будет много вычислений и выражение четвертой степени.
Может быть, сделаем проще? Представим дробь в виде суммы дробей и .
Продолжаем упрощать левую часть:
Теперь можно и привести дроби к одному знаменателю.
Все, больше ничего не пишем. Решаем неравенство методом интервалов.

Ответ: .
Неравенства
При решении неравенств используют следующие правила:
1. Любой член неравенства можно перенести из одной части
неравенства в другую с противоположным знаком, при этом знак неравенства не меняется.
2. Обе части неравенства можно умножить или разделить на одно
и то же положительное число, не изменив при этом знак неравенства.
3. Обе части неравенства можно умножить или разделить на одно
и то же отрицательное число, изменив при этом знак неравенства на
противоположный.
Пример:
Решить неравенство −8x +11<−3x−4
Решение.
1. Перенесём член −3x в левую часть неравенства, а член 11 — в правую часть неравенства, при этом поменяем знаки на противоположные у −3x и у 11.
Тогда получим
−8x+3x <−4−11
−5x<−15
2. Разделим обе части неравенства −5x<−15 на отрицательное число −5, при этом знак неравенства <, поменяется на >, т.е. мы перейдём к неравенству противоположного смысла.
Получим:
−5x<−15|:(−5)
x>−15:(−5)
x>3
x>3 — решение заданного неравенства.
Обрати внимание!
Для записи решения можно использовать два варианта: x>3 или в виде числового промежутка.
Отметим множество решений неравенства на числовой прямой и запишем ответ в виде числового промежутка.
x∈(3;+∞)
Ответ: x>3 или x∈(3;+∞)
Алгебраические неравенства.
Квадратные неравенства. Рациональные неравенства высших степеней.
Дробно-рациональные неравенства.
Методы решения неравенств зависят в основном от того, к какому классу относятся функции, составляющие неравенство.
- I. Квадратные неравенства, то есть неравенства вида
ax2 + bx + c > 0 (< 0), a ≠ 0.
Будем считать, что a>0. Если это не так, то умножив обе части неравенства на -1 и изменив знак неравенства на противоположный, получим желаемое.
Чтобы решить неравенство можно:
- Квадратный трехчлен разложить на множители, то есть неравенство записать в виде
a (x — x1) (x — x2) > 0 (< 0).
- Корни многочлена нанести на числовую ось. Корни разбивают множество действительных чисел на промежутки, в каждом из которых соответствующая квадратичная функция будет знакопостоянной.
- Определить знак a (x — x1) (x — x2) в каждом п
Рациональное неравенство — это неравенство, которое можно свести к виду \[\Large{\dfrac{P(x)}{Q(x)}\lor 0}\]где \(P(x),\
Q(x)\) — многочлены.
(\(\lor\) — один из знаков \(\geqslant,
\ \leqslant, \ >, \ <\))
Например, следующие неравенства являются рациональными: \[\dfrac1{x+1}>0,\qquad x+2+\dfrac{x-1}{x+3}<1,\qquad x^2+x-2\leqslant 0\]
\[{\Large{\text{Линейные неравенства}}}\] Линейные неравенства – это неравенства вида \[ax+b \lor 0, \qquad
\lor — \text{ один из знаков } \geqslant, \ \leqslant, \ >, \
<;\quad a,b — \text{ числа,}\]или сводящиеся к такому виду.
Область допустимых значений \(x\) (ОДЗ) таких неравенств — все вещественные числа (\(x\in \mathbb{R}\)).
Общее правило решения линейных неравенств:
1) Для того, чтобы решить данное неравенство, необходимо привести его к виду \(ax\lor -b\), то есть перенести число \(b\) в правую часть.
2) Если коэффициент \(a\) перед \(x\) – положительный, то неравенство равносильно \(x\lor -\dfrac ba\), то есть после деления обеих частей неравенства на \(a\) знак неравенства не меняется.
3) Если коэффициент \(a\) перед \(x\) – отрицательный, то неравенство равносильно \(x\land -\dfrac ba\), то есть после деления обеих частей неравенства на \(a\) знак неравенства меняется на противоположный.
4) Если \(a=0\), то неравенство равносильно \(0\lor -b\), что либо верно при всех значениях переменной \(x\) (например, если это \(0>-1\)), либо неверно ни при каких значениях \(x\) (например, если это \(0\leqslant -3\)).
То есть ответом будут либо \(x\in\mathbb{R}\), либо \(x\in
\varnothing\).
Замечание
Заметим, что знаку \(\leqslant\) противоположен знак \(\geqslant\), а знаку \(<\) – знак \(>\). И наоборот.
Пример 1
Решить неравенство \(5-3x>-1\).
Решение. I способ
Сделаем цепочку преобразований:
\[5-3x>-1 \ \Rightarrow \ -3x>-1-5 \ \Rightarrow \ -3x>-6 \
\Rightarrow \ x<\dfrac 63 \ \Rightarrow \ x<2\] Таким образом, ответом будет \(x\in(-\infty;2)\).
Заметим, что т.к. мы делили неравенство на \(-3\), то знак неравенства поменялся.
Решение. II способ
Можно перенести слагаемое \(-3x\) в правую часть, а \(-1\) – в левую:
\[5-3x>-1 \ \Rightarrow \ 5+1>3x \ \Rightarrow \ 3x<6 \ \Rightarrow \ x<2\]
Пример 2
Решить неравенство \((1-\sqrt2)x+2\leqslant 0\).
Решение
Заметим, что перед \(x\) находится отрицательный коэффициент. Поэтому:
\[(1-\sqrt2)x\leqslant -2 \Rightarrow x\geqslant -\dfrac 2{1-\sqrt2}\] Преобразуем число \(-\dfrac 2{1-\sqrt2}\): домножим числитель и знаменатель дроби на сопряженное к \(1-\sqrt2\), то есть на \(1+\sqrt2\), чтобы избавиться от иррациональности в знаменателе:
\[-\dfrac 2{1-\sqrt2}=-\dfrac{2(1+\sqrt2)}{(1-\sqrt2)(1+\sqrt2)}=
-\dfrac{2(1+\sqrt2)}{1-2}=2(1+\sqrt2)\]
Таким образом, ответ \(x\in [2+2\sqrt2;+\infty)\).
Перейдем к квадратичным неравенствам, которые являются очень важным инструментом в решении задач.
\[{\Large{\text{Метод интервалов}}}\]
Приступим к рассмотрению общего метода для решения любого рационального неравенства, то есть неравенства вида
\[(**)\qquad \dfrac{P(x)}{Q(x)}\geqslant 0 \qquad (\text{на месте }\geqslant \text{может стоять любой из} \leqslant, \ <, \ >)\]
Область допустимых значений \(x\) (ОДЗ) таких неравенств — все вещественные числа, кроме нулей знаменателя.
Существует два способа решения таких неравенств:
1 способ: Классический. Т.к. дробь положительна (отрицательна) тогда и только тогда, когда числитель и знаменатель дроби одного знака (разных знаков), то неравенство \((*)\) равносильно совокупности: \[{\large{\left[\begin{gathered} \begin{aligned} &\begin{cases} P(x)\geqslant 0\\ Q(x)>0 \end{cases}\\ &\begin{cases} P(x)\leqslant 0\\ Q(x)<0 \end{cases} \end{aligned} \end{gathered} \right.}}\]
Такой способ подойдет для решения любого неравенства, где слева стоит дробь, а справа — \(0\).
Но, как правило, для решения большинства рациональных неравенств он неудобен. Почему? Вы сможете убедиться в этом после того, как мы рассмотрим метод интервалов.
2 способ: Удобный. Метод интервалов (будем рассматривать этот метод на примере конкретного неравенства, чтобы было понятней).
Заметим, что первые три шага созданы для того, чтобы преобразовать неравенство к более простому виду, что поможет вам не допустить ошибку в решении подобных задач. Метод интервалов – это всего лишь удобный инструмент для решения рациональных неравенств, и если вы будете всегда пользоваться одним и тем же алгоритмом, то вероятность допустить ошибку при решении таких неравенств будет минимальной.
Данный алгоритм специально расписан подробно, чтобы у вас не возникло вопросов; всего после нескольких использований этого алгоритма вы будете решать рациональные неравенства очень быстро и без ошибок!
1 ШАГ. Необходимо перенести все слагаемые в одну часть (пусть это будет левая часть) неравенства так, чтобы в другой части неравенства остался \(0\), и привести эти слагаемые к общему знаменателю так, чтобы в левой части неравенства получилась дробь. Затем нужно разложить числитель и знаменатель полученной дроби, то есть многочлены \(P(x), \ Q(x)\), на множители.
Например, неравенство \(\dfrac1{x+1}<1\) нужно переписать в виде \(\dfrac1{x+1}-1<0\), затем привести к общему
знаменателю \(\dfrac1{x+1}-\dfrac{x+1}{x+1}<0\), затем записать в виде одной дроби левую часть: \(\dfrac{1-(x+1)}{x+1}<0\) и
привести подобные слагаемые: \(\dfrac{-x}{x+1}<0\).
Итак, пусть после разложения на множители неравенство приняло вид \[\dfrac{x^2(x-1)^3(x+1)(2x^2+3x+5)(2x-x^2-3)}{(x+1)^3(3-x)(2-3x)^2} \geqslant0\]
Заметим, что любой многочлен можно (а в нашем способе НУЖНО) разложить до произведения только линейных скобок (\(ax+b\)) и квадратичных скобок с отрицательным дискриминантом \((ax^2+bx+c), \ D<0\).
2 ШАГ. Рассмотрим скобки, в которых остался квадратичный трехчлен с \(D<0\).
\(\bullet\) Если при \(x^2\) находится положительный коэффициент \(a>0\), то при всех значениях \(x\) выражение \(ax^2+bx+c\) положительно (не может быть равно нулю!). Т.к. мы имеем право делить неравенство на любое число/выражение, не равное \(0\), то разделим обе части неравенства на такие скобки (в нашем неравенстве такой скобкой является \((2x^2+3x+5)\)). Причем заметим, что т.к. мы делим на положительное выражение, то знак неравенства не меняется!
\(\bullet\) Если при \(x^2\) находится отрицательный коэффициент \(a<0\), то при всех значениях \(x\) выражение \(ax^2+bx+c\) отрицательно. Т.к. мы имеем право делить неравенство на любое число/выражение, не равное \(0\), то разделим обе части неравенства на такие скобки (в нашем неравенстве такой скобкой является \((2x-x^2-3)\)). Причем заметим, что т.к. мы делим на отрицательное выражение, то знак неравенства должен измениться на противоположный!
Итак, обобщим 2 шаг: квадратичные скобки с отрицательным дискриминантом можно просто вычеркнуть, причем при вычеркивании скобок с \(a>0\) знак неравенства остается прежним, а вот при вычеркивании скобок с \(a<0\) знак неравенства меняется на противоположный столько раз, сколько было таких скобок. Лучше вычеркивать их последовательно по одной, каждый раз меняя знак неравенства на противоположный.
Таким образом, неравенство примет вид \[\dfrac{x^2(x-1)^3(x+1)}{(x+1)^3(3-x)(2-3x)^2} \leqslant 0\]
3 ШАГ. Рассмотрим линейные скобки \((ax+b)\).
Назовем скобку хорошей, если при \(x\) находится положительный коэффициент (такие скобки мы трогать не будем), и плохой, если при \(x\) находится отрицательный коэффициент (в таких скобках необходимо поменять все знаки на противоположные, то есть сделать их хорошими).
Для того, чтобы в одной плохой скобке поменять все знаки на противоположные, необходимо домножить правую и левую части неравенства на \(-1\). Таким образом, после одного такого действия знак неравенства сменится на противоположный. Значит, если плохих скобок четное количество, то знак неравенства не изменится, если нечетное – то знак неравенства изменится на противоположный.
Заметим, что выражение \((ax+b)^n\) — это не что иное, как произведение \(n\) скобок \((ax+b)\).
В нашем неравенстве среди плохих одна скобка \((3-x)\) и две скобки \((2-3x)\) (т.к. \((2-3x)^2=(2-3x)(2-3x)\)), то есть всего три плохих скобки, следовательно, знак неравенства изменится и неравенство примет вид: \[\dfrac{x^2(x-1)^3(x+1)}{(x+1)^3(x-3)(3x-2)^2} \geqslant0\quad (***)\]
Заметим, что множитель \(x^2\) — это скобка \((x-0)^2\), или, что то же самое, \((x-0)(x-0)\) – произведение двух одинаковых линейных скобок.
4 ШАГ. Теперь, когда левая часть неравенства состоит из произведения только хороших линейных скобок (в каких-то степенях), можно приступить к самому методу интервалов.
Его суть состоит в том, что левая часть неравенства — всюду непрерывная функция, кроме тех точек, где знаменатель дроби равен нулю. Поэтому точки, в которых эта функция равна нулю (то есть ее числитель равен нулю) и точки, в которых эта функция не существует (то есть ее знаменатель равен нулю), разбивают область определения этой функции на промежутки, причем на каждом промежутке функция принимает значения строго одного знака.
А нам как раз нужно найти те значения \(x\), при которых функция \(\geqslant 0\). Причем, т.к. наша функция — рациональная, то ее область определения — это все действительные числа (\(\mathbb{R}\)), кроме нулей знаменателя. Поэтому отметим нули каждой скобки на вещественной прямой (а ноль каждой скобки – это как раз ноль числителя или знаменателя), причем нули знаменателя – выколотые, нули числителя – закрашенные (если знак неравенства нестрогий, как в примере, то есть \(\geqslant \) или \(\leqslant \)) или выколотые (если знак неравенства строгий, то есть \(>\) или \(<\)).
Заметим, что если мы отметили \(n\) точек, то числовая прямая разобьется на \(n+1\) промежутков.
Расставим знак на каждом промежутке \(\color{red}{{\Large{\text{справа налево}}}}\). Будем ставить “\(+\)”, если функция на этом промежутке принимает положительные значения, и “\(-\)” — если отрицательные. Нулю функция равна в закрашенных точках.
Первые три шага мы делали для того, чтобы не подставлять точки из каждого промежутка и не вычислять, какого знака будет левая часть неравенства (что бывает неудобно, если числа, которые нужно отмечать на прямой, “некрасивые”). Знаки мы будем расставлять, выявив некоторую закономерность. Какую – вы узнаете дальше.
Но в любом случае способ расстановки знаков путем подстановки чисел остается в нашем арсенале.
Т.к. все скобки – хорошие, то первый знак всегда будет “\(+\,\)” (именно для этого мы и приводили неравенство к такому виду!). Действительно, если подставить любое число, превышающее самый большой корень (у нас самый большой корень \(x=3\)), то каждая скобка будет положительна, значит, и произведение таких скобок будет всегда положительно.
Если какой-то корень входит в четное количество скобок, то при переходе через него (справа налево!) знак меняться не будет. В нашем неравенстве это точки \(-1, \ 0, \ \dfrac23\) (например, точка \(-1\) входит в четное количество скобок: одна в числителе \((x+1)\) и три в знаменателе \((x+1)^3\)).
Если точка входит в нечетное количество скобок, то при переходе через эту точку (справа налево!) знак будет меняться (в нашем неравенстве это точки \(3\) и \(1\)).
Объясним, почему так происходит. Каждая линейная скобка в нечетной степени \((x-a)^{2n+1}\) имеет ровно один корень \(x=a\), причем, т.к. мы сделали ее хорошей, то для всех \(x>a\) она будет положительной, для всех \(x<a\) она будет отрицательной (а для \(x=a\), естественно, равной нулю). Значит, когда \(x\in (1;3)\), то все скобки, кроме \((x-3)\), будут оставаться положительными, и лишь эта скобка \((x-3)\) станет отрицательной. Значит, их произведение также станет отрицательным. Аналогично при переходе через точку \(x=1\).
Каждая линейная скобка в четной степени \((x-b)^{2n}\) также имеет ровно один корень \(x=b\), но т.к. она в четной степени, то при всех \(x\ne b\) она всегда будет положительной! И только при \(x=b\) она будет равна нулю. Именно поэтому при переходе через точку \(x=\dfrac23\), т.е. на \(x\in(0;\frac23)\), скобка \((3x-2)^2\) не сменит свой знак на отрицательный, поэтому вся левая часть останется по знаку такой же, как и была на \((\frac23;1)\) (т.е. положительной). Аналогично при переходе через точки \(0, -1\).
5 ШАГ. Неравенство практически решено и нам остается только записать ответ. В нашем случае, т.к. знак преобразованного \((***)\) неравенства \(\geqslant 0\) (нестрогий), то в ответ пойдут промежутки со знаком “\(+\,\)” (где значение функции больше нуля) и закрашенные точки (где значение функции равно нулю): \[x\in \Big(-\infty;-1\Big)\cup \left(-1;\dfrac23\right)\cup \left(\dfrac23;1\right]\cup\Big(3;+\infty\Big)\]Напоминаем, что если точка не входит в ответ, то она пишется в круглой скобке “\((\)” или “\()\)”, если входит в ответ – то в квадратной скобке “\([\)” или “\(]\)”. Бесконечности всегда пишутся в круглых скобках.
\[{\Large{\text{Квадратичные неравенства}}}\]
Квадратичным неравенством называется любое неравенство вида \[ax^2+bx+c \lor 0, \quad a\ne 0,\]
или сводящееся к такому виду.
Область допустимых значений \(x\) (ОДЗ) таких неравенств — все вещественные числа (\(x\in \mathbb{R}\)).
Квадратичные неравенства – это те же самые рациональные неравенства, следовательно, их также можно решать с помощью метода интервалов. Но давайте рассмотрим еще один способ, при помощи которого, как правило, удобнее решать квадратичные неравенства. Для этого нам понадобится вспомнить про параболу.
Замечание
Вспомним, как преобразуется квадратичный трехчлен \(ax^2+bx+c\) в зависимости от того, сколько корней он имеет.
Если квадратное уравнение \(ax^2+bx+c=0\)
\(\bullet\) имеет два корня \(x_1\) и \(x_2\) (дискриминант \(D>0\)), то \(ax^2+bx+c=a(x-x_1)(x-x_2)\).
\(\bullet\) имеет один корень \(x_1\) (\(D=0\)), то \(ax^2+bx+c=a(x-x_1)^2\).
\(\bullet\) не имеет корней (\(D<0\)), то квадратный трехчлен \(ax^2+bc+c\) никогда не может быть равен нулю и не разлагается на линейные множители.
Шаг 1. Рассмотрим функцию \(f(x)=ax^2+bx+c\). Графиком такой функции является парабола.
Для того, чтобы решить квадратичное неравенство, изобразим схематично параболу: то есть определим, куда направлены ее ветви и в каких точках она пересекает ось \(Ox\).
Если \(a>0\), то ветви направлены вверх, если \(a<0\), то ветви направлены вниз. Корни уравнения \(ax^2+bx+c=0 \ (*)\) и есть абсциссы точек, в которых парабола пересекает ось \(Ox\).
Шаг 2. Таким образом, наша парабола будет одного из 6 видов: 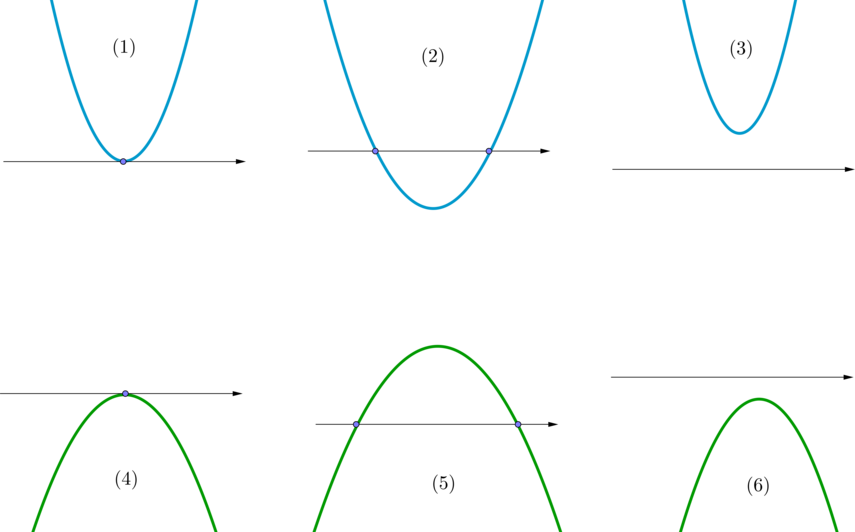
\((1)\) и \((4)\) — когда уравнение \((*)\) имеет один корень;
\((2)\) и \((5)\) — когда уравнение \((*)\) имеет два корня;
\((3)\) и \((6)\) — когда уравнение \((*)\) не имеет корней.
Часть параболы, находящая выше оси \(Ox\), отвечает за \(f(x)>0\);
часть параболы, находящаяся ниже оси \(Ox\), отвечает за \(f(x)<0\);
точки, в которых парабола пересекает ось \(Ox\), отвечают за \(f(x)=0\).
Пример 1.
Решить неравенство \(x^2+3x+2\geqslant 0\).
Решение
Решим уравнение \(x^2+3x+2=0 \Leftrightarrow x_1=-2, x_2=-1\). Таким образом, неравенство можно переписать в виде: \((x+1)(x+2)\geqslant
0\). Ветви параболы направлены вверх, следовательно, схематично она выглядит как \((2)\). Т.к. знак неравенства \(\geqslant\), то решением неравенства будут те значения \(x\), для которых график находится выше оси \(Ox\), а именно \(x\in (-\infty;-2]\cup[-1;+\infty)\).
Заметим, что точки \(-2, -1\) входят в ответ, потому что знак “больше или равно”.
Пример 2.
Решить неравенство \(11x-3x^2-6>0\)
Решение
Решим уравнение \(11x-3x^2-6=0 \quad\Leftrightarrow\quad
x_1=\dfrac23, x_2=3\). Таким образом, неравенство можно переписать в виде: \(-3(x-3)(x-\frac23)>0\).
1 способ. Ветви параболы направлены вниз, следовательно, схематично она выглядит как \((5)\). Т.к. знак неравенства \(>\), то решением неравенства будут \(x\in \left(\dfrac23;3\right)\).
2 способ. Домножим правую и левую части неравенства на \(-1\), получим \(3(x-3)(x-\frac23)<0\) (заметим, что знак сменился на противоположный). У новой параболы \(\Big(f(x)=3(x-3)(x-\frac23)\Big)\) ветви направлены вверх, следовательно, схематично она выглядит как \((2)\). Но знак неравенства уже \(<\). Решением нового неравенства, естественно, будут те же \(x\in \left(\dfrac23;3\right)\).
Таким образом, если в квадратичном неравенстве отрицательный знак при \(x^2\), то можно сначала домножить неравенство на \(-1\) (и не забыть поменять знак неравенства), чтобы ветви параболы всегда были направлены вверх.
Пример 3.
Решить неравенство \(x^2+4x+4 \geqslant 0\).
Решение
Вспомнив формулу сокращенного умножения, получаем \((x+2)^2\geqslant
0\) (это быстрее, чем находить корни через дискриминант :)). Таким образом, парабола пересекает ось \(Ox\) в единственной точке \(x_1=-2\) и выглядит как \((1)\). А т.к. нам нужны те \(x\), для которых график находится не ниже оси \(Ox\), то решением неравенства будут \(x\in
\mathbb{R}\), то есть выражение \((x+2)^2\) всегда больше или равно \(0\).
 Сегодня решаем показательные неравенства.
Сегодня решаем показательные неравенства.
Рассмотрим основные типы показательных неравенств.
При решении показательных неравенств мы будем использовать следующие переходы:

и

Поясним, первый переход возникает в силу возрастания показательной функции 
 , второй – в силу убывания функции
, второй – в силу убывания функции 
 .
.
Показательные неравенства, сводящиеся к простейшим
Задание 1.
Решить неравенство  .
.
Решение:
Перепишем неравенство следующим образом:

А далее вот так:


Так как  – возрастающая функция, то знак неравенства остается без изменения при переходе к новому неравенству:
– возрастающая функция, то знак неравенства остается без изменения при переходе к новому неравенству:


Ответ:  .
.
Задание 2.
Решить неравенство: 
Решение:
Перепишем неравенство следующим образом:

Заметим, что  .
.


В силу того, что основание степени ( ) меньше 1, то есть мы имеем дело с убывающей функцией, переходим к следующему неравенству (не забывая поменять знак
) меньше 1, то есть мы имеем дело с убывающей функцией, переходим к следующему неравенству (не забывая поменять знак  на
на  ):
):





Ответ: 
Однородные показательные неравенства
Задание 3.
Решить неравенство: 
Решение:
Вынесем за скобку 




Тогда переходим к следующему неравенству (в силу того, что основание степени больше 1, знак неравенства не меняется):


Ответ: 
Показательные неравенства, сводящиеся к квадратным
Задание 4.
Решить неравенство 
Решение:


Разделим обе части неравенства на 3:

Мы видим квадратное неравенство относительно  которое будем решать методом интервалов.
которое будем решать методом интервалов.
Имеем:


 или
или 
 или
или 
Ответ: 
Задание 5.
Решить неравенство 
Решение:

Мы видим квадратное неравенство относительно  , которое будем решать методом интервалов.
, которое будем решать методом интервалов.
Находим при помощи дискриминанта корни квадратного трехчлена  . Переходим к следующему неравенству:
. Переходим к следующему неравенству:


Получаем:  или
или  . Заметьте, нет смысла указывать, что
. Заметьте, нет смысла указывать, что  , так как по определению
, так как по определению  положительно.
положительно.
Итак,



Ответ: 
Задание 6.
Решить неравенство 
Решение:
Разделим обе части неравенства на  (можно и на
(можно и на  ,
,  – как хотите…). Заметим,
– как хотите…). Заметим,  .
.

Заметим, что  . Аналогично с
. Аналогично с  .
.



Мы имеем квадратное неравенство относительно 
которое будем решать методом интервалов.
Воспользуемся следующим способом превращения суммы в произведение:
 где
где  – корни уравнения
– корни уравнения  (в случае неотрицательного дискриминанта квадратного трехчлена).
(в случае неотрицательного дискриминанта квадратного трехчлена).
Заготавливаем шаблончик  и находим корни при помощи дискриминанта, тогда
и находим корни при помощи дискриминанта, тогда


То есть 


Ответ: ![Rendered by QuickLaTeX.com [0;1].](http://school37zlat.ru/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
Задание 7.
Решить неравенство 
Решение:
Перепишем неравенство следующим образом:

Домножим обе части неравенства на  (заметим,
(заметим,  ):
):






Ответ: 
Показательные неравенства, сводящиеся к рациональным
Задание 8.
Решить неравенство: 
Решение:
Переносим все в левую сторону неравенства и приводим к общему знаменателю:




Мы можем “отбросить” сумму  в силу ее положительности:
в силу ее положительности:

Неравенство равносильно следующему:





Ответ: 
Неравенства, решаемые графическим методом
Задание 9.
Решить неравенство: 
Решение:
Рассмотрим функции  и
и  Обе они определены на
Обе они определены на  . Первая – возрастает, вторая – убывает. Значит, уравнение
. Первая – возрастает, вторая – убывает. Значит, уравнение  имеет не более одного решения. Несложно заметить, что
имеет не более одного решения. Несложно заметить, что  является корнем указанного уравнения.
является корнем указанного уравнения.

А значит, если вернуться к неравенству и посмотреть на него с графической точки зрения, мы должны взять те значения  , которые отвечают за ту часть графика
, которые отвечают за ту часть графика  , что лежит выше графика
, что лежит выше графика  , то есть
, то есть  .
.
Ответ: 
Для самостоятельной работы:
Решить неравенства:
1. 
Ответ: + показать

2. 
Ответ: + показать
![Rendered by QuickLaTeX.com (-\infty;-2]\cup[2;+\infty)](http://school37zlat.ru/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
3. 
Ответ: + показать
![Rendered by QuickLaTeX.com (-\infty;3]](http://school37zlat.ru/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
4. 
Ответ: + показать
{-2}
5. 
Ответ: + показать

6. 
Ответ: + показать

7. 
Ответ: + показать
(-1;1]
8. 
Ответ: + показать
 .
.
: умножение и деление неравенств — GMAT Math Study Guide
Определения
Неравенство сравнивает два значения.
- Неравенство — сравнение двух значений или выражений.
Например, 10x <50 - это неравенство, тогда как x = 5 - это уравнение. - Уравнение — утверждение, объявляющее равенство двух выражений.
Например, 4x = 8 — это уравнение, тогда как 10x> 20 — это неравенство.
Работа с неравенствами: умножение и деление
Выполнение умножения или деления с неравенством практически идентично умножению или делению частей традиционных уравнений (с одним исключением, которое рассматривается ниже).
Рассмотрим следующие примеры:
10x + 15 <25 + 5x
10x + 15 — 15 <25 - 15 + 5x
10x <10 + 5x
10x — 5x <10 + 5x - 5x
5x <10
x <2
Исключение: отрицательные числа
Существует одно очень важное исключение из правила, согласно которому умножение или деление неравенства такое же, как умножение или деление уравнения.
Всякий раз, когда вы умножаете или делите неравенство на отрицательное число, вы должны перевернуть знак неравенства.
В следующем примере обратите внимание, как знак <становится знаком>, когда неравенство делится на -2
-2x — 10 <2
-2x — 10 + 10 <2 + 10
-2x <12
x> -6 [Для деления на -2 требуется перевернуть знак неравенства]
В следующем примере обратите внимание, как знак <становится знаком>, когда неравенство делится на -2
-2x + 15 <3
-2x + 15 — 15 <3 - 15
-2x <-12
x> 6 [Для деления на -2 требуется перевернуть знак неравенства]
Предупреждение: осторожность при умножении или делении переменных
Одним из очень важных следствий этого правила является: Вы не можете делить на неизвестное (я.переменная), если вы не уверены в ее знаке , так как не знаете, нужно ли менять знак неравенства. Есть много случаев, когда вы узнаете знак переменной, и в результате вы можете умножить или разделить и точно знать, нужно ли вам перевернуть знак неравенства. Однако вы всегда должны спросить себя, знаете ли вы наверняка знак переменной перед делением или умножением при работе с неравенством.
Если 2x5y <10y, каков диапазон потенциальных значений для x?
Вы не можете делить на y или 5y, так как вы не знаете, является ли y отрицательным или положительным, и, следовательно, вы не знаете, следует ли перевернуть неравенство.
Многократное неравенство
Как можно решить два уравнения одновременно, так можно решить два неравенства (или три, или четыре и т. Д.). При решении нескольких одновременных неравенств с использованием умножения или деления наиболее важной частью является решение каждого неравенства в отдельности, а затем их объединение.
Если 2x <150, каков диапазон возможных значений для x? 1.) Решите каждое неравенство в одиночку.
2x <10
x <5 [Примечание: неравенство не переворачивается, так как мы делим на 2, что положительно]
-5x <-10
x> 2 [Поскольку мы делим на -5, отрицательное число, мы переворачиваем знак неравенства]
15x <150
x <10
2.) Объедините каждое неравенство и найдите совпадение (то есть, области, где выполняется каждое неравенство — эта область является решением).
x <5
x> 2
x <10
Область перекрытия, т. Е. Решение множества неравенств, — это где x <5 и x> 2
Для многих студентов вышеупомянутый набор неравенств может быть лучше всего понят графически. Решением множества неравенств является перекрывающаяся графическая область.
,Неравенства в ACT Math: стратегии и практика
Вопросы о неравенстве представлены в ACT в различных формах и формах, но независимо от их формы вы увидите в примерно три вопроса о неравенстве в любом заданном тесте . Это означает, что вопросы неравенства составляют 5% от вашего общего теста по математике ACT. Теперь, 5% вашего теста может показаться не таким уж и большим, но только с помощью быстрого устранения неравенства, это дополнительные 5% ваших вопросов, которые вы непременно должны задеть!
Это будет полное руководство по неравенствам в ACT : что это такое, различные типы математических задач ACT по неравенствам и способы их решения.
Что такое неравенство?
Неравенство — это представление о том, что два значения не равны или что два значения , возможно, не равны. Существуют разные типы неравенств и разные символы для обозначения этих разных отношений.
≠ — знак «неравного». Всякий раз, когда вы видите этот знак, вы знаете, что два значения не равны, но не более того. Мы не знаем, какое значение больше или меньше, просто они не одинаковы.
Если у нас есть $ y ≠ x $, мы не знаем, больше или меньше $ y $, чем $ x $, просто они не равны друг другу.
> — знак «больше чем». Независимо от того, какое число или переменная обращены к открытию знака, всегда большее из двух значений. (Некоторые из вас, возможно, узнали, что знак является «крокодилом» и что крокодил всегда хочет съесть большее значение).
Например, $ x> 14 $ означает, что $ x $ может быть чем-то большим, чем 14 (это может быть даже 14.00000000001), но не может быть 14 и не может быть меньше , чем 14.
<это знак "меньше чем". Какое бы число не было обращено к открытию знака, оно является меньшим из двух значений. Это просто больше, чем знак в обратном порядке.
Таким образом, $ 14 ≥ является знаком «больше или равно». Это действует точно так же, как больший знак, за исключением того факта, что наши значения также могут быть равны. Принимая во внимание, что $ x> 14 $ означает, что $ x $ может быть любым числом больше , чем 14, $ x ≥ 14 $ означает, что $ x $ может быть равно 14 или может быть любым числом больше 14. ≤ — знак «меньше или равно». Решение
Неравенство: обзор (страница
1 из 3) Разделы: линейные неравенства, квадратичные
неравенства, Другие неравенства Решение линейных неравенств
очень похоже на решение
линейные уравнения,
за исключением одной маленькой, но важной детали: вы переворачиваете знак неравенства
всякий раз, когда вы умножаете или делите неравенство на отрицательное.Самый простой
способ показать это с некоторыми примерами: Графически,
решение: Обратите внимание, что
решение неравенства «меньше, но не равно»
обозначается круглыми скобками (или открытой точкой) в конечной точке,
указывая, что конечная точка не включена в решение. Графически,
решение: Обратите внимание, что
« x »
в решении не «должно быть» слева.
Однако зачастую проще представить, что означает решение
с переменной слева. Не бойся переставлять
вещи на ваш вкус. Графически,
решение: Обратите внимание, что
Решение неравенства «меньше или равно»
с квадратной скобкой (или закрытой точкой) на
конечная точка, указывающая, что конечная точка включена в
решение. Графически,
решение: авторское право
© Elizabeth Stapel 1999-2011 Все права защищены. Графически,
решение: Правило для примера 5 выше часто кажется необоснованным студентам, когда они впервые видят его.
Но подумайте о неравенствах с числами вместо переменных.
Вы знаете, что число четыре больше, чем число два: 4
> 2. Умножение
через это неравенство на -1,
мы получаем –4 <–2, который
Номер строки показывает, верно: Если бы мы не перевернули
неравенство, мы бы в конечном итоге «-4
> –2 «, что
явно не правда. Топ | 1 | 2 | 3 | Вернуться к оглавлению Следующая >> Stapel, Елизавета.
«Устранение неравенства: обзор». Purplemath . Доступен с Введите полиномиальное неравенство вместе с переменной, для которой нужно найти решение, и нажмите кнопку «Решить». ЗАКАЗАТЬ ОТНОШЕНИЯ В разделах 1.1 и 2.1 мы видели, что из двух разных чисел график меньшего числа лежит слева от графика большего числа в числовой строке. Эти отношения заказа могут быть выражены с помощью следующих символов: > означает «больше, чем.» ≤ означает «меньше или равно», ≥ означает «больше или равно». Например, «1 меньше 3» можно записать как 1 «7 меньше 9» можно записать как 7 «-3 больше -5» можно записать как -3> -5. «2 меньше или равно x» можно записать как 2 ≤ x. «4 больше или равно y» можно записать как 4 ≥ y. Заявления, которые включают любой из вышеперечисленных символов, называются неравенствами.Неравенства, такие как 1 , как говорят, имеют тот же порядок или тот же смысл, потому что левый элемент меньше, чем правый элемент в каждом случае. Неравенства, такие как 7 -5 , как говорят, имеют противоположный порядок или противоположный смысл, потому что в одном случае левый элемент меньше, чем правый элемент, а в другом случае левый элемент больше, чем правый элемент. СВОЙСТВА НЕРАВЕНСТВ В разделе 3.1 мы увидели, что уравнение первой степени по одной переменной имеет только одно решение. Но неравенство первой степени имеет бесконечное число решений. Например, графики бесконечного числа целочисленных решений неравенства x> 3 показаны на рисунке 3.1. Иногда невозможно определить решения данного неравенства просто проверкой. Но используя следующие свойства, мы можем сформировать эквивалентные неравенства (неравенства с теми же решениями), в которых решение очевидно при проверке. 1. Если одно и то же выражение добавляется или вычитается из каждого члена неравенства, результатом является эквивалентное неравенство в том же порядке. В символах, а эквивалентные неравенства. Пример 1 а. Потому что 3 3 + 4 б. Если х х + 2 c. Если 4 4 + (-2) 2. Если каждый член неравенства умножается или делится на одно и то же положительное число, результатом является эквивалентное неравенство в том же порядке. В символах, эквивалентные неравенства. Пример 2 а. Потому что 2 0, 2 (5) б. Если 3x гр. Если 5 0, то 5 (з) 3. Если каждый член неравенства умножается или делится на одно и то же отрицательное число, результатом является эквивалентное неравенство в обратном порядке. В символах, эквивалентные неравенства. Пример 3 а. Потому что 3 3 (-2)> 5 (-2) или -6> -10 б. Если -3x гр. Если 2 2 (y)> x (y) или 2y> xy Три указанных выше свойства также применимы к неравенствам вида a> b, а также к РЕШЕНИЕ НЕРАВЕНСТВ Теперь давайте посмотрим, как три свойства могут помочь нам решить неравенства. Пример 4 Решить Умножив каждого члена на 2 (положительное число), мы получим Затем разделив каждого члена на 3, мы получим График этого неравенства В приведенном выше примере все неравенства были в том же порядке, потому что мы применили только свойство 2 выше.Теперь рассмотрим следующее неравенство. Пример 5 Решить — 3x + 1> 7, где x — целое число. Добавление решения — 1 каждому члену, мы получаем -3x + 1 + (-1)> 7 + (-1) -3x> 6 Теперь мы применяем свойство 3 и делим каждого члена на -3. В этом случае мы должны обратить порядок неравенства. При решении словесных задач, связанных с неравенством, мы выполняем шесть шагов, описанных на стр. 115, за исключением того, что слово уравнение будет заменено словом неравенство. , если a = b, то b = Большинство проблем, связанных с практическим применением математики, выражены словами. Прежде чем мы сможем решить такие проблемы, мы должны перевести предложения слов в математические уравнения. Затем мы можем использовать методы предыдущих разделов для решения уравнений. В этом разделе мы будем заниматься только написанием алгебраических выражений и уравнений. В следующих разделах мы на самом деле будем решать уравнения. В разделах 1.2 и 1.3 мы связали определенные словосочетания с определенными математическими операциями: Мы можем перевести эти словосочетания в алгебраические выражения, как показано в следующих примерах. Пример 1 Точно так же мы можем переводить предложения слов в уравнения. Пример 2 Распространенные ошибки: при переводе фразы, такой как «вычитается из b», важен порядок. Мы должны написать б — а, а не б — , так как а вычитается из б.Например, перевести «Если семь вычтено из 4 раз целое число, результат будет 17» мы представляем целое число символом, скажем, х, а затем пишем предложение следующим образом. В последнем разделе мы перевели предложения слов в уравнения. Теперь мы решим множество словесных задач. Предлагаются следующие шаги. Чтобы решить словесную задачу: На практике мы обычно объединяем шаги 1 и 2. Выполните шесть шагов, перечисленных выше, чтобы решить следующую проблему слова. Сумма определенного числа и 9 равна четырехкратному числу. Какой номер? Решение Шаги 1-2 Сначала мы напишем, что мы хотим найти (число), в виде словосочетания. Затем мы используем переменную для представления этого числа. Номер: x Шаг 3 Эскиз не применим в этой проблеме. Шаг 4 Запишем уравнение, связывающее известные и неизвестные величины. x + 9 — 4x Шаг 5 Теперь мы решаем полученное уравнение. х + 9 — х = 4х — х 9 = 3x 3 = х Шаг 6 Номер 3. ПОСЛЕДОВАТЕЛЬНЫЕ ИНТЕГЕРЫ Некоторые алгебраические проблемы со словами включают понятия последовательных целых чисел. Последовательные целые числа — это целые числа, которые отличаются на 1 или — 1. Например, 3 и 4 являются последовательными целыми числами, а -2 и -1 — последовательными целыми числами. Если x представляет собой целое число, то следующее последовательное целое число представляется как x + 1. Последовательные четные числа являются четными целыми числами, которые отличаются на 2 или -2.Например, 6 и 8 являются последовательными четными целыми числами, а -4 и -2 — последовательными четными целыми числами. Если x представляет четное целое число, то следующее последовательное четное целое число представляется как x + 2. Последовательные нечетные целые числа — это нечетные целые числа, которые отличаются на 2 или -2. Например, 5 и 7 — последовательные нечетные целые числа, а -3 и -1 — последовательные нечетные целые числа. Если x представляет нечетное целое число, то следующее последовательное нечетное целое число представляется как x + 2. Пример 2 Выполните шесть шагов, перечисленных на стр. 115, чтобы решить следующую проблему со словом. Сумма двух последовательных нечетных целых чисел равна 12. Что такое целые числа? Решение Шаги 1-2 Сначала запишем, что мы хотим найти (целые числа), в виде двух словосочетаний. Затем мы используем переменную для представления целых чисел. Меньшее нечетное целое число: x следующее последовательное нечетное целое число: x + 2 Шаг 3 Эскиз не применим в этой проблеме. Шаг 4 Далее мы пишем уравнение, связывающее известные и неизвестные величины. х + (х + 2) = 12 Шаг 5 Теперь мы решаем полученное уравнение. х + х + 2 = 12 2x + 2 = 12 2x = 10 х = 5 Шаг 6 Целые числа 5 и 5 + 2 или 7. В следующем примере эскиз полезен. Пример 3 Выполните шесть шагов, перечисленных на стр. 115, чтобы решить следующую проблему со словом. Доска длиной 186 сантиметров разрезается на две части, так что одна часть вдвое длиннее другой.Как долго длится каждая из двух частей? Решение Шаги 1-2 Сначала мы напишем то, что мы хотим найти (длины) в виде словосочетаний. Затем мы используем переменную для представления длины. меньший кусок: х Большая часть: 2x Шаг 3 Теперь создадим эскиз и обозначим размеры. Шаг 4 Написание уравнения, связывающего известные и неизвестные величины, дает х + 2х = 186 Шаг 5 Теперь мы решаем уравнение. 3x = 186 х = 62 Шаг 6 Меньшая часть составляет 62 сантиметра, а большая часть составляет 2 (62) или 124 сантиметра.
. Устранение неравенств: обзор
1) Единственная разница между линейным уравнением « x + 3 = 2»
и это линейное неравенство
что у меня есть знак «меньше» вместо «равно»
подписать.Метод решения точно такой же: вычтите 3 из
любая сторона. 2) Единственная разница между линейным уравнением «2
— x = 0 «и
это линейное неравенство является знаком «больше чем»
вместо знака «равно». 3) Единственная разница между линейным уравнением «4 x + 6 = 3 x — 5»
и это неравенство является «меньше или равно»
знак вместо простого знака «равно».Решение
Метод точно такой же. 4) Метод решения здесь состоит в том, чтобы разделить обе стороны на положительные два. 5) Это
это особый случай, отмеченный выше.Когда я разделил на отрицательное два, мне пришлось щелкнуть знак неравенства. Цитировать эту статью
как:
https: // www.purplemath.com/modules/ineqsolv.htm .
Доступ [Дата] [Месяц] 2016 

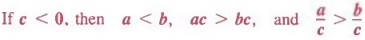
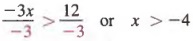
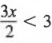 , где x — целое число.
, где x — целое число.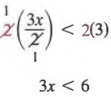
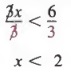

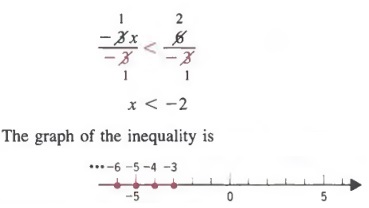
РЕЗЮМЕ ГЛАВЫ
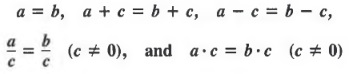
являются эквивалентными уравнениями. Благодаря симметричному свойству равенства члены уравнения могут меняться без каких-либо изменений знака. Таким образом,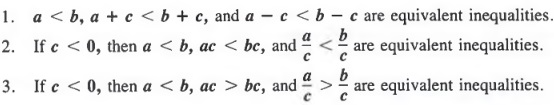
Мы должны обратить неравенство всякий раз, когда мы умножаем или делим оба члена неравенства на отрицательное число. ПЕРЕВОД СЛОВ ПРЕДЛОЖЕНИЯ

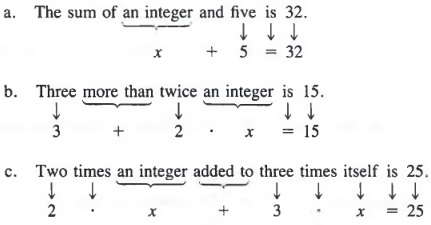
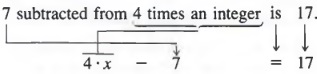
ПРИЛОЖЕНИЯ


Leave A Comment