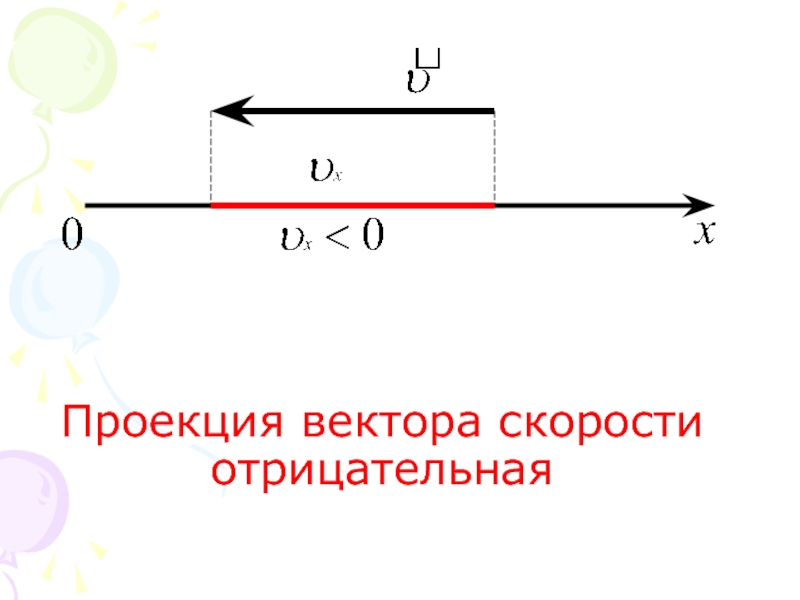
График зависимости проекции ускорения от времени движения. Равнопеременное прямолинейное движение
Вопросы.
1. Запишите формулу, по которой можно рассчитать проекцию вектора мгновенной скорости прямолинейного равноускоренного движения, если известны: а) проекция вектора начальной скорости и проекция вектора ускорения; б) проекция вектора ускорения при том, что начальная скорость равна нулю.
2. Что представляет собой график проекции вектора скорости равноускоренного движения при начальной скорости: а) равной нулю; б) не равной нулю?
3. Чем сходны и чем отличаются друг от друга движения, графики которых представлены на рисунках 11 и 12?
В обоих случаях движение происходит с ускорением, однако в первом случае ускорение положительно, а во-втором отрицательно.
Упражнения.
1. Хоккеист слегка ударил клюшкой по шайбе, придав ей скорость 2 м/с. Чему будет равна скорость шайбы через 4 с после удара, если в результате трения о лёд она движется с ускорением 0,25 м/с 2 ?
2.
3. В одних и тех же координатных осях постройте графики проекции вектора скорости (на ось Х, сонаправленную с вектором начальной скорости) при прямолинейном равноускоренном движении для случаев: а) v ox = 1м/с, a x = 0,5 м/с 2 ; б) v ox = 1м/с, a x = 1 м/с 2 ; в) v ox = 2 м/с, a x = 1 м/с 2 .
Масштаб во всех случаях одинаков: 1см- 1м/с; 1см — 1с.
4. В одних и тех же координатных осях постройте графики проекции вектора скорости (на ось Х, сонаправленную с вектором начальной скорости) при прямолинейном равноускоренном движении для случаев: а) v ox = 4,5 м/с, a x = -1,5 м/с 2 ; б) v ox = 3 м/с, a x = -1 м/с 2
5. На рисунке 13 представлены графики зависимости модуля вектора скорости от времени при прямолинейном движении двух тел. С каким по модулю ускорением движется тело I? тело II?
Равномерное прямолинейное движение – это частный случай неравномерного движения.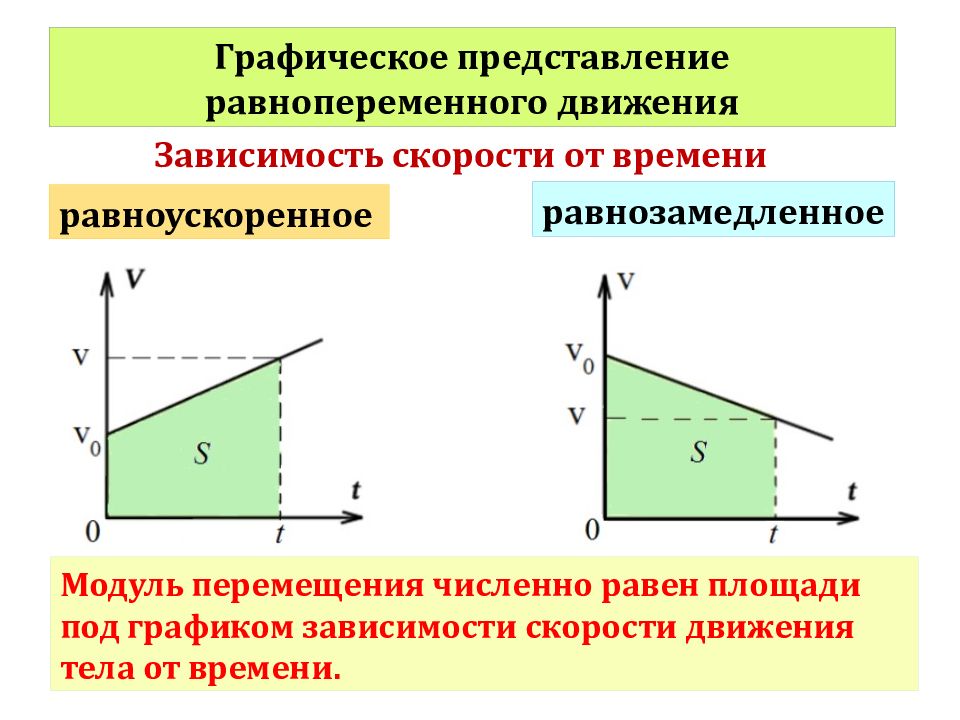
Неравномерное движение
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.
Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).
Равнопеременное движение может быть равноускоренным или равнозамедленным.
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.
Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.
При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.
В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.
Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.
V cp = s / t
– это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:
Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:
Проекция вектора скорости на ось ОХ:
V x = x’
это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).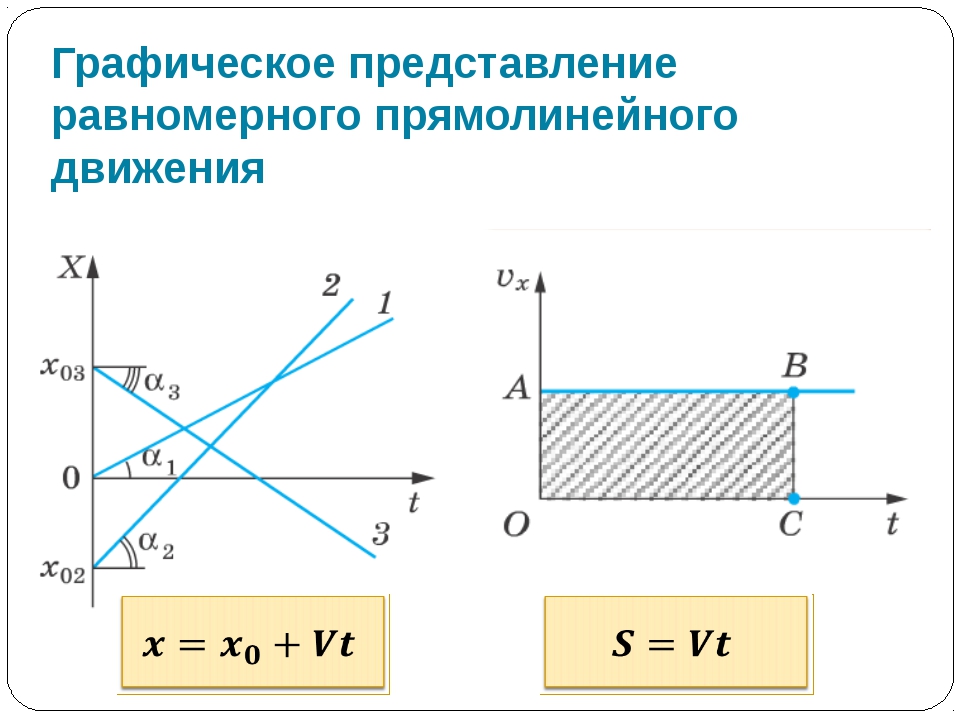
– это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:
Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:
Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:
V x = v 0x ± a x t
Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.
Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).
Рис. 1.15. Зависимость ускорения тела от времени.
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).
Рис. 1.16. Зависимость скорости тела от времени.
График зависимости скорости от времени (рис. 1.16) показывает, что
При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).
Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:
0a = v 0 bc = v
Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:
В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).
График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.
Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.
Рис. 1.18. Зависимость перемещения тела от времени.
Скорость тела в данный момент времени t 1 равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:
Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:
Поможет нам вывести формулу для проекции перемещения:
Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то будет выглядеть следующим образом:
Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При а x
Построение графиков используют, чтобы показать зависимость одной величины от другой. При этом на одной оси откладывают изменение одной величины, а на другой оси — изменение другой величины. При прямолинейном равномерном движении скорость тела остается постоянной, меняются только время и зависимый от него пройденный путь.
При построении такого графика на одной из осей координатной плоскости отмечается изменение времени (t). Например, 1 с, 2 с, 3 с и т. д. Пусть это будет ось x . На другой оси (в данном случае y ) отмечается изменение пройденного пути. Например, 10 м, 20 м, 30 м и т. д.
Начало системы координат принимается за начало движения. Это точка старта, в которой промежуток времени, потраченный на движение, равен нулю, и пройденный путь также равен нулю. Это первая точка графика зависимости пути от времени.
Далее на координатной плоскости находят вторую точку графика. Для этого для какого-либо времени пути находят пройденный за это время путь. Если скорость тела равна 30 м/с, то это может быть точка с координатами (1; 30) или (2; 60) и так далее.
После того, как вторая точка отмечена, проводят луч через две точки (первая — начало координат). Начало луча — это начало координат. Данный луч и является графиком зависимости пути от времени при прямолинейном равномерном движении. У луча нет конца, это говорит о том, что чем больше затраченное на путь время, тем больше будет пройденный путь.
Данный луч и является графиком зависимости пути от времени при прямолинейном равномерном движении. У луча нет конца, это говорит о том, что чем больше затраченное на путь время, тем больше будет пройденный путь.
Вообще говорят, что графиком зависимости пути от времени является прямая, проходящая через начало координат.
Чтобы доказать, что графиком является прямая, а, допустим, не ломаная линия, можно построить ряд точек на координатной плоскости. Например, если скорость равна 5 км/ч, то на координатной плоскости можно отметить точки (1; 5), (2; 10), (3; 15), (4; 20). Затем соединить их последовательно между собой. Вы увидите, что получится прямая.
Чем больше скорость тела, тем быстрее увеличивается пройденный путь. Если на одной и той же координатной плоскости начертить зависимости пути от времени для двух тел, движущихся с разными скоростями, то график тела, которое движется быстрее, будет иметь больший угол с положительным направлением оси времени.
Например, если одно тело движется со скоростью 10 км/ч, а второе — 20 км/ч, то на координатной плоскости можно отметить точки (1; 10) для одного тела и (1; 20) для другого. Понятно, что вторая точка находится дальше от оси времени, и прямая через нее образует больший угол, чем прямая через точку, отмеченную для первого тела.
Понятно, что вторая точка находится дальше от оси времени, и прямая через нее образует больший угол, чем прямая через точку, отмеченную для первого тела.
Графики зависимости пути от времени при прямолинейном равномерном движении можно использовать для быстрого нахождения затраченного времени по известному значению пройденного пути или пути по известному времени. Для этого надо провести перпендикулярную линию из значения координатной оси, которое известно, до пересечения с графиком. Далее из полученной точки пересечения провести перпендикуляр к другой оси, получив тем самым искомое значение.
Кроме графиков зависимости пути от времени, можно построить графики зависимости пути от скорости и скорости от времени. Однако, так как при прямолинейном равномерном движении скорость постоянна, эти графики представляют собой прямые, параллельные осям пути или времени и проходящие на уровне заявленной скорости.
Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).
Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.
Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.
Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости:
V cp = v
Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна:
V x = v, то есть v > 0
Проекция перемещения на ось ОХ равна:
S = vt = x – x 0
где x 0 – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени)
Уравнение движения , то есть зависимость координаты тела от времени х = х(t), принимает вид:
Х = x 0 + vt
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v
Х = x 0 — vt
Зависимость скорости, координат и пути от времени
Зависимость проекции скорости тела от времени показана на рис. 1.11. Так как скорость постоянна (v = const), то графиком скорости является прямая линия, параллельная оси времени Ot.
1.11. Так как скорость постоянна (v = const), то графиком скорости является прямая линия, параллельная оси времени Ot.
Рис. 1.11. Зависимость проекции скорости тела от времени при равномерном прямолинейном движении.
Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 1.12), так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.
Рис. 1.12. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
График зависимости перемещения от времени показан на рис. 1.13. Из графика видно, что проекция скорости равна
V = s 1 / t 1 = tg α
где α – угол наклона графика к оси времени.Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость (больший путь тело проходит за меньшее время). Тангенс угла наклона касательной к графику зависимости координаты от времени равен скорости:
Tg α = v
Рис. 1.13. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
1.13. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
Зависимость координаты от времени показана на рис. 1.14. Из рисунка видно, что
Tg α 1 > tg α 2
следовательно, скорость тела 1 выше скорости тела 2 (v 1 > v 2).
Tg α 3 = v 3
Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть
Х = х 0
Рис. 1.14. Зависимость координаты тела от времени при равномерном прямолинейном движении.
Скорость прямолинейного равноускоренного движения. График скорости
Цель урока. Закрепить представление о прямолинейном равноускоренном движении, рассмотреть, как изменяется скорость тела при прямолинейном равноускоренном движении, график скорости; научить решать задачи с применением формулы для расчета скорости.
Демонстрации. Зависимость скорости от времени при прямолинейном равноускоренном движении.
Содержание опроса. 1. Что понимают под мгновенной скоростью неравномерного движения? 2. Дайте определение ускорения равноускоренного движения. 3. Что характеризует ускорение? 4. Какова единица ускорения в СИ?
1. Что понимают под мгновенной скоростью неравномерного движения? 2. Дайте определение ускорения равноускоренного движения. 3. Что характеризует ускорение? 4. Какова единица ускорения в СИ?
Содержание нового материала. Формулы для определения вектора скорости и его проекции. График зависимости проекции вектора скорости от времени при равноускоренном движении для случаев, когда векторы скорости и ускорения сонаправлены и направлены в противоположные стороны.
Закрепление материала. Решение задачи 1 из упражнения 6, задач 1428 и 1435 из Сборника.
Домашнее задание. § 6. Упражнение 6 (2, 3).
Планируемые результаты обучения
Метапредметные: овладеть навыками самостоятельного приобретения знаний о графическом представлении механического движения тел, регулятивными УУД при решении качественных, расчетных и графических задач.
Личностные: сформировать познавательный интерес и творческую инициативу, самостоятельность в приобретении новых знаний о зависимости проекции вектора скорости от времени при прямолинейном равноускоренном движении, ценностное отношение друг к другу, к учителю, к результатам обучения; уметь принимать самостоятельные решения, обосновывать и оценивать результаты своих действий.
Общие предметные: проводить наблюдения, планировать и проводить эксперимент по изучению прямолинейного равноускоренного движения; объяснять полученные результаты и делать выводы; применять теоретические знания на практике; решать расчетные задачи по определению ускорения, времени, начальной и конечной скоростей движения.
Частные предметные: записывать формулу скорости тела при прямолинейном равноускоренном движении в векторном виде и в виде проекций на выбранную ось; читать и строить графики скорости; решать расчетные и качественные задачи с применением этих формул.
Методические замечания
Урок можно начать с физического диктанта, рассчитанного на 7 мин, а затем перейти к изучению новой темы.
Физический диктант
1. Равноускоренное движение является … (равномерным или неравномерным).
2. Ускорение характеризует … .
3. Вектор ускорения сонаправлен с вектором … .
4. Что такое равноускоренное движение?
5. Единица ускорения в СИ … .
Единица ускорения в СИ … .
6. Что называют мгновенной скоростью неравномерного движения?
7. Как направлен вектор мгновенной скорости при прямолинейном движении тела?
8. Запишите формулу для расчета ускорения в векторном виде.
После выполнения физического диктанта учащиеся самостоятельно проверяют его и оценивают, поменявшись тетрадями с соседом по парте: четыре правильных ответа — 3, пять или шесть правильных ответов — 4, семь или восемь правильных ответов — 5. Для проверки диктанта они могут использовать конспект предыдущего урока, записанный в рабочей тетради. Затем учащиеся вместе с учителем сверяют и обсуждают ответы.
Изложение нового материала следует начать с обсуждения формулы для расчета ускорения в скалярном виде (проекции векторов на ось ОХ). Выразить из этой формулы проекцию вектора конечной скорости. Затем вспомнить из курса математики линейную функцию у = kx + b и график этой функции. Построить, например, график зависимости проекции вектора скорости от времени для разгоняющегося перед взлетом самолета, который движется прямолинейно из состояния покоя с ускорением 1,5 м/с2 в течение 40 с: vx = 1,5t (м/с).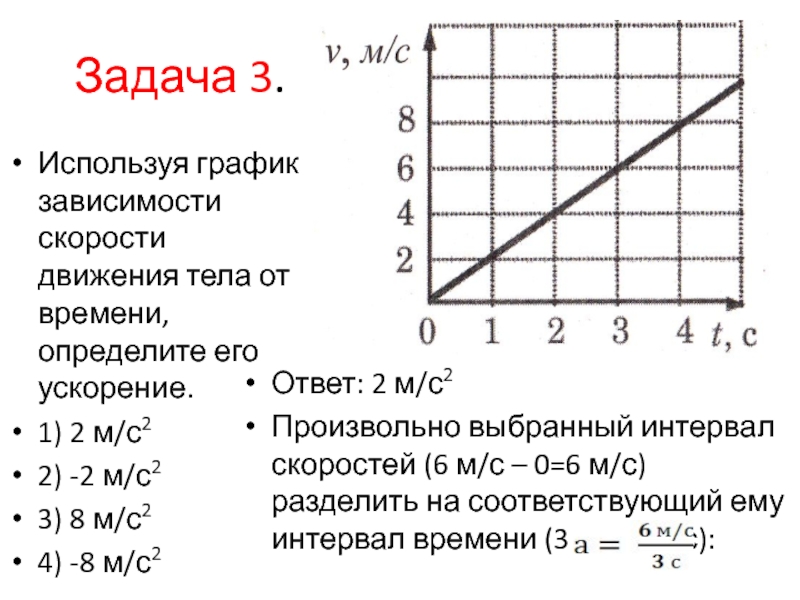
Можно вызвать к доске двух учащихся и дать им задание: построить графики зависимости vx = = 10 + 1,4t (м/с) и vx = 20 — 2t (м/с). Затем проанализировать эти графики.
Равнопеременное прямолинейное движение
Равномерное прямолинейное движение – это частный случай неравномерного движения.
Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.
Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).
Равнопеременное движение может быть равноускоренным или равнозамедленным.
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.
Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.
В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.
Средняя скорость переменного движения определяется путём
деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.
Единица измерения средней скорости – м/с.
vcp = s / tМгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:
Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:
= ‘
Проекция вектора скорости на ось ОХ:
vx = x’это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).
Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:
Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:
= ' = "Учитывая, что 0 – скорость тела в начальный момент времени (начальная скорость), – скорость тела в данный момент времени (конечная скорость), t – промежуток времени, в течение которого произошло изменение скорости, формула ускорения будет следующей:
Отсюда формула скорости равнопеременного движения в любой момент времени:
= 0 + tЕсли тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:
vx = v0x ± axtЗнак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению.
 Аналогично записываются уравнения проекций вектора скорости на другие оси координат.
Аналогично записываются уравнения проекций вектора скорости на другие оси координат.Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).
Рис. 1.15. Зависимость ускорения тела от времени.
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).
Рис. 1.16. Зависимость скорости тела от времени.
График зависимости скорости от времени (рис. 1.16) показывает, что
При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).
Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:
0a = v0 bc = vВысота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна: В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).

Общая формула для определения проекции перемещения:
График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.
Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.
Рис. 1.18. Зависимость перемещения тела от времени.
Скорость тела в данный момент времени t1 равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:
Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:
Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:
Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:
Графиком координаты x(t) также является парабола (как и график перемещения),
но вершина параболы в общем случае не совпадает с началом координат. При аx < 0 и х0 = 0 ветви параболы направлены вниз (рис. 1.18).
При аx < 0 и х0 = 0 ветви параболы направлены вниз (рис. 1.18).
Урок 2. равномерное прямолинейное движение материальной точки — Физика — 10 класс
Физика, 10 класс
Урок 2. Равномерное прямолинейное движение материальной точки
Перечень вопросов, рассматриваемых в теме: 1) основная задача механики; 2) относительность механического движения; 3) система отсчёта, материальная точка, перемещение, траектория, скорость; 4) кинематическое уравнение.
Глоссарий по теме:
Раздел механики, в котором изучается движение тел без выяснения причин, вызывающих данное движение, называют кинематикой.
Механическим движением тела называется изменение положения тела в пространстве относительно других тел с течением времени.
Материальной точкой называют тело, размерами и формой которого в условиях рассматриваемой задачи можно пренебречь. Тело, относительно которого рассматривается движение, называется телом отсчета. Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета.
Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета.
Траектория — линия, по которой движется точка в пространстве.
Длину траектории, по которой двигалось тело в течение какого-то промежутка времени, называют путем, пройденным за этот промежуток времени.
Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением.
Равномерное прямолинейное движение – это движение, при котором за любые равные промежутки времени тело совершает равные перемещения.
Скорость равномерного прямолинейного движения точки – величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло.
Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта
Основная и дополнительная литература по теме урока:
Мякишев Г. Я., Буховцев Б.Б., Сотский Н.Н.. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2016.– С.10-30.
Я., Буховцев Б.Б., Сотский Н.Н.. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2016.– С.10-30.
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.
Открытые электронные ресурсы по теме урока:
http://kvant.mccme.ru/1974/12/byvaet_li_ravnomernoe_dvizheni.htm.
Теоретический материал для самостоятельного изучения
Основная задача классической механики — определить положение тела в пространстве в любой момент времени. По характеру решаемых задач классическую механику делят на кинематику, динамику и статику. В кинематике описывают движение тел без выяснения причин, вызывающих данное движение. Раздел механики, в котором изучаются причины движения, называют динамикой. Статика — раздел механики, в котором изучаются условия равновесия абсолютно твердых тел. Законы сохранения импульса и энергии являются следствиями законов Ньютонов.
Механическим движением тела называется изменение положения тела в пространстве относительно других тел с течением времени.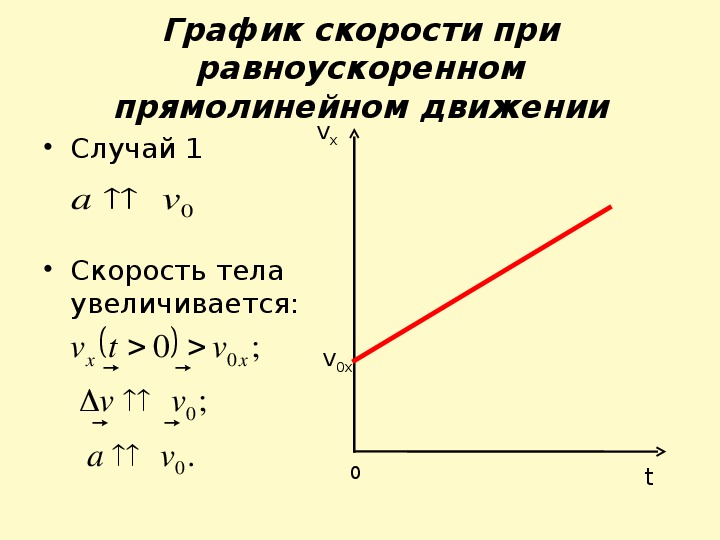 Сформулируем закон относительности движения: характер движения тела зависит от того, относительно каких тел мы рассматриваем движение. Нет абсолютно неподвижных тел.
Сформулируем закон относительности движения: характер движения тела зависит от того, относительно каких тел мы рассматриваем движение. Нет абсолютно неподвижных тел.
Рассмотрим самое простое движение – прямолинейное равномерное движение. Описать движение тела – это значит, указать способ определения его положения в пространстве в любой момент времени.
Для описания движения нужно ввести некоторые понятия: материальная точка, траектория, путь, перемещение, координата, момент времени, промежуток времени, скорость. Материальной точкой называют тело, размерами которого в условиях рассматриваемой задачи можно пренебречь. Это первая физическая модель реальных тел. Практически всякое тело можно рассматривать как материальную точку в тех случаях, когда расстояния, проходимые точками тела, очень велики по сравнению с его размерами. Например, материальными точками считают Землю и другие планеты при изучении их движения вокруг Солнца. В данном случае различия в движении разных точек любой планеты, вызванные её суточным вращением, не влияют на величины, описывающие годовое движение. Но при решении задач, связанных с суточным вращением планет (например, при определении времени восхода солнца в разных местах поверхности земного шара), считать планету материальной точкой нельзя, так как результат задачи зависит от размеров этой планеты и скорости движения точек её поверхности.
Но при решении задач, связанных с суточным вращением планет (например, при определении времени восхода солнца в разных местах поверхности земного шара), считать планету материальной точкой нельзя, так как результат задачи зависит от размеров этой планеты и скорости движения точек её поверхности.
Тело, движущееся поступательно, можно принимать за материальную точку даже в том случае, если его размеры соизмеримы с проходимыми им расстояниями. Поступательным называется такое движение абсолютно твердого тела, при котором любой отрезок, соединяющий любые две точки тела, остается параллельным самому себе.
Что нужно знать для того, чтобы в любой момент времени указать положение тела? Надо, во-первых, знать, где оно было в начальный момент времени; во-вторых, каков вектор перемещения в любой момент времени. Мы уже знаем, что движение любого тела относительно. Поэтому, изучая движение тела, мы обязательно указываем, относительно какого тела это движение рассматривается. Тело, относительно которого рассматривается движение, называется телом отсчета. Чтобы рассчитать положение материальной точки относительно выбранной точки отсчета, надо связать с ним систему координат и измерить время. Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета.
Чтобы рассчитать положение материальной точки относительно выбранной точки отсчета, надо связать с ним систему координат и измерить время. Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета.
Рассмотрим два наиболее часто применяемых способа описания движения тел: координатный и векторный. В координатном способе положение тела в пространстве задается координатами, которые с течением времени меняются.
Рассмотрим движение материальной точки М с координатами (х, y, z) в момент времени t.
Математически это принято записывать в виде:
Количество координат зависит от условия задачи: на прямой – одна, в плоскости – две, в пространстве – три.
В векторном способе используется радиус-вектор. Радиус-вектор – это направленный отрезок, проведенный из начала координат в данную точку. Закон (или уравнение) движения в векторной форме — зависимость радиуса-вектора от времени:
Итак, для задания закона движения материальной точки необходимо указать либо вид функциональной зависимости всех трех ее координат от времени, либо зависимость от времени радиус-вектора этой точки.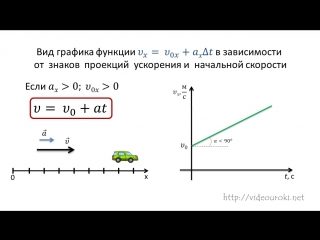
Три скалярных уравнения или эквивалентное им одно векторное уравнение называются кинематическими уравнениями движения материальной точки.
Двигаясь, материальная точка занимает различные положения в пространстве относительно выбранной системы отсчета. При этом она «описывает» в пространстве какую-то линию. Линия, по которой движется точка в пространстве, называется траекторией. По форме траектории все движения делятся на прямолинейные и криволинейные. Траектория движения указывает все положения, которые занимала точка, но, зная траекторию, ничего нельзя сказать о том, быстро или медленно проходила точка отдельные участки траектории. Длину траектории, по которой двигалось тело в течение какого-то промежутка времени, называют путём, пройденным за этот промежуток времени, его обозначают буквой S. Путь – скалярная величина.
Для описания движения тела нужно указать, как меняется положение точек с течением времени. Если участки криволинейные, то изменение координат тела описывают с помощью такого понятия как перемещение. Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением. Обозначается на чертежах как направленный отрезок, соединяющий начальное и конечное положение тела в пространстве:
Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением. Обозначается на чертежах как направленный отрезок, соединяющий начальное и конечное положение тела в пространстве:
Путь и модуль перемещения могут совпадать по значению, только в том случае, если тело движется вдоль одной прямой в одном направлении.
Важной величиной, характеризующей движение тела, является его скорость. Скорость – векторная величина. Она считается заданной, если известен ее модуль и направление. Скорость равномерного прямолинейного движения точки – векторная величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло. Пусть радиус-вектор задает положение точки в начальный момент времени t0, а радиус-вектор- в момент времени t. Тогда промежуток времени:
,
и перемещение:
.
Подставляя выражение для скорости, получим:
Если начальный момент времени t0 принять равным нулю, то скорость равна:
Выразим отсюда радиус-вектор :
Это и есть уравнение равномерного прямолинейного движения точки, записанное в векторной форме.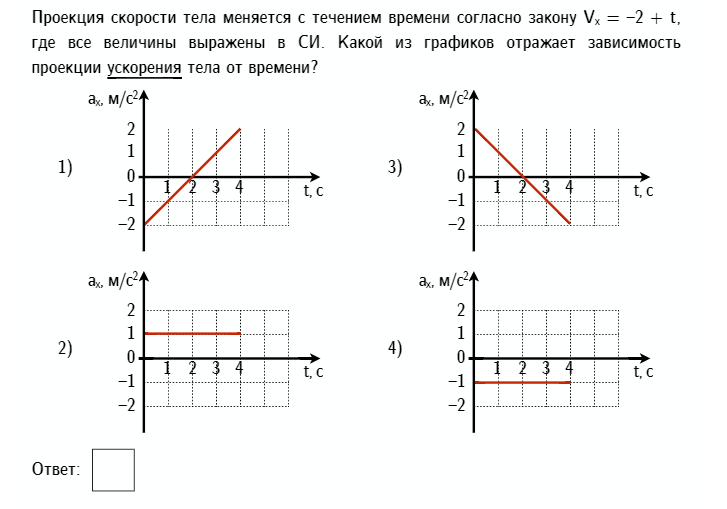 Оно позволяет найти радиус-вектор точки при этом движении в любой момент времени, если известны скорость точки и радиус-вектор, задающий ее положение в начальный момент времени. В проекциях на ось ОХ уравнение можно записать в виде:
Оно позволяет найти радиус-вектор точки при этом движении в любой момент времени, если известны скорость точки и радиус-вектор, задающий ее положение в начальный момент времени. В проекциях на ось ОХ уравнение можно записать в виде:
х=х0+vхt.
Это уравнение есть уравнение равномерного прямолинейного движения точки, записанное в координатной форме. Оно позволяет найти координату х тела при этом движении в любой момент времени, если известны проекция его скорости на ось ОX и его начальная координата х0.
Путь S, пройденный точкой при движении вдоль оси ОХ, равен модулю изменения ее координаты:
Его можно найти, зная модуль скорости
Строго говоря, равномерного прямолинейного движения не существует. Но приближенно на протяжении не слишком большого промежутка времени движение автомобиля можно считать равномерным и прямолинейным с достаточной для практических целей точностью. Таково одно из упрощений действительности, позволяющее без больших усилий описывать многие движения.
Полученные результаты можно изобразить наглядно с помощью графиков. Для прямолинейного равномерного движения график зависимости проекции скорости от времени очень прост. Это прямая, параллельная оси времени.
Как мы уже знаем, зависимость координаты тела от времени описывается формулой х=х0+𝞾хt. График движения представляет собой прямую линию:
Из второго рисунка видим, что углы наклона прямых разные. Угол наклона второй прямой больше угол наклона первой прямой , т.е за одно и тоже время тело, движущееся со скоростью , проходит большее расстояние, чем при движении со скоростью А значит А что же в случае 3, когда угол α < 0? В случае 3 тело движется в сторону, противоположную оси ОХ. Проекция скорости в случае 3 имеет отрицательное значение и график проходит ниже оси ОХ. Проекция скорости определяет угол наклона прямой х(t) к оси t и численно равна тангенсу угла
Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта. В рамках классической механики время есть величина абсолютная, то есть протекающее во всех системах отсчета одинаково.
В рамках классической механики время есть величина абсолютная, то есть протекающее во всех системах отсчета одинаково.
Примеры и разбор решения заданий
1. Тело движется равномерно и прямолинейно в положительном направлении оси ОХ. Координата тела в начальный момент времени равна xо = -10м. Найдите координату тела через 5с, если модуль её скорости равен ʋ=2 м/с. Какой путь проделало тело за это время?
Дано: xо = — 10 м, t = 5 c, ʋ = 2 м/с. Найти s, х.
Решение: координату точки найдем по формуле:
х = х0 + 𝞾х t
Так как направление вектора скорости совпадает с направлением оси координат, проекция вектора скорости положительна и равна ʋx=ʋ; тогда вычисляем:
х = — 10 + 2· 5 = 0 (м).
Пройденный путь найдем s = ʋ t; s = 2·5 = 10 м.
2. Равномерно друг за другом движутся два поезда. Скорость первого равна 72 км/ч, а скорость второго — 54 км/ч. Определите скорость первого поезда относительно второго.
Дано:
Найти .
Решение: Из условия задачи ясно, что векторы скоростей поездов направлены в одну сторону. По закону сложения скоростей запишем:
,
где — искомая величина.
Находим проекцию скоростей на ось ОХ и записываем, чему равен модуль искомой величины
Ответ: .
Прямолинейное равноускоренное движение без начальной скорости. Цель:
9 класс Тесты для самоконтроля ТСК 9.1.5
ТСК 9.1.5 1.Какое(-ие) утверждение(-я) верно(-ы)? А: равноускоренное движение является неравномерным движением Б: равноускоренное движение является равномерным движением 1) Только А 3) И А, и Б 2) Только
Подробнее5.
 Прямолинейное равноускоренное движение
Прямолинейное равноускоренное движение5. Прямолинейное равноускоренное движение Прямолинейное равноускоренное движение это движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково, т. е. это движение с постоянным
ПодробнееКинематика 1 1) 1 2) 2 3) 3 4) 4
Кинематика 1 1 Точка движется по окружности радиусом 2 м, и ее перемещение равно по модулю диаметру. Путь, пройденный телом, равен 1) 2 м 2) 4 м ) 6,28 м 4) 12,56 м 2 Камень брошен из окна второго этажа
ПодробнееИНДИВИДУАЛЬНОЕ ЗАДАНИЕ
ВАРИАНТ 1. 1. Велосипедист тормозит с ускорением м/с. Какую скорость приобретает велосипедист через 1 с если его начальная скорость равна 5 м/с?. Проекция скорости материальной точки изменяется по закону:
ПодробнееЦДО «Уникум» РУДН ОЛИМПИАДА ПО ФИЗИКЕ
ЦДО «Уникум» РУДН ОЛИМПИАДА ПО ФИЗИКЕ Задание 1. Дальность полета снаряда, летящего по навесной траектории, равна максимальной высоте подъема. Какова максимальная высота настильной траектории при той же
Дальность полета снаряда, летящего по навесной траектории, равна максимальной высоте подъема. Какова максимальная высота настильной траектории при той же
t, с. 2015г.
Уравнения и графики кинематики (методика решения тестов и задач), м/с 1 8 6 4 1 3 4 5, с 6 7 8 Составили: Жаганюк М., Киргизов А. Мягков А., Неделько М., Шарипов М. Руководитель: учитель МОУ СОШ 31 Лукина
ПодробнееПРЕДИСЛОВИЕ генератором тестов
ПРЕДИСЛОВИЕ Пособие предназначено для учащихся средних школ, колледжей и техникумов и может быть использовано как при изучении физики, так и при подготовке к ЕГЭ. В пособии представлено 816 разноуровневых
ПодробнееЗадания к контрольной работе
Задания к контрольной работе Содержание контрольных работ составляют задания с выбором ответа, теоретический вопрос и расчётная задача.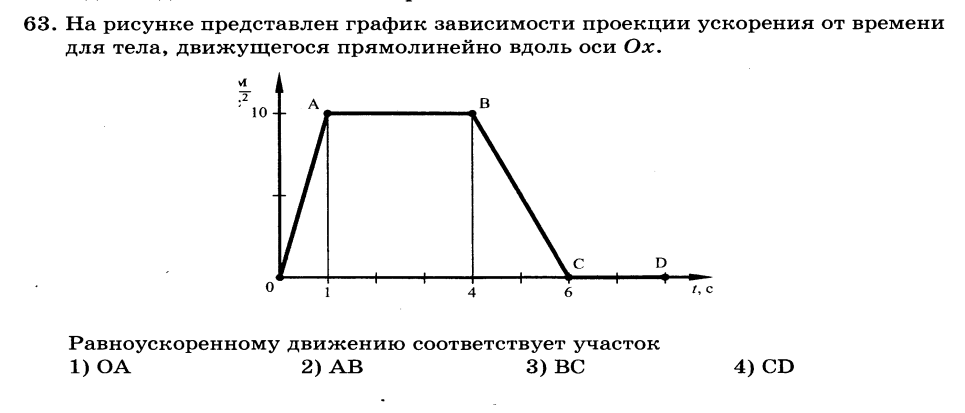 Учитывая результаты исследований по психологии, а также опыт работы
Учитывая результаты исследований по психологии, а также опыт работы
ПРОБНЫЙ ЭКЗАМЕН по теме 1. КИНЕМАТИКА
ПРОБНЫЙ ЭКЗАМЕН по теме. КИНЕМАТИКА Внимание: сначала попытайтесь ответить на вопросы и решить задачи самостоятельно, а потом проверьте свои ответы. Указание: ускорение свободного падения принимать равным
ПодробнееОсновные законы и формулы
1.1. Кинематика материальной точки Основные законы и формулы При движении материальной точки в пространстве радиус-вектор, проведённый из начала координат к точке, и координаты этой точки, представляющие
ПодробнееID_6260 1/5 neznaika.pro
1 Кинематика Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов.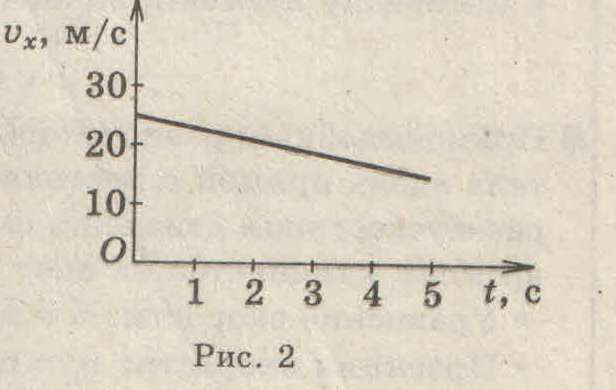 Зависимость координаты
Зависимость координаты
Равноускоренное движение по прямой
ПРАКТИКУМ Равноускоренное движение по прямой АЧЕРНОУЦАН ВСПОМНИМ ОСНОВНЫЕ ФОРМУЛЫ КИНЕМАТИКИ ПРЯмолинейного равноускоренного движения точки Для описания движения точки вдоль некоторой прямой выбирают на
ПодробнееМатериальная точка. Система отсчета
Неравномерное Учебник Касьянов В.А. Автор: Шипкина Е.А. 10 класс. Модуль 1 по теме «Кинематика» — 15 часов Материальная точка Система отсчета Механическое движение Равномерное Периодическое Криволинейное
ПодробнееФИЗИКА 1 триместр 9 класс
Кинематика ФИЗИКА 1 триместр 9 класс Контрольная работа «Кинематика» Демоверсия 1. Решаются две задачи: А: рассчитывается маневр стыковки двух космических кораблей; Б: рассчитываются периоды обращения
ПодробнееРавноускоренное движение
И. В. Яковлев Материалы по физике MathUs.ru Равноускоренное движение Движение с постоянным (как по модулю, так и по направлению ускорением описывается следующими зависимостями скорости и координаты от
В. Яковлев Материалы по физике MathUs.ru Равноускоренное движение Движение с постоянным (как по модулю, так и по направлению ускорением описывается следующими зависимостями скорости и координаты от
Зависимость скорости от времени
И В Яковлев Материалы по физике MathUsru Равноускоренное движение Темы кодификатора ЕГЭ: виды механического движения, скорость, ускорение, уравнения прямолинейного равноускоренного движения, свободное
ПодробнееЗадания к контрольной работе
Задания к контрольной работе Если ученик выполнил все тестовые задания и ответил на теоретический вопрос, то за выполненную работу ставится отметка «4». Отметка «5» ставится за выполнение всех заданий
ПодробнееЗадания к контрольной работе
Задания к контрольной работе Контрольная работа проводится по двум главам: «Законы движения» и «Силы в механике».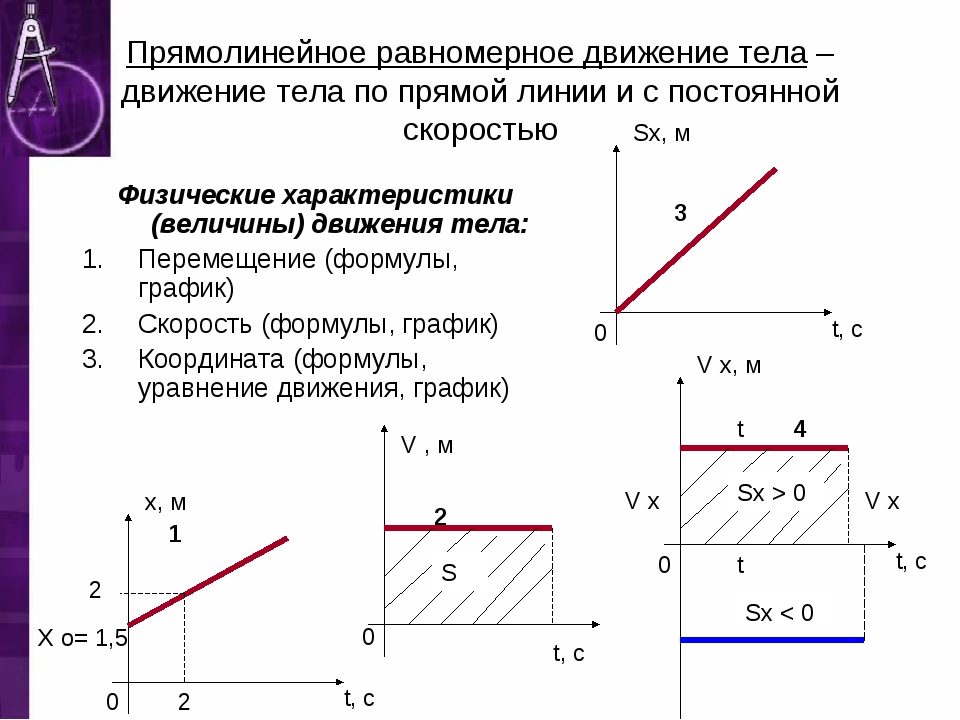 Если ученик выполнил все тестовые задания и ответил на теоретический вопрос, то за выполненную
Если ученик выполнил все тестовые задания и ответил на теоретический вопрос, то за выполненную
если υ 0 а — движение ускоренное
Кинематика Механическое движение изменение положения тела в пространстве с течением времени относительно других тел. Поступательное движение движение, при котором все точки тела проходят одинаковые траектории.
ПодробнееБудем изучать физику вместе
Расскажи мне и я забуду, Покажи мне и я запомню, Вовлеки меня и я научусь! Конфуций (6-й век до нашей эры) Учебник реализует системно-деятельностный поход к изу- Будем изучать физику вместе чению физики.
ПодробнееРавноускоренное движение — материалы для подготовки к ЕГЭ по Физике
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: виды механического движения, скорость, ускорение, уравнения прямолинейного равноускоренного движения, свободное падение.
Равноускоренное движение — это движение с постоянным вектором ускорения . Таким образом, при равноускоренном движении остаются неизменными направление и абсолютная величина ускорения.
Зависимость скорости от времени.
При изучении равномерного прямолинейного движения вопрос зависимости скорости от времени не возникал: скорость была постоянна в процессе движения. Однако при равноускоренном движении скорость меняется с течением времени, и эту зависимость нам предстоит выяснить.
Давайте ещё раз потренируемся в элементарном интегрировании. Исходим из того, что производная вектора скорости есть вектор ускорения:
. (1)
В нашем случае имеем . Что надо продифференцировать, чтобы получить постоянный вектор ? Разумеется, функцию . Но не только: к ней можно добавить ещё произвольный постоянный вектор (ведь производная постоянного вектора равна нулю). Таким образом,
. (2)
Каков смысл константы ? В начальный момент времени скорость равна своему начальному значению: . Поэтому, полагая в формуле (2), получим:
Поэтому, полагая в формуле (2), получим:
.
Итак, константа — это начальная скорость тела. Теперь соотношение (2) принимает свой окончательный вид:
. (3)
В конкретных задачах мы выбираем систему координат и переходим к проекциям на координатные оси. Часто хватает двух осей и прямоугольной декартовой системы координат, и векторная формула (3) даёт два скалярных равенства:
, (4)
. (5)
Формула для третьей компоненты скорости, если она необходима, выглядит аналогично.)
Закон движения.
Теперь мы можем найти закон движения, то есть зависимость радиус-вектора от времени. Вспоминаем, что производная радиус-вектора есть скорость тела:
Подставляем сюда выражение для скорости, даваемое формулой (3):
(6)
Сейчас нам предстоит проинтегрировать равенство (6). Это несложно. Чтобы получить , надо продифференцировать функцию . Чтобы получить , нужно продифференцировать . Не забудем добавить и произвольную константу :
.
Ясно, что — это начальное значение радиус-вектора в момент времени . В результате получаем искомый закон равноускоренного движения:
. (7)
Переходя к проекциям на координатные оси, вместо одного векторного равенства (7) получаем три скалярных равенства:
. (8)
. (9)
. (10)
Формулы (8) — (10) дают зависимость координат тела от времени и поэтому служат решением основной задачи механики для равноускоренного движения.
Снова вернёмся к закону движения (7). Заметим, что — перемещение тела. Тогда
получаем зависимость перемещения от времени:
.
Прямолинейное равноускоренное движение.
Если равноускоренное движение является прямолинейным, то удобно выбрать координатную ось вдоль прямой, по которой движется тело. Пусть, например, это будет ось . Тогда для решения задач нам достаточно будет трёх формул:
,
,
,
где — проекция перемещения на ось .
Но очень часто помогает ещё одна формула, являющаяся их следствием. Выразим из первой формулы время:
Выразим из первой формулы время:
и подставим в формулу для перемещения:
.
После алгебраических преобразований (проделайте их обязательно!) придём к соотношению:
.
Эта формула не содержит времени и позволяет быстрее приходить к ответу в тех задачах, где время не фигурирует.
Свободное падение.
Важным частным случаем равноускоренного движения является свободное падение. Так называется движение тела вблизи поверхности Земли без учёта сопротивления воздуха.
Свободное падение тела, независимо от его массы, происходит с постоянным ускорением свободного падения , направленным вертикально вниз. Почти во всех задачах при расчётах полагают м/с.
Давайте разберём несколько задач и посмотрим, как работают выведенные нами формулы для равноускоренного движения.
Задача. Найти скорость приземления дождевой капли, если высота тучи км.
Решение. Направим ось вертикально вниз, расположив начало отсчёта в точке отрыва капли. Воспользуемся формулой
Воспользуемся формулой
.
Имеем: — искомая скорость приземления, . Получаем: , откуда . Вычисляем: м/с. Это 720 км/ч, порядка скорости пули.
На самом деле капли дождя падают со скоростью порядка нескольких метров в секунду. Почему такое расхождение? Сопротивление воздуха!
Задача. Тело брошено вертикально вверх со скоростью м/с. Найти его скорость через c.
Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу
.
Здесь , так что . Вычисляем: м/с. Значит, скорость будет равна 20 м/с. Знак проекции указывает на то, что тело будет лететь вниз.
Задача. С балкона, находящегося на высоте м, бросили вертикально вверх камень со скоростью м/с. Через какое время камень упадёт на землю?
Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу
.
Имеем: так что , или . Решая квадратное уравнение, получим c.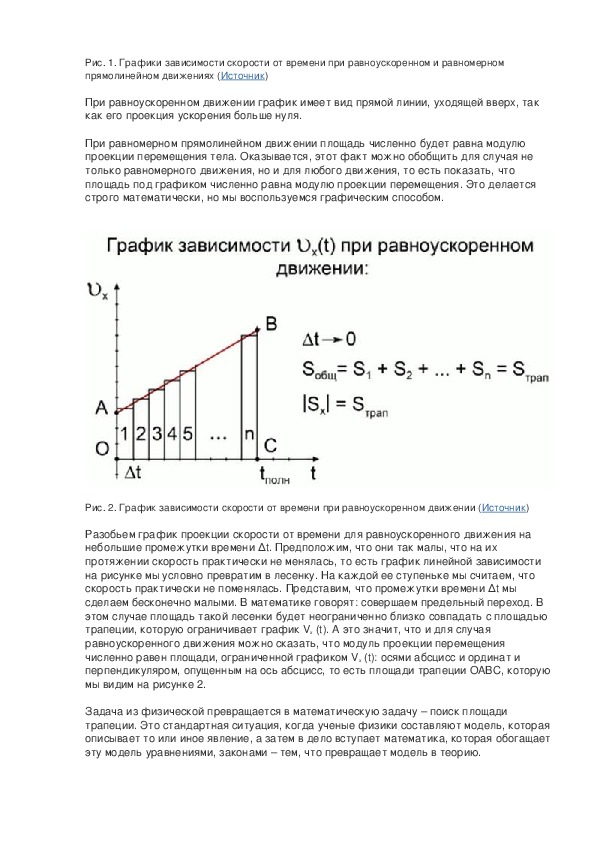
Горизонтальный бросок.
Равноускоренное движение не обязательно является прямолинейным. Рассмотрим движение тела, брошенного горизонтально.
Предположим, что тело брошено горизонтально со скоростью с высоты . Найдём время и дальность полёта, а также выясним, по какой траектории происходит движение.
Выберем систему координат так, как показано на рис. 1.
| Рис. 1. Горизонтальный бросок |
Используем формулы:
В нашем случае . Получаем:
. (11)
Время полёта найдём из условия, что в момент падения координата тела обращается в нуль:
.
Дальность полёта — это значение координаты в момент времени :
.
Уравнение траектории получим, исключая время из уравнений (11). Выражаем из первого уравнения и подставляем во второе:
.
Получили зависимость от , которая является уравнением параболы. Следовательно, тело летит по параболе.
Следовательно, тело летит по параболе.
Бросок под углом к горизонту.
Рассмотрим несколько более сложный случай равноускоренного движения: полёт тела, брошенного под углом к горизонту.
Предположим, что тело брошено с поверхности Земли со скоростью , направленной под углом к горизонту. Найдём время и дальность полёта, а также выясним, по какой траектории двигается тело.
Выберем систему координат так, как показано на рис. 2.
| Рис. 2. Бросок под углом к горизонту |
Начинаем с уравнений:
,
.
В нашем случае . Получаем:
.
Дальше действуем так же, как и в случае горизонтального броска. В результате приходим к соотношениям:
,
,
.
(Обязательно проделайте эти вычисления самостоятельно!) Как видим, зависимость от снова является уравнением параболы. Попробуйте также показать, что максимальная высота подъёма определяется формулой:
Попробуйте также показать, что максимальная высота подъёма определяется формулой:
.
ПЛАН | ||||
Временное планирование | Планируемые мероприятия | Ресурсы | ||
Начало
0-8 | Для постановки целей урока можно провести два эксперимента и обсудить их особенности.
Эксперимент 1 Взять в руки мяч и разжать пальцы. Как изменяется скорость? (При падении мяча скорость его быстро нарастает.)
Эксперимент 2 Приведем в движение
легкую тележку, непродолжительным толчком. Как изменится скорость? (Скорость
тележки, движущейся по столу, уменьшается с течением времени до полной
остановки.
Можно задать учащимся следующие вопросы: — Как изменяется скорость движения мяча и тележки в каждом конкретном случае? — Как называется такое движение? — Какая величина характеризует изменение скорости? — Чем отличается значение ускорения в этих двух случаях? — Как рассчитать ускорение и какое определение вы дали бы этой величине? |
Мяч, тележка | ||
Середина
8- 15
16-20
20-35
|
Учащиеся раскрыли своими ответами
на вопросы самые важные понятия урока. Вывести формулу ускорения можно совместно с учениками по предложенному ими определению, а формулу перемещения при равноускоренном движении можно из графика, находя площадь фигуры под графиком. Из этой формулы достаточно легко и просто выводятся две остальные формулы для перемещения при равноускоренном движении. Решение расчетных задач. 1 этап – тренировка вывода искомых величин из формул(в парах). 2 этап – работа над задачами, в которых требуется производить расчеты одновременно по нескольким формулам (индивидуально). 3 этап – работа над задачей, требующей применение полученных знаний в непривычной и нестандартной задаче (индивидуально). |
Задания формативного оценивания
Презентация
Анимация «Относительность движения, траектория»
Задачи на карточках
| ||
Конец
35-40 |
Обсудить
затруднения и различия в полученных результатах (если есть).
|
| ||
Начало (2 урок)
0-10мин
| Получение графика равноускоренного движения при помощи электронных датчиков. Проводится сравнение графиков ускорения, скорости и перемещения при равномерном и равноускоренном движении.
| Измерительный модуль Spark
| ||
Середина
11-25
26-35
| Работа с графиками. На
этапе отработки материала учащиеся показывают, что происходит при движении,
представленном на графиках, показывая это движение на начерченной на полу
координатной оси. Работа с уравнениями движения. По предложенным графикам движения предлагается определить значение ускорения, написать уравнение движения, и построить график зависимости координаты от времени.
|
Презентация- слайды с вопросами
Карточки с заданиями | ||
Конец
35-40 |
Домашнее задание :задания на карточках |
| ||
Дополнительная информация | ||||
Дифференциация – как вы планируете оказать дополнительную поддержку? Какие задания вы планируете дать наиболее способным учащимся? | Оценка — как вы планируете проверить знания учащихся? | Межучебные связи Проверка соблюдения правил охраны здоровья и безопасности ИКТ связи Связи значений | ||
Все учащиеся будут: Знать, как отличаются понятия траектория, путь, перемещение. Умеют находить векторную и скалярную скорость. Большинство учащихся будут: По графикам записывать уравнения движения по уравнениям движения строить графики. Некоторые учащиеся будут: Связывать полученные знания с реальными жизненными. | (1) Обсуждение демонстраций в начале урока (2) Групповая работа по нахождению суммы и разности векторов. (4)Решение задач. (5) Групповое и индивидуальное решение задач на логику. (6)Опрос усвоенных материалов урока, таких как скалярные и векторные, действия над векторами . | В процессе обработки результатов интерактивных опытов учащимися развивается критическое и логическое мышление. При обсуждении результатов работы в группах и коллективной, развивается уважение к чужому мнению, умение выражать свои мысли и общаться должным образом со сверстниками и одноклассниками. Соблюдение инструкций по технике безопасности в кабинете демонстрирует ответственность и уважение к жизни и здоровью других. | ||
Рефлексия Реалистичны ли задачи урока/учебные задачи? Что вы выучили сегодня? Какова была учебная атмосфера? Удачно ли была подготовлена мной учебная дифференциация? Соблюдал ли я время? Какие изменения внесены в план и почему? | Место, оставленное ниже, используйте для комментариев по проведенному уроку. Ответьте на наиболее важные вопросы, приведенные в графе слева. | |||
| ||||
Итоговая оценка
Какие два момента наиболее успешны (рассмотрите преподавание и обучение)? 1:
2:
Какие два момента улучшили урок (рассмотрите преподавание и обучение)? 1:
2:
Что я узнал из урока о классе и отдельных людях, что я расскажу на следующем уроке?
| ||||
векторов и снарядов — с ответами № 1
Перейдите к:
Обзор сессии Главная — Список темВекторы и снаряды — Главная || Версия для печати || Вопросы и ссылки
Ответы на вопросы: Все || # 1-9 || # 10-45 || # 46-55 || # 56-72
[# 1 | # 2 | # 3 | # 4 | # 5 | # 6 | # 7 | # 8 | # 9]
Часть A: множественный-множественный выбор
1.Какие из следующих утверждений верны для скаляров и векторов? Перечислите все, что ИСТИННО.
- Векторная величина всегда имеет направление.
- Скалярная величина может иметь связанное с ней направление.
- Векторы можно складывать вместе; скалярные величины не могут.
- Векторы могут быть представлены стрелкой на масштабированной диаграмме; длина стрелки представляет величину вектора, а направление, которое она указывает, представляет направление вектора.
Ответ: н.э.
а. ИСТИНА — Векторы определяются как величины, которые полностью описываются как своей величиной, так и направлением. По определению, с вектором связано направление. Если бы этого не было, то это НЕ было бы вектором.
г. FALSE — Скаляры определяются как величины, которые полностью описываются только своей величиной. Скаляры не обращают внимания на направление, и бессмысленно связывать направление с такой величиной.Если бы с величиной действительно было связано направление, то это количество не было бы вектором.
г. FALSE — И векторы, и скаляры можно складывать вместе. Правила сложения векторов уникальны для векторов и не могут использоваться при сложении скаляров. При сложении двух векторов необходимо учитывать направление вектора. При добавлении скаляров направление не имеет значения.
г. ИСТИНА — Именно так и сделано во всем блоке.
[# 1 | # 2 | # 3 | # 4 | # 5 | # 6 | # 7 | # 8 | # 9]
2. Какие из следующих величин являются векторами? Включите все, что применимо.
- пройденное расстояние
- рабочий объем
- средняя скорость
- средняя скорость
- мгновенная скорость
- ускорение
Ответ: BDEF
Из пяти перечисленных здесь кинематических величин (расстояние, смещение, скорость, скорость и ускорение) три являются векторами.Смещение, скорость (как средняя, так и мгновенная) и ускорение — все требует упоминания направления, чтобы полностью описать величину.
[# 1 | # 2 | # 3 | # 4 | # 5 | # 6 | # 7 | # 8 | # 9]
3. Числовые значения и направления указаны для различных величин. Какие из этих утверждений представляют собой векторное описание? Включите все, что применимо.
- 20 метров, запад
- 9,8 м / с / с
- 35 миль / ч, юг
- 16 лет
- 60 минут
- 3.5 м / с / с, юг
- -3,5 м / с / с
- +20 градусов Цельсия
Ответ: ACFG
Выражения векторных величин включают величину (число, значение и т. Д.) И направление. Направление можно описать как север, юг, восток, запад или влево, вправо, вверх, вниз. Иногда для описания направления используется знак «+» или «-». Поскольку математические вычисления на калькуляторах плохо справляются с набором слова «юг», знак «-» часто заменяется на заданное направление.В случае g единицы указывают величину ускорения. Знак «-» указывает направление. Следует быть осторожным, предполагая, что знак «+» или «-» является верным признаком того, что величина, являющаяся направлением, для других не векторных величин также может использовать такие знаки (как в случае h ).
[# 1 | # 2 | # 3 | # 4 | # 5 | # 6 | # 7 | # 8 | # 9]4. Какие из следующих утверждений верны для диаграмм сложения векторов, вычитания векторов и сложения векторов? Перечислите все подходящие варианты.
- Векторы A, B и C складываются как A + B + C. Если порядок, в котором они добавляются, изменить на C + B + A, то результат будет другим.
- Векторы A, B и C складываются вместе как A + B + C. Если порядок, в котором они добавляются, меняется на C + B + A, то результатом будет вектор с той же величиной, но в противоположном направлении. .
- При построении векторной диаграммы для A + B + C не обязательно, чтобы векторы B и C использовали тот же масштаб, который используется вектором A.
- Результирующий элемент на диаграмме сложения векторов всегда простирается от начала последнего вектора до хвоста первого вектора.
- Если векторы A и B сложены под прямым углом друг к другу, то можно быть уверенным, что результирующая величина будет больше, чем величины любого из отдельных векторов A и B.
- Если векторы A и B сложить под прямым углом друг к другу, то можно быть уверенным, что результирующая величина будет меньше арифметической суммы величин A и B.
- Диаграммы сложения векторов не могут использоваться для определения результата при операции вычитания векторов.
Ответ: EF
а. FALSE — Изменение порядка добавления трех векторов не влияет на результат процесса сложения. A + B + C = C + B + A. Каждый порядок операций дает результат с одинаковой величиной и направлением.
г. FALSE — Как упоминалось выше в a, изменение порядка, в котором добавляются три вектора, не влияет на результат процесса сложения.Изменение порядка на противоположное дает результат с той же величиной и тем же направлением.
г. ЛОЖЬ — При построении диаграммы сложения векторов необходимо выбрать масштаб и придерживаться его. Масштаб, который использовался для рисования вектора A, также должен использоваться для векторов B и C. Нельзя переключать лошадей в середине потока .
г. FALSE — Результат на диаграмме сложения векторов рисуется от хвоста первого вектора (начальная точка ) до головы последнего вектора (конечная точка ).
e. ИСТИНА — Предположим, что A = 3 единицы и B = 4 единицы, и что два вектора направлены под прямым углом друг к другу. Векторная сумма или результат A + B составляет 5 единиц, что явно больше, чем любой из добавляемых векторов. В общем случае результирующая в таком случае будет представлена на диаграмме сложения векторов как гипотенуза прямоугольного треугольника. Гипотенуза всегда больше двух других катетов треугольника. Так что это утверждение всегда верно.
ф. ИСТИНА — Предположим, что A = 3 единицы и B = 4 единицы, и что два вектора направлены под прямым углом друг к другу. Векторная сумма или результат A + B составляет 5 единиц, тогда как арифметическая сумма составляет 7 единиц. В этом случае и во всех случаях векторная сумма двух прямоугольных векторов всегда будет меньше арифметической суммы. То есть Sqrt (a 2 + b 2 ) всегда будет меньше a + b.
г. FALSE — Когда выполняется операция вычитания вектора, обычно рекомендуется просто преобразовать ее в операцию сложения вектора.Это достигается путем добавления отрицательного значения вычитаемого вектора. Таким образом, A — B будет эквивалентно A + (-B). Таким образом, диаграмма сложения векторов может использоваться для определения результата.
[# 1 | # 2 | # 3 | # 4 | # 5 | # 6 | # 7 | # 8 | # 9]
5. Какие из следующих описаний движущихся объектов точно изображают снаряд? Перечислите все подходящие варианты.
- объект, который движется по воздуху и не касается какой-либо поверхности
- падающий парашютист с раскрытым парашютом
- Любой объект с незначительным сопротивлением воздуха
- свободно падающий объект
- Объект, единственная значимая сила которого — сила тяжести
- падающее перо
- падающее перо в вакуумной камере
- падающее перо в падающей вакуумной камере.
Ответ: DEGH
Снаряд — это объект, на который действует только сила тяжести. Сопротивление воздуха должно быть незначительным или отсутствовать вовсе. Не должны присутствовать другие силы, возникающие из-за того, что люди или предметы тянут или толкают, прикрепленные веревки или контакт с поверхностями.
а. NO — Самолет движется по воздуху и не касается поверхности. Но самолет явно не снаряд.
г. NO — Падающий парашютист обычно испытывает значительное сопротивление воздуха. — популярный термин для описания таких парашютистов как в свободном падении . Это ошибочное использование термина.
г. NO — Когда вы сидите в кресле, сопротивление воздуха незначительно. Вы точно не снаряд (по крайней мере, мы надеемся, что нет).
г. ДА — Снаряд — это объект в свободном падении.
e. ДА — Объект, на который единственная значимая сила — это сила тяжести, соответствует определению снаряда (при условии, что значительный означает «имеющий влияние»).
ф. NO — Падающие перья сталкиваются с сопротивлением воздуха, которое препятствует ускорению вниз и заставляет перо падать с почти постоянной скоростью.
г. ДА — Когда перо падает в вакууме, сопротивление воздуха устраняется, и перо может свободно падать.
ч. ДА — Когда перо может упасть в вакууме, и вакуум также падает свободно, сопротивление воздуха устраняется, и наблюдатель может заметить, что и вакуумная камера, и перо находятся в свободном падении.
[# 1 | # 2 | # 3 | # 4 | # 5 | # 6 | # 7 | # 8 | # 9]
6. Какие из следующих утверждений верны в отношении снарядов? Перечислите все подходящие варианты.
- Снаряд — это свободно падающий объект.
- Снаряд испытывает незначительное сопротивление воздуха или не имеет его вообще.
- Снаряд должен двигаться вниз.
- Снаряд должен двигаться вниз с ускорением.
- Снаряд не должен иметь горизонтального движения.
- Снаряд может начать движение с нисходящей скоростью.
- Снаряд не обязательно должен «падать».
Ответ: ABDEF и, возможно, G
а. ИСТИНА — Свободно падающие объекты, такие как снаряды, являются объектами, единственная значительная сила которых действует на них — это сила тяжести.
г. ИСТИНА — Единственная сила, действующая на снаряд — это сила тяжести; сопротивление воздуха не должно присутствовать или не должно влиять на движение снаряда.
г. FALSE — Снаряды могут двигаться вверх или вниз или под углом к вертикали. Однако они должны ускоряться вниз в соответствии с действием силы тяжести на объект.
г. ИСТИНА — Сила тяжести действует прямо на объект вниз, вызывая ускорение вниз. Любой снаряд должен ускоряться вниз независимо от других особенностей его движения.
e. TRUE — Снаряд может двигаться строго в вертикальном направлении без горизонтального движения.Таким случаем может быть подброшенный в воздух мяч.
ф. ИСТИНА — Нет правила относительно того, в каком направлении должен двигаться снаряд в момент его выброса. Он мог начать движение с начальной нисходящей скоростью.
г. ИСТИНА — Слово «падение» может означать разные вещи для разных людей. Если «падение» предполагает движение вниз в любой момент времени, то снаряд не обязательно должен «падать». Для многих «падение» означает притяжение силы тяжести вниз.В этом случае снаряд должен «падать».
[# 1 | # 2 | # 3 | # 4 | # 5 | # 6 | # 7 | # 8 | # 9]
7. Какие из следующих утверждений верны относительно горизонтального движения снарядов? Перечислите все подходящие варианты.
- Снаряд не имеет горизонтальной скорости.
- Снаряд с правым компонентом движения будет иметь правый компонент ускорения.
- Горизонтальная скорость снаряда изменяется на 9.8 м / с каждую секунду.
- Снаряд с горизонтальной составляющей движения будет иметь постоянную горизонтальную скорость.
- Горизонтальная скорость снаряда составляет 0 м / с на пике его траектории.
- На горизонтальную скорость снаряда не влияет вертикальная скорость; эти две составляющие движения не зависят друг от друга.
- Горизонтальное смещение снаряда зависит от времени полета и начальной горизонтальной скорости.
- Конечная горизонтальная скорость снаряда всегда равна начальной горизонтальной скорости.
- По мере того, как снаряд поднимается к пику своей траектории, горизонтальная скорость будет уменьшаться; по мере того, как он падает с пика своей траектории, его горизонтальная скорость будет уменьшаться.
- Рассмотрим снаряд, выпущенный с уровня земли с фиксированной скоростью пуска и переменным углом и приземляющийся на уровне земли. Горизонтальное смещение (т.е. диапазон ) снаряда всегда будет увеличиваться при увеличении угла пуска с 0 до 90 градусов.
- Рассмотрим снаряд, выпущенный с уровня земли с фиксированным углом пуска и переменной скоростью пуска и приземлением на уровне земли. Горизонтальное смещение (т.е. диапазон ) снаряда всегда будет увеличиваться с увеличением скорости запуска.
Ответ: DFGHK
а. FALSE — Многие снаряды движутся слева направо и справа налево, одновременно свободно падая. Такие снаряды имеют горизонтальное движение.Снаряд может двигаться в горизонтальном направлении, но не может иметь горизонтальное ускорение. Какое бы движение он ни имел в горизонтальном измерении, он должен быть движением с постоянной скоростью.
г. FALSE — Снаряд, движущийся вправо (в дополнение к вертикальному движению), будет иметь постоянную скорость в правом направлении. Это означает, что у него нет горизонтального ускорения.
г. FALSE — Снаряд имеет постоянную горизонтальную скорость.Вертикальная скорость будет изменяться на 9,8 м / с каждую секунду.
г. ИСТИНА — Абсолютно верно! Снаряды — это объекты, на которые действует только сила тяжести. Таким образом, есть вертикальное ускорение, но нет горизонтального ускорения. Горизонтальная скорость снаряда равна нулю или имеет постоянное ненулевое значение.
e. FALSE — Вертикальная скорость снаряда составляет 0 м / с на пике его траектории; но горизонтальная составляющая скорости на пике — это значение, которое было при первом запуске .
ф. ИСТИНА — Для любого двухмерного движения (будь то движение снаряда или проблемы с речным судном или …) перпендикулярные компоненты движения не зависят друг от друга. Любое изменение вертикального компонента не повлияет на горизонтальные компоненты движения.
г. ИСТИНА — Горизонтальное смещение (x) можно рассчитать по формуле x = v ox • t, где v ox — начальная горизонтальная скорость, а t — время.Это две переменные, которые влияют на горизонтальное смещение снаряда.
ч. ИСТИНА — Поскольку у снаряда нет горизонтального ускорения, начальная горизонтальная скорость равна конечной горизонтальной скорости.
и. FALSE — Это верное описание вертикальной составляющей скорости. Горизонтальная скорость неизменна на всей траектории полета снаряда.
Дж. FALSE — Диапазон (или горизонтальное смещение) будет увеличиваться при увеличении угла с 0 до 45 градусов.Максимальный диапазон составляет 45 градусов. При дальнейшем увеличении угла до значений более 45 градусов горизонтальное смещение уменьшается.
к. ИСТИНА — По мере увеличения скорости запуска компоненты начальной скорости (как горизонтальная, так и вертикальная) также увеличиваются. Это заставляет снаряд оставаться в воздухе в течение более длительного периода времени и быстрее перемещаться в горизонтальном направлении. В результате увеличение скорости запуска всегда приводит к увеличению горизонтальных смещений.
[# 1 | # 2 | # 3 | # 4 | # 5 | # 6 | # 7 | # 8 | # 9]
8. Какие из следующих утверждений верны относительно вертикального движения снарядов? Перечислите все подходящие варианты.
- Вертикальная составляющая скорости снаряда имеет постоянное значение 9,8 м / с.
- Вертикальная составляющая скорости снаряда постоянна.
- Вертикальная составляющая скорости снаряда меняется.
- Вертикальная составляющая скорости снаряда изменяется с постоянной скоростью.
- Снаряд с восходящей составляющей движения будет иметь восходящую составляющую ускорения.
- Снаряд с нисходящей составляющей движения будет иметь нисходящую составляющую ускорения.
- Величина вертикальной скорости снаряда изменяется на 9,8 м / с каждую секунду.
- Вертикальная скорость снаряда составляет 0 м / с на пике его траектории.
- На вертикальную скорость снаряда не влияет горизонтальная скорость; эти две составляющие движения не зависят друг от друга.
- Конечная вертикальная скорость снаряда всегда равна начальной вертикальной скорости.
- Вертикальное ускорение снаряда составляет 0 м / с / с, когда он находится на пике своей траектории.
- Когда снаряд поднимается к пику своей траектории, вертикальное ускорение будет уменьшаться; когда он падает с пика своей траектории, его вертикальное ускорение будет уменьшаться.
- Когда снаряд поднимается к пику своей траектории, вертикальное ускорение направлено вверх; когда он падает с пика своей траектории, его вертикальное ускорение направлено вниз.
- Пиковая высота, на которую снаряд поднимается над местом запуска, зависит от начальной вертикальной скорости.
- По мере того, как снаряд поднимается к пику своей траектории, вертикальная скорость будет уменьшаться; когда он падает с пика своей траектории, его вертикальная скорость будет уменьшаться.
- Рассмотрим снаряд, выпущенный с уровня земли с фиксированной скоростью пуска и переменным углом и приземляющийся на уровне земли. Вертикальное смещение снаряда на первой половине его траектории (т.е., высота пика () всегда будет увеличиваться при увеличении угла запуска с 0 до 90 градусов.
- Рассмотрим снаряд, выпущенный с уровня земли с фиксированным углом пуска и переменной скоростью пуска и приземлением на уровне земли. Вертикальное смещение снаряда в течение первой половины его траектории (то есть пиковая высота ) всегда будет увеличиваться по мере увеличения скорости запуска.
Ответ: CDFGHINPQ
а. FALSE — Вертикальная составляющая скорости снаряда постоянно меняется. Это ускорение, которое имеет значение 9,8 м / с / с.
г. FALSE — Снаряды — это объекты, на которые действует только сила тяжести. Таким образом, существует вертикальное ускорение; вертикальная скорость не постоянна, а меняется.
г. ИСТИНА — См. Часть b выше.
г. TRUE — Снаряд имеет вертикальное ускорение 9,8 м / с / с по всей траектории.Это значение ускорения постоянно. Это означает, что вертикальная скорость изменяется на одинаковую величину — 9,8 м / с — в течение каждой секунды его движения. Вертикальная скорость изменяется на постоянную величину.
e. FALSE — Все снаряды испытывают ускорение вниз независимо от того, движутся они вверх или вниз. Снаряды, движущиеся вверх, имеют восходящую скорость, но фактические значения скорости становятся меньше; то есть снаряд замедляется на пути к своему пику.
ф. ИСТИНА — Это верное утверждение. Можно также сказать, что снаряд с восходящей составляющей движения также имеет ускорение вниз. Все снаряды ускоряются в направлении вниз. Период.
г. ИСТИНА — Это абсолютно верно.
ч. ИСТИНА — На пике своей траектории снаряд находится в процессе изменения направления . Вертикальная скорость должна измениться с положительного значения (+ для движения вверх) на отрицательное значение (- для движения вниз).Этот переход означает, что значение вертикальной скорости в какой-то момент должно быть между числами + и -. Промежуточное число составляет 0 м / с, и это происходит на пике.
и. ИСТИНА — Для любого двухмерного движения (будь то движение снаряда или проблемы с речным судном или …) перпендикулярные компоненты движения не зависят друг от друга. Любое изменение вертикального компонента не повлияет на горизонтальные компоненты движения.
Дж. FALSE — Снаряд, выпущенный под углом, формирует параболическую траекторию.Предположим, что нужно было проследить движение снаряда вперед во времени от пика и назад во времени от пика. Если бы это было сделано, можно было бы обнаружить, что значение вертикальной скорости имеет одинаковую величину в течение равного количества раз, отслеживаемых вперед и назад от пика. Таким образом, в одно и то же время до и после пика снаряд имеет одинаковую скорость. Однако некоторые снаряды не запускаются с той же высоты, на которой они приземляются. Конечная высота не совпадает с начальной высотой, и поэтому время подъема до пика не равно времени падения с пика.В таких случаях начальная вертикальная скорость не равна конечной вертикальной скорости.
к. ЛОЖЬ — Нет! Нет! Нет! Вертикальная скорость составляет 0 м / с на пике, а вертикальное ускорение -9,8 м / с / с по всей траектории.
л. FALSE — Это было бы правильным описанием вертикальной скорости. Но вертикальное ускорение имеет постоянное значение 9,8 м / с / с на всей траектории.
г. FALSE — Не только величина вертикального ускорения является постоянной величиной на всей траектории снаряда, но и направление также является постоянным.Снаряд в любое время, независимо от любой другой переменной, будет ускоряться вниз со скоростью 9,8 м / с / с. Это, пожалуй, самая важная истина о снарядах, которую нужно усвоить.
п. ИСТИНА — Начальная вертикальная скорость влияет на время, необходимое снаряду, чтобы подняться до своего пика. Это также влияет на среднюю скорость снаряда, когда он приближается к своему пику. В результате любое изменение вертикальной скорости приведет к изменению максимальной высоты снаряда.
о. FALSE — Снаряды, поднимающиеся вверх, имеют ускорение вниз; это означает, что они замедляются по мере подъема. Величина их скорости уменьшается. Снаряды, летящие вниз, также имеют ускорение вниз; это означает, что они ускоряются. Величина их скорости увеличивается.
с. ИСТИНА — Увеличение угла запуска (от 0 до 90 градусов) всегда увеличивает вертикальную составляющую начальной скорости (v iy ).Это увеличение v и приведет к увеличению времени подъема снаряда к своему пику. А увеличенный угол заставляет снаряд двигаться с большей средней скоростью на пути к пику. Оба эти эффекта приводят к тому, что пиковая высота снаряда будет увеличиваться по мере увеличения угла запуска от 0 до 90 градусов.
кв. ИСТИНА — По мере увеличения скорости запуска компоненты начальной скорости (как горизонтальная, так и вертикальная) также увеличиваются.Это заставляет снаряд оставаться в воздухе в течение более длительного периода времени и быстрее перемещаться в вертикальном направлении. В результате увеличенная скорость запуска всегда приводит к увеличению высоты снарядов.
[# 1 | # 2 | # 3 | # 4 | # 5 | # 6 | # 7 | # 8 | # 9]
9. Какие из следующих утверждений верны относительно времени полета снаряда? Перечислите все подходящие варианты.
- Время нахождения снаряда в воздухе зависит от горизонтальной составляющей начальной скорости.
- Время нахождения снаряда в воздухе зависит от вертикальной составляющей начальной скорости.
- Для снаряда, который приземляется на той же высоте, с которой он летит, время подъема до пика равно времени падения с пика до исходной высоты.
- При тех же углах запуска вверх снаряды будут оставаться в воздухе дольше, если начальная скорость будет увеличена.
- Предположим, что мяч, брошенный ногой в футболе, является снарядом.Если мячу требуется 3 секунды, чтобы подняться до пика своей траектории, то ему потребуется 6 секунд, чтобы упасть с пика своей траектории на землю.
Ответ: BCD
а. FALSE — Время, в течение которого снаряд поднимется вертикально до своего пика (и затем упадет обратно на землю), зависит от начальной вертикальной скорости. Изменение горизонтальной скорости приведет только к большему горизонтальному смещению снаряда (x).
г. ИСТИНА — Абсолютно верно. Снаряды с большей вертикальной составляющей начальной скорости будут находиться в воздухе более длительное время (при условии, что направление v iy направлено вверх). Изменение значения v iy изменит время полета снаряда, независимо от направления v iy .
г. ИСТИНА — Для снарядов, выпущенных под углом вверх и приземляющихся на исходной высоте, время подъема до пика равно времени падения с пика.Если для подъема вверх требуется 3 секунды, для падения потребуется 3 секунды.
г. ИСТИНА — При постоянном угле запуска увеличение начальной скорости (v i ) увеличит вертикальную скорость (v iy ). Это приводит к увеличению времени замедления снаряда до 0 м / с по мере его подъема к своему пику. Таким образом, снаряду требуется больше времени, чтобы добраться до пика, больше времени, чтобы упасть с пика, и в целом дольше находится в воздухе.
e. FALSE — Близко, но очень ложно.Если для подъема до пика требуется 3 секунды, то для спуска с пика требуется 3 секунды; 6 секунд — это общее время полета снаряда.
[# 1 | # 2 | # 3 | # 4 | # 5 | # 6 | # 7 | # 8 | # 9]Перейдите к:
Обзор сессии Главная — Список темВекторы и снаряды — Главная || Версия для печати || Вопросы и ссылки
Ответы на вопросы: Все || # 1-9 || # 10-45 || # 46-55 || # 56-72
Вам тоже может понравиться…
Пользователи The Review Session часто ищут учебные ресурсы, которые предоставляют им возможности для практики и обзора, которые включают встроенную обратную связь и инструкции. Если это то, что вы ищете, то вам также может понравиться следующее:- Блокнот калькулятора
Блокнот калькулятора включает в себя текстовые задачи по физике, организованные по темам. Каждая проблема сопровождается всплывающим ответом и аудиофайлом, в котором подробно объясняется, как подойти к проблеме и решить ее.Это идеальный ресурс для тех, кто хочет улучшить свои навыки решения проблем.
Посещение: Панель калькулятора На главную | Планшет калькулятора — Векторы и снаряды
- Minds On Physics App Series
Minds On Physics the App («MOP the App») представляет собой серию интерактивных модулей вопросов для учащихся, которые серьезно настроены улучшить свое концептуальное понимание физики. Каждый модуль этой серии посвящен отдельной теме и разбит на подтемы.«Опыт MOP» предоставит учащемуся сложные вопросы, отзывы и помощь по конкретным вопросам в контексте игровой среды. Он доступен для телефонов, планшетов, Chromebook и компьютеров Macintosh. Это идеальный ресурс для тех, кто желает усовершенствовать свои способности к концептуальному мышлению. В первую часть серии входят «Векторы» и «Снаряды».
Посетите: MOP the App Home || MOP приложение — часть 1
4.2 Вектор ускорения — Университетская физика, том 1
Цели обучения
К концу этого раздела вы сможете:
- Рассчитайте вектор ускорения с учетом функции скорости в единичном векторе.
- Опишите движение частицы с постоянным ускорением в трех измерениях.
- Используйте одномерные уравнения движения вдоль перпендикулярных осей, чтобы решить задачу в двух или трех измерениях с постоянным ускорением.
- Выразите ускорение в единичном векторе.
Мгновенное ускорение
Помимо получения векторов смещения и скорости движущегося объекта, мы часто хотим знать его ускорение вектор в любой момент времени вдоль его траектории. Этот вектор ускорения представляет собой мгновенное ускорение, и его можно получить из производной по времени функции скорости, как мы видели в предыдущей главе.Единственная разница в двух или трех измерениях состоит в том, что теперь это векторные величины. Взяв производную по времени
находим
Ускорение по компонентам
Кроме того, поскольку скорость является производной функции положения, мы можем записать ускорение в терминах второй производной функции положения:
Пример
Нахождение вектора ускорения
Частица имеет скорость
(а) Что такое функция ускорения? (б) Каков вектор ускорения при t = 2.0 с? Найдите его величину и направление.
Решение
[show-answer q = ”362804 ″] Показать ответ [/ show-answer]
[hidden-answer a =” 362804 ″] (a) Мы берем первую производную по времени функции скорости, чтобы найти ускорение . Производная берется покомпонентно:
(b) Оценка
дает нам направление в обозначении единичного вектора. Величина ускорения
[/ hidden-answer]
Значение
В этом примере мы обнаруживаем, что ускорение зависит от времени и изменяется на протяжении всего движения.Давайте рассмотрим другую функцию скорости частицы.
Пример
Обнаружение ускорения частиц
Частица имеет функцию положения
(а) Какая скорость? б) Что такое ускорение? (c) Опишите движение от до = 0 с.
Стратегия
Мы можем получить некоторое представление о проблеме, посмотрев на функцию положения. Оно линейно по y и z , поэтому мы знаем, что ускорение в этих направлениях равно нулю, когда мы берем вторую производную.Также обратите внимание, что положение в направлении x равно нулю для t = 0 с и t = 10 с.
Решение
(a)
[show-answer q = ”186733 ″] Показать ответ [/ show-answer]
[hidden-answer a =” 186733 ″] Взяв производную по времени функции положения, мы находим
Функция скорости линейна во времени в направлении x и постоянна в направлениях y и z. [/ Hidden-answer]
(b)
[Показать-ответ q = ”713695 ″] Показать ответ [/ Показать-ответ]
[Скрытый-ответ a =” 713695 ″] Взяв производную функции скорости, находим
Вектор ускорения постоянен в отрицательном направлении оси x.[/ hidden-answer]
(c) [раскрыть-ответ q = ”368016 ″] Показать ответ [/ раскрыть-ответ]
[hidden-answer a = ”368016 ″] Траекторию частицы можно увидеть на (Рисунок).
Давайте сначала посмотрим в направлениях y и z. Положение частицы постоянно увеличивается в зависимости от времени с постоянной скоростью в этих направлениях. Однако в направлении x частица следует по положительному положительному x до тех пор, пока t = 5 с, когда она меняет направление на противоположное. Мы знаем это, глядя на функцию скорости, которая в этот момент становится равной нулю, а затем становится отрицательной.Мы также знаем это, потому что ускорение отрицательное и постоянное, то есть частица замедляется или ускоряется в отрицательном направлении. Положение частицы достигает 25 м, после чего она меняет направление и начинает ускоряться в отрицательном направлении оси x. Положение достигает нуля при t = 10 с.
Рисунок 4.9 Частица начинается в точке (x, y, z) = (0, 0, 0) с вектором положения.Показана проекция траектории на плоскость xy.Значения y и z линейно увеличиваются как функция времени, тогда как x имеет точку поворота в t = 5 с и 25 м, когда он меняет направление. В этот момент компонент x скорости становится отрицательным. При t = 10 с частица возвращается на 0 м в направлении x.
[/ hidden-answer]
Значение
Изобразив траекторию частицы, мы можем лучше понять ее движение, что определяется численными результатами кинематических уравнений.
Проверьте свое понимание
Предположим, что функция ускорения имеет вид
, где a, b, и c — константы.Что можно сказать о функциональном виде функции скорости?
[show-answer q = ”fs-id1165038330863 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165038330863 ″]
Вектор ускорения постоянный и не меняется со временем. Если a, b и c не равны нулю, то функция скорости должна быть линейной во времени. У нас
, поскольку взятие производной функции скорости дает
Если любой из компонентов ускорения равен нулю, то этот компонент скорости будет постоянным.
[/ hidden-answer]
Постоянное ускорение
Многомерное движение с постоянным ускорением можно рассматривать так же, как показано в предыдущей главе для одномерного движения. Ранее мы показали, что трехмерное движение эквивалентно трем одномерным движениям, каждое по оси, перпендикулярной другим. Чтобы разработать соответствующие уравнения для каждого направления, давайте рассмотрим двумерную задачу о частице, движущейся в плоскости xy с постоянным ускорением, игнорируя на данный момент компонент z .Вектор ускорения
Каждый компонент движения имеет отдельный набор уравнений, подобных (рисунок) — (рисунок) из предыдущей главы об одномерном движении. Мы показываем только уравнения для положения и скорости в направлениях x и y . Аналогичный набор кинематических уравнений может быть записан для движения в направлении z — направление:
Здесь индекс 0 обозначает начальное положение или скорость.(Рисунок) на (Рисунок) можно заменить на (Рисунок) и (Рисунок) без компонента z , чтобы получить вектор положения и вектор скорости как функцию времени в двух измерениях:
Следующий пример иллюстрирует практическое использование кинематических уравнений в двух измерениях.
Пример
Лыжник (рисунок) показывает лыжника, движущегося с ускорением
.вниз по склону
при т = 0.С началом системы координат в передней части ложи, ее начальное положение и скорость равны
.и
(a) Каковы составляющие x- и y положения и скорости лыжника как функции времени? (b) Каковы ее положение и скорость при t = 10,0 с?
Рисунок 4.10 У лыжника ускорениевниз по склону
Начало системы координат находится в лыжной базе.
Стратегия
Поскольку мы оцениваем компоненты уравнений движения в направлениях x и y , нам нужно найти компоненты ускорения и поместить их в кинематические уравнения. Компоненты ускорения находятся в системе координат на (Рисунок). Затем, вставив компоненты начального положения и скорости в уравнения движения, мы можем найти ее положение и скорость в более позднее время t .
Решение
(a)
[Показать-ответ q = ”216061 ″] Показать ответ [/ Показать-ответ]
[hidden-answer a =” 216061 ″] Начало системы координат находится на вершине холма с y- ось вертикально вверх и ось x горизонтально. Глядя на траекторию лыжника, можно увидеть, что x-составляющая ускорения положительна, а y-составляющая отрицательна. Поскольку угол
вниз по склону, находим
Вставив начальное положение и скорость в (рисунок) и (рисунок) для x, мы имеем
Для y имеем
(b) Теперь, когда у нас есть уравнения движения для x и y как функции времени, мы можем вычислить их при t = 10.0 с:
Положение и скорость при t = 10,0 с, наконец,
Величина скорости лыжника на 10,0 с составляет 25 м / с, что составляет 60 миль / ч. [/ Hidden-answer]
Значение
Полезно знать, что, учитывая начальные условия положения, скорости и ускорения объекта, мы можем найти положение, скорость и ускорение в любое более позднее время.
С (Рисунок) — (Рисунок) мы завершили набор выражений для положения, скорости и ускорения объекта, движущегося в двух или трех измерениях. Если траектории объектов выглядят как «красные стрелки» на начальном рисунке главы, то выражения для положения, скорости и ускорения могут быть довольно сложными. В следующих разделах мы исследуем два частных случая движения в двух и трех измерениях, рассматривая движение снаряда и круговое движение.
Сводка
- В двух и трех измерениях вектор ускорения может иметь произвольное направление и не обязательно указывать вдоль заданного компонента скорости.
- Мгновенное ускорение вызывается изменением скорости за очень короткий (бесконечно малый) период времени. Мгновенное ускорение — это вектор в двух или трех измерениях. Он находится путем взятия производной функции скорости по времени.
- В трех измерениях, ускорение
можно записать как векторную сумму одномерных ускорений
по осям x- , y — и z- .
- Кинематические уравнения для постоянного ускорения могут быть записаны как векторная сумма уравнений постоянного ускорения в направлениях x , y и z .
Концептуальные вопросы
Если функция положения частицы является линейной функцией времени, что можно сказать о ее ускорении?
Если объект имеет постоянную составляющую скорости x и внезапно испытывает ускорение в направлении x , изменяется ли составляющая x- его скорости?
[показывать-ответ q = ”fs-id1165038328884 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165038328884 ″]
Нет, движения в перпендикулярных направлениях независимы.
[/ hidden-answer]
Если объект имеет постоянную составляющую скорости x- и внезапно испытывает ускорение под углом
в направлении x , изменяется ли составляющая скорости x- ?
Проблемы
Положение частицы
(a) Определите его скорость и ускорение как функции времени. (б) Каковы его скорость и ускорение в момент времени t = 0?
Ускорение частицы
При t = 0 его положение и скорость равны нулю.а) Каковы положение и скорость частицы в зависимости от времени? (б) Найдите уравнение пути частицы. Нарисуйте оси x- и y- и нарисуйте траекторию частицы.
[show-answer q = ”fs-id1165038340090 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165038340090 ″]
а.
,
б.
[/ hidden-answer]
Лодка покидает причал при t = 0 и направляется в озеро с ускорением
.Сильный ветер толкает лодку, придавая ей дополнительную скорость
.(а) Какова скорость лодки при т = 10 с? (b) Каково положение лодки при т = 10 с? Нарисуйте эскиз траектории и положения лодки при t = 10 с, показывая оси x- и y .
Положение частицы для t > 0 определяется как
(а) Какова скорость как функция времени? б) Что такое ускорение как функция времени? (c) Какова скорость частицы при t = 2,0 с? (d) Какова его скорость при т, = 1,0 с и т, = 3,0 с? (e) Какова средняя скорость между t = 1,0 с и t = 2,0 с?
[показывать-ответ q = ”fs-id1165038304047 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165038304047 ″]
а.
,
б.
,
г.
,
г.
,
e.
[/ hidden-answer]
Ускорение частицы постоянно. При t = 0 скорость частицы
При t = 4 с скорость
(а) Каково ускорение частицы? б) Как положение и скорость меняются со временем? Предположим, что частица изначально находится в начале координат.
Частица имеет функцию положения
, где аргументы функций косинуса и синуса выражены в радианах. а) Что такое вектор скорости? б) Что такое вектор ускорения?
[показывать-ответ q = ”fs-id1165038303762 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165038303762 ″]
а.
, г.
[/ hidden-answer]
Реактивный самолет Lockheed Martin F-35 II Lighting взлетает с авианосца с длиной взлетно-посадочной полосы 90 м и скоростью взлета 70 м / с в конце взлетно-посадочной полосы.Самолеты катапультируются в воздушное пространство с палубы авианосца с двумя источниками движения: реактивным движением и катапультой. В момент выхода из палубы авианосца ускорение F-35 уменьшается до постоянного ускорения
.в
по горизонтали. (а) Каково начальное ускорение F-35 на палубе авианосца, чтобы он поднялся в воздух? (b) Запишите положение и скорость F-35 в единичном векторе от точки, когда он покидает палубу авианосца.(c) На какой высоте находится истребитель через 5,0 с после выхода из палубы авианосца? (г) Каковы его скорость и скорость в это время? д) Как далеко он прошел по горизонтали?
Глоссарий
- Вектор ускорения
- мгновенное ускорение, полученное путем взятия производной функции скорости по времени в обозначении единичного вектора
Краткое содержание урока прямолинейное равноускоренное движение с мгновенной скоростью.Прямолинейное равноускоренное движение. Ускорение. I. Организационный этап
Тема урока: «Прямолинейное, равноускоренное движение.
Решение проблем. »
Цель занятия: Систематизировать знания о методах решения задач с равномерно ускоренным движением.
Задачи урока :
Сформировать умения распознавать ускоренное движение и характеризовать его с помощью физических величин — ускорения, скорости.
Научитесь строить график скорости.
Узнайте, как составить уравнение скорости в соответствии с графиком скорости.
Научитесь составлять уравнение скорости.
Во время занятий.
1. Организационный этап
Приветствие, проверка готовности студентов к учебному занятию, раскрытие целей урока и его плана.
Фронтальная съемка.
1) Что называется ускорением равноускоренного движения?
2) Что такое равноускоренное движение?
3) Что характеризует ускорение? Какая формула рассчитывается? (a x =
4) При каком условии увеличивается модуль вектора скорости движущегося тела? Уменьшается?
5) Запишите формулу, по которой можно рассчитать проекцию вектора мгновенной скорости
(V x = V 0 x + axt)
В сегодняшнем уроке мы рассмотрим следующие вопросы:
Как сделать составить уравнение скорости;
Как определить направление скорости и ускорения из уравнения скорости;
Как построить график проекции скорости с помощью уравнения скорости:
Как составить уравнение скорости в соответствии с графиком проекции скорости.
Задача 1 Используя этот рисунок, составьте уравнение проекции скорости:
3 м / с 2 1 м / с 2
1 тело : V x = 6 — 3 t, поскольку вектор скорости сонаправлен. с осью X, то V 0 x = 6 м / с, вектор ускорения направлен противоположно оси X, то ax = -3 м / с 2.
2 body : V x = 2 + t, поскольку вектор скорости совмещен с осью X, то V 0 x = 2 м / с, вектор ускорения также совмещен с осью X, то ax = 1 м / с 2.
Задача 2 . (независимо).
В соответствии с уравнениями проекции скорости нарисуйте положение тел на координатной линии.
В х = -10 + 2 т 2) В х = -6 — 3 т
2 м / с 2 3 м / с 2
10 м / с 6 м / с X
Задача 3. Используя приведенные уравнения проекции скорости, построить графики проекции скорости. (Из условий первой задачи)
1) V x = 6 — 3 t 2) V x = 2 + t
Графики этих функций представляют собой прямые линии, построенные по точкам.
Вопросы для студентов:
1. Как двигается первое тело? Второе тело? (Первое тело тормозит, второе ускоряется)
2. Что означает точка пересечения графиков? (скорости тел через 1 сек после начала движения сравнялись)
Task4 . Используя этот график проекции скорости, напишите уравнение для проекции скорости. (рис. А)
(рис. А)
Ответ: по графику определяем, что V 0x = 3м / с.Чему равно ускорение? а x =
ии x = 2 м / с 2. Подставляя числа в уравнение, имеем: V x = 3 +2 t.
Крепление:
Какое из следующих уравнений описывает движение, при котором скорость тела увеличивается?
На рисунке 1 показан график зависимости скорости тела от времени. Какое уравнение соответствует этому графику?
(рис.1)
Какой из графиков (рис. 2) соответствует уравнению скорости V = 2-t?
(рис. 2)
Какой из графиков (рис. 3) соответствует равноускоренному движению тела, в котором вектор ускорения направлен противоположно вектору скорости?
(рис. 3)
По графику зависимости скорости от времени (рис. 4) определите ускорение тела в момент времени t = 4с.
(рис.4)
Результаты. Домашнее задание. §6.Upr. 6 (3.4)
Список использованной литературы
1. Перышкин А.В., Гутник Е.М. Физика. 9 класс –М. Дрофа 2005.
2. Лукашик В.И., Иванова Е.В. Сборник задач по физике 7–9 классов — М .: Просвещение, 2008.
3. Марон А.Е., Марон Е.А. Физика. Дидактические материалы. 9 класс. — М. Дрофа. 2008
Прямолинейное равноускоренное движение. Ускорение.
На занятиях
I.Организационная фаза
II. Проверка домашнего задания.
1 слайд: Test.
1. Среди значений ниже выберите только вектор.
A: пройденное расстояние
B: перемещение
B: проекция смещения
2. При прямолинейном движении тела проекция вектора смещения на ось считается положительной, если. . . .
направление вектора смещения совпадает с направлением оси
направление вектора смещения противоположно направлению оси
направление вектора смещения перпендикулярно направлению оси
длина вектора равна нулю
3.Автобус переместился из точки с координатой x 0 = 200 м в точку с координатой x 1 = -200 м. Определите проекцию движения автобуса.
A) 0 м B) -200 м C) -400 м D) 400 м
4. Определите конечную координату мотоциклиста, если он покинул точку x 0 = 30 м, и проекцию смещения на ось OX — S x = 240 м.
A) 0 м B) 30 м C) 210 м D) 270 м
5. Спортсмен переместился из точки с координатой x 0 = -100 м в точку с координатой x 1 = 500 м.Определите проекцию движения спортсмена.
A) 0 м B) 400 м C) -400 м D) 600 м
2 слайда: III. Изучение нового материала
Тема урока: «Прямолинейное, равномерно ускоренное движение. Ускорение ». Чтобы описать такое движение, мы вводим важную величину — ускорение . Напомним, что в предыдущих занятиях мы обсуждали вопрос о прямолинейном равномерном движении, то есть таком движении, когда скорость остается постоянной.
3 слайд:
А если скорость меняется, то что? В этом случае говорят, что движение неравномерное. Из всех видов неравномерного движения рассмотрим самый простой — прямолинейный равноускоренный, при котором тело движется по прямой линии, а проекция вектора скорости тела изменяется одинаково для любых равных интервалов времени (в данном случае модуль вектора скорости может как увеличиваться, так и уменьшаться).
4 слайд:
Для характеристики неравномерности движения введена новая физическая величина — мгновенная скорость .
Определение: мгновенная скорость — это скорость тела в данный момент или в данной точке траектории.
Устройство, показывающее мгновенную скорость, есть на любом движущемся транспортном средстве: в машине, поезде и т. Д. Это устройство, называемое спидометром (от англ. — скорость («скорость»)). Обращаем ваше внимание на то, что мгновенная скорость определяется как отношение смещения ко времени, в течение которого это смещение произошло. Но это определение не отличается от нашего более раннего определения скорости в RPD.Для более точного определения следует отметить, что временной интервал и соответствующее движение взяты очень маленькими, стремящимися к нулю. Тогда скорость не успевает сильно измениться, и мы можем воспользоваться формулой, которая была введена ранее:
Обратите внимание на рис. . x 0 и x 1 — координаты вектора смещения. Если этот вектор очень мал, то изменение скорости произойдет довольно быстро. В данном случае мы характеризуем это изменение изменением мгновенной скорости.
Таким образом неравномерное движение имеет смысл характеризовать изменение скорости от точки к точке по тому, насколько быстро это происходит. Это изменение скорости характеризуется величиной, называемой ускорением. Указывается ускорение, это векторная величина.
Определение: Ускорение определяется как отношение изменения скорости ко времени, в течение которого это изменение произошло.
Ускорение измеряется в м / с 2.
6 слайд: Ускорение тела, движущегося прямолинейно и с равномерным ускорением, можно рассчитать с помощью следующего уравнения, которое включает проекции векторов ускорения и скорости:
Мы показываем на конкретных примерах, как обнаруживается ускорение.На рисунке а изображены сани, которые одинаково ускоряются с горы.
Известно, что AV-санный участок пути прошел за 4 с. Причем в точке А у них была скорость 0,4 м / с, а в точке Б — 2 м / с (за материальную точку были взяты сани).
Определим, с каким ускорением сани двигались на участке AB.
В этом случае за точку отсчета времени следует брать момент прохождения санями точки А, поскольку, согласно условию, именно с этого момента интервал времени, для которого модуль вектора скорости изменился с 0.Считается от 4 до 2 м / с.
Теперь проведите ось X параллельно вектору скорости салазок и направьте в том же направлении. Мы проецируем на него начало и конец векторов v 0 и v. Получившиеся отрезки v 0x и v x являются проекциями векторов v 0 и v на ось X. Обе эти проекции положительны и равны модулям соответствующих векторов: v 0x = 0,4 м / с, v x = 2 м / с.
Записываем условие проблемы и решаем.
Проекция вектора ускорения на ось X оказалась положительной, это означает, что вектор ускорения совмещен с осью X и скоростью салазок.
Если векторы скорости и ускорения направлены в одну сторону, то скорость увеличивается.
Теперь рассмотрим другой пример, в котором сани, скатившись с горы, движутся по горизонтальному участку КД (рис. Б).
В результате действия силы трения на салазки их скорость непрерывно уменьшается, и в точке D салазки останавливаются, то есть их скорость равна нулю. Известно, что в точке C сани развивали скорость 1,2 м / с, а отрезок CD был пройден ими за 6 с.
Рассчитываем ускорение саней в этом случае, т.е. определяем, насколько изменилась скорость саней за каждую единицу времени.
Проведите ось X параллельно сегменту CD и совместите ее со скоростью салазок, как показано на рисунке. В этом случае проекция вектора скорости саней на ось X в любой момент их движения будет положительной и равна модулю вектора скорости. В частности, при t 0 = 0 v 0x = 1,2 м / с, а при t = 6 s v x = 0.
Записываем данные и рассчитываем ускорение.
Проекция ускорения на ось X отрицательная. Это означает, что вектор ускорения a направлен противоположно оси X и, соответственно, противоположно скорости движения. В этом случае скорость саней уменьшилась.
Таким образом, если векторы скорости и ускорения движущегося тела направлены в одну сторону, то модуль вектора скорости тела увеличивается, а если в противоположном — уменьшается.
7 слайд: IV. Домашнее задание.
пункт 5, вопросы, упражнение 5 (2,3)
\ Документы \ Учителю физикиПри использовании материалов сайта — и размещение баннера-ОБЯЗАТЕЛЬНО !!!
Урок разработан и отправлен: Калинин В.Н., студент ПГПУ им. Белинского
Конспект занятия.
Тема урока: Прямолинейное равноускоренное движение.Ускорение.
Задачи урока: Познакомить учащихся с одинаково изменчивым типом движений. Представьте понятие ускорения, мгновенной скорости.
Во время занятий.
Этапы урока:
- 1.Org. Момент
- 2. Повторить. Фронтальный обзор
- 3. Изучение новой темы. Разговор, рассказ
- 4. Обеспечение изученного материала. Разговор
- 5.D / W
1.Запись на доске
1. Повторить. Проверьте домашнее задание.
Учитель: Мы закончили последний урок, решив задачу, в которой, используя график зависимости координаты от времени, нашли место и время встречи машин. Дома нужно было проверить результаты аналитически.
Учитель: Ну согласились ли ответы?
Учитель: Хорошо! Решим еще одну проблему.
Задача. Движения 2 велосипедистов описываются уравнениями
Найдите время и место для встречи с велосипедистами. (Подзываю ученика к доске)
Учитель: Давайте сначала запишем данное. Теперь вспомните, что такое график зависимости координаты от времени.
Учеников: Прям
Учитель: Хорошо. Тогда скажите мне, сколько точек достаточно, чтобы провести линию?
9 класс по физике Предмет: Прямолинейное равноускоренное движение.Ускорение.Задачи урока:
Образовательные: повторение, углубление и систематизация доступной студентам информации о механических явлениях; формировать новые знания и умения: определение прямолинейного равнопеременного движения, ускорения, единицы ускорения, проекции ускорения.
Разработка: развитие мышления, эмоционально-волевой и потребности-мотивационной сфер; умственная деятельность (выполнять операции анализа, синтеза, классификации, умение наблюдать, делать выводы,
Образовательная: формирование системы мировоззрений, умение следовать стандартам поведения.
Тип урока: комбинированный.
Методы: словесный, визуальный, практический.
Оснащение:
План урока.
Организационное время
Повторение (решение проблемы).
Освоение нового материала.
Домашнее задание
Подведение итогов урока.
Отражение
Во время занятий.
Орг. Момент.
Повторение.
Решение задач, упражнение 2 (1-3).
1. В начальный момент времени тело находилось в точке с координатами x 0 = — 2м и на 0 = 4м. Тело переместилось в точку с координатами x . = 2м и при = 1м. Найдите проекции вектора смещения на оси x и y. Нарисуйте вектор смещения.
2. Из начальной точки с координатами x 0 = — 3м и на 0 = 1м тело каким-то образом ушло, так что проекция вектора смещения на ось х оказалось 5.2 м, а по оси на — 3м. Найдите координаты конечного положения тела. Нарисуйте вектор смещения. Чему равен его модуль?
3. Путешественник прошел 5 км на юг, а затем еще 12 км на восток. Каков модуль движения, которое он выполнял?
Освоение нового материала.
Презентация «Векторы и действия на них». Повторим четко, что такое векторы и какие действия над ними можно производить.
Вопрос: Какое движение называется равномерным?
Ответ: Движение, при котором тело проходит одинаковое расстояние за любые равные промежутки времени.
Движение с постоянной скоростью.
Вопрос: Что называется скоростью прямолинейного равномерного движения?
Ответ: Постоянное значение вектора, равное отношению смещения к периоду времени, в течение которого произошло это изменение.
В = с / т .
Вопрос: Тогда скажите, как вы понимаете: скорость автомобиля 60 км / ч?
Ответ: За час машина проезжает 60 км.
Вопрос: Скорость скалярная или векторная величина?
Ответ: Скалярный. Следовательно, он характеризуется направлением и модулем (числовым значением).
Вопрос: В каких случаях проекция вектора скорости положительна, а в каких — отрицательна?
Ответ: Положительный, если проекция вектора скорости совмещена с осью.
Отрицательно, если проекция скорости и выбранная ось противоположны.
Вопрос: Определите знак проекции вектора скорости
Ответ : 1-положительный.
2-положительный.
3-отрицательный.
4- равно 0
Вопрос: Запомните формулу, по которой можно в любой момент узнать положение тела.
Ответ: х = х 0 + в х т
Основной материал.
До этого приходилось иметь дело с равномерным движением. Еще раз повторим.
Униформа — это движение, при котором тело проходит равные расстояния за любые равные промежутки времени. С другой стороны, движение с постоянной скоростью на практике не очень распространено. Чаще приходится иметь дело с таким движением, скорость которого со временем меняется. Это движение называется равно переменным.
При простейшей форме равномерного движения он равномерно ускоряется. В котором тело движется по прямой, а проекция вектора скорости тела на любые равные промежутки времени изменяется одинаково.Предположим, автомобиль движется по дороге, и бензин капает из бака через равные промежутки времени и оставляет следы.
Время, каждые 2 секунды.
Мы видим, что через равные промежутки времени скорость меняется одинаково. Это движение называется равномерно ускоренным.
Учитель: Давайте запишем в тетрадь определение равноускоренного движения.
Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называется равномерно ускоренным.
При рассмотрении равноускоренного движения вводится понятие мгновенной скорости.
Мгновенная скорость — скорость в каждой конкретной точке траектории в соответствующий момент времени.
Рассмотрим движение, при котором в начальный момент времени скорость тела была равна V 0. , а по прошествии времени t оказалось равным V,
, тогда передаточное число — это скорость изменения скорости.
Тех. скорость изменения скорости называется ускорением.
а =
В 0 — начальная скорость, скорость в момент времени t = 0
V — скорость, которую тело имело в конце промежутка t.
Величина вектора ускорения.
— [а] = м / с 2
По формуле можно найти значение скорости в определенный момент.
Сначала записываем значение скорости в векторном виде, а затем скалярно.
В = V 0 + при
В = V 0 — at
Ускорением тела называют величину, характеризующую скорость изменения скорости; он равен отношению изменения скорости к периоду времени, в течение которого это изменение произошло.
Равноускоренное движение — это движение с постоянным ускорением.
Поскольку ускорение является векторной величиной, это означает, что оно имеет направление.
Как определить, куда направлен вектор ускорения?
Предположим, что тело движется прямолинейно, и его скорость со временем увеличивается. Изображаем это на рисунке.
В этом случае вектор ускорения направлен с той же скоростью, что и вектор скорости.
Если тело движется и его скорость со временем уменьшается (замедляется), вектор ускорения противоположен вектору скорости.
Если векторы скорости и ускорения движущегося тела направлены в одном направлении, то модуль вектора скорости увеличивается.
Если в противоположных направлениях, то модуль вектора скорости уменьшается.
Домашнее задание
§4 контроль 3.
Подведение итогов.
1. Какое движение называется равноускоренным или равно переменным?
2.Что называется ускорением?
3. Какая формула выражает значение ускорения?
4. В чем разница между «ускоренным» прямолинейным движением и «замедленным» движением?
Таким образом, прямолинейное движение рассматривается двух типов: равномерное и равно переменное (с ускорением). Равномерный с постоянной скоростью, равномерный с постоянным ускорением. Ускорение характеризует скорость изменения скорости.
Отражение.
Урок полезный…
Я был…
Я узнал…
В этом уроке по теме: «Прямолинейное, равноускоренное движение. Разгон »рассмотрим неравномерное движение и его особенности. Будет указано, что такое линейное неравномерное движение и чем оно отличается от равномерного движения, рассматривается определение ускорения.
Тема занятия: «Неравномерное прямолинейное движение, прямолинейное равноускоренное движение. Ускорение ». Для описания такого движения введем важную величину — ускорение .
В предыдущих классах обсуждалась проблема прямолинейного равномерного движения, то есть такого движения, когда скорость остается постоянной. Но что, если скорость изменится? В этом случае говорят, что движение неравномерное, то есть скорость от точки к точке меняется. Важно понимать, что скорость может увеличиваться, затем движение будет ускоряться, либо уменьшаться (рис. 1) (в данном случае мы будем говорить о замедленном движении).
Рис. 1. Движение с изменением скорости
В целом изменение скорости может характеризоваться уменьшением или увеличением скорости.
средняя скорость
Когда мы говорим о неравномерном движении, помимо понятия «мгновенная скорость», которое мы часто будем использовать, понятие «средняя скорость» также чрезвычайно важно. Более того, именно эта концепция позволит нам дать правильное определение мгновенной скорости.
Какая средняя скорость? Это можно понять на простом примере. Представьте, что вы едете из Москвы в Санкт-Петербург и проезжаете 700 км за 7 часов. Какова была ваша скорость во время этого движения? Если автомобиль проехал 700 км за 7 часов, то его скорость была 100 км / ч.Но это не значит, что спидометр в любой момент времени показывал 100 км / ч, потому что где-то машина была в пробке, где-то ускорялась, где-то обгоняла или даже останавливалась. В этом случае можно сказать, что мы искали не мгновенную скорость, а какую-то другую.
Именно для таких ситуаций в физике вводится понятие средней скорости (а также средней путевой скорости). Сегодня мы рассмотрим одно и другое и выясним, какой из них удобнее и практичнее в использовании.
Средняя скорость — это отношение абсолютного перемещения тела ко времени, в течение которого это перемещение выполнено :.
Представим себе пример: вы пошли в магазин за покупками и вернулись домой, модуль вашего движения равен нулю, но скорость не равна нулю, поэтому понятие средней скорости в данном случае неудобно.
Перейдем к более практичному понятию — средней путевой скорости. Средняя путевая скорость — это отношение общего пути, пройденного телом, к общему времени, которое прошло этот путь :.
Эта концепция удобна, потому что путь — это скалярная величина, она может только расти. Часто понятия средней скорости и средней путевой скорости путают, и мы также часто подразумеваем среднюю путевую скорость как среднюю скорость.
При нахождении средней скорости возникает много интересных задач, наиболее интересные из которых мы скоро рассмотрим.
Определение мгновенной скорости по средней скорости
Чтобы описать неравномерное движение, мы вводим понятие мгновенной скорости, называя ее скоростью в данной точке траектории в данный момент времени.Но такое определение будет неверным, потому что нам известны только два определения скорости: скорость равномерного прямолинейного движения и средняя скорость, которую мы используем в случае, когда мы хотим найти отношение полного пути к полному времени. Эти определения в данном случае не подходят. Как правильно найти мгновенную скорость? Здесь можно использовать понятие средней скорости.
Давайте посмотрим на рисунок, на котором показан произвольный участок криволинейной траектории с точкой A, на котором нам нужно найти мгновенную скорость (рис.4). Для этого рассмотрите область, содержащую точку A, и нарисуйте вектор смещения в этой области. Средняя скорость в этом разделе будет отношением смещения ко времени. Мы сократим этот участок и найдем аналогичным образом среднюю скорость уже для меньшего участка. Выполняя таким образом предельный переход от к и т. Д., Мы приходим к очень небольшому смещению за очень короткий период времени.
Рис. 3. Определение мгновенной скорости по средней скорости
Конечно, сначала средняя скорость будет сильно отличаться от мгновенной скорости в точке А, но чем ближе мы приближаемся к точке А, тем меньше меняются условия движения за это время, тем больше движение будет напоминать движение. равномерное движение, для которого мы знаем, что такое скорость.
Итак, когда временной интервал стремится к нулю, средняя скорость практически совпадает со скоростью в данной точке траектории, и мы переходим к мгновенной скорости. Мгновенная скорость в данной точке траектории — это отношение небольшого смещения, которое совершает тело, ко времени, в течение которого оно произошло.
Интересно, что в английском языке для понятия скорости есть два отдельных определения: скорость (модуль скорости), следовательно, спидометр; скорость, первая буква которой — v, отсюда и обозначение вектора скорости.
Мгновенная скорость имеет направление. Вспомните, когда мы говорили о мгновенной скорости, мы рисовали движения и т. Д. (Рис. 4). Что касается участка криволинейной траектории, они секущие. Если подойти ближе к точке А, они станут касательными (рис. 5). Мгновенная скорость на участке пути всегда направлена по касательной к пути.
Рис. 4. При уменьшении сечения секущие приближаются к касательной
Например, во время дождя, когда проезжающая машина забрызгивает нас каплями, они летят точно по касательной к окружности, а этот круг — колесо машины (рис.6).
Рис. 5. Падение
Другой пример: если камень привязан к жгуту и раскручен, то, когда камень оторвется, он также полетит по касательной к пути, по которому движется жгут.
Рассмотрим другие примеры при изучении равноускоренного движения.
Для характеристики неравномерности движения введена новая физическая величина — мгновенная скорость . Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.Устройство, показывающее мгновенную скорость, есть на любом транспортном средстве: в машине, поезде и т. Д. Это устройство, называемое спидометром (от английского speed — «скорость»).
Обращаем ваше внимание на то, что мгновенная скорость определяется как отношение смещения ко времени, в течение которого это смещение произошло. Если движение будет уменьшаться, стремиться к точке, то в этом случае можно говорить о мгновенной скорости :.
Обратите внимание, что и — координаты тела (рис.2). Если временной интервал очень мал, то изменение координат произойдет очень быстро, и изменение скорости на небольшом интервале будет незаметным. Скорость на этом интервале мы характеризуем мгновенной скоростью.
Рис. 2. Об определении мгновенной скорости
Таким образом, имеет смысл охарактеризовать неравномерное движение, изменяя скорость от точки к точке, и насколько быстро это происходит. Это изменение скорости характеризуется величиной, называемой ускорением.Указывается ускорение, это векторная величина.
Ускорение — это физическая величина, характеризующая скорость изменения скорости. Фактически, скорость изменения скорости — это ускорение. Поскольку это вектор, значение проекции ускорения может быть как отрицательным, так и положительным.
Ускорение измеряется в единицах и определяется по формуле :. Ускорение определяется как отношение изменения скорости ко времени, в течение которого это изменение произошло.
Важным моментом является разница векторов скорости.Обратите внимание, что мы обозначаем разницу (рис. 3).
Рис. 6. Вычитание векторов скорости
В заключение отметим, что проекция ускорения на ось, как и любая векторная величина, может иметь отрицательные и положительные значения в зависимости от направления. Важно отметить, что куда направлено изменение скорости, туда и будет направлено ускорение (рис. 7). Особое значение это приобретает при криволинейном движении, когда изменяется не только значение скорости, но и направление.
Рис. 7. Проекция вектора ускорения на ось
Список литературы
- Кикоин И.К., Кикоин А.К. Физика: учебник для 9 класса средней школы. — М .: Просвещение.
- Слободянюк А.И. Физика 10. Часть 1. Механика. Электричество.
- Физика. Механика. 10 класс / Под ред. Мякишева Г.Я. — М .: Дрофа.
- Филатов Е.Н. Физика 9. Часть 1. Кинематика. — ВШМ: Авангард.
Домашнее задание
- В чем разница между средней скоростью и мгновенной скоростью?
- Начальная скорость велосипедиста — 36 км / ч, затем он сбавил скорость до 18 км / ч. Он тормозил на 10 секунд. На какое ускорение двигался велосипедист и куда оно было направлено?
- Мальчик вышел из точки B и направился в точку C, пройдя 400 м, а оттуда вернулся в точку A. Какова средняя путевая скорость, если расстояние от точки A до точки B составляет 150 метров, и мальчик потратил на это 12 минут? все путешествие?
Движение в двух измерениях | Безграничная физика
Постоянная скорость
Объект, движущийся с постоянной скоростью, должен иметь постоянную скорость в постоянном направлении.
Цели обучения
Изучите термины для постоянной скорости и их применимость к ускорению
Основные выводы
Ключевые моменты
- Постоянная скорость означает, что движущийся объект движется по прямой с постоянной скоростью.
- Эта строка может быть представлена алгебраически как: [latex] \ text {x} = \ text {x} _0 + \ text {vt} [/ latex], где [latex] \ text {x} _0 [/ latex] представляет положение объекта в [latex] \ text {t} = 0 [/ latex], а наклон линии указывает скорость объекта.
- Скорость может быть положительной или отрицательной и указывается знаком нашего наклона. Это говорит нам, в каком направлении движется объект.
Ключевые термины
- постоянная скорость : Движение, которое не меняется ни по скорости, ни по направлению.
Движение с постоянной скоростью — одна из простейших форм движения. Этот тип движения возникает, когда объект движется (или скользит) в присутствии небольшого или незначительного трения, подобно тому, как хоккейная шайба скользит по льду.Чтобы иметь постоянную скорость, объект должен иметь постоянную скорость в постоянном направлении. Постоянное направление заставляет объект двигаться по прямой траектории.
Второй закон Ньютона ([latex] \ text {F} = \ text {ma} [/ latex]) предполагает, что когда к объекту прикладывается сила, объект испытывает ускорение. Если ускорение равно 0, объект не должен подвергаться воздействию внешних сил. Математически это можно представить следующим образом:
[латекс] \ text {a} = \ frac {\ text {dv}} {\ text {dt}} = 0 ~ \ Rightarrow ~ \ text {v} = \ text {const} [/ latex].
Если объект движется с постоянной скоростью, график зависимости расстояния от времени ([latex] \ text {x} [/ latex] vs. [latex] \ text {t} [/ latex]) показывает такое же изменение положение по каждому интервалу времени. Следовательно, движение объекта с постоянной скоростью представлено прямой линией: [latex] \ text {x} = \ text {x} _0 + \ text {vt} [/ latex], где [latex] \ text {x} _0 [/ latex] — это смещение, когда [latex] \ text {t} = 0 [/ latex] (или в точке пересечения оси Y).
Движение с постоянной скоростью : Когда объект движется с постоянной скоростью, он не меняет ни направления, ни скорости, и поэтому отображается как прямая линия на графике как расстояние во времени.
Вы также можете получить скорость объекта, если знаете его след во времени. Имея график, как в, мы можем вычислить скорость по изменению расстояния с течением времени. Графически скорость можно интерпретировать как наклон линии. Скорость может быть положительной или отрицательной и указывается знаком нашего наклона. Это говорит нам, в каком направлении движется объект.
Постоянное ускорение
Анализ двумерного движения снаряда выполняется путем разбиения его на два движения: по горизонтальной и вертикальной осям.
Цели обучения
Анализировать двумерное движение снаряда по горизонтальной и вертикальной осям
Основные выводы
Ключевые моменты
- Постоянное ускорение при движении в двух измерениях обычно следует за образцом снаряда.
- Движение снаряда — это движение объекта, брошенного или выброшенного в воздух, при условии только (вертикального) ускорения силы тяжести.
- Мы анализируем двумерное движение снаряда, разбивая его на два независимых одномерных движения по вертикальной и горизонтальной осям.
Ключевые термины
- кинематика : движение или кинематика или относящиеся к ней
Движение снаряда — это движение объекта, брошенного или выброшенного в воздух, подверженное только силе тяжести. Объект называется снарядом, а его путь называется его траекторией. Движение падающих предметов — это простой одномерный тип движения снаряда, при котором нет горизонтального движения. В двумерном движении снаряда, например футбольного мяча или другого брошенного объекта, есть как вертикальная, так и горизонтальная составляющие движения.
Движение снаряда : Бросок камня или удар ногой по мячу, как правило, создает образец движения снаряда, который имеет как вертикальную, так и горизонтальную составляющие.
Самый важный факт, о котором следует помнить, это то, что движения по перпендикулярным осям независимы и поэтому могут быть проанализированы отдельно. Ключ к анализу двумерного движения снаряда состоит в том, чтобы разбить его на два движения, одно по горизонтальной оси, а другое — по вертикали. Чтобы описать движение, мы должны иметь дело со скоростью и ускорением, а также со смещением.2} [/ latex] (мы предполагаем, что движение происходит на достаточно малых высотах у поверхности земли, чтобы ускорение свободного падения было постоянным). Поскольку ускорение свободного падения происходит вдоль вертикального направления только , [latex] \ text {a} _ \ text {x} = 0 [/ latex]. Таким образом, можно использовать кинематические уравнения, описывающие движение по направлениям [latex] \ text {x} [/ latex] и [latex] \ text {y} [/ latex] соответственно:
[латекс] \ text {x} = \ text {x} _0 + \ text {v} _ \ text {x} \ text {t} [/ latex]
[латекс] \ text {v} _ \ text {y} = \ text {v} _ {0 \ text {y}} + \ text {a} _ \ text {y} \ text {t} [/ latex ]
[латекс] \ text {y} = \ text {y} _0 + \ text {v} _ {0 \ text {y}} \ text {t} + \ frac {1} {2} \ text {a} _ \ text {y} \ text {t} ^ 2 [/ latex]
[латекс] \ text {v} _ \ text {y} ^ 2 = \ text {v} _ {0 \ text {y}} ^ 2 + 2 \ text {a} _ \ text {y} (\ text {y} — \ text {y} _0) [/ latex]
Мы анализируем двумерное движение снаряда, разбивая его на два независимых одномерных движения по вертикальной и горизонтальной осям.Горизонтальное движение простое, потому что [latex] \ text {a} _ \ text {x} = 0 [/ latex] и [latex] \ text {v} _ \ text {x} [/ latex], таким образом, является постоянным. Скорость в вертикальном направлении начинает уменьшаться по мере подъема объекта; в самой высокой точке вертикальная скорость равна нулю. Когда объект снова падает на Землю, вертикальная скорость снова увеличивается по величине, но указывает в направлении, противоположном начальной вертикальной скорости. Движения [latex] \ text {x} [/ latex] и [latex] \ text {y} [/ latex] можно рекомбинировать, чтобы получить общую скорость в любой заданной точке траектории.
разгон | Безграничная физика
Графическая интерпретация
Графическое представление ускорения во времени может быть получено с помощью графика положения объекта во времени.
Цели обучения
Определите разницу между построением графика скорости и графиком ускорения
Основные выводы
Ключевые моменты
- Ускорение — это скорость, с которой скорость тела изменяется со временем.
- Ускорение — это вектор, который указывает в том же направлении, что и изменение скорости, хотя он не всегда может быть в направлении движения.
- Поскольку ускорение — это скорость в м / с, деленная на время в с, мы можем построить график ускорения из графика скорости или положения объекта.
Ключевые термины
- ускорение : величина, на которую увеличивается скорость или скорость (и, следовательно, скалярная величина или векторная величина).
- скорость : векторная величина, которая обозначает скорость изменения положения относительно времени или скорость с направленным компонентом.
- позиция : место или местонахождение.
В физике ускорение — это скорость, с которой скорость тела изменяется со временем. Это векторная величина, имеющая как величину, так и направление. Ускорение сопровождается силой, как это описано во втором законе Ньютона; сила, как вектор, является произведением массы ускоряемого объекта и ускорения (вектора), или [latex] \ text {F} = \ text {ma} [/ latex]. 2} [/ latex]
Ускорение — это вектор, указывающий в том же направлении, что и изменение скорости, хотя он не всегда может быть в направлении движения.Например, когда объект замедляется или замедляется, его ускорение происходит в направлении, противоположном его движению.
Движение объекта можно изобразить графически, построив положение объекта во времени. Этот график расстояние-время можно использовать для создания другого графика, показывающего изменения скорости во времени. Поскольку ускорение — это скорость в [latex] \ displaystyle \ frac {\ text {m}} {\ text {s}} [/ latex], деленная на время в s, мы можем дополнительно вывести график ускорения из графика объекта скорость или положение.
— график положения объекта во времени. Этот график похож на движение автомобиля. Вначале положение объекта меняется медленно, по мере того, как он набирает скорость. В середине скорость постоянна, а положение изменяется с постоянной скоростью. По мере того, как он замедляется к концу, положение изменяется медленнее. Из этого графика мы можем получить график зависимости скорости от времени.
График положения и времени : Обратите внимание, что положение объекта изменяется медленно в начале путешествия, а затем все быстрее и быстрее, когда он набирает скорость.Затем его положение меняется медленнее по мере замедления в конце пути. В середине пути, когда скорость остается постоянной, положение меняется с постоянной скоростью.
Показывает скорость объекта во времени. Скорость объекта увеличивается вначале по мере того, как он ускоряется в начале, затем остается постоянной в середине, прежде чем он замедлится к концу. Обратите внимание, что этот график представляет собой наклон графика предыдущей позиции в зависимости от времени.Из этого графика мы можем получить график зависимости ускорения от времени.
Скорость в зависимости от времени : Скорость объекта увеличивается по мере его ускорения в начале пути. Он остается неизменным в середине пути (где нет ускорения). Оно уменьшается по мере замедления объекта в конце пути.
Для этого мы также построим наклон графика зависимости скорости от времени. На этом графике ускорение постоянно на трех различных стадиях движения.Как мы отмечали ранее, вначале объект увеличивает скорость и медленно меняет положение. График ускорения показывает, что в это время объект увеличивался с положительным постоянным ускорением. В середине, когда объект менял положение с постоянной скоростью, ускорение было 0. Это потому, что объект больше не меняет свою скорость и движется с постоянной скоростью. Ближе к концу движения объект замедляется. Это отображается как отрицательное значение на графике ускорения.Обратите внимание, что в этом примере объект все еще движется вперед (положительно), но поскольку он замедляется, ускорение отрицательное.
График зависимости ускорения от времени : У объекта положительное ускорение, поскольку он ускоряется в начале пути. У него нет ускорения, поскольку он движется с постоянной скоростью в середине пути. Его ускорение отрицательное, так как он замедляется в конце пути.
Графическое изображение движения : Краткое введение в диаграммы частиц и графики движения.
Движение с постоянным ускорением
Постоянное ускорение происходит, когда скорость объекта изменяется на равную величину за каждый равный период времени.
Цели обучения
Опишите, как постоянное ускорение влияет на движение объекта
Основные выводы
Ключевые моменты
- Предположение, что ускорение является постоянным, не серьезно ограничивает ситуации, которые мы можем изучить, и не ухудшает точность нашего лечения.
- Из-за алгебраических свойств постоянного ускорения существуют кинематические уравнения, которые можно использовать для вычисления смещения, скорости, ускорения и времени.
- Расчеты с постоянным ускорением могут выполняться как для одномерного, так и для двухмерного движения.
Ключевые термины
- ускорение : величина, на которую увеличивается скорость или скорость (и, следовательно, скалярная величина или векторная величина).
- кинематика : движение или кинематика или относящиеся к ней
Одномерное движение : когда вы роняете объект, он падает вертикально к центру Земли из-за постоянного ускорения силы тяжести.2} [/ латекс]
Предположение, что ускорение является постоянным, не серьезно ограничивает ситуации, которые мы можем изучить, и не ухудшает точность нашего лечения, потому что в большом количестве ситуаций ускорение является постоянным . Когда это не так, мы можем рассматривать его как отдельные части постоянного ускорения или использовать среднее ускорение за определенный период времени.
Движение падающих предметов — это простой одномерный тип движения снаряда, при котором нет горизонтального движения.Например, если вы вытащите камень и уроните его, камень упадет только вертикально вниз к земле. Если бы вы бросили камень вместо того, чтобы просто уронить его, он был бы более похож на снаряд, похожий на тот, за которым следует удар по мячу.
Движение снаряда — это движение объекта, брошенного в воздух и подверженное только ускорению свободного падения. Брошенный объект называется снарядом, а путь объекта называется его траекторией. В двумерном движении снаряда есть как вертикальная, так и горизонтальная составляющие.
Из-за алгебраических свойств постоянного ускорения существуют кинематические уравнения, которые связывают смещение, начальную скорость, конечную скорость, ускорение и время. Краткое изложение этих уравнений приведено ниже.
[латекс] \ text {x} = \ text {x} _0 + \ bar {\ text {v}} \ text {t} [/ latex]
[латекс] \ displaystyle \ bar {\ text {v}} = \ frac {\ text {v} _0 + \ text {v}} {2} [/ latex]
[латекс] \ text {v} = \ text {v} _0 + \ text {at} [/ latex]
[латекс] \ displaystyle \ text {x} = \ text {x} _0 + \ text {v} _0 \ text {t} + \ frac {1} {2} \ text {at} ^ 2 [/ latex]
[латекс] \ text {v} ^ 2 = \ text {v} _0 ^ 2 + 2 \ text {a} (\ text {x} — \ text {x} _0) [/ latex]
Постоянное ускорение с помощью векторов и алгебры : Это видео отвечает на вопрос «что такое ускорение? «.
Равномерно ускоренное движение в общей теории относительности: полнота нерастяжимых траекторий
Бим, Дж. К., Эрлих, П. Э., Изли, К. Л .: Глобальная лоренцианская геометрия. Марсель Деккер, Чистая и прикладная математика 202 , (1996)
Кандела А.М., Ромеро А., Санчес М .: Полнота траекторий релятивистских частиц в стационарных магнитных полях. Int. J. Geom. Методы Мод. Phys., 10 , 1360007 (1–8), (2013)
Кандела А.М., Ромеро А., Санчес М .: Полнота траекторий частиц, связанных с общим силовым полем. Arch. Рацион. Мех. Анальный. 208 , 255–274 (2013)
Артикул МАТЕМАТИКА MathSciNet Google Scholar
Чен Б.Ю .: Геометрия подмногообразий и ее приложения. Токийский научный университет, Токио (1981)
MATH Google Scholar
Кобаяси С., Номидзу К .: Основы дифференциальной геометрии, т. II. Уайли, Нью-Йорк (1969)
MATH Google Scholar
Фридман, Ю., Скар, Т .: Создание ковариантного уравнения релятивистской динамики: явные решения для движения под действием постоянной силы. Phys. Scr. 86 , 065008 (7pp) (2012)
Фридман Ю., Скарр Т .: Преобразования пространства-времени из равномерно ускоренной системы отсчета, Phys.Scr. 87 , 055004 (8 стр.) (2013)
Икава, Т .: О кривых и подмногообразиях в неопределенно-римановом многообразии. Цукуба. J. Math. 9 , 353–371 (1985)
MATH MathSciNet Google Scholar
Мардер, Л .: О равномерном ускорении в специальной и общей теории относительности. Математика. Proc. Camb. Фил. Soc. 53 , 194–198 (1957)
Артикул ОБЪЯВЛЕНИЯ МАТЕМАТИКА MathSciNet Google Scholar
Машхун, Б., Мюнч, У .: Измерение длины в ускоренных системах. Аня. Phys. 11 , 532–547 (2002)
Артикул МАТЕМАТИКА Google Scholar
Макмиллан Э.М.: «Парадокс часов» и космические путешествия. Наука 126 , 381–384 (1957)
Статья ОБЪЯВЛЕНИЯ Google Scholar
Миснер К.В., Торн К.С., Уиллер Дж. А .: Гравитация.W.H. Фриман и Ко, Лондон (1973)
Google Scholar
Номидзу К., Яно К .: Об окружностях и сферах в римановой геометрии. Математика. Аня. 210 , 163–170 (1974)
Артикул МАТЕМАТИКА MathSciNet Google Scholar
О’Нил, Б .: Полуриманова геометрия. Academic Press, Massachusetts (1983)
MATH Google Scholar
Ponge, R., Reckziegel, H .: Скрученные произведения в псевдоримановой геометрии. Геом. Dedicata 48 , 15–25 (1993)
Артикул МАТЕМАТИКА MathSciNet Google Scholar
Риндлер У. Гиперболическое движение в искривленном пространстве-времени. Phys. Ред. 119 , 2082–2089 (1960)
Артикул ОБЪЯВЛЕНИЯ МАТЕМАТИКА MathSciNet Google Scholar
Риндлер, В .: Парадокс сокращения длины. Являюсь. J. Phys. 24 , 365–366 (1961)
Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar
Ромеро, А., Санчес, М .: Полнота компактных лоренцевых многообразий, допускающих времяподобное конформное векторное поле Киллинга. Proc. Являюсь. Математика. Soc. 123 , 2831–2833 (1995)
Артикул МАТЕМАТИКА Google Scholar
Сакс, Р.К., Ву, Х .: Общая теория относительности для математиков. Град. Тексты по математике, т. 48. Springer, New York (1977)
MATH. Google Scholar
Санчес, М .: О геометрии обобщенного пространства-времени Робертсона – Уокера: геодезические. Gen. Relativ. Gravit. 30 , 914–932 (1998)
Google Scholar
Движение снаряда
Снаряд — это любой объект, который после запуска или падения продолжает движение по собственной инерции и на него влияет только сила тяжести, направленная вниз.
Движение снаряда , также известное как параболическое движение , является примером композиции движения в двух измерениях: ед. на горизонтальной оси и u.a.r.m. по вертикальной оси. В этом разделе мы изучим:
Начнем?
Концепция и представление
Движение снаряда , также известное как параболическое движение , состоит в том, что запускает тело со скоростью, которая образует угол α с горизонтом .На следующем рисунке вы можете увидеть представление о ситуации.
Параболическое движение
Это движение характерно для снарядов, движущихся объектов действует только сила тяжести. По оси x тело движется с постоянной скоростью v 0x (u.r.m.), а по оси y — с постоянным ускорением свободного падения (u.a.r.m.).
Характеризуется тем, что в наивысшей точке траектории скорость тела всегда v 0x (нет v y ).
Движение снаряда или параболическое движение является результатом композиции равномерного прямолинейного движения ( горизонтальный urm ) и равномерно ускоренного прямолинейного движения запуска вверх или вниз ( вертикальное uarm ).
Уравнения
Уравнения движения снаряда:
Поскольку, как мы сказали выше, скорость образует угол α с горизонталью, компоненты x и y определяются с использованием наиболее распространенных тригонометрических соотношений:
Разложение вектора скорости
Любой вектор, включая скорость, может быть разбит на 2 вектора, v x и v y , которые имеют те же направления, что и декартовы оси.Величину обоих векторов можно вычислить из угла, который вектор образует с горизонталью, с помощью выражений, показанных на рисунке.
Наконец, принимая во внимание вышесказанное, что y 0 = H , x 0 = 0 , и что a y = -g, , мы можем переписать формулы, как показано в следующем списке. Это окончательные выражения для расчета кинематических величин при движении снаряда или параболическом движении :
Экспериментируй и учись
Данные
г = 9.8 м / с 2 | |
Движение снаряда
Синий шар на рисунке представляет тело, подвешенное над землей. Вы можете перетащить его на нужную начальную высоту H и выбрать начальную скорость (v 0 ), с которой он будет под углом запущен под углом (α) к горизонтали . Серая линия представляет траекторию, по которой он будет двигаться в зависимости от выбранных вами значений.
Затем нажмите кнопку воспроизведения. Перетащите время и наблюдайте, как положение (x и y) и скорость (v x и v y ) рассчитываются для каждого момента его спуска на землю.
Убедитесь, что проекция по оси Y (зеленый) описывает вертикальное движение запуска, а по оси X (красный) — равномерное прямолинейное движение.
Уравнение положения и траектории движения снаряда
Уравнение положения тела помогает нам узнать, в какой точке оно находится в каждый момент времени.В случае движения тела в двух измерениях помните, что в целом оно описывается следующим образом:
Подставляя приведенные выше выражения положения по горизонтальной оси (u.r.m.) и по вертикальной оси (u.a.r.m.) в общее уравнение положения, мы можем получить выражение уравнения положения для параболического движения.
Уравнение положения движения снаряда определяется по формуле:
r → = (x0 + v0x⋅t) · i → + (H + v0y · t-12 · g · t2) · j →
С другой стороны, чтобы узнать, по какой траектории следует тело, то есть его уравнение траектории, мы можем объединить приведенные выше уравнения, чтобы исключить t , получив:
y = H + v0y · (xv0x) -12 · g · (xv0x) 2 = H + k1 · x-k2 · x2k1 = v0yvx; k2 = 12 · v0x2 · g
Как и ожидалось, это уравнение параболы.
С другой стороны, часто в упражнениях вам будут предлагаться некоторые из следующих значений.
Максимальная высота
Это значение достигается, когда скорость по оси y , v y , равна 0. Исходя из уравнения скорости по оси y и составляя v y = 0 , мы получить время t , которое требуется телу, чтобы добраться до этой высоты. С этого времени и из уравнений положения мы можем вычислить расстояние до начала координат по обеим осям, по оси x и оси y .
Время полета
Рассчитано для y = 0 , вертикальной составляющей позиции. То есть время полета — это время, необходимое для того, чтобы высота стала равной 0 (снаряд достигнет земли).
Диапазон
Это максимальное расстояние по горизонтали от начальной точки движения до точки падения тела на землю. Как только будет получено сильное время полета > , просто подставьте в уравнение положения горизонтальный компонент.
Угол траектории
Угол траектории в данной точке совпадает с углом, который образует вектор скорости с горизонтом в этой точке. Для его вычисления мы получаем компоненты v x и v y и из тригонометрического определения тангенса угла вычисляем α :
tanα = противоположная сторона смежная сторона = vyvx⇒α = tan-1vyvx
Пример
Минута 90 игры… Лопера приближается к мячу и наносит штрафной удар в 40 метрах от ворот, делает два шага назад и наносит удар. Мяч взлетает на высоте 20 ° … и ГООООООЛЛ !!! ГООООООООЛЛЛ !!!! Мяч проходит через верхний угол на высоте 1,70 м !!!. Сможете ли вы, послушав эту радиопередачу, ответить на следующие вопросы?
а) Сколько времени прошло от удара Лоперы до взятия ворот? и какова была начальная скорость мяча в момент удара?
б) Какова максимальная высота мяча?
c) Насколько быстро летел мяч, когда достиг цели?

 )
) Затем им предлагается самостоятельно
предложить и обосновать соостветствие примеров, графиков и схематических
рисунков равномерного, равноускоренного движения. Большинство учащихся чаще
всего хорошо справляются с подобными заданиями.
Затем им предлагается самостоятельно
предложить и обосновать соостветствие примеров, графиков и схематических
рисунков равномерного, равноускоренного движения. Большинство учащихся чаще
всего хорошо справляются с подобными заданиями.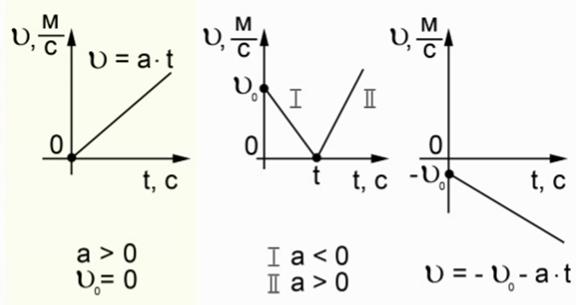
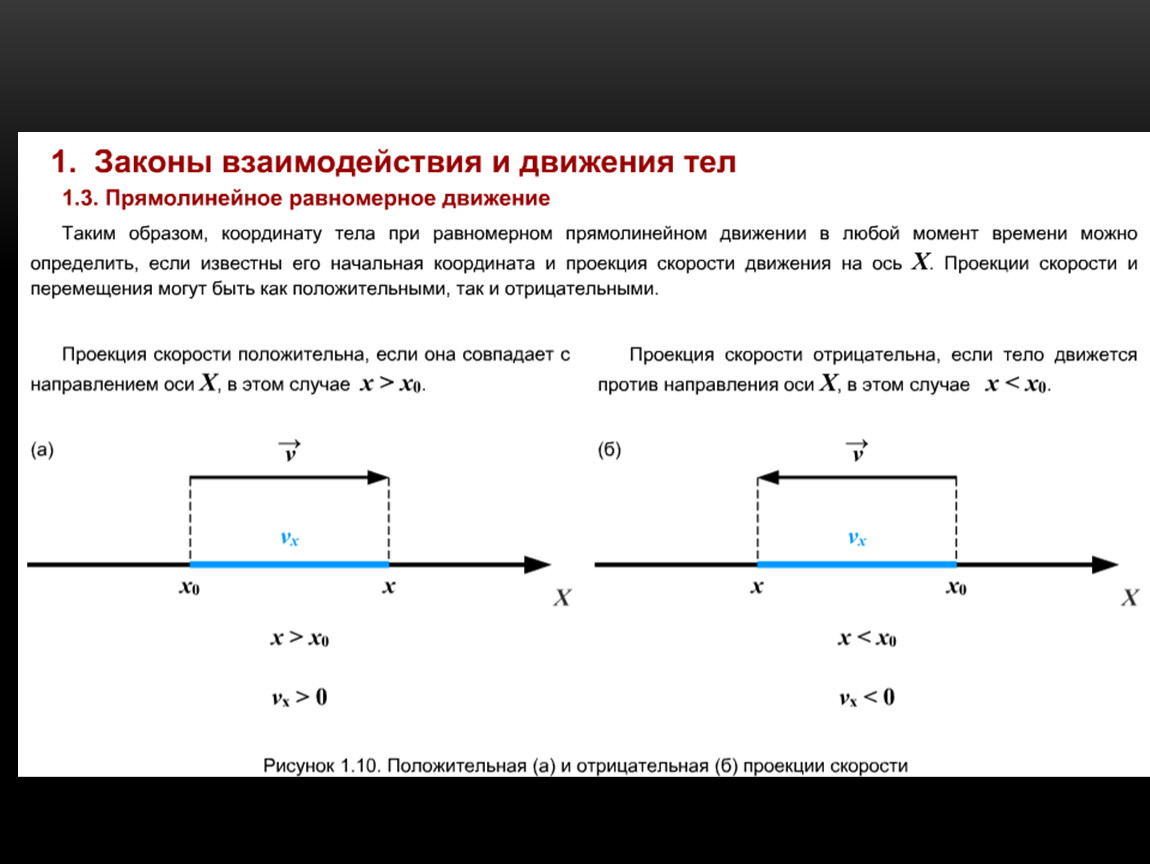 Обязательно учитывается значение ускорения(положительного и
отрицательного), и показывается равноускоренное и равнозамедленное движения.
Обязательно учитывается значение ускорения(положительного и
отрицательного), и показывается равноускоренное и равнозамедленное движения.
Leave A Comment