1. Запишите формулу, по которой можно рассчитать проекцию вектора мгновенной скорости прямолинейного равноускоренного движения, если известны: а) проекция вектора начальной скорости и проекция вектора ускорения; б) проекция вектора ускорения при том, что начальная скорость равна нулю.

2. Что представляет собой график проекции вектора скорости равноускоренного движения при начальной скорости: а) равной нулю; б) не равной нулю?
.jpg)
3. Чем сходны и чем отличаются друг от друга движения, графики которых представлены на рисунках 11 и 12?

Упражнения.
1. Хоккеист слегка ударил клюшкой по шайбе, придав ей скорость 2 м/с. Чему будет равна скорость шайбы через 4 с после удара, если в результате трения о лёд она движется с ускорением 0,25 м/с2?
.jpg)
2. Лыжник съезжает с горы из состояния покоя с ускорением, равным 0,2 м/с2. Через какой промежуток времени его скорость возрастёт до 2 м/с?
.jpg)
3. В одних и тех же координатных осях постройте графики проекции вектора скорости (на ось Х, сонаправленную с вектором начальной скорости) при прямолинейном равноускоренном движении для случаев: а) vox= 1м/с, ax= 0,5 м/с2; б) vox= 1м/с, ax= 1 м/с2; в) vox= 2 м/с, ax= 1 м/с2.
Масштаб во всех случаях одинаков: 1см- 1м/с; 1см — 1с.
.jpg)
4. В одних и тех же координатных осях постройте графики проекции вектора скорости (на ось Х, сонаправленную с вектором начальной скорости) при прямолинейном равноускоренном движении для случаев: а) v
Масштаб выберите сами.
.jpg)
5. На рисунке 13 представлены графики зависимости модуля вектора скорости от времени при прямолинейном движении двух тел. С каким по модулю ускорением движется тело I? тело II?
.jpg)
Физика 9 кл. Скорость прямолинейного равноускоренного движения. График скорости
- Подробности
- Просмотров: 82
1. Как выглядят формулы, по которой можно рассчитать проекцию вектора мгновенной скорости прямолинейного равноускоренного движения, если известны: а) проекция вектора начальной скорости и проекция вектора ускорения; б) проекция вектора ускорения при том, что начальная скорость равна нулю?
а) Формула проекции вектора мгновенной скорости прямолинейного равноускоренного движения, если известны проекция вектора начальной скорости и проекция вектора ускорения:
б) Формула проекции вектора мгновенной скорости прямолинейного равноускоренного движения, если известны проекция вектора ускорения при том, что начальная скорость равна нулю:
2. Что представляет собой график проекции вектора скорости равноускоренного движения при начальной скорости: а) равной нулю: б) не равной нулю?
В обоих случаях — это прямая линия.
а) Функция vx = v0x + axt — линейная функция с аргументом t, постоянным коэффициентом ах и свободным членом v0x аналогична функции y = kx + b.
Графиком этой функции должна быть прямая.
Построение графика проекции вектора скорости в зависимости от времени:
Сонаправим ось vx со скоростью движения.
Тогда проекции векторов скорости и ускорения будут положительны.
Для построения заданной прямой достаточно знать координаты (т. е. t и vx) двух любых её точек.
Задав два произвольных значения t, по формуле vx = axt можно определить соответствующие значения vx.
По координатам первой из найденных точек видно, что график зависимости скорости от времени пройдёт через начало координат.
б) Если начальная скорость движения vо не равна нулю, то начальная точка графика будет лежать на вертикальной оси и соответствовать значению vох.
Дальнейшее построение графика аналогично случаю а).
3. Чем сходны и чем отличаются друг от друга движения, графики которых представлены на рисунках?
а) Движение прямолинейное равноускоренное с начальной скоростью 10 м/с.
Тело разгоняется с ускорением 1,4 м/с2.
Вектор скорости и ускорения направлены в одну сторону.
Проекция вектора ускорения положительная.
ах = (14,2 м/с — 10 м/с) : 3 с = 4,2 м/с : 3 с = 1,4 м/с
Модуль вектора ускорения:
а = |ax| = 1,4 м/с2
б) Движение прямолинейное равноускоренное с начальной скоростью 20 м/с.
Тело тормозит с ускорением 2 м/с2.
Вектор скорости и ускорения направлены в противоположные стороны.
Проекция вектора ускорения отрицательная.
ах = (0 м/с — 20 м/с) : 10 с = — 2 м/с2
Модуль вектора ускорения:
а = |ax| = 2 м/с2
Следующая страница — смотреть
Назад в «Оглавление» — смотреть
Равноускоренное движение
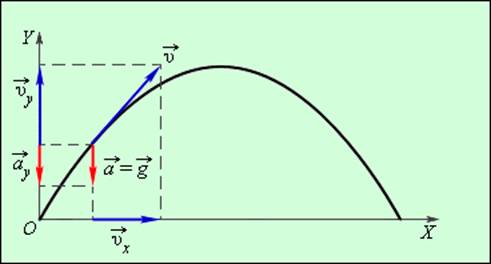
В общем случае равноускоренным движением называют такое движение, при котором вектор ускорения 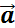 остается неизменным по модулю и направлению. Примером такого движения является движение камня, брошенного под некоторым углом к горизонту (без учета сопротивления воздуха). В любой точке траектории ускорение камня равно ускорению свободного падения
остается неизменным по модулю и направлению. Примером такого движения является движение камня, брошенного под некоторым углом к горизонту (без учета сопротивления воздуха). В любой точке траектории ускорение камня равно ускорению свободного падения 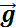 . Для кинематического описания движения камня систему координат удобно выбрать так, чтобы одна из осей, например ось OY, была направлена параллельно вектору ускорения. Тогда криволинейное движение камня можно представить как сумму двух движений – прямолинейного равноускоренного движения вдоль оси OY и равномерного прямолинейного движения в перпендикулярном направлении, т. е. вдоль оси OX (рис. 1.4.1).
. Для кинематического описания движения камня систему координат удобно выбрать так, чтобы одна из осей, например ось OY, была направлена параллельно вектору ускорения. Тогда криволинейное движение камня можно представить как сумму двух движений – прямолинейного равноускоренного движения вдоль оси OY и равномерного прямолинейного движения в перпендикулярном направлении, т. е. вдоль оси OX (рис. 1.4.1).
Таким образом, изучение равноускоренного движения сводится к изучению прямолинейного равноускоренного движения. В случае прямолинейного движения векторы скорости 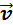 и ускорения
и ускорения 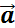 направлены вдоль прямой движения. Поэтому скорость υ и ускорение a в проекциях на направление движения можно рассматривать как алгебраические величины.
направлены вдоль прямой движения. Поэтому скорость υ и ускорение a в проекциях на направление движения можно рассматривать как алгебраические величины.
|
Рисунок 1.4.1. Проекции векторов скорости |
При равноускоренном прямолинейном движении скорость тела определяется формулой
 (*)
(*)
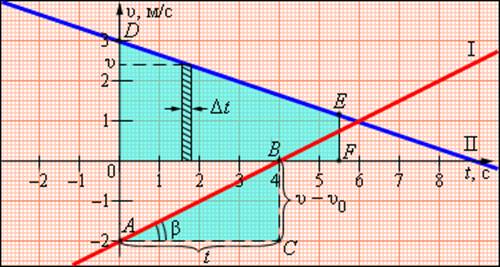
В этой формуле υ0 – скорость тела при t = 0 (начальная скорость), a = const – ускорение. На графике скорости υ (t) эта зависимость имеет вид прямой линии (рис. 1.4.2).
|
Рисунок 1.4.2. Графики скорости равноускоренного движения |
По наклону графика скорости может быть определено ускорение a тела. Соответствующие построения выполнены на рис. 1.4.2 для графика I. Ускорение численно равно отношению сторон треугольника ABC:
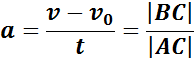
Чем больше угол β, который образует график скорости с осью времени, т. е. чем больше наклон графика (крутизна), тем больше ускорение тела.
Для графика I: υ0 = –2 м/с, a = 1/2 м/с2.
Для графика II: υ0 = 3 м/с, a = –1/3 м/с2
График скорости позволяет также определить проекцию перемещения s тела за некоторое время t. Выделим на оси времени некоторый малый промежуток времени Δt. Если этот промежуток времени достаточно мал, то и изменение скорости за этот промежуток невелико, т. е. движение в течение этого промежутка времени можно считать равномерным с некоторой средней скоростью, которая равна мгновенной скорости υ тела в середине промежутка Δt. Следовательно, перемещение Δs за время Δt будет равно Δs = υΔt. Это перемещение равно площади заштрихованной полоски (рис. 1.4.2). Разбив промежуток времени от 0 до некоторого момента t на малые промежутки Δt, получим, что перемещение s за заданное время t при равноускоренном прямолинейном движении равно площади трапеции ODEF. Соответствующие построения выполнены для графика II на рис. 1.4.2. Время t принято равным 5,5 с.
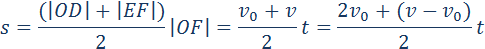
Так как υ – υ0 = at, окончательная формула для перемещения s тела при равномерно ускоренном движении на промежутке времени от 0 до t запишется в виде:
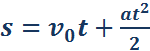 (**)
(**)
Для нахождения координаты y тела в любой момент времени t нужно к начальной координате y0 прибавить перемещение за время t:
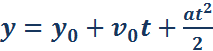 (***)
(***)
Это выражение называют законом равноускоренного движения.
При анализе равноускоренного движения иногда возникает задача определения перемещения тела по заданным значениям начальной υ0 и конечной υ скоростей и ускорения a. Эта задача может быть решена с помощью уравнений, написанных выше, путем исключения из них времени t. Результат записывается в виде
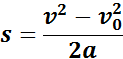
Из этой формулы можно получить выражение для определения конечной скорости υ тела, если известны начальная скорость υ0, ускорение a и перемещение s:
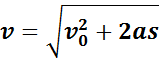
Если начальная скорость υ0 равна нулю, эти формулы принимают вид
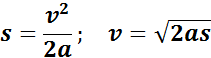
Следует еще раз обратить внимание на то, что входящие в формулы равноускоренного прямолинейного движения величины υ0, υ, s, a, y0 являются величинами алгебраическими. В зависимости от конкретного вида движения каждая из этих величин может принимать как положительные, так и отрицательные значения.
Список вопросов теста
Вопрос 1
Варианты ответов
- прямая, параллельная оси времени
- прямая, перпендикулярная оси времени
- прямая, перпендикулярная оси ускорения
Вопрос 2
График зависимости какой величины от времени представлен на рисунке?
Цели урока:
обучающая: рассмотреть и сформировать навыки построения графиков зависимости кинематических величин от времени при равномерном и равноускоренном движении; научить учащихся анализировать эти графики; путем решения задач закрепить полученные знания на практике;
развивающая: развитие умения наблюдать, анализировать конкретные ситуации; выделять определенные признаки;
воспитывающая: воспитание дисциплины и норм поведения, творческого отношения к изучаемому предмету; стимулировать активность учащихся.
Методы:
словесный — беседа;
наглядный — видеоурок, записи на доске;
контролирующий — тестирование или устный (письменный) опрос, решение задач).
Связи:
межпредметные: математика — линейная зависимость, график линейной функции; квадратичная функция и ее график;
внутрипредметные: равномерное и равноускоренное движение.
Ход урока:
1. Организационный этап.
Добрый день. Прежде чем мы приступим к уроку, хотелось бы, чтобы каждый из вас настроился на рабочий лад.
2. Актуализация знаний.
3. Объяснение нового материала.
Скачать этот видеоурок
Мы с вами знаем, что механическое движение — это изменение положения тела (или частей тела) в пространстве относительного других тел с течением времени.
В свою очередь механическое движение бывает двух видов — равномерное, при котором тело за любые равные промежутки времени совершает одинаковые перемещения, и неравномерным, при котором тело за любые равные промежутки времени совершает разные перемещения.
Давайте вспомним основные формулы, которые мы выучили для равномерного и неравномерного движения.
Если движение равномерное, то:
1. Скорость тела не меняется с течением времени;
2. Что бы найти скорость тела, необходимо путь, который прошло тело за некоторый промежуток времени, разделить на этот промежуток времени;
3. Уравнение перемещения имеет вид:
4. И — кинематическое уравнение равномерного движения.
Для равноускоренного:
1. Ускорение тела не изменяется с течением времени;
2. Ускорение есть величина, равная отношению изменения скорости тела, к промежутку времени, в течении которого это изменение произошло
3. Уравнение скорости для равноускоренного движения имеет вид:
4. — уравнение перемещения для равноускоренного движения;
5. — кинематическое уравнение равноускоренного движения.
Для большей наглядности движение можно о
Тестирование онлайн
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают
Графики равномерного движения
Зависимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость a(t) — прямая линия, которая лежит на оси времени.
Зависимость скорости от времени. Скорость со временем не изменяется, график v(t) — прямая линия, параллельная оси времени.
Правило определения пути по графику v(t): Численное значение перемещения (пути) — это площадь прямоугольника под графиком скорости.
Зависимость пути от времени. График s(t) — наклонная линия.
Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.
Графики равноускоренного движения
Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) — прямая линия, параллельная оси времени.
Зависимость скорости от времени. При равномерном движении путь изменяется, согласно линейной зависимости . В координатах . Графиком является наклонная линия.
Правило определения пути по графику v(t): Путь тела — это площадь треугольника (или трапеции) под графиком скорости.
Правило определения ускорения по графику v(t): Ускорение тела — это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.
Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости . В координатах зависимость имеет вид . Графиком является ветка параболы.
График движения при . График движения при
График движения при . График движения при
Сравнительная таблица графиков

1. Реальное механическое движение — это движение с изменяющейся скоростью. Движение, скорость которого стечением времени изменяется, называют неравномерным движением.
При неравномерном движении координату тола уже нельзя определить но формуле \( x=x_0+v_xt \), так как значение скорости движения не является постоянным. Поэтому для характеристики быстроты изменения положения тела с течением времени при неравномерном движении вводят величину, называемую средней скоростью.
Средней скоростью \( \vec{v}_{ср} \) неравномерного движения называют физическую величину, равную отношению перемещении \( \vec{s} \) тела ко времени \( t \), за которое оно произошло: \( \vec{v}_{ср}=\frac{s}{t} \).
Записанная формула определяет среднюю скорость как векторную величину. В практических целях этой формулой можно воспользоваться для определения модуля средней скорости лишь в том случае, когда тело движется вдоль прямой в одну сторону. Если же нужно определить среднюю скорость движения автомобиля от Москвы до Санкт-Петербурга и обратно, чтобы рассчитать расход бензина, то эту формулу применить нельзя, поскольку перемещение в этом случае равно нулю и средняя скорость тоже равна нулю. Поэтому на практике при определении средней скорости пользуются величиной, равной отношению пути \( l \) ко времени \( t \), за которое этот путь пройден: \( v_{ср}=\frac{l}{t} \). Эта скорость обычно называется средней путевой скоростью.
2. Важно, что, зная среднюю скорость неравномерного движения на каком-либо участке траектории, нельзя определить положение тела на этой траектории в любой момент времени. Например, если средняя скорость движения автомобиля за 2 часа 50 км/ч, то мы не можем сказать, где он находился через 0,5 часа от начала движения, через 1 час, 1,5 часа и т.п., поскольку он мог первые полчаса двигаться со скоростью 80 км/ч, затем какое-то время стоять, а какое-то время ехать в пробке со скоростью 20 км/ч.
3. Двигаясь по траектории, тело проходит последовательно все её точки. В каждой точке траектории оно находится в определённые моменты времени и имеет какую-то скорость.
Мгновенной скоростью называют скорость тела в данный момент времени в данной точке траектории.
Предположим, некоторое тело совершает неравномерное прямолинейное движение (рис. 17), его скорость в точке О можно определить следующим образом: выделим на траектории участок AB, внутри которого находится точка О. Перемещение тела на этом участке — \( \vec{s}_1 \) совершено за время \( t_1 \). Средняя скорость движения на этом участке – \( \vec{v}_{ср.1}=\frac{s_1}{t_1} \). Уменьшим перемещение тела. Пусть оно равно \( \vec{s}_2 \), а время движения — \( t_2 \). Тогда средняя скорость за это время: \( \vec{v}_{ср.2}=\frac{s_2}{t_2} \). Еще уменьшим перемещение, средняя скорость на этом участке: \( \vec{v}_{ср.3}=\frac{s_3}{t_3} \).
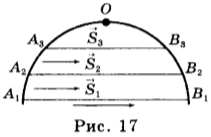

При дальнейшем уменьшении перемещения и соответственно времени движения тела они станут такими маленькими, что прибор, например спидометр, перестанет фиксировать изменение скорости, и движение за этот малый промежуток времени можно считать равномерным. Средняя скорость на этом участке и есть мгновенная скорость тела в т.О.
Таким образом, мгновенной скоростью называют векторную физическую величину, равную отношению малого перемещения (\( \Delta{\vec{s}} \)) к малому промежутку времени \( \Delta{t} \), за которое это перемещение произошло: \( \vec{v}=\frac{\Delta{s}}{\Delta{t}} \).
4. Одним из видов неравномерного движения является равноускоренное движение. Равноускоренным движением называют движение, при котором скорость тела за любые равные промежутки времени изменяется на одно и то же значение.
Слова «любые равные промежутки времени» означают, что какие бы равные промежутки времени (2 с, 1 с, доли секунды и т.п.) мы ни взяли, скорость всегда будет изменяться одинаково. При этом её модуль может как увеличиваться, так и уменьшаться.
5. Характеристикой равноускоренного движения, помимо скорости и перемещения, является ускорение.
Пусть в начальный момент времени \( t_0=0 \) скорость тела равна \( \vec{v}_0 \). В некоторый момент времени \( t \) она стала равной \( \vec{v} \). Изменение скорости за промежуток времени \( t-t_0=t \) равно \( \vec{v}-\vec{v}_0 \) (рис.18). Изменение скорости за единицу времени равно: \( \frac{\vec{v}-\vec{v}_0}{t} \). Эта величина и есть ускорение тела, она характеризует быстроту изменения скорости \( \vec{a}=\frac{\vec{v}-\vec{v}_0}{t} \).

Ускорение тела при равноускоренном движении — векторная физическая величина, равная отношению изменения скорости тела к промежутку времени, за который это изменение произошло.
Единица ускорения \( [a]=[v]/[t] \); \( [a] \) = 1 м/с/1 с = 1 м/с2. 1 м/с2 — это такое ускорение, при котором скорость тела изменяется за 1 с на 1 м/с.
Направление ускорения совпадает с направлением скорости движения, если модуль скорости увеличивается, ускорение направлено противоположно скорости движения, если модуль скорости уменьшается.
6. Преобразовав формулу ускорения, можно получить выражение для скорости тела при равноускоренном движении: \( \vec{v}=\vec{v}_0+\vec{a}t \). Если начальная скорость тела \( v_0=0 \), то \( \vec{v} = \vec{a}t \).
Чтобы определить значение скорости равноускоренного движения в любой момент времени, следует записать уравнение для проекции скорости на ось ОХ. Оно имеет вид: \( v_x = v_{0x} + a_xt \); если\( v_{0x}=0 \), то \( v_x = a_xt \).
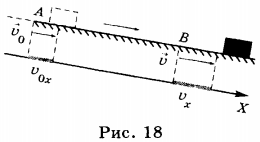
7. Как видно из формулы скорости равноускоренного движения, она линейно зависит от времени. Графиком зависимости модуля скорости от времени является прямая, составляющая некоторый угол с осью абсцисс (осью времени). На рисунке 19 приведены графики зависимости модуля скорости от времени.

График 1 соответствует движению без начальной скорости с ускорением, направленным так же, как и скорость; график 2 — движению с начальной скоростью \( v_{02} \) и с ускорением, направленным так же, как и скорость; график 3 — движению с начальной скоростью \( v_{03} \) и с ускорением, направленным в сторону, противоположную направлению скорости.
8. На рисунке приведены графики зависимости проекции скорости равноускоренного движения от времени (рис. 20).


График 1 соответствует движению без начальной скорости с ускорением, направленным вдоль положительного направления оси X; график 2 — движению с начальной скоростью \( v_{02} \), с ускорением и скоростью, направленными вдоль положительного направления оси X; график 3 — движению с начальной скоростью \( v_{03} \) : до момента времени \( t_0 \) направление скорости совпадает с положительным направлением оси X, ускорение направлено в противоположную сторону. В момент времени \( t_0 \) скорость равна нулю, а затем и скорость, и ускорение направлены в сторону, противоположную положительному направлению оси X.
9. На рисунке 21 приведены графики зависимости проекции ускорения равноускоренного движения от времени.

График 1 соответствует движению, проекция ускорения которого положительна, график 2 — движению, проекция ускорения которого отрицательна.
10. Формулу перемещения тела при равноускоренном движении можно получить, используя график зависимости проекции скорости этого движения от времени (рис. 22).
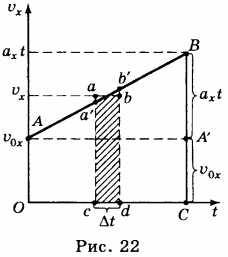

Выделим на графике малый участок \( ab \) и опустим перпендикуляры из точек \( a \) и \( b \) на ось абсцисс. Если промежуток времени \( \Delta{t} \), соответствующий участку \( cd \) на оси абсцисс мал, то можно считать, что скорость в течение этого промежутка времени не изменяется и тело движется равномерно. В этом случае фигура \( cabd \) мало отличается от прямоугольника и её площадь численно равна проекции перемещения тела за время, соответствующее отрезку \( cd \).
На такие полоски можно разбить всю фигуру ОАВС, и её площадь равна сумме площадей всех полосок. Следовательно, проекция перемещения тела за время \( t \) численно равна площади трапеции ОАВС. Площадь трапеции равна произведению полусуммы её оснований на высоту: \( S_x= \frac{1}{2}(OA+BC)OC \).
Как видно из рисунка, \( OA=v_{0x},BC=v_x,OC=t \). Отсюда следует, что проекция перемещения выражается формулой \( S_x= \frac{1}{2}(v_{0x}+v_x)t \). Так как \( v_x = v_{0x} + a_{xt} \), то \( S_x= \frac{1}{2}(2v_{0x} + a_xt)t \), отсюда \( S_x=v_{0x}t+ \frac{a_xt^2}{2} \). Если начальная скорость равна нулю, то формула имеет вид \( S_x=\frac{at^2}{2} \). Проекция перемещения равна разности координат \( S_x=x-x_0 \), поэтому: \( x-x_0=v_{0x}t+\frac{at^2}{2} \), или \( x=x_{0x}+v_{0x}t+\frac{at^2}{2} \).
Полученная формула позволяет определить положение (координату) тела в любой момент времени, если известны начальная скорость, начальная координата и ускорение.
11. На практике часто используют формулу или \( v^2_x-v^2_{0x}=2a_xs_x \), или \( v^2-v^2_{0}=2as \).
Если начальная скорость тела равна нулю, то: \( v^2_x=2a_xs_x \).
Полученная формула позволяет рассчитать тормозной путь транспортных средств, т.е. путь, который проезжает, например, автомобиль до полной остановки. При некотором ускорении движения, которое зависит от массы автомобиля и силы тяги двигателя, тормозной путь тем больше, чем больше начальная скорость автомобиля.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Hа рисунке приведены графики зависимости пути и скорости тела от времени. Какой график соответствует равноускоренному движению?


2. Автомобиль, начав двигаться из состояния покоя но прямолинейной дороге, за 10 с приобрел скорость 20 м/с. Чему равно ускорение автомобиля?
1) 200 м/с2
2) 20 м/с2
3) 2 м/с2
4) 0,5 м/с2
3. На рисунках представлены графики зависимости координаты от времени для четырёх тел, движущихся вдоль оси \( Оx \). У какого из тел в момент времени \( t_1 \) скорость движения равна нулю?
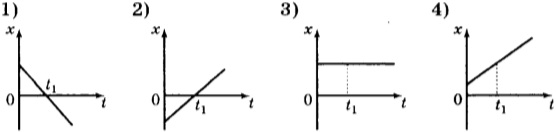

4. На рисунке представлен график зависимости проекции ускорения от времени для тела, движущегося прямолинейно вдоль оси \( Оx \).
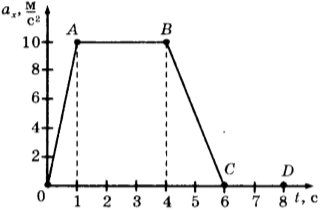

Равноускоренному движению соответствует участок
1) только ОА
2) только АВ
3) только ОА и ВС
4) только CD
5. При изучении равноускоренного движения измеряли путь, пройденный телом из состояния покоя за последовательные равные промежутки времени (за первую секунду, за вторую секунду и т.д.). Полученные данные приведены в таблице.


Чему равен путь, пройденный телом за третью секунду?
1) 4 м
2) 4,5 м
3) 5 м
4) 9 м
6. На рисунке представлены графики зависимости скорости движения от времени для четырёх тел. Тела движутся по прямой.
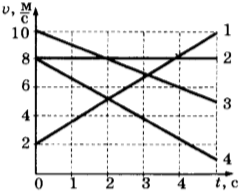

Для какого(-их) из тел — 1, 2, 3 или 4 — вектор ускорения направлен противоположно вектору скорости?
1) только 1
2) только 2
3) только 4
4) 3 и 4
7. Используя график зависимости скорости движения тела от времени, определите его ускорение.
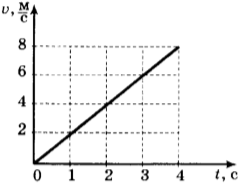

1) 1 м/с2
2) -1 м/с2
3) 2 м/с2
4) -2 м/с2
8. При изучении равноускоренного движения измеряли скорость тела в определённые моменты времени. Полученные данные, приведены в таблице. Чему равна скорость тела в момент времени 3 с?


1) 0 м/с
2) 2 м/с
3) 4 м/с
4) 14 м/с
9. На рисунке приведены графики зависимости скорости движения четырёх тел от времени. Ускорение какого из тел равно -1,5 м/с?


1) 1
2) 2
3) 3
4) 4
10. Используя график зависимости скорости движения тела от времени, определите скорость тела в конце 30-й секунды. Считать, что характер движения тела не изменился.
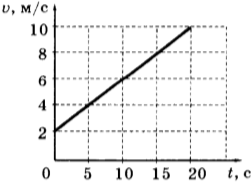

1) 14 м/с
2) 20 м/с
3) 62 м/с
4) 69,5 м/с
11. Два тела движутся по оси \( Оx \). На рисунке представлены графики зависимости проекции скорости движения тел 1 и 2 от времени.
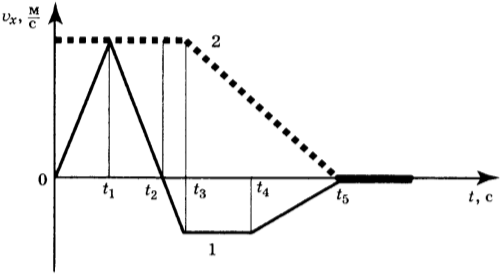

Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.
1) В промежутке времени \( t_3-t_5 \) тело 2 движется равноускоренно.
2) К моменту времени \( t_2 \) от начала движения тела прошли одинаковые пути.
3) В промежутке времени \( 0-t_3 \) тело 2 находится в покое.
4) В момент времени \( t_5 \) тело 1 останавливается.
5) В промежутке времени \( t_3-t_4 \) ускорение \( a_x \) тела 1 отрицательно.
12. На рисунке представлен график зависимости проекции скорости от времени для тела, движущегося вдоль оси Ох.
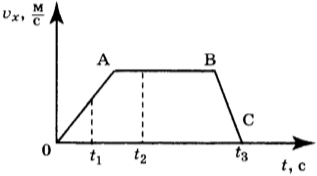

Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.
1) Участок ОА соответствует ускоренному движению тела.
2) Участок АВ соответствует состоянию покоя тела.
3) В момент времени \( t_1 \) тело имело максимальное по модулю ускорение.
4) Момент времени \( t_3 \) соответствует остановке тела.
5) В момент времени \( t_2 \) тело имело максимальное по модулю ускорение.
Часть 2
13. Зависимость координаты от времени для некоторого тела описывается уравнением \( x=12t-t^2 \). В какой момент времени скорость движения равна нулю?
Ответы

Скорость. Ускорение. Равноускоренное прямолинейное движение
3 (60%) 2 votes90000 How to Find Acceleration Using a Velocity Time Graph 90001 90002 What Is Acceleration 90003 90004 90005 90006 90007 Rate of change of velocity is called acceleration. It is a vector quantity 90008 90008 where u is the initial velocity of the object, v is its final velocity and t is the time taken. 90010 90007 Unit of acceleration = m / s 90012 2 90013 or ms 90012 -2 90013 90010 90007 If the velocity of a body decreases, then it will experience a negative acceleration which is called deceleration or retardation.90010 90007 Figure shows a car moving along a straight line. The speedometer of the car shows that it is moving with increasing velocity. The car is accelerating. 90008 90010 90007 We say that an object is undergoing a deceleration or retardation when it is slowing down. The rate of change of velocity of the object then has a negative value. Figure shows a car decelerating. The speedometer of the car shows that it is moving with decreasing velocity. 90010 90024 90004 90005 90027 90028 Types of acceleration 90029 90030 90004 90028 Uniform acceleration: 90029 If a body travels in a straight line and its velocity increases by equal amounts in equal intervals of time then it is said to be in state of uniform acceleration.90008 e.g. motion of a freely falling body. 90005 90004 90028 Non uniform acceleration: 90029 A body has a non-uniform acceleration if its velocity increases by unequal amounts in equal intervals of time. 90005 90004 90028 Instantaneous acceleration: 90029 The acceleration of a body at any instant is called its instantaneous acceleration. 90005 90004 90028 Acceleration is determined by the slope of time-velocity graph. 90029 90008 90005 90049 90007 If the time velocity graph is a straight line, acceleration 90028 remains constant 90029.90010 90007 If the slope of the straight line is positive, 90028 positive 90029 acceleration occurs. 90010 90007 If the slope of the straight line is negative, 90028 negative 90029 acceleration or retardation occurs. 90010 90062 90004 90028 Analysing Motion 90029 90005 90049 90007 Figure shows a set-up of apparatus to analyse motion in the laboratory. 90010 90007 (a) A ticker timer is an apparatus that gives a permanent record of motion for further analysis. When connected to an alternating current (a.c.) power supply (usually 12 V), it vibrates at a frequency of 50 Hz. 90008 (b) The ticker timer makes a series of dots at a rate of 50 dots per second on a piece of ticker tape as it is pulled through the timer by a trolley. Therefore, the time interval of a dot and the next dot which is also known as one 90028 tick 90029 is 1/50 or 0.02 s. 90008 (c) The distance between two dots is equal to the distance travelled by the trolley during the time interval between the dots. 90008 (d) The ticker tape can be analysed to determine the time, displacement, average velocity, acceleration and type of motion of an object.90010 90007 The ticker tape can be cut into strips of equal time (equal number of ticks) and pasted together to form a chart for analysing the motion of a trolley. 90010 90007 Figure shows three charts formed from strips of ticker tape, each consisting of ten ticks. 90010 90007 For motion with uniform acceleration or deceleration, its value can be determined by analysing the chart. Figure shows a chart formed from strips of ticker tape with ten ticks each. 90008 90008 90010 90062 90002 90028 Acceleration Using A Velocity Time Graph Example Problems With Solutions 90029 90003 90004 90028 Example 1.90029 A van accelerates uniformly from a velocity of 10 m s 90012 -1 90013 to 20 m s 90012 -1 90013 in 2.5 s. What is the acceleration of the van? 90008 90028 Solution: 90029 Initial velocity, u = 10 ms 90012 -1 90013 90008 Final velocity, v = 20 ms 90012 -1 90013 90008 Time taken, t = 2.5 s 90008 90005 90004 90028 Example 2. 90029 A car travelling at 24 ms 90012 -1 90013 slowed down when the traffic light turned red. After undergoing uniform deceleration for 4 s, it stopped in front of the traffic light.Calculate the acceleration of the car. 90028 90008 Solution: 90029 Initial velocity, u = 24ms 90012 -1 90013 90008 Final velocity, v = 0 ms 90012 -1 90013 90008 Time taken, t = 4 s 90008 90005 90004 90028 Example 3. 90029 Time-velocity graph of a body is shown in the figure. Find its acceleration in m / s 90012 2 90013. 90008 90028 Solution: 90029 As it is clear from the figure, 90008 At t = 0 s, v = 20 m / s 90008 At t = 4 s, v = 80 m / s 90008 90008 90008 90008 90005 90004 90028 Example 4.90029 Time-velocity graph of a particle is shown in figure. Find its instantaneous acceleration at following intervals 90008 90008 (i) at t = 3s 90008 (ii) at t = 6s 90008 (iii) at t = 9s 90008 90028 Solution: 90029 90028 (i) 90029 Instantaneous acceleration at t = 3s, is given by 90008 a = slope of line AB = zero 90008 90028 (ii) 90029 Instantaneous acceleration at t = 6 s, is given by a = slope of line BC 90008 90008 90028 (iii) 90029 Instantaneous acceleration at t = 9 s, is given by a = slope of line CD 90008 90005 90004 90028 Example 5.90029 Starting from rest, Deepak paddles his bicycle to attain a velocity of 6 m / s in 30 seconds then he applies brakes so that the velocity of the bicycle comes down to 4 m / s in the next 5 seconds. Calculate the acceleration of the bicycle in both the cases. 90008 90028 Solution: 90029 90028 (i) 90029 Initial velocity, u = 0, final velocity, 90008 v = 6 m / s, time, t = 30 s 90008 Using the equation v = u + at, we have 90008 90008 substituting the given values of u, v and t in the above equation, we get 90008 90008 which is positive acceleration.90008 90028 (ii) 90029 Initial velocity, u = 6 m / s, final velocity, 90008 v = 4 m / s, time, t = 5 s, then 90008 90008 which is retardation. 90008 90028 Note: 90029 The acceleration of the case (i) is positive and is negative in the case (ii). 90005 90004 90028 Example 6. 90029 A trolley pulled a ticker tape through a ticker timer while moving down an inclined plane. Figure 2.10 shows the ticker tape produced. 90008 90008 Determine the average velocity of the trolley. 90008 90028 Solution: 90029 90008 90005 90004 90028 Example 7.90029 Figure shows ticker tapes produced from the motion of a trolley. 90008 90008 Describe the type of motion of the trolley for each ticker tape. 90008 90028 Solution: 90029 90008 (a) The distances between two neighbouring dots are the same throughout the tape. Therefore, the trolley moved with uniform velocity. 90008 (b) The distances between two neighbouring dots are increasing. Therefore, the trolley moved with increasing velocity The trolley was accelerating. 90008 (c) The distances between two neighbouring dots are decreasing.Therefore, the trolley moved with decreasing velocity. The trolley was decelerating. 90008 90005 90004 90028 Example 8. 90029 Figure shows a chart representing the movement of a trolley with uniform acceleration. 90008 90008 Determine its acceleration. 90008 90028 Solution: 90029 90008 90005 90004 90028 Example 9. 90029 A trolley travelled down an inclined plane pulling along a ticker tape. Figure shows a chart formed by cutting and arranging the ticker tape into strips of ten ticks each.90008 90008 Determine the acceleration of the trolley. 90008 90028 Solution: 90029 90008 90005 90004 90028 Example 10. 90029 Figure shows a strip of ticker tape depicting the motion of a toy car with uniform acceleration. 90008 90008 Determine the acceleration of the toy car. 90008 90028 Solution: 90029 90008 90005.90000 Constant Acceleration Motion Graphs 90001 90002 The 90003 uniformly accelerated rectilinear motion (u.a.r.m.) 90004, also known as 90003 constant acceleration motion 90004, is a rectilinear motion that has a constant acceleration, which is different from zero. In this section we are going to study: 90007 90008 Constant acceleration motion graphs 90009 90010 Position-time (90011 x 90012 — 90011 t 90012) graph 90015 90002 x = x0 + v0t + 12at2 90007 90002 The 90003 graph position-time (90011 x 90012 — 90011 t 90012) 90004 of a constant acceleration motion, or uniformly accelerated rectilinear motion (u.a.r.m.), represents time on the horizontal axis (90011 t-axis 90012) and position on the vertical axis (90011 x-axis 90012). Observe as the position (normally the 90011 x-coordinate 90012) increases (or decreases) uniformly with time. This happens because as time passes, the magnitude of the velocity varies. We can distinguish two cases, when the velocity is positive or when it is negative: 90007 90002 90033 90007 90010 Velocity-time (90011 v 90012 — 90011 t 90012) graph 90015 90002 v = v0 + a⋅t 90007 90002 The 90011 90003 graph velocity-time (v-t) 90004 90012 of a constant acceleration motion, or uniformly accelerated rectilinear motion (u.a.r.m.), represents time on the horizontal axis (90011 t-axis 90012) and velocity on the vertical axis (90011 x-axis 90012). Observe as the velocity increases (or decreases) uniformly with the passage of time. This happens as the result of the acceleration. Again, we can distinguish two cases: 90007 90002 90054 90007 90002 We can get the velocity from the angle α. To do it just remember that 90011 in a right triangle the tangent of each of its angles is defined as the opposite side (cathetus) divided by the adjacent one 90012: 90007 90002 tanα = opposite sideadjacent side = ΔvΔt = v-v0t = a 90007 90002 The value of the slope is the magnitude of the acceleration.Therefore, the greater the slope of the straight line, the higher the acceleration of the body. 90007 90002 Notice that 90011 the area under the curve v between two instants of time, numerically matches the distance traveled 90012. Could you tell why? 90007 90002 90069 90007 90002 The area under the curve can be calculated as the area of the rectangleo 90011 S 90073 1 90074 90012 that would correspond to a uniform rectilinear motion (u.r.m.) to which we will add the area of the triangle 90011 S 90073 2 90074: 90012 90007 90002 Δx = x-x0 = S1 + S2 = ⏞1v0t + v-v0t2 = ⏞2v0t + 12at2 90007 90002 Where have we applied: 90007 90085 90086 S1 = v0tS2 = Srectangle2 = v-v0t2 90087 90086 v-v0 = at 90087 90090 90010 Acceleration time (90011 a 90012 — 90011 t 90012) graph 90015 90002 a = cst 90007 90002 The 90003 graph acceleration-time (90011 a 90012 — 90011 t 90012) 90004 of a constant acceleration motion, or uniformly accelerated rectilinear motion (u.a.r.m.), shows that the acceleration remains constant over time. It is the 90011 average acceleration 90012, which in the case of u.a.r.m. is the same as the 90011 instantaneous acceleration 90012. Again, we can distinguish two cases: 90007 90002 90112 90007 90002 Notice that 90011 the area under the curve, enclosed between two instants of time, numerically matches the experienced increase of velocity 90012. Do you know why? 90007 .
Leave A Comment