Числа a, b и c таковы, что a+b+c=8 и 1/(a+b)+1/(b+c)+1/(c+a)=0,7 Найдите значение выражения: a/(b+c)+b/(c+a)+c/(a+b) — вопрос №1892592 — Учеба и наука

Лучший ответ по мнению автора
24. 03.16
Лучший ответ по мнению автора

Eleonora Gabrielyan
Читать ответы

Михаил Александров
Читать ответы

Андрей Андреевич
Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его .

.. 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.

Решено

1) Число 111…111,состоящее из 999 единиц,разделили на 3. Сколько нулей будет у получившегося числа? 2) Маша сложила нить пополам, получившуюся

Решено

В математическом тесте школьникам предлагалось 30 задач. За каждый верный ответ начислялось 7 баллов, а за каждый неверный — снималось 3 балла. Костя

Решено

в зоопарке живут крокодилы и страусы. В сумме у них 40 голов и 94 ноги. Сколько там крокодилов и страусов?

диаметр шара равен высоте конуса,образующая…

Пользуйтесь нашим приложением

Основные приемы решения задач о делимости чисел

1. Основные приемы решения задач о делимости чисел

Л.М. Самойлов,
д.ф.-м.н., член жюри всероссийской
олимпиады школьников по математике
Разложение на простые множители
1. Петя хочет записать по кругу 2017 натуральных чисел так,
чтобы для каждых двух соседних чисел частное от деления
большего на меньшее было простым числом. Возможно ли
это?
2. Докажите, что по кругу можно расставить 8 чисел так,
чтобы выполнялось условие: любые стоящие рядом числа не
взаимно просты, а любые стоящие не рядом числа — взаимно
просты.
3. Приведите пример 3-х натуральных чисел, не делящихся
друг на друга, но чтобы при этом произведение любых двух
чисел делилось бы на третье число. То же самое, но числа
>100.
4. Докажите, что 100! не является квадратом целого числа.
Разложение на простые множители
5. Каково наименьшее натуральное число n такое, что n!
делится на 990?
6. К числу, написанному на доске, разрешается прибавлять одну
треть или одну седьмую его текущего значения. Докажите, что
число когда-нибудь перестанет быть целым. (Вопрос. Как
меняется разложение числа на множители при одной
операции?)
7. 2+x — квадрат
Взаимная простота.
5. Про семь натуральных чисел известно, что сумма любых шести из
них делится на 5. Докажите, что каждое из этих чисел делится на 5.
6. Найдите все пары простых чисел p и q, обладающие следующим
свойством: 7p + 1 делится на q, а 7q + 1 делится на p.
7. Перед боем с белогвардейцами у Василия Ивановича и Петьки
было поровну патронов. Василий Иванович израсходовал в бою в 8 раз
меньше патронов, чем Петька, а осталось у него в 9 раз больше
патронов, чем у Петьки. Докажите, что изначальное количество
патронов у Василия Ивановича делилось на 71.
8. При каких натуральных n число n² – 1 является степенью простого
числа?
9. Простые числа a, b, c таковы, что ab+a+b делится на c, bc+b+c
делится на a, ac+a+c делится на b. Докажите, что среди чисел a, b, c
есть одинаковые.
а ⁞ bc, тогда a ⁞ b
1. Найдите все простые p, q, r, для которых pq+qr+rp ⁞
pqr.
2. Найдите все пары натуральных чисел a и b, для
которых число a^{2018}+b делится на ab. 2.
Деление с остатком.
1. Число a кратно 3. Может ли остаток при делении a на 12
равняться 2?
2. Натуральное число A при делении на 1981 дало в остатке 35, при
делении на 1982 оно дало в остатке также 35. Каков остаток от
деления числа A на 14?
3. Маша поделила некоторое натуральное число N с остатком на
29 и получила, что остаток равен неполному частному. Потом она
поделила число N с остатком на 38 и снова остаток оказался равен
неполному частному. Напишите через пробел все варианты, чему
могло равняться число N.
4. Остаток от деления одного натурального числа на 11 равен
остатку от деления другого на 13, а остаток от деления первого
числа на 13 равен остатку от деления второго на 11. Докажите, что
остаток от деления суммы этих чисел на 143 не превосходит 20.

16. Спасибо за внимание!

Если a,b,c — различные действительные числа такие, что a+(1)/(b)=b+(1)/(c )=c+(1)/(a), то оцените abc.

ПУБЛИКАЦИЯ OSWAL-ОЛИМПИАДА 2019-20-3.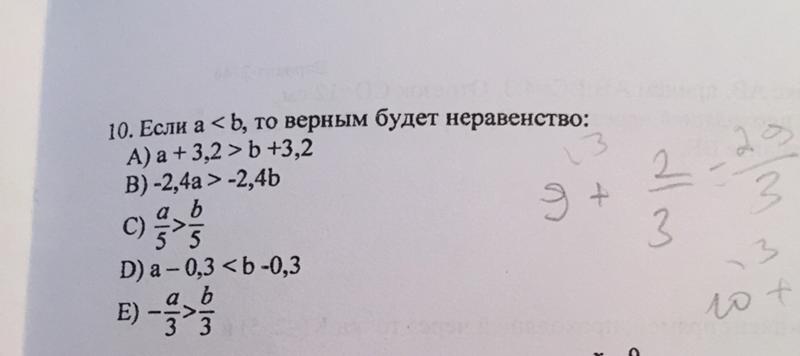 Пара линейных уравнений с двумя переменными.

2 видео.

Обновлено: 27-06-2022

लिखित उत्तर

Ответ

Правильный ответ D

9(3))/((c-a)(c-b))>=3

Если a, b, c положительные действительные числа, тогда √a−1b × √b-1 c × √c-1a равно: (а) 1 (б) абв (с) √abc (D) 1ABC

1408787

यदि a, b, c अशून्य संख्याऐं है तथा a+1b = 1 और b+1c = 1 है तो abc का म ज्ञात क क क।।

22544917

Пусть a, b, c ne три различных ненулевых действительных числа, удовлетворяющих системе уравнений 1a+1a−1+1a−2=1 , (b)+1b−1+1b−2=1 , 1с+1с-1+1с-2=1. Тогда abc=

39605107

Если a, b, c — различные положительные действительные числа такие, что a+1b=4,b+1c=1,c+1d=4 и d+1a=1, то

53794000

Если a, b, c — три различных положительных действительных числа, то наименьшее значение
(1+a+a2)(1+b+b2)(1+c+c2)abc равно

53794011

Если a+b+c=1 и a, b, c — положительные действительные числа такие, что
(1−a)(1−b)(1−c)≥λ abc, то λ=

53794033

если ∣∣ ∣∣111abcbccaab∣∣ ∣∣=∣∣ ∣ ∣∣111abca3b3c3∣∣ ∣ ∣, где a, b, c являются различными положительными реальными, тогда возможные значения ABC составляют/являются

6

55

यदि a b c तीन विभिन धन धनात्मक वास्तविक संखшить संख है तब (a+b+c) (1a+1b+1c) है है है (a+b+c)

618426143

если ∣∣ ∣∣111abcbccaab∣∣ ∣∣=∣∣ ∣ ∣∣111abca3b3c3∣∣ ∣ ∣∣ где a,b,c — различные положительные действительные числа, тогда возможные значения abc равны

642552461

Докажите, что a4+b4+c4>abc(a+b+c). [a,b,c — различные положительные действительные числа]..

644047226

Если a, b, c — различные положительные действительные числа такие, что a+1b=4,b+1c=1,c+1d=4 и d+1a=1, тогда

644740029

Если a, b, c — три различных положительных действительных числа, то наименьшее значение
(1+a+a2)(1+b+b2)(1+c+c2)abc равно

644740038

Если a+b+c=1 и a, b, c — положительные действительные числа такие, что

(1−a)(1−b)(1−c)≥λ abc, тогда λ=

644740055

Пусть a , b , c ne три различных ненулевых действительных числа, удовлетворяющих системе уравнений (1) /(а)+(1)/(а-1)+(1)/(а-2)=1 , (1)/(б)+(1)/(б-1)+(1)/( б-2)=1, (1)/(в)+(1)/(в-1)+(1)/(в-2)=1. Тогда abc=

645285677

РЕКЛАМА

  • OSWAL PUBLICATION-OLYMPIAD 2019-20-3. Пара линейных уравнений с двумя переменными

  • Если a,b,c — различные вещественные числа такие, что a+(1)/(b)=b+(1)/(c )=c+(1…

    03 :26

  • Число троек (x,y,z), такое, что любое из этих чисел равно. ..

    Перейти к содержимому

    Практические задачи во многих областях знаний, таких как биология, бизнес, химия, информатика, экономика, электроника, инженерия, физика и социальные науки, часто можно свести к решению системы линейных уравнений. Линейная алгебра возникла в результате попыток найти систематические методы решения этих систем, поэтому естественно начать эту книгу с изучения линейных уравнений.

    Если , , и действительные числа, график уравнения вида

       

    — прямая линия (если и оба не равны нулю), поэтому такое уравнение называется линейным уравнением в переменных и . Однако часто удобно записывать переменные как , особенно когда задействовано более двух переменных. Уравнение вида

       

    называется линейным уравнением в переменных . Здесь обозначают действительные числа (называемые коэффициенты , соответственно), а также является числом (называемым постоянным членом  уравнения). Конечная совокупность линейных уравнений с переменными называется системой линейных уравнений с этими переменными. Следовательно,

       

    — линейное уравнение; коэффициенты , , и , , и , а постоянный член . Обратите внимание, что каждая переменная в линейном уравнении встречается только в первой степени.

     

    Учитывая линейное уравнение, последовательность чисел называется решение уравнения если

       

    , то есть если уравнение удовлетворяется при произведенных заменах. Последовательность чисел называется решением системы уравнений, если она является решением каждого уравнения в системе.

     

    Система может вообще не иметь решения, или она может иметь единственное решение, или может иметь бесконечное множество решений. Например, система , не имеет решения, потому что сумма двух чисел не может быть одновременно равна 2 и 3. Система, не имеющая решений, называется 9.0123 противоречивый ; система, имеющая хотя бы одно решение, называется непротиворечивой .

     

     

     

    Покажите, что для произвольных значений и

       

    это решение системы

       

     

    Просто подставьте эти значения , , и в каждое уравнение.

       

    Поскольку выполняются оба уравнения, это решение для всех вариантов и .

     

    Величины и в этом примере называются параметрами , а набор решений, описанный таким образом, называется параметрической формой и называется общим решением системы. Оказывается, что решения каждой системы уравнений (если являются решениями) могут быть заданы в параметрической форме (т. е. переменные , , заданы через новые независимые переменные , и т. д. .).

     

    Когда участвуют только две переменные, решения систем линейных уравнений могут быть описаны геометрически, потому что график линейного уравнения представляет собой прямую линию, если и не равны нулю. Более того, точка с координатами и лежит на прямой тогда и только тогда, когда, т. е. когда , является решением уравнения. Следовательно, решения системы линейных уравнений соответствуют точкам, лежащим на всех рассматриваемых прямых.

    В частности, если система состоит всего из одного уравнения, решений должно быть бесконечно много, потому что точек на прямой бесконечно много. Если в системе два уравнения, есть три возможности для соответствующих прямых линий:

    • Линии пересекаются в одной точке. Тогда система имеет 90 123 единственного решения 90 124, соответствующего этой точке.
    • Линии параллельны (и различны) и поэтому не пересекаются. Тогда в системе нет решения .
    • Линии идентичны. Тогда система имеет 90 123 бесконечно много 90 124 решений — по одному для каждой точки на (общей) прямой.

     

    С тремя переменными можно показать, что график уравнения представляет собой плоскость, что опять-таки дает «картину» набора решений. Однако этот графический метод имеет свои ограничения: когда задействовано более трех переменных, физическое изображение графиков (называемых гиперплоскостями) невозможно. Необходимо обратиться к более «алгебраическому» методу решения.

    Перед описанием метода введем понятие, упрощающее связанные с ним вычисления. Рассмотрим следующую систему

       

    из трех уравнений с четырьмя переменными. Массив чисел

       

    , встречающаяся в системе, называется расширенной матрицей системы. Каждая строка матрицы состоит из коэффициентов переменных (по порядку) из соответствующего уравнения вместе с постоянным членом. Для наглядности константы разделены вертикальной чертой. Расширенная матрица — это просто другой способ описания системы уравнений. Массив коэффициентов переменных

       

    называется матрицей коэффициентов системы, а
    называется постоянной матрицей системы.

     

    Элементарные операции

    Алгебраический метод решения систем линейных уравнений описывается следующим образом. Две такие системы называются 90 123 эквивалентными 90 124, если они имеют одинаковый набор решений. Система решается путем написания ряда систем, одна за другой, каждая из которых эквивалентна предыдущей системе. Каждая из этих систем имеет тот же набор решений, что и исходная; цель состоит в том, чтобы в конечном итоге получить систему, которую легко решить. Каждая система в ряду получается из предыдущей системы путем простой манипуляции, выбранной таким образом, чтобы она не меняла множество решений.

    В качестве иллюстрации решим систему таким образом. На каждом этапе отображается соответствующая расширенная матрица. Исходная система

       

    Сначала дважды вычтите первое уравнение из второго. Получившаяся система равна

    .

       

    , что эквивалентно оригиналу. На данном этапе получаем умножением второго уравнения на . В результате получается эквивалентная система

    .

       

    Наконец, мы дважды вычтем второе уравнение из первого, чтобы получить еще одну эквивалентную систему.

       

    Теперь эту систему легко решить! И поскольку он эквивалентен исходной системе, он обеспечивает решение этой системы.

    Обратите внимание, что на каждом этапе над системой (и, следовательно, над расширенной матрицей) выполняется определенная операция для создания эквивалентной системы.

    Следующие операции, называемые элементарными операциями , можно регулярно выполнять над системами линейных уравнений для получения эквивалентных систем.

    1. Поменять местами два уравнения.
    2.  Умножить одно уравнение на ненулевое число.
    3. Добавить множитель одного уравнения к другому уравнению.

     

    Предположим, что над системой линейных уравнений выполняется последовательность элементарных операций. Тогда результирующая система имеет то же множество решений, что и исходная, поэтому эти две системы эквивалентны.

    Элементарные операции, выполняемые над системой уравнений, производят соответствующие манипуляции с строк расширенной матрицы. Таким образом, умножение строки матрицы на число означает умножение каждого элемента строки на . Добавление одной строки к другой строке означает добавление каждой записи этой строки к соответствующей записи другой строки. Вычитание двух строк выполняется аналогично. Обратите внимание, что мы рассматриваем две строки как равные, когда соответствующие записи одинаковы.

    В ручных расчетах (и в компьютерных программах) мы оперируем строками расширенной матрицы, а не уравнениями. По этой причине мы переформулируем эти элементарные операции для матриц.

    Следующие действия называются элементарными операциями со строками  на матрице.

    1. Поменяйте местами два ряда.
    2. Умножить одну строку на ненулевое число.
    3. Добавить кратное одной строки в другую строку.

     

    На иллюстрации выше серия таких операций привела к матрице вида

       

    , где звездочки обозначают произвольные числа. В случае трех уравнений с тремя переменными цель состоит в том, чтобы получить матрицу вида

       

    Это происходит не всегда, как мы увидим в следующем разделе. Вот пример, в котором это действительно происходит.

     

       

     

    Решение:
    Расширенная матрица исходной системы равна

    .

       

    Чтобы создать в верхнем левом углу, мы могли бы умножить строку с 1 на . Однако можно получить без введения дробей, вычитая 2-ю строку из 1-й. Результат равен

    .

       

    Верхний левый угол теперь используется для «очистки» первого столбца, то есть создания нулей в других позициях в этом столбце. Сначала вычтите строку 1 из строки 2, чтобы получить

    .

       

    Далее вычтите время строки 1 из строки 3. Результат равен

    .

       

    Это завершает работу над столбцом 1. Теперь мы используем во второй позиции второй строки, чтобы очистить второй столбец, вычитая строку 2 из строки 1, а затем добавляя строку 2 к строке 3. Для удобства обе операции строки делается за один шаг. Результат

       

    Обратите внимание, что последние две манипуляции не повлияли на  первый столбец (во второй строке там стоит ноль), поэтому наши предыдущие усилия не были подорваны. Наконец, мы очищаем третий столбец. Начните с умножения строки 3 на, чтобы получить

       

    Теперь вычтите время строки 3 из строки 1, а затем прибавьте время строки 3 к строке 2, чтобы получить

       

    Соответствующие уравнения , , и , которые дают (единственное) решение.

     

     

    Алгебраический метод, представленный в предыдущем разделе, можно резюмировать следующим образом: для заданной системы линейных уравнений используйте последовательность элементарных операций со строками, чтобы преобразовать расширенную матрицу в «хорошую» матрицу (это означает, что соответствующие уравнения легко решить). ). В примере 1.1.3 эта красивая матрица приняла вид

    .

       

    Следующие определения идентифицируют хорошие матрицы, возникающие в этом процессе.

     

     

    Говорят, что матрица имеет форму ступенчатых строк (и будет называться матрицей ступенчатых строк , если она удовлетворяет следующим трем условиям:

    1. Все нулевые строки (состоящие полностью из нулей) находятся внизу
    2. Первая ненулевая запись слева в каждой ненулевой строке — это , называемая ведущей для этой строки.
    3. Каждый ведущий находится справа от всех ведущих в строках над ним.

    Говорят, что матрица ступенчатых строк находится в сокращенной ступенчатой ​​форме (и будет называться сокращенной матрицей ступенчатых строк , если, кроме того, она удовлетворяет следующему условию:

    4.     Каждый ведущий единственная ненулевая запись в своем столбце

     

     

     

    Строко-ступенчатые матрицы имеют «лестничную» форму, как показано в следующем примере (звездочки обозначают произвольные числа).

       

    Ведущие s проходят через матрицу «вниз и вправо». Записи выше и справа от начального s произвольны, но все записи ниже и слева от них равны нулю. Следовательно, матрица в форме строки-эшелона находится в сокращенной форме, если, кроме того, все элементы непосредственно над каждым начальным элементом равны нулю. Обратите внимание, что матрицу в форме строки-эшелона можно с помощью еще нескольких операций со строками привести к сокращенной форме (используйте операции со строками для последовательного создания нулей над каждой ведущей единицей, начиная справа).

    Важность ступенчато-строчных матриц вытекает из следующей теоремы.

    Каждая матрица может быть приведена к (редуцированной) строчно-ступенчатой ​​форме с помощью последовательности элементарных операций со строками.

    На самом деле мы можем дать пошаговую процедуру для фактического нахождения матрицы строки-эшелона. Заметьте, что, хотя существует множество последовательностей операций со строками, которые приведут матрицу к эшелонированной форме, та, которую мы используем, является систематической и ее легко программировать на компьютере. Обратите внимание, что алгоритм имеет дело с матрицами вообще, возможно, со столбцами нулей.

    Шаг 1. Если матрица полностью состоит из нулей, остановитесь — она уже имеет строчно-ступенчатую форму.

    Шаг 2. В противном случае найдите первый столбец слева, содержащий ненулевую запись (назовем ее ), и переместите строку, содержащую эту запись, на верхнюю позицию.

    Шаг 3. Теперь умножьте новую верхнюю строку на, чтобы создать начальный .

    Шаг 4. Вычитая числа, кратные этой строке, из строк ниже нее, сделайте каждую запись ниже начального нуля. Это завершает первую строку, и все дальнейшие операции выполняются над оставшимися строками.

    Шаг 5. Повторите шаги 1–4 для матрицы, состоящей из оставшихся строк.

    Процесс останавливается, когда либо на шаге 5 не остается строк, либо оставшиеся строки полностью состоят из нулей.

     

    Обратите внимание, что алгоритм Гаусса является рекурсивным: после получения первого интерлиньяжа процедура повторяется для оставшихся строк матрицы. Это упрощает использование алгоритма на компьютере. Обратите внимание, что решение примера 1.1.3 не использовало алгоритм Гаусса, как написано, потому что первый интерлиньяж не был создан путем деления строки 1 на . Причина этого в том, что он избегает дробей. Однако общая схема ясна: создайте начальные s слева направо, используя каждый из них по очереди, чтобы создать нули под ним. Вот один пример.

       

    Решение:

    Соответствующая расширенная матрица равна

    .

       

    Создайте первую ведущую, поменяв местами строки 1 и 2

       

    Теперь вычтите время строки 1 из строки 2 и вычтите время строки 1 из строки 3. Результат

       

    Теперь вычтите строку 2 из строки 3, чтобы получить

    .

       

    Это означает, что следующая редуцированная система уравнений

       

    эквивалентен исходной системе. Другими словами, они имеют одинаковые решения. Но эта последняя система явно не имеет решения (последнее уравнение требует, чтобы , и удовлетворяли , а таких чисел не существует). Следовательно, исходная система не имеет решений.

    Для решения линейной системы расширенная матрица приводится к уменьшенной строчно-эшелонной форме, а переменные, соответствующие ведущим, называются ведущими переменными . Поскольку матрица имеет редуцированную форму, каждая ведущая переменная встречается ровно в одном уравнении, так что это уравнение можно решить, чтобы получить формулу для ведущей переменной через неведущие переменные. Неведущие переменные принято называть «свободными» переменными, а маркировать их новыми переменными, называемыми параметры . Каждый выбор этих параметров приводит к решению системы, и каждое решение возникает таким образом. Эта процедура работает в целом и получила название

    .

    Чтобы решить систему линейных уравнений, выполните следующие действия:

    1.  Перенести расширенную матрицу\индекс{расширенную матрицу}\индекс{матрицу!расширенную матрицу} к сокращенной матрице строк-эшелонов, используя элементарные операции над строками.
    2.  Если возникает строка, система несовместима.
    3.  В противном случае назначьте неведущие переменные (если они есть) в качестве параметров и используйте уравнения, соответствующие сокращенной матрице строк-ступеней, чтобы найти ведущие переменные с точки зрения параметров.

     

    Существует вариант этой процедуры, при котором расширенная матрица приводится только к строчно-эшелонной форме. Неведущие переменные назначаются как параметры, как и раньше. Затем последнее уравнение (соответствующее ступенчато-строковой форме) используется для решения последней ведущей переменной в терминах параметров. Затем эта последняя ведущая переменная подставляется во все предыдущие уравнения. Затем предпоследнее уравнение дает предпоследнюю ведущую переменную, которая также подставляется обратно. Процесс продолжает давать общее решение. Эта процедура называется обратная замена . Можно показать, что эта процедура численно более эффективна, и поэтому она важна при решении очень больших систем.

    Ранг

    Можно доказать, что редуцированная строчно-эшелонная форма матрицы однозначно определяется . То есть независимо от того, какая последовательность операций со строками используется для перехода к сокращенной матрице строк-ступеней, результатом всегда будет одна и та же матрица. Напротив, это неверно для матриц строк-эшелонов: разные серии операций со строками могут переносить одну и ту же матрицу в разные матрицы строк-эшелонов. Действительно, матрица может быть перенесена (с помощью одной операции со строками) в матрицу со строками , а затем с помощью другой операции со строками в (уменьшенную) матрицу со строками . Однако это равно верно, что количество ведущих единиц должно быть одинаковым в каждой из этих матриц строк-ступеней (это будет доказано позже). Следовательно, число зависит только от того, а не от того, каким образом доводится до рядно-ступенчатой ​​формы.

    ранг матрицы — это количество ведущих s в любой ступенчато-строковой матрице, к которым можно перейти с помощью операций со строками.

     

    Вычислить ранг .

    Решение:

    Приведение к рядно-эшелонному виду равно

       

    Поскольку в этой ступенчато-строковой матрице два ведущих s, ранг .

    Предположим, что ранг , где матрица со строками и столбцами. Затем, потому что начальные s лежат в разных строках и потому что начальные s лежат в разных столбцах. Кроме того, ранг имеет полезное приложение к уравнениям. Напомним, что система линейных уравнений называется совместной, если она имеет хотя бы одно решение.

    Предположим, что система уравнений в переменных непротиворечива и что ранг расширенной матрицы равен .

    1. В набор решений входят именно параметры.
    2. Если система имеет бесконечно много решений.
    3. Если система имеет единственное решение.

    Доказательство:

    Тот факт, что ранг расширенной матрицы равен, означает, что имеются ровно ведущие переменные и, следовательно, ровно неведущие переменные. Все эти неведущие переменные назначаются в качестве параметров в алгоритме Гаусса, поэтому множество решений включает именно параметры. Следовательно, если существует хотя бы один параметр, а значит, бесконечно много решений. Если , то параметров нет, а значит, единственное решение.

     

    Теорема 1.2.2 показывает, что для любой системы линейных уравнений существует ровно три возможности:

    1. Нет решения . Это происходит, когда ряд возникает в форме ряд-эшелон. Это тот случай, когда система несовместима.
    2.   Уникальное решение . Это происходит, когда каждая переменная является ведущей переменной.
    3.   Бесконечное множество решений . Это происходит, когда система непротиворечива и есть хотя бы одна неведущая переменная, поэтому задействован хотя бы один параметр.

     https://www.geogebra.org/m/cwQ9uYCZ
    Пожалуйста, ответьте на эти вопросы после того, как откроете веб-страницу:
    1.   Для данной линейной системы, что представляет каждый из них?

    2. Судя по графику, что можно сказать о решениях? Система имеет одно решение, не имеет решений или бесконечно много решений? Почему

    3. Измените постоянный член в каждом уравнении на 0, что изменилось на графике?

    4. Для следующей линейной системы:

       

    Сможете ли вы решить ее методом исключения Гаусса? Когда вы смотрите на график, что вы видите?

     

     

    Многие важные задачи включают линейных неравенства вместо линейных уравнений Например, условие для переменных и может принимать форму неравенства, а не равенства . Существует метод (называемый симплексным алгоритмом ) для нахождения решений системы таких неравенств, который максимизирует функцию вида где и — фиксированные константы.

     

     

    Система уравнений в переменных называется однородной , если все постоянные члены равны нулю, т. е. каждое уравнение системы имеет вид

       

    Очевидно, это решение для такой системы; это называется тривиальным решением . Любое решение, в котором хотя бы одна переменная имеет ненулевое значение, называется нетривиальным решением.
    Наша главная цель в этом разделе — дать полезное условие того, что однородная система имеет нетривиальные решения. Поучителен следующий пример.

    Покажите, что следующая однородная система имеет нетривиальные решения.

       

    Решение:

    Приведение расширенной матрицы к сокращенной форме строки-эшелона описано ниже.

       

    Ведущими переменными являются , , и , поэтому назначается в качестве параметра, скажем . Тогда общее решение , , , . Отсюда, взяв (скажем), получим нетривиальное решение: , , , .

    Существование нетривиального решения в примере 1.3.1 обеспечивается наличием параметра в решении. Это связано с тем, что есть неведущая переменная (в данном случае). Но здесь должно быть неведущей переменной, потому что есть четыре переменных и только три уравнения (и, следовательно, самое большее  три ведущие переменные). Это обсуждение обобщается до доказательства следующей фундаментальной теоремы.

     

    Если в однородной системе линейных уравнений переменных больше, чем уравнений, то она имеет нетривиальное решение (фактически бесконечное множество).

    Доказательство:

    Предположим, что есть уравнения в переменных, где , и пусть обозначают редуцированную строчно-эшелонную форму расширенной матрицы. Если есть ведущие переменные, есть неведущие переменные и, следовательно, параметры. Следовательно, достаточно показать, что . Но потому что есть ведущие 1 и строки, и по гипотезе. Итак, что дает.

    Обратите внимание, что утверждение, обратное теореме 1.3.1, неверно: если однородная система имеет нетривиальные решения, она не обязана иметь больше переменных, чем уравнений (система , имеет нетривиальные решения, но . )

    Теорема 1.3.1 очень полезна в приложениях. В следующем примере представлена ​​иллюстрация из геометрии.

    Мы называем график уравнения коническим , если числа , , и не все равны нулю. Докажите, что через любые пять точек плоскости, не лежащих на одной прямой, проходит хотя бы одна коника.

    Решение:

    Пусть координаты пяти точек будут , , , и . График проходов if

       

    Это дает пять уравнений, по одному для каждого , линейных относительно шести переменных , , , , и . Следовательно, по теореме 1.1.3 существует нетривиальное решение. Если , то все пять точек лежат на прямой с уравнением , вопреки предположению. Следовательно, один из отличен от нуля.

     

    Линейные комбинации и основные решения

    Что касается строк, два столбца считаются равными , если они имеют одинаковое количество записей и соответствующие записи одинаковы. Пусть и будут столбцами с одинаковым количеством записей. Что касается элементарных операций со строками, то их сумма получается путем сложения соответствующих записей и, если это число, скалярное произведение определяется путем умножения каждой записи на . Точнее:

       

    Сумма скалярных множителей нескольких столбцов называется линейной комбинацией  этих столбцов. Например, является линейной комбинацией и для любого выбора чисел и .

    Если и
    тогда .

     

    Пусть
    и . Если
    и ,
    определите, являются ли и линейными комбинациями , и .

     

    Решение:

    Для , мы должны определить, существуют ли числа , , и такие, что , т. е.

       

    Приравнивание соответствующих записей дает систему линейных уравнений , , и для , , и . Путем исключения Гаусса решение , , и где параметр. Взяв , мы видим, что это линейная комбинация , и .

    Обратившись к , снова ищем , , и такое, что ; то есть

       

    приводит к уравнениям , , и для действительных чисел , и . Но на этот раз нет решения, как может убедиться читатель, так же как и не  линейная комбинация , , и .

    Наш интерес к линейным комбинациям обусловлен тем, что они обеспечивают один из лучших способов описания общего решения однородной системы линейных уравнений. При решении
    такой системы с переменными запишите переменные в виде матрицы-столбца: . Тривиальное решение обозначается . В качестве иллюстрации общее решение в
    примере 1.3.1 имеет вид , , и , где параметр, и теперь мы выражаем это как
    говоря, что общее решение , где произвольно.

    Пусть теперь и — два решения однородной системы с переменными. Тогда любая линейная комбинация этих решений снова оказывается решением системы. В общем:

       

    В самом деле, предположим, что типичным уравнением в системе является , и предположим, что

    , являются решениями. Потом и
    .
    Следовательно, это тоже решение, потому что

       

    Аналогичное рассуждение показывает, что утверждение 1. 1 верно для линейных комбинаций более чем двух решений.

     

    Замечательно то, что каждое решение однородной системы является линейной комбинацией некоторых частных решений и, на самом деле, эти решения легко вычисляются с помощью алгоритма Гаусса. Вот пример.

    Решить однородную систему с матрицей коэффициентов

       

    Решение:

    Приведение расширенной матрицы к уменьшенной форме равно

       

    , поэтому решения равны , , и методом исключения Гаусса. Следовательно, мы можем записать общее решение в матричной форме

       

    Здесь и – частные решения, определяемые алгоритмом Гаусса.

    Решения и в примере 1.3.5 обозначаются следующим образом:

    Алгоритм Гаусса систематически производит решения любой однородной линейной системы, называемые базовыми решениями , по одному для каждого параметра.

    Кроме того, алгоритм дает обычный способ выразить каждое решение в виде линейной комбинации основных решений, как в примере 1. 3.5, где общее решение принимает вид

       

    Следовательно, вводя новый параметр, мы можем умножить исходное базовое решение на 5 и, таким образом, исключить дроби.

    По этой причине:

    Любое ненулевое скалярное кратное базового решения по-прежнему будет называться базовым решением.

     

    Таким же образом алгоритм Гаусса дает базовые решения для каждой однородной системы, по одному для каждого параметра (основных решений нет , если система имеет только тривиальное решение). При этом каждое решение задается алгоритмом как линейная комбинация
    этих основных растворов (как в примере 1.3.5). Если имеет ранг , теорема 1.2.2 показывает, что есть точно параметры, а значит, и основные решения. Это доказывает:

    Позвольте быть матрицей ранга , и рассмотреть однородную систему в переменных с как матрица коэффициентов. Тогда:

    1. Система имеет ровно базовые решения, по одному на каждый параметр.