2

Угловой коэффициент прямой

  Угловой коэффициент прямой. В этой статье мы с вами рассмотрим задачи связанные с координатной плоскостью включённые в ЕГЭ по математике. Это задания на:

— определение углового коэффициента прямой, когда известны две точки через которые она проходит;
— определение абсциссы или ординаты точки пересечения двух прямых на плоскости.

Что такое абсцисса и ордината точки было описано в прошлой статье данной рубрики. В ней мы уже рассмотрели несколько задач связанных с координатной плоскостью. Что необходимо понимать для рассматриваемого типа задач? Немного теории.

Уравнение прямой на координатной плоскости имеет вид:

где k – это и есть угловой коэффициент прямой.

Следующий момент! Угловой коэффициент прямой равен тангенсу угла наклона прямой. Это угол между данной прямой и осью ох.

 

Он лежит в пределах от 0 до 180 градусов.

То есть, если мы приведём уравнение прямой к виду y = kx + b, то далее всегда сможем определить коэффициент k (угловой коэффициент).

Так же, если мы исходя из условия сможем определить тангенс угла наклона прямой, то тем самым найдём её угловой коэффициент.

Следующий теоретический момент! Уравнение прямой походящей через две данные точки. Формула имеет вид:

Подробнее об этой формуле рассказано в этой статье!

Рассмотрим задачи (аналогичные задачам из открытого банка заданий):

Найдите угловой коэффициент прямой, проходящей через точки с координатами (–6;0) и (0;6).

В данной задаче самый рациональный путь решения это найти тангенс угла между осью ох и данной прямой. Известно, что он равен угловому коэффициенту. Рассмотрим прямоугольный треугольник образованный прямой и осями ох и оу:

Тангенсом угла в прямоугольном треугольнике является отношение противолежащего катета к прилежащему:

*Оба катета равны шести (это их длины).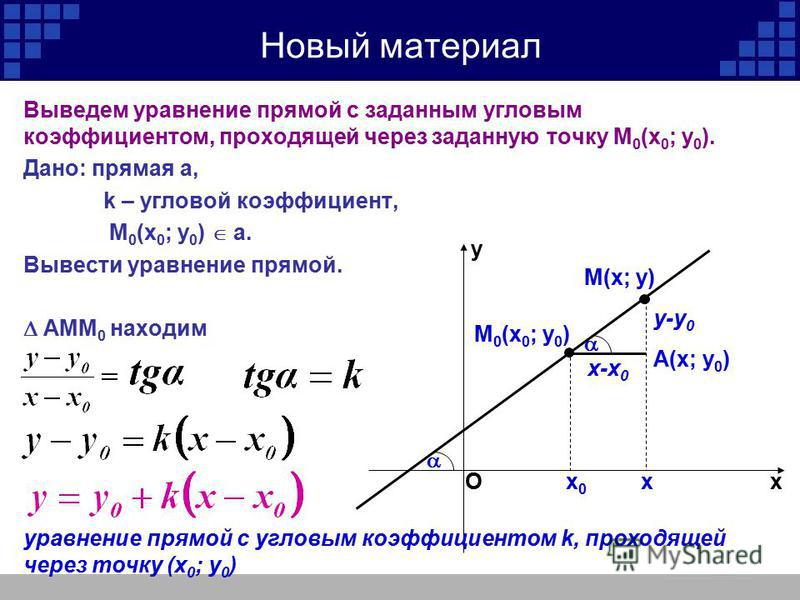

Конечно, данную задачу можно решить используя формулу нахождения уравнения прямой проходящей через две данные точки. Но это будет более длительный путь решения.

Ответ: 1

Найдите угловой коэффициент прямой, проходящей через точки с координатами (5;0) и (0;5).

Формула уравнения прямой походящей через две данные точки имеет вид:

Наши точки  имеют координаты (5;0) и (0;5). Значит,

Приведём формулу к виду  y = kx + b   

Получили, что угловой коэффициент  k = – 1.

Ответ: –1

Прямая a проходит через точки с координатами (0;6) и (8;0). Прямая b проходит через точку с координатами (0;10) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью оx.

В данной задаче можно найти уравнение прямой a, определить угловой коэффициент для неё. У прямой b угловой коэффициент будет такой же, так как они параллельны.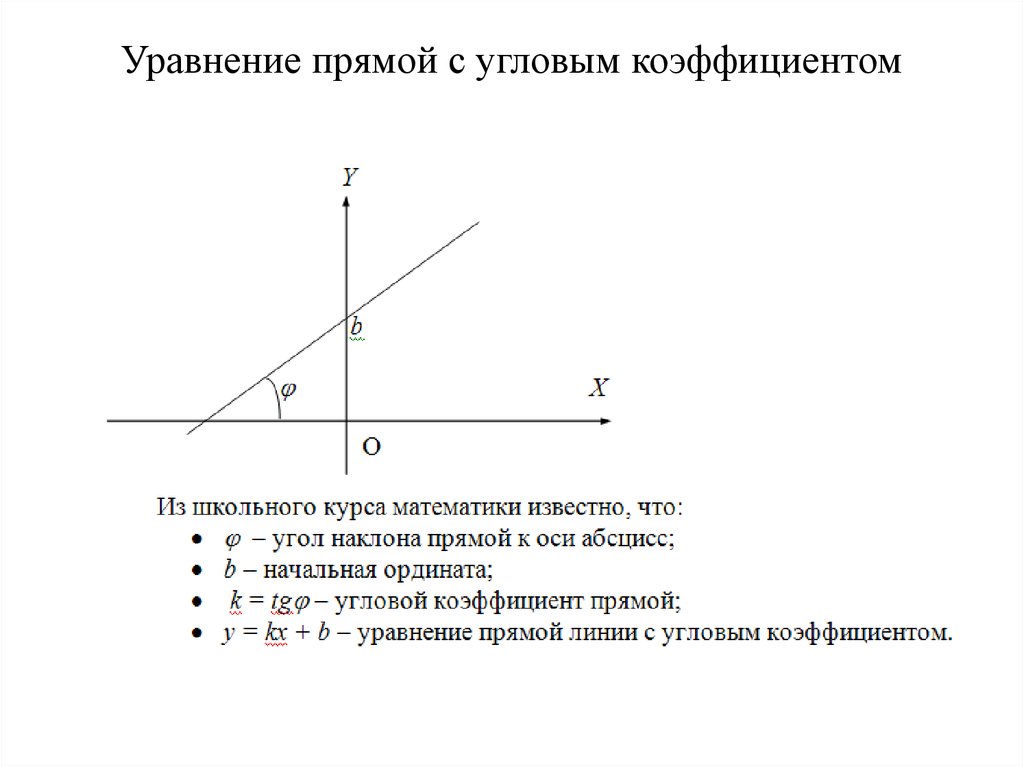 Далее можно найти уравнение прямой b. А затем, подставив в него значение y = 0, найти абсциссу. НО!

В данном случае, проще использовать свойство подобия треугольников.

Прямоугольные треугольники, образованные данными (параллельными) прямыми о осями координат подобны, а это значит, что отношения их соответствующих сторон равны.

Искомая абсцисса равна 40/3.

Ответ: 40/3

Прямая a проходит через точки с координатами (0;8) и (–12;0). Прямая b проходит через точку с координатами (0; –12) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью оx.

Для данной задачи самый рациональный путь решения — это применение свойства подобия треугольников. Но мы решим её другим путём.

Нам известны точки, через которые проходит прямая а. Можем составить уравнение прямой. Формула уравнения прямой походящей через две данные точки имеет вид:

По условию точки  имеют координаты (0;8) и (–12;0).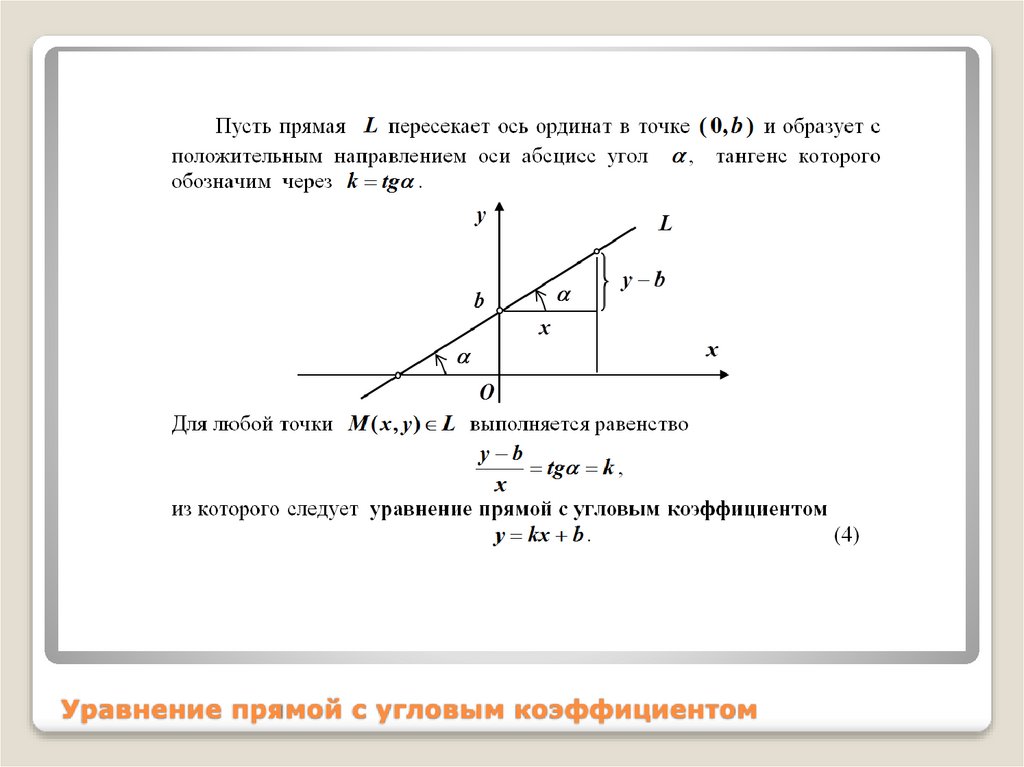 Значит,

Приведём к виду   y = kx + b:

Получили, что угловой  k = 2/3.

*Угловой коэффициент можно было найти через тангенс угла в прямоугольном треугольнике с катетами 8 и 12.

Известно, у параллельных прямых угловые коэффициенты равны. Значит уравнение прямой проходящей через точку (0;-12) имеет вид:

Найти величину b  мы можем подставив абсциссу и ординату в уравнение:

Таким образом, прямая имеет вид:

Теперь чтобы найти искомую абсциссу точки пересечения прямой с осью ох, необходимо подставить у = 0:

Ответ: 18

Найдите ординату точки пересечения оси оy и прямой, проходящей через точку В(10;12) и параллельной прямой, проходящей через начало координат и точку А(10;24).

Найдём уравнение прямой проходящей через точки с координатами (0;0) и (10;24).

Формула уравнения прямой походящей через две данные точки имеет вид:

Наши точки  имеют координаты (0;0) и (10;24). Значит,

Приведём к виду   y = kx + b   

Угловые коэффициенты параллельных прямых равны. Значит, уравнение прямой, проходящей через точку В(10;12) имеет вид:

Значение b  найдём подставив в это уравнение координаты точки В(10;12):

Получили уравнение прямой:

Чтобы найти ординату точки пересечения этой прямой с осью оу  нужно подставить в найденное уравнение х = 0:

*Самый простой способ решения. При помощи параллельного  переноса сдвигаем данную прямую вниз вдоль оси оу до точки (10;12). Сдвиг происходит на 12 единиц, то есть точка А(10;24) «перешла» в точку В(10;12), а точка О(0;0) «перешла» в точку (0;–12). Значит, полученная прямая будет пересекать ось оу в точке (0;–12).

Искомая ордината равна  –12.

Ответ: –12

Найдите ординату точки пересечения прямой, заданной уравнением 

3х + 2у = 6, с осью Oy.

Координата точки пересечения заданной прямой с осью оу имеет вид (0;у). Подставим в уравнение абсциссу х = 0, и найдём ординату:

Ордината  точки пересечения прямой с осью оу равна 3.

*Решается система:

Ответ: 3

Найдите ординату точки пересечения прямых, заданных уравнениями 

3х + 2у = 6   и  у = – х.

Когда заданны две прямые, и стоит вопрос о нахождении координат точки пересечения этих прямых, решается система из данных уравнений:

В первом уравнении подставляем    – х   вместо у:

Ордината равна минус шести.

Ответ: – 6

Найдите угловой коэффициент прямой, проходящей через точки с координатами (–2;0) и (0;2).

Посмотреть решение

Найдите угловой коэффициент прямой, проходящей через точки с координатами (2;0) и (0;2).

Посмотреть решение

Прямая a проходит через точки с координатами (0;4) и (6;0).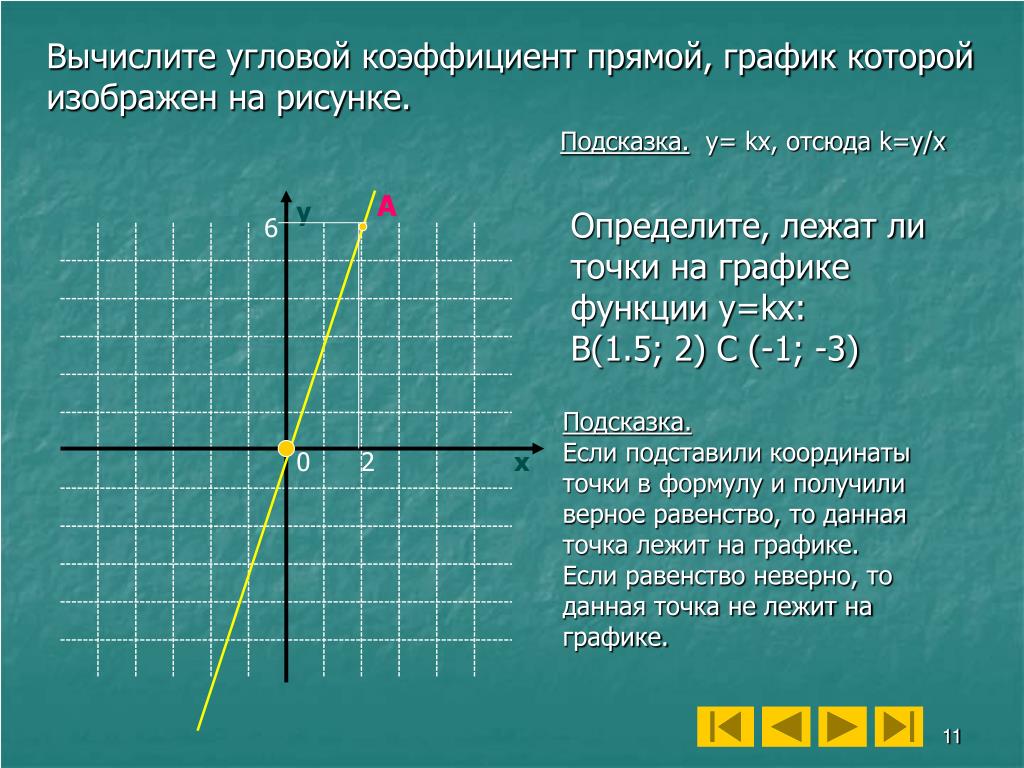 Прямая b проходит через точку с координатами (0;8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.

Посмотреть решение

Прямая a проходит через точки с координатами (0;4) и (–6;0). Прямая b проходит через точку с координатами (0; –6) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.

Посмотреть решение

Найдите ординату точки пересечения оси оy и прямой, проходящей через точку B (6;4) и параллельной прямой, проходящей через начало координат и точку A (6;8).

Посмотреть решение

Найдите абсциссу точки пересечения прямой, заданной уравнением 2х + 2у = 6, с осью ох.

Посмотреть решение

Найдите абсциссу точки пересечения прямых, заданных уравнениями 3х + 2у = 6  и у = х.

Посмотреть решение

Конечно, некоторые задачи, которые мы рассмотрели можно было решить более рациональными способами. Но ставилась цель показать разные подходы к решению. Надеюсь, это удалось.

 

1. Необходимо чётко усвоить, что угловой коэффициент прямой равен тангенсу угла наклона прямой. Это поможет вам при решении многих задач данного типа.

2. Формулу нахождения прямой проходящей через две данные точки нужно понимать обязательно. С её помощью всегда найдёте уравнение прямой, если даны координаты двух её точек.

3. Помните о том, что угловые коэффициенты параллельных прямых равны.

4. Как вы поняли, в некоторых задачах удобно использовать признак подобия треугольников. Задачи решаются практически устно.

5. Задачи в которых даны две прямые и требуется найти абсциссу или ординату точки их пересечения можно решить графическим способом. То есть, построить их на координатной плоскости (на листе в клетку) и определить точку пересечения визуально. *Но этот способ применим не всегда.

6. И последнее. Если дана прямая и координаты точек её пересечения с осями координат, то в таких задачах удобно находить угловой коэффициент через нахождение тангенса угла в образованном прямоугольном треугольнике. Как «увидеть» этот треугольник при различных расположениях прямых на плоскости схематично показано ниже:

>> Угол наклона прямой от 0 до 90 градусов <<

>> Угол наклона прямой от 90 до 180 градусов <<

В данных двух случаях, по свойству тангенса:

То есть, чтобы найти уголвой коэффициент прямой, необходимо вычислить тангенс бетта в полученном прямоугольном треугольнике и записать результат с отрицательным знаком.

В данной рубрике продолжим рассматривать задачи, не пропустите!

На этом всё. Успеха Вам!

С уважением, Александр.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Нахождение уклона по двум точкам

Нахождение уклона по двум точкам — это всего лишь применение формулы уклона подъем/спуск. Существуют разные формулы для нахождения наклона с различными типами доступной информации о линии. Формула нахождения наклона по двум точкам специально используется, когда заданы две точки на линии.

Давайте посмотрим, как вывести формулу для нахождения уклона по двум точкам, а также решим несколько примеров, используя формулу.

1. Определение уклона по формуле двух точек
2. Расчет уклона по двум точкам деривации
3. шагов для нахождения уклона из двух точек
4. Уклон от двух точек Примеры
5. Часто задаваемые вопросы по нахождению уклона по двум точкам

Определение уклона по формуле двух точек

Формула для нахождения уклона по двум точкам (x₁, y₁) и (x₂, y₂) на прямой: m = (y₂ — y₁) / (x₂ — x₁). Здесь

  • м = уклон линии
  • x₁ = x-координата первой точки
  • y₁ = координата y первой точки
  • x₂ = x-координата второй точки
  • y₂ = x-координата второй точки

Мы знаем, что находим наклон линии по ее графику, используя формулу подъем/спуск. Мы можем использовать ту же формулу, чтобы вывести приведенную выше формулу. Рассмотрим прямую с двумя точками A (x₁, y₁) и B (x₂, y₂) на ней.

Затем подъем из А в В = y₂ — y₁

Бег из А в В = x₂ — x₁

Тогда наклон, m = подъем/бег = (y₂ — y₁) / (x₂ — x₁)

Следовательно, мы вывели формулу наклона. Мы можем визуализировать это на рисунке ниже.

Вычисление уклона по двум производным точкам

Помимо метода, который уже показан выше, мы можем вывести формулу нахождения уклона по двум точкам разными методами. Давайте посмотрим на них. В каждом из этих методов рассмотрим две точки A(x₁, y₁) и B(x₂, y₂) на прямой.

Метод 1

Пусть θ будет углом, образованным линией с положительным направлением оси x. Проведите горизонтальную и вертикальную линии из двух точек A и B соответственно так, чтобы они пересекались в точке C.

По свойству соответствующих углов угол при A = θ. Применяя тангенс к треугольнику ABC,

тангенс θ = (Противоположный)/(Смежный)

тангенс θ = (y₂ — y₁) / (x₂ — x₁) .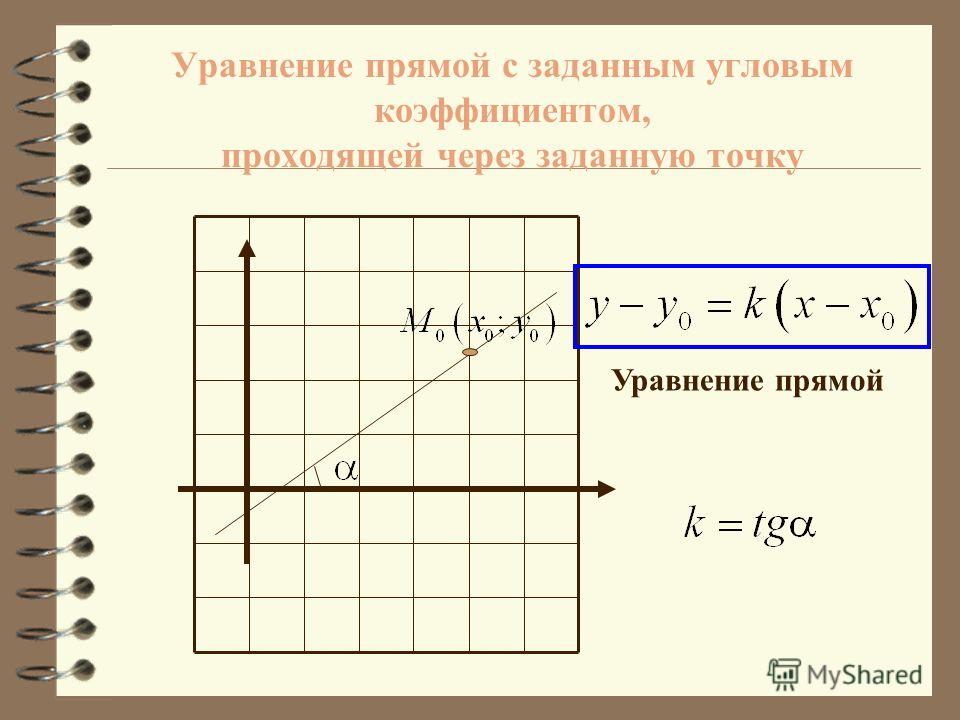 .. (1)

Мы знаем, что если θ равно угол, образуемый прямой линией с положительным направлением оси x, тогда ее наклон равен

м = tan θ … (2)

Из (1) и (2),

м = (y₂ — y₁) / (x₂ — x₁)

Метод 2

Мы знаем, что форма пересечения наклона линии есть y = mx + b.

  • Поскольку A(x₁, y₁) лежит на прямой, y₁ = mx₁ + b … (3)
  • Так как B(x₂, y₂) лежит на прямой, y₂ = mx₂ + b … (4)

Решим (3) и (4) методом подстановки. Фрма (3), b = y₁ — mx₁. Подставляя это в (4):

y₂ = mx₂ + y₁ — mx₁

Вычитая y₁ с обеих сторон,

y₂ — y₁ = mx₂ — mx₁ ₁ = m(x₂ — x₁)

Разделив обе части на x₂ — x₁,

м = (у₂ — у₁) / (х₂ — х₁)

Шаги для нахождения уклона из двух точек

Вот шаги, чтобы найти наклон линии по двум точкам на ней.

  • В первой точке обозначьте координату x с помощью x₁ и обозначьте координату y с помощью y₁.
  • Во второй точке обозначьте координату x с помощью x₂ и обозначьте координату y с помощью y₂.
  • Найдите разности y₂ — y₁ и x₂ — x₁.
  • Разделите разницу координат y на разницу координат x, чтобы найти уклон (м). т. е. m = (y₂ — y₁) / (x₂ — x₁).

Примечание: Мы можем поменять местами точки при нахождении уклона, не влияя на ответ.

Пример: Найдите наклон линии, проходящей через точки (1, -2) и (3, -6).

Решение:

Пусть (1, -2) = (x₁, y₁)

и (3, -6) = (x₂, y₂)

Тогда x₁ = 1, y₁ = -2, x₂ = 3, а у₂ = -6.

Уклон, м = (y₂ — y₁) / (x₂ — x₁)
= (-6 — (-2)) / (3 — 1)
= (-6 + 2) / (3 — 1)
= (-4) / 2
= -2

Таким образом, наклон данной линии равен -2.

Важные примечания по расчету наклона по двум точкам:

  • Можно рассчитать наклон линии по двум точкам (x₁, y₁) и (x₂, y₂)
    либо используя m = (y₂ — y₁) / (x₂ — x₁)
    или используя m = (y₁ — y₂) / (x₁ — x₂)
  • Порядок, которому мы следуем, должен быть одинаковым в числителе и знаменателе. то есть это не может быть что-то вроде (y₁ — y₂) / (x₂ — x₁).
  • Мы получаем одинаковый наклон линии независимо от того, какие две точки на ней мы используем.
  • Наклон линии равен 0, если разница координат y равна 0, и в этом случае линия горизонтальна.
  • Наклон линии не определен, если разница координат x равна 0 и в этом случае линия является вертикальной.

☛ Связанные темы:

  • Определение уклона по двум точкам Калькулятор
  • Калькулятор формы уклона точки
  • Калькулятор формы пересечения уклона
  • Уравнение линейного калькулятора

Часто задаваемые вопросы по нахождению уклона по двум точкам

Какая формула для нахождения уклона по двум точкам?

Для нахождения наклона по двум точкам линии (x₁, y₁) и (x₂, y₂) используем формулу (y₂ — y₁) / (x₂ — x₁). т. е. это отношение разности координат y к разнице координат x, такое, что разности вычисляются в одном и том же порядке.

Как найти уравнение прямой с двумя точками?

Чтобы найти уравнение прямой с двумя точками (x₁, y₁) и (x₂, y₂):

  • Вычислите ее наклон по формуле m = (y₂ — y₁) / (x₂ — x₁)
  • Используйте форму точки-наклона формулы линии, чтобы найти уравнение: y — y₁ = m(x₂ — x₁).

Можем ли мы использовать (y1-y2)/(x1-x2) для вычисления наклона линии по двум точкам?

Если (x₁, y₁) и (x₂, y₂) — две точки на прямой, то обычная формула, которую мы используем для вычисления наклона, это (y₂ — y₁) / (x₂ — x₁). Но если мы возьмем -1 в качестве общего множителя как из числителя, так и из знаменателя, тогда -1 будет отменено, и мы останемся с (y₁ — y₂) / (x₁ — x₂). Так что эта формула применима и для нахождения наклона линии с двумя точками.

Как найти наклон прямой, проходящей через две точки?

Если мы рассмотрим две точки (x₁, y₁) и (x₂, y₂) на прямой, где первая точка лежит ниже, чем верхняя точка на возрастающей прямой, то подъем = y₂ — y₁ и пробег = x₂ — x₁ . Тогда наклон = подъем/спуск = (y₂ — y₁) / (x₂ — x₁). Это формула, которую мы используем, чтобы найти наклон линии, проходящей через две заданные точки.

Как написать форму пересечения наклона с использованием двух точек?

Чтобы найти уравнение линии в форме точки пересечения, когда на прямой заданы две точки (x₁, y₁) и (x₂, y₂),

  • Найдите наклон, используя m = (y₂ — y₁) / (x₂ — x₁).
  • Подставьте его в уравнение y = mx + b.
  • Подставьте любую из заданных точек на (x, y) в приведенном выше уравнении и найдите b.
  • Подставьте значение b обратно в то же уравнение (из второго шага).

Как найти наклон линии на графике?

Чтобы найти наклон линии, когда она показана на графике:

  • Найдите на ней одну случайную точку и обозначьте ее (x₁, y₁).
  • Найдите на нем еще одну точку и обозначьте ее (x₂, y₂).
  • Примените формулу (y₂ — y₁) / (x₂ — x₁).

Уравнение — уравнение линии, проходящей через два балла

алгебраический метод представления набора точек, которые вместе образуют линию в системе координат.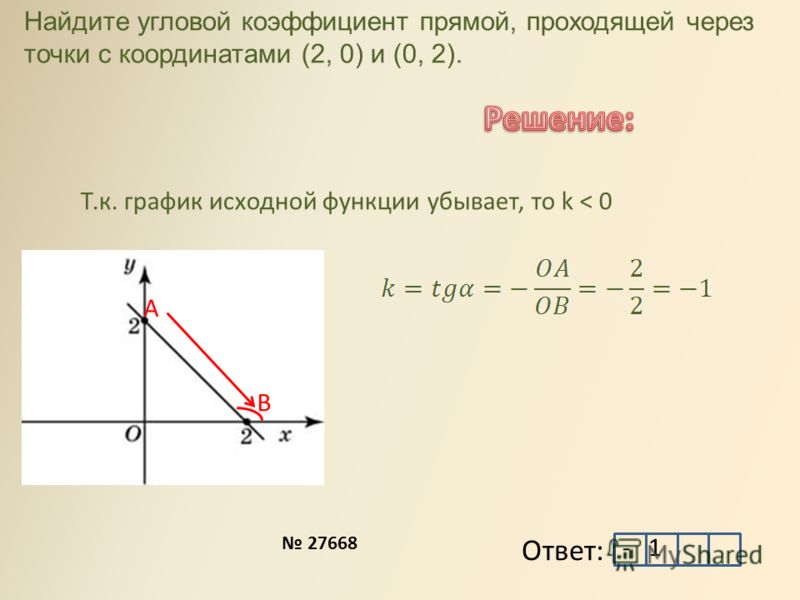 Различные точки, которые вместе образуют линию на оси координат, могут быть представлены в виде набора переменных (x, y), чтобы сформировать алгебраическое уравнение, также называемое уравнением линии. Используя уравнение прямой, можно найти, лежит ли данная точка на прямой.

Уравнение любой прямой является линейным уравнением, имеющим степень один. Давайте прочитаем всю статью, чтобы больше узнать о различных формах уравнения линии и о том, как мы можем определить уравнение линии.

Сегмент линии может быть определен как соединение между двумя точками. Любые две точки в двумерной геометрии можно соединить отрезком или просто прямой линией. Уравнение прямой можно найти тремя способами.

  1. Метод пересечения наклона 

  2. Метод измерения уклона точки 

  3. Стандартный метод

Когда даются две точки, лежащие на определенной линии, обычно используется метод уклона точки.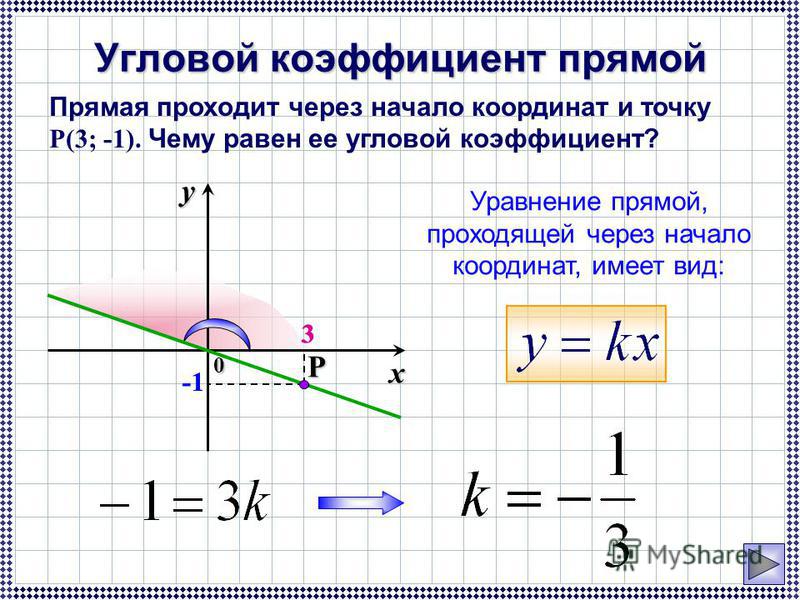

Уравнение прямой имеет вид \[y — y_{1} = m(x — x_{1})\], где \[y_{1}\] — координата оси Y, m — наклон , а \[x_{1}\] — координата по оси X.

Нахождение наклона прямой, проходящей через две заданные точки

Наклон или уклон линии — это изменение высоты линии относительно оси X. Для каждой единицы X изменение Y на линии известно как наклон линии.

(Изображение будет загружено в ближайшее время)

Для расчета уклона используется формула \[m = \frac{y_{2} — y_{1}}{x_{2} — x_{1}}\] .

Здесь точки (2,5) и (6,7).

Итак, сравнивая точку с общими обозначениями координат на декартовой плоскости, т. е. (x, y), получаем \[x_{1}, y_{1} = (2, 5) и x_{2} , у_{2} = (6, 7) \]

Подставляя значения в формулу, ?

Что произойдет, если мы поменяем местами значения \[x_{1}, y_{1} и x_{2}, y_{2}\]?

Значение m остается неизменным. Расположение координат не влияет на значение наклона.

Взяв тот же пример, что и выше, но поменяв местами значения \[x_{1}, y_{1} и x_{2}, y_{2}\], мы получим \[x_{1}, y_{1} = (6,7) и x_{2}, y_{2} = (2,5)\].

\[m = \frac{5 — 7}{ 2 — 6}\]

\[m = \frac{-2}{-3} = \frac{2}{3}\]

Отсюда , любая из двух координат может быть использована как \[x_{1}, y_{1} \], а другая как \[x_{2}, y_{2} \].

Нахождение уравнения прямой, проходящей через две заданные точки

Чтобы найти уравнение прямой, проходящей через две заданные точки, выполните следующие действия:

  1. Найдите наклон/уклон линии.

  2. Подставьте значения наклона и любую из заданных точек в формулу.

  3. Упростите, чтобы получить уравнение, напоминающее стандартное уравнение прямой, т. е. Ax + By + C = 0, где A, B и C — константы.

Взяв приведенный выше пример, где \[x_{1}, y_{1} и x_{2}, y_{2}\], мы получаем \[x_{1}, y_{1} = (2 ,5) и x_{2}, y_{2} = (6,7)\] и наклон рассчитывается как \[m = \frac{2}{3}\], подставьте значение m и любое точка в формуле \[y — y_{1} = m(x — x_{1})\].

\[y — y_{1} = m(x — x_{1})\]

\[y — 5 =  \frac{2}{3} (x — 2)\]

Перемножить и упростить:

\[y — 5 =  \frac{2}{3} (x — 2 )\]

\[ \Стрелка вправо 3 (y — 5) = 2 (x — 2)\]

\[ \Стрелка вправо 3y — 15 = 2x — 4\]

\[ \Стрелка вправо 3y — 2x = 15 — 4\]

\[ \Стрелка вправо 3y — 2x = 11\]

Это же уравнение можно выразить в форме пересечения наклона, составив уравнения относительно y, как показано ниже.

\[ \Стрелка вправо 3y — 2x = 11\]

\[ \Стрелка вправо 3y = 2x + 11\]

\[ \Rightarrow y = \frac{2}{3}x + \frac{11}{3}\]

Решенные примеры

1.

Найти уравнение прямой, проходящей через точки (2,3 ) и (-1,0).

Для расчета наклона используется формула \[m = \frac{y_{2} — y_{1}}{x_{2} — x_{1}}\].

Здесь точки (2,3) и (-1,0)

Итак, сопоставляя точку с общим обозначением координат на декартовой плоскости, т. е. (x, y), получаем (x1, y1) = (2,3) и (x2,y2) = (-1,0).

Подставляя значения в формулу, 

\[ \Rightarrow m = \frac{0 — 3}{-1 — 2}\].

\[ \Стрелка вправо m = \frac{-3}{-3}\].

\[ \Стрелка вправо m = 1 \].

Подставьте значение m и любую координату в формулу \[y — y_{1} = m(x — x_{1})\].

\[y — y_{1} = m(x — x_{1})\]

\[y — 0 = 1(x — (-1)\]

Упростим уравнения: 

\[ y — 0 = 1(x — (-1)\]

\[ \Стрелка вправо y = x + 1 \]

\[ \Стрелка вправо y — x = 1 \]

То же самое уравнение можно выразить в форме пересечения наклона, составив уравнения через y.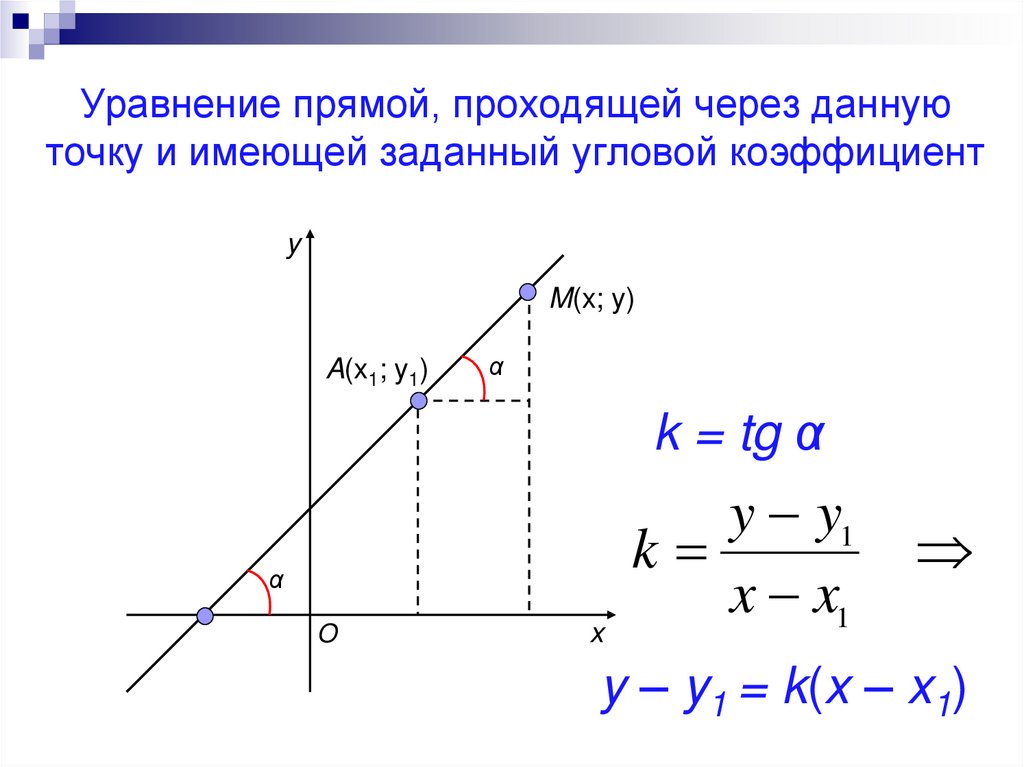

y = x + 1

Уравнение прямой, проходящей через точки (2,3) и (-1,0), имеет вид y = x + 1 или y — x = 1.

2. Найти уравнение линии, проходящей через точку (1,3) и имеющей наклон \[\frac{1}{3}\].

Подставьте значение m и координату в формулу \[y — y_{1} = m(x — x_{1})\].

 \[y — y_{1} = m(x — x_{1})\]

\[ \Стрелка вправо y — 3 = m(x — x_{1})\]

\[ \Стрелка вправо y — 3 = \frac{1}{3}(x — 1)\]

Перекрестное умножение и упростим уравнения:

\[ \Стрелка вправо y — 3 = \frac{1}{3}(x — 1)\]

\[ \Стрелка вправо 3(y — 3) = 1(x — 1)\ ]

Упростим уравнения дальше:

\[ \Стрелка вправо 3(y — 3) = 1(x — 1)\]

\[ \Стрелка вправо 3y — 9 = x — 1\]

\[ \Стрелка вправо 3y — x = 8\]

То же уравнение можно выразить в форме пересечения наклона, составив уравнения через y.