Радиус вписанной окружности, формулы, задачи.

Окружность, вписанная в треугольник

 

Существование окружности, вписанной в треугольник

      Напомним определение биссектрисы угла.

      Определение 1. Биссектрисой угла называют луч, делящий угол на две равные части.

      Теорема  1 (Основное свойство биссектрисы угла). Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).

Рис. 1

      Доказательство. Рассмотрим произвольную точку D, лежащую на биссектрисе угла BAC, и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE, а гипотенуза AD – общая. Следовательно,

DF = DE,

что и требовалось доказать.

      Теорема 2 (обратная теорема к теореме 1). Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).

Рис. 2

      Доказательство. Рассмотрим произвольную точку D, лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE, а гипотенуза AD – общая. Следовательно,

что и требовалось доказать.

      Определение 2

. Окружность называют окружностью, вписанной в угол, если она касается сторон этого угла.

      Теорема 3. Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.

      Доказательство. Пусть точка D – центр окружности, вписанной в угол BAC, а точки E и F – точки касания окружности со сторонами угла (рис.3).

Рис.3

      Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности), а гипотенуза

AD – общая. Следовательно

AF = AE,

что и требовалось доказать.

      Замечание. Теорему 3 можно сформулировать и по-другому: отрезки касательных, проведенных к окружности из одной точки, равны.

      Напомним определение биссектрисы треугольника.

      Определение 3. Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.

      Теорема 4. В любом треугольнике все

три биссектрисы пересекаются в одной точке.

      Доказательство. Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC, и обозначим точку их пересечения буквой O (рис. 4).

Рис. 4

      Опустим из точки O перпендикуляры OD, OE и OF на стороны   треугольника. Поскольку точка O лежит на биссектрисе угла BAC, то в силу теоремы 1 справедливо равенство:

OD = OE,

      Поскольку точка

O лежит на биссектрисе угла ACB, то в силу теоремы 1 справедливо равенство:

OD = OF,

      Следовательно, справедливо равенство:

OE = OF,

откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC. Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать

 

Фигура

Рисунок

Формула

Обозначения

Произвольный треугольник

Посмотреть вывод формулы

a, b, c – стороны треугольника, 
S –площадь, 

r –  радиус вписанной окружности, 
p – полупериметр

.

Посмотреть вывод формулы

Равнобедренный треугольник

Посмотреть вывод формулы

a – боковая сторона равнобедренного треугольника, 
b – основание,   r –  радиус вписанной окружности

Равносторонний треугольник

Посмотреть вывод формулы

a – сторона равностороннего треугольника,  r  –  радиус вписанной окружности

Прямоугольный треугольник

Посмотреть вывод формул

a, b – катеты прямоугольного треугольника,   
c  – гипотенуза,  r – радиус вписанной окружности

     Определение 4. Окружностью, вписанной в треугольник, называют окружность, которая касается всех сторон треугольника (рис.5).  В этом случае треугольник называют

треугольником, описанным около окружности.

Рис. 5

      Следствие. В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.

Формулы для радиуса окружности, вписанной в треугольник

      Формулы, позволяющие найти радиус вписанной в треугольник окружности, удобно представить в виде следующей таблицы.

Вывод формул для радиуса окружности, вписанной в треугольник

      Теорема 5 . Для произвольного треугольника справедливо равенство

,

где a, b, c – стороны треугольника,  r –  радиус вписанной окружности,–  полупериметр (рис.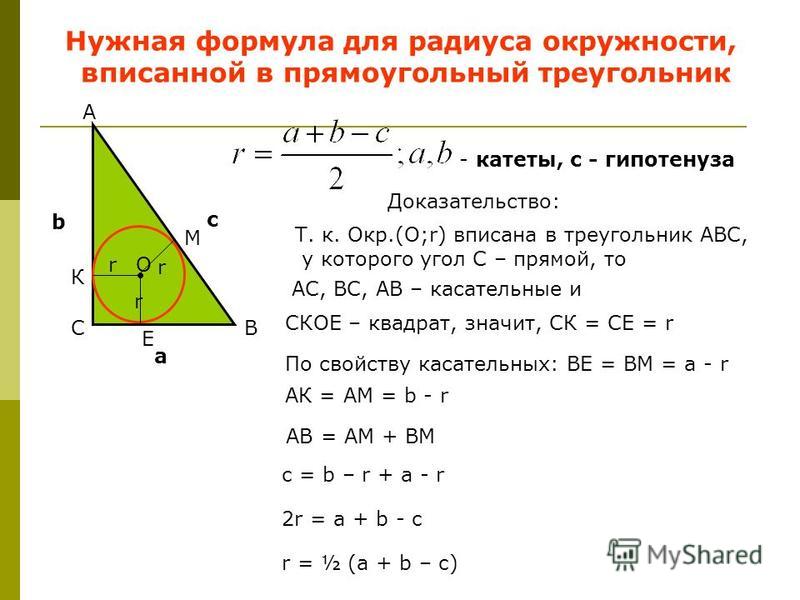 6).

Рис. 6

      Доказательство. Из формулы

с помощью формулы Герона получаем:

что и требовалось.

      Теорема 6 . Для равнобедренного треугольника справедливо равенство

,

где a – боковая сторона равнобедренного треугольника, b – основание,  r –  радиус вписанной окружности (рис. 7).

Рис. 7

      Доказательство. Поскольку для произвольного треугольника справедлива формула

,

где

,

то, в случае равнобедренного треугольника, когда

получаем

что и требовалось.

      Теорема 7 . Для равностороннего треугольника справедливо равенство

где a – сторона равностороннего треугольника,  r –  радиус вписанной окружности (рис. 8).

Рис. 8

      Доказательство. Поскольку для равнобедренного треугольника справедлива формула

,

то, в случае равностороннего треугольника, когда

b = a,

получаем

что и требовалось.

      Замечание. Я рекомендую вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.

      Теорема 8 . Для прямоугольного треугольника справедливо равенство

где a, b – катеты прямоугольного треугольника,   c  –  гипотенуза,  r –  радиус вписанной окружности.

      Доказательство. Рассмотрим рисунок 9.

Рис. 9

      Поскольку четырёхугольник CDOF является прямоугольником, у которого соседние стороны

DO и OF равны, то этот прямоугольник – квадрат. Следовательно,

СВ = СF= r,

      В силу теоремы 3 справедливы равенства

      Следовательно, принимая также во внимание теорему Пифагора, получаем

что и требовалось.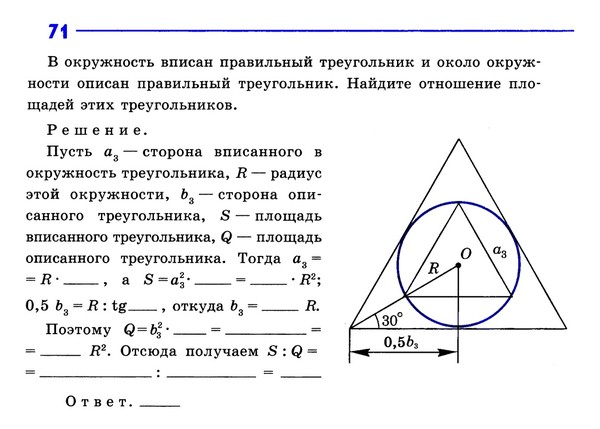

Подборка задач по теме «Окружность, вписанная в треугольник».

1.

Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

 

2.

Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.

 

 

 

3

В треугольнике ABC  АС=4, ВС=3, угол C равен 90º. Найдите радиус вписанной окружности.

 

 

 

 

4.

Катеты равнобедренного прямоугольного треугольника равны 2+. Найдите радиус окружности, вписанной в этот треугольник.

 

 

5.

Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 2. Найдите гипотенузу c этого треугольника. В ответе укажите с(–1).

 

Приведем ряд задач  из ЕГЭ с решениями.

. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .

Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .

Запишем площадь треугольника АВС двумя способами:

Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .

В ответ запишем .

Ответ: .

Задача 2.

 

Задача 3.

Задача 4.

 

1. В произвольном  две боковые стороны 10см и 6см (AB и BC).   Найти радиусы описанной и вписанной окружностей
Задача решается самостоятельно с комментированием.

Решение: 

Задача 5.

В .

1) Найти:   
2) Доказать:  и найти СK 
3) Найти: радиусы описанной и вписанной окружностей

Решение:

Задача 6.

Радиус окружности вписанной в квадрат равен . Найти радиус окружности описанной около этого квадрата.
Дано:

·                                 треугольник ОСЕ – равнобедренный и прямоугольный;

·                                 ОЕ=ЕС=;

·                                 ОЕС=90°;

·                                 ЕОС=ОСЕ=45°;

Найти: ОС=?
Решение: в данном случае задачу можно решить, воспользовавшись либо теоремой Пифагора, либо формулой для R. Второй случай будет проще, поскольку формула для R выведена из теоремы.


Задача 7.

Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 2. Найдите гипотенузу с этого треугольника. В ответе укажите .

Воспользуемся формулой радиуса окружности вписанной в треугольник:

где a, b, c – стороны треугольника

S – площадь треугольника

Нам неизвестны ни стороны треугольника, ни его площадь. Обозначим катеты как х, тогда гипотенуза будет равна:

А площадь  треугольника будет  равна 0,5х2.

Значит

Таким образом, гипотенуза будет равна:

В ответе требуется записать:

Ответ: 4

Задача 8.

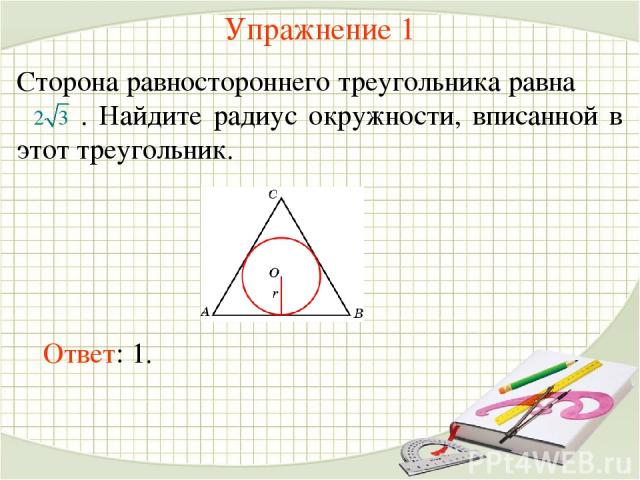
В треугольнике ABC АС = 4, ВС = 3, угол C равен 900. Найдите радиус вписанной окружности.

Воспользуемся формулой радиуса окружности вписанной в треугольник:

где a, b, c – стороны треугольника

S –  площадь треугольника

Две стороны известны (это катеты), можем вычислить третью (гипотенузу), также можем вычислить и площадь.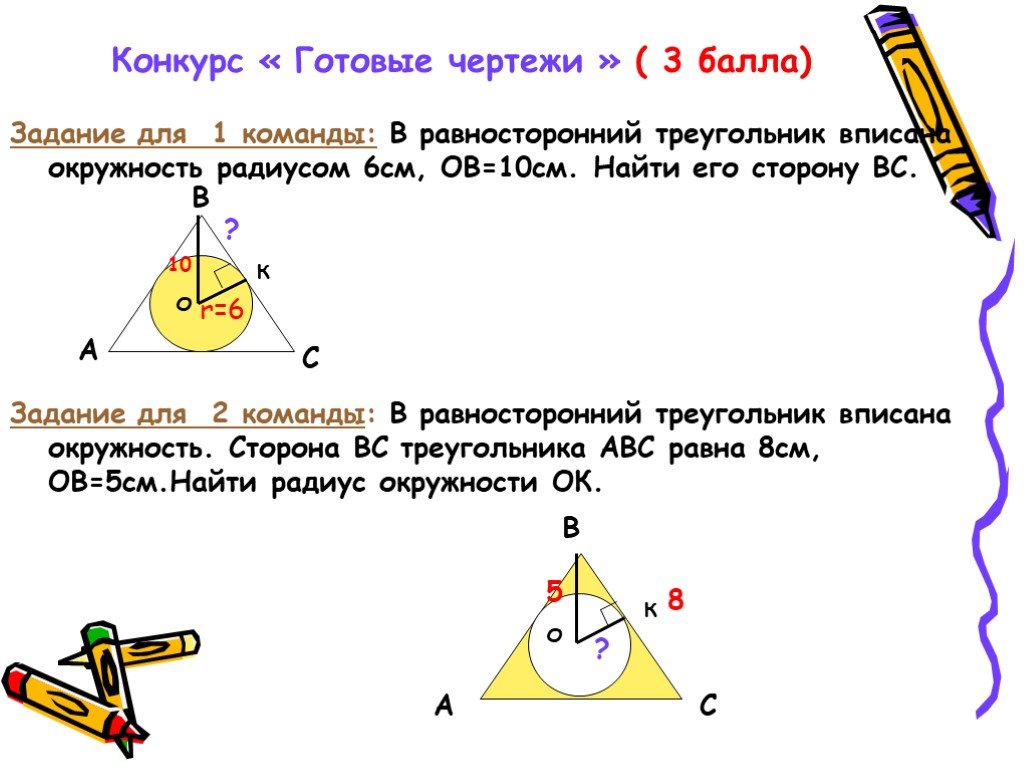

По теореме Пифагора:

Найдём площадь:

Таким образом:

Ответ: 1

 Задача 9.

Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.

Воспользуемся формулой радиуса окружности вписанной в треугольник:

где a, b, c –  стороны треугольника

S – площадь треугольника

Известны все стороны, вычислим и площадь. Её мы можем найти по формуле Герона:

Тогда

Таким образом:

Ответ: 1,5

Задача 10. (Из банка ЕГЭ)

 

Задача 11. (Из банка ЕГЭ)

Задача 12. (Из банка ЕГЭ)

Задача 13. (Из банка ЕГЭ)

Задача 14. (Из банка ЕГЭ)

Задача 15.

Найдите радиусы окружностей, вписанной в правильный треугольник и описанный около него, если их разность равна 4см.

Сторона правильного треугольника вычисляется по формуле a = R√3, где R – радиус описанной окружности, и a = 2r√3 , где r – радиус вписанной окружности, приравняем стороны R√3  = 2·r√3 , отсюда R = 2r,  сдругой сторони по условию задачи R – r = 4 cм, отсюда r = 4 см,  тогда R = 2·4 см = 8 см

Ответ: 4 см, 8 см

 

 Задача 16.
Катеты прямоугольного треугольника равны 12 и 5. Найти:
а) радиусы вписанной окружности;
б) радиусы описанной окружности;
в) расстояние от центра вписанной окружности до вершины наименьшего угла.
Решение:
1. По теореме Пифагора 
2. О – центр описанной окружности, 

Задача 17.

В треугольнике с углами  и   вписана окружность. Найти углы треугольника, вершинамикоторого являются точки касания окружности со сторонами треугольника.

Дано: точки касания вписанной окружности.

Найти: 

Решение:

1.

2. Из 

3. Из 

4. Из  

5.

Задача 18.

В равнобедренную трапецию с основаниями 1 и 9 вписана окружность. Найти: а) боковую сторону; б) радиус вписанной окружности; в) высоту; г) диагональ.

 

 

Приведу пример возможной самостоятельной работы по теме «Вписанная и описанная окружность».

 

Карточки с задачами.
1) В ABC AB = 8, BC = 10, . Найти высоту, опущенную из вершины B и  BAC.
2) В ABC AB=12, BC = 9. Площадь треугольника 9. Найти радиусы вписанной и описанной окружностей.

 

Пример математического диктанта.

I. Математический диктант
I вариант
1. В любой треугольник можно вписать окружность? (Да/Нет)
2. Центр вписанной в треугольник окружности является …
3. Вокруг любого треугольника можно описать окружность? (Да/Нет)
4. Центр окружности описанной около треугольника является …
5. Если центр вписанной и описанной окружности совпадают, то это треугольник …
6. Центр окружности, описанной около прямоугольного треугольника, совпадает с …
7. Если в трапецию можно вписать окружность, то …
8. Если вокруг трапеции можно описать окружность, то …
9. Если центр окружности, описанной около треугольника находится вне его, то этот треугольник …
10. Если центр окружности, описанной около треугольника, находится внутри его, то треугольник …
Использовать взаимопроверку, заготовить заранее ответы на доске. Анализ ошибок.

 

Радиус вписанной окружности в треугольник

Главная » геометрия

Обновлено

Радиус вписанной в треугольник окружности
рассчитать и выразить через периметр, площадь,
высоту, основание, стороны, диаметр. Формулы
радиуса окружности вписанной в треугольник.

Центр вписанной в треугольник окружности — это одна
из замечательных точек треугольника, она расположена
в точке пересечения биссектрис треугольника, её
иногда называют инцентром.

Центр вписанной окружности правильного треугольника — это
точка, где пересекаются высоты, медианы и биссектрисы.

В любой треугольник можно вписать только одну
окружность, которая находится внутри треугольника.
Центр вписанной окружности равноудален от всех
сторон треугольника. Точка, где окружность пересекается
со стороной треугольника, называется точкой касания.

Все отрезки, которые проведены от точки касания к центру
вписанной окружности имеют одинаковую длину.

Чтобы найти радиус окружности вписанной в треугольник
надо площадь разделить на полупериметр.

Диаметр вписанной окружности в треугольник численно
равен двум радиусам вписанной окружности. Радиус
вписанной окружности можно найти по разным
формулам, все зависит от того, какой треугольник.

Всего различают четыре вида треугольников:

  • Разносторонний / любой
  • Правильный / равносторонний
  • Равнобедренный /  равнобочный
  • Прямоугольный / прямой

Содержание

  1. Радиус вписанной окружности в любой треугольник
  2. Радиус вписанной окружности в правильный треугольник
  3. Радиус вписанной окружности в равнобедренный треугольник
  4. Радиус вписанной окружности в прямоугольный треугольник

Радиус вписанной окружности в любой треугольник

  1. Радиус вписанной окружности в любой треугольник через площадь и полупериметр

    \[ r = \frac{S}{p} \]

    S — площадь; p — полупериметр;

  2. Радиус вписанной окружности в любой треугольник через все стороны и полупериметр

    \[ r = \sqrt\frac{{(p-a)(p-b)(p-c)}}{p} \]

    a, b, c — стороны; p — полупериметр;

  3. Радиус вписанной окружности в любой треугольник через основание, высоту и полупериметр

    \[ r = \frac{\frac{1}{2}a \cdot h}{p} \]

    a — основание, сторона на которую падает высота; h — высота; p — полупериметр;

  4. Радиус вписанной окружности в любой треугольник через диаметр вписанной окружности

    \[ r = \frac{D}{2} \]

    D — диаметр вписанной окружности;

Радиус вписанной окружности в правильный треугольник

  1. Радиус вписанной окружности в правильный треугольник через сторону

    \[ r = \frac{a}{2\sqrt 3} \]

    a — сторона;

  2. Радиус вписанной окружности в правильный треугольник через радиус описанной окружности

    \[ r = \frac{R}{2} \]

    R — радиус описанной окружности;

  3. Радиус вписанной окружности в правильный треугольник через диаметр вписанной окружности

    \[ r = \frac{D}{2} \]

    D — диаметр вписанной окружности;

Радиус вписанной окружности в равнобедренный треугольник

  1. Радиус вписанной окружности в равнобедренный треугольник через боковые стороны и основание

    \[ r = \frac{b}{2} \cdot \sqrt{\frac{2a-b}{2a+b}} \]

    a — боковая сторона; b — основание;

  2. Радиус вписанной окружности в равнобедренный треугольник через высоту и основание

    \[ r = \frac{bh}{b + \sqrt{4h^2+b^2}} \]

    b — основание; h — высота;

  3. Радиус вписанной окружности в равнобедренный треугольник через диаметр вписанной окружности

    \[ r = \frac{D}{2} \]

    D — диаметр вписанной окружности;

Радиус вписанной окружности в прямоугольный треугольник

  1. Радиус вписанной окружности в прямоугольный треугольник через два катета и гипотенузу

    \[ r = \frac{a+b-c}{2} \]

    a, b — катеты; с — гипотенуза.

  2. Радиус вписанной окружности в прямоугольный треугольник через гипотенузу и два катета

    \[ r = \frac{ab}{a+b+c} \]

    c — гипотенуза; a, b — катеты;

  3. Радиус вписанной окружности в прямоугольный треугольник через диаметр вписанной окружности

    \[ r = \frac{D}{2} \]

    D — диаметр вписанной окружности;

Вписанная окружность в треугольник — это окружность,
которая вписана в треугольник и касается всех его сторон.

Радиус вписанной окружности в треугольник — это отрезок,
проведенный от центра вписанной окружности до любой стороны.

Длина радиуса вписанной окружности, диаметра
вписанной окружности а также других величин
измеряется в мм, см, м, км и так далее.

В любом треугольнике все радиусы и диаметры
равны, имеют одинаковую длину.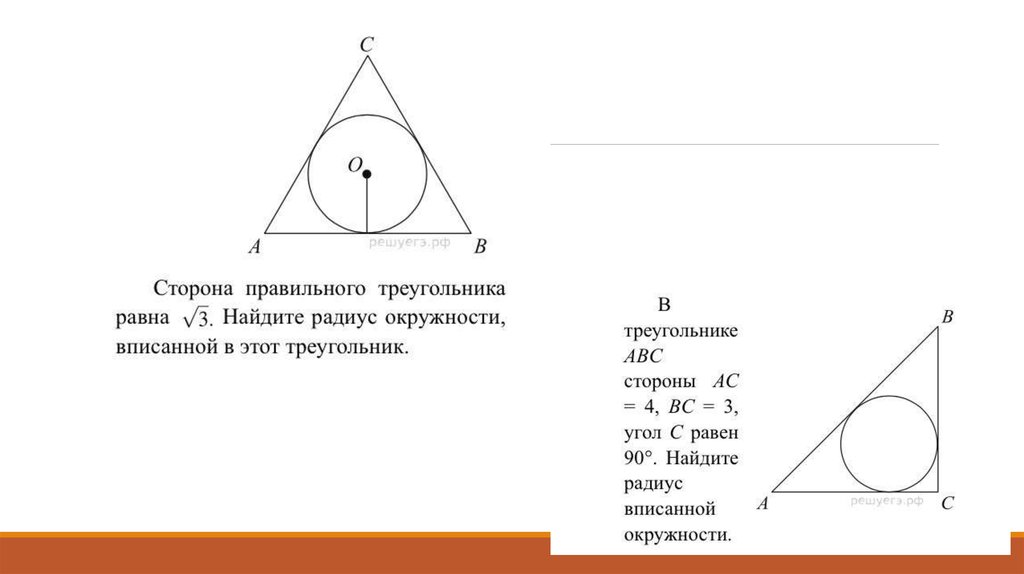

Площадь круга, вписанного в равносторонний треугольник

Главная » Окружности » Вписанные фигуры » Площадь круга, вписанного в равносторонний треугольник

Последнее обновление: Идо Сариг · Этот веб-сайт получает доход от рекламы и использует файлы cookie · Условия использования · Политика конфиденциальности

Мы можем использовать свойства равностороннего треугольника и прямоугольного треугольника 30-60-90 найти площадь круга, вписанного в равносторонний треугольник, используя только длину стороны треугольника.

Задача

В равносторонний треугольник со стороной x вписана окружность. Найдите площадь круга через х.

Стратегия

Мы знаем, что окружность полностью определяется длиной своего радиуса r, поэтому ключом здесь будет найти это — длину сегмента OD.

Есть несколько быстрых способов найти эту длину, которые основаны на свойствах центроида — точки, где сходятся все три медианы треугольника. Центроид равностороннего треугольника лежит на медианах, которые также перпендикулярны основаниям, и разбивает медианы на два отрезка, равные ⅓ длины и ⅔ длины соответственно.

Но доказать эти свойства центроида (например, тот факт, что все три медианы действительно пересекаются в одной точке или что центроид также является центром окружности) довольно сложно и выходит за рамки школьной геометрии.

Вместо этого я буду использовать более длительный процесс, основанный только на вещах, которые мы уже доказали с помощью конгруэнтности треугольников.

Окружность вписана в треугольник, поэтому два радиуса, OE и OD, перпендикулярны сторонам треугольника (AB и BC) и равны друг другу. BE=BD, используя теорему о двух касательных.

BEOD, таким образом, является воздушным змеем, и мы можем использовать свойства воздушного змея, чтобы показать, что ΔBOD представляет собой треугольник 30-60-90. Тогда, если мы найдем длину одной из его сторон, мы сможем найти все три стороны, включая OD.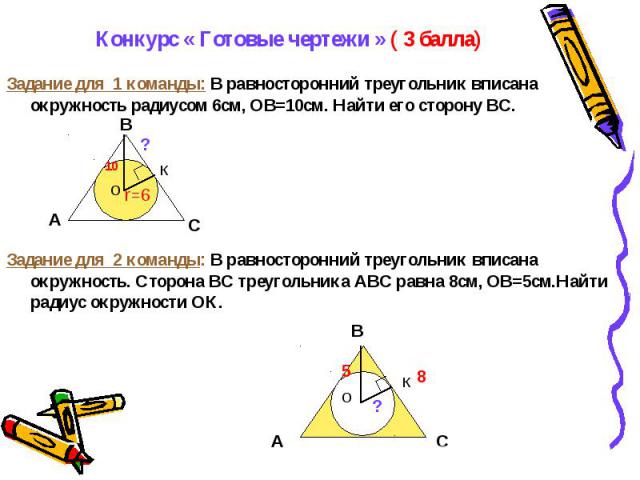

Показав конгруэнтность треугольников ΔBOD и ΔCOD, мы обнаружим, что BD составляет половину BC и равен x/2, тогда OD будет (x/2)/√3, и мы закончим.

Доказательство

Вот как найти площадь круга, вписанного в равносторонний треугольник:

(1) OE = OD = r // все радиусы круга равны друг другу
(2) BE=BD // Теорема о двух касательных
(3) BEOD — воздушный змей //(1), (2) , определение воздушного змея
(4) m∠ODB=∠OEB=90° //радиусы перпендикулярны касательной
(5) м∠ABD = 60° //Дано, ΔABC равностороннее
(6) м∠OBD = 30° // (3) В воздушном змее диагональ делит пополам углы между двумя равными сторонами
(7) ΔBOD — треугольник 30-60-90 //(4), (5), (6)
(8) r=OD=BD/√3 //Свойства треугольника 30-60-90
(9 ) m∠OCD = 30° //повторить шаги (1) -(6) для треугольника ΔOCD, симметрия
(10) ∠OCD≅∠OBD //(6),(9))
(11) ∠DOB≅∠DOC //(10), (4), сумма углов в треугольнике
(12) OD=OD // общая сторона, рефлексивное свойство равенства
(13) ΔBOD≅ΔCOD / /Угол-сторона-Угол постулат
(14) BD=CD=x/2 //Соответствующие стороны в конгруэнтных треугольниках (CPCTC)
(15) OD=(x/2)/√3 //(8), подстановка
(16) Площадь круг =πr 2
(17) Площадь = π[(x/2)/√3] 2
(18) Площадь = πx 2 /12

Об авторе

Идо Сариг — руководитель отдела высоких технологий со степенью бакалавра вычислительной техники. Его цель — помочь вам разработать лучший подход к решению геометрических задач. Вы можете связаться с ним по адресу [email protected]

Равносторонний треугольник со стороной 9 см вписан в окружность Найдите радиус окружности…

Перейти к

  • Круговое упражнение 12А
  • Круговое упражнение 12B
  • Круговое упражнение 12C
  • Системы счисления
  • Полиномы
  • Факторизация многочленов
  • Линейные уравнения с двумя переменными
  • Координатная геометрия
  • Введение в геометрию Евклида
  • Линии и углы
  • Треугольники
  • Конгруэнтность треугольников и неравенства в треугольнике
  • Четырехугольники
  • Площади параллелограммов и треугольников
  • Круги
  • Геометрические построения
  • Площади треугольников и четырехугольников
  • Объем и площадь поверхности твердых тел
  • Средняя медиана и режим разгруппированных данных
  • Вероятность

Главная > Решения RS Aggarwal Класс 9 Математика > Глава 12 — Круги > Круговое упражнение 12А > Вопрос 20

Вопрос 20 Круги Упражнение 12A

В окружность вписан равносторонний треугольник со стороной 9 см.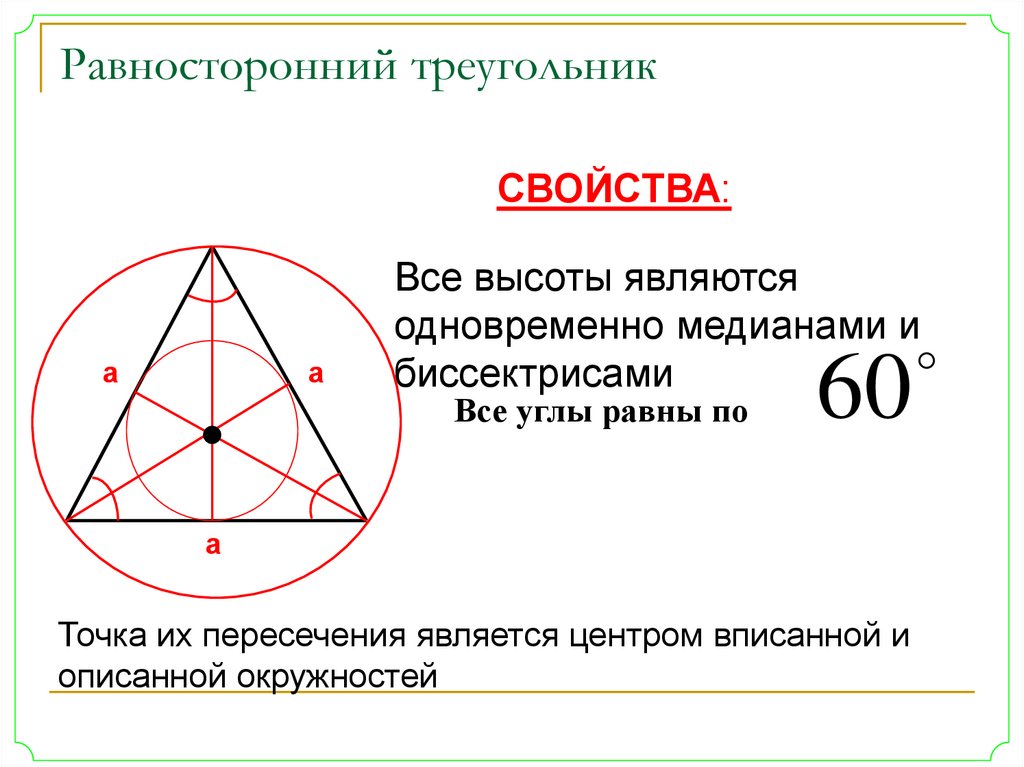 Найдите радиус окружности.

Ответ:

Рассмотрим △ ABC как равносторонний треугольник со стороной 9 см

Возьмем AD как одну из его медиан

Мы знаем, что

AD ⊥ BC

Это можно записать как

BD × 90½ BC

Подставляя значения

BD = ½ × 9

Получаем

BD = 4,5 см 92 = 81 – 81/4

Извлекая квадратный корень

AD = 9√3/2 см

Мы знаем, что в равностороннем треугольнике центр тяжести и центр описанной окружности совпадают

AG: GD = 2:1

Радиус можно записать как

AG = 2/3 AD

Подставив значения

AG = (2/3) × (9√3/2)

Таким образом, мы получим

AG = 3√3 см.

Следовательно, радиус окружности равен 3√3 см.

Похожие вопросы

В окружности радиусом 10 см проведена хорда длиной 16 см.