Человек массой 60 кг стоит на платформе масса которой 30 кг: Человек массой 60 кг стоит на платформе, масса которой 30 кг. Платформа подвешена на

Человек массой 60 кг стоит на платформе, масса которой 30 кг. Платформа подвешена на

РУССКИЙ ЯЗЫК ПОМОГИТЕ ПОЖАЛУЙСТА646. Прочитайте текст. Определите его тип. Объясните, как вы понимаете выражение «близкие люди». Спишите, вставляя про … пущенные буквы. Обозначьте разряд и падеж местоимений и прилагательных.Невозможно даже пр..дставить, сколько пр..красных слов можно сказать своим близк.., любим.. людям. Не бойтесь повторит(?)ся. (Не)ст.. сияйтесь г..ворить о своих чу(?)ствах друг другу. А особенно будьте бл..годарны мамам. Любите своих мам, не забывайте каждый день повторять: «Моя мама — самая лу..шая! Моя мама — мой самый лу..ший друг!»(С. Дудниченко)

Сантос Дюмон, один из первых конструкторов управляемого аэростата, построил шар объёмом в 113 м³ и наполнил его водородом. Масса оборудования составил … а 27,5кг. Укажи, мог ли на таком шаре подняться человек массой 117 кг. Принять =9,8Н/кг. Используй таблицу плотности. 1. Архимедова сила, действующая на шар, равна (округли до десятых) Н. Сила тяжести шара с оборудованием и человеком равна (округли до десятых) Н. 2. Человек массой 117 кг на таком шаре подняться (запиши: «мог» или «не мог») . Ответить!

Масса снаряжения воздушного шара (оболочки, сетки, корзины) составляет 448 кг. Объём шара — 1600м³. Найди, какой подъёмной силой будет обладать этот ш … ар при наполнении его водородом. (Принять плотность газа ρводорода=0,09кг/м3 и =9,8Н/кг). Плотность некоторых газов ρ=кгм3 ρ=гсм3 Хлор 3,210 0,00321 Оксид углерода (IV) (углекислый газ) 1,980 0,00198 Кислород 1,430 0,00143 Воздух 1,290 0,00129 Азот 1,250 0,00125 Оксид углерода (II) (угарный газ) 1,250 0,00125 Природный газ 0,800 0,0008 Водяной пар (при =100°) 0,590 0,00059 Гелий 0,180 0,00018 Водород 0,090 0,00009 Ответ (округли до сотых): воздушный шар будет обладать подъёмной силой кН. Ответить!

Срочно! Грудка мідного купоросу важить у гасі 7Н, а у повітрі 11Н. Знайдіть густину мідного купоросу.

Стріла, випущена вертикально вгору, повертається до лучника через 10 с. Якої найбільшої висоти досягла стріла? а)75 м б)250 м в)125 м г)50м

Тіло кинуто вертикально вгору з початковою швидкістю 20 м/с. Який модуль швидкості тіла через 0,5 с після початку руху? Опір повітря не враховувати. * … а)15 м/с б)10 м/с в)5 м/с г)20 м/с

З аеростата, який завис над Землею, впав вантаж. Через 10 с він досяг поверхні Землі. На якій висоті знаходився аеростат? Опір повітря дуже малий. а) … 1000 б)100 в)50 г)500

Гелікоптер летить горизонтально на висоті 200 м зі швидкістю 360 км/год. За скільки кілометрів до цілі льотчик має скинути вантаж?

Невеликий камінь, який кинули з рівної горизонтальної поверхні землі під кутом до горизонту, впав назад на землю в 20 м від місця кидання. Чому дорівн … ювала швидкість каменя через 1 с після кидання, якщо в цей момент вона була напрямлена горизонтально.

До джерела струму приєднали три однакових резистори, з’єднані паралельно. Як зміниться сила струму через джерело, якщо видалити з кола один резистор? … Напруга на полюсах джерела є незмінною.

Человек массой 60 кг стоит на платформе, масса которой 30 кг. Платформа подвешена на

Используй таблицу плотности. 1. Архимедова сила, действующая на шар, равна (округли до десятых) Н. Сила тяжести шара с оборудованием и человеком равна (округли до десятых) Н. 2. Человек массой 117 кг на таком шаре подняться (запиши: «мог» или «не мог») . Ответить!

Срочно! Грудка мідного купоросу важить у гасі 7Н, а у повітрі 11Н. Знайдіть густину мідного купоросу.

2)/2=12-4.9=7.1 (м)Ответ:7,1м

11 месяцев назад

вращается вокруг вертикальной оси проходящей

Задача 10059

Горизонтальная платформа массой m₁ = 150 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой n = 8 мин^–1. Человек массой m₂ = 70 кг стоит при этом на краю платформы. С какой угловой скоростью ω начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу круглым, однородным диском, а человека — материальной точкой.

Задача 10549

На краю горизонтальной платформы, имеющей форму диска радиусом R = 2 м, стоит человек. Масса платформы m₁ = 200 кг, масса человека m₂ = 80 кг. Платформа может вращаться вокруг вертикальной оси, проходящей через ее центр. Пренебрегая трением, найти, с какой угловой скоростью будет вращаться платформа, если человек будет идти вдоль ее края со скоростью v = 2 м/с относительно платформы.

Задача 40675

На краю горизонтальной платформы стоит человек массой 80 кг. Платформа представляет собой круглый однородный диск массой 160 кг, вращающийся вокруг вертикальной оси, проходящей через ее центр, с частотой 6 об/мин. Сколько оборотов в минуту будет делать платформа, если человек перейдет от края платформы к ее центру? Момент инерции человека рассчитывать как для материальной точки.

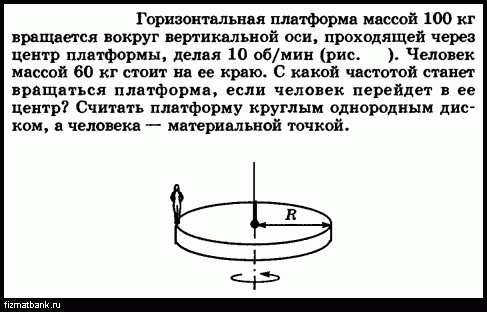
Задача 25961

Горизонтальная платформа массой 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, делая 10 об/мин. Человек весом 60 кг стоит при этом на краю платформы. С какой скоростью начнет вращаться платформа, если человек перейдет к ее центру? Считать платформу круглым однородным диском, а человека — точечной массой.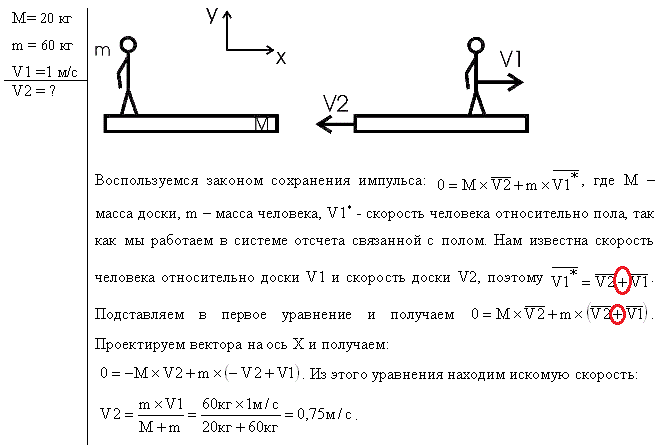

Задача 14666

Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой n₁ = 10 об/мин. Человек массой m₀ = 60 кг стоит при этом на краю платформы. С какой частотой n₂ начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека — точечной массой.

Задача 11164

На краю горизонтальной платформы, имеющей форму диска радиусом R = 2 м, стоит человек массой m₁ = 80 кг. Масса m

2 платформы равна 240 кг. Платформа может вращаться вокруг вертикальной оси, проходящей через ее центр. Пренебрегая трением, найти, с какой угловой скоростью ω будет вращаться платформа, если человек будет идти вдоль ее края со скоростью v = 2 м/с относительно платформы.

Задача 26317

Однородный шар массой m₁ = 5 кг может вращаться вокруг вертикальной оси, проходящей через его центр. На «экватор» шара намотана нить, другой конец которой, перекинутый через цилиндрический блок массой m = 1 кг, привязан к грузу массой m₂ = 10 кг. Определить ускорение груза, если блок и шар вращаются без трения.

Задача 11011

Ha горизонтальной платформе, имеющей форму диска радиусом R = 4 м находится человек массой m = 80 кг. Масса платформы М = 440 кг. Платформа может вращаться вокруг вертикальной оси, проходящей через ее центр. Человек идет вдоль ее окружности со скоростью v = 1,5 м/с относительно платформы. Угловая скорость платформы ω = 0,2 рад/с. Определить на каком расстоянии от оси вращения находится человек. Трением пренебречь.

Задача 12162

На горизонтальной платформе, вращающейся вокруг вертикальной оси, проходящей через ее центр, стоит человек и держит на вытянутых руках две одинаковые гири массой по 2 кг каждая, при этом расстояние от оси платформы до каждой гири 0,75 м. Платформа вращается, делая 1 об/с. Человек сближает гири так, что их расстояние до оси платформы становится равным 0,4 м, а частота оборотов увеличивается до 1,2 об/с. Определить момент инерции платформы с человеком, считая его постоянным, а гири материальными точками.

Задача 13198

Однородная прямоугольная пластина может свободно вращаться вокруг вертикальной оси, проходящей по ее плоскости через середину. В край пластины перпендикулярно ее плоскости упруго ударяется горизонтально летящий со скоростью V = 3 м/с шарик (рис.4). Найдите скорость шарика после удара, если масса пластины в 1,5 раза больше массы шарика.

Задача 13552

Однородная прямоугольная пластина может свободно вращаться вокруг вертикальной оси, проходящей по ее плоскости через середину. В край пластины перпендикулярно ее плоскости упруго ударяется горизонтально летящий со скоростью v = 3 м/с шарик (рис.4). Масса пластины в 1,5 раза больше массы шарика. Найдите угловую скорость вращения пластины сразу после удара. Длина ее горизонтальной стороны l = 80 см.

Задача 17338

Человек массы m = 60 кг находится на краю круглой неподвижной платформы, которая может свободно вращаться вокруг вертикальной оси, проходящей через ее центр. Радиус R платформы равен 1 м. С какой угловой скоростью |ω| начнет вращаться платформа, если человек пойдет по краю платформы со скоростью u = 2 м/с относительно платформы? Момент инерции J платформы принять равным 180 кг·м². Момент инерции человека рассчитывать как для материальной точки.

Задача 19195

Платформа в виде горизонтально расположенного диска может вращаться вокруг вертикальной оси, проходящей через центр платформы. На платформе находится человек, которого в условии задачи можно рассматривать как материальную точку. Расходом энергии на преодоление сил трения пренебречь. Человек массой 60 кг стоит на краю неподвижной платформы.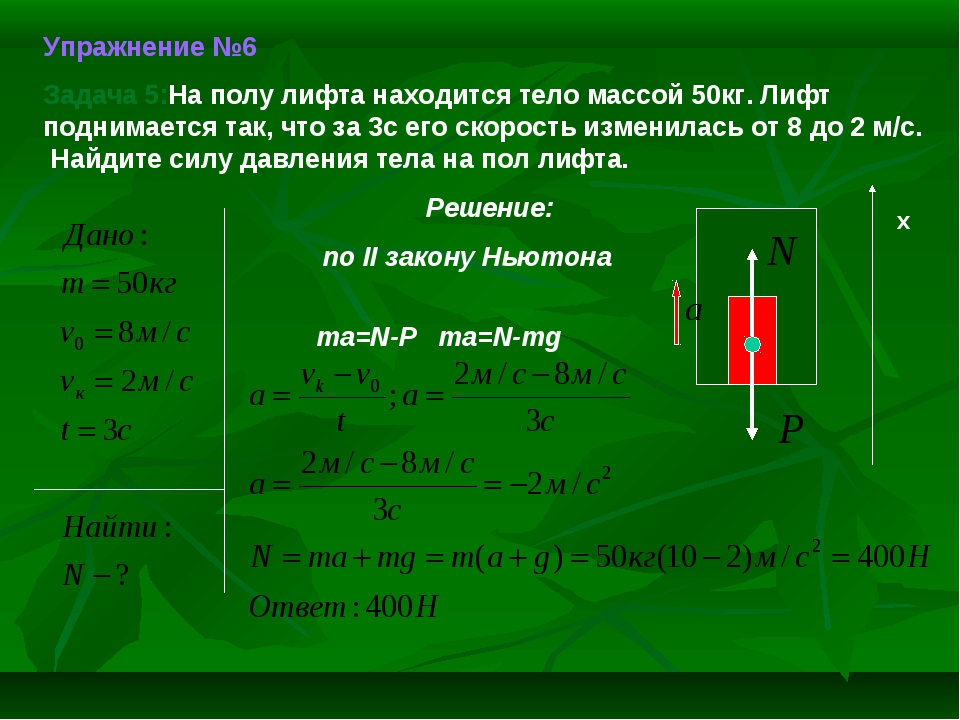 С какой скоростью (относительно платформы) должен пойти человек вдоль края платформы, чтобы она начала вращаться со скоростью, соответствующей 3,0 об/мин? Масса платформы 120 кг, ее радиус 2,0 м.

Задача 21318

Горизонтальная платформа массой M = 90 кг вращается вокруг вертикальной оса, проходящей через центр платформы. На платформе на расстоянии r₁ = 15,0 м от ее центра стоит человек массой m = 64 кг. Если человек перейдет на расстояние r₂ от центра платформы, частота ее вращения изменится в n = 1,75 раз. Найти r₂ (считать платформу однородным диском радиусом R = 16,0 м, а человека — точечной массой).

Задача 21233

Платформа в виде горизонтально расположенного диска может вращаться вокруг вертикальной оси, проходящей через центр платформы. На платформе находится человек, которого в условии задачи можно рассматривать как материальную точку. Расходом энергии на преодоление сил трения пренебречь. Человек массой 75 кг стоит на краю платформы, делающей 3 об/мин. С какой скоростью должен идти человек вдоль края платформы, чтобы его скорость относительно Земли стала равной нулю? Масса платформы 100 кг, ее радиус 1,6 м.

Задача 21347

Платформа в виде горизонтально расположенного диска может вращаться вокруг вертикальной оси, проходящей через центр платформы. На платформе находится человек, которого в условии задачи можно рассматривать как материальную точку. Расходом энергии на преодоление сил трения пренебречь. Человек массой 60 кг стоит на краю платформы массой 120 кг, делающей 3 об/мин. Сколько оборотов в минуту будет делать платформа, если человек перейдет на середину между краем и центром платформы?

StudyPort.Ru — Механика твердого тела

Страница 1 из 3

129. Выведите формулу для момента инерции тонкого кольца радиусом R и массой m относительно оси симметрии.

131. Выведите формулу для момента инерции сплошного шара радиусом R и массой m относительно оси, проходящей через центр масс шара.

132. Выведите формулу для момента инерции полого шара относительно оси, проходящей через его центр. Масса шара равна m, внутренний радиус r, внешний R.

133. Вывести формулу для момента инерции цилиндрической муфты относительно оси, совпадающей с её осью симметрии. Масса муфты равна m, внутренний радиус r, внешний R.

134. Определите момент инерции сплошного однородного диска радиусом R = 40 см и массой m = 1 кг относительно оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска.

135. Определить момент инерции J тонкого однородного стержня длиной l = 50 см и массой m = 360 г относительно оси, перпендикулярной стержню и проходящей через: 1) конец стержня; 2) точку, отстоящую от конца стержня на 1/6 его длины.

136. Шар и сплошной цилиндр, изготовленные из одного и того же материала, одинаковой масса катятся без скольжения с одинаковой скоростью. Определить, во сколько раз кинетическая энергия шара меньше кинетической энергии сплошного цилиндра.

137. Полная кинетическая энергия T диска, катящегося по горизонтальной поверхности, равна 24 Дж. Определите кинетическую энергию T₁ поступательного и T₂ вращательного движения диска.

138. Полый тонкостенный цилиндр массой m = 0,5 кг, катящийся без скольжения, ударяется о стену и откатывается от нее. Скорость цилиндра до удара о стену v₁ = 1,4 м/с, после удара v`₁ = 1 м/с. Определить выделившееся при ударе количество теплоты.

139. К ободу однородного сплошного диска массой m = 10 кг, насаженного на ось, приложена постоянная касательная сила F = 30 Н. Определить кинетическую энергию через время t = 4 с после начала движения силы.

Задачи по динамике с подробными решениями

Задачи по динамике с решениями

Сила, импульс, законы Ньютона

2. 1.1 Тело движется прямолинейно под действием силы 16 Н. Зависимость пути от времени
2.1.2 Тело массой 3 кг движется горизонтально с ускорением 4 м/с2. Определить
2.1.3 На тело массой 5 кг подействовали горизонтальной силой 4 Н. Какую скорость
2.1.4 Под действием какой силы прямолинейное движение частицы массой 100 г
2.1.5 Под действием горизонтальной силы, равной 12 Н, тело движется по горизонтальной
2.1.6 Определить плотность тела массой 100 г и объемом
2.1.7 Определить вес человека массой 70 кг в лифте, опускающемся равнозамедленно
2.1.8 С какой силой давит человек массой 70 кг на вертикальную спинку сиденья
2.1.9 К нити подвешен груз массой 1 кг. Определить силу натяжения нити, если нить
2.1.10 К нити подвешен груз массой 1 кг, который опускается с ускорением 5 м/с2
2.1.11 Поезд, подъезжая к станции со скоростью 72 км/ч, начинает тормозить. Каково
2.1.12 Поезд, подъезжая к станции со скоростью 60 км/ч, тормозит. За какое минимальное
2.1.13 При каком ускорении разорвется трос, прочность которого на разрыв равна
2.1.14 Груз массой 2 кг подвешен на динамометре. Снизу груз тянут с силой 10 Н
2.1.15 Автомобиль массой 1,2 т движется с места с ускорением 0,8 м/с2. Какую силу тяги
2.1.16 Под действием силы 30 Н тело поднимается вверх с ускорением 10 м/с2. Определить
2.1.17 Тело массой 3 кг падает в воздухе вертикально вниз с ускорением 8 м/с2
2.1.18 С какой силой давит тело массой 2 кг на пол лифта, поднимающегося с ускорением
2.1.19 Шар массой 0,1 кг движется со скоростью 5 м/с. После удара о стенку шар стал
2.1.20 Автомобиль массой 2 т, двигаясь равноускоренно, через 4 с достиг скорости 2 м/с
2.1.21 На тело массой 15 кг, лежащее на земле, действует направленная вверх сила 45 Н
2.1.22 Автомобиль массой 2 т, трогаясь с места, прошел путь 100 м за 10 с. Найти
2.1.23 Тело массой 50 г, падающее со скоростью 2 м/с, упруго соударяется с горизонтальной
2.1.24 Из орудия вылетает снаряд массой 10 кг со скоростью 500 м/с. Найти силу давления
2.1.25 Скорость автомобиля изменяется по закону v=10+0,5t. Найдите результирующую
2.1.26 Два автомобиля массами m и 2m движутся в одном направлении с одинаковыми
2.1.27 Пуля массой 10 г, летевшая со скоростью 400 м/с, пробив доску толщиной 5 см
2.1.28 Пуля массой 9 г, летевшая со скоростью 600 м/с, попадает в деревянную стену
2.1.29 На тело, движущееся по горизонтальной поверхности, действуют следующие силы
2.1.30 На участке дороги, где для автотранспорта установлена предельная скорость 30 км/ч
2.1.31 Найти модуль изменения импульса шарика массой 20 г за 3 с свободного падения
2.1.32 Определить натяжение каната, к которому подвешена клеть подъемной машины
2.1.33 Парашютист, достигнув в затяжном прыжке скорости 55 м/с, раскрыл парашют
2.1.34 Канат может выдержать нагрузку 2,5 кН. С каким максимальным ускорением можно
2.1.35 Летящая пуля попадает в мешок с песком и углубляется на 15 см. На какую глубину
2.1.36 Металлический шарик массой 100 г падает на горизонтальную плоскость с высоты 20 см
2.1.37 Мяч массой 0,15 кг ударяется о гладкую стенку под углом 30 градусов к ней
2.1.38 Вор, масса которого вместе с добычей 125 кг, убегая, налетает на камень. Столкновение
2.1.39 Два автомобиля с одинаковыми массами m движутся со скоростями v и 2v
2.1.40 Две стальные проволоки одинаковой длины, диаметр первой в 3 раза больше
2.1.41 Ракета на старте с поверхности Земли движется вертикально вверх с ускорением
2.1.42 С каким ускорением будет опускаться груз на нити, если сила натяжения нити в 1,25
2.1.43 С какой минимальной силой, направленной горизонтально, нужно прижать плоский
2.1.44 С какой силой давит человек массой 70 кг на пол лифта, движущегося вниз с ускорением
2.1.45 С какой силой следует придавить тело массой 4,5 кг к вертикальной стене, чтобы
2.1.46 Автомобиль идет по горизонтальной дороге со скоростью 72 км/ч. Найти тормозной
2.1.47 Тело массой 5 кг покоится на горизонтальной поверхности.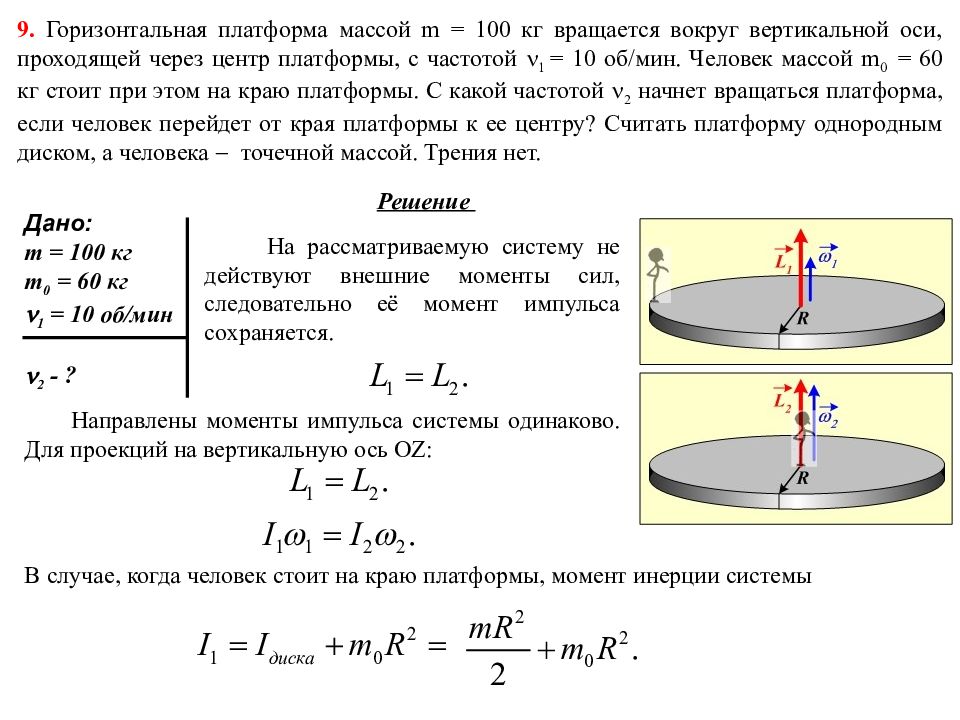 К телу приложена сила
2.1.48 Тело, брошенное вертикально вверх с начальной скоростью 30 м/с, достигло высшей
2.1.49 Три бруска, массы которых 0,5, 0,3 и 0,1 кг, связаны нитями и лежат на столе
2.1.50 Тело массой 1,5 кг движется вверх по вертикальной стенке под действием силы 20 Н
2.1.51 Тело массой 100 кг движется по горизонтальной поверхности под действием силы
2.1.52 Тело массой 200 кг упало на грунт со скоростью 100 м/с и погрузилось в него
2.1.53 Брусок массой 50 кг прижимается к вертикальной стенке с силой 100 Н. Какая сила
2.1.54 Троллейбус, масса которого 12 т, трогаясь с места, за 5 с проходит по горизонтальному
2.1.55 Через сколько секунд тело, брошенное вертикально вверх со скоростью 44,8 м/с
2.1.56 Чтобы на неподвижном блоке поднимать равномерно груз, требуется усилие 270 Н
2.1.57 На гладкой доске лежат два тела массами 2 и 3 кг, соединенные легкой нерастяжимой
2.1.58 Человек везет двое связанных между собой саней, прикладывая к веревке силу 120 Н
2.1.59 Тело массой 100 г движется вверх по вертикальной стенке под действием силы 2 Н
2.1.60 Груз массой 1 кг падает с высоты 240 м и углубляется в землю на 0,2 м. Определить
2.1.61 Дождевая капля массой 0,02 г под влиянием горизонтально дующего ветра падает
2.1.62 Материальная точка массой 1 кг движется со скоростью, которая изменяется по закону
2.1.63 Канат лежит на плоской горизонтальной крыше так, что часть его свешивается
2.1.64 Мяч массой 0,2 кг движется к стене под углом 30 градусов к ней со скоростью 6 м/с
2.1.65 Пуля массой 0,3 г, выпущенная из пневматической винтовки вертикально вверх, упала
2.1.66 Стержень длиной 0,9 м движется с ускорением под действием приложенной к его
2.1.67 Тело массой 2 кг начинает движение под действием постоянной по направлению
2.1.68 Что покажут пружинные весы в лифте при измерении веса груза массой 1 кг
2.1.69 Хоккейная шайба, имея начальную скорость 5 м/с, скользит до удара о борт площадки
2. 1.70 Два соприкасающихся бруска лежат на горизонтальном столе, по которому они могут
2.1.71 Есть два способа закинуть льдинку: бросить её под углом 45 градусов к горизонту или
2.1.72 К вертикальной стенке с силой 40 Н, направленной горизонтально, прижимается брусок
2.1.73 На гладкой поверхности лежит доска массой 5 кг, на ней находится тело массой 3 кг
2.1.74 Струя сечением 6 см2 ударяет из брандспойта в стенку под углом 60 градусов к нормали
2.1.75 На скользкой дороге коэффициент трения между дорогой и колесами мотоцикла
2.1.76 Груз массой 10 кг привязан к свободно свисающему концу веревки, намотанной
2.1.77 Координаты тела массы m=1 кг, движущегося прямолинейно вдоль оси x, меняются
2.1.78 Камень брошен под углом 60 градусов к горизонту. Как соотносятся между собой
2.1.79 Молекула массы m, летящая со скоростью v, ударяется о стенку сосуда под углом a
2.1.80 К невесомой нити подвешен груз массы 1 кг. Точка подвеса нити движется
2.1.81 Четыре одинаковых кубика, связанные невесомыми нитями, движутся по гладкому
2.1.82 Два тела масс m1 и m2, связанные невесомой нитью, лежат на гладкой горизонтальной
2.1.83 Стержень длины L движется по гладкой горизонтальной поверхности. Какая упругая
2.1.84 Тело массы 10 кг движется по горизонтальной плоскости под действием силы
2.1.85 В кузове автомобиля лежит груз. При каком минимальном ускорении автомобиля груз
2.1.86 На шероховатой горизонтальной поверхности лежит тело массы 1 кг. Коэффициент
2.1.87 Тело массы m движется под действием силы F. Как изменится модуль ускорения тела
2.1.88 Тело массы m движется под действием двух равных по модулю взаимно
2.1.89 Тело массы 2 кг движется с результирующим ускорением 5 м/с2 под воздействием
2.1.90 На материальную точку массы 1 кг действует две постоянные взаимно перпендикулярные

Неподвижный блок

2.2.1 Через неподвижный блок перекинута нить с грузами массой 3 и 5 кг. С каким ускорением
2.2.2 Три груза массами m1=1 кг, m2=2 кг, m3=3 кг соединены легкими нитями, проходящими
2. 2.3 Через неподвижный блок перекинута нить, к концам которой подвешены грузы
2.2.4 Два грузика массами m1=0,3 кг и m2=0,2 кг соединены нитью, перекинутой через блок
2.2.5 Два одинаковых груза массами 0,1 кг связаны между собой нитью, перекинутой
2.2.6 Две гири неравной массы висят на концах нити, перекинутой через невесомый блок
2.2.7 Через невесомый блок перекинута нерастяжимая нить, к одному из концов которой
2.2.8 К концам нерастянутой нити, перекинутой через застопоренный блок, подвешенный
2.2.9 К одному концу невесомой и нерастяжимой нити, перекинутой через невесомый блок

Наклонная плоскость

2.3.1 Тело скользит с постоянной скоростью вниз по наклонной плоскости с углом наклона
2.3.2 Льдинка скользит по инерции вверх по наклонной плоскости с углом наклона
2.3.3 По канатной дороге, идущей с уклоном 30 градусов к горизонту, опускается вагонетка
2.3.4 По наклонной плоскости с углом наклона 30 градусов к горизонту скользит вниз тело
2.3.5 Санки можно удержать на ледяной горке с уклоном 0,2 (отношение высоты к длине)
2.3.6 Тело массой 1 кг, имеющее у основания наклонной плоскости скорость 6 м/с
2.3.7 Тело скользит равномерно по наклонной плоскости, угол наклона которой 30 градусов
2.3.8 Тело соскальзывает без начальной скорости с наклонной плоскости. Угол наклона
2.3.9 Автомобиль при полностью включенных тормозах (колеса не вращаются) может
2.3.10 С ледяной горки высотой 3 м и длиной основания 5 м съезжают санки, которые
2.3.11 Брусок массой 3 кг находится на наклонной плоскости, составляющей угол 45 градусов
2.3.12 Брусок сползает без начальной скорости с высоты 2 м по доске, наклоненной
2.3.13 Ледяная гора составляет с горизонтом угол 30 градусов, по ней снизу вверх пускают
2.3.14 Ледяная горка составляет с горизонтом угол 10 градусов. По ней пускают вверх камень
2.3.15 С каким ускорением движутся грузы m1=0,5 кг и m2=0,6 кг, если высота наклонной
2.3.16 С горы высотой 2 м и основанием 5 м съезжают санки, которые затем останавливаются
2. 3.17 Чему должен быть равен минимальный коэффициент трения между шинами
2.3.18 Два бруска одинаковой массы 0,2 кг поставили на наклонную плоскость с углом
2.3.19 На тележке, скатывающейся без трения с наклонной плоскости, установлен стержень
2.3.20 По наклонной плоскости с углом наклона 60 градусов соскальзывает без трения клин
2.3.21 Груз поднимают с помощью ленточного транспортера, расположенного под углом
2.3.22 На горизонтальной доске лежит брусок. Коэффициент трения скольжения между бруском

Центростремительное ускорение

2.4.1 Мальчик массой 50 кг качается на качелях с длиной подвеса 4 м. С какой силой он давит
2.4.2 Автомобиль едет по выпуклому мосту, имеющему радиус кривизны 60 м. При какой
2.4.3 Автомобиль массой 5 т движется с постоянной по модулю скоростью 10 м/с
2.4.4 Гирька массой 0,05 кг, привязанная к нити длиной 0,26 м, описывает в горизонтальной
2.4.5 Гиря массой 100 г равномерно вращается на нити в вертикальной плоскости
2.4.6 Горизонтально расположенный диск равномерно вращается вокруг вертикальной оси
2.4.7 Диск вращается с частотой 70 об/мин. На каком расстоянии от оси вращения можно
2.4.8 На горизонтальной вращающейся платформе на расстоянии 1,15 м от её вертикальной
2.4.9 Определить силу, действующую на летчика, выводящего самолет из пикирования
2.4.10 Поезд движется по закруглению радиуса 765 м со скоростью 72 км/ч. Определить
2.4.11 Трактор массой 8 т проходит по мосту со скоростью 36 км/ч. Какова сила давления
2.4.12 Конькобежец движется по закруглению ледяной дорожки радиусом 2,5 м со скоростью
2.4.13 Шоссе имеет вираж с уклоном 10 градусов при радиусе закругления дороги в 100 м
2.4.14 Камень, подвешенный к потолку на веревке, движется в горизонтальной плоскости
2.4.15 В желобе, наклоненном под углом 30 градусов к горизонту и вращающемся с частотой
2.4.16 Гирька массой 0,1 кг, привязанная легкой нерастяжимой нитью, описывает окружность
2.4.17 Груз массой 1 кг, привязанный к нити, отклоняют на 90 градусов от положения
2. 4.18 Груз, подвешенный на нити длиной 5 м, равномерно движется по окружности
2.4.19 Груз, подвешенный на нити длиной 98 см, равномерно вращается по окружности
2.4.20 Лыжник съезжает с вершины горы. На какой высоте от начала движения его давление
2.4.21 Люстра массой 10 кг висит на цепи, прочность которой 196 Н. На какой максимальный угол
2.4.22 На легкой нерастяжимой нити подвешен тяжелый шарик. На какой угол нужно отвести
2.4.23 Нить может выдержать силу натяжения 25,4 Н. На нити подвесили тело массой 2 кг
2.4.24 По гладкому столу вращается груз, прикрепленный к центру вращения пружиной
2.4.25 Поезд движется по закруглению со скоростью 50 км/ч. Шарик, подвешенный в вагоне
2.4.26 Подвешенный на нити шарик массой 0,3 кг совершает колебания в вертикальной
2.4.27 Шарик массой 200 г на нити длиной 3 м описывает в горизонтальной плоскости
2.4.28 Тело массой 4 кг вращают в вертикальной плоскости с помощью резинового шнура
2.4.29 К потолку лифта на нити длиной 40 см прикреплен шар массой 800 г, который вращается
2.4.30 Какова должна быть максимальная длина выпуклого симметричного относительно
2.4.31 Маленький шарик, подвешенный на нити, движется по окружности так, что нить
2.4.32 Мотоциклист движется по цилиндрической стенке диаметра 12 м. При каком коэффициенте
2.4.33 Спортивный молот – ядро на тросике длиной L, бросают, раскрутив вокруг себя
2.4.34 Тележка, скатившаяся по наклонному желобу с высоты 10 м, описывает в вертикальной
2.4.35 Чаша в форме полусферы радиусом 0,8 м вращается с постоянной угловой скоростью
2.4.36 Автомобиль движется по выпуклому мосту радиусом 40 м. Какое максимальное
2.4.37 Тело массой 0,1 кг вращается в вертикальной плоскости на нити длиной 1 м. Ось
2.4.38 На горизонтально расположенном диске, вращающемся с частотой 60 об/мин, помещают
2.4.39 На конце стержня длиной 10 см укреплен груз массы 0,4 кг, приводимый во вращение
2.4.40 Бусинка может скользить вдоль гладкого кольца радиуса R, расположенного
2. 4.41 Цилиндр радиуса R, расположенный вертикально, вращается вокруг своей оси
2.4.42 Цилиндр радиуса R, расположенный вертикально, вращается вокруг своей оси с постоянной
2.4.43 В сельском хозяйстве применяются дисковые разбрасыватели удобрений. Какой должна

Закон всемирного тяготения

2.5.1 Во сколько раз уменьшится сила тяготения тела к Земле при удалении его
2.5.2 Определить силу взаимодействия тела массой 2 кг и Земли, если тело удалено от
2.5.3 Во сколько раз ускорение свободного падения около поверхности Земли больше
2.5.4 Искусственный спутник Земли движется на высоте 12800 км. Найти скорость движения
2.5.5 Каково ускорение свободного падения на поверхности Солнца, если радиус Солнца
2.5.6 На какое расстояние от поверхности Земли нужно удалить тело, чтобы сила тяготения
2.5.7 Определить первую космическую скорость для планеты, масса и радиус которой в два
2.5.8 На некоторой планете сила тяжести, действующая на тело массой 4 кг, равна 8 Н. Найти
2.5.9 На сферической планете вес тела на полюсе в 3 раза больше веса тела на экваторе
2.5.10 Сколько метров пройдет тело, свободно падая без начальной скорости в течение трех
2.5.11 Чему равно ускорение свободного падения на высоте, равной половине радиуса
2.5.12 Определить, с каким ускорением падают тела на поверхность Луны, зная, что радиус
2.5.13 Человек на Земле прыгает на высоту 1 м. На какую высоту, совершив ту же работу, он
2.5.14 Во сколько раз период обращения искусственного спутника, совершающего движение
2.5.15 Определить плотность шарообразной планеты, если вес тела на полюсе в 2 раза больше
2.5.16 На экваторе некоторой планеты тела весят вдвое меньше, чем на полюсе. Плотность
2.5.17 На экваторе некоторой планеты тела весят втрое меньше, чем на полюсе. Период
2.5.18 Тело поднялось на высоту 1600 км над поверхностью Земли. На сколько процентов
2.5.19 Определить минимальный период обращения спутника нейтронной звезды. Её плотность
2.5.20 Радиус Земли равен 6400 км. Какую скорость имеют точки земной поверхности на широте
2.5.21 На каком расстоянии от центра Земли (в долях радиуса Земли R) ускорение свободного
2.5.22 Радиус Земли равен 6400 км. На каком расстоянии от поверхности Земли сила притяжения

Упругая сила

2.6.1 Для сжатия пружины на 2 см надо приложить силу 10 Н. Определить энергию упругой
2.6.2 Какую работу надо совершить, чтобы удлинить на 0,1 м резиновый шнур с коэффициентом
2.6.3 Под действием силы 4 Н пружина удлинилась на 2 см. Чему равна при этом
2.6.4 Какова начальная скорость шарика массой 1 г, которым выстрелили из пружинного
2.6.5 При вращении шарика, прикрепленного к пружине длиной 20 см, с частотой вращения
2.6.6 Груз массой 1 кг, прикрепленный к пружине, равномерно тянут по горизонтальной
2.6.7 Каков коэффициент жесткости буксировочного троса, если при буксировке автомобиля
2.6.8 Найти удлинение буксирного троса с жесткостью 100 кН/м при буксировке автомобиля
2.6.9 Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины
2.6.10 Тело массой 2 кг тянут по горизонтальной поверхности с помощью пружины, которая
2.6.11 Сила в 6 Н растягивает пружину на 2 см. Какую работу надо произвести, чтобы
2.6.12 К резинке длиной 50 см привязана гирька массой 20 г. При вращении гирьки
2.6.13 Груз массой 4 кг подвешен на пружине жесткостью 1 кН/м. Определите дополнительную
2.6.14 Какую минимальную работу необходимо совершить, чтобы передвинуть по
2.6.15 Деревянный брусок массы 2 кг тянут равномерно по горизонтальной доске с помощью

Работа, мощность, энергия

2.7.1 Какую работу надо совершить, чтобы растянуть пружину с жесткостью 40 кН/м
2.7.2 Какую работу совершает постоянная сила по перемещению на 5 м тела массой 3 кг
2.7.3 Определить работу, необходимую для поднятия груза массой 3 кг на высоту 10 м
2.7.4 Автомобиль поднимается в гору со скоростью 36 км/ч. Определить силу тяги мотора
2.7.5 Пуля массой 10 г вылетает из винтовки со скоростью 600 м/с. Определить работу
2.7.6 Автомобиль массой 1800 кг, двигаясь с ускорением 2 м/с2, прошел 100 м пути
2.7.7 Найти кинетическую энергию стрелы массой 0,5 кг, пущенную вертикально вверх
2.7.8 Мальчик везет санки, прилагая к веревке силу 10 Н, которая образует угол 30 градусов
2.7.9 При подъеме тела массой 10 кг на высоту 2 м совершена работа 230 Дж
2.7.10 Санки тянут на пути 100 м с силой 80 Н за веревку, составляющую угол 30 градусов
2.7.11 Во сколько раз изменится запас потенциальной энергии упруго деформированного тела
2.7.12 При торможении автомобиля массой 1 т скорость уменьшилась от 72 км/ч до 36 км/ч
2.7.13 Автомобиль массой 1500 кг, двигаясь равноускоренно, проходит путь 20 м за 2 с
2.7.14 На какой высоте над поверхностью Луны тело будет обладать такой же потенциальной
2.7.15 Определить работу, которую нужно произвести для того, чтобы сжать пружину на 10 см
2.7.16 Определить массу тела, имеющего кинетическую энергию 16 Дж, а импульс
2.7.17 Тело массой 1 кг начинает свободно падать. Определить мощность силы тяжести
2.7.18 Автомобиль массой 1,5 т едет со стоянки с постоянным ускорением 2 м/с2. Коэффициент
2.7.19 Автомобиль движется со скоростью 72 км/ч. Мощность двигателя 60 кВт, его КПД 30%
2.7.20 Вертолет весит 3 т. На его подъем тратится 30% мощности мотора. Определить
2.7.21 Двигатели электровоза при движении со скоростью 72 км/ч потребляют мощность
2.7.22 Какая работа совершается внешней силой при поднятии тела массой 5 кг на высоту
2.7.23 Какую работу должен совершить двигатель, чтобы разогнать по горизонтальной
2.7.24 Какую работу надо совершить, чтобы поднять груз массой 30 кг на высоту 10 м
2.7.25 Какую работу надо совершить, чтобы поднять груз массой 3000 кг на высоту 10 м
2.7.26 Какую среднюю мощность и силу тяги должен развивать электровоз, чтобы состав массой
2.7.27 Камень брошен под углом 30 градусов к горизонту. 3 (м). Определите
2.7.38 Футбольный мяч весом 8 Н летит со скоростью 15 м/с. Вратарь ловит мяч и за 0,1 с
2.7.39 Пуля летит со скоростью v0. Она пробивает доску толщиной 3,6 см и продолжает полет
2.7.40 Максимальная высота подъема тела массой 2 кг, брошенного с поверхности Земли
2.7.41 На рисунке приведена зависимость потенциальной энергии от времени движения
2.7.42 Начальная скорость пули 600 м/с, её масса 10 г. Под каким углом к горизонту она
2.7.43 Самолет массой 2 т летит со скоростью 50 м/с. На высоте 420 м он переходит на снижение
2.7.44 Тело массой 3 кг падает вертикально вниз с начальной скоростью 2 м/с. Найти работу
2.7.45 Трактор имеет тяговую мощность на крюке, равную 72 кВт. С какой скоростью может
2.7.46 Трактор массой 10 т и мощностью 150 кВт поднимается в гору со скоростью 5 м/с
2.7.47 Ядро массой 8 кг, выпущенное метателем под углом 45 градусов к горизонту с высоты
2.7.48 Допустим, что сила, которая заставляет баржу двигаться по каналу, прямо пропорциональна
2.7.49 Конькобежец движется по горизонтальному пути равномерно, а затем с разгона проезжает
2.7.50 Для растяжения недеформированной пружины на 1 см требуется сила, равная 30 Н
2.7.51 Шайба массы 0,1 кг, пущенная по льду с начальной скоростью 0,5 м/с, остановилась
2.7.52 На тело массы 5 кг действует постоянная сила 10 Н. Чему будет равна кинетическая
2.7.53 Какой кинетической энергией обладает свободно падающее тело массой 0,1 кг
2.7.54 Чему равна кинетическая энергия тела массы 0,2 кг, брошенного вертикально вверх
2.7.55 Камень брошен под углом 60 градусов к горизонту. Как соотносятся между собой
2.7.56 Тело брошено вертикально вверх со скоростью 30 м/с. Если принять потенциальную
2.7.57 Шарик, подвешенный на нити, качается в вертикальной плоскости так, что его ускорения

Законы сохранения энергии и импульса

2.8.1 Камень массой 1 кг бросили вертикально вверх с начальной скоростью 2 м/с
2.8.2 Найти скорость винтовки при отдаче, если её масса в 500 раз больше массы пули
2. 8.3 Снаряд массой 20 кг, летевший горизонтально, попадает в платформу с песком массой
2.8.4 Тело находится на краю горизонтальной плоскости. Затем этот край плоскости
2.8.5 Какую скорость приобретает ракета массой 2 кг, если продукты горения массой
2.8.6 Тело массой 2 кг падает с высоты 10 м и углубляется в песок на глубину 0,5 м
2.8.7 Брусок массой 1 кг первоначально покоился на вершине наклонной плоскости
2.8.8 Велосипедист движется со скоростью 8 м/с. Определить расстояние, пройденное
2.8.9 Мальчик, стреляя из рогатки, натянул резиновый шнур так, что шнур растянулся
2.8.10 Винтовка массой 2,8 кг подвешена горизонтально на двух параллельных нитях
2.8.11 Во сколько раз изменится потенциальная энергия пружины при увеличении
2.8.12 Два шарика движутся навстречу друг другу со скоростями 1 и 0,5 м/с. После удара
2.8.13 Камень массой 2 кг брошен вертикально вверх, его начальная кинетическая энергия
2.8.14 Маленький шарик массой m, закрепленный на нерастяжимой нити в поле силы
2.8.15 Мальчик раскачивается на качелях. При максимальном отклонении от положения
2.8.16 Оконная штора массой 1 кг и длиной 2 м навертывается на валик, расположенный
2.8.17 Под каким углом к горизонту нужно бросить камень, чтобы в верхней точке траектории
2.8.18 При выстреле из орудия снаряд получил начальную скорость 300 м/с и летит
2.8.19 Телеграфный столб длиной 7 м и массой 140 кг при установке перемещается
2.8.20 Укажите график зависимости кинетической энергии свободно падающего тела
2.8.21 Чему равна работа по подъему лежащей цепи массой 50 кг и длиной 2 м, если
2.8.22 Подъемный кран поднимает груз массой 8 т на высоту 15 м. Определить время
2.8.23 Мяч бросили под углом к горизонту со скоростью 20 м/с. Найти скорость мяча
2.8.24 Какую минимальную работу необходимо совершить, чтобы лежащий на столе груз
2.8.25 На тело массой 1 кг, брошенное с поверхности Земли вертикально вверх с начальной
2.8.26 Пуля, летящая горизонтально со скоростью 510 м/с, попадает в ящик, лежащий
2. 8.27 Для откачки воды из шахты глубиной 20 м поставлен насос с двигателем мощностью
2.8.28 Какую работу надо совершить, чтобы поставить однородный куб массой 10 кг
2.8.29 Камень бросили под углом 60 градусов к горизонту со скоростью 15 м/с. Найдите
2.8.30 На нити длиной 1 м подвешено тело массой 1 кг. На какой максимальный угол
2.8.31 Пуля, летящая горизонтально со скоростью 400 м/с, попадает в ящик, лежащий
2.8.32 С какой начальной скоростью v0 нужно бросить вниз мяч с высоты h, чтобы он
2.8.33 Шарик массой m, подвешенный на нити, отклонен от положения равновесия на угол
2.8.34 Шарик подбросили вверх, сообщив ему кинетическую энергию 20 Дж. Через
2.8.35 Мяч падает с высоты 7,5 м на гладкий пол. Какую скорость нужно сообщить мячу
2.8.36 Тело, брошенное с вышки высотой 10 м, упало на землю со скоростью 15 м/с
2.8.37 Мяч скатился с горы высотой 20 м и после короткого горизонтального участка упал
2.8.38 Пуля массой 9 г, летевшая вертикально вверх со скоростью 200 м/с, пробила
2.8.39 Горизонтально летящая пуля массой 10 г насквозь пробивает первоначально
2.8.40 На вершине шара радиусом 30 см лежит небольшая шайба. После легкого толчка
2.8.41 Определите время подъема камня массой 1 кг, брошенного под углом к горизонту
2.8.42 Пуля массой 10 г подлетает к доске массой 1 кг со скоростью 600 м/с и, пробив ее
2.8.43 Тело скользит вниз по наклонной плоскости, плавно переходящей в вертикальную
2.8.44 В школьном опыте с “мертвой петлей” шарик массой 0,1 кг отпущен с высоты h=3R
2.8.45 Вертикальный невесомый стержень длиной 6 м подвешен одним концом к оси
2.8.46 Колодец, имеющий глубину 5 м, площадь дна 0,5 м2, наполовину заполнен водой
2.8.47 Небольшое тело скользит с вершины полусферы вниз. На какой высоте h от вершины
2.8.48 Небольшое тело соскальзывает вниз по наклонному скату, переходящему в мертвую
2.8.49 Небольшое тело соскальзывает по наклонной плоскости, переходящей в мертвую
2.8.50 Плавательный бассейн площадью 100 м2 заполнен водой до глубины 2 м. Требуется
2.8.51 Подвешенному на нити длиной 1 м шарику сообщили начальную скорость такую
2.8.52 При ударе шарика об идеально гладкую горизонтальную поверхность теряется третья
2.8.53 Шарик на нити отклонили от вертикали на 60 градусов и отпустили без начальной

Абсолютно упругий удар

2.9.1 Тело массой 1 кг упруго ударяется о покоящееся тело массой 3 кг и летит обратно
2.9.2 Шарик массой 100 г упал с высоты 2,5 м на горизонтальную плиту, масса которой
2.9.3 Во сколько раз уменьшится энергия нейтрона n при столкновении с ядром углерода C
2.9.4 Гранату бросают от поверхности земли под углом 30 градусов к горизонту
2.9.5 Два упругих стальных шара массами m1=0,2 кг и m2=0,1 кг подвешены рядом
2.9.6 Шарик подлетает к неподвижной вертикальной стенке сверху со скоростью 10 м/с
2.9.7 На горизонтальной поверхности в 3 м от вертикальной стенки находится шар массой

Абсолютно неупругий удар

2.10.1 По абсолютно гладкой поверхности движется со скоростью 6 м/с ящик с песком
2.10.2 Тележка массой 100 кг движется со скоростью 2 м/с. Когда она проезжает мимо
2.10.3 Найти количество теплоты, выделившееся при лобовом абсолютно неупругом ударе
2.10.4 Охотник стреляет из ружья. Определить силу отдачи, если масса дроби 35 г
2.10.5 Шары массами 1 и 2 кг движутся навстречу друг другу. Скорость первого шара 5 м/с
2.10.6 Два шара массами 0,3 и 0,2 кг движутся навстречу друг другу. Скорость первого шара
2.10.7 Охотник стреляет с легкой надувной лодки, находящейся в покое. Какую скорость
2.10.8 Груз массой 0,5 кг падает с некоторой высоты на плиту массой 1 кг, укрепленную
2.10.9 Масса пушки 800 кг. Пушка выстреливает ядро массой 10 кг с начальной скоростью
2.10.10 На вагонетку массой 800 кг, катящуюся по горизонтальным рельсам со скоростью
2.10.11 На тележку с песком массой 49 кг, движущуюся по прямой со скоростью 1 м/с, падает
2.10.12 Пушка, стоящая на горизонтальной поверхности, стреляет под углом 30 градусов
2. 10.13 Свинцовый шар массой 500 г, движущийся со скоростью 10 м/с, соударяется
2.10.14 Стоящий на льду человек массой 60 кг ловит мяч массой 0,5 кг, который летит
2.10.15 Тележка движется по горизонтальной поверхности со скоростью 0,5 м/с. Её догоняет
2.10.16 Конькобежец, стоя на льду, бросил вперед гирю массой 5 кг и вследствие отдачи
2.10.17 Два мальчика играют в мяч, стоя на льду на расстоянии 10 м друг от друга
2.10.18 Вагон массой 50 т движется со скоростью 12 км/ч и встречает стоящую на пути
2.10.19 Конькобежец, стоя на льду, бросает горизонтально с высоты 1,5 м груз массой 10 кг
2.10.20 Кусок пластилина массой m=32 г попадает в брусок массой 6m, двигавшийся
2.10.21 На горизонтальном столе лежит деревянный брусок массой 5 кг. В брусок попадает
2.10.22 По горизонтальной поверхности стола скользит брусок массой m и сталкивается
2.10.23 Пуля массой 10 г застревает в первоначально покоящемся бруске, масса которого 0,1 кг
2.10.24 Мальчик, стоя на Земле, бросает камень горизонтально со скоростью 5 м/с
2.10.25 В покоящийся шар массой 1 кг, подвешенный на стержне, попадает пуля массой
2.10.26 Найти количество теплоты, выделившейся при абсолютно неупругом ударе свинцового
2.10.27 Два груза массами 0,04 и 0,01 кг соединены невесомой нитью, переброшенной
2.10.28 В шар массой 1,5 кг, подвешенный на нерастяжимой нити длиной 55 см, попадает
2.10.29 Какая доля кинетической энергии перейдет в теплоту при неупругом столкновении
2.10.30 Тележка стоит на гладких рельсах. Человек переходит с одного её конца на другой
2.10.31 Человек массой 80 кг захотел спуститься по веревочной лестнице из свободно
2.10.32 Два шарика массами 2 и 3 г движутся в горизонтальной плоскости со скоростями
2.10.33 Космический корабль на скорости 10 км/с попадает в неподвижное облако
2.10.34 На горизонтальной плоскости сделан выстрел из винтовки, ствол которой направлен
2.10.35 С незакрепленной горки (клина) массой 1 кг соскальзывает тело массой 500 г. Угол
2.10.36 Снаряд, выпущенный из пушки под углом 45 градусов к горизонту, разрывается
2.10.37 Человек, сидящий в лодке, бросает камень под углом 60 градусов к горизонту. Масса

Новосибирский государственный архитектурно-строительный университет — Сибстрин

Губернатор Андрей Травников поручил ускорить внедрение цифровых технологий в строительной отрасли региона

26 марта 2021 года на базе Новосибирского государственного архитектурно-строительного университета (Сибстрин) состоялся круглый стол регионального Министерства строительства «Применение BIM-технологий в строительной отрасли Новосибирской области», участие в котором принял Губернатор А.А. Травников. В ходе круглого стола представители Правительства региона, НГАСУ (Сибстрин) и строительного сообщества обсудили вопросы применения BIM-технологий в строительной отрасли. В частности, рассматривались вопросы подготовки в Новосибирской области специалистов по технологиям информационного моделирования, практического применения BIM-технологий при проектировании конкретных объектов, например, физкультурно-оздоровительного комплекса с искусственным льдом в Калининском районе Новосибирска.

В эту субботу НГАСУ (Сибстрин) приглашает на День открытых дверей!

27 марта 2021 года в 12.00 в Новосибирском государственном архитектурно-строительном университете (Сибстрин) состоится день открытых дверей для абитуриентов, их родителей и всех желающих. http://www.sibstrin.ru/ День открытых дверей – это замечательная возможность получить представление о будущей профессии, встретиться с профессорско-преподавательским составом и студентами, получить консультации по вопросам поступления, проникнуться уникальной атмосферой, царящей в университете. В программе мероприятия: Встреча с руководством НГАСУ (Сибстрин). Консультации по вопросам поступления, об изменениях в правилах приема в университет.

Информационная программа о факультетах, институтах и кафедрах. Выставки, мастер-классы, экскурсии по университету.

НГАСУ (Сибстрин) посетил Губернатор Новосибирской области А.А. Травников

26 марта 2021 года Новосибирский государственный архитектурно-строительный университет (Сибстрин) посетил глава Новосибирской области А.А. Травников. Встреча началась со знакомства Губернатора и прибывших с ним официальных лиц – заместителя Губернатора С.А. Нелюбова, министра строительства Новосибирской области И.И. Шмидта, министра образования Новосибирской области С.В. Федорчука и помощника Губернатора по вопросам образования, науки и инноваций М.И. Ананич, с презентацией университета. Как рассказал ректор Ю.Л. Сколубович, в настоящее время НГАСУ (Сибстрин) является одним из значимых для Новосибирской области вузов, поскольку готовит специалистов в области архитектуры, строительства и жилищно-коммунального хозяйства – тех базовых отраслей…

В НГАСУ (Сибстрин) пройдет XIV Международная научно-техническая конференция «Актуальные вопросы архитектуры и строительства»

Уважаемые коллеги! В период с 30 марта по 1 апреля 2021 года Новосибирский государственный архитектурно-строительный университет (Сибстрин) проводит XIV Международную научно-техническую конференцию «Актуальные вопросы архитектуры и строительства». В программе конференции предусмотрены доклады профессорско-преподавательского состава, представителей строительных, проектных и научно-исследовательских организаций, государственных учреждений, а также отдельных исследователей. Мероприятие пройдет в смешанном формате.

человек весом 60 кг. Он стоит на весах в лифте, который движется 1) вверх с

. ВНИМАНИЕ !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

В случае, если яблоко стоит на столе, яблоко не падает, даже если направленная вниз сила (т. е. сила тяжести, действующая на яблоко), происходит из-за направленной вверх силы, действующей на яблоко, которая равна силе гравитации и имени этой силы — нормальная сила.

Как мы знаем, гравитационная сила, действующая на тело (F) = масса * сила тяжести

R = F

R = m * g

См. Диаграмму выше

Всякий раз, когда две силы действуют на тело и они равны силы, то тело не двигается, как в случае с яблоком.Другой пример из реальной жизни — перетягивание каната, когда на обе стороны действуют равные силы, и веревка не перемещается ни в какую сторону.

Когда скорость / скорость остаются неизменными (то есть равное расстояние / смещение, пройденное телом за равное время, это означает, что автомобилю требуется 2 метра, чтобы преодолеть 5 минут

, а в следующие 5 минут он преодолевает те же 2 метра и продолжает движение. быть таким же), тогда ускорение равно нулю {Как мы знаем, ускорение = изменение скорости (конечная скорость — начальная скорость) / время, следовательно, как в приведенном выше примере ускорения автомобиля = 2-2 / 5 + 5 = 0}

Как мы движемся вверх в лифте с увеличивающейся скоростью / скоростью, тогда ускорение не будет равно нулю, так как скорость меняется (конечная скорость больше начальной)

Поскольку лифт движется вверх, это означает, что нормальная сила (восходящая сила) увеличивается

R = mg + ma

По мере того, как мы движемся вниз в лифте с увеличением скорости / скорости, тогда ускорение не будет нулевым, но здесь сила тяжести (направленная вниз сила) увеличивается

mg = R + ma

Поскольку скорость постоянная, следовательно, ускорение равно нулю, но m двигаясь вверх, введите формулу, как указано выше, R = mg + ma.R = мг (как ускорение, т.е. a = 0). R = 60 * 10 = 600 Н или 600/10 = 60 кгс
Так как ускорение равномерное и он движется вниз, введите формулу, как указано выше, mg = R + ma. 60 * 10 = R + 60 * 4 R = 600N-240N = 360N или 360/10 = 36 кгс
Поскольку ускорение равномерное и движется вверх, введите формулу, как указано выше. R = mg + ma R = 60 * 10 + 60 * 4 R = 600 + 240 R = 840N или 840/10 = 84 кгс

Глава 4: Законы движения Ньютона

Пр. 4, 6, 11, 21, 22, 27, 31, 34, 36, 43; Пб 2, 3, 5

Упражнения (Обсуждение Вопросы)

Пр. 4.4 При отрыве бумажного полотенца или полиэтиленового пакета от перекат, почему быстрый резкий рывок более эффективен, чем длинный медленный тянуть?

Быстрый резкий рывок означает большее ускорение и большее ускорение означает большее усилие . А это сила разрывает бумажное полотенце или полиэтиленовый пакет.

Пример 4.6 До времен Галилея и Ньютона это считалось многие ученые ученые утверждали, что камень упал с вершины высокого мачта движущегося корабля упадет вертикально и ударится о палубу позади мачта на расстояние, равное тому, насколько далеко продвинулся корабль пока камень падал.В свете вашего понимания Законы Ньютона, что вы думаете по этому поводу?

Как мы видели на The Mechanical Video , и как я пытался продемонстрировать ходьбу взад и вперед перед в классе при броске мяча мяч или камень должны упасть и удариться о палубу у основания мачты.

Пример 4.11 Какова ваша собственная масса в килограммах? Ваш вес в ньютоны?

Напомним, что масса 1 кг соответствует весу 2.2 фунта. Найти массу в килограммах, возьмите свой вес в фунтах и разделите на 2,2 (это означает, что вес 2,2 фунта соответствует массе 1,0 фунта или вес 22 фунта соответствует массе 10 кг или весу 220 фунтов соответствует массе 100 кг.)

Напомним, что вес 1 кг составляет 9,8 ньютона. Чтобы найти свой вес в ньютонах, возьмите массу в килограммах и умножить на 9,8 .

Вот короткая таблица:

вес (в фунтах)	масса (в килограммах)	вес (в ньютонах)
100	45.5	446
125	56,8	557
150	68,2	668
175	79,5	779
200	90.9	891
225	102,3	1 003

Пр. 4.21 Нелли Ньютон неподвижно висит на концах веревки. как показано. Как показания на шкале соотносятся с ней? масса?

Ее тянут вверх две силы — сила, создаваемая каждая веревка на каждой руке.Те две силы уравновешиваются ею собственный вес. Таким образом, сила, оказываемая веревкой, равна , что составляет половину ее силы. вес . Сила, прилагаемая веревкой, называется натяжением . в тросе.

Пр. 4.22 Гарри художник меняет год через год с кресла боцмана. Его вес 500 Н и веревка, неизвестно ему, имеет предел прочности 300 Н. Почему веревка не сломаться, когда его поддерживают, как показано здесь, обоими концами веревки прикреплен к его стулу боцмана?

Однажды Гарри рисует возле флагштока и, для разнообразия, свободный конец веревки он привязывает к флагштоку, а не к своему стул, как показано здесь.Почему Гарри ушел в отпуск рано?

В его обычном методе подвешивания к стулу боцмана (показано на справа), веревка тянет Гарри вверх с двумя силами, так что каждый сила составляет всего , половина веса Гарри , а это всего 250 № . Но на скетче слева одним концом веревки прикрепленный к флагштоку, веревка тянется вверх только за за один силы, так что она должна быть равна всего веса Гарри , и что это 500 N .Но прежде чем это произойдет, веревка порвется (и Гарри падает!).

Ex 4.27 Два груза по 100 Н прикреплены к пружинной шкале в качестве показано. Показывает ли шкала 0, 100 или 200 Н, или дает другой чтение?

Каждая струна прилагает усилие 100 Н , чтобы подвешивать масса, к которой он прикреплен. Это означает, что натяжение в строка 100 N . Таким образом, масштаб будет 100 N .

Пример 4. 31 Какова чистая сила, действующая на яблоко, которое весит 1 Н, когда вы держите его в покое над полом? Какова чистая сила на нем, когда вы его отпускаете?

Для или в состоянии покоя чистая сила равна нулю.

Когда вы отпускаете яблоко, только усилие на нем является сила тяжести, которую мы называем вес яблока, и нам говорят, что это один Ньютон.

Пример 4.34 Почему можно прикладывать большее усилие к педалям велосипед, если за руль тянуть?

Когда вы тянете вверх на руле велосипеда, они сила вниз на вас, которую вы можете передать педали.

Пр. 4.36. Предположим, что две тележки, одна вдвое массивнее другой, разлетятся при отпускании соединяющей их сжатой пружины.Как быстрее катится более тяжелая тележка по сравнению с более легкой тележкой?

Силы на двух тележках будут одинаковыми (но противоположными направления). У более тяжелой тележки будет , половина . ускорение более легкого, так как у него вдвое больше масса.

Пример 4.43 Как вес падающего тела соотносится с весом сопротивление воздуха, с которым он сталкивается незадолго до достижения терминала скорость? После?

Не достигнув предельной скорости, падающее тело все еще ускоряется, поэтому его вес (сила тяжести) еще больше чем сила из-за сопротивления воздуха.

Достигнув предельной скорости, падающее тело падает с постоянная скорость, поэтому результирующая сила, действующая на него, должна быть равна нулю. Это означает сила тяжести (его вес), действующая вниз , просто уравновешивается силой действующего сопротивления воздуха вверх .

Pb 4.2 Если масса 1 кг ускоряется на 1 м / с ² силой 1 Н, что было бы ускорением 2 кг, на которое воздействует сила 2 Н?

Используйте второй закон Ньютона,

F = m a

2 = 2 х?

2 = 2 х

а = 1

a = 1 м / с ²

Пб 4.2 Сколько разгоняется гигантский реактивный самолет 747 массой 30? 000 кг стажа на взлете при тяге каждой по четырех двигателей это 30 000 Н (для общая тяга 120 000 Н)?

Снова воспользуйтесь Вторым законом Ньютона,

. F = m a

120 000 = (30 000) а

а = 4

a = 4 м / с ²

Pb 4.3 Если вы стоите у стены на скейтборде без трения и толкаем стену с силой 30 Н, насколько сильно стена толкает Вы? Если ваша масса 60 кг, какое у вас ускорение?

Из третьего закона Ньютона, закона действия и противодействия, мы знаем что стена также давит на вас с силой 30 Н .Теперь мы снова используем Второй закон Ньютона,

. F = m a

30 = (60) а

а = 0,5

a = 0,5 м / с ²

Pb 4.5 Пожарный массой 50 кг сползает с вертикального столба с ускорением 5 м / с ². Что делает сила трения полюс приложить к ней?

Во-первых, мы можем найти чистую силу , поскольку это всегда F который появляется во втором законе Ньютона,

F _net = F = m a

F _{, нетто} = (50 кг) (5 м / с ²)

F _сеть = 250 Н

Какие силы составляют эту чистую силу F _net? Гравитация тянет вниз с массой пожарного

w = m g

w = (50 кг) (10 м / с ^w)

ш = 500 Н

Затем следует сила трения , F _f, которая противится ее движению.Значит сила трения F _f должна указывать вверх . Чистая сила F _Чистая состоит из этих две силы,

F _сеть = w — F _f

250 N = 500 N — F _f

F _F = 250 Н

Дополнительные упражнения

Пр. 4. (*** экстра ***) Может ли собака вилять хвостом без хвоста в очередь «вилять собакой»? Объяснять. (Рассмотрим собаку с относительно массивный хвост.)

Третий закон Ньютона говорит нам, что хвост будет оказывать сила на собаке, как собака воздействует на хвост.Следовательно хвост тоже будет «вилять собакой».

Типичные вопросы с несколькими ответами:

1. Первый закон Ньютона гласит, что в отсутствие чистая сила, движущийся объект будет

а) в конце концов остановится
б) продолжать движение, но замедлиться, пока не остановится
в) продолжать движение с той же скоростью по той же прямая
г) продолжать по той же прямой с уменьшением скорость

2.Масса — мера

а) объем объекта
б) размер объекта
c) насколько сложно изменить движение объекта
г) скорость объекта

3. Вес предмета

а) то же, что и масса объекта
б) сумма всех сил на объекте
в) сила тяжести на объекте
г) всегда меньше массы даже в вакууме

4.Чистая сила, действующая на объект массой 1 кг в состоянии покоя, составляет

а) 9,8 Н
б) 4.9 с.ш.
c) 1.00 N
г) ноль

5. Чистое усилие на предмет весом 1 кг при свободном падении составляет

а) 9,8 Н
б) 4.9 с.ш.
c) 1.00 N
г) ноль

6. Гарри-Художник весит 500 Н. Когда он подвешен. как показано на рисунке, каково натяжение веревки?

а) 1000 Н
б) 500 Н
в) 250 Н
г) 25 Н

7.Сила 24 Н действует на объект массой 6 кг. Этот заставляет объект ускоряться на

а) 2 м / с ²
б) 4 м / ^с2
в) 6 м / с ²
г) 10 м / с ²

8. Автомобиль массой 1 000 кг ускоряется со скоростью 2 м / с ². Чистая сила, прилагаемая к автомобилю, должна составлять

а) 500 Н
б) 1,000 N
в) 2,000 Н
г) 10,000 Н

9.Масса автомобиля массой 1000 кг —

кг.

а) 500 Н
б) 1,000 N
в) 2,000 Н
г) 10,000 Н

10. Пожарный весом 500 Н скользит по шесту с ускорение 3 м / с2. Силы, которые действуют на него, — это его вес притягивая его вниз, и сила трения подтягивает его, чтобы замедлить его вниз. Сила трения должна быть

а) 90 Н
б) 150 Н
в) 350 Н
г) 500 Н

Ответы на типичные вопросы с несколькими вариантами ответов:

1.Первый закон движения Ньютона гласит, что в отсутствие чистая сила, движущийся объект будет

а) в конце концов остановится
б) продолжать движение, но замедлиться, пока не остановится
c) продолжить движение тем же скорость по той же прямой
г) продолжать по той же прямой с уменьшением скорость

2. Масса — это мера

а) объем объекта
б) размер объекта
в) насколько сложно поменять движение объекта
г) скорость объекта

3.Вес объекта

а) то же, что и масса объекта
б) сумма всех сил на объекте
c) сила тяжести на объект
г) всегда меньше массы даже в вакууме

4. Сила нетто на объект массой 1 кг в состоянии покоя составляет

а) 9,8 Н
б) 4.9 с.ш.
c) 1.00 N
г) ноль

5.Чистая сила, действующая на объект массой 1 кг при свободном падении, составляет

а) 9,8 Н
б) 4.9 с.ш.
c) 1.00 N
г) ноль

6. Гарри-Художник весит 500 Н. Когда он подвешен. как показано на рисунке, каково натяжение веревки?

а) 1000 Н
б) 500 Н
c) 250 Н
г) 25 Н
Гравитация тянет вниз на художника при его весе 500 Н.Веревка тянет вверх на маляре. дважды с этими силами равными натяжению в веревке. Поскольку художник не двигается, сумма сил вверх должен уравновесить силу вниз. Каждый конец веревки тянется вверх с напряжение 250 Н.

7. Сила 24 Н действует на объект массой 6 кг. Этот заставляет объект ускоряться на

а) 2 м / с ²
б) 4 м / с ²
в) 6 м / с ²
г) 10 м / с ²
F = m a
24 N = (6 кг) (а)
24 Н = (6 кг) (4 м / с ²)
a = 4 м / с ²

8.Автомобиль массой 1000 кг разгоняется со скоростью 2 м / с ². Чистая сила, прилагаемая к автомобилю, должна составлять

а) 500 Н
б) 1,000 N
c) 2,000 Н
г) 10,000 Н

9. Масса автомобиля массой 1000 кг

а) 500 Н
б) 1,000 N
в) 2,000 Н
г) 10,000 Н
w = мг
w = (1000 кг) (10 м / с ²)
w = 10 000 N

10.Пожарный, вес которого составляет 500 Н, скользит по шесту с ускорение 3 м / с ². Силы, которые действуют на него, — это его вес тянет его вниз и сила трения тянет вверх чтобы замедлить его. Сила трения должна быть

а) 90 Н
б) 150 Н
c) 350 Н
г) 500 Н
F = ma
F _сеть = ma
F _нетто = F _{плотность} — F _фрикт
F _{Плотность} = w = m g
500 Н = м (10 м / с ²)
м = 50 кг
F _нетто = ma = (50 кг) (3 м / с ²)
F _нетто = 150 (кг м / с ²)
F _сеть = 150 Н
F _нетто = F _{плотность} — F _фрикт
150 Н = 500 Н — F _фрикт
F _трение = 500 Н — 150 Н = 350 №
F _фрик = 350 №

Крутящий момент

— AP Physics 1

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как как ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

12.2 Примеры статического равновесия — University Physics Volume 1

Цели обучения

К концу этого раздела вы сможете:

Выявление и анализ ситуаций статического равновесия
Создание диаграммы свободного тела для протяженного объекта в статическом равновесии
Установка и решение условий статического равновесия для объектов, находящихся в равновесии в различных физических ситуациях

Все примеры в этой главе относятся к планарным задачам.Соответственно, мы используем условия равновесия в компонентной форме от (Рисунок) до (Рисунок). Мы ввели стратегию решения проблем на (Рисунок), чтобы проиллюстрировать физический смысл условий равновесия. Теперь мы обобщим эту стратегию в виде списка шагов, которые необходимо соблюдать при решении задач статического равновесия для протяженных твердых тел. Мы выполняем пять практических шагов.

Стратегия решения проблем: статическое равновесие

Укажите объект для анализа. Для некоторых систем, находящихся в равновесии, может потребоваться рассмотреть более одного объекта.Определите все силы, действующие на объект. Определите вопросы, на которые вам нужно ответить. Определите информацию, содержащуюся в проблеме. В реальных задачах некоторая ключевая информация может быть скрыта в ситуации, а не предоставлена явно.
Создайте диаграмму свободного тела для объекта. (a) Выберите для задачи справочную рамку xy . Нарисуйте для объекта диаграмму свободного тела, включая только силы, действующие на него. Если возможно, представьте силы в виде их компонентов в выбранной системе отсчета.Когда вы делаете это для каждой силы, вычеркните исходную силу, чтобы ошибочно не включить одну и ту же силу в уравнения. Обозначьте все силы — это понадобится вам для правильного расчета чистых сил в направлениях x и y . Для неизвестной силы направление должно быть задано произвольно; думайте об этом как о «рабочем направлении» или «предполагаемом направлении». Правильное направление определяется знаком, который вы получаете в окончательном решении. Знак плюс
означает, что рабочее направление является фактическим направлением.Знак минус
означает, что фактическое направление противоположно предполагаемому рабочему направлению. (б) Выберите положение оси вращения; Другими словами, выберите точку поворота, относительно которой вы будете вычислять моменты действующих сил. На схеме свободного тела укажите расположение оси и плеч рычага действующих сил — это понадобится вам для правильного расчета крутящих моментов. При выборе шарнира имейте в виду, что шарнир можно разместить где угодно, но руководящий принцип заключается в том, что лучший выбор максимально упростит расчет чистого крутящего момента вдоль оси вращения.
Составьте уравнения равновесия для объекта. (a) Используйте диаграмму свободного тела, чтобы записать правильное состояние равновесия (рисунок) для компонентов силы в направлении x . (b) Используйте диаграмму свободного тела, чтобы записать правильное состояние равновесия (рисунок) для компонентов силы в направлении y . (c) Используйте диаграмму свободного тела, чтобы записать правильное состояние равновесия (рисунок) для крутящих моментов вдоль оси вращения. Используйте (Рисунок), чтобы оценить величины и значения крутящего момента.
Упростите и решите систему уравнений равновесия, чтобы получить неизвестные величины. На данный момент ваша работа связана только с алгеброй. Имейте в виду, что количество уравнений должно быть таким же, как и количество неизвестных. Если количество неизвестных больше, чем количество уравнений, проблема не может быть решена.
Оцените выражения для неизвестных величин, которые вы получили в своем решении. В ваших окончательных ответах должны быть правильные числовые значения и правильные физические единицы.В противном случае используйте предыдущие шаги, чтобы отследить ошибку до ее источника и исправить ее. Кроме того, вы можете самостоятельно проверить свои числовые ответы, переместив точку поворота в другое место и снова решив проблему, что мы и сделали на (рисунок).

Обратите внимание, что построение диаграммы свободного тела для задачи равновесия твердого тела является наиболее важным компонентом в процессе решения. Без правильной настройки и правильной диаграммы вы не сможете записать правильные условия равновесия.Также обратите внимание, что диаграмма свободного тела для протяженного твердого тела, которое может совершать вращательное движение, отличается от диаграммы свободного тела для тела, которое испытывает только поступательное движение (как вы видели в главах, посвященных законам движения Ньютона). В поступательной динамике тело представляется как его ЦМ, в котором все силы прилагаются к телу, а крутящие моменты отсутствуют. Это не относится к динамике вращения, где протяженное твердое тело не может быть представлено одной точкой. Причина этого в том, что при анализе вращения мы должны идентифицировать крутящие моменты, действующие на тело, а крутящий момент зависит как от действующей силы, так и от плеча рычага.Здесь диаграмма свободного тела для протяженного твердого тела помогает нам определить внешние моменты.

Пример

Баланс крутящего момента

Три гири прикреплены к единой измерительной линейке, как показано на (Рисунок). Масса измерительного стержня составляет 150,0 г, а масса слева от точки опоры составляет

Найдите массу

, который уравновешивает систему, когда она прикреплена к правому концу ручки, и нормальную силу реакции на опоре, когда система уравновешена.

Рис. 12.9 При балансировке крутящего момента горизонтальная балка поддерживается в точке опоры (обозначена буквой S), а массы прикрепляются к обеим сторонам оси. Система находится в статическом равновесии, когда балка не вращается. Он уравновешен, когда луч остается ровным.

Стратегия

Для схемы, показанной на рисунке, мы определяем следующие пять сил, действующих на измерительную линейку:

— масса массы

— вес всей измерительной линейки;

— масса неизвестной массы

— нормальная сила реакции в точке опоры S .

Мы выбираем систему отсчета, в которой направление оси y — это направление силы тяжести, направление оси x — вдоль измерительной ручки и ось вращения (ось z ). ) перпендикулярна оси x и проходит через точку опоры S . Другими словами, мы выбираем ось в точке соприкосновения измерительной линейки с опорой. Это естественный выбор для поворота, потому что эта точка не перемещается при вращении ручки.Теперь мы готовы создать диаграмму свободного тела для измерительной ручки. Мы указываем ось и присоединяем пять векторов, представляющих пять сил, вдоль линии, представляющей стержень измерителя, располагая силы относительно оси (рисунок). На этом этапе мы можем идентифицировать рычаги пяти сил, учитывая информацию, предоставленную в задаче. Для трех подвешенных грузов проблема заключается в их расположении вдоль стержня, но информация о расположении груза w дается неявно.Ключевое слово здесь — «униформа». Из наших предыдущих исследований мы знаем, что ЦМ однородной палки находится в ее средней точке, поэтому именно здесь мы прикрепляем груз w на отметке 50 см.

Рисунок 12.10 Диаграмма свободного тела для измерительной ручки. Поворот выбирается в точке поддержки S.

Решение

Используя (Рисунок) и (Рисунок) для справки, мы начинаем с нахождения плеч рычагов пяти сил, действующих на палку:

Теперь мы можем найти пять крутящих моментов относительно выбранной оси:

Второе условие равновесия (уравнение для крутящих моментов) для измерительного стержня —

При подстановке значений крутящего момента в это уравнение мы можем опустить крутящие моменты, дающие нулевой вклад.Таким образом, второе условие равновесия —

Выбор

— направление параллельно

первое условие равновесия ручки —

Подставляя силы, первое условие равновесия становится

Мы решаем эти уравнения одновременно для неизвестных значений

В (рисунок) мы отменяем коэффициент g и переставляем члены, чтобы получить

Для получения

делим обе стороны на

, так что у нас

Чтобы найти нормальную силу реакции, переставляем члены на (Рисунок), переводя граммы в килограммы:

Значение

Обратите внимание, что (рисунок) не зависит от значения г .Таким образом, баланс крутящего момента может использоваться для измерения массы, поскольку изменения значений г на поверхности Земли не влияют на эти измерения. Это не относится к пружинным весам, поскольку они измеряют силу.

Проверьте свое понимание

Повторите (рисунок), используя левый конец измерительной ручки для расчета крутящего момента; то есть, поместив ось на левый конец измерительной ручки.

[показывать-ответ q = ”fs-id11637134

″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id11637134

″]

316.7 г; 5.8 N

[/ hidden-answer]

В следующем примере мы покажем, как использовать первое условие равновесия (уравнение для сил) в векторной форме, заданной (Рисунок) и (Рисунок). Мы представляем это решение, чтобы проиллюстрировать важность правильного выбора системы отсчета. Хотя все инерциальные системы отсчета эквивалентны, а численные решения, полученные в одном кадре, такие же, как и в любом другом, неподходящий выбор системы отсчета может сделать решение довольно длинным и запутанным, тогда как мудрый выбор системы отсчета делает решение простым.Мы покажем это в эквивалентном решении той же проблемы. Этот конкретный пример иллюстрирует применение статического равновесия к биомеханике.

Пример

Силы в предплечье

Тяжелоатлет держит в предплечье гирю весом 50,0 фунтов (эквивалент 222,4 Н), как показано на (Рисунок). Его предплечье находится на отметке

относительно его плеча. Предплечье поддерживается сокращением двуглавой мышцы, которое вызывает крутящий момент вокруг локтя.Предполагая, что напряжение в двуглавой мышце действует в вертикальном направлении, определяемом силой тяжести, какое напряжение должна прикладывать мышца, чтобы удерживать предплечье в показанном положении? Какая сила действует на локтевой сустав? Предположим, что вес предплечья незначителен. Дайте окончательные ответы в единицах СИ.

Рисунок 12.11 Предплечье вращается вокруг локтя (E) за счет сокращения двуглавой мышцы, что вызывает напряжение.

Стратегия

Мы идентифицируем три силы, действующие на предплечье: неизвестная сила

в локтевом суставе; неизвестное напряжение

в мышце; и вес

с магнитудой

Мы принимаем систему отсчета с осью x вдоль предплечья и шарниром в локте.Вертикальное направление — это направление веса, которое совпадает с направлением плеча. Ось x составляет угол

с вертикалью. Ось y перпендикулярна оси x . Теперь создадим диаграмму свободного тела для предплечья. Сначала мы рисуем оси, точку поворота и три вектора, представляющие три идентифицированные силы. Затем располагаем угол

и представьте каждую силу ее компонентами x и y , не забывая перечеркнуть исходный вектор силы, чтобы избежать двойного счета.Наконец, мы помечаем силы и их рычаги. Схема свободного тела для предплечья показана на (Рисунок). На этом этапе мы готовы создать условия равновесия для предплечья. Каждая сила имеет компоненты x и y ; следовательно, у нас есть два уравнения для первого условия равновесия, по одному уравнению для каждой составляющей чистой силы, действующей на предплечье.

Рис. 12.12 Диаграмма свободного тела для предплечья: шарнир расположен в точке E (локоть).

в (рисунок). Для компонентов y у нас есть

в (рисунок). Также обратите внимание, что крутящий момент силы в локте равен нулю, потому что эта сила прилагается к оси поворота.Таким образом, вклад в чистый крутящий момент вносят только крутящие моменты

Решение

Из диаграммы свободного тела видно, что составляющая x чистой силы удовлетворяет уравнению

и y -компонент чистой силы удовлетворяет

(рисунок) и (рисунок) — это два уравнения первого условия равновесия (для сил).Затем мы читаем из диаграммы свободного тела, что чистый крутящий момент вдоль оси вращения равен

(рисунок) — второе условие равновесия (по крутящим моментам) для предплечья. На диаграмме свободного тела показано, что рычаги имеют длину

На этом этапе нам не нужно преобразовывать дюймы в единицы СИ, потому что, пока эти единицы согласованы на (Рисунок), они сокращаются. Снова используя диаграмму свободного тела, находим величины составляющих сил:

Мы подставляем эти величины в (Рисунок), (Рисунок) и (Рисунок), чтобы получить, соответственно,

Когда мы упрощаем эти уравнения, мы видим, что остались только два независимых уравнения для двух неизвестных величин силы, F и T , потому что (Рисунок) для компонента x эквивалентен (Рисунок) для компонента y .Таким образом, мы получаем первое условие равновесия для сил

и второе условие равновесия моментов

Величина напряжения в мышце получается путем решения (Рисунок):

Сила в локте определяется решением (рисунок):

Отрицательный знак в уравнении говорит нам, что действительная сила в локте антипараллельна рабочему направлению, принятому для построения диаграммы свободного тела.В окончательном ответе мы конвертируем силы в единицы силы СИ. Ответ

Значение

Здесь стоит отметить два важных момента. Первый касается преобразования в единицы СИ, который может быть выполнен в самом конце решения, если мы сохраняем согласованность в единицах. Второй важный вопрос касается шарнирных соединений, например, локтевого. При первоначальном анализе проблемы следует всегда предполагать, что шарнирные соединения действуют в произвольном направлении , а затем вы должны решать все компоненты шарнирной силы независимо.В этом примере сила в локтевом суставе оказывается вертикальной, потому что задача предполагает, что напряжение бицепса также является вертикальным. Однако такое упрощение не является общим правилом.

Решение

что силы

(соответственно) производят со своими рычагами. В определении крутящего момента, данном (Рисунок), угол

— угол направления вектора

отсчитывает против часовой стрелки на от радиального направления плеча рычага, который всегда направлен от оси вращения.По такому же соглашению угол

измеряется против часовой стрелки от радиального направления плеча рычага до вектора

При таком выполнении ненулевой крутящий момент легче всего вычислить путем прямой подстановки в (рисунок) следующим образом:

Рис. 12.13 Диаграмма свободного тела для предплечья для эквивалентного решения. Ось находится в точке Е (колено).

Второе условие равновесия,

теперь можно записать как

Из диаграммы свободного тела первое условие равновесия (для сил) равно

(рисунок) идентичен (рисунок) и дает результат

(рисунок) дает

Мы видим, что эти ответы идентичны нашим предыдущим ответам, но второй выбор системы отсчета приводит к эквивалентному решению, которое является более простым и быстрым, поскольку не требует разделения сил на их прямоугольные составляющие.

Проверьте свое понимание

Повторите (рисунок), предполагая, что предплечье представляет собой объект однородной плотности, который весит 8,896 Н.

[show-answer q = ”fs-id1163709773449 ″] Показать решение [/ show-answer]

[скрытый-ответ a = ”fs-id1163709773449 ″]

[/ hidden-answer]

Пример

Лестница, упирающаяся в стену

Единая лестница

в длину и весит 400.0 Н. Лестница упирается в скользкую вертикальную стену, как показано на (Рисунок). Угол наклона лестницы к черновому полу —

Найдите силы реакции пола и стены на лестницу и коэффициент трения покоя

на стыке лестницы с полом, что предотвращает скольжение лестницы.

Рисунок 12.14 Лестница длиной 5,0 м упирается в стену без трения.

Стратегия

Мы можем выделить четыре силы, действующие на лестницу. Первая сила — это сила нормальной реакции Н, от пола в вертикальном направлении вверх. Вторая сила — это сила трения покоя

направлен горизонтально по полу к стене — эта сила предотвращает скольжение лестницы. Эти две силы действуют на лестницу в точке ее контакта с полом. Третья сила — это вес на лестницы, прикрепленный к ее CM, расположенной посередине между ее концами.Четвертая сила — это сила нормального противодействия F от стены в горизонтальном направлении от стены, приложенная в точке контакта со стеной. Других сил нет, потому что стена скользкая, что означает отсутствие трения между стеной и лестницей. На основе этого анализа мы принимаем систему отсчета с осью y в вертикальном направлении (параллельно стене) и осью x в горизонтальном направлении (параллельно полу).В этом кадре каждая сила имеет либо горизонтальную, либо вертикальную составляющую, но не обе, что упрощает решение. Подбираем ось в точке соприкосновения с полом. На схеме со свободным телом для лестницы мы указываем ось, все четыре силы и их плечи рычагов, а также углы между плечами рычагов и силами, как показано на (Рисунок). При нашем выборе положения оси вращения отсутствует крутящий момент ни от нормальной силы реакции N , ни от статического трения f , потому что они оба действуют на шарнир.

Рисунок 12.15 Схема свободного тела для лестницы, упирающейся в стену без трения.

Решение

На диаграмме свободного тела чистая сила в направлении x составляет

чистая сила в направлении y составляет

, а чистый крутящий момент по оси вращения в точке поворота равен

где

— это крутящий момент массы w и

— момент реакции F .Из диаграммы свободного тела мы определяем, что плечо рычага реакции у стены равно

и плечо рычага веса

С помощью диаграммы свободного тела мы определяем углы, которые будут использоваться на (Рисунок) для крутящих моментов:

для крутящего момента от силы реакции со стенкой и

для крутящего момента из-за веса. Теперь мы готовы использовать (рисунок) для вычисления крутящих моментов:

Подставляем крутящие моменты в (рисунок) и решаем

Мы получаем нормальную силу реакции с полом, решая (рисунок):

Величина трения получается путем решения (рисунок):

Коэффициент трения покоя

Чистая сила, действующая на лестницу в точке контакта с полом, представляет собой векторную сумму нормальной реакции пола и сил статического трения:

Его величина —

и его направление

Здесь следует выделить два общих замечания о практическом использовании.Во-первых, обратите внимание, что когда мы выбираем точку поворота, нет никаких ожиданий, что система действительно развернется вокруг выбранной точки. Лестница в этом примере совсем не вращается, а твердо стоит на полу; тем не менее, его точка контакта с полом — хороший выбор для шарнира. Во-вторых, обратите внимание, когда мы используем (рисунок) для расчета отдельных крутящих моментов, нам не нужно разделять силы на их нормальные и параллельные составляющие по отношению к направлению плеча рычага, и нам не нужно учитывать смысл крутящий момент.Если угол на (Рис.) Правильно определен — с помощью диаграммы свободного тела — как угол, измеренный против часовой стрелки от направления плеча рычага к направлению вектора силы, (Рис.) Дает как величину и чувство крутящего момента. Это связано с тем, что крутящий момент является векторным произведением вектора рычага на плечо, пересекаемого с вектором силы, и (рисунок) выражает прямоугольную составляющую этого векторного произведения вдоль оси вращения.

Значение

наши результаты остаются в силе. Но лестница соскользнет, если чистый крутящий момент станет отрицательным (рисунок). Это происходит для некоторых углов, когда коэффициент статического трения недостаточен для предотвращения скольжения лестницы.

Проверьте свое понимание

Для ситуации, описанной на (Рисунок), определите значения коэффициента

статического трения, при котором лестница начинает скользить, учитывая, что

— угол между лестницей и полом.

[показывать-ответ q = ”fs-id1163713423927 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1163713423927 ″]

[/ hidden-answer]

Пример

Усилие на дверных петлях

Распашная дверь весом

поддерживается петлями A, и B, , так что дверь может вращаться вокруг вертикальной оси, проходящей через петли (рисунок). Дверь имеет ширину

и дверная плита имеет однородную массовую плотность.Петли располагаются симметрично у края двери таким образом, чтобы вес двери равномерно распределялся между ними. Расстояние между петлями составляет

Найдите силы на петлях, когда дверь приоткрыта.

Рисунок 12.16 Распашная вертикальная дверь 400-N поддерживается двумя петлями, прикрепленными в точках A и B.

Стратегия

от петли

неизвестная сила

от петли

и известная масса

прикреплен в центре масс дверной плиты. CM расположен в геометрическом центре двери, потому что плита имеет однородную массовую плотность.Мы принимаем прямоугольную систему отсчета с осью y вдоль направления силы тяжести и осью x в плоскости плиты, как показано на панели (a) (Рисунок), и распределяем все силы на их прямоугольные составляющие. Таким образом, у нас есть четыре неизвестных составляющих силы: две составляющие силы

и две составляющие силы

На схеме свободного тела мы представляем две силы на шарнирах их векторными компонентами, предполагаемые ориентации которых произвольны.Потому что есть четыре неизвестных

мы должны составить четыре независимых уравнения. Одно уравнение — это условие равновесия сил в направлении x . Второе уравнение — это условие равновесия сил в направлении y . Третье уравнение — это условие равновесия крутящих моментов при вращении вокруг шарнира. Поскольку вес равномерно распределяется между петлями, мы имеем четвертое уравнение:

Чтобы установить условия равновесия, мы рисуем диаграмму свободного тела и выбираем точку поворота на верхнем шарнире, как показано на панели (b) (Рисунок).Наконец, мы решаем уравнения для неизвестных компонентов силы и находим силы.

Рисунок 12.17 (a) Геометрия и (b) диаграмма свободного тела двери.

Решение

Из диаграммы свободного тела для двери мы имеем первое условие равновесия сил:

Выбираем шарнир в точке P (верхний шарнир, согласно диаграмме свободного тела) и записываем второе условие равновесия для крутящих моментов при вращении вокруг точки P :

Мы используем диаграмму свободного тела, чтобы найти все члены в этом уравнении:

При оценке

мы используем геометрию треугольника, показанного в части (а) рисунка.Теперь подставляем эти моменты в (рисунок) и вычисляем

Следовательно, значения горизонтальных составляющих сил равны

Силы на двери

Силы на петлях находятся из третьего закона Ньютона как

Значение

Обратите внимание, что если бы задача была сформулирована без предположения о том, что вес равномерно распределен между двумя петлями, мы не смогли бы ее решить, потому что количество неизвестных было бы больше, чем количество уравнений, выражающих условия равновесия.

Проверьте свое понимание

Решите проблему, показанную на (Рисунок), приняв положение поворота в центре масс.

[показывать-ответ q = ”fs-id1163713175857 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1163713175857 ″]

[/ hidden-answer]

Проверьте свое понимание

Человек массой 50 кг стоит на расстоянии 1,5 м от одного конца унифицированных лесов длиной 6,0 м и массой 70,0 кг. Найдите натяжение двух вертикальных тросов, поддерживающих подмости.

[показать-ответ q = ”478065 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 478065 ″] 711,0 N; 466.0 N [/ hidden-answer]

Проверьте свое понимание

Знак 400.0-N висит на конце форменной стойки. Стойка имеет длину 4,0 м и вес 600,0 Н. Стойка поддерживается шарниром у стены и тросом, другой конец которого привязан к стене на высоте 3,0 м над левым концом стойки. Найти напряженность в опорном кабеле и сила шарнира на стойках.

[показать-ответ q = ”723276 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 723276 ″] 1167 N; 980 с.ш. направлено вверх на

над горизонтом [/ hidden-answer]

Сводка

Разнообразные инженерные задачи могут быть решены путем применения условий равновесия для твердых тел.
В приложениях идентифицируйте все силы, которые действуют на твердое тело, и отметьте их рычаги, вращающиеся вокруг выбранной оси вращения.Постройте диаграмму свободного тела для тела. Чистые внешние силы и крутящие моменты можно четко определить по правильно построенной диаграмме свободного тела. Таким образом, вы можете установить первое условие равновесия для сил и второе условие равновесия для крутящих моментов.
При создании условий равновесия мы можем принять любую инерциальную систему отсчета и любое положение точки поворота. Все варианты приводят к одному ответу. Однако некоторые варианты могут чрезмерно усложнить процесс поиска решения.Независимо от того, какой выбор мы делаем, мы получаем один и тот же ответ. Единственный способ овладеть этим навыком — практиковаться.

Концептуальные вопросы

Можно ли упереть лестницу в неровную стену, когда пол без трения?

Покажите, как с помощью пружинных весов и простой точки опоры можно взвесить объект, вес которого превышает максимальное показание на весах.

[показывать-ответ q = ”fs-id1163709751583 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1163709751583 ″]

(Проба)

[/ hidden-answer]

Художник поднимается по лестнице.Будет ли лестница соскользнуть с большей вероятностью, когда художник находится внизу или вверху?

Проблемы

Равномерная доска стоит на ровной поверхности, как показано ниже. Доска имеет массу 30 кг и длину 6,0 м. Какую массу можно поместить на его правый конец, прежде чем он наклонится? ( Подсказка: Когда доска собирается опрокинуться, она соприкасается с поверхностью только по краю, который становится мгновенной осью вращения.)

Унифицированные качели, показанные ниже, уравновешены на опоре, расположенной 3.0 м от левого конца. Маленький мальчик справа имеет массу 40 кг, а больший мальчик слева имеет массу 80 кг. Какая масса у доски?

[show-answer q = ”929303 ″] Показать решение [/ show-answer]
[hidden-answer a =” 929303 ″] 40 кг [/ hidden-answer]

Чтобы вытащить свою машину из грязи, мужчина привязывает один конец веревки к переднему бамперу, а другой конец — к дереву на расстоянии 15 м, как показано ниже. Затем он тянет за центр веревки с силой 400 Н, в результате чего ее центр смещается на 0.30 м, как показано. Какова сила троса на машине?

Унифицированные подмости весом 40,0 кг и длиной 6,0 м поддерживаются двумя световыми кабелями, как показано ниже. Маляр весом 80,0 кг стоит на расстоянии 1,0 м от левого конца строительных лесов, а его малярное оборудование — в 1,5 м от правого конца. Если натяжение левого троса вдвое больше, чем правого троса, найдите натяжение тросов и массу оборудования.

[показать-ответ q = ”512258 ″] Показать ответ [/ показать-ответ]
[скрытый-ответ a =” 512258 ″] правый кабель, 444.3 Н; левый кабель, 888,5 Н; вес оборудования 156,8 Н; 16,0 кг [/ hidden-answer]

Когда конструкция, показанная ниже, поддерживается в точке P , она находится в состоянии равновесия. Найдите величину силы F и силу, приложенную в точке P . Вес конструкции незначительный.

Чтобы подняться на крышу, человек (массой 70,0 кг) приставляет алюминиевую лестницу длиной 6,00 м (массой 10,0 кг) к дому на бетонную площадку с основанием лестницы 2.00 м от дома. Лестница упирается в пластиковый водосточный желоб, который, как мы можем предположить, не имеет трения. Центр масс лестницы находится на расстоянии 2,00 м от низа. Человек стоит в 3,00 м от дна. Найдите нормальные силы реакции и трения лестницы у ее основания.

[показывать-ответ q = ”fs-id1163713204708 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1163713204708 ″]

784 N, 376 N

[/ hidden-answer]

Единая горизонтальная стойка весит 400 г.0 Н. Один конец стойки прикреплен к шарнирной опоре у стены, а другой конец стойки прикреплен к знаку, который весит 200,0 Н. Стойка также поддерживается тросом, прикрепленным между концом стойки. и стена. Предполагая, что весь вес знака прикреплен к самому концу стойки, найдите натяжение троса и усилие на шарнире стойки.

Предплечье, показанное ниже, расположено под углом

относительно плеча и 5.Масса 0 кг удерживается в руке. Общая масса предплечья и кисти составляет 3,0 кг, а их центр масс находится на расстоянии 15,0 см от локтя. (а) Какова величина силы, которую двуглавая мышца прилагает к предплечью для

(b) Какова величина силы, действующей на локтевой сустав для того же угла? (c) Как эти силы зависят от угла

[show-answer q = ”233949 ″] Показать решение [/ show-answer]
[hidden-answer a =” 233949 ″] a.539 Н; б. 461 Н; c. не зависят от ракурса [/ hidden-answer]

Унифицированная стрела, показанная ниже, весит 3000 Н. Она поддерживается горизонтальной растяжкой и шарнирной опорой в точке A . Какие силы действуют на стрелу из-за троса и опоры на A ? Действует ли сила A вдоль стрелы?

Унифицированная стрела, показанная ниже, весит 700 Н, а объект, свисающий с ее правого конца, весит 400 Н. Стрела поддерживается световым кабелем и шарниром на стене.Рассчитайте натяжение троса и усилие на шарнире на стреле. Действует ли сила на шарнире вдоль стрелы?

[раскрыть-ответ q = ”612620 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 612620 ″] натяжение 778 Н; на петле 778 Н на

выше горизонтали; нет [/ hidden-answer]

Стрела 12,0 м, AB , крана, поднимающего груз массой 3000 кг, показана ниже. Центр масс стрелы находится в ее геометрическом центре, а масса стрелы составляет 1000 кг.Для показанного положения рассчитайте натяжение T в тросе и усилие на оси A .

Унифицированный люк, показанный ниже, имеет размер 1,0 м на 1,5 м и весит 300 Н. Он поддерживается одной петлей (H) и легкой веревкой, привязанной между серединой двери и полом. Дверь удерживается в показанном положении, где ее плита составляет

Угол

с горизонтальным полом и веревкой составляет

угол с полом.Найдите натяжение веревки и усилие на петле.

[раскрыть-ответ q = ”460173 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 460173 ″] 1500 Н; 1620 N при

[/ hidden-answer]

Мужчина весом 90 кг ходит на козле, как показано ниже. Длина козлы 2,0 м, высота 1,0 м, масса 25,0 кг. Рассчитайте нормальную силу реакции на каждую ногу в точке контакта с полом, когда человек находится на расстоянии 0,5 м от дальнего конца козлы.( Подсказка: На каждом конце сначала найдите общую силу реакции. Эта сила реакции представляет собой векторную сумму двух сил реакции, каждая из которых действует вдоль одной ноги. Нормальная сила реакции в точке контакта с полом является нормальной (с относительно пола) составляющая этой силы.)

Ваша масса 55 кг. Вы стоите на весах в лифте на Земле. Что показывает шкала, когда лифт движется вверх с постоянной скоростью?

Если человек не двигался, на шкале было бы # 539N [«вниз»] #:

#F_ «g» = мг #
# = 55 (9.8) #
# = 539 #

Если лифт движется вверх, мы не можем точно сказать, что будет на цифре. Что мы действительно знаем, так это то, что это число будет больше, чем # 539 #.

Я объясню.

Как мы все знаем, масса составляет , а не вес. Разница в том, что вес включает в себя силу тяжести, а масса используется для определения того, насколько важен ваш макияж.

Когда вы стоите на весах, весы измеряют вашу силу тяжести, также известную как вес.2 #), к полу прилагается меньшая нормальная сила, что приводит к меньшему числу на шкале.

Имейте в виду, что ваша масса не меняется, это влияние вашего ускорения.

Эти отношения прекрасно проиллюстрированы на следующем изображении:

Как видите, когда лифт поднимается, вес рыбы увеличивается.

Когда элеватор опускается, вес рыбы уменьшается.

Физическое тело рыбы не изменилось — материя была удалена / получена.Только его ускорение, которое в конечном итоге изменило #F_ «g» # — его вес.

Надеюсь, это поможет 🙂

Я перешел с 60 кг на более 100 кг — вот что я узнал. | Тим Деннинг

Я продолжал тренироваться в спортзале и ел.

Эта новая жизнь казалась мне комфортной, и я думал, что никогда не сдамся. Все изменилось, когда однажды мне позвонили. По сути, этот звонок стал началом конца моей карьеры. У меня был бизнес, и он стремительно рос.Начались проблемы, и я все больше и больше чувствовал, что должен все это оставить. Это означало, что я оставил много денег и даже BMW, на котором я ездил в спортзал каждый день.

Я приехал в спортзал в один из понедельников на день Бэка и Би около 17:00. Мой тренер снова взвесил меня, и теперь я весил около 98 кг. Я был так близок к своей цели. Во время тренировок мне нравилось разговаривать со своим тренером. Он был простым парнем, но очень хорошо делал то, что делал. Он был генеральным менеджером крупной сети фитнес-центров, а также вел свой бизнес по личным тренировкам.Я всегда восхищался его трудовой этикой и тем, как он заставлял людей чувствовать.

В тот понедельник я поговорил с ним по душам и рассказал ему, что назревает в моем бизнесе. Я хотел, чтобы он знал, что этот образ жизни в спортзале может прийти к краху. Я объяснил финансовые последствия того, что происходило, и то, что 30 тысяч долларов в год, которые я тратил на поддержание этого образа жизни, могут прекратиться. Мой тренер был таким прекрасным человеком и был так вдохновлен тем, чего я достиг, что предложил тренировать меня бесплатно. Я сказал ему, что никогда не приму это предложение, если оно произойдет, и он не стал спорить со мной.

Последующие недели были одними из самых тяжелых в моей жизни.

Чтобы заглушить боль, я тренировался усерднее, чем когда-либо. Я менял каждое упражнение, которое делал, чтобы шокировать мышцы, и быстро увеличивал веса, которые поднимал. Мы начали делать отрицательные повторения, когда он помогал мне на подъеме, чтобы еще больше истощить мышцы. Было больше кряхтения, больше пота и еще больше еды.

Несколько недель спустя пришло время снова взвесить.Я знал, что этот день по какой-то причине будет знаменательным. Я встал на весы и стал ждать чтения. Я сейчас весил 101 кг. Я сделал это !!! С большой гордостью я записал 101 кг в дневник спортзала. Мы оба отметили этот момент. В тот день мой тренер честно сказал мне, что он никогда не думал, что я продержусь больше двух недель.

Он сказал, что я был сюрпризом в его личной тренировочной карьере и показал ему, насколько важна психологическая стойкость. Я никогда не говорил ему о том, насколько слаб мой разум.Я не хотела показывать ему настоящую себя — только сильную сторону.

Это то, за что он меня знал, и я не собирался отказываться от этой игры.

Как только я достиг этой важной вехи, весь мой мир рухнул.

Прошло двенадцать месяцев с того дня, как я начал тренироваться со своим тренером, и все внимание, которое я уделял спортзалу, заставило меня потерять концентрацию на остальной части моей жизни. Я был усталым, больным, измученным, у меня давно не было отпуска, я столкнулся с финансовыми трудностями и собирался оставить свой любимый бизнес.

Настали тяжелые дни, и они пришли быстро.

В следующий понедельник я зашла в спортзал и сообщила своему тренеру плохие новости: я ухожу из спортзала и скрываюсь. Он пытался отговорить меня от этого, но меня ничто не остановило. Мне нужно было сосредоточиться на том, чтобы выбраться из этого очень темного места, и я должен был найти время для себя. Попытка соответствовать идеальному образу тела каждого разрушала того самого человека, которым я хотел стать.

Теперь речь шла о выживании.
Мне пришлось бросить спортзал.

12.2 Примеры статического равновесия

Цели обучения

К концу этого раздела вы сможете:

Выявление и анализ ситуаций статического равновесия
Создание диаграммы свободного тела для протяженного объекта в статическом равновесии
Установка и решение условий статического равновесия для объектов, находящихся в равновесии в различных физических ситуациях

Стратегия решения проблем: статическое равновесие

Укажите объект для анализа. Для некоторых систем, находящихся в равновесии, может потребоваться рассмотреть более одного объекта.Определите все силы, действующие на объект. Определите вопросы, на которые вам нужно ответить. Определите информацию, содержащуюся в проблеме. В реальных задачах некоторая ключевая информация может быть скрыта в ситуации, а не предоставлена явно.
Создайте диаграмму свободного тела для объекта. (a) Выберите для задачи справочную рамку xy . Нарисуйте для объекта диаграмму свободного тела, включая только силы, действующие на него. Если возможно, представьте силы в виде их компонентов в выбранной системе отсчета.Когда вы делаете это для каждой силы, вычеркните исходную силу, чтобы ошибочно не включить одну и ту же силу в уравнения. Обозначьте все силы — это понадобится вам для правильного расчета чистых сил в направлениях x и y . Для неизвестной силы направление должно быть задано произвольно; думайте об этом как о «рабочем направлении» или «предполагаемом направлении». Правильное направление определяется знаком, который вы получаете в окончательном решении. Знак плюс [латекс] (+) [/ латекс] означает, что рабочее направление является фактическим направлением.Знак минус [латекс] (-) [/ латекс] означает, что фактическое направление противоположно предполагаемому рабочему направлению. (б) Выберите положение оси вращения; Другими словами, выберите точку поворота, относительно которой вы будете вычислять моменты действующих сил. На схеме свободного тела укажите расположение оси и плеч рычага действующих сил — это понадобится вам для правильного расчета крутящих моментов. При выборе шарнира имейте в виду, что шарнир можно разместить где угодно, но руководящий принцип заключается в том, что лучший выбор максимально упростит расчет чистого крутящего момента вдоль оси вращения.
Составьте уравнения равновесия для объекта. (a) Используйте диаграмму свободного тела, чтобы записать правильное состояние равновесия (рисунок) для компонентов силы в направлении x . (b) Используйте диаграмму свободного тела, чтобы записать правильное состояние равновесия (рисунок) для компонентов силы в направлении y . (c) Используйте диаграмму свободного тела, чтобы записать правильное состояние равновесия (рисунок) для крутящих моментов вдоль оси вращения. Используйте (Рисунок), чтобы оценить величины и значения крутящего момента.
Упростите и решите систему уравнений равновесия, чтобы получить неизвестные величины. На данный момент ваша работа связана только с алгеброй. Имейте в виду, что количество уравнений должно быть таким же, как и количество неизвестных. Если количество неизвестных больше, чем количество уравнений, проблема не может быть решена.
Оцените выражения для неизвестных величин, которые вы получили в своем решении. В ваших окончательных ответах должны быть правильные числовые значения и правильные физические единицы.В противном случае используйте предыдущие шаги, чтобы отследить ошибку до ее источника и исправить ее. Кроме того, вы можете самостоятельно проверить свои числовые ответы, переместив точку поворота в другое место и снова решив проблему, что мы и сделали на (рисунок).

Пример

Баланс крутящего момента

Три гири прикреплены к единой измерительной линейке, как показано на (Рисунок). Масса измерительного стержня составляет 150,0 г, а массы слева от точки опоры составляют [латекс] {m} _ {1} = 50,0 \, \ text {g} [/ latex] и [латекс] {m} _ {2} = 75,0 \, \ text {g}. [/ latex] Найдите массу [латекс] {m} _ {3} [/ latex], которая уравновешивает систему, когда она прикреплена к правому концу ручки, и нормальную силу реакции в точке опоры, когда система уравновешена .

Рисунок 12.9 При балансировке крутящего момента горизонтальная балка опирается на точку опоры (обозначена буквой S), а массы прикрепляются к обеим сторонам оси. Система находится в статическом равновесии, когда балка не вращается. Он уравновешен, когда луч остается ровным.

Стратегия

Для схемы, показанной на рисунке, мы определяем следующие пять сил, действующих на измерительную линейку:

[латекс] {w} _ {1} = {m} _ {1} г [/ латекс] — масса [латекса] {m} _ {1}; [/ latex] [latex] {w} _ {2} = {m} _ {2} g [/ latex] — масса [латекса] {m} _ {2}; [/ латекс]

[латекс] w = мг [/ латекс] — вес всей измерительной линейки; [латекс] {w} _ {3} = {m} _ {3} g [/ latex] — вес неизвестной массы [латекс] {m} _ {3}; [/ латекс]

[латекс] {F} _ {S} [/ латекс] — нормальная сила реакции в точке опоры S .

Рисунок 12.10 Диаграмма свободного тела для дозатора. Пивот выбирается в точке поддержки S.

Решение

[латекс] \ begin {array} {ccc} \ hfill {r} _ {1} & = \ hfill & 30.0 \, \ text {cm} +40.0 \, \ text {cm} = 70.0 \, \ text {cm} \ hfill \\ \ hfill {r} _ {2} & = \ hfill & 40.0 \, \ text { cm} \ hfill \\ \ hfill r & = \ hfill & 50.0 \, \ text {cm} -30.0 \, \ text {cm} = 20.0 \, \ text {cm} \ hfill \\ \ hfill {r} _ { S} & = \ hfill & 0.0 \, \ text {cm} \, \ text {(потому что} \, {F} _ {S} \, \ text {прикреплен к опоре)} \ hfill \\ \ hfill {r} _ {3} & = \ hfill & 30.0 \, \ text {см.} \ hfill \ end {array} [/ latex]

Теперь мы можем найти пять крутящих моментов относительно выбранной оси:

[латекс] \ begin {array} {ccccc} \ hfill {\ tau} _ {1} & = \ hfill & + {r} _ {1} {w} _ {1} \ text {sin} \, 90 \ text {°} = \ text {+} {r} _ {1} {m} _ {1} g \ hfill & & \ text {(вращение против часовой стрелки, положительное значение)} \ hfill \\ \ hfill {\ tau } _ {2} & = \ hfill & + {r} _ {2} {w} _ {2} \ text {sin} \, 90 \ text {°} = \ text {+} {r} _ {2 } {m} _ {2} g \ hfill & & \ text {(вращение против часовой стрелки, положительное значение)} \ hfill \\ \ hfill \ tau & = \ hfill & + rw \, \ text {sin} \, 90 \ text {°} = \ text {+} rmg \ hfill & & \ text {(гравитационный момент)} \ hfill \\ \ hfill {\ tau} _ {S} & = \ hfill & {r} _ {S} { F} _ {S} \ text {sin} \, {\ theta} _ {S} = 0 \ hfill & & \ text {(потому что} \, {r} _ {S} = 0 \, \ text {см )} \ hfill \\ \ hfill {\ tau} _ {3} & = \ hfill & \ text {-} {r} _ {3} {w} _ {3} \ text {sin} \, 90 \ text {°} = \ text {-} {r} _ {3} {m} _ {3} g \ hfill & & \ text {(вращение по часовой стрелке, отрицательное значение)} \ hfill \ end {array} [/ latex]

Второе условие равновесия (уравнение для крутящих моментов) для измерительного стержня —

[латекс] {\ tau} _ {1} + {\ tau} _ {2} + \ tau + {\ tau} _ {S} + {\ tau} _ {3} = 0.[/ латекс]

При подстановке значений крутящего момента в это уравнение мы можем опустить крутящие моменты, дающие нулевой вклад. Таким образом, второе условие равновесия —

[латекс] + {r} _ {1} {m} _ {1} g + {r} _ {2} {m} _ {2} g + rmg- {r} _ {3} {m} _ { 3} г = 0. [/ латекс]

Если выбрать направление [latex] + y [/ latex], параллельное [latex] {\ overset {\ to} {F}} _ {S}, [/ latex], первое условие равновесия для ручки —

[латекс] \ text {-} {w} _ {1} — {w} _ {2} -w + {F} _ {S} — {w} _ {3} = 0. [/ латекс]

Подставляя силы, первое условие равновесия становится

[латекс] \ text {-} {m} _ {1} g- {m} _ {2} g-mg + {F} _ {S} — {m} _ {3} g = 0.[/ латекс]

Мы решаем эти уравнения одновременно для неизвестных значений [латекс] {m} _ {3} [/ latex] и [латекс] {F} _ {S}. [/ latex] В (Рисунок) мы отменяем коэффициент g и переставляем члены, чтобы получить

[латекс] {r} _ {3} {m} _ {3} = {r} _ {1} {m} _ {1} + {r} _ {2} {m} _ {2} + rm . [/ латекс]

Чтобы получить [латекс] {m} _ {3} [/ latex], мы делим обе стороны на [latex] {r} _ {3}, [/ latex], получаем

[латекс] \ begin {array} {cc} \ hfill {m} _ {3} & = \ frac {{r} _ {1}} {{r} _ {3}} \, {m} _ { 1} + \ frac {{r} _ {2}} {{r} _ {3}} \, {m} _ {2} + \ frac {r} {{r} _ {3}} \, m \ hfill \\ & = \ frac {70} {30} \, (50.{2}} = 5.8 \, \ text {N}. \ Hfill \ end {array} [/ latex]

Значение

Обратите внимание, что (рисунок) не зависит от значения г . Таким образом, баланс крутящего момента может использоваться для измерения массы, поскольку изменения значений г на поверхности Земли не влияют на эти измерения. Это не относится к пружинным весам, поскольку они измеряют силу.

Проверьте свое понимание

Пример

Силы в предплечье

Тяжелоатлет держит в предплечье гирю весом 50,0 фунтов (эквивалент 222,4 Н), как показано на (Рисунок). Его предплечье расположено на [latex] \ beta = 60 \ text {°} [/ latex] относительно его плеча. Предплечье поддерживается сокращением двуглавой мышцы, которое вызывает крутящий момент вокруг локтя.Предполагая, что напряжение в двуглавой мышце действует в вертикальном направлении, определяемом силой тяжести, какое напряжение должна прикладывать мышца, чтобы удерживать предплечье в показанном положении? Какая сила действует на локтевой сустав? Предположим, что вес предплечья незначителен. Дайте окончательные ответы в единицах СИ.

Рисунок 12.11 Предплечье вращается вокруг локтя (E) за счет сокращения мышцы двуглавой мышцы, что вызывает напряжение [латекс] {\ overset {\ to} {T}} _ {\ text {M}}. [/ латекс]

Стратегия

Мы идентифицируем три силы, действующие на предплечье: неизвестная сила [латекс] \ overset {\ to} {F} [/ латекс] в локте; неизвестное напряжение [латекс] {\ overset {\ to} {T}} _ {\ text {M}} [/ latex] в мышце; и вес [латекс] \ overset {\ to} {w} [/ latex] с величиной [латекс] w = 50 \, \ text {lb}.[/ latex] Мы принимаем систему отсчета с осью x вдоль предплечья и осью в локте. Вертикальное направление — это направление веса, которое совпадает с направлением плеча. Ось x образует угол [latex] \ beta = 60 \ text {°} [/ latex] с вертикалью. Ось y перпендикулярна оси x . Теперь создадим диаграмму свободного тела для предплечья. Сначала мы рисуем оси, точку поворота и три вектора, представляющие три идентифицированные силы.Затем мы определяем угол [latex] \ beta [/ latex] и представляем каждую силу ее компонентами x и y , не забывая перечеркнуть исходный вектор силы, чтобы избежать двойного счета. Наконец, мы помечаем силы и их рычаги. Схема свободного тела для предплечья показана на (Рисунок). На этом этапе мы готовы создать условия равновесия для предплечья. Каждая сила имеет компоненты x и y ; следовательно, у нас есть два уравнения для первого условия равновесия, по одному уравнению для каждой составляющей чистой силы, действующей на предплечье.

Рисунок 12.12 Диаграмма свободного тела для предплечья: шарнир расположен в точке E (локоть).

Обратите внимание, что в нашей системе отсчета вклад во второе условие равновесия (для крутящих моментов) происходит только от y -компонент сил, потому что x -компоненты сил параллельны плечам их рычагов, поэтому что для любого из них у нас есть [latex] \ text {sin} \, \ theta = 0 [/ latex] на (Рисунок). Для компонентов y мы имеем [latex] \ theta = ± 90 \ text {°} [/ latex] на (Рисунок).Также обратите внимание, что крутящий момент силы в локте равен нулю, потому что эта сила прилагается к оси поворота. Таким образом, вклад в чистый крутящий момент происходит только от крутящих моментов [латекса] {T} _ {y} [/ latex] и [латекса] {w} _ {y}. [/ латекс]

Решение

Из диаграммы свободного тела видно, что составляющая x чистой силы удовлетворяет уравнению

[латекс] + {F} _ {x} + {T} _ {x} — {w} _ {x} = 0 [/ латекс]

и y -компонент чистой силы удовлетворяет

[латекс] + {F} _ {y} + {T} _ {y} — {w} _ {y} = 0.[/ латекс]

(рисунок) и (рисунок) — это два уравнения первого условия равновесия (для сил). Затем мы читаем из диаграммы свободного тела, что чистый крутящий момент вдоль оси вращения равен

[латекс] + {r} _ {T} {T} _ {y} — {r} _ {w} {w} _ {y} = 0. [/ латекс]

(рисунок) — второе условие равновесия (по крутящим моментам) для предплечья. На диаграмме свободного тела показано, что плечи рычага представляют собой [латекс] {r} _ {T} = 1.5 \, \ text {in} \ text {.} [/ Latex] и [латекс] {r} _ {w} = 13,0 \, \ текст {в} \ текст {.} [/ latex] На этом этапе нам не нужно преобразовывать дюймы в единицы СИ, потому что, пока эти единицы согласованы на (рис.), они сокращаются. Снова используя диаграмму свободного тела, находим величины составляющих сил:

[латекс] \ begin {array} {ccc} \ hfill {F} _ {x} & = \ hfill & F \, \ text {cos} \, \ beta = F \, \ text {cos} \, 60 \ text {°} = F \, \ text {/} \, 2 \ hfill \\ \ hfill {T} _ {x} & = \ hfill & T \, \ text {cos} \, \ beta = T \ , \ text {cos} \, 60 \ text {°} = T \, \ text {/} \, 2 \ hfill \\ \ hfill {w} _ {x} & = \ hfill & w \, \ text { cos} \, \ beta = w \, \ text {cos} \, 60 \ text {°} = w \, \ text {/} \, 2 \ hfill \\ \ hfill {F} _ {y} & = \ hfill & F \, \ text {sin} \, \ beta = F \, \ text {sin} \, 60 \ text {°} = F \ sqrt {3} \, \ text {/} \, 2 \ hfill \\ \ hfill {T} _ {y} & = \ hfill & T \, \ text {sin} \, \ beta = T \, \ text {sin} \, 60 \ text {°} = T \ sqrt {3} \, \ text {/} \, 2 \ hfill \\ \ hfill {w} _ {y} & = \ hfill & w \, \ text {sin} \, \ beta = w \, \ text { sin} \, 60 \ text {°} = w \ sqrt {3} \, \ text {/} \, 2.\ hfill \ end {array} [/ latex]

Мы подставляем эти величины в (Рисунок), (Рисунок) и (Рисунок), чтобы получить, соответственно,

[латекс] \ begin {array} {ccc} \ hfill F \, \ text {/} \, 2 + T \, \ text {/} \, 2-w \, \ text {/} \, 2 & = \ hfill & 0 \ hfill \\ \\ \ hfill F \ sqrt {3} \, \ text {/} \, 2 + T \ sqrt {3} \, \ text {/} \, 2-w \ sqrt { 3} \, \ text {/} \, 2 & = \ hfill & 0 \ hfill \\ \\ \ hfill {r} _ {T} T \ sqrt {3} \, \ text {/} \, 2- { r} _ {w} w \ sqrt {3} \, \ text {/} \, 2 & = \ hfill & 0. \ hfill \ end {array} [/ latex]

[латекс] Ж + Т-ш = 0 [/ латекс]

и второе условие равновесия моментов

[латекс] {r} _ {T} T- {r} _ {w} w = 0. [/ латекс]

Величина напряжения в мышце получается путем решения (Рисунок):

[латекс] T = \ frac {{r} _ {w}} {{r} _ {T}} \, w = \ frac {13.0} {1.5} \, \ text {(50 фунтов)} = 433 \, \ frac {1} {3} \ text {lb} \ simeq 433.3 \, \ text {lb.} [/ latex]

Сила в локте определяется решением (рисунок):

[латекс] F = w-T = 50.0 \, \ text {lb} -433.3 \, \ text {lb} = — 383.3 \, \ text {lb.} [/ Latex]

Отрицательный знак в уравнении говорит нам, что действительная сила в локте антипараллельна рабочему направлению, принятому для построения диаграммы свободного тела. В окончательном ответе мы конвертируем силы в единицы силы СИ. Ответ

[латекс] \ begin {array} {c} F = 383,3 \, \ text {lb} = 383,3 (4,448 \, \ text {N}) = 1705 \, \ text {N вниз} \\ T = 433,3 \ , \ text {lb} = 433.3 (4.448 \, \ text {N}) = 1927 \, \ text {N вверх.} \ end {array} [/ latex]

Значение

Здесь стоит отметить два важных момента.Первый касается преобразования в единицы СИ, который может быть выполнен в самом конце решения, если мы сохраняем согласованность в единицах. Второй важный вопрос касается шарнирных соединений, например, локтевого. При первоначальном анализе проблемы следует всегда предполагать, что шарнирные соединения действуют в произвольном направлении , а затем вы должны решать все компоненты шарнирной силы независимо. В этом примере сила в локтевом суставе оказывается вертикальной, потому что задача предполагает, что напряжение бицепса также является вертикальным.Однако такое упрощение не является общим правилом.

Решение

Предположим, мы используем систему отсчета с направлением оси y вдоль 50-фунтового груза и осью, расположенной в колене. В этой системе отсчета все три силы имеют только y -компонент, поэтому у нас есть только одно уравнение для первого условия равновесия (для сил). Мы рисуем диаграмму свободного тела для предплечья, как показано на (Рисунок), с указанием оси поворота, действующих сил и их плеч рычагов по отношению к оси поворота, а также углов [латекс] {\ theta} _ {T} [/ латекс] и [латекс] {\ theta} _ {w} [/ latex], которые заставляют [латекс] {\ overset {\ to} {T}} _ {\ text {M}} [/ latex] и [латекс ] \ overset {\ to} {w} [/ latex] (соответственно) сделать своими рычагами.В определении крутящего момента, приведенном на (Рисунок), угол [латекс] {\ theta} _ {T} [/ latex] — это угол направления вектора [латекс] {\ overset {\ to} {T}} _ {\ text {M}}, [/ latex] отсчитали против часовой стрелки на от радиального направления плеча рычага, который всегда указывает от оси. По тому же соглашению угол [латекс] {\ theta} _ {w} [/ latex] измеряется против часовой стрелки от радиального направления плеча рычага к вектору [латекс] \ overset {\ to} {w} . [/ latex] Выполненный таким образом ненулевой крутящий момент легче всего вычислить путем прямой подстановки в (рисунок) следующим образом:

[латекс] \ begin {array} {cc} {\ tau} _ {T} = {r} _ {T} T \, \ text {sin} \, {\ theta} _ {T} = {r} _ {T} T \, \ text {sin} \, \ beta = {r} _ {T} T \, \ text {sin} \, 60 \ text {°} = + {r} _ {T} T \ sqrt {3} \, \ text {/} \, 2 \\ {\ tau} _ {w} = {r} _ {w} w \, \ text {sin} \, {\ theta} _ {w } = {r} _ {w} w \, \ text {sin} (\ beta +180 \ text {°}) = \ text {-} {r} _ {w} w \, \ text {sin} \ , \ beta = \ text {-} {r} _ {w} w \ sqrt {3} \, \ text {/} \, 2.\ end {array} [/ latex]

Второе условие равновесия, [латекс] {\ tau} _ {T} + {\ tau} _ {w} = 0, [/ latex] теперь может быть записано как

[латекс] {r} _ {T} T \ sqrt {3} \, \ text {/} \, 2- {r} _ {w} w \ sqrt {3} \, \ text {/} \, 2 = 0. [/ латекс]

Из диаграммы свободного тела первое условие равновесия (для сил) равно

[латекс] \ text {-} F + T-w = 0.[/ латекс]

(рисунок) идентичен (рисунок) и дает результат [латекс] T = 433,3 \, \ text {lb}. [/ latex] (рисунок) дает

[латекс] F = T-w = 433,3 \, \ text {lb} -50,0 \, \ text {lb} = 383,3 \, \ text {lb.} [/ Latex]

Проверьте свое понимание

Повторите (рисунок), предполагая, что предплечье представляет собой объект одинаковой плотности, который весит 8.896 Н.

Показать решение

[латекс] T = \ text {1963 N}; \, \ text {F} = 1732 \, \ text {N} [/ latex]

Пример

Лестница, упирающаяся в стену

Унифицированная лестница имеет длину [латекс] L = 5,0 \, \ text {m} [/ latex] и весит 400,0 Н. Лестница упирается в скользкую вертикальную стену, как показано на (Рисунок). Угол наклона между лестницей и черновым полом составляет [латекс] \ beta = 53 \ text {°}. [/ latex] Найдите силы реакции пола и стены на лестнице и коэффициент статического трения [латекс] {\ mu} _ {\ text {s}} [/ latex] на стыке лестницы с пол, предотвращающий скольжение лестницы.

Рисунок 12.14 Лестница длиной 5,0 м упирается в стену без трения.

Стратегия

Мы можем выделить четыре силы, действующие на лестницу. Первая сила — это сила нормальной реакции Н, от пола в вертикальном направлении вверх. Вторая сила — это сила статического трения [латекс] f = {\ mu} _ {\ text {s}} N [/ latex], направленная горизонтально по полу к стене — эта сила предотвращает скольжение лестницы. Эти две силы действуют на лестницу в точке ее контакта с полом.Третья сила — это вес на лестницы, прикрепленный к ее CM, расположенной посередине между ее концами. Четвертая сила — это сила нормального противодействия F от стены в горизонтальном направлении от стены, приложенная в точке контакта со стеной. Других сил нет, потому что стена скользкая, что означает отсутствие трения между стеной и лестницей. На основе этого анализа мы принимаем систему отсчета с осью y в вертикальном направлении (параллельно стене) и осью x в горизонтальном направлении (параллельно полу).В этом кадре каждая сила имеет либо горизонтальную, либо вертикальную составляющую, но не обе, что упрощает решение. Подбираем ось в точке соприкосновения с полом. На схеме со свободным телом для лестницы мы указываем ось, все четыре силы и их плечи рычагов, а также углы между плечами рычагов и силами, как показано на (Рисунок). При нашем выборе положения оси вращения отсутствует крутящий момент ни от нормальной силы реакции N , ни от статического трения f , потому что они оба действуют на шарнир.

Рис. 12.15 Схема свободного тела для лестницы, упирающейся в стену без трения.

Решение

На диаграмме свободного тела чистая сила в направлении x составляет

[латекс] + f-F = 0 [/ латекс]

чистая сила в направлении y составляет

[латекс] + N = 0 [/ латекс]

, а чистый крутящий момент по оси вращения в точке поворота равен

[латекс] {\ tau} _ {w} + {\ tau} _ {F} = 0. [/ латекс]

, где [latex] {\ tau} _ {w} [/ latex] — это крутящий момент веса w , а [latex] {\ tau} _ {F} [/ latex] — крутящий момент реакции F. .Из диаграммы свободного тела мы определяем, что плечо рычага реакции у стены — это [латекс] {r} _ {F} = L = 5,0 \, \ text {m} [/ латекс], а плечо рычага вес [латекс] {r} _ {w} = L \, \ text {/} \, 2 = 2.5 \, \ text {m}. [/ latex] С помощью диаграммы свободного тела мы определяем углы, которые будут использоваться на (Рисунок) для крутящих моментов: [latex] {\ theta} _ {F} = 180 \ text {°} — \ beta [ / latex] для крутящего момента от силы реакции со стеной и [latex] {\ theta} _ {w} = 180 \ text {°} + (90 \ text {°} — \ beta) [/ latex] для крутящий момент из-за веса.Теперь мы готовы использовать (рисунок) для вычисления крутящих моментов:

[латекс] \ begin {array} {cc} {\ tau} _ {w} = {r} _ {w} w \, \ text {sin} \, {\ theta} _ {w} = {r} _ {w} w \, \ text {sin} (180 \ text {°} +90 \ text {°} — \ beta) = — \ frac {L} {2} w \, \ text {sin} (90 \ text {°} — \ beta) = — \ frac {L} {2} w \, \ text {cos} \, \ beta \\ {\ tau} _ {F} = {r} _ {F} F \, \ text {sin} \, {\ theta} _ {F} = {r} _ {F} F \, \ text {sin} (180 \ text {°} — \ beta) = LF \, \ text {sin} \, \ beta. \ end {array} [/ latex]

Подставляем значения крутящего момента в (рисунок) и решаем для [латекс] F: [/ латекс]

[латекс] \ begin {array} {} \\ \ hfill — \ frac {L} {2} w \, \ text {cos} \, \ beta + LF \, \ text {sin} \, \ beta & = \ hfill & 0 \ hfill \\ \ hfill F = \ frac {w} {2} \, \ text {cot} \, \ beta = \ frac {400.0 \, \ text {N}} {2} \, \ text {cot} \, 53 \ text {°} & = \ hfill & 150.7 \, \ text {N} \ hfill \ end {array} [/ latex ]

Мы получаем нормальную силу реакции с полом, решая (рисунок): [латекс] N = w = 400.0 \, \ text {N}. [/ latex] Величина трения получается путем решения (рисунок): [latex] f = F = 150,7 \, \ text {N}. [/ latex] Коэффициент статического трения [латекс] {\ mu} _ {\ text {s}} = f \, \ text {/} \, N = 150,7 \, \ text {/} \, 400,0 = 0,377. [/ латекс]

[латекс] {\ overset {\ to} {F}} _ {\ text {floor}} = \ overset {\ to} {f} + \ overset {\ to} {N} = \ text {(150.{-1} (400.0 \, \, \ text {/} \, 150.7) = 69.3 \ text {°} \, \ text {над полом.} [/ Latex]

Здесь следует выделить два общих замечания о практическом использовании. Во-первых, обратите внимание, что когда мы выбираем точку поворота, нет никаких ожиданий, что система действительно развернется вокруг выбранной точки. Лестница в этом примере совсем не вращается, а твердо стоит на полу; тем не менее, его точка контакта с полом — хороший выбор для шарнира. Во-вторых, обратите внимание, когда мы используем (рисунок) для расчета отдельных крутящих моментов, нам не нужно разделять силы на их нормальные и параллельные составляющие по отношению к направлению плеча рычага, и нам не нужно учитывать смысл крутящий момент.Если угол на (Рис.) Правильно определен — с помощью диаграммы свободного тела — как угол, измеренный против часовой стрелки от направления плеча рычага к направлению вектора силы, (Рис.) Дает как величину и чувство крутящего момента. Это связано с тем, что крутящий момент является векторным произведением вектора рычага на плечо, пересекаемого с вектором силы, и (рисунок) выражает прямоугольную составляющую этого векторного произведения вдоль оси вращения.

Значение

Этот результат не зависит от длины лестницы, поскольку L отменяется во втором состоянии равновесия (рисунок).Независимо от длины или длины лестницы, если ее вес составляет 400 Н, а угол с полом составляет [латекс] 53 \ text {°}, [/ latex], наши результаты остаются в силе. Но лестница соскользнет, если чистый крутящий момент станет отрицательным (рисунок). Это происходит для некоторых углов, когда коэффициент статического трения недостаточен для предотвращения скольжения лестницы.

Проверьте свое понимание

Для ситуации, описанной на (Рисунок), определите значения коэффициента [латекс] {\ mu} _ {\ text {s}} [/ latex] статического трения, при котором лестница начинает скользить, учитывая, что [латекс] \ beta [/ latex] — угол между лестницей и полом.

Показать решение

[латекс] {\ mu} _ {s} <0,5 \, \ text {cot} \, \ beta [/ latex]

Пример

Усилие на дверных петлях

Распашная дверь весом [латекс] w = 400,0 \, \ text {N} [/ latex] поддерживается петлями A и B , так что дверь может вращаться вокруг вертикальной оси, проходящей через петли (рис. ). Дверь имеет ширину [латекс] b = 1,00 \, \ text {m}, [/ latex], а дверная плита имеет однородную массовую плотность. Петли располагаются симметрично у края двери таким образом, чтобы вес двери равномерно распределялся между ними.Петли разделены расстоянием [латекс] a = 2,00 \, \ text {m}. [/ latex] Найдите силы на петлях, когда дверь приоткрыта.

Рисунок 12.16 Распашная вертикальная дверь 400-N поддерживается двумя петлями, прикрепленными в точках A и B.

Стратегия

Силы, которые дверь оказывает на петли, можно найти, просто изменив направление сил, которые петли воздействуют на дверь. Следовательно, наша задача найти силы от петель на двери.На дверную плиту действуют три силы: неизвестная сила [латекс] \ overset {\ to} {A} [/ latex] от петли [латекс] A, [/ latex] неизвестная сила [латекс] \ overset {\ to} {B} [/ latex] из петли [латекс] B, [/ latex] и известного веса [латекс] \ overset {\ to} {w} [/ latex], прикрепленного в центре масс дверной плиты. CM расположен в геометрическом центре двери, потому что плита имеет однородную массовую плотность. Мы принимаем прямоугольную систему отсчета с осью y вдоль направления силы тяжести и осью x в плоскости плиты, как показано на панели (a) (Рисунок), и распределяем все силы на их прямоугольные составляющие.Таким образом, у нас есть четыре неизвестных составляющих силы: две составляющие силы [латекс] \ overset {\ to} {A} [/ latex] [latex] ({A} _ {x} [/ latex] и [latex] {A} _ {y}), [/ latex] и два компонента силы [latex] \ overset {\ to} {B} [/ latex] [latex] ({B} _ {x} [/ latex] и [латекс] {B} _ {y}). [/ latex] На схеме свободного тела мы представляем две силы на шарнирах их векторными компонентами, предполагаемые ориентации которых произвольны. Поскольку есть четыре неизвестных [латекс] ({A} _ {x}, [/ latex] [latex] {B} _ {x}, [/ latex] [latex] {A} _ {y}, [/ latex ] и [latex] {B} _ {y}), [/ latex] мы должны составить четыре независимых уравнения.Одно уравнение — это условие равновесия сил в направлении x . Второе уравнение — это условие равновесия сил в направлении y . Третье уравнение — это условие равновесия крутящих моментов при вращении вокруг шарнира. Поскольку вес равномерно распределяется между петлями, мы получаем четвертое уравнение [латекс] {A} _ {y} = {B} _ {y}. [/ latex] Чтобы установить условия равновесия, мы рисуем диаграмму свободного тела и выбираем точку поворота на верхнем шарнире, как показано на панели (b) (Рисунок).Наконец, мы решаем уравнения для неизвестных компонентов силы и находим силы.

Рисунок 12.17 (a) Геометрия и (b) диаграмма свободного тела двери.

Решение

Из диаграммы свободного тела для двери мы имеем первое условие равновесия сил:

[латекс] \ begin {array} {} \\ \ text {in} \, x \ text {-direction:} \ hfill & \, — {A} _ {x} + {B} _ {x} = 0 \ enspace⇒ \ enspace {A} _ {x} = {B} _ {x} \ hfill \\ \ text {in} \, y \ text {-direction:} \ hfill & + {A} _ {y } + {B} _ {y} -w = 0 \ enspace⇒ \ enspace {A} _ {y} = {B} _ {y} = \ frac {w} {2} = \ frac {400.0 \, \ text {N}} {2} = 200.0 \, \ text {N.} \ Hfill \ end {array} [/ latex]

[латекс] \ text {pivot at} \, P \ text {:} \, {\ tau} _ {w} + {\ tau} _ {Bx} + {\ tau} _ {By} = 0. [/ латекс]

Мы используем диаграмму свободного тела, чтобы найти все члены в этом уравнении:

[латекс] \ begin {array} {ccc} \ hfill {\ tau} _ {w} & = \ hfill & dw \, \ text {sin} (\ text {-} \ beta) = \ text {-} dw \, \ text {sin} \, \ beta = \ text {-} dw \ frac {b \, \ text {/} \, 2} {d} = \ text {-} w \ frac {b} { 2} \ hfill \\ \ hfill {\ tau} _ {Bx} & = \ hfill & a {B} _ {x} \ text {sin} \, 90 \ text {°} = + a {B} _ { x} \ hfill \\ \ hfill {\ tau} _ {By} & = \ hfill & a {B} _ {y} \ text {sin} \, 180 \ text {°} = 0.\ hfill \ end {array} [/ latex]

При оценке [latex] \ text {sin} \, \ beta, [/ latex] мы используем геометрию треугольника, показанную в части (a) рисунка. Теперь подставляем эти моменты в (рисунок) и вычисляем [латекс] {B} _ {x}: [/ latex]

[латекс] \ text {pivot at} \, P \ text {:} \, \ text {-} w \, \ frac {b} {2} + a {B} _ {x} = 0 \ enspace⇒ \ enspace {B} _ {x} = w \, \ frac {b} {2a} = (400.0 \, \ text {N}) \, \ frac {1} {2 · 2} = 100.0 \, \ text {N.} [/ латекс]

Следовательно, величины горизонтальных составляющих сил равны [латекс] {A} _ {x} = {B} _ {x} = 100.0 \, \ text {N}. [/ latex] Силы на двери

[латекс] \ begin {array} {} \\ \ text {на верхнем шарнире:} \, {\ overset {\ to} {F}} _ {A \, \ text {on door}} = — 100,0 \, \ text {N} \ hat {i} +200.0 \, \ text {N} \ hat {j} \ hfill \\ \ text {на нижнем шарнире:} {\ overset {\ to} {F}} _ {B \, \ text {на двери}} = \ text {+} 100.0 \, \ text {N} \ hat {i} +200.0 \, \ text {N} \ hat {j}. \ Hfill \ end {array} [/ latex]

Силы на петлях находятся из третьего закона Ньютона как

[латекс] \ begin {array} {cc} \ text {на верхнем шарнире:} \, {\ overset {\ to} {F}} _ {\ text {door on} \, A} = 100.0 \, \ text {N} \ hat {i} -200.0 \, \ text {N} \ hat {j} \ hfill \\ \ text {на нижнем шарнире:} \, {\ overset {\ to} { F}} _ {\ text {door on} \, B} = — 100.0 \, \ text {N} \ hat {i} -200.0 \, \ text {N} \ hat {j}. \ Hfill \ end { array} [/ latex]

Значение

Проверьте свое понимание

Решите проблему, показанную на (Рисунок), приняв положение поворота в центре масс.

Показать решение

[латекс] {\ overset {\ to} {F}} _ {\ text {door on} \, A} = 100.0 \, \ text {N} \ hat {i} -200.0 \, \ text {N} \ hat {j} \, \ text {;} \, {\ overset {\ to} {F}} _ {\ text {door on} \, B} = — 100.0 \, \ text {N} \ hat { i} -200.0 \, \ text {N} \ hat {j} [/ latex]

Проверьте свое понимание

Человек массой 50 кг стоит на расстоянии 1,5 м от одного конца унифицированных лесов длиной 6,0 м и массой 70.0 кг. Найдите натяжение двух вертикальных тросов, поддерживающих подмости.

Показать решение

711,0 Н; 466.0 с.

Проверьте свое понимание

Показать решение

1167 Н; 980 Н направлено вверх на [латекс] 18 \ text {°} [/ latex] над горизонтом

Сводка

Разнообразные инженерные задачи могут быть решены путем применения условий равновесия для твердых тел.
В приложениях идентифицируйте все силы, которые действуют на твердое тело, и отметьте их рычаги, вращающиеся вокруг выбранной оси вращения. Постройте диаграмму свободного тела для тела. Чистые внешние силы и крутящие моменты можно четко определить по правильно построенной диаграмме свободного тела.Таким образом, вы можете установить первое условие равновесия для сил и второе условие равновесия для крутящих моментов.
При создании условий равновесия мы можем принять любую инерциальную систему отсчета и любое положение точки поворота. Все варианты приводят к одному ответу. Однако некоторые варианты могут чрезмерно усложнить процесс поиска решения. Независимо от того, какой выбор мы делаем, мы получаем один и тот же ответ. Единственный способ овладеть этим навыком — практиковаться.

Концептуальные вопросы

Можно ли упереть лестницу в неровную стену, когда пол без трения?

Художник поднимается по лестнице. Будет ли лестница соскользнуть с большей вероятностью, когда художник находится внизу или вверху?

Проблемы

Чтобы вытащить свою машину из грязи, мужчина привязывает один конец веревки к переднему бамперу, а другой конец — к дереву на расстоянии 15 м, как показано ниже. Затем он тянет за центр веревки с силой 400 Н, в результате чего ее центр смещается на 0,30 м, как показано. Какова сила троса на машине?

Униформа 40.Подмости 0 кг длиной 6,0 м поддерживаются двумя световыми кабелями, как показано ниже. Маляр весом 80,0 кг стоит на расстоянии 1,0 м от левого конца строительных лесов, а его малярное оборудование — в 1,5 м от правого конца. Если натяжение левого троса вдвое больше, чем правого троса, найдите натяжение тросов и массу оборудования.

Покажи ответ

кабель правый, 444,3 Н; левый кабель, 888,5 Н; вес оборудования 156,8 Н; 16,0 кг

Когда конструкция, показанная ниже, поддерживается в точке P , она находится в состоянии равновесия.Найдите величину силы F и силу, приложенную в точке P . Вес конструкции незначительный.

Чтобы подняться на крышу, человек (массой 70,0 кг) ставит алюминиевую лестницу длиной 6,00 м (массой 10,0 кг) на бетонную площадку с основанием лестницы на расстоянии 2,00 м от дома. Лестница упирается в пластиковый водосточный желоб, который, как мы можем предположить, не имеет трения. Центр масс лестницы находится на расстоянии 2,00 м от низа. Человек стоит 3.00 м от дна. Найдите нормальные силы реакции и трения лестницы у ее основания.

Единая горизонтальная стойка весит 400,0 Н. Один конец стойки прикреплен к шарнирной опоре у стены, а другой конец стойки прикреплен к знаку, который весит 200,0 Н. Стойка также поддерживается прикрепленным тросом. между концом подкоса и стеной. Предполагая, что весь вес знака прикреплен к самому концу стойки, найдите натяжение троса и усилие на шарнире стойки.

Предплечье, показанное ниже, расположено под углом [латекс] \ тета [/ латекс] по отношению к плечу, а в руке удерживается груз весом 5,0 кг. Общая масса предплечья и кисти составляет 3,0 кг, а их центр масс находится на расстоянии 15,0 см от локтя. (a) Какова величина силы, которую мышца двуглавой мышцы оказывает на предплечье для [latex] \ theta = 60 \ text {°} \ text {?} [/ latex] (b) Какова величина силы на локтевом суставе на такой же угол? (c) Как эти силы зависят от угла [латекс] \ theta? [/ латекс]

Показать решение

а.539 Н; б. 461 Н; c. не зависят от угла

Показать решение

напряжение 778 Н; на петле 778 N на [латексе] 45 \ text {°} [/ latex] выше горизонтали; нет

Стрела 12,0 м, AB , крана, поднимающего груз массой 3000 кг, показана ниже. Центр масс стрелы находится в ее геометрическом центре, а масса стрелы составляет 1000 кг. Для показанного положения рассчитайте натяжение T в тросе и усилие на оси A .

Унифицированный люк, показанный ниже, имеет размер 1,0 м на 1,5 м и весит 300 Н.