Боковая сторона равнобедренного треугольника равна: Боковая сторона равнобедренного треугольника равна 4.Угол при вершине, противолежащий основанию, равен 120 градусов. Найдите диаметр...

Боковая сторона равнобедренного треугольника – построение

4.6

Средняя оценка: 4.6

Всего получено оценок: 61.

4.6

Средняя оценка: 4.6

Всего получено оценок: 61.

Боковая сторона равнобедренного треугольника достаточно интересное явление, поскольку ее часто просят найти в простых геометрических задач. Главное в нахождении боковой стороны знать основной метод решения, а сам процесс трудности не представляет.

Равнобедренный треугольник

Равнобедренный треугольник – это треугольник, две стороны которого равны, а третья является основанием.

Рис. 1. Равнобедренный треугольник

Только в равнобедренном треугольнике основание имеет реальное практическое применение. Для лучшего визуального восприятия фигуры стоит располагать чертеж так, чтобы основание располагалось снизу. При этом равносторонний треугольник считается частным случаем равнобедренного. В равностороннем треугольнике любая сторона может считаться как основанием, так и боковой. При этом равносторонний треугольник можно построить, зная только одну сторону. Построение равнобедренного треугольника по боковой стороне невозможно, нужно знать значение основания или угол между сторонами.

Рис. 2. Равносторонний треугольник

Свойства равнобедренного треугольника

Свойств равнобедренного треугольника не так много. В решениях школьных задач даже старших классов используется всего 3 свойства:

Боковые стороны треугольника равны.
Биссектриса треугольника совпадает с медианой и высотой.
Углы при основании равнобедренного треугольника равны.

Этих свойств вполне достаточно, чтобы использовать стиль решения неприменимый для любого другого треугольника.

Боковая сторона треугольника

Равнобедренный отличается от остальных фигур тем, что достаточно двух показателей, из которых хотя бы один должен быть стороной, чтобы решить весь треугольник.

Если известно основание и любой из углов, то найти боковую сторону совсем не сложно. Если опустить на основание высоту, которая совпадет с медианой и биссектрисой, то получится два малых равных между собой прямоугольных треугольника, в которых боковая сторона будет являться гипотенузой.

Рис. 3. Высота равнобедренного треугольника

Сторону можно найти из тригонометрической функции синуса или косинуса. Выбор функции зависит от того, какой угол известен. Для этого понадобится один из катетов. Один из катетов является высотой и его найти не всегда возможно. Чаще всего используют катет, равный половине основания. А почему он равен половине основания?

Потому что основание делится проведенной высотой пополам, так как совпадает с медианой.
Вторая боковая сторона равна найденной. К слову, такой стиль решения применяется практически во всех задачах с равнобедренными треугольниками, поэтому стоит его запомнить.

Тригонометрическую функцию известного угла можно определить по таблицам Брадиса. В этих таблицах рассчитаны значения для всех существующих целых и промежуточных углов.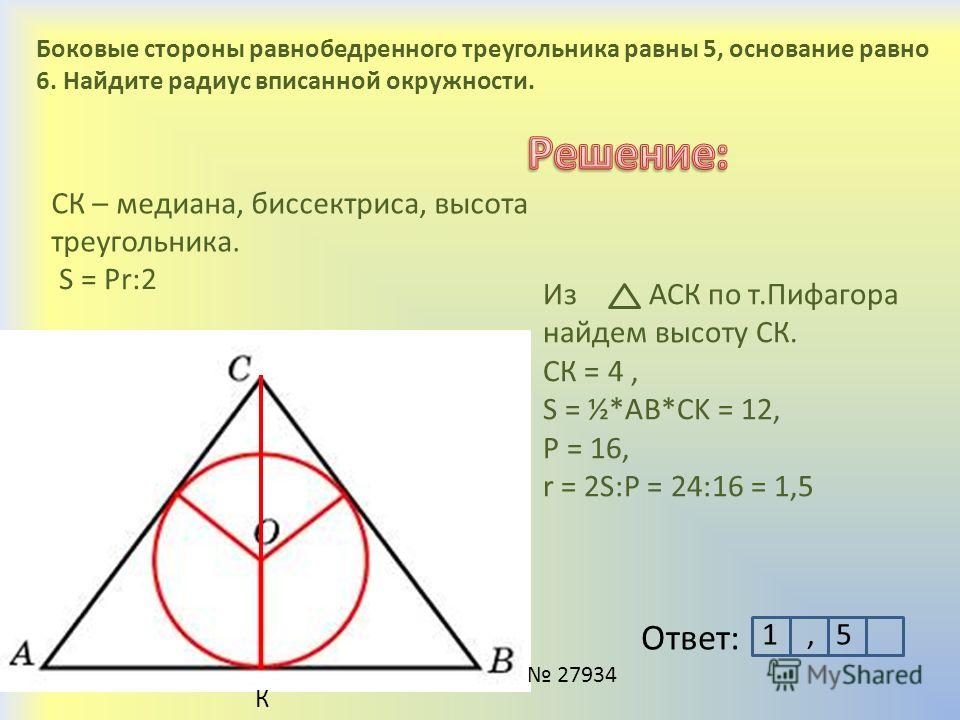

Равнобедренный треугольник нельзя решить, если:

известны только 2 боковые стороны;
известны только углы;
известно только основание;
известна только величина любого из характеризующих отрезков: высоты, медианы, биссектрисы и т.д.

Во всех остальных случаях треугольник можно решить, даже если известна только площадь и один из углов. Зачем знать варианты, когда решение точно невозможно? Чтобы не попасть в ловушку не решаемых задач. Такие редко, но встречаются. Предоставляя их к решению, составители проверяют уровень знаний учеников о фигуре.

Что мы узнали?

Мы поговорили о том, что такое равнобедренный треугольник, выделили основные его свойства и поговорили о методах нахождения сторон равнобедренного треугольника. Также мы выделили в отдельности боковую сторону и рассказали, как просто и быстро определить значение боковой стороны равнобедренного треугольника.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка статьи

4.6

Средняя оценка: 4.6

Всего получено оценок: 61.

А какая ваша оценка?

Боковая сторона равнобедренного треугольника в 5 раз больше основания,…





Ответы

пусть х см — основание треугольника
тогда 5х см — каждая из двух боковых сторон треугольника
(х + 5х + 5х) см — периметр треугольника
зная, что периметр треугольника равен 99 см, составим уравнение:
х + 5х + 5х = 99
11х = 99
х = 99:11
х = 9
9 см — основание треугольника
9*5 = 45 см — каждая из двух боковых сторон треугольника
Ответ: 9 см, 45 см, 45 см

08.

12.16

Михаил Александров

Читать ответы

Андрей Андреевич

Читать ответы

Eleonora Gabrielyan

Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука

Похожие вопросы

Решено

Если два художника могут разрисовать 2 комнаты, за 2 часа. . Сколько художников надо, чтобы разрисовать 18 комнат за 6 часов.. И подробно обьснить решение

Решено

Помогите пожалуйста решить задачу 4-го класса. Если около каждого дома посадить по 9 саженцев, то не зватит 100 саженцев, а если по 5 саженцев, то 20 саженцев останется. Сколько домов? Сколько

Тонкая собирающая линза диаметром D 2 см имеет фокусное расстояние F1 10 см. Вдоль ее оптической оси просверлили круглое отверстие диаметром d 1см и

В стеклянный стакан массой 100 г имеющий температуру 20 градусов цельсия налили воду при температуре 80 градусов цельсия. Через некоторое время…

король разделил свой прямоугольный сад на несколько квадратных участков разного размера в саду есть колодец 1 на 1 метр нужно записать длину и

Пользуйтесь нашим приложением

Свойства равнобедренных треугольников | Brilliant Math & Science Wiki

Ниранджан Хандерия, Архит Бубна, Александр Кац, и

способствовал

Содержимое

Терминология
Основные свойства
Расширенные свойства
Проблемы
Смотрите также

В равнобедренном треугольнике две равные стороны называются катетами , а оставшаяся сторона называется основанием . Угол, лежащий против основания, называется 9.0023 угол вершины , а точка, связанная с этим углом, называется вершиной . Два равных угла называются равнобедренными углами .

Если треугольник также равносторонний, то любую из трех сторон можно считать основанием.

Поскольку углы, противоположные равным сторонам, сами по себе равны, в равнобедренном треугольнике есть два равных угла (против двух равных сторон). Таким образом, по двум равным сторонам и одному углу можно определить всю структуру треугольника. Точно так же, зная два равных угла и длину любой стороны, можно определить структуру треугольника. 92\sin\alpha}{2}\).

Высота до основания также удовлетворяет важным свойствам:

Высота до основания является серединным перпендикуляром к основанию.
Высота до основания равна биссектрисе угла при вершине.
Высота основания — это линия симметрии треугольника.
Высота до основания равна медиане от вершины до основания.

Это означает, что центр вписанной окружности, центр тяжести и ортоцентр лежат на высоте основания, что делает высоту основания линией Эйлера треугольника. 9{\circ}\] на сумму углов треугольника. \(_\квадрат\)

Свойства равносторонних треугольников

Процитировать как: Свойства равнобедренных треугольников. Brilliant.org . Извлекаются из https://brilliant.org/wiki/properties-of-isosceles-triangles/

Формулы для равнобедренных треугольников. Что такое формулы для равнобедренных треугольников? Примеры

Равнобедренный треугольник в геометрии — это треугольник, две стороны которого имеют одинаковую длину. Два угла, лежащие напротив равных сторон, равны и всегда острые. Различные формулы для равнобедренных треугольников объясняются ниже. Две важные формулы для равнобедренных треугольников – площадь треугольника и периметр треугольника.

Что такое формулы равнобедренных треугольников?

Равнобедренный треугольник имеет две стороны одинаковой длины и две равные стороны, соединяющиеся под одинаковым углом к основанию, т. е. к третьей стороне. Таким образом, в равнобедренном треугольнике высота перпендикулярна от вершины, которая является общей для равных сторон. Такие особые свойства равнобедренного треугольника помогают нам рассчитать его площадь, а также его высоту с помощью формул равнобедренного треугольника.

Формулы равнобедренного треугольника 9{2}}{4}}\)

(Здесь а — равная сторона, а b — основание треугольника.)

Площадь = 1/2 × abSinα
(Здесь a и b — длины двух сторон, а α — угол между этими сторонами.)

Периметр равнобедренного треугольника : В равнобедренном треугольнике три стороны: две равные стороны и одно основание. Для вычисления периметра равнобедренного треугольника используется выражение 2a + b , 9{2}}{4}}\)

Давайте проверим несколько примеров, чтобы лучше понять использование формул для равнобедренных треугольников.

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Примеры использования формул для равнобедренных треугольников

Пример 1: Определить площадь равнобедренного треугольника, у которого основание «b» равно 8 единицам, а боковая сторона «a» равна 5 единицам?

Solution: Applying Pythagoras’ theorem:

a ² = (b/2) ² + h ²

h ² = a ² — (b/2) ² = 5 ² — 4 ² что дает h = 3

Площадь ‘A’ = (1/2) × b × h = (1/2) 8 × 3 = 12 единиц ²

Ответ: площадь равнобедренного треугольника – 12 единиц ² .
Пример 2: Найдите боковую сторону равнобедренного треугольника площадью 20 единиц ² и база из 10 единиц?
Решение: Используя формулу площади равнобедренного треугольника:
A = (1/2) b h = 20
Учитывая b = 10,
Найти: боковая сторона
h = 40 / 10 4
Применение теоремы Пифагоры:
A ² = (B/2) ²+ H ² = √ (5 ²+ 4 ²) = √ √419999 + 4 ²) = √419168 + 4 ²) = √4169 + 4 ²) = √4.99168 2 + 4 ²) =.0024
Ответ: боковая сторона равнобедренного треугольника равна √41.
Пример 3: Вычислите площадь, высоту и периметр равнобедренного треугольника, если две его равные стороны имеют длину 6 единиц, а третья сторона равна 8 единицам.
Решение:
Учитывая a = b = 6 единиц, c = 8 единиц
Чтобы найти: площадь, высоту и периметр равнобедренного треугольника
Периметр равнобедренного треугольника,
P = 2×a + b
P = 2×6 + 8
= 20 ед. 8 ² /4)
h = √(36−16)
h = √20 ед. 8×√20
= √20/4 квадратных единиц
Ответ:
Часто задаваемые вопросы о формулах для равнобедренных треугольников
Что такое формула равнобедренного треугольника в геометрии? 9{2}}{4}}\)
Площадь = 1/2 × abSinα
(Здесь a и b — длины двух сторон, а α — угол между этими сторонами.)
Как использовать формулу равнобедренного треугольника?
Мы можем использовать формулы равнобедренного треугольника следующим образом:
Шаг 1: Проверьте параметр (площадь, периметр или высоту), который нужно получить или рассчитать.
Шаг 2. Определите сторону равнобедренного треугольника и подставьте значение в нужную формулу — площадь, периметр или высоту.