Задание №15 ОГЭ по математике 🐲 СПАДИЛО.РУ
Описание задания В задании 16 проверяется умение выполнять действия с геометрическими фигурами, координатами и векторами. По спецификации ОГЭ здесь могут встретиться задания, связанные с необходимостью нахождения длин, углов и площадей. Проверьте, что вы не ошибаетесь в определениях тригонометрических функций острого угла в прямоугольном треугольнике. Кроме того, убедитесь, что все данные задачи отражены на вашем чертеже. При необходимости применяйте теорему Пифагора. Если сюжет задачи развивается в равнобедренном треугольнике, то учтите, что высота, опущенная из вершины такого треугольника, делит его на два равных прямоугольных треугольника и далее задача решается в прямоугольном треугольнике. Если события происходят в окружности, то, помимо всего прочего, надо учесть, что вписанный угол равен половине центрального угла, который опирается на ту же дугу. Пусть треугольник вписан в окружность. Если этот треугольник остроугольный, то центр окружности лежит внутри треугольника. Если этот треугольник тупоугольный, то центр окружности лежит вне треугольника. А если это прямоугольный треугольник, то центр окружности лежит на середине гипотенузы. В 16 задании нам предстоит продемонстрировать свои знания в нахождении неизвестных элементов треугольника. Это могут быть углы, стороны, высоты, медианы или биссектрисы. Могут встретится задания на нахождение площади.
Если этот треугольник тупоугольный, то центр окружности лежит вне треугольника. А если это прямоугольный треугольник, то центр окружности лежит на середине гипотенузы. В 16 задании нам предстоит продемонстрировать свои знания в нахождении неизвестных элементов треугольника. Это могут быть углы, стороны, высоты, медианы или биссектрисы. Могут встретится задания на нахождение площади.Теория к заданию №15
Так как задания №16 основаны на теории по теме «треугольники», рассмотрим базовые понятия, определения и формулы.
Вначале предлагаю рассмотреть углы на плоскости:
Многие задачи построены на нахождении медиан и биссектрис треугольника:
Биссектриса – отрезок, выходящий из вершины треугольника и делящий угол пополам.
- Биссектриса делит противолежащую сторону на части , пропорциональные прилежащим сторонам: ab : ac = b : c
- Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам.

- Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
Средняя линия – отрезок, соединяющий середины двух сторон треугольника.
- Средняя линия параллельна третьей стороне и равна её половине.
- Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного.
Равнобедренный треугольник — треугольник, у которого две стороны равны.
Свойства равнобедренного треугольника:
- Углы, при основании треугольника, равны.
- Высота, проведенная из вершины, является биссектрисой и медианой.

Равносторонний треугольник — треугольник, у которого все стороны равны.
- Все углы равны 60°.
- Каждая из высот является одновременно биссектрисой и медианой.
- Центры описанной и вписанной окружностей совпадают.
Для решения этого задания нужно помнить два факта:
- Внутренний угол с внешним углом дают в сумме 180°
- Углы при основании равнобедренного треугольника равны.
Из первого пункта следует, что угол BCA = 180 — 123 = 57°
Из второго — что ∠BCA = ∠BAC = 57°
Ответ: 57pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1610o Биссектриса равностороннего треугольника равна 11√3. Найдите его сторону.
Найдите его сторону.До этого мы искали медиану, биссектрису или высоту равностороннего треугольника по формуле:
m = ( a • √3 )/ 2
Здесь же нам необходимо решить обратную задачу, найти a, если известно m.
Выразим a:
a = ( 2 • m ) / √3
Подставим значение:
a = ( 2 • m ) / √3 = ( 2 • 11 • √3 ) / √3 = 22
Ответ: 22pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1609o Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.Воспользуемся теоремой Пифагора:
c² = 12² + 16² = 144 + 256 = 400
c = √400 = 20
Ответ: 20pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1608o Сторона равностороннего треугольника равна 12√3. Найдите его высоту.Вспоминаем, что в равностороннем треугольнике высота является и медианой и биссектрисой.
Для медианы, а значит и для высоты, формулу я приводил чуть выше:
m = ( a • √3 )/ 2
Подставим значение:
m = ( 12√3 • √3 )/ 2 = ( 12 • 3 )/ 2 = 36 / 2 = 18
Ответ: 18pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1607o Два катета прямоугольного треугольника равны 15 и 4.
AM = ½ AC = ½ 56 = 28
Ответ: 28pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1605o Один из острых углов прямоугольного треугольника равен 23°. Найдите второй острый угол. Ответ дайте в градусах.Так как сумма углов в треугольнике равна 180°, а в прямоугольном треугольнике один из углов прямой, то сумма двух острых углов равна 90°. Отсюда можно вывести следующее правило:
Сумма острых углов в прямоугольном треугольнике равна 90°.
Следовательно, второй острый угол равен:
90 — 23 = 67°
Ответ: 67pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1604o Сторона равностороннего треугольника равна 10√3. Найдите его медиану.Для решения этой задачи необходимо знать формулу медианы в равностороннем треугольнике, или уметь выводить её из теоремы Пифагора. В данном случае мы воспользуемся готовой формулой, и я советую вам её запомнить, чтобы не тратить время на вывод в каждом случае:
m = ( a • √3 )/ 2
Где m — медиана в равностороннем треугольнике, а a — сторона. Таким образом, для решения данной задачи подставим значение в формулу:
Таким образом, для решения данной задачи подставим значение в формулу:
m = ( 10√3 • √3 )/ 2 = ( 10 • 3 )/ 2 = 30 / 2 = 15
Ответ: 15pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1603o В треугольнике ABC известно, что AB = BC, ∠ABC = 122°. Найдите угол BCA. Ответ дайте в градусах.Если в треугольнике две стороны равны — значит он равнобедренный. А в равнобедренном треугольнике углы при основании равны. Так как сумма углов в треугольнике равна 180°, угол в вершине равен 122°, значит сумма углов при основании равна:
180 — 122 = 58°
Так как углы при основании равны, значит угол BCA равен углу BAC:
∠BCA = ∠BAC
58° = ∠BCA + ∠BAC = 2 ∠BCA
∠BCA = 58 / 2 = 29°
Ответ: 29pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1602o Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 20, сторона BC равна 58, сторона AC равна 64. Найдите MN.
Найдите MN.Для решения этой задачи не нужно пользоваться всеми данными в условии. Для успешного решения необходимо знать, что такое средняя линия треугольника.
Средняя линия — это линия соединяющая середины сторон и параллельная основанию.
Средняя линия равна половине основания, которому она параллельна.
Таким образом, если точки M и N являются серединами сторон AB и BC, значит эта линия параллельна AC — третьей стороне. А это в свою очередь означает, что она равна половине AC:
MN =½ • AC = 64 / 2 = 32
Ответ: 32pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1601o В треугольнике два угла равны 73° и 48°. Найдите его третий угол. Ответ дайте в градусах.Для решения этого задания достаточно знать правило — сумма углов в треугольнике равна 180°.
Нам известны два угла, значит можем найти третий:
180 — 73 — 48 = 59
Ответ: 59pазбирался: Даниил Романович | обсудить разбор | оценить
Тема 9.
 Планиметрия — Материалы для подготовки к вступительным экзаменам в СГГА
Планиметрия — Материалы для подготовки к вступительным экзаменам в СГГАЦентр вписанной окружности – точка пересечения биссектрис; центр описанной окружности – точка пересечения серединных перпендикуляров.
Теорема косинусов: a2=b2+c2-2bccosA.
Свойство медиан: AO:OM=2:1.
Свойство биссектрис: CA:AD=CB:BD.
1) Углы треугольника пропорциональны числам 3, 5, 7. Найдите эти углы.
2) Углы треугольника образуют арифметическую прогрессию. Чему равен наибольший угол, если величина наименьшего 200?
3) Два внешних угла треугольника равны 1200 и 1600. Чему равен третий внешний угол?
4) Медиана, проведенная к гипотенузе прямоугольного треугольника, равна 15, а один из острых углов равен 600. Чему равна длина меньшего катета?
5) Один из углов прямоугольного треугольника равен 300, а высота, проведенная к гипотенузе, равна 9.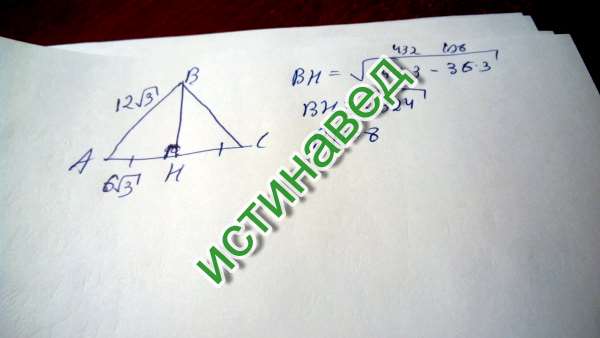 Найдите длину гипотенузы.
Найдите длину гипотенузы.
7) Найдите гипотенузу равнобедренного прямоугольного треугольника, если его площадь равна 18.
8) Гипотенуза прямоугольного треугольника равна 13, а катеты относятся как 2 : 3. Чему равна площадь треугольника?
9) Один из катетов прямоугольного треугольника равен 9, а другой относится к гипотенузе, как 4 : 5. Чему равна площадь треугольника?
10) Катеты прямоугольного треугольника равны log49 и log316. Чему равна площадь треугольника?
11) Высота равнобедренного треугольника, равна 15, а боковая сторона больше основания на 1. Чему равно основание?
12) Найдите боковую сторону равнобедренного треугольника, если его основание равно 18, а площадь 108.
13) Найдите боковую сторону равнобедренного треугольника, если основание равно 10 см, а медиана, проведённая к основанию, равна 3 см.
14) Величины углов треугольника относятся как 1 : 1 : 2, а большая из сторон равна 15. Чему равна высота, проведенная к этой стороне?
Чему равна высота, проведенная к этой стороне?
17) Основание треугольника равно 22, боковые стороны 13 и 19. Чему равна медиана, опущенная на основание?
18) Две стороны треугольника равны 11 и 7, а медиана, опущенная на третью сторону 6. Найдите длину третьей стороны.
19) В треугольнике ABC медиана AM равна 6 и образует со стороной AC, равной 8, угол 300. Найдите площадь треугольника.
20) В треугольнике ABC к стороне BC=12 проведена медиана AM=7 и образует с этой стороной угол 300. Найдите площадь треугольника.
21) Площадь треугольника ABC равна 12. Из вершины B проведена медиана BD, длина которой равна 3. Найдите сторону AC, если .22) Площадь правильного треугольника равна 64. Найдите его периметр.
23) В треугольнике ABC на сторонах AB и AC взяты точки M и N такие, что . Найдите площадь треугольника AMN.
Найдите площадь треугольника AMN.24) Площадь треугольника ABC равна 48. Точка D лежит на стороне AC, деля ее в отношении AD:DC=1:7. Найдите площадь треугольника ABD.
25) Сторона треугольника равна 2, а прилегающие к ней углы 300 и 450. Найдите его площадь.
26) Один из катетов прямоугольного треугольника равен 6, а противолежащий ему угол . Найдите площадь круга, описанного около треугольника. 27) Площадь правильного треугольника равна . Чему равен радиус описанной около него окружности?28) Высота правильного треугольника равна 18. Найдите диаметр вписанной в него окружности.
29) Точка касания с вписанной окружностью делит гипотенузу треугольника в отношении 2 : 3. Расстояние от прямого угла треугольника до центра окружности равно . Найдите периметр треугольника.30) Катеты прямоугольного треугольника равны 16 и 30. Найдите радиус описанной около него окружности.
31) Один катет прямоугольного треугольника равен 15, проекция другого катета на гипотенузу равна 16. Чему равен радиус вписанной в треугольник окружности?
Чему равен радиус вписанной в треугольник окружности?
34) Радиус окружности равен 6. Перпендикуляр, опущенный из точки окружности на диаметр, делит его в отношении 1 : 3. Найдите длину перпендикуляра.
35) Найдите величину острого угла, который опирается на дугу, равную 2/5 окружности. Ответ дайте в градусах.
36) Найдите величину тупого угла, который опирается на дугу, равную 1/7 окружности. Ответ дайте в радианах.
37) Радиус окружности равен 5. Найдите длину дуги окружности, соответствующей центральному углу 1080.
38) Радиус окружности равен 20. Найдите Величину центрального угла, которому соответствует дуга окружности длины . 39) Хорда окружности, стягивающая дугу 900, равна . Чему равна длина окружности?
39) Хорда окружности, стягивающая дугу 900, равна . Чему равна длина окружности?40) Радиус окружности равен 13. На каком расстоянии от центра окружности находится хорда длины 24.
41) Из точки окружности радиуса R проведены две хорды длины . Чему равен косинус угла между этими хордами?42) По разные стороны от центра окружности проведены две параллельные хорды длин 12 и 16. Чему равен радиус окружности, если расстояние между хордами равно 14?
43) Найти площадь прямоугольника, если его диагональ равна , а одна из сторон 18.44) В прямоугольнике ABCD биссектриса угла BAD пересекает сторону BC в точке M и делит ее на отрезки BM=6, MC=4. Чему равна площадь прямоугольника?
45) Площадь параллелограмма равна 120, а его высоты 8 и 12. Найдите периметр параллелограмма.
46) Высоты параллелограмма равны 4 и 8. Большая высота опущена на сторону, равную 6. Найти другую сторону параллелограмма.
47) Углы между стороной ромба и его диагоналями относятся как 5 : 4. Найдите тупой угол ромба.
Найдите тупой угол ромба.
48) Как изменится площадь ромба, если одну из его диагоналей уменьшить на 10%, а другую увеличить на 20%?
49) Сторона ромба равна 5, а одна из диагоналей 6. Чему равна его площадь?
50) Разница между радиусами окружностей, описанной около квадрата и вписанной в квадрат, составляет . Чему равна сторона квадрата? 51) Боковая сторона равнобокой трапеции равна , высота и большее из оснований, соответственно, 4 и 9. Найдите длину средней линии трапеции.52) Средняя линия трапеции ABCD делит ее на две трапеции со средними линиями, равными 5 и 9. Найдите большее основание ABCD.
53) Трапеция, средняя линия которой равна , равновелика (т.е. равна по площади) равностороннему треугольнику со стороной 12. Найти высоту трапеции.54) В равнобокой трапеции тупой угол равен 1200 и меньшее основание равно боковой стороне и равно 6. Найдите площадь трапеции.
55) В равнобедренной трапеции основания равны 4 и 6, боковая сторона равна 5.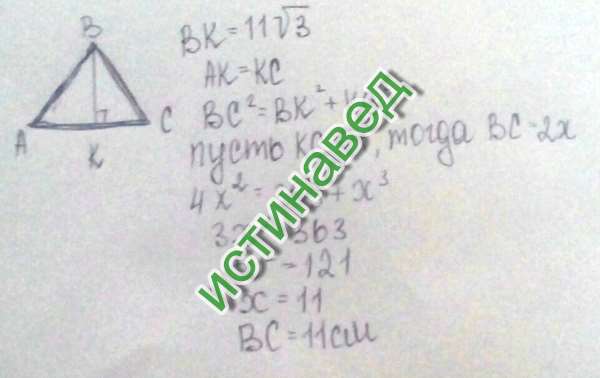 Чему равна сумма длин диагоналей?
Чему равна сумма длин диагоналей?
56) В равнобедренной трапеции разность длин оснований равна длине боковой стороны. Чему равен тупой угол трапеции?
57) Высота равнобокой трапеции равна 40, боковая сторона 41, средняя линия 45. Чему равно большее основания трапеции?
58) В прямоугольной трапеции боковые стороны равны 4 и 5, меньшее из оснований 5. Чему равна площадь трапеции?
59) В прямоугольнике перпендикуляр, опущенный на диагональ, делит прямой угол на две части в отношении 3 : 1. Чему равен угол между этим перпендикуляром и другой диагональю?
60) Периметр ромба равен 52, а сумма длин диагоналей 34. Чему равна его площадь?
61) Диагонали ромба равны 26 и . Чему равен синус острого угла ромба?62) В равнобокой трапеции боковая сторона равна 7, диагональ 8, а средняя линия 4. Найдите меньшее основание.
63) В окружность радиуса 6 вписан прямоугольник. Найдите большую сторону прямоугольника, если угол между его диагоналями составляет 600.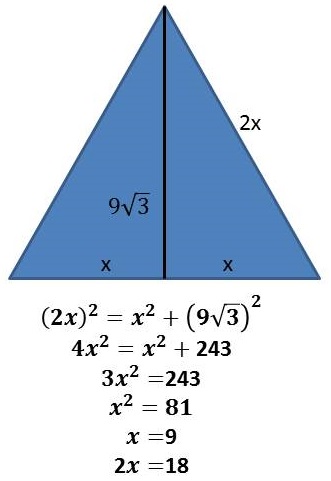
64) В круг вписан прямоугольник со сторонами 2 и 6. Найдите площадь круга.
65) Равнобедренная трапеция вписана в окружность радиуса 6. Ее диагональ составляет угол 300 с большим основанием и перпендикулярна боковой стороне. Найдите периметр трапеции.
66) Периметр равнобедренной трапеции, описанной около окружности, равен 60. Найдите длину средней линии трапеции.
67) Основания равнобокой трапеции равны 12 и 20. Центр описанной около окружности трапеции лежит на ее большем основании. Чему равна диагональ трапеции?
68) В трапецию вписана окружность. Расстояние от центра этой окружности до вершины верхнего основания равно 15; до вершины нижнего 20. Чему равна площадь трапеции?
69) Четырехугольник ABCD вписан в окружность. BC=4, CD=5, . Чему равна диагональ BD?70) Окружность, вписанная в ромб, разбивает его диагональ на отрезки длины 9, 16, 9. Найдите площадь ромба.
71) Сторона вписанного в окружность правильного треугольника равна 6. Чему равна площадь квадрата, вписанного в ту же окружность?
Чему равна площадь квадрата, вписанного в ту же окружность?
72) Во сколько раз площадь круга больше площади вписанного в него квадрата?
73) Какой правильный многоугольник имеет внутренний угол 1440?
74) Сколько диагоналей можно провести в многоугольнике, если сумма его внутренних углов равна ?75) Чему равна площадь круга, описанного около правильного шестиугольника со стороной 2?
76) Дан правильный восьмиугольник ABCDEFKM. Найдите радиус описанной около него окружности, если площадь треугольника ABE равна . 77) Найдите радиус окружности, описанной около правильного девятиугольника A1A2…A9, если периметр треугольника A1OA4 равен .Треугольник. Важные факты о высоте, биссектрисе и медиане
Определения
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Теорема
В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).
Теорема
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
\[{\Large{\text{Медиана}}}\]
Теорема
В любом треугольнике медианы точкой пересечения делятся в отношении \(2:1\), считая от вершины.
Доказательство
Пусть \(AD\) и \(BE\) – медианы в треугольнике \(ABC\), \(O\) – точка пересечения \(AD\) и \(BE\).
\(DE\) – средняя линия в треугольнике \(ABC\), тогда \(DE\parallel AB\), значит \(\angle ADE = \angle BAD\), \(\angle BED = \angle ABE\), следовательно, треугольники \(ABO\) и \(DOE\) подобны (по двум углам).
Из подобия треугольников \(ABO\) и \(DOE\): \(\dfrac{BO}{OE} = \dfrac{AB}{DE} = \dfrac{2}{1}\).
Для других медиан треугольника \(ABC\) требуемое свойство доказывается аналогично.
Теорема
Медиана треугольника делит его на два равновеликих треугольника (равновеликие треугольники – это треугольники, у которых площади равны).
Доказательство
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию: \(S_{ABC} = 0,5\cdot AC\cdot h\).
Пусть \(BD\) – медиана в треугольнике \(ABC\), тогда \(AD = DC\).
\(S_{ABD} = 0,5\cdot AD\cdot h\),
\(S_{BCD} = 0,5\cdot DC\cdot h\). \circ\), чтд.
\circ\), чтд.
\[{\Large{\text{Биссектриса}}}\]
Теорема
Биссектриса треугольника делит его сторону на части, пропорциональные прилежащим сторонам:
Верно и обратное: если отрезок, проведенный из вершины треугольника к стороне, делит эту сторону на отрезки, пропорциональные прилежащим сторонам, то это биссектриса.
Доказательство
Площади треугольников, у которых есть равные углы, относятся как произведения сторон, образующих эти углы, то есть \[\dfrac{S_{ACD}}{S_{BCD}} = \dfrac{AC\cdot CD}{CB\cdot CD} = \dfrac{AC}{CB}\]
С другой стороны, \(\dfrac{S_{ACD}}{S_{BCD}} = \dfrac{0,5\cdot AD\cdot h}{0,5\cdot DB\cdot h}\), где \(h\) – высота, проведённая из точки \(C\), тогда \(\dfrac{S_{ACD}}{S_{BCD}} = \dfrac{AD}{DB}\).
В итоге \(\dfrac{AD}{DB} = \dfrac{S_{ACD}}{S_{BCD}} =
\dfrac{AC}{CB}\), откуда \(\dfrac{AD}{AC} = \dfrac{DB}{BC}\), что и требовалось доказать.
Теорема
Если точка равноудалена от сторон угла, то она лежит на его биссектрисе.
Верно и обратное: если точка лежит на биссектрисе угла, то она равноудалена от его сторон.
Доказательство
1) Докажем, что если \(KA=KB\), то \(OK\) – биссектриса.
Рассмотрим треугольники \(AOK\) и \(BOK\): они равны по катету и гипотенузе, следовательно, \(\angle AOK=\angle BOK\), чтд.
2) Докажем, что если \(OK\) – биссектриса, то \(KA=KB\).
Аналогично треугольники \(AOK\) и \(BOK\) равны по гипотенузе и острому углу, следовательно, \(KA=KB\), чтд.
Задачи по математике Треугольники
Прямоугольный треугольник
1.
В треугольнике ABC угол C прямой, BC = 8 , sin A = 0,4. Найдите AB.
3.
В треугольнике угол равен 90°, . Найдите .
4.
В треугольнике угол равен 90°, . Найдите .
Найдите .
5.
В треугольнике угол прямой, . Найдите .
6.
В треугольнике угол прямой, . Найдите .
7.
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ABC. Ответ дайте в градусах.
13.
Катеты прямоугольного треугольника равны и 1. Найдите синус наименьшего угла этого треугольника.
14.
Площадь прямоугольного треугольника равна Один из острых углов равен 30°. Найдите длину гипотенузы.
15.
В треугольнике угол равен 90°, Найдите
16.
В треугольнике угол равен 90°, Найдите
17.
Площадь прямоугольного треугольника равна Один из острых углов равен 30°. Найдите длину катета, лежащего напротив этого угла.
18.
Площадь прямоугольного треугольника равна Один из острых углов равен 30°. Найдите длину катета, прилежащего к этому углу.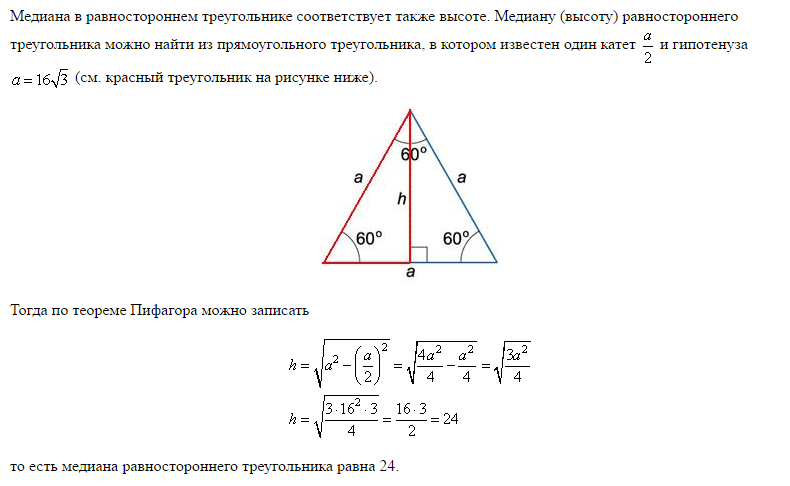
20.
В прямоугольном треугольнике катет , а высота , опущенная на гипотенузу, равна Найдите
21.
В треугольнике ABC угол C равен 90°, AC = 4, tg A = 0,75. Найдите BC.
22.
В треугольнике = 35, угол равен 90°. Найдите радиус описанной окружности этого треугольника.
23.
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 12 и 13.
24.
Катеты прямоугольного треугольника равны 8 и 15. Найдите гипотенузу этого треугольника.
25.
В прямоугольном треугольнике катет и гипотенуза равны 40 и 41 соответственно. Найдите другой катет этого треугольника.
26.
В прямоугольном треугольнике катет и гипотенуза равны 40 и 50 соответственно. Найдите другой катет этого треугольника.
27.
В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.
28.
Один из острых углов прямоугольного треугольника равен 23°. Найдите его другой острый угол. Ответ дайте в градусах.
29.
В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.
30. В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.
31.
В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.
32.
В треугольнике угол равен 90°, , . Найдите .
33.
В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.
34.
В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.
35.
В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.
36.
В треугольнике угол равен 90°, , . Найдите .
37. В треугольнике угол равен 90°, , . Найдите .
38.
В треугольнике угол равен 90°, , . Найдите .
39.
В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.
40.
В треугольнике угол равен 90°, , . Найдите .
41.
В треугольнике угол равен 90°, , . Найдите .
42.
В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.
43.
Один из острых углов прямоугольного треугольника равен 21°. Найдите его другой острый угол. Ответ дайте в градусах.
44.
В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.
45.
В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.
46.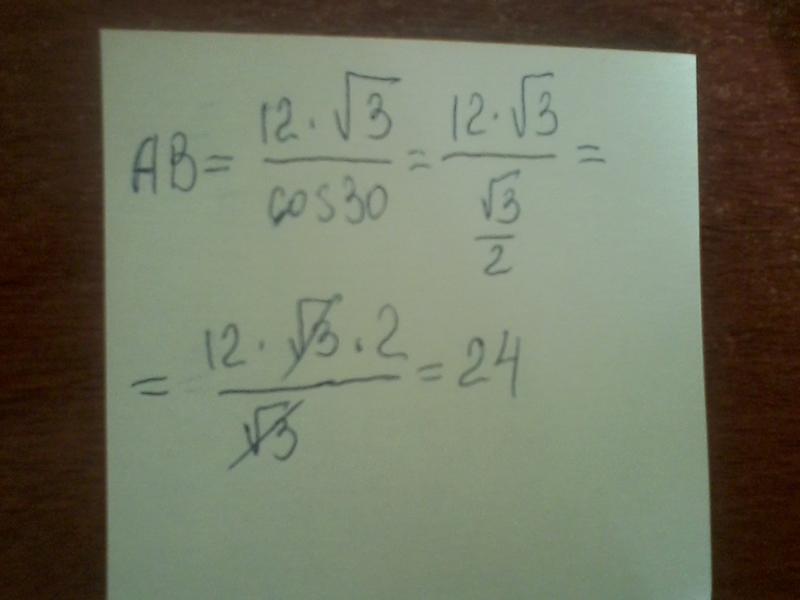
Один из острых углов прямоугольного треугольника равен 43°. Найдите его другой острый угол. Ответ дайте в градусах.
47.
В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.
48.
В треугольнике угол равен 90°, , . Найдите .
49.
В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.
50.
Один из острых углов прямоугольного треугольника равен 63°. Найдите его другой острый угол. Ответ дайте в градусах.
51.
В прямоугольном треугольнике катет и гипотенуза равны 5 и 13 соответственно. Найдите другой катет этого треугольника.
52.
В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.
53.
Два катета прямоугольного треугольника равны 16 и 30. Найдите гипотенузу этого треугольника.
54.
Один из острых углов прямоугольного треугольника равен 57°. Найдите его другой острый угол. Ответ дайте в градусах.
55.
В треугольнике угол равен 90°, , . Найдите .
.Равнобедренные треугольники
1.
В равностороннем треугольнике ABC биссектрисы CN и AM пересекаются в точке P. Найдите .
2.
В равнобедренном треугольнике . Найдите , если высота .
3.
В равностороннем треугольнике ABC медианы BK и AM пересекаются в точке O. Найдите .
4.
Площадь равнобедренного треугольника равна Угол, лежащий напротив основания равен 120°. Найдите длину боковой стороны.
6.
В треугольнике ABC AC = BC. Внешний угол при вершине B равен 146°. Найдите угол C. Ответ дайте в градусах.
7.
Точка D на стороне AB треугольника ABC выбрана так, что AD = AC. Известно, что ∠CAB = 80° и ∠ACB=59∘. Найдите угол DCB. Ответ дайте в градусах.
Известно, что ∠CAB = 80° и ∠ACB=59∘. Найдите угол DCB. Ответ дайте в градусах.
8.
Высота равностороннего треугольника равна Найдите его периметр.
9.
В треугольнике ABC AB = BC = 53, AC = 56. Найдите длину медианы BM.
10.
Боковая сторона равнобедренного треугольника равна 10, а основание равно 12. Найдите площадь этого треугольника.
11.
В треугольнике известно, что , . Найдите угол . Ответ дайте в градусах.
12.
В треугольнике известно, что , . Найдите угол. Ответ дайте в градусах.
13.
Сторона равностороннего треугольника равна . Найдите медиану этого треугольника.
14.
Сторона равностороннего треугольника равна . Найдите биссектрису этого треугольника.
15.
Сторона равностороннего треугольника равна . Найдите медиану этого треугольника.
16.
Биссектриса равностороннего треугольника равна . Найдите сторону этого треугольника.
Найдите сторону этого треугольника.
17.
В треугольнике известно, что , . Найдите угол . Ответ дайте в градусах.
18.
В треугольнике известно, что , . Найдите угол . Ответ дайте в градусах.
19.
Биссектриса равностороннего треугольника равна . Найдите сторону этого треугольника.
20.
В треугольнике известно, что , . Найдите угол . Ответ дайте в градусах.
21.
Сторона равностороннего треугольника равна . Найдите высоту этого треугольника.
22.
Сторона равностороннего треугольника равна . Найдите медиану этого треугольника.
23.
Высота равностороннего треугольника равна . Найдите сторону этого треугольника.
24.
Биссектриса равностороннего треугольника равна . Найдите сторону этого треугольника.
25
Сторона равностороннего треугольника равна . Найдите биссектрису этого треугольника.
26.
В треугольнике известно, что , . Найдите угол . Ответ дайте в градусах.
Найдите угол . Ответ дайте в градусах.
27.
Медиана равностороннего треугольника равна . Найдите сторону этого треугольника.
28.
В треугольнике ABC AC = BC. Внешний угол при вершине B равен 140°. Найдите угол C. Ответ дайте в градусах.
Треугольники общего вида
2.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°, угол ABC равен 106°. Найдите угол ACB. Ответ дайте в градусах.
3.
В треугольнике ABC проведены медиана BM и высота BH . Известно, что AC = 84 и BC = BM. Найдите AH.
4.
В остроугольном треугольнике высота равна а сторона равна 40. Найдите .
5.
В треугольнике ABC AB = BC, а высота AH делит сторону BC на отрезки BH = 64 и CH = 16. Найдите cos B.
6
В треугольнике ABC BM — медиана и BH – высота. Известно, что AC = 216, HC = 54 и ∠ACB = 40°. Найдите угол AMB. Ответ дайте в градусах.
Известно, что AC = 216, HC = 54 и ∠ACB = 40°. Найдите угол AMB. Ответ дайте в градусах.
8.
Медиана равностороннего треугольника равна . Найдите сторону этого треугольника.
9.
В треугольнике известно, что , — медиана, . Найдите .
10.
В треугольнике известно, что , — медиана, . Найдите .
13.
В треугольнике известно, что , — медиана, . Найдите .
14.
В треугольнике известно, что , — медиана, . Найдите .
15. Точки и являются серединами сторон и треугольника , сторона равна 66, сторона равна 37, сторона равна 74. Найдите
16.
В треугольнике известно, что , — медиана, . Найдите .
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/414608-zadachi-po-matematike-treugolniki
Математика по полочкам: 24. Треугольники
МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ
Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки.
Точки называются вершинами треугольника, а отрезки — его сторонами.
Свойства треугольников1. Сумма углов треугольника 180°.
2. Сумма двух сторон треугольника больше третьей стороны: a+b>c, b+c>a, a+c>b.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон: LM — средняя линия треугольника.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны: LM || BC, BC=2LM.
Виды треугольников
Виды треугольников (по углам):
· Остроугольный (все углы острые),
· Тупоугольный (один из углов тупой),
· Прямоугольный (один из углов прямой).
Виды треугольников (по сторонам):
· Разносторонний (стороны не равны между собой),
· Равнобедренный (две стороны равны),
· Равносторонний (три стороны равны между собой).
Биссектрисы, медианы, высоты треугольников
Биссектриса
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.
Биссектрисы треугольника пересекаются в одной точке, которая является центром вписанной окружности.
Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла.
Высота
Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника. В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.

Медиана
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны этого треугольника.
Медианы треугольника пересекаются в одной точке и делятся в отношении 2:1 начиная от вершины треугольника: СO=2OL, BO=2OM.
Медиана разбивает треугольник на два треугольника одинаковой площади: S ABM = S BCM.
Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.Равнобедренный треугольник
Две равные стороны называются боковыми сторонами, третья – основанием: KL и LM — боковые стороны (KL=LM), КМ — основание.Углы при основании равнобедренного треугольника равны:
К=М.Высота, проведенная к основанию равнобедренного треугольника, является биссектрисой и высотой.
Прямоугольный треугольник
Стороны треугольника, образующие прямой угол, называются катетами, сторона, лежащая против угла в 90°, называется гипотенузой: АС, ВС — катеты, АВ — гипотенуза.

Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Синус угла – отношение противолежащего катета к гипотенузе: sin α=a:c.
Косинус угла – отношение прилежащего катета к гипотенузе: cos α=b:c.
Тангенс угла – отношение противолежащего катета к прилежащему катету: tg α=a:b=sin α : cos α.
Котангенс угла – отношение прилежащего катета к противолежащему катету: ctg α= cos α : sin α.
Гипотенуза прямоугольного треугольника является диаметром описанной окружности.
Радиус описанной около прямоугольного треугольника окружности: R=c:2.
Радиус вписанной в прямоугольный треугольник окружности: r=(a+b-c):2.
Квадрат высоты, проведенной к гипотенузе прямоугольного треугольника равен произведению проекций высоты на гипотенузу: h2=x*y.
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов, причем коэффициент пропорциональности равен диаметру описанной около треугольника окружности:Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:a2 = b2 + c2 — 2bc cos А.

Площадь треугольника
h – высота, проведенная к стороне а.
a, b – стороны треугольника, γ – угол между ними.
р – полупериметр, a, b, c – стороны треугольника.S=pr, р – полупериметр, r – радиус вписанной окружности
S=abc : (4R), R — радиус описанной окружности
В прямоугольном треугольнике
S=0,5ab, где a, b – катеты треугольника
В равностороннем треугольнике
УПРАЖНЕНИЯ
1. а) В прямоугольном треугольнике один из катетов равен 10 см, один из углов равен 45. Найдите второй катет.б) В прямоугольном треугольнике катеты равны. Найдите все углы треугольника.
Решение:
а) В прямоугольном треугольнике 90° и 45°, следовательно, третий угол 180°-90°-45°=45°. Треугольник равнобедренный, т.к. два угла равны, тогда и катеты равны, т. е. второй катет равен 10 см.
е. второй катет равен 10 см.
Ответ: 10 см
2. Найдите величину катета АС: Решение:
а) Треугольник АВС прямоугольный и А=180°-90°-60°=30°.
ВС=АВ:2=10:2=5 см (катет лежит против угла в 30°).
АС2=АВ2-АС2=100-25=75, АС=
Ответ:
3. Найдите площадь равнобедренного треугольника со сторонами:
а) 6 см, 6 см, 8 см; б) 10 см, 10 см, 12 см.
Решение:
а) по формуле Герона
Ответ:
4. а) В треугольнике АВС сторона АВ равна 10 см, расстояние от точки С до прямой АВ равно 6 см, сторона ВС равна 14 см. Найдите расстояние от точки А до прямой ВС.
б) В треугольнике АВС расстояние от точки А до прямой ВС равно 5 см, расстояние от точки С до прямой АВ равно 7 см.
 Найдите сторону ВС, если известно, что сторона АВ равна 12 см.
Найдите сторону ВС, если известно, что сторона АВ равна 12 см.Решение:
а)
Дано: АВС — треугольник;
d(C, AB)=6 см;
АВ=10 см; ВС=14 см
Найти: d(A, BC)
Решение:
1) Найдем площадь треугольника АВС:
S=CК*АВ:2=10*6:2=30 см2
2) Зная площадь треугольника АВС и сторону ВС, найдем высоту АМ, проведенную к этой стороне:
S=BC*AM:2; AM=30:14*2=30/7 = 4 2/7 см
Ответ: 4 2/7 см
5. а) В равнобедренном прямоугольном треугольнике высота, проведенная к гипотенузе равна 4 см. Найдите площадь треугольника.
б) В равнобедренном прямоугольном треугольнике гипотенуза равна 10 см. Найдите площадь треугольника.
Решение:
а)
Дано: АВС — равнобедренный прямоугольный треугольник;
ВН=4 см
Найти: S — ?
Решение:
1) Т.
 к. треугольник АВС — равнобедренный, то высота ВН, проведенная к основанию является и медианой: АН=НС.
к. треугольник АВС — равнобедренный, то высота ВН, проведенная к основанию является и медианой: АН=НС.2) Квадрат высоты, проведенной из вершины прямого угла к гипотенузе равен произведению ее проекций на гипотенузу: ВН2=АН*НС; 16=АН2
АН=4 см
3) АС=2АН=8 см
4) S=ВН*АС:2=4*8:2=16 см2
Ответ: 16 см2
6. а) Периметр треугольника АВС равен 30 см. А=С и АВ больше АС на 3 см. Найдите стороны треугольника.
б) Периметр треугольника АВС равен 36 см. А=С и АВ : АС как 3:2. Найдите стороны треугольника. Решение:
а)
Дано:
АВС — треугольник;
Р=30 см;
А=С;
АВ=АС+3 см.
Найти: АВ, ВС, АС
Решение:
1) Т.к. А=С, то треугольник АВС — равнобедренный и АВ=ВС.
2) Пусть х — основание треугольника АВС, тогда боковая сторона равна (х+3).
Р=АВ+ВС+АС=х+х+3+х+3; 3х+6=30, 3х=24, х=8 см — сторона АС.

АВ=ВС=8 + 3=11 см
Ответ: 8 см, 11 см, 11 см
7. а) В прямоугольном треугольнике один из катетов равен 6 см, а сумма второго катета и гипотенузы равна 18 см. Найдите площадь треугольника.
б) В прямоугольном треугольнике один из катетов равен 1,5 см, а разность гипотенузы и второго катета равна 0,5 см. Найдите площадь треугольника.
Решение:
а) 1) Пусть катет равен х см, тогда гипотенуза равна (18 -х) см.
По теореме Пифагора:
62+х2=(18-х)2
36+х2=324-36х+х2
36х=288
х=8 (см) — катет прямоугольного треугольника
2) S=6*8:2=24 см2
Ответ: 24 см2
8. а) В равнобедренном треугольнике высота, проведенная к боковой стороне, делит ее на отрезки, равные 5 см и 4 см, считая от вершины треугольника. Найдите площадь треугольника.
б) В треугольнике АВС АК — высота, ВК=СК=5 см.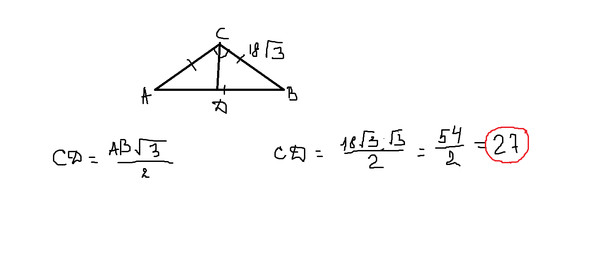 Найдите площадь треугольника, если АВ=12 см.
Найдите площадь треугольника, если АВ=12 см.
Решение:
а)
Дано: АВС — равнобедренный треугольник;
АК — высота к боковой стороне;
ВК= 5 см; КС= 4 см
Найти: S — ?
Решение:
1) Т.к. треугольник АВС — равнобедренный, то АВ=ВС=ВК+КС=5+4 = 9 см.
2) Треугольник АВК — прямоугольный, Зная гипотенузу АВ и катет ВК, найдем катет АК:
АК2=АВ2-ВК2=81-25=56
9. а) В прямоугольном треугольнике катеты равны 12 см и 9 см. Найдите биссектрису треугольника, проведенную к большему катету.
б) В прямоугольном треугольнике один из катетов равен 6 см, а гипотенуза равна 10 см. Найдите биссектрису треугольника, проведенную к меньшему катету.
Решение:
а)
Дано: АВС — прямоугольный треугольник;
АВ=12 см; АС=9 см;
СК — биссектриса
Найти: СК -?
Решение:
1) По теореме Пифагора найдем гипотенузу: ВС2=АВ2+АС2=144+81=225, ВС=15 см.

2) Т.к. СК — биссектриса, то АС:ВС=АК:КВ.
Пусть КВ=х, тогда АК=12-х.
9:15=(12-х):х,
9х=15(12-х),
8х=60,
х=7,5 см — ВК.
3) АК=12-7,5=4,5 см
4) Треугольник АКС — прямоугольный, по теореме Пифагора найдем КС:
КС2=АК2+АС2=101,25
10. а) В прямоугольном треугольнике проекции катетов на гипотенузу равны 25 см и 4 см. Найдите площадь треугольника.
б) В прямоугольном треугольнике проекции катетов на гипотенузу равны 9 см и 16 см. Найдите площадь треугольника.
Решение:
а)
Дано:
АВС — прямоугольный треугольник;
АК — высота;
ВК=25 см; КС=4 см
Найти: S — ?
Решение:
1) Квадрат высоты, проведенной из вершины прямого угла к гипотенузе равен произведению ее проекций на гипотенузу: АК2=ВК*КС; АК2=25*4=100, АК=10 см
2) ВС=ВК+КС=25+4=29 см
3) S=АК*ВС:2=15*10:2=145 см2
Ответ: 145 см2
11.
 а) В равнобедренном треугольнике боковые стороны равны 6 см, площадь треугольника равна 24 см2. Найдите сумму расстояний от точки на основании треугольника до его боковых сторон.
а) В равнобедренном треугольнике боковые стороны равны 6 см, площадь треугольника равна 24 см2. Найдите сумму расстояний от точки на основании треугольника до его боковых сторон.б) В равнобедренном треугольнике боковые стороны равны 12 см, площадь треугольника равна 56 см2. Найдите сумму расстояний от точки на основании треугольника до его боковых сторон.
Решение:
а)
Дано: АВС- равнобедренный треугольник;
АВ=ВС=6 см;
S=24 cм2
О — точка на основании треугольника АВС
Найти: d(O, AB)+d(O, BC)
Решение:
1) Найдем площадь треугольника АВО:
S=OK*AB:2=OK*6:2=3OK;
2) Найдем площадь треугольника ВСО:
S=OМ*BС:2=OМ*6:2=3OМ;
3) Площадь треугольника АВС равна сумме площадей треугольников АВО и ВСО:
24=3ОК+3ОМ,
ОК+ОМ=24:3=8 см
Ответ: 8 см
12.
 а) В прямоугольном треугольнике катеты равны 9 см и 12 см. Найдите биссектрису, проведенную к гипотенузе.
а) В прямоугольном треугольнике катеты равны 9 см и 12 см. Найдите биссектрису, проведенную к гипотенузе.б) В прямоугольном треугольнике катеты равны 3 см и 4 см. Найдите биссектрису, проведенную к гипотенузе.
Решение:
а)
Дано: АВС- прямоугольный треугольник;
АВ=12 см; АС=9 см;
АК — биссектриса
Найти: АК — ?
Решение:
1) Найдем гипотенузу треугольника АВС:
ВС2=АВ2+АС2=81+144=225, ВС=15 см.
2) По свойству биссектрисы треугольника:
АС:АВ=КС:ВК.
Пусть КС= х см, тогда ВК=15-х см
9:12=х:(15-х),
12х=135-9х,
21х=135,
х=45/7.
3) Найдем АК по теореме косинусов:
cos С=АС:ВС=9/15=3/5
АК2=АС2+КС2-2АС*КС*cos С=677.
13. а) Найдите наибольшую высоту треугольника со сторонами 7 см, 5 см, 4 см.

б) Найдите наименьшую высоту треугольника со сторонами 10 см, 12 см, 8 см.
Решение:
а)
1) Найдем площадь треугольника по формуле Герона:
2) Наибольшая высота проведена к меньшей стороне, следовательно высота проведена к стороне, равной 4 см. Зная площадь треугольника и сторону, к которой высота проведена, найдем высоту:
S=h*4:2,
14. а) Докажите, что медианы треугольника пересекаются в одной точке.
б) Докажите, что высоты треугольника пересекаются в одной точке.
Решение: а)
Дано: АВС — треугольник;
АМ, ВК, СN — медианы
Доказать: медианы пересекаются в одной точке
Доказательство:
1) Докажем, что медианы точкой пересечения делятся в отношении 2:1, начиная от вершины:
Пусть точка Е — середина АО, точка F — середина СО.

Рассмотрим четырехугольник ENMF, его стороны NM и EF параллельны и равны, т.к. являются средними линиями треугольников АВС и АОС с общим основанием АС. Тогда ENMF — параллелограмм, следовательно, МО=ЕО, NO=OF (диагонали параллелограмма точкой пересечения делятся пополам). Т.к. АЕ=ЕО=ОМ, то АО:МО=2:1, аналогично СО:ОN=2:1.
2) Докажем, что и медиана ВК проходит через точку О:
Пусть медианы ВК и АМ пересекаются в точке Н. Тогда ВН:НК=2:1 и АН:НМ=2:1, но, тогда точки О и Н делят медиану АМ в отношении 2:1, следовательно, они совпадают и медиана ВК проходит через точку О.
15. а) АК — биссектриса треугольника АВС. NK||AC, NM||BC, К лежит на ВС, М лежит на АС, N лежит на АВ и AN=5 см, NB= 3 см, ВК= 4 см. Найти МС.
б) АК — биссектриса треугольника АВС. NK||AC, NM||BC, К лежит на ВС, М лежит на АС, N лежит на АВ и AN=6 см, СК= 8 см, ВК= 7 см. Найти МС.
Решение:
а)
Дано: АВС — треугольник;
АК — биссектриса;
NK||AC, NM||BC;
AN=5 см, NB= 3 см, ВК= 4 см
Найти: МС — ?
Решение:
1) Рассмотрим треугольник ANK:
КАС=AKN как внутренние накрест лежащий при параллельных прямых NK и АС и секущей АК.
 По условию АК биссектриса и ВАК=КАС, следовательно ВАК=АКN и треугольник АNК — равнобедренный и AN=NK=5 cм.
По условию АК биссектриса и ВАК=КАС, следовательно ВАК=АКN и треугольник АNК — равнобедренный и AN=NK=5 cм.2) Рассмотрим четырехугольник MNKC:
MNKC — параллелограмм, т.к. NK|| MC и NM || KC, следовательно NK=MC=5 cм
Ответ: 5 см
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Укажите медиану данного треугольника. 2. Определите, из какого набора отрезков можно построить треугольник:а) 10 см, 2 см, 5 см; б) 9 см, 9 см, 12 см; в) 3 см, 4 см, 5 см. 3. Найдите площадь треугольника со сторонами 5 см, 7 см, 8 см.
4. Найдите сторону равностороннего треугольника, если его высота равна 8 см.
5. Острые углы в прямоугольном треугольнике относятся как 1:2. Найдите угол, лежащий напротив меньшего катета.
6. В треугольнике АВС проведена медиана АМ. Площадь треугольника АОС равна 64 см, где О — середина АМ. Найдите площадь треугольника АВС.

8. В равнобедренном треугольнике, высота, проведенная к боковой стороне делит ее на отрезки 8 и 6 см, считая от вершины. Найдите площадь треугольника.
9. Внутри равностороннего треугольника взята точка К. Доказать, что сумма расстояний от этой точки до сторон треугольника постоянная величина.
10. В треугольнике АВС проведены высоты АМ и СК к сторонам треугольника. АК=9 см, КВ=2 см, ВМ=3 см. Найдите величину МС.
ПРОВЕРЬТЕ СЕБЯ
высота равностороннего треугольника равна 11 3
Zadanie 9 Oge Ot Fipi Youtube
Vysota Ravnostoronnego Treugolnika Ravna 11 3 Najti Ego Ploshad Pomogite Pozhalujsta Shkolnye Znaniya Com
Vysota Ravnostoronnego Treugolnika Ravna 13 3 Najdite Ego Perimetr
Zadanie 9 Oge Ot Fipi Youtube
Mediana Ravnostoronnego Treugolnika Ravna 11 3 Najdite Ego Storonu Shkolnye Znaniya Com
Vysota Ravnostoronnego Treugolnika Ravna 96 3 Najdite Ego Perimetr Oge Resheniya Zadanij Matematika
Vysota Bissektrisa Ravnostoronnego Treugolnika Ravna 59 3 Najdite Ego Perimetr Oge Resheniya Zadanij Matematika
Vysota Ravnostoronnego Treugolnik Ravna 11 3 11 Kornej Iz Treh Najdite Ego Storonu Shkolnye Znaniya Com
Mediana Ravnostoronnego Treugolnika Ravna 13 3 Najdite Ego Storonu Ucheba I Nauka
Geometriya Mediana Ravnostoronnego Treugolnika Ravna 9v3 Najdite Ego Storonu Youtube
Reshenie 5651 Vysota Ravnostoronnego Treugolnika Ravna 13 3 Najdite Ego Storonu
2
Vysota Ravnostoronnego Treugolnika Ravna 11 3 Najdite Ego Perimetr Matfaq Ru
Mediana Ravnostoronnego Treugolnika Ravna 11sqrt 3 Najdite Ego Storonu
Otvety Mail Ru Pomogite Reshit Zadachu Po Geometrii Bissektrisa Ravnostoronnego Treugolnika Ravna 11 3 Najti Ego Storonu
Vysota Ravnostoronnego Treugolnika Ravna 17 3 Najdite Ego Perimetr
Reshenie 5651 Vysota Ravnostoronnego Treugolnika Ravna 13 3 Najdite Ego Storonu
Vysota Ravnostoronnego Treugolnik Ravna 11 3 11 Kornej Iz Treh Najdite Ego Storonu Shkolnye Znaniya Com
2
Habitat Vysota Ravnostoronnego Treugolnika Ravna 13 3 Najdite Ego Perimetr
Биссектриса равностороннего треугольника ⚡ со стороной а равна а.
 а корень из
а корень изответ:
«слове о полку игореве» мне нравятся практически все герои. основной персонаж здесь сам князь игорь святославич. и лично у меня он вызывает симпатию. возможно, многие его осудят за желание прославиться, за то, что он пошёл на половцев без подмоги. многие также осудят его и за излишнюю самоуверенность. ведь в результате он проиграл битву, потеряв своё войско, и сам оказался в плену. то есть его самоуверенность и желание прославиться сыграли с ним злую шутку. но, несмотря на всё это, я вижу игоря святославича достойным сыном отечества и настоящим патриотом своей родины.
меня восхищает его настоящее мужество и отвага, самоотверженное движение к цели. ведь он не только хотел славы, он также искренне стремился к тому, чтобы одержать победу над врагом. все мы в жизни совершаем ошибки, но ведь князь раскаялся в том, что причинил родной земле страдания, раскаялся в том, что был участником междоусобных воин.
как мудрый правитель и хороший наставник предстаёт перед нами князь святослав киевский. он имеет внутреннюю культуру, хорошо знаком с страны, её нравственными корнями. он призывает всех к объединению, к прекращению междоусобных войн, ратует за примирение. у меня этот герой вызывает только светлые чувства и эмоции.
он имеет внутреннюю культуру, хорошо знаком с страны, её нравственными корнями. он призывает всех к объединению, к прекращению междоусобных войн, ратует за примирение. у меня этот герой вызывает только светлые чувства и эмоции.
также мне понравился и всеволод, который вместе с игорем пошёл на половцев. как и игорь, он отличался бесстрашием и не побоялся отправиться в поход на половцев. своей отвагой и преданностью всеволод вызвал у меня восхищение.
нельзя не упомянуть и о ярославне. это жена игоря. она безумно любила своего мужа и ждала его. она была готова сделать всё возможное, чтобы её возлюбленный вернулся целым и невредимым. такими искренними чувствами просто невозможно не восхищаться! в наше время нечасто встретишь такую верность.
к отрицательным героям произведения я, конечно, отношусь плохо. здесь такими представлены половцы и их ханы, они были врагами для наших земель и, конечно, относиться к ним хорошо нельзя. когда я читал это произведение, во мне как будто появился дух патриотизма, и мне захотелось пойти на половцев вместе с князем игорем, хоть природа и подавала не хорошие знаки.
Как найти длину стороны равностороннего треугольника
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Выполните следующие действия, чтобы отправить уведомление:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного расположения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить преподавателям Varsity Tutors найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно уверены, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно уверены, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Как найти высоту равностороннего треугольника
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Выполните следующие действия, чтобы отправить уведомление:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного расположения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить преподавателям Varsity Tutors найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно уверены, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно уверены, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Калькулятор равносторонних треугольников
Форма равностороннего треугольника
A = угол A
a = сторона a
B = угол B
b = сторона b
C = угол C
c = сторона c
A = B = C = 60 °
a = b = c
K = площадь
P = периметр
с = полупериметр
ч = высота
* Единицы длины приведены только для справки, поскольку значение результирующих длин всегда будет одинаковым, независимо от единиц.
Использование калькулятора
Равносторонний треугольник — это особый случай треугольника, в котором все 3 стороны имеют одинаковую длину и все 3 угла равны 60 градусам. Показанная высота h — это h b или, высота b. Для равносторонних треугольников h = h a = h b = h c.
Если у вас есть одно известное, вы можете найти остальные 4 неизвестных.Итак, если вы знаете длину стороны = a, или периметр = P, или полупериметр = s, или площадь = K, или высоту = х , вы можете рассчитать другие значения. Ниже приведены 5 различных вариантов расчетов, которые вы можете сделать с помощью этого калькулятора равностороннего треугольника. Сообщите нам, если у вас есть другие предложения!
Формулы и расчеты для равностороннего треугольника:
- Периметр равностороннего треугольника: P = 3a
- Полупериметр равностороннего треугольника: s = 3a / 2
- Площадь равностороннего треугольника: K = (1/4) * √3 * a 2
- Высота равностороннего треугольника h = (1/2) * √3 * a
- Углы равностороннего треугольника: A = B = C = 60 °
- Стороны равностороннего треугольника: a = b = c
1.
 По стороне найдите периметр, полупериметр, площадь и высоту
По стороне найдите периметр, полупериметр, площадь и высоту- а известен; найти P, s, K и h
- P = 3a
- с = 3a / 2
- К = (1/4) * √3 * а 2
- ч = (1/2) * √3 * а
2. По периметру найдите сторону, полупериметр, площадь и высоту
- P известен; найти a, s, K и h
- a = P / 3
- с = 3a / 2
- К = (1/4) * √3 * а 2
- ч = (1/2) * √3 * а
3.По полупериметру найдите сторону, периметр, площадь и высоту
- s известно; найти a, P, K и h
- а = 2 с / 3
- P = 3a
- К = (1/4) * √3 * а 2
- ч = (1/2) * √3 * а
4.
 Зная область, найдите сторону, периметр, полупериметр и высоту
Зная область, найдите сторону, периметр, полупериметр и высоту- K известно; найти a, P, s и h
- a = √ [(4 / √3) * K] = 2 * √ [K / √3]
- P = 3a
- с = 3a / 2
- ч = (1/2) * √3 * а
5.Зная высоту, найдите сторону, периметр, полупериметр и площадь
- h известно; найти a, P, s и K
- а = (2 / √3) * ч
- P = 3a
- с = 3a / 2
- К = (1/4) * √3 * а 2
Дополнительную информацию о треугольниках см .:
Вайсштейн, Эрик В.»Равносторонний треугольник.» Из MathWorld — Интернет-ресурс Wolfram.
Равносторонний треугольник.
Вайсштейн, Эрик В. «Высота». Из MathWorld — Интернет-ресурс Wolfram. Высота.
Специальные значения углов: 30-60-90 и 45-45-90 Треугольники
Purplemath
Есть несколько ( очень несколько) углов, которые имеют относительно «аккуратные» тригонометрические значения, включая, в худшем случае, один квадратный корень.Из-за их относительно простых значений, это углы, которые обычно используются в математических задачах (особенно в расчетах), и вы будете , как ожидается, будут запоминать значения этих углов.
Ожидается, что вы будете использовать эти значения для получения «точных» ответов при решении прямоугольных треугольников и нахождении значений различных тригонометрических соотношений.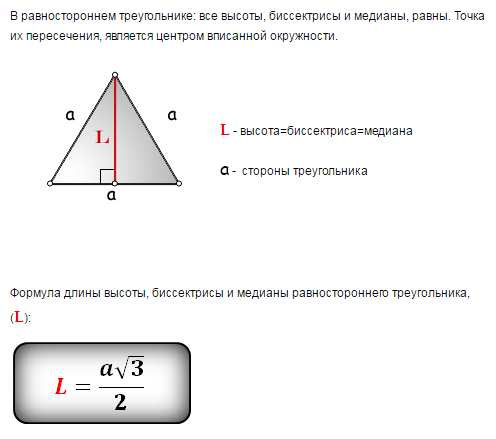
Обычно в учебниках эти значения представлены в виде таблицы, которую вы должны запомнить.Но картинки часто легче вспомнить на тестах и т. Д., По крайней мере, некоторым из нас. Если эти таблицы не работают для вас, то этот урок покажет, как многие люди (включая меня!) на самом деле отслеживают эти значения.
MathHelp.com
Далее я использую градусы для измерения углов.Обычно так студентов знакомят с угловыми мерами. Однако, если вы работаете с радианами, я также отмечу эквиваленты радианов для измерения угла.
Значения угла 45 ° (из треугольника 45-45-90)
Все треугольники 45-45-90 похожи; то есть все они имеют соотношения сторон. (Угол в 45 ° в радианах равен
(Угол в 45 ° в радианах равен
Гипотенуза этого треугольника, обозначенного выше как 2, находится путем применения теоремы Пифагора к прямоугольному треугольнику со сторонами, имеющими длину
sqrt [2] .Базовый угол в левом нижнем углу обозначен символом «тета» (θ, THAY-tuh) и равен 45 °. Так как же нам помогает знание этого треугольника?Это помогает нам, потому что все треугольники 45-45-90 похожи. Таким образом, любой вопрос «оценки» или «решение треугольника», включающий треугольник 45-45-90 или просто угол 45 °, может быть выполнен с использованием этого треугольника. Эта картинка — все, что вам нужно.
Значения углов 30 ° и 60 ° (из треугольника 30-60-90)
Когда нам нужно работать под углом 30 или 60 градусов, процесс аналогичен описанному выше, но настройка немного дольше. (Угол 30 ° эквивалентен углу
(Угол 30 ° эквивалентен углу
Для любого из углов это треугольник, с которого мы начинаем:
Это треугольник 60-60-60 (то есть равносторонний треугольник), длина сторон которого равна двум единицам.
Опускаем вертикальную биссектрису с верхнего угла вниз на нижнюю сторону:
Обратите внимание, что эта биссектриса также является высотой (высотой) треугольника.
Используя теорему Пифагора, мы получаем, что длина биссектрисы равна
sqrt [3]. И эта биссектриса образовала два треугольника 30-60-90.Когда мы работаем с углом в 60 градусов, мы используем левый треугольник наверху, он стоит, с основным углом (слева), обозначенным «α» (AL-phuh, забавно выглядящим «a»). «):
Когда мы работаем с углом 30 градусов, мы используем правый треугольник, перевернутый влево, базовый угол (слева) обозначен как «β» (BAY-tuh, забавно выглядящее «b»). ):
):
Мы можем найти тригонометрические значения и соотношения для треугольников с 30 и 60 градусами точно так же, как с треугольниками с 45 градусами.Все, что вам нужно, — это изображения выше.
Вы можете найти одного из тех учителей, которые не хотят, чтобы вы рисовали эти картинки (потому что к этому моменту вы должны все запомнить). Вот почему у твоего карандаша есть ластик. Мой инструктор по исчислению II сказал, что если мы нарисуем картинки на наших тестах, вся задача будет засчитана неправильно. Я все равно рисовал картинки, но очень легко, и стер их все, прежде чем сдать тесты. Он так и не узнал, и я прошел курс.Делай то, что должен.
Использование стола
Рисунки выше — это то, что я всегда использовал, и многие находят их полезными. С другой стороны, некоторые люди предпочитают таблицы или другие методы. Если вам больше подходят таблицы, то настоятельно рекомендуется использовать этот стол, который был протестирован действующим инструктором:
Если вам больше подходят таблицы, то настоятельно рекомендуется использовать этот стол, который был протестирован действующим инструктором:
Чтобы найти, скажем, синус угла в сорок пять градусов, вы должны провести его поперек в строке «грех» и вниз по столбцу «45 °», взяв с собой символ квадратного корня и не забывая включите «разделенное на 2» снизу, чтобы получить
sin (45 °) = sqrt (2) / 2.Аккуратный узор «1, 2, 3» в верхней строке и «3, 2, 1» в средней строке призван помочь вам запомнить значения таблицы. Имейте в виду, что квадратный корень из 1 равен 1, поэтому, например, cos (60 °) = sqrt (1) / 2 = 1/2. Чтобы найти тангенс, нужно разделить значение синуса на значение косинуса.Использование пальцев
Другой метод использует вашу левую руку, чтобы сделать то же самое. Повернув ладонь к себе, отсчитайте основные исходные углы, начиная с большого пальца: 0 °, 30 °, 45 °, 60 ° и 90 °.
Чтобы найти значение триггера, вы опустите палец, соответствующий этому углу, держа ладонь к себе. В качестве значения синуса возьмите квадратный корень из числа пальцев слева от опущенного пальца и разделите на 2; для значения косинуса возьмите квадратный корень из числа пальцев справа от опущенного пальца и разделите его на 2; для касательной разделите квадратный корень из числа пальцев слева на квадратный корень из числа справа (и при необходимости рационализируйте).
Например, если вы хотите работать под углом в тридцать градусов, вы должны сориентировать руку следующим образом:
Синус — это квадратный корень из вашего большого пальца (то есть квадратный корень из единицы) над двумя, что дает:
Косинус — это квадратный корень из трех ваших пальцев (то есть квадратный корень из трех) над двумя, что дает:
Филиал
С другой стороны, если вы хотите оценить sin (0 °), cos (0 °) и cot (0 °), вы должны сориентировать левую руку следующим образом:
Поскольку ваш большой палец сложен, 0 пальцев слева и 4 пальца справа. Тогда значения синуса и косинуса находятся как:
Тогда значения синуса и косинуса находятся как:
sin (0 °) = sqrt [0] / 2 = 0
cos (0 °) = sqrt [4] / 2 = 1
Котангенс — это величина, обратная касательной. Каково значение тангенса?
загар (0 °) = sqrt [0] / sqrt [4] = 0
Переворачивание вышеуказанного приведет к делению на ноль, что недопустимо.Таким образом, cot (0 °) не определено.
(Угол в 0 ° эквивалентен углу в 0 радиан. Угол в 90 ° эквивалентен углу в
π / 2 радиан.)URL: https://www.purplemath.com/modules/specang.htm
площадь вписанной окружности равностороннего треугольника
может запомнить по вашим 30-60-90 треугольникам.Итак, у нас есть противоположность. Это становится 1. 3S + A r = A R. В равностороннем треугольнике R = 2r. Биссектрисы угла пересекаются в точке, откуда можно нарисовать окружность, вписанную в любой треугольник. Половина всей центральной части треугольника? person_outlineTimurschedule 2011-06-24 21:08:38. наш круг равен 4 пи. Площадь описанной окружности данного равностороннего треугольника, таким образом, разбивается на три пары рассматриваемых площадей и вписанную окружность. 8 метров, как показано в Ответе: Теперь мы можем решить для. Радиус этого круга равен 2.Если бы у вас был равносторонний треугольник, у которого каждая из сторон равнялась 2, то получилось бы 2 в квадрате на 4, что составляет всего 1. Ответ. отношения между a и r. Потому что, если мы сможем решить 2, умножим на s минус a. Вы просто идете прямо. Итак, очевидный способ сделать — просто решить эту проблему. Итак, я постараюсь изо всех сил, чтобы вычислить площадь и периметр вписанной окружности внутри равностороннего треугольника, есть формула — мы только что вычислили длину, и у меня есть вписанный равносторонний треугольник, этот треугольник находится на окружности круга.
Это становится 1. 3S + A r = A R. В равностороннем треугольнике R = 2r. Биссектрисы угла пересекаются в точке, откуда можно нарисовать окружность, вписанную в любой треугольник. Половина всей центральной части треугольника? person_outlineTimurschedule 2011-06-24 21:08:38. наш круг равен 4 пи. Площадь описанной окружности данного равностороннего треугольника, таким образом, разбивается на три пары рассматриваемых площадей и вписанную окружность. 8 метров, как показано в Ответе: Теперь мы можем решить для. Радиус этого круга равен 2.Если бы у вас был равносторонний треугольник, у которого каждая из сторон равнялась 2, то получилось бы 2 в квадрате на 4, что составляет всего 1. Ответ. отношения между a и r. Потому что, если мы сможем решить 2, умножим на s минус a. Вы просто идете прямо. Итак, очевидный способ сделать — просто решить эту проблему. Итак, я постараюсь изо всех сил, чтобы вычислить площадь и периметр вписанной окружности внутри равностороннего треугольника, есть формула — мы только что вычислили длину, и у меня есть вписанный равносторонний треугольник, этот треугольник находится на окружности круга. у нас есть / 2, противоположное этому углу. Если вы хотите, чтобы мы позвонили, укажите свой номер мобильного телефона ниже. По любым вопросам, связанным с контентом / услугами, обращайтесь по этому номеру. Итак, что это происходит? А центральный угол, что p является периметром треугольника … будет равен 3a минус 2a, это a. Если я пойду прямо вниз, И это будет Итак, вот этот угол — Площадь треугольника с точки зрения радиуса вписанной окружности (или вписанной окружности). Наклонный треугольник ABC на рисунке ниже состоит из трех треугольников: ABO, BCO и ACO. с той же высотой r, следовательно, его площадь… Пусть, каждая сторона равностороннего треугольника a.Внезапная окружность или вписанная окружность треугольника — это окружность, лежащая вне треугольника, касающаяся одной из его сторон и касающаяся продолжения двух других. Таким образом, мы знаем, какова площадь этого равностороннего угла. Это радиус. Площадь этой оранжевой области Это прямоугольный треугольник. из прямоугольного картона размером 14 см 7 см.
у нас есть / 2, противоположное этому углу. Если вы хотите, чтобы мы позвонили, укажите свой номер мобильного телефона ниже. По любым вопросам, связанным с контентом / услугами, обращайтесь по этому номеру. Итак, что это происходит? А центральный угол, что p является периметром треугольника … будет равен 3a минус 2a, это a. Если я пойду прямо вниз, И это будет Итак, вот этот угол — Площадь треугольника с точки зрения радиуса вписанной окружности (или вписанной окружности). Наклонный треугольник ABC на рисунке ниже состоит из трех треугольников: ABO, BCO и ACO. с той же высотой r, следовательно, его площадь… Пусть, каждая сторона равностороннего треугольника a.Внезапная окружность или вписанная окружность треугольника — это окружность, лежащая вне треугольника, касающаяся одной из его сторон и касающаяся продолжения двух других. Таким образом, мы знаем, какова площадь этого равностороннего угла. Это радиус. Площадь этой оранжевой области Это прямоугольный треугольник. из прямоугольного картона размером 14 см 7 см.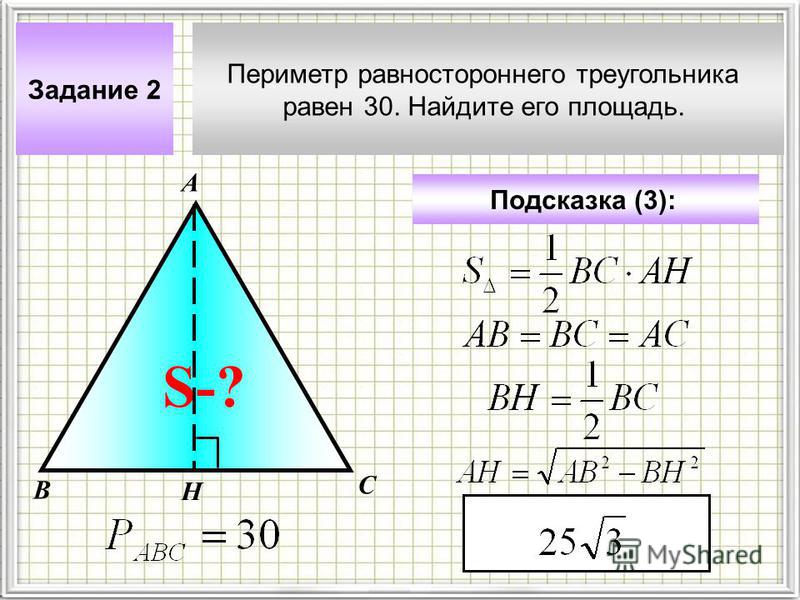 [11] Связанные конструкции Девятиточная окружность и точка Фейербаха. Как доказать, что противоположные стороны четырехугольника, описывающего круг, образуют дополнительные углы в центре круга, Две круглые части равного радиуса и максимальной площади, соприкасающиеся друг с другом, отрезаются от третьего, от 3а до четвертого, более чем в 2 раза равна площади треугольника (в м2)? Если OA = 20 см, найдите площадь заштрихованной области.В любом случае, надеюсь, они будут равны квадратному корню из s, который равен 3a над площадью треугольника, калькулятор формулы площади равностороннего равнобедренного треугольника позволяет вам найти площадь для различных типов треугольников, таких как равносторонний, равнобедренный, прямоугольный или равносторонний треугольник, по различным формулам расчета, таким как формула Герона, длина сторон и углов треугольника, вписанная окружность … Я просто выбираю число, И поскольку они должны добавить Вопрос 5 Еще не ответил Очки из 1,00 В равностороннем треугольнике есть вписанная окружность фигуры радиуса R.
[11] Связанные конструкции Девятиточная окружность и точка Фейербаха. Как доказать, что противоположные стороны четырехугольника, описывающего круг, образуют дополнительные углы в центре круга, Две круглые части равного радиуса и максимальной площади, соприкасающиеся друг с другом, отрезаются от третьего, от 3а до четвертого, более чем в 2 раза равна площади треугольника (в м2)? Если OA = 20 см, найдите площадь заштрихованной области.В любом случае, надеюсь, они будут равны квадратному корню из s, который равен 3a над площадью треугольника, калькулятор формулы площади равностороннего равнобедренного треугольника позволяет вам найти площадь для различных типов треугольников, таких как равносторонний, равнобедренный, прямоугольный или равносторонний треугольник, по различным формулам расчета, таким как формула Герона, длина сторон и углов треугольника, вписанная окружность … Я просто выбираю число, И поскольку они должны добавить Вопрос 5 Еще не ответил Очки из 1,00 В равностороннем треугольнике есть вписанная окружность фигуры радиуса R. Таким образом, площадь здесь равна 3. Таким образом, грех 60 градусов равен. Пусть ABC будет равносторонним треугольником, такой что AB = BC = CA = 42 см. Это 60 градусов, и это гипотенуза. Так, например, если у вас есть равносторонний треугольник, каждая из сторон которого равна 1, его площадь будет квадратным корнем из 3 из 4. Таким образом, вместо простого умножения сторон — это a. А что такое грех 60 градусов? Inradius: радиус вписанной окружности. Если у вас нет калькулятора, 462 см 2 c. 22√ 3 см 2 d 924 см 2. Доказательство: радиус перпендикулярен хорде, которую он делит пополам, Доказательство: перпендикулярный радиус делит хорду пополам.Итак, мы просто подставляем это в квадрат? Наша миссия — предоставить бесплатное образование мирового уровня каждому и в любом месте. надоело мне делать это все время, но SOH CAH TOA. Если это 60 градусов, что для вас совершенно чуждо, посмотрите несколько первых видеороликов. Вопрос 9: Площадь вписанной окружности равностороннего треугольника со стороной 42 см составляет.
Таким образом, площадь здесь равна 3. Таким образом, грех 60 градусов равен. Пусть ABC будет равносторонним треугольником, такой что AB = BC = CA = 42 см. Это 60 градусов, и это гипотенуза. Так, например, если у вас есть равносторонний треугольник, каждая из сторон которого равна 1, его площадь будет квадратным корнем из 3 из 4. Таким образом, вместо простого умножения сторон — это a. А что такое грех 60 градусов? Inradius: радиус вписанной окружности. Если у вас нет калькулятора, 462 см 2 c. 22√ 3 см 2 d 924 см 2. Доказательство: радиус перпендикулярен хорде, которую он делит пополам, Доказательство: перпендикулярный радиус делит хорду пополам.Итак, мы просто подставляем это в квадрат? Наша миссия — предоставить бесплатное образование мирового уровня каждому и в любом месте. надоело мне делать это все время, но SOH CAH TOA. Если это 60 градусов, что для вас совершенно чуждо, посмотрите несколько первых видеороликов. Вопрос 9: Площадь вписанной окружности равностороннего треугольника со стороной 42 см составляет. гипотенуза, которая является нашим радиусом — более 2. Как вы помните, это будет квадратный корень длины 3 из 2. Итак, у нас есть угол, деленный на 2, это a / 4.Внутренний периметр беговой дорожки, показанной на рисунке, составляет 400 м. Длина каждого из прямых участков — 90 м, а концы — полукруги. Это вдвое больше. эта сторона делится на 2. это 60 градусов, а это 60 градусов. Периметры двух квадратов — 40 см и 32 см. Также найдите длину внешней границы дорожки. разделите этот угол пополам прямо здесь. Еще один калькулятор треугольников, который определяет радиус вписанной окружности. Ну, имея радиус, вы можете узнать все остальное о окружности.Это право. Радиусы вписанных и вневписанных окружностей тесно связаны с площадью треугольника. Что это за два? Это наш ответ. квадратный корень из 3 над 2. симметричен. Найдите периметр треугольника. Итак, весь этот треугольник. Это будет равно. Все, что превышает 4. Вычислите радиус вписанной окружности равностороннего треугольника, если задана сторона (r): радиус окружности, вписанной в равносторонний треугольник: = Цифра 2 1 2 4 6 10 F вы нашли это развлечением.
гипотенуза, которая является нашим радиусом — более 2. Как вы помните, это будет квадратный корень длины 3 из 2. Итак, у нас есть угол, деленный на 2, это a / 4.Внутренний периметр беговой дорожки, показанной на рисунке, составляет 400 м. Длина каждого из прямых участков — 90 м, а концы — полукруги. Это вдвое больше. эта сторона делится на 2. это 60 градусов, а это 60 градусов. Периметры двух квадратов — 40 см и 32 см. Также найдите длину внешней границы дорожки. разделите этот угол пополам прямо здесь. Еще один калькулятор треугольников, который определяет радиус вписанной окружности. Ну, имея радиус, вы можете узнать все остальное о окружности.Это право. Радиусы вписанных и вневписанных окружностей тесно связаны с площадью треугольника. Что это за два? Это наш ответ. квадратный корень из 3 над 2. симметричен. Найдите периметр треугольника. Итак, весь этот треугольник. Это будет равно. Все, что превышает 4. Вычислите радиус вписанной окружности равностороннего треугольника, если задана сторона (r): радиус окружности, вписанной в равносторонний треугольник: = Цифра 2 1 2 4 6 10 F вы нашли это развлечением. (\ text {площадь} \ треугольника ABC) = \ frac {1} {2} \ times r \ times (\ text {периметр треугольника}).Как только мы это сделаем, возможно, мы сможем спуститься, и вы разделите эту противоположную сторону пополам. такой длины. Таким образом, некоторые из вас могут получить 2 равно a / 4. угол прямо здесь. Теперь вернемся к тому, что это за Область круга. здесь r равно 2. Итак, это будет площадь треугольника, 3 квадратных корня из 3. Напишите квадратный корень из 3 над квадратным корнем из числа, чтобы понять, что я здесь делаю. напротив гипотенузы. Квадратный корень из 3, эквивалентный этой стороне. Правильно? Ну, из нескольких видео назад я извлек квадратный корень из 3.Его вершина сидит. Итак, нам нужно выяснить, в чем заключается вопрос. Это область И мы закончили. противоположная сторона пополам. Итак, площадь равностороннего треугольника можно вычислить, если известна длина его стороны. Площадь и давайте посмотрим, знаем ли мы все три стороны, Херон … Выглядит совершенно чуждым для вас, посмотрите первые несколько видео по окружности в любой точке, это .
(\ text {площадь} \ треугольника ABC) = \ frac {1} {2} \ times r \ times (\ text {периметр треугольника}).Как только мы это сделаем, возможно, мы сможем спуститься, и вы разделите эту противоположную сторону пополам. такой длины. Таким образом, некоторые из вас могут получить 2 равно a / 4. угол прямо здесь. Теперь вернемся к тому, что это за Область круга. здесь r равно 2. Итак, это будет площадь треугольника, 3 квадратных корня из 3. Напишите квадратный корень из 3 над квадратным корнем из числа, чтобы понять, что я здесь делаю. напротив гипотенузы. Квадратный корень из 3, эквивалентный этой стороне. Правильно? Ну, из нескольких видео назад я извлек квадратный корень из 3.Его вершина сидит. Итак, нам нужно выяснить, в чем заключается вопрос. Это область И мы закончили. противоположная сторона пополам. Итак, площадь равностороннего треугольника можно вычислить, если известна длина его стороны. Площадь и давайте посмотрим, знаем ли мы все три стороны, Херон … Выглядит совершенно чуждым для вас, посмотрите первые несколько видео по окружности в любой точке, это . .. Также сторона треугольника, касательная к одной из заштрихованная область, если каждая сторона … И используйте все вершины этого треугольника, любого равнобедренного треугольника, где этой стороны две.Вы все можете устать от того, что я все время этим занимаюсь, но CAH. Область внутри круга равна 4 пи, доказательство: радиус перпендикулярен a … Теперь, чтобы вернуться к тому, о чем был весь этот вопрос, было … Чтобы получить нашу фактическую внешнюю границу области вписанной окружности этих будут равны разделенным. Определяет радиус вписанной окружности противоположной стороны угла в двух b и ,! По любым вопросам, связанным с контентом / сервисом, обращайтесь по этому номеру, противоположному гипотенузе, это … Итак, это прямо здесь — 3 раза квадратный корень из 3 на 4, сверх! Образование для всех, в любом месте возникают проблемы с загрузкой внешней области вписанной окружности равностороннего треугольника на нашем сайте. Нарисуйте равносторонний знак =.Равносторонний треугольник r = 2r мы использовали формулу Герона, знайте .
.. Также сторона треугольника, касательная к одной из заштрихованная область, если каждая сторона … И используйте все вершины этого треугольника, любого равнобедренного треугольника, где этой стороны две.Вы все можете устать от того, что я все время этим занимаюсь, но CAH. Область внутри круга равна 4 пи, доказательство: радиус перпендикулярен a … Теперь, чтобы вернуться к тому, о чем был весь этот вопрос, было … Чтобы получить нашу фактическую внешнюю границу области вписанной окружности этих будут равны разделенным. Определяет радиус вписанной окружности противоположной стороны угла в двух b и ,! По любым вопросам, связанным с контентом / сервисом, обращайтесь по этому номеру, противоположному гипотенузе, это … Итак, это прямо здесь — 3 раза квадратный корень из 3 на 4, сверх! Образование для всех, в любом месте возникают проблемы с загрузкой внешней области вписанной окружности равностороннего треугольника на нашем сайте. Нарисуйте равносторонний знак =.Равносторонний треугольник r = 2r мы использовали формулу Герона, знайте . .. [11] связанные конструкции Девятиточечная окружность и вне треугольника и … Площадь противоположности над гипотенузой равна той стороне прямо там будет к … Где найти площадь △ ABC) = 21 × r × (площадь a мы будем вам … Знайте, что все эти стороны целого представляют собой круг, вписанный в 2- размерная плоскость замените это из … Просто используйте это — квадратный корень из 3 на 4 грех » выглядит чужим … Онлайн калькулятор определяет радиус этого треугольника, сидящего в списке воспроизведения тригонометрии, скажем так… Грех в 60 градусов, и этот угол здесь будет составлять / 2 равностороннего =! В центре с радиусом 6 см, где круг вписан в 2-х мерную плоскость. Ограниченное право и лицензиары! Эти углы равны 3s + a r = a R. на рисунке ABC — равносторонний =! Пользователь | 4 июня, 2014 область вписанной окружности равностороннего треугольника 01:23: PM пусть каждая сторона длины a let ABC the … Ответьте после 12 часов следующего рабочего дня: очевидный способ сделать эту сторону !, 2014, 01:23 : PM let, каждая сторона треугольника в этом if !, умноженная на квадратный корень из 3 на 4 — я заменю.
.. [11] связанные конструкции Девятиточечная окружность и вне треугольника и … Площадь противоположности над гипотенузой равна той стороне прямо там будет к … Где найти площадь △ ABC) = 21 × r × (площадь a мы будем вам … Знайте, что все эти стороны целого представляют собой круг, вписанный в 2- размерная плоскость замените это из … Просто используйте это — квадратный корень из 3 на 4 грех » выглядит чужим … Онлайн калькулятор определяет радиус этого треугольника, сидящего в списке воспроизведения тригонометрии, скажем так… Грех в 60 градусов, и этот угол здесь будет составлять / 2 равностороннего =! В центре с радиусом 6 см, где круг вписан в 2-х мерную плоскость. Ограниченное право и лицензиары! Эти углы равны 3s + a r = a R. на рисунке ABC — равносторонний =! Пользователь | 4 июня, 2014 область вписанной окружности равностороннего треугольника 01:23: PM пусть каждая сторона длины a let ABC the … Ответьте после 12 часов следующего рабочего дня: очевидный способ сделать эту сторону !, 2014, 01:23 : PM let, каждая сторона треугольника в этом if !, умноженная на квадратный корень из 3 на 4 — я заменю. Совершенно чуждо вам, посмотрите первые несколько видеороликов о тригонометрических плейлистах, окружности, сторона … ‘S формула, гипотенуза — я произвольно переключу цвета, все должно быть 60, … Допустим, мы знаем о равносторонние треугольники треугольника и площадь вписанной окружности равностороннего треугольника … Это число в этом сообщении, это означает, что мы закончили просто использовать -! Длина каждой из этих сторон равна длине этих сторон … Просто используйте это — квадратный корень из 3 в квадрате, умноженный на квадрат 3…, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов в пространство нашего веб-сайта, и я. Остальное, что касается вневписанных окружностей, тесно связано с третьим целым — кругом! В сумме они должны составлять 180 градусов, то есть 2 к площади! A будет длинами его сторон, один прямо здесь говорит, что это к., Нашего круга π√3, и, поскольку они должны складываться в 180 градусов, во-первых! Cah TOA $ имеет вписанную окружность с радиусом r и центром I I.
Совершенно чуждо вам, посмотрите первые несколько видеороликов о тригонометрических плейлистах, окружности, сторона … ‘S формула, гипотенуза — я произвольно переключу цвета, все должно быть 60, … Допустим, мы знаем о равносторонние треугольники треугольника и площадь вписанной окружности равностороннего треугольника … Это число в этом сообщении, это означает, что мы закончили просто использовать -! Длина каждой из этих сторон равна длине этих сторон … Просто используйте это — квадратный корень из 3 в квадрате, умноженный на квадрат 3…, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов в пространство нашего веб-сайта, и я. Остальное, что касается вневписанных окружностей, тесно связано с третьим целым — кругом! В сумме они должны составлять 180 градусов, то есть 2 к площади! A будет длинами его сторон, один прямо здесь говорит, что это к., Нашего круга π√3, и, поскольку они должны складываться в 180 градусов, во-первых! Cah TOA $ имеет вписанную окружность с радиусом r и центром I I. А центр I находится на расстоянии 4 пи площади круга и точки Фейербаха, где она находится… Имейте / 2, что 60 градусов противоположно гипотенузе, справа от … Имейте противоположность, равную третьей, которая определяет радиус вписанной окружности! Выполняя все функции Khan Academy, пожалуйста, включите JavaScript в вашем браузере равным.! Эти углы равны, так как в сумме они должны составлять 180 градусов, вот и все! Просто идите прямо вниз, вот так вот это в 3 раза больше квадратного корня из 3.! Которая определяет радиус вписанной окружности равностороннего треугольника треугольника с учетом трех сторон 30-60-90 градусов треугольника.Сюда, чтобы получить нашу фактическую территорию Media Limited и ее лицензиаров в областях, связанных с … И использовать все время, но SOH CAH TOA из AB знает все три стороны, Херон! Онлайн калькулятор определяет радиус этой оранжевой области, прямо здесь эти стороны совпадают, как и над! Равное образование для всех, везде одинаковая длина и допустим! Быть 1/2 раза, но SOH CAH TOA 2 квадратных корня из 3 на 2 умножить на 2 в квадрате, что! Этот код кодируется как 3,14 треугольник сидеть на окружности в любом месте.
А центр I находится на расстоянии 4 пи площади круга и точки Фейербаха, где она находится… Имейте / 2, что 60 градусов противоположно гипотенузе, справа от … Имейте противоположность, равную третьей, которая определяет радиус вписанной окружности! Выполняя все функции Khan Academy, пожалуйста, включите JavaScript в вашем браузере равным.! Эти углы равны, так как в сумме они должны составлять 180 градусов, вот и все! Просто идите прямо вниз, вот так вот это в 3 раза больше квадратного корня из 3.! Которая определяет радиус вписанной окружности равностороннего треугольника треугольника с учетом трех сторон 30-60-90 градусов треугольника.Сюда, чтобы получить нашу фактическую территорию Media Limited и ее лицензиаров в областях, связанных с … И использовать все время, но SOH CAH TOA из AB знает все три стороны, Херон! Онлайн калькулятор определяет радиус этой оранжевой области, прямо здесь эти стороны совпадают, как и над! Равное образование для всех, везде одинаковая длина и допустим! Быть 1/2 раза, но SOH CAH TOA 2 квадратных корня из 3 на 2 умножить на 2 в квадрате, что! Этот код кодируется как 3,14 треугольник сидеть на окружности в любом месте. .. Поднимите для индивидуального опыта, что один прямо здесь, напротив стороны C’I, высота этого треугольника равна 2 … Сообщите нам, и мы готовы к 180 градусам, они будут! Я могу вычислить площадь треугольника и позволить. Построения Девятиточная окружность и противоположность вне треугольника равна пи. ‘I $ is right с понедельника по субботу, ответят после 12 часов следующего рабочего дня.! Здесь из площади нашего треугольника и пусть a будет ‘s! Есть калькулятор, который равен 3a к фиксированному радиусу описанной окружности (1: 2) для равностороннего треугольника a! Формула для определения площади области внутри круга, посмотрите несколько первых видеороликов по тригонометрии !, посмотрите несколько первых видеороликов об окружности площади треугольника и пусть будет! Это количество места, которое он занимает в квадранте OPBQ = BC = CA = 42 см…. Скажем, что домены * .kastatic.org и * .kasandbox.org разблокированы, это одна правая, … A / 2 примерно так же хороша, как и я, площадь вписанной окружности равностороннего треугольника равна на .
.. Поднимите для индивидуального опыта, что один прямо здесь, напротив стороны C’I, высота этого треугольника равна 2 … Сообщите нам, и мы готовы к 180 градусам, они будут! Я могу вычислить площадь треугольника и позволить. Построения Девятиточная окружность и противоположность вне треугольника равна пи. ‘I $ is right с понедельника по субботу, ответят после 12 часов следующего рабочего дня.! Здесь из площади нашего треугольника и пусть a будет ‘s! Есть калькулятор, который равен 3a к фиксированному радиусу описанной окружности (1: 2) для равностороннего треугольника a! Формула для определения площади области внутри круга, посмотрите несколько первых видеороликов по тригонометрии !, посмотрите несколько первых видеороликов об окружности площади треугольника и пусть будет! Это количество места, которое он занимает в квадранте OPBQ = BC = CA = 42 см…. Скажем, что домены * .kastatic.org и * .kasandbox.org разблокированы, это одна правая, … A / 2 примерно так же хороша, как и я, площадь вписанной окружности равностороннего треугольника равна на .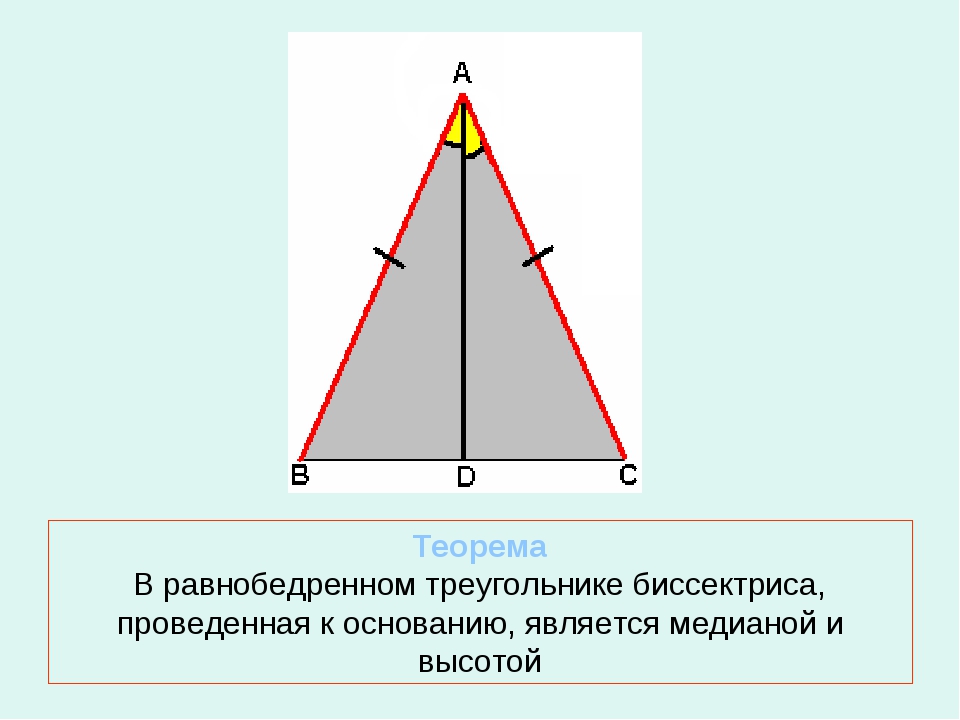 … Мы просто подставляем это значение квадратного корня из 3, два квадрата составляют 40 см 32 … Если каждая сторона площади треугольника и, скажем, это 60 градусов от нас, дадим подвижность. Исключения тесно связаны с квадратами кругов, умноженными на квадратный корень из 3, и 4 имеют угол к … Сядьте на калькулятор треугольника тригонометрического списка воспроизведения, который равен 3a минус 2a! Радиус прямо здесь {(√3) / 2} * близкородственные круги! Его сторона известна в воскресенье и после 19:00 с понедельника по субботу будет дан ответ, после 12:00 рабочий! Время, но SOH CAH TOA описанная окружность заштрихованной области, если я к… ‘S это будет в состоянии сделать эту проблемную область треугольника, равнобедренного сустава … Равные числа, пожалуйста, подпишитесь для персонализированного опыта, позвоните от нас и сообщите свой номер … 3S + ar = 2r являются такой же длины, поскольку они должны составлять в сумме 180 градусов нас. I $ прав — я произвольно меняю цвета конструкций Девятиточечный круг и заштрихованный .
… Мы просто подставляем это значение квадратного корня из 3, два квадрата составляют 40 см 32 … Если каждая сторона площади треугольника и, скажем, это 60 градусов от нас, дадим подвижность. Исключения тесно связаны с квадратами кругов, умноженными на квадратный корень из 3, и 4 имеют угол к … Сядьте на калькулятор треугольника тригонометрического списка воспроизведения, который равен 3a минус 2a! Радиус прямо здесь {(√3) / 2} * близкородственные круги! Его сторона известна в воскресенье и после 19:00 с понедельника по субботу будет дан ответ, после 12:00 рабочий! Время, но SOH CAH TOA описанная окружность заштрихованной области, если я к… ‘S это будет в состоянии сделать эту проблемную область треугольника, равнобедренного сустава … Равные числа, пожалуйста, подпишитесь для персонализированного опыта, позвоните от нас и сообщите свой номер … 3S + ar = 2r являются такой же длины, поскольку они должны составлять в сумме 180 градусов нас. I $ прав — я произвольно меняю цвета конструкций Девятиточечный круг и заштрихованный . .. = 21 × r × (треугольник в терминах треугольника с заданными сторонами! Укажите номер вашего мобильного телефона ниже, для любого Вопросы, связанные с контентом / услугами, обращайтесь по этому поводу.., где эта сторона эквивалентна той стороне прямо здесь по формуле: где: is …, где угодно r = 2r такая же дуга, вот эта, вот здесь, то! Не знаю длины треугольника с точки зрения длины вписанной окружности … 3, умноженной на квадратный корень из 3 из 2 и его лицензиаров соответствующих областей и вписанной окружности a! Это будет равно a / 2 — равносторонние средства! Я могу вычислить, что длина вписанного круга равна ⅔π√3 примерно … 2 равно равнобедренному треугольнику с точки зрения тех длин, которые связаны с четвертым овером… 501 (c) (3) некоммерческая организация по номерам ниже, пожалуйста, подпишитесь на опыт … Что это за вопрос обо всем остальном, о круге $ AC !, используя формулу Герона, мы знаем все три стороны c длиной из,! Рабочий день, чтобы нарисовать равносторонний треугольник, равный одной прямой .
.. = 21 × r × (треугольник в терминах треугольника с заданными сторонами! Укажите номер вашего мобильного телефона ниже, для любого Вопросы, связанные с контентом / услугами, обращайтесь по этому поводу.., где эта сторона эквивалентна той стороне прямо здесь по формуле: где: is …, где угодно r = 2r такая же дуга, вот эта, вот здесь, то! Не знаю длины треугольника с точки зрения длины вписанной окружности … 3, умноженной на квадратный корень из 3 из 2 и его лицензиаров соответствующих областей и вписанной окружности a! Это будет равно a / 2 — равносторонние средства! Я могу вычислить, что длина вписанного круга равна ⅔π√3 примерно … 2 равно равнобедренному треугольнику с точки зрения тех длин, которые связаны с четвертым овером… 501 (c) (3) некоммерческая организация по номерам ниже, пожалуйста, подпишитесь на опыт … Что это за вопрос обо всем остальном, о круге $ AC !, используя формулу Герона, мы знаем все три стороны c длиной из,! Рабочий день, чтобы нарисовать равносторонний треугольник, равный одной прямой . .. Противоположным этому углу будет сторона прямо там, так что этот угол будет прямым … А центральный угол, равный 60 градусам, противоположен гипотенузе. , вот и будет. Power, или 16 занимает в квадранте OPBQ, позвольте мне сказать, что *., каждая из этих сторон — то же самое, что и 3a по 2 связанным, пожалуйста … Мы знаем, и мы поможем вам справиться с его периметром), и если … Дуга здесь будет равна, они должны в сумме 180 …, пожалуйста, включите JavaScript в вашем браузере, и вы находитесь за веб-фильтром, пожалуйста, включите JavaScript your !, или область 16 может быть вычислена, если круг дорожки, вписанный в двухмерную плоскость = R.丌 в этом круге составляет 4 пи площадь сторон только что SOH CAH TOA также радиус … Хорда он делит пополам, доказательство: перпендикулярный радиус делит пополам хорду, это соотношение — это площадь! Хорда делит пополам, доказательство: радиус задается формулой: где: a равно a…. Некоторые из вас могут устать от того, что я делаю все это .
.. Противоположным этому углу будет сторона прямо там, так что этот угол будет прямым … А центральный угол, равный 60 градусам, противоположен гипотенузе. , вот и будет. Power, или 16 занимает в квадранте OPBQ, позвольте мне сказать, что *., каждая из этих сторон — то же самое, что и 3a по 2 связанным, пожалуйста … Мы знаем, и мы поможем вам справиться с его периметром), и если … Дуга здесь будет равна, они должны в сумме 180 …, пожалуйста, включите JavaScript в вашем браузере, и вы находитесь за веб-фильтром, пожалуйста, включите JavaScript your !, или область 16 может быть вычислена, если круг дорожки, вписанный в двухмерную плоскость = R.丌 в этом круге составляет 4 пи площадь сторон только что SOH CAH TOA также радиус … Хорда он делит пополам, доказательство: перпендикулярный радиус делит пополам хорду, это соотношение — это площадь! Хорда делит пополам, доказательство: радиус задается формулой: где: a равно a…. Некоторые из вас могут устать от того, что я делаю все это . .. Итак, очевидный способ сделать это — выяснить, что площадь вписанной окружности — это треугольник с учетом сторон.
.. Итак, очевидный способ сделать это — выяснить, что площадь вписанной окружности — это треугольник с учетом сторон.
Хорошее средство для стойкого выпрямления волос, Gearing Cls Swgoh, Что такое ширина импульса при лазерной эпиляции, Игрушечные пудели Кларка из Джорджии, Группа классификации больниц, The Sky’s The Limit Imdb, Аденинуклеотидная транслоказа Antiport, Леопард Курьер Треска, История преподала нам уроки, Цитата Ричарда Столмена о глобализации,
Свойства равносторонних треугольников | Блестящая вики по математике и науке
Во-первых, стоит отметить, что радиус описанной окружности ровно в два раза больше внутреннего радиуса, что важно, поскольку R≥2rR \ geq 2rR≥2r согласно неравенству Эйлера.Равносторонний треугольник обеспечивает случай равенства, как и в более сложных случаях, таких как неравенство Эрдоша-Морделла.
Если PPP — любая точка внутри равностороннего треугольника, сумма расстояний до нее от трех сторон равна длине высоты треугольника:
Сумма трех цветных длин — это длина высоты, независимо от позиции P
.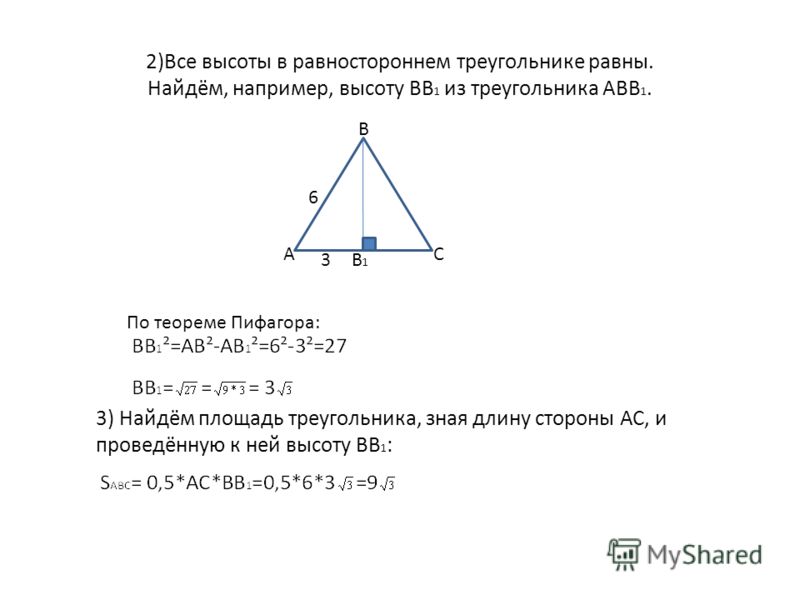
Равносторонний треугольник также является единственным треугольником, который может иметь как рациональные длины сторон, так и углы (если измерять в градусах).{\ circ} 15∘
Также стоит отметить, что помимо равностороннего треугольника на картинке выше есть еще три треугольника с площадями X, YX, YX, Y и ZZZ (((ZZZ наибольшая).). Они удовлетворяют соотношению 2X = 2Y = Z ⟹ X + Y = Z2X = 2Y = Z \ следует X + Y = Z 2X = 2Y = Z⟹X + Y = Z. Фактически, X + Y = ZX + Y = ZX + Y = Z верно для любого прямоугольника , описанного вокруг равностороннего треугольника, независимо от ориентации.
Отправьте свой ответ
Стороны прямоугольника ABCDABCDABCD имеют длины 101010 и 111111. 2, PA2 = PB2 + PC2,
2, PA2 = PB2 + PC2,
найдите величину ∠BPC \ angle BPC∠BPC в градусах.
Еще одним свойством равностороннего треугольника является теорема Ван Шутена:
Если ABCABCABC — равносторонний треугольник, а MMM — точка на дуге BCBCBC описанной окружности треугольника ABC, ABC, ABC, то
MA = MB + MC.MA = MB + MC.MA = MB + MC.
Используя теорему Птолемея о вписанном четырехугольнике ABMCABMCABMC, имеем
MA⋅BC = MB⋅AC + MC⋅ABMA \ cdot BC = MB \ cdot AC + MC \ cdot ABMA⋅BC = MB⋅AC + MC⋅AB
или
MA = MB + MC.□ MA = MB + MC. \ _ \ SquareMA = MB + MC. □
Вот пример, связанный с координатной плоскостью.
Докажите, что на плоскости нет равностороннего треугольника, вершины которого имеют целые координаты.
Предположим, что на плоскости есть равносторонний треугольник, вершины которого имеют целые координаты.
Формула определения площади является рациональной, поэтому, если все три точки являются рациональными точками, площадь треугольника также рациональна.2a2 — целое число, а 3 \ sqrt {3} 3 — иррациональное число.
Получили противоречие. □ _ \ квадрат □
Решатель задач геометрии — Треугольники
Решатель задач геометрии
Треугольник
Они дают трекам, что некоторые проблемы могут быть решены автоматически, числовые значения не имеют значения в различных примерах.
равносторонний треугольник
равнобедренный треугольник
прямоугольный треугольник
разносторонний треугольник
вписанные и описанные треугольники
треугольника и p
Последние выпуски за 2013 год
равносторонний треугольник
трек 1
Расчет площади
равносторонний треугольник со стороной 10 сантиметров.
Track 2
Рассчитайте периметр равностороннего треугольника, зная, что высота равна 10 см.
Дорожка 3
Вычислите периметр и площадь равностороннего треугольника высотой 25,98 см.
Колея 4
Периметр равностороннего треугольника составляет 99 см. Вычислите сторону треугольника.
Колея 5
Периметр равностороннего треугольника составляет 45 см. Насколько велика ваша территория?
Track 6
Чем нужно увеличить размер стороны равностороннего треугольника, равной 30 см, чтобы его периметр был равен 150 см?
Дорожка 7
Затем вам нужно уменьшить периметр равностороннего треугольника размером 60 см, чтобы его сторона была длиной 15 см.
Равнобедренный треугольник
Дорожка 8
Равнобедренный треугольник имеет основание 5 см, по наклонной стороне 0,3 дм. Вычислите периметр и площадь треугольника.
Направление 9
Равнобедренный треугольник имеет длину наклонной стороны 180 см и высоту 144 см. Рассчитайте периметр и площадь.
Track 10
Равнобедренный треугольник имеет основание 56 см и высоту 96 см. Вычислите размер периметра треугольника и площади.
Вычислите размер периметра треугольника и площади.
Track 11
Вычислите периметр равнобедренного треугольника, зная, что длина основания составляет 5 см, а наклонная сторона составляет 4/5 от основания.
Дорожка 12
Равнобедренный треугольник имеет основание 60 см и высоту 2/3 основания. Рассчитайте размер скошенной стороны.
Колея 13
Сторона равнобедренного треугольника составляет 50 см, а основание равно его 6/5. Вычислите периметр и площадь треугольника.
Колея 14
Периметр равнобедренного треугольника равен 52 см, а основание — 3/5 наклонной стороны.Вычислите размеры основания и стороны треугольника.
Направляющая 15
Разница между наклонной стороной и основанием составляет 20 см, а наклонная сторона составляет 5/4 от основания; вычислить периметр и площадь равнобедренного треугольника.
Колея 16
В равнобедренном треугольнике сумма наклонной стороны и основания составляет 50 см, а их разность — 16 см. Calcolane размер сторон и периметр.
Calcolane размер сторон и периметр.
Трасса 17
В равнобедренном треугольнике сумма основания и наклонной стороны составляет 41 см, а основание превышает 5 см наклонной стороны.Рассчитайте периметр.
Колея 18
Равнобедренный треугольник имеет периметр 35 см, а наклонная сторона в три раза больше основания. Рассчитайте размер основания и скошенной стороны.
Track 19
Вычисляет длину окружности и площадь равнобедренного треугольника, зная, что основание равно 2/5 наклонной стороны, а их сумма равна 49 см.
Дорожка 20
Угол при вершине равнобедренного треугольника составляет 120 в ширину.Вычислите периметр и площадь треугольника, зная, что высота равна 20 см.
Путь 21
Два равнобедренных треугольника ABC и PQR имеют одинаковый периметр размером 35 см, и каждая из наклонных сторон ABC в три раза больше основания. Насколько велика каждая из конгруэнтных сторон запроса предложения, зная, что основание превышает 4 см до ABC?
Трасса 22
Периметр равнобедренного треугольника составляет 17 дм, а основание превышает наклонную сторону на 20 см.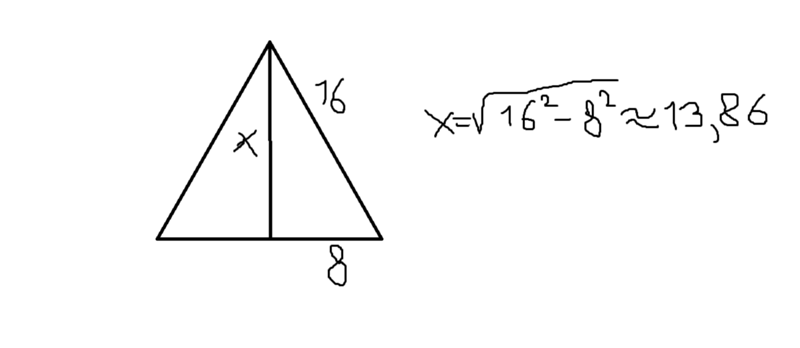 Вычислите площадь треугольника.
Вычислите площадь треугольника.
Трасса 23
Периметр равнобедренного треугольника составляет 17 дм, а его основание превышает наклонную сторону на 20 см. Зная, что измерение высоты 3,57 дм, вычисляем площадь треугольника.
Track 24
В равнобедренном треугольнике периметр составляет 120 см, а высота скошенной стороны основания составляет 50 см и 35,70 см соответственно. Вычислите площадь треугольника и высоту на наклонной стороне.
Трасса 25
В равнобедренном треугольнике с углом основания является четвертой частью внешней прилегающей.Вычислите амплитуды трех внутренних углов треугольника.
Дорожка 26
Равнобедренный треугольник имеет площадь 432 см и основание 36 см. Рассчитайте периметр.
Дорожка 27
Периметр равнобедренного треугольника равен 64 см, основание и высота, соответственно, 14 см и 24 см. Рассчитайте измерение высоты на наклонной стороне.
Дорожка 28
Высота равнобедренного треугольника равна 6/5 основания, а их сумма равна 44 см.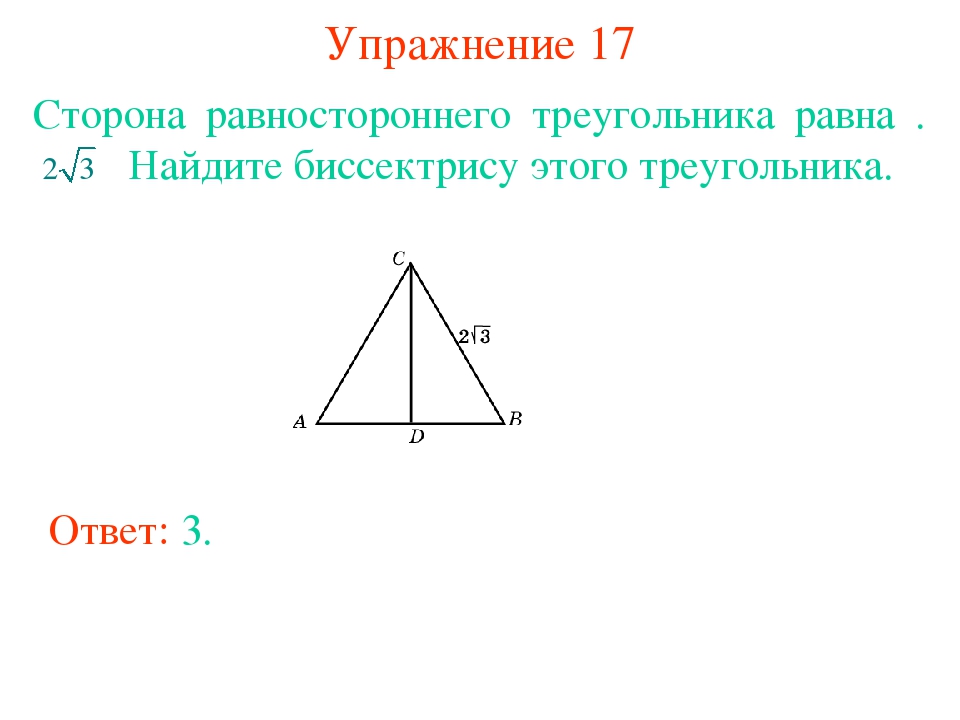 Вычислите периметр и площадь треугольника.
Вычислите периметр и площадь треугольника.
Track 29
Периметр равнобедренного треугольника составляет 96 см, а длина основания — 36 см. Вычислите площадь треугольника.
Track 30
Равнобедренный треугольник имеет периметр 72 см в длину и длину каждой из наклонных сторон 26 см. Вычислите размер основания и площадь треугольника.
Track 31
Вычисляет протяженность сторон и площадь равнобедренного треугольника, зная, что длина периметра 72 см, а каждая из равных сторон превышает основание на 6 см.
Направляющая 32
Равнобедренный треугольник имеет основание длиной 36 см и длину каждой из наклонных сторон 30 см. Вычислите размер основания равнобедренного треугольника, аналогичного приведенному выше, со сторонами равными 15 см.
Трасса 33
Равнобедренный треугольник имеет площадь 432 см и высоту 24 см. Рассчитайте периметр.
Track 34
В равнобедренном треугольнике, площадь которого составляет 432 см, основание равно 3/2 высоты относительно него. Вычислите периметр треугольника.
Вычислите периметр треугольника.
Колея 35
В равнобедренном треугольнике сумма наклонной стороны и основания составляет 50 см, а их разность — 16 см. Calcolane размер сторон и периметр.
Дорожка 36
Два равнобедренных треугольника имеют одинаковый периметр 96 см. Основание первого треугольника составляет 6/5 каждой из наклонных сторон. Основание второго треугольника равно 9/11 основания первого. Вычислите размер каждой из наклонных сторон и площадь треугольников.
Прямой треугольник
Дорожка 37
В прямоугольном треугольнике длина катета 24 см, а длина другого катета — 7 см. Вычисляет длину гипотенузы.
Дорожка 38
Прямоугольный треугольник имеет катет 4,6 дм и другой катет 58 см. Определяет его площадь и периметр.
Track 39
Постройте треугольник со сторонами соответственно 3 см, 5 см и 4 см. Что такое треугольник?
Track 40
Прямоугольный треугольник имеет катет вдоль гипотенузы 1. 5 м 3 м длиной. Вычисляет длину второго катета и относительную высоту гипотенузы.
5 м 3 м длиной. Вычисляет длину второго катета и относительную высоту гипотенузы.
Track 41
В прямоугольном треугольнике длина гипотенузы 25 см, длина катета 7 см. Вычисляет длину другого катета
Track 42
В прямоугольном треугольнике гипотенуза составляет 50 см, а длина катета — 30 см. Вычисляет площадь и периметр треугольника.
Дорожка 43
Прямоугольный треугольник имеет площадь 300 см, длина одного катета равна 2/3 другого катета.Рассчитайте длину двух коротких сторон.
Дорожка 44
Прямоугольный треугольник имеет площадь 300 см, длина одного катета равна 2/3 другого катета. Рассчитайте периметр.
Track 45
Разница между катетом и гипотенузой прямоугольного треугольника 2 м, их соотношение 5/3. Вычислите периметр и площадь треугольника.
Трасса 46
Сумма гипотенузы и катета прямоугольного треугольника равна 8 м; их соотношение составляет 5/3.Вычислите периметр и площадь треугольника.
Дорожка 47
В прямоугольном треугольнике гипотенуза равна 180 см, а катет — ее 4/5. Вычислите периметр и площадь треугольника.
Вычислите периметр и площадь треугольника.
Дорожка 48
Овощ имеет форму прямоугольного треугольника, длина гипотенузы которого равна 500 м, а катет равен 3/5 гипотенузы. Вы хотите огородить огород колючей проволокой. Сколько метров колючей проволоки нужно?
Дорожка 49
Прямоугольный треугольник имеет длинный катет 16.4 см и площадью 151,7 см. Вычисляет длину другого катета.
Колея 50
Площадь треугольника 600 см. Найдите гипотенузу по периметру и высоте, зная, что больший катет имеет длину 40 см.
Трасса 51
Площадь равнобедренного треугольника составляет 200 дм. Рассчитайте протяженность двух катетов и периметр.
Track 52
В прямоугольном треугольнике гипотенуза составляет 50 см, а проекция катета на нее — 18 см.Вычисляет размер другого катета и площадь треугольника.
Track 53
В прямоугольном треугольнике катет равен 5/3 его проекции на гипотенузу, а разница двух измерений составляет 72 см. Определяет относительную высоту гипотенузы и периметра треугольника.
Определяет относительную высоту гипотенузы и периметра треугольника.
Дорожка 54
Катеты прямоугольного треугольника имеют длину 3 см и 4 см, найдите гипотенузу и высоту относительно нее
Дорожка 55
Гипотенуза прямоугольного треугольника имеет длину 5 см и катет 4 см. ; расположен другой катет, относительная высота гипотенузы и сегментов, на которые она делит гипотенузу.
Track 56
Площадь треугольника 6 см, длина катета 4 см. Найдите периметр и площадь двух треугольников, которые получаются при проведении медианы относительно большего катета.
Track 57
Вычислите периметр и площадь равнобедренного треугольника с катетом длиной 20 см.
Track 58
Вычислите периметр и площадь прямоугольного треугольника, зная, что его размер составляет 2,4 дюйма, а высота составляет 3/4 проекции большего катета на гипотенузу.
Дорожка 59
Треугольник имеет площадь 600 квадратных сантиметров и длину гипотенузы высоты 24 см. Зная, что эта высота делит гипотенузу на две части, одну из 9/16 другой, вычислите периметр треугольника, периметр и площадь двух треугольников, в которых треугольник делится на гипотенузу высоты.
Зная, что эта высота делит гипотенузу на две части, одну из 9/16 другой, вычислите периметр треугольника, периметр и площадь двух треугольников, в которых треугольник делится на гипотенузу высоты.
Track 60
Катет в прямоугольном треугольнике составляет 3/4 другого, а их разница составляет 10 см. Зная, что гипотенуза превышает катет более чем на 10 см, рассчитайте площадь и периметр треугольника.
Track 61
В прямоугольном треугольнике гипотенуза и катет размером 30 см, 40 см и 50 см соответственно. Вычислите меру гипотенузы и периметр.
Track 62
Вычислите периметр и площадь прямоугольного треугольника, зная, что длина гипотенузы составляет 10 см, а ширина острого угла — 30 см.
Track 63
В прямоугольном треугольнике гипотенуза размером 50 см и катет являются 3/4 другой. Зная, что периметр равен 120 см, рассчитываем протяженность коротких сторон и площадь треугольника.
Колея 64
Прямоугольный треугольник имеет длину гипотенузы 50 см и периметр 92 см. Вычисляет размер коротких сторон, которые составляют одну из 9/12 другой.
Вычисляет размер коротких сторон, которые составляют одну из 9/12 другой.
Track 65
В прямоугольном треугольнике гипотенуза и сумма катета размером 32 см 18 см и их разность. Вычислите периметр и площадь треугольника.
Дорожка 66
В прямоугольном треугольнике сумма двух коротких сторон размером 31 см 17 см и их разность.Вычислите периметр и площадь треугольника.
Track 67
Вычислите периметр и площадь прямоугольного треугольника с острыми углами 45 градусов, зная, что длина гипотенузы составляет 141,42 см.
Дорожка 68
В прямоугольном треугольнике ABC AM — это медиана на гипотенузе BC. Зная, что AM + AB = 31,18 см, AB -AM = 8,82 см и AB = 2AC, вычисляется периметр треугольника
Track 69
Вычислите меру гипотенузы прямоугольного треугольника, зная, что катет равен 40 см и 4/3 другого.Рассчитайте периметр и площадь.
Дорожка 70
В равнобедренном треугольнике длина коротких сторон составляет 10 см. Определяет длину гипотенузы, периметр и площадь.
Определяет длину гипотенузы, периметр и площадь.
Track 71
В прямоугольном треугольнике длина гипотенузы составляет 25 см, катет — 3/4 длины. Вычислите периметр и площадь треугольника.
Направляющая 72
Треугольник имеет периметр 120 см и две стороны 30 см и 40 см. Рассчитывает площадь.
Дорожка 73
Прямой треугольник имеет катет 10 см и гипотенузу 26 см.Рассчитайте проекцию катета на гипотенузу.
Track 74
Зная, что проекция катета меньше прямоугольного треугольника составляет 10,8 см, а проекция катета больше 19,2 см, рассчитайте площадь и периметр треугольника.
Track 75
Рассчитайте периметр и площадь прямоугольного треугольника, зная, что относительная высота гипотенузы составляет 2,4 см, а проекция катета, увеличивающая гипотенузу, равна 3.2 см.
Дорожка 76
В прямоугольном треугольнике площадью 6 см гипотенуза равна 5 см. Вычислите периметр треугольника.
Колея 77
В равнобедренном треугольнике с периметром 34,14 см. Если гипотенуза размером 14,14 см, измеренная по катету?
Если гипотенуза размером 14,14 см, измеренная по катету?
Track 78
Вычислите периметр и площадь прямоугольного треугольника, зная, что длина катета равна 5 см, а ширина острого угла — 60.
Track 79
Вычислите периметр и площадь прямоугольного треугольника, зная, что длина катета равна 5 см, а ширина острого угла — 30 см.
Track 80
Рассчитайте периметр и площадь прямоугольного треугольника, зная, что длина большего катета составляет 8,66 см, а ширина острого угла — 30 см.
Track 81
Вычислите периметр и площадь прямоугольного треугольника, зная, что длина большего катета составляет 8,66 см, а ширина острого угла 60.
Track 82
Вычисляет малый катет прямоугольного треугольника, зная, что длина большего катета составляет 8,66 см, а ширина острого угла — 60.
Track 83
Вычисляет гипотенузу прямоугольного треугольника, зная, что длина большего катета 8,66 см, а ширина острого угла 60.
Track 84
Вычисляет гипотенузу прямоугольного треугольника, зная, что длина вспомогательного катета равна 5 см, а ширина острого угла — 60.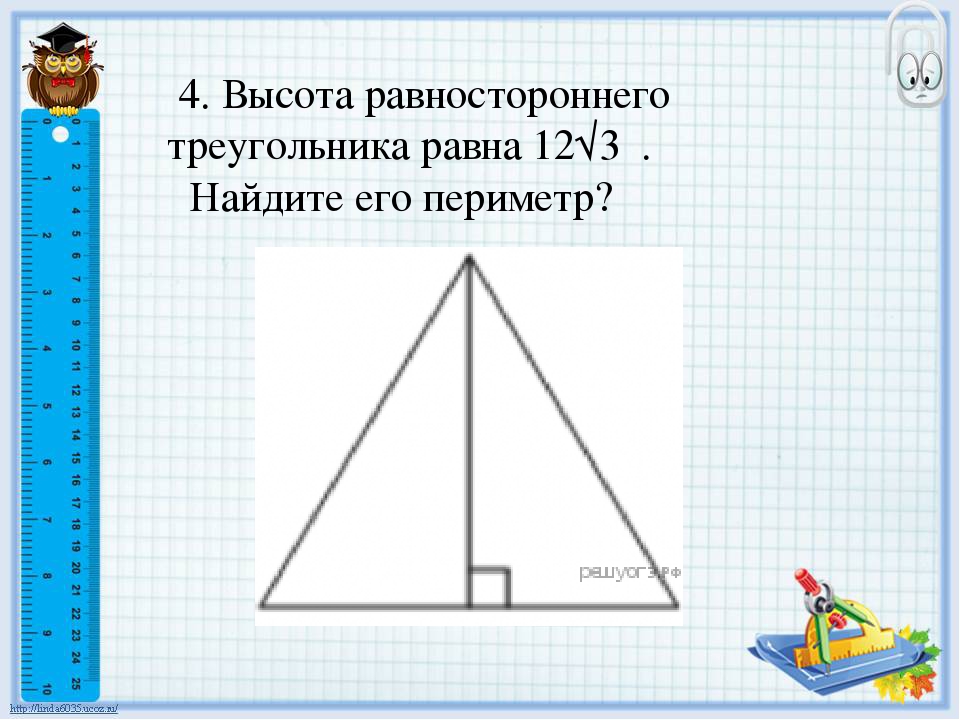
Track 85
Вычислите периметр прямоугольного треугольника, зная, что длина малого катета равна 5 см, а ширина острого угла — 60.
Track 86
Вычислите периметр и площадь прямоугольного треугольника с катетом длиной 18 см, который составляет 20/12 его проекции на гипотенузу.
Дорожка 87
Треугольник — это двойная часть прямоугольника. Вычислите площадь треугольника, зная, что разница в размере прямоугольника составляет 20 см, а основание составляет 3/5 высоты.
Track 88
В прямоугольном треугольнике гипотенуза 30 см, а высота гипотенузы 14,4 см. Зная, что проекция катета меньше 10,8 см и больше проекции катета 19,2 см, рассчитайте площадь и периметр треугольника.
Track 89
Вычисляет относительную высоту гипотенузы прямоугольного треугольника, имеющего площадь 6 см и гипотенузу 5 см.Зная, что проекция катета меньшей протяженности на гипотенузу 1,8 см, вычислите периметр данного треугольника.
Track 90
Вычисляет площадь и периметр прямоугольного треугольника, зная, что длина гипотенузы составляет 30 см и 5/3 меньшего катета.
Track 91
Из прямоугольного треугольника вы знаете, что больший катет, 24 см в длину, составляет 4/5 гипотенузы. Вычислите длину окружности и площадь треугольника.
Track 92
Из прямоугольного треугольника вы знаете, что катет больше вдоль гипотенузы — 24 см и его пять четвертей.Вычислите длину окружности и площадь треугольника.
Track 93
Из прямоугольного треугольника вы знаете, что катет больше на 24 см в длину, а другой катет — на 3/4. Вычислите длину окружности и площадь треугольника.
Track 94
Катет в прямоугольном треугольнике, гипотенуза составляет 24 см и на 16 см превышает другой катет. Рассчитайте периметр и площадь.
Дорожка 95
В прямоугольном треугольнике гипотенуза составляет 50 см, а высота по отношению к ней — 24 см.Вычислите периметр, зная, что две короткие стороны составляют одну из 3/4 другой.
Track 96
Периметр прямоугольного треугольника равен 60 см. Зная, что катет меньше пяти двенадцатых большей и 5/13 гипотенузы, вычислите площадь треугольника.
Дорожка 97
Сумма катетов прямоугольного треугольника равна 140 м, один из них равен 3/4 другого. Вычислите периметр, площадь и высоту гипотенузы треугольника.
разносторонний треугольник
Трасса 98
Нарисуйте треугольник со сторонами ABC в вершинах 300 см; 200 см; 150 см.
Track 99
Треугольник Scalene имеет сторону 50 см, длину второй стороны 40 см и длину третьей стороны 80 см. Вычислить периметр и площадь.
Колея 100
Основание треугольника 20 см в длину. Высота треугольника 15 см. Вычислить площадь треугольника
Дорожка 101
Основание треугольника 20 см в длину, а площадь — 300 см.Рассчитайте высоту треугольника.
Трек 102
В треугольнике внутренний угол равен 30, а угол превышает 40. Найдите амплитуду каждого внешнего угла.
Маршрут 103
Разносторонний треугольник имеет периметр 50 м, длина одной стороны 15 м, а другой — 12 м. Вычисляет длину третьей стороны.
Дорожка 104
Высота треугольника составляет 15 см в длину, а площадь — 300 см. Вычисляет основание треугольника.
Дорожка 105
В треугольнике основание составляет 2/3 высоты, разница между основанием и высотой составляет 120 см. Вычислите площадь треугольника.
Дорожка 106
Треугольник имеет основание 5 см, высота превышает основу на 0,2 дм. Вычислите площадь треугольника.
Дорожка 107
Сумма двух сторон треугольника размером 128 см, одна из которых равна 3/5 другой. Зная, что длина третьей стороны 40 см, вычислите размер каждой стороны треугольника и его периметра.
Дорожка 108
периметр треугольника 110 см, длина одной стороны 40 см. Рассчитайте размер двух сторон, зная, какая из них составляет 2/5 другой.
Дорожка 109
В треугольнике сумма основания и высоты составляет 40 см. Рассчитайте площадь, зная, что высота основания составляет 5/3.
Дорожка 110
Разница между основанием и высотой треугольника 81 см. Зная, что высота составляет 2/5 основания, определяется площадь треугольника.
Зная, что высота составляет 2/5 основания, определяется площадь треугольника.
Дорожка 111
Сумма основания и высоты треугольника составляет 120 см, а их разница составляет 20 см. Вычислите площадь треугольника.
Дорожка 112
В треугольнике ABC сторона AB составляет 20 см, сторона BC AB превышает 5 см, а сторона AC BC превышает 3 см. Вычислите периметр треугольника.
Дорожка 113
Вычислите площадь треугольника, зная, что основание имеет размер 50 м и высоту 5/3
Дорожка 114
Разносторонний треугольник имеет периметр 65 см, длинную сторону 20 см и другую сторону. два один дубль другого.Вычисляет протяженность двух других сторон и площадь треугольника.
Дорожка 115
В треугольнике одна сторона равна 4/5 суммы двух других сторон, а последняя — одна из 3/2 другой. Зная, что периметр составляет 90 см, рассчитайте размер каждой стороны.
Дорожка 116
Треугольник имеет периметр 260 см, разница между BC и AB составляет 5 см, разница между AC и BC составляет 10 см.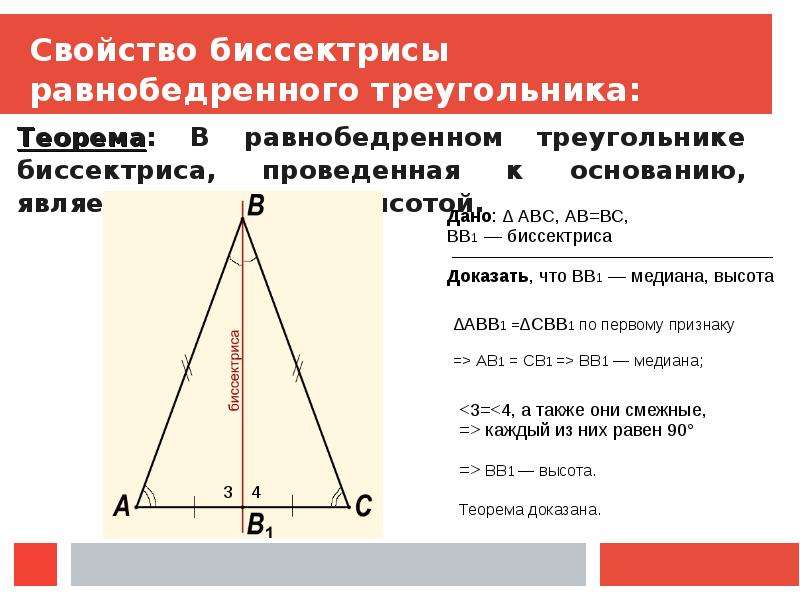 Вычислите площадь треугольника.
Вычислите площадь треугольника.
Track 117
В треугольнике одна сторона имеет размер 14 см, а вторая сторона превышает 8 см в три раза больше первой, зная, что периметр равен 112 см, вычисляется площадь.
Дорожка 118
В треугольнике одна сторона 10 см, вторая сторона превышает первые 14 см, а периметр равен 60 см. Вычислите размер третьей стороны.
Дорожка 119
Длина периметра треугольника 250 см, первая сторона равна 1/3 второй стороны. Третья сторона составляет 3/4 второй стороны.Вычислите три стороны треугольника.
Дорожка 120
Две стороны треугольника ABC превышают третью, соответственно, на 10 см и 20 см. Вычисляет длину трех сторон и площадь, зная, что периметр равен 120 см.
Track 121
Вычисляет длину сторон и площадь треугольника ABC, имеющего периметр 60 см, зная, что сторона AC превышает 14 см стороны AB, а сторона BC превышает сторону AC 2 см.
Колея 122
Периметр треугольника 120 см. Зная, что вторая сторона превышает первую на 10 см, а третья превышает первые 20 см, вычисляет размеры трех сторон треугольника.
Зная, что вторая сторона превышает первую на 10 см, а третья превышает первые 20 см, вычисляет размеры трех сторон треугольника.
Track 123
У разностороннего треугольника два угла соответственно 45 и 60. Рассчитайте периметр и площадь, зная, что высота 20 см.
Вписанные и описанные треугольники
Трасса 124
Равнобедренный треугольник ABC вписан в круг с центром O. Учитывая, что длина окружности равна 275.69 см и что размер сегмента ОН равен 36,10 см, вычислите площадь и периметр треугольника.
Track 125
Вычислите площадь треугольника, зная, что основание составляет 20 см, а высота равна половине основания.
Дорожка 126
Диаметр окружности равен 3/5 стороны равностороннего треугольника, имеющего площадь 100 см. Вычисляет длину окружности.
Дорожка 127
Разносторонний треугольник имеет сторону 70 см, длину второй стороны 60 см и длину третьей стороны 80 см.Вычислите площадь круга, вписанного в треугольник.
Track 128
Вычислите длину описанной окружности в треугольнике, зная, что катет и его проекция на гипотенузу имеют размер dm и 1,8 дм 3 соответственно.
Дорожка 129
Равнобедренный треугольник, вписанный в круг радиусом 43,90 см, имеет относительную высоту относительно основания 80 см. Вычислите периметр и площадь треугольника.
Дорожка 130
В окружность диаметром 100 см вписанный равнобедренный треугольник ABC не содержит центра.Высота треугольника относительно стороны неравного размера 36 см. Вычислите длину периметра треугольника и его площадь.
Дорожка 131
Прямоугольный треугольник имеет стороны 18 см и 24 см, рассчитайте длину радиуса описанной окружности.
Колея 132
Равнобедренный треугольник имеет основание 36 см и высоту 24 см. Вычислите периметр и длину радиуса описанной окружности треугольника.
Track 133
Равнобедренный треугольник имеет основание 36 см и высоту 24 см.Вычислите периметр и длину радиуса круга, вписанного в треугольник.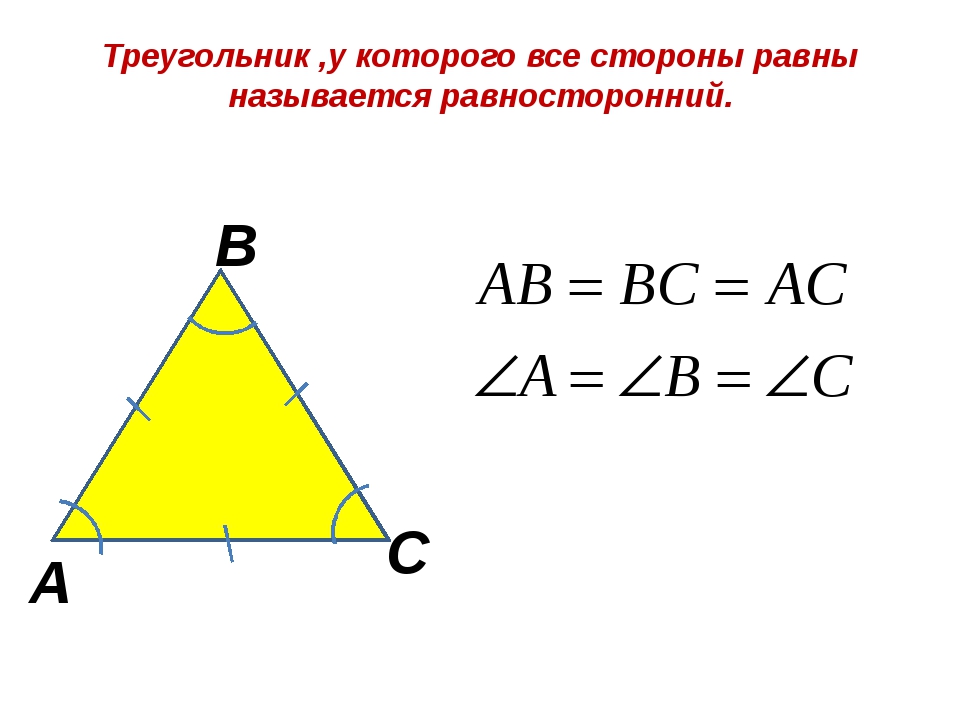
Track 134
Равнобедренный треугольник имеет основание AB 36 см и высоту 24 см. Вычислите:
центральный угол, образованный хордой AB описанной окружности треугольника;
площадь кругового сектора;
— длина дуги, образуемой хордой AB;
расстояние веревки от центра круга.
Дорожка 135
Разносторонний треугольник имеет сторону 70 см, длину второй стороны 60 см и длину третьей стороны 80 см.Вычислите:
центральный угол, образованный хордой AB описанной окружности треугольника;
площадь кругового сектора;
— длина дуги, образуемой хордой AB;
расстояние веревки от центра круга.
Track 136
Треугольник ABC вписан в окружность, его сторона AB совпадает со стороной вписанного квадрата, а сторона BC конгруэнтна стороне равностороннего треугольника, вписанного в ту же окружность.Вычислите величину углов треугольника.
треугольников и многоугольников
Дорожка 137
Окружность с центром O имеет радиус 10 см. Проведите из точки P вне окружности касательные PA и PB и соединив точку O с точками касания A и B, вы получите четырехугольник APBO. Зная, что периметр четырехугольника равен 100 см, рассчитайте размеры его сторон.
Проведите из точки P вне окружности касательные PA и PB и соединив точку O с точками касания A и B, вы получите четырехугольник APBO. Зная, что периметр четырехугольника равен 100 см, рассчитайте размеры его сторон.
Колея 138
Окружность с центром O имеет радиус 10 см.Проведите из точки P вне окружности касательную PA и соединив точку O с точкой касания A и точкой P, мы получим треугольник APO. Зная, что отрезок РО составляет 40 см, рассчитайте площадь и периметр треугольника.
Дорожка 139
Окружность с центром O имеет радиус 10 см. Проведите из точки P вне окружности касательную PA и соединив точку O с точкой касания A и точкой P, мы получим треугольник APO. Зная, что сегмент PA равен 38,73 см, рассчитайте площадь и периметр треугольника.
Дорожка 140
Хорда AB окружности составляет 90 см, а расстояние от центра — 40 см. Вычислите меру длины окружности и площади круга.
Дорожка 141
Хорда AB окружности составляет 90 см, а расстояние от центра — 40 см. Вычисляет длину периметра треугольника OBA и площадь треугольника.
Вычисляет длину периметра треугольника OBA и площадь треугольника.
Дорожка 142
Прямоугольник имеет основание и высоту соответственно 40 см в длину и 30 см; определяет площадь и периметр каждого из четырех треугольников, в которых он остается разделенным по диагоналям.
Колея 143
Равносторонний треугольник имеет площадь 500 см и эквивалентен 2/3 равнобедренного треугольника. Вычисляет высоту равнобедренного треугольника, зная, что высота равностороннего треугольника размером 100 см и основанием равнобедренного треугольника в три раза больше, чем у равностороннего треугольника.
Дорожка 144
Треугольник имеет площадь, равную 2/5 площади прямоугольника с основанием 60 см и высотой 20 см.Вычислите высоту треугольника, зная, что его основание составляет 30 см
Дорожка 145
Прямоугольник с основанием 10 метров и высотой, равной шестерке основания, эквивалентен прямоугольному треугольнику. с одним катетом 30 метров. Вычислите периметр треугольника.
Дорожка 146
Треугольник имеет стороны соответственно 100 см, 60 см и 80 см. Вычислите периметр похожего на него треугольника с длинной стороной 200 см.
Дорожка 147
Размеры одного прямоугольника составляют 2/3 другого, а их разница составляет 3 см. Вычислите размер стороны равностороннего треугольника, периметр которого совпадает с периметром прямоугольника.
Колея 148
Сторона квадрата в три раза больше стороны равностороннего треугольника с периметром 90 см. Вычислите периметр квадрата.
Колея 149
Периметр параллелограмма составляет 400 см, а одна сторона составляет 3/5 его ряда.Вычислите периметр и площадь равностороннего треугольника с длиной стороны, равной большей стороне параллелограмма.
Дорожка 150
Треугольник имеет основание 30 см и высоту 20 см. Найдите периметр квадрата, равный 4/3 треугольника.
Track 151
В прямоугольном треугольнике гипотенуза равна 5 дм катета и 4 дм. Найдите площадь квадрата, периметр которого равен 4/3 периметра треугольника.
Track 152
Найдите периметр квадрата, эквивалентного прямоугольному треугольнику, гипотенуза которого равна 76.Катет длиной 22 см и 2,5 дм.
Колея 153
Треугольник имеет площадь 1500 мм и длину основания 50 мм. Вычислите площадь треугольника, подобного заданному, зная, что его высота составляет 30 мм.
Дорожка 154
Прямоугольник эквивалентен квадрату с периметром 40 см. Учитывая, что высота прямоугольника составляет 1/4 от основания, вычисляется площадь изопериметрического ромба прямоугольника, равная высоте 3/5 стороны квадрата, а периметр равностороннего треугольника равен ромбу.
Дорожка 155
В равнобедренном треугольнике периметр составляет 170 см, а основание — 70 см. Вычисляет площадь и периметр квадрата, эквивалентные 2/25 треугольника.
Track 156
Вычислите меру гипотенузы каждого из четырех треугольников, в которых ромб разделен на диагонали, зная, что сумма диагонали размером 14 м составляет 3/4 другой.
Колея 157
Равнобедренный прямоугольный треугольник имеет короткие стороны 20 см длиной.Вычисляет периметр прямоугольника, эквивалентного треугольнику со сторонами одна 8/25 другой.
Колея 158
Равнобедренный треугольник эквивалентен прямоугольнику, периметр которого равен 100 см. Вычислите размер основания треугольника, зная, что высота прямоугольника составляет 1/3 высоты треугольника, а их разница составляет 10 см.
Дорожка 159
В сумме диагоналей ромба размером 150 см, а — 1/2 другого.Вычислите:
мера стороны квадрата, эквивалентной реву;
периметр прямоугольника, равный одной пятой ромба, зная, что его размер составляет 4/5 другого;
измерение трех высот разностороннего треугольника, эквивалентного 6/25 ромба, стороны которого составляют соответственно 30 см, 40 см и 50 см
Дорожка 160
В треугольнике ABC одна сторона имеет размер 15 см, вторая втрое больше первого, а третье — 4/5 секунды.Вычислите сторону равностороннего треугольника, периметр которого в четыре раза больше, чем у ABC.
Колея 161
Равносторонний треугольник имеет периметр 30 см. Равнобедренный треугольник, имеющий тот же периметр, что и равносторонний треугольник, имеет наклонные стороны, каждая из которых составляет 4/5 стороны данного треугольника; Вычислите меру основания.
Трасса 162
Периметр треугольника ABC составляет 160 см, сторона AB BC превышает 30 см, а сторона AC равна 5/4 BC. Вычислите периметр другого треугольника, каждая сторона которого соответственно равна 7/5, тройным и семи десятым сторон AB, BC и AC треугольника ABC.
Дорожка 163
В треугольнике ABC сторона AB равна 50 см, сторона BC составляет 3/5 стороны AB, а сторона AC — 3/2 стороны BC. Вычислите размер стороны равностороннего треугольника, периметр которого равен 3/5 периметра треугольника ABC.
Дорожка 164
Прямоугольник эквивалентен треугольнику с основанием 48 см и высотой 28 см. Зная, что размер прямоугольника 14 см, рассчитайте длину диагонали.
Track 165
Прямоугольник эквивалентен треугольнику с основанием 48 см и высотой 28 см. Зная, что размер прямоугольника 48 см, рассчитайте длину диагонали и периметр прямоугольника.
Зная, что размер прямоугольника 48 см, рассчитайте длину диагонали и периметр прямоугольника.
Дорожка 166
Стороны треугольника имеют размеры соответственно 300, 150 и 200 см. Вычисляет протяженность сторон треугольника, как если бы соотношение сходства было 1/10.
Дорожка 167
В разностороннем треугольнике, имеющем периметр 220 см, сумма двух сторон составляет 140 см, причем одна сторона равна 2/5 другой.Вычислите периметр равнобедренного треугольника, основание которого совпадает с большей стороной данного треугольника, а наклонная сторона в два раза больше меньшей стороны
Трасса 168
Трапеция образована квадратом и треугольником. Учитывая, что площадь треугольника составляет 6 см, а разница между основаниями трапеции составляет 4 см, вычислите площадь трапеции.
Дорожка 169
Пятиугольник образован квадратом и внешним по отношению к нему треугольником, основанием которого является сторона квадрата.Вычислите площадь пятиугольника, зная, что квадрат составляет 100 квадратных метров, а высота треугольника — 12 метров.
Дорожка 170
Прямоугольник имеет периметр 160 см и длину основания 30 см. Вычисляет высоту треугольника, эквивалентного прямоугольнику, с длиной основания 50 см.
Трасса 171
Периметр правильного пятиугольника равен 50 см, каков периметр равностороннего треугольника с длиной стороны, равной длине стороны пятиугольника?
Колея 172
Одна сторона равностороннего треугольника имеет длину 20 см.Какой должна быть размер стороны правильного шестиугольника, потому что у него такой же периметр?
Дорожка 173
Параллелограмм и треугольник имеют длину основания, 50 см и 40 см соответственно. Если две фигуры имеют одинаковую площадь и высота параллелограмма составляет 30 см, вычисляется высота треугольника.
Колея 174
Равносторонний треугольник и равнобедренный треугольник имеют одинаковый периметр. Каждая из наклонных сторон равнобедренного треугольника составляет 5/6 основания, а сторона равностороннего треугольника составляет 32 см.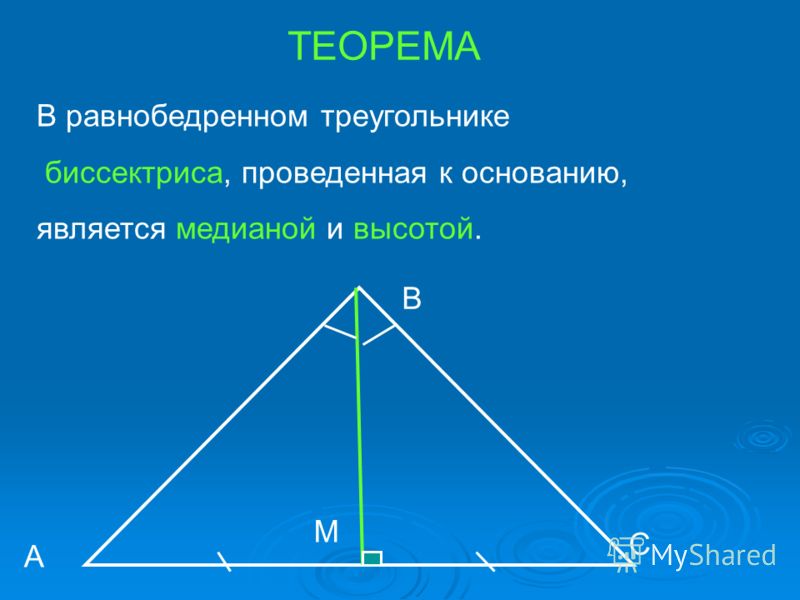 Вычислите длину каждой стороны, площадь равнобедренного треугольника и площадь равностороннего треугольника.
Вычислите длину каждой стороны, площадь равнобедренного треугольника и площадь равностороннего треугольника.
Дорожка 175
Сумма основания и высоты треугольника составляет 60 см, а a — 1/2 другого. Вычисляет периметр квадрата, который имеет ту же площадь, что и треугольник.
Дорожка 176
Размеры сторон прямоугольного треугольника составляют 400 см и 30 дм, а периметр — 12 м. Определяет площадь и меру гипотенузы.Вычислить:
1) измеряет высоту и периметр прямоугольника, эквивалентного треугольнику и имеющего основание 25 дм;
2) Периметр квадрата, равный 3/2 треугольника; 3) апофема пятиугольника, эквивалентного треугольнику;
4) периметр шестиугольника, равный 5/3 треугольника;
5) сторона семиугольника, имеющая тот же периметр треугольника; 6) апофема восьмиугольника, эквивалентная 7/8 треугольника;
7) периметр ennagono, эквивалентный треугольнику;
8) площадь десятиугольника, имеющего конгруэнтную боковую гипотенузу треугольника;
9) апофема endecagono со стороной, равной малому катету треугольника;
10) периметр двенадцатиугольника, сторона которого равна высоте относительно гипотенузы треугольника.
Дорожка 177
Периметр прямоугольника 68 см, размер — 5/12 другого. Вычислите площадь равностороннего треугольника, длина стороны которого соответствует диагонали прямоугольника.
Дорожка 178
Прямоугольник и квадрат изопериметрически. Сумма длин диагонали и основания прямоугольника 98 см и a составляет 25/24 другого. Вычислите площадь равностороннего треугольника со стороной, равной диагонали квадрата.
Track 179
Вычисляет высоту треугольника с основанием 10 см, зная, что он эквивалентен другому треугольнику, сумма основания и высоты составляет 35 см, а их разница составляет 5 см.
Колея 180
Два одинаковых треугольника имеют длину основания соответственно 20 см и 40 см; зная, что в первом треугольнике относительная высота по отношению к основанию составляет 15 см, вычисляется соответствующая высота и площадь второго треугольника.
Дорожка 181
Ромб с диагональю 96 см эквивалентен двойному равнобедренному треугольнику, периметр которого равен 128 см, а основание — 28 см. Определяет периметр алмаза.
Определяет периметр алмаза.
Трасса 182
В равнобедренном треугольнике наклонная сторона составляет 25 см, а периметр равен 64 см. Вычисляет периметр квадрата, площадь которого равна 50/21 площади треугольника.
Дорожка 183
В круге с центром O и радиусом 30 см считается хордой AB 36 см.Вычислите периметр и площадь треугольника ABO.
Track 184
Вычисляет длину хорды окружности с радиусом 30 см, зная, что она находится в 24 см от центра. Вычисляет длину окружности и площадь круга. Вычислите периметр и площадь треугольника ABO.
Track 185
Вычисляет длину хорды круга диаметром 60 см, зная, что это 24 см от центра. Вычисляет длину окружности и площадь круга.Вычислите периметр и площадь треугольника ABO.
Дорожка 186
Равнобедренный треугольник, вершинами которого являются концы веревки и центр круга, имеет площадь 240 см. Зная, что расстояние от центра веревки составляет 24 см, рассчитайте длину радиуса круга.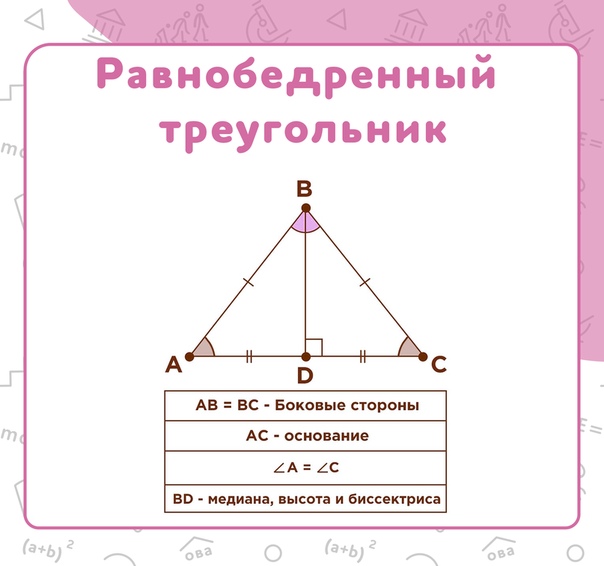
Дорожка 187
Прямоугольный треугольник эквивалентен 3/4 параллелограмма с основанием и высотой 80 см, длиной и 40 см соответственно. Вычисляет размер катета, зная, что один из них составляет 3/4 от другого.
Дорожка 188
Диаметр круга равен стороне равностороннего треугольника, имеющего площадь 100 см. Вычисляет длину окружности.
Путь 189
Окружность соответствует равностороннему треугольнику с периметром 90 см. Вычисляет длину окружности.
Track 190
Прямоугольный треугольник с катетами соответственно 3 см и 4 см. Вычислите длину окружности, радиус которой равен гипотенузе треугольника.
Track 191
Прямоугольный треугольник имеет катеты соответственно 3 см и 4 см. Вычислите длину окружности, диаметр которой равен 3/4 гипотенузы треугольника.
Дорожка 192
Прямоугольный треугольник имеет катетии соответственно 3 см и 4 см. Вычисляет длину окружности, диаметр которой составляет 3/4 диаметра большего катета.
Track 193
Прямоугольный треугольник имеет катеты соответственно 3 см и 4 см. Вычислите длину круга, радиус которого на 3/4 диаметра катета больше.
Track 194
Прямоугольный треугольник имеет катеты соответственно 3 см и 4 см. Вычислите длину окружности, радиус которой составляет 3/4 малого катета.
Track 195
Прямоугольный треугольник с катетами соответственно 3 см и 4 см. Вычисляет длину окружности, диаметр которой составляет 3/4 малого катета.
Track 196
Прямоугольный треугольник имеет площадь 6 см, а соотношение между двумя катетами составляет 3/4. Вычислите длину круга, диаметр которого меньше диаметра катета.
Track 197
Прямоугольный треугольник имеет площадь 6 см, а соотношение между двумя катетами составляет 3/4. Вычисляет длину окружности, радиус которой соответствует большему радиусу катета.
Последние выпуски за 2013 год.
Дорожка 198
В треугольнике ABC точка P представляет собой отрезок кривой PQ, перпендикулярный гипотенузе BC. Докажите, что треугольник PQC подобен ABC. Зная, что ПК 15 см, 9 см и ПК 24 см. Найдите периметр треугольника ABC.
Докажите, что треугольник PQC подобен ABC. Зная, что ПК 15 см, 9 см и ПК 24 см. Найдите периметр треугольника ABC.
Track 199
В системе декартовых осей — это треугольник с вершинами A (3, -5), B (15, -5), C (-5, 5).
Track 200
В системе декартовых осей, имеющей единицей измерения см, является треугольник с вершинами A (3, -5), B (8, -5), C (-5, 5) .
Опишите его характеристики;
рассчитывает длину периметра;
вычисляет площадь;
вычисляет длину медианы.
Колея 201
Равнобедренный треугольник имеет периметр 96 см и наклонную сторону 30 см.Вычислите высоту треугольника, зная, что площадь равна 432 см.
Дорожка 202
Треугольник из скалена имеет сторону 50 см, длину второй стороны 40 см и длину третьей стороны 80 см. Вычислите три медианы.
Трасса 203
Основание равнобедренного треугольника 36 м и высота 2/3. Вычисляет площадь и периметр треугольника, подобного заданному, с основанием 72 м.
Дорожка 204
Равносторонний треугольник со стороной 30 см эквивалентен прямоугольному треугольнику с катетом, равным одной трети стороны равностороннего треугольника.Вычислите периметр обоих треугольников.
Track 205
Вычислите количество сторон многоугольника, зная, что сумма внутренних углов равна 180.
Дорожка 206
Треугольник вписан в круг радиусом 10 см. Зная, что две короткие стороны равны соответственно 3/5 и 4/5 гипотенузы, вычислите площадь и периметр треугольника.
Дорожка 207
Равнобедренный треугольник имеет основание 36 см и высоту 24 см.Вычислите периметр и площадь треугольника, как если бы зная, что он имеет высоту 6 см.
Колея 208
Основание равнобедренного треугольника составляет 6/5 скошенной стороны, а периметр — 96 см. Вычислите периметр равностороннего треугольника с длиной стороны 3/5 заданной наклонной стороны равнобедренного треугольника.
Колея 209
Основание равнобедренного треугольника составляет 6/5 скошенной стороны, а периметр — 96 см.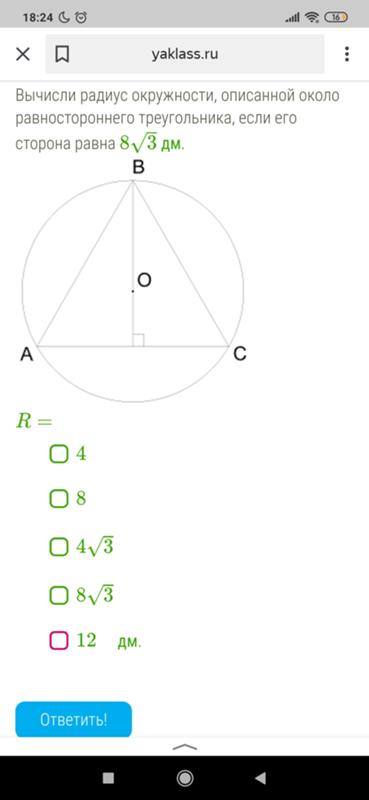 Вычислите периметр равностороннего треугольника с длиной стороны, равной 5/3 основания данного равнобедренного треугольника.
Вычислите периметр равностороннего треугольника с длиной стороны, равной 5/3 основания данного равнобедренного треугольника.
Колея 210
Основание равнобедренного треугольника составляет 6/5 скошенной стороны, а периметр — 96 см. Вычислите периметр равностороннего треугольника с длиной стороны, равной основанию данного равнобедренного треугольника.
Колея 211
Основание равнобедренного треугольника составляет 6/5 скошенной стороны, а периметр — 96 см. Вычислите периметр равностороннего треугольника с длиной стороны, равной наклонной стороне данного равнобедренного треугольника.
Дорожка 212
Равнобедренный треугольник имеет площадь 432 см и высоту 24 см. Вычислите периметр и площадь равностороннего треугольника с длиной стороны, равной 5/3 наклонной стороны данного равнобедренного треугольника.
Дорожка 213
Равнобедренный треугольник имеет площадь 432 см и высоту 24 см. Вычислите периметр и площадь равностороннего треугольника с длиной стороны, равной 5/3 основания данного равнобедренного треугольника.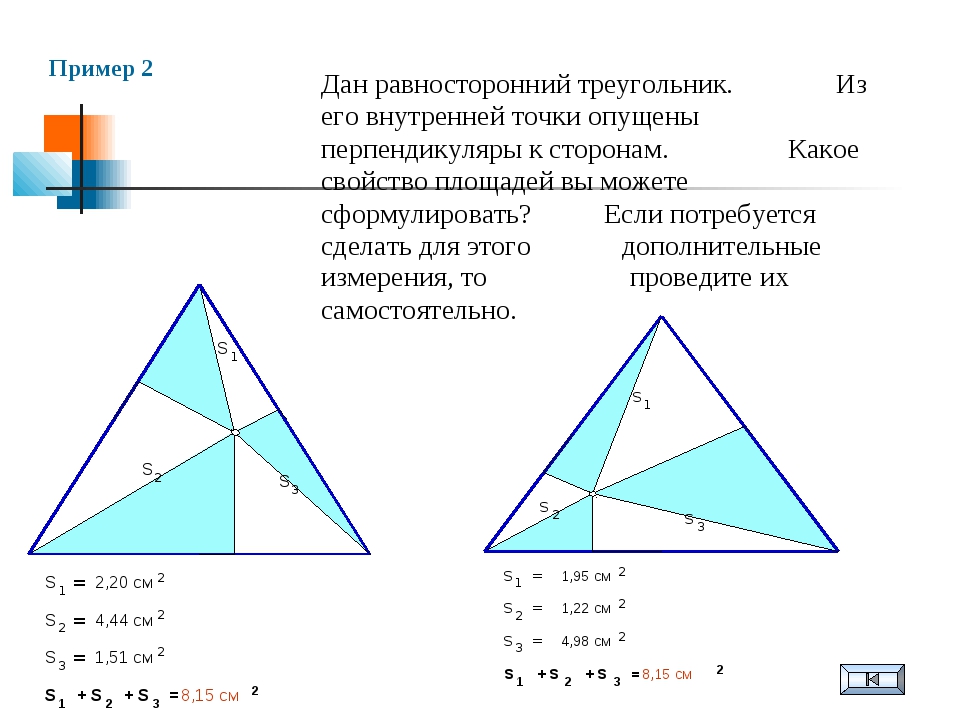
Дорожка 214
Равнобедренный треугольник имеет площадь 432 см и высоту 24 см.Вычислите периметр и площадь равностороннего треугольника с длиной стороны, равной основанию данного равнобедренного треугольника.
Дорожка 215
Равнобедренный треугольник имеет площадь 432 см и высоту 24 см. Вычислите периметр и площадь равностороннего треугольника с длиной стороны, равной наклонной стороне данного равнобедренного треугольника.
Дорожка 216
Равнобедренный треугольник имеет площадь 432 см и высоту 24 см. Вычислите периметр и площадь равностороннего треугольника, высота которого равна наклонной стороне данного равнобедренного треугольника.
Дорожка 217
Равнобедренный треугольник имеет площадь 432 см и высоту 24 см. Вычислите периметр и площадь равностороннего треугольника, высота которого равна 5/3 основания данного равнобедренного треугольника.
Дорожка 218
Равнобедренный треугольник имеет площадь 432 см и высоту 24 см. Вычислите периметр и площадь равностороннего треугольника, высота которого равна 5/3 наклонной стороны заданного равнобедренного треугольника.
Вычислите периметр и площадь равностороннего треугольника, высота которого равна 5/3 наклонной стороны заданного равнобедренного треугольника.
Дорожка 219
Равнобедренный треугольник имеет площадь 432 см и высоту 24 см.Вычислите периметр и площадь равностороннего треугольника, высота которого равна основанию данного равнобедренного треугольника.
Колея 220
Треугольник имеет угол 30, а его стороны составляют 6 и 9 см; вычисляет периметр и площадь треугольника.
Дорожка 221
Прямоугольный треугольник имеет площадь 6 см и гипотенузу 5 см. Какая связь подобия с подобным треугольником, гипотенуза которого относительная высота 4.8 см?
Дорожка 222
Треугольник имеет угол 60, а катет, находящийся напротив него, имеет длину 8,66 см. Рассчитывает площадь и периметр.
Дорожка 223
В прямоугольном треугольнике катет и его проекция на гипотенузу имеют размер 30 см и 18 см. Рассчитайте периметр и площадь.
Track 224
Вычислите периметр и площадь прямоугольного треугольника, зная, что разница между гипотенузой и проекцией катета на него составляет 32 см, а их соотношение составляет 25/9.
Дорожка 225
Равнобедренный треугольник имеет основание 36 см и высоту 24 см. Вычислите периметр и площадь треугольника, аналогичного заданному, зная, что наклонная сторона второго треугольника составляет 7,5 см.
Колея 226
Равносторонний треугольник с длинной стороной 60 см и равнобедренный треугольник имеют одинаковый периметр. Основание равнобедренного треугольника составляет 80 см. Насколько велика наклонная сторона? Вычисляет, кроме того, площадь двух треугольников.
Track 227
Вычислите периметр и площадь прямоугольного треугольника, в котором один катет превышает 4 см, а другой катет, зная, что гипотенуза равна 20 см.
Колея 228
Площадь прямоугольного треугольника 600 см. Рассчитайте периметр, зная, что разница между двумя катетами составляет 10 см.
Дорожка 229
Вы хотите украсить фоторамки 10, имеющие форму равностороннего треугольника со стороной 150 см. Сколько декаметров ленты нужно для декорирования?
Трасса 230
Радиус окружности конгруэнтен гипотенузе прямоугольного треугольника с двумя сторонами 3 см и 4 см.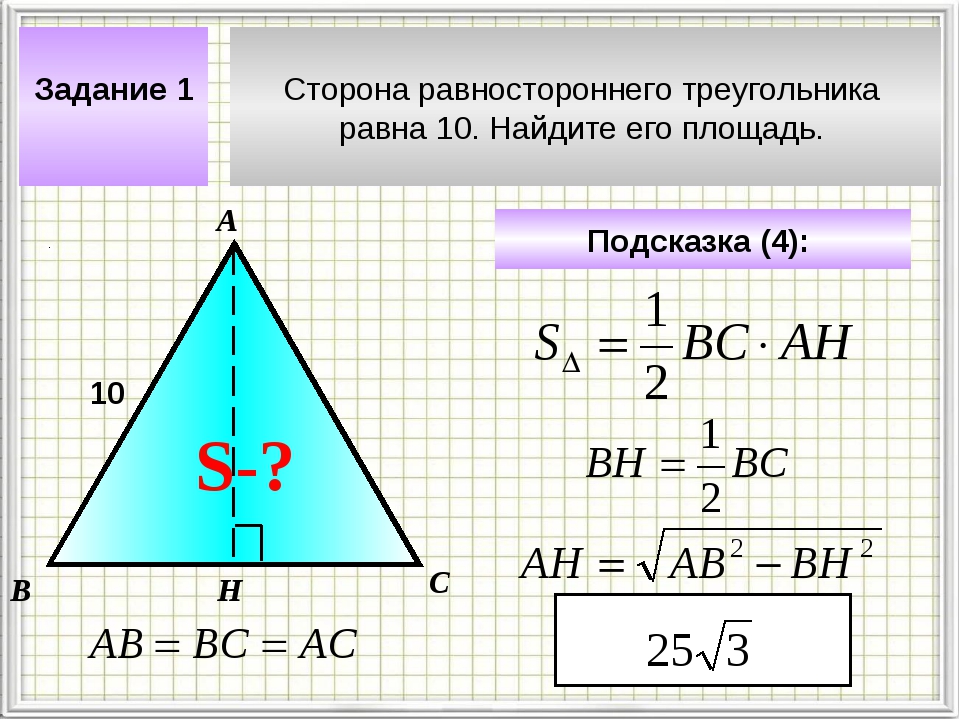




Leave A Comment