Бесконечная арифметическая прогрессия: Арифметическая прогрессия — урок. Алгебра, 9 класс.

Арифметическая прогрессия. Учебник по ЕГЭ и ГИА

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Числовая последовательность

Итак, сядем и начнем писать какие-нибудь числа. Например:
Писать можно любые числа, и их может быть сколько угодно (в нашем случае их ). Сколько бы чисел мы не написали, мы всегда можем сказать, какое из них первое, какое – второе и так далее до последнего, то есть, можем их пронумеровать. Это и есть пример числовой последовательности:

Числовая последовательность – это множество чисел, каждому из которых можно присвоить уникальный номер.
Например, для нашей последовательности:

Присвоенный номер характерен только для одного числа последовательности. Иными словами, в последовательности нет трех вторых чисел. Второе число (как и -ное число) всегда одно.

Число с номером называется -ным членом последовательности.

Всю последовательность мы обычно называем какой-нибудь буквой (например, ), и каждый член этой последовательности – той же буквой с индексом, равным номеру этого члена: .

В нашем случае:

Арифметическая прогрессия

Допустим, у нас есть числовая последовательность, в которой разница между соседствующими числами одинакова и равна .
Например:

и т.д.
Такая числовая последовательность называется арифметической прогрессией.
Термин «прогрессия» был введен римским автором Боэцием еще в 6 веке и понимался в более широком смысле, как бесконечная числовая последовательность. Название «арифметическая» было перенесено из теории непрерывных пропорций, которыми занимались древние греки.

Арифметическая прогрессия – это числовая последовательность, каждый член которой равен предыдущему, сложенному с одним и тем же числом. Это число называется разностью арифметической прогрессии и обозначается .

Попробуй определить, какие числовые последовательности являются арифметической прогрессией, а какие нет:

a)
b)
c)
d)

Разобрался? Сравним наши ответы:
Является арифметической прогрессией – b, c.
Не является арифметической прогрессией – a, d.

Вернемся к заданной прогрессии ( ) и попробуем найти значение ее -го члена. Существует два способа его нахождения.

1. Способ

Мы можем прибавлять к предыдущему значению числа прогрессии , пока не дойдем до -го члена прогрессии. Хорошо, что суммировать нам осталось немного – всего три значения:

Итак, -ой член описанной арифметической прогрессии равен .

2. Способ

А что если нам нужно было бы найти значение -го члена прогрессии? Суммирование заняло бы у нас не один час, и не факт, что мы не ошиблись бы при сложении чисел.
Разумеется, математики придумали способ, при котором не нужно прибавлять разность арифметической прогрессии к предыдущему значению. Присмотрись внимательно к нарисованному рисунку… Наверняка ты уже заметил некую закономерность, а именно:

Если нам нужно найти значение числа прогрессии с порядковым номером, мы прибавляем к первому члену арифметической прогрессии количество , которое

на одно значение меньше порядкового номера искомого числа.

Например, посмотрим, из чего складывается значение -го члена данной арифметической прогрессии:

Иными словами:

Попробуй самостоятельно найти таким способом значение члена данной арифметической прогрессии.

Рассчитал? Сравни свои записи с ответом:

Обрати внимание, что у тебя получилось точно такое же число, как и в предыдущем способе, когда мы последовательно прибавляли к предыдущему значению членов арифметической прогрессии.

Попробуем «обезличить» данную формулу – приведем ее в общий вид и получим:

— уравнение арифметической прогрессии.

Кстати, таким образом мы можем посчитать и -ой член данной арифметической прогрессии (да и -ый тоже можем, да и любой другой вычислить совсем несложно). Попробуй посчитать значения -го и -го членов, применив полученную формулу.

Арифметические прогрессии бывают возрастающие, а бывают убывающие.

Возрастающие – прогрессии, в которых каждое последующее значение членов больше предыдущего.
Например:

Убывающие – прогрессии, в которых каждое последующее значение членов меньше предыдущего.
Например:

Выведенная формула применяется в расчете членов как в возрастающих, так и в убывающих членах арифметической прогрессии.
Проверим это на практике.
Нам дана арифметическая прогрессия, состоящая из следующих чисел: Проверим, какое получится -ое число данной арифметической прогрессии, если при его расчете использовать нашу формулу:

Заметим, что так как арифметическая прогрессия убывающая, то значение будет отрицательным, ведь каждый последующий член меньше предыдущего.

Так как , то:

Таким образом, мы убедились, что формула действует как в убывающей, так и в возрастающей арифметической прогрессии.
Попробуй самостоятельно найти -ой и -ый члены этой арифметической прогрессии.

Сравним полученные результаты:

Свойство арифметической прогрессии

Усложним задачу — выведем свойство арифметической прогрессии.
Допустим, нам дано такое условие:
— арифметическая прогрессия, найти значение .
Легко, скажешь ты и начнешь считать по уже известной тебе формуле:

Пусть , а , тогда:

Абсолютно верно. Получается, мы сначала находим , потом прибавляем его к первому числу и получаем искомое . Если прогрессия представлена маленькими значениями, то ничего сложного в этом нет, а если нам в условии даны числа ? Согласись, есть вероятность ошибиться в вычислениях.
А теперь подумай, можно ли решить эту задачу в одно действие с использованием какой-либо формулы? Конечно да, и именно ее мы попробуем сейчас вывести.

Обозначим искомый член арифметической прогрессии как , формула его нахождения нам известна – это та самая формула, выведенная нами в начале:
, тогда:

предыдущий член прогрессии это :
последующий член прогрессии это :

Просуммируем предыдущий и последующий члены прогрессии:

Получается, что сумма предыдущего и последующего членов прогрессии – это удвоенное значение члена прогрессии, находящегося между ними. Иными словами, чтобы найти значение члена прогрессии при известных предыдущих и последовательных значениях, необходимо сложить их и разделить на .

— свойство членов арифметической прогрессии.

Попробуем посчитать значение , используя выведенную формулу:

Все верно, мы получили это же число. Закрепим материал. Посчитай значение для прогрессии самостоятельно, ведь это совсем несложно.

Молодец! Ты знаешь о прогрессии почти все! Осталось узнать только одну формулу, которую по легендам без труда вывел для себя один из величайших математиков всех времен, «король математиков» — Карл Гаусс…

Сумма первых n членов арифметической прогрессии

Когда Карлу Гауссу было 9 лет, учитель, занятый проверкой работ учеников других классов, задал на уроке следующую задачу: «Сосчитать сумму всех натуральных чисел от до (по другим источникам до ) включительно». Каково же было удивление учителя, когда один из его учеников (это и был Карл Гаусс) через минуту дал правильный ответ на поставленную задачу, при этом, большинство одноклассников смельчака после долгих подсчетов получили неправильный результат…

Юный Карл Гаусс заметил некоторую закономерность, которую без труда заметишь и ты.
Допустим, у нас есть арифметическая прогрессия, состоящая из -ти членов: Нам необходимо найти сумму данных членов арифметической прогрессии. Конечно, мы можем вручную просуммировать все значения, но что делать, если в задании необходимо будет найти сумму ее членов, как это искал Гаусс?

Изобразим заданную нам прогрессию. Присмотрись внимательно к выделенным числам и попробуй произвести с ними различные математические действия.

Попробовал? Что ты заметил? Правильно! Их суммы равны

А теперь ответь, сколько всего наберется таких пар в заданной нам прогрессии? Конечно, ровно половина всех чисел, то есть .
Исходя из того, что сумма двух членов арифметической прогрессии равна , а подобных равных пар , мы получаем, что общая сумма равна:
.
Таким образом, формула для суммы первых членов любой арифметической прогрессии будет такой:

, где – количество значений.

В некоторых задачах нам неизвестен -й член, но известна разность прогрессии. Попробуй подставить в формулу суммы, формулу -го члена.
Что у тебя получилось?

, где – количество значений.

Молодец! Теперь вернемся к задаче, которую задали Карлу Гауссу: посчитай самостоятельно, чему равна сумма чисел, начиная от -го, и сумма чисел начиная от -го.

Сколько у тебя получилось?
У Гаусса получилось, что сумма членов равна , а сумма членов . Так ли ты решал?

На самом деле формула суммы членов арифметической прогрессии была доказана древнегреческим ученым Диофантом еще в 3 веке, да и на протяжении всего этого времени остроумные люди вовсю пользовались свойствами арифметической прогрессии.
Например, представь Древний Египет и самую масштабную стройку того времени – строительство пирамиды… На рисунке представлена одна ее сторона.

Где же здесь прогрессия скажешь ты? Посмотри внимательно и найди закономерность в количестве песчаных блоков в каждом ряде стены пирамиды.

Чем не арифметическая прогрессия? Посчитай, сколько всего блоков необходимо для строительства одной стены, если в основание кладется блочных кирпичей. Надеюсь, ты не будешь считать, водя пальцем по монитору, ты же помнишь последнюю формулу и все, что мы говорили об арифметической прогрессии?

В данном случае прогрессия выглядит следующим образом: .
Разность арифметической прогрессии .
Количество членов арифметической прогрессии .
Подставим в последние формулы наши данные (посчитаем количество блоков 2 способами).

Способ 1.

Способ 2.

А теперь можно и на мониторе посчитать: сравни полученные значения с тем количеством блоков, которое есть в нашей пирамиде. Сошлось? Молодец, ты освоил сумму -ных членов арифметической прогрессии.
Конечно, из блоков в основании пирамиду не построишь, а вот из ? Попробуй рассчитать, сколько необходимо песчаных кирпичей, чтобы построить стену с таким условием.
Справился?
Верный ответ – блоков:

Тренировка

Задачи:

Маша приходит в форму к лету. Ежедневно она увеличивает количество приседаний на . Сколько раз будет приседать Маша через недели, если на первой тренировке она сделала приседаний.
Какова сумма всех нечетных чисел, содержащихся в .
Лесорубы при хранении бревен укладывают их таким образом, что каждый верхний слой содержит на одно бревно меньше, чем предыдущий. Сколько бревен находится в одной кладке, если основанием кладки служат бревен.

Ответы:

Определим параметры арифметической прогрессии. В данном случае
( недели = дней).

Ответ: Через две недели Маша должна приседать раз в день.
Первое нечетное число , последнее число .
Разность арифметической прогрессии .
Количество нечетных чисел в – половина, однако, проверим этот факт, используя формулу нахождения -ного члена арифметической прогрессии:

В числах действительно содержится нечетных чисел.
Имеющиеся данные подставим в формулу:

Ответ: Сумма всех нечетных чисел, содержащихся в , равна .
Вспомним задачу про пирамиды. Для нашего случая , a , так как каждый верхний слой уменьшается на одно бревно, то всего в кучке слоев, то есть .
Подставим данные в формулу:

Ответ: В кладке находится бревен.

Подведем итоги

Арифметическая прогрессия – числовая последовательность, в которой разница между соседними числами одинакова и равна . Она бывает возрастающей и убывающей .
Формула нахождения -го члена арифметической прогрессии записывается формулой — , где – количество чисел в прогрессии.
Свойство членов арифметической прогрессии — — где – количество чисел в прогрессии.
Сумму членов арифметической прогрессии можно найти двумя способами:
, где – количество значений.
, где – количес

Арифметическая прогрессия: определение, формулы, свойства

Арифметическая прогрессия – это числовая последовательность, в которой, начиная со второго числа, каждое последующее равняется предыдущему плюс постоянное слагаемое.

Общий вид арифметической прогрессии

a₁, a₁ + d, a₁ + 2d, … a₁ + (n – 1) d, …

d – шаг или разность прогрессии; это и есть постоянное слагаемое.

Члены прогрессии:

a₁
a₂ = a₁ + d
a₃ = a₂ + d = a₁ + 2d
и т.д.

Цифры 1,2,3… – это их порядковые номера, т.е. место, которое они занимают в последовательности.

Свойства и формулы арифметической прогрессии

1. Нахождение общего n-ого члена (a_n)

a_n = a_n-1 + d
a_n = a₁ + (n – 1) d
a_n = a_m – (m – n) d

2. Разность прогрессии

d = a_n – a_n-1

Также для нахождения шага используется такая формула:

3. Характеристическое свойство

Последовательность чисел a₁, a₂, a₃ … является арифметической прогрессией, если для любого ее члена выполняется следующее условие:

4. Сумма первых членов прогрессии

Чтобы найти сумму первых членов арифметической прогрессии, необходимо воспользоваться формулой:

n – количество суммируемых членов.

Если a_n заменить на a₁ + (n – 1) d, то получится:

5. Сумма членов прогрессии с n-ого по m-ный

(m – n + 1) – количество суммируемых членов.

Если a_m заменить на a_n + (m – n) d, то получим:

6. Сходимость прогрессии

Арифметическая прогрессия сходится при d = 0, во всех остальных случаях она расходится.

При этом, если:

d > 0, прогрессия называется возрастающей;
d < 0 – убывающей;
d = 0 – стационарной.

Арифметическая прогрессия | umath.ru

Определение арифметической прогрессии

Определение. Числовая последовательность, каждый член которой получается из предыдущего прибавлением одного и того же числа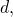

называется арифметической прогрессией. Число

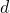называется разностью арифметической прогрессии.

То есть арифметическая прогрессия определяется рекуррентным соотношением

$a_{n+1} = a_n + d.$

Например, последовательность нечётных натуральных чисел

$1, 3, 5, 7, 9, \ldots$

является арифметической прогрессией, так как любой её член отличается от предыдущего на 2.

Общий член арифметической прогрессии 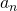задаётся формулой

$a_n = d(n - 1) + a_1.$

Например, последовательность 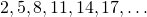$2, 5, 8, 11, 14, 17,\ldots$ образует арифметическую прогрессию с разностью 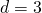d = 3 и первым членом 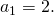Поэтому её общий член может быть задан соотношением

$a_n = 2 + 3(n-1) = 3n - 1.$

Пример 1. Найти одиннадцатый член арифметической прогрессии, если её первый член 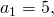а разность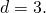 d = 3.

Решение. По формуле для общего члена арифметической прогрессии имеем

$a_{11} = 5 + 3(11 - 1) = 35.$

Теорема. Последовательность 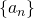$\{a_n\}$ тогда и только тогда является арифметической прогрессией, когда каждый её член, начиная со второго, равен полусумме предыдущего и последующего членов:

$a_n = \frac{a_{n - 1} + a_{n+1}}{2}.$

Доказательство. По определению арифметической прогрессии для всех 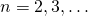$n = 2, 3, \ldots$ имеем

$d = a_n - a_{n-1} = a_{n+1} - a_n.$

Отсюда

$2a_n = a_{n-1} + a_{n+1},$

то есть

$a_n = \frac{a_{n-1} + a_{n+1}}{2}.$

Сумма первых n членов арифметической прогрессии

В качестве примера найдём сумму всех натуральных чисел от 1 до 100, то есть вычислим сумму

$S = 1 + 2 + 3 + \ldots + 99 + 100.$

Решение. Можно сидеть и долго складывать все числа по порядку. Но есть более простой способ. Запишем сумму этих чисел, а под ней — ту же сумму, но в обратной последовательности:

$\begin{array}{cccccccccc} S = & 1& + & 2& + & 3& + \ldots + &99& + &100, \\ S = &100& + &99& + &98& + \ldots + & 2& + & 1. \end{array}$

Теперь почленно сложим эти суммы:

$2S = (1 + 100) + (2 + 99) + (3 + 98) + \ldots + (100 + 1)=$

$= \underbrace{101 + 101 + \ldots + 101}_{100} = 100 \cdot 101 = 10100.$

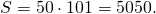
Отсюда $S = 50\cdot 101 = 5050.$

По легенде, школьный учитель математики, надеясь надолго занять детей, предложил им сосчитать эту сумму. Среди тех детей был будущий великий математик Карл Гаусс. Юный Гаусс быстро заметил, что попарные суммы членов с противоположных концов равны: 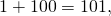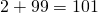и т.д, и уже через несколько минут подошёл к учителю с ответом: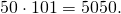 $50\cdot 101 = 5050.$

Этим же приёмом удобно воспользоваться и при вычислении суммы первых 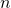членов арифметической прогрессии, если заметить, что

$a_k + a_{n+1-k} = a_1 + a_n.$

Действительно,

$a_k + a_{n+1-k} = a_1 + d(k - 1) + a_1 + d(n-k) =$

$a_1 + (a_1 + d(n-1)) = a_1 + a_n.$

Сумма первых n членов арифметической прогресиии

$S_n = a_1 + a_2 + \ldots + a_n$

равна полусумме первого и n-ного её членов, умноженной на число членов, то есть

$S_n = \frac{a_1 + a_n}{2}\cdot n.$

Доказательство. Запишем сумму 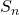S_n сначала в прямом порядке, а затем — в обратном:

$S_n = a_1 + a_2 + \ldots + a_{n-1} + a_n,$

$S_n = a_n + a_{n-1} + \ldots + a_2 + a_1.$

Сложим почленно эти два равенства и воспользуемся тем, что 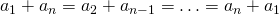$a_1 + a_n = a_2 + a_{n-1} = \ldots = a_n + a_1$ :

$2S_n = (a_1 + a_n) + (a_2 + a_{n-1}) + \ldots + (a_n + a_1) =$

$=(a_1 + a_n)n.$

Отсюда находим

$S_n = \frac{a_1 + a_n}{2}\cdot n.$

Арифметическая прогрессия | Онлайн калькулятор

Арифметическая прогрессия — это некая последовательность чисел, каждый следующий член которой отличается от предыдущего на одно и то же число d, называемое шаг прогрессии или разность прогрессии. Калькулятор арифметической прогрессии, используя следующие формулы, может найти первый член арифметической прогрессии , n-ный член прогрессии, найти сумму первых членов или разность.

Арифметическая прогрессия как последовательность, составленная из действительных чисел, связывает их между собой заданной закономерностью ряда. Как правило, числовой ряд начинается с того, что дан первый член арифметической прогрессии, как отправная точка. Далее каждый следующий член прогрессии получается путем прибавления к предыдущему одного и того же параметра, называемого разность арифметической прогрессии или шаг арифметической прогрессии. Если разность является положительным числом, то вся последовательность будет стремиться к плюс бесконечности, так как значения членов будут увеличиваться по мере возрастания их порядковых номеров.

Если разность арифметической прогрессии представлена отрицательным числом, каждый следующий член будет меньше предыдущего и вся последовательность будет стремиться к минус бесконечности. В некоторых случаях предел арифметической прогрессии будет конкретным числом. Это происходит, если шаг прогрессии (разность) равен нулю, тогда первый член арифметической прогрессии совпадает со всеми остальными.

Формулы арифметической прогрессии включают в себя следующие равенства:

• формула первого члена арифметической прогрессии;

• формула n-ного члена прогрессии;

• формула разности арифметической прогрессии;

• формула суммы первых членов арифметической прогрессии или суммы определенной выборки членов.

По всем формулам онлайн калькулятор рассчитывает необходимые значения, используя условия, по которым дана арифметическая прогрессия. Числа, выстроенные в симметричной последовательности, дают возможность вычислить любой член или сумму прогрессии, опираясь всего на два или три параметра в зависимости от уровня сложности задания.

Арифметическая прогрессия. Задачи на прогрессии.

Всем привет! Сегодня вспоминаем прогрессии. Задачи на прогрессии встречаются как в блоке текстовых задач ЕГЭ (задачи типа В14), так и среди задач ГИА (В4).

Сначала вспомним арифметическую прогрессию и порешаем задачи, связанные с ней. Кому нужна геометрическая – смотри тут.

В любой последовательности каждый элемент должен иметь “адрес”, по которому можно было бы этот элемент отыскать. Этот “адрес” – это порядковый номер элемента. Например, понятно, что элемент – первый, а – “живет” в сотой “квартире”.

Также между номером элемента и его значением есть зависимость. Если последовательность возрастающая, то, чем больше номер “квартиры”, тем “толще” жилец, а если убывающая, то наоборот (все это – непостоянные последовательности). Существуют также последовательности, у которых все члены – одинаковы. Такие последовательности называются постоянными последовательностями (например: 5, 5, 5, …).

Задать последовательность можно по-разному.

Часто встречается такой способ задания: “Дана последовательность 30; 28; 26;…” – по сути, это табличный способ задания. Интуитивно понятно, что 30 здесь – первый член последовательности, и можно сразу “увидеть” разность такой прогрессии – это “расстояние между соседями”.

Также задают последовательности формулой n-ного члена, например: a_n=n+6 . Чтобы найти элемент такой последовательности, нужно подставить нужное n в формулу.

В случае же, когда член последовательности задан с помощью одного или нескольких предыдущих членов, то, чтобы найти этот член последовательности, необходимо знать и эти предыдущие члены также, то есть нужно как бы позвонить им в квартиры и спросить адрес их соседа. Такое задание называется рекуррентным от итальянского слова recurro (спешить обратно).Пример: $a_{n+1}=a_n+6$ .

Арифметической прогрессией называется последовательность чисел, в которой каждое последующее число отличается от предыдущего на одну и ту же величину, которая называется разностью прогрессии и обозначается

Разность может быть положительной, отрицательной и нулевой. Так как она постоянна, то между соседями “расстояние” будет , а “расстояние” между членами, которые стоят “через одного” – . Отсюда свойство прогрессии:

$a_n={a_{n-1}+a_{n+1}}/2$

Понятно, что это свойство относится и к другим членам, отстоящим от “центра” на одинаковое количество номеров: $a_n={a_{n-m}+a_{n+m}}/2$

Найти n-ный член прогрессии просто, если знаешь первый и разность прогрессии. Ведь если вы знаете, где первая квартира в доме, вы легко отыщете сотую, верно?

Еще нужно знать формулу суммы прогрессии. Когда это может понадобиться? Например, население города увеличивается каждый месяц на 1000 жителей. Сколько новых жителей появится в городе через год или два, сколько строить новых школ или поликлиник?

Сумму прогрессии можно найти по формулам:

Ну вот, теперь мы вооружены, можем и задачи порешать попробовать.

1. Дана арифметическая прогрессия: -30; -24; -18;… Найти сумму первых десяти членов.

Первый член a_1=-30 . Разность прогрессии можно найти, вычтя из a_2 (последующего члена) (предыдущий). (Или из – a_2 ):

Теперь воспользуемся формулой для суммы – берем вторую формулу:

Ответ: -30

2. Дана арифметическая прогрессия: 35; 28;21;… Найти сумму членов с 12 по 18 включительно.

Первый член a_1=35 . Разность прогрессии можно найти, вычтя из a_2 (последующего члена) (предыдущий). (Или из – a_2 ):

Теперь найдем сумму 18 первых членов, и вычтем из нее сумму 11 первых членов – тогда останется то, что нам и надо::

Вторая сумма равна 0, поэтому ответ: -441.

3. Арифметическая прогрессия задана условиями: a_1=5 , $a_n=a_{n+1}+3$ . Найти .

Так как между последующим и предыдущим членами (из условия) разность равна 3, то это и есть разность прогрессии. По формуле для нахождения n-ного члена определяем :

Ответ: 38

4. Последовательности заданы несколькими первыми членами. Какая из них – арифметическая прогрессия?

а) 1; 2; 3; 5;… б) 1; 2; 4; 8;… в) 1; 3; 5; 7;… г).

Надо выбрать такую последовательность, где разность между соседними членами была бы одинаковой. Первая не подойдет: четвертый член выбивается из общего ряда. Вторая тоже, очевидно, не подойдет: здесь соседние члены отличаются не “на”, а “в” – каждый следующий вдвое больше. Третья годится: разность равна 2. Четвертая тоже не подойдет: разность между соседними дробями не одинакова.

Ответ: в)

5. Выписаны несколько членов арифметической прогрессии: 3; 6; 9; 12;… Какое из следующих чисел есть среди членов этой прогрессии?

а) 85 б) 73 в) 117 г) 254.

Конечно, задан первый член и можно определить разность – она равна 3 – но неужели предстоит просчитать каждое число по формуле n-ного члена, чтобы определить нужное? НЕТ! Все гораздо проще! Заметим, что все члены прогрессии делятся на 3. И разность прогрессии 3, значит, если число входит в прогрессию, то оно тоже должно делиться на три! Вы помните признак делимости на три? Правильно: если сумма чисел делится на три, то и все число делится. Считаем: 8+5=13 – на три не делится; 7+3=10 – не делится; 1+1+7=9 – число 117 делится на три, и является членом прогрессии. 2+5+4=11 – не подходит.

Ответ: в)

6. Арифметические прогрессии заданы формулами n-ного члена:, y_n=3n , . Укажите те из них, у которых разность равна 3.

Просто подставив в каждую формулу 1 и 2 вместо n, посмотрим, какая разность получится между членами прогрессий:

Первая прогрессия отвечает требованию.

Вторая:

Вторая также подойдет.

Третья:

– очевидно, что такая разность нам не подходит.

Ответ:

7. Сумма третьего и пятого членов арифметической прогрессии равна 16, а шестой ее член на 12 больше второго. Найдите разность и первый член данной прогрессии.

Составим уравнения по условиям:

Перепишем второе уравнение:

Теперь можем определить разность:

4d=12

d=3

Перепишем первое уравнение:

Ответ:

8. Выписано несколько последовательных членов арифметической прогрессии: …; 10; x; –14; –26; … Найдите член прогрессии, обозначенный буквой x.

По свойству прогрессии неизвестный член равен полусумме своих соседей: . Также можно было найти разность прогрессии и прибавить ее к числу “до” х, или отнять от числа “после”.

9. В первом ряду кинозала 50 мест, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в ряду с номером n?

Если число мест в каждом ряду выписать в ряд, получим арифметическую прогрессию. Арифметическую – потому что число мест все время увеличивается на одно и то же число. Понятно, что разность этой прогрессии 2. И вот здесь-то и хочется сказать, что в ряду n число мест , но это неверно! Ведь тогда в первом ряду получается 52 места! Поэтому правильно .

10. Дана арифметическая прогрессия: 35; 27; 19; … . Найдите первый отрицательный член этой прогрессии.

Можно, конечно, найти, на сколько последующий член меньше предыдущего (прогрессия убывающая), то есть разность прогрессии, и затем вычитать последовательно это число до тех пор, пока результат не станет отрицательным.

11. Дана арифметическая прогрессия 13, 8, 3, … Какое число стоит в этой последовательности на 81-м месте?

Первый член a_1=13 . Разность прогрессии можно найти, вычтя из a_2 (последующего члена) (предыдущий):

Находим 81 член прогрессии:

Ответ: -387

12. Какое наибольшее число последовательных натуральных чисел, начиная с 1, можно сложить, чтобы получившаяся сумма была меньше 528?

“Начиная с 1” – значит, . Натуральные числа – ряд последовательных чисел, отличающихся на 1 – значит, d=1 .

Формула суммы прогрессии: – здесь нам неизвестно число членов прогрессии – n.

Подставим 528 и попробуем определить n:

$S_n={{2+(n-1)}/2}n={2n+n^2-n}/2=528$

Получили квадратное уравнение:

Второй корень – отрицательный, его можно даже не считать.

Получается, что сумма 32 членов дает 528, а нам нужно, чтобы сумма была бы меньше – тогда берем 31 член прогрессии.

Ответ: 31.

13. Найдите сумму всех отрицательных членов арифметической прогрессии –17; –16; -15; …

Первый член прогрессии . Разность прогрессии d=1 .

Формула n-ного члена: . Найдем, сколько таких отрицательных членов у нас получится:

a_n<0

Тогда отрицательных членов 17. Находим их сумму:

Ответ: -153.

14. Руслану надо решить 420 задач. Ежедневно он решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что за первый день Руслан решил 13 задач. Определите, сколько задач Руслан решил в последний день, если со всеми задачами он справился за 12 дней.

Сначала разберемся, какие сведения содержит в себе условие. Похоже, фраза “на одно и то же количество задач больше” говорит о том, что мы имеем дело с прогрессией. Общий объем работы, предстоящий Руслану – это сумма прогрессии. 13 задач, решенных в первый день – это первый член нашей прогрессии. Ну и 12 дней, отведенных на это сложное дело – это количество членов прогрессии.

Найти надо количество задач, решенных в последний день – то есть 12 член прогрессии.

– в формуле n-ного члена нам неизвестна разность этой прогрессии. Поэтому воспользуемся суммой:

$S_12={{2a_1+(n-1)d}/2}n={{2(13)+11d}/2}12=420$

11d=44

Находим 12 член прогрессии:

Ответ: 57

15. Улитка ползет от одного дерева до другого. Каждый день она проползает на одно и то же расстояние больше, чем в предыдущий день. Известно, что за первый и последний дни улитка проползла в общей сложности 10 метров. Определите, сколько дней улитка потратила на весь путь, если расстояние между деревьями равно 150 метрам.

Сумма прогрессии равна 150. Сумма первого и последнего членов – 10. Зная это, можем найти, какое количество дней улитка затратила на свой путь (количество членов прогрессии):

$S_n={10n}/2=150$

Откуда n=30

Ответ: 30

Сумма арифметической прогрессии | Онлайн калькулятор

Когда речь идет о таком параметре, как сумма арифметической прогрессии, подразумевается всегда сумма первых членов арифметической прогрессии или сумма членов прогрессии с k по n, то есть количество членов, которые берутся для суммы, строго ограничено в заданных условием пределах. В противном случае задание не будет иметь решения, так как вся числовая последовательность именно арифметической прогрессии начинается с конкретного числа — первого члена a₁, и продолжается бесконечно.

Бытует мнение, что формула суммы арифметической прогрессии была открыта еще Гауссом, как быстрый и точный способ расчета суммы чисел в определенной последовательности. Он заметил, что такая прогрессия является симметричной, то есть сумма симметрично расположенных с начала и конца членов прогрессии является постоянной для данного ряда.

a₁+a_n=a₂+a_(n-1)=a₃+a_(n-2)=⋯

Соответственно, он нашел данную сумму и умножил ее на половину от общего количества чисел в последовательности, участвующих в расчете суммы. Таким образом, была выведена формула суммы арифметической прогрессии

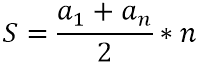
Пример. Предположим, задано условие: «Найдите сумму первых десяти (10) членов арифметической прогрессии». Для этого понадобится следующие данные: разность прогрессии и первый ее член. Если в задаче дан какой-либо n член арифметической прогрессии вместо первого, тогда сначала нужно воспользоваться разделом, где представлена формула нахождения первого члена прогрессии, и найти его. Затем исходные данные вбиваются в калькулятор и он производит расчеты, складывая первый и десятый члены, и умножая полученную сумму на половину от общего количества складываемых членов – на 5. Аналогично происходит, если нужно найти сумму первых шести членов или любого другого количества.

В случае, когда необходимо найти сумму членов арифметической прогрессии, начинающихся не с первого, а с пятого члена, к примеру, тогда среднее арифметическое остается тем же, а общее количество членов берется как увеличенная на единицу разность между порядковыми номерами взятых членов.

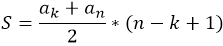
Смотрите также

Геометрическая прогрессия — YouClever.org

Числовая последовательность

Если ты уже читал тему «Арифметическая прогрессия» ты можешь смело пропускать этот блок и переходить к самой сути. Если нет, то советую ознакомиться, чтобы иметь общее представление о том, что такое прогрессия в целом и с чем ее едят.

Итак, сядем и начнем писать какие-нибудь числа. Например:

Писать можно любые числа, и их может быть сколько угодно (в нашем случае их ). Сколько бы чисел мы не написали, мы всегда можем сказать, какое из них первое, какое – второе и так далее до последнего, то есть, можем их пронумеровать. Это и есть пример числовой последовательности:

Числовая последовательность – это множество чисел, каждому из которых можно присвоить уникальный номер.

Например, для нашей последовательности:

Число с номером называетмя -ным членом последовательности.

В нашем случае:

Самые распространенные виды прогрессии это арифметическая и геометрическая. В этой теме мы поговорим о втором виде – геометрической прогрессии.

Для чего нужна геометрическая прогрессия и ее история возникновения.

Еще в древности итальянский математик монах Леонардо из Пизы (более известный под именем Фибоначчи) занимался решением практических нужд торговли. Перед монахом стояла задача определить, с помощью какого наименьшего количества гирь можно взвесить товар? В своих трудах Фибоначчи доказывает, что оптимальной является такая система гирь: Это одна из первых ситуаций, в которой людям пришлось столкнуться с геометрической прогрессией, о которой ты уже наверное слышал и имеешь хотя бы общее понятие. Как только полностью разберешься в теме, подумай, почему такая система является оптимальной?

В настоящее время, в жизненной практике, геометрическая прогрессия проявляется при вложении денежных средств в банк, когда сумма процентов начисляется на сумму, скопившуюся на счете за предыдущий период. Иными словами, если положить деньги на срочный вклад в сберегательный банк, то через год вклад увеличится на от исходной суммы, т.е. новая сумма будет равна вкладу, умноженному на . Ещё через год уже эта сумма увеличится на , т.е. получившаяся в тот раз сумма вновь умножится на и так далее. Подобная ситуация описана в задачах на вычисление так называемых сложных процентов – процент берется каждый раз от суммы, которая есть на счете с учетом предыдущих процентов. Об этих задачах мы поговорим чуть позднее.

Есть еще много простых случаев, где применяется геометрическая прогрессия. Например, распространение гриппа: один человек заразил человек, те в свою очередь заразили еще по человека, и таким образом вторая волна заражения – человек, а те в свою очередь, заразили еще … и так далее…

Кстати, финансовая пирамида, та же МММ – это простой и сухой расчет по свойствам геометрической прогрессии. Интересно? Давай разбираться.

Геометрическая прогрессия.

Допустим, у нас есть числовая последовательность:

Ты сразу же ответишь, что это легко и имя такой последовательности — арифметическая прогрессия с разностью ее членов . А как на счет такого:

Если ты будешь вычитать из последующего числа предыдущее, то ты увидишь, что каждый раз получается новая разница ( и т.д.), но последовательность определенно существует и ее несложно заметить – каждое следующие число в раз больше предыдущего!

Такой вид числовой последовательности называется геометрической прогрессией и обозначается .

Геометрическая прогрессия { } — это числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же число . Это число называют знаменателем геометрической прогрессии.

Ограничения, что первый член { } не равен и не случайны. Допустим, что их нет, и первый член все же равен , а q равно, хм.. пусть , тогда получается:

и так далее.

Согласись, что это уже никакая не прогрессия.

Как ты понимаешь, те же самые результаты мы получим, если будет каким-либо числом, отличным от нуля, а . В этих случаях прогрессии просто не будет, так как весь числовой ряд будут либо все нули, либо одно число, а все остальные нули.

Теперь поговорим поподробнее о знаменателе геометрической прогрессии, то есть о .

Повторим: – это число, во сколько раз изменяется каждый последующий член геометрической прогрессии.

Как ты думаешь, каким может быть ? Правильно, положительным и отрицательным, но не нулем (мы говорили об этом чуть выше).

Допустим, что у нас положительное. Пусть в нашем случае , а . Чему равен второй член и ? Ты без труда ответишь, что:

Все верно. Соответственно, если , то все последующие члены прогрессии имеют одинаковый знак – они положительны.

А что если отрицательное? Например, , а . Чему равен второй член и ?

Это уже совсем другая история

Попробуй посчитать член данной прогрессии. Сколько у тебя получилось? У меня . Таким образом, если , то знаки членов геометрической прогрессии чередуются. То есть, если ты увидишь прогрессию, с чередующимися знаками у ее членов, значит ее знаменатель на отрицательный. Это знание может помочь тебе проверять себя при решении задач на эту тему.

Теперь немного потренируемся: попробуй определить, какие числовые последовательности являются геометрической прогрессией, а какие арифметической:

Разобрался? Сравним наши ответы:

Геометрическая прогрессия – 3, 6.
Арифметическая прогрессия – 2, 4.
Не является ни арифметической, ни геометрической прогрессиями — 1, 5, 7.

Вернемся к нашей последней прогрессии , а и попробуем так же как и в арифметической найти ее член. Как ты уже догадываешься, есть два способа его нахождения.

Последовательно умножаем каждый член на .

Итак, -ой член описанной геометрической прогрессии равен .

Как ты уже догадываешься, сейчас ты сам выведешь формулу, которая поможет найти тебе любой член геометрической прогрессии. Или ты ее уже вывел для себя, расписывая, как поэтапно находить -ой член? Если так, то проверь правильность твоих рассуждений.

Если нам нужно найти значение числа прогрессии с порядковым номером, то мы умножаем первый член геометрической прогрессии на знаменатель в степени, которая на единицу меньше, чем порядковый номер искомого числа.

Проиллюстрируем это на примере нахождения -го члена данной прогрессии:

Иными словами:

Найди самостоятельно значение члена заданной геометрической прогрессии.

Получилось? Сравним наши ответы:

Обрати внимание, что у тебя получилось точно такое же число, как и в предыдущем способе, когда мы последовательно умножали на каждый предыдущий член геометрической прогрессии.
Попробуем «обезличить» данную формулу – приведем ее в общий вид и получим:

— уравнение членов геометрической прогрессии.

Выведенная формула верна для всех значений — как положительных, так и отрицательных. Проверь это самостоятельно, рассчитав и члены геометрической прогрессии со следующими условиями: , а .

Посчитал? Сравним полученные результаты:

Согласись, что находить член прогрессии можно было бы так же как и член, однако, есть вероятность неправильно посчитать . А если мы нашли уже -ый член геометрической прогрессии, а , то что может быть проще, чем воспользоваться «обрезанной» частью формулы .

Бесконечно убывающая геометрическая прогрессия.

Совсем недавно мы говорили о том, что может быть как больше, так и меньше нуля, однако, есть особые значения при которых геометрическая прогрессия называется бесконечно убывающей.

При – прогрессия называется бесконечно убывающей.

Как ты думаешь, почему такое название?
Для начала запишем какую-нибудь геометрическую прогрессию, состоящую из членов.
Допустим, , а , тогда:

Мы видим, что каждый последующий член меньше предыдущего в раза, но будет ли какое-либо число ? Ты сразу же ответишь – «нет». Вот поэтому и бесконечно убывающая – убывает, убывает, а нулем никогда не становится.

Чтобы четко понять, как это выглядит визуально, давай попробуем нарисовать график нашей прогрессии. Итак, для нашего случая формула приобретает следующий вид:

На графиках нам привычно строить зависимость от , поэтому:

Суть выражения не изменилась: в первой записи у нас была показана зависимость значения члена геометрической прогрессии от его порядкового номера, а во второй записи – мы просто приняли значение члена геометрической прогрессии за , а порядковый номер обозначили не как , а как . Все, что осталось сделать – построить график.
Посмотрим, что у тебя получилось. Вот какой график получился у меня:

Видишь? Функция убывает, стремится к нулю, но никогда его не пересечет, поэтому она бесконечно убывающая. Отметим на графике наши точки, а заодно и то, что обозначает координата и :

Попробуй схематично изобразить график геометрической прогрессии при , если первый ее член также равен . Проанализируй, в чем разница с нашим предыдущим графиком?

Справился? Вот какой график получился у меня:

Теперь, когда ты полностью разобрался в основах темы геометрической прогрессии: знаешь, что это такое, знаешь, как найти ее член, а также знаешь, что такое бесконечно убывающая геометрическая прогрессия, перейдем к ее основному свойству.

Свойство геометрической прогрессии.

Помнишь свойство членов арифметической прогрессии? Да, да, как найти значение определенного числа прогрессии, когда есть предыдущее и последующее значения членов данной прогрессии. Вспомнил? Вот это:

— свойство членов арифметической прогрессии.

Теперь перед нами стоит точно такой же вопрос для членов геометрической прогрессии. Чтобы вывести подобную формулу, давай начнем рисовать и рассуждать. Вот увидишь, это очень легко, и если ты забудешь, то сможешь вывести ее самостоятельно.

Возьмем еще одну простую геометрическую прогрессию, в которой нам известны и . Как найти ? При арифметической прогрессии это легко и просто, а как здесь? На самом деле в геометрической тоже нет ничего сложного — необходимо просто расписать по формуле каждое данное нам значение.

Ты спросишь, и что теперь нам с этим делать? Да очень просто. Для начала изобразим данные формулы на рисунке, и попытаемся сделать с ними различные манипуляции, чтобы прийти к значению .

Абстрагируемся от чисел, которые у нас даны, сосредоточимся только на их выражении через формулу. Нам необходимо найти значение, выделенное оранжевым цветом, зная соседствующие с ним члены. Попробуем произвести с ними различные действия, в результате которых мы сможем получить .

Сложение.
Попробуем сложить два выражения и , мы получим:

Из данного выражения, как ты видишь, мы никак не сможем выразить , следовательно, будем пробовать другой вариант – вычитание.

Вычитание.

Как ты видишь, из этого мы тоже не можем выразить , следовательно, попробуем умножить данные выражения друг на друга.

Умножение.

А теперь посмотри внимательно, что мы имеем, перемножая данные нам члены геометрической прогрессии в сравнении с тем, что необходимо найти:

Догадался о чем я говорю? Правильно, чтобы найти нам необходимо взять квадратный корень от перемноженных друг на друга соседствующих с искомым чисел геометрической прогрессии:

Ну вот. Ты сам вывел свойство геометрической прогрессии. Попробуй записать эту формулу в общем виде. Получилось?

, при

Забыл условие при ? Подумай, почему оно важно, например, попробуй самостоятельно просчитать , при . Что получится в этом случае? Правильно, полная глупость так как формула выглядит так:

Соответственно, не забывай это ограничение.

Теперь посчитаем, чему же равно

Правильный ответ – ! Если ты при расчете не забыл второе возможное значение, то ты большой молодец и сразу можешь переходить к тренировке, а если забыл – прочитай то, что разобрано далее и обрати внимание, почему в ответе необходимо записывать оба корня.

Нарисуем обе наши геометрические прогрессии – одну со значением , а другую со значением &nb

NCERT Решения для математики класса 10 Глава 5 Арифметические прогрессии

Вы можете выбрать главу 5 — Арифметические прогрессии Решения NCERT для математики в формате PDF для предстоящих экзаменов, а также вы можете найти решения всех глав по математике ниже.

Решения NCERT для математики класса 10

Арифметическая прогрессия

Задумывались ли вы, почему числа такие удивительные? Глава 5 Арифметические прогрессии в NCERT Class 10 дает вам краткое представление об одном из самых замечательных числовых паттернов в математике.Он проведет вас через определение, примеры и несколько других понятий, связанных с арифметическими прогрессиями. Эта глава состоит из четырех разделов и трех упражнений.

Список покрываемых упражнений и тем:

Упражнение 5.1: Арифметическая прогрессия.
Упражнение 5.2: n-й срок AP.
Упражнение 5.3: Иррациональные числа
Упражнение 5.4: Рациональные числа и их десятичные разложения.

Фантазия чисел: арифметическая прогрессия:

Мы сталкиваемся с бесконечным количеством математических структур в нашей повседневной жизни. Большинство из нас просто лелеют при виде этих паттернов и двигаются один, а лишь немногие задаются вопросом: «ЧТО ТАКОЕ МАТЕМАТИКА ЗА НАСТОЯЩИМ УСТРОЙСТВОМ !!» Один такой удивительный шаблон чисел описан в главе 5 по математике, класс 10. Арифметические прогрессии — одна из самых важных и интересных тем в учебнике NCERT класса 10. Глава описывает определение арифметической прогрессии с примерами.Это также объясняет общую форму представления арифметических прогрессий. В этой главе также рассматривается большое количество задач, в которых объясняются шаги по определению n-го члена арифметической последовательности и суммы членов в арифметической последовательности.

Упражнение 5.1: Введение и арифметическая прогрессия

Упражнение 5.2: N-й член арифметической прогрессии

Упражнение 5.3: Сумма терминов в арифметической прогрессии

Упражнение 5.4: Дополнительные вопросы

Сумма и Вещество Ch 5 Класс 10 Математика :

Арифметическая прогрессия — это последовательность чисел, в которой разность между любыми двумя последовательными числами является постоянной, если числа взяты в одном и том же порядке.Поскольку разница между терминами постоянна во всей последовательности, она называется общей разницей.
Арифметическая прогрессия записывается в общем виде как:

a, a + d, a + 2d, a + 3d, …… .., a + (n-1) d

Замечания по ревизии для математики Глава 5 — Арифметические прогрессии (10-й класс)

Арифметические прогрессии

Арифметическая прогрессия - это последовательность чисел, в которой мы получаем каждый член, добавляя определенное число к предыдущему члену, кроме первого.

Каждое число в последовательности известно как термин .
Фиксированное число, то есть разница между каждым термином и его предыдущим термином, называется общей разницей . Это может быть положительным, отрицательным или нулевым. Он представлен как « d ».

Некоторые примеры арифметических прогрессий

Общая разница	Значение d	Пример
d> 0, положительный	10	20, 30, 40, 50,…
d <0, отрицательное	-25	100, 75, 50, 25, 0
d = 0, ноль	0	5, 5, 5, 5 ,.,

Общая форма арифметической прогрессии

Если первый член равен «а» , а общая разница равна «d» .

Пример

Данная последовательность: 2, 5, 8, 11, 14,…

Здесь a = 2 и d = 3

d = 5 — 2 = 8 — 5 = 11 — 8 = 3

Первый член = 2

Второй член — это + d = 2 + 3 = 5

Третий член — это + 2d = 2 + 6 = 8 и так далее.

Конечные или бесконечные арифметические прогрессии

1. Конечная арифметическая прогрессия

Если в последовательности есть только ограниченное число терминов, то это называется конечной Арифметической прогрессией.

229, 329, 429, 529, 629

2. Бесконечная арифметическая прогрессия

Если в последовательности есть бесконечное число членов, то это называется бесконечной арифметической прогрессии .

2, 4, 6, 8, 10, 12, 14, 16, 18… ..…

n ^th член арифметической прогрессии

Если _n — это n-й член, ₁ — это первый член, n — это число членов в последовательности, а d — это общее различие, то n-й член арифметической прогрессии будет равен

Пример

Найдите 11-й член AP: 24, 20, 16,…

Решение

Дано a = 24, n = 11, d = 20 — 24 = — 4

a _n = a + (n — 1) d

a ₁₁ = 24 + (11-1) — 4

= 24 + (10) — 4

= 24 — 40

= -16

Арифметическая серия

Арифметический ряд является суммой всех членов арифметической последовательности.

Арифметическая серия в форме

{a + (a + d) + (a + 2d) + (a + 3d) + ………}

Сумма первых n слагаемых арифметической серии

Сумма первых n членов последовательности рассчитывается по

Пример

Если Радха каждый месяц будет копить деньги в своей копилке, то сколько денег будет в ее копилке через 12 месяцев, если деньги будут в последовательности 100, 150, 200, 250,….соответственно?

Решение

Данная последовательность —

100, 150, 200, 250,…

а = 100 (первый семестр)

d = 50 (общая разница)

n = 12 (так как мы должны рассчитать деньги за 12 месяцев)

Теперь мы будем ставить значения в формулу

Таким образом, деньги, собранные в ее банке за 12 месяцев, составляют рупии. 4500.

Но когда у нас конечной арифметической прогрессии или мы знаем последний член последовательности, тогда сумма всех заданных членов прогрессии будет вычислена на

, где l = a + (n — 1) d i.е. последний член конечной арифметической прогрессии.

Примечание: Сумма бесконечной арифметической последовательности не существует.

Пример

Найдите сумму последовательности 38, 36, 34, 32, 30.

Решение

Учитывая

Геометрическая прогрессия

Геометрическая прогрессия — это последовательность чисел, в которой мы получаем каждый член путем умножения или деления определенного числа на предыдущий член, кроме первого.

Соотношение между каждым членом к следующему члену является постоянным.

n ^th член геометрической последовательности

a _n = a ₁ r ^{n — 1}

Сумма геометрической серии

Гармоническая прогрессия

Это обратная арифметическая прогрессия. Если a, a + d, a + 2d… ..is арифметическая прогрессия, то гармоническая прогрессия равна

n ^th срок Гармонической прогрессии

Примечание: Специальной формулы для нахождения суммы ряда гармоник не существует, поэтому мы можем вычислить сумму арифметического ряда и затем взять ее обратную величину, которая будет суммой ряда гармоник.

Серия гармоник расходится до бесконечности.

Среднее арифметическое

Среднее арифметическое — это среднее из двух чисел. Если a, b и c находятся в арифметической прогрессии, то среднее арифметическое значений a и c будет равно

Некоторые важные моменты

Сумма первых n положительных целых чисел задается
Разница между суммой первых n слагаемых и первых (n — 1) слагаемых также является n-м слагаемым данной Арифметической прогрессии.

a _n = S _n — S _n-1

Среднее геометрическое

Среднее геометрическое — это среднее из двух чисел. Если a и b — два числа, то среднее геометрическое будет

Отношения между А.М. и Г.М.

Как мы видели выше, формула для среднего арифметического и среднего геометрического значения следующие:

Где a и b — два заданных положительных числа.

. Пусть A и G — A.M. и Г.М.

, т.

Теперь давайте вычтем два средства друг с другом

Это показывает, что A ≥ G

Свойства отношений А.М. и Г.М.

Свойство I: Если среднее арифметическое и среднее геометрическое двух положительных чисел a и b равны A и G соответственно, то

A> G

As A — G> 0

Свойство II: Если A — среднее арифметическое, а G — среднее геометрическое между двумя положительными числами a и b, то квадратное уравнение с корнями a, b равно

x ² — 2Ax + G ² = 0

Свойство III: Если A — это Арифметическое Средство, а G — Геометрическое Средство между двумя положительными числами, а затем числа равны

A ± √A ² — G ²

Среднее гармоническое

Среднее гармоническое значение рассчитывается путем деления количества элементов на сумму обратных величин всех элементов.

Гармоническое среднее используется при экстремальных наблюдениях. Нравится

В этом случае, если мы будем использовать среднее арифметическое значение, чтобы найти среднее значение, то получим неточное среднее значение.

Отношение между AM, GM и HM

Если a и b два положительных действительных числа, то

AM ≥ GM

GM ≥ HM

Сочетание двух вышеупомянутых неравенств показывает, что

AM ≥ GM ≥ HM

Особенности курса

728 видео лекций
Редакция Примечания
Предыдущий год Документы
Карта разума
Планировщик исследования
NCERT Solutions
Дискуссионный форум
с Video Solution

Арифметическая прогрессия — учебный материал для ИИТ JEE

Значение арифметической прогрессии (А.П.)

Арифметическая прогрессия — это последовательность чисел, так что разница между двумя последовательными членами всегда постоянна. И эта разница называется Общая разница . Он также известен как Арифметическая последовательность .

Первый член последовательности называется начальным термином , который обозначается как «a».
Разница, на которую последовательные числа последовательности увеличиваются или уменьшаются, называется Common Difference , которая обозначается как «d».
Общий термин , то есть n-й член арифметической прогрессии с начальным слагаемым a и общей разницей d равен

a _n = a + (n-1) d

Пример

Рассмотрим правильную цифру —

Здесь последовательность дана как

1, 3, 5, 7, 9, 11, 13, 15

с учетом а = 1 и д = 2

Давайте проверим значение термина 5 ^th, используя формулу n-го термина.

a _n = a + (n-1) d

a ₅ = 1 + (5 -1) 2

= 1 + 8

= 9

На правильном рисунке дано, что термин 5 ^th равен 9.

Конечная и бесконечная арифметическая прогрессия

Арифметическая прогрессия с ограниченным числом терминов называется Finite Sequence . У него есть последний срок.

Пример

2, 9, 16, 23,…, 86

Это конечная последовательность с a = 2 и d = 7

Арифметическая прогрессия с неограниченным количеством терминов называется Бесконечная последовательность .У него нет последнего срока.

Пример

1, 3, 5, 7,…

Это бесконечная последовательность с a = 1 и d = 2

Положительная и отрицательная общая разница

Это зависит от значения общей разницы, что арифметическая прогрессия увеличивается или уменьшается.

Если общая разность «d» положительна, то арифметическая прогрессия будет увеличиваться в сторону положительной бесконечности, то есть это будет увеличивающаяся последовательность .

Если d> 0 и удовлетворяет, что _n-1 <_n, то

a ₁ 2 3 …

Пример

11, 22, 33, 44, 55,…

Это возрастающая последовательность с a = 11 и d = 11.

Если общая разность «d» отрицательна, то арифметическая прогрессия будет расти в сторону отрицательной бесконечности, то есть это будет убывающая последовательность .

Если d <0 и удовлетворяет, что _n-1> a _n, то

a ₁> a ₂> a ₃…

Пример

20, 10, 0, -10, -20,…

Это убывающая последовательность с a = 20 и d = -10.

Особенности курса

731 Видео Лекции
Редакция Примечания
Документы предыдущего года
Карта разума
Планировщик исследования
NCERT Solutions
Дискуссионный форум
с Video Solution

NCERT Solutions Class 10 Maths Глава 5 Арифметические прогрессии

- Классы
  Класс 1 — 3
  Класс 4 — 5
  Класс 6 — 10
  Класс 11 — 12
- КОНКУРСЫ
  BBS
  000000000 Книги
  NCERT Книги для 5 класса
  NCERT Книги Класс 6
  NCERT Книги для 7 класса
  NCERT Книги для 8 класса
  NCERT Книги для 9 класса
  NCERT Книги для 10 класса
  NCERT Книги для 11 класса
  NCERT Книги для 12-го класса
  NCERT Exemplar
  NCERT Exemplar Class 8
  NCERT Exemplar Class 9
  NCERT Exemplar Class 10
  NCERT Exemplar Class 11
  NCERT Exemplar Class 12
  9000al Aggar Agaris Agard Agard Agard Agard Agard 2000 12000000
  Решения RS Aggarwal класса 10
  Решения RS Aggarwal класса 11
  Решения RS Aggarwal класса 10
  90 003 Решения RS Aggarwal класса 9
  Решения RS Aggarwal класса 8
  Решения RS Aggarwal класса 7
  Решения RS Aggarwal класса 6
  Решения RD Sharma
  Решения класса RD Sharma
  Решения класса 9 Шарма 7 Решения RD Sharma Class 8
  Решения RD Sharma Class 9
  Решения RD Sharma Class 10
  Решения RD Sharma Class 11
  Решения RD Sharma Class 12
  ФИЗИКА
  Механика
  000000 Электромагнетизм
  ХИМИЯ
  Органическая химия
  Неорганическая химия
  Периодическая таблица
  МАТС
  Теорема Пифагора
  Отношения и функции
  Последовательности и серии
  Таблицы умножения
  Детерминанты и матрицы
  Прибыль и убыток
  Полиномиальные уравнения
  Делительные дроби
  000 ФОРМУЛЫ
  Математические формулы
  Алгебровые формулы
  Тригонометрические формулы
  Геометрические формулы
  КАЛЬКУЛЯТОРЫ
  Математические калькуляторы
  S000
  S0003
  Pегипс Класс 6
  Образцы документов CBSE для класса 7
  Образцы документов CBSE для класса 8
  Образцы документов CBSE для класса 9
  Образцы документов CBSE для класса 10
  Образцы документов CBSE для класса 11
  Образец образца CBSE pers for Class 12
  CBSE Документ с вопросами о предыдущем году
  CBSE Документы за предыдущий год Class 10
  CBSE Вопросы за предыдущий год Class 12
  HC Verma Solutions
  HC Verma Solutions Класс 11 Физика
  Решения HC Verma Class 12 Physics
  Решения Lakhmir Singh
  Решения Lakhmir Singh Class 9
  Решения Lakhmir Singh Class 10
  Решения Lakhmir Singh Class 8
  Примечания
  CBSE
  Notes
  CBSE Класс 7 Примечания CBSE
  Класс 8 Примечания CBSE
  Класс 9 Примечания CBSE
  Класс 10 Примечания CBSE
  Класс 11 Примечания CBSE
  Класс 12 Примечания CBSE
  Примечания пересмотра
  CBSE Редакция
  CBSE
  CBSE Class 10 Примечания к пересмотру
  CBSE Class 11 Примечания к пересмотру 9000 4
  Замечания по пересмотру CBSE класса 12
  Дополнительные вопросы CBSE
  Дополнительные вопросы CBSE 8 класса
  Дополнительные вопросы CBSE 8 по естественным наукам
  CBSE 9 класса Дополнительные вопросы
  CBSE 9 дополнительных вопросов по науке CBSE
  9000 Класс 10 Дополнительные вопросы по математике
  CBSE Класс 10 Дополнительные вопросы по науке
  Класс CBSE
  Класс 3
  Класс 4
  Класс 5
  Класс 6
  Класс 7
  Класс 8
  Класс 9
  Класс 10
  Класс 11
  Класс 12
  Решения для учебников
- Решения NCERT
  Решения NCERT для класса 11
  Решения NCERT для физики класса 11
  Решения NCERT для класса 11 Химия
  Решения для класса 11 Биология
  NCERT Решения для класса 11 Математика
  9 0003 NCERT Solutions Class 11 Бухгалтерия
  NCERT Solutions Class 11 Бизнес исследования
  NCERT Solutions Class 11 Экономика
  NCERT Solutions Class 11 Статистика
  NCERT Solutions Class 11 Коммерция
  NCERT Solutions для класса 12
  NCERT Solutions для Класс 12 Физика
  Решения NCERT для 12 класса Химия
  Решения NCERT для 12 класса Биология
  Решения NCERT для 12 класса Математика
  Решения NCERT Класс 12 Бухгалтерский учет
  Решения NCERT Класс 12 Бизнес исследования
  Решения NCERT Класс 12 Экономика
  NCERT Solutions Class 12 Бухгалтерский учет Часть 1
  NCERT Solutions Class 12 Бухгалтерский учет Часть 2
  NCERT Solutions Class 12 Микроэкономика
  NCERT Solutions Class 12 Коммерция
  NCERT Solutions Class 12 Макроэкономика
  NCERT Solutions Для Класс 4
  Решения NCERT для математики класса 4
  Решения NCERT для класса 4 EVS
  Решения NCERT для класса 5
  Решения NCERT для математики класса 5
  Решения NCERT для класса 5 EVS
  Решения NCERT для класса 6
  Решения NCERT для класса 6 Maths
  Решения NCERT для класса 6 Science
  Решения NCERT для класса 6 Общественные науки
  Решения NCERT для класса 6 Английский
  Решения NCERT для класса 7
  Решения NCERT для класса 7 Математика
  Решения NCERT для 7 класса Science
  Решения NCERT для 7 класса Общественные науки
  Решения NCERT для 7 класса Английский
  Решения NCERT для 8 класса Математические решения
  для 8 класса Математика
  Решения NCERT для класса 8 Science
  Решения NCERT для класса 8 Общественные науки
  NCERT Solutio ns для класса 8 Английский
  Решения NCERT для класса 9
  Решения NCERT для класса 9 Общественные науки
  Решения NCERT для класса 9 Математика
  Решения NCERT для класса 9 Математика Глава 1
  Решения NCERT Для класса 9 Математика 9 класса Глава 2
  Решения NCERT для математики 9 класса Глава 3
  Решения NCERT для математики 9 класса Глава 4
  Решения NCERT для математики 9 класса Глава 5
  Решения NCERT для математики 9 класса Глава 6
  Решения NCERT для Математика 9 класса Глава 7
  Решения NCERT для математики 9 класса Глава 8
  Решения NCERT для математики 9 класса Глава 9
  Решения NCERT для математики 9 класса Глава 10
  Решения NCERT для математики 9 класса Глава 11
  Решения NCERT для Математика 9 класса Глава 12
  Решения NCERT для математики 9 класса Глава 13
  Решения NCERT для математики 9 класса Глава 14
  Решения NCERT для математики класса 9 Глава 15
  Решения NCERT для науки 9 класса
  Решения NCERT для науки 9 класса Глава 1
  Решения NCERT для науки 9 класса Глава 2
  Решения NCERT для класса 9 Наука Глава 3
  Решения NCERT для 9 класса Наука Глава 4
  Решения NCERT для 9 класса Наука Глава 5
  Решения NCERT для 9 класса Наука Глава 6
  Решения NCERT для 9 класса Наука Глава 7
  Решения NCERT для 9 класса Научная глава 8
  Решения NCERT для 9 класса Научная глава
  Научные решения NCERT для 9 класса Научная глава 10
  Научные решения NCERT для 9 класса Научная глава 12
  Научные решения NCERT для 9 класса Научная глава 11
  Решения NCERT для 9 класса Научная глава 13
  Решения NCERT для 9 класса Научная глава 14
  Решения NCERT для класса 9 Science Глава 15
  Решения NCERT для класса 10
  Решения NCERT для класса 10 Общественные науки
  Решения NCERT для математики класса 10
  Решения NCERT для математики класса 10 Глава 1
  Решения NCERT для математики класса 10 Глава 2
  решения NCERT для математики класса 10 глава 3
  решения NCERT для математики класса 10 глава 4
  решения NCERT для математики класса 10 глава 5
  решения NCERT для математики класса 10 глава 6
  решения NCERT для математики класса 10 Глава 7
  решения NCERT для математики класса 10 глава 8
  решения NCERT для математики класса 10 глава 9
  решения NCERT для математики класса 10 глава 10
  решения NCERT для математики класса 10 глава 11
  решения NCERT для математики класса 10, глава 12
  Решения NCERT для математики класса 10, глава 13
  соль NCERT Решения для математики класса 10 Глава 14
  Решения NCERT для математики класса 10 Глава 15
  Решения NCERT для науки 10 класса
  Решения NCERT для науки 10 класса Глава 1
  Решения NCERT для науки 10 класса Глава 2
  Решения NCERT для науки 10 класса, глава 3
  Решения NCERT для науки 10 класса, глава 4
  Решения NCERT для науки 10 класса, глава 5
  Решения NCERT для науки 10 класса, глава 6
  Решения NCERT для науки 10 класса, глава 7
  Решения NCERT для науки 10 класса, глава 8
  Решения NCERT для науки 10 класса, глава 9
  Решения NCERT для науки 10 класса, глава 10
  Решения NCERT для науки 10 класса, глава 11
  Решения NCERT для науки 10 класса, глава 12
  Решения NCERT для 10 класса Science Глава 9
  Решения NCERT для 10 класса Science Глава 14
  Решения NCERT для науки 10 класса Глава 15
  Решения NCERT для науки 10 класса Глава 16
  Программа NCERT
  NCERT
- Коммерция
  Класс 11 Коммерческая программа Syllabus
  Учебный курс по бизнес-классу 11000
  Учебная программа по экономическому классу
- Учебная программа по коммерческому классу
  Учебная программа по 12 классу
  Учебная программа по 12 классу
  Учебная программа по экономическому классу
  000000000000000000
  Образцы коммерческих документов класса 11
  Образцы коммерческих документов класса 12
  Решения TS Grewal
  Решения TS Grewal Класс 12 Бухгалтерский учет
  Решения TS Grewal Класс 11 Бухгалтерский учет
  Отчет о движении денежных средств
  eurship
  Защита потребителей
  Что такое фиксированный актив
  Что такое баланс
  Формат баланса
  Что такое акции
  Разница между продажами и маркетингом
- P000S Документы ICSE
- ML Решения Aggarwal
  ML Решения Aggarwal Class 10 Maths
  ML Решения Aggarwal Class 9 Математика
  ML Решения Aggarwal Class 8 Maths
  ML Решения Aggarwal Class 7 Математические решения
  ML 6 0004
  ML 6
- Selina Solutions
  Selina Solution для 8 класса
  Selina Solutions для 10 класса
  Selina Solution для 9 класса 9
- Frank Solutions
  Frank Solutions для класса 10 Maths
  Frank Solutions для класса 9 Maths
- ICSE Class 9000 2
- ICSE Class 6
- ICSE Class 7
- ICSE Class 8
- ICSE Class 9
- ICSE Class 10
- ISC Class 11
- ISC Class 12