Автомобиль массой 2000 кг стоит на участке шоссе с наклоном 10: Автомобиль массой 2000 кг кг стоит на участке шоссе с наклоном 10 градусов к горизонтальной поверхности. Макс. значение коэффициента трения покоя равно 0,5. Найти силу трения покоя, действующую на авт...

Как определить индуктивность катушки. — вопрос №1610148 — Учеба и наука






Лучший ответ по мнению автора

01.

09.15

Лучший ответ по мнению автора

Ответ понравился автору вопроса

Михаил Александров

Читать ответы

Андрей Андреевич

Читать ответы

Владимир

Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Физика

Похожие вопросы

Залежність пройденого тілом шляху від часу дається рівнянням S= A+Bt+Ct2-Dt3,де С= 2м\с2 і D=1м\с3. 2 раз 5) нет верного ответа

Автомобиль массой 2000 кг кг стоит на участке шоссе с наклоном 10 градусов к горизонтальной поверхности. Макс. значение коэффициента трения покоя…

В явлении Комптона энергия падающего фотона распределяется поровну между рассеянным фотоном и электроном отдачи. Угол рассеяния равен 90 градусов. Найти энергию и импульс рассеянного фотона.

Пользуйтесь нашим приложением

Ł Старые понятные учебники советских времен по физике, математике. Акупунктура, похудение

КАБАРДИН О.Ф. «ФИЗИКА (справочные материалы)», 1991

ГЛАВНАЯ СТРАНИЦА / МЕНЮ САЙТА / СОДЕРЖАНИЕ ДАННОЙ СТАТЬИ

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

1. После удара о поверхность Земли мяч движется вертикально вверх со скоростью 15 м/с. Найдите координату мяча над поверхностью Земли через 1 с и через 2 с после начала движения. Дайте объяснение полученному результату.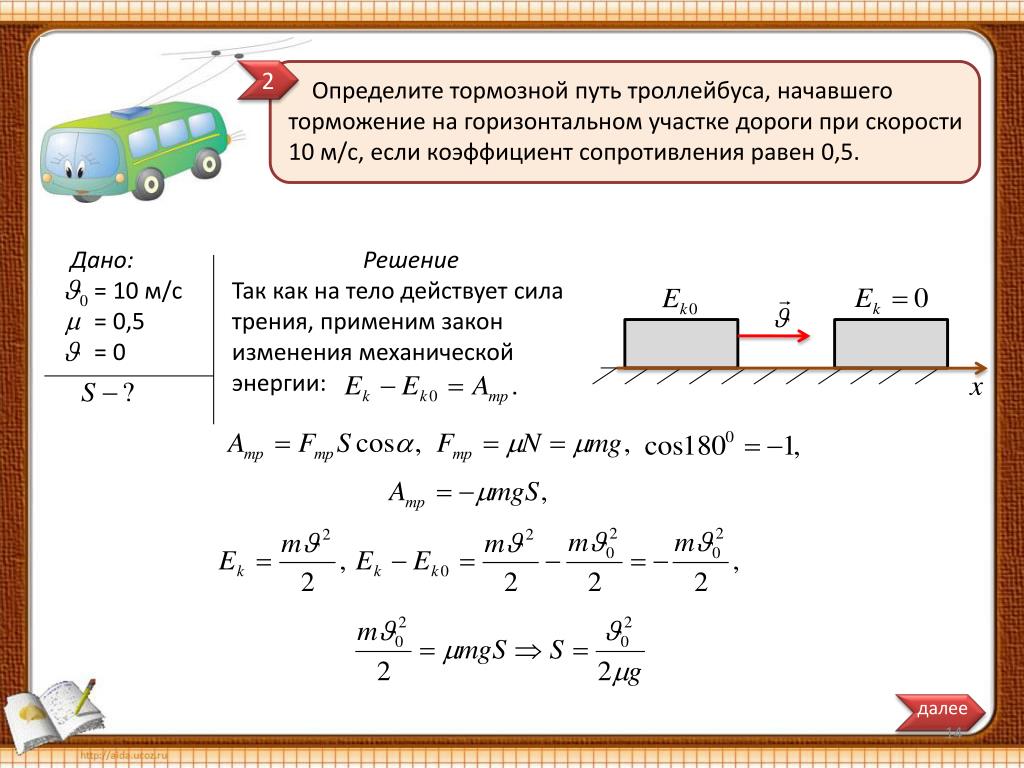

Решение

Координата тела при равноускоренном прямолинейном движении определяется по формуле

Координатную ось 𝑂𝑌 направим по вертикали вверх, начало отсчета находится на поверхности Земли.

Тогда . Так как направление вектора начальной скорости совпадает с направлением оси 𝑂𝑌, а направление вектора противоположно направлению оси 𝑂𝑌, то проекция начальной скорости положительна, а ускорения отрицательна: .

Тогда

Через 1 с и через 2 с после начала движения мяч находится в одной и той же точке пространства. В момент времени с он проходит через эту точку во время движения вверх, в момент времени c во время движения вниз.

2. Лодка движется перпендикулярно берегу реки. Ее скорость относительно воды равна 2 м/с. Определите время движения лодки к другому берегу, если ширина реки 80 м, а скорость течения 1 м/с.

Решение

Для нахождения времени движения лодки через реку необходимо найти скорость лодки относительно берега. Скорость лодки относительно берега равна сумме векторов (скорости течения воды) и (скорости лодки относительно воды):

Вектор скорости лодки относительно берега перпендикулярен вектору скорости течения реки. В векторном треугольнике (рис. 73) они являются катетами, а вектор — гипотенузой. Модуль вектора из этого треугольника равен

Рис. 73

Время движения лодки от одного берега к другому равно

3. Человек массой 60 кг катается на карусели. Найдите значение силы упругости, действующей на человека при его движении в горизонтальной плоскости со скоростью 10 м/с по окружности радиусом 12 м.

Решение

Движение человека по окружности, лежащей в горизонтальной плоскости, происходит под действием равнодействующей сил тяжести и упругости . Вектор лежит в горизонтальной плоскости и направлен к центру окружности (рис. 74).

Рис. 74

По второму закону Ньютона модуль равнодействующей равен

Так как вектор перпендикулярен вектору , то вектор является гипотенузой в прямоугольном треугольнике с катетами и . Модуль вектора силы упругости равен

4. Велосипедист массой 80 кг движется со скоростью 10 м/с по вогнутому мосту, траектория его движения является дугой окружности радиусом 20 м. Определите силу упругости, действующую на велосипедиста в нижней точке моста.

Решение

Движение велосипедиста по дуге окружности является движением с центростремительным ускорением , равным по модулю

В нижней точке моста вектор центростремительного ускорения направлен вертикально вверх. Это ускорение по второму закону Ньютона определяется равнодействующей векторов силы тяжести , направленной вертикально вниз, и силы упругости , действующей со стороны моста и направленной вертикально вверх (рис. 75):

Рис. 75

Направим ось 𝑂𝑌 вертикально вверх и запишем это уравнение в проекциях на эту ось

Проекции векторов и на эту ось положительны, а проекция вектора отрицательна, поэтому уравнение для модулей сил имеет вид

Отсюда получаем формулу для вычисления модуля силы упругости

5. Труба массой 100 кг лежит на двух горизонтальных опорах. Длина трубы 6 м, одна опора находится у конца трубы, вторая — на расстоянии 1 м от второго конца трубы. Определите силы реакции опор.

Решение

Изобразим все действующие на трубу силы (рис. 76). Сила тяжести направлена вертикально вниз и приложена к центру масс трубы, находящемуся на равных расстояниях от концов трубы. Силы реакции опор и направлены вертикально вверх. Так как труба не движется поступательно, геометрическая сумма векторов сил, действующих на трубу, равна нулю:

Рис. 76

Направим ось 𝑂𝑌 вертикально вверх. Тогда для проекций сил на эту ось имеем равенство

а для модулей —

Так как труба не вращается, алгебраическая сумма моментов всех сил, действующих на нее, равна нулю для любой оси вращения. Выберем в качестве оси вращения горизонтальную прямую, проходящую через центр масс трубы перпендикулярно плоскости чертежа. На основании правила моментов запишем равенство

Так как вектор силы тяжести проходит через ось вращения ( ), момент этой силы равен нулю. Вектор силы реакции опоры создает вращение против часовой стрелки, поэтому вращательный момент этой силы взят с отрицательным знаком. Таким образом, для решения задачи мы получили систему из двух уравнений

Решаем эту систему:

По условию задачи м, м, поэтому

6. Тепловоз массой 130 т приближается со скоростью 2 м/с к неподвижному составу массой 1170 т. С какой скоростью будет двигаться состав после сцепления с тепловозом?

Решение

По закону сохранения импульса проекции вектора полного импульса системы из тепловоза и состава на ось координат, направленную по вектору скорости, до сцепления и после сцепления одинаковы:

Так как состав был неподвижным, векторы скорости тепловоза до сцепления и скорости тепловоза вместе с составом после сцепления параллельны и проекции векторов и можно заменить их модулями:

отсюда скорость тепловоза и состава после сцепления равна

7. Человек массой 70 кг спускается по лестнице длиной 20 м, расположенной под углом 30° к горизонтальной плоскости. Найдите работу силы тяжести.

Решение

Работа силы тяжести равна произведению модуля вектора силы на модуль вектора перемещения и косинус угла между вектором силы и вектором перемещения:

Угол равен 60°, поэтому работа равна

= 70 кг · 9,8 м/с² · 20 м · 0,5 ≈ 6860 Дж ≈ 7 кДж.

8. Вычислите работу силы упругости при изменении деформации пружины жесткостью 200 Н/м от см до см.

Решение

По закону Гука проекция вектора силы упругости на ось 𝑂𝑋, направленную по вектору перемещения конца пружины при ее деформации, равна

Так как сила упругости изменяется пропорционально деформации, то для вычисления работы можно найти среднее значение ее проекции при изменении деформации пружины от 2 см до 6 см:

Работа силы упругости равна произведению модуля среднего значения силы на модуль перемещения и косинус угла между этими векторами:

При растяжении пружины вектор силы упругости направлен противоположно вектору перемещения, поэтому угол между ними равен 180°, a . Тогда работа силы упругости будет равна

= 8 H·4·10^-2 м (–1) = –0,32 Дж.

Работа силы упругости может быть найдена и по изменению потенциальной энергии пружины:

9. Кран поднимает груз массой 2 т на высоту 24 м за 2 мин. Найдите механическую мощность. Силами трения пренебречь.

Решение

Механическая мощность равна .

Механическая работа внешних сил при подъеме груза равна изменению его потенциальной энергии:

Поэтому механическая мощности равна

10. Самолет Ил-62 имеет четыре двигателя, сила тяги каждого 103 кН. Какова полезная мощность двигателей при полете самолета со скоростью 864 км/ч?

Решение

Полезная мощность двигателей равна отношению механической работы ко времени :

Механическая работа при совпадении направлений вектора силы и перемещения равна

Отсюда для механической мощности имеем

Так как при равномерном прямолинейном движении

11. На высоте 2,2 м от поверхности Земли мяч имел скорость 10 м/с. С какой скоростью будет двигаться мяч у поверхности Земли? Сопротивлением воздуха пренебречь, ускорение свободного падения принять равным 10 м/с².

Решение

Хотя в условии задачи не указаны направление вектора скорости мяча и масса мяча, задача имеет однозначное решение.

Так как на мяч действует только сила тяготения со стороны Земли, к замкнутой системе «Земля — мяч» применим закон сохранения механической энергии. Согласно этому закону полная механическая энергия системы «Земля — мяч» остается неизменной, а изменение кинетической энергии мяча равно изменению его потенциальной энергии, взятому с противоположным знаком:

Обозначим массу мяча получим

Разделим обе части равенства на и умножим на 2:

Отсюда скорость мяча у поверхности Земли равна

12. Крупнейшая в мире Саяно-Шушенская гидроэлектростанция будет вырабатывать 23,5 млрд. кВт·ч электроэнергии в год. Сколько воды должно проходить за год через гидротурбины станции? Высота плотины — 222 м. Считать, что потенциальная энергия воды полностью превращается в электрическую энергию.

Решение

По закону сохранения энергии электроэнергия, вырабатываемая гидроэлектростанцией, получается за счет превращения кинетической энергии движущейся воды в энергию электрического тока. Кинетическая энергия воды в свою очередь получается в результате превращения потенциальной энергии воды у вершины плотины в кинетическую у основания плотины. Если не учитывать потери, то вся выработанная гидроэлектростанцией электроэнергия равна изменению потенциальной энергии воды, прошедшей через гидроагрегаты станции, взятому с противоположным знаком:

. (1)

Массу воды выразим через ее объем и плотность :

. (2)

Из равенств (1) и (2) найдем выражение для объема воды, прошедшей через гидроагрегаты станции:

13. Определите минимальное значение тормозного пути автомобиля, начавшего торможение на горизонтальном участке шоссе при скорости движения 20 м/с. Коэффициент трения равен 0,5.

Решение

Тормозной путь автомобиля будет иметь минимальное значение при максимальном значении силы трения. Модуль максимального значения силы трения равен

Вектор силы трения при торможении направлен противоположно векторам скорости и перемещения .

При прямолинейном равноускоренном движении проекция перемещения автомобиля на ось, параллельную вектору скорости автомобиля, равна

Переходя к модулям величин, получаем уравнение

Значение времени можно найти из условия

Тогда для модуля перемещения получаем

(Модуль перемещения можно найти и с помощью выражения 2.10.)

Так как

то

Тот же результат можно получить на основе использования теоремы о кинетической энергии:

Так как вектор силы трения направлен противоположно вектору перемещения, угол равен 180°, .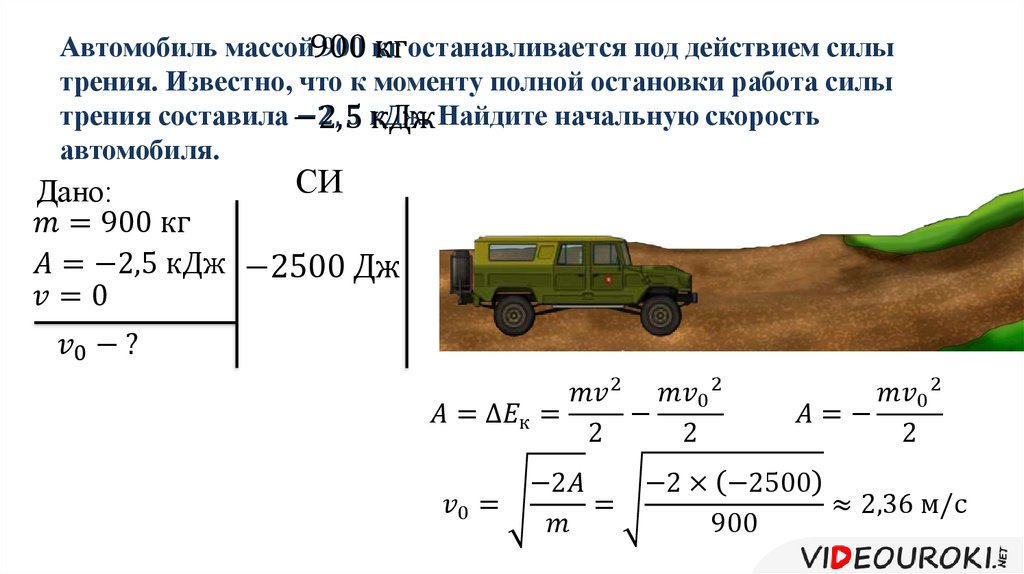 Поэтому

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

14. Парашютист раскрыл свой парашют на высоте 1 км от поверхности Земли и далее двигался равномерно и прямолинейно со скоростью 7 м/с по вертикали вниз. На каком расстоянии от поверхности Земли он находился через 1 мин после раскрывания парашюта?

15. На прямолинейном участке шоссе автомобиль увеличивает свою скорость от 18 км/ч до 72 км/ч за 20 с. С каким ускорением двигался автомобиль, если движение было равноускоренным?

16. Автомобиль двигался со скоростью 54 км/ч. Какой будет скорость автомобиля через 4 с после начала торможения, если при торможении ускорение постоянно и равно по модулю 3 м/с²? Какой путь пройдет автомобиль за это время?

17. Какую скорость приобретает после прохождения пути 200 м электропоезд, начинающий равноускоренное прямолинейное движение с ускорением 1 м/с²?

18. С горы начинают скатываться сани с ускорением 0,5 м/с². Какой путь проходят сани, если скорость их в конце горы 36 км/ч?

19. Какой длины должна быть взлетная полоса аэродрома для самолета ИЛ-62, если для взлета самолету необходимо иметь скорость 300 км/ч, а его двигатели могут обеспечить движение по взлетной полосе с ускорением 1,6 м/с²?

20. Шарик, скатываясь с наклонной плоскости, за первую секунду прошел путь, равный 10 см. Чему равен путь, пройденный шариком за четвертую секунду?

21. Тормоз грузового автомобиля считается исправным, если при движении по сухой и ровной дороге со скоростью 36 км/ч тормозной путь не превышает 12,5 м. Определите ускорение при таком торможении.

22. Пуля, летящая со скоростью 600 м/с, пробивает доску толщиной 0,1 м и вылетает из нее со скоростью 400 м/с. Чему равен модуль ускорения пули в доске?

23. С каким минимальным ускорением должен двигаться автомобиль для экстренной остановки перед перекрестком, если его скорость в начале торможения 72 км/ч, а расстояние от перекрестка 50 м?

24. Космонавт проходит тренировку на центрифуге радиусом 15 м. С какой скоростью движется космонавт, если его центростремительное ускорение равно 40 м/с²?

25. Лодка движется равномерно поперек течения реки; ее скорость относительно берега 2 м/с, скорость течения реки 3 м/с. С какой скоростью движется лодка относительно воды?

26. Человек переплывает реку шириной 100 м по прямой, перпендикулярной ее берегам. Скорость пловца относительно берега 0,3 м/с, скорость течения 0,4 м/с. Какое расстояние преодолевает пловец относительно воды?

27. Сила 10 Н сообщает телу ускорение 3 м/с². Какая сила сообщает этому телу ускорение 1,5 м/с²?

28. Тело массой 5 кг под действием некоторой силы приобретает ускорение 1 м/с². Какое ускорение сообщит эта сила телу массой 10 кг?

29. На каком расстоянии от поверхности Земли сила гравитационного притяжения, действующая на тело, в 2 раза меньше, чем у поверхности Земли?

30. Масса орбитальной космической станции 19 т, масса космонавта в скафандре 100 кг. Оцените силу гравитационного взаимодействия между станцией и космонавтом на расстоянии 100 м. За какое приблизительно время под действием этой силы космонавт приблизится к станции на расстояние 1 м, если в начальный момент времени относительная скорость станции и космонавта была равна нулю?

31. Определите первую космическую скорость для Венеры. Масса Венеры 4,87·10²⁴ кг, радиус 6,06·10⁶ м.

32. Спутник планеты Марс Фобос обращается по орбите радиусом 9,4·10⁶ м с периодом 7 ч 39 мин. Определите массу планеты Марс.

33. Каким должен быть радиус круговой орбиты искусственного спутника Земли, для того чтобы он все время находился над одной точкой земной поверхности на экваторе?

34. Автомобиль «Москвич-412» массой 10³ кг движется со скоростью 36 км/ч по выпуклому мосту. Траектория движения автомобиля является дугой окружности радиусом 50 м. Определите вес автомобиля в верхней точке моста.

35. Какие «перегрузки» испытывает белье в центрифуге стиральной машины диаметром 0,3 м при частоте вращения 3000 об/мин?

36. При какой продолжительности суток на Земле вес тела на экваторе был бы равен нулю? Радиус Земли 6,4·10⁶ м.

37. После скатывания с горы сани начинают движенце по горизонтальной поверхности со скоростью 10 м/с. Коэффициент трения между полозьями саней и дорогой равен 0,1. Какой путь пройдут сани за 5 с и за 15 с?

38. Определите минимальный тормозной путь автомобиля на горизонтальном участке шоссе при начальной скорости 36 км/ч, если максимальное значение коэффициента трения покоя шин на шоссе 0,55.

39. Определите максимальное значение скорости автомобиля при движении на повороте по дуге окружности радиусом 50 м, если максимальное значение коэффициента трения покоя шин на шоссе равно 0,4.

40. Автомобиль массой 2000 кг стоит на участке шоссе с наклоном 10° к горизонтальной поверхности. Максимальное значение коэффициента трения покоя 0,5. Определите силу трения покоя, действующую на автомобиль.

41. Во сколько раз нужно увеличить силу тяги двигателей самолета для увеличения скорости его движения в два раза, если сила сопротивления при движении в воздухе возрастает пропорционально квадрату скорости?

42. Железнодорожный вагон массой 15 т движется по горизонтальному участку железнодорожного пути со скоростью 1 м/с. Его догоняет второй вагон массой 20 т, движущийся со скоростью 2 м/с. Какой будет скорость вагонов после их сцепления?

43. С какой примерно скоростью будет двигаться ракета массой 20 кг после вылета из нее продуктов сгорания топлива массой 1 кг со скоростью 2 км/с?

44. Определите силу тяги ракетного двигателя с расходом топлива 2000 кг/с при скорости истечения газов 3,5 км/с.

45. Какую работу совершает равнодействующая всех сил при разгоне автомобиля массой 5 т из состояния покоя до скорости 36 км/ч на горизонтальном участке пути?

46. Сани движутся равномерно и прямолинейно по горизонтальному участку дороги. Какую работу совершает сила 50 Н, приложенная к веревке, при перемещении саней на 100 м, если веревка тянется под углом 30° к горизонтальной плоскости?

47. Человек массой 70 кг поднимается по лестнице длиной 20 м на высоту 10 м. Какую работу совершает при этом сила тяжести?

48. Спортсмен массой 60 кг прыгает с высоты 9 м на упругую сетку — батут. Найдите максимальное значение потенциальной энергии упругой деформации сетки, если ее максимальный прогиб равен 1 м.

49. Стальной трос жесткостью 5·10 Н/м растянут на 2 мм. Вычислите потенциальную энергию упругой деформации троса.

50. Камень массой 1 кг брошен со скоростью 20 м/с под углом 25° к горизонту. С какой скоростью будет двигаться камень в тот момент, когда расстояние от него до поверхности Земли увеличится на 1 м по сравнению с начальным значением?

51. Высота плотины Красноярской ГЭС 120 м, мощность станции 6000 МВт. Сколько кубометров воды должно проходить через гидротурбины станции при КПД, равном 90%?

52. Найдите полезную работу, совершенную энергетической машиной с КПД 0,7 при затратах энергии 2·10⁶ Дж.

53. Груз массой 1 кг на тонкой нити длиной 1 м совершает свободные колебания, максимальный угол отклонения нити от вертикального положения 5°. Определите силу упругости нити при прохождении грузом положения равновесия.

54. Гимнаст совершает большие обороты на перекладине. Во сколько раз его вес при прохождении нижнего вертикального положения больше веса в состоянии покоя? Скорость движения гимнаста в верхнем вертикальном положении считать равной нулю.

55. Для определения скорости пули массой производится выстрел в ящик с песком массой , подвешенный на тросе длиной . Пуля застревает в песке, и ее удар приводит ящик в движение. При максимальном удалении ящика от положения равновесия трос отклоняется от вертикального положения на угол . Выведите формулу для вычисления скорости пули по известным значениям и .

⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨

ГЛАВНАЯ СТРАНИЦА / МЕНЮ САЙТА / СОДЕРЖАНИЕ ДАННОЙ СТАТЬИ

Страница не найдена — Фонд Наффилда

Страница, которую вы ищете, не может быть найдена. Пожалуйста, попробуйте использовать либо главное меню, либо поиск по сайту.

Поиск проектов, новостей, воздействия, событий

Поиск

Образование 653 Когнитивные и некогнитивные навыки 33Curriculum и субъект. 31-й годы 165education. образование и навыки 95primary Education 134Q-шаг 26School Эффективность 45 Сторонного образования 156 Специальные потребности в образовании и инвалидность 56 Проблемы с учетом образования. интеллект 3Помощь при смерти 1Дополненная реальность 0Преимущества 52Обязанности по уходу 27Сообщества и социальная сплоченность 63Страна рождения 24COVID-19327Прогнозирование преступности 2Данные для общественного блага 27Цифровой вред и дезинформация 33Цифровое включение и исключение 14Цифровые навыки 16Цифровое общество 48Инвалидность 14Экономика, государственные расходы и услуги 181Этническая принадлежность 48Семья и семейная динамика 117Гендер 43Глобальное неравенство в отношении здоровья и нуждающиеся дети 73Психическое здоровье 92Заболевания опорно-двигательного аппарата 18Пенсии 16Физическое здоровье 50Бедность и уровень жизни 109Productivity and innovation 7Public health 150Social media 2Socioeconomics of ageing 24Socioeconomics of early adulthood 41Sports science 1Substance misuse 11Tax 48Trust in democracy 65Valuing data 5

ProjectsNewsEventsImpactOpinionPublicationsSeriesReportsEducation 653Cognitive and non-cognitive skills 33Curriculum and subject choice 31Early years 165Education workforce 75Educational assessment 29Higher education 92Language and literacy 79Lifelong обучение 15Nuffield Research Placement 23Числа 83Воспитание детей 75Педагогика 20Образование и навыки после 16 лет 95primary Education 134Q-шаг 26School Эффективность 45 Сторонного образования 156 Специальные потребности в образовании и инвалидность 56 Проблемы с учетом образования. интеллект 3Помощь при смерти 1Дополненная реальность 0Преимущества 52Обязанности по уходу 27Сообщества и социальная сплоченность 63Страна рождения 24COVID-19327Прогнозирование преступности 2Данные для общественного блага 27Цифровой вред и дезинформация 33Цифровое включение и исключение 14Цифровые навыки 16Цифровое общество 48Инвалидность 14Экономика, государственные расходы и услуги 181Этническая принадлежность 48Семья и семейная динамика 117Гендер 43Глобальное неравенство в отношении здоровья и нуждающиеся дети 73Психическое здоровье 92Заболевания опорно-двигательного аппарата 18Пенсии 16Физическое здоровье 50Бедность и уровень жизни 109Производительность и инновации 7Общественное здравоохранение 150Социальные сети 2Социоэкономика старения 24Социоэкономика раннего взросления 41Спортивная наука 1Злоупотребление психоактивными веществами 11Налоги 48Доверие к демократии 65Оценка данных 5

Ознакомьтесь с нашими проектами

Новый

Образование | 2023 – 2025

Посмотреть проект

Увидеть все

Последние

Ускорение автомобиля

Если вы знаете начальную и конечную скорость автомобиля (или что-то еще) — и затраченное время — среднее ускорение можно рассчитать как

A = DV / DT
= (V _F — V _S) / DT (1)
, где
ACCELERES фут/с ² )
dv = изменение скорости (м/с, фут/с)
v _f = конечная скорость (м/с, фут/с) v _с = начальная скорость (м/с, фут/с)
dt = использованное время (с) м/с = 0–96,6 км/ч
0–100 км/ч = 0–27,8 м/с = 0–62,1 миль/ч начальная скорость (км/ч)
конечная скорость (км/ч)
использованное время (с)
масса объекта (кг)
Обратите внимание, , что сила, работа и мощность рассчитываются только для массового ускорения. Силы сопротивления воздуха (лобового сопротивления) и трения качения не учитываются.
миль в час
Начальная скорость (миль на мик.)
Конечная скорость (миль на мик)
Используется время (S)
Moment V.S. Power и RPM
1919
V.S. Power и RPM
199991910
— Power and Power и RPM
191999910
.0356 км/ч
Скачать и распечатать график ускорения автомобиля
Диаграмма ускорения автомобиля —
миль в час
Скачать и распечатать график ускорения автомобиля
рассчитывать как
A = 2 DS / DT ² (2)
, где
DS = расстояние перемещено (M, FT)
0003
Ускорение некоторых известных автомобилей
Сила ускорения
Сила ускорения может быть рассчитана как
F = M A (3)
, где
96. _f )
m = масса автомобиля (кг, слизней)
Работа по ускорению
Работа по ускорению может быть рассчитана как
W = F L (4)
, где
W = работа (NM, J, FT LB _F )
L = расстояние (M, FT)
6 L = расстояние (M, FT)
6 L = расстояние (M, FT)
Ускорение мощности
Мощность ускорения может быть рассчитана как
P = W /DT (5)
, где
P = Power (J /S, W, FT LB _F /S) 77777777777777777. .
Пример — ускорение автомобиля
Автомобиль массой 1000 кг (2205 фунтов _м ) ускоряется с 0 м/с (0 фут/с) до 21,0 км/ч , 91,1 фут/с, 62,1 миль/ч) в 10 с .
Ускорение можно рассчитать по ур. 1 as
a = ((27,8 м/с) — (0 м/с)) / (10 с)

   = 2,78 м/с ²

Ускорение можно рассчитать из уравнения 3 как
F = (1000 кг) (2,78 м/с ² )
   = 2780 Н
Пройденное расстояние можно рассчитать, переставив уравнение 2 to
ds = a dt ² / 2
    = (2.78 m/s ² ) (10 s) ² / 2
    = 139 m
The acceleration work можно рассчитать из уравнения 4 как
Вт = (2780 Н) (139 м)
    = 386420 Дж
Сила ускорения может быть рассчитана по ур. 5 AS
P = (386420 J) / (10 S)
= 38642 W
= 38,6 KW
. Также можно сделать в Imperial. вычислить из уравнения 1 как
a = ((91,1 фут/с) — (0 фут/с)) / (10 с)

   = 9,11 фут/с ²
Масса измеряется в Британской системе мер в слизнях где 1 порция = 32,17405 фунта _м
Ускоряющую силу можно рассчитать по формуле 3 as
F = (( 2205 lb _m ) (1/32.17405 (slugs/ lb _m )) ) (9.11 ft/s ² )
   = 624 lb _f

Пройденное расстояние можно рассчитать, переставив уравнение от 2 до
ds = a dt ² / 2
    = (9,11 фут/с ² ) (10 с) ² / 2
    = 455 футов
Работа ускорения может быть рассчитана по уравнению 4 as
W = (624 lb _f ) (455 ft)
    = 284075 ft lb _f

1 ft lb _f = 1.

Как определить индуктивность катушки. — вопрос №1610148 — Учеба и наука

Лучший ответ по мнению автора

Михаил Александров

Андрей Андреевич

Владимир

Ł Старые понятные учебники советских времен по физике, математике. Акупунктура, похудение

Страница не найдена — Фонд Наффилда

Поиск проектов, новостей, воздействия, событий

Ознакомьтесь с нашими проектами

Целенаправленная и эффективная практическая работа по естествознанию начальных классов

Широкие плечи: повышение налогов в топ-

Оптимизация и осуществимость родительской программы Triple P для дистанционного обучения

Продление трудовой жизни людям с заболеваниями опорно-двигательного аппарата

Ювенильные ревматические заболевания: образование, профессиональная подготовка и трудоустройство

Испытание PAW: осуществимость и приемлемость инструментария Pain-at-Work Toolkit

Приоритеты образования на следующих всеобщих выборах

Дистанционное наставничество по остеоартриту для малообеспеченных людей

Психологические, социальные и экономические последствия заболеваний опорно-двигательного аппарата

Физические наказания и последствия для детей в Великобритании

Оптимизация и осуществимость родительской программы Triple P для дистанционного обучения

Понимание использования прав на дошкольное образование

Переосмысление особых образовательных потребностей

Артрит, работа и благополучие: исследование смешанных методов с рекомендациями по политике

Испытание PAW: осуществимость и приемлемость инструментария Pain-at-Work Toolkit

Психологические, социальные и экономические последствия заболеваний опорно-двигательного аппарата

Дистанционное наставничество по остеоартриту для малообеспеченных людей

Ювенильные ревматические заболевания: образование, профессиональная подготовка и трудоустройство

Региональный индекс регенерации для отслеживания социально-экономического «повышения уровня»

Пути развития после 16 лет: роль сверстников, семейное положение и ожидания

Разработка инклюзивной удаленной и гибридной работы для поддержки работников с ограниченными возможностями

Влияние выявления потребностей в дополнительном обучении в Уэльсе

Изучение расового неравенства при отвлечении от системы ювенальной юстиции

Административная справедливость в цифровом государстве всеобщего благосостояния

Прозрачность и судебный контроль: исследование долга откровенности

Влияние автоматического зачисления на пенсию и COVID-19 на сберегательное поведение

Долгосрочное влияние пособия на содержание образования

Дистанционное наставничество по остеоартриту для малообеспеченных людей

Ювенильные ревматические заболевания: образование, профессиональная подготовка и трудоустройство

Продление трудовой жизни людям с заболеваниями опорно-двигательного аппарата

Изменение выбора школы для более справедливого обучения в Англии

Среднесрочное влияние пандемии COVID-19 на учащихся с SEND

Этические принципы, лежащие в основе совместного производства с молодежью

Могут ли математические приложения повысить ценность обучения?

Реалии COVID: малообеспеченные семьи в период пандемии

Как население Великобритании получает информацию о COVID-19

Влияние заболеваний опорно-двигательного аппарата на исходы других заболеваний

Систематический обзор дипломов и путей трудоустройства

Измерение разрыва в уровнях образования в 16-19 лет

«Неуправляемые» школы: может ли решение Ofsted помешать устойчивому улучшению?

Исследовательская программа Nuffield Languages ​​​​Inquiry и Nuffield Languages ​​Program

Ускорение автомобиля

миль в час

Диаграмма ускорения автомобиля —

Ускорение некоторых известных автомобилей

Сила ускорения

Работа по ускорению

Пример — ускорение автомобиля

Share This Story, Choose Your Platform!

Related Posts

Приставки рос рас роз рас рос: Ошибка 403 — доступ запрещён

2 х 5 9: решите уравнение 2(x-5)=9 — Школьные Знания.com

Какие свойства человека относят к биологическим: 1. Какие свойства человека относят к биологическим? 2. Что, по вашему мнению, произошло бы с

Высшим исполнительным органом рф является: Статья 32. Высший исполнительный орган субъекта Российской Федерации \ КонсультантПлюс

Leave A Comment Отменить ответ

Исследовательская программа Nuffield Languages Inquiry и Nuffield Languages Program