Алгебра формула: Алгебра – основные понятия и формулы. Готовимся к ЕГЭ по Математике

Алгебра – основные понятия и формулы. Готовимся к ЕГЭ по Математике

Оглавление:

• Арифметический квадратный корень
• Модуль числа
• Свойства модулей
• Корни и степени
• Логарифмы

В школьном курсе алгебры не так уж много теории. Намного больше практики, то есть секретов и приемов решения задач. Хороший репетитор-математик вряд ли будет читать вам на каждом уроке длинные лекции. Он скажет: «Смотри, как решаются такие задачи!»

И все-таки минимальное знание теории необходимо. Основные понятия и формулы надо знать наизусть.

Например, что такое квадратный корень из неотрицательного числа?

Что такое модуль числа?

Для каких чисел существуют логарифмы?

Чем действительные числа отличаются от рациональных?

Как узнать, что число делится на 11?

На этой странице – все основные темы и понятия алгебры, необходимые учащимся 10-11 класса. И еще – полезная информация о том, как считать быстро и без калькулятора и как легко запоминать формулы.

Числовые множества

Делимость чисел

Правила округления чисел 

Таблица квадратов натуральных чисел и формулы сокращенного умножения

ЕГЭ без ошибок. Считаем быстро и без калькулятора

Как запоминать формулы

Основы логики. Система условий, совокупность условий

Квадратный корень

Корни и степени

Логарифмы

Модуль числа

Число e

Проверь себя. Помнишь ли ты основные понятия алгебры?

к оглавлению ▴

Арифметический квадратный корень

— Арифметический квадратный корень из числа a — это такое неотрицательное число, квадрат которого равен a.

Посмотрим, какие задания на тему «Арифметический квадратный корень» чаще всего встречаются в вариантах ЕГЭ и ОГЭ по математике.

1. Вычислите:

Решение:

Мы применили одну из формул сокращенного умножения – квадрат разности.

Ответ: 18.

2. Избавьтесь от иррациональности в знаменателе:
(в алгебре считается, что в задаче ответ без квадратных корней в знаменателе выглядит более красиво).

a) б)

Решение:

а) Числитель и знаменатель дроби умножим на одно и то же число, равное знаменателю дроби.

б) Числитель и знаменатель дроби умножим на одно и то же число, сопряженное знаменателю.

Что значит «сопряженное»?

Выражение a+b называют сопряженным выражению a-b, а выражение a-b будет сопряженным выражению a+b.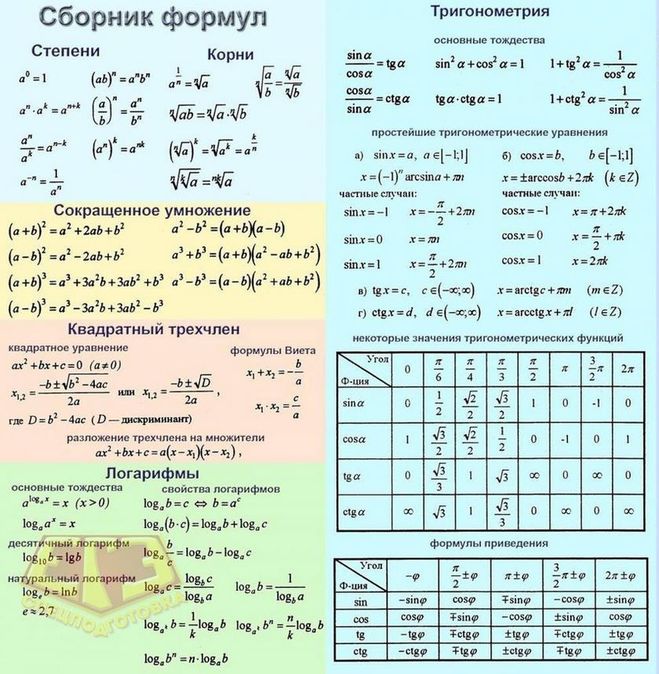

Мы используем формулу разности квадратов:

Поэтому

Получим:

Ответ: а) б)

В вариантах ОГЭ по математике есть также задачи на сравнение арифметических квадратных корней.

3. Сравните числа и

Решение:

Мы не будем искать приближенное значение корня из 3,26. Ясно, что без калькулятора это сделать сложно. Зато два рациональных числа можно легко сравнить между собой.

Запишем число 1,8 как

Мы сравниваем и Из этих чисел больше то, для которого больше подкоренное выражение. Сравним числа 3,26 и 3,24. Конечно, тогда значит,

Ответ:

4. Между какими целыми последовательными числами заключено число ?

Решение:

Так как то значит

Ответ:

к оглавлению ▴

Модуль числа

— Определение модуля числа:

— Что такое ?  Запомним:

5. Вычислите а) б) в)

Решение:

а) Мы применили формулу

б)

в)

Ответ: а) ; б) ; в)

6. Вычислите значение выражения при

Решение:

Если то

Ответ: 5

к оглавлению ▴

Свойства модулей

1) Модуль любого числа неотрицателен.

2) любые числа.

3) любые числа.

4) любые числа.

5) любое число,

к оглавлению ▴

Корни и степени

— Знаешь ли ты, что корни второй, третьей, четвертой, пятой, n-ной степени можно записывать просто как степени? И это намного удобнее. Например,

Напомним, что корень третьей степени из а – такое число, при возведении которого в третью степень получается число а.

Аналогично, корень четвертой степени из а – такое неотрицательное число, при возведении которого в четвертую степень получается число

а.

Тема Корни и степени подробно здесь.

к оглавлению ▴

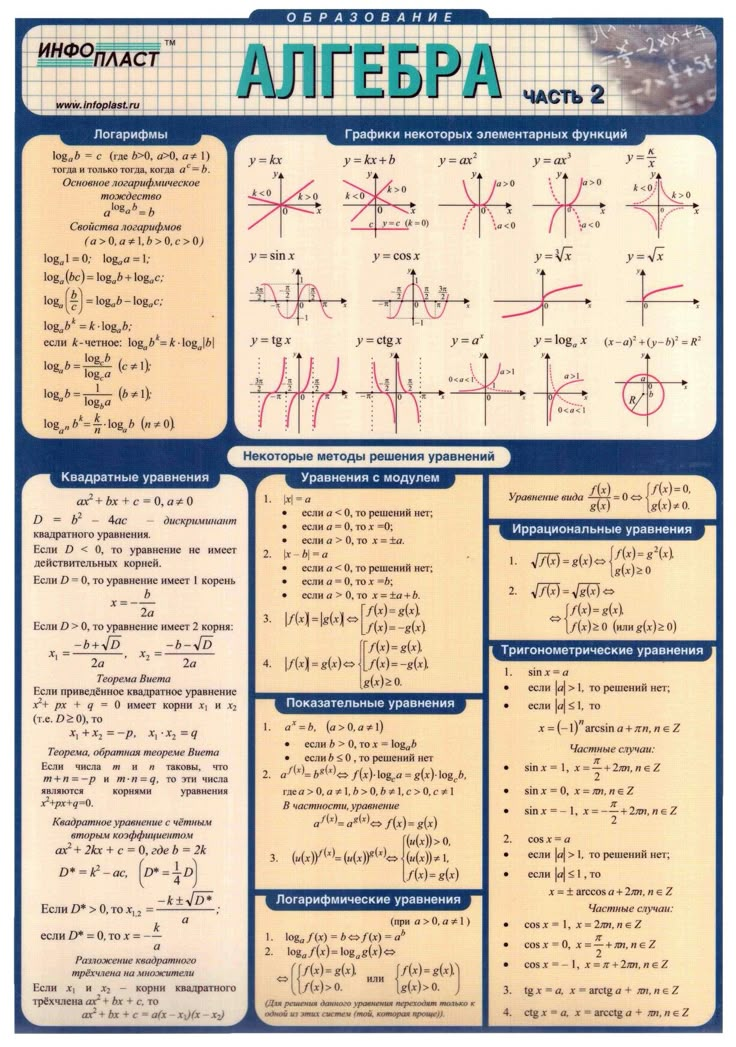
Логарифмы

Логарифм положительного числа b по основанию a — это показатель степени, в которую надо возвести a , чтобы получить b.

При этом

Перечислим основные формулы для логарифмов:

По определению, — это показатель степени, в которую надо возвести число a, чтобы получить число b:

Формула (1) называется основным логарифмическим тождеством.

Вот еще один вариант записи основного логарифмического тождества:

Логарифм произведения равен сумме логарифмов:

Логарифм частного равен разности логарифмов:

Логарифм степени – это показатель степени, умноженный на логарифм:

Есть также формула, когда основанием логарифма является число в некотоой степени. Показатель степени основания логарифма тоже «спрыгивает», но в виде обратного числа:

Наконец, важнейшая формула перехода к новому основанию:

В частности, если c = b, то , и тогда:

Из этих формул можно получать новые.

7. Например, докажем полезное свойство логарифма:

Доказательство:

По формуле перехода к новому основанию получим:

Отсюда

8. Докажем тождество:

Доказательство:

Решим примеры на вычисление.

9. Вычислите:

Решение: Применили формулы перехода к новому основанию и логарифма произведения.

10. Вычислите:

Решение:

Применили формулу перехода к новому основанию и формулу логарифма степени.

Спасибо за то, что пользуйтесь нашими статьями. Информация на странице «Алгебра – основные понятия и формулы» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена: 08.04.2023

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра — Формулы сокращенного умножения

Справочник по математике

Алгебра

Формулы сокращенного умножения

      Формулы сокращенного умножения включают в себя следующие группы формул:

	Степень суммы
	Степень разности
	Квадрат многочлена
	Куб трехчлена
	Сумма нечетных степеней
	Разность нечетных степеней
	Разность четных степеней

Степень суммы

      Группа формул «Степень суммы» составляет Таблицу 1. Эти формулы можно получить, выполняя вычисления в следующем порядке:

(x + y)2 = (x + y)(x + y) , (x + y)3 = (x + y)2(x + y) , (x + y)4 = (x + y)3(x + y)

и т.д.

      Группу формул «Степень суммы» можно получить также с помощью треугольника Паскаля и с помощью бинома Ньютона, которым посвящены специальные разделы нашего справочника.

      Таблица 1. – Степень суммы

Название формулы	Формула
Квадрат (вторая степень) суммы	(x + y)2 = x2 + 2xy + y2
Куб (третья степень) суммы	(x + y)3 = x3 + 3x2y + 3xy2 + y3
Четвертая степень суммы	(x + y)4 = x4 + 4x3y + 6x2y2 + 4xy3 + y4
Пятая степень суммы	(x + y)5 = x5 + 5x4y + 10x3y2 + 10x2y3 + 5xy4 + y5
Шестая степень суммы	(x + y)6 = x6 + 6x5y + 15x4y2 + 20x3y3 + 15x2y4 + 6xy5 + y6
…	…

Квадрат (вторая степень) суммы (x + y)2 = x2 + 2xy + y2

Куб (третья степень) суммы (x + y)3 = = x3 + 3x2y + 3xy2 + y3

Четвертая степень суммы (x + y)4 = x4 + 4x3y + + 6x2y2 + 4xy3 + y4

Пятая степень суммы (x + y)5 = x5 + 5x4y + + 10x3y2 + + 10x2y3 + + 5xy4 + y5

Шестая степень суммы (x + y)6 = x6 + 6x5y + + 15x4y2 + + 20x3y3 + + 15x2y4 + 6xy5 + y6

…

      Общая формула для вычисления суммы

(x + y)ⁿ

с произвольным натуральным значением   n рассматривается в разделе «Бином Ньютона» нашего справочника.

Степень разности

      Если в формулах из Таблицы 1 заменить  y  на  – y ,  то мы получим группу формул «Степень разности» (Таблица 2.):

      Таблица 2. – Степень разности

Название формулы	Формула
Квадрат (вторая степень) разности	(x – y)2 = x2 – 2xy + y2
Куб (третья степень) разности	(x – y)3 = x3 – 3x2y + 3xy2 – y3
Четвертая степень разности	(x – y)4 = x4 – 4x3y + 6x2y2 – 4xy3 + y4
Пятая степень разности	(x – y)5 = x5 – 5x4y + 10x3y2 – 10x2y3 + 5xy4– y5
Шестая степень разности	(x – y)6 = x6 – 6x5y + 15x4y2 – 20x3y3 + 15x2y4 – 6xy5 + y6
…	…

Квадрат (вторая степень) разности (x – y)2 = x2 – 2xy + y2

Куб (третья степень) разности (x – y)3 = = x3 – 3x2y + 3xy2 – y3

Четвертая степень разности (x – y)4 = x4 – 4x3y + + 6x2y2 – 4xy3 + y4

Пятая степень разности (x – y)5 = x5 – 5x4y + + 10x3y2 – – 10x2y3 + + 5xy4– y5

Шестая степень разности (x – y)6 = x6 – 6x5y + + 15x4y2 – – 20x3y3 + + 15x2y4 – 6xy5 + y6

…

Квадрат многочлена

      Следующая формула применяется достаточно часто и называется «Квадрат многочлена»:

      Словами эту формулу можно выразить так: — «Квадрат многочлена равен сумме квадратов всех его членов плюс сумма всевозможных удвоенных произведений его членов».

Куб трехчлена

      Следующая формула называется «Куб трехчлена»:

(x + y + z)³ =
= x³ + y³ + z³ + 3x²y +
+ 3x²z + 3xy² +
+ 3xz² +
+ 3y²z + 3yz² + 6xyz .

     Другие формулы сокращенного умножения приведены в разделе «Формулы сокращенного умножения: сумма степеней, разность степеней» нашего справочника.

Формулы алгебры

• Главная

• Узнать

• Алгебра

• Что такое алгебра
• Алгебра в повседневной жизни
• Основные алгебраические термины
• Методы решения по алгебре
• Линейные, нелинейные уравнения
• Алгебра Формулы
• Коммутативные Ассоциативные законы
• Формула расстояния
• Метод фольги
• Формула средней точки
• Скобки Правила
• Квадратное уравнение
• Квадратичная формула
• Полиномиальные операции
• Полиномиальное сложение
• Полиномиальное вычитание
• Полиномиальное умножение
• Многочлен длинного деления
• Графики полиномиальных функций 92` + 10`x` + 25

  Explanation:

  ---

  Binomial Theorem Example

  
  

  Example 1:

  
  

  Example 2:

  ---

  Sum / Difference Formula Example

  
  

  Example 1:

  
  

  Example 2:

  Популярные ссылки по алгебре

  
  
  • Что такое алгебра
  • Алгебра в повседневной жизни
  • Основные алгебраические термины
  • Методы решения по алгебре
  • Линейные, нелинейные уравнения
  • Алгебра Формулы
  • Коммутативные ассоциативные законы
  • Формула расстояния
  • Метод фольги
  • Формула средней точки
  • Скобки Правила
  • Квадратное уравнение
  • Квадратичная формула
  • Полиномиальные операции
  • Полиномиальное сложение
  • Полиномиальное вычитание
  • Полиномиальное умножение
  • Многочлен длинного деления
  • Графики полиномиальных функций
  Спираль

  Станьте участником сегодня!

   Зарегистрируйтесь (бесплатно)

  Вы член? Войти!

   Войдите в свою учетную запись

  Все алгебраические формулы PDF, математические тождества для классов 10 и 12

  Содержание

  Алгебраическая формула

  Алгебраическая формула является частью 10-го класса в Индии. Одной из важнейших областей математики является алгебра. Многие дисциплины, в том числе квадратные уравнения, многочлены, координатная геометрия, исчисление, тригонометрия, вероятность и другие, могут быть решены с помощью алгебраических формул. В формулах алгебры мы использовали числа вместе с буквами. Чаще всего в алгебраических уравнениях и задачах используются буквы X, Y, A и B. Эти формулы алгебры позволяют нам быстро и эффективно решать трудоемкие алгебраические задачи. Здесь мы включили все важные формулы алгебры вместе с их решениями, чтобы учащиеся могли получить к ним доступ в одном месте.

  Алгебра-формулы

  Алгебра-формулы в основном представляют собой алгебраические уравнения, образованные алгебраическими и математическими фразами и символами. Эти алгебраические формулы содержат неизвестную переменную x, которую можно получить при упрощении уравнения. Эти алгебраические уравнения легко решают сложные алгебраические вычисления.
  Для примера формул алгебры:

  (a+b)³ =a³+ 3a²b+3ab²+b³
  В приведенных выше формулах алгебры обе части по отдельности представляют собой алгебраическое уравнение. Где (a³ + 3a²b+3ab²+b³) — это упрощенное выражение (a+b)³.

  Квадрат формул алгебры для класса 10

  Вот некоторые формулы алгебры, включающие квадраты.
  • a²– b² = (a – b)(a + b)
  • (a + b)²=  a²+ 2ab + b²
  • a²+ b²= (a + b)²– 2ab
  • (a – b )² = a²– 2ab+ b²
  • (a + b + c)² = a² + b² + c²+ 2ab + 2bc + 2ca
  • (a – b – c)² = a²+ b²+ c²– 2ab + 2bc – 2ca

  Куб формул алгебры для SSC CGL

  Вот некоторые формулы алгебры, использующие кубы.

  • (a + b)³ = a³+ 3a²b + 3ab²+ b³
  •  (a + b)³ = a³ + b³ + 3ab(a + b)
  • (a – b)³= a³ – 3a²b + 3ab² – b³
  • (a – b)³= a³ – b³ – 3ab( a – b)
  • a³ – b³ = (a – b)(a²+ ab + b²)
  • a³ + b³ = (a + b)(a²– ab + b²)

  Еще несколько формул алгебры –
  • (a + b)⁴= a⁴+ 4a³b + 6a²b² + 4ab³ + b²
  • (a – b)⁴= a4 – 4a³b + 6a²b² – 4ab³+ b⁴ b)(a² + b²)
  • a⁵ – b⁵= (a – b)(a⁴ + a³b + a²b² + ab³+ b⁴)

  Алгебраические формулы – натуральные числа

  Алгебраические формулы для натуральных чисел За исключением 0 и отрицательных чисел, остальные числа [от 2 до бесконечности] в системе счисления, которые люди могут считать, известны как натуральные числа. Некоторые алгебраические формулы применяются при выполнении операций над натуральными числами. Они есть.
  Считайте n натуральным числом.

  1. (a ⁿ  – b ⁿ  )= (a – b)(a ^n-1  + a ^n-2 b+…+ b ^n-2 a2 + b-902 )
  2. ( 9где n четно , (n = k + 1) ]
  3. (a ⁿ  + b ⁿ )= (a + b)(a ^n-1  – a ^n-2 b +a ^n-3 b ² …- 9 n-902 2 a + b ^n-1 ) [где n нечетное, (n = 2k + 1)  ]

  Алгебраические формулы-

  Законы экспонент

  В алгебраических формулах Экспонента или степень используется для демонстрации многократного умножения числа. Например, 3 × 3 × 3 × 3 можно записать как 3⁴, где 4 — показатель степени числа 3. В общем случае показатели степени или степени указывают, сколько раз можно умножать число. Существуют различные правила работы с показателем степени для сложения, вычитания и умножения, которые легко решаются с помощью алгебраических формул.

  Формула алгебры: законы экспоненты

  Формулы алгебры – квадратные уравнения

  Формулы алгебры для квадратных уравнений – одна из самых важных тем в программе 9 и 10 классов. Чтобы найти корень данных квадратных уравнений, мы использовали следующие формулы алгебры

  Если ax²+bx+c =0 является квадратным уравнением, то

  Формула алгебры: квадратные уравнения

   

  Из приведенной выше формулы мы можем сделать вывод, что , Если корнями квадратного уравнения являются α и β
  1. Уравнение будет (x − α)(x − β) = 0,
  2. Значение (α + β ) = (-b / a) и α × β = (c / a).

  Формулы алгебры для иррациональных чисел (SSC CGL)

  Формулы алгебры, используемые для решения уравнений, основанных на иррациональных числах, следующие:

  1. √ab = √a √b
  2. √а/б = √а / √б
  3. ( √a + √b )  ( √a – √b ) = a-b
  4. ( √a + √b )²= a + 2 √ab + b
  5. ( а +√b )( а -√b )= а² – b

  Список формул по алгебре и лист

  Здесь представлен список всех важных формул алгебры. Студенты должны пройти по списку, чтобы решить сложные алгебраические уравнения очень быстро.

  	Важные формулы алгебры
  1	а²– b² = (а – b)(а + b)
  2	(а + b)²=  a²+ 2ab + b²
  3	а²+ b²= (а + b)²– 2ab
  4	(а – б)² = а²– 2аб+ б²
  5	(a + b + c)² = a² + b² + c²+ 2ab + 2bc + 2ca
  6	(a – b – c)² = a²+ b²+ c²– 2ab + 2bc – 2ca
  7	(а + b)³ = а³+ 3a²b + 3ab²+ b³
  8	(а + b)³ = a³ + b³ + 3ab(a + b)
  9	(a – b)³= a³ – 3a²b + 3ab² – b³
  10	(a – b)³= a³ – b³ – 3ab(a – b)
  11	a³ – b³ = (a – b)(a²+ ab + b²)
  12	a³ + b³ = (a + b)(a²– ab + b²)
  13	(а + b)⁴= а⁴+ 4a³b + 6a²b² + 4ab³ + b²
  14	(a – b)⁴= a4 – 4a³b + 6a²b² – 4ab³+ b⁴
  15	а⁴ – b⁴= (а – b)(а + b)(а² + b²)
  16	а⁵ – b⁵= (a – b)(a⁴ + a³b + a²b² + ab³+ b⁴)

  Алгебраические формулы в формате PDF

  Ознакомьтесь с алгебраическими формулами в формате PDF для учащихся 10 класса. Щелкните здесь- Алгебраические формулы

  Алгебраические формулы с примерами (решено)

  Пример 1. Найдите значение 20²- 15²
  Решение: Чтобы решить уравнение, мы используем формулу
  a² -b² = (a +b) (a-b)
  = (20+15)(20-15)
  = 35 × 5
  = 175 (ответ)

  Пример 2: (x-y) =2 и x²+ y² =20, затем найдите значение x и y [где x,y >0]
  Решение: Здесь x²+ y² =20
  (x-y)² +2xy =20
  Или, (2)²+ 2xy =20
  Или, 2xy = 20-4  = 16
  Или,xy = 8
  Теперь (x+y)²= (x-y)² +4xy = (2)² +4,8 =36
  Или,x+y = ± 6
  Итак, x+y = 6 [x,y >0] …. (1)
  Также получаем , x- y =2 ……(2)
  Решая два уравнения, получаем ,
  x = 4 и y = 2 (Ответ)

  Пример 3 : Разделить( a³ + b³ + c³ – 3abc) на (a+b+c) и частное. Определите величину.

  Решение: a+b³ + c3 – 3abc

  =(a+b+c)(a²+b²+c2-ab-ac-bc)

  Определяющее частное =
  [(a+b+c)(a²+b²+ c²-ab-ac-bc)] ÷ (a+b+c)

  = a²+b²+c²-ab-be-ca.

  Величина частного равна  2. (Ответ)

  Пример 4
  Найдите их последовательное произведение (x + y), (x – y),  (x² + y²).

  Решение: Произведение определителя =
  (x + y) (x – y) (x² + y²)
  = (x²-y²)(x² + y²)
  = (x²)² – (y²)²
  = х⁴ – у ⁴.(Ответ)

  Алгебраические формулы- Вопросы

  1. Если x+y = 3 и xy = 2, каково значение (x – y) ² ?
  2. Если a+b = 8 и ab = 15, каковы будут значения a и b?
  3. Если a+b = 5 и ab = 6, Найдите значение a² – b²?
  4. Если x = 29 и y = 14, каково значение (4x² + 9y²+ 12xy )?

  Формулы алгебраической идентичности на хинди

  बीजगणित सूत्र कक्षा 10 के

  यह कुछ बीजगणित सूत सूत सूत गए हैं व व व व व श हैं बीजगणित सूत दिए हैं हैं व व व व श कुछ सूत दिए गए हैं व व व व श कुछ सूत दिए हैं जिनमें व व व व व दिए दिए गए जिनमें जिनमें व व व व व व व व व व व व व व व व व व व व व व व व व व व व व व व व व व व
  • а²– b² = (а – b)(а + b)
  • (a + b)²=  a²+ 2ab + b²
  • a²+ b²= (a + b)²– 2ab
  • (ए – बी)² = ए²– 2ab+ बी²
  • (a + b + c) ² = a²+ b²+ c²+ 2ab+ 2bc+ 2ca
  • (ए-बी-सी) ² = ए²+ बी²+ सी² 2 ab+ 2bc-2ca

  एसएससी के के बीजगणित सूत्ve

  गए हैं जिनमें घन शामिल हैं।

  • (a + b)³ = a³+ 3a²b + 3ab²+ b³
  •  (a + b)³ = a³ + b³ + 3ab(a + b)
  • (a – b)³= a³ – 3a²b + 3ab² – b³
  • (a – b)³= a³ – b³ – 3ab(a – b)
  • a³ – b³ = (a – b)(a²+ ab + b²)
  • a³ + b³ = (a + b) (a²– ab + b²)

  कुछ औ बीजगणित बीजगणित सूत्र हैं —
  • (a + b) ⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b²
  • (a — B + 6A² + 4ab³ + b²
  )⁴= a4 – 4a³b + 6a²b² – 4ab³+ b⁴
  • a⁴ – b⁴= (a – b)(a + b)(a² + b²)
  • a⁵ – b⁵= (a – b)(a⁴ + a³b + a²b² + ab³+ b⁴)

  Связанный пост:

  • Законы движения Ньютона – примеры для детей 9 и 11 классов
  • Простая схема микроскопа, формула, определение, открытие и увеличение силы
  • Законы движения — первый, второй, третий закон с приложениями
  • Правило большого пальца левой руки Флеминга используется для
  • Uidai. Gov.In Aadhar — Новая регистрация, обновление, загрузка для школы
  • Столицы штатов и союзных территорий Индии 2022
  • Чрезвычайная ситуация в Индии и ее последствия
  • Формула куба — объем, площадь поверхности в математике для класса 10
  • Схема круговорота воды для детей 3 класса с объяснением
  • Квадрат и куб от 1 до 30 [ Скачать PDF ]
  • Тригонометрическая таблица (от 0 до 360): формула, значение, диаграмма, отношение, PDF

  Алгебраические формулы — QNA

  В. Какие формулы используются для решения задач по алгебре?

  Широко используются следующие формулы основной алгебры:

  • a²– b² = (a – b)(a + b)
  • (a + b)²=  a²+ 2ab + b² б)²– 2ab
  • (a – b)² = a²– 2ab+ b²
  • (a + b + c)² = a² + b² + c²+ 2ab + 2bc + 2ca

  •(a + b)³ = a³+ 3a²b + 3ab²+ b³
  •  (a + b)³ = a³ + b³ + 3ab(a + b)
  • (a – b)³= a³ – 3a²b + 3ab² – b³
  • (a – b)³ = а³ – b³ – 3ab(a – b)
  • a³ – b³ = (a – b)(a²+ ab + b²)
  • a³ + b³ = (a + b)(a²– ab + b²)

  В.