Abcd трапеция описанная около окружности ab cd: ABCD — трапеция, описанная около окружности, АВ = CD. Зив Б.Г. 10 класс Геометрия. Повторение планиметрии 1. Вариант 7 – Рамблер/класс

Решение №2583 Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.

Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.

а) Докажите, что треугольник АОВ прямоугольный.
б) Найдите отношение большего основания трапеции к меньшему, если известно, что АВ = CD, а площадь четырёхугольника с вершинами в точках касания окружности со сторонами трапеции составляет \frac{16}{81} площади трапеции ABCD.

Источник: Ященко ЕГЭ 2022 (36 вар)

Решение:

а) Доказать, что в ΔАОВ ∠АОВ = 90° (тогда он прямоугольный).

    Окружность вписана в углы: ∠ВAD, ∠ADC, ∠DCB и ∠CBA. Центр окружности, которая вписана в угол, расположен на биссектрисе этого угла, значит АО, DO, СО, ВО – биссектрисы и делят соответствующие углы пополам. {\circ}

    Получили:

∠AOB = ∠COD = 90°

    Что и требовалось доказать.

б) Найти: \frac{AD}{BC}, если АВ = СD, S_{KMNL}=\frac{16}{81}\cdot S_{ABCD}:

    Отрезки касательных к окружности, проведённые из одной точки, равны:

BM = BK
CM = CN
AK = AL
DL = DN

    Т.к. AB = CD, то:

BK = СN = BM = CM = x
AK = DN = AL = DL = y

    Проведём радиусы из точки О к касательным ВС и AD, тогда ОМ⊥ВС, OL⊥AD, точка О∈OM, O∈OL, значит МL это одна прямая и высота трапеции:

    Проведём ещё одну высоту трапеции СН:

    MC = LH, МCHL – прямоугольник, значит MC = LH = x, найдём HD:

HD = LD – LH = y – x

    Из прямоугольного ΔСHD по теореме Пифагора найдём СН:

СН² + HD² = CD²
CH² + (y – x)² = (y + x)²
CH² = (y + x)² – (y – x)² = y² + 2xy + x² – y² + 2xy – x² = 4xy
CH=\sqrt{4xy}=2\sqrt{xy}

    Выразим площадь S_ABCD^:

S_{ABCD}=\frac{BC+AD}{2}\cdot CH=\frac{2x + 2y}{2}\cdot 2\sqrt{xy}=(x+y)\cdot 2\sqrt{xy}

    В четырёхугольнике проведём KMNL диагональ KN, прямые ВС и KN отсекают равные отрезки ВК = СN = x, значит они по теорема Фалеса параллельны ВС||KN, т. к. BC⊥LM, то KM⊥ML, значит угол между диагоналями ∠MSK = 90°.
    Диагональ ML = 2\sqrt{xy}, как высота трапеции.
    Проведём BF||CD и пересекающая KN в точке Е. BCDF – параллелограмм, значит EN = BC = 2x. 

    ΔАВF подобен ΔВКЕ (∠В – общий, ∠ВКЕ = ∠ВАF – соответственные). Из пропорциональности сторон найдём КЕ:

\frac{KE}{AF}=\frac{BK}{BA}
\frac{KE}{AD-FD}=\frac{x}{x+y}
\frac{KE}{2y-BC}=\frac{x}{x+y}
\frac{KE}{2y-2x}=\frac{x}{x+y}
KE=\frac{(2y-2x)\cdot x}{x+y}

    Найдём диагональ KN:

KN = КЕ + ЕN = \frac{(2y-2x)\cdot x}{x+y}+2x=\frac{2x(y-x)+2x(x+y)}{x+y}=\frac{2x(y-x+x+y)}{x+y}=\frac{4xy}{x+y}

    Выразим площадь S_KMNL:

S_{KMNL}=\frac{1}{2 }\cdot ML\cdot KN\cdot \sin \angle MSK=\frac{1}{2 }\cdot 2\sqrt{xy}\cdot \frac{4xy}{x+y}\cdot \sin 90^{\circ}=\sqrt{xy}\cdot \frac{4xy}{x+y}\cdot 1= \frac{4xy\sqrt{xy}}{x+y}

    Подставим выраженные площади с исходное отношение:

S_{KMNL}=\frac{16}{81}\cdot S_{ABCD}
\frac{4xy\sqrt{xy}}{x+y}=\frac{16}{81}\cdot (x+y)\cdot 2 \sqrt{xy}
\frac{4xy\sqrt{xy}}{x+y}=\frac{32(x+y)\sqrt{xy}}{81}
\frac{xy}{x+y}=\frac{8(x+y)}{81}
81ху = 8(х + у)²
8х² + 16ху – 81ху + 8y² = 0 
8х² – 65ху + 8y² = 0 | :x²
8 – 65\frac{y}{x} + 8(\frac{y}{x})^{2} = 0
8(\frac{y}{x})^{2} – 65\frac{y}{x} + 8 = 0
D = (–65)² – 4·8·8 = 3969 = 63²
\frac{y}{x}_{1}=\frac{65-63}{2\cdot 8}=\frac{2}{16}=\frac{1}{8}
\frac{y}{x}_{2}=\frac{65+63}{2\cdot 8}=\frac{128}{16}=8

    Т. к. у нас у большее основание, а х меньшее, то их отношение равно 8.

Ответ: б) 8.

Урок 15. Теория. Задание 16. Часть III (фипи)

Пример 1. Трапеция ABCD с основаниями AD и BC описана около окружности, AB = 11, BC = 6, CD = 9. Найдите AD.

Ответ: 14

Пример 2. Основания трапеции равны 3 и 9, а высота равна 5. Найдите среднюю линию этой трапеции.

Средняя линия трапеции равна полусумме оснований. Все значения нам известны.

Ответ: 6

Пример 3. Сторона квадрата указана на рисунке. Найдите диагональ этого квадрата.

Диагональ квадрата разбивает квадрат на два равных прямоугольных треугольника.

Квадрат — это прямоугольник с равными сторонами. Зная две стороны прямоугольного треугольника, по теореме Пифагора можно найти третью сторону.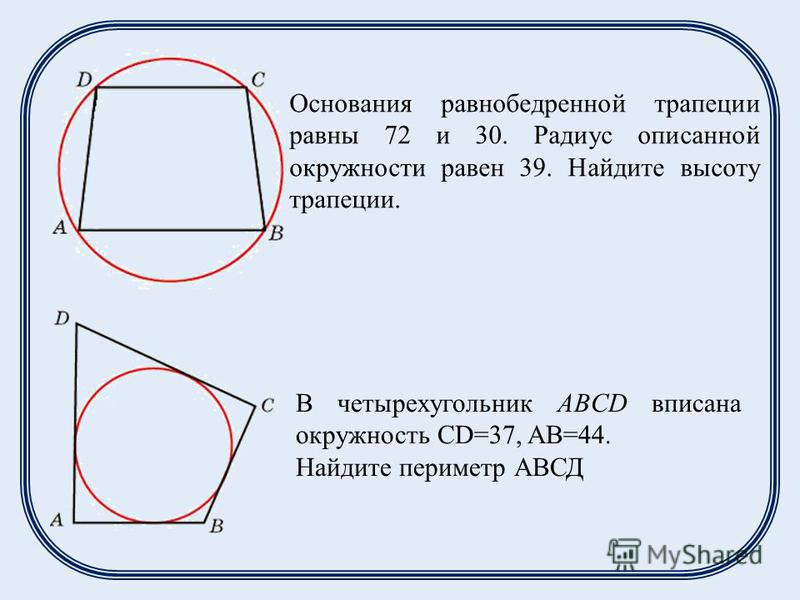

Ответ: 14

Пример 4. Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=12, BD=20, AB=7. Найдите DO.

Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

Ответ: 10

Пример 5. Диагонали AC и BD прямоугольника ABCD пересекаются в точке O, BO=7, AB=6. Найдите AC.

Диагонали прямоугольника равны, пересекаются и точкой пересечения делятся пополам.

Ответ: 14

Пример 6. Катеты прямоугольного треугольника равны 20 и 21. Найдите гипотенузу этого треугольника.

Зная две стороны в прямоугольном треугольнике, всегда можно найти третью сторону по теореме Пифагора.

Теорема Пифагора: Квадрат гипотенузы равен сумме квадратов катетов. Катеты — стороны, пересекающиеся под углом 90 градусов, гипотенуза — сторона, лежащая напротив прямого угла.

Ответ: 29

Пример 7. В прямоугольном треугольнике катет и гипотенуза равны 8 и 17 соответственно. Найдите другой катет этого треугольника.

Зная две стороны в прямоугольном треугольнике, всегда можно найти третью сторону по теореме Пифагора.

Теорема Пифагора: Квадрат гипотенузы равен сумме квадратов катетов. Катеты — стороны, пересекающиеся под углом 90 градусов, гипотенуза — сторона, лежащая напротив прямого угла.

Ответ: 15

Пример 8. В треугольнике ABC известно, что AC = 14, BM — медиана, BM = 10. Найдите AM.

Медиана треугольника — это отрезок, выходящий из вершины треугольника и пересекающий противоположную сторону деля ее на две равные части.

т.е. если BM — медиана  =>  AM=MC=0,5AC

Ответ: 7

Пример 9. Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 21, сторона BC равна 22, сторона AC равна 28. Найдите MN.

Средняя линия треугольника — это отрезок, соединяющий середины двух сторон, параллельна третьей стороне и равна ее половине.

Ответ: 14

Пример 10. Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 15°. Ответ дайте в градусах.

Параллелограмм — это четырехугольник у которого противоположные стороны параллельны.

Биссектриса — это луч, выходящий из вершины угла и делящий этот угол на две равные части.

Если две прямые параллельны ( BC || AD), то накрест лежащие углы равны (<BKA=<KAD).

Ответ: 30

Пример 11. Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 8 и 15. Найдите длину основания BC.

Трапеция — это четырехугольник с двумя параллельными сторонами (основаниями) и двумя не параллельными сторонами (боковыми сторонами).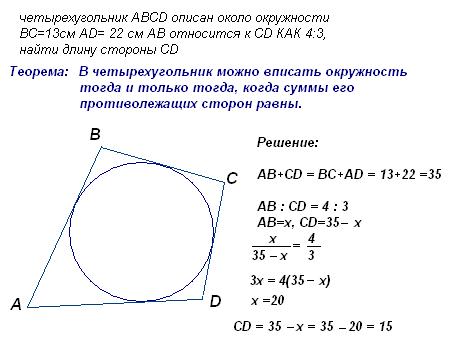

В равнобедренной трапеции боковые стороны равны и углы при основаниях равны,

Ответ: 7

ABCD — трапеция, в которой AB параллельна CD и AB = 4 (CD). Диагонали трапеции пересекаются в точке О. Каково отношение площади треугольника DCO к площади треугольника ABO?

ПУБЛИКАЦИЯ ЧЕМПИОНА-2017 TIER-II БУМАГА(11)-УПРАЖНЕНИЕ

20 видео

РЕКЛАМА

Ab Padhai каро бина адс ке

Khareedo DN Про и дехо сари видео бина киси ад ки рукаават ке!

Ответить

Пошаговое решение, разработанное экспертами, чтобы помочь вам в решении вопросов и получении отличных оценок на экзаменах.

---

Видео по теме

Диагонали трапеции ABCD с AB || DC пересекают друг друга в точке O. Если AB = 2 CD, найдите отношение площадей треугольников AOB и COD.

एक समलम्ब abcd जिसमें ab∣dc है, के विकर्ण परस्पर बिन्दु o पर पшить करते हैं।।।।।।।। प प् Как यदि ab = 2 Cd हो तो त्रिभुजों aob और Cod के क्षेत्रफलों का अनुपात ज्ञात कीजिए।।।।।।।।।।

76132141

Диагональ трапеции ABCD, в которой AB//CD пересекаются в точке ‘O’ . ЕСЛИ AB=2CD, то отношение площадей треугольников AOB и COD равно ……….

161135286

Диагонали трапеции ABCd с AB∣∣DC пересекаются в точке O. Если AB = 2 CD , найдите отношение площадей треугольников AOB и COD.

203474863

Диагонали трапеции ABCD с AB || DC пересекают друг друга в точке O. Если AB = 2 CD, найдите отношение площадей треугольников AOB и COD.

571222545

Диагонали трапеции ABCD с AB∣∣DC пересекаются в точке O. Если AB=2CD, найдите отношение площадей треугольников AOB и COD.

642723092

एक समलंब चतुर्भुज □ABCD में, AB ∣∣ CD औथ AB = 2 CD Ac तथा db का पшить बिंदु बिंदु o हैं, तो Δaob तथ ΔCod के क्षेत्रफलों का अनुपात ज्ञात कीजिए।।।।।।।।

643048949

ABCD — трапеция, у которой AB||CD и AB=2CD. Если его диагонали пересекаются в точке O, то отношение площадей треугольников AOB и COD равно:

643476618

ABCD — равнобедренная трапеция. AB||CD Диагонали AD=BC пересекаются в точке O, площадь ABO = 84 см2 найти площадь ΔCOD

643555888

Диагонали трапеции ABCD с AB∣∣DC пересекаются в точке O.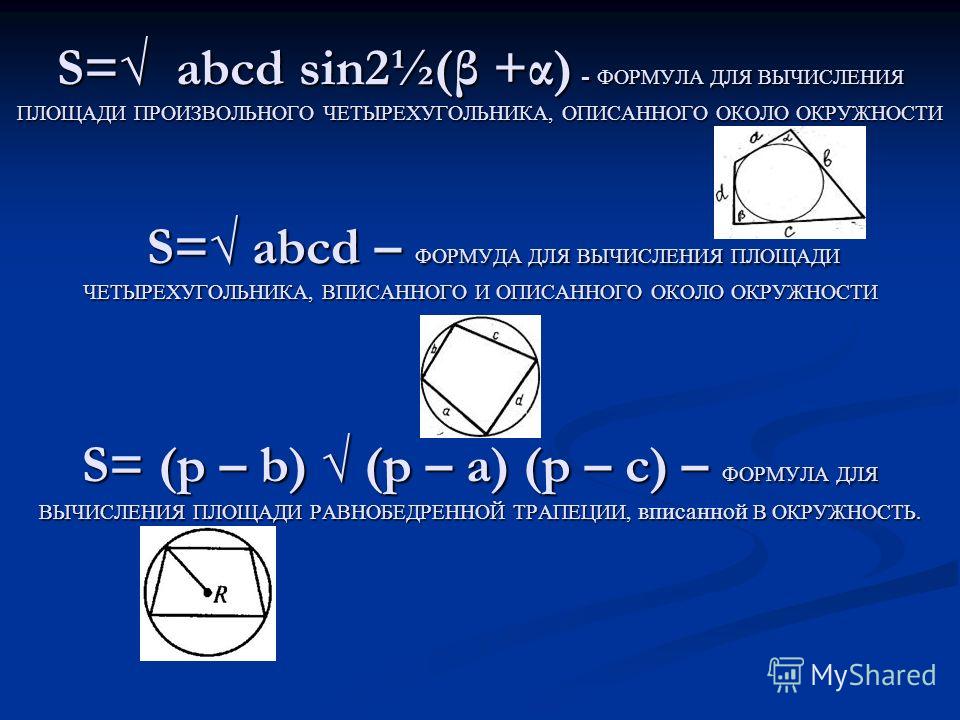 Если AB=2CD, найдите отношение площадей треугольника AOB и COD.

643863192

Диагонали трапеции ABCD с AB||DC пересекаются в точке O. Если AB=2CD, найдите отношение площадей треугольников AOB и COD.

644836053

В трапеции ABCD, AB∣∣CD и AB = 2CD. Если площадь △AOB=84см2,
найти площадь △COD.

645188753

ABCD — трапеция, в которой AB∣∣CD и AB=2CD. Если его диагонали пересекаются в точке O, то отношение площадей треугольника AOB и COD равно

646303081

ABCD — трапеция, в которой AB параллельна CD и AB = 4 (CD). Диагонали трапеции пересекаются в точке О. Каково отношение площади треугольника DCO к площади треугольника ABO?

646931885

Диагонали трапеции ΔBCD с AB || CD пересекаются в точке O. Если AB = 2CD, то отношение площадей ΔAOB и ΔCOD равно 9(2), тогда площадь Delta Cod равен

647449125

Ololol — âm nhạc 6 — nguyễn đng khoa

ngày đng: 25/10/2022, 19:00

Geometry Geometry. Задачи по геометрии со страницы блога IMO http //imogeometry blogspot gr/ Группа романтиков геометрии в facebook https //web facebook com/gr[.] Задачи по геометрии со среднеевропейских математических олимпиад 2007–2017 [со ссылками aops] MEMO 2007 Individual Let k be окружность и k1, k2, k3 и k4 четыре меньшие окружности с центрами O1, O2, O3 и O4 соответственно на k Для i = 1, 2, 3 и k5 = k1 окружности ki и ki+1 пересекаются в точках Ai и Bi такое, что Ai лежит на k Точки O1, A1, O2, A2, O3, A3, O4, A4 лежат в этом порядке на k и попарно различны Докажите, что B1B2B3B4 — прямоугольник (Швейцария) MEMO 2008 Individual Пусть ABC равнобедренный треугольник с AC = BC. Вписанная окружность касается AB и BC в точках D и E соответственно. Прямая (отличная от AE) проходит через шероховатой A и пересекает вписанную окружность в точках F и G. Прямые EF и EG пересекают прямую AB в точках K и L соответственно. Докажите, что DK = DL (Hungary) MEMO 2008 Team Дан остроугольный треугольник ABC, пусть E — точка, расположенная по другую сторону прямой AC от B, и пусть D — внутренняя точка отрезка AE.

Предположим, что ADB = CDE, BAD = ECD и ACB = EBA. Докажите, что B, C и E равны коллинеар (Словения) MEMO 2009Индивидуум Пусть ABCD — выпуклый четырехугольник такой, что AB и CD не параллельны и AB = CD. Середины диагоналей AC и BD равны E и F. Прямая EF пересекает отрезки AB и CD в точках G и H соответственно. Покажите, что AGH = DHG (Венгрия) MEMO 2009 Team Пусть ABCD — параллелограмм с BAD = 60°, и обозначим через E пересечение его диагоналей. Окружность, описанная около треугольника ACD, пересекает прямую BA в точке K ≠ A, прямую BD в точке P ≠ D и прямая BC в точке L ≠ C. Прямая EP пересекает описанную окружность треугольника CEL в точках E и M. Докажите, что треугольники KLM и CAP равны (Словения) MEMO 2009Команда Предположим, что ABCD — вписанный четырехугольник и CD = DA. Точки E и F принадлежат отрезкам AB и BC соответственно, а ADC = EDF. Отрезки DK и DM — высота и медиана треугольника DEF соответственно L — точка, симметричная в K относительно M Докажите, что прямые DM и BL параллельны (Польша) Задачи по геометрии со страницы блога IMO: Романтики геометрии Группа facebook: http://imogeometry.

blogspot.gr/ https://web.facebook.com /groups/parmenides52/ Задачи по геометрии со среднеевропейских математических олимпиад MEMO 2010 Individual Нам дан вписанный четырехугольник ABCD с точкой E на диагонали AC такой, что AD=AE и CB = CE. Пусть M – центр описанной окружности k окружности. треугольник BDE Окружность k пересекает прямую AC в точках E и F. Докажите, что прямые FM, AD и BC пересекаются в одной точке (Швейцария) MEMO 2010 Team Вписанная окружность треугольника ABC касается сторон BC, CA и AB в точках D, E и F соответственно. Пусть K — точка, симметричная D относительно центра вписанной плоскости. Прямые DE и FK пересекаются в точке S. Докажите, что AS параллельна BC (Польша) MEMO 2010 Team Пусть A, B, C, D, E — такие точки, что ABCD — вписанный четырехугольник, а ABDE — параллелограмм Диагонали AC и BD пересекаются в точке S, а лучи AB и DC пересекаются в точке F. Докажите, что AFS = ECD (Хорватия) MEMO 2011 Individual На плоскости окружности K1 и K2 с центрами I1 и I2 соответственно пересекаются по двум точки A и B Предположим, что I1AI2 тупая Касательная к K1 в A снова пересекает K2 в C, а касательная к K2 в A снова пересекает K1 в D Пусть K3 — описанная окружность треугольника BCD Пусть E — середина этой дуги CD треугольника K3, содержащего B. Прямые AC и AD снова пересекают K3 в K и L соответственно. Докажите, что прямая AE перпендикулярна KL (Ник Стопар, Словения). MEMO 2011 Team Пусть ABCDE — выпуклый пятиугольник, все пять сторон которого равны между собой. длина Диагонали AD и EC пересекаются в S с ASE = 60o. Докажите, что ABCDE имеет пару параллельных сторон. (Michal Szabados, Словакия) MEMO 2011 Team Пусть ABC — остроугольный треугольник. Обозначим через B0 и C0 основания высот из вершин B и C соответственно. Пусть X — точка внутри треугольника ABC, такая, что прямая BX касается описанная окружность треугольника AXC0, а прямая CX касается описанной окружности треугольника AXB0. Покажите, что прямая AX перпендикулярна BC (Михал Ролинек, Йозеф Ткадлец, Чешская Республика). http://imogeometry.blogspot.gr/ https://web.facebook.com/groups/parmenides52/ Задачи по геометрии среднеевропейских математических олимпиад MEMO 2012 Индивидуальные В данной трапеции ABCD с AB параллельно CD и AB > CD, прямая BD делит пополам угол ADC Прямая, проведенная через C, параллельная AD, пересекает отрезки BD и AB в E и F соответственно. Пусть O — центр описанной окружности треугольника BEF. Предположим, что ACO = 60ο. Докажите равенство CF = AF + FO ( Хорватия) MEMO 2012 Team Let K be the mid точка стороны AB данного треугольника ABC. Пусть L и M — точки на сторонах AC и BC соответственно такие, что CLK = KMC. Докажите, что перпендикуляры к сторонам AB, AC и BC, проходящие через точки K, L , и M соответственно параллельны (Польша) MEMO 2012 Team Пусть ABCD — выпуклый четырехугольник без пары параллельных сторон, такой что ABC = CDA. четырехугольник EFGH. Пусть K — пересечение диагоналей треугольника EFGH. Докажите, что прямые AB и CD пересекаются по описанной окружности треугольника BKD (Хорватия) MEMO 2013 Individual. Пусть ABC — равнобедренный треугольник с AC = BC. Пусть N — точка внутри треугольника. такой треугольник, что 2ANB = 180ο + ACB. Пусть D — пересечение прямой BN и прямой, параллельной AN, проходящей через точку C. Пусть P — пересечение биссектрисы углов CAN и ABN. Покажите, что прямые DP и AN перпендикулярны (Matija Basic, Хорватия) MEMO 2013 Team Пусть ABC — остроугольный треугольник.

Постройте треугольник PQR такой, что AB = 2PQ, BC = 2QR, CA = 2RP, а прямые PQ, QR и RP проходят через точки A, B и C соответственно (все шесть точек A , B, C, P, Q и R различны.) (Герд Барон, Австрия) MEMO 2013 Team Пусть K — точка внутри остроугольного треугольника ABC, такая, что BC — общая касательная окружностей, описанных вокруг треугольников AKB и AKC. Пусть D — пересечение прямых CK и AB, а E — пересечение прямых BK и AC. Пусть F — пересечение прямой BC и серединного перпендикуляра к отрезку DE. Окружность, описанная вокруг ABC, и окружность k с центром F и радиус FD пересекаются в точках P и Q Докажите, что отрезок PQ является диаметром k (Патрик Бак, Словакия) Задачи по геометрии со страницы блога ИМО: Романтики геометрии в группе facebook: http://imogeometry.blogspot.gr/ https ://web.facebook.com/groups/parmenides52/ Задачи по геометрии Среднеевропейских математических олимпиад MEMO 2014 Индивидуальный Пусть ABC — треугольник с AB 45o и центром описанной окружности O Точка P лежит внутри нее так, что точки A, P, O, B лежат на окружности, а BP перпендикулярна CP Точка Q лежит на отрезке BP так, что AQ параллелен PO Докажите, что QCB=PCO (Патрик Бак, Словакия) MEMO 2016 Team Пусть ABC — остроугольный треугольник, где AB ≠ AC, и пусть O — его центр описанной окружности. Прямая AO пересекает описанную окружность ω треугольника ABC второй раз в точке D , а прямая BC в точке E Окружность, описанная вокруг CDE, пересекает прямую CA второй раз в точке P Прямая PE пересекает прямую AB в точке Q Прямая через O, параллельная PE, пересекает высоту треугольника ABC, проходящего через A в точке F Докажите, что FP = FQ (Хорватия) MEMO 2016 Team Пусть ABC — треугольник, в котором AB ≠AC. Точки K, L, M — середины сторон BC, CA, AB соответственно. Вписанная окружность ABC с центром I касается стороны BC в точке D Прямая g, проходящая через середину отрезка ID и перпендикулярная IK, в пересекает прямую LM в точке P. Докажите, что PIA = 90 ο (Польша) MEMO 2017 Individual Пусть ABCDE — выпуклый пятиугольник. Пусть P — пересечение прямых CE и BD. Предположим, что PAD = ACB и CAP = EDA. Докажите, что центры описанных окружностей треугольников ABC и ADE совпадают. с P (Патрик Бак, Словакия) MEMO 2017 Team Пусть ABC — остроугольный треугольник с AB > AC и описанной окружностью Γ. Пусть M — середина меньшей дуги BC дуги Γ, а D — пересечение лучей AC и BM Пусть E ≠ C — пересечение внутренней биссектрисы угла ACB и описанной окружности треугольника BDC. Предположим, что E лежит внутри треугольника ABC и существует пересечение N прямой DE и окружности Γ такое, что E — середина отрезка DN. Покажите, что N — середина отрезка IBIC, где IB и IC — эксцентры ABC, противоположные B и C соответственно (Хорватия) MEMO 2017 Team Пусть ABC — остроугольный треугольник с треугольником AB ≠ AC, центр описанной окружности O и описанная окружность Γ. Пусть касательные к Γ через B и C пересекаются в точке D , и пусть прямая AO пересекает BC в точке E. Обозначим середину BC через M и пусть AM снова пересекает Γ в точке N ≠ A. Наконец, пусть F ≠ A — точка на Γ такая, что A, M, E и F концикличны. что FN делит пополам отрезок MD (Патрик Бак, Словакия) Задачи геометрии со страницы блога IMO: Романтика геометрии, группа facebook: http://imogeometry.blogspot.gr/ https://web.facebook.com/groups/parmenides52/ .