7 класс алгебра все правила и формулы: Основные правила математики с примерами. 7 класс Алгебра.

Основные правила математики с примерами. 7 класс Алгебра.

Основные правила математики с примерами. 7 класс Алгебра.

Содержание

• Уравнения. Равносильные уравнения. Свойства
• Линейное уравнение
• Одночлены и многочлены
• Формулы сокращенного умножения
• Степень. Свойства степени с целым показателем
• Функция. Область определения и область значений функции
• Линейная функция, её график и свойства
• Системы линейных уравнений с двумя переменными
• Графический метод решения системы двух линейных уравнений с двумя переменными
• Решение системы двух линейных уравнений с двумя переменными методом подстановки
• Решение систем линейных уравнений методом сложения

Уравнения. Равносильные уравнения. Свойства

Корень уравнения

• Корнем уравнения называют значение переменной, при котором уравнение обращается в верное числовое равенство.
• Решить уравнение означает найти все его корни или убедиться, что их вообще нет. Также можно сказать, что решить уравнение — это значит найти множество его корней.

2 x  + 6 =36x = 15 —корень уравнения, поскольку2 · 15  + 6 =3636 = 36 —верное равенство.5x — 5x = 100 —не имеет корней, посколькуx(5 — 5)∥0 = 100  0 = 100  — неверно.

Равносильные уравнения

Два уравнения называют равносильными, если они имеют одно и тоже множество корней.

2x — 5 = 5 ≡равносильно 4x — 10 =10,поскольку x = 5 корень и для 1—го, и для 2—го уравнения.

 

Свойства уравнений

• Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, равносильное данному.

2x — 5 = 7 +52x — 5 + 5 = 7 + 52x = 12x = 12 : 2x = 6

• Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, равносильное данному.

2x — 5 =+5→ 72x = 7 + 52x =12x = 12 : 2x =6

• Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, равносильное данному

12x = 24  : 1212x :12 = 24 : 12x = 2. x5 = 3  · 5×5 · 5  = 3 · 5x = 15

Линейное уравнение

Уравнение вида   , где — переменная,  и некоторые числа, называют линейным уравнением с одной переменной.

Значения и
Корни уравнения		-любое число	корней нет

2x = 0, 5y —3 = 12 — линейные уравненияx2 —4 = 0,  5x = 8 —нелинейные уравнения

Одночлены и многочлены

Одночлены

• Выражения, являющиеся произведениями чисел, переменных и их степеней, называют одночленами.

2x,  356x2y,  0,2a20,  b, 15 — одночлены.

• Одночлен, содержащий только один отличный от нуля числовой множитель, стоящий на первом месте, а все остальные множители которого — степени с разными основаниями, называют одночленом стандартного вида. К одночленам стандартного вида также относят числа, отличные от нуля, переменные и их степени.

2x,  356x2y,  0,2a20 — одночлены стандартного вида.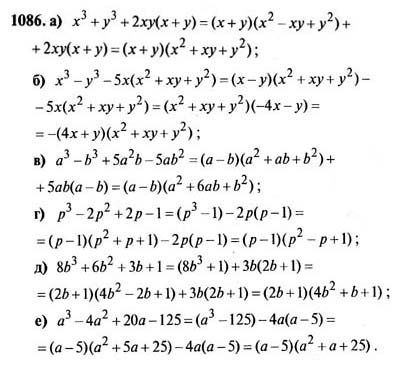

• Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена.

2x,  356x2y,  0,2a20.2,  356,  0,2 —коэффициенты.

• Одночлены, имеющие одинаковые буквенные части, называют подобными. Степенью одночлена называют сумму показателей степеней всех переменных, входящих в него. Степень одночлена, являющегося числом, отличным от нуля, считают равной нулю.

2x2y3z ,  —15x2y3z,    0,5x2y3z —подобные.2x2y3z и  2x2y3 — не подобные.

• Нуль-одночлен степени не имеет.

Многочлены

• Выражение, являющееся суммой нескольких одночленов, называют многочленом.

2x + 3x2y

• Одночлены, из которых состоит многочлен, называют членами многочлена.

2x + 3x2y —многочлен;2x и  3x2y — его одночлены

• Одночлен является частным случаем многочлена. Считают, что такой многочлен состоит из одного члена.

 Умножение одночлена на многочлен

Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый член многочлена и полученные произведения сложить.

Умножение многочлена на многочлен

Чтобы умножить многочлен на многочлен, можно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.

Формулы сокращенного умножения

Разность квадратов двух выражений

Разность квадратов двух выражений равна произведению разности этих выражений и их суммы:

Произведение разности и суммы двух выражений

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений:

Квадрат суммы и квадрат разности двух выражений

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения:

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражении:

Преобразование многочлена в квадрат суммы или разности двух выражений

Формулы

позволяют «свернуть» трёхчлен в квадрат двучлена.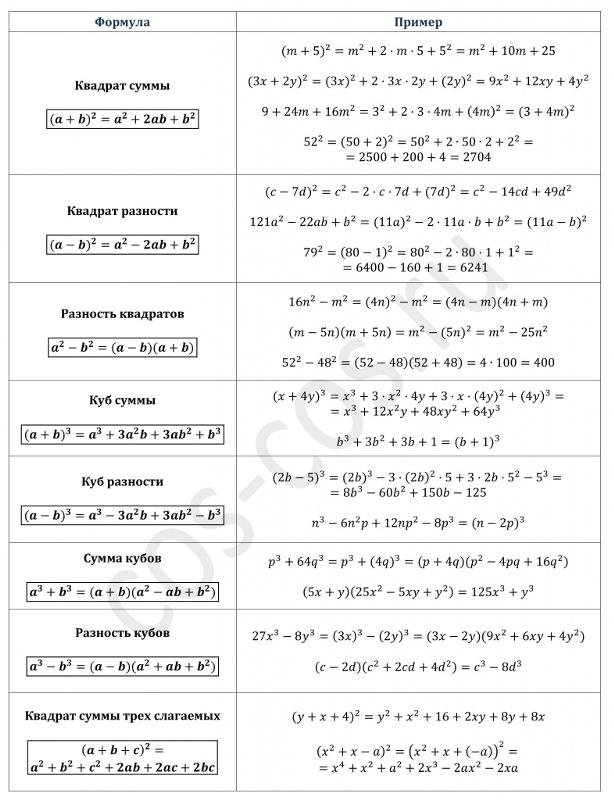

Трёхчлен, который можно представить в виде квадрата двучлена, называют полным квадратом.

Сумма и разность кубов двух выражений

Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности:

Многочлен  называют неполным квадратом суммы.

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы:

Многочлен   называют неполным квадратом разности.

Степень. Свойства степени с целым показателем

Свойства степени с целым показателем

Для любого и любых целых  выполняются равенства:

Для любых , и любого целого   выполняются равенства:

Функция. Область определения и область значений функции

Функция

Правило, с помощью которого по каждому значению независимой переменной можно найти единственное значение зависимой переменной, называют функцией, а соответствующую зависимость одной пeременной от другой — функциональной.
Обычно независимую переменную обозначают ,  зависимую обозначают  , функцию(правило) — .
Независимую переменную называют аргументом функции. Значение зависимой переменной   называют значением функции.
Тогда функциональную зависимость обозначают .
Значения, которые принимает аргумент, образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.

Способы задания функции

Описательный, табличный, с помощью формулы, графический.

График функции

Графиком функции называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.

Линейная функция, её график и свойства

• Функцию, которую можно задать формулой вида , где и  — некоторые числа, — независимая переменная, называют линейной.
• Графиком линейной функции является прямая.
• Линейную функцию, заданную формулой , где , называют прямой пропорциональностью.

Системы линейных уравнений с двумя переменными

 Уравнение с двумя переменными

Пару значений переменных, обращающую уравнение с двумя переменными в верное равенство, называют решением уравнения с двумя переменными.

Решить уравнение с двумя переменными — значит найти все его решения или показать, что оно не имеет решений.

Графиком уравнения с двумя переменными называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, координаты которых (пары чисел) являются решениями данного уравнения.

Если некоторая фигура является графиком уравнения, то выполняются два условия:

•  все решения уравнения являются координатами точек, принадлежащих графику;
•  координаты любой точки, принадлежащей графику, — это пара чисел, являющаяся решением данного уравнения.

Графический метод решения системы двух линейных уравнений с двумя переменными

Графический метод решения системы уравнений заключается в следующем:

• построить в одной координатной плоскости графики уравнений, входящих в систему;
• найти координаты всех точек пересечения построенных графиков;
• полученные пары чисел и будут искомыми решениями.

Если графиками уравнений, входящих в систему линейных уравнении, являются прямые, то количество решений этой системы зависит от взаимного расположения двух прямых на плоскости:

• если прямые пересекаются, то система имеет единственное решение.
• если прямые совпадают, то система имеет бесконечно много решении.
• если прямые параллельны, то система решений не имеет.

Решение системы двух линейных уравнений с двумя переменными методом подстановки

Чтобы решить систему линейных уравнений методом подстановки, следует:

• выразить из любого уравнения системы одну переменную через другую;
• подставить в уравнение системы вместо этой переменной выражение, полученное на первом шаге;
• решить уравнение с одной переменной, полученное на втором шаге;
• подставить найденное значение переменной в выражение, полученное на первом шаге;
• вычислить значение второй переменной;
• записать ответ.

Решение систем линейных уравнений методом сложения

Чтобы решить систему линейных уравнений методом сложения, следует:

• подобрать такие множители для уравнений, чтобы после преобразований коэффициенты при одной из переменной стали противоположными числами
• сложить почленно левые и правые части уравнений, полученных на первом шаге
• решить уравнение с одной переменной, полученной на втором шаге
• подставить найденное на третьем шаге значение переменной в любое из уравнений исходной системы;
• вычислить значение второй переменной;
• записать ответ.

Данная информация взята  из  УМК  А.Г.Мерзляк, В.Б.Полонский, М.С. Якир

Все формулы по физике за 7 класс с пояснениями — таблица и шпаргалки

Шпаргалки по физике за 7 класс

В рамках одной статьи сложно охватить весь курс по физике, но мы осветили основные темы за 7 класс и этого достаточно, чтобы освежить знания в памяти. Скачайте и распечатайте обе шпаргалки — одна из них (подробная) пригодится для вдумчивой подготовки к ОГЭ и ЕГЭ, а вторая (краткая) послужит для решения задач.

Скачать шпаргалку со всеми формулами и определениями по физике за 7 класс (мелко на одной странице).

Для тех, кто находится на домашнем обучении или вынужден самостоятельно изучать материал ввиду пропусков по болезни, рекомендуем также учебник по физике А. В. Перышкина с формулами за 7 класс и легкими, доступными пояснениями по всем темам. Он был написан несколько десятилетий назад, но до сих пор очень популярен и востребован.

Полезные подарки для родителей

В колесе фортуны — гарантированные призы, которые помогут наладить учебный процесс и выстроить отношения с ребёнком!

Измерение физических величин

Измерением называют определение с помощью инструментов и технических средств числового значения физической величины. Результат измерения сравнивают с неким эталоном, принятым за единицу. В итоге значением физической величины считается полученное число с указанием единиц измерения.

В курсе по физике за 7 класс изучают правила измерений с использованием приборов со шкалой. Если цена деления шкалы неизвестна, узнать ее можно с помощью следующей формулы:

ЦД = (max − min) / n, где ЦД — цена деления, max — максимальное значение шкалы, min — минимальное значение шкалы, n — количество делений между ними.

Вместо максимального и минимального можно взять любые другие значения шкалы, числовое выражение которых нам известно.

Выделяют прямое и косвенное измерение:

• при прямом измерении результат можно увидеть непосредственно на шкале инструмента;

• при косвенном измерении значение величины вычисляется через другую величину (например, среднюю скорость определяют на основе нескольких замеров скорости).

Для удобства и стандартизации измерений в 1963 году была принята Международная система единиц СИ. Она регламентирует, какие единицы измерения считать основными и использовать для формул. Обозначения этих единиц также учат в программе по физике за 7 класс.

Механическое движение: формулы за 7 класс

Механическое движение — перемещение тела в пространстве, в результате которого оно меняет свое положение относительно других тел. Закономерности такого движения изучают в рамках механики и конкретно ее раздела — кинематики.

Для того, чтобы описать движение, требуется тело отсчета, система координат, а также инструмент для измерения времени. Это составляющие системы отсчета.

Изучение механического движения в курсе по физике за 7 класс включает следующие термины:

• Перемещение тела — минимальное расстояние, которое соединяет две выбранные точки траектории движения.

• Траектория движения — мысленная линия, вдоль которой перемещается тело.

• Путь — длина траектории тела от начальной до конечной точки.

• Скорость — быстрота перемещения тела или отношение пройденного им пути ко времени прохождения.

• Ускорение — быстрота изменения скорости, с которой движется тело.

Равномерное движение — механическое движение, при котором тело за любые равные промежутки времени проходит одно и то же расстояние.

Формула скорости равномерного прямолинейного движения:

V = S / t, где S — путь тела, t — время, за которое этот путь пройден.

Формула скорости равномерного криволинейного движения:

где S₁ и S₂ — отрезки пути, а t₁ и t₂ — время, за которое был пройден каждый из них.

Единица измерения скорости в СИ: метр в секунду (м/с).

Формула скорости равноускоренного движения:

V = V₀ + at, где V₀— начальная скорость, а — ускорение.

Единица измерения ускорения в СИ: м/с².

Сила тяжести, вес, масса, плотность

Формулы, понятия и определения, описывающие эти физические характеристики, изучают в 7 классе в рамках такого раздела физики, как динамика.

Вес тела или вещества — это физическая величина, которая характеризует, с какой силой оно действует на горизонтальную поверхность или вертикальный подвес.

Обратите внимание: вес тела измеряется в ньютонах, масса тела — в граммах и килограммах.

Формула веса:

P = mg, где m — масса тела, g — ускорение свободного падения.

Ускорение свободного падения возникает под действием силы тяжести, которой подвержены все находящиеся на нашей планете тела.

g = 9,806 65 м/с² или 9,8 Н/кг

Если тело находится в покое или в прямолинейном равномерном движении, его вес равен силе тяжести.

F_тяж = mg

Но эти понятия нельзя отождествлять: сила тяжести действует на тело ввиду наличия гравитации, в то время как вес — это сила, с которой само тело действует на поверхность.

Плотность тела или вещества — величина, указывающая на то, какую массу имеет данное вещество, занимая единицу объема. Плотность прямо пропорциональна массе и обратно пропорциональна объему.

Формула плотности:

ρ = m / V, где m — масса тела или вещества, V — занимаемый объем.

Единица измерения плотности в СИ: кг/м³.

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

Механический рычаг, момент силы

О механическом рычаге говорил еще Архимед, когда обещал перевернуть Землю, если только найдется подходящая точка опоры. Это простой механизм, который помогает поднимать грузы, закрепленные на одном его конце, прилагая силу к другому концу. При этом вес груза намного превосходит прилагаемое усилие. В 7 классе физические формулы, описывающие этот процесс, изучаются в том же разделе динамики.

Рычаг — это некое твердое тело, способное вращаться вокруг неподвижной точки опоры, на один конец которого действует сила, а на другом находится груз. Перпендикуляр, проведенный от точки опоры до линии действия силы, называется плечом силы.

Рычаг находится в равновесии, если произведение силы на плечо с одной его стороны равно произведению силы на плечо с другой стороны.

Уравнение равновесия рычага:

F₁ × l₁ = F₂ × l₂

Из этого следует, что рычаг уравновешен, когда модули приложенных к его концам сил обратно пропорциональны плечам этих сил.

Момент силы — это физическая величина, равная произведению модуля силы F на ее плечо l.

Формула момента силы:

M = F × l, где F — модуль силы, l — длина плеча.

Единица измерения момента силы в СИ: ньютон-метр (Н·м).

Эта формула верна, если сила приложена перпендикулярно оси рычага. Если же она прилагается под углом, такой случай выходит за рамки курса физики за 7 класс и подробно изучается в 9 классе.

Правило моментов: рычаг уравновешен, если сумма всех моментов сил, которые поворачивают его по часовой стрелке, равна сумме всех моментов сил, которые поворачивают его в обратном направлении.

Можно сказать иначе: рычаг в равновесии, если сумма моментов всех приложенных к нему сил относительно любой оси равна нулю.

М₁ + М₂ + М_n + … = 0

Давление, сила давления

Прилагая одну и ту же силу к предмету, можно получить разный результат в зависимости от того, на какую площадь эта сила распределена. Объясняют этот феномен в программе 7 класса физические термины «давление» и «сила давления».

Давление — это величина, равная отношению силы, действующей на поверхность, к площади этой поверхности. Сила давления направлена перпендикулярно поверхности.

Формула давления:

p = F / S, где F — модуль силы, S — площадь поверхности.

Единица измерения давления в СИ: паскаль (Па).

1 Па = 1 Н/м²

Понятно, что при одной и той же силе воздействия более высокое давление испытает та поверхность, площадь которой меньше.

Формулу для расчета силы давления вывести несложно:

F = p × S

В задачах по физике за 7 класс сила давления, как правило, равна весу тела.

Давление газов и жидкостей

Жидкости и газы, заполняющие сосуд, давят во всех направлениях: на стенки и дно сосуда. Это давление зависит от высоты столба данного вещества и от его плотности.

Формула гидростатического давления:

р = ρ × g × h, где ρ — плотность вещества, g — ускорение свободного падения, h — высота столба.

g = 9,8 м/с²

Единица измерения давления жидкости или газа в СИ: паскаль (Па).

Однородная жидкость или газ давит на стенки сосуда равномерно, поскольку это давление создают хаотично движущиеся молекулы. И внешнее давление, оказываемое на вещество, тоже равномерно распределяется по всему его объему.

Закон Паскаля: давление, производимое на поверхность жидкого или газообразного вещества, одинаково передается в любую его точку независимо от направления.

Внешнее давление, оказываемое на жидкость или газ, рассчитывается по формуле:

p = F / S, где F — модуль силы, S — площадь поверхности.

Сообщающиеся сосуды

Сообщающимися называются сосуды, которые имеют общее дно либо соединены трубкой. Уровень однородной жидкости в таких сосудах всегда одинаков, независимо от их формы и сечения.

Если ρ₁ = ρ₂, то h₁ = h₂ и ρ₁gh₁ = ρ₂gh₂, где:

p — плотность жидкости,

h — высота столба жидкости,

g = 9,8 м/с².

Если жидкость в сообщающихся сосудах неоднородна, т. е. имеет разную плотность, высота столба в сосуде с более плотной жидкостью будет пропорционально меньше.

Высоты столбов жидкостей с разной плотностью обратно пропорциональны плотностям.

Гидравлический пресс — это механизм, созданный на основе сообщающихся сосудов разных сечений, заполненных однородной жидкостью. Такое устройство позволяет получить выигрыш в силе для оказания статического давления на детали (сжатия, зажимания и т. д.).

Если под поршнем 1 образуется давление p₁ = f₁/s₁, а под поршнем 2 будет давление p₂ = f₂/s₂, то, согласно закону Паскаля, p₁ = p₂

Следовательно,

Силы, действующие на поршни гидравлического пресса F₁ и F₂, прямо пропорциональны площадям этих поршней S₁ и S₂.

Другими словами, сила поршня 1 больше силы поршня 2 во столько раз, во сколько его площадь больше площади поршня 2. Это позволяет уравновесить в гидравлической машине с помощью малой силы многократно бóльшую силу.

Закон Архимеда

На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу объема жидкости или газа, вытесненного частью тела, погруженной в жидкость или газ.

Формула архимедовой силы:

F_a = ρ × g × V, где ρ — плотность жидкости, V — объем погруженной части тела, g — ускорение 9,8 м/с².

Закон Архимеда помогает рассчитать, как поведет себя тело при погружении в среды разной плотности. Верны следующие утверждения:

• если плотность тела выше плотности среды, оно уйдет на дно;

• если плотность тела ниже, оно всплывет на поверхность.

Другими словами, тело поднимется на поверхность, если архимедова сила больше силы тяжести.

Работа, энергия, мощность

Механическая работа — это физическая величина, которая равна произведению перемещения тела на модуль силы, под действием которой было выполнено перемещение.

Формула работы в курсе физики за 7 класс:

A = F × S, где F — действующая сила, S — пройденный телом путь.

Единица измерения работы в СИ: джоуль (Дж).

Такое понятие, как мощность, описывает скорость выполнения механической работы. Оно говорит о том, какая работа была совершена в единицу времени.

Мощность — это физическая величина, равная отношению работы к временному промежутку, потребовавшемуся для ее выполнения.

Формула мощности:

N = A / t, где A — работа, t — время ее совершения.

Также мощность можно вычислить, зная силу, воздействующую на тело, и среднюю скорость перемещения этого тела.

N = F × v, где F — сила, v — средняя скорость тела.

Единица измерения мощности в СИ: ватт (Вт).

Тело может совершить какую-либо работу, если оно обладает энергией — кинетической и/или потенциальной.

• Кинетической называют энергию движения тела. Она говорит о том, какую работу нужно совершить, чтобы придать телу определенную скорость.

• Потенциальной называется энергия взаимодействия тела с другими телами или взаимодействия между частями одного целого. Потенциальная энергия тела, поднятого над Землей, характеризует, какую работу должна совершить сила тяжести, чтобы опустить это тело снова на нулевой уровень.

Таблица с формулами по физике за 7 класс для вычисления кинетической и потенциальной энергии:

Кинетическая энергия	Пропорциональна массе тела и квадрату его скорости.	Ek = mv2/2
Потенциальная энергия	Равна произведению массы тела, поднятого над Землей, на ускорение свободного падения и высоту поднимания.	Ep= mgh
Полная механическая энергия	Складывается из кинетической и потенциальной энергии.	E = Ek+Ep
Сохранение и превращение энергии	Если механическая энергия не переходит в другие формы, то сумма потенциальной энергии и кинетической представляет собой константу.	Ek+ Ep= const

Для того, чтобы понять, какая часть совершенной работы была полезной, вычисляют коэффициент полезного действия или КПД. С его помощью определяется эффективность различных механизмов, инструментов и т. д.

Коэффициент полезного действия (КПД) отражает полезную часть выполненной работы. Также его можно выразить через отношение полезно использованной энергии к общему количеству полученной энергии.

Формула для расчета КПД:

где А_п— полезная работа, А_з— затраченная работа.

КПД выражается в процентах и составляет всегда меньше 100%, поскольку часть энергии затрачивается на трение, повышение температуры воздуха и окружающих тел, преодоление силы тяжести и т. д.

Удачи на экзаменах!

Алгебраическая формула, класс 7 — Решенные примеры, загружаемый файл PDF

Алгебра помогает представлять задачи в виде математических выражений. Он состоит из переменных, констант и математических операций, которые вместе образуют выражение. Изучение алгебраических формул для 7 класса важно для учащихся, поскольку помогает в решении различных задач. Чтобы помочь им облегчить процесс обучения и сделать алгебру интересной, в этой статье дается составленный список алгебраических формул класса 7, их применения и несколько быстрых советов по их запоминанию.

Список алгебраических формул 7-го класса

Краткий список основных формул, которые используются в алгебре 7-го класса, приведен ниже.

• (а + б) ² = а ² + 2аб + б ²
• (a — b) ³ = a ³ — b ³  — 3ab(a — b)
• (a — b) ² = a ²  — 2ab + b ²
• (а + b)(a — b) = a ² — b ²   

Применение алгебраических формул Класс 7

Алгебра используется во всех разделах математики, таких как тригонометрия, исчисление, координатная геометрия. Помимо этого, он используется в нашей повседневной жизни. Несколько приложений алгебраических формул приведены ниже.

• Алгебраические выражения используются для записи математических формул. Например, формула площади прямоугольника может быть выражена как l × b, где «l» — длина прямоугольника, а «b» — его ширина.
• Алгебраические формулы используются для решения текстовых задач, связанных с несколькими темами, такими как среднее, расстояние, унитарный метод.
• Алгебру можно использовать для оценки нашего ежедневного расписания каждый день, чтобы измерить время, которое мы тратим на чистку зубов, принятие душа, завтрак и походы в школу или на работу.

Советы по запоминанию алгебраических формул Класс 7

Существует множество способов легкого запоминания алгебраических формул. Следующие советы могут помочь учащимся быстро выучить алгебраические формулы для эффективного обучения.

• Попробуйте связать формулы с историей или сплести историю вокруг формул и понятий. Это сделает предмет интересным, и можно будет легко вспомнить основы в виде истории.
• Студенты должны попробовать учиться со своими друзьями, это поможет обменяться идеями, а также мгновенно прояснить сомнения.
• Учащиеся 7 класса могут выучить алгебраические формулы, используя свои смартфоны и ноутбуки. Они могут загрузить изображения формул из Интернета и установить их в качестве экранных заставок. Это гарантирует, что они могут иметь свою версию всякий раз, когда они используют свое устройство.

Алгебраические формулы Класс 7 Примеры

Пример 1: Добавьте все подобные члены и упростите выражение: , нам нужно изменить термины,

6M ² -8M + 2M-2M ² -3M + 5

= 6M ² -2M ² -8M + 2M + 5

= = =. 4м ²  — 9м + 5

Пример 2: Мать Джона в три раза старше Джона. Если матери Джона 39 лет, найдите возраст Джона.

Решение:

Пусть возраст Джона равен x.

Возраст матери Джона 3x = 39

x = 39/3 = 13.

Следовательно, возраст Джона = 13 лет. Алгебраические формулы класса 7

Какие важные алгебраические формулы класса 7?

Краткий список важных алгебраических формул для класса 7 приведен ниже:

• (a + b) ² = a ² + 2ab + b ²
• (a — b) ³ = a ³ — b ³  — 3ab(a — b)
• (a — b) ² = a ²  — 2ab + b ²
• (а + b) (а — b) = а ² — b ²

Что такое основные алгебраические формулы класса 7?

Базовые алгебраические формулы 7 класса охватывают понятия переменных, констант и упрощают алгебраические выражения, собирая одинаковые и неодинаковые термины по отдельности и складывая их. Неизвестную величину также можно вычислить, представив словесную задачу в алгебраическое уравнение. Существуют и другие формулы, которые можно использовать для решения таких задач, как (a + b) (a — b) = a ² — b ² , (a + b) ² = a ² + 2ab + b ²  и т.  д.

Сколько формул в алгебраических формулах 7 класса?

Алгебраические формулы класса 7 охватывают четыре важные формулы, приведенные ниже. Эти формулы помогают в факторизации алгебраических выражений, а также в упрощении сложных уравнений.

• (a — b) ² = a ²  — 2ab + b ²
• (а + b) (а — b) = а ² — b ²
• (а + b) ² = а ² + 2ab + b ²
• (а — б) ³ = а ³ — б ³ — 3аб(а — б)

Как запомнить алгебраические формулы 7 класса?

Принимая во внимание важность алгебры, становится важным, чтобы учащиеся хорошо знали основные понятия и алгебраические формулы в классе 7. Таким образом, следующие советы могут помочь им эффективно запомнить эти формулы:

• Истории легко запомнить. Таким образом, учащиеся могут попытаться связать основные понятия и алгебраические формулы с какой-либо историей или придумать собственную историю. Это помогает быстро вспомнить понятия и формулы.
• Студенты должны попытаться учиться вместе со своими друзьями, так как это позволит им поделиться идеями и получить немедленные ответы на все свои сомнения. Когда логика формул понятна, запомнить их несложно.
• Учащиеся также могут использовать свои смартфоны и ноутбуки для изучения алгебраических формул в классе 7. Они могут использовать изображения формул в качестве заставок, загрузив их из Интернета. Таким образом, они смогут пересматривать их всякий раз, когда используют свой смартфон или ноутбук.

Скачать БЕСПЛАТНЫЕ учебные материалы

Математические формулы 7 класс

Математические формулы для 7 класса Карточки

Похожие карточки

Пожалуйста, войдите, чтобы добавлять в папки.

Войти

Вы создали 2 папки. Пожалуйста, обновитесь до Cram Premium, чтобы создавать сотни папок!

Обновление

• Перемешать

  Включить

  Выключить

• В алфавитном порядке

  Включить

  Выключить

• Передний Первый

  Включить

  Выключить

• Обе стороны

  Включить

  Выключить

• Читать

  Включить

  Выключить

Чтение.