4Bc16 в десятичной системе счисления: Перевод 4bc16 из шестнадцатеричной в десятичную систему счисления

Автор — Лада Борисовна Есакова.

Перед тем, как приступить к решению задач, нам нужно понять несколько несложных моментов.

Рассмотрим десятичное число 875. Последняя цифра числа (5) – это остаток от деления числа 875 на 10. Последние две цифры образуют число 75 – это остаток от деления числа 875 на 100. Аналогичные утверждения справедливы для любой системы счисления:

Последняя цифра числа – это остаток от деления этого числа на основание системы счисления.

Последние две цифры числа – это остаток от деления числа на основание системы счисления в квадрате.

Например, . Разделим 23 на основание системы 3, получим 7 и 2 в остатке (2 – это последняя цифра числа в троичной системе). Разделим 23 на 9 (основание в квадрате), получим 18 и 5 в остатке (5 = ).

Вернемся опять к привычной десятичной системе. Число = 100000. Т.е. 10 в степени k– это единица и k нулей.

Аналогичное утверждение справедливо для любой системы счисления:

Основание системы счисления в степени k в этой системе счисления записывается как единица и k нулей.

Например, .

1. Поиск основания системы счисления

Пример 1.

В системе счисления с некоторым основанием десятичное число 27 записывается в виде 30. Укажите это основание.

Решение:

Обозначим искомое основание x. Тогда .Т.е. x = 9.

Ответ: 9

Пример 2.

В системе счисления с некоторым основанием десятичное число 13 записывается в виде 111. Укажите это основание.

Решение:

Обозначим искомое основание x. Тогда

Решаем квадратное уравнение, получаем корни 3 и -4. Поскольку основание системы счисления не может быть отрицательным, ответ 3.

Ответ: 3

Пример 3

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 29 оканчивается на 5.

Решение:

Если в некоторой системе число 29 оканчивается на 5, то уменьшенное на 5 число (29-5=24) оканчивается на 0. Ранее мы уже говорили, что число оканчивается на 0 в том случае, когда оно без остатка делится на основание системы. Т.е. нам нужно найти все такие числа, которые являются делителями числа 24. Эти числа: 2, 3, 4, 6, 8, 12, 24. Заметим, что в системах счисления с основанием 2, 3, 4 нет числа 5 (а в формулировке задачи число 29 оканчивается на 5), значит остаются системы с основаниями: 6, 8, 12,

Ответ: 6, 8, 12, 24

Пример 4

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 71 оканчивается на 13.

Решение:

Если в некоторой системе число оканчивается на 13, то основание этой системы не меньше 4 (иначе там нет цифры 3).

Уменьшенное на 3 число (71-3=68) оканчивается на 10. Т.е. 68 нацело делится на искомое основание системы, а частное от этого при делении на основание системы дает в остатке 0.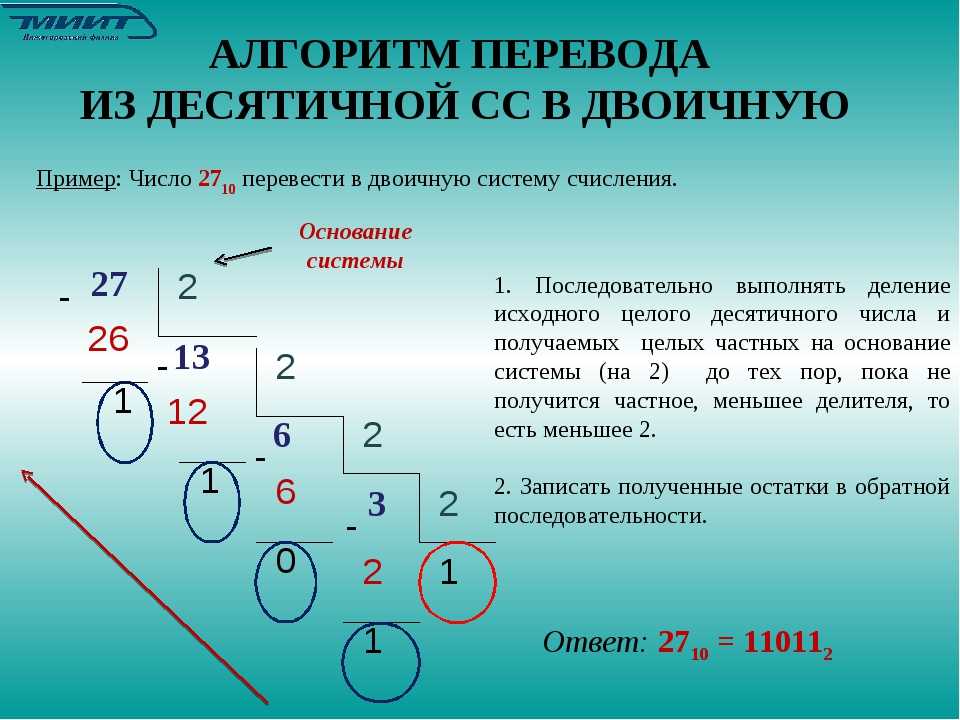

Выпишем все целые делители числа 68: 2, 4, 17, 34, 68.

2 не подходит, т.к. основание не меньше 4. Остальные делители проверим:

68:4 = 17; 17:4 = 4 (ост 1) – подходит

68:17 = 4; 4:17 = 0 (ост 4) – не подходит

68:34 = 2; 2:17 = 0 (ост 2) – не подходит

68:68 = 1; 1:68 = 0 (ост 1) – подходит

Ответ: 4, 68

2. Поиск чисел по условиям

Пример 5

Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием четыре оканчивается на 11?

Для начала выясним, как выглядит число 25 в системе счисления с основанием 4.

. Т.е. нам нужно найти все числа, не больше , запись которых оканчивается на 11. По правилу последовательного счета в системе с основанием 4,
получаем числа и . Переводим их в десятичную систему счисления:

Ответ: 5, 21

3. Решение уравнений

Пример 6

Решите уравнение:

Ответ запишите в троичной системе (основание системы счисления в ответе писать не нужно).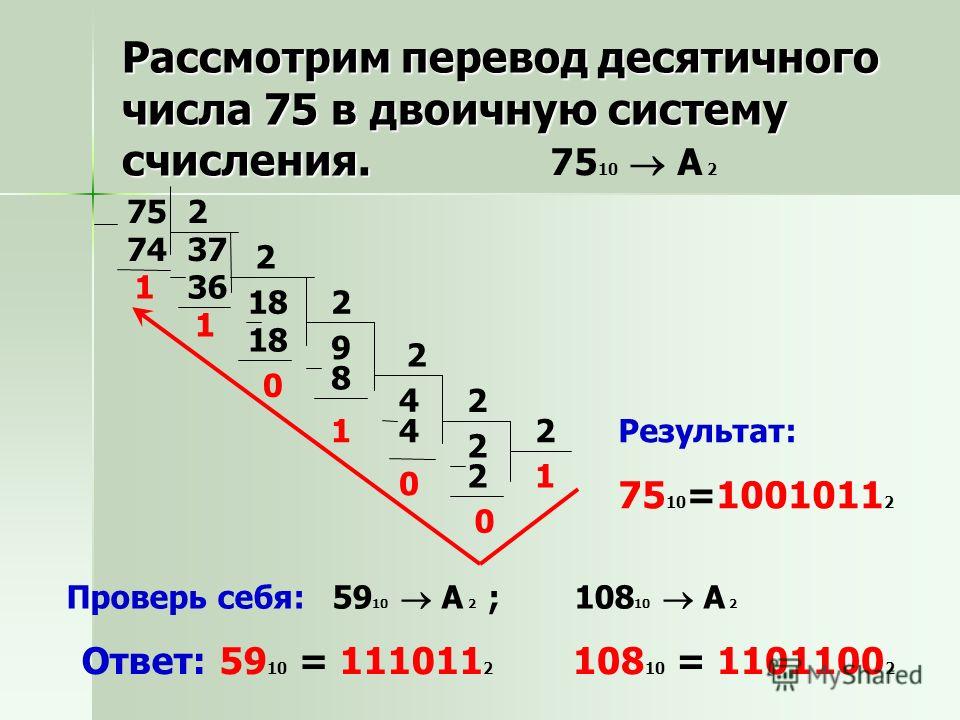

Решение:

Переведем все числа в десятичную систему счисления:

Квадратное уравнение имеет корни -8 и 6. (т.к. основание системы не может быть отрицательным). .

Ответ: 20

4. Подсчет количества единиц (нулей) в двоичной записи значения выражения

Для решения этого типа задач нам нужно вспомнить, как происходит сложение и вычитание «в столбик»:

При сложении происходит поразрядное суммирование записанных друг под другом цифр, начиная с младших разрядов. В случае, если полученная сумма двух цифр больше или равна основанию системы счисления, под суммируемыми цифрами записывается остаток от деления этой суммы на основание системы, а целая часть от деления этой суммы на основание системы прибавляется к сумме следующих разрядов.

При вычитании происходит поразрядное вычитание записанных друг под другом цифр, начиная с младших разрядов. В случае, если первая цифра меньше второй, мы «занимаем» у соседнего (большего) разряда единицу.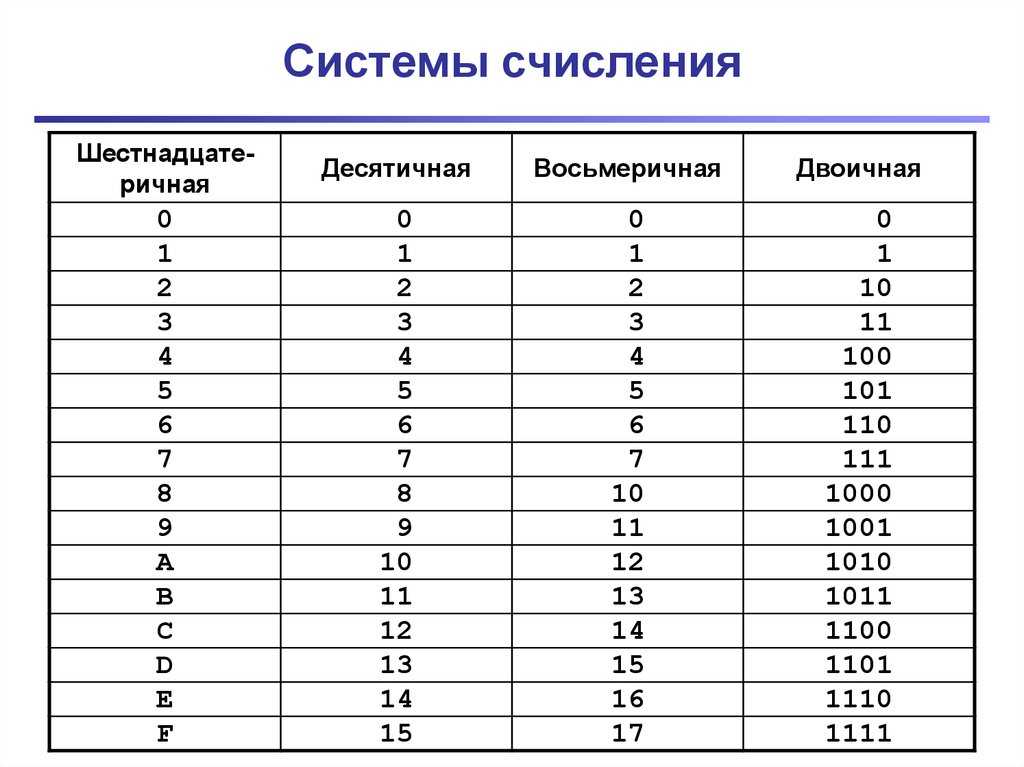 Занимаемая единица в текущем разряде равна основанию системы счисления. В десятичной системе это 10, в двоичной 2, в троичной 3 и т.д.

Пример 7

Сколько единиц содержится в двоичной записи значения выражения: ?

Решение:

Представим все числа выражения, как степени двойки:

В двоичной записи двойка в степени n выглядит, как 1 и n нулей. Тогда суммируя и , получим число, содержащее 2 единицы:

Теперь вычтем из получившегося числа 10000. По правилам вычитания занимаем у следующего разряда.

Теперь прибавляем к получившемуся числу 1:

Видим, что у результата 2013+1+1=2015 единиц.

Ответ: 2015.

Спасибо за то, что пользуйтесь нашими статьями. Информация на странице «Задача №16. Поиск основания системы по окончанию числа, уравнения и различные кодировки, арифметические действия в различных системах.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.

Публикация обновлена: 07.04.2023

Как преобразовать 4bc из шестнадцатеричной системы в двоичную

Что такое 4bc в шестнадцатеричной системе счисления? 4bc из шестнадцатеричной системы счисления в двоичную — это 10010111100. Здесь мы покажем вам, как записать 0x4bc в двоичной системе и как преобразовать 4bc из шестнадцатеричной системы счисления в двоичную.

Число:

От: двоичный [с основанием 2] троичный [с основанием 3] четверичный [с основанием 4] пятеричный [с основанием 5] десятеричный [с основанием 6] семеричный [с основанием 7] восьмеричный [с основанием 8] ненарочный [с основанием 9] десятичный [ с основанием 10] одиннадцатеричный [с основанием 11] двенадцатеричный [с основанием 12] трехдесятеричный [с основанием 13] четырехдесятичный [с основанием 14] пятидесятичный [с основанием 15] шестнадцатеричный [с основанием 16] семидесятеричный [с основанием 17] октодесятеричный [с основанием- 18] шестнадцатеричный [основание-19] десятичный [по основанию-20] недесятеричный [по основанию-21] двенадцатеричный [по основанию-22] трехдесятеричный [по основанию-23] тетрадесятичный [по основанию-24] пятидесятеричный [по основанию-25] тройничный [по основанию-30] двенадцатеричный [по основанию-32]

К: двоичный [с основанием 2] троичный [с основанием 3] четверичный [с основанием 4] пятеричный [с основанием 5] десятеричный [с основанием 6] семеричный [с основанием 7] восьмеричный [с основанием 8] ненарочный [с основанием 9] десятичный [ с основанием 10] одиннадцатеричный [с основанием 11] двенадцатеричный [с основанием 12] трехдесятеричный [с основанием 13] четырехдесятичный [с основанием 14] пятидесятичный [с основанием 15] шестнадцатеричный [с основанием 16] семидесятеричный [с основанием 17] октодесятеричный [с основанием- 18] шестнадцатеричный [основание-19] десятичный [по основанию-20] недесятеричный [по основанию-21] двенадцатеричный [по основанию-22] трехдесятеричный [по основанию-23] тетрадесятичный [по основанию-24] пятидесятеричный [по основанию-25] тройничный [по основанию-30] двенадцатеричный [по основанию-32]

10010111100 ₂

В системе счисления мы знаем, что шестнадцатеричная система счисления — это основание 16, а двоичное — основание 2. Чтобы преобразовать шестнадцатеричное число 4bc в двоичное, выполните следующие действия:

Сначала преобразовать 4bc ₁₆ into decimal, by using above steps:

= 4bc ₁₆
= 4 × 16 ² b × 16 ¹ c × 16 ⁰
= 1212 ₁₀

Now, we have to convert 1212 ₁₀ в двоичный код

1212 / 2 = 606 с остатком 0
606 / 2 = 303 с остатком 0
303 / 2 = 151 с остатком 1
151 / 2 = 75 с остатком 7 = 7 / 3 95029 остаток 1
37 / 2 = 18 с остатком 1
18 / 2 = 9 с остатком 0
9 / 2 = 4 с остатком 1
4 / 2 = 2 с остатком 0
2 / 2 = 1 с остатком 0
1 / 2 = 0 с остатком 1

Затем просто запишите остатки в обратном порядке, чтобы получить Таким образом, шестнадцатеричное число 4bc, преобразованное в двоичное, равно:

10010111100

Вот еще несколько примеров преобразования шестнадцатеричного в двоичное

• 0022
• 4BF из шестнадцатеричной в двоичную
• 4C0 из шестнадцатеричной в двоичную

[РЕШЕНО] Преобразование 1001011110000001100 из двоичного в десятичное



Ответ

Предупреждение

1. Введите число в двоичной, шестнадцатеричной или десятичной форме.
2. Выберите двоичный, шестнадцатеричный или десятичный вывод, затем вычислите число.

Номер для преобразования

Бинарный

восьмеричный

Десятичная дробь

шестнадцатеричный

Выход

Бинарный

восьмеричный

Десятичная дробь

шестнадцатеричный

Бинарная Бонанза! Увлекательная игра для тренировки преобразования чисел в двоичные и обратно

Игра Cisco с двоичными числами Классическая игра для тренировки преобразования чисел в двоичные и обратно

Почему компьютеры используют двоичные числа?

Что такое двоичное число

Двоичные, шестнадцатеричные и восьмеричные уроки

См.