Урок 24. логарифмы. свойства логарифмов — Алгебра и начала математического анализа — 10 класс

Алгебра и начала математического анализа, 10 класс

Урок № 24. Логарифм. Свойства логарифмов.

Перечень вопросов, рассматриваемых в теме

1. Определение логарифма.

2. Основное логарифмическое тождество.

3. Свойства логарифмов.

Глоссарий по теме

Логарифмом положительного числа по основанию , называется показатель степени, в которую надо возвести чтобы получить .

Логарифмирование – это действие нахождения логарифма числа.

Основное логарифмическое тождество:

Свойства логарифмов. При , справедливы равенства:

— логарифм произведения: ;

— логарифм частного: ;

— логарифм степени: .

Основная литература:

Колягин Ю. М., Ткачева М. В., Фёдорова Н.Е. и др. Математика: алгебра и начала математического анализа, геометрия.

Алгебра и начала математического анализа. 10 класс. Базовый и углублённый уровни. – М.: Просвещение, 2014. – 384 с.

Открытые электронные ресурсы:

http://fipi.ru/

Теоретический материал для самостоятельного изучения

При решении простейших показательных уравнений не всегда можно найти точный ответ. Например, уравнение имеет корень 5, т. к. значит , В уравнении число 5 не является степенью 2, значит предыдущий способ решения не подходит. Нам известно, что уравнение имеет единственный корень. Посмотрим это на графике.

Абсцисса точки пересечения – единственное решение данного уравнения. Это число и называют логарифмом 5 по основанию 2.

Дадим определение логарифма.

Логарифмом положительного числа по основанию , называется показатель степени, в которую надо возвести чтобы получить .

Т. е. логарифм числа по основанию , есть некоторое число такое, что .

Пример 1.

, т. к. выполнены все условия определения:

1) 216 > 0; 2) 6 > 0, 6 ≠ 1; 3) .

Пример 2.

, т. к. выполнены все условия определения:

1) ; 2) 2 > 0, 2 ≠ 1; 3) .

Это действие называется логарифмированием.

Логарифмирование – это действие нахождения логарифма числа.

Существует краткая запись определения логарифма:

так называемое основное логарифмическое тождество. Его используют при вычислениях.

Пример 3.

(Читают: 4 в степени логарифм 5 по основанию 4 равен 5)

Пример 4.

(Читают: одна треть в степени логарифм 6 по основанию одна треть равен 6)

Решим несколько задач с использованием определения логарифма.

Задача 1. Вычислить .

Решение. Пусть тогда по определению логарифма Приведем левую и правую части к одному основанию. 27 = 33, 81 = 34, значит . Отсюда следует, что

Задача 2. Вычислить .

Решение. Для вычисления воспользуемся свойствами степеней: 1) , 2) и основным логарифмическим тождеством: .

.

Для решения более сложных задач потребуется знание свойств логарифмов. Рассмотрим их.

1. Логарифм произведения.

Логарифм произведения чисел по основанию равен сумме логарифма по основанию и логарифма по основанию .

Пример 5.

2. Логарифм частного.

Логарифм частного чисел по основанию равен разности логарифма по основанию и логарифма по основанию .

Пример 6.

3. Логарифм степени.

Логарифм числа по основанию равен произведению показателя и логарифма по основанию .

Пример 7.

Важно! Свойства выполняются при ,

Примеры и разбор решения заданий тренировочного модуля

№ 1. Вычислите: .

Решение:

Чтобы выполнить это задание нам понадобятся следующие определения и свойства:

  2. ;
  3. .

Представим в виде степени с рациональным показателем: . Далее воспользуемся свойством нахождения логарифма степени: . Вспоминаем таблицу квадратов: , значит , . Ответ: .

№ 2. Вычислите

Решение:

Чтобы выполнить это задание нам понадобятся следующие определения и свойства:

  1. ;
  2. ;
  3. ;
  5. .

.

Свойства логарифмов и примеры их решений (ЕГЭ — 2021)

То есть и аргумент, и основание должны быть больше нуля, а основание еще и не может равняться \( 1\).

Почему так?

Начнем с простого: допустим, что \( a=1\). Тогда, например, число не существует, так как в какую бы степень мы не возводили \( 1\), всегда получается \( 1\).

Более того, \( \displaystyle {{\log }_{1}}b\) не существует ни для какого \( \displaystyle b\ne 1\).

Но при этом \( \displaystyle {{\log }_{1}}1\) может равняться чему угодно (по той же причине – \( 1\) в любой степени равно \( 1\)). {\frac{1}{2}}}=\sqrt{4}=2\)), а вот \( \displaystyle {{\log }_{-4}}2\) не существует.

Поэтому и отрицательные основания проще выбросить, чем возиться с ними.

Ну а поскольку основание a у нас бывает только положительное, то в какую бы степень мы его ни возводили, всегда получим число строго положительное.

Значит, аргумент должен быть положительным.

Например, \( \displaystyle {{\log }_{2}}\left( -4 \right)\) не существует, так как \( 2\) ни в какой степени не будет отрицательным числом (и даже нулем, поэтому \( \displaystyle {{\log }_{2}}0\) тоже не существует).

В задачах с логарифмами первым делом нужно записать ОДЗ. 

Приведу пример:

Решим уравнение \( \displaystyle {{\log }_{x}}\left( x+2 \right)=2\).

Вспомним определение: логарифм \( \displaystyle {{\log }_{x}}\left( x+2 \right)\) – это степень, в которую надо возвести основание \( x\), чтобы получить аргумент \( \displaystyle \left( x+2 \right)\).

И по условию, эта степень равна \( 2\): \( \displaystyle {{x}^{2}}=x+2\). {2}}-x-2=0\).

Решим его с помощью теоремы Виета: сумма корней равна \( 1\), а произведение \( -2\). Легко подобрать, это числа \( 2\) и \( -1\).

Но если сразу взять и записать оба этих числа в ответе, можно получить 0 баллов за задачу на ЕГЭ.

Почему?

Давайте подумаем, что будет, если подставить эти корни в начальное уравнение?

\( \displaystyle x=2\text{: }{{\log }_{2}}\left( 2+2 \right)={{\log }_{2}}4=2\) – верно.

\( \displaystyle x=-1\text{: }{{\log }_{-1}}\left( -1+2 \right)=2\) – это явно неверно, так как основание не может быть отрицательным, то есть корень \( x=-1\) – «сторонний».

Чтобы избежать таких неприятных подвохов, нужно записать ОДЗ еще до начала решения уравнения:

\( \displaystyle \left\{ \begin{array}{l}x>0\\x\ne 1\\x+2>0\end{array} \right.\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}x>0\\x\ne 1.\end{array} \right.\)

Тогда, получив корни \( x=2\) и \( x=-1\), сразу отбросим корень \( -1\), и напишем правильный ответ. {2}}-4=0\text{ }\Leftrightarrow \text{ }\left[ \begin{array}{l}x=2\\x=-2.\end{array} \right.\)

Казалось бы, меньший корень равен \( \displaystyle -2\). Но это не так: согласно ОДЗ корень \( \displaystyle x=-2\) – сторонний, то есть это вообще не корень данного уравнения. Таким образом, уравнение имеет только один корень: \( \displaystyle x=2\).

Ответ: \( \displaystyle x=2\).

тестовые задания по теме Корни, степени, логарифмы

РАССМОТРЕНО УТВЕРЖДАЮ

на заседании МК зам по ОД

естественно-математического цикла

председатель МК __________И.Е.Ермолаева _______Т.В. Бунакова

КОНТРОЛЬНЫЙ СРЕЗ ПО МАТЕМАТИКЕ по теме « Корни, степени, логарифмы»

ВАРИАНТ 1

УРОВЕНЬ 1

№

ВОПРОСЫ

ВАРИАНТЫ ОТВЕТОВ

1

Вычислите

а) 2,4

б) 1,5

в) 4

г) 1,2

2

Упростите выражение

а)

б)

в)

г)

3

Представьте в виде степени с основанием x:

а)

б)

в)

г)

4

Найдите значение выражения: 81 +

а) 84

б) 35

в) 81

г) 48

5

Допишите правую часть формулы

_____, где a , xиy – любые действительные числа.

а)

б)

в)

г)

6

Представьте в виде степени с рациональным показателем

а)

б)

в)

г)

7

Допишите правую часть формулы

_____, где , ≠1,

x0 иy

а) b

б)

в)

г)

8

Вычислите по определению логарифма:

а) 3

б) 8

в) 0

г) 16

9

Найдите значение выражения:

+

а) 3

б) 4

в) 1

г) 0

10

Решите уравнение:

= -1

а)

б)

в) 1

г)

УРОВЕНЬ 2

ВАРИАНТ 1

1. Допишите предложение: Степенью числаa с натуральным показателем n, большим 1, называется _______________________________________________________________ .

2. Вставьте пропущенные слова: Арифметическим корнем натуральной степени n 2 из неотрицательного числа aназывается _______________ _______, n –я степень которого равна a.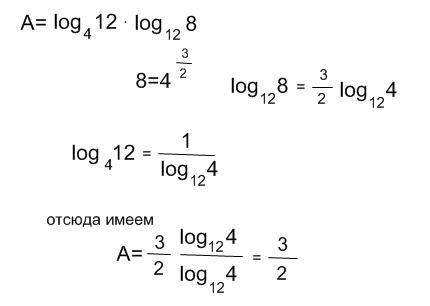

3. Вычислите: +

4. Представьте в виде степени с рациональным показателем: :

5. Вычислите:

РАССМОТРЕНО УТВЕРЖДАЮ

на заседании МК зам по ОД

естественно-математического цикла

председатель МК __________И.Е.Ермолаева _______Т.В. Бунакова

КОНТРОЛЬНЫЙ СРЕЗ ПО МАТЕМАТИКЕ по теме « Корни, степени, логарифмы»

УРОВЕНЬ 1ВАРИАНТ 2

№

ВОПРОСЫ

ВАРИАНТЫ ОТВЕТОВ

1

Вычислить

а) 2,4

б) 1,5

в) 4

г) 1,2

2

Упростите выражение

а)

б)

в)

г)

3

Представьте в виде степени с основанием x:

а)

б)

в)

г)

4

Найдите значение выражения: 52 —

а) 84

б) 35

в) 81

г) 48

5

Допишите правую часть формулы

_____, где , xи y-любые действительные числа.

а)

б)

в)

г)

6

Представьте в виде степени с рациональным показателем

а)

б)

в)

г)

7

Допишите правую часть формулы

_____, где , ≠1,

x0 иyНайдите число b, если

а) b

б)

в)

г)

8

Вычислите

а) 3

б) 8

в) 1

г) 1

9

Найдите значение выражения:

—

а) 3

б) 4

в) 1

г) 0

10

Решите уравнение:

= -2

а)

б)

в)

г)

ВАРИАНТ 2

УРОВЕНЬ 2

1. Степень любого числа a, не равного нулю, с нулевым показателем равна ______________

2. Вставьте пропущенные слова: Логарифмом положительного числа b по основанию a, где , ≠1, называется__________________ ___________, в которую надо возвести aчтобы получить b .

3. Вычислите: —

4. Представьте в виде степени с рациональным показателем: ∙

5. Вычислите:

РАССМОТРЕНО УТВЕРЖДАЮ

на заседании МК зам по ОД

естественно-математического цикла

председатель МК __________И.Е.Ермолаева _______Т.В. Бунакова

КОНТРОЛЬНЫЙ СРЕЗ ПО МАТЕМАТИКЕ по теме « Корни, степени, логарифмы»

ВАРИАНТ 3 УРОВЕНЬ 1

№

ВОПРОСЫ

ВАРИАНТЫ ОТВЕТОВ

1

Вычислить

а) 2,4

б) 1,5

в) 4

г) 1,2

2

Упростите выражение

а)

б)

в)

г)

3

Представьте в виде степени с основанием x:

а)

б)

в)

г)

4

Найдите значение выражения: 18 —

а) 84

б) 35

в) 14

г) 48

5

Допишите правую часть формулы

y, где , x иy -любые действительные числа.

а)

б)

в)

г)

6

Представьте в виде степени с рациональным показателем

а)

б)

в)

г)

7

Допишите правую часть формулы

_____, где , ≠1,

x0 иp — любое действительное число.

а) b

б)

в)

г)

8

Вычислите

а) 3

б) 4

в) 1

г) 16

9

Найдите значение выражения:

+

а) 3

б) 4

в) 1

г) 0

10

Решите уравнение:

= -3

а)

б)

в)

г)

ВАРИАНТ 3

УРОВЕНЬ 2

1. Допишите предложение: Логарифм числа по основанию е,

называют______________________________________ .

2. Вставьте пропущенное слово: При любом числе x и любом a0 степень является ___________________ действительным числом.

3. Вычислите: + 0,5

4. Представьте в виде степени с рациональным показателем: ∙

5. Вычислите:

РАССМОТРЕНО УТВЕРЖДАЮ

на заседании МК зам по ОД

естественно-математического цикла

председатель МК __________И.Е.Ермолаева _______Т.В. Бунакова

КОНТРОЛЬНЫЙ СРЕЗ ПО МАТЕМАТИКЕ по теме « Корни, степени, логарифмы»

ВАРИАНТ 4 УРОВЕНЬ 1

№

ВОПРОСЫ

ВАРИАНТЫ ОТВЕТОВ

1

Вычислить

а) 2,4

б) 1,5

в) 4

г) 1,2

2

Упростите выражение

а)

б)

в)

г)

3

Представьте в виде степени с основанием x:

а)

б)

в)

г)

4

Найдите значение выражения: 8 +

а) 84

б) 35

в) 81

г) 48

5

Допишите правую часть формулы

, где , x -любое действительное число.

а)

б)

в)

г)

6

Представьте в виде степени с рациональным показателем

а)

б)

в)

г)

7

Допишите правую часть формулы

_____, где , ≠1,

b0.

а) b

б)

в)

г)

8

Вычислите

а) 3

б) 8

в) 1

г) 16

9

Найдите значение выражения:

+

а) 3

б) 4

в) 1

г) 0

10

Решите уравнение:

= 0

а)

б)

в)

г)

ВАРИАНТ 4

УРОВЕНЬ 2

1. Допишите предложение: Логарифм числаb по основанию 10,

называют_____________________________________

2. Вставьте пропущенные слова: При умножении степеней с одинаковыми показателями ___________ оставляют прежним, а показатели ______________ .

3. Вычислите: +

4. Представьте в виде степени с рациональным показателем: ∙

5. Вычислите:

Эталоны ответов к контрольному срезу знаний по математике по теме « Корни, степени, логарифмы»

Уровень 1

№

1 вариант

2 вариант

3 вариант

4 вариант

1

а

б

в

г

2

г

в

б

а

3

б

г

в

а

4

а

г

в

б

5

г

б

а

в

6

а

в

г

б

7

б

г

в

а

8

в

г

б

а

9

г

в

б

а

10

а

б

г

в

Уровень 2

№

1 вариант

2 вариант

3 вариант

4 вариант

1

Произведение n множителей, каждый из которых равен a.

единице

Натуральным логарифмом

Десятичным логарифмом

2

Неотрицательное число

Показатель степени, в которую нужно возвести a, чтобы получить b.

положительным

Основаниями,

складывают

3

-3+0,5 ∙ 2=-3+1 = -2

0,75∙2 + 6= 7,5

3+0,5∙(-10)=3-5= -2

0,2∙5-3=1-3= -2

4

=

5

-3

2

2

1

Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/82606-testovye-zadanija-po-teme-korni-stepeni-logar

Правила логарифма

— ChiliMath

В этом уроке вам будут представлены общие правила логарифмов, также известные как «правила журнала». Эти семь (7) логарифмов полезны при расширении логарифмов, сжатии логарифмов и решении логарифмических уравнений. Кроме того, поскольку логарифмическая функция, обратная логарифмической функции, является экспоненциальной функцией, я бы также рекомендовал вам изучить правила экспоненты. Поверьте, они всегда идут рука об руку.

Если вам когда-либо было интересно, почему работают правила логарифма, ознакомьтесь с моим уроком о доказательствах или обоснованиях свойств логарифмов.

Правила логарифмов

Описание правил логарифмов

Правило 1: Правило произведения

Логарифм произведения — это сумма логарифмов факторов.

Правило 2: Правило частных

Логарифм отношения двух величин — это логарифм числителя минус логарифм знаменателя.

Правило 3: Правило мощности

Логарифм экспоненциального числа — это показатель степени, умноженный на логарифм основания.

Правило 4: Правило нуля

Логарифм 1 такой, что b> 0, но b ≠ 1 равняется нулю.

Правило 5: Правило идентичности

Логарифм аргумента (внутри скобок), в котором аргумент такой же, как основание, равен 1. Поскольку аргумент равен основанию, b должно быть больше 0, но не может быть равно 1.

Правило 6: Логарифм правила экспоненты (логарифм от основания до правила мощности)

Логарифм экспоненциального числа, основание которого совпадает с основанием журнала, равен экспоненте.

Правило 7: Правило экспоненты логарифмической мощности (основание для правила логарифмической мощности)

Возведение логарифма числа к основанию равняется числу.

Примеры применения правил журнала

Пример 1: Вычислите приведенное ниже выражение с помощью правил журнала.

{\ log _2} 8 + {\ log _2} 4

Express 8 и 4 как экспоненциальные числа с основанием 2. Затем примените Power Rule, а затем Identity Rule. После этого вы добавляете полученные значения, чтобы получить окончательный ответ.

Итак, ответ \ color {blue} 5.

Пример 2: Вычислите выражение ниже, используя правила журнала.

{\ log _3} 162 — {\ log _3} 2

Мы не можем выразить 162 как экспоненциальное число с основанием 3. Похоже, мы застряли, поскольку нет правил, которые можно было бы применить в прямом манера.

Однако можно применять правила логарифма в обратном порядке! Обратите внимание, что логарифмическое выражение может быть выражено в виде одного или одного логарифмического числа с помощью обратного правила Quotient Rule.Звучит как план.

Мы сделали это! Применяя правила в обратном порядке, мы сгенерировали одно легко разрешимое логарифмическое выражение. Окончательный ответ здесь \ color {blue} 4.

Пример 3: Вычислите выражение ниже.

Похоже, одновременно происходит так много всего. Во-первых, проверьте, можно ли упростить каждое из логарифмических чисел. Если нет, подумайте о некоторых логарифмических правилах, которые, очевидно, применимы.

Наблюдением мы видим, что здесь задействованы две основы: 5 и 4. Так почему бы не сложить выражения вместе с одной и той же основой? Давайте упростим их отдельно.

Для журнала с основанием 5 сначала примените правило мощности, а затем правило коэффициента. Для журнала с базой 4 немедленно примените Правило продукта. Затем получите окончательный ответ, сложив два найденных значения.

Ага, окончательный ответ \ color {blue} 7.

Пример 4: Разверните логарифмическое выражение ниже.5}} \ right)

В скобках указано произведение множителей. Примените правило продукта, чтобы разбить их как сумму отдельных выражений журнала. Убедитесь, что вы стараетесь изо всех сил сводить числовые выражения к точным значениям, когда это возможно. Используйте Правило 5 (Правило идентификации) как можно чаще, потому что оно может упростить процесс упрощения.

Верно! Последняя строка в подробном решении, как показано выше, является окончательным ответом. Хотя надо признать, что они выглядят несколько «недоделанными».Пока мы знаем, что правильно применяем правила, это не должно нас беспокоить.

Пример 5 : развернуть логарифмическое выражение.

Подход состоит в том, чтобы сначала применить правило частного как разность двух логарифмических выражений, поскольку они имеют дробную форму. Затем используйте правило произведения, чтобы разделить произведение факторов как сумму логарифмических выражений.

Пример 6 : развернуть логарифмическое выражение.

Значит, у этого есть радикальное выражение в знаменателе.{{1 \ over 2}}}. Как и в случае с проблемой №5, примените правило Quotient для журналов, а затем используйте правило продукта.

Пример 7 : развернуть логарифмическое выражение.

Подобная проблема может вызвать у вас сомнения, действительно ли вы пришли к правильному ответу, потому что окончательный ответ все еще может выглядеть «незаконченным». Однако, если вы правильно применяете правила журнала на каждом этапе, беспокоиться не о чем.

Вы могли заметить, что сначала нам нужно применить правило частного, потому что выражение имеет дробную форму.

Вас также могут заинтересовать:

Сжатые логарифмы

Расширяющиеся логарифмы

Объяснение логарифма

Решение логарифмических уравнений

Доказательства логарифмического уравнения

Логарифмические свойства

Логарифмические свойства

совсем как логарифмы.

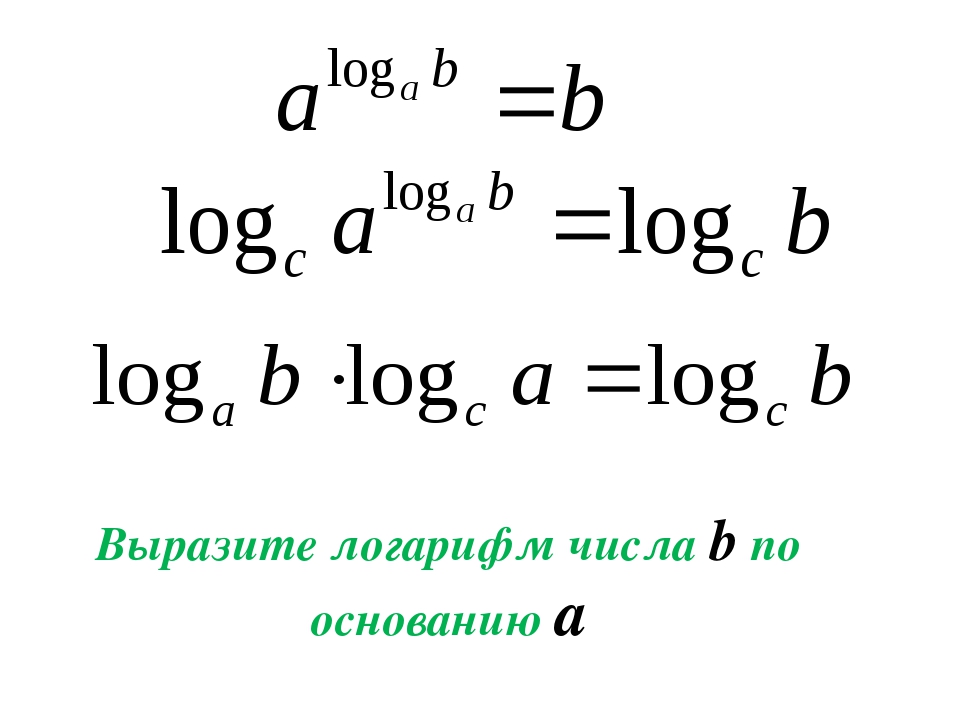Они громоздки, ими трудно манипулировать, и для некоторых они немного загадочны. К счастью, есть простой способ избавить ваше уравнение от этих надоедливых математических выражений.Все, что вам нужно сделать, это помнить, что логарифм — это величина, обратная экспоненте. Хотя основание логарифма может быть любым числом, наиболее распространенными основаниями, используемыми в науке, являются 10 и е, что является иррациональным числом, известным как число Эйлера. Чтобы различать их, математики используют «log», когда основание равно 10, и «ln», когда основание равно e.

TL; DR (слишком долго; не читал)

Чтобы избавить уравнение от логарифмов, возведите обе стороны до той же степени, что и основание логарифмов. В уравнениях со смешанными членами соберите все логарифмы с одной стороны и сначала упростите.

Что такое логарифм?

Понятие логарифма простое, но его сложно выразить словами. Логарифм — это количество раз, которое вам нужно умножить на одно число, чтобы получить другое число. Другой способ сказать, что логарифм — это степень, до которой необходимо возвести определенное число, называемое основанием, для получения другого числа. Степень называется аргументом логарифма.

Например, log 8 2 = 64 просто означает, что возведение 8 в степень 2 дает 64.В уравнении log x = 100 под основанием понимается 10, и вы можете легко найти аргумент x , потому что он отвечает на вопрос: «10 в какой степени равно 100?» Ответ: 2.

Логарифм — это величина, обратная экспоненте. Уравнение log x = 100 — это еще один способ записи 10_ x _ = 100. Это соотношение позволяет убрать логарифмы из уравнения, возведя обе части в один и тот же показатель степени, равный основанию логарифма.2 — x — 2 = 0.

Решения: x = −2; x = 1.

В уравнениях, которые содержат смесь логарифмов и других алгебраических членов, важно собрать все логарифмы на одной стороне уравнения. Затем вы можете складывать или вычитать термины. 3 \\ x = 1000x — 2000 \\ -999x = -2000 \\ x = \ frac {2000} {999} = 2.002

Используйте формулу замены основания для логарифмов

Большинство калькуляторов могут вычислять только обычные и натуральные логарифмы. Чтобы вычислить логарифмы с основанием, отличным от 10 или [латекс] e [/ latex], мы используем формулу изменения базы , чтобы переписать логарифм как частное от логарифмов любого другого основания; при использовании калькулятора мы изменили бы их на обычные или натуральные журналы.

Чтобы вывести формулу замены основания, мы используем свойство

«один к одному» и правило мощности для логарифмов .{y} \ right) \ hfill & = {\ mathrm {log}} _ {n} M \ hfill & \ text {Применить однозначное свойство}. \ hfill \\ y {\ mathrm {log}} _ {n} b \ hfill & = {\ mathrm {log}} _ {n} M \ hfill & \ text {Применить правило степени для логарифмов}. \ hfill \\ y \ hfill & = \ frac {{\ mathrm {log}} _ {n} M} {{\ mathrm {log}} _ {n} b} \ hfill & \ text {Isolate} y. \ hfill \\ {\ mathrm {log}} _ {b} M \ hfill & = \ frac {{\ mathrm {log}} _ {n} M} {{\ mathrm {log}} _ {n} b} \ hfill & \ text {Заменить} y. \ hfill \ end { case} [/ latex]

Например, чтобы вычислить [latex] {\ mathrm {log}} _ {5} 36 [/ latex] с помощью калькулятора, мы должны сначала переписать выражение как частное от обычных или натуральных логарифмов.Мы будем использовать общий журнал.

[латекс] \ begin {case} {\ mathrm {log}} _ {5} 36 \ hfill & = \ frac {\ mathrm {log} \ left (36 \ right)} {\ mathrm {log} \ left ( 5 \ right)} \ hfill & \ text {Примените изменение базовой формулы, используя базу 10} \ text {.} \ Hfill \\ \ hfill & \ приблизительно 2.2266 \ text {} \ hfill & \ text {Используйте калькулятор, чтобы оценивается до 4 знаков после запятой} \ text {.} \ hfill \ end {cases} [/ latex]

Общее примечание: Формула смены базы

Формула замены основания может использоваться для вычисления логарифма с любым основанием.

Для любых положительных действительных чисел M , b и n , где [латекс] n \ ne 1 [/ latex] и [latex] b \ ne 1 [/ latex],

[латекс] {\ mathrm {log}} _ {b} M \ text {=} \ frac {{\ mathrm {log}} _ {n} M} {{\ mathrm {log}} _ {n} b }[/латекс].

Отсюда следует, что формулу замены основания можно использовать для перезаписи логарифма с любым основанием в качестве частного от обычных или натуральных логарифмов.

[латекс] {\ mathrm {log}} _ {b} M = \ frac {\ mathrm {ln} M} {\ mathrm {ln} b} [/ latex]

и

[латекс] {\ mathrm {log}} _ {b} M = \ frac {\ mathrm {log} M} {\ mathrm {log} b} [/ латекс]

Как сделать: учитывая логарифм в форме [латекс] {\ mathrm {log}} _ {b} M [/ latex], используйте формулу замены базы, чтобы переписать его как частное от логарифмов с любым положительным основанием. [латекс] n [/ латекс], где [латекс] n \ ne 1 [/ латекс].

  1. Определите новую базу n , помня, что общий журнал, [latex] \ mathrm {log} \ left (x \ right) [/ latex], имеет основание 10, а натуральный журнал, [latex] \ mathrm {ln} \ left (x \ right) [/ latex], имеет базу e .
  2. Перепишите журнал как частное, используя формулу замены базы
    • В числителе частного будет логарифм с основанием n и аргументом M .
    • Знаменателем частного будет логарифм с основанием n и аргументом b .

Пример 13: Замена логарифмических выражений на выражения, содержащие только натуральные логарифмы

Замените [латекс] {\ mathrm {log}} _ {5} 3 [/ latex] на частное от натуральных логарифмов.

Решение

Поскольку мы будем выражать [латекс] {\ mathrm {log}} _ {5} 3 [/ latex] как частное от натуральных логарифмов, новое основание n = e .

Мы переписываем журнал как частное, используя формулу замены базы. В числителе частного будет натуральный логарифм с аргументом 3.Знаменателем частного будет натуральный логарифм с аргументом 5.

[латекс] \ begin {case} {\ mathrm {log}} _ {b} M \ hfill & = \ frac {\ mathrm {ln} M} {\ mathrm {ln} b} \ hfill \\ {\ mathrm {log}} _ {5} 3 \ hfill & = \ frac {\ mathrm {ln} 3} {\ mathrm {ln} 5} \ hfill \ end {case} [/ latex]

Попробовать 13

Замените [latex] {\ mathrm {log}} _ {0.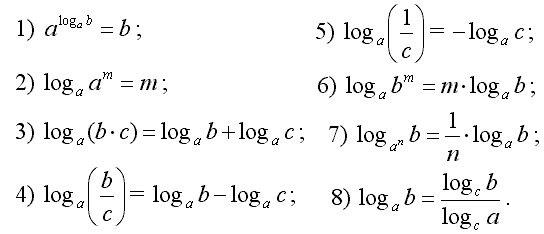 5} 8 [/ latex] на частное от натуральных логарифмов.

Решение

Вопросы и ответы

Можно ли заменить десятичный логарифм на натуральный?

Да.Помните, что [латекс] \ mathrm {log} 9 [/ latex] означает [латекс] {\ text {log}} _ {\ text {10}} \ text {9} [/ latex]. Итак, [латекс] \ mathrm {log} 9 = \ frac {\ mathrm {ln} 9} {\ mathrm {ln} 10} [/ latex].

Пример 14: Использование формулы изменения базы в калькуляторе

Вычислите [латекс] {\ mathrm {log}} _ {2} \ left (10 \ right) [/ latex] с помощью калькулятора по формуле замены базы.

Решение

Согласно формуле замены базы, мы можем переписать логарифм по основанию 2 как логарифм любого другого основания.Поскольку наши калькуляторы могут вычислять натуральный логарифм, мы можем использовать натуральный логарифм, который представляет собой логарифм с основанием e .

[латекс] \ begin {cases} {\ mathrm {log}} _ {2} 10 = \ frac {\ mathrm {ln} 10} {\ mathrm {ln} 2} \ hfill & \ text {Применить изменение базовая формула с использованием base} e. \ hfill \\ \ приблизительно 3.3219 \ hfill & \ text {Используйте калькулятор для вычисления до 4 знаков после запятой}. \ hfill \ end {cases} [/ latex]

Попробуйте 14

Вычислить [латекс] {\ mathrm {log}} _ {5} \ left (100 \ right) [/ latex], используя формулу замены базы.

Решение

журналов и экспонент


Одно из основных свойств чисел состоит в том, что они могут быть выражены в экспоненциальной форме. Все мы знакомы с представлением 1000 = 10 3 или 0,001 = 10 -3 . Более общий способ изложения это свойство означает, что любое число (N) может быть выражено как основание (B) в степени (x) или N = B x

В приведенных выше примерах формула основана на 10. Дополнительные примеры с использованием основание 10, основание 2 и основание e (где e = 2.718 …) приведены ниже в таблице 1.

Таблица 1
Число = 10 x Число = 2 x Число = e x
, 01 10 -2 1 2 0 . 01 е -4,605 ​​
1 10 0 2 2 1 ​​ 1 e 0
10 10 1 ​​ 4 2 2 10 и 2.303
1000 10 3 8 2 3 1000 е 6,908
2 10 .301 2 e 0,693
4 10 . 602 4 е 1,386
8 10 .903 8 е 2,079

Первые четыре записи в разделе base-10 выглядят естественно, как и записи в базе 2, но немногие студенты сразу догадаются .301 как соответствующий показатель степени для 2 = 10 x . Далее натуральная база e (e = 2,71828 ..), вероятно, поначалу кажется нелогичным основанием для представления числа.Как будет показано ниже, экспоненциальные функции типа y = ae bx очень часто используются при описании физических и химических систем, и необходимо базовое понимание этого типа функций.

ЛОГАРИФМЫ

Математическое утверждение N = B x служит основой для определяющие логарифмы. Логарифм числа (N) по основанию (B) определяется как (х).

логарифм (В) Н = х

Обычно используются две базы: 10 и e.Стенографические представления находятся:

логарифм по основанию 10 10 N = лог 10 N = журнал N
и
по основанию e («натуральный» логарифм) логарифм e N = внутренний N
Таким образом, логарифм числа — это просто степень, в которой основание должно быть поднятым, чтобы дать номер. Таблица 2 показывает логарифм и ln чисел. в таблице 1.
Таблица 2
Число бревно пер
.0100 -2,000 -4,605
1,00 0 0
10. 0 1.000 2.303
1000 3.000 6,908
2,00 0,301 0,693
4.00 0,602 1,386
8.00 0.903 2,079

ПРИМЕЧАНИЕ:
Только числа справа от десятичной точки в логарифме значимые фигуры. Число слева от десятичной точки просто, по сути, сообщает нам, где находится десятичная точка, и не считается значимая цифра.

Есть несколько основных правил обработки логарифмов. Приведены примеры в базе 10, но правила применимы к любой базе.

Правило 1: журнал (a x b) = журнал a + журнал b
Примеры:

журнал (2000) = журнал (2 x 1000) = журнал 2 + журнал 1000 = 0,301 + 3 = 3,301
журнал (0,004) = журнал (4 x 0,001) = журнал 4 + журнал 0,001 = 0,602 — 3 = -2,398
Правило 2: журнал (а / б) = журнал а — журнал б
Примеры:
журнал (2/4) = журнал 2 — журнал 4 = . 301 — .602 = -.301
журнал (2 / .4) = журнал 2 — журнал .4 = журнал 2 — [журнал (4 x .1)] = .301 — [.602 — 1] = 0,699
Правило 3: log (a) b = b log a
Примеры:
журнал (4) 3 = 3 журнал 4 = 3 x.602 = 1,806
журнал (8) 1/2 = 1/2 журнал 8 = 1/2 x 0,903 = 0,452
Правило 4: журнал (10) x = x
Примеры:
журнал 10 -8 = -8
по 4 = 4
Если у кого-то есть логарифм числа и он хочет его найти, просто возводит основание в степень логарифма. Это называется взятием антилогарифм.

Примеры:

антилогарифм .301 = 10 .301 = 2
антилогарифмический 1.806 = 10 1.806 = 64
антилог -2.398 = 10 -2,398 = 0,004
antiln 2.303 = e 2.303 = 10
antiln 1.386 = e 1.386 = 4
Примечание: На большинстве калькуляторов антилогарифмы могут приниматься
  • INV + log или INV + ln

    • или
  • 10 x или e x

    • или
  • y x , где y = BASE.
Хотя логарифмы интересны и полезны сами по себе, они наибольшая применимость для нас при работе с экспоненциальными функциями. ЛОГАРИФМИЧЕСКИЙ И ЭКСПОНЕНЦИАЛЬНЫЕ ФУНКЦИИ

Одно из наиболее распространенных функциональных соотношений, возникающих из экспериментальных наблюдения — это экспоненциальное увеличение или уменьшение. Это требует форма выражения как

y = e x и y = e -x

В более общем виде это выглядит как

y = e ax и y = e -ax

, где a группирует вместе любые количества, которые могут рассматриваться как константа при изменении x и y.На графике эти функции появляются, как показано на рисунке 1 (обратите внимание, что когда x = 0, y становится = 1). Основание Логарифмы можно преобразовать в логарифмы по основанию 10.

Рисунок 1. Экспоненциальные функции

Поскольку получить точный вид коэффициента очень сложно a из таких графиков, становится удобнее применять логарифмы к функциям в этой форме. Таким образом,
y = e ax становится ln y = ax; y = 10 a’x становится журнал y = a’x

или 2.3 журнал y = ax. [Обратите внимание, что a ‘= a / 2.3]

и график зависимости ln (или log) y от x даст прямую линию наклон которого будет «а». Те же соображения применимы к этим выражениям когда они прямые, как любые прямые.

В простом случае рассмотрим данные из таблицы 3 для разложения перекиси водорода. Показаны два способа графического представления этих данных. ниже: (а) концентрация в зависимости от времени в прямоугольных координатах, (б) log концентрация против времени по прямоугольным координатам.Это проиллюстрировано на рисунках 2а — 2б.

Таблица 3
Разложение перекиси водорода
Время Концентрация Лог концентрации
0 22,8 1,358
5 17,6 1,245
10 13,8 1. 140
15 10.5 1.021
20 8,25 0,916

Рисунок 2а. Разложение пероксида водорода
График концентрации от времени

Рисунок 2б. Разложение пероксида водорода
График журнала Концентрация от времени

Используется ли для таких отношений логарифмическая или экспоненциальная форма зависит от того, что предстоит определить.Математически экспоненциальная форма имеет определенные преимущества, в то время как графически логарифмическая форма более информативна. Любые функциональные отношения в этой форме имеют узнаваемые характеристики. что становится более очевидным, когда в общее выражение включается еще один символ. Таким образом,

y = y o e -ax

, где y o — постоянная, определяемая тем, что при x = 0, значение e -ax = 1 и при этих условиях y = y o . Следующие ниже примеры иллюстрируют общие характеристики этого типа. функции. «A» — это конкретная константа в каждом примере.

  1. Уменьшение концентрации реагирующего материала c в единицу времени t пропорционально концентрации и выражается как

    2. c = c o e -at
    , где c o — концентрация в момент времени t = 0 (в начале эксперимента).
  2. Уменьшение интенсивности падающего света I пропорционально на глубину l поглощающего материала и выражается как

    3. I = I o e -al
    где I o — интенсивность падающего излучения на l = 0, прежде чем он пройдет через поглощающий материал.
  3. Давление атмосферы P уменьшается со скоростью, пропорциональной высота h и выражается как

    4. P = P o e -ah
    , где P o — давление при h = 0 на уровне моря.
Общие Подход к созданию уравнения из данных
  1. Нанесите указанные числовые значения для x и y на миллиметровую бумагу, используя y как вертикальная ось (ордината) и x как горизонтальная ось (абсцисса). Если доступна программа построения графиков для микрокомпьютера, она обеспечивает удобный Способ пойти изучить график, не прибегая к бумажной копии.Экспериментально независимое значение обычно наносится на ось x, а экспериментально измеряемая, зависимая, переменная по оси y.
  2. Если полученный график показывает прямую линию, уравнение для исходного числовые значения легко определяются, так как уравнение прямой строка

    3. у = mx + b
    , где m = наклон и b = пересечение линии с осью y (при x = 0).
Рисунок A. Положительный наклон
уклон = м = подъем / спуск = 2/3

Рисунок B.Отрицательный уклон
уклон = м = подъем / спуск = -2/2 = -1

    Рассчитайте или прочтите значения m и b, затем вставьте m и b значений в уравнение y = mx + b. В результате должно получиться уравнение Вы ищете. Чтобы дважды проверить свою работу, попробуйте некоторые из оригинальных заданные значения x в вашем уравнении и посмотрите, получится ли y, как ожидалось. Уравнение линии на рис. A имеет вид y = 2x / 3 + 5/3, а для рис. B — у = -х + 5 = 5 — х.

  1. Если сюжет, полученный в результате шага I, не является прямой линией, вы не особенно Вероятно, это произойдет при осмотре.Т.е. тот факт, что если x = 3, y = 9, (одна точка) не означает, что уравнение имеет вид y = x 2 (справедливо для всех точек). Один из способов — преобразовать исходные данные в прямая линия. В этом курсе мы встретимся с несколькими отношениями форма

    2. y = ae -b / T
    где y — некоторое свойство системы, a и b — константы, а T это температура в Кельвинах. Все эти функции линеаризуются, если взять натуральный логарифим выражения.

    ln y = ln a — b / T. График зависимости ln y от 1 / T даст прямую линию с наклон -b и пересечение ln a.

Задачи

4.3 — Свойства логарифмов

4.3 — Свойства логарифмов

Изменение базовой формулы

Одна дилемма состоит в том, что в вашем калькуляторе есть логарифмы только для двух оснований. База 10 (журнал) и база e (ln). Что произойдет, если вы захотите узнать логарифм для какой-то другой базы? Вам не повезло?

№ Есть изменение базовой формулы для преобразования между разными базами.К найти базу журнала a, где a предположительно некоторое число, отличное от 10 или e , в противном случае вы просто использовали бы калькулятор,

Возьмите логарифм аргумента, разделенный на логарифм основания.

журнал a x = (журнал b x) / (журнал b a)

Там нет необходимости использовать основание 10 или основание e , но поскольку это два у вас есть на калькуляторе, вероятно, это те два, которые вы собираетесь использовать больше всего.Я предпочитаю натуральный журнал (ln всего 2 буквы, а журнал 3, плюс есть дополнительная выгода, о которой я знаю из расчетов). База, которая вы используете не имеет значения, только то, что вы используете одну и ту же базу для числителя и знаменатель.

журнал a x = (журнал x) / (журнал a) = (ln x) / (ln a)

Пример: журнал 3 7 = (ln 7) / (ln 3)

Логарифмы — экспоненты

Помните, что логарифмы — это показатели степени, поэтому свойства показателей свойства логарифмов.

Умножение

Какое правило, когда вы умножаете два значения с одинаковым основанием вместе (x 2 * x 3 )? Правило состоит в том, что вы сохраняете базу и добавляете экспоненты. Хорошо, помните, что логарифмы — это показатели, и когда вы умножаете, вы собираетесь сложить логарифмы.

журнал продукта — это сумма журналов.

журнал a xy = журнал a x + журнал a y

Дивизион

Правило при делении двух значений с одинаковым основанием — вычитание экспоненты.Поэтому правило деления — вычитание логарифмов.

логарифм частного — это разница журналов.

журнал a (x / y) = журнал a x — журнал a y

Возведение к власти

Когда вы возводите количество в степень, правило состоит в том, что вы умножаете показатели вместе. В этом случае одним из показателей будет лог, а другим — экспонента будет степенью, до которой вы увеличиваете количество.

экспонента на аргументе — коэффициент журнала.

журнал a x r = r * журнал a x

Мелодическая математика

Некоторые из приведенных выше утверждений очень мелодичны. То есть звучат хорошо. Это может помочь вам запомнить мелодическую математику, а не формулы.

  • Журнал продукта — это сумма журналов
  • Сумма журналов — это журнал продуктов
  • Логарифм частного — разность бревен
  • Разница журналов — это журнал частного
  • Показатель степени аргумента — это коэффициент журнала
  • Коэффициент при логарифме — это показатель степени при аргументе

Ладно, последние два не такие мелодичные.

Общие ошибки

Я почти не решаюсь поместить сюда этот раздел. Кажется, когда я пытаюсь указать ошибка, которую люди собираются совершить, что больше людей совершают ее.

  • The журнал суммы НЕ является суммой журналов. Сумма журналов — это журнал продукт. Журнал суммы не может быть упрощен.
    журнал a (x + y) ≠ журнал a x + журнал a y
  • The журнал разницы НЕ является разницей журналов.Разница журналы — это журнал частного. Журнал разницы не может быть упрощен.
    журнал a (x — y) ≠ журнал a x — журнал a y
  • An показатель степени в журнале НЕ является коэффициентом журнала. Только когда аргумент возведен в степень, можно превратить показатель степени в коэффициент. Когда весь логарифм возведен в степень, то его нельзя упростить.
    (журнал a x) r ≠ r * журнал a x
  • The журнал частного не является частным из журналов. Частное бревен от изменения базовой формулы. Журнал частного — это разница журналов.
    журнал a (x / y) ≠ (журнал a x ) / (журнал а г)

logfunc

logfunc ЛОГАРИФМИЧЕСКИЙ ФУНКЦИИ

А логарифмическая функция является обратной по отношению к экспоненциальной функции. Обратный Функция получается путем замены x и y в функции. Логарифмический функцию можно записать в виде x = a y
дюйм В предыдущем разделе мы нарисовали уравнения этой формы.

Переписывание в форме журнала: когда мы пишем логарифмическую функцию как x = a y , мы говорим, что это экспоненциальная форма. Альтернатива — логарифмическая форма написана y = log a x, который читается как «логарифм по основанию x» или «логарифм по основанию а».

Определение журнала: log a x определяется как показатель степени, необходимый для возведения a до, чтобы получить x.

  • журнал 3 81 равно 4, так как 3 нужно возвести в 4-ю степень, чтобы получить 81
  • журнал 3 3 m равно m, так как 3 необходимо возвести в m-ю степень в чтобы получить 3 м
  • бревно x x равен 1, так как x необходимо возвести в 1-ю степень, чтобы получить х
  • бревно x 1 равно 0, так как x необходимо возвести в нулевую степень, чтобы получить 1
Преобразование между экспоненциальной и логарифмической формой:
х = у и у = log a x оба указывают одно и то же отношения между x и y.Оба они указывают на то, что если вы повысите до мощность y вы получите x. Нам нужно попрактиковаться в конвертации из одной формы к другому.
Журнал из экспоненциальной формы:
The база для обеих форм -. Чтобы сделать это преобразование, начните с основания. В показатель для основания будет по другую сторону от равенства. Далее положить в знак равенства и напишите выражение с другой стороны от равенства знак.
экспоненциальный из формы в журнал:
Старт со словом log и основанием в качестве подстрочного индекса.Ставим показатель степени обратная сторона знака равенства. (Журнал равен экспоненте.) Теперь заполните журнал с выражением.
форма журнала экспоненциальная форма
журнал 2 8 = 3 2 3 = 8
журнал p w = в p c = w
журнал 10 1000 = 3 10 3 = 1000
журнал 10 0.1 = -1 10 -1 = 0,1
Решение Простые логарифмические уравнения:
Вкл. уравнения вида y = log a x где a или x неизвестны, возможно решить для x путем перехода к экспоненциальной форме.
  • Решить для x: журнал 5 x = 3 Переход на экспоненциальная форма дает решение x = 5 3 или x = 125
  • Решить для x: log x 25 = 2 Переход к экспоненциальному форма дает x 2 = 25 Поскольку основание должно быть положительным, единственное решение это x = 5.
В поисках Журналы на калькуляторе: Логи по базе 10 называются общие журналы и когда база не записана, предполагается, что это база 10. Log 100 означает журнал 10 100 или 2. На калькуляторе есть кнопка журнала, которая будет дайте журналам базу 10 любого числа.

функция журнала | R Документация

Логарифмы и экспоненты

log вычисляет логарифмы, по умолчанию натуральные логарифмы, log10 вычисляет общие (т. е.е., основание 10) логарифмы, и log2 вычисляет двоичные (т. Е. С основанием 2) логарифмы. Общая форма log (x, base) вычисляет логарифмы с основанием база .

log1p (x) вычисляет \ (\ log (1 + x) \) точно также для \ (| х | \ ll 1 \).

exp вычисляет экспоненциальную функцию.

expm1 (x) вычисляет \ (\ exp (x) — 1 \) точно также для \ (| х | \ ll 1 \).

Ключевые слова
математика
Использование
  журнал (x, основание = exp (1))
logb (x, основание = ехр (1))
log10 (x)
log2 (x) 
 log1p (x) 
 
 exp (x)
экспм1 (х)
Аргументы
x

числовой или комплексный вектор.

база

положительное или комплексное число: основание, по которому вычисляются логарифмы. По умолчанию \ (e \) = exp (1) .

Детали

Все, кроме logb , являются универсальными функциями: можно определять методы для них индивидуально или через Math группа родовая.

log10 и log2 — это только удобные обертки, но журналы к базам 10 и 2 (независимо от того, вычислено ли через журнал или обертки) будут вычисляться более эффективно и точно там, где это поддерживается ОС.Методы могут быть установлены для них индивидуально (в противном случае методы для будет использоваться журнал ).

logb — это оболочка для log для совместимости с S. Если (S3 или S4) методы установлены для журнала, они будут отправлены. Не устанавливайте методы S4 на самом logb .

Все, кроме log , являются примитивными функциями.

Значение

Вектор той же длины, что и x , содержащий преобразованный значения. log (0) дает -Inf , а log (x) для отрицательные значения x — NaN . exp (-Inf) равно 0 .

Для сложных входных данных функций журнала значение представляет собой комплексное число. с мнимой частью в диапазоне \ ([- \ pi, \ pi] \): который конец диапазона может зависеть от платформы.

S4 методы

exp , expm1 , log , log10 , log2 и log1p являются универсальными S4 и являются членами Math группа generic.

Обратите внимание, что это означает, что общий S4 для журнала имеет подпись только с одним аргументом, x , но эта база может передаваться в методы (но не будет использоваться для выбора метода). На с другой стороны, если вы установите метод только для группы Math общий, то аргумент base из log будет проигнорирован для твой класс.

Список литературы

Беккер, Р. А., Чемберс, Дж.М. и Уилкс А. Р. (1988) Новый язык S . Уодсворт и Брукс / Коул. (для log , log10 и exp .)

Чемберс, Дж. М. (1998) Программирование с данными. Руководство по языку S . Springer. (для logb .)

См. Также

Триг , кв. , г. Арифметика .

Псевдонимы
  • журнал
  • лог
  • журнал10
  • log2
  • log1p
  • эксп.
  • экспм1
Примеры

библиотека (базовая) # NOT RUN { журнал (exp (3)) log10 (1e7) # = 7 х <- 10 ^ - (1 + 2 * 1: 9) cbind (x, журнал (1 + x), log1p (x), exp (x) -1, expm1 (x)) #}

Документация воспроизведена из базы пакета, версия 3. 6.2, Лицензия: Часть R 3.6.2

Примеры сообщества

[email protected] в 16 сен.2017 основание v3.4.1

x1 <- c (1,1, -2,3, 2,5, 0,5, -3,2, -4, 5,2, -2,2, -2,2, 3) y3 <- log2 (x1) y3

.