3 в квадрате плюс 2 в квадрате: 2 в квадрате +3 в квадрате сколько будет?

Таблица квадратов

Таблица квадратов

Определение Калькулятор — квадрат числа Таблица квадратов

Скачать таблицу квадратов Определение. Квадрат числа — есть данное число, возведенное во вторую степень (число умноженное само на себя).

a² = a · a

«Квадратом» оно называется, потому что такая операция аналогична вычислению площади квадрата.

Калькулятор для вычисления квадрата числа

² = 49 ≈ 0.4444444444444444

Ниже приведены две удобные таблицы квадратов натуральных чисел от 1 до 100.

Таблица квадратов чисел от 1 до 100

12 = 1 22 = 4 32 = 9 42 = 16 52 = 25 62 = 36 72 = 49 82 = 64 92 = 81 102 = 100	112 = 121 122 = 144 132 = 169 142 = 196 15 2 = 225 162 = 256 172 = 289 182 = 324 192 = 361 202 = 400	212 = 441 222 = 484 232 = 529 242 = 576 252 = 625 262 = 676 272 = 729 282 = 784 292 = 841 302 = 900	312 = 961 322 = 1024 332 = 1089 342 = 1156 352 = 1225 362 = 1296 372 = 1369 382 = 1444 392 = 1521 402 = 1600	412 = 1681 422 = 1764 432 = 1849 442 = 1936 452 = 2025 462 = 2116 472 = 2209 482 = 2304 492 = 2401 502 = 2500
512 = 2601 522 = 2704 532 = 2809 542 = 2916 552 = 3025 562 = 3136 572 = 3249 582 = 3364 592 = 3481 602 = 3600	612 = 3721 622 = 3844 632 = 3969 642 = 4096 652 = 4225 662 = 4356 672 = 4489 682 = 4624 692 = 4761 702 = 4900	712 = 5041 722 = 5184 732 = 5329 742 = 5476 752 = 5625 762 = 5776 772 = 5929 782 = 6084 792 = 6241 802 = 6400	812 = 6561 822 = 6724 832 = 6889 842 = 7056 852 = 7225 862 = 7396 872 = 7569 882 = 7744 892 = 7921 90 2 = 8100	912 = 8281 922 = 8464 932 = 8649 942 = 8836 952 = 9025 962 = 9216 972 = 9409 982 = 9604 992 = 9801 1002 = 10000

 Распечатать таблицу квадратов

Таблица квадратов

	0	1	2	3	4	5	6	7	8	9
0	0	1	4	9	16	25	36	49	64	81
1	100	121	144	169	196	225	256	289	324	361
2	400	441	484	529	576	625	676	729	784	841
3	900	961	1024	1089	1156	1225	1296	1369	1444	1521
4	1600	1681	1764	1849	1936	2025	2116	2209	2304	2401
5	2500	2601	2704	2809	2916	3025	3136	3249	3364	3481
6	3600	3721	3844	3969	4096	4225	4356	4489	4624	4761
7	4900	5041	5184	5329	5476	5625	5776	5929	6084	6241
8	6400	6561	6724	6889	7056	7225	7396	7569	7744	7921
9	8100	8281	8464	8649	8836	9025	9216	9409	9604	9801

 Распечатать таблицу квадратов

© 2011-2023 Довжик Михаил
Копирование материалов запрещено.

Добро пожаловать на OnlineMSchool

.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне [email protected]

Степени и возведение в степень, вторая, третья, четвёртая степени

Когда число умножается само на себя, произведение называется степенью.

Так      2.2 = 4, квадрат или вторая степень 2-х
     2.2.2 = 8, куб или третья степень.
     2.2.2.2 = 16, четвёртая степень.

Также,      10.10 = 100, вторая степень 10.

     10.10.10 = 1000, третья степень.
    10.10.10.10 = 10000 четвёртая степень.

И      a.a = aa, вторая степень a
     a.a.a = aaa, третья степень a
     a. a.a.a = aaaa, четвёртая степень a

Первоначальное число называется корнем степени этого числа, потому что это число, из которого были созданы степени.

Однако не совсем удобно, особенно в случае высоких степеней, записывать все множители, из которых состоят степени. Поэтому используется сокращенный метод обозначения. Корень степени записывается только один раз, а справа и немного выше возле него, но чуть меньшим шрифтом записывается сколько раз

выступает корень как множитель. Это число или буква называется показателем степени или степенью числа. Так, а² равно a.a или aa, потому что корень a дважды должен быть умножен сам на себя, чтобы получилось степень aa. Также, a³ означает aaa, то есть здесь a повторяется три раза как множитель.

Показатель первой степени есть 1, но он обычно не записывается. Так, a¹ записывается как a.

Вы не должны путать степени с коэффициентами. Коэффициент показывает, как часто величина берётся как

часть целого. Степень показывает, как часто величина берётся как множитель в произведении.
Так, 4a = a + a + a + a.      Но a⁴ = a.a.a.a

Схема обозначения со степенями имеет своеобразное преимущество, позволяя нам выражать неизвестную степень. Для этой цели в показатель степени вместо числа записывается буква. В процессе решения задачи, мы можем получить величину, которая, как мы можем знать, есть некоторой степенью другой величины. Но пока что мы не знаем, это квадрат, куб или другая, более высокая степень. Так, в выражении a^x, показатель степени означает, что это выражение имеет

некоторую степень, хотя не определено какую степень. Так, b^m и dⁿ возводятся в степени m и n. Когда показатель степени найден, число подставляется вместо буквы. Так, если m=3, тогда b^m = b³; но если m = 5, тогда b^m=b⁵.

Метод записи значений с помощью степеней является также большим преимуществом в случае использования выражений . Tак, (a + b + d)³ есть (a + b + d).(a + b + d).(a + b + d), то есть куб трёхчлена (a + b + d). Но если записать это выражение после возведения в куб, оно будет иметь вид

a³ + 3a²b + 3a²d + 3ab² + 6abd + 3ad² + b³ + d³.

Если мы возьмем ряд степеней, чьи показатели увеличиваются или уменьшаются на 1, мы обнаружим, что произведение увеличивается на общий множитель или уменьшается на общий делитель, и этот множитель или делитель есть первоначальным числом, которое возводится в степень.

Так, в ряде      aaaaa, aaaa, aaa, aa, a;
или        a⁵, a⁴, a³, a², a¹;
показатели , если считать справа налево, равны 1, 2, 3, 4, 5; и разница между их значениями равна 1. Если мы начнем справа

умножатьна a, мы успешно получим несколько значений.

Tак a.a = a², второй член. И a³. a = a⁴
     a².a = a³, третий член. a⁴.a = a⁵.

Если мы начнем слева делить на a,
мы получим a⁵:a = a⁴      и a³:a = a².
a⁴:a = a³       a²:a = a¹

Но такой процесс деления может быть продолжен и далее, и мы получаем новый набор значений.

Так, a:a = a/a = 1. (1/a):a = 1/aa
     1:a = 1/a      (1/aa):a = 1/aaa.

Полный ряд будет: aaaaa, aaaa, aaa, aa, a, 1, 1/a, 1/aa, 1/aaa.

Или a⁵, a⁴, a³, a², a, 1, 1/a, 1/a², 1/a³.

Здесь значения справа от единицы есть обратными значениям слева от единицы. Поэтому эти степени могут быть названы обратными степенями a. Можно также сказать, что степени слева есть обратными к степеням справа.

Так, 1:(1/a) = 1.(a/1) = a. И 1:(1/a³) = a³.

Тот же самый план записи может применяться к многочленам. Так, для a + b, мы получим множество,
(a + b)³, (a + b)², (a + b), 1, 1/(a + b), 1/(a + b)², 1/(a + b)³.

Для удобства используется еще одна форма записи обратных степеней.

Согласно этой форме, 1/a или 1/a¹ = a^-1. И 1/aaa или 1/a³ = a^-3.
1/aa или 1/a² = a^-2. 1/aaaa или 1/a⁴ = a^-4.

А чтобы сделать с показателями законченный ряд с 1 как общая разница, a/a или 1, рассматривается как такое, что не имеет степени и записывается как a⁰.

Тогда, учитывая прямые и обратные степени
вместо aaaa, aaa, aa, a, a/a, 1/a, 1/aa, 1/aaa, 1/aaaa
можно записать      a⁴, a³, a², a¹, a⁰, a^-1, a^-2, a^-3, a^-4.
Или      a⁺⁴, a⁺³, a⁺², a⁺¹, a⁰, a^-1, a^-2, a^-3, a^-4.

А ряд только отдельно взятых степеней будет иметь вид:
     +4,+3,+2,+1,0,-1,-2,-3,-4.

Корень степени может выражен более чем одной буквой.

Так, aa.aa или (aa)² есть второй степенью aa.
И aa.aa.aa или (aa)³ есть третьей степенью aa.

Все степени цифры 1 одинаковы: 1.1 или 1.1.1. будет равно 1.

Возведение в степень есть нахождение значения любого числа путем умножения этого числа само на себя. Правило возведения в степень:

Умножайте величину саму на себя столько раз, сколько указано в степени числа.

Это правило является общим для всех примеров, которые могут возникнуть в процессе возведения в степень. Но будет правильно дать объяснение, каким образом оно применяется к частным случаям.

Если в степень возводится только один член, то он умножается сам на себя столько раз, сколько указывает показатель степени.

Четвертая степень a есть a⁴ или aaaa. (Art. 195.)
Шестая степень y есть y⁶ или yyyyyy.
N-ая степень x есть xⁿ или xxx….. n раз повторенное.

Если необходимо возвести в степень выражение из нескольких членов, применяется принцип, согласно которому степень произведения нескольких множителей равна произведению этих множителей, возведенных в степень.

Tак (ay)² =a²y²; (ay)² = ay.ay.
Но ay.ay = ayay = aayy = a²y².
Так, (bmx)³ = bmx.bmx.bmx = bbbmmmxxx = b³m³x³.

Поэтому, в нахождении степени произведения мы можем или оперировать со всем произведением сразу, или мы можем оперировать с каждым множителем отдельно, а потом умножить их значения со степенями.

Пример 1. Четвертая степень dhy есть (dhy)⁴, или d⁴h⁴y⁴.

Пример 2. Третья степень 4b, есть (4b)³, или 4³b³, или 64b³.

Пример 3. N-ая степень 6ad есть (6ad)ⁿ или 6ⁿaⁿdⁿ.

Пример 4. Третья степень 3m.2y есть (3m.2y)³, или 27m³.8y³.

Степень двочлена, состоящего из членов, соединенных знаком + и -, вычисляется умножением его членов. Tак,

(a + b)¹ = a + b, первая степень.
(a + b)¹ = a² + 2ab + b², вторая степень (a + b).
(a + b)³ = a³ + 3a²b + 3ab² + b³, третья степень.
(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴, четвертая степень.

Квадрат a — b, есть a² — 2ab + b².

3 + 3a² + 3a + 1.

Квадрат a + b + h есть a² + 2ab + 2ah + b² + 2bh + h²

Упражнение 1. Найдите куб a + 2d + 3

Упражнение 2. Найдите четвертую степень b + 2.

Упражнение 3. Найдите пятую степень x + 1.

Упражнение 4. Найдите шестую степень 1 — b.

Квадраты суммы суммы и разницы двочленов встречаются так часто в алгебре, что необходимо их знать очень хорошо.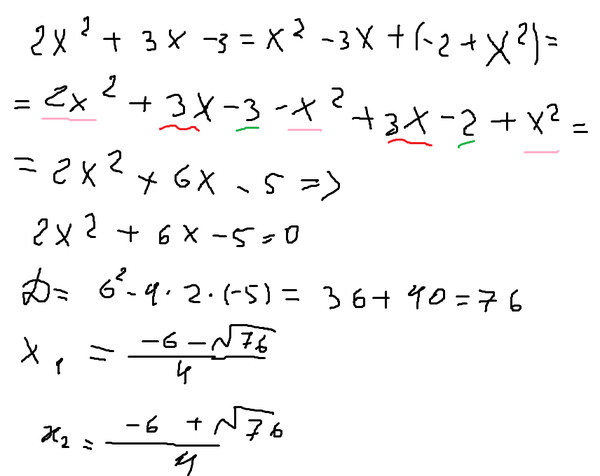

Если мы умножаем a + h само на себя или a — h само на себя,
мы получаем: (a + h)(a + h) = a² + 2ah + h²      также, (a — h)(a — h) = a² — 2ah + h².

Отсюда видно, что в каждом случае, первый и последний члены есть квадраты a и h, а средний член есть удвоеннное произведение a на h. Отсюда, квадрат суммы и разницы двочленов может быть найден, используя следующее правило.

Квадрат двочлена, оба члена которых положительны, равен квадрату первого члена + удвоенное произведение обоих членов, + квадрат последнего члена.

Квадрат разницы двочленов равен квадрату первого члена минус удвоенное произведение обоих членов плюс квадрат второго члена.

Пример 1. Квадрат 2a + b, есть 4a² + 4ab + b².

Пример 2. Квадрат ab + cd, есть a²b² + 2abcd + c²d².

Пример 3. Квадрат 3d — h, есть 9d₂ + 6dh + h².

Пример 4. Квадрат a — 1 есть a² — 2a + 1.

Чтобы узнать метод нахождения более высоких степеней двочленов, смотрите следующие разделы.

Во многих случаях является эффективным записывать степени без умножения.

Так, квадрат a + b, есть (a + b)².
N-ая степень bc + 8 + x есть (bc + 8 + x)ⁿ

В таких случаях, скобки охватывают все члены под степенью.

Но если корень степени состоит из нескольких множителей, скобки могут охватывать всё выражение, или могут применяться отдельно к множителям в зависимости от удобства.

Так, квадрат (a + b)(c + d) есть или [(a + b).(c + d)]² или (a + b)².(c + d)².

Для первого из этих выражений результатом есть квадрат произведения двух множителей, а для второго — произведением их квадратов. Но они равны друг другу.

Куб a.(b + d), есть [a.(b + d)]³, или a³.(b + d)³.

Необходимо также учитывать и знак перед вовлеченными членами. Очень важно помнить, что когда корень степени положительный, все его положительные степени также положительны. Но когда корень отрицательный, значения с нечетными степенями отрицательны, в то время как значения чётных степеней есть положительными.

Вторая степень (- a) есть +a²
Третья степень (-a) есть -a³
Четвёртая степень (-a) есть +a⁴
Пятая степень (-a) есть -a⁵

Отсюда любая нечётная степень имеет тот же самый знак, что и число. Но чётная степень есть положительна вне зависимости от того, имеет число отрицательный или положительный знак.
Так, +a.+a = +a²
И -a.-a = +a²

Величина, уже возвёденная в степень, еще раз возводится в степень путем умножения показателей степеней.

Третья степень a² есть a^2.3 = a⁶.

Для a² = aa; куб aa есть aa.aa.aa = aaaaaa = a⁶; что есть шестой степенью a, но третьей степенью a².

Четвертая степень a³b² есть a^3.4b^2.4 = a¹²b⁸

Третья степень 4a²x есть 64a⁶x³.

Пятая степень (a + b)² есть (a + b)¹⁰.

N-ая степень a³ есть a³ⁿ

N-ая степень (x — y)^m есть (x — y)^mn

(a³.b³)² = a⁶.b⁶

(a³b²h⁴)³ = a⁹b⁶h¹²

Правило одинаково применяется к отрицательным степеням.

Пример 1. Третья степень a^-2 есть a^-3.3=a^-6.

Для a^-2 = 1/aa, и третья степень этого
(1/aa).(1/aa).(1/aa) = 1/aaaaaa = 1/a⁶ = a^-6

Четвертая степень a²b^-3 есть a⁸b^-12 или a⁸/b¹².

Квадрат b³x^-1, есть b⁶x^-2.

N-ая cтепень ax^-m есть x^-mn или 1/x.

Однако, здесь надо помнить, что если знак, предшествующий степени есть «-«, то он должен быть изменен на «+» всегда, когда степень есть четным числом.

Пример 1. Квадрат -a³ есть +a⁶. Квадрат -a³ есть -a³.-a³, которое, согласно правилам знаков при умножении, есть +a⁶.

2. Но куб -a³ есть -a⁹. Для -a³.-a³.-a³ = -a⁹.

3. N-ая степень -a³ есть a³ⁿ.

Здесь результат может быть положительным или отрицательным в зависимости от того, какое есть n — чётное или нечётное.

Если дробь возводится в степень, то возводятся в степень числитель и знаменатель.

Квадрат a/b есть a²/b². Согласно правилу умножению дробей,
     (a/b)(a/b) = aa/bb = a²b²

Вторая, третья и n-ая степени 1/a есть 1/a², 1/a³ и 1/aⁿ.

Примеры двочленов, в которых один из членов является дробью.

1. Найдите квадрат x + 1/2 и x — 1/2.
(x + 1/2)² = x² + 2.x.(1/2) + 1/2² = x² + x + 1/4
(x — 1/2)² = x² — 2.x.(1/2) + 1/2² = x² — x + 1/4

2. Квадрат a + 2/3 есть a² + 4a/3 + 4/9.

3. Квадрат x + b/2 = x² + bx + b²/4.

4 Квадрат x — b/m есть x² — 2bx/m + b²/m².

Ранее было показано, что дробный коэффициент может быть перемещен из числителя в знаменатель или из знаментеля в числитель. Используя схему записи обратных степеней, видно, что любой множитель также может быть перемещен, если будет изменен знак степени.

Так, в дроби ax^-2/y, мы можем переместить x из числителя в знаменатель.
Тогда ax_-2/y = (a/y).x^-2 = (a/y).(1/x² = a/yx².

В дроби a/by³ мы можем переместить у из знаменателя в числитель.
Тогда a/by₂ = (a/b).(1/y³) = (a/b).y^-3 = ay^-3/b.

Таким же образом мы можем переместить множитель, который имеет положительный показатель степени в числитель или множитель с отрицательной степенью в знаменатель.

Так, ax³/b = a/bx^-3. Для x³ обратным есть x_-3, что есть x³ = 1/x^-3.

Следовательно, знаменатель любой дроби может быть полностью удален, или числитель может быть сокращен до единицы, что не изменит значение выражения.

Так, a/b = 1/ba^-1, or ab^-1.

2 = 3 \ умножить на 3 = 9 \]

Поделитесь этой ссылкой для ответа: help
Вставьте эту ссылку в электронное письмо, текст или социальные сети.

Получить виджет для этого калькулятора

© Calculator Soup

Поделитесь этим калькулятором и страницей

Калькулятор Использование

Найдите квадрат числа n. Введите положительные или отрицательные целые числа или десятичные числа или научную нотацию E.

Возведение в квадрат отрицательных чисел

Если вы хотите возвести в квадрат отрицательные числа в этом калькуляторе, используйте круглые скобки при вводе.

• -5² означает -(5 × 5) = -25
• -(5)² означает -(5 × 5) = -25
• (-5)² означает (-5 × -5) = 25

Например, чтобы возвести -4 в квадрат, введите его в калькулятор как (-4) со скобками. Чтобы взять отрицательное число 4 в квадрате, введите его как -(4) или -4.

Когда выражение степени записывается с положительным значением, таким как 4², большинству легко понять, что это означает 4 × 4 = 16

Однако, когда оно записывается как отрицательное значение без круглых скобок, значение неоднозначно. Для разных людей это имеет разное значение.

Различные возможные интерпретации -4²:

1. минус (4 в квадрате) равен -4² = -(4)² = -(4 × 4) = -16

2. (минус 4) в квадрате равен (- 4)² = (-4 × -4) = 16

Используйте круглые скобки, чтобы четко указать, какое вычисление вы действительно хотите выполнить.

В квадрате

Число n в квадрате записывается как n² и n² = n × n. Если n — целое число, то n² — полный квадрат.

Например, 3 в квадрате записывается как 3², а 3² = 3 × 3 = 9. Девять — это полный квадрат.

Числа от 0 до 10 в квадрате

• 0 в квадрате равно 0² = 0 × 0 = 0
• 1 в квадрате равно 1² = 1 × 1 = 1
• 2 в квадрате равно 2² = 2 × 2 = 4
• 3 в квадрате равно 3² = 3 × 3 = 9
• 4 в квадрате равно 4² = 4 × 4 = 16
• 5 в квадрате равно 5² = 5 × 5 = 25
• 6 в квадрате равно 6² = 6 × 6 = 36
• 7 в ​​квадрате равно 7² = 7 × 7 = 49
• 8 в квадрате равно 8² = 8 × 8 = 64
• 9 в квадрате равно 9² = 9 × 9 = 81
• 10 в квадрате равно 10² = 10 × 10 = 100

Ссылки/ Дополнительная литература

Гудман, Лен и Вайсштейн, Эрик В. «Квадратное число». От MathWorld — Веб-ресурс Wolfram. Квадратный номер

Википедия «Квадратный номер» на https://en.wikipedia.org/wiki/Квадратное_число

 

Подписаться на калькуляторSoup:

Калькулятор дробей

Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.

Правила выражений с дробями:

Дроби — для деления числителя на знаменатель используйте косую черту, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.

Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .

Математические символы

Символ	Название символа	Символ Значение	Пример
+	плюс	сложение	1/2 + 1/3
—	минус	вычитание	90 112 1 1/2 — 2/3
*	звездочка	умножение	2/3 * 3/4 ​​
×	знак умножения	умножение	2/3 × 5/6
:	знак деления	деление 91/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 ​​ • квадратный корень дроби: sqrt(1/16) • сокращение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций . Наиболее распространенные мнемоники для запоминания этого порядка операций: PEMDAS — Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание. BEDMAS — скобки, возведение в степень, деление, умножение, сложение, вычитание BODMAS — Скобки, Порядок, Деление, Умножение, Сложение, Вычитание. GEMDAS — символы группировки — скобки (){}, показатели степени, умножение, деление, сложение, вычитание. MDAS — Умножение и деление имеют тот же приоритет, что и сложение и вычитание. Правило MDAS является частью порядка операций правила PEMDAS. Будь осторожен; всегда выполняйте умножение и деление перед сложением и вычитанием . Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны оцениваться слева направо. Использование денег Из 575 000,00, переданных школе, было использовано 25 000,00. Какая часть от общей суммы была использована? Упростить 12 Упростить {1/3 + 1/12} ÷ {2/3 — 5/8} Дети 9 В комнате 11 детей. Шесть детей — девочки. Какую часть детей составляют девочки? Следующие 3 Следующая дробь сокращена до наименьшего члена, кроме единицы. Какой из них: А.98/99 B.73/179 C.1/250 D.81/729 В дробях Муравей поднимается на 2/5 шеста за первый час и 1/4 шеста за следующий час. Какую часть шеста преодолевает муравей за два часа? Коричневый или черный У Макса 13 пар носков. Отсюда шесть пар синих, три пары коричневых, две черных и две белых. Какая часть носков Макса коричневого или черного цвета? Дроби 80134 В школе 420 учеников. Двести пятьдесят два ученика переходят на 1-й уровень. Напишите дробью, какая часть учеников идет в 1-й класс, а какая во 2-й. Сократите обе дроби до их основной формы. Младенцы Двое взрослых, двое детей и четверо младенцев в автобусе. Какую часть населения составляют младенцы? Вычислить выражение Вычислить значение выражения z/3 — 2 z/9 + 1/6, для z = 2 Ферма 6 На ферме 20 животных. Share This Story, Choose Your Platform! FacebookTwitterLinkedInRedditWhatsappGoogle+TumblrPinterestVkEmail Related Posts Насморк при прорезывании зубов у детей: причины, симптомы и лечение Насморк при прорезывании зубов у детей: причины, симптомы и лечение Как развивать ребенка в 10 месяцев: игры и занятия для малыша Как развивать ребенка в 10 месяцев: игры и занятия для малыша Во сколько месяцев можно ставить мальчиков в ходунки: оптимальный возраст и безопасность использования Во сколько месяцев можно ставить мальчиков в ходунки: оптимальный возраст и безопасность использования УЗИ брюшной полости у детей: подготовка, проведение и расшифровка результатов УЗИ брюшной полости у детей: подготовка, проведение и расшифровка результатов Когда и как вводить прикорм грудному ребенку: рекомендации педиатров Когда и как вводить прикорм грудному ребенку: рекомендации педиатров Leave A Comment Отменить ответ Comment Save my name, email, and website in this browser for the next time I comment.