2 деленное на корень из 3
Вы искали 2 деленное на корень из 3? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 2 корень из 2 поделить на 3, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «2 деленное на корень из 3».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 2 деленное на корень из 3,2 корень из 2 поделить на 3,2 корень из 3 делить на 2,2 корней из 3 делить на 2,2 корня из 2 делить на 3,2 корня из 3 делить на 3,3 деленное на 2 корень из 3,3 делить на 2 корня из 2,3 делить на 2 корня из 3,3 делить на 3 корня из 2,3 корень из 2 деленное на 2,3 корня из 3 делить на 2,корень из 2 деленное на 3,корень из 2 делить на 3,корень из 3 деленное на 2,корень из 3 делить на 2.
Где можно решить любую задачу по математике, а так же 2 деленное на корень из 3 Онлайн?
Решить задачу 2 деленное на корень из 3 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
методы умножения, примеры с объяснением
 Однако знак корня означает не только алгебраическое действие, но и применяется в деревообрабатывающем производстве — в расчете относительных размеров.
Однако знак корня означает не только алгебраическое действие, но и применяется в деревообрабатывающем производстве — в расчете относительных размеров.Если вы хотите узнать, как умножить корни «с» или «без» множителей, то эта статья для вас. В ней мы рассмотрим методы умножения корней:
- без множителей;
- с множителями;
- с разными показателями.
Метод умножения корней без множителей
Алгоритм действий:
Убедиться, что у корня одинаковые показатели (степени). Вспомним, что степень записывается слева над знаком корня. Если нет обозначения степени, это значит, что корень квадратный, т.е. со степенью 2, и его можно умножать на другие корни со степенью 2.
ПримерПример 1: 18×2=?
Пример 2: 10×5=?
Пример 3: 33×93=?
Далее необходимо перемножить числа под корнем.
ПримерПример 1: 18×2=36
Пример 2: 10×5=50
Пример 3: 33×93=273
Упростить подкоренные выражения.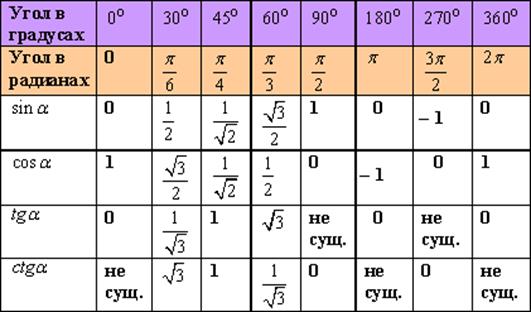 Когда мы умножаем корни друг на друга, мы можем упростить полученное подкоренное выражение до произведения числа (или выражения) на полный квадрат или куб:
Когда мы умножаем корни друг на друга, мы можем упростить полученное подкоренное выражение до произведения числа (или выражения) на полный квадрат или куб:
Пример 1: 36=6. 36 — квадратный корень из шести (6×6=36).
Пример 2: 50=(25×2)=(5×5)×2=52. Число 50 раскладываем на произведение 25 и 2. Корень из 25 — 5, поэтому выносим 5 из-под знака корня и упрощаем выражение.
Пример 3: 273=3. Кубический корень из 27 равен 3: 3×3×3=27.
Слишком сложно?
Не парься, мы поможем разобраться и подарим скидку 10% на любую работу
Опиши заданиеМетод умножения показателей с множителями
Алгоритм действий:
Умножить множители. Множитель — число, которое стоит перед знаком корня. В случае отсутствия множителя, он, по умолчанию, считается единицей. Далее необходимо перемножить множители:
Пример 1: 32×10=3?3×1=3
Пример 2: 43×36=12?4×3=12
Умножить числа под знаком корня. Как только вы перемножили множители, смело умножайте числа, стоящие под знаком корня:
Как только вы перемножили множители, смело умножайте числа, стоящие под знаком корня:
Пример 1: 32×10=3(2×10)=320
Пример 2: 43×36=12(3×6)=1218
Упростить подкоренное выражение. Далее следует упростить значения, которые стоят под знаком корня, — требуется вынести соответствующие числа за знак корня. После этого, необходимо перемножить числа и множители, которые стоят перед знаком корня:
Пример 1: 320=3(4×5)=3(2×2)×5=(3×2)5=65
Пример 2: 1218=12(9×2)=12(3×3)×2=(12×3)2=362
Метод умножения корней с разными показателями
Алгоритм действий:
Найти наименьшее общее кратное (НОК) показателей. Наименьшее общее кратное — наименьшее число, делящееся на оба показателя.
ПримерНеобходимо найти НОК показателей для следующего выражения:
53×22
Показатели равны 3 и 2. Для этих двух чисел наименьшим общим кратным является число 6 (оно делится без остатка и на 3, и на 2). Для умножения корней необходим показатель 6.
Для умножения корней необходим показатель 6.
Записать каждое выражение с новым показателем:
56×26
Найти числа, на которые нужно умножить показатели, чтобы получить НОК.
В выражении 53 необходимо умножить 3 на 2, чтобы получить 6. А в выражении 22 — наоборот, необходимо умножить на 3, чтобы получить 6.
Возвести число, которое стоит под знаком корня, в степень равную числу, которое было найдено в предыдущем шаге. Для первого выражения 5 нужно возвести в степень 2, а втором — 2 в степень 3:
2→56=5263→26=236
Возвести в степень выражения и записать результат под знаком корня:
526=(5×5)6=256236=(2×2×2)6=86
Перемножить числа под корнем:
(8×25)6
Записать результат:
(8×25)6=2006
По возможности необходимо упростить выражение, но в данном случае оно не упрощается.
Возведение в степень и извлечение корня из числа онлайн.
Корень из числа
Корень нечётной степени из положительного числа
В результате вычисления корня нечётной степени из положительного числа будет положительное число: .
Пример Вычислим корни нечётной степени из 8, 27, 125, 243
Корни 3 степени также называют кубическими корнями.
В результате вычисления корней 5-ой степени из положительных чисел, получили также положительные числа.
Корень нечётной степени из отрицательного числа
В результате вычисления корня нечётной степени из отрицательного числа будет отрицательное число: .
Пример Найдем корни 3 и 5 степеней из отрицательных чисел.
Корень четной степени из положительного числа
Корень чётной степени из положительного числа имеет два значения, положительное и отрицательное: .
Пример Вычислим корни 2 и 4 степени.
Корень 2-й степени называют квадратный корнем.
Корень четной степени из отрицательного числа
Корень любой степени из нуля
Числа в степени -1, 0, 1
Число в -1 степени
Число 3 в -1 степени можно представить в виде дроби .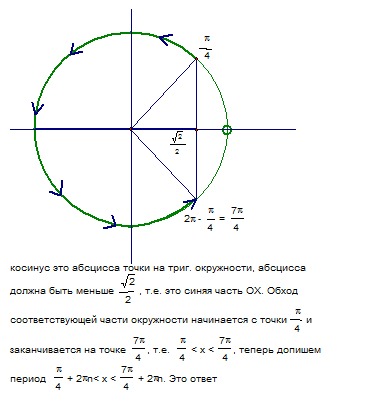 Обратная операция также верна ,
любую дробь можно представить как число в -1 степени, для этого нужно поменять числить и знаменатель местами.
Обратная операция также верна ,
любую дробь можно представить как число в -1 степени, для этого нужно поменять числить и знаменатель местами.
Число является обратным числом 5, т.е. их произведение равно единице , такое равенство выполнено для любого числа
Пример Представить дробь в степени -1
Число в 1 степени
Число в первой степени является самим числом a1=a
Число в 0 степени
Любое число в степени ноль равно единице a0=1
Квадратный корень из 3;2;5 — Квадратный Корень
Квадратный корень из числа 3 — положительное действительное число, которое при умножении само на себя даёт число 3.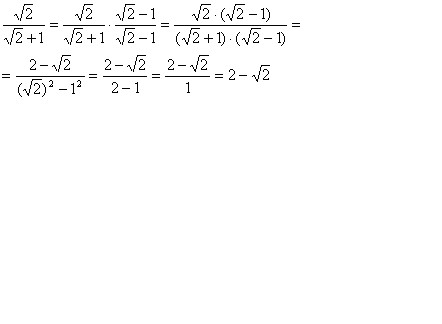
Его приблизительным значением с 69 цифрами после запятой является:
Округленное значение 1.732 является правильным с точностью до 0,01 %. Приблизительной правильной дробью является (1,7321 42857…).
Квадратный корень из 3 является иррациональным числом. Также известен как Феодоровская постоянная, названная в честь Феодора Киренского.
Может быть выражен в виде непрерывной дроби [1; 1, 2, 1, 2, 1, 2, …].
Геометрия
Квадратный корень из 3 равен длине между параллельными сторонами правильного шестиугольника со сторонами 1.Если равносторонний треугольник со сторонами длиной 1 делится на две равные половины, пересечением внутреннего угла для составления прямого угла с одной стороной, то получившийся прямоугольный треугольник имеет гипотенузу со стороной 1 и катеты длиной 1/2 и Поэтому тангенс 60° равен
Так же, это расстояние между параллельными сторонами правильного шестиугольника со сторонами 1.
является длиной диагонали куба со стороной 1.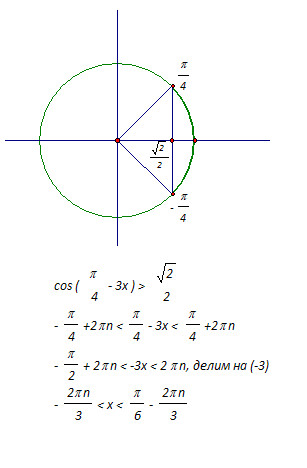
Использование в других областях
Энергетика
При трехфазной системе токов модуль напряжения между двумя фазами (линейное напряжение) в больше модуля фазного напряжения
Квадратный корень из числа 2 — положительное вещественное число, которое при умножении само на себя даёт число 2. Обозначение: Приведём значение корня из 2 с 65 знаками после запятой:
- 1,414 213 562 373 095 048 801 688 724 209 698 078 569 671 875 376 948 073 176 679 737 99…
Геометрически корень из 2 можно представить как длину диагонали квадрата со стороной 1 (это следует из теоремы Пифагора). Вероятно, это было первое известное в истории математики иррациональное число (то есть число, которое нельзя точно представить в виде дроби).
Квадратный корень из 2 равен длине гипотенузы в прямоугольном треугольнике с длиной катетов 1. Квадратный корень из 2.Хорошим и часто используемым приближением к является дробь .
Несмотря на то, что числитель и знаменатель дроби лишь двузначные
целые, оно отличается от реального значения меньше, чем на 1/10000.
История
Вавилонская глиняная табличка с примечаниями.Вавилонская глиняная табличка (ок. 1800—1600 до н. э.) даёт приближённое значение в четырёх шестидесятеричных цифрах, что составляет 8 десятичных цифр:
Другое раннее приближение этого числа в древнеиндийском математическом тексте, Шульба-сутры (ок. 800—200 до н. э.) даётся следующим образом:
Пифагорейцы обнаружили, что диагональ квадрата несоизмерима с его стороной, или на современном языке, что квадратный корень из двух является иррациональным. Мало что известно с определённостью о времени и обстоятельствах этого выдающегося открытия, но традиционно его авторство приписывается Гиппасу из Метапонта.
Алгоритмы вычисления
Существует множество алгоритмов для вычисления значения квадратного
корня из двух. В результате алгоритма получается приблизительное
значение в виде обыкновенной или десятичной дроби.
Самый популярный алгоритм для этого, который используется во многих
компьютерах и калькуляторах, это вавилонский метод вычисления квадратных
корней.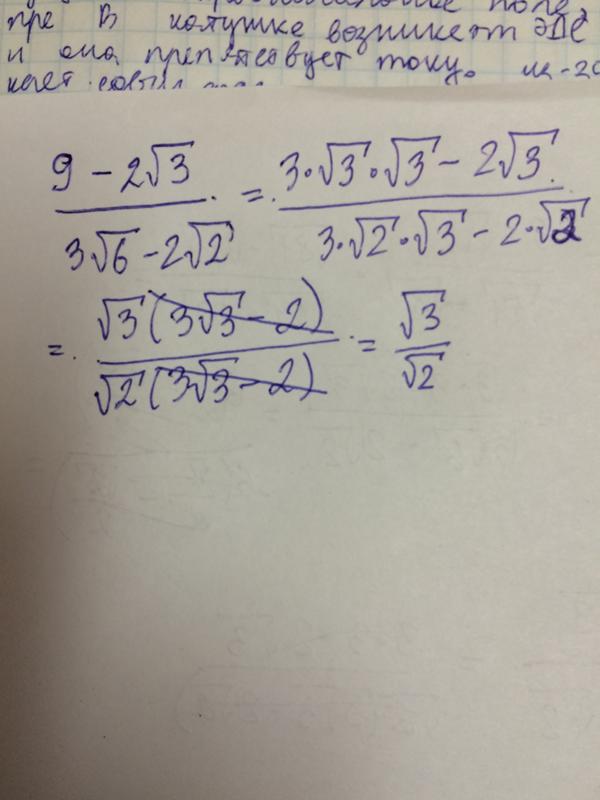 Он состоит в следующем:
Он состоит в следующем:
Чем больше повторений в алгоритме (то есть, чем больше «n»), тем лучше приближение квадратного корня из двух. Каждое повторение приблизительно удваивает количество правильных цифр. Приведём несколько первых приближений:
- 3/2 = 1.5
- 17/12 = 1.416…
- 577/408 = 1.414215…
- 665857/470832 = 1.4142135623746…
В 1997 году Ясумаса Канада вычислил значение √2 до 137,438,953,444 десятичных знаков после запятой. В феврале 2007 года рекорд был побит: Сигэру Кондо вычислил 200 миллиардов десятичных знаков после запятой в течение 13 дней и 14 часов, используя процессор 3.6 GHz с 16 ГБ ОЗУ. Среди математических констант только было вычислено более точно.
Свойства квадратного корня из двух
Половина √2 приблизительно равна 0.70710 67811 86548; эта величина даёт в геометрии и тригонометрии координаты единичного вектора, образующего угол 45° с координатными осями:
Одно из интересных свойств √2 состоит в следующем:
- .
 Потому что
Потому что
Это является результатом свойства серебряного сечения.
Другое интересное свойство √2:
Квадратный корень из двух может быть выражен в мнимых единицах i используя только квадратные корни и арифметические операции:
- и
Квадратный корень из 2 является единственным числом, отличным от 1, чья бесконечная тетрация равна его квадрату.
Квадратный корень из двух может быть также использован для приближения :
С точки зрения высшей алгебры, является корнем многочлена и поэтому является целым алгебраическим числом. Множество чисел вида , где — рациональные числа, образует алгебраическое поле. Оно обозначается и является подполем поля вещественных чисел.
Доказательство иррациональности
Применим доказательство от противного: допустим, рационален, то есть представляется в виде несократимой дроби , где и — целые числа. Возведём предполагаемое равенство в квадрат:
- .

Отсюда следует, что чётно, значит, чётно и . Пусть , где целое. Тогда
Следовательно, чётно, значит, чётно и . Мы получили, что и чётны, что противоречит несократимости дроби . Значит, исходное предположение было неверным, и — иррациональное число.
Непрерывная дробь
Квадратный корень из двух может быть представлен в виде непрерывной дроби:
Подходящие дроби данной непрерывной дроби дают приближённые значения, быстро сходящиеся к точному квадратному корню из двух. Способ их вычисления прост: если обозначить предыдущую подходящую дробь , то последующая имеет вид . Скорость сходимости здесь меньше, чем у метода Ньютона, но вычисления гораздо проще. Выпишем несколько первых приближений:
Квадрат последней приведенной дроби равен (округлённо) 2,000000177.
Размер бумаги
Квадратный корень из двух является пропорцией формата бумаги ISO 216.
Соотношение сторон таково, что при разрезании листа пополам параллельно
его короткой стороне получатся два листа той же пропорции.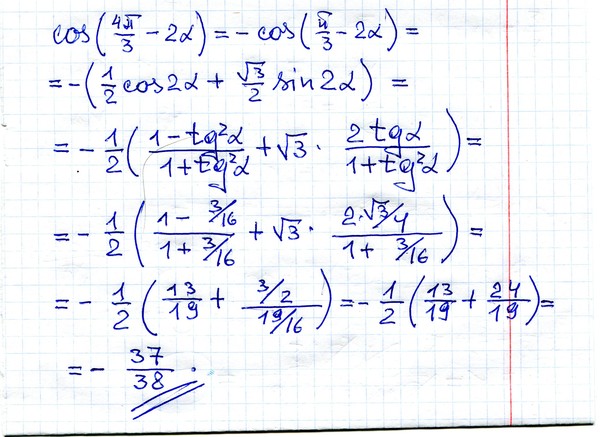
Квадратный корень из числа 5 — положительное действительное число, которое при умножении само на себя даёт число 5. Это иррациональное и алгебраическое число.[1]
Его приблизительное значение с 59 цифрами после запятой является:
Округлённое значение 2.236 является правильным с точностью до 0,01 %. Компьютерная вычисленная точность составляет не менее 1 000 000 знаков.[2]
Может быть выражено в виде непрерывной дроби [2; 4, 4, 4, 4, 4, 4, …], последовательно это дроби:
Вавилонский метод
Вычисление корня из 5, начиная с r0 = 2, где rn+1 = (rn + 5/rn) / 2:
Золотое сечение
√5/2 — диагональ половины квадрата, представляет собой геометрическое представление о золотом сечении.Золотое сечение φ — среднее арифметическое 1 и корня из 5.[3]
() алгебраически можно выразить так:
Числа Фибоначчи могут быть выражены через корень из 5 так:
Отношение √5 к φ и наоборот дают интересные зависимости непрерывных дробей с числами Фибоначчи и числами Люка:[4]
Алгебра
Кольцо содержит числа вида , где a и b целые числа и мнимое число . Это кольцо является примером области целостности, не являющейся факториальным кольцом.
Это кольцо является примером области целостности, не являющейся факториальным кольцом.
Число 6 представляется в данном кольце двумя способами:
Поле — абелево расширение рациональных чисел.
Теорема Кронекера — Вебера утверждает, что корень из 5 можно выразить линейной комбинацией корней из единицы:
Тождества Рамануджана
Корень из 5 появляется во множестве тождеств Рамануджана с непрерывными дробями.[5][6]
Например, случай непрерывных дробей Роджерса-Рамануджана:
Корни и степени. Квадратный корень, кубический корень.
Степенью называется выражение вида .
Здесь — основание степени, — показатель степени.
Степень с натуральным показателем
Проще всего определяется степень с натуральным (то есть целым положительным) показателем.
По определению, .
Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.
.
Возвести число в куб — значит умножить его само на себя три раза.
.
Возвести число в натуральную степень — значит умножить его само на себя раз:
Степень с целым показателем
Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.
По определению,
.
Это верно для . Выражение 00 не определено.
Определим также, что такое степень с целым отрицательным показателем.
Конечно, все это верно для , поскольку на ноль делить нельзя.
Например,
Заметим, что при возведении в минус первую степень дробь переворачивается.
Показатель степени может быть не только целым, но и дробным, то есть рациональным числом. В статье «Числовые множества» мы говорили, что такое рациональные числа. Это числа, которые можно записать в виде дроби , где — целое, — натуральное.
Здесь нам понадобится новое понятие — корень -степени. Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.
Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен .
Согласно определению,
В школьной математике мы извлекаем корень только из неотрицательных чисел. Выражение для нас сейчас имеет смысл только при .
Выражение всегда неотрицательно, т.е. . Например, .
Свойства арифметического квадратного корня:
Кубический корень
Аналогично, кубический корень из — это такое число, которое при возведении в третью степень дает число .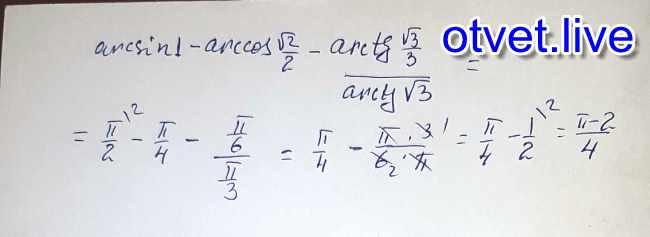
Например, , так как ;
, так как ;
, так как .
Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.
Теперь мы можем дать определение корня -ной степени для любого целого .
Корень -ной степени
Корень -ной степени из числа — это такое число, при возведении которого в -ную степень получается число .
Например,
Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.
Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.
Итак, — такое число, что . Оказывается, корни можно записывать в виде степеней с рациональным показателем. Это удобно.
По определению,
в общем случае .
Сразу договоримся, что основание степени больше 0.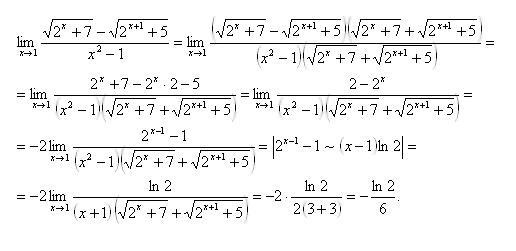
Например,
Выражение по определению равно .
При этом также выполняется условие, что больше 0.
Например,
Запомним правила действий со степенями:
— при перемножении степеней показатели складываются
— при делении степени на степень показатели вычитаются
— при возведении степени в степень показатели перемножаются
Ты нашел то, что искал? Поделись с друзьями!
Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:
1.
Внесли все под общий корень, разложили на множители, сократили дробь и извлекли корень.
2.
3.
Здесь мы записали корни в виде степеней и использовали формулы действий со степенями.
Задача 5 — разбор задания ЕГЭ по предмету Математика
Решение №1
Первое, что делаем, когда видим корень — определяем Область Допустимых Значений:
Подкоренное выражение должно быть больше нуля, то есть 3 — х > 0 или x < 3 — Другие значения переменной нам не подходят!
ОДЗ: x<3
Следующий шаг — возведение правой и левой части в квадрат, чтобы избавиться от корня.
Обратите внимание! Необходимо при этом убедиться, что правая часть будет точно больше нуля. Иначе мы можем получить решения, которые будут выглядеть правильными, но не подойдут для ответа. Для примера рассмотрим значения наших выражений до и после возведения в квадрат при, например, х = 2:
Равенство НЕ выполнено. Если же рассмотреть квадраты:
Равенство ВЫПОЛНЯЕТСЯ — мы получили корень x = 2, которого на самом деле нет!
Поэтому добавим в наше ОДЗ условие 1 — x > 0 или x < 1
ОДЗ: x<3, x<1 т.к. если х<1 то он точно меньше 3, можно упростить ОДЗ: x<1
Теперь можно перейти к собственно решению. Возводим обе части в квадрат и получаем обычное квадратное уравнение:
Воспользуемся формулой для нахождения дискриминанта:
И подставим полученный дискриминант в формулу корней уравнения:
Мы получили два корня, причём первый входит в ОДЗ: -1<1, а вот второй — нет: 2>1,
Значит у первоначального уравнения только один корень: -1
Ответ: -1
Заметьте, что если пропустить шаги определения ОДЗ, то мы получим два корня, причём наибольшим из них будет 2 — в итоге ответ будет неправильным.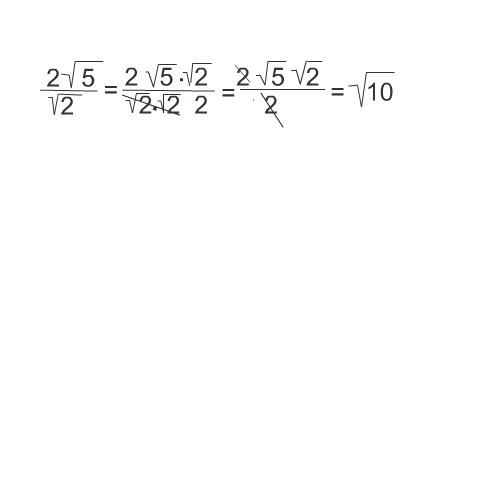 Следует всегда аккуратно записывать ОДЗ
Следует всегда аккуратно записывать ОДЗ
Центр Подготовки к ОГЭ ЕГЭ Развитие. Комплексная подготовка школьников к экзаменам ОГЭ ЕГЭ в мини-группах до 5 человек или индивидуально с увлеченными и профессиональными преподавателями. Гарантированно.
квадратный корень — Перевод на английский — примеры русский
На основании Вашего запроса эти примеры могут содержать грубую лексику.
На основании Вашего запроса эти примеры могут содержать разговорную лексику.
Инверсный квадратный корень числа с плавающей запятой используется для вычисления нормализованного вектора.
The inverse square root of a floating point number is used in calculating a normalized vector. Затем добавляете результат к другому числу и извлекаете квадратный корень.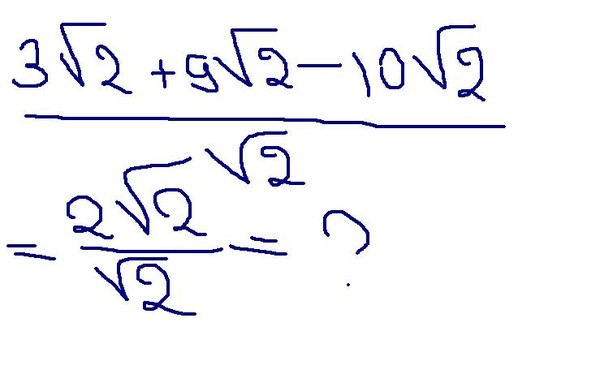
Показывает стандартное отклонение (квадратный корень отклонения).
Displays the standard deviation (square root of the variance).Какой будет квадратный корень из икс?
В школе мы выучили, что квадратный корень из девяти — это три.
We learned at school that the square root of nine is three.Реальный пример можно найти в коде Quake III — см. Быстрый обратный квадратный корень.
For a practical example popularized by Quake III, see fast inverse square root.
Скажем так: меньше, чем квадратный корень из 64.
Степень алгебры А означает квадратный корень из размерности А как к-векторного пространства.
The degree of A means the square root of the dimension of A as a k-vector space.Типичным методом комбинирования является квадратный корень из суммы квадратов (SRSS), если модальные частоты не близки.
A typical combination method is the square root of the sum of the squares (SRSS) if the modal frequencies are not close.Выполняя участок программы дважды, программа вычисляет квадратный корень двух чисел, введенных пользователем.
By executing a program section twice, the program calculates the square root of two numbers that are entered by the user.
Любое числовое выражение, для которого нужно вычислить квадратный корень.
A numerical expression of which you want the square root.Кризис в их доктрине возник, когда они обнаружили что квадратный корень из двух был иррациональным числом.
So a crisis in doctrine occurred when they discovered that the square root of two was irrational.Девять девятых, квадратный корень, нажмите на целое.Это всё.
Put in nine nines, take the square root and press the integer.Лили, милая, чему равен квадратный корень из 64?
Тогда, скольки равен квадратный корень из девяти?
Некоторые подполя R имеют нетривиальные автоморфизмы, которые, однако, нельзя распространить на всё поле R (поскольку они не сохраняют свойство числа иметь квадратный корень в R). {2} ot \geq n} and so the modulus is not involved when squaring.
{2} ot \geq n} and so the modulus is not involved when squaring.
Сколько будет квадратный корень из Пи умноженного на десять и деленное на скорость света с квадрате?
What is the square root of pi times ten divided by the speed of light squared.Итак, скорость диффузии равна чему-то… умноженному на квадратный корень… из чего-то…
So, the rate of diffusion equals something… times the square root of something-Калькулятор корня
Калькулятор квадратного корня
Калькулятор кубического корня
Калькулятор общего корня
Калькулятор связанных показателей | Научный калькулятор | Калькулятор журнала
В математике общий корень или корень n th числа a — это другое число b , которое при умножении на себя n раз равно a . В формате уравнения:
В формате уравнения:
n √a = b
б н = а
Оценка корня
Некоторые общие корни включают квадратный корень, где n = 2, и кубический корень, где n = 3.Вычисление квадратных корней и корней n th довольно сложно. Это требует оценки, проб и ошибок. Существуют более точные и эффективные способы вычисления квадратных корней, но ниже приведен метод, который не требует глубокого понимания более сложных математических концепций. Для расчета √a:
- Оценить число b
- Разделите a на b . Если возвращаемое число c является точным до желаемого десятичного разряда, остановитесь.
- Среднее значение b и c и использование результата в качестве нового предположения
- Повторите шаг два
| EX: | Найти √27 до 3 знаков после запятой |
Предположение: 5. 125 125 27 ÷ 5,125 = 5,268 (5,125 + 5,268) / 2 = 5,197 27 ÷ 5,197 = 5,195 (5,195 + 5,197) / 2 = 5,196 27 ÷ 5,196 = 5,196 |
Оценка n th Корень
Вычисление корней n th можно выполнить с помощью аналогичного метода, но с изменениями для работы с n .Вычисление квадратного корня полностью вручную утомительно. Оценить более высокие корни n th , даже если использовать калькулятор для промежуточных шагов, значительно утомительнее. Для тех, кто разбирается в рядах, см. Здесь более математический алгоритм для вычисления корней n th . Для более простого, но менее эффективного метода перейдите к следующим шагам и примеру. Для расчета n √a:
- Оценить число b
- Разделите a на b n-1 .Если возвращаемое число c является точным до желаемого десятичного разряда, остановитесь.

- Среднее значение: [b × (n-1) + c] / n
- Повторите шаг два
| EX: | Найти 8 √15 до 3 знаков после запятой |
| Предположение: 1.432 15 ÷ 1,4327 = 1,405 (1,432 × 7 + 1,405) / 8 = 1,388 15 ÷ 1,388 7 = 1,403 (1,403 × 7 + 1,388) / 8 = 1.402 |
Тогда должно быть ясно, что дальнейшие вычисления приведут к числу, которое будет округляться до 1,403, в результате чего 1,403 будет окончательной оценкой с точностью до 3 знаков после запятой.
Калькулятор кубического корня
Использование калькулятора
Воспользуйтесь этим калькулятором, чтобы найти кубический корень из положительных или отрицательных чисел. Учитывая число x , кубический корень x — это число a , такое что a 3 = x . Если x положительный, будет положительным, если x — отрицательное значение — — отрицательное значение. Кубические корни — это особая форма нашего общего
Калькулятор радикалов.
Если x положительный, будет положительным, если x — отрицательное значение — — отрицательное значение. Кубические корни — это особая форма нашего общего
Калькулятор радикалов.
Пример корней куба:
- Третий корень 64, или 64, радикал 3, или кубический корень из 64 записывается как \ (\ sqrt [3] {64} = 4 \).
- Корень 3-го числа из -64, или -64, радикал 3, или кубический корень из -64 записывается как \ (\ sqrt [3] {- 64} = -4 \).{\ frac {1} {3}} \). Распространенное определение кубического корня отрицательного числа таково:
(-x) 1/3 = — (x 1/3 ) . [1] Например:- Кубический корень из -27 записывается как \ (\ sqrt [3] {- 27} = -3 \).
- Кубический корень -8 записывается как \ (\ sqrt [3] {- 8} = -2 \).

- Кубический корень из -64 записывается как \ (\ sqrt [3] {- 64} = -4 \).
Кубические корни (для целочисленных результатов от 1 до 10)
- Кубический корень из 1 1
- Корень кубический из 8 равен 2
- Корень кубический из 27 равен 3
- Кубический корень из 64 равен 4
- Кубический корень из 125 составляет 5
- Кубический корень из 216 равен 6
- Корень кубический из 343 равен 7
- Кубический корень из 512 равен 8
- Кубический корень из 729 составляет 9
- Кубический корень из 1000 составляет 10
Для вычисления дробных показателей используйте наш калькулятор для Дробные экспоненты.
Список литературы
[1] Вайсштейн, Эрик В.
 «Кубический корень». От MathWorld — Интернет-ресурс Wolfram.
Кубический корень
«Кубический корень». От MathWorld — Интернет-ресурс Wolfram.
Кубический кореньДополнительная литература о кубических корнях:
Математический форум 0 — это идеальный квадрат?
Математика — это забавные кубические корни
Упрощение квадратного корня
Чтобы упростить извлечение квадратного корня: сделайте число внутри квадратного корня как можно меньшим (но все же целым числом):
Пример: √12 проще как 2√3
Возьмите калькулятор и проверьте, хотите ли вы: они оба имеют одинаковое значение!
Вот правило: когда a и b не отрицательны
А вот как им пользоваться:
Пример: упрощение √12
12 — это 4 умножить на 3:
√12 = √ (4 × 3)
Используйте правило:
√ (4 × 3) = √4 × √3
И квадратный корень из 4 равен 2:
√4 × √3 = 2√3
Итак, √12 проще как 2√3
Другой пример:
Пример: упрощение √8
√8 = √ (4 × 2) = √4 × √2 = 2√2
(поскольку квадратный корень из 4 равен 2)
И еще:
Пример: упрощение √18
√18 = √ (9 × 2) = √9 × √2 = 3√2
Часто помогает разложить числа (лучше всего на простые числа):
Пример: упростить √6 × √15
Сначала мы можем объединить два числа:
√6 × √15 = √ (6 × 15)
Затем мы множим их:
√ (6 × 15) = √ (2 × 3 × 3 × 5)
Потом видим две тройки и решаем «вытащить их»:
√ (2 × 3 × 3 × 5) = √ (3 × 3) × √ (2 × 5) = 3√10
Дроби
Для дробей действует аналогичное правило:
Пример: упрощение √30 / √10
Сначала мы можем объединить два числа:
√30 / √10 = √ (30/10)
Затем упростите:
√ (30/10) = √3
Примеры посложнее
Пример: упрощение √20 × √5 √2
Посмотрите, сможете ли вы выполнить следующие шаги:
√20 × √5 √2
√ (2 × 2 × 5) × √5 √2
√2 × √2 × √5 × √5 √2
√2 × √5 × √5
√2 × 5
5√2
Пример: упрощение 2√12 + 9√3
Первое упрощение 2√12:
2√12 = 2 × 2√3 = 4√3
Теперь оба члена имеют √3, мы можем их сложить:
4√3 + 9√3 = (4 + 9) √3 = 13√3
Surds
Примечание: корень, который не может упростить , называется Surd.
 Итак, √3 — сюрд. Но √4 = 2 — это не сюрприз.
Итак, √3 — сюрд. Но √4 = 2 — это не сюрприз.Сложение и вычитание радикалов (квадратные корни)
Purplemath
Так же, как и «обычные» числа, квадратные корни можно складывать. Но, возможно, вы не сможете упростить сложение до одного числа. Как «нельзя добавлять яблоки и апельсины», так и нельзя комбинировать «непохожие» радикальные термины.Чтобы можно было объединить радикальные термины вместе, эти термины должны иметь одну и ту же радикальную часть.
Упростить:
Поскольку радикал в каждом члене один и тот же (является квадратным корнем из трех), то это «одинаковые» термины. Это означает, что я могу комбинировать термины.
MathHelp.
 com
comУ меня два радикала копии, добавлены еще три копии. Всего получается пять копий:
Этот средний шаг в круглых скобках показывает рассуждение, которое оправдывает окончательный ответ.Возможно, вам никогда не понадобится «показывать» этот шаг, но это то, о чем вы должны подумать.
Упростить:
Коренная часть одинакова в каждом термине, поэтому я могу добавить это дополнение. Чтобы помочь мне понять, что первый термин означает «одну копию квадратного корня из трех», я вставлю «понял» «1»:
Не думайте, что выражения с непохожими радикалами нельзя упростить.
 Возможно, что после упрощения радикалов выражение действительно может быть упрощено.
Возможно, что после упрощения радикалов выражение действительно может быть упрощено.Упростить:
Чтобы упростить радикальное сложение, я должен сначала посмотреть, могу ли я упростить каждый радикальный термин. В данном конкретном случае квадратные корни упрощаются «полностью» (то есть до целых чисел):
Упростить:
У меня есть три копии радикала плюс еще две копии, что дает мне … Погодите! Я могу упростить эти радикалы до целых чисел:
Не волнуйтесь, если вы не увидите упрощения сразу.Если бы я не заметил до конца, что радикальное упрощение, мои шаги были бы другими, но мой окончательный ответ был бы таким же:
Упростить:
Могу объединить только радикалы «лайки».
 Первый и последний члены содержат квадратный корень из трех, поэтому их можно комбинировать; средний член содержит квадратный корень из пяти, поэтому его нельзя комбинировать с другими.Итак, в этом случае в моем ответе будет два термина.
Первый и последний члены содержат квадратный корень из трех, поэтому их можно комбинировать; средний член содержит квадратный корень из пяти, поэтому его нельзя комбинировать с другими.Итак, в этом случае в моем ответе будет два термина.Я начну с перестановки терминов, чтобы соединить «похожие» термины вместе, и вставив «понятый» 1 во второй член квадратного корня из трех:
Насколько мне известно, нет предпочтительного упорядочивания терминов в такого рода выражениях, поэтому выражение
также должно быть приемлемым ответом.Упростить:
Насколько мне известно, это «непохожие» термины, и я не могу их объединить.Но восьмерка в радикале первого члена множится как 2 × 2 × 2. Это означает, что я могу вытащить 2 из радикала. В этот момент у меня будут термины «нравится», которые я могу комбинировать.

Упростить:
Я могу упростить большинство радикалов, и это позволит сделать хотя бы небольшое упрощение:
Упростить:
В этих двух терминах есть «непохожие» радикальные части, и я не могу извлечь ничего из любого радикала.Тогда я не могу дальше упрощать выражение
, и мой ответ должен быть таким:(выражение уже полностью упрощено)
Развернуть:
Чтобы расширить это выражение (то есть умножить его, а затем упростить), мне сначала нужно извлечь квадратный корень из двух через круглые скобки:
Как видите, упрощение включало превращение продукта радикалов в один радикал, содержащий значение продукта (2 × 3 = 6).
 Вы должны ожидать, что вам придется манипулировать радикальными продуктами в обоих «направлениях».
Вы должны ожидать, что вам придется манипулировать радикальными продуктами в обоих «направлениях».Развернуть:
Как и в предыдущем примере, мне нужно умножить через круглые скобки.
Развернуть:
Наверное, проще будет это умножение «по вертикали».
Упрощение дает мне:
Делая умножение по вертикали, я мог лучше отслеживать свои шаги. Вы должны использовать тот метод умножения, который лучше всего подходит для вас. Но знайте, что вертикальное умножение — это не временная уловка для начинающих студентов; Я до сих пор использую эту технику, потому что обнаружил, что при этом я постоянно быстрее и точнее.

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в нахождении радикалов. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
URL: https: // www.purplemath.com/modules/radicals3.htm
Умножение и деление радикальных выражений
Умножение радикальных выражений
При умножении радикальных выражений на один и тот же индекс мы используем правило произведения для радикалов. Если a и b представляют положительные действительные числа,
Пример 1: Умножение: 2⋅6.

Решение: Эта задача представляет собой произведение двух квадратных корней. Примените правило произведения для радикалов, а затем упростите.
Ответ: 23
Пример 2: Умножение: 93⋅63.
Решение: Эта проблема является продуктом кубических корней. Примените правило произведения для радикалов, а затем упростите.
Ответ: 3 23
Часто перед радикалами стоят коэффициенты.
Пример 3: Умножение: 23⋅52.
Решение: Используя правило произведения радикалов и тот факт, что умножение является коммутативным, мы можем перемножить коэффициенты и подкоренные выражения следующим образом.
Обычно первый шаг, связанный с применением коммутативного свойства, не показан.

Ответ: 106
Пример 4: Умножение: −2 5×3⋅3 25×23.
Раствор:
Ответ: −30x
Используйте свойство распределенности при умножении рациональных выражений более чем на один член.
Пример 5: Умножить: 43 (23-36).
Решение: Примените свойство распределения и умножьте каждый член на 43.
Ответ: 24−362
Пример 6: Умножение: 4×23 (2×3−5 4×23).
Решение: Примените свойство распределения, а затем упростите результат.
Ответ: 2x − 10x⋅2×3
Процесс умножения радикальных выражений на несколько членов — это тот же процесс, который используется при умножении многочленов.
 Примените свойство распределения, упростите каждый радикал, а затем объедините одинаковые термины.
Примените свойство распределения, упростите каждый радикал, а затем объедините одинаковые термины.Пример 7: Умножение: (5 + 2) (5−4).
Решение: Начните с применения свойства распределения.
Ответ: −3−25
Пример 8: Умножение: (3x − y) 2.
Раствор:
Ответ: 9x − 6xy + y
Попробуй! Умножить: (23 + 52) (3−26).
Ответ: 6-122 + 56-203
Выражения (a + b) и (a − b) называются сопряженными. Множители (a + b) и (a − b) являются сопряженными.. При умножении конъюгатов сумма произведений внутреннего и внешнего членов дает 0.
Пример 9: Умножение: (2 + 5) (2−5).
Решение: Примените свойство распределения, а затем объедините похожие термины.

Ответ: −3
Важно отметить, что при умножении сопряженных радикальных выражений мы получаем рациональное выражение.Это верно в целом и часто используется при изучении алгебры.
Следовательно, для неотрицательных действительных чисел a и b мы имеем следующее свойство:
Деление радикальных выражений (рационализация знаменателя)
Чтобы разделить радикальные выражения с одинаковым индексом, мы используем правило частного для радикалов. Если a и b представляют собой неотрицательные числа, где b ≠ 0, то мы имеем
Пример 10: Разделить: 8010.
Решение: В этом случае мы видим, что 10 и 80 имеют общие множители. Если мы применим правило частного для радикалов и запишем его как единый квадратный корень, мы сможем уменьшить дробное подкоренное выражение.

Ответ: 22
Пример 11: Разделить: 16x5y42xy.
Раствор:
Ответ: 2x2y2y
Пример 12: Разделить: 54a3b5316a2b23.
Раствор:
Ответ: 3b⋅a32
Когда делитель радикального выражения содержит радикал, обычно находят эквивалентное выражение, в котором знаменатель является рациональным числом. Нахождение такого эквивалентного выражения называется рационализацией знаменателя Процесс определения эквивалентного радикального выражения с рациональным знаменателем ..
Для этого умножьте дробь на единицу особого вида, чтобы подкоренное выражение в знаменателе можно было записать со степенью, соответствующей индексу.После этого упростите и удалите радикал в знаменателе.
 Например,
Например,Помните, чтобы получить эквивалентное выражение, вы должны умножить числитель и знаменатель на один и тот же ненулевой коэффициент.
Пример 13: Рационализируйте знаменатель: 32.
Решение: Цель состоит в том, чтобы найти эквивалентное выражение без радикала в знаменателе. В этом примере умножьте на 1 в форме 22.
Ответ: 62
Пример 14: Рационализируйте знаменатель: 123x.
Решение: Подкоренное выражение в знаменателе определяет факторы, которые необходимо использовать для его обоснования. В этом примере умножьте на 1 в форме 3x3x.
Ответ: 3x6x
Как правило, мы обнаруживаем необходимость уменьшить или отменить после рационализации знаменателя.
Пример 15: Рационализируйте знаменатель: 525ab.

Решение: В этом примере мы умножим на 1 в форме 5ab5ab.
Обратите внимание, что a и b не отменяются в этом примере. Не отменяйте факторы внутри радикала с теми, которые находятся снаружи.
Ответ: 10abab
Попробуй! Рационализируем знаменатель: 4a3b.
Ответ: 23ab3b
До этого момента мы видели, что умножение числителя и знаменателя на квадратный корень с одним и тем же корнем дает рациональный знаменатель. В общем, это верно, только когда знаменатель содержит квадратный корень. Однако это не относится к кубическому корню. Например,
Обратите внимание, что умножение на тот же коэффициент в знаменателе не дает рационального объяснения. В этом случае, если мы умножим на 1 в форме x23x23, то мы можем записать подкоренное выражение в знаменателе как степень 3.
 Затем упрощение результата дает рационализированный знаменатель. Например,
Затем упрощение результата дает рационализированный знаменатель. Например,Поэтому, чтобы рационализировать знаменатель радикальных выражений с одним радикальным членом в знаменателе, начните с факторизации подкоренного выражения знаменателя. Коэффициенты этого подкоренного выражения и индекса определяют, на что мы должны умножать. Умножьте числитель и знаменатель на корень n -й степени из множителей, что дает n -ю степень всех множителей в подкоренном выражении знаменателя.
Пример 16: Рационализируйте знаменатель: 1253.
Решение: Радикал в знаменателе эквивалентен 523. Чтобы рационализировать знаменатель, он должен быть 533. Чтобы получить это, нам нужен еще один множитель 5. Следовательно, умножьте на 1 в форме 5353.
Ответ: 535
Пример 17: Рационализируйте знаменатель: 27a2b23.

Решение: В этом примере мы умножим на 1 в форме 22b322b3.
Ответ: 34ab32b
Пример 18: Рационализируем знаменатель: 1 4×35.
Решение: В этом примере мы умножим на 1 в форме 23x2523x25.
Ответ: 8x252x
Когда в знаменателе появляются два члена с квадратными корнями, мы можем рационализировать это с помощью очень специальной техники.Этот метод заключается в умножении числителя и знаменателя дроби на сопряжение знаменателя. Напомним, что умножение радикального выражения на его сопряжение дает рациональное число.
Пример 19: Рационализируйте знаменатель: 13−2.
Решение: В этом примере сопряжение знаменателя равно 3 + 2. Следовательно, умножьте на 1 в виде (3 + 2) (3 + 2).

Ответ: 3 + 2
Обратите внимание, что члены, содержащие квадратный корень в знаменателе, исключаются путем умножения на сопряжение.Мы можем использовать свойство (a + b) (a − b) = a − b, чтобы ускорить процесс умножения выражений в знаменателе.
Пример 20: Рационализируйте знаменатель: 2−62 + 6.
Решение: Умножьте на 1 в форме 2−62−6.
Ответ: −2 + 3
Пример 21: Рационализируйте знаменатель: x + yx − y.
Решение: В этом примере мы умножим на 1 в форме x − yx − y.
Ответ: x − 2xy + yx − y
Попробуй! Рационализируйте знаменатель: 35 + 525−3.
Ответ: 195 + 4511
Ключевые выводы
- Чтобы умножить два одночленных радикальных выражения, умножьте коэффициенты и умножьте подкоренные выражения.
 По возможности упростите результат.
По возможности упростите результат. - Применить свойство распределения при умножении радикальных выражений на несколько членов.Затем упростите и объедините все похожие радикалы.
- Умножение двухчленного радикального выражения, содержащего квадратные корни, на его сопряжение, дает рациональное выражение.
- Принято писать радикальные выражения без радикалов в знаменателе. Процесс поиска такого эквивалентного выражения называется рационализацией знаменателя.
- Если выражение имеет один член в знаменателе, включающий радикал, то рационализируйте его, умножив числитель и знаменатель на n корень -й степени из множителей подкоренного выражения, чтобы их степени равнялись индексу.
- Если радикальное выражение имеет в знаменателе два члена, включающих квадратные корни, то рационализируйте его, умножив числитель и знаменатель на его сопряжение.
Тематические упражнения
Часть A: Умножение радикальных выражений
Умножить.
 ( Предположим, что все переменные неотрицательны. )
( Предположим, что все переменные неотрицательны. ) 1. 3⋅5
2.7⋅3
3. 2⋅6
4. 5⋅15
5. 7⋅7
6. 12⋅12
7. 25⋅710
8. 315⋅26
9. (25) 2
10. (62) 2
11. 2x⋅2x
12. 5лет 5лет
13. 3a⋅12
14. 3a⋅2a
15. 42x⋅36x
16. 510–22 года
17.53⋅253
18. 43⋅23
19. 43⋅103
20. 183⋅63
21. (5 93) (2 63)
22. (2 43) (3 43)
23. (2 23) 3
24. (3 43) 3
25. 3a23⋅9a3
26. 7b3⋅49b23
27. 6×23⋅4×23
28. 12y3⋅9y23
29.
 20x2y3⋅10x2y23
20x2y3⋅10x2y2330.63xy3⋅12x4y23
31,5 (3-5)
32. 2 (3−2)
33,37 (27−3)
34. 25 (6−310)
35. 6 (3−2)
36,15 (5 + 3)
37. х (х + ху)
38. у (ху + у)
39. 2ab (14a − 210b)
40. 6ab (52a − 3b)
41. (2−5) (3 + 7)
42. (3 + 2) (5-7)
43.(23−4) (36 + 1)
44. (5−26) (7−23)
45. (5−3) 2
46. (7−2) 2
47. (23 + 2) (23−2)
48. (2 + 37) (2−37)
49. (a − 2b) 2
50. (ab + 1) 2
51. Каковы периметр и площадь прямоугольника длиной 53 сантиметра и шириной 32 сантиметра?
52. Каковы периметр и площадь прямоугольника длиной 26 сантиметров и шириной 3 сантиметра?
53.
 Если основание треугольника 62 метра, а высота 32 метра, то какова площадь?
Если основание треугольника 62 метра, а высота 32 метра, то какова площадь?54. Если основание треугольника составляет 63 метра, а высота — 36 метров, то какова площадь?
Часть B: Деление радикальных выражений
Разделить.
55. 753
56. 36010
57. 7275
58. 9098
59.90x52x
60. 96y33y
61. 162x7y52xy
62. 363x4y93xy
63. 16a5b232a2b23
64. 192a2b732a2b23
Рационализируйте знаменатель.
65,15
66,16
67. 23
68. 37
69. 5210
70. 356
71.3−53
72. 6−22
73. 17x
74. 13лет
75.
 a5ab
a5ab76. 3b223ab
77. 2363
78. 1473
79. 14×3
80. 13y23
81. 9x⋅239xy23
82. 5y2⋅x35x2y3
83. 3a2 3a2b23
84. 25н3 25м2н3
85.327x2y5
86. 216xy25
87. ab9a3b5
88. abcab2c35
89. 310-3
90,26-2
91. 15 + 3
92. 17−2
93. 33 + 6
94. 55 + 15
95. 105-35
96. −224-32
97. 3 + 53−5
98. 10−210 + 2
99.23−3243 + 2
100. 65 + 225−2
101. х + ух-у
102. х − yx + y
103. a − ba + b
104. ab + 2ab − 2
105.
 x5−2x
x5−2x106. 1x-y
Часть C: Обсуждение
107. Изучите и обсудите некоторые причины, по которым рациональное использование знаменателя является обычной практикой.
108. Объясните своими словами, как рационализировать знаменатель.
ответы
1: 15
3: 23
5: 7
7: 702
9: 20
11: 2x
13: 6a
15: 24×3
17: 5
19: 2 53
21:30 23
23: 16
25: 3a
27: 2x⋅3×3
29: 2xy⋅25×3
31: 35−5
33: 42-321
35: 32−23
37: x + xy
39: 2a7b − 4b5a
41: 6 + 14−15−35
43: 182 + 23−126−4
45: 8−215
47: 10
49: a − 22ab + 2b
51: Периметр: (103 + 62) см; площадь: 156 квадратных сантиметров
53: 18 квадратных метров
55: 5
57: 265
59: 3×25
61: 9x3y2
63: 2a
65: 55
67: 63
69: 104
71: 3−153
73: 7x7x
75: ab5b
77: 633
79: 2x232x
81: 3 6x2y3y
83: 9ab32b
85: 9x3y45xy
87: 27a2b453
89: 310 + 9
91: 5-32
93: −1 + 2
95: −5-352
97: −4−15
99: 15−7623
101: x2 + 2xy + yx2 − y
103: a − 2ab + ba − b
105: 5x + 2×25−4x
Учебное пособие по делению квадратного корня с примерами, практическими задачами и бесплатный рабочий лист с ключом ответа
Пополнение словарного запаса
Подкоренное выражение относится к числу под знаком корня.
 В нижнем радикале подкоренное выражение — это цифра «5».
В нижнем радикале подкоренное выражение — это цифра «5».Еще раз о важном правиле деления квадратных корней:
Правило, описанное ниже, является важной частью того, как мы собираемся делить квадратные корни, поэтому убедитесь, что у вас есть секунда, чтобы освежить его в памяти. (Или узнайте впервые;)
Когда вы делите два квадратных корня, вы можете «поместить» числитель и знаменатель в один квадратный корень.Ниже приведен пример этого правила с использованием чисел
.Как видите, «23» и «2» можно переписать внутри одного радикального знака.
Видео о том, как разделить квадратные корни
youtube.com/embed/o0HnTr6UtTM» frameborder=»0″ allowfullscreen=»»/>
Примеры деления квадратного корня
Пример 1 умножения квадратных корней
Шаг 1Объединить квадратные корни под 1 подкоренное число
Шаг 2Разделить (если возможно).Так как 150 делится на 2, мы можем это сделать.
Шаг 3Практика Деление квадратного корня
Указания: Разделите квадратные корни и выразите свой ответ в простейшей радикальной форме
Задача 1
Покажи ответЭта проблема похожа на пример 1.
Шаг 1
Объединить квадратные корни под 1 подкоренное число
шаг 1 ответ Шаг 2Разделить (если возможно).Так как 200 делится на 10, мы можем это сделать.
шаг 1 ответ Шаг 3 шаг 1 ответЗадача 2
Покажи ответЭта проблема похожа на пример 1
Шаг 1Объединить квадратные корни под 1 подкоренное число
шаг 1 ответ Шаг 2Разделить (если возможно).
шаг 1 ответ Шаг 3 шаг 1 ответ Так как 140 делится на 5, мы можем это сделать.
Так как 140 делится на 5, мы можем это сделать.

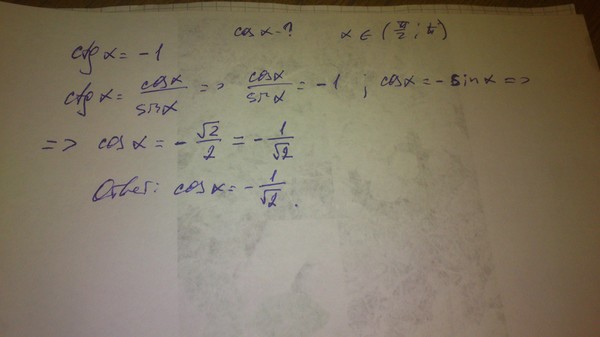
 Потому что
Потому что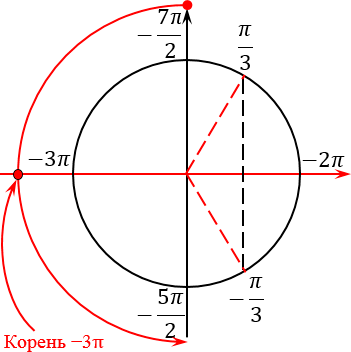


 «Кубический корень». От MathWorld — Интернет-ресурс Wolfram.
Кубический корень
«Кубический корень». От MathWorld — Интернет-ресурс Wolfram.
Кубический корень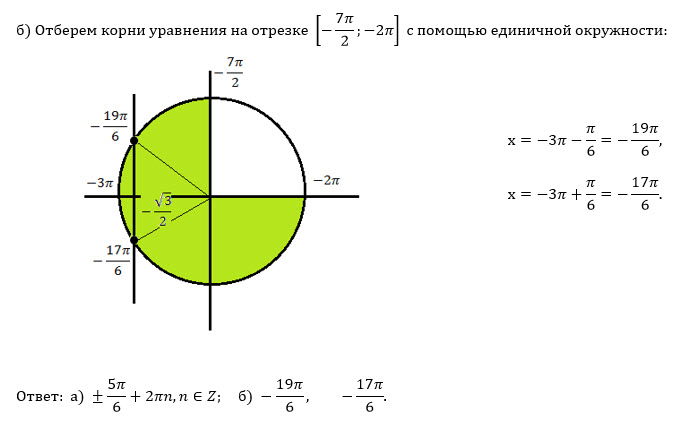 Итак, √3 — сюрд. Но √4 = 2 — это не сюрприз.
Итак, √3 — сюрд. Но √4 = 2 — это не сюрприз. com
com Возможно, что после упрощения радикалов выражение действительно может быть упрощено.
Возможно, что после упрощения радикалов выражение действительно может быть упрощено. Первый и последний члены содержат квадратный корень из трех, поэтому их можно комбинировать; средний член содержит квадратный корень из пяти, поэтому его нельзя комбинировать с другими.Итак, в этом случае в моем ответе будет два термина.
Первый и последний члены содержат квадратный корень из трех, поэтому их можно комбинировать; средний член содержит квадратный корень из пяти, поэтому его нельзя комбинировать с другими.Итак, в этом случае в моем ответе будет два термина.
 Вы должны ожидать, что вам придется манипулировать радикальными продуктами в обоих «направлениях».
Вы должны ожидать, что вам придется манипулировать радикальными продуктами в обоих «направлениях».
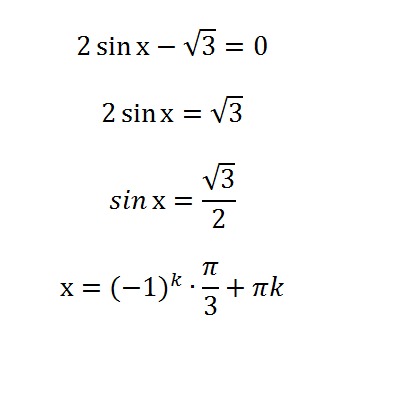

 Примените свойство распределения, упростите каждый радикал, а затем объедините одинаковые термины.
Примените свойство распределения, упростите каждый радикал, а затем объедините одинаковые термины.

 Например,
Например,
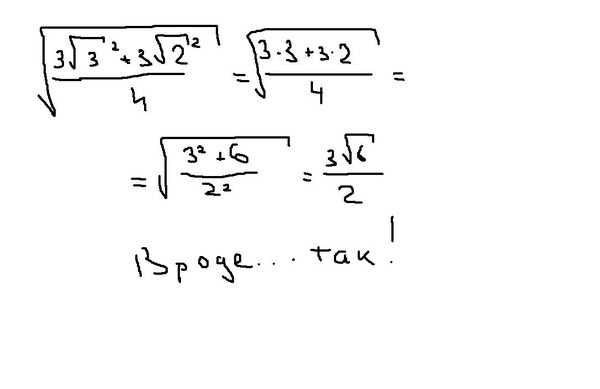 Затем упрощение результата дает рационализированный знаменатель. Например,
Затем упрощение результата дает рационализированный знаменатель. Например,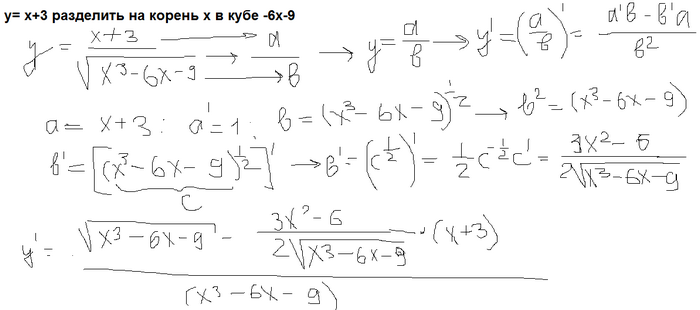

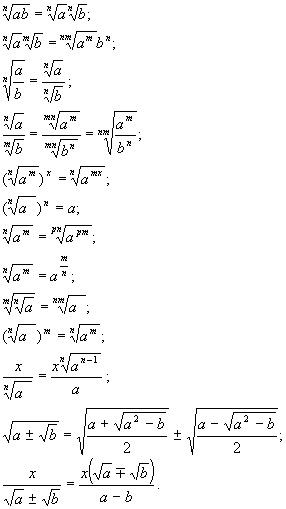 По возможности упростите результат.
По возможности упростите результат. ( Предположим, что все переменные неотрицательны. )
( Предположим, что все переменные неотрицательны. ) 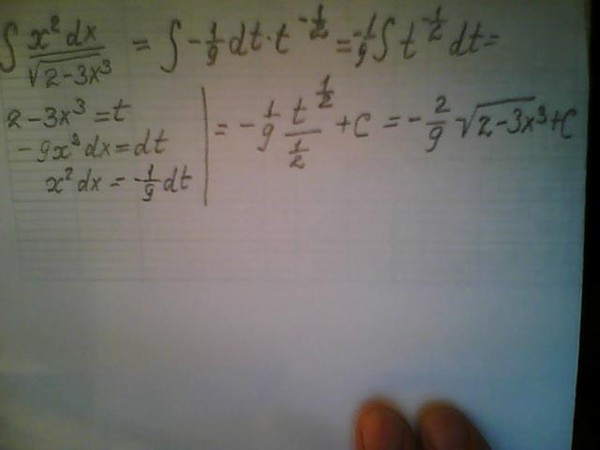 20x2y3⋅10x2y23
20x2y3⋅10x2y23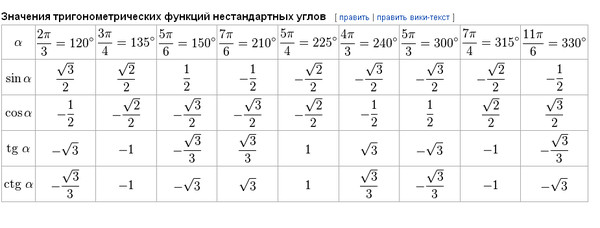 Если основание треугольника 62 метра, а высота 32 метра, то какова площадь?
Если основание треугольника 62 метра, а высота 32 метра, то какова площадь? a5ab
a5ab x5−2x
x5−2x В нижнем радикале подкоренное выражение — это цифра «5».
В нижнем радикале подкоренное выражение — это цифра «5».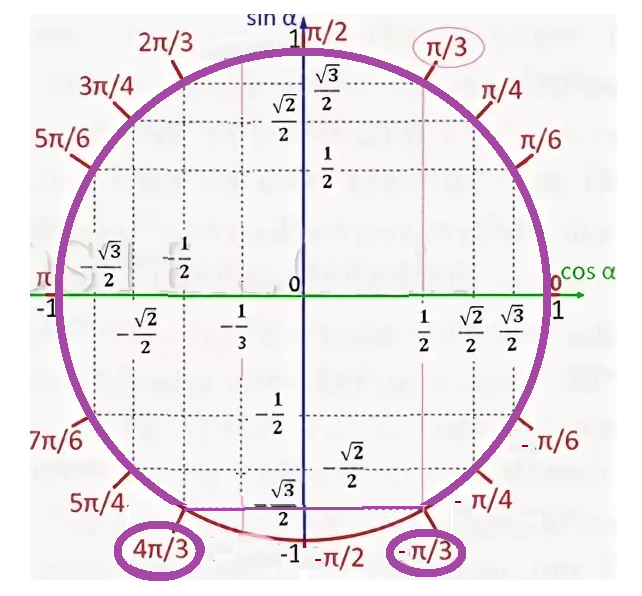
 Так как 140 делится на 5, мы можем это сделать.
Так как 140 делится на 5, мы можем это сделать.
 Итак, когда мы рационализируем знаменатель или числитель
мы хотим избавить его от радикалов.
Итак, когда мы рационализируем знаменатель или числитель
мы хотим избавить его от радикалов. Умножьте числитель и знаменатель на корень
это избавит от радикала в знаменателе.
Умножьте числитель и знаменатель на корень
это избавит от радикала в знаменателе. 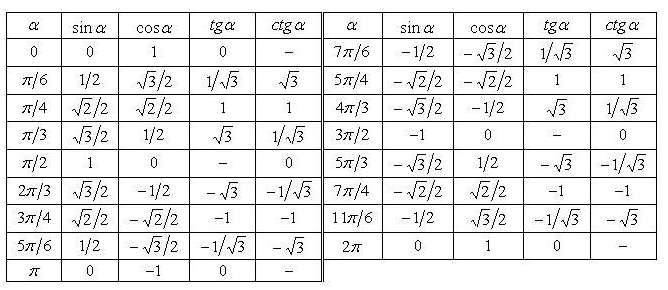
 Умножьте числитель и знаменатель на корень
это избавит от радикала в знаменателе.
Умножьте числитель и знаменатель на корень
это избавит от радикала в знаменателе.  число и ден. корнем из 6
число и ден. корнем из 6  Вы не можете этого сделать, если
они оба находятся внутри одного радикала или оба вне радикала, как
4 в числителе и 6 в знаменателе были во втором
до последней дроби.
Вы не можете этого сделать, если
они оба находятся внутри одного радикала или оба вне радикала, как
4 в числителе и 6 в знаменателе были во втором
до последней дроби.


 число и ден. корнем квадратным из 5
число и ден. корнем квадратным из 5 
 число и ден. кубическим корнем из
число и ден. кубическим корнем из 


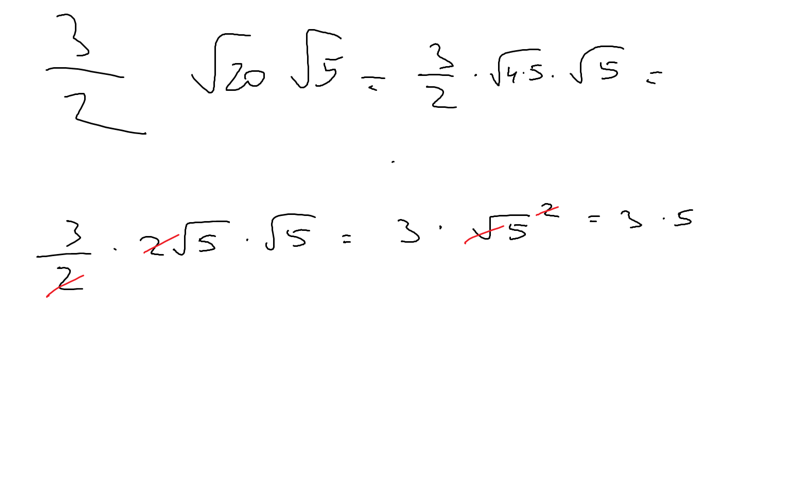

 корень из 4 равен 2
корень из 4 равен 2 
Leave A Comment