Трапеция: свойства, признаки, площадь, средняя линия
Т. А. Унегова
Определения:
Трапеция — это называется четырехугольник, у которого две стороны параллельны, а две другие — не параллельны.
Параллельные стороны называются основаниями трапеции, а непараллельные — боковыми сторонами трапеции.
Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.
Если боковые стороны равны, трапеция называется равнобедренной.
Высотой трапеции называется перпендикуляр, проведенный из любой точки одного из оснований трапеции к прямой, содержащей другое основание.
Трапеция называется вписанной в окружность, если каждая ее вершина принадлежит окружности.
Трапеция называется описанной вокруг окружности, если каждая ее сторона касается окружности.
Трапеция называется равнобедренной (равнобокой, равнобочной), если ее боковые стороны равны.
Трапеция, один из углов которой прямой, называется прямоугольной.
Теоремы о средней линии и диагоналях трапеции
Теорема 1. Средняя линия трапеции параллельна основаниям и равна их полусумме: .
Теорема 2. Диагонали трапеции делят среднюю линию трапеции на три отрезка. Средний из них равен полуразности оснований, а два крайних равны между собой: .
Теорема 3. Средняя линия треугольника, составленного из диагоналей и суммы оснований трапеции, равна средней линии трапеции: .
Теорема 4. Четыре точки: середины оснований трапеции, точка пересечения ее диагоналей и точка пересечения продолжений ее боковых сторон — лежат на одной прямой.
Эта теорема называется также «Замечательное свойство трапеции».
Теорема 5. Диагонали трапеции делят ее на четыре треугольника. Два из них, содержащие боковые стороны, равновелики (имеют равные площади), а два других, содержащие основания, подобны.
Диагонали трапеции делят ее на четыре треугольника. Два из них, содержащие боковые стороны, равновелики (имеют равные площади), а два других, содержащие основания, подобны.
Теоремы о площади трапеции
Теорема 6. Площадь трапеции равна произведению полусуммы ее оснований на высоту: .
Теорема 7. Площадь трапеции равна произведению ее средней линии на высоту: .
Теорема 8. Площадь трапеции (как и всякого выпуклого четырехугольника) равна половине произведения ее диагоналей на синус угла между ними: , где (Вместо можно брать
Теорема 9. Если в трапецию можно вписать окружность, то (как и для всякого описанного многоугольника) площадь трапеции равна произведению ее полупериметра на радиус вписанной окружности: . Таким образом, .
Теорема 10. Площадь трапеции равна площади треугольника, составленного из диагоналей и суммы оснований этой трапеции. (Сравни эту теорему и теорему 3. )
)
Теоремы о вписанных и описанных трапециях
Теорема 11. Если трапеция вписана в окружность, то она равнобедренная. И наоборот, если трапеция равнобедренная, то около нее можно описать окружность.
Теорема 12. Если трапеция описана около окружности, то сумма оснований трапеции равна сумме ее боковых сторон.
Задачи ЕГЭ и ОГЭ по теме: Трапеция
Задача 1.
Найдите высоту трапеции ABCD, опущенную из вершины B, если стороны квадратных клеток равны .
Решение:
Высота трапеции— это отрезок, перпендикулярный ее основаниям. Проведем высоту из вершины . Так как сторона квадратной клетки равна , то по теореме Пифагора получаем, что .
Ответ: 2.
Задача 2.
Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол . Найдите площадь трапеции.
Решение:
Углы ABC и BAH — односторонние, их сумма равна , и тогда BAH
Из ABH найдем высоту BH. Катет, лежащий против угла в , равен половине гипотенузы. Получаем, что BH = 3,5.
Катет, лежащий против угла в , равен половине гипотенузы. Получаем, что BH = 3,5.
Площадь трапеции равна .
Ответ: 42.
Задача 3.
Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции ее диагональ.
Решение:
Напомним, что средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. Средняя линия треугольника параллельна третьей его стороне и равна половине этой стороны. Из ACD находим, что
Ответ: 5.
Задача 4.
Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.
Решение:
Проведем PQ — среднюю линию трапеции, PQ = 2,5 и . Отсюда получаем, что середина отрезка AC, то есть PM — средняя линия треугольника ABC и PM = 1.
Ответ: 0,5.
Задача 5.
Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.
Решение:
Периметр треугольника равен сумме его сторон, то есть
Периметр трапеции равен
Ответ: 23.
Задача 6.
В равнобедренной трапеции ABCD диагональ AC является биссектрисой острого угла трапеции и образует со стороной CD угол . Найдите углы трапеции.
Решение:
Пусть CAD , тогда CAB и BAD , так как трапеция равнобедренная.
Сумма углов , откуда
Итак, , а.
Ответ: .
Задача 7.
В равнобедренной трапеции основания равны 10 м и 24 м, боковая сторона 25 м. Найдите высоту трапеции.
Решение:
В равнобедренной трапеции проведем высоты. Получим прямоугольник и два равных прямоугольных треугольника. Тогда основание каждого треугольника равно 7 и Отсюда,
Ответ: 24.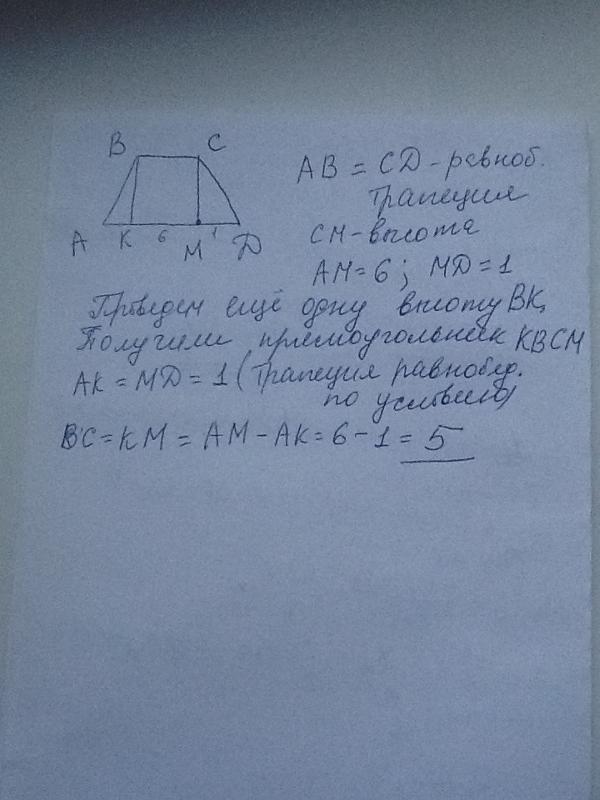
Задача 8.
Тупой угол равнобедренной трапеции равен , а высота, проведенная из вершины этого угла, делит большее основание на отрезки 1,4 см и 3,4 см. Найдите площадь трапеции.
Решение:
Проведем две высоты. Они разделят трапецию на три части: прямоугольник и два равных прямоугольных треугольника с острым углом .
Каждый треугольник равнобедренный, поэтому h = 1,4.
Нетрудно видеть, что верхнее основание трапеции равно 2, а нижнее — 4,8. Отсюда площадь трапеции равна .
Ответ: 4,76.
Задача 9.
Площадь трапеции равна 60м а основания 8 м и 12 м. Найдите высоту трапеции.
Решение:
Так как площадь трапеции , то , откуда h = 6.
Ответ: 6.
Задача 10.
В равнобедренной трапеции диагонали перпендикулярны и равны Найдите площадь трапеции.
Решение:
Проведем CE BD и DE — продолжение AD.
Так как BCDE — параллелограмм, то CE = a.
По теореме 10 получим, что .
Ответ:
Задач 11.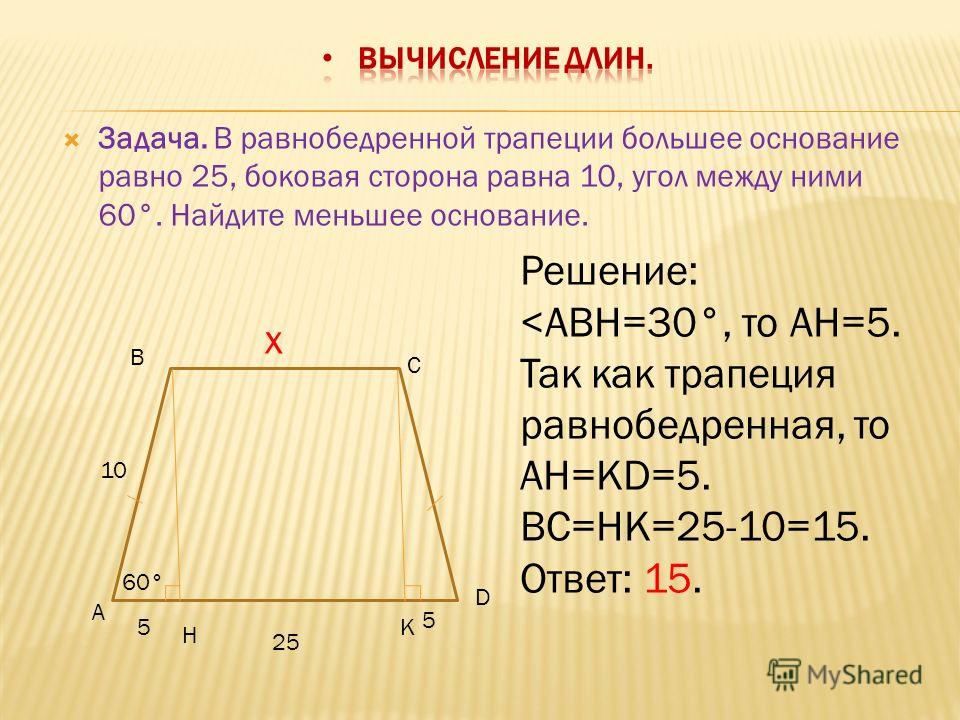
В трапеции ABCD с большим основанием AD диагональ AC перпендикулярна к боковой стороне CD и является биссектрисой угла A.
Найдите AD, если периметр трапеции равен 20, а угол D равен .
Решение:
По условию задачи в прямоугольном ACD
D , следовательно, CAD .
Так как AC — биссектриса, то CAB , откуда DAB , то есть, трапеция равнобедренная. BCA CAD как накрест лежащие, поэтому ABC — равнобедренный.
Обозначим длины боковых сторон ABC буквой x.
Тогда AB = BC = CD = x, и AD = 2x, так как в прямоугольном ACD против угла в лежит катет, равный половине гипотенузы.
Таким образом, периметр трапеции, равный 20, составляет 5x, отсюда
x = 4 и AD = 8.
Ответ: 8.
Задача 12.
В равнобедренной трапеции ABCD с острым углом меньшее основание BC равно 2, а боковая сторона AB равна 10. Продолжения боковых сторон трапеции пересекаются в точке M. Во сколько раз площадь трапеции больше площади треугольника BCM?
Решение:
Нетрудно видеть, что BCM равносторонний и BM = 2, тогда AM = 12 и BCM подобен ADM c коэффициентом .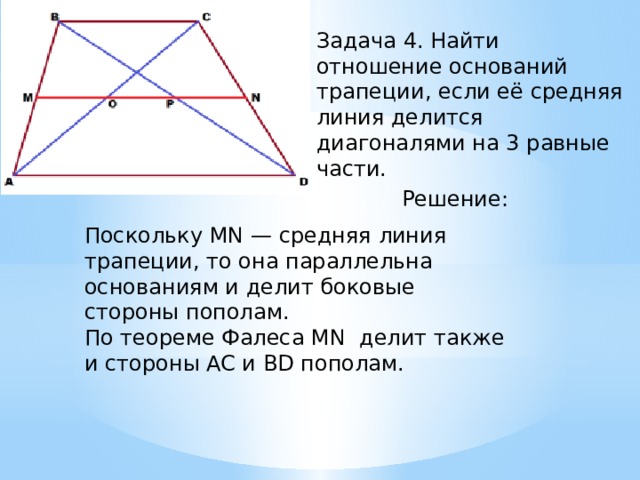
Пусть, , тогда
Площадь трапеции будет равна
Ответ: 35.
Задача 13.
Сумма углов при одном из оснований трапеции равна . Найдите длину отрезка, соединяющего середины оснований, если основания равны 6 и 10.
Решение:
Продолжим боковые стороны до пересечения в точке E и отметим точки F и G — середины оснований трапеции.
Так как сумма углов при основании трапеции равна , то , поэтому EF и EG — медианы в прямоугольных треугольниках BEC и AED соответственно.
Известно, что медиана, проведенная к гипотенузе, равна ее половине, значит
Ответ: 2.
Задача 14.
Найдите радиус окружности, вписанной в равнобочную трапецию, если средняя линия трапеции равна 10, а ее площадь 24.
Решение:
Так как площадь трапеции равна , а высота трапеции равна диаметру вписанной окружности, то есть то , откуда .
Ответ: 1,2.
Задача 15.
Периметр прямоугольной трапеции равен 32, а большая боковая сторона равна 10. Найдите радиус r вписанной в трапецию окружности.
Найдите радиус r вписанной в трапецию окружности.
Решение:
По свойствам описанной трапеции сумма ее боковых сторон равна сумме оснований, поэтому
откуда
Сторона AB равна диаметру окружности, поэтому .
Ответ: 3.
Задача 16.
Около окружности описана трапеция, сумма боковых сторон которой равна 40. Найдите длину ее средней линии.
Решение:
Длина средней линии трапеции равна полусумме оснований. Если трапеция описана вокруг окружности, то в ней сумма оснований равна сумме боковых сторон, поэтому
Ответ: 20.
Задача 17.
В окружность вписана трапеция так, что диаметр окружности служит основанием трапеции, а вершины другого основания делят полуокружность на три равные части. Найдите тупые углы трапеции. Ответ выразите в градусах.
Решение:
Так как AD — диаметр окружности, то дуга ABCD равна . Она делится на три равные части по
Вписанный угол D опирается на дугу ABC, которая равна , отсюда и, стало быть,
Ответ: 120.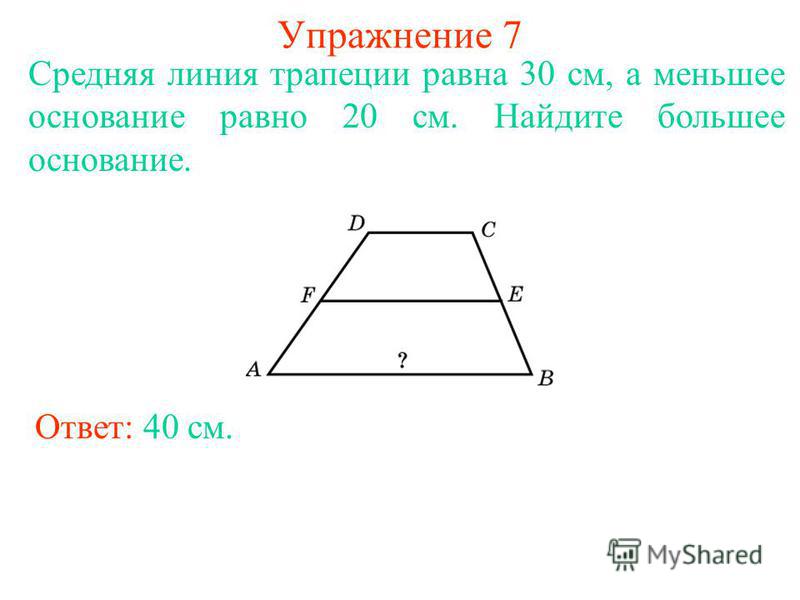
Благодарим за то, что пользуйтесь нашими статьями. Информация на странице «Трапеция и ее свойства» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена: 07.02.2023
Решутест. Продвинутый тренажёр тестов
Решутест. Продвинутый тренажёр тестов- Главная
- ЕГЭ
- Математика профильная
- Планиметрия
- Трапеция
Решил заданий
Не решил заданий
Осталось заданий
История решения
4697 — не приступал 3103 — не приступал 1546 — не приступал 9220 — не приступал 8532 — не приступал 8963 — не приступал 7494 — не приступал 2314 — не приступал 9338 — не приступал 2836 — не приступал 7776 — не приступал 6862 — не приступалФормат ответа: цифра или несколько цифр, слово или несколько слов. Вопросы на соответствие «буква» — «цифра» должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.
Вопросы на соответствие «буква» — «цифра» должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.
Примеры ответов: 7 или здесьисейчас или 3514
Раскрыть Скрыть
№1Средняя линия трапеции равна 11, а меньшее основание равно 5. Найдите большее основание трапеции.
№2Основания трапеции равны 1 и 3, высота равна 1. Найдите площадь трапеции.
№3Средняя линия и высота трапеции равны соответственно 3 и 2. Найдите площадь трапеции.
№4Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
№5Периметр трапеции равен 50, а сумма непараллельных сторон равна 20. Найдите среднюю линию трапеции.
№6Высота трапеции равна 10, площадь равна 150. Найдите среднюю линию трапеции.
№7
Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 1 : 2.
№8Основания равнобедренной трапеции равны 7 и 19, а ее периметр равен 46. Найдите площадь трапеции.
№9
Основания равнобедренной трапеции равны 7 и 19, а ее площадь равна 104. Найдите боковую сторону трапеции.
№10
Основания трапеции равны 20 и 25. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции ее диагональ.
№11
Основание трапеции равно 3, высота равна 13, а площадь равна 65. Найдите второе основание трапеции.
№12Основания трапеции равны 12 и 18, боковая сторона, равная 10, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.
Так твой прогресс будет сохраняться.
Регистрация
Мы отправили код на:
ИзменитьПолучить код повторно через 00:00
Я прочитал(-а) Политику конфиденциальности и согласен(-на) с правилами использования моих персональных данных
Ништяк!
Решено верно
Браво!
Решено верно
Крутяк!
Решено верно
Зачёт!
Решено верно
Чётко!
Решено верно
Бомбезно!
Решено верно
Огонь!
Решено верно
Юхууу!
Решено верно
Отпад!
Решено верно
Шикарно!
Решено верно
Блестяще!
Решено верно
Волшебно!
Решено верно
Калькулятор трапеций: найти A и P
Создано Maciej Kowalski, кандидатом наук
Отзыв Стивена Вудинга
Последнее обновление: 14 ноября 2022 г.
- Что такое трапеция?
- Формула периметра трапеции и углы трапеции
- Как вычислить площадь трапеции
- Как найти высоту трапеции
- Пример: с помощью калькулятора трапеции
- FAQ
Похоже, есть что обсудить, так что давайте приступим, не так ли?
Что такое трапеция?
Трапеция — это четырехугольник (форма с четырьмя сторонами), по крайней мере одна пара противоположных сторон которого параллельна друг другу. Обратите внимание, что мы сказали « по крайней мере одна пара сторон» — если фигура имеет две такие пары, это просто прямоугольник. И не заблуждайтесь – каждый прямоугольник является трапецией . Обратное, конечно, неверно.
Обратите внимание, что мы сказали « по крайней мере одна пара сторон» — если фигура имеет две такие пары, это просто прямоугольник. И не заблуждайтесь – каждый прямоугольник является трапецией . Обратное, конечно, неверно.
Две параллельные стороны обычно называются основаниями . Обычно мы рисуем трапеции так, как мы это делали выше, что может объяснить, почему мы часто различаем их, говоря снизу и вверху основания . Две другие непараллельные стороны называются катетами (аналогично двум сторонам прямоугольного треугольника).
Здесь мы хотели бы упомянуть несколько частных случаев трапеций.
Прямоугольник
Мы уже упоминали об этом в начале этого раздела – это трапеция, имеющая две пары противоположных сторон, параллельных друг другу .
Равнобедренная трапеция
Трапеция, у которой катетов имеют одинаковую длину (аналогично тому, как мы определяем равнобедренные треугольники).

Правая трапеция
Трапеция, у которой одна сторона перпендикулярна основаниям . Во-первых, обратите внимание, что здесь требуется, чтобы только одна из сторон удовлетворяла этому условию — другая может быть, а может и нет. Во-вторых, обратите внимание, что если катет перпендикулярен одному из оснований, то он автоматически перпендикулярен и другому, поскольку они параллельны.
Имея в виду эти особые случаи, зоркий глаз может заметить, что прямоугольника удовлетворяют условиям 2 и 3 . В самом деле, если бы кто-то не знал, что такое прямоугольник, мы могли бы просто сказать, что это равнобедренная трапеция, которая также является прямоугольной трапецией. Довольно причудливое определение по сравнению с обычным, но оно заставляет нас звучать изощренно, не так ли?
Прежде чем мы перейдем к следующему разделу, упомянем еще два отрезка, которые есть у всех трапеций.
Высота трапеции — это расстояние между основаниями, т. е. длина линии, соединяющей два , которая перпендикулярна обоим. На самом деле, это значение имеет решающее значение, когда мы обсуждаем, как вычислить площадь трапеции, и, следовательно, получает отдельный выделенный раздел.
е. длина линии, соединяющей два , которая перпендикулярна обоим. На самом деле, это значение имеет решающее значение, когда мы обсуждаем, как вычислить площадь трапеции, и, следовательно, получает отдельный выделенный раздел.
Медиана трапеции — линия, соединяющая середины катетов. Другими словами, имея в виду рисунок выше, это линия, разрезающая трапецию горизонтально пополам . Он всегда параллелен основаниям, и с обозначениями, как на рисунке, мы имеем median=(a+b)/2\mathrm{median} = (a + b)/2median=(a+b)/2. Если вам интересно название, обязательно ознакомьтесь с калькулятором медианы Omni (примечание: он не касается трапеций).
Хорошо, мы достаточно хорошо изучили нашу форму ; мы даже видели одну формулу трапеции! Давайте сделаем еще один шаг и попробуем еще лучше понять тему. Мы начнем этот углубленный анализ с формулы периметра трапеции и ее внутренних углов .
Формула периметра трапеции и углы трапеции
Периметр многоугольника равен сумме длин его сторон . Для героя сегодняшней статьи история ничем не отличается. С обозначениями, как на рисунке в первом разделе (и в калькуляторе трапеций), мы выводим формулу периметра трапеции:
Для героя сегодняшней статьи история ничем не отличается. С обозначениями, как на рисунке в первом разделе (и в калькуляторе трапеций), мы выводим формулу периметра трапеции:
P=a+b+c+dP = a + b + c + dP=a+b +c+d
Довольно просто, не так ли?
Далее, поговорим об углах . Как и в любом другом четырехугольнике, сумма углов в трапеции составляет 360°360\градус 360° (или 2π2\pi2π радиан. Однако условие трапеции (т.е. наличие пары параллельных сторон) навязывает дополнительных свойства на отдельных.Если быть точным, пара углов вдоль одного из катетов являются дополнительными углами.Это означает, что их сумма должна равняться 180°180\градус180° (или π\piπ радиан), как вы можете узнать на наш дополнительный калькулятор углов.В обозначениях из рисунка в первом разделе это переводится как:
α+β+γ+δ=180°\alpha+\beta+\gamma+\delta=180\степеньα+β+γ+δ=180°
Обратите внимание, что наш инструмент также упоминает углы в нижнем наборе переменных поля. Таким образом, он также может служить калькулятором угла трапеции всякий раз, когда мы ищем эти числа. И действительно, они часто пригодятся – они играют существенную роль , когда мы учимся находить высоту трапеции, а та, в свою очередь, появляется при изучении того, как вычислить площадь трапеции. Однако начнем с последнего вопроса.
Таким образом, он также может служить калькулятором угла трапеции всякий раз, когда мы ищем эти числа. И действительно, они часто пригодятся – они играют существенную роль , когда мы учимся находить высоту трапеции, а та, в свою очередь, появляется при изучении того, как вычислить площадь трапеции. Однако начнем с последнего вопроса.
Как вычислить площадь трапеции
Вернемся к картинке из первого раздела, чтобы вам не приходилось пролистывать всю статью всякий раз, когда вы захотите вспомнить обозначения.
Площадь трапеции по формуле выглядит следующим образом:
A=(a+b)×h3A=\frac{(a+b)\times h}{2}A=2(a+b)× h
Обратите внимание, что действительно, как мы уже упоминали пару раз, очень важно знать, как найти высоту трапеции, чтобы вычислить ее площадь. Кроме того, ноги никогда не появляются в уравнении. Конечно, они определяют форму нашего четырехугольника, но их длины используются только в формуле периметра трапеции, которую мы обсуждали в предыдущем разделе.
Наконец, давайте проясним, что по порядку операций не имеет значения, в какой момент мы делим на 222 в приведенной выше области формулы трапеции. Мы можем либо сначала вычислить (a+b)×h(a + b) \times h(a+b)×h, а затем разделить все это на 222, либо сначала найти h/2h/2h/2, а только потом умножьте его на (a+b)(a+b)(a+b). На самом деле, зоркий глаз заметит, что (a+b)/2(a+b)/2(a+b)/2 равно медиане , которую мы упоминали в первом разделе. Другими словами, в качестве альтернативы мы можем использовать формулу A=медиана×hA = \mathrm{медиана} \times hA=медиана×h, чтобы найти AAA.
Хорошо, мы научились вычислять площадь трапеции, и все кажется простым, если нам дают все данные на табличке. А если нет? Базы довольно просты, но как насчет hhh? Что ж, пора посмотреть , как найти высоту трапеции.
Как найти высоту трапеции
Важным фактом, который мы используем для нахождения высоты трапеции, является то, что это отрезок, перпендикулярный основаниям . Это дает нам прямой угол в обеих конечных точках, что позволяет нам использовать прямоугольные треугольники. И первое, что приходит на ум, когда мы слышим словосочетание прямоугольный треугольник — это, конечно же, теорема Пифагора.
Это дает нам прямой угол в обеих конечных точках, что позволяет нам использовать прямоугольные треугольники. И первое, что приходит на ум, когда мы слышим словосочетание прямоугольный треугольник — это, конечно же, теорема Пифагора.
Проведем из одной из верхних вершин линию, падающую на нижнее основание aaa под углом 90°90\градус90°. (Обратите внимание, что для тупых трапеций, таких как та, что на правом рисунке, над высотой hhh попадает за пределы формы, т. е. на прямую, содержащую aaa, а не саму aaa. Тем не менее, то, что мы опишем ниже, по-прежнему справедливо для таких четырехугольников.) длина этой линии равна высоте нашей трапеции, так что именно то, что мы ищем. Обратите внимание, что по тому, как мы нарисовали линию, образует прямоугольный треугольник с одной из сторон ccc или ddd (в зависимости от того, какую вершину мы выбрали).
Если у нас есть длина катета трапеции и мы можем вычислить другую сторону прямоугольного треугольника (т. е. eee или fff на рисунке выше), то мы знаем, как найти высоту трапеции – мы используем Теорема Пифагора . Однако есть и другой способ расчета.
е. eee или fff на рисунке выше), то мы знаем, как найти высоту трапеции – мы используем Теорема Пифагора . Однако есть и другой способ расчета.
Если вы немного разбираетесь в тригонометрии, вы сможете найти высоту с использованием внутреннего угла трапеции . Если быть точным, глядя на углы трапеций в нашем калькуляторе (т.е. на обозначение на картинке), мы можем использовать определение тригонометрических функций, чтобы написать:
h=c×sin(α)=d×sin (δ)h = c\times\sin(\alpha)=d\times\sin(\delta)h=c×sin(α)=d×sin(δ)
Где sin\sinsin — функция синуса . На самом деле может случиться, что угол равен 30°30\градус30°, 45°45\градус45° или 60°60\градус60°, и в этом случае мы можем просто использовать свойства специальных прямоугольных треугольников с такими внутренними углами.
🙋 Чтобы узнать больше о математике, которую мы использовали в последних шагах, посетите наш калькулятор тригонометрических функций и наш специальный калькулятор прямоугольных треугольников!
Наконец, отметим, что весь этот поиск hhh очень прост в особом случае – когда у нас есть правильная трапеция . Тогда высота нашей трапеции — это просто катет, лежащий рядом с прямым углом. Обратите внимание, что в этом случае приведенная выше тригонометрическая формула все еще работает, поскольку sin(90°)=1\sin(90\градус) = 1sin(90°)=1.
Тогда высота нашей трапеции — это просто катет, лежащий рядом с прямым углом. Обратите внимание, что в этом случае приведенная выше тригонометрическая формула все еще работает, поскольку sin(90°)=1\sin(90\градус) = 1sin(90°)=1.
Уф, это было много теории . Самое время воспользоваться этими формулами трапеции и посмотреть как вычислить площадь и периметр трапеции на практике .
Пример: с помощью калькулятора трапеций
Давайте проверим , как найти площадь и периметр трапеции со сторонами и углами, обозначенными как в калькуляторе трапеций, и следующими данными:
a=8 inb=5 ind =3 в\начать{разделить} a&=8\\mathrm{in}\\ b&=5\\mathrm{in}\\ d&=3\\mathrm{in} \end{split}abd=8 in=5 in=3 in
А:
α=90°δ=45°\begin{split} \альфа&=90\градус\\ \дельта &= 45\градус \end{split}αδ=90°=45°
Вроде не много, но давайте посмотрим, что здесь можно сделать . Во-первых, однако, давайте заметим, что наш калькулятор трапеций может легко справиться с нашей задачей даже с таким небольшим количеством информации. Действительно, если мы введем вышеуказанные числа в наш инструмент (обратите внимание, как мы можем переключаться на другие единицы, щелкая по ним и выбирая подходящую из списка), заполнит все остальные поля . Например, в качестве калькулятора угла трапеции он будет использовать тождества, упомянутые во втором разделе, для вычисления β\betaβ и γ\gammaγ. Также обратите внимание, что мы можем дополнительно зайти в расширенный режим и посмотреть длину медианы.
Действительно, если мы введем вышеуказанные числа в наш инструмент (обратите внимание, как мы можем переключаться на другие единицы, щелкая по ним и выбирая подходящую из списка), заполнит все остальные поля . Например, в качестве калькулятора угла трапеции он будет использовать тождества, упомянутые во втором разделе, для вычисления β\betaβ и γ\gammaγ. Также обратите внимание, что мы можем дополнительно зайти в расширенный режим и посмотреть длину медианы.
Если инструмент может это сделать, сможем и мы! Давайте посмотрим, как вычислить площадь и периметр трапеции вручную.
Прежде всего обратите внимание, что мы имеем дело с прямой трапецией , так как α=90°\альфа=90\градус α=90° (на самом деле у нас тоже β=90°\бета = 90\градус β=90°). Это означает, что сторона ccc перпендикулярна основаниям и, следовательно, равна высоте c=hc = hc=h. Однако мы не знаем ccc, так что нам еще предстоит найти .
Для этого нарисуйте высоту нашей трапеции , которая идет от вершины между bbb и ddd. Вместе с ddd и частью aaa, образует прямоугольный треугольник . Более того, нам известен один из его углов – δ=45°\delta = 45\градус δ=45°. Значит, это один из частных случаев – это половина квадрата. Следовательно, hhh равно нижней стороне треугольника, а ddd — это, по сути, диагональ квадрата, а значит:
ч=d2=3 дюйм2=1,52 дюйм≈2,1213 дюйм\начало{разделение} h &=\frac{d}{\sqrt{2}} = \frac{3\ \mathrm{in}}{\sqrt{2}}\\ &= 1,5\sqrt{2}\\mathrm{дюйм} \приблизительно 2,1213\ \mathrm{дюйм} \end{split}h=2
d=2
3 in=1,52
in ≈2,1213 in
(последнее равенство получаем, рационализируя знаменатель).
Теперь у нас есть все необходимое для поиска ААА. Вспомните из специального раздела, как вычислить площадь трапеции, и используйте информацию, чтобы получить 92} \end{split}A=2(a+b)×h=2(8 in+5 in)×1,52
in=9,752
in2≈13,789 in2
Мы также собрали все данные для нахождения PPP, поскольку c=h=1,52 inc = h = 1,5\sqrt{2}\ \mathrm{in}c=h=1,52 in . По формуле периметра трапеции из второго сечения получаем
По формуле периметра трапеции из второго сечения получаем
P=a+b+c+d=8 дюйм + 5 дюйм + 1,52 дюйм + 3 дюйм=16 дюйм+1,52 дюйм≈18,12 дюйм\ начинать {разделять} P& = a + b + c + d \\ &= 8\ \mathrm{in}\!+\! 5\ \mathrm{in} \!+\! 1.5\sqrt{2}\\mathrm{in} \!+\! 3\\mathrm{в} \\ &= 16\ \mathrm{in}+ 1,5\sqrt{2}\ \mathrm{in}\\ & \примерно 18.12\\mathrm{in} \end{split}P=a+b+c+d=8 дюймов+5 дюймов+1,52
дюйм+3 дюйм=16 дюйм+1,52
дюйм≈18,12 дюйм
Не так уж и плохо, не правда ли? Стороны и углы, которые мы получили в начале, казались довольно случайным набором, но нам удалось найти им хорошее применение. Если вы чувствуете, что изголодались по геометрии и формулам , обязательно ознакомьтесь с другими калькуляторами 2D-форм на веб-сайте Omni — у нас есть все!
Часто задаваемые вопросы
Как найти высоту трапеции, зная площадь и основания?
Для определения высоты h из области A и оснований a и b :
- Сумма длин оснований:
a + b.
- Разделите дважды площадь на результат шага 1:
2A/(a + b). - Вот оно! Вы нашли высоту трапеции.
Какова высота трапеции с площадью 10 и сторонами 2 и 3?
Высота имеет длину 4. Действительно, формула для высоты гласит: h = 2A/(a+b) .
Подставляя значения a = 2 , b = 3 и A = 10 , мы получаем h = 2 × 10 /(2 + 3) = 4 .
Является ли трапеция параллелограммом?
№ . У параллелограмма две пары параллельных сторон, а у трапеции должна быть только одна пара параллельных сторон. Следовательно, общая трапеция не является параллелограммом.
Является ли параллелограмм трапецией?
Да , каждый параллелограмм является трапецией. То же самое верно для каждого ромба, каждого прямоугольника и каждого квадрата. Однако воздушный змей (дельтовидная) не является трапецией.
У каждой трапеции есть 2 пары противоположных параллельных сторон?
Нет , у трапеции должна быть хотя бы одна пара параллельных сторон, а это значит, что она может иметь ровно одну такую пару и при этом быть совершенно правильной трапецией. Если у него две пары параллельных сторон, то это, по сути, параллелограмм.
Если у него две пары параллельных сторон, то это, по сути, параллелограмм.
Сколько осей симметрии у трапеции?
Обычная трапеция имеет ноль линий симметрии. Однако есть частный случай 9.0023 равнобедренные трапеции: у них есть одна линия симметрии, которая проходит через середины их оснований.
Maciej Kowalski, кандидат в PhD
A (основание)
B (основание)
H (высота)
Область (A)
Периметр
Периметр (P)
. похожие калькуляторы 2d геометрии 📏
ПлощадьПлощадь прямоугольникаПлощадь полумесяца… еще 20
Как найти длину стороны трапеции
Все ресурсы промежуточной геометрии
8 Диагностические тесты 250 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Справка по геометрии среднего уровня » Плоская геометрия » Четырехугольники » Трапеции » Как найти длину стороны трапеции
Предположим, площадь трапеции равна , высота и основание . Какой должна быть длина второго основания?
Какой должна быть длина второго основания?
Возможные ответы:
Правильный ответ:
Пояснение:
Напишите формулу нахождения площади трапеции.
Подставьте данные и решите по любому основанию.
Сообщить об ошибке
Если площадь трапеции , высота трапеции , а длина основания , то какой должна быть длина другого основания?
Возможные ответы:
Правильный ответ:
Пояснение:
Напишите формулу площади трапеции.
Подставьте все данные значения и найдите основание.
Сообщить об ошибке
Основание равнобедренной трапеции равно и . Периметр трапеции равен . Найдите длину одной из двух оставшихся сторон.
Периметр трапеции равен . Найдите длину одной из двух оставшихся сторон.
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы решить эту задачу, сначала заметьте, что у равнобедренной трапеции два параллельных основания неодинаковой длины. Кроме того, у равнобедренной трапеции должны быть две непараллельные стороны, которые имеют одинаковую длину. Поскольку в этой задаче указана длина обоих оснований, а также общий периметр, недостающие стороны можно найти по следующей формуле: две равные непараллельные стороны.
Таким образом, решение:
Проверьте решение, подключив Ответ:
Отчет о ошибке
Asosceles Trapezoid Trapezoid на базовых измерениях и. Кроме того, равнобедренная трапеция имеет высоту . Найдите длину одной из двух недостающих сторон.
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы решить эту задачу, сначала заметьте, что у равнобедренной трапеции два параллельных основания неравной длины. Кроме того, у равнобедренной трапеции должны быть две непараллельные стороны, которые имеют одинаковую длину.
Эта задача дает длины для каждого из оснований, а также высоту равнобедренной трапеции. Чтобы найти длину одного из двух эквивалентных непараллельных катетов трапеции, сначала используйте высоту трапеции, чтобы сформировать прямоугольные треугольники внутри трапеции, каждый из которых имеет длину основания . См. изображение ниже:
Примечание: длину основания можно найти, вычитая длины двух оснований, а затем разделив эту разницу пополам:
. ножки трапеции.
Таким образом, решение:
Сообщить об ошибке
Размеры основания равнобедренной трапеции, показанной выше, равны и .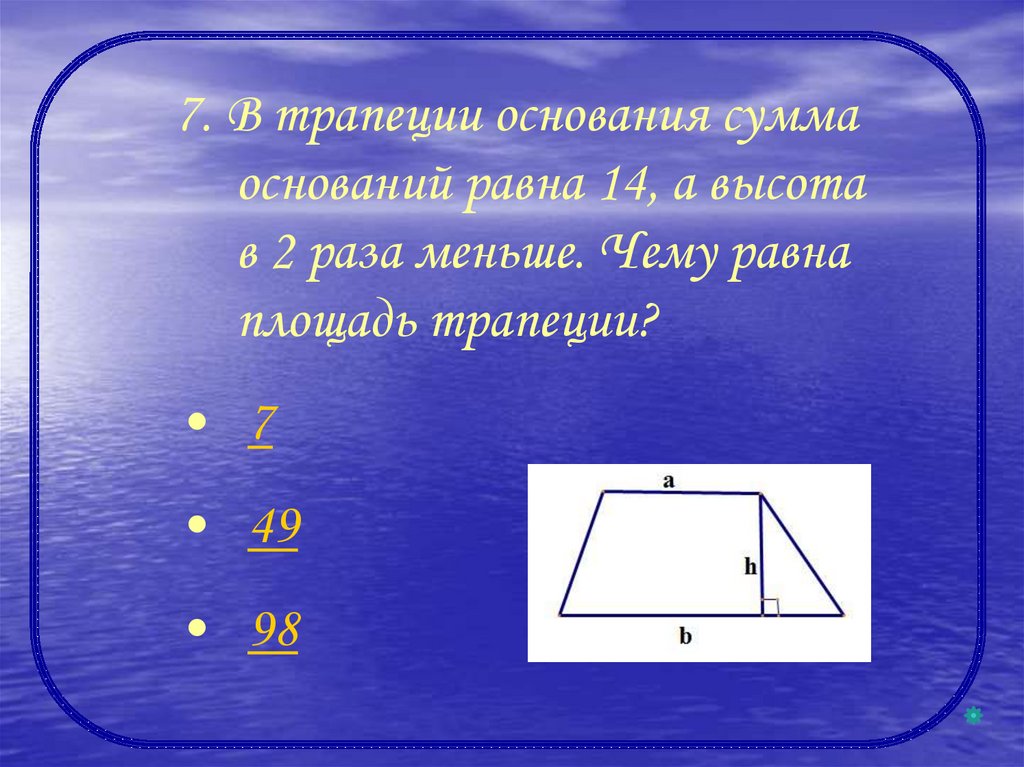 Кроме того, трапеция имеет высоту . Найдите длину стороны.
Кроме того, трапеция имеет высоту . Найдите длину стороны.
Возможные ответы:
Правильный ответ:
Пояснение:
В этой задаче длины всех оснований и высоты равнобедренной трапеции указаны в подсказке. Чтобы найти длину одного из двух эквивалентных непараллельных катетов трапеции (сторона ), сначала используйте высоту трапеции, чтобы сформировать прямоугольные треугольники внутри трапеции, каждый из которых имеет длину основания .
Основание внутренних треугольников равно , потому что разница между двумя основаниями равна . И эта разница должна быть разделена поровну пополам, потому что равнобедренная трапеция симметрична — из-за двух эквивалентных непараллельных сторон и двух неэквивалентных параллельных оснований.
Теперь применим теорему Пифагора: , где .
Таким образом,
Сообщить об ошибке
Используя показанную выше равнобедренную трапецию, найдите длину одной из двух непараллельных сторон.
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы решить эту задачу, сначала заметьте, что у равнобедренной трапеции два параллельных основания неодинаковой длины. Кроме того, у равнобедренной трапеции должны быть две непараллельные стороны, которые имеют одинаковую длину. Поскольку в этой задаче указана длина обоих оснований, а также общий периметр, недостающие стороны можно найти по следующей формуле: две равные непараллельные стороны.
Таким образом, решение:
Сообщить об ошибке
Равнобедренная трапеция имеет одно основание, длина которого равна , а длина одной из сторон равна . Периметр трапеции равен . Найдите длину другого основания трапеции.
Возможные ответы:
В этой задаче недостаточно информации.
Правильный ответ:
Пояснение:
Чтобы решить эту задачу, сначала заметьте, что у равнобедренной трапеции два параллельных основания неодинаковой длины. Кроме того, у равнобедренной трапеции должны быть две непараллельные стороны, которые имеют одинаковую длину.
Таким образом, используйте данную информацию, чтобы применить формулу:
Периметр = Основание один Основание два (отрезок), где длина «отрезка» – одна из двух эквивалентных непараллельных сторон.
Таким образом, решение:
Сообщить об ошибке
Равнобедренная трапеция имеет размеры основания и , соответственно. Кроме того, высота равнобедренной трапеции равна длине большего основания. Найдите длину одной из двух равных непараллельных сторон.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, сначала заметьте, что у равнобедренной трапеции два параллельных основания неодинаковой длины. Кроме того, у равнобедренной трапеции должны быть две непараллельные стороны, которые имеют одинаковую длину.
Кроме того, у равнобедренной трапеции должны быть две непараллельные стороны, которые имеют одинаковую длину.
Эта задача дает длины для каждого из оснований, а также информацию о высоте равнобедренной трапеции. Чтобы найти длину одного из двух эквивалентных непараллельных катетов трапеции, используйте высоту трапеции, чтобы сформировать прямоугольные треугольники внутри трапеции, каждый из которых имеет длину основания . Длину основания внутреннего треугольника можно найти, вычитая длины двух оснований, а затем разделив эту разницу пополам:
Чтобы вычислить точную высоту равнобедренной трапеции (а также внутреннего треугольника), найдите большее основание. Так как наибольшее основание трапеции равно , высота трапеции равна:
Теперь у вас достаточно информации, чтобы применить формулу , где одна из недостающих сторон.
Окончательное решение:
Сообщить об ошибке
Основание равнобедренной трапеции равно и .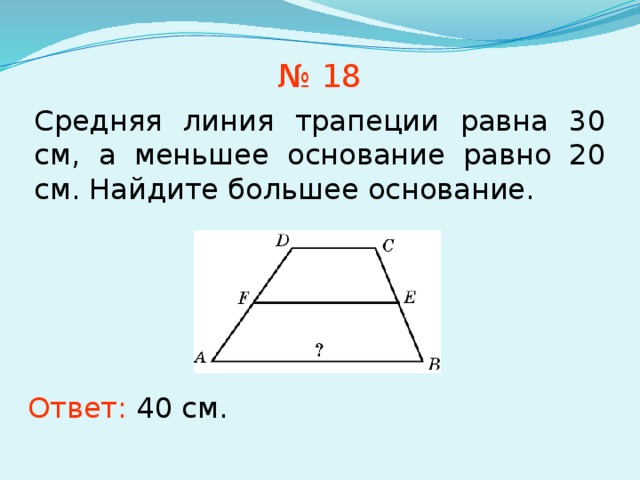 Периметр трапеции равен . Найдите длину одной из двух оставшихся сторон.
Периметр трапеции равен . Найдите длину одной из двух оставшихся сторон.
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы решить эту задачу, сначала заметьте, что у равнобедренной трапеции два параллельных основания неодинаковой длины. Кроме того, у равнобедренной трапеции должны быть две непараллельные стороны, которые имеют одинаковую длину. Поскольку в этой задаче указана длина обоих оснований, а также общий периметр, недостающие стороны можно найти по следующей формуле: две равные непараллельные стороны.
Таким образом, решение:
Проверьте решение. непараллельных сторон. Периметр трапеции равен . Найдите длину другого основания трапеции.
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы решить эту задачу, сначала заметьте, что у равнобедренной трапеции два параллельных основания неодинаковой длины.



Leave A Comment