средняя линия, как найти площадь, формула
Содержание:
- Окружность, описанная около трапеции
-
Как найти радиус описанной окружности
- Если известны угол и диагональ трапеции
- Если известны диагональ, стороны трапеции и площадь одного из треугольников
- Если известны длины сторон треугольника
-
Как найти центр описанной окружности
-
Если угол прямой
- Если угол острый
- Если угол тупой
-
Если угол прямой
- Задачи с решениями
Содержание
- Окружность, описанная около трапеции
-
Как найти радиус описанной окружности
- Если известны угол и диагональ трапеции
- Если известны диагональ, стороны трапеции и площадь одного из треугольников
- Если известны длины сторон треугольника
-
Как найти центр описанной окружности
-
Если угол прямой
- Если угол острый
- Если угол тупой
-
Если угол прямой
- Задачи с решениями
Окружность, описанная около трапеции
Трапеция — это выпуклый четырехугольник, две стороны которого параллельны, а две другие — не параллельны.
Около четырехугольника можно описать окружность, если сумма его противолежащих углов равна 180°. Поэтому окружность можно описать только вокруг равнобедренной трапеции.
Как найти радиус описанной окружности
Самый распространенный способ найти радиус окружности, описанной около трапеции — через радиус окружности, описанной около треугольника, имеющего 3 любые общие вершины с данной трапецией.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Каждая диагональ делит трапецию на два треугольника. Описанная окружность проходит через все вершины трапеции, значит она проходит через все вершины каждого из этих треугольников и также является для них описанной окружностью.
Формула 1
\(R=\frac а{2\cdot\sin\alpha},\)
где R — радиус описанной окружности,
а — сторона треугольника,
α — угол треугольника, противолежащий стороне а. \circ-\beta\right)}\).
\circ-\beta\right)}\).
Формула 2
\(R=\frac{abc}{4S}\),
где R — радиус описанной окружности,
а, b, c — стороны треугольника,
S — площадь треугольника.
Если известны длины сторон треугольникаФормула 3
\(R=\frac{abc}{4\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}},\)
где R — радиус описанной окружности,
а, b, c — стороны треугольника,
p — ½ периметра треугольника.
Как найти центр описанной окружности
Центр описанной окружности может лежать как внутри трапеции, так и вне ее. Определить его местонахождение помогает угол между диагональю трапеции и боковой стороной.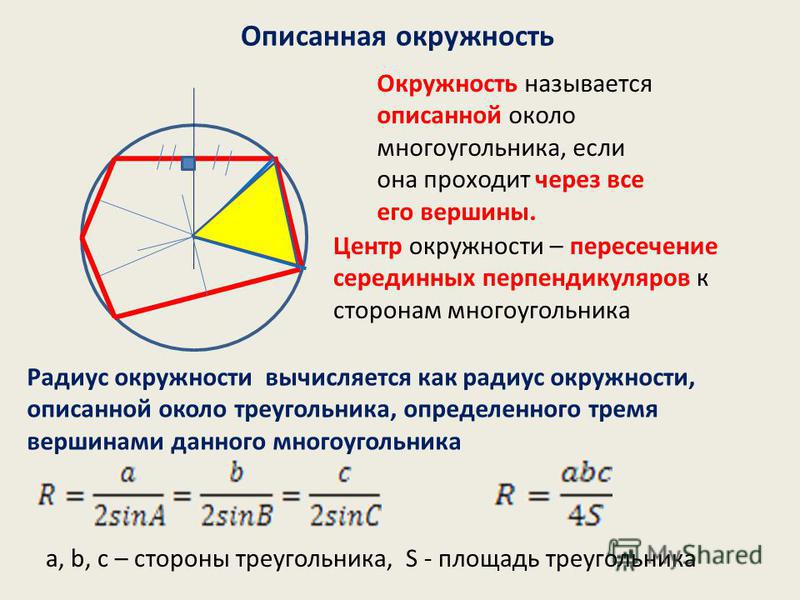
Если диагональ трапеции перпендикулярна ее боковой стороне, то центр описанной окружности будет лежать на середине большего основания. Тогда большее основание будет равно диаметру описанной окружности.
Формула 4
\(R=\frac12а,\)
где R — радиус описанной окружности,
Если диагональ трапеции и боковая сторона образуют острый угол, то центр описанной около трапеции окружности лежит внутри трапеции.
Если угол тупойЕсли диагональ трапеции и боковая сторона образуют тупой угол, то центр описанной около трапеции окружности будет лежать вне трапеции за ее большим основанием.
Задачи с решениями
Задача
Дано: трапеция с описанной окружностью.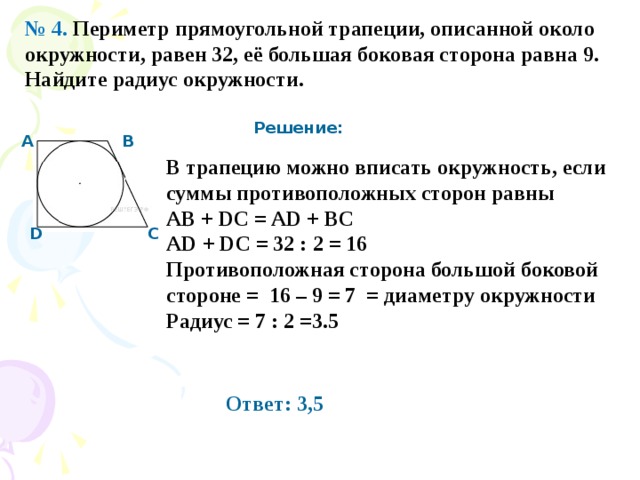
Найти: боковую сторону трапеции.
Решение: Так как около трапеции описана окружность, эта трапеция — равнобедренная. Удвоенная средняя линия трапеции равна сумме ее оснований (10 см). Сумма двух боковых сторон равна 22-10=12 (см). Боковая сторона трапеции равна 6 см.
Ответ: 6 см.
Примечание
Дано: основания трапеции ВС=11 см и AD=21 см. Диагональ трапеции ВD=20 см.
Найти: радиус описанной окружности.
Решение
- Трапеция ABCD равнобедренная, AB=CD, так как описать окружность можно только около равнобедренной трапеции.
- ВЕ — высота трапеции. Отрезок \(АЕ=(21-11):2=5 (см)\) по свойству равнобедренной трапеции. Отрезок ЕD=21-5=16 (см).
- Треугольник BED прямоугольный.
 2}=13 (см).\)
2}=13 (см).\) - \(sin∠BAD=\frac{12}{13}\) по определению синуса.
- \(R=\frac{BD}{2\sin\angle A}=10\frac56 (см).\)
Ответ: \(10\frac56 см.\)
Насколько полезной была для вас статья?
Рейтинг: 1.25 (Голосов: 4)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Описанная окружность и трапеция
Не откладывайте! ЗАГОВОРИТЕ на Английском!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2015-12-05
Описанная окружность и трапеция. Здравствуйте! Для вас ещё одна публикация, в которой рассмотрим задачи с трапециями. Задания входят в состав экзамена по математике. Здесь они объединены в группу, дана не просто одна трапеция, а комбинация тел – трапеция и окружность. Большинство из таких задачек решаются устно. Но есть и такие на которые нужно обратить особое внимание, например, задача 27926.
Какую теорию необходимо помнить? Это:
1. Свойство сторон четырёхугольника описанного около окружности.
2. Теорему Пифагора. *Куда мы без неё )
3. Понятие средней линии трапеции.
Задачи с трапециями, которые имеются на блоге можно посмотреть здесь.
27924. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.
Отметим, что описать окружность можно только около равнобедренной трапеции. Нам дана средняя линия, значит можем определить сумму оснований, то есть:
Значит сумма боковых сторон будет равна 22–10=12 (периметр минус основания). Так как боковые стороны равнобедренной трапеции равны, то одна сторона будет равна шести.
Ответ: 6
27925. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 600, большее основание равно 12. Найдите радиус описанной окружности этой трапеции.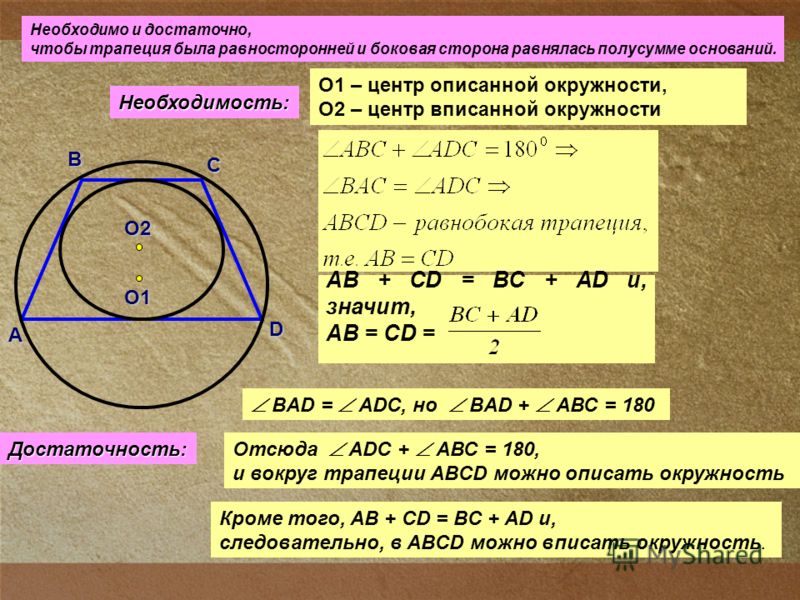
Если вы решали задачи с окружностью и вписанным в неё шестиугольником, то сразу озвучите ответ – радиус равен 6. Почему?
Посмотрите: равнобедренная трапеция с углом при основании равным 600 и равными сторонами AD, DC и CB, представляет собой половину правильного шестиугольника:
В таком шестиугольнике отрезок соединяющий противоположные вершины проходит через центр окружности. *Центр шестиугольника и центр окружности совпадают, подробнее здесь п.6
То есть большее основание этой трапеции совпадает с диаметром описанной окружности. Таким образом радиус равен шести.
*Конечно, можно рассмотреть равенство треугольников ADO, DOС и OCB. Доказать что они равносторонние. Далее сделать вывод о том, что угол AOB равен 1800 и точка О равноудалена от вершин A, D, C и B, а и значит АО=ОВ=12/2=6.
Ответ: 6
27926. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.
Отметим, что центр описанной окружности лежит на оси симметрии, при чём если построить высоту трапеции проходящую через этот центр, то она при пересечении с основаниями разделит их пополам. Покажем это на эскизе, также соединим центр с вершинами:
Отрезок EF является высотой трапеции, его нам нужно найти.
В прямоугольном треугольнике OFC нам известна гипотенуза (это радиус окружности), FC=3 (так как DF=FC). По теореме Пифагора можем вычислить OF:
В прямоугольном треугольнике OEB нам известна гипотенуза (это радиус окружности), EB=4 (так как AE=EB). По теореме Пифагора можем вычислить OE:
Таким образом EF=FO+OE=4+3=7.
Ответ: 7
Теперь важный нюанс!
В этой задаче на рисунке чётко показано, что основания лежат по разные стороны от центра окружности, поэтому задача решается именно так.
А если бы в условии не было дано эскиза?
Тогда у задачи было бы два ответа. Почему? Посмотрите внимательно – в любую окружность можно вписать две трапеции с заданными основаниями:
*То есть при данных основаниях трапеции и радиусе окружности существует две трапеции.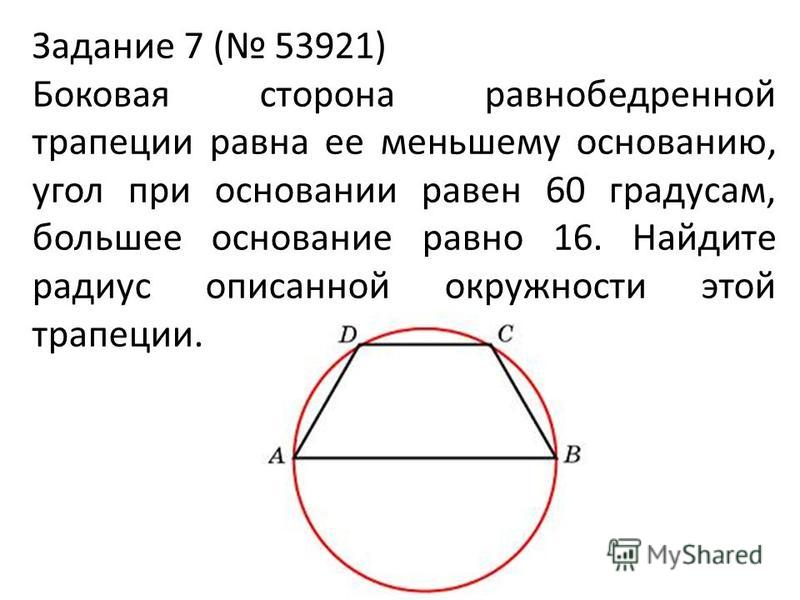
И решение будет «второго варианта» будет следующим.
По теореме Пифагора вычисляем OF:
Также вычислим OE:
Таким образом EF=FO–OE=4–3=1.
Конечно, в задаче с кратким ответом на ЕГЭ двух ответов быть не может, и подобная задача без эскиза дана не будет. Поэтому обратите особое внимание на эскиз! А именно: как расположены основания трапеции. А вот в заданиях с развёрнутым ответом такая в прошлые годы присутствовала (немного с усложнённым условием). Тот, кто рассматривал только один вариант расположения трапеции теряли балл на этом задании.
27937. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.
Здесь сразу следует вспомнить свойство четырёхугольника описанного около окружности:
Суммы противоположных сторон любого четырёхугольника описанного около окружности равны.
Значит
А средняя линия равна половине суммы оснований, то есть 10.
Ответ: 10
27938. Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.
Радиус окружности равен половине высоты. Используя свойство указанное в предыдущей задаче получим:
Большая сторона у нас это СВ, следовательно можем вычислить AD=11–CB=11–7=4. Таким образом, радиус будет равен 2.
Ответ: 2
27915. Найдите высоту трапеции, в которую вписана окружность радиуса 1.
Посмотреть решение
27936. Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.
Посмотреть решение
На этом всё, успеха вам!
С уважением, Александр Крутицких.
*Расскажите о сайте в социальных сетях.
Категория: Четырёхугольники | ЕГЭ-№1Трапеция
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
геометрия — Нахождение радиуса окружности, вписанной в трапецию
Когда ничего не помогает, возьмите молоток побольше
…что я и сделал и обнаружил, что ответ $R=6$.
Я не буду объяснять, почему $AC$, $BD$, $PR$ и $QS$ совпадают в $F$. это просто частный случай Теорема Брианшона. Итак, давайте начнем оттуда. Обратите внимание на углы $\angle CAB=\angle ACD=\alpha$, $\angle ABD=\angle BDC=\beta$ и отрезок $OF=x$. Мы будем использовать их постоянно. Для простоты я также введу следующие символы: $AK=p_1$, $LC=p_2$, $BM=q_1$, $DN=q_2$. Мы знаем, что $p_1p_2=16$ и $q_1q_2=9/4$.
Сначала попробуем найти $p_1=AK$. Тот же подход будет использован для нахождения отрезков $p_2,q_1,q_2$
Взглянем на четырехугольник $AQOK$:
$$AQ=FQ\cot\alpha=AK\cos \alpha+OK\sin\varphi $$
$$QO=AK\sin\alpha+OK\cos\varphi$$
Это приводит к следующим уравнениям:
$$p_1\cos\alpha+R\sin\varphi=(R+x )\кот\альфа$$ $$p_1\sin\alpha+R\cos\varphi=R$$
или:
$$R\sin\varphi=(R+x)\cot\alpha-p_1\cos\alpha$$ $$R\cos\varphi=R-p_1\sin\alpha$$ 92}=36\подразумевается R=6$$
Урок Радиус окружности, вписанной в равнобедренную трапецию
Урок Радиус окружности, вписанной в равнобедренную трапециюАлгебра -> Настраиваемые средства решения задач Word ->
|

 2}=13 (см).\)
2}=13 (см).\)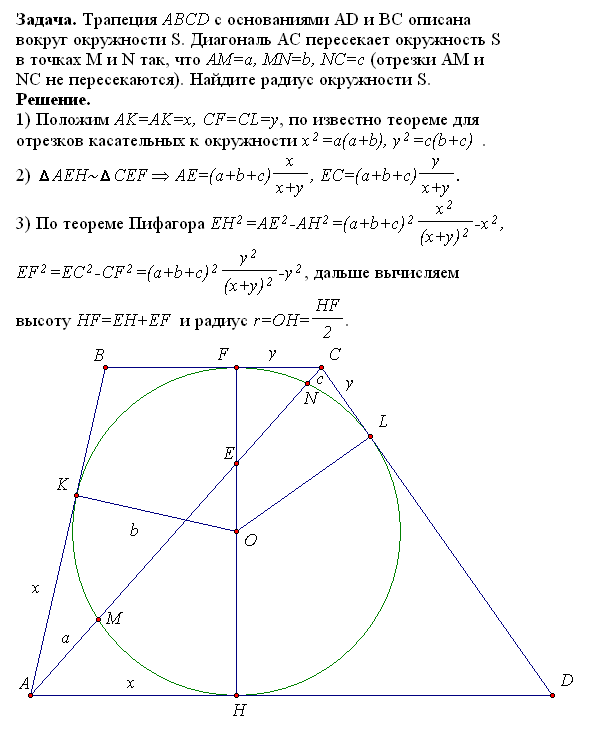 com
com 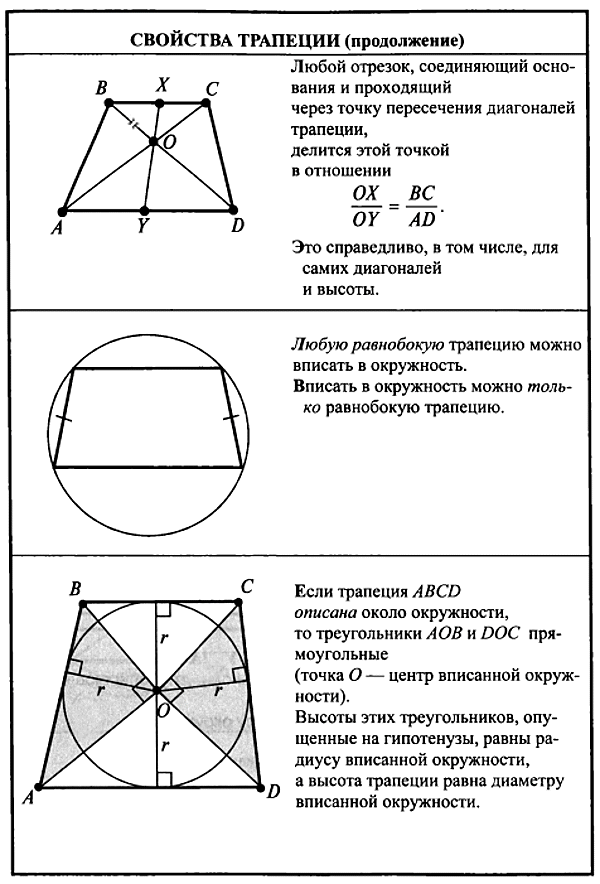 В трапецию вписана окружность.
В трапецию вписана окружность. 
Leave A Comment