Тесты ОГЭ по математике 2021
Тесты ОГЭ по математике 2021
Структура
Модуль «Алгебра» содержит 11 заданий: в части 1 – 8 заданий; в части 2 – 3 задания.
Модуль «Геометрия» содержит 8 заданий: в части 1 – 5 заданий; в части 2 – 3 задания.
Модуль «Реальная математика» содержит 7 заданий.
Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня.
Шкала перевода баллов в оценки
«2» – от 0 до 7
«3» – от 8 до 14
«4» – от 15 до 21
«5» – от 22 до 32
Система оценивания выполнения отдельных заданий и экзаменационной работы в целом
Для оценивания результатов выполнения работ выпускниками используется общий балл. Максимальный балл за работу в целом – 32. Задания, оцениваемые 1 баллом, считаются выполненными верно, если указан номер верного ответа (в заданиях с выбором ответа), или вписан верный ответ (в заданиях с кратким ответом), или правильно соотнесены объекты двух множеств и записана соответствующая последовательность цифр (в заданиях на установление соответствия).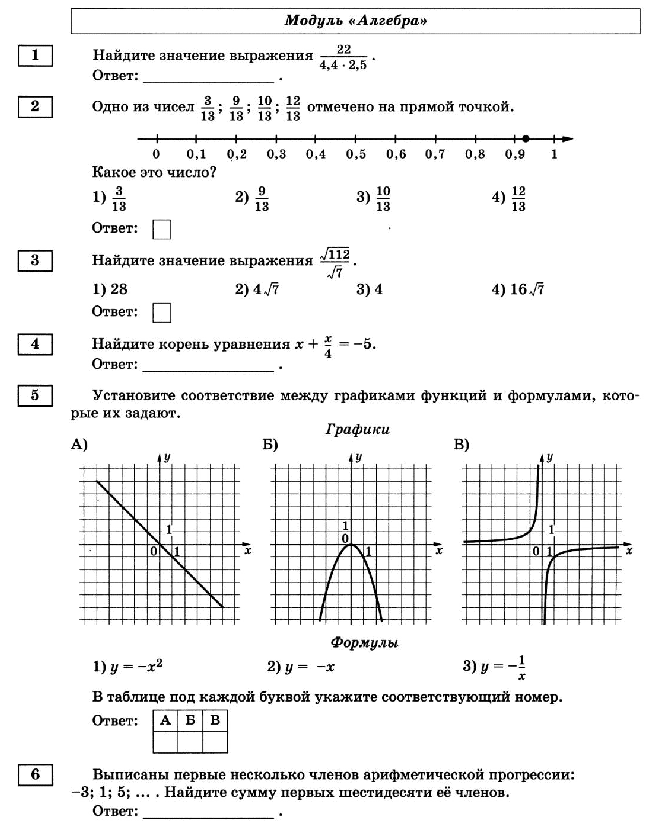
Задания, оцениваемые в 2 балла, считаются выполненными верно, если обучающийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется полный балл, соответствующий данному заданию. Если в решении допущена ошибка, не имеющая принципиального характера и не влияющая на общую правильность хода решения, то участнику выставляется 1 балл.
Дополнительные материалы и оборудование
Участникам разрешается использовать справочные материалы, содержащие основные формулы курса математики, выдаваемые вместе с работой. Разрешается использовать линейку. Калькуляторы на экзамене не используются.
На выполнение экзаменационной работы отводится 235 минут
Любой учитель или репетитор может отслеживать результаты своих учеников по всей группе или классу. Для этого нажмите ниже на кнопку «Создать класс», а затем отправьте приглашение всем заинтересованным.
Ознакомьтесь с подробной видеоинструкцией по использованию модуля.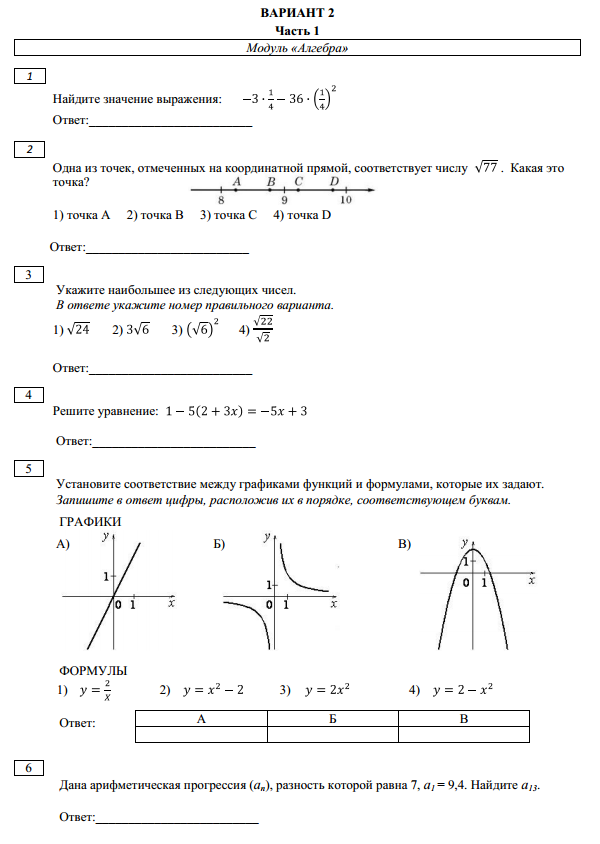
| 2131 | Тренировочная работа №4 по математике 9 класс 05.03.2020 СтатГрад — Варианты МА1990601, МА1990602, Ответы, Критерии | Статград 9 класс Тренировочная работа №4 по математике 05.03.2020 !Варианты МА1990601, МА1990602, Критерии PDF | |
| 2087 | На стороне KM остроугольного треугольника PKM (PK не равно PM) как на диаметре построена полуокружность, пересекающая высоту PS в точке T, PS=8, TS=6, H -точка пересечения высот треугольника PKM. Найдите PH Решение | На стороне KM остроугольного треугольника PKM (PK не равно PM) как на диаметре построена полуокружность ! Лысенко ОГЭ 2020 Математика 40 вариантов — Вариант 3 Задание 26# Апробация КИМ ОГЭ 06-02-2020 Санкт-Петербург Задание 26 # Задача-аналог 278 | |
| 2072 | Апробация КИМ ОГЭ математика 9 класс Санкт-Петербург 06. 02.2020 02.2020Решение | Пробный ОГЭ математика 9 класс Санкт-Петербург 06.02.2020 ! Апробация КИМ ОГЭ 6 февраля 2020 года | |
| 2069 | Тренировочная работа №2 по математике 9 класс СтатГрад Варианты МА1990303, МА1990304, Критерии Решение | Статград 9 класс Тренировочная работа №3 по математике 04.02.2020 !Варианты МА1990303, МА1990304 PDF Ответы, Критерии | |
| 2068 | Тренировочная работа №2 по математике 9 класс СтатГрад Варианты МА1990301, МА1990302, Критерии Решение | Статград 9 класс Тренировочная работа №3 по математике 04.02.2020 !Варианты МА1990301, МА1990302 PDF Ответы, Критерии | |
| 1974 | Краевая диагностическая работа по математике 9 класс декабрь 2019 Решение | КДР математика 9 класс 18-12-2019 4 варианта | |
| 1950 | Упростите выражение (x-9)/(x-6sqrt(x)+9)-6/(sqrt(x)-3) Решение График | Диагностическая работа по алгебре и геометрии Статград 12-12-2019 профильный уровень Вариант МА1990402 Задание 2 | |
| 1949 | Найдите целые решения неравенства (x^2+x-6)/(x^2+4x+4)<=0 Решение График | Диагностическая работа по алгебре и геометрии Статград 12-12-2019 профильный уровень Вариант МА1990402 Задание 2 | |
| 1948 | Решите уравнение abs(2x+5)-abs(3x-1)=5 Решение График | Диагностическая работа по алгебре и геометрии Статград 12-12-2019 профильный уровень Вариант МА1990402 Задание 4 | |
| 1947 | Постройте график функции y=(3x-6)/(x^2-2x) и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку Решение График | Диагностическая работа по алгебре и геометрии Статград 12-12-2019 профильный уровень Вариант МА1990402 Задание 5 | |
Демонстрационные варианты (демоверсии) ОГЭ по математике
Демонстрационные варианты по математике (алгебре) 2010 года представлены в двух видах: демонстрационный вариант 1 и демонстрационный вариант 2.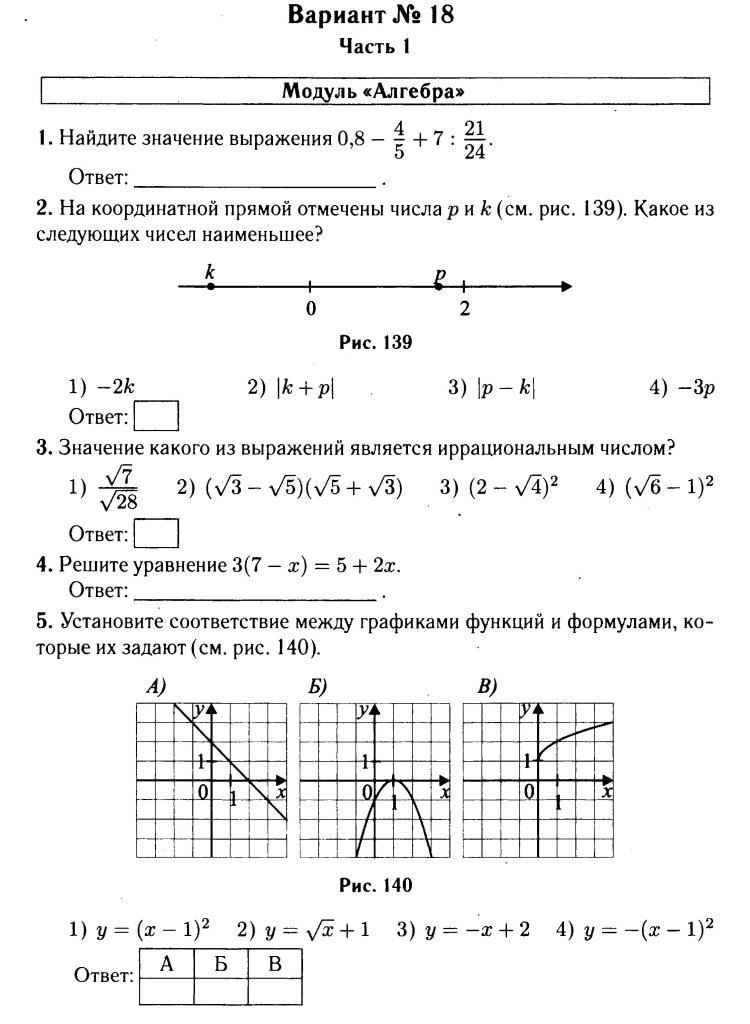 Отличие между ними заключается в том, что первая часть демонстрационного варианта 2 содержит на две задачи больше, чем первая часть демонстрационного варианта 1 (задачи 17 и 18) Эти задачи относятся к теории вероятностей и статистике. Других отличий нет.
Отличие между ними заключается в том, что первая часть демонстрационного варианта 2 содержит на две задачи больше, чем первая часть демонстрационного варианта 1 (задачи 17 и 18) Эти задачи относятся к теории вероятностей и статистике. Других отличий нет.
Демонстрационный вариант ОГЭ по математике (алгебре) 2011 года почти полностью совпадает с демонстрационным вариантом 2 ОГЭ по математике (алгебре) 2010 года. Отличие заключается лишь в заданиях №10 и №22.
В 2011 году в ряде регионов в порядке эксперимента для проведения ОГЭ-9 по математике была использована перспективная модель КИМов, проект демонстрационного варианта которой мы также размещаем.
В 2012 году в демонстрационный вариант ОГЭ по математике были включены не только задания по алгебре, теории вероятностей и статистике, но также и задания по геометрии.
Демонстрационные варианты ОГЭ по математике 2013-2017 годов отличаются от вариантов предыдущих лет. В них
В них
- Работа состоит из трёх модулей: «Алгебра», «Геометрия», «Реальная математика». Модули «Алгебра» и «Геометрия» состоят из двух частей: во второй части задачи более сложные по сравнению с первой частью.
- За каждое правильно выполненное задание части 1 выставляется 1 балл. В каждом модуле части 2 задания расположены по нарастанию сложности и оцениваются в 2 балла (в 2, 3 и 4 балла в демонстрационных вариантах по математике 2013-2015 годов).
- Рекомендуемый минимальный порог выполнения экзаменационной работы – 8 баллов, набранные в сумме за выполнение заданий всех трёх модулей, при условии, что по модулю «Алгебра» набрано не менее 3 баллов, по модулю «Геометрия» набрано не менее 2 баллов и по модулю «Реальная математика»набрано не менее 2 баллов.

Демонстрационный вариант ОГЭ по математике 2014 годапрактически полностью совпадает с демонстрационным вариантом ОГЭ по математике 2013 года. Небольшое отличие имеется лишь в задаче №13, где требуется указать номера верных утверждений: в 2013 году условие этой задачи содержало 3 утверждения, а 2014 году к этим трем утверждениям было добавлено еще одно.
В демонстрационном варианте ОГЭ по математике 2015 года по сравнению с демонстрационным вариантом 2014 года были заменены задачи 1, 2, 3, 4, 6, 7, 10 и 17 на другие по той же тематике. Задачи 8 и 12 претерпели лишь косметические изменения. Из чертежа задачи 11 по геометрии удалены лишние данные. Остальные задачи были оставлены без изменений. Кроме того, в 2015 году была изменена форма записи ответа в задачах с выбором ответа: ответ стало нужно записывать цифрой с номером правильного ответа (а не обводить кружком).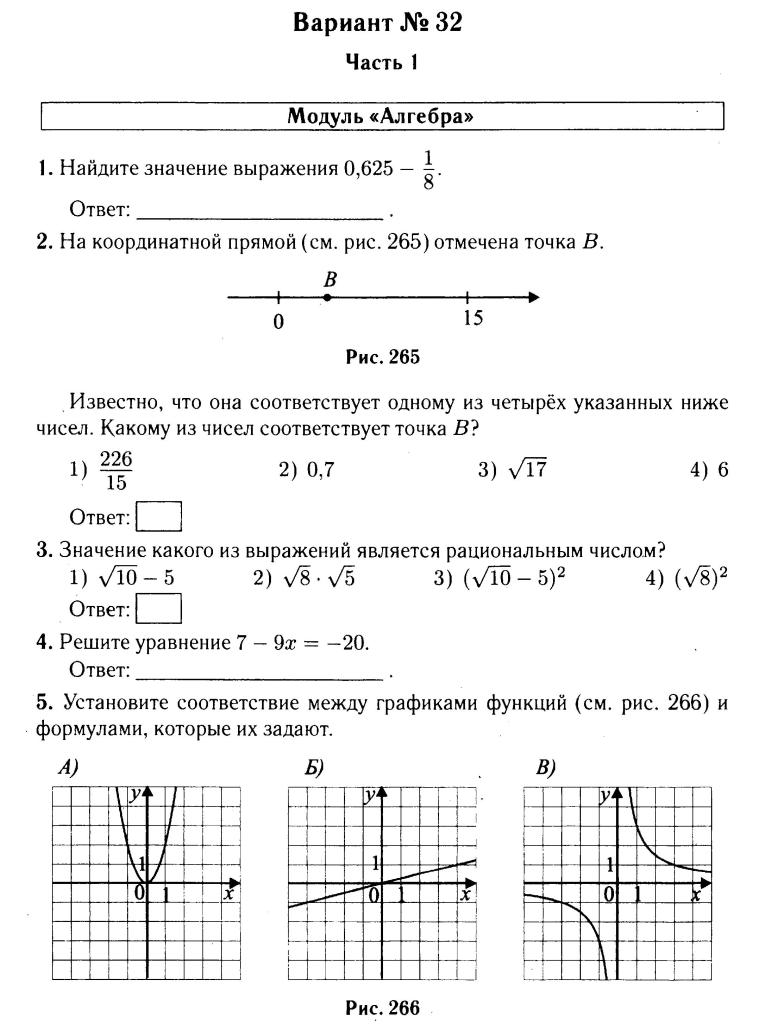
В демонстрационных вариантах ОГЭ по математике 2016-2017 годов по сравнению с демонстрационным вариантом 2015 года изменений нет. Снижен максимальный первичный балл за всю работу с 38 до 32 за счет того, что правильное выполнение каждого из заданий части 2 в демонстрационных вариантах ОГЭ по математике 2016-2017 годов оценивается в 2 балла.
В демонстрационный вариант ОГЭ по математике 2018 года по сравнению с демонстрационным вариантом 2017 года были внесены следующие изменения: из демонстрационного варианта был исключен модуль «Реальная математика», а задания, входившие в этот модуль, были распределены по модулям «Алгебра» и «Геометрия». При этом общее количество заданий и максимальный балл за всю работу не изменились.
В демонстрационном варианте ОГЭ по математике 2019 года по сравнению с демонстрационным вариантом 2018 года изменений не было.
В демонстрационном варианте ОГЭ по математике 2020 года по сравнению с демонстрационным вариантом 2019 года были заменены задания 2, 5, 7, 8, 15 на блок практико-ориентированных заданий 1-5, объединенных единым сюжетом.
В демонстрационный вариант ОГЭ по математике 2021 года по сравнению с демонстрационным вариантом 2020 года были внесены следующие изменения:
- Были объединены в одно задания 13 и 8 на преобразование выражений
- Задание 12 заменено на задание с практическим содержанием, направленное на проверку умения применять знания о последовательностях и прогрессиях в прикладных ситуациях
- Изменен порядок заданий в соответствии с тематикой и сложностью
- Максимальный балл уменьшен с 32 до 31
Пробный экзамен по математике 9 класс. 1-4 варианты с ответами
Решение.
Сумма углов выпуклого четырёхугольника равна 360°. Имеем: Так как , и — общая треугольника ABD и BDC. Из равенства треугольников следует, что . Таким образом, .
Ответ: 95.
Ответ: 95
17. Короткое плечо шлагбаума имеет длину 1 м, а длинное плечо – 3 м. На какую высоту (в метрах) опустится конец короткого плеча, когда конец длинного плеча поднимается на 1,8 м?
Решение.
Найдём синус угла, на который поднимается длинное плечо:
Угол подъема длинного плеча равен углу на который опустится короткое плечо. Пусть x — высота, на которую опустится короткое плечо, имеем:
Таким образом, короткое плечо опустится на 0,6 м.
Ответ: 0,6.
Ответ: 0,6
18 На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 12 млн пользователей.Какое из следующих утверждений неверно?
1) Пользователей из России больше, чем пользователей из Белоруссии и Украины вместе.
2) Пользователей из Украины больше, чем пользователей Латвии.
3) Примерно две трети общего числа пользователей — из России.
4) Пользователей из Украины больше 3 миллионов.
В ответ запишите номер выбранного утверждения.
Решение.
Разъясним каждый вариант ответа:
1) Очевидно, что пользователей из России больше, чем пользователей из Украины и Белоруссии вместе.
2) Сектор «Украина» занимает большую площадь диаграммы, чем сектор «Другие страны», а т. к. «Латвия» включена в «Другие страны», имеем: пользователей из Украины больше, чем пользователей из Латвии.
3) Сектор в две трети диаграммы отсекается углом в 2·360°/3 = 240°. Очевидно, что угол, отсекающий сектор «Россия» примерно равен 240°, значит примерно две трети общего числа пользователей — из России.
4) Видно, что пользователей из Украины меньше четверти всех пользователей, значит, меньше 12/4=3 миллионов.
Ответ: 4.
Ответ: 4
19. В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
Решение.
Вероятность благоприятного случая() — отношение количества благоприятных случаев к количеству всех случаев. В данной задаче благоприятным случаем является старт спортсмена не из России под номером 1. Всего благоприятных случаев 2 + 5 = 7, а количество всех случаев 13 + 2 + 5 = 20. Отношение соответственно равно
Ответ: 0,35.
Ответ: 0,35
20. Площадь трапеции можно вычислить по формуле , где — основания трапеции, — высота (в метрах). Пользуясь этой формулой, найдите высоту , если основания трапеции равны и , а её площадь .
Часть 2
Решение.
Выразим высоту трапеции из формулы площади:
Подставляя, получаем:
Ответ: 4.
Приведём другое решение.
Подставим в формулу известные значения величин:
Ответ: 4
21. Разложите на множители .
Решение.
Имеем:
.
Ответ: .
22.Два оператора, работая вместе, могут набрать текст газеты объявлений за 8 ч. Если первый оператор будет работать 3 ч, а второй 12 ч, то они выполнят только 75% всей работы. За какое время может набрать весь текст каждый оператор, работая отдельно?
23.Постройте график функции и определите, при каких значениях прямая имеет с графиком ровно три общие точки.
Решение.
Раскрывая модуль, получим, что график функции можно представить следующим образом:
Этот график изображён на рисунке:
Из графика видно, что прямая имеет с графиком функции ровно три общие точки при и
Ответ: 0; 4.
24. Диагонали и трапеции пересекаются в точке . Площади треугольников и равны соответственно и . Найдите площадь трапеции.
Решение.
Заметим, что площади двух треугольников, общей вершиной которых является точка пересечения диагоналей трапеции, а основаниями — боковые стороны, равны. Это следует, например, из того, что площади треугольников и равны (поскольку эти треугольники имеют общее основание , и их высоты, проведенные к этому основанию, равны как высоты трапеции), а . По условию, , поэтому и являются не боковыми сторонами, а основаниями трапеции. Тогда треугольники и подобны по двум углам, и отношение их площадей равно квадрату коэффициента подобия . Поэтому . Поскольку треугольники и имеют общую высоту, проведённую из вершины , то отношение их площадей равно отношению их оснований, т. е. . Значит, . Поэтому и . Но тогда .
Это следует, например, из того, что площади треугольников и равны (поскольку эти треугольники имеют общее основание , и их высоты, проведенные к этому основанию, равны как высоты трапеции), а . По условию, , поэтому и являются не боковыми сторонами, а основаниями трапеции. Тогда треугольники и подобны по двум углам, и отношение их площадей равно квадрату коэффициента подобия . Поэтому . Поскольку треугольники и имеют общую высоту, проведённую из вершины , то отношение их площадей равно отношению их оснований, т. е. . Значит, . Поэтому и . Но тогда .
Ответ: .
25.В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BOC.
Решение.
Проведём высоту так, чтобы она проходила через точку Углы и равны друг другу как вертикальные. Вспомним также, что диагонали делятся точкой пересечения пополам, следовательно, Рассмотрим треугольники и , они прямоугольные, имеют равные углы и равные гипотенузы, следовательно эти треугольники равны, а значит равны отрезки и . Таким образом,
Вспомним также, что диагонали делятся точкой пересечения пополам, следовательно, Рассмотрим треугольники и , они прямоугольные, имеют равные углы и равные гипотенузы, следовательно эти треугольники равны, а значит равны отрезки и . Таким образом,
Площадь параллелограмм равна а площадь треугольника
26. Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
ВАРИАНТ № 2
Часть 1 МОДУЛЬ «АЛГЕБРА»
1. Вычислите:
Решение.
Приведём к общему знаменателю:
Ответ: 3,7.
Ответ: 3,7
2.На координатной прямой отмечены числа a, b и c:
Значение какого из следующих выражений отрицательно?
1)−a 2)a+c 3)b−c 4) c − a
Решение.
Заметим, что −2 < a < −1, 1 < b < 2 и 3 < c < 4. Тогда выражение −a положительно. Для выражения a + c верно двойное неравенство 1 < a + c < 3. Для выражения b − c верно двойное неравенство −2 < b − c < −1. Для выражения c − a верно двойное неравенство 4 < c − a < 6.
Таким образом, отрицательным является выражение b − c.
Правильный ответ указан под номером 3.
Ответ: 3
3.В какое из следующих выражений можно преобразовать дробь ?
1) 2) 3) 4)
Решение.
Упростим дробь:
Правильный ответ указан под номером 3.
Ответ: 3
4. Решите уравнение (x + 2)2 = (x − 4)2.
Решение.
Последовательно получаем:
Ответ: 1.
Приведем другое решение.
Возведем обе части уравнения в квадрат:
Приведем другое решение.
Воспользуемся формулой разности квадратов:
Ответ: 1
5.График какой из приведенных ниже функций изображен на рисунке?
1)
2)
3)
4)
Решение.
Ветви изображённой на рисунке гиперболы лежат во II и IV четверти, её график растянут вдоль оси ординат в два раза. Этим условиям соответствует вариант 1
Этим условиям соответствует вариант 1
Графику соответствует вариант под номером 1.
Ответ: 1
6. Геометрическая прогрессия задана формулой n — го члена . Укажите третий член этой прогрессии.
Решение.
По формуле n-го члена геометрической прогрессии имеем:
Ответ: 12.
Ответ: 12
7.Представьте в виде дроби выражение и найдите его значение при . В ответ запишите полученное число.
Решение.
Упростим выражение:
Найдем значение выражения при
Ответ: −10.
Ответ: -10
8.Решите неравенство:
1) 2)3) 4)
МОДУЛЬ «ГЕОМЕТРИЯ»
Решение.
Решим неравенство: Корнями уравнения являются числа -23 и 0. Поэтому
Правильный ответ указан под номером 4.
Ответ: 4
9. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма.
Решение.
Сумма смежных углов параллелограмма равна 180°. Тогда величина меньшего угла параллелограмма будет равна:
Ответ:
Ответ: 65
10. В окружности с центром в точке проведены диаметры и , угол равен 25°. Найдите величину угла .
Решение.
Углы OCD и OAB являются вписанными и опираются на одну дугу BD. Таким образом,
Ответ: 25.
Ответ: 25
11. Найдите площадь параллелограмма, изображённого на рисунке.
Решение.
Площадь параллелограмма равна произведению основания на высоту: 7 · 4 = 28.
Ответ: 28.
Ответ: 28
12. Найдите тангенс угла треугольника , изображённого на рисунке.
Решение.
Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему. Треугольник ABC — прямоугольный, поэтому
Ответ: 0,75.
Ответ: 0,75
13.Какие из следующих утверждений верны?
1) Каждая сторона треугольника меньше разности двух других сторон.
2) В равнобедренном треугольнике имеется не более двух равных углов.
3) Если сторона и угол одного треугольника соответственно равны стороне и углу другого треугольника, то такие треугольники равны.
4) В треугольнике ABC, для которого AB = 3, BC = 4, AC = 5, угол C наименьший.
МОДУЛЬ «РЕАЛЬНАЯ МАТЕМАТИКА»
Решение.
Проверим каждое из утверждений:
1)«Каждая сторона треугольника меньше разности двух других сторон.» — неверно, так как если имеем, что
2) «В равнобедренном треугольнике имеется не более двух равных углов.» — неверно, в равнобедренном треугольнике углы при основании равны.
3)«Если сторона и угол одного треугольника соответственно равны стороне и углу другого треугольника, то такие треугольники равны.» — неверно, равенство определяется по трем элементам.
4)«В треугольнике ABC, для которого AB = 3, BC = 4, AC = 5, угол C наименьший.» — верно, в треугольнике против большего угла лежит большая сторона.
Ответ: 4.
Ответ: 4
14. Учёный Иванов выезжает из Москвы на конференцию в Санкт-Петербургский университет. Работа конференции начинается в 10:00. В таблице дано расписание ночных поездов Москва — Санкт-Петербург
Номерпоезда
Отправление из
Москвы
Прибытие в
Санкт-Петербург
026А
23:00
06:30
002А
23:55
07:55
038А
00:44
08:46
016А
01:00
08:38
Путь от вокзала до университета занимает полтора часа. Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят учёному Иванову.
1)026А 2)002А 3)038А 4) 016А
Решение.
Поскольку путь от вокзала до университета занимает полтора часа, поезд должен прибыть на вокзал не позднее 08:30. Этому условию удовлетворяют поезда под номерами: 026А и 002А. Из них позже отправляется поезд под номером 002А.
Правильный ответ указан под номером 2.
Ответ: 2
15.В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.
Вещество
Дети от 1 года
до 14 лет
Мужчины
Женщины
Жиры
40—97
70—154
60—102
Белки
36—87
65—117
58—87
Углеводы
170—420
257—586
Какой вывод о суточном потреблении жиров, белков и углеводов 7-летней девочкой можно сделать, если по подсчётам диетолога в среднем за сутки она потребляет 42 г жиров, 35 г белков и 190 г углеводов? В ответе укажите номера верных утверждений.
1) Потребление жиров в норме.
2) Потребление белков в норме.
3) Потребление углеводов в норме.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
Решение.
Проанализируем каждое утверждение.
1) Для семилетней девочки нормой является употребление от 40 до 97 граммов жиров в сутки, 42 грамма укладываются в этот промежуток. Первое утверждение верно.
2) Для семилетней девочки нормой является употребление от 36 до 87 граммов белков в сутки, 35 граммов не укладываются в этот промежуток. Второе утверждение неверно.
2) Для семилетней девочки нормой является употребление от 170 до 420 граммов углеводов в сутки, 190 граммов укладываются в этот промежуток. Третье утверждение верно.
Ответ: 1; 3.
Ответ: 1; 3
16.Площадь земель крестьянского хозяйства, отведённая под посадку сельскохозяйственных культур, составляет 24 га и распределена между зерновыми и овощными культурами в отношении 5:3. Сколько гектаров занимают овощные культуры?
Решение.
Овощные культуры занимают:
Ответ: 9.
Ответ: 9
17. Сколько досок длиной 3,5 м, шириной 20 см и толщиной 20 мм выйдет из четырехугольной балки длиной 105 дм, имеющей в сечении прямоугольник размером 30 см 40 см?
Решение.
Найдем объем доски : 350 · 20 · 2 = 14 000 см3. Найдем объем балки: 1050 · 30 · 40 = 1 260 000 см3.
Поэтому количество досок равно 1 260 000 : 14 000 = 90.
Ответ: 90.
Ответ: 90
18. На диаграмме представлены семь крупнейших по площади территории (в млн км2) стран мира.
Какое из следующих утверждений неверно
1) По площади территории Австралия занимает шестое место в мире.
2) Площадь территории Бразилии составляет 7,7 млн км2.
3) Площадь Индии меньше площади Китая.
4) Площадь Канады меньше площади России на 7,1 млн км2.
В ответе запишите номер выбранного утвержденияРешение.
Проверим каждое утверждение:
1) На диаграмме видно, что Австралия — шестая по площади страна в мире. Значит первое утверждение верно.
2) Из диаграммы видно, что площадь Бразилии — 8,5 млн км2. Второе утверждение неверно.
3) Из диаграммы видно, что площадь Индии меньше площади Китая. Третье утверждение верно.
4) Из диаграммы видно, что площадь Канады меньше площади России на 17,1-10,0=7,1 млн км2. Четвёртое утверждение верно.
Неверным является утверждение под номером 2.
Ответ: 2
Решение.
Проанализируем все утверждения.
1) Пользователей из России больше всех, тем самым, их больше чем пользователей из Украины.
2) Сектор «Беларусь» занимает большую площадь диаграммы, чем сектор «Другие страны», а т. к. «Швеция» включена в «Другие страны» пользователей из Беларуси больше чем пользователей из Швеции.
3) Сектор в треть диаграммы имеет угол 360° : 3 = 120°. Угол сектора «Украина» меньше 90°, следовательно, меньше трети пользователей сети из Украины.
4) Пользователей из России больше половины всех пользователей, значит, больше 9 : 2 = 4,5 млн, а значит, больше 4 миллионов.
Ответ:3.
Ответ: 3
19. Какова вероятность того, что случайно выбранное натуральное число от 15 до 29 делится на 5?
Решение.
Чисел от 15 до 29 — 15 штук. Среди них на 5 делится только 3 числа. Таким образом, вероятность того, что случайно выбранное натуральное число от 15 до 29 делится на 5 равна
Ответ: 0,2
20.Объём пирамиды вычисляют по формуле , где — площадь основания пирамиды, — её высота. Объём пирамиды равен 40, площадь основания 15. Чему равна высота пирамиды?
Часть 2
Решение.
Выразим высоту пирамиды из формулы для ее объема:
Подставляя, получаем:
Ответ: 8.
Ответ: 8
21.Сократите дробь , если .
Решение.
Имеем:
Ответ: 1.
22.Пристани и расположены на реке, скорость течения которой на этом участке равна 3 км/ч. Лодка проходит туда и обратно без остановок со средней скоростью 8 км/ч. Найдите собственную скорость лодки.
Решение.
Пусть км/ч — собственная скорость лодки. Тогда скорость движения по течению равна км/ч, а скорость движения против течения равна км/ч. Обозначим расстояние между пристанями. Время, затраченное на весь путь, равно
.
По условию средняя скорость равна 8 км/ч, а весь путь равен . Следовательно,
.
Решим это уравнение:
Получаем: или . Корень −1 не является решением задачи. Значит, скорость лодки равна 9 км/ч.
Ответ: 9 км/ч.
23.Постройте график функции
и определите, при каких значениях прямая будет иметь с графиком единственную общую точку.
Решение.
Построим график функции (см. рисунок).
Из графика видно, что прямая будет иметь с графиком функции единственную точку пересечения при принадлежащем множеству [0; 1).
Ответ: [0; 1).
24. Медианы треугольника пересекаются в точке . Найдите длину медианы, проведённой к стороне , если угол равен 47°, угол равен 133°, .
Решение.
Обозначим середину стороны за . Продлим на свою длину за точку до точки . Четырёхугольник — параллелограмм, потому что и . Значит, = 133°, поэтому четырёхугольник — вписанный. Тогда .
Ответ: 6.
25. В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём СF = АM, BE = DK. Докажите, что EFKM — параллелограмм.
Решение.
Противоположные стороны параллелограмма равны и по условию следовательно:
В параллелограмме противоположные углы равны: , Рассмотри треугольники и , в этих треугольниках , , следовательно эти треугольники равны, а значит, . Аналогично равны треугольники и а следовательно равны отрезки и Противоположные стороны четырехугольника равны, следовательно, по признаку параллелограмма, этот четырёхугольник — параллелограмм.
26.Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
ВАРИАНТ № 3
Часть 1 МОДУЛЬ «АЛГЕБРА»
1. Вычислите:
Решение.
Приведём к общему знаменателю:
Ответ: 1,03.
Ответ: 1,03
2.На координатной прямой отмечены числа и Какое из следующих утверждений неверно?
1) 2)
3) 4)
Решение.
Заметим, что и , и проверим все варианты ответа:
1) — неверно.
2) — верно, поскольку каждый множитель отрицателен.
3) — верно.
4) — верно.
Неверным является утверждение 1.
Ответ: 1
3. Какое из чисел больше: или ?
1)
2)
3)
Решение.
В силу цепочки неравенств
первое число меньше второго.
Правильный ответ указан под номером 1.
Ответ: 1
4. Найдите корни уравнения
Если корней несколько, в ответе запишите их сумму.
Решение.
Перенесём всё в уравнении в одну сторону:
По теореме, обратной теореме Виета, сумма корней равна 1, а их произведение равно −12. Тем самым, это числа −3 и 4.
Ответ: −3; 4.
Ответ: -3;4
5.Укажите соответствие между графиками функций и формулами, которые их задают.
1) 2)
3) 4)
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке
АБ
В
Решение.
Определим вид графика каждой из функций.
1) уравнение прямой, которая пересекает ось абсцисс в точке 2 ; ось ординат в точке −2.
2) уравнение степенной функции с положительным дробным показателем. График проходит через точку (1; 0).
3) уравнение параболы, ветви которой направлены вверх.
4) уравнение степенной функции с положительным дробным показателем. График проходит через точку (−1; 0).
Таким образом, искомое соответствие: A — 4, Б — 3, В — 1.
Ответ: 431.
Ответ: 431
6. Последовательность задана условиями , . Найдите .
Решение.
Будем вычислять последовательно:
Данная последовательность образует арифметическую прогрессию. Найдем разность арифметической прогрессии:
тогда
Примечание.
Зная разность и первый член арифметической прогрессии, можно найти посредственно:
Ответ: −9.
Ответ: -9
7. Сократите дробь
Решение.
Сократим дробь:
Ответ: 84.
Ответ: 84
8.На каком рисунке изображено множество решений неравенства
1)
2)
3)
4)
МОДУЛЬ «ГЕОМЕТРИЯ»
9.В равностороннем треугольнике ABC биссектрисы CN и AM пересекаются в точке P. Найдите .
Решение.
В равностороннем треугольнике ABC все углы равны 60°. Биссектрисы CN и AM делят уголы пополам, поэтому = = Сумма углов в треугольнике равна 180°, поэтому Вертикальные углы равны, следовательно,
Ответ: 120.
Ответ: 120
10 . Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 48°.
Решение.
Угол AOB является центральным углом, ACB — вписанным. Оба угла опираются на одну и ту же дугу, следовательно, угол AOB в два раза больше угла ACB.
Ответ: 24.
Ответ: 24
11. Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.
Решение.
Диагонали ромба пересекаются под углом 90° и точкой пересечения делятся пополам. Из прямоугольного треугольника, катетами которого являются половины диагоналей ромба, а гипотенузой — сторона ромба, по теореме Пифагора найдем половину неизвестной диагонали: Тогда вся неизвестная диагональ равна 8.
Площадь ромба равна половине произведения диагоналей:
Ответ: 24.
Ответ: 24
12. Найдите тангенс угла AOB, изображенного на рисунке.
Решение.
Опустим перпендикуляр BH на отрезок OA и рассмотрим прямоугольный треугольник OBH:
Ответ: 2.
Ответ: 2
13.Какие из следующих утверждений верны?
1) Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.
2) Если радиусы двух окружностей равны 5 и 7, а расстояние между их центрами равно 3, то эти окружности не имеют общих точек.
3) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность пересекаются.
4) Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°.
МОДУЛЬ «РЕАЛЬНАЯ МАТЕМАТИКА»
14. В таблице представлены нормативы по технике чтения в 3 классе.
Какую отметку получит третьеклассник, прочитавший в апреле 68 слов за минуту?
1)«2» 2)«3» 3)«4» 4) «5»
Решение.
Проверка техники чтения происходила во втором полугодии. Из таблицы видно, что 68 прочитанных за минуту слов попадают в интервал «69 и менее» слов. Это соответствует отметке «2».
Правильный ответ указан под номером 1.
Ответ: 1
15.В таблице приведены результаты двух полуфинальных забегов на дистанцию 60 м. В финальном забеге 6 участников. Из каждого полуфинала в финал выходят два спортсмена, показавших первый и второй результаты. К ним добавляют еще двух спортсменов, показавших лучшее время среди всех остальных участников полуфиналов.Запишите в ответ номера спортсменов, не попавших в финал.
Решение.
В полуфинале 1, лучшее время у спортсмена №4 и у спортсмена №1, таким образом, они выходят в финал.
В полуфинале 2, лучшее время у спортсмена №6 и у спортсмена №7 таким образом, они также выходят в финал.
Лучшее время из оставшихся спортсменов у спортсмена №2 и №5. таким образом таким образом, они тоже выходят в финал.
Таким образом, в финал не попали спортсмены под намерами 3 и 8.
Ответ: 38|3,8|8,3|83
16.На молочном заводе пакеты молока упаковываются по 12 штук в коробку, причём в каждой коробке все пакеты одинаковые. В партии молока, отправляемой в магазин «Уголок», коробок с полуторалитровыми пакетами молока втрое меньше, чем коробок с литровыми пакетами. Сколько литров молока в этой партии, если коробок с литровыми пакетами молока 45?
Решение.
Найдём количество коробок с полуторалитровыми пакетами молока: 45 : 3 = 15. Теперь рассчитаем количество литров молока в этой партии: 45 · 12 · 1 + 15 · 12 · 1,5 = 810 л.
Ответ: 810.
Ответ: 810
17. На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
Решение.
Пусть неизвестное расстояние равно х м. Рассмотрим два прямоугольных треугольника, выделенные на рисунке красным и зелёным. Они имеют общий угол и, следовательно, подобны. Поэтому отношения их катетов равны:
Тем самым, искомое расстояние равно 3,5 м.
Ответ: 3,5.
Ответ: 3,5
18.На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 9 млн пользователей.Какое из следующих утверждений неверно?
1) Пользователей из Беларуси меньше, чем пользователей из Украины.
2) Пользователей из России больше 4 миллионов.
3) Пользователей из Украины больше четверти общего числа пользователей.
4) Пользователей из Беларуси больше, чем пользователей из Финляндии.
В ответе запишите номер выбранного утверждения.
Решение.
Разъясним каждый вариант ответа.
1) Очевидно, что пользователей из Беларуси меньше, чем пользователей из Украины.
2) Видно, что пользователей из России больше половины всех пользователей, значит, больше 9/2 = 4,5 млн, а значит, больше 4 миллионов.
3) Сектор в четверть диаграммы отсекается углом в 360°/4 = 90°. Очевидно, что угол, отсекающий сектор «Украина» меньше 90°, значит, меньше четверти пользователей сети — из Украины.
4) Сектор «Беларусь» занимает большую площадь диаграммы, чем сектор «Другие страны», а т. к. «Финляндия» включена в «Другие страны», имеем: пользователей из Белоруссии больше, чем пользователей из Финляндии.
Ответ: 3.
Ответ: 3
19. В фирме такси в данный момент свободна 21 машина: 11 черных, 2 желтых и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси. Полученный ответ округлите до сотых.
Решение.
Вероятность того, что приедет зеленая машина равна отношению количества зеленых машин к общему количеству машин:
Ответ: 0,38.
Ответ: 0,38
20.Площадь параллелограмма можно вычислить по формуле , где — стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь параллелограмма, если его стороны 10 м и 12 м и .
Часть 2
Решение.
Подставим в формулу известные значения величин:
Ответ: 60.
Ответ: 60
21.Решите систему уравнений:
Решение.
Сложим два уравнения системы:
откуда получаем или
Вычтем из первого уравнения системы второе:
Таким образом, решения систему
Ответ:
22. Две трубы наполняют бассейн за 8 часов 45 минут, а одна первая труба наполняет бассейн за 21 часов. За сколько часов наполняет бассейн одна вторая труба?
Решение.
По условию первая труба за одну минуту наполняет часть бассейна, а две трубы вместе за одну минуту наполняют часть бассейна. Таким образом, одна вторая труба за минуту наполняет часть бассейна, то есть она наполнит весь бассейн за 15 часов.
Ответ: 15.
23.При каком значении прямая имеет с параболой ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении .
Решение.
График функции изображён на рисунке.
Запишем условие общей точки:
Прямая будет иметь с параболой единственную общую точку при условии, что дискриминант полученного квадратного уравнения равен нулю: откуда Подставив значение параметра в уравнение, находим
Ответ: (-2;0).
24. Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 140°.
Решение.
Проведём радиус OA. Треугольник AOC — прямоугольный, ∠A = 90°. ∠COA = 180° − ∠AOD = 180° − 140° = 40°; ∠ACO = 90° − 40° = 50°.
Ответ: 50.
25.Дана равнобедренная трапеция . Точка лежит на основании и равноудалена от концов другого основания. Докажите, что — середина основания .
Решение.
Треугольник равнобедренный. Поэтому .
В равнобедренной трапеции .
Отсюда следует, что . Значит, треугольники и равны по двум сторонам и углу между ними. Следовательно, .
26. Диагонали четырёхугольника , вершины которого расположены на окружности, пересекаются в точке . Известно, что = 74°, = 102°, = 112°. Найдите .
ВАРИАНТ № 4
Часть 1 МОДУЛЬ «АЛГЕБРА»
1.Найдите значение выражения .
Решение.
Вынесем общий множитель за скобки:
Ответ: −3.
Ответ: -3
2. Одна из точек, отмеченных на координатной прямой, соответствует числу . Какая это точка?
1) точкаM 2) точкаN
3) точкаP 4) точка Q
Решение.
Возведём в квадрат числа 6, 7, 8:
Число 45 лежит между числами 36 и 49 и находится ближе к числу 49, поэтому соответствует точке N.
Правильный ответ указан под номером 2.
Ответ: 2
3 Какое из чисел больше: или?
1)
2)
3)
Решение.
В силу цепочки неравенств
первое число меньше второго.
Правильный ответ указан под номером 1.
Ответ: 1
4.Найдите корни уравнения .
Если корней несколько, запишите в ответе наименьший.
5.На одном из рисунков изображен график функции . Укажите номер этого рисунка.
1)
2)
3)
4)
Решение.
График функции проходит через точку (1; 0). Этому условию удовлетворяет только график, изображённый на рисунке 4.
Таким образом, верный ответ указан под номером 4.
Ответ: 4
6. Дана арифметическая прогрессия: 33; 25; 17; … Найдите первый отрицательный член этой прогрессии.
Решение.
Для члена имеем: По формуле нахождения n-го члена арифметической прогрессии имеем:
Первое число, которое удовлетворяет этому условию, число 6. Следовательно, первым отрицательным членом прогрессии является
Таким образом, правельный ответ указан под номером 1.
Ответ: 1.
Ответ: 1
7.Найдите значение выражения при .
Решение.
Упростим выражение:
Найдем значение выражения при
Ответ: 2,5.
Ответ: 2,5
8.На каком рисунке изображено множество решений неравенства ?
1)1 2)2 3)3 4) 4
МОДУЛЬ «ГЕОМЕТРИЯ»
9.Сумма трех углов выпуклого четырехугольника равна 300°. Найдите четвертый угол. Ответ дайте в градусах.
Решение.
Так как сумма углов выпуклого четырехугольника равна 360°, четвертый угол равен 360° − 300° = 60°.
Ответ: 60.
Ответ: 60
10.Боковая сторона равнобедренного треугольника равна 5. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.
Решение.
Воспользуемся теоремой косинусов:
Здесь и — боковые стороны равнобедренного треугольника, — основание.
Диаметр описанной окружности вычислим по формуле:
Ответ: 10.
Ответ: 10
11. Найдите площадь трапеции, изображённой на рисунке.
Решение.
Площадь трапеции вычисляется по формуле где и — основания, а — высота трапеции.
Ответ: 270.
Ответ: 270
12. Найдите тангенс угла С треугольника ABC , изображённого на рисунке.
Решение.
Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Ответ: 0,75.
Ответ: 0,75
13. Какие из следующих утверждений верны?
1) Около любого правильного многоугольника можно описать не более одной окружности.
2) Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника.
3) Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.
4) Около любого ромба можно описать окружность
МОДУЛЬ «РЕАЛЬНАЯ МАТЕМАТИКА»
14. На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 9 млн пользователей.
Какое из следующих утверждений неверно?
1) Пользователей из Украины больше, чем пользователей из Беларуси.
2) Пользователей из Украины меньше четверти общего числа пользователей.
3) Пользователей из Беларуси больше, чем пользователей из Эстонии.
4) Пользователей из России больше 8 миллионов.
Решение.
Проверим каждое утверждение:
1) Из диаграммы видно, что число пользователей из Украины больше, чем пользователей из Беларуси. Первое утверждение верно.
2) Из диаграммы видно, что пользователей из Украины меньше четверти общего числа пользователей. Второе утверждение верно.
3) Из диаграммы видно, что пользователей из Беларуси больше, чем пользователей из «других стран», а значит, и больше, чем пользователей из Эстонии. Третье утверждение верно.
4) Из диаграммы видно, что пользователей из России примерно две трети от общего числа пользователей. Всего пользователей 9 млн, значит пользователей из России около 6 млн, что меньше 8 млн. Четвёртое утверждение неверно.
Неверным является утверждение под номером 4.
Ответ: 4
15.На графике показано, сколько человек зарегистрировалось с 25 декабря 2012 года по 13 февраля 2013 года в качестве участников конференции. По горизонтали указаны числа месяцев, а по вертикали — количество человек.
Во сколько раз возросло количество зарегистрировавшихся с 4 января по 3 февраля?
Решение.
Из графика видно, что число зарегестрировавшихся на4 января состваляло 30 человек, а 3 февраля — 270. Следовательно, число зарегистрировавшихся возросло в 270 : 30 = 9 раз.
Ответ: 9.
Ответ: 9
16. На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 120 человек. Голоса между кандидатами распределились в отношении 3:5. Сколько голосов получил победитель?
Решение.
Пусть x голосов приходится на одну часть, тогда 5x приходится на второго кандидата, а 3x — на первого. Зная, что в голосовании участвовало 120 человек составим уравнение:
Таким образом, победитель получил:
.
Ответ: 75.
Ответ: 75
17. Какой угол (в градусах) описывает минутная стрелка за 10 мин?
Решение.
Часовыми делениями циферблат разбит на 12 круговых секторов. Угол каждого из них равен 360° : 12 = 30°. Между минутной и часовой стрелкой два часовых деления. Они образуют угол 60°.
Ответ: 60.
Ответ: 60
18. Рок-магазин продаёт значки с символикой рок-групп. В продаже имеются значки пяти цветов: чёрные, синие, зелёные, серые и белые. Данные о проданных значках представлены на столбчатой диаграмме.
Определите по диаграмме, значков какого цвета было продано меньше всего. Сколько примерно процентов от общего числа значков составляют значки этого цвета?
1) 5 2) 10 3) 15 4) 20
Решение.
Из диаграммы видно, что было продано меньше всего значков зелёного цвета в количестве 150 штук. Определим сколько процентов от общего числа составляют зелёные значки:
Значит зелёных значков примерно 15% от общего числа.
Ответ: 3.
Ответ: 3
19. На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с яблоками
Решение.
Всего было подготовлено 25 билетов. Среди них 16 двузначных. Таким образом, вероятность взять билет с двухзначным номером равна
Ответ: 0,64
20. Из закона всемирного тяготения
выразите массу и найдите её величину (в килограммах), если и гравитационная постоянная
Часть 2
Решение.
Выразим массу: Подставим значения переменных:
Ответ: 1000.
Ответ: 1000
21. Решите неравенство
Решение.
Умножим на 10, приведём подобные слагаемые и разложим на множители:
Произведение двух сомножителей будет меньше нуля, если сомножители имеют разный знак (см. рисунок). Таким образом, получаем ответ:
Ответ:
22. Железнодорожный состав длиной в 1 км прошёл бы мимо столба за 1 мин., а через туннель (от входа локомотива до выхода последнего вагона) при той же скорости — за 3 мин. Какова длина туннеля (в км)?
Решение.
Поезд проходит через туннель за 3 минуты, при этом за одну минуту поезд проходит мимо выхода из туннеля, следовательно, от входа локомотива в туннель до выхода проходит 2 минуты. Мимо столба поезд длиной 1 км проходит за 1 минуту, поэтому его скорость равна 1 км/мин. Значит, за 2 минуты поезд пройдет 2 км, поэтому длина туннеля равна 2 км.
Ответ: 2.
23.Постройте график функции и определите, при каких значениях прямая имеет с графиком ровно три общие точки.
Решение.
Раскрывая модуль, получим, что график функции можно представить следующим образом:
Этот график изображён на рисунке:
Из графика видно, что прямая имеет с графиком функции ровно три общие точки при и
Ответ: 0; 4.
24. Диагонали и трапеции пересекаются в точке . Площади треугольников и равны соответственно и . Найдите площадь трапеции.
Решение.
Заметим, что площади двух треугольников, общей вершиной которых является точка пересечения диагоналей трапеции, а основаниями — боковые стороны, равны. Это следует, например, из того, что площади треугольников и равны (поскольку эти треугольники имеют общее основание , и их высоты, проведенные к этому основанию, равны как высоты трапеции), а . По условию, , поэтому и являются не боковыми сторонами, а основаниями трапеции. Тогда треугольники и подобны по двум углам, и отношение их площадей равно квадрату коэффициента подобия . Поэтому . Поскольку треугольники и имеют общую высоту, проведённую из вершины , то отношение их площадей равно отношению их оснований, т. е. . Значит, . Поэтому и . Но тогда .
Ответ: .
25.В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BOC.
Решение.
Проведём высоту так, чтобы она проходила через точку Углы и равны друг другу как вертикальные. Вспомним также, что диагонали делятся точкой пересечения пополам, следовательно, Рассмотрим треугольники и , они прямоугольные, имеют равные углы и равные гипотенузы, следовательно эти треугольники равны, а значит равны отрезки и . Таким образом,
Площадь параллелограмм равна а площадь треугольника
26. Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
как сдать ОГЭ по математике — Учёба.ру
Чем раньше начнешь готовиться к ЕГЭ,
тем выше будет балл Поможем подготовиться, чтобы сдать экзамены на максимум и поступить в топовые вузы на бюджет. Первый урок бесплатно
Ольга Евсеева,
преподаватель математики физико-математической школы Института довузовской подготовки
Московского технологического университета (МИРЭА, МИТХТ, МГУПИ)
По вашему мнению, насколько хорошо девятиклассники сейчас знают математику? Насколько сложен для них этот ОГЭ?
Не сказала бы, что школьники не знают математику. Как правило, к нам на занятия приходят ребята с неплохим начальным уровнем, с хорошими навыками выполнения арифметических действий и преобразования выражений, знакомые с методами решения линейных, квадратных уравнений и неравенств — то есть со всем тем, что они должны знать к началу 9 класса. Конечно, глубина знаний и умение ими пользоваться напрямую зависят от количества часов математики в школе: при изучении предмета на базовом уровне это три-четыре часа алгебры и два часа геометрии в неделю, на углубленном уровне — пять-семь часов алгебры и три часа геометрии. Поскольку ОГЭ состоит из двух частей, первая из которых проверяет базовый уровень подготовки, а вторая включает более сложные задания, ребятам, изучающим в школе базовую математику, необходимо выделить дополнительное время для подготовки.
Иногда школьных уроков и самостоятельной работы достаточно, чтобы сдать ОГЭ на хорошо и отлично. В качестве подспорья можно использовать различные сайты и учебную литературу в открытом доступе. Возникающие вопросы можно обсудить на форумах или со школьным учителем. Но занятия на курсах помогают последовательно разобрать темы, систематизировать материал, проверить глубину его усвоения. Ведь после ОГЭ ребят через два года ждет более трудное испытание — ЕГЭ, в котором часть базовых заданий аналогичны заданиям повышенной и высокой сложности из ОГЭ. Девятиклассники впервые сдают экзамен, содержащий так много заданий, и его длительность составляет 3 часа 55 минут. Безусловно, для ребят это непросто.
Расскажите про структуру экзамена и систему начисления баллов. За какие задания на ОГЭ по математике ставится наибольшее количество баллов?
Всего школьникам предлагается 26 заданий. До недавнего времени экзамен состоял из трех частей — «Математика», «Реальная математика» и «Геометрия». С 2018 года раздела «Реальная математика» в ОГЭ больше нет, а его задания распределены между модулями «Алгебра» и «Геометрия».
Ребятам предстоит решить 17 задач по алгебре (14 задач в части 1 и три в части 2) и девять задач по геометрии (шесть задач в части 1 и три в части 2). Задания части 1 требуют краткого ответа в виде числа или последовательности цифр, которые вносятся в бланк ответов № 1. Развернутые решения заданий части 2 и ответы к ним записываются на бланке ответов № 2. За правильный ответ на каждое из заданий № 1-20 ставится 1 балл. Эти задания проверяются автоматически при сканировании бланков. Задания № 21-26 проверяют двое независимых экспертов, хотя при значительном расхождении оценок назначается проверка третьим экспертом. Эти задания могут быть оценены от 0 до 2 баллов. Таким образом, максимально за работу можно получить 32 первичных балла. Пятерка ставится за результат от 22 баллов, четверка — от 15 баллов, тройка — от 8 баллов (из них не менее 4 баллов по алгебре и 2 баллов по геометрии).
Как видите, для положительной оценки достаточно решить лишь восемь задач из части 1, а для пятерки — безошибочно выполнить базовую часть экзамена и только одно из заданий повышенной сложности. Вроде бы задача «сдать ОГЭ на отлично» не кажется такой уж сложной. Однако с заданиями повышенной сложности из части 2 ребятам придется снова столкнуться на ЕГЭ, уже в его базовой части. Например, задание № 22 повышенного уровня сложности — «текстовая задача» — аналогично заданию № 11 из части 1 ЕГЭ. Поэтому, как мне кажется, ребятам уже в 9 классе надо освоить методы и приемы решения заданий из части 2.
По вашему опыту преподавания, какие разделы математики самые сложные для школьников и вызывают наибольшее затруднение? Какие темы самые простые?
В модуле «Алгебра» это, прежде всего, исследование функций и построение их графиков. Задания на эту тему входят и в часть 1, и в часть 2 ОГЭ. В задании № 10 нужно установить соответствие между графиками функции и формулами, которые их задают. Здесь школьники часто ошибаются, пытаясь угадать ответ вместо того, чтобы рассуждать логически. В части 1 можно еще отметить задания на преобразование и вычисление выражений, если там содержатся радикалы: задание № 4, где надо найти значение выражения, и задание № 12, где сначала выражение надо упростить, а потом вычислить. Работать с корнями правильно получается далеко не у всех. Также не всегда ребятам удается справиться с заданием № 13 — «задачей прикладного содержания», где из несложной формулы нужно выразить одну из величин, найти ее значение, а ответ записать в указанных единицах измерения. Сложность здесь как раз заключается в переходе от одной размерности к другой.
В модуле «Геометрия» в части 1 включены задачи, относящиеся к ключевым разделам курса геометрии. И все же, если в задании встречаются такие темы, как «вписанная и описанная окружности», «вписанные углы», «соотношения между сторонами и углами прямоугольного треугольника», «подобие треугольников», показатель его решаемости падает.
Меньше всего ошибок девятиклассники допускают в заданиях на чтение таблиц и диаграмм, нахождение вероятности случайного события.
Какие есть «подводные камни» в заданиях части 2? На что нужно обратить внимание при подготовке к заданиям повышенной сложности?
| Задание № 21 | В этом задании необходимо решить уравнение или неравенство, преобразовать алгебраическое выражение. При решении рациональных и дробно-рациональных уравнений, а также уравнений высших степеней необходимо обращать внимание на возможность потери решения (при сокращении на выражение, которое может быть равным нулю) или получение посторонних решений (которые обнуляют знаменатель или обращают исходное уравнение в выражение, не имеющее смысла). При решении неравенств надо помнить, что при умножении неравенства на отрицательное выражение оно меняет знак. Зачастую школьники либо просто не обращают внимание на знак величины, на которую умножают неравенство, либо умножают неравенство на выражение, содержащее переменную. |
| Задание № 22 | Это текстовая задача, как правило, на «движение», «работу», «концентрации растворов» или «смеси и сплавы». Для ее решения необходимо составить уравнение или систему уравнений. Я бы посоветовала ребятам для наглядности обязательно заполнять таблицу, в которую вносятся известные по условию величины, выбранная переменная или переменные, после чего в пустые клетки вписываются соответствующие им величины, выраженные через введенные переменные, и только потом приступать к составлению уравнения (или системы). |
| Задание № 23 | Построение графика функции. Для правильного выполнения этого задания необходимо знать свойства следующих функций: линейная, квадратичная, либо функция, описывающая обратно пропорциональную зависимость. Также необходимо уметь строить графики этих функций, знать правила преобразования графиков. Очень часто встречаются задания, в которых формулу, задающую исходную функцию, можно преобразовать, после чего она значительно упрощается. Здесь необходимо помнить, что область определения исходной и получившейся функции могут не совпадать. |
| Задание № 24 | Геометрическая задача вычислительного характера. Школьник должен решить планиметрическую задачу, применяя различные теоретические знания из курса геометрии. |
| Задание № 25 | Геометрическая задача на доказательство с использованием стандартных приемов. Здесь надо обратить внимание на умение математически грамотно и ясно записать решения, приведя все необходимые обоснования и пояснения. |
| Задание № 26 | Для решения этой задачи школьникам нужно владеть широким спектром приемов и способов рассуждений. Здесь возможно потребуются и дополнительные построения, и знание утверждений, не так часто используемых в школьном курсе. Например, теорема об угле между касательной и хордой; теорема о секущих и касательной; свойства высоты прямоугольного треугольника, опущенной из прямого угла; свойства биссектрис, медиан, высот треугольника; теорема Чевы; теорема Менелая. |
Что нужно делать школьнику, чтобы подготовиться к экзамену наилучшим образом? Как вы посоветуете им распределить свое время?
На занятиях со школьниками я обычно придерживаюсь следующей стратегии. Во-первых, мы полностью проходим программу 9 класса, начиная с отработки основных навыков и умений по следующим темам: преобразование алгебраических выражений, решение уравнений и неравенств, числовые последовательности, функции, их свойства и графики, элементы статистики и теории вероятностей. Постепенно повышая уровень заданий, мы переходим к решению задач повышенной и высокой сложности и стараемся уделить этим заданиям как можно больше внимания. Не менее трети времени следует посвятить геометрии, и здесь также нужно двигаться «от простого к сложному».
Во-вторых, необходимо готовиться к самому формату ОГЭ, к его структуре. Если ученик хорошо умеет решать задачи, но ни разу не пробовал написать работу в этом формате, ему сложно будет оценить количество затрачиваемого времени на часть 1 и 2. Обязательно нужно научиться правильно распределять свои силы.
Многие девятиклассники не используют предлагаемое на экзамене время полностью, у них просто не хватает усидчивости. Ребята сдают работу раньше, хотя еще остались нерешенными задания повышенной сложности. Зачастую и в заданиях части 1 бывают ошибки по невнимательности, которые сам школьник не смог найти и исправить. На ЕГЭ же складывается обратная ситуация. Выпускники прилежно готовятся к экзамену, считают, что времени мало. Им хочется еще раз проверить свои решения и подумать над заданиями высокой сложности.
Какие источники вы рекомендуете использовать для самостоятельной подготовки к экзамену?
- «Сайт ФИПИ». На нем вы найдете открытый банк заданий ОГЭ.
- Сборник «ОГЭ. Математика 2018. Типовые и тестовые задания». Таких сборников очень много, нужно обращать внимание на гриф «рекомендовано ФИПИ».
- Учебные пособия Центра непрерывного математического образования. Например, сборник «Подготовка к ОГЭ по математике. Методические указания. Разбор задач». На 500 страницах здесь можно найти подробный разбор каждой из 26 задач экзамена и множество вариантов каждой из них для самостоятельного решения.
- «Сайт Alexlarin.net». Здесь каждую неделю выкладывается новый вариант ОГЭ и новый вариант ЕГЭ. Ребятам дается семь дней на размышление. Они могут обсуждать свои решения на специальном форуме. Потом вывешиваются правильные ответы.
- «РешуЕГЭ». На сайте доступен большой банк заданий. Тесты можно составлять самостоятельно, выбирая лишь те темы, над которыми необходимо поработать. Небольшой минус — тесты часто получаются похожими друг на друга.
Пробный ОГЭ 2021 9 класс в СПб
Всем привет! Меня зовут Дарина, и я ходила на курсы подготовки по математике в 2016-2017 году в центр «Опять Пятерка», преподавал Байбуз Дмитрий Викторович.
Расскажу свою историю. Математику я любила, и она у меня хорошо шла до 9 класса включительно. А потом поменялся учитель… В общем, весь 10 класс в математике я плавала… Вроде понимала, но как-то поверхностно и всё равно оставалось много неясного, везде было достаточно зыбко, и я думала только бы пережить контрольную и забыть эту тему. Так и происходило, т.к. всё понимала с большим трудом, не до конца и соответственно математика уже перестала быть такой привлекательной… Но я планировала идти на программиста, соответственно мне было не обойтись без ЕГЭ по математике. Да и не верила я в то, что резко разлюбила математику. Летом я просматривала вариант за вариантом, но результат совсем не утешал, писала на 40-50. С такими баллами о бюджете можно и не мечтать. Я понимала, что самой мне хорошо не подготовиться.
Если честно, я не знаю, почему курсы, а не репетитор. Да и вообще на эти курсы я пришла просто потому, что они были не далеко от дома. Если вкратце — уже в феврале я написала пробник на 88 баллов. В апреле на 86, но там были три глупейшие ошибки…
А теперь подробнее. На уроке мы качественно прорабатывали каждую тему, разбирали домашнее задание, учитель спокойно отвечал на все вопросы, даже если они задавались не в первый раз и возникали только у кого-то одного. Мне иногда было неловко задать вопрос, когда всем остальным вроде было всё ясно. Но лучше признать, что ты чего-то не понял и разобраться в этом, чем изобразить умного, а самому не понять задачу, которая по закону подлости 100% потом где-нибудь всплывёт. Мне очень понравился учитель. Дмитрий Викторович действительно хорошо всё объяснет, а ещё любит шутить. Второе для меня было не менее важно, т.к. (простите меня за выражения) на нервной почве крыша ехала, а смех как-никак помогал расслабиться, поднимал настроение и укреплял боевой дух. И, конечно, шутки никогда не занимали значимую часть урок. Мы действительно занимались математикой. И я снова её полюбила! Вот серьёзно. Я поняла, что математика для меня увлекательная и интересная.
На курсах, в отличие от репетитора, для меня был плюс в том, что рядом со мной занимались мои ровесники, и я могла себя сравнить с ними. Если вся группа не решила какую-то задачу, то мне становилось ясно, что это не у меня с мозгами плохо, а задание действительно сложное, ну и заодно была возможность пообщаться, обсудить пробник или домашнее задание. Ещё Дмитрий Викторович находил самые сложные задания. Это было огромным плюсом, т.к. неизвестно, что попадётся на экзамене, да и после разбора они уже не казались такими сложными. Ещё в мозгу наконец-то всё структурировалось, и я начала понимать какие баллы и откуда берутся. Нам объясняли нюансы: где и что нужно писать, чтобы не потерять баллы. Ещё мне очень понравилось, что нам давали распечатки с формулами. Теперь они не разбросаны по всем тетрадям, а есть на отдельных листах. Это действительно очень удобно. Дмитрий Викторович рассказал про способы решения заданий, которые существенно облегчали жизнь, а в школе про них не было сказано ни слова (по крайней мере, у меня). На курсы ходила с большим удовольствием на полном серьёзе. Уходила чаще всего жутко вымотанная, но внутри было чувство удовлетворения, и результат того стоил. Дело даже не в баллах за ЕГЭ. Вернее не только в них. Я чувствую, насколько сильно поднялся мой уровень в математике. Я наконец-то перестала в ней «плавать», начала чувствовать себя гораздо увереннее. Да и просто я поняла, что мне стоит связывать дальнейшее обучение с математикой. А это тоже не мало.
А теперь немного того, что не лежит на поверхности. Домашних заданий было много. Это был действительно большой объём и иногда на решение какой-нибудь геометрической задачи уходил не один час. Это курсы. Тут никто не поставит 2 за невыполненное домашнее задание. В принципе, можно не делать. Но я сомневаюсь, что тогда будет хороший результат. Я сидела над заданиями долго и упорно. И я помню свой восторг, когда наконец-то одолела трудную задачу! Курсы это не волшебная палочка, когда знания появляются сами собой. Нужно работать. И работать нужно много. На уроке дают формулы. Их нужно учить! Не будет ни малейшего толка от того, что эта распечатка будет пылиться в ящике или даже стоять в красивой рамке. Само собой ничего не получится, какие бы деньги вы не заплатили. Дмитрий Викторович был строгим учителем. И я за это ему благодарна. Потому что любой мелкий недочёт может привести на ЕГЭ к потере баллов.
В завершение я скажу, что это моя история. Я не знаю, какого мнения о курсах другие ученики. Но я довольна! И даже очень. Я прошла на бюджет во всех ВУЗах, куда подавала. В итоге я поступила в ЛЭТИ и довольна своим выбором.
Спасибо Дмитрию Викторовичу за знания, за шутки, за терпение. Просто спасибо!
P.S. Есть один неприятный момент. Когда-нибудь курсы закончатся… И придётся расставаться. У меня за 15 минут до конца последнего занятия слёзы начали капать прямо на тетрадь просто от той мысли, что я больше не буду сидеть в этом кабинете, слушая объяснение какой-то задачи или историю из жизни Дмитрия Викторовича. Но с другой стороны, глупо не пускать в свою жизнь что-то замечательное только из-за того, что с этим придётся расставаться.
Всем удачи и хороших баллов!
Расписание ОГЭ-2021 | Lancman School
Курсы ОГЭ и ЕГЭ Lancman School подготовили для вас самый подробный календарь выпускника 9 классов 2021 года. В нем вы найдёте не только даты экзаменов, но и сроки проверки экзаменационных работ по всем предметам, а также информацию по срокам апелляций.
Итоговое собеседование по русскому языку
В 2021 году все учащиеся 9 классов должны будут получить допуск к выпускным экзаменам. Для этого в феврале 2021 года они должны будут получить «зачёт» на итоговом собеседовании. Пересдать экзамен можно будет дважды.
10 февраля 2021 года (среда) — основной период. Результаты станут известны не позднее 15 февраля 2021 г. (проверяют обычно 5 рабочих дней)
10 марта 2021 года (среда) — пересдача
17 мая 2021 года (понедельник) — пересдача
Контрольные работы (вместо ОГЭ по выбору)
| Дата ОГЭ | Предмет | Сроки проверки ОГЭ |
|---|---|---|
| 18.05.2021 (вторник) | Биология, литература, информатика и ИКТ | Не позднее 21.05.2021 |
| 19.05.2021 (среда) | Физика, история | Не позднее 22.05.2021 |
| 20.05.2021 (четверг) | Обществознание, химия | Не позднее 23.05.2021 |
| 21.05.2021 (пятница) | География, иностранные языки | Не позднее 24.05.2021 |
ОГЭ по выбору в связи с эпидемией коронавируса в 2021 году отменены. Рособрнадзор и Министерство просвещения РФ приняли решение заменить их на контрольные работы по выбору.
Каждый ученик 9 класса должен выбрать предмет, по которому он напишет в конце года контрольную работу. Учащиеся с ОВЗ могут отказаться от участия.
Формат контрольных будет приближен к заданиям демоверсий ОГЭ 2021 года, но формат их будет облегчённый, так как регионам разрешено убирать из КИМов ОГЭ по предметам практическую часть.
До 30 апреля 2021 года каждый выпускник 9 класса должен не только определиться с выбором предмета, но и написать заявление. Пройдут к/р по выбору в своих школах, оценки не будут влиять на допуск школьников к прохождению государственной итоговой аттестации, но результаты этих к/р могут быть использованы при наборе в профильные классы. Выставление полученной за контрольную работу оценки в классный журнал носит рекомендательный характер.
Основной период ОГЭ 2021
| Дата ОГЭ | Предмет | Сроки проверки ОГЭ |
|---|---|---|
| 24.05.2021 (понедельник) | Русский язык | Не позднее 31.05.2021 |
| 25.05.2021 (вторник) | Русский язык | Не позднее 02.06.2021 |
| 27.05.2021 (четверг) | Математика | Не позднее 02.06.2021 |
| 28.05.2021 (пятница) | Математика | Не позднее 04.06.2021 |
| Резервные дни: | ||
| 08.065.2021 (вторник) | Русский язык | Не позднее 15.06.2021 |
| 16.06.2021 (среда) | Математика | не позднее 22.06.2021 |
| 30.06.2021 (среда) | Русский язык | Не позднее 06.07.2021 |
| 02.07.2021 (пятница) | Математика | Не позднее 08.07.2021 |
После проверки экзаменационных работ первичные баллы переводятся в оценки и официальные результаты становятся известны выпускникам. Информированием о количестве баллов и полученной оценке за тот или иной предмет обычно занимается образовательное учреждение (школа). Если вы не преодолели минимальный порог по одному из экзаменов, не надо отчаиваться. Для вас предусмотрен повторный экзамен в резервные сроки.
Читайте также:
Дополнительный период ОГЭ-2021
| Дата ОГЭ | Предмет | Сроки проверки ОГЭ |
|---|---|---|
| 03.09.2021 (пятница) | Русский язык | Не позднее 09.09.2021 |
| 06.09.2021 (понедельник) | Математика | Не позднее 13.09.2021 |
|
|
Резервные дни: | |
|
13.09.2021 (четверг) |
Русский язык | Не позднее 20.09.2021 |
|
15.09.2021 (среда) |
Математика | Не позднее 21.10.2021 |
Сроки апелляций ОГЭ-2021
Если вы не согласны с выставленными баллами и оценками за экзамен, если вы нашли ошибку при проверке вашей работы, обязательно стоит попробовать отвоевать свои баллы на апелляции.
Что для этого необходимо сделать? В течение двух рабочий дней (суббота тоже считается) вам необходимо прийти в свою школу и подать заявление на апелляцию о не согласии с выставленными баллами. В школе вам помогут правильно составить этот документ, а также передадут все необходимые сведения в Конфликтную комиссию. Далее вам назначат дату и время апелляции.
Как готовиться к апелляции?
Обязательно необходимо обсудить все слабые места вашей работ с учителем. Он укажет, где можно попробовать настоять на повышении баллов. Но запомните: задания с кратким ответом на апелляции не рассматриваются, черновые записи не учитываются.
И ещё: количество ранее выставленных баллов после прохождения вами процедуры апелляции могут измениться как в сторону увеличения, так и в сторону уменьшения (если будет выявлена незамеченная экспертами ошибка/ошибки).
Курсы ОГЭ и ЕГЭ Lancman School желают вам удачи на экзаменах! Если понадобится апелляция результатов, то наши преподаватели помогут проанализировать работу и сопроводят вас по нотариальной доверенности на саму апелляцию.
Читайте также:
Ваш ребёнок — школьник 1-11 класса? Вы учитель? Отлично! Мы пишем для вас. Узнавайте от нас первыми новости образования, актуальную информацию об экзаменах и просто полезные советы. Кнопка подписки прямо под постом!
Редактор канала — топовый образовательный блогер Мария Кучерова (mel.fm, newtonew.com).
% PDF-1.4 % 163 0 объект > эндобдж xref 163 74 0000000016 00000 н. 0000002574 00000 н. 0000002721 00000 н. 0000003284 00000 н. 0000003748 00000 н. 0000003775 00000 н. 0000004352 00000 п. 0000004601 00000 п. 0000005036 00000 н. 0000005400 00000 н. 0000005512 00000 н. 0000005626 00000 н. 0000005758 00000 п. 0000006178 00000 п. 0000006228 00000 н. 0000006768 00000 н. 0000009224 00000 н. 0000009404 00000 н. 0000009594 00000 н. 0000010043 00000 п. 0000010298 00000 п. 0000010722 00000 п. 0000011024 00000 п. 0000011350 00000 п. 0000011550 00000 п. 0000011748 00000 п. 0000012090 00000 н. 0000012252 00000 п. 0000012631 00000 п. 0000013227 00000 н. 0000013391 00000 п. 0000013684 00000 п. 0000014156 00000 п. 0000014436 00000 п. 0000014740 00000 п. 0000015298 00000 п. 0000015467 00000 п. 0000015561 00000 п. 0000015894 00000 п. 0000016202 00000 п. 0000027375 00000 п. 0000061879 00000 п. 0000061949 00000 п. 0000062045 00000 п. 0000079745 00000 п. 0000080008 00000 п. 0000080359 00000 п. 0000082565 00000 п. 0000083329 00000 п. 0000109456 00000 п. 0000127905 00000 н. 0000128024 00000 н. 0000128094 00000 н. 0000128178 00000 н. 0000130628 00000 н. 0000130905 00000 н. 0000131081 00000 н. 0000131108 00000 н. 0000131408 00000 н. 0000131548 00000 н. 0000133113 00000 п. 0000133506 00000 н. 0000133873 00000 н. 0000133900 00000 н. 0000134197 00000 н. 0000134337 00000 н. 0000134711 00000 н. 0000135026 00000 н. 0000140017 00000 н. 0000140277 00000 н. 0000140580 00000 н. 0000149770 00000 н. 0000002397 00000 н. 0000001776 00000 н. трейлер ] / Назад 365361 / XRefStm 2397 >> startxref 0 %% EOF 236 0 объект > поток hb«f`0a`g«9 Ā
Oak Grove Elementary PTA — Math Superstars
Добро пожаловать в Math Superstars — виртуальное дополнение!Math Superstars — это спонсируемая PTA добровольная программа углубленного изучения математики, охватывающая все классы от Pre-K до 5-го класса.
Ссылки для присвоения оценок
Pre-K класс 3
Детский сад 4 класс
1 класс 5
2 класс
Цели программы для классов от Pre-K до 5:
(1) Развить понимание математики.
(2) Для улучшения математических навыков учащихся.
(3) Стимулировать математический диалог между учеником и воспитателем.
Как принять участие- ВИРТУАЛЬНЫЙ СТИЛЬ
- Выберите и распечатайте (односторонние) задания уровня ученика.
- Задания чередуются между заданиями «Звездный взрыв» (25 баллов) и «Суперзвезды» (50 баллов).
- Студентам рекомендуется выполнять задания по порядку, однако студенты могут пропустить их.
- Распечатайте все 12 заданий и скрепите каждое отдельно. В качестве дополнительной меры предосторожности убедитесь, что имя вашего ученика и учитель указаны на каждой странице.
- Студенты могут работать в своем собственном темпе. Нет поздней работы.
- Первый «срок оплаты» — конец ноября (обновлено). За пределами школы мы установим ящик для сдачи заданий.
- Мы не будем собирать задания в цифровом виде. Нам нужны бумажные копии.
Даты получения — ВИРТУАЛЬНЫЙ СТИЛЬ
Завершенную студенческую работу можно сдать через ящик для писем Math Superstars.Он находится напротив главного входа в школу. Работы с оценками будут сохранены, а за их выполнение будут вручены призы. призов будут вручены участвующим студентам волонтерами! Убедитесь, что ваш адрес указан на работе.
20 ноября (обновлено)
18 декабря
26 февраля
30 апреля (последний сбор)
Starburst vs Superstar Рабочие листы
Звездообразования (25 баллов) различаются по размеру и ближе к учебной программе на уровне класса.Большинство Starburst — это одна тема с разной степенью сложности.
Superstar (50 баллов) обычно выше уровня класса и предлагают учащимся более высокий уровень сложности.
Признание и награды виртуально
Все участвующие студенты получат «звезду», а их баллы будут размещены на доске объявлений Math Superstars за входной дверью.
0-50 баллов Уровень участия, малый приз
51-200 баллов Средний приз-сюрприз
201-300 баллов Брелок Superstars
300-425 баллов Случайный БОЛЬШОЙ Squishy (будет доступен для обмена позже)
426+ баллов Фоторамка, опубликовано фото на доска объявлений и подушка SuperStar!
Math Superstars предлагает дополнительные баллы на вечере STEM в феврале.Студенты, которые не могут присутствовать, могут отправить электронное письмо координатору суперзвезд для получения дополнительного задания. Будем надеяться, что мы снова в школе !!
Дополнительные призы выдаются в конце года за три лучших результата в каждом классе.
Пожалуйста, сохраните оцененные рабочие листы и проекты на случай расхождения в итоговых результатах в конце года.
Роль опекунов
Math Superstars — это возможность для учащихся заниматься математикой более высокого уровня и решать проблемы.Это дополнительная программа. Не все студенты добираются до вершины горы. Математика.
Роль родителей — поощрять и способствовать решению проблем. Рабочие листы и проекты будут содержать новые концепции вне учебной программы. Если вашему ребенку нужна помощь в решении этих проблем, пожалуйста, объясните концепцию, используя числа, отличные от приведенных на самом деле.
Поймите, что эти задачи выше уровня класса: они требуют значительных усилий от вашего ребенка и от вас.Попытки быстро решить проблемы редко приводят к успеху. Родители НЕ должны давать ответ или показывать ребенку, как именно решить проблему. Мы призываем родителей позволить вашему ребенку самостоятельно обдумать проблему и придумать ответ.
Постарайтесь проявлять позитивный настрой в общении и позволяйте ребенку совершать ошибки. Даже если ребенок не получит правильный ответ, частичное замечание может быть присуждено за приложенные усилия. ПОСЛЕ того, как рабочие листы были оценены и возвращены, мы призываем родителей сесть со своим ребенком и обсудить любые проблемы, которые они пропустили.
Участие в программе подтверждает понимание родителями того, что все находятся в системе чести. Другими словами, родители НЕ должны решать проблемы, а должны направлять ребенка в процессе. Наконец, полученные баллы НЕ засчитываются в школьные оценки, поскольку программа Math Superstar спонсируется PTA.
* Специальное примечание для родителей учеников Pre-K и K: Возможно, ваши дети еще плохо читают. Они не могут работать над проблемами самостоятельно.Вы должны прочитать им проблемы, а затем направить их к пониманию проблемы и, наконец, к ответу. Хороший способ сделать это — задать им несколько вопросов, похожих на те, что указаны в рабочих листах, и показать, как они решаются; тогда вы можете позволить им решать проблемы с листами без вашей непосредственной помощи.
Ссылка не работает? Вопросы и конструктивный отзыв? электронная почта [email protected]
Я классификатор Superstars.
Астрономия. Авиация. Безопасность. Биология. Бухгалтерский учет. География
- основной
- О сайте
- В какой стране он был создан?
- «Указ о бесплатных лезвиях»
- Колледж, признанный ценностью в энциклопедии Брокгауза и колледж иностранных дел Эфрона
- Жизнь на «золотой» карьере: от верха до низа
- «Секретные материалы» в бразильском Джордано Бруно, Бразилия
- Как американцы превратили райский остров в ядерную пустыню
- Рассказы пяти американцев, исследующих русских под руководством американцев Русский язык
- Частная жизнь русской женщины XVIII век
- Ольденбург Правление императора Николая II
- Описание Земли Камчатка Текст Крашенинникова Земля Описание Камчатка 1755
- Император Александр I, его жизнь и царствование Сестра Александра Первая
- Система образования в России: особенности, понятие, структура и особенности Образование и его учебно-методическое обеспечение
- Федор Михайлович Достоевский
- Три жизненно важных проблемы Какие жизненно важные проблемы позволяет решить 9 0070 Властелин эмоций: как справиться со страхом, гневом и грустью
- Как начать действовать прямо сейчас
- Мысли мудрых о знаниях, воспитании, образовании и культуре
- Психологическая характеристика противоположной целостности —
- Техника изменения веры
- Что представляет собой правило 6 p.
- Наши взгляды, как часы — все показывают разное время, но каждый верит только своим взглядам как очерку часов
- Традиции и обычаи народов мира с точки зрения химии
- Под Севастополем, археологи обнаружили «Скифское золото затерянный храм Мусасир»
- Как проходят археологические раскопки во время археологических раскопок в
- Легко общаться Простота общения
- Влияние ИК-лазера на зрение
- Какое полушарие мозга более развито слева
- Каким образом секретный советский бункер
- Рейтинг аудиокниг: Список, обзоры и обзоры Читатели 900 71
- Скачать аудиокнигу lion cassile
- Детская литература Слушать аудио-рассказы онлайн для детей 11 12 лет
- Сказка Разное Пиратские истории Сказка Придумали дети про пиратов
- Книга Летучий корабль Читать онлайн Аудиокниги Андрей Белянин Летучий корабль
- Джозеф Джейкобс Английский Сказки
- Все аудиокниги Джон Хмелевская
- Александра Маринина: знающая маринина, знающая 5-ю
- Игорь Марченко — Цикл Тёмной планеты Тёмная планета
- Цикл Тёмной планеты Тёмная планета Аудиокниги
- Аудиокнига Шелыгина Зона смерти
- Сказки народы Северного Кавказа
- Астрономия, авиация
- Безопасность
- Биографии
- Биология
- Биология и химия
- Бухгалтерский учет
- География
Популярное
- В какой стране он был создан?
- «Указ о бесплатных лезвиях
- Жизнь на «золотой» карьере: от верхнего края к низу
- Истории пяти американцев, изучающих русских под руководством американцев Русский язык
- Личная жизнь русской женщины XVIII век
- Ольденбург Время правления императора Николая II
- Описание Земли Камчатка Текст Крашенинникова Земля Описание Камчатка 1755
- Император Александр I, его жизнь и правление Сестра Александра Первая
- Система образования в России: особенности, понятие, структура и особенности Образование и его учебно-методическое обеспечение
- Достоевский Федор Михайлович


Leave A Comment