Все формулы для радиуса вписанной окружности
1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол
a — сторона ромба
D — большая диагональ
d — меньшая диагональ
α — острый угол
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в ромб через диагонали ( r ) :
Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :
Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :
Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :
2. Радиус вписанной окружности ромба, равен половине его высоты
a — сторона ромба
h — высота
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в ромб ( r ) :
www-formula.ru
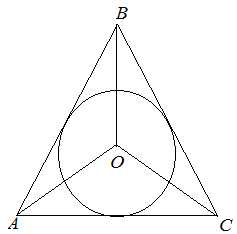
Окружность, вписанная в правильный треугольник
Окружность, вписанная в правильный треугольник, помимо свойств вписанной в произвольный треугольник окружности, обладает своими собственными свойствами.
1) Центр вписанной в треугольник окружности — точка пересечения его биссектрис.
Поскольку в равностороннем треугольнике биссектрисы, медианы и высоты совпадают, то центр вписанной в правильный треугольник окружности является точкой пересечения не только его биссектрис, но также медиан и высот.
Например, в правильном треугольнике ABC AB=BC=AC=a
точка O — центр вписанной окружности.
AK, BF и CD — биссектрисы, медианы и высоты треугольника ABC.
2) Расстояние от центра вписанной окружности до точки касания её со стороной треугольника равно радиусу. Так как центр вписанной в правильный треугольник окружности лежит на пересечении его медиан, а медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины, то радиус вписанной в равносторонний треугольник окружности равен одной третьей длины медианы:
Таким образом, формула для радиуса вписанной в правильный треугольник окружности
Обратно, сторона равностороннего треугольника через радиус вписанной окружности:
3) Так как формула для нахождения площади равностороннего треугольника через сторону
можем найти площадь через r:
Таким образом, формула площади правильного треугольника через радиус вписанной окружности —
3) Все отрезки, на которые стороны равностороннего треугольника делятся точками касания вписанной окружности, равны половине его стороны:
4) Центр вписанной в правильный треугольник окружности является также центром описанной около него окружности.
5) Радиус вписанной в равносторонний треугольник окружности в два раза меньше радиуса описанной окружности:
www.treugolniki.ru
Окружность, вписанная в правильный треугольник
Определение и формулы окружности, вписанной в правильный треугольник
Окружность, касающаяся всех трех сторон треугольника, называется его вписанной окружностью.
Центр вписанной окружности лежит на пересечении биссектрис углов треугольника.
В любой треугольник можно вписать окружность, причем, только одну.
Если окружность вписана в правильный треугольник (в тот, у которого все стороны равны между собой), то ее радиус вычисляется по формуле
где – площадь треугольника, а – его полупериметр; или его можно выразить через сторону следующим образом:
Примеры решения задач
ru.solverbook.com
Радиус вписанной окружности | Треугольники
Удобно, когда все формулы, по которым можно найти радиус вписанной в треугольник и в многоугольник окружности, размещены на одной странице.
Радиус вписанной в многоугольник окружности
Если в многоугольник можно вписать окружность, то
где p — полупериметр, то есть полусумма длин всех сторон этого многоугольника.
Например, для пятиугольника со сторонами a, b, c, d, e радиус вписанной окружности находится по формуле
откуда
По этой же формуле ищут радиус вписанной в треугольник окружности.
Радиус вписанной в треугольник окружности
Формула для нахождения радиуса вписанной в треугольник окружности (верна для треугольника любого вида)
где p — полупериметр,
где a, b, c — стороны треугольника.
Радиус вписанной в прямоугольный треугольник окружности
Формула для нахождения радиуса окружности, вписанной в прямоугольный треугольник
где a и b — катеты, c — гипотенуза.
Радиус окружности, вписанной в правильный многоугольник
Формула радиуса вписанной в правильный многоугольник окружности
где a — сторона многоугольника, n — количество сторон.
Частные случаи — правильный (равносторонний) треугольник, правильный четырехугольник (квадрат) и правильный шестиугольник.
Радиус окружности, вписанной в правильный треугольник
Формула радиуса вписанной окружности для правильного треугольника:
В правильном треугольнике радиус вписанной окружности вдвое меньше радиуса описанной окружности:
Радиус окружности, вписанной в квадрат
Формула радиуса вписанной в квадрат окружности:
где a — сторона квадрата.
Радиус окружности, вписанной в правильный шестиугольник
Формула радиуса вписанной в правильный шестиугольник окружности:
где a — сторона правильного шестиугольника.
Для любого многоугольника центр вписанной окружности лежит в точке пересечения его биссектрис.
Правильный треугольник, площадь правильного треугольника
Правильный треугольник — треугольник, у которого все стороны равны. Каждый угол правильного треугольника равен градусов.
Правильный треугольник называют еще равносторонним.
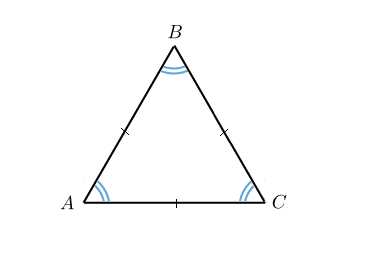
Каждая из высот правильного треугольника является также его медианой и биссектрисой.
Центры вписанной и описанной окружностей правильного треугольника совпадают.
Пусть сторона правильного треугольника равна .
Высота правильного треугольника:
Радиус окружности, вписанной в правильный треугольник: .
Радиус описанной окружности в два раза больше: .
Площадь правильного треугольника: .
Все эти формулы легко доказать. Если вы нацелены на решение задач части — докажите их самостоятельно.
. Сторона правильного треугольника равна . Найдите радиус окружности, вписанной в этот треугольник.
Задача решается в одну строчку. Радиус вписанной окружности .
. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна .
Сравним формулы для высоты правильного треугольника и радиуса вписанной окружности. Очевидно, радиус вписанной окружности равен высоты.
Ответ: .
. Сторона правильного треугольника равна . Найдите радиус окружности, описанной около этого треугольника.
Радиус окружности, описанной вокруг правильного треугольника, равен .
Ответ: .
Звоните нам: 8 (800) 775-06-82
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Планиметрия
Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
Напомним определение биссектрисы угла.
Определение 1. Биссектрисой угла называют луч, делящий угол на две равные части.
Теорема 1 (Основное свойство биссектрисы угла). Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).
Рис. 1
Доказательство. Рассмотрим произвольную точку D, лежащую на биссектрисе угла BAC, и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE, а гипотенуза AD – общая. Следовательно,
DF = DE,
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1). Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).
Рис. 2
Доказательство. Рассмотрим произвольную точку D, лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE, а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Определение 2. Окружность называют окружностью, вписанной в угол, если она касается касается сторон этого угла.
Теорема 3. Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.
Доказательство. Пусть точка D – центр окружности, вписанной в угол BAC, а точки E и F – точки касания окружности со сторонами угла (рис.3).
Рис.3
Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности радиусы окружности), а гипотенуза AD – общая. Следовательно
AF = AE,
что и требовалось доказать.
Замечание. Теорему 3 можно сформулировать и по-другому: отрезки касательных касательных, проведенных к окружности из одной точки, равны.
Напомним определение биссектрисы треугольника.
Определение 3. Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.
Теорема 4. В любом треугольнике все три биссектрисы пересекаются в одной точке.
Доказательство. Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC, и обозначим точку их пересечения буквой O (рис. 4).
Рис. 4
Опустим из точки O перпендикуляры OD, OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC, то в силу теоремы 1 справедливо равенство:
OD = OE,
Поскольку точка O лежит на биссектрисе угла ACB, то в силу теоремы 1 справедливо равенство:
OD = OF,
Следовательно, справедливо равенство:
OE = OF,
откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC. Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать
Определение 4. Окружностью, вписанной в треугольник, называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности.
Рис. 5
Следствие. В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.
Формулы для радиуса окружности, вписанной в треугольник
Формулы, позволяющие найти радиус вписанной в треугольник окружности, удобно представить в виде следующей таблицы.
| Фигура | Рисунок | Формула | Обозначения |
| Произвольный треугольник | Посмотреть вывод формулы | a, b, c – стороны треугольника, . | |
Посмотреть вывод формулы | |||
| Равнобедренный треугольник | Посмотреть вывод формулы | a – боковая сторона равнобедренного треугольника, | |
| Равносторонний треугольник | Посмотреть вывод формулы | a – сторона равностороннего треугольника, | |
| Прямоугольный треугольник | Посмотреть вывод формул | a, b – катеты прямоугольного треугольника, |
| Произвольный треугольник | |
где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
| Равнобедренный треугольник | |
где Посмотреть вывод формулы | |
| Равносторонний треугольник | |
где Посмотреть вывод формулы | |
| Прямоугольный треугольник | |
где Посмотреть вывод формул | |
| Произвольный треугольник |
где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
| Равнобедренный треугольник |
где Посмотреть вывод формулы |
| Равносторонний треугольник |
где Посмотреть вывод формулы |
| Прямоугольный треугольник |
где Посмотреть вывод формулы |
Вывод формул для радиуса окружности, вписанной в треугольник
Теорема 5 . Для произвольного треугольника справедливо равенство
где a, b, c – стороны треугольника, r – радиус вписанной окружности, – полупериметр (рис. 6).
Рис. 6
Доказательство. Из формулы
с помощью формулы Герона получаем:

что и требовалось.
Теорема 6 . Для равнобедренного треугольника справедливо равенство
где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).
Рис. 7
Доказательство. Поскольку для произвольного треугольника справедлива формула
где
то, в случае равнобедренного треугольника, когда
получаем
что и требовалось.
Теорема 7 . Для равностороннего треугольника справедливо равенство
где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).
Рис. 8
Доказательство. Поскольку для равнобедренного треугольника справедлива формула
то, в случае равностороннего треугольника, когда
b = a,
получаем

что и требовалось.
Замечание. Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.
Теорема 8 . Для прямоугольного треугольника справедливо равенство
где a, b – катеты прямоугольного треугольника, c – гипотенуза, r – радиус вписанной окружности.
Доказательство. Рассмотрим рисунок 9.
Рис. 9
Поскольку четырёхугольник CDOF является прямоугольникомпрямоугольником, у которого соседние стороны DO и OF равны, то этот прямоугольник – квадратквадрат. Следовательно,
СD = СF= r,
В силу теоремы 3 справедливы равенства
Следовательно, принимая также во внимание теорему Пифагора, получаем
что и требовалось.
Замечание. Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в прямоугольный треугольник, с помощью общей формулы для радиуса окружности, вписанной в произвольный треугольник.
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Радиус вписанной в треугольник окружности
Радиус вписанной в треугольник окружности можно найти по одной общей формуле.
Кроме того, для правильного и прямоугольного треугольников существуют дополнительные формулы.
Радиус вписанной в треугольник окружности для произвольного треугольника
Формула для нахождения радиуса окружности, вписанной в произвольный треугольник:
где S — площадь треугольника, p — его полупериметр.
Для треугольника со сторонами a, b, c полупериметр
и формулу можно записать так:
Если нужно найти радиус вписанной в треугольник окружности по его сторонам, то площадь треугольника ищут по формуле Герона, соответственно, формула для нахождения радиуса треугольника по трем сторонам имеет вид:
Радиус вписанной в прямоугольный треугольник окружности
Формула для нахождения радиуса вписанной в прямоугольный треугольник окружности:
где a, b — длины катетов, c — длина гипотенузы.
Радиус окружности, вписанной в правильный (то есть равносторонний) треугольник
Формула для нахождения радиуса окружности, вписанной в правильный треугольник:
или (без иррациональности в знаменателе):
где a -длина стороны правильного треугольника.
В правильном треугольнике радиус вписанной окружности также можно найти через радиус описанной окружности:
www.treugolniki.ru

Leave A Comment