| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | cos(30 град. ) | ||
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) |
|
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | 45 | ||
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) |
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) |
|
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) |
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | ||
| 100 | Преобразовать из градусов в радианы | 88 град. |
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) |
|
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) |
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) |
|
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) |
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Формулы приведения тригонометрических функций
Формулы приведения тригонометрических функцийФормулы привидения тригонометрических функций представлены в виде таблицы. Ниже находятся некоторые формулы приведения в табличном виде. Еще ниже эти формулы приведения расписаны для некоторых тригонометрических функций в виде тригонометрических тождеств.Таблицы значений тригонометрических функций находятся на другой странице.
Формулы привидения для синуса выглядят так:
sin (π/2 + α) = cos α
sin (π + α) = — sin α
sin (3π/2 + α) = — cos α
sin (π/2 — α) = cos α
sin (π — α) = sin α
sin (3π/2 — α) = — cos α
sin (2π — α) = — sin α
Формулы приведения для тригонометрической функции синус будут следующие. Синус угла пи пополам (пи/2) плюс или минус угол альфа равняется косинусу угла альфа. Синус угла пи плюс угол альфа или угла два пи минус альфа по формуле приведения будет равен минус синусу угла альфа. Синус угла три вторых пи (3пи/2) плюс или минус альфа равен минус косинусу альфа. Если угол равняется пи минус альфа, то синус такого угла равняется синусу угла альфа. Тригонометрия формулы и тригонометрические тождества. Перевод синуса в косинус.
Тригонометрические формулы привидения для косинуса приобретают такой вид:
cos (π/2 + α) = — sin α
cos (π + α) = — cos α
cos (3π/2 + α) = sin α
cos (π/2 — α) = sin α
cos (π — α) = — cos α
cos (3π/2 — α) = — sin α
cos (2π — α) = cos α
Для косинуса формулы приведения имеют следующий вид.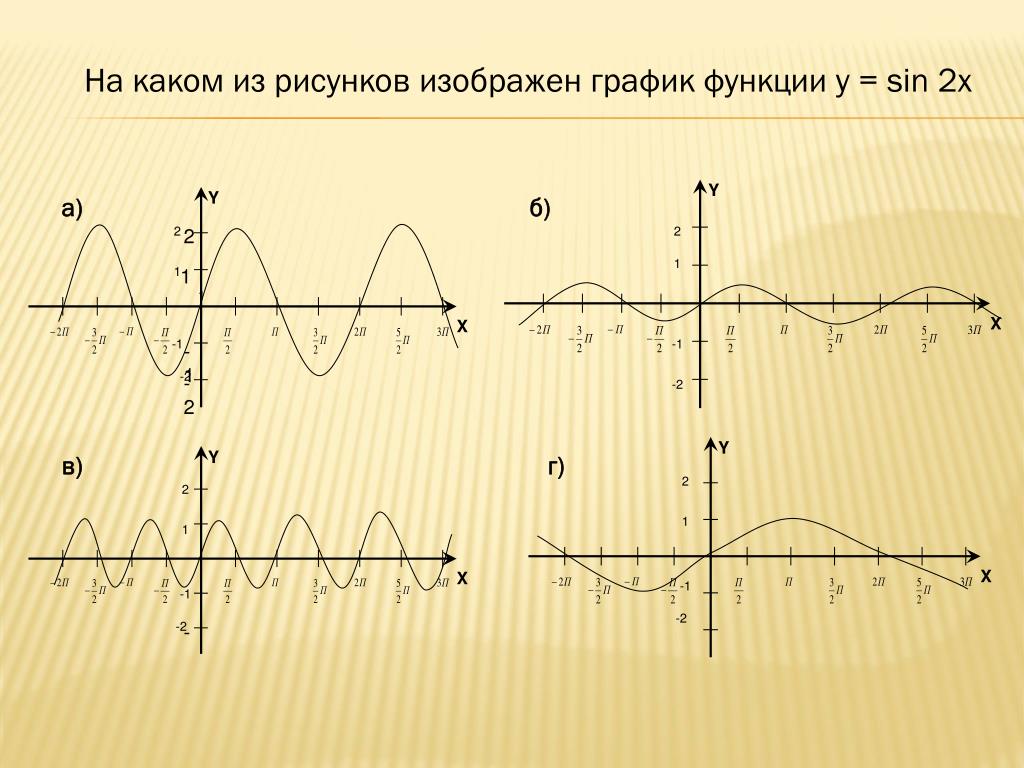
Косинус угла пи пополам (пи/2) плюс угол альфа и косинус три вторых пи минус альфа равняются минус синусу угла альфа. Косинус угла пи плюс или минус угол альфа в результате равен минус косинусу альфа. Формула приведения для косинуса угла (3пи/2) три вторых пи плюс угол альфа и пи пополам минус альфа равняется синусу угла альфа. Тригонометрическая функция косинус пи пополам (1/2 пи) минус альфа равняется тригонометрической функции косинус угла альфа. Тригонометрия формулы. Перевод косинуса в синусы.
Тригонометрическая функция тангенс имеет следующие формулы привидения:
tg (π/2 + α) = — ctg α
tg (π + α) = tg α
tg (3π/2 + α) = — ctg α
tg (π/2 — α) = ctg α
tg (π — α) = — tg α
tg (3π/2 — α) = ctg α
tg (2π — α) = tg α
Тригонометрические формулы приведения функции тангенс tg. Тангенс угла пи деленное на два плюс альфа и угла три вторых пи плюс альфа приравниваются минус котангенсу угла альфа. Тригонометрическая функция тангенс угла пи на два или три пи деленное на два (3/2 пи) минус альфа равна котангенсу альфа. Тангенс угла пи минус альфа равен минус тангенсу угла альфа. Формулы приведения для тангенса пи плюс альфа и тангенса два пи минус альфа равняются тангенсу угла альфа. Тригонометрические тождества. Перевод тангенса в котангенсы.
Тригонометрическая функция тангенс имеет следующие формулы привидения:
ctg (π/2 + α) = — tg α
ctg (π + α) = ctg α
ctg (3π/2 + α) = — tg α
ctg (π/2 — α) = tg α
ctg (π — α) = — ctg α
ctg (3π/2 — α) = tg α
ctg (2π — α) = ctg α
Формулы приведения функции котангенс ctg угла.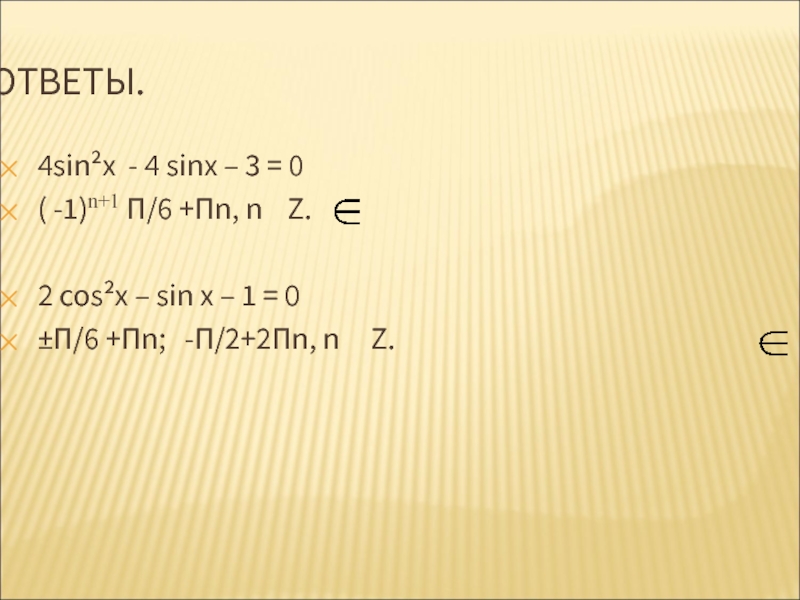
Для угла 1/2 пи плюс альфа и угла 3/2 пи плюс альфа котангенс равняется минус тангенсу -tg угла альфа. Если в этих же выражениях угол альфа не прибавляется, а вычитается, тогда котангенс такого угла равняется тангенсу угла альфа. Функция котангенс пи минус альфа равна минус котангенсу угла альфа. Котангенс угла пи плюс альфа и 2 пи минус альфа будет равен котангенсу угла альфа. Тригонометрические тождества и формулы тригонометрия. Перевод котангенсов в тангенсы.
Если вам понравилась публикация и вы хотите знать больше, помогите мне в работе над другими материалами.
17 января 2010 года — 1 декабря 2018 года..
© 2006 — 2021 Николай Хижняк. Все права защищены.
SIN (функция SIN) — Служба поддержки Office
В этой статье описаны синтаксис формулы и использование функции SIN в Microsoft Excel.
Описание
Возвращает синус заданного угла.
Синтаксис
SIN(число)
Аргументы функции SIN описаны ниже.
Замечание
Если аргумент задан в градусах, умножьте его на ПИ()/180 или преобразуйте в радианы с помощью функции РАДИАНЫ.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel.
Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Формула | Описание | Результат |
|---|---|---|
|
=SIN(ПИ()) |
Синус пи радиан (0, приблизительно). |
0,0 |
|
=SIN(ПИ()/2) |
Синус пи/2 радиан. |
1,0 |
|
=SIN(30*ПИ()/180) |
Синус угла 30 градусов. |
0,5 |
|
=SIN(РАДИАНЫ(30)) |
Синус 30 градусов. |
0,5 |
Четверть числовой окружности
Если посмотреть на числовую окружность, то можно заметить, что оси абсцисс и ординат разбивают ее на четыре части. Эти части называют четвертями и нумеруют в том порядке как их проходят, двигаясь в положительном направлении (против часовой стрелки).
|
\((\)\(\frac{π}{2}\)\(;π)\)- вторая четверть |
\((0;\)\(\frac{π}{2}\)\()\) — первая четверть |
|
|
|
|
|
|
\((π;\)\(\frac{3π}{2}\)\()\) — третья четверть |
\((\)\(\frac{3π}{2}\)\(;2π)\) — четвертая четверть |
Почему так важно определять какой четверти принадлежит угол?
Дело в том, что каждая четверть уникальна в плане знаков тригонометрических функций.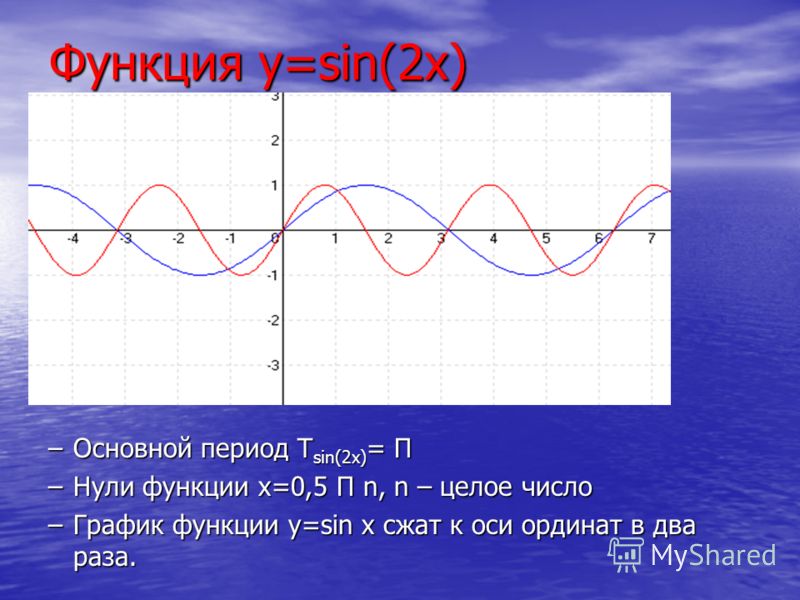
2a=0,64\)
\(\sina=0,8\) или \(\sina=-0,8\)
У нас два ответа, и оба нам подходят. Но у угла не может быть два синуса! Один лишний! А какой?
Вот тут нам и поможет знание о четвертях: обратите внимание, что у нас в условии есть двойное неравенство \(π<a<\) \(\frac{3π}{2}\), то есть угол \(a\) такой, что больше \(π\), но меньше \(\frac{3π}{2}\).
Значит он лежит в третьей четверти. А в третьей четверти синус отрицателен. Поэтому верный ответ: \(-0,8\).
Ответ: \(\sina=-0,8\).
Про непостоянство четвертей:
Важно понимать, что, например, первой четверти принадлежат не только углы от \(0\) до \(\frac{π}{2}\), но и углы от \(2π\) до \(\frac{5π}{2}\), и от \(4π\) до \(\frac{9π}{2}\), и от \(6π\) до \(\frac{13π}{2}\) и так далее. Ведь как только мы заканчиваем полный оборот – кончается четвертая четверть и опять начинается первая.
Кроме того, нужно помнить, что углы могут откладываться в отрицательную сторону (по часовой стрелке), и тогда мы попадем в первую четверть только в конце круга. Ведь сначала мы пройдем четвертую четверть, потом в третью и т.д.
|
\((-π;-\)\(\frac{3π}{2}\)\()\)- вторая четверть |
\((-\)\(\frac{3π}{2}\)\(;-2π)\) — первая четверть |
|
|
|
|
|
|
\((-\)\(\frac{π}{2}\)\(;-π)\) — третья четверть |
\((0;-\)\(\frac{π}{2}\)\()\) — четвертая четверть |
Ну и, конечно, мы можем в отрицательную сторону делать обороты, так же как и в положительную.
Смотрите также:
Числовая окружность (шпаргалка)
Тригонометрическая таблица с кругом
Как обозначать точки на числовой окружности
Скачать статью 3 (\ theta) + \ cdots, \ end {align} cos (nθ) sin (nθ) = cosn (θ) −1⋅2n (n − 1) cosn − 2 (θ) ⋅sin2 (θ) + 1⋅2⋅3⋅4n (n −1) (n − 2) (n − 3) cosn − 4 (θ) ⋅sin4 (θ) + ⋯ = ncosn − 1 (θ) ⋅sin (θ) −1⋅2⋅3n (n − 1) (n − 2) cosn − 3 (θ) ⋅sin3 (θ) + ⋯,
, где члены обеих вышеуказанных серий попеременно положительные и отрицательные. Кроме того, каждая серия продолжается до тех пор, пока один из множителей в числителе не станет равным нулю, а затем прекращается. Значит, доказано.
Чтобы доказать для tan (nθ) \ tan (n \ theta) tan (nθ), заметим, что
tan (nθ) = sin (nθ) cos (nθ) = ∑r = 02r + 1≤n (−1) r (n2r + 1) cosn − 2r − 1 (θ) sin2r + 1 (θ) ∑r = 02r≤n (−1) r (n2r) cosn − 2r (θ) sin2r (θ).n}, \) \ (\ sinh x, \) \ (\ ch x, \) \ (\ tanh x, \) \ (\ text {coth} x, \) \ (\ text {sech} x, \ ) \ (\ text {csch} x, \) \ (\ sin x, \) \ (\ cos x, \) \ (\ tan x, \) \ (\ cot x, \) \ (\ ln x, \) \ (\ arcsin x, \) \ (\ arccos x, \) \ (\ arctan x \)
Аргумент (независимая переменная): \ (x \)
Натуральные числа: \ (n \), \ (m \)
Действительные числа: \ (a \), \ (b \), \ (c \)
- Чтобы найти некоторые интегралы, мы можем использовать формулы приведения. Эти формулы позволяют уменьшить степень подынтегральной функции и вычислить интегралы за конечное число шагов.{n — 1}}}} \ normalsize}, \) \ (n \ ne 1. \)
Интегрирование по формулам редукции — доказательства и рабочие примеры
Интегрирование по формулам редукции
Предположим, вам нужно ∫e x sin (x) dx.
Мы используем интеграцию по частям для получения результата, но натолкнулись на небольшую загвоздку:
u = e x ; dv / dx = sin x
Итак, du / dx = e x ; v = -cos x
∫e x sin (x) dx = -e x cos x + ∫ e x cos x dx 1
Теперь нам нужно повторить процесс интегрирования для ∫ e x cos x dx, который выглядит следующим образом:
u = e x ; dv / dx = cos x
du / dx = e x ; v = грех х
Итак, e x cos x dx = e x sin x — ∫ e x sin x dx 2
Как видите, теперь мы движемся к бесконечному циклу; следовательно, мы должны использовать другой подход.
Давайте сделаем ∫ e x cos x dx объектом из обоих уравнений и приравняем их.
Из 1 => ∫e x sin (x) dx + e x cos x = ∫ e x cos x dx 3
Из 2 => ∫ e x cos x dx = e x sin x — ∫ e x sin x dx 4
Поскольку 3 = 4 => ∫e x sin (x) dx + e x cos x = e x sin x — e x sin x dx
2∫e x sin (x) dx = e x sin x — e x cos x
∫e x sin (x) dx = 1 / 2e x [sin x — cos x]
Нам удается найти интеграл, но знак интеграции по-прежнему остается частью решения!
Есть множество случаев, когда процесс интеграции непрост и непрост. Интегрирование по формулам редукции — один из таких методов.
Интегрирование по формулам приведения
В этом методе мы постепенно уменьшаем мощность функции, пока не дойдем до стадии, на которой ее можно интегрировать. Обычно это достигается путем интеграции по частям методом .
Например.∫ [ln x] n dx
Воспользуемся методом интегрирования по частям:
u = [ln x] n => du / dx = n / x [ln x] n-1 ; dv / dx = 1 => v = x
∫ [ln x] n dx = x [ln x] n — n / x∫x [ln x] n-1
= x [ln x] n — n∫ [ln x] n-1
Если ∫ [ln x] n dx = I n , то ∫ [ln x] n-1 = I n-1
Следовательно,
I n = x [ln x] n — n I n-1
Это формула приведения для интегрирования [ln x] n относительно x.На данном этапе это не дает никакого результата; следовательно. посмотрим, как это на самом деле работает.
Предположим, вы хотите найти ∫ [ln x] 3 dx, то есть I 3 .
I 3 = x [ln x] 3 — 3 I 2
= x (ln x) 3 — 3 [x (ln x) 2 — 2 I 1 ]
= x (ln x) 3 — 3x (ln x) 2 + 6 I 1
= x (ln x) 3 — 3x (ln x) 2 + 6 [x (ln x) 1 — I 0 ]
= x (ln x) 3 — 3x (ln x) 2 + 6x (ln x) 1 — 6I 0
= x (ln x) 3 — 3x (ln x) 2 + 6x (ln x) — 6 [x (ln x) 0 — 0 I -1 ]
= x (ln x) 3 — 3x (ln x) 2 + 6 x (ln x) — 6x + c
Итак, ∫ [ln x] 3 dx = x (ln x) 3 — 3x (ln x) 2 + 6x (ln x) — 6x + c
Теперь давайте докажем, что интеграл, полученный с помощью формулы редукции, действительно является интегралом ∫ [ln x] 3 dx, путем дифференцирования первого:
Доказательство
Давайте применим правило продукта и правило цепочки для их дифференциации
d [x (ln x) 3 — 3x (ln x) 2 + 6x (ln x) — 6x] / dx = x (3) [ln x] 2 (1 / x) + [ln x] 3 — 6ln x — 3 [ln x] 2 + 6 + 6 ln x -6
= [ln x] 3
Формулы редукции могут быть расширены до ряда функций.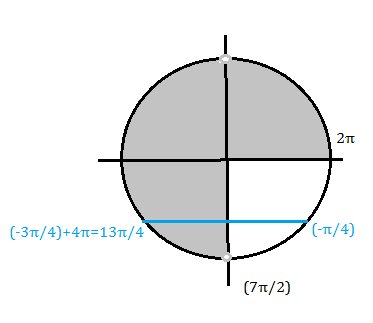
Однако процедура не одинакова для всех функций.
Например, 1
Найдите формулу редукции для интегрирования ∫sin n x dx и, следовательно, найдите ∫sin 4 x dx.
∫sin n x dx = ∫sin n-1 x sin x dx
Пусть u = ∫sin n-1 x и dv / dx = sin x
Итак, du / dx = (n-1) sin n-2 x cos x; v = -cos x
∫sin n x dx = -sin n-1 x cos x + ∫ cos x (n-1) sin n-2 x cos x dx
= -sin n-1 x cos x + ∫ cos 2 x (n-1) sin n-2 x dx
= -sin n-1 x cos x + ∫ [1 — sin 2 x] (n-1) sin n-2 x dx
= -sin n-1 x cos x + ∫ (n-1) sin n-2 x dx — ∫ (n-1) sin 2 x sin n-2 x dx
= -sin n-1 x cos x + ∫ (n-1) sin n-2 x dx — ∫ (n-1) sin n x dx
∫n sin n x dx = -sin n-1 x cos x + ∫ (n-1) sin n-2 x dx
∫sin n x dx = -1 / n sin n-1 x cos x + ∫ (n-1) / n sin n-2 x dx
I n = -1 / n sin n -1 x cos x + (n-1) / n I n-2
sin 4 x dx = -1/4 sin 3 x cos x + ∫ 3/4 sin 2 x dx
= -1/4 sin 3 x cos x + 3/4 [-1/2 cos x sin x + ∫ 1/2 sin 0 x dx]
= -1/4 sin 3 x cos x -3/8 cos x sin x + 3/8 x + c dx
= -1/4 sin 3 x cos x -3/8 sin x cos x + 3/8 x + c
поскольку sin 2x = 2 sin x cos x
∫ sin 4 x dx = -1/4 sin 3 x cos x — 3/16 sin 2x + 3/8 x + c
E.г.2
Найдите формулу редукции для интегрирования ∫cos n x dx и, следовательно, найдите ∫cos 4 x dx.
∫cos n x dx = ∫cos n-1 x cos x dx
Пусть u = ∫cos n-1 x и dv / dx = cos x
Итак, du / dx = — (n-1) cos n-2 x sin x; v = грех х
∫cos n x dx = -cos n-1 x sin x + ∫ sin x (n-1) cos n-2 x sin x dx
= cos n-1 x sin x + ∫ sin 2 x (n-1) cos n-2 x dx
= cos n-1 x sin x + ∫ [1 — cos 2 x] (n-1) cos n-2 x dx
= cos n-1 x sin x + ∫ (n-1) cos n-2 x dx — ∫ (n-1) cos n x dx
∫n cos n x dx = cos n-1 x sin x + ∫ (n-1) cos n-2 x dx
∫cos n x dx = 1 / n cos n-1 x sin x + ∫ (n-1) / n cos n-2 x dx
I n = 1 / n cos n- 1 x sin x + (n-1) / n I n-2
∫ cos 4 x dx = 1/4 cos 3 x sin x + ∫ 3/4 cos 2 x dx
= 1/4 cos 3 x sin x + 3/4 [1/2 cos x sin x + ∫ 1/2 cos 0 x dx]
= 1/4 cos 3 x sin x + 3/8 cos x sin x + 3/8 x + c
Поскольку sin 2x = 2 sin x cos x
∫ cos 4 x dx = 1/4 cos 3 x sin x + 3/16 sin 2x + 3/8 x + c
E.
г.3
Найдите формулу редукции для интегрирования ∫ tan n x dx и, следовательно, найдите ∫tan 4 x dx.
∫tan n x dx = ∫tan n-2 x tan 2 x dx
u = tan n-2 x => du / dx = n-2 tan n-3 x sec 2 x; dv / dx tan 2 x = sec 2 x — 1 => v = tan x — x
Интеграция приводит к следующей формуле:
∫tan n x dx = 1 / n-1 tan n-1 x — ∫tan n-2 x dx
I n = 1 / n-1 I n-1 — I п-2
∫tan 4 x dx = 1/3 tan 3 x — ∫tan 2 x dx
= 1/3 загар 3 x — [загар x — ∫ dx]
= 1/3 загар 3 x — загар x + x + c
E.г.4
Найдите формулу сокращения для интегрирования ∫ e x x n x dx и, следовательно, найдите ∫e x x 3 dx.
u = x n => du / dx = nx n-1 ; dv / dx = e x => e x
∫ e x x n x dx = x n e x — n∫e x x n-1 dx
I n = x n e x — nI п-1
∫ e x x 3 x dx = x 3 e x — 3 e x x 2 dx
= x 3 e x — 3 [x 2 e x — 2∫e x x dx]
= x 3 e x — 3x 2 e x + 6∫e x x dx
= x 3 e x — 3x 2 e x + 6 [xe x x — ∫e x x 0 dx]
= x 3 e x — 3x 2 e x + 6xe x x — 6∫e x dx
= x 3 e x — 3x 2 e x + 6xe x x — 6e x + c
Здесь вы можете интерактивно попрактиковаться в графическом представлении вышеуказанных интегралов.
2 (х). Затем нажмите ввод.
Синяя кривая — функция, которую нужно интегрировать; красная кривая — интегрированная функция.
Wolfram | Alpha Примеры: исчисление и анализ
Другие примеры
ИнтегралыВычислить определенные и неопределенные интегралы от функций. Интегрировать по одной или нескольким переменным.
Вычислить неопределенный интеграл:
Вычислить определенный интеграл:
Вычислить неправильный интеграл:
Другие примеры
Другие примеры
Производные Возьмем производную от функций одного или нескольких переменных.
Вычислить частную производную выражений с более чем одной переменной.
Вычислить производную функции:
Вычислить высшие производные:
Вычислить частные производные:
Другие примеры
Другие примеры
ПределыИсследуйте предельное поведение функции, когда она приближается к единственной точке или асимптотически приближается к бесконечности.
Вычислить односторонний предел:
Другие примеры
Другие примеры
Последовательности Вычисляйте и исследуйте последовательности целых чисел или других числовых значений.
Найдите продолжения и формулы для известных или неизвестных последовательностей.
Вычислите возможную формулу и продолжение для последовательности:
Другие примеры
Другие примеры
СуммыВычислить значение проиндексированных сумм или сумм последовательностей значений.Вычислить бесконечные суммы и найти условия сходимости.
Другие примеры
Другие примеры
Товары Вычислить индексированный продукт путем умножения конечного или бесконечного числа членов.
Вычислить проиндексированный продукт:
Вычислить бесконечное произведение:
Другие примеры
Другие примеры
Расширения серийНайдите серию Тейлора, серию Лорана и многое другое по любому вопросу.
Найдите расширение ряда Тейлора:
Укажите центральную точку и порядок расширения:
Другие примеры
Другие примеры
Приложения исчисления Используйте инструменты исчисления, такие как интегралы и производные, для вычисления свойств кривых, поверхностей, твердых тел и плоских областей.
Вычислите площадь, ограниченную двумя кривыми:
Найдите точки перегиба функции:
Другие примеры
Другие примеры
Векторный анализПримените ротор, градиент и другие дифференциальные операторы к скалярным и векторным полям.
Вычислить градиент функции:
Вычислить альтернативные формы выражения векторного анализа:
Другие примеры
Другие примеры
Интегральные преобразованияВычислить преобразование Фурье, преобразование Лапласа и другие интегральные преобразования функций.
Вычислить преобразование Фурье:
Вычислить преобразование Лапласа:
Другие примеры
Другие примеры
Домен и диапазонВычислить область и диапазон реальных математических функций.Нанесите на числовую линию домен и диапазон.
Вычислить область определения функции:
Вычислить диапазон функции:
Другие примеры
Другие примеры
НепрерывностьНайдите разрывы и непрерывные интервалы функции.Также определите, являются ли определенные разрывы устранимыми или бесконечными из-за асимптоты.
Определите, является ли функция непрерывной:
Найдите разрывы функции:
Другие примеры
Получение триггерных тождеств с помощью формулы Эйлера
Написано наставником Джеффри Д.
В этом уроке мы рассмотрим вывод нескольких тригонометрических тождеств, а именно
cos ( x + y ) = cos x cos y — sin x sin y
и
sin ( x + y ) = sin x cos y + sin x cos y
также
cos 2 x = cos 2 x — sin 2 x
вместе с
sin 2 x = 2 sin x cos x
и, наконец, Формула ДеМуавра,
(cos x + i sin x ) n = cos nx + i sin nx
с использованием формулы Эйлера.Чтобы хорошо понять, что происходит, вам потребуются предварительные знания о расширениях рядов и комплексных числах! Вы можете сначала освежить свои знания по этим предметам.
Расширения серии Power
Начнем с изучения разложения в степенной ряд функций e x , sin x и cos x . Степенный ряд функции обычно выводится из ряда Тейлора функции для случая, когда a = 0.Этот случай, когда a = 0, называется серией Маклаурина. Серия Тейлор:
Случай, когда a = 0 — это серия Маклаурина:
Эти ряды используются для аппроксимации значений функций вокруг определенной точки. Это все, что я скажу по этому поводу. Силовой ряд e x ; cos x и sin x взяты из их представления серии MacLaurin:
для всех x.
для всех x.
для всех x.
Комплексные числа и
e xКомплексное число — это число в форме a + bi , где i — корень уравнения x 2 + 1 = 0 и a и b — действительные числа. Отметив это, мы можем использовать i в нашем степенном ряду ex , поскольку это верно для всех x .
для всех x.
Принимая во внимание, что x 2 + 1 = 0 → x = i и поэтому √-1 = i → i 2 = -1, i 3 = — и , и т. Д. Итак, применяя мощности выборочно, получаем
Теперь мы можем переставить члены и разложить на множители i так, чтобы у нас было
Теперь, если мы оглянемся на наши последовательные представления cos x и sin x , мы получим
e ix = cos x + i sin x
Это огромный вывод. Она известна как формула Эйлера . Отсюда мы можем вывести некоторые тригонометрические тождества, а также составить формулы для общих случаев.Давайте сначала рассмотрим простой вывод:
e ix e iy = (cos x + i sin x ) (cos y + i sin y )
Но напомним, что e x e y = e x + y . Следовательно, имеем
e ix + iy = cos ( x + y ) + i sin ( x + y ) = (cos x + i sin x ) ( cos y + i sin y )
= cos x cos y + i sin x cos y + i sin y cos x + i 2 sin x sin 3 y
А теперь мы можем переставить это так, чтобы сложная часть и действительная часть были разделены.
Итак, у нас
e ix + iy = cos ( x + y ) + i sin ( x + y ) = (cos x + i sin x ) ( cos y + i sin y )
= cos x cos y + i sin x cos y + i sin y cos x + i 2 sin x sin y = (cos x cos y — sin x sin y ) + ( i sin x cos y + i sin y cos x )
Взяв действительные части и приравняв их, мы получим знакомую формулу тригонометрической суммы:
cos ( x + y ) = cos x cos y — sin x sin y
, а также
sin ( x + y ) = sin x cos y + sin y cos x
Теперь предположим, что у нас есть что-то вроде этого:
e ix e ix = e ix + ix = e i2x = cos ( x + x ) + i ( x + x )
= (cos x + i sin x ) (cos x + i sin x )
= cos x cos x + i sin x cos x + i sin x cos x + i 2 sin x sin 3 x
Если приравнять действительные части уравнения
cos 2 x = cos 2 x — sin 2 x
А еще у нас
sin 2 x = 2 sin x cos x
В общем, таким образом мы можем получить формулу для любого угла, кратного углу.Это приводит нас к другой известной формуле, известной как формула ДеМуавра. Формулу ДеМуавра можно получить, взяв n -й случай формулы Эйлера.
e inx = cos nx + i sin nx
Мы заинтересованы в том, чтобы показать, что
(cos x + i sin x ) n = cos nx + i sin nx
, что составляет , точнее, Формула ДеМуавра.Очевидно, что это верно для любого n . Мы можем показать, что это верно для всех n , используя индукцию.
(cos x + i sin x ) n +1 = (cos x + i sin x ) n (cos x + sin x )
Отсюда мы применяем то, что мы знаем о случае n , приведенном выше.
= (cos nx + i sin nx ) (cos x + i sin x )
Теперь мы можем умножать.
= cos nx cos x + i sin x cos nx + i sin nx cos x + i 2 sin nx263 sin
И из нашей работы выше мы уже показали, что их можно упростить в наши формулы суммы как таковые:
cos ( nx + x ) + i sin ( nx + x ) = cos ( n + 1) x + i sin ( n + 1) x
Итак, мы показали, что
(cos x + i sin x ) n = cos nx + i sin nx
верно для всех n .Таким образом, мы показали, что некоторые очень распространенные тригонометрические тождества связаны и могут быть получены из разложений в ряды и комплексных чисел!
Бесплатно зарегестрироваться чтобы получить доступ к дополнительным математическим ресурсам, например Ресурсы Wyzant содержат блоги, видео, уроки и многое другое по математике и более чем 250 другим предметам. Прекратите бороться и начните учиться сегодня с тысячами бесплатных ресурсов! .
Leave A Comment