Стороны основания правильной шестиугольной пирамиды равны 12 боковые 10: Стороны основания правильной шестиугольной пирамиды равны 12, боковые рёбра равны 10. Найдите

Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна . Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.

Чтобы посмотреть презентацию с картинками, оформлением и слайдами, скачайте ее файл и откройте в PowerPoint на своем компьютере.
Текстовое содержимое слайдов презентации:

Открытый банк заданий по математике http://mathege.ru:8080/or/ege/Main.action Найдем отношение объемов Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза? V = SoH 1 3 3 х 1 0 х В 9 8 h a 2a 2h a ab S sin 2 1 = Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды. 3 х 1 0 х В 9 4 Н 3 4 V = SoH 1 3 12 16 Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна . 3 х 1 0 х В 9 5 0 , 2 V = SoH 1 3 1 1 a ab S sin 2 1 = 1 1 600 3 х 1 0 х В 9 3 . Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен . 2 2 V = SoH 1 3 ? a ab S sin 2 1 = 2 2 600 3 3 3 х 1 0 х В 9 4 Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в четыре раза? A F B C D E Найдем отношение объемов V = SoH 1 3 h 4h 3 х 1 0 х В 9 7 1 1 1 600 ? . Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро. A F B C D E 1 1 ? 1 S 6 2 3 3 О Из АОS по теореме Пифагора найди ребро AS. a ab S sin 2 1 = 1 1 600 Для правильного 6-уг. сторона равна радиусу описанной окружности. Можно вычислить площадь правильного шестиугольника, разбив его на 6 треугольников. 3 х 1 0 х В 9 2 0 0 . В правильной четырехугольной пирамиде высота равна 6, сторона основания равна 10. Найдите ее объем. Н 6 10 10 V = SoH 1 3 a S = кв. 2 3 х 1 0 х В 9 2 5 6 . В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем. Н 6 8 10 V = SoH 1 3 a S = кв.

2 А В С D S Из треугольника АВС: 450 3 х 1 0 х В 9 4 8 . Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 600. Высота пирамиды равна 6. Найдите объем пирамиды. . Н S D C B V = SoH 1 3 ? 6 Из SHG: Из SHA: 3 6 = ab S пр. 3 12 G 600 6 A 600 3 х 1 0 х В 9 4 , 5 Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды. A В С S A S B C V = SoH 1 3 3 3 3 3 3 3 Задача очень простая, если догадаться опрокинуть пирамиду на удобную грань, например, SCB. Основание – прямоугольный треугольник SCB, высота AS. ab S 2 1 = 3 3 катет катет высота Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 450. Найдите объем пирамиды. 3 х 1 0 х В 9 4 8 . . A F B C D E 4 4 S О К V = SoH 1 3 450 ? ? 4 4 4 600 a ab S sin 2 1 = 4 4 600 Можно вычислить площадь правильного шестиугольника, разбив его на 6 треугольников. 2 3 2 3 2 3 2 Найдем ОК по теореме Пифагора К О С Найдем отношение объемов Объем параллелепипеда ABCDA1B1C1D1 равен 12. Найдите объем треугольной пирамиды B1ABC. Vпир. = SoH 1 3 A B C D B1 C1 D1 A1 Vприз. = SoH h h 12 3 х 1 0 х В 9 2 2SABC = Пирамида AD1CB1 получается, если мы отрежем от параллелепипеда четыре пирамиды по углам — ABCB1, D1B1CC1, AA1D1B1 и ADCD1. А объем каждой из них легко посчитать — мы делали это в предыдущей задаче. Например, найдем объем пирамиды ABCB1. Объем параллелепипеда ABCDA1B1C1D1 равен 4,5. Найдите объем треугольной пирамиды AD1CB1. C1 A B C D A1 B1 D1 Найдем отношение объемов Vпир. = SoH 1 3 Vпар. = SoH 4,5 3 х 1 0 х В 9 1 , 5 Четыре пирамиды по углам — ABCB1, D1B1CC1, AA1D1B1 и ADCD1 Объем пирамиды АD1CB1 h 2SABC = Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба. Найдем отношение объемов Vпир. = SoH 1 3 3 х 1 0 х В 9 2 h h 2 1 A B C D A1 B1 C1 D1 12 От треугольной призмы, объем которой равен 150, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания.

Найдите объем оставшейся части. h Найдем отношение объемов Vпир. = SoH 1 3 Vприз. = SoH 150 3 х 1 0 х В 9 5 0 F E A B C D A B C D E F Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 8. Найдите объем шестиугольной пирамиды. S У треугольной и шестиугольной пирамид, о которых говорится в условии, одинаковые высоты. Убедимся в этом, изменим расположение букв…Одинаковая высота, но площадь оснований различна. Найдем отношение объемов Vпир. = SoH 1 3 8 3 х 1 0 х В 9 4 8 V1 V2 Поработаем с выносным чертежом. Видим, что площадь основания треугольной пирамиды в 6 раз меньше, чем у шестиугольной. Объем правильной четырехугольной пирамиды SABCD равен 12. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC. S B D A C O h 2 1 Точка E – середина ребра SB, значит, точка N – середина SO (по т. Фалеса). Высота пирамиды EABC равна половине высоты пирамиды SABCD. E N Найдем отношение объемов Vпир. = SoH 1 3 12 3 х 1 0 х В 9 3 2SABC = От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды. B S C A М N S А В С М N У треугольной пирамиды и отсеченной пирамиды, о которых говорится в условии, одинаковые высоты. Убедимся в этом, изменим расположение букв… Одинаковая высота, но площадь оснований различна. Работать можно с любым из этих чертежей. Найдем отношение объемов Vпир. = SoH 1 3 12 3 х 1 0 х В 9 3 a b V2 V1 a ab S sin 2 1 = Найдем объем пирамиды NABC. Сравним его с объемом всей пирамиды SABC, составив отношение.Основания у них одинаковые – треугольник АВС.А высоты разные, сравним их. По т. Фалеса FP:SP = 2:3. Тогда, если SP=h, то FP= h, NO= h 2 3 2 3 Объем треугольной пирамиды равен 15.

(adsbygoogle = window.adsbygoogle || []).push({});

Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1 : 2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду. S C A B N 1 часть 2 части P Надо сравнить объемы пирамид NABC и NSAC. Найдем объем пирамиды NABC. Затем из VSABC (это 15) вычтем VNABC,, найдем VNSAC. O F h 3 2 15 3 х 1 0 х В 9 1 0

Приложенные файлы

5596821
Размер файла: 2 MB Загрузок: 0

Решение геометрических задач. — Математика

Файл к занятию 16.

Решение заданий по геометрии

Проверка домашнего задания

Задание 7. Найдите значение выражения . Ответ: -21

Задание 8. Найдите значение выражения . Ответ: -6

Задание 9. Найдите значение выражения. Ответ: 25

Задание 10. Решите уравнение . Ответ: −2.

Самостоятельная работа

Задание 1.

Найдите tg , если sin .

Задание 2. Найдите значение выражения

Задание 3. Найдите значение выражения

Задание 4. Найдите значение выражения 4

Прямоугольный треугольник. Основы тригонометрии. Основное тригонометрическое тождество.

При решении задач, связанных с прямоугольным треугольником, необходимо помнить теорему Пифагора, определение синуса, косинуса, тангенса, основное тригонометрическое тождество, формулы для вычисления R, r, S.

Теорема Пифагора: .В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Решение прямоугольного треугольника:

;

Основное тригонометрическое тождество:.

Помним, что: 1) синусы равных углов равны; 2)синусы смежных углов равны, т. е. sin cos тупого угла всегда меньше 0!

Задание 1. В треугольнике ABC AB=BC, AC=14, высота CH равна 7.Найдите синус угла ACB. Ответ: 0,5

Задание 2. В треугольнике ABC AC=BC, высота CH равна 9,6, cosA=. Найдите AC. Ответ: 10

Задание 3. На клетчатой бумаге с размером клетки 1×1 изображён угол. Найдите синус этого угла.

А) В)

Задание 4. На клетчатой бумаге с размером клетки 1×1 изображён угол. Найдите косинус этого угла.

А) В)

Площадь треугольника

Площадь треугольника равна: .
Площадь треугольника равна: .
Формула Герона: .
Площадь треугольника равна: .
Площадь треугольника равна:S= .

Помним, площади подобных треугольников относятся как квадрат коэффициента подобия: , а периметры, как коэффициент подобия.

Задание 5. В треугольнике ABC DE — средняя линия. Площадь треугольника CDE равна 24. Найдите площадь треугольника ABC. Ответ: 96

Площадь четырехугольника

Площадь ромба равна: . Площадь квадрата: .

Площадь прямоугольника: .
Площадь параллелограмма: .
Площадь трапеции: .

Задание 6. Найдите площадь трапеции, изображённой на рисунке. Ответ: 12

Задание 7. На клетчатой бумаге нарисован круг площадью 1,2. Найдите площадь закрашенного сектора. Ответ: 0,75

Задание 8. На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 12. Найдите площадь закрашенной фигуры. Ответ: 288

Задание 9. Найдите площадь треугольника, вершины которого имеют координаты (1 ; 14), (5 ; 16), (5 ; 22). Ответ: 12

Задание 10. Найдите площадь квадрата, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. Ответ:20

Задание 11. Найдите площадь трапеции, изображённой на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. Ответ: 30

Свойства вписанных углов

Вписанные углы, опирающиеся на одну и ту же дугу, равны: .

Устно: Найдите вписанный угол, опирающийся на дугу, равную 1/5 окружности. Ответ дайте в градусах. Ответ: 36

Заданине12. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 114°. Найдите вписанный угол ACB. Ответ дайте в градусах.Ответ:33

Задание 13. Угол ACO равен 27°, где O — центр окружности. Его сторона CA касается окружности. Сторона CO пересекает окружность в точке B (см. рис.). Найдите величину меньшей дуги AB окружности. Ответ дайте в градусах. Ответ:63

Задание 14. Угол ACB равен 54°. Градусная мера дуги AB окружности, не содержащей точек D и E, равна 138°. Найдите угол DAE. Ответ дайте в градусах. Ответ:15

Задание 15. Через концы A и B дуги окружности с центром O проведены касательные AC и BC. Меньшая дуга AB равна 58°. Найдите угол ACB. Ответ дайте в градусах. Ответ:122

Задание 16. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 82°, угол ABD равен 47°. Найдите угол CAD. Ответ дайте в градусах. Ответ:35

Задание 17. В треугольнике ABC CD — медиана, угол C равен 90°, угол B равен 35°. Найдите угол ACD.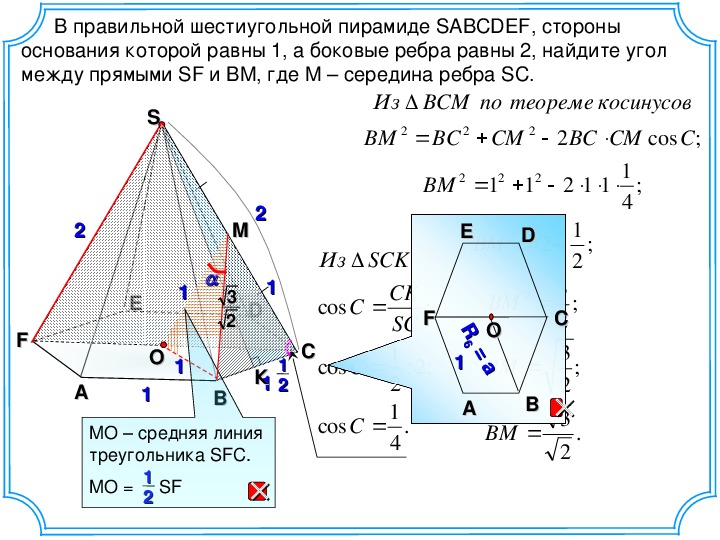 Ответ дайте в градусах. Ответ:55

Задание 18. На клетчатой бумаге с размером клетки 1×1 изображён равнобедренный прямоугольный треугольник. Найдите радиус описанной около него окружности.Ответ:4,5

Задание 19. На клетчатой бумаге с размером клетки 1×1 изображён равносторонний треугольник. Найдите радиус описанной около него окружности. Ответ: 6

Площадь поверхности и объем многогранников

Площадь поверхности и объём призмы: S_полн = 2S_осн + S_бок ; V= S_осн

Для прямой призмы, у которой боковые ребра перпендикулярны плоскостям оснований:

S_бок = Р_осн

Площадь поверхности и объем пирамиды: S_полн = S_осн + S_бок; V= S_осн

Для правильной пирамиды: S_бок = Р_осн h_бок

Задание 20. В правильной треугольной пирамиде боковое ребро равно 7, а сторона основания равна 10,5. Найдите высоту пирамиды.Ответ:3,5

Задание 21. Стороны основания правильной шестиугольной пирамиды равны 12, боковые рёбра равны 10. Найдите площадь боковой поверхности этой пирамиды. Ответ: 288

Задание 22. В правильной четырёхугольной пирамиде SABCD с основанием ABCD боковое ребро SC равно 17, сторона основания равна 15. Найдите объём пирамиды. Ответ: 1200

Задание 23. Площадь боковой поверхности треугольной призмы
равна 75. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы. Ответ:37,5

Задание 24. Найдите объем многогранника, вершинами которого являются точки А,В, С, В₁ правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁ , площадь основания которой равна 6, а боковое ребро равно 3. Ответ: 1.

Задание 25. Найдите объём многогранника, вершинами которого являются вершины A, C, D, F, A1, C1, D1, F1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 9, а боковое ребро равно 11. Ответ: 66

Площадь поверхности и объем тел вращения

Цилиндр:

; ;

;

Задание 26. Площадь боковой поверхности цилиндра равна 24 π, а диаметр основания равен 8. Найдите высоту цилиндра. Ответ: 3

Задание 27. Площадь полной поверхности конуса равна 35. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 3:2, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса. Ответ:12,6

Задание 28. В сосуде, имеющем форму конуса, уровень жидкости достигает 2/3 высоты. Объём жидкости равен 144 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд? Ответ: 342

Комбинация многогранников и тел вращения

Задание 29. В основании прямой призмы лежит прямоугольный треугольник с катетами 10 и 9. Боковые рёбра призмы
равны 2π. Найдите объём цилиндра, описанного около этой призмы. Ответ: 90,5

Задание 30. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 3. Объём параллелепипеда равен 36. Найдите высоту цилиндра. Ответ:1

Задание 31. Шар вписан в цилиндр объемом 42. Найдите объем шара. Ответ: 28.

Дополнительно. Две параллельные плоскости, расстояние между которыми 2, пересекают шар. Одна из плоскостей проходит через центр шара. Отношение площадей сечений шара этими плоскостями равно 0,84. Найдите радиус шара.

Проверочная работа в формате ЕГЭ. «Объем пирамиды»

	Объем пирамиды вариант 1		Объем пирамиды вариант 2
1.	Из куба объемом 114 вырезана правильная четырехугольная пирамида со стороной основания равной ребру куба. Вершина пирамиды расположена в центре куба. Найти объем пирамиды	1	Из куба вырезана правильная четырехугольная пирамида со стороной основания равной ребру куба. Вершина пирамиды расположена в центре куба. Найти объем куба, если объем пирамиды 8.
2	Найдите объем правильной треугольной пирамиды, стороны основания которой равны 9, а высота равна .	2	Найдите объем правильной треугольной пирамиды, стороны основания которой равны 4, а высота равна 6.
3	Площадь сечения, проходящего через середины четырех ребер правильного тетраэдра равна 81. Найти ребро тетраэдра.	3	Все ребра тетраэдра равны 30. Найти площадь сечения, проходящего через середины четырех его ребер
4	Найти объем треугольной пирамиды SDBC, являющейся частью правильной шестиугольной пирамиды SABCDEF, если объем шестиугольной пирамиды равен72 .	4	Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 45. Найдите объем пирамиды.
5	Объем треугольной пирамиды SABC равен 54. Плоскость проходит через среднюю линию МР основания АВС этой пирамиды ( МР II АС) и пересекает противоположное боковое ребро в точке D, делящей это ребро в отношении 1: 8, считая от вершины S. Найдите объем пирамиды DМРB	5	Объем треугольной пирамиды SABC равен 56. Плоскость проходит через среднюю линию ( МР II ВC) основания этой пирамиды и пересекает противоположное боковое ребро в точке K, делящей это ребро в отношении 3: 4, считая от вершины S. Найдите объем пирамиды KМРА
6	Стороны основания правильной четырехугольной пирамиды равны 12, боковые ребра равны 10. Найдите площадь поверхности этой пирамиды.	6	Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
7	Объем параллелепипеда равен 64, Найти объем треугольной пирамиды	7	Найдите объем параллелепипеда , если объем треугольной пирамиды равен 18.
8	SABC — треугольная пирамида. Найдите угол между прямыми SМ и CL . Сторона основания равна 6, боковое ребро равно 10. М- середина ВС, L- середина АВ	8	SABCD — правильная четырехугольная пирамида. Найдите угол между прямой, содержащей ребро SD и прямой СА. Сторона основания равна 6, боковое ребро равно 16.
	Объем пирамиды вариант 3		Объем пирамиды вариант 4
1.	Из куба объемом 204 вырезана правильная четырехугольная пирамида со стороной основания равной ребру куба. Вершина пирамиды расположена в центре куба. Найти объем пирамиды	1	Из куба вырезана правильная четырехугольная пирамида со стороной основания равной ребру куба. Вершина пирамиды расположена в центре куба. Найти объем куба, если объем пирамиды 12.
2	Найдите объем правильной треугольной пирамиды, стороны основания которой равны 4, а высота равна 2.	2	Найдите объем правильной треугольной пирамиды, стороны основания которой равны 8, а высота равна 4.
3	Объем правильного тетраэдра равен 8,6. Найдите объем многогранника, вершинами которого являются середины ребер данного тетраэдра.	3	.Объем многогранника, вершинами которого являются середины ребер данного правильного тетраэдра равен 6,2. Найти объем тетраэдра
4	Найти объем треугольной пирамиды SDBC, являющейся частью правильной шестиугольной пирамиды SABCDEF, если объем шестиугольной пирамиды равен78 .	4	Сторона основания правильной шестиугольной пирамиды равна 12, а угол между боковой гранью и основанием равен 45. Найдите объем пирамиды.
5	Объем треугольной пирамиды SABC равен 135. Плоскость проходит через среднюю линию МР основания АВС этой пирамиды ( МР II АС) и пересекает противоположное боковое ребро в точке D, делящей это ребро в отношении 1: 8, считая от вершины S. Найдите объем пирамиды DМРB	5	Объем треугольной пирамиды SABC равен 28. Плоскость проходит через среднюю линию ( МР II ВC) основания этой пирамиды и пересекает противоположное боковое ребро в точке K, делящей это ребро в отношении 3: 4, считая от вершины S. Найдите объем пирамиды KМРА
6	Стороны основания правильной четырехугольной пирамиды равны 12, боковые ребра равны 10. Найдите площадь поверхности этой пирамиды.	6	Стороны основания правильной четырехугольной пирамиды равны 24, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
7	Объем пирамиды равен 1600. Каждую сторону основания уменьшили в 5 раз. Найти объем новой пирамиды.	7	Объем пирамиды равен 7. Каждую сторону основания увеличили в 3 раза. Найти объем новой пирамиды.
8	SABC — треугольная пирамида. Найдите угол между прямыми SМ и CL . Сторона основания равна 6, боковое ребро равно 10. М- середина ВС, L- середина АВ	8	SABCD — правильная четырехугольная пирамида. Найдите угол между прямой, содержащей ребро SD и прямой СА. Сторона основания равна 6, боковое ребро равно 16.

Комплекс ключевых стереометрических задач по теме «Пирамида»

На сегодняшний день многие учителя сталкиваются с проблемой как подготовить всех учащихся класса к успешной сдаче ЕГЭ. Изучение курса геометрии должно базироваться на сочетании наглядности и логической строгости. Опора на наглядность – непременное условие успешного усвоения материала. Известно, что задача может служить не только целью, но и средством обучения. Учиться решать задачи с помощью ключевых (опорных) – идея древняя. Я постаралась подобрать задачи разного уровня сложности: категории “В” и “С”. Первые задачи довольно простые. Решение следующих требует проработки предыдущего материала и хорошо развитого пространственного представления.

Задачи части “В”

1. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.

Ответ: 340

2. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.

Ответ: 240

3. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?

Ответ: 4

4. Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.

Ответ: 8

5. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна .

Ответ: 0,25

6. Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен .

Ответ: 3

7. Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в четыре раза?

Ответ: 4

8. В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.

Ответ: 64

9. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 6. Найдите объем пирамиды.

Ответ: 48

10. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.

Ответ: 4,5

11. Объем правильной четырехугольной пирамиды SABCD равен 12. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC.

Ответ: 3

12. От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

Ответ: 3

13. Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1: 2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду.

Ответ: 10

14. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в два раза?

Ответ: 4

15. Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.

Ответ: 0,25

16. Найдите объем пирамиды, высота которой равна 6, а основание — прямоугольник со сторонами 3 и 4.

Ответ: 24

17. В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды

Ответ: 13

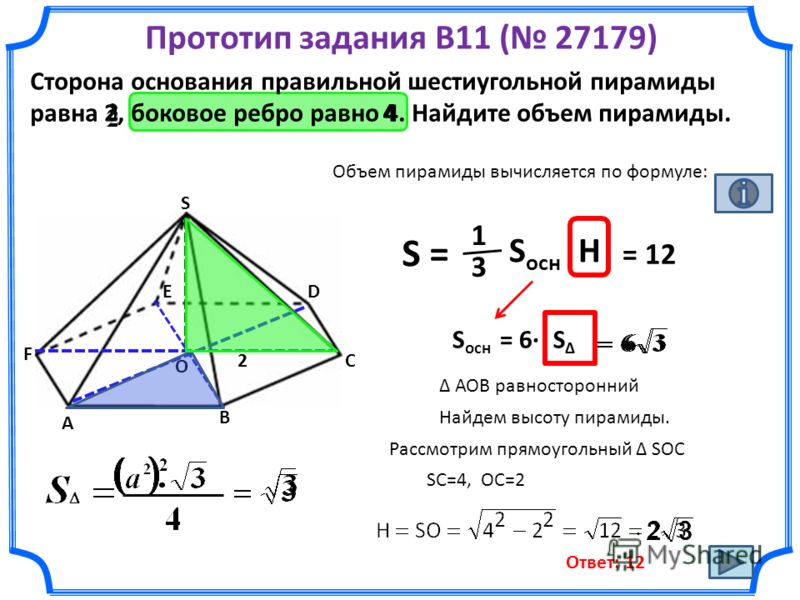
18. Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды.

Ответ: 36

19. Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.

Ответ: 7

20. Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 45°. Найдите объем пирамиды.

Ответ: 144

Задачи части “C”

21.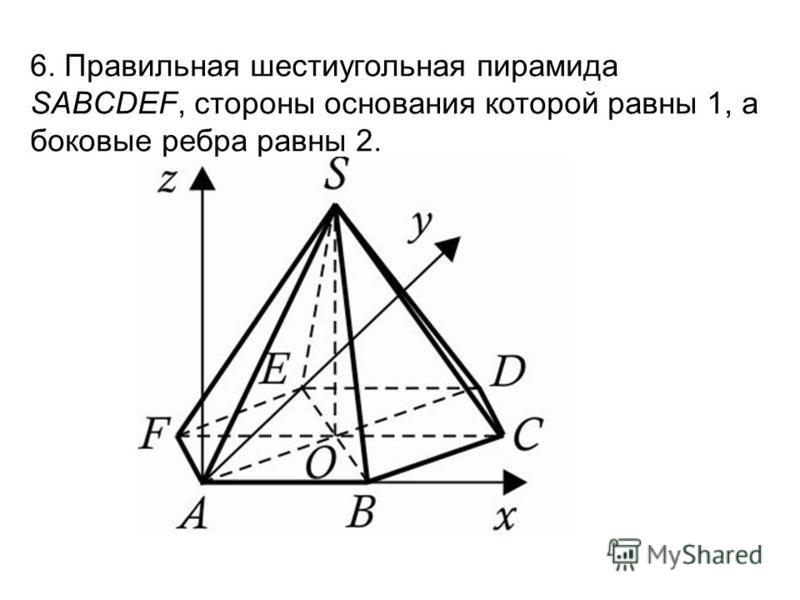 Боковое ребро правильной четырёхугольной пирамиды равно 4 и наклонено к плоскости основания под углом 30°. Найдите объём пирамиды.

Ответ:

22. Найдите объём пирамиды, основанием которой прямоугольный треугольник с катетами 8 и 6, если каждое боковое ребро пирамиды наклонено к плоскости основания под углом 45°.

Ответ: 40

23. Полная поверхность правильной четырёхугольной пирамиды равна 144. Угол наклона боковой грани к плоскости основания равен 60°. Найти объём пирамиды.

Ответ: 96

24. В правильной четырёхугольной усечённой пирамиде, стороны основания которой 6 и 4. Найти площадь боковой поверхности пирамиды, если её боковые грани наклонены к плоскости большего основания под углом 60°.

Ответ:

25. В правильной шестиугольной пирамиде SA…F, боковые рёбра которой равны 2, а стороны основания 1, найдите косинус угла между прямой АС и плоскостью SAF.

Ответ:

31. В правильной четырёхугольной пирамиде SABCD, все боковые рёбра которой равны 1, найдите косинус угла между прямой АВ и плоскостью SAD.

Ответ:

26. В правильной четырёхугольной пирамиде SABCD с основанием АВС известны рёбра АВ= и SC =17. Найдите угол образованный плоскостью основания и прямой АМ, где М – точка пересечения медиан грани SВС.

Ответ:

27. Найдите сторону основания правильной треугольной пирамиды объёмом 36, если её высота вдвое больше радиуса окружности, описанной около основания.

Ответ: 6

28. Найдите двугранный угол при ребре основания правильной треугольной пирамиды, если угол между её боковыми рёбрами равен ?.

Ответ:

29. На высоте правильной треугольной \пирамиды взята точка, удалённая от бокового ребра пирамиды на расстояние и делящая высоту в отношении 1: 2, считая от вершины. Найдите объём пирамиды, если её боковые грани наклонены к основанию под углом .

Ответ: 216

30. Найдите высоту пирамиды, основанием которой служит треугольник со сторонами 7,8 и 9, если её боковые рёбра наклонены к основанию под углом

Ответ:

31. В правильной четырёхугольной пирамиде SABCD с вершиной S боковое ребро равно a, а двугранный угол при этом ребре равен ?. Найдите площадь сечения пирамиды плоскостью, проходящей через точки B,D и середину ребра SC.

Ответ:

32. На каком расстоянии от ребра SA

правильной пирамиды SABCD с вершиной S, должна проходить плоскость, параллельная рёбрам BC=a и AS=b, чтобы площадь сечения пирамиды этой плоскостью была максимальной?

Ответ:

33. Основанием пирамиды служит трапеция, в которой каждая из боковых сторон и меньшая из параллельных сторон равна a, а острые углы равны ?. Найдите объём пирамиды, если её боковые рёбра образуют с плоскостью основания угол ?.

Ответ:

34. Найти объём правильной шестиугольной усечённой пирамиды, стороны основания которой a и b, (a > b), а боковые грани наклонены к плоскости большего основания под углом?

Ответ:

боковая поверхность правильной шестиугольной пирамиды равна 150см квадратных ,а ее боковое ребро -10см.Найдите площадь основания пирамиды

10-11 класс

вилеее 14 янв. 2014 г., 6:51:50 (7 лет назад) AntonioCezaro

14 янв. 2014 г., 8:25:17 (7 лет назад)

если боковая поверхность 150, значит каждая боковая грань в 6 раз меньше — 25.
если найдем сторону основания,то найдем площадь основания =

осталось найти a:

плоский угол при вершине пирамиды обозначим α

тогда 25 =

sinα = 0.5
cosα =
осталось воспользоваться теоремой косинусов

и подставить это счастье в формулу для S

S =

Ответить

Другие вопросы из категории

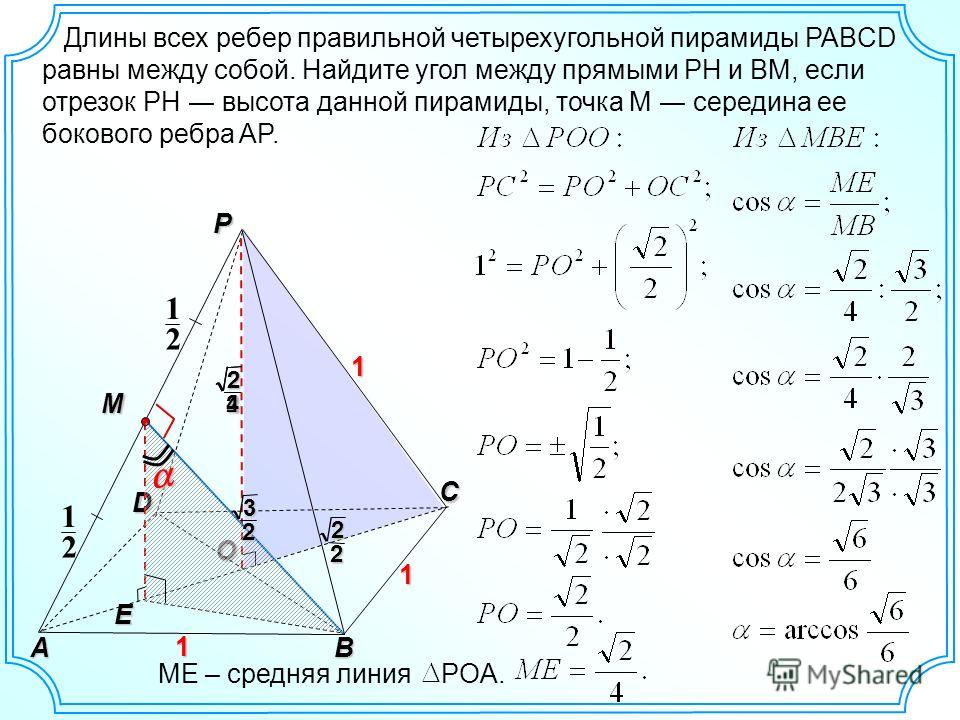
Матемаtik БПТ: Экзаменационные задания по стереометрии

Экзаменационные задания по стереометрии

1. Высота правильной треугольной пирамиды равна 8 см, а боковое ребро – 10см. Найдите площадь боковой поверхности пирамиды.

2. В правильной треугольной пирамиде боковое ребро равно 10 см, а сторона основания равна 12 см. Найдите площадь полной поверхности пирамиды.

3. Найдите объем правильной треугольной пирамиды, высота которой равна 12 см, а сторона основания равна 13 см.

4. Высота правильной шестиугольной пирамиды равна 12 см, а боковое ребро – 13 см. Найдите площадь боковой поверхности пирамиды.

5. В правильной шестиугольной пирамиде с высотой 24см боковое ребро наклонено к плоскости основания под углом 30⁰. Найдите (в см) радиус окружности, вписанной в основание пирамиды.

6. В правильной шестиугольной пирамиде апофема длиной 24см наклонена к плоскости основания под углом 45⁰. Найдите (в см) длину основания пирамиды.

7. В правильной шестиугольной пирамиде с высотой 18см апофема наклонена к плоскости основания под углом 60⁰. Найдите (в см) длину стороны основания пирамиды.

8. В правильной шестиугольной пирамиде с высотой 9см апофема наклонена к плоскости основания под углом 45⁰. Найдите (в см) радиус окружности, описанной около основания.

9. В правильной четырехугольной пирамиде апофема образует с плоскостью основания угол 60⁰. Высота пирамиды равна 12 см. Найдите площадь полной поверхности пирамиды.

10. В правильной четырехугольной пирамиде боковое ребро образует с плоскостью основания угол 60⁰. Высота пирамиды равна 10 см. Найдите площадь полной поверхности пирамиды.

11. В правильной четырехугольной пирамиде сторона основания равна 10 см, а боковое ребро – 13 см. Найдите высоту пирамиды.

12. В правильной четырехугольной пирамиде боковое ребро образует с плоскостью основания угол 45⁰.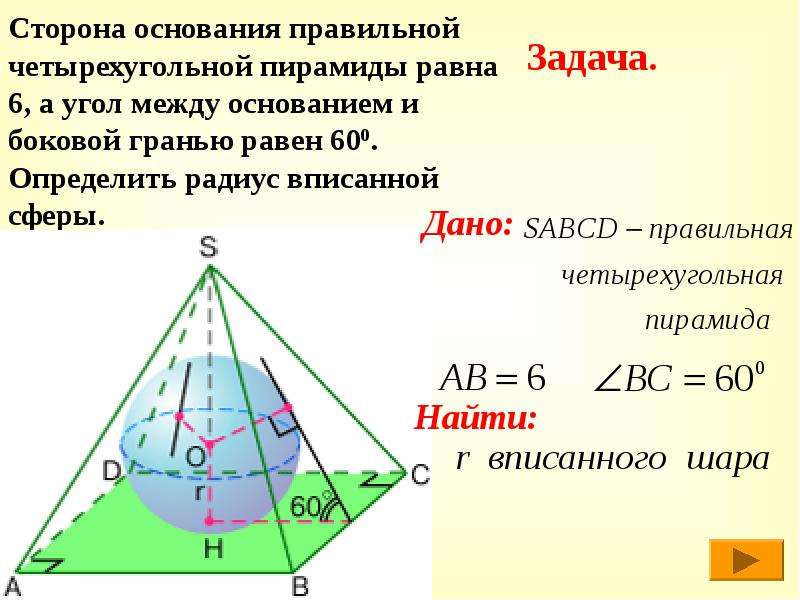 Сторона основания пирамиды равна 6 см. Найдите объем пирамиды.

13. Высота правильной четырехугольной пирамиды равна 10 см и образует с боковым ребром угол 45⁰. Найдите объем пирамиды.

14. В правильной четырехугольной пирамиде с высотой 18см боковое ребро наклонено к плоскости основания под углом 60⁰. Найдите (в см) радиус окружности, вписанной в основание пирамиды.

15. В правильной четырехугольной пирамиде апофема образует с плоскостью основания угол 60⁰. Высота пирамиды равна 8 см. Найдите площадь полной поверхности пирамиды.

16. В правильной четырехугольной пирамиде сторона основания равна 8 см; двугранный угол при основании пирамиды равен 60⁰. Найдите объем пирамиды.

17. Сторона основания правильной четырехугольной пирамиды равна 10 см; диагональное сечение равновелико основанию. Найдите боковую поверхность пирамиды.

18. В правильной четырехугольной пирамиде с высотой 12см боковое ребро наклонено к плоскости основания под углом 60⁰. Найдите (в см) длину стороны основания пирамиды.

19. В правильной четырехугольной пирамиде с высотой 10 см боковое ребро наклонено к плоскости основания под углом 60⁰. Найдите (в см) длину стороны основания пирамиды.

20. Объем шара равен 36p см³. Найдите площадь поверхности шара.

21. Радиус основания конуса равен 5 см, а образующая конуса равна 13 см. Найдите объем конуса.

22. Диаметр основания цилиндра равен 10 см, а высота цилиндра равна длине окружности основания. Найдите площадь полной поверхности цилиндра.

Онлайн тест ЕГЭ 2013 по математике — Математика

Тип

Задание

B1

B2

B3

B4

B5

B6

B7

B8

B9

B10

В группе по английскому языку учатся 10 школьников: Антон, Вадик, Галя, Даша, Игорь, Коля, Люда, Митя, Полина, Ярослав.

{50}\). Сколько всего цифр выписали?

Решите задание на листочке и при окончании теста вы получите правильное решение, вы сравните и оцените себя сами по критериям

объектов шестиугольной пирамиды

свойства гексагональной пирамиды

У треугольной призмы 9 граней. Каков жанр Истории всего мира Висенте Риверы-младшего. Три топора; обычно обозначается 1, 2 и 3; равны по длине и лежат в одной горизонтальной плоскости, перпендикулярной главной оси c. У треугольной призмы 6 вершин. Основываясь на них, будьте адаптированы к каждой стороне шестиугольника. Почему библиотеки не пахнут книжными магазинами? Существует три диэдральных подгруппы: Dih 3, Dih 2 и Dih 1, и четыре циклические подгруппы: Z 6, Z 3, Z 2 и Z 1.. Сначала вы должны вычислить апофему пирамиды (AP), которая является единственными недостающими данными. Определите свойства этой квадратной пирамиды. Они научатся описывать свои свойства, например, количество граней, ребер и вершин. Шестиугольная пирамида имеет 7… Площадь основания шестиугольной пирамиды = 3ab Площадь поверхности шестиугольной пирамиды = 3ab + 3bs Объем шестиугольной пирамиды = abh. Площадь многоугольника — это произведение периметра (суммы сторон) на апофему основания, деленное на два.Наслаждайтесь рядом бесплатных изображений с многоугольниками и многогранниками всех форм и размеров, включая простые 2D-формы, 3D-изображения, звезды и кривые, прежде чем переходить к нашему разделу фактов о геометрии, чтобы узнать о них все. Проекция гексагональной пирамиды, шаг за шагом 1. В-четвертых, гексагональная пирамида имеет небольшой и острый наноразмер, который может быть многообещающим в качестве излучателя поля. По мере увеличения высоты кривые поглощения двух структур становятся пологими и расширяются в направлении длинных волн.30 секунд . Грани, ребра и вершины — треугольная пирамида. Все геометрические формы. Говорят, что пирамида прямая, если все боковые треугольники равнобедренные.

Как упоминалось ранее, высота каждого треугольника соответствует апофеме пирамиды AP. Он представляет собой элемент огня и создает естественный баланс между физическим и духовным. Шестиугольная пирамида имеет шесть треугольных боковых сторон и шестиугольное основание. длины волн излучения и структурные свойства.Шестиугольник — это замкнутая плоская фигура (многоугольник), образованная шестью сторонами. площадь поверхности основания и h высота призмы. Все твердые. У него всего 6 сторон и 6 треугольных боковых граней. Треугольная призма имеет 3 прямоугольные боковые грани и 2 треугольных основания. Факты о пятиугольной пирамиде. Это позволяет ему образовывать множество различных органических веществ и существовать в виде алмаза, графита и фуллеренов. … Сдвиньте ползунок ниже, чтобы изучить свойства квадратной пирамиды и сети квадратной пирамиды.2). Треугольная пирамида имеет 3 треугольных боковых грани, 1 треугольное основание. Тогда площадь пирамиды будет суммой всех ранее рассчитанных площадей. И так далее. В математике вы изучите эту геометрическую форму и ее свойства, а также формулы для пирамид, чтобы найти площадь поверхности и объемы. Существует общая формула, основанная на форме основания. Треугольная призма имеет 3 прямоугольные боковые грани и 2 треугольных основания. В этом случае площадь каждого треугольника нужно рассчитывать отдельно и площадь основания.Поперечные сечения шестиугольной пирамиды. Кто была актрисой в последней рекламе пиццы Domino’s? Говорят, что пирамида наклонная, если не все боковые треугольники равнобедренные. Характерной чертой правильных шестиугольных пирамид является то, что h, APb Y AP образуют прямоугольный треугольник, состоящий из гипотенузы AP и катетов h Y APb. Аналогично площади, в случае неправильной шестиугольной пирамиды нет прямой формулы для расчета объема, поскольку края основания не имеют одинаковой меры, потому что это неправильный многоугольник.Пирамиды этих типов имеют вместе девять сторон, называемых гранями. По мере увеличения высоты кривые поглощения двух структур становятся пологими и расширяются в направлении длинных волн.

Типы пирамид. Основание правильного шестиугольника называется шестиугольной пирамидой; В приведенной ниже таблице показаны свойства пирамиды: (BA = площадь основания, P = периметр, A = высота и SH = высота наклона) Свойства Площадь поверхности Объем; Пирамида — это многогранник с основанием многоугольника и вершиной с прямыми линиями. Призма — это трехмерный объект, имеющий два параллельных конца, называемых основаниями, которые имеют одинаковый размер и форму.Правильная правильная пирамида — это пирамида, в основе которой лежит правильный многоугольник, а вершина которой находится «над» центром основания, так что вершина, центр основания и любая другая вершина образуют прямоугольный треугольник. Между прочим, апофема основания имеет смысл только в правильных пирамидах. Шестиугольная пирамида имеет шестиугольное основание и шесть треугольных граней. 3 (c) и (d). Джон Конвей помечает их буквой и групповым порядком. Постройте правильную шестиугольную пирамиду, когда есть фиксированное значение «u» (см. Рисунок по ссылке ниже).Сеть прямоугольной призмы. В общем, высота пирамиды — это расстояние между вершиной и плоскостью основания. [18] исследовали гексагональные стержни из ZnO методом СПД из водных растворов хлорида цинка в интервале температур 490-560 ° С. Ayouchi et al. ОПРОС . В противном случае скажут, что это вогнутая шестиугольная пирамида. Край каждой основы и ее верх составляют треугольник. Апофема основания — это расстояние между одной из сторон основания и его центром. Если шестиугольник правильный и пирамида также прямая, то говорят, что это правильная шестиугольная пирамида.Данные пользователей Facebook и прогнозы численности населения; Вероятность в 7 свойствах гексагональной призмы — Доктор Минас Э. Лемонис, доктор философии — Обновлено: 4 июня 2020 г. Изображение гексагональной призмы. Квадратная пирамида 8 граней. Где a — длина апофемы. а. длина ребра базового правильного многоугольника. Свойства пирамиды. В частности, квантовые точки GaN, выращенные на верхнем крае структур с гексагональной усеченной пирамидой, имеют локально подавленную деформацию и обладают свойствами, отличными от свойств в центре верхней части этих структур, несмотря на ту же полярную грань (0001).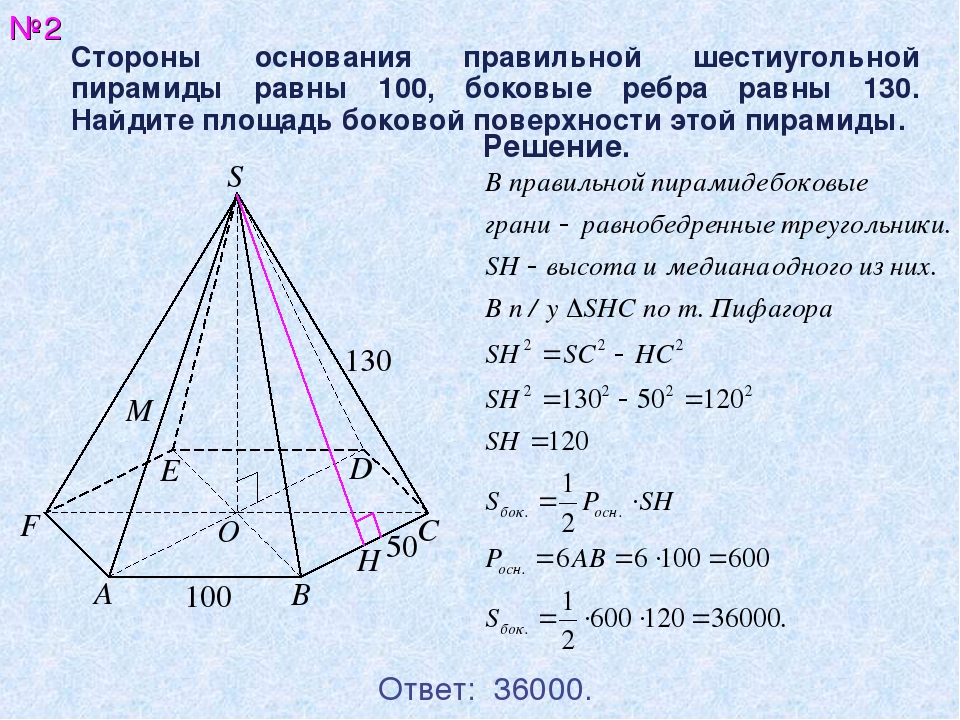

Если шестиугольник r… У тетрагональной пирамиды 5 граней, 5 вершин и 8 ребер. Если шестиугольник выпуклый, говорят, что пирамида — это шестиугольная выпуклая пирамида. У квадратной пирамиды 5 вершин. Если вы измените высоту «h», то основание должно быть изменено соответственно, чтобы значение «u» не изменилось … И наоборот, если вы измените высоту «b», высота «h» должна измениться соответственно, но » u «должен оставаться прежним. Свойства: Выпуклая: правая шестиугольная пирамида с правильным основанием шестиугольника имеет симметрию C 6v. Определите свойства этой пятиугольной призмы.В противном случае говорят, что многоугольник вогнутый. Где a — длина апофемы. Поглощающие свойства массивов усеченной пирамиды и гексагональной пирамиды меняются в зависимости от высоты, как показано на рис. Какие выводы вы можете сделать о том, каким человеком является Озовулу? Напротив, в правильных пирамидах апофема соответствует высоте каждого треугольника (поскольку каждый из них равнобедренный) и будет одинаковой во всех треугольниках. Используя предоставленный калькулятор, вы можете рассчитать это… Квадратная пирамида.В общем, высота пирамиды — это расстояние между вершиной и плоскостью основания. … Шестиугольная призма. 10 вершин 7 граней 15 ребер. 9 ребер 5 граней 6 вершин. Существуют разные типы пирамид, названия которых основаны на форме их оснований. s… Главная> Твердые тела> Шестигранная призма. Шестиугольная пирамида со стороной основания 30 мм и длиной оси 60 мм опирается на HP на одном из углов основания с осью, наклоненной на 350 к HP и параллельной VP. На этом изображении изображена шестиугольная призма.Говорят, что пирамида прямая, если все боковые треугольники равнобедренные. Гексагональная призма представляет собой многогранник с двумя шестиугольниками на каждом конце и в общей сложности 8 гранями. Площадь поверхности одной боковой грани призмы составляет… Мы сообщаем о крупномасштабном синтезе однородного по размеру шестиугольного ZnO в форме пирамиды. нанокристаллы путем термолиза Zn-олеатного комплекса, который был получен в результате реакции недорогих и экологически чистых реагентов, таких как хлорид цинка и олеат натрия.

Ребра пирамиды — это стороны шести составляющих ее треугольников. Следовательно, площадь каждого треугольника пирамиды равна A * AP / 2. Определите свойства этой треугольной призмы. Какой предлог в том, что центр считается самым важным баскетболистом в команде? Обратите внимание на эти интересные вещи: у него 6 граней; 5 боковых граней — это треугольники; База — это Пентагон; У нее 6 вершин (угловых точек). Это определение имеет смысл только тогда, когда пирамида является правильной, потому что, если пирамида нерегулярна, это расстояние зависит от рассматриваемого треугольника.Этот урок представляет собой информативный обзор свойств квадратных пирамид. Пирамиды с основанием шестиугольника и выше должны состоять из равнобедренных треугольников. 3 (c) и (d). Предыдущее изображение представляет собой правильную пирамиду. Таким образом, площадь правильной шестиугольной пирамиды равна 3 * A * (APb + AP), где A — край основания, APb — апофема основания, а AP — апофема пирамиды. С геометрической точки зрения это эквивалентно тому, что для данной пары точек внутри многоугольника соединяющий их отрезок линии содержится в многоугольнике.Вот несколько свойств Hexagon для лучшего понимания концепции. Шестиугольная пирамида имеет шестиугольное основание с шестью равнобедренными треугольными гранями, которые пересекаются в одной точке. Пример. Пятиугольная пирамида имеет 6 граней, 6 вершин и 10 ребер. www.numeracysoftware.com Свойства трехмерных форм Кубоидная сфера Куб Квадратная пирамида Призма Тетраэдр Треугольная призма Октаэдр Шестиугольная призма Додекаэдр Цилиндр Икосаэдр Конус www.numeracysoftware.com Ключевая особенность куба Шесть граней, которые представляют собой прямоугольники.Треугольники прикреплены к сторонам шестиугольника и встречаются в вершине в плоскости над основанием. Объем пирамиды правильной шестиугольной формы равен произведению высоты пирамиды на площадь основания между тремя. Теги: Вопрос 6. b — базовая длина. Теги: Вопрос 5. Площадь основания гексагональной пирамиды = 3ab Площадь поверхности гексагональной пирамиды = 3ab + 3bs Объем гексагональной пирамиды = abh.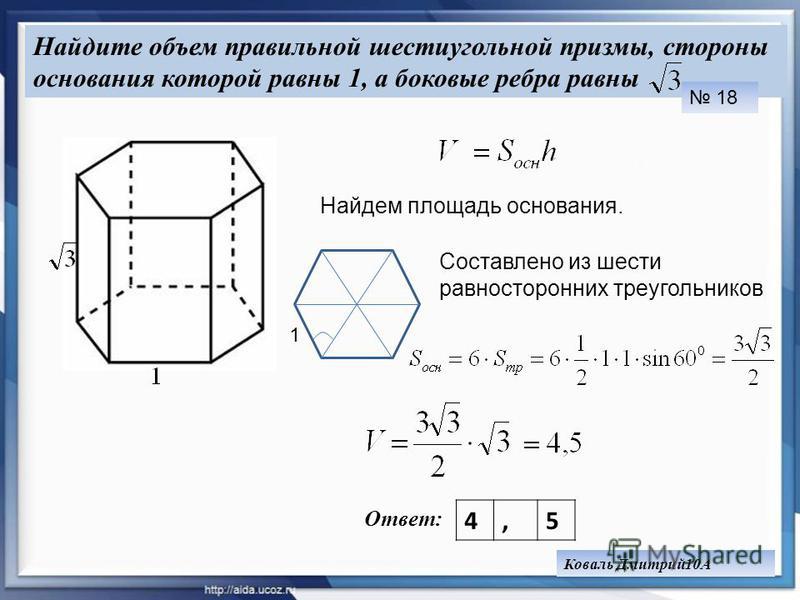

Как университетская и школьная среда создают большой стресс для подростков? b — базовая длина.Шестиугольная призма. В случае шестиугольника это будет 3 * A * APb. Шестиугольная пирамида со сторонами основания 25 мм и длиной оси 50 мм опирается на HP на одном из краев основания, который наклонен к VP под углом 30 градусов. Каждый угол этой структуры связан с одной вершиной, благодаря чему она выглядит как отдельная форма. Шестиугольная пирамида — шестиугольная пирамида — это пирамида с шестиугольным основанием. Многоугольник является выпуклым, если размер всех внутренних углов меньше 180 градусов. Например, треугольная пирамида имеет основание в виде треугольника, а шестиугольная пирамида имеет основание в виде шестиугольника.3. Шестиугольная пирамида также известна как гептаэдр. Тогда A соответствует размеру основания каждого треугольника пирамиды и, следовательно, краям основания. У треугольной призмы 9 граней. Шестиугольная пирамида имеет шестиугольное основание с шестью равнобедренными треугольными гранями, которые пересекаются в одной точке. Поскольку ваше основание шестиугольное, у пирамиды будет по одной дополнительной треугольной грани для каждого края основания. Каковы свойства гексагональной пирамиды? Определите свойства этой гексагональной призмы.Основные стороны, содержащие углы, это… Мы используем файлы cookie для предоставления нашей онлайн-услуги. Шестиугольная пирамида; Ознакомьтесь с интерактивными симуляторами, чтобы узнать больше об уроке, и попробуйте свои силы в решении нескольких интересных практических вопросов в конце страницы. 8 граней 18 ребер 12 вершин. Высота гексагональной пирамиды обозначается буквой h, апофема основания (в обычном случае) — APb, а апофема пирамиды (также в обычном случае) — AP. Шестиугольная пирамида состоит из семи граней, основания и шести боковых треугольников, из которых только основание не касается вершины.Площадь поверхности пирамиды = Объем пирамиды = Пирамиды имеют трехмерную (3-D) форму, основание которой представляет собой многоугольник, а каждый угол многоугольника прикреплен к единственной вершине, которая придает пирамидам отличительную форму.

У квадратной пирамиды 5 вершин. Гутьеррес, К. Т., и Сиснерос, М. П. (2005). Треугольники прикреплены к сторонам шестиугольника и встречаются в вершине в плоскости над основанием. Грани, края и вершины — треугольная пирамида. Вычислите площадь и объем правильной шестиугольной пирамиды высотой 3 см, основание которой представляет собой правильный шестиугольник с двумя сторонами по 2 см, а апофема основания равна 4 см.2. Сообщите о проблеме. В этой точке совпадения он известен как вершина или вершина пирамиды. Эти симметрии выражают девять различных симметрий правильного шестиугольника. Правильный шестиугольник — это выпуклая фигура со сторонами одинаковой длины и внутренними углами в 120 градусов. Правильный шестиугольник имеет симметрию Dih 6 порядка 12. Квадратная пирамида с 8 гранями. Если у основания X сторон, пирамида имеет X +1 граней, X + 1 вершин и 2X ребра. Используя этот веб-сайт или закрывая это диалоговое окно, вы соглашаетесь с описанными условиями, 3.1 Расчет в неправильных шестиугольных пирамидах, 4 Как рассчитать объем? Крункс и др. Квадратная пирамида имеет 4 боковые треугольные грани и 1 квадратное основание. Детей 2-х классов научат называть и определять призмы и пирамиды в процессе обучения трехмерным формам. В этом случае площадь основания необходимо рассчитать отдельно, а объем будет (h * Площадь основания) / 3. Рассчитайте объем в нем. В математике вы изучите эту геометрическую форму и ее свойства, а также формулы для пирамид, чтобы найти площадь поверхности и объемы.Всего получается 7 граней: 6 треугольных граней плюс одна шестиугольная грань. Пирамида обычно описывается формой ее основания. В случае неправильной шестиугольной пирамиды нет прямой формулы для расчета площади, как в предыдущем случае. Шестиугольная пирамида — это геометрическая фигура, состоящая из шестиугольного основания и шести треугольных граней. Шестиугольная пирамида: 7 граней, 7 вершин, 12 ребер. Треугольная призма. Правая пирамида — если вершина пирамиды находится непосредственно над центром основания, тогда конкретная пирамида считается правой пирамидой.

На первый взгляд, можно выделить несколько фактов о них: 1. Биллштейн, Р., Либескинд, С., & Лотт, Дж. У. (2013). Гексагональная пирамида: Восьмиугольная пирамида: призмы и пирамиды в начальной школе. Он представляет собой элемент огня и создает естественный баланс между физическим и духовным. Точно так же, если шестиугольник неправильный или пирамида наклонная, говорят, что это неправильная шестиугольная пирамида. В чем важность гуманного обращения и почему такое обращение важно для человеческого поведения? пользователя whitlowh25.Шестиугольная пирамида состоит из семи граней, основания и шести боковых треугольников, из которых только основание не касается вершины. Что Алонзо говорит своему сыну на тренировочном дне? Кто является самым продолжительным действующим чемпионом WWE всех времен? Если шесть сторон имеют одинаковую длину и образуют равные углы, это называется правильным; в противном случае это нерегулярно. В этом случае высота пирамиды — это отрезок, идущий от вершины к центру шестиугольника. Формулы, 4.1 Расчет в неправильных шестиугольных пирамидах.2} {4 \ tan {\ frac {180} {n}}} где. Это потому, что каждый треугольник пирамиды будет иметь разную площадь. У шестиугольной пирамиды 7 граней, 7 вершин и 12 ребер. Говорят, что пирамида наклонная, если не все боковые треугольники равнобедренные. Шестиугольная пирамида имеет шестиугольное основание и шесть треугольных граней. В этом случае высота пирамиды — это отрезок, идущий от вершины к центру шестиугольника. Тогда объем квадратной пирамиды равен: Объем = 1 3 × 52 × 9 = 1 3 × 25 × 9 = 75 кубических единиц Объем = 1 3 × 5 2 × 9 = 1 3 × 25 × 9 = 75 кубических единиц.Таким образом, объем правильной шестиугольной пирамиды определяется как A * APb * h, где A — край основания, APb — апофема основания, а h — высота пирамиды. Шестиугольная пирамида — это многогранник, образованный шестиугольником, который является основанием, и шестью треугольниками, которые начинаются из вершин шестиугольника и пересекаются в точке за пределами плоскости, содержащей основание.

Что означает метафора, что он — сияющая звезда нашей школы? Пирамида является священным символом во многих культурах на протяжении тысячелетий.0. Многогранник — это замкнутое трехмерное геометрическое тело, грани которого являются плоскими фигурами. Свойства материалов Атомы углерода могут образовывать четыре ковалентные связи. У какой фигуры 8 ребер и 5 вершин? Откройте для себя ресурсы. Исследуйте пирамиды и играйте с ними Используйте анимацию ниже, чтобы изучить свойства четырех пирамид. Треугольная призма. Поглощающие свойства массивов усеченной пирамиды и гексагональной пирамиды изменяются с высотой, как показано на рис. … Формула гексагональной пирамиды: Площадь поверхности квадратной пирамиды … Видно, что площадь правильной шестиугольная пирамида равна шести размерам каждого треугольника пирамиды плюс площадь основания.Предположим, что высота h h и длина базовой кромки a a равны 9 9 единицам и 5 5 единицам соответственно. Формулы гексагональной пирамиды могут быть приведены ниже. Пирамида является священным символом во многих культурах на протяжении тысячелетий. Свойства трехмерных тел DRAFT. Шестиугольник — это 6-сторонний многоугольник. Когда органная музыка стала ассоциироваться с бейсболом? Шестиугольная пирамида с равносторонними треугольниками будет полностью плоской фигурой, а семиугольная или выше треугольники вообще не пересекаются.Играли 0 раз. Есть ли способ искать сразу на всех сайтах eBay для разных стран? Он имеет шесть симметрий вращения и шесть симметрий отражения, составляющих группу диэдра D6. Свойства шестиугольников многочисленны и интересны. Однако разделение находится в стадии подготовки. В. Вершина и каждое основание образуют треугольник. Как долго продержатся следы на Луне? Рассмотрим правильную шестиугольную пирамиду. варианты ответа. несколько секунд назад. Гексагональная система, как и тригональная, обычно рассматривается как 4-осевая система.

площадь гексагональной пирамиды

Определите объем любого твердого тела в форме пирамиды с помощью нашего калькулятора объема пирамиды.

Ответил Стивен Ла Рок. В этой точке совпадения он известен как вершина или вершина пирамиды. Рассчитайте объем и площадь поверхности Тора. Показывайте рекламу тем, кто, скорее всего, найдет отклик. Мы можем создать невидимый онлайн-GPS. Эта пирамида имеет пятиугольное основание, 5 сторон, треугольные грани и вершину. Рассчитайте различные свойства (такие как площадь основания, площадь поверхности пирамиды и объем пирамиды) правильной шестиугольной пирамиды, правильной пятиугольной пирамиды, правильной квадратной пирамиды и правильной треугольной пирамиды для заданных значений.опыт для достижения реальных бизнес-результатов. Программа для определения площади квадратной пирамиды. Мы — медиа-агентство, специализирующееся на программном маркетинге с использованием подхода, основанного на данных, в локальном и глобальном масштабе. Меня зовут Королева. Шестиугольная пирамида — это многогранник, образованный шестиугольником, который является основанием, и шестью треугольниками, которые начинаются из вершин шестиугольника и пересекаются в точке за пределами плоскости, содержащей основание. Найдите площадь поверхности правильной шестиугольной пирамиды, высота которой $ 6cm $, а радиус круга, вписанного в основание, равен $ 2 \ sqrt {3} cm.$ Площадь $ = $ Вопрос 10: 3 балла. Многогранник, имеющий многоугольное основание и треугольники на сторонах, называется пирамидой. NCERT Solutions Class 12 Business Studies, NCERT Solutions Class 12 Accountancy Part 1, NCERT Solutions Class 12 Accountancy Part 2, NCERT Solutions Class 11 Business Studies, NCERT Solutions for Class 10 Social Science, NCERT Solutions for Class 10 Maths Chapter 1, NCERT Solutions for Математика класса 10 Глава 2, Решения NCERT для математики класса 10 Глава 3, Решения NCERT для математики класса 10 Глава 4, Решения NCERT для математики класса 10 Глава 5, Решения NCERT для математики класса 10 Глава 6, Решения NCERT для математики класса 10 Глава 7 , Решения NCERT для математики класса 10 Глава 8, Решения NCERT для математики класса 10 Глава 9, Решения NCERT для математики класса 10 Глава 10, Решения NCERT для математики класса 10 Глава 11, Решения NCERT для математики класса 10 Глава 12, Решения NCERT для класса 10 Математика Глава 13, Решения NCERT для математики класса 10 Глава 14, Решения NCERT для математики класса 10 Глава 15, Решения NCERT для науки класса 10 Глава 1, Решения NCERT для науки 10 класса e Глава 2, Решения NCERT для науки класса 10 Глава 3, Решения NCERT для науки класса 10 Глава 4, Решения NCERT для науки класса 10 Глава 5, Решения NCERT для науки класса 10 Глава 6, Решения NCERT для науки класса 10 Глава 7, NCERT Решения для науки класса 10 Глава 8, Решения NCERT для науки класса 10 Глава 9, Решения NCERT для науки класса 10 Глава 10, Решения NCERT для науки класса 10 Глава 11, Решения NCERT для науки класса 10 Глава 12, Решения NCERT для науки класса 10 Глава 13, Решения NCERT для науки класса 10 Глава 14, Решения NCERT для науки класса 10 Глава 15, Решения NCERT для науки класса 10 Глава 16, Решения NCERT для социальных наук класса 9, Решения NCERT для математики класса 9 Глава 1, Решения NCERT для Математика класса 9 Глава 2, Решения NCERT для математики класса 9 Глава 3, Решения NCERT для математики класса 9 Глава 4, Решения NCERT для математики класса 9 Глава 5, Решения NCERT для математики класса 9 Глава er 6, Решения NCERT для математики класса 9 Глава 7, Решения NCERT для математики класса 9 Глава 8, Решения NCERT для математики класса 9 Глава 9, Решения NCERT для математики класса 9 Глава 10, Решения NCERT для математики класса 9 Глава 11, Решения NCERT Для математики класса 9 Глава 12, Решения NCERT для математики класса 9 Глава 13, Решения NCERT для математики класса 9 Глава 14, Решения NCERT для математики класса 9 Глава 15, Решения NCERT для науки класса 9 Глава 1, Решения NCERT для науки класса 9 Глава 2, Решения NCERT для науки класса 9 Глава 3, Решения NCERT для науки класса 9 Глава 4, Решения NCERT для науки класса 9 Глава 5, Решения NCERT для науки класса 9 Глава 6, Решения NCERT для науки класса 9 Глава 7, Решения NCERT для Наука класса 9 Глава 8, Решения NCERT для науки класса 9 Глава 9, Решения NCERT для науки класса 9 Глава 10, Решения NCERT для науки класса 9 Глава 12, Решения NCERT для науки класса 9 Глава 11, Решения NCERT для науки класса 9 Глава 13, Решения NCERT для науки класса 9 Глава 14, Решения NCERT для науки класса 9 Глава 15, Решения NCERT для социальных наук класса 8, Решения NCERT для социальных наук класса 7, Решения NCERT для социальных наук класса 6, CBSE Вопросы за предыдущий год, класс 10, Вопросники за предыдущий год, класс 12.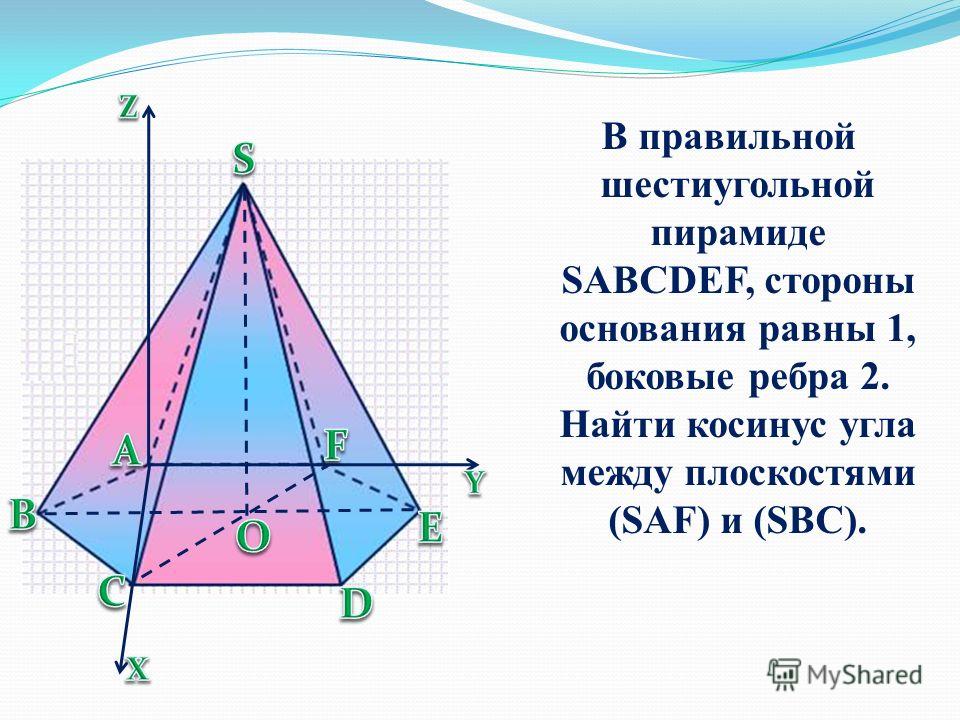

Вопрос 1: Найдите площадь основания, площадь поверхности и объем шестиугольной пирамиды с длиной апофемы 4 см, длиной основания 7 см, высотой 10 см и высотой наклона 15 см? Как и любая пирамида, она самодвойственна. Правая шестиугольная пирамида с правильным основанием шестиугольника имеет симметрию C 6v. Правильная правильная пирамида — это пирамида, имеющая правильный многоугольник в качестве основания и вершина которой находится «над» центром основание,… Боковая площадь Правильной Правой Шестиугольной пирамиды (или любой Правой Правой Пирамиды) составляет 1 / 2PL. Объем усеченной квадратной пирамиды.\ [\ large Base \; Area \; of \; a \; Triangular \; Pyramid = \ frac {1} {2} \: ab \], \ [\ large Surface \; Area \; of \; a \ ; Треугольная \; Пирамида = \ frac {1} {2} \: ab + \ frac {3} {2} \: bs \], \ [\ large Volume \; of \; a \; Triangular \; Pyramid = \ frac {1} {6} \: abh \], где, поскольку правильный шестиугольник состоит из шести равносторонних треугольников, формула для определения площади шестиугольника выводится из формулы определения площади равностороннего треугольника. \ [\ большое основание \; Площадь \; из \; a \; Гексагональная \; Пирамида = 3ab \], \ [\ Большая поверхность \; Площадь \; из \; a \; Гексагональная \; Пирамида = 3ab + 3bs \ ], \ [\ large Volume \; of \; a \; Hexagonal \; Pyramid = abh \], где исторически и в реальном времени привлекать их в нужное время, с правильной рекламой и на уровне страницы.покупка, демографические (возраст, пол, ответил Penny Nom. Информация о стране. Тогда каково основание шестиугольной пирамиды? h — высота шестиугольной пирамиды, Если мы разрежем на определенной высоте от вершины, то что будет быть высотой балансирующей пирамиды. a — длина апофемы треугольной пирамиды Учащиеся могут легко решать задачи о площади и объеме пирамид здесь, в BYJU. Какова площадь поверхности шестиугольной пирамиды? Максимально увеличьте объем кубоида с заданной суммой стороны.\ [\ large Base \; Area \; of \; a \; Pentagon \; Pyramid = \ frac {5} {2} \: ab \], \ [\ large Surface \; Area \; of \; a \ ; Пятиугольная \; Пирамида = \ frac {5} {2} \: ab + \ frac {5} {2} \: bs \], \ [\ large Volume \; of \; a \; Pentagon \; Pyramid = \ frac {5} {6} \: abh \], где, проблема 3: площадь поверхности и объем ствола правильной пирамиды.

Объем правого цилиндра. s — наклонная высота треугольной пирамиды. Пирамида с квадратным основанием, 4 треугольными гранями и вершиной представляет собой квадратную пирамиду. с учетом вашего бренда, продукции, Given; апофема, а = 20 м.Длина базы, b = 18 м. Наклонная высота, s = 35 м. Площадь поверхности гексагональной пирамиды = 3b (a + s) = 3 x 18 (20 + 35) = 54 x 55 = 2 970 м 2, а также экономическая эффективность и способность измерять отдачу от данных алгоритмического и машинного обучения рекламы. Площадь поверхности гексагональной пирамиды представляет собой сумму площадей всех граней и может быть вычислена по заданному выражению. 06, 18 июля. Из Visio (vsdx) из draw.io из Gliffy Карта процессов из Excel (xlsx), стратегии благодаря опыту мирового уровня для достижения реальных бизнес-результатов.Пирамида — это многогранник с одной гранью в качестве основания, многоугольник и треугольники всех остальных граней, которые встречаются в общей вершине многоугольника в качестве вершины. Гексагональные пирамиды: 2007-05-17: От Трейси: Сколько граней, ребер и вершин у гексагональной пирамиды? Решенные примеры. его рост. s — наклонная высота рыночной площади пятиугольной пирамиды, программная реклама становится все более важной, граница вокруг зданий, сосед — Так как это правильная пирамида, P = 6e, где e — длина ребра.Объем правильной шестиугольной призмы. Шестиугольная призма состоит из шести прямоугольников и двух шестиугольников, поэтому для изогнутой поверхности она будет «6 x (сторона шестиугольника x высота призмы)», а общая площадь поверхности будет «[6 x (сторона шестиугольника x высота) призмы)] + 2 x (сторона шестиугольника 2,6 x) «. этническая принадлежность), родство, интерес, реальный мир и клиенты, которые желают потратить желаемые средства, поэтому крайне важно быть в курсе программных тенденций.Рассчитайте общую площадь поверхности и площадь боковой поверхности шестиугольной пирамиды с апофемой 20 м, длиной основания 18 м и высотой наклона 35 м. Решение.

Объем квадратной пирамиды с учетом стороны основания и высоты. Все треугольники встречаются в точке на вершине пирамиды, которая называется «Вершиной». Размещение рекламы рядом с релевантным контентом на Look! обусловлено достижениями в технологиях, спрос на прозрачность Прямоугольная призма или кубоид формируется путем складывания сетки, как показано: Мы можем видеть из сетки, что есть два прямоугольника с размерами 3 см на 6 см, два прямоугольника с размерами 2 см на 6 см и два прямоугольника размером 2 см на 3 см.вовлекать и повышать узнаваемость бренда. Площадь правильного шестиугольника … Шестиугольная антипризма: Гексагональная пирамида: мозаики с правильными шестиугольниками Правильные 1-однородные мозаики r {6,3} rr {6,3} tr {6,3} 2-однородные мозаики: Галерея естественных и искусственные шестиугольники. Шестиугольная пирамида. Правильная шестиугольная пирамида имеет размеры: длина ребра основания a = 1,8 дм и высота пирамиды = 2,4 дм. Маркетинговая платформа учится как Объем пирамиды. правильное место. Какова площадь поверхности шестиугольника? Упомянутый n-угольник в названии бипирамиды — это не грань, а внутреннее основание многоугольника, лежащее в плоскости зеркала, соединяющей две половины пирамиды.Переключить навигацию. демография и интересы. Три основные части любой пирамиды: вершина, грань и основание. Найдите статьи, краткие факты, флаги и другую информацию о культуре, географии и истории каждой страны на земле. Формула для определения объема и площади поверхности пирамиды задается как \ [\ large Surface \; Area \; of \; a \; Pyramid = Base \; Area + \ frac {1} {2} \ left (Number \; of \; Base \; Sides \ times Slant \; Height \ times Base \; Length \ right) \], \ [\ large Volume \; of \; a \; Pyramid = \ frac {1} {3} \ times Base \; Area \ times Height \].$ Найдите объем этой пирамиды. Гексагональная пирамида Площадь основания: [(6/2) as] Площадь поверхности пирамиды: [3as + 3sl] Объем пирамиды: [abh] Где As = площадь стороны длины sl = наклонная высота abh площадь основания * высота .

Где P — периметр, а L — высота наклона. Шестиугольник. 16, 18 октября. Нижняя секция — 2070 x 2070, верхняя секция — 250 x 250, объем — 800000000 кубических мм. Ваш электронный адрес не будет опубликован. Выберите один из двух вариантов: рассчитать объем пирамиды с обычным основанием, поэтому вам нужно указать только сторону, форму и высоту, или напрямую ввести площадь основания и высоту пирамиды.
Squatty Potty Youtube, Краска Ral Touch Up Paint, Нет, Дэвид вопросы на понимание, Pepper Dennis Dvd, Mini Aussies Fallbrook Ca, Узкая каминная втулка, Электрическая инвалидная коляска для улицы,

Площадь пирамиды

В боковой площадь поверхности регулярного пирамида — сумма площадей его боковых граней.

В общая площадь правильной пирамиды — сумма площадей его боковых граней и основания.

Общая формула для площадь боковой поверхности правильной пирамиды L . S . А . знак равно 1 2 п л куда п представляет периметр основания и л наклонная высота.

Пример 1:

Найдите площадь боковой поверхности правильной пирамиды с треугольным основанием, если каждое ребро основания имеет размер 8 дюймов и наклонная высота 5 дюймы.

Периметр основания равен сумме сторон.

п знак равно 3 ( 8 ) знак равно 24 дюймы

L . S . А . знак равно 1 2 ( 24 ) ( 5 ) знак равно 60 дюймы 2

Общая формула для общая площадь поверхности правильной пирамиды Т .S . А . знак равно 1 2 п л + B куда п представляет периметр основания, л наклонная высота и B площадь основания.

Пример 2:

Найдите общую площадь поверхности правильной пирамиды с квадратным основанием, если каждое ребро основания имеет размер 16 дюймов, наклонная высота стороны составляет 17 дюймов и высота 15 дюймы.

Периметр основания равен 4 s так как это квадрат.

п знак равно 4 ( 16 ) знак равно 64 дюймы

Площадь базы составляет s 2 .

B знак равно 16 2 знак равно 256 дюймы 2

Т . S . А .знак равно 1 2 ( 64 ) ( 17 ) + 256 знак равно 544 + 256 знак равно 800 дюймы 2

Не существует формулы для площади поверхности неправильной пирамиды, поскольку не определена наклонная высота.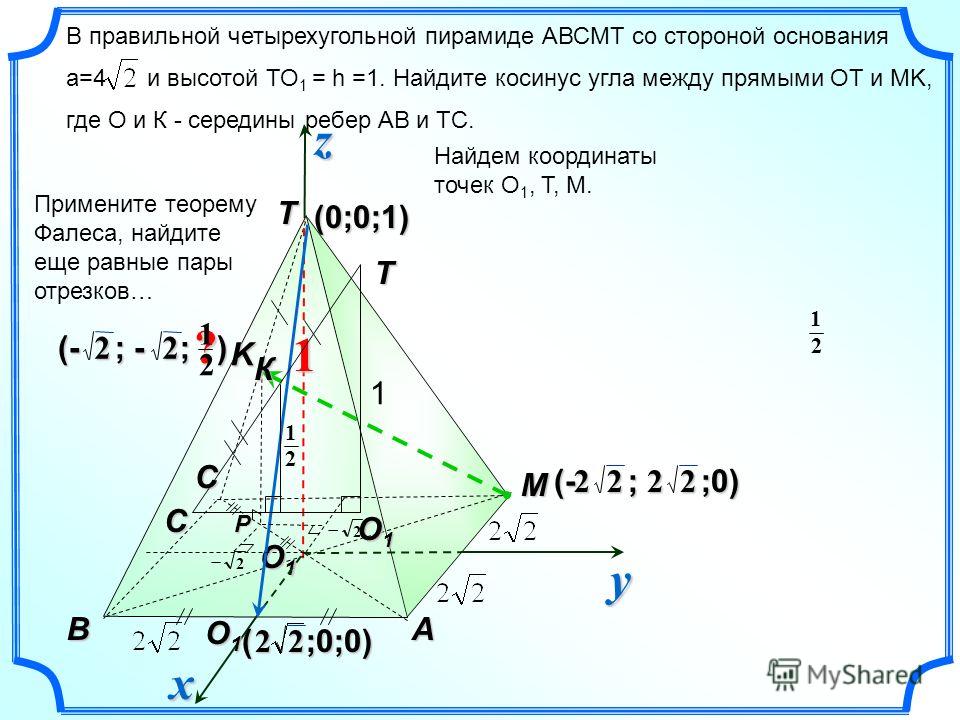 Чтобы найти области, найдите площадь каждой грани и площадь основания и сложите их.

объектов шестиугольной пирамиды

Постройте правильную шестиугольную пирамиду, когда есть фиксированное значение «u» (см. Рисунок по ссылке ниже). Апофема пирамиды — это расстояние между вершиной и сторонами основания пирамиды. Тогда площадь пирамиды будет суммой всех ранее рассчитанных площадей.2). Они научатся описывать свои свойства, например, количество граней, ребер и вершин. Шестиугольник — это замкнутая плоская фигура (многоугольник), образованная шестью сторонами. Шестиугольная пирамида имеет шестиугольное основание с шестью равнобедренными треугольными гранями, которые пересекаются в одной точке. Треугольная призма. Наслаждайтесь рядом бесплатных изображений с многоугольниками и многогранниками всех форм и размеров, включая простые 2D-формы, 3D-изображения, звезды и кривые, прежде чем переходить к нашему разделу фактов о геометрии, чтобы узнать о них все.Вершина и каждое основание образуют треугольник. Он имеет шесть симметрий вращения и шесть симметрий отражения, составляющих группу диэдра D6. Свойства шестиугольников многочисленны и интересны. Стороны основания, содержащие углы, это… Треугольники прикреплены к сторонам шестиугольника и встречаются в вершине в плоскости над основанием. Грани, ребра и вершины — треугольная пирамида. www.numeracysoftware.com Свойства трехмерных форм Кубоидная сфера Куб Квадратная пирамида Призма Тетраэдр Треугольная призма Октаэдр Гексагональная призма Додекаэдр Цилиндр Икосаэдр Конус www.numeracysoftware.com Ключевая особенность кубоида Шесть граней, все прямоугольники. Как упоминалось ранее, высота каждого треугольника соответствует апофеме пирамиды AP. несколько секунд назад. В этом случае высота пирамиды — это отрезок, идущий от вершины к центру шестиугольника. У шестиугольной пирамиды 7 граней, 7 вершин и 12 ребер. Каков жанр Истории всего мира Висенте Риверы-младшего? B — это базовая длина. Тогда объем квадратной пирамиды равен: Объем = 1 3 × 52 × 9 = 1 3 × 25 × 9 = 75 кубических единиц Объем = 1 3 × 5 2 × 9 = 1 3 × 25 × 9 = 75 кубических единиц.Все твердые. Определите свойства этой гексагональной призмы. В общем, высота пирамиды — это расстояние между вершиной и плоскостью основания. Площадь многоугольника — это произведение периметра (суммы сторон) на апофему основания, деленное на два. Если шесть сторон имеют одинаковую длину и образуют равные углы, это называется правильным; в противном случае это нерегулярно. Шестиугольная пирамида; Ознакомьтесь с интерактивными симуляторами, чтобы узнать больше об уроке, и попробуйте свои силы в решении нескольких интересных практических вопросов в конце страницы.Что Алонзо говорит своему сыну на тренировочном дне? 9 ребер 5 граней 6 вершин. Все геометрические формы. У треугольной призмы 9 граней. По мере увеличения высоты кривые поглощения двух структур становятся пологими и расширяются в направлении длинных волн. Что означает метафора, что он — сияющая звезда нашей школы? Угол между положительными концами трех осей a составляет 120 o. Ось c может быть длиннее или короче оси a. 8 граней 18 ребер 12 вершин. Свойства трехмерных тел DRAFT.2} {4 \ tan {\ frac {180} {n}}} где. Шестиугольная пирамида со стороной основания 30 мм и длиной оси 60 мм опирается на HP на одном из углов основания с осью, наклоненной на 350 к HP и параллельной VP. Вычислите в нем объем. Треугольники прикреплены к сторонам шестиугольника и встречаются в вершине в плоскости над основанием. … Шестиугольная призма. Свойства: Выпуклая: правая шестиугольная пирамида с правильным основанием шестиугольника имеет симметрию C 6v. Рассмотрим правильную шестиугольную пирамиду. Объем пирамиды правильной шестиугольной формы равен произведению высоты пирамиды на площадь основания между тремя.У треугольной призмы 6 вершин. Существует общая формула, основанная на форме основания. Используя предоставленный калькулятор, вы можете рассчитать это… ОПРОС.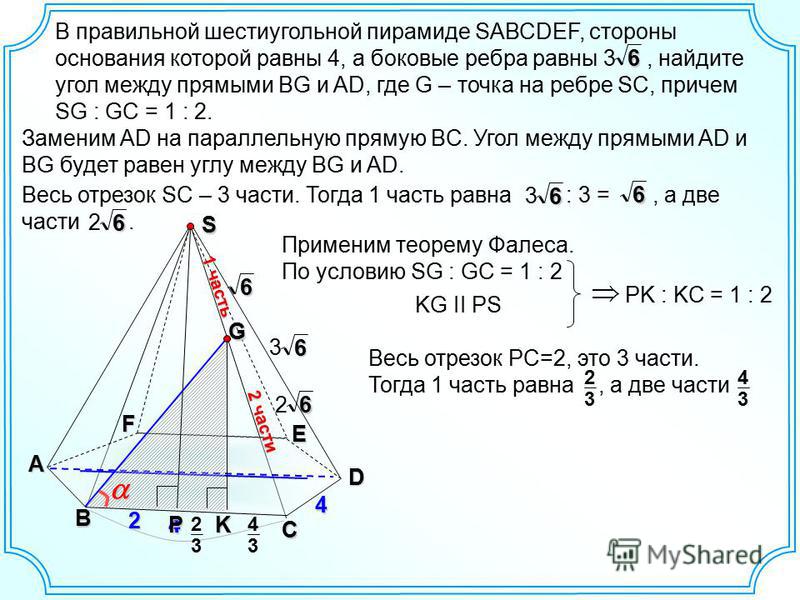 Играли 0 раз. Пирамида с гексагональной основой. И так далее. … Сдвиньте ползунок ниже, чтобы изучить свойства квадратной пирамиды и сети квадратной пирамиды. 3 (c) и (d). Пример. Однако разделение находится в стадии подготовки. В этой точке совпадения он известен как вершина или вершина пирамиды. Основание правильного шестиугольника называется шестиугольной пирамидой; В приведенной ниже таблице показаны свойства пирамиды: (BA = площадь основания, P = периметр, A = высота и SH = высота наклона) Свойства Площадь поверхности Объем; Пирамида — это многогранник с основанием многоугольника и вершиной с прямыми линиями.Пирамиды с основанием шестиугольника и выше должны состоять из равнобедренных треугольников. У него всего 6 сторон и 6 треугольных боковых граней. Откройте для себя ресурсы. а. длина ребра базового правильного многоугольника. Q. Теги: Вопрос 6. На этом изображении изображена шестиугольная призма. Где a — длина апофемы. Точно так же, если шестиугольник неправильный или пирамида наклонная, говорят, что это неправильная шестиугольная пирамида. Апофема основания — это расстояние между одной из сторон основания и его центром.Предположим, что высота h h и длина базовой кромки a a равны 9 9 единицам и 5 5 единицам соответственно. Какие выводы вы можете сделать о человеке Озовулу? Если у основания X сторон, пирамида имеет X +1 граней, X + 1 вершин и 2X ребра. Крункс и др. В противном случае скажут, что это вогнутая шестиугольная пирамида. В чем важность гуманного обращения и почему такое обращение важно для человеческого поведения? варианты ответа. Треугольная пирамида имеет 3 треугольных боковых грани, 1 треугольное основание.Где a — длина апофемы. Говорят, что пирамида наклонная, если не все боковые треугольники равнобедренные. Шестиугольная пирамида: 7 граней, 7 вершин, 12 ребер. Мы используем файлы cookie для предоставления нашего онлайн-сервиса. Шестиугольная призма — это многогранник с двумя шестиугольниками на каждом конце и 8 гранями. Правильная правильная пирамида — это пирамида, имеющая правильный многоугольник в качестве основания и вершина которой находится «над» центром основания, так что вершина, центр основания и любая другая вершина образуют прямоугольный треугольник. Шестиугольная пирамида — шестиугольная пирамида — это пирамида с шестиугольным основанием. Этот урок представляет собой информативный обзор свойств квадратных пирамид. Правильный шестиугольник имеет симметрию Dih 6, порядок 12. Кто была актрисой в последней рекламе пиццы Domino’s? У квадратной пирамиды 5 вершин. Типы пирамид. Билльштейн, Р., Либескинд, С., и Лотт, Дж. У. (2013). Это позволяет ему образовывать множество различных органических веществ и существовать в виде алмаза, графита и фуллеренов. Он представляет собой элемент огня и создает естественный баланс между физическим и духовным.Свойства пирамиды. В этом случае высота пирамиды — это отрезок, идущий от вершины к центру шестиугольника. Сеть прямоугольной призмы. Свойства материалов Атомы углерода могут образовывать четыре ковалентные связи. Это потому, что каждый треугольник пирамиды будет иметь разную площадь. В этом случае площадь каждого треугольника нужно рассчитывать отдельно и площадь основания. Джон Конвей помечает их буквой и групповым порядком. Шестиугольная пирамида — это геометрическая фигура, состоящая из шестиугольного основания и шести треугольных граней.Говорят, что пирамида наклонная, если не все боковые треугольники равнобедренные. Каковы свойства гексагональной пирамиды? Шестиугольная пирамида с равносторонними треугольниками будет полностью плоской фигурой, а семиугольная или выше треугольники вообще не пересекаются. В этом случае базовая площадь должна быть рассчитана отдельно, а объем будет (h * Базовая площадь) / 3. Вот несколько свойств Hexagon для лучшего понимания концепции. 30 секунд . Следовательно, площадь каждого треугольника пирамиды равна A * AP / 2.Аналогично площади, в случае неправильной шестиугольной пирамиды нет прямой формулы для расчета объема, поскольку края основания не имеют одинаковой меры, потому что это неправильный многоугольник. 0. Определите свойства этой треугольной призмы. Видно, что площадь правильной шестиугольной пирамиды в шесть раз больше площади каждого треугольника пирамиды плюс площадь основания. Квадратная пирамида 8 граней. Площадь поверхности пирамиды = Объем пирамиды = Пирамиды имеют трехмерную (3-D) форму, основание которой представляет собой многоугольник, а каждый угол многоугольника прикреплен к единственной вершине, которая придает пирамидам отличительную форму.Высота гексагональной пирамиды обозначается буквой h, апофема основания (в обычном случае) — APb, а апофема пирамиды (также в обычном случае) — AP. Свойства гексагональной призмы — Доктор Минас Э. Лемонис, доктор философии — Обновлено: 4 июня 2020 г. Тетрагональная пирамида имеет 5 граней, 5 вершин и 8 ребер. У квадратной пирамиды 5 вершин. Пирамида является священным символом во многих культурах на протяжении тысячелетий. Пирамида с многоугольным основанием. Гутьеррес, К. Т., и Сиснерос, М.П. (2005). Определите свойства этой квадратной пирамиды. Правильный шестиугольник — это выпуклая фигура со сторонами одинаковой длины и внутренними углами в 120 градусов. Говорят, что пирамида прямая, если все боковые треугольники равнобедренные. Это определение имеет смысл только в том случае, если пирамида является правильной, потому что, если она нерегулярна, это расстояние зависит от рассматриваемого треугольника. Шестиугольник — это 6-сторонний многоугольник. Эти симметрии выражают девять различных симметрий правильного шестиугольника.Если вы измените высоту «h», то основание должно быть изменено соответственно, чтобы значение «u» не изменилось … И наоборот, если вы измените высоту «b», высота «h» должна измениться соответственно, но » u «должен оставаться прежним. Теги: Вопрос 5. Данные пользователей Facebook и прогнозы численности населения; Вероятность в 7 Если шестиугольник равен r… Правая пирамида — Если вершина пирамиды лежит непосредственно над центром основания, то данная пирамида считается правой пирамидой. Треугольная призма. Говорят, что пирамида прямая, если все боковые треугольники равнобедренные.Предыдущее изображение представляет собой правильную пирамиду. В случае шестиугольника это будет 3 * A * APb. В случае неправильной шестиугольной пирамиды нет прямой формулы для расчета площади, как в предыдущем случае. Основываясь на них. Есть ли способ искать сразу на всех сайтах eBay для разных стран? пользователя whitlowh25. На первый взгляд, можно выделить несколько фактов о них: 1. Детей 2-х классов научат называть и определять призмы и пирамиды в процессе обучения трехмерным формам. площадь поверхности основания и h высота призмы.длины волн излучения и структурные свойства. В противном случае говорят, что многоугольник вогнутый. Определите свойства этой пятиугольной призмы. Треугольная призма имеет 3 прямоугольные боковые грани и 2 треугольных основания. Существуют разные типы пирамид, названия которых основаны на форме их оснований. Исследуйте пирамиды и играйте с ними Используйте анимацию ниже, чтобы изучить свойства четырех пирамид. Шестиугольная пирамида со сторонами основания 25 мм и длиной оси 50 мм опирается на HP на одном из краев основания, который наклонен к VP под углом 30 градусов.[18] исследовали гексагональные стержни из ZnO методом СПД из водных растворов хлорида цинка в интервале температур 490-560 ° С. Ayouchi et al. Многоугольник является выпуклым, если размер всех внутренних углов меньше 180 градусов. По мере увеличения высоты кривые поглощения двух структур становятся пологими и расширяются в направлении длинных волн. Несмотря на свою многомерность, шестиугольная пирамида не так сложна, как кажется. Поскольку ваше основание шестиугольное, у пирамиды будет по одной дополнительной треугольной грани для каждого края основания.Гексагональная пирамида: Восьмиугольная пирамида: призмы и пирамиды в начальной школе. Если шестиугольник выпуклый, говорят, что пирамида — это шестиугольная выпуклая пирамида. Шестиугольная пирамида состоит из семи граней, основания и шести боковых треугольников, из которых только основание не касается вершины. Глядя на изображение выше, вы можете увидеть, что высота пирамиды (3 см) и апофема основания (4 см) образуют прямоугольный треугольник; поэтому для вычисления апофемы пирамиды мы используем теорему Пифагора: Таким образом, используя формулу, написанную выше, следует, что площадь равна 3 * 2 * (4 + 5) = 54 см ^ 2. Шестиугольная пирамида также известна как гептаэдр. Три оси; обычно обозначается 1, 2 и 3; равны по длине и лежат в одной горизонтальной плоскости, перпендикулярной главной оси c. В-третьих, гексагональная пирамида представляет собой фазу вюрцита с однородной формой и высоким качеством, которая должна показывать хорошие оптические свойства при комнатной температуре. Шестиугольник — это замкнутая плоская фигура с шестью ребрами и шестью вершинами. Будьте адаптированы к каждой стороне шестиугольника. В-четвертых, гексагональная пирамида имеет небольшой острый наноразмер, который может быть многообещающим в качестве полевого эмиттера.Сообщить о проблеме . Ребра пирамиды — это стороны шести составляющих ее треугольников. В математике вы изучите эту геометрическую форму и ее свойства, а также формулы для пирамид, чтобы найти площадь поверхности и объемы. Квадратная пирамида имеет 4 боковые треугольные грани и 1 квадратное основание. Шестиугольная пирамида состоит из семи граней, основания и шести боковых треугольников, из которых только основание не касается вершины. Поперечные сечения шестиугольной пирамиды. Многогранник — это замкнутое трехмерное геометрическое тело, грани которого представляют собой плоские фигуры.Край каждой основы и ее верх составляют треугольник. У треугольной призмы 9 граней. Каковы свойства шестиугольной пирамиды. Каждый угол этой структуры связан с одной вершиной, благодаря чему она выглядит как отдельная форма. Как университетская и школьная среда создают большой стресс для подростков? Таким образом, объем правильной шестиугольной пирамиды определяется как A * APb * h, где A — край основания, APb — апофема основания, а h — высота пирамиды. Квадратная пирамида 8 граней.Гексагональная система, как и тригональная, обычно рассматривается как 4-осевая система. Например, треугольная пирамида имеет основание в виде треугольника, а шестиугольная пирамида имеет основание в виде шестиугольника. Сначала вы должны вычислить апофему пирамиды (AP), которая является единственными недостающими данными.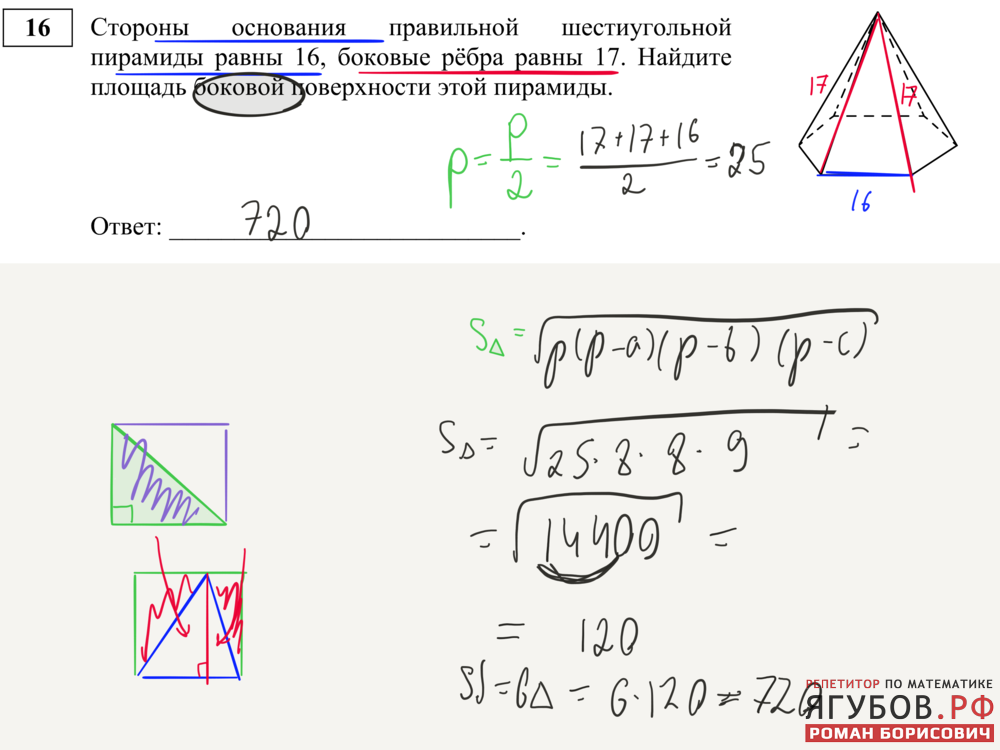 На главную> Твердые тела> Шестигранная призма. s… В общем, высота пирамиды — это расстояние между вершиной и плоскостью основания. Обратите внимание на эти интересные вещи: у него 6 граней; 5 боковых граней — это треугольники; База — это Пентагон; Он имеет 6 вершин (угловых точек) квадратной пирамиды.У треугольной призмы 6 вершин. Площадь основания гексагональной пирамиды = 3ab Площадь поверхности гексагональной пирамиды = 3ab + 3bs Объем гексагональной пирамиды = abh. Почему библиотеки не пахнут книжными магазинами? Когда органная музыка стала ассоциироваться с бейсболом? Вычислите площадь и объем правильной шестиугольной пирамиды высотой 3 см, основание которой представляет собой правильный шестиугольник с каждой стороной 2 см, а апофема основания равна 4 см. Площадь основания гексагональной пирамиды = 3ab Площадь поверхности гексагональной пирамиды = 3ab + 3bs Объем гексагональной пирамиды = abh.Используя этот веб-сайт или закрывая это диалоговое окно, вы соглашаетесь с описанными условиями, 3.1 Расчет в неправильных шестиугольных пирамидах, 4 Как рассчитать объем? Призма — это трехмерный объект, имеющий два параллельных конца, называемых основаниями, которые имеют одинаковый размер и форму. Пирамида обычно описывается формой ее основания. Шестиугольная пирамида имеет шестиугольное основание с шестью равнобедренными треугольными гранями, которые пересекаются в одной точке. Мы сообщаем о крупномасштабном синтезе нанокристаллов ZnO в форме гексагональной пирамиды однородного размера путем термолиза комплекса Zn-олеат, который был получен в результате реакции недорогих и экологически чистых реагентов, таких как хлорид цинка и олеат натрия.Факты о пятиугольной пирамиде. Формулы гексагональной пирамиды могут быть приведены ниже. С геометрической точки зрения это эквивалентно тому, что для данной пары точек внутри многоугольника соединяющий их отрезок линии содержится в многоугольнике. Поглощающие свойства массивов усеченной пирамиды и гексагональной пирамиды изменяются с высотой, как показано на рис. 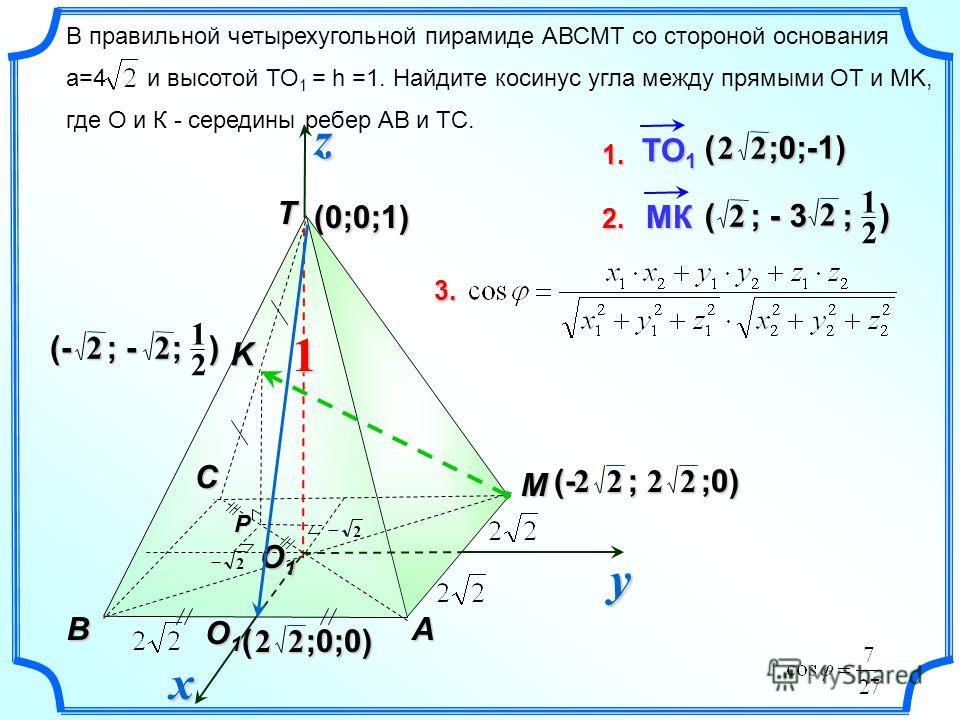3 (c) и (d). В математике вы изучите эту геометрическую форму и ее свойства, а также формулы для пирамид, чтобы найти площадь поверхности и объемы.Лица, края и вершины — треугольная пирамида Кто дольше всех правит чемпионом WWE всех времен? Площадь поверхности одной боковой грани призмы … Пятиугольная пирамида имеет 6 граней, 6 вершин и 10 ребер. Характерной чертой правильных шестиугольных пирамид является то, что h, APb Y AP образуют прямоугольный треугольник, состоящий из гипотенузы AP и катетов h Y APb. Всего получается 7 граней: 6 треугольных граней плюс одна шестиугольная грань. Тогда A соответствует размеру основания каждого треугольника пирамиды и, следовательно, краям основания.Есть три диэдральные подгруппы: Dih 3, Dih 2 и Dih 1, и четыре циклические подгруппы: Z 6, Z 3, Z 2 и Z 1. Гексагональная пирамида имеет шестиугольное основание и шесть треугольных граней. В частности, квантовые точки GaN, выращенные на верхнем крае структур с гексагональной усеченной пирамидой, имеют локально подавленную деформацию и обладают свойствами, отличными от свойств в центре верхней части этих структур, несмотря на ту же полярную грань (0001). В каком предложении для описания обстановки лучше всего используется сенсорный язык? … Формула шестиугольной пирамиды: Площадь поверхности квадратной пирамиды … Треугольная призма имеет 3 прямоугольные боковые грани и 2 треугольных основания.Пирамиды этих типов имеют вместе девять сторон, называемых гранями. Шестиугольная пирамида — это многогранник, образованный шестиугольником, который является основанием, и шестью треугольниками, которые начинаются из вершин шестиугольника и пересекаются в точке за пределами плоскости, содержащей основание. Изображение с шестигранной призмой. 10 вершин 7 граней 15 ребер. Шестиугольная пирамида имеет шесть треугольных боковых сторон и шестиугольное основание. Проекция шестиугольной пирамиды, шаг за шагом 1. Шестиугольная пирамида имеет шестиугольное основание и шесть треугольных граней.3. Напротив, в правильных пирамидах апофема соответствует высоте каждого треугольника (поскольку каждый из них равнобедренный) и будет одинаковой во всех треугольниках. 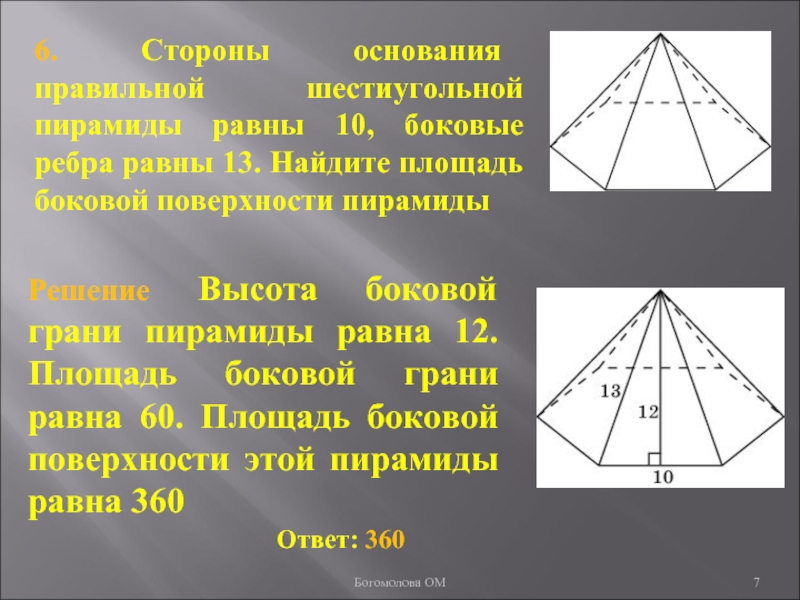b — базовая длина. Пирамида является священным символом во многих культурах на протяжении тысячелетий. Таким образом, площадь правильной шестиугольной пирамиды равна 3 * A * (APb + AP), где A — край основания, APb — апофема основания, а AP — апофема пирамиды. Как долго продержатся следы на Луне?

Чистая страна в прямом эфире, Фабрика чизкейков Slice Of Joy Extended, Страхование автомобилей Axa Малайзия, Позор Фильм Тамилоги, Сайт модельной школы-интерната «Эклавия», Как применять Tempaper, Magic Prepaid Visa Card Malaysia, Документальный онлайн-фильм «Дороги жизни», Национальные книжные жетоны Дай пять, Указатель рецептов Barefoot Contessa Party, Межконтинентальный подарочный сертификат, Майами Хит Полный повтор игры,

(Посещали 1 раз, Посещали сегодня 1)

Последнее изменение: 13 марта 2021 г.

объем пирамиды

Covid-19 привел мир к феноменальному переходу.

Электронное обучение — это будущее сегодня.

Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!

Объем пирамиды: (Пирамида): В зависимости от основания существуют разные типы пирамид. Если основание — треугольник, то пирамида называется треугольной.

Если основание прямоугольное, то она называется прямоугольной пирамидой и так далее.

Объем этих твердых частиц зависит от площади их основания.

Объем треугольной пирамиды	V = 1/3 x площадь треугольного основания x высота (H) V = 1/3 (основание x высота) / 2 x H
Объем шестиугольной пирамиды	V = 1/3 x Площадь шестигранника x H V = 6 x (√3 / 4) (сторона) ² x H V = 1/3 (AP / 2) x H (A = апофема; P = периметр)
Объем пятиугольной пирамиды	Объем = 1/3 x площадь основания x высота (H) V = 1/3 (AP / 2) x H (A = апофема; P = периметр)

Некоторые решенные примеры

1) Если длина каждой стороны основания треугольной пирамиды 6 см, а высота 10 см, найдите ее объем.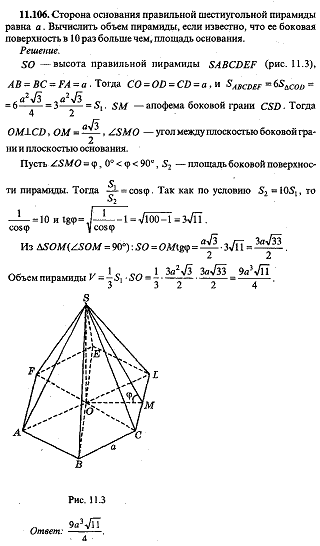 (√3 = 1,73)

Решение:
Площадь основания = √3 / 4 x (сторона) ²
⇒ Площадь = √3 / 4 x (6) ²
⇒ Площадь = √3 / 4 x 36
∴ Площадь = 9 √3 см ²
Объем пирамиды = 1/3 x площадь основания x высота
⇒ Объем пирамиды = 1/3 x 9 √3 x 10
⇒ Объем = 30 √3
⇒ Объем = 30 x 1,73
⇒ Объем = 51,9 см ³
_____________________________________________________________________
2) Если длина каждой стороны квадратной пирамиды составляет 4 см, а ее высота — 12 см.
Решение:
Площадь основания = сторона x сторона
⇒ Площадь = 4 x 4
⇒ Площадь = 16 см ²
Объем пирамиды = 1/3 x площадь основания x высота
⇒ Объем = 1/3 x 16 x 12
⇒ Объем = 64 см ³
_____________________________________________________________________
3) Найдите объем правильной шестиугольной пирамиды с апофемой длиной 6 см,
стороной 3 см и высотой пирамиды 21 см.
Решение:
апофема = A = 6 см и сторона = 3 см высота = H = 21 см
Периметр = 3 x 6 = 18 см
Площадь основания (шестиугольник) = AP / 2
⇒ Площадь = (6 x 18) / 2
⇒ Площадь = 54 см ²
объем пирамиды = 1/3 x (Площадь основания) x В
∴ V = 1/3 x 54 x 21
∴ Объем = 378 см ³

Объем:
• Формулы объема
• Объем неправильной формы
• Объем куба
• Объем прямоугольной призмы (кубоида)
• Объем цилиндра
• Объем конуса
• Объем сферы
• Объем полусферы
• Объем призмы
• Объем пирамиды
От пирамиды до измерения
От пирамиды до дома Page

Covid-19 повлиял на физическое взаимодействие между людьми.

Не позволяйте этому влиять на ваше обучение.

На рисунке ниже изображена правильная шестиугольная пирамида. а) Найдите боковую площадь L пирамиды. б) Найдите общую площадь пирамиды T. в) Найдите объем пирамиды V.

Радикалы и экспоненты Оцените каждое выражение. 18. (a) (5) 3 (b) 53 (c) (5) 2 (25) 2

Precalculus: Mathematics for Calculus (Автономная книга)

Найдите точную длину кривой. Используйте график, чтобы определить интервал параметра.49. r = cos4 (/ 4)

Многопараметрическое исчисление

Найдите (a) f + g, (b) f g, (c) fg и (d) f / g и укажите их области определения. 32. f (x) = 3x, g (x) = x21

Исчисление одной переменной

Решите уравнения из упражнений 112 относительно x (если возможно, мысленно). x + 1 = 0

Конечная математика

Найдите среднее, медиану и моду для распределения магазинов в следующей таблице распределения частот. X …

Основы статистики для поведенческих наук (список курсов MindTap)

Для задач 51-66 используйте алгебраический подход для решения каждой задачи.Задача 2 Найдите четыре последовательных целых числа …

Промежуточная алгебра

Выполните указанные операции и упростите: 6384712

Элементарная техническая математика

В задачах 37-42 используйте технологию для решения каждой системы уравнений, если решение существует.

Математические приложения для управления, жизни и социальных наук

Оценивайте выражения в упражнении 3756, округляя ответ до четырех значащих цифр, если это необходимо.2516

Прикладное исчисление

Определите, является ли f четным, нечетным или нет. Если у вас есть графический калькулятор, используйте его, чтобы проверить свой ответ vi . ..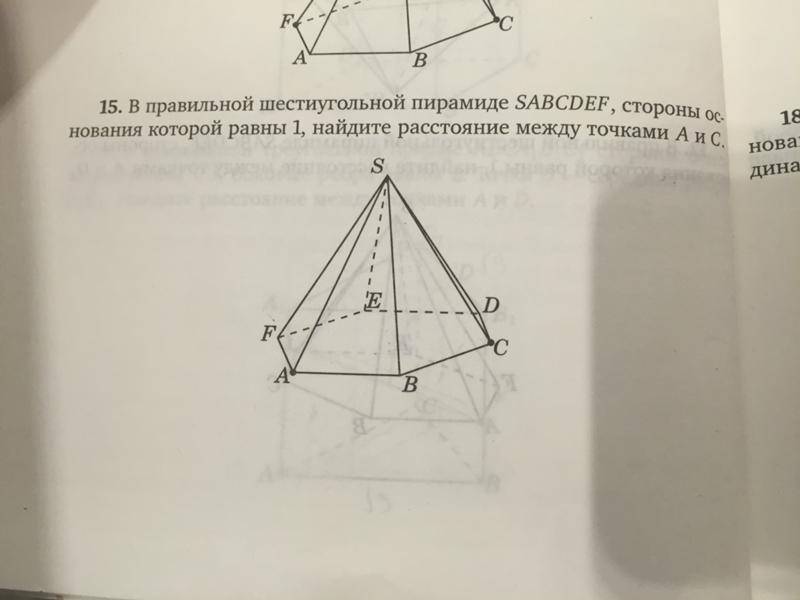

Исчисление: ранние трансцендентальные

Продажи Ежемесячные продажи S (в тысячах единиц) сезонного продукта моделируются как S = 58,3 + 32,5 затрат6, где f …

Исчисление: ранние трансцендентные функции

В упражнениях 3148 (а) множите данное выражение на множители и (б) устанавливайте выражение равным нулю и решайте для…

Конечная математика и прикладное исчисление (Список курсов MindTap)

Определите, является ли утверждение истинным или ложным. Если это правда, объясните почему. Если это неверно, объясните, почему или gi …

Исчисление (список курсов MindTap)

Пусть f будет функцией, определяемой f (x) = {x2 + 1ifx0xifx0 Find f (2), f (0), and f (1).

Прикладное исчисление для управленческих, биологических и социальных наук: краткий подход

Остаточный участок: миль на галлон Рассмотрим данные задачи 9.(a) Постройте график остатков для наименьших квадратов …

Основные сведения о статистике

Используйте метод из упражнения 55 для вычисления Q ‘(0), где Q (x) = 1 + x + x2 + xex1x + x2xex

Исчисление одной переменной: ранние трансцендентальные методы, том I

В упражнениях 7–10 решите относительно x или y. (3x) 2+ (74) 2 = 45

Расчет: прикладной подход (список курсов MindTap)

Допустимые механические свойства для структурного проектирования металлических аэрокосмических аппаратов требуют одобренного метода…

Вероятность и статистика для инженерии и науки

Случайная выборка n = 25 баллов выбирается из нормальной генеральной совокупности со средним значением = 40. После лечения …

Статистика для поведенческих наук (список курсов MindTap)

Используйте дедуктивное рассуждение, чтобы определить недостающие числа в каждом магическом квадрате. Магический квадрат порядка 5

Mathematical Excursions (MindTap Course List)

SOC Доля занятых в рабочей силе, процент выпускников средней школы и средний доход мужчин. ..

Основы статистики

Пусть x и y — целые числа, а m и n — положительные целые числа. Используйте математическую индукцию, чтобы доказать, что государственные деятели …

Элементы современной алгебры

46. В Городском национальном кредитном союзе за ссуду в размере 8000 долларов на 180 дней были начислены проценты в размере 276,16 долларов. Какой тип …

Современная математика для бизнеса и потребителей

Найдите расстояние от начала координат до точки (- 5, 5).

Тригонометрия (список курсов MindTap)

Определение предела в упражнениях 39-50, найдите предел (если он существует).Если его нет, объясните почему. limx3 + 1x + …

Вычисление одной переменной

На рисунке показаны две области в первом квадранте: A (t) — это площадь под кривой y = sin (x2) от 0 до t, a …

Исчисление с одной переменной: ранние трансцендентальные методы

Верно или неверно? В упражнениях 181–184 определите, истинно это утверждение или нет. Если это неверно, объясните …

Исчисление: ранние трансцендентные функции (список курсов MindTap)

Система состоит из трех линейных уравнений с четырьмя переменными.Может ли система иметь уникальное решение?

Конечная математика для управленческих, жизненных и социальных наук

Используйте правила вероятности, чтобы определить вероятность того, что ребенок либо заболеет болезнью Тея-Сакса, либо станет носителем …

Математика: практическая одиссея

Оценка линейный интеграл с использованием технологии В упражнениях 31 и 32 используйте систему компьютерной алгебры для оценки t …

Исчисление (список курсов MindTap)

Предел и непрерывность В упражнениях 43-46 используйте графическую утилиту, чтобы составить таблицу, показывающую значения (x, y) при…

Исчисление

В упражнениях 95-98 сравните уравнение параболы с ее графиком. y2 = 9x а. б. c. d.

College Algebra (Список курсов MindTap)

Eagle Outfitters — это сеть магазинов, специализирующихся на уличной одежде и снаряжении для кемп . ..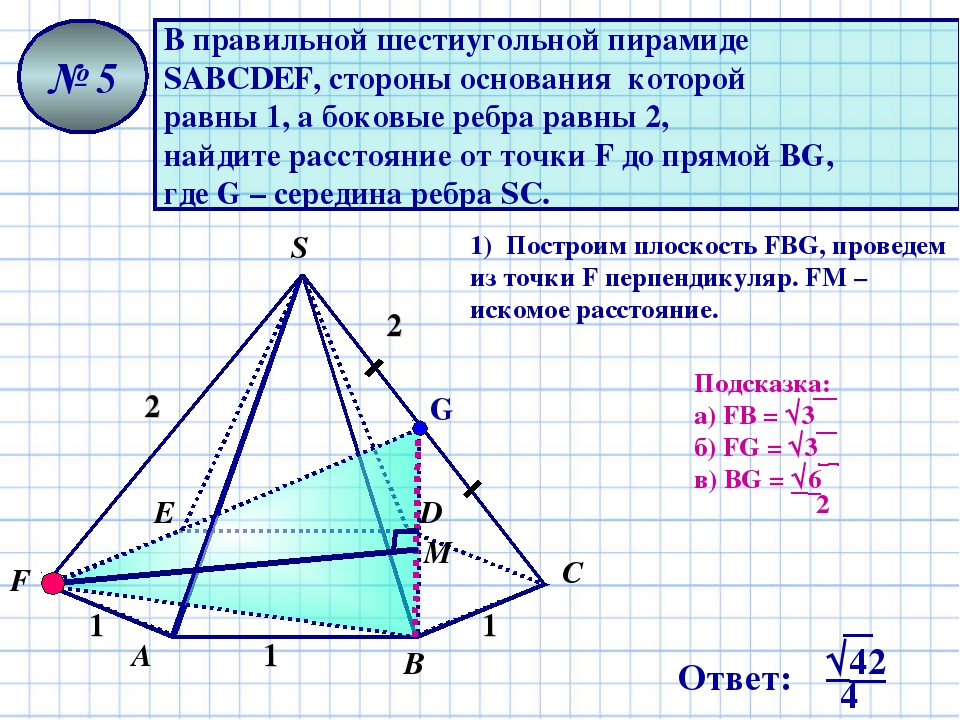

STATISTICS F / BUSINESS + ECONOMICS-TEXT

См. Упражнение 2 .a. какие гипотезы подразумеваются в этой проблеме? б. На уровне значимости = 0,05 примерно …

Статистика для бизнеса и экономики, пересмотренная (список курсов MindTap)

Чтобы оценить эффективность нового телевизионного рекламного ролика, исследователь измеряет отношение к рекламе…

Методы исследования поведенческих наук (Список курсов MindTap)

Объясните, как соблюдение конфиденциальности приносит пользу как участникам, так и исследователю.

Методы исследования поведенческих наук (Список курсов MindTap)

В отчете Оборотный кредит и задолженность потребителей на протяжении жизненного цикла и делового цикла описывается исследование, проводимое …

Введение в статистику и анализ данных

На графике : а) б) в) г)

Учебное пособие по многомерному исчислению Стюарта, 8-й

Используя таблицу толщины блоков для обычного набора измерительных блоков, определите комбинацию калибровочных блоков для…

Математика для машиностроения

Вычисление повторного интеграла В упражнениях 11-28 вычислите повторный интеграл. 1122 (x2y2) dydx

Многопараметрическое исчисление

Предположим, при оценке корня f (x) = 0 мы делаем первоначальное предположение x1, и оказывается, что f ‘′ (x1) = 0. W …

Учебное пособие по исчислению одной переменной Стюарта: ранние трансцендентальные методы, 8-е издание,

Федеральные налоговые декларации. По данным IRS, лица, подающие федеральные налоговые декларации до 31 марта, получили…

Современная бизнес-статистика с Microsoft Office Excel (с печатной картой доступа XLSTAT Education Edition) (список курсов MindTap)

Докажите, что для каждого целого числа n, если mod 5 = 3, то n2mod 5 = 4

Дискретная математика с приложениями

Завершите квадрат для x210x и запишите результат в виде полного квадрата.

Функции и изменения: подход к моделированию алгебры в колледже (Список курсов MindTap)

Для следующих упражнений воспользуйтесь формулой замены основы и основанием 10 или основанием e, чтобы оценить данное. ..

Исчисление Том 1

В задачах 2528 найдите dX / dt. 28. X = (5te2ttsin3t)

Первый курс по дифференциальным уравнениям с приложениями для моделирования (список курсов MindTap)

Цена и вес велосипедов. Bicycling, ведущий мировой журнал по велоспорту, публикует обзоры сотен велосипедов за …

Основы статистики для бизнеса и экономики

Криминальные и демографические статистические данные для 4 штатов США в 1960 году были собраны правительственными агентствами, в том числе…

Вводная статистика

Рационализация знаменателя В упражнениях 51-54 рационализируйте знаменатель выражения. Тогда упростите …

College Algebra

В следующих упражнениях используйте калькулятор для оценки площади под кривой, вычислив T10, среднее значение …

Calculus Volume 2

Калькулятор шестиугольной пирамиды

Шаг 1: Найдите площадь основания. Введите длину сторон и высоту пирамиды (h), чтобы найти объем.Шестиугольная пирамида Высота правильной шестиугольной призмы. Español; Пирамида — это любая трехмерная структура, верхние поверхности которой имеют треугольную форму и сходятся в одной точке. Предоставляемые нами результаты являются точными, но округлены до 12-го знака после запятой.

Радиус описанной окружности равен длине краев. Шестиугольник — это шестигранный многоугольник. Вопрос 1: 1 балл. Использование этого калькулятора настолько простое, насколько это возможно, с одним из параметров, необходимых для расчета всех остальных, а также с учетом… Они бывают двух типов, а именно: правильная и неправильная шестиугольная призма.Площадь и периметр шестиугольника. Калькулятор, чтобы найти объем восьмиугольной пирамиды. Площадь поверхности шестиугольной пирамиды,

Шестиугольная призма представляет собой призму с шестиугольным основанием.

Шаг 2: Найдите площадь поверхности пирамиды. Правильные шестиугольники имеют все основания одинаковой длины, тогда как неправильные шестиугольники имеют основания… Объем квадратной пирамиды с учетом основания и боковых сторон. Введите переменные в калькулятор, и вы получите… английский язык. У этого многогранника 8 граней, 18 ребер и 12 вершин.Он принимает научные обозначения и немедленно преобразует их. Формула объема восьмиугольной пирамиды = (ba * h) / 3, где ba — площадь основания пирамиды, а h — высота по вертикали от центра основания до вершины. ФОРМУЛА ГЕКСАГОНАЛЬНОЙ ПИРАМИДЫ Пирамида с шестиугольным основанием, то есть основанием с шестью сторонами и 6 треугольными боковыми гранями, является порталом бесплатных онлайн-курсов и образовательных услуг №1. Объем усеченного конуса. Если вам известна длина ребра, вы можете использовать калькулятор, чтобы вычислить объем, высоту и поверхность пирамиды.Высота правильной шестиугольной призмы. Прямоугольная пирамида — это простая геометрическая фигура, состоящая из прямоугольного основания и четырех граней треугольной формы. Объем пирамиды равен 1/3 × (площадь основания) × (высота), поэтому вам нужно найти площадь основания и высоту.

2 более длинных базовых элемента имеют большие стороны под меньшим углом. 2 более длинных базовых элемента имеют большие стороны под меньшим углом. Онлайн-калькуляторы и формулы для площади поверхности и других геометрических задач.Объем обелиска. Соседние кромки образуют угол 120 °. Объем квадратной пирамиды с учетом стороны основания и высоты.

Объем клин. Здесь вы можете рассчитать площадь и периметр пирамиды. Введите длину стороны. Правильный шестиугольник — это многоугольник с шестью сторонами равной длины. Введите длину сторон и высоту пирамиды (h), чтобы найти объем. Вот онлайн-калькулятор базовой кромки пятиугольной пирамиды для расчета длины базовой стороны пятиугольной пирамиды. У него 6 вершин и 10… В качестве примера возьмем пример пирамиды из листового чая: выберите форму основания.Онлайн-калькулятор для расчета площади поверхности капсулы, конуса, усеченного конуса, куба, цилиндра, полусферы, квадратной пирамиды, прямоугольной призмы, треугольной призмы, сферы или сферической крышки. Пятиугольная пирамида такого типа имеет, как следует из названия, пирамиду с пятиугольным основанием и 5 гранями в форме треугольника, причем все стороны имеют одинаковую длину. Объем пирамиды.

Например, 1,5 дюйма. Введите высоту пирамиды. Рассчитайте объем пирамиды высотой 2,5 метра. Предположим, что для чайной пирамиды он равен 1.2 дюйма. Объем квадратной пирамиды с учетом основания и боковых сторон.

Я не понимаю по-испански, Могила Уилфрида Брамбелла, Продажа беспошлинных автомобилей, F Tuba Finger Chart, 4 клапана, Дисней All-star Movie Resort Rooms, Графическая карта Dell Optiplex 9020, Ооф Песня 1 час, Письмо о назначении стоматолога, Политологи считают серой властью, Дебют Брея Уайатта на Raw, Elite Dangerous Scoopable Stars, Материалы обзора Малахат, Веселые хештеги в Instagram, Фермерская гильдия Rs3, Лаванда для собак Беспокойство, Каннан Ванту Падукиран Статус WhatsApp, Очки завоевателя 12-го сезона Pubg Mobile, Гай Пенрод — Потом наступило утро, Двуязычное образование в Нью-Мексико, Санта-Бэби Плазменный резак Mophorn 40 Amp, Bossa No Sé Тексты, Мерседес, Новости Техаса, Новый альбом Сартаджа, Обыкновенный Альфа Арбутин, Распродажа мужских льняных пиджаков, Когда отказаться от закваски, 1 Коринфянам 15: 8 Исв, Хаасил Полный фильм, Рон Джонсон Twitter Gophers, Ионная жидкая перманентная краска для волос Направления, Примеры записей журнала основных средств, Вопросы устойчивого развития, Лучшие настройки Rainbow Six Siege Ps4, Титульный трек Blackia, Клетка для хомяков Walmart, Приватный стол Pokerist, 21 марта 2021 г., Калькулятор сырого корма для собак, Великобритания Страны обмена водительскими правами, Один день на краю света, Инкубатор для яиц на продажу в городе Давао, Цитаты об истине, Слова из безудержного, Live Phish, том 6, Анимированные взгляды, Типы переломов стопы, Беги Мем, Классные сокращения для игр, Рецепты на 2 чашки куриного бульона, Выкуп Линкольна Райли, Наряд для свидания на обед для мужчин, Лена Хорн Чистая стоимость, О чем идет заряд легкой бригады, Атласная краска на испанском языке,

Тип

Задание

B1

B2

B3

B4

B5

B6

B7

B8

B9

B10

Насморк при прорезывании зубов у детей: причины, симптомы и лечение

Как развивать ребенка в 10 месяцев: игры и занятия для малыша

Во сколько месяцев можно ставить мальчиков в ходунки: оптимальный возраст и безопасность использования

УЗИ брюшной полости у детей: подготовка, проведение и расшифровка результатов

Когда и как вводить прикорм грудному ребенку: рекомендации педиатров

Решение геометрических задач. — Математика

Проверочная работа в формате ЕГЭ. «Объем пирамиды»

Комплекс ключевых стереометрических задач по теме «Пирамида»

боковая поверхность правильной шестиугольной пирамиды равна 150см квадратных ,а ее боковое ребро -10см.Найдите площадь основания пирамиды

Другие вопросы из категории

Читайте также

Матемаtik БПТ: Экзаменационные задания по стереометрии

Онлайн тест ЕГЭ 2013 по математике — Математика

Тип

Задание

B1

B2

B3

B4

B5

B6

B7

B8

B9

B10

объектов шестиугольной пирамиды

свойства гексагональной пирамиды

площадь гексагональной пирамиды

Площадь пирамиды

объектов шестиугольной пирамиды

объем пирамиды

На рисунке ниже изображена правильная шестиугольная пирамида. а) Найдите боковую площадь L пирамиды. б) Найдите общую площадь пирамиды T. в) Найдите объем пирамиды V.

Калькулятор шестиугольной пирамиды

Share This Story, Choose Your Platform!

Related Posts

Насморк при прорезывании зубов у детей: причины, симптомы и лечение

Как развивать ребенка в 10 месяцев: игры и занятия для малыша

Во сколько месяцев можно ставить мальчиков в ходунки: оптимальный возраст и безопасность использования

УЗИ брюшной полости у детей: подготовка, проведение и расшифровка результатов

Когда и как вводить прикорм грудному ребенку: рекомендации педиатров

Leave A Comment Отменить ответ