Бросаем под углом к горизонту. Олимпиадная подготовка, 9 класс.
В этой статье будем бросать тела горизонтально и под углом к горизонту, и рассчитывать расстояния между ними или их скорости спустя некоторое время. Подробнее про треугольники скоростей и перемещений можно почитать здесь: “Геометрический подход к баллистическим задачам”
Задача 1. Мяч, брошенный одним игроком другому под углом к горизонту со скоростью м/с, достиг высшей точки траектории через с. На каком расстоянии друг от друга находились игроки? Сопротивление воздуха не учитывать, ускорение свободного падения принять равным м/. Ответ дать в метрах, округлив до целых. Высота игроков одинаковая.
Решение.
Весь полет в силу симметрии параболы длился по времени . Применим треугольник перемещений, в котором учтем, что вектор перемещения – горизонтален. Следовательно – сам треугольник – прямоугольный! Тогда можно воспользоваться теоремой Пифагора , откуда
Ответ: 35 м.
Задача 2. Тело брошено горизонтально со скоростью м/с. Определите величину скорости тела через с после начала полета. Ускорение свободного падения м/. Ответ дать в м/с, округлив до десятых.
Решение.
Воспользуемся треугольником скоростей. Так как он прямоугольный, по теореме Пифагора найдем модуль конечной скорости.
Получим м/с.
Ответ: 14,1 м/с.
Задача 3. Тело брошено с балкона башни вверх под углом к горизонту со скоростью м/с. Определите модуль угла наклона скорости тела к горизонту через 2 с после начала полета. Ускорение свободного падения м/. Ответ дать в градусах, округлив до целых.
Решение.
Из треугольника скоростей, с учетом , нетрудно заметить, что угол между начальной и конечной скоростью . Следовательно, угол между конечной скоростью и горизонтом .
Ответ: .
Задача 4. Со скалы, возвышающейся над морем, бросили камень под углом . к горизонту. Найти время полёта камня , если известно, что непосредственно перед падением в воду его скорость была равна м/с и направлена под углом к горизонту. Ускорение свободного падения м/. Ответ дать в секундах, округлив до десятых.
к горизонту. Найти время полёта камня , если известно, что непосредственно перед падением в воду его скорость была равна м/с и направлена под углом к горизонту. Ускорение свободного падения м/. Ответ дать в секундах, округлив до десятых.
Решение.
Воспользуемся треугольником скоростей. Из условия задачи следует, что он прямоугольный. Изменение скорости , откуда с.
Ответ: 2,3 с.
Задача
Решение.
Воспользуемся треугольником скоростей. Угол между вектором начальной скорости и вектором изменения скорости равен . По теореме косинусов можно найти модуль вектора конечной скорости
Ответ: 5 м/с.
«БрошеННый» или «брошеНый» (камень, мяч, человек), как правильно пишется?
Слово «брошенный» правильно пишется с -нн- в суффиксе -енн-.
Обычно все отглагольные прилагательные или причастия, образованные от глаголов совершенного вида, имеют приставку в морфемном составе и соответственно пишутся с -нн-, например:
- (что сделать?) исправить — исправленная рукопись;
- закоптить — закопченный котелок;
- залатать — залатанный рукав;
- застирать — застиранное пятно.
В составе интересующего нас слова «брошенный» нет приставки:
брошенный — корень/суффикс/окончание.
И всё же, как это уже видно из этой записи, рассматриваемое слово правильно пишется с -нн-. Выясним, почему.
Брошенный пишется с -н- или -нн-?
Чтобы узнать, как правильно пишется слово «брошенный» или «брошеный» (камень, мяч, человек), с одной буквой «н» или с -нн-, определим, к какой части речи оно принадлежит.
Брошенный им пятак зазвенел на камнях (Анатолий Рыбаков. Кортик).
Подлежащее «пятак» определяет слово «брошенный», которое имеет признак действия (пятак бросили), имеет зависимое слово и отвечает на вопрос какой?
По этим грамматическим признакам, выясним, что это страдательное причастие, которое образовано от глагола «бросить». Определим вид глагола:
что сделать? бросить.
Теперь вполне обоснованно установим, что хотя производящий глагол является бесприставочным, но он обозначает действие, которое уже состоялось, причастие пишется с -нн- в суффиксе.
Слово «брошенный», образованное от бесприставочного глагола совершенного вида «бросить», пишется с -нн- в суффиксе -енн-.
Алексашка на лету подхватил брошенный рубль (Алексей Толстой. Пётр Первый).
Сравним с написанием слов:
Понаблюдаем за написанием форм анализируемого страдательного причастия.
Примеры предложений
Какая неведомая катастрофа искрошила этот огромный мыс, брошенный между двух океанов! (Жюль Верн. Дети капитана гранта).
Это дикое проявление жизненного брожения, этот буйный мятеж и вызов, брошенный ему движущейся материей, поразили и заинтересовали его (Джек Лондон. Морской волк).
Брошенное кем-то, это предложение было принято с восторгом, но, к счастью, пробило одиннадцать часов (Александр Дюма. Три мушкетёра).
Он радовался, видя, как рыба, брошенная в воду, уплыла, весело махнув хвостом (Александр Беляев. Человек-амфибия).
Первые шесть лодок, подхваченные прибоем и брошенные на скалы, превратились в щепки еще до того, как находившиеся в них люди смогли броситься в воду (Рафаэль Сабатини.
Одиссея капитана Блада).
Это написание с -нн- имеют все слова, образованные от бесприставочных глаголов совершенного вида.
Правописание слов, образованных от бесприставочных глаголов
Такое же написание с -нн- прослеживается у всех слов, образованных от бесприставочных глаголов совершенного вида. Перечислим их:
бросить, встретить, воспитать, дать, кончить, купить, лишить, обидеть, основать, пленить, простить, пустить и пр.
Убедимся в этом:
- (что сделать?) купить — купленный шкаф;
- лишить — лишенный слова;
- решить — решенный вопрос;
- пустить — пущенная стрела.
В составе некоторых устойчивых словочетаний имеются омонимичные прилагательные, которые пишутся с одной буквой «н». Запомним их написание.
Исключения:
- названый брат;
- названая сестра;
- конченый человек;
- посажёный отец;
- посажёная мать;
- Прощёное Воскресенье.
Будет ли мяч, брошенный прямо в поезд, приземлиться в том же месте (в реальном мире)?
Нет, мяч не приземляется точно в одно и то же место, даже при отсутствии какого-либо воздуха. Однако в реальном мире эффекты в поезде, вероятно, слишком малы, чтобы их можно было наблюдать без тщательной экспериментальной установки.
Ответ dmckee описывает физику в инерциальной системе отсчета. Однако, поскольку Земля вращается, шар испытывает зависящую от скорости силу Кориолиса . Эта сила исходит от движения шара и вращения Земли, поэтому ее величина порядка м в / т м v / T , с v v скорость мяча, м м его масса, и T T время, необходимое для вращения Земли — один день. Точная величина зависит от угла между скоростью поезда и осью Земли. Сила перпендикулярна скорости шара.
Если эта сила отталкивает шар в сторону от его траектории, расстояние, на которое он уходит, должно быть порядка т 2 T 2 с ускорение и T T время в воздухе. Если он находится в воздухе около секунды, отклонение мало, потому что секунда мала по сравнению с днем. Вы получите что-то вокруг 10 — 5 V S 10 — 5 v s так что даже если поезд идет 100 м / с 100 м / s Вы все еще получаете только миллиметры отклонения.
Если он находится в воздухе около секунды, отклонение мало, потому что секунда мала по сравнению с днем. Вы получите что-то вокруг 10 — 5 V S 10 — 5 v s так что даже если поезд идет 100 м / с 100 м / s Вы все еще получаете только миллиметры отклонения.
Если поезд движется с постоянной скоростью, любые колебания, вызванные некоторое время назад ускорением, должны уравновеситься, и воздух должен быть подобен обычному неподвижному воздуху (за исключением повторения сил Кориолиса в воздухе). Как упоминал Рон Маймон, это происходит довольно быстро. Как быстро? Попробуйте петь в душе. Когда вы получите хороший резонанс, внезапно прекратите петь и посмотрите, как долго звучит нота. Может быть, десятая часть секунды. Физически это примерно тот же механизм, поэтому колебания воздуха, вызванные ускорением поезда, исчезнут в аналогичном масштабе времени, плюс или минус на порядок, чтобы приспособиться к размеру вагона и граничным условиям на стены.
Как насчет объемного движения воздуха? Попробуйте включить вентилятор, а затем внезапно остановить его палкой? Как долго ты еще чувствуешь ветер? Может быть, немного дольше, порядка секунд на этот раз, но опыт все же сообщает нам, что это тоже быстро умирает. Я думаю, что замечание Рона в комментариях о том, что по существу нет колебаний или токов, установленных ускорением поезда, является правильным. Шкала времени, в течение которой воздух уравновешивается, является быстрой по сравнению со временем, в течение которого поезд ускоряется, поэтому воздух по существу всегда находится в равновесии.
Рон Маймон Затухание звука происходит по другому механизму (тепловой поток между соседними адиабатически сжатыми областями), чем затухание скорости для объемной циркуляции воздуха, и нет никакой связи между шкалой времени. Если вы настроите движение воздуха в душе, оно будет циркулировать гораздо дольше, чем будет звучать звуковая волна. Что касается силы Кориолиса, то она исчезнет, когда поезд движется с востока на запад по экватору, и я полагаю, что плакат должен был игнорировать этот эффект.
Марк Айхенлауб
@ Рон Кориолис исчезает, когда вы двигаетесь с севера на юг по экватору, а не с востока на запад. Когда вы двигаетесь с востока на запад, это параллельно гравитации. Я подумаю больше о том, что вы сказали об ослаблении звука.
Рон Маймон
Сила Кориолиса не будет параллельна гравитации — она будет толкать шар в направлении вращения Земли при падении, это прямая сила. Движение шаров вверх-вниз, а сила Кориолиса перпендикулярна движению и оси вращения. Я был совершенно неправ. Вам придется идти в любом направлении на полюсах. Но этот эффект не является целью вопроса — циркуляция воздуха.
Марк Айхенлауб
@ Рон Я рассчитывал Кориолиса из-за движения поезда, а не из-за движения вверх / вниз. Вопрос заключался в том, что «если я брошу мяч прямо в закрытом поезде вагоне, движущемся с постоянной скоростью, я считаю, что в базовых учебниках по физике говорится, что он приземлится в том же месте. Но так ли это на самом деле?». Кориолис имеет отношение к этому. ОП не обсуждал это, скорее всего потому, что не знал об этом. Я согласен с тем, что существуют разные механизмы рассеивания энергии в воздухе, но поскольку я непосредственно обращался к вибрациям, я оставлю аналогию со звуком, добавив примечание о объемном движении.
Дейв
Спасибо Марк. Я пренебрег Кориолисом из-за этой проблемы. Меня больше интересовало, как воздух передает силу, как указал Рон.
Волчата удивили учёных: они впервые принесли брошенный им мяч
Если бросить мячик домашнему псу – он скорее всего его принесёт. Новое исследование показало, что волчата тоже умеют приносить мяч.
Считалось, что собачья способность понимать социальные и коммуникационные сигналы человека появилась только после приручения – около 15 000 лет назад. Оказывается, эта уникальная способность есть и у волков.
Последние три года исследователь Кристина Хансен Уит из Стокгольмского университета разводила волков и собак в одинаковых условиях.![]() Она собирала данные для того, чтобы выяснить – каким образом собаки стали лучшими друзьями человека. Ее команда наблюдала за 13 щенками волков из трех разных помётов.
Она собирала данные для того, чтобы выяснить – каким образом собаки стали лучшими друзьями человека. Ее команда наблюдала за 13 щенками волков из трех разных помётов.
Каждое животное воспитывалось человеком с десятидневного возраста и подвергалось различным поведенческим тестам. Один из них: незнакомец (животное видит человека впервые) бросает теннисный мяч и просит щенка принести его. Щенков оценивали по пятибалльной шкале, где единица – полное игнорирование мяча, а пятёрка – реагирование и возвращение игрушки человеку.
Первые два помёта не интересовались мячом, и ученые решили, что эксперимент провалился. Но третий помёт оказался более дружелюбным. Три восьминедельных волчонка проявили интерес к мячу: один из них принёс игрушку три раза из трёх, два остальных – два из трёх.
«Когда я увидела, как первый волчонок берёт в зубы мяч и возвращает его, по моей спине буквально пробежали мурашки», – сказала Кристина Хансен Уит.
По мнению учёных, качества, которыми обладают домашние собаки, появились не после приручения. Они – природная вариация поведения. Древние люди просто брали на воспитание самых послушных и дружелюбных волков.
Команда исследователей продолжит изучать данные, собранные за три года, чтобы подробнее изучить поведенческие различия и сходства собак и волков.
Источник
Футболист «Барселоны» съел брошенный ему с трибуны банан
Автор фото, Reuters
Подпись к фото,Дани Алвес выступает за ужесточение наказаний за проявления расизма на трибунах
Защитник «Барселоны» Дани Алвес поднял брошенный в него во время футбольного матча банан, очистил его и надкусил. Это произошло в гостевом матче чемпионата Испании против «Вильярреала».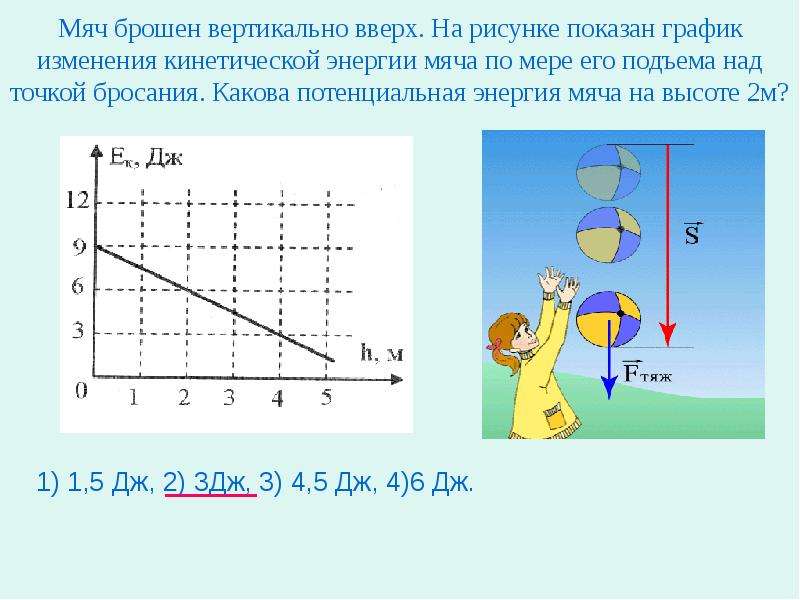 Прожевав банан, бразильский футболист ввел мяч в игру.
Прожевав банан, бразильский футболист ввел мяч в игру.
Экс-игрок «Барселоны» и сборной Англии, комментатор Би-би-си Гари Линекер похвалил Алвеса за такой жест: «Совершенно блестящая реакция Алвеса. Отнестись к расистской тупости с полным презрением!».
Стадиону «Эль Мадригал» в пригороде Валенсии за расистскую выходку одного из болельщиков теперь может грозить дисквалификация и штраф.
Алвес оказался причастен к двум голам своей команды в игре, которую «Барселона» выиграла со счетом 3:2. За три тура до финиша испанского чемпионата каталонский клуб на четыре очка отстает от мадридского «Атлетико».
Против расизма
Алвес, который уже 12 лет играет в Испании, заявил после матча, что над подобными выходками отсталых людей нужно просто смеяться.
Партнер футболиста по клубу и бразильской сборной Неймар назвал этот инцидент позорным.
«Мы все обезьяны, и мы все одинаковые. Скажите нет расизму!», — написал Неймар на своей странице в Instagram, где он также выложил собственную фотографию с бананом в руке.
В январе 2013 года Дани Алвес заявил, что подвергся расистским оскорблениям во время матча против «Реала» в Мадриде со стороны болельщиков.
Бразильский легионер не раз призывал испанскую футбольную лигу ужесточить наказания за любые проявления расизма на стадионах.
Бананы в России
За последние несколько лет в футбольном чемпионате России произошло несколько инцидентов с бананами. В 2011 году дважды объектом оскорблений становился чемпион мира в составе сборной Бразилии Роберто Карлос, выступавший за «Анжи» из Махачкалы.
Тогда Роберто Карлос в знак протеста снял с себя капитанскую повязку и покинул поле, не дожидаясь финального свистка, сел на скамейку запасных и накрылся полотенцем. По словам именитого футболиста, он испытал «сильнейшее разочарование».
В 2012 году банан бросили в другого игрока «Анжи», конголезца Кристофера Самба. Это произошло на московском стадионе «Локомотив». Самба в ответ поднял банан и кинул его обратно на трибуну.
Это произошло на московском стадионе «Локомотив». Самба в ответ поднял банан и кинул его обратно на трибуну.
В прошлом году дисциплинарный комитет УЕФА распорядился закрыть одну из трибун стадиона «Арена Химки» заоскорбительные выкрики болельщиков ЦСКАв адрес игрока «Манчестер Сити» Яя Туре во время матча Лиги чемпионов.
Защитник «Барселоны» съел брошенный в него банан во время матча :: Футбол :: РБК Спорт
Во время матча испанской Примеры «Вильярреал» — «Барселона» фанаты хозяев бросили в защитника каталонцев Даниэла Алвеса с трибуны банан.
Читайте нас в
Новости НовостиФото: AP
Интересно, что «Барселона» проигрывала в данном матче со счетом 2:0, но в итоге одержала победу. Сначала сам Алвес исполнил прострел и мяч рикошетом от Паулисты залетел в ворота хозяев, а уже после того, как футболист подкрепился, заставил ошибиться Музаккьо.
Победную точку в матче поставил Лионель Мессси на 83-й минуте.
Я живу в Испании уже 11 лет. Над этими отсталыми людьми можно только посмеяться», — приводит слова игрока испанская пресса.
Поддержал Алвеса его партнер по команде Неймар. «Мы все обезьяны», — написал бразилец в своем инстаграм.
Фото — Инстаграм Неймара
Чемпионат Испании. Примера. 35-й тур
«Вильярреал» (Вильярреал) – «Барселона» (Барселона) – 2:3 (1:0)
Голы: Кани, 45, Тригерос, 55 — Паулиста, 65 (автогол), Музаккьо, 78 (автогол), Месси, 83
1) Мяч, брошенный вертикально вверх, падает на землю. Найдите график зависимости от времени проекции скорости на вертикальную ось, направленную вверх.
Решение задач ЕГЭ части С: Электростатика
С1.1. Около небольшой металлической пластины, укрепленной на изолирующей подставке, подвесили на шелковой нити легкую металлическую незаряженную гильзу. Когда пластину подсоединили к клемме высоковольтного
Подробнее2,5 2,5. a x, м/с 2 2,5
Часть 1 Ответами к заданиям 1 4 являются цифра, число или последовательность цифр. Запишите ответ в поле ответа в тексте работы, а затем перенесите в БЛАНК ОТВЕТОВ 1 справа от номера соответствующего задания,
ПодробнееВариант Задание 1
Параграфы 88-93 повторить выполнить упражнение 12. Выполнить тест Вариант 3679536 1. Задание 1 На рисунке изображены графики зависимости модуля скорости движения четырёх автомобилей от времени. Один из
Выполнить тест Вариант 3679536 1. Задание 1 На рисунке изображены графики зависимости модуля скорости движения четырёх автомобилей от времени. Один из
Класс Фамилия, имя (полностью) Дата 2015 г.
Класс Фамилия, имя (полностью) Дата 05 г Инструкция по выполнению работы На выполнение работы по физике отводится 90 минут Работа состоит из частей, включающих в себя 0 заданий Часть содержит 5 заданий
ПодробнееОтложенные задания (25)
Отложенные задания (25) В области пространства, где находится частица с массой 1 мг и зарядом 2 10 11 Кл, создано однородное горизонтальное электрическое поле. Какова напряжённость этого поля, если из
ПодробнееЗадание 1. Ответ: 31.
Задание 1. Установите соответствие между физическими величинами, описывающими протекание постоянного тока через резистор, и формулами для их расчёта. В формулах использованы обозначения: R сопротивление
Подробнее/6 A Б В Г Д
Вариант 3366482 1. На рисунке приведен график зависимости проекции скорости тела от времени. Чему равна проекция ускорения тела в момент времени 45 с? Ответ выразите в м/с 2. 2. На брусок массой 5 кг,
ПодробнееФизика ЕГЭ 2015 Тренировочный вариант 2
Часть 1 1. После толчка брусок скользит вверх по наклонной плоскости. В системе отсчета, связанной с плоскостью, направление оси 0x показано на рисунке. Направления векторов скорости бруска, его ускорения
ПодробнееЧасть А. n n A A 3) A
ЭЛЕКТРОДИНАМИКА Кириллов А.М., учитель гимназии 44 г. Сочи (http://kirilladrey7. arod.ru/) Данная подборка тестов сделана на основе учебного пособия «Веретельник В.И., Сивов Ю.А., Толмачева Н.Д., Хоружий
arod.ru/) Данная подборка тестов сделана на основе учебного пособия «Веретельник В.И., Сивов Ю.А., Толмачева Н.Д., Хоружий
Вариант 1 Часть
Вариант 1 При выполнении заданий части 1 запишите номер выполняемого задания, а затем номер выбранного ответа или ответ. Единицы физических величин писать не нужно. 1. По проводнику течѐт постоянный электрический
ПодробнееФизика ЕГЭ 2015 Тренировочный вариант 1
Часть 1 1. Тело начинает двигаться из начала координат вдоль оси Ох, причем проекция скорости v x меняется с течением времени по закону, приведенному на графике. Через 2 с ускорение тела равно 1) 0 м/с
ПодробнееКраевая диагностическая работа по ФИЗИКЕ
ФИЗИКА, класс Вариант, Октябрь 2009 Краевая диагностическая работа по ФИЗИКЕ ВАРИАНТ При выполнении заданий А А8 в бланке ответов под номером выполняемого задания поставьте знак «х» в клеточку, номер которой
ПодробнееID_969 1/8 neznaika.pro
Вариант 1 Часть 1 Ответами к заданиям 1 23 являются слово, число или последовательность цифр или чисел. Запишите ответ в соответствующее поле справа. Каждый символ пишите без пробелов. Единицы измерения
ПодробнееОтвет: 35. Ответ: 21.
Задачи по теме «Электродинамика» (тексты Демидовой М.Ю. ЕГЭ-2017) Вариант 1 Задание 14. Пять одинаковых резисторов с сопротивлением 1 Ом соединены в электрическую цепь, через которую течёт ток I = 2 А
Подробнееmυ 2 /R = qυb. sin α = d/r
Задача 1 Альфа-частица, пройдя ускоряющую разность потенциалов U, влетает в однородное магнитное поле с индукцией В. Толщина области поля d. Определите, на сколько изменится ее импульс за время пролета
Толщина области поля d. Определите, на сколько изменится ее импульс за время пролета
ν моль гелия, а в другой ν = 3
Второй (заключительный) этап академического соревнования Олимпиады школьников «Шаг в будущее» по образовательному предмету «Физика», З А Д А Ч А весна 7 г Вариант 3 Два тела, находящиеся на одной высоте,
ПодробнееОбразец возможного решения
Физика. 11 класс. Вариант 1 1 Критерии оценивания заданий с развёрнутым ответом C1 Медный стержень укреплен на штативе в горизонтальном положении. К нижней поверхности стержня на равных расстояниях друг
ПодробнееБанк заданий по физике 10 класс
Банк заданий по физике 1 класс МЕХАНИКА Равномерное и равноускоренное прямолинейное движение 1 На рисунке приведён график зависимости координаты тела от времени при его прямолинейном движении по оси x.
ПодробнееЧасть 3. задания Ответ В1 123 В2 43 В3 150 В В5 2,7
Инструкция по проверке и оценке работ учащихся по физике Вариант Часть За правильный ответ на каждое задание части ставится балл. Если указаны два и более ответов (в том числе правильный), неверный ответ
ПодробнееОлимпиада «Физтех» по физике 2017
Олимпиада «Физтех» по физике 217 Класс 11 Билет 11-3 Шифр 1. На наклоненной под углом ( cos 3/ 4 ) к горизонту поверхности лежит брусок, прикрепленный к упругой невесомой и достаточно длинной пружине (см.
ПодробнееОЛИМПИАДА ПО ФИЗИКЕ Вариант А
ОЛИМПИАДА ПО ФИЗИКЕ 7 Вариант А. С какой горизонтальной скоростью нужно бросить камень с вершины горы, склон которой образует угол с горизонтом, чтобы он упал на склон горы на расстоянии L от вершины?
ПодробнееЗадача одномерной кинематики: мяч, брошенный прямо вверх — Физика
Шаг 1:
Скорость, когда мяч покинул вашу руку (точка 1) — это информация, запрошенная в части а) задачи.
————————————————- ——————————————-
Шаг 2:
В части b) задачи запрашивается количество времени, в течение которого мяч находился в воздухе (между точками 1 и 3.) Никаких дополнительных математических решений не требуется.
В постановке задачи указаны все вертикальные положения относительно земли, поэтому я выбрал землю в качестве точки y = 0.
Первый момент, описанный в задаче, — это когда мяч покидает вашу руку. В этой точке мяч находится на высоте 1,2 м над землей, которая была выбрана в качестве контрольной точки y = 0. Вы не знаете, с какой скоростью движется мяч, покидая вашу руку, поэтому v 1 неизвестно.
Мяч поднимается на высоту 3.3 м над землей или 3,3 м над точкой y = 0. На этом этапе у вас также есть информация о скорости. Вы знаете, что гравитация заставляет объект замедляться при движении вверх и ускоряться при движении вниз. В верхней части движения (наивысшая точка) вертикальная (или y) составляющая скорости объекта равна нулю.
В последней точке задачи мяч достигает земли или нулевой высоты. Очень распространенная ошибка полагать, что скорость мяча в этой точке равна нулю.Но помните, что кинематические уравнения применимы только в периоды постоянного ускорения. Как только мяч касается земли, земля очень быстро замедляет его — у него больше нет ускорения, равного g. Итак, точка 3 — это точка непосредственно перед тем, как мяч коснется земли.
В этом случае мяч движется строго вертикально. У вас есть только движение в направлении y. Следовательно, вам не нужно разделять какие-либо переменные на их x- и y-компоненты.
Я нарисовал движение мяча по параболе, а не по прямой вверх и вниз, только для того, чтобы четко обозначить точки 1, 2 и 3 на рисунке.
t в кинематических уравнениях относится к интервалу времени между двумя точками в уравнении, причем y 0 происходит в более ранний момент времени. Я использую Δt вместо t, чтобы явно указать, что это временной интервал (t — t 0 ), а не момент времени.
Я использую Δt вместо t, чтобы явно указать, что это временной интервал (t — t 0 ), а не момент времени.
В некоторых учебниках приводится более трех кинематических уравнений — например, они могут содержать «уравнения дальности» или различные версии уравнений для горизонтального и вертикального движения. Это как раз те три уравнения, которые решаются для частных случаев.На мой взгляд, лучше знать и понимать три уравнения, которые всегда будут работать, чем запоминать множество уравнений, характерных только для определенных ситуаций.
Вам предлагается найти скорость мяча в точке 1 (когда он покидает вашу руку), чтобы он имел необходимое движение в точке 2 (достигает высоты 3,3 м). Следовательно, «y 0 » и «y» равны «y 1 » и «y 2 » соответственно.
Ускорение мяча (из-за силы тяжести) направлено вниз, что является отрицательным y-направлением, выбранным в этой задаче.Поскольку a, v и y являются векторными величинами, их значениям должны быть присвоены знаки + или — для обозначения направления всякий раз, когда они вводятся в любое из кинематических уравнений.
Многие из наиболее распространенных ошибок в кинематических задачах можно избежать, внимательно следя за бухгалтерским учетом. Когда мы рисовали картинку, мы были осторожны, чтобы пометить каждую точку интереса другим нижним индексом, и когда мы заполняем уравнение, мы должны быть осторожны, чтобы ввести правильное значение для правильной точки.Мы не можем предположить, что нулевые значения совпадают с более ранним моментом времени. Фактически в этом выражении нулевая скорость возникает в верхней части движения (точка 2), а не в начале (точка 1).
В тексте задачи приведены только две значащие цифры, поэтому в решение включены только две значащие цифры.
Вас просят определить количество времени, которое требуется мячу, чтобы добраться от точки 1 (когда он покидает вашу руку) до земли (точка 3.) Следовательно, «y 0 » и «y» равны «y 1 » и «y 3 » соответственно.
Чтобы найти Δt в этом уравнении, примите во внимание, что у вас есть квадратное уравнение: оно имеет вид a Δt 2 + b Δt + c = 0, где a = -4,9, b = 6,4 и c = 1,2. (Быстрый взгляд на единицы измерения показывает, что Δt должно быть в секундах, поэтому я не буду переносить единицы измерения в алгебру для решения квадратного уравнения просто потому, что я хочу избежать путаницы, когда вы сосредотачиваетесь на математике.)
Решение квадратного уравнения дается выражением:
Обратите внимание, что квадратная формула всегда дает два решения. По сути, это формула для полной параболической дуги, и двумя решениями будут времена, когда объект находится на любой заданной высоте в этой дуге (один раз поднимается, а один раз возвращается). В этом случае мяч не был брошен с земли. Если бы было брошено с земли (с такой скоростью, чтобы следовать по тому же пути), он получил бы 0.16 с, чтобы попасть с земли в руку. Чтобы вернуться от руки к земле, требуется еще 1,5 секунды, а это именно та информация, которую вы хотите найти.
Ускорение мяча (из-за силы тяжести) направлено вниз, что является отрицательным направлением оси y, выбранным в этой задаче. Поскольку a, v и y являются векторными величинами, их значениям должны быть присвоены знаки + или — для обозначения направления всякий раз, когда они вводятся в любое из кинематических уравнений.
В тексте задачи приведены только две значащие цифры, поэтому в решение включены только две значащие цифры.
Многие из наиболее распространенных ошибок в кинематических задачах можно избежать, внимательно следя за бухгалтерским учетом. Когда мы рисовали картинку, мы были осторожны, чтобы пометить каждую точку интереса другим нижним индексом, и когда мы заполняем уравнение, мы должны быть осторожны, чтобы ввести правильное значение для правильной точки. Мы не можем предположить, что нулевые значения совпадают с более ранним моментом времени. Фактически в этом выражении положение y = 0 происходит в конце движения (точка 3), а не в начале (точка 1. )
)
Обратите внимание, что квадратная формула всегда дает два решения. По сути, это формула для полной параболической дуги, и двумя решениями будут времена, когда объект находится на любой заданной высоте в этой дуге (один раз поднимается, а один раз возвращается). В этом случае мяч не был брошен с земли. Если бы он был брошен с земли (с такой скоростью, чтобы следовать по тому же пути), ему потребовалось бы 0,16 с, чтобы добраться от земли до вашей руки. Требуется дополнительный 1.5 секунд, чтобы вернуться из руки в землю, и это информация, которую вы хотите найти.
Как выбрать y = 0?
Все, что имеет значение для описания движения, — это то, что вы явно указываете, где находится ваша контрольная точка. В этом случае проблема давала высоту относительно земли, поэтому я выбрал точку отсчета. Если вы выбрали начальную точку (вашу руку) как y = 0, тогда земля будет на y = -1,2 м, а y 2 будет 2.1 мес. В любом случае вы получите одинаковые ответы.
Почему вы нарисовали траекторию мяча в виде параболы, а не показывали его прямо вверх и вниз?
Это просто для удобства отображения всех трех точек на диаграмме. Точка 3 действительно находится прямо под точкой 1.
В моей книге в уравнениях используется «t», а не «Δt». Это нормально?
или жеВ моей книге приведено более трех уравнений. Почему вы используете только эти три?
t в кинематических уравнениях относится к интервалу времени между двумя точками в уравнении, причем y 0 происходит в более ранний момент времени.Я использую Δt, а не t, чтобы явно указать, что это временной интервал (t — t 0 ), а не момент времени.
В некоторых учебниках приводится более трех кинематических уравнений — например, они могут содержать «уравнения дальности» или различные версии уравнений для горизонтального и вертикального движения. Это как раз те три уравнения, которые решаются для частных случаев. На мой взгляд, лучше знать и понимать три уравнения, которые всегда будут работать, чем запоминать множество уравнений, характерных только для определенных ситуаций.
Как вы узнали, какие две точки выбрать?
Вас просят определить количество времени, которое требуется мячу, чтобы добраться от точки 1 (когда он покидает вашу руку) до земли (точка 3). Следовательно, «y 0 » и «y» равны «y». 1 »и« y 3 »соответственно.
Почему 9,8 м / с
2 отрицательно?Ускорение мяча (из-за силы тяжести) направлено вниз, что является отрицательным направлением оси y, выбранным в этой задаче.Поскольку a, v и y являются векторными величинами, их значениям должны быть присвоены знаки + или — для обозначения направления всякий раз, когда они вводятся в любое из кинематических уравнений.
Почему v
2 0 вместо v 1 ?Многие из наиболее распространенных ошибок в кинематических задачах можно избежать, внимательно следя за бухгалтерским учетом. Когда мы рисовали картинку, мы были осторожны, чтобы пометить каждую точку интереса другим нижним индексом, и когда мы заполняем уравнение, мы должны быть осторожны, чтобы ввести правильное значение для правильной точки.Мы не можем предположить, что нулевые значения совпадают с более ранним моментом времени. Фактически в этом выражении положение y = 0 происходит в конце движения (точка 3), а не в начале (точка 1).
Мои числа близки, но не совсем те, которые показаны в уравнении. Достаточно ли я близок?
В тексте задачи приведены только две значащие цифры, поэтому в решение включены только две значащие цифры.
Как вы узнали, какие две точки выбрать?
Вас просят определить количество времени, которое требуется мячу, чтобы добраться от точки 1 (когда он покидает вашу руку) до земли (точка 3.) Следовательно, «y 0 » и «y» равны «y 1 » и «y 3 » соответственно.
Почему 9,8 м / с
2 отрицательно? Ускорение мяча (из-за силы тяжести) направлено вниз, что является отрицательным направлением оси y, выбранным в этой задаче. Поскольку a, v и y являются векторными величинами, их значениям должны быть присвоены знаки + или — для обозначения направления всякий раз, когда они вводятся в любое из кинематических уравнений.
Поскольку a, v и y являются векторными величинами, их значениям должны быть присвоены знаки + или — для обозначения направления всякий раз, когда они вводятся в любое из кинематических уравнений.
Почему v
3 0 вместо y 1 ?Многие из наиболее распространенных ошибок в кинематических задачах можно избежать, внимательно следя за бухгалтерским учетом.Когда мы рисовали картинку, мы были осторожны, чтобы пометить каждую точку интереса другим нижним индексом, и когда мы заполняем уравнение, мы должны быть осторожны, чтобы ввести правильное значение для правильной точки. Мы не можем предположить, что нулевые значения совпадают с более ранним моментом времени. Фактически в этом выражении положение y = 0 происходит в конце движения (точка 3), а не в начале (точка 1).
Как вы решили для Δt?
Чтобы найти Δt в этом уравнении, примите во внимание, что у вас есть квадратное уравнение: оно имеет вид a Δt 2 + b Δt + c = 0, где a = -4.9, b = 6,4 и c = 1,2. (Быстрый взгляд на единицы показывает, что Δt должно быть в секундах, поэтому я не буду переносить единицы измерения в алгебру для решения квадратного уравнения просто потому, что я хочу избежать путаницы, когда вы сосредотачиваетесь на математике.)
Решение квадратного уравнения дается выражением:
Обратите внимание, что квадратная формула всегда дает два решения. По сути, это формула для полной параболической дуги, и двумя решениями будут времена, когда объект находится на любой заданной высоте в этой дуге (один раз поднимается, а другой возвращается назад.) В этом случае мяч не был брошен с земли. Если бы было брошено с земли (с такой скоростью, чтобы следовать по тому же пути), то чтобы добраться от земли до вашей руки, потребовалось бы 0,16 с. Чтобы вернуться от руки к земле, требуется еще 1,5 секунды, а это именно та информация, которую вы хотите найти.
Мои числа близки, но не совсем те, которые показаны в уравнении.
 Достаточно ли я близок?
Достаточно ли я близок?В тексте задачи приведены только две значащие цифры, поэтому в решение включены только две значащие цифры.
Какое ускорение у мяча? Откуда вы знаете?
В этой задаче вам явно предлагается игнорировать сопротивление воздуха. (Даже если вы этого не сделали, сопротивление воздуха объектам, предназначенным для использования в качестве снарядов, движущихся с низкой скоростью, обычно довольно мало.) Следовательно, единственной существенной причиной ускорения мяча является сила тяжести. Для всех объектов у поверхности Земли ускорение силы тяжести g, направленное вниз, имеет значение 9.8 м / с 2 . (Если вы уже изучили силы, вы можете быстро увидеть это на диаграмме свободного тела.)
Как выбрать y = 0?
Все, что имеет значение для описания движения, — это то, что вы явно указываете, где находится ваша контрольная точка. В этом случае проблема давала высоту относительно земли, поэтому я выбрал точку отсчета. Если вы выбрали начальную точку (вашу руку) как y = 0, тогда земля будет на y = -1,2 м, а y 2 будет 2.1 мес. В любом случае вы получите одинаковые ответы.
Мяч был брошен прямо вверх. Почему вы показали это параболическим путем?
Это просто для удобства отображения всех трех точек на диаграмме. Точка 3 действительно находится прямо под точкой 1.
В моей книге используются такие переменные, как y, y
0 , v, v 0 и t. Почему вы используете 1, 2 и 3 в качестве индексов, а Δt вместо t? Кинематические уравнения связывают положение и скорость в любых двух точках движения.Поскольку многие задачи предоставляют или запрашивают информацию более чем в двух точках, я помечаю каждую точку своим собственным индексом, чтобы они оставались правильными. Затем я могу выбрать любые две точки как y 0 и y, когда я использую уравнения. T в кинематических уравнениях относится к интервалу времени между двумя точками в уравнении, причем y 0 происходит в более раннее время. Я использую Δt вместо t, чтобы явно указать, что это временной интервал (t — t 0 ), а не момент времени.
Я использую Δt вместо t, чтобы явно указать, что это временной интервал (t — t 0 ), а не момент времени.
Projectile Motion
Projectile Motion Движение снаряда| Объект подбрасывается прямо с вершины здания высотой h футов с начальной скоростью v футов в секунду. Высота объекта как функция времени может быть смоделирована функцией h (t) = –16t 2 + vt + h, где h (t) — высота объекта (в футах) через t секунд после него. брошен. Если нам задана начальная скорость (или скорость) объекта и высота здания, мы можем использовать эту модель, чтобы определить, сколько времени требуется, чтобы объект достиг разной высоты.В этой модели предполагается, что объект не попадает в верхнюю часть здания на обратном пути к земле и что сопротивление ветра минимально. |
Вот шаги, необходимые для решения проблем движения снаряда:
| Шаг 1 : | Установите данное уравнение равным соответствующей высоте. |
| Шаг 2 : | Решите уравнение, найденное на шаге 1, приравняв уравнение нулю и разложив уравнение на множители. |
| Шаг 3 : | В зависимости от проблемы определите, какой ответ или ответы верны. Не забудьте указать единицы в своем окончательном ответе. |
Пример 1 — Мяч подбрасывается прямо с вершины здания высотой 128 футов с начальной скоростью 32 фута в секунду. Высота шара как функция времени может быть смоделирована функцией h (t) = –16t 2 + 32t + 128.Сколько времени потребуется, чтобы мяч коснулся земли?
Шаг 1 : Установите данное уравнение равным соответствующей высоте. В этом случае мы устанавливаем уравнение равным нулю, потому что высота земли равна нулю. В этом случае мы устанавливаем уравнение равным нулю, потому что высота земли равна нулю. | |
| Шаг 2 : Решите уравнение, найденное на шаге 1, установив уравнение равным нулю и разложив уравнение на множители. | |
| Шаг 3 : В зависимости от проблемы определите, какой ответ или ответы верны.Не забудьте указать единицы в своем окончательном ответе. В этом случае есть только один положительный ответ, который имеет смысл, потому что мяч ударяется о землю только один раз. |
Пример 2 — Мяч подбрасывается прямо с вершины здания высотой 288 футов с начальной скоростью 48 футов в секунду. Высота мяча как функция времени может быть смоделирована функцией h (t) = –16t 2 + 48t + 288. Когда мяч достигнет высоты 320 футов?
| Шаг 1 : Установите данное уравнение равным соответствующей высоте.В этом случае мы устанавливаем уравнение равным 320, потому что мы хотим определить, когда высота будет 320 футов. | |
| Шаг 2 : Решите уравнение, найденное на шаге 1, установив уравнение равным нулю и разложив уравнение на множители. | |
| Шаг 3 : В зависимости от проблемы определите, какой ответ или ответы верны. Не забудьте указать единицы в своем окончательном ответе.В этом случае есть два положительных ответа, которые имеют смысл, потому что мяч достигнет 320 футов один раз на пути вверх и еще раз на пути вниз. |
Нажмите здесь для практических задач
Пример 3 — Ракета запускается прямо с вершины здания высотой 24 фута с начальной скоростью 92 фута в секунду. Высота ракеты как функция времени может быть смоделирована функцией h (t) = –16t 2 + 92t + 24.Сколько времени потребуется, чтобы ракета упала на землю?
Высота ракеты как функция времени может быть смоделирована функцией h (t) = –16t 2 + 92t + 24.Сколько времени потребуется, чтобы ракета упала на землю?
| Шаг 1 : Установите данное уравнение равным соответствующей высоте. В этом случае мы устанавливаем уравнение равным нулю, потому что высота земли равна нулю. | |
| Шаг 2 : Решите уравнение, найденное на шаге 1, установив уравнение равным нулю и разложив уравнение на множители. | |
| Шаг 3 : В зависимости от проблемы определите, какой ответ или ответы верны.Не забудьте указать единицы в своем окончательном ответе. В этом случае есть только один положительный ответ, который имеет смысл, потому что мяч ударяется о землю только один раз. |
Нажмите здесь для практических задач
Пример 4 — Мяч падает прямо в воздухе с высоты 4 фута с начальной скоростью 64 фута в секунду. Высота шара как функция времени может быть смоделирована функцией h (t) = –16t 2 + 64t + 4.Когда мяч достигнет высоты 52 футов?
| Шаг 1 : Установите данное уравнение равным соответствующей высоте. В этом случае мы устанавливаем уравнение равным 52, потому что мы хотим определить, когда высота будет 52 фута. | |
| Шаг 2 : Решите уравнение, найденное на шаге 1, установив уравнение равным нулю и разложив уравнение на множители. | |
Шаг 3 : В зависимости от проблемы определите, какой ответ или ответы верны.Не забудьте указать единицы в своем окончательном ответе. В этом случае есть два положительных ответа, которые имеют смысл, потому что мяч достигнет 52 футов один раз на пути вверх и еще раз на пути вниз. В этом случае есть два положительных ответа, которые имеют смысл, потому что мяч достигнет 52 футов один раз на пути вверх и еще раз на пути вниз. |
Нажмите здесь для практических задач
домашних заданий и упражнений — Что происходит с импульсом системы земля-шар, когда мяч подбрасывается вверх?
Я бы сказал о линейном импульсе везде, где я использовал слово импульс.
Я увидел вопрос, который был задан в моем учебнике: —
Когда мяч брошен вверх от поверхности земли, тогда: —
- Земля и шар движутся навстречу друг другу.
- Земля неподвижна, и мяч движется вверх.
- Земля и шар удаляются друг от друга.
- Ничего из этого.
Ответ: — (3) Земля и шар удаляются друг от друга, чтобы сохранить импульс.
Ниже приводится последовательность событий, через которые я прошел: —
Событие 1
Прочитал вопрос и попытался решить.Я подумал, что ответом будет ни один из них, потому что, во-первых, вопрос довольно неясен, потому что он не описывает, каким образом мяч подбрасывается вверх? Я подумал о следующем конкретном случае: —
На этом изображении мужчина держит мяч в руке и может бросить его вверх.
Если мы возьмем землю и шар в качестве нашей системы, то внешние силы в этой системе равны
.Нормальная реакция на земле из-за веса человека.
Сила, с которой он подбрасывает мяч вверх.
С этими мыслями я предположил, что количество движения этой системы не сохраняется.
В следующий момент я предположил, что человек безмассовый (имеющий незначительную массу), тогда нормальная реакция между землей и человеком исчезает, но все еще существует чистая внешняя сила, которая представляет собой силу, приложенную рукой человека к мячу.
Проведя анализ, я пришел к выводу, что импульс системы не сохраняется.
Событие 2
Я спросил своего учителя о своих предположениях.Он сказал, что они правы, но сказал, что импульс все еще сохраняется. Он объяснил причину, по которой, когда мяч брошен вверх, время контакта между рукой и мячом очень мало, а сила контакта слишком мала, так что импульс передаваемый в систему, очень мал, которым можно пренебречь.
Событие 3
Я снова проанализировал аргументы своего учителя и пришел к выводу: —
- Даже если импульс небольшой, но импульс системы все равно изменяется.{-5} \ frac {m} {s} $, то по-прежнему изменение импульса составляет $ 10 \ frac {kg.m} {s} $.
С этими аргументами я совершенно не понимаю, будет ли сохраняться импульс или нет?
ньютоновских механиков — Мяч, брошенный из движущегося поезда
Позвольте мне сначала пройти через это без трения или сопротивления воздуха.
Вы говорите $ v_y $ по оси $ x $, и поезд движется с $ v_x $ по оси $ z $. Это немного непоследовательно. Я буду использовать скорости, но не ваше описание осей.Итак, поезд движется в направлении $ x $, мяч бросается в направлении $ y $, а в направлении $ z $ — вверх-вниз.
Судя по наблюдателю в поезде, мяч будет двигаться с постоянным значением $ v_y $ от поезда. Нет ничего, что могло бы его замедлить. Также отсутствует компонента $ v_x $ в движении мяча относительно поезда . Таким образом, человек в поезде увидит мяч прямо перед собой, который летит еще дальше и начинает падать с $ v_z = — g t $. Будет кривая траектория, парабола в плоскости $ y $ — $ z $, плоскости, в которой поезд движется перпендикулярно.
Это выглядит так:
Вы можете записать это с векторами следующим образом, где $ g $ — ускорение свободного падения: $$ \ vec v (t) = v_y \, \ hat y — g t \, \ hat z = \ begin {pmatrix} 0 \\ v_y \\ — gt \ end {pmatrix} $$
Затем вы можете интегрировать это снова относительно $ t $ и получить позицию $ \ vec r $ вашего шара. Я установил для всех констант интеграции значение 0, чтобы упростить задачу. В принципе, они допускают любую отправную точку. Я просто предполагаю, что отправной точкой является начало системы координат.2 \ end {pmatrix} $$
Я установил для всех констант интеграции значение 0, чтобы упростить задачу. В принципе, они допускают любую отправную точку. Я просто предполагаю, что отправной точкой является начало системы координат.2 \ end {pmatrix} $$
Если вы являетесь наблюдателем, и поезд движется относительно вас, вы увидите, как мяч движется с постоянной скоростью в $ x $ и $ y $, но также увидите, как он начинает падать. Итак, вы видите параболу в плоскости, перпендикулярной осям.
Я сделал еще один снимок, вы смотрите на переднюю часть поезда, немного перекошенную, чтобы увидеть трехмерные оси:
Скорости аналогичны, за исключением того, что вы также должны включить движение поезда.2 \ end {pmatrix} $$
Преобразование Галилея
В качестве альтернативы вы можете применить к нему преобразование Галилея. Я постараюсь быть педантичным, поскольку преобразования из систем координат трудно сделать правильно. Я только что несколько месяцев изучал общую теорию относительности, поэтому я знаю, насколько это сложно 🙂
Пусть системой поезда будет система $ \ Sigma $, где координаты — $ \ vec r $ и $ \ vec v $. Система на земле должна иметь вид $ \ tilde \ Sigma $, где координаты — $ \ tilde {\ vec r} $ и $ \ tilde {\ vec v} $.2 \ end {pmatrix} $$ который у нас уже был.
Сопротивление воздуха заставит мяч замедляться на каждой из своих скоростей, еще больше изгибая кривую.
Если вы посмотрите сверху, это то же самое, что игнорировать гравитацию. Выглядит это так:
Когда вы находитесь в поезде, вы увидите, как рельсы движутся под вами, и мяч просто будет двигаться в вашем $ y $ -направлении:
Когда вы выйдете на улицу, вы увидите, как движется поезд.Мяч всегда будет перед тем, кто его бросил. Поэтому он будет двигаться по диагональной линии. Однако эта линия прямая!
ньютоновских механик — Бросание мяча вверх в ускоряющем поезде
Пользователь Sahil Chadha уже ответил на вопрос, но вот математика и красивая картинка для всех, кто не убежден в вашей правоте. 2 $ значений ускорения поезда
2 $ значений ускорения поезда
С точки зрения человека, сидящего в поезде, мяч летит назад по своего рода деформированной параболе, но чем меньше ускорение, тем больше он выглядит так, как если бы вы бросили мяч в вертикальном направлении. ускоренный поезд.
с отличием по физике: свободное падение
Фон
Исследование свободно падающих тел восходит к временам Аристотеля. В то время Аристотель считал, что более массивные объекты будут падать быстрее, чем менее массивные. Он верил в это во многом из-за того, что при рассмотрении камня и пера, падающего с одной высоты, становится ясно, что камень первым ударяется о землю. При дальнейшем рассмотрении становится ясно, что Аристотель ошибался в своей гипотезе.
В качестве доказательства возьмите баскетбольный мяч и лист бумаги. Бросьте их одновременно с одной и той же высоты … приземляются ли они одновременно? Возможно нет. Теперь возьмите этот лист бумаги, скомкайте его в плотный клубок и повторите эксперимент. Что вы видите сейчас? Вы должны увидеть, что и мяч, и бумага приземляются одновременно. Таким образом, можно сделать вывод, что предсказания Аристотеля не учитывали влияние сопротивления воздуха. В рамках этого курса не принимаются во внимание силы сопротивления, такие как сопротивление воздуха.
В 17 веке Галилео Галилей начал новое исследование движения падающих тел. Галилей, осознавая, что сопротивление воздуха влияет на движение падающего тела, провел свой знаменитый мысленный эксперимент, в котором постоянно спрашивал, что произойдет, если эффект сопротивления воздуха будет устранен. Командир Аполлона-15 Дэвид Скотт провел этот эксперимент, находясь на Луне. Он одновременно уронил молот и перо и заметил, что они достигли земли одновременно.
Со времени экспериментов Галилея ученые пришли к лучшему пониманию того, как гравитационное притяжение Земли ускоряет свободно падающие тела. Путем экспериментов было определено, что местная напряженность гравитационного поля (g) на поверхности Земли составляет 9,8 Н / кг, что дополнительно указывает на то, что все объекты в свободном падении (без учета сопротивления воздуха) испытывают эквивалентное ускорение 9,8 м. / с 2 к центру Земли.
Путем экспериментов было определено, что местная напряженность гравитационного поля (g) на поверхности Земли составляет 9,8 Н / кг, что дополнительно указывает на то, что все объекты в свободном падении (без учета сопротивления воздуха) испытывают эквивалентное ускорение 9,8 м. / с 2 к центру Земли.
(ПРИМЕЧАНИЕ: если вы оторветесь от поверхности Земли, местная напряженность гравитационного поля и, следовательно, ускорение свободного падения изменится.)
Вы можете смотреть на свободно падающие тела как на предметы, которые падают с некоторой высоты или отбрасывают вертикально вверх. В этом экзамене вы проанализируете движение каждого состояния.
Падающие предметы
Объекты, стартующие в состоянии покоя, имеют начальную скорость, равную нулю, что дает вам первую кинематическую величину, необходимую для решения проблемы. Кроме того, если вы назовете направление начального движения (вниз) положительным, объект будет иметь положительное ускорение и ускоряться при падении.
Важным первым шагом в анализе объектов в свободном падении является решение, какое направление по оси Y вы собираетесь назвать положительным, а какое, следовательно, отрицательным. Хотя вы можете установить свое положительное направление любым удобным вам способом и получить правильный ответ, следование приведенным ниже советам может упростить вашу работу, чтобы постоянно находить правильный ответ.
- Определите направление первоначального движения объекта и назначьте его положительным направлением.В случае падения объекта положительное направление оси Y будет направлено к нижней части бумаги.
- Теперь, когда ось идентифицирована, вы можете идентифицировать и записывать заданную кинематическую информацию. Не забывайте, что у падающего объекта начальная скорость равна нулю.
- против 0 = 0
- v =?
- Δy =?
- a = 9,8 м / с 2
- т =?
- Обратите внимание на направление, в котором нарисованы векторные стрелки — если скорость и ускорение указывают в одном направлении, объект ускоряется.
 Если они указывают в противоположных направлениях, объект замедляется.
Если они указывают в противоположных направлениях, объект замедляется.
КЛЮЧЕВАЯ КОНЦЕПЦИЯ: Величина ускорения свободного падения (g) постоянна 9,81 м / с 2 на поверхности Земли.
Вопрос: Какова скорость 2,5-килограммовой массы после того, как она свободно упала из состояния покоя на расстояние 12 метров?
Переменная Значение v 0 0 v НАЙТИ Δy 12 м и 9.8 м / с 2 т ? Ответ: Вертикальная проблема: Укажите положительное направление вниз. Это означает, что ускорение, которое также уменьшается, является положительной величиной.
Объекты, запущенные вверх
Изучение движения объекта, запущенного вертикально вверх, выполняется почти так же, как вы исследовали движение объекта, падающего из состояния покоя.Основное отличие состоит в том, что вы должны смотреть не на один, а на два сегмента его движения: вверх и вниз.
Прежде чем вы приступите к установлению системы отсчета и проработке количественного анализа, вы должны построить твердое концептуальное понимание того, что происходит, когда мяч находится в воздухе. Представьте, что мяч подбрасывается вертикально в воздух, как показано на рисунке.
Чтобы мяч двигался вверх, его начальная скорость должна быть больше нуля.Когда мяч поднимается, его скорость уменьшается, пока он не достигнет максимальной высоты, где он останавливается, а затем начинает падать. Когда мяч падает, его скорость увеличивается. Другими словами, мяч ускоряется все время, пока он находится в воздухе, как на пути вверх, в момент остановки в самой высокой точке, так и на пути вниз.
Когда мяч падает, его скорость увеличивается. Другими словами, мяч ускоряется все время, пока он находится в воздухе, как на пути вверх, в момент остановки в самой высокой точке, так и на пути вниз.
Причина ускорения мяча — сила тяжести. Все время, пока мяч находится в воздухе, его ускорение составляет 9,8 м / с 2 вниз при условии, что это происходит на поверхности Земли.Обратите внимание, что ускорение может быть 9,8 м / с 2 или -9,8 м / с 2 . Знак ускорения зависит от направления, которое вы указали как положительное, но во всех случаях направление ускорения силы тяжести направлено вниз, к центру Земли.
Вы уже установили, что ускорение мяча за все время, пока он находится в воздухе, составляет 9,8 м / с. 2 вниз. Это ускорение приводит к тому, что скорость мяча уменьшается с постоянной скоростью, пока он не достигнет максимальной высоты, после чего он разворачивается и начинает падать.Чтобы повернуться, скорость мяча должна пройти через ноль. Следовательно, на максимальной высоте скорость мяча должна быть равна нулю.
Вопрос: Мяч, брошенный вертикально вверх, достигает максимальной высоты 30 метров над поверхностью Земли. На максимальной высоте скорость мяча составляет:
Ответ: 0 м / с. Мгновенная скорость любого снаряда на максимальной высоте равна нулю.
Поскольку сила тяжести обеспечивает одинаковое ускорение мяча при движении вверх (замедляя его) и при спуске (ускоряя его), время достижения максимальной высоты совпадает с временем возврата в исходное положение.Точно так же начальная скорость мяча на пути вверх будет равна скорости мяча в тот момент, когда он достигнет точки, из которой он был запущен на пути вниз. Другими словами, время подъема равно времени спуска, а начальная скорость подъема равна конечной скорости вниз (при условии, что объект начинается и заканчивается на одной и той же высоте над землей).
Теперь, когда концептуальное понимание движения мяча установлено, вы можете работать над количественным решением.Следуя ранее установленному эмпирическому правилу, вы можете начать с определения положительного направления движения мяча. Помните, что назначение положительных и отрицательных направлений совершенно произвольно. У вас есть свобода назначать их так, как вы считаете нужным. Однако, назначив их, не меняйте их.
После того, как это положительная ссылка направление было установлено, все остальные скорости и перемещения назначаются соответственно. Например, если вверх — положительное направление, ускорение свободного падения будет отрицательным, потому что ускорение силы тяжести направлено вниз, к центру Земли.В своей наивысшей точке шар будет иметь положительное смещение и нулевое смещение, когда он вернется в свою начальную точку. Если мяч не пойман, но продолжит движение к Земле мимо начальной точки, он будет иметь отрицательное смещение.
«Уловка» для решения задач свободного падения включает в себя симметрию. Время, необходимое объекту для достижения своей наивысшей точки, равно времени, необходимому для возврата в то же вертикальное положение. Скорость, с которой снаряд начинает свой путь вверх, равна скорости снаряда, когда он возвращается на ту же высоту (хотя, конечно, его скорость в противоположном направлении).Если вы хотите упростить задачу, по вертикали, в самой высокой точке, вертикальная скорость равна 0. Эта дополнительная информация может помочь вам в заполнении таблицы вертикальных перемещений. Если вы сократите движение объекта вдвое, вы можете упростить решение проблемы, но не забывайте, что если вы хотите, чтобы общее время в воздухе находилось в воздухе, вы должны удвоить время, необходимое для того, чтобы объект поднялся до своей наивысшей точки.
Вопрос: Баскетболист прыгнул прямо, чтобы отскочить.Если она была в воздухе 0,80 секунды, насколько высоко она прыгнула?
Переменная Значение v 0 ? v 0 м / с Δy НАЙТИ и -9,8 м / с 2 т 0. 40 с
Ответ: Определите вверх как положительное направление оси Y. Обратите внимание: если баскетболист находится в воздухе 0,80 секунды, он достигает своего максимального роста за 0,40 секунды, после чего его скорость равна нулю.
Невозможно найти Δx напрямую с данной информацией, поэтому сначала найдите v 0 .
Теперь, когда известно v 0 , решите для Δx.
Вопрос: Какой график лучше всего отображает взаимосвязь между ускорением объекта, свободно падающего около поверхности Земли, и временем, в которое он падает?
Ответ: (4) Ускорение свободного падения является постоянным 9.8 м / с 2 вниз по поверхности Земли.
Физика бейсбола: как далеко вы можете забросить?
Ключевые концепции
Физика
Движение
Гравитация
Сопротивление
Уголки
Введение
Вы когда-нибудь видели длинный выигрышный пас в футбольном матче, бейсболиста, который забрасывает мяч с дальнего поля или футбольного вратаря, отбрасывающего мяч по всему полю? Во всех этих действиях игрок пытается бросить или ударить по мячу как можно дальше.За этими бросками и ногами стоит некоторая наука. А иногда все дело в угле. Угол может повлиять на то, как далеко мяч может унести мяч при броске или ударе. Что делать: мелкий бросок (прямо, параллельно земле), крутой бросок (подбрасывание мяча высоко в воздух) или что-то среднее между ними? Попробуйте этот научный спортивный проект, чтобы узнать!
Фон
Объект, который бросают, пинают или иным образом запускают по воздуху, называется снарядом.Изучение того, как снаряды движутся по воздуху, называется движением снаряда. Когда снаряд запущен, он имеет начальную скорость (скорость и направление движения). Однако, когда снаряд движется по воздуху, на него действует сила тяжести, которая заставляет его двигаться вниз к Земле. Он также подвержен силе сопротивления воздуха, которое замедляет снаряд.
Когда снаряд запущен, он имеет начальную скорость (скорость и направление движения). Однако, когда снаряд движется по воздуху, на него действует сила тяжести, которая заставляет его двигаться вниз к Земле. Он также подвержен силе сопротивления воздуха, которое замедляет снаряд.
Когда сопротивление воздуха очень низкое, снаряд движется в форме параболы — типа математической кривой.(Вы можете выполнить поиск в Интернете по запросу «парабола», чтобы увидеть, как он выглядит.) Путь, по которому мяч следует (называемый его траекторией), будет определять, как далеко он уйдет, прежде чем упадет на землю. Регулировка начального угла мяча и поддержание постоянной начальной скорости — это один из способов найти лучший угол, чтобы бросить мяч как можно дальше. В этом эксперименте вы будете бросать мяч изо всех сил, изменяя начальный угол мяча относительно земли. Как вы думаете, под каким углом мяч уйдет дальше всего?
Материалы
- Спортивный мяч по вашему выбору (бейсбол, теннисный мяч, футбол и т. Д.)
- Большая открытая площадка для броска мяча
- По три разных объекта, чтобы отметить приземление мяча на землю (например, три клюшки, три камня и три мяча для гольфа)
- Помощник
Подготовка
- Убедитесь, что у вас есть большое открытое пространство для броска и что на пути нет других людей или предметов.
- Перед началом эксперимента сделайте несколько упражнений на растяжку или разминку — это будет связано с большим количеством метаний!
- Выберите место для стойки на большом открытом пространстве. Отметьте место на земле, чтобы вы знали, что всегда нужно бросать мяч с этого места.
- Выберите направление, чтобы бросить мяч. (Если сегодня ветреный день, убедитесь, что вы выбрали постоянное направление относительно ветра.)
- Какой угол, по вашему мнению, позволит получить наибольшее расстояние — мелкий, крутой или средний?
Процедура
- Бросьте мяч так сильно, как только можете, относительно прямо вперед под «неглубоким» углом — настолько параллельно земле, насколько это возможно.
 Если вы знакомы с измерением углов в градусах, представьте, что вы пытаетесь бросить мяч под углом примерно 15 градусов относительно земли. Можете ли вы назвать время, когда этот тип броска был бы лучшим?
Если вы знакомы с измерением углов в градусах, представьте, что вы пытаетесь бросить мяч под углом примерно 15 градусов относительно земли. Можете ли вы назвать время, когда этот тип броска был бы лучшим? - Пусть ваш помощник отметит место приземления мяча (например, камнем).
- Повторите бросок под этим углом еще два раза. Старайтесь постоянно бросать мяч как можно сильнее, чтобы его начальная скорость была постоянной. Пусть ваш волонтер отметит каждую до конца. Как вы думаете, почему важно выполнить один и тот же тест хотя бы несколько раз?
- Теперь повторите процедуру для «среднего» угла (наружу и вверх) около 45 градусов три раза.Не забывайте стараться и постоянно бросать мяч как можно сильнее. Используйте другой объект-маркер для того, где приземляются эти броски. Как это расстояние по сравнению с мелким углом?
- Теперь сделайте то же самое для «крутого» угла (вверх в воздухе и немного вперед, но не прямо вверх) около 75 градусов. Как вы думаете, это расстояние будет сравниваться с другими? Не забывайте стараться бросать мяч как можно сильнее. Для этой серии бросков используйте маркер другого типа.
- Теперь проанализируйте результаты своего эксперимента, глядя на маркеры. Какие броски прошли дальше всего? Какой угол, по вашему мнению, лучше всего, если вы хотите забросить мяч как можно дальше?
- Экстра: Попробуйте поэкспериментировать с разными типами мячей. Как вы думаете, размер, вес и форма мяча повлияют на то, под каким углом лучше всего бить с дальнего расстояния? У вас были разные результаты?
- Дополнительно: Повторите упражнение, на этот раз вместо этого ударив по мячу. Как вы думаете, углы дадут относительно одинаковые расстояния? У вас были результаты, отличные от результатов, когда вы бросали мяч?
Наблюдения и результаты
В большинстве случаев вы должны увидеть, что средний угол в 45 градусов заставлял мяч лететь дальше всего.

 Одиссея капитана Блада).
Одиссея капитана Блада). Если они указывают в противоположных направлениях, объект замедляется.
Если они указывают в противоположных направлениях, объект замедляется. 40 с
40 с Если вы знакомы с измерением углов в градусах, представьте, что вы пытаетесь бросить мяч под углом примерно 15 градусов относительно земли. Можете ли вы назвать время, когда этот тип броска был бы лучшим?
Если вы знакомы с измерением углов в градусах, представьте, что вы пытаетесь бросить мяч под углом примерно 15 градусов относительно земли. Можете ли вы назвать время, когда этот тип броска был бы лучшим?
Leave A Comment