Внутренняя энергия 1-й закон термодинамики. | |
Сумма кинетических энергий хаотического движения всех частиц тела относительно центра масс тела (молекул, атомов) и потенциальных энергий их взаимодействия друг с другом называется внутренней энергией. | |
Внимание!
| U=U(T,V) |
Для идеального газа: U=U(T), т.к. взаимодействием на расстоянии пренебрегаем. — внутренняя энергия идеального одноатомного газа. Внутренняя энергия — однозначная функция состояния (с точностью до произвольной постоянной) и в замкнутой системе сохраняется. Обратное неверно(!) — одной и той же энергии могут соответствовать разные состояния. | Идеальный газ:
|
Опыты Джоуля доказали эквивалентность работы и количества теплоты, т.е. и та и другая величины являются мерой изменения энергии, их можно измерять в одинаковых единицах: 1 кал = 4,1868 Дж ≈ 4,2 Дж. Эта величина наз. механическим эквивалентом теплоты. |
|
Р.Майер, Д.Джоуль, Г.Гельмгольц — закон сохранения энергии для тепловых процессов — 1-й закон термодинамики. |
|
Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:
| |
Изменений внутренней энергии не зависит от способа, которым осуществляется этот переход. Т.о. существует два способа изменения внутренней энергии: совершение механической работы и теплопередача (теплообмен). Работа и количество теплоты характеризуют процесс изменения внутренней энергии, но не саму внутреннюю энергию. |
|
Если А — работа внешних сил, а А’ — работа газа, то А = — А’ (в соответствии с 3-м законом Ньютона). Тогда: — другая форма записи первого закона термодинамики.Количество теплоты, переданное системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами. | |
Невозможность создания вечного двигателя 1-го рода. Вечный двигатель первого рода — устройство, которое могло бы совершать неограниченное количество работы без затраты энергии. Тогда Q=0. Следовательно: A’= — ΔU. Т.е. такой двигатель должен совершать работу за счет убыли внутренней энергии. Но ее запасы конечны. После того, как запас энергии будет исчерпан, двигатель остановится. |
|
Идеальный одноатомный газ, теория и примеры
Определение идеального одноатомного газа
Количество атомов в молекуле оказывает влияние на то, как распределяется энергия по степеням свободы.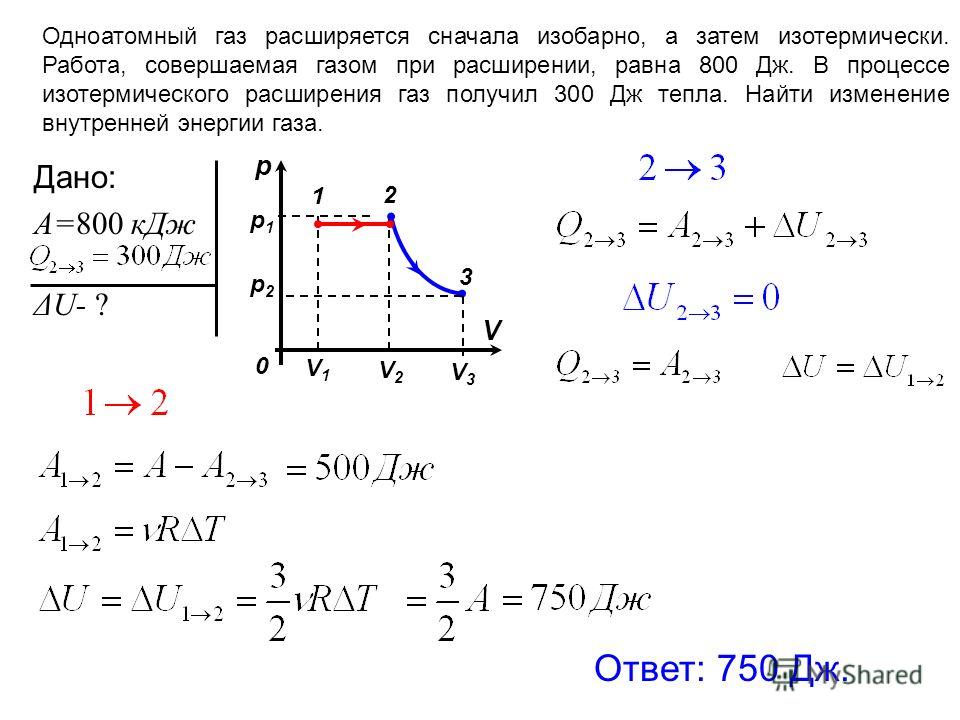 Так для одноатомного газа молекула имеет три степени свободы (). Формулу для расчета внутренней энергии идеального одноатомного газа очень просто получить.
Так для одноатомного газа молекула имеет три степени свободы (). Формулу для расчета внутренней энергии идеального одноатомного газа очень просто получить.
Внутренняя энергия одноатомного идеального газа
Учтем, что молекулы идеального газа представлены как материальные точки, которые не взаимодействуют на расстоянии. Отсутствие сил взаимодействия между молекулами обозначает, что потенциальная энергия взаимодействия молекул постоянна. Суммарная энергия покоя самих молекул также неизменна, так как молекулы при тепловых процессах не изменяются. Следовательно, внутренняя энергия идеального одноатомного газа является суммой кинетических энергий поступательного движения молекул и еще некоторая постоянная.
Обозначим внутреннюю энергию газа как U, тогда сказанное выше запишем как:
где – сумма кинетических энергий поступательного движения молекул; N – число молекул в газе. Примем во внимание то, что средняя кинетическая энергия молекулы () равна:
По закону о равномерном распределении энергии по степеням свободы имеем:
для одноатомного газа:
– постоянная Больцмана; T – температура по шкале Кельвина.
Внутреннюю энергию одноатомного идеального газа можно записать как:
Обычно постоянную величину в выражении (5) опускают, так как в расчётах она роли не играет.
Выражение (5) говорит о том, что внутренняя энергия идеального газа определена его температурой. Она является функцией состояния и не зависит от процесса который провели для того чтобы газ пришел в состояние с этой температурой. При этом изменение внутренней энергии идеального газа определено только его начальным и конечным состояниями, и не связано с характером процесса.
Выражение (5) часто используют в виде:
где m – масса газа; – молярная масса газа; – универсальная газовая постоянная; – количество вещества.
Теплоемкость одноатомного идеального газа
Для изохорного процесса, проводимого в идеальном газе работа равна нулю (A), поэтому первое начало термодинамики:
запишем как:
где – теплоемкость газа при постоянном объеме. Используя выражения (8) и (6) получим:
Используя выражения (8) и (6) получим:
Используя формулу (10) можно вычислить молярную теплоемкость любого одноатомного газа при постоянном объеме:
Молярная теплоемкость одноатомного газа при изобарном процессе () связана с соотношением Майера:
Примеры решения задач
4. Внутренняя энергия одноатомного идеального газа вычисляется по формуле: A) p*ΔV Б) m/M
Сделать 6 задач по физики олимпиада 1 РЕБЯТА КУПИЛИ ГЕЛИЕВЫЕ ШАРИКИ К ПРАЗДНИКУ, К НОВОМУ ГОДУ, КОГДА ОНИ ВЫШЛИ НА УЛИЦУ, ШАРИКИ ИСПОРТИЛИСЬ, РЕБЯТА Н
… Е ЗНАЛИ, ПОЧЕМУ ТАК ПРОИЗОШЛО. И ЖЕ ТЕПЕРЬ ДЕЛАТЬ. ОПИШИТЕ, ЧТО ПРОИЗОШЛО ШАРИКАМИ НА МОРОЗЕ. И КАК НУЖНО ПОСТУПИТЬ РЕБЯТАМ. 2 РЕБЯТА В ОБРАЗОВАТЕЛЬНОМ ЦЕНТРЕ СИРИУС, РАЗРАБАТЫВАЛИ МОДЕЛЬ ЛОДКИ. ОНИ ЗАПУСКАЛИна побережье ЧЁрного моря, лодка прошла все испытания. но когда ребята вернулись домой и запустили ее на НАБЕРЕЖНОЙ РЕКИ ТУРА, У ЛОДКИ ОКАЗАЛАСЬ СЛИШКОМ БОЛЬШАЯ ОСАДКА. НАПИШИТЕ, В ЧЕМ БЫЛА ПРИЧИНА.3 ДВА ВОДОЛАЗЫ ПОГРУЗИЛИСЬ НА ОДИНАКОВУЮ ГЛУБИНУ. ОДИН НАХОДИТСЯ НА ДНЕ В ОТКРЫТОМ МОРЕ, А ДРУГОЙ В ПЕЩЕРЕ ПОД ВОДОЙ НА ТОЙ ЖЕ ГЛУБИНЕ. НА КАКОГО ВОДОЛАЗА ДЕЙСТВУЕТ БОЛЬШЕЕ ДАВЛЕНИЕ ПОЧЕМУ?4 ФОКУСНИК ПОКАЗЫВАЕТ ВАМ ВОЛШЕБНУЮ КОРОБКУ, КОТОРАЯ «НЕ ПОДДАЕТСЯ ЗАКОНАМ ФИЗИКИ». ОНА СТОИТ НА КРАЮ СТОЛА, МЕНЬШЕЙ ЧАСТЬЮ, БОЛЬШАЯ ЕЁ ЧАСТЬ ВИСИТ НАД ПОЛОМ. НО ФОКУСНИК НЕ УЧЁЛ, ВЫ ОТЛИЧНО РАЗБИРАЕТЕСЬ В ФИЗИКЕ И ВЫ ЛЕГКОСТЬЮ ОБЪЯСНЯЕТ, КАК ЭТО СДЕЛАТЬ. ЧТО ВЫ СКАЖЕТокуснику?5 ТРИ ХОЗЯЙКИ ПОСТАВИЛИ НА ПЛИТУ КАСТРЮЛИ. НЕОБХОДИМО БЫЛО, КАК МОЖНО БЫСТРЕЕ ВСКИПЯТИТЬ ВОДУ. МОЩНОСТЬ ПЛИТ ОДИНАКОВАЯ. ОДНА ВЗЯЛА КАСТРЮЛЮ, НАЛИЛА ВОДУ И СТАЛА ЖДАТЬ, ВТОРАЯ ЗАКРЫЛА ВОДУ НО ПОСТОЯННО ОТКРЫВАЛА И ПОМЕШИВАЛА ВОДУ. А ТРЕТЬЯ ЗАКРЫЛА ВОДУ КРЫШКОЙ И НЕ ОТКРЫВАЛА ЕЕ. У КАКОЙ ХОЗЯЙКИ ВОДА ЗАКИПИТ БЫСТРЕЕ ВСЕГО?6 У АЛЕНЫ В КЛУМБЕ РАСЦВЕЛИ 10 ТЮЛЬПАНОВ (СМ. РИС. АЛЕНА ХОЧЕТ РАСПОЛть ЦВЕТЫ В КЛУМБЕ ПО-ОСОБОМУ. И ПОЭТОМУ ПЕРЕСАДИЛА ТЮЛЬПАНЫ ТАК, ЧТО ОБРАЗОВАЛОСЬ ПЯТЬ РЯДОВ ПО 4 ТЮЛЬПАНА В КАЖДОМ. КАК ТЕПЕРЬ ВЫГЛЯДИТ КЛУМБА? СХЕМАТИЧНО НАРИСУЙТЕ РАСПОЛОЖЕНИЕ ТЮЛЬПАНОВ ПОСЛЕ ИХ ПЕРЕСАДКИ.
5. Почему мы сначала видимМОЛНИЮ, а только потом слышим звук?а)скорость звука меньше скорости Светаб)Сначала происходит световое явление,потом звуково … ев)явление которое производит гром находится дальше от явления которое производит свет
Наше ухо воспринимает только колебания, частота которых:а)не реже 17 колебаний и не чаще 20 000 в секундуб)не реже 170 колебаний и не чаще 20 00 в сек … ундув)не реже 1700 колебаний и не чаще 20 000
Знайдіть червону межу фотоефекту, якщо робота виходу для даної речовини становить 2 МеВ
1. Два тела имеют одинаковую скорость. Масса первого тела в 2 раза меньше массы второго тела. При этом импульс второго тела…. … больше в 2 раза меньше в 2 раза меньше в 4 раза больше в 4 раза2. Какие из ниже приведенных утверждений НЕ справедливы (несколько ответов)? Импульс – векторная величина Сила, действующая на тело, противоположна направлению изменения импульса тела Сила, действующая на тело, равна произведению импульса тела на время Импульс сонаправлен с изменением скорости3. Чему равен импульс тела массой 9 кг движущегося со скоростью 2 м/с? А) 1 кг ∙м/сВ) 6 кг ∙м/сС) 9 кг ∙м/сD) 18 кг ∙м/с4.. . Два шара, массы которых 600 г и 200 г, движутся по гладкой горизонтальной поверхности друг за другом со скоростями 4м/с и 3 м/с соответственно. Столкновение не упругоеа) Вычислите импульс первого и второго шара до столкновения. Покажите полное решение. b) Запишите закон сохранения импульса в векторном виде для данной задачи. c) Вычислите скорость шаров после столкновения. Покажите полное решение.
Источник света излучает ежесекундно n=2*1019 квантов на длине волны лямбда=690нм, Найдите мощность источника,если в световую энергию переходит 10% по … требляемой энергии?
СРОЧНО!!!!Пожалуйста,помогите решить задачу по физике 8 класса
Что из перечисленного работает на основе сообщающихся сосудов? Выбери все верные. Фонтан Лейка Кружка Шлюз Насос Аквариум Водонапорная башня (Я знаю т … олько что лейка на основе сообщающихся сосудов)
ОЧЕНЬ СРОЧНО, ПОЖАЛУЙСТА!!
ЗАДАЧИ :
1) Резиновый шар содержит 2 л воздуха, находящегося при температуре 20 °С и под атмосферным давлением 780 мм рт.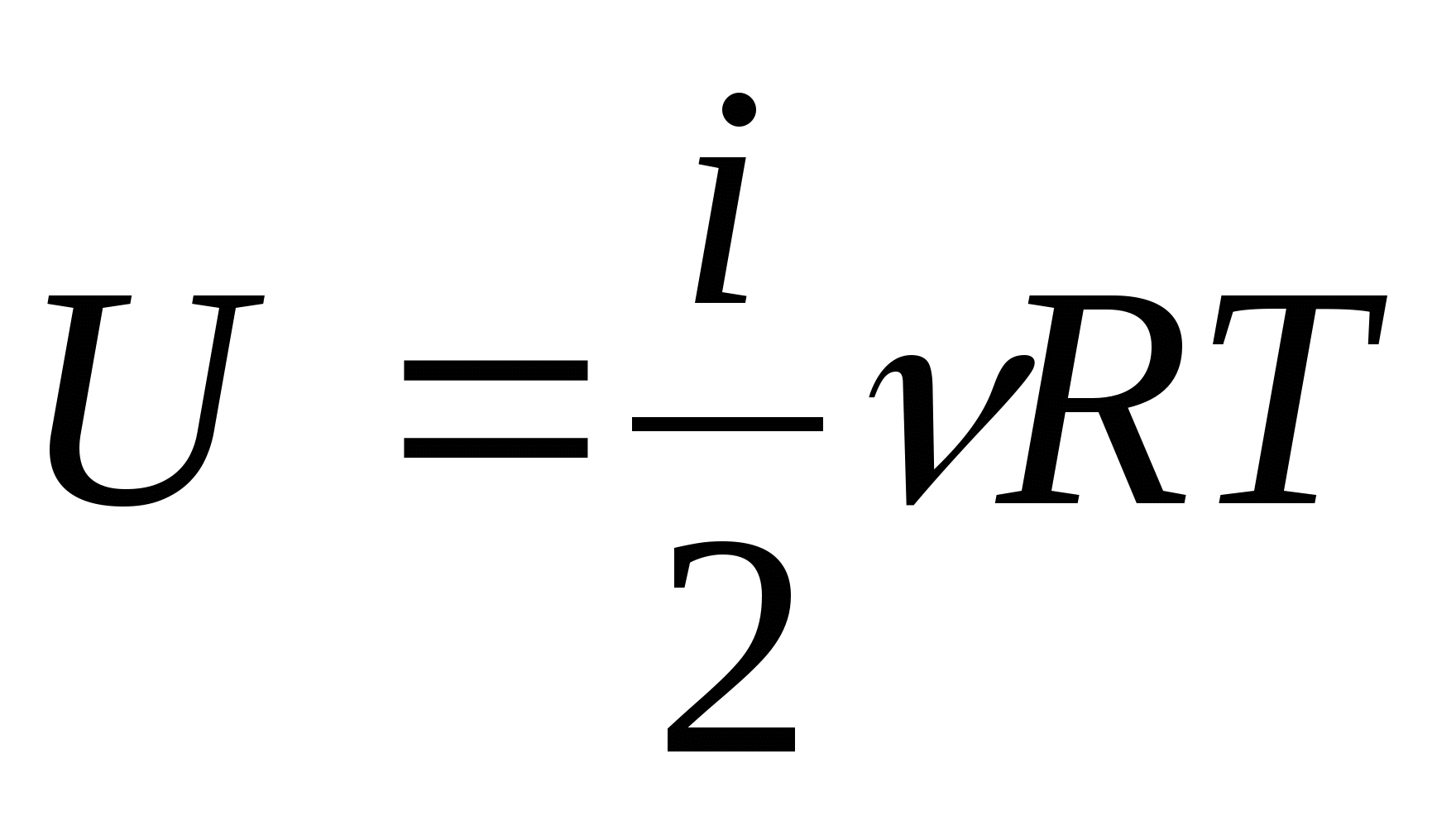 с
… т. Какой объем займет воздух, если шар будет опущен в воду на глубину 10 м? Температура воды 4 °С.
2) Бутылку, заполненную газом, плотно закрыли пробкой площадью поперечного сечения 2,5 см2. Чтобы удерживать пробку, нужно прикладывать силу 12 Н. До какой температуры нужно нагреть газ, чтобы пробка вылетела из бутылки? Начальная температура -3⁰С, атмосферное давление 105 Па.
3) На рисунке в координатах p, V изображен замкнутый газовый процесс (цикл). Постройте этот цикл в координатах V, T и p, T. ( картинка 1 )
с
… т. Какой объем займет воздух, если шар будет опущен в воду на глубину 10 м? Температура воды 4 °С.
2) Бутылку, заполненную газом, плотно закрыли пробкой площадью поперечного сечения 2,5 см2. Чтобы удерживать пробку, нужно прикладывать силу 12 Н. До какой температуры нужно нагреть газ, чтобы пробка вылетела из бутылки? Начальная температура -3⁰С, атмосферное давление 105 Па.
3) На рисунке в координатах p, V изображен замкнутый газовый процесс (цикл). Постройте этот цикл в координатах V, T и p, T. ( картинка 1 )
Женя с папой катаясь на коньках, решили узнать массу папы. Стоя на коньках, они взялись за концы длинной веревки и потянули (каждый в свою сторону) Ок … азалось что к моменту столкновения папа проехал 3 м, а Женя-9м. Чему равно масса папы, если масса Жени-40кг?
Глава 14. Термодинамика
Изучение энергетических превращений в молекулярных системах составляет содержание термодинамики. Для решения задач на термодинамику необходимо знать определения внутренней энергии, количества теплоты, теплоемкости и ряда других величин. Необходимо также понимать и уметь использовать в простейших случаях первый закон термодинамики как балансовое соотношение, описывающее процессы превращения энергии из одних форм в другие. Также нужно знать основные свойства процессов перехода вещества из одних агрегатных состояний в другие. Рассмотрим эти вопросы.
Внутренней энергией тела называется сумма кинетической энергии молекул и потенциальной энергии их взаимодействия друг с другом. Для жидкостей и твердых тел из-за сильного взаимодействия молекул друг с другом вычислить внутреннюю энергию не удается. Внутреннюю энергию можно вычислить только для идеальных газов, в которых можно пренебречь энергией взаимодействия молекул друг с другом и считать, что внутренняя энергия равна сумме кинетических энергий молекул. Для одноатомного газа (т.е. газа, каждая молекула которого состоит из одного атома) внутренняя энергия определяется соотношением
(14. |
где — количество вещества газа (число молей), — универсальная газовая постоянная, — абсолютная температура. Заметим, что с помощью закона Клапейрона-Менделеева формула (14.1) может быть преобразована к виду
(14.2) |
где — давление, — объем газа.
Внутренняя энергия тела может измениться при теплообмене, когда молекулы тела сталкиваются с более быстрыми или более медленными молекулами других тел и получают от них или отдают им энергию, или в процессе совершения механической работы над этим телом внешними силами. В связи с эти вводят следующие определения. Количеством теплоты, переданным некоторому телу, называют энергию, переданную этому телу в процессе хаотических столкновений молекул. Процесс передачи энергии в виде теплоты называют процессом теплопередачи. Если внешние силы не совершают над телом работы, для процесса теплопередачи справедливо следующее балансовое соотношение
(14.3) |
где — изменение внутренней энергии тела, — количество переданной этому телу теплоты. Поскольку изменение внутренней энергии тела может быть и положительным , и отрицательным , из закона (14.3) следует, что количеству теплоты следует придать алгебраический смысл: если энергия передается телу, количество переданной этому телу теплоты нужно считать положительным , если забирается — отрицательным .
Внутренняя энергия тела изменяется при сжатии тела, трении и ряде других механических процессах. В этом случае на изменение внутренней энергии расходуется работа , совершаемая над телом внешними силами
(14.4) |
(конечно, здесь подразумевается, что работа не расходуется на энергию движения тела как целого, а только на изменение внутреннего движения, т. е. все перемещения тела как целого или его макроскопических частей должны происходить бесконечно медленно). Очевидно, работа внешних сил положительна, если эти силы сжимают тело и его объем уменьшается, и отрицательна — если объем тела увеличивается. В первом случае, как это следует из (14.4), внутренняя энергия тела возрастает (), во втором убывает ().
е. все перемещения тела как целого или его макроскопических частей должны происходить бесконечно медленно). Очевидно, работа внешних сил положительна, если эти силы сжимают тело и его объем уменьшается, и отрицательна — если объем тела увеличивается. В первом случае, как это следует из (14.4), внутренняя энергия тела возрастает (), во втором убывает ().
Одновременно с внешними силами при сжатии или расширении тел совершают работу и сами эти тела. Рассмотрим, например, газ, находящийся в цилиндрическом сосуде и отделенный от атмосферы поршнем (см. рисунок). И при сжатии, и при расширении газа силы, действующие на поршень со стороны газа, совершают над ним работу (в первом случае отрицательную, во втором положительную). При этом, поскольку поршень перемещается бесконечно медленно, силы, действующие на него со стороны газа и внешние силы практически равны друг другу как при сжатии, так и при расширении газа (в противном случае в балансе энергии необходимо было учитывать кинетическую энергию, приобретенную поршнем). Поэтому работа, совершенная газом и внешними силами над газом равны по величине, но отличаютсязнаком1. Очевидно, работа газа положительна, если газ расширяется, и отрицательна, если газ сжимается.
При решении задач на термодинамику следует помнить одно важное свойство работы газа, которое во многих случаях позволяет ее легко вычислить. Работа газа в некотором процессе численно равна площади фигуры под графиком зависимости давления от объема в этом процессе. В частности в изобарическом процессе при давлении , в котором объем газа изменился от значения до значения , газ совершает работу (см. рисунок; площадь графика, соответствующая работе, выделена):
(14.5) |
где — количество вещества газа, — изменение температуры в рассматриваемом процессе.
Если газ участвует в процессе, в котором одновременно имеет место и теплообмен, и совершается работа, то справедливо соотношение
(14. |
которое называется первым законом термодинамики (здесь — работа газа).
Закон (14.6) позволяет найти одну из входящих в него величин, если заданы две других. Если задается только одна из величин, входящих в закон (14.6), но как-то определяется процесс, происходящий с газом, то две остальные величины могут быть определены. Например, в изохорическом процессе не совершается работа, поэтому
(14.7) |
В изотермическом процессе не меняется внутренняя энергия газа, поэтому
(14.8) |
В адиабатическом процессе (процессе без теплообмена с окружающей средой) , поэтому
(14.9) |
В изобарическом процессе есть связь между изменением внутренней энергии газа и его работой. Из формул (14.1) и (14.5) заключаем, что работа одноатомного идеального газа и изменение его внутренней энергии в изобарическом процессе связаны соотношением
(14.10) |
Для характеристики процессов нагрева-остывания тела вводят понятие теплоемкости тела , которая определяется как
(14.11) |
где — количество теплоты, сообщенное телу в некотором процессе, — изменение его температуры в этом процессе. Подчеркнем, что и в формуле (14.11) не независимы, а связаны друг с другом: — это то изменение температуры, которое происходит благодаря сообщению телу количества теплоты . Поэтому теплоемкость (14.11) не зависит от и , а зависит от свойств тела и происходящего с ним процесса.
Если тело однородно, то его теплоемкость пропорциональна его массе . Поэтому отношение является характеристикой вещества тела и называется его удельной теплоемкостью. Удельная теплоемкость представляет собой экспериментально измеряемую (табличную) характеристику веществ. Из определения удельной теплоемкости следует, что если телу массой , изготовленному из вещества с удельной теплоемкостью , сообщить количество теплоты , то будет справедливо соотношение
(14.12) |
где — изменение температуры тела.
Приведем теперь решения данных в первой части задач.
В задаче 14.1.1 внутренняя энергии газа увеличится согласно формуле (14.1) — ответ 1.
Для ответа на вопрос задачи 14.1.2 удобно использовать формулу для внутренней энергии газа в виде (14.2). По этой формуле находим, что внутренняя энергия увеличилась в 3/2 раза (ответ 2). Обратим внимание читателя, что причина изменения давления и объема может быть любой — ответ от этого не зависит. Может измениться или температура газа, или количество вещества, или и то и другое одновременно.
Поскольку температура и количество вещества газа не изменялись в рассматриваемом в задаче 14.1.3 процессе, внутренняя энергия газа не изменилась (ответ 3).
В задаче 14.1.4 следует воспользоваться определением теплоемкости (14.11). Для этого рассмотрим, например, ин-тервал времени , выделенный жирным на оси времени (см. рисунок). За этот интервал оба тела получили одинаковое количество теплоты , поскольку нагреватели одинаковы. Изменение температур тел и можно определить по графику — эти величины отмечены фигурными скобками на оси температур. Поскольку из формулы (14.11) заключаем, что — ответ 2.
В задаче 14. 1.5 следует воспользоваться определением удельной теплоемкости. По формуле (14.12) находим
1.5 следует воспользоваться определением удельной теплоемкости. По формуле (14.12) находим
(ответ 1).
Для совершения работы необходимо механическое движение. Поскольку объем газа в задаче 14.1.6 не меняется, механическое движение отсутствует, работа газа равна нулю (ответ 4).
Применяя к рассматриваемому в задаче 14.1.7 процессу первый закон термодинамики (14.6) и учитывая, что в изохорическом процессе работа газа равна нулю, заключаем, что (ответ 3).
В изотермическом процессе не меняется внутренняя энергия идеального газа. Поэтому , и работа , совершенная над газом, определяется соотношением (14.4), (14.6): (задача 14.1.8 — ответ 2).
Адиабатический процесс происходит без теплообмена с окружающими телами: . Поэтому из первого закона термодинамики (14.6) получаем в задаче 14.1.9 для работы газа (ответ 2).
Применяя первый закон термодинамики (14.6) к процессу, происходящему с газом в задаче 14.1.10, найдем, что внутренняя энергия газа увеличилась на 10 Дж (ответ 2).
Для решения задачи 14.2.1 можно использовать то обстоятельство, что работа газа численно равна площади фигуры, ограниченной графиком зависимости давления от объема и осью объемов. Из рисунка следует, что наибольшей является площадь под графиком процесса 1. Поэтому бóльшую работу газ совершает в процессе 1 (ответ 1).
В задаче 14.2.2 следует применить ко всем трем процессам, графики которых даны на рисунке к решению предыдущей задачи, первый закон термодинамики (14.6) . Учитывая, что начальная и конечная температура газа во всех трех процессах одинакова, и, следовательно, одинаковы изменения внутренней энергии газа , а работа наибольшая в процессе 1 (см. решение предыдущей задачи), заключаем, что газ получил большее количество теплоты в процессе 1 (ответ 1).
Работа газа положительна, если газ расширяется. Для доказательства этого утверждения представим газ в сосуде, ограниченном подвижным поршнем. Если газ расширяется, то и перемещение поршня и сила, действующая на него со стороны газа, направлены одинаково, поэтому работа газа положительна. При сжатии газа его работа отрицательна. Поэтому в задаче 14.2.3 работа газа положительна в процессе 3 (ответ 3).
Так как графики процессов 1–2 и 3–4 в задаче 14.2.4 — прямые, проходящие через начало координат, эти процессы — изохорические, и газ не совершает в них работу. А поскольку изменение внутренней энергии газа в этих процессах одинаково, то одинаковы и количества теплоты, сообщенные газу в этих процессах (ответ 3).
Задача 14.2.5 аналогична предыдущей. Рассматриваемый процесс — изохорический, поэтому изменение внутренней энергии газа равно сообщенному количеству теплоты = 100 кДж (ответ 2).
Вычисляя площадь под графиком процесса в задаче 14.2.6, находим работу газа (ответ 2).
В условии задачи 14.2.7 дано количество теплоты , которое забрали у газа. Первый закон термодинамики, в который входит эта величина, имеет вид
где — работа, совершенная над газом в рассматриваемом процессе. Подставляя в эту формулу данные в условии величины, находим = –5 Дж (ответ 1).
Чтобы понять, расширялся или сжимался газ в рассматриваемом в задаче 14.2.8 процессе, из первого закона термодинамики найдем работу газа: если она окажется положительной, газ расширялся, если отрицательной — сжимался. Из закона (14.6) находим
Поэтому газ сжимался (ответ 1).
Чтобы найти долю количества теплоты, которая пошла на увеличение внутренне энергии газа в изобарическом процессе (задача 14. 2.9) воспользуемся формулой (14.5) для работы газа в этом процессе . Поскольку изменение внутренней энергии одноатомного идеального газа равно , заключаем, что изменение внутренней энергии газа составляет 3/2 от его работы. Поэтому 2/5 количества теплоты, сообщенного газу в изобарическом процессе тратится на работу, 3/5 — на изменение внутренней энергии газа (ответ 3).
2.9) воспользуемся формулой (14.5) для работы газа в этом процессе . Поскольку изменение внутренней энергии одноатомного идеального газа равно , заключаем, что изменение внутренней энергии газа составляет 3/2 от его работы. Поэтому 2/5 количества теплоты, сообщенного газу в изобарическом процессе тратится на работу, 3/5 — на изменение внутренней энергии газа (ответ 3).
Чтобы найти теплоемкость газа в изотермическом процессе (задача 14.2.10), применим к этому процессу определение теплоемкости (14.11)
Поскольку в изотермическом процессе при ненулевом количестве сообщенной теплоты, то теплоемкость газа равна бесконечности. Это означает следующее — в изотермическом процессе газу сообщают теплоту, а он не нагревается, что и означает бесконечную теплоемкость газа (теплота расходуется только на совершение работы).
Урок 23. внутренняя энергия. работа. количество теплоты — Физика — 10 класс
Физика, 10 класс
Урок 23. Внутренняя энергия. Работа. Количество теплоты
Список вопросов, рассмотренных в уроке: внутренняя энергия; способы изменения внутренней энергии; различные виды теплообмена; уравнение теплового баланса; работа в термодинамике; нахождение численного значения работы в различных тепловых процессах.
Глоссарий по теме
Термодинамическая система представляет собой систему тел, которые взаимодействуют и обмениваются энергией и веществом.
Состояние равновесия — это состояние системы, в которой нет теплообмена между телами, составляющими систему.
Термодинамический процесс — процесс изменения состояния системы, который изменяет параметры системы.
Внутренняя энергия представляет собой сумму кинетической энергии хаотичного теплового движения и потенциальной энергии взаимодействия всех молекул, составляющих тело.
Теплоемкость представляет собой энергию, которая численно равна количеству тепла, которое выделяется или поглощается, когда температура тела изменяется на 1 К.
Теплопередача- это передача энергии от одного тела другому без выполнения работы.
Количество тепла является количественной мерой изменения внутренней энергии во время теплообмена.
Работа в термодинамике — это взаимодействие системы с внешними объектами, в результате чего изменяются параметры системы.
Список литературы
Г.Я. Мякишев., Б. Буховцев., Н. Н. Соцкий. Физика.10. Учебник для образовательных организаций М .: Просвещение, 2017. — С. 243-254.
Рымкевич А.П. Сборник задач по физике. 10-11 класс М.: Дрофа, 2009.- с.75-84
Основное содержание урока
Внутренняя энергия тела — это полная энергия всех молекул, которые его составляют. Внутренняя энергия идеального газа пропорциональна его температуре.
U = 3/2 · ν · R · T
Чтобы изменить внутреннюю энергию вещества, надо сообщить ему некоторое количество тепла или совершить работу.
Работа в термодинамике равна изменению внутренней энергии системы: A = ΔU.
Работа газа в изобарном процессе равна A = P · ΔV. Если газ расширяется, то А > 0, если газ сжимается, то А < 0.
Кроме того, работа газа может быть определена с использованием графика давления в зависимости от объема.
Работа газа численно равна площади под графиком давления.
Количество теплоты — это энергия, которую система получает или теряет во время теплообмена.
Количество тепла для различных термических процессов определяется по-разному.
При нагревании и охлаждении: Q = c_ ∙ m ∙ ΔT;
Во время плавления и кристаллизации: Q = ℷ ∙ m;
Во время испарения и конденсации; Q = r ∙ m;
При сжигании: Q = q ∙ m.
Для замкнутой и адиабатически изолированной системы тел выполняется уравнение теплового баланса: Q1 + Q2 + … + Qn = 0
Выражение для внутренней энергии одноатомного идеального или разреженного реального газа имеет следующий вид:
U = 3/2 ν ∙ R ∙ T
Для идеального газа из молекул с двумя, тремя или более атомами необходимо учитывать кинетическую энергию вращения молекул (они больше не могут считаться материальными точками), поэтому выражение для их внутренней энергии отличается от U = 3/2 ν ∙ R ∙ T числовым коэффициентом.
Для двухатомного газа (например, O2, CO и т. д.):
U = 5/2 ν ∙ R ∙ T
Для газа с тремя атомами или более (например, O3, Ch5):
U = 3ν · R · T
Изменить внутреннюю энергию вещества можно, передав ему некоторое количество тепла или выполнить над ним работу.
Существует три типа теплопередачи:
1) Теплопроводность представляет собой процесс переноса энергии от более теплого тела к менее нагретому телу с прямым контактом или от более нагретых частей тела к менее нагретым, осуществляемый хаотично движущимися частицами тела (атомы, молекулы, электроны , и т.д.). Простым примером является нагревание чашки, в которую выливают горячий чай.
2) Конвекция — это своего рода передача тепла, в которой внутренняя энергия передается снизу вверх струями или потоками жидкости или газа. Пример: нагревание воды в чайнике, который стоит на горячей плите.
3) Лучистый обмен или излучение — это процесс передачи энергии через электромагнитное излучение. Простой пример: солнечный свет.
Механическая работа изменяет механическую энергию тела. Термодинамическая работа изменяет внутреннюю энергию газа.
Если газ расширяется, то работа газа считается положительной. Если он сжат, то отрицательной.
Формула для нахождения работы газа в изобарном процессе имеет следующий вид:
A = p · ΔV
Для изотермического процесса формула принимает следующий вид: A = ν ∙ R ∙ T ∙ ln (V_2 / V_1)
Разбор тренировочных заданий
1. Объём газа, расширяющегося при постоянном давлении 100 кПа, увеличился на 20 литров. Работа, выполняемая газом в этом процессе, — _____.
Варианты ответов:
2000 Дж;
20 000 Дж;
200 Дж;
50 МДж.
Правильный вариант / варианты (или правильные комбинации вариантов): 3) 2000 Дж.
Совет: используйте формулу работы.
2. Чтобы из 5 кг снега, при температуре 0ºС, получить воду при 20ºС, необходимо сжигать в печке с КПД 40% __ кг дров.
Решение: при сгорании дров выделится количество теплоты:
из этого количества на полезную работу пойдёт только:
Для плавления снега необходимо количество теплоты:
для нагревания воды понадобится:
Согласно уравнению теплового баланса:
Отсюда следует:
Подставим числовые значения в формулу:
Ответ: 0,5175 кг. 2} – 1} \right) = 1996,1\;ДЖ\]
2} – 1} \right) = 1996,1\;ДЖ\]
Ответ: 1996,1 Дж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Внутренняя энергия идеального газа — Комшилова В.А.
Домашнее
задание: §77(учебник- Физика 10,
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Москва,
«Просвещение» 2004), №541,542(сборник задач по физике, А.П.Рымкевич,
П.А.Рымкевич0.
Тема урока: Внутренняя энергия идеального газа
Опрос:
1.Какие виды энергии вы знаете?
2.Какие виды механической энергии вы знаете?
3.Какая энергия называется кинетической?
4.Написать формулу для кинетической энергии.
5.Какая энергия называется потенциальной?
6.Какие виды потенциальной энергии вы знаете?
7.Написать формулу для потенциальной энергии тела, поднятого над землёй.
8.Написать формулу для потенциальной энергии тела деформированного тела.
9.Из чего состоит тело?
10.Как ведут себя молекулы тела?
11.Могут ли молекулы перестать двигаться?
12.Обладают ли молекулы кинетической энергией?
13.Взаимодействуют ли молекулы физического тела между собой?
14.Как называется энергия взаимодействия между молекулами тела?
15Что называется внутренней энергией тела?
16. Может ли механическая энергия тела быть равной нулю?
17.Может ли внутренняя энергия тела быть равной нулю?
Теория тепловых процессов, в которой не учитывается молекулярное строение тел называется термодинамикой.
Термодинамика была создана в середине 19 века после открытия закона сохранения энергии.
Вывод: Внутренняя энергия макроскопического тела складывается из
кинетической энергии хаотичного теплового движения молекул(атомов) и
потенциальной энергии их взаимодействия.
Внутренняя энергия идеального газа.
1.Дать характеристику идеального газа.
2.Описать молекулу идеального газа.
3.Как взаимодействуют молекулы идеального газа?
4.Какими видами механической энергии обладают молекулы идеального газа.
5.Можно ли сжать идеальный газ до объёма равного нулю? А реальный?
6.Может ли идеальный газ при сильном сжатии превратится в жидкость? А реальный?
Вывод: Внутренняя энергия идеального газа представляет собой кинетическую энергию беспорядочного движения его молекул
Написать формулу для средней кинетической
энергии молекулы газа:
E=3kT|/2 (1)
Написать формулу для определения количества молекул в данной массе газа:
N=mNa∕M (2)
Внутренняя энергия газа обозначается буквой U и определяется по формуле:
U=NE (3)
Изменение внутренней энергии газа определяется по формуле:
ΔU-изменение внутренней энергии газа.
Формулы (4) и (5) справедливы
только для идеальных и одноатомных реальных разряжённых газов.
Задача.
Какова внутренняя энергия 20 моль одноатомного газа при 67°С?
Закон об идеальном газе| Безграничная физика
Уравнения состояния
Закон идеального газа — это уравнение состояния гипотетического идеального газа (в котором нет взаимодействия между молекулами).
Цели обучения
Опишите, как был получен закон идеального газа.
Основные выводы
Ключевые моменты
- Закон идеального газа был получен эмпирическим путем путем объединения закона Бойля и закона Чарльза.
- Хотя эмпирический вывод уравнения не учитывает микроскопические детали, закон идеального газа может быть выведен из первых принципов классической термодинамики.2} [/ латекс].
Ключевые термины
- моль : В Международной системе единиц — основная единица количества вещества; количество вещества системы, которая содержит столько же элементарных единиц, сколько атомов в 12 г углерода-12.
 Символ: мол.
Символ: мол. - идеальный газ : гипотетический газ, молекулы которого не взаимодействуют друг с другом и подвергаются упругому столкновению друг с другом и со стенками контейнера.
- Число Авогадро : количество составляющих частиц (обычно атомов или молекул) в одном моль данного вещества.Он имеет размеры обратного моля и его значение равно 6.02214129 · 1023 моль-1 .
Закон идеального газа — это уравнение состояния гипотетического идеального газа (иллюстрация приведена в). В идеальном газе нет взаимодействия молекулы с молекулой, и разрешены только упругие столкновения. Это хорошее приближение к поведению многих газов во многих условиях, хотя у него есть несколько ограничений. Впервые это было высказано Эмилем Клапейроном в 1834 году как комбинация закона Бойля и закона Шарля.
Атомы и модули в газе : Атомы и молекулы в газе обычно широко разделены, как показано. Поскольку силы между ними на таких расстояниях довольно малы, они часто описываются законом идеального газа.
Эмпирический вывод
Закон Бойля гласит, что давление P и объем V данной массы ограниченного газа обратно пропорциональны:
[латекс] \ text {P} \ propto \ frac {1} {\ text {V}} [/ latex],
, в то время как закон Чарльза гласит, что объем газа пропорционален абсолютной температуре T газа при постоянном давлении
[латекс] \ text {V} \ propto \ text {T} [/ latex].
Объединив два закона, мы получим
[латекс] \ frac {\ text {PV}} {\ text {T}} = \ text {C} [/ latex],
, где C — постоянная величина, прямо пропорциональная количеству газа n (представляющая количество молей).
Коэффициент пропорциональности — это универсальная газовая постоянная R, то есть C = nR.
Отсюда и закон идеального газа
[латекс] \ text {PV} = \ text {nRT} [/ latex].
Эквивалентно его можно записать как [latex] \ text {PV} = \ text {NkT} [/ latex],
где k — постоянная Больцмана, а N — количество молекул. 2}} {3 \ text {V}} [/ latex],
2}} {3 \ text {V}} [/ latex],
где P — давление, N — количество молекул, m — масса молекулы, v — скорость молекул, а V — объем газа.2} [/ латекс].
Изотермы
Изотермический процесс — это изменение системы, в которой температура остается постоянной: ΔT = 0.
Цели обучения
Укажите условия, при которых могут происходить изотермические процессы.
Основные выводы
Ключевые моменты
- Изотермические процессы обычно происходят, когда система находится в контакте с внешним тепловым резервуаром (тепловой ванной), и изменение происходит достаточно медленно, чтобы позволить системе постоянно приспосабливаться к температуре резервуара посредством теплообмена.
- Для идеального газа, согласно закону идеального газа PV = NkT, PV остается постоянным в результате изотермического процесса. Кривая на диаграмме P-V, созданная уравнением PV = const, называется изотермой.
- Для изотермического обратимого процесса работа, совершаемая газом, равна площади под соответствующей изотермой «давление-объем». Он задается как [латекс] \ text {W} _ {\ text {A} \ to \ text {B}} = \ text {NkT} \ ln {\ frac {\ text {V} _ \ text {B} } {\ text {V} _ \ text {A}}} [/ latex].
Ключевые термины
- адиабатический : Происходит без увеличения или уменьшения тепла.
- внутренняя энергия : сумма всей энергии, присутствующей в системе, включая кинетическую и потенциальную энергию; эквивалентно, энергия, необходимая для создания системы, за исключением энергии, необходимой для перемещения ее окружения.
- идеальный газ : гипотетический газ, молекулы которого не взаимодействуют друг с другом и подвергаются упругому столкновению друг с другом и со стенками контейнера.
Изотермический процесс — это изменение системы, в которой температура остается постоянной: ΔT = 0.Обычно это происходит, когда система находится в контакте с внешним тепловым резервуаром (тепловой ванной), и изменение происходит достаточно медленно, чтобы позволить системе постоянно приспосабливаться к температуре резервуара посредством теплообмена. Напротив, адиабатический процесс происходит, когда система не обменивается теплом с окружающей средой (Q = 0). Другими словами, в изотермическом процессе значение ΔT = 0, но Q ≠ 0, а в адиабатическом процессе ΔT ≠ 0, но Q = 0.
Напротив, адиабатический процесс происходит, когда система не обменивается теплом с окружающей средой (Q = 0). Другими словами, в изотермическом процессе значение ΔT = 0, но Q ≠ 0, а в адиабатическом процессе ΔT ≠ 0, но Q = 0.
Для идеального газа произведение PV (P: давление, V: объем) является постоянным, если газ поддерживается в изотермических условиях (закон Бойля).Согласно закону идеального газа, значение постоянной равно NkT, где N — количество молекул газа, а k — постоянная Больцмана.
Это означает, что [латекс] \ text {p} = {\ text {N} \ text {k} \ text {T} \ over \ text {V}} = {\ text {Constant} \ over \ text {V }} [/ latex] держится.
Семейство кривых, генерируемых этим уравнением, показано на графике, представленном на. Каждая кривая называется изотермой. Такие графики называются индикаторными диаграммами — они впервые использовались Джеймсом Ваттом и другими для мониторинга эффективности двигателей.{\ text {V} _ \ text {B}} \ text {P} \, \ text {dV} [/ latex].
(Это уравнение получено в нашем атоме «Постоянное давление» в соответствии с кинетической теорией. Обратите внимание, что P = F / A. Это определение согласуется с нашим определением работы как силы, умноженной на расстояние.)
Для изотермического обратимого процесса этот интеграл равен площади под соответствующей изотермой давление-объем и обозначен синим цветом in для идеального газа. Опять же, применяется P = nRT / V, и при постоянном T (поскольку это изотермический процесс) мы имеем:
Работа, выполненная газом во время расширения : Синяя область представляет «работу», совершаемую газом во время расширения для этого изотермического изменения.{\ text {V} _ \ text {B}} \ frac {\ text {NkT}} {\ text {V}} \ text {dV} \\ & = \ text {NkT} \ ln {\ frac {\ текст {V} _ \ text {B}} {\ text {V} _ \ text {A}}} \ end {align} [/ latex].
По соглашению, работа определяется как работа, которую система выполняет в своей среде. Если, например, система расширяется поршнем, движущимся в направлении силы, приложенной внутренним давлением газа, то работа считается положительной.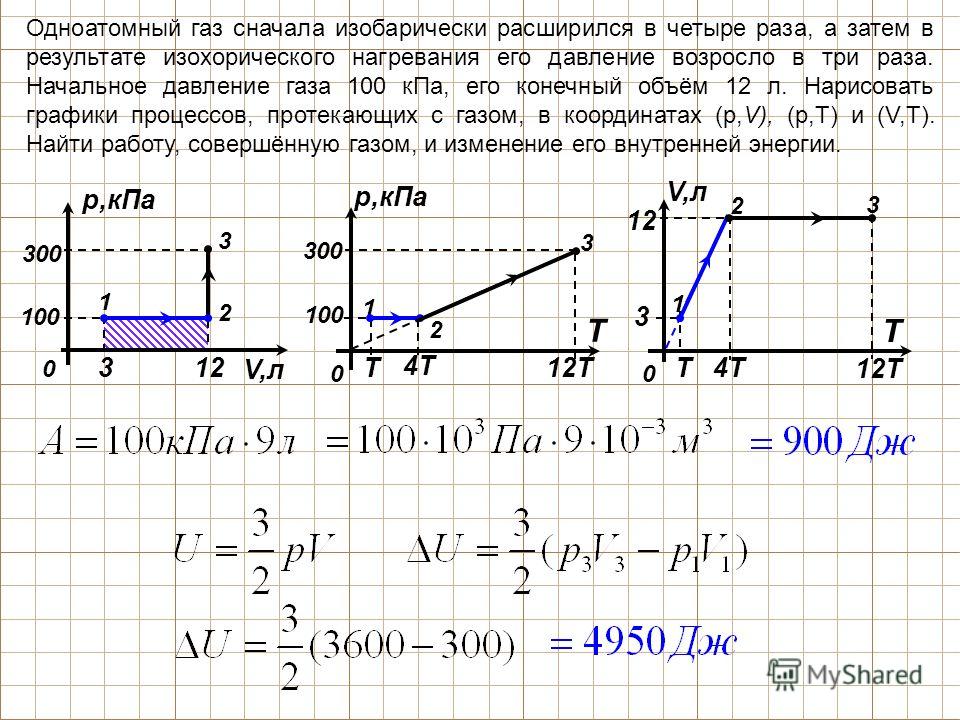 Поскольку эта работа выполняется за счет использования внутренней энергии системы, в результате внутренняя энергия уменьшается.И наоборот, если окружающая среда воздействует на систему так, что ее внутренняя энергия увеличивается, эта работа считается отрицательной (подробности о внутренней энергии см. В нашем Атоме «Внутренняя энергия идеального газа»).
Поскольку эта работа выполняется за счет использования внутренней энергии системы, в результате внутренняя энергия уменьшается.И наоборот, если окружающая среда воздействует на систему так, что ее внутренняя энергия увеличивается, эта работа считается отрицательной (подробности о внутренней энергии см. В нашем Атоме «Внутренняя энергия идеального газа»).
Постоянное давление
Изобарический процесс — это термодинамический процесс, в котором давление остается постоянным (при постоянном давлении работа, выполняемая газом, равна [latex] \ text {P} \ Delta \ text {V} [/ latex]).
Цели обучения
Описать поведение одноатомного газа во время изобарных процессов.
Основные выводы
Ключевые моменты
- Газы могут расширяться или сжиматься при определенных ограничениях. В зависимости от ограничения конечное состояние газа может измениться.
- Тепло, передаваемое системе, работает, но также изменяет внутреннюю энергию системы. В изобарическом процессе для одноатомного газа тепло и изменение температуры удовлетворяют следующему уравнению: [latex] \ text {Q} = \ frac {5} {2} \ text {N} \ text {k} \ Delta \ text {T} [/ латекс].
- Для одноатомного идеального газа удельная теплоемкость при постоянном давлении равна [латекс] \ frac {5} {2} \ text {R} [/ latex].
Ключевые термины
- первый закон термодинамики : версия закона сохранения энергии: изменение внутренней энергии замкнутой системы равно количеству тепла, подаваемого в систему, за вычетом количества работы, выполняемой системой на его окрестностях.
- удельная теплоемкость : Отношение количества тепла, необходимого для повышения температуры единицы массы вещества на единицу градуса, к количеству тепла, необходимому для повышения температуры той же массы воды на такое же количество.
При определенных ограничениях (например, давлении) газы могут расширяться или сжиматься; в зависимости от типа ограничения конечное состояние газа может измениться. Например, идеальный газ, который расширяется при постоянной температуре (так называемый изотермический процесс), будет существовать в другом состоянии, чем газ, который расширяется при постоянном давлении (так называемый изобарический процесс). Этот Атом обращается к изобарическому процессу и коррелированным условиям. Мы обсудим изотермический процесс в следующем атоме.
Например, идеальный газ, который расширяется при постоянной температуре (так называемый изотермический процесс), будет существовать в другом состоянии, чем газ, который расширяется при постоянном давлении (так называемый изобарический процесс). Этот Атом обращается к изобарическому процессу и коррелированным условиям. Мы обсудим изотермический процесс в следующем атоме.
Изобарический процесс
Изобарный процесс — это термодинамический процесс, в котором давление остается постоянным: ΔP = 0. Для идеального газа это означает, что объем газа пропорционален его температуре (исторически это называется законом Чарльза). Давайте рассмотрим случай, когда газ действительно воздействует на поршень при постоянном давлении P, ссылаясь на рис. 1 в качестве иллюстрации. Поскольку давление постоянно, прилагаемая сила постоянна, а проделанная работа выражается как W = Fd, где F (= PA) — сила, прикладываемая к поршню со стороны давления, а d — смещение поршня.Следовательно, работа, совершаемая газом (Вт), равна:
[латекс] \ text {W} = \ text {PAd} [/ латекс].
Поскольку изменение объема цилиндра равно его площади поперечного сечения A, умноженной на смещение d, мы видим, что Ad = ΔV, изменение объема. Таким образом,
[латекс] \ text {W} = \ text {P} \ Delta \ text {V} [/ latex]
(как видно на рис. 2 — изобарный процесс). Примечание: если ΔV положительно, тогда W положительно, что означает, что работа выполняется газом во внешнем мире. Используя закон идеального газа PV = NkT (P = const),
Рис. 2 : График зависимости давления от объема для постоянного или изобарного процесса.Площадь под кривой равна работе, совершаемой газом, поскольку W = PΔV.
[латекс] \ text {W} = \ text {Nk} \ Delta \ text {T} [/ latex]
(уравнение 1) для идеального газа, подвергающегося изобарическому процессу.
Одноатомный газ
Согласно первому закону термодинамики,
[латекс] \ text {Q} = \ Delta \ text {U} + \ text {W} \, [/ latex]
(уравнение 2), где W — работа, совершаемая системой, U — внутренняя энергия, Q — тепло. Закон гласит, что тепло, передаваемое системе, действительно работает, но также изменяет внутреннюю энергию системы.Так как,
[латекс] \ text {U} = \ frac {3} {2} \ text {NkT} [/ latex] для одноатомного газа, мы получаем [латекс] \ Delta \ text {U} = \ frac {3} {2} \ text {Nk} \ Delta \ text {T} [/ latex]
(уравнение 3; подробности о внутренней энергии см. В нашем Атоме «Внутренняя энергия идеального газа»). Используя уравнения 1 и 3, уравнение. 2 можно записать как:
[латекс] \ text {Q} = \ frac {5} {2} \ text {N} \ text {k} \ Delta \ text {T} [/ latex] для одноатомного газа в изобарическом процессе.
Удельная теплоемкость
Удельная теплоемкость при постоянном давлении определяется следующим уравнением:
[латекс] \ text {Q} = \ text {n} \ text {c} _ \ text {P} \ Delta \ text {T} [/ latex].
Здесь n — количество частиц в газе, выраженное в молях. Отметив, что N = N A n и R = кН A (N A : число Авогадро, R: универсальная газовая постоянная), получаем:
[латекс] \ text {c} _ \ text {P} = \ frac {5} {2} \ text {kN} _ \ text {A} = \ frac {5} {2} \ text {R} [ / латекс] для одноатомного газа.
Решение проблем
С помощью закона идеального газа мы можем вычислить давление, объем или температуру, а также количество молей газа при идеальных термодинамических условиях.
Цели обучения
Укажите шаги, используемые для решения уравнения идеального газа.
Основные выводы
Ключевые моменты
- Запишите всю информацию, которую вы знаете о газе, и при необходимости преобразуйте известные значения в единицы СИ.
- Выберите соответствующее уравнение закона газа, которое позволит вам вычислить неизвестную переменную, и подставьте известные значения в уравнение. Затем вычислите неизвестную переменную.
- Общее уравнение газа применимо только в том случае, если молярное количество газа фиксировано.
Ключевые термины
- идеальный газ : гипотетический газ, молекулы которого не взаимодействуют друг с другом и подвергаются упругому столкновению друг с другом и со стенками контейнера.
- Единицы СИ : Международная система единиц (сокращенно СИ от французского: Le Système international d’unités). Это современная форма метрической системы.
Закон идеального газа — это уравнение состояния гипотетического идеального газа. Это хорошее приближение к поведению многих газов во многих условиях, хотя у него есть несколько ограничений.Он наиболее точен для одноатомных газов при высоких температурах и низких давлениях.
Закон идеального газа имеет вид:
[латекс] \ text {PV} = \ text {nRT} [/ latex],
, где R — универсальная газовая постоянная, и с ее помощью мы можем найти значения давления P, объема V, температуры T или числа молей n при определенных идеальных термодинамических условиях . Обычно вам дается достаточно параметров, чтобы вычислить неизвестное. Вариации уравнения идеального газа могут помочь легко решить проблему.Вот несколько общих советов.
Закон идеального газа также может иметь форму:
[латекс] \ text {PV} = \ text {NkT} [/ latex],
где N — количество частиц в газе, а k — постоянная Больцмана.
Для решения уравнения идеального газа:
- Запишите всю информацию, которую вы знаете о газе.
- При необходимости преобразуйте известные значения в единицы СИ.
- Выберите соответствующее уравнение закона газа, которое позволит вам вычислить неизвестную переменную.
- Подставьте известные значения в уравнение. Рассчитайте неизвестную переменную.
Помните, что общее уравнение газа применимо только в том случае, если молярное количество газа фиксировано. Например, если газ смешивается с другим газом, вам, возможно, придется применить уравнение отдельно для отдельных газов.
Пример
Представим, что в начале пути шина грузовика имеет объем 30 000 см 3 и внутреннее давление 170 кПа.Температура шины составляет 16 C. К концу поездки объем шины увеличился до 32000 см 3 , а температура воздуха внутри шины составляет 40 ∘ C. Что такое давление в шинах в конце пути?
Давление в шинах : Давление в шинах может значительно измениться во время эксплуатации автомобиля. В основном это связано с изменением температуры воздуха в шинах.
Решение:
Шаг 1. Запишите всю информацию, которую вы знаете о газе: P 1 = 170 кПа и P 2 неизвестно.V 1 = 30 000 см 3 и V 2 = 32 000 см 3 . T 1 = 16 C и T 2 = 40 ∘ C.
Шаг 2. Преобразуйте известные значения в единицы СИ, если необходимо: Здесь температуру необходимо перевести в Кельвины. Следовательно, T 1 = 16 + 273 = 289 K, T 2 = 40 + 273 = 313 K
Шаг 3. Выберите соответствующее уравнение закона газа, которое позволит вам вычислить неизвестную переменную: Мы можем использовать общее уравнение газа для решения этой проблемы: [latex] \ frac {\ text {P} _1 \ text {V} _1 } {\ text {T} _1} = \ frac {\ text {P} _2 \ text {V} _2} {\ text {T} _2} [/ latex].
Следовательно, [латекс] \ text {P} _2 = \ frac {\ text {P} _1 \ times \ text {V} _1 \ times \ text {T} _2} {\ text {T} _1 \ times \ text {V} _2} [/ латекс].
Шаг 4. Подставьте известные значения в уравнение. Вычислить неизвестную переменную:
[латекс] \ text {P} _2 = \ frac {170 \ times 30 000 \ times 313} {289 \ times 32 000} = 173 ~ \ text {кПа} [/ latex].
Давление в шине в конце пути 173 кПа.
Обратите внимание, что на шаге 2 мы не удосужились преобразовать значения объема в м 3 .На шаге 4 давление появляется как в числителе, так и в знаменателе. В этом случае преобразование не требовалось.
Число Авогадора
Число молекул в молье называется числом Авогадро (N A ) и определяется как 6,02x 10 23 моль -1 .
Цели обучения
Объясните связь между числом Авогадро и родинкой.
Основные выводы
Ключевые моменты
- Авогадро предположил, что равные объемы газа при одинаковом давлении и температуре содержат одинаковое количество молекул, независимо от типа газа.
- Постоянная Авогадро — это коэффициент масштабирования между макроскопическими и микроскопическими (атомный масштаб) наблюдениями за природой. Он обеспечивает связь между другими физическими константами и свойствами.
- Альберт Эйнштейн предположил, что число Авогадро можно определить на основе величин, наблюдаемых в броуновском движении. Впервые числовая апертура была измерена Жаном Батистом Перреном в 1908 году.
Ключевые термины
- газовая постоянная : Универсальная постоянная R, которая появляется в законе идеального газа (PV = nRT), полученная из двух фундаментальных констант, постоянной Больцмана и числа Авогадро (R = NAk).
- Постоянная Фарадея : Величина электрического заряда на моль электронов.
- Броуновское движение : Случайное движение взвешенных в жидкости частиц, возникающее в результате столкновения этих частиц с отдельными молекулами жидкости.
При измерении количества вещества иногда проще работать с единицей измерения, отличной от количества молекул. Моль (сокращенно моль) — основная единица Международной системы единиц (СИ). Он определяется как любое вещество, содержащее столько атомов или молекул, сколько содержится ровно в 12 граммах (0.012 кг) углерода-12. Фактическое количество атомов или молекул в одном моль, по признанию итальянского ученого Амедео Авогадро, называется постоянной Авогадро (N A ) .
Амадео Авогадро : Амедео Авогадро (1776–1856). Он установил, что соотношение между массами одного и того же объема разных газов (при одинаковых температуре и давлении) соответствует соотношению между их соответствующими молекулярными массами.
Число Авогадро (N) обозначает количество молекул в одной грамм-молекуле кислорода.Это указывает на количество вещества, а не на независимое измерение. В 1811 году Амедео Авогадро впервые предположил, что объем газа (при данном давлении и температуре) пропорционален количеству атомов или молекул, независимо от природы газа (т. Е. Это число универсально и не зависит от типа газа). газ). В 1926 году Жан Перрен получил Нобелевскую премию по физике, в основном за его работу по определению постоянной Авогадро (несколькими различными методами). Значение постоянной Авогадро N A оказалось равным 6.{-1}} [/ латекс].
Измерение N
AОпределение N A имеет решающее значение для расчета массы атома, поскольку последняя получается делением массы моля газа на постоянную Авогадро. В своем исследовании броуновского движения в 1905 году Альберт Эйнштейн предположил, что эта постоянная может быть определена на основе величин, наблюдаемых в броуновском движении. Впоследствии идея Эйнштейна была подтверждена, что привело к первому определению N A в 1908 году в результате экспериментальной работы Жана Батиста Перрена.
Абсолютная температура
Абсолютная температура — это наиболее часто используемая термодианмическая единица измерения температуры и стандартная единица измерения температуры.
Цели обучения
Опишите взаимосвязь между абсолютной температурой и кинетической энергией.
Основные выводы
Ключевые моменты
- Температура возникает из кинетической энергии случайных движений компонентов материи, таких как молекулы или атомы. Поэтому разумно выбрать в качестве точки отсчета абсолютный ноль, при котором все классическое движение прекращается.
- Согласно международному соглашению, единица измерения кельвина и ее шкала определяются двумя точками: абсолютным нулем и тройной точкой стандартизированной воды.
- При абсолютном нуле частицы, составляющие материю, имеют минимальное движение и не могут стать холоднее. Они сохраняют минимальное квантово-механическое движение.
Ключевые термины
- абсолютный ноль : самая низкая из возможных температур: ноль по шкале Кельвина и приблизительно -273,15 ° C и -459.67 ° F. Полное отсутствие тепла; температура, при которой движение всех молекул прекратится.
- Международная система единиц : (СИ): Стандартный набор основных единиц измерения, используемый в мировой научной литературе.
- Венский стандарт для средней океанической воды : Стандарт, определяющий стандартизованный изотопный состав воды.
Термодинамическая температура — это абсолютная мера температуры. Это один из основных параметров термодинамики и кинетической теории газов.Термодинамическая температура — это «абсолютная» шкала, потому что это мера фундаментального свойства, лежащего в основе температуры: ее нулевая или нулевая точка («абсолютный ноль») — это температура, при которой частицы, составляющие материю, имеют минимальное движение и не могут стать холоднее. То есть, они имеют минимальное движение, сохраняя только квантово-механическое движение, как показано на схеме.
График зависимости давления от температуры : График зависимости давления от температуры для различных газов, поддерживаемых в постоянном объеме.Обратите внимание, что все графики экстраполированы на нулевое давление при одной и той же температуре
В самом простом случае, «температура» возникает из кинетической энергии случайных движений составляющих материальных частиц, таких как молекулы или атомы, как показано на рисунке. Следовательно, разумно выбрать абсолютный ноль, когда все классическое движение прекращается, в качестве эталона. точка (T = 0) нашей температурной системы. Используя шкалу абсолютных температур (система Кельвина), которая является наиболее часто используемой термодинамической температурой, мы показали, что средняя поступательная кинетическая энергия (KE) частицы в газе имеет простую связь с температурой:
Поступательное движение гелия : Реальные газы не всегда ведут себя в соответствии с идеальной моделью при определенных условиях, таких как высокое давление.Здесь размер атомов гелия относительно их расстояния показан в масштабе при давлении 1950 атмосфер.
[латекс] \ overline {\ text {KE}} = \ frac {3} {2} \ text {kT} [/ latex].
Обратите внимание, что это уравнение не выглядело бы так элегантно, если бы вместо него использовалась шкала Фаренгейта.
Шкала Кельвина
Кельвин (или «абсолютная температура») — это стандартная термодианмическая единица измерения температуры. Это одна из семи основных единиц Международной системы единиц (СИ), которой присвоен символ единицы K.По международному соглашению единица измерения кельвина и ее шкала определяются двумя точками: абсолютным нулем и тройной точкой Венской стандартной средней океанской воды (вода с определенной смесью изотопов водорода и кислорода). Абсолютный ноль, минимально возможная температура, определяется как 0 K и −273,15 ° C. Тройная точка воды определяется точно как 273,16 K и 0,01 ° C.
Процессы идеального газа — Химия LibreTexts
В этом разделе мы поговорим о взаимосвязи идеальных газов с точки зрения термодинамики.Мы увидим, как с помощью термодинамики мы сможем лучше понять идеальные газы.
Введение
В области химии мы часто видим много взаимосвязей между первой и ее связью с физикой. Используя и химию, и физику, мы можем лучше понять оба упомянутых аспекта. Мы будем использовать то, что мы знаем об идеальных газах и термодинамике, чтобы попытаться понять конкретные процессы, происходящие в системе.
Краткий обзор термодинамикиПрежде чем мы продолжим обсуждение, давайте сделаем очень краткий обзор важных аспектов термодинамики, которые важно знать для процессов с идеальным газом.Некоторые из них будут кратким обзором, а некоторые будут относительно новыми, если вы не видели их на своем уроке физики.
Итак, прежде всего давайте сформулируем Первый закон термодинамики:
\ (\ Delta {U} = Q + W \)
Весь смысл формулировки этого уравнения состоит в том, чтобы напомнить нам, что энергия в любой данной системе сохраняется. Это означает, что энергия НИКОГДА не создается и не уничтожается, а просто преобразуется из одной формы в другую, например, тепло для работы и наоборот.
Если вас могут смутить некоторые из этих символов, вот краткое пояснение в таблице.
| ΔU | Это полное изменение внутренней энергии газа. |
| Q | Это общий тепловой поток газа. • Когда Q отрицательно (-), тепло отводится из системы • Когда Q положительно (+), в систему добавляется тепло |
| Вт | Это общая работа, выполненная на газе или им. • Когда W отрицательно (-), работа выполняется системой • Когда W положительный (+), работа выполняется в системе |
Ниже приведены два уравнения, которые описывают взаимосвязь между внутренней энергией системы одноатомного газа и двухатомного газа.В одноатомном газе ( одно- : один) газ, поскольку он имеет только одну молекулу, способы получения энергии будут меньше, чем у двухатомного газа ( di- : два), поскольку двухатомный газ имеет больше способов получить энергию. энергия (Следовательно, двухатомный газ имеет фактор 5/2, а одноатомный газ — 3/2).
Глядя на эти два уравнения, мы также делаем вывод, что внутренняя энергия (ΔU) влияет только на кинетическую энергию молекул газа (движение). Нигде в этих двух уравнениях мы не видим влияния на потенциальную энергию.
Одноатомный идеальный газ
Одноатомное уравнение идеального газа:
\ (\ Delta {U} = \ frac {3} {2} nR \ Delta {T} \)
В одноатомном газе он имеет всего три режима поступательной кинетической энергии (отсюда 3 /2).
Двухатомный идеальный газ
Уравнение двухатомного идеального газа:
\ (\ Delta {U} = \ frac {5} {2} nR \ Delta {T} \)
В двухатомном газе он имеет в общей сложности три режима поступательной кинетической энергии и два режима вращательной энергии (отсюда 5 /2).
Работа в идеальных газах
Что касается первого закона термодинамики, мы можем видеть, что добавлением тепла (Q) или работы (W) внутренняя энергия газовой системы может быть увеличена. Кроме того, во время сжатия системы объем газа будет уменьшаться, а его температура будет увеличиваться, и, таким образом, внутренняя энергия системы также увеличится, поскольку температура связана с энергией. И это верно, за исключением изотермической системы (о которой мы поговорим позже).Поэтому при сжатии газа работа положительная, а при сжатии — отрицательная.
Также может быть полезно знать, что область под кривой — рабочая. Если вы использовали исчисление, вы можете запомнить интеграл, поскольку он используется для определения площади под кривой (или графиком), как показано ниже.
\ [W = — \ displaystyle \ int P dV \]
ИЛИ
W = — (площадь под кривой)
В этом случае можно буквально взять площадь треугольника или работать с интегралами.
Работа = Площадь = (1/2) основание x высота
или
Работа = ∫F (x) dx
Теплоемкость и функции состояния
Когда определенные функции состояния (P, V, T) поддерживаются постоянными, это влияет на удельную теплоемкость газа.
Ниже приводится универсальная формула молекулы газа при постоянном давлении:
\ (c_p = c_v + R \)
При изменении этой формулы мы получаем тепловую мощность газа, когда его объем остается постоянным:
\ (c_v = R — c_p \)
Типы процессов идеального газа
Существует четыре типа термодинамических процессов.В основном это означает, что в системе одна или несколько переменных остаются постоянными. Для простоты ниже приведены примеры того, как может привести к сохранению определенной переменной в системной константе.
Изобарический
• Это процесс, при котором давление в системе поддерживается постоянным.
• P = 0
• Примером может быть вода, кипящая в кастрюле над горелкой. В этом случае между горелкой и кастрюлей происходит обмен теплом, но давление остается постоянным.
Чтобы вывести этот процесс, мы начнем с использования того, что мы знаем, и это первый закон термодинамики:
\ (\ Delta {U} = Q + W \)
Немного изменив это уравнение, получим:
\ (Q = \ Delta {U} + W \)
Далее, поскольку давление равно W ΔV, его можно обозначить как:
\ (Q = \ Delta {U} + p \ Delta {V} \)
Теперь можно применить закон идеального газа (PV = nRΔT), и, поскольку давление постоянно:
\ (Q = ΔU + nR \ Delta {T} \)
Для следующего шага мы предположим, что это количество молей газа остается постоянным на протяжении всего процесса:
\ (Q = n \ c_V \ \ Delta {T} + nR \ Delta {T} \)
Еще раз упростив уравнение, вычтя nΔT из обоих уравнений, мы получим:
\ (Q = n \ (c_V + R) \ \ Delta {T} \)
Зная, что c p = c v + R, мы можем заменить cp:
\ (Q = n \ c_P \ \ Delta {T} \)
Теперь мы получили уравнение изобарного процесса!
Рисунок: Изобарический процесс в графической формеИзохорный
• Это процесс, при котором объем системы поддерживается постоянным.
• ΔV = 0
• Примером этого может быть случай, когда газообразный гелий запечатан в контейнере, и есть объект (например, поршень), толкающий контейнер вниз (оказывающий давление). Но молекулы газа не входят в систему и не выходят из нее.
Давайте найдем уравнение для этого процесса, как раньше, давайте начнем с первого закона термодинамики:
\ (\ Delta {U} = Q + W \)
Немного изменив это уравнение, получим:
\ (Q = \ Delta {U} + W \)
В этом случае, поскольку объем постоянный, ΔV = 0:
\ (Q = \ Delta {U} \)
Поскольку внутренняя энергия системы равна количеству переданного тепла, мы можем заменить ΔU уравнением для тепла идеального газа:
\ (Q = nC_V \ Delta {T} \)
Выше уравнение идеального газа для изохорного процесса!
Рисунок: Изохорный процесс в графической форме
Изотермический
• Это процесс, при котором температура системы поддерживается постоянной.
ΔU = 0, ΔT = 0
• При увеличении объема давление будет уменьшаться, и наоборот.
ΔT = 0, тогда: ΔV ↑ и P ↓ OR ΔV ↓ и P ↑ (обратная зависимость)
• Например, молекулы газа запечатаны в контейнере, но объект наверху контейнера ( например, поршень) давит на контейнер очень медленно, этого недостаточно, чтобы изменить его температуру.
Чтобы вывести уравнение изотермического процесса, мы должны сначала написать первый закон термодинамики:
\ (\ Delta {U} = Q + W \)
Немного изменив это уравнение, получим:
\ (Q = \ Delta {U} + W \)
Так как ΔT = 0.Остается только работа:
\ (Q = W \)
Таким образом получаем:
\ (W = -p \ Delta {V} \)
Превращая это уравнение в уравнение идеального газа, получаем:
\ (W = \ frac {nRt} {V} \)
Чтобы перейти к следующему шагу, нам нужно использовать некоторые вычисления:
\ (Q = nRT ln \ frac {V_f} {V_i} \)
И вот так! Уравнение изотермического процесса.
Адиабатический
• Это процесс, при котором система не нагревается и не удаляется.
• Или можно просто сформулировать так: в системе не происходит теплопередачи (или теплового потока).
• На первом курсе химии нужна только основная идея этого процесса, и это когда нет теплопередачи, Q = 0.
Задачи для практики
1
Объем газа в баллоне увеличился с 1 л до 3 л при выпуске поршня вверх.На следующем графике найдите объем работы, связанный с расширением газа.
\ (f (x) = x + 3 \) из [1, 3]
Задача 2
Кальвин наблюдает за неизвестной одноатомной молекулой газа (запечатанной внутри контейнера) в своей химической лаборатории для первокурсников. Инструктор лаборатории сообщил ему, что в контейнере находится четыре моля неопознанного газа. Когда он начал работу в лаборатории, температура в лабораторной комнате была изначально установлена на уровне комнатной, но к тому времени, когда он почти закончил с лабораторией, температура поднялась на 10 ° C.Какова полная внутренняя энергия этого неизвестного газообразного вещества к моменту окончания лабораторного сеанса Кальвина?
Задача 3
В изохорной системе три моля газообразного водорода удерживаются внутри закрытого контейнера с поршнем наверху. Общее количество внутренней энергии газовой системы составляет 65 Дж, а температура системы снизилась с 25 ° C до 19 ° C. Какова удельная теплоемкость молекул газа?
Задача 4
Просматривая некоторые из своих лабораторных данных, студентка-химик замечает, что она забыла записать количество молей молекулы газа, на которую она смотрела.Эксперимент, который она провела в тот день, поддерживал постоянное давление, а в процессе эксперимента температура упала на два градуса. Если предположить, что все переменные также идеальны, со сколькими родинками она имела дело?
Задача 5
Студент-химик изучает 5,00 граммов одноатомного гелия, помещенного в контейнер, который расширяется с 10 до 13 литров. Контейнер находится в закрытой системе при постоянной температуре 30 ° C. а) Какова полная энергия системы? (б) Давление в системе увеличивается, уменьшается или не изменяется?
Решение проблемы 1
Как указано выше, мы знаем, что объем работы равен площади под кривой.В этом случае мы можем искать формы, площадь которых легко найти.
Здесь у нас есть форма, похожая на прямоугольник.
Работа = Площадь = Длина x Ширина
= (3) (3-1)
= (3) (2)
= 6
Работа = 6 Джоулей
Решение проблемы 2
Из задачи мы знаем, что неизвестное газообразное вещество одноатомное, поэтому нам пришлось бы использовать уравнение для одноатомного газа:
\ (\ Delta {U} = \ frac {3} {2} nR \ Delta {T} \)
Также из проблемы мы знаем, что вещество имеет комнатную температуру и 25 ° C, но это была просто дополнительная информация, и нам не нужно было знать это, чтобы решить проблему.Поскольку мы знаем, что изменение температуры от начала до конца было + 10 °.
\ (\ Delta {T} = + 10K \)
Задача также дала нам количество родинок в контейнере:
\ (п = 4 моль \)
В качестве значения R мы можем выбрать любую константу R, но, чтобы немного упростить эту задачу, мы выберем константу R, которая компенсирует любые другие единицы, кроме джоулей.
\ (R = 8,3145 \ frac {J} {mol K} \)
Подставляя все эти значения в уравнение, мы получаем:
\ (\ Delta {U} = \ frac {3} {2} (4 моль) (8.3145 \ frac {J} {mol K}) (10K) \)
\ (= 498 Дж \)
Решение проблемы 3
Поскольку система является изохорной системой, изменение объема будет нулевым, следовательно:
\ (\ Delta {V} = 0 \)
И уравнение для изохорной системы будет:
\ (Q = nC_V \ Delta {T} \)
Из уравнения мы знаем следующее:
\ (n = 3 моль \)
\ (Q = \ Delta {T} = (25-19) K = 6K \)
(поскольку мы только пытаемся найти разницу между начальной и конечной точками, нам не нужно выполнять преобразование в градусы Кельвина)
\ (Q = 65 Дж \)
Перед тем, как подставить значения, давайте изменим изохорическое уравнение и установим для него то, что мы пытаемся найти:
\ (C_V = \ frac {Q} {n \ Delta {T}} \)
Теперь мы можем вставить значения:
\ (C_V = \ frac {65J} {(3 моль) (6K)} \)
\ (= 3.6 \ frac {J} {mol k} \)
Решение проблемы 4
Из задачи получаем следующее:
\ (\ Delta {T} = + 2K \)
\ (\ Delta {U} = Q = 110 Дж \)
Так как указано, что давление газа поддерживалось постоянным:
\ (C_p = 14 \ frac {J} {K mol} \)
У нас достаточно доказательств, чтобы сделать вывод, что это изобарный процесс:
\ (Q = n \ c_P \ \ Delta {T} \)
Преобразуя уравнение в соответствии с тем, что мы пытаемся найти, мы получаем:
\ (n = \ frac {Q} {\ c_P \ \ Delta {T}} \)
Теперь мы можем ввести наши значения:
\ (n = \ frac {110 Дж} {14 \ frac {J} {K mol} 2K} \)
\ (= 4 моля газа \)
Решение проблемы 5
А)
Сначала перечислим, что дано в задаче:
\ (V_i = 10 л \)
\ (V_f = 13 л \)
Переводя температуру из Цельсия в Кельвин, получаем:
\ (Т = (30 + 273.15) К = 303,15К \)
А поскольку температура постоянна, это изотермический процесс:
\ (Q = nRT ln \ frac {V_f} {V_i} \)
Чтобы использовать это уравнение, нам нужно преобразовать газообразный гелий в моль:
\ (n = \ frac {grams} {\ frac {grams} {мол}} \)
\ (= \ frac {5,00 г He} {\ frac {4,00 г He} {mol He}} \)
\ (= 1,25 моль He \)
Мы выберем универсальную R-константу, которая легко исключает все единицы, которые помогут нам получить ответ без каких-либо других преобразований:
\ (= 8.31451 \ frac {J} {K mol} \)
Подставляя все эти значения в изотермическое уравнение, получаем:
\ (Q = (1,25 моль) (8,31451 \ frac {J} {K mol}) (303,15 K) ln \ frac {13 L} {10 L} \)
\ (= 827 Дж \)
В)
Как правило, в изотермическом процессе объем и давление имеют обратную зависимость. Это означает, что один идет вверх, а другой должен опускаться. В этом случае объем увеличился, поэтому давление должно было снизиться .
Внутренняя энергия — Идеальный газ — Одноатомный, Двухатомный газ
Удельная теплоемкость при постоянном объеме и постоянном давлении
Удельная теплоемкость — это свойство, связанное с внутренней энергией , которое очень важно в термодинамике.Интенсивные свойства c v и c p определены для чистых простых сжимаемых веществ как частные производные внутренней энергии u (T, v) и энтальпии ч. (Т, п) , соответственно:
, где индексы v и p обозначают переменные, фиксированные во время дифференцирования. Свойства c v и c p упоминаются как удельная теплоемкость (или теплоемкость ), потому что при определенных особых условиях они связывают изменение температуры системы с количеством энергии, добавляемой теплопередача.Их единицы СИ: Дж / кг K или Дж / моль K . Для газов определены две удельные теплоты: одна для постоянного объема (c v ) и одна для постоянного давления (c p ) .
Согласно первому закону термодинамики , для процесса постоянного объема с одноатомным идеальным газом молярная удельная теплоемкость будет:
C v = 3 / 2R = 12,5 Дж / моль K
потому что
U = 3 / 2nRT
Можно вывести, что молярная теплоемкость при постоянном давлении составляет:
C p = C v + R = 5 / 2R = 20.8 Дж / моль K
Это C p больше, чем молярная удельная теплоемкость при постоянном объеме C v , потому что теперь необходимо подавать энергию. не только с до поднимает температуру газа , но и для газа для работы , потому что в этом случае объем изменяется.
Идеальные одноатомные газы
Идеальные одноатомные газыДалее: Парадокс Гибба Up: Приложения статистической термодинамики Предыдущий: Функции разделения
Идеальные одноатомные газы Попрактикуемся в вычислении термодинамических соотношений с использованием разбиения функция, рассмотрев пример, с которым мы уже хорошо знакомы: и.е. , г. идеальный одноатомный газ. Рассмотрим газ, состоящий из одинаковых одноатомных молекулы массы заключены в контейнер объема. Обозначим положение и импульс векторов молекулы th по и , соответственно. Поскольку газ идеален, межатомные силы отсутствуют, и полная энергия представляет собой просто сумму отдельных кинетических энергий молекул:
| (427) |
куда .
Давайте подойдем к проблеме классически.В этом подходе мы разделяем фазовое пространство
в ячейки равного объема. Здесь — количество степеней
свободы, и является небольшой постоянной с размерами углового момента, который
параметризует точность, с которой положения и импульсы молекул
определены (см. раздел 3.2).
Каждая ячейка в фазовом пространстве соответствует своему состоянию.
Статистическая сумма представляет собой сумму фактора Больцмана по всем возможным состояниям, где — энергия состояния.
Классически мы можем аппроксимировать суммирование по ячейкам в фазовом пространстве
как интеграция по всему фазовому пространству.Таким образом,
| (428) |
где — число степеней свободы одноатомного газа, содержащего молекулы. Используя уравнение. (427), вышесказанное выражение сводится к
| (429) |
Обратите внимание, что интеграл по координатам заданного молекула просто дает объем контейнера, так как энергия не зависит от расположение молекул в идеальном газе.Такие интегралы есть, поэтому получаем множитель в приведенном выше выражении. Отметим также, что каждый из интегралов по импульсам молекул в формуле. (429) идентичны: они отличаются только нерелевантными фиктивными переменными интегрирования. Отсюда следует, что статистическая сумма газа складывается из произведения идентичные множители: то есть ,
| (430) |
куда
| (431) |
— статистическая сумма отдельной молекулы.Конечно, это результат очевиден, поскольку мы уже показали, что статистическая сумма для система, состоящая из ряда слабо взаимодействующих подсистем, — это просто произведение функций распределения подсистем (см. раздел 7.5).
Интеграл в уравнении. (431) легко оценивается:
где использовалась формула. (79). Таким образом,
| (433) |
и
| (434) |
Выражение для среднего давления (414) дает
| (435) |
которое сводится к уравнению состояния идеального газа
| (436) |
где использовались и .Согласно формуле. (399) среднее энергия газа определяется выражением
| (437) |
Обратите внимание, что внутренний энергия зависит только от температуры и не зависит от объем. Молярная теплоемкость при постоянном объеме газа определяется выражением
| (438) |
так что среднюю энергию можно записать
| (439) |
Мы видели все вышеперечисленные результаты
перед.Разрешите нам
теперь используйте функцию распределения для вычисления нового результата. Энтропия
газ можно довольно просто рассчитать из выражения
| (440) |
Таким образом,
| (441) |
или же
| (442) |
куда
| (443) |
Приведенное выше выражение для энтропии идеального газа, безусловно, ново.К сожалению, это также совершенно очевидно неверно!
Далее: Парадокс Гибба Up: Приложения статистической термодинамики Предыдущий: Функции разделения Ричард Фицпатрик 2006-02-02
Теплоемкость одноатомного идеального газа при постоянном давлении — калькулятор
Описание
Теплоемкость или теплоемкость — это физическая величина, равная отношению тепла, добавляемого к объекту (или отводимого от него), к результирующему изменению температуры.
Единица измерения теплоемкости в системе СИ — джоуль на кельвин (Дж / К). Однако в прошлом для этого количества использовалось несколько других единиц измерения, которые до сих пор используются в определенных контекстах.
Теплоемкость — это обширное свойство материи, что означает, что она пропорциональна размеру объекта. Чтобы выразить соответствующее интенсивное свойство вещества, теплоемкость образца делится на количество вещества в нем.
Если принять за массу образца, результатом будет удельная теплоемкость, часто называемая просто удельной теплоемкостью (в системе СИ — джоуль на кельвин на килограмм, Дж / К / кг).Если принять количество молей вещества, получится молярная теплоемкость (в системе СИ — джоуль на кельвин на моль, Дж / К / моль). Если количество берется за объем образца (как это иногда делается в инженерии), получается объемная теплоемкость (в системе СИ — джоуль на кельвин на кубический метр, Дж / К / м3). В физике и химии одноатомный — это комбинация слов «моно» и «атомный» и означает «отдельный атом». Обычно это применяется к газам: одноатомный газ — это газ, в котором атомы не связаны друг с другом.Все химические элементы будут одноатомными в газовой фазе при достаточно высоких температурах. Термодинамическое поведение одноатомного газа чрезвычайно просто по сравнению с многоатомным газом, поскольку он не содержит вращательной или колебательной энергии. Движение одноатомного газа является трансляционным (электронное возбуждение не имеет значения при комнатной температуре). Таким образом, в адиабатическом процессе одноатомные газы имеют идеализированный γ-фактор (Cp / Cv) 5/3, в отличие от 7/5 для идеальных двухатомных газов, где вращение (но не вибрация при комнатной температуре) также способствует.Также для идеальных одноатомных газов. Связанные формулы2.3 Теплоемкость и равнораспределение энергии — Общая физика с использованием исчисления I
OpenStax и Паула Эррера-Сиклоди
К концу этого раздела вы сможете:
- Решить проблемы, связанные с передачей тепла к идеальным одноатомным газам и от них, объемы которых поддерживаются постоянными
- Решить аналогичные задачи для немонатомных идеальных газов на основе числа степеней свободы молекулы
- Оценить теплоемкость металлов с помощью модели на основе степеней свободы
В главе, посвященной температуре и теплу, мы определили удельную теплоемкость с помощью уравнения [латекс] Q = mc \ Delta T [/ latex] или [латекс] c = (1 / m) Q / \ Delta T [/ латекс].Однако свойства идеального газа напрямую зависят от количества молей в образце, поэтому здесь мы определяем удельную теплоемкость в терминах количества молей, а не массы. Более того, говоря о твердых телах и жидкостях, мы игнорируем любые изменения объема и давления при изменении температуры — хорошее приближение для твердых тел и жидкостей, но для газов мы должны сделать некоторые условия на изменения объема или давления. Здесь мы сосредотачиваемся на теплоемкости при неизменном объеме. Мы можем рассчитать это для идеального газа.
Мы определяем молярную теплоемкость при постоянном объеме [латекс] C_V [/ латекс] как
[latex] C_V = \ frac {1} {n} \ frac {Q} {\ Delta T}, \ text {с постоянным V.} [/ Latex]
Это часто выражается в форме
[латекс] \ begin {уравнение} \ tag {2.13} Q = nC_V \ Delta T. \ end {уравнение} [/ латекс]
Если объем не изменяется, общее смещение отсутствует, поэтому работа не выполняется, а единственное изменение внутренней энергии связано с тепловым потоком [латекс] \ Delta E_ \ text {int} = Q [/ latex] .(Этот оператор обсуждается далее в следующей главе.) Мы используем уравнение [latex] E_ \ text {int} = 3nRT / 2 [/ latex] для записи [latex] \ Delta E_ \ text {int} = 3nR \ Delta T / 2 [/ latex] и замените [latex] \ Delta E [/ latex] на Q , чтобы найти [latex] Q = 3nR \ Delta T / 2 [/ latex], что дает следующий простой результат для идеального одноатомный газ:
[латекс] C_V = \ frac {3} {2} R. [/ Латекс]
Он не зависит от температуры, что оправдывает использование нами конечных разностей вместо производной.\ circ \ text {C} [/ latex], теплота Q составляет 180 Дж, а масса м ксенона составляет 0,125 кг.
Молярная масса ксенона 131.3 г, поэтому получаем
[латекс] n = \ frac {125 \ text {g}} {131,3 \ text {g / mol}} = 0,952 \ text {mol}, [/ latex]
[латекс] \ Delta T = \ frac {2Q} {3nR} = \ frac {2 (180 \ text {J})} {3 (0,952 \ text {mol}) (8.31 \ text {Дж / моль} \ cdot ° \ text {C})} = 15,2 ° \ text {C}. [/ latex]
Следовательно, конечная температура составляет 35,2 ° C. Проблема также может быть решена в градусах Кельвина; поскольку градус Кельвина равен градусу Цельсия изменения температуры, вы получите [латекс] \ Delta T = 15,2 \ text {K} [/ latex].
Значение
Нагрев идеального или почти идеального газа при постоянном объеме важен для автомобильных двигателей и многих других практических систем.
Предположим, что 2 моля газообразного гелия при 200 К смешаны с 2 молями газообразного криптона при 400 К в калориметре. Какая конечная температура?
Мы хотели бы обобщить наши результаты на идеальные газы с более чем одним атомом на молекулу. В таких системах молекулы могут иметь другие формы энергии помимо поступательной кинетической энергии, такие как кинетическая энергия вращения, кинетическая и потенциальная энергии колебаний. Мы увидим, что простое правило позволяет нам определять средние энергии, присутствующие в этих формах, и решать проблемы во многом так же, как мы это делаем для одноатомных газов.2_z} [/ латекс]. Таким образом, мы можем рассматривать нашу энергию [латекса] \ frac {3} {2} k_ \ text {B} T [/ latex] как сумму вкладов [латекса] \ frac {1} {2} k_ \ текст {B} T [/ latex] от каждого из трех измерений поступательного движения. Переходя к газу в целом, мы видим, что 3 в формуле [латекс] C_V = \ frac {3} {2} R [/ latex] также отражает эти три измерения. Мы определяем степеней свободы как независимое возможное движение молекулы, такое как каждое из трех измерений трансляции. Тогда, если d представляет число степеней свободы, молярная теплоемкость при постоянном объеме одноатомного идеального газа будет [латекс] C_V = \ frac {d} {2} R [/ latex], где [латекс] d = 3 [/ латекс].
Раздел физики, называемый статистической механикой, говорит нам, и эксперимент подтверждает, что [латекс] C_V [/ латекс] любого идеального газа задается этим уравнением, независимо от количества степеней свободы. Этот факт следует из более общего результата, теоремы о равнораспределении , которая выполняется в классической (неквантовой) термодинамике для систем, находящихся в тепловом равновесии при технических условиях, которые выходят за рамки наших возможностей. Здесь мы упоминаем только, что в системе энергия распределяется между степенями свободы за счет столкновений.
Энергия равновесной термодинамической системы распределяется поровну между ее степенями свободы. Соответственно, молярная теплоемкость идеального газа пропорциональна его количеству степеней свободы d:
.[латекс] \ begin {уравнение} \ tag {2.14} C_V = \ frac {d} {2} R. \ end {Equation} [/ latex]
Этот результат был получен шотландским физиком Джеймсом Клерком Максвеллом (1831–1871 гг.), Имя которого еще несколько раз встречается в этой книге.
Например, рассмотрим двухатомный идеальный газ (хорошая модель для азота, [латекса] N_2 [/ латекса] и кислорода, [латекса] O_2 [/ латекса]).Такой газ имеет больше степеней свободы, чем одноатомный газ. Помимо трех степеней свободы перемещения, он имеет две степени свободы вращения перпендикулярно своей оси. Кроме того, молекула может колебаться вдоль своей оси. Это движение часто моделируется представлением пружины, соединяющей два атома, и мы знаем из простого гармонического движения, что такое движение имеет как кинетическую, так и потенциальную энергию. Каждой из этих форм энергии соответствует определенная степень свободы, что дает еще две.
Можно ожидать, что для двухатомного газа мы должны использовать 7 как число степеней свободы; классически, если бы молекулы газа обладали только поступательной кинетической энергией, столкновения между молекулами вскоре заставили бы их вращаться и колебаться. Однако, как объяснялось в предыдущем модуле, квантовая механика определяет, какие степени свободы активны. Результат показан на Рисунке 2.13. И вращательная, и колебательная энергии ограничены дискретными значениями. При температурах ниже примерно 60 К энергии молекул водорода слишком низки для того, чтобы столкновение привело к тому, что вращательное или колебательное состояние молекулы перешло от самой низкой энергии ко второй самой низкой, поэтому единственной формой энергии является поступательная кинетическая энергия, и [латекс] d = 3 [/ латекс] или [латекс] C_V = 3R / 2 [/ латекс] как в одноатомном газе.Выше этой температуры начинают вносить вклад две вращательные степени свободы, то есть некоторые молекулы переходят во вращательное состояние со второй по величине энергией. (Эта температура намного ниже, чем при вращении одноатомных газов, потому что двухатомные молекулы имеют гораздо более высокую инерцию вращения и, следовательно, гораздо более низкую энергию вращения.) От примерно комнатной температуры (немного меньше 300 К) до примерно 600 К вращательная инерция степени свободы полностью активны, а колебательные — нет, и [латекс] d = 5 [/ латекс].Затем, наконец, выше примерно 3000 K, колебательные степени свободы полностью активны, и [латекс] d = 7 [/ латекс], как предсказывала классическая теория.
Рис. 2.13 Молярная теплоемкость водорода как функция температуры (в логарифмической шкале). Три «ступеньки» или «плато» показывают разное количество степеней свободы, которых должна достигнуть типичная энергия молекул для активации. Поступательная кинетическая энергия соответствует трем степеням свободы, вращательная — двум другим, а колебательная — еще двум.Многоатомные молекулы обычно имеют одну дополнительную степень свободы вращения при комнатной температуре, поскольку они имеют сравнимые моменты инерции вокруг любой оси. Таким образом, при комнатной температуре они имеют [латекс] d = 6 [/ латекс], а при высокой температуре [латекс] d = 8 [/ латекс]. Обычно мы предполагаем, что газы имеют теоретические значения комнатной температуры d .
Как показано в Таблице 2.3, результаты хорошо согласуются с экспериментами для многих одноатомных и двухатомных газов, но согласие для трехатомных газов только удовлетворительное.\ circ \ text {C} [/ latex] и 1 атм
А как насчет внутренней энергии двухатомных и многоатомных газов? Для таких газов [латекс] C_V [/ латекс] является функцией температуры (рис. 2.13), поэтому у нас нет такого простого результата, как для одноатомных идеальных газов.
Идея равнораспределения приводит к оценке молярной теплоемкости твердых элементов при обычных температурах.Мы можем смоделировать атомы твердого тела как прикрепленные к соседним атомам пружинами (рис. 2.14).
Рис. 2.14. В простой модели твердого элемента каждый атом связан с другими шестью пружинами, по две для каждого возможного движения: x , y и z . Каждое из трех движений соответствует двум степеням свободы: одной для кинетической энергии, а другой — для потенциальной. Таким образом, d = 6.Аналогично обсуждению вибрации в предыдущем модуле, каждый атом имеет шесть степеней свободы: одну кинетическую и одну потенциальную для каждого из направлений x -, y — и z -направлений.Соответственно, молярная теплоемкость металла должна быть 3 R . Этот результат, известный как закон Дюлонга и Пети, довольно хорошо работает экспериментально при комнатной температуре. (Для каждого элемента он не работает при низких температурах по квантово-механическим причинам. Поскольку квантовые эффекты особенно важны для частиц с малой массой, закон Дюлонга и Пти уже не работает при комнатной температуре для некоторых легких элементов, таких как бериллий и углерод. Он также не работает с некоторыми более тяжелыми элементами по разным причинам, которые мы не можем охватить.)
Стратегия решения этих проблем такая же, как и в случае изменения фазы для эффектов теплопередачи. Единственная новая особенность заключается в том, что вы должны определить, применим ли к проблеме только что представленный случай — идеальные газы при постоянном объеме. (Для твердых элементов определение удельной теплоемкости обычно лучше, чем ее оценка по закону Дюлонга и Пти.) В случае идеального газа определите число d степеней свободы по количеству атомов в молекулу газа и используйте ее для вычисления [латекс] C_V [/ latex] (или используйте [latex] C_V [/ latex], чтобы найти d ).\ circ \ text {C} [/ latex] в изолированном контейнере. Когда воздух достигает равновесия с галлием, 202 г галлия расплавляются. Исходя из этих данных, какова теплота плавления галлия? Предположим, что объем воздуха не меняется и других теплообменников нет.
Стратегия
Мы будем использовать уравнение [латекс] Q_ \ text {hot} + Q_ \ text {cold} = 0 [/ latex]. Поскольку часть галлия не плавится, мы знаем, что конечной температурой остается точка плавления. Тогда единственный [латекс] Q_ \ text {hot} [/ latex] — это тепло, теряемое при охлаждении воздуха, [латекс] Q_ \ text {hot} = n_ \ text {air} C_V \ Delta T [/ latex], где [латекс] C_V = 5R / 2 [/ латекс].{\ circ} \ text {C}) + (0.202 \ text {kg}) \ text {L} _ \ text {f} = 0. [/ latex]
Решаем найти, что теплота плавления галлия составляет 80,2 кДж / кг.
РЕШЕНИЕ: Идеальный одноатомный газ сжимается в iso…
Расшифровка стенограммы
серебряная партия. Проделанная работа будет равна отрицательному давлению. Время менять и объем. Это будет равно двум отрицательным 1,50 умноженным на 10 к пятому. Паскаля умножить на 0.500 кубометров, минус 1,25 кубометра. Таким образом, проделанная работа будет равна 21,13 умноженным на 10 к пятому. Жюль, это будет наш окончательный ответ на четвертый карп. Мы знаем, что изменение внутренней энергии было бы во столько раз больше, чем моляр. У него емкость постоянного объема, умноженная на изменение температуры. У нас есть монотонный газ, поэтому мы можем сказать, что наша постоянная мощность Мюллера при постоянном объеме будет равна количеству степеней свободы на атомной траве.Три степени свободы, умноженные на постоянную идеального газа, делятся на два. Итак, мы знаем, что для закона идеального газа, применяемого к процессу постоянного давления, количество молей, умноженное на изменение температуры, будет равно давлению, умноженному на изменение объема, деленное на постоянную идеального газа. Энергия будет равна Мёллеру. Емкость три больше двух, умноженная на давление, умноженное на изменение объема, деленное на наш, и это дает нам 3/2 кратное давление, умноженное на изменение объема.Таким образом, изменение нашей внутренней энергии будет в три раза больше, умноженных на 1,50, умноженных на 10, до пятой величины, умноженной на 0,500 минус 1,25 кубических метра. И это дает нам отрицательные 1,69 умноженные на 10 к пятому. Жюль. Таким образом, это было бы нашим ответом на наши изменения в нашей внутренней энергии для части B, четыре части. Понимаете, мы собираемся использовать первый закон термодинамики. Где здесь Изменение внутренней энергии равно приложению тепла плюс работа. Таким образом, тепло будет равно изменению внутренней энергии за вычетом работы.И это будет равно отрицательным 1,69 умноженным на 10 для пятого, и Жюля минус 1,13 умноженным на 10 для пятого Джулса.


 1)
1)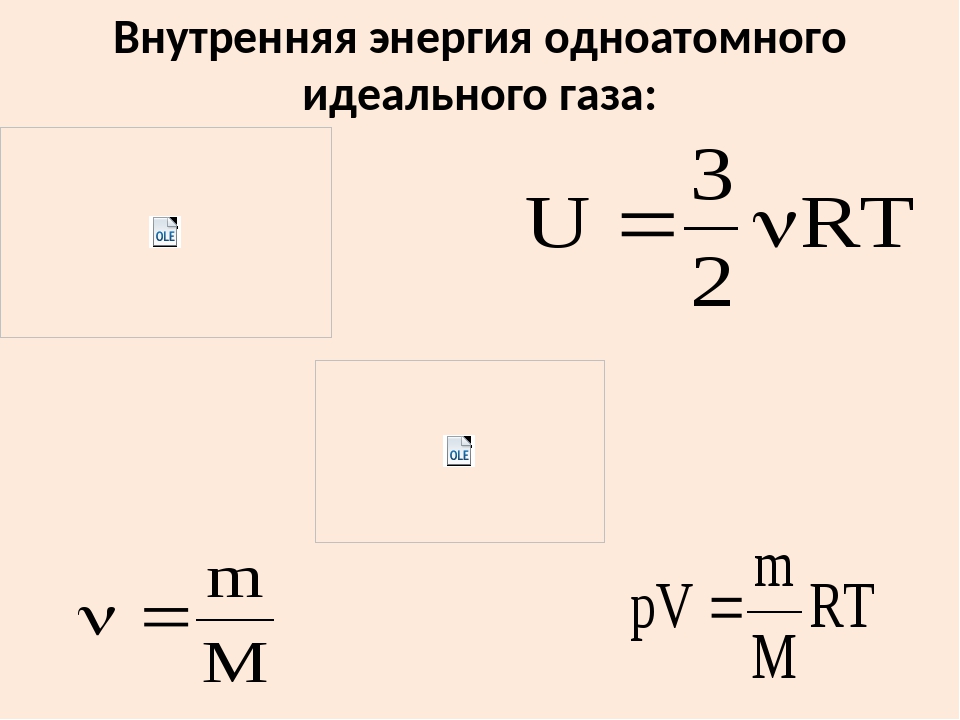 6)
6) Символ: мол.
Символ: мол.
Leave A Comment