к каждому элементу первого столбца подберите соответствующийэлемент из второго столбца. ВЕЛИЧИНЫ ЗНАЧЕНИЯ А) масса человека 1) 460 т Б) масса шариковой ручки 2) 80 кг В) масса автомобиля 3) 1,3 т Г) масса железнодорожного состава 4) 10 г . Математика базовая 22970
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | ЗНАЧЕНИЯ | ||
| А) | масса человека | 1) |
460 т |
| Б) | масса шариковой ручки | 2) |
80 кг |
| В) | масса автомобиля | 3) |
1,3 т |
| Г) | масса железнодорожного состава | 4) |
10 г |
Тесты.
 Задание №9 ЕГЭ базовый уровень
Задание №9 ЕГЭ базовый уровеньТест №1 – Б9
1. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
А) площадь почтовой маркиБ) площадь письменного стола
В) площадь города Санкт-Петербурга
Г) площадь волейбольной площадки
1) 162 кв. м
2) 1,2 кв. м
3) 1439 кв. км
4) 5,2 кв. см
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
2. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) масса автомобиляВ) расстояние от Москвы до Сочи
Г) объём воды в Азовском море
1) 256 км3
2) 1300 кг
3) 1600 км
4) 1439 кв. км
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
3.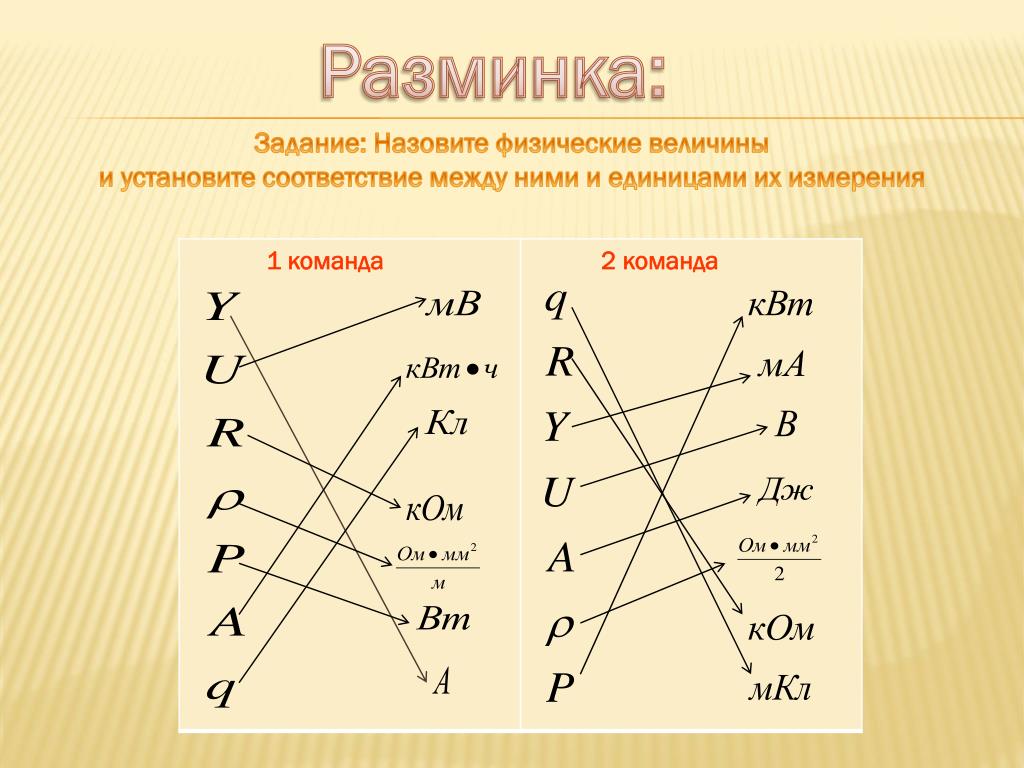 Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) объём ящика комода
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) объём ящика комодаВ) объём пакета ряженки
Г) объём железнодорожного вагона
1) 0,75 л
2) 78 200 км3
3) 96 л
4) 90 м3
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
4. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) масса футбольного мячаБ) масса дождевой капли
В) масса взрослого бегемота
Г) масса стиральной машины
1) 18 кг
2) 2,8 т
3) 20 мг
4) 750 г
В таблице под каждой буквой укажите соответствующий номер. АБВГ
5. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
Б) ширина окна
В) высота горы Эверест
Г) диаметр монеты
1) 20 мм
2) 120 см
3) 8848 м
4) 3530 км
В таблице под каждой буквой укажите соответствующий номер. АБВГ
6. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
Б) длительность эпизода мультипликационного сериала
В) время одного оборота барабана стиральной машины при отжиме
Г) время одного оборота Плутона вокруг Солнца
1) 25 минут
2) 90 553 суток
3) 0,06 секунды
4) 8 часов
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
7. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) площадь города Санкт-Петербурга
А) площадь города Санкт-ПетербургаВ) площадь поверхности тумбочки
Г) площадь баскетбольной площадки
1) 420 кв. м
2) 300 кв. мм
3) 1439 кв. км
4) 0,2 кв. м
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: АБВГ
8. Установите соответствие между величинами и их возможными значениями:
А) скорость движения автомобиляБ) скорость движения пешехода
В) скорость движения улитки
Г) скорость звука в воздушной среде
1) 0,5 м/мин
2) 60 км/час
3) 330 м/сек
4) 4 км/час
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Б) Объём пакета кефира
В) Объём бассейна
Г) Объём ящика для фруктов
1) 1 л
2) 23 615,39 км3
3) 72 л
4) 600 м3
В таблице под каждой буквой укажите соответствующий номер.
В) длительность прямого авиаперелёта Москва — Южно-Сахалинск
Г) продолжительность взмаха крыла колибри
1) 40 минут
2) 8 часов 45 минут
3) 0,01 секунды
4) 88 суток
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: АБВГ
11. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
А) объём воды в Онежском озереБ) объём бутылки воды
В) объём туристического рюкзака для взрослого человека
Г) объём контейнера для мебели
1) 0,5 л
2) 60 м3
3) 90 л
4) 295 км3
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
12. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) масса кухонного холодильника
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) масса кухонного холодильникаБ) масса автобуса
В) масса новорождённого ребёнка
Г) масса карандаша
1) 3500 г
2) 15 г
3) 18 т
4) 38 кг
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
13. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) расстояние от дома до школыБ) расстояние от Земли до Марса
В) расстояние от Амстердама до Парижа
Г) расстояние между глазами человека
1) 65 мм
2) 1 км
3) 500 км
4) 55 · 106 км
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: АБВГ
14. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
Б) длина реки Москвы
В) масса таблетки лекарства
Г) площадь тарелки
1) 502 мг
2) 502 кв. см
3) 502 км
4) 502 м3
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
15. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) крейсерская скорость самолётаБ) скорость мотоциклиста
В) скорость муравья
Г) скорость света
1) 80 км/ч
2) 900 км/ч
3) 5 см/с
4) 300 000 км/с
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: АБВГ
Тест №2 – Б9
16. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
А) масса двухлитрового пакета сокаБ) масса взрослого кита
В) масса косточки персика
Г) масса таблетки лекарства
1) 130 т
2) 2 кг
3) 400 мг
4) 8 г
В таблице под каждой буквой укажите соответствующий номер.
Б) площадь тарелки
В) площадь Ладожского озера
Г) площадь одной стороны монеты
1) 300 кв. мм
2) 3 кв. м
3) 17,6 тыс. кв. км
4) 600 кв. см
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
18. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) объём воды в Азовском мореБ) объём ящика с инструментами
В) объём грузового отсека транспортного самолёта
Г) объём бутылки растительного масла
1) 150 м
2) 1 л
3) 36 л
4) 256 км
19. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.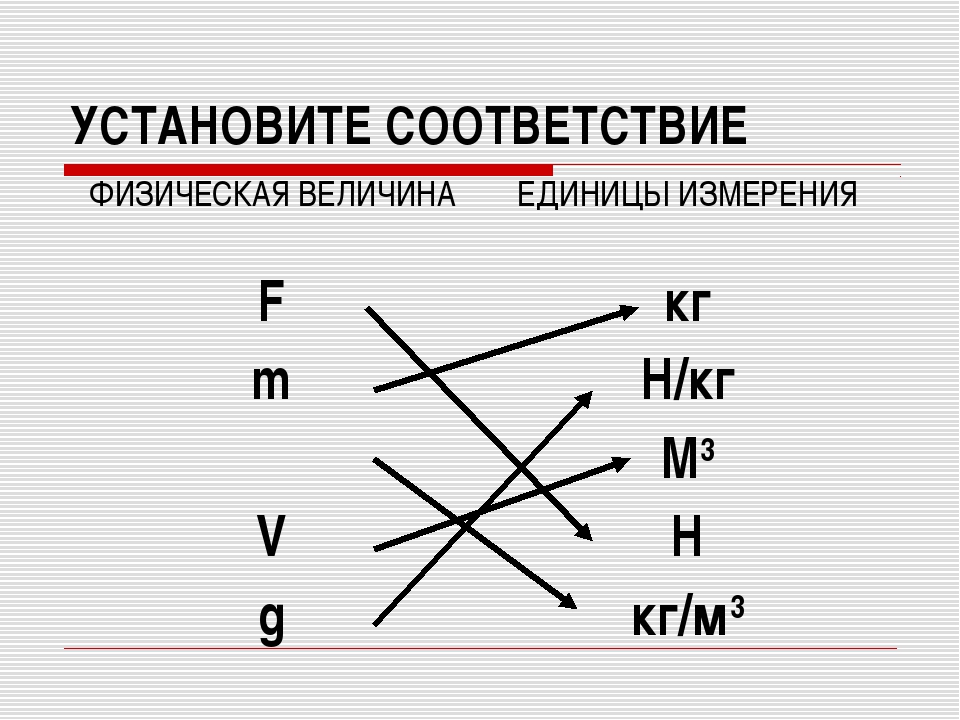
Б) бронзовый норматив ГТО по бегу на 100 м для мальчиков 16–17 лет
В) время одного оборота Нептуна вокруг Солнца
Г) длительность эпизода мультипликационного сериала
1) 14,6 секунды
2) 60190 суток
3) 13 часов
4) 22 минуты
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: АБВГ
20. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
А) масса взрослого человекаБ) масса грузового автомобиля
В) масса книги
Г) масса пуговицы
1) 8 т
2) 5 г
3) 65 кг
4) 300 г
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
21. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент второго столбца. А) Объём комнаты
А) Объём комнатыБ) Объём воды в Каспийском море
В) Объём ящика для овощей
Г) Объём банки сметаны
1) 78 200 км3
2) 75 м3
3) 50 л
4) 0,5 л
В таблице под каждой буквой укажите соответствующий номер. АБВГ
22. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
А) площадь города Санкт-ПетербургБ) площадь одной стороны монеты
В) площадь поверхности тумбочки
Г) площадь баскетбольной площадки
1) 420 кв. м
2) 400 кв. мм
3) 1439 кв. км
4) 0,2 кв. м
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
23. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) масса мобильного телефонаБ) масса одной ягоды клубники
В) масса взрослого слона
Г) масса курицы
1) 12,5 г
2) 4 т
3) 3 кг
4) 100 г
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
24. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) частота вращения минутной стрелки
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) частота вращения минутной стрелкиБ) частота вращения лопастей вентилятора
В) частота обращения Земли вокруг своей оси
Г) частота обращения Венеры вокруг Солнца
1) 1 об/день
2) 1,6 об/год
3) 24 об/день
4) 50 об/с
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: АБВГ
25. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
А) объём ящика с яблоками
Б) объём воды в озере Ханка
В) объём бутылки соевого соуса
Г) объём бассейна в спорткомплексе
1) 108 л
2) 900 м3
3) 0,2 л
4) 18,3 км3
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
26. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) расстояние между троллейбусными остановками
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) расстояние между троллейбусными остановкамиБ) расстояние от Земли до Луны
В) расстояние от Москвы до Сочи
Г) расстояние между глазами кошки
1) 25 мм
2) 300 м
3) 385 000 км
4) 1636 км
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
27. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) длительность урокаБ) серебряный норматив ГТО по бегу на 100 м для девочек 16–17 лет
В) время в пути поезда Санкт-Петербург – Минеральные Воды
Г) время одного оборота Урана вокруг Солнца
1) 17,6 секунды
2) 45 минут
3) 30685 суток
4) 45 часов
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
28. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) объём бутылки газировки
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) объём бутылки газировкиБ) объём багажника автомобиля
В) объём грузового отсека транспортного самолёта
Г) объём воды в Чёрном море
1) 2 л
2) 200 л
3) 555 000 км3
4) 400 м3
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: АБВГ
29. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
А) масса человекаБ) масса шариковой ручки
В) масса автомобиля
Г) масса железнодорожного состава
1) 460 т
2) 80 кг
3) 1,3 т
4) 10 г
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
30. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) масса взрослого кита
А) масса взрослого китаБ) объём железнодорожного вагона
В) площадь волейбольной площадки
Г) ширина футбольного поля
1) 162 кв. м
2) 100 т
3) 120 м
4) 68 м
В таблице под каждой буквой укажите соответствующий номер. АБВГ
Тест №3 – Б9
31. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
А) площадь монитора компьютераБ) площадь города Санкт-Петербурга
В) площадь ногтя на пальце взрослого человека
Г) площадь Краснодарского края
1) 75 500 кв. км
2) 1439 кв. км
3) 100 кв. мм
4) 1020 кв. см
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
32. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) длительность полнометражного мультипликационного фильма
А) длительность полнометражного мультипликационного фильмаБ) время обращения Марса вокруг Солнца
В) длительность звучания одной песни
Г) продолжительность вспышки фотоаппарата
1) 4 минуты
2) 90 минут
3) 687 суток
4) 0,2 секунды
В таблице под каждой буквой укажите соответствующий номер.
33. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) высота горы ЭверестБ) длина реки Волги
В) ширина окна
Г) диаметр монеты
1) 3530 км
2) 120 см
3) 20 мм
4) 8848 м
В таблице под каждой буквой укажите соответствующий номер. АБВГ
34. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
А) объём грузового отсека транспортного самолётаБ) длина реки Москвы
В) масса таблетки лекарства
Г) площадь тарелки
1) 502 мг
2) 502 кв. см
см
3) 502 км
4) 502 м
В таблице под каждой буквой укажите соответствующий номер. АБВГ
35. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
А) скорость гоночной машиныБ) скорость улитки
В) скорость пешехода
Г) скорость звука
1) 1,5 мм/с
2) 200 км/ч
3) 1,5 м/с
4) 330 м/с
36. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
А) площадь города Санкт-ПетербургаБ) площадь одной стороны монеты
В) площадь поверхности тумбочки
Г) площадь баскетбольной площадки
1) 420 кв. м
2) 400 кв. мм
3) 1439 кв. км
4) 0,2 кв. м
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: АБВГ
37. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
Б) масса грузовой машины
В) масса кота
Г) масса дождевой капли
1) 8 т
2) 32 г
3) 20 мг
4) 8 кг
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
38. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) объём воды в Азовском мореБ) объём ящика с инструментами
В) объём грузового отсека транспортного самолёта
Г) объём бутылки растительного масла
1) 150 м3
2) 1 л
3) 76 л
4) 256 км3
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
39. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) длина тела кошки
А) длина тела кошкиБ) высота потолка в комнате
В) высота Исаакиевского собора в Санкт-Петербурге
Г) длина реки Обь
1) 102 м
2) 2,8 м
3) 3650 км
4) 54 см
40. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
А) длительность полнометражного мультипликационного фильмаБ) время одного оборота Марса вокруг Солнца
В) длительность звучания одной песни
Г) продолжительность вспышки фотоаппарата
1) 4 минуты
2) 90 минут
3) 687 суток
4) 0,2 секунды
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
41. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
А) объём железнодорожного вагонаБ) объём бытового холодильника
В) объём воды в Ладожском озере
Г) объём пакета сока
1) 300 л
2) 120 м3
3) 908 км3
4) 1,5 л
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
42. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) масса куриного яйца
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) масса куриного яйцаБ) масса детской коляски
В) масса взрослого бегемота
Г) масса активного вещества в таблетке
1) 2,5 мг
2) 14 кг
3) 50 г
4) 3 т
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
43. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца. А) масса новорождённого ребёнкаБ) длина реки Обь
В) объём воды в озере Мичиган
Г) площадь озера Байкал
1) 3650 км
2) 3500 г
3) 31500 кв. км
4) 4918 км
В таблице под каждой буквой укажите соответствующий номер.
44. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
Б) площадь тарелки
В) площадь Ладожского озера
Г) площадь одной стороны монеты
1) 300 кв. мм
2) 3 кв. м
3) 17,6 тыс. кв. км
4) 600 кв. см
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: АБВГ
45. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
А) серебряный норматив ГТО по бегу на 2 км для мальчиков 16–17 летБ) длительность полнометражного художественного фильма
В) время одного оборота Сатурна вокруг Солнца
Г) продолжительность вспышки фотоаппарата
1) 0,1 секунды
2) 10 759 суток
3) 8 минут 50 секунд
4) 132 минуты
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Тест №1,2,3 – Б91
4231
2
2431
3
3214
4
4321
5
4231
6
4132
7
3241
8
2413
9
2143
10
4123
11
4132
12
4312
13
2431
14
4312
15
2134
16
2143
17
2431
18
4312
19
3124
20
3142
21
2134
22
3241
23
4123
24
3412
25
1432
26
2341
27
2143
28
1243
29
2431
30
2314
31
4231
32
2314
33
4123
34
4312
35
2134
36
3241
37
2143
38
4312
39
4213
40
2314
41
2134
42
3241.
43
2143
44
2431
45
3421
Тест №9 ЕГЭ по математике (база) 🐲 СПАДИЛО.РУ
ПравильноА) длительность лекции в вузе. Здесь нужно вспомнить, сколько времени традиционно длятся занятия в вузах. Это время обычно составляет 1,5 часа (подряд либо в виде 2 частей по 45 мин с небольшим перерывом).
Б) время одного оборота барабана стиральной машины при отжиме. Вращение барабана происходит очень быстро, поскольку именно это обеспечивает эффект подсушивания мокрого белья. Поэтому время 1 оборота может измеряться только в секундах, но никак не в минутах, часах или, тем более, сутках.
В) время одного оборота Венеры вокруг Солнца. Венера расположена ближе к Солнцу, чем Земля. Это означает, что полный оборот вокруг Солнца Венера совершает быстрее, чем Земля. Однако все равно длительность его измеряется не в часах или минутах, а в сутках.
Г) время в пути поезда Волгоград – Санкт-Петербург. Тут подходящее значение можно определить по остаточному принципу, поскольку остался только вариант №2. Но все-таки вспомним, что от Волгограда до С-Петербурга не менее 1,5 тыс.км, скорость пассажирского поезда равна 50-90 км/ч, а потому время движения без остановок должно составить порядка 17-30 часов, что соизмеримо со значением, равным 32 часа.
НеправильноА) длительность лекции в вузе. Здесь нужно вспомнить, сколько времени традиционно длятся занятия в вузах. Это время обычно составляет 1,5 часа (подряд либо в виде 2 частей по 45 мин с небольшим перерывом).
Б) время одного оборота барабана стиральной машины при отжиме. Вращение барабана происходит очень быстро, поскольку именно это обеспечивает эффект подсушивания мокрого белья. Поэтому время 1 оборота может измеряться только в секундах, но никак не в минутах, часах или, тем более, сутках.
В) время одного оборота Венеры вокруг Солнца. Венера расположена ближе к Солнцу, чем Земля. Это означает, что полный оборот вокруг Солнца Венера совершает быстрее, чем Земля. Однако все равно длительность его измеряется не в часах или минутах, а в сутках.
Это означает, что полный оборот вокруг Солнца Венера совершает быстрее, чем Земля. Однако все равно длительность его измеряется не в часах или минутах, а в сутках.
Г) время в пути поезда Волгоград – Санкт-Петербург. Тут подходящее значение можно определить по остаточному принципу, поскольку остался только вариант №2. Но все-таки вспомним, что от Волгограда до С-Петербурга не менее 1,5 тыс.км, скорость пассажирского поезда равна 50-90 км/ч, а потому время движения без остановок должно составить порядка 17-30 часов, что соизмеримо со значением, равным 32 часа.
4) 110 см Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Размеры пуговиц и собак
Размеры пуговиц и собак 1.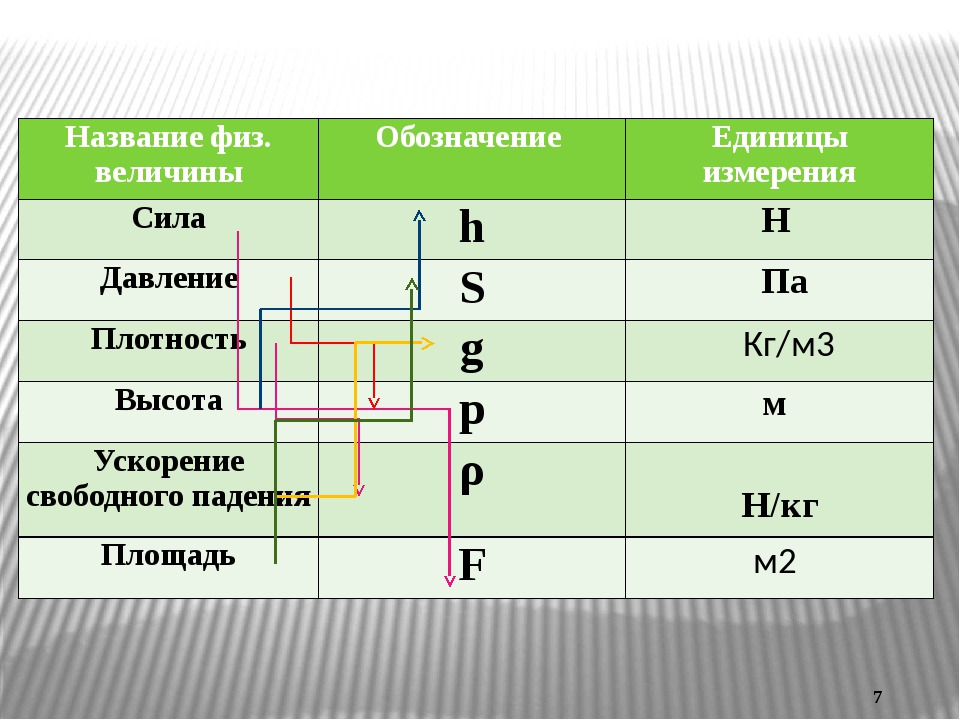 Задание 9 506128. Установите соответствие между величинами и их возможными значениями: к каждому А) рост ребѐнка Б) толщина листа бумаги В) длина автобусного маршрута Г) высота
Задание 9 506128. Установите соответствие между величинами и их возможными значениями: к каждому А) рост ребѐнка Б) толщина листа бумаги В) длина автобусного маршрута Г) высота
Размеры пуговиц и собак
Размеры пуговиц и собак 1. А) рост ребёнка Б) тол щи на листа бумаги В) длина ав то бус но го маршрута Г) вы со та жи ло го дома 1) 32 км 2) 30 м 3) 0,2 мм 4) 110 см 2. Установите со от вет ствие между
ПодробнееРазмеры пуговиц и собак
Размеры пуговиц и собак 1. А) рост ребёнка Б) тол щи на листа бумаги В) длина ав то бус но го маршрута Г) вы со та жи ло го дома 1) 32 км 2) 30 м 3) 0,2 мм 4) 110 см Рост ребёнка может быть равен 110 см,
ПодробнееID_4262 1/12 neznaika.pro
1 Размеры и единицы измерения Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов. 1 А) Скорость
Запишите ответ без пробелов, запятых и других дополнительных символов. 1 А) Скорость
ID_8710 1/5 neznaika.pro
1 Размеры и единицы измерения Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов. 1 А) плотность
ПодробнееИнструкция для обучающихся
Томский областной институт повышения квалификации и переподготовки работников образования Центр мониторинга и оценки качества образования Измерительная работа по математике 10 класс (апрель, 016 г.) (Базовый
ПодробнееТест 6 (базовый)
Тест 6 (базовый) 06.02.2017 (Выполняем тест и присылаем на следующий день вместе с решением и таблицей ответов, после выдачи д. з. до 10 00 [email protected]) 1. Найдите значение выражения 2. Найдите
з. до 10 00 [email protected]) 1. Найдите значение выражения 2. Найдите
дифференцированные задачи
дифференцированные задачи Движение это жизнь! Самостоятельная I работа I СИСТЕМА ОТСЧЕТА. ТРАЕКТОРИЯ. ПУТЬ И ПЕРЕМЕЩЕНИЕ Из рекомендаций врача < Начальный уровень 1. Автомобиль движется по горной дороге
ПодробнееМатериальная точка. Система отсчета
Неравномерное Учебник Касьянов В.А. Автор: Шипкина Е.А. 10 класс. Модуль 1 по теме «Кинематика» — 15 часов Материальная точка Система отсчета Механическое движение Равномерное Периодическое Криволинейное
ПодробнееВариант 2. Математика Базовый уровень
Вариант 2 Математика Базовый уровень Ответом к каждому заданию является конечная десятичная дробь, целое число или последовательность цифр. Запишите ответы к заданиям в поле ответа справа от номера соответствующего
Запишите ответы к заданиям в поле ответа справа от номера соответствующего
Математические диктанты 4 класс
Математические диктанты 4 класс Работа 1 1. 25 увеличить в 100 раз. 2. Чему равно второе слагаемое, если первое слагаемое- 60, а сумма- 310? 3. Найди частное 360 и 4. 4. 500 без 59. 5. На сколько надо
ПодробнееРазноуровневые задания
Разноуровневые задания РЗ-9.1. Прямолинейное равномерное дни* жение. Относительность движения Задания уровня «А» 1. Велосипедист, двигаясь равномерно, проезжает 20 м за 2 с. Какой путь он проедет при движении
ПодробнееИнструкция по выполнению работы
Репетиционный экзамен. Математика (базовый уровень) 11 класс Вариант 110202 1/7 Инструкция по выполнению работы Экзаменационная работа включает в себя 20 заданий.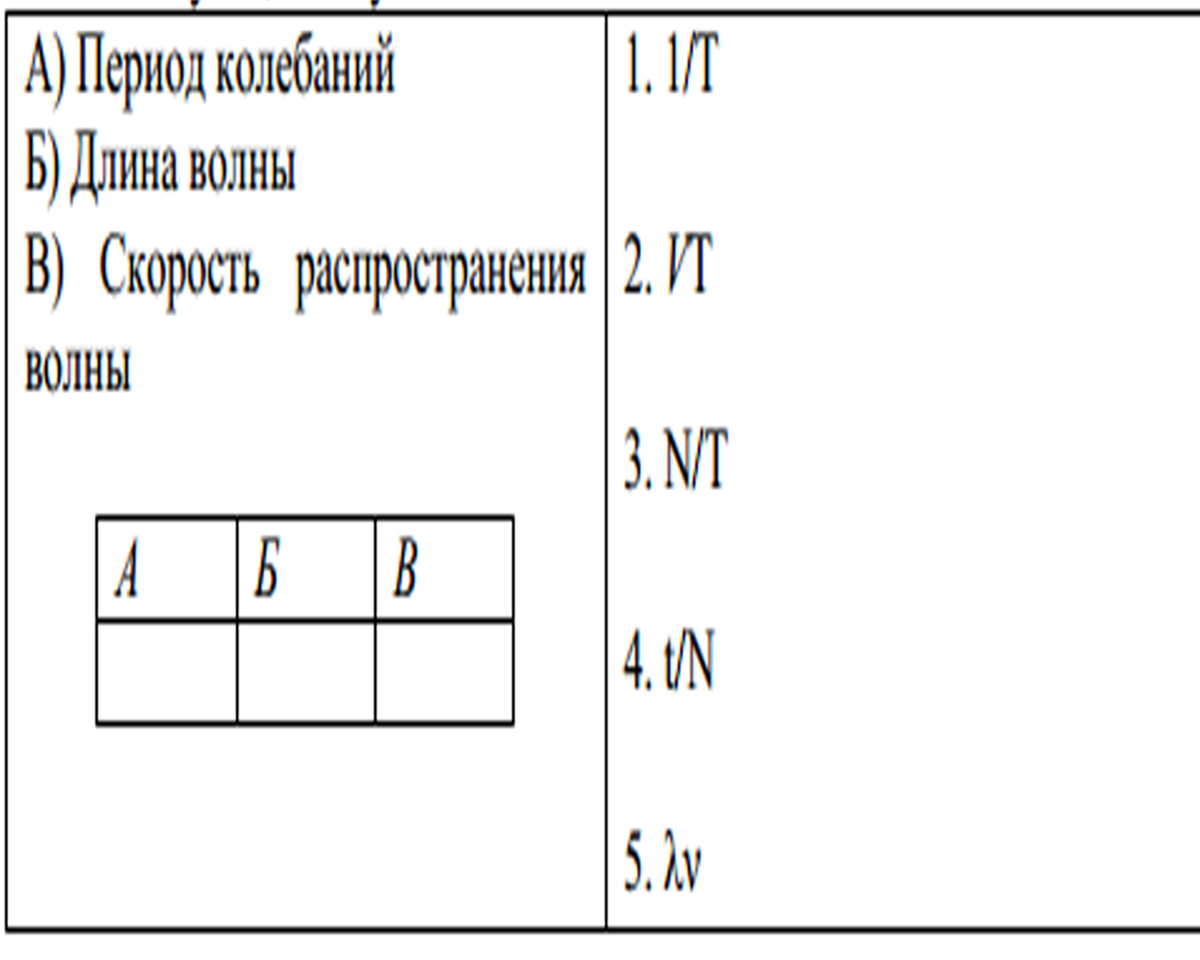 На выполнение работы отводится 3 часа
На выполнение работы отводится 3 часа
К УЧЕНИКУ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
К УЧЕНИКУ Юный друг! Ты только начинаешь изучать физику. Можно только позавидовать тебе так много нового и интересного ждет на этом пути. Этот путь не пройден и никогда не будет пройден до конца Природа
Подробнее7Ф Раздел 1. Понятия, определения
7Ф Раздел 1. Понятия, определения 1.1 Продолжите фразу: «Материя это всё, что..». 1.2 Продолжите фразу: «Молекула-это.» 1.3 Продолжите фразу : «Диффузия-это явление» 1.4 Продолжите фразу: «Масса-это физическая
ПодробнееID_332 1/5 neznaika.pro
Вариант 20 Математика Базовый уровень Ответом к каждому заданию является конечная десятичная дробь, целое число или последовательность цифр. Запишите ответы к заданиям в поле ответа справа от номера соответствующего
ПодробнееЗАДАНИЯ ДЛЯ ОЛИМПИАДЫ
ЗАДАНИЯ ДЛЯ ОЛИМПИАДЫ 1. В каждом ряду зачеркни «лишнее». а) Днепр, Волга, Байкал, Енисей. б) Юг, запад, право, север. в) Антарктида, Франция, Африка, Европа. г) Петербург, Индия, Россия, Германия. О т
ПодробнееЗадание 7 ЕГЭ по физике
Механика. Установление соответствия между графиками и физическими величинами, между физическими величинами и формулами.
В. З. Шапиро
Это задание повышенного уровня сложности. Тема – различные разделы механики. Здесь необходимо найти соответствие между физическими величинами и формулами, графическими зависимостями и физическими величинами.
1. Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 15 + 6t – 3t2 (все величины выражены в СИ).
Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
Кинетическую энергию тела можно рассчитать по формуле Для нахождения зависимости скорости от времени надо взять производную по времени от координаты.
Для нахождения перемещения тела надо использовать зависимость для равноускоренного движения.
Ответ: 24.
Секрет решения: Такие кинематические задачи можно также решать, используя известные формулы для равноускоренного движения. Но решение с использованием производной функции является более рациональным и менее трудоёмким.
2. Шайба массой m, скользящая по гладкой горизонтальной поверхности со скоростью абсолютно неупруго сталкивается с покоящейся шайбой массой М. Установите соответствие между физическими величинами и формулами, выражающими их в рассматриваемой задаче.
К каждой позиции первого столбца подберите соответствующую позицию
из второго и запишите в таблицу выбранные цифры.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ФОРМУЛЫ |
| А) кинетическая энергия покоившейся шайбы после столкновения Б) импульс первоначально движущейся шайбы после столкновения | 1) 2) 3) 4) |
Ответ:
Для решения задачи необходимо применить закон сохранения импульса системы тел. При этом надо учесть, что при абсолютно неупругом столкновении тела после взаимодействия движутся как единое целое с постоянной скоростью.Согласно закону сохранения импульса системы тел:
Ответ: 43.
Секрет решения: При решении задач на столкновение тел надо знать различия между абсолютно упругим и абсолютно неупругим ударом. В таких задачах всегда используется закон сохранения импульса тел и, при необходимости, закон сохранения энергии.
3. После удара в момент t=0 шайба начинает скользить вверх по гладкой наклонной плоскости с начальной скоростью как показано на рисунке, и в момент времени возвращается в исходное положение. Графики А и Б отображают изменение с течением времени физических величин, характеризующих движение шайбы.
Установите соответствие между графиками и физическими величинами, изменение которых со временем эти графики могут отображать.
К каждой позиции первого столбца подберите соответствующую позицию второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
После удара тело начинает подниматься вверх по наклонной плоскости. Это движение происходит с уменьшающейся скоростью, так как равнодействующая направлена в сторону, противоположенную движению тела. Поэтому график А будет относиться к первому утверждению. График Б будет характеризовать проекцию скорости на ось ОY, которая с течением времени уменьшается до нуля, а потом тело начинает двигаться в обратном направлении. При этом его проекция на ось ОY становится отрицательной.
Ответ: 13.
Секрет решения: В подобных задачах можно провести рассуждения «от противного», доказав, что эти графики не могут характеризовать кинетическую или потенциальную энергии. Тем самым, отбрасывая неверные утверждения, можно прийти к правильному ответу.
Как удалить подписчиков в Инстаграме: методы 2021
До рассказа о том, как удалить подписчиков в инстаграме, хочу у Вас спросить: уверены ли Вы, что хотите удалить именно “мусор”?
Знаю, знаю, Вы хотите очистить аккаунт, фейковых страниц, удалить ботов из подписчиков в инстаграме… НО! Есть и другие категории лишних подписчиков, которые портят статистику, и Ваш Инстаграм от них страдает. А некоторые профили наоборот нужно оставить (не о банальном). Поэтому сразу объясню, что к чему:
- Оставляйте арабов. Не всегда, но часто они являются, к общему удивлению, очень активной аудиторией;
- Фильтруйте коммерческие аккаунты. Не все коммерческие профили бесполезны, ведь за ними также скрываются люди;
- Будьте осторожней с неактивными. Если человек не проявляет активность, это не значит, что он не купит;
- Изучайте вовлеченность. Её нормальный уровень 5-10% (считать тут в приложении по промокоду “INSCALE” скидка 30% +7 дней доступа), но не факт, что проблема в ботах;
- Бойтесь сомнительных сервисов. Если они без гибкой настройки, то могут удалить нужных подписот;
- Не удаляйте большое количество. Сколько подписчиков можно удалять? Не более 1 000 в день, иначе заблокируют.
Как удалить подписчикОВ
Есть несколько методов удаления нежелательных подписчиков в инстаграм. Я расскажу подробно и об автоматизированном, и о ручном удалении.
1. С помощью сервиса
Онлайн-инструментов, специализирующихся на очистке профилей, не так уж много. Собрала для Вас ТОП-5 площадок, которые справятся с этой задачей быстро и качественно, а главное, не нанесут вреда аккаунту.
| Сервис | Стоимость | Бесплатный период | Кого/что можно удалить |
| InstaHero | 99 руб/мес | Есть | Ботов, массфоловеров, иностранцев, неактивных подписчиков, коммерческие аккаунты, аудитория определенной страны/города. |
| InstaPlus | 399 руб/мес | 5 дней | Ботов, массфоловеров, неактивных подписчиков. |
| Zeus | 69 руб/мес | 7 дней | Ботов, иностранцев, неактивных подписчиков, коммерческие аккаунты. |
| SocialKit | 1 100 руб/мес лицензия | Нет | Ботов, неактивных подписчиков, коммерческие аккаунты. |
| Spam Guard | от 259 руб/мес | Нет | Ботов, иностранцев, неактивных подписчиков, коммерческие аккаунты, спам в Директе, спам-отметки. |
Все сервисы работают по одному принципу. Разберем, как очистить аккаунт от ботов в один клик на примере InstaHero.
Шаг 1. Добавление аккаунта
Выполните вход в сервис, добавьте аккаунт для бесплатного анализа. После этого запустится анализ Вашей аудитории. Обратите внимание, это будет бесплатный анализ – сервис проверит 30% фолловеров, но не более 1 000 человек.
Чтобы получить информацию обо всех подписчиках на аккаунте, оплатите полный анализ. Кстати, если выполнить его в течение трех часов после бесплатного анализа, можно получить скидку.
Добавление аккаунта на анализПосле того, как Вы проведете полный анализ, откроется вся подробная информация по Вашим подписчикам, а также доступ к блоку ботов. Очистить инстаграм от ботов возможно только за отдельную плату.
Для быстрых зайчиков. Если Вы уже поняли, что чистить профиль важно и нужно, то быстрее переходите по ссылке -> InstaHero (по промокоду “INSCALE” скидка 30% на полный анализ).
Шаг 2. Выбор способа чистки
Далее определитесь, будете Вы сами чистить подписчиков или оставите эту задачу сервису.
– Автоматическая чистка
Если Вам нужен этот вариант, выберите “автоматическое удаление”.
Подождите несколько минут, и данные для удаления будут внесены в раздел “чистка” и подраздел “автоматическая”.
Перейдите в “автоматическую” чистку, выберите, сколько ботов в день Вы будете удалять или блокировать (на выбор). Рекомендуем не больше 50-100 человек в день. Да, порой это долго, но спешить не стоит – в инстаграме есть лимит на безопасное удаление подписчиков.
Автоматическая чисткаВнизу будет информация о том, за сколько дней будет очищен аккаунт, и сколько их найдено для удаления. Нажмите “сохранить” внесенные данные и “запустить” для запуска удаления. Отслеживать все действия можно в “журнале аккаунта”.
– Чистка по параметрам
Если Вы хотите самостоятельно задать параметры для удаления ботов, воспользуйтесь удалением “по параметрам”. Задайте необходимые для удаления параметры. Сервис покажет, сколько найдено человек, в правом нижнем углу.
Настройте удаление ботов, выбрав, сколько в день Вы будете удалять или блокировать. Ниже будет указано, за сколько дней заданное число будет удалено. Как проходит удаление можно также отслеживать в разделе “журнал аккаунта”.
Ручная чисткаЛайфхак. Новый тренд Инстаграм – чат-бот. Он ответит клиентам за 4 секунды, напомнит о важных событиях/акциях через рассылку в директ, и в следствии увеличит продажи в 3 раза. Внедряйте, пока это не сделали конкуренты + по промокоду “inscale” 5 дней в подарок. Кликайте -> BossDirect.
2. Через приложение
Второй способ быстро и безопасно очистить список подписчиков – воспользоваться мобильными приложениями. В таблице ниже ТОП-5 инструментов для iOS и Android, которые автоматически удалят ботов и другой “мусор” из Вашего аккаунта.
| Приложение | Платформа | Кого/что можно удалить |
| InsPlus | Android | – Ботов; – Неактивных подписчиков. |
| Follower Manager | Android/iOS | – Ботов; – Неактивных подписчиков. |
| Followers & Unfollowers | Android/iOS | – Ботов; – Неактивных подписчиков; – Невзаимных подписок. |
| iMetric | Android/iOS | – Невзаимных подписок. |
| Twitly | Android/iOS | – Невзаимных подписок. |
Для примера покажу, как массово удалить подписчиков с телефона в приложении Follower Manager. Оно стабильно работает как на iOS, так и на Android.
Шаг 1. Добавление аккаунта
Скачайте приложение в AppStore или GooglePlay и подключите профиль в Instagram. Для этого введите логин и пароль.
АвторизацияШаг 2. Удаление подписчиков
На вкладке “Ghosts” Вы можете просмотреть и удалить список подписчиков, которые не ставят Вам лайки, то есть ботов и неактивную аудиторию. Эта функция доступна по тарифу PRO.
Удаление подписчиков3. Вручную
Этот метод, конечно, долгий и муторный (особенно, если Вы накопили много “мусора” в аккаунте), зато абсолютно бесплатный.
3.1. Без блокировки
Зайдите с телефона в само приложение Инстаграм, потом в раздел “Подписчики”. Здесь можно выбрать аккаунты из общего списка или воспользоваться автоматическими подборками профилей, на которые Вы не подписались в ответ или с кем меньше всего взаимодействуете. Далее около нужного аккаунта просто нажмите кнопку “Удалить”.
Кстати. Продвигайте Инстаграм с сервисом – Tooligram (по ссылке 100 подписчиков бесплатно). Пока Вы отдыхаете, он раскрутит Ваш аккаунт, и это 100% безопасно (сами им пользуемся).
Таким образом можно удалить любую нежелательную аудиторию: коммерческие профили, мертвые аккаунты, неактивных подписчиков и т.д.
Удаление вручную без блокировки3.2. С блокировкой
Наиболее бесполезных подписчиков в инстаграме (спамеров или ботов) можно заблокировать, чтобы ограничить для них доступ в Ваш аккаунт. Для этого перейдите в профиль фолловера, нажмите три точки в правом верхнем углу, далее кликните “Заблокировать” в выпадающем списке.
Удаление вручную с блокировкойВажно. Удалить мертвых подписчиков в Инстаграм этим методом сложно. Способ применим на страницах с числом до 350 фолловеров. Поэтому не мучайте себя и пользуйтесь Spam Guard.
как не навредить профилю
Многие пользователи Instagram считают удаление ботов панацеей, которая мгновенно повысит охваты и улучшит статистику профиля. На деле часто все оказывается не так радужно. Более того, за резкую массовую отписку можно схлопотать бан. Поэтому собрала для Вас ТОП советов, которые обезопасят Ваш аккаунт в процессе тотальной чистки.
- Изучите ЦА. Чтобы удалить именно нецелевую, холодную аудиторию, у Вас должен быть четкий портрет клиента. Иначе можно лишиться в аккаунте живых людей, которые способны на целевые действия;
- Не торопитесь. Удаляйте медленно. Помните о том, что быстрая очистка повлечет за собой резкое уменьшение охватов (особенно, если Вы удаляете живых), что может активировать проблемы с рекламодателями;
- Соблюдайте лимиты. Если у Вас молодой аккаунт, не совершайте более 200 отписок в сутки. Если профилю более 1 года допускается удалять до 1 000 невзаимных и столько же взаимных фолловеров. При этом средний интервал отписок должен быть 40-60 секунд;
- Привлекайте аудиторию. Восполняйте баланс подписчиков. Это должны быть реальные люди, поэтому для привлечения лучше воспользоваться таргетированной рекламой на заинтересованных пользователей;
- Запускайте акции. Привлекайте новых фолловеров с помощью акций и конкурсов: дарите скидки на первую покупку за подписку на аккаунт или разыгрывайте призы среди подписчиков, оставивших комментарий под конкурсным постом;
- Не используйте массфоловинг. Не применяйте серые методы привлечения аудитории во время автоматического удаления ботов, иначе Инстаграм заблокирует Вас за подозрительную активность.
частые вопросы
В блоке собрала ТОП актуальных вопросов об отписках, которые волнуют каждого владельца профиля в Инстаграм.
– Чем отличается удаление от блокировки подписчиков?
Если Вы заблокировали пользователя, он больше не сможет видеть Ваш профиль, комментировать публикации и писать в Директ. При стандартном удалении доступ к Вашему аккаунту не будет ограничен, и человек сможет повторно подписаться на Вас в любое время.
– Как вернуть удаленного подписчика?
Автоматически вернуть подписчика нельзя. Если Вы удалили пользователя по ошибке, но запомнили его ник, можете написать ему сообщение с приглашением подписаться обратно.
– Как разблокировать пользователя?
Зайдите в настройки Инстаграм, выберите пункт “Конфиденциальность”. Далее нажмите на кнопку “Заблокированные аккаунты” и разблокируйте нужных пользователей. После этого человек снова сможет просматривать Вашу страницу и активничать на ней.
– Как удалить массово?
Массово удалить ботов или нежелательных подписчиков можно с помощью онлайн-сервисов или мобильных приложений. В начале статье представлены инструменты для этих целей.
НАС УЖЕ БОЛЕЕ 32 000 чел.
ВКЛЮЧАЙТЕСЬ
Коротко о главном
Как удалить ненужных подписчиков в Инстаграм без вреда для аккаунта, разобрались. Если Вы все еще сомневаетесь, то ловите инфу о том, что может случиться с профилем при наличии лишнего “мусора”.
- Уменьшение вовлеченности. При обилии мусорных подписчиков показатели вовлеченности будут снижаться, это понесет за собой ряд других негативов;
- Снижение доверия. Большое число недоброкачественных фолловеров может вызвать подозрение, что это боты, и Вы их купили, а сами рассылаете спам;
- Понижение ранжирования. Алгоритмы Instagram опускают в ленте посты с аккаунтов, у которых в профиле много неактивных подписчиков, то есть пост может потеряться в ленте;
- Низкая стоимость рекламных постов. Если Вы блогер и занимаетесь продажей рекламы, то с мертвой базой Вам точно не видать золотых гор.
Интересно. Добавьте в профиль мультиссылку. Она позволит связываться напрямую через мессенджеры, а также использовать несколько ссылок вместо одной -> taplink.ru (по промокоду “INSCALE7” 7 дней бесплатно).
Напоследок хочу отметить, что главное – это качество фолловеров, а не их количество. И помните, что после очистки аккаунта вовлеченность не взлетит до небес, так как очистка – это всего лишь один инструмент из десятка.
По теме:
Фишки Инстаграм: ТОП-60 от SMMщика
Полезные приложения для Инстаграм: ТОП-50
| Теория квантовой механики утверждает, что в атоме электроны находятся на орбиталях, и каждая орбиталь имеет характерную энергию. Орбитальный означает «малая орбита». Нас интересуют два свойства орбитали — их энергии и формы. Их энергия важный потому что мы обычно находим атомы в их наиболее стабильных состояниях, которые мы вызов их основных состояний , в которых электроны находятся на самом низком уровне возможный энергии. |
| |
| Главное квантовое число, n |
| Квантовое число n называется принципом
квантовое число.
Вы уже знаете это как оболочку. Снаряду «К» присвоено значение n = 1, оболочке «L» присвоено значение n =
2. п. 1 2 3 4… оболочка K L M № … |
| |
| Основное квантовое число служит для определения размера из орбиталь, или как далеко электрон простирается от ядра. В выше значение n чем дальше от ядра мы можем ожидать найти Это. По мере увеличения n увеличивается и требуемая энергия. потому что чем дальше от ядра вы уходите, тем больше энергии электрон должен должны оставаться на орбите.В работе Бора учтено только это первый главное квантовое число. Его теория работала для водорода, потому что водород просто оказывается единственным элементом, в котором все орбитали, имеющие одно и тоже значение n также имеют такую же энергию. Теория Бора не удалось для атомов, отличных от водорода, однако, поскольку орбитали с одинаковыми значение n может иметь разные энергии, когда у атома больше чем один электрон. |
| |
| Вторичное квантовое число, л |
| Вторичный квант
номер, l , разделяет оболочки на более мелкие группы подоболочек, называемых
орбитали.
Значение n определяет возможные значения для l .
За
для любой данной оболочки количество подоболочек можно найти как l = n -1. Это означает, что для первой оболочки n = 1 существует
Только л = 1-1 = 0 подоболочек. т.е. оболочка и подоболочка идентичны. Когда н =
2 есть два набора подоболочек; л = 1 и л =
0.
Номер может использоваться для идентификации подоболочки, однако во избежание
путаница
между числовыми значениями n и l l значениям присваивается буквенный код. значение л 0
1 2 3 4 ….. |
| |
| Для обозначения конкретной подоболочки записываем количество
оболочка
за самим собой следует обозначение подоболочки. n l Это иллюстрирует отношение между «n» и «l». 1 s с первой оболочкой связан один орбитальный тип. 2 с п вторая оболочка имеет два связанных с ней орбитальных типа. 3 с п d и т. д. 4 с п д ф 5 с п д ж |
| |
| Главное квантовое число описывает размер и энергию,
но
второе квантовое число описывает форму.Подоболочки в любом заданном
орбитальный
немного отличаются по энергии, при этом энергия в подоболочке увеличивается
с
увеличение л . Это означает, что в данной оболочке s
подоболочка имеет наименьшую энергию, p — следующая наименьшая, за ней следует d, затем
е и так далее. Например: 4s <4p <4d <4f ---> увеличение энергии |
| |
| Магнитное квантовое число, м л |
| Известно третье квантовое число, m l .
как
магнитное квантовое число.Он разбивает подоболочки на отдельные
орбитали.
Эта орбиталь описывает, как орбиталь ориентирована в пространстве относительно
к
другие орбитали. то есть дает трехмерную информацию. Первые «с»
подоболочка
имеет магическое число «1». Подоболочка «p» имеет магнитный
номер
из «3». Простая числовая прогрессия дает нам: s p d
ж <--- имя подоболочки * Орбиталь может содержать всего два электрона. Он не может содержать никого, один или два, но не более двух . |
| |
| Спиновое магнитное число, м с |
| Четвертое и последнее квантовое число используется для обозначения ориентация двух электронов на каждой орбитали.Значения для м с равны +1/2 и -1/2. Атом наиболее стабилен, когда его электроны иметь минимально возможную энергию. Электроны получают как можно меньше энергия когда они занимают самые низкие из возможных энергетических орбиталей. Но Какие определяет, как электроны «заполняют» орбитали? Два электрона может заполнить каждую орбиталь. Как могут два электрона с отрицательным зарядом, и следовательно, взаимно отталкивающие держаться вместе на одной орбите? |
| |
| Концепция спина электрона основана на том факте, что электроны ведут себя как крошечные магниты.Электрон вращается вокруг своей оси так же, как игрушка верх. Вращающийся электрический заряд создает магнитное поле. (В одно и тоже эффект заставляет электродвигатели и генераторы работать.) Электрон может вращение в двух направлениях: по часовой стрелке или против часовой стрелки. С помощью Правило левой руки для магнитных полей вращение электронов по часовой стрелке создайте северный полюс вверху и южный полюс внизу. В против часовой стрелки вращающиеся электроны генерируют северный полюс внизу и южный полюс на вершине. |
| |
| В 1925 году физик Вольфганг Паули (1900-1958), выразил важность спина электрона в определении электронных конфигурации. Принцип исключения Паули гласит, что никакие два электрона в одном и том же атом может иметь одинаковые значения для всех четырех квантовых чисел. Этот означает, что два электрона, заполняющие любую конкретную орбиталь, должны иметь противоположные вращения. Что произойдет, если орбиталь содержит только 1 электрон? Тогда его магнитное поле не отменяется и его можно притягивать к другие внешние магнитные поля.Атомы, имеющие хотя бы один a непарных электронов парамагнитны и могут притягиваться к магнитному полю. поля. Атомы без неспаренных электронов называются диамагнитными и не считаются магнитными. |
| |
| В общем, количество электронов в оболочке 2 n 2 . номер оболочки
подоболочек максимальное количество электронов |
Определить функцию | Промежуточная алгебра
Результаты обучения
- Определите функцию с помощью таблиц
- Определить, создает ли набор упорядоченных пар функцию
- Определите домен и диапазон функции, представленной в виде таблицы или набора упорядоченных пар
Есть много видов отношений.Отношения — это просто соответствие между наборами значений или информации. Подумайте о членах вашей семьи и их возрасте. Спаривание каждого члена вашей семьи и их возраст являются отношениями. Каждого члена семьи можно сопоставить с возрастом из набора возрастов членов вашей семьи. Другой пример взаимосвязи — объединение штата и его сенаторов США. Каждый штат может быть сопоставлен с двумя людьми, каждый из которых был избран сенатором. В свою очередь, каждому сенатору можно сопоставить одно конкретное государство, которое он или она представляет.Оба эти примера реальных отношений.
Первое значение отношения — это входное значение, а второе значение — выходное значение. Функция — это особый тип отношения, в котором каждое входное значение имеет одно и только одно выходное значение. Вход — это независимое значение , а выход — это зависимое значение , поскольку оно зависит от значения входа.
Обратите внимание, что в первой таблице ниже, где вход — «имя», а выход — «возраст», каждый вход соответствует ровно одному выходу.Это пример функции.
| Имя члена семьи (ввод) | Возраст члена семьи (Вывод) |
|---|---|
| Нелли | [латекс] 13 [/ латекс] |
| Маркос | [латекс] 11 [/ латекс] |
| Есфирь | [латекс] 46 [/ латекс] |
| Самуэль | [латекс] 47 [/ латекс] |
| Нина | [латекс] 47 [/ латекс] |
| Пол | [латекс] 47 [/ латекс] |
| Катрина | [латекс] 21 [/ латекс] |
| Андрей | [латекс] 16 [/ латекс] |
| Мария | [латекс] 13 [/ латекс] |
| Ана | [латекс] 81 [/ латекс] |
Сравните это со следующей таблицей, где входными данными является «возраст», а выходными данными — «имя.«Некоторые входы приводят к более чем одному выходу. Это пример соответствия , а не функции.
| Возраст члена семьи (ввод) | Имя члена семьи (вывод) |
|---|---|
| [латекс] 11 [/ латекс] | Маркос |
| [латекс] 13 [/ латекс] | Нелли, Мария |
| [латекс] 16 [/ латекс] | Андрей |
| [латекс] 21 [/ латекс] | Катрина |
| [латекс] 46 [/ латекс] | Есфирь |
| [латекс] 47 [/ латекс] | Самуэль, Нина, Пол |
| [латекс] 81 [/ латекс] | Ана |
Теперь давайте посмотрим на некоторые другие примеры, чтобы определить, являются ли отношения функциями или нет и при каких обстоятельствах.Помните, что отношение является функцией, если для каждого входа существует только один выход .
Пример
Заполните таблицу.
| Ввод | Выход | Функция? | Почему или почему нет? |
|---|---|---|---|
| Имя сенатора | Название государства | ||
| Название государства | Имя сенатора | ||
| Истекшее время | Высота подбрасываемого мяча | ||
| Высота подбрасываемого мяча | Истекшее время | ||
| Кол-во вагонов | Кол-во шин | ||
| Кол-во шин | Количество вагонов |
| Ввод | Выход | Функция? | Почему или почему нет? |
|---|---|---|---|
| Имя сенатора | Название государства | Есть | Для каждого входа будет только один выход, потому что сенатор представляет только одно состояние. |
| Название государства | Имя сенатора | № | Для каждого штата, являющегося входом, будет получено 2 имени сенаторов, потому что в каждом штате есть два сенатора. |
| Истекшее время | Высота подбрасываемого мяча | Есть | В определенное время мяч имеет определенную высоту. |
| Высота подбрасываемого мяча | Истекшее время | № | Помните, что мяч подбрасывался и упал.Таким образом, для данной высоты может быть два разных момента, когда мяч находился на этой высоте. Высота входа может привести к более чем одному выходу. |
| Кол-во вагонов | Кол-во шин | Есть | Для любого ввода определенного количества автомобилей есть один конкретный результат, представляющий количество шин. |
| Кол-во шин | Количество вагонов | Есть | Для любого ввода определенного количества шин существует один конкретный результат, представляющий количество автомобилей. |
Отношения могут быть записаны как упорядоченные пары чисел или как числа в таблице значений. Изучая входные данные (координаты x ) и выходы (координаты y ), вы можете определить, является ли отношение функцией. Помните, что в функции каждый вход имеет только один выход.
Есть имя для набора входных значений и другое имя для набора выходных значений для функции. Набор входных значений называется областью функции .Набор выходных значений называется диапазоном функции .
Если у вас есть набор упорядоченных пар, вы можете найти домен, перечислив все входные значения, которые являются координатами x . Чтобы найти диапазон, перечислите все выходные значения, которые представляют собой координаты y .
Рассмотрим следующий набор упорядоченных пар:
[латекс] \ {(- 2,0), (0,6), (2,12), (4,18) \} [/ латекс]
У вас есть:
[латекс] \ begin {array} {l} \ text {Domain:} \ {- 2,0,2,4 \} \\\ text {Range:} \ {0,6,12,18 \} \ конец {массив} [/ латекс]
А теперь попробуйте сами.
Пример
Укажите домен и диапазон для следующей таблицы значений, где x — это входные данные, а y — выходные.
| x | y |
|---|---|
| [латекс] −3 [/ латекс] | [латекс] 4 [/ латекс] |
| [латекс] -2 [/ латекс] | [латекс] 4 [/ латекс] |
| [латекс] -1 [/ латекс] | [латекс] 4 [/ латекс] |
| [латекс] 2 [/ латекс] | [латекс] 4 [/ латекс] |
| [латекс] 3 [/ латекс] | [латекс] 4 [/ латекс] |
Домен описывает все входные данные, и мы можем использовать обозначение набора с квадратными скобками {}, чтобы составить список.
[латекс] \ text {Домен}: \ {- 3, -2, -1,2,3 \} [/ латекс]
Диапазон описывает все выходы.
[латекс] \ text {Диапазон}: \ {4 \} [/ латекс]
Мы указали [latex] 4 [/ latex] только один раз, потому что нет необходимости перечислять его каждый раз, когда он появляется в диапазоне.
В следующем видео мы предоставляем еще один пример определения того, представляет ли таблица значений функцию, а также определения домена и диапазона каждой из них.
Пример
Определите домен и диапазон для следующего набора упорядоченных пар и определите, является ли данное отношение функцией.
[латекс] \ {(- 3, −6), (- 2, −1), (1,0), (1,5), (2,0) \} [/ латекс]
Показать решениеМы перечисляем все входные значения как домен. Входные значения представлены первыми в упорядоченной паре по соглашению.
Домен: {[latex] -3, -2,1,2 [/ latex]}
Обратите внимание на то, что мы не ввели повторяющиеся значения более одного раза; это не обязательно.
Диапазон — это список выходов для отношения; они вводятся вторыми в упорядоченной паре.
Диапазон: {[латекс] -6, -1, 0, 5 [/ латекс]}
Организация упорядоченных пар в таблице может помочь вам определить, является ли это отношение функцией.По определению, входы функции имеют только один выход.
| x | y |
|---|---|
| [латекс] −3 [/ латекс] | [латекс] −6 [/ латекс] |
| [латекс] -2 [/ латекс] | [латекс] -1 [/ латекс] |
| [латекс] 1 [/ латекс] | [латекс] 0 [/ латекс] |
| [латекс] 1 [/ латекс] | [латекс] 5 [/ латекс] |
| [латекс] 2 [/ латекс] | [латекс] 0 [/ латекс] |
Отношение не является функцией, потому что вход [latex] 1 [/ latex] имеет два выхода: [latex] 0 [/ latex] и [latex] 5 [/ latex].
В следующем видео мы покажем, как определить, является ли отношение функцией, и как найти домен и диапазон.
Пример
Найдите область и диапазон отношения и определите, является ли это функцией.
[латекс] \ {(- 3, 4), (- 2, 4), (-1, 4), (2, 4), (3, 4) \} [/ латекс]
Показать решениеДомен: {[latex] -3, -2, -1, 2, 3 [/ latex]}
Диапазон: {[латекс] 4 [/ латекс]}
Чтобы помочь вам определить, является ли это функцией, вы можете реорганизовать информацию, создав таблицу.
| x | y |
|---|---|
| [латекс] −3 [/ латекс] | [латекс] 4 [/ латекс] |
| [латекс] -2 [/ латекс] | [латекс] 4 [/ латекс] |
| [латекс] -1 [/ латекс] | [латекс] 4 [/ латекс] |
| [латекс] 2 [/ латекс] | [латекс] 4 [/ латекс] |
| [латекс] 3 [/ латекс] | [латекс] 4 [/ латекс] |
Каждый вход имеет только один выход, и тот факт, что это один и тот же выход (4), не имеет значения.
Это отношение является функцией.
Сводка: определение того, является ли отношение функцией- Определите входные значения — это ваш домен.
- Определите выходные значения — это ваш диапазон.
- Если каждое значение в домене приводит только к одному значению в диапазоне, классифицируйте отношение как функцию. Если какое-либо значение в домене приводит к двум или более значениям в диапазоне, не классифицируйте отношение как функцию.
Функция: Определение Функция — это соответствие первого набора, называемого доменом, второму набору, называемому диапазоном, так что каждый элемент в.
Презентация на тему: «Функция: определение Функция — это соответствие первого набора, называемого доменом, второму набору, называемому диапазоном, так что каждый элемент в.» — стенограмма презентации:
1 Функция: определение Функция — это соответствие первого набора, называемого доменом, второму набору, называемому диапазоном, так что каждый элемент в домене соответствует ровно одному элементу в диапазоне.Элементы домена называются входами. Элементы диапазона называются выходами.
2 Независимая переменная x обозначает член домена, а зависимая переменная y обозначает член диапазона. Мы говорим: «y является функцией x». Функция: Определение В этом курсе членами каждого набора являются действительные числа. На данный момент x будет представлять действительное число из домена, а y или f (x) будет представлять действительное число из диапазона.
3 Функция: представление диаграммы сопоставления Функция может быть представлена с использованием набора упорядоченных пар (x, y), таблицы значений, уравнения, графика и диаграммы сопоставления. Вот пример функции, представленной диаграммой отображения. 5 17 02 — 2-4
4 Правила, регулирующие соответствие между двумя наборами, следующие: 1.Умножьте значение домена на три. 2. Добавьте два к результату. Функция: отображение диаграммы отображения Здесь левый овал представляет домен. Правый овал представляет диапазон. 5 17 02 — 2-4
5 Вот та же функция, представленная набором упорядоченных пар: {(- 2, — 4), (0, 2), (5, 17)}. Функция: упорядоченные пары 5 17 02-2-4
6 Функция: Табличные представления 5 17 02 — 2- 4 Вот та же функция, представленная таблицей значений: x y — 2 — 4 0 2 5 17
7 Допустим, отображение — это всего лишь частичное представление бесконечного числа упорядоченных пар.Тогда вот та же функция, представленная уравнением: y = 3x + 2 или f (x) = 3x + 2. Функция: Уравнение 5 17 02-2-4
8 Функция: Графические представления 5 17 02 — 2- 4 Вот та же функция, представленная графиком (изображена оранжевая линия).
9 Функция
Выравнивание множества выявляет соответствие между транскриптомом отдельной клетки и динамикой эпигенома
Введение
Понимание механизмов, которые регулируют экспрессию генов в пространстве и времени, является фундаментальной проблемой в биологии.Известно, что эпигенетические модификации, такие как метилирование ДНК, гистоновые метки и доступность хроматина, регулируют экспрессию генов, но точные детали этой регуляции не совсем понятны. Одноклеточные геномные технологии выявляют гетерогенность популяций клеток, включая сложные ткани, опухоли и клетки, претерпевающие временные изменения [1, 2]. Кроме того, поскольку объемные данные состоят из измерений, усредненных по популяции клеток, геномные данные отдельных клеток, в принципе, позволяют гораздо более точно изучить, как эпигенетические изменения и экспрессия генов изменяются вместе.
Single cell RNA-seq был с большим успехом применен для изучения последовательных клеточных процессов, таких как дифференцировка и репрограммирование [3–7]. В таких экспериментах предполагается, что каждая секвенированная клетка находится в одной точке процесса, и секвенирование достаточного количества клеток может выявить прогрессию изменений экспрессии генов, которые происходят во время процесса [8, 9]. Совсем недавно было разработано несколько экспериментальных методов для выполнения эпигенетики отдельных клеток [10–17], и первоначальный анализ продемонстрировал, что эпигенетические данные отдельных клеток можно использовать для выяснения серии изменений в последовательном процессе [16, 18, 19]. .
Выявление корреляций между динамикой эпигенома и транскриптома позволит более полно понять последовательные изменения, которым клетки подвергаются во время биологических процессов. Измерение нескольких геномных величин из одной клетки или многомерное профилирование [20, 21] было бы лучшим способом выявления таких корреляций. К сожалению, выполнение многомерного профилирования одной клетки очень сложно экспериментально, потому что анализ хроматина или РНК разрушает соответствующие молекулы, и только крошечные количества ДНК и РНК присутствуют в одной клетке.В некоторых случаях можно анализировать РНК и ДНК [14, 22–24] или РНК и белки [25, 26] из одной и той же клетки, но экспериментальное выполнение нескольких анализов хроматина или РНК из одной и той же клетки в настоящее время является возможным. невозможно.
Наши знания об эпигенетической регуляции предполагают, что любые большие изменения в экспрессии генов, такие как те, которые происходят во время дифференцировки, сопровождаются эпигенетическими изменениями. Следовательно, в принципе должна быть возможность сделать вывод о последовательных изменениях клеточного эпигенетического состояния во время процесса.Более того, если клетки, претерпевающие общий процесс, секвенируются с использованием нескольких геномных методов, исследование любого количества генома должно выявить один и тот же базовый биологический процесс. Например, основное различие между клетками, подвергающимися дифференцировке, будет заключаться в степени прогресса их дифференцировки, независимо от того, смотрите ли вы на профили экспрессии генов или профили доступности хроматина клеток.
Мы пришли к выводу, что это свойство данных отдельной клетки можно использовать для вывода соответствия между различными типами геномных данных.Чтобы вывести соответствия отдельных ячеек, мы используем технику, называемую совмещением многообразий [27, 28]. Интуитивно, выстраивание многообразия конструирует низкоразмерное представление (многообразие) для каждого из наблюдаемых типов данных, а затем проецирует эти представления в общее пространство (выравнивание), в котором измерения различных типов напрямую сравниваются. Насколько нам известно, множественное выравнивание никогда не использовалось в геномике. Однако другие области применения признают этот метод как мощный инструмент для мультимодального слияния данных, такого как получение изображений на основе текстового описания и многоязычный поиск без прямого перевода [28].
Мы называем наш метод MATCHER (Выравнивание многообразия для характеристики экспериментальных взаимосвязей). Используя MATCHER, мы определили корреляции между транскриптомными и эпигенетическими изменениями в одиночных эмбриональных стволовых клетках мыши по мере их продвижения по траектории от плюрипотентности к состоянию примирования дифференцировки.
Результаты
Обзор MATCHER
Выравнивание коллектора ранее использовалось для построения общего низкоразмерного представления, которое резюмирует известную информацию о соответствии между двумя разными типами данных [27, 28].Простейшим примером совмещения многообразий является канонический корреляционный анализ (CCA), в котором выравниваются линейные проекции каждого пространства. Гауссовские модели скрытых переменных процесса также использовались для выполнения множественного выравнивания путем изучения полностью [29, 30] или частично [29] общих скрытых представлений многомерных, мультимодальных данных. Учитывая набор изображений и соответствующих текстовых описаний, можно использовать выравнивание по множеству, чтобы идентифицировать низкоразмерное представление, которое позволяет предсказывать заголовок для нового изображения.Это в некоторой степени аналогично проблеме получения соответствующего эпигенетического измерения для данного транскриптома отдельной клетки. Однако в контексте геномных данных одной клетки информация о соответствии обычно недоступна для обучения модели, поскольку в большинстве случаев невозможно измерить более одной величины на одной клетке. Поэтому мы разработали новый подход к выравниванию коллекторов без соответствия, который использует уникальные аспекты этой проблемы.
Мы предполагаем, что:
Геномные данные отдельной клетки от клеток, проходящих через биологический процесс, лежат вдоль одномерного коллектора.Другими словами, различия между ячейками можно объяснить, главным образом, единственной скрытой переменной («псевдовремя»), соответствующей положению в процессе.
Каждая из рассматриваемых геномных величин изменяется в ответ на один и тот же основной процесс.
Биологический процесс монотонен, что означает, что прогресс происходит только в одном направлении. Процессы, которые попеременно идут вперед и назад или повторяются циклически, нарушили бы это предположение.
Клетки в каждом эксперименте отбираются из одной и той же популяции, процесса и типа клеток.
При этих предположениях существует только три возможных типа различий между одномерными представлениями каждого типа данных: ориентация, масштаб и «деформация времени» (рис. 1a). Мы можем выполнить выравнивание коллектора без информации о соответствии, учитывая эти три типа различий. Различия в ориентации могут возникать, если биологический процесс соответствует увеличению множества координат для одного типа геномных данных и уменьшению координат для другого типа данных.Мы можем согласовать различные ориентации, просто изменив порядок одного набора координат многообразия. Невозможно вывести правильную ориентацию из данных, поэтому мы используем предварительные биологические знания, чтобы выбрать правильную ориентацию для многообразия, выведенного из каждого типа данных. Чтобы устранить различия в масштабе, мы можем нормализовать множественные координаты, чтобы они лежали между 0 и 1. Эффект искажения времени может возникать, если разные геномные количества изменяются с разной скоростью. Например, изменения экспрессии генов могут происходить медленно в начале процесса и постепенно ускоряться, в то время как изменения в доступности хроматина могут показывать прямо противоположную тенденцию во время процесса (рис.1а). Мы учитываем эффекты искажения времени, изучая функцию монотонного искажения для каждого типа данных (подробности см. Ниже).
Рис. 1: Обзор метода MATCHER(a) Мы делаем вывод о множественных представлениях каждого набора данных, используя модель скрытых переменных гауссовского процесса (GPLVM). Однако полученные значения «псевдовремени» из разных типов геномных данных нельзя напрямую сравнивать из-за различий в ориентации, масштабе и «деформации времени». И цвет многообразия (от черного к желтому), и морфология клетки (от пятна до продолговатого) указывают на положение внутри этого гипотетического процесса.(b) — (c) Чтобы учесть эти эффекты, псевдовремя для каждого типа данных моделируется как нелинейная функция (функция деформации) основного времени с использованием гауссовского процесса. (d) MATCHER определяет «основное время», в котором шаги биологического процесса соответствуют значениям, равномерно распределенным между 0 и 1, и сопоставимы между различными типами данных. Однако разные наборы данных измеряются из разных физических ячеек и, таким образом, могут отбирать разные точки в биологическом процессе и даже разное количество клеток.(e) Диаграмма, показывающая, как генеративная модель MATCHER может вывести соответствующие измерения клеток. Сгенерированная ячейка отображается с прозрачностью, чтобы указать, что это предполагаемая, а не наблюдаемая величина. (f) Применение MATCHER к нескольким типам данных обеспечивает точно соответствующие измерения для наблюдаемых ячеек и ненаблюдаемых ячеек (обозначенных прозрачностью), сгенерированных MATCHER.
Мы используем гауссовскую модель скрытых переменных процесса (GPLVM), чтобы вывести значения псевдовремени отдельно для каждого типа данных.GPLVM — это нелинейный, вероятностный, генеративный метод уменьшения размерности, который моделирует многомерные наблюдения как функцию одной или нескольких скрытых переменных [31]. Ключевым свойством GPLVM является то, что производящая функция является гауссовским процессом, который позволяет байесовский вывод скрытых переменных, нелинейно связанных с многомерными наблюдениями [32, 33]. Нелинейный характер этой модели делает ее более гибкой и устойчивой к шумам, чем линейная модель, такая как анализ главных компонентов (PCA).Фактически, PCA может быть получен как частный случай GPLVM, в котором производящая функция гауссовского процесса использует линейное ядро [31]. Важно отметить, что GPLVM также являются генеративными моделями, что означает, что они могут ответить на контрфактический вопрос о том, как будет выглядеть ненаблюдаемая многомерная точка данных в определенном месте на коллекторе . Генеративная природа GPLVM особенно важна для нашего подхода: мы используем это свойство, чтобы сделать вывод о соответствии между геномными количествами отдельных клеток, измеренными разными способами.Мы отмечаем, что GPLVM ранее использовались для вывода латентных переменных, лежащих в основе различий между профилями экспрессии генов отдельных клеток [34–36]; наш подход отличается от этих предыдущих подходов в том, что мы используем GPLVM как часть подхода выравнивания коллектора и генерируют измерений из ненаблюдаемых ячеек, чтобы интегрировать нескольких типов измерений отдельных ячеек.
После вывода псевдовремени отдельно для каждого типа данных мы узнаем монотонную функцию деформации (рис.1b-c), который преобразует значения псевдовремени в значения «основного времени», которые равномерно распределены между 0 и 1 (рис. 1d). Это эквивалентно выравниванию квантилей псевдовременного распределения для соответствия квантилям однородной случайной величины. Значения основного времени, выведенные из разных типов данных, затем напрямую сравниваются, что соответствует одним и тем же точкам в базовом биологическом процессе.
Модель (рис. 1e), которую мы используем для вывода основных значений времени, позволяет нам сгенерировать измерений соответствующих ячеек даже из наборов данных, где измерения проводились на разных отдельных ячейках.Различные типы измерений могут производить наборы данных с клетками с разных позиций в биологическом процессе и даже с разным количеством клеток (рис. 1e). Чтобы сгенерировать соответствующее измерение для ячейки, мы берем главное значение времени, выведенное для данной ячейки, например, измеренное с помощью RNA-seq. Затем мы сопоставляем это главное значение времени с помощью функции деформации со значением псевдовремени для другого типа данных, например ATAC-seq. Используя GPLVM, обученный на данных ATAC-seq, мы можем вывести соответствующую ячейку на основе этого значения псевдовремени.Как показано на рис. 1f, генеративный характер модели позволяет MATCHER сделать вывод, какие ненаблюдаемые клетки, измеренные с помощью одного экспериментального метода , будут выглядеть , если они точно соответствуют клеткам, измеренным с использованием другого метода. Затем эти соответствующие клеточные измерения можно использовать различными способами, например, для вычисления корреляции между экспрессией генов и доступностью хроматина.
Хотя в целом очень сложно измерить несколько геномных количеств в одной и той же клетке, был разработан один конкретный протокол (scM & T-seq) для измерения метилирования ДНК и экспрессии генов в одной и той же отдельной клетке [14].Возможно, что будущие протоколы позволят проводить другие совместные измерения. В таких случаях мы можем включить известную информацию о соответствии в нашу модель, используя совместно используемую GPLVM [29], чтобы вывести совместно используемую скрытую переменную псевдовременности для обоих типов данных.
Описание и обработка данных
Было разработано несколько высокопроизводительных одноклеточных версий эпигенетических анализов, включая бисульфитное секвенирование отдельных клеток (метилирование ДНК) [14], ATAC-seq (доступность хроматина) [13] и ChIP-seq (гистоновая модификация) [12].В каждом из первых исследований, в которых впервые использовались эти методы, они применялись к эмбриональным стволовым клеткам мыши (mESC), выращенным в сыворотке, — классической модельной системе биологии стволовых клеток. Клетки в этой системе неоднородны, различаются в зависимости от того, где они расположены, в диапазоне от плюрипотентного основного состояния до состояния примирования дифференцировки [37]. Обратите внимание, что mESCs, выращенные в сыворотке, обладают другими свойствами, чем mESCs, культивируемые в среде 2i, которые намного более гомогенны и различаются, прежде всего, стадией их клеточного цикла [34, 37].
Мы собрали общедоступные данные из этих статей. Всего у нас есть четыре типа данных об отдельных клетках из 4974 клеток: 250 клеток с данными экспрессии генов [37], 61 с метилированием ДНК [14], 76 с доступностью хроматина [13] и 4587 с h4K4me2 ChIP [ 12]. Данные о метилировании ДНК были собраны с использованием протокола scM & T-seq, который измеряет экспрессию генов и метилирование ДНК одновременно в одной клетке [14].
Обработка эпигенетических данных отдельных клеток сложнее, чем RNA-seq, потому что эпигенетические данные почти бинарны в каждой геномной позиции (кроме аллель-специфичных эффектов и вариаций числа копий) и чрезвычайно редки, всего несколько тысяч считываний. на ячейку во многих случаях.Это очень затрудняет извлечение какой-либо значимой информации при разрешении пары оснований из одной ячейки. Вместо этого мы следовали этапам обработки данных, изложенным в каждой из соответствующих статей, в которых разрабатывались эти методы, и агрегировали считывания по связанным геномным интервалам. Например, мы последовали примеру авторов при суммировании значений данных о доступности хроматина из ATAC-seq в данной клетке по всем сайтам связывания для данного фактора транскрипции. Выполнение этого для каждого из 186 факторов транскрипции приводит к матрице из 186 сигнатур доступности хроматина для набора клеток.Данные о метилировании ДНК и данные о h4K4me2 ChIP-seq были агрегированы аналогичным образом. Мы получили обработанные данные о метилировании ДНК и ChIP-seq из исходных публикаций. Обработанные данные ATAC-seq не являются общедоступными, поэтому мы обработали данные, реализовав конвейер, описанный в статье. Мы обнаружили, что данные о метилировании ДНК показали самый высокий уровень обнаружения на клетку; данные ChIP-seq имели самую низкую скорость обнаружения. Следовательно, мы смогли агрегировать данные о метилировании ДНК по относительно небольшим геномным интервалам, таким как отдельные промоторы или островки CpG.
Данные транскриптома отдельных клеток и эпигенома демонстрируют общие способы вариации.
Кажется вероятным, что экспрессия генов, метилирование ДНК, доступность хроматина и модификации гистонов будут меняться во время перехода от плюрипотентности к состоянию примирования дифференцировки. Однако мы хотели выяснить, выполняется ли это ключевое предположение в данной конкретной системе.
Чтобы проверить нашу гипотезу о том, что каждый из этих эпигенетических типов данных изменяется в ходе общего основного процесса, мы сначала попытались построить траекторию клетки для каждого типа данных.Используя SLICER, метод, который мы разработали ранее [9], мы визуализировали каждый тип данных как двумерную проекцию и вывели одномерный порядок для ячеек. Двухмерные проекции показывают, что каждый тип данных напоминает одномерную траекторию, а не двумерный блок точек (рис. 2a-d). Обратите внимание, что эти 2D-проекции не заставляют данные принимать одномерные формы; графики могут выглядеть как диффузное облако точек, и тот факт, что они вместо этого напоминают траектории, показывает, что различия между ячейками преимущественно одномерны.Кроме того, проекции каждого типа данных поразительно похожи визуально (рис. 2a-d).
Рисунок 2: Данные транскриптома и эпигенома отдельной клетки показывают общие способы вариации.(a) — (d): траектории отдельных клеток, построенные с помощью SLICER из RNA-seq, бисульфитного секвенирования, ATAC-seq и h4K4me2 ChIP-seq эмбриональных стволовых клеток мыши, выращенных в сыворотке. (e) — (l) Уровни экспрессии важных генов, метилирования ДНК, доступности хроматина и маркеров h4K4me2 на всех траекториях. Примечание: мы использовали SLICER для анализа на этом рисунке, потому что это ранее опубликованный метод построения траекторий клеток, который позволил нам исследовать гипотезу о том, что измерения транскриптома одной клетки и эпигенома имеют общие источники вариаций.SLICER и MATCHER — это совершенно разные методы; MATCHER никоим образом не полагается на SLICER; и SLICER нельзя было использовать для интеграции нескольких типов измерений, как это делает MATCHER, потому что SLICER не может генерировать измерения ненаблюдаемых ячеек.
Мы дополнительно исследовали эти траектории, чтобы определить, соответствуют ли они одному и тому же основному процессу. Траектория, построенная на основе данных РНК, показывает снижение экспрессии генов плюрипотентности, таких как SOX2, в соответствии с ранее опубликованными анализами [37] (рис.2д). Метилирование ДНК тела гена Rex1 , гена, который отключается во время перехода от плюрипотентности к примированию дифференцировки [38], увеличивается во время процесса (рис. 2f). Данные ATAC-seq для отдельных клеток показывают, что доступность хроматина для сайтов связывания для фактора транскрипции SOX2 снижается в течение псевдодвремени (Fig. 2g). Сходным образом уровни h4K4me2, модификации гистона, связанной с активными энхансерами и промоторами, снижаются на сайтах связывания SOX2 (рис. 2h).Данные RNA-seq показывают увеличение экспрессии ранее идентифицированных маркеров дифференцировки [37], таких как Krt8 (рис. 2i). Метилирование ДНК промотора Mael увеличивается, что согласуется с предыдущими открытиями [38] (Рис. 2j). Доступность хроматина (Рис. 2k) и уровни h4K4me2 (Рис. 2l) в сайтах связывания REST увеличиваются, что согласуется с известной ролью REST в репрессии ключевых генов, определяющих клон [39, 40]. Таким образом, наш анализ показывает, что каждый тип данных отдельных клеток изменяется вдоль траектории, устанавливая континуум, который варьируется от плюрипотентности до состояния примирования дифференцировки.
Мы использовали SLICER для выполнения этого первоначального исследовательского анализа, но для остальной части этого исследования мы используем MATCHER, который полностью отделен от SLICER и никоим образом не зависит от метода. Однако мы подтвердили, что основные значения времени, полученные с помощью MATCHER, сильно коррелируют со значениями псевдовремени, полученными с помощью SLICER (дополнительный рисунок 1). Также обратите внимание, что SLICER нельзя использовать для интеграции нескольких типов измерений отдельных ячеек так, как это делает MATCHER, потому что модель, лежащая в основе SLICER, не является генеративной.
Дополнительный рисунок 1: Главное время MATCHER сильно коррелировано с псевдовремени SLICER.График разброса псевдовременности SLICER и основного времени MATCHER для (a) РНК-seq, (b) бисульфитного секвенирования, (c) ATAC-seq и (d) h4K4me2 ChIP-seq. Точки раскрашены псевдовремени SLICER.
MATCHER точно моделирует синтетические и реальные данные
Чтобы оценить точность MATCHER, мы сгенерировали синтетические данные, для которых известно время наземного мастера. Мы сгенерировали данные путем выборки 100 основных значений времени равномерно случайным образом из интервала [0,1], а затем сопоставили их со значениями псевдовремени с помощью функции деформации.Используя полученные значения псевдодействия, мы сгенерировали 600 «генов», каждый из которых следовал немного отличающемуся «паттерну экспрессии» (функция псевдовремени). К каждому значению экспрессии гена добавляли нормально распределенный шум. Затем мы использовали MATCHER для определения основного времени из этих смоделированных значений экспрессии генов и измерили точность как корреляцию между истинными и предполагаемыми значениями основного времени. Обратите внимание, что мы используем корреляцию Пирсона, а не Спирмена, потому что мы ожидаем, что истинное и предполагаемое основное время будут линейно связаны (фактически равны), а нелинейная связь будет указывать на неточность процесса вывода.Результаты нашего моделирования показывают, что MATCHER точно определяет общее время по ряду различных функций деформации и уровней шума (дополнительные рисунки 2-3). Этот метод очень устойчив к шуму в смоделированных генах, давая корреляцию 0,92 при уровне шума σ = 9, что превышает 50% диапазона смоделированных функций.
Дополнительный рисунок 2: Результаты синтетических данных, сгенерированных различными базовыми функциями деформации.Предполагаемые функции деформации для (а) линейных, (б) квадратного корня, (в) квадратичного и (г) логита истинных основных функций деформации.(e) — (h) Диаграмма рассеяния истинного и предполагаемого основного времени для соответствующих функций деформации панелей (a) — (d).
Дополнительный рисунок 3: Результаты синтетических данных для увеличения уровня шума.Мы также протестировали MATCHER на реальных данных. Мы использовали данные scM и T-seq, в которых метилирование ДНК и экспрессия генов измеряются в одних и тех же отдельных клетках [14], так что истинное соответствие между измерениями отдельных клеток известно. Обратите внимание, что мы использовали известную информацию о соответствии ячеек только для проверки, а не во время процесса вывода.Сначала мы проверили взаимосвязь между основным временем, выведенным MATCHER из RNA-seq, и данными метилирования ДНК, вычислив корреляцию между предполагаемыми значениями основного времени для соответствующего метилирования ДНК и RNA-seq клеток. Это показало, что основные значения времени, хотя и не идентичны, очень согласованы (Пирсон ρ = 0,63). Прогнозирование ковариации нескольких геномных величин в отдельных клетках — одно из ключевых приложений MATCHER. Поэтому в качестве дополнительного теста мы исследовали, может ли MATCHER точно вывести корреляции между событиями метилирования ДНК и экспрессией генов.Здесь мы использовали корреляцию Спирмена, потому что нас интересуют как линейные, так и нелинейные отношения. Мы выбрали набор генов и проксимальных метилированных локусов, которые показали статистически значимую корреляцию в исходном анализе данных scM и T-seq [14]. Angermueller et al. сгруппировали эти пары в соответствии с типом области, в которой происходит сайт метилирования. Мы выбрали три типа областей с наибольшим количеством значимых пар (области с низким метилированием, пики h4K27me3 и сайты связывания P300).Затем для каждой значимой пары мы сравнили истинную корреляцию (вычисленную с использованием истинных соответствий ячеек) и корреляцию, полученную с помощью MATCHER (вычисленную с использованием предполагаемых соответствий ячеек). Мы также использовали MATCHER для вычисления корреляций для одних и тех же пар ген-локус, используя набор данных RNA-seq для одной клетки, опубликованный другой лабораторией [37]. В этом наборе данных клетки, измеренные с помощью RNA-seq, относятся к тому же типу клеток, но не к тем же физическим клеткам, что и клетки, исследованные на метилирование ДНК Angermueller et al.В обоих случаях предполагаемые корреляции полностью совпадают с истинными корреляциями (рис. 3). Корреляции, вычисленные с использованием данных Колодзейчика, показывают немного меньшее соответствие с реальной истиной, вероятно, из-за неизбежных биологических и технических вариаций, которые возникают, когда разные лаборатории повторяют эксперимент. Даже в этом случае подавляющее большинство предполагаемых корреляций имеет правильный знак, и относительная величина корреляций, как правило, сохраняется.
Рисунок 3: MATCHER точно выводит известные корреляции между метилированием ДНК и экспрессией генов.(a) — (c) Тепловые карты, сравнивающие истинные корреляции между экспрессией генов и метилированием ДНК связанных областей (пики h4K27me3, LMR и сайты связывания P300). Первый столбец каждой тепловой карты показывает истинную корреляцию на основе известной информации о соответствии, второй столбец показывает корреляцию, выведенную MATCHER в том же наборе данных, а третий столбец представляет собой корреляцию, выведенную MATCHER с использованием совершенно другого набора данных RNA-seq с одной ячейкой из мЭСК, выращенные в сыворотке. (d) — (e) Диаграмма рассеяния результатов, показанных в (a) — (c).Панель (d) содержит корреляции, вычисленные с использованием данных Ангермюллера; панель (e) — корреляции, рассчитанные на основе данных Колодзейчика. Каждая точка представляет собой истинную и предполагаемую корреляцию для одной пары ген-сайт; идеальные результаты лежат на линии y = x . Обратите внимание, что знак предполагаемой корреляции верен для подавляющего большинства пар.
Корреляции между экспрессией генов отдельных клеток, доступностью хроматина и модификациями гистонов
Затем мы использовали MATCHER для исследования взаимосвязей между экспрессией гена, доступностью хроматина и модификациями гистонов во время перехода от плюрипотентности к состоянию примирования дифференцировки.Насколько нам известно, это первый раз, когда исследование взаимосвязи между этими тремя геномными величинами было выполнено в отдельных клетках.
Поскольку h4K4me2 является модификацией гистона, связанной с активацией промотора и энхансера, мы ожидаем, что уровни модификации положительно коррелируют с доступностью хроматина. Мы подтвердили, что это действительно так, сделав вывод о корреляциях между доступностью хроматина и h4K4me2 в соответствующих областях, связанных 186 факторами транскрипции и ДНК-связывающими белками (рис.4а). Большинство этих корреляций строго положительные, указывая на то, что активирующие модификации гистонов и доступность хроматина имеют тенденцию изменяться в унисон во время подготовки к дифференцировке.
Рисунок 4: Корреляция между экспрессией генов отдельных клеток, доступностью хроматина и модификациями гистонов.(a) Скрипичный график корреляций между доступностью хроматина и h4K4me2 сайтов связывания факторов транскрипции для 186 факторов транскрипции. Обратите внимание, что большинство корреляций строго положительные.(b) Корреляция между доступностью хроматина и данными h4K4me2 показывает, что мишени факторов плюрипотентности / комплекса NuRD и мишени белков Polycomb Group / Trithorax Group антикоррелированы в отдельных клетках. (c) Корреляция между сигнатурами экспрессии генов и сигнатурами доступности хроматина. (d) Корреляция между сигнатурами экспрессии генов и сигнатурами h4K4me2. (e) Корреляция между экспрессией генов ДНК-связывающих белков и доступностью хроматина для их мишеней.
При исследовании корреляции между h4K4me2 и доступностью хроматина мы обнаружили, что участки связывания генома сгруппированы в две основные группы: (1) факторы транскрипции плюрипотентности и комплекс NuRD и (2) факторы ремоделирования хроматина, которые репрессируют или активируют гены, специфичные для клонов ( Инжир.4б). Rotem et al. отметили аналогичную взаимосвязь в данных h4K4me2 [12]. Доступность сайтов связывания для OCT4 (также известных как POU5F1), NANOG и SOX2, хорошо зарекомендовавших себя факторов транскрипции плюрипотентности, в значительной степени антикоррелирована с доступностью сайтов связывания для EZh3, RING1B и SUZ12, которые являются белками группы Polycomb (PcG ) [41]. Мишени фактора транскрипции YY1, который рекрутирует белки PcG [42], демонстрируют сходную тенденцию с белками PcG. Принимая во внимание, что белки PcG играют ключевую роль в репрессии генов нейрональных клонов в плюрипотентных клетках [43], эта антикорреляция указывает на то, что хроматин ремоделируется на первичные клон-специфические гены, в то же время закрывая области, связанные с плюрипотентностью.REST и COREST демонстрируют сходную картину с белками PcG; эти белки, как известно, совместно ассоциируют с репрессивным комплексом polycomb (PRC2), а также репрессируют ключевые клон-специфические гены в плюрипотентных клетках [39, 40]. Интересно, что мишени USF1, который, как известно, рекрутирует белки Trithorax Group (TrxG) [44], также обнаруживают паттерн увеличения доступности хроматина. Белки TrxG являются активаторами хроматина, которые регулируют гены дифференцировки клонов [43–45], подтверждая, что активация определенных генов дифференцировки происходит, в то время как их репрессия с помощью PRC2 снимается.Наконец, мишени LSD1, MI2, HDAC1 и HDAC2, компонентов комплекса NuRD, обнаруживают положительную корреляцию с мишенями факторов плюрипотентности. Комплекс NuRD содержит белки ремоделирования хроматина, которые удаляют метки метилирования гистонов и ацетилирования гистонов и функционируют для «вывода из строя» усилителей плюрипотентности во время ранней дифференцировки [46]. Таким образом, наш анализ корреляции между доступностью хроматина и метками h4K4me2 показывает, что общая тенденция в обоих типах данных направлена на изменения хроматина, которые отключают плюрипотентность и начинают снимать репрессию клонов при подготовке к дифференцировке.
Мы также вычислили корреляции между экспрессией генов и доступностью хроматина, а также между экспрессией генов и h4K4me2. Чтобы идентифицировать популяции молекул РНК с четкой связью с агрегированными областями генома, используемыми для вычисления измерений доступности хроматина, мы объединили уровни экспрессии генов из генов, промоторы которых перекрывают сайты связывания для нескольких белков. Мы специально изучили области связывания для EZh3, RING1B, TCF3, OCT4, SOX2 и NANOG. После обнаружения генов, промоторы которых перекрывают каждую из этих областей связывания, мы отфильтровали наборы генов, чтобы удалить гены, которые встречаются во множестве областей связывания.Затем мы нормализовали экспрессию каждого гена (нулевое среднее, единичная дисперсия) и рассчитали совокупную экспрессию для каждого набора генов. Совокупная экспрессия этих наборов генов хорошо коррелирует с доступностью хроматина и h4K4me2 промоторов генов (Fig. 4c-d), за исключением OCT4. Экспрессия мишеней OCT4 слабо коррелирует с доступностью агрегированного хроматина и h4K4me2. Дополнительные рисунки 4 и 5 показывают соответствующие значения, выведенные MATCHER для экспрессии гена, доступности хроматина и значений h4K4me2 в одних и тех же отдельных клетках.
Дополнительный рисунок 4: Соответствующие значения, выведенные MATCHER для экспрессии генов и сигнатур доступности хроматина.Каждая точка представляет собой предполагаемое соответствие из одной ячейки. По оси абсцисс показано значение сигнатуры экспрессии гена в этой ячейке, а по оси ординат — значение сигнатуры доступности хроматина. Точки окрашены в соответствии с предполагаемым основным временем. Обратите внимание, что это данные, используемые для генерации значений на диагонали тепловой карты на рис. 4c.
Дополнительный рисунок 5: Соответствующие значения, выведенные MATCHER для экспрессии гена и сигнатур h4K4me2.Каждая точка представляет собой предполагаемое соответствие из одной ячейки. По оси абсцисс показано значение сигнатуры экспрессии гена в этой ячейке, а по оси ординат — значение сигнатуры h4K4me2. Точки окрашены в соответствии с предполагаемым основным временем. Обратите внимание, что эти данные используются для генерации значений на диагонали тепловой карты на рис. 4d.
Наконец, мы спросили, как уровни экспрессии РНК ключевых факторов плюрипотентности и белков ремоделирования хроматина связаны с доступностью хроматина их сайтов связывания (рис.4д). Используя те же факторы транскрипции и ДНК-связывающие белки, что и на рис. 4а, мы вычислили корреляцию между уровнем экспрессии каждого гена и общей доступностью хроматина на сайтах, где его белковый продукт связывается с геномом. Факторы транскрипции плюрипотентности ESRRB, NANOG, POU5F1 и SOX2 каждый показывают положительную корреляцию между экспрессией и доступностью хроматина. Это указывает на то, что экспрессия этих генов отключается на уровне РНК, в то время как связывание факторов отключается на уровне хроматина.Интересно, что экспрессия Tcf7l2 обнаруживает сильную отрицательную корреляцию с доступностью хроматина для его мишеней. Мы предполагаем, что эта отрицательная корреляция может быть связана с тем фактом, что TCF7L2 функционирует в первую очередь как репрессор транскрипции [47], и, таким образом, повышенная экспрессия приведет к большей репрессии его мишеней. В отличие от факторов плюрипотентности, экспрессия генов, участвующих в ремоделировании хроматина, обнаруживает слабую отрицательную корреляцию с доступностью их сайтов связывания.Тот факт, что эти корреляции почти нулевые, указывает на то, что изменения в доступности хроматина для мишеней этих ремоделирующих комплексов хроматина происходят в основном без сопутствующих изменений в уровнях экспрессии генов ремоделеров. Единственным исключением является Rest , экспрессия которого показывает сильную отрицательную корреляцию с доступностью его сайтов связывания.
Функции деформации, выведенные MATCHER, предполагают быстрый переход между двумя метастабильными состояниями
После проверки функций деформации, выведенных MATCHER для экспрессии гена, доступности хроматина и данных h4K4me2, мы заметили, что все кривые имеют схожую форму (рис.5а-в). Набор данных Angermueller RNA-seq по одиночным клеткам [14] также демонстрирует похожую закономерность (см. Дополнительный рисунок 6, где представлены графики всех функций деформации). Функции деформации почти плоские в начале и в конце псевдовремени и имеют крутой наклон между ними. Одним из возможных объяснений этого паттерна является процесс, при котором клетки быстро переходят из одного метастабильного состояния в другое. Мы предполагаем, что формы функций деформации могут отражать биологию эмбриональных стволовых клеток, выращенных в сыворотке, в которой некоторые плюрипотентные клетки начинают «терять контроль» и переходить в состояние примирования дифференцировки [37, 38].В поддержку этой гипотезы недавняя работа с использованием FISH для одиночных клеток охарактеризовала такой переход между метастабильными состояниями в эмбриональных стволовых клетках мышей [38]. Интересно, что функция деформации для данных метилирования ДНК не обнаруживает этого переключателя (Fig. 5d). Мы подозреваем, что это может быть связано с частичным разделением метилирования ДНК и изменений экспрессии генов (см. Следующий раздел).
Дополнительный рисунок 6: Предполагаемые функции деформации для всех экспериментальных наборов данных, проанализированных в статье.(a) данные одноклеточной РНК-seq Колодзейчика, (b) данные метилирования scM и T-seq Ангермюллера, (c) ATAC-seq, (d) данные ChIP h4K4me2, (e) данные экспрессии генов scM и T-seq Ангермюллера, и (f ) функция деформации, полученная в результате линейной интерполяции данных h4K4me2 ChIP-seq.
Рис. 5: Функции деформации, полученные с помощью MATCHER, предполагают быстрый переход между двумя метастабильными состояниями.(a) — (d) Гауссовские функции деформации процесса для (a) RNA-seq, (b) ATAC-seq, (c) ChIP-seq и (d) scM & T-seq.Примечание. Поскольку среднее значение гауссовской функции деформации процесса для ChIP-seq не является монотонным в наблюдаемом диапазоне данных, мы использовали линейную интерполяцию для функции деформации ChIP-seq во всех анализах, представленных в статье.
Включение известной информации о клеточном соответствии
Исследование, которое впервые привело к scM & T-seq, обнаружило вариабельность силы связи между экспрессией генов и метилированием ДНК в наборе клеток [14]. Мы исследовали этот феномен дополнительно, построив график зависимости времени основного метилирования ДНК от времени мастера РНК (рис.6а). Этот график выявил интригующую тенденцию: метилирование ДНК и мастер-время РНК довольно хорошо отслеживаются вместе до определенного момента в мастер-времени РНК. После этого степень сцепления внезапно уменьшается. Мы предполагаем, что эта тенденция может иметь место, потому что специфические изменения метилирования ДНК необходимы для запуска ключевого этапа в процессе изменений экспрессии генов, которые происходят при переходе от плюрипотентного к примированному состоянию. После этого момента в процессе последовательные изменения экспрессии генов происходят в некоторой степени независимо от изменений метилирования ДНК.В поддержку этой гипотезы клетки, в которых метилирование ДНК и экспрессия генов совпадают, обнаруживают высокие уровни экспрессии Rex1 , тогда как остальные клетки обнаруживают гораздо более низкую экспрессию (рис. 6a). Ранее было показано, что ген Rex1 является маркером двух различных метастабильных состояний экспрессии в эмбриональных стволовых клетках мыши [38]. Переход между этими двумя состояниями зависит от активности ферментов ДНК-метилтрансферазы (DNMT), и отключение активности DNMT значительно увеличивает долю клеток в высоком состоянии Rex1 [38].
Рисунок 6: Включение известной информации о соответствии ячеек.(a) Диаграмма рассеяния основного времени, полученного с использованием экспрессии генов (ось x) и метилирования ДНК (ось y) из одних и тех же отдельных клеток. Точки раскрашены выражением Rex1 . (b) Диаграмма разброса общего основного времени, полученного как по экспрессии гена, так и по метилированию ДНК (ось x), и основного времени, полученного с использованием только метилирования ДНК (ось y). (c) Диаграмма разброса общего основного времени, выведенного как из экспрессии гена, так и из метилирования ДНК (ось x), и основного времени, выведенного с использованием только экспрессии генов (ось y).
Чтобы проверить значимость частичного разделения между метилированием ДНК и экспрессией генов, мы вычислили отдельные значения корреляции Пирсона для клеток с мастер-временем RNA-seq менее 0,5 и более 0,5. Затем мы выполнили преобразование Фишера r -to- z для корреляций и вычислили значение p для нулевой гипотезы о равенстве двух корреляций (односторонний тест). Значение p составляло 0,0039, что указывает на очень значимую разницу.
Затем мы использовали MATCHER, чтобы вывести общее значение основного времени, используя данные метилирования ДНК и экспрессии генов для каждой клетки (рис. 6b-c). Полученные общие значения основного времени согласовывают последовательность изменений, происходящих в обеих геномных величинах. Корреляция Пирсона между мастер-временем метилирования ДНК и мастер-временем РНК составляет 0,63. Напротив, корреляция между мастер-временем метилирования ДНК и общим мастер-временем составляет 0,93, а корреляция между мастер-временем РНК и общим мастер-временем равна 0.84. Таким образом, мы использовали MATCHER для определения основного времени, которое отражает известную информацию о соответствии, доступную из данных scM и T-seq. Это демонстрирует способность MATCHER моделировать данные отдельных ячеек с использованием или без использования известной информации о соответствии.
Обсуждение
В этом исследовании мы использовали MATCHER для характеристики соответствующих транскриптомных и эпигенетических изменений в эмбриональных стволовых клетках, претерпевающих переход от плюрипотентности к состоянию примирования дифференцировки.Интересные направления будущих исследований включают расширение модели для выравнивания многообразий с размерностью выше единицы, а также адаптацию метода для популяций клеток, клетки которых попадают в дискретные кластеры, а не на один непрерывный спектр. Кроме того, наша модель не учитывает явным образом ветвящиеся траектории, которые могут возникать в биологических процессах с множественными исходами [3, 9]. Простой способ справиться с такими ситуациями — назначить ячейки ветвям перед запуском MATCHER, а затем выполнить выравнивание коллектора для каждой ветви отдельно.
Хотя протокол Hi-C для измерения конформации хроматина был адаптирован для одиночных клеток [10], мы не включили данные Hi-C одиночных клеток в это исследование по двум причинам. Во-первых, насколько нам известно, не существует опубликованных наборов данных Hi-C по отдельным клеткам эмбриональных стволовых клеток мыши. Кроме того, данные Hi-C представляют собой набор парных взаимодействий (матрица для каждой ячейки, а не вектор), и неясно, как построить траекторию из этого типа данных. Необходима дальнейшая работа, чтобы выяснить, показывает ли конформация хроматина последовательные изменения во время биологических процессов, а также найти лучшие способы сделать вывод о таких последовательных изменениях и интегрировать их с другими типами данных.
Одно из многообещающих применений метода — объединение измерений отдельных клеток в биологически значимые группы. Ячейки можно сгруппировать по предполагаемым основным значениям времени, а измерения в этих группах можно агрегировать. В экспериментах с тысячами клеток это, вероятно, позволит корреляцию между отдельными локусами и родственными генами, что в настоящее время невозможно из-за крайней редкости эпигенетических данных. Вычислительная агрегация измерений из множества одинаковых отдельных клеток может быть наиболее быстрым способом решения проблемы разреженности эпигенетических измерений отдельных клеток, хотя экспериментальные протоколы, вероятно, улучшатся в долгосрочной перспективе.
MATCHER дает представление о последовательных изменениях геномной информации, позволяя использовать как экспрессию гена отдельной клетки, так и эпигенетические данные при построении клеточных траекторий. Кроме того, он выявляет связи между этими изменениями, что позволяет исследовать механизмы регуляции генов при разрешении отдельных клеток. MATCHER обещает быть полезным для изучения множества биологических процессов, таких как дифференциация, перепрограммирование, активация иммунных клеток и туморогенез.
Методы
Обработка данных РНК-seq
Мы получили обработанные данные РНК-seq для 250 клеток от Kolodziejczyk et al. [37] В исходной статье количественная оценка генов проводилась с использованием счетчиков считываний, нормализованных для глубины секвенирования и пакетных эффектов [37]. Мы преобразовали эти нормализованные подсчеты в журнал и использовали наш ранее опубликованный метод дисперсии соседства, чтобы выбрать информативное подмножество генов для передачи в MATCHER.
Чтобы идентифицировать популяции молекул РНК с четкой связью с агрегированными областями генома, используемыми для расчета доступности хроматина и измерений модификации гистонов (см. Ниже), мы вычислили аналогичные агрегированные измерения экспрессии генов.Мы сделали это, идентифицировав гены, промоторы которых перекрывают сайты связывания для каждого из 6 белков (EZh3, RING1B, TCF3, OCT4, SOX2 и NANOG). Затем мы отфильтровали списки генов, чтобы данный ген появился только в одном из шести списков. Затем мы масштабировали и центрировали каждый ген, чтобы получить нулевое среднее значение и единичную дисперсию, и вычислили сумму генов в каждом списке на ячейку, а также общую сумму экспрессированных генов в каждой ячейке. Конечные значения, используемые для вычисления корреляций, показанные на рис. 4c-d, представляют собой центрированные и масштабированные разности суммы для каждого списка генов и общей суммы экспрессии генов на клетку.
Обработка данных ATAC-seq
Обработанные данные ATAC-seq отдельной ячейки не являются общедоступными, поэтому мы реализовали конвейер обработки данных, описанный Buenrostro et al. [13] Для каждой ячейки мы выровняли показания до мм10 с помощью Bowtie2, удалили дубликаты ПЦР и подсчитали количество считываний, совпадающих с каждым из 50000 пиков, указанных в исходной статье [13]. Мы преобразовали эти целочисленные счетчики считывания, которые преимущественно равны 1 или 0 на заданном пике, в двоичные значения (1 для доступного хроматина, 0 для недоступного), чтобы избежать потенциальных мешающих факторов, которые могут вызвать большое количество, таких как вариации числа копий и повторяющиеся элементы.Затем мы использовали FIMO [48], чтобы определить для каждого пика, какой из 186 мотивов факторов транскрипции в базе данных JASPAR [49] встречается в области пика. Используя это сопоставление пиков с TF, мы суммировали количество пиков для каждой клетки путем суммирования пиков для каждого мотива фактора транскрипции. Это дало матрицу с 186 функциями в 96 ячейках. Впоследствии мы удалили все клетки с менее чем 1000 пиков, обнаруженных на клетку, оставив 77 клеток. Снижение размерности с использованием PCA и GPLVM на 77 ячейках показало, что одна ячейка была значительным выбросом, поэтому мы удалили эту дополнительную ячейку.Остальные 76 ячеек использовали для всех последующих анализов. Затем мы нормализовали матрицу подсчета 186 × 76, чтобы учесть различия между ячейками в количестве обнаруженных пиков. Мы нормализовали значение f ij (признак i в ячейке j ) путем умножения на следующий масштабный коэффициент:, где t j — общее количество доступных пиков в ячейка j . (1000 в знаменателе масштабного коэффициента масштабирует измерения так, чтобы f ij были близки к 1.)
Обработка данных ChIP-seq
Мы получили обработанные данные от Rotem et al. [12], который состоит из h4K4me2 ChIP-seq, считываемых из 4587 клеток, агрегированных с использованием 91 сигнатуры хроматина. Мы обнаружили, что эти данные требуют дальнейшей нормализации для общей суммы значений сигнатур на ячейку. Мы нормализовали значение f ij (подпись i в ячейке j ) путем умножения на следующий масштабный коэффициент:, где t j — общая сумма подписей в ячейке j .(Число 10 в числителе масштабного коэффициента масштабирует измерения таким образом, что f ij близки к 1.)
Обработка данных scM и T-seq
Данные метилирования РНК и ДНК от Angermueller et al. . [14] общедоступны в полностью обработанной форме, поэтому мы не проводили никакой дальнейшей обработки. В исходной статье уровни экспрессии генов были рассчитаны путем подсчета уникальных молекулярных идентификаторов (UMI) и впоследствии нормализованы. Значения метилирования ДНК по Angermueller также были нормализованы в исходной статье [14].
Сначала мы попытались использовать значения метилирования из всех позиций в геноме, но результаты PCA и GPLVM для полного набора данных не показали систематических вариаций, связанных с плюрипотентностью и дифференцировкой. Это вероятно потому, что только часть сайтов метилирования демонстрирует систематические биологические вариации, превышающие технические вариации во время перехода от плюрипотентности к примированию дифференцировки. Поэтому мы выбрали сайты метилирования на основе ранее проверенного маркера, Mael , метилирование которого, как известно, изменяется во время перехода к состоянию примированного дифференцировки [38].Мы выбрали все сайты метилирования, корреляция которых с метилированием промотора Mael была не менее 0,2. Это дало набор из приблизительно 13000 сайтов метилирования. По существу не было сайтов метилирования, антикоррелированных с Mael , что согласуется с тем фактом, что плюрипотентные клетки глобально деметилированы, так что изменения метилирования при подготовке к дифференцировке происходят в основном в одном направлении. Мы также обнаружили, что использование только данных из регионов с низким уровнем метилирования (LMRs), которые, как известно, резко изменяют состояние метилирования во время дифференцировки, дает аналогичные результаты [50].
Выведение псевдовремени и изучение функций искажения
Мы выводим псевдовремя, используя модель скрытых переменных процесса Гаусса (GPLVM) с единственной скрытой переменной t . Для более подробного введения в гауссовские процессы и GPLVM см. Расмуссен [51] или Дамиану [33]. В рамках нашей модели наблюдаемые многомерные данные (RNA-seq, ATAC-seq, ChIP-seq, метилирование ДНК и т. Д.) Генерируются из t функцией f с добавлением гауссовского шума: где ∊ ∼ 𝒩 ( 0 , σ 2 I ).
Ключевым свойством GPLVM является то, что предыдущее распределение f является гауссовским процессом:
Линейное ядро дает модель, эквивалентную вероятностному PCA, но если мы выберем функцию ядра k как нелинейную, GPLVM может вывести нелинейные отношения между t и Y . Мы используем популярное ядро радиальной базисной функции (RBF), также называемое экспоненциальным ядром в квадрате.
Поскольку гауссовский процесс представляет собой набор случайных величин, для которых ковариация любого конечного множества является многомерной гауссовой, мы имеем: где K ff — ковариационная матрица, определяемая функцией ядра k .Простым подходом к выводу скрытой переменной t было бы найти значения, которые максимизируют апостериорное распределение:
Вместо оценки MAP мы используем метод Damianou [33], который оценивает апостериорную оценку с использованием вариационного приближения. Ключевым преимуществом этого подхода является то, что он обеспечивает оценку распределения скрытых переменных, а не просто точечную оценку. Аппроксимация основана на введении вспомогательных переменных, называемых побуждающими входными данными, для получения аналитической нижней границы предельного правдоподобия.Затем выполняется вывод, максимизируя нижнюю границу в отношении индуцирующих входов и гиперпараметров, и -1. Мы использовали 10 побуждающих входов для всех наших анализов, хотя мы подтвердили, что результаты устойчивы к количеству использованных побуждающих входов.
Чтобы изучить функции деформации от псевдовремени к главному времени, мы вычисляем выборочные квантили псевдовремени для заданного числа квантилей, а затем выравниваем эти выборочные квантили с теоретическими квантилями однородной (0,1) случайной величины.Мы использовали 50 квантилей для всех анализов в рукописи, но обнаружили, что функции деформации устойчивы к количеству используемых квантилей. Регрессия гауссовского процесса является привлекательным выбором для изучения функции деформации из-за способности улавливать нелинейные эффекты и неопределенность, но гауссовские процессы теоретически не гарантируют монотонность. На практике мы обнаружили, что среднее значение гауссовского процесса в большинстве случаев является монотонным, поскольку обучающие данные представляют собой монотонно возрастающие квантили.Для случаев, когда среднее значение гауссовского процесса не является монотонным (как в случае данных ChIP-seq с одной ячейкой), мы используем линейную интерполяцию. Монотонность квантилей гарантирует, что линейная интерполяция будет монотонной.
Когда использовать и не использовать анализ корреспонденции
Анализ корреспонденции — один из тех редких инструментов науки о данных, которые упрощают работу. Вы начинаете с большой таблицы, которую трудно читать, и заканчиваете относительно простой визуализацией.В этом посте я объясню, как можно определить, подходит ли таблица для анализа корреспонденции.
Анализ соответствия полезен, когда у вас есть таблица, содержащая как минимум две строки и два столбца, без пропущенных данных, без отрицательных значений, и все данные имеют тот же масштаб . Единственное, что сложно понять, — это «одинаковый масштаб», которому и посвящены приведенные здесь примеры.
Таблицы непредвиденных обстоятельств (ОК)
Классическим приложением для анализа соответствий является анализ таблиц непредвиденных обстоятельств .Таблица непредвиденных обстоятельств — это перекрестная таблица , в которой категории строк являются взаимоисключающими, а категории столбцов также взаимоисключающими. Когда ваши данные выглядят так, обычно помогает анализ соответствий.
В приведенном ниже примере я почти показываю таблицу непредвиденных обстоятельств. Я говорю «почти», потому что я включил итоги по строкам и столбцам (обозначенные как NET ). Если бы я провел анализ соответствий для этой таблицы, он был бы недействителен, потому что итоговые значения находятся в другом масштабе, чем остальные данные.
Есть простой способ разобраться в этой проблеме. Разве таблица теряет смысл, если она отсортирована по любой из ее строк или столбцов? Рассмотрим ряд с кока-колой. Сортировка по этой строке переместит NET в начало этой строки, добавит ли она понимания? Нет, это не так. Вероятно, это просто создаст путаницу. К счастью, большинство приложений для анализа данных достаточно умны, чтобы оставить итоги по строкам и столбцам вне анализа корреспонденции, поэтому я не буду снова говорить об этом тривиальном случае. После удаления итогов эта таблица идеально подходит для анализа соответствий.
Мы также могли бы провести анализ соответствия, если бы вместо этого отображали процентные значения строк, столбцов или значения индекса. Однако каждый из них даст разные результаты, поскольку каждый анализ подчеркивает разные аспекты данных, и эти аспекты подчеркиваются в результате анализа соответствия.
Квадратные столы (ОК)
В таблице ниже показан специальный тип таблицы, в которой строки и столбцы имеют одинаковые метки. В этой таблице показаны варианты выбора автомобилей, где строки представляют автомобили, принадлежащие ранее, а столбцы представляют автомобили, которые в настоящее время принадлежат выборке покупателей.Такие таблицы имеют различные имена, например, матрицы переключения , таблицы переходов, матрицы ошибок и . Все они могут быть проанализированы с помощью анализа соответствий, но есть (небольшое) преимущество в использовании специального варианта анализа соответствий, разработанного для таких квадратных таблиц .
График ниже создан с использованием специального варианта анализа соответствий, предназначенного для квадратных таблиц. Основное практическое преимущество этого метода заключается в том, что мы не наносим на график метки столбца и строки и, таким образом, можем интерпретировать отношения, глядя на то, насколько близко друг к другу отображаются метки.В этом примере в анализе преобладает Porche. Глядя на необработанные данные, мы видим, что у них небольшой размер выборки. У нас есть три варианта:
- Мы можем просто удалить его с графика (это можно сделать перетаскиванием). В этом случае переоценка карты не выполняется. Скорее всего, он по-прежнему включает в анализ Porche, так что это, вероятно, не идеальное решение.
- Объедините похожие бренды и повторите анализ.
- Повторите анализ, удалив марку.Обычно это мой предпочтительный вариант.
Таблицы с множественной статистикой (плохо)
В таблице ниже показаны как количество, так и процентное соотношение столбцов. Данные здесь явно представлены в двух разных шкалах, что делает анализ соответствия неуместным. Мы могли бы масштабировать подсчеты, превратив их в проценты, но тогда у нас были бы одни и те же данные дважды, что было бы бессмысленно.
Несколько таблиц, соединенных вместе (плохо, если не масштабировано)
Приведенная ниже таблица, в которой показано предпочтение колы по возрасту и полу, не подходит для анализа корреспонденции.Почему? Проблема в том, что не все данные имеют одинаковый масштаб. Есть простой способ увидеть это. Если все данные имеют одинаковый масштаб, это означает, что имеет смысл отсортировать таблицу по любой из ее строк и столбцов. Если бы мы отсортировали эту таблицу по первой строке, мы бы сначала увидели Male и Female, потому что они имеют большие базовые размеры, а не потому, что сортировка будет иметь смысл.
Это дает нам некоторое представление о том, как решить проблему. Нам нужно каким-то образом преобразовать данные, чтобы все они были в одном масштабе.Мы можем добиться этого, разделив каждое число на общую сумму столбца ( NET внизу таблицы), что дает нам таблицу ниже. В этой таблице имеет смысл сортировать по первой строке (которая показывает, что предпочтения Coca-Cola гораздо шире различаются по возрасту, чем по полу). Также целесообразно отсортировать таблицу по любому из столбцов.
Следующий пример также был построен с использованием двух таблиц. В последнем столбце показан средний балл отношения к каждому бренду, полученный по 5-балльной шкале.Надеюсь, легко увидеть, что данные в этой таблице не в одном масштабе, что делает ее непригодной для анализа соответствий.
В следующей таблице снова показаны те же данные, но «фиксированные», так что в сумме получается 100. Эта таблица в порядке? Нет. Лучший способ осознать проблему — сосредоточиться на диетической Pepsi. У Diet Pepsi самый низкий балл среди всех брендов в рейтинге Attitude. Однако, если мы прочитаем строку Diet Pepsi, мы увидим, что Diet Pepsi в конечном итоге получает свой «лучший» балл по Attitude.Если бы вы применили анализ корреспонденции, он бы сказал, что Pepsi «владеет» Attitude.
Таблицы и сетки множественных ответов (ОК)
Большинство таблиц, которые показывают данные множественных ответов , также можно использовать с анализом соответствий. Приведенная ниже таблица, которую исследователи рынка называют сеткой ассоциаций брендов , состоит из данных по 63 различным переменным. Каждый из 800 респондентов в наборе данных указал, какие бренды и какое отношение имеют.Поскольку данные неотрицательны и все находятся в одном масштабе, они являются основным кандидатом для анализа соответствий.
Таблицы средних значений (ОК)
В таблице ниже приведены средние значения. Он отвечает всем требованиям к анализу корреспонденции. (Хотя, поскольку есть только две строки данных, итоговая карта покажет все точки данных, организованные по прямой линии, что может вызвать у вас небольшую панику, если вы этого не ожидаете.)
Корреляции (обычно плохие)
В следующей таблице показаны корреляции между двумя наборами переменных.Анализ корреспонденции здесь не работает, так как у нас отрицательные значения.
Следующая таблица такая же, как и предыдущая, за исключением того, что я добавил 1 к каждому числу. Это значит, что отрицательных результатов больше нет. Теперь эти данные соответствуют требованиям для анализа соответствий. Конечно, есть, возможно, лучшие методы, такие как канонический корреляционный анализ , , но мы можем извлечь информацию из этой таблицы, используя анализ соответствий.
Исходные данные (обычно в порядке)
В таблице ниже показаны исходные данные, которые мы использовали для вычисления корреляций выше.Каждая строка представляет человека. В каждом столбце указано потребление различных брендов дома или вне дома. Это нормально? Необработанные данные обычно подходят, если они двоичные или числовые. И необработанные данные для неупорядоченных категориальных переменных (например, род занятий, предпочтения бренда) не будут работать, поскольку данные не имеют значимого масштабирования (т.е. средние значения не имеют смысла). В этом конкретном случае у нас есть несколько строк без данных, и это вызывает проблему. Но как только они будут удалены, мы сможем получить полезную карту, как показано ниже.
Самое замечательное в использовании сырых данных — это то, что мы можем понять распределение респондентов в данных. Однако сложность заключается в том, что применимы все обычные правила интерпретации, поэтому эти сюжеты может быть довольно сложно интерпретировать правильно.
Создайте свой собственный анализ корреспонденции!
Данные временного ряда (например, данные о продажах)
Последний пример, показанный ниже, показывает продажи по разным категориям розничных продавцов по месяцам. Хотя вы можете не думать о данных о продажах как о подходящих для анализа корреспонденции, они удовлетворяют всем критериям.
Визуализация ниже основана на данных о продажах. Он показывает, что продажи универмага и одежды / аксессуаров сильно связаны с декабрем.
Сводка
Анализ соответствий — мощный инструмент для упрощения таблиц. При условии, что ваши данные подходят — два или более измерения, без негативов, согласованно масштабируются — он справится со своей задачей.
Если у вас есть данные, но вы не знаете, с чего начать, вы можете создать свой собственный анализ корреспонденции, используя шаблон ниже!
Соответствие Карри-Ховарда между программами и доказательствами
Этот пост объяснит связь между языками программирования и логическими доказательствами, известную как соответствие Карри-Ховарда.Я приведу несколько примеров этого соответствия, чтобы помочь вам выработать работающее интуитивное представление о том, как эти два поля соотносятся друг с другом.
В переписке Карри-Ховарда говорится, что:
- Логические предложения соответствуют типам программирования
- Логические доказательства соответствуют программным значениям
- Доказательство предложения соответствует созданию значения данного типа
Я буду использовать свой язык программирования Dhall, чтобы проиллюстрировать вышеупомянутые связи, поскольку Dhall — это тотальный язык программирования с явной типизацией без каких-либо выходных штрихов.Если вы не знакомы с Dhall, вы можете прочитать руководство по Dhall, и я также буду проводить аналогии с Haskell по пути.
Предложения
Начнем со следующего логического предложения:
∀ (a ∈ Prop): a ⇒ a Вы можете прочитать это как «для любого предложения (которое мы будем обозначать буквой a ), если утверждение a истинно, то утверждение a истинно». Это верно независимо от предложения a .Например, предположим, что a были следующим утверждением:
a = {Небо голубое} Тогда мы могли бы сделать вывод, что «если небо голубое, значит небо голубое»:
{Небо голубое} ⇒ {Небо голубое} Здесь двойная стрелка вправо ( ⇒ ) обозначает логическое следствие. Везде, где вы видите ( A ⇒ B ), вы должны читать, что «если утверждение A верно, то утверждение B верно».Вы также можете сказать «предложение A подразумевает предложение B » или просто « A подразумевает B » для краткости.
Однако что, если бы a было другим предложением, например:
a = {Небо зеленое} дает нам:
{Небо зеленое} ⇒ {Небо зеленое} Это правда, даже если небо может быть не зеленым. Мы только утверждаем, что «, если небо зеленое, то небо зеленое», что определенно верно, независимо от того, зеленое небо или нет.
Перевернутая буква A (т.е. ∀ ) в нашем исходном предложении — это математическое сокращение, означающее «для всех» (хотя я иногда описываю это как «для любого»). Символ ∈ является сокращением для «входящего» (т. Е. Установленного членства). Так что всякий раз, когда вы видите это:
∀ (a ∈ S): p … можно прочитать, что «для любого элемента a в наборе S утверждение p верно». Обычно набор S — это Prop (т.е.е. набор всех возможных предложений), но мы увидим несколько примеров ниже, где S может быть другим набором.
Типы
Это логическое предложение:
∀ (a ∈ Prop): a ⇒ a … соответствует следующему типу Dhall:
∀ (a: Тип) → a → … который можно читать как «для любого типа (который мы будем обозначать буквой a ), это тип функции, которая преобразует вход типа a в выход типа a «.Вот соответствующая функция этого типа:
λ (a: Тип) → λ (x: a) → x Это анонимная функция двух аргументов:
- первый аргумент называется
aиaявляетсяТип - второй аргумент называется
x, аxимеет типa
Результат — второй аргумент функции (т. Е. x ), который по-прежнему имеет тип a .
Эквивалентная функция Haskell — id , функция полиморфной идентичности:
id :: a -> a
id x = x
- или используя расширение языка ExplicitForAll
id :: forall a. а -> а
id x = x Основное отличие состоит в том, что Haskell не требует явного связывания полиморфного типа и в качестве дополнительного аргумента. Dhall действительно требует этого, потому что Dhall — это язык с явной типизацией.
Переписка
В переписке Карри-Ховарда говорится, что мы можем использовать средство проверки типов языка программирования в качестве средства проверки.Каждый раз, когда мы хотим доказать логическое предположение, мы:
- преобразовать логическое предложение в соответствующий тип на нашем языке программирования
- создать значение на нашем языке программирования с заданным типом
- используйте проверку типов, чтобы убедиться, что наше значение имеет указанный тип
Если мы найдем значение данного типа, это завершит доказательство нашего исходного предложения.
Например, если мы хотим доказать это утверждение:
∀ (a ∈ Prop): a ⇒ a … затем переводим предложение в соответствующий тип на языке программирования Dhall:
∀ (a: Тип) → a → … затем определите значение на языке Dhall, имеющее этот тип:
λ (a: Тип) → λ (x: a) → x … а затем используйте средство проверки типов Dhall, чтобы убедиться, что это значение имеет заданный тип:
$ dhall <<< 'λ (a: Тип) → λ (x: a) → x'
∀ (a: Тип) → ∀ (x: a) → a
λ (a: Тип) → λ (x: a) → x Первая строка - это предполагаемый тип нашего значения, а вторая строка - это нормальная форма значения (которая в данном случае совпадает с исходным значением).
Обратите внимание, что предполагаемый тип немного отличается от исходного типа, который мы ожидали:
- Что мы ожидали:
∀ (a: Тип) → a → a
- Что сделал компилятор:
∀ (a: Тип) → ∀ (x: a) → a Они оба все того же типа. Разница в том, что предполагаемый тип компилятора также включает имя второго аргумента: x . Если бы мы вернули это обратно в нотацию логических предложений, мы могли бы написать:
∀ (a ∈ Prop): ∀ (x ∈ a): a ... которое можно было бы читать как: «для любого предложения с именем a , при условии доказательства a с именем x , утверждение a истинно». Это эквивалентно нашему первоначальному предложению, но теперь мы дали имя (например, x ) доказательству a .
Причина, по которой это работает, состоит в том, что вы также можете думать о предложении как о множестве, где элементы множества являются доказательствами этого предложения. Некоторые предложения ложны и не содержат элементов (т.е. нет действительных доказательств), в то время как другие предложения могут иметь несколько элементов (т.е. несколько действительных доказательств).
Точно так же вы можете думать о типе как о наборе, где элементы набора являются значениями, имеющими этот тип. Некоторые типы пусты и не имеют элементов (то есть значений этого типа), в то время как другие типы могут иметь несколько элементов (то есть несколько значений этого типа).
Вот пример предложения, имеющего несколько действительных доказательств:
∀ (a ∈ Prop): a ⇒ a ⇒ a Соответствующий тип:
∀ (a: тип) → a → a → a ... и есть два значения, которые имеют указанный выше тип. Первое значение:
λ (a: Тип) → λ (x: a) → λ (y: a) → x ... а второе значение:
λ (a: Тип) → λ (x: a) → λ (y: a) → y Мы даже можем перевести эти два значения обратно в неформальные логические доказательства. Например, это значение:
λ (a: Тип) → λ (x: a) → λ (y: a) → x ... соответствует этому неофициальному доказательству:
За каждую «а» в наборе всех предложений:
Имея доказательство того, что «а» истинно [назовем это доказательство «х»]
Имея доказательство того, что «а» истинно [назовем это доказательство «у»]
Мы можем заключить, что «а» истинно, согласно доказательству «х».
QED Аналогично это значение:
λ (a: Тип) → λ (x: a) → λ (y: a) → y ... соответствует этому неофициальному доказательству:
За каждую «а» в наборе всех предложений:
Имея доказательство того, что «а» истинно [назовем это доказательство «х»]
Имея доказательство того, что «а» истинно [назовем это доказательство «у»]
Мы можем заключить, что «a» истинно, согласно доказательству «y»
QED Мы действительно можем придать этим доказательствам формальную структуру, которая соответствует нашему коду, но это выходит за рамки этой публикации.
Функциональный состав
Теперь рассмотрим это более сложное предложение:
∀ (a ∈ Prop):
∀ (b ∈ Prop):
∀ (c ∈ Prop):
(б ⇒ в) ⇒ (а ⇒ б) ⇒ (а ⇒ в) Вы можете прочитать это как высказывание: «для любых трех предложений с именами a , b и c , если b подразумевает c , то если a подразумевает b , то a подразумевает c ".
Соответствующий тип:
∀ (a: Тип)
→ ∀ (b: Тип)
→ ∀ (c: Тип)
→ (б → в) → (а → б) → (а → в) ... и мы можем определить значение этого типа, чтобы доказать, что утверждение верно:
λ (a: Тип)
→ λ (b: Тип)
→ λ (c: Тип)
→ λ (f: b → c)
→ λ (g: a → b)
→ λ (х: а)
→ f (г x) ... и компилятор сделает вывод, что наше значение имеет правильный тип:
$ дхалл
λ (a: Тип)
→ λ (b: Тип)
→ λ (c: Тип)
→ λ (f: b → c)
→ λ (g: a → b)
→ λ (х: а)
→ f (g x)
∀ (a: Тип) → ∀ (b: Тип) → ∀ (c: Тип) → ∀ (f: b → c) → ∀ (g: a → b) → ∀ (x: a) → c
λ (a: Тип) → λ (b: Тип) → λ (c: Тип) → λ (f: b → c) → λ (g: a → b) → λ (x: a) → f (gx) Обратите внимание, что эта функция эквивалентна оператору композиции функций Haskell (т.е. (.) ):
(.) :: (b -> c) -> (a -> b) -> (a -> c)
(е. ж) х = е (г х) Это потому, что доказательства и программы эквивалентны друг другу: всякий раз, когда мы доказываем логическое предложение, мы бесплатно получаем потенциально полезную функцию.
Круговое рассуждение
Есть некоторые утверждения, которые мы не можем доказать, например, это:
∀ (a ∈ Prop): a ... который можно прочитать как "все предложения верны".Это предложение неверно, потому что если мы переведем предложение на соответствующий тип:
... тогда в языке Dhall нет значения, имеющего этот тип. Если бы такое значение было, мы могли бы автоматически создать любое значение любого типа.
Однако в Haskell есть значения, относящиеся к вышеуказанному типу, например, этот:
пример :: a
пример = пусть x = x in x
- или используя расширение языка ExplicitForAll:
example :: forall a. а
пример = пусть x = x in x Это значение просто обманывает и бесконечно зацикливается, что удовлетворяет требованиям средства проверки типов в Haskell, но не дает полезной программы.Такая неограниченная рекурсия является программным эквивалентом «кругового рассуждения» (т.е. попытки утверждать, что a истинно, потому что a истинно).
Мы не можем обмануть так в Dhall, и если мы попробуем, мы просто получим эту ошибку:
$ dhall <<< 'пусть x = x in x'
Для получения подробных сведений об ошибках используйте "dhall --explain".
Ошибка: несвязанная переменная
Икс
(стандартный ввод): 1: 9 Вы не можете определить x в терминах самого себя, потому что Dhall не допускает никакой рекурсии и, следовательно, не допускает циклических рассуждений при использовании в качестве средства проверки.
и
Мы будем использовать символ ∧ для обозначения логического «и», поэтому вы можете прочитать следующее предложение:
∀ (a ∈ Prop): ∀ (b ∈ Prop): (a ∧ b) ⇒ a ... как говорится: «для любых двух предложений a и b , если a и b истинны, то a истинно»
Эквивалент логического "и" на уровне типа - это запись с двумя полями:
∀ (a: Тип) → ∀ (b: Тип) → {fst: a, snd: b} → a ... что эквивалентно этому типу Haskell:
(а, б) -> а
- или используя ExplicitForAll:
для всех а б. (а, б) -> а Программируемое значение этого типа:
λ (a: Тип) → λ (b: Тип) → λ (r: {fst: a, snd: b}) → r.fst ... что эквивалентно этому значению Haskell:
Аналогичным образом можно сделать вывод, что:
∀ (a ∈ Prop): ∀ (b ∈ Prop): (a ∧ b) ⇒ b ... что соответствует этому типу:
∀ (a: Тип) → ∀ (b: Тип) → {fst: a, snd: b} → b ... и это значение того типа в качестве доказательства:
λ (a: Тип) → λ (b: Тип) → λ (r: {fst: a, snd: b}) → r.snd Теперь давайте попробуем немного более сложное предложение:
∀ (a ∈ Prop): ∀ (b ∈ Prop): (a ∧ (a ⇒ b)) ⇒ b Вы можете прочитать это как высказывание «для любых предложений a и b , если утверждение a истинно, а a подразумевает b , то утверждение b истинно».
Что соответствует этому типу:
∀ (a: Тип) → ∀ (b: Тип) → {fst: a, snd: a → b} → b ... и следующее значение того типа, которое доказывает истинность предложения:
λ (a: Тип)
→ λ (b: Тип)
→ λ (r: {fst: a, snd: a → b})
→ r.snd r.fst Вот немного более сложный пример:
∀ (a ∈ Prop): ∀ (b ∈ Prop): ∀ (c ∈ Prop): ((a ∧ b) ⇒ c) ⇒ (a ⇒ b ⇒ c) Вы можете прочитать это как высказывание: «для любых трех предложений с именами a , b и c , если a и b подразумевают c , то a подразумевает, что b подразумевает c ".
Вот соответствующий тип:
∀ (a: Тип)
→ ∀ (b: Тип)
→ ∀ (c: Тип)
→ ({fst: a, snd: b} → c) → (a → b → c) ... и соответствующее значение этого типа:
λ (a: Тип)
→ λ (b: Тип)
→ λ (c: Тип)
→ λ (f: {fst: a, snd: b} → c)
→ λ (х: а)
→ λ (y: b)
→ f {fst = x, snd = y} Обратите внимание, что это эквивалентно функции Haskell curry :
карри :: ((a, b) -> c) -> (a -> b -> c)
карри f x y = f (x, y) или
Мы будем использовать символ ∨ для обозначения логического «или», поэтому вы можете прочитать следующее предложение:
∀ (a ∈ Prop): ∀ (b ∈ Prop): a ⇒ a ∨ b ... как говорится: «для любых предложений a и b , если a истинно, то либо a истинно, либо b истинно».
Эквивалент логического «ИЛИ» на уровне типа является типом суммы:
∀ (a: Тип) → ∀ (b: Тип) → a → <Слева: a | Справа: b> ... что эквивалентно этому типу Haskell:
a -> Либо a b
- или используя ExplicitForAll
для всех а б. a -> Либо a b ... и значение этого типа:
λ (a: Тип) → λ (b: Тип) → λ (x: a) → ... что эквивалентно этому значению Haskell:
Аналогично для этого предложения:
∀ (a ∈ Prop): ∀ (b ∈ Prop): b ⇒ a ∨ b ... эквивалентный тип:
∀ (a: Тип) → ∀ (b: Тип) → b → <Влево: a | Справа: b> ... и значение этого типа:
λ (a: Тип) → λ (b: Тип) → λ (x: b) → Рассмотрим более сложный пример:
∀ (a ∈ Prop): a ∨ a ⇒ a ... который гласит: «для любого предложения a , если a истинно или a истинно, то a истинно».
Соответствующий тип:
∀ (a: Тип) → <Слева: a | Справа: a> → a ... что эквивалентно этому типу Haskell:
Либо a -> a
- или используя ExplicitForAll
для всех а. Либо a -> a ... и мы можем создать значение этого типа путем сопоставления с образцом для типа суммы:
λ (a: Тип)
→ λ (s: <Слева: a | Справа: a>)
→ объединить
{Left = λ (x: a) → x
, Вправо = λ (x: a) → x
}
s
: ... что эквивалентно этому коду Haskell:
пример :: Либо a -> a
пример (Left x) = x
пример (Правый x) = x Вы можете прочитать это «доказательство» следующим образом: «Есть две возможности. Первая возможность (названная« Левая ») состоит в том, что a истинно, поэтому a должно быть истинным в этом случае. Вторая возможность (названная "Правильно") означает, что a истинно, поэтому в этом случае должно быть истинно a . Поскольку a истинно в обоих случаях, мы можем заключить, что a истинно, точка.«
Истинно
Мы будем использовать True для обозначения логического утверждения, которое всегда верно:
Истинно ... и соответствующий тип - пустая запись без полей:
... что эквивалентно типу "единицы" в Haskell:
Литерал пустой записи - единственное значение, имеющее тип пустой записи:
... что эквивалентно "единичному" значению Haskell:
Ложь
Мы будем использовать False , чтобы обозначить логическое утверждение, которое никогда не является истинным:
Ложь ... и соответствующий тип является пустым типом суммы (то есть типом без конструкторов / альтернатив):
... что эквивалентно типу Void в Haskell.
Не существует значения с указанным выше типом, поэтому вы не можете доказать утверждение False .
Логический «принцип взрыва» гласит, что если вы сделаете предположение False , то вы сможете доказать любое другое утверждение. Другими словами:
Ложь ⇒ ∀ (a ∈ Prop): a ... что вы можете прочитать как высказывание: «если вы принимаете ложное предложение, то для любого предложения с именем a вы можете доказать, что a истинно».
Соответствующий тип:
<> → ∀ (a: Тип) → a ... и значение, принадлежащее указанному выше типу:
λ (s: <>) → λ (a: Тип) → объединить {=} s: a Вы можете прочитать это «доказательство» следующим образом: «Возможностей ноль. Поскольку мы рассмотрели все возможности, утверждение a должно быть истинным.«Эта линия рассуждений называется« пустой истиной », что означает, что если нет случаев для рассмотрения, то любое ваше утверждение технически верно для всех случаев.
Эквивалентный тип Haskell:
... и эквивалентное значение Haskell этого типа будет:
Не
Мы будем использовать , а не , чтобы опровергнуть логическое утверждение, что означает:
not (True) = False
not (False) = True Мы можем закодировать логический , а не с точки зрения логического следования и логического Ложь , например:
not (a) = a ⇒ False
not (True) = True ⇒ False = False
not (Ложь) = Ложь ⇒ Ложь = Истина Если логический , а не , является функцией от предложения к другому предложению, то уровень типа , а не должен быть функцией от типа к типу:
λ (a: Тип) → (a → <>) Мы можем сохранить указанную выше функцию уровня типа в файл, чтобы создать удобный файл ./ not Утилита , которую мы будем использовать позже:
$ echo 'λ (a: Тип) → a → <>'> ./not Теперь попробуем доказать утверждение типа:
нет (Верно) ⇒ Неверно Соответствующий тип:
... который расширяется до:
... и значение этого типа:
λ (f: {} → <>) → f {=} Двойное отрицание
Однако предположим, что мы пытаемся доказать «двойное отрицание»:
∀ (a ∈ Prop): not (not (a)) ⇒ a ... который говорит, что «если a не ложь, то a должно быть истинным».
Соответствующий тип:
∀ (a: Тип) → ./not (./not a) → a ... который расширяется до:
∀ (a: Тип) → ((a → <>) → <>) → a ... но в языке Dhall нет значения, имеющего этот тип!
Причина в том, что каждое средство проверки типов соответствует определенной логической системе, а не все логические системы одинаковы.Каждая логическая система имеет разные правила и аксиомы о том, что вы можете доказать в рамках системы.
Проверка типовДхалла основана на Системе Fω, которая соответствует интуиционистской (или конструктивной) логике. Такая логическая система не предполагает закона исключенного третьего.
Закон исключенного третьего гласит, что каждое предложение должно быть истинным или ложным, что мы можем записать так:
∀ (a ∈ Prop): a ∨ not (a) Вы можете прочитать это как высказывание: «любое предложение a либо истинно, либо ложно».Это кажется вполне разумным, пока вы не попытаетесь перевести предложение на соответствующий тип:
∀ (a: Тип) → <Слева: a | Справа: a → <>> ... что в Haskell будет:
пример :: Either a (a -> Void) Мы не можем создать такое значение, потому что, если бы мы могли, это означало бы, что для любого типа мы могли бы либо:
- создать значение этого типа, или:
- создать «контрпример», создав
Пустотуиз любого значения этого типа
Хотя мы можем сделать это для некоторых типов, наша программа проверки типов не позволяет нам делать это автоматически для каждого типа.
Это та же самая причина, по которой мы не можем доказать двойное отрицание, которое неявно предполагает, что есть только два варианта (то есть «истина или ложь»). Однако, если мы не примем закон исключенного третьего, тогда могут быть другие варианты, например: «Я не знаю».
Однако не вся надежда потеряна! Несмотря на то, что наша программа проверки типов не поддерживает аксиому выбора, мы все равно можем свободно добавлять новые аксиомы в нашу логическую систему. Все, что нам нужно сделать, это принять их так же, как мы предполагаем другие предложения.
Например, мы можем изменить наше первоначальное предложение, чтобы теперь сказать:
(∀ (b ∈ Prop): b ∨ not (b)) ⇒ (∀ (a ∈ Prop): not (not (a)) ⇒ a) ... который можно прочесть как высказывание: «если мы предполагаем, что все предложения истинны или ложны, то, если предложение не ложно, оно должно быть истинным».
Что соответствует этому типу:
(∀ (b: Тип) → <Слева: b | Справа: b → <>>)
→ (∀ (a: Тип) → ((a → <>) → <>) → a) ... и мы можем создать значение этого типа:
λ (noMiddle: ∀ (b: Type) → >)
→ λ (a: Тип)
→ λ (двойное отрицание: (a → <>) → <>)
→ объединить
{Left = λ (x: a) → x
, Right = λ (x: a → <>) → merge {=} (doubleNegation x): a
}
(нетСредний а)
: ... который, как подтверждает проверка типов, имеет правильный тип:
$ дхалл
λ (noMiddle: ∀ (b: Type) → >)
→ λ (a: Тип)
→ λ (двойное отрицание: (a → <>) → <>)
→ объединить
{Left = λ (x: a) → x
, Right = λ (x: a → <>) → merge {=} (doubleNegation x): a
}
(нетСредний а)
: а
∀ (noMiddle: ∀ (b: Type) → >) → ∀ (a: Type) → ∀ (doubleNegation: (a → <>) → <>) → a
λ (noMiddle: ∀ (b: Type) → >) → λ (a: Type) → λ (doubleNegation: (a → <>) → <>) → merge {Left = λ (x: a) → x, Right = λ (x: a → <>) → merge {=} (doubleNegation x): a} (noMiddle a): a Вы можете прочитать это доказательство следующим образом:
- Закон исключенного третьего гласит, что есть две возможности: либо
aистинно, либоaложно- Если
aистинно, тогда все готово: мы тривиально заключаем, чтоaистинно - Если
aложно, то наше предположение оnot (not (a))также неверно- мы можем заключить что угодно из ложного предположения, поэтому мы заключаем, что
aистинно
- мы можем заключить что угодно из ложного предположения, поэтому мы заключаем, что
- Если
Что хорошо в этом, так это то, что компилятор механически проверяет процесс рассуждений.Вам не нужно понимать или доверять моему объяснению того, как работает доказательство, потому что вы можете делегировать свое доверие компилятору, который сделает всю работу за вас.
Заключение
Этот пост дает краткий обзор того, как вы можете конкретно перевести логические предложения и доказательства в типы и программы. Это может позволить вам использовать свою логическую интуицию, чтобы рассуждать о типах, или, наоборот, использовать интуицию программирования, чтобы рассуждать о предложениях. Например, если вы можете доказать ложное утверждение в логической системе, то это обычно выход в соответствующей системе типов.Точно так же, если вы можете создать значение пустого типа на языке программирования, это означает, что соответствующая логика не работает.
Существует много видов систем типов, точно так же, как существует много видов логических систем. Для каждой новой логической системы (например, линейной логики) вы бесплатно получаете систему типов (например, линейные типы). Например, средство проверки типов в Rust является примером системы аффинных типов, которая соответствует системе аффинной логики.
Насколько мне известно, в академической литературе больше логических систем, чем систем типов, реализованных для языков программирования.Это, в свою очередь, говорит о том, что есть много замечательных систем типов, ожидающих реализации.
Функционально-ориентированное соответствие с использованием спектральной регуляризации
FOCUSR: Функционально-ориентированное соответствие с использованием спектральной регуляризацииFOCUSR [1,2] - это новый алгоритм для плотного соответствия вершин между двумя поверхностными сетками. Он извлекает выгоду из скорости прямого сопоставления элементов по поверхности и использует спектральное соответствие как среднее значение регуляризации .Спектральные методы использовались для согласования формы путем сравнения самых низкочастотных (гладких) собственных векторов лапласиана графа (представляющих геометрические свойства поверхностей сетки, см. Рис. 1). FOCUSR использует преимущество гладкости этих низкочастотных собственных векторов для регуляризации вложения, содержащего любой набор дополнительных функций (например, метрики, полученные из сетки, или внешние меры).
Собственные векторы графического лапласиана сетки представляют геометрические свойства, присущие этой поверхности. За вершины, пусть - взвешенная матрица смежности, описывающая связи между вершинами.Учитывая метрику расстояния между точками и :
| (1) |
Метрика расстояния может быть основана на расстоянии между вершинами: , или если дополнительные функции используются (например, кривизна поверхности, текстура сетки, практически любых дополнительных измерений):
| (2) |
куда является конкатенацией значений трехмерных координат с значения характеристик , пока - это весовой параметр для каждой функции.
Общий лапласов оператор формулируется как матрица вида:
| (3) |
куда матрица степеней (диагональная матрица с ), и - диагональная матрица весов узлов. Обычно в спектральном соответствии установлен на идентичность , или в . Однако предлагается установить как любые значимых узловых весов (например, положительный признак величин ):
| (4) |
куда степень узла (т.е., ), - ранее упомянутые веса функций, и - это функция, которая применяет положительные значения (например, или же ). Знаменатель в формуле. (5) содержит сумму влияний каждого признака на вершину . Мы использовали для обеспечения соответствия между узлами, имеющими наибольшие компоненты функций (которые, как мы предполагаем, указывают на наибольшую значимость).
| (5) |
куда степень узла, ранее упомянутые веса функций и функция, которая обеспечивает положительные значения весов узлов (например,грамм., или же ).
Правые собственные векторы матрицы Лапласа составляют спектр графа . Значения по поверхностям для пяти собственных векторов с самой низкой частотой показаны на рис. 1 и иллюстрируют стабильность этих собственных векторов между шарнирно-сочлененными или сильно деформируемыми формами. здесь, представляет трехмерную координату в пространстве (т. е. ), а надстрочный представляет th спектральная координата (т.е. th собственный вектор лапласиана графа. Каждый собственный вектор матрица-столбец с значения, и представляет другую (взвешенную) гармонику на поверхности сетки, которая соответствует внутреннему свойству геометрии сетки.В значения дать спектральные координаты узла (т.е. координата в спектральной области ).
Первый собственный вектор - тривиальный (равномерный) собственный вектор, а собственные векторы, связанные с нижними ненулевыми собственными значениями (например, ) представляют собой грубые (т.е. низкочастотные) внутренние геометрические свойства формы. Первый из них называется вектором Фидлера , в то время как собственные векторы, связанные с более высокими собственными значениями (например, ) представляют собой прекрасные (высокочастотные) геометрические свойства.Например, на рис.1 значения увеличиваются вдоль виртуальной центральной линии, отображающей общую форму моделей (грубое внутреннее свойство), в то время как значения изображаем мельчайшие детали моделей.
Только первый низкочастотные собственные векторы ( и ) представляют интерес. На практике эти собственные векторы на обеих сетках необходимо переупорядочить (их знак может быть изменен, а из-за алгебраической множественности собственные векторы близких собственных значений могут быть переставлены местами). Переупорядочивание выполняется путем проверки значений этих собственных векторов между парами ближайших точек на поверхности сетки ( на сетке ближайшая точка на сетке ).Матрица собирает все различия между собственным вектором и :
Венгерский алгоритм может найти оптимальную перестановку так что каждый собственный вектор соответствует .
Начальные векторы признаков и расширены переупорядоченными собственными векторами и для формирования расширенного спектрального вложения:
куда являются весовыми параметрами, основанными на частотах собственных векторов и достоверности их переупорядочения, и параметр взвешивания для каждой функции (например,грамм., уравнения (2)).
Эти спектральные вложения регуляризованы с использованием нежесткого соответствия множеств точек. Используется когерентный дрейф точки (CPD) [1].
Расширенные спектральные вложения регуляризованы с учетом гладкости их спектральных компонент. Ближайшие точки между этими выровненными вложениями показывают соответствующие точки между обеими сетками. Карта соответствия может быть дополнительно упорядочена в пространстве, чтобы учитывать пространственную окрестность сеток.Дается окончательная карта соответствия так, что:
| (8) |
FOCUSR работает с обычными сетками при использовании простейших настроек (никаких дополнительных функций не требуется). На рисунке ниже показано, что поиск ближайших точек в пространстве сталкивается с проблемой работы непосредственно в пространственной области , в то время как соответствия становятся более ясными в спектральной области . FOCUSR использует другой подход, поскольку он использует плавность самых низких гармоник для регуляризации согласования.
FOCUSR может соответствовать сеткам, претерпевающим важные нежесткие преобразования, и сочлененным сеткам. Ниже приведены примеры скачущих животных и различных выражений лица.
FOCUSR также может использоваться для точного и точного соответствия при медицинской визуализации. Ниже показано соответствие между двумя корками головного мозга, которые представляют собой сильно извитые поверхности. FOCUSR совпадает с точностью современного алгоритма сопоставления мозга с тем преимуществом, что по своей сути является чрезвычайно быстрым.
КОД ПЕРЕСМОТРЕН И ДОСТУПЕН ТОЛЬКО ДЛЯ ПРОВЕРКИ В ТЕКУЩЕМ ФОРМЕ
http://step.polymtl.ca/~rv101/spectral-correspondence.zip
- 1
- Ломберт, Х.; Grady, L .; Полимени, Дж. Р. и Чериет, Ф. FOCUSR: Ориентированное на признаки соответствие с использованием спектральной регуляризации - метод точного согласования поверхностей. ПАМИ, 2013.
- 2
- Lombaert, H .; Grady, L .; Полимени, Дж. Р. и Шериет, Ф. Быстрое сопоставление мозга со спектральным соответствием. ИПМИ, 2005.
- 1
- Мироненко А. и Сонг X. Регистрация точек: когерентный дрейф точек. ПАМИ, 2010.
Эрве 2013-01-28 .

Leave A Comment