3. Биссектрисы углов А и Д параллелограмма АВСД пересекаются в точке М, лежащей на стороне. ВС. другой. 6. В ромбе АВСД диагонали АС и ВД пересекаются в точке О, угол Д равен 120°.
Чтобы посмотреть этот PDF файл с форматированием и разметкой, скачайте его и откройте на своем компьютере.
Геометрия
–
8
1.
Сколько сторон имеет выпуклый многоугольник, если каждый его угол равен 108°.
2.
Найдите боковые стороны равнобедренной трапеции, основания которой равны 14 см и 8 см, а
один из углов 120°.
3.
Биссектрисы углов А и Д параллелограмма АВСД
пересекаются в точке М, лежащей на стороне
ВС. Найдите стороны параллелограмма, если его периметр равен 36 см.
4.
Найдите меньшую боковую сторону прямоугольной трапеции, основания которой 10 см и 6 см, а
один из углов равен 45°.
5.
Периметр прямоугольника равен
36 см. Найдите его стороны, если одна из них на 6 см меньше
другой.
6.
В ромбе АВСД диагонали АС и ВД пересекаются в точке О, угол Д равен 120°. Найдите углы
7.
Сколько потребуется кафельных плиток квадратной формы со стороной 20 см, чтобы обли
цевать
ими часть стены, имеющей форму прямоугольника со сторонами 3 м и 2,4 м?
8.
Пол комнаты имеет форму ква
драта со стороной 4 м. Сколько надо паркетных дощечек
прямоугольной формы со сторонами 5 см и 20 см, чтобы покрыть весь пол паркетом?
9.
Площадь прямоуго
льника равна 40 см
2
, а его периметр 26 см. Найдите его стороны.
10.
Стороны АВ и ВС треугольника АВС равны соответственно 32 см и 44 см. Высота, проведённая к
стороне АВ, равна 22 см. Найдите высоту, проведённую к стороне ВС.
11.
Сторона ромба равна 12 см, а оди
н из его углов равен 30°. Найдите площадь ромба.
12.
Найдите площадь прямоугольной трапеции, две меньшие стороны которой равны 30 см, а больший
угол равен 135°.
13.
Площадь прямоугольного треугольника равна 64 см
2
. Найдите его катеты, если один из них в 2
раза бол
ьше другого.
14.
Стороны параллелограмма равны 18 см и 30 см, а высота, проведённая к большей стороне, равна
6 см. Найдите высоту, проведённую к меньшей стороне параллелограмма.
15.
Острый угол равнобедренной трапеции равен 45°, а высота, проведённая из вершины ту
делит основание на отрезки 14 см и 34 см. Найдите площадь трапеции.
16.
В треугольнике стороны равны 10 см, 10 см и 12 см. Найдите высоту, проведённую к большей
стороне, и площадь треугольника.
17.
В прямоугольной трапеции
основания равны 22 см и 6 см,
большая боковая сторона
–
20 см.
Найдите площадь трапеции.
18.
В прямоугольной трапеции боковые стороны 7 см и 25 см, а меньшее основание равно 2 см.
Найдите площадь трапеции.
19.
Диагональ прямоугольника равна 52 мм, а стороны относятся как 5 : 12.
риметр.
20.
В треугольнике АВС угол А равен 45°, ВС = 13, а высота ВД отсекает на стороне АС отрезок ДС,
равный 12 см. Найдите площадь треугольника АВС.
Приложенные файлы
- 11652910
Размер файла: 187 kB Загрузок: 0
Биссектрисы углов А и D параллелограмма ABCD
Здравствуйте! В этой публикации мы с вами рассмотрим задачу по геометрии. На её примере вы отметите для себя довольно важные моменты, которые можно упустить при решении планиметрической задачи. Например, на экзамене, построив эскиз и рассмотрев вариант решения, можно торжествуя приступить к решению следующей задачи и не обратить внимание на то, что имеются ещё варианты.
*Источник: задачи из сборника Дмитрия Мальцева «Математика. ЕГЭ-2017. Профильный уровень» Глава 2. Планиметрия. Задача 1 и 2. При желании вы можете приобрести его на портале my-shop.ru *Введите на сайте в строке поиска запрос «Мальцев ЕГЭ» и увидите все книги автора.
Биссектрисы углов А и D параллелограмма ABCD пересекают прямую ВС в точках M и N так, что BM:MN=2:3. Найдите длину стороны ВС этого параллелограмма, если АВ=6.
Построим эскиз:
Сразу отметим, что треугольники АВМ и MDC равнобедренные, так как:
Вывод: АВ=BN=6 и CD=MC=6.
Сказано, что BM:MN=2:3. Можем записать: 2х+3х=6 => х=6/5. Значит:
Вычислим NC:
Таким образом:
Казалось бы ответ получен и можно «успокоиться». Но вы при решении всегда задавайте себе вопросы: а есть ли ещё варианты решения? Как ещё можно произвести построение? Какие варианты возможны?
В данном случае — если просто мысленно «вытянуть» параллелограмм, то ещё один вариант решения очевиден.
Случай 2:
Так как АВ=ВМ, то можем записать: 2х=6 => х=3.
Следовательно МN=3х=9. Таким образом:
А теперь «сожмём» параллелограмм.
Случай 3:
Треугольники NCD и АВМ равнобедренные. Так как BM:MN=2:3, то можем записать:
Так как BM:MN=2:3, то можем записать:
Значит NМ=3∙3=9, CM = NM – NC = 9 – 6 = 3.
Таким образом
*Теперь внимание! Необходимо рассмотреть ещё случай, когда положение обозначений M и N изменены. Дело в том, что в условии не сказано как точки располагаются относительно друг друга. Конечно, в первом и втором случае очевидно, что по-другому их и не расположить, так как по условию у нас BM<MN. А в-третьем случае это под вопросом…
Проверим:
Так как по условию BM:MN=2:3, то можем записать:
Значит BN=x=6 и MB=2∙x=12. А этого быть не может, так как МС=6 и отрезок МВ должен быть меньше чем 6. То есть при данном расположении точек и указанных в условии данных построить такой параллелограмм невозможно.
Ответ: 8,4; 21 и 3
*Почему мы рассмотрели случай с переменой положения точек M и N? Вы это поймёте при решении следующей задачи, аналогичной этой.
В параллелограмме ABCD биссектрисы углов при стороне AD пересекают прямую ВС в точках M и N так, что BM:MN=1:3.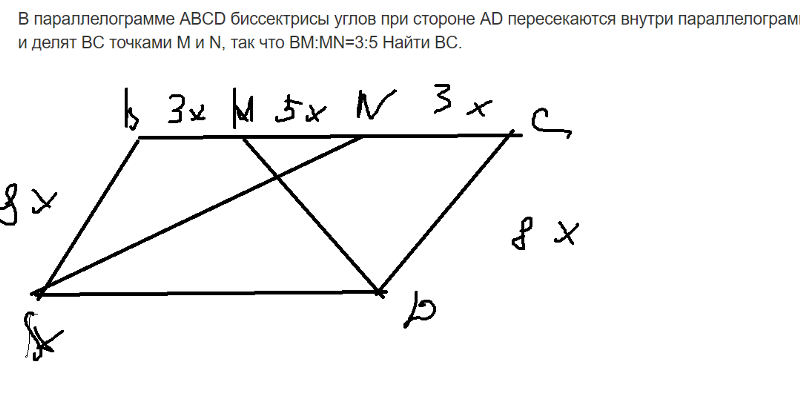 Найдите длину стороны ВС этого параллелограмма, если АВ=8.
Найдите длину стороны ВС этого параллелограмма, если АВ=8.
Построим эскиз:
Треугольники АВМ и MDC равнобедренные. Значит АВ=BN=8 и CD=MC=8.
Сказано, что BM:MN=1:3. Можем записать: х+3х=8 => х=2. Значит
Вычислим NC:
Таким образом:
Случай 2:
Отметим, что АВ=ВМ=CD=NC=8. Так как BM:MN=1:3, то можем записать что BM=х=8 Следовательно МN=3∙8=24. Таким образом:
Случай 3:
Треугольники NCD и АВМ равнобедренные. Так BM:MN=1:3, то мы можем записать:
Значит NМ=3∙8=24, CM = NM – NC = 24 – 8 = 16. А это невозможно, так как у нас BM>CM.
Рассмотрим случай, когда M и N расположены по другому:
Треугольники NCD и АВМ равнобедренные. Так BM:MN=1:3, то можем записать:
Значит BM=4, NМ=3∙4=12, CN = NM – CM = 12 – 8 = 4. Таким образом
Ответ: 10, 40 и 4.
Вывод:
— необходимо всегда ставить вопрос о возможности существования других вариантов решения и рассматривать все обнаруженные случаи.
— обращайте внимание на возможность иного (взаимного) расположения точек.
С уважением, Александр Крутицких.
*Делитесь информацией в социальных сетях
часть 2 «сложные задачи»
1) Через точку O пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны BC и AD в точках K и M соответственно. Докажите, что BK=DM.
2) В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали
3) В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK,СF = АM. Докажите, что EFKM — параллелограмм
4)В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
5) В параллелограмме ABCDABCDдиагонали ACAC и BDBD пересекаются в точке KK. Докажите, что площадь параллелограммаABCDABCD в четыре раза больше площади треугольника CKD.
Докажите, что площадь параллелограммаABCDABCD в четыре раза больше площади треугольника CKD.
6) Сторона AD параллелограмма ABCD вдвое больше стороны AB.
Точка G — середина стороны AD. Докажите, что BG — биссектриса
угла ABC.
7) Высоты AA1 иCC1остроугольного треугольника ABC пересекаются
в точке E. Докажите, что углы CC1A1 и CAA1 равны.
8) Биссектрисы углов C и D параллелограмма ABCD пересекаются
в точке K, лежащей на стороне AB. Докажите, что K — середина AB.
9) На средней линии трапеции ABCDABCD с основаниями ADAD и BCBC выбрали произвольную точку KK. Докажите, что сумма площадей треугольников BKCBKC и AKDAKD равна половине площади трапеции.
10) Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=15 и MB=16. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
11) Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 9 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине.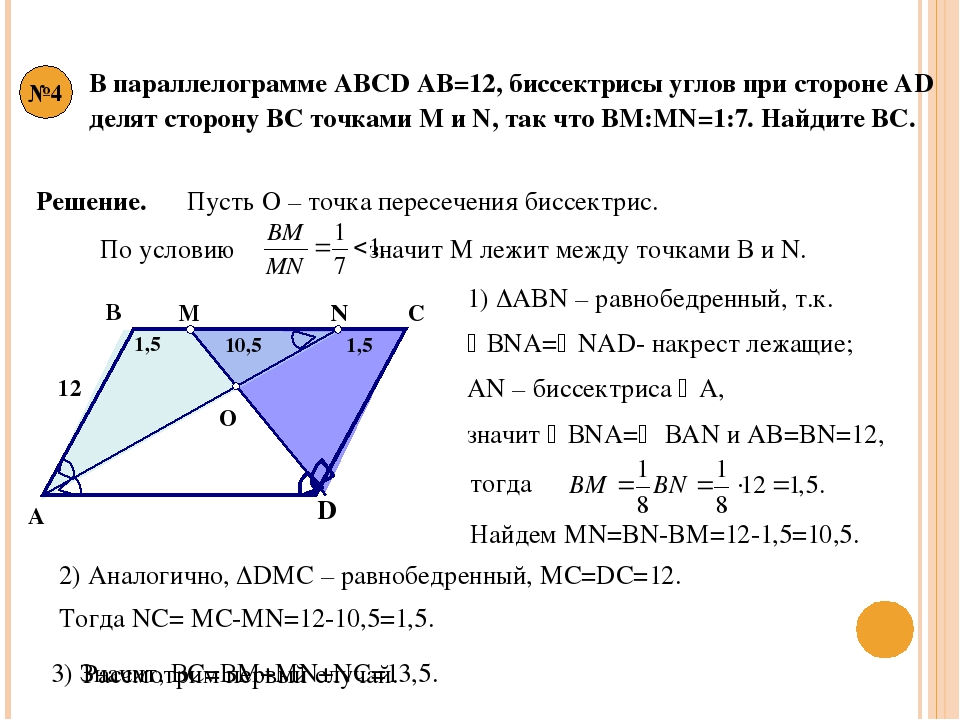 Найдите радиус окружности, вписанной в треугольник ABC.
Найдите радиус окружности, вписанной в треугольник ABC.
12) Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AD и BC четырёхугольника пересекаются в точке K. Докажите, что треугольники KAB и KCD подобны.
13) Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
14) Точка E — середина боковой стороны AB трапеции ABCD. Докажите,
что площадь треугольника ECD равна половине площади трапеции.
15) Окружности с центрами в точках P и Q пересекаются в точках K и L, причём точки P и Q лежат по одну сторону от прямой KL. Докажите,
что прямые PQ и KL перпендикулярны.
16) Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:7:8. Найдите радиус окружности, если меньшая из сторон равна 20.
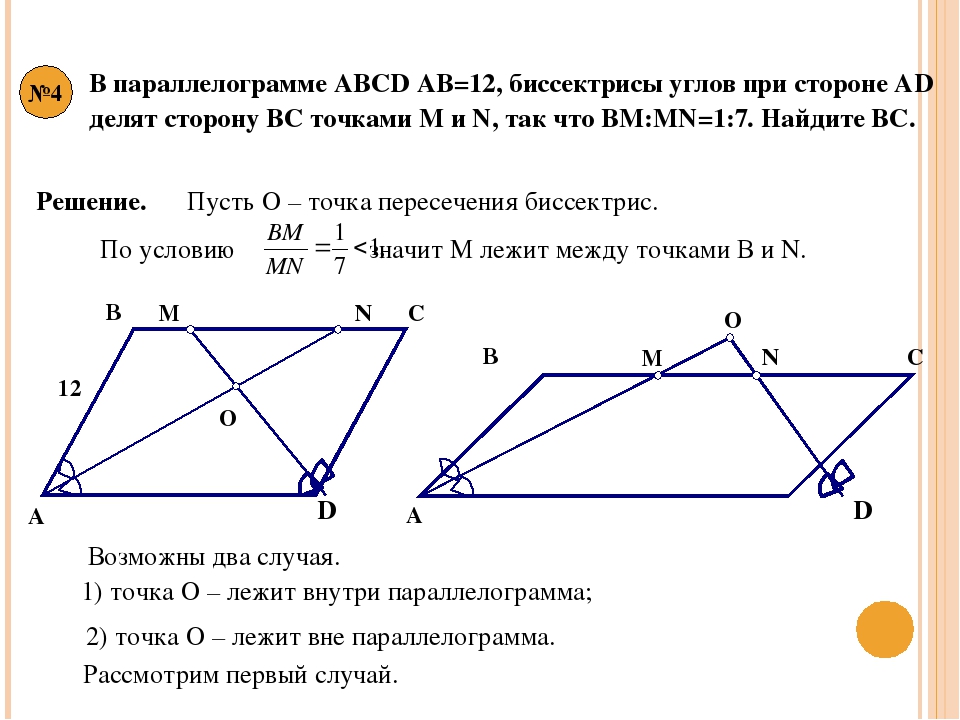 Найдите длину
Найдите длину отрезка EF, если AD=25, BC=15, CF:DF=3:2.
18) В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 13.
19) Окружность пересекает стороны AB и AC треугольника ABC в точках K
и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=9, а сторона BC в 3 раза меньше стороны AB.
20) Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность
21) В трапецию, сумма длин боковых сторон которой равна 22, вписана окружность. Найдите длину средней линии трапеции.
Начало формы
| 22) Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB=30, а расстояния от центра окружности до хорд AB и CD равны соответственно 20 и 15. |
Конец формы
23) Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC.
24) В треугольнике ABC известно, что AC=39, BC= , угол C равен 90°. Найдите радиус описанной окружности этого треугольника.
25) В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 8 и 5. Найдите площадь параллелограмма ABCD.
26) На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку K. Докажите, что сумма площадей треугольников BKC и AKD равна половине площади трапеции.
27) Известно, что около четырёхугольника ABCD можно описать окружность
и что продолжения сторон AB и CD четырёхугольника пересекаются
28) В параллелограмме ABCD точка M — середина стороны AB. Известно, что MC=MD. Докажите, что данный параллелограмм — прямоугольник.
29) Окружности радиусов 45 и 55 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC
Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC
и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
30) В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.
31) Катеты прямоугольного треугольника равны 15 и 20. Найдите высоту, проведённую к гипотенузе.
32) На стороне BC остроугольного треугольника ABC ( AB≠AC ) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=81, MD=45, H — точка пересечения высот треугольника ABC. Найдите AH.
33) В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 84. Найдите стороны треугольника ABC.
34) Боковые стороны AB и CD трапеции ABCD равны соответственно 12 и 20, а основание BC равно 2. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Найдите площадь трапеции.
35) Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 48, тангенс угла BAC равен 1235. Найдите радиус окружности, вписанной в треугольник ABC.
36) В треугольнике ABC на его медиане BM отмечена точка K так, что BK:KM=7:6. Прямая AK пересекает сторону BC в точке P. Найдите отношение площади треугольника BKP к площади треугольника ABC.
37) Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 33, тангенс угла BAC равен 34. Найдите радиус окружности, вписанной в треугольник ABC.
38) В треугольнике ABC на его медиане BM отмечена точка K так, что BK:KM=2:11. Прямая AK пересекает сторону BC в точке P. Найдите отношение площади треугольника BKP к площади треугольника AKM.
39) Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 45:4, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 16.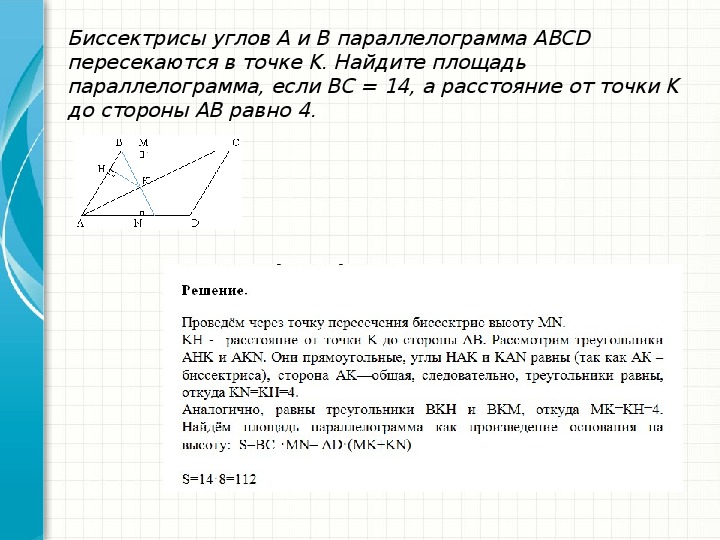
40) Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=5, а расстояние от точки K до стороны AB равно 5.
41) Две касающиеся внешним образом в точке K окружности, радиусы которых равны 36 и 39, касаются сторон угла с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
42) В трапеции ABCD основания AD и BC равны соответственно 34 и 9, а сумма углов при основании AD равна 90∘. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=10.
43) Середина M стороны AD выпуклого четырёхугольника равноудалена от всех его вершин. Найдите AD, если BC=9, а углы B и C четырёхугольника равны соответственно 98∘ и 142∘.
44) Найдите площадь трапеции, диагонали которой равны 13 и 11, а средняя линия равна 10.
45) Углы при одном из оснований трапеции равны 48∘ и 42∘, а отрезки, соединяющие середины противоположных сторон трапеции, равны 6 и 3.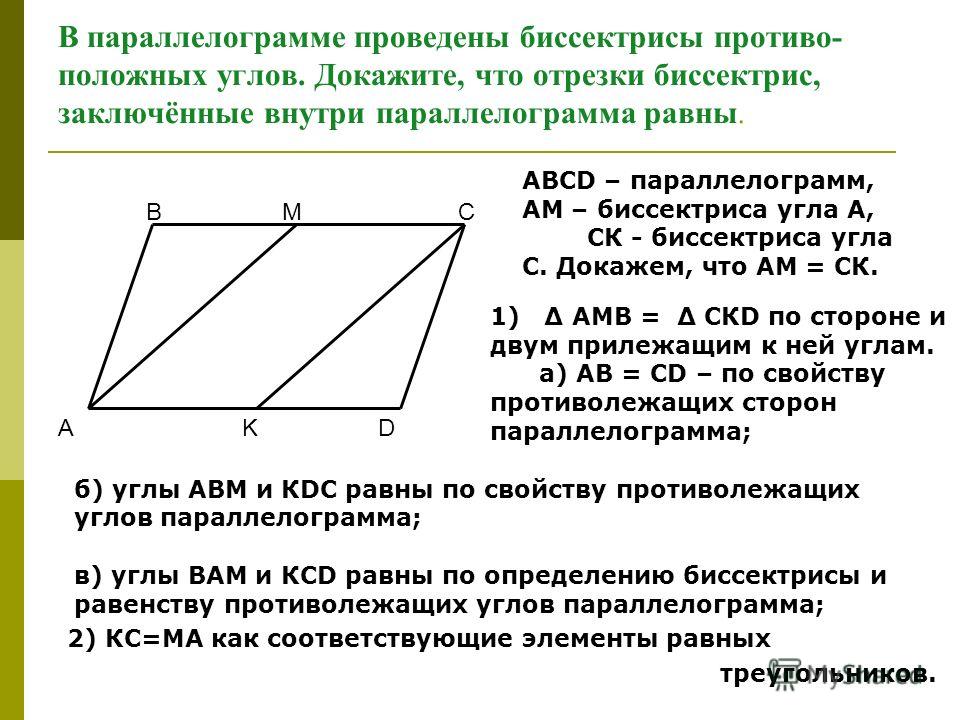 Найдите основания трапеции.
Найдите основания трапеции.
46) Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 16.
47) Основания трапеции относятся как 2:3. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции?
48) В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 10, 8 и 6. Найдите площадь параллелограмма ABCD.
49) На стороне AB треугольника ABC взята точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=12, BC=30 и CD=10.
50) Четырёхугольник ABCD со сторонами AB=19 и CD=28 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60∘. Найдите радиус окружности, описанной около этого четырёхугольника.
Найдите радиус окружности, описанной около этого четырёхугольника.
51) Окружности радиусов 29 и 87 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
52) Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC относится к длине стороны AB как 5:7. Найдите отношение площади четырёхугольника KPCM к площади треугольника ABC.
53) В треугольнике ABC известны длины сторон AB=8, AC=64, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D.
Найдите CD.
54) Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 60, тангенс угла BAC равен 43. Найдите радиус окружности, вписанной в треугольник ABC.
55) Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 16, а площадь равна 32 .
56) В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точкиE до прямой CD, если AD=9, BC=6.
57) Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 20, а площадь равна 50 .
58) В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=72, SQ=1.
59) Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=7, а сторона BC в 1,4 раза меньше стороны AB.
60) Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 8, а AB=3.
61) Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=19.
Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=19.
62) Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
63) Стороны AC, AB, BC треугольника ABC равны 2 , и 1 соответственно. Точка K расположена вне треугольника ABC, причём отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K, A и C подобен исходному. Найдите косинус угла AKC, если ∠KAC>90°.
64) В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=85, SQ=17.
65) В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=15, BC=12.
Найдите расстояние от точки E до прямой CD, если AD=15, BC=12.
Упражнения: Параллелограмм. Свойства параллелограмма
Геометрия 8 класс (УМК Мерзляк, Полонский, Якир). Упражнения по теме «Параллелограмм. Свойства параллелограмма». Материал предназначен для составления самостоятельных проверочных работ. Раздел состоит из трёх однотипных вариантов задач по проверяемой теме.
Параллелограмм. Свойства параллелограмма
Вариант 1
- В четырёхугольнике ABCD (рис. 1) ∠1 = ∠2, ∠3 = ∠4. Докажите, что четырёхугольник ABCD — параллелограмм.
- Периметр параллелограмма равен 56 см. Найдите его стороны, если одна из них на 6 см больше другой.
- Периметр параллелограмма равен 126 см. Найдите его стороны, если две из них относятся как 4 : 5.
- Найдите углы параллелограмма, если:
1) один из его углов равен 46°; 2) сумма двух его углов равна 186°; 3) один из его углов на 56° больше другого; 4) один из его углов в 3 раза меньше другого; 5) два его угла относятся как 5 : 7.
- Даны два параллелограмма ABCD и KMNP. Могут ли одновременно выполняться неравенства: ∠А > ∠К и ∠B > ∠M?
- На рисунке 2 изображены параллелограммы. Определите, не выполняя измерений, на каких рисунках величины углов или длины отрезков обозначены неверно (длины отрезков даны в сантиметрах).
- Диагонали параллелограмма ABCD пересекаются в точке О. Найдите разность периметров треугольников COD и AOD, если АВ = 7 см, ВС = 4 см.
- На рисунке 3 изображены параллелограммы. Определите, не выполняя измерений, на каких рисунках величины углов или длины отрезков обозначены неправильно (длины отрезков даны в сантиметрах).
- Биссектрисы углов А к В параллелограмма ABCD пересекаются в точке О. Найдите сторону АВ параллелограмма, если ОА = 8 см и ∠ABO = 30°.
- В параллелограмме ABCD известно, что АВ = 7 см, AD = 12 см. Биссектриса угла А пересекает сторону ВС в точке Е. Найдите отрезки BE и ЕС.
- Биссектриса угла А параллелограмма ABCD делит сторону CD в отношении 1:3, считая от вершины угла С.
 Найдите стороны параллелограмма, если его периметр равен 84 см.
Найдите стороны параллелограмма, если его периметр равен 84 см. - В параллелограмме ABCD угол А равен 60°. Высота BE делит сторону AD в отношении 3 : 8, считая от вершины острого угла. Найдите стороны параллелограмма, если его периметр равен 68 см.
- Два угла параллелограмма относятся как 1:5. Найдите угол между высотами параллелограмма, проведёнными из вершины острого угла.
- В параллелограмме ABCD проведены высоты ВМ и ВК. Найдите периметр параллелограмма, если ВМ = 6 см, ВК = 9 см, ∠ADC = 150°.
- На основании равнобедренного треугольника отмечена произвольная точка и через неё проведены прямые, параллельные его боковым сторонам. Найдите периметр полученного параллелограмма, если боковая сторона равнобедренного треугольника равна 6 см.
- Постройте параллелограмм ABCD, если заданы точки М, N и К — середины сторон АВ, ВС и CD соответственно.
- Постройте параллелограмм ABCD, если заданы его вершины А и В и точка О — точка пересечения диагоналей параллелограмма.

Вариант 2
- В четырёхугольнике ABCD (рис. 42) ∠1 = ∠2 = ∠3. Докажите, что четырёхугольник ABCD — параллелограмм.
- Периметр параллелограмма равен 84 см. Найдите стороны параллелограмма, если одна из них на 12 см меньше другой.
- Периметр параллелограмма равен 90 см. Найдите его стороны, если две из них относятся как 2:3.
- Найдите углы параллелограмма, если:
1) один из его углов равен 52°; 2) сумма двух его углов равна 174°; 3) один из его углов на 28° больше другого; 4) один из его углов в 4 раза меньше другого; 5) два его угла относятся как 4:5. - Даны два параллелограмма ABCD и EFGH. Могут ли одновременно выполняться неравенства: ∠B < ∠F и ∠C < ∠G?
- На рисунке 43 изображены параллелограммы. Определите, не выполняя измерений, на каких рисунках величины углов или длины отрезков обозначены неверно (длины отрезков даны в сантиметрах).
- Диагонали параллелограмма ABCD пересекаются в точке О. Найдите разность периметров треугольников ВОС и COD, если АВ = 9 см, AD = 14 см.

- На рисунке 44 изображены параллелограммы. Определите, не выполняя измерений, на каких рисунках величины углов или длины отрезков обозначены неверно (длины отрезков даны в сантиметрах).
- Биссектрисы углов С и D параллелограмма ABCD пересекаются в точке О. Найдите отрезок СО, если CD = 10 см и ∠DCO = 60°.
- Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке К, ВК = 4 см и КС = 3 см. Найдите стороны параллелограмма.
- Биссектриса угла В параллелограмма ABCD делит сторону AD в отношении 2:3, считая от вершины угла А. Найдите стороны параллелограмма, если его периметр равен 42 см.
- В параллелограмме ABCD угол А равен 120°. Высота АК делит сторону CD в отношении 3 : 5, считая от вершины тупого угла. Найдите стороны параллелограмма, если его периметр равен 108 см.
- Два угла параллелограмма относятся как 3 : 7. Найдите угол между высотами параллелограмма, проведёнными из вершины тупого угла.
- В параллелограмме ABCD проведены высоты AM и AN.
 Найдите периметр параллелограмма, если AM -= 8 см, AN = 11 см, ∠BCD = 30°.
Найдите периметр параллелограмма, если AM -= 8 см, AN = 11 см, ∠BCD = 30°. - На основании равнобедренного треугольника отмечена произвольная точка и через неё проведены прямые, параллельные его боковым сторонам. Периметр полученного параллелограмма равен 24 см. Найдите боковую сторону треугольника.
- Постройте параллелограмм ABCD, если заданы его вершина А и точки Ми N — середины сторон АВ и CD соответственно.
- Постройте параллелограмм ABCD, если заданы его вершина А, точка М — середина стороны АВ, точка О — точка пересечения диагоналей параллелограмма.
Вариант 3
- В четырёхугольнике ABCD (рис. 83) ∠1 = ∠2, ∠3 = ∠4. Докажите, что четырёхугольник ABCD — параллелограмм.
- Периметр параллелограмма равен 80 см. Найдите стороны параллелограмма, если одна из них на 14 см меньше другой.
- Периметр параллелограмма равен 98 см. Найдите его стороны, если две из них относятся как 4:3.
- Найдите углы параллелограмма, если:
1) один из его углов равен 63°; 2) сумма двух его углов равна 134°; 3) один из его углов на 44° меньше другого; 4) один из его углов в 11 раз меньше другого; 5) два его угла относятся как 5:13.
- Даны два параллелограмма ABCD и PKTF. Могут ли одновременно выполняться неравенства: ∠C > ∠T и ∠D > ∠F4
- На рисунке 84 изображены параллелограммы. Определите, не выполняя измерений, на каких рисунках величины углов или длины отрезков обозначены неверно (длины отрезков даны в сантиметрах).
- Диагонали параллелограмма ABCD пересекаются в точке О. Найдите разность периметров треугольников АОВ и ВОС, если CD =11 см, AD = 6 см.
- На рисунке 85 изображены параллелограммы. Определите, не выполняя измерений, на каких рисунках величины углов или длины отрезков обозначены неверно (длины отрезков даны в сантиметрах).
- Биссектрисы углов В и С параллелограмма ABCD пересекаются в точке О. Найдите сторону ВС параллелограмма, если ОС = 6 см и ∠BCO = 60°.
- В параллелограмме ABCD известно, что AD = 8 см, CD = 11 см. Биссектриса угла D пересекает сторону АВ в точке К. Найдите отрезки АК и КВ.
- Биссектриса угла С параллелограмма ABCD делит сторону АВ в отношении 1 : 4, считая от вершины угла А.
 Найдите стороны параллелограмма, если его периметр равен 72 см.
Найдите стороны параллелограмма, если его периметр равен 72 см. - В параллелограмме ABCD угол В равен 60°. Высота АН делит сторону ВС в отношении 4 : 7, считая от вершины острого угла. Найдите стороны параллелограмма, если его периметр равен 76 см.
- Два угла параллелограмма относятся как 5 : 7. Найдите угол между высотами параллелограмма, проведёнными из вершины острого угла.
- В параллелограмме ABCD проведены высоты ВН и DE. Найдите периметр параллелограмма, если ВН = 10 см, DE = 7 см, ∠ABC = 150°.
- На основании равнобедренного треугольника отмечена произвольная точка и через неё проведены прямые, параллельные его боковым сторонам. Найдите периметр полученного параллелограмма, если боковая сторона равнобедренного треугольника равна 10 см.
- Постройте параллелограмм ABCD, если заданы точки М и N — середины сторон АВ и ВС соответственно и точка О — точка пересечения диагоналей параллелограмма.
- Постройте параллелограмм ABCD, если заданы его вершина А, точка М — середина стороны ВС, точка О — точка пересечения диагоналей параллелограмма.

Вы смотрели: Геометрия 8 класс (УМК Мерзляк, Полонский, Якир). Упражнения по теме «Параллелограмм. Свойства параллелограмма». Материал в первую очередь предназначен для составления самостоятельных проверочных работ. Будьте внимательны: при транскрипте цитат возможны опечатки!
Вернуться к Списку упражнений по геометрии УМК Мерзляк
Просмотров: 3 292
2. Из вершины В параллелограмма ABCD с острым углом А проведен перпендикуляр ВК к прямой AD ВК АВ/2. Докажите, что точки М и К находятся на одинаковом расстоянии от точки пересечения диагоналей четырехугольника.
Разноуровневый материал по теме: «Четырёхугольники»Самостоятельная работа обучающего характера с последующей самопроверкой по теме: «Многоугольники»
I уровень I вариант
1. Найдите сумму углов выпуклого двенадцати угольника.
2. В выпуклом пятиугольнике две стороны равны, третья сторона на 3 см больше, а четвертая в 2 раза больше первой стороны, пятая — на 4 см меньше четвертой. Найдите стороны пятиугольника, если известно, что его периметр равен 34 см.
Найдите стороны пятиугольника, если известно, что его периметр равен 34 см.
I уровень II вариант
1. Найдите сумму углов выпуклого тринадцати угольника.
2. В выпуклом шестиугольнике три стороны равны, четвертая в 2 раза больше первой стороны, пятая — на 3 см меньше четвертой, а шестая на 1 см больше второй. Найдите стороны шестиугольника, если известно, что его периметр равен 30 см.
2 уровень I вариант
1. Сколько сторон имеет выпуклый многоугольник, если сумма его углов равна 2160°?
2. Выпуклый четырехугольник ABCD имеет две пары равных между собой смежных сторон: АВ = AD, ВС = CD, О — точка пересечения диагоналей четырехугольника. Сравните периметры пятиугольников ABCOD и ABOCD.
2 уровень II вариант
1. Сколько сторон имеет выпуклый многоугольник, если сумма его углов равна 2520°?
2. Диагональ АС невыпуклого четырехугольника A BCD разделяет этот четырехугольник на два треугольника, причем АВ > ВС, АВ = AD, DC = CD, а прямые, содержащие диагонали четырехугольника, пересекаются в точке О. Сравните периметры пятиугольников BCODA и DCOBA.
Сравните периметры пятиугольников BCODA и DCOBA.
3 уровень I вариант
1. Каждый угол выпуклого многоугольника равен 162°. Найдите число сторон этого многоугольника.
2. В выпуклом шестиугольнике ABCDEF все стороны равны. Большая диагональ, проведенная из вершины А, параллельна стороне ВС, (BAD = (CDA. Сравните периметры пятиугольников ABDEF и ACDEF.
3 уровень II вариант
1. Каждый угол выпуклого многоугольника равен 165°. Найдите число сторон этого многоугольника.
2. В выпуклом пятиугольнике ABCDE все стороны имеют равные длины. Диагональ, проведенная из вершины А, параллельна стороне ED, (EAC = (DCA. Сравните периметры четырехугольников ЕАВС и DCBA.
РЕШЕНИЯ
I уровень I вариант
1. 180° ( (12-2) =1800°.
2. Рис.70.
х + х + х + 3 + 2х + 2х – 4 = 34; х = 5.
Ответ: 5 см, 5 см, 8 см, 10 см, 6 см.
I уровень II вариант
1. 180° ( (13-2) =1980°.
2. Рис.71.
х + х + х + 2х + 2х – 3 + х + 1 = 30; х = 4
Ответ: 4 см, 4 см, 4 см, 8 см, 5 см, 5 см.
2 уровень I вариант
1. 180° ( (n — 2) = 2160°.
Ответ: четырнадцать сторон.
2. См. рис. 72. Докажи, что:
1)
·АВС =
· ADC
2)
·CBO =
·CDO
3) PBCODA = PABOCD
2 уровень II вариант
1. 180° ( (n — 2) = 2520°.
Ответ: шестнадцать сторон
2. См. рис. 73. Докажи, что:
1)
·ABC =
·ADC
2)
·ABO =
·ADO
3) РBCODA = РDCOBA
III уровень I вариант
1. 180 o ( (n — 2) : n = 162°.
2. См. рис. 74. Докажи, что:
1)
·АBD =
·DCА;
2) PABDEF = PACDEF
3 уровень 2 вариант
1. 180° (п — 2) : п = 165°.
2. См. рис. 75. Докажи, что:
2) РЕАВС = PDCВА
Самостоятельная работа по теме «Параллелограмм»
I уровень I вариант
1. В четырехугольнике ABCD AB || CD, AC = 20 см, BD = 10 см, АВ = 13 см. Диагонали ABCD пересекаются в точке О. Найдите периметр
·COD.
2. Из вершины В параллелограмма ABCD с острым углом А проведен перпендикуляр ВК к прямой AD; ВК = АВ/2. Найдите (C, (D.
Найдите (C, (D.
3. Середина отрезка BD является центром окружности с диаметром АС, причем точки А, В, С, D нe лежат на одной прямой. Докажите, что ABCD — параллелограмм.
I уровень II вариант
1. В четырехугольнике ABCD АВ || CD, ВС || AD, О — точка пересечения диагоналей. Периметр
·AOD равен 25 см, АС = 16 см, BD = 14 см. Найдите ВС.
2. В параллелограмме ABCD с острым углом А из вершины В опущен перпендикуляр ВК к прямой AD, AD = ВК. Найдите (C, (D.
3. Дан параллелограмм ABCD. На продолжении диагонали АС за вершины А и С отмечены точки М и N соответственно так, что AM = CN. Докажите, что MBND — параллелограмм.
II уровень I вариант
1. В четырехугольнике ABCD (A + (B = 180°, АВ || CD. На сторонах ВС и AD отмечены точки М и К соответственно так, что ВМ = KD. Докажите, что точки М и К находятся на одинаковом расстоянии от точки пересечения диагоналей четырехугольника.
2. На сторонах РК и МН параллелограмма МРКН взяты точки А и В соответственно, МР = РВ = АК; MPB = 60°. Найдите углы параллелограмма и сравните отрезки ВМ и АН.
Найдите углы параллелограмма и сравните отрезки ВМ и АН.
3. На основании АС равнобедренного треугольника ABC отмечена точка К, а на сторонах АВ и ВС точки М и Р соответственно, причем РК = МВ, (KPC = 80°, (С = 50°. Докажите, что КМВР — параллелограмм.
II уровень II вариант
1. В четырехугольнике МРКН (PMK = (HKM, РК || МН. Через точку пересечения диагоналей проведена прямая, пересекающая стороны РК и МН в точках А и В соответственно. Докажите, что АР = НВ.
2. На сторонах ВС и AD параллелограмма ABCD взяты точки М и К, АВ = ВМ = KD, (AMB = 30°. Найдите углы параллелограмма и сравните отрезки AM и СК.
3. В треугольнике МРК (M = 65°. На сторонах МК, МР, РК отмечены точки А, В, С соответственно так, что середина стороны РК -точка С, AM = КС, ВР = АС, (BAM = 50°. Докажите, что ВРСА — параллелограмм.
III уровень I вариант
1. В выпуклом четырехугольнике ABCD (A + (B = (B + (C = 180°. Через точку О пересечения диагоналей четырехугольника проведена прямая, пересекающая стороны DC и AD в точках М и К соответственно; (BOM= 90°. Докажите, что ВК = ВМ.
Докажите, что ВК = ВМ.
2. На сторонах ВС и CD параллелограмма ABCD отмечены точки М и Н соответственно так, что отрезки ВН и MD пересекаются в точке О; (BHD = 95°, (DMС = 90°, (ВОD = 155°. Найдите отношение длин отрезков АВ и MD и углы параллелограмма.
3. Точки М и К являются соответственно серединами сторон АВ и ВС треугольника AВС. Через вершину С вне треугольника проведена прямая, параллельная АВ и пересекающая луч МК в точке Е. Докажите, что КЕ = АС/2.
III уровень II вариант
1. В выпуклом четырехугольнике МРКН (M + (P = 180°, (MKH = (KMP. На сторонах МН и РК отмечены точки А и В так, что РВ = РА. Отрезок АВ проходит через точку пересечения диагоналей четырехугольника. Докажите, что HP ( AB.
2. На сторонах ВС и CD параллелограмма ABCD взяты точки К и М соответственно. Отрезки ВМ и KD пересекаются в точке О; (BOD = 140°, (DKB =110°, (BMC = 90°. Найдите отношение длин отрезков МС и AD и углы параллелограмма.
3. Точки А и В принадлежат соответственно сторонам РЕ и ЕТ треугольника PET. Прямая, проходящая через вершину Т вне треугольника, пересекает луч АВ в точке К, АР = КТ, АВ = ВК = РТ/2. Докажите, что точка А является серединой отрезка РЕ.
Прямая, проходящая через вершину Т вне треугольника, пересекает луч АВ в точке К, АР = КТ, АВ = ВК = РТ/2. Докажите, что точка А является серединой отрезка РЕ.
Самостоятельная работа обучающего характера с последующей самопроверкой по теме: «Теорема Фалеса»
I уровень
1. В трапеции ABCD ВС — меньшее основание. На отрезке AD взята точка Е так, что BE (( CD, (ABE = 70°, (BEA = 50°. Найдите углы трапеции.
2. В прямоугольной трапеции острый угол равен 45°. Меньшая боковая сторона и меньшее основание равны по 10 см. Найдите большее основание.
II уровень
1. В равнобедренной трапеции диагональ составляет с боковой стороной угол в 120°. Боковая сторона равна меньшему основанию. Найдите углы трапеции.
2. В прямоугольной трапеции острый угол и угол, который составляет меньшая диагональ с меньшим основанием, равны по 60°. Найдите отношение оснований.
III уровень
1.Из вершины тупого угла равнобедренной трапеции ABCD проведен перпендикуляр СЕ к прямой AD, содержащей большее основание. Докажите, что АЕ = (AD + ВС)/2.
Докажите, что АЕ = (AD + ВС)/2.
2. В прямоугольной трапеции диагонали взаимно перпендикулярны. Большая диагональ составляет с меньшей боковой стороной угол в 60°. Докажите, что меньшая диагональ равна полусумме оснований трапеции.
Самостоятельная работа обучающего характера с последующей самопроверкой по теме: «Многоугольники, обобщение»
I уровень
1. Найдите углы ромба, если его диагонали составляют с его стороной углы, один из которых на 30° меньше другого.
2. Угол между диагоналями прямоугольника равен 80°. Найдите углы между диагональю прямоугольника и его сторонами.
II уровень
1. В ромбе ABCD биссектриса угла ВАС пересекает сторону ВС и диагональ BD соответственно в точках М и N. Найдите угол ANB, если (AMC= 120°.
2. Через точку пересечения диагоналей квадрата проведены две взаимно перпендикулярные прямые. Докажите, что точки пересечения этих прямых со сторонами квадрата являются вершинами еще одного квадрата.
Самостоятельная работа проверочного характера
по теме: «Многоугольники, обобщение»
I УРОВЕНЬ I вариант
1. В прямоугольнике ABCD диагонали пересекаются в точке О. Е — середина стороны АВ, (BAC = 50°. Найдите угол EOD.
В прямоугольнике ABCD диагонали пересекаются в точке О. Е — середина стороны АВ, (BAC = 50°. Найдите угол EOD.
2. В ромбе ABCD диагонали пересекаются в точке О, (A = 31о Найдите углы треугольника ВОС
3. Дан отрезок, равный перпендикуляру, опущенному из вершины некоторого квадрата на диагональ. Постройте этот квадрат.
I УРОВЕНЬ II вариант
1. В прямоугольнике МРКН диагонали пересекаются в точке О. Отрезок ОА является высотой треугольника МОР, (AOP = 15°. Найдите (ОНK.
2. В ромбе МРКН диагонали пересекаются в точке Е. Один из углов треугольника РКЕ равен 16°30′. Найдите остальные углы этого треугольника и угол РМH.
3. Дан отрезок, равный перпендикуляру, проведенный из точки пересечения диагоналей некоторого квадрата на его сторону. Постройте этот квадрат.
I УРОВЕНЬ I вариант
1. В прямоугольнике ABCD диагонали пересекаются в точке О. Е — середина стороны АВ, (BAC = 50°. Найдите угол EOD.
2. В ромбе ABCD диагонали пересекаются в точке О, (A = 31о Найдите углы треугольника ВОС
3. Дан отрезок, равный перпендикуляру, опущенному из вершины некоторого квадрата на диагональ. Постройте этот квадрат.
Дан отрезок, равный перпендикуляру, опущенному из вершины некоторого квадрата на диагональ. Постройте этот квадрат.
I УРОВЕНЬ II вариант
1. В прямоугольнике МРКН диагонали пересекаются в точке О. Отрезок ОА является высотой треугольника МОР, (AOP = 15°. Найдите (ОНK.
2. В ромбе МРКН диагонали пересекаются в точке Е. Один из углов треугольника РКЕ равен 16°30′. Найдите остальные углы этого треугольника и угол РМH.
3. Дан отрезок, равный перпендикуляру, проведенный из точки пересечения диагоналей некоторого квадрата на его сторону. Постройте этот квадрат.
III УРОВЕНЬ I вариант
1. В прямоугольнике ABCD точки М и К — середины сторон АВ и AD соответственно. На прямой А С взята точка Р, на прямой BD точка Е, МР ( А С, КЕ ( ВD Известно, что 4КЕ = АD. Найдите отношения сторон АР : РС.
2. В ромбе ABCD угол В тупой. На стороне AD взята точка К, ВК ( АD Прямые ВК и А С пересекаются в точке О, А С = 2ВK . Найдите угол АОВ.
3. Постройте прямоугольник по углу между стороной и диагональю и перпендикуляру, проведенному из вершины прямоугольника к прямой, содержащей эту диагональ.
III УРОВЕНЬ II вариант
1. В прямоугольнике МРКН О — точка пересечения диагоналей.
Точки А и В — середины сторон МР и МН соответственно. Точка С делит отрезок МК в отношении 1 : 7, считая от точки М, А С ( MK. Найдите отношение ВО : РH.
2. В ромбе МРКН угол М острый. Отрезок РЕ является перпендикуляром к прямой МК, О — точка пересечения диагоналей, Т — общая точка прямых РЕ и МН, (MTP= 120o, ОН= а. Найдите РЕ.
3. Постройте ромб по острому углу и отрезку, длина которого равна расстоянию между прямыми, содержащими противоположные стороны ромба.
Контрольная работа по теме: «Многоугольники»
I УРОВЕНЬ I вариант
1. Диагонали прямоугольника ABCD пересекается в точке О, (ABO = 36о. Найдите угол AOD.
2. Найдите углы прямоугольной трапеции, если один из ее углов равен 20о.
3. Стороны параллелограмма относятся как 1 : 2, а его периметр равен 30 см. Найдите стороны параллелограмма.
4. В равнобокой трапеции сумма углов при большем основании равна 96о. Найдите углы трапеции.
Найдите углы трапеции.
5*. Высота ВМ, проведенная из вершины угла ромба ABCD образует со ‘стороной АВ угол 30о, АМ = 4 см. Найдите длину диагонали BD ромба, если точка М лежит на стороне AD.
I УРОВЕНЬ II вариант
1. Диагонали прямоугольника MNKP пересекаются в точке О, (MON= 64о. Найдите угол ОМР.
2. Найдите углы равнобокой трапеции, если один из ее углов на 30о больше второго.
3. Стороны параллелограмма относятся как 3 : 1, а его периметр равен 40 см. Найдите стороны параллелограмма.
4. В прямоугольной трапеции разность углов при одной из боковых сторон равна 48о. Найдите углы трапеции.
5*. Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 30о, длина диагонали АС равна 6 см. Найдите АМ, если точка М лежит на продолжении стороны AD.
II УРОВЕНЬ II вариант
1. Периметр параллелограмма 60 см. Одна из его сторон на 6 см меньше другой. Найдите длины сторон параллелограмма.
2. Угол между диагоналями прямоугольника равен 80о.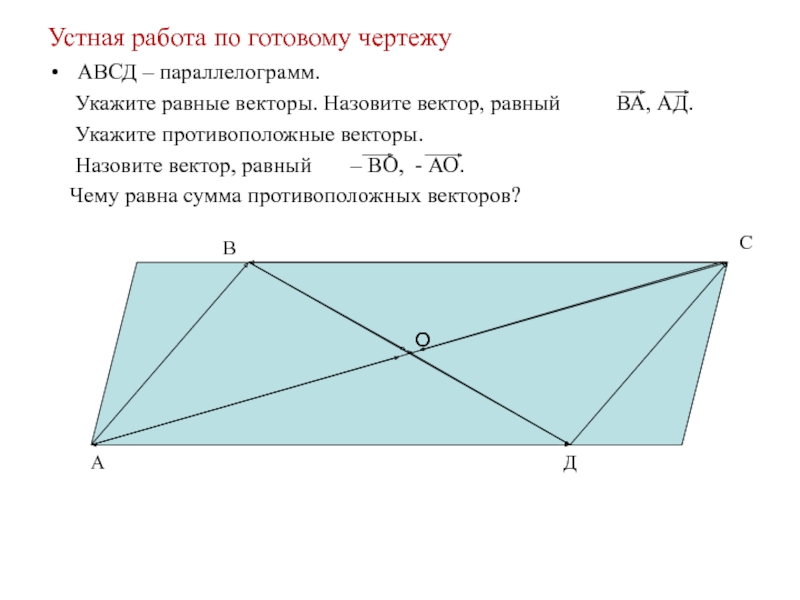 Найдите угол между диагональю и меньшей стороной прямоугольника.
Найдите угол между диагональю и меньшей стороной прямоугольника.
3. Найдите углы параллелограмма, если одна из его диагоналей является высотой и равна половине неперпендикулярной к ней стороны параллелограмма.
4. В трапеции ABCD диагональ А С перпендикулярна боковой стороне CD и является биссектрисой угла А. Найдите длину АВ, если периметр трапеции равен 35 см, (D = 60о.
5*. В параллелограмме ABCD AD = 6 см. Биссектрисы углов АВС и BCD пересекаются в точке М1,. На прямых АВ и CD взяты точки К и Р так, что А — В — К, D — С — Р. Биссектрисы углов КВС и ВСР пересекаются в точке М2 Найдите М1М2
II УРОВЕНЬ I вариант
1. Периметр параллелограмма 50 см. Одна из его сторон на 5 см больше другой. Найдите длины сторон параллелограмма.
2. Найдите угол между диагоналями прямоугольника, если каждая из них делит угол прямоугольника в отношении 4 : 5.
3. Найдите углы параллелограмма, если одна из его диагоналей является высотой и равна одной из его сторон.
4. В трапеции ABCD диагональ BD перпендикулярна боковой стороне АВ, (ADB = (BDC = 30о. Найдите длину AD, если периметр трапеции 60 см.
В трапеции ABCD диагональ BD перпендикулярна боковой стороне АВ, (ADB = (BDC = 30о. Найдите длину AD, если периметр трапеции 60 см.
5*. В параллелограмме ABCD биссектрисы углов АВС и BCD пересекаются в точке М1,. На прямых АВ и CD взяты точки К и Р так, что А — В — К, D — С — Р. Биссектрисы углов КВС и ВСР пересекаются в точке М2, М1М2 = 8 см. Найдите AD.
III УРОВЕНЬ I вариант
1. В равнобокой трапеции длина боковой стороны 2d, длины оснований 5d и 7d. Найдите углы трапеции.
2. В параллелограмме ABCD известно, что (A = 60о, АВ = 10, AD = 16. Найдите расстояния от вершин В и D до биссектрисы (BCD.
3. В ромбе ABCD биссектриса угла DCA перпендикулярна стороне AD. Найдите углы ромба.
4. Внутри квадрата ABCD выбрана точка М так, что треугольник AMD равносторонний. Найдите угол АМВ.
5*. Биссектриса угла С параллелограмма ABCD пересекает сторону AD в точке М и продолжение стороны АВ за точку А в точке N. Найдите периметр параллелограмма, если AN = 4, DM = 3.
III УРОВЕНЬ II вариант
1. В равнобокой трапеции боковая сторона равна меньшему основанию, а диагональ перпендикулярна боковой стороне. Найдите углы трапеции.
2. В параллелограмме KМNP угол М равен 120о, КМ= 8, КР = 10.
Найдите расстояния от вершин М и Р до биссектрисы угла МКР.
3. Высота ромба делит его сторону пополам. Найдите углы ромба.
4. Внутри квадрата ABCD выбрана точка N так, что треугольник BNC равносторонний. Найдите угол NAD.
5*. В параллелограмме ABCD биссектриса угла А пересекает сторону ВС в точке F и продолжение стороны CD за точку С — в точке Е. Найдите периметр параллелограмма, если ВР = 2 см, ЕС = 3 см.
15
ЕГЭ по математике 2019, Ященко 20 вариантов, решение заданий 6 (тематическая рабочая тетрадь) — Решения вариантов ЕГЭ по математике: 2017, 2018, 2019, 2020
Задачи из книжки https://yadi.sk/i/NZcoB3vn4T_c5w или https://yadi.sk/i/05jYXhJFpGw-9w (то же самое)
Подготовительные задания
youtube.com/embed/waGOMtGEYL0″ frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
1. Угол между высотой и биссектрисой, проведёнными из вершины
прямого угла прямоугольного треугольника, равен 15°. Найдите ги-
потенузу, если меньший катет равен 5.
2. Биссектриса тупого угла параллелограмма делит противоположную
сторону в отношении 4 : 3, считая от вершины острого угла. Найди-
Найди-
те большую сторону параллелограмма, если его периметр равен 88.
3. Основания трапеции равны 12 и 17. Найдите больший из отрезков,
на которые диагональ трапеции делит среднюю линию.
4. Биссектриса угла, смежного с углом параллелограмма, параллельна
одной из его диагоналей. Найдите угол, под которым пересекаются
диагонали параллелограмма. Ответ дайте в градусах.
5. Периметр параллелограмма АВС равен 72. На диагонали АС
отмечена точка О, такая что АО : ОС = 5 : 3. Через точку О проведе-
ны две прямые, параллельные сторонам ВС и АР параллелограмма,
и они пересекают стороны АВ и АР, соответственно, в точках К и
М. Найдите периметр четырёхугольника АКОМ.
6. Хорда АВ делит окружность на две дуги, градусные величины кото-
рых относятся как 5: 7. Под каким углом видна эта хорда из точки
С, принадлежащей меньшей дуге окружности? Ответ дайте в граду-
сах.
7. Найдите угол АСО, если его сторона СА касается окружности, О —
центр окружности, а большая дуга АР окружности, заключенная
внутри этого угла, равна 116°. Ответ дайте в градусах.
Ответ дайте в градусах.
8. Около трапеции, один из углов которой равен 35°, описали окруж-
ность. Найдите меньший из остальных углов трапеции. Ответ дайте в
градусах.
9. Радиус окружности, вписанной в прямоугольный треугольник, ра-
вен 6. Найдите гипотенузу этого треугольника, если его катеты отно-
сятся как 8 : 15.
10. Периметр прямоугольной трапеции, описанной около окружности,
равен 22, её большая боковая сторона равна 7. Найдите радиус ок-
ружности.
11. Прямая, параллельная стороне АС треугольника АВС, пересекает
стороны АВ и ВС в точках К и М соответственно. Найдите АС, если
ВК :КА=6:5, КМ = 18.
12. В прямоугольном треугольнике, один из острых углов которого ра-
вен 60°, гипотенуза равна 19. Найдите меньший катет этого тре-
угольника.
13. В трапеции АВСР с основаниями АВ и СР диагонали пересекаются
в точке О. Найдите АО, если СО = 217, ОС = 30, АВ = 20.
14. Один из углов параллелограмма на 56° меньше другого угла.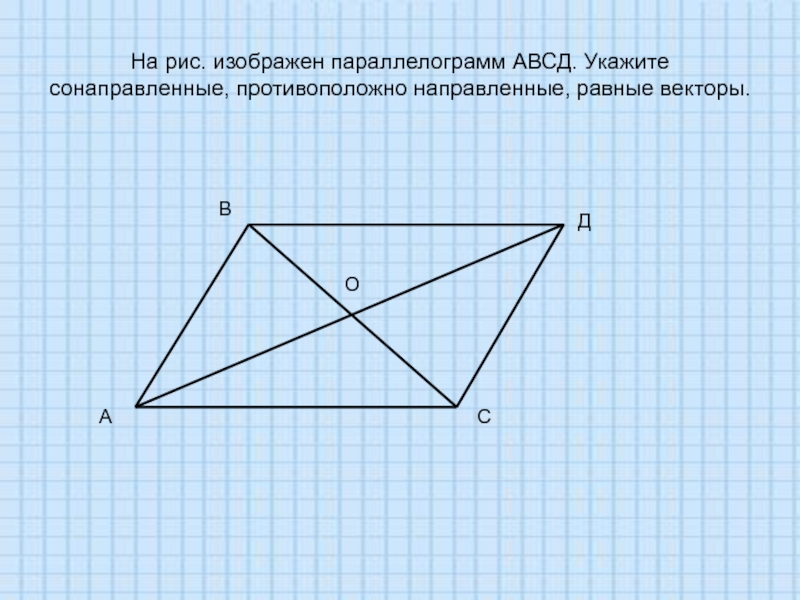 Най-
Най-
дите величину тупого угла параллелограмма. Ответ дайте в граду-
сах.
15. Биссектрисы углов А и О параллелограмма АВСО пересекаются
в точке, лежащей на стороне ВС. Найдите ВС, если АВ = 13.
16. Площадь параллелограмма АВСШ равна 60. Точка Е — середина сто-
роны СР. Найдите площадь треугольника АРЕ.
17. Найдите площадь прямоугольного треугольника, если его катеты
равны 7 и 14.
18. Найдите площадь прямоугольного треугольника, если его катет и ги-
потенуза равны соответственно 16 и 20.
19. В треугольнике со сторонами 9 и 6 проведены высоты к этим сторо-
нам. Высота, проведённая к первой из этих сторон, равна 2. Чему
равна высота, проведённая ко второй стороне?
20. Найдите площадь прямоугольной трапеции, основания которой рав-
ны 14 и 26, большая боковая сторона составляет с основанием угол
45°.
Вы тонете в океане математики и физики? Давайте спасаться вместе!
Получи запись бесплатного вебинара
с разбором задач, которые были на реальном ЕГЭ-2019 (29 мая 2019г.
 ),
), получи условия и ссылки на решения некоторых задач
с реальных ЕГЭ-2017 (2 июня 2017) и ЕГЭ-2018 (26 июня 2018),
получи видеоразбор решений 11й,12й,13й,14й,15й, 16й,17й,18й задач
из варианта 7 книжки «Ященко 36 вариантов 2019»,
видеозаписи прошлых вебинаров
Получить ссылки на вебинар и на видео. Нажимай!
C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru
Врожденные пороки сердца — факты о дефекте атриовентрикулярной перегородки
Дефект атриовентрикулярной перегородки (произносится как EY-tree-oh-ven-TRIC-u-lar SEP-tal DEE-fekt) или AVSD — это порок сердца, поражающий клапаны между верхней и нижней камерами сердца и стенки между камерами.
Что такое дефект атриовентрикулярной перегородки?
Дефект атриовентрикулярной перегородки (AVSD) — это порок сердца, при котором есть отверстия между камерами правой и левой сторон сердца, и клапаны, контролирующие поток крови между этими камерами, могут быть неправильно сформированы. Это состояние также называется дефектом атриовентрикулярного канала (AV-канала) или дефектом эндокардиальной подушки. При АВСД кровь течет туда, где она обычно не должна идти. В крови также может быть меньше кислорода, чем обычно, и дополнительная кровь может поступать в легкие. Эта дополнительная кровь, закачиваемая в легкие, заставляет сердце и легкие усердно работать и может привести к застойной сердечной недостаточности .
Это состояние также называется дефектом атриовентрикулярного канала (AV-канала) или дефектом эндокардиальной подушки. При АВСД кровь течет туда, где она обычно не должна идти. В крови также может быть меньше кислорода, чем обычно, и дополнительная кровь может поступать в легкие. Эта дополнительная кровь, закачиваемая в легкие, заставляет сердце и легкие усердно работать и может привести к застойной сердечной недостаточности .
В зависимости от того, какие структуры сформированы неправильно, могут возникать два основных типа AVSD:
- Полная AVSD
Полная AVSD возникает, когда есть большое отверстие в центре сердца, которое позволяет крови течь между всеми четырьмя камерами сердца.Это отверстие возникает там, где обычно встречаются перегородки (стенки), разделяющие две верхние камеры ( предсердий ) и две нижние камеры ( желудочков ). Также имеется один общий атриовентрикулярный клапан в центре сердца вместо двух отдельных клапанов — трехстворчатый клапан на правой стороне сердца и митральный клапан на левой стороне сердца. Этот общий клапан часто имеет створки (створки), которые могут быть неправильно сформированы или закрываются неплотно.Полный AVSD возникает во время беременности, когда общий клапан не может разделиться на два отдельных клапана (трикуспидальный и митральный клапаны) и когда перегородки (стенки), разделяющие верхнюю и нижнюю камеры сердца, не растут полностью, чтобы встретиться в центр сердца.
Этот общий клапан часто имеет створки (створки), которые могут быть неправильно сформированы или закрываются неплотно.Полный AVSD возникает во время беременности, когда общий клапан не может разделиться на два отдельных клапана (трикуспидальный и митральный клапаны) и когда перегородки (стенки), разделяющие верхнюю и нижнюю камеры сердца, не растут полностью, чтобы встретиться в центр сердца. - Частичный или неполный AVSD
Частичный или неполный AVSD возникает, когда сердце имеет некоторые, но не все дефекты полного AVSD. Обычно в стенке предсердия или в стенке желудочка около центра сердца имеется отверстие.Частичный АВСД обычно имеет как митральный, так и трикуспидальный клапаны, но один из клапанов (обычно митральный) может не закрыться полностью, что позволяет крови течь назад из левого желудочка в левое предсердие.
Узнайте больше о том, как работает сердце »
происшествие
По оценкам Центров по контролю и профилактике заболеваний (CDC), около 2118 младенцев (1 из 1859 младенцев) рождаются с АВСД каждый год в Соединенных Штатах. 1
1
Причины и факторы риска
Причины врожденных пороков сердца, таких как AVSD, у большинства младенцев неизвестны.Некоторые дети имеют пороки сердца из-за изменений в их генах или хромосомах . В частности, АВСД часто встречается у детей с синдромом Дауна, генетическим заболеванием, которое включает дополнительную хромосому 21 (также называемую трисомией 21). Считается, что врожденные пороки сердца также вызваны сочетанием генов и других факторов риска, таких как факторы, с которыми мать контактирует в своем окружении, что она ест или пьет, или определенные лекарства, которые она использует во время беременности.
Подробнее о работе CDC по причинам и факторам риска »
Диагностика
AVSD может быть диагностирован во время беременности или вскоре после рождения ребенка.
Во время беременности
Во время беременности проводятся скрининговые тесты (также называемые пренатальными тестами) для выявления врожденных дефектов и других состояний. AVSD может быть диагностирован во время беременности с помощью ультразвукового исследования (которое создает изображения ребенка с помощью звуковых волн), но то, можно ли увидеть дефект с помощью ультразвукового исследования, зависит от размера или типа (частичный или полный) AVSD.Поставщик медицинских услуг может запросить эхокардиограмму плода для подтверждения диагноза, если есть подозрение на AVSD. Эхокардиограмма плода — это ультразвуковое исследование сердца ребенка, которое показывает больше деталей, чем обычное пренатальное ультразвуковое исследование. Эхокардиограмма плода может показать проблемы со структурой сердца и насколько хорошо оно работает.
AVSD может быть диагностирован во время беременности с помощью ультразвукового исследования (которое создает изображения ребенка с помощью звуковых волн), но то, можно ли увидеть дефект с помощью ультразвукового исследования, зависит от размера или типа (частичный или полный) AVSD.Поставщик медицинских услуг может запросить эхокардиограмму плода для подтверждения диагноза, если есть подозрение на AVSD. Эхокардиограмма плода — это ультразвуковое исследование сердца ребенка, которое показывает больше деталей, чем обычное пренатальное ультразвуковое исследование. Эхокардиограмма плода может показать проблемы со структурой сердца и насколько хорошо оно работает.
После рождения ребенка
Во время медицинского осмотра младенца можно заподозрить полный AVSD. Используя стетоскоп, врач часто слышит шум в сердце (ненормальный свистящий звук, вызванный кровотечением, протекающим через аномальное отверстие).Однако не все шумы в сердце присутствуют при рождении. Младенцы с полным АВСД обычно проявляют признаки проблем в течение первых нескольких недель после рождения. Когда симптомы действительно возникают, они могут включать
Когда симптомы действительно возникают, они могут включать
- Проблемы с дыханием
- Бьющееся сердце
- Слабый пульс
- Пепельный или голубоватый цвет кожи
- Плохое питание, медленное прибавление в весе
- Легко утомляет
- Отек ног или живота
При частичных AVSD, если отверстия между камерами сердца невелики, признаки и симптомы могут не проявляться в период новорожденности или младенчества.В этих случаях людям с частичным АВСД может не ставиться диагноз в течение многих лет.
Симптомы, которые могут указывать на ухудшение полного или частичного AVSD у ребенка, включают
- Аритмия, нарушение сердечного ритма. Из-за аритмии сердце может биться слишком быстро, слишком медленно или хаотично. Когда сердце не бьется должным образом, оно не может эффективно перекачивать кровь.
- Застойная сердечная недостаточность, когда сердце не может перекачивать кровь и кислород, достаточные для удовлетворения потребностей организма.

- Легочная гипертензия, вид высокого кровяного давления, поражающий артерии легких и правую часть сердца.
Поставщик медицинских услуг может запросить один или несколько тестов для подтверждения диагноза AVSD. Самый распространенный тест — это эхокардиограмма. Это ультразвуковое исследование сердца, которое может показать проблемы со структурой сердца, такие как отверстия между камерами правой и левой стороны сердца, а также любой нерегулярный кровоток. Электрокардиограмма (ЭКГ), которая измеряет электрическую активность сердца, рентген грудной клетки и другие медицинские тесты также могут использоваться для постановки диагноза.Поскольку многие дети с синдромом Дауна имеют АВСД, всем младенцам с синдромом Дауна необходимо пройти эхокардиограмму для поиска АВСД или других пороков сердца.
Процедуры
Все AVSD, как частичные, так и полные, обычно требуют хирургического вмешательства. Во время операции любые отверстия в камерах закрываются заплатами. Если митральный клапан не закрывается полностью, его ремонтируют или заменяют. Для полного AVSD общий клапан разделен на два отдельных клапана — один с правой стороны, а другой — с левой.
Если митральный клапан не закрывается полностью, его ремонтируют или заменяют. Для полного AVSD общий клапан разделен на два отдельных клапана — один с правой стороны, а другой — с левой.
Возраст, в котором проводится операция, зависит от здоровья ребенка и конкретной структуры AVSD. Если возможно, операция должна быть сделана до того, как легкие будут повреждены из-за слишком большого количества крови, перекачиваемой в легкие. Лекарства могут использоваться для лечения застойной сердечной недостаточности, но это только краткосрочная мера, пока ребенок не станет достаточно сильным для операции.
Младенцы, перенесшие хирургическое вмешательство по поводу АВСД, не излечены; у них могут быть пожизненные осложнения. Наиболее частым из этих осложнений является негерметичность митрального клапана.Это когда митральный клапан не закрывается полностью, чтобы кровь могла течь в обратном направлении через клапан. Негерметичный митральный клапан может привести к тому, что сердце будет работать тяжелее, чтобы получить достаточно крови для остального тела; негерметичный митральный клапан, возможно, придется исправить хирургическим путем. Ребенку или взрослому с АВСД потребуются регулярные контрольные посещения кардиолога (кардиолога), чтобы следить за его или ее прогрессом, избегать осложнений и проверять наличие других состояний здоровья, которые могут развиться по мере взросления ребенка.При правильном лечении большинство детей с АВСД вырастают и ведут здоровую и продуктивную жизнь.
Ребенку или взрослому с АВСД потребуются регулярные контрольные посещения кардиолога (кардиолога), чтобы следить за его или ее прогрессом, избегать осложнений и проверять наличие других состояний здоровья, которые могут развиться по мере взросления ребенка.При правильном лечении большинство детей с АВСД вырастают и ведут здоровую и продуктивную жизнь.
Номер ссылки
- Mai CT, Isenburg JL, Canfield MA, et al. для Национальной сети профилактики врожденных дефектов. Национальные популяционные оценки основных врожденных дефектов, 2010-2014 гг. Врожденные дефекты Res 2019; 1–16. Https://doi.org/10.1002/bdr2.1589.
Изображения находятся в общественном достоянии и, следовательно, свободны от каких-либо ограничений авторских прав. В порядке любезности мы просим, чтобы поставщик контента (Центры по контролю и профилактике заболеваний, Национальный центр по врожденным дефектам и порокам развития) был указан и уведомлен о любом публичном или частном использовании этого изображения.
Изображения находятся в общественном достоянии и, следовательно, свободны от каких-либо ограничений авторских прав. В порядке любезности мы просим, чтобы поставщик контента (Центры по контролю и профилактике заболеваний, Национальный центр по врожденным дефектам и порокам развития) был указан и уведомлен о любом публичном или частном использовании этого изображения.
Параллелограмм равен половине произведения его диагоналей. Решение геометрических задач: решение четырехугольников
Тогда (Так как в прямоугольном треугольнике катет, лежащий под углом 30 °, равен половине гипотенузы).
Но CD = AB. Тогда AB: НD = 2: 1.
3.
4.
Ответ: AB: НD = 2: 1,
Задача 4.
Одна из диагоналей параллелограмма длиной 4√6 составляет угол 60 ° с основанием, а вторая диагональ составляет угол 45 ° с тем же основанием. Найдите вторую диагональ.
Решение.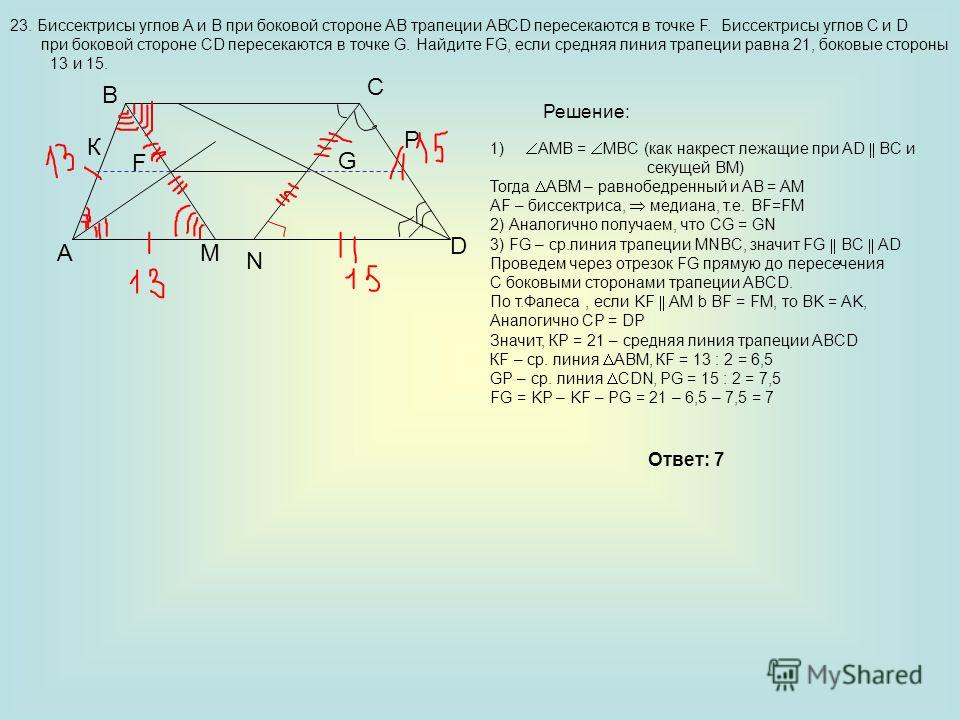
1. АО = 2√6.
2. Применим теорему синусов к треугольнику AOD.
АО / sin D = OD / sin A.
2√6 / sin 45 о = OD / sin 60 о.
OD = (2√6sin 60 о) / sin 45 о = (2√6 · √3 / 2) / (√2 / 2) = 2√18 / √2 = 6.
Ответ: 12.
Задача 5.
У параллелограмма со сторонами 5√2 и 7√2 меньший угол между диагоналями равен меньшему углу параллелограмма.Найдите сумму длин диагоналей.
Решение.
Пусть d 1, d 2 — диагонали параллелограмма, а угол между диагоналями и меньшим углом параллелограмма равен f.
1. Посчитайте двумя разными
способами его площадь.
S ABCD = AB · AD · sin A = 5√2 · 7√2 · sin f,
S ABCD = 1/2 AC · BD · sin AOB = 1/2 · d 1 d 2 sin f.
Получаем равенство 5√2 · 7√2 · sin f = 1 / 2d 1 d 2 sin f или
2 · 5√2 · 7√2 = d 1 d 2;
2.Используя соотношение сторон и диагоналей параллелограмма, запишем равенство
(AB 2 + AD 2) · 2 = AC 2 + BD 2.
((5√2) 2 + (7√2) 2) · 2 = d 1 2 + d 2 2.
d 1 2 + d 2 2 = 296.
3. Составьте систему:
(d 1 2 + d 2 2 = 296,
(d 1 + d 2 = 140.
Умножаем второе уравнение системы на 2 и прибавляем его к первому.
Получаем (d 1 + d 2) 2 = 576. Следовательно, Id 1 + d 2 I = 24.
Поскольку d 1, d 2 — длины диагоналей параллелограмма, то d 1 + d 2 = 24.
Ответ: 24.
Задание 6.
Стороны параллелограмма равны 4 и 6. Острый угол между диагоналями составляет 45 °. Найдите площадь параллелограмма.
Решение.
1. Из треугольника AOB, используя теорему косинусов, запишем соотношение между стороной параллелограмма и диагоналями.
AB 2 = AO 2 + VO 2 2 · AO · VO · cos AOV.
4 2 = (d 1/2) 2 + (d 2/2) 2 — 2 · (d 1/2) · (d 2/2) cos 45 о;
d 1 2/4 + d 2 2/4 — 2 · (d 1/2) · (d 2/2) √2 / 2 = 16.
d 1 2 + d 2 2 — d 1 · d 2 √2 = 64.
2. Аналогично запишем соотношение для треугольника AOD.
Учтем, что
Получаем уравнение d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
3. Имеем систему
(d 1 2 + d 2 2 — d 1 · d 2 √2 = 64,
(d 1 2 + d 2 2 + d 1 d 2 √ 2 = 144.
Вычитая первое из второго уравнения, получаем 2d 1 · d 2 √2 = 80 или
d 1d 2 = 80 / (2√2) = 20√2
4. S ABCD = 1/2 AC · BD · sin AOB = 1/2 · d 1 d 2 sin α = 1/2 · 20√2 · √2 / 2 = 10.
Примечание: В этой и предыдущей задачах нет необходимости решать всю систему, предполагая, что в этой задаче для вычисления площади нам понадобится произведение диагоналей.
Ответ: 10.
Задание 7.
Площадь параллелограмма равна 96, а его стороны равны 8 и 15. Найдите квадрат меньшей диагонали.
Решение.
1. S ABCD = AB · AD · sin BAD. Сделаем замену в формуле.
Получаем 96 = 8 · 15 · sin BAD.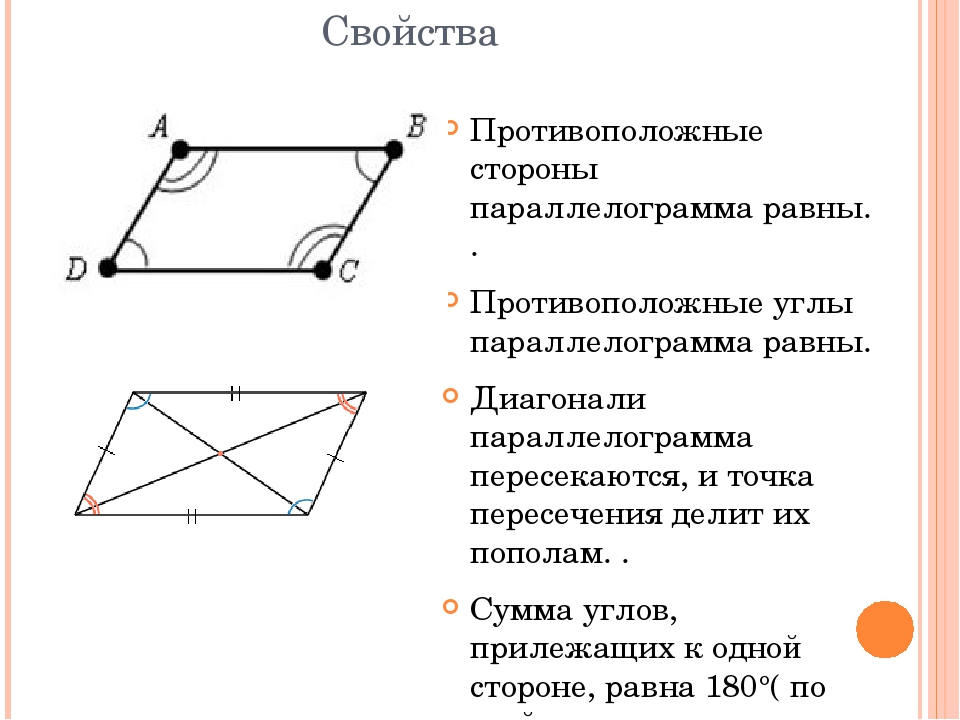 Следовательно sin ПЛОХО = 4/5.
Следовательно sin ПЛОХО = 4/5.
2. Найдите cos BAD. sin 2 BAD + cos 2 BAD = 1.
(4/5) 2 + cos 2 BAD = 1.cos 2 BAD = 9/25.
По условию задачи находим длину меньшей диагонали. Диагональ BD будет меньше, если угол BAD острый. Тогда cos BAD = 3/5.
3. Из треугольника ABD по теореме косинусов находим квадрат диагонали BD.
BD 2 = AB 2 + AD 2 — 2 · AB · BD · cos BAD.
БД 2 = 8 2 + 15 2 — 2 · 8 · 15 · 3/5 = 145.
Ответ: 145.
Остались вопросы? Не знаете, как решить геометрическую задачу?
Чтобы получить помощь репетитора — зарегистрируйтесь.
Первое занятие бесплатно!
, при полном или частичном копировании материала ссылка на источник обязательна.
Примечание . Это часть урока с задачами по геометрии (раздел о параллелограммах). Если вам нужно решить задачу по геометрии, которой здесь нет, напишите об этом на форуме. Символ √ или sqrt () используется для обозначения действия по извлечению квадратного корня при решении задач; кроме того, в скобках указано радикальное выражение.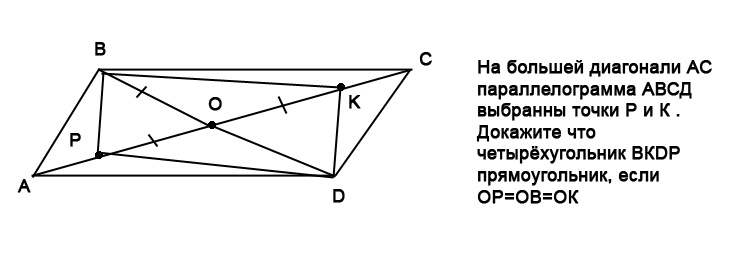
Теоретический материал
Пояснения к формулам для нахождения площади параллелограмма:
- Площадь параллелограмма равна произведению длины одной из его сторон на высоту, опущенную на эту сторону
- Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними
- Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними
Задачи на поиск площади параллелограмма
Задача .В параллелограмме меньшая высота и меньшая сторона равны 9 см и корню 82 соответственно. Большая диагональ — 15 см. Найдите площадь параллелограмма.
Решение .
Обозначим высоту нижнего параллелограмма ABCD, опущенного из точки B на большее основание AD, как BK.
Найдите значение катета прямоугольного треугольника ABK, образованного меньшей высотой, меньшей стороной и частью большего основания. По теореме Пифагора:
AB 2 = BK 2 + AK 2
82 = 9 2 + AK 2
AK 2 = 82 — 81
AK = 1
Продолжим верхнее основание параллелограмма BC и опустите высоту AN от его нижнего основания. AN = BK как стороны прямоугольника ANBK. В получившемся прямоугольном треугольнике ANC находим боковой катет NC.
AN = BK как стороны прямоугольника ANBK. В получившемся прямоугольном треугольнике ANC находим боковой катет NC.
AN 2 + NC 2 = AC 2
9 2 + NC 2 = 15 2
NC 2 = 225 — 81
NC 2 = √144
NC = 12
Теперь найдите большее основание BC параллелограмм ABCD.
BC = NC — NB
Учтем, что NB = AK как стороны прямоугольника, то
BC = 12 — 1 = 11
Площадь параллелограмма равна произведению основания и высоту этого основания.
S = ah
S = BC * BK
S = 11 * 9 = 99
Ответ : 99 см 2.
Задача
В параллелограмме АВСД перпендикуляр ВО опущен к диагонали АС. Найдите площадь параллелограмма, если АО = 8, ОС = 6, а БО = 4. Решение .
Опустим еще один перпендикуляр DK на диагональ AC.
Соответственно, треугольники AOB и DKC, COB и AKD попарно равны.Одна из сторон является противоположной стороной параллелограмма, один из углов — это прямая линия, поскольку она перпендикулярна диагонали, а один из оставшихся углов — это внутренний крест, лежащий для параллельных сторон параллелограмма и секущей.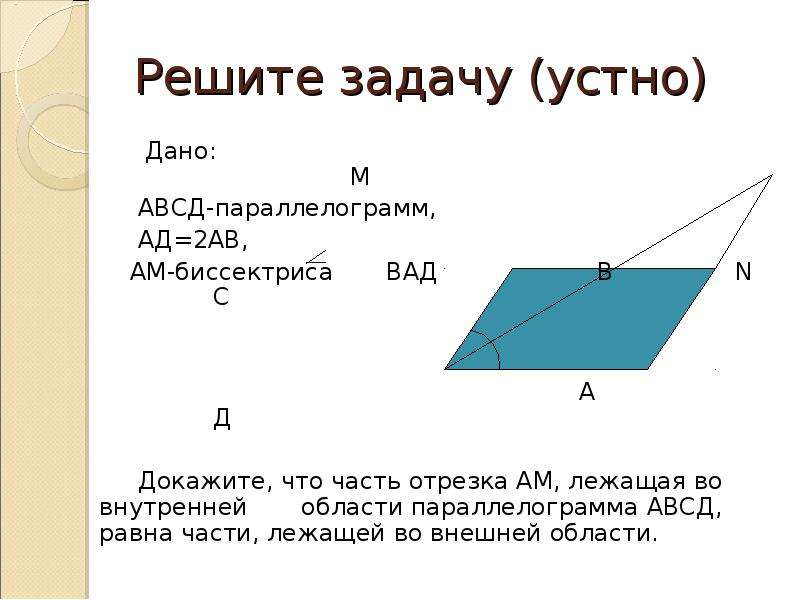 диагональ.
диагональ.
Таким образом, площадь параллелограмма равна площади этих треугольников. Т.е.
Sparal = 2S AOB + 2S BOC
Площадь прямоугольного треугольника равна половине произведения катетов.Где от
S = 2 (1/2 8 * 4) + 2 (1/2 6 * 4) = 56 см 2
Ответ : 56 см 2.
Теорема 1 Площадь трапеции равна произведению половины суммы ее оснований на высоту:
Теорема 2 Диагонали трапеции делят ее на четыре треугольника, два из которых похожи, а два других имеют одинаковую площадь:
Теорема 3 Площадь параллелограмма равна произведению основания на высоту, опущенную до этого основания, или произведению двух сторон на синус угла между ними:
Теорема 4 В параллелограмме сумма квадратов диагоналей равна сумме квадратов его сторон:
Теорема 5 Площадь произвольного выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними:
Теорема 6 Площадь четырехугольника, описанного вокруг круга, равна произведению полупериметра этого четырехугольника на радиус этого круга:
Теорема 7 Четырехугольник, вершинами которого являются середины сторон произвольного выпуклого четырехугольника, является параллелограммом, площадь которого равна половине площади исходного четырехугольника:
Теорема 8. Если диагонали выпуклого четырехугольника взаимно перпендикулярны, то суммы квадратов противоположных сторон этого четырехугольника равны:
Если диагонали выпуклого четырехугольника взаимно перпендикулярны, то суммы квадратов противоположных сторон этого четырехугольника равны:
AB2 + CD2 = BC2 + AD2.
Статья опубликована при поддержке компании ДКРОСТ. Детские горки, домики, песочницы и многое другое — изготовление и продажа детских площадок оптом и в розницу. Самые низкие цены, скидки, короткие сроки выполнения заказа, выезд и консультации специалистов, гарантия качества.Узнать больше о компании, посмотреть каталог товаров, цены и контакты можно на сайте, который находится по адресу: http://dkrost.ru/.
Доказательства некоторых теорем
Доказательство теоремы 2 . Пусть ABCD — заданная трапеция, AD и BC — ее основания, O — точка пересечения диагоналей AC и BD этой трапеции. Докажем, что треугольники AOB и COD имеют одинаковую площадь. Для этого опустите перпендикуляры BP и CQ из точек B и C на линию AD.Тогда площадь треугольника ABD равна
.А площадь треугольника ACD равна
Поскольку BP = CQ, то S∆ABD = S∆ACD. Но площадь треугольника AOB — это разница площадей треугольников ABD и AOD, а площадь треугольника COD — это разница площадей треугольников ACD и AOD. Следовательно, площади треугольников AOB и COD равны, как требуется.
Но площадь треугольника AOB — это разница площадей треугольников ABD и AOD, а площадь треугольника COD — это разница площадей треугольников ACD и AOD. Следовательно, площади треугольников AOB и COD равны, как требуется.
Доказательство теоремы 4 .Пусть ABCD — параллелограмм, AB = CD = a , AD = BC = b,
AC = d1, BD = d2, ∠BAD = α, ∠ADC = 180 ° — α. Применяем теорему косинусов к треугольнику ABD:
Теперь, применяя теорему косинусов к треугольнику ACD, получаем:
Суммируя почтовые равенства, получаем q.E.D.
Доказательство теоремы 5. Пусть ABCD — произвольный выпуклый четырехугольник, E — точка пересечения его диагоналей, AE = a , BE = b,
CE = c, DE = d, ∠AEB = ∠CED = ϕ, ∠BEC =
= ∠AED = 180 ° — ϕ.У нас:
q.E.D.
Доказательство теоремы 6 . Пусть ABCD — произвольный четырехугольник, описанный около круга, O — центр этой окружности, OK, OL, OM и ON — перпендикуляры, опущенные из точки O на прямые AB, BC, CD и AD соответственно. У нас:
У нас:
где r — радиус окружности, а p — полупериметр четырехугольника ABCD.
Доказательство теоремы 7 .Пусть ABCD — произвольный выпуклый четырехугольник, K, L, M и N — середины сторон AB, BC, CD и AD соответственно. Поскольку KL является средней линией треугольника ABC, прямая KL параллельна прямой AC и аналогично, прямая MN параллельна прямой AC и, следовательно, KLMN является параллелограммом. Рассмотрим треугольник KBL. Его площадь равна четверти площади треугольника ABC. Площадь треугольника MDN также равна четверти площади треугольника ACD.Следовательно,
Аналогично
Это означает, что
откуда следует, что
Доказательство теоремы 8 . Пусть ABCD — произвольный выпуклый четырехугольник, диагонали которого взаимно перпендикулярны, пусть E — точка пересечения его диагоналей,
AE = a , BE = b, CE = c, DE = d. Применим теорему Пифагора к треугольникам ABE и CDE:
AB2 = AE2 + BE2 = a 2 + b2,
CD2 = CE2 + DE2 = c2 + d2,
следовательно,
AB2 + CD2 = а 2 + b2 + c2 + d2.
Теперь применив теорему Пифагора к треугольникам ADE и BCE, получим:
AD2 = AE2 + DE2 = a 2 + d2,
BC2 = BE2 + CE2 = b2 + c2, откуда следует
, что
AD2 + BC2 = a 2 + b2 + c2 + d2.
Следовательно, AB2 + CD2 = AD2 + BC2, что и требуется.
Решения задач
Задача 1 . Трапеция с углами у основания α и β описана около круга.Найдите отношение площади трапеции к площади круга.
Решение . Пусть ABCD — заданная трапеция, AB и CD — их основания, DK и CM — перпендикуляры, опущенные из точек C и D на прямую AB. Желаемое соотношение не зависит от радиуса круга. Поэтому считаем, что радиус равен 1. Тогда площадь круга равна π, находим площадь трапеции. Поскольку треугольник ADK прямоугольный, то
Аналогично из прямоугольного треугольника BCM находим, что Поскольку в эту трапецию можно вписать круг, суммы противоположных сторон равны:
AB + CD = AD + BC,
где находим
Значит площадь трапеции
и желаемое соотношение
Ответ :
Задача 2 . В выпуклом четырехугольнике ABCD угол A равен 90 °, а угол C не превышает 90 °. Из вершин B и D перпендикуляры BE и DF падают на диагональ AC. Известно, что AE = CF. Докажите, что угол C прямой.
В выпуклом четырехугольнике ABCD угол A равен 90 °, а угол C не превышает 90 °. Из вершин B и D перпендикуляры BE и DF падают на диагональ AC. Известно, что AE = CF. Докажите, что угол C прямой.
Доказательства . Поскольку угол A равен 90 °,
и угол C не превышает 90 °, то точки E и F лежат на диагонали AC. Без ограничения общности можно считать, что AE ∠EBC = β, ∠FDA = γ, ∠FDC = δ.Нам достаточно доказать, что α + β + γ + δ = π. Как
, откуда мы получаем то, что требовалось для доказательства.
Задача 3 . Периметр равнобедренной трапеции, описанной около круга, равен p. Найдите радиус этого круга, если известно, что острый угол у основания трапеции равен α.
Решение . Пусть ABCD — заданная равнобедренная трапеция с основаниями AD и BC, пусть BH — высота этой трапеции, опущенной из вершины B.
Поскольку в эту трапецию можно вписать круг, то
Следовательно,
Из прямоугольного треугольника ABH находим
Ответ :
Задача 4 . Дана трапеция ABCD с основаниями AD и BC. Диагонали AC и BD пересекаются в точке O, а прямые AB и CD пересекаются в точке K. Прямая KO пересекает стороны BC и AD в точках M и N соответственно, а угол BAD равен 30 °. Известно, что в трапеции ABMN и NMCD можно вписать круг.Найдите отношение площадей треугольника BKC и трапеции ABCD.
Дана трапеция ABCD с основаниями AD и BC. Диагонали AC и BD пересекаются в точке O, а прямые AB и CD пересекаются в точке K. Прямая KO пересекает стороны BC и AD в точках M и N соответственно, а угол BAD равен 30 °. Известно, что в трапеции ABMN и NMCD можно вписать круг.Найдите отношение площадей треугольника BKC и трапеции ABCD.
Решение . Как известно, для произвольной трапеции прямая линия, соединяющая точку пересечения диагоналей и точку пересечения продолжений сторон, делит каждое из оснований пополам. Итак, БМ = МС и АН = НД. Далее, поскольку в трапеции ABMN и NMCD можно вписать круг, то
BM + AN = AB + MN,
MC + ND = CD + MN.
Отсюда следует, что AB = CD, то есть трапеция ABCD равнобедренная. Желаемое соотношение площадей не зависит от масштаба, поэтому можно считать, что KN = x, KM = 1. Из прямоугольных треугольников AKN и BKM получаем это, записав соотношение, уже использованное выше
BM. + АН = АБ + МН ⇔
Нам нужно вычислить соотношение:
Здесь мы использовали тот факт, что площади треугольников AKD и BKC называются квадратами сторон KN и KM, то есть x2.
Ответ:
Задача 5. В выпуклом четырехугольнике ABCD точки E, F, H, G — середины сторон AB, BC, CD, DA соответственно, а O — точка пересечения отрезков EH и FG. Известно, что EH = a , FG = b, Найдите длины диагоналей четырехугольника.
Решение . Известно, что если соединить последовательно середины сторон произвольного четырехугольника, то получится параллелограмм.В нашем случае EFHG — параллелограмм, а O — точка пересечения его диагоналей. Тогда
Применим теорему косинусов к треугольнику FOH:
Поскольку FH является средней линией треугольника BCD, то
Аналогичным образом, применяя теорему косинусов к треугольнику EFO, мы находим, что
Ответ :
Задача 6. Стороны трапеции равны 3 и 5. Известно, что в трапецию можно вписать окружность.Средняя линия трапеции делит ее на две части, соотношение площадей которых равно Найти основание трапеции.
Решение . Пусть ABCD — заданная трапеция, AB = 3 и CD = 5 — ее боковые стороны, точки K и M — середины сторон AB и CD соответственно. Пусть для определенности AD> BC, тогда площадь трапеции AKMD будет больше площади трапеции KBCM. Поскольку KM является средней линией трапеции ABCD, трапеции AKMD и KBCM имеют одинаковую высоту.Поскольку площадь трапеции равна произведению половины суммы оснований на высоту, справедливо равенство
Далее, поскольку в трапецию ABCD можно вписать круг, то AD + BC = AB + CD = 8. Тогда KM = 4 как средняя линия трапеции ABCD. Пусть BC = x, тогда AD = 8 — x. Имеем:
Следовательно, ВС = 1 и н.э. = 7.
Ответ: 1 и 7.
Задача 7 .Основание AB трапеции ABCD вдвое длиннее основания CD и вдвое длиннее стороны AD. Длина диагонали AC равна a , а длина стороны BC равна b. Найдите площадь трапеции.
Решение . Пусть E — точка пересечения продолжений сторон трапеции и CD = x, тогда AD = x, AB = 2x. Отрезок CD параллелен отрезку AB и составляет половину его длины, что означает, что CD является средней линией треугольника ABE.Следовательно, CE = BC = b и DE = AD = x, откуда AE = 2x. Итак, треугольник ABE равнобедренный (AB = AE) и AC — его медиана. Следовательно, AC также является высотой этого треугольника, и, следовательно,
Отрезок CD параллелен отрезку AB и составляет половину его длины, что означает, что CD является средней линией треугольника ABE.Следовательно, CE = BC = b и DE = AD = x, откуда AE = 2x. Итак, треугольник ABE равнобедренный (AB = AE) и AC — его медиана. Следовательно, AC также является высотой этого треугольника, и, следовательно,
Поскольку треугольник DEC аналогичен треугольнику AEB с коэффициентом подобия,
Ответ :
Задача 8 . Диагонали трапеции ABCD пересекаются в точке E. Найдите площадь треугольника BCE, если длины оснований трапеции AB = 30, DC = 24, боковой стороны AD = 3 и угла DAB составляет 60 °.
Решение . Пусть DH — высота трапеции. Из треугольника ADH находим, что
Поскольку высота треугольника ABC, исключенная из вершины C, равна высоте DH трапеции, имеем:
Ответ :
Задача 9 . В трапеции средняя линия равна 4, а углы у одного из оснований равны 40 ° и 50 °. Найдите основания трапеции, если отрезок, соединяющий середины оснований, равен 1.
Найдите основания трапеции, если отрезок, соединяющий середины оснований, равен 1.
Решение . Пусть ABCD — заданная трапеция, AB и CD — ее основания (AB AB + CD = 8. Продолжим стороны DA и CB до пересечения в точке E. Рассмотрим треугольник ABE, в котором ∠EAB = 50 °. ∠EBA = 40 °,
, следовательно, AEB = 90 °. Медиана EM этого треугольника, проведенная из вершины прямого угла, равна половине гипотенузы: EM = AM. Пусть EM = x , то AM = x, DN = 4 — x. По условию задачи MN = 1, следовательно,
EN = x + 1.Из подобия треугольников AEM и DEN имеем:
Это означает, что AB = 3 и CD = 5.
Ответ : 3 и 5.
Задача 10 . Выпуклый четырехугольник ABCD описывается около круга с центром в точке O, при этом AO = OC = 1, BO = OD = 2. Найдите периметр четырехугольника ABCD.
Решение . Пусть K, L, M, N — точки касания окружности со сторонами AB, BC, CD, DA соответственно, r — радиус окружности. Поскольку касательная к окружности перпендикулярна радиусу, проведенному до точки касания, треугольники AKO, BKO, BLO, CLO, CMO, DMO, DNO, ANO имеют прямоугольную форму. Применяя к этим треугольникам теорему Пифагора, получаем
Поскольку касательная к окружности перпендикулярна радиусу, проведенному до точки касания, треугольники AKO, BKO, BLO, CLO, CMO, DMO, DNO, ANO имеют прямоугольную форму. Применяя к этим треугольникам теорему Пифагора, получаем
Следовательно, AB = BC = CD = DA, то есть ABCD — ромб. Диагонали ромба перпендикулярны друг другу, а точка их пересечения — центр вписанной окружности. Отсюда легко найти, что стороны ромба равны, а это значит, что периметр ромба равен
Ответ :
Задачи для самостоятельного решения
С-1. Равнобедренная трапеция ABCD описана вокруг круга радиуса r. Пусть E и K — точки касания этой окружности со сторонами трапеции. Угол между основанием AB и боковой стороной AD трапеции составляет 60 °. Докажите, что EK параллельно AB, и найдите площадь трапеции ABEK.
С-2. У трапеции диагонали 3 и 5, а отрезок, соединяющий середины оснований, равен 2. Найдите площадь трапеции.
С-3 . Можно ли описать окружность вокруг четырехугольника ABCD, если ∠ADC = 30 °, AB = 3, BC = 4, AC = 6?
Можно ли описать окружность вокруг четырехугольника ABCD, если ∠ADC = 30 °, AB = 3, BC = 4, AC = 6?
С-4. В трапеции ABCD (AB — основание) углы DAB, BCD, ADC, ABD и ADB образуют арифметическую прогрессию (в том порядке, в котором они написаны). Найдите расстояние от вершины C до диагонали BD, если высота трапеции равна h.
С-5. Дана равнобедренная трапеция, в которую вписан круг и вокруг которой описывается круг.Отношение высоты трапеции к радиусу описанной окружности равно Найти углы трапеции.
С-6. Площадь прямоугольника ABCD равна 48, а длина диагонали — 10. На плоскости, в которой расположен прямоугольник, выбирается точка O так, чтобы OB = OD = 13. Найти расстояние от точки O до самой дальней от него вершины прямоугольника.
С-7. Периметр параллелограмма ABCD равен 26. Угол ABC равен 120 °.Радиус вписанной в треугольник BCD окружности равен Найти длины сторон параллелограмма, если известно, что AD> AB.
С-8. Четырехугольник ABCD вписан в круг с центром в точке O. Радиус OA перпендикулярен радиусу OB, а радиус OC перпендикулярен радиусу OD. Длина перпендикуляра, опущенного из точки C на линию AD, равна 9. Длина отрезка BC в два раза меньше длины отрезка AD.Найдите площадь треугольника AOB.
Радиус OA перпендикулярен радиусу OB, а радиус OC перпендикулярен радиусу OD. Длина перпендикуляра, опущенного из точки C на линию AD, равна 9. Длина отрезка BC в два раза меньше длины отрезка AD.Найдите площадь треугольника AOB.
С-9. В выпуклом четырехугольнике ABCD вершины A и C противоположны, а длина стороны AB равна 3. Угол ABC равен углу BCD. Найдите длину стороны AD, если известно, что площадь четырехугольника
S-10. Диагонали AC и BD начерчены в выпуклом четырехугольнике ABCD. Известно, что
AD = 2, ∠ABD = ∠ACD = 90 °, а расстояние между точкой пересечения биссектрис треугольника ABD и точкой пересечения биссектрис треугольника ACD равно Find длина стороны ВС.
С-11. Пусть M — точка пересечения диагоналей выпуклого четырехугольника ABCD, в котором стороны AB, AD и BC равны друг другу. Найдите угол CMD, если известно, что DM = MC,
и ∠CAB ≠ ∠DBA.
С-12. В четырехугольнике ABCD известно, что ∠A = 74 °, ∠D = 120 °.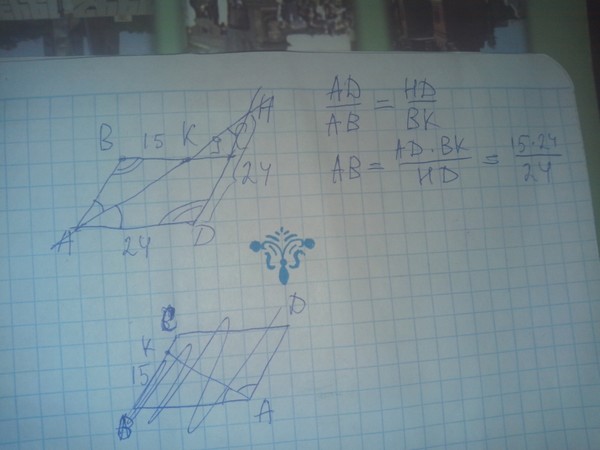 Найдите угол между биссектрисами углов B и C.
Найдите угол между биссектрисами углов B и C.
S-13. В ABCD можно вписать круг. Пусть K — точка пересечения его диагоналей.Известно, что AB> BC> KC, а периметр и площадь треугольника BKC равны 14 и 7. Найдите DC.
С-14. В описанной по кругу трапеции известно, что BC AD, AB = CD, ∠BAD =
= 45 °. Найдите AB, если площадь трапеции ABCD равна 10.
S-15. В трапеции ABCD с основаниями AB и CD известно, что ∠CAB = 2∠DBA. Найдите площадь трапеции.
С-16. В параллелограмме ABCD известно, что AC = a , ∠CAB = 60 °. Найдите площадь параллелограмма.
С-17 . В четырехугольнике ABCD диагонали AC и BD пересекаются в точке K. Точки L и M являются серединами сторон BC и AD соответственно. Отрезок LM содержит точку K. Четырехугольник ABCD таков, что в него можно вписать окружность. Найдите радиус этой окружности, если AB = 3, а LK: KM = 1: 3.
S-18. Диагонали AC и BD нарисованы в выпуклом четырехугольнике ABCD.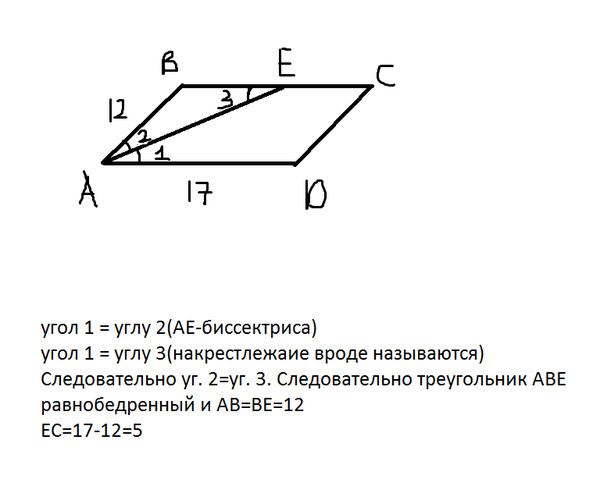 Причем ∠BAC =
Причем ∠BAC =
= ∠BDC, а площадь описанной окружности возле треугольника BDC равна
а) Найдите радиус окружности, описанной вокруг треугольника ABC.
б) Зная, что BC = 3, AC = 4, ∠BAD = 90 °, найдите площадь четырехугольника ABCD.
Формула для площади параллелограмма
Площадь параллелограмма равна произведению его стороны на высоту, опущенную на эту сторону.
Доказательства
Если параллелограмм является прямоугольником, то равенство выполняется по теореме о площади прямоугольника.Далее считаем, что углы параллелограмма не прямые.
Пусть угол $ \ angle BAD $ острый в параллелограмме $ ABCD $ и $ AD> AB $. В противном случае переименуйте вершины. Тогда высота $ BH $ от вершины $ B $ до прямой $ AD $ падает в сторону $ AD $, так как катет $ AH $ короче гипотенузы $ AB $, а $ AB
Сравните площадь параллелограмма $ ABCD $ и площадь прямоугольника $ HBCK $. Площадь параллелограмма больше на $ \\ треугольник ABH $, но меньше на $ \\ треугольник DCK $.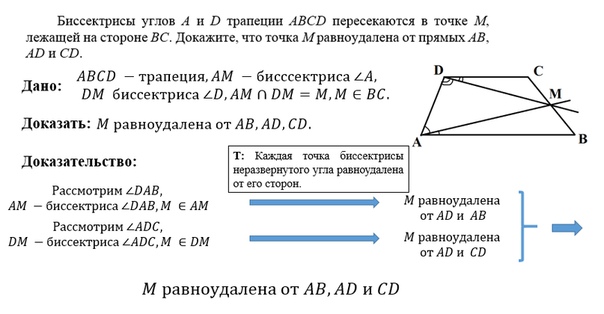 \ circ — \ \ angle AOD $.Следовательно, синусы углов на пересечении диагоналей равны $ \\ sin \\ alpha $.
\ circ — \ \ angle AOD $.Следовательно, синусы углов на пересечении диагоналей равны $ \\ sin \\ alpha $.
$ S_ (ABCD) = S _ (\ треугольник AOB) + S _ (\ треугольник BOC) + S _ (\ треугольник COD) + S _ (\ треугольник AOD) $
по аксиоме площадь измерения. Применяем формулу площади треугольника $ S_ (ABC) = \ dfrac (1) (2) \ cdot AB \ cdot BC \ sin \ angle ABC $ для этих треугольников и углов при пересечении диагоналей. Стороны каждой равны половине диагоналей, синусы тоже равны.Следовательно, площади всех четырех треугольников равны $ S = \ dfrac (1) (2) \ cdot \ dfrac (AC) (2) \ cdot \ dfrac (BD) (2) \ cdot \ \ sin \ alpha = \ dfrac (AC \ Суммируя все вышесказанное, получаем
$ S_ (ABCD) = 4S = 4 \ cdot \ dfrac (AC \ cdot BD) (8) \ sin \ alpha = \ dfrac (AC \ cdot BD \ cdot \ грех \ альфа) (2) $
Параллелограмм равен половине произведения его диагоналей. Площадь параллелограмма. Задачи на поиск площади параллелограмма
Формула площади параллелограмма
Площадь параллелограмма равна произведению его стороны на высоту, опущенную на эту сторону.
Доказательства
Если параллелограмм прямоугольник, то равенство выполняется по теореме о площади прямоугольника. Далее считаем, что углы параллелограмма не прямые.
Пусть в параллелограмме $ ABCD $ угол $ \ angle BAD $ острый и $ AD> AB $. В противном случае переименуйте вершины. Тогда высота $ BH $ от вершины $ B $ до прямой $ AD $ падает на сторону $ AD $, так как катет $ AH $ короче гипотенузы $ AB $, а $ AB
Сравним площадь параллелограмма $ ABCD $ и площадь прямоугольника $ HBCK $.Площадь параллелограмма больше на площадь $ \\ треугольника ABH $, но меньше на площадь $ \\ треугольника DCK $. Поскольку эти треугольники равны, значит, их площади равны. Это означает, что площадь параллелограмма равна площади прямоугольника с длиной сторон в сторону и высотой параллелограмма.
Формула площади параллелограмма через стороны и синус
Площадь параллелограмма равна произведению соседних сторон на синус угла между ними.
Доказательства
Высота параллелограмма $ ABCD $, опущенного в сторону $ AB $, равна произведению отрезка $ BC $ на синус угла $ \ angle ABC $. Осталось применить предыдущее утверждение.
Осталось применить предыдущее утверждение.
Формула площади параллелограмма через диагонали
Площадь параллелограмма равна половине произведения диагоналей и синуса угла между ними.
Доказательства
Пусть диагонали параллелограмма $ ABCD $ пересекаются в точке $ O $ под углом $ \ alpha $.\\ circ — \\ угол AOD $. Это означает, что синусы углов на пересечении диагоналей равны $ \\ sin \\ alpha $.
$ S_ (ABCD) = S _ (\ треугольник AOB) + S _ (\ треугольник BOC) + S _ (\ треугольник COD) + S _ (\ треугольник AOD) $
по аксиоме измерения площади. Примените формулу площади треугольника $ S_ (ABC) = \ dfrac (1) (2) \ cdot AB \ cdot BC \ sin \ angle ABC $ для этих треугольников и углов на пересечении диагоналей.Стороны каждой равны половине диагоналей, синусы тоже равны. Следовательно, площади всех четырех треугольников равны $ S = \ dfrac (1) (2) \ cdot \ dfrac (AC) (2) \ cdot \ dfrac (BD) (2) \ cdot \ \ sin \ alpha = \ dfrac (AC \ Суммируя все вышесказанное, получаем
$ S_ (ABCD) = 4S = 4 \ cdot \ dfrac (AC \ cdot BD) (8) \ sin \ alpha = \ dfrac (AC \ cdot BD \ cdot \ грех \ альфа) (2) $
Теорема 1. Площадь трапеции равна произведению полусуммы ее оснований на высоту:
Площадь трапеции равна произведению полусуммы ее оснований на высоту:
Теорема 2. Диагонали трапеции делят ее на четыре треугольника, два из которых похожи, а два других имеют одинаковую площадь:
Теорема 3. Площадь параллелограмма равна произведению основания и высоты, пониженной на данное основание, или произведению двух сторон на синус угла между ними:
Теорема 4. В параллелограмме сумма квадратов диагоналей равна сумме квадратов его сторон:
Теорема 5. Площадь произвольного выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними:
Теорема 6. Площадь четырехугольника, описанного вокруг окружности, равна произведению полупериметра этого четырехугольника на радиус этой окружности:
Теорема 7. Четырехугольник, вершинами которого являются середины сторон произвольного выпуклого четырехугольника, является параллелограммом, площадь которого равна половине площади исходного четырехугольника:
Теорема 8. Если диагонали выпуклого четырехугольника взаимно перпендикулярны, то суммы квадратов противоположных сторон этого четырехугольника равны:
Если диагонали выпуклого четырехугольника взаимно перпендикулярны, то суммы квадратов противоположных сторон этого четырехугольника равны:
AB2 + CD2 = BC2 + AD2.
Статья опубликована при поддержке компании ДКРОСТ. Детские горки, домики, песочницы и многое другое — производство и продажа детских площадок оптом и в розницу. Самые низкие цены, скидки, короткие сроки изготовления, выезд и консультация специалиста, гарантия качества.Узнать больше о компании, посмотреть каталог товаров, цены и контакты можно на сайте, который находится по адресу: http://dkrost.ru/.
Доказательства некоторых теорем
Доказательство теоремы 2 … Пусть ABCD — заданная трапеция, AD и BC — ее основания, O — точка пересечения диагоналей AC и BD этой трапеции. Докажем, что треугольники AOB и COD имеют одинаковую площадь. Для этого опускаем перпендикуляры BP и CQ из точек B и C на линию AD.Тогда площадь треугольника ABD равна
.А площадь треугольника ACD равна
Поскольку BP = CQ, то S∆ABD = S∆ACD. Но площадь треугольника AOB — это разница между площадями треугольников ABD и AOD, а площадь треугольника COD — это разность площадей треугольников ACD и AOD. Следовательно, площади треугольников AOB и COD равны, как требуется.
Но площадь треугольника AOB — это разница между площадями треугольников ABD и AOD, а площадь треугольника COD — это разность площадей треугольников ACD и AOD. Следовательно, площади треугольников AOB и COD равны, как требуется.
Доказательство теоремы 4 … Пусть ABCD — параллелограмм, AB = CD = a , AD = BC = b,
AC = d1, BD = d2, ∠BAD = α, ∠ADC = 180 ° — α. Применим теорему косинусов к треугольнику ABD:
Теперь применив теорему косинусов к треугольнику ACD, мы получим:
Складывая полученные почленные равенства, получаем, что q.E.D.
Доказательство теоремы 5. Пусть ABCD — произвольный выпуклый четырехугольник, E — точка пересечения его диагоналей, AE = a , BE = b,
CE = c, DE = d, ∠AEB \ u003d ∠CED = ϕ, ∠BEC =
= ∠AED = 180 ° — ϕ.У нас:
q.E.D.
Доказательство теоремы 6 … Пусть ABCD — произвольный четырехугольник, описанный вокруг окружности, O — центр этой окружности, OK, OL, OM и ON — перпендикуляры, опущенные из точки O на прямые AB, BC, CD и AD соответственно.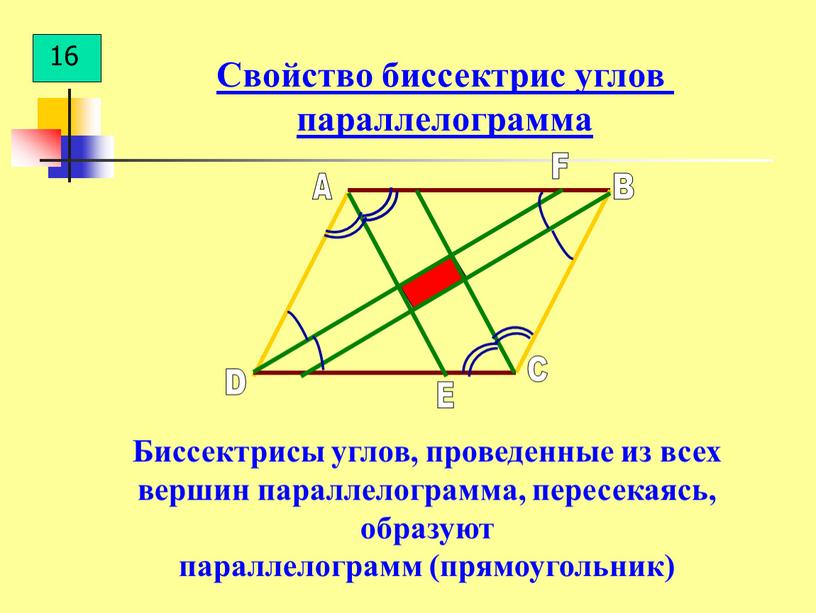 У нас:
У нас:
где r — радиус окружности, а p — полупериметр четырехугольника ABCD.
Доказательство теоремы 7 … Пусть ABCD — произвольный выпуклый четырехугольник, K, L, M и N — середины сторон AB, BC, CD и AD соответственно. Поскольку KL является средней линией треугольника ABC, прямая KL параллельна прямой AC и аналогично, прямая MN параллельна прямой AC, и, следовательно, KLMN является параллелограммом. Рассмотрим треугольник KBL. Его площадь равна четверти площади треугольника ABC. Площадь треугольника MDN также равна четверти площади треугольника ACD.Следовательно,
Аналогично
Это означает, что
откуда следует, что
Доказательство теоремы 8 … Пусть ABCD — произвольный выпуклый четырехугольник, диагонали которого взаимно перпендикулярны, пусть E — точка пересечения его диагоналей,
AE = a , BE = b, CE = c , DE = d. Применим теорему Пифагора к треугольникам ABE и CDE:
AB2 = AE2 + BE2 = a 2 + b2,
CD2 = CE2 + DE2 = c2 + d2,
следовательно,
AB2 + CD2 = а 2 + b2 + c2 + d2.
Теперь применив теорему Пифагора к треугольникам ADE и BCE, получим:
AD2 = AE2 + DE2 = a 2 + d2,
BC2 = BE2 + CE2 = b2 + c2, откуда следует
, что
AD2 + BC2 = a 2 + b2 + c2 + d2.
Следовательно, AB2 + CD2 = AD2 + BC2, что и требуется.
Решение проблем
Задача 1 … Трапеция с углами α и β в основании описывается по окружности. Найдите отношение площади трапеции к площади круга.
Решение … Пусть ABCD — заданная трапеция, AB и CD — ее основания, DK и CM — перпендикуляры, опущенные из точек C и D на линию AB. Желаемое соотношение не зависит от радиуса круга. Поэтому будем считать, что радиус равен 1. Тогда площадь окружности равна π, находим площадь трапеции. Поскольку треугольник ADK прямоугольный,
Аналогично из прямоугольного треугольника BCM находим, что Поскольку в эту трапецию можно вписать круг, суммы противоположных сторон равны:
AB + CD = AD + BC,
где находим
Следовательно, площадь трапеции равна
и желаемое соотношение
Ответ :
Задача 2 . .. В выпуклом четырехугольнике ABCD угол A равен 90 °, а угол C не превышает 90 °. Перпендикуляры BE и DF опущены из вершин B и D на диагональ AC. Известно, что AE = CF. Докажите, что угол C прямой.
.. В выпуклом четырехугольнике ABCD угол A равен 90 °, а угол C не превышает 90 °. Перпендикуляры BE и DF опущены из вершин B и D на диагональ AC. Известно, что AE = CF. Докажите, что угол C прямой.
Evidence … Поскольку угол A равен 90 °,
и угол C не превышает 90 °, то точки E и F лежат на диагонали AC. Без ограничения общности можно считать, что AE ∠EBC = β, ∠FDA = γ, ∠FDC = δ.Нам достаточно доказать, что α + β + γ + δ = π. Потому что
, что и требовалось доказать.
Задача 3 … Периметр равнобедренной трапеции, описанной вокруг окружности, равен p. Найдите радиус этого круга, если известно, что острый угол у основания трапеции равен α.
Решение … Пусть ABCD — заданная равнобедренная трапеция с основаниями AD и BC, пусть BH — высота этой трапеции, опущенной из вершины B.
Так как в эту трапецию можно вписать круг, то
Следовательно,
Из прямоугольного треугольника ABH находим,
Ответ :
Задача 4 .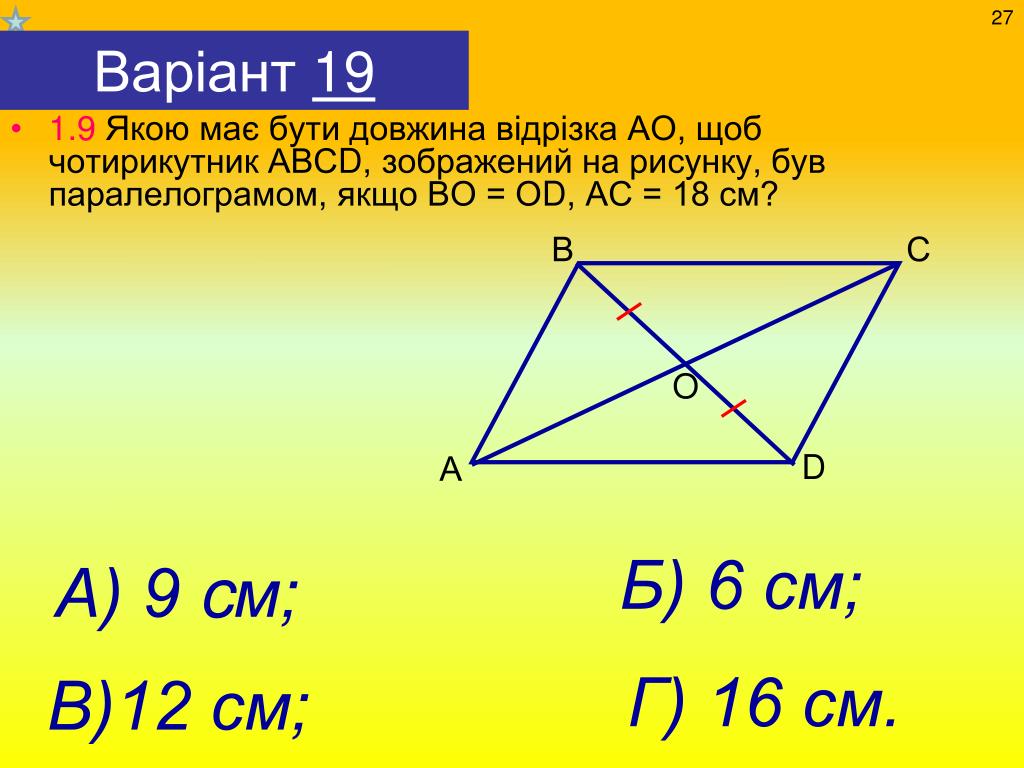 .. Вам дана трапеция ABCD с основаниями AD и BC. Диагонали AC и BD пересекаются в точке O, а прямые AB и CD пересекаются в точке K. Прямая KO пересекает стороны BC и AD в точках M и N соответственно, а угол BAD равен 30 °. Известно, что круг можно вписать в трапеции ABMN и NMCD.Найдите соотношение площадей треугольника BKC и трапеции ABCD.
.. Вам дана трапеция ABCD с основаниями AD и BC. Диагонали AC и BD пересекаются в точке O, а прямые AB и CD пересекаются в точке K. Прямая KO пересекает стороны BC и AD в точках M и N соответственно, а угол BAD равен 30 °. Известно, что круг можно вписать в трапеции ABMN и NMCD.Найдите соотношение площадей треугольника BKC и трапеции ABCD.
Решение … Как известно, для произвольной трапеции линия, соединяющая точку пересечения диагоналей и точку пересечения продолжений боковых сторон, делит каждое из оснований пополам. Итак, БМ = МС и АН = НД. Далее, поскольку круг можно вписать в трапеции ABMN и NMCD, то
BM + AN = AB + MN,
MC + ND = CD + MN.
Отсюда следует, что AB = CD, то есть трапеция ABCD равнобедренная. Искомое соотношение площадей не зависит от масштаба, поэтому можно считать, что KN = x, KM = 1. Из прямоугольных треугольников AKN и BKM получаем, что Записывая соотношение уже использованное выше
BM + AN = AB + MN ⇔
Нам нужно вычислить соотношение:
Здесь мы использовали тот факт, что площади треугольников AKD и BKC связаны как квадраты сторон KN и KM, то есть как x2.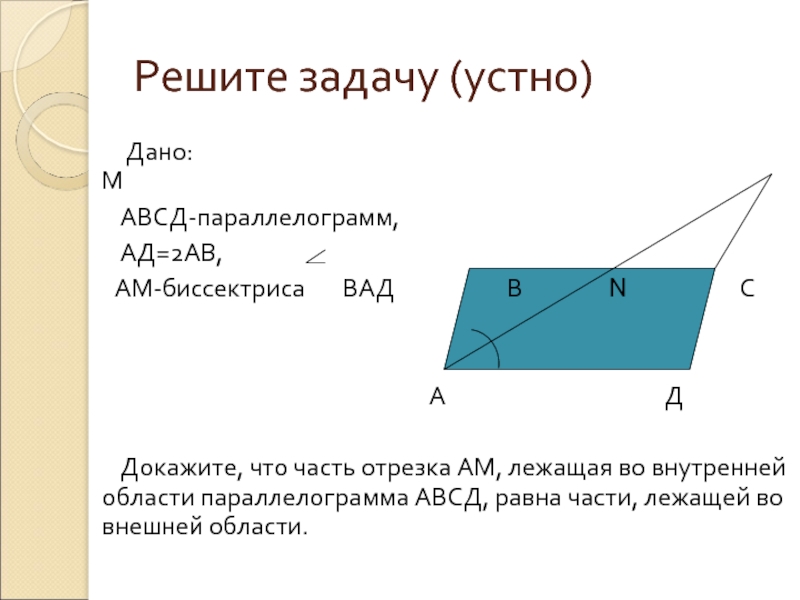
Ответ:
Цель 5. В выпуклом четырехугольнике ABCD точки E, F, H, G — середины сторон AB, BC, CD, DA соответственно, а O — точка пересечения отрезков EH и FG. Известно, что EH = a , FG = b, Найдите длины диагоналей четырехугольника.
Решение … Известно, что если соединить последовательно середины сторон произвольного четырехугольника, получится параллелограмм.В нашем случае EFHG — параллелограмм, а O — точка пересечения его диагоналей. Тогда
Примените теорему косинусов к треугольнику FOH:
Поскольку FH является средней линией треугольника BCD, то
Аналогичным образом, применяя теорему косинусов к треугольнику EFO, мы находим, что
Ответ :
Задание 6. Стороны трапеции равны 3 и 5. Известно, что в трапецию можно вписать окружность.Средняя линия трапеции делит ее на две части, отношение площадей которых равно Найти основания трапеции.
Решение … Пусть ABCD — заданная трапеция, AB = 3 и CD = 5 — ее боковые стороны, точки K и M — середины AB и CD соответственно. Пусть для определенности AD> BC, тогда площадь трапеции АКМД будет больше площади трапеции КВСМ. Поскольку KM является средней линией трапеции ABCD, трапеции AKMD и KBCM имеют одинаковую высоту.Поскольку площадь трапеции равна произведению полусуммы оснований и высоты, то справедливо равенство
Далее, поскольку круг можно вписать в трапецию ABCD, то AD + BC = AB + CD = 8. Тогда KM = 4 как средняя линия трапеции ABCD. Пусть BC = x, тогда AD = 8 — x. Имеем:
Это значит до н.э. = 1 и н.э. = 7.
Ответ: 1 и 7.
Задача 7 … Основание AB трапеции ABCD вдвое длиннее основания CD и вдвое длиннее боковой стороны AD. Длина диагонали AC равна a , а длина стороны BC равна b. Найдите площадь трапеции.
Решение … Пусть E — точка пересечения продолжений боковых сторон трапеции и CD = x, тогда AD = x, AB = 2x. Отрезок CD параллелен отрезку AB и на половину его длины, поэтому CD — это средняя линия треугольника ABE.Следовательно, CE = BC = b и DE = AD = x, откуда AE = 2x. Итак, треугольник ABE — равнобедренный (AB = AE), а AC — его медиана. Следовательно, AC также является высотой этого треугольника, и, следовательно,
Отрезок CD параллелен отрезку AB и на половину его длины, поэтому CD — это средняя линия треугольника ABE.Следовательно, CE = BC = b и DE = AD = x, откуда AE = 2x. Итак, треугольник ABE — равнобедренный (AB = AE), а AC — его медиана. Следовательно, AC также является высотой этого треугольника, и, следовательно,
Так как треугольник DEC аналогичен треугольнику AEB с коэффициентом подобия, то
Ответ :
Задача 8 … Диагонали трапеции ABCD пересекаются в точке E. Найти площадь треугольника BCE, если длины оснований трапеции равны AB = 30, DC = 24, длина стороны AD = 3, а угол DAB — 60 °.
Решение … Пусть DH будет высотой трапеции. Из треугольника ADH находим, что
Поскольку высота треугольника ABC, опущенного из вершины C, равна высоте DH трапеции, имеем:
Ответ :
Задача 9 … В трапеции средняя линия равна 4, а углы на одном из оснований составляют 40 ° и 50 °. Найдите основания трапеции, если отрезок прямой, соединяющий середины оснований, равен 1.
Найдите основания трапеции, если отрезок прямой, соединяющий середины оснований, равен 1.
Решение … Пусть ABCD — заданная трапеция, AB и CD — ее основания (AB AB + CD = 8. Продолжим стороны DA и CB до пересечения в точке E. Рассмотрим треугольник ABE, в котором ∠ EAB = 50 °. ∠EBA = 40 °,
, следовательно, AEB = 90 °. Медиана EM этого треугольника, проведенная из прямого угла вершины, равна половине гипотенузы: EM = AM. Пусть EM = x, тогда AM = x, DN = 4 — x. По условию задачи MN = 1; следовательно,
EN = x + 1.Из подобия треугольников AEM и DEN имеем:
Это означает AB = 3 и CD = 5.
Ответ : 3 и 5.
Задача 10 … Выпуклый четырехугольник ABCD описан около окружности с центром в точке O, при этом AO = OC = 1, BO = OD = 2. Найдите периметр четырехугольника ABCD.
Решение … Пусть K, L, M, N — точки касания окружности со сторонами AB, BC, CD, DA соответственно, r — радиус окружности. Поскольку касательная к окружности перпендикулярна радиусу, проведенному к точке касания, треугольники AKO, BKO, BLO, CLO, CMO, DMO, DNO, ANO имеют прямоугольную форму. Применяя к этим треугольникам теорему Пифагора, получаем, что
Поскольку касательная к окружности перпендикулярна радиусу, проведенному к точке касания, треугольники AKO, BKO, BLO, CLO, CMO, DMO, DNO, ANO имеют прямоугольную форму. Применяя к этим треугольникам теорему Пифагора, получаем, что
Следовательно, AB = BC = CD = DA, то есть ABCD — ромб. Диагонали ромба перпендикулярны друг другу, а точка их пересечения — центр вписанной окружности. Отсюда легко находим, что стороны ромба равны и, следовательно, периметр ромба равен
Ответ :
Задачи для самостоятельного решения
С-1. Равнобедренная трапеция ABCD описана вокруг круга радиуса r. Пусть E и K — точки касания этой окружности боковыми сторонами трапеции. Угол между основанием AB и боковой стороной AD трапеции составляет 60 °. Докажите, что EK параллельно AB и найдите площадь трапеции ABEK.
С-2. У трапеции диагонали 3 и 5, а отрезок, соединяющий середины оснований, равен 2. Найдите площадь трапеции.
S-3 . .. Можно ли описать окружность вокруг четырехугольника ABCD, если ∠ADC = 30 °, AB = 3, BC = 4, AC = 6?
.. Можно ли описать окружность вокруг четырехугольника ABCD, если ∠ADC = 30 °, AB = 3, BC = 4, AC = 6?
С-4. В трапеции ABCD (AB — основание) углы DAB, BCD, ADC, ABD и ADB образуют арифметическую прогрессию (в том порядке, в котором они написаны). Найдите расстояние от вершины C до диагонали BD, если высота трапеции равна h.
С-5. Вам дана равнобедренная трапеция, в которую вписан круг и вокруг которого описывается круг.Отношение высоты трапеции к радиусу описанной окружности равно Найти углы трапеции.
С-6. Площадь прямоугольника ABCD равна 48, а длина диагонали — 10. На плоскости, в которой расположен прямоугольник, выбирается точка O так, чтобы OB = OD = 13. Найти расстояние от наведите точку O на самую дальнюю от нее вершину прямоугольника.
С-7. Периметр параллелограмма ABCD равен 26. Угол ABC равен 120 °. Радиус окружности, вписанной в треугольник BCD, равен Найти длины сторон параллелограмма, если известно, что AD> AB.
С-8. Четырехугольник ABCD вписан в окружность с центром в точке O. Радиус OA перпендикулярен радиусу OB, а радиус OC перпендикулярен радиусу OD. Длина перпендикуляра, опущенного из точки C в линию AD, равна 9. Длина отрезка BC составляет половину длины отрезка AD. Найдите площадь треугольника AOB.
Радиус OA перпендикулярен радиусу OB, а радиус OC перпендикулярен радиусу OD. Длина перпендикуляра, опущенного из точки C в линию AD, равна 9. Длина отрезка BC составляет половину длины отрезка AD. Найдите площадь треугольника AOB.
С-9. В выпуклом четырехугольнике ABCD вершины A и C противоположны, а длина стороны AB равна 3. Угол ABC равен углу BCD равен Найдите длину стороны AD, если известно, что площадь четырехугольника равна
С-10. Выпуклый четырехугольник ABCD содержит диагонали AC и BD. Известно, что
AD = 2, ∠ABD = ∠ACD = 90 °, а расстояние между пересечением биссектрис треугольника ABD и пересечением биссектрис треугольника ACD равно Найти длину отрезка сторона BC.
С-11. Пусть M — точка пересечения диагоналей выпуклого четырехугольника ABCD, в котором стороны AB, AD и BC равны друг другу. Найдите угол CMD, если известно, что DM = MC,
и ∠CAB ≠ ∠DBA.
С-12. В четырехугольнике ABCD известно, что ∠A = 74 °, ∠D = 120 °. Найдите угол между биссектрисами углов B и C.
Найдите угол между биссектрисами углов B и C.
S-13. В четырехугольник ABCD можно вписать круг. Пусть K — точка пересечения его диагоналей. Известно, что AB> BC> KC, а периметр и площадь треугольника BKC равны 14 и 7 соответственно. Найдите DC.
С-14. В описанной около окружности трапеции известно, что BC AD, AB = CD, ∠BAD =
= 45 °.Найдите AB, если площадь трапеции ABCD равна 10.
S-15. В трапеции ABCD с основаниями AB и CD известно, что ∠CAB = 2∠DBA. Найдите площадь трапеции.
С-16. В параллелограмме ABCD известно, что AC = a , ∠CAB = 60 °. Найдите площадь параллелограмма.
S-17 … В четырехугольнике ABCD диагонали AC и BD пересекаются в точке K. Точки L и M являются серединами сторон BC и AD соответственно.Отрезок LM содержит точку K. Четырехугольник ABCD таков, что в него можно вписать окружность. Найдите радиус этой окружности, если AB = 3 и LK: KM = 1: 3.
S-18. Выпуклый четырехугольник ABCD содержит диагонали AC и BD. Причем ∠BAC =
Причем ∠BAC =
= ∠BDC, а площадь описанной окружности вокруг треугольника BDC равна
а) Найдите радиус окружности, описанной вокруг треугольника ABC.
б) Зная, что BC = 3, AC = 4, ∠BAD = 90 °, найдите площадь четырехугольника ABCD.
При решении задач по этой теме, кроме основных свойств параллелограмма и соответствующих формул, можно запомнить и применить следующее:
- Биссектриса внутреннего угла параллелограмма отсекает от него равнобедренный треугольник
- Биссектрисы внутренних углов, примыкающих к одной из сторон параллелограмма, взаимно перпендикулярны
- Биссектрисы, выходящие из противоположных внутренних углов параллелограмма, параллельны друг другу или лежат на одной прямой
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон
- Площадь параллелограмма равна половине произведения диагоналей и синуса угла между ними
Рассмотрим задачи, при решении которых используются эти свойства.
Цель 1.
Биссектриса угла C параллелограмма ABCD пересекает сторону AD в точке M и продолжение стороны AB за точку A в точке E. Найти периметр параллелограмма, если AE = 4, DМ = 3.
Решение.
1. Треугольник CMD равнобедренный. (Свойство 1). Следовательно, CD = MD = 3 см.
2. Треугольник EAM равнобедренный.
Следовательно, АЕ = АМ = 4 см.
3. AD = AM + MD = 7 см.
4. Периметр ABCD = 20 см.
Ответ. 20 см.
Цель 2.
В выпуклом четырехугольнике ABCD начерчены диагонали. Известно, что площади треугольников ABD, ACD, BCD равны. Докажите, что данный четырехугольник — параллелограмм.
Решение.
1. Пусть BE — высота треугольника ABD, CF — высота треугольника ACD.Поскольку по условию задачи площади треугольников равны и имеют общее основание AD, высоты этих треугольников равны. BE = CF.
2. BE, CF перпендикулярны AD. Точки B и C расположены по одну сторону от линии AD. BE = CF. Следовательно, прямая ВС || ОБЪЯВЛЕНИЕ. (*)
Точки B и C расположены по одну сторону от линии AD. BE = CF. Следовательно, прямая ВС || ОБЪЯВЛЕНИЕ. (*)
3. Пусть АL — высота треугольника АСD, BK — высота треугольника BCD. Поскольку по условию задачи площади треугольников равны и имеют общее основание CD, то высоты этих треугольников равны.АЛ = БК.
4. AL и BK перпендикулярны CD. Точки B и A расположены по одну сторону от прямой CD. АЛ = БК. Следовательно, прямая AB || CD (**)
5. Из условий (*), (**) следует — параллелограмм ABCD.
Ответ. Проверено. ABCD — параллелограмм.
Цель 3.
На сторонах BC и CD параллелограмма ABCD соответственно отмечены точки M и H, так что отрезки BM и HD пересекаются в точке O;
Решение.
1. В треугольнике DOM
2. В прямоугольном треугольнике DHC
(
Тогда (Так как в прямоугольном треугольнике катет, лежащий под углом 30 °, равен половине гипотенузы)
Но CD = AB. Тогда AB: HD = 2: 1.
Тогда AB: HD = 2: 1.
3.
4.
Ответ: AB: НD = 2: 1,
Задача 4.
Одна из диагоналей параллелограмма длиной 4√6 составляет угол 60 ° с основанием, а вторая диагональ составляет угол 45 ° с тем же основанием.Найдите вторую диагональ.
Решение.
1. АО = 2√6.
2. Применим теорему о синусах к треугольнику AOD.
АО / sin D = OD / sin A.
2√6 / sin 45 о = OD / sin 60 о.
ОD = (2√6sin 60 о) / sin 45 о = (2√6 √3 / 2) / (√2 / 2) = 2√18 / √2 = 6.
Ответ: 12.
Цель 5.
У параллелограмма со сторонами 5√2 и 7√2 меньший угол между диагоналями равен меньшему углу параллелограмма.Найдите сумму длин диагоналей.
Решение.
Пусть d 1, d 2 — диагонали параллелограмма, а угол между диагоналями и меньшим углом параллелограмма равен φ.
1. Посчитаем два разных
пути его площади.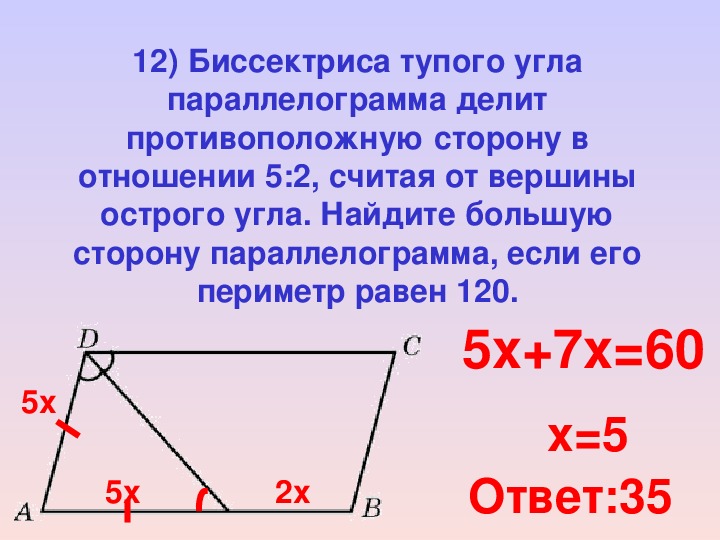
S ABCD = AB AD sin A = 5√2 7√2 sin φ,
S ABCD = 1/2 AC ВD sin AОВ = 1/2 d 1 d 2 sin ф.
Получаем равенство 5√2 7√2 sin φ = 1 / 2d 1 d 2 sin φ или
2 5√2 7√2 = d 1 d 2;
2.Используя соотношение сторон и диагоналей параллелограмма, запишем равенство
(AB 2 + AD 2) 2 = AC 2 + BD 2.
((5√2) 2 + (7√2) 2) 2 = d 1 2 + d 2 2.
d 1 2 + d 2 2 = 296.
3. Составим систему:
(d 1 2 + d 2 2 = 296,
(d 1 + d 2 = 140.
Умножаем второе уравнение системы на 2 и прибавляем его к первому.
Получаем (d 1 + d 2) 2 = 576. Отсюда Id 1 + d 2 I = 24.
Поскольку d 1, d 2 — длины диагоналей параллелограмма, то d 1 + d 2 = 24.
Ответ: 24.
Задание 6.
Стороны параллелограмма равны 4 и 6. Острый угол между диагоналями составляет 45 градусов. Найдите площадь параллелограмма.
Решение.
1. Из треугольника AOB, используя теорему косинусов, запишем отношение между стороной параллелограмма и диагоналями.
Из треугольника AOB, используя теорему косинусов, запишем отношение между стороной параллелограмма и диагоналями.
AB 2 = AO 2 + BO 2 2 AO VO cos AOB.
4 2 = (d 1/2) 2 + (d 2/2) 2 — 2 · (d 1/2) · (d 2/2) cos 45 о;
d 1 2/4 + d 2 2/4 — 2 (d 1/2) (d 2/2) √2 / 2 = 16.
d 1 2 + d 2 2 — d 1 d 2 √2 = 64.
2. Аналогично запишем соотношение для треугольника AOD.
Учтем, что
Получаем уравнение d 1 2 + d 2 2 + d 1 d 2 √2 = 144.
3. Имеем систему
(d 1 2 + d 2 2 — d 1 d 2 √2 = 64,
(d 1 2 + d 2 2 + d 1 d 2 √2 = 144.
Вычитая первое из второго уравнения, получаем 2d 1 d 2 √2 = 80 или
d 1 d 2 = 80 / (2√2) = 20√2
4.S ABCD = 1/2 AC · ВD · sin AОВ = 1/2 · d 1 d 2 sin α = 1/2 · 20√2 · √2 / 2 = 10.
Примечание: В этой и в предыдущей задаче нет необходимости полностью решать систему, предвидя, что в этой задаче для вычисления площади нам понадобится произведение диагоналей.
Ответ: 10.
Задание 7.
Площадь параллелограмма 96, а его стороны 8 и 15. Найдите квадрат меньшей диагонали.
Решение.
1.S ABCD = AB · AD · sin BAD. Сделаем замену в формуле.
Получаем 96 = 8 15 sin BAD. Следовательно sin ВAD = 4/5.
2. Найдите cos BAD. sin 2 VAD + cos 2 VAD = 1.
(4/5) 2 + cos 2 BAD = 1.cos 2 BAD = 9/25.
По постановке задачи находим длину меньшей диагонали. Диагональ BD будет меньше, если угол BAD острый. Тогда cos BAD = 3/5.
3. Из треугольника ABD по теореме косинусов находим квадрат диагонали BD.
BD 2 = AB 2 + AD 2 — 2 AB BD cos BAD.
ВD 2 = 8 2 + 15 2 — 2 8 15 3/5 = 145.
Ответ: 145.
Остались вопросы? Не знаете, как решить геометрическую задачу?
Чтобы получить помощь репетитора — зарегистрируйтесь.
Первое занятие бесплатно!
, при полном или частичном копировании материала ссылка на источник обязательна.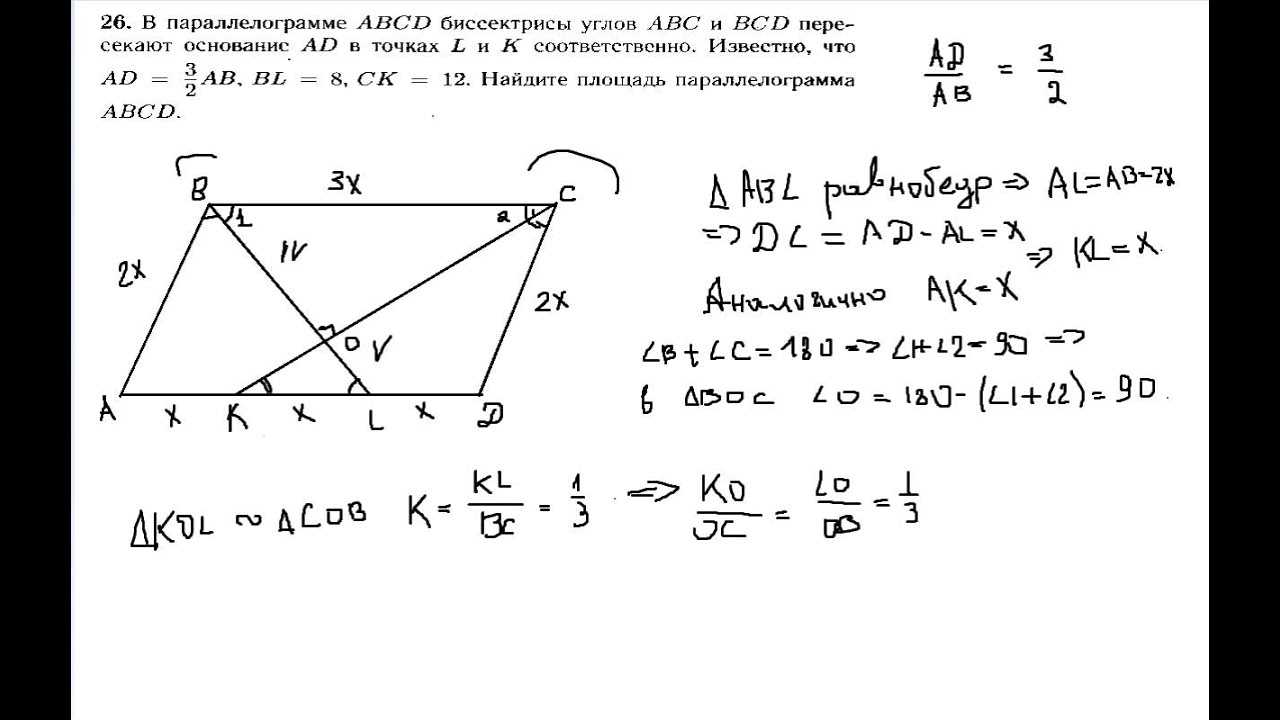
Примечание … Это часть урока с задачами геометрии (параллелограмм сечения). Если вам нужно решить геометрическую задачу, которой здесь нет, напишите об этом на форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ или sqrt () с радикальным выражением в скобках.
Теоретический материал
Пояснения к формулам для нахождения площади параллелограмма:
- Площадь параллелограмма равна произведению длины одной из его сторон на высоту, опущенную в эту сторону
- Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними
- Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними
Задачи на поиск площади параллелограмма
Задача .В параллелограмме меньшая высота и меньшая сторона равны 9 см и корню 82 соответственно. Большая диагональ — 15 см. Найдите площадь параллелограмма.
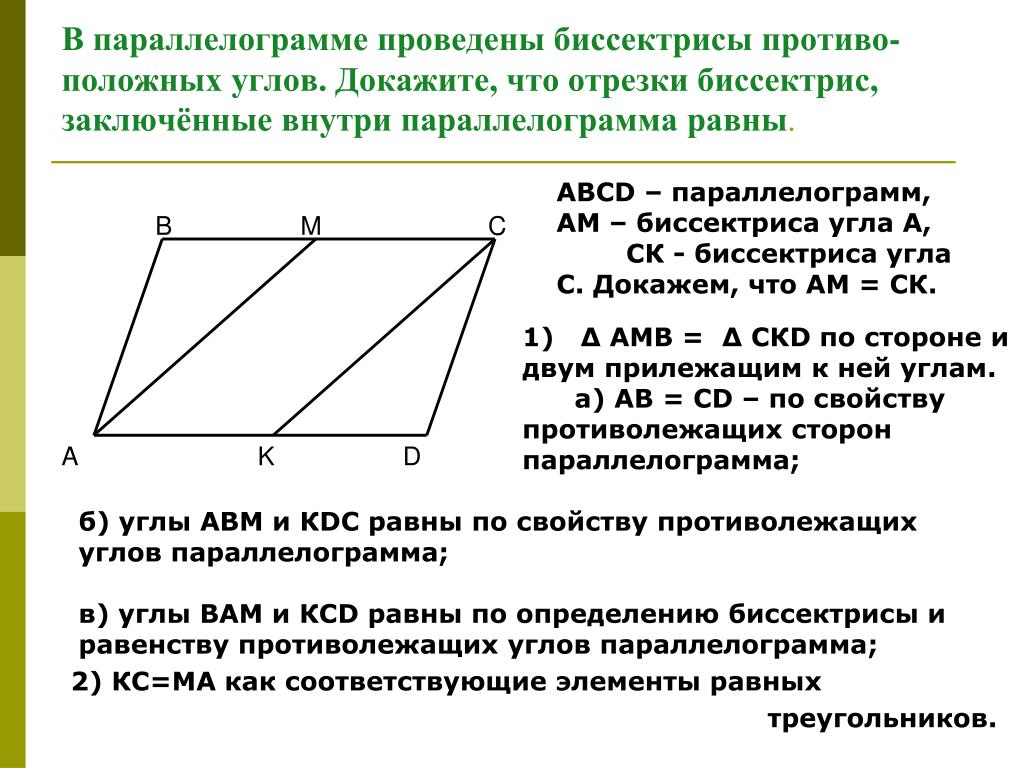
Решение .
Обозначим нижнюю высоту параллелограмма ABCD, опущенную от точки B к большему основанию AD, как BK.
Найдите значение катета прямоугольного треугольника ABK, образованного меньшей высотой, меньшей стороной и частью большего основания. По теореме Пифагора:
AB 2 = BK 2 + AK 2
82 = 9 2 + AK 2
AK 2 = 82 — 81
AK = 1
Продолжим верхнее основание параллелограмма BC и опустите на него высоту AN с нижнего основания.AN = BK как стороны прямоугольника ANBK. В получившемся прямоугольном треугольнике ANC найти катет NC.
AN 2 + NC 2 = AC 2
9 2 + NC 2 = 15 2
NC 2 = 225 — 81
NC 2 = √144
NC = 12
Теперь найдите большее основание BC параллелограмм ABCD.
BC = NC — NB
Учтем, что NB = AK как стороны прямоугольника, то
BC = 12 — 1 = 11
Площадь параллелограмма равна произведению основания и высоту до этого основания.
S = ah
S = BC * BK
S = 11 * 9 = 99
Ответ : 99 см 2.
Задание
В параллелограмме АВСД перпендикуляр ВО опускается на Диагональ переменного тока. Найдите площадь параллелограмма, если AO = 8, OC = 6 и BO = 4. Решение .
Опустим еще один перпендикуляр DK на диагональ AC.
Соответственно, треугольники AOB и DKC, COB и AKD попарно равны.Одна из сторон является противоположной стороной параллелограмма, один из углов является прямым, так как он перпендикулярен диагонали, а один из оставшихся углов — это внутренний крест, лежащий для параллельных сторон параллелограмма и секущей диагонали.
Таким образом, площадь параллелограмма равна площади указанных треугольников. Т.е.
Parall = 2S AOB + 2S BOC
Площадь прямоугольного треугольника равна половине произведения катетов.Откуда
S = 2 (1/2 8 * 4) + 2 (1/2 6 * 4) = 56 см 2
Ответ : 56 см 2.
При решении задач по этой теме, кроме основных свойств параллелограмма и соответствующих формул, можно запомнить и применить следующее:
- Биссектриса внутреннего угла параллелограмма отсекает от него равнобедренный треугольник
- Биссектрисы внутренних углов, примыкающих к одной из сторон параллелограмма, взаимно перпендикулярны
- Биссектрисы, выходящие из противоположных внутренних углов параллелограмма, параллельны друг другу или лежат на одной прямой
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон
- Площадь параллелограмма равна половине произведения диагоналей и синуса угла между ними
Рассмотрим задачи, при решении которых используются эти свойства.
Цель 1.
Биссектриса угла C параллелограмма ABCD пересекает сторону AD в точке M и продолжение стороны AB за точку A в точке E. Найти периметр параллелограмма, если AE = 4, DМ = 3.
Решение.
1. Треугольник CMD равнобедренный. (Свойство 1). Следовательно, CD = MD = 3 см.
2. Треугольник EAM равнобедренный.
Следовательно, АЕ = АМ = 4 см.
3. AD = AM + MD = 7 см.
4. Периметр ABCD = 20 см.
Ответ. 20 см.
Цель 2.
В выпуклом четырехугольнике ABCD начерчены диагонали. Известно, что площади треугольников ABD, ACD, BCD равны. Докажите, что данный четырехугольник — параллелограмм.
Решение.
1. Пусть BE — высота треугольника ABD, CF — высота треугольника ACD.Поскольку по условию задачи площади треугольников равны и имеют общее основание AD, высоты этих треугольников равны. BE = CF.
2. BE, CF перпендикулярны AD. Точки B и C расположены по одну сторону от линии AD. BE = CF. Следовательно, прямая ВС || ОБЪЯВЛЕНИЕ. (*)
Точки B и C расположены по одну сторону от линии AD. BE = CF. Следовательно, прямая ВС || ОБЪЯВЛЕНИЕ. (*)
3. Пусть АL — высота треугольника АСD, BK — высота треугольника BCD. Поскольку по условию задачи площади треугольников равны и имеют общее основание CD, то высоты этих треугольников равны.АЛ = БК.
4. AL и BK перпендикулярны CD. Точки B и A расположены по одну сторону от прямой CD. АЛ = БК. Следовательно, прямая AB || CD (**)
5. Из условий (*), (**) следует — параллелограмм ABCD.
Ответ. Проверено. ABCD — параллелограмм.
Цель 3.
На сторонах BC и CD параллелограмма ABCD соответственно отмечены точки M и H, так что отрезки BM и HD пересекаются в точке O;
Решение.
1. В треугольнике DOM
2. В прямоугольном треугольнике DHC
(
Тогда (Так как в прямоугольном треугольнике катет, лежащий под углом 30 °, равен половине гипотенузы)
Но CD = AB. Тогда AB: HD = 2: 1.
Тогда AB: HD = 2: 1.
3.
4.
Ответ: AB: НD = 2: 1,
Задача 4.
Одна из диагоналей параллелограмма длиной 4√6 составляет угол 60 ° с основанием, а вторая диагональ составляет угол 45 ° с тем же основанием.Найдите вторую диагональ.
Решение.
1. АО = 2√6.
2. Применим теорему о синусах к треугольнику AOD.
АО / sin D = OD / sin A.
2√6 / sin 45 о = OD / sin 60 о.
ОD = (2√6sin 60 о) / sin 45 о = (2√6 √3 / 2) / (√2 / 2) = 2√18 / √2 = 6.
Ответ: 12.
Цель 5.
У параллелограмма со сторонами 5√2 и 7√2 меньший угол между диагоналями равен меньшему углу параллелограмма.Найдите сумму длин диагоналей.
Решение.
Пусть d 1, d 2 — диагонали параллелограмма, а угол между диагоналями и меньшим углом параллелограмма равен φ.
1. Посчитаем два разных
пути его площади.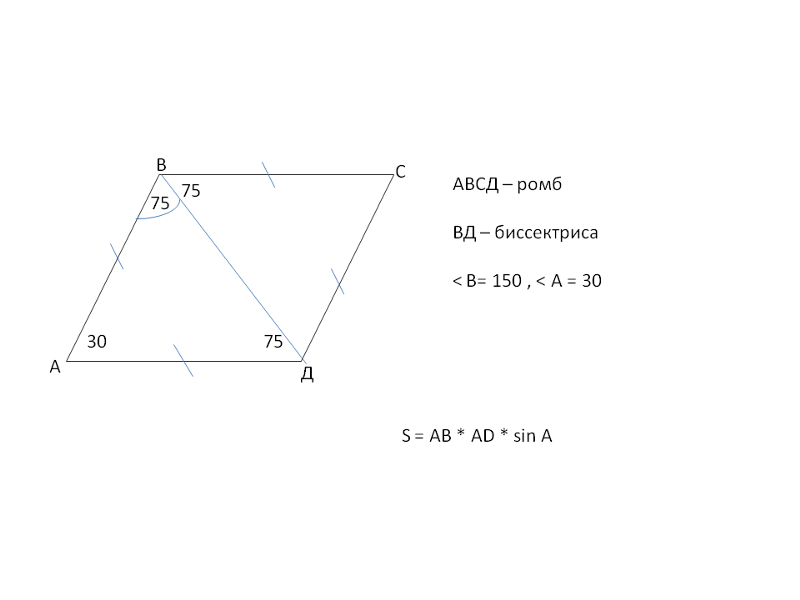
S ABCD = AB AD sin A = 5√2 7√2 sin φ,
S ABCD = 1/2 AC ВD sin AОВ = 1/2 d 1 d 2 sin ф.
Получаем равенство 5√2 7√2 sin φ = 1 / 2d 1 d 2 sin φ или
2 5√2 7√2 = d 1 d 2;
2.Используя соотношение сторон и диагоналей параллелограмма, запишем равенство
(AB 2 + AD 2) 2 = AC 2 + BD 2.
((5√2) 2 + (7√2) 2) 2 = d 1 2 + d 2 2.
d 1 2 + d 2 2 = 296.
3. Составим систему:
(d 1 2 + d 2 2 = 296,
(d 1 + d 2 = 140.
Умножаем второе уравнение системы на 2 и прибавляем его к первому.
Получаем (d 1 + d 2) 2 = 576. Отсюда Id 1 + d 2 I = 24.
Поскольку d 1, d 2 — длины диагоналей параллелограмма, то d 1 + d 2 = 24.
Ответ: 24.
Задание 6.
Стороны параллелограмма равны 4 и 6. Острый угол между диагоналями составляет 45 градусов. Найдите площадь параллелограмма.
Решение.
1. Из треугольника AOB, используя теорему косинусов, запишем отношение между стороной параллелограмма и диагоналями.
Из треугольника AOB, используя теорему косинусов, запишем отношение между стороной параллелограмма и диагоналями.
AB 2 = AO 2 + BO 2 2 AO VO cos AOB.
4 2 = (d 1/2) 2 + (d 2/2) 2 — 2 · (d 1/2) · (d 2/2) cos 45 о;
d 1 2/4 + d 2 2/4 — 2 (d 1/2) (d 2/2) √2 / 2 = 16.
d 1 2 + d 2 2 — d 1 d 2 √2 = 64.
2. Аналогично запишем соотношение для треугольника AOD.
Учтем, что
Получаем уравнение d 1 2 + d 2 2 + d 1 d 2 √2 = 144.
3. Имеем систему
(d 1 2 + d 2 2 — d 1 d 2 √2 = 64,
(d 1 2 + d 2 2 + d 1 d 2 √2 = 144.
Вычитая первое из второго уравнения, получаем 2d 1 d 2 √2 = 80 или
d 1 d 2 = 80 / (2√2) = 20√2
4.S ABCD = 1/2 AC · ВD · sin AОВ = 1/2 · d 1 d 2 sin α = 1/2 · 20√2 · √2 / 2 = 10.
Примечание: В этой и в предыдущей задаче нет необходимости полностью решать систему, предвидя, что в этой задаче для вычисления площади нам понадобится произведение диагоналей.
Ответ: 10.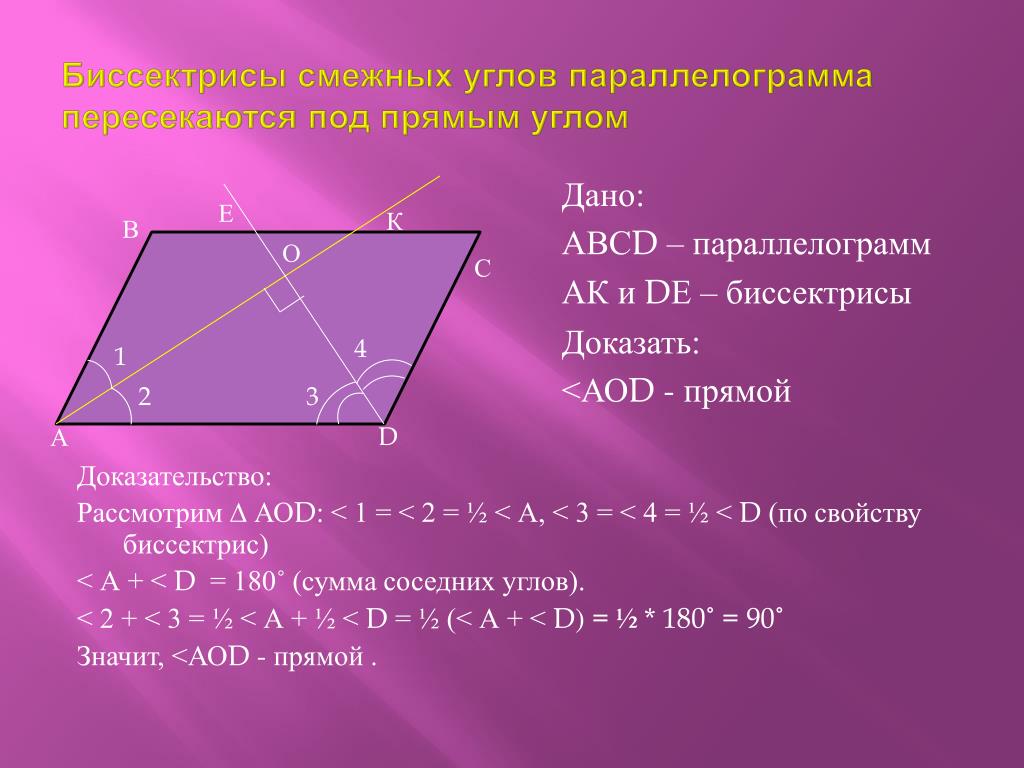
Задание 7.
Площадь параллелограмма 96, а его стороны 8 и 15. Найдите квадрат меньшей диагонали.
Решение.
1.S ABCD = AB · AD · sin BAD. Сделаем замену в формуле.
Получаем 96 = 8 15 sin BAD. Следовательно sin ВAD = 4/5.
2. Найдите cos BAD. sin 2 VAD + cos 2 VAD = 1.
(4/5) 2 + cos 2 BAD = 1.cos 2 BAD = 9/25.
По постановке задачи находим длину меньшей диагонали. Диагональ BD будет меньше, если угол BAD острый. Тогда cos BAD = 3/5.
3. Из треугольника ABD по теореме косинусов находим квадрат диагонали BD.
BD 2 = AB 2 + AD 2 — 2 AB BD cos BAD.
ВD 2 = 8 2 + 15 2 — 2 8 15 3/5 = 145.
Ответ: 145.
Остались вопросы? Не знаете, как решить геометрическую задачу?
Чтобы получить помощь репетитора -.
Первое занятие бесплатно!
блог. сайт, при полном или частичном копировании материала ссылка на источник обязательна.
Найдите площадь параллелограмма по сторонам. Параллелограмм в задачах
Параллелограмм Четырехугольник, стороны которого попарно параллельны.
На этом рисунке противоположные стороны и углы равны друг другу. Диагонали параллелограмма пересекаются в одной точке и делятся ею пополам.Формулы площади параллелограмма позволяют найти значение в терминах сторон, высоты и диагоналей. Параллелограмм также можно представить в частных случаях. Их принято считать прямоугольником, квадратом и ромбом.
Для начала рассмотрим пример расчета площади параллелограмма по высоте и той стороны, на которую он опускается.
Дело считается классическим и не требует дополнительного расследования. Лучше рассмотрите формулу расчета площади через две стороны и угол между ними.При расчете используется тот же метод. Если стороны и угол между ними заданы, то площадь рассчитывается следующим образом:
Пусть задан параллелограмм со сторонами a = 4 см, b = 6 см. Угол между ними α = 30 °. Найдите площадь:
Угол между ними α = 30 °. Найдите площадь:
Площадь параллелограмма по диагоналям
Формула площади параллелограмма в пересчете на диагонали позволяет быстро найти значение.
Для расчетов нужно значение угла, расположенного между диагоналями.
Рассмотрим пример вычисления площади параллелограмма по диагоналям. Пусть дан параллелограмм с диагоналями D = 7 см, d = 5 см. Угол между ними α = 30 °. Подставим данные в формулу:
Пример вычисления площади параллелограмма по диагонали дал нам отличный результат — 8,75.
Зная формулу площади параллелограмма через диагональ, можно решить множество интересных задач.Давайте посмотрим на один из них.
Задание: Дан параллелограмм площадью 92 кв. См. Точка F расположена посередине его стороны ВС. Найдем площадь трапеции ADFB, которая будет лежать в нашем параллелограмме. Для начала нарисуем все, что мы получили по условиям.
Приступим к решению:
По нашим условиям ah = 92, и соответственно площадь нашей трапеции будет равна
Примечание . .. Это часть урока с задачами по геометрии (секционный параллелограмм). Если вам нужно решить геометрическую задачу, которой нет здесь, напишите об этом на форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ или sqrt () с радикальным выражением в скобках.
.. Это часть урока с задачами по геометрии (секционный параллелограмм). Если вам нужно решить геометрическую задачу, которой нет здесь, напишите об этом на форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ или sqrt () с радикальным выражением в скобках.
Теоретический материал
Пояснения к формулам для нахождения площади параллелограмма:
- Площадь параллелограмма равна произведению длины одной из его сторон на высоту, опущенную в эту сторону
- Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними
- Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними
Задачи на поиск площади параллелограмма
Задача .В параллелограмме меньшая высота и меньшая сторона равны 9 см и корню 82 соответственно. Большая диагональ — 15 см. Найдите площадь параллелограмма.
Решение .
Обозначим нижнюю высоту параллелограмма ABCD, опущенную от точки B к большему основанию AD, как BK.
Найдите значение катета прямоугольного треугольника ABK, образованного меньшей высотой, меньшей стороной и частью большего основания. По теореме Пифагора:
AB 2 = BK 2 + AK 2
82 = 9 2 + AK 2
AK 2 = 82 — 81
AK = 1
Продолжим верхнее основание параллелограмма BC и опустите на него высоту AN с нижнего основания.AN = BK как стороны прямоугольника ANBK. В получившемся прямоугольном треугольнике ANC найти катет NC.
AN 2 + NC 2 = AC 2
9 2 + NC 2 = 15 2
NC 2 = 225 — 81
NC 2 = √144
NC = 12
Теперь найдите большее основание BC параллелограмм ABCD.
BC = NC — NB
Учтем, что NB = AK как стороны прямоугольника, то
BC = 12 — 1 = 11
Площадь параллелограмма равна произведению основания и высоту до этого основания.
S = ah
S = BC * BK
S = 11 * 9 = 99
Ответ : 99 см 2.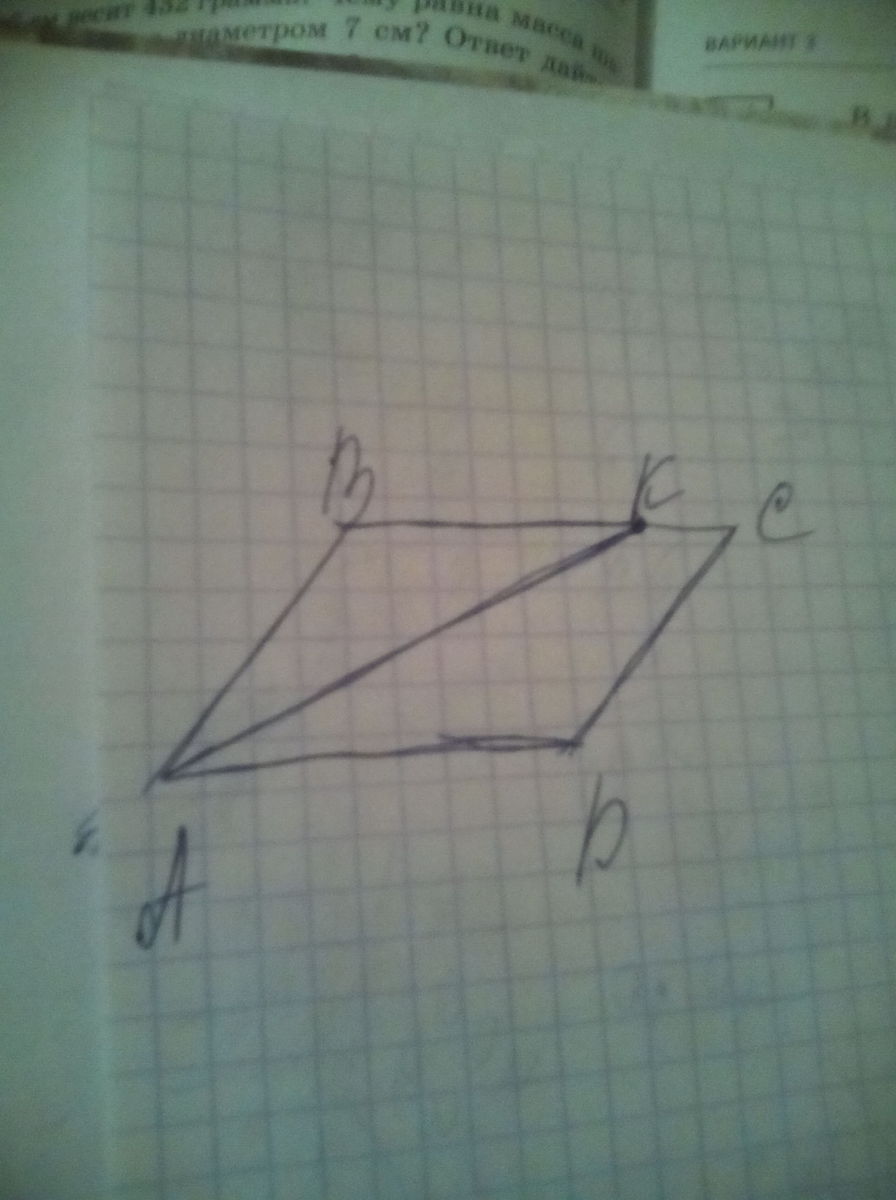
Задание
В параллелограмме АВСД перпендикуляр ВО опускается на Диагональ переменного тока. Найдите площадь параллелограмма, если AO = 8, OC = 6 и BO = 4. Решение .
Опустим еще один перпендикуляр DK на диагональ AC.
Соответственно, треугольники AOB и DKC, COB и AKD попарно равны.Одна из сторон является противоположной стороной параллелограмма, один из углов является прямым, так как он перпендикулярен диагонали, а один из оставшихся углов — это внутренний крест, лежащий для параллельных сторон параллелограмма и секущей диагонали.
Таким образом, площадь параллелограмма равна площади указанных треугольников. Т.е.
Parall = 2S AOB + 2S BOC
Площадь прямоугольного треугольника равна половине произведения катетов.Откуда
S = 2 (1/2 8 * 4) + 2 (1/2 6 * 4) = 56 см 2
Ответ : 56 см 2.
Видеокурс «Получи пятерку» включает в себя все темы, необходимые для успешной сдачи экзамена по математике на 60-65 баллов. Полностью все задания 1-13 Профильного единого государственного экзамена по математике. Также подходит для сдачи базового экзамена по математике. Если вы хотите сдать экзамен на 90-100 баллов, вам нужно решить часть 1 за 30 минут и без ошибок!
Полностью все задания 1-13 Профильного единого государственного экзамена по математике. Также подходит для сдачи базового экзамена по математике. Если вы хотите сдать экзамен на 90-100 баллов, вам нужно решить часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 классов, а также для учителей.Все необходимое для решения части 1 ЕГЭ по математике (первые 12 задач) и задачи 13 (тригонометрия). А это больше 70 баллов на ЕГЭ, и без них не обойтись ни стобалловый, ни гуманитарий.
Вся необходимая теория. Быстрые решения, ловушки и секреты экзамена. Были проанализированы все соответствующие задачи части 1 от Банка задач ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, 2.По 5 часов. Каждая тема дана с нуля, просто и понятно.
Сотни экзаменационных заданий. Проблемы со словом и теория вероятностей. Простые и легко запоминающиеся алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех видов заданий ЕГЭ.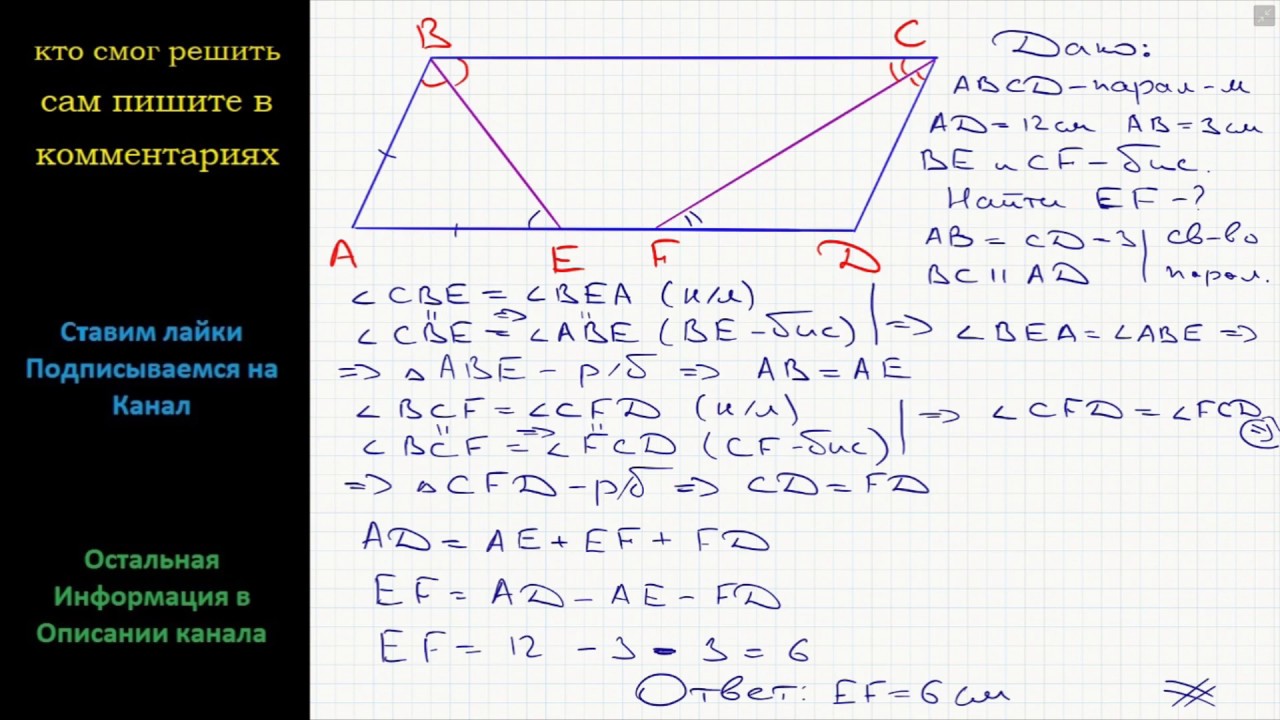 Стереометрия. Хитрые решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля до задачи 13. Понимание вместо зубрежки. Визуальное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функции и производные.Основа для решения сложных задач 2-й части экзамена.
Стереометрия. Хитрые решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля до задачи 13. Понимание вместо зубрежки. Визуальное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функции и производные.Основа для решения сложных задач 2-й части экзамена.
Площадь параллелограмма. В очень многих задачах по геометрии, связанных с расчетом площадей, в том числе в задачах к экзамену, используются формулы площади параллелограмма и треугольника. Их несколько, здесь мы их рассмотрим.
Перечислить эти формулы было бы слишком просто, этого товара уже достаточно в справочниках и на разных сайтах. Хочу передать суть — чтобы вы их не впихивали, а понимали и легко запоминали в любой момент.Изучив материал статьи, вы поймете, что изучать эти формулы совсем не нужно. Объективно говоря, они настолько часты в решениях, что запоминаются надолго.
1. Итак, давайте посмотрим на параллелограмм. Определение гласит:
Почему? Это так просто! Чтобы наглядно показать, в чем смысл формулы, выполним некоторые дополнительные построения, а именно нанесем высоты:
Площадь треугольника (2) равна площади треугольника (2).![]() u200b треугольник (1) — второй признак равенства прямоугольных треугольников «вдоль катета и гипотенузы».«А теперь мысленно« отрежем »второй и перенесем, наложив на первый — получим прямоугольник, площадь которого будет равна площади исходного параллелограмма:
u200b треугольник (1) — второй признак равенства прямоугольных треугольников «вдоль катета и гипотенузы».«А теперь мысленно« отрежем »второй и перенесем, наложив на первый — получим прямоугольник, площадь которого будет равна площади исходного параллелограмма:
Известно, что площадь прямоугольника равна произведению его смежных сторон. Как видно из эскиза, одна сторона получившегося прямоугольника равна стороне параллелограмма, а другая равна высоте параллелограмма.Таким образом, получаем формулу площади параллелограмма S = a ∙ h a
2. Продолжим, еще одна формула для его площади. Имеем:
Площадь параллелограмма по формуле
Обозначим стороны как a и b, угол между ними γ «гамма», высота h a. Рассмотрим прямоугольный треугольник:
При решении задач по этой теме, кроме основных свойств параллелограмма и соответствующих формул, можно запомнить и применить следующее:
- Биссектриса внутреннего угла параллелограмма отсекает от него равнобедренный треугольник
- Биссектрисы внутренних углов, примыкающих к одной из сторон параллелограмма, взаимно перпендикулярны
- Биссектрисы, выходящие из противоположных внутренних углов параллелограмма, параллельны друг другу или лежат на одной прямой
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон
- Площадь параллелограмма равна половине произведения диагоналей и синуса угла между ними
Рассмотрим задачи, при решении которых используются эти свойства.
Цель 1.
Биссектриса угла C параллелограмма ABCD пересекает сторону AD в точке M и продолжение стороны AB за точку A в точке E. Найти периметр параллелограмма, если AE = 4, DМ = 3.
Решение.
1. Треугольник CMD равнобедренный. (Свойство 1). Следовательно, CD = MD = 3 см.
2. Треугольник EAM равнобедренный.
Следовательно, АЕ = АМ = 4 см.
3. AD = AM + MD = 7 см.
4. Периметр ABCD = 20 см.
Ответ. 20 см.
Цель 2.
В выпуклом четырехугольнике ABCD начерчены диагонали. Известно, что площади треугольников ABD, ACD, BCD равны. Докажите, что данный четырехугольник — параллелограмм.
Решение.
1. Пусть BE — высота треугольника ABD, CF — высота треугольника ACD.Поскольку по условию задачи площади треугольников равны и имеют общее основание AD, высоты этих треугольников равны. BE = CF.
2. BE, CF перпендикулярны AD. Точки B и C расположены по одну сторону от линии AD. BE = CF. Следовательно, прямая ВС || ОБЪЯВЛЕНИЕ. (*)
Точки B и C расположены по одну сторону от линии AD. BE = CF. Следовательно, прямая ВС || ОБЪЯВЛЕНИЕ. (*)
3. Пусть АL — высота треугольника АСD, BK — высота треугольника BCD. Поскольку по условию задачи площади треугольников равны и имеют общее основание CD, то высоты этих треугольников равны.АЛ = БК.
4. AL и BK перпендикулярны CD. Точки B и A расположены по одну сторону от прямой CD. АЛ = БК. Следовательно, прямая AB || CD (**)
5. Из условий (*), (**) следует — параллелограмм ABCD.
Ответ. Проверено. ABCD — параллелограмм.
Цель 3.
На сторонах BC и CD параллелограмма ABCD отмечены точки M и H соответственно, так что отрезки BM и HD пересекаются в точке O;
Решение.
1. В треугольнике DOM
2. В прямоугольном треугольнике DHC
(
Тогда (Так как в прямоугольном треугольнике катет, лежащий под углом 30 °, равен половине гипотенузы)
Но CD = AB. Тогда AB: HD = 2: 1.
Тогда AB: HD = 2: 1.
3.
4.
Ответ: AB: НD = 2: 1,
Задача 4.
Одна из диагоналей параллелограмма длиной 4√6 составляет угол 60 ° с основанием, а вторая диагональ составляет угол 45 ° с тем же основанием.Найдите вторую диагональ.
Решение.
1. АО = 2√6.
2. Применим теорему о синусах к треугольнику AOD.
АО / sin D = OD / sin A.
2√6 / sin 45 о = OD / sin 60 о.
ОD = (2√6sin 60 о) / sin 45 о = (2√6 √3 / 2) / (√2 / 2) = 2√18 / √2 = 6.
Ответ: 12.
Цель 5.
У параллелограмма со сторонами 5√2 и 7√2 меньший угол между диагоналями равен меньшему углу параллелограмма.Найдите сумму длин диагоналей.
Решение.
Пусть d 1, d 2 — диагонали параллелограмма, а угол между диагоналями и меньшим углом параллелограмма равен φ.
1. Посчитаем два разных
пути его площади.
S ABCD = AB AD sin A = 5√2 7√2 sin φ,
S ABCD = 1/2 AC ВD sin AОВ = 1/2 d 1 d 2 sin ф.
Получаем равенство 5√2 7√2 sin φ = 1 / 2d 1 d 2 sin φ или
2 5√2 7√2 = d 1 d 2;
2.Используя соотношение сторон и диагоналей параллелограмма, запишем равенство
(AB 2 + AD 2) 2 = AC 2 + BD 2.
((5√2) 2 + (7√2) 2) 2 = d 1 2 + d 2 2.
d 1 2 + d 2 2 = 296.
3. Составим систему:
(d 1 2 + d 2 2 = 296,
(d 1 + d 2 = 140.
Умножаем второе уравнение системы на 2 и прибавляем его к первому.
Получаем (d 1 + d 2) 2 = 576. Отсюда Id 1 + d 2 I = 24.
Поскольку d 1, d 2 — длины диагоналей параллелограмма, то d 1 + d 2 = 24.
Ответ: 24.
Задание 6.
Стороны параллелограмма равны 4 и 6. Острый угол между диагоналями составляет 45 °. Найдите площадь параллелограмма.
Решение.
1. Из треугольника AOB, используя теорему косинусов, запишем отношение между стороной параллелограмма и диагоналями.
AB 2 = AO 2 + BO 2 2 AO VO cos AOB.
4 2 = (d 1/2) 2 + (d 2/2) 2 — 2 (d 1/2) (d 2/2) cos 45 o;
d 1 2/4 + d 2 2/4 — 2 (d 1/2) (d 2/2) √2 / 2 = 16.
d 1 2 + d 2 2 — d 1 d 2 √2 = 64.
2. Аналогично записываем соотношение для треугольника AOD.
Учтем, что
Получаем уравнение d 1 2 + d 2 2 + d 1 d 2 √2 = 144.
3. Имеем систему
(d 1 2 + d 2 2 — d 1 d 2 √2 = 64,
(d 1 2 + d 2 2 + d 1 d 2 √2 = 144.
Вычитая первое из второго уравнения, получаем 2d 1 d 2 √2 = 80 или
d 1 d 2 = 80 / (2√2) = 20√2
4.S ABCD = 1/2 AC · ВD · sin AОВ = 1/2 · d 1 d 2 sin α = 1/2 · 20√2 · √2 / 2 = 10.
Примечание: В этой и предыдущей задачах нет необходимости полностью решать систему, предвидя, что в этой задаче для вычисления площади нам понадобится произведение диагоналей.
Ответ: 10.
Задание 7.
Площадь параллелограмма 96, а его стороны 8 и 15. Найдите квадрат меньшей диагонали.
Найдите квадрат меньшей диагонали.
Решение.
1.S ABCD = AB · AD · sin BAD. Сделаем замену в формуле.
Получаем 96 = 8 15 sin BAD. Следовательно sin ВAD = 4/5.
2. Найдите cos BAD. sin 2 BAD + cos 2 BAD = 1.
(4/5) 2 + cos 2 BAD = 1.cos 2 BAD = 9/25.
По постановке задачи находим длину меньшей диагонали. Диагональ BD будет меньше, если угол BAD острый. Тогда cos BAD = 3/5.
3. Из треугольника ABD по теореме косинусов находим квадрат диагонали BD.
BD 2 = AB 2 + AD 2 — 2 · AB · BD · cos BAD.
ВD 2 = 8 2 + 15 2 — 2 8 15 3/5 = 145.
Ответ: 145.
Остались вопросы? Не знаете, как решить геометрическую задачу?
Чтобы получить помощь репетитора — зарегистрируйтесь.
Первое занятие бесплатно!
, при полном или частичном копировании материала ссылка на источник обязательна.
Площадь параллелограмма сбоку и по высоте. Вычисляем сумму углов и площади параллелограмма: свойства и знаки
Видеокурс «Получи пятерку» включает в себя все темы, необходимые для успешной сдачи экзамена по математике на 60-65 баллов. Полностью выполнены все задания 1-13 основного экзамена по математике.Также подходит для сдачи базового экзамена по математике. Если вы хотите сдать экзамен на 90-100 баллов, вам нужно решить часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 классов, а также для учителей. Все, что нужно для решения части 1 экзамена по математике (первые 12 задач) и задачи 13 (тригонометрия). А это больше 70 баллов по ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарным наукам.
Вся необходимая теория.Быстрые решения, ловушки и секреты экзамена. Все соответствующие задачи Части 1 из Банка задач ФИПИ отсортированы. Курс полностью соответствует требованиям экзамена.
Курс состоит из 5 больших тем по 2,5 часа каждая. Каждая тема дана с нуля, просто и понятно.
Сотни экзаменационных заданий. Текстовые задачи и теория вероятностей. Простые и легко запоминающиеся алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ.Стереометрия. Хитрые уловки, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — к задаче 13. Понимание вместо зубрежки. Визуальное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функции и производные. База для решения сложных задач 2 части экзамена.
Примечание . Это часть урока с задачами по геометрии (раздел о параллелограммах). Если вам нужно решить задачу по геометрии, которой здесь нет, напишите об этом на форуме.Символ √ или sqrt () используется для обозначения действия по извлечению квадратного корня при решении задач; кроме того, в скобках указано радикальное выражение.
Теоретический материал
Пояснения к формулам для нахождения площади параллелограмма:
- Площадь параллелограмма равна произведению длины одной из его сторон на высоту, опущенную на эту сторону
- Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними
- Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними
Задачи на поиск площади параллелограмма
Задача .В параллелограмме меньшая высота и меньшая сторона равны 9 см и корню 82 соответственно. Большая диагональ — 15 см. Найдите площадь параллелограмма.
Решение .
Обозначим высоту нижнего параллелограмма ABCD, опущенного из точки B в большее основание AD, как BK.
Найдите значение катета прямоугольного треугольника ABK, образованного меньшей высотой, меньшей стороной и частью большего основания. По теореме Пифагора:
AB 2 = BK 2 + AK 2
82 = 9 2 + AK 2
AK 2 = 82 — 81
AK = 1
Продолжим верхнее основание параллелограмма BC и опустите высоту AN от его нижнего основания.AN = BK как стороны прямоугольника ANBK. В получившемся прямоугольном треугольнике ANC находим боковой катет NC.
AN 2 + NC 2 = AC 2
9 2 + NC 2 = 15 2
NC 2 = 225 — 81
NC 2 = √144
NC = 12
Теперь найдите большее основание BC параллелограмм ABCD.
BC = NC — NB
Учтем, что NB = AK как стороны прямоугольника, то
BC = 12 — 1 = 11
Площадь параллелограмма равна произведению основания и высоту этого основания.
S = ah
S = BC * BK
S = 11 * 9 = 99
Ответ : 99 см 2.
Задача
В параллелограмме АВСД перпендикуляр ВО находится понижен до диагонали AS. Найдите площадь параллелограмма, если АО = 8, ОС = 6, а БО = 4. Решение .
Опустим еще один перпендикуляр DK на диагональ AC.
Соответственно, треугольники AOB и DKC, COB и AKD попарно равны.Одна из сторон является противоположной стороной параллелограмма, один из углов — это прямая линия, поскольку она перпендикулярна диагонали, а один из оставшихся углов — это внутренний крест, лежащий для параллельных сторон параллелограмма и секущей. диагональ.
Таким образом, площадь параллелограмма равна площади этих треугольников. Т.е.
Sparal = 2S AOB + 2S BOC
Площадь прямоугольного треугольника равна половине произведения катетов.Где от
S = 2 (1/2 8 * 4) + 2 (1/2 6 * 4) = 56 см 2
Ответ : 56 см 2.
Параллелограмм — это четырехугольник, стороны которого попарно параллельны.
На этом рисунке противоположные стороны и углы равны друг другу. Диагонали параллелограмма пересекаются в одной точке и делятся пополам. Формулы площади параллелограмма позволяют найти значение по сторонам, высоте и диагоналям. Параллелограмм также может быть представлен в особых случаях.Их считают прямоугольником, квадратом и ромбом.
Для начала рассмотрим пример расчета площади параллелограмма по высоте и стороне, на которую он опускается.
Это дело считается классическим и не требует дополнительных разбирательств. Лучше рассмотрите формулу для расчета площади двух сторон и угла между ними. При расчете используется тот же метод. Если стороны и угол между ними заданы, то площадь рассчитывается следующим образом:
Пусть задан параллелограмм со сторонами a = 4 см, b = 6 см.Угол между ними α = 30 °. Найдите площадь:
Площадь параллелограмма по диагоналям
Формула площади параллелограмма по диагоналям позволяет быстро найти значение.
Для расчетов нужно значение угла, расположенного между диагоналями.
Рассмотрим пример вычисления площади параллелограмма по диагоналям. Пусть дан параллелограмм с диагоналями D = 7 см, d = 5 см.Лежащий между ними угол α = 30 °. Подставляем данные в формулу:
Пример расчета площади параллелограмма по диагонали дал нам отличный результат — 8,75.
Зная формулу площади параллелограмма по диагонали, можно решить много интересных задач. Посмотрим на один из них.
Задание: Дан параллелограмм площадью 92 квадратных метра. см. Точка F расположена посередине своей стороны от солнца.Найдем площадь трапеции ADFB, которая будет лежать в нашем параллелограмме. Для начала нарисуем все, что получили по условиям.
Приступаем к решению:
По нашим условиям ах = 92, и соответственно площадь нашей трапеции будет равна
параллелограмм они называют четырехугольником, в котором противоположные стороны параллельны друг другу. Основные задачи школы по этой теме — вычислить площадь параллелограмма, его периметр, высоту, диагонали.Указанные значения и формулы для их расчета будут приведены ниже.
Свойства параллелограмма
Противоположные стороны параллелограмма, а также противоположные углы равны между собой:
AB = CD, BC = AD,
Диагонали параллелограмма в точке пересечения разделены на две равные части:
АО = OC, OB = OD.
Углы, прилегающие к каждой стороне (смежные углы), в сумме составляют 180 градусов.2).
Основные признаки параллелограммов:
1. Четырехугольник, в котором противоположные стороны попарно параллельны, является параллелограммом.
2. Четырехугольник с равными противоположными сторонами — параллелограмм.
3. Четырехугольник с равными и параллельными противоположными сторонами является параллелограммом.
4. Если диагонали четырехугольника в точке пересечения делятся пополам, то это параллелограмм.
5. Четырехугольник, в котором противоположные углы попарно равны, представляет собой параллелограмм
Биссектрисы параллелограмма
Биссектрисы противоположных углов в параллелограмме могут быть параллельны или совпадать.
Биссектрисы смежных углов (смежных с одной стороной) пересекаются под прямым углом (перпендикулярно).
Высота параллелограмма
Высота параллелограмма — это отрезок, который рисуется под углом, перпендикулярным основанию. Отсюда следует, что с каждого угла можно нарисовать две высоты.
Формула площади параллелограмма
Площадь параллелограмма равна произведению стороны на начерченную высоту.Формула площади имеет следующий вид:
Вторая формула не менее популярна в расчетах и определяется следующим образом: площадь параллелограмма равна произведению соседних сторон на синус угла между ними
На основе приведенных выше формул вы будете знать, как рассчитать площадь параллелограмма.
Периметр параллелограмма
Формула для расчета периметра параллелограмма имеет вид
то есть периметр равен удвоенному значению суммы сторон.Задачи на параллелограмме будут рассмотрены в соседних материалах, а пока изучим формулы. Большинство задач по вычислению сторон, диагоналей параллелограмма довольно просты и сводятся к знанию теоремы синусов и теорем Пифагора.
При решении задач по этой теме кроме основных свойств параллелограмма и соответствующих формул можно запомнить и применить следующее:
- Биссектриса внутреннего угла параллелограмма отсекает от него равнобедренный треугольник
- Биссектрисы внутренних углов, примыкающих к одной из сторон параллелограмма, взаимно перпендикулярны
- Биссектрисы, выходящие из противоположных внутренних углов параллелограмма, параллельны друг другу или лежат на одной прямой
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон
- Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними
Рассмотрим задачи, для решения которых используются данные свойства.
Задача 1
Биссектриса угла C параллелограмма ABCD пересекает сторону AD в точке M и продолжение стороны AB за точку A в точке E. Найти периметр параллелограмма, если AE = 4, DM = 3.
Решение.
1. Треугольник CMD равнобедренный. (Свойство 1). Следовательно, CD = MD = 3 см.
2. Треугольник ЕАМ равнобедренный.
Следовательно, АЕ = АМ = 4 см.
3.AD = AM + MD = 7 см.
4. Периметр ABCD = 20 см.
Ответ. 20 см
Задача 2
В выпуклом четырехугольнике ABCD начерчены диагонали. Известно, что площади треугольников ABD, ACD, BCD равны. Докажите, что этот четырехугольник — параллелограмм.
Решение.
1. Пусть BE — высота треугольника ABD, CF — высота треугольника ACD.Поскольку по условию задачи площади треугольников равны и имеют общее основание AD, высоты этих треугольников равны. BE = CF.
2. BE, CF перпендикулярны AD. Точки B и C расположены с одной стороны относительно прямой AD. BE = CF. Следовательно, прямая линия || ОБЪЯВЛЕНИЕ. (*)
3. Пусть AL — высота треугольника ACD, BK — высота треугольника BCD. Поскольку по условию задачи площади треугольников равны и имеют общее основание CD, то высоты этих треугольников равны.АЛ = БК.
4. AL и BK перпендикулярны CD. Точки B и A расположены с одной стороны относительно прямой CD. АЛ = БК. Следовательно, прямая AB || CD (**)
5. Из условий (*), (**) следует — параллелограмм ABCD.
Ответ. Доказано. ABCD — параллелограмм.
Задача 3.
На сторонах BC и CD параллелограмма ABCD отмечены точки M и H соответственно, так что отрезки BM и HD пересекаются в точке O;
Решение.
1. В треугольнике DOM
2. В прямоугольном треугольнике DC
(
Тогда (Поскольку в прямоугольном треугольнике катет, лежащий под углом 30 °, равен половине гипотенузы)
Но CD = AB. Тогда AB: НD = 2: 1.
3.
4.
Ответ: AB: НD = 2: 1,
Задача 4.
Одна из диагоналей параллелограмма длиной 4√6 составляет угол 60 ° с основанием, а вторая диагональ составляет угол 45 ° с тем же основанием.Найдите вторую диагональ.
Решение.
1. АО = 2√6.
2. Применим теорему синусов к треугольнику AOD.
АО / sin D = OD / sin A.
2√6 / sin 45 о = OD / sin 60 о.
OD = (2√6sin 60 о) / sin 45 о = (2√6 · √3 / 2) / (√2 / 2) = 2√18 / √2 = 6.
Ответ: 12.
Задача 5.
У параллелограмма со сторонами 5√2 и 7√2 меньший угол между диагоналями равен меньшему углу параллелограмма.Найдите сумму длин диагоналей.
Решение.
Пусть d 1, d 2 — диагонали параллелограмма, а угол между диагоналями и меньшим углом параллелограмма равен f.
1. Посчитайте двумя разными
способами его площадь.
S ABCD = AB · AD · sin A = 5√2 · 7√2 · sin f,
S ABCD = 1/2 AC · BD · sin AOB = 1/2 · d 1 d 2 sin f.
Получаем равенство 5√2 · 7√2 · sin f = 1 / 2d 1 d 2 sin f или
2 · 5√2 · 7√2 = d 1 d 2;
2.Используя соотношение сторон и диагоналей параллелограмма, запишем равенство
(AB 2 + AD 2) · 2 = AC 2 + BD 2.
((5√2) 2 + (7√2) 2) · 2 = d 1 2 + d 2 2.
d 1 2 + d 2 2 = 296.
3. Составляем систему:
(d 1 2 + d 2 2 = 296,
(d 1 + d 2 = 140.
Умножаем второе уравнение системы на 2 и прибавляем его к первому.
Получаем (d 1 + d 2) 2 = 576. Следовательно, Id 1 + d 2 I = 24.
Поскольку d 1, d 2 — длины диагоналей параллелограмма, то d 1 + d 2 = 24.
Ответ: 24.
Задание 6.
Стороны параллелограмма равны 4 и 6. Острый угол между диагоналями составляет 45 °. Найдите площадь параллелограмма.
Решение.
1. Из треугольника AOB, используя теорему косинусов, запишем соотношение между стороной параллелограмма и диагоналями.
AB 2 = AO 2 + VO 2 2 · AO · VO · cos AOV.
4 2 = (d 1/2) 2 + (d 2/2) 2 — 2 · (d 1/2) · (d 2/2) cos 45 о;
d 1 2/4 + d 2 2/4 — 2 · (d 1/2) · (d 2/2) √2 / 2 = 16.
d 1 2 + d 2 2 — d 1 · d 2 √2 = 64.
2. Аналогично запишем соотношение для треугольника AOD.
Учтем, что
Получаем уравнение d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
3. Имеем систему
(d 1 2 + d 2 2 — d 1 · d 2 √2 = 64,
(d 1 2 + d 2 2 + d 1 d 2 √ 2 = 144.
Вычитая первое из второго уравнения, получаем 2d 1 · d 2 √2 = 80 или
d 1d 2 = 80 / (2√2) = 20√2
4. S ABCD = 1/2 AC · BD · sin AOB = 1/2 · d 1 d 2 sin α = 1/2 · 20√2 · √2 / 2 = 10.
Примечание: В этой и предыдущей задачах нет необходимости решать всю систему, предполагая, что в этой задаче для вычисления площади нам понадобится произведение диагоналей.
Ответ: 10.
Задание 7.
Площадь параллелограмма равна 96, а его стороны равны 8 и 15. Найдите квадрат меньшей диагонали.
Решение.
1. S ABCD = AB · AD · sin BAD. Сделаем замену в формуле.
Получаем 96 = 8 · 15 · sin BAD. Следовательно sin ПЛОХО = 4/5.
2. Найдите cos BAD. sin 2 BAD + cos 2 BAD = 1.
(4/5) 2 + cos 2 BAD = 1.cos 2 BAD = 9/25.
По условию задачи находим длину меньшей диагонали. Диагональ BD будет меньше, если угол BAD острый. Тогда cos BAD = 3/5.
3. Из треугольника ABD по теореме косинусов находим квадрат диагонали BD.
BD 2 = AB 2 + AD 2 — 2 · AB · BD · cos BAD.
БД 2 = 8 2 + 15 2 — 2 · 8 · 15 · 3/5 = 145.
Ответ: 145.
Остались вопросы? Не знаете, как решить геометрическую задачу?
Чтобы получить помощь репетитора — зарегистрируйтесь.
Первое занятие бесплатно!
, с полным или частичным копированием материала, ссылка на источник обязательна.
Дефект атриовентрикулярной перегородки или AV-канал (AVSD) | Детская больница CS Mott
Что такое дефект атриовентрикулярной перегородки или атриовентрикулярного канала?
Дефект атриовентрикулярной перегородки (AVSD) или AV-канал — это порок сердца, который затрагивает клапаны между верхней и нижней камерами сердца и стенки между камерами.Другие термины, используемые для описания этой проблемы, включают дефект эндокардиальной подушки и дефект AV-канала. Подобная, но менее серьезная форма дефекта атриовентрикулярной перегородки называется первичным дефектом межпредсердной перегородки или неполным или частичным дефектом атриовентрикулярной перегородки. Причина дефекта атриовентрикулярной перегородки неизвестна. В целом это довольно редко и составляет 4% диагностированных пороков сердца у детей. Однако это довольно часто встречается у детей с синдромом Дауна и встречается примерно у 25% этих детей.Верхние камеры сердца называются предсердиями, а нижние камеры — желудочками. Стенка между верхними камерами называется межпредсердной перегородкой, а стенка между нижними камерами — межжелудочковой перегородкой. В нормальном сердце клапан между правым предсердием и правым желудочком называется трехстворчатым клапаном, а клапан между левым предсердием и левым желудочком называется митральным клапаном. У детей с АВСД трикуспидальный и митральный клапаны не развиваются нормально, что затем влияет на рост межпредсердной и межжелудочковой перегородок.В большинстве случаев существует один «общий» клапан, разделяющий верхнюю и нижнюю камеры сердца (1), а не два отдельных клапана. Кроме того, имеется отверстие в межпредсердной перегородке (2), называемое дефектом межпредсердной перегородки, и отверстие в межжелудочковой перегородке (3), называемое дефектом межжелудочковой перегородки. При первичном дефекте межпредсердной перегородки есть два отдельных клапана между верхней и нижней камерами сердца, но они не полностью нормальны и имеется дефект межпредсердной перегородки.
Как этот дефект влияет на здоровье моего ребенка?
Дефект атриовентрикулярной перегородки — серьезная проблема с сердцем, которая обычно вызывает сердечные симптомы.В отличие от некоторых пороков сердца, проблема не решается со временем, и большинству детей требуется операция на сердце. Хорошая новость заключается в том, что эта операция обычно бывает очень успешной, и у большинства детей все хорошо. Некоторые пациенты с первичным дефектом межпредсердной перегородки не нуждаются в хирургическом вмешательстве, потому что клапаны имеют небольшую утечку или ее отсутствие, а дефект межпредсердной перегородки небольшой. Эффекты AVSD вызваны отверстиями в стенках сердца и утечкой из аномального клапана. Отверстия позволяют крови с левой стороны сердца (насыщенная кислородом или красная кровь, которая вернулась из легких) течь обратно в правую сторону сердца.Это приводит к образованию большого количества крови, которое правая сторона сердца должна снова перекачивать в легкие. Сердце должно работать намного тяжелее, чем обычно, чтобы перекачивать достаточно крови к телу, потому что большая ее часть возвращается в правую сторону сердца. Нагрузка еще больше увеличивается из-за утечки сердечного клапана. В результате дополнительной нагрузки у большинства детей с АВСД появляются признаки застойной сердечной недостаточности, такие как учащенное дыхание, проблемы с кормлением, медленное увеличение веса, низкая энергия и холодное липкое потоотделение.Эти симптомы обычно появляются в возрасте от 4 до 8 недель, но у некоторых младенцев могут возникать и раньше. Еще один возможный эффект AVSD для здоровья — гипертензия легочной артерии. Эта проблема развивается медленнее и вызвана внелегочным кровотоком. Легочные артерии, по которым кровь от правой стороны сердца поступает в легкие, плохо приспособлены к повышенному давлению, вызванному дополнительным кровотоком. Со временем, если проблема не будет устранена, легочные артерии станут толстыми и жесткими, что заставит сердце работать еще больше.Это очень серьезная проблема, без эффективного лечения. По неизвестным причинам дети с синдромом Дауна очень подвержены этой проблеме, поэтому операции на сердце часто делают, когда ребенку 4-6 месяцев. Рекомендации по упражнениям: Рекомендации по упражнениям лучше всего делать врачом пациента, чтобы при принятии решения можно было учесть все соответствующие факторы. В общем, ограничения физических упражнений для пациентов с восстановленными дефектами атриовентрикулярной перегородки не являются необходимыми, и дети могут участвовать в соревновательной и активной спортивной деятельности.Дети с синдромом Дауна чаще страдают аномалиями позвоночника, что требует некоторых ограничений в активности.
Как диагностируется эта проблема?
Клинические данные: Большинство новорожденных с АВСД не имеют сердечных симптомов, однако застойная сердечная недостаточность обычно развивается в течение первых 1-2 месяцев жизни. Проблемы с медленным ростом и медленным двигательным развитием не редкость. У некоторых детей с AVSD губы и / или под ногтями выглядят немного посиневшими, особенно когда они плачут.Это называется цианозом и возникает, когда кровь с правой стороны сердца течет к левой стороне сердца (и выходит к телу) через одно из отверстий. Физические данные: Шум в сердце часто является первым признаком того, что у ребенка AVSD. У многих детей шум слышен сразу после рождения, но может не слышаться до достижения ребенком возраста 6-8 недель. Если у ребенка застойная сердечная недостаточность, он не прибавит в весе, частота сердечных сокращений и частота дыхания будут выше нормы, а печень увеличится. Медицинские тесты: Первые тесты, которые часто назначает врач, — это электрокардиограмма, рентген грудной клетки и тест на сатурацию кислорода. AVSD изменяет расположение проводящей или электрической системы сердца, что часто проявляется как отклонение от нормы на электрокардиограмме. Уровень кислорода в крови обычно нормальный, но может быть немного низким. Рентген грудной клетки часто показывает большее, чем обычно, сердце и дополнительный приток крови к легким. Диагноз дефекта атриовентрикулярной перегородки может быть поставлен со 100% точностью с помощью эхокардиограммы.Катетеризация сердца выполняется, если есть какие-либо вопросы, на которые нет четкого ответа на эхокардиограмме, или если есть опасения по поводу легочной гипертензии.
Как лечится проблема?
Как описано ранее, хирургическое вмешательство почти всегда требуется детям с АВСД. Если возможно, операцию откладывают до тех пор, пока ребенку не исполнится 4-6 месяцев, чтобы ребенок мог расти. Перед операцией целью лечения является контроль симптомов застойной сердечной недостаточности и обеспечение адекватного набора веса.Это можно сделать, давая ребенку сердечные лекарства, такие как дигоксин (ланоксин) и фуросемид (лазикс). Иногда используется лекарство, поддерживающее уровень калия, под названием спиронолактон (альдактон). Лекарства, понижающие артериальное давление, такие как каптоприл, также иногда используются для уменьшения работы сердца. Для увеличения веса полезны более богатые смеси или добавки к грудному молоку, поскольку младенцам с застойной сердечной недостаточностью требуется больше калорий, чем другим младенцам. Если ребенок все еще не может набрать вес, операцию можно сделать раньше.Операция на открытом сердце — это основа лечения детей с АВСД. Ремонт включает в себя установку одной или двух заплаток, чтобы разделить общий клапан на правую и левую стороны и закрыть отверстия. Это выполняется после начала искусственного кровообращения, чтобы поддержать кровообращение во время самого ремонта. В клапан также накладываются швы, чтобы уменьшить утечку клапана. Результаты хирургического вмешательства очень хорошие, и 95% пациентов чувствуют себя хорошо без серьезных осложнений. Осложнения включают нарушение сердечного ритма и остаточную утечку клапана.
Клиники
Уход и услуги для пациентов с этой проблемой предоставляются в клиниках врожденной сердечной и сердечно-сосудистой хирургии при Медицинском центре Мичиганского университета в Анн-Арборе.
Каковы перспективы для детей с дефектом атриовентрикулярной перегородки?
Хирургические результаты продолжают улучшаться, и прогноз у большинства детей хороший. Некоторым детям требуется повторная операция из-за утечки клапана, имплантации кардиостимулятора или нарушения кровотока в сердце.Поздние смерти от этой проблемы довольно редки.
Список литературы
Merrill WH, Hoff SJ и Bender HW. Хирургическое лечение дефекта атриовентрикулярной перегородки. В C Mavroudis & C Backer (Eds) Детская кардиохирургия. Сент-Луис, Миссури: Мосби, 1994, 225-236. Автор: С. Лерой, RN, MSN Рецензент: Э. Бов, доктор медицины Дата отзыва: январь 2010 г.
Дефект атриовентрикулярной перегородки (AVSD) | Детская Миннесота
Дефект атриовентрикулярной перегородки (AVSD), также называемый дефектом атриовентрикулярного канала или дефектом эндокардиальной подушки, представляет собой сложный порок сердца, состоящий из нескольких структурных проблем.
Здоровое сердце — это мощный мышечный насос, который нагнетает кровь по системе кровообращения, доставляя кислород и питательные вещества к телу. Сердце имеет четыре камеры — две справа и две слева. Кровь прокачивается через эти камеры и регулируется клапанами, которые открываются и закрываются, как крошечные дверцы, так что кровь может двигаться только в одном направлении.
После путешествия по телу для доставки кислорода кровь приобретает синий цвет, потому что она больше не богата кислородом. Голубая кровь возвращается к сердцу через правые камеры и перекачивается через легочную артерию в легкие.В легких он набирает больше кислорода и становится ярко-красным. Затем он возвращается через легочную вену в левые камеры и снова перекачивается через аорту в тело.
В сердце с АВСД несколько дефектов мешают нормальной работе сердца:
- Дефект межпредсердной перегородки: Отверстие, которое позволяет обогащенной кислородом (красной) крови из левого предсердия смешиваться с бедной кислородом (синей) кровью в правом предсердии.
- Дефект межжелудочковой перегородки: Другое отверстие, которое позволяет богатой кислородом (красной) крови из левого желудочка смешиваться с бедной кислородом (синей) кровью в правом желудочке.
- Патологии митрального или трехстворчатого клапанов: Эти дефекты позволяют крови, которая должна течь вперед через систему, вместо этого течь назад.
Есть два типа AVSD:
- Частичный AVSD: В стенке между верхними камерами сердца имеется отверстие, и клапан между левыми камерами не закрывается полностью.
- Complete AVSD: Большое отверстие существует в центре сердца, где встречаются стенки между верхней и нижней камерами.Вместо двух отдельных клапанов справа и слева один большой общий клапан находится между верхней и нижней камерами. Часто этот клапан закрывается неплотно.
В любом случае AVSD позволяет крови, богатой и бедной кислородом, проходить через отверстие в стенке сердца, а аномальные клапаны пропускают кровь в нижние камеры сердца. Эти проблемы заставляют сердце работать тяжелее, вызывая его увеличение.
В результате у младенцев с АВСД могут возникать проблемы с дыханием, и они могут не расти нормально.При отсутствии лечения к потенциальным осложнениям АВСД также относятся:
- Пневмония: Отсутствие лечения AVSD может привести к повторным проблемам с этой легочной инфекцией.
- Увеличение сердца (кардиомегалия): Увеличение кровотока через сердце заставляет его работать тяжелее, что приводит к его увеличению.
- Застойная сердечная недостаточность: При отсутствии лечения AVSD вызывает застойную сердечную недостаточность, состояние, при котором сердце не может перекачивать кровь, достаточную для удовлетворения потребностей организма.
- Высокое кровяное давление в легких (легочная гипертензия): Когда сердце слабеет и не может перекачивать достаточно крови, это увеличивает кровяное давление в сердце и легких. Высокое кровяное давление в кровеносных сосудах легких может вызвать повреждение легких.
- Бактериальный эндокардит: Серьезная инфекция внутренней оболочки сердца.
Что вызывает AVSD?
Дефект атриовентрикулярной перегородки возникает в течение первых восьми недель внутриутробного развития плода, когда формируется сердце.
Сердце начинается как полая трубка. Затем образуются перегородки, или стенки, которые разделяют трубку на четыре камеры. AVSD возникает, когда стенки между правой и левой сторонами сердца формируются не полностью, оставляя отверстия, которых там не должно быть. Кроме того, клапаны, разделяющие верхнюю и нижнюю камеры сердца, также не развиваются должным образом.
НаAVSD приходится около 4–10% всех врожденных пороков сердца, возникающих примерно у двух из каждых 10 000 живорождений.Он одинаково проявляется у мальчиков и девочек.
Хотя точная причина AVSD неизвестна и в большинстве случаев ее невозможно предотвратить, несколько факторов риска могут увеличить риск рождения вашего ребенка с этим заболеванием. Дети, рожденные с синдромом Дауна, подвержены повышенному риску врожденных пороков сердца. Сорок пять процентов детей с синдромом Дауна страдают врожденными пороками сердца. Из них 20-25% процентов имеют АВСД.
К другим факторам риска относятся мать, у которой во время беременности было вирусное заболевание (например, корь), мать, страдающая диабетом, злоупотребление алкоголем во время беременности, использование некоторых лекарств во время беременности, а также родитель, у которого был врожденный порок сердца.Четырнадцать процентов матерей с атриовентрикулярным дефектом рожают ребенка с этим заболеванием.
Каковы признаки и симптомы?
Размер отверстий влияет на тип и тяжесть симптомов, а также на возраст, в котором они впервые возникают. Чем больше отверстия, тем серьезнее состояние.
Если у вашего ребенка Complete AVSD , признаки и симптомы обычно проявляются в первые несколько недель жизни. Симптомы различаются для каждого ребенка, но обычно включают:
- Затрудненное или затрудненное дыхание
- Плохой аппетит или плохая прибавка в весе
- Отсутствие интереса или необычная усталость во время кормления
- Цианоз: голубой оттенок кожи, губ или ногтей
- Бледная, прохладная или потная кожа
- Слишком быстрое сердцебиение
Полный AVSD может привести к застойной сердечной недостаточности.Если у вашего ребенка развивается застойная сердечная недостаточность, признаки и симптомы могут включать:
- Утомляемость, слабость и отсутствие бдительности
- Внезапное увеличение веса или отек ног, лодыжек, ступней или живота
- Нерегулярное или слишком быстрое сердцебиение
- Не прекращающийся кашель или хрипы, иногда с белой или розовой мокротой с кровью
Если у вашего ребенка частичный AVSD , признаки и симптомы могут не проясняться в течение недель, месяцев или даже лет.У некоторых людей с частичным АВСД симптомы не проявляются до тех пор, пока они не станут взрослыми в возрасте от 20 до 30 лет, из-за чего у них могут развиться такие состояния, как нарушение сердечного ритма, застойная сердечная недостаточность и высокое кровяное давление в легких.
Врач вашего ребенка также может заподозрить частичную АВСД, если он или она слышит шум в сердце — ненормальный свистящий шум, слышимый при осмотре стетоскопом, который может указывать на проблемы с кровотоком. Большинство сердечных шумов называют «невинными сердечными шумами». Дети с невинными сердечными шумами не имеют порока сердца и не испытывают проблем с сердцем.Однако, если шум в сердце присутствует наряду с другими симптомами, ваш врач может захотеть провести дополнительное расследование, назначив другие тесты.
Как диагностируется AVSD?
Обычно детям с АВСД требуется коррекционная операция к шести месяцам. У детей с АВСД и синдромом Дауна проблемы с легкими могут развиться раньше, чем у других детей, и им может потребоваться операция в более раннем возрасте.
Многие дети, перенесшие корректирующую операцию по поводу АВСД, не нуждаются в дальнейшем хирургическом вмешательстве и будут вести здоровый образ жизни, при этом уровень активности, аппетит и рост в конечном итоге вернутся к норме.
Четкий диагноз — это первый шаг к лечению. Детский кардиолог (детский кардиолог) может использовать несколько тестов, чтобы подтвердить диагноз вашего ребенка. Эти тесты могут включать:
- Рентген грудной клетки: Луч электромагнитной энергии создает на пленке изображения, которые показывают внутренние структуры тела вашего ребенка.
- Магнитно-резонансная томография сердца (MRI ): этот тест позволяет получить трехмерное изображение сердца, чтобы врачи вашего ребенка могли исследовать кровоток и работу сердца во время его работы.
- Электрокардиограмма (ЭКГ или ЭКГ) : этот тест, проводимый путем прикрепления участков с проводами (электродами) к коже ребенка, регистрирует электрическую активность сердца. Он покажет, есть ли нарушения сердечного ритма (аритмии или аритмии) и напряжение сердечной мышцы.
- Эхокардиограмма (эхо) : В этом тесте используются высокочастотные звуковые волны для создания движущегося изображения сердца на видеоэкране. Это похоже на ультразвук. У ребенка с дефектом атриовентрикулярного канала на эхокардиограмме выявляется отверстие в стенке между камерами сердца и аномальными клапанами.Поскольку этот тест может отслеживать кровоток, он также показывает, что кровь движется через отверстие от левой стороны к правой стороне сердца, позволяя смешиваться крови, богатой и бедной кислородом.
- Катетеризация сердца : Во время этой процедуры ваш врач вставляет тонкую гибкую трубку (катетер) в кровеносный сосуд в паху, а затем направляет ее внутрь сердца. Краситель, вводимый через катетер, делает структуры сердца видимыми на рентгеновских снимках. Катетер также измеряет кровяное давление и уровень кислорода.
Как лечится?
После постановки диагноза лечение вашего ребенка может варьироваться в зависимости от его или ее индивидуальных потребностей. Врач вашего ребенка может прописать лекарства, которые помогут сердцу и легким функционировать в условиях стресса, пока ваш ребенок не будет готов к операции.
Врачи часто рекомендуют операцию в течение первого года жизни для коррекции АВСД путем закрытия отверстия и реконструкции клапанов.
Хирургические процедуры различаются, но обычно дефекты закрываются пластырем, сделанным либо из куска сердечной оболочки, либо из синтетического материала.Пластырь остается на месте навсегда, и сердце со временем вырастает поверх него. Вероятность успеха операции высока.
При частичном дефекте атриовентрикулярного канала операция также включает восстановление митрального клапана, чтобы он плотно закрылся. Если ремонт невозможен, может потребоваться замена клапана.
Если у вашего ребенка полный дефект предсердно-желудочкового канала, операция также включает разделение единственного клапана на два клапана, один с левой стороны, а другой с правой стороны восстановленной перегородки.Если реконструкция одного клапана в два клапана невозможна, может потребоваться замена сердечного клапана.
После корректирующей операции вашему ребенку потребуется пожизненное наблюдение у кардиолога (кардиолога), специализирующегося на врожденных пороках сердца. Возможные осложнения в более позднем возрасте, такие как утечка сердечного клапана, могут потребовать дополнительного лечения. Вашему ребенку также необходимо будет принимать антибиотики перед стоматологическими и другими хирургическими процедурами, чтобы предотвратить бактериальную инфекцию сердца
О лечении АВСД у детей
Дефект атриовентрикулярной перегородки лечится в рамках Детской сердечно-сосудистой программы, одной из крупнейших и старейших детских сердечно-сосудистых программ в регионе.


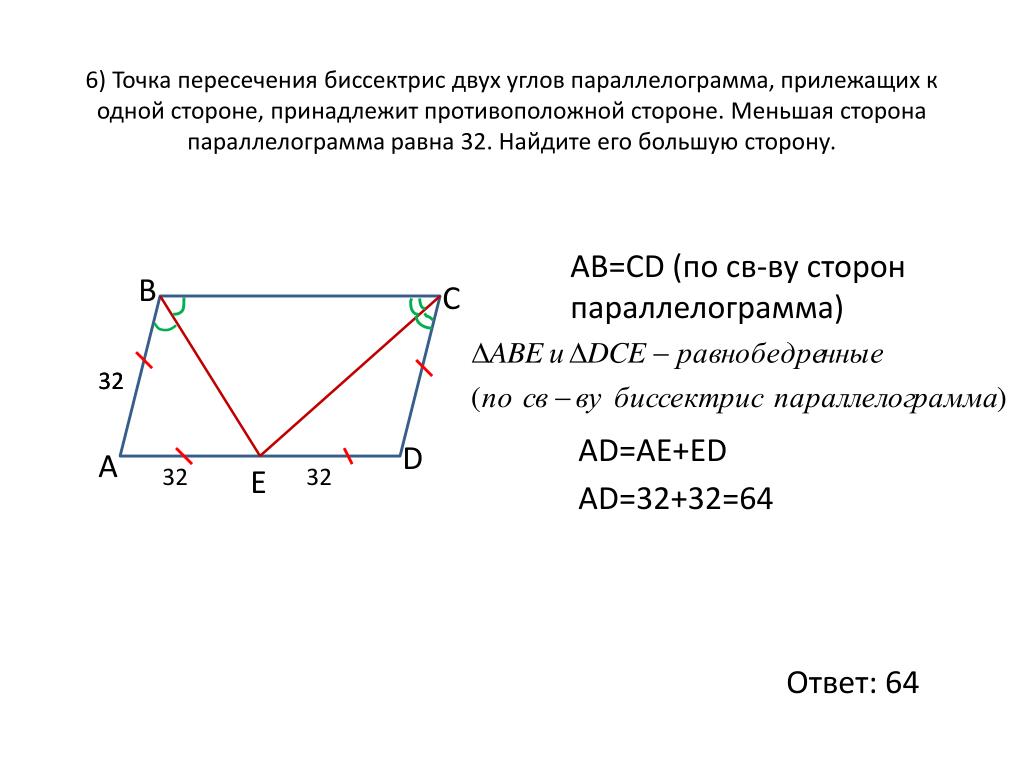

 Найдите стороны параллелограмма, если его периметр равен 84 см.
Найдите стороны параллелограмма, если его периметр равен 84 см.

 Найдите периметр параллелограмма, если AM -= 8 см, AN = 11 см, ∠BCD = 30°.
Найдите периметр параллелограмма, если AM -= 8 см, AN = 11 см, ∠BCD = 30°.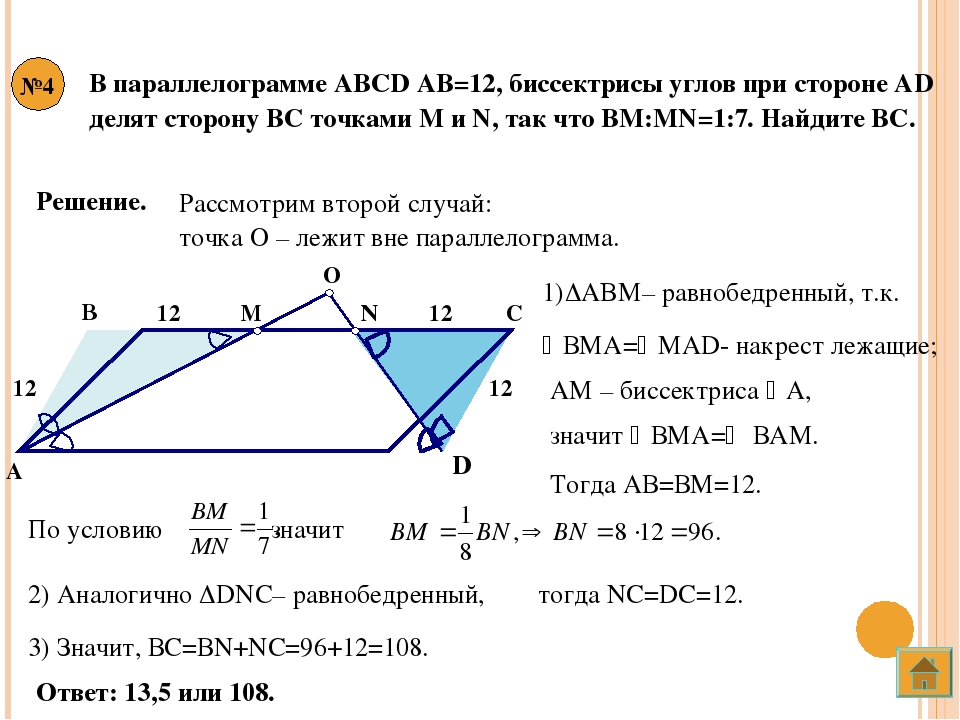
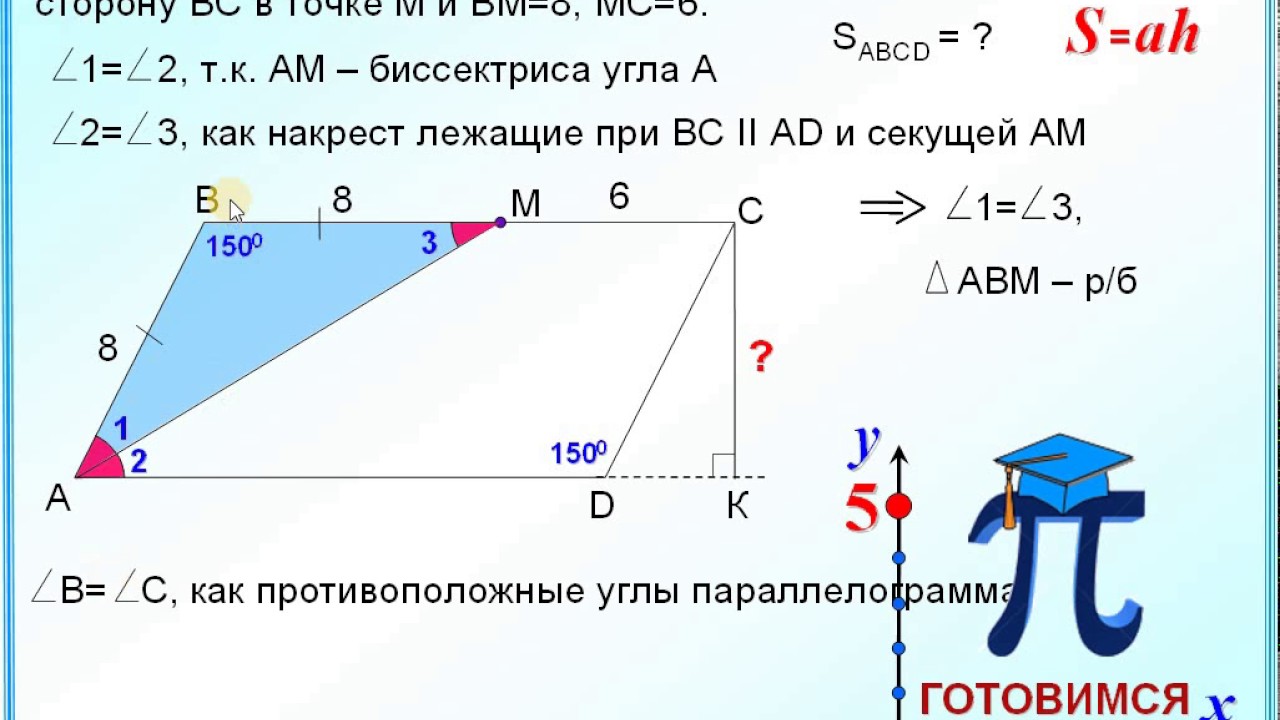 Найдите стороны параллелограмма, если его периметр равен 72 см.
Найдите стороны параллелограмма, если его периметр равен 72 см.
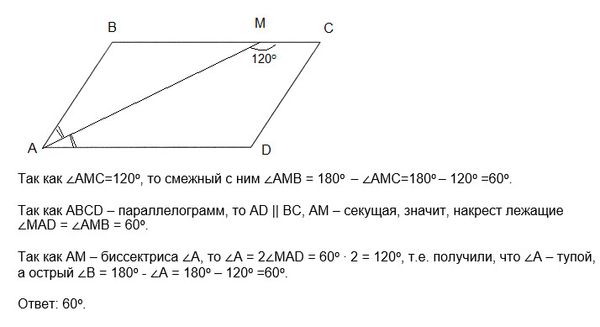 Этот общий клапан часто имеет створки (створки), которые могут быть неправильно сформированы или закрываются неплотно.Полный AVSD возникает во время беременности, когда общий клапан не может разделиться на два отдельных клапана (трикуспидальный и митральный клапаны) и когда перегородки (стенки), разделяющие верхнюю и нижнюю камеры сердца, не растут полностью, чтобы встретиться в центр сердца.
Этот общий клапан часто имеет створки (створки), которые могут быть неправильно сформированы или закрываются неплотно.Полный AVSD возникает во время беременности, когда общий клапан не может разделиться на два отдельных клапана (трикуспидальный и митральный клапаны) и когда перегородки (стенки), разделяющие верхнюю и нижнюю камеры сердца, не растут полностью, чтобы встретиться в центр сердца.
Leave A Comment