Производная x делить на x: Найти производную y' = f'(x) = x/2 (х делить на 2)

1 делить на х производная

Вы искали 1 делить на х производная? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и x в квадрате производная, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «1 делить на х производная».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 1 делить на х производная,x в квадрате производная,икс в квадрате производная,как вычислить производную функции,как производные считать,как считать производную,как считать производные,производная 1 равна,производная 1 х в квадрате 1,производная 1 чему равна,производная 2 в степени x 2 в степени,производная 2 в степени х,производная x в квадрате,производная а в степени х,производная икс в квадрате,производная икса,производная от 0,производная от x чему равна,производная от икс,производная от икс в квадрате,производная от х в 3 степени,производная от х в степени 2,производная от х в степени а,производная от числа,производная от числа в степени,производная от числа в степени х,производная равна 1,производная х в квадрате,производная х в степени 2,производная чему равна,производная числа в степени х,производная числа пи,х в квадрате производная,чему равна производная,чему равна производная 1,чему равна производная 1 x,чему равна производная x 1,чему равна производная от x.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 1 делить на х производная. Просто введите задачу в окошко и нажмите «решить» здесь (например, икс в квадрате производная).

Где можно решить любую задачу по математике, а так же 1 делить на х производная Онлайн?

Решить задачу 1 делить на х производная вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Онлайн калькулятор: Производная функции

Данный калькулятор вычисляет производную функции и затем упрощает ее.

— возведение в степень.
Допускаются также следующие функции: sqrt — квадратный корень, exp — e в указанной степени, lb — логарифм по основанию 2, lg — логарифм по основанию 10, ln — натуральный логарифм (по основанию e), sin — синус, cos — косинус, tg — тангенс, ctg — котангенс, sec — секанс, cosec — косеканс, arcsin — арксинус, arccos — арккосинус, arctg — арктангенс, arcctg — арккотангенс, arcsec — арксеканс, arccosec — арккосеканс, versin — версинус, vercos — коверсинус, haversin — гаверсинус, exsec— экссеканс, excsc — экскосеканс, sh — гиперболический синус, ch — гиперболический косинус, th — гиперболический тангенс, cth — гиперболический котангенс, sech — гиперболический секанс, csch — гиперболический косеканс, abs — абсолютное значение (модуль), sgn — сигнум (знак), logP — логарифм по основанию P, например log7(x) — логарифм по основанию 7, rootP — корень степени P, например root3(x) — кубический корень.

Таблица синтаксиса математических выражений

ГруппаКонстанты и переменныеОперацииТригонометрические функцииОбратные тригонометрические функцииГиперболические функции
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Загрузить close
content_copy Ссылка save Сохранить extension Виджет
Вычисление производной
Вычисление производной — дело нехитрое, достаточно знать несколько простых правил и формулы дифференцирования простых функций; сложнее в этом онлайн калькуляторе было сделать интерпретатор математических выражений и алгоритм упрощения полученного результата, но об этом как-нибудь в другой раз…

Правила дифференцирования
1) производная суммы:

2) производная произведения:

3) производная частного:

4) производная сложной функции равна произведению производных:
Таблица производных
Производная степенной функции:

Производная показательной функции:

Производная экспонециальной функции:

Производная логарифмической функции:

Производные тригонометрических функций:
,
,
,

Производные обратных тригонометрических функций:
,
,
,

Производные гиперболических функций:

Как найти производную.
Таблица производных.
Как мы знаем,
Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
Математический смысл этого определения понять не очень просто, поскольку в школьном курсе алгебры понятие предела функции либо не изучают совсем, либо изучают очень поверхностно. Но для того, чтобы научиться находить производные различных функций, это и не обязательно.
Тем, кто все же хочет понять, что такое предел числовой последовательности, я предлагаю посмотреть ВИДЕОУРОК:

Операция нахождения производной функции называется дифференцированием. В результате выполнения этой операции мы по определенным правилам получаем другую функцию:
В этом равенстве — функция, от которой мы берем производную,
— функция, которая получается в результате этой операции.
Для того, чтобы каждый раз не искать производные элементарных функций, используя определение производной, существует таблица производных элементарных функций:
1. Производная константы равна нулю:

2. Производная степенной функции:
Заметим, что может принимать любые действительные значения.
Примеры.
1.
2.
3.
3. Производная показательной функции:
Пример.
Частный случай этой формулы:
4. Производная логарифма:
Частный случай этой формулы:
5. Производные тригонометрических функций:
6. Производные обратных тригонометрических функций:

Правила дифференцирования:
1. Производная суммы двух функций:

2. Производная произведения двух функций:
3. Производная дроби:
4. Производная произведения функции на число равна произведению числа на производную функции (число «выносится» за знак производной):
Чтобы правильно найти производную функции , полезно придерживаться такого алгоритма:
1. Выделите, какие элементарные функции входят в состав уравнения функции.
2. Отделите в явном виде коэффициенты.
3. Если возможно, упростите выражение , используя свойства степени, свойства логарифмов или тригонометрические формулы в зависимости от того, какие элементарные функции входят в состав функции

4. Вспомните, чему равны производные этих функций или посмотрите в таблице производных.
5. Обратите внимание на то, какими арифметическими действиями связаны между собой элементарные функции, которые входят в состав функции и вспомните правило, по которому находится производная суммы, разности, произведения или частного двух функций.
Пример 1. Найти производную функции:
Используя свойства логарифмов, упростим выражение в правой части уравнения функции:

Так как по условию , следовательно,
Таким образом:
Пример 2. Найти производную функции:
1. Упростим каждую дробь, используя свойства степени :
Мы видим, что наша функция представляет собой сумму степенных функций.
Следовательно:
Пример 3. Найти производную функции
Сначала запишем каждое слагаемое в виде степени и выделим в явном виде числовые коэффициенты:
Теперь легко найти производную:
Пример 4. Найти производную функции:
Мы видим, что наша функция представляет собой дробь, в числителе которой стоит степенная функция, а в знаменателе сумма косинуса и константы.
Найдем производную функции по формуле производной дроби:
В нашем случае:
Отсюда:
КАК ИСКАТЬ ПРОИЗВОДНУЮ СЛОЖНОЙ ФУНКЦИИ читайте здесь
Видеоурок «Производная сложной функции» смотрите здесь.
И.В. Фельдман, репетитор по математике.
Урок 10. определение производной. физический смысл производной — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №10. Определение производной. Физический смысл производной.
Перечень вопросов, рассматриваемых в теме
1) Определение производной;
2) Физический смысл производной;
2) Приращение функции;
3) Скорость материальной точки в заданный момент времени по данному закону движения.
Глоссарий по теме
Пусть функция y=f(x) определена в точках x₀ и x₁. Разность x₁−x₀ называют приращением аргумента (при переходе от точки x₀ к точке x₁), а разность f(x₁)-f(x₀) называют приращением функции.
Определение. Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.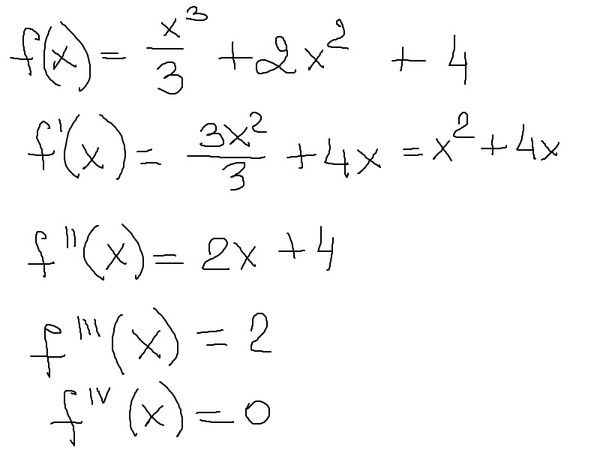
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Изучая поведение функции y=f(x) около конкретной точки x₀, важно знать, как меняется значение функции при изменении значения аргумента. Для этого используют понятия приращений аргумента и функции.
Пусть функция y=f(x) определена в точках x₀ и x₁. Разность x₁−x₀ называют приращением аргумента (при переходе от точки x₀ к точке x₁), а разность f(x₁)-f(x₀) называют приращением функции.
Приращение аргумента обозначают Δx (читают: дельта икс; Δ — прописная буква греческого алфавита «дельта»; соответствующая строчная буква пишется так: δ). Приращение функции обозначают Δy или Δf.
Итак, x₁-x₀=Δx, значит, x₁=x₀+Δx.
f(x₁)-f(x₀)=Δy, значит,
Δy=f(x₀+Δx)-f(x₀). (1)
Нельзя истолковывать термин «приращение» как «прирост».
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Найдем приращение Δx и Δf в точке x_0,если f(x)= x², x₀=2 и х=1,9
Решение:
Δx= x₁−x₀=1,9-2=-0,1
Δf= f(1,9) –f(2)=1,9²-2²=-0,39
Ответ: Δx=-0,1; Δf =-0,39
Пример 2.
Найдем приращение Δx и Δf в точке x_0,если f(x)= x², x₀=2 и х=2,1
Решение:
Δx= x₁−x₀=2,1-2=0,1
Δf= f(1,9) –f(2)=2,1²-2²=0,41
Ответ: Δx=0,1; Δf =0,41
Пример 3.
Найдем приращение Δf функции в точке x₀,если приращение аргумента равно x₀.
Решение:
по формуле (1) находим:
.
Ответ: .
С помощью введенных обозначений приращений удобно также выражать среднюю скорость движения за промежуток времени [t₀; t₀+∆t]. Если точка движется по прямой и известна ее координата x(t), то
Эта формула верна и для ∆t<0 (для промежутка [t₀+∆t; t₀]).
Аналогично выражение называют средней скорость изменения функции на промежутке с концами х₀ и х₀+∆х.
Определение. Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Обозначение: y’ или f’(x)
Если функция f(x) имеет производную в точке х, то эта функция называется дифференцируемой в этой точке. Если функция f(x) имеет производную в каждой точке некоторого промежутка, то эта функция дифференцируема на этом промежутке. Операция нахождения производной называется дифференцированием.
Схема вычисления производной функции
Найти приращение функции на отрезке [x; x+Δx]:
∆y=y(x+∆x)-y(x)
Разделить приращение функции на приращение аргумента:
Найти предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Пример 4.
Вычислить производную функции y=x²
Решение: Используем схему вычисления производной по действиям:
∆y=y(x+∆x)-y(x)= (х+∆х)²-х²= х²+2х·∆х+ ∆х²-х²= 2х·∆х+ ∆х²
Ответ: y’=2x.
Физический смысл производной: если положение точки при её движении задаётся функцией пути S(t), где t – время движения, то производная функции S есть мгновенная скорость движения в момент времени t: v(t)=S’(t).
Таким образом, скорость – есть производная от пути по времени.
Пример 5.
Точка движется по закону s(t)=1-2t. Найдите среднюю скорость движения за промежуток времени от t=0,8 до t=1.
Решение:
найдем ∆t= 1-0,8=0,2
S(0,8)= 1-2·0,8= -0,6=S(t)
S(1)= 1-2·1= -1=S(t+∆t)
.
Ответ: _.
Необходимое и достаточное условие дифференцируемости
Теорема 1. Для того, чтобы функция f(x) была дифференцируема в точке x₀, необходимо и достаточно, чтобы в этой точке она имела конечную производную. Следствие. Функция, дифференцируемая в точке, непрерывна в этой точке.
Замечание. Дифференциалом dx независимой переменной будем считать приращение Δx, т.е. dx ≡ Δx.
Операции c функциями — сложение, вычитание, умножение и деление
Операции c функциями
Функции можно складывать
Функции можно вычитать
Функции можно умножать
Функции можно делить
Функции могут быть составлены друг с другом
Давайте возьмем две функции
f(x) = x² and g(x) = x
Сумма этих функций:
f(x) + g(x) = x² + x
Сумма двух функций f и g определяется как f + g
Определение операций с функциями
(f + g)(x) = f(x) + g(x) Сложение
(f — g)(x) = f(x) — g(x) Вычитание
(f. g)(x) = f(x).g(x) Умножение
(f/g)(x) = f(x)/g(x) Деление
Для функции f + g, f — g, f.g, области определяются как пересечение областей f и g
Для f/g, область есть пересечение областей f и g кроме точек, где g(x) = 0
Пример
f(x) = 1 + √x — 2 and g(x) = x — 1
Тогда их сумма определяется как
(f + g)(x) = f(x) + g(x) = (1 + √x — 2) + (x — 1) = x + √x — 2
Теперь давайте сравним области первоначальных функций f и g с их суммой:
Функция Область
f(x) = 1 + √x — 2 [2; +∞)
g(x) = x — 1 (-∞ +∞)
(f + g)(x) = x + √x — 2 [2; ∞)∩(-∞ +∞) = [2; ∞)
Пример:
Рассмотрим две функции
f(x) = 3√x and g(x) = √x
Тогда их произведение определяется как
(f. g)(x) = f(x).g(x) = (3√x)(√x) = 3x
Обратите внимание, что
Натуральная область 3x есть (-∞; +∞)
Теперь сравним области первоначальных функций f и g, и их произведение:
Функция Область
f(x) = 3√x [0; +∞)
g(x) = √x [0; +∞)
(f.g)(x) = 3x, x ≥ 0 [0; +∞) ∩ [0; +∞) = [0; +∞)
Иногда произведение двух одинаковых функций записывается как
f²(x) = f(x).f(x)
В целом, если n есть положительным целым, тогда hen
fⁿ(x) = f(x).f(x)…f(x)
Например,
sin(x).sin(x) = (sin(x))² = sin²x
Допустим, что есть две функции
f(x) = x³ и g(x) = x + 4
Если мы заменим g(x) на x в формуле для f, мы получим новую функцию, определенную
(f o g)(x) = f(g(x)) = (g(x))³ = (x + 4)³

Чтобы вычислить f(g(x)) необходимо вычислить сначала g(x) для x из области g, а тогда необходимо g(x) в области f вычислить f(g(x))
Пример:
Есть
f(x) = x² + 3 g(x) = √x
Тогда составная этих функций есть
(f o g)(x) = f(g(x)) = (g(x))² + 3 = (√x)² + 3 = x + 3
Теперь сравним областя оригинальных функций f и g, и их составную функцию
Функция Область
f(x) = x² + 3 (-∞; +∞)
g(x) = √x [0; +∞)
(f o g)(x) = x + 3 Все x в [0; +∞) такие, что g(x)
лежит в (-∞; +∞) отсюда область
is (-∞; +∞)
Рассмотрим функцию
h(x) = (x + 1)²
мы можем разбить функцию h как
f(x) = x + 1
g(x) = x²
h(x) = g(f(x))
Примечание:
Обратите внимание, что мы можем выразить функцию как
(x² + 1)¹⁰ = [(x² + 1)²]⁵ = f(g(x))
g(x) = (x² + 1)², f(x) = x⁵
Также мы можем записать (x² + 1) = [(x² + 1)³]^10/3 = f(g(x))
g(x) = (x² + 1)³, f(x) = x^10/3
Обратите внимание, что в целом мы не можем записать
(f o g) ≠ (g o f)
Область (f o g) состоит из всех x в области g для которых g(x) в области f
Схема Горнера.
2-30x+100$ равна $6$. После деления на два заданных бинома степень заданного многочлена уменьшится на $2$, т.е. станет равна $4$.
Конечно, данный метод подбора малоэффективен в общем случае, когда корни не являются целыми числами, но для целочисленных корней метод довольно-таки неплох.
Нейронные сети — математический аппарат
В наши дни возрастает необходимость в системах, которые способны не только выполнять однажды запрограммированную последовательность действий над заранее определенными данными, но и способны сами анализировать вновь поступающую информацию, находить в ней закономерности, производить прогнозирование и т.д. В этой области приложений самым лучшим образом зарекомендовали себя так называемые нейронные сети – самообучающиеся системы, имитирующие деятельность человеческого мозга. Рассмотрим подробнее структуру искусственных нейронных сетей (НС) и их применение в конкретных задачах.
Искусственный нейрон
Несмотря на большое разнообразие вариантов нейронных сетей, все они имеют общие черты. {-ax}}$, (3)
Основное достоинство этой функции в том, что она дифференцируема на всей оси абсцисс и имеет очень простую производную:
$f’\,(x) = \alpha f(x)\,\bigl(1\,-\,f\,(x)\bigr)$, (4)
При уменьшении параметра a сигмоид становится более пологим, вырождаясь в горизонтальную линию на уровне 0,5 при a=0. При увеличении a сигмоид все больше приближается к функции единичного скачка.
Нейронные сети обратного распространения
Нейронные сети обратного распространения – это мощнейший инструмент поиска закономерностей, прогнозирования, качественного анализа. Такое название – сети обратного распространения (back propagation) они получили из-за используемого алгоритма обучения, в котором ошибка распространяется от выходного слоя к входному, т. е. в направлении, противоположном направлению распространения сигнала при нормальном функционировании сети.
Нейронная сеть обратного распространения состоит из нескольких слоев нейронов, причем каждый нейрон слоя i связан с каждым нейроном слоя i+1, т. 2$, (5)
где
y_j – значение j-го выхода нейросети,
d_j – целевое значение j-го выхода,
p – число нейронов в выходном слое.
Обучение нейросети производится методом градиентного спуска, т. е. на каждой итерации изменение веса производится по формуле:
$\Delta\,w_{ij} = -\,\eta\,\cdot\,\frac{\partial\,E}{\partial\,w_{ij}}$, (6)
где h – параметр, определяющий скорость обучения.
$\frac{\partial\,E}{\partial\,w_{ij}} = \frac{\partial\,E}{\partial\,y_i}\,\cdot\,\frac{dy_i}{dS_j}\,\cdot\,\frac{\partial\,S_j}{\partial\,w_{ij}}$, (7)
где
y_j – значение выхода j-го нейрона,
S_j – взвешенная сумма входных сигналов, определяемая по формуле (1).
При этом множитель
$\frac{\partial\,S_j}{\partial\,w_{ij}} = x_i$, (8)
где
x_i – значение i-го входа нейрона. {(n)}\,(t\,-\,1)$ , (13.1)
Дополнительным преимуществом от введения момента является способность алгоритма преодолевать мелкие локальные минимумы.
Представление входных данных
Основное отличие НС в том, что в них все входные и выходные параметры представлены в виде чисел с плавающей точкой обычно в диапазоне [0..1]. В то же время данные предметной области часто имеют другое кодирование. Так, это могут быть числа в произвольном диапазоне, даты, символьные строки. Таким образом данные о проблеме могут быть как количественными, так и качественными. Рассмотрим сначала преобразование качественных данных в числовые, а затем рассмотрим способ преобразования входных данных в требуемый диапазон.
Качественные данные мы можем разделить на две группы: упорядоченные (ординальные) и неупорядоченные. Для рассмотрения способов кодирования этих данных мы рассмотрим задачу о прогнозировании успешности лечения какого-либо заболевания. Примером упорядоченных данных могут, например, являться данные, например, о дополнительных факторах риска при данном заболевании.
нет
ожирение
алкоголь
курение
гипертония
А также возможным примером может быть, например, возраст больного:
до 25 лет
25-39 лет
40-49 лет
50-59 лет
60 и старше
Опасность каждого фактора возрастает в таблицах при движении слева направо.
В первом случае мы видим, что у больного может быть несколько факторов риска одновременно. В таком случае нам необходимо использовать такое кодирование, при котором отсутствует ситуация, когда разным комбинациям факторов соответствует одно и то же значение. Наиболее распространен способ кодирования, когда каждому фактору ставится в соответствие разряд двоичного числа. 1 в этом разряде говорит о наличии фактора, а 0 о его отсутствии. Параметру нет можно поставить в соответствии число 0. Таким образом для представления всех факторов достаточно 4-х разрядного двоичного числа. Таким образом число 1010₂ = 10₁₀ означает наличие у больного гипертонии и употребления алкоголя, а числу 0000₂ соответствует отсутствие у больного факторов риска. Таким образом факторы риска будут представлены числами в диапазоне [0..15].
Во втором случае мы также можем кодировать все значения двоичными весами, но это будет нецелесообразно, т.к. набор возможных значений будет слишком неравномерным. В этом случае более правильным будет установка в соответствие каждому значению своего веса, отличающегося на 1 от веса соседнего значения. Так, число 3 будет соответствовать возрасту 50-59 лет. Таким образом возраст будет закодирован числами в диапазоне [0..4].
В принципе аналогично можно поступать и для неупорядоченных данных, поставив в соответствие каждому значению какое-либо число. Однако это вводит нежелательную упорядоченность, которая может исказить данные, и сильно затруднить процесс обучения. В качестве одного из способов решения этой проблемы можно предложить поставить в соответствие каждому значению одного из входов НС. В этом случае при наличии этого значения соответствующий ему вход устанавливается в 1 или в 0 при противном случае. К сожалению, данный способ не является панацеей, ибо при большом количестве вариантов входного значения число входов НС разрастается до огромного количества. Это резко увеличит затраты времени на обучение. В качестве варианта обхода этой проблемы можно использовать несколько другое решение. В соответствие каждому значению входного параметра ставится бинарный вектор, каждый разряд которого соответствует отдельному входу НС.
Литература
Dirk Emma Baestaens, Willem Max Van Den Bergh, Douglas Wood, «Neural Network Solution for Trading in Financial Markets», Pitman publishing
R. M. Hristev, «Artifical Neural Networks»
С. Короткий, «Нейронные сети: Алгоритм обратного распространения»
С. Короткий, «Нейронные сети: Основные положения»
Правило частного.
Неявное дифференцирование
8
Правило частного
Доказательство правила частного
Неявное дифференцирование
Производная обратной функции
Правило частного
Следующее называется правилом частного:
«Производная частного двух функций равна
.
знаменатель, умноженный на производную числителя
минус числитель, умноженный на производную знаменателя
, все делится на квадрат знаменателя.«
Например, если на момент принять, что производная sin x равна cos x (Урок 12):
Задача 1. Вычислить производную x ²
sin x .
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!
sin x · 2 x — x ² cos x
sin ² x
Проблема 2. Используйте цепное правило для вычисления производной
.
x ³ · 2 sin x cos x — sin ² x · 3 x ²
x ⁶ = x ² sin x (2 x cos x — 3 sin x )
x ⁶
= sin x (2 x cos x — 3 sin x )
x ⁴
Проблема 3.Вычислить производную от x ² — 5 x — 6
2 x + 1 .
(2 x + 1) (2 x — 5) — ( x ² — 5 x — 6) · 2
(2 x + 1) ² = 4 x ² — 8 x — 5 — 2 x ² + 10 x + 12
(2 x + 1) ²
= 2 x ² + 2 x + 7
(2 x + 1) ²
Проблема 4. Вычислить производную от 3 x ² — x + 4
.
См. Пример, Урок 6 и Урок 22 по алгебре.
=
=
=
Доказательство правила частного
ТЕОРЕМА.
Доказательство. Поскольку г = г ( x ), то
d
dx 1
г = d
dg 1
г · dg
dx = — 1
г ² г ‘
согласно цепному правилу и задаче 4 урока 5.
Следовательно, согласно правилу продукта (Урок 6),
Это правило частного, которое мы хотели доказать.

Неявное дифференцирование
Рассмотрим следующее:
x ² + y ² = r ²
Это уравнение окружности радиусом r . (Урок 17 книги Precalculus.)
Давайте посчитаем.
Для этого мы могли бы найти и , а затем взять производную. Но вместо этого мы возьмем производную каждого члена. Что касается y ², мы рассматриваем его неявно как функцию x , и поэтому мы можем применить к нему цепное правило. Тогда будем решать за.
d
dx x ² + d
dx y ² = d
dx r ²
2 x + 2 y dy
dx = 0
dy
dx = – x
y .
Это называется неявным дифференцированием. Мы рассматриваем y как функцию от x и применяем цепное правило. Производная, которая получается в результате, обычно содержит как x , так и y .
Задача 5. 15 л + 5 л ³ + 3 y ⁵ = 5 x ³. Вычислите y ‘.
15 y ‘ + 15 y ² y’ + 15 y ⁴ y ‘ = 15 x ²
y ‘ (1 + y ² + y ⁴) = x ²
г = x ²
1 + y ² + y ⁴
Проблема 6. Вычислить y ‘.
Проблема 7.
а) В этом круге
x ² + y ² = 25,
а) какова координата y , когда x = −3?
y = 4 или −4. Для,
(−3) ² + (± 4) ² = 5 ²
б) Каков наклон касательной к окружности в точке (−3, 4)?
c) Каков наклон касательной к окружности в точке (−3, −4)?
Проблема 8.В первом квадранте, каков наклон касательной к этой окружности,
( x — 1) ² + ( y + 2) ² = 169,
, когда x = 6?
[Подсказка: 5 ² + 12 ² = 13 ² — тройка Пифагора.]
В первом квадранте, когда x = 6, y = 10.
(6-1) ² + (10 + 2) ² = 13 ².
г ‘ = — x — 1
y + 2 . Следовательно, уклон — 6 — 1
10 + 2 = — 5
12
Задача 9. Вычислите наклон касательной к этой кривой в точке (2, −1):
x ³ — 3 x y ² + y ³ = 1
3 x ² — (3 x · 2 y y ‘ + y ² · 3) + 3 y ² y’ = 0
согласно правилу продукта.
3 x ² — 6 x y y ‘ — 3 y ² + 3 y ² y’ = 0
x ² — 2 x y y ‘ — y ² + y ² y’ = 0
y ‘ ( y ²-2 xy ) = y ² — x ²
г = y ² — x ²
y ² — 2 xy
Следовательно, в (2, −1):
г = (-1) ²-2 ²
(-1) ²-2 · 2 · -1
= −3
5
= – 3
5
Производная обратной функции
Когда у нас есть функция y = f ( x ) — например
y = x ²
— тогда мы часто можем решить для x . В данном случае
При обмене переменных получаем
называется функцией, обратной y = x ².
Напишем
f ( x ) = x ²
г ( x ) =
И позвольте нам называть f прямой функцией и g обратной функцией .Формальное соотношение между f и g следующее:
f ( g ( x )) = g ( f ( x )) = x .
(Тема 19 Precalculus.)
Вот другие пары прямых и обратных функций:
f ( x ) = грех x г ( x ) = арксин x
f ( x ) = a ^x г ( x ) = бревно _a x
f ( x ) = x ³ г ( x ) =
Теперь, когда мы знаем производную прямой функции f , то из нее мы можем определить производную g .
Таким образом, пусть g ( x ) будет обратной величиной f ( x ). Тогда
f ( г ( x )) = x .
Теперь возьмем производную по отношению к x :
Это означает следующее:
Теорема. Если g ( x ) является обратной величиной f ( x ), то
«Производная обратной функции равна
.
величина, обратная производной прямой функции
, если его аргумент — обратная функция.«
Пример. Пусть f ( x ) = x ² и Тогда f ( г ) = г ².
Следовательно,
Следующий урок: Мгновенная скорость и скорость изменения
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]

Введение в производные инструменты
Все дело в наклоне!
Наклон = Изменение Y Изменение X
Мы можем найти средний уклон между двумя точками.
Но как найти наклон в точке ?
Измерять нечем!
Но с производными мы используем небольшую разницу …
… затем уменьшите его до нуля .
Давайте найдем производную!
Чтобы найти производную функции y = f (x), воспользуемся формулой наклона:
Наклон = Изменение в Y Изменение в X = Δy Δx
И (из диаграммы) видим, что:
С С
x отличается от х по х + Δx
г отличается от f (x) по ф (х + Δx)
Теперь выполните следующие действия:
Заполните эту формулу наклона: Δy Δx = f (x + Δx) — f (x) Δx
Упростите как можно лучше
Затем уменьшите Δx до нуля.
Как это:
Пример: функция
f (x) = x ²
Мы знаем f (x) = x ² , и мы можем вычислить f (x + Δx) :
Начать с: f (x + Δx) = (x + Δx) ²
Развернуть (x + Δx) ²: f (x + Δx) = x ² + 2x Δx + (Δx) ²
Формула наклона: f (x + Δx) — f (x) Δx
Положим f (x + Δx) и f (x) : x ² + 2x Δx + (Δx) ² — x ² Δx
Упростить (x ² и −x ² отменить): 2x Δx + (Δx) ² Δx
Еще больше упростить (разделить на Δx): = 2x + Δx
Тогда , поскольку Δx направляется к 0 , мы получаем: = 2x
Результат: производная x ² равна 2x
Другими словами, наклон в точке x равен 2x
Мы пишем dx вместо «Δx головки в сторону 0″ .
А «производная от» обычно пишется:
x ² = 2x
«Производная x ² равна 2x »
или просто «d dx x ² равно 2x »
Что означает x
² = 2x?
Это означает, что для функции x ² наклон или «скорость изменения» в любой точке составляет 2x .
Итак, когда x = 2 , наклон равен 2x = 4 , как показано здесь:
Или, когда x = 5 , наклон равен 2x = 10 и так далее.
Примечание: иногда f ’(x) также используется для обозначения» производной от «:
f ’(x) = 2x
» Производная f (x) равна 2x «
или просто » f-тире x равно 2x «
Попробуем другой пример.
Пример: Что такое x
³?
Мы знаем f (x) = x ³ и можем вычислить f (x + Δx) :
Начать с: f (x + Δx) = (x + Δx) ³
Развернуть (x + Δx) ³: f (x + Δx) = x ³ + 3x ² Δx + 3x (Δx) ² + (Δx) ³
Формула наклона: f (x + Δx) — f (x) Δx
Положим f (x + Δx) и f (x) : x ³ + 3x ² Δx + 3x (Δx) ² + (Δx) ³ — x ³ Δx
Упростить (x ³ и −x ³ отменить): 3x ² Δx + 3x (Δx) ² + (Δx) ³ Δx
Еще больше упростить (разделить на Δx): = 3x ² + 3x Δx + (Δx) ²
Тогда , поскольку Δx направляется к 0 , мы получаем: = 3x ²
Результат: производная x ³ равна 3x ²
Поиграйте с этим с помощью плоттера производных.
Производные от других функций
Мы можем использовать тот же метод для вычисления производных других функций (например, синуса, косинуса, логарифмов и т. Д.).
Пример: какова производная от sin (x)?
В правилах производных финансовых инструментов он указан как cos (x)
Готово.
Использование правил может быть непростым делом!
Пример: какова производная от cos (x) sin (x)?
Вы не можете просто найти производную cos (x) и умножить ее на производную sin (x)… вы должны использовать «Правило продукта», как описано на странице «Производные правила».
На самом деле получается cos ² (x) — sin ² (x)
Итак, это ваш следующий шаг: научитесь использовать правила.
Обозначение
«Сжатие до нуля» на самом деле записывается как предел, например:

«Производная f равна пределу, поскольку Δx стремится к нулю f (x + Δx) — f (x) по Δx»
Или иногда производная записывается так (объяснено в Производных как dy / dx):
Процесс нахождения производной называется «дифференцированием».
Вы, , проводите дифференциацию … до получаете производную.
Куда дальше?
Иди и узнай, как находить деривативы с помощью правил деривативов, и получи много практики:
Найдите производный инструмент, используя правило частного
Быстро! Мне нужна помощь с: Выберите элемент справки по математике … Исчисление, Производные вычисления, Интеграционное вычисление, Частное правило Монеты, Подсчет комбинаций, Поиск всех сложных чисел, Сложение сложных чисел, Вычисление с комплексными числами, Умножение комплексных чисел, Степень комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование скорости, Преобразование длины , VolumeData Analysis, Find the AverageData Analysis, Find the Standard DeviationData Analysis, HistogramsDecimals, Convert to a дробь Электричество, Стоимость разложения, Целые числа, Наибольшие общие факторы, Наименьшие общие фракции, AddingFractions, Сравнение фракций, Преобразование фракций, Преобразование в десятичные дроби, Преобразование в десятичные дроби, Преобразование дробей в десятичные дроби, Преобразование в десятичные дроби ВычитаниеФракции, Что это такое: Геометрия, Коробки, Геометрия, Круги, Геометрия, Цилиндры, Геометрия, Прямоугольники, Геометрия, Правые треугольники, Геометрия, Сферы, Геометрия, Квадраты, Графики, Линии, Графики, Любая функция, Графики, Круги hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Equation from point and slopeLines, Equation from slopeLines Theotation, The Equation from slopeLines Theotation, The Equation from slopeLines Theotation и Y-intation , Поиск шансов, Математика, Практика многочленов, Математика, Практика основ Квадратные многочлены, Деление многочленов, Факторизация разности квадратов многочленов, Факторизация триномов многочленов, Факторинг с GCF Полиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Квадратные уравнения ormulaQuadratic Equations, Solve by FactoringRadicals, Other RootsRadicals, Square RootsRatios, Что они из себя представляют, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Упрощение, Упрощение продуктов, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение , Правые треугольники, Ветер, Рисунок
Mathway | Популярные задачи
1 Найдите производную — d / dx квадратный корень x
2 Найдите производную — d / dx натуральное бревно х
3 Оцените интеграл интеграл натурального логарифма x относительно x
4 Найдите производную — d / dx e ^ x
5 Оцените интеграл интеграл от e ^ (2x) относительно x
6 Найдите производную — d / dx 1 / х
7 Найдите производную — d / dx х ^ 2
8 Оцените интеграл интеграл e ^ (- x) относительно x
9 Найдите производную — d / dx 1 / (х ^ 2)
10 Найдите производную — d / dx грех (х) ^ 2
11 Найдите производную — d / dx сек (x)
12 Оцените интеграл интеграл e ^ x относительно x
13 Оцените интеграл интеграл x ^ 2 относительно x
14 Оцените интеграл интеграл квадратного корня x относительно x
15 Оценить натуральное бревно 1
16 Оценить e ^ 0
17 Оценить грех (0)
18 Найдите производную — d / dx cos (x) ^ 2
19 Оцените интеграл интеграл 1 / x относительно x
20 Оценить cos (0)
21 Оцените интеграл интеграл sin (x) ^ 2 относительно x
22 Найдите производную — d / dx х ^ 3
23 Найдите производную — d / dx сек (x) ^ 2
24 Найдите производную — d / dx 1 / (х ^ 2)
25 Оцените интеграл интеграл arcsin (x) относительно x
26 Оцените интеграл интеграл cos (x) ^ 2 относительно x
27 Оцените интеграл интеграл от sec (x) ^ 2 относительно x
28 Найдите производную — d / dx е ^ (х ^ 2)
29 Оцените интеграл интеграл от 0 до 1 кубического корня из 1 + 7x относительно x
30 Найдите производную — d / dx грех (2x)
31 Оцените интеграл интеграл натурального логарифма x относительно x
32 Найдите производную — d / dx загар (x) ^ 2
33 Оцените интеграл интеграл от e ^ (2x) относительно x
34 Оцените интеграл интеграл от 1 / (x ^ 2) относительно x
35 Найдите производную — d / dx 2 ^ х
36 График натуральное бревно из
37 Оценить e ^ 1
38 Оцените интеграл интеграл от 1 / (x ^ 2) относительно x
39 Оценить бревно 0
40 Найдите производную — d / dx cos (2x)
41 Найдите производную — d / dx хе ^ х
42 Оцените интеграл интеграл 1 / x относительно x
43 Оцените интеграл интеграл 2x по отношению к x
44 Найдите производную — d / dx (натуральный логарифм x) ^ 2
45 Найдите производную — d / dx натуральный логарифм (x) ^ 2
46 Найдите производную — d / dx 3x ^ 2
47 Оценить натуральное бревно из 2
48 Оцените интеграл интеграл xe ^ (2x) относительно x
49 Найдите производную — d / dx 2e ^ x
50 Найдите производную — d / dx натуральное бревно 2х
51 Найдите производную — d / dx -sin (х)
52 Оценить загар (0)
53 Найдите производную — d / dx 4x ^ 2-x + 5
54 Найдите производную — d / dx y = 16 корень четвертой степени из 4x ^ 4 + 4
55 Найдите производную — d / dx 2x ^ 2
56 Оцените интеграл интеграл e ^ (3x) относительно x
57 Оцените интеграл интеграл от cos (2x) относительно x
58 Оцените интеграл интеграл cos (x) ^ 2 относительно x
59 Найдите производную — d / dx 1 / (квадратный корень из x)
60 Оцените интеграл интеграл e ^ (x ^ 2) относительно x
61 Оценить сек (0)
62 Оценить e ^ бесконечность
63 Оценить 2 ^ 4
64 Найдите производную — d / dx х / 2
65 Оценить 4 ^ 3
66 Найдите производную — d / dx -cos (x)
67 Найдите производную — d / dx грех (3x)
68 Оценить полено натуральное 1 / е
69 Оцените интеграл интеграл x ^ 2 относительно x
70 Упростить 1 / (кубический корень из x ^ 4)
71 Найдите производную — d / dx 1 / (х ^ 3)
72 Оцените интеграл интеграл e ^ x относительно x
73 Оцените интеграл интеграл tan (x) ^ 2 относительно x
74 Оцените интеграл интеграл 1 по x
75 Найдите производную — d / dx х ^ х
76 Найдите производную — d / dx х натуральное бревно х
77 Оцените интеграл интеграл sin (x) ^ 2 относительно x
78 Найдите производную — d / dx х ^ 4
79 Оценить предел предел, когда x приближается к 3 из (3x-5) / (x-3)
80 Оцените интеграл интеграл от x ^ 2 натурального логарифма x относительно x
81 Найдите производную — d / dx f (x) = квадратный корень из x
82 Найдите производную — d / dx х ^ 2sin (х)
83 Оцените интеграл интеграл sin (2x) относительно x
84 Найдите производную — d / dx 3e ^ x
85 Оцените интеграл интеграл xe ^ x относительно x
86 Найдите производную — d / dx у = х ^ 2
87 Найдите производную — d / dx квадратный корень из x ^ 2 + 1
88 Найдите производную — d / dx грех (x ^ 2)
89 Оцените интеграл интеграл от e ^ (- 2x) относительно x
90 Оцените интеграл интеграл натурального логарифма квадратного корня x относительно x
91 Оценить 2 ^ 5
92 Найдите производную — d / dx e ^ 2
93 Найдите производную — d / dx х ^ 2 + 1
94 Оцените интеграл интеграл sin (x) относительно x
95 Оценить 2 ^ 3
96 Найдите производную — d / dx арксин (х)
97 Оценить предел предел, когда x приближается к 0 из (sin (x)) / x
98 Оценить e ^ 2
99 Оцените интеграл интеграл e ^ (- x) относительно x
100 Оцените интеграл интеграл 1 / x относительно x
6.
Производные продукты и коэффициенты
М. Борна
ПРАВИЛО ПРОДУКТА
Если u и v — две функции x , то производная от произведения uv дается как …
`(d (uv)) / (dx) = u (dv) / (dx) + v (du) / dx`
На словах это можно запомнить как:
«Производная произведения двух функций — это первое, умноженное на производное второго, плюс второе, умноженное на производное первого.«
Откуда взялась эта формула? Как и все встречающиеся нам формулы дифференцирования, она основана на производных от первых принципов.
Пример 1
Если у нас есть такой товар, как
y = (2 x ² + 6 x ) (2 x ³ + 5 x ²)
мы можем найти производную, не умножая выражение справа. 2) `(в главе« Дифференциация трансцендентных функций ».) Это выражение нельзя умножить почленно, поэтому нам нужен метод, чтобы дифференцировать произведения таких функций.
Примечание
Мы можем написать правило продукта разными способами:
`(d (uv)) / (dx) = uv’ + vu’`
ИЛИ
`(d (fg)) / (dx)` `= f (x) d / (dx) g (x) + g (x) d / (dx) f (x)`… и т. Д.
ЧАСТНОЕ ПРАВИЛО
(частное — это всего лишь дробь.2) `
Формулы первой производной функции
y — функция y = y (x)
C = константа, производная (y ‘) константы равна 0
у = С => у ‘= 0
Пример: y = 5, y ‘= 0
Если y является функцией типа y = x ⁿ формула производной:
y = x ⁿ => y ‘= nx ^n-1
Пример: y = x ³ y ‘= 3x ^3-1 = 3x ²
y = x ^-3 y’ = -3x ^-4
Из верхней формулы для производной y ‘функции y = x = x ¹ можно сказать, что:
если y = x, то y ‘= 1
y = f ₁ (x) + f ₂ (x) + f ₃ (x). .. =>
y ‘= f’ ₁ (x) + f ‘₂ (x) + f’ ₃ (x) …
Эта формула представляет собой производную функции, которая является суммой функций.
Пример: если у нас есть две функции f (x) = x ² + x + 1 и g (x) = x ⁵ + 7 и y = f (x) + g (x), тогда y ‘= f’ (x) + g ‘(x) =>
y’ = (x ² + x + 1) ‘+ (x ⁵ + 7)’ = 2x ¹ + 1 + 0 + 5x ⁴ + 0 = 5x ⁴ + 2x + 1
Если функция является кратной из двух функций, производная определяется следующим образом:
у = f (х).g (x) => y ‘= f’ (x) g (x) + f (x) g ‘(x)
Если f (x) = C (C — константа) и y = f (x) g (x)
y = Cg (x) y ‘= C’.g (x) + C.g’ (x) = 0 + C.g ‘(x) = C.g’ (x)
у = Cf (x) => y ‘= C.f’ (x)
В разделе задач есть примеры следующих формул.
y = г ‘=
f ‘(x) g (x) — f (x) g’ (x)
g ² (x)
y = ln x => y ‘= ¹/_x
y = e ^x => y ‘= e ^x
у = грех х => у ‘= соз х
y = cos x => y ‘= -sin x
y = tan x => y ‘= ¹/_{cos ² x}
y = детская кроватка x => y ‘= — ¹/_{sin ² x}
Когда функция является функцией функции: u = u (x)
y = f (u) => y ‘= f’ (u). ты
Пример: давайте зададим y = sin (x ²)
Здесь u = x ², f (u) = sin (u), производные будут f ‘(u) = cos (u), u’ = 2x
y ‘= (sin (u))’ ⋅u ‘= cos (x ²) ⋅2x = 2⋅x⋅cos (x ²)
Проблемы с производными
1) f (x) = 10x + 4y, Какая первая производная f ‘(x) =?
Решение: Мы можем использовать формулу для производной функции, которая является суммой функции
f (x) = f ₁ (x) + f ₂ (x), f ₁ (x) = 10x, f ₂ (x) = 4y для функции f ₂ (x) = 4y, y является константой, поскольку аргумент f ₂ (x) равен x поэтому f ‘₂ (x) = (4y)’ = 0.Следовательно, производная функция f (x) равна: f ‘(x) = 10 + 0 = 10.
2) Вычислить производную f (x) =
Решение: У нас есть две функции: h (x) = x ¹⁰ и g (x) = 4,15 + cos x
, функция f (x) — это h (x), деленная на g (x). h ‘(x) = 10x ⁹ g’ (x) = 0 — sin x = -sin x
f ‘(x) =
h ‘(x) .g (x) — h (x) .g’ (x)
(g (x)) ²
f ‘(x) =
10x ⁹ (4.15 + cos x) — x ¹⁰ (-sin x)
(4,15 + cosx) ²
=
x ¹⁰ sin x + 10 (60 + cos x) x ⁹
(60 + cosx) ²
3) f (x) = ln (sinx). какова производная функции f (x)?
Решение: Для решения задачи необходимо использовать последнюю формулу. Как мы видим, f (x) является функцией функции функции f (x) = h (g (x)), где h = ln и g = sin x
Калькулятор производных
Подробнее о производных на математическом форуме
Регистрация на форуме
Математическая сцена — Производные, урок 5
Математическая сцена — Производные, урок 5 — Цепное правило
2009 Rasmus ehf & Jhann sak
Производные
Урок 5
Цепное правило
Пример 1
Дифференцировать f (x) = (x ³ +1) ².
Только так у нас есть пока это делается путем умножения скобок, а затем дифференцируя. Если мы это сделаем, то получим
f (x) = x ⁶ + 2x ³ +1 и, следовательно, f (x) = 6x ⁵ + 6x ².
Это не проблема с простой пример, такой как приведенный выше, но что произойдет, если, например, у нас есть f (x) = (x ³ +1) ⁶?
В этом случае требуется слишком много усилий, чтобы перемножить скобки перед дифференцируя.
Чтобы различать такие составные функции, мы используем так называемое правило цепочки. Сделаем пример 1 еще раз, чтобы увидеть, как это работает.
f (x) является примером составная функция, как было введено в функциях 2.
Его можно записать как f (u) = u ², где u = x ³ +1, u равно функция от x, то есть u (x) = x ³ +1.
Цепное правило гласит, что мы сначала дифференцируйте f (u), рассматривая u как переменную, и получите f (u) = 2u (так же, как (x ²) = 2x)
Далее дифференцируем u и получаем и (х) = 3х ². Наконец, мы умножаем два результата вместе и получаем f (x) = 2u3x ². Возвращая значение u, получаем f (x) = 2 (x ³ +1) 3x ² = 6x ⁵ + 6x ²
^{Это дает нам правило
называется цепным правилом, которое гласит, что}
(f (u (x)) = f (u (x)) u (x)
Мы только указали здесь правило, но его легко доказать для всех непрерывных дифференцируемых функции.
Пример 2
Различайте композицию функция f (x) = sin ² x.
Обозначение грех ² х это другой способ записи (sin x) ² так что квадрат является внешней функцией, а sin x — внутренней функцией. Начать мы разделим это на две части, но с практикой это не будет необходимо.
f (x) = (грех х) ² можно записать как f (u) = u ² где u = sin x.
f (u) = 2u и u = cos x, так что умножая вместе получаем
f (x) = 2ucos x = 2 sin x cos x
Цепное правило гласит, что дифференцируем составную функцию, мы дифференцируем внешнюю функцию и умножьте на производную внутренней функции.
Пример 2 +
Продифференцируем f (x) = sin x ². Это можно записать как f (u) = sin u, где u = х ²
Итак, в этом случае синус — это внешняя функция, а квадрат внутренний функция
ф (х) = cos x ² 2x
Пример 3
Мы можем использовать правила cos x = sin (/ ₂ x) и sin x = cos (/ ₂ x), чтобы найти производную cos x.
cos x = f (x) = sin (/ ₂ x)
Производная синуса, внешняя функция является cos и производной от (/ ₂ x), внутренняя функция равна 1, поэтому мы получаем
ф (х) = cos (/ ₂ x) (1)
= грех х (1)
= грех х
Пример 4
Найдите производную f (x) = sin ² x ².
Это можно записать как f (x) = (sin x ²) ² так что у нас есть тройная составная функция. Самая внешняя функция — квадратичная, затем синус и, наконец, еще один квадратичный.
Мы можем написать f = u ² , где u = sinv и v = х ². Различение каждой функции и умножение дает 2 u cos v 2x, и, возвращая значения u и v, получаем результат:
f (x) = 2 sin x ² cos x ² 2x
Первая дифференцируем квадрат, оставляя sin x ² без изменений.Затем мы дифференцируем синусоидальную функцию, чтобы получить cos и оставить х ² без изменений, наконец, мы дифференцируем х ² и получите 2x.
Пример 5
a) f (x) = e ^2x
f (x) = e ^2x 2
Дифференцирование экспоненциальной функции не меняет ее. производная 2x равна 2.
Дифференцирование экспоненциальной функции не меняет ее, производная от x ² + 1 равна 2x.
c) f (x) = e ^{sin
x} f (x) = e ^{^{sin
x}} cos x
Дифференцирование экспоненциальной функции не меняет ее, производная sin x равна cos x.
Теперь мы хотим найти правило для дифференциации f (x) = ln x.
Мы используем метод под названием неявное дифференцирование , что означает различение обеих сторон уравнение.
Если f (x) = ln x, то e ^{f (x)} = х. Если мы продифференцируем обе части уравнения, мы получим следующее:
e ^{f (x)} = х
e ^{f (x)} f (x) = 1 Использование правила цепочки.
Решая для f (x), получаем
f (x) = 1 / e ^{f (x)}
= 1 / х Помните, что x = e ^{f (x)}.
Теперь мы можем найти производную от других логарифмические функции.
Найдите производную от f (x) = log x.
Сначала мы должны напомнить себе о правила логарифмирования и отношения между бревнами с разными основаниями. Этот Правило, которое нам нужно:
Таким образом мы можем переписать любой логарифм как натуральный логарифм ln x.
Логарифм ln 10 — константа, не влияющая на производная, остальное несложно.
Аналогичные расчеты работают для любой функции журнала, поэтому мы можем резюмировать следующие три правила:
Пример 6
Продифференцируем f (x) = ln (x ² + 1).
Пример 7
Продифференцируем f (x) = xln х х + 5.
f (x) = 1lnx + x1 / x 1 = ln x
Обобщение производных
Производная:
к = 0 k = постоянная Икс = 1
(x ⁿ) = nx ⁿ¹ n может быть любым действительным числом.
(e ^x) = e ^x
(^x) = ^x дюйм
(грех х) = cos x
(соз х) = грех х
Правила:
(УФ) = УФ + УФ
(е (г (х)) = е (г (х)) г (х)
Попрактикуйтесь в этих методах, а затем пройдите тест 5 по производным.
шт. Запомните свой контрольный список.
.