При игре в крестики нолики второй игрок после первого хода первого игрока получает количество
PascalABC -> uses System.Windows.Forms TabControl -> TabPage -> listView1 ______________________________________ Кто объяснит почему таблица … не создается ?
В словаре employee поменяйте зарплату сотрудника John на 300000. employee = { ’employee1′: {‘name’: ‘Sam’, ‘age’: 35, ‘salary’: 400000}, ’employee2′: … {‘name’: ‘Anna’, ‘age’: 29, ‘salary’: 350000}, ’employee3′: {‘name’: ‘John’, ‘age’: 25, ‘salary’: 250000} } Вывод: employee = { ’employee1′: {‘name’: ‘Sam’, ‘age’: 35, ‘salary’: 400000}, ’employee2′: {‘name’: ‘Anna’, ‘age’: 29, ‘salary’: 350000}, ’employee3′: {‘name’: ‘John’, ‘age’: 25, ‘salary’: 300000} }
Дана последовательность из N вещественных чисел, начинающаяся с положительного числа. Определить, какое количество положительных чисел записано в нача … ле последовательности. Условный оператор не использовать. Решить задачу используя циклическую конструкцию while
Запишите определение одномерного массива(1б)Необходимо заполнить массив числами (количество вводимых чисел определяет пользователь), вывести его на пе
… чать, отсортировать его в порядке возрастания и убывания.
Помогите пожалуйста по информатике
Дана последовательность из N вещественных чисел, начинающаяся с положительного числа. Определить, какое количество положительных чисел записано в нача … ле последовательности. Условный оператор не использовать. Решить задачу используя циклическую конструкцию while
Помогите пожалуйста срочно
Дана последовательность из n вещественных чисел, начинающаяся с положительного числа. Определить, какое количество положительных чисел записано в нача … ле последовательности. Условный оператор не использовать. Решить задачу используя циклическую конструкцию while.
) К присва пС ДАДЮ155 БАЛЛОВ
4. Определите синтаксическую ошибку программного кода.a = int input()b = int (input())c = a + bprint (T)
Какое количество информации получит второй игрок при игре в крестики-нолики на поле 4х4, после первого хода первого игрока, играющего крестиками?
Количество информации
10 класс
ВАРИАНТ 1
5 бит
4 бита
3 бита
2 бита
Производится бросание симметричной четырехгранной пирамидки.

1 бит
4 бит
1 байт
2 бита
Группа школьников пришла в бассейн, в котором 4 дорожки для плавания. Тренер сообщил, что группа будет плавать на дорожке №3. сколько информации получили школьники из этого сообщения?
1 бит
2 бита
2 байта
1 байт
В течении 5 минут со скоростью 20 байт/с вождь племени Мульти передавал информационное сообщение.
 Сколько оно содержало символов, если
алфавит племени состоит из 32 символов.
Сколько оно содержало символов, если
алфавит племени состоит из 32 символов.Во сколько раз увеличится информационный объем страницы текста (текст не содержит управляющих символов форматирования) при его преобразовании из кодировки MS-DOS (таблица кодировки содержит 256 символов) в кодировку Unicode (таблица кодировки содержит 65536 символов)?
|
|
|
|
Обычный дорожный светофор без дополнительных секций подает шесть видов сигналов (непрерывные красный, желтый и зеленый, мигающие желтый и зеленый, красный и желтый одновременно). Электронное устройство управления светофором последовательно воспроизводит записанные сигналы.

Световое табло состоит из лампочек, каждая из которых может находиться в двух состояниях («включено» или «выключено»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 50 различных сигналов?
Метеорологическая станция ведет наблюдение за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100 процентов, которое записывается при помощи минимально возможного количества бит. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.
1)
80 бит
2)
3)
80 байт
4)
560 байт
Для передачи секретного сообщения используется код, состоящий из десятичных цифр.
 При этом все цифры
кодируются одним и тем же (минимально
возможным) количеством бит. Определите
информационный объем сообщения длиной
в 150 символов.
При этом все цифры
кодируются одним и тем же (минимально
возможным) количеством бит. Определите
информационный объем сообщения длиной
в 150 символов.1)
600 бит
2)
750 бит
3)
1200 бит
4)
60 байт
На полке находятся учебники по физике, географии и информатике, причем учебников по географии в 3 раза меньше, чем по физике, а учебников по информатике 8. Сообщение о том, что с полки достали учебник по информатике, содержит два бита информации. Количество учебников по физике равно.

В теннисном турнире принимали участие теннисисты А, В и С. Информационный объём сообщения, что победил не А, равен 4 — log23 — log25 бит. Информационный объём сообщения, что победил В, равен 4 — log211 бит. Определить, сколько бит информации содержит сообщение, что победил на турнире теннисист С.
Информационный объём первого сообщения в 7 раза меньше, чем информационный объём второго сообщения. Количество символов первого сообщения в 2 раза меньшем, чем количество символов второго сообщения. Найти размер алфавита для первого сообщения, если на каждый символ приходится целое число бит, а мощности обеих алфавитов не превышают 240 символов
Информационный объём текста равен 2 Кбайтам. Текст записан на 4 страницах по 32 символа в строке, 16-символьным алфавитом. Определить количество строк на странице.
ВАРИАНТ 2
Какое количество информации получит при игре в шахматы играющий черными после первого хода белых (при условии, что ходить конями запрещено)?
2 бита
3 бита
4 бита
5 бит
Вы подошли к светофору, когда горел желтый свет.
 После этого
загорелся зеленый. Какое количество
информации вы при этом получили?
После этого
загорелся зеленый. Какое количество
информации вы при этом получили?1 бит
2 бита
0 бит
1 байт
Происходит выбор одной карты из колоды в 32 карты. Какое количество информации мы получаем в зрительном сообщении о выборе определенной карты?
32 бита
8 бит
5 бит
1 бит
Алфавит племени Мульти состоит из 8 символов.
 Вождь племени
говорит со скоростью 20 символов в
минуту. Какова в этом случае скорость
информационного потока?
Вождь племени
говорит со скоростью 20 символов в
минуту. Какова в этом случае скорость
информационного потока?60 бит/с
1 бит/с
60 байт/с
1 байт/с
Во сколько раз уменьшится информационный объем страницы текста (текст не содержит управляющих символов форматирования) при его преобразовании из кодировки Unicode (таблица кодировки содержит 65536 символов) в кодировку Windows CP-1251 (таблица кодировки содержит 256 символов)?
в 2 раза
в 8 раз
в 16 раз
в 256 раз
Обычный дорожный светофор без дополнительных секций подает 5 видов сигналов (непрерывные красный, желтый и зеленый, мигающий и зеленый, красный и желтый одновременно).
 Электронное устройство управления
светофором последовательно воспроизводит
записанные сигналы. Подряд записано
50 сигналов светофора. В байтах данный
информационный объем составляет
Электронное устройство управления
светофором последовательно воспроизводит
записанные сигналы. Подряд записано
50 сигналов светофора. В байтах данный
информационный объем составляет
Азбука Морзе позволяет кодировать символы для радиосвязи, задавая комбинацию точек и тире. Сколько различных символов (цифр, букв, знаков пунктуации и т.д.) можно закодировать, используя код Морзе длиной не менее пяти и не более шести сигналов (точек и тире)?
1)
80
2)
120
3)
112
4)
96
1)
64
2)
50
3)
32
4)
20
Сколько существует различных последовательностей из символов «плюс» и «минус», длиной ровно в пять символов?
Световое табло состоит из лампочек.
 Каждая лампочка может
находиться в одном из трех состояний
(«включено», «выключено» или «мигает»).
Какое наименьшее количество лампочек
должно находиться на табло, чтобы с его
помощью можно было передать 18 различных
сигналов?
Каждая лампочка может
находиться в одном из трех состояний
(«включено», «выключено» или «мигает»).
Какое наименьшее количество лампочек
должно находиться на табло, чтобы с его
помощью можно было передать 18 различных
сигналов?
Книга состоит из 5 глав, причем число страниц в третьей главе в 3 раза меньше, а в пятой в 2 раза больше, чем в первой. Объем второй и четвертой главы составляет по 70 страниц каждая. Количество информации в сообщении о том, что наугад открыли страницу четвертой главы равно 3 битам. Объем книги равен…
В аудитории находятся 16 студентов только с именами Александр, Борис, Владимир и Денис, причем Александров в 3 раза больше, чем Денисов. Информационный объём сообщения, что из аудитории вышел не Борис, равен 6 — log224 — log25 + log23 бит. Информационный объём сообщения, что из аудитории вышел не Владимир, равен 5log228 бит.
 Определить, сколько студентов с
именем Денис находилось в аудитории.
Определить, сколько студентов с
именем Денис находилось в аудитории.Информационный объём первого сообщения в 5 раза меньше, чем информационный объём второго сообщения. Количество символов первого сообщения в 4 раза меньшем, чем количество символов второго сообщения. Найти размер алфавита для первого сообщения, если на каждый символ приходится целое число бит, а мощности обоих алфавитов не превышают 32 символов.
Информационный объём текста равен 12 Кбайтам. Текст записан на 8 страницах по 32 строки на каждой странице по 64 символа в каждой строке. Определить мощность алфавита, с помощью которого записан текст.
как выиграть в крестики-нолики. Хитрая стратегия за крестики
В школе я был чемпионом в крестики нолики, играл не зная поражаения. Эта игра была любимым способом скоротать время до перемены на скучных уроках.
Когда не было компьютерных игр и приложений для смартфонов, нам для игры достаточно было тетрадного листка в клетку и карандаша.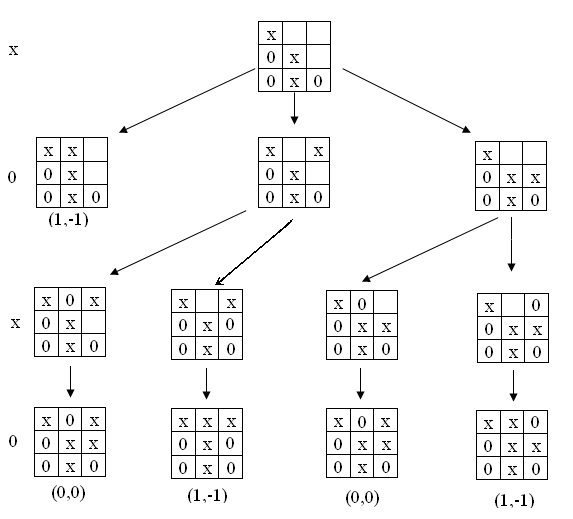 Зимой в крестики-нолики играли на улице, начертив игровое поле веточкой на снегу.
Зимой в крестики-нолики играли на улице, начертив игровое поле веточкой на снегу.
Сейчас игры детства приобрели «мобильный» характер и доступны онлайн. Но правила игры и стратегия победы остались прежними. Освоив простой алгоритм из этой заметки, вы легко сможете выиграть крестики нолики у зои, победить 5 в ряд в мета школе и никогда не проиграете живому человеку.
Крестики-нолики, правила игры
Игровое поле представляет собой квадрат размером 3х3 нарисованный на листке бумаги и расчерченный на девять клеток. Две линии проводятся вдоль квадрата, две линии поперек.
Варианты, когда игровое поле имеет размеры от 4 х 4 до бесконечности, рассмотрим ниже, после разбора комбинаций игры в поле 3х3.
Базовые принципы общие, и освоив алгоритм «три в ряд», вы сможете уверенно играть в более сложные и интересные варианты этой древней игры.
Первым ход делает игрок, играющий крестиками. Второй ход за игроком, играющим ноликами. Крестики уже заняли одну клетку, и нолики для хода выбирают пустую, из оставшихся клеток.
Игроки по очереди меняются, кому играть за крестиков и ноликов.
Древние китайцы вместо рисованных символов «Х» и «0» на поле ставили камни, черные и белые. Сейчас дома в качестве поля можно использовать шахматную доску и шашками обозначать клетку, на которую сделан ход.
Побеждает игрок, который первым построил (в пределах игрового поля) линию из трех своих символов: горизонтальную, вертикальную или по диагонали.
Стратегия победы пошагово видеоразбор
Небольшой видео ролик, для тех, кому так проще воспринимать информацию. Кому интереснее читать, листаем дальше.
- Вы победили.
- Ничья. Закончились пустые клетки на игровом поле и ходить больше некуда.
Возможны два варианта исхода игры:
Вариант «Вы проиграли», мы не рассматриваем, так как тем, кто до конца дочитал эту статью проигрыш не грозит. Все время выигрывать я вас не научу, но расскажу, как можно всегда свести игру к ничьей.
Для удобства рассказа, я каждый квадрат игрового поля обозначил цифрами, от 1 до 9.
(5) — центральная клетка.
(1), (3), (7), (9) — угловые клетки.
(2), (4), (6), (8) — боковые клетки.
Чтоб не растягивать повествование, я для каждого варианта первого хода буду рассматривать по одной комбинации. Если в моем примере нолики сходили в угловую клетку (1), а в вашем случае в угловую клетку (3), (7) или (9), то мысленно разверните поле и продолжайте ходить по изложенному мной алгоритму.
Ситуация №1, крестики ходят в центр
Когда крестики первым ходом занимают центральную клетку (5), ноликам остается ходить в угловую клетку или в боковую.
На этом ходу уже все решается. Сходили нолики в угловую клетку — это ничья. Если нолики сходили в любую боковую клетку — вы победили. Можно начинать новую партию, эта игра дальше не имеет смысла.
В нашем примере нолики сходили в боковую клетку (8).
Крестики ответным ходом занимают любую угловую клетку, для примера клетку (1) и получают линию из двух крестиков (см. рисунок).
Главная премудрость игры и основа всей тактики держится на двух принципах:
Принцип 1. Занимай ту клетку, которая принесет тебе немедленную победу;
Принцип 2. Если такой клетки нет, занимай клетку, которая принесет немедленную победу сопернику.
Нолики сейчас своим ходом выиграть не могут и по второму принципу занимают клетку (9), в свою очередь образуя линию из двух ноликов, см. шаг 4.
Крестики занимая клетку (7) нейтрализуют угрозу со стороны ноликов и одновременно с этим строят две линии из своих фигур. Для победы в следующем ходе крестикам нужно будет занять клетку (3) или (4). См. шаг 5.
Такое построение, когда одним ходом создается две угрозы, называется ВИЛКА.
Нолики в шестом шаге заняв клетку (3) закрывают одну угрозу со стороны крестиков.
Крестики по принципу 1, ходят в клетку (4) и одерживают победу.
Ситуация №2, крестики ходят в центр
Предположим, что теперь вы играете ноликами. Чтоб не проиграть эту встречу, первым ходом нужно занять угловую клетку. Без разницы какую, на ваш вкус (1), (3), (7) или (9). Для примера возьмем (1), см. рисунок ниже, шаг 2.
Без разницы какую, на ваш вкус (1), (3), (7) или (9). Для примера возьмем (1), см. рисунок ниже, шаг 2.
Крестики, опять же без разницы, куда бы ни сходили, получат линию из двух фигур. см. шаг 3.
Нолики закрывают линию крестиков, и создают свою угрозу — см. шаг 4.
Крестики по принципу 2 ходят в квадрат (4), нолики отвечают в квадрат (6). См. шаг 5 и 6.
Независимо от того, каким был предыдущий ход у крестиков, ноликам следует занимать оставшуюся свободную боковую клетку (2) или (8). Крестики занимают последнюю свободную клетку — игра закончена ничьей.
Вилку крестикам при таком начале игры построить не получится, но и ноликам не дадут. Если по невнимательности, после 6-го шага, нолики сходят в угловую клетку (9) вместо боковой (2) или (8), то крестики одержат победу построив горизонтальную линию (2)-(5)-(8).
Ситуация №3, крестики ходят в угол
Вы снова играете крестиками, теперь для разнообразия сходим в угол, без разницы какая угловая клетка.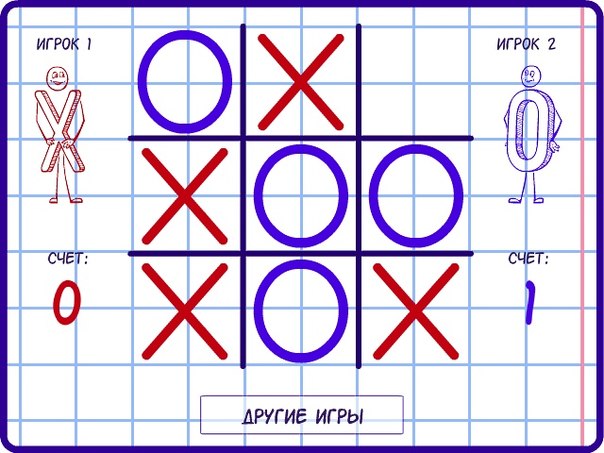 См. рис. ниже, шаг1.
См. рис. ниже, шаг1.
Ход ноликов, как и в ситуации №1, от этого хода зависит исход игры. Если нолики сходили в боковую клетку, то вы построите вилку и победите.
В случае, если нолики первым ходом займут центр или угловую клетку, то будет ничья. Ноликам останется уповать на вашу невнимательность, которая подарит им победу. Но в нашем примере такой исход событий не предусмотрен.
В случае хода ноликами на боковую клетку, шаг 2, вы занимаете еще одну угловую клетку, образуя угрозу — линию из двух фигур. См. шаг 3.
Центр, клетку (5) умышленно оставим пустой для ноликов. Часто, нолики вместо того, чтоб закрыть вашу угрозу ходом в боковую клетку (2), радостно занимают центр.
Если противник попался на уловку и сходил в клетку (5), мы занимаем клетку (2) и линия построена (1)-(2)-(3)
Не будем недооценивать соперника, и он в шаге 4 закрыл нашу угрозу ходом на боковую клетку (2)
Крестикам ничего не остается, как по первому принципу занять центральную клетку (5) и построить вилку.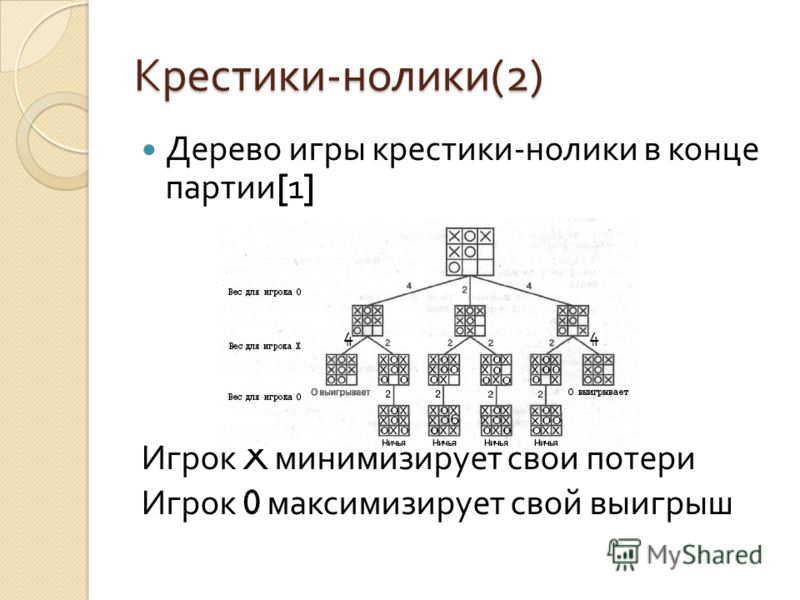
Теперь, см. шаг 6, куда бы нолик не ткнулся, у нас останется свободной одна из двух угловых клеток (7) или (9), ход в которую и принесет нам победу.
Ситуация №4, крестики ходят на боковую клетку
Ход сам по себе в плане будущей победы не оправдан. Варианты исходов — ничья, или проигрыш по невнимательности.
Комбинацию, когда вы с первого хода ставите себя в тактически невыгодное положение можете рассмотреть самостоятельно, опираясь на указанные выше два принципа игры.
Рендзю, жемчужная нить, гомоку, пять в ряд
Когда вам стало тесно и скучно в игровом поле 3х3, и играть три в ряд уже не спортивно, переходим на большую игровую площадь.
Рендзю — настояльная логическая игра для двух игроков, была известна еще в древнем Китае и Японии. Спортивный вариант классических крестиков-ноликов.
Игровое поле для рендзю имеет размеры от 15х15 и больше. Вот здесь уже начинается простор для стратегий и тактик. Каждая партия носит уникальный характер.
Побеждает так же игрок, первым построивший линию из пяти фигур своего цвета. Линия может быть в любом направлении — по диагонали, по вертикали, по горизонтали.
Для удобства игры в длинные линии (пять в ряд), крестики и нолики должны отличаться цветом. Иначе, глаз замылится и чужие фишки можно принять за свои, т.к. они одного цвета, хоть и разной формы. В классическом варианте фишки (камни, кружочки) которыми ходят игроки, — имеют черный и беый цвет.
По правилам, первый ход делают черные и им запрещено делать вилки 3х3, 4х4, а так же ряд из 6 и более «камней» своего цвета подряд.
Зато черные могут делать вилки размером 3х4, когда за один ход образуются две перекрещивающиеся линии — одна длиной три камня, вторая из 4 камней. Так что нет повода расслабляться у того, кто играет белыми.
- Могут строить вилки любого размера и любой кратности;
- Победу белым приносит линия не только 5 в ряд, но и из большего числа камней;
- Для своей победы белые могут вынудить построить черных линию из 6 и более камней подряд.

Белые, за то, что ходят вторыми — имеют следующие преимущества:
Ничья
Игрок, может пропустить ход, если ему в данный момент не выгодно менять расположение своих камней на игровом поле.
Если оба игрока подряд отказались от хода, объявляется ничья.
Закончились все свободные клетки — ничья.
Получается, игрок еще может пропустить ход, потому что ему некуда ходить.
Гомоку, отличия от рендзю
- Для черных отсутсвуют фолы (запрещенные ходы), и черные могут строить вилки любой кратности и длины.
- Ряд из шести и более камней одного цвета не приносит победы ни одной из сторон.
Гомоку имеют более мягкие правила, для удобства игры в обычной жизни. Правила рендзю ориентированы на спортивные состязания.
Сервисы, где можно играть онлайн
У всех сервисов для игры онлайн реализованы режимы игры с компьютером, с другим пользователем и вторым игроком, который находится рядом с вами.
Так же почти у всех есть вариант игры рендзю. Ссылки даны ниже, на всех сайтах я лично играл. Обязательная регистрация не требуется.
Обязательная регистрация не требуется.
Реомендую сервис, где ваш соперник живой человек . Есть сервисы, где компьютер очень слабый , есть где сильно играет или нестандартно выглядит игра . Но все компьютеры слабо играют в длинный вариант пять в ряд. Если в крестики нолики была ничья, то в рендзю компьютер проигрывает.
На этой ноте я с вами прощаюсь и до новых встреч на страницах моего дневника. Не забудьте подписаться на обновления — в следующий раз я расскажу как всегда выигрывать в морской бой.
С вами был Александр Утышев
Знаете ли вы, что с помощью стратегий в игру крестики-нолики можно выигрывать с 80% вероятностью? Рассказываем об этом далее в статье!
Данная статья предназначена для лиц старше 18 лет
А вам уже исполнилось 18?
Игра в крестики-нолики хорошо знакома и взрослому, и малышу. Играя в нее, важно оставить за собой последнее решение. Если крестики или нолики игрока не выстроятся в ряд или по диагонали, то он одержит поражение. Чтобы не попасть в неприятное положение, нужно знать секрет того, как выиграть в крестики-нолики.
Как выиграть в крестики-нолики?
Самой популярной является игра на девятиклеточном поле. Поле представляет собой три квадрата по горизонтали и три по вертикали.
Как всегда, сначала рисуют поле и выбирают крестик и нолик. Первый вопрос, который хотелось бы уточнить — это vожно ли выиграть у соперника, если ты крестик? Ответ утвердительный, так как крестик в этой схватке всегда ходит первым.
По правилам соревнования нужно выставить по горизонтали или по диагонали три одинаковых хода. И сделать этj нужно быстрее, чем партнер по игре. Первым в соревновании ходит крестик. Для первого игрока появляется больше шансов на выигрыш. Второй ход будет предназначен для нолика.
Как легко и быстро победить крестиком?
Самым выгодным первым шагом является позиция в центре поля. Эта ячейка дает преимущество игроку ходить не только прямо, но и по диагонали. У игрока появляется шанс выстроить три фигуры в ряд по:
- диагонали — две линии;
- вертикали — одна линия;
- горизонтали — одна линия.

После второго шага противника на поле появится первый нолик. В зависимости от того, куда противник его поставил, выстраивается дальнейшая линия обороны.
Теоретически противник имеет два варианта:
- поставить нолик в одну из четырех боковых крайних клеток;
- поставить нолик в позицию ячеек, не проходящих через диагональ под номером 2, 4, 6, 8. Этот шаг может стать решающим для исхода сражения.
Теперь у игрока, ходящего крестиком, появляется большая вероятность победить, а не быть побежденным. Второй шаг — это выстраивание нападения. Нужно поставить крестик в свободную угловую ячейку. Необходимо, чтобы через нее проходила диагональ. Эта позиция побудит соперника выстроить линию защиты.
Третьим ходом крестика станет захват еще одной угловой клетки. Это необходимо для того, чтобы получить как можно большее количество рядов, в которых не хватает по одной фигуре. Таким образом, вы идете на одну позицию впереди соперника. В какую бы точкe нолик не поставил свою фигуру, у крестика всегда будет в запасе еще один вариант.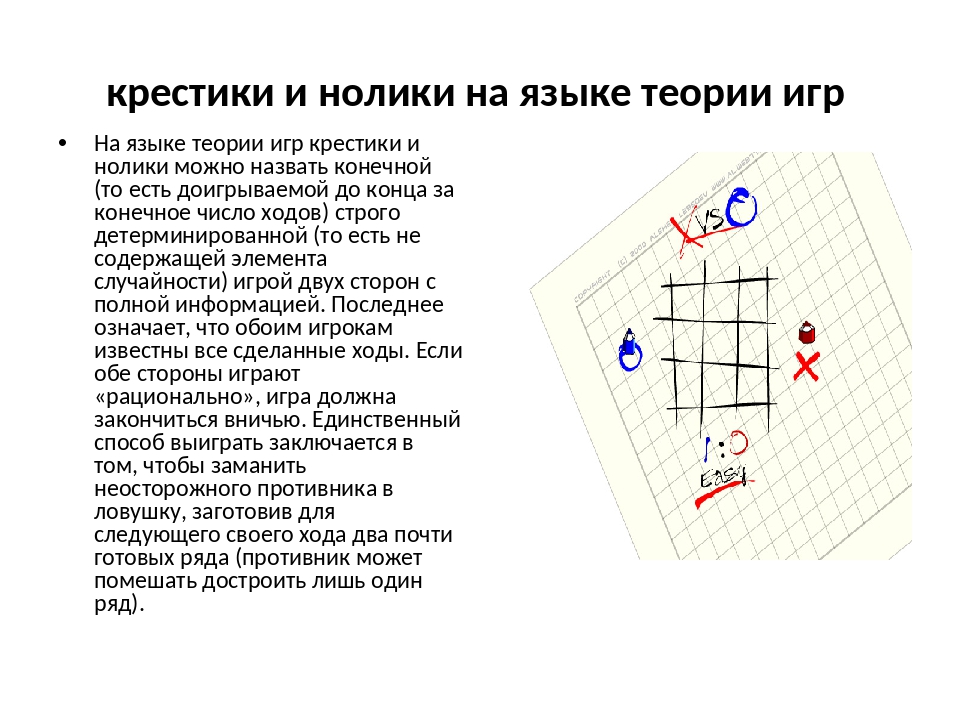
Если же противник на втором шаге вашего боя поставил фигуру на одну из ячеек под номером 1, 3, 7, 9 — шансы на победу становятся невысокими, хотя и зависят от невнимательности противника.
Стратегия победы заключается в построении линии из трех одинаковых фигур по горизонтали или по вертикали. Как легко увеличить шанс на выигрыш? Нужно поставить первую фигуру в центр или в угол.
Схема ходов для нолика
Для игроков, сражающихся за победу ноликов, выиграть намного сложнее. Ведь право первого удара в этой игре дорогого стоит. Здесь нужно попытаться выйти на ничью, а в случае невнимательности или неопытности оппонента даже появляется шанс на выигрыш.
Первый шаг нолика (в случае, если оппонент не поставил свою фигуру в центр) — поставить нолик в ячейку номер 5. Дальнейшая тактика будет похожа на ту, которая была предписана крестикам. Если же ячейка номер 5 будет занята крестиком, нужно выбрать диагональные ячейки с номерами 1, 3, 7, 9.
Следующие удары оппонентов должны идти параллельно и не допустить построения ряда из трех фигур.
Узнать, как постоянно выигрывать, можно с помощью изучения схемы.
Если крестик сделал свой первый ход не через центральную, а через угловую клеточку, то у противника появляется два варианта развития стратегии игры.
Как только нолик походит в центр, противнику нужно быстро походить в противоположный от первого хода угол. В этом случае у нолика на выбор будет два шага. Какой из них будет выбран — таким и станет исход сражения. Допустим, нолик поставит фигурку не в угловую клетку. Тогда крестик начнет защищаться, и битва закончится дружбой. Но если позиция противника будет обозначена в угловой ячейке, крестики смогут сделать своего рода «вилку» и занять оставшийся угол.
Как сделать так, чтобы крестик все время выигрывал? Нужно придерживаться следующей тактики:
- занять центр;
- заставить ноликов начать защиту;
- построить «вилку» из крестиков.
Существует такая стратегия, когда нолик ставят в угол, а крестики выставляют по прямой.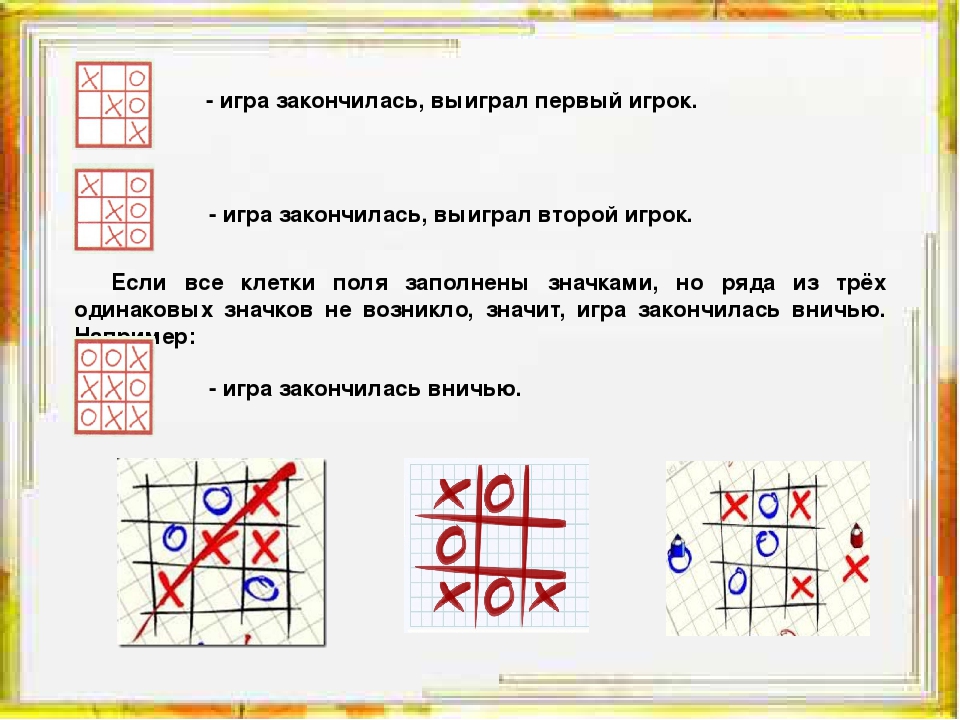 Тогда нолик начинают выстраивать по диагонали, но крестик и тут занимает последний свободный угол. В результате получается вилка.
Тогда нолик начинают выстраивать по диагонали, но крестик и тут занимает последний свободный угол. В результате получается вилка.
Как выиграть в крестики-нолики 3×3 и больше клеточек?
Эта популярная игра очень полезна для развития логики и мышления, ведь в ее основе лежат азы программирования и математики.
В игре 3 на 3 клеточки главной причиной проигрыша одного из игроков является допущенный промах во время первого хода. Именно он определяет дальнейшую цепочку событий. Чтобы второй игрок имел фору и не проиграл, ему нужно в свой первый ход, который будет сделан после начального удара, поставить свою фигуру в центр поля или в один из углов. Это позволит ему занять стратегически важное место, и в случае необходимости с любой точки блокировать угрозу. В соревновании 3 на 3 самым важным является именно стратегия первого удара.
Интересной разновидностью боя являются трехмерные 3 на 3 на 3. Здесь соревнование ведется в кубе. Выигрыш присваивается тому игроку, который займет верхнее центральное поле. В этой борьбе не может быть ничьей. Победить можно, заняв центральное положение на поле, а также с помощью ходов, диаметрально противоположных друг другу.
В этой борьбе не может быть ничьей. Победить можно, заняв центральное положение на поле, а также с помощью ходов, диаметрально противоположных друг другу.
Для усложнения соревнования и увеличения выигрыша, для игроков было придумано игровое поле Силвермэна размером 4 на 4 к. В этом бою целью игрока является составление прямой из четырех одинаковых фигур. Стратегия боя для первого игрока заключается в атаке и перекрывании ходов соперника. В этом варианте игры ничьей не бывает. Худшим вариантом для начала соревнования на поле 4 на 4 является противопоставление по диагонали. Но и в этом случае у первого игрока всегда есть шесть вариантов ходов. Как показывает практика и анализ боя, у игроков, сделавших первый ход в этой игре, есть огромные преимущества. Для того чтобы изменить условия и усложнить игру, главные диагонали для победы не считаются. В этом случае для выигрыша первый ход не нужно делать по главной диагонали.
На доске 4 на 4 можно играть в интересный вариант игры — «Безумные крестики-нолики». Здесь фигуры не ставят в привязку к игрокам. Выиграет тот, кто соберет первым ряд из любых четырех фигур.
Здесь фигуры не ставят в привязку к игрокам. Выиграет тот, кто соберет первым ряд из любых четырех фигур.
Как играть в крестики-нолики 5 на 5 клеточек?
Игра 5 на 5 интересная, но принцип ее действия такой же, как и в игре на поле из девяти клеточек. Главная тактика соревнования — это составление вилок, которые не дадут противнику возможности построить ряд из 5 фигур. Чтобы игра была длинной и интересной, для первого игрока устанавливают специальные правила. Нельзя строить больше двух вилок, а также запрещено создавать вилки на площадке из клеточек 3 на 3 и 4 на 4. Соблюдение этих условий открывает перед вторым игроком шансы на победу. Примечательно, что в этом варианте соревнования можно пропустить один ход. Но, если и второй игрок пропустит ход, то игра заканчивается ничьей.
Как играть в крестики-нолики 10 на 10 клеточек?
Игровые поля 10×10 и 15×15 представляют собой доски, которые называются гомоку. Это увлекательная спортивная игра, которая популярна во всем мире. Основным моментом соревнования является составление ряда из пяти одинаковых фигур. Для расчета ходов существует множество алгоритмов и проведены даже компьютерные расчеты.
Основным моментом соревнования является составление ряда из пяти одинаковых фигур. Для расчета ходов существует множество алгоритмов и проведены даже компьютерные расчеты.
Нужно знать, что одна фигура оказывает влияние на другие фигуры в пределах пяти клеточек с каждой стороны от фигуры. Главная цель игроков — не допустить, чтобы противник выставил три фигуры подряд.
Действовать нужно по цепочке, строя сначала цепочку из двух фигур, потом трех, четырех и так до победы. Как и в простом уровне, второй игрок всегда идет на шаг позади первого, поэтому ему необходимо тщательно продумывать каждый свой ход.
Игра пришла к нам из древности. Сегодня известно множество вариантов соревнования: на бумаге, с камнями на компьютере. В Интернете существуют виртуальные игры, в которые играют реальные люди, делают ставки и зарабатывают реальные деньги. Но нужно помнить, что сложность боя возрастает с ростом игрового поля. При онлайн игре нет гарантии, что твой противник не машина, которая на один ход имеет несколько решений и алгоритмов.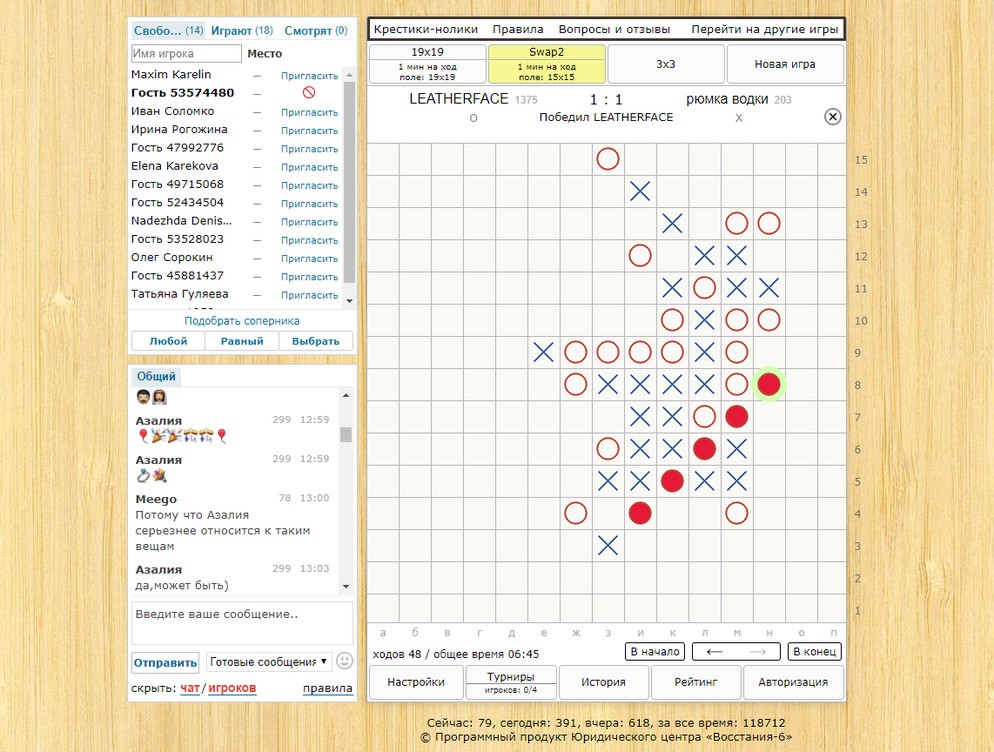 Именно поэтому онлайн игра требует от человека внимания и сосредоточенности.
Именно поэтому онлайн игра требует от человека внимания и сосредоточенности.
Не потеряйте. Подпишитесь и получите ссылку на статью себе на почту.
Каждый из нас хотя бы раз в жизни играл в знаменитые крестики-нолики, пытаясь построить в ряд или по диагонали 3 крестика или 3 нолика на девятиклеточном поле. Если вы достаточно тренировались в этой игре, то, наверняка, знаете, что два опытных игрока всегда заканчивают партию вничью, и это делает игру для них неинтересной. В этой статье вы прочитаете о том, как выиграть в крестики-нолики или, по крайней мере, не проиграть, а также узнаете все хитрости и секреты прохождения этой популярной игры.
Немного о правилах. Цель игры выстроить на девятиклеточном поле подряд 3 одинаковых фигуры (3 крестика или 3 нолика) по горизонтали, по вертикали или по диагонали раньше, чем это сделает ваш партнер по игре. Игра в крестики-нолики начинается с хода игрока, который ставит крестик в любой клетке на игровом поле три на три (отметим сразу, что у него гораздо больше шансов выиграть, чем у противника). После этого второй игрок ставит в любой свободной ячейке нолик. Затем снова ходит крестик. Потом опять нолик. И так продолжается до тех пор, пока:
После этого второй игрок ставит в любой свободной ячейке нолик. Затем снова ходит крестик. Потом опять нолик. И так продолжается до тех пор, пока:
- Кто-то из игроков не построит в ряд или по диагонали 3 крестика или 3 нолика, и в результате чего будет признан победителем;
- Не останется свободных клеток, и на поле не будет присутствовать трех идущих подряд одинаковых фигур — в этом случае объявляется ничья.
Тактика крестиков
Первый ход крестиков. Самой выгодной позицией является середина игрового поля, или как отмечено на схеме клетка №5. Именно сюда следует вписывать вашу фигуру, если эта ячейка является свободной, и именно поэтому начинающие крестики всегда имеют преимущество. Через центральную ячейку вы можете построить наибольшее количество возможных вариантов выигрыша: две диагонали, одну горизонталь и одну вертикаль.
Второй ход крестиков. После того как вы сделали первый ход, поставив крестик по центру, вам остается ждать ход противника.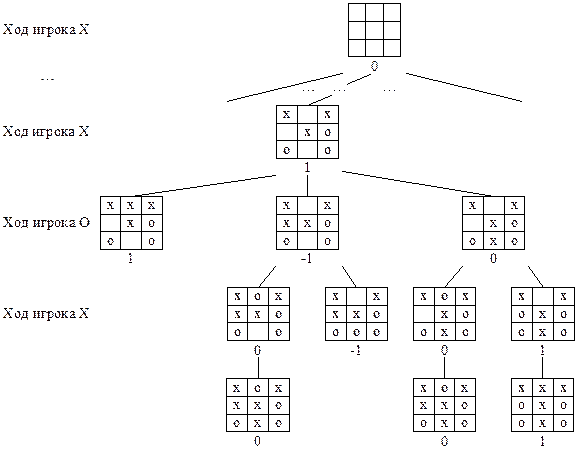 В целом, у него есть всего 2 возможных варианта действий: поставить нолик в одной из «угловых» ячеек (№1, №3, №7 и №9) или поместить свою фигуру в ячейки №2, №4, №6 или №8. И следует сразу отметить, что от этого хода уже коренным образом зависит ваша возможность выиграть.
В целом, у него есть всего 2 возможных варианта действий: поставить нолик в одной из «угловых» ячеек (№1, №3, №7 и №9) или поместить свою фигуру в ячейки №2, №4, №6 или №8. И следует сразу отметить, что от этого хода уже коренным образом зависит ваша возможность выиграть.
Если игрок выбирает одну из недиагональных ячеек №2, №4, №6 или №8, то у вас появляется беспроигрышная стратегия. Другими словами вы сможете победить с вероятностью 100%, если знаете, как верно действовать. Этот алгоритм описан в схеме ниже. В первую очередь вам нужно поставить крестик своим вторым ходом в угловую клетку, вынудив соперника защищаться. А после этого вы занимаете еще одну свободную угловую клетку, в результате чего вы имеете 2 ряда, где не хватает всего одного крестика (это показано на последнем поле схемы). Куда бы соперник ни поставил свой нолик, вы в любом случае побеждаете, имея запасную стратегию.
Если же ваш соперник своим первым ходом выбирает ячейки №1, №3, №7 и №9, тогда вы не имеете абсолютной выигрышной стратегии, и вам следует уповать лишь на дальнейшую невнимательность второго игрока, что в такой простой игре бывает достаточно редко.
Третий и последующие ходы крестиков. Дальнейшие ходы «крестиков» должны быть направлены на построение в ряд 3-х собственных фигур, а также на пресечение маловероятных, но все-таки возможных попыток «ноликов» поставить подряд 3 фигуры.
Также, «крестики» для того, чтобы выиграть могут начинать не только с центральной клетки, но и с угловой. Подробнее об этом .
Алгоритмы ходов ноликов
Если вам выпало играть ноликами, то в большинстве случаев вам предстоит бороться только за ничью. Однако у вас есть шансы победить, если вы играете с совсем неискушенным игроком.
Первый ход ноликов. Если игрок №1 почему-то не занял центральную клетку – смело ставьте туда нолик и действуйте дальше, опираясь на стратегию крестиков, описанную выше. Но, скорее всего, центральная ячейка к моменту вашего начального хода будет уже занята. В этом случае не совершайте непростительную ошибку и не ставьте нолик в ячейки №2, №4, №6 или №8, а выбирайте только диагональные ячейки №1, №3, №7 и №9.
Второй и последующие ходы. Дальнейшие ходы «ноликов» должны быть направлены на пресечение попыток «крестиков» поставить подряд 3 фигуры, а также при возможности, на построение в ряд 3-х ноликов, что является практически невозможным.
Все стратегии игры
На графике, представленном ниже, который можно найти в Википедии , приведены возможные стратегии побед и ничьих в игре крестики-нолики на поле в 9 клеток.
***
Надеюсь, эта статья стала для вас помощником в хитростях крестиков-ноликов, в том числе на деньги и на раздевание, и вы теперь знаете некоторые необходимые тактики и стратегии для того, чтобы выиграть (или, по меньшей мере, не проиграть) в эту замечательную игру. А если у вас есть комментарии, отзывы и предложения – оставляйте их ниже.
В первой статье разобраны различные варианты решения задачи, но нет реализации в виде игры, во второй — игра есть, но компьютер «играет» слабовато. Я решил сделать свой вариант игры гомоку с блэкджеком достаточно сильной игрой компьютера. Публикация о том, что в итоге получилось. Для тех, кто любит сразу в бой — сама игра .
Публикация о том, что в итоге получилось. Для тех, кто любит сразу в бой — сама игра .
Для начала хочу определиться с основными моментами. Во-первых, существует множество разновидностей игры гомоку, я остановился на таком варианте: игровое поле 15х15, крестики ходят первыми, выигрывает тот, кто первый построит 5 в ряд. Во-вторых, игровой алгоритм расчета хода компьютером для простоты буду называть AI.
Спасибо за внимание. Надеюсь, вам было также приятно читать и играть, как мне — реализовывать:)
P.S. Небольшая просьба, если будете легко выигрывать — прикрепите, пожалуйста, скриншот игры и ходы (из логов консоли) для анализа и улучшения алгоритма.
Update 1
1. На 10% увеличил значимость весов для атаки. Теперь атака для AI предпочтительнее защиты при прочих равных. Например, если 4ка у AI и у пользователя, то AI предпочтет выиграть.2. Изменил значения весов по шаблонам. При более четкой балансировки весов можно добиться лучшей игры AI.
Значения весов у шаблонов сейчас такие:
99999 — xxxxx — пять в ряд (финальная выигрышная линия)
7000 — _xxxx_ — открытая четверка
4000 — _xxxx — полузакрытая четверка (две таких четверки предпочтительнее одной открытой, возможно «интереснее игра» будет)
2000 — _x_xxx, _xx_xx, _xxx_x — полузакрытая четверка с брешью (2 таких четверки равны одной открытой четверке и «предпочтительнее» открытой тройки; но если только 1 такая четверка, то открытая тройка предпочтительнее)
3000 — _xxx_ — открытая тройка
1500 — _xxx — полузакрытая тройка
800 — _xx_x, _x_xx — полузакрытая тройка с брешью
200 — _xx_ открытая двойка
Также небольшие веса (от 1 до 20-30) есть вокруг всех ходов, для создания «небольшой случайности хода».
Здравствуйте, читатели моего блога, сегодня я расскажу вам о том, как выиграть в крестики нолики.
Замечательная игра, которая не требует много подготовки, нашли ручку или карандаш, листик и напарника.
На самом деле, игра простая и, одновременно, сложная. Многие подходят к ней не серьезно, поэтому проигрывают. Скажу честно, я сам не понимал, как можно в нее играть, но затем, проанализировал все возможные ходы и понял, что здесь все упирается в математику.
Почему данная игра, очень простая? Все дело в том, что здесь всего 9 клеток, то есть у вас есть 1 из 9 начальных вариантов, а затем это количество уменьшается на 1. То есть, если вы сделали свой ход, то у вашего противника уже появляется не 9 вариантов, а всего лишь 8, потому, что 1 клетка уже занята.
Ну, думаю, это вы и без меня поняли, я сегодня, прям «капитан очевидность». Почему сложная, потому, что здесь есть возможные комбинации и если вы хотите научится именно выигрывать в данную игру, то вам потребуется ручка, а также чистый листик.
Как выигрывать в крестики нолики
Основные понятия, которые нужно знать:
Поле – условное поле 3×3 клетки, где и происходит битва.
Крестики – вот такие значки «х», они ходят первые.
Нолики – вот такие значки «0», они ходят вторые.
Победа – когда игрок собирает подряд 3 крестика или 3 нолика.
Вот пример поля.
Для того, чтобы вы могли правильно анализировать давайте пронумеруем каждую клетку.
Вот хотя бы так, чтобы вы понимали, где какое поле.
Стратегия выигрыша в 3×3
Запомните, что если вы играете за нолики, то есть вам нужно делать вторым ход, то против сильного противника вы сделаете лишь ничью. Ноликами сложно выиграть, так как они ходят вторыми и, практически, всегда обороняются от угроз, которые создают крестики (они первые ходят).
Вы не удивляйтесь тому, что я пишу, как для новичков, я хочу, чтобы вы поняли, как правильно выигрывать за крестики и как делать ничью за нолики.
Начнемс…
Самая лучшая стратегия. Крестики делают ход на 5 клетку, которая находится в середине.
Дальше, ЗАПОМНИТЕ, что если нолики делают свой второй ход не на ДИАГОНАЛЬНУЮ КЛЕТКУ, то они проигрывают. Не важно, на какую клетку, они делают ход: 2, 4, 6, 8, если они поставили нолик на любое из этих полей, то они форсировано проигрывают.
Для примера, вы поставили на 5, они поставили на 2, теперь вы ставите на 1 или 3, угрожая сделать 3 крестика по диагонали. Ну, ок, вы поставили на 1, получается, что если вы поставите на поле 9 крестик, то вы выиграете. Вы вынуждаете поставить нолик на поле 9, но теперь вы изысканно побеждаете, ставя крестик на поле 7.
Получается, что вы угрожаете поставить три крестика по диагонали ходом 3 и по вертикали ходом – 4. Красота, не правда ли?
Лучшая защита за нолики – это, после ходя 5 за крестики, делать ходы: 1, 3, 7, 9, в таком случае, вы, при внимательности, всегда будете делать ничью. Запомните это простое правило и вы никогда не проиграете.
Хитрая стратегия за крестики
Но, ведь игрок, вовсе, не обязан делать первый ход в середину, то есть на клетку – 5. Тут, есть весьма крутая ловушка, вы делаете первый ход на угловое поле.
Лучшей защитой здесь будет занятие ноликами поле – 5, раз оно освободилось, то его нужно занять. В таком случае, всегда нолики будут делать ничью, тем, что будут угрожать постоянно самим поставить три в ряд.
Если, к примеру, крестики делают ход на клетку – 1, то ошибкой будет делать ход – 4 и 9, в этих случаях, форсировано выигрывают крестики.
Давайте разберем эти варианты:
А) Крестики – 1, нолики – 4, крестики – 5, нолики – 9 (вынуждено), крестики – 3 с выигрышем на поля 2 или 7 в зависимости от ответа ноликов.
В) Крестики – 1, нолики – 9, крестики – 3, нолики – 2 (вынуждено), крестики – 7 с выигрышем на поля 4 или 5 в зависимости от ответа ноликов.
Ну, вот и все, друзья, надеюсь, что теперь вы знаете, как выиграть в крестики нолики 3х3. В ней (игре) нет ничего сложного, при правильной защите, здесь всегда будет ничья, но, как видите, за крестики есть интересные варианты, в которые можно словить нолики.
В ней (игре) нет ничего сложного, при правильной защите, здесь всегда будет ничья, но, как видите, за крестики есть интересные варианты, в которые можно словить нолики.
Я желаю вам побед, если я что-то забыл написать, то напомните мне, можно даже в комментарии.
Всем удачи, пока!
С уважением, Юрий Ваценко!
Определение количества информации. Вероятностный подход. ЕГЭ
ЕГЭ Определениеколичестваинформации( ) вероятностный подход( ) вероятностный подход Урок2 Существует формула, которая связывает между собой количество возможных событийN и количество информацииI:N = 2I По этой формуле можно легко определить количество возможных событий, если известно количество информации.Например, если мы получили4 бита информации, то количество возможных событий составлялоN = 24 =16 Наоборот, для определения количества информации, если известно количество событий, необходимо решить показательное уравнение относительноI.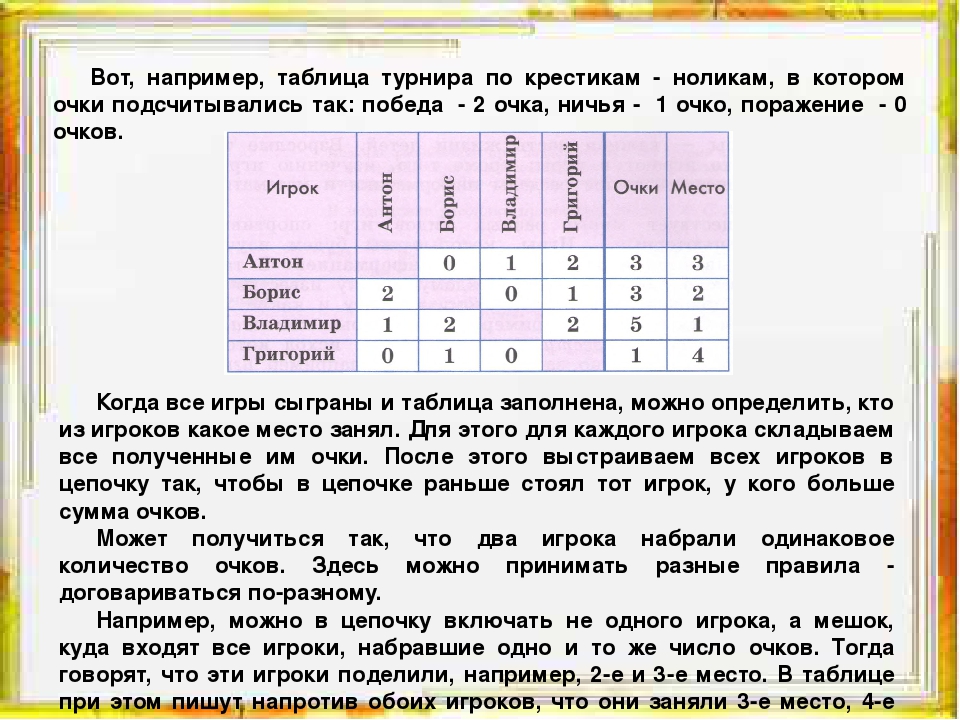
Решение задач 1.
Определить количество информации, полученной вторым игроком после первого хода первого игрока, в игре «крестики-нолики» на поле размером 8х8 клеток.
Решение: Перед первым ходом существует64 возможных события (64 различных варианта расположения «крестика»), тогда уравнениеN = 2I принимает вид: 64 = 2I Так как 64 = 26 , то26 = 2I .
Таким образом,I =6 битов , т.е.
количество информации, полученной вторым игроком после первого хода первого игрока, составляет 6 битов.
Ответ: 6 битов2.
В рулетке общее количество лунок равно 32.
Какое количество информации (с точки зрения вероятностного подхода) мы получаем в зрительном сообщении об остановке шарика в одной из лунок? 1) 8 битов 2) 5 битов 3) 2 бита 4) 1 бит Решение:N = 2I 32 = 2I т.к.
32=25 , то 25 = 2I, I = 5 Ответ: 5 битов 3.
Каково было количество возможных событий, если после реализации одного из них получено количество информации, равное 3 битам? Решение:N = 2IN = 23 8 = 23 N = 8 Ответ:84.
Световое табло состоит из лампочек.
Каждая лампочка может находиться в одном из трех состояний («включено», «выключено» или «мигает»).
Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 18 различных сигналов? Решение: С помощью одной лампочки можно передать 3 сигнала, с помощью двух 32 = 9 сигналов, с помощью трех 33 = 27 сигналов.
Значит, чтобы подать 18 сигналов, нужно не менее трех лампочек.
Ответ:3 Другой способ: 3 состояния лампочки, 18 сигналовN = 3I , 18 = 3I , 27 = 3I = 33,I =3 Домашняя работа №2 (задания из ЕГЭ!) 1.
Производится бросание симметричной четырехгранной пирамидки.
Какое количество информации (с точки зрения вероятностного подхода) мы получаем в зрительном сообщении о ее падении на одну из граней? 1) 1 бит 2) 2 бита 3) 4 бита 4) 8 битов 2.
Какое количество информации (с точки зрения вероятностного подхода) получит второй игрок при игре в крестики-нолики на поле 4х4, после первого хода первого игрока, играющего крестиками? 1) 1 бит 2) 2 бита 3) 4 бита 4) 8 битов (10 задач) 3.
В рулетке общее количество лунок равно 128.
Какое количество информации мы получаем в зрительном сообщении об остановке шарика в одной из лунок? 1) 1 бит 2) 4 бита 3) 7 бит 4) 8 4.
Сколько различных последовательностей длиной в 7 символов можно составить из цифр 0 и 1? 5.
В корзине лежат 8 шаров.
Все шары разного цвета.
Сколько информации несет сообщение о том, что из корзины выкатился синий шар? 6.
Какое максимальное количество бит потребуется для кодирования целых положительных чисел меньших 60? 7.
Игровое клетчатое поле состоит из 15 строк и 5 столбцов.
Партия записана последовательностью из 10 координат, соответствующих ходам игроков по клеткам.
Какой объем информации в битах несет эта запись, если для кодирования координат одной клетки поля использовали двоичный код минимальной длины? 1) 50 2) 60 3) 70 4) 80 8.
В некоторой стране пользуются двоичной системой счисления.
Какое минимальное количество знаков потребуется для написания различных почтовых индексов для 718 городов? 9.
В кинотеатре 16 рядов по 32 места в каждом.
Какое количество информации в битах содержит сообщение о том, что продан один билет в 8-ом ряду место №4? 1) 5 2) 8 3) 9 4) 16 10.
Сколько существует различных вариантов составления
Крестики Нолики
Кре́стики но́лики — логическая игра между двумя противниками на квадратном поле 3 на 3 клетки или бо́льшего размера (вплоть до «бесконечного поля»). Один из игроков играет «крестиками», второй — «ноликами».
Содержание
1 Классический вариант
1.1 Правила игры
1.2 Анализ
1.2.1 За крестики
1.2.2 За нолики
1.3 Дерево игровых ситуаций
1.4 Компьютерное решение
2 Обобщения
2.1 Более длинные линии
2.2 Модификация поля
2.3 Обмен значков
2.4 Изменение условия выигрыша
2.5 Удлинение хода
Классический вариант игры крестики нолики
Правила игры
Выигранная партия в крестики нолики
Игроки по очереди ставят на свободные клетки поля 3х3 знаки (один всегда
крестики, другой всегда нолики). Первый, выстроивший в ряд 3 своих
фигуры по вертикали, горизонтали или диагонали, выигрывает. Первый ход
делает игрок, ставящий крестики.
Первый, выстроивший в ряд 3 своих
фигуры по вертикали, горизонтали или диагонали, выигрывает. Первый ход
делает игрок, ставящий крестики.
Обычно по завершении партии выигравшая сторона зачёркивает чертой свои три знака (нолика или крестика), составляющих сплошной ряд.
Анализ игры крестики нолики
Для каждой из сторон общеизвестны алгоритмы, которые гарантируют ничью при любой игре противника, а при его ошибке позволяет выиграть. Таким образом, игра находится в состоянии «ничейной смерти».
Ниже приведены некоторые из таких стратегий. Считается, что игрок всегда
соблюдает два правила, имеющие приоритет над всеми остальными:
Правило 1. Если игрок может немедленно выиграть, он это делает.
Правило 2. Если игрок не может немедленно выиграть, но его
противник мог бы немедленно выиграть, сделав ход в какую-то клетку,
игрок сам делает ход в эту клетку, предотвращая немедленный проигрыш.
За крестики
Первый ход сделать в центр. Остальные ходы, если неприменимы правила 1-2, делаются в тот из свободных углов, который дальше всего от предыдущего хода ноликов, а если и это невозможно — в любую клетку.
Докажем, что эта стратегия приводит к победе или ничьей. Если нолик
пойдёт на сторону, то позиция (с точностью до симметрии) окажется
такова:
.0.
.Х.
Х..
После чего правила 1 и 2 приведут к позиции:
Х00
.Х.
Х..
Выигрыш.
Если же нолик пойдёт в угол, позиция (с точностью до симметрии) будет
следующая:
0..
.Х.
..Х
В зависимости от следующего хода нолика, возникнет одна из трёх позиций:
00Х 0Х0 0..
.Х. .Х. .Х0
..Х ..Х Х.Х
В первой и третьей позиции — выигрыш. Во второй — ничья
За нолики
(Напоминаем, что правила 1-2, если они применимы, имеют приоритет над
всем, написанным ниже. )
)
Если крестики сделали первый ход в центр, до конца игры ходить в любой
угол, а если это невозможно — в любую клетку.
Если крестики сделали первый ход в угол, ответить ходом в центр.
Следующим ходом занять угол, противоположный первому ходу крестиков, а
если это невозможно — пойти на сторону.
Если крестики сделали первый ход на сторону, ответить ходом в центр.
Если следующий ход крестиков — в угол, занять противоположный угол:
.Х0
.0.
Х..
Если следующий ход крестиков — на противоположную сторону, пойти в любой
угол:
0Х.
.0.
.Х.
Если следующий ход крестиков — на сторону рядом с их первым ходом, пойти
в угол рядом с обоими крестиками
0Х.
Х0.
…
Дерево игровых ситуаций игры крестики нолики
Частичное дерево игровых ситуаций для игры крестики нолики
Дерево игровых ситуаций для игры крестики нолики, где игрок за
«крестики» ходит первым и поступает по приведенному выше алгоритму, а
игрок за «нолики» может поступать как угодно (причем приведено по одной
вершине для рационального и для нерационального поступка, то есть любого
другого), состоит из 50-ти узлов.
Компьютерное решение
Для решения такого рода игр на компьютере строится дерево игровых ситуаций в соответствии с методом мини-макс. Полное число узлов в таком дереве равно 255168. Это число получается как сумма всех возможных вариантов ходов — 9 вариантов на первом шаге, 8 — для каждого из 9 на втором шаге, 7 — на каждом из 72 вариантов на третьем шаге и т. д., за вычетом ситуаций досрочного окончания игры (выигрыша).
Обобщения
Более длинные линии
Можно рассматривать игру, в которой победителем считается игрок, первым построивший одинаковых знаков на достаточно большом для этого прямоугольном поле. При этом можно ограничить поле каким-нибудь размером (начиная с ), либо вовсе не ограничивать (в этом случае говорят о «бесконечном» поле)
Игра до 4 одинаковых знаков на бесконечном поле неинтересна, ибо
начинающий довольно быстро строит «вилку» и выигрывает. Игра при также
неинтересна из-за «ничейной смерти». Существуют стратегии, не дающие
противнику построить нужную линию никогда. Однако при игра становится
намного содержательнее. Такой вариант имеет специальное название —
гомоку. Изначально в гомоку играли на доске размером 19х19, позже она
была уменьшена до размера в 15х15 клеток.
Игра при также
неинтересна из-за «ничейной смерти». Существуют стратегии, не дающие
противнику построить нужную линию никогда. Однако при игра становится
намного содержательнее. Такой вариант имеет специальное название —
гомоку. Изначально в гомоку играли на доске размером 19х19, позже она
была уменьшена до размера в 15х15 клеток.
Основной победной тактикой при игре на бесконечном поле считается построение пересечений («вилок»), которые не дают противнику возможности блокировать все возможные пути построения пятёрки. Чтобы не проиграть, необходимо своевременно прерывать линии противника длиной в три фигуры.
Практика показала, что при равных правилах для игроков тот, кто делает
первый ход, имеет преимущество, позволяющее при достаточно
квалифицированной игре одержать победу. Для сохранения интереса к игре
предлагались различные варианты модификации правил игры. Так, с
введением фолов (запрещенных ходов) для игрока, начинающего первым — ему
запрещено строить вилки 3х3, 4х4, а также построение «длинного ряда» из
своих фигур — получилась новая игра под названием рэндзю, с совершенно
иными стратегиями выигрыша.
Модификация поля
Увеличение размера поля уже обсуждалось выше. Самым простейшим, но увеличивающим тактическое богатство игры, является добавление одной клетки вдоль одной из сторон поля 3х3.
Другим вариантом является изменение топологии поля. Например, можно считать противоположные стороны поля склеенными, образуя при этом либо поверхность цилиндра или тора, либо проективную плоскость. Также можно увеличивать размерность, например, играть в кубе 4x4x4, в гиперкубе, и так далее.
Возможный алгоритм для игры крестики нолики в кубе 4x4x4:
1. Проверяем наличие своих трёх подряд стоящих фигур, если нашли, то ставим четвёртую и выходим (игра завершается).
2. Проверяем наличие трёх подряд стоящих фигур противника, если нашли, то ставим четвёртую свою и выходим.
3. Проверяем наличие своих двух подряд стоящих фигур, если нашли, то
ставим третью на любую позицию в этом ряду и выходим.
4. Проверяем наличие двух подряд стоящих фигур противника, если нашли, то ставим третью свою на любую позицию в этом ряду и выходим.
5. Ищем любой ряд, имеющий три пустых клетки и одну содержащую свою
фигуру и ставим на любую позицию в этом ряду свою фигуру, при чём
предпочтение отдаётся наличию ряда в пространстве.
Обмен значков
Можно отменить правило, указывающее игрокам ставить только свой вид
значков. Например, вариантом игры может быть: игроки ставят крестик или
нолик (что захотят), первый выигрывает, если кто-нибудь построит линию
нужной длины из одинаковых значков, второй — если до заполнения поля
этого не произойдёт.
Изменение условия выигрыша
Вместо того, чтобы заканчивать игру построением первой линии нужной
длины, можно на этом не останавливаться и продолжить до полного
заполнения поля. Например, на любом поле можно играть на то, кто больше
построит «четвёрок» из своих знаков.
Удлинение хода
Ещё один вариант модификации игры крестики нолики — выставлять на каждом ходе не один свой знак, а два или более. Такова игра Connect6, в которой чёрные делают первый ход, выставляя один знак, после чего игроки поочерёдно выставляют по два знака, побеждает первый, построивший линию из 6 или более своих знаков.
Удачи вам в игре крестики нолики!
Крестики Нолики Онлайн:
Крестики Нолики скачать:
Скачать Крестики Нолики
29_game-theory
Игра как граф¶
В общем случае состояния игры могут представлять из себя гораздо более сложную структуру, чем «N спичек». А именно, представим себе ориентированный граф:
- Вершины — это состояния игры
- Ребра — это переходы между ними
- В одной из вершин стоит фишка — текущее состояние игры
- Два игрока по очереди двигают фишку по одному из ребер.

- Кто не может двигать фишку — тот проиграл
На таком графе так же легко считать проигрышные и выигрышные состояния. А именно, вершины, из которых не выходят ребра — очевидно проигрышные. Вершины с ребрами в проигрышные — это выигрышные. А вершины с ребрами только в выигрышные — это проигрышные.
Очень удобно сделать топологическую сортировку графа. После этого все ребра будут смотреть в одну сторон, и можно за один проход по массиву посчитать выигрышность и проигрышность каждой вершины.
Но! Может ничего не выйти, если в графе есть цикл. В циклическом графе могут быть ничейные вершины — из которых у обоих игроков есть стратегия, при которой игра будет длиться вечно.
Поэтому обычно рассматривают конечные ациклические игры, в которых граф конечен и ацикличен. Благодаря тому, что для них работает топологическая сортировка и переход динамики для подсчета выигрышных и проигрышных состояний, мы уже практически доказали, что в них в каждой вершине существует либо выигрышная стратегия у первого игрока, либо у второго игрока.
Задание¶
Посчитайте у каждого состояние в этом графе-игре, выигрышное оно или нет. А также найдите для каждой вершины, куда оттуда идти оптимальнее всего:
Решение¶
Расмотрим такие игры:
- Есть шахматная доска NxM, в верхней правой клетке стоит ферзь. Два игрока по очереди двигают его либо вниз, либо влево, либо вниз-влево по диагонали на сколько угодно клеток. Проигрывает тот, кто не может ходить.
- Крестики-нолики на доске 3×3.
- Шахматы.
Задание¶
Придумайте, как представить эти игры в виде графов. Что является состоянием игры? Являются ли игры ациклическими?
Решение¶
- Состояние игры — это пара (x, y) — координаты ферзя. Есть ходы из (x, y) в (x — k, y), (x, y — k) и (x — k, y — k), где k — любое. Игра ациклическая — после каждого хода обе координаты не возрастают, и хотя бы одна убывает.
- Состояние игры — это доска с уже поставленными крестиками и ноликами.
 По доске однозначно считается, кто ходит следующий. Во все возможные доски, в которые можно походить, в графе стоит ребро. Игра ациклическая — после каждого хода заполняется езе одна клетка.
По доске однозначно считается, кто ходит следующий. Во все возможные доски, в которые можно походить, в графе стоит ребро. Игра ациклическая — после каждого хода заполняется езе одна клетка. Состояние игры — это пара (доска с фигурами, чей сейчас ход). Особенность шахмат в том, что здесь бывают ничьи. Можно расширить нашу модель графа, введя ничейные вершины. А можно поставить во всех ничейных вершинах петлю — если ты попал в нее, то ты будешь вечно ходить по петле, и в соответствии с нашим старым определением, это действительно ничья.
Еще шахматы циклические — игроки могут вернуться в то же положение. Ха, вообще-то нет! Есть правило, согласно которому одно положение не может повторяться более 3 раз. Поэтому можно сделать состоянием игры (доска с фигурами, чей сейчас ход, статистика о том сколько раз встретилось каждая доска). При этом, если какая-то доска встретилась 3 раза, объявляем ничью. Тогда игра становится ациклической — статистика всегда в одной доске возрастает.
 При всем огромном числе возможных досок шахматы — игра конечная. Досок конечное число, и на каждой можно побывать не более 6 раз (3 раза с ходом белым, 3 раза с ходом черных), это все еще конечное число. А значит, в шахматах точно существует либо выигрышная стратегия для белых, либо для черных, либо ничейная у обоих.
При всем огромном числе возможных досок шахматы — игра конечная. Досок конечное число, и на каждой можно побывать не более 6 раз (3 раза с ходом белым, 3 раза с ходом черных), это все еще конечное число. А значит, в шахматах точно существует либо выигрышная стратегия для белых, либо для черных, либо ничейная у обоих.
Задание¶
Решите 4, 5 и 6 задачи в этом контесте:
https://informatics.msk.ru/mod/statements/view3.php?id=33386
В них самое сложное — придумать, чем является состояние игры. Также рекомендуем использовать ленивую динамику, чтобы не думать о том, в каком порядке проходить состояния.
Результат игры¶
В прошлом разделе мы столкнулись с тем, что помимо проигрышных и выгрышных состояний бывают ничейные. Очень часто в играх вместо таких однозначных итогов вводят гораздо более сложные и интересные итоги. Например, можно считать, что результат игры — это пара чисел (A, B), где A — это выигрыш (в условных монетах) первого игрока, а B — выигрыш второго игрока. И оба игрока стремятся максимизировать свой выигрыш.
И оба игрока стремятся максимизировать свой выигрыш.
Очень часто рассматриваются игры с нулевой суммой: A + B = 0, то есть сколько монет выиграл один, столько проиграл второй
Можно считать, что в каждой вершине-листе (то есть откуда некуда идти) написан результат игры: первое число получает тот, кто должен ходить из листа, а второе число должен писать тот, кто туда пришел.
Для такой модели существует аналог выигрышных-проигрышных позиций. А именно, давайте в win[x] хранить пару — лучший результат первого игрока, если он начнет играть с этой вершины, и сколько в этом случае получит второй игрок. Если это игра с нулевой суммой, то второй игрок потеряет ровно столько, сколько получит первый, в этом случае можно не хранить пару, а только выигрыш первого.
Тогда такая динамика пересчитывается просто — если ты хочешь узнать результат игры в вершине X, то нужно просто максимизировать выигрыш второго игрока во всех состояниях, куда можно прийти из X. При этом результат первого игрока становится результатом второго игрока в вершине X. Конечно, при этом писать топологическую сортировку не надо, достаточно считать динамику прямо ленивой динамикой (DFS по графу игры).
При этом результат первого игрока становится результатом второго игрока в вершине X. Конечно, при этом писать топологическую сортировку не надо, достаточно считать динамику прямо ленивой динамикой (DFS по графу игры).
Задание¶
Посчитайте у каждого состояние в этом графе-игре результат игры. А также найдите для каждой вершины, куда оттуда идти оптимальнее всего:
Решение¶
В общем, может быть сколько угодно моделей игры. Монетки могут получаться не только в листьях — они могут лежать на ребрах, и игрок получает их, если проходит по ребру, или в вершинах. Но идеи подсчета результата игры можно использовать и в таких задачах: главное — понимать, что такое состояние в динамике.
Задание¶
Решите 2 последние задачи в этом контесте:
https://informatics.msk.ru/mod/statements/view3.php?id=33386
Стратегия крестиков-ноликов — Стивен Остермиллер
Игра с нулевой суммой
Если вы знаете, что делаете, вы не можете проиграть в крестики-нолики. Если ваш противник знает, что делает, вы не сможете выиграть в крестики-нолики. Игра представляет собой игру с нулевой суммой. Если оба игрока используют оптимальную стратегию, каждая игра заканчивается вничью.
Если ваш противник знает, что делает, вы не сможете выиграть в крестики-нолики. Игра представляет собой игру с нулевой суммой. Если оба игрока используют оптимальную стратегию, каждая игра заканчивается вничью.
На удивление мало людей знают оптимальную стратегию «крестики-нолики». Да, есть люди (и компьютеры), которых вы никогда не победите, но они относительно редки.Зная это, вы сможете стать мастером крестиков-ноликов.
Перед тем, как начать, откройте игровую доску «Крестики-нолики» в новом окне браузера, чтобы вы могли экспериментировать, читая эту статью.
Игроков
В крестики-нолики есть четыре типа игроков.
- Начинающий игрок делает случайные ходы
- Промежуточный игрок блокирует победу своего противника
- Опытный игрок знает, что игра на определенных первых клетках проиграет игру
- Опытный игрок никогда не проиграет
Столкнув этих игроков друг с другом, вы увидите, что во всех случаях лучший игрок побеждает больше.
| Второй игрок | |||||
|---|---|---|---|---|---|
| Новичок | Средний | Опытный | Эксперт | ||
| Первый игрок | Новичок | 1 побед: 57,1% 2 победы: 30,6% Ничьи: 12,3% | 1 побед: 6,40% 2 победы: 68,3% Ничьи: 25,3% | 1 побед: 2,60% 2 победы: 76,4% Ничьи: 21,0% | 1 побед: 0.00% 2 победы: 79,6% Ничьи: 20,4% |
| Промежуточный | 1 побед: 90,4% 2 победы: 1,60% Ничьи: 8,00% | 1 побед: 31,6% 2 победы: 17,1% Ничьи: 51,3% | 1 побед: 16,1% 2 победы: 10,3% Ничьи: 73,6% | 1 побед: 0,00% 2 победы: 16,1% Ничьи: 83,9% | |
| Опытный | 1 побед: 90,8% 2 победы: 0,700% Ничьи: 8,50% | 1 побед: 35,5% 2 победы: 11,7% Ничьи: 52.  8% 8% | 1 побед: 13,3% 2 победы: 0,800% Ничьи: 85,9% | 1 побед: 0,00% 2 победы: 1,70% Ничьи: 98,3% | |
| Эксперт | 1 побед: 97,8% 2 победы: 0,00% Ничьи: 2,20% | 1 побед: 76,6% 2 победы: 0,00% Ничьи: 23,4% | 1 побед: 27,1% 2 победы: 0,00% Ничьи: 72,9% | 1 побед: 0,00% 2 победы: 0,00% Ничьи: 100% | |
Эксперт — игрок, который не может проиграть
На игровом поле «Крестики-нолики», которое вы открыли в новом окне, выберите тип «Эксперт» для каждого игрока и нажмите «Новая игра».Убедитесь, что результатом каждой игры является ничья (кошачья игра).
| O | х | O |
| O | х | х |
| х | O | х |
Ни один из компьютерных игроков не может быть побежден, потому что они играют так же хорошо, как и в игру. Компьютер делает это, разыгрывая каждую игру в крестики-нолики заранее и выясняя, какие ходы хороши, а какие плохи.Компьютер может это сделать, потому что возможных игр не так много. Первый ход можно сделать в любом из девяти квадратов, второй — в любом из восьми, третий — в любом из семи квадратов и так далее. Это означает, что существует не более девяти факториалов или 362 880 возможных игр. Компьютер может пройти 400 000 игр в мгновение ока. На самом деле, он должен играть гораздо меньше игр, чем это. Есть только 125 168 игр в крестики-нолики, потому что кто-то выигрывает большинство из них до того, как все поля будут заполнены.Крестики-нолики симметричны, и если компьютер сможет понять, что многие игры одинаковы, потому что он может вращать доску, игр будет еще меньше. Достаточно сказать, что компьютеры побеждают с помощью грубой силы.
Компьютер делает это, разыгрывая каждую игру в крестики-нолики заранее и выясняя, какие ходы хороши, а какие плохи.Компьютер может это сделать, потому что возможных игр не так много. Первый ход можно сделать в любом из девяти квадратов, второй — в любом из восьми, третий — в любом из семи квадратов и так далее. Это означает, что существует не более девяти факториалов или 362 880 возможных игр. Компьютер может пройти 400 000 игр в мгновение ока. На самом деле, он должен играть гораздо меньше игр, чем это. Есть только 125 168 игр в крестики-нолики, потому что кто-то выигрывает большинство из них до того, как все поля будут заполнены.Крестики-нолики симметричны, и если компьютер сможет понять, что многие игры одинаковы, потому что он может вращать доску, игр будет еще меньше. Достаточно сказать, что компьютеры побеждают с помощью грубой силы.
Так как же человек может стать непобедимым в крестики-нолики? У человека даже нет времени разыграть в уме сотню игр и при этом сделать ход в разумные сроки. Однако человек может компенсировать это с помощью опыта и рассуждений.
Однако человек может компенсировать это с помощью опыта и рассуждений.
| O | х | |
| O | х | |
Новичок — глупая случайная игра
Победить «Новичка» может любой желающий практически в любой игре. Сделайте одного игрока новичком, а другого человека и понаблюдайте, как легко победить новичка.
Новичок просто ставит отметку в любой пустой клетке. Эта стратегия очень плохая и почти никогда не выигрывает.
| O | х | |
| O | ||
| х |
Промежуточный — реакционная игра
Большинство игроков в крестики-нолики начинают как реакционные игроки. Реакционные игроки будут блокировать своих противников по три подряд или брать любые три подряд, которые могут.В противном случае они играют как новички и выбирают случайные ходы. Именно этот стиль игры использует компьютерный игрок среднего уровня.
Реакционные игроки будут блокировать своих противников по три подряд или брать любые три подряд, которые могут.В противном случае они играют как новички и выбирают случайные ходы. Именно этот стиль игры использует компьютерный игрок среднего уровня.
Опытный — умеет завести
Опытный игрок знает лучшие стартовые ходы. Приведенные ниже стратегии подробно объясняют эти шаги.
Стратегии
Move First
Если два игрока среднего уровня играют много игр. Игрок, идущий первым, выигрывает примерно в два раза чаще, чем игрок, идущий вторым. Убедитесь в этом сами, настроив двух игроков среднего уровня друг против друга и наблюдая за статистикой, когда вы заставляете их играть во многие новые игры.
В некотором смысле это имеет смысл. На доске Tic-Tac-Toe всего девять квадратов, первый игрок получит пять из них, а второй игрок только четыре.
Когда играют два эксперта, игра всегда заканчивается вничью. Во всех остальных случаях игрок, который ходит первым, выигрывает гораздо больше, чем если бы его противник пошел первым.
Знай плохие первые шаги
Игрок 1
Если вы идете первым, знайте безопасные первые шаги.Уловка состоит в том, чтобы избегать краев. Углы и центр — безопасные ходы:
Игрок 2
Есть две возможности. Либо игрок 1 занял угловой, либо центр.
|
|
Игрок 1 может быть безжалостным
Если игрок 1 делает первый ход в углу, игрок 2 должен занять центр. Если игрок 1 играет против новичка, игрок 1 может быть безжалостным и всегда первым играть в углу. Это оставляет много доски для выбора новичку, и игрок 1 будет выигрывать чаще.
Если игрок 1 играет против новичка, игрок 1 может быть безжалостным и всегда первым играть в углу. Это оставляет много доски для выбора новичку, и игрок 1 будет выигрывать чаще.
Стать экспертом
Первые ходы (или открывающая книга) вычислить труднее всего. Помимо первого хода, не нужно много практики, чтобы из опытного игрока стать опытным игроком. Один из хороших способов решить эту проблему — сыграть дурака с опытным компьютерным игроком и посмотреть, как вас побьют.Попробуйте известные плохие первые ходы и посмотрите, как компьютер каждый раз может вас перехитрить. Помимо этого, я оставляю читателю упражнение на то, чтобы стать экспертом.
Кто выигрывает крестики-нолики, если второй игрок выигрывает только в случае ничьей? Ft. ScamSchool. Теория игр по вторникам — помните о своих решениях
В стандартных крестики-нолики первый игрок (X) и второй игрок (O) пытаются собрать по три подряд. Если оба играют оптимально, игра заканчивается вничью.
Теперь рассмотрим вариант: первый игрок выигрывает, если Xs или Os выпадут 3 подряд, а второй игрок выигрывает, только если на доске заканчивается ничья.Кто теперь выиграет игру?
Это кажется честной игрой, но это далеко не так! ScamSchool представила почему в видео, так что проверьте это.
Выиграй крестики-нолики, проиграв ?!
Или продолжайте читать мои объяснения.
.
.
«Все будет хорошо, если вы будете использовать свой разум для принятия решений, и думать только о своих решениях». С 2007 года я посвятил свою жизнь разделению радости теории игр и математики. MindYourDecisions теперь имеет более 1000 бесплатных статей без рекламы благодаря поддержке сообщества! Помогите и получите ранний доступ к сообщениям с обещанием на Patreon.
..
.
.
.
.
M
I
N
D
.
Y
O
U
R
.
D
E
C
I
S
I
O
N
S
.
.
.
.
.
Ответьте на вопрос, кто выиграет крестики-нолики, если второй игрок выиграет только при ничьей.
Это кажется честной игрой, но на самом деле первый игрок может добиться победы третьим ходом. Проблема в том, что второй игрок должен блокировать и крестики, и против образовывать тройку подряд, а первый игрок может вызвать «двойную атаку» всего за три хода.
Давайте рассмотрим случаи, чтобы понять, почему. Предположим, первый игрок начинает с центрального квадрата.
| |
————-
| X |
————-
| |
Второй игрок может играть в углу или на краю. В любом случае первый игрок может добиться победы всего за несколько ходов. Пройдемся по кейсам.
(a) Второй игрок играет в угол
Без ограничения общности, мы можем сделать его верхним левым углом.
O | |
————-
| X |
————-
| |
Теперь первый игрок может играть в любом углу, примыкающем к тому, где играл второй игрок (а не в противоположном углу).В этом случае первый игрок играет в левом углу третьего ряда.
O | |
————-
| X |
————-
X | |
Теперь второй игрок должен блокировать в первом ряду.
O | | O
————-
| X |
————-
X | |
Теперь первый игрок может играть в средней колонке третьего ряда, создавая двойную атаку.
O | | O
————-
| X |
————-
X | X |
Второй игрок застрял. Любой из игроков два блокирует три подряд крестика, тем самым делая три «О» подряд.Или второй игрок перемещается в другое место, позволяя первому игроку сделать три крестика подряд в следующий ход.
(b) Второй игрок играет край
Без ограничения общности, мы можем сделать его верхним центральным краем.
| O |
————-
| X |
————-
| |
Теперь первый игрок играет в углу, примыкающем к ходу второго игрока. В данном случае берется правый верхний угол:
X | O |
————-
| X |
————-
| |
Второй игрок должен заблокировать.
X | O |
————-
| X |
————-
| | O
И это позволяет игроку 1 создать двойную атаку, играя на краю рядом с крестиками в углу и центре.
X | O |
————-
X | X |
————-
| | O
Как и в обычных крестиках-ноликах, второй игрок не может блокировать и атаки, и поражения.
Первый игрок также может выиграть, играя в угловом квадрате.
Первый игрок может играть в центре, и это легкий выигрыш.Но есть и другие простые способы выиграть, например, если игрок 1 начинает игру в углу.
X | |
————-
| |
————-
| |
Теперь есть больше случаев для рассмотрения, потому что второй игрок может играть либо в (а) центре, (б) в соседнем углу, (в) на соседнем крае, (г) в противоположном углу, или (д) на противоположном крае. . Давайте работать над каждым случаем.
В каждом случае я продемонстрирую стратегию, в которой первый игрок может добиться победы. (Могут быть и другие методы, но это те пути, которые я видел)
(a) Второй игрок делает ход по центру
Это ход второго игрока.
X | |
————-
| O |
————-
| |
Теперь первый игрок может выбрать соседнее ребро.
X | X |
————-
| O |
————-
| |
Игрок 2 должен заблокировать угол, где игрок 1 угрожает тройкой подряд.
X | X | O
————-
| O |
————-
| |
И теперь первый игрок может играть другим соседним краем.
X | X | O
————-
X | O |
————-
| |
Теперь второй игрок застрял.Если второй игрок блокирует O в углу, то второй игрок делает 3 подряд и проигрывает. В противном случае первый игрок сделает три крестика подряд в следующий ход. Так что это потеря для второго игрока.
(b) Второй игрок делает ход в соседний угол
Это ход второго игрока.
X | | O
————-
| |
————-
| |
Теперь первый игрок может играть в центре.
X | | O
————-
| X |
————-
| |
Второй игрок должен блокировать в углу.
X | | O
————-
| X |
————-
| | O
И теперь игрок 1 может создать двойную атаку, играя в левый край.
X | | O
————-
X | X |
————-
| | O
И снова второй игрок застрял. В отличие от обычных крестиков-ноликов, если второй игрок блокирует ряд с помощью O, то второй игрок делает 3 подряд и проигрывает. Таким образом, второй игрок не может выиграть в этот ход, а второй игрок не может одновременно блокировать атаки среднего ряда и первого столбца.
(c) Второй игрок делает ход по соседнему краю
Это ход второго игрока.
X | O |
————-
| |
————-
| |
Теперь первый игрок играет в центре.
X | O |
————-
| X |
————-
| |
Теперь у второго игрока есть блок в углу.
Затем первый игрок выбирает другой соседний край.
X | O |
————-
X | X |
————-
| | O
Это двойная атака крестиков в первом столбце и среднем ряду, и игрок 2 не может заблокировать оба.
(d) Второй игрок делает ход в противоположный угол
Это ход второго игрока.
X | |
————-
| |
————-
| | O
Теперь первый игрок занимает соседнее ребро.
X | |
————-
X | |
————-
| | O
Это заставляет второго игрока блокировать угол.
X | |
————-
X | |
————-
O | | O
Теперь первый игрок играет вторым соседним краем.
X | X |
————-
X | |
————-
O | | O
Второй игрок должен заблокировать первый ряд.
X | X | O
————-
X | |
————-
O | | O
И теперь игрок 1 создает двойную атаку, взяв центр.
X | X | O
————-
X | X |
————-
O | | O
Если второй игрок блокирует любую точку, то второй игрок делает три «О» подряд и проигрывает.
(e) Второй игрок делает ход на противоположной стороне
Это ход второго игрока.
X | |
————-
| |
————-
| O |
Первый игрок занимает центр.
X | |
————-
| X |
————-
| O |
Теперь второй игрок блокирует угол.
X | |
————-
| X |
————-
| O | O
Первый игрок создает двойную атаку в углу.
X | |
————-
| X |
————-
X | O | O
Это поражение для второго игрока, точно так же, как и обычные крестики-нолики.
Первый игрок также может выиграть за преимущество
Оказывается, первый игрок может выиграть и за ребра, то есть первый игрок выигрывает независимо от того, каким будет первый ход.
Предположим, что первый ход — это преимущество.
| |
————-
X | |
————-
| |
Есть 5 возможных ответов от второго игрока: (а) центр, (б) соседний угол, (в) смежный край, (г) противоположный угол и (д) противоположный край.
Анализ аналогичен тому, как игрок 1 может выиграть, играя в углу.Для полноты картины я рассмотрю каждый случай.
(a) Второй игрок берет центр
Вот поле для игры после одного хода.
| |
————-
X | O |
————-
| |
Первый игрок может занять соседний угол.
X | |
————-
X | O |
————-
| |
Теперь второй игрок должен блокировать.
X | |
————-
X | O |
————-
O | |
Теперь первый игрок берет край, примыкающий к углу.
X | X |
————-
X | O |
————-
O | |
Это двойная атака в этой игре: либо игрок два блокирует, делая три «О» подряд, который проигрывает, либо второй игрок не блокирует и допускает три «крестика» подряд.
(b) Второй игрок занимает соседний угол
Вот поле для игры после одного хода.
O | |
————-
X | |
————-
| |
Теперь первый игрок занимает противоположную сторону.
O | |
————-
X | | X
————-
| |
Это заставляет второго игрока блокировать в центре.
O | |
————-
X | O | X
————-
| |
Теперь игрок 1 может провести двойную атаку в противоположном углу, как показано на рисунке:
O | | X
————-
X | O | X
————-
| |
Второй игрок должен либо заблокировать его (и проиграть с тремя «О»), либо второй игрок не блокирует и позволяет первому игроку сделать три «крестика».
(c) Второй игрок берет соседний край
Вот поле для игры после одного хода.
| O |
————-
X | |
————-
| |
Первый игрок занимает центр.
| O |
————-
X | X |
————-
| |
Второй игрок должен заблокировать.
| O |
————-
X | X | O
————-
| |
Теперь игрок 1 делает двойную атаку, играя в углу.
X | O |
————-
X | X |
————-
| |
Игрок 2 не может блокировать обе атаки в следующий ход, поэтому игрок 1 может выиграть.
(d) Второй игрок занимает противоположный угол
Вот поле для игры после одного хода.
| | O
————-
X | |
————-
| |
Первый игрок подает угол, противоположный ходу второго игрока.
| | O
————-
X | |
————-
X | |
Второй игрок должен заблокировать.
O | | O
————-
X | |
————-
X | |
Теперь первый игрок играет в центре.
O | | O
————-
X | X |
————-
X | |
Второй игрок снова должен блокировать.
O | | O
————-
X | X | O
————-
X | |
Теперь игрок 1 делает двойную атаку в последнем ряду.
O | | O
————-
X | X | O
————-
X | X |
Если второй игрок блокирует любую точку, второй игрок делает три «О» подряд и проигрывает.
(e) Второй игрок занимает противоположный край
Вот поле для игры после одного хода.
| |
————-
X | | O
————-
| |
Первый игрок может занять соседний угол.
X | |
————-
X | | O
————-
| |
Вынуждает второго игрока заблокировать.
X | |
————-
X | | O
————-
O | |
Теперь первый игрок может взять край, примыкающий к углу X.
X | X |
————-
X | | O
————-
O | |
Это снова заставляет второго игрока блокировать.
X | X | O
————-
X | | O
————-
O | |
Теперь первый игрок создает двойную атаку.
X | X | O
————-
X | | O
————-
O | X |
Игрок второй застрял: в любом месте выпадает три О подряд.
Заключение
Этот вариант крестиков-ноликов кажется справедливым, но игрок 1 на самом деле может заставить выиграть любой из начальных ходов!
Как выиграть крестики-нолики
Вы когда-нибудь задавались вопросом, как выиграть в крестики-нолики, иначе известные как крестики-нолики? В этом посте будут подробно описаны все способы добиться успеха в игре, и вскоре вы всегда будете либо выигрывать, либо рисовать.Если вы будете следовать этим простым правилам, вы больше никогда не проиграете ни одной игры в крестики-нолики.
Правила для крестиков-ноликов
Правила игры в крестики-нолики довольно просты. Ниже приведен исчерпывающий список правил игры в крестики-нолики:
- Игра требует двух игроков, X и O.
- Игровое поле представляет собой сетку 3×3, в которую игроки помещают свой символ, чтобы получить этот сегмент.
- X обычно сначала игроки, затем игроки по очереди.
- Цель состоит в том, чтобы заявить три сегмента сетки подряд по горизонтали, вертикали или диагонали.
- Никакие дополнительные стороны не могут быть добавлены к сетке.
- Игра заканчивается либо когда один игрок достигает трех сегментов подряд, либо когда сетка заполняется так, что никто не достигает трех сегментов подряд.
Хотя эти правила просты для понимания, в игре есть потенциал для создания 26 830 различных вариаций, но это включает в себя все идентичные повороты и зеркальное отображение каждой доски.Если убрать эти повторения, в таблице будет всего 765 различных результатов.
Крестики-нолики
Существует несколько различных стратегий, которые можно использовать для обеспечения победы при игре в крестики-нолики, но есть также несколько простых приемов, которые новые игроки могут использовать, чтобы повысить свои шансы. Помните, что эта игра известна как «решенная игра», что означает, что существует определенная стратегия, которую можно использовать для победы каждый раз.Однако, если оба игрока применяют одну и ту же непобедимую стратегию, игра каждый раз приводит к ничьей. Вот несколько приемов для новых игроков:
- Играя первым, займите угловую позицию вместо центральной.
- Играя вторым, захватите центральный сегмент, если первый игрок этого не сделал.
- При игре вторым занять угловое место, если первый игрок занял центральный сегмент.
- Всегда делайте ходы на основе стратегии.
- Большинство ходов либо блокируют, либо побеждают, либо настраивают на победу в следующий ход.
Это лишь некоторые из самых простых приемов для начинающих игроков, но игра включает в себя еще несколько нюансов для финальных ходов.
Те, кто может захотеть чего-то посложнее, могут попробовать трехмерные крестики-нолики, которые в основном похожи на три отдельные игры в крестики-нолики, но накладываются друг на друга. Это создает трехмерные крестики-нолики, в которых возможны выигрышные ряды по три во всех трех измерениях. Интересно, что применяются те же правила, и нужно использовать многие из тех же стратегий, если вы надеетесь выиграть в этом более сложном типе игры.
Как выиграть крестики-нолики, если вы идете вторым
Даже будучи вторым, можно выиграть игру, особенно если первый игрок не применяет непобедимую стратегию. Играя вторым, легко добиться ничьей, но выиграть немного сложнее. Вот лучшая стратегия для выигрыша, играя вторым:
- Если ваш оппонент понимает стратегию игры, он, скорее всего, сделает свой первый ход либо в центральном сегменте, либо в угловом сегменте.Если они это сделают и продолжат играть безупречно, ваш единственный выход — добиться ничьей.
- Если ваш противник не полностью понимает правила игры, и он все еще играет либо в центральном сегменте, либо в угловом сегменте, он может выиграть, если он сделает ошибку. Будьте внимательны и следите за ошибками с их стороны.
- Если ваш противник сделает свой первый ход в одном из боковых сегментов, у вас будет шанс добиться победы. Как всегда, сделайте свой ход в центральном квадрате после того, как они заняли сторону.На этом этапе ваша победа будет определяться ходом вашего оппонента. Если они размещают свой второй ход в той же строке, что и первые два хода, создавая полную строку или столбец, вашим следующим ходом должен быть один из углов. Если они не смогут заблокировать ваш ход, вы выиграете на следующем ходу.
Следует отметить, что эта стратегия требует как минимум двух ошибок от игрока, который пошел первым, поэтому ее можно использовать редко. В большинстве случаев, если вы играете вторым, ваша главная цель — добиться ничьей.
Как никогда не проиграть в крестики-нолики
Некоторые игроки хотят научиться всегда побеждать, а другие просто хотят знать, как никогда не проигрывать, что, по сути, означает, что они хотят знать, как добиться ничьей в любой ситуации. В этой игре довольно легко добиться ничьей, если вы знаете стандартную стратегию блокировки. Вот несколько лучших стратегий принуждения к ничьей:
- Если вы играете первым, форсировать ничью довольно легко. Они лишь требуют, чтобы игрок не упускал никаких шансов заблокировать победу у соперника.Игра первым — лучший способ выиграть, а проиграть при правильной стратегии практически невозможно.
- Если вы играете вторым, ваша главная цель — добиться ничьей. Победа со второй позиции довольно сложна и требует от соперника нескольких ошибок. Если первый игрок делает свой первый ход в углу, что является рекомендуемым первым ходом, второй игрок должен занять центральный сегмент. Затем первый игрок сделает свой второй ход, а второй игрок должен взять одну из граней.Возьмите только угловую фигуру, чтобы не дать вашему противнику получить три подряд. Если эта стратегия будет применена, наверняка будет достигнута ничья.
- Если вы играете вторым и первый игрок занимает центральный сегмент, вашим первым ходом должен быть угол. После этого второй игрок должен сосредоточиться только на блокировании первого игрока.
Как выигрывать крестики-нолики каждый раз
К сожалению, нет способа гарантировать, что игрок выиграет каждую игру в крестики-нолики, в которые он играет.Победа, поражение или ничья определяется взаимодействием обоих игроков. Если оба игрока действуют безупречно, всегда будет ничья. Лучшие стратегии для победы:
- Попытка пойти первым и потребовать угловой сегмент.
- Играйте вторым и надейтесь, что ваш оппонент ошибается.
- Сосредоточьтесь на блокировании и смотрите как минимум на два хода вперед.
Модели сообщества пользователей NetLogo:
Модели сообщества пользователей NetLogo
(назад к моделям сообщества пользователей NetLogo)
Загрузить |
ЧТО ЭТО?
Это знакомая игра «Крестики-нолики», запрограммированная в NetLogo, где вы можете играть против компьютера.
КАК ЭТО РАБОТАЕТ
Программа собирает все возможные позиции крестиков-ноликов в список, а затем переупорядочивает список по количеству сделанных ходов. В игре возможно не более 9 ходов. После 9 ходов легко определить, кто выиграл или была ли это ничья.Затем программа разбивает все позиции длины k, k = 1,2, …, 8 (то есть было сделано k ходов) на три списка: список выигрышных позиций, список проигравших позиций и список ничьи позиции. Список выигрышных позиций длины k состоит из всех позиций длины k, в которых игрок, чей ход следующий, может добиться выигрыша. Список проигрышных позиций длины k состоит из всех позиций длины k, в которых игрок, чей ход следующий, либо проигрывает k-м ходом, либо другой игрок может форсировать выигрыш.Если такое разбиение было установлено для позиций длины k, то оно может быть установлено для позиций длины k-1 следующим образом. Программа назначает каждую позицию длины k-1 списку выигрышей, проигрышей или ничьей в зависимости от того, что происходит с каждым возможным следующим ходом. Обратите внимание, что для каждой данной позиции есть только несколько возможных следующих ходов. Программа индуктивно переходит от k = 8 к k = 1.
Игра может начаться после того, как все позиции будут разделены на выигрышные, проигрышные и ничейные.Компьютер сначала проверяет, есть ли выигрышный ход. Если его нет, он выбирает ход ничьей. Это возможно только потому, что списки галстуков длины 1 и длины 2 не пусты. Поскольку список выигрышных ходов длиной 1 пуст, ни первый, ни второй игрок не могут добиться выигрыша.
КАК ИСПОЛЬЗОВАТЬ
Сначала нажмите кнопку настройки игры. Это может занять некоторое время, но вам нужно сделать это только один раз. Затем нажмите кнопку игры. Если переключить «сначала компьютер»? включен, то компьютер сделает первый ход.В противном случае компьютер будет ждать вашего хода. Чтобы сделать ход, просто нажмите на игровое поле по вашему выбору. Вам нужно дать компьютеру около 1 секунды, чтобы сделать ход, иначе вы можете столкнуться с ошибкой.
ИНФОРМАЦИЯ ДЛЯ УВЕДОМЛЕНИЯ
Компьютер никогда не проигрывает.
КРЕДИТЫ И ССЫЛКИ
Эта программа была написана Бертрамом Зиннером, 2004.
Крестики-нолики 2.0 | Кружки учителей математики
Новое принимает во внимание старую классику
Кэтрин Пуллин Лейн и Линн М.Пахновски
Твитнуть
Нравится MTCircular ? Подпишитесь на наш бесплатный полугодовой журнал.
Игра в крестики-нолики, или, как ее называют британцы, «крестики-нолики», имеет многовековые корни. Игровые доски в виде сетки были найдены в Древнем Египте, во времена Римской империи и в наше время на салфетках во многих ресторанах, став спасательным кругом для родителей, пытающихся развлечь шевелящихся детей.
Те, кто играл в крестики-нолики достаточно раз, возможно, обнаружили, что если игрок, который делает первый ход, является стратегическим, этот игрок всегда либо выигрывает, либо игра заканчивается ничьей (также известная как «кошачья игра». ).Как только игроки узнают эту стратегию, они могут потерять интерес. В конце концов, играть не так уж и весело, если ты знаешь, что не можешь выиграть! Тем не менее, наш кружок учителей математики наткнулся на связанную игру под названием «Gobblet Gobblers», которая снова переключает вызов в крестики-нолики и увлекала нас на несколько часов.
Разминка с помощью крестиков-ноликов
По-настоящему основанный на запросах, сеанс начинается с увлекательной ситуации. Учителя играют с партнером в игру в крестики-нолики, а затем их спрашивают: «Что вы замечаете? Что вам интересно? » Их обсуждение обычно начинается с таких комментариев, как: «Я заметил, что игрок, который начинает, обычно тот, кто побеждает» или «Интересно, есть ли способ быть вторым игроком и гарантировать победу.”
Второй этап каждого хорошего урока, основанного на запросах, — дать учащимся возможность исследовать. Итак, на нашем занятии учителя играют еще в несколько игр, уделяя больше внимания некоторым своим вопросам. Через несколько минут мы просим учителей объяснить свои стратегии, что является третьим этапом урока, основанного на запросах. Последующее обсуждение часто включает преимущества или недостатки различных подходов. Учителя обычно предполагают, что лучшая первая игра — играть в углу или в центре.На одном занятии учительница заявила, что предпочитает первую игру играть в центре, потому что у нее больше возможностей для победы. Ее аргумент состоял в том, что начальный ход в угол оставляет три возможных победы, а начальный ход в центр оставляет четыре возможных победы. Этот аргумент является естественным продолжением группы, разрабатывающей исчерпывающее описание выигрышной стратегии Игрока 1. В «Компьютерных науках для развлечения» есть отличное занятие по информатике, «Intelligent Paper», которое предоставляет письменное описание стратегии.Стратегия также может быть инкапсулирована в блок-схему или дерево решений (как показано здесь). Еще одно отличное направление для исследования — определить количество различных возможных игр, включая количество различных позиций «кошачьей игры». (Спойлер: последних всего три!) Также посетите страницу Википедии о крестиках-ноликах, чтобы получить хороший обзор этих и многих других математических вопросов, связанных с игрой.
Все эти дискуссии о крестиках-ноликах показывают, что это проблема «множественных точек входа».«В каком бы классе мы ни учили, и независимо от нашего конкретного математического опыта, мы можем опираться на общий опыт работы с крестиками-ноликами и исследовать вопросы о стратегиях.
Крестики-нолики с поворотом
Gobblet Gobblers — это вариация игры Tic-Tac-Toe. Коммерческую версию игры, производимую Blue Orange, можно недорого купить и она завоевала несколько престижных наград. Части игровой коробки включают:
- Четыре стержня, которые можно расположить в сетку три на три
- Шесть оранжевых «гоблеров» (по два маленьких, средних и больших)
- Шесть синих «гоблеров» (опять же, по два маленьких, средних и больших)
Игра может быть легко модифицирована для большой группы, сделав сетки на больших листах бумаги и используя три разных размера непрозрачных чашек двух цветов.По сути, за несколько пачек чашек и большой бумаги можно играть до тридцати человек.
Чтобы начать игру, дайте Игроку 1 шесть оранжевых гоблеров, а Игроку 2 — шесть синих гоблеров. Как и в Tic-Tac-Toe, цель игры состоит в том, чтобы выстроить три ваши фигуры. За ход вы можете:
- Поместите любого гублера на доску в пустое место или над меньшим гоблером, или
- Переместите любого гублера, уже находящегося на доске, в пустое место или над меньшим гоблером.
Как только вы дотронетесь до гобблера на доске, вы должны его переместить.
Учителей просят поиграть и быть готовыми описать то, что они замечают и удивляются. После игры учителя делятся своими наблюдениями, которые обычно включают такие вопросы, как: «Что лучше начать с больших глотков или с маленьких?» «Стоит ли начинать с угла, как крестики-нолики?» «Какая защита лучше: блокировать на открытом пространстве или« сожрать »противника?» «Есть ли ситуация, в которой вы должны« съесть »свой кусок?»
Другой естественный вопрос — есть ли в Gobblet Gobblers выигрышная стратегия или стратегии.Создание дерева решений, подобного тому, которое используется в нашей более простой игре «Крестики-нолики», может стать очень многослойным и представляет собой насыщенное и интересное занятие, способствующее расследованию.
Мы обнаружили, что игра в одиночку занимает около 45 минут, в то время как включение дополнительных следственных действий легко увеличивает время сеанса до двух часов. По нашему опыту, учителям полезно играть в Gobblet Gobblers группами по четыре человека. Это дает возможность обсуждать пьесы вслух и наблюдать за игрой других. Чтобы разработать выигрышную стратегию, парам или группам может потребоваться совместная, а не соревновательная игра, отмечая выбор и решения.
После представления Gobblet Gobblers в сети MTC, мы прогнозируем, что она станет постоянным хитом и станет одной из тех классических игр, которые доступны на семинарах по погружению и других собраниях. Учителя рассказывают, что они вернули его в свои классы на всех уровнях обучения, не говоря уже о том, что он также нашел свое применение во многих кухонных столах в нашем районе.
Кэтрин Пуллин Лейн (Университет Болдуина Уоллеса) и Линн М. Пахновски (Университет Акрона) — руководители MTC Rubber City в Акроне, штат Огайо.
Твитнуть
Эта статья была впервые опубликована в MTCircular , выпущенном осенью 2019 года.
Крестики-нолики с использованием Python — AskPython
В этой статье мы рассмотрим этапы создания крестиков-ноликов с использованием языка Python с нуля.
Крестики-ноликиОб игре
Крестики-нолики — это игра для двух игроков, в которой используется квадратная сетка 3 × 3. Каждый игрок по очереди занимает ячейку с целью размещения трех отметок по горизонтали, вертикали или диагонали.Один игрок использует крест 'X' в качестве маркера, а другой использует нулевое значение 'O' .
Шаг 1: Дизайн крестиков-ноликов
Мы будем играть в крестики-нолики в командной строке, поэтому первое, что нам нужно сделать, это создать дизайн для наших крестиков-ноликов.
Крестики-нолики Дизайн Если игрок должен отметить конкретную ячейку, он должен ввести соответствующий номер, показанный в сетке. Предположим, мы хотим занять центральный блок, тогда мы введем 5 в терминал.Эту сетку можно создать с помощью:
# Функция для печати крестиков-ноликов
def print_tic_tac_toe (значения):
печать ("\ п")
печать ("\ t | |")
print ("\ t {} | {} | {}". формат (значения [0], значения [1], значения [2]))
print ('\ t _____ | _____ | _____')
печать ("\ t | |")
print ("\ t {} | {} | {}". формат (значения [3], значения [4], значения [5]))
print ('\ t _____ | _____ | _____')
печать ("\ t | |")
print ("\ t {} | {} | {}". формат (значения [6], значения [7], значения [8]))
печать ("\ t | |")
печать ("\ п")
В приведенном выше коде функция создает нашу игру в крестики-нолики в соответствии со значениями, переданными в качестве аргумента.Здесь аргумент значений — это список, содержащий статус каждой ячейки в сетке.
Шаг 2. Сохранение информации с использованием структур данных
В основе любой игры лежит игровая механика. Поскольку эту игру довольно легко создать, задействованная механика также проста.
В любой момент нам нужны две важные информации:
- Статус сетки — У нас должна быть структура данных, в которой хранится состояние каждой ячейки, то есть занята она или свободна.
- Ходы каждого игрока — Мы должны каким-то образом знать прошлые и настоящие ходы каждого игрока, то есть позиции, занятые
'X'и'O'.
Примечание: Обе информации можно было бы получить, используя статус сетки, но требовалось бы пересекать ее каждый раз, когда нам нужны позиции игрока. Это можно назвать компромиссом между временем и сложностью пространства. Это общий метод экономии времени.
# Функция для одиночной игры в крестики-нолики
def single_game (cur_player):
# Представляет крестики-нолики
values = ['' для x в диапазоне (9)]
# Сохраняет позиции, занятые X и O
player_pos = {'X': [], 'O': []}
Статус сетки управляется списком символов, который может иметь три возможных значения,
-
''— Свободная ячейка -
'X'— Ячейка, занятая игроком X -
'O'— Ячейка, занятая игроком O
Ходы каждого игрока сохраняются как словарь списка целых чисел.Ключи: 'X' и 'O' для соответствующего игрока. Соответствующие им списки содержат номера, присвоенные ячейкам сетки, которые они занимают.
Примечание: Переменная
cur_playerхранит текущего игрока, делающего ход, как в'X'или'O'.
Шаг 3: игровой цикл
Каждая игра имеет своего рода игровой цикл, который длится до тех пор, пока какой-либо игрок не выиграет или игра не закончится ничьей.В крестики-нолики каждая итерация цикла относится к одному ходу, который делает любой игрок.
# Игровой цикл для одиночной игры в крестики-нолики в то время как True: print_tic_tac_toe (значения)
Шаг 4. Обработка ввода игрока
На каждой итерации игры игрок должен ввести свой ход.
# Попробовать блок исключений для ввода MOVE
пытаться:
print ("Игрок", cur_player, "поворот. Какой ящик?:", end = "")
переместить = int (вход ())
кроме ValueError:
print («Неверный ввод !!! Попробуйте еще раз»)
Продолжить
# Проверка работоспособности для MOVE inout
если ход <1 или ход> 9:
print («Неверный ввод !!! Попробуйте еще раз»)
Продолжить
# Проверить, не занят ли ящик
если значения [move-1]! = '':
print ("Место уже заполнено.Попробуйте еще раз!!")
Продолжить
Создаем блок try на случай, если игрок введет какое-то непреднамеренное значение. Такое событие не должно останавливать игру, поэтому мы обрабатываем исключение ValueError и продолжаем нашу игру.
Нам нужно выполнить некоторые проверки работоспособности, например, введенное значение является действительной позицией, и если это действительная позиция, она уже занята?
Шаг 5: Обновите информацию
Согласно вводу игрока, нам необходимо обновить информацию для бесперебойного функционирования игры.
# Обновить информацию об игре # Обновление статуса сетки значения [move-1] = cur_player # Обновление позиций игроков player_pos [cur_player] .append (переместить)
Список значений обновляет ячейку, занятую в соответствии с текущим игроком. Позиция игрока добавляет позицию, только что занятую текущим игроком.
После обновления списка значений и вызова функции print_tic_tac_toe () сетка выглядит так:
Последний ход: «X» на 2
Шаг 6: Проверьте выигрыш или ничью
После каждого хода мы должны проверять, выиграл ли какой-либо игрок игру или игра была сделана вничью. Его можно проверить по:
Вызов функций:
# Вызов функции для проверки выигрыша
если check_win (player_pos, cur_player):
print_tic_tac_toe (значения)
print ("Игрок", cur_player, "выиграл игру !!")
печать ("\ п")
вернуть cur_player
# Вызов функции для проверки розыгрыша игры
если check_draw (player_pos):
print_tic_tac_toe (значения)
print ("Игра нарисована")
печать ("\ п")
вернуть 'D'
Если любой игрок выигрывает, то функция single_game () возвращает текущего игрока, который сделал ход.В случае ничьей, 'D' отправляется обратно.
Функции:
# Функция, чтобы проверить, выиграл ли какой-либо игрок def check_win (player_pos, cur_player): # Все возможные выигрышные комбинации soln = [[1, 2, 3], [4, 5, 6], [7, 8, 9], [1, 4, 7], [2, 5, 8], [3, 6, 9] » , [1, 5, 9], [3, 5, 7]] # Цикл, чтобы проверить, удовлетворена ли какая-либо выигрышная комбинация для x в soln: если все (y в player_pos [cur_player] для y в x): # Возвращаем True, если какая-либо выигрышная комбинация удовлетворяет вернуть True # Возвращаем False, если комбинация не удовлетворяет вернуть ложь # Функция проверки, нарисована ли игра def check_draw (player_pos): если len (player_pos ['X']) + len (player_pos ['O']) == 9: вернуть True вернуть ложь
check_win () — Функция содержит все выигрышные комбинации.Все, что он делает, это проверяет, удовлетворяется ли какая-либо из выигрышных комбинаций текущими позициями игрока. Если это так, он возвращает True . Если ни одна из комбинаций не удовлетворена, функция возвращает False .
check_draw () — Условие розыгрыша довольно простое, поскольку игра заканчивается, когда все «девять» позиций заняты.
Шаг 7: переключить текущего игрока
Поскольку каждый игрок движется только один раз за раз, поэтому после каждого успешного хода мы должны менять местами текущего игрока.
# Сменить ходы игрока если cur_player == 'X': cur_player = 'О' еще: cur_player = 'X'
Что касается одиночной игры, это все, что нам нужно сделать. Но в этой статье также представлена система табло для отслеживания, если игроки хотят сыграть в несколько игр.
Шаг 8: Введите имена игроков
Имя каждого игрока обязательно должно отображаться на любом табло.
если __name__ == "__main__":
print ("Игрок 1")
player1 = input ("Введите имя:")
печать ("\ п")
print ("Игрок 2")
player2 = input ("Введите имя:")
печать ("\ п")
Шаг 9. Сохраните информацию об игре
Необходимо сохранить такую информацию, как текущий игрок, выбор игроков (взять крестик или ноль), доступные варианты (крестик и ноль) и табло.
# Сохраняет игрока, который выбирает X и O
cur_player = player1
# Хранит выбор игроков
player_choice = {'X': "", 'O': ""}
# Сохраняет параметры
options = ['X', 'O']
# Хранит табло
score_board = {player1: 0, player2: 0}
По умолчанию текущий игрок — это игрок, который первым ввел имя.
Шаг 10: Дизайн табло
Табло хранится в виде словаря, где ключи — это имена игроков, а значения — их выигрышные числа.
# Функция для печати табло
def print_scoreboard (Score_board):
Распечатать("--------------------------------")
print ("ДОСКА СЧЕТОВ")
Распечатать("--------------------------------")
игроки = список (score_board.keys ())
print ("", игроки [0], "", Score_board [игроки [0]])
print ("", игроки [1], "", Score_board [игроки [1]])
print ("-------------------------------- \ n")
Для отображения табло нам нужны имена игроков. Ключи извлекаются с помощью .keys () , а затем преобразуется в список, чтобы его можно было проиндексировать при отображении результатов.
Шаг 11: Внешний игровой цикл
Нам нужен еще один игровой цикл, чтобы управлять множеством матчей в крестики-нолики. В каждом матче текущий игрок выбирает свою отметку ( 'X' или 'O' ). Меню для выбора должно отображаться на каждой итерации игры:
# Game Loop для серии Tic Tac Toe
# Цикл длится до тех пор, пока игроки не выйдут
в то время как True:
# Меню выбора игрока
print ("Поверните, чтобы выбрать", cur_player)
print ("Введите 1 для X")
print ("Введите 2 вместо O")
print («Введите 3, чтобы выйти»)
Табло и меню выглядят так:
Табло и менюШаг 12: Обработка и назначение выбора игрока
На каждой итерации мы должны обрабатывать и сохранять выбор текущего игрока.
# Попробуйте исключение для ввода CHOICE
пытаться:
выбор = int (вход ())
кроме ValueError:
print («Неправильный ввод !!! Попробуйте еще раз \ n»)
Продолжить
# Условия выбора игрока
если выбор == 1:
player_choice ['X'] = cur_player
если cur_player == player1:
player_choice ['O'] = player2
еще:
player_choice ['O'] = player1
elif choice == 2:
player_choice ['O'] = cur_player
если cur_player == player1:
player_choice ['X'] = player2
еще:
player_choice ['X'] = player1
elif choice == 3:
print («Окончательные результаты»)
print_scoreboard (табло_счетов)
перемена
еще:
print ("Неправильный выбор !!!! Попробуйте снова \ n")
По выбору игрока данные сохранены.Это важно, так как после завершения каждой игры мы узнаем, какой игрок выиграл.
Шаг 13: Выполнить сопоставление
После сохранения всей необходимой информации пора выполнить независимый матч и сохранить выигрышный знак.
# Сохраняет победителя в одиночной игре в крестики-нолики победитель = single_game (варианты [выбор-1])
Шаг 14: Обновите табло
Нам нужно обновлять табло после каждого матча крестики-нолики.
# Обновляет табло в соответствии с победителем если победитель! = 'D': player_won = player_choice [победитель] Score_board [player_won] = Score_board [player_won] + 1 print_scoreboard (табло_счетов)
Если игра не закончилась вничью, то обновляем табло.
Шаг 15: Сменить игрока
Это прекрасная идея, что у каждого игрока должна быть возможность выбрать, какой знак он хочет. Для этого меняем местами значение cur_player .
# Сменить игрока, который выбирает X или O если cur_player == player1: cur_player = player2 еще: cur_player = player1
Полный рабочий код
# Функция для печати крестиков-ноликов
def print_tic_tac_toe (значения):
печать ("\ п")
печать ("\ t | |")
print ("\ t {} | {} | {}". формат (значения [0], значения [1], значения [2]))
print ('\ t _____ | _____ | _____')
печать ("\ t | |")
print ("\ t {} | {} | {}". формат (значения [3], значения [4], значения [5]))
print ('\ t _____ | _____ | _____')
печать ("\ t | |")
print ("\ t {} | {} | {}".формат (значения [6], значения [7], значения [8]))
печать ("\ t | |")
печать ("\ п")
# Функция для печати табло
def print_scoreboard (Score_board):
print ("\ t --------------------------------")
print ("\ t ДОСКА СЧЕТОВ")
print ("\ t --------------------------------")
игроки = список (score_board.keys ())
print ("\ t", игроки [0], "\ t", табло [игроки [0]])
print ("\ t", игроки [1], "\ t", табло [игроки [1]])
print ("\ t -------------------------------- \ n")
# Функция, чтобы проверить, выиграл ли какой-либо игрок
def check_win (player_pos, cur_player):
# Все возможные выигрышные комбинации
soln = [[1, 2, 3], [4, 5, 6], [7, 8, 9], [1, 4, 7], [2, 5, 8], [3, 6, 9] » , [1, 5, 9], [3, 5, 7]]
# Цикл, чтобы проверить, удовлетворена ли какая-либо выигрышная комбинация
для x в soln:
если все (y в player_pos [cur_player] для y в x):
# Возвращаем True, если какая-либо выигрышная комбинация удовлетворяет
вернуть True
# Возвращаем False, если комбинация не удовлетворяет
вернуть ложь
# Функция проверки, нарисована ли игра
def check_draw (player_pos):
если len (player_pos ['X']) + len (player_pos ['O']) == 9:
вернуть True
вернуть ложь
# Функция для одиночной игры в крестики-нолики
def single_game (cur_player):
# Представляет крестики-нолики
values = ['' для x в диапазоне (9)]
# Сохраняет позиции, занятые X и O
player_pos = {'X': [], 'O': []}
# Игровой цикл для одиночной игры в крестики-нолики
в то время как True:
print_tic_tac_toe (значения)
# Попробовать блок исключений для ввода MOVE
пытаться:
print ("Игрок", cur_player, "поворот.Какая коробка? : ", end =" ")
переместить = int (вход ())
кроме ValueError:
print («Неверный ввод !!! Попробуйте еще раз»)
Продолжить
# Проверка работоспособности для MOVE inout
если ход <1 или ход> 9:
print («Неверный ввод !!! Попробуйте еще раз»)
Продолжить
# Проверить, не занят ли ящик
если значения [move-1]! = '':
print («Место уже заполнено. Попробуйте еще раз !!»)
Продолжить
# Обновить информацию об игре
# Обновление статуса сетки
значения [move-1] = cur_player
# Обновление позиций игроков
player_pos [cur_player].добавить (переместить)
# Вызов функции для проверки выигрыша
если check_win (player_pos, cur_player):
print_tic_tac_toe (значения)
print ("Игрок", cur_player, "выиграл игру !!")
печать ("\ п")
вернуть cur_player
# Вызов функции для проверки розыгрыша игры
если check_draw (player_pos):
print_tic_tac_toe (значения)
print ("Игра нарисована")
печать ("\ п")
вернуть 'D'
# Сменить ходы игрока
если cur_player == 'X':
cur_player = 'О'
еще:
cur_player = 'X'
если __name__ == "__main__":
print ("Игрок 1")
player1 = input ("Введите имя:")
печать ("\ п")
print ("Игрок 2")
player2 = input ("Введите имя:")
печать ("\ п")
# Сохраняет игрока, который выбирает X и O
cur_player = player1
# Хранит выбор игроков
player_choice = {'X': "", 'O': ""}
# Сохраняет параметры
options = ['X', 'O']
# Хранит табло
score_board = {player1: 0, player2: 0}
print_scoreboard (табло_счетов)
# Game Loop для серии Tic Tac Toe
# Цикл длится до тех пор, пока игроки не выйдут
в то время как True:
# Меню выбора игрока
print ("Поверните, чтобы выбрать", cur_player)
print ("Введите 1 для X")
print ("Введите 2 вместо O")
print («Введите 3, чтобы выйти»)
# Попробуйте исключение для ввода CHOICE
пытаться:
выбор = int (вход ())
кроме ValueError:
print («Неправильный ввод !!! Попробуйте еще раз \ n»)
Продолжить
# Условия выбора игрока
если выбор == 1:
player_choice ['X'] = cur_player
если cur_player == player1:
player_choice ['O'] = player2
еще:
player_choice ['O'] = player1
elif choice == 2:
player_choice ['O'] = cur_player
если cur_player == player1:
player_choice ['X'] = player2
еще:
player_choice ['X'] = player1
elif choice == 3:
print («Окончательные результаты»)
print_scoreboard (табло_счетов)
перемена
еще:
print ("Неправильный выбор !!!! Попробуйте снова \ n")
# Сохраняет победителя в одиночной игре в крестики-нолики
победитель = single_game (варианты [выбор-1])
# Редактирует табло в соответствии с победителем
если победитель! = 'D':
player_won = player_choice [победитель]
Score_board [player_won] = Score_board [player_won] + 1
print_scoreboard (табло_счетов)
# Сменить игрока, который выбирает X или O
если cur_player == player1:
cur_player = player2
еще:
cur_player = player1
Пора поиграть!
Все шаги по созданию игры завершены.Пришло время поиграть в игру.
Игрок 1 Введите имя: Луффи Игрок 2 Введите имя: Санджи -------------------------------- ТАБЛО -------------------------------- Луффи 0 Санджи 0 -------------------------------- Повернись, чтобы выбрать Луффи Введите 1 для X Введите 2 для O Введите 3, чтобы выйти 1 | | | | _____ | _____ | _____ | | | | _____ | _____ | _____ | | | | | | Игрок X ход.Какая коробка? : 5 | | | | _____ | _____ | _____ | | | X | _____ | _____ | _____ | | | | | | Игрок O ход. Какая коробка? : 1 | | O | | _____ | _____ | _____ | | | X | _____ | _____ | _____ | | | | | | Игрок X ход. Какая коробка? : 9 | | O | | _____ | _____ | _____ | | | X | _____ | _____ | _____ | | | | Икс | | Игрок O ход.Какая коробка? : 2 | | O | O | _____ | _____ | _____ | | | X | _____ | _____ | _____ | | | | Икс | | Игрок X ход. Какая коробка? : 3 | | O | O | Икс _____ | _____ | _____ | | | X | _____ | _____ | _____ | | | | Икс | | Игрок O ход. Какая коробка? : 7 | | O | O | Икс _____ | _____ | _____ | | | X | _____ | _____ | _____ | | O | | Икс | | Игрок X ход.Какая коробка? : 6 | | O | O | Икс _____ | _____ | _____ | | | X | Икс _____ | _____ | _____ | | O | | Икс | | Игрок X выиграл игру !! -------------------------------- ТАБЛО -------------------------------- Луффи 1 Санджи 0 -------------------------------- Повернись, чтобы выбрать Санджи Введите 1 для X Введите 2 для O Введите 3, чтобы выйти 2 | | | | _____ | _____ | _____ | | | | _____ | _____ | _____ | | | | | | Игрок O ход.Какая коробка? : 5 | | | | _____ | _____ | _____ | | | O | _____ | _____ | _____ | | | | | | Игрок X ход. Какая коробка? : 3 | | | | Икс _____ | _____ | _____ | | | O | _____ | _____ | _____ | | | | | | Игрок O ход. Какая коробка? : 2 | | | O | Икс _____ | _____ | _____ | | | O | _____ | _____ | _____ | | | | | | Игрок X ход.Какая коробка? : 8 | | | O | Икс _____ | _____ | _____ | | | O | _____ | _____ | _____ | | | X | | | Игрок O ход. Какая коробка? : 1 | | O | O | Икс _____ | _____ | _____ | | | O | _____ | _____ | _____ | | | X | | | Игрок X ход. Какая коробка? : 9 | | O | O | Икс _____ | _____ | _____ | | | O | _____ | _____ | _____ | | | X | Икс | | Игрок O ход.Какая коробка? : 6 | | O | O | Икс _____ | _____ | _____ | | | O | О _____ | _____ | _____ | | | X | Икс | | Игрок X ход. Какая коробка? : 7 | | O | O | Икс _____ | _____ | _____ | | | O | О _____ | _____ | _____ | | X | X | Икс | | Игрок X выиграл игру !! -------------------------------- ТАБЛО -------------------------------- Луффи 2 Санджи 0 -------------------------------- Повернись, чтобы выбрать Луффи Введите 1 для X Введите 2 для O Введите 3, чтобы выйти 3 Итоговые результаты -------------------------------- ТАБЛО -------------------------------- Луффи 2 Санджи 0 --------------------------------
Заключение
Мы надеемся, что эта статья была интересной и информативной для читателя.Я также загрузил код на Github. Вы можете посетить здесь для получения кода. Если есть какие-то предложения по игре, не стесняйтесь комментировать.
Введение в информатику, глава 10: Пример: крестики-нолики
Этот компьютер, сделанный из деталей Тинкер-Той, играет крестики-нолики. Простая схема: введение в информатику, глава 10: Пример: крестики-ноликиПростая схема: Введение в информатику 2 / e Copyright (C) 1999 MIT
Глава 10
Теперь, когда вы узнали о функциях высшего порядка, мы рассмотрим большой пример, который их широко использует.С использованием методы, которые вы изучили до сих пор, мы собираемся написать программу, которая воспроизводит идеальные крестики-нолики.
Вы можете загрузить нашу программу в Scheme, набрав
(нагрузка «ттт.см»)
(см. Приложение A, если это не сработает для вас.)
Предупреждение
Программы не всегда выходят правильно с первого раза. Одна из наших целей в эта глава призвана показать вам, как разрабатывается программа, поэтому мы представляем ранние версии процедур. К ним относятся некоторые ошибки, которые мы сделали, и также некоторые постфактум упрощения, чтобы наши объяснения Полегче.Если вы введете эти ранние версии, они не будут работать. Мы покажем вам, как мы исправляли эти «ошибки», а также представим полную, правильную версия в конце главы.
Для обозначения незавершенных версий процедур будем использовать комментарии типа «первая версия» или «не совсем часть игры».
Технические термины в крестиках-ноликах
Пронумеруем клетки доски следующим образом:
Мы будем называть частично заполненную доску позицией.»
Для компьютера эта же позиция будет представлена словом __o_xox_x . Девять букв слова соответствуют квадратам с первого по
девять из доски. (Мы заранее продумываем возможность использования элемента для извлечения n -го квадрата данной позиции.)
Размышляя о структуре программы
Наша процедура верхнего уровня, ttt , вернет следующий ход компьютера
учитывая текущую позицию.Требуется два аргумента: текущая позиция
и играет ли компьютер X или O. Если компьютер O и
доска выглядит так, как показано выше, тогда мы вызываем ttt следующим образом:
(ttt '__o_xox_x' o)
Вот пример игры:
> (ттт '____x____' о); Человек идет первым в квадрате 5 1; Компьютер движется в квадрате 1 > (ttt 'o__xx____' o); Человек движется в квадрате 4 6; Компьютерные блоки в квадрате 6 > (ttt 'o_xxxo___' o); Человек движется в квадрате 3 7; Компьютер снова блокируется > (ttt 'o_xxxoox_' o) 2
Это не полная игровая программа! Позже, когда мы поговорим о вводе и вывода, вы увидите, как написать интерактивную программу, отображающую доска графически, спрашивает игрока, куда двигаться, и так далее.А пока мы просто напишите процедуру стратегии , которая выбирает следующий двигаться. Как платежеспособный покупатель, вы не будете удовлетворены этим частичная программа, но с точки зрения программиста, это более интересная часть.
Давайте спланируем компьютерную стратегию на английском языке, прежде чем мы начнем писать компьютерная программа. Как ты играешь в крестики-нолики? У вас есть несколько правила стратегии в вашей голове, некоторые из которых более важны, чем другие. За Например, если вы можете выиграть этим ходом, то вы просто делаете это, не задумываясь ни о чем другом.Но если нет ничего более быстрого, вы рассмотреть менее срочные вопросы, например, как этот шаг может повлиять на то, происходит двумя ходами позже.
Итак, мы представим этот набор правил гигантским выражением cond :
(определить (ttt position me) ;; первая версия
(cond ((я-могу-выиграть?)
(выбрать-выигрышный ход))
((противник может выиграть?)
(блок-оппонент-победа))
((Я-могу-выиграть-в следующий раз?)
(подготовить-выиграть))
(еще (что угодно))))
Мы придумываем множество вспомогательных процедур. Я могу выиграть? посмотрит
доску и скажите, есть ли у компьютера немедленный выигрышный ход. Если это так, выбирает-выигрышный ход найдет этот конкретный ход. Противник может выиграть? возвращает истину, если игрок-человек немедленно
выигрышный ход. Блок-оппонент-победа вернет ход, предотвращающий
компьютерный противник от победы и так далее.
На самом деле мы не начали с написания этого определения ttt . В
конкретные имена вспомогательных процедур — всего лишь предположения, потому что мы не
пока что спланировал стратегию крестиков-ноликов в деталях.Но мы знали, что это
будет общей структурой нашей программы. Эта большая картина не
автоматически сообщать нам, что делать дальше; разные программисты могут заполнить
детали по-разному. Но об этом следует помнить во время
остальная часть работы.
Нашим первым практическим шагом было подумать о структурах данных в нашей программе. Структура данных — это способ организация нескольких фрагментов информации в большой кусок. Например, предложение — это структура данных, которая объединяет несколько слов в последовательность (что есть в порядке слева направо).
В первой, ручной версии ttt , процедуры стратегии, такие как я могу выиграть? вызываются без аргументов, но мы, конечно, знали, что они
потребуется некоторая информация о позиции доски. Мы начали с размышлений
о том, как представить эту информацию в программе.
Первый шаг: утроение
Человек, смотрящий на доску для крестиков-ноликов, смотрит на строки, столбцы и диагонали. На вопрос «есть ли у меня выигрышный ход?» эквивалентен вопрос «есть ли в линии три квадрата, два из которых мои? а последняя пуста? »На самом деле, в игре нет ничего важного. помимо этих потенциальных выигрышных комбинаций.
Есть восемь возможных выигрышных комбинаций: три ряда, три
столбцы и две диагонали. Рассмотрим комбинацию, содержащую три
квадраты 1, 5 и 9. Если он содержит как x , так и o , тогда
никто не может выиграть с этой комбинацией и думать не о чем.
Но если он содержит два размера x и свободный квадрат, нас очень интересует
комбинация. В частности, мы хотим знать, какой квадрат
бесплатно, так как мы хотим двигаться в этом квадрате, чтобы выиграть или заблокировать.
В целом, единственные квадраты, в которых числа нас интересуют, — это
те, в которые мы могли бы захотеть переехать, а именно бесплатные. Так что единственный
Интересная информация о квадрате: имеет ли он разрешение x или o , а если нет, то каков его номер.
Информация о том, что 1, 5, 9 является потенциальной выигрышной комбинацией, и
информация о том, что квадрат 1 содержит x , квадрат 5 пуст, а квадрат 9 содержит еще x может быть объединено в одно слово x5x .Глядя на это слово, мы сразу видим, что в этой «тройке» есть два x , а свободный квадрат равен 5. Итак, когда мы
хотите узнать о комбинации из трех квадратов, мы превратим ее в
тройка этой формы.
Вот пример расположения платы:
и вот предложение всех его троек:
(1xo 4x6 o89 14o xx8 o69 1x9 oxo)
Найдите минутку, чтобы убедиться, что это предложение действительно говорит вам все, что вам нужно знать о соответствующей позиции доски.Один раз наша стратегическая процедура находит тройки для позиции на доске, она никогда не собираюсь снова взглянуть на исходное положение.
Этот метод преобразования данных из одной формы в другую, чтобы их можно было легче манипулировать — важная идея в информатике. Есть на самом деле три представления одного и того же. Вот такая картинка:
, а также слово _xo_x_o__ и предложение (1xo 4x6
o89 14o xx8 o69 1x9 oxo) .Все три формата имеют одинаковые
информации, но удобны по-разному. Изобразительная форма
удобно, потому что это имеет смысл для человека, который играет в крестики-нолики.
К сожалению, вы не можете ввести это изображение в компьютер, поэтому нам нужен
другой формат, слово _xo_x_o__ , которое содержит , содержимое из девяти квадратов на картинке, но без линий
разделяющие квадраты и без двухмерной формы.
Третий формат, предложение, довольно неудобно для человека существа.Вы бы никогда не захотели так думать о доске для крестиков-ноликов
вы сами, потому что это предложение не имеет визуальной простоты, которая позволяет
вы принимаете позу крестики-нолики с первого взгляда. Но приговор троек
это наиболее удобное представление для нашей программы. Ttt будет иметь
чтобы ответить на вопросы типа «может ли x выиграть на следующем ходу?» Для этого он
придется рассмотреть эквивалентный, но более подробный вопрос: «Для каждого
из восьми возможных выигрышных комбинаций может составить x комбинацию на следующем ходу? »На самом деле не имеет значения,
комбинация — это строка или столбец; что имеет значение, так это то, что каждый из восьми
комбинации должны быть легко доступны для проверки программой.В
представление троек скрывает часть доступного
информация (какая комбинация где), чтобы выделить другую часть (создание
восемь явных комбинаций, а не неявных в девяти полях
диаграмму).
Представление дробей в виде «смешанных чисел», например 2 1 / 3 , и как «неправильные дроби», например 7 / 3 , является непрограммируемым пример этой идеи о множественных представлениях.Смешанная цифра делает человеку легче определить, насколько велико число, но неправильный дробь упрощает арифметику.
В поисках троек
Мы сказали, что объединим текущую позицию на доске с номера квадратов в восьми потенциальных выигрышных комбинациях по порядку для вычисления того, что мы называем тройками. Это была наша первая задача в написание программы.
Наша программа начнется с этого предложения всех выигрышных комбинаций:
(123 456 789 147 258 369 159 357)
и слово позиции, такое как _xo_x_o__ ; он вернет
предложение троек, таких как
(1xo 4x6 o89 14o xx8 o69 1x9 oxo)
Все, что необходимо, — это заменить некоторые числа на x s и o с.Такой пословный перевод предложения — хорошая работа.
для каждые .
(определить (найти позицию троек) ;; первая версия (каждый заменитель-тройка '(123 456 789 147 258 369 159 357)))
Мы придумали имя -тройка-заменитель для процедуры, которой у нас нет
написано еще. Это совершенно нормально, если мы напишем это до того, как попытаемся
вызвать найти-троек . Функция замены-тройки примет
три цифры, например 258 , и возвращают тройку, например 2x8 :
(определить (комбинация замещающей тройки) ;; первая версия (каждая комбинация заменяющих букв))
Эта процедура использует каждые для вызова с замещающим письмом на
все три буквы.
Но есть небольшая проблема. Каждый всегда возвращает предложение, и
мы хотим, чтобы наша тройка была словом. Например, мы хотим превратить потенциал
выигрышная комбинация 258 в слово 2x8 , но каждые будет
верните предложение (2 x 8) . Итак, вот наша следующая версия замещающего тройного :
(определить (замещающая тройная комбинация) ;; вторая версия (накопить слово (каждую комбинацию заменяющих букв)))
Замещающая буква знает букву номер 3 слова, которая
обозначает, что доска соответствует содержимому квадрата 3 доски.Это означает, что он может просто позвонить элемент с заданным квадратным номером и
доска, чтобы узнать, что в этом квадрате. Если он пуст, мы возвращаем
само квадратное число; в противном случае мы возвращаем содержимое квадрата.
(определить (квадрат заменяющей буквы) ;; первая версия
(если (равно? '_ (позиция элемента в квадрате))
квадрат
(позиция элемента в квадрате)))
Ой! Ты видишь проблему?
> (заменяющая буква 5) ОШИБКА: переменная POSITION не связана.
Использование
каждые с двухаргументными процедурами Наша процедура принимает только один аргумент, квадрат , но ей нужно знать
положение, чтобы он мог узнать, что находится в данном квадрате. Итак, вот
реальный замещающая буква :
(определить (положение квадрата замещающей буквы)
(если (равно? '_ (позиция элемента в квадрате))
квадрат
(позиция элемента в квадрате)))
> (замещающая буква 5 '_xo_x_o__)
Икс
> (замещающая буква 8 '_xo_x_o__)
8
Теперь замещающая буква может выполнять свою работу, так как она имеет доступ к
позиция.Но нам придется изменить замещающий тройной , чтобы вызвать замещающая буква с двумя аргументами.
Это немного сложно. Давайте еще раз посмотрим, как мы используем замещающую букву внутри замещающую тройку :
(определить (комбинация замещающей тройки) ;; снова вторая версия (накопить слово (каждую комбинацию заменяющих букв)))
Придавая замещающую букву еще один аргумент, мы сделали
эта ранее правильная процедура неверна.Первый аргумент каждые должен быть функцией одного аргумента, а не двух. Это именно та
ситуация, в которой нам может помочь лямбда : у нас есть функция двух
аргументы, и нам нужна функция одного аргумента, которая делает то же самое,
но с одним из фиксированных аргументов.
Процедура, возвращаемая
(лямбда (квадрат) (квадратная позиция замещающей буквы))
делает именно то, что нужно; он принимает квадрат в качестве аргумента и возвращает содержимое позиции в этом квадрате.
Вот окончательная версия с заменой тройки :
(определить (замещающая-тройная комбинация) (накапливайте слово (каждые (лямбда (квадрат) (квадратная позиция замещающей буквы)) сочетание))) > (заменитель-тройка 456 '_xo_x_o__) «4X6» > (подставка-тройка 147 '_xo_x_o__) «14О» > (заменитель-тройка 357 '_xo_x_o__) OXO
Как видите, Scheme печатает некоторые из этих слов с двойные кавычки. Правило состоит в том, что слово, которое не является числом, а начинается с цифрой должны быть заключены в двойные кавычки.Но в готовой программе мы не собираюсь напечатать такие слова вообще; мы просто показываем вам работу вспомогательная процедура. Точно так же в этой главе мы покажем прямые вызовы вспомогательных процедур, в которых некоторые аргументы являются строками, но пользователю всей программы не нужно использовать это обозначение.
Мы исправили проблему с замещающей буквой , предоставив замещающую тройку дополнительным аргументом, поэтому нам придется пройти через
тот же процесс с находками-тройками .Вот правильная версия:
(определить (найти-тройное положение)
(каждые (лямбда (гребешок) (положение тройной гребенки-заменителя))
'(123 456 789 147 258 369 159 357)))
Это тот же трюк. Заместитель-тройка — процедура
из двух аргументов. Мы используем лямбда , чтобы преобразовать его в процедуру
одного аргумента для использования с каждые .
Мы завершили поисков-троек , одну из самых важных процедур в
игра.
> (найти троек '_xo_x_o__)
("1XO" "4X6" O89 "14O" XX8 O69 "1X9" OXO)
> (найти троек x_____oxo)
(X23 456 OXO X4O "25X" "36O" X5O "35O")
Здесь снова представлены задания всех трех процедур, которые мы написали до сих пор:
Замещающее письмо | находит букву в единственном квадрате. |
Заменитель тройной | находит все три буквы, соответствующие трем квадратам. |
Найти-троек | находит все буквы во всех восьми выигрышных комбинациях. |
Мы сделали все это, потому что думаем, что остальная часть программы может использовать тройки, которые мы вычислили как данные. Итак, мы просто вычислим тройки один раз для всех остальных процедур использовать:
(определить (ттт положение меня)
(ттт-выбери (найди-тройное положение) меня))
(определить (ttt-select меня утроит) ;; первая версия
(cond ((я-могу-выиграть? утроит меня)
(выбрать-выигрыш-ход меня утроит))
((противник может выиграть? утроит меня)
(блок-оппонент-победа утраивает меня))
…))
Может ли компьютер победить в этом шаге?
Очевидный следующий шаг — написать i-can-win? , процедура, которая должна
вернуть #t , если компьютер может выиграть на текущем ходу, то есть, если
в компьютере уже есть два квадрата из тройки, третий квадрат которых пуст.Тройки x6x и oo7 являются примерами.
Итак, нам нужна функция, которая принимает слово и букву в качестве аргументов.
и считает, сколько раз эта буква встречается в слове. В появлений примитивов, которые мы использовали в главе 2 (и
который вы повторно реализовали в упражнении 9.10) выполнит свою работу:
> (появление 'o' oo7) 2 > (появление 'x' oo7) 0
Компьютер «владеет» тройкой, если буква компьютера появляется дважды и
письмо оппонента вообще не появляется.(Второе условие
необходимо исключить такие случаи, как xxo .)
(определить (моя пара? Утроить меня)
(и (= (появляется тройное) 2)
(= (появления (соперник меня) тройной) 0)))
Обратите внимание, что нам нужна функция оппонент , которая возвращает противоположное
письмо от нашего.
(определить (письмо оппонента) (если (равно? буква 'x)' o 'x)) > (противник х) О > (противник о) Икс > (моя пара? 'oo7' o) #T > (моя пара? 'xo7' o) #F > (моя пара? 'oox' o) #F
Наконец, компьютер может выиграть, если он владеет любой из троек:
(определить (я могу выиграть? Утроит меня) ;; первая версия
(не пустой?
(держать (лямбда (тройной) (моя пара? утроить меня))
троек))))
> (я-могу-выиграть? '("1xo" "4x6" o89 "14o" xx8 o69 "1x9" oxo)' x)
#T
> (я-могу-выиграть? '("1xo" "4x6" o89 "14o" xx8 o69 "1x9" oxo)' o)
#F
К настоящему времени вы уже привыкли к этому трюку с лямбда . Моя пара? принимает в качестве аргументов тройку и букву компьютера, но мы
хотите, чтобы функция одного аргумента использовалась с , оставьте .
Если да, то в каком квадрате?
Допустим, я-могу-выиграть? возвращает #t . Затем мы должны найти
конкретный квадрат, который выиграет для нас игру. Это будет включать
повторение той же работы, которую мы уже сделали:
(определить (выбрать-выигрыш-ход меня утроит) ;; на самом деле не часть игры
(сохранить номер? (сначала (сохранить (лямбда (тройной) (моя пара? утроить меня))
троек))))
Мы снова используем Keep , чтобы найти тройки с двумя из
буквы компьютера, но на этот раз мы извлекаем число из первого такого
выигрышный тройной.
Хотелось бы избежать этой неэффективности. Как оказалось, поколения Lisp программисты в прошлом были связаны именно с этим, поэтому они изобрели kludge [1], чтобы обойти это.
Помните, мы говорили вам, что все, кроме #f , считается правдой?
Мы воспользуемся этим, имея единственную процедуру, которая возвращает
номер выигрышного квадрата, если он есть, или #f в противном случае. В
В главе 6 мы назвали такую процедуру «полупредикатом».»Клуджи
часть состоит в том, что cond принимает предложение, содержащее одно выражение
вместо обычных двух выражений; если выражение имеет какое-либо истинное значение,
тогда cond возвращает это значение. Итак, мы можем сказать
(определить (ттт-выбрать меня утроит) ;; вторая версия
(cond ((я могу выиграть? утроит меня))
((противник может выиграть? утроит меня))
…))
, где каждое предложение cond вызывает полупредикат. Мы тогда
модифицировать i-can-win? для желаемого поведения:
(определить (я могу выиграть? Утроит меня)
(выбрать-выиграть
(держать (лямбда (тройной) (моя пара? утроить меня))
троек)))
(определить (выбрать-выиграть-тройки)
(если (пусто? троек)
#f
(сохранить номер? (первые выигрыши-тройки))))
> (я-могу-выиграть? '("1xo" "4x6" o89 "14o" xx8 o69 "1x9" oxo)' x)
8
> (я-могу-выиграть? '("1xo" "4x6" o89 "14o" xx8 o69 "1x9" oxo)' o)
#F
К этому моменту мы начинаем видеть структуру всей программы.Будет несколько процедур, аналогичных i-can-win? , вот попробую
выбрать следующий ход. Я могу выиграть? проверяет, может ли компьютер
win на этом ходу другая процедура проверит, должен ли компьютер
заблокировать победу противника на следующем ходу, и другие процедуры будут проверять
другие возможности. Каждая из этих процедур будет тем, чем мы были
называя «полупредикатами». То есть каждый вернет количество
квадрат, куда компьютер должен двигаться дальше, или #f , если он не может
решать.Осталось только разобраться в остальной части компьютера.
стратегии и напишите больше процедур, таких как i-can-win? .
Второй стих, такой же, как и первый
Теперь пришло время рассмотреть второй вариант стратегии: компьютер не может выиграть на этом ходу, но противник может выиграть, если мы не заблокируем тройной прямо сейчас.
(Что, если и у компьютера, и у оппонента сразу же есть тройные выигрыши? В этом случае мы уже заметили выигрыш компьютера, и, выиграв В игре мы избегаем думать о блокировке соперника.)
И снова нам предстоит пройти непростой бизнес по поиску троек, в которых есть две буквы оппонента и ни одна из букв компьютера письмо — но это уже сделано!
(определите (оппонент может выиграть? Утроит меня)
(я могу выиграть? тройки (соперник меня)))
> (оппонент может победить? '("1xo" "4x6" o89 "14o" xx8 o69 "1x9" oxo)' x)
#F
> (противник может победить? '("1xo" "4x6" o89 "14o" xx8 o69 "1x9" oxo)' o)
8
Это что, удивительно?
Теперь стратегия усложняется
Поскольку наша цель — научить программированию, а не крестики-нолики стратегии, мы просто объясним используемую нами стратегию и не будем история того, как мы его разработали.
Третий шаг, после того, как мы проверим, может ли любой из игроков выиграть на следующем этапе. двигаться, — это искать ситуацию, в которой движение, которое мы делаем сейчас, даст в следующий раз поднимитесь до на две выигрышные тройки . Вот пример:
Ни x , ни o не могут выиграть на этом ходу. Но если компьютер
при игре x перемещение в клетку 4 или 7 приведет к ситуации
с двумя выигрышными тройками. Например, вот что произойдет, если мы переедем в
квадрат 7:
Из этой позиции x может выиграть, переместив любой квадрат
3 или в квадрате 4.Сейчас ход o , но o может заблокировать только один из
эти две возможности. Напротив, если (в более ранней позиции) x ходов в квадрате 3 или поле 6, что создаст единственную выигрышную тройку для
в следующий раз, но o может заблокировать его.
Другими словами, мы хотим найти две троек, в которых один квадрат равен
взяты компьютером, а два других свободны, с одним свободным квадратом
поделены между двумя тройками. (В этом примере мы можем найти два
троек x47 и 3x7 ; что привело бы нас к перемещению в квадрате 7,
тот, что есть у этих троек.) Назовем такую ситуацию
«вилка», и мы будем называть общий квадрат «осью». Этот
нестандартная терминология; мы придумали эти условия, чтобы упростить
поговорим о стратегии.
Для того, чтобы написать процедуру стратегии i-can-fork? мы предполагаем, что
нам понадобится процедура pivots , которая возвращает предложение всех точек поворота
вилки в настоящее время доступны для компьютера. На этой доске 4 и 7 — это
pivots, поэтому процедура pivots вернет предложение (4 7) .Если предположить, что опорных точек , то напишем i-can-fork? это
простой:
(определить (я-могу-форк? Утроит меня)
(первый-если-есть (меняет втрое)))
(определить (первым отправлено)
(если (пусто? отправлено)
#f
(отправлено первым)))
В поисках точек поворота
Pivots должен возвратить предложение, содержащее номера поворота. Вот
план. Начнем с троек:
(xo3 4x6 78o x47 ox8 36o xxo 3x7)
Мы сохраняем тех, у которых есть x и два числа:
(4x6 x47 3x7)
Мы объединяем их в одно огромное слово:
4x6x473x7
Мы сортируем цифры этого слова в девять «ведер», по одной для каждая цифра:
("" "" 3 44 "" 6 77 "" "")
Мы видим, что нет ни единиц, ни двоек, ни одной тройки, двух четверок и скоро.Теперь мы легко можем видеть, что четыре и семь являются поворотными квадратами.
Давайте напишем процедуры для выполнения этого плана. Pivots должен найти
все тройки с одним квадратом, принадлежащим компьютеру, и двумя свободными квадратами, и
затем он должен извлечь квадратные числа, которые встречаются более чем в одном
тройной.
(определить (меняет втрое)
(повторяющиеся числа (сохранить (лямбда (тройной) (мой-одиночный? утроить меня))
троек)))
(определить (мой-одиночный? утроить меня)
(и (= (появляется тройное) 1)
(= (появления (соперник меня) тройной) 0)))
> (мой-сингл? "4x6" 'x)
#T
> (мой-сингл? 'xo3' x)
#F
> (сохранить (лямбда (тройной) (мой-одиночный? тройной 'x))
(найти троек xo__x___o))
("4X6" X47 "3X7")
Мой-сингл? это как моя пара? за исключением того, что выглядит
за одно появление буквы вместо двух.
Repeated-numbers принимает предложение троек в качестве аргумента и имеет
чтобы вернуть предложение всех чисел, которые встречаются более чем в одном
тройной.
(определить (повторные номера отправлены)
(каждый первый
(сохранить (лямбда (wd) (> = (count wd) 2))
(sort-digits (накопить отправленное слово)))))
Мы собираемся прочитать эту процедуру наизнанку, начиная с накапливают и работают наружу.
Почему можно накапливать слово в предложении? Предположим, что число
появляется в двух троек.Все, что нам нужно знать, это это число, а не
конкретные тройки, через которые мы его нашли. Поэтому вместо того, чтобы писать
программа для просмотра нескольких троек по отдельности, с тем же успехом мы можем
объединить тройки в одно длинное слово, оставить только цифры этого слова,
и просто ищите те, которые появляются более одного раза.
> (накопить слово '("4x6" x47 "3x7"))
«4X6X473X7»
Теперь у нас есть одно длинное слово, и мы ищем повторяющиеся цифры. С это сложная проблема, давайте начнем с подзадачи поиска всех копии определенной цифры.
(определить (извлечь цифру желаемую цифру wd) (сохранить (лямбда (вд-цифра) (равно? вд-цифра желаемая-цифра)) вд)) > (извлеките цифру 7 "4x6x473x7") 77 > (извлеките цифру 2 "4x6x473x7") ""
Теперь нам нужно предложение, в котором первое слово — это все 1 s, второе
word — это все 2 s и т. д. Мы могли бы сделать это так:
(se (извлечение цифры 1 "4x6x473x7")
(извлечение цифры 2 "4x6x473x7")
(извлечение цифры 3 "4x6x473x7")
…)
, но это не означает использование мощности компьютеров для
делать такую повторяющуюся работу за нас.Вместо этого мы будем использовать каждые :
(определить (сортировка цифр число-слово) (каждые (лямбда (цифра) (извлечение-цифра-цифра-слово)) '(1 2 3 4 5 6 7 8 9)))
Sort-digits берет слово, полное чисел, и возвращает предложение,
первое слово — все единицы, второе слово — все двойки и т. д. [2]
> (сортировка цифр 12345678
583657) (111 22 333 44 5555 66 777 88 999) > (сортировка цифр "4x6x473x7") ("" "" 3 44 "" 6 77 "" "")
Давайте еще раз посмотрим на повторяющихся номеров :
(определить (повторные номера отправлены)
(каждый первый
(сохранить (лямбда (wd) (> = (count wd) 2))
(sort-digits (накопить отправленное слово)))))
> (повторяющиеся числа '("4x6" x47 "3x7"))
(4 7)
> (сохранить (лямбда (wd) (> = (count wd) 2))
'("" "" 3 44 "" 6 77 "" ""))
(44 77)
> (каждый первый '(44 77))
(4 7)
На этом мы завершаем объяснение точек поворота .Помните тот i-can-fork? выбирает первую точку поворота, если таковая имеется, в качестве хода компьютера.
В наступление
Вот окончательная версия ttt-choose со всеми показанными пунктами:
(определить (ттт-выбрать меня утроит)
(cond ((я могу выиграть? утроит меня))
((противник может выиграть? утроит меня))
((я-могу-вилка? утроит меня))
((я могу продвинуться? утроит меня))
(else (тройки с лучшими свободными квадратами))))
Вы уже знаете о первых трех возможностях.
Так же, как вторая возможность была "зеркальным отображением" первой (блокируя ход противника того же типа, что и компьютер), Было бы разумно, если бы четвертая возможность заблокировала создание вилки противником. Это было бы легко сделать:
(определить (оппонент-может-форк? Утроить меня) ;; на самом деле не часть игры (я-могу-форк? тройки (против меня)))
К сожалению, хотя программирование работает, стратегия - нет. Может быть у соперника две потенциальных вилки ; мы можем заблокировать только один из их.(Почему это не вызывает беспокойства при блокировании побед соперника? - это , но если мы позволили ситуации достичь точки, где есть два способа, которыми оппонент может выиграть следующим ходом, слишком поздно делать что-нибудь с этим.)
Вместо этого наша стратегия - перейти в наступление. Если мы получим два подряд на этом ходу, то на следующем ходу наш противник будет вынужден блокировать, вместо того, чтобы делать вилку. Однако мы хотим убедиться, что не случайно втолкнуть противника в , сделав вилку.
Давайте еще раз посмотрим на эту позицию платы, но с точки зрения o :
X точки поворота - 4 и 7, как мы обсуждали ранее; или не мог взять оба эти квадрата. Вместо этого посмотрите на тройки 369 и 789 , оба из которых являются одиночными и принадлежат к или . Так или должен двигаться в одном из квадратов 3, 6, 7 или 8, заставляя x блокировать
вместо настройки вилки.Но o не должно двигаться в квадрате
8, вот так:
, потому что это заставит x заблокироваться в квадрате 7, настроив
вилка!
Структура алгоритма очень похожа на структуру другой стратегии.
возможности. Мы используем , сохраняем , чтобы найти подходящие тройки, берем
сначала такую тройку, если она есть, а затем решите, какой из двух пустых квадратов в
эта тройка, чтобы переехать.
(определите (я могу продвинуться? Утроит меня)
(лучший ход (сохранить (лямбда (тройной) (мой-одиночный? тройной меня)) тройной)
тройки
мне))
(определите (лучший ход - мои тройки, все тройки меня)
(если (пусто? мои тройки)
#f
(лучшие квадраты (первые мои тройки) все тройки меня)))
Best-move выполняет ту же работу, что и first-if-any , что мы
видел ранее, за исключением того, что он также вызывает наилучшего квадрата на первом
тройной, если он есть.
Поскольку мы уже выбрали соответствующие тройки, прежде чем перейти к , лучший ход , вам может быть интересно, зачем ему все тройки в качестве
дополнительный аргумент. Ответ заключается в том, что с наилучшим квадратом будет выглядеть
в позиции на доске с точки зрения соперника искать вилки.
(определить (лучший квадрат моя тройка меня утроит)
(лучший квадрат-помощник (поворачивает троек (оппонент мне))
(держать номер? мой-тройной)))
(определите (пара оппонент-оппонент, лучший помощник)
(если (член? (первая пара) оппонент-разворачивается)
(первая пара)
(последняя пара)))
Мы сохраняем два числа тройки, которые мы уже выбрали.Мы
также выберите возможные опоры соперника из всех троек. Если
один из двух возможных ходов - это потенциальный поворот для противника, это
тот, в который мы должны войти, чтобы заблокировать вилку. В противном случае мы произвольно
выберите второй ( последних ) свободный квадрат.
> (лучший квадрат "78o" (найти-тройки 'xo__x___o)' o)
7
> (лучший квадрат "36o" (найти-тройки 'xo__x___o)' o)
6
> (лучший ход '("78o" "36o") (найти-тройки' xo__x___o) 'o)
7
> (я-могу-продвинуться? (найти-тройки 'xo__x___o)' o)
7
Что делать, если и квадратов кандидатов являются опорными точками оппонента? В этом случае мы выбрали плохую тройку; перемещение в любой из квадратов сделает мы проиграем.Оказывается, это может произойти только в такой ситуации, как следующий:
Если мы выберем тройку 3o7 , то любое движение вызовет
оппоненту поставить вилку, так что мы проиграем двумя ходами позже. К счастью,
однако вместо этого мы можем выбрать тройку, например 2o8 . Мы можем въехать
любой из этих квадратов, и игра закончится ничьей.
В принципе, мы должны проанализировать тройку кандидатов, чтобы увидеть, свободны ли обе
квадраты создают вилки для противника.Но поскольку мы знаем, что
такая ситуация возникает только по диагоналям, можно полениться. Мы просто перечисляем
диагонали последние в процедуре находят-троек . С тех пор, как мы
возьмите первую доступную тройку, это гарантирует, что мы не будем брать диагональ
если есть другие варианты. [3]
Остатки
Если ничего не помогает, мы просто выбираем квадрат. Однако некоторые квадраты лучше чем другие. Центральный квадрат является частью четырех троек, угловые квадраты каждая является частью трех, а каждый край квадратов равен двум.
Итак, мы выбираем центр, если он свободный, затем угол, затем край.
(определить (тройки с лучшими свободными квадратами) (по первому выбору (накапливаются тройки слов) '(5 1 3 7 9 2 4 6 8))) (определить (предпочтения вариантов первого выбора) (сначала (сохранить (лямбда (квадрат) (возможности члена? квадрата)) предпочтения))) > (первый выбор 12345678
583657 '(5 1 3 7 9 2 4 6 8)) 5 > (первый выбор "1xo4x6o8914oxx8o691x9oxo" '(5 1 3 7 9 2 4 6 8)) 1 > (лучший-свободный квадрат (найти-тройки '_________)) 5 > (лучший-свободный квадрат (найти-тройки '____x____)) 1
Полный листинг программы
;;; ттт.scm
;;; Программа крестики-нолики
(определите (положение меня)
(ттт-выбери (найди-тройное положение) меня))
(определить (найти-тройное положение)
(каждые (лямбда (гребешок) (положение тройной гребенки-заменителя))
'(123 456 789 147 258 369 159 357)))
(определить (позиция комбинации замещающих-тройных))
(накапливайте слово
(каждые (лямбда (квадрат)
(квадратная позиция замещающей буквы))
сочетание)))
(определить (положение квадрата замещающей буквы)
(если (равно? '_ (позиция элемента в квадрате))
квадрат
(позиция элемента в квадрате)))
(определить (ttt-select меня утроит)
(cond ((я могу выиграть? утроит меня))
((противник может выиграть? утроит меня))
((я-могу-вилка? утроит меня))
((я могу продвинуться? утроит меня))
(else (тройки с лучшими свободными квадратами))))
(определить (я могу выиграть? утроит меня)
(выбрать-выиграть
(держать (лямбда (тройной) (моя пара? утроить меня))
троек)))
(определить (моя пара? утроить меня)
(и (= (появляется тройное) 2)
(= (появления (соперник меня) тройной) 0)))
(определить (письмо оппонента)
(если (равно? буква 'x)' o 'x))
(определить (выбрать-выиграть-тройки)
(если (пусто? троек)
#f
(сохранить номер? (первые выигрыши-тройки))))
(определите (оппонент может выиграть? утроит меня)
(я могу выиграть? тройки (соперник меня)))
(определить (я-могу-вилка? утроит меня)
(первый-если-есть (меняет втрое)))
(определить (первым отправлено)
(если (пусто? отправлено)
#f
(отправлено первым)))
(определить (повороты меня втрое)
(повторяющиеся числа (сохранить (лямбда (тройной) (мой-одиночный? утроить меня))
троек)))
(определить (мой-одиночный? утроить меня)
(и (= (появляется тройное) 1)
(= (появления (соперник меня) тройной) 0)))
(определить (отправленные повторяющиеся номера)
(каждый первый
(сохранить (лямбда (wd) (> = (count wd) 2))
(sort-digits (накопить отправленное слово)))))
(определить (сортировка цифр число-слово)
(каждые (лямбда (цифра) (извлечение-цифра-цифра-слово))
'(1 2 3 4 5 6 7 8 9)))
(определить (извлечь цифру желаемую цифру wd)
(сохранить (лямбда (вд-цифра) (равно? вд-цифра желаемая-цифра)) вд))
(определить (я могу продвинуться? утроит меня)
(лучший ход (сохранить (лямбда (тройной) (мой-одиночный? тройной меня)) тройной)
тройки
мне))
(определите (лучший ход - мои тройки, все тройки меня)
(если (пусто? мои тройки)
#f
(лучшие квадраты (первые мои тройки) все тройки меня)))
(определите (моя тройка с лучшим квадратом меня утроит)
(лучший квадрат-помощник (поворачивает троек (оппонент мне))
(держать номер? мой-тройной)))
(определите (пара оппонент-оппонент, лучший помощник)
(если (член? (первая пара) оппонент-разворачивается)
(первая пара)
(последняя пара)))
(определить (тройки с лучшими свободными квадратами)
(по первому выбору (накапливаются тройки слов)
'(5 1 3 7 9 2 4 6 8)))
(определить (предпочтения вариантов первого выбора)
(сначала (сохранить (лямбда (квадрат) (возможности члена? квадрата))
предпочтения)))
Упражнения
10.1 Процедура ttt предполагает, что никто не выиграл игру
пока что. Что произойдет, если вы вызовете ttt с позицией платы, в которой
какой-то игрок уже выиграл? Попытайтесь понять это, просмотрев
программу, прежде чем запускать ее.
Полная программа крестиков-ноликов должна быть остановлена, когда один из двух
игроки выигрывают. Напишите предикат , который уже выиграл? , который требует
позиция доски и буква ( x или o ) в качестве аргументов и возвращаемых значений #t , если этот игрок уже выиграл.
10.2 Программа также не замечает, когда игра закончилась вничью, то есть, когда все девять квадратов уже заполнены. Что будет теперь, если вы попросите двигаться в этой ситуации?
Напишите процедуру галстук-игра? , который в данном случае возвращает #t .
10,3 Настоящий человек, играющий в крестики-нолики, будет смотреть на доску так:
и обратите внимание, что это ничья, а не движение в квадрате 9 .Модифицируйте галстук-игру? из упражнения 10.2, чтобы обратить внимание на эту ситуацию и
возврат # t .
(Можете ли вы еще больше улучшить способность программы распознавать связи? А доски с двумя свободными квадратами?)
10,4 Вот некоторые возможные изменения правил игры в крестики-нолики:
| • | Что, если бы вы могли выиграть игру, имея три квадрата, образующие L-образную форму в углу, например как квадраты 1, 2 и 4? |
|---|
| • | Что, если диагонали не выиграли? |
|---|
| • | Что, если бы вы могли выиграть, имея четыре квадраты в углу, например 1, 2, 4 и 5? |
|---|
Ответьте на следующие вопросы по каждой из этих модификаций отдельно:
Что произойдет, если мы попытаемся реализовать изменение, просто изменив
процитированное предложение потенциальных выигрышных комбинаций в находках-троек ?
Будет ли программа успешно следовать измененным правилам?
10.5 Измените ttt , чтобы играть в шахматы.
[1] Кладж - это программный трюк, который не следует норм но работает все равно как-то. Это не рифмуется со словом «ил»; это больше похоже на «подсказку», за которой следует «j», как в «Джим».
[2] Брайан думает, что это кладж, но Мэтт думает, что это гениально и элегантно.
[3] Мэтт считает, что это kludge, но Брайан считает его блестящим и элегантным.
(вернуться к содержанию)
НАЗАД резьба главы СЛЕДУЮЩАЯ
Брайан Харви, bh @ cs.berkeley.edu .

 Сколько оно содержало символов, если
алфавит племени состоит из 32 символов.
Сколько оно содержало символов, если
алфавит племени состоит из 32 символов.
 При этом все цифры
кодируются одним и тем же (минимально
возможным) количеством бит. Определите
информационный объем сообщения длиной
в 150 символов.
При этом все цифры
кодируются одним и тем же (минимально
возможным) количеством бит. Определите
информационный объем сообщения длиной
в 150 символов.
 После этого
загорелся зеленый. Какое количество
информации вы при этом получили?
После этого
загорелся зеленый. Какое количество
информации вы при этом получили?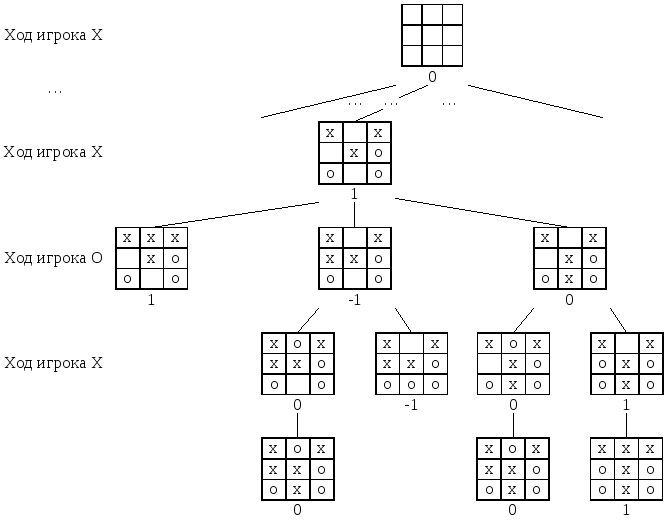 Вождь племени
говорит со скоростью 20 символов в
минуту. Какова в этом случае скорость
информационного потока?
Вождь племени
говорит со скоростью 20 символов в
минуту. Какова в этом случае скорость
информационного потока? Электронное устройство управления
светофором последовательно воспроизводит
записанные сигналы. Подряд записано
50 сигналов светофора. В байтах данный
информационный объем составляет
Электронное устройство управления
светофором последовательно воспроизводит
записанные сигналы. Подряд записано
50 сигналов светофора. В байтах данный
информационный объем составляет Каждая лампочка может
находиться в одном из трех состояний
(«включено», «выключено» или «мигает»).
Какое наименьшее количество лампочек
должно находиться на табло, чтобы с его
помощью можно было передать 18 различных
сигналов?
Каждая лампочка может
находиться в одном из трех состояний
(«включено», «выключено» или «мигает»).
Какое наименьшее количество лампочек
должно находиться на табло, чтобы с его
помощью можно было передать 18 различных
сигналов? Определить, сколько студентов с
именем Денис находилось в аудитории.
Определить, сколько студентов с
именем Денис находилось в аудитории.

 Среди игр,
которые изучаются математически и используются в различных
математических моделях реальности, занимают важное место игры, в
которых присутствует элемент случайности, например, бросается кость. В
других играх игрокам неизвестна (или не полностью известна) позиция,
создавшаяся в игре (в том числе и начальная позиция).
Среди игр,
которые изучаются математически и используются в различных
математических моделях реальности, занимают важное место игры, в
которых присутствует элемент случайности, например, бросается кость. В
других играх игрокам неизвестна (или не полностью известна) позиция,
создавшаяся в игре (в том числе и начальная позиция). 
 С этими детьми
можно обсудить такую задачу: научить другого человека, а потом даже и
компьютер играть в Крестики-нолики. Это поможет им понять смысл
происходящего.
С этими детьми
можно обсудить такую задачу: научить другого человека, а потом даже и
компьютер играть в Крестики-нолики. Это поможет им понять смысл
происходящего.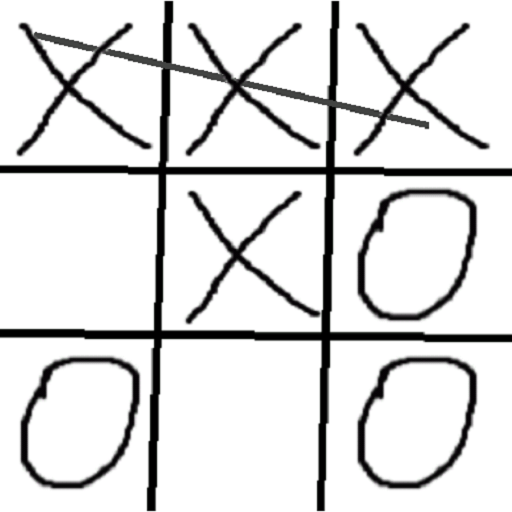 Хотя формально в данной игре у Крестиков нет преимущества
(игру всегда можно свести к ничьей), однако опыт показывает ребятам,
что Крестики выигрывают несколько чаще.
Хотя формально в данной игре у Крестиков нет преимущества
(игру всегда можно свести к ничьей), однако опыт показывает ребятам,
что Крестики выигрывают несколько чаще. 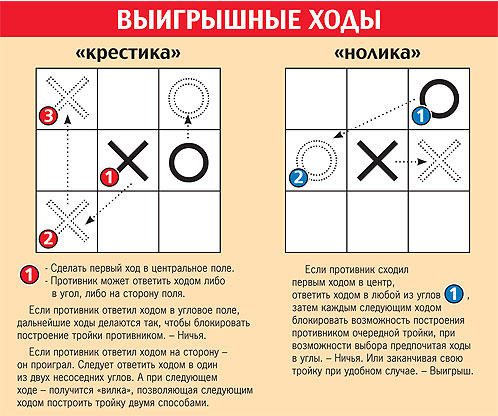 Например, можно в углу пустой клетки
игрока, который играл крестиками, поставить маленький крестик или
пометить очки Первого цветом. После того как сыграны все 5 партий,
учащиеся суммируют очки в каждом столбце. Заканчивается решение задачи
ответами на вопросы. Возможно, при ответе на второй вопрос учащиеся
заметят, что Крестики выигрывали чаще. Ответом на последний вопрос
будет фамилия учащегося, набравшего больше очков, или слово «ничья»,
если очков у игроков поровну. Проследите за тем, чтобы по окончании
решения задачи у каждого учащегося из пары была заполнена своя таблица,
а не одна на двоих.
Например, можно в углу пустой клетки
игрока, который играл крестиками, поставить маленький крестик или
пометить очки Первого цветом. После того как сыграны все 5 партий,
учащиеся суммируют очки в каждом столбце. Заканчивается решение задачи
ответами на вопросы. Возможно, при ответе на второй вопрос учащиеся
заметят, что Крестики выигрывали чаще. Ответом на последний вопрос
будет фамилия учащегося, набравшего больше очков, или слово «ничья»,
если очков у игроков поровну. Проследите за тем, чтобы по окончании
решения задачи у каждого учащегося из пары была заполнена своя таблица,
а не одна на двоих. 



 По доске однозначно считается, кто ходит следующий. Во все возможные доски, в которые можно походить, в графе стоит ребро. Игра ациклическая — после каждого хода заполняется езе одна клетка.
По доске однозначно считается, кто ходит следующий. Во все возможные доски, в которые можно походить, в графе стоит ребро. Игра ациклическая — после каждого хода заполняется езе одна клетка. При всем огромном числе возможных досок шахматы — игра конечная. Досок конечное число, и на каждой можно побывать не более 6 раз (3 раза с ходом белым, 3 раза с ходом черных), это все еще конечное число. А значит, в шахматах точно существует либо выигрышная стратегия для белых, либо для черных, либо ничейная у обоих.
При всем огромном числе возможных досок шахматы — игра конечная. Досок конечное число, и на каждой можно побывать не более 6 раз (3 раза с ходом белым, 3 раза с ходом черных), это все еще конечное число. А значит, в шахматах точно существует либо выигрышная стратегия для белых, либо для черных, либо ничейная у обоих.
Leave A Comment