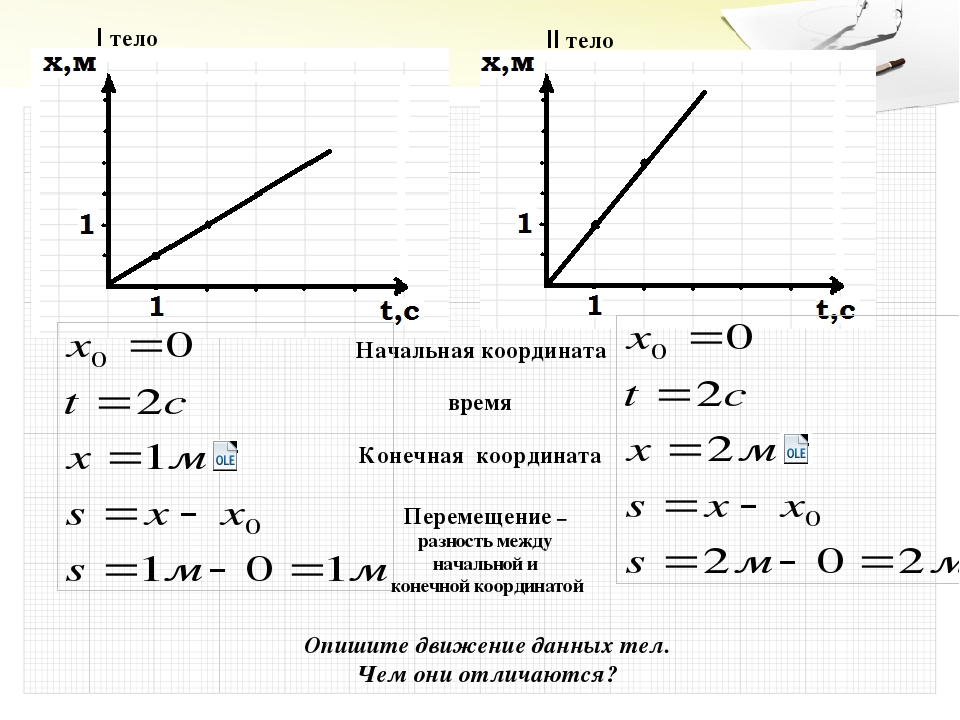
Физика как найти x0: Ошибка: 404 Материал не найден

Формула скорости в физике

Содержание:

Определение и формула скорости

Определение

Мгновенной скоростью (или чаще просто скоростью) материальной точки называется физическая величина равная первой производной от радиус–вектора $\bar{r}$ точки по времени (t). Обозначают скорость обычно буквой v. Это векторная величина. Математически определение вектора мгновенной скорости записывается как:

$$\bar{v}=\frac{d \bar{r}}{d t}=\dot{\bar{r}}(1)$$

Скорость имеет направление указывающее направление движения материальной точки и лежит на касательной к траектории ее движения. Модуль скорости можно определить как первую производную от длины пути (s) по времени:

$$v=\frac{d s}{d t}=\dot{s}(2)$$

Скорость характеризует быстроту перемещения в направлении движения точки по отношениюк рассматриваемой системе координат.

Скорость в разных системах координат

Проекции скорости на оси декартовой системы координат запишутся как:

$$v_{x}=\dot{x} ; v_{y}=\dot{y} ; v_{z}=\dot{z}(3)$$

Следовательно, вектор скоростив декартовых координатах можно представить:

$$\bar{v}=\dot{x} \bar{i}+\dot{y} \bar{j}+\dot{z} \bar{k}(4)$$

где $\bar{i}, \bar{j}, \bar{k}$ единичные орты.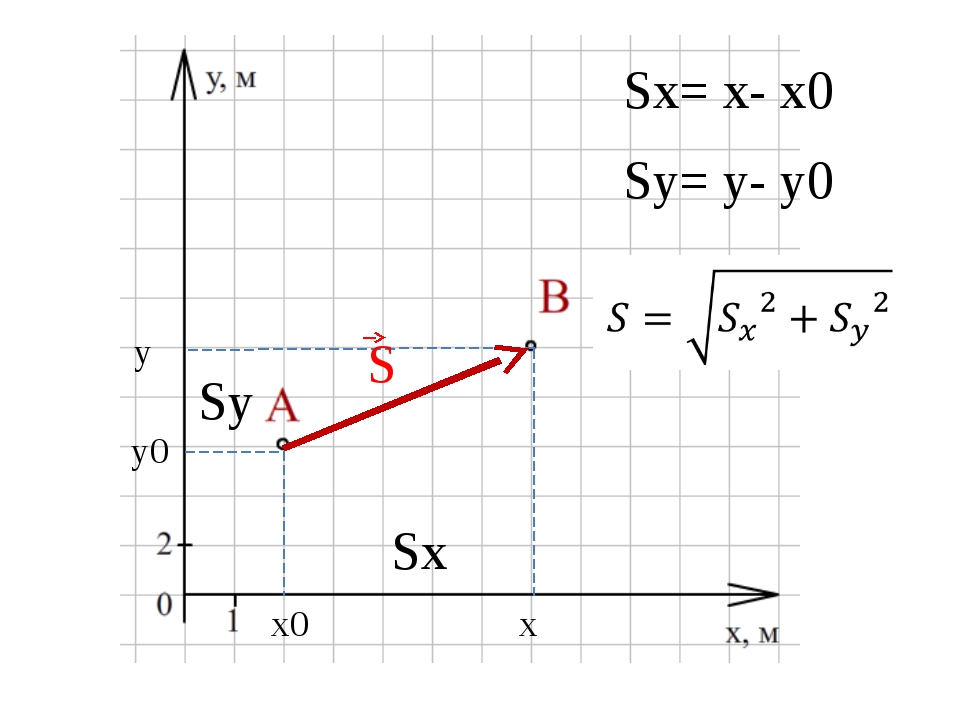 {2}=-10(2.3)$$

При решении уравнения (2.3) нам подойдет корень равный:

$$t_{3}=5+6=11 (c)$$

Ответ. 1) $x=0 \mathrm{~m}$ 2) $t_{1}=8,8 \mathrm{c}, t_{2}=1,13 c, t_{3}=11 c$

Читать дальше: Формула средней скорости.

Теория к заданию 1 из ЕГЭ по физике

Архитектор, инженер, программист, технолог — это далеко не полный список специальностей, для которых нужно сдавать экзамен по физике. Задание 1 из ЕГЭ по этому предмету кажется школьникам простым, однако для его решения нужно выучить большой блок теории. Все задачи из первого номера относятся к теме «Движение». Выпускник должен разбираться в

видах движения, уметь анализировать графики и знать принцип относительности. Если вы понимаете эту тему и хотите освежить знания перед ЕГЭ, наша статья напомнит вам основные формулы и правила.

Также стоит обратить внимание на курсы подготовки к ЕГЭ: там преподаватель объяснит все подробно, с нуля. А чтобы быть уверенным в высоких баллах, можно выбрать комплексную программу, включающую также занятия по русскому языку и профильной математике.

Кинематика

Путь, траектория, перемещение — понятия, без знания которых не решить задание 1 на ЕГЭ по физике. Подготовка должна начинаться с теории. Когда вы будете хорошо ориентироваться в ней, можно переходить к практике. Наука кинематика, о которой идет речь в первом вопросе, изучает механическое движение тел без описания причин этого движения. А механическим движением называют изменение взаимного расположения тел или их частей в пространстве с течением времени. Для его изучения пользуются системами отсчета. В кинематике это

система координат (X, Y, Z), тело отсчета (тело, относительно которого двигаются другие тела) и часы для измерения времени. Форма тел значения не имеет, поэтому в задачах их обозначают материальными точками — объектами, у которых есть масса, а размеры пренебрежимо малые.

Не каждое тело может считаться материальной точкой, главное правило — расстояние, которое оно проходит, должно быть намного больше размера. Если мы исследуем скорость самолета на пути из одного города в другой, он является материальной точкой. Если мы определяем сопротивление воздуха в момент полета, нам важна форма, и представить самолет точкой уже нельзя.

Если материальная точка перемещается в пространстве, у нее есть траектория — это условная линия, описывающая движение. Форма траектории зависит от выбранной системы отсчета, в задачах ЕГЭ траектории обычно рассматривают относительно Земли. Если мы свяжем траекторию с часами, то получим путь — то, что прошло тело за определенный временной промежуток. Путь, как и траектория, может иметь любую форму, но у него есть начальная и конечная точка. Соединив их прямой линией, мы нарисуем вектор перемещения. Он не может быть больше пути, а

иногда вовсе равняется нулю (в том случае, когда тело двигалось по замкнутой линии).

Теория к заданию 1 из ЕГЭ по физике не будет полной без описания принципа относительности движения. Для этого представим, что мы сидим в поезде и видим еще один на соседнем пути. Сначала наш поезд стоит неподвижно, а потом трогается. Если посмотреть на ситуацию относительно Земли, мы двигаемся: были на станции, а теперь отъехали от нее. Относительно самого поезда мы стоим на месте — как сидели у окна, так и сидим. А если взглянуть на соседний состав? Он постепенно удаляется от нас. Несмотря на то, что он по-прежнему стоит на станции, нам кажется, что он перемещается.
Вывод: движение зависит от того, в какой системе координат его изучают.

Виды движения

От теории мы переходим к решению задач. Чаще всего в них фигурируют два понятия: скорость и ускорение. Скорость — это быстрота и направление перемещения. Средняя скорость перемещения находится по формуле u = s / t, средняя путевая — u = l / t. Здесь u — скорость, l — путь, s — перемещение. Первая величина будет векторной, вторая — скалярной. Существует также мгновенная скорость, то есть скорость в определенной точке. Ее можно найти по графику или из уравнения

u = u0 + at. a — ускорение, то есть изменение скорости за единицу времени. Это векторная величина, она рассчитывается следующим образом: a = u / t. При ускоренном движении она направлена так же, как и скорость, при замедленном — противоположно ей. В случае с движением по окружности эти величины перпендикулярны. Перечислим несколько формул для задания 1 ЕГЭ по физике, связанных с видами движения:

равномерное прямолинейное:

x = x0 + ut (x — координата точки в данный момент времени).
s = ut.

u = const.
a = 0.

прямолинейное равноускоренное:

x = x0 + u0t + аt2 / 2.
s = u0t + аt2 / 2.
u= uox+ at.
a = const.

движение по окружности (u = const):

T = t / N = 1 / v — период.
v = N / t = 1 / T — частота.
u = l / t = 2πR / T = 2πRv — линейная скорость.
ω = ϕ / t = 2π / T = 2πv — угловая скорость.
a = u2 / R = ω2R = ωu — ускорение.

движение по параболе с ускорением свободного падения:

x = xo + uoxt + gt2 / 2.
y = yo + uoyt +gt2 / 2.
ux= uox+ gt.
uy= uoy+ gt.
uоx = u0 cosα.
uоy = u0 sinα.

Частные случаи равноускоренного движения под действием силы тяжести

В рамках теории к заданию 1 ЕГЭ по физике нужно знать два частных случая:

движение по вертикали:

при u0 = 0 высота h = gt2 / 2 и u = gt.
при u0↑ и движении вверх h = u0t — gt2 / 2 и u = u0 – gt.
при u0↑ и движении вниз h = -u0t + gt2 / 2 и u = -u0 + gt.
при υ0↓ h = u0t + gt2 / 2 и υ = υ0 + gt.

движение тела, брошенного горизонтально:

h = gt2 / 2 — высота полета.
s = uоt — дальность полета.
υy= gt — скорость относительно оси OY.

Дополнительная информация для частных случаев решения задач

Еще несколько формул для задания 1 ЕГЭ по физике:

модуль вектора: S=sx2+sy2.
средняя скорость: uср = (s1 + s2 + … + sn ) / (t1 + t2 + … + tn) = 2u1u2 / (u1 + u2).
площадь фигуры равна пройденному пути: S = S1 — S2.
физический смысл производной: ux = x΄ и uy = y΄, ах = u΄x = x΄΄ и аy = u΄y = y΄΄.
движение колеса без проскальзывания: uпост = uвращ и u = uпост + uвращ.

Пример решения задач

Задача 1: Велосипедисты движутся по уравнениям x1 = 3t и x2 = 12 — t. Найти координату их встречи.

Решение: В момент встречи велосипедистов их координаты совпадут: x1 = x2, следовательно, 3t = 12 — t. Решив уравнение, найдем, что t = 3 с. Чтобы найти координату, подставим значение в любое из уравнений (для самопроверки лучше подставить в оба): x1 = 3 • 3 = 9.

Ответ: 9.

Задача 2: Первую половину пути супермен пролетел со скоростью 30 км/ч, вторую — со скоростью 50 км/ч. Найти среднюю скорость супермена.

Решение: Нам известны две скорости: u1 и u2, поэтому мы можем воспользоваться формулой uср = 2u1u2 / u1 + u2 = 2 • 30 • 50 / (30 + 50) = 37,5 км/ч.

Ответ: 37,5.

Теперь вы знаете больше теории для ЕГЭ по физике в 2020 году. Задание 1 только кажется очень простым, в нем бывают нетипичные задачи, поэтому стоит уделить внимание его разбору. Грамотно подготовиться к ЕГЭ вам помогут курсы ЦМДО «Уникум» . На них вы разберете каждую тему из экзамена, переходя от простого к сложному. Много времени преподаватели уделяют решению задач, объяснению сложных моментов. Но независимо от того, какой способ подготовки вы выберете, мы желаем вам удачи, высоких баллов и поступления в вуз мечты.

Физика Срочно нужна помощь!!! Надо найти величины: X0=? U0=? a=? Уравнение скорости-

35 баллов физика пожалуйста

Умоляю помогите с физикой

Физика 35 баллов помогите пожалуйста

Найти массу всех тел из 1 варианта (1 задание (1,2,3 дослід) и 2 задание(порожня пляшечка та пляшечка з водою), пожалуйста срочно помогите))

1. Как передают давление жидкости и газы? 2. Пользуясь рисунком 99, объясните, почему жидкости и газы передают давление во все сто роны без изменений. … 3. На каком опыте можно показать особенность передачи давления жидкостями и газами? 4. При изготовлении бу тылок в расплавленное стекло через трубку вдувают воздух, и бес форменная масса принимает нужную форму (см. рис. 29). Какое фи зическое явление здесь используют?

Вопрос №1 ? 2 балла Жидкость создает гидростатическое давление из-за действия . .. силы притяжения силы трения силы упругости силы Паскаля Вопрос №2 ? … 2 балла В какой точке жидкость создает наибольшее давление? во всех трех одинаковое точка А точка С точка В Вопрос №3 ? 2 балла Определите примерное давление, которое создает столбец эфира (жидкость) высотой 14 см. 1 кПа 110 Па 98 кПа 1,4 кПа Вопрос №4 ? 3 балла Аквариум в форме цилиндра высотой 60 см наполовину заполнен водой. Определите силу, с которой вода давит на дно аквариума, если площадь дна составляет 0,35 м2. Ответ запишите в ньютонах. Ускорение свободного падения 10 Н/кг, плотность воды 1000 кг/м3. Ответ Вопрос №5 ? 3 балла Какое давление должен выдерживать батискаф (в МПа), чтобы иметь возможность погрузиться на дно Марианской впадины? Глубина впадины 11 км, плотность соленой воды на 3% больше, плотности пресной воды.

Площадь дна ёмкости равна 1170 см2. Найди, на сколько увеличится давление ёмкости на стол, если в неё налить воду объёмом 4 л. Принять g=9,8 Н/кг. Отв … ет (округли до целого числа): давление ёмкости на стол увеличится на Па.

СРОЧНО НАДО!!!!В течение 13 минут через лампочку протекает электрический ток, значение которого — 160 мА. Электрическое напряжение на этом участке — 5 … ,67 В. Найди работу электрического поля по перемещению заряда, произведённую за это время.

Формулы по физике 9 класс

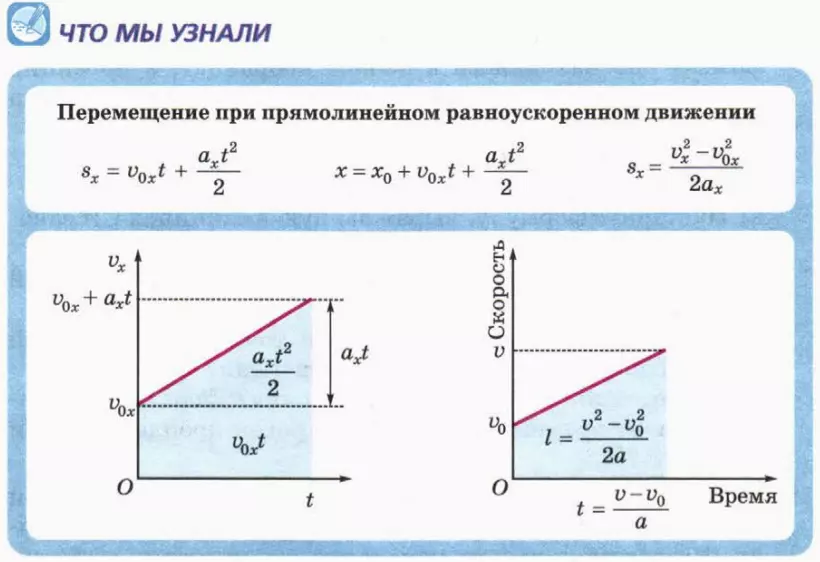
Равномерное движение
Путь	$S=Vt$	метр
Скорость	$V=\frac{S}{t}$	метр/секунда
Ускорение	$a=0$	метр/сек²
Координата	$x = x_0 + vt$
Равноускоренное движение
Ускорение	$а=\frac{V-V_0}{t}$	метр/сек²
Координата	$x=x_0+V_0t+\frac{at^2}{2}$
Путь	$S=V_0t+\frac{at^2}{2} = V^2-\frac{{V_0}^2}{2a}$	метр
Криволинейное движение по окружности
Ускорение	$a_{цс}=\frac{v^2}{r}=w^2r$	метр/сек²
Угловая скорость	$w=\frac{2π}{T}$	радиан/секунда
Вещество
Масса	$m=pv$	килограмм
Силы
Равнодействующая сила	$F=ma$	Ньютон
Сила тяжести, вес	$F=mg$	Ньютон
Сила трения	$F = \mu N$	Ньютон
Сила упругости	$F_{упр}=-kx$	Ньютон
Закон Архимеда	$F = p_ж V_т g$	Ньютон
Закон всемирного тяготения	$F=G\frac{m_1 m_2}{R^2}$	Ньютон
Момент силы	$M=Fl$	Ньютон*метр
Давление
Давление твердых тел	$p=\frac{F}{S}$	Паскаль
Давление в жидкостях	$p=\rho gh$	Паскаль
Гидравлический пресс	$\frac{F_1}{F_2}=\frac{S_2}{S_1}$
Работа, энергия, мощность
Механическая работа	$A=FScos a$	Джоуль
Мощность	$N=\frac{A}{t}$	Ватт
$КПД=\frac{А_п}{A_з}100\%=\frac{Q_п}{Q_з}100\%$		%
Кинетическая энергия	$E=\frac{mv^2}{2}$	Джоуль
Потенциальная энергия	$E=mgh$	Джоуль
Количество теплоты	$Q=cm(t_2-t_1)$	Джоуль
Теплота сгорания	$Q=qm$	Джоуль
Теплота парообразования	$Q=Lm$	Джоуль
Тепловое действие тока	$Q=I^2 Rt$	Джоуль
Работа тока	$A=IUt$	Джоуль
Мощность тока	$P=\frac{A}{t}=UI$	Ватт
Энергия пружины	$E=\frac{kx^2}{2}$	Джоуль
Закон сохранения энергии	$E_{const}=E_{кин} + E_{пот} + E_{внутр}$	Джоуль
Импульс
Импульс	$p=mv$	кг*метр/сек²
Закон сохранения импульса	$mv_1+mv_2={mv_1}’+{mv_2}’$	кг*метр/сек²
Ток
Закон Ома	$I=\frac{U}{R}$	Ампер
Сопротивление проводника	$R=\frac{p l}{s}$	Ом
Последовательное соединение проводников
Сила тока	$I=I_1=I_2$	Ампер
Напряжение	$U=U_1+U_2$	Вольт
Сопротивление	$R=R_1+R_2$	Ом
Параллельное соединение проводников
Сила тока	$I=I_1+I_2$	Ампер
Напряжение	$U=U_1=U_2$	Вольт
Сопротивление	$\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}$	Ом

Открытая Физика.

Сила упругости. Закон Гука

При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Её называют силой упругости.

Простейшим видом деформации являются деформации растяжения и сжатия (рис. 1.12.1).

Деформация растяжения (x > 0) и сжатия (x < 0). Внешняя сила F→=–F→упр.

При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации:

F_x = F_упр = –kx.

Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жёсткостью тела. В системе СИ жёсткость измеряется в ньютонах на метр (Н/м). Коэффициент жёсткости зависит от формы и размеров тела, а также от материала. В физике закон Гука для деформации растяжения или сжатия принято записывать в другой форме. Отношение ε = x / l называется относительной деформацией, а отношение σ = F / S = –F_упр / S, где S – площадь поперечного сечения деформированного тела, называется напряжением. Тогда закон Гука можно сформулировать так: относительная деформация ε пропорциональна напряжению σ:

ε=1Eσ.

Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Модуль Юнга различных материалов меняется в широких пределах. Для стали, например, E ≈ 2∙10¹¹ Н/м², а для резины E ≈ 2∙10⁶ Н/м², т. е. на пять порядков меньше.

Закон Гука может быть обобщен и на случай более сложных деформаций.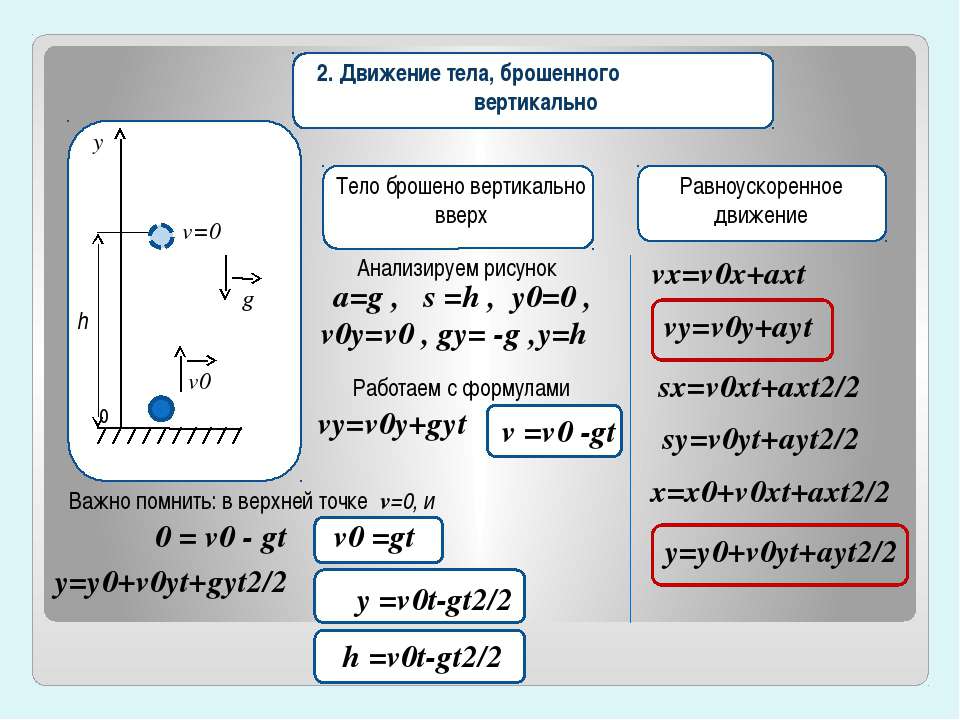 Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах (рис. 1.12.2).

Деформация изгиба. F→упр=–mg→, Fупр=–kx.

Упругую силу N→, действующую на тело со стороны опоры (или подвеса), называют силой реакции опоры. При соприкосновении тел сила реакции опоры направлена перпендикулярно поверхности соприкосновения. Поэтому её часто называют силой нормального давления. Если тело лежит на горизонтальном неподвижном столе, сила реакции опоры направлена вертикально вверх и уравновешивает силу тяжести:N→=–mg→. Сила P→, с которой тело действует на стол, называется весом тела.

В технике часто применяются спиралеобразные пружины (рис. 1.12.3). При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром. Следует иметь в виду, что при растяжении или сжатии пружины в её витках возникают сложные деформации кручения и изгиба.

Деформация растяжения пружины. F→упр=–mg→, Fупр=–kx.

В отличие от пружин и некоторых эластичных материалов (резина) деформация растяжения или сжатия упругих стержней (или проволок) подчиняются линейному закону Гука в очень узких пределах. Для металлов относительная деформация ε = x / l не должна превышать 1 %. При больших деформациях возникают необратимые явления (текучесть) и разрушение материала.

Закон Гука

Формула вершины параболы

☰

Обычно формулу координаты x вершины параболы используют, когда имеют дело с квадратичной функцией.

Квадратичная функция имеет вид: y = ax² + bx + c.

Ее график — это парабола с вершиной, координаты которой определяются по формулам:

Однако формулу координаты y знать и использовать не обязательно. Обычно проще подставить найденное значение x в саму квадратичную функцию и найти оттуда y.

Например, если дана функция y = 2x² – 4x + 5, то координата x ее вершины будет равна:

x = –(–4 / (2 × 2)) = 1

Координату же y вычислим, подставив найденный x в саму функцию:

y = 2 × 12 – 4 × 1 + 5 = 3

Таким образом, вершина графика функции y = 2x² – 4x + 5 находится в точке с координатами (1; 3).

В остальном парабола квадратичной функции вида y = ax² + bx + c такая же как функции вида y = ax². Отличие лишь в сдвиге вершины по сравнению с функцией y = ax². Так в приведенном выше примере (y = 2x² – 4x + 5) парабола будет по форме и направлению ветвей такой же, как для функции y = 2x². Разница лишь в координатах вершин парабол.

Формулы вершины параболы получаются при преобразовании квадратичной функции к виду y = f(x + l) + m. Делается это методом выделения полного квадрата. Как известно функции вида y = f(x + l) + m отличаются от функций y = f(x) сдвигом из графиков по оси x на –l и по оси y на m. Именно l в преобразованной квадратичной функции оказывается равным –b/2a, а m = (4ac – b²) / 4a. То есть l и m — это координаты x₀ и y₀ соответственно.

Доказывается это применением метода выделения полного квадрата к квадратному трехчлену общего вида ax² + bx + c. При этом выполняются следующие преобразования:

Объединим первые два члена многочлена: y = (ax² + bx) + c
Вынесем коэффициент a за скобку, при этом b разделится на a:
Представим, что у нас есть квадрат суммы, в котором x одно из слагаемых, а из выражения в скобках надо получить его полный квадрат суммы. Одночлен (b/a)x умножим на 2 и разделим на 2 одновременно. Также прибавим и вычтем квадрат второго слагаемого квадрата суммы. Получим:
Выделим квадрат суммы:
Умножим на a:
Приведем к общему знаменателю свободные члены:
Поменяем знак:

Таким образом, мы привели функцию y = ax² + bx + c к виду y = a(x + l)² + m, что соответствует функции y = f(x + l) + m, где f(x) = ax². А как строить графики последней известно.

Все формулы по физике 10 класса

МЕХАНИКА
Вычисление перемещения	АВ² = АС² + ВС²	Перемещение – вектор, соединяющий начальную точку движения тела с его конечной точкой.
Проекция вектора перемещения	S_x = x₂ – x₁		x₁ – начальная координата, [м] x₂ – конечная координата, [м] S_x – перемещение, [м]
Формула расчета скорости движения тела	v = s/t	Скорость – физическая величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло.	v – скорость, [м/с] s – путь, [м] t – время, [c]
Уравнение движения	x = x₀ + V_xt		x₀– начальная координата, [м] x – конечная координата, [м] v – скорость, [м/с] t – время, [c]
Формула для вычисления ускорения движения тела	a ⃗ = v ⃗- v₀⃗ /t	Ускорение – физическая величина, которая характеризует быстроту изменения скорости.	a – ускорение, [м/с²] v – конечная скорость, [м/с] v₀ – начальная скорость, [м/с] t – время, [c]
Уравнение скорости	v ⃗ = v₀ ⃗ + a ⃗t		v – конечная скорость, [м/с] v₀ – начальная скорость, [м/с] a – ускорение, [м/с²] t – время, [c]
Уравнение Галилея	S = v₀t + at² / 2		S – перемещение, [м] v – конечная скорость, [м/с] v₀ – начальная скорость, [м/с] a – ускорение, [м/с²] t – время, [c]
Закон изменения координаты тела при прямолинейном равноускоренном движении	x = x₀ + v₀t + at²/2		x₀ – начальная координата, [м] x – конечная координата, [м] v – конечная скорость, [м/с] v₀ – начальная скорость, [м/с] a – ускорение, [м/с²] t – время, [c]
Первый закон Ньютона		Если на тело не действуют никакие тела либо их действие скомпенсировано, то это тело будет находиться в состоянии покоя или двигаться равномерно и прямолинейно.
Второй закон Ньютона	a= F ⃗ / m	Ускорение, приобретаемое телом под действием силы, прямо пропорционально величине этой силы и обратно пропорционально массе тела.	a – ускорение, [м/с²] F – сила, [Н] m – масса, [кг]
Третий закон Ньютона	\|F₁⃗ \|=\|F₂⃗\| F₁⃗ = -F₂⃗	Сила, с которой первое тело действует на второе, равна по модулю и противоположна по направлению силе, с которой второе тело действует на первое.	F – сила, [Н]
Формула для вычисления высоты, с которой падает тело	H = g*t²/2		Н – высота, [м] t – время, [c] g ≈ 9,81 м/с² – ускорение свободного падения
Формула для вычисления высоты при движении вертикально вверх	h=v₀t -gt²/2		h – высота, [м] v₀ – начальная скорость, [м/с] t – время, [c] g ≈ 9,81 м/с² – ускорение свободного падения
Формула для вычисления веса тела при движении вверх с ускорением	P = m (g + a)		P – вес тела, [Н] m – масса тела, [кг] g ≈ 9,81 м/с² – ускорение свободного падения a – ускорение тела, [м/с²]
Формула для вычисления веса тела при движении вниз с ускорением	P = m (g – a)		P – вес тела, [Н] m – масса тела, [кг] g ≈ 9,81 м/с² – ускорение свободного падения a – ускорение тела, [м/с²]
Формула закона всемирного тяготения	F = Gm₁m₂/r²	Закон всемирного тяготения: два тела притягиваются друг к другу с силой, прямо пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними.	F – сила, [Н] G = 6,67 · 10^-11 [Н·м²/кг²] – гравитационная постоянная m – масса тела, [кг] r – расстояние между телами, [м]
Формула расчета ускорения свободного падения на разных планетах	g = GM_пл/R_пл²		g – ускорение свободного падения, [м/с2] G = 6,67 · 10^-11 [Н·м²/кг²] – гравитационная постоянная M – масса планеты, [кг] R – радиус планеты, [м]
Формула расчета ускорения свободного падения	g = GM_з/(R_з+H)²		g – ускорение свободного падения, [м/с2] G = 6,67 · 10^-11 [Н·м²/кг²] – гравитационная постоянная M – масса Земли, [кг] R – радиус Земли, [м] Н – высота тела над Землей, [м]
Формула расчета центростремительного ускорения	а = υ²/r		a – центростремительное ускорение, [м/с²] v – скорость, [м/с] r – радиус окружности, [м]
Формула периода движения по окружности	T = 1/ν = 2πr/υ = t/N		Т – период, [с] ν – частота вращения, [с^-1] t – время, [с] N – число оборотов
Формула расчета угловой скорости	ω = 2π/T = 2πν =υr		ω – угловая скорость, [рад/с] υ – линейная скорость, [м/с] Т – период, [с] ν – частота вращения,[с^-1] r – радиус окружности, [м]
Формула импульса тела	p = mv	Импульсом называют произведение массы тела на его скорость.	p – импульс тела, [кг·м/с] m – масса тела, [кг] υ – скорость, [м/с]
Формула закона сохранения импульса	p₁ + p₂ =p₁’ + p₂’ m₁v + m₂u = m₁v’ + m₁u’
Формула импульса силы	P = Ft		p – импульс тела, [кг·м/с] F – сила, [Н] t – время, [c]
Формула механической работы	A = Fs	Механическая работа – физическая величина, равная произведению модуля силы на величину перемещения тела в направлении действия силы.	A – работа, [Дж] F – сила, [Н] s – пройденный путь, [м]
Формула расчета мощности	N = A/t	Мощность – физическая величина, характеризующая быстроту совершения механической работы.	N – мощность, [Вт] A – работа, [Дж] t – время, [c]
Формула для нахождения коэффициента полезного действия (КПД)	η = A_п/A_з∙ 100%	КПД – отношение полезной работы к затраченной работе.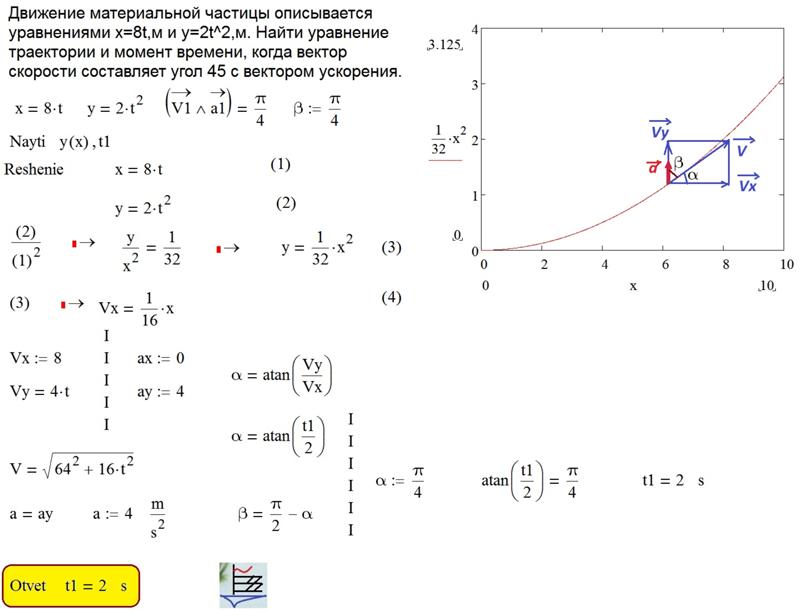	A_п – полезная работа, [Дж] A_з – затраченная работа, [Дж]
Формула расчета потенциальной энергии	E_п = mgh	Потенциальная энергия – это энергия, которая определяется взаимным положением взаимодействующих тел или частей одного и того же тела.	Eп – потенциальная энергия тела, [Дж] m – масса тела, [кг] g ≈ 9,81 м/с² – ускорение свободного падения h – высота тела над поверхностью земли, [м]
Формула расчета кинетической энергии	E_k= mv²/2	Кинетическая энергия – энергия, которой обладает тело вследствие своего движения.	E_k – кинетическая энергия тела, [Дж] m – масса тела, [кг] v – скорость движения тела, [м/с]
Формула закона сохранения полной механической энергии	mv₁²/2 + mgh₁=mv₂²/2 + mgh₂	Закон сохранения полной механической энергии: полная механическая энергия тела, на которое не действуют силы трения и сопротивления, в процессе его движения остается неизменной.	m – масса тела, [кг] g ≈ 9,81 м/с2 – ускорение свободного падения v₁ – скорость тела в начальный момент времени, [м/с] v₂ – скорость тела в конечный момент времени, [м/с] h₁ – начальная высота, [м] h₂ – конечная высота, [м]
Формула силы трения	F_тр = μ mg	Сила трения – сила, возникающая при соприкосновении двух тел и препятствующая их относительному движению.	Fтр – сила трения, [Н] μ – коэффициент трения m – масса тела, [кг] g ≈ 9,81 м/с² – ускорение свободного падения
Уравнение колебаний	x = A cos (ωt + φ₀)		А – амплитуда колебаний, [м] х – смещение, [м] t – время, [c] ω – циклическая частота, [рад/с] φ₀ – начальная фаза, [рад]
Формула периода	T = 1/ν = 2πr/υ = t/N		Т – период, [с] ν – частота колебании, [с^-1] t – время колебании, [с] N – число колебаний
Формула периода для математического маятника	T= 2π √L/g		Т – период, [с] g ≈ 9,81 м/с² – ускорение свободного падения L – длина нити, [м]
Формула периода для пружинного маятника	T= 2π √m/K		Т – период, [с] m – масса груза, [кг] К – жесткость пружины, [Н/м]
Формула длины волны	λ = υТ = υ/ν		λ – длина волны, [м] Т – период, [с] ν – частота, [с^-1] υ – скорость волны, [м/с]
Формула полной механической энергии колебательного движения	E = kA²/2		E – энергия, [Дж] А – амплитуда колебаний, [м] k – жесткость пружины, [Н/м]
Радиус Шварцшильда	R = 2GM/c²	Радиус Шварцшильда – радиус «горизонта событий» черной дыры, из которого ничто не может вырваться.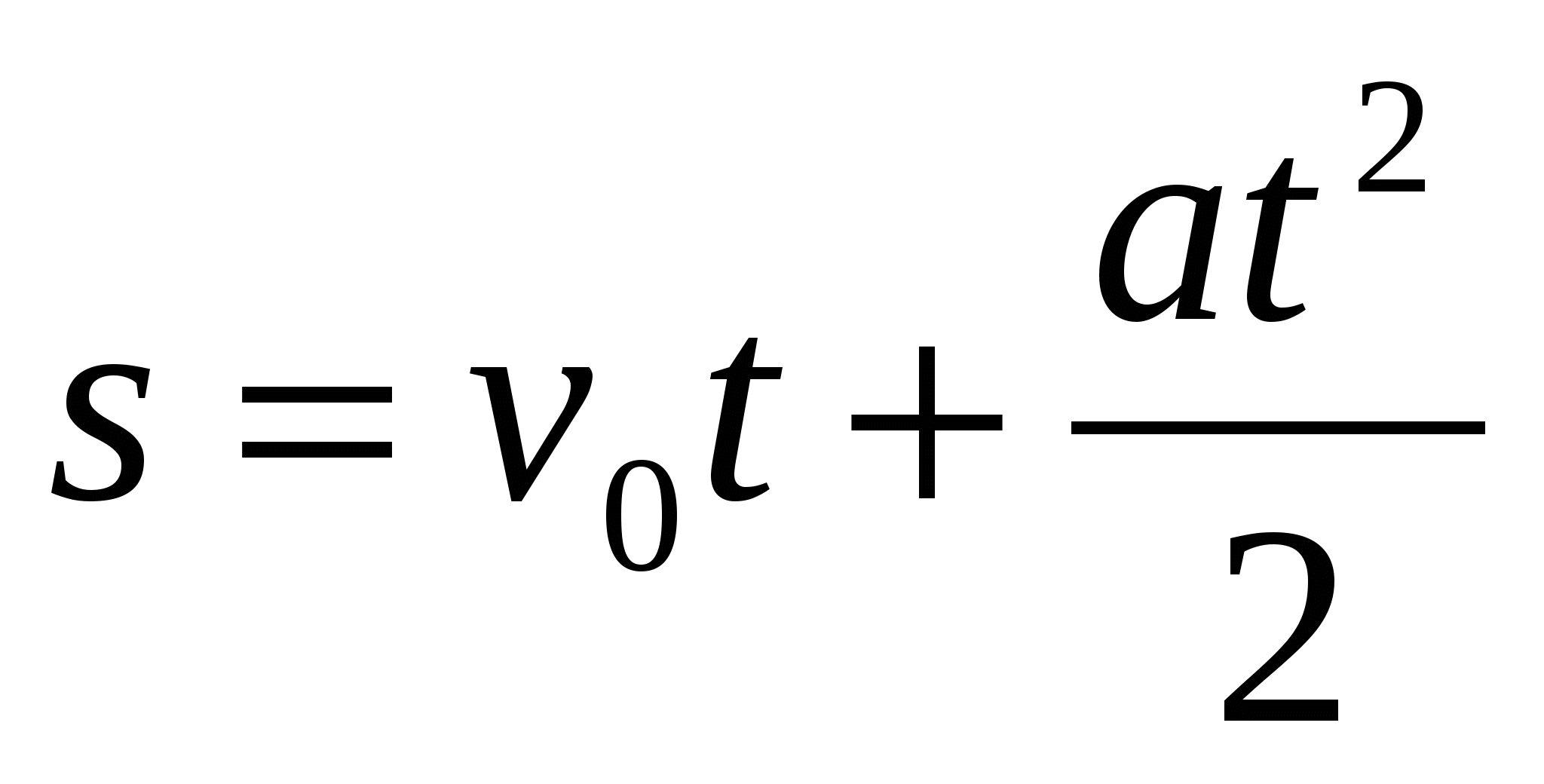	R – радиус Шварцшильда, [м] G = 6,67 · 10^-11 [Н·м2/кг²] – гравитационная постоянная М – масса черной дыры, [кг]
Собственное время	t = T/√1-v²/c²	Собственное время – время, измеренное наблюдателем, движущимся вместе с часами.	t – собственное время, [с] T – время в движущейся системе отсчета, [с] v – скорость движущейся системы отсчета, [м/с] c – скорость света, [м/с]
Масса покоя	m = M/√1-v²/c²2	Масса покоя – масса тела в СО, относительно которой оно покоится.	m – масса тела в СО, относительно которой оно покоится, [кг] M – масса тела в подвижной СО, [кг] v – скорость движущейся системы отсчета, [м/с] c – скорость света, [м/с]
Формула Эйнштейна	E = mc²		E – энергия, [Дж] m – масса, [кг] c – скорость света, [м/с
МОЛЕКУЛЯРНАЯ ФИЗИКА 10 класс
Массовое число	M = Z + N		M – массовое число Z – число протонов (электронов), зарядовое число N – число нейтронов
Формула массы ядра	М_Я = М_А – Z m_e		M_Я – масса ядра, [кг] М_А – масса изотопа , [кг] m_e – масса электрона, [кг]
Формула дефекта масс	∆m = Zm_p + Nm_n – M_Я	Дефект масс – разность между суммой масс покоя нуклонов, составляющих ядро данного нуклида, и массой покоя атомного ядра этого нуклида.	∆m – дефект масс, [кг] m_p – масса протона, [кг] m_n – масса нейтрона, [кг]
Уравнение Менделеева-Клапейрона	pV = m/M RT	Уравнение состояния идеального газа	p – давление, [Па] V – объем, [м³] m – масса, [кг] M – молярная масса, [кг] R = 8,31 [Дж/мольК] – молярная газовая постоянная T – температура, [°С]
Формула давления газа			p – давление, [Па] n – концетрация молекул E – средняя кинетическая энергия молекулы, [Дж] T – температура, [°С] k = 1,38 · 10^-23, [Дж/К] – постоянная Больцмана
Закон Бойля-Мариотта	p₁V₁ = p₂V₂		p – давление, [Па] V – объем, [м³]
Закон Гей-Люссака	V₁/T₁ = V₂/T₂		T – температура, [°С] V – объем, [м³]
Закон Шарля	p₁/T₁= p₂/T₂		T – температура, [°С] p – давление, [Па]
Внутренняя энергия идеального газа	U = i/2 pV		U – энергия, [Дж] p – давление, [Па] V – объем, [м³] i – число степеней свободы молекул газа
Работа, совершаемая газом	A = pΔV		p – давление, [Па] V – объем, [м³] А – работа, [Дж]
Первый закон термодинамики	Q = ΔU + A		Q – количество теплоты, [Дж] А – работа, [Дж] U – энергия, [Дж]
Формула для нахождения коэффициента полезного действия (КПД) теплового двигателя	η = A/Q∙100%		А – работа, [Дж] Q – количество теплоты, полученное от нагревателя, [Дж]
Сила поверхностного натяжения	F = ϭl		F – сила поверхностного натяжения, [Н] ϭ – поверхностное натяжение, [Н/м] l – длина участка поверхности слоя, [м]
Закон Гука	ϭ = Eε	При упругой деформации тела напряжение пропорционально относительному удлинению тела.	ϭ – механическое напряжение, [Па] Е – модуль Юнга, [Па] ε – относительное удлинение тела, [м]
ЭЛЕКТРОДИНАМИКА
Закон Кулона	F = kq₁q₁/r²	Определяет силу электростатического взаимодействия двух точечных зарядов	F – сила Кулона, [Н] k = 9·10⁹ [Нм²/Кл²] q – заряд, [Кл] r – расстояние между зарядами, [м]
Напряженность поля	E = F/q E = kQ/r²		Е – напряженность поля, [Н/Кл] q – пробный положительный заряд, [Кл] F – сила Кулона, [Н] k = 9·10⁹ [Нм²/Кл²]
Потенциал электростатического поля	φ = W/q φ = Q/4πεr		φ – потенциал, [В] W – энергия, [Дж] q – заряд, [Кл]
Потенциальная энергия заряда	W = qφ		W – энергия, [Дж] q – заряд, [Кл] φ – потенциал, [В]
Работа силы электростатического поля	A = qU		А – работа сил, [Дж] q – заряд, [Кл] U – разность потенциалов, [В]
Разность потенциалов в однородном поле	U = Ed		U – разность потенциалов, [В] Е – напряженность поля, [Н/Кл] d – расстояние, [м]
Электроемкость уединенного проводника	C = Q/φ		C – электроемкость, [Ф] φ – потенциал, [В] Q – заряд, [Кл]
Электроемкость конденсатора	C = Q/U		C – электроемкость, [Ф] U – разность потенциалов, [В] Q – заряд, [Кл]
Энергия ЭСП	W = CU²/2		C – электроемкость, [Ф] U – разность потенциалов, [В] W – энергия ЭСП, [Дж

уравнений движения для постоянного ускорения в одном измерении

Обозначение:

t , x , v , a

Прежде всего, сделаем несколько упрощений в обозначениях. Принятие начального времени равным нулю, как если бы время измерялось секундомером, является большим упрощением. Так как прошедшее время Δ t = t _f — t ₀, принимая t ₀ = 0 означает, что Δ t = t _f, последнее время на секундомер.Когда начальное время принимается равным нулю, мы используем индекс 0 для обозначения начальных значений положения и скорости. То есть x ₀ — это начальная позиция , а v ₀ — начальная скорость . Мы не ставим нижние индексы на окончательные значения. То есть t — это конечное время , x — конечное положение , а v — конечная скорость . Это дает более простое выражение для прошедшего времени — теперь Δ t = t .Это также упрощает выражение для смещения, которое теперь составляет Δ x = x — x ₀. Кроме того, это упрощает выражение для изменения скорости, которое теперь составляет Δ v = v — v ₀. Подводя итог, используя упрощенные обозначения, с начальным временем, принятым равным нулю,

[латекс] \ begin {case} {\ Delta} {t} & = & t \\ {\ Delta} {x} & = & x — {{x} _ {0}} \\ {\ Delta} { v} & = & v — {{v} _ {0}} \ end {case} [/ latex]

, где нижний индекс 0 обозначает начальное значение, а отсутствие нижнего индекса означает конечное значение в любом рассматриваемом движении.

Теперь мы делаем важное предположение, что ускорение постоянно . Это предположение позволяет нам избегать использования расчетов для определения мгновенного ускорения. Поскольку ускорение постоянно, среднее и мгновенное ускорения равны. То есть

[латекс] \ bar {a} = a = \ text {constant} [/ latex],

, поэтому мы всегда используем символ a для обозначения ускорения. Предположение, что ускорение является постоянным, не серьезно ограничивает ситуации, которые мы можем изучить, и не снижает точность нашего лечения. Во-первых, ускорение постоянно равно в большом количестве ситуаций. Кроме того, во многих других ситуациях мы можем точно описать движение, приняв постоянное ускорение, равное среднему ускорению для этого движения. Наконец, в движениях, где ускорение резко меняется, например, когда автомобиль разгоняется до максимальной скорости, а затем тормозит до остановки, движение можно рассматривать в отдельных частях, каждая из которых имеет собственное постоянное ускорение.

Решение для смещения (Δ x ) и конечного положения ( x ) по средней скорости, когда ускорение ( a ) является постоянным

Чтобы получить наши первые два новых уравнения, мы начнем с определения средней скорости:

Замена упрощенных обозначений для Δ x и Δ t дает

[латекс] \ bar {v} = \ frac {x- {x} _ {0}} {t} [/ latex]

Решение для x дает

[латекс] x = {x} _ {0} + \ bar {v} t [/ latex],

при средней скорости

[латекс] \ bar {v} = \ frac {{v} _ {0} + v} {2} \ left (\ text {constant} a \ right) [/ latex].

Уравнение [латекс] \ bar {v} = \ frac {{v} _ {0} + v} {2} [/ latex] отражает тот факт, что при постоянном ускорении v — это просто среднее начальной и конечной скоростей. Например, если вы постоянно увеличиваете скорость (то есть с постоянным ускорением) с 30 до 60 км / ч, то ваша средняя скорость во время этого постоянного увеличения составляет 45 км / ч. Используя уравнение [латекс] \ bar {v} = \ frac {{v} _ {0} + v} {2} [/ latex], чтобы проверить это, мы видим, что

[латекс] \ bar {v} = \ frac {{v} _ {0} + v} {2} = \ frac {\ text {30 км / ч} + \ text {60 км / ч}} {2 } = \ text {45 км / ч} [/ latex],

, что кажется логичным.

Пример 1. Расчет смещения: как далеко пробегает бегунок?

Бегун бежит по прямому участку дороги со средней скоростью 4,00 м / с в течение 2,00 мин. Какова его конечная позиция, если исходная позиция равна нулю?

Стратегия

Нарисуйте эскиз.

Конечная позиция x определяется уравнением

[латекс] x = {x} _ {0} + \ bar {v} t [/ latex]. {2} [/ latex].На графике линейные функции выглядят как прямые линии с постоянным наклоном.) Например, в автомобильной поездке мы продвинемся вдвое дальше за заданный промежуток времени, если мы усредним 90 км / ч, чем если бы мы в среднем 45 км / ч.

Решение для окончательной скорости

Мы можем вывести еще одно полезное уравнение, манипулируя определением ускорения.

Подставляя упрощенные обозначения для Δ v и Δ t , получаем

[латекс] a = \ frac {v- {v} _ {0}} {t} \ text {} \ left (\ text {constant} a \ right) [/ latex]

Решение для v дает

[латекс] v = {v} _ {0} + \ text {at} \ text {} \ left (\ text {constant} a \ right) [/ latex]

Пример 2.Расчет конечной скорости: самолет замедляется после приземления

Самолет приземляется с начальной скоростью 70,0 м / с, а затем замедляется со скоростью 1,50 м / с ² в течение 40,0 с. Какова его конечная скорость?

Стратегия

Нарисуйте эскиз. Мы рисуем вектор ускорения в направлении, противоположном вектору скорости, потому что самолет замедляется.

Решение

1. Определите известные. v ₀ = 70.{2} \ right) \ left (\ text {40} \ text {.} \ Text {0 s} \ right) = \ text {10} \ text {.} \ Text {0 м / с} [/ latex ]

Обсуждение

Конечная скорость намного меньше начальной скорости, желательно при замедлении, но все же положительная. С помощью реактивных двигателей обратная тяга могла поддерживаться достаточно долго, чтобы остановить самолет и начать движение назад. На это указывает отрицательная конечная скорость, чего здесь нет.

Уравнение [латекс] v = {v} _ {0} + \ text {at} [/ latex] не только помогает при решении задач, но и дает нам представление о взаимосвязях между скоростью, ускорением и временем.Из него видно, например, что

конечная скорость зависит от того, насколько велико ускорение и как долго оно длится
, если ускорение равно нулю, то конечная скорость равна начальной скорости ( v = v ₀), как и ожидалось (т. е. скорость постоянна)
если a отрицательно, то конечная скорость меньше начальной скорости

(Все эти наблюдения соответствуют нашей интуиции, и всегда полезно исследовать основные уравнения в свете нашей интуиции и опыта, чтобы убедиться, что они действительно точно описывают природу.)

Установление соединений: соединение в реальном мире

Межконтинентальная баллистическая ракета (МБР) имеет большее среднее ускорение, чем космический шаттл, и достигает большей скорости в первые две минуты полета (фактическое время горения межконтинентальной баллистической ракеты засекречено — ракеты с коротким временем горения сложнее для противника. разрушать). Но космический шаттл получает большую конечную скорость, так что он может вращаться вокруг Земли, а не сразу возвращаться вниз, как это делает межконтинентальная баллистическая ракета. Космический шаттл делает это за счет более длительного ускорения.

Решение для конечного положения, когда скорость не постоянна ( a ≠ 0)

Мы можем объединить приведенные выше уравнения, чтобы найти третье уравнение, которое позволяет нам вычислить окончательное положение объекта, испытывающего постоянное ускорение. {2} \ left (\ text {constant} a \ right) \ text {.} [/ latex]

Пример 3. Расчет смещения ускоряющегося объекта: драгстеры

Драгстеры могут развивать среднее ускорение 26,0 м / с ². Предположим, такой драгстер ускоряется из состояния покоя за 5,56 с. Как далеко он пролетит за это время?

Стратегия

Нарисуйте эскиз.

Нас просят найти смещение, которое составляет x , если мы примем x ₀ равным нулю. (Подумайте об этом как о стартовой линии гонки.{2} [/ latex] после того, как мы определим v ₀, a и t из описания проблемы.

Решение

1. Определите известные. Запуск из состояния покоя означает, что v ₀ = 0, a задается как 26,0 м / с ² и t задается как 5,56 с.

2. Подставьте известные значения в уравнение, чтобы найти неизвестное x :

Поскольку начальное положение и скорость равны нулю, это упрощается до

Подстановка идентифицированных значений на и т дает

дает

x = 402 м. {2} + 2a \ left (x- {x} _ {0} \ right) [/ latex] идеально подходит для этой задачи, поскольку он связывает скорости, ускорение и смещение и не требует информации о времени.

Решение

1. Определите известные значения. Мы знаем, что v ₀ = 0, так как драгстер запускается из состояния покоя. Затем заметим, что x — x ₀ = 402 м (это был ответ в примере 3). Наконец, среднее ускорение составило , а = 26.{2} + 2a \ left (x- {x} _ {0} \ right) [/ latex] и решите для v .

v ² = 0 + 2 (26,0 м / с ²) (402 м).

Таким образом,

Чтобы получить против , извлекаем квадратный корень:

Обсуждение

145 м / с составляет около 522 км / ч или около 324 миль / ч, но даже эта головокружительная скорость не достигает рекорда для четверти мили. Также обратите внимание, что квадратный корень имеет два значения; мы взяли положительное значение, чтобы указать скорость в том же направлении, что и ускорение. {2} + 2a \ left (x- {x} _ {0} \ right) [/ latex] может дать дополнительное понимание общих отношений между физическими величинами:

Конечная скорость зависит от того, насколько велико ускорение и расстояние, на котором оно действует
При фиксированном замедлении автомобиль, который едет в два раза быстрее, не просто останавливается на удвоенном расстоянии — для остановки требуется гораздо больше времени. (Вот почему у нас есть зоны с пониженной скоростью возле школ.)

Объединение уравнений

В следующих примерах мы дополнительно исследуем одномерное движение, но в ситуациях, требующих немного большего количества алгебраических манипуляций.Примеры также дают представление о методах решения проблем. В рамке ниже приведены ссылки на необходимые уравнения.

Сводка кинематических уравнений (константа a )

Пример 5. Расчет смещения: как далеко уходит автомобиль при остановке?

На сухом бетоне автомобиль может замедляться со скоростью 7,00 м / с ², тогда как на мокром бетоне он может замедляться только со скоростью 5,00 м / с ². Найдите расстояния, необходимые для остановки движения машины на отметке 30.0 м / с (около 110 км / ч) (а) на сухом бетоне и (б) на мокром бетоне. (c) Повторите оба вычисления, найдя смещение от точки, где водитель видит, что светофор становится красным, принимая во внимание время его реакции 0,500 с, чтобы нажать ногой на тормоз.

Стратегия

Нарисуйте эскиз.

Чтобы определить, какие уравнения лучше всего использовать, нам нужно перечислить все известные значения и точно определить, что нам нужно решить. Мы сделаем это явно в следующих нескольких примерах, используя таблицы для их выделения.

Решение для (a)

1. Определите, что мы знаем и что мы хотим решить. Мы знаем, что v ₀ = 30,0 м / с; v = 0; a = -7,00 м / с ² ( a отрицательно, потому что оно находится в направлении, противоположном скорости). Примем x ₀ равным 0. Ищем смещение Δ x , или x — x ₀.

2. Найдите уравнение, которое поможет решить проблему.Лучшее уравнение для использования —

Это уравнение лучше всего, потому что оно включает только одно неизвестное, x . Нам известны значения всех других переменных в этом уравнении. (Существуют и другие уравнения, которые позволят нам решить для x , но они требуют, чтобы мы знали время остановки, t , которое мы не знаем. Мы могли бы использовать их, но это потребовало бы дополнительных вычислений.)

3. Переставьте уравнение, чтобы найти x .

4. Введите известные значения.{2} \ right)} [/ латекс]

Таким образом,

x = 64,3 м по сухому бетону.

Решение для (b)

Эта часть может быть решена точно так же, как и часть A. Единственная разница в том, что замедление составляет –5,00 м / с ². Результат

x _мокрый = 90,0 м на мокром бетоне.

Решение для (c)

После реакции водителя тормозной путь будет таким же, как в частях A и B для сухого и влажного бетона. Итак, чтобы ответить на этот вопрос, нам нужно вычислить, как далеко проехала машина за время реакции, а затем добавить это время ко времени остановки. Разумно предположить, что скорость остается постоянной в течение времени реакции водителя.

1. Определите, что мы знаем и что мы хотим решить. Мы знаем, что [латекс] \ bar {v} = 30.0 \ text {m / s} [/ latex]; т _{реакция} = 0,500 с; a _{реакция} = 0. Возьмем x _0- _{реакция} = равным 0.Ищем x _{реакция}.

2. Определите лучшее уравнение для использования. [latex] x = {x} _ {0} + \ bar {v} t [/ latex] работает хорошо, потому что единственное неизвестное значение — x , и это то, что мы хотим найти.

3. Подключите известные знания, чтобы решить уравнение.

x = 0+ (30,0 м / с) (0,500 с) = 15,0 м.

Это означает, что автомобиль проезжает 15,0 м, в то время как водитель реагирует, создавая общие перемещения в двух случаях: сухой и мокрый бетон 15. На 0 м больше, чем если бы он среагировал мгновенно.

4. Добавьте смещение за время реакции к смещению при торможении.

x _{торможение} + x _{реакция} = x _всего

64,3 м + 15,0 м = 79,3 м в сухом состоянии
90,0 м + 15,0 м = 105 м во влажном состоянии

Обсуждение

Смещения, найденные в этом примере, кажутся разумными для остановки быстро движущегося автомобиля.Остановка автомобиля на мокром, а не на сухом асфальте займет больше времени. Интересно, что время реакции значительно увеличивает смещения. Но важнее общий подход к решению проблем. Мы идентифицируем известные и определяемые величины, а затем находим соответствующее уравнение. Часто есть несколько способов решить проблему. Фактически, различные части этого примера могут быть решены другими методами, но решения, представленные выше, являются самыми короткими.

Пример 6.

Расчет времени: автомобиль сливается с движением

Предположим, автомобиль выезжает на автомагистраль на съезде длиной 200 м. Если его начальная скорость составляет 10,0 м / с, а ускорение составляет 2,00 м / с ², сколько времени потребуется, чтобы преодолеть 200 м по рампе? (Такая информация может быть полезна транспортному инженеру.)

Стратегия

Нарисуйте эскиз.

Просят решить на время т . Как и раньше, мы идентифицируем известные величины, чтобы выбрать удобную физическую связь (то есть уравнение с одной неизвестной, t ).{2} [/ латекс]

4. Упростите уравнение. Единицы измерения (м) отменяются, потому что они есть в каждом члене. Мы можем получить единицы секунд для отмены, взяв t = ts , где t — величина времени, а s — единица измерения. Остается

200 = 10 т + т ².

5. Используйте формулу корней квадратного уравнения, чтобы найти t .

(a) Переставьте уравнение, чтобы получить 0 на одной стороне уравнения.{2} -4 \ text {ac}}} {2a} [/ latex]

Это дает два решения для т , которые составляют

т = 10,0 и -20,0.

В этом случае время равно t = t в секундах, или

т = 10,0 с и -20,0 с.

Отрицательное значение времени неразумно, так как это будет означать, что событие произошло за 20 секунд до начала движения. Мы можем отказаться от этого решения. Таким образом,

т = 10,0 с.

Обсуждение

Всякий раз, когда уравнение содержит неизвестный квадрат, будет два решения. В некоторых проблемах имеют смысл оба решения, но в других, таких как вышеупомянутое, разумно только одно решение. Ответ 10,0 с кажется разумным для типичной автострады на съезде.

Установив основы кинематики, мы можем перейти ко многим другим интересным примерам и приложениям. В процессе разработки кинематики мы также познакомились с общим подходом к решению проблем, который дает как правильные ответы, так и понимание физических взаимоотношений. В разделе «Основы решения проблем» обсуждаются основы решения проблем и описывается подход, который поможет вам добиться успеха в этой бесценной задаче.

Задачи и упражнения

1. Спринтер олимпийского класса начинает забег с ускорением 4,50 м / с ². (а) Какова ее скорость через 2,40 с? (б) Нарисуйте график ее положения в зависимости от времени за этот период.

2. Хорошо брошенный мяч попадает в мягкую перчатку. Если замедление мяча составляет 2,10 × 10 ⁴ м / с ² и 1.85 мс (1 мс = 10–3 с) проходит с момента первого касания мяча рукавицы до момента остановки. Какова была начальная скорость мяча?

3. Пуля в ружье ускоряется от камеры выстрела до конца ствола со средней скоростью 6,20 × 10 ⁵ м / с ² за 8,10 × 10 ^-4 с. Какова его начальная скорость (то есть конечная скорость)?

4. (a) Пригородный легкорельсовый поезд ускоряется со скоростью 1,35 м / с ². Сколько времени нужно, чтобы достичь максимальной скорости 80?0 км / ч, трогаться с места? (b) Этот же поезд обычно замедляется со скоростью 1,65 м / с ². Сколько времени нужно, чтобы остановиться с максимальной скорости? (c) В аварийных ситуациях поезд может замедляться быстрее, останавливаясь на скорости 80,0 км / ч за 8,30 с. Какое его аварийное замедление в м / с ²?

5. При выезде на автостраду автомобиль ускоряется из состояния покоя со скоростью 2,40 м / с ² за 12,0 с. (а) Нарисуйте набросок ситуации. (б) Перечислите известных в этой проблеме.(c) Как далеко машина уезжает за эти 12,0 с? Чтобы решить эту часть, сначала определите неизвестное, а затем обсудите, как вы выбрали соответствующее уравнение для его решения. После выбора уравнения покажите свои шаги в решении неизвестного, проверьте свои единицы и обсудите, является ли ответ разумным. (d) Какова конечная скорость автомобиля? Решите для этого неизвестного таким же образом, как в части (c), явно показывая все шаги.

6. В конце забега бегун замедляется со скорости 9.00 м / с со скоростью 2,00 м / с ². а) Как далеко она продвинется в следующие 5,00 с? б) Какова ее конечная скорость? (c) Оцените результат. Имеет ли это смысл?

7. Professional Application: Кровь ускоряется из состояния покоя до 30,0 см / с на расстоянии 1,80 см от левого желудочка сердца. (а) Сделайте набросок ситуации. (б) Перечислите известных в этой проблеме. (c) Сколько времени длится ускорение? Чтобы решить эту часть, сначала определите неизвестное, а затем обсудите, как вы выбрали соответствующее уравнение для его решения.После выбора уравнения покажите свои шаги в решении неизвестного, проверяя свои единицы. (г) Является ли ответ разумным по сравнению со временем биения сердца?

8. При нанесении удара по воротам хоккеист ускоряет шайбу со скорости 8,00 м / с до 40,0 м / с в том же направлении. Если этот бросок занимает 3,33 × 10 ^-2, вычислите расстояние, на котором шайба ускоряется.

9. Мощный мотоцикл может разогнаться с места до 26,8 м / с (100 км / ч) всего за 3 секунды.90 с. а) Какое у него среднее ускорение? б) Как далеко он пролетит за это время?

10. Грузовые поезда могут производить только относительно небольшие ускорения и замедления. (a) Какова конечная скорость грузового поезда, который ускоряется со скоростью 0,0500 м / с ² за 8,00 мин, начиная с начальной скорости 4,00 м / с? (b) Если поезд может замедляться со скоростью 0,550 м / с ², сколько времени потребуется, чтобы остановиться с этой скорости? (c) Как далеко он продвинется в каждом случае?

11.Снаряд фейерверка ускоряется из состояния покоя до скорости 65,0 м / с на расстояние 0,250 м. а) Как долго длилось ускорение? (b) Рассчитайте ускорение.

12. Лебедь на озере поднимается в воздух, взмахивая крыльями и бегая по воде. (a) Если лебедь должен достичь скорости 6,00 м / с для взлета, и он ускоряется из состояния покоя со средней скоростью 0,350 м / с ², как далеко он пролетит, прежде чем взлетит? б) Сколько времени это займет?

13. Профессиональное применение: Мозг дятла специально защищен от сильных замедлений с помощью прикрепленных к нему сухожилий внутри черепа. Во время клевания дерева голова дятла останавливается с начальной скорости 0,600 м / с на расстоянии всего 2,00 мм. (a) Найдите ускорение в м / с ² и кратное g ( g = 9,80 м / с ². (b) Рассчитайте время остановки. (c) Сухожилия, удерживающие мозг, растягиваются , делая тормозной путь 4.50 мм (больше головы и, следовательно, меньше торможение мозга). Каково замедление мозга, выраженное кратным г ?

14. Неосторожный футболист сталкивается со стойкой ворот с мягкой подкладкой при беге со скоростью 7,50 м / с и полностью останавливается, сжав подушку и свое тело на 0,350 м. а) Каково его замедление? б) Как долго длится столкновение?

15. Во время Второй мировой войны было зарегистрировано несколько случаев, когда летчики прыгали со своих пылающих самолетов без парашюта, чтобы избежать верной смерти.Некоторые упали с высоты около 20000 футов (6000 м), некоторые выжили, получив несколько опасных для жизни травм. Для этих удачливых пилотов ветки деревьев и снежные заносы на земле позволяли их замедление относительно небольшого. Если предположить, что скорость пилота при столкновении составляла 123 мили в час (54 м / с), то каково было его замедление? Предположим, что деревья и снег остановили его на расстоянии 3,0 м.

16. Представьте серую белку, падающую с дерева на землю. (a) Если мы проигнорируем сопротивление воздуха в этом случае (только ради этой проблемы), определите скорость белки непосредственно перед тем, как упасть на землю, предполагая, что она упала с высоты 3.{2} [/ latex] как проходит. Длина станции 210 м. а) Какова длина носа поезда на станции? б) Как быстро он движется, когда нос покидает станцию? (c) Если поезд имеет длину 130 м, когда конец поезда покидает станцию? г) Какова скорость отходящего поезда?

18. Драгстеры могут развить максимальную скорость 145 м / с всего за 4,45 с — значительно меньше времени, чем указано в Примере 2.10 и Примере 2.11. (а) Рассчитайте среднее ускорение для такого драгстера.(b) Найдите конечную скорость этого драгстера, начиная с состояния покоя и ускоряясь со скоростью, указанной в (a) для 402 м (четверть мили), без использования какой-либо информации о времени. (c) Почему конечная скорость больше той, которая использовалась для определения среднего ускорения? Подсказка: подумайте, справедливо ли предположение о постоянном ускорении для драгстера. Если нет, обсудите, будет ли ускорение больше в начале или в конце пробега и как это повлияет на конечную скорость.

19.Велогонщик бежит в конце гонки, чтобы одержать победу. Гонщик имеет начальную скорость 11,5 м / с и ускоряется со скоростью 0,500 м / с ² за 7,00 с. а) Какова его конечная скорость? (b) Гонщик продолжает движение на этой скорости до финиша. Если он был в 300 м от финиша, когда начал ускоряться, сколько времени он сэкономил? (c) Еще один гонщик был на 5,00 м впереди, когда победитель начал ускоряться, но он не смог ускориться и ехал со скоростью 11,8 м / с до финиша.Насколько далеко впереди (в метрах и секундах) финишировал победитель?

20. В 1967 году новозеландец Берт Манро установил мировой рекорд для индийского мотоцикла на соляных равнинах Бонневиль в штате Юта с максимальной скоростью 183,58 миль / ч.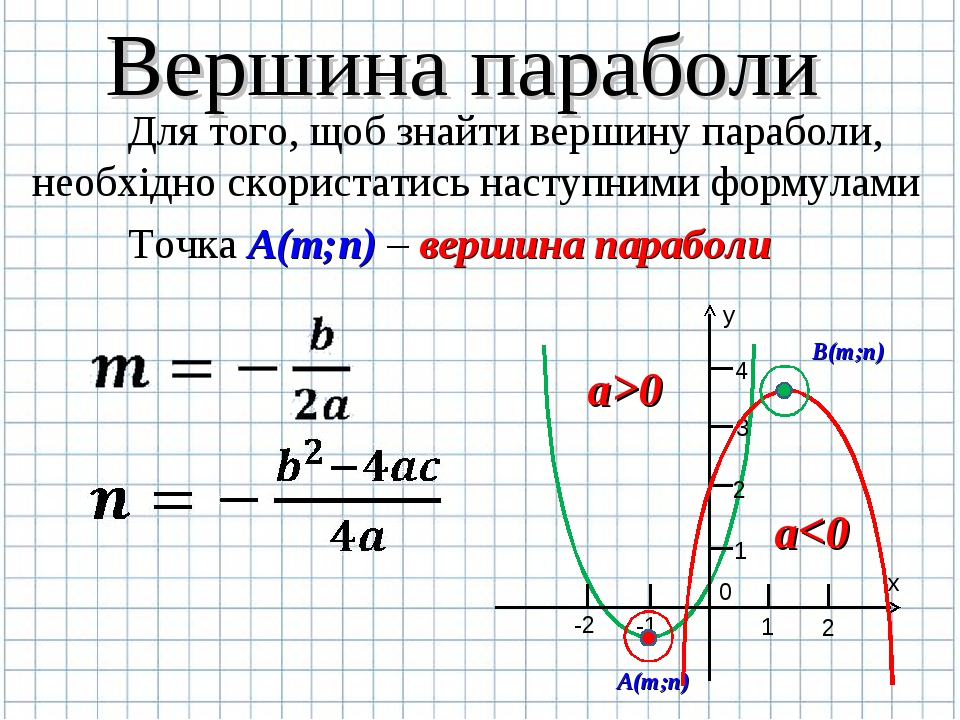 Курс в одну сторону длился 5,00 миль. Скорость ускорения часто описывается временем, необходимое для достижения 60,0 миль / ч из состояния покоя. Если на этот раз было 4,00 с, и Берт ускорялся с этой скоростью, пока не достиг максимальной скорости, сколько времени потребовалось Берту, чтобы пройти курс?

21.(а) Мировой рекорд в беге на 100 метров среди мужчин на Олимпийских играх 2008 года в Пекине был установлен Усэйном Болтом из Ямайки. Болт «выбежал» по финишу со временем 9,69 с. Если мы предположим, что Болт ускорялся в течение 3,00 с, чтобы достичь своей максимальной скорости, и сохранял эту скорость до конца гонки, вычислите его максимальную скорость и его ускорение. (b) Во время той же Олимпиады Болт также установил мировой рекорд в беге на 200 м со временем 19,30 с. Используя те же предположения, что и для бега на 100 м, какова была его максимальная скорость в этой гонке?

Избранные решения проблем и упражнения

1.10,8 м / с

(б)

2. 38,9 м / с (около 87 миль в час)

4. (а) 16,5 с (б) 13,5 с (в) -2,68 м / с ²

6. (a) 20,0 м (b) -1,00 м / с (c) Этот результат не имеет смысла. Если бегун стартует со скоростью 9,00 м / с и замедляет скорость 2,00 м / с ², то она остановится через 4,50 с. Если она продолжит замедляться, она будет бежать назад.

8. 0,799 м

10. (a) 28,0 м / с (b) 50,9 с (c) 7,68 км для разгона и 713 м для замедления

12.(а) 51,4 м (б) 17,1 с

14. (а) -80 м / с ² (б) 9,33 × 10 ^— ² с

16. (а) 7,7 м / с (б) -15 × 10 ² м / с ² Это примерно в 3 раза больше замедления пилотов, падающих с тысячи метров!

18. (a) 36,2 м / с ² (b) 162 м / с (c) v> v _max, потому что предположение о постоянном ускорении недействительно для драгстера. Драгстер переключает передачи и будет иметь большее ускорение на первой передаче, чем на второй передаче, чем на третьей передаче и т. Д.Ускорение будет наибольшим вначале, поэтому он не будет ускоряться со скоростью 32 м / с ² в течение последних нескольких метров, а будет значительно меньше, а конечная скорость будет меньше 162 м / с.

20. 104 с

21. (а) v = 12/2 м / с; a = 4,07 м / с ² (б) v = 11,2 м / с

3.6 Определение скорости и смещения по ускорению — University Physics Volume 1

3 Движение по прямой

Цели обучения

К концу этого раздела вы сможете:

Выведите кинематические уравнения для постоянного ускорения с помощью интегрального исчисления.
Используйте интегральную формулировку кинематических уравнений при анализе движения.
Найдите функциональную форму зависимости скорости от времени с учетом функции ускорения.
Найдите функциональную форму зависимости положения от времени с учетом функции скорости.

В этом разделе предполагается, что у вас достаточно знаний в области вычислений, чтобы быть знакомыми с интеграцией. В разделах «Мгновенная скорость и скорость», «Среднее и мгновенное ускорение» мы ввели кинематические функции скорости и ускорения с использованием производной.Взяв производную функции положения, мы нашли функцию скорости, и аналогичным образом взяв производную функции скорости, мы нашли функцию ускорения. Используя интегральное исчисление, мы можем работать в обратном направлении и вычислять функцию скорости из функции ускорения и функцию положения из функции скорости.

Кинематические уравнения из интегрального исчисления

Начнем с частицы с ускорением , а (t) — известная функция времени.Поскольку производной функции скорости по времени является ускорение,

мы можем взять неопределенный интеграл от обеих сторон, найдя

, где C ₁ — постоянная интегрирования. С

г.

, скорость определяется как

Аналогично, производная по времени функции положения является функцией скорости,

Таким образом, мы можем использовать те же математические манипуляции, которые мы только что использовали, и найти

, где C ₂ — вторая постоянная интегрирования.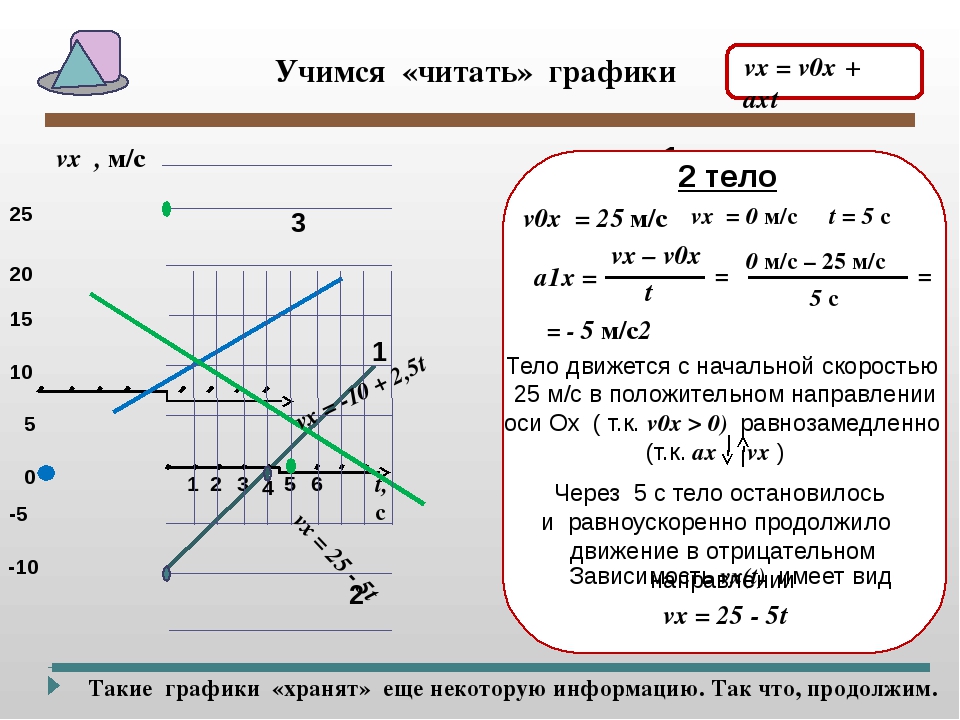

Мы можем вывести кинематические уравнения для постоянного ускорения, используя эти интегралы. Если a ( t ) = a a константа, и выполняя интегрирование в (рисунок), мы находим

Если начальная скорость v (0) = v ₀, то

Тогда, C ₁ = v ₀ и

(Уравнение).Подстановка этого выражения в (рисунок) дает

Делая интеграцию, находим

Если x (0) = x ₀, имеем

так, C ₂ = x ₀. Подставляя обратно в уравнение для x ( t ), мы, наконец, имеем

(Уравнение).

Пример

Движение моторной лодки

Моторная лодка движется с постоянной скоростью 5.0 м / с, когда он начинает замедляться, чтобы прибыть в док. Его ускорение

. а) Какова функция скорости моторной лодки? (б) В какое время скорость достигает нуля? (c) Какова функция местоположения моторной лодки? (d) Каково смещение моторной лодки с момента начала замедления до момента, когда скорость равна нулю? (e) Постройте график функций скорости и положения.

Стратегия

(a) Чтобы получить функцию скорости, мы должны интегрировать и использовать начальные условия, чтобы найти постоянную интегрирования.(b) Мы устанавливаем функцию скорости равной нулю и решаем для t . (c) Точно так же мы должны интегрировать, чтобы найти функцию положения, и использовать начальные условия, чтобы найти постоянную интегрирования. (d) Поскольку начальное положение принимается равным нулю, нам нужно только оценить функцию положения на

Решение

Возьмем t = 0 за время начала замедления лодки.

Из функциональной формы ускорения мы можем решить (рисунок), чтобы получить v ( t ): [раскрыть-ответ q = ”136447 ″] Показать ответ [/ раскрыть-ответ]
[hidden-answer a = ”136447 ″]
При t = 0 имеем v (0) = 5. 0 м / с = 0 + C1, поэтому C1 = 5,0 м / с или
. [/ Hidden-answer]
[show-answer q = ”967265 ″] Показать ответ [/ show-answer]
[hidden-answer a =” 967265 ″]
[/ hidden-answer]
Решить (рисунок): [show-answer q = ”251505 ″] Показать ответ [/ show-answer]
[hidden-answer a = ”251505 ″]
При t = 0 мы устанавливаем x (0) = 0 = x0, так как нас интересует только смещение с момента начала замедления лодки.У нас
Следовательно, уравнение для положения —
[/ hidden-answer]
[show-answer q = ”330950 ″] Показать ответ [/ show-answer]
[hidden-answer a =” 330950 ″] Поскольку начальная позиция принимается равной нулю, нам нужно вычислить x (t) только тогда, когда скорость равна нулю. Это происходит при t = 6,3 с. Следовательно, смещение равно
[/ hidden-answer]

Рис. 3.30 (a) Скорость катера как функция времени.

Катер снижает скорость до нуля за 6,3 с. Иногда скорость становится отрицательной — это означает, что лодка меняет направление. (b) Положение моторной лодки как функция времени. В момент времени t = 6,3 с скорость равна нулю, и лодка остановилась. В разы больше, чем это значение, скорость становится отрицательной — это означает, что если лодка продолжает двигаться с тем же ускорением, она меняет направление и направляется обратно к тому месту, откуда она началась.

Значение

Функция ускорения линейна по времени, поэтому интегрирование включает простые полиномы.На (Рисунок) мы видим, что если мы продолжим решение за точку, когда скорость равна нулю, скорость станет отрицательной, и лодка изменит направление. Это говорит нам о том, что решения могут предоставить нам информацию, выходящую за рамки наших непосредственных интересов, и мы должны быть осторожны при их интерпретации.

Проверьте свое понимание

Частица стартует из состояния покоя и имеет функцию ускорения.

. а) Что такое функция скорости? б) Что такое функция положения? (c) Когда скорость равна нулю?

[show-answer q = ”fs-id1168057352922 ″] Показать решение [/ show-answer]

[скрытый-ответ a = ”fs-id1168057352922 ″]

Функция скорости представляет собой интеграл от функции ускорения плюс постоянную интегрирования.По (Рисунок),
Поскольку v (0) = 0, имеем C ₁ = 0; итак,
По (рисунок),
. Так как x (0) = 0, мы имеем C ₂ = 0 и
Скорость может быть записана как v ( t ) = 5 t (1 — t ), что равно нулю при t = 0 и t = 1 с.

[/ hidden-answer]

Сводка

Интегральное исчисление дает нам более полную формулировку кинематики.
Если известно ускорение a ( t ), мы можем использовать интегральное исчисление для получения выражений для скорости v ( t ) и положения x ( t ).
Если ускорение постоянное, интегральные уравнения сводятся к (Рисунок) и (Рисунок) для движения с постоянным ускорением.

Ключевые уравнения

«>

Рабочий объем
Полный рабочий объем
Средняя скорость
Мгновенная скорость
Средняя скорость
Мгновенная скорость
Среднее ускорение
Мгновенное ускорение
Положение от средней скорости
Средняя скорость
Скорость от разгона
Положение по скорости и ускорению
Скорость на расстоянии
Скорость свободного падения
Высота свободного падения
Скорость свободного падения с высоты
Скорость от разгона
Положение от скорости

Концептуальные вопросы

Если задана функция ускорения, какая дополнительная информация необходима для нахождения функции скорости и функции положения?

Проблемы

Ускорение частицы меняется со временем в соответствии с уравнением

. Изначально скорость и положение равны нулю. а) Какова скорость как функция времени? б) Каково положение как функция времени?

Между t = 0 и t = t ₀, ракета движется прямо вверх с ускорением, определяемым

, где A и B — константы. (a) Если x в метрах, а t в секундах, каковы единицы измерения A и B ? (b) Если ракета стартует из состояния покоя, как изменяется скорость от t = 0 до t = t ₀? (c) Если ее начальное положение равно нулю, каково положение ракеты в зависимости от времени в течение этого же временного интервала?

[показывать-ответ q = ”fs-id1168055134758 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1168055134758 ″]

а.

;
г.

;

г.

[/ hidden-answer]

Скорость частицы, движущейся вдоль оси x- , изменяется со временем в соответствии с

, где A = 2 м / с, B = 0,25 м и

. Определите ускорение и положение частицы при t = 2,0 с и t = 5.0 с. Предположим, что

Покоящаяся частица покидает начало координат со скоростью, увеличивающейся со временем согласно v ( t ) = 3,2 t м / с. На 5,0 с скорость частицы начинает уменьшаться в соответствии с [16,0 — 1,5 ( т — 5,0)] м / с. Это уменьшение продолжается до t = 11,0 с, после чего скорость частицы остается постоянной на уровне 7,0 м / с. а) Каково ускорение частицы как функция времени? (б) Каково положение частицы при t = 2.0 с, т = 7,0 с и т = 12,0 с?

[показывать-ответ q = ”fs-id1168055121296 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1168055121296 ″]

а.

;
г.

[/ hidden-answer]

Дополнительные проблемы

Профессиональный бейсболист Нолан Райан мог подавать бейсбольный мяч со скоростью примерно 160,0 км / ч. При такой средней скорости, сколько времени потребовалось мячу, брошенному Райаном, чтобы достичь своей тарелки, а это 18.4 м от насыпи питчера? Сравните это со средним временем реакции человека на визуальный стимул, которое составляет 0,25 с.

Самолет вылетает из Чикаго и совершает 3000-километровый перелет в Лос-Анджелес за 5,0 ч. Второй самолет вылетает из Чикаго через полчаса и одновременно прибывает в Лос-Анджелес. Сравните средние скорости двух плоскостей. Не обращайте внимания на кривизну Земли и разницу в высоте между двумя городами.

[показывать-ответ q = ”fs-id1168055151090 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1168055151090 ″]

Двигайтесь на запад в положительном направлении.

1-й самолет:

2-й самолет

[/ hidden-answer]

Необоснованные результаты Велосипедист едет на 16,0 км на восток, затем на 8,0 км на запад, затем на 8,0 км на восток, затем на 32,0 км на запад и, наконец, на 11,2 км на восток.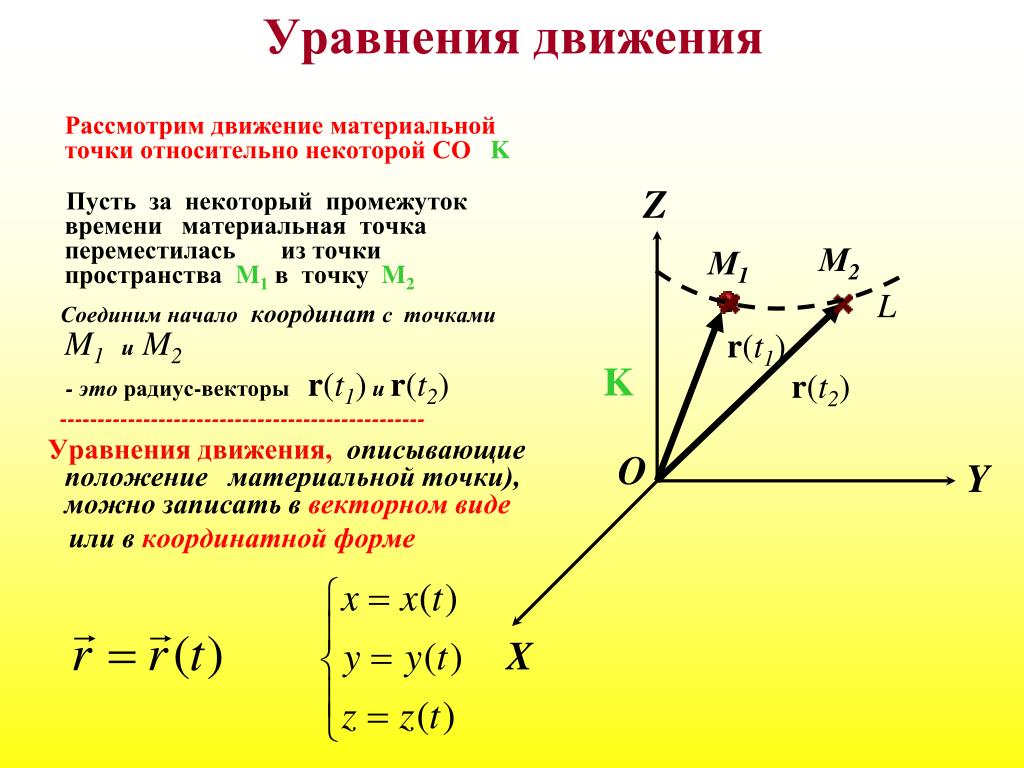 Если его средняя скорость составляет 24 км / ч, сколько времени ему потребовалось, чтобы завершить поездку? Это разумное время?

Объект имеет ускорение

. На

, его скорость

.Определите скорости объекта на

[показывать-ответ q = ”fs-id1168055302745 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1168055302745 ″]

;

[/ hidden-answer]

Частица движется по оси x в соответствии с уравнением

г.Какие скорость и ускорение у

с и

с?

Частица, движущаяся с постоянным ускорением, имеет скорость

при

с и

при

с. Что такое ускорение частицы?

[показывать-ответ q = ”fs-id1168055307822 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1168055307822 ″]

[/ hidden-answer]

Поезд движется по крутому склону с постоянной скоростью (см. Следующий рисунок), когда его камбуз отрывается и начинает свободно катиться по рельсам.Через 5,0 с камбуз отстает от поезда на 30 м. Какое ускорение у камбуза?

Электрон движется по прямой со скоростью

м / с. Он входит в область длиной 5,0 см, где испытывает ускорение

по той же прямой. а) Какова скорость электрона, когда он выходит из этой области? б) Сколько времени нужно электрону, чтобы пересечь область?

[показывать-ответ q = ”fs-id1168055302554 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1168055302554 ″]

а.

;

г.

[/ hidden-answer]

Водитель скорой помощи доставляет пациента в больницу. Двигаясь со скоростью 72 км / ч, она замечает, что светофор на ближайших перекрестках стал желтым. Чтобы добраться до перекрестка до того, как загорится красный свет, она должна проехать 50 м за 2,0 с. (a) Какое минимальное ускорение должно быть у машины скорой помощи, чтобы добраться до перекрестка, прежде чем загорится красный свет? б) Какова скорость машины скорой помощи на перекрестке?

Мотоцикл, который замедляет скорость, равномерно покрывает 2. 0 последовательных км за 80 с и 120 с соответственно. Рассчитайте (а) ускорение мотоцикла и (б) его скорость в начале и в конце 2-километровой поездки.

[show-answer q = ”fs-id1168057524743 ″] Показать решение [/ show-answer]

[скрытый-ответ a = ”fs-id1168057524743 ″]

;

решайте одновременно, чтобы получить

, что составляет

.Скорость в конце пути

.
[/ hidden-answer]

Велосипедист едет из пункта А в пункт Б за 10 мин. В течение первых 2,0 мин поездки она поддерживает равномерное ускорение

. Затем она движется с постоянной скоростью следующие 5,0 мин. Затем она замедляется с постоянной скоростью, так что она приходит в состояние покоя в точке B на 3,0 мин позже. (а) Нарисуйте график зависимости скорости от времени для поездки. (б) Какое ускорение произошло за последние 3 минуты? (c) Как далеко едет велосипедист?

Два поезда движутся со скоростью 30 м / с в противоположных направлениях по одному и тому же пути. Инженеры одновременно видят, что они идут на встречу, и тормозят, когда они находятся на расстоянии 1000 м друг от друга. Предполагая, что оба поезда имеют одинаковое ускорение, каким должно быть это ускорение, если поезда должны останавливаться незадолго до столкновения?

[показывать-ответ q = ”fs-id1168055171872 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1168055171872 ″]

[/ hidden-answer]

Грузовик длиной 10,0 м, движущийся с постоянной скоростью 97.0 км / ч проезжает автомобиль длиной 3,0 м, движущийся с постоянной скоростью 80,0 км / ч. Сколько времени проходит между моментом, когда передняя часть грузовика сравняется с задней частью автомобиля, и моментом, когда задняя часть грузовика сравняется с передней частью автомобиля?

Полицейская машина ждет в укрытии немного в стороне от шоссе. Полицейская замечает мчащуюся машину со скоростью 40 м / с. В тот момент, когда машина, превышающая скорость, проезжает мимо полицейской машины, полицейская машина ускоряется из состояния покоя со скоростью 4 м / с ², чтобы поймать ускоряющуюся машину.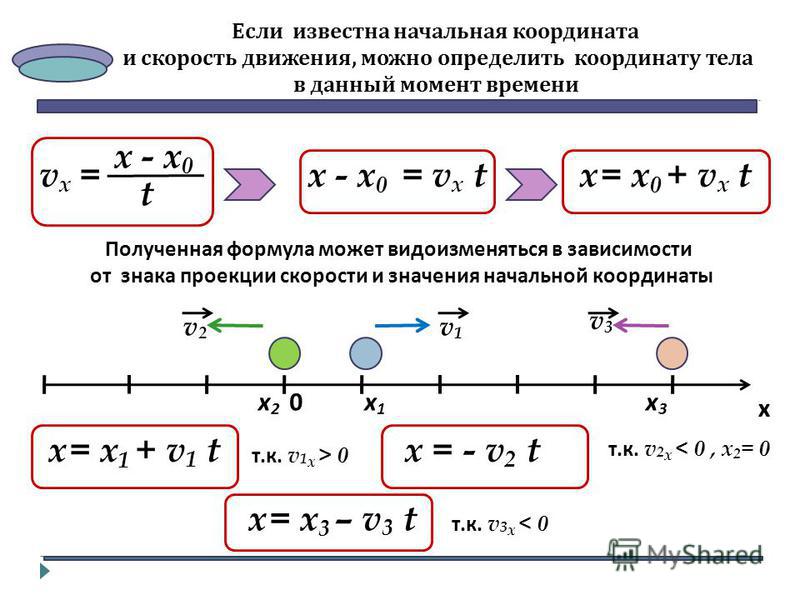 Сколько времени нужно полицейской машине, чтобы догнать мчащуюся машину?

[показывать-ответ q = ”fs-id1168055306834 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1168055306834 ″]

Уравнение для ускоряющегося автомобиля: этот автомобиль имеет постоянную скорость, которая является средней скоростью, и не ускоряется, поэтому используйте уравнение для перемещения с

; Уравнение для полицейской машины: эта машина ускоряется, поэтому используйте уравнение для перемещения с

, так как полицейская машина трогается с места:

; Теперь у нас есть уравнение движения для каждой машины с общим параметром, который можно исключить, чтобы найти решение.В этом случае мы решаем

. Шаг 1, устранение

; Шаг 2, решение для

. Мчащийся автомобиль имеет постоянную скорость 40 м / с, которая является его средней скоростью. Ускорение полицейской машины составляет 4 м / с ². Оценивая t , время, за которое полицейская машина достигает скорости, мы получаем

.
[/ hidden-answer]

Пабло бежит полумарафон со скоростью 3 м / с. Другой бегун, Джейкоб, с той же скоростью отстает от Пабло на 50 метров. Джейкоб начинает ускоряться со скоростью 0,05 м / с ². а) Сколько времени нужно Иакову, чтобы поймать Пабло? б) Какое расстояние преодолел Иаков? в) Какова конечная скорость Иакова?

Неприемлемые результаты Бегун приближается к финишу и находится на расстоянии 75 м; ее средняя скорость в этом положении составляет 8 м / с.В этот момент она замедляется со скоростью 0,5 м / с ². Сколько времени ей нужно, чтобы пересечь финишную черту с расстояния 75 м? Это разумно?

[показывать-ответ q = ”fs-id1168055381859 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1168055381859 ″]

На этом разгоне она доходит до полной остановки в

, но пройденное расстояние —

, что меньше расстояния, на которое она отошла от финиша, поэтому она никогда не финиширует.
[/ hidden-answer]

Самолет ускоряется со скоростью 5,0 м / с ² за 30,0 с. За это время он преодолевает расстояние 10,0 км. Каковы начальная и конечная скорости самолета?

Сравните расстояние, пройденное объектом, скорость которого в два раза превышает начальную скорость, с объектом, который изменяет свою скорость в четыре раза по сравнению с начальной скоростью за тот же период времени. Ускорения обоих объектов постоянны.

[показывать-ответ q = ”fs-id1168055323241 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1168055323241 ″]

[/ hidden-answer]

Объект движется на восток с постоянной скоростью и находится в позиции

.(а) С каким ускорением должен иметь объект, чтобы его полное смещение в дальнейшем стало равным нулю t ? (б) Какова физическая интерпретация решения в случае

Мяч брошен прямо вверх. На своем пути вверх он проходит окно высотой 2,00 м над землей на высоте 7,50 м и проходит за 1,30 с. Какая была начальная скорость мяча?

[показывать-ответ q = ”fs-id11680553

″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id11680553

″]

скорость внизу окна.

[/ hidden-answer]

Монета сбрасывается с воздушного шара, который находится на высоте 300 м над землей и поднимается вверх со скоростью 10,0 м / с. Для монеты найдите (а) максимальную достигнутую высоту, (б) ее положение и скорость через 4,00 с после выпуска и (в) время до того, как она упадет на землю.

Мягкий теннисный мяч падает на твердый пол с высоты 1,50 м и отскакивает от него на высоте 1,10 м. (а) Рассчитайте его скорость непосредственно перед тем, как он ударится об пол.(б) Рассчитайте его скорость сразу после того, как он покинет пол на обратном пути вверх. (c) Рассчитайте его ускорение во время контакта с полом, если этот контакт длится 3,50 мс

(d) Насколько сильно мяч сжался при столкновении с полом, если предположить, что пол абсолютно жесткий?

[показывать-ответ q = ”fs-id1168055325521 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1168055325521 ″]

а.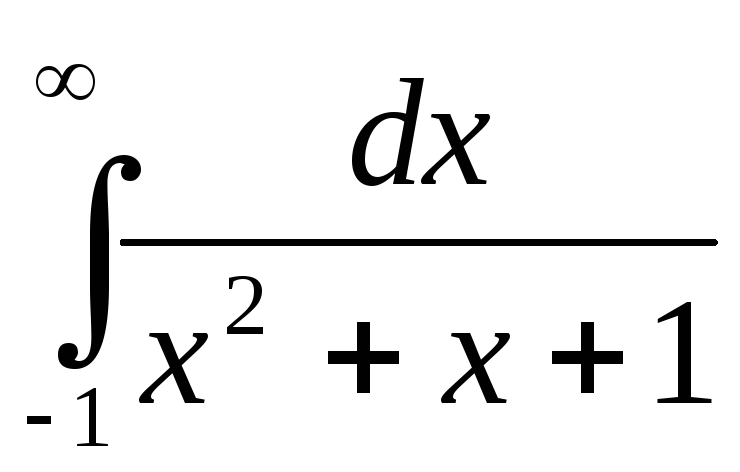

;
г.

;

г.

;

г.

[/ hidden-answer]

Необоснованные результаты . Капля дождя падает из облака на высоте 100 м над землей. Пренебрегайте сопротивлением воздуха. Какова скорость капли дождя, когда она падает на землю? Это разумное число?

Сравните время в воздухе баскетболиста, подпрыгнувшего на 1,0 м вертикально от пола, с временем игрока, прыгнувшего 0.3 м по вертикали.

[show-answer q = ”fs-id1168057418927 ″] Показать решение [/ show-answer]

[скрытый-ответ a = ”fs-id1168057418927 ″]

Рассмотрим падение игроков с высоты 1,0 м и 0,3 м.

0,9 с

0,5 с

[/ hidden-answer]

Предположим, что человеку требуется 0,5 с, чтобы отреагировать и переместить руку, чтобы поймать предмет, который он уронил. (а) Как далеко упадет объект на Земле, где

(b) Как далеко объект падает на Луну, где ускорение свободного падения составляет 1/6 от земного?

Воздушный шар поднимается с уровня земли с постоянной скоростью 3. 0 м / с. Через минуту после старта с воздушного шара случайно падает мешок с песком. Рассчитайте (а) время, необходимое мешку с песком, чтобы достичь земли, и (б) скорость мешка с песком, когда он ударяется о землю.

[показывать-ответ q = ”fs-id1168055469821 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1168055469821 ″]

а.

берет положительный корень;
г.

[/ hidden-answer]

(a) На Олимпийских играх 2008 года в Пекине Усэйн Болт из Ямайки установил мировой рекорд в беге на 100 метров среди мужчин.Болт «выбежал» по финишу со временем 9,69 с. Если мы предположим, что Болт ускорялся в течение 3,00 с, чтобы достичь своей максимальной скорости, и сохранял эту скорость до конца гонки, вычислите его максимальную скорость и его ускорение. (b) Во время той же Олимпиады Болт также установил мировой рекорд в беге на 200 м со временем 19,30 с. Используя те же предположения, что и для бега на 100 м, какова была его максимальная скорость в этой гонке?

Предмет упал с высоты 75,0 м над уровнем земли. (а) Определите расстояние, пройденное за первую секунду. (b) Определите конечную скорость, с которой объект ударяется о землю. (c) Определите расстояние, пройденное за последнюю секунду движения до удара о землю.

[show-answer q = ”fs-id1168055273683 ″] Показать решение [/ show-answer]

[скрытый-ответ a = ”fs-id1168055273683 ″]

а.

;
г.

;

г.

[/ hidden-answer]

Стальной шар падает на твердый пол с высоты 1.50 м и подборы на высоту 1,45 м. (а) Рассчитайте его скорость непосредственно перед тем, как он ударится об пол. (б) Рассчитайте его скорость сразу после того, как он покинет пол на обратном пути вверх. (c) Рассчитайте его ускорение при контакте с полом, если этот контакт длится 0,0800 мс

(d) Насколько сильно мяч сжался при столкновении с полом, если предположить, что пол абсолютно жесткий?

Объект упал с крыши здания высотой х . За последнюю секунду спуска он падает на расстояние ч /3. Рассчитайте высоту здания.

[показывать-ответ q = ”fs-id11680554 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id11680554 ″]

, ч = общая высота и время падения на землю

за т — за 1 секунду падает 2/3 ч

или

т = 5.45 с и ч = 145,5 м. Другой корень меньше 1 с. Проверить на т = 4,45 с

[/ hidden-answer]

Задачи

В беге на 100 м победитель определяется за 11,2 с. Время занявшего второе место — 11,6 с. Как далеко игрок, занявший второе место, отстает от победителя, когда она пересекает финишную черту? Предположим, что скорость каждого бегуна постоянна на протяжении всего забега.

Положение частицы, движущейся по оси x , изменяется со временем в соответствии с

г. Найдите (а) скорость и ускорение частицы как функции времени, (б) скорость и ускорение при t = 2,0 с, (в) время, в которое положение является максимальным, (г) время при скорость которого равна нулю, и (e) максимальное положение.

[show-answer q = ”fs-id1168055269782 ″] Показать решение [/ show-answer]

[скрытый-ответ a = ”fs-id1168055269782 ″]

а.

;
г.

; c.Наклон функции положения равен нулю или скорость равна нулю. Есть два возможных решения: t = 0, что дает x = 0, или t = 10,0 / 12,0 = 0,83 с, что дает x = 1,16 м. Второй ответ — правильный выбор; d. 0,83 с (э) 1,16 м

[/ hidden-answer]

Велосипедист делает спринт в конце гонки, чтобы одержать победу. Она имеет начальную скорость 11,5 м / с и разгоняется со скоростью 0,500 м / с ² за 7.00 с. а) Какова ее конечная скорость? (b) Велосипедист продолжает движение на этой скорости до финиша. Если она находится в 300 м от финиша, когда начинает ускоряться, сколько времени она сэкономила? (c) Победитель, занявший второе место, был на 5,00 м впереди, когда победитель начал ускоряться, но он не смог ускориться и ехал со скоростью 11,8 м / с до финиша. Какая разница во времени финиша в секундах между победителем и занявшим второе место? Как далеко назад был занявший второе место, когда победитель пересек финишную черту?

В 1967 году новозеландец Берт Манро установил мировой рекорд для индийского мотоцикла на соляных равнинах Бонневиль в штате Юта — 295 человек.38 км / ч. Трасса в одну сторону составила 8,00 км. Скорость ускорения часто описывается временем, необходимое для достижения 96,0 км / ч из состояния покоя. Если на этот раз было 4,00 с, и Берт ускорялся с этой скоростью, пока не достиг максимальной скорости, сколько времени потребовалось Берту, чтобы пройти курс?

[показывать-ответ q = ”fs-id1168057239219 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1168057239219 ″]

, 295,38 км / ч = 82,05 м / с,

Пора разогнаться до максимума

расстояние при разгоне

при постоянной скорости

, итого время

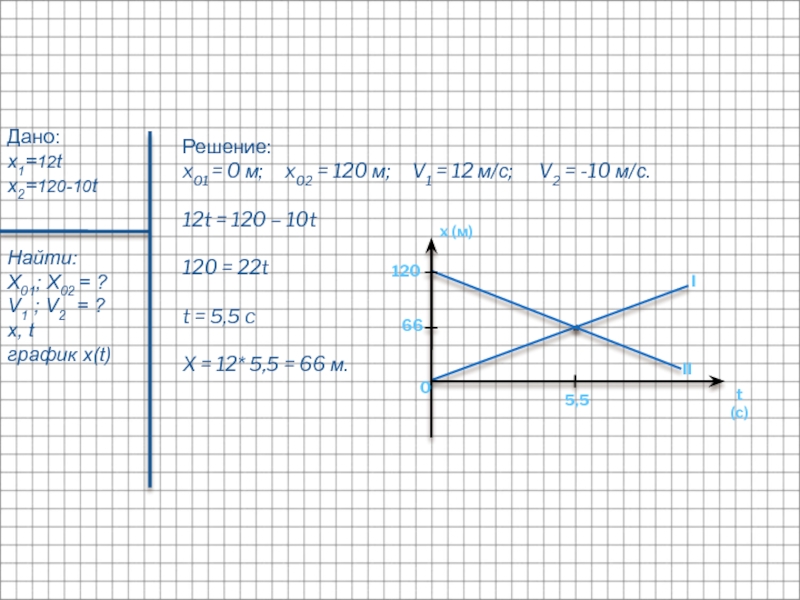
[/ hidden-answer]

Учебные пособия и практические занятия д-ра Юэ-Лин Вонга

Общая физика :: Движение снаряда :: Как рассчитать # 1

Проблема №1: Найти где приземлится пушечное ядро, учитывая начальную скорость ( v ₀ ) и угол стрельбы ( θ ₀ )
(параметры, значения которых известны, выделены красным.Основное направление решения проблемы: попытаться вывести уравнения которые используют эти параметры с известными значениями.)

Пошаговое описание решения:

Разложите вектор начальной скорости на компоненты x и y.
Начальная скорость:
X-компонента: v _x0 = v ₀ × cos θ ₀
Y-компонента: v _y0 = v ₀ × sin θ ₀

Независимый анализ горизонтального и вертикального движения:

Вертикальное движение: использовать постоянную ускорение (g)
v _y = v _y0 — g × t

, где g — сила тяжести (9. 8 м / сек) или в свободном падении ускорение, а t — прошедшее время.

Когда объект достигает вершины его траектория движения параболы, v _y = 0 .

т.е. v _y0 — g × t _max = 0

Þ т _макс = v _y0 / g

где t _max — время, за которое объект достигает максимума высота.

Шаг 2
Вычислить:	т _макс
От:	v _y0
Попробуйте: Используйте значения v _y0 , полученные выше для расчета времени (t _max), когда объект достигает своего максимума высота: т _макс = v _y0 / g т _макс = м / сек. / 9,8 м / сек. = 0,408 сек.

Итак, теперь вы знаете, сколько времени требуется, чтобы объект достиг вершины его траектория движения параболы. После этого он начнет падать.

Что выясняет это время, чтобы выяснить, где пушечное ядро приземлится и горизонтальное положение, когда оно достигнет высшая точка?

Из-за симметрии вертикального движения требуется столько же времени для пушечного ядра, чтобы вернуться на землю (предположим, что пушечное ядро мяч был запущен на уровне земли).Таким образом, весь путь пушки мяч, от выстрела до возвращения на землю, занимает:

Шаг 3
Вычислить:	т _всего
От:	т _макс
Попробуйте: Используйте t _max, полученное выше для расчета общего времени (t _всего) для ядро для возврата на землю: т _всего = 2 × т _макс т _всего = 2 × сек. = 0,816 сек.

Например, если пушечному ядру требуется 3 секунды, чтобы достичь максимума точки на его траектории движения параболы, то для это вернуться с самой высокой точки. Общее время на пушку Возвращение мяча в землю после выстрела составляет 6 секунд.

Эту информацию о времени можно использовать для расчета, где ядро приземлится. (См. Анализ горизонтального движения ниже)

Горизонтальное движение: использовать постоянную скорость (v _x)
v _x = v _x0
горизонтальное расстояние (d _x), пройденное ядром при приземлении на землю:

[при обработке этой директивы произошла ошибка]

Исчисление I — метод Ньютона

Показать мобильное уведомление Показать все заметки Скрыть все заметки
Похоже, вы используете устройство с «узкой» шириной экрана ( i. е. вы, вероятно, пользуетесь мобильным телефоном). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать их, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 4-13: Метод Ньютона
Следующее приложение, которое мы рассмотрим в этой главе, — это важное приложение, которое используется во многих областях.Если вы до сих пор следили за главой, вполне возможно, что у вас сложилось впечатление, что многие из рассмотренных нами приложений созданы нами для того, чтобы вы работали. Это прискорбно, потому что все приложения, которые мы рассмотрели до этого момента, являются реальными приложениями, которые действительно используются в реальных ситуациях. Проблема часто заключается в том, что для работы с более значимыми примерами приложений нам потребуется больше знаний о науке и / или физике, стоящих за этой проблемой, чем мы обычно располагаем.Без этих знаний мы вынуждены приводить довольно упрощенные примеры, которые часто не кажутся очень реалистично, и поэтому трудно понять, что приложение, которое мы рассматриваем, является настоящим приложением.
Это изменится в этом разделе. Это приложение, которое мы все можем понять, и все мы можем понять, что иногда приходится делать это, даже если мы не понимаем физику / науку, лежащую в основе реального приложения.
В этом разделе мы рассмотрим метод приближения решений уравнений.Все мы знаем, что уравнения нужно решать время от времени, и на самом деле мы сами решили довольно много уравнений к этому моменту. Во всех примерах, которые мы рассмотрели до этого момента, мы действительно могли найти решения, но не всегда возможно сделать это точно и / или выполнить работу вручную.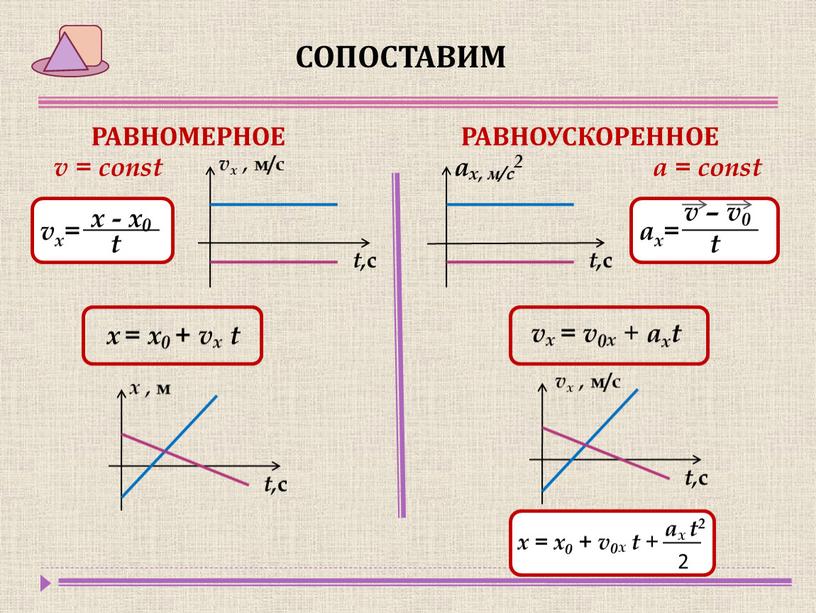 Вот тут-то и пригодится это приложение. Итак, давайте посмотрим, что это за приложение.
Предположим, что мы хотим приблизить решение к \ (f \ left (x \ right) = 0 \), а также предположим, что мы каким-то образом нашли начальное приближение к этому решению, скажем, \ ({x_0} \).Это начальное приближение, вероятно, не так уж и хорошо, на самом деле это может быть не более чем быстрое предположение, которое мы сделали, и поэтому мы хотели бы найти лучшее приближение. Сделать это достаточно просто. Сначала мы получим касательную к \ (f \ left (x \ right) \) в точке \ ({x_0} \).
\ [y = f \ left ({{x_0}} \ right) + f ‘\ left ({{x_0}} \ right) \ left ({x — {x_0}} \ right) \]
Теперь взгляните на график ниже.
Синяя линия (если вы все равно читаете это в цвете…) — это касательная линия в точке \ ({x_0} \).Мы видим, что эта линия пересекает ось \ (x \) гораздо ближе к фактическому решению уравнения, чем \ ({x_0} \). Назовем эту точку, где касательная в \ ({x_0} \) пересекает \ (x \) — ось \ ({x_1} \), и мы будем использовать эту точку в качестве нашего нового приближения к решению.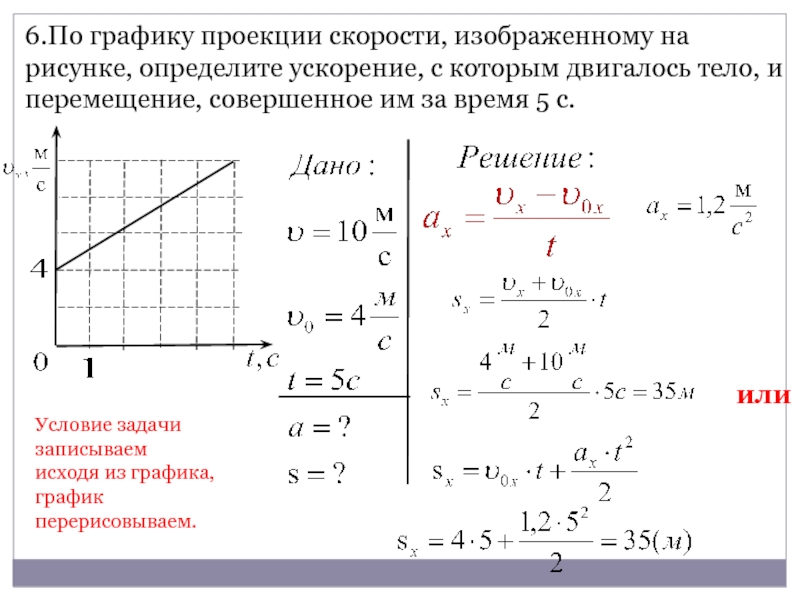
Итак, как нам найти эту точку? Мы знаем его координаты, \ (\ left ({{x_1}, 0} \ right) \), и мы знаем, что он находится на касательной, поэтому подключите эту точку к касательной и решите относительно \ ({x_1} \ ) следующим образом:
\ [\ begin {align *} 0 & = f \ left ({{x_0}} \ right) + f ‘\ left ({{x_0}} \ right) \ left ({{x_1} — {x_0}} \ справа) \\ {x_1} — {x_0} & = — \ frac {{f \ left ({{x_0}} \ right)}} {{f ‘\ left ({{x_0}} \ right)}} \ \ {x_1} & = {x_0} — \ frac {{f \ left ({{x_0}} \ right)}} {{f ‘\ left ({{x_0}} \ right)}} \ end {align * } \]
Итак, мы можем найти новое приближение при условии, что производная не равна нулю в исходном приближении.
Теперь мы повторяем весь процесс, чтобы найти еще лучшее приближение. Мы формируем касательную линию к \ (f \ left (x \ right) \) в \ ({x_1} \) и используем ее корень, который мы назовем \ ({x_2} \), как новое приближение к фактическое решение. Если мы сделаем это, мы придем к следующей формуле.
\ [{x_2} = {x_1} — \ frac {{f \ left ({{x_1}} \ right)}} {{f ‘\ left ({{x_1}} \ right)}} \]
Эта точка также показана на графике выше, и мы можем видеть из этого графика, что если мы продолжим следовать этому процессу, мы получим последовательность чисел, которая очень приближается к фактическому решению.Этот процесс называется методом Ньютона.
Вот общий метод Ньютона
Метод Ньютона
Если \ ({x_n} \) является приближением решения \ (f \ left (x \ right) = 0 \) и если \ (f ‘\ left ({{x_n}} \ right) \ ne 0 \ ) следующее приближение дается выражением,
\ [{x_ {n + 1}} = {x_n} — \ frac {{f \ left ({{x_n}} \ right)}} {{f ‘\ left ({{x_n}} \ right)}} \]
Это должно привести к вопросу, когда нам остановиться? Сколько раз мы проходим этот процесс? Одна из наиболее распространенных точек остановки в процессе — это продолжение до тех пор, пока два последовательных приближения не согласятся с заданным количеством десятичных знаков.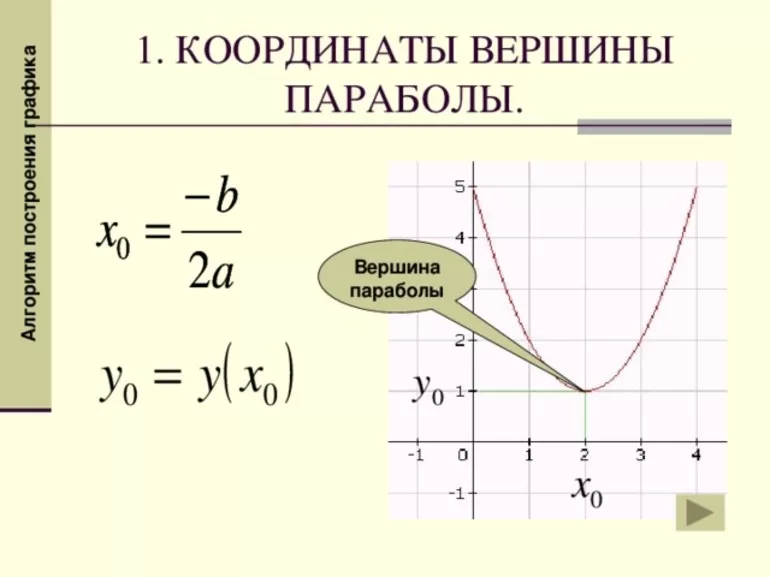
Прежде чем приступить к работе с какими-либо примерами, мы должны решить две проблемы. Во-первых, нам действительно нужно решить \ (f \ left (x \ right) = 0 \), чтобы применить метод Ньютона. На самом деле это не такая уж большая проблема, но мы должны убедиться, что уравнение находится в этой форме, прежде чем использовать метод.
Во-вторых, нам нужно каким-то образом получить начальное приближение к решению (, т.е. , нам нужно как-то \ ({x_0} \)). Один из наиболее распространенных способов получить \ ({x_0} \) — нарисовать график функции и использовать его для получения оценки решения, которое мы затем используем как \ ({x_0} \).Другой распространенный метод: если мы знаем, что есть решение функции в интервале, мы можем использовать середину интервала как \ ({x_0} \).
Давайте рассмотрим пример метода Ньютона.
Пример 1 Используйте метод Ньютона, чтобы определить приближение к решению \ (\ cos x = x \), которое лежит в интервале \ (\ left [{0,2} \ right] \). Найдите приближение до шести знаков после запятой. Показать решение
Во-первых, обратите внимание, что нам не давали первоначального предположения.Однако нам дали время, чтобы посмотреть. Мы будем использовать это, чтобы получить наше первоначальное предположение. Как отмечалось выше, общее практическое правило в этих случаях состоит в том, чтобы принять начальное приближение за середину интервала. Итак, мы будем использовать \ ({x_0} = 1 \) в качестве нашего первоначального предположения.
Затем напомним, что у нас должна быть функция в виде \ (f \ left (x \ right) = 0 \). Поэтому сначала перепишем уравнение как,
\ [\ cos x — x = 0 \]
Теперь мы можем записать общую формулу для метода Ньютона.Это часто немного упрощает работу, поэтому, как правило, это неплохая идея.
\ [{x_ {n + 1}} = {x_n} — \ frac {{\ cos x_ {n} — x_ {n}}} {{- \ sin x_ {n} — 1}} \]
Давайте теперь получим первое приближение.
\ [{x_1} = 1 — \ frac {{\ cos \ left (1 \ right) — 1}} {{- \ sin \ left (1 \ right) — 1}} = 0,7503638679 \]
Здесь мы должны указать, что фраза «шесть знаков после запятой» не означает, что нужно просто получить \ ({x_1} \) до шести знаков после запятой, а затем остановиться.Вместо этого это означает, что мы продолжаем, пока два последовательных приближения не согласятся с шестью десятичными знаками.
Учитывая это условие остановки, нам явно нужно сделать хотя бы один шаг дальше.
\ [{x_2} = 0,7503638679 — \ frac {{\ cos \ left (0,7503638679 \ right) — 0,7503638679}} {{- \ sin \ left ({0,7503638679} \ right) — 1}} = 0,73909 \]
Хорошо, мы делаем успехи. У нас есть приближение к 1 десятичному знаку. Давайте сделаем еще один, оставив детали вычислений вам.
\ [{x_3} = 0,73^{334 \] У нас есть три десятичных знака. Нам понадобится еще один.
\ [{x_4} = 0,73^{332 \] И теперь у нас есть два приближения, которые согласуются с 9 десятичными знаками, и мы можем остановиться. Предположим, что решение приблизительно равно \ ({x_4} = 0,73^{332 \).}
В этом последнем примере мы увидели, что нам не нужно выполнять слишком много вычислений, чтобы метод Ньютона дал нам приближение в желаемом диапазоне точности.Так будет не всегда. Иногда для достижения желаемой точности требуется много итераций процесса, а иногда он может полностью выйти из строя.
Следующий пример немного глупый, но он указывает на сбой метода. Пример 2 Используйте \ ({x_0} = 1 \), чтобы найти приближение к решению \ (\ sqrt [3] {x} = 0 \).
Показать решение Да, это глупый пример. Ясно, что решение — \ (x = 0 \), но это действительно очень важный момент.{- \ frac {2} {3}}}} = {x_n} — 3 {x_n} = — 2 {x_n} \]
На самом деле, здесь нам не нужно делать никаких вычислений. Эти вычисления удаляются все дальше и дальше от решения \ (x = 0 \) с каждой итерацией. Вот несколько вычислений, чтобы понять суть дела.
\ [\ begin {align *} {x_1} & = — 2 \\ {x_2} & = 4 \\ {x_3} & = — 8 \\ {x_4} & = 16 \\ & т. д. \ end {align * } \] Итак, в этом случае метод терпит неудачу, причем совершенно неуспешно.
Итак, нам нужно быть немного осторожнее с методом Ньютона. Обычно он быстро находит приближение к уравнению. Однако бывают случаи, когда это требует много работы или когда это вообще не работает.
Аппроксимация кривой — гипертекст по физике
Обсуждение
введение
Я украл это у «Triple A-S» (Американской ассоциации содействия развитию науки). Они знают, как это делать правильно, так зачем это менять.
Из-за своей абстрактности математика универсальна в том смысле, что другие области человеческой мысли — нет. Он находит полезные применения в бизнесе, промышленности, музыке, исторической науке, политике, спорте, медицине, сельском хозяйстве, инженерии, а также в социальных и естественных науках. Особенно сильна связь между математикой и другими областями фундаментальной и прикладной науки.
Я вижу одиннадцать различных полей, упомянутых в этом единственном предложении.Я занимаюсь только одним из них ежедневно, но я согласен с тем, что все они обязаны математике. Если вы принимаете решения о том, чему вы посвятите свою жизнь (или, по крайней мере, чему будете учиться профессионально), основываясь на некотором понятии «важности», тогда откажитесь от всего, кроме математики. Это одна из древнейших областей человеческого знания. Единственное, что старше, — это сельское хозяйство… эм… да… а еще есть инструменты, огонь и… ну, язык очень важен, а математика — прямо там. Ага по математике!
Что это значит для вас прямо сейчас?
Обычный способ работы.Предполагается, что между отображаемыми на графике величинами существует некоторая математическая связь. Данные стремятся к этому математическому идеалу, но из-за ограниченности людей и их инструментов они только приближаются к нему. Точки данных на графике образуют облако вокруг кривой функции. Если бы только у нас было лучшее «зрение». Если бы только наши устройства лучше записывали фактические значения. Если бы только мы действительно знали, в чем заключается сущность природы, чтобы мы могли назначить эти устройства их предназначенной задаче.Потом. Тогда мы увидим, что каждая точка данных попадает в точную аналитическую кривую. Ах, какой это был бы прекрасный мир. К сожалению, реальные данные никогда не выглядят в точности как идеальные кривые математики.
горизонтальная ось ( x ) вертикальная ось ( y )
независимая переменная зависимая переменная
объясняющая переменная переменная ответа
∞ ∝ α
бесконечность пропорционально Греческая «альфа»
Также.
категориальные переменные — представлены разными символами в одной системе координат
скрытые переменные или скрытые переменные — источник некоторых экспериментальных ошибок
В поисках отношений.
Ваш друг — символ соразмерности.
независимый
Посмотрите на кривую справа. Независимо от того, какое значение принимает переменная x на кривой, переменная y остается неизменной.Это классический пример отношений под названием независимость . Две величины являются независимыми , если одна не влияет на другую. Кривая представляет собой горизонтальную прямую линию, представленную уравнением общего вида…
y = к
, где k — постоянная.
Подходящим выводом из такой взаимосвязи будет то, что…
y не зависит от x .
y не зависит от x .
y константа для всех значений x .
y не зависит от x .
y и x независимы.
Например…
Ускорение свободного падения не зависит от массы. При отсутствии сопротивления воздуха тяжелые предметы падают так же быстро, как и легкие.
Период простого маятника не зависит от его массы. Простые маятники, которые идентичны во всех отношениях, за исключением веса груза на конце, будут качаться взад и вперед одинаковым образом.
Скорость света в вакууме c постоянна для всех значений v , скорости системы отсчета. Независимо от того, как я двигаюсь, скорость света в вакууме всегда остается неизменной.
На силу сухого трения не влияет площадь двух соприкасающихся поверхностей. Перетаскивание прямоугольника за его нижнюю или боковую часть приводит к той же силе трения.
Масса и местоположение не зависят. Если замороженная индейка имеет массу 10 кг в Нью-Йорке, она будет иметь массу 10 кг в Нью-Джерси, в Нью-Дели, на горе Эверест, в самолете, на орбите, на поверхности Луны, в Галактика Андромеды, в…Ну вы поняли.
Независимые отношения могут быть как скучными, так и глубокими. Скучно, когда мы понимаем, что между двумя величинами нет связи. Глубоко, когда мы понимаем, что определили фундаментальный принцип или основополагающую концепцию, имеющую большое значение. Независимость скорости света и скорости системы отсчета — одно из этих утверждений. Скорость света — фундаментальная постоянная, одна из трех или четырех в физике.
прямой
А теперь взгляните на эту кривую.По мере увеличения переменной x увеличивается и переменная y . Но есть много кривых, которые делают это. Что делает его уникальным? Что отличает его от всех остальных кривых, которые монотонно увеличиваются (как говорят математики) ? Ключ в форме — прямой негоризонтальной линии, проходящей через начало координат. С этой конкретной формой происходит нечто особенное.
Укажите точку на линии и запишите ее координаты. Удвойте значение переменной x и посмотрите, как отреагирует переменная y . Новое значение и также должно удвоиться. Попробуйте снова. Только на этот раз сократите переменную x пополам. Переменная y должна была реагировать таким же образом; то есть его тоже нужно разрезать пополам. Что бы ни делал x , y делает то же самое. Это иллюстрирует простейшую, нетривиальную форму пропорциональности — прямую пропорциональность . Две величины прямо пропорциональны , если их соотношение постоянное.
Преобразование этого определения дает нам уравнение в общем виде…
y = kx
, где k — постоянная пропорциональности, которую каждый должен распознать как наклон прямой в плоскости xy .
Подходящим выводом из такой взаимосвязи будет то, что…
y прямо пропорционально x .
y напрямую зависит от x
y и x прямо пропорциональны.
y ∝ x
Например,
Регулярная заработная плата прямо пропорциональна количеству отработанных часов. За сорок часов работы оплачивается в четыре раза больше, чем за десять часов работы.За один час работы оплачивается одна десятая десяти часов работы.
Вес напрямую зависит от массы. В три раза больше массы означает в три раза больше веса. Точно так же половина массы означает половину веса.
Расстояние и время прямо пропорциональны, когда скорость постоянна. Вождение в течение двух часов дает вам вдвое большее расстояние, чем за один час, но только половину до четырех часов.
Внимание! Не думайте, что прямо пропорциональный означает «когда одно увеличивается, другое увеличивается» или «когда одно уменьшается, другое уменьшается».Это более конкретные отношения, чем эти. Приведу противоположный пример. Рабочий, который работает 60 часов, работает в 1,5 раза больше, чем тот, кто затрачивает 40 часов.
Но рабочие, работающие в США более 40 часов в неделю, должны получать сверхурочную оплату, которая обычно в полтора раза превышает их обычную заработную плату. Таким образом, 60-часовой рабочий зарабатывает в 1,75 раза больше, чем 40-часовой рабочий.
1 × 40 обычных часов + 1,5 × 20 сверхурочных часов) = 1.75
1 × 40 в обычное время
Так как изменения не те…
1,75 ≠ 1,5
: заработная плата в этом примере не прямо пропорциональна отработанным часам. Прямые отношения гораздо более специфичны, чем общее утверждение: «когда одно увеличивается, другое увеличивается». Это больше похоже на «когда один изменяется в определенном соотношении, другой изменяется в таком же отношении».
обратное
Двигаемся дальше.Взгляните на эту кривую. Эта форма называется прямоугольной гиперболой — гиперболой, поскольку она имеет асимптоты (линии, к которым кривая приближается, но никогда не пересекает), и прямоугольной, поскольку асимптоты представляют собой оси x и y (которые расположены под прямым углом.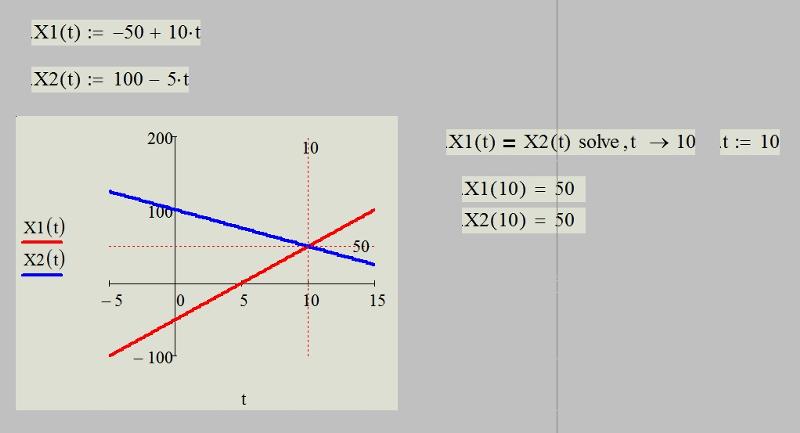 для другого).
Некоторые говорят, что эта кривая показывает поведение, противоположное предыдущему; то есть, когда переменная x увеличивается, переменная y уменьшается, а при уменьшении переменной x увеличивается переменная y .Но, как и в случае с предыдущей кривой, происходит более конкретное изменение. Убедитесь сами. Выберите удобную точку на кривой. Обратите внимание на значения координат в этой точке. Теперь удвойте координату x и посмотрите, что произойдет с координатой y . Он разрезан пополам. Теперь попробуйте обратное. Укажите точку на кривой и разрежьте ее координату x пополам. Координата y теперь в два раза больше исходного значения. Трижды x , вы получите одну треть от y .Уменьшите x до одной четвертой и посмотрите, как y увеличится на четыре. Однако вы изменяете одну из переменных, а другая изменяется на обратную величину. Это иллюстрирует другой простой вид пропорциональности — обратная пропорциональность . Две величины называются обратно пропорциональными , если их произведение является константой.
xy = k
Преобразование этого определения дает нам уравнение общего вида…
, где k — константа пропорциональности.
Подходящим выводом из такого отношения будет то, что…
y обратно пропорционально x .
y изменяется обратно пропорционально x .
y и x обратно пропорциональны.
y ∝ 1/ x
y ∝ x ⁻¹
Например…
Время, необходимое для завершения работы, обратно пропорционально количеству рабочих.Больше рабочих означает меньше времени на выполнение работы. (В два раза больше означает половину времени.) Меньше рабочих означает больше времени. (Если появится только одна треть от нормального числа рабочих, работа займет в три раза больше.)
Объем массы газа обратно пропорционален действующему на него давлению. Поместите баллон в барокамеру и увеличьте давление вдвое — баллон сократится до половины своего первоначального объема. Поместите баллон в вакуумную камеру и уменьшите давление до одной десятой атмосферного — баллон расширится в десять раз в объеме (при условии, что он не сломается первым).
квадрат
Что у нас здесь? Почему это парабола с вершиной в начале координат. Такая кривая получается, когда одно количество пропорционально квадрату другого. Поскольку эта парабола симметрична относительно оси y , это делает ее вертикальной параболой , и мы знаем, что квадрат получает горизонтальная переменная. Вот уравнение общего вида для такой кривой…
y = kx ²
Подходящим выводом из такой взаимосвязи было бы то, что…
y пропорционально квадрату x .
y ∝ x ²
Например…
Расстояние, пройденное объектом, упавшим из состояния покоя, пропорционально квадрату времени. Сколько времени нужно, чтобы упасть на один метр? Удвойте это время, и вы упадете на 4 м, утроите — и вы упадете на 9 м, и так далее.
Скорость, с которой электрическая цепь производит тепло, пропорциональна квадрату силы тока. Удвоение силы тока в тостере увеличивает ее тепловыделение в четыре раза.Уменьшите ток в процессоре компьютера до половины его предыдущего значения, и вы уменьшите тепловыделение до четверти от предыдущего значения.
корень квадратный
Вот еще одна парабола с вершиной в начале координат. Эта парабола наклонена на бок и симметрична относительно оси x . Для горизонтальной параболы , подобной этой, квадрат получает вертикальная переменная. Уравнение общего вида для такой кривой:…
y = k √ x
Подходящим выводом из такой взаимосвязи было бы то, что…
y пропорционально квадратному корню из x .
y ∝ √ x
y ∝ x ^½
Например…
Скорость пропорциональна квадратному корню из расстояния для свободно падающих объектов. Насколько быстро движется объект после падения на один метр? На четырёх метрах он будет иметь вдвое большую скорость; на девяти метрах — тройной; шестнадцать, четырехместные; и так далее.
Что нужно запомнить — квадратный корень не является явной функцией. Это не однозначно.Каждое число имеет два квадратных корня: положительный и отрицательный. Типичное программное обеспечение для построения кривой игнорирует отрицательный корень, поэтому я нарисовал только половину параболы на диаграмме выше. Еще кое-что нужно запомнить — область квадратного корня ограничена неотрицательными значениями. Это причудливый способ сказать, что вы не можете найти квадратный корень из отрицательного числа (то есть не без расширения вашего понятия «число»).
мощность
На данный момент у нас есть пять кривых и пять уравнений общего вида…
• независимый y = k
• прямой y = kx
• обратный y = k / x
• квадрат y = kx ²
• корень квадратный y = k √ x
У них есть три общих компонента…
x = независимая переменная (или объясняющая переменная)
y = зависимая переменная (или переменная ответа)
к = константа пропорциональности
и один другой компонент…
n = степень независимой переменной
Мы могли бы переписать эти общие уравнения с двумя переменными, константой пропорциональности и такой степенью . ..
• независимый y = kx ⁰
• прямой y = kx ¹
• обратный y = kx ⁻¹
• квадрат y = kx ²
• корень квадратный y = kx ^½
Мы могли бы даже пойти дальше и написать уравнение общей формы для всего семейства уравнений…
y = kx ⁿ
Говорят, что любые две переменные, которые связаны друг с другом уравнением этой формы, имеют между собой отношение мощности .
Обобщенные властные отношения мощность общая форма описание внешний вид
0 y = k независимый горизонтальный, прямой
1 y = kx прямой негоризонтальная прямая линия через начало координат
2 y = kx ² квадрат вертикальная парабола с вершиной в начале координат
3 y = kx ³ куб
-1 y = k / x обратная прямоугольная гипербола
-2 y = k / x ² обратный квадрат
−3 y = k / x ³ обратный куб
½ y = k √ x квадратный корень горизонтальная парабола с вершиной в начале координат
⅓ y = k ∛ x кубический корень
линейный
Описание: Сочетание постоянного и прямого. Фиксированная сумма добавляется (или вычитается) через равные промежутки времени.
Общий вид.
y = ax + b
Подходящим выводом из такой взаимосвязи было бы то, что…
y линейно с x .
y изменяется линейно с x .
y является линейной функцией x .
Внешний вид: любая прямая линия, независимо от наклона или точки пересечения оси Y
Пример (ы): счета за коммунальные услуги (всегда есть плата за обслуживание)
квадратичный
Описание: Комбинация квадрата, прямого и постоянного.
Общая форма
y = ax ² + bx + c
Подходящим выводом из такой связи будет то, что…
y является квадратичным с x .
y изменяется квадратично с x .
y — квадратичная функция x .
Внешний вид: Вертикальная парабола на графике. Его вершина может быть где угодно.Его также можно было перевернуть вверх дном.
Пример (ы): расстояние при равномерном ускорении
полином
Описание: Комбинация постоянного, прямого, квадрата, куба,…. Продолжайте идти так далеко, как хотите.
Общий вид.
y = a + bx + cx ² + dx ³ +…
Подходящим выводом из такой взаимосвязи будет то, что…
y может быть аппроксимируется полиномом n-го порядка x .
Полином n-го порядка x соответствовал y .
Внешний вид: любая непериодическая функция без асимптот
Пример (ы): Полиномиальные функции могут использоваться для аппроксимации многих непрерывных однозначных кривых
Обобщенные полиномиальные отношения заказ общая форма название
0 и = и постоянная
1 y = a + bx линейный
2 y = a + bx + cx ² квадратичный
3 y = a + bx + cx ² + dx ³ куб.
4 y = a + bx + cx ² + dx ³ + ex ⁴ квартика
5 y = a + bx + cx ² + dx ³ + ex ⁴ + fx ⁵ квинтик
⋮ ⋮ ⋮
n y = a ₀ x ⁰ + a ₁ x ¹ + a ₂ x ² + 71 3 ² + 71 a x ³ +… + a _n x ⁿ Многочлен n-го порядка
экспоненциальный рост
Описание:
Общий вид.
y = an ^bx
Подходящим выводом из такой взаимосвязи было бы то, что…
y увеличивается экспоненциально с x .
y экспоненциально растет с x .
y ∝ n ^x
Отношение последовательных итераций является постоянным. Количество умножается на фиксированное количество через равные промежутки времени.
Внешний вид: асимптотика с отрицательной осью x , за которой следует неконтролируемое расширение
Пример (ы): неограниченный рост населения, магия сложных процентов
экспоненциальный спад
Описание:
Общий вид.
y = an ^{— bx}
Подходящим выводом из такой взаимосвязи было бы то, что…
y уменьшается экспоненциально с x .
y экспоненциально затухает с x .
y ∝ n ^{— x}
Отношение последовательных итераций является константой. Количество делится на фиксированное количество через равные промежутки времени.
Внешний вид: большое начальное значение, за которым следует резкий коллапс, асимптотически приближается к положительной оси x
Пример (ы): радиоактивный распад, разряд конденсатора, обесточивание катушки индуктивности
экспоненциальный подход
Описание:
Общий вид.
y = a (1 — n ^{— bx}) + c
Подходящим выводом из такой зависимости будет то, что…
y приближается к конечному значению экспоненциально .
Внешний вид: асимптотически приближается к горизонтальной прямой
Пример (ы): зарядка конденсатора, включение индуктора, обучение (половина студентов получает его, затем половина оставшихся студентов получает его, затем половина оставшихся студентов получает его и так далее …)
периодический
Описание:
Общий вид.
y = a sin ( bx + c )
Подходящим выводом из такой взаимосвязи будет следующее:
y периодически меняется на x .
y периодичен с x .
Внешний вид: Синусоидальная кривая — это типичный, а не единственный пример. Любая повторяющаяся кривая периодична.
Пример (ы): Любое ежедневное (суточное), ежемесячное (лунное), годовое (годовое, сезонное) или другое периодическое изменение.
5.6: Движение с постоянным ускорением (часть 2)
Объединение уравнений
В следующих примерах мы продолжаем исследовать одномерное движение, но в ситуациях, требующих немного большего количества алгебраических манипуляций. Примеры также дают представление о методах решения проблем. Следующее примечание предназначено для облегчения поиска необходимых уравнений. Имейте в виду, что эти уравнения не являются независимыми. Во многих ситуациях у нас есть два неизвестных, и нам нужно два уравнения из набора для решения для неизвестных.{2} + 2a (x — x_ {0}) \]
Прежде чем мы перейдем к примерам, давайте более внимательно рассмотрим некоторые уравнения, чтобы увидеть поведение ускорения при экстремальных значениях.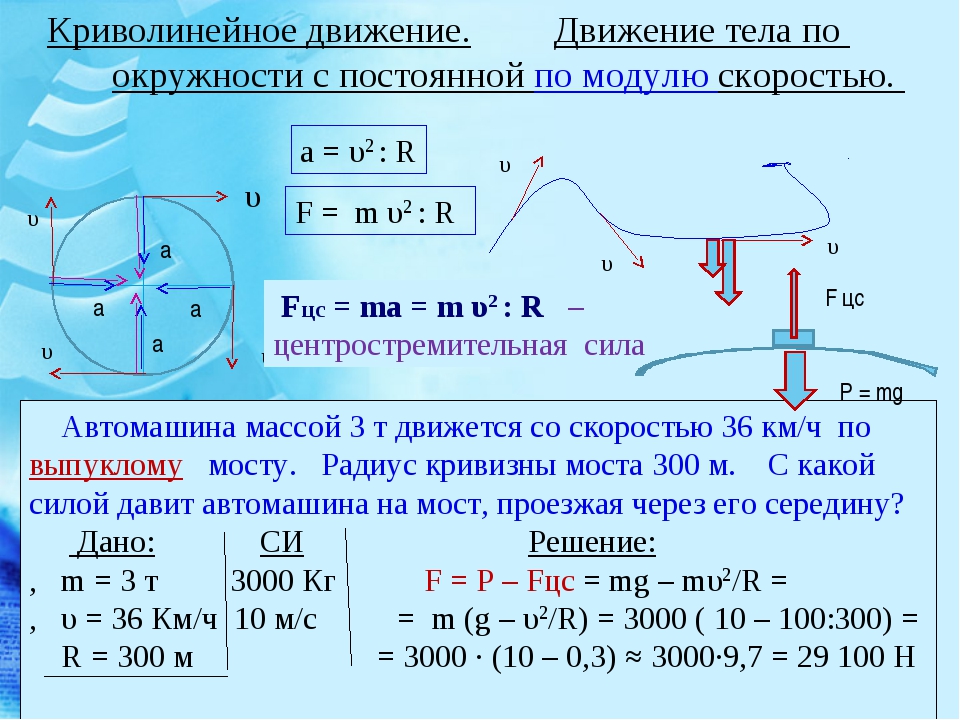 Переставляя \ (v = v_0 + at \), получаем
\ [a = \ frac {v — v_ {0}} {t} \ ldotp \]
Из этого мы видим, что в течение конечного времени, если разница между начальной и конечной скоростями мала, ускорение невелико, приближаясь к нулю в том пределе, когда начальная и конечная скорости равны. Напротив, в пределе t → 0 при конечной разности начальной и конечной скоростей ускорение становится бесконечным.{2}} {2 (x — x_ {0})} \ ldotp \]
Таким образом, при конечной разнице между начальной и конечной скоростями ускорение становится бесконечным, в пределе смещение приближается к нулю. Ускорение приближается к нулю в пределе, разница в начальной и конечной скоростях приближается к нулю для конечного смещения.
Пример 3.10: Как далеко уезжает машина?
На сухом бетоне автомобиль может замедляться со скоростью 7,00 м / с ², тогда как на мокром бетоне он может замедляться только со скоростью 5.00 м / с ². Найдите расстояния, необходимые для остановки автомобиля, движущегося со скоростью 30,0 м / с (около 110 км / ч) по (а) сухому бетону и (б) мокрому бетону. (c) Повторите оба вычисления и найдите смещение от точки, где водитель видит, что светофор становится красным, принимая во внимание время его реакции 0,500 с, чтобы он нажал ногу на тормоз.
Стратегия
Сначала нам нужно нарисовать эскиз Рисунок \ (\ PageIndex {1} \). Чтобы определить, какие уравнения лучше всего использовать, нам нужно перечислить все известные значения и точно определить, что нам нужно решить.
Рисунок \ (\ PageIndex {1} \): образец эскиза для визуализации замедления и тормозного пути автомобиля. Решение
Во-первых, нам нужно определить известные и то, что мы хотим решить. Мы знаем, что v ₀ = 30,0 м / с, v = 0 и a = −7,00 м / с ² (a отрицательно, потому что оно находится в направлении, противоположном скорости). Возьмем x0 равным нулю. Ищем смещение \ (\ Delta \) x, или x — x ₀. Во-вторых, мы определяем уравнение, которое поможет нам решить проблему. {2})} \ ldotp $$ Таким образом, $$ x = 64.3 \; м \; на\; сухой\; бетон \ ldotp $$
Эта часть может быть решена точно так же, как (а). Единственное отличие состоит в том, что ускорение составляет −5,00 м / с ². Результат: $$ x_ {wet} = 90.0 \; м \; на\; смачивать\; бетон \ ldotp $$
Когда водитель реагирует, тормозной путь такой же, как в пунктах (a) и (b) для сухого и влажного бетона. Итак, чтобы ответить на этот вопрос, нам нужно вычислить, как далеко проехал автомобиль за время реакции, а затем добавить это время к времени остановки.Разумно предположить, что скорость остается постоянной в течение времени реакции водителя. Для этого мы, опять же, определяем известные и то, что мы хотим решить. Мы знаем, что \ (\ bar {v} \) = 30,0 м / с, t _{реакции} = 0,500 с, а реакция = 0. Мы принимаем x _{0-реакция} равным нулю. Ищем х _{реакция}. Во-вторых, как и раньше, мы определяем лучшее уравнение для использования. В этом случае x = x ₀ + \ (\ bar {v} \) t работает хорошо, потому что единственное неизвестное значение — это x, которое мы и хотим найти.В-третьих, мы подставляем известные для решения уравнения: $$ x = 0 + (30,0 \; м / с) (0,500 \; с) = 15,0 \; m \ ldotp $$ Это означает, что автомобиль движется на 15,0 м, в то время как водитель реагирует, в результате чего общие смещения в двух случаях с сухим и мокрым бетоном на 15,0 м больше, чем при мгновенной реакции. Наконец, мы добавляем смещение во время реакции к смещению при торможении (рис. \ (\ PageIndex {2} \)), $$ x_ {braking} + x_ {response} = x_ {total}, $$ и находим (a) 64,3 м + 15,0 м = 79,3 м в сухом состоянии и (b) 90.0 м + 15,0 м = 105 м во влажном состоянии.
Рисунок \ (\ PageIndex {2} \): Расстояние, необходимое для остановки автомобиля, сильно варьируется в зависимости от дорожных условий и времени реакции водителя. Здесь показаны значения тормозного пути для сухого и мокрого покрытия, рассчитанные в этом примере для автомобиля, изначально движущегося со скоростью 30,0 м / с. Также показаны общие расстояния, пройденные от точки, когда водитель впервые видит, что свет загорается красным, при условии, что время реакции составляет 0,500 с. Значение
Смещения, найденные в этом примере, кажутся разумными для остановки быстро движущегося автомобиля.Остановка автомобиля на мокром асфальте должна длиться дольше, чем на сухом. Интересно, что время реакции значительно увеличивает смещения, но более важным является общий подход к решению проблем. Мы определяем известные и определяемые величины, а затем находим соответствующее уравнение. Если существует более одного неизвестного, нам нужно столько независимых уравнений, сколько неизвестных необходимо решить. Часто есть несколько способов решить проблему. Фактически, различные части этого примера могут быть решены другими методами, но представленные здесь решения являются самыми короткими.
Пример 3.11: Расчет времени
Предположим, автомобиль выезжает на автомагистраль на съезде длиной 200 м. Если его начальная скорость равна 10,0 м / с, а он ускоряется со скоростью 2,00 м / с ², сколько времени потребуется машине, чтобы преодолеть 200 м по рампе? (Такая информация может быть полезна транспортному инженеру.)
Стратегия
Сначала мы рисуем эскиз Рисунок \ (\ PageIndex {3} \). Нас просят решить для времени t. Как и раньше, мы идентифицируем известные величины, чтобы выбрать удобное физическое соотношение (то есть уравнение с одним неизвестным, t.)
Рисунок \ (\ PageIndex {3} \): эскиз автомобиля, ускоряющегося на съезде с автострады. Решение
Опять же, мы идентифицируем то, что нам известно, и то, что мы хотим решить. Мы знаем, что x ₀ = 0, v ₀ = 10 м / с, a = 2,00 м / с ² и x = 200 м.
Нам нужно решить за t. Уравнение x = x ₀ + v ₀ t + \ (\ frac {1} {2} \) at ² работает лучше всего, потому что единственной неизвестной в уравнении является переменная t, для которой нам нужно решать. {2} — 4ac}} {2a}, \]
, что дает два решения: t = 10,0 и t = -20,0. Отрицательное значение времени неразумно, так как это будет означать, что событие произошло за 20 секунд до начала движения. Мы можем отказаться от этого решения. Таким образом,
\ [t = 10,0 \; s \ ldotp \]
Значение
Всякий раз, когда уравнение содержит неизвестный квадрат, есть два решения. В некоторых проблемах имеют смысл оба решения; в других разумно только одно решение. 10.Ответ 0 кажется разумным для типичной автострады на съезде.
Упражнение 3.5
Пилотируемая ракета ускоряется со скоростью 20 м / с ² во время пуска. Сколько времени требуется ракете, чтобы достичь скорости 400 м / с?
Пример 3.12: Ускорение космического корабля
Космический корабль покинул орбиту Земли и направляется к Луне. Разгоняется со скоростью 20 м / с ² за 2 мин и преодолевает расстояние в 1000 км. Каковы начальная и конечная скорости космического корабля?
Стратегия
Нас просят найти начальную и конечную скорости космического корабля. {2}) (120,0 \; s) = 9533,3 \; м / с \ ldotp \]
Значение
Есть шесть переменных смещения, времени, скорости и ускорения, которые описывают движение в одном измерении. Начальные условия данной задачи могут быть множеством комбинаций этих переменных. Из-за такого разнообразия решения могут быть нелегкими, например простой заменой в одно из уравнений. Этот пример показывает, что решения кинематики могут потребовать решения двух одновременных кинематических уравнений.
Установив основы кинематики, мы можем перейти ко многим другим интересным примерам и приложениям. В процессе разработки кинематики мы также познакомились с общим подходом к решению проблем, который дает как правильные ответы, так и понимание физических взаимоотношений. Следующий уровень сложности в наших задачах кинематики связан с движением двух взаимосвязанных тел, называемых задачами преследования двух тел .
Задачи преследования двух тел
До этого момента мы рассматривали примеры движения с участием одного тела. Даже для задачи с двумя автомобилями и тормозным путем на мокрой и сухой дороге мы разделили эту задачу на две отдельные задачи, чтобы найти ответы. В задаче преследования двух тел движения объектов связаны, то есть искомая неизвестная зависит от движения обоих объектов. Чтобы решить эти проблемы, мы пишем уравнения движения для каждого объекта, а затем решаем их одновременно, чтобы найти неизвестное. Это показано на рисунке \ (\ PageIndex {4} \).
Рисунок \ (\ PageIndex {4} \): Сценарий преследования с двумя телами, где автомобиль 2 имеет постоянную скорость, а автомобиль 1 идет сзади с постоянным ускорением.Автомобиль 1 догонит автомобиль 2 позже. Время и расстояние, необходимое для того, чтобы автомобиль 1 догнал автомобиль 2, зависит от начального расстояния, на которое автомобиль 1 находится от автомобиля 2, а также от скорости обоих автомобилей и ускорения автомобиля 1. Кинематические уравнения, описывающие движение обоих автомобилей, должны быть решил найти эти неизвестные.
Рассмотрим следующий пример.
Пример 3.13: Гепард ловит газель
Гепард прячется за кустом. Гепард замечает пробегающую мимо газель со скоростью 10 м / с.В тот момент, когда газель проходит мимо гепарда, гепард ускоряется из состояния покоя со скоростью 4 м / с ², чтобы поймать газель. а) Сколько времени требуется гепарду, чтобы поймать газель? б) Что такое смещение газели и гепарда?
Стратегия
Мы используем систему уравнений для постоянного ускорения, чтобы решить эту проблему. Поскольку есть два движущихся объекта, у нас есть отдельные уравнения движения, описывающие каждое животное. Но то, что связывает уравнения, — это общий параметр, который имеет одинаковое значение для каждого животного.Если мы внимательно посмотрим на проблему, становится ясно, что общим параметром для каждого животного является их позиция x в более позднее время t. Поскольку оба они начинаются с x ₀ = 0, их смещения будут такими же в более позднее время t, когда гепард догонит газель. {2} — 50 \; m \ ldotp $$ Водоизмещение газели: $$ x = \ bar {v} t = 10 (5) = 50 \; m \ ldotp $$ Мы видим, что оба смещения равны, как и ожидалось.
Значение
Важно анализировать движение каждого объекта и использовать соответствующие кинематические уравнения для описания отдельного движения. Также важно иметь хорошую визуальную перспективу задачи преследования двух тел, чтобы увидеть общий параметр, который связывает движение обоих объектов.
Упражнение 3.6
Велосипед имеет постоянную скорость 10 м / с. Человек начинает с отдыха и бежит, чтобы догнать велосипед через 30 секунд, когда велосипед находится в том же положении, что и человек.Какое ускорение у человека?
А как насчет x = x0 + v0t + 1/2 a t?
Движение с постоянным ускорением
Какой вид движения описывает это уравнение? x (t) = x ₀ + v ₀ t + 1/2 при ² (1) v (t) = v ₀ + a ₀ t (2)
a (t ) = a ₀ (3)
Это движение с постоянным ускорением (a (t) = постоянное).
Уравнения (1) и (2) — важные уравнения, которые следует запомнить, поскольку проблемы с постоянным ускорением очень распространены в этом курсе — например, мы вскоре увидим их, когда начнем говорить о движении снаряда в двух измерениях.Существует третье важное уравнение, которое можно найти таким образом:
Перестановка (2) -> t = (vv ₀) / a ₀ (4)
Подстановка (4) в (1) дает:
x = x ₀ + v ₀ (vv ₀) / a ₀ + 1/2 a ₀ (vv ₀) 2 / a ₀ 2 x = x ₀ + vv ₀ / a ₀ — v ₀ ² / a ₀ +1/2 v2 / a ₀ –vv ₀ / a ₀ + v ₀ 2 / a ₀
x = x ₀ + v ² / 2a ₀ — v ₀ ² / 2a ₀
или: v ² -v ₀ ² = 2a ₀ (xx ₀) (5)
Существует более быстрый способ вывести (5), если мы готовы сделать несколько предположений / предположений. Ясно, что x = x ₀ + v _{среднее значение} t Если предположить, что vaverage = (v + v ₀) / 2 (что в общем случае неверно, но легко показать, что это верно для постоянного ускорение), то имеем:
xx ₀ = v _{среднее значение} (vv ₀) / a ₀ = (v + v ₀) (vv ₀) / 2a ₀ = (v ² -v ₀ ²) / 2a ₀
, как и раньше (здесь мы снова использовали (4) для ‘t’).В любом случае у нас есть метод, который связывает начальную и конечную скорости и положения, не требуя начального или конечного времени. Есть много проблем, для которых это полезно. .}}