По графикам движения определить: А. Проекцию скорости каждого
Ребят помогите пж! Срочно! Задачи две! 1) Тело в воздухе весит 100 н , а воде 65 н. Чему равна выталкивающая сила? 2) Вычислите силу Архимеда , дей … ствующую в воде на тело объемом 1,5 м в кубе? Спасибо!)
Найди заряд тела, на котором в избытке имеются электроны, число которых равно 86! Ответ запиши в аттокулонах без округления.
Два поезда движутся навстречу друг другу со скоростью 54 км/ч каждый. Первый поезд в какой-то момент дат гудок. Как только этот гудок слышит машинист … второго поезда, он двет свой гудок в ответ. Машинист первого поезда услышал ответный гудок через 16,6 секунд после своего сигнала. Какое в этот момент было расстояние между поездами?
Пожалуйста, физика срочно
Расстояние S=15 по течению реки катер прошел за 2 часа. По озеру такое же расстояние катер прошел за 3 часа. Найти:
-скорость катера относительно вод
… ы;
-скорость течения реки;
За какое время катер пройдет путь S=15км.
. Корабль движется по волнующемуся морю со скоростью 36 км/ч перпендикулярно гребням волн. Каждую минуту он дважды выходит на гребень волны. Скорость … движения волн 18 км/ч. Определить длину волны, период и частоту волнения.
. На определенном расстоянии от колокольни, на которой бьют набат, путник заметил, что звук колокола он слышит в тот же момент, когда приходит удар. П … ри этом удары повторялись через каждые 3 секунды. Снова он заметил это явление, когда подошел к колокольне ближе на 950 м. Скорость звука в воздухе равна 330 м/с. Определить скорость ветра. Куда он дует – от человека к колокольне или наоборот? 10 баллов за ответ
У відро масою 4кг налили 4л мастила. Яку силу треба прикласти, щоб утримувати відро в руках? Зробіть пояснювальний рисунок зобразивши сили, що діють н … а відро.
 Вещества можно расположить в ряды, в которых предыдущее тело электризуется положительно, а последующее — отрицательно. Рассмотри ряд Фарадея! (+) ме … х, фланель, слоновая кость, перья, горный хрусталь, флинтглас, бумажная ткань, шёлк, дерево, металл, сера (-)
самая маленькая птица саванн.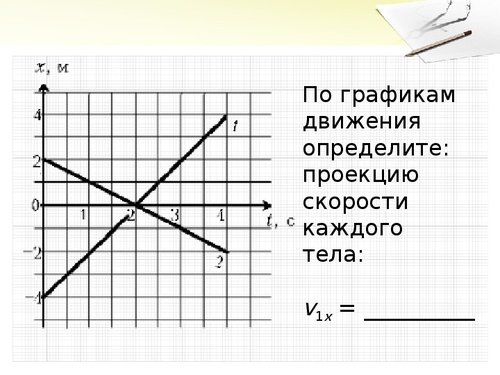 начинается на букву Н , плиз, даю 30 баллов
начинается на букву Н , плиз, даю 30 баллов
Вариант 1 Тест № 1. Равномерное прямолинейное движение 1. Можно ли считать материальной точкой иглу швейной машины в следующих случаях: а) игла падает со стола _ б)
Вариант 1Тест № 1. Равномерное прямолинейное движение
1. Можно ли считать материальной точкой иглу швейной машины в следующих случаях:
а) игла падает со стола _________ ;б) игла движется при работе машины ________?
2. Прямолинейным равномерным движением называется движение, при котором тело ________ совершает __________ .
3. Определите координату пешехода, взяв за тело отсчета:
а) дерево: x = ________ ,б) дорожный указатель:x = _______ .
4. Определите проекции векторов s1 и s2 на оси координат:
s1x = _____ , s2x = ______ ,s2x = _____ , s2y = ______.
5. Если при равномерном прямолинейном движении тело за 20 мин перемещается на 20 км, то:
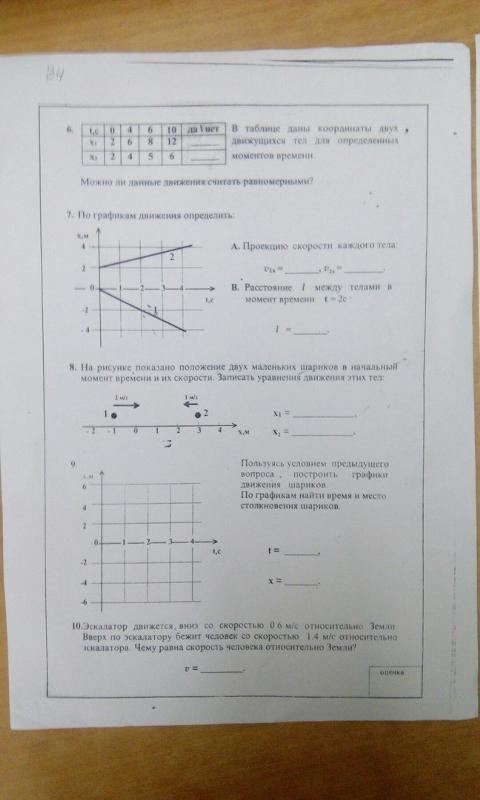
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
[ Cкачайте файл, чтобы посмотреть картинку ]
Можно ли считать данные движения равномерными?
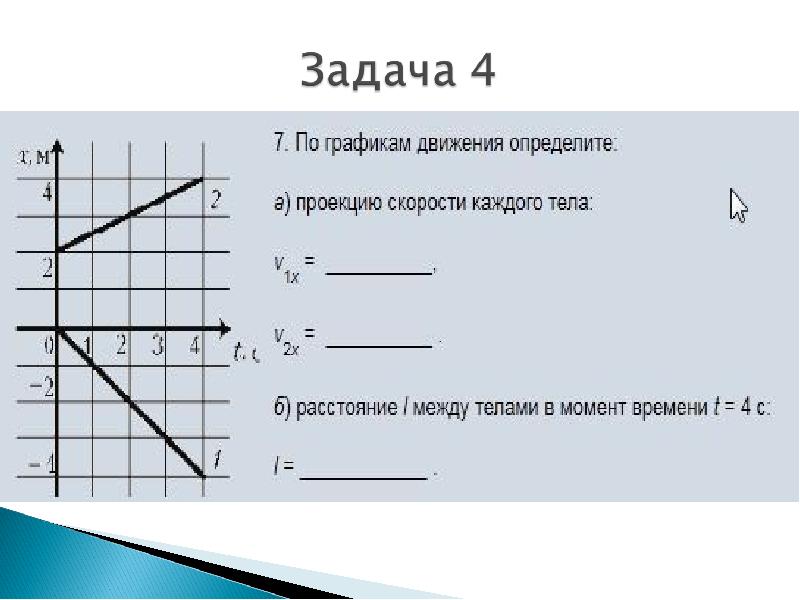
7. По графикам движения определите:
а) проекцию скорости каждого тела:
v1x = __________,
v2x = __________ ;
б) расстояние l между телами в момент времени t = 4 с:l = ____________ .
8. На рисунке показаны положения двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел:
x1 = ___ ,x2 = _____ .
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения:
t = ____________ ,x = _____________ .
10. С какой скоростью относительно Земли будет опускаться парашютист в восходящем потоке воздуха, если скорость парашютиста относительно воздуха 5 м/с, а скорость потока относительно Земли 4 м/с?
v = _____________ .

Вариант 2
Тест № 1. Равномерное прямолинейное движение
1. Можно ли считать космонавта материальной точкой в следующих случаях:
2. Скоростью равномерного прямолинейного движения называется_________________величина, равная _______________ __________________________ к промежутку времени _____________________________________________________ .
3. Определите координату пешехода, взяв за тело отсчета:
[ Cкачайте файл, чтобы посмотреть картинку ]
а) дерево: x = ____________ ,б) дорожный указатель:x = _____________ .
4. Определите проекции векторов s1 и s2 на оси координат:
s1x = ___ , s2x = ___ ,s1y = ___ , s2y = ____.
5. Если при равномерном прямолинейном движении тело за 5 c перемещается на 25 м, то:
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.

[ Cкачайте файл, чтобы посмотреть картинку ]
Можно ли считать данные движения равномерными?
7. По графикам движения определите:
а) проекцию скорости каждого тела:v1x = ______________,v2x = ______________ ;б) расстояние l между телами в момент времени t = 4 с:l = __________________
.
8. На рисунке показаны положения двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел.
x1 = ___________ ,x2 = ___________ ;
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения.
t = ___________ ,x = ___________ .
10. В неподвижной воде пловец плывет со скоростью 2 м/с. Когда он плывет по реке против течения, его скорость относительно берега равна 0,5 м/с вниз по течению. Чему равна скорость течения?
v = ____________
.
Вариант 3
Тест № 1. Равномерное прямолине
·йное движение
1. Можно ли считать поезд материальной точкой в следующих случаях:
2.
 Поступательным называется движение, при котором ___________________ ________________________ .
Поступательным называется движение, при котором ___________________ ________________________ .3. Определите координату пешехода, взяв за тело отсчета:
а) дерево: x = ________ ,б) дорожный указатель:x = _______ .
4. Определите проекции векторов s1 и s2 на оси координат:
s1x = _____ , s2x = ______ ,s1y = _____ , s2y = ______.
5. Если при равномерном прямолинейном движении тело за 2 ч перемещается на 100 км, то:
– за 0,5 ч оно перемещается на ______________ ,– за 3 ч оно перемещается на ________________ .
[ Cкачайте файл, чтобы посмотреть картинку ]
Можно ли считать данные движения равно- мерными?
7. По графикам движения определите:
а) проекцию скорости каждого тела:
v1x = __________,
v2x = __________;
б) расстояние l между телами в момент времени t = 4 с:
l = ____________ .
8. На рисунке показаны положение двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел:
Запишите уравнения движения этих тел:
[ Cкачайте файл, чтобы посмотреть картинку ]
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения:
t = _____________ ,
x = _____________ .
10. По реке, скорость течения которой 2 км/ч, плывет бревно. По бревну в том же направлении бежит мышонок. С какой скоростью относительно бревна бежит мышонок, если его скорость относительно берега 2,5 км/ч?
v = _______________ .
Вариант 4
Тест № 1. Равномерное прямолинейное движение
1. Можно ли считать автомобиль материальной точкой в следующих случаях:
а) автомобиль движется по шоссе _____________;б) автомобиль въезжает в гараж ______________?
2. Скорость тела относительно ______________ системы координат равна _________ сумме скорости ________ относительно ________ и скорости ____________ относительно ___________.
а) дерево: x = ________ ,б) дорожный указатель:x = _______ .

4. Определите проекции векторов s1 и s2 на оси координат:
s1x = ______ , s2x = ______ ,s1y = ______ , s2y = ______.
5. Если при равномерном прямолинейном движении тело за 1 мин перемещается на 120 м, то:
– за 10 с оно перемещается на _________________ – за 5 мин оно перемещается на ________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
Можно ли считать данные движения равно- мерными?
7. По графикам движения определите:
а) проекцию скорости каждого тела:
v1x = __________,
v2x = __________ .
б) расстояние l между телами в момент времени t = 4 с:
l = ____________ .
8. На рисунке показаны положения двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел:
[ Cкачайте файл, чтобы посмотреть картинку ]
x1 = ______ ,x2 = ______ .
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения:
t = _____________ ,x = _____________ .

10. Эскалатор движется вниз со скоростью 0,6 м/с относительно Земли. Вверх по эскалатору бежит человек со скоростью 1,4 м/с относительно эскалатора. Чему равна скорость человека относительно Земли?
v = _______________ .
15
Приложенные файлы
- 3737500
Размер файла: 89 kB Загрузок: 2
Прямолинейное неравномерное движение тест 2 вариант 1. Равномерное прямолинейное движение — тест
Вариант 1
а ) игла падает со стола _________ ;
б ) игла движется при работе машины ________?
2. Прямолинейным равномерным движением называется движение, при котором тело ________ совершает __________ .
а ) дерево:
x = ________ ,
б ) дорожный указатель:
x = _______ .
s 1 и s 2 на оси координат:
s 1x = _____ , s 2x = ______ ,
s 2x = _____ , s 2y = ______.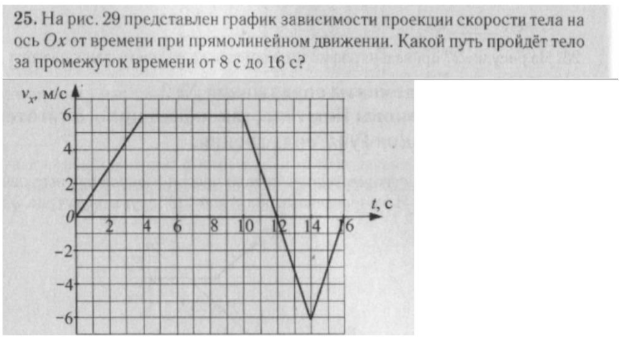
5. Если при равномерном прямолинейном движении тело за 20 мин перемещается на 20 км, то:
– за 5 мин оно перемещается на ____________ ,
– за 2 ч оно перемещается на _______________ .
а
v 1x = __________,
v 2x = __________ ;
б ) расстояние l t = 4 с:
l = ____________ .
x 1
= ___ ,
x 2 = _____
font-size:10.0pt;font-family:» arial cyr>.
t = ____________ ,
x = _____________ .
10. С какой скоростью относительно Земли будет опускаться парашютист в восходящем потоке воздуха, если скорость парашютиста относительно воздуха 5 м/с, а скорость потока относительно Земли 4 м/с?
v = _____________ .
Вариант 2
Тест № 1. Равномерное прямолинейное движение
а ) космонавт перемещается в космическом корабле ____ ;
б ) космонавт в космическом корабле обращается вокруг Земли ___?
2. Скоростью равномерного прямолинейного движения называется_________________величина, равная _______________ __________________________ к промежутку времени _____________________________________________________ .
Скоростью равномерного прямолинейного движения называется_________________величина, равная _______________ __________________________ к промежутку времени _____________________________________________________ .
3. Определите координату пешехода, взяв за тело отсчета:
а ) дерево:
x = ____________ ,
б ) дорожный указатель:
x = _____________ .
4. Определите проекции векторов s 1 и s 2 на оси координат:
s 1x = ___ , s 2x = ___ ,
s 1y = ___ , s 2y = ____.
5. Если при равномерном прямолинейном движении тело за 5 c перемещается на 25 м, то:
– за 2 с оно перемещается на _____________ ,
– за 1 мин оно перемещается на ___________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
7. По графикам движения определите:
а ) проекцию скорости каждого тела:
v 1x = ______________,
v 2x = ______________ ;
б ) расстояние l между телами в момент времени t = 4 с:
l = __________________
8.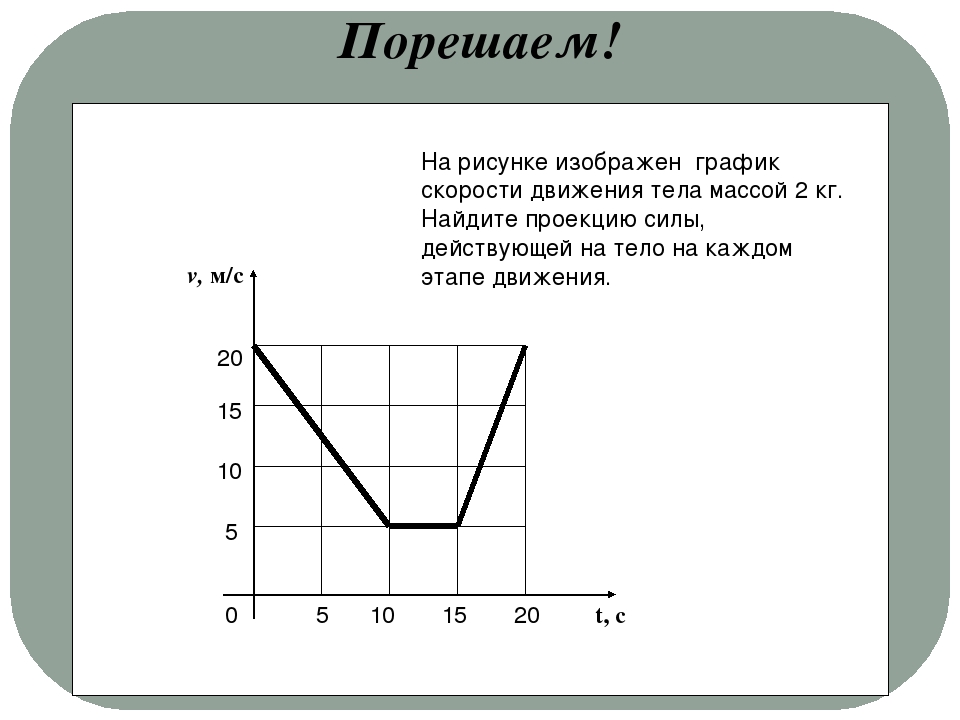 На рисунке показаны положения двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел.
На рисунке показаны положения двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел.
x 1
= ___________ ,
x 2 = ___________ ;
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения.
t = ___________ ,
x = ___________ .
10. В неподвижной воде пловец плывет со скоростью 2 м/с. Когда он плывет по реке против течения, его скорость относительно берега равна 0,5 м/с вниз по течению. Чему равна скорость течения?
v = ____________
.
Вариант 3
Тест № 1. Равномерное прямолинейное движение
а ) поезд въезжает на станцию ________________;
б ) поезд движется между станциями ___________?
2. Поступательным называется движение, при котором ___________________ ________________________ .
3. Определите координату пешехода, взяв за тело отсчета:
а ) дерево:
x = ________ ,
б ) дорожный указатель:
x = _______ .
4. Определите проекции векторов s 1 и s 2 на оси координат:
s 1x = _____ , s 2x = ______ ,
s 1y = _____ , s 2y = ______.
5. Если при равномерном прямолинейном движении тело за 2 ч перемещается на 100 км, то:
– за 0,5 ч оно перемещается на ______________ ,
– за 3 ч оно перемещается на ________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
7. По графикам движения определите:
а ) проекцию скорости каждого тела:
v 1x = __________,
v 2x = __________;
б ) расстояние l между телами в момент времени t = 4 с:
l = ____________ .
8. На рисунке показаны положение двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел:
x 1
= ______ ,
x 2 = ______ .
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения:
t = _____________ ,
x = _____________ .
10. По реке, скорость течения которой 2 км/ч, плывет бревно. По бревну в том же направлении бежит мышонок. С какой скоростью относительно бревна бежит мышонок, если его скорость относительно берега 2,5 км/ч?
v = _______________ .
Вариант 4
Тест № 1. Равномерное прямолинейное движение
а ) автомобиль движется по шоссе _____________;
б ) автомобиль въезжает в гараж ______________?
2. Скорость тела относительно ______________ системы координат равна _________ сумме скорости ________ относительно ________ и скорости ____________ относительно ___________.
3. Определите координату пешехода, взяв за тело отсчета:
а ) дерево:
x = ________ ,
б ) дорожный указатель:
x = _______ .
4. Определите проекции векторов s 1 и s 2 на оси координат:
s 1x = ______ , s 2x = ______ ,
s 1y = ______ , s 2y = ______.
5. Если при равномерном прямолинейном движении тело за 1 мин перемещается на 120 м, то:
– за 10 с оно перемещается на _________________
– за 5 мин оно перемещается на ________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
Можно ли считать данные движения равно — мерными?
7. По графикам движения определите:
а ) проекцию скорости каждого тела:
v 1x = __________,
v 2x = __________ .
б ) расстояние l между телами в момент времени t = 4 с:
l = ____________ .
8. На рисунке показаны положения двух маленьких шариков в начальный момент времени и их скорости.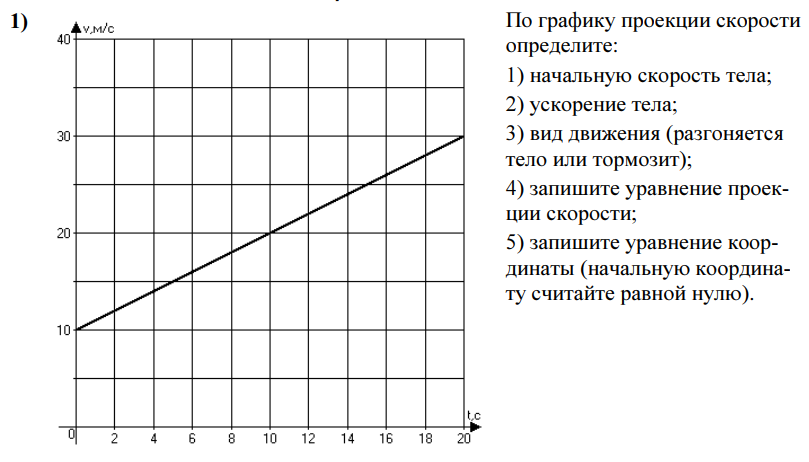 Запишите уравнения движения этих тел:
Запишите уравнения движения этих тел:
x 1
= ______ ,
x 2 = ______ .
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения:
t = _____________ ,
x = _____________ .
10. Эскалатор движется вниз со скоростью 0,6 м/с относительно Земли. Вверх по эскалатору бежит человек со скоростью 1,4 м/с относительно эскалатора. Чему равна скорость человека относительно Земли?
v = _______________ .
с. 1
Вариант 1
а ) игла падает со стола _________ ;
б ) игла движется при работе машины ________?
2. Прямолинейным равномерным движением называется движение, при котором тело ________ совершает __________ .
а ) дерево:
x = ________ ,
б ) дорожный указатель:
x = _______ .
s 1 и s 2 на оси координат:
s 1 x = _____ , s 2 x = ______ ,
s 2 x = _____ , s 2 y = ______.
5. Если при равномерном прямолинейном движении тело за 20 мин перемещается на 20 км, то:
– за 5 мин оно перемещается на ____________ ,
– за 2 ч оно перемещается на _______________ .
7. По графикам движения определите:
а
v 1 x = __________,
v 2 x = __________ ;
б ) расстояние l t = 4 с:
l = ____________ .
x 1 = ___ ,
x 2 = _____ .
t = ____________ ,
x = _____________ .
10. С какой скоростью относительно Земли будет опускаться парашютист в восходящем потоке воздуха, если скорость парашютиста относительно воздуха 5 м/с, а скорость потока относительно Земли 4 м/с?
v = _____________ .
Вариант 2
Тест № 1. Равномерное прямолинейное движение
а ) космонавт перемещается в космическом корабле ____ ;
б ) космонавт в космическом корабле обращается вокруг Земли ___?
2.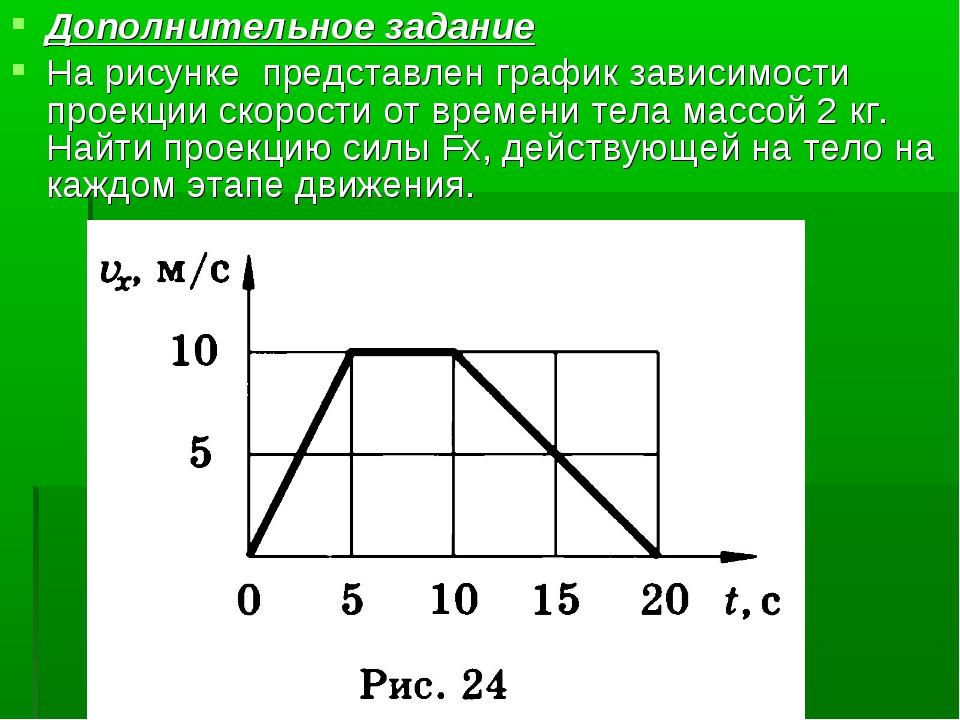 Скоростью равномерного прямолинейного движения называется_________________величина, равная _______________ __________________________ к промежутку времени _____________________________________________________ .
Скоростью равномерного прямолинейного движения называется_________________величина, равная _______________ __________________________ к промежутку времени _____________________________________________________ .
3. Определите координату пешехода, взяв за тело отсчета:
а ) дерево:
x = ____________ ,
б ) дорожный указатель:
x = _____________ .
4. Определите проекции векторов s 1 и s 2 на оси координат:
s 1 x = ___ , s 2 x = ___ ,
s 1 y = ___ , s 2 y = ____.
5. Если при равномерном прямолинейном движении тело за 5 c перемещается на 25 м, то:
– за 2 с оно перемещается на _____________ ,
– за 1 мин оно перемещается на ___________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
а ) проекцию скорости каждого тела:
v 1 x = ______________,
v 2 x = ______________ ;
б ) расстояние l между телами в момент времени t = 4 с:
l = __________________
8. На рисунке показаны положения двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел.
На рисунке показаны положения двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел.
x 1 = ___________ ,
x 2 = ___________ ;
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения.
t = ___________ ,
x = ___________ .
10. В неподвижной воде пловец плывет со скоростью 2 м/с. Когда он плывет по реке против течения, его скорость относительно берега равна 0,5 м/с вниз по течению. Чему равна скорость течения?
v = ____________
Вариант 3
Тест № 1. Равномерное прямолинейное движение
а ) поезд въезжает на станцию ________________;
б ) поезд движется между станциями ___________?
2. Поступательным называется движение, при котором ___________________ ________________________ .
3. Определите координату пешехода, взяв за тело отсчета:
а ) дерево:
x = ________ ,
б ) дорожный указатель:
x = _______ .
4. Определите проекции векторов s 1 и s 2 на оси координат:
s 1 x = _____ , s 2 x = ______ ,
s 1 y = _____ , s 2 y = ______.
5. Если при равномерном прямолинейном движении тело за 2 ч перемещается на 100 км, то:
– за 0,5 ч оно перемещается на ______________ ,
– за 3 ч оно перемещается на ________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
М
7. По графикам движения определите:
а ) проекцию скорости каждого тела:
v 1 x = __________,
v 2 x = __________;
б ) расстояние l между телами в момент времени t = 4 с:
l = ____________ .
8. На рисунке показаны положение двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел:
x 1 = ______ ,
x 2 = ______ .
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения:
t = _____________ ,
x = _____________ .
10. По реке, скорость течения которой 2 км/ч, плывет бревно. По бревну в том же направлении бежит мышонок. С какой скоростью относительно бревна бежит мышонок, если его скорость относительно берега 2,5 км/ч?
v = _______________ .
Вариант 4
Тест № 1. Равномерное прямолинейное движение
а ) автомобиль движется по шоссе _____________;
б ) автомобиль въезжает в гараж ______________?
2. Скорость тела относительно ______________ системы координат равна _________ сумме скорости ________ относительно ________ и скорости ____________ относительно ___________.
3. Определите координату пешехода, взяв за тело отсчета:
а ) дерево:
x = ________ ,
б ) дорожный указатель:
x = _______ .
4. Определите проекции векторов s 1 и s 2 на оси координат:
s 1 x = ______ , s 2 x = ______ ,
s 1 y = ______ , s 2 y = ______.
5. Если при равномерном прямолинейном движении тело за 1 мин перемещается на 120 м, то:
– за 10 с оно перемещается на _________________
– за 5 мин оно перемещается на ________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
Можно ли считать данные движения равно- мерными?
7. По графикам движения определите:
а ) проекцию скорости каждого тела:
v 1 x = __________,
v 2 x = __________ .
б ) расстояние l между телами в момент времени t = 4 с:
l = ____________ .
8. На рисунке показаны положения двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел:
Запишите уравнения движения этих тел:
x 1 = ______ ,
x 2 = ______ .
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения:
t = _____________ ,
x = _____________ .
10. Эскалатор движется вниз со скоростью 0,6 м/с относительно Земли. Вверх по эскалатору бежит человек со скоростью 1,4 м/с относительно эскалатора. Чему равна скорость человека относительно Земли?
v = _______________ .
с. 1
ВСЕРОССИЙСКИЙ ФЕСТИВАЛЬ ПЕДАГОГИЧЕСКОГО ТВОРЧЕСТВА
2016/2017 УЧЕБНОГО ГОДА
Автор: Петренко Надежда Федоровна,
учитель физики высшей квалификационной категории.
Образовательная организация: Муниципальное бюджетное общеобразовательное учреждение Городского округа Балашиха
«Средняя общеобразовательная школа № 7 с углубленным изучением отдельных предметов»
Адрес: 143980, Московская обл., Г. о. Балашиха,
мкр. Железнодорожный, ул. Октябрьская, д. 7.
Железнодорожный, ул. Октябрьская, д. 7.
Дата 2013-2014 уч. год
МБОУ СОШ №7 с УИОП Г.о. Балашиха Московской обл.
Физика – 10 класс.
Урок №4. Тема: «Равномерное прямолинейное движение Решение задач»
Равномерное прямолинейное движение — ТЕСТ
Вариант I
Часть 1
А) троллейбус движется по прямой улице. К каждой следующей остановке он прибывает через равные интервалы времени и через равные интервалы отбывает от них
Б) автомобиль движется по дороге и проходит за любые равные промежутки времени одинаковые расстояния
В каком случае движение тела является равномерным?
Что такое скорость прямолинейного равномерного движения?
Физическая величина, равная отношению перемещения точки к промежутку времени, в течение которого это перемещение произошло.
Физическая величина, равная произведению перемещения точки к промежутку времени, в течение которого это перемещение произошло.
Физическая величина, равная отношению промежутка времени к перемещению, которое совершило тело за этот промежуток времени.
Отношение перемещения точки к промежутку времени, в течение которого это перемещение произошло.
Тело движется прямолинейно равномерно так, что направление вектора скорости противоположно направлению оси координат. Что можно сказать о проекции вектора скорости на данную ось?
положительна 3) равна нулю
Выберите формулу координаты прямолинейного равномерного движения
2) 3) 4)
5; 2 2) 2; -5 3) -5; 2 4) 0; 2
3086100266065I
III
II
t, c
X, м
5
0
— 5
— 10
— 15
00I
III
II
t, c
X, м
5
0
— 5
— 10
— 15
На рисунке представлены графики зависимости координат от времени. Определите проекцию скорости второго тела на ось ОХ
–1,0 м/с
2) 1,0 м/с
3) — 0,5 м/с
4) 0,5 м/с
2971800188595Vx, м/с
4
2
0
— 2
— 4
t, c
2
4
6
8
00Vx, м/с
4
2
0
— 2
— 4
t, c
2
4
6
8
На рисунке приведен график зависимости скорости движения от времени. Определите путь, пройденный телом за первые 8 секунд движения.
Определите путь, пройденный телом за первые 8 секунд движения.
Координата тела меняется с течением времени согласно формуле. Чему равна координата этого тела через 5 с после начала движения?
1) 28 м 2) 12 м 3) — 4 м 4) — 12 м Часть 2
Тело Вид движения
А) первое 1) покоится
Часть 3
Уравнения движения двух тел имеют вид:; . Найдите место и время встречи тел графически и аналитически.
Равномерное движение
Вариант II
Часть 1
К каждому из заданий 1 – 8 даны 4 варианта ответа, из которых только один правильный.
Рассмотрим два вида движения тел:
А) поезд метрополитена движется по прямолинейному пути. Он прибывает на каждую следующую станцию и отправляется от нее через одинаковые промежутки времени
Б) спутник движется по окружности вокруг Земли и за любые равные промежутки времени проходит одинаковые расстояния
В каком случае движение тела не является равномерным?
1) только в А 2) только в Б 3) в А и в Б 4) ни в А, ни в Б
Что характеризует скорость прямолинейного равномерного движения?
направление движения тела
отношение перемещения ко времени, за которое это перемещение совершено.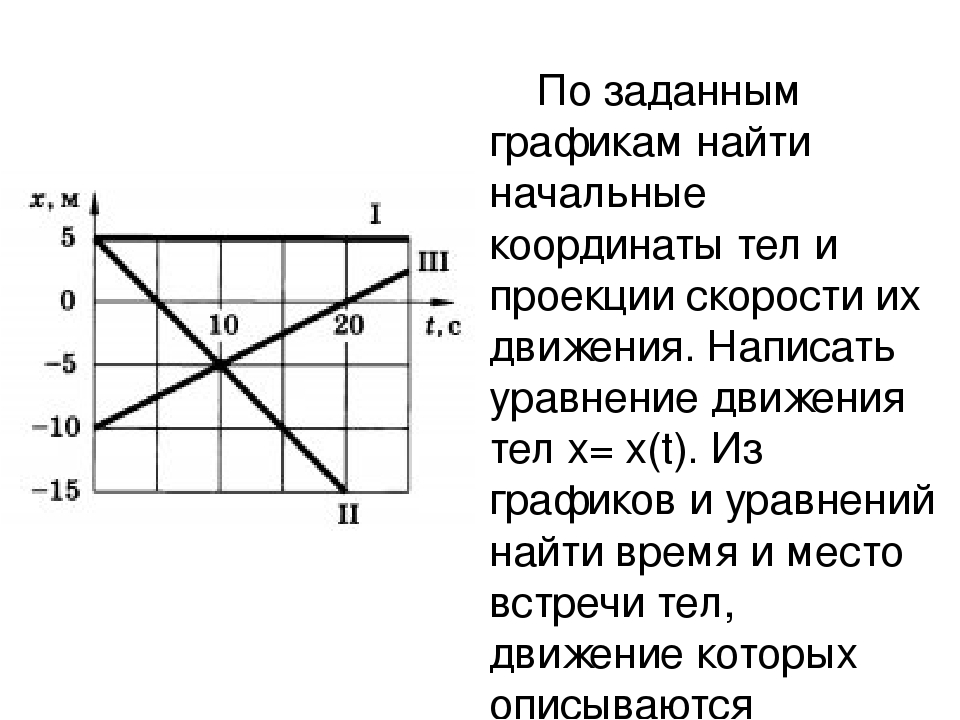
быстроту изменения координаты
произведение перемещения и времени, за которое это перемещение совершено.
Тело движется прямолинейно равномерно так, что направление вектора скорости совпадает с направлением оси координат. Что можно сказать о проекции вектора скорости на данную ось?
положительна 3) равна нулю
отрицательна 4) может быть, как положительной, так и отрицательной.
Выберите формулу скорости прямолинейного равномерного движения
2) 3) 4)
Уравнение движения имеет вид. Определите начальную координату и скорость
0; — 3 2) — 3; 0 3) 0; 3 4) 3; 0
2628900186055I
III
II
t, c
X, м
5
0
— 5
— 10
— 15
00I
III
II
t, c
X, м
5
0
— 5
— 10
— 15
На рисунке представлены графики зависимости координат от времени. Определите проекцию скорости третьего тела на ось ОХ
– 0,5 м/с
2) 2,5 м/с
3) — 2,5 м/с
4) 0,5 м/с
2514600227330Vx, м/с
4
2
0
— 2
— 4
t, c
2
4
6
8
00Vx, м/с
4
2
0
— 2
— 4
t, c
2
4
6
8
На рисунке приведен график зависимости скорости движения от времени. Определите перемещение тела за первые 8 секунд движения.
Определите перемещение тела за первые 8 секунд движения.
1) 4 м 2) 8 м 3) 16 м 4) 0 м
Координата тела меняется с течением времени согласно формуле. Через сколько секунд координата тела станет равной нулю?
1) 2 с 2) 5 с 3) 10 с 4) 4 с
Часть 2
В задании 9 требуется указать последовательность цифр, соответствующих правильному ответу.
Уравнения движения тел имеют вид:; ; . Как и в каком направлении движутся тела?
К каждой позиции первого столбика подберите соответствующую позицию второго столбика. Цифры могут повторяться.
Тело Вид движения
А) первое 1) покоится
Б) второе 2) равномерно по оси
В) третье 3) равномерно против оси
Часть 3
Задание 10 представляет собой задачу, полное решение которой необходимо записать.
Уравнения движения двух тел имеют вид: ; . Найдите место и время встречи тел графически и аналитически.
Ответы
N 1 2 3 4 5 6 7 8 9 10
Вариант I 2 1 2 2 3 1 3 4 231 10 с; 30 мВариант II 1 2 1 3 1 4 4 1 321 10 с; 50 м
1.
 График зависимости скорости от времени при прямолинейном движении с постоянным ускорением
График зависимости скорости от времени при прямолинейном движении с постоянным ускорениемСамое простое из всех неравномерных движений — это прямолинейное движение с постоянным ускорением.
При движении с постоянным ускорением (a→=const→) скорость тела линейно зависит от времени:
v→=v→o+a→t.
В проекциях на ось \(Ox\) данные равенства имеют вид:
ax=const;
vx=vox+axt.
Построим графики зависимостей axt и vxt для случаев ax>0 и ax<0.
Примем vox>0.
Поскольку в обоих случаях ax=const, то графиком зависимости axt ускорения от времени в обоих случаях будет прямая, параллельная оси времени.
Только при ax>0 данная прямая будет лежать в верхней полуплоскости (рис. \(1\)), а при ax<0 — в нижней (рис. \(2\)).
Рис. \(1\)
Рис. \(2\)
Графиком зависимости скорости движения тела от времени vxt является прямая, пересекающая ось скорости в точке v0 и образующая с положительным направлением оси времени острый угол при ax>0 (рис. \(3\)) и тупой угол при ax<0 (рис. \(4\)).
\(3\)) и тупой угол при ax<0 (рис. \(4\)).
Рис. \(3\)
Рис. \(4\)
График на рисунке \(3\) описывает возрастание проекции скорости vx. При этом модуль скорости тела также растёт. Данный график соответствует равноускоренному движению тела.
График на рисунке \(4\) показывает, что проекция vx скорости тела вначале положительна.
Она уменьшается и в момент времени t=tп становится равной нулю.
В этот момент тело достигает точки поворота, в которой направление скорости тела меняется на противоположное, и при t>tп проекция скорости становится отрицательной.
Из последнего графика также видно, что до момента поворота модуль скорости уменьшался — тело двигалось равнозамедленно.
При t>tп модуль скорости растёт — тело движется равноускоренно.
Для любого равнопеременного прямолинейного движения площадь фигуры между графиком vx и осью времени \(t\) численно равна проекции перемещения Δrx.
Рис. \(5\)
Согласно данному правилу, проекция перемещения Δrx при равнопеременном движении определяется площадью трапеции \(ABCD\) (рис. \(5\)). Эта площадь равна полусумме оснований трапеции, умноженной на её высоту:
S=AB+DC2⋅AD.
В результате:
Δrx=vox+vx2⋅Δt.
Из данной формулы получим формулу для среднего значения проекции скорости:
vxср=ΔrxΔt=vox+vx2.
При движении с постоянным ускорением данное отношение выполняется не только для проекций, но и для векторов скорости:
vcp→=vo→+v→2.
Средняя скорость движения с постоянным ускорением равна полусумме начальной и конечной скоростей.
Равномерное движение вариант 1. Равномерное прямолинейное движение — тест
Вариант 1
а ) игла падает со стола _________ ;
б ) игла движется при работе машины ________?
2. Прямолинейным равномерным движением называется движение, при котором тело ________ совершает __________ .
Прямолинейным равномерным движением называется движение, при котором тело ________ совершает __________ .
а ) дерево:
x = ________ ,
б ) дорожный указатель:
x = _______ .
s 1 и s 2 на оси координат:
s 1x = _____ , s 2x = ______ ,
s 2x = _____ , s 2y = ______.
5. Если при равномерном прямолинейном движении тело за 20 мин перемещается на 20 км, то:
– за 5 мин оно перемещается на ____________ ,
– за 2 ч оно перемещается на _______________ .
а
v 1x = __________,
v 2x = __________ ;
б ) расстояние l t = 4 с:
l = ____________ .
x 1
= ___ ,
x 2 = _____
font-size:10.0pt;font-family:» arial cyr>.
t = ____________ ,
x = _____________ .
10. С какой скоростью относительно Земли будет опускаться парашютист в восходящем потоке воздуха, если скорость парашютиста относительно воздуха 5 м/с, а скорость потока относительно Земли 4 м/с?
v = _____________ .
Вариант 2
Тест № 1. Равномерное прямолинейное движение
а ) космонавт перемещается в космическом корабле ____ ;
б ) космонавт в космическом корабле обращается вокруг Земли ___?
2. Скоростью равномерного прямолинейного движения называется_________________величина, равная _______________ __________________________ к промежутку времени _____________________________________________________ .
3. Определите координату пешехода, взяв за тело отсчета:
а ) дерево:
x = ____________ ,
б ) дорожный указатель:
x = _____________ .
4. Определите проекции векторов s 1 и s 2 на оси координат:
s 1x = ___ , s 2x = ___ ,
s 1y = ___ , s 2y = ____.
5. Если при равномерном прямолинейном движении тело за 5 c перемещается на 25 м, то:
– за 2 с оно перемещается на _____________ ,
– за 1 мин оно перемещается на ___________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
7. По графикам движения определите:
а ) проекцию скорости каждого тела:
v 1x = ______________,
v 2x = ______________ ;
б ) расстояние l между телами в момент времени t = 4 с:
l = __________________
8. На рисунке показаны положения двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел.
x 1
= ___________ ,
x 2 = ___________ ;
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения.
t = ___________ ,
x = ___________ .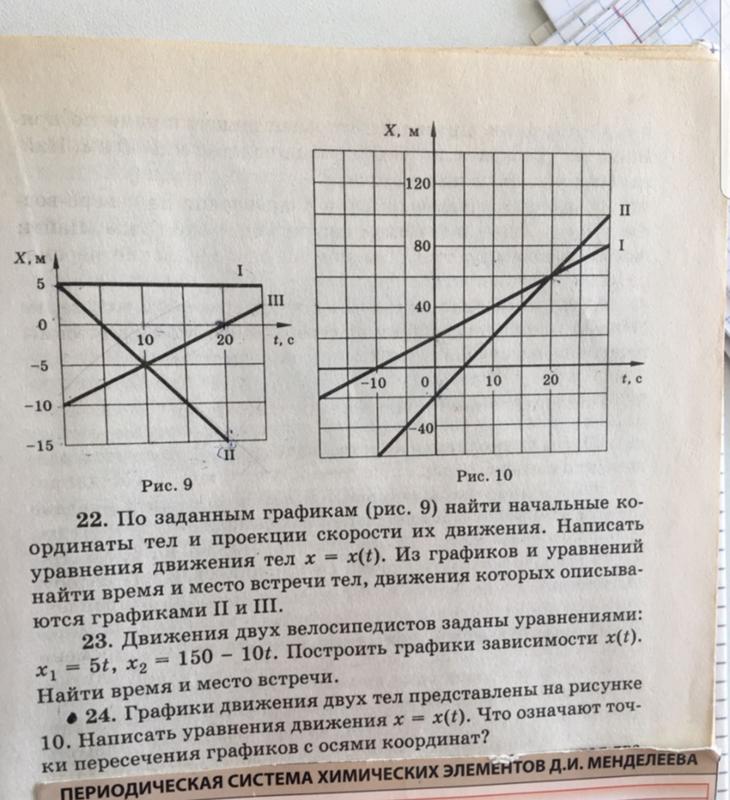
10. В неподвижной воде пловец плывет со скоростью 2 м/с. Когда он плывет по реке против течения, его скорость относительно берега равна 0,5 м/с вниз по течению. Чему равна скорость течения?
v = ____________
.
Вариант 3
Тест № 1. Равномерное прямолинейное движение
а ) поезд въезжает на станцию ________________;
б ) поезд движется между станциями ___________?
2. Поступательным называется движение, при котором ___________________ ________________________ .
3. Определите координату пешехода, взяв за тело отсчета:
а ) дерево:
x = ________ ,
б ) дорожный указатель:
x = _______ .
4. Определите проекции векторов s 1 и s 2 на оси координат:
s 1x = _____ , s 2x = ______ ,
s 1y = _____ , s 2y = ______.
5. Если при равномерном прямолинейном движении тело за 2 ч перемещается на 100 км, то:
– за 0,5 ч оно перемещается на ______________ ,
– за 3 ч оно перемещается на ________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
7. По графикам движения определите:
а ) проекцию скорости каждого тела:
v 1x = __________,
v 2x = __________;
б ) расстояние l между телами в момент времени t = 4 с:
l = ____________ .
8. На рисунке показаны положение двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел:
x 1
= ______ ,
x 2 = ______ .
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения:
t = _____________ ,
x = _____________ .
10. По реке, скорость течения которой 2 км/ч, плывет бревно. По бревну в том же направлении бежит мышонок. С какой скоростью относительно бревна бежит мышонок, если его скорость относительно берега 2,5 км/ч?
v = _______________ .
Вариант 4
Тест № 1. Равномерное прямолинейное движение
а ) автомобиль движется по шоссе _____________;
б ) автомобиль въезжает в гараж ______________?
2. Скорость тела относительно ______________ системы координат равна _________ сумме скорости ________ относительно ________ и скорости ____________ относительно ___________.
3. Определите координату пешехода, взяв за тело отсчета:
а ) дерево:
x = ________ ,
б ) дорожный указатель:
x = _______ .
4. Определите проекции векторов s 1 и s 2 на оси координат:
s 1x = ______ , s 2x = ______ ,
s 1y = ______ , s 2y = ______.
5. Если при равномерном прямолинейном движении тело за 1 мин перемещается на 120 м, то:
– за 10 с оно перемещается на _________________
– за 5 мин оно перемещается на ________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
Можно ли считать данные движения равно — мерными?
7. По графикам движения определите:
а ) проекцию скорости каждого тела:
v 1x = __________,
v 2x = __________ .
б ) расстояние l между телами в момент времени t = 4 с:
l = ____________ .
8. На рисунке показаны положения двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел:
x 1
= ______ ,
x 2 = ______ .
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения:
t = _____________ ,
x = _____________ .
10. Эскалатор движется вниз со скоростью 0,6 м/с относительно Земли. Вверх по эскалатору бежит человек со скоростью 1,4 м/с относительно эскалатора. Чему равна скорость человека относительно Земли?
Чему равна скорость человека относительно Земли?
v = _______________ .
с. 1
Вариант 1
а ) игла падает со стола _________ ;
б ) игла движется при работе машины ________?
2. Прямолинейным равномерным движением называется движение, при котором тело ________ совершает __________ .
а ) дерево:
x = ________ ,
б ) дорожный указатель:
x = _______ .
s 1 и s 2 на оси координат:
s 1 x = _____ , s 2 x = ______ ,
s 2 x = _____ , s 2 y = ______.
5. Если при равномерном прямолинейном движении тело за 20 мин перемещается на 20 км, то:
– за 5 мин оно перемещается на ____________ ,
– за 2 ч оно перемещается на _______________ .
7. По графикам движения определите:
а
v 1 x = __________,
v 2 x = __________ ;
б ) расстояние l t = 4 с:
l = ____________ .
x 1 = ___ ,
x 2 = _____ .
t = ____________ ,
x = _____________ .
10. С какой скоростью относительно Земли будет опускаться парашютист в восходящем потоке воздуха, если скорость парашютиста относительно воздуха 5 м/с, а скорость потока относительно Земли 4 м/с?
v = _____________ .
Вариант 2
Тест № 1. Равномерное прямолинейное движение
а ) космонавт перемещается в космическом корабле ____ ;
б ) космонавт в космическом корабле обращается вокруг Земли ___?
2. Скоростью равномерного прямолинейного движения называется_________________величина, равная _______________ __________________________ к промежутку времени _____________________________________________________ .
3. Определите координату пешехода, взяв за тело отсчета:
а ) дерево:
x = ____________ ,
б ) дорожный указатель:
x = _____________ .
4. Определите проекции векторов s 1 и s 2 на оси координат:
s 1 x = ___ , s 2 x = ___ ,
s 1 y = ___ , s 2 y = ____.
5. Если при равномерном прямолинейном движении тело за 5 c перемещается на 25 м, то:
– за 2 с оно перемещается на _____________ ,
– за 1 мин оно перемещается на ___________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
а ) проекцию скорости каждого тела:
v 1 x = ______________,
v 2 x = ______________ ;
б ) расстояние l между телами в момент времени t = 4 с:
l = __________________
8. На рисунке показаны положения двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел.
x 1 = ___________ ,
x 2 = ___________ ;
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения.
Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения.
t = ___________ ,
x = ___________ .
10. В неподвижной воде пловец плывет со скоростью 2 м/с. Когда он плывет по реке против течения, его скорость относительно берега равна 0,5 м/с вниз по течению. Чему равна скорость течения?
v = ____________
Вариант 3
Тест № 1. Равномерное прямолинейное движение
а ) поезд въезжает на станцию ________________;
б ) поезд движется между станциями ___________?
2. Поступательным называется движение, при котором ___________________ ________________________ .
3. Определите координату пешехода, взяв за тело отсчета:
а ) дерево:
x = ________ ,
б ) дорожный указатель:
x = _______ .
4. Определите проекции векторов s 1 и s 2 на оси координат:
s 1 x = _____ , s 2 x = ______ ,
s 1 y = _____ , s 2 y = ______.
5. Если при равномерном прямолинейном движении тело за 2 ч перемещается на 100 км, то:
– за 0,5 ч оно перемещается на ______________ ,
– за 3 ч оно перемещается на ________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
М
7. По графикам движения определите:
а ) проекцию скорости каждого тела:
v 1 x = __________,
v 2 x = __________;
б ) расстояние l между телами в момент времени t = 4 с:
l = ____________ .
8. На рисунке показаны положение двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел:
x 1 = ______ ,
x 2 = ______ .
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения:
t = _____________ ,
x = _____________ .
10. По реке, скорость течения которой 2 км/ч, плывет бревно. По бревну в том же направлении бежит мышонок. С какой скоростью относительно бревна бежит мышонок, если его скорость относительно берега 2,5 км/ч?
v = _______________ .
Вариант 4
Тест № 1. Равномерное прямолинейное движение
а ) автомобиль движется по шоссе _____________;
б ) автомобиль въезжает в гараж ______________?
2. Скорость тела относительно ______________ системы координат равна _________ сумме скорости ________ относительно ________ и скорости ____________ относительно ___________.
3. Определите координату пешехода, взяв за тело отсчета:
а ) дерево:
x = ________ ,
б ) дорожный указатель:
x = _______ .
4. Определите проекции векторов s 1 и s 2 на оси координат:
s 1 x = ______ , s 2 x = ______ ,
s 1 y = ______ , s 2 y = ______.
5. Если при равномерном прямолинейном движении тело за 1 мин перемещается на 120 м, то:
– за 10 с оно перемещается на _________________
– за 5 мин оно перемещается на ________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
Можно ли считать данные движения равно- мерными?
7. По графикам движения определите:
а ) проекцию скорости каждого тела:
v 1 x = __________,
v 2 x = __________ .
б ) расстояние l между телами в момент времени t = 4 с:
l = ____________ .
8. На рисунке показаны положения двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел:
x 1 = ______ ,
x 2 = ______ .
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения:
t = _____________ ,
x = _____________ .
10. Эскалатор движется вниз со скоростью 0,6 м/с относительно Земли. Вверх по эскалатору бежит человек со скоростью 1,4 м/с относительно эскалатора. Чему равна скорость человека относительно Земли?
v = _______________ .
с. 1
ВСЕРОССИЙСКИЙ ФЕСТИВАЛЬ ПЕДАГОГИЧЕСКОГО ТВОРЧЕСТВА
2016/2017 УЧЕБНОГО ГОДА
Автор: Петренко Надежда Федоровна,
учитель физики высшей квалификационной категории.
Образовательная организация: Муниципальное бюджетное общеобразовательное учреждение Городского округа Балашиха
«Средняя общеобразовательная школа № 7 с углубленным изучением отдельных предметов»
Адрес: 143980, Московская обл., Г. о. Балашиха,
мкр. Железнодорожный, ул. Октябрьская, д. 7.
Дата 2013-2014 уч. год
МБОУ СОШ №7 с УИОП Г.о. Балашиха Московской обл.
Физика – 10 класс.
Урок №4. Тема: «Равномерное прямолинейное движение Решение задач»
Равномерное прямолинейное движение — ТЕСТ
Вариант I
Часть 1
А) троллейбус движется по прямой улице.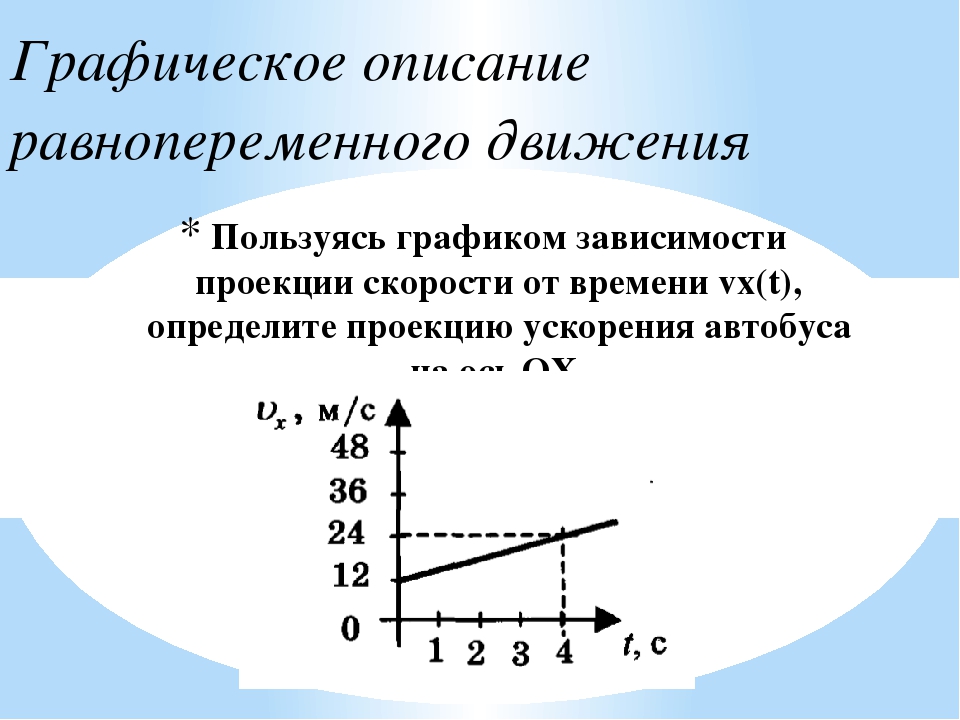 К каждой следующей остановке он прибывает через равные интервалы времени и через равные интервалы отбывает от них
К каждой следующей остановке он прибывает через равные интервалы времени и через равные интервалы отбывает от них
Б) автомобиль движется по дороге и проходит за любые равные промежутки времени одинаковые расстояния
В каком случае движение тела является равномерным?
Что такое скорость прямолинейного равномерного движения?
Физическая величина, равная отношению перемещения точки к промежутку времени, в течение которого это перемещение произошло.
Физическая величина, равная произведению перемещения точки к промежутку времени, в течение которого это перемещение произошло.
Физическая величина, равная отношению промежутка времени к перемещению, которое совершило тело за этот промежуток времени.
Отношение перемещения точки к промежутку времени, в течение которого это перемещение произошло.
Тело движется прямолинейно равномерно так, что направление вектора скорости противоположно направлению оси координат. Что можно сказать о проекции вектора скорости на данную ось?
положительна 3) равна нулю
Выберите формулу координаты прямолинейного равномерного движения
2) 3) 4)
5; 2 2) 2; -5 3) -5; 2 4) 0; 2
3086100266065I
III
II
t, c
X, м
5
0
— 5
— 10
— 15
00I
III
II
t, c
X, м
5
0
— 5
— 10
— 15
На рисунке представлены графики зависимости координат от времени. Определите проекцию скорости второго тела на ось ОХ
Определите проекцию скорости второго тела на ось ОХ
–1,0 м/с
2) 1,0 м/с
3) — 0,5 м/с
4) 0,5 м/с
2971800188595Vx, м/с
4
2
0
— 2
— 4
t, c
2
4
6
8
00Vx, м/с
4
2
0
— 2
— 4
t, c
2
4
6
8
На рисунке приведен график зависимости скорости движения от времени. Определите путь, пройденный телом за первые 8 секунд движения.
Координата тела меняется с течением времени согласно формуле. Чему равна координата этого тела через 5 с после начала движения?
1) 28 м 2) 12 м 3) — 4 м 4) — 12 м Часть 2
Тело Вид движения
А) первое 1) покоится
Часть 3
Уравнения движения двух тел имеют вид:; . Найдите место и время встречи тел графически и аналитически.
Равномерное движение
Вариант II
Часть 1
К каждому из заданий 1 – 8 даны 4 варианта ответа, из которых только один правильный.
Рассмотрим два вида движения тел:
А) поезд метрополитена движется по прямолинейному пути. Он прибывает на каждую следующую станцию и отправляется от нее через одинаковые промежутки времени
Он прибывает на каждую следующую станцию и отправляется от нее через одинаковые промежутки времени
Б) спутник движется по окружности вокруг Земли и за любые равные промежутки времени проходит одинаковые расстояния
В каком случае движение тела не является равномерным?
1) только в А 2) только в Б 3) в А и в Б 4) ни в А, ни в Б
Что характеризует скорость прямолинейного равномерного движения?
направление движения тела
отношение перемещения ко времени, за которое это перемещение совершено.
быстроту изменения координаты
произведение перемещения и времени, за которое это перемещение совершено.
Тело движется прямолинейно равномерно так, что направление вектора скорости совпадает с направлением оси координат. Что можно сказать о проекции вектора скорости на данную ось?
положительна 3) равна нулю
отрицательна 4) может быть, как положительной, так и отрицательной.
Выберите формулу скорости прямолинейного равномерного движения
2) 3) 4)
Уравнение движения имеет вид.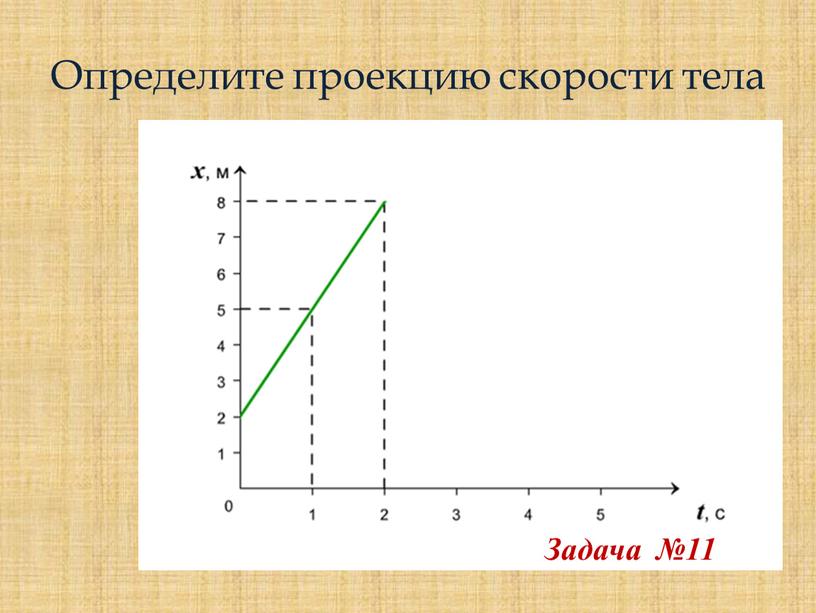 Определите начальную координату и скорость
Определите начальную координату и скорость
0; — 3 2) — 3; 0 3) 0; 3 4) 3; 0
2628900186055I
III
II
t, c
X, м
5
0
— 5
— 10
— 15
00I
III
II
t, c
X, м
5
0
— 5
— 10
— 15
На рисунке представлены графики зависимости координат от времени. Определите проекцию скорости третьего тела на ось ОХ
– 0,5 м/с
2) 2,5 м/с
3) — 2,5 м/с
4) 0,5 м/с
2514600227330Vx, м/с
4
2
0
— 2
— 4
t, c
2
4
6
8
00Vx, м/с
4
2
0
— 2
— 4
t, c
2
4
6
8
На рисунке приведен график зависимости скорости движения от времени. Определите перемещение тела за первые 8 секунд движения.
1) 4 м 2) 8 м 3) 16 м 4) 0 м
Координата тела меняется с течением времени согласно формуле. Через сколько секунд координата тела станет равной нулю?
1) 2 с 2) 5 с 3) 10 с 4) 4 с
Часть 2
В задании 9 требуется указать последовательность цифр, соответствующих правильному ответу.
Уравнения движения тел имеют вид:; ; . Как и в каком направлении движутся тела?
К каждой позиции первого столбика подберите соответствующую позицию второго столбика. Цифры могут повторяться.
Тело Вид движения
А) первое 1) покоится
Б) второе 2) равномерно по оси
В) третье 3) равномерно против оси
Часть 3
Задание 10 представляет собой задачу, полное решение которой необходимо записать.
Уравнения движения двух тел имеют вид: ; . Найдите место и время встречи тел графически и аналитически.
Ответы
N 1 2 3 4 5 6 7 8 9 10
Вариант I 2 1 2 2 3 1 3 4 231 10 с; 30 мВариант II 1 2 1 3 1 4 4 1 321 10 с; 50 м
Равномерное прямолинейное движение — тест. Равномерное прямолинейное движение — тест Тест номер 1 равномерное прямолинейное движение
с. 1
Вариант 1
а ) игла падает со стола _________ ;
б ) игла движется при работе машины ________?
2. Прямолинейным равномерным движением называется движение, при котором тело ________ совершает __________ .
а ) дерево:
x = ________ ,
б ) дорожный указатель:
x = _______ .
s 1 и s 2 на оси координат:
s 1 x = _____ , s 2 x = ______ ,
s 2 x = _____ , s 2 y = ______.
5. Если при равномерном прямолинейном движении тело за 20 мин перемещается на 20 км, то:
– за 5 мин оно перемещается на ____________ ,
– за 2 ч оно перемещается на _______________ .
7. По графикам движения определите:
а
v 1 x = __________,
v 2 x = __________ ;
б ) расстояние l t = 4 с:
l = ____________ .
x 1 = ___ ,
x 2 = _____ .
t = ____________ ,
x = _____________ .
10. С какой скоростью относительно Земли будет опускаться парашютист в восходящем потоке воздуха, если скорость парашютиста относительно воздуха 5 м/с, а скорость потока относительно Земли 4 м/с?
v = _____________ .
Вариант 2
Тест № 1. Равномерное прямолинейное движение
а ) космонавт перемещается в космическом корабле ____ ;
б ) космонавт в космическом корабле обращается вокруг Земли ___?
2. Скоростью равномерного прямолинейного движения называется_________________величина, равная _______________ __________________________ к промежутку времени _____________________________________________________ .
3. Определите координату пешехода, взяв за тело отсчета:
а ) дерево:
x = ____________ ,
б ) дорожный указатель:
x = _____________ .
4. Определите проекции векторов s 1 и s 2 на оси координат:
s 1 x = ___ , s 2 x = ___ ,
s 1 y = ___ , s 2 y = ____.
5. Если при равномерном прямолинейном движении тело за 5 c перемещается на 25 м, то:
– за 2 с оно перемещается на _____________ ,
– за 1 мин оно перемещается на ___________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
а ) проекцию скорости каждого тела:
v 1 x = ______________,
v 2 x = ______________ ;
б ) расстояние l между телами в момент времени t = 4 с:
l = __________________
8. На рисунке показаны положения двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел.
x 1 = ___________ ,
x 2 = ___________ ;
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения.
t = ___________ ,
x = ___________ .
10. В неподвижной воде пловец плывет со скоростью 2 м/с. Когда он плывет по реке против течения, его скорость относительно берега равна 0,5 м/с вниз по течению. Чему равна скорость течения?
v = ____________
Вариант 3
Тест № 1. Равномерное прямолинейное движение
Равномерное прямолинейное движение
а ) поезд въезжает на станцию ________________;
б ) поезд движется между станциями ___________?
2. Поступательным называется движение, при котором ___________________ ________________________ .
3. Определите координату пешехода, взяв за тело отсчета:
а ) дерево:
x = ________ ,
б ) дорожный указатель:
x = _______ .
4. Определите проекции векторов s 1 и s 2 на оси координат:
s 1 x = _____ , s 2 x = ______ ,
s 1 y = _____ , s 2 y = ______.
5. Если при равномерном прямолинейном движении тело за 2 ч перемещается на 100 км, то:
– за 0,5 ч оно перемещается на ______________ ,
– за 3 ч оно перемещается на ________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
М
7. По графикам движения определите:
По графикам движения определите:
а ) проекцию скорости каждого тела:
v 1 x = __________,
v 2 x = __________;
б ) расстояние l между телами в момент времени t = 4 с:
l = ____________ .
8. На рисунке показаны положение двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел:
x 1 = ______ ,
x 2 = ______ .
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения:
t = _____________ ,
x = _____________ .
10. По реке, скорость течения которой 2 км/ч, плывет бревно. По бревну в том же направлении бежит мышонок. С какой скоростью относительно бревна бежит мышонок, если его скорость относительно берега 2,5 км/ч?
v = _______________ .
Вариант 4
Тест № 1. Равномерное прямолинейное движение
а ) автомобиль движется по шоссе _____________;
б ) автомобиль въезжает в гараж ______________?
2. Скорость тела относительно ______________ системы координат равна _________ сумме скорости ________ относительно ________ и скорости ____________ относительно ___________.
Скорость тела относительно ______________ системы координат равна _________ сумме скорости ________ относительно ________ и скорости ____________ относительно ___________.
3. Определите координату пешехода, взяв за тело отсчета:
а ) дерево:
x = ________ ,
б ) дорожный указатель:
x = _______ .
4. Определите проекции векторов s 1 и s 2 на оси координат:
s 1 x = ______ , s 2 x = ______ ,
s 1 y = ______ , s 2 y = ______.
5. Если при равномерном прямолинейном движении тело за 1 мин перемещается на 120 м, то:
– за 10 с оно перемещается на _________________
– за 5 мин оно перемещается на ________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
Можно ли считать данные движения равно- мерными?
7. По графикам движения определите:
а ) проекцию скорости каждого тела:
v 1 x = __________,
v 2 x = __________ .
б ) расстояние l между телами в момент времени t = 4 с:
l = ____________ .
8. На рисунке показаны положения двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел:
x 1 = ______ ,
x 2 = ______ .
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения:
t = _____________ ,
x = _____________ .
10. Эскалатор движется вниз со скоростью 0,6 м/с относительно Земли. Вверх по эскалатору бежит человек со скоростью 1,4 м/с относительно эскалатора. Чему равна скорость человека относительно Земли?
v = _______________ .
с. 1
ВСЕРОССИЙСКИЙ ФЕСТИВАЛЬ ПЕДАГОГИЧЕСКОГО ТВОРЧЕСТВА
2016/2017 УЧЕБНОГО ГОДА
Автор: Петренко Надежда Федоровна,
учитель физики высшей квалификационной категории.
Образовательная организация: Муниципальное бюджетное общеобразовательное учреждение Городского округа Балашиха
«Средняя общеобразовательная школа № 7 с углубленным изучением отдельных предметов»
Адрес: 143980, Московская обл.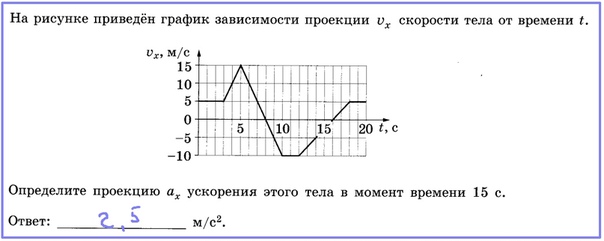 , Г. о. Балашиха,
, Г. о. Балашиха,
мкр. Железнодорожный, ул. Октябрьская, д. 7.
Дата 2013-2014 уч. год
МБОУ СОШ №7 с УИОП Г.о. Балашиха Московской обл.
Физика – 10 класс.
Урок №4. Тема: «Равномерное прямолинейное движение Решение задач»
Равномерное прямолинейное движение — ТЕСТ
Вариант I
Часть 1
А) троллейбус движется по прямой улице. К каждой следующей остановке он прибывает через равные интервалы времени и через равные интервалы отбывает от них
Б) автомобиль движется по дороге и проходит за любые равные промежутки времени одинаковые расстояния
В каком случае движение тела является равномерным?
Что такое скорость прямолинейного равномерного движения?
Физическая величина, равная отношению перемещения точки к промежутку времени, в течение которого это перемещение произошло.
Физическая величина, равная произведению перемещения точки к промежутку времени, в течение которого это перемещение произошло.
Физическая величина, равная отношению промежутка времени к перемещению, которое совершило тело за этот промежуток времени.
Отношение перемещения точки к промежутку времени, в течение которого это перемещение произошло.
Тело движется прямолинейно равномерно так, что направление вектора скорости противоположно направлению оси координат. Что можно сказать о проекции вектора скорости на данную ось?
положительна 3) равна нулю
Выберите формулу координаты прямолинейного равномерного движения
2) 3) 4)
5; 2 2) 2; -5 3) -5; 2 4) 0; 2
3086100266065I
III
II
t, c
X, м
5
0
— 5
— 10
— 15
00I
III
II
t, c
X, м
5
0
— 5
— 10
— 15
На рисунке представлены графики зависимости координат от времени. Определите проекцию скорости второго тела на ось ОХ
–1,0 м/с
2) 1,0 м/с
3) — 0,5 м/с
4) 0,5 м/с
2971800188595Vx, м/с
4
2
0
— 2
— 4
t, c
2
4
6
8
00Vx, м/с
4
2
0
— 2
— 4
t, c
2
4
6
8
На рисунке приведен график зависимости скорости движения от времени. Определите путь, пройденный телом за первые 8 секунд движения.
Определите путь, пройденный телом за первые 8 секунд движения.
Координата тела меняется с течением времени согласно формуле. Чему равна координата этого тела через 5 с после начала движения?
1) 28 м 2) 12 м 3) — 4 м 4) — 12 м Часть 2
Тело Вид движения
А) первое 1) покоится
Часть 3
Уравнения движения двух тел имеют вид:; . Найдите место и время встречи тел графически и аналитически.
Равномерное движение
Вариант II
Часть 1
К каждому из заданий 1 – 8 даны 4 варианта ответа, из которых только один правильный.
Рассмотрим два вида движения тел:
А) поезд метрополитена движется по прямолинейному пути. Он прибывает на каждую следующую станцию и отправляется от нее через одинаковые промежутки времени
Б) спутник движется по окружности вокруг Земли и за любые равные промежутки времени проходит одинаковые расстояния
В каком случае движение тела не является равномерным?
1) только в А 2) только в Б 3) в А и в Б 4) ни в А, ни в Б
Что характеризует скорость прямолинейного равномерного движения?
направление движения тела
отношение перемещения ко времени, за которое это перемещение совершено.
быстроту изменения координаты
произведение перемещения и времени, за которое это перемещение совершено.
Тело движется прямолинейно равномерно так, что направление вектора скорости совпадает с направлением оси координат. Что можно сказать о проекции вектора скорости на данную ось?
положительна 3) равна нулю
отрицательна 4) может быть, как положительной, так и отрицательной.
Выберите формулу скорости прямолинейного равномерного движения
2) 3) 4)
Уравнение движения имеет вид. Определите начальную координату и скорость
0; — 3 2) — 3; 0 3) 0; 3 4) 3; 0
2628900186055I
III
II
t, c
X, м
5
0
— 5
— 10
— 15
00I
III
II
t, c
X, м
5
0
— 5
— 10
— 15
На рисунке представлены графики зависимости координат от времени. Определите проекцию скорости третьего тела на ось ОХ
– 0,5 м/с
2) 2,5 м/с
3) — 2,5 м/с
4) 0,5 м/с
2514600227330Vx, м/с
4
2
0
— 2
— 4
t, c
2
4
6
8
00Vx, м/с
4
2
0
— 2
— 4
t, c
2
4
6
8
На рисунке приведен график зависимости скорости движения от времени. Определите перемещение тела за первые 8 секунд движения.
Определите перемещение тела за первые 8 секунд движения.
1) 4 м 2) 8 м 3) 16 м 4) 0 м
Координата тела меняется с течением времени согласно формуле. Через сколько секунд координата тела станет равной нулю?
1) 2 с 2) 5 с 3) 10 с 4) 4 с
Часть 2
В задании 9 требуется указать последовательность цифр, соответствующих правильному ответу.
Уравнения движения тел имеют вид:; ; . Как и в каком направлении движутся тела?
К каждой позиции первого столбика подберите соответствующую позицию второго столбика. Цифры могут повторяться.
Тело Вид движения
А) первое 1) покоится
Б) второе 2) равномерно по оси
В) третье 3) равномерно против оси
Часть 3
Задание 10 представляет собой задачу, полное решение которой необходимо записать.
Уравнения движения двух тел имеют вид: ; . Найдите место и время встречи тел графически и аналитически.
Ответы
N 1 2 3 4 5 6 7 8 9 10
Вариант I 2 1 2 2 3 1 3 4 231 10 с; 30 мВариант II 1 2 1 3 1 4 4 1 321 10 с; 50 м
Вариант 1
а ) игла падает со стола _________ ;
б ) игла движется при работе машины ________?
2. Прямолинейным равномерным движением называется движение, при котором тело ________ совершает __________ .
Прямолинейным равномерным движением называется движение, при котором тело ________ совершает __________ .
а ) дерево:
x = ________ ,
б ) дорожный указатель:
x = _______ .
s 1 и s 2 на оси координат:
s 1x = _____ , s 2x = ______ ,
s 2x = _____ , s 2y = ______.
5. Если при равномерном прямолинейном движении тело за 20 мин перемещается на 20 км, то:
– за 5 мин оно перемещается на ____________ ,
– за 2 ч оно перемещается на _______________ .
а
v 1x = __________,
v 2x = __________ ;
б ) расстояние l t = 4 с:
l = ____________ .
x 1
= ___ ,
x 2 = _____
font-size:10.0pt;font-family:» arial cyr>.
t = ____________ ,
x = _____________ .
10. С какой скоростью относительно Земли будет опускаться парашютист в восходящем потоке воздуха, если скорость парашютиста относительно воздуха 5 м/с, а скорость потока относительно Земли 4 м/с?
v = _____________ .
Вариант 2
Тест № 1. Равномерное прямолинейное движение
а ) космонавт перемещается в космическом корабле ____ ;
б ) космонавт в космическом корабле обращается вокруг Земли ___?
2. Скоростью равномерного прямолинейного движения называется_________________величина, равная _______________ __________________________ к промежутку времени _____________________________________________________ .
3. Определите координату пешехода, взяв за тело отсчета:
а ) дерево:
x = ____________ ,
б ) дорожный указатель:
x = _____________ .
4. Определите проекции векторов s 1 и s 2 на оси координат:
s 1x = ___ , s 2x = ___ ,
s 1y = ___ , s 2y = ____.
5. Если при равномерном прямолинейном движении тело за 5 c перемещается на 25 м, то:
– за 2 с оно перемещается на _____________ ,
– за 1 мин оно перемещается на ___________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
7. По графикам движения определите:
а ) проекцию скорости каждого тела:
v 1x = ______________,
v 2x = ______________ ;
б ) расстояние l между телами в момент времени t = 4 с:
l = __________________
8. На рисунке показаны положения двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел.
x 1
= ___________ ,
x 2 = ___________ ;
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения.
t = ___________ ,
x = ___________ .
10. В неподвижной воде пловец плывет со скоростью 2 м/с. Когда он плывет по реке против течения, его скорость относительно берега равна 0,5 м/с вниз по течению. Чему равна скорость течения?
v = ____________
.
Вариант 3
Тест № 1. Равномерное прямолинейное движение
а ) поезд въезжает на станцию ________________;
б ) поезд движется между станциями ___________?
2. Поступательным называется движение, при котором ___________________ ________________________ .
3. Определите координату пешехода, взяв за тело отсчета:
а ) дерево:
x = ________ ,
б ) дорожный указатель:
x = _______ .
4. Определите проекции векторов s 1 и s 2 на оси координат:
s 1x = _____ , s 2x = ______ ,
s 1y = _____ , s 2y = ______.
5. Если при равномерном прямолинейном движении тело за 2 ч перемещается на 100 км, то:
– за 0,5 ч оно перемещается на ______________ ,
– за 3 ч оно перемещается на ________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
7. По графикам движения определите:
а ) проекцию скорости каждого тела:
v 1x = __________,
v 2x = __________;
б ) расстояние l между телами в момент времени t = 4 с:
l = ____________ .
8. На рисунке показаны положение двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел:
x 1
= ______ ,
x 2 = ______ .
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения:
t = _____________ ,
x = _____________ .
10. По реке, скорость течения которой 2 км/ч, плывет бревно. По бревну в том же направлении бежит мышонок. С какой скоростью относительно бревна бежит мышонок, если его скорость относительно берега 2,5 км/ч?
v = _______________ .
Вариант 4
Тест № 1. Равномерное прямолинейное движение
а ) автомобиль движется по шоссе _____________;
б ) автомобиль въезжает в гараж ______________?
2. Скорость тела относительно ______________ системы координат равна _________ сумме скорости ________ относительно ________ и скорости ____________ относительно ___________.
3. Определите координату пешехода, взяв за тело отсчета:
а ) дерево:
x = ________ ,
б ) дорожный указатель:
x = _______ .
4. Определите проекции векторов s 1 и s 2 на оси координат:
s 1x = ______ , s 2x = ______ ,
s 1y = ______ , s 2y = ______.
5. Если при равномерном прямолинейном движении тело за 1 мин перемещается на 120 м, то:
– за 10 с оно перемещается на _________________
– за 5 мин оно перемещается на ________________ .
6. В таблице даны координаты двух движущихся тел для определенных моментов времени.
Можно ли считать данные движения равно — мерными?
7. По графикам движения определите:
а ) проекцию скорости каждого тела:
v 1x = __________,
v 2x = __________ .
б ) расстояние l между телами в момент времени t = 4 с:
l = ____________ .
8. На рисунке показаны положения двух маленьких шариков в начальный момент времени и их скорости. Запишите уравнения движения этих тел:
x 1
= ______ ,
x 2 = ______ .
9. Пользуясь условием предыдущего вопроса, постройте графики движения шариков и найдите время и место их столкновения:
t = _____________ ,
x = _____________ .
10. Эскалатор движется вниз со скоростью 0,6 м/с относительно Земли. Вверх по эскалатору бежит человек со скоростью 1,4 м/с относительно эскалатора. Чему равна скорость человека относительно Земли?
Чему равна скорость человека относительно Земли?
v = _______________ .
Представление свободного падения с графиками p-t и v-t
В начале урока 1 было упомянуто, что существует множество способов описания движения объектов. Одним из таких средств описания движения объектов является использование графиков — графика зависимости положения от времени и скорости от времени. В этой части Урока 5 движение свободного падения будет представлено с использованием этих двух основных типов графиков.
Представление свободного падения с помощью графиков положения и времениГрафик зависимости положения от времени для свободно падающего объекта показан ниже.
Обратите внимание, что линия на графике изгибается. Как было сказано ранее, изогнутая линия на графике зависимости положения от времени означает ускоренное движение. Поскольку свободно падающий объект испытывает ускорение (g = 9,8 м / с / с), можно было бы ожидать, что его график положения-времени будет искривленным. Дальнейший взгляд на график положение-время показывает, что объект начинает с небольшой скорости (медленной) и заканчивается с большой скоростью (быстро). Поскольку наклон любой позиции vs.Временной график — это скорость объекта (как показано в Уроке 3), небольшой начальный наклон указывает на небольшую начальную скорость, а большой конечный наклон указывает на большую конечную скорость. Наконец, отрицательный наклон линии указывает на отрицательную (т.е. нисходящую) скорость.
Дальнейший взгляд на график положение-время показывает, что объект начинает с небольшой скорости (медленной) и заканчивается с большой скоростью (быстро). Поскольку наклон любой позиции vs.Временной график — это скорость объекта (как показано в Уроке 3), небольшой начальный наклон указывает на небольшую начальную скорость, а большой конечный наклон указывает на большую конечную скорость. Наконец, отрицательный наклон линии указывает на отрицательную (т.е. нисходящую) скорость.
График зависимости скорости от времени для свободно падающего объекта показан ниже.
Обратите внимание, что линия на графике представляет собой прямую диагональную линию. Как было сказано ранее, диагональная линия на графике зависимости скорости от времени означает ускоренное движение. Поскольку свободно падающий объект испытывает ускорение (g = 9,8 м / с / с, вниз), можно было бы ожидать, что его график скорости-времени будет диагональным. Дальнейший взгляд на график скорость-время показывает, что объект начинается с нулевой скорости (как видно из графика) и заканчивается большой отрицательной скоростью; то есть объект движется в отрицательном направлении и набирает скорость.Говорят, что объект, который движется в отрицательном направлении и ускоряется, имеет отрицательное ускорение (при необходимости проверьте векторную природу ускорения). Поскольку наклон любого графика зависимости скорости от времени — это ускорение объекта (как показано в Уроке 4), постоянный отрицательный наклон указывает на постоянное отрицательное ускорение. Этот анализ наклона на графике согласуется с движением свободно падающего объекта — объекта, движущегося с постоянным ускорением 9,8 м / с / с в направлении вниз.
Дальнейший взгляд на график скорость-время показывает, что объект начинается с нулевой скорости (как видно из графика) и заканчивается большой отрицательной скоростью; то есть объект движется в отрицательном направлении и набирает скорость.Говорят, что объект, который движется в отрицательном направлении и ускоряется, имеет отрицательное ускорение (при необходимости проверьте векторную природу ускорения). Поскольку наклон любого графика зависимости скорости от времени — это ускорение объекта (как показано в Уроке 4), постоянный отрицательный наклон указывает на постоянное отрицательное ускорение. Этот анализ наклона на графике согласуется с движением свободно падающего объекта — объекта, движущегося с постоянным ускорением 9,8 м / с / с в направлении вниз.
Движение в двух измерениях | Безграничная физика
Постоянная скорость
Объект, движущийся с постоянной скоростью, должен иметь постоянную скорость в постоянном направлении.
Цели обучения
Изучите термины для постоянной скорости и их применение к ускорению
Основные выводы
Ключевые моменты
- Постоянная скорость означает, что движущийся объект движется по прямой с постоянной скоростью.
- Эта строка может быть представлена алгебраически как: [latex] \ text {x} = \ text {x} _0 + \ text {vt} [/ latex], где [latex] \ text {x} _0 [/ latex] представляет положение объекта в [latex] \ text {t} = 0 [/ latex], а наклон линии указывает скорость объекта.
- Скорость может быть положительной или отрицательной и обозначена знаком нашего наклона. Это говорит нам, в каком направлении движется объект.
Ключевые термины
- постоянная скорость : Движение, которое не меняется ни по скорости, ни по направлению.
Движение с постоянной скоростью — одна из простейших форм движения. Этот тип движения возникает, когда объект движется (или скользит) в присутствии небольшого или незначительного трения, подобно тому, как хоккейная шайба скользит по льду. Чтобы иметь постоянную скорость, объект должен иметь постоянную скорость в постоянном направлении. Постоянное направление заставляет объект двигаться по прямой траектории.
Чтобы иметь постоянную скорость, объект должен иметь постоянную скорость в постоянном направлении. Постоянное направление заставляет объект двигаться по прямой траектории.
Второй закон Ньютона ([latex] \ text {F} = \ text {ma} [/ latex]) предполагает, что когда к объекту прикладывается сила, объект испытывает ускорение.Если ускорение равно 0, объект не должен подвергаться воздействию внешних сил. Математически это можно представить следующим образом:
[латекс] \ text {a} = \ frac {\ text {dv}} {\ text {dt}} = 0 ~ \ Rightarrow ~ \ text {v} = \ text {const} [/ latex].
Если объект движется с постоянной скоростью, график зависимости расстояния от времени ([latex] \ text {x} [/ latex] vs. [latex] \ text {t} [/ latex]) показывает такое же изменение положение по каждому интервалу времени. Поэтому движение объекта с постоянной скоростью представлено прямой линией: [latex] \ text {x} = \ text {x} _0 + \ text {vt} [/ latex], где [latex] \ text {x} _0 [/ latex] — это смещение, когда [latex] \ text {t} = 0 [/ latex] (или в точке пересечения оси Y).
Движение с постоянной скоростью : Когда объект движется с постоянной скоростью, он не меняет ни направления, ни скорости, и поэтому отображается в виде прямой линии на графике как расстояние во времени.
Вы также можете получить скорость объекта, если знаете его след во времени. Имея график, как в, мы можем вычислить скорость по изменению расстояния с течением времени. Графически скорость можно интерпретировать как наклон линии.Скорость может быть положительной или отрицательной и указывается знаком нашего наклона. Это говорит нам, в каком направлении движется объект.
Постоянное ускорение
Анализ двумерного движения снаряда осуществляется путем разбиения его на два движения: по горизонтальной и вертикальной осям.
Цели обучения
Анализировать двумерное движение снаряда по горизонтальной и вертикальной осям
Основные выводы
Ключевые моменты
- Постоянное ускорение при движении в двух измерениях обычно следует за образцом снаряда.

- Движение снаряда — это движение объекта, брошенного или выброшенного в воздух, с учетом только (вертикального) ускорения силы тяжести.
- Мы анализируем двумерное движение снаряда, разбивая его на два независимых одномерных движения по вертикальной и горизонтальной осям.
Ключевые термины
- кинематика : движение или кинематика или относящиеся к ней
Движение снаряда — это движение объекта, брошенного или выброшенного в воздух, подверженное только силе тяжести.Объект называется снарядом, а его путь называется его траекторией. Движение падающих предметов — это простой одномерный тип движения снаряда, при котором нет горизонтального движения. В двумерном движении снаряда, например футбольного мяча или другого брошенного объекта, есть как вертикальная, так и горизонтальная составляющие движения.
Движение снаряда : Бросок камня или удар ногой по мячу, как правило, создает образец движения снаряда, который имеет как вертикальную, так и горизонтальную составляющие.
Самый важный факт, о котором следует помнить, это то, что движения по перпендикулярным осям независимы и поэтому могут быть проанализированы отдельно. Ключ к анализу двумерного движения снаряда — разбить его на два движения, одно по горизонтальной оси, а другое по вертикали. Чтобы описать движение, мы должны иметь дело со скоростью и ускорением, а также со смещением.
Предположим, что все силы, кроме силы тяжести (например, сопротивление воздуха и трение), незначительны.2} [/ latex] (мы предполагаем, что движение происходит на достаточно малых высотах у поверхности земли, чтобы ускорение свободного падения было постоянным). Поскольку ускорение свободного падения происходит в вертикальном направлении , только , [latex] \ text {a} _ \ text {x} = 0 [/ latex]. Таким образом, можно использовать кинематические уравнения, описывающие движение по направлениям [latex] \ text {x} [/ latex] и [latex] \ text {y} [/ latex] соответственно:
[латекс] \ text {x} = \ text {x} _0 + \ text {v} _ \ text {x} \ text {t} [/ latex]
[латекс] \ text {v} _ \ text {y} = \ text {v} _ {0 \ text {y}} + \ text {a} _ \ text {y} \ text {t} [/ latex ]
[латекс] \ text {y} = \ text {y} _0 + \ text {v} _ {0 \ text {y}} \ text {t} + \ frac {1} {2} \ text {a} _ \ text {y} \ text {t} ^ 2 [/ latex]
[латекс] \ text {v} _ \ text {y} ^ 2 = \ text {v} _ {0 \ text {y}} ^ 2 + 2 \ text {a} _ \ text {y} (\ text {y} — \ text {y} _0) [/ latex]
Мы анализируем двумерное движение снаряда, разбивая его на два независимых одномерных движения по вертикальной и горизонтальной осям.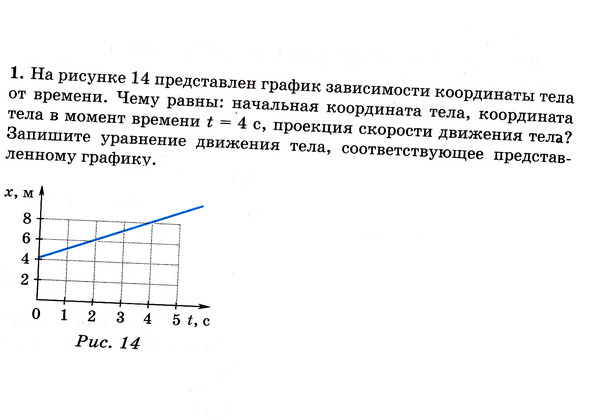 Горизонтальное движение простое, потому что [latex] \ text {a} _ \ text {x} = 0 [/ latex] и [latex] \ text {v} _ \ text {x} [/ latex], таким образом, является постоянным. Скорость в вертикальном направлении начинает уменьшаться по мере подъема объекта; в самой высокой точке вертикальная скорость равна нулю. Когда объект снова падает на Землю, вертикальная скорость снова увеличивается по величине, но указывает в направлении, противоположном начальной вертикальной скорости. Движения [latex] \ text {x} [/ latex] и [latex] \ text {y} [/ latex] можно рекомбинировать, чтобы получить общую скорость в любой заданной точке траектории.
Горизонтальное движение простое, потому что [latex] \ text {a} _ \ text {x} = 0 [/ latex] и [latex] \ text {v} _ \ text {x} [/ latex], таким образом, является постоянным. Скорость в вертикальном направлении начинает уменьшаться по мере подъема объекта; в самой высокой точке вертикальная скорость равна нулю. Когда объект снова падает на Землю, вертикальная скорость снова увеличивается по величине, но указывает в направлении, противоположном начальной вертикальной скорости. Движения [latex] \ text {x} [/ latex] и [latex] \ text {y} [/ latex] можно рекомбинировать, чтобы получить общую скорость в любой заданной точке траектории.
Одномерное (прямолинейное) движение.
Кинематика — это «геометрия движения». Он описывает движение без использования понятий силы и массы. В этой главе нас интересуют новаторские работы Галилея в области кинематики, посвященные проблемам движения с постоянным ускорением, включая движение падающих тел.
Определения:
Скорость: v = (x 2 — x 1 ) / (t 2 — t 1 ), что может быть записано v = Δx / Δt
Ускорение: a = (v 2 — v 1 ) / (t 2 — t 1 ), что может быть записано a = Δv / Δt
|
Символ Δ — это оператор, означающий «изменение». Мы будем использовать жирные символы для положения, смещения, скорости и ускорения в наших уравнениях, чтобы подчеркнуть, что это величины, которые могут иметь как положительные, так и отрицательные знаки, и что этот знак указывает направление движения вдоль линии. Очень важно, чтобы вы указали направление, которое вы выбрали для вызова «+», прежде чем приступить к проблеме, поскольку относительные знаки имеют значение. Сделав этот выбор, не меняйте его, решая задачу.Мы также ожидаем того факта, что эти величины являются векторными величинами, и когда мы расширим это представление, включив в него двух- и трехмерное движение, мы будем нуждаться в том, чтобы рассматривать определенные физические величины как векторы, а жирный шрифт — традиционный способ обозначить, что величины являются векторами.
Приведенные выше уравнения действительны для любого вида движения, если вы возьмете предел исчисления правых частей, поскольку Δt стремится к нулю. Но в частном случае прямолинейного движения, когда ускорение постоянно, скорость одинакова независимо от того, используете ли вы большой или малый интервал времени, Δt, и, поскольку ускорение постоянно, оно также не зависит от размера временной интервал.График скорость-время представляет собой прямую линию, и мы можем написать:
Но в частном случае прямолинейного движения, когда ускорение постоянно, скорость одинакова независимо от того, используете ли вы большой или малый интервал времени, Δt, и, поскольку ускорение постоянно, оно также не зависит от размера временной интервал.График скорость-время представляет собой прямую линию, и мы можем написать:
|
Эти два могут быть немедленно объединены, чтобы получить уравнение
для любых двух точек 1 и 2 на прямой. d = x 2 — x 1 — это смещение положения, которое происходит в течение интервала времени t.
Это последний раз, когда мы будем использовать понятие средней скорости, поскольку оно бесполезно при решении проблем. По правде говоря, он используется здесь только для того, чтобы не вводить исчисление, но его использование законно в этом частном случае постоянного ускорения.
По правде говоря, он используется здесь только для того, чтобы не вводить исчисление, но его использование законно в этом частном случае постоянного ускорения.
Предполагаемые начальные условия: Тело имеет смещение d = 0 при t = 0, а его скорость при t = 0 составляет v o .Иногда мы называем t = 0 и t «начальной» и «конечной» скоростями, но на самом деле это просто моменты времени, в которые движущееся тело оказывается в двух разных положениях, выбранных потому, что они представляют для нас особый интерес. в решении проблем. Метки «начальный» и «конечный» относятся только к конечным точкам рассматриваемого временного интервала.
Приведенные ниже уравнения являются результатами, действительными только для случая постоянного ускорения.
Используйте уравнение 5, записанное для «начальной» и «конечной» скоростей v o и v .Затем решите уравнение для d .
Решите уравнение 7 для v
Поместите это в уравнение 9.
Наконец, умножьте уравнение 7 на уравнение 9 и переставьте, чтобы получить:
Мы выделили ускорение и смещение жирным шрифтом, чтобы напомнить вам, что в этом уравнении знаки этих векторных величин все еще важны. Символ • можно рассматривать просто как означающий «умножение величин, включая их знаки».Позже, когда мы займемся двух- и трехмерным движением, этот символ приобретет новое значение.
Уравнения 9, 11 и 12 иногда называют «уравнениями движения Галилея», но помните, что у Галилея не было преимуществ алгебраических обозначений, которые мы здесь используем. Важным моментом является то, что эти уравнения следуют из определений скорости и ускорения Галилео путем непосредственной алгебраической манипуляции. Здесь мы видим способность математики преобразовывать простые предложения в более полезные формы: уравнения, которые мы можем использовать для анализа движения и прогнозирования результатов движения в конкретных случаях.
Двумерное движение (в плоскости).
Galileo расширил кинематику на случаи падения тел и снарядов (ядер). Он представил для этого инновационную концепцию. Он предположил, что движение снаряда можно рассматривать как комбинацию двух более простых движений, объединенных «принципом суперпозиции». Это так.
Предположим, что пушка стреляет горизонтально с высокой скалы. Результирующее движение включает поступательное движение и падающее движение.Представим, что мы можем рассмотреть их по отдельности. Если бы ядро было просто сброшено со скалы без какого-либо прямого (горизонтального) толчка и без толчка вниз, его начальная скорость равна нулю, и уравнение 11 сводится к
.Чтобы не усложнять, мы рассматриваем движение, которое должно быть описано в декартовой системе координат, где «x» — горизонтальное расстояние, «y» — вертикальное, а «+» — направленное вниз.
А теперь представьте, что «отключает» движение ядра вниз.Галилей понял, что величина ускорения движущегося тела зависит от угла движения к вертикали, и что в этих условиях горизонтально движущееся тело не ускоряется или не замедляется.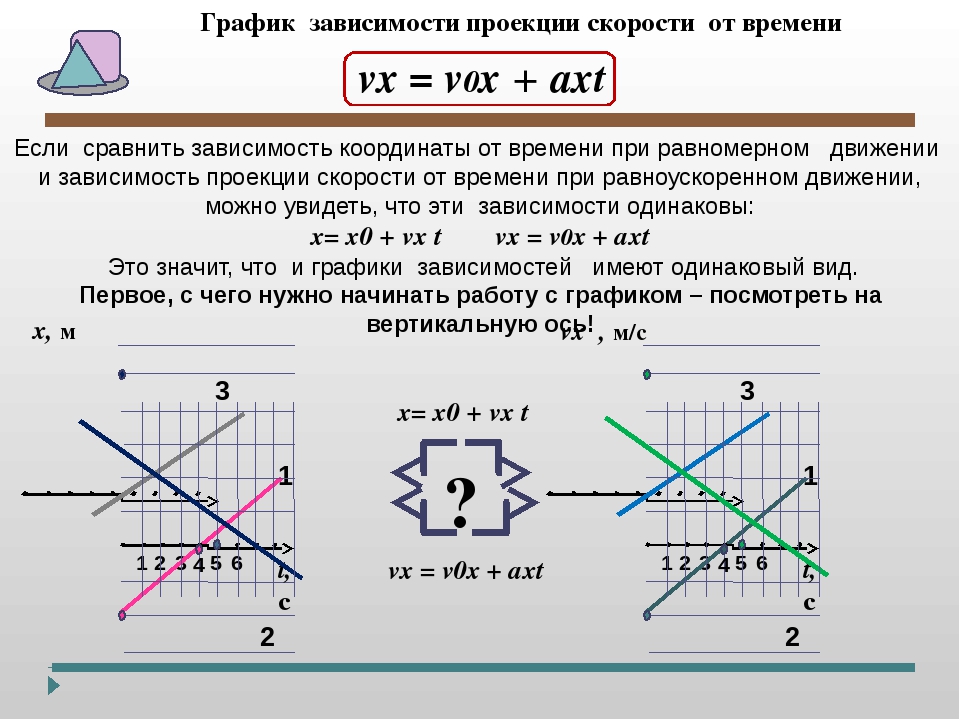 Он подробно обсудил это, поскольку это довольно сложный аргумент, учитывая, что ему пришлось отбросить такие осложнения, как сопротивление воздуха, трение и т. Д. Итак, Галилей сказал, что такое движение, строго горизонтальное, имеет нулевое ускорение, и поэтому уравнение 11 уменьшается до
Он подробно обсудил это, поскольку это довольно сложный аргумент, учитывая, что ему пришлось отбросить такие осложнения, как сопротивление воздуха, трение и т. Д. Итак, Галилей сказал, что такое движение, строго горизонтальное, имеет нулевое ускорение, и поэтому уравнение 11 уменьшается до
Тело движется вперед на равные расстояния за равное время с постоянной скоростью, равной начальной скорости v o .
Теперь, если и «падение», и «поступательное движение» происходят одновременно, Галилей сказал, что мы можем комбинировать (совмещать) эти два движения, чтобы определить фактическое движение. Просто выберите значение времени, в которое вы хотите знать, где находится пушечное ядро, поместите это синто-уравнение 13 и 14, и вы получите положение тела, выраженное в единицах горизонтального расстояния x от начальной точки, и вертикальное расстояние падения y, измеренное от начальной точки. [Мы выражаем это на языке координатной геометрии Декарта, которая была разработана позже Галилея, но мы видим концептуальную основу, предвосхищенную в работах Галилея и других исследователей проблемы движения. Фактически, анализ Галилея предвосхитил важное развитие концепции вектора в математике, которая не была сформулирована полностью и явно не использовалась в физике до 19 века!
Фактически, анализ Галилея предвосхитил важное развитие концепции вектора в математике, которая не была сформулирована полностью и явно не использовалась в физике до 19 века!
Схема показывает, что происходит. Он показывает горизонтальные и вертикальные смещения от начальной точки вверху слева. Вдоль горизонтальной линии представьте стрелки с хвостами в начальной точке. Показаны их головы. Стрелки вниз представляют смещения от этой горизонтальной линии из-за «падения».Длины отрисовываются с равными интервалами времени и в соответствии с уравнениями 13 и 14. Наложение горизонтальных и вертикальных движений достигается путем добавления вертикальных и горизонтальных смещений для каждого времени, комбинируя стрелки, помещая их лицом к хвосту в строка из двух. Эта строка имеет один «хвост» стрелки в начальной точке и другой «наконечник» стрелки в положении тела в то время. Смещение тела в этот момент представлено стрелкой (не показана), которая проходит от начальной точки до только что построенной стрелки.
Эта процедура работает правильно даже для стрельбы под другим углом к горизонтали, например, когда пушка стреляет под углом вверх. Эта процедура позволяет проследить траекторию движения тела. Используя разработанные нами уравнения, этот путь будет математической кривой, называемой параболой . В реальном мире необходимо учитывать влияние воздуха, замедляющего движение, — эффект, более значительный для больших скоростей.К сожалению, это осложнение потребовало бы анализа с использованием математического анализа.
Сложение вектора.
Показанный нами процесс очень важен для физики, так что мы могли бы взглянуть на него более внимательно. Эти стрелки, которые мы нарисовали, представляют векторов , в частности векторов смещения. Многие величины в физике комбинируются посредством процесса объединения векторов путем сложения векторов процесса помещения «стрелочного» представления векторных величин в строку «голова к хвосту». Сумма этих векторов и есть вектор, проведенный от свободного хвоста к свободной голове.
Сумма этих векторов и есть вектор, проведенный от свободного хвоста к свободной голове.
Скаляры и векторы
Скаляр — это физическая величина, определение которой никоим образом не путь зависит от направления в пространстве. Скаляры включают время, массу, объем, температуру, плотность и другие. Размер скалярной величины представлен в виде числа. В физических уравнениях скаляры подчиняются алгебре чисел.
|
Вектор — это физическая величина, зависящая от направления в пространстве. Вектор имеет размер и направление , и оба должны быть задан для уникальной характеристики вектора. К векторам относятся смещение, скорость, ускорение, импульс, угловой момент и другие.
Некоторые векторные величины могут вас удивить. Рассмотрим кусок поверхности. Поскольку площадь поверхности имеет ориентацию в пространстве,
его часто нужно рассматривать как вектор, его направление — это линия, нормальная к поверхности.
Поскольку площадь поверхности имеет ориентацию в пространстве,
его часто нужно рассматривать как вектор, его направление — это линия, нормальная к поверхности.
Направление векторной величины в физике должно быть указано, так как оно так же важно, как размер вектора при определении эффекта вектора. Два вектора называются равными , только если их размеры Направления и совпадают. Когда мы пишем A = B , мы говорим, что эти два вектора равны по размеру и направлены в одном направлении. Знак равенства, выделенный жирным шрифтом, говорит нам, что это векторное уравнение. Когда мы пишем A = B, мы говорим, что два вектора равны только по размеру, а знак равенства световых граней представляет только равенство размеров.
Векторы в физических уравнениях подчиняются алгебре, совершенно отличной от
что скалярной алгебры. Одно полезное и интуитивно понятное графическое представление вектора
это стрела. Длина стрелки представляет размер вектора, а
Направление стрелки представляет направление вектора в пространстве.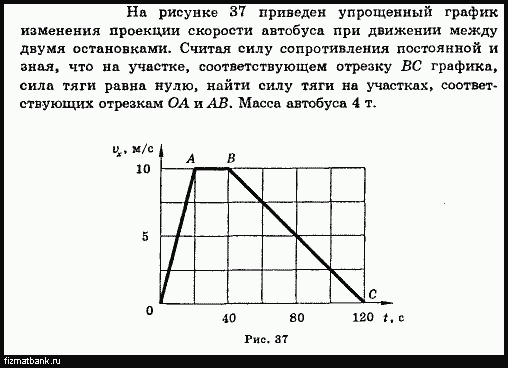 С помощью этого представления мы можем проиллюстрировать отношения между
векторов геометрически, и это облегчает использование геометрии для решения некоторых задач.
С помощью этого представления мы можем проиллюстрировать отношения между
векторов геометрически, и это облегчает использование геометрии для решения некоторых задач.
Размер (или величина ) векторной величины является скаляр, т.е.е., ряд. Обозначается размер вектора V | В |. (Обратите внимание, что V выделено жирным шрифтом, так как это вектор, но световые скобки «абсолютное значение», | |, указывают, что вся величина является скаляром. Т.е. берем абсолютное значение вектора, которое дает скалярный результат). мы можем просто написать буквенный символ вектора lightface, чтобы указать, что он представляет только размер вектора.
Сумму двух векторов можно найти, геометрически расположив стрелки, представляющие векторы голова к хвосту. Тогда сумма может быть найдено путем рисования нового вектора от свободного хвоста к свободной голове.
Разница между двумя векторами A — B находится сложением
векторы A и −B где −B — вектор
тот же размер, что и B , но противоположный по направлению.
Проекция вектора на линию равна В cosθ , где θ — угол между вектор и линия, а V — размер вектора. Это может быть найдено геометрически построения линии, перпендикулярной к опорной линии и от головы и хвост вектора. Длина по контрольной линии, лежащей между Строительные линии — это «проекция вектора на эту линию».
|
Компоненты векторов . При работе с векторами алгебраически
вектор полезно представлять его компонентами. Компонент вектора
является проекцией этого вектора на выбранную координатную ось.
Компонент вектора обычно рассматривается как скалярная величина.
Хотя ось координат может быть
любая линия, мы обычно используем оси декартовой системы координат,
с указанием компонентов вектора x, y, и z .Когда это будет сделано, любой вектор в пространстве однозначно определяется путем указания
оси координат и компоненты вектора вдоль этих осей (x, y, z).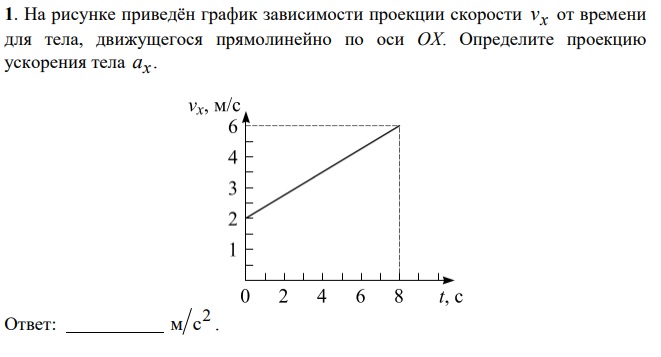 Иногда даже полезно иметь набор осей координат
которые не являются ортогональными (перпендикулярными), если оси «охватывают пространство»
(способны однозначно представить любой вектор в пространстве его компонентами).
Это требование выполняется, если три оси выполняют , а не все.
лежат в одной плоскости и никакие два не лежат на одной прямой.
Иногда даже полезно иметь набор осей координат
которые не являются ортогональными (перпендикулярными), если оси «охватывают пространство»
(способны однозначно представить любой вектор в пространстве его компонентами).
Это требование выполняется, если три оси выполняют , а не все.
лежат в одной плоскости и никакие два не лежат на одной прямой.
Обычно хвосты векторов не находятся на оси координат. Отбросьте два перпендикуляра к оси из головы вектора и из его хвоста. Тогда компонент на этой оси — это длина между ножками. этих перпендикуляров. На иллюстрации показаны лежащие векторы в плоскости x, y, но тот же принцип используется с тремя размерные ситуации.
|
Компоненты векторов — числа со знаком; они могут
имеют положительный или отрицательный знак. Вычтите проекцию хвоста
значение из значения проекции головы, чтобы получить это число со знаком.
Если компоненты двух векторов равны (x 1 , y 1 , z 1 ) и (x 2 , y 2 , z 2 ), тогда сумма этих трех векторов может быть записана в компонентной нотации как (x 1 + x 2 , y 1 + y 2 , z 1 + z 2 ).
Произведение вектора и скаляра, V s, является вектором размера | V | с. Он имеет то же направление, что и V .
Два вида векторных произведений полезны в физике, и они будут будут определены позже, когда они нам понадобятся.
Уравнения Галилея в векторной записи.
Как мы видели, векторные величины складываются геометрическим способом, совершенно отличным от способа сложения обычных чисел (скаляров).Два вектора размера 3 и 5 обычно не складываются с вектором размера 8. Мы получаем этот результат только тогда, когда они оказываются в одном направлении. Но этот процесс сложения векторов может быть представлен расширенной алгеброй, включающей векторы и скаляры. Мы отличаем векторы от скаляров, используя жирный шрифт для векторных величин и светлый шрифт для скалярных величин. Когда символ математической операции, такой как «+» или «-», стоит между двумя терминами, которые являются векторами, символы представляют собой сложение и вычитание векторов только что описанного типа.Когда такие операторы стоят между скалярами, они представляют собой обычное скалярное сложение чисел. Две векторные величины равны только тогда, когда их размеры и направлений равны.
Мы отличаем векторы от скаляров, используя жирный шрифт для векторных величин и светлый шрифт для скалярных величин. Когда символ математической операции, такой как «+» или «-», стоит между двумя терминами, которые являются векторами, символы представляют собой сложение и вычитание векторов только что описанного типа.Когда такие операторы стоят между скалярами, они представляют собой обычное скалярное сложение чисел. Две векторные величины равны только тогда, когда их размеры и направлений равны.
Давайте посмотрим, как это работает, попробовав преобразовать кинематические уравнения Галилея в векторную нотацию.
Определения:
Скорость: v = (x 2 — x 1 ) / (t 2 — t 1 ), что может быть записано v = Δx / Δt
Ускорение: a = (v 2 — v 1 ) / (t 2 — t 1 ), что может быть записано a = Δv / Δt
Величины Δx и Δv теперь представляют собой векторные перемещения и скорости соответственно.
Как и раньше, мы можем написать выражение для средней скорости в случае, когда вектор ускорения постоянен. Нарисуйте картинку, представляющую уравнения 23 и 24.
|
Службы борьбы с вредителями Сакраменто — Службы борьбы с вредителями в жилых и коммерческих помещениях Сакраменто
ПРОСТО
3 ПРОСТОГО ШАГА К ДОМУ, БЕЗ ВРЕДНЫХШАГ 1
БЕСПЛАТНЫЙ ОСМОТР / КОНСУЛЬТАЦИЯ
ШАГ 2
ЛЕЧЕНИЕ ОТ ВРЕДИТЕЛЕЙ
Семьи и компании в регионе Сакраменто полагаются на нас, чтобы предоставить лучшие в отрасли решения по борьбе с вредителями и сорняками.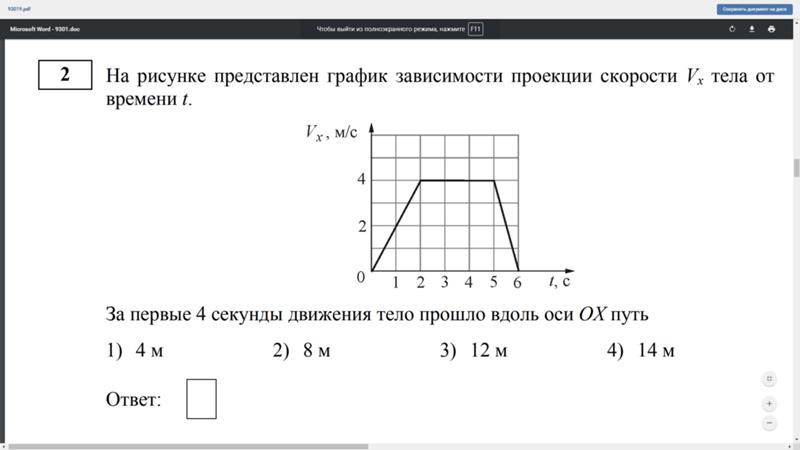 Мы специализируемся на уничтожении ваших сорняков и вредителей! Наши клиенты награждают эти функции, оставаясь верными ежегодно.
Мы специализируемся на уничтожении ваших сорняков и вредителей! Наши клиенты награждают эти функции, оставаясь верными ежегодно.
Наша команда технических специалистов оценит, определит, предложит решение и устранит ряд проблем, связанных с вредителями или садоводством, в рамках вашего бюджета. Вам не нужно тратить деньги на наши услуги по борьбе с вредителями Sacramento .
После завершения первоначального обслуживания мы будем возвращаться к вам домой каждый квартал, чтобы повторно установить внешний барьер. Во время нашего ежеквартального визита мы будем обрабатывать участок от четырех до пяти футов по периметру вашего дома.Уведомление будет оставлено на вашей входной двери, чтобы вы знали, что ваша защита была продлена. Мы вас прикрываем.
Мы предоставляем лучшие услуги по борьбе с вредителями в Сакраменто. Взгляните на наши обзоры! Если у вас возникла проблема внутри вашего дома, которую необходимо решить, мы с радостью предоставим внутреннюю услугу в удобное для вас время без дополнительной оплаты.
Позвольте нам предоставить вашему дому необходимые средства от вредителей и / или сорняков. В Центре борьбы с вредителями мы относимся к вашему дому как к своему!
ПРЕИМУЩЕСТВА НАЙМА УСЛУГ ПО БЕЗОПАСНОСТИКогда вы ходите по своему чистому и аккуратному дому, последнее, что вы хотите видеть, — это паутина, отверстия, сделанные крысами в ваших картонных коробках или шкафах с хлопьями, или даже муравьи, выставляющие напоказ вашу кладовую.Насекомых и грызунов приятно наблюдать в лесу или на открытом воздухе, но когда они попадают в наши дома, это уже не такое приятное зрелище. Но не волнуйтесь, эта статья и услуг по борьбе с вредителями Sacramento вас охватят.
Часто мы пытаемся бороться с вредителями только потому, что они беспокоят, но мы можем не до конца понимать, почему борьба с ними чрезвычайно важна. Давайте посмотрим, почему нам нужна борьба с вредителями. Борьба с вредителями необходима по следующей причине. Служба борьбы с вредителями Сакраменто:
Служба борьбы с вредителями Сакраменто:
• Вызывает неудобства и стресс.
• Угрожает безопасности пищевых продуктов
• Угрожает здоровью
• Конкурирует за еду и воду
• Уничтожает имущество и имущество
• Вызывает аллергию
ВЫЗЫВАЕТ НЕУДОБСТВО И СТРЕСС
Простое присутствие вредителей в вашем доме — серьезная тревога для стресса. Их устранение становится навязчивой мыслью, от которой, кажется, невозможно избавиться, пока вредители не будут удалены, взяты под контроль или полностью устранены.Кроме того, большинство вредителей всегда оставляют в доме следы, которые не так уж и красивы. Это означает, что вам придется больше заниматься уборкой или пытаться убить насекомых самостоятельно.
JEOPARDIZES БЕЗОПАСНОСТЬ ПИЩЕВЫХ ПРОДУКТОВ
Когда насекомые (насекомые и грызуны) ползают вокруг, они собирают грязь и микроорганизмы. Когда вредители контактируют с вашей пищей, эти диеты и микробы (которые они носят с собой) заражают пищу и делают ее нездоровой для употребления.
УГРОЗА ЗДОРОВЬЮ
Вредители являются основными переносчиками болезней.Вредители являются одной из 3 самых смертоносных причин болезней из-за их способности передавать их. Мыши и крысы являются переносчиками хантавируса, клещи переносят болезнь Лайма, а комары способны переносить множество различных болезней, от вируса Западного Нила до вируса Зика и даже малярии. Тараканы распространяют такие болезни, как сальмонеллез, передаваемый через пищевые продукты, а комнатные мухи переносят сальмонеллы, кишечную палочку, вибрионы и шигеллы. Укусы муравьев и пауков иногда смертельны или ядовиты. Этот список можно продолжить.
УНИЧТОЖАЕТ ИМУЩЕСТВА И ПРИНАДЛЕЖНОСТИ
Вредители, такие как термиты и грызуны, могут привести в ярость к вашему имуществу и имуществу. Обычно это дорогостоящая вещь, потому что вам придется потратить немного денег на ремонт собственности, или это может быть даже полной потерей, если это связано с такими вещами, как ваши сертификаты или документы.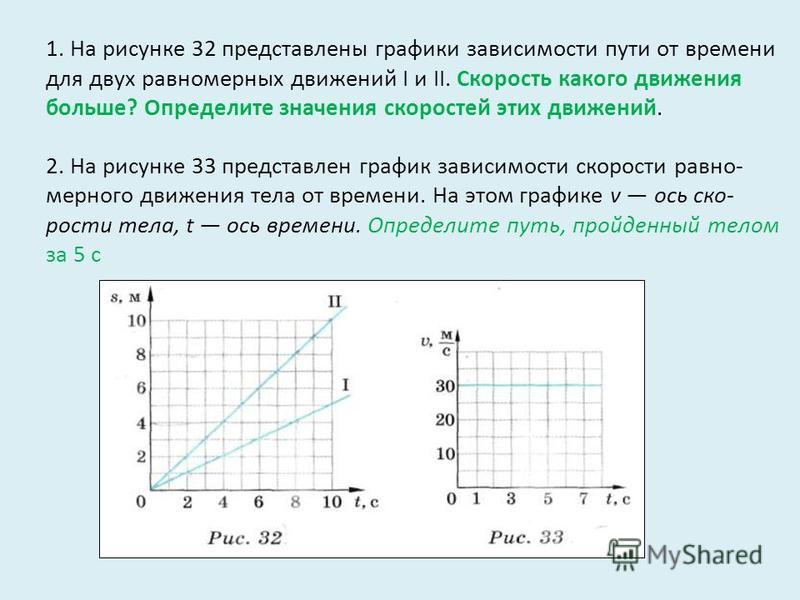
ТРИГГЕРЫ АЛЛЕРГИИ
Некоторые вредители могут вызывать аллергические реакции в организме, когда кусают вас или выделяют химические вещества.
Кто должен заниматься вашей борьбой с вредителями?
Борьба с вредителями — серьезное дело, с которым не стоит заниматься самостоятельно. Потому что для получения наилучших результатов (а это именно то, чего вы хотите) вам нужны профессионалы, которые сделают эту работу.
Преимущества найма служб по борьбе с вредителями
Благодаря этим преимуществам услуги по борьбе с вредителями — лучший выбор, когда речь идет о борьбе с вредителями.
• Целостный подход
• Лучшее оборудование и инструменты
• Безопасность
• Экономия денег
• Экономия времени
• Обучение
• Последующие действия
ЦЕЛОСТНЫЙ ПОДХОД
Компания по борьбе с вредителями не просто занимается уничтожением вредителей.Они начинают с осмотра, чтобы определить источник, причину и уровень заражения до лечения.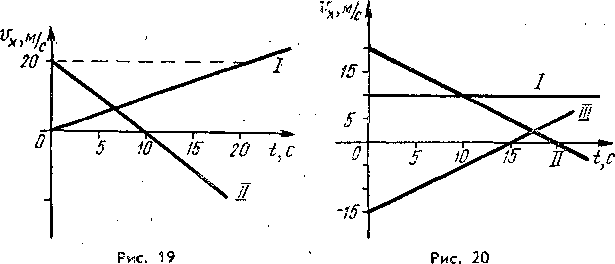 Они также проводят наблюдение после лечения. Такой подход носит систематический характер и гарантирует, что вы будете свободны от вредителей на долгое время.
Они также проводят наблюдение после лечения. Такой подход носит систематический характер и гарантирует, что вы будете свободны от вредителей на долгое время.
ЛУЧШЕЕ ОБОРУДОВАНИЕ И ИНСТРУМЕНТЫ
Всегда интересно позаботиться о вредителях самостоятельно, потому что вы можете зайти в магазин и купить химикаты. Но есть ли у вас или даже знаете, какие инструменты или оборудование нужно использовать? Вот почему службы по борьбе с вредителями так важны.У этих компаний есть нужные инструменты; это дает им технологическое преимущество для очень хорошего выполнения работы.
БЕЗОПАСНОСТЬ
Услуги по борьбе с вредителями означают, что безопасность превыше всего. Эти профессионалы понимают влияние пестицидов и следят за тем, чтобы они использовали правильные (в нужном количестве) и применяли их таким образом, чтобы вы и ваша семья подвергались небольшому риску или вовсе не подвергались риску после применения.
ЭКОНОМИЯ ДЕНЬГИ
Подумайте о сумме денег, которая уйдет на ветер, если вы продолжите пробовать пестицид за пестицидом.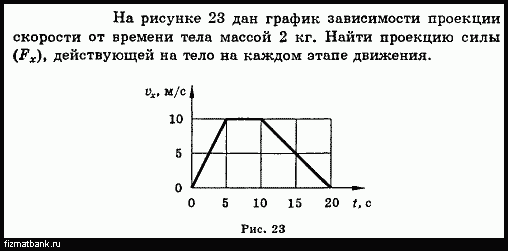 Компании по борьбе с вредителями знают, какой пестицид следует использовать в любой ситуации, что позволяет сэкономить много средств.
Компании по борьбе с вредителями знают, какой пестицид следует использовать в любой ситуации, что позволяет сэкономить много средств.
ЭКОНОМИЯ ВРЕМЕНИ
Когда вы нанимаете компанию по борьбе с вредителями, вы можете тратить это время на другие важные дела. Это также означает, что вы можете спокойно спать, не бегая вокруг, чтобы убить пауков, и не искать совета по борьбе с вредителями у друзей и семьи. Кроме того, компании по борьбе с вредителями позаботятся обо всем, включая очистку от мертвых вредителей. Об этом тебе тоже не нужно беспокоиться.
ОБРАЗОВАНИЕ
Компании по борьбе с вредителями не только справятся с вашей ситуацией с вредителями, но и дадут вам информацию о том, как избежать или уменьшить заражение в будущем. Это знание обычно спасает жизнь.
ПОСЛЕДУЮЩИЕ ДЕЙСТВИЯ
Для профессиональных компаний по борьбе с вредителями борьба с вредителями не заканчивается обработкой. Они совершают последующий визит, чтобы проверить свою работу и проверить наличие новых заражений.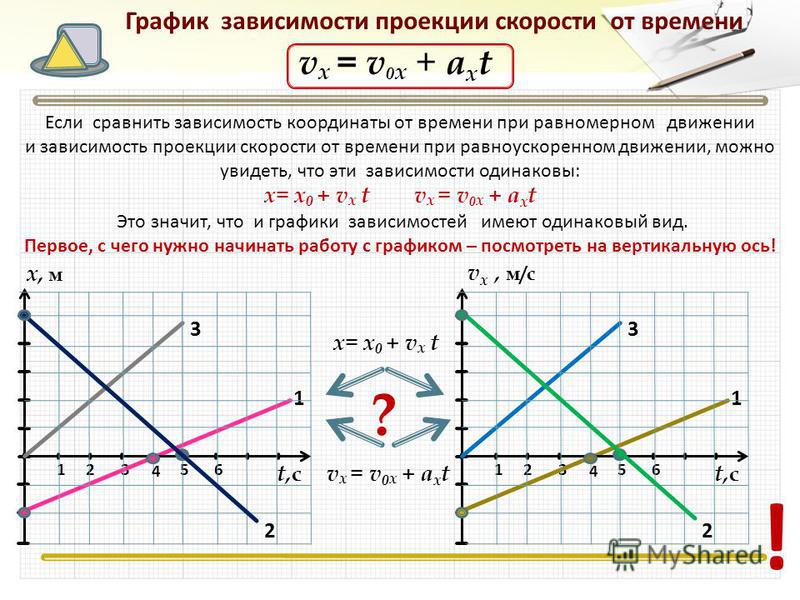
Видите ли, наем службы борьбы с вредителями в конце концов — хорошее использование денег.
Что еще?
Теперь вы понимаете, зачем вам нужны услуги по борьбе с вредителями, Сакраменто, но знаете ли вы, где получить лучшие профессиональные услуги по борьбе с вредителями , Сакраменто ? США — Центр борьбы с вредителями, Inc.
Графики движения — Гипертекст по физике
Обсуждение
введение
Современные математические обозначения — это очень компактный способ кодирования идей. Уравнения могут легко содержать информационный эквивалент нескольких предложений.Описание Галилеем объекта, движущегося с постоянной скоростью (возможно, первое применение математики к движению), потребовало одного определения, четырех аксиом и шести теорем. Все эти отношения теперь можно записать в одном уравнении.
Когда дело доходит до глубины, ничто не сравнится с уравнением.
Ну почти ничего. Вернитесь к предыдущему разделу об уравнениях движения. Вы должны помнить, что три (или четыре) уравнения, представленные в этом разделе, действительны только для движения с постоянным ускорением по прямой.Поскольку, как я правильно указал, «ни один объект никогда не двигался по прямой с постоянным ускорением в любом месте Вселенной в любое время», эти уравнения верны только приблизительно, только время от времени.
Вы должны помнить, что три (или четыре) уравнения, представленные в этом разделе, действительны только для движения с постоянным ускорением по прямой.Поскольку, как я правильно указал, «ни один объект никогда не двигался по прямой с постоянным ускорением в любом месте Вселенной в любое время», эти уравнения верны только приблизительно, только время от времени.
Уравнения отлично подходят для описания идеализированных ситуаций, но не всегда помогают. Иногда вам нужна картинка, чтобы показать, что происходит, — математическая картинка, называемая графиком. Графики часто являются лучшим способом передать описания реальных событий в компактной форме.Графики движения бывают нескольких типов в зависимости от того, какие кинематические величины (время, положение, скорость, ускорение) присвоены какой оси.
время позиции
Начнем с графического представления некоторых примеров движения с постоянной скоростью. На графике справа представлены три разные кривые, каждая с начальным положением нуля.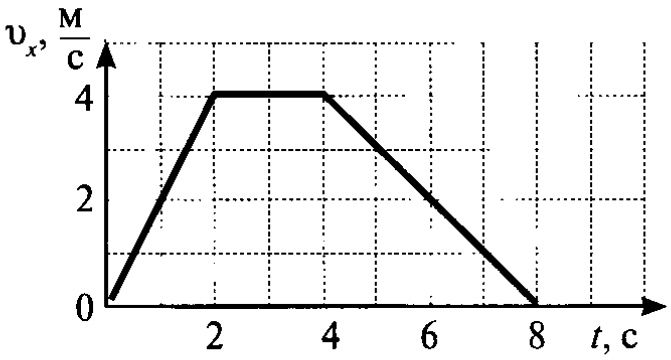 Прежде всего, обратите внимание, что графики все прямые. (Любая линия, нарисованная на графике, называется кривой. Даже прямая линия называется кривой в математике.) Этого следовало ожидать, учитывая линейный характер соответствующего уравнения. (Независимая переменная линейной функции возводится не выше первой степени.)
Прежде всего, обратите внимание, что графики все прямые. (Любая линия, нарисованная на графике, называется кривой. Даже прямая линия называется кривой в математике.) Этого следовало ожидать, учитывая линейный характер соответствующего уравнения. (Независимая переменная линейной функции возводится не выше первой степени.)
Сравните уравнение положения-времени для постоянной скорости с классическим уравнением пересечения наклона, которое преподается во вводной алгебре.
| с = | с 0 | + | v ∆ t |
| y = | a | + | bx |
Таким образом, скорость соответствует наклону, а начальное положение — точке пересечения на вертикальной оси (обычно называемой осью «y»).Поскольку каждый из этих графов имеет точку пересечения в начале координат, каждый из этих объектов имеет одинаковую начальную позицию.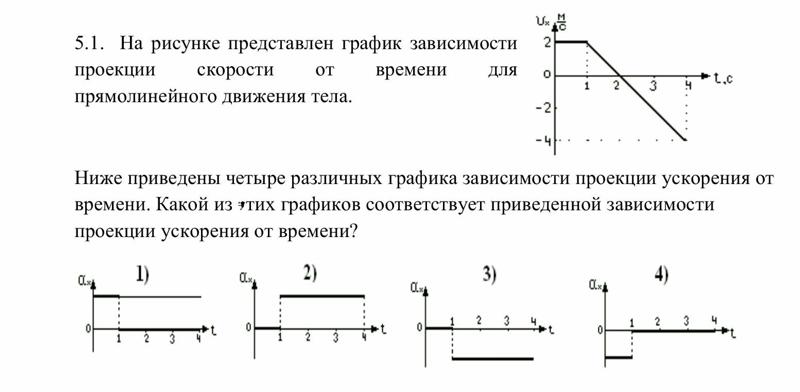 Этот график может представлять собой своего рода гонку, в которой все участники выстраиваются в линию на стартовой линии (хотя на этих скоростях это должна была быть гонка между черепахами). Если бы это была гонка, то участники уже двигались, когда гонка началась, поскольку каждая кривая имеет ненулевой уклон в начале. Обратите внимание, что нулевое начальное положение не обязательно означает, что начальная скорость также равна нулю.Высота кривой ничего не говорит о ее наклоне.
Этот график может представлять собой своего рода гонку, в которой все участники выстраиваются в линию на стартовой линии (хотя на этих скоростях это должна была быть гонка между черепахами). Если бы это была гонка, то участники уже двигались, когда гонка началась, поскольку каждая кривая имеет ненулевой уклон в начале. Обратите внимание, что нулевое начальное положение не обязательно означает, что начальная скорость также равна нулю.Высота кривой ничего не говорит о ее наклоне.
- На графике положение-время …
- наклон скорость
- точка пересечения y — это начальная позиция
- , когда две кривые совпадают, два объекта имеют одинаковое положение в это время
В отличие от предыдущих примеров, давайте изобразим положение объекта с постоянным ненулевым ускорением, начиная с момента покоя в начале координат.Основное различие между этой кривой и кривой на предыдущем графике состоит в том, что эта кривая фактически изгибается. Отношение между положением и временем квадратично, когда ускорение постоянное, и поэтому эта кривая представляет собой параболу . (Переменная квадратичной функции возводится не выше второй степени.)
Отношение между положением и временем квадратично, когда ускорение постоянное, и поэтому эта кривая представляет собой параболу . (Переменная квадратичной функции возводится не выше второй степени.)
| с = с 0 + v 0 ∆ t + | 1 | a ∆ t 2 | |
| 2 | |||
| y = a + bx + cx 2 | |||
В качестве упражнения давайте вычислим ускорение этого объекта по его графику.Он пересекает начало координат, поэтому его начальное положение равно нулю, в примере указано, что начальная скорость равна нулю, а график показывает, что объект прошел 9 м за 10 с. Затем эти числа можно ввести в уравнение.
| с = |
| ||||
| = | |||||
| = |
|
Когда график положения-времени изогнут, невозможно вычислить скорость по его наклону. Наклон — это свойство только прямых линий. Такой объект не имеет — скорость , потому что у него нет наклона — . Слова «the» и «a» подчеркнуты здесь, чтобы подчеркнуть идею о том, что при этих обстоятельствах не существует единственной скорости .Скорость такого объекта должна изменяться. Он ускоряется.
- На графике положение-время …
- прямые сегменты подразумевают постоянную скорость
- сегмент кривой подразумевает ускорение
- объект, испытывающий постоянное ускорение , следует части параболы
Хотя у нашего гипотетического объекта нет единой скорости, у него все же есть средняя скорость и непрерывный набор мгновенных скоростей.Среднюю скорость любого объекта можно найти, разделив общее изменение положения (также известное как смещение) на изменение во времени.
Это то же самое, что и расчет наклона прямой, соединяющей первую и последнюю точки кривой, как показано на диаграмме справа. В этом абстрактном примере средняя скорость объекта была…
| против = | ∆ с | = | 9,5 м | = 0.95 м / с |
| ∆ т | 10,0 с |
Мгновенная скорость — это предел средней скорости при сокращении временного интервала до нуля.
| против = | ∆ с | = | DS | |
| ∆ т | дт |
По мере того, как концы линии средней скорости становятся ближе друг к другу, они становятся лучшим индикатором фактической скорости.Когда две точки совпадают, прямая касается кривой. Этот процесс ограничения представлен на анимации справа.
- На графике положение-время …
- средняя скорость — наклон прямой линии, соединяющей конечные точки кривой
- мгновенная скорость — наклон касательной к кривой в любой точке
Семь касательных были добавлены к нашему общему графику положения-времени в анимации, показанной выше.Обратите внимание, что угол наклона равен нулю дважды — один раз в верхней части выступа при 3,0 с и снова в нижней части вмятины при 6,5 с. (Выступ — это локальный максимум , а вмятина — это локальный минимум . В совокупности такие точки известны как локальные экстремумы .) Наклон горизонтальной линии равен нулю, что означает, что объект в то время был неподвижен . Поскольку график не плоский, объект находился в состоянии покоя лишь на мгновение, прежде чем снова начал двигаться. Хотя его положение в то время не менялось, его скорость была.Это понятие, с которым у многих возникают трудности. Можно ускоряться и при этом не двигаться, но только на мгновение.
Отметим также, что наклон отрицательный в интервале между выступом в 3,0 с и вмятиной в 6,5 с. Некоторые интерпретируют это как движение в обратном направлении, но так ли это вообще? Что ж, это абстрактный пример. Это не сопровождается никаким текстом. Графики содержат много информации, но без названия или другой формы описания они не имеют смысла.Что представляет собой этот график? Персона? Автомобиль? Лифт? Носорог? Астероид? Пылинка? Почти все, что мы можем сказать, это то, что этот объект сначала двигался, замедлился до остановки, изменил направление, снова остановился, а затем возобновил движение в том направлении, в котором он начал (в каком бы направлении он ни был). Отрицательный уклон не означает автоматически движение назад, ходьбу налево или падение. Выбор знаков всегда произвольный. В общем, все, что мы можем сказать, это то, что когда наклон отрицательный, объект движется в отрицательном направлении.
- На графике положение-время …
- положительный наклон подразумевает движение в положительном направлении
- отрицательный наклон подразумевает движение в отрицательном направлении
- нулевой наклон подразумевает состояние покоя
скорость-время
Самое важное, что нужно помнить о графиках скорость-время, — это то, что это графики скорость-время, а не графики положения-времени. В линейном графике есть что-то такое, что заставляет людей думать, что они смотрят на путь объекта.Распространенная ошибка новичков — смотреть на график справа и думать, что линия v = 9,0 м / с соответствует объекту, который «выше» других объектов. Не думай так. Это не правильно.
Не смотрите на эти графики и думайте о них как о движущемся объекте. Вместо этого думайте о них как о записи скорости объекта. На этих графиках выше означает, что быстрее, не дальше. Линия v = 9,0 м / с выше, потому что этот объект движется быстрее других.
Эти конкретные графики все горизонтальные. Начальная скорость каждого объекта такая же, как конечная скорость такая же, как и каждая промежуточная скорость. Скорость каждого из этих объектов постоянна в течение этого десятисекундного интервала.
Для сравнения, когда кривая на графике скорость-время прямая, но не горизонтальная, скорость меняется. Три кривые справа имеют разный наклон. График с самым крутым наклоном испытывает наибольшую скорость изменения скорости.Этот объект имеет наибольшее ускорение. Сравните уравнение скорости-времени для постоянного ускорения с классическим уравнением пересечения наклона, которое преподается во вводной алгебре.
| v = | v 0 | + | a ∆ t |
| y = | a | + | bx |
Вы должны увидеть, что ускорение соответствует наклону, а начальная скорость — точке пересечения на вертикальной оси.Поскольку каждый из этих графов имеет точку пересечения в начале координат, каждый из этих объектов изначально находился в состоянии покоя. Однако начальная скорость, равная нулю, не означает, что начальное положение также должно быть нулевым. Этот график ничего не говорит нам о начальном положении этих объектов. Насколько нам известно, они могут находиться на разных планетах.
- На графике скорость-время …
- крутизна ускорение
- точка пересечения y — начальная скорость
- , когда две кривые совпадают, два объекта имеют одинаковую скорость в это время
Кривые на предыдущем графике были прямыми линиями.Прямая линия — это кривая с постоянным наклоном. Поскольку наклон — это ускорение на графике скорость-время, каждый из объектов, представленных на этом графике, движется с постоянным ускорением. Если бы графики были изогнутыми, ускорение не было бы постоянным.
- На графике скорость-время …
- прямые подразумевают постоянное ускорение
- изогнутые линии означают непостоянное ускорение
- объект, испытывающий постоянное ускорение , идет по прямой
Поскольку у изогнутой линии нет единого наклона, мы должны решить, что мы имеем в виду, когда спрашивают о ускорении объекта .Эти описания вытекают непосредственно из определений среднего и мгновенного ускорения. Если требуется среднее ускорение, нарисуйте линию, соединяющую конечные точки кривой, и вычислите ее наклон. Если требуется мгновенное ускорение, возьмите предел этого наклона по мере сокращения временного интервала до нуля, то есть возьмите наклон касательной.
- На графике скорость-время …
- среднее ускорение — наклон прямой, соединяющей концы кривой
- На графике скорость-время …
- мгновенное ускорение — наклон касательной к кривой в любой точке
| = | ∆ v | = | дв | |
| ∆ т | дт | |||
Семь касательных были добавлены к нашему общему графику скорость-время в анимации, показанной выше.Обратите внимание, что угол наклона равен нулю дважды — один раз в верхней части выступа при 3,0 с и снова в нижней части вмятины при 6,5 с. Наклон горизонтальной линии равен нулю, что означает, что в это время объект мгновенно прекращает ускорение. В эти два момента ускорение могло быть нулевым, но это не означает, что объект остановился. Чтобы это произошло, кривая должна пересекать горизонтальную ось. Это произошло только один раз — в начале графика. В обоих случаях, когда ускорение было нулевым, объект все еще двигался в положительном направлении.
Вы также должны заметить, что наклон был отрицательным от 3,0 до 6,5 с. За это время скорость снижалась. Однако в целом это не так. Скорость уменьшается всякий раз, когда кривая возвращается в исходное положение. Выше горизонтальной оси это будет отрицательный наклон, но ниже это будет положительный наклон. Об отрицательном наклоне графика скорость-время можно сказать только то, что в течение такого интервала скорость становится более отрицательной (или менее положительной, если хотите).
- На графике скорость-время …
- положительный наклон подразумевает увеличение скорости в положительном направлении
- отрицательный наклон подразумевает увеличение скорости в отрицательном направлении
- нулевой наклон подразумевает движение с постоянной скоростью
В кинематике есть три величины: положение, скорость и ускорение. Имея график любой из этих величин, всегда можно в принципе определить две другие.Ускорение — это скорость изменения скорости во времени, поэтому ее можно определить по наклону касательной к кривой на графике скорость-время. Но как определить позицию? Давайте рассмотрим несколько простых примеров, а затем выведем взаимосвязь.
Начните с простого графика скорость-время, показанного справа. (Для простоты предположим, что начальная позиция равна нулю.) На этом графике есть три важных интервала. Во время каждого интервала ускорение постоянно, как показывают отрезки прямой линии.Когда ускорение постоянно, средняя скорость — это просто среднее значение начального и конечного значений в интервале.
0–4 с: этот сегмент треугольный. Площадь треугольника равна половине основания, умноженной на высоту. По сути, мы только что вычислили площадь треугольного сегмента на этом графике.
| ∆ с = v ∆ t ∆ s = ½ ( v + v 0 ) ∆ t ∆ с м = 8 ) (4 с) ∆ с = 16 м |
Суммарное пройденное расстояние в конце этого интервала составляет…
16 кв.м
4–8 с: Этот сегмент имеет форму трапеции.Площадь трапеции (или трапеции ) равна среднему значению двух оснований, умноженному на высоту. По сути, мы только что рассчитали площадь трапециевидного сегмента на этом графике.
| ∆ с = v ∆ t ∆ s = ½ ( v + v 0 ) ∆ t ∆ s м / с + 8 м / с) (4 с) ∆ с = 36 м |
Суммарное пройденное расстояние в конце этого интервала составляет…
16 м + 36 м = 52 м
8–10 с: этот сегмент прямоугольный.Площадь прямоугольника равна его высоте, умноженной на ширину. По сути, мы только что вычислили площадь прямоугольного сегмента на этом графике.
| ∆ с = v ∆ t ∆ s = (10 м / с) (2 с) ∆ с = 20 м |
Суммарное пройденное расстояние в конце этого интервала составляет…
16 м + 36 м + 20 м = 72 м
Надеюсь, сейчас вы заметили тенденцию. Площадь под каждым сегментом — это изменение положения объекта в течение этого интервала.Это верно, даже когда ускорение непостоянно.
Любой, кто прошел курс математического анализа, должен был знать это, прежде чем читать здесь (или, по крайней мере, когда они читали это, они должны были сказать: «О да, я это помню»). Первая производная положения по времени — это скорость. Производная функции — это наклон прямой, касательной к ее кривой в данной точке. Обратная операция производной называется интегралом. Интеграл функции — это совокупная площадь между кривой и горизонтальной осью на некотором интервале.Эта обратная связь между действиями производной (наклон) и интеграла (площадь) настолько важна, что ее называют фундаментальной теоремой исчисления . Это означает, что это важные отношения. Узнать его! Это «фундаментально». Ты еще не видел этого.
- На графике скорость-время …
- область под кривой — это изменение позиции
время разгона
График ускорения-времени любого объекта, движущегося с постоянной скоростью, одинаков.Это верно независимо от скорости движения объекта. Самолет, летящий со скоростью 270 м / с (600 миль в час), ленивец, идущий с постоянной скоростью 0,4 м / с (1 миль в час), и лежащий на диване картофель, неподвижно лежащий перед телевизором часами, будут иметь одинаковое ускорение. -временные графики — горизонтальная линия, коллинеарная горизонтальной оси. Это потому, что скорость каждого из этих объектов постоянна. Они не ускоряются. Их ускорения равны нулю. Как и в случае графиков скорость-время, важно помнить, что высота над горизонтальной осью не соответствует положению или скорости, она соответствует ускорению .
Если вы споткнетесь и упадете по дороге в школу, ваше ускорение по отношению к земле будет больше, чем у всех, кроме нескольких высокопроизводительных автомобилей с «педалью до металла». Ускорение и скорость — разные величины. Быстрая езда не означает быстрого ускорения. Эти две величины не зависят друг от друга. Большое ускорение соответствует быстрому изменению скорости на , но оно ничего не говорит вам о значениях самой скорости.
При постоянном ускорении кривая ускорения-время представляет собой горизонтальную линию.Скорость изменения ускорения во времени обсуждается нечасто, поэтому наклон кривой на этом графике пока игнорируется. Если вам нравится знать названия вещей, это количество называется рывок . На первый взгляд, единственная информация, которую можно почерпнуть из графика ускорения-времени, — это ускорение в любой момент времени.
- На графике время разгона …
- наклон рывок
- точка пересечения «y» равна начальному ускорению
- , когда две кривые совпадают, два объекта имеют одинаковое ускорение в это время
- объект, испытывающий постоянное ускорение , очерчивает горизонтальную линию
- нулевой наклон подразумевает движение с постоянным ускорением
Ускорение — это скорость изменения скорости во времени.Преобразование графика скорости-времени в график ускорения-времени означает вычисление наклона линии, касательной к кривой в любой точке. (В расчетах это называется нахождением производной.) Обратный процесс влечет за собой расчет совокупной площади под кривой. (В исчислении это называется нахождением интеграла.) Это число представляет собой изменение значения на графике скорость-время.
Учитывая начальную скорость, равную нулю (и предполагая, что падение положительное), конечная скорость человека, падающего на графике справа, составляет…
| ∆ v = | a ∆t |
| ∆ v = | (9.8 м / с 2 ) (1,0 с) |
| ∆ v = | 9,8 м / с = 22 миль / ч |
а конечная скорость разгоняемого автомобиля составляет…
| ∆ v = | a ∆t |
| ∆ v = | (5,0 м / с 2 ) (6,0 с) |
| ∆ v = | 30 м / с = 67 миль / ч |
- На графике время разгона …
- Площадь под кривой равна изменению скорости
О графиках времени разгона можно сказать еще много чего, но по большей части они тривиальны.
фазовое пространство
Есть четвертый график движения, который связывает скорость с положением. Он так же важен, как и другие три типа, но редко привлекает внимание ниже продвинутого уровня бакалавриата. Когда-нибудь я напишу что-нибудь об этих графиках, называемых диаграммами фазового пространства , , но не сегодня.
Движение снаряда
Снаряд — это любой объект, который после запуска или падения продолжает движение по собственной инерции, и на него влияет только сила тяжести, направленная вниз.
Движение снаряда , также известное как параболическое движение , является примером композиции движения в двух измерениях: ед. на горизонтальной оси и u.a.r.m. по вертикальной оси. В этом разделе мы изучим:
Начнем?
Концепция и представление
Движение снаряда , также известное как параболическое движение , состоит в том, что запускает тело со скоростью, которая образует угол α с горизонтом .На следующем рисунке вы можете увидеть представление ситуации.
Параболическое движение
Это движение характерно для снарядов, движущихся объектов действует только сила тяжести. По оси x тело движется с постоянной скоростью v 0x (u.r.m.), а по оси y — с постоянным ускорением свободного падения (u.a.r.m.).
Характеризуется тем, что в наивысшей точке траектории скорость тела всегда v 0x (нет v y ).
Движение снаряда или параболическое движение является результатом композиции равномерного прямолинейного движения ( по горизонтали ) и равномерно ускоренного прямолинейного движения при запуске вверх или вниз ( по вертикали ).
Уравнения
Уравнения движения снаряда:
Поскольку, как мы сказали выше, скорость образует угол α с горизонталью, компоненты x и y определяются с использованием наиболее распространенных тригонометрических соотношений:
Разложение вектора скорости
Любой вектор, включая скорость, может быть разбит на 2 вектора, v x и v y , которые имеют те же направления, что и декартовы оси.Величину обоих векторов можно вычислить из угла, который вектор образует с горизонталью, с помощью выражений, показанных на рисунке.
Наконец, принимая во внимание вышесказанное, что y 0 = H , x 0 = 0 , и что a y = -g, , мы можем переписать формулы, как показано в следующем списке. Это окончательные выражения для расчета кинематических величин при движении снаряда или параболическом движении :
Экспериментируй и учись
Данные
г = 9.8 м / с 2 | |
Движение снаряда
Синий шар на рисунке представляет тело, подвешенное над землей. Вы можете перетащить его на нужную начальную высоту H и выбрать начальную скорость (v 0 ), с которой он будет запускать под углом (α) к горизонтальному . Серая линия представляет траекторию, по которой он будет двигаться в зависимости от выбранных вами значений.
Затем нажмите кнопку воспроизведения. Перетащите время и наблюдайте, как положение (x и y) и скорость (v x и v y ) рассчитываются для каждого момента его спуска на землю.
Убедитесь, что проекция по оси Y (зеленый) описывает вертикальное движение запуска, а по оси X (красный) — равномерное прямолинейное движение.
Уравнение положения и траектории движения снаряда
Уравнение положения тела помогает нам узнать, в какой точке оно находится в каждый момент времени.В случае движения тела в двух измерениях помните, что в целом оно описывается следующим образом:
Подставляя приведенные выше выражения положения на горизонтальной оси (u.r.m.) и на вертикальной оси (u.a.r.m.) в общее уравнение положения, мы можем получить выражение уравнения положения для параболического движения.
Уравнение движения снаряда определяется по формуле:
r → = (x0 + v0x⋅t) · i → + (H + v0y · t-12 · g · t2) · j →
С другой стороны, чтобы узнать, по какой траектории следует тело, то есть его уравнение траектории, мы можем объединить приведенные выше уравнения, чтобы исключить t , получив:
y = H + v0y · (xv0x) -12 · g · (xv0x) 2 = H + k1 · x-k2 · x2k1 = v0yvx; k2 = 12 · v0x2 · g
Как и ожидалось, это уравнение параболы.
С другой стороны, часто в упражнениях вам будут предлагаться некоторые из следующих значений.
Максимальная высота
Это значение достигается, когда скорость по оси y , v y равна 0. Исходя из уравнения скорости по оси y и составляя v y = 0 , мы получить время t , которое требуется телу, чтобы добраться до этой высоты. С этого момента и из уравнений положения мы можем вычислить расстояние до начала координат по обеим осям, оси x и оси y .
Время полета
Рассчитано для y = 0 , вертикальной составляющей позиции. То есть время полета — это время, необходимое для того, чтобы высота стала равной 0 (снаряд достигнет земли).
Диапазон
Это максимальное расстояние по горизонтали от начальной точки движения до точки падения тела на землю. Как только будет получено сильное> время полета , просто подставьте в уравнение положения горизонтальный компонент.
Угол траектории
Угол траектории в данной точке совпадает с углом, который образует вектор скорости с горизонтом в этой точке. Для его вычисления получаем компоненты v x и v y и из тригонометрического определения тангенса угла вычисляем α :
tanα = противоположная сторона смежная сторона = vyvx⇒α = tan-1vyvx
Пример
Минута 90 игры… Лопера приближается к мячу и наносит штрафной удар в 40 метрах от ворот, делает два шага назад и делает удар ногой. Мяч взлетает на высоте 20 ° … и ГООООООЛЛ !!! ГООООООООЛЛЛ !!!! Мяч проходит через верхний угол на высоте 1,70 м !!!. Сможете ли вы, прослушав эту радиопередачу, ответить на следующие вопросы?
а) Сколько времени прошло от удара Лоперы до взятия ворот? и какова была начальная скорость мяча в момент удара?
б) Какова максимальная высота мяча?
c) Насколько быстро летел мяч, когда достиг цели?
Страница не найдена | MIT
Перейти к содержанию ↓- Образование
- Исследование
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов
Предложения или отзывы?
.

 Затем решите уравнение для d .
Затем решите уравнение для d .
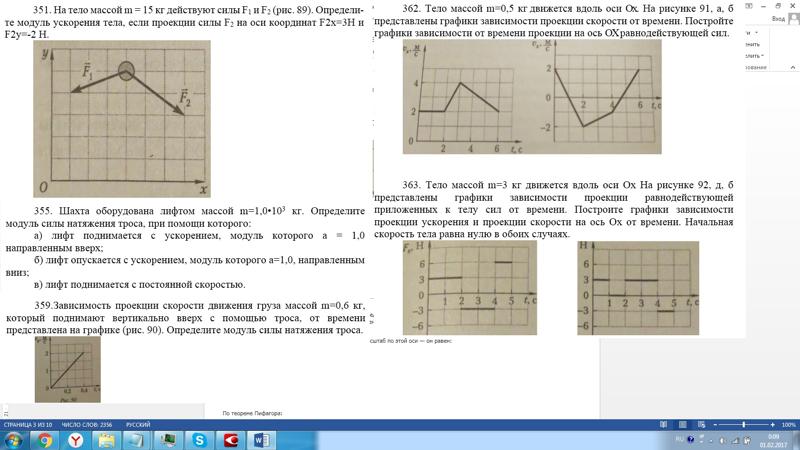
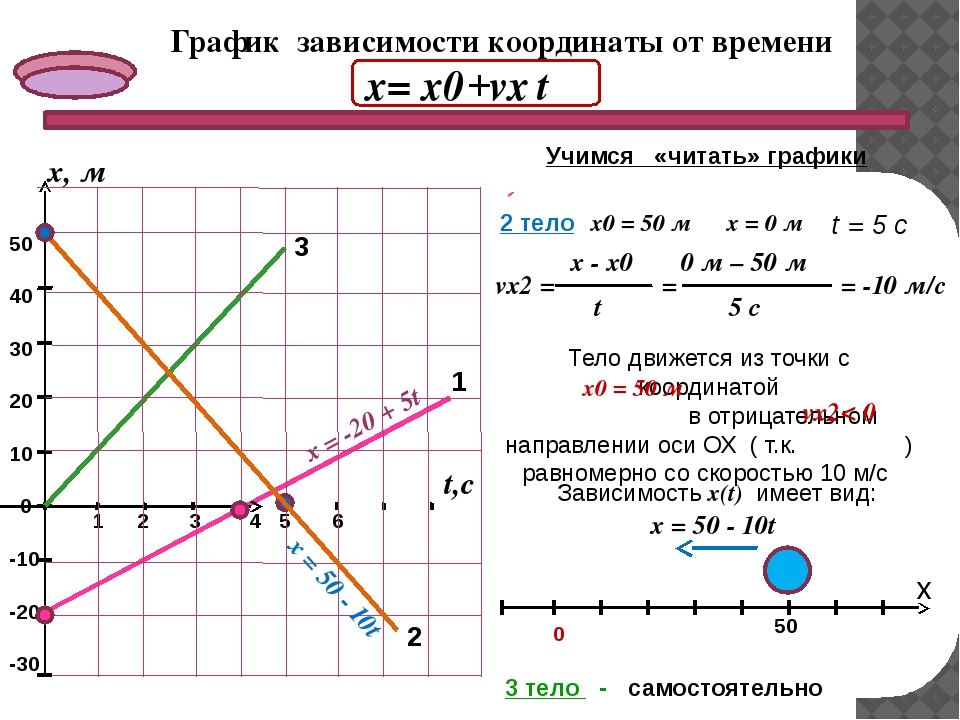 Разве они оба не описывают движение и не используют одно и то же «сырье»? В ранней истории физики этот вопрос долгое время занимал некоторые великие умы, прежде чем стало ясно, что оба они абсолютно необходимы. Кинетическая энергия — это скалярная величина, которая зависит от квадрата скорости, поэтому сама по себе не может сказать нам о направлениях движущихся тел. Импульс — это векторная величина, зависящая от первой степени скорости.Но это также не говорит нам всего о движении. Верно, что иногда физическая проблема может быть решена для желаемой величины, используя только энергию или только импульс. Но многие задачи требуют одновременного применения обоих уравнений. Даже такая простая задача, как отскок мяча от пола. Посмотрите, как шар с документами отскакивает от массивной стены.
Разве они оба не описывают движение и не используют одно и то же «сырье»? В ранней истории физики этот вопрос долгое время занимал некоторые великие умы, прежде чем стало ясно, что оба они абсолютно необходимы. Кинетическая энергия — это скалярная величина, которая зависит от квадрата скорости, поэтому сама по себе не может сказать нам о направлениях движущихся тел. Импульс — это векторная величина, зависящая от первой степени скорости.Но это также не говорит нам всего о движении. Верно, что иногда физическая проблема может быть решена для желаемой величины, используя только энергию или только импульс. Но многие задачи требуют одновременного применения обоих уравнений. Даже такая простая задача, как отскок мяча от пола. Посмотрите, как шар с документами отскакивает от массивной стены.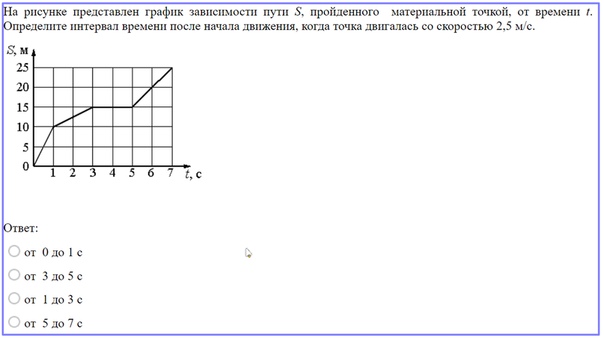 Учебники редко представляют это так, как это делал Галилей. Хороший веб-документ об этом — «Маятник снова качается: математическое обоснование эксперимента Галилея с наклонными плоскостями» Александра Хана.
Учебники редко представляют это так, как это делал Галилей. Хороший веб-документ об этом — «Маятник снова качается: математическое обоснование эксперимента Галилея с наклонными плоскостями» Александра Хана.
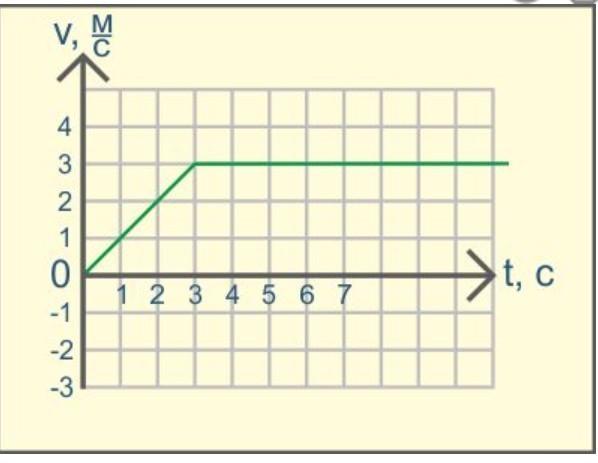
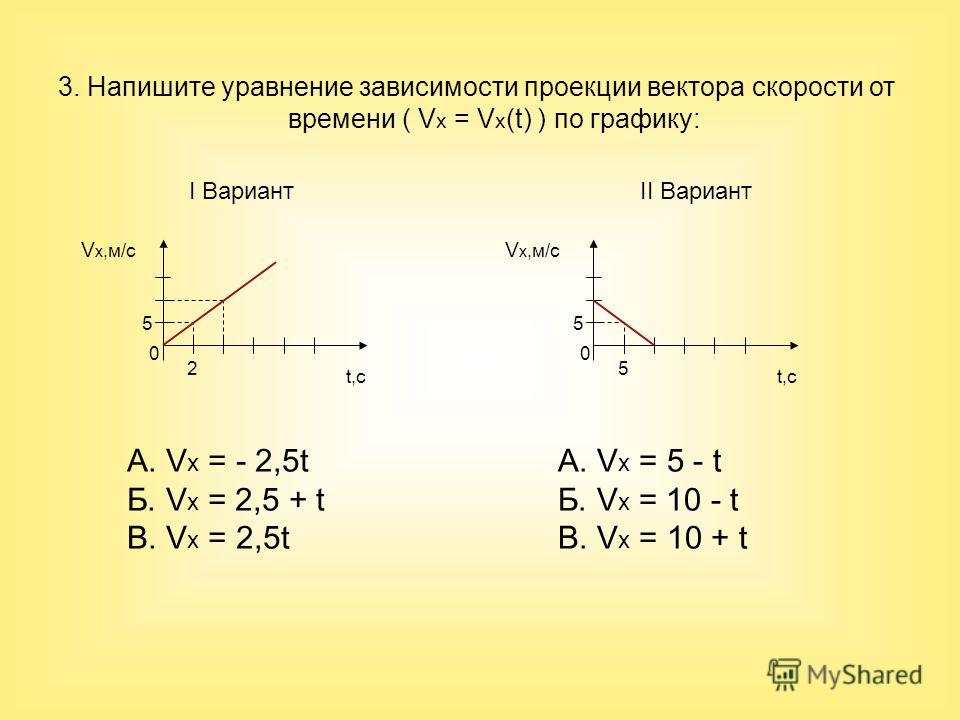 Пуля упадет на одинаковое количество за одно и то же время и, следовательно, поразит обезьяну. Нарисуйте векторы v o t и (1/2) gt 2 лицом к хвосту, чтобы увидеть это. Вы знаете, что эта проблема существует много-много лет, потому что в настоящее время мы не хотим поощрять отстрел обезьян.
Пуля упадет на одинаковое количество за одно и то же время и, следовательно, поразит обезьяну. Нарисуйте векторы v o t и (1/2) gt 2 лицом к хвосту, чтобы увидеть это. Вы знаете, что эта проблема существует много-много лет, потому что в настоящее время мы не хотим поощрять отстрел обезьян.
 Представьте себе самолет, который движется со скоростью 200 миль в час прямо на восток в неподвижном воздухе. Но затем он встречает боковой ветер со скоростью 30 миль в час, дующий на юг. Вы хотите узнать скорость и курс самолета по ветру, предполагая, что самолет не меняет свой курс намеренно.
Представьте себе самолет, который движется со скоростью 200 миль в час прямо на восток в неподвижном воздухе. Но затем он встречает боковой ветер со скоростью 30 миль в час, дующий на юг. Вы хотите узнать скорость и курс самолета по ветру, предполагая, что самолет не меняет свой курс намеренно. Вектор V pg является гипотенузой и имеет размер, определяемый теоремой Пифагора (200 2 + 30 2 ) 1/2 = 202 миль в час. Если пилот не корректирует курс, новое направление полета будет под углом к югу от востока, размером, указанным из tan θ = 30/200.Итак, θ = 8,53 °.
Вектор V pg является гипотенузой и имеет размер, определяемый теоремой Пифагора (200 2 + 30 2 ) 1/2 = 202 миль в час. Если пилот не корректирует курс, новое направление полета будет под углом к югу от востока, размером, указанным из tan θ = 30/200.Итак, θ = 8,53 °.
Leave A Comment