Свобода выбора или комбинаторный разнобой на правила суммы и произведений
Южная математическая смена 1-24 ноября 2016
ДЕНЬ ДЕВЯТЫЙ 14 ноября 2016 1. В левом нижнем углу прямоугольника 5 6 стоит фишка. За один ход фишку разрешается передвинуть на одну клетку вправо или вверх. Сколько существует путей прохода фишки в правый
ПодробнееКомбинаторика. Правило произведения
И. В. Яковлев Материалы по математике MathUs.ru Комбинаторика. Правило произведения При решении комбинаторных задач часто приходится умножать число способов выбора одного объекта на число способов выбора
ПодробнееКраткий конспект по комбинаторике
Комбинаторика Краткий конспект по комбинаторике раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного
ПодробнееТрушин Б.
 В., 2015 г. Рис. 1:
В., 2015 г. Рис. 1:Комбинаторика Часть первая. Введение Что такое комбинаторика? Комбинаторикой (или комбинаторным анализом) называется раздел математики, который решает задачи подсчета количества объектов, удовлетворяющих
c Трушин Б.В., г. Троицк, 2 декабря 2006 г.
Тема I. Четность Задача 1. Квадратная таблица 25 25 раскрашена в 25 цветов так, что в каждой строке и в каждом столбце представлены все цвета. Докажите, что если расположение цветов симметрично относительно
ПодробнееНайдите все такие значения x.
Числа и их свойства 1. Дано трёхзначное натуральное число (число не может начинаться с нуля), не кратное 100. а) Может ли частное этого числа и суммы его цифр быть равным 90? б) Может ли частное этого
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ.

ЭЛЕМЕНТЫ КОМБИНАТОРИКИ. Правило произведения. Если существует n вариантов выбора первого элемента и для каждого из них имеется m вариантов выбора второго элемента, то всего существует n m различных пар
ПодробнееКомбинаторика. Перебор вариантов
И. В. Яковлев Материалы по математике MathUs.ru Комбинаторика. Перебор вариантов Сколькими способами можно выбрать три яблока из корзины? Сколько имеется вариантов школьного расписания? Такого рода вопросами
0:1 Маша написала фразу: «Я хочу участвовать в Лиге Открытий», посчитала количество букв в каждом слове и перемножила полученные числа. Какой результат должен получиться? 0:0 Сколько всего квадратов изображено
ПодробнееError! Reference source not found. 1
Error! Reference source not found. 1 2 Электронная физико-техническая школа Решебник для 8-9 класса 1 Первая часть задания Задача 1 Камень весит 6 кг, еще треть камня и еще половину камня. Сколько весит
1 2 Электронная физико-техническая школа Решебник для 8-9 класса 1 Первая часть задания Задача 1 Камень весит 6 кг, еще треть камня и еще половину камня. Сколько весит
Математический квадрат
Комбинаторная геометрия КГ4. Отметьте на листе бумаги две красные, две желтые и две зеленые точки и соедините их отрезками так, чтобы получилось пять равносторонних треугольников с разноцветными вершинами.
ПодробнееГрафы. Лемма о рукопожатиях. Связность.
Лемма о рукопожатиях. Связность. Графы Почему 2017 марсиан не могут взяться за руки? Упр 1. Даша натянула веревки для белья. Причем к 6 гвоздикам она прикрепила по 7 веревок, к 4 гвоздикам по 6 веревок,
6 класс. обозначают шесть разных цифр. Какая цифра обозначена буквой Д? 6.2. Прямые, параллельные сторонам квадрата, образуют квадратик,
6 класс 6. 1. В числовом примере АБВ+9 = ГДЕ буквы А, Б, В, Г, Д и Е обозначают шесть разных цифр. Какая цифра обозначена буквой Д? 6.2. Прямые, параллельные сторонам квадрата, образуют квадратик, центр
1. В числовом примере АБВ+9 = ГДЕ буквы А, Б, В, Г, Д и Е обозначают шесть разных цифр. Какая цифра обозначена буквой Д? 6.2. Прямые, параллельные сторонам квадрата, образуют квадратик, центр
7 класс, высшая лига, 3 тур, 26 ноября
7 класс, высшая лига, 3 тур, 26 ноября 1. Треугольник ABC разрезали на несколько равносторонних треугольника. Обязательно ли треугольник ABC должен был быть равносторонним? 2. Расстоянием между вершинами
Задачник по комбинаторике
Министерство образования Московской области Государственное бюджетное образовательное учреждение среднего профессионального образования Московской области «Балашихинский промышленно-экономический колледж»
Подробнее6 класс, цифры. 6 класс, цифры.
6 класс, цифры.
Правила суммы и произведения
И. В. Яковлев Материалы по математике MathUs.ru Содержание Правила суммы и произведения 1 Правило суммы……………………………….. 1 2 Правило произведения…………………………….
ПодробнееВЕРОЯТНОСТЬ СЛУЧАЙНОГО СОБЫТИЯ
ВЕРОЯТНОСТЬ СЛУЧАЙНОГО СОБЫТИЯ Аксиомы Колмогорова В 1933 г. А. Н. Колмогоров в книге «Основные понятия теории вероятностей» дал аксиоматическое обоснование теории вероятностей. «Это означает, что, после
ПодробнееРЕШЕНИЯ ЗАДАЧ 4 КЛАССА
РЕШЕНИЯ ЗАДАЧ 4 КЛАССА Задача 1. Нотки До, Ре, Ми, Фа и Ля организовали концерт. При этом двое играли на барабанах, а трое на гитарах. До и Ре играли на одинаковых инструментах, До и Фа на разных, как
Нотки До, Ре, Ми, Фа и Ля организовали концерт. При этом двое играли на барабанах, а трое на гитарах. До и Ре играли на одинаковых инструментах, До и Фа на разных, как
1. Закон сложения в комбинаторикерия:
Тема 10. Комбинаторика 1. Закон сложения в комбинаторикерия: В вазе лежит 5 яблок, 4 груши и 3 мандарина. Сколько существует возможностей взять один фрукт из вазы? Если взять яблоко, то существует 5 возможностей,
Подробнее0:1 В парке семь деревьев посадили в ряд. Расстояние между соседними деревьями 2 м. Какое расстояние между крайними деревьями? 0:0 Использовав три тройки, три пятерки и три семерки, а также знаки скобок
ПодробнееII этап 7 класс
II этап 7 класс 4.12.2016 Работа рассчитана на 180 минут 1. Поставьте в каждом из шести чисел по одной запятой так, чтобы равенство стало верным: 2016 + 2016 + 2016 + 2016 + 2016 = 46368.
Примеры и конструкции
И. В. Яковлев Материалы по математике MathUs.ru Примеры и конструкции 1. (Всеросс., 2018, ШЭ, 5.2 ) Девочка заменила каждую букву в своём имени её номером в русском алфавите. Получилось число 2011533.
ПодробнееU n? (читается Р из n ).
Тема 1 1 Комбинаторные формулы Пусть имеется множество, состоящее из элементов. Обозначим его U. Перестановкой из элементов называется заданный порядок во множестве U. Примеры перестановок: 1)распределение
Электронная школа Знаника
0 Электронная школа Знаника Разбор заданий 1-5. 2-3 класс 1 Разбор заданий 1-5 2-3 класс Задание 1 (1 балл) У мальчика были сломанные очки, они меняли черный цвет на белый, а белый на черный. Что увидит
ПодробнееЛекция 1.

Лекция 1. Тема: «Элементы комбинаторики» Определение. Комбинаторика — это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить
ПодробнееПОЯСНИТЕЛЬНАЯ ЗАПИСКА
2 КЛАСС МАТЕМАТИКА УЧЕБНИК И РАБОЧАЯ ТЕТРАДЬ: Моро М. И., Бантова М. А., Бельтюкова Г. В. и др. Математика. 2кл. в 2ч. М.: Просвещение. Моро М. И., Волкова С. И. Тетрадь по математике. 2кл. в 2ч. М.: Просвещение.
ПодробнееВступительная олимпиада в 8 класс год
Вступительная олимпиада в 8 класс. 2013 год 1. У Вани на 90 конфет больше, чем у Маши. Одновременно Ваня и Маша отдали друг другу треть всех конфет, которые у них были. На сколько конфет больше теперь
Подробнее4 класс, первая лига, 3 тур, 6 ноября
X Ижевский омандный Турнир Математиков, 4-6 ноября 2017 4 класс, первая лига, 3 тур, 6 ноября 1. В семье есть Андрей, Богдан, Василий, Анна, Дарья и Жанна. Сколькими способами их можно посадить на диван
В семье есть Андрей, Богдан, Василий, Анна, Дарья и Жанна. Сколькими способами их можно посадить на диван
Задания С6 ЕГЭ олимпиадного характера
Задания С6 ЕГЭ олимпиадного характера 1. Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 11 раз больше, либо в 11 раз
ПодробнееЗадание 21 Числа и их свойства
Задание 21 Числа и их свойства 1. Дано трёхзначное натуральное число (число не может начинаться с нуля), не кратное 100. а) Может ли частное этого числа и суммы его цифр быть равным 90? б) Может ли частное
ПодробнееТема №7354 Задачи по теории вероятностей 127
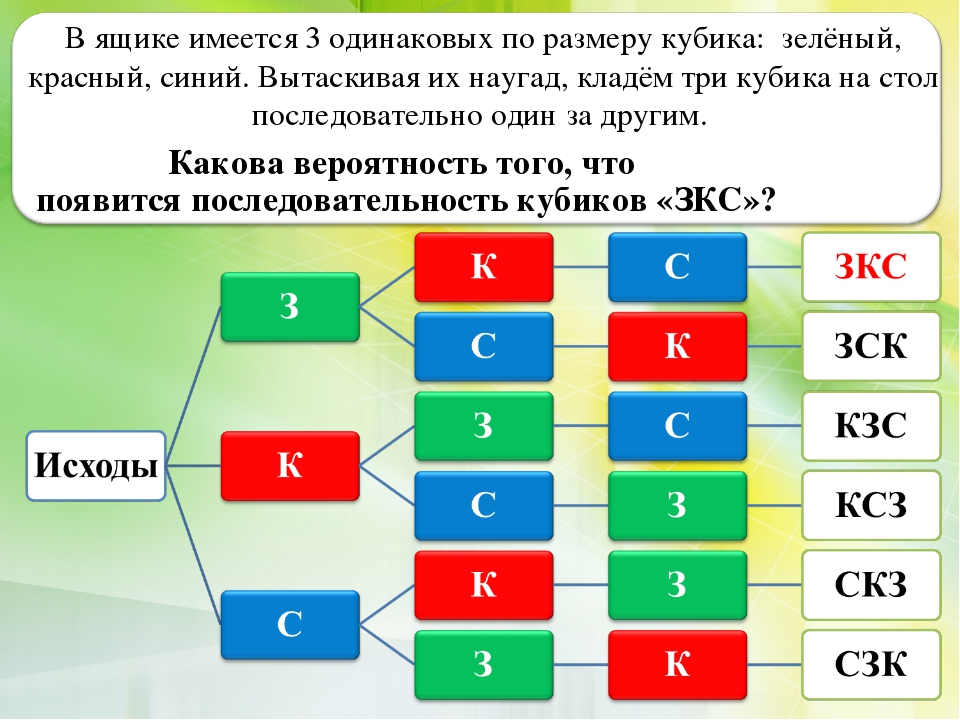
Здесь находится описание темы Задачи по теории вероятностей 127, изучаемой по предмету Математика. Ниже вы разберете ответы на все ваши разнообразные вопросы. Если представленный текст вам не помог, то вы смело можете задать свои вопросы ниже.
Ниже вы разберете ответы на все ваши разнообразные вопросы. Если представленный текст вам не помог, то вы смело можете задать свои вопросы ниже.
Задачи
1. Наудачу выбрано двузначное число. Какова вероятность того, что это
число кратно 5?
2. В урне 4 желтых и 6 красных шаров. Какова вероятность того, что
наудачу извлеченный шар из этой урны окажется белым?
3. В урне 4 желтых и 6 красных шаров. Какова вероятность того, что
наудачу извлеченный шар из этой урны окажется желтым?
4. В урне 4 желтых и 6 красных шаров. Какова вероятность того, что
наудачу извлеченный шар из этой урны окажется окрашенным?
5. В урне 4 желтых и 6 красных шаров. Из этой урны вынули один желтый
шар. После этого из урны берут еще один шар. Какова вероятность того,
что этот шар также желтый?
6. В урне 4 желтых и 6 красных шаров. Из этой урны вынули один желтый
шар. После этого из урны берут еще один шар. Какова вероятность того,
что этот шар белый?
7. Какова вероятность того, что в наудачу выбранном двузначном числе все
Какова вероятность того, что в наудачу выбранном двузначном числе все
цифры одинаковы?
8. Какова вероятность наугад вынуть из кошелька единственную монету в 1
рубль из 10 разных монет?
9. Какова вероятность, не посмотрев на номер, сесть не в тот автобус, если
на остановке из 8 автобусов в нужном направлении едут 3.
10. Наудачу выбрано двузначное число. Какова вероятность того, что
выбранное число делится на 10?
11. Какова вероятность выпадения числа 3 при бросании игральной кости?
12. Какова вероятность, не посмотрев на номер, сесть в правильный автобус,
если на остановке из 5 автобусов в нужном направлении едут 2.
13. В урне 5 шаров: 2 красных, 2 синих и 1 белый. Найти вероятность
появления цветного шара.
14. В урне 5 шаров: 2 красных, 2 синих и 1 белый. Найти вероятность
появления белого шара.
15. В урне 5 шаров: 2 красных, 2 синих и 1 белый. Найти вероятность
появления зеленого шара.
16. Набирая семизначный номер телефона, абонент забыл одну цифру и
набрал ее наудачу. Найти вероятность того, что набрана нужная цифра.
17. В лаборатории посеяно 1000 семян, из которых 234 не взошли. Какова
частота нормального всхода семян?
18. В роддоме из 598 детей 312 оказались мальчиками. Какова частота
рождения девочек?
19. Частота встречаемости второй группы крови в исследовании оказалась
0.25. Сколько человек имело вторую группу крови, если в исследовании
приняло участие 500 человек?
20. За три летних месяца 27 дней были дождливыми. Найдите частоту
дождливых дней.
21. Экзаменационные билеты пронумерованы от 1 до 35. Какова вероятность
того, что наудачу взятый билет имеет номер, кратный пяти?
22. Из урны, содержащей 9 белых, 9 черных, 9 синих и 9 красных шаров,
наудачу извлекли 3 шара. Какова вероятность, что это окажутся белые
или черные шары.
23. В чемпионате по гимнастике участвуют 50 спортсменок: 17 из России, 22
В чемпионате по гимнастике участвуют 50 спортсменок: 17 из России, 22
из США, остальные – из Китая. Порядок, в котором выступают
гимнастки, определяется жребием. Найдите вероятность того, что
спортсменка, выступающая первой, окажется из Китая.
24. В среднем из 500 садовых насосов, поступивших в продажу, 4 подтекают.
Найдите вероятность того, что один случайно выбранный для контроля
насос не подтекает.
25. Фабрика выпускает сумки. В среднем на 80 качественных сумок
приходится одна сумка со скрытыми дефектами. Найдите вероятность
того, что купленная сумка окажется качественной. Результат округлите
до сотых.
26. В соревнованиях по толканию ядра участвуют 4 спортсмена из Эстонии, 6
спортсменов из Латвии, 3 спортсмена из Литвы и 7 – из Польши.
Порядок, в котором выступают спортсмены, определяется жребием.
Найдите вероятность того, что спортсмен, который выступает последним,
окажется из Литвы.
27. Научная конференция проводится в 4 дня. Всего запланировано 50
докладов – первые два дня по 11 докладов, остальные распределены
поровну между третьим и четвертым днями. Порядок докладов
определяется жеребьёвкой. Какова вероятность, что доклад профессора
М. окажется запланированным на последний день конференции?
28. На семинар приехали 2 ученых из Польши, 3 из Бельгии и 5 из Болгарии.
Порядок докладов определяется жеребьёвкой. Найдите вероятность того,
что девятым окажется доклад ученого из Бельгии.
29. В сборнике билетов по химии всего 50 билетов, в 20 из них встречается
вопрос по углеводородам. Найдите вероятность того, что в случайно
выбранном на экзамене билете школьнику достанется вопрос по
углеводородам.
30. В сборнике билетов по истории всего 60 билетов, в 18 из них встречается
вопрос по смутному времени. Найдите вероятность того, что в случайно
выбранном на экзамене билете школьнику не достанется вопроса по
смутному времени.
31. На чемпионате по прыжкам в воду выступают 25 спортсменов, среди них
8 прыгунов из России и 9 прыгунов из Парагвая. Порядок выступлений
определяется жеребьёвкой. Найдите вероятность того, что шестым будет
выступать прыгун из Парагвая.
Задачи
1. В семье 2 ребенка. Найти вероятность того, что оба ребёнка мальчики.
2. В семье 2 ребенка. Найти вероятность того, что оба ребёнка мальчики,
если известно что первый – мальчик.
3. Бросают две монеты. Найти вероятность того, что появятся «Орёл» и
«Решка».
4. Брошены монета и игральная кость. Найти вероятность совмещения
событий: «появилась “решка”» и «появилось 3 очка».
5. У большой популяции дрозофилы 25% мух имеют мутацию глаз,
50% – мутацию крыльев, двойных мутаций нет ни у одной мухи.
Какова вероятность того, что у наудачу выбранной мухи окажется
какая-либо мутация?
6. Имеется 5 видов конвертов без марок и 4 вида марок одинаковой
стоимости. Сколькими способами можно выбрать конверт с маркой для
Сколькими способами можно выбрать конверт с маркой для
посылки письма?
7. На вершину горы ведут 5 тропинок. Сколькими способами турист
может подняться в гору и потом спуститься с нее? Подъем и спуск
а) должны происходить по разным тропинкам,
б) могут происходить по одинаковым тропинкам
8. У одного студента 5 книг, у другого – 9. Все книги различные.
Сколькими способами студенты могут произвести обмен:
а) одной книги на книгу?
б) 2 книги на 2 книги за 1 раз?
в) 2 книги на 2 книги за 2 раза?
9. Сколько словарей надо издать, чтобы можно было непосредственно
выполнить переводы с любого из 5 языков: русского, английского,
французского, немецкого, итальянского – на любой другой из этих 5
языков?
10. В урне 5 белых и 5 черных шаров. Из этой урны последовательно
извлечены черный и белый шары по одному. Какова вероятность того,
что следующий шар будет белым?
11. В урне 5 белых и 5 черных шаров. Из этой урны последовательно
В урне 5 белых и 5 черных шаров. Из этой урны последовательно
извлечены подряд два шара. Какова вероятность того, что
а) оба шара белые
б) сначала был белый шар, потом черный
12. Брошены 3 игральные кости. Какова вероятность того, что на всех
костях выпадает четное число?
13. Игральная кость брошена 3 раза. Какова вероятность того, что при этом
все выпавшие грани равны 2?
14. Вероятность попадания в мишень при одном выстреле для первого
стрелка равна р, а для второго – 0.7. Известно, что вероятность
попадания при одном выстреле обоих стрелков равна 0.35. Найдите р.
15. В ящике 10 деталей, среди которых 7 окрашенных. Сборщик наудачу
достает 4 детали. Найдите вероятность того, что все взятые детали
окрашенные.
16. Игральная кость брошена 3 раза. Какова вероятность того, что при этом
все выпавшие грани различны?
17. На 6 одинаковых карточках написаны буквы «а», «в», «к», «М», «о»,
«с». Эти карточки наудачу разложены в ряд. Какова вероятность того,
Эти карточки наудачу разложены в ряд. Какова вероятность того,
что получится слово «Москва»?
18. 2 стрелка сделали по одному выстрелу по мишени. Известно, что
вероятность попадания в мишень для одного из стрелков равна 0.6, а
для другого – 0.7. Найдите вероятность того, что:
а) только один из стрелков попадет в мишень;
б) хотя бы один из стрелков попадет в мишень;
в) оба стрелка попадут в мишень;
г) ни один из стрелков не попадет в мишень;
д) ни один из стрелков не попадет в мишень.
19. Вероятность дождливого дня составляет 0.7. Найдите вероятность того,
что:
а) только один день будет дождливым;
б) хотя бы один день будет дождливым;
в) оба дня будут дождливыми;
г) оба дня будут ясными;
д) только первый день будет дождливым.
20. Вероятность попадания в цель при одном выстреле равна 0.2.
Произведено 10 выстрелов. Найдите вероятность поражения цели, если
для этого достаточно хотя бы одно попадание.
21. Вероятность выигрыша по одному билету лотереи равна 0.5. Какова
вероятность, купив 5 билетов, выиграть:
а) по всем пяти билетам;
б) ни по одному билету;
в) хотя бы по одному билету?
22. Студент успел подготовить к экзаменам 20 вопросов из 25. В билете 3
вопроса, выбранных случайно. Какова вероятность того, что из 3
наудачу выбранных вопросов
а) студент знает все 3?
б) студент не знает ни один?
в) студент знает только 2?
г) студент знает не менее 2?
23. В первой урне содержится 10 шаров, из них 8 белых; во второй урне —
20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному
шару, а затем из этих шаров наудачу взят один шар. Найдите
вероятность того, что взят белый шар.
24. В пассажирском поезде 9 вагонов. Сколькими способами можно
рассадить в поезде 4 человек при условии, что все они должны ехать в
различных вагонах?
25.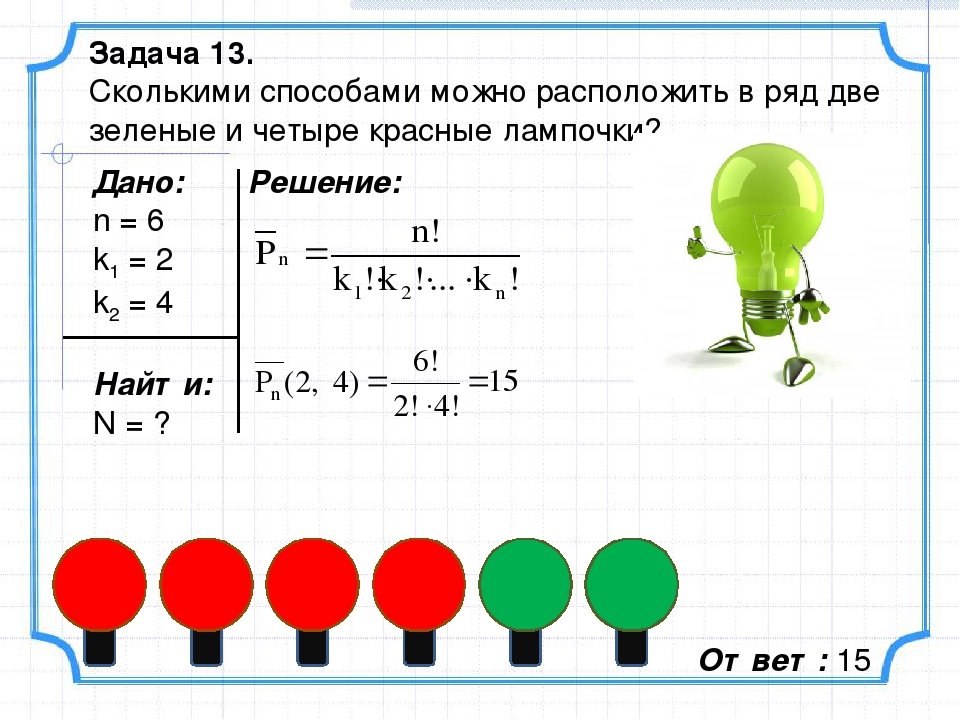 Сколькими способами 3 различных подарка А, В и С можно сделать
Сколькими способами 3 различных подарка А, В и С можно сделать
каким-то 3 из 15 лиц, если:
а) никто не должен получать более одного подарка;
б) подарок А должно получить лицо номер 1?
26. В группе 9 человек. Сколько можно образовать разных подгрупп при
условии, что в подгруппу входит
а) 5 человек?
б) не менее 5 человек?
27. Сколько существует различных автомобильных номеров, которые
состоят из трех цифр?
28. Пятитомное собрание сочинений расположено на полке в случайном
порядке. Какова вероятность того, что книги стоят слева направо в
порядке нумерации томов (от 1 до 5)?
29. Два стрелка сделали по одному выстрелу в мишень. Вероятность
попадания в мишень для первого стрелка равна 0.6, а для второго – 0.3.
В мишени оказалась одна пробоина. Найти вероятность того, что она
принадлежит первому стрелку.
30. В одной урне 3 белых и 8 черных шаров, а в другой 5 белых и 7 черных
шаров. Из первой урны вынимают 1 шар и опускают во вторую урну.
Из первой урны вынимают 1 шар и опускают во вторую урну.
После этого из второй урны также случайно вынимают 1 шар. Найти
вероятность того, что шар, вынутый из второй урны, белый.
31. Вероятность того, что цель поражена при одном выстреле первым
стрелком р1=0.35, вторым p2=0.49. Первый сделал n1=3, второй n2=2
выстрела. Определить вероятность того, что цель не поражена.
32. На полке в случайном порядке расставлено 40 книг, среди которых
находится трехтомник Пушкина. Найти вероятность того, что эти тома
стоят в порядке возрастания номера слева направо, но не обязательно
рядом.
33. На каждой из пяти одинаковых карточек напечатана одна из
следующих букв: «а», «м», «р», «т», «ю». Карточки тщательно
перемешаны. Найти вероятность того, что на четырех вынутых по
одной карточке можно прочесть слово «юрта».
34. Ребенок имеет на руках 5 кубиков с буквами: А, К, К, Л, У. Какова
вероятность того, что ребенок соберет из кубиков слово «кукла»?
35. У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней подряд она
У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней подряд она
выдает по одному фрукту. Сколькими способами это может быть
сделано?
36. Сколькими способами на шахматной доске можно указать:
а) две клетки;
б) две клетки одного цвета;
в) две клетки разного цвета?
37. Имеются три письма, каждое из которых нужно послать по шести
различным адресам. Сколькими способами можно осуществить
рассылку писем, если:
а) никакие два письма не посылать по одному адресу;
б) по одному адресу посылать более одного письма?
38. Из цифр 1, 2, 3, 4, 5 составляются всевозможные числа, каждое из
которых состоит не более чем из трех цифр. Сколько таких чисел
можно составить, если:
а) повторение цифр в числах не разрешается;
б) разрешается повторение цифр?
39. Сколькими способами три различных подарка А, В и С можно сделать
каким-то трем из пятнадцати лиц, если:
а) никто не должен получить более одного подарка;
б) подарок А должен получить определенное лицо?
40. В группе девять человек. Сколько можно образовать разных подгрупп
В группе девять человек. Сколько можно образовать разных подгрупп
при условии, что в подгруппу входит не менее двух человек?
41. Сколько существует различных автомобильных номеров, которые
состоят из пяти цифр, если первая цифра не равна нулю?
42. Проверьте то, что число трехбуквенных «слов», которые можно
образовать из букв слова «гипотенуза», равно числу всех возможных
перестановок букв слова «призма»?
43. Три дороги соединяют города А и В, четыре дороги соединяют города
В и С. Сколькими способами можно совершить поездку из А в С через
В и вернуться в А также через В?
44. Сколькими способами можно расставить на полке семь различных
книг, если:
а) две определенные книги должны стоять рядом;
б) эти две книги не должны стоять рядом?
45. Группу из двадцати студентов нужно разделить на три бригады,
причем в первую бригаду должны входить три человека, во вторую —
пять и в третью — двенадцать. Сколькими способами это можно
Сколькими способами это можно
сделать?
46. Сколько шестизначных чисел можно образовать из цифр 1, 2, 3, 4, 5, 6,
7, 8, 9, если каждое число должно состоять из три четных и три
нечетных цифр, причем никакая цифра не входит в число более одного
раза?
47. В течение четырех недель студенты сдают четыре экзамена, в том
числе два экзамена по математике. Сколькими способами можно
распределить экзамены по неделям так, чтобы экзамены по математике
не следовали один за другим?
48. Восемь человек должны сесть в два автомобиля, причем в каждом
должно быть, по крайней мере, три человека. Сколькими способами
они могут это сделать?
49. Сколько различных чисел можно получить, переставляя цифры числа
2 233 344 455?
50. Сколькими способами можно в строчку написать шесть плюсов и
четыре минуса?
51. Найдите число всевозможных «слов» из букв слова «зоология».
Сколько таких слов, в которых три буквы «о» стоят рядом?
52. Имеются двадцать наименований товаров. Сколькими способами их
Имеются двадцать наименований товаров. Сколькими способами их
можно распределить по трем магазинам, если известно, что в первый
магазин должно быть доставлено восемь наименований, во второй —
семь наименований и в третий — пять наименований товаров?
53. Сколько различных вариантов хоккейной команды можно составить из
десяти нападающих, пяти защитников и трех вратарей, если в состав
каждой команды должно войти три нападающих, два защитника и один
вратарь?
54. Сколькими способами можно распределить шесть различных
предметов между тремя лицами так, чтобы каждое лицо получило по
два предмета?
55. Пять девушек и три юноши играют в баскетбол. Сколькими способами
они могут разбиться на две команды по четыре игрока, если в каждой
команде должно быть не менее одного юноши?
56. На десяти карточках написаны цифры 0. 1, 2, 3, 4, 5, 6, 7, 8, 9. Берут
четыре карточки и составляют из цифр, записанных на них,
четырехзначное число. Сколько различных четырехзначных чисел
Сколько различных четырехзначных чисел
можно составить таким образом?
57. Сколько можно подать сигналов из пяти различных флажков,
одинаково поднимая их вверх в любом количестве и в любом порядке?
58. Эксперт оценивает качественный уровень трех видов изделий по
потребительским признакам. Вероятность того, что изделию первого
вида будет присвоен знак качества, равна 0.9; для изделия второго
вида – 0.7. Найти вероятность того, что знак качества будет присвоен:
а) всем изделиям;
б) только одному изделию;
в) хотя бы одному изделию.
59. В партии товара, состоящей из 30 мужских пальто, находится 20
изделий местного производства. Товаровед наудачу отбирает три
изделия. Какова вероятность, что все три изделия окажутся:
а) местного производства;
б) не местного производства?
60. В группе 9 человек. Сколько можно образовать разных подгрупп при
условии, что в подгруппу входит не менее 2 человек?
61. Группу из 20 студентов нужно разделить на 3 бригады, причем в
Группу из 20 студентов нужно разделить на 3 бригады, причем в
первую бригаду должны входить 3 человека, во вторую — 5 и в третью —
12. Сколькими способами это можно сделать.
62. Для участия в команде тренер отбирает 5 мальчиков из 10. Сколькими
способами он может сформировать команду, если 2 определенных
мальчика должны войти в команду?
63. В шахматном турнире принимали участие 15 шахматистов, причем
каждый из них сыграл только одну партию с каждым из остальных.
Сколько всего партий было сыграно в этом турнире?
64. Экспедиция издательства отправила газеты в три почтовых отделения.
Вероятность своевременной доставки газет в первое отделение равна
0.95, во второе – 0.9, в третье – 0.8. Найти вероятность следующих
событий:
а) только одно отделение получит газеты вовремя;
б) хотя бы одно отделение получит газеты с опозданием.
65. Для сигнализации об аварии установлены два независимо работающих
сигнализатора. Вероятность того, что при аварии сигнализатор
Вероятность того, что при аварии сигнализатор
сработает, равна 0.95 для первого сигнализатора и 0.9 для второго.
Найти вероятность того, что при аварии сработает только один
сигнализатор.
66. Вероятность хотя бы одного попадания в цель при четырех выстрелах
равна 0.9984. Найти вероятность попадания в цель при одном выстреле.
67. В первой урне находятся 10 белых и 4 черных шаров, а во второй 5
белых и 9 черных шаров. Из каждой урны вынули по шару. Какова
вероятность того, что оба шара окажутся черными?
68. Трое учащихся на экзамене независимо друг от друга решают одну и ту
же задачу. Вероятности ее решения этими учащимися равны 0.8, 0.7 и
0.6 соответственно. Найдите вероятность того, что хотя бы один
учащийся решит задачу.
69. Брошены две игральные кости. Событие А={выпадение шестерки на
первой кости}. Событие В={сумма выпавших очков равна 7}.
Являются ли события А и В независимыми?
70. В партии из 23 деталей находятся 10 бракованных. Вынимают из
В партии из 23 деталей находятся 10 бракованных. Вынимают из
партии наудачу две детали. Используя классическое определение
теории вероятности определить, какова вероятность того, что обе
детали окажутся бракованными.
71. В ящике лежат шары: 4 белых, 10 красных, 8 зеленых, 9 коричневых.
Из ящика вынимают один шар. Пользуясь теоремой сложения
вероятностей определить, какова вероятность, что шар окажется
цветным (не белым)?
72. В вопросах к зачету имеются 75% вопросов, на которые студенты
знают ответы. Преподаватель выбирает из них два вопроса и задает их
студенту. Определить вероятность того, что среди полученных
студентом вопросов есть хотя бы один, на который он знает ответ.
73. На складе находятся 26 деталей, из которых 13 стандартные. Рабочий
берет наугад две детали. Пользуясь теоремой умножения вероятностей
зависимых событий, определить вероятность того, что обе детали
окажутся стандартными.
74. В случайном эксперименте бросают две игральные кости. Найдите
вероятность того, что в сумме выпадет 6 очков. Результат округлите до
сотых.
75. В случайном эксперименте симметричную монету бросают дважды.
Найдите вероятность того, что орел выпадет ровно один раз.
76. В случайном эксперименте бросают три игральные кости. Найдите
вероятность того, что в сумме выпадет 4 очка. Результат округлите до
сотых.
77. Имеется пять видов конвертов без марок и четыре вида марок
одинаковой стоимости. Сколькими способами можно выбрать конверт
с маркой для посылки письма?
78. В магазин поступает минеральная вода в бутылках от двух
изготовителей: местного и иногороднего, причем местный
изготовитель поставляет 40% всей продукции. Вероятность того, что
при транспортировке бутылка окажется разбитой, для местной
продукции 0.5%, а для иногородней 2%. Найти вероятность, того, что
взятая наудачу бутылка окажется неразбитой. Какова ожидаемая доля
Какова ожидаемая доля
(в %) разбитых бутылок?
79. Магазин приобретает чай у двух фабрик, при этом первая из них
поставляет
всего товара. Продукция высшего сорта для первой
фабрики составляет 90%, а для второй 80%.Найти вероятность того,
что купленная наугад пачка чая будет высшего сорта.
80. Для трех розничных торговых предприятий определен плановый
уровень прибыли. Вероятность того, что первое предприятие выполнит
план по прибыли, равна 90%, для второго она составляет 95%, для
третьего 100%. Какова вероятность того, что плановый уровень
прибыли будет достигнут:
а) всеми предприятиями;
б) только двумя предприятиями;
в) хотя бы одним предприятием?
81. Для магазина потребительской кооперации куплены два холодильника.
Вероятность того, что каждый из них выдержит гарантийный срок
службы, составляет 90%. Найти вероятность того, что в течение
гарантийного срока:
а) оба холодильника не потребуют ремонта;
б) только один из них потребует ремонта;
в) хотя бы один не потребует ремонта.
82. Произведено три выстрела по цели из орудия. Вероятность попадания
при первом выстреле равна 0.75; при втором – 0.8; при третьем – 0.9.
Определить вероятность того, что будет:
а) три попадания;
б) хотя бы одно попадание.
83. Контролер ОТК, проверив качество сшитых 20 пальто, установил, что
16 из них первого сорта, а остальные – второго. Найти вероятность
того, что среди взятых наудачу из этой партии трех пальто одно будет
второго сорта.
84. Среди 20 поступающих в ремонт часов 8 нуждаются в общей чистке
механизма. Какова вероятность того, что среди взятых одновременно
наудачу 8 часов по крайней мере двое нуждаются в общей чистке
механизма?
85. Среди 15 лампочек 4 стандартных. Одновременно берут наудачу две
лампочки. Найти вероятность того, что хотя бы одна из них
нестандартная.
86. Какова вероятность того, что наудачу брошенная в круг точка окажется
внутри вписанного в него квадрата?
87. Найти вероятность того, что из 10 книг, расположенных в случайном
Найти вероятность того, что из 10 книг, расположенных в случайном
порядке, 3 определенные книги окажутся рядом.
88. В коробке 10 красных, 3 синих и 7 желтых карандашей. Наудачу
вынимают 3 карандаша. Какова вероятность того, что все они:
а) разных цветов;
б) одного цвета?
89. Пакеты акций, имеющихся на рынке ценных бумаг, могут дать доход
владельцу с вероятностью 0.5 (для каждого пакета). Сколько пакетов
акций различных фирм нужно приобрести, чтобы с вероятностью, не
меньшей 0.96875, можно было ожидать доход хотя бы по одному
пакету акций?
90. На связке 5 ключей. К замку подходит только один ключ. Найти
вероятность того, что потребуется не более двух попыток открыть
замок, если опробованный ключ в дальнейших испытаниях не
участвует.
91. В магазине 10 телевизоров, 3 из них имеют дефекты. Какова
вероятность того, что посетитель купит телевизор, если для выбора
телевизора без дефектов понадобится не более трех попыток?
92. Радист трижды вызывает корреспондента. Вероятность того, что будет
Радист трижды вызывает корреспондента. Вероятность того, что будет
принят первый вызов, равна 0.2, второй – 0.3, третий – 0.4. События,
состоящие в том, что данный вызов будет услышан, независимы. Найти
вероятность того, что корреспондент услышит вызов радиста.
93. Из 20 сбербанков 10 расположены за чертой города. Для обследования
случайным образом отобрано 5 сбербанков. Какова вероятность того,
что среди отобранных окажется в черте города:
а) 3 сбербанка;
б) хотя бы один?
94. В магазине 30 телевизоров, причем 20 из них импортных. Найти
вероятность того, что среди 5 поданных в течение дня телевизоров
окажется более трех импортных телевизоров, предполагая, что
вероятности покупки телевизоров разных марок одинаковы.
95. Наудачу взятый телефонный номер состоит из 5 цифр. Известно, что
номер телефона не начинается с нуля. Какова вероятность того, что в
нем все цифры:
а) различные;
б) одинаковые;
в) нечетные?
96. В одной урне 5 белых и 6 черных шаров, а в другой – 4 белых и 8
В одной урне 5 белых и 6 черных шаров, а в другой – 4 белых и 8
черных шаров. Из первой урны случайным образом вынимают 3 шара и
опускают во вторую урну. После этого из второй урны также случайно
вынимают 4 шара. Какова вероятность того, что все шары, вынутые из
второй урны, белые.
97. При приеме партии изделий подвергается проверке половина изделий.
Условие приемки – наличие брака в выборке менее 2 %. Какова
вероятность того, что партия из 100 изделий, содержащая 5% брака,
будет принята.
98. Вероятность своевременного выполнения студентом контрольной
работы по каждой из трех дисциплин равно соответственно 0.6, 0.5 и
0.8. Найти вероятность своевременного выполнения контрольной
работы студентом:
а) по 2 дисциплинам;
б) хотя бы по 2 дисциплинам.
99. На фирме работают 8 аудиторов, из которых 3 – высокой
квалификации, и 5 программистов, из которых 2 – высокой
квалификации. В командировку надо отправить группу из 3 аудиторов
В командировку надо отправить группу из 3 аудиторов
и 2 программистов. Какова вероятность того, что в этой группе
окажется по крайней мере 1 аудитор высокой квалификации и хотя бы
один программист высокой квалификации, если каждый специалист
имеет равные возможности поехать в командировку?
100.
В данный район изделия поставляются тремя фирмами в
отношении 5:8:7. Среди продукции первой фирмы стандартные
изделия составляют 90%, второй – 85%, третьей – 75%. Найти
вероятность того, что:
а) приобретенное изделие окажется стандартным;
б) приобретенное изделие оказалось стандартным.
Какова вероятность того, что оно изготовлено третьей фирмой.
101.
Для проведения соревнования 16 волейбольных команд разбиты
по жребию на 2 подгруппы (по 8 команд в каждой). Найти вероятность
того, что две наиболее сильные команды окажутся:
а) в разных подгруппах;
б) в одной подгруппе.
102.
Комиссия по качеству раз в месяц проверяет качество продуктов
в двух из 30 магазинов, среди которых находятся и два известным всем
магазина. Какова вероятность того, что в течение месяца они оба будут
проверены?
Задачи
1. Какова вероятность того, что в 8 семьях родится 5 девочек?
2. По данным статистики 2% приготовленных растворов неправильные.
Найдите вероятность того, что из 6 растворов 2 неправильные.
3. В семье 5 детей. Найдите вероятность того, что среди детей 2
мальчика, если вероятность рождения мальчика принимается 0.5.
4. Найдите наиболее вероятное число выпаданий шестерки при 46
бросаниях игральной кости.
5. Контрольное задание состоит из 10 вопросов, предусматривающих
ответы «да» и «нет». Найдите наиболее вероятное число правильных
ответов, которые даст учащийся, если он станет выбирать ответ по
каждому вопросу наудачу. Найдите вероятность наиболее вероятного
числа правильных ответов А если существует 4 варианта ответа?
6. Вероятность изготовления стандартной детали 0.95. Сколько деталей
Вероятность изготовления стандартной детали 0.95. Сколько деталей
должно быть в партии, чтобы наиболее вероятное число нестандартных
деталей в ней равнялось 55?
7. На автобазе имеется 12 автомашин. Вероятность выхода на линию
каждой из них равна 0.8. Найдите вероятность нормальной работы
автобазы в ближайший день, если для этого необходимо иметь на
линии не меньше 8 автомашин.
8. Вероятность того, что игровой автомат при опускании монеты
сработает на выигрыш, равна 0.03. Найдите наиболее вероятное число
случаев проигрыша и выигрыша, если будет опущено 150 монет.
9. Вероятность того, что денежный приемник автомата при опускании
одной монеты сработает правильно, равна 0.97. Сколько нужно
опустить монет, чтобы наиболее вероятное число случаев правильной
работы автомата было равно 100?
10. Контрольное задание состоит из 5 вопросов, на каждый из которых
дается 4 варианта ответа, причем один из них правильный, а остальные
неправильные. Найдите вероятность того, что учащийся, не знающий
Найдите вероятность того, что учащийся, не знающий
ни одного вопроса, даст:
а) 3 правильных ответа;
б) не менее 3 правильных ответов
(предполагается, что учащийся выбирает ответы наудачу).
11. Производится 10 независимых выстрелов по цели, вероятность
попадания в которую при одном выстреле равна 0.2. Найдите:
а) наиболее вероятное число попаданий;
б) вероятность того, что число попаданий равно наиболее вероятному
числу попаданий.
12. Проведено 5 независимых испытаний, каждое из которых заключается
в одновременном подбрасывании 2 монет. Найдите вероятность того,
что ровно в 3 испытаниях появились по 2 герба.
13. Представить закон распределения Х для серии испытаний в виде
таблицы при n = 3; p(А) = 0.1.
14. Представить закон распределения Х для серии испытаний в виде
таблицы при n = 3; p(А) = 0.2.
15. Представить закон распределения Х для серии испытаний в виде
таблицы при n = 4; p(А) = 0. 3.
3.
16. Представить закон распределения Х для серии испытаний в виде
таблицы при n = 3; p(А) = 0.4.
17. Представить закон распределения Х для серии испытаний в виде
таблицы при n = 3; p(А) = 0.5.
18. Эксперимент с бросанием монеты проведен 4 раза. Какова вероятность
того, что герб выпадет не более:
а) 1 раза;
б) 2 раз;
в) 3 раз;
г) 4 раз.
19. В среднем пятая часть поступающих в продажу автомобилей
некомплектны. Найти вероятность того, что среди десяти автомобилей
имеют некомплектность:
а) три автомобиля;
б) менее трех.
20. В магазине продаются 5 отечественных и 3 импортных телевизора.
Составить закон распределения случайной величины – числа
импортных из четырех наудачу выбранных телевизоров.
21. Вероятность того, что изготовленная на первом станке деталь будет
первосортной, равна 0.7. При изготовлении такой же детали на втором
станке эта вероятность равна 0. 8. На первом станке изготовлены две
8. На первом станке изготовлены две
детали, на втором – три. Найти вероятность того, что детали первого
сорта.
22. Всхожесть семян некоторого растения составляет 80%. Найти
вероятность того, что из 6 посеянных семян взойдут:
а) три;
б) не менее трех;
в) четыре.
23. В урне содержится 6 черных и 5 белых шаров. Случайным образом
вынимают 4 шаров. Найти вероятность, что среди них имеются:
а) 3 белых шаров;
б) меньше, чем 3 белых шаров;
в) хотя бы один белый шар.
24. Бросают три монеты. Найти вероятность того, что:
а) на всех монетах появится герб
б) хотя бы на одной монете появится герб;
в) только на двух монетах появиться герб;
г) только на одной монете появится герб;
д) на ни одной монете не появится герб.
25. Вероятность выигрыша в лотерею на один билет равна 0.6. Куплено 16
билетов. Найти наивероятнейшее число выигрышных билетов и
соответствующую вероятность.
26. Абонент забыл последнюю цифру семизначного номера телефона и
поэтому набирает её наугад. Определить вероятность того, что ему
придётся звонить не более чем в 3 места.
27. В случайном эксперименте симметричную монету бросают четырежды.
Найдите вероятность того, что орел не выпадет ни разу.
Линейное программирование — тест с ответами
Математика дается не всем. Но сдавать её нужно чтобы получить за нее зачет или какую либо оценку. Сейчас чаще всего проводится проверка знаний в виде тестирования. Мы собрали частые вопросы встречающиеся в тестах на этой странице. Обратите внимание что правильные варианты ответов выделены символом [+].
Каждую секунду бактерия делится на две новые бактерии. Известно, что весь объём одного стакана бактерии заполняют за 1 час. За сколько секунд бактерии заполняют половину стакана?
[+] Ответ: 3599
На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 15 кусков, если по жёлтым — 5 кусков, а если по зелёным — 7 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
Если распилить палку по красным линиям, получится 15 кусков, если по жёлтым — 5 кусков, а если по зелёным — 7 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
[+] Ответ: 25
Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за один прыжок. Кузнечик начинает прыгать из начала координат. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 11 прыжков?
[+] Ответ: 12
Саша пригласил Петю в гости, сказав, что живёт в седьмом подъезде в квартире № 462, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом семиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)
[+] Ответ: 5
Саша пригласил Петю в гости, сказав, что живёт в восьмом подъезде в квартире № 468, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом двенадцатиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)
На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)
[+] Ответ: 10
Саша пригласил Петю в гости, сказав, что живёт в двенадцатом подъезде в квартире № 465, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом пятиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)
[+] Ответ: 4
Саша пригласил Петю в гости, сказав, что живёт в десятом подъезде в квартире № 333, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом девятиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)
[+] Ответ: 3
Тренер посоветовал Андрею в первый день занятий провести на беговой дорожке 15 минут, а на каждом следующем занятии увеличивать время, проведённое на беговой дорожке, на 7 минут. За сколько занятий Андрей проведёт на беговой дорожке в общей сложности 2 часа 25 минут, если будет следовать советам тренера?
[+] Ответ: 5
Врач прописал пациенту принимать лекарство по такой схеме: в первый день он должен принять 3 капли, а в каждый следующий день — на 3 капли больше, чем в предыдущий. Приняв 30 капель, он ещё 3 дня пьёт по 30 капель лекарства, а потом ежедневно уменьшает приём на 3 капли. Сколько пузырьков лекарства нужно купить пациенту на весь курс приёма, если в каждом содержится 20 мл лекарства (что составляет 250 капель)?
Приняв 30 капель, он ещё 3 дня пьёт по 30 капель лекарства, а потом ежедневно уменьшает приём на 3 капли. Сколько пузырьков лекарства нужно купить пациенту на весь курс приёма, если в каждом содержится 20 мл лекарства (что составляет 250 капель)?
[+] Ответ: 2
Врач прописал пациенту принимать лекарство по такой схеме: в первый день он должен принять 20 капель, а в каждый следующий день — на 3 капли больше, чем в предыдущий. После 15 дней приёма пациент делает перерыв в 3 дня и продолжает принимать лекарство по обратной схеме: в 19-й день он принимает столько же капель, сколько и в 15-й день, а затем ежедневно уменьшает дозу на 3 капли, пока дозировка не станет меньше 3 капель в день. Сколько пузырьков лекарства нужно купить пациенту на весь курс приёма, если в каждом содержится 200 капель?
[+] Ответ: 7
Произведение десяти идущих подряд чисел разделили на 7. Чему может быть равен остаток?
[+] Ответ: 0
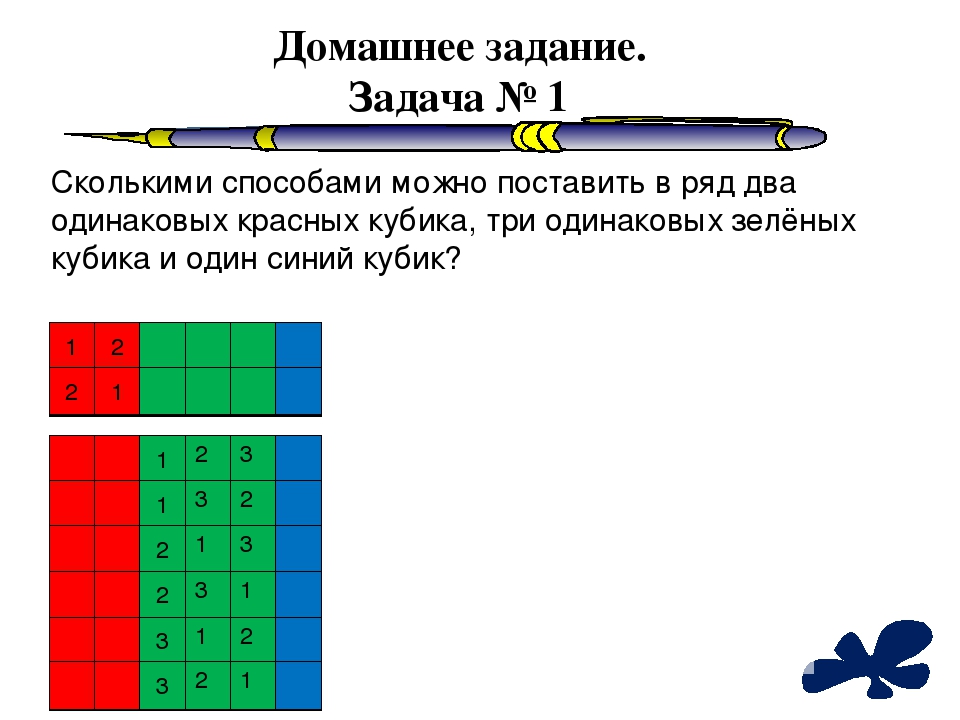
Сколькими способами можно поставить в ряд два одинаковых красных кубика, три одинаковых зелёных кубика и один синий кубик?
[+] Ответ: 60
В бак объёмом 38 литров каждый час, начиная с 12 часов, наливают полное ведро воды объёмом 8 литров. Но в днище бака есть небольшая щель, и из неё за час вытекает 3 литра. В какой момент времени (в часах) бак будет заполнен полностью.
Но в днище бака есть небольшая щель, и из неё за час вытекает 3 литра. В какой момент времени (в часах) бак будет заполнен полностью.
[+] Ответ: 18
Какое наименьшее число идущих подряд чисел нужно взять, чтобы их произведение делилось на 7?
[+] Ответ: 2
В результате паводка котлован заполнился водой до уровня 2 метра. Строительная помпа непрерывно откачивает воду, понижая её уровень на 20 см в час. Подпочвенные воды, наоборот, повышают уровень воды в котловане на 5 см в час. За сколько часов работы помпы уровень воды в котловане опустится до 80 см?
[+] Ответ: 8
В меню ресторана имеется 6 видов салатов, 3 вида первых блюд, 5 видов вторых блюд и 4 вида десерта. Сколько вариантов обеда из салата, первого, второго и десерта могут выбрать посетители этого ресторана?
[+] Ответ: 360
Нефтяная компания бурит скважину для добычи нефти, которая залегает, по данным геологоразведки, на глубине 3 км. В течение рабочего дня бурильщики проходят 300 метров в глубину, но за ночь скважина вновь «заиливается», то есть заполняется грунтом на 30 метров. За сколько рабочих дней нефтяники пробурят скважину до глубины залегания нефти?
В течение рабочего дня бурильщики проходят 300 метров в глубину, но за ночь скважина вновь «заиливается», то есть заполняется грунтом на 30 метров. За сколько рабочих дней нефтяники пробурят скважину до глубины залегания нефти?
[+] Ответ: 11
Какое наименьшее число идущих подряд чисел нужно взять, чтобы их произведение делилось на 9?
[+] Ответ: 2
В обменном пункте можно совершить одну из двух операций: • за 2 золотых монеты получить 3 серебряных и одну медную; • за 5 серебряных монет получить 3 золотых и одну медную. У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 50 медных. На сколько уменьшилось количество серебряных монет у Николая?
[+] Ответ: 10
На поверхности глобуса фломастером проведены 12 параллелей и 22 меридиана. На сколько частей проведённые линии разделили поверхность глобуса? Меридиан — это дуга окружности, соединяющая Северный и Южный полюсы. Параллель — это окружность, лежащая в плоскости, параллельной плоскости экватора.
Параллель — это окружность, лежащая в плоскости, параллельной плоскости экватора.
[+] Ответ: 286
В корзине лежит 50 грибов: рыжики и грузди. Известно, что среди любых 28 грибов имеется хотя бы один рыжик, а среди любых 24 грибов хотя бы один груздь. Сколько груздей в корзине?
[+] Ответ: 27
Группа туристов преодолела горный перевал. Первый километр подъёма они преодолели за 50 минут, а каждый следующий километр проходили на 15 минут дольше предыдущего. Последний километр перед вершиной был пройден за 95 минут. После десятиминутного отдыха на вершине туристы начали спуск, который был более пологим. Первый километр после вершины был пройден за час, а каждый следующий на 10 минут быстрее предыдущего. Сколько часов группа затратила на весь маршрут, если последний километр спуска был пройден за 10 минут.
[+] Ответ: 8,5
На кольцевой дороге расположены четыре бензоколонки: A, B, C и D. Расстояние между A и B — 35 км, между A и C — 20 км, между C и D — 20 км, между D и A — 30 км (все расстояния измеряются вдоль кольцевой дороги в кратчайшую сторону). Найдите расстояние между B и C. Ответ дайте в километрах.
Найдите расстояние между B и C. Ответ дайте в километрах.
[+] Ответ: 15
На кольцевой дороге расположены четыре бензоколонки: A, B, C и D. Расстояние между A и B — 50 км, между A и C — 40 км, между C и D — 25 км, между D и A — 35 км (все расстояния измеряются вдоль кольцевой дороги в кратчайшую сторону). Найдите расстояние между B и C.
[+] Ответ: 10
В классе учится 25 учащихся. Несколько из них ходили в кино, 18 человек ходили в театр, причём и в кино, и в театр ходили 12 человек. Известно, что трое не ходили ни в кино, ни в театр. Сколько человек из класса ходили в кино?
[+] Ответ: 16
По эмпирическому закону Мура среднее число транзисторов на микросхемах каждый год удваивается. Известно, что в 2005 году среднее число транзисторов на микросхеме равнялось 520 млн. Определите, сколько в среднем миллионов транзисторов было на микросхеме в 2003 году.
[+] Ответ: 130
В первом ряду кинозала 24 места, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в восьмом ряду?
Сколько мест в восьмом ряду?
[+] Ответ: 38
На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 5 кусков, если по жёлтым — 7 кусков, а если по зелёным — 11 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
[+] Ответ: 21
В магазине бытовой техники объём продаж холодильников носит сезонный характер. В январе было продано 10 холодильников, и в три последующих месяца продавали по 10 холодильников. С мая продажи увеличивались на 15 единиц по сравнению с предыдущим месяцем. С сентября объём продаж начал уменьшаться на 15 холодильников каждый месяц относительно предыдущего месяца. Сколько холодильников продал магазин за год?
[+] Ответ: 360
В обменном пункте можно совершить одну из двух операций: 1) за 3 золотых монеты получить 4 серебряных и одну медную; 2) за 6 серебряных монет получить 4 золотых и одну медную. У Николы были только серебряные монеты. После посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 35 медных. На сколько уменьшилось количество серебряных монет у Николы?
У Николы были только серебряные монеты. После посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 35 медных. На сколько уменьшилось количество серебряных монет у Николы?
[+] Ответ: 10
Саша пригласил Петю в гости, сказав, что живёт в седьмом подъезде в квартире № 462, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом семиэтажный. На каком этаже живёт Саша? (На каждом этаже число квартир одинаково, номера квартир в доме начинаются с единицы.)
[+] Ответ: 5
Во всех подъездах дома одинаковое число этажей, а на каждом этаже одинаковое число квартир. При этом число этажей в доме больше числа квартир на этаже, число квартир на этаже больше числа подъездов, а число подъездов больше одного. Сколько этажей в доме, если всего в нём 110 квартир?
[+] Ответ: 11
Решение задач № 20 ЕГЭ (базовый уровень)
Математика Базовый уровень. Решение задания 20.
Решение задания 20.
Обмен фишек
- Петя меняет маленькие фишки на большие, зайдя на обмен он получает 6 больших фишек отдав 9 маленьких. Сначала у Пети было 100 фишек (больших и маленьких), Осталось 79 сколько обменов он совершил?
Решение:
- 9-6=3. этим действием мы узнаем сколько Петя теряет (назовём это так) фишек за 1 обмен.
- 100-79=21 фишку он потерял
- 21:3 и получаем 7 Ответ: 7
Обмен наклеек
- Петя обменивался наклейками. Одну наклейку он меняет на 5 других Вначале у него была 1 наклейка. Сколько наклеек у него будет после 50 обменов?
1)50*5=250 – всего получит наклеек
2)но при обмене он отдавал по 1 наклейке получается 250-49=201. Ответ. 201
Оценка за четверть
- В конце четверти Петя выписал подряд все свои отметки по одному из предметов, их оказалось 5, и поставил между некоторыми из них знаки умножения. Произведение получившихся чисел оказалось равным 3530.
 Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2″, «3″, «4″ или «5″ и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округленным по правилам округления?
Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2″, «3″, «4″ или «5″ и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округленным по правилам округления? - Решение:
Число 3530 разложим на множители таким образом, чтобы остаток от разложения состоял из чисел 2, 3, 4 и 5 (т.к. только такие оценки ставит учитель). 3530=2⋅5⋅353, при этом оценки 353 не бывает, но оно записано в виде ряда оценок 3, 5 и 3.
Таким образом, получается ряд оценок 2, 5, 353 (как и по условию у нас оценок получилось 5 штук). Найдем среднее арифметическое данных оценок 2+5+3+5+3=3,6, округлив до целого получим оценку 4.
Ответ: 4.
- В конце четверти Петя выписал подряд все свои отметки по одному из предметов, их оказалось 5, и поставил между некоторыми из них знаки умножения. Произведение получившихся чисел оказалось равным 3495. Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2″, «3″, «4″ или «5″ и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округленным по правилам округления? ()
- Ответ: 3
Среднее арифметическое
- Среднее арифметическое 6 различных натуральных чисел равно 8.
 На сколько нужно увеличить наибольшее из этих чисел, чтобы их среднее арифметическое стало на 1 больше?
На сколько нужно увеличить наибольшее из этих чисел, чтобы их среднее арифметическое стало на 1 больше? - Решение:
Ответ: 6
Партия в теннис
- Миша, Коля и Леша играют в настольный теннис: игрок, проигравший партию, уступает место игроку, не участвовавшему в ней. В итоге оказалось, что Миша сыграл 12 партий, а Коля — 25. Сколько партий сыграл Леша?
- Решение:
Ответ: 13
Чёрно-белое поле
- Клетки таблицы 6 х 5 раскрашены в черный и белый цвета. Пар соседних клеток разного цвета 26, пар соседних клеток черного цвета всего 6. Сколько пар соседних клеток белого цвета?
- Решение:
Ответ: 17
Договор о дружбе
- Из десяти стран семь подписали договор о дружбе ровно с тремя другими странами, а каждая из оставшихся трех — ровно с семью. Сколько всего было подписано договоров?
- Решение:
Ответ: 21
Плоскость
- Три луча, выходящие из точки, разбивают плоскость на 3 разных угла, измеряемых целым числом градусов.
 Наибольший угол в 3 раза больше наименьшего. Сколько значений может принимать величина среднего угла?
Наибольший угол в 3 раза больше наименьшего. Сколько значений может принимать величина среднего угла? - Решение:
Ответ: 20
Задача о столбах
- Семь столбов соединены между собой проводами так, что от каждого столба отходит ровно 4 провода. Сколько всего проводов протянуто между этими семью столбами?
- Решение:
Ответ: 14
- Десять столбов соединены между собой проводами так, что от каждого столба отходит ровно 8 проводов. Сколько всего проводов протянуто между этими десятью столбами?
Ответ: 40
Вазы с розами
- На прилавке цветочного магазина стоят 3 вазы с розами: черная, зеленая и оранжевая. Слева от черной вазы 32 розы, справа от оранжевой вазы 9 роз. Всего в вазах 37 роз. Сколько роз в зеленой вазе?
- Решение:
- На прилавке цветочного магазина стоят 3 вазы с розами: белая, синяя и красная. Слева от красной вазы 15 роз, справа от синей вазы 12 роз.
 Всего в вазах 22 розы. Сколько роз в белой вазе?
Всего в вазах 22 розы. Сколько роз в белой вазе?
Ответ: 5
Маша и медведь
- Маша и Медведь съели 160 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь — печенье, но в какой-то момент они поменялись. Медведь и то, и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенье они съели поровну?
- Решение:
Ответ: 144
Маша и Медведь съели 51 печенье и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь-печенье, но в какой-то момент они поменялись. Медведь и то, и другое ест в четыре раза быстрее. Сколько печений съел Медведь, если варенья они съели поровну?
Маша и Медведь съели 100 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь – печенья, но в какой-то момент они поменялись. Медведь и то, и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну?
Порванная книга
- Из книги выпало несколько идущих подряд листков.
 Номер последней страницы перед выпавшими листами — 352, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало?
Номер последней страницы перед выпавшими листами — 352, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало? - Решение:
Ответ: 85
- Про натуральные числа A, B и C известно, что каждое из них больше 4, но меньше 8. Загадали натуральное число, затем его умножили на А, потом прибавили к полученному произведению B и вычли C. Получилось 165. Какое число было загадано?
- Решение:
Цветные линии
- На палке отмечены поперечные линии красного, желтого и зеленого цвета. Если распилить палку по красным линиям, получится 8 кусков, если по желтым – 12 кусков, а если по зеленым — 6 кусков. Сколько кусков получится, если распилить палку по линиям всех трех цветов?
- Решение:
Ответ: 24
ЕГЭ — 2017
- На ленте с разных сторон от середины отмечены две поперечные полоски: синяя и красная. Если разрезать ленту по синей полоске, то одна часть будет длиннее другой на A см.
 Если разрезать по красной, то одна часть будет длиннее другой на B см. Найдите расстояние от красной до синей полоски.
Если разрезать по красной, то одна часть будет длиннее другой на B см. Найдите расстояние от красной до синей полоски. - Решение:
Ответ: 30
Деление амёб. Способ 1
- Биологи открыли разновидность амёб, каждая из которых ровно через минуту делится на две. Биолог кладёт амёбу в пробирку, и ровно через час пробирка оказывается полностью заполненной амёбами. Сколько минут потребуется, чтобы вся пробирка заполнилась амёбами, если в неё положить не одну, а четыре амёбы?
- Решение:
Переведем часы в минуты, так как ответ должен быть в минутах:
1 час = 60 минут
Через 60 минут одна амеба произведет полную пробирку амеб. Если амеб будет 4, то за тот же час будет заполнено 4 пробирки. Однако пробирка лишь одна, поэтому каждой амебе нужно заполнить лишь 1/4 от пробирки.
Если 1 амеба заполняет всю пробирку за 60 минут, то 1/2 пробирки (половина) будет заполнена 1 амебой за 59 минут, а 1/4 пробирки (половина от половины) будет заполнена ею за 58 минут. Поскольку все 4 амебы будут делиться одновременно, за 58 минут они полностью заполнят пробирку.
Поскольку все 4 амебы будут делиться одновременно, за 58 минут они полностью заполнят пробирку.
Способ 2
- Переведем часы в минуты, так как ответ должен быть в минутах:
- 1 час = 60 минут
- Пусть количество минут, которое будет происходить деление, равно x. Тогда за это время 1 амеба поделится на 2x амеб, а 4 амебы – на 4 ⋅ 2x. При этом они полностью заполнят пробирку. Кроме этого известно, что 1 амеба за 60 минут полностью заполнит пробирку, то есть при этом получится 260 амеб. Составляем уравнение и решаем его:
- 260 = 4 ⋅ 2x
- 260 = 2log24 ⋅ 2x
- 260 = 2x + log24
- 60 = x + log24
- x = 60 – log24 = 60 – 2 = 58 минут
- Заметим, что при вычислениях нам понадобилось привести число 4 к степени с основанием 2. Для этого было использовано основное логарифмическое тождество:
Ответ: 58
Манекенщицы
- При демонстрации летней одежды наряды каждой манекенщицы отличаются хотя бы одним из трёх элементов: блузкой, юбкой и туфлями.
 Всего модельер приготовил для демонстрации 5 видов блузок, 3 вида юбок и 4 вида туфель. Сколько различных нарядов будет показано на этой демонстрации?
Всего модельер приготовил для демонстрации 5 видов блузок, 3 вида юбок и 4 вида туфель. Сколько различных нарядов будет показано на этой демонстрации? - Решение:
Поскольку существует 5 видов блузок, 3 вида юбок и 4 вида туфель, число различных нарядов равно произведению этих чисел:
5 ⋅ 3 ⋅ 4 = 60
Ответ: 60
Кубики
- Сколькими способами можно поставить в ряд два одинаковых красных кубика, три одинаковых зелёных кубика и один синий кубик?
- Решение:
Нам важен порядок кубиков, поэтому нам нужно посчитать количество перестановок всех кубиков: Р = (2 + 3 + 1)! = 6! Однако у нас есть одинаковые кубики, от перемены мест которых результат не изменится: 3 зеленых (это 3! перестановок) и 2 красных (это 2! перестановок). Нужно разделить получившееся число перестановок при всех разных кубиках на число перестановок зеленых и красных кубиков, чтобы исключить повторы:
6! / (2! ⋅ 3!) = 1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 ⋅ 6 / (1 ⋅ 2 ⋅ 1 ⋅ 2 ⋅ 3) = 2 ⋅ 5 ⋅ 6 = 60
ОТВЕТ: 60
Горный перевал
- Группа туристов преодолела горный перевал.
 Первый километр подъёма они преодолели за 50 минут, а каждый следующий километр проходили на 15 минут дольше предыдущего. Последний километр перед вершиной был пройден за 95 минут. После десятиминутного отдыха на вершине туристы начали спуск, который был более пологим. Первый километр после вершины был пройден за час, а каждый следующий на 10 минут быстрее предыдущего. Сколько часов группа затратила на весь маршрут, если последний километр спуска был пройден за 10 минут.
Первый километр подъёма они преодолели за 50 минут, а каждый следующий километр проходили на 15 минут дольше предыдущего. Последний километр перед вершиной был пройден за 95 минут. После десятиминутного отдыха на вершине туристы начали спуск, который был более пологим. Первый километр после вершины был пройден за час, а каждый следующий на 10 минут быстрее предыдущего. Сколько часов группа затратила на весь маршрут, если последний километр спуска был пройден за 10 минут. - Решение:
Ответ: 8,5
Произведение чисел
- Произведение десяти идущих подряд чисел разделили на 7. Чему может быть равен остаток?
- Решение:
Так как количество чисел, произведение которых берется, больше заданного делителя, остаток от деления будет равен 0. Поскольку среди чисел из произведения обязательно найдется число, которое делится нацело на заданный делитель.
Приведем несколько примеров:
1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 ⋅ 6 ⋅ 7 ⋅ 8 ⋅ 9 ⋅ 10 / 7 = 1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 ⋅ 6 ⋅ 8 ⋅ 9 ⋅ 10
16 ⋅ 17 ⋅ 18 ⋅ 19 ⋅ 20 ⋅ 21 ⋅ 22 ⋅ 23 ⋅ 24 ⋅ 25 / 7 = 3 ⋅ 16 ⋅ 17 ⋅ 18 ⋅ 19 ⋅ 20 ⋅ 22 ⋅ 23 ⋅ 24 ⋅ 25
Ответ: 0
Места в кинозале
- В первом ряду кинозала 24 места, а в каждом следующем на 2 больше, чем в предыдущем.
 Сколько мест в восьмом ряду?
Сколько мест в восьмом ряду? - Решение:
Вычислим количество мест в каждом ряду кинозала последовательно:
Ряд 1: 24
Ряд 2: 24 + 2 = 26
Ряд 3: 26 + 2 = 28
Ряд 4: 28 + 2 = 30
Ряд 5: 30 + 2 = 32
Ряд 6: 32 + 2 = 34
Ряд 7: 34 + 2 = 36
Ряд 8: 36 + 2 = 38
Ответ: 38
Закон Мура
- По эмпирическому закону Мура среднее число транзисторов на микросхемах каждый год удваивается. Известно, что в 2005 году среднее число транзисторов на микросхеме равнялось 520 млн. Определите, сколько в среднем миллионов транзисторов было на микросхеме в 2003 году.
- Решение:
Пусть в 2003 году было x миллионов транзисторов, тогда в 2005 году их стало:
x ⋅ 2 ⋅ 2 = 4x = 520
Осталось найти значение x:
x = 520 / 4 = 130
Ответ: 130
Продажа холодильников
По условию задачи в апреле было продано 10 холодильников. С мая по август (4 месяца) продажи увеличивались на 15 холодильников каждый месяц. Получили арифметическую прогрессию a1 = 10 d = 15 n = 5 Число n равно 5, так как в расчеты мы включили месяц апрель. Необходимо найти сумму 5 членов арифметической прогрессии. Воспользуемся формулами: Sn = (a1 + an) ⋅ n / 2 an = a1 + d(n — 1) Вычислим n-ый член арифметической прогрессии и сумму n членов: a5 = a1 + d(n — 1) = 10 + 15 ⋅ (5 – 1) = 10 + 60 = 70 S5 = (10 + 70) ⋅ 5 / 2 = 80 ⋅ 5 / 2 = 400 / 2 = 200 С сентября объем продаж начал уменьшаться на 15 холодильников каждый месяц (4 месяца). Значит в сентябре было продано: 70 – 15 = 55 холодильников Получили убывающую арифметическую прогрессию: a1 = 55 d = –15 n = 4 Вычислим n-ый член арифметической прогрессии и сумму n членов: a4 = a1 + d(n — 1) = 55 – 15 ⋅ (4 – 1) = 55 – 45 = 10 S4 = (55 + 10) ⋅ 4 / 2 = 65 ⋅ 4 / 2 = 260 / 2 = 130 холодильников Таким образом, в январе, феврале и марте было продано по 10 холодильников, с апреля по август включительно было продано 200 холодильников, а с сентября по декабрь включительно было продано 130 холодильников.
Получили арифметическую прогрессию a1 = 10 d = 15 n = 5 Число n равно 5, так как в расчеты мы включили месяц апрель. Необходимо найти сумму 5 членов арифметической прогрессии. Воспользуемся формулами: Sn = (a1 + an) ⋅ n / 2 an = a1 + d(n — 1) Вычислим n-ый член арифметической прогрессии и сумму n членов: a5 = a1 + d(n — 1) = 10 + 15 ⋅ (5 – 1) = 10 + 60 = 70 S5 = (10 + 70) ⋅ 5 / 2 = 80 ⋅ 5 / 2 = 400 / 2 = 200 С сентября объем продаж начал уменьшаться на 15 холодильников каждый месяц (4 месяца). Значит в сентябре было продано: 70 – 15 = 55 холодильников Получили убывающую арифметическую прогрессию: a1 = 55 d = –15 n = 4 Вычислим n-ый член арифметической прогрессии и сумму n членов: a4 = a1 + d(n — 1) = 55 – 15 ⋅ (4 – 1) = 55 – 45 = 10 S4 = (55 + 10) ⋅ 4 / 2 = 65 ⋅ 4 / 2 = 260 / 2 = 130 холодильников Таким образом, в январе, феврале и марте было продано по 10 холодильников, с апреля по август включительно было продано 200 холодильников, а с сентября по декабрь включительно было продано 130 холодильников. Общее количество проданных за год холодильников равно: 10 + 10 + 10 + 200 + 130 = 360 холодильников
Общее количество проданных за год холодильников равно: 10 + 10 + 10 + 200 + 130 = 360 холодильников
- В магазине бытовой техники объём продаж холодильников носит сезонный характер. В январе было продано 10 холодильников, и в три последующих месяца продавали по 10 холодильников. С мая продажи увеличивались на 15 единиц по сравнению с предыдущим месяцем. С сентября объём продаж начал уменьшаться на 15 холодильников каждый месяц относительно предыдущего месяца. Сколько холодильников продал магазин за год?
- Решение:
Ответ: 360
Таблица чисел
- В таблице три столбца и несколько строк. В каждую клетку таблицы вписали по натуральному числу так, что сумма всех чисел в первом столбце равна 103, во втором — 97, в третьем — 93, а сумма чисел в каждой строке больше 21, но меньше 24. Сколько всего строк в таблице?
- Решение:
Вычислим сумму натуральных чисел во всей таблице, для этого нужно сложить суммы чисел во всех столбцах:
103 + 97 + 93 = 293
Теперь найдем диапазон, в котором лежит число строк таблицы. Для этого разделим сумму чисел в таблице на сумму чисел в строке.
Для этого разделим сумму чисел в таблице на сумму чисел в строке.
Поскольку сумма чисел в строке больше 21, но меньше 24, она может быть равна 22 или 23. Если сумма в строке равна 22, то:
293 / 22 ≈ 13,3
Если сумма чисел в строке равна 23, то:
293 / 23 ≈ 12,7
Получается, что число строк в таблице лежит в диапазоне от 12,7 и 13,3. Единственное целое число, лежащее в данном диапазоне, равно 13.
Использованные источники:
- http://www.ege-math.ru
- http://worksbase.ru/matematika/kak-reshat/egeb-20
— сколькими способами можно расположить 3 красных, 3 синих и 3 зеленых шара так, чтобы никакие два шара одного цвета не были последовательными (с точностью до симметрии)?
У нас есть девять позиций, которые нужно заполнить тремя синими, тремя зелеными и тремя красными шарами. Мы можем заполнить три из девяти позиций синими шарами способами $ \ binom {9} {3} $, три из оставшихся позиций зелеными шарами способами $ \ binom {6} {3} $, а оставшиеся три позиции с красными шарами $ \ binom {3} {3} $ способами. Следовательно, количество различимых расположений из трех синих, трех зеленых и трех красных шаров равно
$$ \ binom {9} {3} \ binom {6} {3} \ binom {3} {3} = \ frac {9!} {3! 3! 3!} $$
Множители $ 3! $ В знаменателе представляют собой количество способов, которыми шары одного цвета могут быть переставлены между собой в рамках заданного расположения, поскольку перестановка шаров одного цвета между собой не приводит к расположению, которое отличается от данного расположения.
Следовательно, количество различимых расположений из трех синих, трех зеленых и трех красных шаров равно
$$ \ binom {9} {3} \ binom {6} {3} \ binom {3} {3} = \ frac {9!} {3! 3! 3!} $$
Множители $ 3! $ В знаменателе представляют собой количество способов, которыми шары одного цвета могут быть переставлены между собой в рамках заданного расположения, поскольку перестановка шаров одного цвета между собой не приводит к расположению, которое отличается от данного расположения.
Из них мы должны исключить те расстановки, в которых есть хотя бы одна пара соседних шаров одного цвета.
Пара соседних шаров одного цвета: Есть три способа выбрать цвет. У нас есть восемь объектов, которые нужно расположить: блок из двух соседних шаров, другой шар того же цвета и шесть других шаров. Нам нужно заполнить восемь вакансий.
Допустим, блок состоит из синих шаров. Затем мы можем заполнить три из этих восьми позиций зелеными шарами способами $ \ binom {8} {3} $, три из оставшихся позиций красными шарами способами $ \ binom {5} {3} $, поместить блок в одну из двух оставшихся позиций по $ 2 $, а второй синий шар поместите в последнюю открытую позицию одним способом. Следовательно, есть
$$ \ binom {8} {3} \ binom {5} {3} 2! = \ frac {8!} {3! 3!} $$
такие договоренности. Поскольку есть три способа выбора цвета, есть
$$ \ binom {3} {1} \ frac {8!} {3! 3!} $$
расположения, в которых пара соседних шаров одного цвета.
Следовательно, есть
$$ \ binom {8} {3} \ binom {5} {3} 2! = \ frac {8!} {3! 3!} $$
такие договоренности. Поскольку есть три способа выбора цвета, есть
$$ \ binom {3} {1} \ frac {8!} {3! 3!} $$
расположения, в которых пара соседних шаров одного цвета.
Две пары соседних шаров одного цвета: Возможны два случая.
Обе пары соседних шаров одного цвета. : Это означает, что все три шара этого цвета являются смежными. Таким образом, у нас есть семь объектов, которые нужно расположить, блок из трех шаров одного цвета и шесть других объектов.Поскольку есть три способа выбрать цвет, количество комбинаций, в которых есть две пары соседних шаров одного цвета, равно $$ \ binom {3} {1} \ frac {7!} {3! 3!} $$
Два цвета, в которых есть пара соседних шаров того же цвета. : Есть $ \ binom {3} {2} $ способы выбрать цвета пар. У нас есть семь объектов, которые нужно расположить: два блока, два отдельных шара этих цветов и три шара другого цвета. Таким образом, есть
$$ \ binom {3} {2} \ frac {7!} {3!} $$
расположения, в которых есть два цвета, в которых есть пара соседних шаров этого цвета.
Таким образом, есть
$$ \ binom {3} {2} \ frac {7!} {3!} $$
расположения, в которых есть два цвета, в которых есть пара соседних шаров этого цвета.
Три пары соседних шаров одного цвета: И снова два случая.
Две пары соседних шаров одного цвета и одна пара соседних шаров другого цвета : Есть три способа выбрать цвет, в котором есть две пары соседних шаров, и два способа выбрать другой цвет, в котором есть одна пара соседних шаров этого цвета. У нас есть шесть объектов, которые нужно расположить: блок из трех шаров, пара, другой шар этого цвета и три шара оставшегося цвета.Следовательно, есть $$ \ binom {3} {1} \ binom {2} {1} \ frac {6!} {3!} $$ устройства этого типа.
Три цвета, в которых есть пара соседних шаров этого цвета. : У нас есть шесть объектов, которые нужно расположить, три блока и три отдельных шара. Поскольку все объекты различны, есть $$ 6! $$ устройства этого типа.
Четыре пары соседних шаров одного цвета: У нас снова два случая.
Два цвета, в которых есть две пары соседних шаров этого цвета. : Есть $ \ binom {3} {2} $ способы выбрать два цвета.У нас есть пять объектов, которые нужно расположить: два блока из трех смежных шаров одного цвета и три шара третьего цвета. Следовательно, есть $$ \ binom {3} {2} \ frac {5!} {3!} $$ устройства этого типа.
Один цвет, в котором есть две пары соседних шаров этого цвета, и два других цвета, в которых есть одна пара соседних шаров этого цвета : Есть три способа выбрать цвет с двумя парами соседних шаров этого цвета цвет. У нас есть пять объектов, которые нужно расположить: блок из трех шаров, два блока из двух шаров и два других шара.Поскольку пять объектов различны, есть $$ \ binom {3} {1} 5! $$ устройства этого типа.
Пять пар соседних шаров одного цвета: Должны быть два цвета, в которых есть две пары соседних шаров этого цвета, а также должна быть пара соседних шаров третьего цвета. Есть $ \ binom {3} {2} $ способы выбора двух цветов, в которых есть две пары соседних шаров этого цвета. У нас есть четыре объекта, которые нужно расположить: два блока по три шара, блок из двух шаров и другой шар того же цвета.Поскольку объекты различны, есть
$$ \ binom {3} {2} 4! $$
устройства этого типа.
У нас есть четыре объекта, которые нужно расположить: два блока по три шара, блок из двух шаров и другой шар того же цвета.Поскольку объекты различны, есть
$$ \ binom {3} {2} 4! $$
устройства этого типа.
Шесть пар соседних шаров одного цвета: Должно быть две пары соседних шаров одного цвета каждого из трех цветов. Следовательно, нам нужно расположить три объекта: блок из трех синих шаров, блок из трех зеленых шаров и блок из трех красных шаров. Поскольку эти объекты различны, есть $$ 3! $$ устройства этого типа.
Согласно принципу включения-исключения, количество различимых комбинаций из трех синих, трех зеленых и трех красных шаров, в которых нет двух шаров одного цвета, является смежным, равно $$ \ frac {9!} {3! 3! 3!} — \ binom {3} {1} \ frac {8!} {3! 3!} + \ binom {3} {1} \ frac {7 !} {3! 3!} + \ Binom {3} {2} \ frac {7!} {3!} — \ binom {3} {1} \ binom {2} {1} \ frac {6!} {3!} — 6! + \ binom {3} {2} \ frac {5!} {3!} + \ binom {3} {1} 5! — \ binom {3} {2} 4! + 3! $$
Это подводит нас к вопросу о симметрии. Обратите внимание, что ни одна из этих схем за 174 $ не может быть палиндромом, поскольку для двух цветов, которые не занимают среднюю позицию, должно быть нечетное количество шаров этого цвета на одной стороне среднего шара и четное количество шаров того же цвета на другой стороне среднего шара. Если мы приравняем два расположения, которые могут быть получены путем отражения, у нас останется 87 $ различимых расположений шаров.
Обратите внимание, что ни одна из этих схем за 174 $ не может быть палиндромом, поскольку для двух цветов, которые не занимают среднюю позицию, должно быть нечетное количество шаров этого цвета на одной стороне среднего шара и четное количество шаров того же цвета на другой стороне среднего шара. Если мы приравняем два расположения, которые могут быть получены путем отражения, у нас останется 87 $ различимых расположений шаров.
Какими способами мы можем расположить 3 красных цветка 4 желтых класса 12 по математике CBSE
Подсказка : Найдите общее количество цветов, а затем количество композиций, используя формулу для неидентичных объектов, которая задается как; когда имеется n объектов, из которых $ {n_1} $ идентичны, $ {n_2} $ идентичны и т. д., то количество компоновок задается как:Количество компоновок $ = \ dfrac {{n!} } {{{n_1}! \ times {n_2}! \ times \ ldots \ times {n_k}!}} $
Полное пошаговое решение :
Мы указали, что есть красные цветы за 3 доллара, желтые цветы за 4 доллара и белые цветы за 5 долларов.
Цель состоит в том, чтобы найти количество способов, которыми мы можем расположить эти цветы в ряд, а затем найти количество способов, если белые цветы будут разделены в любом порядке.
Мы подарили цветы,
— красные цветы — 3 доллара, желтые цветы — 4 доллара, белые цветы — 5 долларов.
Тогда общее количество цветов:
Всего цветов $ = 3 + 4 + 5 = 12 $ цветов
Тогда количество способов расположить эти цветы в ряд дается как:
Количество композиций $ = \ dfrac {{ 12!}} {{3! {\ Text {}} \ times 4! {\ Text {}} \ times 5!}} $
Упростите указанную выше дробь, чтобы получить количество расположений цветов в ряду.
Число расстановок $ = \ dfrac {{12 \ times 11 \ times 10 \ times 9 \ times 8 \ times 7 \ times 6 \ times 5!}} {{3 \ times 2 \ times 4 \ times 3 \ times 2 \ times 5!}} $
Число расстановок $ = \ dfrac {{12 \ times 11 \ times 10 \ times 9 \ times 8 \ times 7 \ times 6}} {{3 \ times 2 \ times 4 \ times 3 \ times 2}} $
Количество композиций $ = 27720 $
Итак, существует $ 27720 $ способов расставить цветы по $ 12 $ в ряд.
Чтобы получить решение второй части, подумайте о количестве способов расположить в ряд красный и 4 желтых цветка по $ 3 $.
Тогда общее количество цветов будет $ \ left ({3 + 4 = 7} \ right) $.
Итак, количество композиций из 3 $ красных и 4 желтых цветов в ряду можно представить как:
Количество композиций $ = \ dfrac {{7!}} {{3! {\ Text {}} \ times 4 {\ text {!}}}} $
Упростите указанную выше дробь:
Номер расположения $ = \ dfrac {{7 \ times 6 \ times 5 \ times 4!}} {{3 \ times 2 \ times 4 {\ text {!}}}} $
Число композиций $ = 7 \ times 5 $
Число композиций $ = 35 $
Таким образом, существует 35 способов расположить 3 $ красных и 4 желтых цветка в ряд.5 {C_8} = 56 $
Итак, общее количество аранжировок дается как:
Количество путей $ = 35 \ times 56 $
Количество путей $ = 1960 $
Итак, требуемое количество способов составляет $ 1960. $
Примечание : данные красные, желтые и белые цветы идентичны, поэтому, если мы используем их вместо друг друга, это не вносит никаких изменений, поэтому при нахождении общих способов расстановки цветов мы должны извлечь количество повторений аранжировок из общего количества, и, следовательно, перестановка имеет вид:
$ P = \ dfrac {{7!}} {{3! {\ text {}} \ times 4! {\ text {}} \ times 5!}} $
Проблема Башен | Оценка: прототипы для экзамена по математике
Обоснование для математического сообщества Проблемы или ситуации, связанные с систематическим подсчетом количества способов, которыми что-то может быть сделано, предоставляют учащимся хорошие возможности для решения проблем, рассуждений и передачи результатов другим. Хотя такие задачи дискретной математики явно не требуются в Стандарте K-4 , они описаны в стандартах для старших классов. Основы дискретной математики можно заложить на раннем этапе, особенно с помощью манипуляций.
Хотя такие задачи дискретной математики явно не требуются в Стандарте K-4 , они описаны в стандартах для старших классов. Основы дискретной математики можно заложить на раннем этапе, особенно с помощью манипуляций.
Анализ видеозаписей пилотных тестов по этому заданию показал, что устные объяснения четвероклассников в небольших группах часто были намного более подробными и сложными, чем их письменные объяснения. То есть «письма», которые они пишут своим больным одноклассникам, часто не отражают их полного понимания задачи.Можно было бы ожидать, что расхождение между письменными и устными объяснениями будет уменьшаться по мере того, как учащиеся приобретут больший опыт в тех видах математического общения, которые подчеркиваются в Стандарте Стандарты .
Несоответствие может возникать отчасти из-за того, что студенты знают, что их коллеги по малой группе не примут неточных или неясных устных объяснений, тогда как письменное письмо не дает немедленной обратной связи. Однако этот недостаток необходимо устранить, поскольку развитие коммуникативных навыков учащихся является важной целью реформы.
Однако этот недостаток необходимо устранить, поскольку развитие коммуникативных навыков учащихся является важной целью реформы.
Рекомендации по разработке задания: Это отличное задание, чтобы проиллюстрировать важность точной формулировки вопросов. Заманчиво сказать «использовать два цвета» вместо «когда у вас было два цвета для работы». Но некоторые дети (правильно) интерпретируют «использование двух цветов» как означающее, что в каждой башне должны использоваться оба цвета, и приходят к выводу, что всего шесть трехблочных башен используют , ровно два цвета . Конечно, нет ничего плохого в задаче определения количества башен, которые используют ровно два цвета, но это не то же самое, что задача определения количества башен, в которых используется не более двух цветов .Существенным моментом здесь является то, что небольшие изменения в формулировках вопросов могут иметь значительные и часто непредвиденные последствия. Обычно цель задания не заключается в том, чтобы дети делали эти тонкие различия, поэтому важно
% PDF-1. 5
%
1 0 obj
>
endobj
2 0 obj
> поток
2013-08-02T10: 09: 48 + 01: 002013-08-02T10: 09: 48 + 01: 002013-08-02T10: 09: 48 + 01: 00ENG Персонал 1-е приложение MID / pdfuuid: 7276b425-9851-4336-b63b -b325d1fb0bf4uuid: 600c2c47-21bc-4bed-af2b-ddcaa79222acKONICA MINOLTA bizhub C552 конечный поток
endobj
3 0 obj
>
endobj
5 0 obj
>
endobj
6 0 obj
>
endobj
7 0 obj
>
endobj
21 0 объект
>>> / Повернуть 0 / Тип / Страница >>
endobj
22 0 объект
>>> / Повернуть 0 / Тип / Страница >>
endobj
23 0 объект
>>> / Повернуть 0 / Тип / Страница >>
endobj
24 0 объект
>>> / Повернуть 0 / Тип / Страница >>
endobj
25 0 объект
>>> / Повернуть 0 / Тип / Страница >>
endobj
34 0 объект
> поток
q
595.
5
%
1 0 obj
>
endobj
2 0 obj
> поток
2013-08-02T10: 09: 48 + 01: 002013-08-02T10: 09: 48 + 01: 002013-08-02T10: 09: 48 + 01: 00ENG Персонал 1-е приложение MID / pdfuuid: 7276b425-9851-4336-b63b -b325d1fb0bf4uuid: 600c2c47-21bc-4bed-af2b-ddcaa79222acKONICA MINOLTA bizhub C552 конечный поток
endobj
3 0 obj
>
endobj
5 0 obj
>
endobj
6 0 obj
>
endobj
7 0 obj
>
endobj
21 0 объект
>>> / Повернуть 0 / Тип / Страница >>
endobj
22 0 объект
>>> / Повернуть 0 / Тип / Страница >>
endobj
23 0 объект
>>> / Повернуть 0 / Тип / Страница >>
endobj
24 0 объект
>>> / Повернуть 0 / Тип / Страница >>
endobj
25 0 объект
>>> / Повернуть 0 / Тип / Страница >>
endobj
34 0 объект
> поток
q
595. 080 0 0 841.680 0 0 см
/ JI38a Do
Q конечный поток
endobj
35 0 объект
> поток
080 0 0 841.680 0 0 см
/ JI38a Do
Q конечный поток
endobj
35 0 объект
> поток
Если вам удастся разгадать следующие загадки за 7 секунд, у вас будет уникальный мозг
Если вы любознательны и думаете, что все в этом мире можно объяснить логикой, то загадки в этой статье для вас. Если вам нужно быстро разогреть мозг и проснуться, то эта статья также для вас. Мы предлагаем вам разгадать каждую загадку за 7 секунд. На старт, внимание, марш!
AdMe.ru собрал для вас интересные, а главное простые головоломки, которые вы можете решить, а также запомнить, чтобы потом развлечь друзей уютным вечером.
1.
Убийцу приговорили к смертной казни. Он должен выбрать одну из 3 комнат: в первой бушуют пожары, во второй полно убийц с заряженными ружьями, а в третьей — группа львов, которые не ели 3 года.
Вопрос : какая из этих комнат будет самой безопасной?
2.
Мастера, изготавливающие сувениры, могут поместить лодку внутрь бутылки.
Вопрос : можете ли вы придумать способ положить целый неразрезанный огурец в бутылку и не повредить бутылку?
3.
Однажды во время завтрака девушка уронила кольцо в чашку, полную кофе.
Вопрос : как кольцо оставалось сухим?
4.
Вопрос : где реки, но без воды, города, но без зданий, и леса, но без деревьев?
5.
Выдается человеку трижды — первый 2 раза бесплатно, в третий раз придется платить.
Вопрос : что это?
6.
Разделите 30 на 1/2 и прибавьте 10.
Вопрос : каков результат?
7.
Царь велел своим дочерям поставить на плиту одновременно 3 одинаковых чайника с одинаковым количеством воды. Если вода закипит быстрее, то наследником короля будет муж дочери. Первым закипел чайник младшей дочери, которая совсем не хотела выходить замуж.
Вопрос : почему?
8.
В Турции многие чистильщики обуви предлагают свои услуги прохожим бесплатно. Однако, если они решат воспользоваться предложением, прохожие сами платят уборщицам деньги.
Вопрос : почему?
9.
Ваше окружение использует его чаще, чем вы, однако оно принадлежит вам.
Вопрос : что это?
10.
Джеймс провел в больнице 3 дня. Он не был болен и не получил травм, однако его пришлось нести, когда он выходил из больницы.
Вопрос : почему?
Ответы:
1.
Комната со львами, потому что они уже давно умерли от голода.
2.
Не отрывая плодоножки, поместите огурец в бутылку, пока он еще маленький.Дайте ему вырасти в бутылке.
3.
Кофе был в зернах, молотый или растворимый.
4.
Это карта мира.
5.
6.
70. Обычно люди считают это так: 30: 2 + 10 = 25. Но при делении число нужно умножить на обратную дробь, то есть 30 * 2 + 10.
7.
Остальные продолжали поднимать крышку, чтобы проверить, кипит ли вода.Вот почему им потребовалось больше времени для закипания воды.
8.
Чистят один сапог бесплатно, а чтобы не выглядеть дураком в одном начищенном сапоге, прохожий вынужден платить за чистку второго.
9.
10.
Он только что родился в этой больнице.
Сколько времени у вас ушло на решение всех этих загадок? А знаете какие еще интересные загадки? Делитесь ими в комментариях!
| Вероятность Страница вероятности слова Уэйна Рандомизированный флиппер для монет: шансы 50-50 для орла или решки Бесплатные сценарии JavaScripts от источника JavaScript Сводка элементарной вероятности Пять монет имеют в общей сложности 32 перестановки: H = голова и T = хвост
Вероятность броска пары игральных костей Миниатюрные игральные кости на пенни США. Каждая матрица имеет сторону 4 мм. Вероятность для двух пятерок составляет 1/36 или 3/36, всего 10 точек. Всего 36 различных комбинаций: 6 X 6 = 36
Вероятность получения флеш-рояля Вытягивание карт по порядку из случайно перемешанной колоды
Вероятность выигрыша в лотерее Калифорнии Выбор шести из 53 номеров одним билетом
Вероятность определения пола у людей Определение пола более сложно, чем бросание монеты
| ||||||||||||||
| ’62 Центр театра и танца, ’62 Центр | ||
| касса | 597-2425 | |
| Магазин костюмов | 597-3373 | |
| Менеджер мероприятий / Помощник менеджера | 597-4808 | 597-4815 факс |
| Производство | 597-4474 факс | |
| Магазин сцен | 597-2439 | |
| ’68 Центр карьерного роста, Мирс | 597-2311 | 597-4078 факс |
| Academic Resources, Paresky | 597-4672 | 597-4959 факс |
| Служба поддержки инвалидов, Парески | 597-4672 | |
| Прием, Вестон Холл | 597-2211 | 597-4052 факс |
| Affirmative Action, Hopkins Hall | 597-4376 | |
| Africana Studies, Hollander | 597-2242 | 597-4222 факс |
| Американские исследования, Шапиро | 597-2074 | 597-4620 факс |
| Антропология и социология, Холландер | 597-2076 | 597-4305 факс |
| Архивы и специальные коллекции, Sawyer | 597-4200 | 597-2929 факс |
| Читальный зал | 597-4200 | |
| Искусство (История, Студия), Spencer Studio Art / Lawrence | 597-3578 | 597-3693 факс |
| Архитектурная студия, Spencer Studio Art | 597-3134 | |
| Фотография Студия, Spencer Studio Art | 597-2030 | |
| Printmaking Studio, Spencer Studio Art | 597-2496 | |
| Скульптурная студия, Spencer Studio Art | 597-3101 | |
| Senior Studio, Spencer Studio Art | 597-3224 | |
| Видео / фотостудия, Spencer Studio Art | 597-3193 | |
| Asian Studies, Hollander | 597-2391 | 597-3028 факс |
| Астрономия / Астрофизика, Thompson Physics | 597-2482 | 597-3200 факс |
| Департамент легкой атлетики, физическое воспитание, отдых, Ласелл | 597-2366 | 597-4272 факс |
| Спортивный директор | 597-3511 | |
| Лодочный домик, Озеро Онота | 443-9851 | |
| Автобусы | 597-2366 | |
| Фитнес-центр | 597-3182 | |
| Hockey Rink Ice Line, Lansing Chapman | 597-2433 | |
| Intramurals, Атлетический центр Чандлера | 597-3321 | |
| Физическое воспитание | 597-2141 | |
| Pool Wet Line, Атлетический центр Чандлера | 597-2419 | |
| Sports Information, Hopkins Hall | 597-4982 | 597-4158 факс |
| Спортивная медицина | 597-2493 | 597-3052 факс |
| Площадки для игры в сквош | 597-2485 | |
| Поле для гольфа Taconic | 458-3997 | |
| Биохимия и молекулярная биология, Thompson Biology | 597-2126 | |
| Биоинформатика, геномика и протеомика, Бронфман | 597-2124 | |
| Биология, Thompson Biology | 597-2126 | 597-3495 факс |
| Охрана и безопасность кампуса, Хопкинс-холл | 597-4444 | 597-3512 факс |
| Карты доступа / системы сигнализации | 597-4970 / 4033 | |
| Служба сопровождения, Хопкинс Холл | 597-4400 | |
| Офицеры и диспетчеры | 597-4444 | |
| Секретарь, удостоверения личности | 597-4343 | |
| Коммутатор | 597-3131 | |
| Центр развития творческого сообщества, 66 Stetson Court | 884-0093 | |
| Центр экономики развития, 1065 Main St | 597-2148 | 597-4076 факс |
| Компьютерный зал | 597-2522 | |
| Вестибюль | 597-4383 | |
| Центр экологических исследований, класс 1966 г. Экологический центр | 597-2346 | 597-3489 факс |
| Лаборатория экологических наук, Морли | 597-2380 | |
| Экологические исследования | 597-2346 | |
| Лаборатория ГИС | 597-3183 | |
| Центр иностранных языков, литератур и культур, Холландер | 597-2391 | 597-3028 факс |
| Арабские исследования, Холландер | 597-2391 | 597-3028 факс |
| Сравнительная литература, Холландер | 597-2391 | |
| Критические языки, Холландер | 597-2391 | 597-3028 факс |
| лингафонный кабинет | 597-3260 | |
| Русский, Hollander | 597-2391 | |
| Центр обучения в действии, Brooks House | 597-4588 | 597-3090 факс |
| Библиотека редких книг Чапина, Сойер | 597-2462 | 597-2929 факс |
| Читальный зал | 597-4200 | |
| Офис капелланов, Парески | 597-2483 | 597-3955 факс |
| Еврейский религиозный центр, 24 Стетсон-Корт | 597-2483 | |
| Мусульманская молельная комната, часовня Томпсона (нижний уровень) | 597-2483 | |
| Католическая часовня Ньюмана, часовня Томпсона (нижний уровень) | 597-2483 | |
| Химия, Thompson Chemistry | 597-2323 | 597-4150 факс |
| Классика (греческий и латинский), Hollander | 597-2242 | 597-4222 факс |
| Когнитивная наука, Бронфман | 597-4594 | |
| College Marshal, Thompson Physics | 597-2008 | |
| Отношения с колледжем | 597-4057 | |
| Программа 25-го воссоединения, Фогт | 597-4208 | 597-4039 факс |
| Программа 50-го воссоединения, Фогт | 597-4284 | 597-4039 факс |
| Advancement Operations, Мирс Вест | 597-4154 | 597-4333 факс |
| Мероприятия для выпускников, Vogt | 597-4146 | 597-4548 факс |
| Фонд выпускников | 597-4153 | 597-4036 факс |
| Связи с выпускниками, Мирс Вест | 597-4151 | 597-4178 факс |
| Alumni / Development Mail Services, Мирс-Уэст | 597-4369 | |
| Девелопмент, Фогт | 597-4256 | |
| Отношения с донорами, Vogt | 597-3234 | 597-4039 факс |
| Офис по планированию подарков, Vogt | 597-3538 | 597-4039 факс |
| Офис грантов, Мирс-Уэст | 597-4025 | 597-4333 факс |
| Программа крупных подарков, Vogt | 597-4256 | 597-4548 факс |
| Parents Fund, Vogt | 597-4357 | 597-4036 факс |
| Prospect Management & Research, Мирс | 597-4119 | 597-4178 факс |
| Начало занятий и академические мероприятия, Jesup | 597-2347 | 597-4435 факс |
| Коммуникации, Хопкинс Холл | 597-4277 | 597-4158 факс |
| Sports Information, Hopkins Hall | 597-4982 | 597-4158 факс |
| Web Team, Southworth Schoolhouse | ||
| Williams Magazines (ранее Alumni Review), Hopkins Hall | 597-4278 | |
| Компьютерные науки, Thompson Chemistry | 597-3218 | 597-4250 факс |
| Conferences & Events, Парески | 597-2591 | 597-4748 факс |
| Запросы Elm Tree House, Mt.Надежда Ферма | 597-2591 | |
| Офис контролера, Хопкинс Холл | 597-4412 | 597-4404 факс |
| Accounts Payable & Data Entry, Hopkins Hall | 597-4453 | |
| Bursar & Cash Receipts, Hopkins Hall | 597-4396 | |
| Финансовые информационные системы, Хопкинс-холл | 597-4023 | |
| Purchasing Cards, Hopkins Hall | 597-4413 | |
| Студенческие ссуды, Хопкинс Холл | 597-4683 | |
| Dance, 62 Центр | 597-2410 | |
| Центр Дэвиса (ранее Мультикультурный центр), Дженнесс | 597-3340 | 597-3456 факс |
| Харди Хаус | 597-2129 | |
| Jenness House | 597-3344 | |
| Райс Хаус | 597-2453 | |
| Декан колледжа, Хопкинс-холл | 597-4171 | 597-3507 факс |
| Декан факультета Хопкинс Холл | 597-4351 | 597-3553 факс |
| Столовая, капельницы | 597-2121 | 597-4618 факс |
| ’82 Гриль, Парески | 597-4585 | |
| Кондитерская, Парески | 597-4511 | |
| Общественное питание, факультет | 597-2452 | |
| Driscoll Dining Hall, Дрисколл | 597-2238 | |
| Eco Café, Научный центр | 597-2383 | |
| Grab ‘n Go, Парески | 597-4398 | |
| Lee Snack Bar, Парески | 597-3487 | |
| Обеденный зал Mission Park, Mission Park | 597-2281 | |
| Whitmans ‘, Paresky | 597-2889 | |
| Economics, Schapiro | 597-2476 | 597-4045 факс |
| английский, Hollander | 597-2114 | 597-4032 факс |
| Сооружения, здание служебного помещения | 597-2301 | |
| College Car Request | 597-2302 | |
| Скорая помощь вечером / в выходные дни | 597-4444 | |
| Запросы на работу объектов | 597-4141 факс | |
| Особые мероприятия | 597-4020 | |
| Кладовая | 597-2143 | 597-4013 факс |
| Клуб преподавателей, Дом факультетов / Центр выпускников | 597-2451 | 597-4722 факс |
| Бронирование | 597-3089 | |
| Fellowships Office, Hopkins Hall | 597-3044 | 597-3507 факс |
| Financial Aid, Weston Hall | 597-4181 | 597-2999 факс |
| Geosciences, Clark Hall | 597-2221 | 597-4116 факс |
| Немецко-русский, Hollander | 597-2391 | 597-3028 факс |
| Глобальные исследования, Холландер | 597-2247 | |
| Программа магистратуры по истории искусств, Кларк | 458-2317 факс | |
| Службы здравоохранения и хорошего самочувствия, Thompson Ctr Health | 597-2206 | 597-2982 факс |
| Медицинское просвещение | 597-3013 | |
| Услуги интегративного благополучия (консультирование) | 597-2353 | |
| Чрезвычайные ситуации с опасностью для жизни | Позвоните 911 | |
| Медицинские услуги | 597-2206 | |
| История, Холландер | 597-2394 | 597-3673 факс |
| История науки, Бронфман | 597-4116 факс | |
| Лес Хопкинса | 597-4353 | |
| Розенбург-центр | 458-3080 | |
| Отдел кадров, B&L Building | 597-2681 | 597-3516 факс |
| Услуги няни, корпус B&L | 597-4587 | |
| Льготы | 597-4355 | |
| Программа помощи сотрудникам | 800-828-6025 | |
| Занятость | 597-2681 | |
| Заработная плата | 597-4162 | |
| Ресурсы для супруга / партнера | 597-4587 | |
| Занятость студентов | 597-4568 | |
| Погодная линия (ICEY) | 597-4239 | |
| Humanities, Schapiro | 597-2076 | |
| Информационные технологии, Jesup | 597-2094 | 597-4103 факс |
| Пакеты для чтения курсов, ящик для сообщений Office | 597-4090 | |
| Центр ссуды на оборудование, приложение Додда | 597-4091 | |
| Служба поддержки преподавателей / сотрудников, [адрес электронной почты защищен] | 597-4090 | |
| Медиауслуги и справочная служба | 597-2112 | |
| Служба поддержки студентов, [электронная почта] | 597-3088 | |
| Телекоммуникации / телефоны | 597-4090 | |
| Междисциплинарные исследования, Hollander | 597-2552 | |
| Международное образование и учеба, Хопкинс-холл | 597-4262 | 597-3507 факс |
| Инвестиционный офис, Хопкинс Холл | 597-4447 | |
| Бостонский офис | 617-502-2400 | 617-426-5784 факс |
| Еврейские исследования, Мазер | 597-3539 | |
| Справедливость и закон, Холландер | 597-2102 | |
| Latina / o Studies, Hollander | 597-2242 | 597-4222 факс |
| Исследования лидерства, Шапиро | 597-2074 | 597-4620 факс |
| Морские исследования, Бронфман | 597-2297 | |
| Математика и статистика, Bascom | 597-2438 | 597-4061 факс |
| Музыка, Бернхард | 597-2127 | 597-3100 факс |
| Concertline (записанная информация) | 597-3146 | |
| Неврология, Thompson Biology | 597-4107 | 597-2085 факс |
| Окли Центр, Окли | 597-2177 | 597-4126 факс |
| Управление институционального разнообразия и справедливости, Хопкинс-холл | 597-4376 | 597-4015 факс |
| Управление счетов студентов, Hopkins Hall | 597-4396 | 597-4404 факс |
| Performance Studies, ’62 Center | 597-4366 | |
| Философия, Шапиро | 597-2074 | 597-4620 факс |
| Физика, Thompson Physics | 597-2482 | 597-4116 факс |
| Планетарий / Обсерватория Хопкинса | 597-3030 | |
| Театр Old Hopkins Observatory | 597-4828 | |
| Бронирование | 597-2188 | |
| Политическая экономия, Шапиро | 597-2327 | |
| Политология, Шапиро | 597-2168 | 597-4194 факс |
| Офис президента, Хопкинс Холл | 597-4233 | 597-4015 факс |
| Дом президента | 597-2388 | 597-4848 факс |
| Услуги печати / почты для преподавателей / сотрудников, ’37 House | 597-2022 | |
| Программа обучения, Бронфман | 597-4522 | 597-2085 факс |
| Офис Провоста, Хопкинс Холл | 597-4352 | 597-3553 факс |
| Психология, психологические кабинеты и лаборатории | 597-2441 | 597-2085 факс |
| Недвижимость, B&L Building | 597-2195 / 4238 | 597-5031 факс |
| Ипотека для преподавателей / сотрудников | 597-4238 | |
| Аренда жилья для преподавателей и сотрудников | 597-2195 | |
| Офис регистратора, Хопкинс Холл | 597-4286 | 597-4010 факс |
| Религия, Холландер | 597-2076 | 597-4222 факс |
| Romance Languages, Hollander | 597-2391 | 597-3028 факс |
| Планировщик помещений | 597-2555 | |
| Соответствие требованиям безопасности и охраны окружающей среды, класс ’37 Дом | 597-3003 | |
| Библиотека Сойера, Сойер | 597-2501 | 597-4106 факс |
| Службы доступа | 597-2501 | |
| Приобретения / Серийные номера | 597-2506 | |
| Каталогизация / Службы метаданных | 597-2507 | |
| Межбиблиотечный абонемент | 597-2005 | 597-2478 факс |
| Исследовательские и справочные службы | 597-2515 | |
| Стеллаж | 597-4955 | 597-4948 факс |
| Системы | 597-2084 | |
| Научная библиотека Шоу, Научный центр | 597-4500 | 597-4600 факс |
| Исследования в области науки и технологий, Бронфман | 597-2239 | |
| Научный центр, Бронфман | 597-4116 факс | |
| Магазин электроники | 597-2205 | |
| Машинно-модельный цех | 597-2230 | |
| Безопасность | 597-4444 | |
| Специальные академические программы, Харди | 597-3747 | 597-4530 факс |
| Sports Information, Hopkins Hall | 597-4982 | 597-4158 факс |
| Студенческая жизнь, Парески | 597-4747 | |
| Планировщик помещений | 597-2555 | |
| Управление студенческими центрами | 597-4191 | |
| Организация студенческих мероприятий | 597-2546 | |
| Студенческий дом, Парески | 597-2555 | |
| Участие студентов | 597-4749 | |
| Программы проживания для старших классов | 597-4625 | |
| Студенческая почта, Паресский почтовый кабинет | 597-2150 | |
| Устойчивое развитие / Центр Зилха, Харпер | 597-4462 | |
| Коммутатор, Хопкинс Холл | 597-3131 | |
| Книжный магазин Уильямса | 458-8071 | 458-0249 факс |
| Театр, 62 Центр | 597-2342 | 597-4170 факс |
| Trust & Estate Administration, Sears House | 597-4259 | |
| Учебники | 597-2580 | |
| вице-президент по кампусу Life, Hopkins Hall | 597-2044 | 597-3996 факс |
| вице-президент по связям с колледжем, Мирс | 597-4057 | 597-4178 факс |
| вице-президент по финансам и администрированию, Хопкинс-холл | 597-4421 | 597-4192 факс |
| Центр визуальных ресурсов, Лоуренс | 597-2015 | 597-3498 факс |
| Детский центр Williams College, Детский центр Williams | 597-4008 | 597-4889 факс |
| Музей искусств колледжа Уильямс (WCMA), Лоуренс | 597-2429 | 597-5000 факс |
| Подготовка музея | 597-2426 | |
| Служба безопасности музея | 597-2376 | |
| Музейный магазин | 597-3233 | |
| Уильямс Интернэшнл | 597-2161 | |
| Уильямс Outing Club, Парески | 597-2317 | |
| Оборудование / стол для студентов | 597-4784 | |
| Проект Уильямса по экономике высшего образования, Мирс-Вест | 597-2192 | |
| Williams Record, Парески | 597-2400 | 597-2450 факс |
| Программа Уильямса-Эксетера в Оксфорде, Оксфордский университет | 011-44-1865-512345 | |
| Программа Williams-Mystic, Mystic Seaport Museum | 860-572-5359 | 860-572-5329 факс |
| Исследования женщин, гендера и сексуальности, Schapiro | 597-3143 | 597-4620 факс |
| Написание программ, Хопкинс-холл | 597-4615 | |
| Центр экологических инициатив «Зилха», Харпер | 597-4462 |

 Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2″, «3″, «4″ или «5″ и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округленным по правилам округления?
Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2″, «3″, «4″ или «5″ и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округленным по правилам округления? На сколько нужно увеличить наибольшее из этих чисел, чтобы их среднее арифметическое стало на 1 больше?
На сколько нужно увеличить наибольшее из этих чисел, чтобы их среднее арифметическое стало на 1 больше? Наибольший угол в 3 раза больше наименьшего. Сколько значений может принимать величина среднего угла?
Наибольший угол в 3 раза больше наименьшего. Сколько значений может принимать величина среднего угла? Всего в вазах 22 розы. Сколько роз в белой вазе?
Всего в вазах 22 розы. Сколько роз в белой вазе? Номер последней страницы перед выпавшими листами — 352, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало?
Номер последней страницы перед выпавшими листами — 352, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало? Если разрезать по красной, то одна часть будет длиннее другой на B см. Найдите расстояние от красной до синей полоски.
Если разрезать по красной, то одна часть будет длиннее другой на B см. Найдите расстояние от красной до синей полоски. Всего модельер приготовил для демонстрации 5 видов блузок, 3 вида юбок и 4 вида туфель. Сколько различных нарядов будет показано на этой демонстрации?
Всего модельер приготовил для демонстрации 5 видов блузок, 3 вида юбок и 4 вида туфель. Сколько различных нарядов будет показано на этой демонстрации? Первый километр подъёма они преодолели за 50 минут, а каждый следующий километр проходили на 15 минут дольше предыдущего. Последний километр перед вершиной был пройден за 95 минут. После десятиминутного отдыха на вершине туристы начали спуск, который был более пологим. Первый километр после вершины был пройден за час, а каждый следующий на 10 минут быстрее предыдущего. Сколько часов группа затратила на весь маршрут, если последний километр спуска был пройден за 10 минут.
Первый километр подъёма они преодолели за 50 минут, а каждый следующий километр проходили на 15 минут дольше предыдущего. Последний километр перед вершиной был пройден за 95 минут. После десятиминутного отдыха на вершине туристы начали спуск, который был более пологим. Первый километр после вершины был пройден за час, а каждый следующий на 10 минут быстрее предыдущего. Сколько часов группа затратила на весь маршрут, если последний километр спуска был пройден за 10 минут. Сколько мест в восьмом ряду?
Сколько мест в восьмом ряду?
Leave A Comment